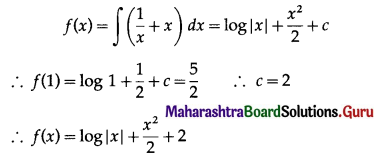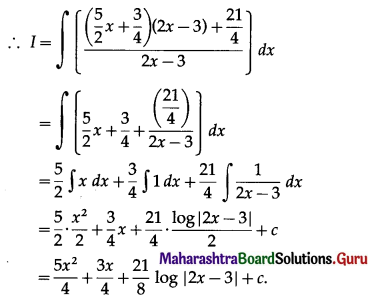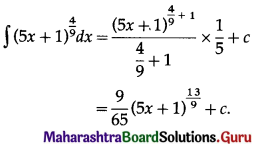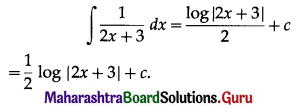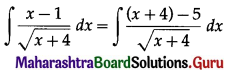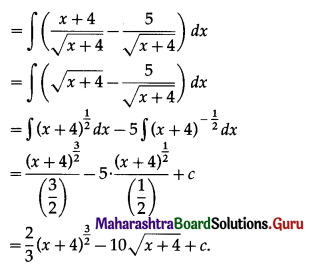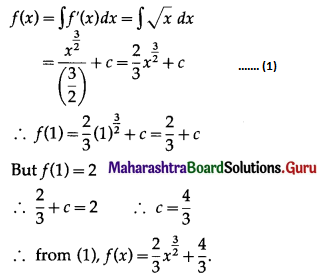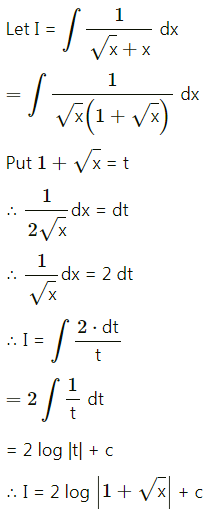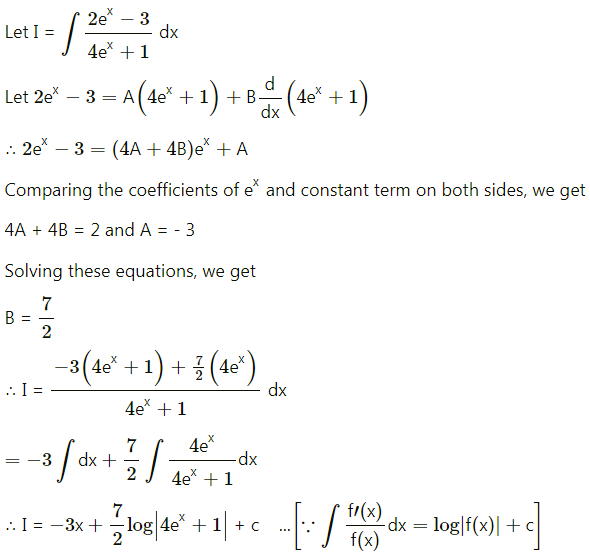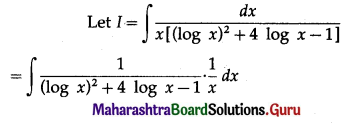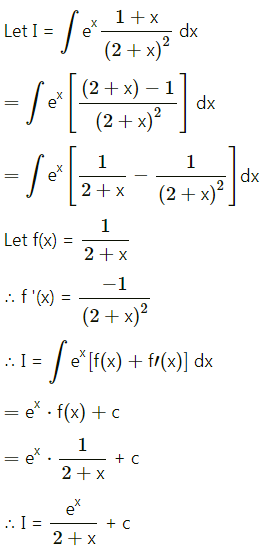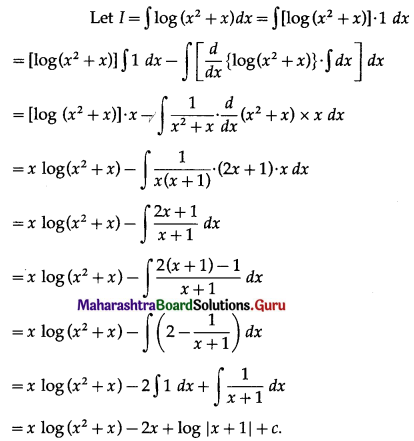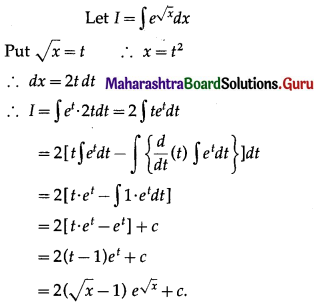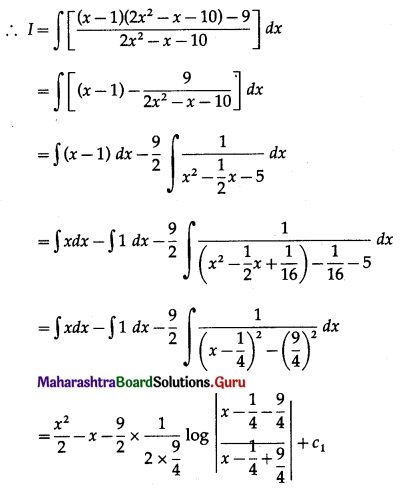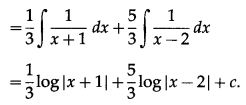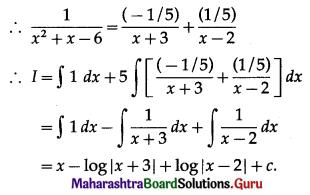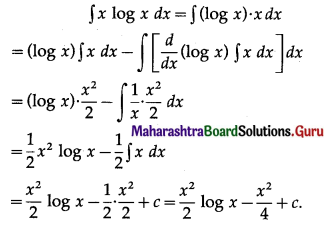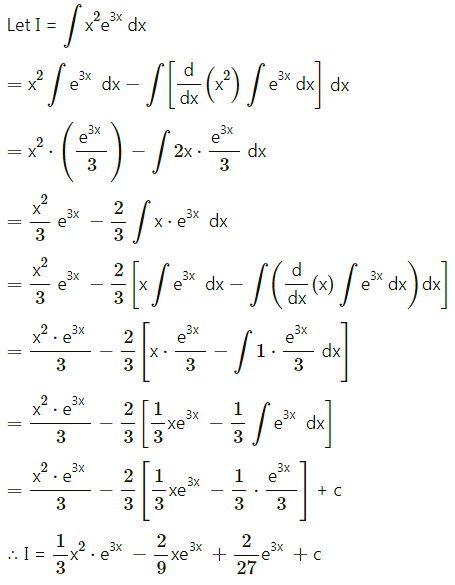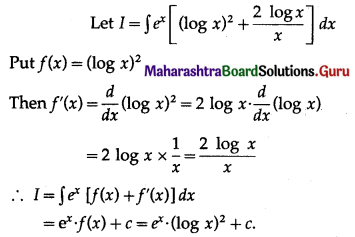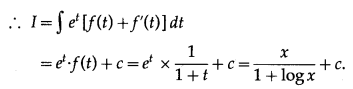Class 12

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Ex 6.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 6 Definite Integration Ex 6.1

Evaluate the following definite integrals:

Question 1.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:

Question 2.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:

Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:

Question 4.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:

Question 5.
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:
Let I = \(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Let \(\frac{x}{(x+2)(x+3)}=\frac{A}{x+3}+\frac{B}{x+2}\)
∴ x = A(x + 2) + B(x + 3)
Put x + 3 = 0, i.e. x = -3, we get
-3 = A(-1) + B(0)
∴ A = 3
Put x + 2 = 0, i.e. x = -2, we get
-2 = A(0) + B(1)
∴ B = -2

Question 6.
\(\int_{1}^{2} \frac{d x}{x^{2}+6 x+5}\)
Solution:

Question 7.
If \(\int_{0}^{a}(2 x+1) d x\) = 2, find the real values of ‘a’.
Solution:
Let I = \(\int_{0}^{a}(2 x+1) d x\)
= \(\left[2 \cdot \frac{x^{2}}{2}+x\right]_{0}^{a}\)
= a² + a – 0
= a² + a
∴ I = 2 gives a² + a = 2
∴ a² + a – 2 = 0
∴ (a + 2)(a – 1) = 0 1
∴ a + 2 = 0 or a – 1 = 0
∴ a = -2 or a = 1.

Question 8.
If \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\) = 11, find ‘a’.
Solution:
Let I = \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\)
= \(\left[3\left(\frac{x^{3}}{3}\right)+2\left(\frac{x^{2}}{2}\right)+x\right]_{1}^{a}\)
= \(\left[x^{3}+x^{2}+x\right]_{1}^{a}\)
= (a³ + a² + a) – (1 + 1 + 1)
= a³ + a² + a – 3
∴ I = 11 gives a³ + a² + a – 3 = 11
∴ a³ + a² + a – 14 = 0
∴ (a³ – 8) + (a² + a – 6) = 0
∴ (a – 2)(a² + 2a + 4) + (a + 3)(a – 2) = 0
∴ (a – 2)(a² + 2a + 4 + a + 3) = 0
∴ (a – 2)(a² + 3a + 7) = 0
∴ a – 2 = 0 or a² + 3a + 7 = 0
∴ a = 2 or a = \(\frac{-3 \pm \sqrt{9-28}}{2}\)
The latter two roots are not real.
∴ they are rejected.
∴ a = 2.

Question 9.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:

Question 10.
\(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\) = \(\int_{1}^{2} \frac{3 x}{(3 x)^{2}-1} d x\)
Put 3x = t
∴ 3 dx = dt
∴ dx = \(\frac{d t}{3}\)
When x = 1, t = 3 × 1 = 3
When x = 2, t = 3 × 2 = 6

Question 11.
\(\int_{1}^{3} \log x d x\)
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Miscellaneous Exercise 5

(I) Choose the correct alternative from the following:

Question 1.
The value of \(\int \frac{d x}{\sqrt{1-x}}\) is
(a) 20\(\sqrt{1-x}\) + c
(b) -2\(\sqrt{1-x}\) + c
(c) √x + c
(d) x + c
Answer:
(b) -2\(\sqrt{1-x}\) + c

Question 2.
\(\int \sqrt{1+x^{2}} d x\) =
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)
(b) \(\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}+c\)
(c) \(\frac{1}{3}\left(1+x^{2}\right)+c\)
(d) \(\frac{(x)}{\sqrt{1+x^{2}}}+c\)
Answer:
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)

Question 3.
\(\int x^{2}(3)^{x^{3}} d x\) =
(a) \(\text { (3) }^{x^{3}}+c\)
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
(c) \(\log 3(3)^{x^{3}}+c\)
(d) \(x^{2}(3)^{x 3}\)
Answer:
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
Hint:
Put x³ = t

Question 4.
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=p \int \frac{4 x+6}{2 x^{2}+6 x+5} d x\) + \(\frac{1}{2} \int \frac{d x}{2 x^{2}+6 x+5}\), then p = __________
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) 2
Answer:
(c) \(\frac{1}{4}\)
Hint:
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=\int \frac{\frac{1}{4}(4 x+6)+\frac{1}{2}}{2 x^{2}+6 x+5} d x\)

Question 5.
\(\int \frac{d x}{\left(x-x^{2}\right)}\) = ________
(a) log x – log(1 – x) + c
(b) log(1 – x²) + c
(c) -log x + log(1 – x) + c
(d) log(x – x²) + c
Answer:
(a) log x – log(1 – x) + c

Question 6.
\(\int \frac{d x}{(x-8)(x+7)}\) = __________
(a) \(\frac{1}{15} \log \left|\frac{x+2}{x-1}\right|+c\)
(b) \(\frac{1}{15} \log \left|\frac{x+8}{x+7}\right|+c\)
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)
(d) (x – 8)(x – 7) + c
Answer:
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)

Question 7.
\(\int\left(x+\frac{1}{x}\right)^{3} d x\) = _________
(a) \(\frac{1}{4}\left(x+\frac{1}{x}\right)^{4}+c\)
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
(c) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x+\frac{1}{x^{2}}+c\)
(d) \(\left(x-x^{-1}\right)^{3}+c\)
Answer:
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
Hint:
\(\left(x+\frac{1}{x}\right)^{3}=x^{3}+3 x+\frac{3}{x}+\frac{1}{x^{3}}\)

Question 8.
\(\int\left(\frac{e^{2 x}+e^{-2 x}}{e^{x}}\right) d x\)
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)
(b) \(e^{x}+\frac{1}{3 e^{3 x}}+c\)
(c) \(e^{-x}+\frac{1}{3 e^{3 x}}+c\)
(d) \(e^{-x}-\frac{1}{3 e^{3 x}}+c\)
Answer:
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)

Question 9.
∫(1 – x)^-2 dx = ___________
(a) (1 + x)^-1 + c
(b) (1 – x)^-1 + c
(c) (1 – x)^-1 – 1 + c
(d) (1 – x)^-1 + 1 + c
Answer:
(b) (1 – x)^-1 + c

Question 10.
\(\int \frac{\left(x^{3}+3 x^{2}+3 x+1\right)}{(x+1)^{5}} d x\) = _______
(a) \(\frac{-1}{x+1}+c\)
(b) \(\left(\frac{-1}{x+1}\right)^{5}+c\)
(c) log(x + 1) + c
(d) log|x + 1|⁵ + c
Answer:
(a) \(\frac{-1}{x+1}+c\)
Hint:
x³ + 3x² + 3x + 1 = (x + 1)³

(II) Fill in the blanks.

Question 1.
\(\int \frac{5\left(x^{6}+1\right)}{x^{2}+1}\)dx = x⁴ + ___x³ + 5x + c.
Answer:
\(-\frac{5}{3}\)
Hint:
x⁶ + 1 = (x² + 1)(x⁴ – x² + 1)

Question 2.
\(\int \frac{x^{2}+x-6}{(x-2)(x-1)} d x\) = x + ______ + c
Answer:
4 log|x – 1|
Hint:
x² + x – 6 = (x + 3)(x – 2)

Question 3.
If f'(x) = \(\frac{1}{x}\) + x and f(1) = \(\frac{5}{2}\) then f(x) = log x + \(\frac{x^{2}}{2}\) + _______
Answer:
2
Hint:

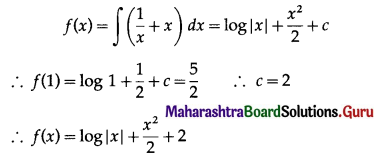
Question 4.
To find the value of \(\int \frac{(1+\log x) d x}{x}\) the proper substitution is __________
Answer:
1 + log x = t

Question 5.
\(\int \frac{1}{x^{3}}\left[\log x^{x}\right]^{2} d x\) = p(log x)³ + c, then p = _______
Answer:
\(\frac{1}{3}\)
Hint:
\(\frac{1}{x^{3}}\left(\log x^{x}\right)^{2}=\frac{1}{x^{3}}(x \log x)^{2}=\frac{(\log x)^{2}}{x}\)

(III) State whether each of the following is True or False:

Question 1.
The proper substitution for \(\int x\left(x^{x}\right)^{x}(2 \log x+1) d x \text { is }\left(x^{x}\right)^{x}=t\)
Answer:
True

Question 2.
If ∫x e^2x dx is equal to e^2x f(x) + c where c is constant of integration, then f(x) is \(\frac{(2 x-1)}{2}\).
Answer:
False

Question 3.
If ∫x f(x) dx = \(\frac{f(x)}{2}\), then f(x) = \(e^{x^{2}}\).
Answer:
True

Question 4.
If \(\int \frac{(x-1) d x}{(x+1)(x-2)}\) = A log|x + 1| + B log|x – 2|, then A + B = 1.
Answer:
True

Question 5.
For \(\int \frac{x-1}{(x+1)^{3}} e^{x} d x\) = e^x f(x) + c, f(x) = (x + 1)².
Answer:
False

(IV) Solve the following:

1. Evaluate:

(i) \(\int \frac{5 x^{2}-6 x+3}{2 x-3} d x\)
Solution:

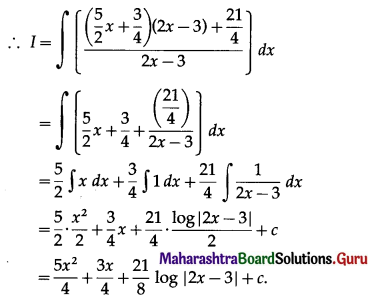
(ii) \(\int(5 x+1)^{\frac{4}{9}} d x\)
Solution:

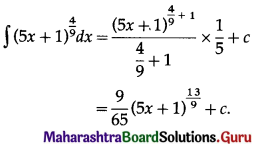
(iii) \(\int \frac{1}{2 x+3} d x\)
Solution:

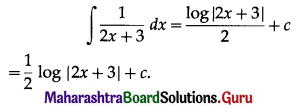
(iv) \(\int \frac{x-1}{\sqrt{x+4}} d x\)
Solution:

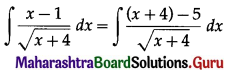
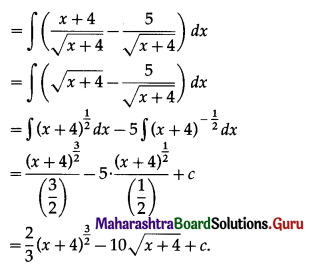
(v) If f'(x) = √x and f(1) = 2, then find the value of f(x).
Solution:
By the definition of integral

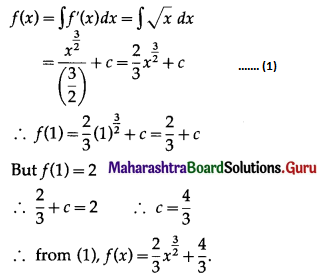
(vi) ∫|x| dx if x < 0
Solution:
∫|x| dx = ∫-x dx …..[∵ x < 0]
= -∫x dx
= \(-\frac{x^{2}}{2}\) + c

2. Evaluate:

(i) Find the primitive of \(\frac{1}{1+e^{x}}\)
Solution:
Let I be the primitive of \(\frac{1}{1+e^{x}}\)

(ii) \(\int \frac{a e^{x}+b e^{-x}}{\left(a e^{x}-b e^{-x}\right)^{2}} d x\)
Solution:

(iii) \(\int \frac{1}{2 x+3 x \log x} d x\)
Solution:

(iv) \(\int \frac{1}{\sqrt{x}+x} d x\)
Solution:

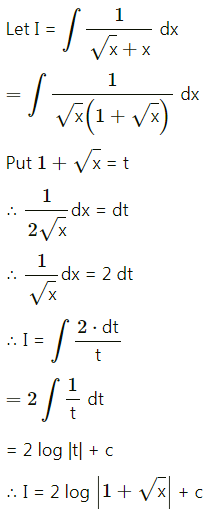
(v) \(\int \frac{2 e^{x}-3}{4 e^{x}+1} d x\)
Solution:

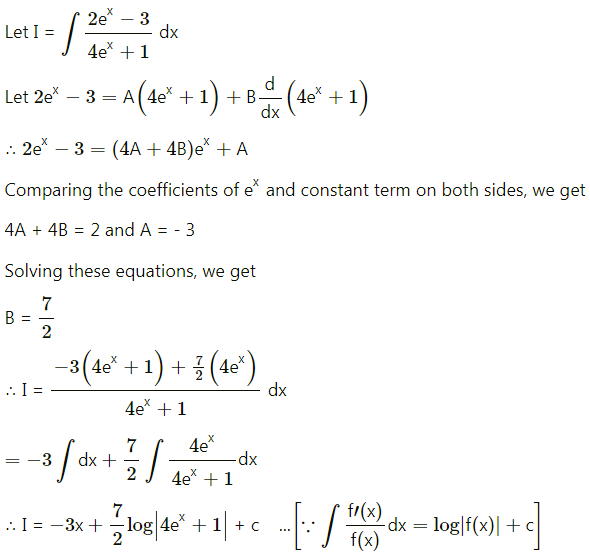
3. Evaluate:

(i) \(\int \frac{d x}{\sqrt{4 x^{2}-5}} d x\)
Solution:

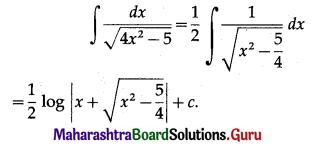
(ii) \(\int \frac{d x}{3-2 x-x^{2}} d x\)
Solution:

(iii) \(\int \frac{d x}{9 x^{2}-25}\)
Solution:

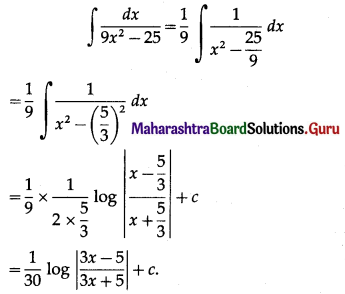
(iv) \(\int \frac{e^{x}}{\sqrt{e^{2 x}+4 e^{x}+13}} d x\)
Solution:

(v) \(\int \frac{d x}{x\left[(\log x)^{2}+4 \log x-1\right]}\)
Solution:

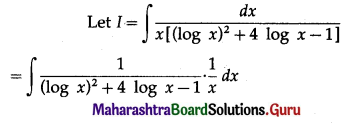
(vi) \(\int \frac{d x}{5-16 x^{2}}\)
Solution:

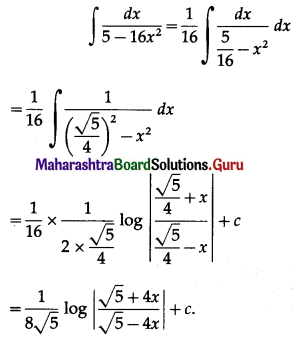
(vii) \(\int \frac{d x}{25 x-x(\log x)^{2}}\)
Solution:

(viii) \(\int \frac{e^{x}}{4 e^{2 x}-1} d x\)
Solution:

4. Evaluate:

(i) ∫(log x)² dx
Solution:

(ii) \(\int e^{x} \frac{1+x}{(2+x)^{2}} d x\)
Solution:

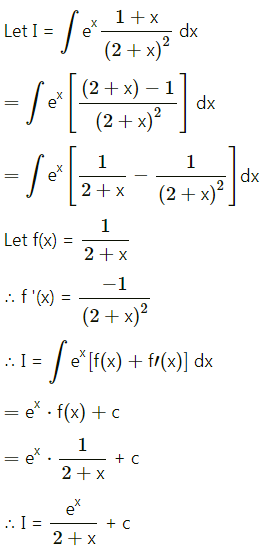
(iii) ∫x e^2x dx
Solution:

(iv) ∫log(x² + x) dx
Solution:

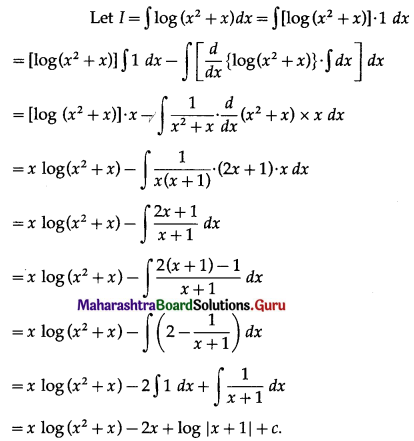
(v) \(\int e^{\sqrt{x}} d x\)
Solution:

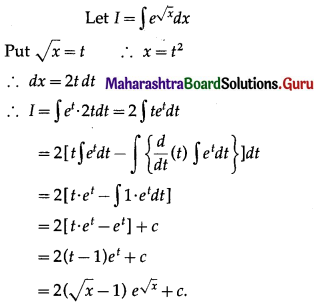
(vi) \(\int \sqrt{x^{2}+2 x+5} d x\)
Solution:

(vii) \(\int \sqrt{x^{2}-8 x+7} d x\)
Solution:

5. Evaluate:

(i) \(\int \frac{3 x-1}{2 x^{2}-x-1} d x\)
Solution:

(ii) \(\int \frac{2 x^{3}-3 x^{2}-9 x+1}{2 x^{2}-x-10} d x\)
Solution:

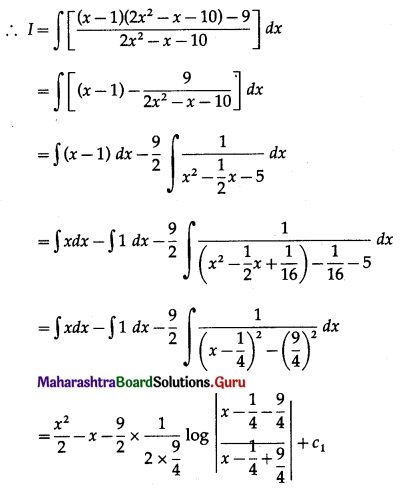
(iii) \(\int \frac{1+\log x}{x(3+\log x)(2+3 \log x)} d x\)
Solution:

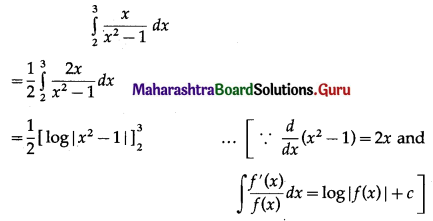
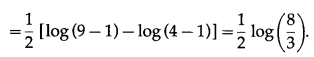
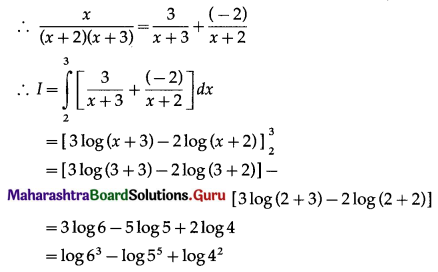
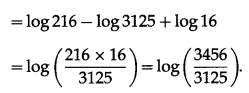
Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.6 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.6

Evaluate:

Question 1.
\(\int \frac{2 x+1}{(x+1)(x-2)} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{(x+1)(x-2)} d x\)
Let \(\frac{2 x+1}{(x+1)(x-2)}=\frac{A}{x+1}+\frac{B}{x-2}\)
∴ 2x + 1 = A(x – 2) + B(x + 1)
Put x + 1 = 0, i.e. x = -1, we get
2(-1) + 1 = A(-3) + B(0)
∴ A = \(\frac{1}{3}\)
Put x – 2 = 0, i.e. x = 2, we get
2(2) + 1 = A(0) + B(3)
∴ B = \(\frac{5}{3}\)

Question 2.
\(\int \frac{2 x+1}{x(x-1)(x-4)} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{x(x-1)(x-4)} d x\)
Let \(\int \frac{2 x+1}{x(x-1)(x-4)}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{x-4}\)
∴ 2x + 1 = A(x – 1)(x – 4) + Bx(x – 4) + Cx(x – 1)
Put x = 0, we get
2(0) + 1 = A(-1)(-4) + B(0)(-4) + C(0)(-1)
∴ 1 = 4A
∴ A = \(\frac{1}{4}\)
Put x – 1 = 0, i.e. x = 1, we get
2(1) + 1 = A(0)(-3) + B(1)(-3) + C(1)(0)
∴ 3 = -3B
∴ B = -1
Put x – 4 = 0, i.e x = 4, we get
2(4) + 1 = A(3)(0) + B(4)(0) + C(4)(3)
∴ 9 = 12C
∴ C = \(\frac{3}{4}\)

Question 3.
\(\int \frac{x^{2}+x-1}{x^{2}+x-6} d x\)
Solution:

∴ 1 = A(x – 2) + B(x + 3)
Put x + 3 = 0, i.e. x = -3, we get
1 = A(-5) + B (0)
∴ A = \(\frac{-1}{5}\)
Put x – 2 = 0, i.e. x = 2, we get
1 = A(0) + B(5)
∴ B = \(\frac{1}{5}\)

Question 4.
\(\int \frac{x}{(x-1)^{2}(x+2)} d x\)
Solution:
Let I = \(\int \frac{x}{(x-1)^{2}(x+2)} d x\)
Let \(\frac{x}{(x-1)^{2}(x+2)}=\frac{A}{x-1}+\frac{B}{(x-1)^{2}}+\frac{C}{x+2}\)
∴ x = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)²
Put x – 1 = 0, i.e. x = 1, we get
1 = A(0)(3) + B(3) + C(0)
∴ B = \(\frac{1}{3}\)
Put x + 2 = 0, i.e. x = -2, we get
-2 = A (-3)(0) + B(0) + C(9)
∴ C = \(-\frac{2}{9}\)
Put x = -1, we get,
-1 = A(-2)(1) + B(1) + C(4)
But B = \(\frac{1}{3}\) and C = \(-\frac{2}{9}\)

Question 5.
\(\int \frac{3 x-2}{(x+1)^{2}(x+3)} d x\)
Solution:
Let I = \(\int \frac{3 x-2}{(x+1)^{2}(x+3)} d x\)
Let \(\frac{3 x-2}{(x+1)^{2}(x+3)}=\frac{A}{x+1}+\frac{B}{(x+1)^{2}}+\frac{C}{x+3}\)
∴ 3x – 2 = A(x + 1)(x + 3) + B(x + 3) + C(x + 1)²
Put x + 1 = 0, i.e. x = -1, we get
3(-1) – 2 = A(0)(2) + B(2) + C(0)
∴ -5 = 2B
∴ B = \(-\frac{5}{2}\)
Put x + 3 = 0, i.e. x = -3, we get
3(-3) – 2 = A(-2)(0) + B(0) + C(4)
∴ -11 = 4C
∴ C = \(-\frac{11}{4}\)
Put x = 0, we get
3(0) – 2 = A(1)(3) + B(3) + C(1)
∴ -2 = 3A + 3B + C
But B = \(-\frac{5}{2}\) and C = \(-\frac{11}{4}\)

Question 6.
\(\int \frac{1}{x\left(x^{5}+1\right)} d x\)
Solution:
Let I = \(\int \frac{1}{x\left(x^{5}+1\right)} d x\)
= \(\int \frac{x^{4}}{x^{5}\left(x^{5}+1\right)} d x\)

Question 7.
\(\int \frac{1}{x\left(x^{n}+1\right)} d x\)
Solution:

Question 8.
\(\int \frac{5 x^{2}+20 x+6}{x^{3}+2 x^{2}+x} d x\)
Solution:

Let \(\frac{5 x^{2}+20 x+6}{x(x+1)^{2}}=\frac{A}{x}+\frac{B}{x+1}+\frac{C}{(x+1)^{2}}\)
∴ 5x² + 20x + 6 = A(x + 1)² + Bx(x + 1) + Cx
Put x = 0, we get
0 + 0 + 6 = A(1) + B(0)(1) + C(0)
∴ A = 6
Put x + 1 = 0, i.e. x = -1, we get
5(1) + 20(-1) + 6 = A(0) + B(-1)(0) + C(-1)
∴ -9 = -C
∴ C = 9
Put x = 1, we get
5(1) + 20(1) + 6 = A(4) + B(1)(2) + C(1)
But A = 6 and C = 9
∴ 31 = 24 + 2B + 9
∴ B = -1

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.5

Evaluate the following.

Question 1.
∫x log x
Solution:

Question 2.
∫x² e^4x dx
Solution:

Question 3.
∫x² e^3x dx
Solution:

Question 4.
\(\int x^{3} e^{x^{2}} d x\)
Solution:

Question 5.
\(\int e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right) d x\)
Solution:

Question 6.
\(\int e^{x} \frac{x}{(x+1)^{2}} d x\)
Solution:

Question 7.
\(\int e^{x} \frac{x-1}{(x+1)^{3}} d x\)
Solution:

Question 8.
\(\int e^{x}\left[(\log x)^{2}+\frac{2 \log x}{x}\right] d x\)
Solution:

Question 9.
\(\int\left[\frac{1}{\log x}-\frac{1}{(\log x)^{2}}\right] d x\)
Solution:

Question 10.
\(\int \frac{\log x}{(1+\log x)^{2}} d x\)
Solution:

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Ex 1.5

Question 1.
Use qualifiers to convert each of the following open sentences defined on N, into a true statement:
(i) x² + 3x – 10 = 0
Solution:
∃ x ∈ N, such that x² + 3x – 10 = 0 is a true statement
(x = 2 ∈ N satisfy x² + 3x – 10 = 0)

(ii) 3x – 4 < 9
Solution:
∃ x ∈ N, such that 3x – 4 < 9 is a true statement.
(x = 1, 2, 3, 4 ∈ N satisfy 3x – 4 < 9)

(iii) n² ≥ 1
Solution:
∀ n ∈ N, n² ≥ 1 is a true statement.
(All n ∈ N satisfy n² ≥ 1)

(iv) 2n – 1 = 5
Solution:
∃ x ∈ N, such that 2n – 1 = 5 is a true statement.
(n = 3 ∈ N satisfy 2n – 1 = 5)

(v) y + 4 > 6
Solution:
∃ y ∈ N, such that y + 4 > 6 is a true statement.
(y = 3, 4, 5, … ∈ N satisfy y + 4 > 6

(vi) 3y – 2 ≤ 9
Solution:
∃ y ∈ N, such that 2y ≤ 9 is a true statement.
(y = 1, 2, 3 ∈ N satisfy 3y – 2 ≤ 9).

Question 2.
If B = {2, 3, 5, 6, 7}, determine the truth value of each of the following:
(i) ∀ x ∈ B, x is a prime number.
Solution:
(i) x = 6 ∈ B does not satisfy x is a prime number.
So, the given statement is false, hence its truth value is F.

(ii) ∃ n ∈ B, such that n + 6 > 12.
Solution:
Clearly n = 7 ∈ B satisfies n + 6 > 12.
So, the given statement is true, hence its truth value is T.

(iii) ∃ n ∈ B, such that 2n + 2 < 4.
Solution:
No element n ∈ B satisfy 2n + 2 < 4.
So, the given statement is false, hence its truth value is F.

(iv) ∀ y ∈ B, y² is negative.
Solution:
No element y ∈ B satisfy y² is negative.
So, the given statement is false, hence its truth value is F.

(v) ∀ y ∈ B, (y – 5) ∈ N.
Solution:
y = 2 ∈ B, y = 3 ∈ B and y = 5 ∈ B do not satisfy (y – 5) ∈ N.
So, the given statement is false, hence its truth value is F.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Ex 1.4

Question 1.
Write the following statements in symbolic form:
(i) If the triangle is equilateral, then it is equiangular.
Solution:
Let p : Triangle is equilateral.
q : It is equiangular.
Then the symbolic form of the given statement is p → q.

(ii) It is not true that ‘i’ is a real number.
Solution:
Let p : ‘i’ is a real number.
Then the symbolic form of the given statement is ~p.

(iii) Even though it is not cloudy, it is still raining.
Solution:
Let p : It is cloudy.
q : It is still raining.
Then the symbolic form of the given statement is ~p ∧ q.

(iv) Milk is white if and only if the sky is not blue.
Solution:
Let p : Milk is white.
q : Sky is blue.
Then the symbolic form of the given statement is p ↔ (~q).

(v) Stock prices are high if and only if stocks are rising.
Solution:
Let p : Stock prices are high.
q : stocks are rising.
Then the symbolic form of the given statement is p ↔ q

(vi) If Kutub-Minar is in Delhi, then Taj Mahal is in Agra.
Solution:
Let p : Kutub-Minar is in Delhi.
q : Taj Mahal is in Agra.
Then the symbolic form of the given statement is p → q

Question 2.
Find the truth value of each of the following statements:
(i) It is not true that 3 – 7i is a real number.
Solution:
Let p : 3 – 7i be a real number.
Then the symbolic form of the given statement is ~p.
The truth value of p is F.
∴ the truth value of ~p is T. ….[~F ≡ T]

(ii) If a joint venture is a temporary partnership, then a discount on purchase is credited to the supplier.
Solution:
Let p : Joint venture is a temporary partnership.
q : Discount on purchases is credited to the supplier.
Then the symbolic form of the given statement is p → q.
The truth values of p and q are T and F respectively.
∴ the truth value of p → q is F. …..[T → F ≡ F]

(iii) Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
Solution:
Let p : Every accountant is free to apply his own accounting rules.
q : Machinery is an asset.
Then the symbolic form of the given statement is p ↔ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ↔ q is F. ….[F ↔ T ≡ F]

(iv) Neither 27 is a prime number nor divisible by 4.
Solution:
Let p : 27 is a prime number.
q : 27 is divisible by 4.
Then the symbolic form of the given statement is ~p ∧ ~q.
The truth values of both p and q are F.
∴ the truth value of ~p ∧ ~q is T. …..[~F ∧ ~F ≡ T ∧ T ≡ T]

(v) 3 is a prime number and an odd number.
Solution:
Let p : 3 be a prime number.
q : 3 is an odd number.
Then the symbolic form of the given statement is p ∧ q
The truth values of both p and q are T.
∴ the truth value of p ∧ q is T. …..[T ∧ T ≡ T]

Question 3.
If p and q are true and r and s are false, find the true value of each of the following statements:
(i) p ∧ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∧ (q ∧ r) ≡ T ∧ (T ∧ F)
≡ T ∧ F
≡ F
Hence, the truth value of the given statement is false.

(ii) (p → q) ∨ (r ∧ s)
Solution:
(p → q) ∨ (r ∧ s) ≡ (T → T) ∨ (F ∧ F)
≡ T ∨ F
≡ T
Hence, the truth value of the given statement is true.

(iii) ~[(~p ∨ s) ∧ (~q ∧ r)]
Solution:
~[(~p ∨ s) ∧ (~q ∧ r)] ≡ ~[(~ T ∨ F) ∧ (~T ∧ F)]
≡ ~[(F ∨ F) ∧ (F ∧ F)]
≡ ~(F ∧ F)
≡ ~F
≡ T
Hence, the truth value of the given statement is true.

(iv) (p → q) ↔ ~(p ∨ q)
Solution:
(p → q) ↔ ~(p ∨ q) = (T → T) ↔ ~(T ∨ T)
≡ T ↔ ~ (T)
≡ T ↔ F
≡ F
Hence, the truth value of the given statement is false.

(v) [(p ∨ s) → r] ∨ [~(p → q) ∨ s]
Solution:
[(p ∨ s) → r] ∨ ~[~(p → q) ∨ s]
≡ [(T ∨ F) → F] ∨ ~[ ~(T → T) ∨ F]
≡ (T → F) ∨ ~(~T ∨ F)
≡ F ∨ ~ (F ∨ F)
≡ F ∨ ~F
≡ F ∨ T
≡ T
Hence, the truth value of the given statement is true.

(vi) ~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
Solution:
~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
≡ ~[T ∨ (F ∧ F)] ∧ ~[(F ∧ ~F) ∧ T]
≡ ~[T ∨ F] ∧ ~[(F ∧ T) ∧ T]
≡ ~T ∧ ~(F ∧ T)
≡ F ∧ ~F
≡ F ∧ T
≡ F
Hence, the truth value of the given statement is false.

Question 4.
Assuming that the following statements are true:
p : Sunday is a holiday.
q : Ram does not study on holiday.
Find the truth values of the following statements:
(i) Sunday is not holiday or Ram studies on holiday.
Solution:
The symbolic form of the statement is ~p ∨ ~q.

∴ the truth value of the given statement is F.

(ii) If Sunday is not a holiday, then Ram studies on holiday.
Solution:
The symbolic form of the given statement is ~p → ~q.

∴ the truth value of the given statement is T.

(iii) Sunday is a holiday and Ram studies on holiday.
Solution:
The symbolic form of the given statement is p ∧ q.

∴ the truth value of the given statement is F.

Question 5.
If p : He swims.
q : Water is warm.
Give the verbal statements for the following symbolic statements:
(i) p ↔ ~q
Solution:
p ↔ ~ q
He swims if and only if the water is not warm.

(ii) ~(p ∨ q)
Solution:
~(p ∨ q)
It is not true that he swims or water is warm.

(iii) q → p
Solution:
q → p
If water is warm, then he swims.

(iv) q ∧ ~p
Solution:
q ∧ ~p
The water is warm and he does not swim.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Ex 1.3

Question 1.
Write the negation of each of the following statements:
(i) All men are animals.
Solution:
Some men are not animals.

(ii) 3 is a natural number.
Solution:
-3 is not a natural number.

(iii) It is false that Nagpur is the capital of Maharashtra.
Solution:
Nagpur is the capital of Maharashtra.

(iv) 2 + 3 ≠ 5.
Solution:
2 + 3 = 5.

Question 2.
Write the truth value of the negation of each of the following statements:
(i) √5 is an irrational number.
Solution:
Let p : √5 is an irrational number.
The truth value of p is T.
Therefore, the truth value of ~p is F.

(ii) London is in England.
Solution:
Let p : London is in England.
The truth value of p is T.
Therefore, the truth value of ~p is F.

(iii) For every x ∈ N, x + 3 < 8.
Solution:
Let p : For every x ∈ N, x + 3 < 8.
The truth value of p is F.
Therefore, the truth value of ~p is T.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Ex 1.2

Question 1.
Express the following statements in symbolic form:
(i) e is a vowel or 2 + 3 = 5.
Solution:
Let p : e is a vowel.
q: 2 + 3 = 5.
Then the symbolic form of the given statement is p ∨ q.

(ii) Mango is a fruit but potato is a vegetable.
Solution:
Let p : Mango is a fruit.
q : Potato is a vegetable.
Then the symbolic form of the given statement is p ∧ q.

(iii) Milk is white or grass is green.
Solution:
Let p : Milk is white.
q : Grass is green.
Then the symbolic form of the given statement is p ∨ q.

(iv) I like playing but not singing.
Solution:
Let p : I like playing.
q : I am not singing.
Then the symbolic form of the given statement is p ∧ q.

(v) Even though it is cloudy, it is still raining.
Solution:
The given statement is equivalent to:
It is cloudy and it is still raining.
Let p : It is cloudy.
q : It is still raining.
Then the symbolic form of the given statement is p ∧ q.

Question 2.
Write the truth values of the following statements:
(I) Earth is a planet and Moon is a star.
Solution:
Let p : Earth is a planet.
q : Moon is a star.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. …[T ∧ F ≡ F]

(ii) 16 is an even number and 8 is a perfect square.
Solution:
Let p : 16 is an even number.
q : 8 is a perfect square.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. ….[T ∧ F ≡ F]

(iii) A quadratic equation has two distinct roots or 6 has three prime factors.
Solution:
Let p : A quadratic equation has two distinct roots.
q : 6 has three prime factors.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are F.
∴ the truth value of p ∨ q is F. …..[F ∨ F ≡ F]

(iv) The Himalayas are the highest mountains but they are part of India in the northeast.
Solution:
Let p : the Himalayas are the highest mountains.
q : They are part of India in the northeast.
Then the symbolic form of the given statement is p ∧ q.
The truth values of both p and q are T.
∴ the truth value of p ∧ q is T. …..[T ∧ T ≡ T]

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Ex 1.1

State which of the following sentences are statements. Justify your answer. In case of statements, write down the truth value:

Question (i).
A triangle has ‘ n’ sides.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (ii).
The sum of interior angles of a triangle is 180°.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (iii).
You are amazing!
Solution:
It is an exclamatory sentence, hence it is not a statement.

Question (iv).
Please grant me a loan.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (v).
√-4 is an irrational number.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (vi).
x² – 6x + 8 = 0 implies x = -4 or x = -2.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (vii).
He is an actor.
Solution:
It is an open sentence, hence it is not a statement.

Question (viii).
Did you eat lunch yet?
Solution:
It is an interrogative sentence, hence it is not a statement.

Question (ix).
Have a cup of cappuccino.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (x).
(x + y)² = x² + 2xy + y² for all x, y ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is ‘T’.

Question (xi).
Every real number is a complex number.
Solution:
It is a statement that is true, hence its truth value is ‘T.

Question (xii).
1 is a prime number.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (xiii).
With the sunset, the day ends.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xiv).
1! = 0.
Solution:
It is a statement that is false, hence its truth value is

Question (xv).
3 + 5 > 11.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (xvi).
The number π is an irrational number.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xvii).
x² – y² = (x + y)(x – y) for all x, y ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is ‘T’.

Question (xviii).
The number 2 is only even a prime number.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xix).
Two coplanar lines are either parallel or intersecting.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xx).
The number of arrangements of 7 girls in a row for a photograph is 7!
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xxi).
Give me a compass box.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (xxii).
Bring the motor car here.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (xxiii).
It may rain today.
Solution:
It is an open sentence, hence it is not a statement.

Question (xxiv).
If a + b < 7, where a ≥ 0 and b ≥ 0, then a < 7 and b < 7.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xxv).
Can you speak English?
Solution:
It is an interrogative sentence, hence it is not a statement.

Maharashtra State Board HSC 12th Commerce Maths & Statistics Digest Pdf, 12th Commerce Maharashtra State Board Maths Solution Book Pdf Part 1 & 2 free download in English Medium and Marathi Medium 2021-2022.

Maharashtra State Board 12th Commerce Maths Digest Pdf

12th Commerce Maths Digest Pdf Part 1

Maharashtra State Board Std 12th Commerce Maths Textbook Solutions Chapter 1 Mathematical Logic

• Chapter 1 Mathematical Logic Ex 1.1
• Chapter 1 Mathematical Logic Ex 1.2
• Chapter 1 Mathematical Logic Ex 1.3
• Chapter 1 Mathematical Logic Ex 1.4
• Chapter 1 Mathematical Logic Ex 1.5
• Chapter 1 Mathematical Logic Ex 1.6
• Chapter 1 Mathematical Logic Ex 1.7
• Chapter 1 Mathematical Logic Ex 1.8
• Chapter 1 Mathematical Logic Ex 1.9
• Chapter 1 Mathematical Logic Ex 1.10
• Chapter 1 Mathematical Logic Miscellaneous Exercise 1

12th Commerce Maths Book Pdf Chapter 2 Matrices

• Chapter 2 Matrices Ex 2.1
• Chapter 2 Matrices Ex 2.2
• Chapter 2 Matrices Ex 2.3
• Chapter 2 Matrices Ex 2.4
• Chapter 2 Matrices Ex 2.5
• Chapter 2 Matrices Ex 2.6
• Chapter 2 Matrices Miscellaneous Exercise 2

Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 3 Differentiation

• Chapter 3 Differentiation Ex 3.1
• Chapter 3 Differentiation Ex 3.2
• Chapter 3 Differentiation Ex 3.3
• Chapter 3 Differentiation Ex 3.4
• Chapter 3 Differentiation Ex 3.5
• Chapter 3 Differentiation Ex 3.6
• Chapter 3 Differentiation Miscellaneous Exercise 3

12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives

• Chapter 4 Applications of Derivatives Ex 4.1
• Chapter 4 Applications of Derivatives Ex 4.2
• Chapter 4 Applications of Derivatives Ex 4.3
• Chapter 4 Applications of Derivatives Ex 4.4
• Chapter 4 Applications of Derivatives Miscellaneous Exercise 4

12th Commerce Maths Notes Chapter 5 Integration

• Chapter 5 Integration Ex 5.1
• Chapter 5 Integration Ex 5.2
• Chapter 5 Integration Ex 5.3
• Chapter 5 Integration Ex 5.4
• Chapter 5 Integration Ex 5.5
• Chapter 5 Integration Ex 5.6
• Chapter 5 Integration Miscellaneous Exercise 5

12th Commerce Maths Digest Pdf Chapter 6 Definite Integration

• Chapter 6 Definite Integration Ex 6.1
• Chapter 6 Definite Integration Ex 6.2
• Chapter 6 Definite Integration Miscellaneous Exercise 6

12th Maharashtra State Board Maths Solution Book Pdf Part 1 Chapter 7 Application of Definite Integration

• Chapter 7 Application of Definite Integration Ex 7.1
• Chapter 7 Application of Definite Integration Miscellaneous Exercise 7

12th Maths 1 Digest Pdf Chapter 8 Differential Equation and Applications

• Chapter 8 Differential Equation and Applications Ex 8.1
• Chapter 8 Differential Equation and Applications Ex 8.2
• Chapter 8 Differential Equation and Applications Ex 8.3
• Chapter 8 Differential Equation and Applications Ex 8.4
• Chapter 8 Differential Equation and Applications Ex 8.5
• Chapter 8 Differential Equation and Applications Ex 8.6
• Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

12th Commerce Maths Solution Book Pdf Part 2

HSC Maths Textbook Pdf Chapter 1 Commission, Brokerage and Discount

• Chapter 1 Commission, Brokerage and Discount Ex 1.1
• Chapter 1 Commission, Brokerage and Discount Ex 1.2
• Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1

12th Maths Digest Pdf Part 2 Chapter 2 Insurance and Annuity

• Chapter 2 Insurance and Annuity Ex 2.1
• Chapter 2 Insurance and Annuity Ex 2.2
• Chapter 2 Insurance and Annuity Miscellaneous Exercise 2

12 Maths Book Pdf State Board Chapter 3 Linear Regression

• Chapter 3 Linear Regression Ex 3.1
• Chapter 3 Linear Regression Ex 3.2
• Chapter 3 Linear Regression Ex 3.3
• Chapter 3 Linear Regression Miscellaneous Exercise 3

12th Maths 2 Digest Pdf Chapter 4 Time Series

• Chapter 4 Time Series Ex 4.1
• Chapter 4 Time Series Miscellaneous Exercise 4

12th Maths Part 2 Digest Pdf Chapter 5 Index Numbers

• Chapter 5 Index Numbers Ex 5.1
• Chapter 5 Index Numbers Ex 5.2
• Chapter 5 Index Numbers Ex 5.3
• Chapter 5 Index Numbers Miscellaneous Exercise 5

12th Statistics Book Chapter 6 Linear Programming

• Chapter 6 Linear Programming Ex 6.1
• Chapter 6 Linear Programming Ex 6.2
• Chapter 6 Linear Programming Miscellaneous Exercise 6

12th Commerce Maths Book Pdf Chapter 7 Assignment Problem and Sequencing

• Chapter 7 Assignment Problem and Sequencing Ex 7.1
• Chapter 7 Assignment Problem and Sequencing Ex 7.2
• Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7

12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions

• Chapter 8 Probability Distributions Ex 8.1
• Chapter 8 Probability Distributions Ex 8.2
• Chapter 8 Probability Distributions Ex 8.3
• Chapter 8 Probability Distributions Ex 8.4
• Chapter 8 Probability Distributions Miscellaneous Exercise 8

Maharashtra State Board Class 12 Textbook Solutions