Bhagya

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 3 सच हम नहीं; सच तुम नहीं Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 3 सच हम नहीं; सच तुम नहीं

12th Hindi Guide Chapter 3 सच हम नहीं; सच तुम नहीं Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) कविता की पंक्ति पूर्ण कीजिए :
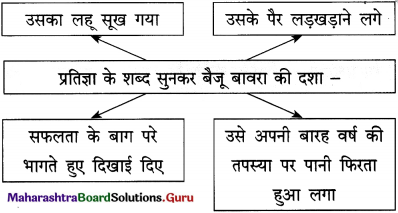
(1) अपने हृदय का सत्य, – ……………………….
(2) आदर्श हो सकती नहीं, – ……………………….
(3) बेकार है मुस्कान से ढकना, – ……………………….
(4) अपने नयन का नीर, – ……………………….
उत्तर :
(1) अपने हृदय का सत्य, अपने-आप हमको खोजना।
(2) आदर्श हो सकती नहीं, तन और मन की भिन्नता।
(3) बेकार है मुस्कान से ढकना, हृदय की खिन्नता।
(4) अपने नयन का नीर, अपने-आप हमको पोंछना।

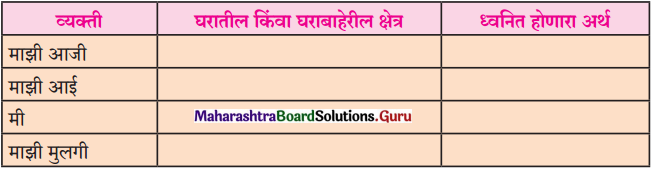
(आ) लिखिए :

(a) जीवन यही है
(1) जीवन यही है –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
जीवन यही है –
(i) नत न होना।
(ii) पंथ भूलने पर भी न रुकना।
(iii) हार देखकर भी न झुकना।
(iv) मृत्यु को भी जीत लेना।

(b) मिलना वही है –
(1) मिलना वही है – ……………………….
(2) यह जिंदगी जिंदगी नहीं है – ……………………….
(3) हर राही को इससे दिशा मिलती है – ……………………….
(4) कवि तब तक इस राह को सही नहीं मानेगा – ……………………….
उत्तर :
(1) जो मँझधार को मोड़ दे।
(2) जो सिर्फ पानी-सी बहती रहे।
(3) भटकने के बाद।
(4) जब तक जीवन बँधा होगा और जब तक प्यार पर दुख की गहरी छाया होगी।

शब्द संपदा

प्रश्न 2.
प्रत्येक शब्द के दो पर्यायवाची शब्द लिखिए :
(1) पंथ – [ ] [ ]
(2) काँटा – [ ] [ ]
(3) कुसुम – [ ] [ ]
(4) हार – [ ] [ ]
उत्तर :
(1) पंथ – [ रास्ता ] [ डगर ]
(2) काँटा – [ शूल ] [ कंटक ]
(3) कुसुम – [ पुष्प ] [ प्रसून ]
(4) हार – [ पराजय ] [ पराभव ]

अभिव्यक्ति

प्रश्न 3.
(अ) ‘जीवन निरंतर चलते रहने का नाम है’, इस विचार की सार्थकता स्पष्ट कीजिए।
उत्तर :
जीवन का उद्देश्य निरंतर आगे-ही-आगे बढ़ते रहना है। जीवन में ठहराव आने को मृत्यु की संज्ञा दी जाती है। अनेक महापुरुषों ने अपने उद्देश्य की पूर्ति के लिए जीवनभर संघर्ष किया है और उनका नाम अमर हो गया है। जीवन का मार्ग आसान नहीं ३ है। उस पर पग-पग पर कठिनाइयाँ आती रहती हैं। इन कठिनाइयों 1 से उसे जूझना पड़ता है। उसमें हार भी होती है और जीत भी होती ३ है। असफलताओं से मनुष्य को घबराना नहीं चाहिए।

बल्कि उनका ३ दृढ़तापूर्वक सामना करके उसमें से अपना मार्ग प्रशस्त करना और ३ निरंतर आगे बढ़ते रहना चाहिए। एक दिन मंजिल अवश्य मिलेगी। जीवन संघर्ष कभी न खत्म होने वाला संग्राम है। इसका सामना करने का एकमात्र मार्ग है निरंतर चलते रहना और हर स्थिति में संघर्ष जारी रखना।

(आ) ‘संघर्ष करने वाला ही जीवन का लक्ष्य प्राप्त करता है, इस विषय पर अपने विचार प्रकट कीजिए।
उत्तर :
दुनिया में दो प्रकार के मनुष्य होते हैं। एक वे जो सामान्य रूप से चलनेवाली जिंदगी जीना पसंद करते हैं और आगे बढ़ने के लिए किए जानेवाले उठा-पटक को पसंद नहीं करते। दूसरे तरह के वे लोग होते हैं, जो अपना लक्ष्य निर्धारित कर लेते हैं और उसे प्राप्त करने के लिए संघर्ष का रास्ता चुनते हैं। ऐसे लोगों का जीवन आसान नहीं होता। इन्हें पग-पग पर विभिन्न रुकावटों का सामना करना पड़ता है।

पर ऐसे लोग इन रुकावटों से डरते नहीं, बल्कि हँसते-हँसते इनका सामना करते हैं। सामना करने में अनेक बार असफलता भी इनके हाथ लगती है। पर ये इससे हताश नहीं होते। ये फिर अपनी गलतियों को सुधारते हैं और नए सिरे से संघर्ष करने में जुट जाते हैं। परिस्थितियाँ कैसी भी हों, वे न झुकते हैं और न हताश होते हैं। उनके सामने सदा उनका लक्ष्य होता है। उसे प्राप्त करने के लिए वे निरंतर संघर्ष करते रहते हैं।

ऐसे लोग अपनी निष्ठा और लगन के बल पर एक-न-एक दिन अवश्य सफल हो जाते हैं। वे संघर्ष के बल पर अपने जीवन का लक्ष्य प्राप्त करके रहते हैं।

रसास्वादन

प्रश्न 4.
‘आँसुओं को पोंछकर अपनी क्षमताओं को पहचानना ही जीवन है’, इस सच्चाई को समझाते हुए कविता का रसास्वादन कीजिए।
उत्तर :
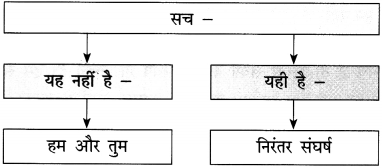
डॉ. जगदीश गुप्त द्वारा लिखित कविता ‘सच हम नहीं, सच तुम नहीं’ में जीवन में निरंतर संघर्ष करते रहने का आह्वान किया गया है।

कवि पानी-सी बहने वाली सीधी-सादी जिंदगी का विरोध करते हुए संघर्षपूर्ण जीवन जीने की बात करते हैं। वे कहते हैं, जो जहाँ भी हो, उसे संघर्ष करते रहना चाहिए।

संघर्ष में मिली असफलता से निराश होने की आवश्यकता नहीं है। ऐसी हालत में हमें किसी के सहयोग की आशा नहीं करनी। हमें अपने आप में खुद हिम्मत लानी होगी और अपनी क्षमता को पहचानकर नए सिरे से संघर्ष करना होगा। मन में यह विश्वास रखकर काम करना होगा कि हर राही को भटकने के बाद दिशा मिलती ही है और उसका प्रयास व्यर्थ नहीं जाएगा। उसे भी दिशा मिलकर रहेगी।

कवि ने सीधे-सादे शब्दों में प्रभावशाली ढंग से अपनी बात कही है। अपनी बात कहने के लिए उन्होंने ‘अपने नयन का नीर पोंछने’ शब्द समूह के द्वारा हताशा से अपने आपको उबार कर स्वयं में नई शक्ति पैदा करने तथा ‘आकाश सुख देगा नहीं, धरती पसीजी है नहीं’ से यह कहने का प्रयास किया है कि भगवान तुम्हारी सहायता के लिए नहीं आने वाले हैं और धरती के लोग तुम्हारे दुख से द्रवित नहीं होने वाले हैं। इसलिए तुम स्वयं अपने आप को सांत्वना दो और नए जोश के साथ आगे बढ़ो। तुम अपने लक्ष्य पर पहुँचने में अवश्य कामयाब होंगे।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
जानकारी दीजिए :
(अ) ‘नई कविता’ के अन्य कवियों के नाम –
(आ) कवि डॉक्टर जगदीश गुप्त की प्रमुख साहित्यिक कृतियों के नाम –
उत्तर :
(अ) ‘नई कविता’ के अन्य कवियों के नाम – [रामस्वरूप चतुर्वेदी, विजयदेव साही]
(आ) कवि डॉक्टर जगदीश गुप्त की प्रमुख साहित्यिक कृतियों के नाम – [‘नाँव के पाँव, शब्द दंश, हिम विद्ध, गोपा-गौतम’] (काव्य संग्रह), ‘शंबूक’ (खंडकाव्य), ‘भारतीय कला के पदचिहन, नयी कविता : स्वरूप और समस्याएँ, केशवदास’ (आलोचनाएँ) तथा ‘नयी कविता’ (पत्रिका)।]

प्रश्न 6.
निम्नलिखित वाक्यों में अधोरेखांकित शब्दों का लिंग परिवर्तन कर वाक्य फिर से लिखिए :

(1) बहुत चेष्टा करने पर भी हरिण न आया।
उत्तर :
बहुत चेष्टा करने पर भी हरिणी न आई।

(2) सिद्धहस्त लेखिका बनना ही उनका एकमात्र सपना था।
उत्तर :
सिद्धहस्त लेखक बनना ही उनका एकमात्र सपना था।

(3) तुम एक समझदार लड़की हो।
उत्तर :
तुम एक समझदार लड़के हो।

(4) मैं पहली बार वृद्धाश्रम में मौसी से मिलने आया था।
उत्तर :
मैं पहली बार वृद्धाश्रम में मौसा से मिलने आया था।

(5) तुम्हारे जैसा पुत्र भगवान सब को दे।
उत्तर :
तुम्हारी जैसी पुत्री भगवान सब को दे।

(6) साधु की विद्वत्ता की धाक दूर-दूर तक फैल गई थी।
उत्तर :
साध्वी की विद्वत्ता की धाक दूर-दूर तक फैल गई थी।

(7) बूढ़े मर गए।
उत्तर :
बुढ़ियाँ मर गईं।

(8) वह एक दस वर्ष का बच्चा छोड़ा गया।
उत्तर :
वह एक दस वर्ष की बच्ची छोड़ी गई।

(9) तुम्हारा मौसेरा भाई माफी माँगने पहुंचा था।
उत्तर :
तुम्हारी मौसेरी बहन माफी माँगने पहुंची थी।

(10) एक अच्छी सहेली के नाते तुम उसकी पारिवारिक पृष्ठभूमि का अध्ययन करो।
उत्तर :
एक अच्छे मित्र के नाते तुम उसकी पारिवारिक पृष्ठभूमि का अध्ययन करो।

Hindi Yuvakbharati 12th Digest Chapter 3 सच हम नहीं; सच तुम नहीं Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
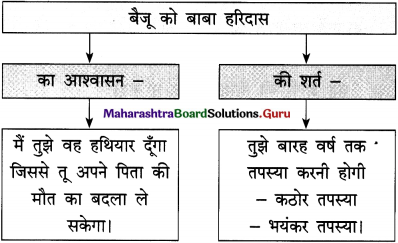
पद्यांश क्र. 1

प्रश्न. निम्नलिखितपद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

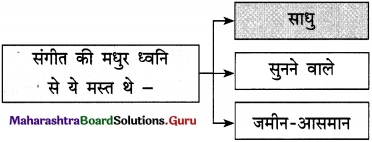
प्रश्न 1.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
जीवन का संदेश
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
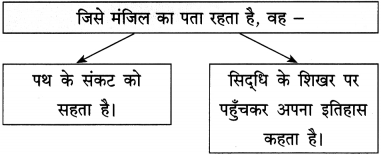
जीवन का संदेश –
(i) जीवन में कहीं जड़ता नहीं होनी चाहिए।
(ii) अपनी-अपनी जगह पर खुद से लड़ाई जारी रखनी चाहिए।
(iii) हर तरह की परिस्थिति का सामना करने की तैयारी होनी चाहिए।
(iv) इन्सान को कभी टूटना-हारना नहीं चाहिए।

प्रश्न 3.
उत्तर लिखिए :
(1) नत होने से मृत जैसा होने की तुलना की गई है इससे – …………………………….
(2) काँटे चुभे, कलियाँ खिलें का अर्थ – …………………………….
उत्तर :
(1) नत होने से मृत जैसा होने की तुलना की गई है इससे – [डंठल से झरे फूल से।]
(2) काँटे चुभे, कलियाँ खिलें का अर्थ – [स्थिति चाहे प्रतिकूल हो अथवा अनुकूल।]

पदयांश क्र. 2
प्रश्न. निम्नलिखितपद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
पद्यांश पर आधारित दो ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों :
(1) आकाश
(2) धरती
उत्तर :
(1) कौन सुख नहीं देगा?
(2) कौन नहीं पसीजती है?

कृति 2 : (शब्द संपदा)

प्रश्न 1.
प्रत्येक शब्द के दो-दो पर्यायवाची शब्द लिखिए :
(1) फूल – [ ] [ ]
(2) नीर – [ ] [ ]
(3) नयन – [ ] [ ]
(4) धरती – [ ] [ ]
उत्तर :
(1) फूल – [ पुष्प ] [ कुसुम ]
(2) नीर – [ अंबु ] [ जल ]
(3) नयन – [ चक्षु ] [ आँख ]
(4) धरती – [ पथ्वी ] [ अवनि ]

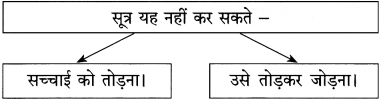
(2) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) तोड़ना x …………………………
(2) सच x …………………………
(3) दुख x …………………………
(4) बेकार x …………………………
उत्तर :
(1) तोड़ना x जोड़ना
(3) दुख x सुख
(2) सच x झूठ
(4) बेकार x साकार।

रसास्वादन मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर सच हम नहीं; सच तुम नहीं’ कविता का रसास्वादन कीजिए।
उत्तर :
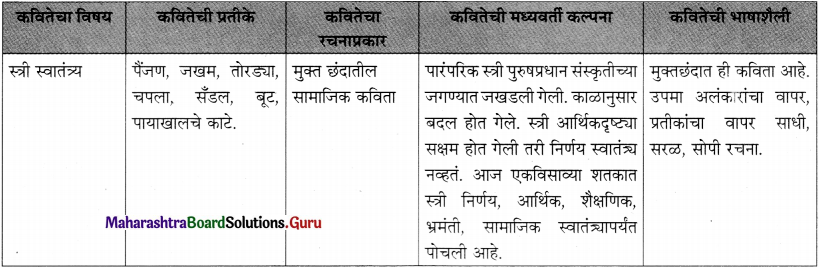
(1) रचना का शीर्षक : सच हम नहीं; सच तुम नहीं।
(2) रचनाकार : डॉ. जगदीश गुप्त।
(3) कविता की केंद्रीय कल्पना : प्रस्तुत कविता में निरंतर आगे बढ़ते रहने, संघर्ष करते रहने और मार्ग में आनेवाली रुकावटों की परवाह न करके अपने लक्ष्य की प्राप्ति की ओर अग्रसर होने की प्रेरणा दी गई है। यही इस कविता की केंद्रीय कल्पना है।
(4) रस-अलंकार : –
(5) प्रतीक विधान : इस कविता में संघर्ष का मार्ग त्याग कर नत हो जाने यानी किसी की अधीनता स्वीकार कर लेने वाले को मृतक के समान हो जाना कहा गया है। कवि ने इस तरह के मृत व्यक्ति के लिए ‘डाल से झड़े हुए फूल’ का प्रतीक के रूप में उपयोग किया है।
(6) कल्पना : जीवन में दृढ़तापूर्वक संघर्ष का मार्ग अपनाना और निराश हुए बिना उस पर अडिग रहना ही जीवन की एकमात्र सच्चाई है।
(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
अपने हृदय का सत्य,
अपने आप हम को खोजना।
अपने नयन का नीर,
अपने आप हम को पोंछना।.

इन पंक्तियों में अपनी समस्याओं को पहचानने और उनका समाधान ढूँढ़ने के लिए बिना किसी की सहायता की उम्मीद किए स्वयं कमर कस कर तैयार होने की प्रेरणा मिलती है।

(8) कविता पसंद आने का कारण : कवि ने इस पंक्ति में यह बताया है कि संघर्ष में असफलता हाथ लगे, तो भी निराश होने की जरूरत नहीं है। हमें अपने आप अपनी आँखों के आँसू पौंछकर फिर से हिम्मत के साथ संघर्ष में जुट जाना है।

व्याकरण

अलंकार :

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त अलंकार पहचान कर उनके नाम लिखिए :
(1) हरि पद कोमल कमल से।
(2) झूठे जानि न संग्रही मन मुँह निकसे बैन। यहि ते मानहुँ किए, बातनु को बिघि नैन।
(3) पायो जी मैंने राम रतन धन पायो।
(4) हनूमान की पूँछ में लग न पाई आग। लंका सिगरी जल गई, गए निशाचर भाग।
(5) एक म्यान में दो तलवारें कभी नहीं रह सकतीं। किसी और पर प्रेम पति का नारियाँ नहीं सह सकी।
उत्तर :
(1) उपमा अलंकार
(2) उत्प्रेक्षा अलंकार
(3) रूपक अलंकार
(4) अतिशयोक्ति अलंकार
(5) दृष्टांत अलंकार।

रस:

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त रस पहचान कर लिखिए :
(1) काहु न तखा सो चरित विसेरना। सो सरूप नृप कन्या देखा।
मर्कट वदन भयंकर देही। देखत हृदय क्रोध मा तेही।
जेहि दिसि बैठे नारद फूली। सो दिसि तेहि न विलोकी भूली।
पुनि-पुनि मुनि उकसहिं अकुलाहीं। देखि दसा हर गन मुसुकाहीं।

(2) जो हौं तव अनुशासन पावौं
तौ चंद्रमहिं निचोरि चैल ज्यों आनि सुधा सिर नावौं।
कै पाताल दलौं व्यालावलि अमृत कुंड महि लावौ।
भेदि भुवन, करि भानु बाहियें तुरत राहु दै ताबौ।।
विबुध बैद बरबस आनौं धरि, तौ प्रभु अनुग कहावौं।
पटकौं मीच नीच मूषक ज्यों सबहिं को पाप कहावौं।

(3) कहुँ सुलगत कोउ चिता, कहुँ कोउ जात लगाई।
एक लगाई जात, एक की राख बुझाई।
विविध रंग की उठति ज्वाल दुर्गन्धिति महकति,
कहु चरबी सी चटचटाति कहुँ दह-दह दहकति।
उत्तर :
(1) हास्य रस
(2) वीर रस
(3) वीभत्स रस।

मुहावरे :

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) गुड़ गोबर करना।
अर्थ : बने काम को बिगाड़ देना।
वाक्य : चित्रकार का चित्र तैयार था तभी एक छोटे बच्चे ने आकर उस पर ऐसी कूँची फिराई की सारा गुड़ गोबर हो गया।

(2) जहर का चूंट पीना।
अर्थ : अपमान को चुपचाप सह लेना।
वाक्य : मुंशीजी अपने चपरासी से कभी-कभी जब पैर दबा देने की बात करते थे तब वह जहर का यूंट पीकर रह जाता था।

(3) तिल का ताड़ बनाना।
अर्थ : छोटी बात को बढ़ा-चढ़ा कर कहना।
वाक्य : रमेश की बात विश्वास करने लायक नहीं होती, उसकी तो तिल का ताड़ बनाने की आदत है।

(4) मुट्ठी गर्म करना।
अर्थ : रिश्वत देना।
वाक्य : गाँवों में छोटा-मोटा काम करवाने के लिए भी अधिकारियों की मुट्ठी गर्म करनी पड़ती है।

(5) पत्थर की लकीर।
अर्थ : पक्की बात।
वाक्य : गाँव के लोग वकील साहब की बात को पत्थर की लकीर मानते थे।

काल परिवर्तन :

प्रश्न 1.
सूचनाओं के अनुसार काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) वह पंथ भूल कर नहीं रुकता है। (पूर्ण भूतकाल)
(2) वह हार देख कर नहीं झुका। (सामान्य भविष्यकाल)
(3) आकाश सुख नहीं देगा। (अपूर्ण वर्तमानकाल)
(4) धरती नहीं पसीजती है। (पूर्ण वर्तमानकाल)
(5) हर एक राही को भटक कर दिशा मिलती है। (अपूर्ण भूतकाल)
उत्तर :
(1) वह पंथ भूल कर नहीं रुका था।
(2) वह हार देख कर नहीं झुकेगा।
(3) आकाश सुख नहीं दे रहा है।
(4) धरती नहीं पसीजी है।
(5) हर एक राही को भटक कर दिशा मिल रही थी।

वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) वह उसका काम कर रहा हैं।
(2) उस बगीचे में अनेकों फूले खिले हैं।
(3) पुस्तक की ढेर देख मैं दंग रह गया।
(4) उसे मात्र केवल दो दिन की छुट्टी चाहिएँ।
(5) मैं तुमको धन्यवाद करता हूँ।
उत्तर :
(1) वह अपना काम कर रहा है।
(2) उस बगीचे में अनेक फूल खिले हैं।
(3) पुस्तकों का ढेर देख में दंग रह गया।
(4) उसे केवल दो दिन की छुट्टी चाहिए।
(5) मैं तुम्हें धन्यवाद देता हूँ।

सच हम नहीं; सच तुम नहीं Summary in Hindi

सच हम नहीं; सच तुम नहीं कवि का परिचय

सच हम नहीं; सच तुम नहीं कवि का नाम : डॉ. जगदीश गुप्त। (जन्म 1924; निधन 2001.)
प्रमुख कृतियाँ : नाँव के पाँव, शब्द दंश, हिम विद्ध, गोपा-गौतम (काव्य संग्रह), ‘शंबूक’ (खंडकाव्य), भारतीय कला के पदचिह्न,
नयी कविता : स्वरूप और समस्याएँ, केशवदास (आलोचनाएँ) तथा ‘नयी कविता’ (पत्रिका) आदि।
विशेषता : प्रयोगवाद के बाद जिस नयी कविता का प्रारंभ हुआ, उसके प्रवर्तकों में जगदीश गुप्त का नाम प्रमुख रूप से लिया जाता है।
विधा : नई कविता। नए भावबोधों की अभिव्यक्ति के साथ नए मूल्यों और नए शिल्प विधान का अन्वेषण नई कविता की विशेषता है।

विषय प्रवेश : प्रस्तुत नई कविता में कवि ने संघर्ष करने की प्रेरणा दी है। संघर्ष ही जीवन की सच्चाई है। जो मनुष्य कठिनाइयों और मुसीबतों का सामना करते हुए बिना झुके या रुके आगे बढ़ता रहता है, वही सच्चा मनुष्य है। जिंदगी लीक से हटकर चलने का नाम है। लीक से भटककर भी मंजिल अवश्य मिलती है। कवि का कहना है कि हमें अपनी समस्याएँ खुद सुलझानी होंगी। हमारी लड़ाई – कोई दूसरा लड़ने नहीं आएगा। हमें खुद योद्धा बनकर अपनी लड़ाई लड़नी है।

सच हम नहीं; सच तुम नहीं कविता का सरल अर्थ

सच हम नहीं …………………………………………….. है जीवन वही।
कवि कहते हैं कि न मेरी बात सच है और न तुम्हारी बात सच है। सच है तो निरंतर संघर्ष करना। संघर्ष ही जीवन है। हमें संघर्ष का रास्ता अपनाना चाहिए। कवि के अनुसार संघर्ष से हटकर जीने की बात ही नहीं करनी चाहिए। बिना संघर्ष का जीवन भी भला कोई जीवन है!

कवि कहते हैं कि जिसने अधीनता स्वीकार ली, वह मृतक के समान हो गया। उसकी हालत डाल से झड़े हुए फूल जैसी होती है। जो व्यक्ति संघर्ष के मार्ग पर चलता हआ भटक जाने पर भी अपनी मंजिल पर बढ़ने से नहीं रुका अथवा अपने प्रयास में असफल हो जाने पर भी जिसने हार नहीं मानी अथवा जिसने मृत्यु से भी मोर्चा लिया हो और उसको परास्त कर दिया हो, उसी का जीवन जीवन कहलाने के योग्य है। यही सच्चाई है।

ऐसा करो जिससे …………………………………………….. यौवन का यही।
कवि कहते हैं कि मनुष्य में कहीं भी कोई ठहराव नहीं आना चाहिए। जो जहाँ है उसे वहीं चुपचाप अपना संघर्ष जारी रखना चाहिए। वे कहते हैं कि परिस्थितियाँ कैसी भी हों चाहे प्रतिकूल स्थिति हो अथवा अनुकूल स्थिति, मनुष्य को हताश होकर अपना संघर्ष कभी भी त्यागना नहीं चाहिए। जीवन का यही संदेश है।

हमने रचा जाओ …………………………………………….. पानी-सी बही।
कवि कहते हैं कि यथास्थिति में जीने का हमने जो नियम बनाया था, आओ, अब हम उसे तोड़ दें। यह भी कोई जीवन है। जीवन तो वह है, जो मँझधार को भी मोड़ने की शक्ति रखता हो। जिसने संघर्ष किया ही नहीं और यथास्थिति को ही सुखमय मानकर जीवन जीता आ रहा हो और दूसरों के इशारों पर चलता आ रहा हो, उसकी भला कोई जिंदगी है? वह जिंदगी तो यथास्थिति को स्वीकार लेने और लीक पर चलनेवाला जीवन है। (इसमें संघर्ष का नामोनिशान नहीं है।)

अपने हृदय का …………………………………………….. दिशा मिलती रही।

कवि कहते हैं कि हमें अपने दुखों को पहचानना होगा। उन्हें दूर करने के लिए हमें स्वयं प्रयास करना होगा। अपनी आँखों के आँसू हमें खुद पोंछने होंगे। हमें अपनी सहायता के लिए किसी अन्य से आशा नहीं करनी है। किसी अन्य की कृपा का भरोसा करना व्यर्थ है। हमें खुद योद्धा बनना होगा। हर संघर्ष करने वाले को कोई-नकोई मार्ग अवश्य मिलता है। मनुष्य मार्ग भटकने के बाद अपने लक्ष्य पर अवश्य पहुँचता है, इस बात को हमें गाँठ बाँध लेनी चाहिए।

बेकार है मुस्कान से …………………………………………….. राह को ही मैं सही।
कवि कहते हैं कि हृदय के कष्ट को बाह्य मुस्कान से दबाया नहीं जा सकता। इस तरह के प्रयास का कोई लाभ नहीं होता। इसे आदर्श नहीं माना जा सकता है। मनुष्य को भीतर और बाहर दोनों से एक-सा ही रहना चाहिए, यही आदर्श है। कवि कहते हैं कि जब तक विचारों पर अंकुश लगा रहेगा और जब तक प्यार पर दुख की गहरी छाया बनी रहेगी, तब तक इस मार्ग को किसी भी कीमत पर उचित नहीं माना जा सकता।

सच हम नहीं; सच तुम नहीं शब्दार्थ

• नत = झुका हुआ
• जड़ता = अचलता, ठहराव
• पसीजना = मन में दया भाव आना
• वृंत = डंठल
• मँझधार = नदी की बीच की धारा
• चेतना = जागृत अवस्था

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 5.1 गुरुबानी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 5.1 गुरुबानी

12th Hindi Guide Chapter 5.1 गुरुबानी Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) संजाल पूर्ण कीजिए :

उत्तर :

(आ) कृति पूर्ण कीजिए :
(a) आकाश के दीप

उत्तर :

शब्द संपदा

प्रश्न 2.
लिखिए :

उत्तर:

अभिव्यक्ति

प्रश्न 3.
(अ) ‘गुरु बिन ज्ञान न होई उक्ति पर अपने विचार लिखिए।
उत्तर :
ज्ञान की कोई सीमा नहीं है। विभिन्न क्षेत्रों में भिन्न-भिन्न प्रकार के ज्ञान की आवश्यकता होती है। यह ज्ञान हमें किसी-नकिसी व्यक्ति से मिलता है। जिस व्यक्ति से हमें यह ज्ञान मिलता है, वही हमारे लिए गुरु होता है। बचपन में बच्चे का पालन-पोषण कर उसे बड़ा करके बोलने-चालने और बोली-भाषा सिखाने का काम माता करती है। उस समय वह बच्चे की गुरु होती है। बड़े होने पर बच्चे को विद्यालय में शिक्षकों से ज्ञान प्राप्त होता है।

पढ़-लिखकर। जीवन में पदार्पण करने पर हर व्यक्ति को किसी-न-किसी से अपने काम-काज करने का ढंग सीखना पड़ता है। इस तरह के लोग हमारे लिए गुरु के समान होते हैं। मनुष्य गुरुओं से ही सीखकर विभिन्न कलाओं में पारंगत होता है। बड़े-बड़े विद्वान, विचारक, राजनेता,। समाजशास्त्री, वैज्ञानिक, अर्थशास्त्री अपने-अपने गुरुओं से ज्ञान। प्राप्त करके ही महान हुए हैं। अच्छी शिक्षा देने वाला गुरु होता है। गुरु की महिमा अपरंपार है।

गुरु ही हमें गलत या सही में भेद करना सिखाते हैं। वे अपने मार्ग से भटके हुए लोगों को सही मार्ग दिखाते हैं। यह सच है कि गुरु के बिना ज्ञान नहीं होता।

(आ) ‘ईश्वर भक्ति में नामस्मरण का महत्त्व होता है’, इस विषय पर अपना मंतव्य लिखिए।
उत्तर :
ईश्वरभक्ति के अनेक मार्ग बताए गए हैं। उनमें सबसे सरल मार्ग ईश्वर का नाम स्मरण करना है। नाम स्मरण करने का कोई नियम नहीं है। भक्त जहाँ भी हो, चाहे जिस हालत में हो, ईश्वर का नाम स्मरण कर सकता है। अधिकांश लोग ईश्वर भक्ति का यही मार्ग अपनाते हैं।

उठते-बैठते, आते-जाते तथा काम करते हुए नाम स्मरण किया जा सकता है। भजन-कीर्तन भी ईश्वर के नाम स्मरण का ही एक रूप है। ईश्वर भक्ति के इस मार्ग में प्रभु के गुणों का वर्णन किया जाता है। इसमें धार्मिक पूजा-स्थलों में जाने की जरूरत नहीं होती।

गृहस्थ अपने घर में ईश्वर का नाम स्मरण कर उनके गुणों का बखान कर सकता है। इससे नाम स्मरण करने वालों को मानसिक शांति मिलती हैं और मन प्रसन्न होता है। कहा गया है – ‘कलियुग केवल नाम अधारा, सुमिरि-सुमिर नर उतरें पारा।’ इसमें ईश्वर भक्ति में नाम स्मरण का ही महत्त्व बताया गया है।

रसास्वादन

प्रश्न 4.
‘गुरुनिष्ठा और भक्तिभाव से ही मानव श्रेष्ठ बनता है’ इस कथन के आधार पर कविता का रसास्वादन कीजिए।
उत्तर :
गुरु नानक का कहना है कि बिना गुरु के मनुष्य को ज्ञान नहीं मिलता। मनुष्य के अंतःकरण में अनेक प्रकार के मनोविकार होते हैं, जिनके वशीभूत होने के कारण उसे वास्तविकता के दर्शन नहीं होते। वह अहंकार में डूबा रहता है और उसमें गलत-सही का विवेक नहीं रह जाता।

ये मनोविकार दूर होता है गुरु से ज्ञान प्राप्त होने पर। यदि गुरु के प्रति सच्ची श्रद्धा और उनमें पूरा विश्वास हो तो मनुष्य के अंतःकरण के इन विकारों को दूर होने में समय नहीं लगता। मन के विकार दूर हो जाने पर मनुष्य में सबको समान दृष्टि से देखने की भावना उत्पन्न हो जाती है।

उसके लिए कोई बड़ा या छोटा अथवा ऊँच-नीच नहीं रह जाता। उसे मनुष्य में ईश्वर के दर्शन होने लगते हैं। उसके लिए ईश्वर की भक्ति भी सुगम हो जाती है। गुरु नानक ने अपने पदों में इस बात को सरल ढंग से कहा है। … इस तरह गुरु के प्रति सच्ची निष्ठा और भक्ति-भावना से मनुष्य श्रेष्ठ मानव बन जाता है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) गुरु नानक जी की रचनाओं के नाम :
…………………………………………………………
उत्तर :
गुरुग्रंथसाहिब आदि।

(आ) गुरु नानक जी की भाषाशैली की विशेषताएं:
…………………………………………………………
…………………………………………………………
उत्तर :
गुरु नानक जी सहज-सरल भाषा में अपनी बात कहने में माहिर हैं। आपकी काव्य भाषा में फारसी, मुल्तानी, पंजाबी, सिंधी, खड़ी बोली और अरबी भाषा के शब्द समाए हए हैं। आपने पद शैली में रचना की है। ‘पद’ काव्य रचना की गेय शैली है।

प्रश्न 6.
निम्नलिखित वाक्यों में अधोरेखांकित शब्दों का वचन परिवर्तन करके वाक्य फिर से लिखिए :

(1) सत्य का मार्ग सरल है।
उत्तर :
सत्य के मार्ग सरल हैं।

(2) हथकड़ियाँ लगाकर बादशाह अकबर के दरबार को ले चले।
उत्तर :
हथकड़ी लगाकर बादशाह अकबर के दरबार को ले चले।

(3) चप्पे-चप्पे पर काटों की झाड़ियाँ हैं।
उत्तर :
चप्पे-चप्पे पर काँटे की झाड़ी है।

(4) सुकरात के लिए यह जहर का प्याला है।
उत्तर :
सुकरात के लिए ये जहर के प्याले हैं।

(5) रूढ़ि स्थिर है, परंपरा निरंतर गतिशील है।
उत्तर :
रूढ़ियाँ स्थिर हैं, परंपराएँ निरंतर गतिशील हैं।

(6) उनकी समस्त खूबियों-खामियों के साथ स्वीकार कर अपना लें।
उत्तर :
उनकी समस्त खूबी-कमी के साथ स्वीकार कर अपना लें।

(7) वे तो रुपये सहेजने में व्यस्त थे।
उत्तर :
वह तो रुपया सहेजने में व्यस्त था।

(8) ओजोन विघटन के खतरे क्या-क्या हैं?
उत्तर :
ओजोन विघटन का खतरा क्या है?

(9) शब्द में अर्थ छिपा होता है।
उत्तर :
शब्दों में अर्थ छिपे होते हैं।

(10) अभी से उसे ऐसा कोई कदम नहीं उठाना चाहिए।
उत्तर :
अभी से उसे ऐसे कोई कदम नहीं उठाने चाहिए।

Hindi Yuvakbharati 12th Digest Chapter 5.1 गुरुबानी Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)
पदयाश क्र. 1
प्रश्न. निम्नलिखितपद्यांशपढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : गुरु को महत्त्व न देने वाले ऐसे होते हैं –
(1) ……………………………………..
(2) ……………………………………..
(3) ……………………………………..
(4) ……………………………………..
उत्तर :
(1) व्यर्थ ही उगने वाले तिल की झाड़ियों के समान।
(2) केवल ऊपर से फलते-फूलते दिखाई देते हैं।
(3) उनके अंदर गंदगी और मैल भरा होता है।
(4) लोग उनसे किनारा कर लेते हैं।

प्रश्न 2.
उत्तर लिखिए :
(1) मन के लिए यह कहा गया है – ……………………………………..
(2) संसार में ऐसे लोग विरले होते हैं – ……………………………………..
(3) साधक को अपना ध्यान इसमें लगाना है – ……………………………………..
(4) प्रभु के दर्शन के लिए आवश्यक है – ……………………………………..
उत्तर :
(1) दिन-रात भगवान के गुणों का स्मरण करना।
(2) जो एक क्षण भी भगवान का नाम नहीं भूलते।
(3) भगवान में।
(4) साधक को अहंभाव का त्याग करना।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) तन = …………………………….
(2) मसि = …………………………….
(3) मति = …………………………….
(4) विरले = …………………………….
उत्तर :
(1) (1) तन = शरीर।
(2) मसि = स्याही।
(3) मति = बुद्धि।
(4) बिसरे = भूले।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

(2) संजाल पूर्ण कीजिए :

उत्तर :

रसास्वादन। मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर दोहो-पदों का रसास्वादन कीजिए:
उत्तर :
(1) रचना का शीर्षक : गुरुवाणी।
(2) रचनाकार : गुरु नानक
(3) कविता की केंद्रीय कल्पना : प्रस्तुत दोहों-पदों में गुरु के .. महत्त्व, ईश्वर की महिमा तथा प्रभु का नाम स्मरण करने से ईश्वर प्राप्ति की बात कही गई है।

(4) रस-अलंकार :
गगन में थाल, रवि-चंद्र दीपक बने।
तारका मंडल जनक मोती।
धूप मलयानिल, पवनु चैवरो करे।
सकल वनराइ कुलंत जोति।।

यहाँ कहा गया है कि गगन ही थाल है; सूर्य-चंद्रमा ही दीपक हैं; तारका मंडल ही मोती है; मलयानिल ही धूप-गंध है; जंगल की समस्त वनस्पतियाँ फूल हैं। इसलिए रूपक अलंकार है।

(5) प्रतीक विधान : प्रस्तुत कविता में कवि ने गुरु का चिंतन न करने वालों तथा अपने आप को ही ज्ञानी समझने वालों को बिना संरक्षक वाले व्यक्ति कहा गया है। इसके लिए कवि ने निर्जन स्थान पर उगी हुई तिल्ली के पौधे का प्रतीक के रूप में उपयोग किया है।

(6) कल्पना : जीवन में गुरु का महत्त्व, कर्म की महानता तथा प्रभु के नाम का स्मरण ही प्रभु प्राप्ति का मार्ग है।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
नानक गुरु न चेतनी मनि आपणे सुचेत।
छूते तिल बुआड़ जिऊ सुएं अंदर खेत।
खेते अंदर छुट्टया कहु नानक सऊ नाह।
फली अहि फूली अहि बपुड़े भी तन विच स्वाह।

इन पंक्तियों में कवि ने गुरु का महत्त्व न समझने और अपने को ज्ञानी मानने वालों को मरुस्थल में पाई जानेवाली तिल्ली की फली में मिलने वाली राख कहा है, जो बहुत ही सटीक है।

(8) कविता पसंद आने का कारण : गुरु नानक ने इन पंक्तियों में यह बताया है कि कुछ लोग ऐसे होते हैं, जो गुरु को महत्त्व नहीं देते और अपने आप को ही ज्ञानी मान बैठते हैं। गुरु नानक जी ऐसे लोगों की तुलना उस तिल के पौधे से करते हैं, जो किसी निर्जन स्थान पर अपने आप उग आता है और उसको खाद-पानी देने वाला कोई भी नहीं होता। इसलिए उस पौधे का विकास नहीं हो पाता। ऐसे पौधे में फूल भी लगते हैं और फली भी लगती है, पर फली के अंदर दाने नहीं पड़ते, उसमें गंदगी और राख ही होती है। वैसी ही हालत बिना गुरु के मनुष्य की होती है। ऐसे लोगों का मानसिक विकास नहीं हो पाता।

1. अलंकार :

निम्नलिखित काव्य पंक्तियों में प्रयुक्त अलंकार पहचानकर लिखिए :
(1) तरुवर की छायानुवाद सी,
उपमा-सी-भावुकता-सी,
अविदित भावाकुल भाषा-सी,
कटी-छूटी नव कविता-सी।

(2) उदित उदय गिरि मंच पर, रघुवर बाल पतंग।
विकसे संत सरोज सब हरषे लोचन भंग।

(3) जिन दिन देखे वे कुसुम, गई सो बीति बहार।
अब अलि रही गुलाब में, अपत कँटीली डार।

(4) छिप्यो छबीली मुँह लसै नीले अंचल चीर।
मनो कलानिधि झलमले, कालिंदी के तीर।

(5) छाले परिबे के डरनि, सकै न हाथ छुवाय।
झिझकत हिये गुलाब के सँवा सँवावत पाय।
उत्तर :
(1) उपमा अलंकार
(2) रूपक अलंकार
(3) अन्योक्ति अलंकार
(4) उत्प्रेक्षा अलंकार
(5) अतिशयोक्ति अलंकार।

2. रस :

निम्नलिखित काव्य पंक्तियों में प्रयुक्त रस पहचानकर लिखिए :
(1) भूषन बसन बिलोकत सिय के।
प्रेम-बिबस मन, कंप पुलक तनु
नीरज नयन नीर भरे पिय के।
सकुचत, कहत, सुमिरि उर उमगत
सील, सनेह सुगुन गुन तिय के।

(2) लीन्हों उखारि पहार बिसाल
चल्यौ तेहि काल, बिलंब न लायौ।
मारुत नंदन मारुत को, मन को
खगराज को बेगि लजायो।।

(3) रामहि बाम समेत पठै बन,
शोक के भार में भुंजौ भरत्थहि।
जो धनु हाथ धरै रघुनाथ तो
आज अनाथ करौं दशरत्थहि।
उत्तर :
(1) शृंगार रस
(2) अद्भुत रस
(3) रौद्र रस।

3. मुहावरे :

निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :

(1) सिर खपाना।
अर्थ : कठिन परिश्रम करना।
वाक्य : कई साल तक सिर खपाने के बाद आखिरकार उस युवक को सी.ए. की डिग्री मिल ही गई।

(2) उगल देना।
अर्थ : भेद बता देना।
वाक्य : पुलिस का डंडा पड़ते ही चोर ने चुराई गई संपत्ति को छिपाकर रखे जाने के स्थान की बात उगल दी।

(3) कब्र में पैर लटकना।
अर्थ : मरने के समीप होना।
वाक्य : कोरोना के प्रसार से अनेक मरीजों के पैर कब्र में लटक गए हैं।

(4) पापड़ बेलना।
अर्थ : कड़ी मेहनत करना।
वाक्य : आज जो लड़का जिलाधीश के पद पर आसीन है, इस पद तक पहुँचने में इसने बहुत पापड़ बेले हैं।

(5) मरने की फुरसत न होना।
अर्थ : कामों में बहुत व्यस्त होना।
वाक्य : मुनीम जी तो अपने काम में इतने व्यस्त हैं कि उन्हें मरने की भी फुरसत नहीं है।

4. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों को कोष्ठक में सूचित काल में परिवर्तन कीजिए :
(1) वे सभी धर्मों को समान दृष्टि से देखते थे। (सामान्य वर्तमानकाल)
(2) दिन रात महान आरती होती है। (अपूर्ण भूतकाल)
(3) अनहद नाद का वाद्य बज रहा है। (सामान्य भविष्यकाल)
(4) श्रद्धा भक्त की सबसे बड़ी भेंट होगी। (पूर्ण भूतकाल)
(5) तुम्हारे अनेक रंग हैं। (भविष्यकाल)
उत्तर :
(1) वे सभी धर्मों को समान दृष्टि से देखते हैं।
(2) दिन-रात महान आरती हो रही थी।
(3) अनहद नाद का वाद्य बजेगा।
(4) श्रद्धा भक्त की सबसे बड़ी भेंट थी।
(5) तुम्हारे अनेक रंग होंगे।

5. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) गुरू के बिना ग्यान नहीं होता।
(2) उसने भगवान की नाम का माला पहन ली है।
(3) सभी जंगल की वनस्पतियाँ फूल चढ़ा रही है।
(4) श्रद्धा ही भक्त का सबसे बड़ा भेट है।
(5) तू दीन-रात भगवान के गुणों का स्मरण कर।
उत्तर :
(1) गुरु के बिना ज्ञान नहीं होता।
(2) उसने भगवान के नाम की माला पहन ली है।
(3) जंगल की सभी वनस्पतियाँ फूल चढ़ा रही हैं।
(4) श्रद्धा ही भक्त की सबसे बड़ी भेंट है।
(5) तू दिन-रात भगवान के गुणों का स्मरण कर।

गुरुबानी Summary in Hindi

गुरुबानी कवि का परिचय

कवि का नाम : गुरु नानक। (जन्म 15 अप्रैल, 1469; निधन 1539.)

प्रमुख कृतियाँ : गुरुग्रंथसाहिब आदि।

विशेषता : आप सर्वेश्वरवादी हैं और सभी धर्मों को समान दृष्टि से देखते हैं। आपके भावुक व कोमल हृदय ने प्रकृति से एकात्म होकर अनूठी अभिव्यक्ति की है। आप सहज-सरल भाषा द्वारा अपनी बात कहने में सिद्धहस्त हैं।

विधा : दोहे, पद। पदकाव्य रचना की एक गेय शैली है। इसके विकास का मूल स्रोत लोकगीतों की परंपरा रही है। हिंदी साहित्य में ‘पद शैली’ की दो परंपराएँ मिलती हैं – एक संतों की ‘शबद’ और दूसरी ‘कृष्ण भक्तों की परंपरा’।

विषय प्रवेश : मनुष्य के जीवन को उत्तम और सदाचार से परिपूर्ण बनाने के लिए गुरु का मार्गदर्शन अत्यंत आवश्यक होता है। इसी से शिक्षा प्राप्त कर मनुष्य उत्तम कार्य करता है। प्रस्तुत दोहों और पदों में गुरु नानक ने गुरु की महिमा, कर्म की महानता तथा सच्ची शिक्षा आदि के बारे में अपने अमूल्य विचारों से परिचित कराया है। वे गुरु द्वारा दिए गए ज्ञान को शिष्य की सबसे बड़ी पूँजी मानते हैं। उन्होंने प्रभु की महिमा का वर्णन करते हुए नाम स्मरण को प्रभु प्राप्ति का मार्ग बताया है और कर्मकांड और बाह्याडंबर का घोर विरोध किया है।

गुरुबानी कविता (पदों) का सरल अर्थ

(1) नानक गुरु न चेतनी …………………………………….. तन बिच स्वाह।

गुरु नानक कहते हैं कि जो लोग गुरु का चिंतन नहीं करते, गुरु से लापरवाही बरतते हैं और अपने आप को ही ज्ञानी समझते हैं, वे व्यर्थ ही उगने वाली तिल की उन झाड़ियों के समान होते हैं, जिनकी देखभाल करने वाला कोई नहीं होता। वे ऊपर से फलतीफूलती दिखाई देती है, पर उन फलियों के अंदर गंदगी और मैल भरा होता है। लोग ऐसे लोगों से किनारा कर लेते हैं।

(2) जलि मोह धसि …………………………………….. अंत न पारावार।

गुरु नानक कहते हैं कि मोह को जलाकर और घिसकर स्याही बनाओ। अपनी बुद्धि को श्रेष्ठ कागज समझो। प्रेम-भाव की कलम बनाओ। चित को लेखक समझो और गुरु से पूछकर लिखो – नाम की स्तुति। साथ ही यह सच्चाई भी लिखो कि प्रभु का न कोई आदि है और न कोई अंत।

(3) मन रे अहिनिसि …………………………………….. मेले गरु संजोग।

हे मन! तू दिन-रात भगवान के गुणों का स्मरण कर। जिन्हें एक क्षण के लिए भी ईश्वर का नाम नहीं भूलता, संसार में ऐसे लोग विरले ही होते हैं। अपना ध्यान उसी ईश्वर में लगाओ और उसकी ज्योति से तुम भी प्रकाशित हो जाओ। जब तक तुझमें अहंभाव रहेगा, तब तक तुझे प्रभु के दर्शन नहीं हो सकते। जिसने अपने हृदय में भगवान के नाम की माला पहन ली है, उसे ही प्रभु के दर्शन होते हैं।

(4) तेरी गति मिति …………………………………….. दजा और न कोई।

हे प्रभो! अपनी शक्ति के सब रहस्यों को केवल तुम्हीं जानते हो। उनकी व्याख्या कोई दूसरा नहीं कर सकता है। तुम ही अप्रकट रूप भी हो और तुम ही प्रकट रूप भी हो। तुम्हारे अनेक रंग हैं। अनगिनत भक्त, सिद्ध, गुरु और शिष्य तुम्हें ढूँढ़ते फिरते हैं। हे प्रभु! जिन्होंने नाम स्मरण किया उन्हें प्रसाद (भिक्षा) में तुम्हारे दर्शन की प्राप्ति हुई है। प्रभु! तुम्हारे इस संसार के खेल को केवल कोई गुरुमुख ही समझ सकता है। प्रभु! अपने इस संसार में युग-युग से तुम्हीं बिराजमान रहते हो, कोई दूसरा नहीं।।

(5) गगन में थाल …………………………………….. शबद बाजत भेरी। (संसार में दिन-रात महान आरती हो रही है।)

आकाश की थाल में सूर्य और चंद्रमा के दीपक जल रहे हैं। हजारों तारे-सितारे – मोती बने हैं। मलय की खुशबूदार हवा वाला धूप (गुग्गुल) महक रहा है। वायु हवा से चँवर कर रही है। जंगल की सभी वनस्पतियाँ फूल चढ़ा रही हैं। हृदय में अनहद नाद का वाद्य बज रहा है। हे मनुष्य! इस महान आरती के होते हुए तेरी आरती का क्या महत्त्व है। अर्थात भगवान की असली आरती तो मन में उतारी जाती है। श्रद्धा ही भक्त की सबसे बड़ी भेंट है।

गुरुबानी शब्दार्थ

• बूआड़ = बुआई करना
• सउ = ईश्वर
• चितु = चित्त
• गुपता = अप्रकट, गुप्त
• सगल = संपूर्ण
• सुंजे = सूने
• मसु = स्याही
• अहिनिसि = दिन-रात
• जुग = युग
• भेरी = बड़ा ढोल

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 2 निराला भाई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 2 निराला भाई

12th Hindi Guide Chapter 2 निराला भाई Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
लिखिए :

(अ) लेखिका के पास रखे तीन सौ रुपये इस प्रकार समाप्त हो गए :
(1) ……………………………………………
(2) …………………………………………..
(3) ……………………………………………
(4) ……………………………………………
उत्तर :
लेखिका के पास रखे तीन सौ रुपए इस प्रकार समाप्त हो गए –
(1) किसी विद्यार्थी का परीक्षा शुल्क देने के लिए 50 रुपए लिए।
(2) किसी साहित्यिक मित्र को देने के लिए 60 रुपए लिए।
(3) तांगेवाले की माँ को मनीआर्डर करने के लिए 40 रुपए लिए।
(4) दिवंगत मित्र की भतीजी के विवाह के लिए 100 रुपए लिए। तीसरे दिन जमा पैसे समाप्त।

(आ) अतिथि की सुविधा हेतु निराला जी ये चीजें ले आए :
(1) ……………………………………………
(2) ……………………………………………
(3) ……………………………………………
(4) ……………………………………………
उत्तर :
अतिथि की सुविधा हेतु निराला जी ये चीजें ले आए –
(1) नया घड़ा खरीदकर लाए।
(2) उसमें गंगाजल भर लाए।
(3) धोती।
(4) चादर।

शब्द संपदा

प्रश्न 2.
निम्न शब्दों के समानार्थी शब्द लिखिए :
(1) प्रहरी – ……………………………………………
(2) अतिथि – ……………………………………………
(3) प्रयास – ……………………………………………
(4) स्मृति – ……………………………………………
उत्तर :
(1) प्रहरी = द्वारपाल
(2) अतिथि = मेहमान
(3) प्रयास = प्रयत्न
(4) स्मृति = याद

अभिव्यक्ति

प्रश्न 3.
(अ) ‘भाई-बहन का रिश्ता अनूठा होता है, इस विषय पर अपना मत लिखिए।
उत्तर :
एक माता से उत्पन्न भाइयों अथवा भाई-बहनों का रिश्ता निराला होता है। यह रिश्ता अटूट होता है। बचपन में वे साथ-साथ खेलते, बढ़ते और पढ़ते हैं। जीवन में घटने वाली अनेक अच्छी बुरी घटनाओं के साक्षी होते हैं। बड़े होने पर बहन की शादी हो जाने पर उसका नया घर बस जाता है। फिर भी उसका लगाव अपने मायके के परिवार के साथ बना रहता है। जब भी पीहर आने का कोई मौका आता है, वह उसे कभी गँवाना नहीं चाहती।

पीहर में आकर उसे जो खुशी मिलती है, उसका वर्णन नहीं किया जा सकता। रक्षाबंधन के त्योहार पर वह कहीं भी हो, अपने भाई की कलाई पर राखी बाँधने और उसकी आरती उतारने जरूर पहुँचती है। भाई-बहन का यह मिलन अनूठा होता है। भाई भी इस अवसर पर उसे अपनी क्षमता के अनुसार अच्छे-से-अच्छा उपहार देने से नहीं चूकता। यह उनके अटूट प्यार और अनूठे रिश्ते का ही प्रमाण है।

(आ) ‘सभी का आदरपात्र बनने के लिए व्यक्ति का सहृदयी और संस्कारशील होना आवश्यक है’, इस कथन पर अपने विचार लिखिए।
उत्तर :
मनुष्य एक सामाजिक प्राणी है। वह अपने परिवार और समाज में सबके साथ हिल-मिल कर रहना चाहता है। उसे सबके दुख-सुख में शामिल होना अच्छा लगता है। जीवों पर दया करना और मन में करुणा के भाव उत्पन्न होना मनुष्य का स्वाभाविक गुण है। ऐसे व्यक्ति संस्कारशील कहलाते हैं।

ऐसे व्यक्ति का सभी लोग आदर करते हैं और उसे अपना प्यार देते हैं। मगर सब लोग ऐसे नहीं होते। कुछ लोग विभिन्न कारणों से समाज से कटे-कटे रहते हैं और ‘अपनी डफली अपना राग’ विचार वाले होते हैं। वे अपने घमंड में चूर रहते हैं और किसी अन्य की परवाह नहीं करते।

ऐसे लोगों को समाज तो क्या कोई भी पसंद नहीं करता। ऐसे लोगों को समाज में सम्मान नहीं मिलता। इसलिए मनुष्य को सहृदयी और संस्कारशील होना जरूरी है।

पाठ पर आधारित लघूत्तरी प्रश्न –

प्रश्न 4.
(अ) निराला जी की चारित्रिक विशेषताएँ लिखिए।
उत्तर :
निराला जी मानवता के पुजारी थे। उनमें मानवीय गुण कूट-कूट कर भरे हुए थे। उन्हें स्वयं से अधिक दूसरों की अधिक चिंता होती थी। खुद निर्धनता में जीवन बिताते रहे, पर दूसरों के आर्थिक दुखों का भार उठाने के लिए सदा तत्पर रहते थे। आतिथ्य करने में उनका जवाब नहीं था।

अतिथियों को सदा हाथ पर लिये रहते थे। उनके लिए खुद भोजन बनाने और बर्तन माँजने में उन्हें हर्ष होता था। घर में सामान न होने पर अतिथियों के लिए मित्रों से कुछ चीजें माँग लाने में शर्म नहीं करते थे। उदार इतने थे कि अपने उपयोग की वस्तुएँ भी दूसरों को दे देते थे और खुद कष्ट उठाते थे।

साथी साहित्यकारों के लिए उनके मन में बहुत लगाव था। एक बार कवि सुमित्रानंदन पंत के स्वर्गवास की झूठी खबर सुनकर वे व्यथित हो गए थे और उन्होंने पूरी रात जाग कर बिता दी थी।

निराला जी पुरस्कार में मिले धन का भी अपने लिए उपयोग नहीं करते थे। अपनी अपरिग्रही वृत्ति के कारण उन्हें मधुकरी खाने ३ तक की नौबत भी आई थी। इस बात को वे बड़े निश्छल भाव से बताते थे।

उनका विशाल डील-डौल देखने वालों के हृदय में आतंक पैदा कर देता था, पर उनके मुख की सरल आत्मीयता इसे दूर कर देती थी।

निराला जी से अन्याय सहन नहीं होता था। इसके विरोध में उनका हाथ और उनकी लेखनी दोनों चल जाते थे। निराला जी आचरण से क्रांतिकारी थे। वे किसी चीज का विरोध करते हुए कठिन चोट करते थे। पर उसमें द्वेष की भावना नहीं होती थी। निराला जी के प्रशंसक तथा आलोचक दोनों थे। कुछ लोग जहाँ उनकी नम्र उदारता की प्रशंसा करते थे, वहीं कुछ लोग उनके उद्धत व्यवहार की निंदा करते नहीं थकते थे।

निराला जी अपने युग की विशिष्ट प्रतिभा रहे हैं। उनके सामने अनेक प्रतिकूल परिस्थितियाँ आईं पर वे कभी हार नहीं माने।

(आ) निराला जी का आतिथ्य भाव स्पष्ट कीजिए।
उत्तर :
निराला जी में आतिथ्य सत्कार का पुराना संस्कार था। वे अतिथि को देवता के समान मानते थे। अपने अतिथि की सुविधा में कोई कसर बाकी नहीं रखते थे। वे अतिथि को अपने कक्ष में ठहराते थे। उसके लिए स्वयं भोजन तैयार करते थे। बर्तन भी वे खुद माँजते थे। अतिथि सत्कार के लिए आवश्यक सामान घर में न होता तो वे अपने हित-मित्रों से माँगकर ले आते थे, पर अतिथि सेवा में कोई कमी नहीं रखते थे। कई बार तो वे कवयित्री महादेवी वर्मा के यहाँ से भोजन बनाने के लिए लकड़ियाँ तथा घी आदि माँगकर ले आए थे।

निराला जी की आर्थिक स्थिति अच्छी नहीं थी। उनका कक्ष भी सुविधाओं से रहित था, पर अतिथि के लिए उनके दिल में अपार श्रद्धा थी। एक बार प्रसिद्ध कवि मैथिलीशरण गुप्त निराला जी का आतिथ्य ग्रहण करने आए थे। उस समय उन्होंने उनका जो सत्कार किया था वह देखते ही बनता था। निराला जी गुप्त जी के बिछौने का बंडल खुद बगल में दबाकर और दियासलाई की तीली के प्रकाश में तंग सीढ़ियों का मार्ग दिखाते हुए उन्हें अपने कक्ष में ले गए थे।

कक्ष प्रकाश और सुख सुविधा से रहित था, पर निराला जी की विशाल आत्मीयता से भरा हुआ था। वे गुप्त जी की सुविधा के लिए नया घड़ा खरीदकर उसमें गंगाजल ले आए। घर में धोती-चादर जो कुछ मिल सका सब तख्त पर बिछा कर गुप्त जी को प्रतिष्ठित किया था। निराला जी का आतिथ्य भाव अपनी किस्म का निराला था।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) ‘निराला’ जी का मूल नाम – [ ]
(आ) हिंदी के कुछ आलोचकों द्वारा महादेवी वर्मा को दी गई उपाधि – [ ]
उत्तर :
(अ) निराला जी का मूल नाम – सूर्यकांत त्रिपाठी।
(आ) कुछ हिंदी आलोचकों द्वारा महादेवी वर्मा को दी गई उपाधि – [आधुनिक मीरा]

रस

काव्यशास्त्र में आचार्यों ने रस को काव्य की आत्मा माना है। विभाव, अनुभाव, व्यभिचारी (संचारी) भाव और स्थायी भाव रस के अंग हैं और इन अंगों अर्थात तत्त्वों के संयोग से रस की निष्पत्ति होती है।

साहित्यशास्त्र में नौ प्रकार के रस माने गए हैं। कालांतर में अन्य दो रसों को सम्मिलित किया गया है।
रस – स्थायी भाव – रस – स्थायी भाव

• शृंगार – प्रेम
• शांत – शांति
• करुण – शोक
• हास्य – हास
• भयानक – भय
• रौद्र – क्रोध
• बीभत्स – घृणा
• वीर – उत्साह
• अद्भुत – आश्चर्य
• वात्सल्य – ममत्व
• भक्ति – भक्ति

ग्यारहवीं कक्षा की युवकभारती पाठ्यपुस्तक में हमने करुण, हास्य, वीर, भयानक और वात्सल्य रस के लक्षण एवं उदाहरणों का अध्ययन किया है। इस वर्ष हम शेष रसों – रौद्र, बीभत्स, अद्भुत, शृंगार, शांत और भक्ति रस का अध्ययन करेंगे।

रौद्र रस : जहाँ पर किसी के असह्य वचन, अपमानजनक व्यवहार के फलस्वरूप हृदय में क्रोध का भाव उत्पन्न होता है; वहाँ रौद्र रस उत्पन्न होता है। इस रस की अभिव्यंजना अपने किसी प्रिय अथवा श्रद्धेय व्यक्ति के प्रति अपमानजनक, असह्य व्यवहार के प्रतिशोध के रूप में होती है।

उदा. –
(१) श्रीकृष्ण के वचन सुन, अर्जुन क्रोध से जलने लगे।
सब शोक अपना भूलकर, करतल युगल मलने लगे।

(२) कहा – कैकयी ने सक्रोध
दूर हट! दूर हट! निर्बोध!
द्विजिव्हे रस में, विष मत घोल।

बीभत्स रस : जहाँ किसी अप्रिय, अरुचिकर, घृणास्पद वस्तुओं, पदार्थों के प्रसंगों का वर्णन हो, वहाँ बीभत्स रस उत्पन्न होता है।

उदा. –
(१) सिर पर बैठो काग, आँखि दोऊ खात
खींचहि जीभहि सियार अतिहि आनंद उर धारत।
गिद्ध जाँघ के माँस खोदि-खोदि खात, उचारत हैं।
(२) सुडुक, सुडुक घाव से पिल्लू (मवाद) निकाल रहा है,
नासिका से श्वेत पदार्थ निकाल रहा है।

Hindi Yuvakbharati 12th Digest Chapter 2 निराला भाई Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए)
गद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

(1)

उत्तर :

(2)

उत्तर :

प्रश्न 2.
उत्तर लिखिए : निराला जी ने
(1) यह रचा – ………………………………..
(2) यह किया – ………………………………..
उत्तर :
निराला जी ने
(1) यह रचा – दिव्य वर्ण-गंधवाले मधुर गीत।
(2) यह किया – बर्तन मांजने, पानी भरने जैसे कठिन काम।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) कच्चे x ………………………………..
(2) प्रश्न x ………………………………..
(3) कठिन x ………………………………..
(4) जीवन x ………………………………..
उत्तर :
(1) कच्चे x पक्के
(2) प्रश्न – उत्तर
(3) कठिन x सरल
(4) जीवन x मरण।

प्रश्न 2.
गद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए :
(1) ………………………………..
(2) ………………………………..
उत्तर :
(1) वर्ण-गंध
(2) दिन-रात।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
किसी अन्य का कष्ट दूर करने के लिए लुप्त हो गई वस्तुएँ –
(1) …………………………..
(2) …………………………..
उत्तर :
किसी अन्य का कष्ट दूर करने के लिए लुप्त हो गई वस्तुएँ –
(1) रजाई
(2) कोट।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) आदेश = ……………………………….
(2) दुष्कर = ……………………………….
(3) अंतर्धान = ……………………………….
(4) दिवंगत = ……………………………….
उत्तर :
(1) आदेश = हुकम
(3) अंतर्धान = अदृश्य
(2) दुष्कर = कठिन
(4) दिवंगत = मृत।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘निर्बंध उदारता’ के बारे में अपना मत 40 से 50 शब्दों में व्यक्त किजिए।
उत्तर :
मनुष्य ही मनुष्य के काम आता है। किसी के दुखदर्द से सहानुभूति रखना अथवा उसकी आर्थिक मदद करना मनुष्य का धर्म है। इससे जरूरतमंद व्यक्ति को राहत और नैतिक सहयोग मिलता है। अनेक संपन्न व्यक्ति एवं बड़ी-बड़ी संस्थाएँ इस प्रकार का सहयोग देने का कार्य करती हैं। कई साधारण व्यक्ति भी अपनी क्षमता के अनुसार अपने जान-पहचान वाले लोगों की मदद करते हैं।

पर सामान्य लोगों के लिए किसी की आर्थिक सहायता करने की एक सीमा होती है। उसे सबसे पहले अपना घर-बार देखना पड़ता है। अगर कोई व्यक्ति अपनी क्षमता से अधिक उदारता बरतने लगता है, तो उसकी आर्थिक स्थिति अस्त-व्यस्त हो जाती है। ‘अति’ किसी की अच्छी नहीं होती। हर काम अपनी सीमा में ही फबता है। इसलिए निबंध उदारता अनुचित ही नहीं है, यह किसी की भी आर्थिक स्थिति को डाँवाडोल कर सकती है।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : निराला जी का कक्ष ऐसा था –
(1) ………………………….
(2) ………………………….
(3) सुख-सुविधाहीन।
(4) ………………………….
उत्तर :
(1) निराला जी का कक्ष ऐसा था –
(2) कक्ष में जाने का मार्ग तंग सीढ़ियों से होकर था।
(3) प्रकाश रहित था।
(4) सुख-सुविधाहीन।

प्रश्न 2.
अतिथि के लिए निराला जी माँग लिया करते थे –
(1) ………………………….
(2) ………………………….
उत्तर :
अतिथि के लिए निराला जी माँग लिया करते थे
(1) लकड़ियाँ
(2) थोड़ा घी।

प्रश्न 3.
अतिथि देवता के लिए निराला जी शौक से ये करते थे-
(1) ………………………….
(2) ………………………….
उत्तर :
अतिथि देवता के लिए निराला जी शौक से ये करते थे –
(1) अतिथि के लिए भोजन बनाने का काम।
(2) उनके जूठे बर्तन माँजना।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘अतिथि देवो भव’ के बारे में अपने विचार 40 से 50 शब्दों में लिखिए।
उत्तर :
अतिथियों का स्वागत-सत्कार करना हमारे देश के लोगों के संस्कार का एक अंग रहा है। अतिथि के स्वागत में लोग कोई कसर बाकी नहीं रखते। घर में कोई सामान न हो, तो किसी के यहाँ से माँग-जाँच कर ले आने में भी लोग नहीं हिचकते। पर अतिथि की सेवा करने में कोई कसर नहीं रखते।

सुशील अतिथि मेजबान की क्षमता को ध्यान में रखते हैं और उसके साथ पूरा सहयोग करते हैं। मेजबान की तरफ से कहीं कोई कमी भी रह जाती है तो भी उसके साथ सहयोग करते हैं। ऐसे अतिथि मेजबान के लिए देव स्वरूप होते हैं। पर कुछ अतिथि ऐसे होते हैं, जो मेजबान की तरफ से आवभगत में कहीं कोई कमी रह जाने पर उसकी निंदा करने से भी नहीं चूकते।

कुछ अतिथि ‘मान न मान मैं तेरा मेहमान’ की तरह मेजबान के घर आ धमकते हैं और जाने का नाम ही नहीं लेते। ऐसे अतिथि मेजबान के लिए भार स्वरूप होते हैं। जो अतिथि मेजबान की सुविधा-असुविधा का ध्यान रखते हैं, वही अतिथि देव स्वरूप होते हैं।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :
कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
चौखट पूर्ण कीजिए :
(1) गेरू में रंगे हुए वस्त्र।
(2) शरीर पर इस वस्त्र का अभाव था। –
(3) गद्यांश में प्रयुक्त दो वृक्ष।
(4) कवि का गैरिक शरीर ऐसा लगता था। –
उत्तर :
(1) गेरू में रंगे हुए वस्त्र। – [दोनों अधोवस्त्र और उत्तरीय]
(2) शरीर पर इस वस्त्र का अभाव था। – [अंगोछा]
(3) गद्यांश में प्रयुक्त दो वृक्ष। – [नीम-पीपल]
(4) कवि का गैरिक शरीर ऐसा लगता था – [किसी शिखर जैसा।]

प्रश्न 3.
उत्तर लिखिए : कवि के संन्यास से लेखिका को –
(1) लाभ – ………………………….
(2) हानि – ………………………….
उत्तर :
कवि के संन्यास से लेखिका को
(1) लाभ – साबुन के पैसे बचेंगे।
(2) हानि – जाने कहाँ-कहाँ छप्पर डलवाने पड़ेंगे।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदल कर लिखिए :
(1) निधियाँ – ………………………..
(2) वस्त्रों – ………………………..
(3) रोटियाँ – ………………………..
(4) पुत्रौं – ………………………..
उत्तर :
(1) निधियाँ – निधि
(3) रोटियाँ – रोटी
(2) वस्त्रों – वस्त्र
(4) पुत्रौं – पुत्र

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘साधु-संन्यासियों से जनता का मोहभंग’ इस विषय पर 40 से 50 शब्दों में अपना मत व्यक्त कीजिए।
उत्तर :
एक समय था जब लोग साधु-संतों और संन्यासियों का बड़ा सम्मान करते थे। वे समाज में बड़े सम्मान की दष्टि से देखे जाते थे। वे समाज-सुधार और जनता के हित के कार्य किया करते थे और बदले में जनता से कोई अपेक्षा नहीं करते थे। लेकिन हाल में जब से साधु-संन्यासियों के वेष में कुछ ढोंगी लोगों ने साधुसंन्यासियों की जमात को अपने समाज-विरोधी कार्यों से बदनाम कर दिया है, तब से लोगों को इनसे घृणा हो गई है।

ऐसा नहीं है कि सच्चे साधु-संन्यासी हैं ही नहीं। हैं, लेकिन इन ढोंगी साधु संन्यासियों ने उनकी छबि-धूमिल कर दी है। ढोंगी साधु-संन्यासियों के बीच सच्चे साधु-संन्यासियों को पहचानना मुश्किल हो गया है। साधु-संन्यासियों से जनता का मोहभंग ढोंगी साधु-संन्यासियों की जमात के कारण हुआ है। सच्चे साधु-संन्यासियों की जनता आज भी मुरीद है।

गद्यांश क्र. 5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई। सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : निराला जी इस दृष्टि से निराले थे –
(1) ………………………..
(2) जीवन में ………………………..
(3) ………………………..
उत्तर :
निराला जी इस दृष्टि से निराले थे –
(1) अपने शरीर की दृष्टि से।
(2) जीवन में।
(3) अपने साहित्य की दृष्टि से।

प्रश्न 2.
उत्तर लिखिए :
(1) देखने वालों के हृदय में इससे आतंक उत्पन्न होता था –
(2) सत्य दृष्टा ऐसे होते हैं –
(3) अन्याय के प्रतिकार का निराला जी का तरीका –
(4) निराला जी की लेखनी की विशेषता –
उत्तर :
(1) देखने वालों के हृदय में इससे आतंक उत्पन्न होता था – [निराला जी का विशाल डील-डौल देखकर।]
(2) सत्यदृष्टा ऐसे होते हैं – [बालकों जैसे सरल और विश्वासी।]
(3) अन्याय के प्रतिकार का निराला जी का तरीका – [लेखनी के पहले हाथ उठाना।]
(4) निराला जी की लेखनी की विशेषता – [उनकी लेखनी हाथ से अधिक कठोर प्रहार करती थी।]

प्रश्न 3.
संबंध निरूपित कीजिए :
(1) क्रूरता – ………………………..
(2) कायरता – ………………………..
उत्तर :
(1) क्रूरता – वृक्ष की जड़ के अव्यक्त रस में
(2) कायरता – वृक्ष के फल के व्यक्त स्वाद में।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) शरीर = ………………………………………
(2) सत्य = ………………………………………
(3) प्रतिकार = ………………………………………
(3) कठोर = ………………………………………
उत्तर :
(1) शरीर = तन
(2) सत्य = सच्चाई
(3) प्रतिकार = विरोध
(4) कठोर = कड़ा

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘अन्याय सहन करना भी अन्याय है।’ इस विषय पर 40 से 50 . शब्दों में अपने विचार लिखिए।
उत्तर :
सभी मनुष्य समान हैं। किसी को भी किसी के साथ अन्याय करने का अधिकार नहीं है। इसके बावजूद कुछ लोग ऐसे होते हैं, जो अपने से कमजोर व्यक्तियों पर अत्याचार करने से नहीं चूकते। कभी किन्हीं कारणों से जिनके साथ अन्याय होता है, वे उसका विरोध भी नहीं कर पाते।

वे समझते हैं कि विरोध करने का परिणाम उल्टा होगा और अत्याचारी उसे और सताने की कोशिश करेगा। लेकिन यह सोच उचित नहीं है। अन्याय का विरोध न करने से अत्याचारी का मन और बढ़ जाता है। वह समझ जाता है कि उसके अत्याचार का विरोध करने की संबंधित व्यक्ति में शक्ति नहीं है।

इसलिए ऐसे लोगों पर अत्याचार करना अपना अधिकार मान लेता है और वह निडर होकर उन पर अत्याचार करता रहता है। इस तरह अत्याचार सहन करना अपने आप पर अन्याय हो जाता मुक्ति मिल सकती है।

गद्यांश क्र. 6 प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : निराला जी के व्यवहार के बारे में जन-मत –
(1) – …………………………………..
(2) – …………………………………..
उत्तर :
(1) कोई उनकी उदारता की भूरि-भूरि प्रशंसा करता था।
(2) कोई उनके उद्धत व्यवहार की निंदा करते नहीं हारता था।

प्रश्न 2.
संजाल पूर्ण कीजिए :

उत्तर :

प्रश्न 3.
कृति पूर्ण कीजिए :
(1) निराला अपने युग की यह हैं – …………………………………..
(2) उनके जीवन के चारों ओर यह नहीं है – …………………………………..
(3) उनके लिए परिवार के कोंपल यह बन गए – …………………………………..
(4) आर्थिक कारणों से उन्हें यह नहीं मिली – …………………………………..
उत्तर :
(1) विशिष्ट प्रतिमा
(2) परिवार का लौहसार घेरा।
(3) पत्नी वियोग के पतझड़।
(4) अपनी संतान के प्रति कर्तव्य-निर्वाह की सुविधा।

प्रश्न 4.

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त उपसर्गयुक्त शब्द ढूँढ़ कर लिखिए :
(1) …………………………………….
(2) …………………………………….
(3) …………………………………….
(4) …………………………………….
उत्तर :
(1) असफलता
(2) निष्फल
(3) सजातीय
(4) अभिशाप।

व्याकरण

1. मुहावरे :

• निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) आँखों में धूल झोंकना।
अर्थ : धोखा देना।
वाक्य : साइबर क्राइम से अच्छे-अच्छे लोगों की आँखों में धूल झोंककर लाखों रुपए ऐंठ लिए जाते हैं।

(2) आँखें बिछाना।
अर्थ : अति उत्साह से स्वागत करना।
वाक्य : स्वामी जी के दर्शन के लिए श्रद्धालु आँखें बिछाए हुए थे।

(3) कान में कौड़ी डालना।
अर्थ : गुलाम बनाना।
वाक्य : अंग्रेजों ने भारी संख्या में भारतीय मजदूरों के कान में कौड़ी डाल रखा था।

2. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों का काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) कौन बहिन हम जैसे भुक्खड़ को भाई बनाएगी। (सामान्य वर्तमानकाल)
(2) उनके अस्त-व्यस्त जीवन को व्यवस्थित करने के असफल प्रयासों का स्मरण कर मुझे आज भी हँसी आ जाती है। (अपूर्ण भूतकाल)
(3) उनकी व्यथा की सघनता जानने का मुझे एक अवसर मिला था। (पूर्ण वर्तमानकाल)
(4) पंत के साथ तो रास्ता कम अखरता था, पर अब सोचकर ही थकावट होती है। (सामान्य भविष्यकाल)
(5) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण हैं। (पूर्ण भूतकाल)
उत्तर :
(1) कौन बहिन हम जैसे भुक्खड़ को भाई बनाती है।
(2) उनके अस्त-व्यस्त जीवन को व्यवस्थित करने के असफल प्रयासों का स्मरण कर मुझे आज भी हँसी आ रही थी।
(3) उनकी व्यथा की सघनता जानने का मुझे एक अवसर मिला है।
(4) पंत के साथ तो रास्ता कम अखरता था, पर अब सोचकर ही थकावट होगी।
(5) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण थे।

3. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) निराला जी अपनी युग के विशिष्ट प्रतिभा हैं।
(2) सत्य की मार्ग सरल हैं।
(3) मनुष्य जाती की नासमझी की इतिहास क्रूर और लंबा है।
(4) निराला जी अपना शरीर, जीवन और साहित्य सभी में असाधारण है।
(5) उनके जीवन पर संघर्श के जो आघात हैं, वे उनकी हार के नहीं शक्ती के प्रमाणपत्र हैं।
उत्तर :
(1) निराला जी अपने युग की विशिष्ट प्रतिभा हैं।
(2) सत्य का मार्ग सरल है।
(3) मनुष्य जाति की नासमझी का इतिहास क्रूर और लंबा है।
(4) निराला जी अपने शरीर, जीवन और साहित्य सभी में असाधारण हैं।
(5) उनके जीवन पर संघर्ष के जो आघात हैं, वे उनकी हार के नहीं शक्ति के प्रमाणपत्र हैं।

निराला भाई Summary in Hindi

निराला भाई लेखक का परिचय

निराला भाई लेखक का नाम : श्रीमती महादेवी वर्मा। (जन्म 26 मार्च, 1907; निधन 1987.)

प्रमुख कृतियाँ : नीहार, रश्मि, नीरजा, दीपशिखा, सांध्यगीत, यामा (कविता संग्रह), अतीत के चलचित्र, स्मृति की रेखाएँ, मेरा परिवार (रेखाचित्र), श्रृंखला की कड़ियाँ तथा साहित्यकार की आस्था (निबंध)।

विधा : संस्मरण।

विषय प्रवेश : प्रसिद्ध कवि सूर्यकांत त्रिपाठी “निराला’ की गणना हिंदी के श्रेष्ठ कवियों में की जाती है। वे हिंदी साहित्य में छायावादी कवि एवं क्रांतिकारी व्यक्तित्व के रूप में जाने जाते हैं। प्रसिद्ध कवयित्री महादेवी वर्मा एवं निराला जी दोनों का कार्यक्षेत्र प्रयागराज रहा है। इसलिए भी कवयित्री निराला जी को नजदीक से जानती-समझती और उनके व्यक्तित्व से गहराई से परिचित रही हैं।

प्रस्तुत संस्मरण में उन्होंने निराला जी को जिन विभिन्न रूपों में देखा और परखा है, उसे उन्होंने बेबाकी से शब्दांकित किया है। – इस संस्मरण से हमें निराला जी के फक्कड़पन, उनके व्यक्तित्व, उनकी निर्धनता, उदारता, संवेदनशीलता, आतिथ्य सत्कार की भावना तथा पारिवारिक दशा आदि के बारे में अनेक अनछुई बातों की जानकारी मिलती है।

निराला भाई पाठ का सार

कवयित्री महादेवी वर्मा प्रसिद्ध कवि निराला जी के साथ घटित कई घटनाओं की साक्षी रही हैं। उन्होंने उन्हें नजदीक से देखा-समझा है। उन्होंने इस संस्मरण में उनके साथ घटी हुई अनेक घटनाओं और उनके स्वभाव एवं व्यवहार का चित्रण किया है।

निराला जी संवेदनशील उदार, आतिथ्यप्रेमी, सहृदय, फक्कड़ किस्म के और सदा निर्धनता में जीवन बिताने वाले कवि रहे हैं। वे स्पष्टवादी व्यक्ति थे और अपने बारे में सही बात कहने से नहीं चूकते थे। एक बार रक्षाबंधन त्योहार के अवसर पर कवयित्री ने उनकी सूनी कलाइयाँ देखकर इसके बारे में पूछा तो उन्होंने जवाब दिया, “कौन बहन मुझ भुक्खड़ को भाई बनाएगी।”

कवि अपनी उदारता और दूसरों का दुख दूर करने की प्रवृत्ति के कारण सदा तंगी में रहे। वे खुद कष्ट सह लेते थे पर दूसरों का कष्ट दूर करके रहते थे। एक बार तो उन्होंने अपने लिए बनवाई गई रजाई और कोट भी किसी ठिठुरते हुए को दे दिया और खुद काँपते हुए मजे से सर्दियाँ काट दीं।

आर्थिक संकट सदा उनका साथी रहा। इसके कारण वे अपनी मातृविहीन संतान की भी उचित देखभाल न कर पाए। पुत्री के अंतिम क्षणों में असहाय बने रहे और पुत्र को उचित शिक्षा न दे पाए।

एक बार तो उन्होंने कवयित्री को 300 रुपए देकर अपने खर्च का बजट बनाने के लिए कहा था। पर बजट बनते-बनते तक सारे पैसे लेकर जरूरतमंद लोगों को दे डाले।

एक बार प्रसिद्ध कवि मैथिलीशरण गुप्त ने उनका आतिथ्य ग्रहण किया था। जब वे आए तो वे दियासलाई के प्रकाश में उन्हें लेकर तंग सीढ़ियों से होकर अपने सुविधा रहित कक्ष में पहुँचे तो वहाँ ढंग का बिस्तर भी नहीं था। फिर उन्होंने घर में धोती, चादर जो कुछ मिला उसे तख्त पर बिछाकर बड़े प्यार से उन्हें प्रतिष्ठित किया था। अतिथि का सत्कार करने के लिए उन्होंने कवयित्री से एक बार जलावन लकड़ी और घी तक माँग लिया था।

समकालीन साहित्यकारों की व्यथा के बारे में सुनकर वे विचलित हो जाते थे। एक बार सुमित्रानंदन पंत की मृत्यु की झूठी खबर पढ़कर वे बेचैन हो गए थे और सच्चाई जानने के लिए सारी रात जागते हुए इंतजार करते रहे।

एक बार तो उन्होंने अपने दोनों अधोवस्त्र और उत्तरीय गेरू में रंग डाले थे। कवयित्री उनका रूप देखती रह गई थीं। कहने लगे, “अब ठीक है। जहाँ पहुँचे, किसी नीम या पीपल के पेड़ के नीचे बैठ गए। दो रोटियाँ माँग कर खा लीं और गीत लिखने लगे।”

निराला जी के विशाल डील-डौल से देखने वाले के हृदय में आतंक उत्पन्न हो जाता था, पर उनकी आत्मीयता से यह भय तिरोहित हो जाता था।

निराला ऐसे व्यक्तित्व थे जिनके बारे में अलग-अलग व्यक्तियों की अलग-अलग धारणाएँ थीं। कोई उनकी उदारता की प्रशंसा करते नहीं थकता तो कोई उनके उद्धत व्यवहार की निंदा करते नहीं हारता। पर उन्हें समझ पाना हर किसी के वश की बात नहीं थी।

निराला जी अपने युग की विशिष्ट प्रतिभा थे। वे एक विद्रोही साहित्यकार थे। कवयित्री का मानना है कि निराला जी किसी दुर्लभ सीप में ढले सुडौल मोती नहीं थे, वे तो अनगढ़ पारस के भारी शिलाखंड थे। पारस की अमूल्यता दूसरों का मूल्य बढ़ाने में होती है। उसके मूल्य में तो न कोई कुछ जोड़ सकता है, न कुछ घटा सकता है।

निराला भाई शब्दार्थ

• भुक्खड़ = जिसके पास कुछ न हो, कंगाल
• औढरदानी = अत्यंत उदारतापूर्वक दान करने वाला
• अक्षुण्ण = अखंडित
• लौहसार = लोहे का कठघरा
• अछोर = ओर-छोर रहित, असीम
• महाघ = बहुमूल्य
• कुहेलिका = कोहरा, धुंध
• नापित = नाई
• मधुकरी = भोजन की भिक्षा
• डीलडौल = कदकाठी
• कोंपल = नई पत्ती
• अकूल = बिना किनारेवाला
• अनगढ़ = जिसे व्यवस्थित गढ़ा न गया हो
• संसृति = संसार, सृष्टि

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 4 आदर्श बदला Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 4 आदर्श बदला

12th Hindi Guide Chapter 4 आदर्श बदला Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.

(अ) कृति पूर्ण कीजिए :
साधुओं की एक स्वाभाविक विशेषता – ………………………………
उत्तर :
एक स्थान से दूसरे स्थान पर जाते रहना और भजन तथा भक्तिगीत गाते-बजाते रहना।

(आ) लिखिए :

(a) आगरा शहर का प्रभातकालीन वातावरण –
………………………………………………………………
………………………………………………………………
उत्तर :

(b) साधुओं की मंडली आगरा शहर में यह गीत गा रही थी –
………………………………………………………………
………………………………………………………………
उत्तर :
सुमर-सुमर भगवान को,
मूरख मत खाली छोड़ इस मन को।

शब्द संपदा

प्रश्न 2.
लिंग बदलिए:

(1) साधु
(2) नवयुवक
(3) महाराज
(4) दास
उत्तर :
(1) साधु – साध्वी
(2) नवयुवक – नवयुवती
(3) महाराज – महारानी
(4) दास – दासी।

अभिव्यक्ति

प्रश्न 3.

(अ) ‘मनुष्य जीवन में अहिंसा का महत्त्व’, इस विषय पर अपने विचार लिखिए।
उत्तर :
हिंसा क्रूरता और निर्दयता की निशानी है। इससे किसी.। का भला नहीं हो सकता। इस संसार के सभी जीव ईश्वर की संतान हैं और समान हैं। सृष्टि में सबको जीने का अधिकार है। कोई कितना भी शक्तिमान क्यों न हो, किसी को उससे उसका जीवन छीनने का अधिकार नहीं है। जब कोई किसी को जीवन दे नहीं सकता तब वह किसी का जीवन ले भी नहीं सकता। बड़े-बड़े मनीषियों और महापुरुषों ने अहिंसा को ही धर्म कहा है – अहिंसा परमोधर्मः।

अहिंसा का अस्त्र सबसे बड़ा माना जाता है। राष्ट्रपिता महात्मा गांधी ने अहिंसा के बल पर शक्तिशाली अंग्रेज सरकार को झुका दिया था और अंग्रेज सरकार देश को आजाद करने पर विवश हो गई थी। जीवन का मूलमंत्र ‘जियो और जीने दो’ है। किसी के प्रति ईर्ष्या की भावना रखना या किसी का नुकसान करना भी एक प्रकार की हिंसा है। इससे हमें बचना चाहिए।

(आ) ‘सच्चा कलाकार वह होता है जो दूसरों की कला का सम्मान करता हैं, इस कथन पर अपना मत व्यक्त कीजिए।
उत्तर :
कलाकार को कोई कला सीखने के लिए गुरु के सान्निध्य में रह कर वर्षों तक तपस्या करनी पड़ती है। कला की छोटीछोटी बारीक बातों की जानकारी करनी पड़ती है। इसके साथ ही निरंतर रियाज करना पड़ता है। गुरु से कला की जानकारियाँ प्राप्त करते-करते अपनी कला में वह प्रवीण होता है।

सच्चा कलाकार किसी कला को सीखने की प्रक्रिया में होने वाली कठिनाइयों से परिचित होता है। इसलिए उसके दिल में अन्य कलाकारों के लिए सदा सम्मान की भावना होती है। वह छोटे-बड़े हर कलाकार को समान समझता है और उनकी कला का सम्मान करता है। सच्चे कलाकार का यही धर्म है। इससे कला को प्रोत्साहन मिलता है और वह फूलती-फलती है।

पाठ पर आधारित लघूत्तरी प्रश्न –

प्रश्न 4.

(अ) ‘आदर्श बदला’ कहानी के शीर्षक की सार्थकता स्पष्ट कीजिए।
उत्तर :
अपने पिता को मृत्युदंड दिए जाने पर बैजू विक्षिप्त हो गया था। और अपनी कुटिया में विलाप कर रहा था। उस समय बाबा हरिदास ने उसकी कुटिया में आकर उसे ढाढ़स बंधाया था। तब बालक बैजू ने बाबा को बताया था कि उसे अब बदले की भूख है। वे उसकी इस भूख को मिटा दें। बाबा हरिदास ने उसे वचन दिया था कि वे उसे ऐसा हथियार देंगे, जिससे वह अपने पिता की मौत का बदला ले सकेगा।

बाबा हरिदास ने बारह वर्षों तक बैजू को संगीत की हर प्रकार की बारीकियाँ सिखाकर उसे पूर्ण गंधर्व के रूप में तैयार कर दिया। मगर इसके साथ ही उन्होंने उससे यह वचन भी ले लिया कि वह इस राग विद्या से किसी को हानि न पहुँचाएगा।

इसके बाद वह दिन भी आया जब बैजू आगरा की सड़कों पर गाता हुआ निकला और उसके पीछे उसकी कला के प्रशंसकों की अपार भीड़ थी। आगरा में गाने के नियम के अनुसार उसे बादशाह के समक्ष पेश किया गया और शर्त के अनुसार तानसेन से उसकी संगीत प्रतियोगिता हुई, जिसमें उसने तानसेन को बुरी तरह परास्त कर दिया। तानसेन बैजू बावरा के पैरों पर गिरकर अपनी जान की भीख माँगने लगा। इस मौके पर बैजू बावरा उससे अपने पिता की मौत का बदला लेकर उसे प्राणदंड दिलवा सकता था। पर उसने ऐसा नहीं किया। बैजू ने तानसेन की जान बख्श दी।

उसने उससे केवल इस निष्ठुर नियम को उड़वा देने के लिए कहा, जिसके अनुसार किसी को आगरे की सीमाओं में गाने और तानसेन की जोड़ का न होने पर मरवा दिया जाता था। इस तरह बैजू बावरा ने तानसेन का गर्व नष्ट कर उसे मुँह की खिलाकर उससे अनोखा बदला लेकर उसे श्रीहीन कर दिया था। यह अपनी तरह का आदर्श बदला था। समूची कहानी इस बदले के आसपास घूमती है। इसलिए ‘आदर्श बदला’ शीर्षक इस कहानी के उपयुक्त है।

(आ) ‘बैजू बावरा संगीत का सच्चा पुजारी है’, इस विचार को स्पष्ट कीजिए।
उत्तर :
सच्चा कलाकार उसे कहते हैं, जिसे अपनी कला से सच्चा लगाव हो। वह अपने गुरु की कही हुई बातों पर अमल करे तथा गुरु से विवाद न करे। इसके अलावा उसे अपनी कला पर अहंकार न हो। बैजू बावरा ने बारह वर्ष तक बाबा हरिदास से संगीत सीखने की कठिन तपस्या की थी।

वह उनका एक आज्ञाकारी शिष्य था। उसकी संगीत शिक्षा पूरी हो जाने के बाद बाबा हरिदास ने जब उससे यह प्रतिज्ञा करवाई कि वह इस राग विद्या से किसी को हानि नहीं पहुँचाएगा, तो भी उसने रक्त का यूंट पी कर इस गुरु आदेश को स्वीकार कर लिया था, जबकि उसे मालूम था कि इससे उसके हाथ में आई हुई प्रतिहिंसा की छुरी कुंद कर दी गई थी। फिर भी गुरु के सामने उसके मुँह से एक शब्द भी नहीं निकला।

बैजू बावरा की संगीत कला की धाक दूर-दूर तक फैल गई थी। है उसके संगीत में जादू का असर था। बैजू बावरा को संगीत ज्ञान है पर तानसेन की तरह कोई अहंकार नही था। बल्कि इसके विपरीत उसके हृदय में दया की भावना थी। गानयुद्ध में तानसेन को पराजित करने पर भी वह अपनी जीत और संगीत का प्रदर्शन नहीं करता।

बल्कि वह तानसेन को जीवनदान दे देता है। वह उससे केवल यह माँग करता है कि वह इस नियम को खत्म करवा दे कि जो कोई आगरा की सीमा के अंदर गाए, वह अगर तानसेन की जोड़ का न हो, तो मरवा दिया जाए। उसकी इस माँग में भी गीत-संगीत की ५ रक्षा करने की भावना निहित है।

इस प्रकार इसमें कोई संदेह नहीं है कि बैजू बावरा संगीत का सच्चा पुजारी था।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.

(अ) सुदर्शन जी का मूल नाम : ……………………………………
उत्तर :
सुदर्शन जी का मूल नाम बदरीनाथ है।

(आ) सुदर्शन ने इस लेखक की लेखन परंपरा को आगे बढ़ाया है : ……………………………………
उत्तर :
सुदर्शन ने मुंशी प्रेमचंद की लेखन परंपरा को आगे बढ़ाया है।

रस

अद्भुत रस : जहाँ किसी के अलौकिक क्रियाकलाप, अद्भुत, आश्चर्यजनक वस्तुओं को देखकर हृदय में विस्मय अथवा आश्चर्य का भाव जाग्रत होता है; वहाँ अद्भुत रस की व्यंजना होती है।

उदा. –

(१) एक अचंभा देखा रे भाई।
ठाढ़ा सिंह चरावै गाई।
पहले पूत पाछे माई।
चेला के गुरु लागे पाई।।

(२) बिनु-पग चलै, सुनै बिनु काना।
कर बिनु कर्म कर, विधि नाना।
आनन रहित सकल रस भोगी।
बिनु वाणी वक्ता, बड़ जोगी।।

शृंगार रस : जहाँ नायक और नायिका अथवा स्त्री-पुरुष की प्रेमपूर्ण चेष्टाओं, क्रियाकलापों का शृंगारिक वर्णन हो; वहाँ शृंगार रस की व्यंजना होती है।

उदा. –
(१) राम के रूप निहारति जानकी, कंकन के नग की परछाही,
यातै सबै सुधि भूलि गई, कर टेकि रही पल टारत नाही।

(२) कहत, नटत, रीझत, खिझत, मिलत, खिलत, लजियात।
भरे भौन में करत हैं, नैननु ही सौं बात।।

शांत रस : (निर्वेद) जहाँ भक्ति, नीति, ज्ञान, वैराग्य, धर्म, दर्शन, तत्त्वज्ञान अथवा सांसारिक नश्वरता संबंधी प्रसंगों का वर्णन हो; वहाँ शांत रस उत्पन्न होता है।

उदा. –
(१) माला फेरत जुग भया, गया न मन का फेर।
कर का मनका डारि कै, मन का मनका फेर।।

(२) माटी कहै कुम्हार से, तू क्या रौंदे मोहे।
एक दिन ऐसा आएगा, मैं रौंदूंगी तोहे।।

भक्ति रस : जहाँ ईश्वर अथवा अपने इष्ट देवता के प्रति श्रद्धा, अलौकिकता, स्नेह, विनयशीलता का भाव हृदय में उत्पन्न होता है; वहाँ भक्ति रस की व्यंजना होती है।

उदा. –
(१) तू दयालु दीन हौं, तू दानि हौं भिखारि।
हौं प्रसिद्ध पातकी, तू पाप पुंजहारि।

(२) समदरसी है नाम तिहारो, सोई पार करो,
एक नदिया इक नार कहावत, मैलो नीर भरो,
एक लोहा पूजा में राखत, एक घर बधिक परो,
सो दुविधा पारस नहीं जानत, कंचन करत खरो।

Hindi Yuvakbharati 12th Digest Chapter 4 आदर्श बदला Additional Important Questions and Answers

गद्यांश क्र. 1
कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए।

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
साधु इस तरह गाते थे गीत –
(1) ……………………………………..
(2) ……………………………………..
(3) ……………………………………..
(4) ……………………………………..
उत्तर :
(1) कोई ऊँचे स्वर में गाता था।
(2) कोई मुँह में गुनगुनाता था।
(3) सब अपने राग में मगन थे।
(4) उन्हें सुर-ताल की परवाह नहीं थी।

प्रश्न 3.
तानसेन द्वारा बनवाया गया कानून –
(1) ……………………………………..
(2) ……………………………………..
उत्तर :
(1)जो आदमी राग-विद्या में तानसेन की बराबरी न कर सके, है वह आगरे की सीमा में गीत न गाए।
(2) ऐसा आदमी जो आगरे की सीमा में गीत गाए, उसे मौत की सजा दी जाए।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग बदलकर लिखिए :
(1) पत्ते – …………………………………..
(2) स्वामी – …………………………………..
(3) राग – …………………………………..
(4) आदमी – …………………………………..
उत्तर :
(1) पत्ते – पत्तियाँ
(2) स्वामी – स्वामिनी
(3) राग – रागिनी (4) आदमी – औरत

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
साधु-संतों को राग विद्या की जानकारी न होने के कारण मौत की सजा दिया जाना क्या उचित है? इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
साधु-संत दीन-दुनिया से विरक्त ईश्वर आराधना में लीन रहने वाले लोग होते हैं। वे अपने साथी साधु-संतों से सुने-सुनाए भजन-कीर्तन अपने ढंग से गाते हैं। उन्हें राग, छंद और संगीत का समुचित ज्ञान नहीं होता। भजन भी वे अपनी आत्म-संतुष्टि और ईश्वर आराधना के लिए गाते हैं।

उनका उद्देश्य उसे राग में गा कर किसी को प्रसन्न करना नहीं होता। आगरा शहर में बिना सुर-ताल की परवाह किए हुए और बादशाह के कानून से अनभिज्ञ ये साधु गाते हुए जा रहे थे। इन्हें इस जुर्म में पकड़ लिया गया था कि वे आगरा की सीमा में गाते हुए जा रहे हैं। अकबर के मशहूर रागी तानसेन ने यह नियम बनवा दिया था कि जो आदमी राग विद्या में उसकी बराबरी न कर सके वह आगरा की सीमा में न गाए। यदि गाए तो उसे मौत की सजा दी जाए।

अतः इन्हें मौत की सजा दे दी गई। इस तरह साधुओं को मौत की सजा देना उनके साथ बिलकुल अन्याय है। इस तरह के कानून से तानसेन के अभिमान की बू आती है।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर :

उत्तर :

प्रश्न 2.
उत्तर लिखिए :

(1) बैजू ने हरिदास के चरणों में और ज्यादा लिपट कर यह कहा –
(i) ……………………………………
(ii) ……………………………………
(iii) ……………………………………
(iv) ……………………………………
उत्तर :
(i) महाराज (मेरी) शांति जा चुकी है।
(ii) अब मुझे बदले की भूख है।
(iii) अब मुझे प्रतिकार की प्यास है।
(iv) आप मेरी प्यास बुझाइए।

(2)

उत्तर :

(3)

उत्तर :

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर :

प्रश्न 4.
बैजू ने दिया बाबा हरिदास को यह वचन –
(i) ……………………………………
(ii) ……………………………………
(iii) ……………………………………
(iv) ……………………………………
उत्तर :
(i) मैं बारह जीवन देने को तैयार हूँ।
(ii) मैं तपस्या करूँगा।
(iii) मैं दुख झेलूँगा, मैं मुसीबतें उठाऊँगा।
(iv) मैं अपने जीवन का एक-एक क्षण आपको भेंट कर दूंगा।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग बदल कर लिखिए :
(1) बेटा – ……………………………………
(2) बच्चा – ……………………………………
(3) सेवक – ……………………………………
(4) सूना – ……………………………………
उत्तर :
(1) बेटा – बेटी
(2) बच्चा – बच्ची
(3) सेवक – सेविका
(4) आखिरी = अंतिम।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) संसार = ……………………………………
(2) तबाह = ……………………………………
(3) चरण = ……………………………………
(4) आखिरी = ……………………………………
उत्तर :
(1) संसार = दुनिया
(2) तबाह = बर्बाद
(3) चरण = पाँव
(4) सूना – सूनी।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘बिनु गुरु होय न ज्ञान’ इस कथन के बारे में 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
मनुष्य को बचपन से लेकर अंतिम समय तक विभिन्न . कार्यों को पूर्ण करने के लिए ज्ञान की आवश्यकता होती है। यह ज्ञान विभिन्न रूपों में हमें किसी-न-किसी गुरु से मिलता है। बचपन में बच्चे का पालन-पोषण कर उसे बड़ा करके बोलने-चालने और बोली-भाषा सिखाने का काम माता करती है।

उस समय वह उसकी गुरु होती है। बड़े होने पर विद्यालय में शिक्षकों से बच्चे को ज्ञान की प्राप्ति होती है। तरह-तरह की कलाओं को सीखने के लिए गुरु से ज्ञान प्राप्त करने की आवश्यकता होती है। गुरु से ज्ञान प्राप्त करके ही कलाकार नाम कमाते हैं।

प्रसिद्ध क्रिकेट खिलाड़ी सचिन तेंदुलकर के क्रिकेट के क्षेत्र में महारत हासिल करने में उनके क्रिकेट गुरु रमाकांत आचरेकर का विशेष योगदान रहा है।

इसी तरह छत्रपति शिवाजी महाराज की सफलता में उनके गुरु का काफी योगदान रहा है। गुरु ही हमें सही या गलत में भेद करना सिखाते हैं। वे ही भूले-भटके हओं को सही राह दिखाते हैं। इस तरह गुरु की महिमा अपरंपार है।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए : जवान बैजू के संगीत की विशेषताएँ –
(1) …………………………
(2) …………………………
(3) …………………………
(4) …………………………
उत्तर :
(1) उसके स्वर में जादू था और तान में आश्चर्यमयी मोहिनी थी।
(2) गाता था तो पत्थर तक पिघल जाते थे।
(3) पशु-पंछी तक मुग्ध हो जाते थे।
(4) लोग सुनते थे और झूमते थे तथा वाह-वाह करते थे।

प्रश्न 3.
बैजू की राग विद्या की शिक्षा पूरी होने पर हरिदासजी ने यह कहा –
(1) …………………………
(2) …………………………
उत्तर :
(1) वत्स! मेरे पास जो कुछ था, वह मैंने तुझे दे डाला।
(2) अब तू पूर्ण गंधर्व हो गया है।

प्रश्न 4.
संजाल पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) उजड़ना x ……………………………..
(2) बूढ़े x ……………………………..
(3) कृतज्ञता x ……………………………..
(4) उपकार x ……………………………..
उत्तर :
(1) उजड़ना – बसना
(3) कृतज्ञता – कृतघ्नता
(2) बूढ़े x जवान
(4) उपकार x अपकार।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘कृतज्ञता मनुष्य का उत्तम गुण है’ इस विषय पर 40 से 50 शब्दों में अपना मत लिखिए।
उत्तर :
कृतज्ञता का अर्थ है अपने साथ किसी के द्वारा किए गए किसी अच्छे कार्य के लिए व्यक्ति का एहसान मानना। प्रत्येक मनुष्य के जीवन में कभी-न-कभी ऐसा समय आता है, जब उसे किसी रूप में किसी व्यक्ति से छोटी-बड़ी मदद लेनी पड़ती है अथवा किसी का एहसान लेना पड़ता है। उस समय इस प्रकार की मदद अथवा उपकार करने वाला व्यक्ति हमें किसी फरिश्ते से कम नहीं लगता।

ऐसे समय हमारे मन में उसके प्रति श्रद्धा और सम्मान की भावना जाग उठती है। इसे हम एहसान करने वाले के पैर छू करः अथवा उसे धन्यवाद दे कर प्रदर्शित करते हैं। इतना ही नहीं हम सदा उसके एहसान को याद रखते हैं। कृतज्ञता व्यक्त करने से एहसान करने वाले व्यक्ति को भी प्रसन्नता होती है।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :

(1) सिपाहियों ने साधु को इस रूप में देखा –
(i) ………………………………..
(ii) ………………………………..
(iii) ………………………………..
(iv) ………………………………..
उत्तर :
(i) साधु के मुँह से तेज की किरणें फूट रही थीं। .
(ii) उन किरणों में जादू था, मोहिनी थी और मुग्ध करने की शक्ति थी।
(iii) उसके मुँह पर सरस्वती का वास था।
(iv) उसके मुँह से संगीत की मधुर ध्वनि की धारा बह रही थी।

(2)

उत्तर :

प्रश्न 2.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 3.
लिखिए : तानसेन ने नवयुवक (साधु) से यह कहा –
(1) ………………………………..
(2) ………………………………..
(3) ………………………………..
(4) ………………………………..
उत्तर :
(1) शायद आपके सिर पर मौत सवार है।
(2) आप नियम जानते हैं न?
(3) नियम कड़ा है और मेरे दिल में दया नहीं है।
(4) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार हैं।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदल कर लिखिए :
(1) हथकड़ियाँ – ………………………………………
(2) आँखें – ………………………………………
(3) बाजारों – ………………………………………
(4) श्रोता – ………………………………………
उत्तर :
(1) हथकड़ियाँ – हथकड़ी
(2) आँखें – आँख
(3) बाजारों – बाजार
(4) श्रोताँ – श्रोतागण।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘घमंड मनुष्य का सबसे बड़ा शत्रु है’ इस विषय पर अपने विचार 40 से 50 शब्दों में लिखिए।
उत्तर :
मनुष्य के अंदर सद् और असद् दो प्रवृत्तियाँ होती हैं। सद् का अर्थ है अच्छा और असद् का अर्थ है जो अच्छा न हो यानी बुरा। घमंड मनुष्य की बुरी वृत्ति है। घमंडी व्यक्ति को अच्छे और बुरे का विवेक नहीं होता। वह अपने घमंड के नशे में चूर रहता है और अपना भला-बुरा भी भूल जाता है।

घमंडी व्यक्ति को अपनी गलती का अहसास तब होता है, जब उसकी की गई गलतियों का परिणाम उसके सामने आता है। घमंड का परिणाम बहुत बुरा होता है। इसके कारण बड़े-बड़े ज्ञानी पुरुषों को भी मुँह की खानी पड़ती है।

रावण जैसा महाज्ञानी पंडित भी अपने घमंड के कारण अपने कुल परिवार सहित नष्ट हो गया। घमंड मनुष्य का सबसे बड़ा शत्रु है और उसकी मंजिल है दारुण दुख। इसलिए मनुष्य को घमंड का मार्ग त्याग कर प्रेम और सद्गुण का मार्ग अपनाना चाहिए।

गद्यांश क्र. 5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
उत्तर लिखिए :
(1) बैजू बावरा ने अपने सितार के पदों को हिलाया, तो यह हुआ –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
(i) जनता ब्रह्मानंद में लीन हो गई।
(ii) पेड़ों के पत्ते तक निःशब्द हो गए।
(iii) वायु रुक गई।
(iv) सुनने वाले मंत्रमुग्धवत सुधिहीन हुए सिर हिलाने लगे।

प्रश्न 3.
बैजू बावरा की उँगलियाँ जब सितार पर दौड़ी, तब –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
(i) तारों पर राग विद्या निछावर हो रही थी।
(ii) लोगों के मन उछल रहे थे।
(iii) लोग झूम रहे थे, थिरक रहे थे।
(iv) जैसे सारे विश्व की मस्ती वहीं आ गई थी।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द समूहों के लिए गद्यांश में से ढूँढकर एकएक शब्द लिखिए :
(1) ब्रह्म स्वरूप के साक्षात्कार का दर्शन।
(2) जहाँ किसी प्रकार का शब्द न होता हो।
(3) जो होश से रहित हो।
(4) किसी से भी न डरने की भावना।
उत्तर :
(1) ब्रह्मानंद
(2) निःशब्द
(3) सुधिहीन
(4) निर्भयता

गद्यांश क्र. 6
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए : गानयुद्ध-स्थल पर दर्शक यह देखकर हैरान रह गए –
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
उत्तर :
(1) कुछ हरिण छलाँगें मारते हुए आए और बैजू बावरा के पास खड़े हो गए।
(2) हरिण संगीत सुनते रहे, सुनते रहे।
(3) हरिण मस्त और बेसुध थे।
(4) बैजू ने सितार रखकर उनके गले में फूलमालाएँ पहनाईं तब उन्हें सुध आई और भाग खड़े हुए।

प्रश्न 2.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 3.
लिखिए : तानसेन ने इस तरह बजाया सितार –
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
उत्तर :
(1) पूर्ण प्रवीणता के साथ।
(2) पूर्ण एकाग्रता के साथ।
(3) वह बजाया, जो कभी न बजाया था।
(4) वह बजाया, जो कभी न बजा सकता था।

प्रश्न 4.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित उपसर्ग जोड़कर शब्द बनाकर लिखिए :
(1) अ – …………………………….
(2) बे – …………………………….
(3) निर् – …………………………….
(4) परा – …………………………….
उत्तर
(1) अ – असाधारण
(2) बे – बेसुध
(3) निर् – निरादर
(4) परा – पराजय

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘संगीत का प्रभाव’ विषय पर 40 से 50 शब्दों में अपने विचार व्यक्त कीजिए।
उत्तर :
संगीत ऐसी कला है, जो श्रोताओं को अपनी स्वर लहरियों से आह्लादित कर देती है। संगीत एक गूढ़ विद्या है। संगीत-साधक इसमें जितनी गहराई तक जाता है, उसे उतने ही मोती मिलते हैं। संगीत का आनंद संगीत विशेषज्ञ तो उठाते ही हैं, जिन लोगों में संगीत कला की समझ नहीं होती, वे भी संगीत की स्वर लहरियों को सुन कर झूमने लगते हैं। संगीत की मधुर ध्वनि से लोग अपनी सुध-बुध खो बैठते हैं। संगीत सुनने से मन प्रसन्न होता है।

संगीत तनाव कम करने में सहायक होता है और उससे मानसिक शांति मिलती है।

संगीत का प्रभाव अद्भुत होता है। उससे केवल मनुष्य ही नहीं, वातावरण, पशु-पक्षी, पेड़-पौधे सभी प्रभावित होते हैं। संगीत से पौधों की वृद्धि और दुधारू पशुओं के अधिक दूध देने तक की बातें कही जाती रही हैं। गुणी संगीतकार के संगीत-वादन से वर्षा होने लगती है।

मधुर संगीत से प्रभावित होकर लोगों के मन उछलने लगते हैं, उनके मन थिरकने लगते हैं। लोग मस्ती में डूब जाते हैं। संगीत में जादू-सा प्रभाव होता है। संसार में शायद ही ऐसा कोई प्राणी होगा, जो संगीत की मधुर ध्वनि की धारा में न बह जाता हो।

गद्यांश क्र. 7
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
लिखिए : हरिण बुला पाने में असमर्थ तानसेन की बौखलाहट –
(1) ………………………………..
(2) ………………………………..
(3) ………………………………..
(4) ………………………………..
उत्तर :
(1) उसकी आँखों के सामने मौत नाचने लगी।
(2) उसकी देह पसीना-पसीना हो गई।
(3) लज्जा से उसका मुँह लाल हो गया।
(4) वह खिसिया गया।

प्रश्न 2.
उत्तर लिखिए :

(a) दुबारा बैजू बावरा ने सितार पकड़ा, तो यह हुआ –
(i) …………………………………
(ii) …………………………………
(iii) …………………………………
(iv) …………………………………
उत्तर :
(i) एक बार फिर संगीतलहरी वायुमंडल में लहराने लगी।
(ii) फिर सुनने वाले संगीत-सागर की तरंगों में डूबने लगे।
(iii) हरिण बैजू बावरा के पास फिर आए।
(iv) बैजू ने (उनके गले से) मालाएँ उतार लीं और हरिण छलाँग लगाते चले गए।

(b) अकबर का निर्णय सुन कर तानसेन ने यह किया –
(i) …………………………………
(ii) …………………………………
(iii) …………………………………
(iv) …………………………………
उत्तर :
(i) काँपता हुआ उठा।
(ii) काँपता हुआ आगे बढ़ा।
(iii) काँपता हुआ बैजू बावरा के पाँव में गिर पड़ा।
(iv) उससे गिड़गिड़ाया, ‘मेरे प्राण न लो।’

(c) बैजू बावरा ने तानसेन को यह जवाब दिया –
(i) …………………………………
(ii) …………………………………
उत्तर :
(i) मुझे तुम्हारे प्राण लेने की चाह नहीं।
(ii) तुम इस नियम को उड़वा दो कि यदि आगरे की सीमा में गाने वाला तानसेन की जोड़ का न हो, तो उसे मरवा दिया जाए।

(d) बैजू बावरा ने तानसेन को यह पुरानी बात बताई –
(i) …………………………………
(ii) …………………………………
उत्तर :
(i) बारह साल पहले आपने एक बच्चे की जान बचाई (बख्शी ) थी।
(ii) आज उस बच्चे ने आपकी जान बख्शी है।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्द ढूँढ़कर लिखिए : .
(1) ………………………………
(2) ………………………………
(3) ………………………………
(4) ………………………………
उत्तर :
(1) संगीतलहरी – संगीतलहर + ई।
(2) मालाएँ – माला + एँ।
(3) होकर – हो + कर।
(4) दीनता – दीन + ता।

1. मुहावरे :

निम्नलिखित मुहावरों का अर्थ लिखकर अपने वाक्यों में प्रयोग कीजिए :

(1) अगर-मगर करना।
अर्थ : टाल-मटोल करना।
वाक्य : सिपाही ने आरोपी से कहा, अगर-मगर मत करो, सीधे-सीधे मेरे साथ थाने चलो।

(2) अपना राग अलापना।
अर्थ : अपनी ही बातें करते रहना।
वाक्य : श्यामसुंदर की तो आदत है, दूसरे की बात न सुनना और अपना ही राग अलापते रहना।

(3) चाँदी काटना।
अर्थ : बहुत लाभ कमाना।
वाक्य : आजकल जब लोग कोरोना के डर से घरों में दुबके हैं, कुछ सब्जी बेचने वाले चाँदी काट रहे हैं।

(4) कान भरना।
अर्थ : चुगली करना।
वाक्य : मुनीमजी का चपरासी आफिस के अन्य लोगों के बारे में उनके कान भरता रहता है।

(5) जली-कटी सुनाना।
अर्थ : कटु बात करना।
वाक्य : रघु की माँ अकारण अपनी बहू को जली-कटी सुनाती रहती है।

2. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों का काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) प्रकाश की किरणें संसार पर नवीन जीवन की वर्षा कर रही थीं। (सामान्य वर्तमानकाल)
(2) जो जवान थे उनके बाल सफेद हो गए। (सामान्य भविष्यकाल)
(3) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार हैं। (पूर्ण भूतकाल)
(4) बैजू बावरा की उँगलियाँ सितार पर दौड़ रही थीं। (अपूर्ण वर्तमानकाल)
(5) बहुत अच्छा! दोबारा बुलाकर दिखा देता हूँ। (सामान्य भविष्यकाल)
उत्तर :
(1) प्रकाश की किरणें संसार पर नवीन जीवन की वर्षा करती हैं।
(2) जो जवान होंगे उनके बाल सफेद हो जाएंगे।
(3) मेरी आँखें दूसरों की मौत को देखने के लिए हर समय तैयार थीं।
(4) बैजू बावरा की उँगलियाँ सितार पर दौड़ रही हैं।
(5) बहुत अच्छा! दोबारा बुलाकर दिखा दूंगा।

3. वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्यों को शुद्ध करके लिखिए :
(1) मैं तेरे को वह हथियार दूँगा, जिससे तू तेरे पिता की मौत का बदला ले सकेगा।
(2) हरिदास की धीरज की दीवार आँसुओं के बौछार न सह सकी।
(3) बैजू हाथों बाँधकर खड़े हो गया।
(4) अब मेरी पास और कुछ नहीं, जो तुजे दूँ।
(5) साधु की प्रार्थना में सर्वसाधारण को भी उसकी जीवन और मृत्यु का तमाशा देखने की आज्ञा दे दी गई थी।
उत्तर :
(1) मैं तुझे वह हथियार दूँगा, जिससे तू अपने पिता की मौत का बदला ले सकेगा।
(2) हरिदास के धीरज की दीवार आँसुओं की बौछार न सह सकी।
(3) बैजू हाथ बाँधकर खड़ा हो गया।
(4) अब मेरे पास और कुछ नहीं जो तुझे दूँ।
(5) साधु की प्रार्थना पर सर्वसाधारण को भी उसके जीवन और मृत्यु का तमाशा देखने की आज्ञा दे दी गई थी।

आदर्श बदला Summary in Hindi

आदर्श बदला लेखक का परिचय

आदर्श बदला लेखक का नाम : सुदर्शन। (मूल नाम : बदरीनाथ) (जन्म 29 मई, 1895, सियालकोट ; निधन 9 मार्च, 1967.)

प्रमुख कृतियाँ : पुष्पलता, सुदर्शन सुधा, तीर्थयात्रा, पनघट (कहानी संग्रह)। सिकंदर, भाग्यचक्र (नाटक)। भागवती (उपन्यास)। आनररी मजिस्ट्रेट (प्रहसन)।

विशेषता : आपने प्रेमचंद की लेखन-परंपरा को आगे बढ़ाया है। आपकी रचनाएँ आदर्शोन्मुख यथार्थवाद को रेखांकित करती हैं। साहित्य को लेकर आपका दृष्टिकोण सुधारवादी रहा है। आपने हिंदी फिल्मों की पटकथाएँ और गीत भी लिखे हैं। आपकी प्रथम कहानी ‘हार की जीत’ हिंदी साहित्य में विशिष्ट स्थान रखती है।

विधा : कहानी। कहानी भारतीय साहित्य की प्राचीन विद्या है। आपकी कहानियों की भाषा सरल, पात्रानुकूल तथा प्रभावोत्पादक हैं। मुहावरों का सटीक प्रयोग, प्रवाहमान शैली कहानी की प्रभावोत्पादकता में वृद्धि करती है।

विषय प्रवेश : बदला लेने वाले व्यक्ति के मन में अकसर क्रोध अथवा हिंसा की भावना प्रमुख होती है। इतना ही नहीं, मौत का बदला मौत से लेने की अनेक घटनाएँ प्रसिद्ध हैं। पर प्रस्तुत कहानी में लेखक ने बदला लेने का अनूठा आदर्श प्रस्तुत किया है। ‘बचपन में बैजू अपने पिता को भजन गाने के अपराध में तानसेन की क्रूरता का शिकार होता हुआ देखता है। परंतु वही बैजू बावरा तानसेन को संगीत-प्रतियोगिता में हरा कर उसे जीवन-दान दे देता है। लेखक ने इस कहानी के माध्यम से बैजू बावरा को आदर्श बदला लेते हुए दर्शाया है।

आदर्श बदला पाठ का सार

आगरा शहर में सुबह-सुबह साधुओं की एक मंडली अपने ढंग से भजन गाते-गुनगुनाते प्रवेश कर रही थी। इस मंडली में एक छोटा बच्चा भी था। साधु अपने राग में मगन थे, तभी राज्य के सिपाहियों ने उन्हें गिरफ्तार कर लिया और उन्हें बादशाह अकबर के सामने पेश कर दिया गया।

अकबर के मशहूर संगीतकार तानसेन ने यह कानून बनवा दिया था कि जो आदमी राग विद्या में उसकी बराबरी न कर सके, वह आगरा की सीमा में गीत न गाए और जो गाए तो उसे मौत की सजा दी जाए। बेचारे साधुओं को इसकी जानकारी नहीं थी। साधु संगीत विद्या से अनभिज्ञ थे। अतः उन्हें मृत्युदंड की सजा हुई। पर उस बच्चे पर दया करके उसे छोड़ दिया गया।

वह बच्चा रोता-तड़पता आगरा की बाजारों से निकल कर जंगल में अपनी कुटिया में पहुँचा और विलाप करता रहा। तभी खड़ाऊँ पहने, हाथ में माला लिए हुए, राम नाम का जप करते हुए बाबा हरिदास कुटिया के अंदर आए और उन्होंने उसे शांत रहने के लिए कहा। पर उस बच्चे के मन में शांति कहाँ थी! उसका तो संसार उजड़ चुका था। तानसेन ने उसे तबाह कर दिया था।

यह बच्चा बैजू बावरा था। उसने अपने साथ हुई सारी दुर्घटना बाबा हरिदास को बताई और अपने बदले की भूख और प्रतिकार की प्यास मिटाने की उनसे प्रार्थना की। E अंत में हरिदास ने उसे आश्वस्त किया कि वे उसे ऐसा हथियार देंगे, जिससे वह अपने पिता का बदला ले सके।

इसके लिए उन्होंने बैजू से बारह वर्ष तक (संगीत की) तपस्या E करने का वचन लिया। बाबा ने बारह वर्ष में बैजू बावरा को वह सब कुछ सिखा दिया, जो उनके पास था। अब बैजू पूर्ण गंधर्व हो गया था। उसके स्वर में जादू था।

लेकिन संगीत-तपस्या पूरी होने के साथ ही बैजू बावरा को बाबा हरिदास के सामने यह प्रतिज्ञा भी करनी पड़ी कि वह इस राग विद्या से किसी को हानि नहीं पहुँचाएगा। इस प्रतिज्ञा से उसे लगा कि प्रतिहिंसा की छुरी हाथ में आई भी तो गुरु ने प्रतिज्ञा लेकर उसे कुंद कर दी।

कुछ दिनों बाद यही सुंदर युवक साधु आगरा के बाजारों में गाता हुआ जा रहा था। लोगों ने सोचा कि इसकी भी मौत आ गई है। वे उसे नगर की रीति की सूचना देने निकले। पर उसके निकट पहुँचने के पहले ही वे उससे मुग्ध होकर अपनी सुधबुध खो बैठे। सिपाही उसे पकड़ने दौड़े तो उसका गीत सुन कर उन्हें अपनी हथकड़ियों की भी सुध न रही। लोग नवयुवक के गीत पर मुग्ध थे। चलते-चलते यह जन-समूह मौत के द्वार यानी तानसेन के महल के सामने था।

तानसेन बाहर निकला और उसने फब्ती कसी, ‘तो शायद आपके सिर पर मौत सवार है।’ यह सुन कर बैजू के होठों पर मुस्कराहट आ गई। उसने कहा, “मैं आपके साथ गान-विद्या पर चर्चा करना चाहता हूँ।” तानसेन ने कहा, “जानते हैं नियम कड़ा है। मेरे दिल में दया नहीं है। मेरी आँखें दूसरों की मौत देखने के लिए हर समय तैयार हैं।” इस पर बैजू बावरा ने कहा, “और मेरे दिल में जीवन का मोह नहीं है। मैं मरने के लिए हर समय तैयार हूँ।”

दरबार की ओर से शर्ते सुनाई गई। राग-युद्ध नगर के बाहर वन में आयोजित किया गया था। लगता था वन में नगर बस गया है। बैजू ने सितार उठाया। उसने पदों को हिलाया तो जनता ब्रह्मानंद में लीन हो गई। उसकी उँगलियाँ सितार पर दौड़ने लगीं। लगा, सारे विश्व की मस्ती वहीं आ गई हो। तभी संगीत से प्रभावित होकर कुंछ हरिण छलांगें मारते हुए वहाँ आ पहुँचे। वे संगीत सुनते रहे।

बैजू ने सितार बजाना बंद किया और अपने गले से फूलमालाएँ उतार कर हरिणों को पहना दीं। हरिण चौकड़ी भरते हुए गायब हो गए। बैजू ने तानसेन से कहा, “ तानसेन, मेरी फूलमालाएँ यहाँ मँगवा दें, तब जानूँ कि आप राग-विद्या जानते हैं।”

तानसेन सितार हाथ में लेकर बजाने लगा। इतनी एकाग्रता के साथ उसने अपने जीवन में कभी सितार नहीं बजाया था। आज वह अपनी पूरी कला दिखा देना चाहता था। आज वह किसी तरह जीतना चाहता था। आज वह किसी भी तरह जिंदा रहना चाहता था। सितार बजता रहा, पर आज लोगों ने उसे पसंद नहीं किया। तानसेन का शरीर पसीना-पसीना हो गया, पर हरिण न आए। वह खिसिया गया। बोला, “वे हरिण राग की तासीर से नहीं आए थे। हिम्मत है तो दुबारा बुला कर दिखाओ।”

यह सुन कर बैजू ने फिर सितार पकड़ लिया। सितार बजने लगा। वे हरिण फिर बैजू बावरा के पास आ गए। बैजू ने उनके गले से मालाएँ उतार लीं। अकबर ने अपना निर्णय सुना दिया, “बैजू बावरा जीत गया, तानसेन हार गया।’ यह सुन कर तानसेन बैजू बावरा के पाँव में गिर पड़ा और उससे अपने प्राणों की भीख माँगने लगा। बैजू बावरा ने कहा, “मुझे तुम्हारे प्राण लेने की चाह नहीं है। तुम इस निष्ठुर नियम को खत्म करवा दो कि यदि आगरा की सीमा में गाने वाला व्यक्ति तानसेन की जोड़ का न हो, तो उसे मरवा दिया जाए।”

यह सुन कर अकबर ने उसी समय उस नियम को खत्म कर दिया। तानसेन ने बैजू बावरा के चरणों में गिर कर कहा, “मैं यह उपकार जीवन भर नहीं भूलूँगा।’ बैजू बावरा ने उसे याद दिलाया, ‘बारह बरस पहले उसने एक बच्चे की जान बख्शी थी। आज उस बच्चे ने उसकी जान बख्शी है।’

मुहावरे : अर्थ और वाक्य प्रयोग

(1) तूती बोलना।
अर्थ : अधिक प्रभाव होना।
वाक्य : आज उद्योग के क्षेत्र में देश के कुछ घरानों की ही तूती बोलती है।

(2) वाह वाह करना।
अर्थ : प्रशंसा करना।
वाक्य : सितारवादक रविशंकर का सितार वादन सुन कर। श्रोता वाह वाह कर उठते थे।

(3) लहू सूखना।
अर्थ : भयभीत हो जाना।
वाक्य : कोरोना वायरस का नाम सुनते ही लहू सूखने लगता है।

(4) कंठ भर आना।
अर्थ : भावुक हो जाना।
वाक्य : बेटी की बिदाई के समय पिता का कंठ भर आया।

(5) बिलख-बिलख कर रोना।
अर्थ : विलाप करना, जोर-जोर से रोना।
वाक्य : दुर्घटना में घायल पिता की मृत्यु का समाचार सुन कर बेटा बिलख-बिलख कर रोने लगा।

(6) समाँ बँधना।
अर्थ : रंग जमना, वातावरण निर्माण होना।
वाक्य : मदारी ने बंदरों से ऐसा नृत्य करवाया कि समाँ बँध गया।

(7) ब्रह्मानंद में लीन होना।
अर्थ : अलौकिक आनंद का अनुभव करना।
वाक्य : तबलावादक सामताप्रसाद का तबला वादन सुन कर श्रोता ब्रह्मानंद में लीन हो जाते थे।

(8) जान बख्शना।
अर्थ : जीवन दान देना।
वाक्य : डाकुओं ने सेठ की संपत्ति लूट ली, पर उनकी जान बख्श दी।

(9) संसार उजड़ जाना।
अर्थ : सब कुछ व्यर्थ हो जाना।
वाक्य : पति के असामयिक निधन से बेचारी राधा का संसार उजड़ गया।

(10) खरीद लेना।
अर्थ : गुलाम बना लेना।
वाक्य : गाँवों में पहले कुछ लोग मजदूरों को थोड़ा-बहुत कर्ज देकर जैसे उन्हें खरीद ही लेते थे।

(11) रक्त का चूँट पी कर रह जाना।
अर्थ : अपना क्रोध या दुःख प्रकट न होने देना।
वाक्य : मुनीमजी ने बार-बार चपरासी को बुरा-भला कहा, पर वह रक्त का चूंट पी कर रह गया।

(12) पसीना-पसीना होना।
अर्थ : बहुत अधिक परेशान होना।
वाक्य : जंगल से जाते हुए किसान ने हिरन पर झपट्टा मारते हुए चीते को देखा तो वह पसीना-पसीना हो गया।

आदर्श बदला शब्दार्थ

• सुमर = स्मरण करना
• प्रतिकार = बदला, प्रतिशोध
• अवहेलना = अनादर
• चाँदनिया = शामियाना
• नि:शब्द = मौन, चुप
• तासीर = प्रभाव, परिणाम
• खड़ाऊँ = लकड़ी की बनी खूटीदार पादुका
• कुंद = भोथरा, बिना धार का
• कनात = मोटे कपड़े की दीवार या परदा
• उद्विग्नता = घबराहट, आकुलता
• सुधिहीन = बेहोश
• अगाध = अपार, अथाह

आदर्श बदला मुहावरे

• तूती बोलना = अधिक प्रभाव होना
• वाह-वाह करना = प्रशंसा करना
• लहू सूखना = भयभीत हो जाना
• कंठ भर आना = भावुक हो जाना
• बिलख-बिलखकर रोना = विलाप करना/जोर-जोर से रोना
• समाँ बँधना = रंग जमना, वातावरण निर्माण होना
• ब्रह्मानंद में लीन होना = अलौकिक आनंद का अनुभव करना
• जान बख्शना = जीवन दान देना

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest निबंध लेखन Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati निबंध लेखन

1. अबला! नव्हे सबला!

समाजात पुरुष व महिला यांची निर्मिती निसर्गानेच केली. केवळ मानवी समाजातच नव्हे तर सर्व पशू व पक्ष्यांच्या अनेक जातींमध्येही ती व्यवस्था आहे. निसर्गनियमाप्रमाणे दोघेही समान हवेत. पण प्रत्यक्षात निसर्गाने मादीवर, स्त्रीवर पुनरुत्पत्तीची महत्त्वाची जबाबदारी सोपवली. असे असल्यामुळे खरे तर तिचे स्थान अधिक महत्त्वाचे हवे, पण प्रत्यक्षात जगातील विविध खंड, देश, प्रांत, धर्म, जाती, वर्ण या सर्व व्यवस्थांमध्ये महिलेचे स्थान बहुधा दुय्यम राहिले.

खरे तर या शतकभरात सर्वच क्षेत्रांत स्त्रियांनी उत्तुंग झेप घेतली आहे. अगदी खास पुरुषांसाठी राखीव असलेल्या क्षेत्रांतही आपल्या बुद्धीच्या जोरावर त्या शिरल्या आहेत. अन्यायाला प्रतिकार करण्याचे सामर्थ्य तिला प्राप्त होत आहे. लोकसंख्याशिक्षणाच्या प्रसारामुळे कुटुंब मर्यादित राखण्याची वृत्ती बळावत आहे. त्यामुळे स्त्रीवरील कौटुंबिक कामाचा ताण कमी होत आहे. विज्ञानजनित साधनांच्या वापरामुळे हा दैनंदिन कामाचा ताण सुसह्य होतो आहे. प्रसारमाध्यमांद्वारे ज्ञानविज्ञानात स्त्रीची गती वाढत आहे. अनेक क्षेत्रांत स्त्री-प्रतिमा उजळून निघाली आहे.

आजच्या स्त्रीमध्ये आत्मविश्वास, धडाडी आहे. तिच्या कर्तृत्वाची क्षितिजे विस्तारलेली आहेत. जीवनातील प्रत्येक संधी टिपण्यास ती उत्सुक असते. अतिशय हुशार आणि हिशेबी अशी आजच्या स्त्रियांची ओळख आहे. आजच्या स्पर्धेत त्या संसार, नोकरी आणि करिअर अशा तिन्ही क्षेत्रांमध्ये आघाडीवर आहेत. मागील पिढीच्या तुलनेत प्रचंड महत्त्वाकांक्षी असलेल्या आजच्या मुली जीवनाचा सर्वार्थाने आस्वाद घेण्यास उत्सुक असतात.

या मुलींमध्ये लोकसेवेची जाण अधिक आहे. म्हणूनच मेधा पाटकर, किरण बेदी, मंदा आमटे, राणी बंग या सामाजिक क्षेत्रांत झोकून देणाऱ्या महिलांचे कर्तृत्व ठळकपणे जाणवते. आपल्यावर अन्याय झाल्यानंतर घर सोडून हजारो अनाथ मुलांची आई होणाऱ्या सिंधुताई सपकाळ यांना अबला कोण म्हणेल?

अशक्यप्राय गोष्टीही प्रतिकूल परिस्थितीत जिद्द आणि प्रामाणिक प्रयत्नांनी करता येऊ शकतात. हे आजच्या स्त्रीने सिद्ध करून दाखविले आहे. मग ती शिखरे सर करणारी कृष्णा पाटील असो किंवा दोन्ही ध्रुवांवर पॅराजंपिग करणारी शीतल महाजन असो.

प्रस्थापित राजकारणाच्या चौकटीतही स्त्रियांचा सहभाग वाढतच आहे. राष्ट्रपती या सर्वोच्च घटनापदी प्रतिभा पाटील आहेत. तर लोकसभेत विरोधी पक्षनेत्या सुषमा स्वराज आहेत. लोकसभेचे अध्यक्षपदही मीराकुमारीच भूषवित आहेत. पंतप्रधानपदी श्रीमती इंदिरा गांधी यांनी गाजवलेल्या कर्तृत्वाची आठवण आजही समाज काढत आहे. राजकारणात स्त्रियांसाठी ५० टक्के जागा राखीव ठेवल्या आहेत. आजच्या स्त्रीने घर आणि काम दोन्ही गोष्टी नजाकतीने पेलायची शक्ती आणलीय.

अर्थार्जनाच्या क्षेत्रात स्त्री रुळू लागली आहे. पाळण्याची दोरी हाती धरणाऱ्या स्त्रीच्या अंगी जगाचा उद्धार करण्याचे सामर्थ्य आले आहे. भारतासह इंग्लंड, कॅनडा, आखाती देश, हाँगकाँग, सिंगापूर या देशांमधल्या आर्थिक बाजारातले आय. सी. आय. सी. आय. बँकचे सर्व प्रकारचे व्यवहार हाताळणारी शिल्पा शिरगावकर असो किंवा वैमानिक सौदामिनी देशमुख असो किंवा मोटारवुमन सुरेखा नाहीतर अंतराळवीर कल्पना चावला असो.

या साऱ्याजणी आता अबला नव्हे सबला असल्याचे दाखवून देत आहेत. आजची स्त्री वाऱ्याच्या वेगाने, कात टाकून सर्वार्थाने नव्या जगण्याकडे निघाली आहे.

2. माझा आवडता संत

महाराष्ट्र ही संतांची पावन-भूमी आहे. अनंत काळापासून या संतांनी समाजाला सन्मार्ग आणि सत्कर्माची दिशा दाखवली आहे. अज्ञानाच्या अंधारातून ज्ञानाच्या प्रकाशाकडे वाटचाल करण्यासाठी योग्य मार्गदर्शन करण्याचे महान कार्य या संत-महंतांनी केले आहे. संत कबीर, संत तुलसीदास, संत ज्ञानेश्वर, संत तुकाराम, संत नामदेव, संत रामदास, संत तुकडोजी महाराज, संत गाडगेबाबा अशा असंख्य संतांनी या भूमीची माती पवित्र केली. या असंख्य संतांपैकी माझा आवडता संत म्हणजे ज्ञानियाचा राजा – संत ज्ञानेश्वर.

१२७५ मध्ये संत ज्ञानदेवांचा जन्म झाला. महाराष्ट्रात ज्ञानाचा उदय झाला. विठ्ठलपंत आणि रुक्मिणी यांच्या पोटी या रत्नाने जन्म घेतला. . निवत्ती, ज्ञानदेव, सोपान आणि मक्ताबाई या चार भावंडांना त्या काळातील समाजाकडून त्रास सहन करावा लागला. समाजाने उपेक्षा केली तरी जन्मजात विद्वान आणि ज्ञानी असणाऱ्या संत ज्ञानदेवांची प्रतिभा बहरू लागली. बालपणातच ते विठ्ठल भक्तीत रमून गेले. वारकरी पंथाचे (संप्रदाय) त्यांनी पुनरुज्जीवन केले. म्हणूनच ‘ज्ञानदेवे रचिला पाया’ असे म्हटले जाते. महाराष्ट्रातील असंख्य भाविकांची माऊली म्हणजे संत ज्ञानेश्वर.

संत ज्ञानदेव योगी, तत्त्वज्ञ, आणि प्रतिभासंपन्न कवी होते. साऱ्या जगाला तत्त्वज्ञान आणि काव्य यांचे सुंदर दर्शन घडविणारा ‘ज्ञानेश्वरी’ हा ग्रंथ त्यांनी लिहिला. ‘अमृतानुभव’, ‘चांगदेव पासष्टी’, ‘हरिपाठाचे व इतर अभंग’ ही त्यांची साहित्यसंपदा. सुंदर कल्पना, आलंकारिक पण ओघवती व प्रासादिक भाषा हे त्यांच्या लेखनाचे विशेष होते. संत ज्ञानेश्वरांनी समाजजागृती केली. अथक परिश्रम केल्यानंतर ते अवघ्या महाराष्ट्राचे ‘ज्ञानमाऊली’ झाले.

संत ज्ञानदेवांनी पसायदान मागितले.
दुरितांचे तिमिर जावो, विश्व स्वधर्मेसूर्ये पाहो।
जो जे वांच्छिल तो ते लाहो प्राणिजात।।

‘या जगातून दुष्कर्माचा अंधार नाहीसा होवो, ज्याला जे जे हवे ते ते मिळो’ अशी विश्वकल्याणाची प्रार्थना त्यांनी केली.

ही प्रार्थना सगळ्या जगासाठी आहे. चराचरासाठी आहे. ‘भूतां परस्परें जडो मैत्र जीवांचे’ ही तळमळ त्यामागे आहे. ‘वसुधैव कुटुंबकम्’ ही अवघे विश्व कवटाळणारी कल्पना संत ज्ञानेश्वरांनी तेराव्या शतकात केली होती.

‘ज्ञानेश्वर माऊली, ज्ञानराज माऊली तुकाराम’ अशा जयघोषामध्ये आज संपूर्ण महाराष्ट्रात वारकरी तल्लीन होऊन जातात. घराघरात संत ज्ञानेश्वरांचे अभंग गायले जातात. महाराष्ट्रातील सामान्य जनतेच्या हृदयात अढळ स्थान प्राप्त करणाऱ्या ज्ञानेश्वरांनी वयाच्या २१व्या वर्षी आळंदी येथे संजीवन समाधी घेतली. असा हा माझा आगळा-वेगळा आवडता संत तुम्हा सर्वांनाही आवडेलच.

3. नाट्यशिबिरातील आनंददायी क्षण

उन्हाळ्याची सुट्टी लागली होती. यावर्षी कुठेही बाहेर फिरायला जायचे नव्हते. दहावीचा क्लास सुरू होणार होता. त्यामुळे वाचन, अभ्यास यात दोन महिने जाणार होते. पण त्या व्यतिरिक्त काहीतरी आपण वेगळं शिकायला हवे असे मला सतत वाटायचे. योगा, पोहणे वा नाटक असं काहीतरी. पण ही संधी अगदी घरी चालून आल्यासारखी झाली. आमच्या कॉलनीतील हॉलमध्ये ८ दिवसांचे एक नाट्यशिबिर आयोजित करण्यात आले होते.

सकाळी ८ ते १० वेळ असल्यामुळे माझ्या अभ्यासाचा खोळंबा होणार नव्हता. त्यामुळे मी लगेचच या शिबिरासाठी प्रवेश घेतला.

चार दिवसांनी शिबिर सुरू झाले. अगदी पहिल्याच दिवशी आमच्या ताईंनी आम्हा सर्वांची ओळख करून घेतली. शिबिरासाठी विविध वयाची साधारण ३०-३५ मुले मुली आम्ही होतो. ताईने नाटक म्हणजे काय? नाटकं करणं म्हणजे काय, अभिनय म्हणजे काय या गोष्टी अगदी गप्पा गोष्टी करत समजावून सांगितल्या. दुसऱ्या दिवसापासून तिने पॅक्टिकली या गोष्टी समजावून सांगणार असे सांगितले आणि तिने पुस्तकातील एक नाट्यउतारा पाठ करून यायला सांगितले होते.

दुसऱ्या दिवशी ताईसोबत दोन दादाही आले होते. आमचे ५ ग्रुप करण्यात आले आणि ताईने आम्हाला बोलण्याचे काही खेळ शिकविले. केवळ ‘ळ’, ‘क’, ‘च’, ‘ठ’ या अक्षरांचा वापर करून त्याच्या गमतीजमती शिकता शिकता हसून हसून पुरेवाट लागली. या शाब्दिक खेळानंतर आम्हाला ताईने आरोह-अवरोह शिकवले. वाक्यातील कोणत्या शब्दावर जोर दिला की वाक्याचा कसा अर्थ बदलतो याचे प्रात्यक्षिक तिने आमच्याकडून करून घेतले.

हे करत असताना श्वासाचा कसा वापर करायचा हे तिने समजावून सांगितले. तिने एकाग्रतेसाठी श्वास रोखणे, जप करणे, योगा करणे किती महत्त्वाचे आहे हे तिच्या बोलण्यातून जाणवले.

या शिबिरात केवळ नाटकाचे संवादच नाही तर कवितेचेही अभिवाचन कसे करावे, कथा कशी वाचावी याचे मार्गदर्शन केले. मी नेहमी एकसूरी वाचणारी होते पण ताईदादांनी सांगितल्याप्रमाणे मी प्रकट वाचन करू लागले आणि माझ्या वाचनात कमालीचा बदल झाला. अभिनय करताना कसे उभे रहावे, कोणता कोन ठेवावा, प्रेक्षकांकडे दृष्टी कशी ठेवावी, केवळ आवाजावर भर न देता, चेहऱ्यावरील हावभाव, आवाजातील कंपनं, हंकार, श्वास यांचा मार्मिक वापरही आवश्यक असतो हे शिकायला मिळाले. केवळ कुणाचे तरी अनुकरण न करता त्यात आपली काही वैशिष्ट्ये घालून तो अभिनय परिपूर्ण करता येऊ शकतो.

आमच्या ५ ग्रुपला ताईने वेगवेगळे विषय दिले आणि त्यावर आम्हांला एक नाटुकलं लिहायला सांगितले. कोणत्याही विषयाकडे पाहताना तो विषय किती सखोल विचार करून लिहिता येतो ते दादांनी शिकविले. संवाद लिहिताना पल्लेदार व विशेषणांनी युक्त वाक्य लिहिण्यापेक्षा साध्या वाक्यरचनेतही संवाद लिहिता येतो याची जाणीव झाली. त्यात आणखी एक नवउपक्रम हाती घेतला तो म्हणजे चित्र काढण्याचा, त्या क्षणी जे मनात आहे ते उतरवणं काम होते पण त्यामधून प्रत्येकाच्या मनात धावणाऱ्या विविध भावभावनांचा वेध कसा घेता येतो याची परिपक्वता आली.

या सगळ्याबरोबर काही खेळही आम्ही खेळलो. ज्यात सतत आव्हाने होती. जीवनातही अनेक आव्हाने पेलण्याचे सामर्थ्य आपल्यांत असते. त्यासाठी हवा असतो तो आत्मविश्वास. आपल्या समोरची परिस्थिती कायमस्वरूपी नसते, त्यामध्ये चढउतार असणारच पण स्वत:वर विश्वास ठेवून त्या त्या परिस्थितीला सामोरे जायचे असते ही शिकवण या खेळांतून मिळाली.

शेवटच्या दोन दिवसात आम्ही तयारी करून एक छोटंसं नाटुकलं करून दाखवलं. त्या दोन दिवसांत आम्ही अगदी रंगभूमी वरचढ असल्याचा आवेश होता. घरीही तशाच पद्धतीने आम्ही बोलत होतो, घरीही सगळी गम्मत वाटत होती.

शेवटी ताईने पालकांसोबत आमचं एक गेट टुगेदर ठेवलं. आम्ही आमची नाटुकली पालकांसमोर सादर केली आणि त्यानंतर खाणं पिणं झाले. पालकांची मते मांडून झाल्यावर ताईने आमच्यापैकी ४-५ जणांना आपला अनुभव व्यक्त करायला सांगितला. वर्गात कधीही न उत्तर देणारी मी त्या दिवशी भरभरून बोलले. या शिबिरातून केवळ नाटकच नव्हे तर अभ्यास करतानाही काही क्लृप्त्या कशा वापराव्या, आयुष्यातही कसे वागावे याचा परिपाठ शिकायला मिळाला होता. असे हे नाट्यशिबिर माझ्या आयुष्याला कलाटणी देणारे ठरले खरे.

4. वाचाल, तर वाचाल

वाचन आणि त्यातून मिळालेलं ज्ञान किती मोलाचं असतं याबाबत डॉ. बाबासाहेब आंबेडकर सांगतात की, ‘वाचाल, तर वाचाल’. हाच विचार मनात घेऊन प्रत्येकाने आपल्या मनाला वाचनाची सवय लावली पाहिजे. ‘दिसामाजी काहीतरी लिहावे। प्रसंगी अखंडित वाचित जावे’ असा लेखन व वाचनाचा मंत्र समर्थ रामदास स्वामींनी सांगितला आहे. तुम्ही कोणत्याही ज्ञानशाखेचे विदयार्थी असू दया. आपल्या ज्ञानाला अदययावत ठेवण्यासाठी सतत वाचन हाच पर्याय आहे. जीवनातील कोणत्याही क्षेत्रात तुम्हाला यशस्वी व्हायचे असेल तर त्या क्षेत्रातील नवे नवे ज्ञान व माहिती आत्मसात करावी लागते. त्यासाठी का होईना प्रत्येकाने वाचलेच पाहिजे.

नानाविध पुस्तकांचे जो वाचन करतो, त्यांतील विचार समजून घेतो तो जीवनप्रवासात नेहमीच इतरांच्या पुढे जातो. वाचनामुळेच आपले व्यक्तिमत्त्व समृद्ध बनते. वाचनामुळेच आपली वैचारिक श्रीमंती वाढते. नवनवीन विचारांना स्फुरण मिळते. कल्पनाशक्ती तरल बनते. बहुश्रुत होण्यासाठी आपण सतत वाचलेच पाहिजे. ‘वाचनानंद’ हा एक वेगळाच अनुभव आहे. आपण वाचलेली माहिती केव्हा व कोठे उपयोगी पडेल ते सांगता येत नाही.

वाचलेल्या माहितीचे आदान-प्रदान केल्यास बऱ्याचदा नवीन मुद्देही मिळतात. विदयार्थी दशेत समजून घेऊन वाचनाची सवय मनाला लावली तर कोणताही अभ्यासविषय नक्कीच सुलभ वाटू लागतो. मन लावून अभ्यास केला तर यश नक्कीच मिळते. केवळ वरवरचे उथळ असे वाचन काहीही कामाचे नाही.

विदयार्थी दशेतच अभ्यासाबरोबरच अवांतर वाचनाची सवय मनाला लावल्यास आपले विचार प्रगल्भ होतात. प्रगल्भ विचारांमुळे भविष्यातील जीवनवाटचाल सुकर व यशस्वी होते.

माहिती तंत्रज्ञानाच्या युगात वेगवेगळ्या वेबसाईट्स्वर एका क्लिक् सरशी जगभरातल्या लेखकांची पुस्तके हव्या त्या भाषेत उपलब्ध होतात. अनेकजण ती आवडीने वाचतात. नवनवीन साईट्स्वर जाऊन माहिती मिळवतात. मिळवलेली माहिती ब्लॉग वा इतर सोशल मिडीयाद्वारे शेअरही करतात. म्हणूनच वाचनसंस्कृती लोप पावली नाही तर बदलत्या कालमान परिस्थितीनुसार वाचन संस्कृतीनेही आपली कूस बदलली असे वाटते. वाचनाची माध्यमे बदलली.

पूर्वीच्या पुस्तकांची जागा ई-बुक्सनी घेतली. छोट्या घरात पुस्तके ठेवायला जागा नाही हा अनेकांचा प्रश्न डिजिटल क्रांतीने, अनेक पुस्तकांच्या ऑनलाईन आवृत्त्यांनी खरोखरच सोडवला. संस्कृतात ‘वचने किम् दरिद्रता’ असे एक वचन आहे. बोलण्यात कंजुषी कशाला करावी असा त्याचा अर्थ आहे. ‘वचने’ या शब्दात (एक काना, एक मात्रेचा) बदल करून वाचन करण्यात कसली आली आहे कंजुषी असे म्हणायला हरकत नाही.

जे उपलब्ध होईल ते व्यक्तीने वाचून समजून घ्यावे. चौफेर अशा वाचनामुळेच तुमच्यात चतुरस्रता निर्माण होणार आहे. जीवनात यशस्वी होण्यासाठी प्रत्येकाने वाचन केलेच पाहिजे. विविधांगी व विधांगी वाचनामुळेच लेखनाची प्रवृत्ती प्रबळ होते. रसिकता वाढीस लागते. सहृदयता म्हणजेच दुसऱ्याच्या दुःखांची जाणीव असणाऱ्या संवेदनक्षम मनास खतपाणी मिळते.

5. झाड बोलू लागले तर…..

नमस्कार ! मी तुमचा मित्र, झाड बोलत आहे. पण तुम्ही खरेच माझे मित्र आहात का? तुम्हाला वाटेल मी असे का बोलत आहे? पण मी आज जे अनुभवत आहे ते तुम्हांला सांगावसे वाटले म्हणून हा प्रयत्न.

तुम्ही म्हणता ना झाडे मानवाचा मित्र आहेत. परंतु तुम्ही माझ्याबरोबर मित्रासारखे वागता का?

मी तुमच्या खूप उपयोगी पडतो. मी प्रत्येक सजीवाला नि:स्वार्थवृत्तीने काही ना काही देतच असतो. माझ्या सुगंधी फुलांनी तुमचे मन प्रफुल्लित होते. माझी गोड फळे चाखून तुम्ही किती खुश होता. मी इंधनासाठी, घरे बांधण्यासाठी लाकूड देतो. थकल्या भागल्या वाटसरूला शीतल छाया देतो. पक्ष्यांना माझ्यामुळे आश्रय मिळतो. प्राणी माझ्या सावलीत विश्रांती घेतात.

तुमच्या रोजच्या जीवनात उपयोगी पडणाऱ्या कागद, रबर, ब्रश, गोंद कितीतरी वस्तू माझ्यामुळे तुम्हाला उपलब्ध होतात. मध, औषधे तयार केली जातात. माझा प्रत्येक अवयव तुमच्या उपयोगी पडतो.

माझ्या मुळांमुळे जमिनीची धूप थांबते. माझी वाढ झाली तर पाऊस पडतो. पृथ्वीवर पर्जन्यवृष्टी झाल्याने सर्व सजीव तृप्त होतात. दुष्काळ आणि पूर दोन्ही आटोक्यात येतात. सर्व सजीवसृष्टीला जगण्यासाठी मी प्राणवायूचा पुरवठा करतो आणि मानवाला अपायकारक असणारा कार्बनडाय ऑ क्साइड वायू शोषून घेतो.

परंतु आता माझे महत्त्व तुम्ही विसरत चालले आहात. ‘वृक्षवल्ली आम्हा सोयरी वनचरी’ या ओळी आता फक्त पुस्तकातच राहिल्या आहेत. आजच्या गतिमान वैज्ञानिक युगात माझ्यावर तुम्ही आक्रमण करू लागला आहात. सिमेंट, काँक्रीटच्या इमारती उभारण्यासाठी, रस्ते दुरुस्ती करण्यासाठी, विकासाच्या नावाखाली तुम्ही मोठ्या प्रमाणात वृक्षतोड करत आहात. तुम्ही माझ्यावर कु-हाड चालवता तेव्हा मला खूप दुःख होते रे!

माझा संहार करू लागल्याने पावसाचे प्रमाण कमी झाले आहे. वातावरणात बदल होऊन उष्णतेचे प्रमाण वाढले आहे. जंगलातील प्राणी-पक्ष्यांची संख्या कमी होत चालली आहे. नदया कोरड्या झाल्या आहेत. शेतकऱ्यांचे आत्महत्यांचे प्रमाण वाढले आहे.

म्हणून मी तुम्हाला मन:पूर्वक विनंती करतो की मी नसलो तर तुमचे संपूर्ण जीवन रुक्ष होईल. सर्व सजीवसृष्टी संपुष्टात येईल. याचे दुष्परिणाम भावी पिढीला भोगावे लागतील. अनेक संकटांना सामोरे जावे लागेल.

पर्यावरणाचा हास थांबवण्यासाठी तुम्ही जेव्हा प्रयत्न करता, वृक्षारोपणाचे महत्त्व पटवून देता तेव्हा मला खूप आनंद होतो. निसर्गाबाबत तुमची स्वार्थी वृत्ती पाहून मला खंतही वाटते आणि तुमची काळजीही. पर्यावरणाची काळजी घ्या. निसर्ग संवर्धन करा. ती काळाची गरज आहे. आजूबाजूच्या परिसरात खूप झाडे लावा. त्यांची जोपासना करा. कारण मला रुजायला, फुलायला, वाढायला खूप काळ लागतो. बदलणारे निसर्गाचे चक्र पूर्ववत करण्याची जबाबदारी तुमच्यासारख्या सुजाण नागरिकांचीच आहे. मला जगवाल तर तुम्ही जगाल याचा विचार करण्याची वेळ आली आहे. माझ्या सहवासात राहून आनंदी, निरोगी रहा आणि दीर्घायुषी व्हा.

6. ‘मायबोलीचे मनोगत

‘झाडावरून प्राजक्त ओघळतो
त्याचा आवाज होत नाही
याचा अर्थ असा होत नाही
त्याला वेदना होत नाही’

मी मायबोली राजभाषा मराठी! तुम्हाला दिसतोय तो राजभाषेचा सोनेरी मुकुट, पण माझ्या मनीचे दुःख मात्र तुम्हाला दिसत नाही. माझ्या दयनीय अवस्थेचे रडगाणे सर्वचजण गातात. पण माझी स्थिती सुधारण्याचे उपाय मात्र योजले जात नाहीत.

तेराव्या शतकात देवी शारदेच्या दरबारातील एक मानकरी – माझा सुपुत्र – संत ज्ञानेश्वरांनी माझा पाया रचला. केवढा अभिमान वाटत असे त्यांना माझा! ‘माझा मराठाचि बोलु कौतुके, परि अमृतातेही पैजा जिंके’ या शब्दांत त्यांनी माझा गौरव केला. माझी कूस धन्य झाली.

खरे तर माझी जन्मदात्री गीर्वाण भाषा संस्कृत. तिच्याच उदरी माझा जन्म झाला. देवाने माझ्यासाठी महाराष्ट्राचा पाळणा केला. त्याला सहयाद्री व सातपुड्याची खेळणी लावली. कृष्णा-गोदेचा गोफ विणून पाळणा हलवायला दोरी बनवली. देवी रेणुकामाता व देवी तुळजाभवानी यांनी माझ्यासाठी पाळणा म्हटला. पुढे संत ज्ञानेश्वर, संत नामदेव, संत एकनाथ, संत तुकाराम, संत रामदास या संतांनी तर वामन पंडित, मुक्तेश्वर, मोरोपंत या पंडितांनी तसेच त्यानंतर शाहीर अमरशेख, शाहीर होनाजीबाळा यांनी मला समृद्ध केले.

मी जशी संत ज्ञानेश्वरांची, संत तुकारामांची तशी छत्रपती शिवरायांची आणि पेशव्यांच्या बाजीरावांची! जशी ज्योतीबा फुल्यांची तशी चाफेकर बंधूंची! मी लोकमान्य टिळक – गोपाळ गणेश आगरकरांची तशी बाबासाहेब आंबेडकरांची! जशी परक्या सत्तेविरुद्ध बंड पुकारणारी तशी क्रांतीच्या जयजयकाराला ज्ञानपीठावर गौरवित करणारी!

काळाबरोबर मी अनेक भाषाभगिनींना माझ्यात सामावून घेत गेले. दिसामासांनी मी वाढत होते. वि. स. खांडेकर, आचार्य अत्रे, केशवसुत, कुसुमाग्रज, पु. ल. देशपांडे, विंदा करंदीकर यांच्या बाळगुटीने मी बाळसे धरू लागले होते. म्हणूनच राजभाषेचा मानही मला मिळाला. किती आनंद झाला मला त्या दिवशी! पण हा आनंद अळवावरच्या पाण्यासारखाच निघाला.

माझ्याच सुपुत्रांनी मला दरिद्री केले. माझी अवस्था दयनीय झाली असे रडगाणे गात त्यांनी माझा अपप्रचारच केला. माझा वापर करणे त्यांना कमीपणाचे वाटते. आपल्या मुलांना मराठी शाळेत घालणे त्यांना मागासलेपणाचे लक्षण वाटते. मराठीच्या प्रचाराच्या गोष्टी करणारे हे महाभाग स्वत:च्या मुलांना व नातवांना मात्र इंग्रजी माध्यमाच्या शाळेत शिकायला पाठवतात. माझ्या विकासासाठी कसलेही प्रयत्न होताना दिसत नाहीत.

ज्या माझ्या सुपुत्रांनी मला वैभवशिखरावर पोहोचवले होते, त्याच सुपुत्रांच्या आजच्या राजकारणी वारसदारांनी मात्र मला देशोधडीला लावण्याचेच काम केले. आज माझ्यात दर्जेदार साहित्यनिर्मिती होत नाही, अशी ओरड होऊ लागली आहे. माझ्या माध्यमाच्या शाळा ओस पडून बंद पडू लागल्या आहेत. मी संपेन की काय अशी भीती व्यक्त केली जात आहे.

या सर्वांना मी ठणकावून सांगू इच्छिते की मी अशी-तशी संपणार नाही. ज्ञानदेवाने जिचा पाया इतका मजबूत रचला आहे ती मी अशी सहजा सहजी ढासळणार नाही. अर्थात माझं गतवैभव परत मिळवायला मला तुम्हा सर्वांच्या मदतीची गरज आहे. आज सारे ज्ञान-विज्ञान इंग्रजी भाषेत निर्माण होत आहे, संगणकाची भाषासुद्धा इंग्रजी आहे. तुम्हा सर्वांना माझी विनंती आहे की तुम्ही प्रत्येकाने परकीय भाषांतील ज्ञान-विज्ञान माझ्यात निर्माण करा.

रटाळ, लांबलचक माहिती लिहिलेली पुस्तके लिहिण्यापेक्षा रंगीत चित्रांनी युक्त मोजक्या शब्दांत माहिती लिहिलेली आकर्षक पुस्तके निर्माण करा. काळाप्रमाणे बदलायला शिका. नवीन नवीन बदल स्वीकारा. ‘जुने ते सर्वच चांगले व नवीन ते सर्वच वाईट’ असे समजू नका. संगणकात माझ्या भाषेत माहिती निर्माण करा. त्या दृष्टीने तंत्रज्ञान विकसित करा. मराठीतून बोलण्याची, शिकण्याची लाज बाळगू नका. मुख्य म्हणजे माझा अपप्रचार थांबवा.

मग बघा मला पुन्हा माझे गतवैभव प्राप्त होते की नाही?

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest व्याकरण पारिभाषिक शब्द Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati Solutions व्याकरण पारिभाषिक शब्द

पारिभाषिक शब्द :

विज्ञान-तंत्रज्ञान, उदयोग, कृषी, शिक्षण, प्रशासन, विधी, वाणिज्य, कला संस्कृती इत्यादी क्षेत्रांशी संबंधित संकल्पनांच्या प्रकटीकरणासाठी पारिभाषिक शब्दांचा उपयोग केला जातो. त्यांच्या वापरामुळे त्या-त्या क्षेत्रांमधील ज्ञानव्यवहार अधिक नेमका तसेच सुस्पष्ट होतो. त्यादृष्टीने पारिभाषिक शब्दांना अनन्यसाधारण महत्त्व असते. याठिकाणी तुमच्या माहितीसाठी काही महत्त्वाचे पारिभाषिक शब्द दिले आहेत.

Academics	विदयाभ्यास
Elected	निर्वाचित
Administration	प्रशासन
Encyclopedia	विश्वकोश
Agenda	कार्यक्रम पत्रिका
Enrolment	नावनोंदणी
Auditor	लेखापरीक्षक
File	संचिका
Backlog	अनुशेष
Felicitation	गौरव
Barometer	वायुभारमापक
Foundation	प्रतिष्ठान
Barcode	दंडसंकेत
Gazette	राजपत्र
Broadband	विस्तारित वहन
Geology	भूशास्त्र
Circular	परिपत्रक
Guest House	अतिथीगृह
Commissioner	आयुक्त
Guard of Honour	मानवंदना
Criticism	समीक्षा
Herald	अग्रदूत
Dean	अधिष्ठाता
Habitat	प्राकृतिक वसतिस्थान
Director	संचालक
Honorary	मानद, मानसेवी
Domain	अधिक्षेत्र
Hygiene	आरोग्यशास्त्र
Domicile	अधिवास
Iceberg	हिमनग
Draft	मसुदा, धनाकर्ष
Incentive	प्रोत्साहनपर
Increment	वाढ
Recommendation	शिफारस
Industrialization	औदयोगिकीकरण
Rest House	विश्रामगृह
Journal	नियतकालिक
Runway	धावपट्टी
Jubilee	महोत्सव
Self defence	स्वसंरक्षण
Junction	महास्थानक
Senate	अधिसभा
Keep pending	प्रलंबित ठेवणे
Share Certificate	समभागपत्र
Keyboard	कळफलक
Superintendent	अधीक्षक
Kindergarten	बालकमंदिर
Symposium	परिसंवाद
Labour welfare	कामगार कल्याण
Technician	तंत्रज्ञ
Land holder	भूधारक
Telecommunication	दूरसंपर्क
Lawyer	विधिज्ञ/वकील
Terminology	परिभाषा
Layout	आखणी, मांडणी
Thesis	प्रबंध
Meteorology	हवामानशास्त्र
Unbiased opinion	पूर्वग्रहविरहीत मत
Migration Certificate	स्थलांतर प्रमाणपत्र
Upgradation	उन्नयन
Minute book	कार्यवृत्त पुस्तक
Up to date	अदययावत
Motto	ब्रीदवाक्य
Utility	उपयुक्तता
Nationalism	राष्ट्रवाद
Vacancy	रिक्त पद
Nervous System	चेतासंस्था
Validity	वैधता
Notification	अधिसूचना
Verification	पडताळणी
Noteworthy	उल्लेखनीय
Official	कार्यालयीन
Organisation	संघटना
Organic Farming	सेंद्रिय शेती
Paediatrician	बालरोगतज्ज्ञ
Pedestrian	पादचारी
Personal Assistant	स्वीय सहायक
Procession	मिरवणूक
Qualified	अर्हतापात्र
Quality Control	गुणवत्ता नियंत्रण
Quick Disposal	त्वरित निकाली काढणे
Quorum	गणसंख्या
Vocational School	व्यवसाय शिक्षण शाळा
Waiting list	प्रतीक्षासूची
World Record	विश्वविक्रम
Working Capital	खेळते भांडवल
Writ	न्यायलेख
X-ray	क्ष-किरण
Xerox	नक्कलप्रत
Yard	आवार
Yearbook	संवत्सरिका
Zero Hour	शून्यकाळ
Zoologist	प्राणिशास्त्रज्ञ
Zone	परिमंडळ, विभाग
Reader	प्रपाठक, वाचक

इंग्रजी आणि मराठी म्हणी

1. A bad workman always blames his tools नाचता येईना अंगण वाकडे

2. Jack of all trades and master of none. एक ना धड भाराभर चिंध्या.

3. No pains, no gains. कष्टाविण फळ नाही.

4. Listen to people, but obey your conscious. ऐकावे जनाचे पण करावे मानाचे.

5. A fig for the doctor when cured. गरज सरो नि वैदय मरो.

6. Many a little makes a mickle. थेंबे थेंबे तळे साचे.

7. An empty vessel makes much noise. उथळ पाण्याला खळखळाट फार

8. Might is right. बळी तो कान पिळी.

9. As you sow, so you reap. दाम करी काम.

10. Money makes the mare go. पेराल तसे उगवेल.

11. Necessity is the mother of invention. बुडत्याला काडीचा आधार.

12. A drowning man will clutch at a straw. गरज ही शोधाची जननी आहे.

13. Between two stools we come to the ground. नवी विटी नवे राज्य.

14. New lords, new laws. दोन्ही घरचा पाहुणा उपाशी.

15. No rose without a thorn. गर्जेल तो पडेल काय?

16. Barking dogs seldom bite काट्यावाचून गुलाब नाही.

17. Doctor after death जुने ते सोने.

18. Old is gold. वरातीमागून घोडे.

19. Out of sight, out of mind. चार दिवस सासूचे, चार दिवस सुनेचे.

20. Every dogs has his day. दृष्टीआड सृष्टी.

21. Too many cooks spoil the broth. घरोघरी मातीच्या चुली.

22. Every house has its skeleton. बारा सुगरणी तरी आमटी आळणी.

23. First come first served. हाजीर तो वजीर.

24. Union is strength. एका हाताने टाळी वाजत नाही.

25. It takes two to make a quarrel. एकी हेच बळ.

26. Where there is a will, there is a way. इच्छा तेथे मार्ग.

काही साहित्यिकांची टोपण नावे व पूर्ण नावे

टोपणनाव	लेखक
मोरोपंत	मोरेश्वर रायाजी पराडकर
काव्यविहारी	धोंडो वामन गद्रे
लोकहितवादी	गोपाळ हरी देशमुख
यशवंत	यशवंत दिनकर पेंढरकर
रे. टिळक	नारायण वामन टिळक
अनिल	आत्माराम रावजी देशपांडे
केशवसुत	कृष्णाजी केशव दामले
विभावरी शिरुरकर	मालतीबाई विश्राम बेडेकर
माधवानुज	काशीनाथ हरी मोडक
राष्ट्रसंत तुकडोजी महाराज	माणिक बंडोजी ठाकूर
बी	नारायण मुरलीधर गुप्ते
मनमोहन	गोपाळ नरहर नातू
नाथमाधव	द्वारकानाथ माधवराव पितळे
बी. रघुनाथ	भगवान रघुनाथ कुळकर्णी
बाळकराम (नाटक) गोविंदाग्रज (कविता)	राम गणेश गडकरी
अमरशेख	शेख महबूब हसन
बालकवी	त्र्यंबक बापूजी ठोमरे
आरती प्रभु	चिंतामण त्र्यंबक खानोलकर
गिरीश	शंकर केशव कानेटकर
चारुता सागर	दिनकर दत्तात्रय भोसले
माधव ज्युलियन	माधव त्रिंबक पटवर्धन
दया पवार	दगडू मारुती पवार
विनोबा	विनायक नरहर भावे
ग्रेस	माणिक सितारामपंत गोडघाटे
कुंजविहारी	हरिहर गुरुनाथ कुळकर्णी
प्रेमानंद गज्वी	आनंद शंकर गजभिये
अज्ञातवासी	दिनकर गंगाधर केळकर
पठे बापूराव	श्रीधर कृष्णाजी कुळकर्णी
ठणठणपाळ	जयवंत द्वारकानाथ दळवी

काही साहित्यिक व त्यांच्या प्रसिद्ध रचना

साहित्यिकाचे नाव	पुस्तक
लक्ष्मीबाई टिळक	स्मृतिचित्रे
श्री. म. माटे	उपेक्षितांचे अंतरंग
श्री. ज. जोशी	आनंदीगोपाळ
वि. वा. शिरवाडकर	नटसम्राट
विश्राम बेडेकर	रणांगण
गोदावरी परुळेकर	जेव्हा माणूस जागा होतो
वसंत कानेटकर	रायगडाला जेव्हा जाग येते
जी. ए. कुलकर्णी	काजळमाया
गंगाधर गाडगीळ	एका मुंगीचे महाभारत
ना. सं. इनामदार	राऊ
श्री. ना. पेंडसे	रथचक्र
गो. नी. दांडेकर	पडघवली
विंदा करंदीकर	अष्टदर्शने
अण्णाभाऊ साठे	फकिरा
शंकरराव खरात	तराळ अंतराळ
शांता शेळके	चौघीजणी
महेश एलकुंचवार	वाडा चिरेबंदी
किरण नगरकर	सात सक्कं त्रेचाळीस
प्र. ई. सोनकांबळे	आठवणींचे पक्षी
अनिल अवचट	माणसं
नारायण सुर्वे	माझे विदयापीठ
सुनीता देशपांडे	आहे मनोहर तरी
व्यंकटेश माडगूळकर	बनगरवाडी
द. मा. मिरासदार	मिरासदारी
रणजित देसाई	स्वामी
मंगेश पाडगांवकर	सलाम
मारुती चितमपल्ली	पक्षी जाय दिगंतरा
नरहर कुरुंदकर	धार आणि काठ
मधु मंगेश कर्णिक	माहिमची खाडी
आनंद यादव	झोंबी
दया पवार	बलुतं
लक्ष्मण माने	उपरा
रंगनाथ पठारे	ताम्रपट
नरेंद्र जाधव	आमचा बाप आन् आम्ही
लक्ष्मण गायकवाड	उचल्या
उत्तम कांबळे	आई समजून घेताना
अरुणा ढेरे	कृष्णकिनारा
विश्वास पाटील	पानिपत
राजन गवस	तणकट
सदानंद देशमुख	बारोमास
किशोर शांताबाई काळे	कोल्हाट्याचं पोर
भालचंद्र नेमाडे	कोसला

ज्ञानपीठ पुरस्कारप्राप्त मराठी साहित्यिक

साहित्यिकाचे नाव

विष्णु सखाराम खांडेकर

विष्णू वामन शिरवाडकर (कुसुमाग्रज)

गोविंद विनायक करंदीकर (विंदा करंदीकर)

भालचंद्र वनाजी नेमाडे

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest Chapter 11 वाङ्‌मयीन लेण्याचा शिल्पकार Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati Solutions Chapter 11 वाङ्‌मयीन लेण्याचा शिल्पकार

11th Marathi Digest Chapter 11 वाङ्‌मयीन लेण्याचा शिल्पकार Textbook Questions and Answers

कृती

1. खालील कृती पूर्ण करा.

अ. टॉलस्टॉयच्या ज्ञानेंद्रियांच्या तल्लख संवेदनेची पाठातील उदाहरणे देऊन खालील तक्ता पूर्ण करा.

प्रश्न 1.

उत्तरः

ज्ञानेंद्रिये	संवेदनांची उदाहरणे
डोळे	दाईचे मोकळे हात दिसतात
कान	पाण्याशी खेळताना पाण्याचा आवाज ऐकू येतो
नाक	सुगंधी द्रव्याचा वास जाणवतो
त्वचा	टबच्या आतील गुळगुळीत स्पर्श कळतो

2. आकृत्या पूर्ण करा.

प्रश्न 1.

उत्तरः

प्रश्न 2.

उत्तरः

प्रश्न 3.

उत्तरः

प्रश्न 4.

उत्तरः

इ. सूचनेप्रमाणे सोडवा.

प्रश्न 1.
खालील शब्दांसाठी पाठात आलेल्या उपमा लिहा.
अ. मन:पटलावरील प्रतिमा [ ]
आ. ‘युद्ध आणि शांती’ ही कादंबरी [ ]
उत्तरः
अ. शोभादर्शक
आ. न भूतो न भविष्यति अशा स्वरूपाचे कैलास लेणे

प्रश्न 2.
‘कादंबरी’ हे उत्तर येईल असा प्रश्न तयार करा.
उत्तरः
‘युद्ध आणि शांती’ हे अवाढव्य लिखाण साहित्यातील कोणत्या प्रकारात मोडते?

2. खालील शब्दसमूहांचा तुम्हांला समजलेला अर्थ स्पष्ट करा.

प्रश्न 1.
अ. मनाची कोरी पाटी.
आ. लोकोत्तर कल्पनाशक्ती.
इ. तपशिलांचा महासागर.
उत्तरः
अ. मनाची कोरी पाटी : ज्या मनात कोणत्याही प्रकारचे विचार नसतात किंवा जे मन निरागस असते. चांगले किंवा वाईट यांचा विचार न करणारे मन म्हणजेच निर्विकार मन होय. लहान मुलांचे मन असे असते. जे समोर असते तेच त्यांच्यासाठी वास्तव असते. समोरचे वास्तव ते सहजपणे स्वीकारतात. त्यातल्या चांगल्या किंवा वाईट परिणामांचा विचार करण्याची त्यांची तयारी नसते किंवा त्यांचे मन तेवढे प्रगल्भ नसते. त्यामुळे त्या वयात त्यांच्याकडून झालेल्या चुकासुद्धा क्षम्य असतात. कारण त्यांच्या मनाची पाटी कोरी असते. जी गोष्ट त्यांच्यासमोर असते त्याच गोष्टीचा ते विचार करीत असतात. बालमन कधीही अमूर्तासंबंधी विचार करीत नसते. ज्या ठिकाणी बालमन जाईल त्या सर्व गोष्टींचा ते मनापासून आनंद घेते कारण त्यांच्या मनाची पाटी कोरी असते.

आ. लोकोत्तर कल्पनाशक्ती : लोकोत्तर कल्पनाशक्ती म्हणजे विलक्षण असामान्य, अलौकिक अशी कल्पनाशक्ती, सर्वसामान्य माणसांमध्ये अशी विचार करण्याची क्षमता नसते. तत्त्वज्ञ, कवी, शास्त्रज्ञ, लेखक इत्यादी असामान्य माणसेच वेगळा विचार करू शकतात. त्यांच्या कल्पनाशक्तीची धाव असीम असते. जिथपर्यंत आपण साधारण माणसे पोहचू शकत नाही, अशी विलक्षण, असामान्य, अलौकिक अशा कल्पनाशक्तीची टॉलस्टॉयला जणू देणगीच लाभलेली होती. म्हणूनच या अजरामर, उदात्त, कितीतरी वेगळ्या, श्रेष्ठ कलाकृतींची निर्मिती झाली.

इ. तपशिलांचा महासागर : महासागर म्हणजे मोठा समुद्र. समुद्राच्या पाण्याची खोली किंवा व्याप्ती आपण मोजू शकत नाही. लेखिकेने टॉलस्टॉय यांनी लिहिलेल्या ‘युद्ध आणि शांती’ या अवाढव्य कादंबरीच्या लिखाणासाठी त्यांनी जे तपशील, संदर्भ गोळा केले त्यांना तपशिलांचा महासागर अशी उपमा दिली आहे. त्यावरून त्याने जमवलेल्या तपशिलांच्या माहितीची कल्पना येते. त्याने विविध प्रकारचे संदर्भ ग्रंथ रशियाचा इतिहास, रशियातील लोकांच्या जीवनपद्धतीचा अभ्यास केला मुलाखती घेतल्या. त्याने प्रवासातून, वाचनातून, लोकांच्या मनांतून, इतिहासातून इ. विविध माध्यमांतून तपशील गोळा केले व समुद्रमंथन करून एक अवाढव्य कलाकृती जगासमोर आणली.

3. व्याकरण.

अ. तक्ता पूर्ण करा.

प्रश्न 1.

उत्तरः

विशेषणे	विशेष्ये
अर्थपूर्ण	आठवण
अमर्याद	शक्ती
वाङ्मयीन	शिल्प
अजोड	कलाकृती

आ. खालील शब्दसमूहांचा वाक्यांत उपयोग करा.

प्रश्न 1.

1. न्यून असणे
2. मातीशी मसलत करणे
3. अवाक् होणे
4. अभ्यासाचे डोंगर पेलणे

उत्तरः

1. न्यून असणे : आई गेल्यावर रमेशच्या मनात काहीतरी न्यून असल्याची भावना निर्माण झाली.
2. मातीशी मसलत करणे : पाऊस पडल्यानंतर शेतकरी विविध कामांच्या आधारे मातीशी मसलत करतात.
3. अवाक होणे : गणेशला दहावीच्या परीक्षेत नव्वद टक्के गुण मिळल्याचे ऐकून घरातले सगळेच अवाक झाले.
4. अभ्यासाचे डोंगर पेलणे : डॉक्टर होण्यासाठी खूप अभ्यासाचे डोंगर पेलावे लागतात.

4. स्वमत.

प्रश्न अ.
टॉलस्टॉयच्या तरल संवेदनेची सूचक आठवण तुमच्या शब्दांत वर्णन करा.
उत्तरः
सत्य, शांती, त्याग, सेवा या मूल्यांचे उपासक असणारे थोर तत्वचिंतक, शिक्षणशास्त्रज्ञ आणि प्रतिभासंपन्न साहित्यिक लिओ निकोल्विच टॉलस्टॉय हे विश्वशांतीचे मार्गदर्शक होते. लहानपणापासूनच त्यांच्या तरल संवेदनांची जाणीव लेखनातून स्पष्ट होते. त्यांची आई गेल्यानंतर त्यांच्या आत्याने त्यांचा संभाळ केला, त्यांना कुठेही आईची कमतरता जाणवू दिली नाही. त्यांनी त्यांच्या तान्हेपणाच्या दोन आठवणी लिहून ठेवल्या आहेत. त्यांच्या संवेदनांची आठवण सांगताना ते सांगतात की त्यांना दुपट्यात घट्ट गुंडाळून ठेवले आहे. त्यांना हतपाय हालवता येत नाहीत, त्यांना मोकळेपणा हवा आहे. म्हणून ते जोरजोरात रडत आहेत.

पण त्यांची व्यथा कोणीही समजू शकत नाही. दुसरी आठवण अशी की, पहिल्यांदाच त्यांना त्यांच्या चिमुकल्या देहाचे अस्तित्व जाणवले. त्यांना दाईचे मोकळे हात दिसतात, त्यांना सगंधी द्रव्याचा वास येतो, पाण्याची उष्णता जाणवते, पाण्याशी खेळताना पाण्याचा आवाज ऐकू येतो, टबच्या आतील मऊ स्पर्श कळतो इतक्या लहानपणी संवेदना कळून प्रत्यक्षात त्यांचे वर्णन करणारा टॉलस्टॉय हा कदाचित जगातील पहिला माणूस असेल. मऊ, काळाभोर लाकडाचा टब, बाहया मागे दुमडलेला दाईंचा हात, पाण्याच्या कढत वाफा, चिमुकल्या हातांनी पाण्याशी खेळताना होणारा आवाज या सर्व संवेदनांची संकलित जाणीव आनंद देणारी आहे. त्यांच्या या तरल संवेदनांमुळेच मोठेपणी त्यांच्या हातून लिखाणाचे महान कार्य घडत गेले. प्रत्येक ज्ञानेंद्रियाच्या त्यांच्या संवेदना लहानपणापासून खूप तल्लख असल्याचे त्यावरून स्पष्ट होते.

प्रश्न आ.
‘युद्ध आणि शांती’ ही कादंबरी लिहिण्यासाठी टॉलस्टॉयने केलेल्या अभ्यासाचे वर्णन तुमच्या शब्दांत लिहा.
उत्तरः
‘युद्ध आणि शांती’ ही कादंबरी लिहिण्यासाठी टॉलस्टॉय यांनी परिपूर्ण अभ्यास केला. कादंबरी दर्जेदार होण्यासाठी अनेक वेळा पुनर्लेखन केले. त्यामुळे ‘वॉर अण्ड पिस’ हे जगातील साहित्यातील वाङ्मयीन लेणे ठरले. लग्नानंतरची 15 – 16 वर्षे टॉलस्टॉयचा जीवनप्रवाह फारशी वळणे न घेता अनिरूद्धपणे वाहत राहिला. 1863 च्या अखेरीस ‘युद्ध आणि शांती’ या कादंबरीच्या लेखनास त्याने सुरुवात केली. ही कादंबरी लिहून पूर्ण करण्यासाठी त्यांना सहा वर्षे लागली, या कादंबरीच्या लिखाणासाठी टॉलस्टॉय यांनी प्रचंड कष्ट घेतले. वास्तवाच्या चारही बाजूंचा अभ्यास करून त्यांनी लिखाण केले, त्यांच्या अभ्यासाचा आवाका फारच मोठा होता. त्यासाठी त्यांनी अनेक संदर्भग्रंथांचा अभ्यास केला आणि हा अभ्यास त्यांनी लिखाण पूर्ण होईपर्यंत चालू ठेवला.

अधिकृत इतिहास, रशियन व फ्रेंच इतिहासकारांनी लिहिलेला, त्या कालखंडाचा परामर्श घेताना एकाच घटनेतून दोन विरुद्ध पक्षांचे लोक असा काय अर्थ काढतात त्याचे सबंध, अन्वयार्थ त्याने समजावून घेतले. नेपोलियनविषयी प्रसिद्ध झालेले अपरंपार लिखाण हे सारे काही त्याने अक्षरश: घुसळून काढले. जणू काही तो त्याच काळात जगत होता, इतका अभ्यास त्याने या कादंबरीच्या लिखाणासाठी केला.

या सगळ्या अभ्यासामुळेच कादंबरीतली पात्रे जणू देहधारण करून त्याच्याशी वार्तालाप करू लागली होती. कादंबरी लिखाणासाठी त्याने विविध तपशिलांचा अतिशय चिकित्सकपणे अभ्यास केला, ज्या जमिनीत कथाबीज पेरायचे तिची त्याने खूप कसून नांगरणी केली, म्हणजेच शेतकरी ज्याप्रमाणे जमिनीची खूप मशागत करतो व त्यानंतर पीक घेतो, त्याचप्रमाणे टॉलस्टॉयने कादंबरी लिखाणाअगोदर विविध संदर्भाचा व दाखल्यांचा प्रचंड अभ्यास केला.

प्रश्न इ.
स्वत:चे लेखन परिपूर्ण होण्यासाठी टॉलस्टॉयने केलेले परिश्रम तुमच्या शब्दांत लिहा.
उत्तरः
टॉलस्टॉयला स्वत:च्या सुप्तशक्तीवर विश्वास होता. लेखनवाचनाच्या बाबतीतही तो खूप चिकित्सक होता. त्याचे बालमनही त्या काळात प्रचंड व्यापक होते. विशेष म्हणजे त्याला दैनंदिनी लिहायची सवय लहानपणापासून होती. लहानपणापासूनच आपण इतरांसारखे सामान्य जीवन जगण्यासाठी जन्माला आलेलो नाही ही त्याला जाणीव होती.

‘युद्ध आणि शांती’ या कादंबरीच्या लिखाणासाठी टॉलस्टॉयने जी मेहनत घेतली, अभ्यास केला ते पाहून आश्चर्यचकित व्हायला होते. स्वतःचे लिखाण परिपूर्ण होण्यासाठी टॉलस्टॉयने कादंबरीचा मूळ आराखडाच तीन वेळा बदलला. कित्येक व्यक्तिरेखा मूळ आराखड्यात नव्हत्या. त्यांना नंतर प्रवेश मिळाला. त्यांच्या अभ्यासूवृत्तीमुळेच हे शक्य झाले. त्याने विविध ऐतिहासिक घटनांचा तपशीलवार अभ्यास करून एकाच घटनेतून दोन विरुद्ध पक्षाचे लोक कसा काय अर्थ काढतात त्याचे सर्व अन्वयार्थ त्याने समजावून घेतले.

युद्धाचे वर्णन प्रत्ययकारी होण्यासाठी त्याने बोरोडिनोच्या युद्धभूमीस भेट दिली. त्याने कादंबरी लिखाणाला सुरुवात केली आणि कमीत-कमी बारा – पंधरा वेळा लिखाण थांबवले. तो रोज दिवसभर लिखाण करायचा आणि संध्याकाळी तो पत्नीच्या टेबलवर आणून ठेवी, त्यातील तिने केलेल्या खाणाखुणांसह तो परत लिखाण करीत असे. त्यात खऱ्याखुऱ्या ऐतिहासिक घटनांच्या संदर्भात लिखाण करायचे होते त्यामुळेच त्याने ही दोन हजार पानांची कादंबरी 1869 साली पूर्ण केली. ‘युद्ध आणि शांती’ या कादंबरीच्या लिखाणासाठी त्याने अपार कष्ट घेतले, जणू काही तो 1863 ते 1869 या काळात नेपोलियनच्या काळातच जगत होता. त्याने या कादंबरीच्या लिखाणासाठी अगणित संदर्भग्रंथांचे वाचन केले. कदाचित त्याच्याएवढे कष्ट कादंबरी लिखाणासाठी खूप कमी लोकांनी घेतले असतील.

5. अभिव्यक्ती.

प्रश्न अ.
‘टॉलस्टॉय पहिल्या दर्जाचा कलावंत ठरतो, या विधानाची यथार्थता पटवून दया.
उत्तरः
लेखिका सुमती देवस्थळे यांनी प्रसिद्ध साहित्यिक टॉलस्टॉय यांच्या संबंधी मराठीत लिखाण केले आहे आणि हे लिखाण पहिल्यांदा प्रसिद्ध करण्याचे श्रेयही त्यांना मिळाले आहे. कोणताही साहित्विक हा आत्मनिरीक्षण व आत्मपरीक्षणाच्या जोरावर साहित्यनिर्मिती करत असतो. साहित्यिकाला जर आपल्या लिखाणाबदद्ल समाधान वाटत नसेल तर अगदी मनाला समाधान मिळेपर्यंत वारंवार लिखाण करीत असतो. ‘युद्ध आणि शांती’ या कादंबरीच्या निर्मितीसाठी टॉलस्टॉय यांनी अपार कष्ट घेतले.

टॉलस्टॉयला मुळातच वाचनाची आवड होती. वाचनाची आवड असल्यामुळे त्याचे लिखाणही उत्तम दर्जाचे झाले. त्याच्या लिखाणात मानवतावाद दिसून येतो. टॉलस्टॉयने कादंबरी लिखाणाअगोदर असंख्य व्यक्तिरेखा अभ्यासल्या. अनेक लहान – मोठ्या घटनांचा भव्य विस्तार, नेपोनियनची रशियावर स्वारी, युद्धातील चित्तथरारक प्रसंग, तत्कालीन खानदानी रशियन लोकांचे आणि सामान्य लोकांचे वैयक्तिक जीवन, लष्करी कारवाया इ. बाबींचा त्याने चिकित्सक पद्धतीने अभ्यास केला. त्याने आपल्या मूळच्या आराखड्यातसुद्धा अनेक वेळा बदल केला.

सुरुवातीला जे चित्रित करायचे होते त्यापेक्षा कितीतरी पटीने श्रेष्ठ व उदात्त लिखाण होत गेले. त्याने अवतीभोवती राहणाऱ्या वयस्कर लोकांच्या अनौपचारिक मनमोकळ्या मुलाखती घेतल्या. युद्ध प्रत्यक्ष पाहिलेल्या माणसाला तो वेड्याच्या इस्पितळात जाऊन भेटला. ऐतिहासिक घटनांच्या पार्श्वभूमीवर मानवी जीवनदर्शन हा त्याच्या कादंबरीचा खरा विषय होता.

या कादंबरीत त्याने 500 पेक्षा जास्त व्यक्तिरेखा रंगवल्या आहेत, त्या व्यक्तिरेखांमध्ये प्रत्येकाला अगदी प्राण्यांनासुद्धा वेगवेगळे, स्वयंपूर्ण, सुस्पष्ट व्यक्तिमत्त्व आहे. केवळ आपण व्यक्तिचित्रणांकडे जरी दृष्टिक्षेप टाकला तरीसुद्धा या कादंबरीने फार मोठे यश साध्य केल्याचे आपणास दिसून येते. म्हणूनच टॉलस्टॉय हा पहिल्या दर्जाचा कलावंत ठरतो.

प्रश्न आ.
‘ज्या जमिनीत कथाबीज पेरायचे तिची खूप कसून नांगरणी चालली होती’, या विधानाचा अर्थ स्पष्ट करा.
उत्तरः
‘युद्ध आणि शांती’ या कादंबरीच्या लिखाणापूर्वी टॉलस्टॉय या महान साहित्यकाराने जी अपार मेहनत घेतली त्यांचे वर्णन या पाठात लेखिका सुमती देवस्थळे यांनी अत्यंत मार्मिकपणे केल्याचे दिसून येते. मोहरीएवढ्या बिजापासून प्रचंड अश्वत्थ वृक्ष उभा राहावा तशी ही कादंबरी वाढत गेली. या कादंबरीतील निसर्गवर्णने कादंबरीच्या पोतात अशी काही एकरूप झालेली आहेत की जणू काही त्यां या कादंबरीतील प्रसंगांना एक प्रकारचा जिवंतपणा आलेला आहे.

वेगवेगळ्या पार्श्वभूमीवर वेगवेगळ्या ऐतिहासिक संदर्भात व्यक्तिमनाचा वेध घेण्यात टॉलस्टॉयने जी मानवी उकल केली आहे. ती केवळ आश्चर्यकारक म्हटली पाहिजे. कादंबरी लिखाणासाठी टॉलस्टॉयने अपार मेहनत घेतली. अभ्यासाचे डोंगर पेलले, अगणित संदर्भ ग्रंथांचा त्याने सतत अभ्यास केला. नेपोलियनविषयी प्रसिद्ध झालेले सर्व लिखाण त्याने अक्षरशः घुसळून काढले. 1863 ते 1869 या सहा वर्षांच्या काळा तो जणूकाही नेपोलियनच्या काळातच जगत होता असे वाटते.

ज्याप्रमाणे एखादा शेतकरी शेतात पीक घेण्याअगोदर अतिशय काळजीपूर्वक शेतीची मशागत करतो व त्यानंतर त्यात पेरणी करतो. व्यवस्थित मशागत केल्यानंतर येणारे पीकही चांगले येते, चांगले पीक आल्यानंतर शेतकऱ्याच्या चेहऱ्यावर समाधान झळकते. त्याचप्रमाणे ‘युद्ध आणि शांती’ कादंबरी लिहिण्याअगोदर त्याने सर्व माहिती गोळा करण्यासाठी प्रचंड कष्ट घेतले, असंख्य व्यक्तिरेखांचा अभ्यास केला, रशियातील त्या काळातील जीवनपद्धतीचा त्याने अभ्यास केला, अवतीभोवती राहणाऱ्या वयस्कर लोकांच्या अनौपचारिक मुलाखती घेतल्या. त्याला जे जे जमते ते त्याने सर्वकाही केले. कोणतीही कमतरता त्याने ठेवली नाही म्हणूनच असे म्हणता येईल की, ज्या जमिनीत कथाबीज पेरायचे तिची खूप कसून नांगरणी चालली होती.

प्रकल्प.

संगणकावर उपलब्ध असणाऱ्या ‘गुगल अॅप’चा वापर करून लिओ टॉलस्टॉय यांच्याविषयी अधिक माहिती मिळवून संपादित करा.

11th Marathi Book Answers Chapter 11 वाङ्‌मयीन लेण्याचा शिल्पकार Additional Important Questions and Answers

आकलन कृती

खालील पठित गदय उताऱ्याच्या आधारे सुचनेनुसार कृती करा.

प्रश्न 1.

उत्तर:

खालील घटनेचे परिणाम लिहा.

प्रश्न 1.

घटना	परिणाम
कादंबरीचा मूळचा आराखडा व नाव तीन वेळा बदलले	………………………..

उत्तर:

घटना	परिणाम
कादंबरीचा मूळचा आराखडा व नाव तीन वेळा बदलले	कित्येक व्यक्तिरेखांना मूळच्या आराखड्यात स्थान नव्हते नंतर प्रवेश मिळाला. जे चित्रित करण्याचे प्रांरभी ठरवले होते, त्याहून कितीतरी वेगळी, कितीतरी श्रेष्ठ, उदात्त अशी कलाकृती हळूहळू तयार होत गेली.

प्रश्न 2.
1869 च्या अखेरीस’ हे उत्तर येईल असा प्रश्न तयार करा.
उत्तरः
‘युद्ध आणि शांती’ या कादंबरीच्या लिखाणास कोणत्या वर्षी सुरुवात झाली?

प्रश्न 3.
स्टॅकॉव्हसारख्या तज्ज्ञ टीकाकाराचा ‘बुद्ध आणि शांती’ या कादंबरीवरील अभिप्राय म्हणजे – [ ]
उत्तरः
स्टॅकॉव्हसारख्या तज्ज्ञ टीकाकाराचा ‘युद्ध आणि शांती’ या कादंबरीवरील अभिप्राय म्हणजे – कादंबरीच्या शिफारशीचा एक ताम्रपटच

उपयोजित कृती

प्रश्न 1.
एखादे लिखाण वाचल्यानंतर स्वत:चे मत मांडणे या अर्थाचा उताऱ्यात आलेला शब्द
उत्तरः
अभिप्राय

प्रश्न 2.
खालील वाक्यातील अधोरेखित शब्दाची जात ओळखा.
प्रत्यक्ष लेखनास पुरी सहा वर्षे लागली.
उत्तरः
सहा – संख्यावाचक विशेषण

प्रश्न 3.
खालील शब्दांसाठी उताऱ्यात वापरलेले पर्यायी शब्द लिहा.
(अ) प्रचंड
(ब) ठिकाण
उत्तरः
(अ) प्रचंड – भव्य
(ब) ठिकाण – स्थान

स्वमतः

प्रश्न 1.
‘युद्ध आणि शांती’ ही कादंबरी वाचकांच्या मनावर अधिराज्य गाजवते, तुमचे मत लिहा.
उत्तरः
सत्य, शांती, त्याग, सेवा या मूल्यांची जोपासना करणारे थोर तत्त्वचिंतक, शिक्षणशास्त्रज्ञ आणि प्रतिभासंपन्न साहित्यिक लिओ टॉलस्टॉय लिखित ‘युद्ध आणि शांती’ ही कादंबरी आहे. या कादंबरी लिखाणाअगोदर टॉलस्टॉय यांनी परिपूर्ण अभ्यास केला. कादंबरीचा दर्जा जपण्याचा त्याने अतोनात प्रयत्न केला. पूर्वीच्या काळी साम्राज्यवादाला महत्त्व असल्यामुळे जो बलवान असेल तो राज्य करीत असे, पण त्याच्यापुढेही साम्राज्य टिकवणे हे आव्हान होते. कारण त्या काळात वर्चस्वासाठी सैन्यातसुद्धा मोठ्या प्रमाणावर बंडाळी होत असे. अनेक साम्राज्ये उभी राहिल्याचा व ती साम्राज्ये जगासमोर आहेत. याचा सखोल अभ्यास टॉयस्टॉय यांनी केला. त्यांनी कादंबरी लिखाणाअगोदर लोकांची मते विचारून घतला. लिखाणात आवश्यक बाबी कोणत्या आहेत? हे त्याने जाणून घेतले.

प्रत्यक्ष युद्धभूमीला त्याने भेट दिली. त्याने ऐतिहासिक माफत लिखाणाला परिपूर्ण अशी सर्व माहिती गोळा केली. जवळजवळ तीन वेळा मूळ लिखाणाचा ढाचा व नाव बदलले. लिखाणात अतिशयोक्ती होणार नाही याची त्याने काळजी घेतली. मानवी जीवनदर्शन अगणित संदर्भ ग्रंथांचा त्याने अभ्यास केला. 1863 साली सुरू झालेले लिखाण 1869 साली पूर्ण झाले. या सहा वर्षांच्या काळात प्रत्यक्ष तो त्याच जगात वावरत होता. इतके परिपूर्ण लिखाण मानवी मनावर व्यापक परिणाम करते. यद्धाच्या माध्यमातून कोणतेही जगातील प्रश्न सुटत नाहीत हा कादंबरीचा मूळ विषय आहे. टॉलस्टॉयच्या लेखन शैलीमुळे वाचक कादंबरी वाचताना खिळून राहतो म्हणूनच ही कादंबरी वाचकांच्या मनावर अधिराज्य गाजवते असे आपल्याला म्हणता येईल.

आकलन कृती

खालील पठित गदव उताऱ्याच्या आधारे सुचनेनुसार कृती करा.

प्रश्न 1.

उत्तर:

प्रश्न 2.
प्रत्यक्षात वावरणाऱ्या व्यक्तीपेक्षा कल्पनासृष्टीतली पाने त्याला अधिक जवळची वाटू लागली कारण ।
उत्तरः
प्रत्यक्षात वावरणाऱ्या व्यक्तीपेक्षा कल्पनासृष्टीतली पात्रे त्याला अधिक जवळची वाटू लागली. कारण कादंबरीतील पात्रे जणू देहधारण करून त्याच्याशी बातचीत करत होती.

प्रश्न 3.

उत्तर:

आकृतिबंध पूर्ण करा.

प्रश्न 1.

उत्तरः

उपयोजित कृती

वाक्यरूपांतर ओळखा.

प्रश्न 1.
कल्पनासृष्टीमुळे उलगडलेला ऐतिहासिक काळ लवकरच बारीकसारीक तपशिलांसह जिवंत होऊ लागला. (विधानार्थी वाक्य)
सूचना : प्रश्नार्थी रूप ओळखा.
पर्याय : 1. कल्पनासृष्टीमुळे उलगडलेला ऐतिहासिक काळ लवकरच बारीकसारीक तपशिलांसह जिवंत होऊ लागला का?
2. कल्पनासृष्टीमुळे उलगडलेला ऐतिहासिक काळ लवकरच बारीकसारीक तपशिलांसह जिवंत होऊ लागला तर !
3. कल्पनासृष्टीमुळे उलगडलेला ऐतिहासिक काळ लवकरच बारीकसारीक तपशिलांसह जिवंत होऊ लागेलच असेही नाही.
उत्तरः
कल्पनासृष्टीमुळे उलगडलेला ऐतिहासिक काळ लवकरच बारीकसारीक तपशिलांसह जिवंत होऊ लागला का?

प्रश्न 2.
गटात न बसणारा शब्द ओळखा कादंबरी, कथासंग्रह, काव्यसंग्रह, संदर्भग्रंथ
उत्तरः
संदर्भग्रंथ

प्रश्न 3.
योग्य विरामचिन्हांचा पर्याय ओळखा.
निर्मितीची प्रक्रिया शक्य तेवढ्या वेगाने सुरू होती ; पण मूळच्या अति चोखंदळपणापायी रचलेला पुष्कळसा आकृतिबंध विस्कटून जात होता.
स्वल्पविराम, पूर्णविराम, दुहेरी अवतरणचिन्ह, पूर्णविराम, स्वल्पविराम, उद्गारचिन्ह., अर्धविराम पूर्णविराम
उत्तरः
(अर्धविराम, पूर्णविराम)

स्वमतः

प्रश्न 1.
लेखकाच्या अतिचोखंदळ वृत्तीमुळे रचलेला पुष्कळसा आकृतिबंध विस्कटून जातो, तुमचे मत लिहा.
उत्तरः
लिखाण परिपूर्ण होण्यासाठी बरेच साहित्यिक चोखंदळ मार्गाचा अवलंब करतात. एखादा विषय जर अर्थपूर्ण किंवा व्यापक असेल तर त्या विषयाच्या मांडणी संदर्भात अतिशय काळजी घेतली जाते. आपल्या लिखाणाचा विषय किंवा अर्थ वाचकांच्या मनाला भिडणारा असावा असा प्रयत्ल लेखकाचा असतो. आपल्यासारखे लिखाण संबंधित विषयावर अजूनपर्यंत कोणीही केलेले नसावे व आपल्याला यश मिळावे हा त्यामागील हेतू असतो. लिखाणाअगोदर विविध गोष्टींचा परामर्श घ्यायचा त्यांचा प्रयत्न असतो. अभ्यासाचे डोंगर पेलायची त्यांची ताकद असते.

दंबरीचा विषय समजून घेताना लिखाणाचा मूळ ढाचा बदलण्याची त्यांची तयारी असते. प्रवास, मुलाखती, चर्चा, भेटीगाठी, विविध संदर्भ ग्रंथ इ. प्रकारच्या मार्गाचा अवलंब ते करतात. त्यामळे लिखाणाला सरुवात होण्यास वेळ ला पात्रे विषयाला अनुसरून असतील याची काळजी घेतली जाते. कल्पनेतले लिखाण वास्तववादी वाले परिणामकारक होण्यासाठी अनेक वेळा लिखाण केले जाते. या चोखंदळ वत्तीमळे रचलेला पुष्कळसा आकृतिबंध खरोखरच विस्कटन गेलेला दिसून येतो कारण मूळ लिखाणामध्ये अनेक बदल झालेले असतात, पण लिखाण मात्र परिणामकारक व वास्तववादाला स्पर्श करते.

वाङ्‌मयीन लेण्याचा शिल्पकार Summary in Marathi

प्रास्ताविकः

सुप्रसिद्ध लेखिका, चरित्रकार, ‘टॉलस्टॉय एक माणूस’, ‘मॅक्झिम गॉर्को’, ‘डॉ. अल्बर्ट श्वाइट्झर’, ‘एक विचारवंत’ (कार्ल मार्क्ससंबंधी) ‘छाया आणि ज्योती’ ही चरित्रे त्यांनी लिहिली. चरित्रलेखनाला आवश्यक असणारी मेहनत, विषयासंबंधीचा जिव्हाळा, समरसता आणि प्रवाही शैली या वैशिष्ट्यांमुळे त्यांच्या लेखनाला आगळेपण प्राप्त झाले आहे. टॉलस्टॉय आणि श्वाइट्झर यांच्यासंबंधी एवढे मार्मिक लेखन मराठीत पहिल्यांदा प्रसिद्ध करण्याचे श्रेयही त्यांना मिळाले आहे.

पाठ परिचयः

सत्य, शांती, त्याग, सेवा या मूल्यांचे उपासक असणारे थोर तत्त्वचिंतक, शिक्षणशास्त्रज्ञ आणि प्रतिभासंपन्न साहित्यिक लिओ निकोल्विच टालस्टॉय हे विश्वशांतीचे मार्गदर्शक होते. सत्याग्रह, असहकार या शांततामय प्रतिकाराचे तत्त्वज्ञान त्यांनी सांगितले. टॉलस्टॉय यांच्या लेखक म्हणून बडणीचे आणि ‘वॉर अॅण्ड पिस’ या महान कादंबरीच्या निर्मिती प्रक्रियेचे प्रत्ययकारी चित्रण ‘टॉलस्टॉय एक माणूस’ या पुस्तकातून आले आहे. या कादंबरी लेखनासाठी टॉलस्टॉय यांनी परिपूर्ण अभ्यास करून कादंबरी दर्जेदार होण्यासाठी अनके वेळा पुनर्लेखन केले. त्यामुळे ‘वॉर अॅण्ड पिस’ हे जागतिक साहित्यातील वाङ्मयीन लेणे ठरले. मानवी जीवनातील गुंतागुतीचे प्रश्न युद्धाने सुटत नसून ते शांती आणि प्रेमाने सुटतात हे टॉलस्टॉय यांनी या कादंबरीत सांगितले आहे.

समानार्थी शब्द / पर्यायी शब्दः

1. मातृविहीन – ज्याला माता नाही तो.
2. न्यून – काहीतरी कमी असल्याचे जाणवणे.
3. उणीव – (less, deficient).
4. उत्तेजित – प्रोत्साहित.
5. चिमुकले – छोटेसे – (very small, tiny).
6. संकलित – एकत्रित – (collected).
7. बालपण – लहानपण – (childhood).
8. छंद – आवड – (liking, hobby).
9. पिंजण – चक्र – (मनातले विचार).
10. दैनंदिनी – रोजनिशी – (diary).
11. सुप्त शक्ती – अंतर्गत शक्ती – (दडलेले ज्ञान).
12. चिकित्सा – संशोधन – (minute examination).
13. अभिप्राय – स्वत:चे मत (एखादया लिखाणावरचे) – (opinion).
14. यातना – त्रास, दुःख – (great pains)
15. बांडगुळ – झाडावरील वाढलेला अतिरिक्त भाग जो झाडाच्या वाढीवर परिणाम करतो – (a parasitical (living an another).
16. मेहनत – कष्ट – (hard work)

वाक्यप्रचारः

1. न्यून असणे – कमी असणे.
2. मातीशी मसलत करणे – मातीची मशागत करणे.
3. अवाक होणे – चकित होणे.
4. अभ्यासाचे डोंगर पेलणे – खूप अभ्यास करणे.
5. कृतकृत्य होणे – समाधानी होणे.
6. अभिप्राय देणे – स्वत:चे एखादया लिखाणाविषयी किंवा कलाकृतीविषयी मत मांडणे.

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest व्याकरण गटात न बसणारा शब्द Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati Solutions व्याकरण गटात न बसणारा शब्द

11th Marathi Book Answers व्याकरण गटात न बसणारा शब्द Additional Important Questions and Answers

गटात न बसणारा शब्द

प्रश्न 1.
नामांकित, कीर्तिमान, कुविख्यात, सर्वज्ञात
उत्तर :
कुविख्यात

प्रश्न 2.
वात, जलद, मेघ, घन
उत्तर :
वात

प्रश्न 3.
सटासट, कटकट, वटवट, झटपट
उत्तर :
सटासट

प्रश्न 4.
अपमान, दुर्लक्ष, निष्काळजी, आदर
उत्तर :
अपमान

प्रश्न 5.
सौदामिनी, प्रकाश, दिप्ती, तेज
उत्तर :
सौदामिनी

प्रश्न 6.
त्याला, त्याचा, तुझा, आणि
उत्तर :
आणि

प्रश्न 7.
संभाषण, भाषण, चर्चा, संवाद
उत्तर : भाषण

प्रश्न 8.
गुजरात, महाराष्ट्र, मुंबई, कर्नाटक
उत्तर :
मुंबई

प्रश्न 9.
फूल, पान, खोड, मासा
उत्तर :
मासा

प्रश्न 10.
पृथ्वी, धरणी, वसुधा, समिधा
उत्तर :
समिधा

प्रश्न 11.
देवूळ, मंदिर, देवालय, देव
उत्तर :
देव

प्रश्न 12.
कर्ण, डोळा, नयन, नेत्र
उत्तर :
कर्ण

प्रश्न 13.
पर्वत, नग, नभ, गिरी
उत्तर :
नभ

प्रश्न 14.
हात, पद, कर, हस्त
उत्तर :
पद

प्रश्न 15.
दैत्य, दानव, राक्षस, सुर
उत्तर :
सुर

प्रश्न 16.
नवल, संकोच, आश्चर्य, विस्मय
उत्तर :
संकोच

प्रश्न 17.
युद्ध, समर, संगम, लढाई
उत्तर :
संगम

प्रश्न 18.
वणवा, वन, जंगल, अरण्य
उत्तर :
वणवा

प्रश्न 19.
शत्रू, वैरी, दुष्मन, दोस्त
उत्तर :
दोस्त

प्रश्न 20.
पिता, वडील, भ्राता, जनक
उत्तर :
भ्राता

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 1 नवनिर्माण Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 1 नवनिर्माण

12th Hindi Guide Chapter 1 नवनिर्माण Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

प्रश्न 1.
(अ) कृति पूर्ण कीजिए :

बल इसके लिए होता है ↓
(a) …………………………………….
(b) …………………………………….
उत्तर :
(a)

(b)

(आ) जिसे मंजिल का पता रहता है वह :

(a) …………………………………….
(b) …………………………………….
उत्तर :
(a) सब के बल बनना – सब की मदद करना।
(b) पथ के संकट सहना – मंजिल पर पहुँचने की कोशिश में होने वाला कष्ट सहन करना।

शब्द संपदा

प्रश्न 2.
निम्नलिखित शब्दों से उपसर्गयुक्त शब्द तैयार कर उनका अर्थपूर्ण वाक्य में प्रयोग कीजिए :

(a) नीति – …………………………………….
(b) बल – …………………………………….
उत्तर :
(a) उपसर्गयुक्त शब्द – अनीति।
वाक्य : अनीति के मार्ग पर नहीं चलना चाहिए।

(b) उपसर्गयुक्त शब्द – आजीवन।
वाक्य : कुछ पाठक पुस्तकालयों के आजीवन सदस्य होते हैं।

अभिव्यक्ति

प्रश्न 3.
(अ) ‘धरती से जुड़ा रहकर ही मनुष्य अपने लक्ष्य को प्राप्त कर सकता है’, इस विषय पर अपना मत प्रकट कीजिए।
उत्तर :
लक्ष्य का अर्थ है निर्धारित उद्देश्य, जिसे प्राप्त करने के लिए गंभीरता पूर्वक नजर रखी जाए और उसे अर्जित करने के लिए यथासंभव प्रयास किया जाए। हर व्यक्ति का अपने-अपने है ढंग से लक्ष्य निर्धारण करने और उसे अर्जित करने का अपना तरीका होता है। कोई इसे हल्के-फुल्के ढंग से लेता है और बड़े से बड़ा लक्ष्य निर्धारित कर लेता है। ऐसे लक्ष्य क्षमता की कमी है और अपर्याप्त साधन के अभाव में कभी पूरे नहीं हो पाते। जो व्यक्ति अपनी क्षमता और अपने पास उपलब्ध साधनों के अनुसार लक्ष्य का निर्धारण और उसकी पूर्ति के लिए तन-मन-धन से प्रयास करता है, वह व्यक्ति अपने लक्ष्य को प्राप्त करने में अवश्य सफल होता है। ऐसे दूरदर्शी व्यक्ति जमीन से जुड़े हुए होते हैं और समझ-बूझ कर अपना लक्ष्य निर्धारित करते तथा उसके निरंतर प्रयासरत रहते हैं।

(आ) ‘समाज का नवनिर्माण और विकास नर-नारी के सहयोग से ही संभव है’, इसपर अपने विचार लिखिए।
उत्तर :
हमारा समाज विभिन्न प्रकार की कुरीतियों और समस्याओं से भरा हुआ है। अनेक समाज सुधारकों के कठिन परिश्रम के बावजूद आज भी हमारे समाज में अनेक प्रकार की विषमताएँ व्याप्त हैं। असमानता, जातीयता, सांप्रदायिकता, प्रांतीयता, अस्पृश्यता आदि समस्याओं के कारण समाज के नर-नारी दोनों समान रूप से व्यथित हैं। जब तक हमारे समाज से ये बुराइयाँ दूर नहीं होती, तब तक समाज का नव निर्माण और विकास होना असंभव है। नर-नारी दोनों रथ के दो पहियों के समान हैं। बिना दोनों के सहयोग से आगे बढ़ना मुश्किल है। समाज की अनेक समस्याएँ ऐसी हैं, जिनके बारे में नारी को नर से अधिक जानकारियाँ होती हैं। नर-नारी दोनों कंधे से कंधा मिलाकर समाज उत्थान के कार्य में जुटेंगे, तभी समाज का . नव निर्माण और विकास संभव हो सकता है।

रसास्वादन

प्रश्न 4.
निम्नलिखित मुद्दों के आधार पर चतुष्पादियों का रसास्वादन कीजिए :
(1) रचनाकार का नाम – …………………………………….
(2) पसंद की पंक्तियाँ – …………………………………….
(3) पसंद आने के कारण – …………………………………….
(4) कविता का केंद्रीय भाव – …………………………………….
उत्तर :
(1) रचना का शीर्षक : नव निर्माण।
(2) रचनाकार : त्रिलोचन (मूलनाम – वासुदेव सिंह)
(3) कविता की केंद्रीय कल्पना : प्रस्तुत कविता में संघर्ष करने, अत्याचार, विषमता तथा निर्बलता पर विजय पाने का आवाहन किया गया है तथा समाज में समानता, स्वतंत्रता एवं मानवता की स्थापना की बात कही गई है।
(4) रस-अलंकार :
(5) प्रतीक विधान : कविता में विश्वास और प्रेरणा की मात्रा दर्शाने के लिए ‘आकाश’ तथा नर-नारी द्वारा नए समाज की रचना करने का कठिन कार्य करने के लिए ‘काँटों के ताज’ लेने जैसे प्रतीकों का सुंदर प्रयोग किया गया है।
(6) कल्पना : दबे-कुचले लोगों के प्रति आशावाद एवं उत्थान के स्वर बुलंद करना।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की । पंक्तियाँ इस प्रकार हैं :
जिसको मंजिल का पता रहता है,
पथ के संकट को वही सहता है,
एक दिन सिद्धि के शिखर पर बैठ
अपना इतिहास वही कहता है।

(8) कविता पसंद आने का कारण : प्रस्तुत पंक्तियों में यह बात कही गई है कि एक बार अपने लक्ष्य का निर्धारण कर लेने के बाद मनुष्य को हर समय उसको पूरा करने के काम में जी-जान से लग जाना चाहिए। फिर मार्ग में कितनी भी कठिनाइयाँ क्यों न आएँ, उन्हें सहते हुए निरंतर आगे ही बढ़ते रहना चाहिए। एक दिन ऐसे व्यक्ति को सफलता मिलकर ही रहती है। ऐसे ही व्यक्ति लोगों के आदर्श बन जाते हैं। लोग उनका गुणगान करते है और उनसे प्रेरणा लेते हैं।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) चतुष्पदी के लक्षण लिखिए।
……………………………………………
……………………………………………
उत्तर :
चतुष्पदी चौपाई की भाँति चार चरणों वाला छंद होता है। इसके प्रथम, द्वितीय तथा चतुर्थ चरण में पंक्तियों के तुक मिलते हैं। तीसरे चरण का तुक नहीं मिलता। प्रत्येक चतुष्पदी भाव और विचार की दृष्टि से अपने आप में पूर्ण होती है और कोई चतुष्पदी किसी दूसरी से संबंधित नहीं होती।

(आ) त्रिलोचन जी के दो काव्य संग्रहों के नाम
……………………………………………
उत्तर :
त्रिलोचन जी के कुल पाँच काव्य संग्रह हैं –

• धरती
• दिगंत
• गुलाब और बुलबुल
• उस जनपद का कवि हूँ
• सब का अपना आकाश।

Hindi Yuvakbharati 12th Digest Chapter 1 नवनिर्माण Additional Important Questions and Answers

निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए :

1. अतिथि आए है, घर में सामान नहीं है।
   ……………………………………………
2. परंतु अम्यान भी अपराध है।
   ……………………………………………
3. उसके सत्य का पराजय हो जाता है।
   ……………………………………………
4. प्रेरणा और ताकद बनकर परस्पर विकास मे सहभागी बनें।
   ……………………………………………
5. दिलीप अपने माँ-बाप की इकलौती संतान थी।
   ……………………………………………
6. आप इस शेष लिफाफे को खोलकर पढ़ लीजिए।
   ……………………………………………
7. उसमें फुल बिछा दें।
   ……………………………………………
8. कहाँ खो गई है आप।
   ……………………………………………
9. एक मैं सफल सूत्र संचालक के रूप में प्रसिद्ध हो गया।
   ……………………………………………
10. चलते-चलते हमारे बीच का अंतर कम हो गया था।
    ……………………………………………

उत्तर :

1. अतिथि आए हैं, घर में सामान नहीं है।
2. परंतु अज्ञान भी अपराध है।
3. उसका सत्य पराजित हो जाता है।
4. प्रेरणा और ताकत बनकर परस्पर विकास में सहभागी बनें।
5. दिलीप अपने माता-पिता की इकलौती संतान था।
6. शेष आप इस लिफाफे को खोल कर पढ़ लीजिए।
7. उसमें फूल बिछा दें।
8. कहाँ खो गई हैं आप?
9. मैं एक सफल सूत्र संचालक के रूप में प्रसिद्ध हो गया।
10. हमारे बीच का अंतर चलते-चलते कम हो गया था।

Hindi Yuvakbharati 12th Textbook Solutions Chapter 1 नवनिर्माण Additional Important Questions and Answers

कृति-स्वाध्याय एवं उत्तर
पद्यांश क्र. 1
कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
प्रश्न. निम्नलिखित पद्यांश पढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :
(a)

उत्तर :

(b)

उत्तर :

प्रश्न 2.
ऐसे दो प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द हों :

(a) उत्तर लिखिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द के अर्थ वाले दो शब्द पद्यांश से ढूँढ कर लिखिए :

उत्तर :

प्रश्न 2.
निम्नलिखित शब्दों के शब्द-युग्म बना कर लिखिए :
(1) तोड़ – ……………………………..
(2) काम – ……………………………..
(3) जाना – ……………………………..
(4) आकाश – ……………………………..
उत्तर :
(1) तोड़ – जोड़
(2) काम – काज
(3) जाना – आना
(4) आकाश – पाताल।

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए :
(1) विश्वास x ……………………………..
(2) अँधेरा x ……………………………..
(3) सत्य x ……………………………..
(4) सामने x ……………………………..
उत्तर :
(1) विश्वास – अविश्वास
(2) अँधेरा x उजाला
(3) सत्य x असत्य
(4) सामने x पीछे।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पद्यांश पढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के उपसर्गयुक्त शब्द तैयार कर उनका अर्थपूर्ण वाक्यों में प्रयोग कीजिए :
*(1) बल
(2) न्याय।
उत्तर :
(1) शब्द : निर् + बल = निर्बल।
वाक्य : निर्बल को सताना नहीं चाहिए।

(2)शब्द : अ + न्याय = अन्याय।
वाक्य : किसी व्यक्ति का अपनी बात कहने का अधिकार छीनना उसके साथ अन्याय करना है।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) सिद्धि – …………………….
(2) इतिहास – …………………….
(3) मंजिल – …………………….
(4) पथ – …………………….
उत्तर :
(1) सिद्धि – स्त्रीलिंग।
(2) इतिहास – पुल्लिंग।
(3) मंजिल – स्त्रीलिंग।
(4) पथ – पुल्लिंग।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘मानव सेवा ही सच्ची सेवा है’ इस विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
सेवा करने का अर्थ है किसी को प्रसन्न करने का प्रयत्न करना। दूसरों का दुख दूर करना सेवा का उद्देश्य है। दीनदुखी हमारे समाज के अंग हैं। अपनी जरूरतों की पूर्ति के लिए वे समाज से ही अपेक्षा रखते हैं। उनकी सेवा-सहायता करना समाज का कर्तव्य है। मानव सेवा विविध रूपों में की जा सकती है। पीड़ित व्यक्ति को बचाया जा सकता है। जिसके साथ अन्याय हो रहा है उसे न्याय दिलाया जा सकता है। निर्धन रोगियों को उनके इलाज का खर्च दिया जा सकता है। गरीब परिवार की कन्याओं के विवाह के लिए आर्थिक मदद की जा सकती है। अनेक संतों और समाज सेवियों ने अपना जीवन ही मानव सेवा को अर्पित कर दिया। दीनदुखियों की सेवा कर हम उनके चेहरों पर खुशी ला सकते हैं। इस तरह मानव सेवा ही सच्ची सेवा है।

पद्यांश क्र. 3
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
उत्तर लिखिए :
(1) आज नर-नारी –
(i) इस तरह निकलेंगे – ………………………..
(ii) यह लेंगे – ………………………..
(iii) दोनों की विशेषताएँ – ………………………..
(iv) दोनों रचना करेंगे – ………………………..
उत्तर :
(i) इस तरह निकलेंगे – साथ-साथ।
(ii) यह लेंगे – काँटों का ताज।
(iii) दोनों की विशेषताएँ – संगी हैं, सहचर हैं।
(iv) दोनों रचना करेंगे – समाज की।

प्रश्न 3.
लिखिए –
(i) काँटों का ताज लेंगे, यानी क्या?
(ii) ‘गीत मेरा भविष्य गाएगा’ से कवि का तात्पर्य?
उत्तर :
(i) महत्त्वपूर्ण जिम्मेदारियाँ सँभालेंगे।
(ii) भविष्य में (जब वर्तमान अतीत हो जाएगा तब) लोग वर्तमान की प्रशंसा करेंगे।

प्रश्न 4.
वर्तमान का कथन –
(i) ………………………..
(ii) ………………………..
(iii) ………………………..
(iv) ………………………..
उत्तर :
(i) अतीत अच्छा था।
(ii) प्राण के पथ का गीत अच्छा था।
(iii) मेरा गीत भविष्य गाएगा।
(iv) अतीत का भी गीत अच्छा था।

प्रश्न 5.
दो ऐसे प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द हों :
(1) समाज की
(2) भविष्य।
उत्तर :
(1) नर-नारी किसकी रचना करेंगे?
(2) वर्तमान के गीत कौन गाएगा?

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के युग्म-शब्द बना कर लिखिए :
(1) ……………………………… मीत
(2) साथ – ………………………………
(3) संगी – ………………………………
(4) अच्छा – ………………………………
उत्तर :
(1) हित – मीत
(2) साथ – साथ
(3) संगी – साथी
(4) अच्छा – बुरा।

रसास्वादन मुद्दों के आधार पर

कृतिपत्रिका के प्रश्न 2 (इ) के लिए

निम्नलिखित मुद्दों के आधार पर ‘नव निर्माण’ कविता का रसास्वादन कीजिए।

रसास्वादन अर्थ के आधार पर

प्रश्न 1.
अन्याय, अत्याचार से दीन-दुखियों को मुक्ति दिलाने के लिए उनका बल बन जाना ही बलवान व्यक्तियों के बल का सही उपयोग हैं। इस कथन के आधार पर ‘नव निर्माण’ कविता का रसास्वादन कीजिए।
उत्तर :
कवि त्रिलोचन द्वारा चतुष्पदी छंद में रचित कविता ‘नव निर्माण’ का मूलतत्त्व जीवन में संघर्ष करना बताया गया है। हमारे समाज में व्याप्त अन्याय, अत्याचार, विषमता आदि का बोलबाला है। कवि इन बुराइयों पर काबू पाने के लिए लोगों को बल और साहस एकत्र करने का आवाहन करते हैं। यह सर्व विदित है कि ये सारी बुराइयाँ कुछ लोगों द्वारा अपने शारीरिक एवं आर्थिक बल का दुरुपयोग करने के कारण पनपती हैं। इसलिए इन पर विजय पाने का मार्ग भी बल का प्रयोग ही है। यहाँ बल प्रयोग से कवि का आशय किसी के विरुद्ध बल का अनावश्यक प्रयोग करने से न होकर सताए हुए, दबाए हुए बलहीन लोगों का बल बन कर दिखाने से है। बलहीन निरीह व्यक्तियों पर होने वाला अन्याय और अत्याचार तभी रुक सकता है और तभी उन्हें समाज में समानता का दर्जा मिल सकता है और वे निर्बलता पर विजय प्राप्त कर सकेंगे। इसी बात को कवि अपनी कविता में बिना किसी लाग-लपेट के सीधे-सादे सरल शब्दों में इस प्रकार कहते हैं –

बल नहीं होता सताने के लिए,
वह है पीड़ित को बचाने के लिए।
बल मिला है, तो बल बनो सबके,
उठ पड़ो न्याय दिलाने के लिए।

कवि ने इस कविता में अपनी बात कहने के लिए न कहीं रसअलंकार वाली शृंगारिक भाषा का प्रयोग किया है और न ही उन्हें अपनी बात कहने के लिए दुरुहता के मायाजाल में ही फँसना पड़ा है। कविता के शाब्दिक शरीर के रूप में सरल शब्दों की अमिघा शक्ति तथा कविता का प्रसाद गुण कविता में व्यक्त भावों को सरलतापूर्वक आत्मसात करने में प्रमुख भूमिका निभाते हैं।

व्याकरण

1. अलंकार :

प्रश्न 1.
निम्नलिखित पंक्तियों में उद्धृत अलंकार पहचानकर उसका नाम लिखिए :
(1) हाय फूल-सी कोमल बच्ची। हुई राख की थी ढेरी।
(2) मैया मैं तो चंद्र खिलौना लैहों।
(3) इस काल मारे क्रोध के तनु काँपने उनका लगा। मानो हवा के जोर से सोता हुआ सागर जगा।
उत्तर :
(1) उपमा अलंकार।
(2) रूपक अलंकार।
(3) उत्प्रेक्षा अलंकार।

2. रस :

प्रश्न 1.
निम्नलिखित पंक्तियों में उद्धृत रस पहचानकर उसका नाम लिखिए :
(1) उस काल मारे क्रोध के तन काँपने उनका लगा।
मानो हवा के जोर से सोता हुआ सागर जगा।
उत्तर :
रौद्र रस

प्रश्न 2.
काहु न लखा सो चरित बिसेरवा। सो स्वरूप नृपकन्या देखा। मर्कट बदन भयंकर देही। देखत हृदय क्रोध भा तेही। जेहि दिसि बैठे नारद फूली। सो दिसि तेहिन विलोकी भूली। पुनि पुनि मुनि उकसहिं अकुलाहीं। देखि दशा हर गान मुसुकाहीं।
उत्तर :
हास्य रस।

3. मुहावरे :

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) अपना उल्लू सीधा करना।
अर्थ : अपना स्वार्थ सिद्ध करना।
वाक्य : रमेश से समाज के हित की उम्मीद करना व्यर्थ है, वह हमेशा अपना उल्लू सीधा करने में लगा रहता है।

(2) दिन दूना रात चौगुना बढ़ना।
अर्थ : दिन प्रतिदिन अधिक उन्नति करना।
वाक्य : जब से मुनीम जी की सलाह से सेठ करोड़ीमल ने काम-काज शुरू किया है, तब से उनका धंधा दिन दूना रात चौगुना बढ़ता जा रहा है।

4. काल परिवर्तन :

प्रश्न 1.
निम्नलिखित वाक्यों के साथ दी गई सूचना के अनुसार काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) तुमने मुझे विश्वास दिया है। (अपूर्ण वर्तमानकाल)
(2) राह में अँधेरा है। (सामान्य भविष्यकाल)
(3) नर-नारी साथ निकलेंगे। (पूर्ण भूतकाल)
उत्तर :
(1) तुम मुझे विश्वास दे रहे हो।
(2) राह में अँधेरा होगा।
(3) नर-नारी साथ निकले थे।

नवनिर्माण Summary in Hindi

नवनिर्माण कवि का परिचय

नवनिर्माण कवि का नाम : त्रिलोचन। वास्तविक नाम वासुदेव सिंह। (जन्म 20 अगस्त, 1917; निधन 2007.)

प्रमुख कृतियाँ : धरती, दिगंत, गुलाब और बुलबुल, उस जनपद का कवि हूँ, सब का अपना आकाश (कविता संग्रह); देशकाल (कहानी संग्रह) तथा दैनंदिनी (डायरी) आदि।

विशेषता : काव्यक्षेत्र में प्रयोग धर्मिता के समर्थक। समाज के दबे-कुचले वर्ग को संबोधित करने वाले साहित्य के रचयिता।

विधा : चतुष्पदी। इस विधा में चार चरणों वाला छंद होता है। यह चौपाई की तरह होता है। इसके प्रथम, द्वितीय और चतुर्थ चरण में तुकबंदी होती है। भाव और विचार की दृष्टि से प्रत्येक चतुष्पदी अपने आप में पूर्ण होती है।

विषय प्रवेश : प्रस्तुत पद्य पाठ में कुल आठ चतुष्पदियाँ दी गई हैं। ये सभी चतुष्पदियाँ भाव एवं विचार की दृष्टि से अपने आप में पूर्ण है। इन चतुष्पदियों में आशावादी दृष्टिकोण प्रस्तुत किया गया है। कवि ने इनके माध्यम से संघर्ष करने तथा अन्याय, अत्याचार, विषमता और निर्बलता पर विजय पाने का आवाहन किया है।

नवनिर्माण चतुष्पदियों का सरल अर्थ

(1) तुमने विश्वास ……………………………….. आकाश दिया है मुझको।
मनुष्य के जीवन में किसी का विश्वास प्राप्त करने तथा किसी से प्रोत्साहन पाने का बड़ा महत्त्व होता है। इनके बल पर मनुष्य बड़े-बड़े काम कर डालता है।

कवि कहते हैं कि, तुमने मुझे जो विश्वास और प्रेरणा दी है वह मेरे लिए बहुत ही महत्त्वपूर्ण है। इन्हें देकर तुमने मुझे असीम संसार दे दिया है। पर मैं इन्हें इस तरह सँभाल कर अपने पास रखूगा कि मैं आकाश में न उहूँ और मेरे पाँव हमेशा जमीन पर रहें। अर्थात मुझे अपनी मर्यादा का हमेशा ध्यान रहे।

(2) सूत्र यह तोड़ ……………………………….. छोड़ नहीं सकते।

कवि मनुष्य के बारे में कहते हैं कि वह चाहे कितना ही बड़ा क्यों न हो जाए, आकाश में उड़ानें भरता हो या अन्य कहीं उड़ कर चला जाए, पर अंत में उसे अपनों के बीच यानी धरती पर तो आना ही पड़ता है। कवि कहते हैं कि, यह बात शाश्वत सत्य है। इस सच्चाई को कोई नियम तोड़-मरोड़ कर झूठा साबित नहीं कर सकता। अर्थात मनुष्य कितना भी आडंबर क्यों न कर ले, पर वह अपनी वास्तविकता को छोड़ नहीं सकता।

(3) सत्य है ……………………………….. सामने अँधेरा है।
कवि संघर्ष करने का आवाहन करते हुए कहते हैं कि आपकी राह अँधेरों से भरी हुई है; भले यह बात सच हो या आपकी प्रगति के द्वार को अवरुद्ध करने के लिए तरह-तरह की कठिनाइयाँ रास्ते में आ रही हों, तब भी आपको संघर्ष के मार्ग पर रुकना नहीं है।

अँधेरे में भी आगे ही आगे बढ़ते जाना है, क्योंकि इसके अलावा आपके सामने और कोई चारा भी तो नहीं है। कवि का कहने का तात्पर्य यह है कि संघर्ष करना जारी रखना चाहिए। संघर्ष से ही सफलता का मार्ग प्रशस्त होता है।

(4) बल नहीं होता ……………………………….. “दिलाने के लिए।

कवि कहते हैं कि मनुष्य को निरर्थक कार्यों के लिए अपने बल का प्रयोग नहीं करना चाहिए। उसका प्रयोग सार्थक कार्यों के लिए होना चाहिए। वे कहते हैं कि मनुष्य के पास बल किसी असहाय, पीड़ित व्यक्ति को सताने के लिए नहीं होता। बल्कि वह किसी असहाय या पीड़ित व्यक्ति की रक्षा करने के लिए होता है। कवि बलवान व्यक्तियों को संबोधित करते हुए कहते हैं, यदि ईश्वर ने तुम्हें शक्ति प्रदान की है, तो तुम सभी कमजोर लोगों के बल बन ३ कर उनको न्याय दिलाने के काम में लग जाओ। तभी तुम्हारे बल की सार्थकता है।

(5) जिसको मंजिल ……………………………….. वही कहता है।

कवि कहते हैं कि जिस व्यक्ति को अपनी सफलता की मंजिल की जानकारी हो जाती है, वह व्यक्ति अपने मार्ग में आने वाली परेशानियों से नहीं डरता। वह हँसते-हँसते इन परेशानियों को झेल लेता है। ऐसे व्यक्तियों को ही जीवन में सफलता मिलती है। इस तरह सफलता के शिखर पर पहुँचने वाले व्यक्ति समाज के लिए इतिहास बन जाते हैं और लोग उससे प्रेरणा लेते हैं।

(6) प्रीति की राह ……………………………….. चले आओ।
कवि प्यार-मोहब्बत और अच्छे आचार-व्यवहार को अपनाने की बात करते हुए लोगों का आवाहन करते हैं कि वे सब के साथ प्यार-मोहब्बत से रहें और सब के साथ अच्छा व्यवहार करें। यही सब के लिए अपनाने वाला सही मार्ग है। वे कहते हैं कि सब को हँसते-गाते जीवन जीने का मार्ग अपनाना चाहिए।

(7) साथ निकलेंगे ……………………………….. “समाज नर-नारी।
कवि स्त्री-पुरुष समानता की बात करते हुए कहते हैं कि स्त्री पुरुष दोनों एक साथ मिल कर विकट समस्याओं को सुलझाने का कार्य करेंगे। दोनों इस दिशा में कंधे से कंधा मिलाकर काम करेंगे और नए समाज की रचना करेंगे, जिसमें सब को समानता का अधिकार मिले।

(8) वर्तमान बोला……………………………….. गीत अच्छा था।

कवि वर्तमान और अतीत की बात करते हुए कहते हैं कि वर्तमान के अनुसार बीता हुआ समय अच्छा था। उस समय जीवन पथ में साथ निभाने वाले अच्छे मित्र थे। वर्तमान कहता है कि भविष्य में (जब हम अतीत हो जाएँगे और) लोग हमारा भी गुणगान करेंगे। वैसे अतीत भी गुणगान करने लायक था।

नवनिर्माण शब्दार्थ

• व्योम = आकाश
• सहचर = साथ-साथ चलने वाला, मित्र
• सिद्धि = सफलता
• मीत = मित्र, दोस्त