Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 7 Assignment Problem and Sequencing Ex 7.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 7 Assignment Problem and Sequencing Ex 7.2
Question 1.
A machine operator has to perform two operations, turning and threading on 6 different jobs. The time required to perform these operations (in minutes) for each job is known. Determine the order in which the jobs should be processed in order to minimize the total time required to complete all the jobs. Also, find the total processing time and idle times for turning and threading operations.
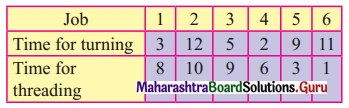
Solution:
Let turning to be A and threading be B.
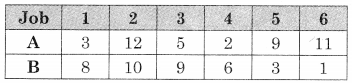
∴ Observe Min{A, B} = 1 for job 6 on B.
![]()
Then the problem reduces to
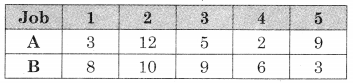
∴ Now Min {A, B} = 2 for job 4 on A
![]()
Then the problem reduce to

Now Min {A, B} = 3 for job 1 on A and job 5 on B
![]()
Then the problem reduces to

Now Min {A, B) = 5 for job 3 on A
![]()
Only job 2 is left so the optimal sequence is
![]()
Worktable is given by
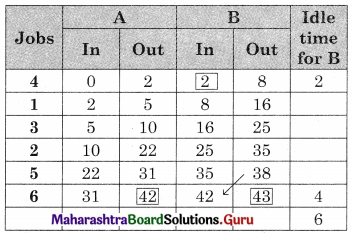
Total elapsed time = 43 minutes
Idle time for A (turning) = 43 – 42 = 1 min
Idle time for B (threshing) = 2 + 4 = 6 min
![]()
Question 2.
A company has three jobs on hand, Each of these must be processed through two departments, in the AB where
Department A: Press shop and
Department B: Finishing
The table below gives the number of days required by each job each department
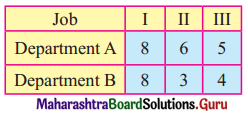
Find the sequence in which the three jobs should be processed so as to take minimum time to finish all the three jobs. Also find idle time for both the departments.
Solution:
Observe Min {A, B} = 3 for job II on B.
![]()
Then the problem is reduced to
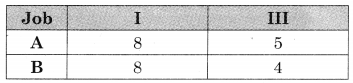
Now Min {A, B} = 4 for job III at B
![]()
Now only job I in left
∴ the optimal sequence is given by
![]()
The work table is
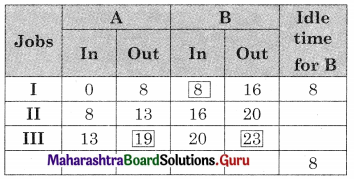
Total elapsed time = 23 days
Idle time for A = 23 – 19 = 4 days
Idle time for B = 8 days
![]()
Question 3.
An insurance company receives three types of policy application bundles daily from its head office for data entry and filing. The time (in minutes) required for each type for these two operations is given in the following table:
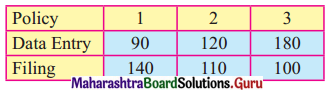
Find the sequence that minimizes the total time required to complete the entire task. Also, find the total elapsed time and idle times for each operation.
Solution:
Let Data entry be A and filing be B. So
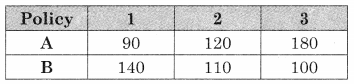
Observe min {A, B} = 90 for policy 1 at A
![]()
Then the problem reduces to

Observe min {A, B} = 100 for policy 3 at B
![]()
Now only policy 2 is left
∴ The optimal sequence is
![]()
Worktable
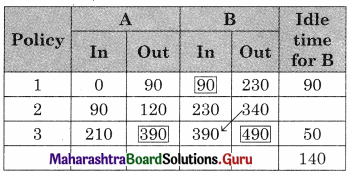
So Total elapsed time = 490 min
Idle time for A (data entry) = 490 – 390 = 100 min
Idle time for B (filing) = 140 min.
![]()
Question 4.
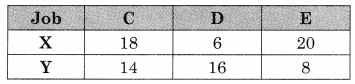
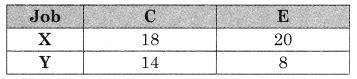
There are five jobs, each of which must go through two machines in the order XY. Processing times (in hours) are given below. Determine the sequence for the jobs that will minimize the total elapsed time. Also, find the total elapse time and idle time for each machine.
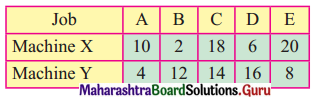
Solution:
Observe min {x, y} = 2 for job B on x
![]()
The problem reduces to
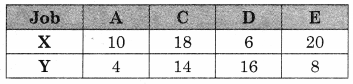
Now min [x, y] = 4 for job A on x
![]()
The problem reduces to
Now min [x, y] = 6 for job D on x
![]()
The problem reduces to
![]()
Now min [x, y] = 8 for job E on y
Now only job C in left
∴ The optimal sequence is
![]()
Worktable
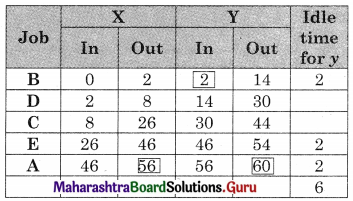
Total elapsed time = 60 hrs
Idle time for X = 60 – 56 = 4 hrs
Idle time for Y = 6 hrs
![]()
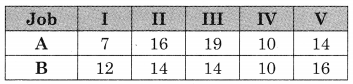
Question 5.
Find the sequence that minimizes the total elapsed time to complete the following jobs in the order AB. Find the total elapsed time and idle times for both machines.
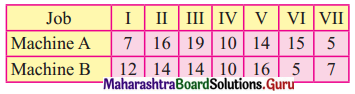
Solution:
Observe min {A, B} = 5 for job VI for B and job VII for A
![]()
The problem reduces to
Now min {A, B] = 7 for job I on A
![]()
The problem reduces to
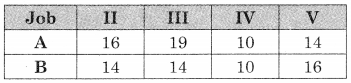
Now min {A, B] = 10 for job IV on A and B so we have two options.
![]()
Or
![]()
we take the 1st one.
The problem reduces to

Now min {A, B} = 14 for job V on A and job II and III for job B.
∴ We have
![]()
Or
![]()
We take the optimal sequence as.
VII – I – IV – V – III – II – VI
Worktable
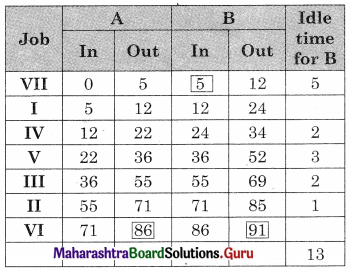
Total elapsed time = 91 units
Idle time for A = 91 – 86 = 5 units
Idle time for B = 13 units
![]()
Question 6.
Find the optimal sequence that minimizes the total time required to complete the following jobs in the order ABC. The processing times are given in hrs.
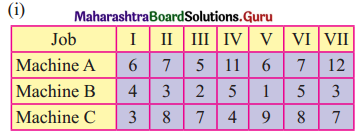
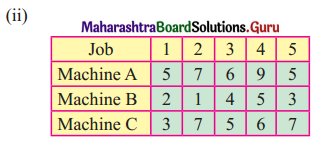
Solution:
(i) Min A = 5, Max B = 5
As min A ≥ max B.
The problem can be converted into two machine problems.
Let G and H be two fictitious machines such that G = A + B and H = B + C we get
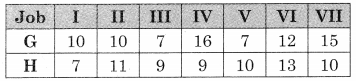
Now min {G, H} = 7 for job III & V for G and job I for H
∴ We have two options
![]()
Or
![]()
We take the first one
The problem reduces to
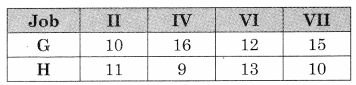
Min {G, H} = 9 for job IV on H
![]()
The problem reduces to
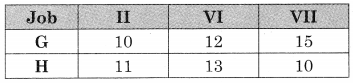
Now min {G, H} = 10 for job II for G and job VII for H
![]()
Now job VI is left
∴ The optimal sequence is
![]()
The work table is
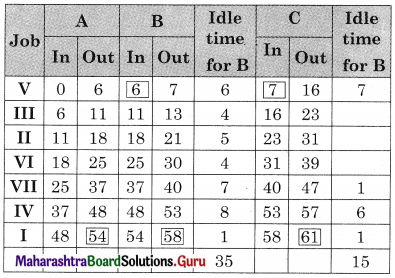
Total elapsed time = 61 hrs
Idle time for A = 61 – 54 = 7 hrs
Idle time for B = 35 + [61 – 58] = 38 hrs
Idle time for C = 15 hrs
![]()
(ii) Min A = 5, Max B = 5
Min A ≥ Max B.
The problem can be converted into two machine problems.
Let G and H be two fictitious machines such that G = A + B and H = B + C we get
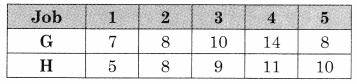
Now min {G, H} = 5 for job 1 for H.
![]()
The problem reduces to
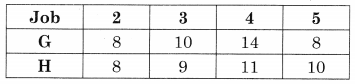
Now min {G, H} = 8 for job 2 for G and job H also job 5 for G
∴ We have two options
![]()
Or
![]()
We take the first one
The problem reduces to
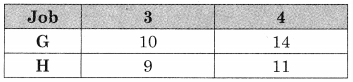
Now min {G, H} = 9 for job 3 for H
![]()
Now only job 4 is left
∴ The optimal sequence is
![]()
Worktable
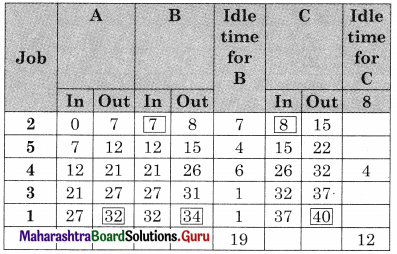
Total elapsed time = 40 hrs
Idle time for A = 40 – 32 = 8 hrs
Idle time for B = 19 + [40 – 34] = 25 hrs
Idle time for C = 12 hrs
![]()
Question 7.
A publisher produces 5 books on Mathematics. The books have to go through composing, printing, and binding was done by 3 machines P, Q, E. The time schedule for the entire task in the proper unit is as follows.
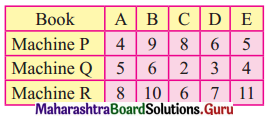
Determine the optimum time required to finish the entire task.
Solution:
Min R = 6, Max Q = 6
As min R ≥ max Q.
The problem can be converted into a two-machine problem.
Let G and H be two fictitious machines such that G = P + Q and H = Q + R we get
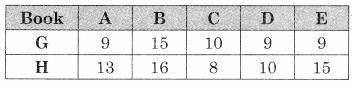
Min {G, H} = 9 for books A, D, E for G.
∴ We have more than one option we take
![]()
The problem reduces to

Min {G, H} = 8 for book C on H
![]()
Now only B is left. So the optimal sequence is
![]()
Worktable
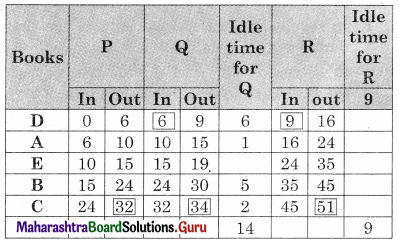
Total elapsed time = 51 units
Idle time for P = 51 – 32 = 19 units
Idle time for Q = 14 + [51 – 34] = 31 units
Idle time for R = 9 units