Maharashtra Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.3

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.3

Question 1.
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of (i) 2 successes (ii) at least 3 successes (iii) at most 2 successes.
Solution:
X: Getting an odd no.
p: Probability of getting an odd no.
A die is thrown 4 times
∴ n = 4
∵ p = \(\frac{3}{6}=\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
∵ X ~ B(3, \(\frac{1}{2}\))
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
(i) P(Two Successes)

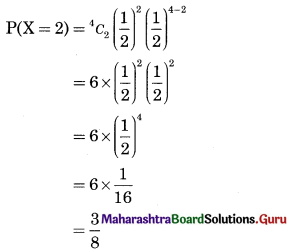
(ii) P(Atleast 3 Successes)

(iii) P(Atmost 2 Successes)

Question 2.
A pair of dice is thrown 3 times. If getting a doublet is considered a success, find the probability of two successes.
Solution:
n: No. of times die is thrown = 3
X: No. of doublets
p: Probability of getting doublets
Getting a doublet means, same no. is obtained on 2 throws of a die
There are 36 outcomes
No. of doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)

Question 3.
There are 10% defective items in a large bulk of items. What is the probability that a sample of 4 items will include not more than one defective item?
Solution:
n: No of sample items = 4
X: No of defective items
p: Probability of getting defective items
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
X ~ B(4, 0.1)
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} \mathrm{q}^{n-x}\)
P(Not include more than 1 defective)
P(X ≤ 1) = p(0) + p(1)
= ⁴C₀ (0.1)⁰ (0.9)⁴ + ⁴C₁ (0.1)¹ (0.9)^4-1
= 1 × 1 × (0.9)⁴ + 4 × 0.1 × (0.9)³
= (0.9)³ [0.9 + 0.4]
= (0.9)³ × 1.3
= 0.977

Question 4.
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Find the probability that (i) all the five cards are spades, (ii) only 3 cards are spades, (iii) none is a spade.
Solution:
X: No. of spade cards
Number of cards drawn
∴ n = 5
p: Probability of getting spade card

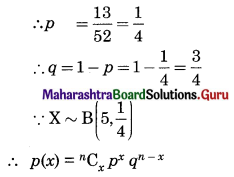
(i) P(All five cards are spades)

(ii) P(Only 3 cards are spades)

(iii) P(None is a spade)

Question 5.
The probability that a bulb produced by a factory will use fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of (i) X = 0, (ii) X ≤ 1, (iii) X > 1, (iv) X ≥ 1.
Solution:
X : No. of bulbs fuse after 200 days of use
p : Probability of getting fuse bulbs
No. of bulbs in a sample
∴ n = 5
∴ p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
∵ X ~ B(5, 0.2)
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
(i) P(X = 0) = ⁵C₀ (0.2)⁰ (0.8)^5-0
= 1 × 1 × (0.8)⁵
= (0.8)⁵

(ii) P(X ≤ 1) = p(0) + p(1)
= ⁵C₀ (0.2)⁰ (0.8)^5-0 + ⁵C₁ (0.2)¹ (0.8)^5-1
= 1 × 1 × (0.8)⁵ + 5 × 0.2 × (0.8)⁴
= (0.8)⁴ [0.8 + 1]
= 1.8 × (0.8)⁴

(iii) P(X > 1) = 1 – [p(0) + p(1)]
= 1 – 1.8 × (0.8)⁴

(iv) P(X ≥ 1) = 1 – p(0)
= 1 – (0.8)⁵

Question 6.
10 balls are marked with digits 0 to 9. If four balls are selected with replacement. What is the probability that none is marked 0?
Solution:
X : No. of balls drawn marked with the digit 0
n : No. of balls drawn
∴ n = 4
p : Probability of balls marked with 0.
∴ p = \(\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
p(x) = \({ }^{n} C_{x} p^{x} q^{n-x}\)
P(None of the ball is marked with digit 0)

Question 7.
In a multiple-choice test with three possible answers for each of the five questions, what is the probability of a candidate getting four or more correct answers by random choice?
Solution:
n: No. of Questions
∴ n = 5
X: No. of correct answers by guessing
p: Probability of getting correct answers

Question 8.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solution:
X : No. of sixes in 6 throws
n : No. of times dice thrown
∴ n = 6
p : Probability of getting six
∴ p = \(\frac{1}{6}\)
∴ q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
∵ X ~ B(6, \(\frac{1}{6}\))
∴ p(x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
P(At most 2 sixes)
P(X ≤ 2) = p(0) + p(1) + p(2)

Question 9.
Given that X ~ B(n, p),
(i) if n = 10 and p = 0.4, find E(X) and Var(X).
(ii) if p = 0.6 and E(X) = 6, find n and Var(X).
(iii) if n = 25, E(X) = 10, find p and Var(X).
(iv) if n = 10, E(X) = 8, find Var(X).
Solution:
∵ X ~ B (n, p), E(X) = np, V(X) = npq, q = 1 – p
(i) E(X) = np = 10 × 0.4 = 4
∵ q = 1 – p = 1 – 0.4 = 0.6
V(X) = npq = 10 × 0.4 × 0.6 = 2.4

(ii) ∵ p = 0.6
∴ q = 1 – p = 1 – 0.6 = 0.4
E(X) = np
∴ 6 = n × 0.6
∴ n = 10
∴ V(X) = npq = 10 × 0.6 × 0.4 = 2.4

(iii) E(X) = np
∴ 10 = 25 × p
∴ p = 0.4
∴ q = 1, p = 1 – 0.4 = 0.6
∴ S.D.(X) = √V(X)
= \(\sqrt{n p q}\)
= \(\sqrt{25 \times 0.4 \times 0.6}\)
= √6
= 2.4494

(iv) ∵ E(X) = np
∴ 8 = 10p
∴ p = 0.8
∴ q = 1 – p = 1 – 0.8 = 0.2
∵ V(X) = npq = 10 × 0.8 × 0.2 = 1.6