Class 12

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 7 Plant Growth and Mineral Nutrition Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 7 Plant Growth and Mineral Nutrition

1. Multiple choice questions

Question 1.
Which of the hormone can replace vernalization?
(a) Auxin
(b) Cytokinin
(c) Gibberellins
(d) Ethylene
Answer:
(c) Gibberellins

Question 2.
The principle pathway of water translocation in angiosperms is ………………..
(a) Sieve cells
(b) Sieve tube elements
(c) Xylem
(d) Xylem and phloem
Answer:
(c) Xylem

Question 3.
Abscissic acid controls ………………..
(a) cell division
(b) leaf fall and dormancy
(c) shoot elongation
(d) cell elongation and wall formation
Answer:
(b) leaf fall and dormancy

Question 4.
Which is employed for artificial ripening of banana fruits?
(a) Auxin
(b) Ethylene
(c) Cytokinin
(d) Gibberellin
Answer:
(b) Ethylene

Question 5.
Which of the following is required for stimulation of flowering in plants?
(a) Adequate oxygen
(b) Definite photoperiod
(c) Adequate water
(d) Water and minerals
Answer:
(b) Definite photoperiod

Question 6.
For short day plants, the critical period is ………………..
(a) light
(b) dark/night
(c) UV rays
(d) Both (a) and (c)
Answer:
(b) dark/night

Question 7.
Which of the following is NOT day neutral plant?
(a) Tomato
(b) Cotton
(c) Sunflower
(d) Soybean
Answer:
(d) Soybean

Question 8.
Essential macro elements are ………………..
(a) manufactured during photosynthesis
(b) produced by enzymes
(c) obtained from soil
(d) produced by growth hormones
Answer:
(c) obtained from soil

Question 9.
Function of Zinc is ………………..
(a) closing of stomata
(b) biosynthesis of 3-IAA
(c) synthesis of chlorophyll
(d) oxidation of carbohydrates
Answer:
(b) biosynthesis of 3-LAA

Question 10.
Necrosis means ………………..
(a) yellow spot on the leaves
(b) death of tissue
(c) darkening of green colour in leaves
(d) wilting of leaves
Answer:
(b) death of tissue

Question 11.
Conversion of nitrates to nitrogen is called ………………..
(a) ammonification
(b) nitrification
(c) nitrogen fixation
(d) denitrification
Answer:
(d) denitrification

Question 12.
How many molecules of ATP are required to fix one molecule of nitrogen?
(a) 12
(b) 20
(c) 6
(d) 16
Answer:
(d) 16

2. Very short answer questions

Question 1.
Enlist the phases of growth in plants.
Answer:
The three phases of growth are phase of cell division, phase of cell enlargement and phase of cell maturation.

Question 2.
Give full form of IAA.
Answer:
Full form is Indole Acetic Acid.

Question 3.
What does it mean by ‘open growth’?
Answer:
In plants the growth is indeterminate and takes place throughout the life at specific regions having meristems.

Question 4.
Plant stress hormone.
Answer:
Abscissic acid.

Question 5.
What is denitrification?
Answer:
Anaerobic bacteria can convert nitrates of soil back into nitrogen gas. That process performed by denitrifying bacteria is denitrification.

Question 6.
Bacteria responsible for conversion of nitrite to nitrate.
Answer:
Nitrobacter.

Question 7.
What is the role of gibberellins in rosette plants?
Answer:
In rosette plants like beet and cabbage, bolting, i.e. elongation of internodes before flowering is observed due to effect of gibberellins.

Question 8.
Vernalization
Answer:
The response of plant to the influence of low temperature on flowering in plants is called vernalization.

Question 9.
Photoperiodism
Answer:
The response of plant to the influence of light for initiation of flowering is known as photoperiodism.

Question 10.
What is grand period of growth?
Answer:
There are three phases of growth and the total time required for all phases to occur is called grand period of growth.

3. Short Answer Questions

Question 1.
(i) Differentiation
Answer:

1. It is a process of maturation of cells derived from apical meristems.
2. Differentiation is a permanent change in structure and function of cells that leads to its maturation.
3. Cell undergoes major anatomical and physiological change during differentiation process.
4. In hydrophytic plants parenchyma cells develop large schizogenous cavities which help them in aeration, buoyancy and mechanical support.

(ii) Redifferentiation
Answer:

1. It is a process in which cells produced by de-differentiation lose their capacity of division and become mature.
2. The cells mature to perform specific function.
3. Interfascicular cambium is formed by process of dedifferentiation loses its capacity to divide.
4. Secondary xylem and secondary phloem is formed form this cambium in vascular cylinder.

Question 2.
Arithmetic growth and Geometric growth
Answer:

Arithmetic growth	Geometric growth
1. In arithmetic growth only one daughter cell continues to divide, while the other undergoes differentiation and maturation.	1. In geometric growth both the daughter cells continue to divide and redivide again and again.
2. Rate of growth is constant.	2 Rate growth is initially slow but later on rapid rate.
3. Linear curve is obtained.	3. Exponential curve is obtained.
4. Mathematical expression is Lt = Lo + rt whereLt = length of time ‘t’ Lo = Length at time zero rt = growth rate, t = time of growth	4. Mathematical expression is Wt = Woe rt where, Wt = final size, Wo = initial size, r = growth rate, t = time of growth E = base of natural logarithm
5. e.g. Elongation of root	5. e.g. Divisions of zygote during embryo development.

Question 3.
Enlist the role and deficiency symptoms of: (a) nitrogen (b) phosphorus (c) potassium.
Answer:
(a) Nitrogen:
Role : Constituent of proteins as amino acids, nucleic acids, vitamins, hormones, coenzymes, ATP and chlorophyll molecule.
Deficiency symptoms : stunted growth and chlorosis.

(b) Phosphorus:
Role : Constituent of cell membrane, certain proteins, nucleic acids and nucleotides, required for all phosphorylation reactions.
Deficiency symptoms : Poor growth, leaves dull green

(c) Potassium :
Role : Determination of anion – cation balance in cell, necessary for protein synthesis, involved in formation of cell membrane, opening and closing of stomata, activates enzymes, helps in maintenance of turgidity of cells.
Deficiency symptom : Yellow edges in leaves, premature death.

Question 4.
What is short day plant? Give any two examples.
Answer:
The plants which flower when the day length or light period is shorter than the critical photoperiod are called short day plants or SDP
SDPs usually flower during winter and late summer.
Examples – Dahlia, Aster, Tobacco, Chrysanthemum, Soybean (Glycine max) and Cocklebur (Xanthium).

Question 5.
What is vernalization? Give its significance.
Answer:
A low temperature or chilling treatment that induces early flowering in plants is known as vernalization.

Significance:

1. Due to chilling treatment crops can be produced earlier.
2. Crops can be grown in areas where they do not grow naturally.

4. Long answer questions

Question 1.
Explain sigmoid growth curve with the help of diagram.
Answer:

1. When growth occurs in plants three distinct phases of growth are noticed.
2. Phase of cell formation is first phase where meristematic cells divide and new cells added.
3. In phase of cell enlargement newly formed cells elongate and with turgidity there is cell enlargement.
4. In phase of cell maturation cells get differentiated.
5. When we compare the growth rate it differs in these three phases.
6. In first phase or lag phase it is slow, while in log phase or exponential phase, growth rate accelerates and it reaches maximum.
7. In stationary phase of maturation growth rate slows down and comes to steady state.
8. When this changing rate of growth is plotted against time duration in a graph a sigmoid or S-shaped growth curve is obtained.

Question 2.
Describe the types of plants on the basis of photoperiod required, with the help of suitable examples.
Answer:

1. Effect of light duration on flowering of plants is known as photoperiodism.
2. Depending on photoperiodic response, plants are categorised into three types – Short day plants, long day plants and day neutral plants.

1. Short day plants : Plants that flower under short day length conditions are called short day plants. Plants such as Dahlia, Xanthium, Soybean, Aster, Tobacco and Chrysanthemum are short day plants or SDR. Short day plants require a long uninterrupted dark period for flowering. Therefore, they are also called long night plants.

2. Long day plants : Plants that flower only when they are exposed to light period longer than their critical photoperiod are called long day plants or LDP Long day plants require a short dark or night period for flowering. Hence, they are also called short night plants. Plants such as radish, spinach, wheat, poppy, cabbage, pea, sugar beet, etc. are long day plants.

3. Day neutral plants : Plants in which the flowering is not affected by the day length period are called day neutral plants or DNP or photoneutral plants. Plants such as cucumber, sunflower, cotton, balsam, maize, tomato, etc. are day neutral plants.

Question 3.
Explain biological nitrogen fixation with example.
Answer:

1. Conversion of atmospheric nitrogen into nitrogenous salts to make it available to plants for its update is described as nitrogen fixation.
2. When living organisms are involved in nitrogen fixation process it is known as biological nitrogen fixation.
3. The process is mainly carried out by prokaryotic organisms, i.e. different kinds of bacteria present in soil.
4. The nitrogen fixing organisms are known as diazotrophs or nitrogen fixers and about 70% nitrogen is fixed by them.
5. The nitrogen fixers are either free living bacteria or symbiotic associated with other higher plants e.g. Rhizobium.
6. The cyanobacteria have specialized cells heterocysts which help in process of nitrogen fixation.
7. Nitrogen fixation is high energy requiring process and 16 ATP molecules are needed for fixation of one molecule of nitrogen to ammonia.
8. Soil bacteria like Nitrosomonas, Nitrosocyccus convert ammonia to nitrate and the Nitrobacter convert nitrite to nitrate. This is known as nitrification, biological oxidation.
9. These bacteria are chemoautotrophic and utilize these processes for their metabolism.
10. Fabaceae plants like pea, bean have root nodules which harbour symbiotic bacterium Rhizobium which fixes nitrogen. It is host specific, soil bacterium, Nitrogen is made available to host plant.

Question 4.
Write on macro and micro nutrients required for plant growth.
Answer:

1. Plants absorb mineral nutrients from their surroundings.
2. For a proper growth of plants about 35 to 40 different elements are required.
3. Plants absorb these nutrients in ionic or dissolved form from soil with their root system e.g. Phosphorus as PO₄^–, Sulphur as SO₄^2- etc.
4. Based on their requirement in quantity, they are classified as major nutrients or macronutrients and those needed in small amounts Eire minor or micronutrients.
5. Macroelements are required in large amounts, as they play nutritive and structural roles e.g. C, H, O, R Mg, N, K, S and Ca. – Ca pectate cell wall component, Mg component of chlorophyll.
6. C, H, O are non-mineral major elements obtained from air and water e.g. CO₂ is source of carbon, Hydrogen from water.
7. Microelements are required in traces as they mainly have catalytic role as co-factors or activators of enzymes.
8. Microelements may be needed for certain activity in life cycle of plant e.g. B for pollen germination, Si has protective role during stress conditions and fungal attacks, Al enhances availability of phosphorus.
9. The important micronutrients for plant growth are Mn, B, Cu, Zn, Cl.

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 6 Plant Water Relation Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 6 Plant Water Relation

1. Multiple Choice Questions

Question 1.
In soil, water available for absorption by root is ……………..
(a) gravitational water
(b) capillary water
(c) hygroscopic water
(d) combined water
Answer:
(b) capillary water

Question 2.
The most widely accepted theory for ascent of sap is ……………..
(a) capillarity theory
(b) root pressure theory
(c) diffusion
(d) transpiration pull theory
Answer:
(d) transpiration pull theory

Question 3.
Water movement between the cells is due to ……………..
(a) T.E
(b) W.P
(c) D.P.D.
(d) incipient plasmolysis
Answer:
(c) D.P.D.

Question 4.
In guard cells, when sugar is converted into starch, the stomata pore ……………..
(a) closes almost completely
(b) opens partially
(c) opens fully
(d) remains unchanged
Answer:
(a) closes almost completely

Question 5.
Surface tension is due to ……………..
(a) diffusion
(b) osmosis
(c) gravitational force
(d) cohesion
Answer:
(d) cohesion

Question 6.
Which of the following type of solution has lower level of solutes than the solution?
(a) Isotonic
(b) Hypotonic
(c) Hypertonic
(d) Anisotonic
Answer:
(b) Hypotonie

Question 7.
During rainy season wooden doors warp and become difficult to open or to close because of ……………..
(a) plasmolysis
(b) imbibition
(c) osmosis
(d) diffusion
Answer:
(b) imbibition

Question 8.
Water absorption takes place through ……………..
(a) lateral root
(b) root cap
(c) root hair
(d) primary root
Answer:
(c) root hair

Question 9.
Due to low atmospheric pressure the rate of transpiration will ……………..
(a) increase
(b) decrease rapidly
(c) decrease slowly
(d) remain unaffected
Answer:
(a) increase

Question 10.
Osmosis is a property of ……………..
(a) solute
(b) solvent
(c) solution
(d) membrane
Answer:
(c) solution

2. Very short answer question

Question 1.
What is osmotic pressure?
Answer:
The pressure exerted due to osmosis is osmotic pressure.

Question 2.
Name the condition in which protoplasm of the plant cell shrinks.
Answer:
Plasmolysis

Question 3.
What happens when a pressure greater than the atmospheric pressure is applied to pure water or a solution?
Answer:
When a pressure greater than the atmospheric pressure is applied to pure water or a solution then water potential of pure water or solution increases.

Question 4.
Which type of solution will bring about deplasmolysis ?
Answer:
Placing a plasmolysed cell in hypotonic solution will bring about deplasmolysis.

Question 5.
Which type of plants have negative root pressure?
Answer:
Plants showing excessive transpiration have negative root pressure.

Question 6.
In which conditions transpiration pull will be affected?
Answer:
Due to temperature fluctuations during day and night gas bubbles may be formed which affects transpiration pull.

Question 7.
Mention the shape of guard cells in Cyperus.
Answer:
Kidney shaped and dumbbell shaped guard cells are seen.

Question 8.
Why do diurnal changes occur in osmotic potential of guard cells?
Answer:
Enzyme activity of phosphorylase converts starch into sugar during daytime and sugar is converted to starch during night. This causes changes in osmotic potential of guard cells.

Question 9.
What is symplast pathway?
Answer:
When water is absorbed by root hair it passes across from one living cell to other living cell through the plasmodesmatal connections between them, then it is called symplast pathway across the root.

3. Answer the Following Questions

Question 1.
Describe mechanism of absorption of water.
Answer:

1. The absorption of water takes place by two modes, i.e. active absorption and passive absorption.
2. Passive absorption is the chief method of absorption (98%).
3. There is no expenditure of energy in passive absorption.
4. Transpiration pull is a driving force and water moves depending upon concentration gradient. Water is pulled upwards.
5. It occurs during daytime when there is active transpiration.
6. Active absorption occurs usually during night time as due to closure of stomata transpiration stops.
7. Water absorption is against D.ED. gradient, A.T.R energy is required which is available from respiration.
8. Active absorption may be osmotic or non- osmotic type.
9. For osmotic absorption root pressure has a role.

Question 2.
Discuss theories of water translocation.
Answer:

1. Translocation of water is transport of water along with dissolved minerals from roots to aerial parts.
2. The movement is against the gravity and described as ascent of sap.
3. The translocation occurs through lumen of water conducting tissue xylem mainly vessels and tracheids.
4. Different theories have been discussed for translocation mechanism like vital force theory (Root pressure), relay pump, physical force (capillary), etc.
5. Cohesion tension theory or transpiration pull theory is most widely accepted theory.

Question 3.
What is transpiration? Describe mechanism of opening and closing of stomata.
Answer:

1. The loss of water in the form of vapour is called transpiration.
2. Stomatal transpiration is a main type of transpiration where minute pores are concerned with it.
3. Stomata are bounded by two guard cells which in turn are surrounded by accessory cells.
4. Opening and closing of stomata is controlled by turgidity of guard cells.
5. When guard cells become turgid due to endosmosis their lateral thin and elastic wall bulges or stretch out.
6. The inner thick and inelastic wall is pulled apart, thus the stoma opens during daytime.
7. At night when guard cells become flaccid due to exosmosis the wall relaxes and stoma closes.
8. Endosmosis and exosmosis takes place due to changes in osmotic potential of guard cells.

Question 4.
What is transpiration? Explain role of transpiration.
Answer:
Transpiration : The loss of water from plant body in the form of vapour is called transpiration.

Role of transpiration:

1. Removal of excess of water
2. Helps in passive absorption of water and minerals
3. Helps in ascent of sap – transpiration pull
4. Maintains turgor of cells
5. Imparts cooling effect by reducing temperature 90% – 93% is stomatal transpiration and hence when stomata are open gaseous exchange takes place.

Question 5.
Explain root pressure theory and its limitations.
Answer:

1. Root pressure theory is proposed by J. Pristley.
2. For translocation of water, activity of living cells of root is responsible.
3. Absorption of water by root hair is a constant and continuous process and due to this a hydrostatic pressure is developed in cortical cells.
4. Owing to this hydrostatic pressure i.e. root pressure, water is forced into xylem and further conducted upwards.
5. Root pressure is an osmotic phenomenon.

Limitation of this theory:

1. Not applicable to tall plants above 20 metres.
2. Even in absence of root pressure ascent of sap is noticed.
3. In actively transpiring plants, root pressure is not developed.
4. In taller gymnosperms, root pressure is zero.
5. Xylem sap is under tension and shows negative hydrostatic pressure.

Question 6.
Explain capillarity theory of water translocation.
Answer:

1. Capillarity theory of water translocation is proposed by Bohem.
2. Capillarity is because of surface tension and cohesive forces and adhesive forces of water molecules.
3. Xylem vessels and tracheids are tubular elements having their lumen.
4. In these elements water column exists due to combined action of cohesive and adhesive forces of water and lignified wall.
5. As a result of this capillarity water is raised upwards.

Question 7.
Why is transpiration called ‘a necessary evil’?
Answer:

1. The loss of water in the form of water vapour is called transpiration.
2. About 90 – 93% of transpiration occurs through stomata, small apertures located in the epidermis of leaves.
3. For this process stomata must remain open and then only gaseous exchange by diffusion takes places.
4. Gaseous exchange is necessary for respiration and photosynthesis. If stomata remain closed then it will affect productivity of plant.
5. The process is necessary evil because water which is important for plant is lost in the process.
6. At the same time it helps in absorption of water and its translocation. Hence it cannot be avoided.
   So Curtis has rightly called it as necessary evil.

Question 8.
Explain movement of water in the root.
Answer:

1. Root hairs absorb water by imbibition then diffusion which is followed by osmosis.
2. As water is taken inside the root hair cell it becomes turgid i.e. increase in turgor pressure (T.E)
3. Root hair cell has less D.ED. but adjacent cortical cell has more D.PD.
4. The inner cortical cell has more osmotic potential so it will suck water from root hair cell.
5. Root hair cell becomes flaccid and ready to absorb soil water.
6. Water is passed on similarly in inner cortical cells.
7. Water moves rapidly through loose cortical cells up to endodermis and through passage cells in pericycle.
8. From pericycle due to hydrostatic pressure developed it is forced into protoxylem.

Question 9.
(i) Osmosis
Answer:
It is a special type of diffusion of solvent through a semipermeable membrane.

(ii) Diffusion
Answer:
It is the movement of ions/ atoms/molecules of a substance from the region of higher concentration to the region of their lower concentration.

(iii) Plasmolysis
Answer:
Exo-osmosis in a living cell when placed in hypertonic solution is called plasmolysis.

(iv) Imbibition
Answer:
It is swelling up of hydrophilic colloids due to adsorption of water.

(v) Guttation
Answer:
The loss of water in the form of liquid is called guttation.

(vi) Transpiration
Answer:
The loss of water from plant body in the form of vapour is called transpiration.

(vii) Ascent of sap
Answer:
The transport of water with dissolved minerals in it from root to other aerial parts of plant against the gravity is called ascent of sap.

(viii) Active absorption
Answer:
Water absorption by activity of root which is against the D.PD. gradient along with expenditure of A.T.E energy generated by respiration is the process of active absorption.

(ix) Diffusion Pressure Deficit (D.P.D.)
Answer:
The difference in the diffusion pressures of pure solvent and the solvent in a solution is called diffusion pressure deficit.

(x) Turgor pressure
Answer:
It is the pressure exerted by turgid cell sap on to the cell membrane and cell wall.

(xi) Water potential
Answer:
Chemical potential of water is called water potential.

(xii) Wall pressure
Answer:
Thick and rigid cell wall exerts a counter pressure to turgor pressure developed on the cell sap is called wall pressure that operates in opposite direction.

(xiii) Root pressure
Answer:
As absorption of water by root hair being a continuous process, a sort of hydrostatic pressure is developed in living cells of root, this is called root pressure.

Question 10.
Osmotic Pressure (O.P) and Turgor Pressure (T.P)
Answer:

Osmotic Pressure (O.R)	Turgor Pressure (T.P.)
1. The pressure exerted due to osmosis is called osmotic pressure.	1. The pressure exerted by turgid cell sap on cell membrane and cell wall, is called turgor pressure.
2. It is pressure caused by water when it moves by osmosis.	2. It is pressure caused by content of cell (cell sap).
3. It is generated by the osmotic flow of water through a semipermeable membrane.	3. It is maintained by osmosis.

Question 11.
How are the minerals absorbed by the plants ?
Answer:

1. Soil is the chief source of minerals for the plants.
2. Minerals get dissolved in the soil water.
3. Minerals are absorbed by the plants in the ionic form mainly through roots.
4. Absorption of minerals is independent of water.
5. Absorbed minerals are pulled upwards along with xylem sap.
6. Mineral ions can be remobilized in the plant body form older parts to young plants E.g. Ions of S, P and N.

4. Long answer questions

Question 1.
Describe structure of root hair.
Answer:

1. Water from soil is absorbed by plants with the help of root hairs.
2. Root hairs are present in zone of absorption.
3. Epidermal cells form unicellular extensions which are short lived (ephemeral) structures i.e. root hairs.
4. Root hairs are nothing but cytoplasmic extensions of epiblema cell.
5. Root hairs are long tube like structures of about 1 to 10 mm.
6. They are colourless, unbranched and very delicate structures.
7. A large central vacuole is surrounded by thin layer of cytoplasm, plasma membrane and outer cell wall.
8. The cell wall of root hair is thin and double layered with outer layer of pectin and inner layer of cellulose which is freely permeable.

Question 2.
Write on journey of water from soil to xylem in roots.
Answer:

1. Unicellular root hairs which are tubular extensions of epiblema cells absorb readily available capillary water from soil.
2. The three physical processes imbibition, diffusion and osmosis are concerned with absorption of water.
3. Water molecules get adsorbed on cell wall of root hair (imbibition).
4. They enter the root hair cell by diffusion through cell wall which is freely permeable.
5. By process of osmosis they enter through plasma membrane which is semipermeable.
6. The root hair cell becomes turgid and hence its turgor pressure increases and D.ED. value decreases.
7. The adjacent cell of cortex has more D.ED. value as its osmotic potential is more.
8. The cortical cell thus takes water from epidermal cell which is turgid. This process goes on due to gradient of suction pressure developed from cell to cell till thin walled passage cells of endodermis.
9. From endodermis it will enter pericycle and then due to hydrostatic pressure it is forced in protoxylem cell.
10. The pathway of water is by apoplast and symplast.
11. When water passes through cell wall and intercellular spaces of cortex it is apoplast pathway.
12. When water passes across living cells through their plasmodesmatal connections it is symplast pathway.

Question 3.
Explain cohesion theory of translocation of water.
Answer:

1. This is very widely accepted theory of ascent of sap proposed by Dixon and Joly.
2. It is based on principles of adhesion and cohesion of water molecules and transpiration by plants.
3. A strong force of attraction existing between water molecules is cohesion and the force of attraction between water molecules and lignified walls of xylem elements is adhesion.
4. Ascent of sap occurs through lumen of xylem elements.
5. Owing to cohesive and adhesive forces a continuous water column is maintained in xylem from root to aerial parts i.e. leaves.
6. Transpiration occurs through stomata and transpiration pull is developed in leaf vessels.
7. This tension or pull is transmitted downwards through vein to roots which triggers ascent of sap.
8. In transpiration, water is lost in vapour form and this increases D.PD. of mesophyll cells that are near guard cells.
9. Mesophyll cells absorb water from xylem in leaf and a gradient of D.PD. or suction pressure (S. E) is set.
10. Owing to this gradient from guard cell to xylem in leaf, a transpiration pull or tension is created in xylem.
11. Hence water column is pulled upward passively against gravity.

Question 4.
Write on mechanism of opening and closing of stomata.
Answer:

1. Transpiration takes place through stomata. Turgidity of guard cells controls opening and closing of stomata
2. Turgor pressure exerted on unevenly thickened wall of guard cell is responsible for the movement.
3. The outer thin wall which is elastic is stretched out which pulls inner thick inelastic wall and thus stomata open.
4. When guard cells are flaccid that results in closure of stomata.
5. According to starch-sugar in ter conversion theory enzyme phosphorylase converts starch to sugar during daytime.
6. Sugar being osmotically active, the O.E of guard cells is increased. The water is absorbed from subsidiary cells. Due to turgidity walls are stretched and stoma opens.
7. During night-time sugar is converted to starch and hence guard cells loose water and become flaccid. Hence there is closure of stomata.
8. According to proton transport theory, the movement is due to transport of H⁺ and K⁺ ions.
9. Subsidiary cells are reservoirs of K⁺ ions. Starch is converted to malic acid which dissociate into malate and proton (H⁺) during day.
10. Proton transported to subsidiary cells and K⁺ ions are taken from it. This forms potassium malate in guard cells.
11. Potassium malate increases osmotic potential and endo osmosis occurs hence turgidity of guard cells. → stomata opens,
12. The uptake of K⁺ and Cl^– ions is stopped by abscissic acid formed during night. This changes permeability. Guard cells become hypotonic and loose water as they become flaccid stomata close.

Question 5.
What is hydroponics? How is it useful in identifying the role of nutrients?
Answer:
(1) Growing plants in aqueous (soilless) medium is known as hydroponics. [Greek word hudor = water and ponos = work]

(2) It is technique of growing plants by supplying all necessary nutrients in the water supply given to plant.

(3) A nutrient medium is prepared by dissolving necessary salts of micronutrients and macronutricnts In desired quantity and roots of plants are suspended in this liquid with appropriate support.

(4) Hydroponics is of great use in studying the deficiency symptoms of different mineral nutrients.

(5) The plants uptake mineral nutrients in the form of dissolved ions with the help of root hairs from the surrounding medium or nutrient solution supplied.

(6) While preparing the required nutricnt medium particular nutrient can be totally avoided and then the effect of lack of that nutrient can be studied in variation of plant growth.

(7) Any visible change noticed from normal structure and function of the plant is the symptom or hunger sign considered.

(8) For e.g. Yellowing of leaf is observed due to loss of chlorophyll pigments or Chiorosis is noticed if Magnesium is lacking as it is a structural componen of chlorophyll pigment.

Question 6.
Explain the active absorption of minerals.
Answer:

1. Plants absorb minerals from the soil with their root system.
2. MInerals are absorbed from the soil In the form of charged particles, positively charged cations and negatively charged anions.
3. The absorption of minerals against the concentration gradient which requires expenditure of metabolic energy is called active absorption.
4. The ATP energy derived from resp’ration in root cells Is utilized for active absrption.
5. Ions get accumulated in the root hair against the concentration gradient.
6. These ions pass into cortical cells and finally reach xylem of roots.
7. Along with the water these minerals are carried to other parts of plant.

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 5 Origin and Evolution of Life Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 5 Origin and Evolution of Life

1. Multiple Choice Questions

Question 1.
Who proposed that the first form of life could have come from pre-existing non-living organic molecules?
(a) Alfred Wallace
(b) Oparin and Haldane
(c) Charles Darwin
(d) Louis Pasteur
Answer:
(b) Oparin and Haldane

Question 2.
The sequence of origin of life may be
(a) Organic materials – inorganic materials – Eobiont – colloidal aggregates – cell.
(b) Inorganic materials – organic materials – colloidal aggregates – Eobiont – cell.
(c) Organic materials – inorganic materials – colloidal aggregates – cell.
(d) Inorganic materials – organic materials – Eobiont – colloidal aggregates – cell.
Answer:
(b) Inorganic materials – organic materials- colloidal aggregates – Eobiont – cell.

Question 3.
In Hardy-Weinberg equation, the frequency of homozygous recessive individual is represented by-
(a) p²
(b) pq
(c) q²
(d) 2pq
Answer:
(c) q²

Question 4.
Select the analogous organs.
(a) Forelimbs of whale and bat
(b) Flippers of dolphins and penguin
(c) Thorn and tendrils of bougainvillea and Cucurbita
(d) Vertebrate hearts or brains
Answer:
(b) Flippers of dolphins and penguin

Question 5.
Archaeopteryx is known as missing link because it is a fossil and share characters of both
(a) Fishes and amphibians
(b) Annelida and Arthropoda
(c) Reptiles and birds
(d) Chordates and non-chordates
Answer:
(c) Reptiles and birds

Question 6.
Identify the wrong statement regarding evolution.
(a) Darwin’s variations are small and directional.
(b) Mutations are random and non- directional.
(c) Adaptive radiations leads to divergent evolution.
(d) Mutations are non-random and directional.
Answer:
(d) Mutations are non-random and directional

Question 7.
Gene frequency in a population remain constant due to ……………….
(a) Mutation
(b) Migration
(c) Random mating
(d) Non-random mating
Answer:
(c) Random mating

Question 8.
Which of the following characteristic is not : shown by the ape?
(a) Prognathous face
(b) Tail is present
(c) Chin is absent
(d) Forelimbs are longer than hind limbs
Answer:
(b) Tail is present

Question 9.
………………. can be considered as connecting link between ape and man.
(a) Australopithecus
(b) Homo habilis
(c) Homo erectus
(d) Neanderthal man
Answer:
(a) Australopithecus

Question 10.
The Cranial capacity of Neanderthal man was ……………….
(a) 600 cc
(b) 940 cc
(c) 1400 cc
(d) 1600 cc
Answer:
(c) 1400 cc

2. Very short answer questions

Question 1.
Define
(i) Gene pool
Answer:
The sum total of genes of all individuals of interbreeding population or Mendelian population is called gene pool.

(ii) Gene frequency
Answer:
The proportion of an allele in the gene pool as compared with other alleles at the same locus is termed as gene frequency.

(iii) Organic evolution
Answer:
Organic evolution can be defined as slow, gradual, continuous and irreversible changes through which the present-day complex forms of the life developed (or evolved) from their simple pre-existing forms.

(iv) Population
Answer:
All individuals of the same species form a group which is called a population.

(v) Speciation
Answer:
Formation of new species from the pre-existing single group of organisms is called speciation.

Question 2.
What is adaptive radiation?
Answer:
The process of evolution which results in transformation of original species to many different varieties is called adaptive radiation.

Question 3.
If the variation occurs in population by chance alone and not by natural selection and bring change in frequencies of an allele, what is it called?
Answer:
If the variation occurs in population by chance alone and not by natural selection to bring change in frequencies of an allele, it is called genetic drift.

Question 4.
State the Hardy-Weinberg equilibrium law.
Answer:
The Hardy-Weinberg equilibrium law states that at equilibrium point both the allelic frequency and genotypic frequency remain constant from generation to generation, in the diploid, sexually reproducing, large, free interbreeding population in which mating is random and there is absence of any other factors that change the allele frequency.

Question 5.
What is homologous organs?
Answer:
Homologous organs are those organs, which are structurally similar but perform different functions.

Question 6.
What is vestigial organ?
Answer:
Vestigial organs are imperfectly developed and non-functional organs which are in degenerate form, they may be functional in some related and other animals or in ancestor.

Question 7.
What is the scientific name of modern man?
Answer:
Homo sapiens sapiens is the scientific name of modern man.

Question 8.
What is coacervate?
Answer:
Coacervates are colloidal aggregations of hydrophobic proteins and lipids which grew in size by taking up material from surrounding aqueous medium.

Question 9.
Which period is known as ‘age of Reptilia’?
Answer:
Jurassic period from Mesozoic era is known as age of Reptilia.

Question 10.
Name the ancestor of human which is described as man with ape brain.
Answer:
Australopithecus, the ancestor of human which is described as man with ape brain.

Short Answer Questions

Question 1.
Genetic drift.
Answer:

1. Genetic drift is random, directionless fluctuation that takes place in allele frequency.
2. It occurs by pure chance, in small sized population.
3. Genetic drift becomes an evolutional factor as it can change the gene frequency.
4. Sewall wright has given this concept and hence it is also known as Sewall wright effect.
5. Due to genetic drift, some alleles of a population are lost or reduced by chance and some others may be increased.
6. Some time, a few individuals become isolated from the large population and they produce new population in new geographical area.
7. Genetic drift is also called founders’ effect because original drifted population becomes ‘founders’ in the new area.
   E.g. Non-adaptive character of huge horns in Antelope is fixed due to genetic drift.

Question 2.
Enlist the different factors that are responsible for changing gene frequency.
Answer:
Gene flow, genetic drift, gene mutations, chromosomal aberrations such as deletion, duplication, inversion and translocation, genetic recombinations, natural selection, isolation are some of the factors which are responsible for changing the gene frequency.

Question 3.
Draw a graph to show that natural selection leads to disruptive change.
Answer:

Question 4.
Significance of fossils
Answer:

1. Fossils are studied under palaeontology. They are used in reconstruction of phylogeny.
2. Fossil study helps in studying various forms and structures of extinct animals.
3. By understanding the structure of fossil, record of missing link between two groups of organisms can be deduced.
4. By studying fossils various body forms and their evolution can be understood. They also help to understand the habit and habitat.
5. Some fossils provide the evolutionary evidences such a connecting links.

Question 5.
Write the objections to Mutation theory of Hugo de Vries.
Answer:
Objections to Mutation Theory:

1. Hugo de Vries observed the large and discontinuous variation. But these were chromosomal aberrations. Only gene mutations usually bring about minor changes.
2. Rate by which mutations take place is very slow as compared to the requirement of evolution.
3. Chromosomal aberrations are very unstable.
4. The organisms with chromosomal aberration are usually sterile and thus chromosomal aberrations have little significance in evolution.

Question 6.
What is disruptive selection? Give example.
Answer:
Disruptive selection:

1. The natural selection that disrupts the mean characters of the population, is called disruptive selection.
2. Greater number of individuals acquire peripheral character value at both ends of the distribution curve. E.g. Finches with large size or small size, both will be selected.
3. Extreme phenotypes are selected in evolutionary process and intermediate forms are eliminated.
4. When distribution curve is plotted it shows two peaks for two extremes.
5. Disruptive selection is rare because, nature always tries to balance the characters.
6. It ensures the effect on the entire gene pool of a population, considering all mating types or systems.

Example of disruptive selection:
African seed cracker finches are types of seed-feeder birds which have different sizes of beak. The seeds available to them were of small and large sized. Large beak sized birds feeds on large seeds while small beak sized birds feed on small seeds.

Such large and small birds thus thrive well. However, intermediate beak sized birds are unable to feed on either type of seeds so they starve and their population was decreased gradually. Natural selection eliminated them and thus the population of finches appear disrupted.

4. Match the columns

Question 1.

Column I	Column II
(1) August Weismann	(a) Mutation theory
(2) Hugo de Vries	(b) Germplasm theory
(3) Charles Darwin	(c) Theory of acquired characters
(4) Lamarck	(d) Theory of natural selection

Answer:

Column I	Column II
(1) August Weismann	(b) Germplasm theory
(2) Hugo de Vries	(a) Mutation theory
(3) Charles Darwin	(d) Theory of natural selection
(4) Lamarck	(c) Theory of acquired characters

5. Long Answer Questions

Question 1.
Would you consider wings of butterfly and bat as homologous or analogous and why?
Answer:
Wings of butterfly are made up of chitin. They neither have bones, nor muscles in the wings. The bat’s wings are actually patagium. They have muscles and bones just as those seen in all vertebrate limb series. Therefore, these two examples cannot be homologous. However, both the animals use the wings for flight. This is an indication that their function is similar but structure is different, hence they are analogous organs.

Question 2.
What is adaptive radiation? Explain with suitable example.
Answer:

1. Adaptive radiation is the process of evolution which results in transformation of original species to many different varieties.
2. The well-known example of adaptive radiation is Darwin’s Finches. When Charles Darwin went on his voyage to Galapagos islands, he noticed finches which is a variety of small birds.
3. According to Darwin’s observations, the American main land species of finches was the original one which must have migrated to the different islands of Galapagos.
4. Since environmental conditions here were different, they adapted in various ways to the differing environmental conditions of these islands.
5. Original bird had a beak suited for eating seeds, but the changed feeding pattern has changed the shape of beaks too. Some birds also show altered beaks for insectivorous mode. Thus, this demonstrated adaptive radiation.
6. Adaptive radiation in Australian Marsupials is also well studied. In Australia, there are many marsupial mammals who evolved from common ancestor.
7. Adaptive radiation leads to divergent evolution.

Question 3.
By talking industrial melanism as one example, explain the concept of natural selection.
OR
Explain natural selection in action by quoting the example of industrial melanism.
Answer:
1. Industrial melanism is the best example of natural selection which was studied by Kettlewell. In U.K. there are two varieties of peppered moths, Biston betularia and Biston carbonaria.

2. Before industrialisation, in Great Britain, Biston betularia were more in number than Biston carbonaria. B. Betularia is greyish white while B.carbonaria is melanic form.

3. These nocturnal moths rest on tree trunk during day. White-winged moth can camouflage well with the lichen covered whitish barks of trees. They thus escaped the attention of the predatory birds. But at the same time melanic forms were visible due to white barks of the trees. Their number was thus reduced as they were preyed upon by birds.

4. Later there was an industrial revolution, which ultimately resulted in air pollution causing dark soot to settle on the barks of the trees. Lichens too were destroyed and the melanic forms were now at advantage. Melanic forms could camouflage with black tree trunks and their number increased. White-winged moth become clearly seen in changed colours of the trees and thus they were easily caught by predatory birds. This caused decrease in their number.

5. Natural selection thus acted in changed environmental conditions and helped in the establishment of a phenotypic traits. The changed traits were more adaptive and hence were selected. Natural selection encourages those genes or traits that assure highest degree of adaptive efficiency between population and its environment.

Question 4.
Describe the Urey and Miller’s experiment.
Answer:

1. Urey and Miller performed an experiment to prove Oparin’s theory of chemical evolution.

2. They selected a spark discharge apparatus that consisted of closed system of glass having tungsten electrodes, flask for water boiling, a side tube connected to a vacuum pump, a cooling jacket and U-shaped trap.

3. The entire apparatus was first evacuated and made sterile and pre-biotic atmosphere was created in it.

4. The flask was filled with some water and mixture of methane, ammonia and hydrogen in the ratio of 1 : 2 : 2 were slowly passed through the stopcock, without allowing air.

5. Heat was supplied to the flask at very low temperature causing water to boil. The flask simulated the ocean present on primitive earth. Process of evaporation and precipitation was simulated by using heating mantle and condenser respectively.

6. Water vapours along with other gases were circulated continuously through continuous electric sparks. These sparks were given to the mixture for several days causing the gases to interact. This too simulated lightning.

7. Mixture of CH₄, NH₃ and H₂ gases passed through a condenser and was condensed to liquid.

8. The liquefied mixture was collected in the U-shaped trap, present at the bottom of the apparatus. It was found that variety of simple organic compounds (urea, amino acids, lactic acid and sugars) were formed in the apparatus.

This experiment provides the evidence in support to the fact that simple molecules present in the earth’s early atmosphere combined to form the organic building blocks of life.

Question 5.
What is Isolation? Describe the different types of reproductive isolations.
Answer:
1. Isolation means separation of the population of a particular species into smaller units. The organisms belonging to these subunits are prevented from interbreeding due to some barrier. These barriers are called isolating mechanisms.

2. They prevent the genetic exchange and gene flow.

3. Due to isolating mechanisms in nature the divergence among organisms takes place gradually leading to speciation. The isolating mechanisms are of two types namely, geographical isolation and reproductive isolation.

I. Geographical Isolation : The barrier in the form of physical distance or geographical barrier is called geographical isolation. The original population gets divided into two or more groups by geographical barriers such as river, ocean, mountain, glacier, etc. Organisms cannot cross the barriers on their own and hence interbreeding is prevented between isolated groups.

The separated groups experience different environmental factors and they acquire new traits by mutations. The separated populations develop distinct gene pool and they do not interbreed. Each subgroup then evolves differently which results into formation of new species. E.g. Darwin’s Finches, African elephant, Loxodonta and Indian elephant, Elephas.

II. Reproductive Isolation : Two populations may be occupying the same area, they may not be separated by geographical barrier, but then also they are reproductively isolated. Such reproductive isolation occurs due to change in genetic material, gene pool and structure of genital organs. Such differences prevent interbreeding between population. Such isolation later leads to speciation.

III. Different types of reproductive isolations : Reproductive isolation is of two types, viz. pre-zygotic and post-zygotic isolating mechanisms.

1. Pre-zygotic or pre-mating isolating mechanisms do not allow individuals to mate with each other at all.
2. By various mechanisms the two groups remain isolated.
3. In post-zygotic or post-mating isolating mechanisms, the two individuals can mate but the result of mating is not favourable.
4. Thus the populations remain isolated without the actual genetic exchange.

Question 6.
What is Genetic variations? Explain the different factors responsible for genetic variations.
Answer:
Genetic variations : The change in gene and gene frequencies is known as genetic variation. Genetic variations are caused by following factors:
(i) Mutations : Sudden permanent heritable change is called mutation. Mutation can occur in the gene, in the chromosome structure and in chromosome number. Mutation that occurs within the single gene is called point mutation or gene mutation. This leads to the change in the phenotype of the organism, causing variations.

(ii) Genetic recombination : In sexually reproducing organisms, during gamete formation, exchange of genetic material occurs between non-sister chromatids of homologous chromosomes. This is called crossing over. It produces new genetic combinations which result in variation. Fertilization between opposite mating gametes leads to various recombinations resulting into the phenotypic variations. These result in change in the frequencies of alleles.

(iii) Gene flow : Gene flow is movement of genes into or out of a population. Gene movement may be in the form of migration of organism, or gametes (dispersal of pollens) or segments of DNA (transformation). Gene flow also alters gene frequency causing evolutionary changes.

(iv) Genetic drift : Any random fluctuation (alteration) in allele frequency, occurring in the natural population by pure chance, is called genetic drift. For example, when the size of a population is severely reduced due to natural disasters like earthquakes, floods, fires, etc. elimination of particular alleles from a population becomes possible. Smaller populations have greater chances for genetic drift. It results in the change in the gene frequency. Genetic drift is also an important factor for evolutionary change.

(v) Chromosomal aberrations : The structural, morphological change in chromosome due to rearrangement of genes is called chromosomal aberrations. Due to changes in the gene arrangement or gene sequence variations are caused.

6. Complete the chart

Era	Dominating group of animals
1. Coenozoic	————–
2. ————-	Reptiles
3. Palaeozoic	————-
4. ————	Lower Invertebrates

Answer:

Era	Dominating group of animals
1. Coenozoic	Mammals
2. Mesozoic	Reptiles
3. Palaeozoic	Insects, Fishes, Amphibians
4. Proterozoic	Lower Invertebrates

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 4 Molecular Basis of Inheritance Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 4 Molecular Basis of Inheritance

1. Multiple Choice Questions

Question 1.
Griffith worked on ………………..
(a) Bacteriophage
(b) Drosophila
(c) Frog eggs
(d) Streptococci
Answer:
(d) Streptococci

Question 2.
The molecular knives of DNA are ………………..
(a) Ligases
(b) Polymerases
(c) Endonucleases
(d) Transcriptase
Answer:
(c) Endonucleases

Question 3.
Translation occurs in the ………………..
(a) Nucleus
(b) Cytoplasm
(c) Nucleolus
(d) Lysosomes
Answer:
(b) Cytoplasm

Question 4.
The enzyme required for transcription is ………………..
(a) DNA polymerase
(b) RNApolymerase
(c) Restriction enzyme
(d) RNase
Answer:
(b) RNA polymerase

Question 5.
Transcription is the transfer of genetic information from ………………..
(a) DNA to RNA
(b) t-RNA to m-RNA
(c) DNA to m-RNA
(d) m-RNA to t-RNA
Answer:
(a) DNA to RNA

Question 6.
Which of the following is NOT part of protein synthesis?
(a) Replication
(b) Translation
(c) Transcription
(d) All of these
Answer:
(a) Replication

Question 7.
In the RNA molecule, which nitrogen base is found in place of thymine?
(a) Guanine
(b) Cytosine
(c) Thymine
(d) Uracil
Answer:
(d) Uracil

Question 8.
How many codons are needed to specify three amino acids?
(a) 3
(b) 6
(c) 9
(d) 12
Answer:
(a) 3

Question 9.
Which out of the following is NOT an example of inducible operon?
(a) Lactose operon
(b) Histidine operon
(c) Arabinose operon
(d) Tryptophan operon
Answer:
(d) Tryptophan operon

Question 10.
Place the following event of translation in the correct sequence ………………..
i. Binding of met-t-RNA to the start codon.
ii. Covalent bonding between two amino acids.
iii. Binding of second t-RNA.
iv. Joining of small and large ribosome subunits.
(a) iii, iv, i, ii
(b) i, iv, iii, ii
(c) iv, iii, ii, i
(d) ii, iii, iv, i
Answer:
(b) i, iv, iii, ii

2. Very Short Answer Questions

Question 1.
What is the function of an RNA primer during protein synthesis?
Answer:
During DNA replication, RNA primer provides 3’ OH to which DNA polymerase enzyme can add nucleotides to synthesize new strand using parental strand of DNA as template.
[Note : RNA primer has no direct role in protein synthesis.]

Question 2.
Why is the genetic code considered as commaless?
Answer:
The triplet codon are arranged one after the other on m-RNA molecule without any gap or space and therefore genetic code is considered as commaless.

Question 3
Genome
Answer:
Genome is the total genetic constitution of an organism or a complete copy of genetic information (DNA) or one complete set of chromosomes (monoploid or haploid) of an organism.

Question 4.
Which enzyme does remove supercoils from replicating DNA?
Answer:
Super-helix relaxing enzyme (Topoisomerase) removes supercoils from replicating DNA.

Question 5.
Why are Okazaki fragments formed on lagging strand only?
Answer:
Okazaki fragments are formed only on lagging template as only short stretch of lagging template becomes available for replication at one time.

Question 6.
When does DNA replication take place?
Answer:
In eukaryotes DNA-replication takes place during S-phase of interphase of cell cycle and in prokaryotes. DNA replicates prior to cell division.

Question 7.
Define term Codogen and Codon
Answer:
Codogen is a triplet of nucleotides present on the DNA which specifies one particular amino acid.
Codon is a triplet of nucleotides present on the m-RNA which specifies one particular amino acid.

Question 8.
What is degeneracy of genetic code?
Answer:
Genetic code is degenerate as 61 codons code for 20 amino acids, that is two or more codons can specify the same amino acid. E.g. Cysteine has two codons, while isoleucine has three codons.

Question 9.
Which are the nucleosomal ‘core’ histones?
Answer:
Two molecules each of histone proteins, viz. H₂A. H₂B, H₃ and H₄ are the nucleosomal ‘core’ histones.

3. Short Answer Questions

Question 1.
DNA packaging in eukaryotic cell.
Answer:

1. In eukaryotic cells, DNA (2.2 metres) is condensed, coiled and supercoiled to be packaged efficiently in the nucleus (10^-16 m).
2. DNA is associated with histone and non-histone proteins.
3. Histones are a set of positively charged, basic proteins, rich in basic amino acid residues lysine and arginine.
4. Nucleosome consists of nucleosome core (two molecules of each of histone proteins viz. H₂A, H₂B, H₃ and H₄ forming histone octamer) and negatively charged DNA (146 bps) that wraps around the histone octamer by 1 3/4 turns.
5. H₁ protein binds the DNA thread where it enters and leaves the nucleosome.
6. Adjacent nucleosomes are linked with linker DNA (varies in length from 8 to 114 bp, average length of linker DNA is about 54 bp).
7. Each nucleosome contains 200 bp of DNA.
8. Packaging involves formation of – Beads on string (10 nm diameter), Solenoid fibre (looks like coiled telephone wire, 30 nm diameter/300Å), Chromatin fibre and Chromosome.
9. Non-Histone Chromosomal Proteins (NHC) contribute to the packaging of chromatin at a higher level.

Question 2.
Enlist the characteristics of genetic code.
Answer:
The characteristics of genetic code are

1. Genetic code is triplet, commaless and non-overlapping.
2. It is degenerate and non-ambiguous.
3. It is universal
4. It has polarity.

Question 3.
Applications of DNA fingerprinting.
Answer:
Applications of DNA fingerprinting are as follows:

1. In forensic science to solve rape and murder cases.
2. Finds out the biological father or mother or both, of the child, in case of disputed parentage.
3. Used in pedigree analysis in cats, dogs, horses and humans.

Question 4.
Explain the role of lactose in ‘Lac Operon’.
Answer:

1. A small amount of beta-galactoside permease enzyme is present in cell even when Lac operon is switched off and it allows a few molecules of lactose to enter into the cell.
2. Lactose binds to repressor and inactivates it.
3. Repressor – lactose complex cannot bind with the operator gene, which is then turned on.
4. RNA polymerase transcribes all the structural genes to produce lac m-RNA which is then translated to produce all enzymes.
5. Thus, lactose acts as an inducer.
6. When the inducer level falls, the operator is blocked again by repressor and structural genes are repressed again. This is negative feedback.

4. Short Answer Questions

Question 1.
Human genome project.
Answer:
1. Human Genome Project (HGP) was initiated in 1990 under the International administration of the Human Genome Organization (HUGO) and it was completed r in 2003.

2. The main aims:

• To sequence 3 billion base pairs of DNA in human genome and to map an estimated 33000 genes.
• To store the information collected from the project in databases.
• To develop tools and techniques for analysis of the data.
• Transfer of the related technologies to the private sectors, such as industries.
• Taking care of the legal, ethical and social issues which may arise from project.
• To sequence the genomes of several other organisms such as bacteria e.g. E.coli, Caenorhabditis elegans, Saccharomyces cerevisiae, Drosophil, rice, Arabidopsis), Mus musculus, etc.

3. Significance:

1. HGP has a major impact in the fields like Medicine, Biotechnology, Bioinformatics and the Life sciences.
2. More understanding of functions of genes, proteins and human evolution.

Question 2.
Describe the structure of operon.
Answer:

1. An operon is a unit of gene expression and regulation.
2. It includes the structural genes and their control elements. Control elements are promoters and operators.
3. The structural genes code for proteins, r-RNA and t-RNA that are necessary for all the cells.
4. Promoters are signal sequences in DNA. They start the RNA synthesis. They also act as sites where the RNA polymerases are bound during transcription.
5. Operators are present between the promoters and structural genes.
6. There is repressor protein that binds to the operator region of the operon.
7. There are regulatory genes which are responsible for the formation of repressors which interact with operators.

Question 3.
In the figure below A, B and C are three types of

Answer:
Answer: A, B and C are A : m-RNA, B : r-RNA, C : t-RNA

Question 4.
Identify the labelled structures on the following diagram of translation.

Part A is the ………………
Part B is the ………………
Part C is the ………………
Answer:
Part A is the anti-codon.
Part B is the amino acid.
Part C is the larger subunit of ribosome.

Question 5.
Match the entries in Column I with those of Column II and choose the correct answer.

Column I	Column II
A. Alkali treatment	i. Separation of DNA fragments on gel slab
B. Southern blotting	ii. Splits DNA fragments into single strands
C. Electrophoresis	iii. DNA transferred to nitrocellulose sheet
D. PCR	iv. X-ray photography
E. Autoradiography	v. Produce fragments different sizes
F. DNA treated with REN	vi. DNA amplification

Answer:

Column I	Column II
A. Alkali treatment	ii. Splits DNA fragments into single strands
B. Southern blotting	iii. DNA transferred to nitrocellulose sheet
C. Electrophoresis	i. Separation of DNA fragments on gel slab
D. PCR	vi. DNA amplification
E. Autoradiography	iv. X-ray photography
F. DNA treated with REN	v. Produce fragments different sizes

5. Long Answer Questions

Question 1.
Explain the process of DNA replication.
Answer:

DNA replication is semi-conservative replication. It involves following steps:
Activation of Nucleotides:

1. Nucleotides (dAMP dGMR dCMP and dTMP) present in the nucleoplasm, are activated by ATP in presence of an enzyme phosphorylase.
2. This phosphorylation results in the formation of deoxyribonucleotide triphosphates i.e. dATE dGTR dCTP and dTTE

Point of Origin or Initiation point:

1. Replication begins at specific point ‘O- Origin and terminates at point ‘T’.
2. At the point ‘O’, enzyme endonuclease nicks (breaks the sugar-phosphate backbone or the phosphodiester bond) one of the strands of DNA, temporarily.

Unwinding of DNA molecule:

1. Enzyme DNA helices breaks weak hydrogen bonds in the vicinity of ‘O’.
2. The strands of DNA separate and unwind. This unwinding is bidirectional.
3. SSBP (Single strand binding proteins) remains attached to both the separated strands and prevent them from recoiling (rejoining).

Replicating fork:

1. Y-shape replication fork is formed due to unwinding and separation of two strands.
2. The unwinding of strands results in strain which is released by super-helix relaxing enzyme.

Synthesis of new strands:

1. Each separated strand acts as a template for the synthesis of new complementary strand.
2. A small RNA primer (synthesized by activity of enzyme RNA primase) get attached to the 3′ end of template strand and attracts complementary nucleotides from surrounding nucleoplasm.
3. These nucleotides bind to the complementary nucleotides on the template strand by hydrogen bonds (i.e. A = T or T = A; G = C or C = G, CEG).
4. The phosphodiester bonds are formed between nucleotides of new strand to form a polynucleotide strand.
5. The enzyme DNA polymerase catalyses synthesis of new complementary strand always in 5′ – 3′ direction.

Leading and Lagging strand:

1. The template strand with free 3′ is called the leading template.
2. The template strand with free 5′ end is called the lagging template.
3. The replication always starts at C-3 end of template strand and proceeds towards C-5 end.
4. New strands are always formed in 5′ → 3′ direction.
5. The new strand which develops continuously towards replicating fork is called the leading strand.
6. The new strand which develops discontinuously away from the replicating fork is called the lagging strand.
7. Maturation of Okazaki fragments : The lagging strand is synthesized in the form of small Okazaki fragments which are joined by enzyme DNA ligase.
8. Later RNA primers are removed by the combined action of RNase H, an enzyme that degrades the RNA strand of RNA-DNA hybrids, and polymerase I.
9. Gaps formed are filled by complementary DNA sequence with the help of DNA polymerase-I in prokaryotes and DNA polymerase-a in eukaryotes.
10. Finally, DNA gyrase (topoisomerase) enzyme forms double helix to form daughter DNA molecules.

Formation of two daughter DNA molecules:

1. In each daughter DNA molecule, one strand is parental and the other one is newly synthesized.
2. Thus, 50% part (i.e. one strand of the helix) is contributed by mother DNA. Hence, it is described as semiconservative replication.

Question 2.
Describe the process of transcription in protein synthesis.
Answer:

Transcription involves three stages, viz. Initiation, Elongation and Termination.
(1) Initiation:

1. RNA polymerase binds to promoter site.
2. It then moves along the DNA and causes local unwinding of DNA duplex into two strands in the region of the gene.
3. Only antisense strand functions as template.

(2) Elongation:

• The complementary ribonucleoside tri-phosphates get attached to exposed bases of DNA template chain.
• As transcription proceeds, the hybrid DNA-RNA molecule dissociates and makes m-RNA molecule free.
• As the m-RNA grows, the transcribed region of DNA molecule becomes spirally coiled and regains double helical form.

(3) Termination:
When RNA polymerase reaches the terminator site on the DNA, both enzyme and newly formed m-RNA (primary transcript) gets released.

Question 3.
Describe the process of translation in protein synthesis.
Answer:

Translation involves the following steps:
1. Activation of amino acids and formation of charged t-RNA (t-RNA – amino acid complex):
i. In the presence of an enzyme amino acyl t-RNA synthetase, the amino acid is activated and then attached to the specific t-RNA molecule at 3’ end to form charged t-RNA (t-RNA – amino acid complex).

ii. ATP is essential for the reaction.

2. Initiation of Polypeptide chain:

• Small subunit of ribosome binds to the m-RNA at 5’ end.
• Start codon is positioned properly at P-site.
• Initiator t-RNA, (carrying amino acid methionine in eukaryotes or formyl methionine in prokaryotes) binds with initiation codon (AUG) of m-RNA, by its anticodon (UAC) through hydrogen bonds.
• The large subunit of ribosome joins with the smaller subunit in the presence of Mg⁺⁺.
• Thus, initiator charged t-RNA occupies the P-site and A – site is vacant.

3. Elongations of polypeptide chain:
Addition of amino acid occurs in 3 Step cycle-
i. Codon recognition.
Anticodon of second (and subsequent) amino acyl t-RNA molecule recognizes and binds with codon at A-site by hydrogen bonds.

ii. Peptide bond formation.

1. Ribozyme catalyzes the peptide bond formation between amino acids on the initiator t-RNA at P-site and t-RNA at A-site.
2. It takes less than 0.1 second for formation of peptide bond.
3. Initiator t-RNA at ‘P’ site is then released from E-site.

iii. Translocation.

1. Translocation is the process in which sequence of codons on m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
2. Due to this A’-site becomes vacant to receive next charged t-RNA molecule.
3. The events like arrival of t-RNA – amino acid complex, formation of peptide bond, ribosomal translocation and release of previous t-RNA, are repeated.
4. As ribosome move over the m-RNA, all the codons on m-RNA are exposed oiie by one for translation.

4. Termination and release of polypeptide:
When stop codon (UAA, UAG, UGA) gets exposed at the A-site, the release factor binds to the stop codon, thereby terminating the translation process
The polypeptide gets released in the cytoplasm.
Two subunits of ribosome dissociate and last t-RNA and m-RNA are released in the cytoplasm.
m-RNA gets denatured by nucleases immediately.

Question 4.
Describe Lac ‘Operon’.
Answer:

Lac operon consists of the following components:
(1) Regulator gene:

• Regulator gene precedes the promoter gene.
• It may not be present immediately adjacent to operator gene.
• Regulator gene codes for a repressor protein which binds with operator gene and represses (stops) its action.

(2) Promoter gene:

• It precedes the operator gene.
• It is present adjacent to operator gene.
• RNA Polymerase enzyme binds at promoter site.
• Promoter gene base sequence determines which strand of DNA acts a template.

(3) Operator gene:

• It precedes the structural genes.
• When operator gene is turned on by an inducer, the structural genes get transcribed to form m-RNA.

(4) Structural gene:

• There are 3 structural genes in the sequence lac-Z, lac-Y and lac-A.
• Enzymes produced are β-galactosidase, β-galactoside permease and transacetylase respectively.
  Inducer Allolactose acts as an inducer. It inactivates the repressor by binding with it.

Question 5.
Justify the statements. If the answer is false, change the underlined word(s) to make the statement true.
(i) The DNA molecule is double stranded and the RNA molecule is single stranded.
Answer:

1. DNA as the genetic material has to be chemically and structurally stable.
2. It should be able to generate its replica.
3. Sugar-phosphate backbone and complementary base pairing between the two strands, give stability to DNA.
4. Both the strands of DNA act as template for synthesis of their complementary strands. This allows accurate replication of DNA.
5. Single stranded RNA can be folded to form complex structures and perform specific functions such as synthesis of proteins.

(ii) The process of translation occurs at the ribosome.
Answer:

1. Translation is the process in which sequence of codons of m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
2. Ribosome has one binding site for m-RNA. It orients m-RNA molecule in such a way that all the codons are properly read.
3. Ribosome has three binding sites for t-RNA : P-site (peptidyl t-RNA-site), A-site (aminoacyl t-RNA-site) and E-site (exit site).
4. t-RNAs place the required amino acids in correct sequence and translate the coded message of RNA.
5. In eukaryotes, a groove which is present between two subunits of ribosomes, protects the polypeptide chain from the action of cellular enzymes and also protects m-RNA from the action of nucleases.
6. Thus ribosome plays an important role in translation.

(iii) The job of m-RNA is to pick up amino acids and transport them to the ribosomes.
Answer:
The job of t-RNA is to pick up amino acids and transport them to ribosomes. t-RNA is an adapter molecule. It reads the codons of m-RNA and also simultaneously transfer specific amino acid to m-RNA Ribosome complex. It binds with amino acid at its 3′ end.

(iv) Transcription must occur before translation may occur.
Answer:
In prokaryotes, translation can start before transcription is complete, as both these processes occur in the same compartment, i.e. cytoplasm. But in eukaryotes, transcription and processing of hnRNA occurs in nucleus. hnRNA then comes out of the nucleus through nuclear pores and then it is translated at ribosomes in the cytoplasm.

Question 6.
Guess
(i) the possible locations of DNA on the collected evidence from a crime scene and
(ii) the possible sources of DNA.

Evidence	Possible location of DNA on the evidence	Sources of DNA
e.g. Eyeglasses	e.g. Earpieces	e.g. Sweat, Skin
Bottle, Can, Glass	Sides, mouthpiece	—————-
————–	Handle	Sweat, skin, blood
Used cigarette	Cigarette butt	—————–
Bite mark	—————–	Saliva
————-	Surface area	Hair, semen, sweat, urine

Answer:

Evidence	Possible location of DNA on the evidence	Sources of DNA
e.g. Eyeglasses	e.g. Earpieces	e.g. Sweat, Skin
Bottle, Can, Glass	Sides, mouthpiece	Saliva
Door	Handle	Sweat, skin, blood
Used cigarette	Cigarette butt	Saliva
Bite mark	Teeth impression	Saliva
Clothes	Surface area	Hair, semen, sweat, urine

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 3 Inheritance and Variation Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 3 Inheritance and Variation

1. Multiple Choice Questions

Question 1.
Phenotypic ratio of incomplete dominance in Mirabilis jalapa.
(a) 2 : 1 : 1
(b) 1 : 2 : 1
(c) 3 : 1
(d) 2 : 2
Answer:
(b) 1 : 2 : 1

Question 2.
In dihybrid cross, F₂ generation offspring show four different phenotypes while the genotypes are ……………….
(a) six
(b) nine
(c) eight
(d) sixteen
Answer:
(b) nine

Question 3.
A cross between an individual with unknown genotype for a trait with recessive plant for that trait is ……………….
(a) back cross
(b) reciprocal cross
(C) monohybrid cross
(d) test cross
Answer:
(d) test cross

Question 4.
When phenotypic and genotypic ratios are the same, then it is an example of ……………….
(a) incomplete dominance
(b) complete dominance
(c) multiple alleles
(d) cytoplasmic inheritance
Answer:
(a) incomplete dominance

Question 5.
If the centromere is situated near the end of the chromosome, the chromosome is called ……………….
(a) Metacentric
(b) Acrocentric
(c) Sub-Metacentric
(d) Telocentric
Answer:
(d) Telocentric

Question 6.
Chromosomal theory of inheritance was proposed by ……………….
(a) Sutton and Boveri
(b) Watson and Crick
(c) Miller and Urey
(d) Oparin and Halden
Answer:
(a) Sutton and Boveri

Question 7.
If the genes are located in a chromosome as p-q-r-s-t, which of the following gene pairs will have least probability of being inherited together ?
(a) p and q
(b) r and s
(c) s and t
(d) p and s
Answer:
(d) p and s

Question 8.
Find the mismatched pair:
(a) Down’s syndrome = 44 + XY
(b) Turner’s syndrome = 44 + XO
(c) Klinefelter’s syndrome = 44 + XXY
(d) Super female = 44 + XXX
Answer:
(a) Down’s syndrome = 44 + XY

Question 9.
A colourblind man marries a woman, who is homozygous for normal colour vision, the probability of their son being colour blind is ……………….
(a) 0%
(b) 25%
(c) 50%
(d) 100%
Answer:
(a) 0%

2. Very Short Answer Questions

Question 1.
Explain the statements
a. Test cross is back cross but back cross is not necessarily a test cross.
b. Law of dominance is not universal.
Answer:
a. (1) Test cross is the cross between F₁ hybrid and its homozygous recessive parent.
(2) Back cross is the cross of offspring with any one of the parents, either dominant or recessive.
(3) Therefore, test cross can be a back cross – but back cross cannot be a test cross.

b. (1) There are many traits in many organisms which show dominance. For example, widow’s peak in human beings is a dominant trait. Yellow seed colour and round seed shape are dominant traits in pea plant.
(2) However, there are characters which are either co-dominant, such as genes for human blood group A and B or incompletely dominant as in flower colour of Mirabilis jalapa.
(3) Therefore the law of dominance is not universally applicable.

Question 2.
Define the following terms:
a. Dihybrid cross
b. Homozygous
c. Heterozygous
d. Test cross
Answer:
a. A cross between parents differing in two heritable traits is called dihybrid cross.
b. An individual possessing identical alleles for a particular trait is called homozygous or pure for that trait. E.g. TT for tallness and tt for dwarfness.
c. An individual possessing contrasting allele for a particular trait is called heterozygous. E.g. Tt showing tallness.
d. The cross of F₁ progeny with homozygous recessive parent is called a test cross.

Question 3.
What are allosomes?
Answer:
Allosomes are the chromosomes which decide the sex of an organism.

Question 4.
What is crossing over?
Answer:
Crossing over is the process of forming new recombinations by interchanging and exchanging non-sister chromatid arms of the homologous chromosomes.

Question 5.
Give one example of autosomal recessive disorder.
Answer:
Thalassemia is an example of autosomal recessive disorder.

Question 6.
What are X-linked genes?
Answer:
Genes located on the non-homologous region of X chromosome are called X-linked genes.

Question 7.
What are holandric traits?
Answer:
Genes located on the non-homologous region of Y chromosome are called Y-linked genes. The traits due to such genes are called holandric traits which are seen only in male sex.

Question 8.
Give an example of chromosomal disorder caused due to non-disjunction of autosomes.
Answer:
Down’s syndrome is an example of chromosomal disorder caused due to non-disjunction of autosomes.

Question 9.
Give one example of complete sex linkage.
Answer:
Sex linkage can be complete X linkage and complete Y linkage. X linkage is haemophilia and Y linkage is hypertrichosis.

3. Short Answer Questions

Question 1.
Enlist seven traits of pea plant selected / studied by Mendel.
Answer:
Seven traits in pea selected by Mendel:

1. Tall habit versus dwarf habit (Height of the plant).
2. Purple flowers versus white flowers. (Colour of flowers)
3. Yellow seeds versus green seeds. (Colour of seeds)
4. Round seeds versus wrinkled seeds. (Shape of seeds)
5. Green pods versus yellow pods. (Colour of pods)
6. Inflated pods versus constricted pods. (Shape of pods)
7. Axial flower versus terminal flower. (Position of a flower)

Question 2.
Why law of segregation is also called the law of purity of gametes?
Answer:
(1) Mendel’s law of segregation is also called Law of purity of gametes because, during formation of gametes, the alleles separate/ segregate from each other and only one allele enters a gamete.

(2) The separation of one allele does not affect other. Since single allele enters a gamete means gametes will be pure for a trait.
E.g. The contrasting characters such as tall (T) and dwarf (t) present in F₁ hybrid (Tt) segregate during the formation of gametes.

(3) Owing to this, two types of gametes i.e. T and t are formed which are pure for the characters which they carry.
(4) Thus for example:

Question 3.
Pleiotropy.
Answer:

1. When a single gene controls two or more different traits, it is called a pleiotropic gene and the phenomenon is known as pleiotropy or pleiotropism.
2. The pleiotropic ratio is always 1 : 2 instead . of normal 3 : 1.
3. Sickle-cell anaemia is caused by the gene HbS. The healthy or normal gene which is dominant is HbA. The heterozygotes or carriers i.e., HbA/Hbs show anaemia as there is deficiency of haemoglobin due to sickling of RBCs. Abnormally low concentration of oxygen can cause sickling of RBCs.
4. The homozygotes possessing the recessive gene HbS die because of fatal anaemia because the gene for sickle-cell anaemia is lethal in homozygous condition and causes sickle-cell trait in heterozygous carrier.
5. Thus a single gene produces two different expressions.
6. When two carriers are married they will produce normal carriers and Sickle-cell anaemic children in the ratio of 1 : 2 : 1. Out of these three children sickle-cell anaemic child will die leaving the ratio 1 : 2 instead of 3 : 1.

Question 4.
What are the reasons of Mendel’s success?
Answer:
Reasons for Mendel’s success:

1. Mendel planned his experiments carefully and these experiments consisted of large sample.
2. He always recorded the results of number of plants of each type and their ratios.
3. The contrasting characters that he chose were easily recognizable.
4. The seven pairs of contrasting characters that he selected were under control of a single factor each. They were present on separate chromosomes and were transmitted from one generation to the next.
5. Mendel studied and introduced concept of dominance and recessiveness.

Question 5.
“Father is responsible for determination of sex of child and not the mother”. Justify.
Answer:

1. Human made is heterogame tic, i.e. he produces two different types of sperms. One is bearing X chromosome along with 22 autosomes and the other is Y bearing sperm with 22 autosomes.
2. Mother, on the other hand, is homogametic, producing all similar types of ova, i.e 22 + X chromosomal combination.
3. If 22+X bearing sperm fertilise an egg, female child is formed while if Y bearing sperm fertilizes an egg, male child is formed.
4. Thus the sex of the child is dependent upon type of sperm that father gives, therefore, it is said that father is responsible for determination of sex of a child and not the mother.

Question 6.
What is linkage? How many linkage groups do occur in human being and maize?
Answer:

1. Linkage is defined as the tendency of the genes to be inherited together because they are present in the same chromosome. Linkage group is group of genes situated on a chromosome.
2. Humans have 23 linkage groups because they have 23 pairs of chromosomes.
3. Maize plant has 10 linkage groups because they have 10 pairs of chromosomes.

Question 7.
PKU.
Answer:

1. PKU means phenylketonuria which is an autosomal recessive inborn error.
2. In this disorder the metabolism of phenylalanine does not occur due to deficiency of phenylalanine hydroxylase (PAH) enzyme.
3. This enzyme is necessary to metabolize the amino acid phenylalanine to the amino acid tyrosine.
4. When PAH activity is reduced, phenylalanine accumulates in blood and cerebrospinal fluid and is converted into phenylpyruvate or phenyl-ketone which is a toxic compound. This may cause mental retardation. Excess phenylalanine is excreted in urine, hence this disease is called phenylketonuria.
5. PKU is caused by mutations in the PAH gene on chromosome no. 12.
6. Untreated PKU causes abnormal phenotype which includes growth failure, poor skin pigmentation, microcephaly, seizures, global developmental delay and severe intellectual impairment. However, at birth if an infant is checked for PKU, the further abnormalities can be avoided.

Question 8.
Compare X-chromosome and Y-chromosome.
Answer:

X-chromosome	Y-chromosome
1. X-chromosome is straight, rod like and longer 1. than Y chromosome. It is metacentric.	1. Y-chromosome is shorter chromosome which is acrocentric.
2. X-chromosome has large amount of euchromatin and small amount of heterochromatin.	2. Y-chromosome has small amount of euchromatin and large amount of heterochromatin.
3. X-chromosome has large amount of DNA, hence it is genetically active due to more genes.	3. Y-chromosome has less amount of DNA, hence it is genetically less active or inert due to lesser genes.
4. Non-homologous region of X-chromosome is longer and contains more genes.	4. Non-homologous region of Y-chromosome is shorter and contains lesser genes.
5. Contains X-linked genes on non-homologous region.	5. Contains Y-linked genes on non-homologous region.
6. X-chromosome is present in men as well as women.	6. Y-chromosome is present only in men.

Question 9.
Explain the chromosomal theory of inheritance.
Answer:
Chromosomal theory of inheritance was put forth by Sutton and Boveri after studying paraillel behaviour of genes and chromosomes during meiotic division. This theory states following points:

1. Chromosomal theory identifies chromosomes as the carrier of genetic material.
2. All the hereditary characters are transmitted by gametes. Nucleus of gametes, i.e. sperms and ova of the parents contain chromosomes which transmit the heredity to offspring.
3. Chromosomes are found in pairs in somatic or diploid cells.
4. During gamete formation, homologous chromosomes pair and segregate independently at meiosis. The diploid condition is converted into haploid condition. Thus each gamete contains only one chromosome of a pair.
5. During fertilization, the union of sperm and egg restores the diploid number of chromosomes.

Question 10.
Observe the given pedigree chart and answer the following questions

(a) Identify whether the trait is sex-linked or autosomal.
(b) Give an example of a trait in human beings which shows such a pattern of inheritance.
Answer:
Pedigree given above shows:

1. First Generation : Carrier woman marrying a sufferer man. Their three children are in following birth order.
2. Second generation : First son is normal, second daughter is carrier and third daughter is sufferer.
3. Third generation : The sufferer daughter marries a normal man. Her children are normal daughter and sufferer son.

(a) The above pedigree show sex-linked (X-linked) trait. Since criss-cross inheritance is seen in the trait, it must be sex-linked inheritance.
(b) Such trait and its inheritance can be seen in colour blindness.

4. Match the Columns

rewrite the matching pairs.

Column I	Column II
(1) 21 trisomy	(a) Turner’s syndrome
(2) X-monosomy	(b) Klinefelter’s syndrome
(3) Holandric traits	(c) Down’s syndrome
(4) Feminized male	(d) Hypertrichosis

Answer:

Column I	Column II
(1) 21 trisomy	(c) Down’s syndrome
(2) X-monosomy	(a) Turner’s syndrome
(3) Holandric traits	(d) Hypertrichosis
(4) Feminized male	(b) Klinefelter’s syndrome

5. Long Answer Questions

Question 1.
What is dihybrid cross? Explain with suitable example and checker board method.
Answer:
1. A cross which involves two pairs of alleles is called a dihybrid cross. A phenotypic ratio of 9 : 3 : 3 : 1 obtained in the F₂ generation of a dihybrid cross is called a dihybrid ratio.

(2) Thus for example, when we cross a true breeding pea plant bearing round and yellow seeds with a true breeding pea plant bearing wrinkled and green seeds we get pea plants bearing round and yellow seeds in the F₁ generation.

(3) When F₁ plants are selfed, we get a ratio of 9 : 3 : 3 : 1 in the F₂ generation, where 9 plants bear yellow round seeds, 3 plants bear yellow wrinkled seeds, 3 plants bear green round seeds and 1 plant bears green wrinkled seeds.

(4) Parents (P₁) : RRYY × rryy
Gametes of P₁ RY and ry
F₁ generation : RrYy(Yellow round)
On selfing F₁ : RrYy × RrYy
Gametes of F₁ : RY, Ry, rY, ry

P₂ generation:

Round Yellow : 9 Round green : 3 Wrinkled yellow : 3 Wrinkled green : 1
Phenotypic ratio : 9 : 3 : 3 : 1
Genotypic ratio : 1 : 2 : 1 : 2 : 4 : 2 : 1 : 2 : 1

Question 2.
Explain with suitable example an independent assortment.
Answer:
(1) The law of independent assortment states that when hybrid possessing two or more pairs of contrasting characters bearing alleles form gametes, the alleles in each pair segregate independently of the other pair. Therefore, the inheritance of one pair of characters is independent of that of the other pair of characters.
(2) For example, when we cross a pea plant which is tall and having purple flowers with dwarf plant having white flowers we obtain all tall plants with purple flowers in F₁ generation. When F₁ generation are selfed, 9 : 3 : 3 : 1 ratio was obtained in F₂ generation with 9 tall and purple flower, 3 tall with white flowers, 3 dwarf with purple flowers and 1 which was dwarf and white. Tallness and purple colour are dominant traits while dwarfness and white colour are recessive traits.

(i) Homozygous tall purple – TTPP
(ii) Homozygous dwarf white – ttpp

Tall purple = 9. Tall white = 3
Dwarf purple = 3, Dwarf white = 1,
Phenotypic ratio = 9 : 3 : 3 : 1
Results : The offspring of F₁ generation will be in the proportion of 9 : 3 : 3 : 1, where 9 are tall purple, 3 are tall white, 3 are dwarf purple and 1 is dwarf white.

Question 3.
Define test cross and explain its significance.
Answer:
1. Definition of test cross : A cross between F₁ offspring and its homozygous recessive parent is called a test cross.
2. Significance of test cross:

• Test cross can be used to find out the genotype of any plant which shows dominant characters.
• Whether the plant is homozygous or heterozygous can be understood by performing test cross.
• Test cross is used to introduce useful recessive traits in the hybrids of self- pollinated plants.
• Test cross is quicker method to improve the variety of crop plants and thus it is useful for breeders and geneticists.
• Test cross can be used for verifying the laws of inheritance.

Question 4.
What is parthenogenesis? Explain the haplodiploid method of sex determination in honey bee.
Answer:
I. Parthenogenesis is a natural form of asexual reproduction in which growth and development of embryos occur without fertilization by sperm. In some insects like honey bees, parthenogenesis means development of an embryo from an unfertilized egg cell.

II. In honey bee:

1. Sex determination is by haplodiploid system.
2. Sex is determined by the number of sets of chromosomes received by an individual.
3. The egg which is fertilized by sperm, becomes diploid and develops into female.
4. The egg which is not fertilized develops by parthenogenesis and develops into a male.
5. The queen and worker bee therefore contain 32 chromosomes. The drone, i.e. male bears 16 chromosomes.
6. The sperms are produced by mitosis while eggs are produced by meiosis.

Question 5.
In the answer for inheritance of X-linked. genes, Madhav had shown carrier male. His answer was marked incorrect. Madhav was wondering why his marks were cut. Explain the reason.
Answer:
Males can never be carriers. They have single X and other Y chromosome. In X linked inheritance, the genes are present on the non-homologous region of X chromosome. Males do not have other X and hence if the genes are present on his X chromosome, they will not be suppressed in them. The Y chromosome does not have dominant gene to hide this expression as there is no homolorous region too. But in case of females, there are double X chromosomes and hence if X-linked gene is recessive, the other X can hide the expression of such X-linked gene.

Thus she becomes a carrier without showing any physical characters. She is physically normal and does not suffer from such X-linked recessive disorder. Thus, Madhav will get his answer wrong due to incorrect concept.

Question 6.
With the help of neat labelled diagram, describe the structure of chromosome.
Answer:

(1) A chromosome is best visible during metaphase, when it is highly condensed.

(2) Chromosome shows two identical halves, called sister chromatids. Chromatids are held together at centromere which is also called primary constriction.

(3) Primary constriction has disc shaped plate called kinetochore. This plate is useful for attachment of spindle fibres at the time of cell division.

(4) Additional narrow areas called secondary constrictions are seen in some chromosomes which are known as nucleolar organizers. They help in the formation of nucleolus. At secondary constriction (i) there is nucleolar organising region. Secondary constriction (ii) shows attachment of satellite body or SAT body.

(5) Each chromatid is made up of sub¬chromatids called chromonemata. Each chromonema consists of a long, unbranched, slender, highly coiled DNA thread. This double stranded DNA molecule extends throughout the length of the chromosome.

(6) The ends of the chromatid arms are called telomeres.

Question 7.
What is criss-cross inheritance? Explain with suitable example.
Answer:
Criss-cross inheritance is the type of inheritance in which the genes are passed on from father to daughter and then to her son, i.e. from male to female and from female to male (grandson). In other words, it is also said that the transmission is from the grandfather to his grandson through his daughter.

I. Inheritance of Colour blindness show criss-cross pattern.
(1) Colour blindness is a sex-linked disorder in which the person concerned cannot distinguish between red and green colours.

(2) It is recessively X-linked disorder, which is expressed in males. It is rarely seen in females.

(3) The genes for normal vision are dominant whereas those for colour blindness are recessive.

(4)

• Gene for normal vision : X^C
• Gene for colour blindness : X^c
• Normal female : X^CX^C
• Normal male : X^CY
• Colour blind female : X^cX^c
• Carrier female : X^CX^c
• Colour blind male : X^c Y

II. Crosses showing the inheritance of colour blindness:
(i) A cross between normal female and colour-blind male.

(ii) A cross of carrier female with normal male.

(1) Normal female with Colour blind male. Such cross produces 50% carrier daughters and 50% normal sons.

(2) Carrier female with normal male. Such a cross produces 25% normal daughters, 25% normal sons, 25% carrier daughters and 25% colour blind sons.

(3) Colour blind father transmits the disorder to his grandson through his carrier daughter. The inheritance of characters from the father to his grandson through his daughter is called criss-cross inheritance.

Question 8.
Describe the different types of chromosomes.
Answer:
I. Chromosomes are classified into the following four types according to the position of the centromere in them:
(1) Metacentric : In metacentric chromosome, the centromere is situated in the middle of the chromosome. The two arms of the chromosome are nearly equal. It appears ‘V’-shaped during anaphase.

(2) Sub-metacentric : In sub-metacentric chromosome, the centromere is situated some distance away from the middle. Due to this, one arm of the chromosome is shorter than the other. It appears T-shaped during anaphase.

(3) Acrocentric : In acrocentric chromosome, the centromere is situated near the end of the chromosome. One arm of the acrocentric chromosome is very short while the other is long making it appear like ‘J’-shaped during anaphase.

(4) Telocentric : In telocentric chromosome, the centromere is situated at the tip of the chromosome. Telocentric chromosome has only one arm thus it appears rod-shaped.

II. Based on the functions, chromosomes are divided into autosomes and allosomes. Autosomes are somatic chromosomes which decide the body characters. Allosomes are sex chromosomes which decide the sex of the individual.

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 2 Reproduction in Lower and Higher Animals Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 2 Reproduction in Lower and Higher Animals

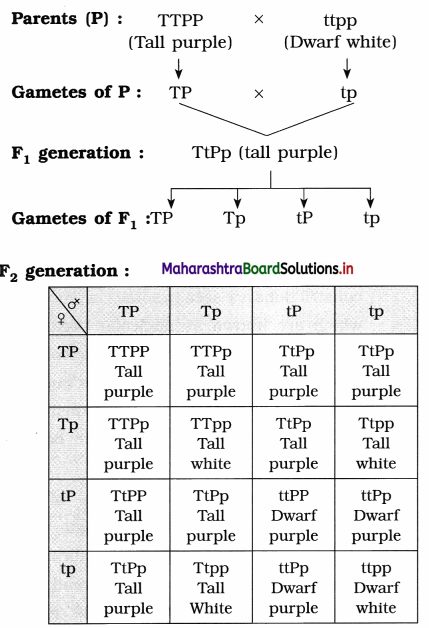
1. Multiple choice questions

Question 1.
The number of nuclei present in a zygote is ……………….
(a) two
(b) one
(c) four
(d) eight
Answer:
(b) one

Question 2.
Which of these is the male reproductive organ in human?
(a) Sperm
(b) Seminal fluid
(c) Testes
(d) Ovary
Answer:
(c) Testes

Question 3.
Attachment of embryo to the wall of the uterus is known as ……………….
(a) fertilization
(b) gestation
(c) cleavage
(d) implantation
Answer:
(d) implantation

Question 4.
Rupturing of follicles and discharge of ova is known as ……………….
(a) capacitation
(b) gestation
(c) ovulation
(d) copulation
Answer:
(c) ovulation

Question 5.
In human females, the fertilized egg gets implanted in uterus ……………….
(a) after about 7 days of fertilization
(b) after about 30 days of fertilization
(c) after about two months of fertilization
(d) after about 3 weeks of fertilization
Answer:
(a) after about 7 days of fertilization

Question 6.
Test tube baby technique is called ……………….
(a) In vivo fertilization
(b) In situ fertilization
(c) In Vitro Fertilization
(d) Artificial Insemination
Answer:
(c) In Vitro Fertilization

Question 7.

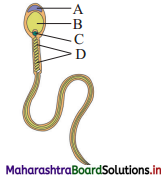
The given figure shows a human sperm. Various parts of it are labelled as A, B, C, and D. Which labelled part represents acrosome?
(a) B.
(b) C
(c) D
(d) A
Answer:
(d) A

Question 8.
Presence of beard in boys is a ……………….
(a) primary sex organ
(b) secondary sexual character
(c) secondary sex organ
(d) primary sexual character
Answer:
(b) secondary sexual character

2. Very short answer questions

Question 1.
What is the difference between a foetus and an embryo?
Answer:
Embryo is a growing egg after fertilization until the main parts of the body and the internal organs have started to take shape while foetus is a stage which has the appearance of a fully developed offspring.

Question 2.
Outline the path of sperm up to the urethra.
Answer:
The path of sperm up to the urethra in male is as follows :
Seminiferous tubules → Rete testis → Vasa efferentia → Epididymis → Vas deferens → Ejaculatory ducts Urethra.

Question 3.
Which glands contribute fluids to the semen?
Answer:
The glands which contribute fluids to the semen are seminal vesicles, prostate gland.

Question 4.
Name the endocrine glands involved in maintaining the sexual characteristics of males.
Answer:
Interstitial cells of Leydig which lie in between the seminiferous tubules are involved in maintaining the sexual characteristics of male by secreting the male hormone androgen or testosterone. Adenohypophysis also regulates this secretion from the testis.

Question 5.
Where does fertilization and implantation occur?
Answer:
Fertilization of ovum takes place in the ampulla region of fallopian tube whereas implantation occur in the endometrium of uterus.

Question 6.
Enlist the external genital organs in female.
Answer:
The external genital organs in female include the following parts such as vestibule, labia minora, clitoris, labia majora and mons Veneris.

Question 8.
What is the difference between embryo and zygote?
Answer:
Zygote is the unicellular diploid structure formed as a result of fusion of sperm and ovum whereas embryo is a multicellular structure formed from zygote in the uterus 3 weeks after fertilization.

3. Fill in the blanks

Question 1.
The primary sex organ in human male is ……………….
Answer:
testis

Question 2.
The ……………… is also called the womb.
Answer:
uterus

Question 3.
Sperm fertilizes ovum in the ……………….. of fallopian tube.
Answer:
ampulla

Question 4.
The disc like structure which helps in the transfer of substances to and from the foetus’s body is called ………………..
Answer:
placenta

Question 5.
Gonorrhoea is caused by ……………….. bacteria.
Answer:
Neisseria gonorrhoeae

Question 6.
The hormone produced by the testis is ……………………
Answer:
testosterone / androgen.

4. Short Answer Questions

Question 1.
Budding in Hydra.
Answer:

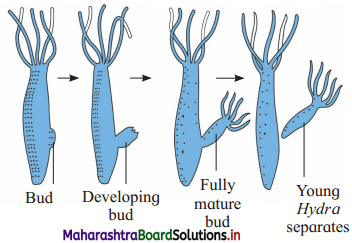
1. Budding is a type of asexual reproduction method seen in Hydra.
2. Budding takes place during favourable period.
3. Towards the basal end of the body, small outgrowth is produced which is called a bud.
4. It grows and forms tentacles and gradually forms a new individual.
5. The young Hydra after complete development detaches from the parent and becomes an independent new organism.

Question 2.
Explain the different methods of reproduction occurring in sponges.
Answer:

1. Sponges reproduce both asexually and sexually and they also possess the power of regeneration. Their sexual reproduction is similar to higher animals even though their body organization is primitive type.
2. Asexual reproduction in sponges takes place by regeneration, budding and gemmule formation.
3. In sponges, during unfavourable period, gemmule is produced. It is an internal bud.
4. Archaeocytes which are dormant cells are seen in the aggregation in gemmule. These cells are capable of developing into a new organism.
5. Amoebocytes are other cells which secrete thick resistant layer of secretion which is coated around archaeocytes.
6. When favourable conditions of water and temperature return back, the gemmules can develop into new individuals by hatching, e.g. Spongilla.

Question 3.
IVF.
Answer:

1. In laboratory under sterile conditions, oocyte and sperms are placed in a test tube or glass plate to form a zygote. This process is called In Vitro Fertilization.
2. The zygote with 8 blastomeres is then transferred into the fallopian tube for further development.
3. IVF technique is used when childless couple wants to have a baby, but there are issues of sterility.
4. IVF is also called test tube baby technique.

Question 4.
Comment on any two mechanical contraceptive methods.
Answer:
Two mechanical contraceptive methods are as follows:
A. Condom or Nirodh:

1. It is a protective barrier in the form of thin rubber sheath which is used by male partner during the sexual coitus. It covers the penis and does not allow semen to flow during copulation.
2. Thus the entry of ejaculated semen into the female reproductive tract is obstructed. This can prevent conception. It is a simple and effective method and has no side effects.
3. “Nirodh” is a condom, most widely used in India as a contraceptive by males.
4. Condom also protects both the partners against sexually transmitted diseases such as AIDS and others.

B. Diaphragm, cervical caps and vaults:

1. Diaphragm and cervical caps are to be used by females as mechanical contraceptive measures.
2. They are made up of rubber. They are fitted on the cervix in vagina so that they prevent the entry of sperms into the uterus.
3. They are kept at least six hours after sexual intercourse in order to inhibit sperms from entering female genital tract.

Question 5.
Tubectomy.
Answer:

1. The permanent birth control method in women, is called tubectomy.
2. It is a surgical method, also called sterilization.
3. In tubectomy, a small part of the fallopian tube is tied and cut.
4. Tubectomy blocks transport of oocytes and also blocks sperms, thus preventing fertilization from reaching the oocyte.

Question 6.
Give the name of causal organism of Syphilis and write on its symptoms.
Answer:
1. Syphilis is a sexually transmitted veneral disease caused by a Spirochaete bacterium Treponema pallidum.

2. The site of infection is the mucous membrane in genital, rectal and oral region.

3. Symptoms of syphilis:

• Primary lesion known as chancre at the site of infection.
• They are seen on the external genitalia in males and inside the vagina in females.
• Skin rashes accompanied by fever, inflammed joints and loss of hair.
• Paralysis
• Degenerative changes in the heart and brain.

Question 7.
What is colostrum?
Answer:

1. The fluid secreted by the mammary glands soon after childbirth is called colostrum.
2. Colostrum is the sticky and yellow fluid. It contains proteins, lactose and mother’s antibodies, e.g. IgA.
3. The fat content in colostrum is low.
4. The antibodies present in colostrum helps in developing resistance for the newborn baby at a time when its own immune response is not fully developed.

5. Answer the Following Questions

Question 1.
Describe the phases of menstrual cycle and their hormonal control.
Answer:
Menstrual cycle (Ovarian cycle):
i. Menstrual cycle involves a series of cyclic, changes in the ovary and uterus. The cyclic events are regulated by gonadotropins from pituitary and the hormones from ovary.
ii. The cyclic events in woman are repeated within approximately 28 days.
iii. Menstrual cycle is divided into following phases, viz.

1. Menstrual phase (Day 1-5)
2. Follicular phase in ovary that coincides with proliferative phase in uterus. Post menstrual phase (Day 5-14)
3. Ovulatory phase (Day 14-15)
4. Luteal phase in ovary which coincides with secretory phase in uterus (Day 16 to 28).

1. Menstrual Phase:

• Menstrual phase occurs in the absence of fertilization.
• During menstruation, uterine endometrium is sloughed off. Level of progesterone and estrogen decrease during this phase resulting into release of prostaglandins which cause this rupture.
• Blood about 45-100 ml, tissue fluid, mucus, endometrial lining and unfertilized oocyte and other cellular debris is discharged through vagina as a menstrual flow. The endometrial lining becomes about 1 mm thin.
• Fibrinolysin does not allow blood to clot during this period.
• Pituitary starts secreting FSH, which further makes many primordial follicles to develop into primary and few of them into secondary follicles.

2. Proliferative phase/Follicular phase/Post menstrual phase:

• During this phase in the ovary the follicles develop while in uterus the endometrium starts proliferating. 6 to 12 secondary follicles start developing but usually only one of them becomes Graafian follicle due to action of FSH.
• Developing secondary follicles secrete the hormone estrogen.
• Estrogen brings about regeneration of endometrium. Further proliferation of endometrium causes formation of endothelial cells, endometrial or uterine glands and network of blood vessels. Endometrium’s thickness becomes 3-5 mm.

(3) Ovulatory phase:

• Ovulation occurs in this phase. Mature Graafian follicle ruptures and secondary oocyte is released into the pelvic region of abdomen.
• Ovulation occurs due to surging quantity of LH from pituitary.

(4) Luteal phase/Secretary phase :
(i) Since the empty Graafian follicle converts itself into corpus luteum under the influence of LH, this phase is called luteal phase in ovary. At the same time, the uterine endometrium thickens and becomes more secretory and hence it is called secretory phase in uterus.

(ii) Corpus luteum secretes progesterone, some amount of estrogens and inhibin. These hormones stimulate the growth of endometrial glands which later start uterine secretions.

(iii) Endometrium becomes more vascularized becomes 8-10 mm. in thickness. These changes are the preparation for the implantation of the ovum if fertilization occurs.

(iv) In absence of fertilization, corpus luteum can survive for only two weeks and then degenerate into a non-secretory white scar called corpus albicans.

(v) If ovum is fertilized, woman becomes pregnant and hormone hCG (human Chorionic Gonadotropin) is secreted by chorionic membrane of embryo which keeps corpus luteum active till the formation of placenta.

Question 2.
Explain the steps of parturition.
Answer:
Parturition involves the following three steps:
1. Dilation stage:

• Dilation stage means dilating the birth canal or passage though which baby is pushed out. In the beginning uterine contractions start from top and baby is moved to cervix. Due to compression of blood vessels and movements of flexible joints in pelvic girdle, mother experiences labour pains.
• Oxytocin is secreted later in more amount causing severe uterine contractions. This pushes baby in a head down position and closer to cervix.
• Cervix and vagina both are dilated.
• This stage lasts for about 12 hours.
• At the end, amniotic sac ruptures and amniotic fluid is passed out.

2. Expulsion stage:

• During second stage of about 20 to 60 minutes, the uterine and abdominal contractions become stronger.
• Foetus moves out with head down position through cervix and vagina.
• The umbilical cord which connects the baby to placenta is tied and cut off close to the baby’s navel.

3. After birth or placental stage : In the last stage of 10 to 45 minutes, once the baby is out then the placenta is also separated from uterine wall and is expelled out as “after birth”. This is accompanied by severe contractions of the uterus.

Question 3.
Explain the histological structure of testis.
Answer:
Histological structure of testis:

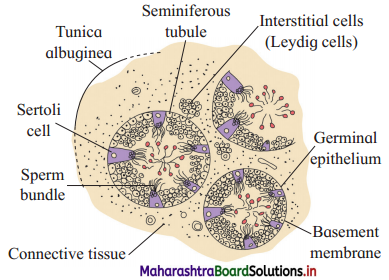
1. The external covering of testis is a fibrous connective tissue called tunica albuginea.
2. Then there is an incomplete peritoneal covering called tunica vaginalis.
3. Interior to this there is a covering called tunica vascularis formed by capillaries.
4. The testis is composed of many seminiferous tubules that are lined by cuboidal germinal epithelial cells.
5. In the seminiferous tubules various stages of developing sperms are seen as spermatogenesis takes place here. These stages are spermatogonia, primary and secondary spermatocytes, spermatids and sperms.
6. Large, pyramidal sub tentacular cells, nurse cells or Sertoli cells are present between germinal epithelium. Sperm bundles remain attached to Sertoli cells with their heads.
7. Seminiferous tubules form sperms whereas Sertoli cells provide nourishment to the sperms till maturation.
8. In between the seminiferous tubules there are interstitial cells of Leydig which are endocrine in nature. They secrete testosterone.

Question 4.
Describe the structure of blastocyst or blastulation
Answer:

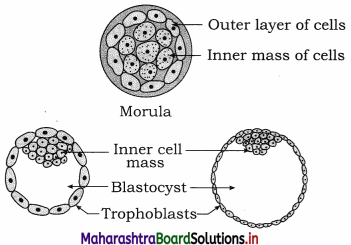
1. The outer layer of cells of the morula is called trophoblast or trophoectoderm. This layer absorbs the nutritive fluid secreted by uterine endometrial membrane.
2. As more and more fluid is absorbed by trophoblast cells, the cells become flat and a cavity called blastocyst cavity or blastocoel or segmentation cavity is formed.
3. This causes trophoblast cells to get separated from inner cell mass except at one side.
4. The trophoblast cells in contact with embryonal knob are known as cells of Rauber. As the quantity of fluid increases, the morula enlarges rapidly and assumes the shape of a cyst. This stage is called blastocyst.
5. The side of the blastocyst to which embryonal knob is attached is known as the embryonic or animal pole and the opposite side as abembryonic pole.
6. The trophoblast produces extra embryonic membranes and does not participate in the formation of embryo proper.
7. Zona pellucida disappears allowing the blastula to increase in size and volume. The blastocyst stage is reached in about five days after fertilization.
8. Blastocyst depends on mother for nutrition which it obtained through placenta.

Question 5.
Explain the histological structure of ovary in human.
Answer:
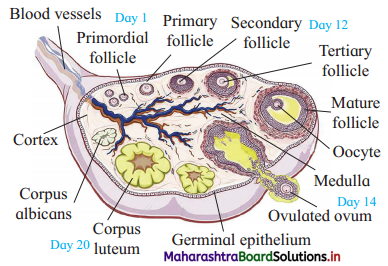
Histological structure of ovary:
(1) Each ovary is a compact structure differentiated into a central part called medulla and the outer part called cortex.

(2) The cortex is covered externally by a layer of germinal epithelium while the medulla contains the stroma or loose connective tissue with blood vessels, lymph vessels and nerve fibres.

(3) Different stages of developing ovarian follicles are seen in the cortex. Each primordial follicle has at its centre a large primary oocyte (2n) surrounded by a single layer of flat follicular cells, then gradually it matures.

(4) In the ovary during each menstrual cycle there is a maturation of primordial follicles into multilayered primary, secondary and Graafian follicles.

(5) Every Graafian follicle has three layers, viz. theca externa, theca interna and membrana granulosa which are from outer to inner side. A space called antrum filled with liquor folliculi is present inside the follicle. There is a small hillock of cells called cumulus oophours or discus proligerus over which the ovum is lodged. The ovum in turn is covered by vitelline membrane, zona pellucida and corona radiata from inner side to outer surface.

(6) Ovarian cortex also shows corpus luteum, or yellow body formed from empty Graafian follicle after ovulation. Corpus luteum is converted into corpus albicans or white body in case of absence of conception.

Question 6.
Describe the various methods of birth control to avoid pregnancy.
Answer:
Birth control/Contraceptive methods are of two main types, viz. temporary and permanent.
A. Temporary methods:
(1) Natural method/Safe period/Rhythm method : A week before and a week after menstrual bleeding is considered the safe period for sexual intercourse. It is based on the fact that ovulation occurs on the 14th day of menstrual cycle.

(2) Coitus Interruptus or withdrawal : In this method, the male partner withdraws his penis from the vagina before ejaculation, so as to avoid insemination. This method also has some drawbacks, as the pre-ejaculation fluid may contain sperms and this can cause fertilization.

(3) Lactational amenorrhoea (absence of menstruation) : This method is based on the fact that ovulation does not occur during the period of intense lactation following parturition so chances of conception are almost negligible. However, this method also has high chances of failure.

(4) Chemical means (spermicides) : In this method chemicals like foam, tablets, jellies and creams are introduced into the vagina before sexual intercourse, they adhere to the mucous membrane, immobilize and kill the sperms.

(5) Mechanical means/Barrier methods:
(i) Condom : It is a thin rubber sheath that is used to cover the penis of the male. Condom should be used before starting coital activity. It also prevents STDs and AIDS.

(ii) Diaphragm, cervical caps and vaults : These devices made of rubber are inserted into the female reproductive tract to cover the cervix diming copulation. They prevent conception by blocking the entry of sperms through the cervix.

(iii) Intra-uterine devices (IUDs) : These are plastic or metal objects placed in the uterus by a doctor. These include Lippes loop, copper releasing IUDs (Cu-T, Cu 7, multiload 375) and hormone releasing IUDs (LNG-20, progestasert). They prevent fertilization of the egg or implantation of the embryo.

(6) Physiological (Oral) Devices : Birth control pills (oral contraceptive pills) check ovulation as they inhibit the secretion of follicle stimulating hormone (FSH) and luteinizing hormone (LH) that are necessary for ovulation. The pill ‘Saheli’ is taken weekly.

(7) Other contraceptives : The birth control implant is similar to that of pills in their mode of action. It is implanted under the skin of the upper arm of the female.

B. Permanent methods surgical operations : In men surgical operation is called vasectomy and in women it is called tubectomy. This method blocks gamete transport and prevent pregnancy.

Question 7.
What are the goals of RCH programmes?
Answer:
Goals of RCH programmes are as follows:

1. Various aspects related to reproduction are made aware to general public.
2. Facilities are provided to people to understand and build up reproductive health.
3. Support is given for building up a reproductively healthy society.
4. Three critical health indicators, i.e. reducing total infertility rate, infant mortality rate and maternal mortality rate are well looked after.

Question 8.
What is parturition? Which hormones are involved in parturition?
Answer:

1. Parturition is the act of expelling out the mature foetus from the uterus of mother via the vagina.
2. When the foetus is fully mature, it starts secreting ACTH (Adreno Cortico Trophic Hormone) from its pituitary.
3. ACTH stimulates adrenal glands of foetus to produce corticosteroids.
4. These corticosteroids diffuse from foetal blood to mother’s blood across the placenta. Corticosteroids accumulate in mother’s blood that results in decreased amount of progesterone. Corticosteroids also increase secretion of prostaglandins.
5. Simultaneously estrogen levels rise bringing about initation of contractions of uterine muscular wall.
6. Reduced progesterone level and increased estrogen level cause secretion of oxytocin from mother’s pituitary. This causes greater stimulation of myometrium of uterus.
7. Prostaglandins cause increased forceful contraction of uterus which expels the foetus out of the uterus.
8. Hormone relaxin secreted by the placenta makes the pubic ligaments and sacroiliac joints of the mother loosen. This causes widening of birth canal which facilitates the normal birth of the baby.

Question 9.
What are the functions of male accessory glands?
OR
Write a brief account of accessory sex glands associated with human male reproductive system.
Answer:
Seminal Vesicles, prostate gland and Cowper’s glands are associated with human male reproductive system.
(i) Seminal Vesicles:

1. Seminal vesicles occur in pair present on the posterior side of urinary bladder. Its secretion consists about 60% of the total volume of the semen. The secretion is an alkaline seminal fluid containing fructose, fibrinogen and prostaglandins.
2. Fructose helps in the movement of sperms by providing energy to them.
3. Semen is coagulated in bolus by fibrinogen. This helps in faster movements of sperms in vagina after insemination.
4. Reverse peristalsis in vagina and uterus for faster movement of sperms towards the egg in the female body is elided by prostaglandins.

(ii) Prostate gland:

1. It is a single gland located under the urinary bladder. It has about 20 to 30 separate lobes which open separately into the urethra.
2. Prostatic fluid secreted by this gland is milky white and slightly acidic. It forms 30 % of the semen and is secreted in urethra.
3. Its contents are citric acid, acid phosphatase and various other enzymes.
4. The sperms are protected from the acidic environment of vagina by acid phosphatase.

(iii) Cowper’s glands (Bulbo-urethral glands):

1. Cowper’s glands occur in pair on either side of urethra. They are small and pea shaped.
2. Cowper’s glands secrete an alkaline, viscous, mucous-like fluid. It helps as lubricant during copulation.

Question 10.
What is capacitation? Give its importance.
Answer:

1. Capacitation is the process by which the sperms are made capable to swim up to the fallopian tubes. This process takes place in 5-6 hours.
2. 50% of ejaculated sperms die due to unfavourable vaginal and uterine conditions.
3. The remaining sperms are capacitated with the help of prostaglandin and vestibular secretions of female tract. It involves the changes in the membrane covering the acrosome.
4. Due to capacitation, acrosome membrane becomes thin, Calcium ions enters the sperm and their tail begin to show rapid whiplash movements.
5. Sperms become extra active and then they ascend upwards to reach fallopian tubes.
6. After capacitation the sperms swim through the vagina and uterus and reach ampulla of fallopian tube within 5 minutes.

Long answer questions

Question 1.
Explain the following parts of male reproductive system along with labelled diagram showing these parts – Testis, vasa deferentia, epididymis, seminal vesicle, prostate gland and penis.
OR
With the help of a neat, labelled diagram, describe the human male reproductive system.
Answer:

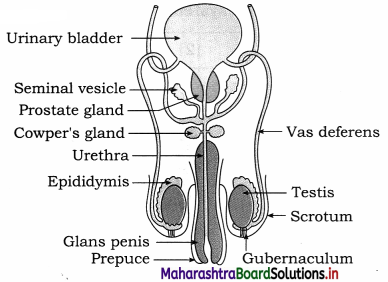
(i) Testis, the male gonad, the accessory ducts and glands along with external genitalia form the male reproductive system.

(ii) Testes:

1. Testes are male gonads with dimensions of about 4.5. cm length, 2.5 cm width and 3 cm thickness.
2. There are about 200 to 300 lobules in each testis in which there are seminiferous tubules that form rete testis.
3. Testes produce sperms and secrete male sex hormone, androgen or testosterone.

(iii) Accessory ducts : Rete testis, vasa efferentia, epididymis, vas deferens, ejaculatory duct and urethra together form the accessory ducts of male reproductive system.
1. Vasa efferentia : Vasa efferentia are 12-20 fine tubules. They arise from rete testis and end into the epididymis. The sperms from the testis are carried by these ducts to the epididymis.

2. Epididymis : Epididymis are long and coiled tubes having three parts, viz. caput, corpus and cauda epididymis. They are located on the posterior border of each testis. The sperms undergo maturation in epididymis.

3. Vasa deferentia:

• Vasa deferentia are a pair of 40 cm long tubular structures that arise from cauda epididymis.
• Each vas deferens enters the abdominal cavity through the inguinal canal and then ascends in the form of spermatic cord.
• Vas deferens of each side is joined by the duct from seminal vesicle to form ejaculatory duct.

4. Ejaculatory duct : About 2 cm long pair of ducts formed by joining of vas deferens and a duct of seminal vesicle are the ejaculatory ducts. Both ejaculatory ducts open into urethra near the prostate gland. Seminal fluid containing spermatozoa are carried by ejaculatory duct to the urethra.

5. Urethra : The male urethra provides a common passage for the urine and semen hence is also called urinogenital duct.

(iv) Accessory glands : Associated with male reproductive system are : (a) Seminal vesicles (b) Prostate gland and (c) Cowper’s or Bulbourethral glands. Every accessory gland has secretion which helps in functions of reproductive system.

(v) External genitalia : External genitalia consists of penis and scrotum.
1. Penis:

• Penis is the copulatory organ used for insemination or deposition of sperms in female genital tract.
• It is cylindrical, erectile and pendulous organ through which passes the urethra.
• It contains three columns of erectile tissues which has abundant blood sinuses.
• The tip is called glans penis while the retractible fold of skin on penis is called prepuce.

2. Scrotum : The scrotum is a pouch of pigmented skin arising from lower abdominal wall. It protects testes within it. Scrotum acts as thermoregulator. Testis are suspended in scrotum by spermatic cord.

Question 2.
Describe female reproductive system of human
Answer:

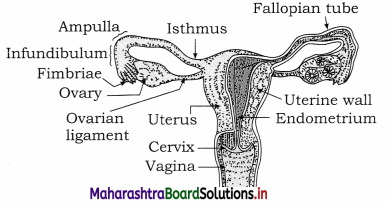
The female reproductive system consists of internal organs and external genitalia.

Internal organs are pair of ovaries and pair of fallopian ducts or oviducts, single median uterus and vagina. External genitalia is called vulva. There are a pair of vestibular glands in external genitalia. Mammary glands or breasts are also associated with reproductive system of female.

(1) Ovaries:

• Ovaries are situated in the abdomen in upper lateral part of the pelvis near the kidneys. Their dimensions are about 3 cm in length, 1.5 cm in breadth and 1.0 cm thick. They are solid, oval or almond shaped organs.
• Ovaries produce ova and they are also endocrine in nature as they produce estrogen, progesterone, relaxin, activin and inhibin.
• Ovarian hormones bring about secondary sexual characters. They also control menstrual cycle, pregnancy and parturition.

(2) Fallopian tubes/oviducts:
(i) Fallopian tubes lie horizontally over peritoneal cavity. These are about 10 to 12 cm long, narrow, muscular structure lined by ciliated epithelium.
(ii) They transport the ovum after ovulation from the ovary to the uterus.
(iii) Fallopian tube can be subdivided into the following three parts:

• The infundibulum which bears a number of finger-like processes called fimbriae at its free border.
• Infundibulum is funnel-shaped having ostium which receives ova released from the ovary.
• The second part is the ampulla where the fertilization takes place.
• The last part is short cornua or isthmus which opens into the uterus.

(3) Uterus/Womb:
(i) Uterus is a pear-shaped, highly muscular, thick walled, hollow organ measuring about 8 cm in length, 5 cm in width and 2 cm in thickness.

(ii) Uterus has the following three parts : Fundus, Body or corpus and Cervix.

(iii) The cervix communicates above with the body of the uterus by an aperture, the internal os and with vagina below by an opening the external os.

(iv) Uterus has three-layered wall. These layers are:

• Perimetrium : An outer serous layer.
• Myometrium : The middle thick muscular layer of smooth muscles.
• Endometrium : The inner highly vascular mucosa that has many uterine glands.

(v) Uterus receives the ovum from fallopian tube. It develops placenta during pregnancy for the nourishment of foetus. At the time of parturition, it expels the young one at birth.

(4) Vagina:

• Vagina is a highly distensible fibro-muscular tube that lies between the cervix and the vestibule.
• It is about 7 to 9 cm in length and is internally lined by stratified and non- keratinised epithelium. The vaginal wall has inner mucous lining.
• Vagina acts as a birth canal as well as copulatory passage. It also allows passage of menstrual flow.
• Vagina opens into vestibule by vaginal orifice which may be covered with hymen which is also a mucous membrane.

(5) External genitalia or vulva or pudendum : The external genitalia consists of five parts; viz. labia majora, labia minora, mons veneris, clitoris and vestibule.

(6) A pair of vestibular glands / Bartholin’s glands : These glands open into the vestibule and release a lubricating fluid.

(7) A pair of mammary glands/breasts : These are the accessory organs of female reproductive system for production and release of milk after parturition.

Question 3.
Describe the process of fertilization.
Answer:
(1) Fertilization is the process of fusion of the haploid male and female gametes which results in the formation of a diploid zygote (2n).

(2) In human beings fertilization is internal. Sperms deposited in vagina, swim across the uterus and fertilize the ovum in ampulla of the fallopian tube.

(3) Fertilization involves the following events:
(i) Insemination : Discharge of semen into the vagina at the time of copulation is called insemination.

(ii) Movement of sperm towards egg : Sperms reaching the vagina undergo capacitation process for 5-6 hours. During capacitation acrosomal membrane of sperm becomes thin and Ca⁺⁺ enters the sperm making it extra active. Sperms reach up to the ampulla by swimming aided with contraction of uterus and fallopian tubes. These contractions are stimulated by oxytocin of female. By capacitation sperm can reach ampulla within 5 minutes, they remain 5 viable for 24 to 48 hours, whereas ovum remains viable for 24 hours.

(iii) Entry of sperm into the egg : Though many sperms reach the ampulla, only a single sperm fertilizes the ovum. The acrosome of sperm after coming in contact with the ovum, releases lysins; hyaluronidase and corona penetrating enzymes. Due to these enzymes cells of corona radiata are separated and dissolved. The sperm head then passes through zona pellucida of egg. The zona pellucida has glycoprotein fertilizin receptor proteins. These bind to specific acid protein-antifertilizin of sperm. This makes sperm and ovum to come together. Fertilizin-Antifertilizin interaction is species- specific.

(iv) Acrosome reaction : When the sperm head comes in contact with the zona pellucida, its acrosome covering ruptures to release lytic enzymes, acrosin or zona lysin. These enzymes dissolve plasma membrane of egg so that the sperm nucleus and the centrioles enter the egg, while other parts remain outside. Now the vitelline membrane of egg changes into fertilization membrane which prevents any further entry of other sperms into the egg, thus polyspermy is prevented.

(v) Activation of ovum : After the entry of sperm head into ovum, it gets activated to resume and complete its meiosis-II. With this it gives out the second polar body. The germinal vesicle organises into female pronucleus. At this stage, it is true ovum.

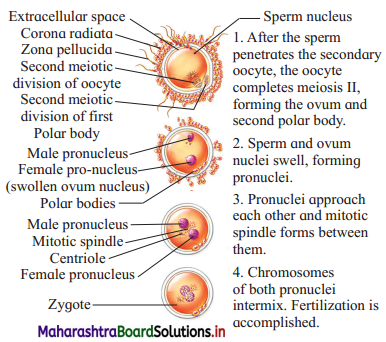
(vi) Fusion of egg and sperm : The coverings of male and female pronuclei degenerate results in the formation of a synkaryon by a process called syngamy or karyogamy. The zygote is thus formed.

Question 4.
Explain the process by which zygote divides and redivides to form the morula.
Answer:
(1) Cleavage is a rapid mitotic division to form a blastula. These divisions takes place immediately after fertilization. The cells formed by cleavage are called blastomeres.

(2) The type of cleavage in human is holoblastic, i.e. the whole zygote gets divided, radial and indeterminate, i.e. fate of each blastomere is not predetermined.

(3) Cleavage show faster synthesis of DNA and high consumption of oxygen.

(4) Since there is no growth phase between the cleavages, the size of blastomeres will be reduced with every successive cleavage.

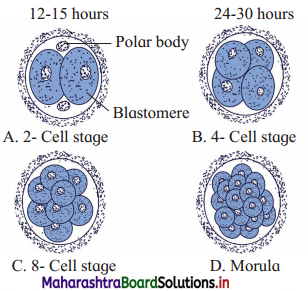
(5) The cleavages occur as follows:

(6) Successive divisions produce a solid ball of cells called morula of 16 cells. It consists of an outer layer of smaller clearer cells and an inner mass of larger cells.

(7) Morula reaches the uterus about 4-6 days after fertilization.

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 1 Reproduction in Lower and Higher Plants Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Biology Solutions Chapter 1 Reproduction in Lower and Higher Plants

1. Multiple Choice Questions

Question 1.
Insect pollinated flowers usually possess ………………
(a) sticky pollen with a rough surface
(b) large quantities of pollens
(c) dry pollen with a smooth surface
(d) light-colored pollens
Answer:
(a) sticky pollen with a rough surface

Question 2.
In ovule, meiosis occurs in ………………
(a) Integument
(b) Nucellus
(c) Megaspore
(d) Megaspore mother cell
Answer:
(d) Megaspore mother cell

Question 3.
The ploidy level is NOT the same in ………………
(a) Integuments and nucellus
(b) Root tip and shoot tip
(c) Secondary nucleus and endosperm
(d) Antipodals and synergids
Answer:
(c) Secondary nucleus and endosperm

Question 4.
Which of the following types require pollination but result is genetically similar to autogamy?
(a) Geitonogamy
(b) Xenogamy
(c) Apogamy
(d) Cleistogamy
Answer:
(a) Geitonogamy

Question 5.
If diploid chromosome number in a flowering plant is 12, then which one of the following will have 6 chromosomes?
(a) Endosperm
(b) Leaf cells
(c) Cotyledons
(d) Synergids
Answer:
(d) Synergids

Question 6.
In angiosperms, endosperm is formed by/ due to ………………
(a) free nuclear divisions of megaspore
(b) polar nuclei
(c) polar nuclei and male gamete
(d) synergids and male gametes
Answer:
(c) polar nuclei and male gamete

Question 7.
Point out the odd one.
(a) Nucellus
(b) Embryo sac
(c) Micropyle
(d) Pollen grain
Answer:
(d) Pollen grain

2. Very Short Answer Questions

Question 1.
The part of gynoecium that determines the compatible nature of pollen grain.
Answer:
Stigmatic surface.

Question 2.
How many haploid cells are present in a mature embryo sac?
Answer:
6 cells, 2 synergids, 1 egg cell, 3 antipodals.

Question 3.
Even though each pollen grain has 2 male gametes why at least 20 pollen grains are required to fertilize 20 ovules in a particular carpel?
Answer:
Angiosperms have phenomenon of double fertilization in which both the male gametes are utilized, one for fusion with egg cell to form zygote and other for fusion with secondary nucleus to form endosperm.

Question 4.
Megasporogenesis
Answer:
It is the process of formation of haploid megaspores from diploid megaspore mother cell.

Question 5.
What is hydrophily?
Answer:
Transfer of pollen grains in pollination process through agency of water is known as hydrophily.

Question 6.
The layer which supplies nourishment to the developing pollen grains.
Answer:
Tapetum

Question 7.
Parthenocarpy
Answer:
The condition in which fruit is developed without the process of fertilization is called parthenocarpy.

Question 8.
Are pollination and fertilization necessary in apomixis?
Answer:
Apomixis is formation of embryos without formation of gametes hence there is no need of pollination and fertilization.

Question 9.
The part of pistil which develops into fruit and seed.
Answer:
Ovary develops into fruit and ovules into seed.

Question 10.
What is the function of filiform apparatus ?
Answer:
Filiform apparatus guides the pollen tube towards egg cell.

3. Short Answer Questions

Question 1.
How polyembryony can be commercially exploited?
Answer:

1. Polyembryony is the development of more than one embryo inside the seed.
2. When such polyembryonic seed germinate we get multiple seedlings from it.
3. This condition increases the chances of survival of new plants.
4. Nucellar embryos are genetically identical to parent plants hence we get uniform plants.
5. In horticulture we can utilize these as rootstock for grafting, hence they have significant role in fruit breeding programmes e.g. Citrus, Mango.

Question 2.
Pollination and seeds formation are very crucial for the fruit formation, Justify.
Answer:

1. After fertilization, ovary is transformed into fruit, where ovary wall becomes fruit wall, i.e pericarp.
2. Mature ovules are transformed into seeds after fertilization.
3. Fertilization is a process where male gametes unites with female gamete to form zygote which develops into embryo.
4. In pollination process pollen grains carrying non-motile male gamete are transferred on stigma.
5. Seeds have embryo which germinate into new plant hence the goal of reproduction to create offspring for next generation is achieved. Hence these are the crucial events for fruit formation.

Question 3.
Incompatibility is a natural barrier in the fusion of gametes. How will you explain this statement?
Answer:

1. Self incompatibility or self-sterility is a genetic mechanism that prevents germination of pollen on stigma of same flower. This favours cross pollination. E.g. Tobacco.
2. In pollen-pistil interaction, when pollen grain is deposited on stigma, pistil has the ability to recognize and allow germination of right type of pollen.
3. Special type of proteins on stigmatic surface determine compatibility or incompatibility.
4. A physiological mechanism operates to ensure successful germination of compatible pollen.
5. Compatible pollen absorbs water and nutrients from stigmatic surface that are absent in pollen and then pollen tube emerges which grow-s through style.

Question 4.
Describe three devices by which cross pollination is encouraged in Angiosperms by avoiding self-pollination?
Answer:

1. Unisexuality, dichogamy, prepotency, heteromorphy and herkogamy are the outbreeding devices.
2. Unisexuality : The plants bear either male or female flowers. Due to unisexual nature, self-pollination is avoided. Plants are either dioecious, e.g. Papaya or monoecious, e.g. maize.
3. Heteromorphy : In same plants different types of flowers are produced. In these flowers, stigmas and anthers are situated at different levels. There is heterostyly and heteroanthy. This prevents self-pollination e.g. Primrose.
4. Herkogamy : In bisexual flowers we may come across mechanical device to prevent self-pollination. Natural physical barrier avoids contact of pollens with stigma. E.g. Calotropis where pollinia are situated below the stigma.

4. Long Answer Questions

Question 1.
Describe the process of double fertilization.
Answer:
Double fertilization:
(1) Out of the two male gametes produced by the male gametophyte in angiosperms, one unites with the female gamete and the other with the secondary nucleus. Since both the male gametes take part in fertilization and fertilization occurs twice, it is called double fertilization.

(2) During double fertilization, the pollen tube on reaching the ovule enters the embryo sac through micropyle and bursts in one of the synergids. Owing to this, the two male gametes contained in the pollen tube, are set free.

(3) Out of the two male gametes, one unites with the egg or female gamete and the other unites with the secondary nucleus of the embryo sac, forming a triploid or triple fusion nucleus, called the primary endosperm nucleus. The process involving the fusion of one of the male gametes with the egg nucleus, resulting in the formation of a diploid zygote is called syngamy.

(4) The reproductive process in which non-motile male nuclei are carried to the egg cell through a pollen tube is called siphonogamy.

(5) After fertilization, zygote develops into an embryo. Certain changes take place in the ovule leading to the development of a seed.

Question 2.
Explain the stages involved in the maturation of microspore into male gametophyte.
OR
Describe the development of male gametophyte before pollination in angiosperms.
OR
Sketch and label male gametophyte in angiosperm.
Answer:

1. Microspore or pollen grain is first cell of male gametophyte.
2. The protoplast of pollen grain divides mitotically to form two unequal cells – a small thin walled generative cell and a large naked vegetative or tube cell.
3. The generative cell possesses thin cytoplasm and a nucleus. It separates and floats in the cytoplasm of vegetative cell.
4. The vegetative, possesses thick cytoplasm, irregular shaped nucleus and the reserved food.
5. In majority of the angiosperms, the pollen grains are liberated at two-celled stage after the dehiscence of the anther.
6. The generative cell of the pollen grain divides by mitosis to form two male non-motile gametes.

Question 3.
Explain the development of dicot embryo.
Answer:
Development of embryo (dicot) in angio- sperm:

The oospore undergoes a transverse division to form a large basal cell towards the micropyle and a small apical or terminal cell towards the chalaza of the embryo sac. This two celled structure is called proembryo. The basal cell or suspensor initial undergoes repeated transverse divisions to form a multicellular structure called suspensor. The suspensor pushes the embryo towards the endosperm to draw its nutrition.

1. The development of embryo from a zygote is called embryogenesis.
2. The fusion of male gamete and an egg cell during fertilization results in the formation of a diploid zygote. The zygote develops a wall around it and is converted into oospore.
3. The apical cell or embryonal initial of the proembryo undergoes a transverse division followed by two vertical divisions at right angles to form an octant stage.
4. From octant, the lower four cells form hypocotyl and radicle while four cells of upper side form plumule with two cotyledons.
5. The lowermost cell of suspensor is hypophysis and by its further division forms part of radicle and root cap.
6. The cells from upper side of octant divide repeatedly to form heart shaped which elongated further to form two lateral cotyledons.
7. Enlargement of hypocotyl and cotyledon results into curved embryo which appears horse shoe shaped.

Question 4.
Draw a diagram of the L.S of anatropous ovule and list the components of embryo sac and mention their fate after fertilization.
Answer:
Components of Embryo sac.

1. Mature embryo sac is 7-celled and 8 nucleate.
2. Egg apparatus at micropylar end – with 2 synergids and egg cell.
3. Central cell with secondary nucleus formed by 2 polar nuclei
4. Antipodal cells at chalazal end – 3 cells.
5. Pollen tube enters the synergids, Synergids guide the growth of pollen tube towards egg.
6. Male gamete fuses with female gamete, i.e. syngamy to form zygote which develops into embryo.
7. One male gamete fuses with secondarynucleus to form primary endosperm nucleus (PEN) which forms endosperm, nutritive tissue for embryo.

5. Fill in the Blanks

Question 1.
The ……………… collects the pollen grains.
Answer:
biotic agents

Question 2.
The male whorl, called the ……………… produces ………………
Answer:
androecium, pollen grains

Question 3.
The pollen grains represent the ………………
Answer:
male

Question 4.
The ……………… contains the egg or ovum.
Answer:
embryo sac

Question 5.
…………….. takes place when one male gamete and the egg fuse together. The fertilized egg grows vs into seed from which the new plants can grow.
Answer:
Fertilization

Question 6.
The ……………… is the base of the flower to which other floral parts are attached.
Answer:
thalamus

Question 7.
……………… is the transfer of pollen grains from anther of the flower to the stigma of the same or a different flower.
Answer:
Pollination

Question 8.
Once the pollen reaches the stigma, pollen tube traverses down the ……………… to the ovary where fertilization occurs.
Answer:
style

Question 9.
The ……………… are coloured to attract the insects that carry the pollen. Some flowers also produce ……………… or ……………… that attracts insects.
Answer:
petals, fragrance, nectar

Question 10.
The whorl ……………… is green that protects the flower until it opens.
Answer:
Calyx.

6. Label the Parts of seed.

Answer:

7. Match the following

Column I (Structure Before seed formation)	Column II (Structure After seed formation)
A. Funiculus	i. Hilum
B. Scar of Ovule	ii. Tegmen
C. Zygote	iii. Testa
D. Inner Integument	iv. Stalk of Seed
	v. Embryo

(a) A-v, B-i, C-ii, D-iv
(b) A-iii, B-iv, C-i, D-v
(c) A-iv, B-i, C-v D-ii
(d) A-iv, B-v C-iii, D-ii
Answer:
(c) A-iv, B-i, C-v D-ii

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Ex 4.3

Question 1.
Find the joint equation of the pair of lines:
(i) Through the point (2, -1) and parallel to lines represented by 2x² + 3xy – 9y² = 0
Solution:
The combined equation of the given lines is
2x² + 3 xy – 9y² = 0
i.e. 2x² + 6xy – 3xy – 9y² = 0
i.e. 2x(x + 3y) – 3y(x + 3y) = 0
i.e. (x + 3y)(2x – 3y) = 0
∴ their separate equations are
x + 3y = 0 and 2x – 3y = 0
∴ their slopes are m₁ = \(\frac{-1}{3}\) and m₂ = \(\frac{-2}{-3}=\frac{2}{3}\).
The slopes of the lines parallel to these lines are m₁ and m₂, i.e. \(-\frac{1}{3}\) and \(\frac{2}{3}\).
∴ the equations of the lines with these slopes and through the point (2, -1) are
y + 1 = \(-\frac{1}{3}\) (x – 2) and y + 1 = \(\frac{2}{3}\)(x – 2)
i.e. 3y + 3= -x + 2 and 3y + 3 = 2x – 4
i.e. x + 3y + 1 = 0 and 2x – 3y – 7 = 0
∴ the joint equation of these lines is
(x + 3y + 1)(2x – 3y – 7) = 0
∴ 2x² – 3xy – 7x + 6xy – 9y² – 21y + 2x – 3y – 7 = 0
∴ 2x² + 3xy – 9y² – 5x – 24y – 7 = 0.

(ii) Through the point (2, -3) and parallel to lines represented by x² + xy – y² = 0
Solution:
Comparing the equation
x² + xy – y² = 0 … (1)
with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 1, b = -1
Let m₁ and m₂ be the slopes of the lines represented by (1).

The slopes of the lines parallel to these lines are m₁ and m₂.
∴ the equations of the lines with these slopes and through the point (2, -3) are
y + 3 = m₁(x – 2) and y + 3 = m₂(x – 2)
i.e. m₁(x – 2) – (y + 3) = 0 and m₂(x – 2) – (y + 3) = 0
∴ the joint equation of these lines is
[m₁(x – 2) – (y + 3)][m₂(x – 2) – (y + 3)] = 0
∴ m₁m₂(x – 2)² – m₁(x – 2)(y + 3) – m₂(x – 2)(y + 3) + (y + 3)² = o
∴ m₁m₂(x – 2)² – (m₁ + m₂)(x – 2)(y + 3) + (y + 3)³ = 0
∴ -(x – 2)² – (x – 2)(y + 3) + (y + 3)² = 0 …… [By (2)]
∴ (x – 2)² + (x – 2)(y + 3) – (y + 3)² = 0
∴ (x² – 4x + 4) + (xy + 3x – 2y – 6) – (y² + 6y + 9) = 0
∴ x² – 4x + 4 + xy + 3x – 2y – 6 – y² – 6y – 9 = 0
∴ x² + xy – y² – x – 8y – 11 = 0.

Question 2.
Show that equation x² + 2xy+ 2y² + 2x + 2y + 1 = 0 does not represent a pair of lines.
Solution:
Comparing the equation
x² + 2xy + 2y² + 2x + 2y + 1 = 0 with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 1, h = 1, b = 2, g = 1, f = 1, c = 1.
The given equation represents a pair of lines, if
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|\) = 0 and h² – ab ≥ 0
Now, D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 1 (2 – 1) – 1(1 – 1) + 1 (1 – 2)
= 1 – 0 – 1 = 0
and h² – ab = (1)² – 1(2) = -1 < 0
∴ given equation does not represent a pair of lines.

Question 3.
Show that equation 2x² – xy – 3y² – 6x + 19y – 20 = 0 represents a pair of lines.
Solution:
Comparing the equation
2x² – xy – 3y² – 6x + 19y – 20 = 0
with ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 2, h = \(-\frac{1}{2}\), b = -3, g = -3, f = \(\frac{19}{2}\), c = -20.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
2 & -\frac{1}{2} & -3 \\
-\frac{1}{2} & -3 & \frac{19}{2} \\
-3 & \frac{19}{2} & -20
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & -1 & -6 \\
-1 & -6 & 19 \\
-6 & 19 & -40
\end{array}\right|\)
= \(\frac{1}{8}\)[4(240 – 361) + 1(40 + 114) – 6(-19 – 36)]
= \(\frac{1}{8}\)[4(-121) + 154 – 6(-55)]
= \(\frac{11}{8}\)[4(-11) + 14 – 6(-5)]
= \(\frac{1}{8}\)(-44 + 14 + 30) = 0
Also h² – ab = \(\left(-\frac{1}{2}\right)^{2}\) – 2(-3) = \(\frac{1}{4}\) + 6 = \(\frac{25}{4}\) > 0
∴ the given equation represents a pair of lines.

Question 4.
Show the equation 2x² + xy – y² + x + 4y – 3 = 0 represents a pair of lines. Also find the acute angle between them.
Solution:
Comparing the equation
2x² + xy — y² + x + 4y — 3 = 0 with
ax² + 2hxy + by² + 2gx + 2fy + c — 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2, c = – 3.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lrr}
2 & \frac{1}{2} & \frac{1}{2} \\
\frac{1}{2} & -1 & 2 \\
\frac{1}{2} & 2 & -3
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & 1 & 1 \\
1 & -2 & 4 \\
1 & 4 & -6
\end{array}\right|\)
= \(\frac{1}{8}\)[4(12 —16) — 1( —6 — 4) + 1(4 + 2)]
= \(\frac{1}{8}\)[4( – 4) – 1(-10) + 1(6)]
= \(\frac{1}{8}\)(—16 + 10 + 6) = 0
Also, h² – ab = \(\left(\frac{1}{2}\right)^{2}\) – 2(-1) = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
∴ the given equation represents a pair of lines. Let θ be the acute angle between the lines
∴ tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\)

Question 5.
Find the separate equation of the lines represented by the following equations :
(i) (x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)² = 0
Solution:
(x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)2 = 0
∴ (x – 2)² – 2(x – 2)(y + 1) – (x – 2)(y + 1) + 2(y + 1)² = 0
∴ (x – 2) [(x – 2) – 2(y + 1)] – (y + 1)[(x – 2) – 2(y + 1)] = 0
∴ (x – 2)(x – 2 – 2y – 2) – (y + 1)(x – 2 – 2y – 2) = 0
∴ (x – 2)(x – 2y – 4) – (y + 1)(x – 2y – 4) = 0
∴ (x – 2y – 4)(x – 2 – y – 1) = 0
∴ (x – 2y – 4)(x – y – 3) = 0
∴ the separate equations of the lines are
x – 2y – 4 = 0 and x – y – 3 = 0.
Alternative Method :
(x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)² = 0 … (1)
Put x – 2 = X and y + 1 = Y
∴ (1) becomes,
X² – 3XY + 2Y² = 0
∴ X² – 2XY – XY + 2Y² = 0
∴ X(X – 2Y) – Y(X – 2Y) = 0
∴ (X – 2Y)(X – Y) = 0
∴ the separate equations of the lines are
∴ X – 2Y = 0 and X – Y = 0
∴ (x – 2) – 2(y + 1) = 0 and (x – 2) – (y +1) = 0
∴ x – 2y – 4 = 0 and x – y – 3 = 0.

(ii) 10(x + 1)² + (x + 1)( y – 2) – 3(y – 2)² = 0
Solution:
10(x + 1)² + (x + 1)( y – 2) – 3(y – 2)² = 0 …(1)
Put x + 1 = X and y – 2 = Y
∴ (1) becomes
10x² + xy – 3y² = 0
10x² + 6xy – 5xy – 3y² = 0
2x(5x + 3y) – y(5x + 3y) = 0
(2x – y)(5x + 3y) = 0
5x + 3y = 0 and 2x – y = 0
5x + 3y = 0
5(x + 1) + 3(y – 2) = 0
5x + 5 + 3y – 6 = 0
∴ 5x + 3y – 1 = 0
2x – y = 0
2(x + 1) – (y – 2) = 0
2x + 2 – y + 2 = 0
∴ 2x – y + 4 = 0

Question 6.
Find the value of k if the following equations represent a pair of lines :
(i) 3x² + 10xy + 3y² + 16y + k = 0
Solution:
Comparing the given equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0,
we get, a = 3, h = 5, b = 3, g = 0, f= 8, c = k.
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af² – bg² – ch² = 0
∴ (3)(3)(k) + 2(8)(0)(5) – 3(8)² – 3(0)² – k(5)² = 0
∴ 9k + 0 – 192 – 0 – 25k = 0
∴ -16k – 192 = 0
∴ – 16k = 192
∴ k= -12.

(ii) kxy + 10x + 6y + 4 = 0
Solution:
Comparing the given equation with
ax² + 2 hxy + by² + 2gx + 2fy + c = 0,
we get, a = 0, h = \(\frac{k}{2}\), b = 0, g = 5, f = 3, c = 4
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af² – bg² – ch² = 0
∴ (0)(0)(4) + 2(3)(5)\(\left(\frac{k}{2}\right)\) – 0(3)² – 0(5)² – 4\(\left(\frac{k}{2}\right)^{2}\) = 0
∴ 0 + 15k – 0 – 0 – k² = 0
∴ 15k – k² = 0
∴ -k(k – 15) = 0
∴ k = 0 or k = 15.
If k = 0, then the given equation becomes
10x + 6y + 4 = 0 which does not represent a pair of lines.
∴ k ≠ o
Hence, k = 15.

(iii) x² + 3xy + 2y² + x – y + k = 0
Solution:
Comparing the given equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0,
we get, a = 1, h = \(\frac{3}{2}\), b = 2, g = \(\frac{1}{2}\), f= \(-\frac{1}{2}\), c = k.
Now, given equation represents a pair of lines.


∴ 2(8k – 1) – 3(6k + 1) + 1(-3 – 4) = 0
∴ 16k – 2 – 18k – 3 – 7 = 0
∴ -2k – 12 = 0
∴ -2k = 12 ∴ k = -6.

Question 7.
Find p and q if the equation px² – 8xy + 3y² + 14x + 2y + q = 0 represents a pair of perpendicular lines.
Solution:
The given equation represents a pair of lines perpendicular to each other
∴ (coefficient of x²) + (coefficient of y²) = 0
∴ p + 3 = 0 p = -3
With this value of p, the given equation is
– 3x² – 8xy + 3y² + 14x + 2y + q = 0.
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we have,
a = -3, h = -4, b = 3, g = 7, f = 1 and c = q.
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
-3 & -4 & 7 \\
-4 & 3 & 1 \\
7 & 1 & q
\end{array}\right|\)
= -3(3q – 1) + 4(-4q – 7) + 7(-4 – 21)
= -9q + 3 – 16q – 28 – 175
= -25q – 200= -25(q + 8)
Since the given equation represents a pair of lines, D = 0
∴ -25(q + 8) = 0 ∴ q= -8.
Hence, p = -3 and q = -8.

Question 8.
Find p and q if the equation 2x² + 8xy + py² + qx + 2y – 15 = 0 represents a pair of parallel lines.
Solution:
The given equation is
2x² + 8xy + py² + qx + 2y – 15 = 0
Comparing it with ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 2, h = 4, b = p, g = \(\frac{q}{2}\), f = 1, c = – 15
Since the lines are parallel, h² = ab
∴ (4)² = 2p ∴ P = 8
Since the given equation represents a pair of lines

i.e. – 242 + 240 + 2q + 2q – 2q² = 0
i.e. -2q² + 4q – 2 = 0
i.e. q² – 2q + 1 = 0
i.e. (q – 1)² = 0 ∴ q – 1 = 0 ∴ q = 1.
Hence, p = 8 and q = 1.

Question 9.
Equations of pairs of opposite sides of a parallelogram are x² – 7x+ 6 = 0 and y² – 14y + 40 = 0. Find the joint equation of its diagonals.
Solution:
Let ABCD be the parallelogram such that the combined equation of sides AB and CD is x² – 7x + 6 = 0 and the combined equation of sides BC and AD is y² – 14y + 40 = 0.
The separate equations of the lines represented by x² – 7x + 6 = 0, i.e. (x – 1)(x – 6) = 0 are x – 1 = 0 and x – 6 = 0.
Let equation of the side AB be x – 1 = 0 and equation of side CD be x – 6 = 0.
The separate equations of the lines represented by y² – 14y + 40 = 0, i.e. (y – 4)(y – 10) = 0 are y – 4 = 0 and y – 10 = 0.
Let equation of the side BC be y – 4 = 0 and equation of side AD be y – 10 = 0.

Coordinates of the vertices of the parallelogram are A(1, 10), B(1, 4), C(6, 4) and D(6, 10).
∴ equation of the diagonal AC is
\(\frac{y-10}{x-1}\) = \(\frac{10-4}{1-6}\) = \(\frac{6}{-5}\)
∴ -5y + 50 = 6x – 6
∴ 6x + 5y – 56 = 0
and equation of the diagonal BD is
\(\frac{y-4}{x-1}\) = \(\frac{4-10}{1-6}\) = \(\frac{-6}{-5}\) = \(\frac{6}{5}\)
∴ 5y – 20 = 6x – 6
∴ 6x – 5y + 14 = 0
Hence, the equations of the diagonals are 6x + 5y – 56 = 0 and 6x – 5y + 14 = 0.
∴ the joint equation of the diagonals is (6x + 5y – 56)(6x – 5y + 14) = 0
∴ 36x² – 30xy + 84x + 30xy – 25y² + 70y – 336x + 280y – 784 = 0
∴ 36x² – 25y² – 252x + 350y – 784 = 0.

Question 10.
∆OAB is formed by lines x² – 4xy + y² = 0 and the line 2x + 3y – 1 = 0. Find the equation of the median of the triangle drawn from O.
Solution:

Let D be the midpoint of seg AB where A is (x₁, y₁) and B is (x₂, y₂).
Then D has coordinates \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\).
The joint (combined) equation of the lines OA and OB is x² – 4xy + y² = 0 and the equation of the line AB is 2x + 3y – 1 = 0.
∴ points A and B satisfy the equations 2x + 3y – 1 = 0
and x² – 4xy + y² = 0 simultaneously.
We eliminate x from the above equations, i.e.,
put x = \(\frac{1-3 y}{2}\) in the equation x² – 4xy + y² = 0, we get,
∴ \(\left(\frac{1-3 y}{2}\right)^{2}\) – 4\(\left(\frac{1-3 y}{2}\right)\)y + y² = 0
∴ (1 – 3y)² – 8(1 – 3y)y + 4y² = 0
∴1 – 6y + 9y² – 8y + 24y² + 4y² = 0
∴ 37y² – 14y + 1 = 0
The roots y₁ and y₂ of the above quadratic equation are the y-coordinates of the points A and B.
∴ y₁ + y₂ = \(\frac{-b}{a}=\frac{14}{37}\)
∴ y-coordinate of D = \(\frac{y_{1}+y_{2}}{2}=\frac{7}{37}\).
Since D lies on the line AB, we can find the x-coordinate of D as
2x + 3\(\left(\frac{7}{37}\right)\) – 1 = 0
∴ 2x = 1 – \(\frac{21}{37}=\frac{16}{37}\)
∴ x = \(\frac{8}{37}\)
∴ D is (8/37, 7/37)
∴ equation of the median OD is \(\frac{x}{8 / 37}=\frac{y}{7 / 37}\),
i.e., 7x – 8y = 0.

Question 11.
Find the co-ordinates of the points of intersection of the lines represented by x² – y² – 2x + 1 = 0.
Solution:
Consider, x² – y² – 2x + 1 = 0
∴ (x² – 2x + 1) – y² = 0
∴ (x – 1)² – y² = 0
∴ (x – 1 + y)(x – 1 – y) = 0
∴ (x + y – 1)(x – y – 1) = 0
∴ separate equations of the lines are
x + y – 1 = 0 and x – y +1 = 0.
To find the point of intersection of the lines, we have to solve
x + y – 1 = 0 … (1)
and x – y + 1 = 0 … (2)
Adding (1) and (2), we get,
2x = 0 ∴ x = 0
Substituting x = 0 in (1), we get,
0 + y – 1 = 0 ∴ y = 1
∴ coordinates of the point of intersection of the lines are (0, 1).

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 4 Pair of Straight Lines Ex 4.2

Question 1.
Show that lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.
Solution:
Comparing the equation 3x² – 4 xy – 3y² = 0 with ax² + 2hxy + by² = 0, we get, a = 3, 2h = -4, b = -3 Since a + b = 3 + (-3) = 0, the lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.

Question 2.
Show that lines represented by x² + 6xy + gy²= 0 are coincident.
Question is modified.
Show that lines represented by x² + 6xy + 9y²= 0 are coincident.
Solution:
Comparing the equation x² + 6xy + 9y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 6, i.e. h = 3 and b = 9
Since h² – ab = (3)² – 1(9)
= 9 – 9 = 0, .
the lines represented by x² + 6xy + 9y² = 0 are coincident.

Question 3.
Find the value of k if lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other.
Solution:
Comparing the equation kx² + 4xy – 4y² = 0 with ax² + 2hxy + by² = 0, we get,
a = k, 2h = 4, b = -4
Since lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other,
a + b = 0
∴ k – 4 = 0 ∴ k = 4.

Question 4.
Find the measure of the acute angle between the lines represented by:
(i) 3x² – 4\(\sqrt {3}\)xy + 3y² = 0
Solution:
Comparing the equation 3x² – 4\(\sqrt {3}\)xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 3, 2h = -4\(\sqrt {3}\), i.e. h = -24\(\sqrt {3}\) and b = 3
Let θ be the acute angle between the lines.

∴ θ = 30°.

(ii) 4x² + 5xy + y² = 0
Solution:
Comparing the equation 4x² + 5xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 5, i.e. h = \(\frac{5}{2}\) and b = 1.
Let θ be the acute angle between the lines.

(iii) 2x² + 7xy + 3y² = 0
Solution:
Comparing the equation
2x² + 7xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 2, 2h = 7 i.e. h = \(\frac{7}{2}\) and b = 3
Let θ be the acute angle between the lines.


tanθ = 1
∴ θ = tan 1 = 45°
∴ θ = 45°

(iv) (a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0
Solution:
Comparing the equation
(a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0, with
Ax² + 2Hxy + By² = 0, we have,
A = a² – 3b², H = 4ab, B = b² – 3a².
∴ H² – AB = 16a²b² – (a² – 3b²)(b² – 3a²)
= 16a²b² + (a² – 3b²)(3a² – b²)
= 16a²b² + 3a⁴ – 10a²b² + 3b⁴
= 3a⁴ + 6a²b² + 3b⁴
= 3(a⁴ + 2a²b² + b⁴)
= 3 (a² + b²)²
∴ \(\sqrt{H^{2}-A B}\) = \(\sqrt {3}\) (a² + b²)
Also, A + B = (a² – 3b²) + (b² – 3a²)
= -2 (a² + b²)
If θ is the acute angle between the lines, then
tan θ = \(\left|\frac{2 \sqrt{H^{2}-A B}}{A+B}\right|=\left|\frac{2 \sqrt{3}\left(a^{2}+b^{2}\right)}{-2\left(a^{2}+b^{2}\right)}\right|\)
= \(\sqrt {3}\) = tan 60°
∴ θ = 60°

Question 5.
Find the combined equation of lines passing through the origin each of which making an angle of 30° with the line 3x + 2y – 11 = 0
Solution:
The slope of the line 3x + 2y – 11 = 0 is m₁ = \(-\frac{3}{2}\) .
Let m be the slope of one of the lines making an angle of 30° with the line 3x + 2y – 11 = 0.
The angle between the lines having slopes m and m1 is 30°.

On squaring both sides, we get,
\(\frac{1}{3}=\frac{(2 m+3)^{2}}{(2-3 m)^{2}}\)
∴ (2 – 3m)² = 3 (2m + 3)²
∴ 4 – 12m + 9m² = 3(4m² + 12m + 9)
∴ 4 – 12m + 9m² = 12m² + 36m + 27
3m² + 48m + 23 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
3\(\left(\frac{y}{x}\right)^{2}\) + 48\(\left(\frac{y}{x}\right)\) + 23 = 0
∴ \(\frac{3 y^{2}}{x^{2}}+\frac{48 y}{x}\) + 23 = 0
∴ 3y² + 48xy + 23x² = 0
∴ 23x² + 48xy + 3y² = 0.

Question 6.
If the angle between lines represented by ax² + 2hxy + by² = 0 is equal to the angle between lines represented by 2x² – 5xy + 3y² = 0 then show that 100(h² – ab) = (a + b)².
Solution:
The acute angle θ between the lines ax² + 2hxy + by² = 0 is given by
tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\) ..(1)
Comparing the equation 2x² – 5xy + 3y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 2, 2h= -5, i.e. h = \(-\frac{5}{2}\) and b = 3
Let ∝ be the acute angle between the lines 2x² – 5xy + 3y² = 0.

This is the required condition.

Question 7.
Find the combined equation of lines passing through the origin and each of which making angle 60° with the Y- axis.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 3 सच हम नहीं; सच तुम नहीं Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 3 सच हम नहीं; सच तुम नहीं

12th Hindi Guide Chapter 3 सच हम नहीं; सच तुम नहीं Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) कविता की पंक्ति पूर्ण कीजिए :
(1) अपने हृदय का सत्य, – ……………………….
(2) आदर्श हो सकती नहीं, – ……………………….
(3) बेकार है मुस्कान से ढकना, – ……………………….
(4) अपने नयन का नीर, – ……………………….
उत्तर :
(1) अपने हृदय का सत्य, अपने-आप हमको खोजना।
(2) आदर्श हो सकती नहीं, तन और मन की भिन्नता।
(3) बेकार है मुस्कान से ढकना, हृदय की खिन्नता।
(4) अपने नयन का नीर, अपने-आप हमको पोंछना।

(आ) लिखिए :

(a) जीवन यही है
(1) जीवन यही है –
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
जीवन यही है –
(i) नत न होना।
(ii) पंथ भूलने पर भी न रुकना।
(iii) हार देखकर भी न झुकना।
(iv) मृत्यु को भी जीत लेना।

(b) मिलना वही है –
(1) मिलना वही है – ……………………….
(2) यह जिंदगी जिंदगी नहीं है – ……………………….
(3) हर राही को इससे दिशा मिलती है – ……………………….
(4) कवि तब तक इस राह को सही नहीं मानेगा – ……………………….
उत्तर :
(1) जो मँझधार को मोड़ दे।
(2) जो सिर्फ पानी-सी बहती रहे।
(3) भटकने के बाद।
(4) जब तक जीवन बँधा होगा और जब तक प्यार पर दुख की गहरी छाया होगी।

शब्द संपदा

प्रश्न 2.
प्रत्येक शब्द के दो पर्यायवाची शब्द लिखिए :
(1) पंथ – [ ] [ ]
(2) काँटा – [ ] [ ]
(3) कुसुम – [ ] [ ]
(4) हार – [ ] [ ]
उत्तर :
(1) पंथ – [ रास्ता ] [ डगर ]
(2) काँटा – [ शूल ] [ कंटक ]
(3) कुसुम – [ पुष्प ] [ प्रसून ]
(4) हार – [ पराजय ] [ पराभव ]

अभिव्यक्ति

प्रश्न 3.
(अ) ‘जीवन निरंतर चलते रहने का नाम है’, इस विचार की सार्थकता स्पष्ट कीजिए।
उत्तर :
जीवन का उद्देश्य निरंतर आगे-ही-आगे बढ़ते रहना है। जीवन में ठहराव आने को मृत्यु की संज्ञा दी जाती है। अनेक महापुरुषों ने अपने उद्देश्य की पूर्ति के लिए जीवनभर संघर्ष किया है और उनका नाम अमर हो गया है। जीवन का मार्ग आसान नहीं ३ है। उस पर पग-पग पर कठिनाइयाँ आती रहती हैं। इन कठिनाइयों 1 से उसे जूझना पड़ता है। उसमें हार भी होती है और जीत भी होती ३ है। असफलताओं से मनुष्य को घबराना नहीं चाहिए।

बल्कि उनका ३ दृढ़तापूर्वक सामना करके उसमें से अपना मार्ग प्रशस्त करना और ३ निरंतर आगे बढ़ते रहना चाहिए। एक दिन मंजिल अवश्य मिलेगी। जीवन संघर्ष कभी न खत्म होने वाला संग्राम है। इसका सामना करने का एकमात्र मार्ग है निरंतर चलते रहना और हर स्थिति में संघर्ष जारी रखना।

(आ) ‘संघर्ष करने वाला ही जीवन का लक्ष्य प्राप्त करता है, इस विषय पर अपने विचार प्रकट कीजिए।
उत्तर :
दुनिया में दो प्रकार के मनुष्य होते हैं। एक वे जो सामान्य रूप से चलनेवाली जिंदगी जीना पसंद करते हैं और आगे बढ़ने के लिए किए जानेवाले उठा-पटक को पसंद नहीं करते। दूसरे तरह के वे लोग होते हैं, जो अपना लक्ष्य निर्धारित कर लेते हैं और उसे प्राप्त करने के लिए संघर्ष का रास्ता चुनते हैं। ऐसे लोगों का जीवन आसान नहीं होता। इन्हें पग-पग पर विभिन्न रुकावटों का सामना करना पड़ता है।

पर ऐसे लोग इन रुकावटों से डरते नहीं, बल्कि हँसते-हँसते इनका सामना करते हैं। सामना करने में अनेक बार असफलता भी इनके हाथ लगती है। पर ये इससे हताश नहीं होते। ये फिर अपनी गलतियों को सुधारते हैं और नए सिरे से संघर्ष करने में जुट जाते हैं। परिस्थितियाँ कैसी भी हों, वे न झुकते हैं और न हताश होते हैं। उनके सामने सदा उनका लक्ष्य होता है। उसे प्राप्त करने के लिए वे निरंतर संघर्ष करते रहते हैं।

ऐसे लोग अपनी निष्ठा और लगन के बल पर एक-न-एक दिन अवश्य सफल हो जाते हैं। वे संघर्ष के बल पर अपने जीवन का लक्ष्य प्राप्त करके रहते हैं।

रसास्वादन

प्रश्न 4.
‘आँसुओं को पोंछकर अपनी क्षमताओं को पहचानना ही जीवन है’, इस सच्चाई को समझाते हुए कविता का रसास्वादन कीजिए।
उत्तर :
डॉ. जगदीश गुप्त द्वारा लिखित कविता ‘सच हम नहीं, सच तुम नहीं’ में जीवन में निरंतर संघर्ष करते रहने का आह्वान किया गया है।

कवि पानी-सी बहने वाली सीधी-सादी जिंदगी का विरोध करते हुए संघर्षपूर्ण जीवन जीने की बात करते हैं। वे कहते हैं, जो जहाँ भी हो, उसे संघर्ष करते रहना चाहिए।

संघर्ष में मिली असफलता से निराश होने की आवश्यकता नहीं है। ऐसी हालत में हमें किसी के सहयोग की आशा नहीं करनी। हमें अपने आप में खुद हिम्मत लानी होगी और अपनी क्षमता को पहचानकर नए सिरे से संघर्ष करना होगा। मन में यह विश्वास रखकर काम करना होगा कि हर राही को भटकने के बाद दिशा मिलती ही है और उसका प्रयास व्यर्थ नहीं जाएगा। उसे भी दिशा मिलकर रहेगी।

कवि ने सीधे-सादे शब्दों में प्रभावशाली ढंग से अपनी बात कही है। अपनी बात कहने के लिए उन्होंने ‘अपने नयन का नीर पोंछने’ शब्द समूह के द्वारा हताशा से अपने आपको उबार कर स्वयं में नई शक्ति पैदा करने तथा ‘आकाश सुख देगा नहीं, धरती पसीजी है नहीं’ से यह कहने का प्रयास किया है कि भगवान तुम्हारी सहायता के लिए नहीं आने वाले हैं और धरती के लोग तुम्हारे दुख से द्रवित नहीं होने वाले हैं। इसलिए तुम स्वयं अपने आप को सांत्वना दो और नए जोश के साथ आगे बढ़ो। तुम अपने लक्ष्य पर पहुँचने में अवश्य कामयाब होंगे।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
जानकारी दीजिए :
(अ) ‘नई कविता’ के अन्य कवियों के नाम –
(आ) कवि डॉक्टर जगदीश गुप्त की प्रमुख साहित्यिक कृतियों के नाम –
उत्तर :
(अ) ‘नई कविता’ के अन्य कवियों के नाम – [रामस्वरूप चतुर्वेदी, विजयदेव साही]
(आ) कवि डॉक्टर जगदीश गुप्त की प्रमुख साहित्यिक कृतियों के नाम – [‘नाँव के पाँव, शब्द दंश, हिम विद्ध, गोपा-गौतम’] (काव्य संग्रह), ‘शंबूक’ (खंडकाव्य), ‘भारतीय कला के पदचिहन, नयी कविता : स्वरूप और समस्याएँ, केशवदास’ (आलोचनाएँ) तथा ‘नयी कविता’ (पत्रिका)।]

प्रश्न 6.
निम्नलिखित वाक्यों में अधोरेखांकित शब्दों का लिंग परिवर्तन कर वाक्य फिर से लिखिए :

(1) बहुत चेष्टा करने पर भी हरिण न आया।
उत्तर :
बहुत चेष्टा करने पर भी हरिणी न आई।

(2) सिद्धहस्त लेखिका बनना ही उनका एकमात्र सपना था।
उत्तर :
सिद्धहस्त लेखक बनना ही उनका एकमात्र सपना था।

(3) तुम एक समझदार लड़की हो।
उत्तर :
तुम एक समझदार लड़के हो।

(4) मैं पहली बार वृद्धाश्रम में मौसी से मिलने आया था।
उत्तर :
मैं पहली बार वृद्धाश्रम में मौसा से मिलने आया था।

(5) तुम्हारे जैसा पुत्र भगवान सब को दे।
उत्तर :
तुम्हारी जैसी पुत्री भगवान सब को दे।

(6) साधु की विद्वत्ता की धाक दूर-दूर तक फैल गई थी।
उत्तर :
साध्वी की विद्वत्ता की धाक दूर-दूर तक फैल गई थी।

(7) बूढ़े मर गए।
उत्तर :
बुढ़ियाँ मर गईं।

(8) वह एक दस वर्ष का बच्चा छोड़ा गया।
उत्तर :
वह एक दस वर्ष की बच्ची छोड़ी गई।

(9) तुम्हारा मौसेरा भाई माफी माँगने पहुंचा था।
उत्तर :
तुम्हारी मौसेरी बहन माफी माँगने पहुंची थी।

(10) एक अच्छी सहेली के नाते तुम उसकी पारिवारिक पृष्ठभूमि का अध्ययन करो।
उत्तर :
एक अच्छे मित्र के नाते तुम उसकी पारिवारिक पृष्ठभूमि का अध्ययन करो।

Hindi Yuvakbharati 12th Digest Chapter 3 सच हम नहीं; सच तुम नहीं Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
पद्यांश क्र. 1

प्रश्न. निम्नलिखितपद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए :

उत्तर :

प्रश्न 2.
जीवन का संदेश
(i) …………………………….
(ii) …………………………….
(iii) …………………………….
(iv) …………………………….
उत्तर :
जीवन का संदेश –
(i) जीवन में कहीं जड़ता नहीं होनी चाहिए।
(ii) अपनी-अपनी जगह पर खुद से लड़ाई जारी रखनी चाहिए।
(iii) हर तरह की परिस्थिति का सामना करने की तैयारी होनी चाहिए।
(iv) इन्सान को कभी टूटना-हारना नहीं चाहिए।

प्रश्न 3.
उत्तर लिखिए :
(1) नत होने से मृत जैसा होने की तुलना की गई है इससे – …………………………….
(2) काँटे चुभे, कलियाँ खिलें का अर्थ – …………………………….
उत्तर :
(1) नत होने से मृत जैसा होने की तुलना की गई है इससे – [डंठल से झरे फूल से।]
(2) काँटे चुभे, कलियाँ खिलें का अर्थ – [स्थिति चाहे प्रतिकूल हो अथवा अनुकूल।]

पदयांश क्र. 2
प्रश्न. निम्नलिखितपद्यांशपढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
पद्यांश पर आधारित दो ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों :
(1) आकाश
(2) धरती
उत्तर :
(1) कौन सुख नहीं देगा?
(2) कौन नहीं पसीजती है?

कृति 2 : (शब्द संपदा)

प्रश्न 1.
प्रत्येक शब्द के दो-दो पर्यायवाची शब्द लिखिए :
(1) फूल – [ ] [ ]
(2) नीर – [ ] [ ]
(3) नयन – [ ] [ ]
(4) धरती – [ ] [ ]
उत्तर :
(1) फूल – [ पुष्प ] [ कुसुम ]
(2) नीर – [ अंबु ] [ जल ]
(3) नयन – [ चक्षु ] [ आँख ]
(4) धरती – [ पथ्वी ] [ अवनि ]

(2) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) तोड़ना x …………………………
(2) सच x …………………………
(3) दुख x …………………………
(4) बेकार x …………………………
उत्तर :
(1) तोड़ना x जोड़ना
(3) दुख x सुख
(2) सच x झूठ
(4) बेकार x साकार।

रसास्वादन मुद्दों के आधार पर
कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर सच हम नहीं; सच तुम नहीं’ कविता का रसास्वादन कीजिए।
उत्तर :
(1) रचना का शीर्षक : सच हम नहीं; सच तुम नहीं।
(2) रचनाकार : डॉ. जगदीश गुप्त।
(3) कविता की केंद्रीय कल्पना : प्रस्तुत कविता में निरंतर आगे बढ़ते रहने, संघर्ष करते रहने और मार्ग में आनेवाली रुकावटों की परवाह न करके अपने लक्ष्य की प्राप्ति की ओर अग्रसर होने की प्रेरणा दी गई है। यही इस कविता की केंद्रीय कल्पना है।
(4) रस-अलंकार : –
(5) प्रतीक विधान : इस कविता में संघर्ष का मार्ग त्याग कर नत हो जाने यानी किसी की अधीनता स्वीकार कर लेने वाले को मृतक के समान हो जाना कहा गया है। कवि ने इस तरह के मृत व्यक्ति के लिए ‘डाल से झड़े हुए फूल’ का प्रतीक के रूप में उपयोग किया है।
(6) कल्पना : जीवन में दृढ़तापूर्वक संघर्ष का मार्ग अपनाना और निराश हुए बिना उस पर अडिग रहना ही जीवन की एकमात्र सच्चाई है।
(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
अपने हृदय का सत्य,
अपने आप हम को खोजना।
अपने नयन का नीर,
अपने आप हम को पोंछना।.

इन पंक्तियों में अपनी समस्याओं को पहचानने और उनका समाधान ढूँढ़ने के लिए बिना किसी की सहायता की उम्मीद किए स्वयं कमर कस कर तैयार होने की प्रेरणा मिलती है।

(8) कविता पसंद आने का कारण : कवि ने इस पंक्ति में यह बताया है कि संघर्ष में असफलता हाथ लगे, तो भी निराश होने की जरूरत नहीं है। हमें अपने आप अपनी आँखों के आँसू पौंछकर फिर से हिम्मत के साथ संघर्ष में जुट जाना है।

व्याकरण

अलंकार :

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त अलंकार पहचान कर उनके नाम लिखिए :
(1) हरि पद कोमल कमल से।
(2) झूठे जानि न संग्रही मन मुँह निकसे बैन। यहि ते मानहुँ किए, बातनु को बिघि नैन।
(3) पायो जी मैंने राम रतन धन पायो।
(4) हनूमान की पूँछ में लग न पाई आग। लंका सिगरी जल गई, गए निशाचर भाग।
(5) एक म्यान में दो तलवारें कभी नहीं रह सकतीं। किसी और पर प्रेम पति का नारियाँ नहीं सह सकी।
उत्तर :
(1) उपमा अलंकार
(2) उत्प्रेक्षा अलंकार
(3) रूपक अलंकार
(4) अतिशयोक्ति अलंकार
(5) दृष्टांत अलंकार।

रस:

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त रस पहचान कर लिखिए :
(1) काहु न तखा सो चरित विसेरना। सो सरूप नृप कन्या देखा।
मर्कट वदन भयंकर देही। देखत हृदय क्रोध मा तेही।
जेहि दिसि बैठे नारद फूली। सो दिसि तेहि न विलोकी भूली।
पुनि-पुनि मुनि उकसहिं अकुलाहीं। देखि दसा हर गन मुसुकाहीं।

(2) जो हौं तव अनुशासन पावौं
तौ चंद्रमहिं निचोरि चैल ज्यों आनि सुधा सिर नावौं।
कै पाताल दलौं व्यालावलि अमृत कुंड महि लावौ।
भेदि भुवन, करि भानु बाहियें तुरत राहु दै ताबौ।।
विबुध बैद बरबस आनौं धरि, तौ प्रभु अनुग कहावौं।
पटकौं मीच नीच मूषक ज्यों सबहिं को पाप कहावौं।

(3) कहुँ सुलगत कोउ चिता, कहुँ कोउ जात लगाई।
एक लगाई जात, एक की राख बुझाई।
विविध रंग की उठति ज्वाल दुर्गन्धिति महकति,
कहु चरबी सी चटचटाति कहुँ दह-दह दहकति।
उत्तर :
(1) हास्य रस
(2) वीर रस
(3) वीभत्स रस।

मुहावरे :

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(1) गुड़ गोबर करना।
अर्थ : बने काम को बिगाड़ देना।
वाक्य : चित्रकार का चित्र तैयार था तभी एक छोटे बच्चे ने आकर उस पर ऐसी कूँची फिराई की सारा गुड़ गोबर हो गया।

(2) जहर का चूंट पीना।
अर्थ : अपमान को चुपचाप सह लेना।
वाक्य : मुंशीजी अपने चपरासी से कभी-कभी जब पैर दबा देने की बात करते थे तब वह जहर का यूंट पीकर रह जाता था।

(3) तिल का ताड़ बनाना।
अर्थ : छोटी बात को बढ़ा-चढ़ा कर कहना।
वाक्य : रमेश की बात विश्वास करने लायक नहीं होती, उसकी तो तिल का ताड़ बनाने की आदत है।

(4) मुट्ठी गर्म करना।
अर्थ : रिश्वत देना।
वाक्य : गाँवों में छोटा-मोटा काम करवाने के लिए भी अधिकारियों की मुट्ठी गर्म करनी पड़ती है।

(5) पत्थर की लकीर।
अर्थ : पक्की बात।
वाक्य : गाँव के लोग वकील साहब की बात को पत्थर की लकीर मानते थे।

काल परिवर्तन :

प्रश्न 1.
सूचनाओं के अनुसार काल परिवर्तन करके वाक्य फिर से लिखिए :
(1) वह पंथ भूल कर नहीं रुकता है। (पूर्ण भूतकाल)
(2) वह हार देख कर नहीं झुका। (सामान्य भविष्यकाल)
(3) आकाश सुख नहीं देगा। (अपूर्ण वर्तमानकाल)
(4) धरती नहीं पसीजती है। (पूर्ण वर्तमानकाल)
(5) हर एक राही को भटक कर दिशा मिलती है। (अपूर्ण भूतकाल)
उत्तर :
(1) वह पंथ भूल कर नहीं रुका था।
(2) वह हार देख कर नहीं झुकेगा।
(3) आकाश सुख नहीं दे रहा है।
(4) धरती नहीं पसीजी है।
(5) हर एक राही को भटक कर दिशा मिल रही थी।

वाक्य शुद्धिकरण :

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके लिखिए :
(1) वह उसका काम कर रहा हैं।
(2) उस बगीचे में अनेकों फूले खिले हैं।
(3) पुस्तक की ढेर देख मैं दंग रह गया।
(4) उसे मात्र केवल दो दिन की छुट्टी चाहिएँ।
(5) मैं तुमको धन्यवाद करता हूँ।
उत्तर :
(1) वह अपना काम कर रहा है।
(2) उस बगीचे में अनेक फूल खिले हैं।
(3) पुस्तकों का ढेर देख में दंग रह गया।
(4) उसे केवल दो दिन की छुट्टी चाहिए।
(5) मैं तुम्हें धन्यवाद देता हूँ।

सच हम नहीं; सच तुम नहीं Summary in Hindi

सच हम नहीं; सच तुम नहीं कवि का परिचय

सच हम नहीं; सच तुम नहीं कवि का नाम : डॉ. जगदीश गुप्त। (जन्म 1924; निधन 2001.)
प्रमुख कृतियाँ : नाँव के पाँव, शब्द दंश, हिम विद्ध, गोपा-गौतम (काव्य संग्रह), ‘शंबूक’ (खंडकाव्य), भारतीय कला के पदचिह्न,
नयी कविता : स्वरूप और समस्याएँ, केशवदास (आलोचनाएँ) तथा ‘नयी कविता’ (पत्रिका) आदि।
विशेषता : प्रयोगवाद के बाद जिस नयी कविता का प्रारंभ हुआ, उसके प्रवर्तकों में जगदीश गुप्त का नाम प्रमुख रूप से लिया जाता है।
विधा : नई कविता। नए भावबोधों की अभिव्यक्ति के साथ नए मूल्यों और नए शिल्प विधान का अन्वेषण नई कविता की विशेषता है।

विषय प्रवेश : प्रस्तुत नई कविता में कवि ने संघर्ष करने की प्रेरणा दी है। संघर्ष ही जीवन की सच्चाई है। जो मनुष्य कठिनाइयों और मुसीबतों का सामना करते हुए बिना झुके या रुके आगे बढ़ता रहता है, वही सच्चा मनुष्य है। जिंदगी लीक से हटकर चलने का नाम है। लीक से भटककर भी मंजिल अवश्य मिलती है। कवि का कहना है कि हमें अपनी समस्याएँ खुद सुलझानी होंगी। हमारी लड़ाई – कोई दूसरा लड़ने नहीं आएगा। हमें खुद योद्धा बनकर अपनी लड़ाई लड़नी है।

सच हम नहीं; सच तुम नहीं कविता का सरल अर्थ

सच हम नहीं …………………………………………….. है जीवन वही।
कवि कहते हैं कि न मेरी बात सच है और न तुम्हारी बात सच है। सच है तो निरंतर संघर्ष करना। संघर्ष ही जीवन है। हमें संघर्ष का रास्ता अपनाना चाहिए। कवि के अनुसार संघर्ष से हटकर जीने की बात ही नहीं करनी चाहिए। बिना संघर्ष का जीवन भी भला कोई जीवन है!

कवि कहते हैं कि जिसने अधीनता स्वीकार ली, वह मृतक के समान हो गया। उसकी हालत डाल से झड़े हुए फूल जैसी होती है। जो व्यक्ति संघर्ष के मार्ग पर चलता हआ भटक जाने पर भी अपनी मंजिल पर बढ़ने से नहीं रुका अथवा अपने प्रयास में असफल हो जाने पर भी जिसने हार नहीं मानी अथवा जिसने मृत्यु से भी मोर्चा लिया हो और उसको परास्त कर दिया हो, उसी का जीवन जीवन कहलाने के योग्य है। यही सच्चाई है।

ऐसा करो जिससे …………………………………………….. यौवन का यही।
कवि कहते हैं कि मनुष्य में कहीं भी कोई ठहराव नहीं आना चाहिए। जो जहाँ है उसे वहीं चुपचाप अपना संघर्ष जारी रखना चाहिए। वे कहते हैं कि परिस्थितियाँ कैसी भी हों चाहे प्रतिकूल स्थिति हो अथवा अनुकूल स्थिति, मनुष्य को हताश होकर अपना संघर्ष कभी भी त्यागना नहीं चाहिए। जीवन का यही संदेश है।

हमने रचा जाओ …………………………………………….. पानी-सी बही।
कवि कहते हैं कि यथास्थिति में जीने का हमने जो नियम बनाया था, आओ, अब हम उसे तोड़ दें। यह भी कोई जीवन है। जीवन तो वह है, जो मँझधार को भी मोड़ने की शक्ति रखता हो। जिसने संघर्ष किया ही नहीं और यथास्थिति को ही सुखमय मानकर जीवन जीता आ रहा हो और दूसरों के इशारों पर चलता आ रहा हो, उसकी भला कोई जिंदगी है? वह जिंदगी तो यथास्थिति को स्वीकार लेने और लीक पर चलनेवाला जीवन है। (इसमें संघर्ष का नामोनिशान नहीं है।)

अपने हृदय का …………………………………………….. दिशा मिलती रही।

कवि कहते हैं कि हमें अपने दुखों को पहचानना होगा। उन्हें दूर करने के लिए हमें स्वयं प्रयास करना होगा। अपनी आँखों के आँसू हमें खुद पोंछने होंगे। हमें अपनी सहायता के लिए किसी अन्य से आशा नहीं करनी है। किसी अन्य की कृपा का भरोसा करना व्यर्थ है। हमें खुद योद्धा बनना होगा। हर संघर्ष करने वाले को कोई-नकोई मार्ग अवश्य मिलता है। मनुष्य मार्ग भटकने के बाद अपने लक्ष्य पर अवश्य पहुँचता है, इस बात को हमें गाँठ बाँध लेनी चाहिए।

बेकार है मुस्कान से …………………………………………….. राह को ही मैं सही।
कवि कहते हैं कि हृदय के कष्ट को बाह्य मुस्कान से दबाया नहीं जा सकता। इस तरह के प्रयास का कोई लाभ नहीं होता। इसे आदर्श नहीं माना जा सकता है। मनुष्य को भीतर और बाहर दोनों से एक-सा ही रहना चाहिए, यही आदर्श है। कवि कहते हैं कि जब तक विचारों पर अंकुश लगा रहेगा और जब तक प्यार पर दुख की गहरी छाया बनी रहेगी, तब तक इस मार्ग को किसी भी कीमत पर उचित नहीं माना जा सकता।

सच हम नहीं; सच तुम नहीं शब्दार्थ

• नत = झुका हुआ
• जड़ता = अचलता, ठहराव
• पसीजना = मन में दया भाव आना
• वृंत = डंठल
• मँझधार = नदी की बीच की धारा
• चेतना = जागृत अवस्था