Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Matrices Ex 2.1
Question 1.
Construct a matrix A = [aij]3×2 whose elements aij isgiven by
(i) aij = \(\frac{(i-j)^{2}}{5-i}\)
Solution:

(ii) aij = i – 3j
Solution:
aij = i – 3j
∴ a11 = 1 – 3(1) = 1 – 3 = -2
a12 = 1 – 3(2) = 1 – 6 = -5
a21 = 2 – 3(1) = 2 – 3 = -1
a22 = 2 – 3(2) = 2 – 6 = -4
a31 = 3 – 3(1) = 3 – 3 = 0
a32 = 3 – 3(2) = 3 – 6 = -3
∴ A = \(\left[\begin{array}{cc}
-2 & -5 \\
-1 & -4 \\
0 & -3
\end{array}\right]\)
![]()
(iii) aij = \(\frac{(i+j)^{3}}{5}\)
Solution:
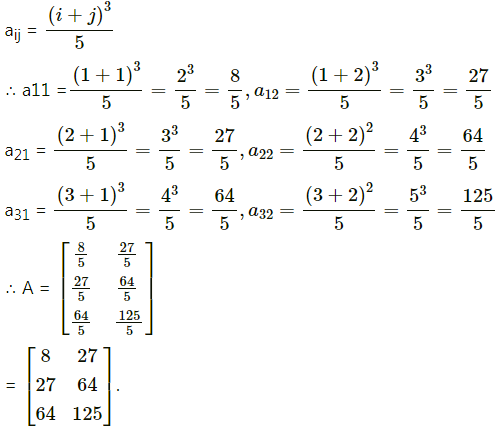
Question 2.
Classify each of the following matrices as a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular matrix:
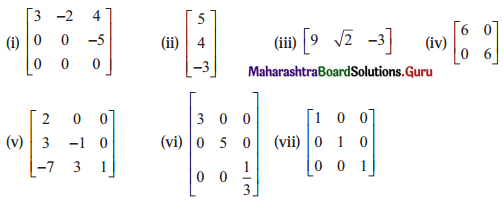
Solution:
(i) Since, all the elements below the diagonal are zero, it is an upper triangular matrix.
(ii) This matrix has only one column, it is a column matrix.
(iii) This matrix has only one row, it is a row matrix.
(iv) Since, diagonal elements are equal and non-diagonal elements are zero, it is a scalar matrix.
(v) Since, all the elements above the diagonal are zero, it is a lower triangular matrix.
(vi) Since, all the non-diagonal elements are zero, it is a diagonal matrix.
(vii) Since, diagonal elements are 1 and non-diagonal elements are 0, it is an identity (or unit) matrix.
Question 3.
Which of the following matrices are singular or non-singular:
(i) \(\left[\begin{array}{ccc}
a & b & c \\
p & q & r \\
2 a-p & 2 b-q & 2 c-r
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{ccc}
5 & 0 & 5 \\
1 & 99 & 100 \\
6 & 99 & 105
\end{array}\right]\)
Solution:
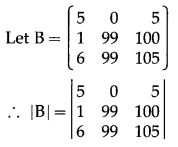

![]()
(iii) \(\left[\begin{array}{ccc}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right]\)
Solution:
Let C = \(\left[\begin{array}{ccc}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right]\)
∴ |C| = \(\left|\begin{array}{rrr}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right|\)
= 3(5 – 8) – 5(-10 – 12) + 7(-4 – 3)
= -9 + 110 – 49
= 52 ≠ 0
∴ C is a non-singular matrix.
(iv) \(\left[\begin{array}{cc}
7 & 5 \\
-4 & 7
\end{array}\right]\)
Solution:
Let D = \(\left[\begin{array}{cc}
7 & 5 \\
-4 & 7
\end{array}\right]\)
∴ |D| = \(\left|\begin{array}{rr}
7 & 5 \\
-4 & 7
\end{array}\right|\)
= 49 – (-20)
= 69 ≠ 0
∴ D is a non-singular matrix.
![]()
Question 4.
Find k, if the following matrices are singular:
(i) \(\left[\begin{array}{cc}
7 & 3 \\
-2 & K
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
7 & 3 \\
-2 & K
\end{array}\right]\)
Since, A is a singular matrix, |A| = 0
∴ \(\left|\begin{array}{rr}
7 & 3 \\
-2 & k
\end{array}\right|\) = 0
∴ 7k – (-6) = 0
∴ 7k = -6
∴ k = \(-\frac{6}{7}\)
(ii) \(\left[\begin{array}{ccc}
4 & 3 & 1 \\
7 & \mathrm{~K} & 1 \\
10 & 9 & 1
\end{array}\right]\)
Solution:
Let B = \(\left[\begin{array}{ccc}
4 & 3 & 1 \\
7 & \mathrm{~K} & 1 \\
10 & 9 & 1
\end{array}\right]\)
Since, B is a singular matrix, |B| = 0
∴ \(\left|\begin{array}{rrr}
4 & 3 & 1 \\
7 & k & 1 \\
10 & 9 & 1
\end{array}\right|\) = 0
∴ 4(k – 9) – 3(7 – 10) + 1(63 – 10k) = 0
∴ 4k – 36 + 9 + 63 – 10k = 0
∴ -6k + 36 = 0
∴ 6k = 36
∴ k = 6.
![]()
(iii) \(\left[\begin{array}{ccc}
K-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right]\)
Solution:
Let C = \(\left[\begin{array}{ccc}
K-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right]\)
Since, C is a singular matrix, |C| = 0
∴ \(\left|\begin{array}{crr}
k-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right|\) = 0
∴ (k – 1)(4 + 4) – 2(12 – 2) + 3(-6 – 1) = 0
∴ 8k – 8 – 20 – 21 = 0
∴ 8k = 49
∴ k = \(\frac{49}{8}\)