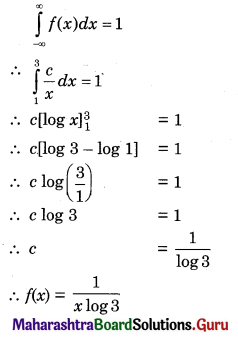Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.2
Question 1.
Check whether each of the following is p.d.f.
(i) \(f(x)= \begin{cases}x & \text { for } 0 \leq x \leq 1 \\ 2-x & \text { for } 1<x \leq 2\end{cases}\)
Solution:
Given function is
f(x) = x, 0 ≤ x ≤ 1
Each f(x) ≥ 0, as x ≥ 0.

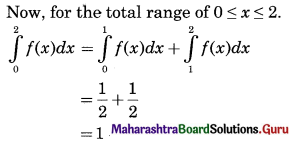
∴ The given function is a p.d.f. of x.
(ii) f(x) = 2 for 0 < x < 1
Solution:
Given function is
f(x) = 2 for 0 < x < 1 Each f(x) > 0,
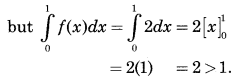
∴ The given function is not a p.d.f.
![]()
Question 2.
The following is the p.d.f. of a r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
Find (i) P(X < 1.5), (ii) P(1 < X < 2), (iii) P(X > 2)
Solution:


Question 3.
It is felt that error in measurement of reaction temperature (in Celsius) in an experiment is a continuous r.v. with p.d.f.
\(f(x)= \begin{cases}\frac{x^{3}}{64} & \text { for } 0 \leq x \leq 4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Verify whether f(x) is a p.d.f.
(ii) Find P(0 < X ≤ 1).
(iii) Find the probability that X is between 1 and 3.
Solution:
(i) f(x) is p.d.f. of r.v. X if
(a) f(x) ≥ 0, ∀ x ∈ R
(b) \(\int_{0}^{4} f(x) d x\) = 1


Question 4.
Find k, if the following function represents the p.d.f. of a r.v. X.
(i) \(f(x)= \begin{cases}k x & \text { for } 0<x<2 \\ 0 & \text { otherwise }\end{cases}\)
Also find P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)]
Solution:

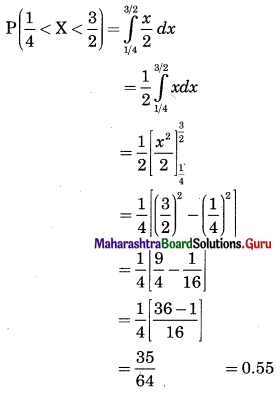
(ii) \(f(x)= \begin{cases}k x(1-x) & \text { for } 0<x<1 \\ 0 & \text { otherwise }\end{cases}\)
Also find (a) P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)], (b) P[X < \(\frac{1}{2}\)]
Solution:
We know that


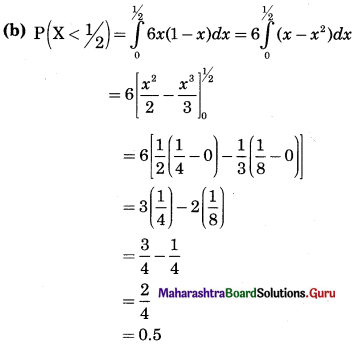
![]()
Question 5.
Let X be the amount of time for which a book is taken out of the library by a randomly selected student and suppose that X has p.d.f.
\(f(x)= \begin{cases}0.5 x & \text { for } 0 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Calculate (i) P(X ≤ 1), (ii) P(0.5 ≤ X ≤ 1.5), (iii) P(X ≥ 1.5).
Solution:
Given p.d.f. of X is f(x) = 0.5x for 0 ≤ x ≤ 2
∴ Its c.d.f. F(x) is given by
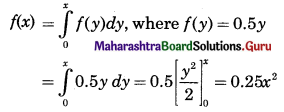
(i) P(X < 1) = F(1)
= 0.25(1)2
= 0.25
(ii) P(0.5 < X < 1.5) = F(1.5) – F(0.5)
= 0.25(1.5)2 – 0.25(0.5)2
= 0.25[2.25 – 0.25]
= 0.25(2)
= 0.5
(iii) P(X ≥ 1.5) = 1 – P(X ≤ 1.5)
= 1 – F(1.5)
= 1 – 0.25(1.5)2
= 1 – 0.25(2.25)
= 1 – 0.5625
= 0.4375
Question 6.
Suppose X is the waiting time (in minutes) for a bus and its p.d.f. is given by
\(f(x)=\left\{\begin{array}{cl}
\frac{1}{5} & \text { for } 0 \leq x \leq 5 \\
0 & \text { otherwise }
\end{array}\right.\)
Find the probability that (i) waiting time is between 1 and 3 minutes, (ii) waiting time is more than 4 minutes.
Solution:
p.d.f. of r.v. X is given by
f(x) = \(\frac{1}{5}\) for 0 ≤ x ≤ 5
This is a constant function.
(i) Probability that waiting time X is between 1 and 3 minutes

(ii) Probability that waiting time X is more than 4 minutes

Question 7.
Suppose error involved in making a certain measurement is a continuous r.v. X with p.d.f.
\(f(x)= \begin{cases}k\left(4-x^{2}\right) & \text { for }-2 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Compute (i) P(X > 0), (ii) P(-1 < X < 1), (iii) P(X < -0.5 or X > 0.5)
Solution:
Since given f(x) is a p.d.f. of r.v. X
Since -2 ≤ x ≤ 2
∴ x2 ≤ 4
∴ 4 – x2 ≥ 0
∴ k(4 – x2) ≥ 0
∴ k ≥ 0 [∵ f(x) ≥ 0]




Question 8.
Following is the p.d.f. of a continuous r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Find an expression for the c.d.f. of X.
(ii) Find F(x) at x = 0.5, 1.7, and 5.
Solution:
The p.d.f. of a continuous r.v. X is
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) c.d.f. of continuous r.v. X is given by
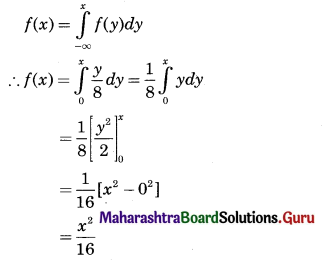
(ii) F(0.5) = \(\frac{(0.5)^{2}}{16}=\frac{0.25}{16}=\frac{1}{64}\) = 0.015
F(1.7) = \(\frac{(1.7)^{2}}{16}=\frac{2.89}{16}\) = 0.18
For any of x greater than or equal to 4, F(x) = 1
∴ F(5) = 1
![]()
Question 9.
The p.d.f. of a continuous r.v. X is
\(f(x)=\left\{\begin{array}{cl}
\frac{3 x^{2}}{8} & \text { for } 0<x<2 \\
0 & \text { otherwise }
\end{array}\right.\)
Determine the c.d.f. of X and hence find (i) P(X < 1), (ii) P(X < -2), (iii) P(X > 0), (iv) P(1 < X < 2).
Solution:
The p.d.f. of a continuous r.v. X is
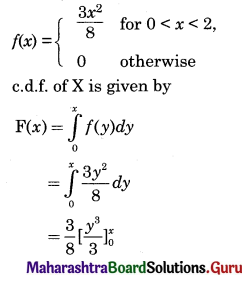

Question 10.
If a r.v. X has p.d.f.
\(f(x)= \begin{cases}\frac{c}{x} & \text { for } 1<x<3, c>0 \\ 0 & \text { otherwise }\end{cases}\)
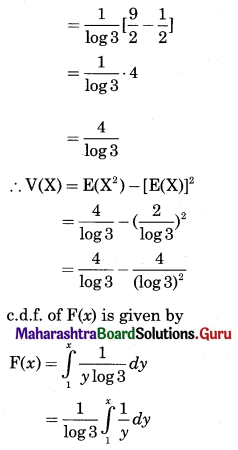
Find c, E(X) and V(X). Also find f(x).
Solution:
The p.d.f. of r.v. X is
f(x) = \(\frac{c}{x}\), 1 < x < 3, c > 0
For p.d.f. of X, we have