Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 1 Commission, Brokerage and Discount Ex 1.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Commission, Brokerage and Discount Ex 1.2
Question 1.
What is the present worth of a sum of ₹ 10,920 due six months hence at 8% p.a simple interest?
Solution:
Given, SD = ₹ 10,920
n = \(\frac{6}{12}\) year = \(\frac{1}{2}\) year
r = 8%
We have,

Thus the present worth is ₹ 10,500
Question 2.
What is the sum due of ₹ 8,000 due 4 months at 12.5% simple interest?
Solution:
Given, PW = ₹ 8,000, n = \(\frac{4}{12}\) year = \(\frac{1}{3}\) year, r = 12.5%
We have,

Thus, the sum due is ₹ 8,333.33
Question 3.
The true discount on the sum due 8 months hence at 12% p.a. is ₹ 560. Find the sum due and present worth of the bill.
Solution:
Given, TD = ₹ 560, n = \(\frac{8}{12}\) year = \(\frac{2}{3}\) year, r = 12%
We have,
TD = \(\frac{\mathrm{PW} \times n \times r}{100}\)
∴ 560 = \(\frac{\mathrm{PW} \times 2 \times 12}{3 \times 100}\)
∴ PW = 560 × \(\frac{25}{2}\) = ₹ 7,000
Now, SD = PW + TD
= 7,000 + 560
= ₹ 7,560
![]()
Question 4.
The true discount on a sum is \(\frac{3}{8}\) of the sum due at 12% p.a. Find the period of the bill.
Solution:

8 × n × 12 = 3(100 + n × 12)
96n = 300 + 36n
60n = 300
∴ n = 5
∴ Period of the bill = 5 years.
Question 5.
20 copies of a book can be purchased for a certain sum payable at the end of 6 months and 21 copies for the same sum in ready cash. Find the rate of interest.
Solution:
Given, n = \(\frac{6}{12}\) year = \(\frac{1}{2}\) year
Let the sum payable be ₹ x
Let the rate of interest be r%
According to given condition,
PW of one book = \(\frac{x}{21}\)
SD of one book = \(\frac{x}{20}\)

Thus, the rate of interest is 10%.
Question 6.
Find the true discount, Banker’s discount, and Banker’s gain on a bill of ₹ 4,240 due 6 months hence at 9% p.a.
Solution:

And, Banker’s Gain (BG) = BD – TD
= 190.80 – 182.58
= ₹ 8.22
Question 7.
The true discount on a bill is ₹ 2,200 and bankers discount is ₹ 2,310. If the bill is due 10 months, hence, find the rate of interest.
Solution:
Given, TD = ₹ 2,200, BD = ₹ 2,310
n = \(\frac{10}{12}=\frac{5}{6}\) year

∴ \(\frac{r}{120}=\frac{1}{20}\)
∴ r = 6%
Thus, rate of interest is 6%
![]()
Question 8.
A bill of ₹ 6,395 drawn on 19th January 2015 for 8 months was discounted on 28th February 2015 at 8% p.a. interest. What is the banker’s discount? What is the cash value of the bill?
Solution:
Face value = ₹ 6,395
Date of drawing = 19/01/2015
Period of the bill = 8 months
Nominal Due date = 19/09/2015
Legal due date = 22/09/2015
Date of discounting = 28/02/2015
Now, the unexpired period = Legal due date – Date of discounting
= 22/09/2015 – 28/02/2015
= days (as shown below)

Cash Value = FV – BD
= 6,395 – 313.12
= ₹ 6,621.38
Question 9.
A bill of ₹ 8,000 drawn on 5th January 1998 for 8 months was discounted for ₹ 7,680 on a certain date. Find the date on which it was discounted at 10% p.a.
Solution:
Bankers discount (BD) = FV – cash value
= 8,000 – 7,680
= ₹ 320
Let the unexpired period be x days
∴ BD = \(\frac{\mathrm{FV} \times x \times r}{365 \times 100}\)
∴ 320 = \(\frac{8,000 \times x \times 10}{365 \times 100}\)
∴ x = 146 days
∴ The unexpired days = 146 days
Date of drawing = 05/01/1998
Period of bill = 8 months
Nominal due date = 05/09/1998
Legal due date = 08/09/1998
Thus, the date of discounting is 146 days before the legal due date
![]()
∴ Date of discounting of the bill is 15th April 1998
Question 10.
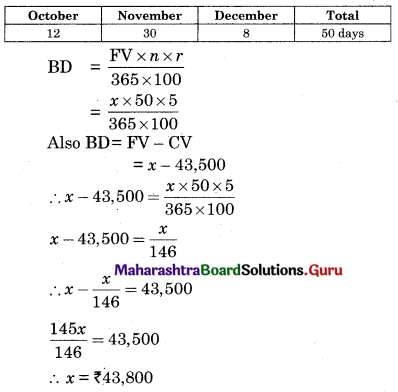
A bill drawn on 5th June for 6 months was discounted at the rate of 5% p.a. on 19th October. If the cash value of the bill is ₹ 43,500, find the face value of the bill.
Solution:
Date of drawing = 5th June
Period of bill = 6 months
Nominal due date = 5th December
Legal due date = 8th December
Date of discounting = 19th October
Rate of interest = 5% p.a.
Let the face value of the bill be ₹ x
The unexpired period
Question 11.
A bill was drawn on 14th April for ₹ 7,000 and was discounted on 6th July at 5% p.a. The Banker paid ₹ 6,930 for the bill. Find the period of the bill.
Solution:
Face value = ₹ 7,000, cash value = ₹ 6,930
∴ Banker’s discount = 7,000 – 6,930 = ₹ 70
Date of drawing = 14/04
Date of discounting = 06/07
Rate of interest = 5%
Let the unexpired period = x days
∴ BD = \(\frac{7,000 \times x \times 5}{365 \times 100}\)
∴ 70 = \(\frac{70 \times x}{73}\)
∴ x = 73 days
∴ Legal due date of the bill is 73 days after the date of discounting.
![]()
∴ Legal due date = 17/09
∴ Nominal due date = 14/09
∴ Period of the bill = 5 months
![]()
Question 12.
If the difference between true discount and banker’s discount on a sum due 4 months hence is ₹ 20. Find true discount, banker’s discount and amount of bill, the rate of simple interest charged is 5% p.a.
Solution:
Banker’s gain (BG) = Banker’s discount (BD) – True Discount (TD)
∴ BG = ₹ 20
Also, BG = \(\frac{\mathrm{TD} \times n \times r}{100}\)
∴ 20 = \(\frac{\mathrm{TD} \times 4 \times 5}{12 \times 100}\)
∴ 20 = \(\frac{\mathrm{TD}}{60}\)
∴ TD = ₹ 1200
Now, BD = BG + TD
= 20 + 1,200
= ₹ 1,220
Also, BD = \(\frac{\mathrm{FV} \times n \times r}{100}\)
∴ 1,220 = \(\frac{\mathrm{FV} \times 4 \times 5}{12 \times 100}\)
∴ FV = 1,200 × 60 = ₹ 73,200
∴ Amounting the bill = ₹ 73,200
Question 13.
A bill of ₹ 51,000 was drawn on 18th February 2010 for 9 months. It was encashed on 28th June 2010 at 5% p.a. Calculate the banker’s gain and true discount.
Solution:
Face Value = ₹ 51,000
Date of drawing = 18/02/2010
Period of the bill = 9 months
Nominal due date = 18/11/2010
Legal due date = 21/11/2010
Date of discounting = 28/06/2010
Unexpired period
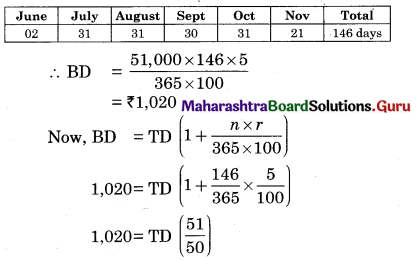
∴ TD = ₹ 1,000
∴ BG = BD – TD
= 1,020 – 1,000
= ₹ 20
Question 14.
A certain sum due 3 months hence is \(\frac{21}{20}\) of the present worth, what is the rate of interest.
Solution:

![]()
Question 15.
A bill of a certain sum drawn on 28th February 2007 for 8 months was encashed on 26th March 2007 for ₹ 10,992 at 14% p.a. Find the face value of the bill.
Solution:
Date drawing = 28/02/2007
Period of the bill = 8 months
Nominal due date = 28/10/2007
Legal due date = 31/10/2007
Date of discounting = 26/03/2007
Cash value = ₹ 10,992
Rate of interest = 14%
Let face value of the bill = ₹ x
Bankers discount = Face value – Cash value = x – 10,992
Also, Banker s discount = \(\frac{F V \times n \times r}{365 \times 100}\)
Where n is the unexpired days
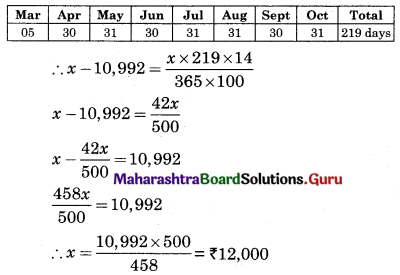
Thus face value of the bill = ₹ 12,000