Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Miscellaneous Exercise 1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Mathematical Logic Miscellaneous Exercise 1
(I) Choose the correct alternative:
Question 1.
Which of the following is not a statement?
(a) Smoking is injurious to health
(b) 2 + 2 = 4
(c) 2 is only even prime number
(d) Come here
Answer:
(d) Come here
Question 2.
Which of the following is an open statement?
(a) x is a natural number
(b) Give me a glass of water
(c) Wish you best of luck
(d) Good morning to all
Answer:
(a) x is a natural number
![]()
Question 3.
Let p ∧ (q ∨ r) = (p ∧ q) ∨ (p ∧ r). Then this law is known as
(a) Commutative law
(b) Associative law.
(c) De Morgan’s law
(d) Distributive law
Answer:
(d) Distributive law
Question 4.
The false statement in the following is:
(a) p ∧ (~p) is a contradiction
(b) (p → q) ↔ (~q → ~p) is a contradiction
(c) ~(~p) ↔ p is a tautology
(d) p ∨ (~p) ↔ p is a tautology.
Answer:
(b) (p → q) ↔ (~q → ~p) is a contradiction
Question 5.
Consider the following three statements
p : 2 is an even number.
q : 2 is a prime number.
r : Sum of two prime numbers is always even.
Then, the symbolic statement (p ∧ q) → ~r means:
(a) 2 is an even and prime number and the sum of two prime numbers is always even.
(b) 2 is an even and prime number and the sum of two prime numbers is not always even.
(c) If 2 is an even and prime number, then the sum of two prime numbers is not always even.
(d) If 2 is an even and prime number, then the sum of two prime numbers is also even.
Answer:
(c) If 2 is an even and prime number, then the sum of two prime numbers is not always even.
Question 6.
If p : He is intelligent.
q : He is strong.
Then, symbolic form of statement: ‘It is wrong that, he is intelligent or strong’ is
(a) ~p ∨ ~p
(b) ~(p ∧ q)
(c) ~(p ∨ q)
(d) p ∨ ~q
Answer:
(c) ~(p ∨ q)
Question 7.
The negation of the proposition ‘If 2 is prime, then 3 is odd’, is
(a) If 2 is not prime, then 3 is not odd
(b) 2 is prime and 3 is not odd
(c) 2 is not prime and 3 is odd
(d) If 2 is not prime, then 3 is odd
Answer:
(b) 2 is prime and 3 is not odd
![]()
Question 8.
The statement (~p ∧ q) ∨ ~q is
(a) p ∨ q
(b) p ∧ q
(c) ~(p ∨ q)
(d) ~(p ∧ q)
Answer:
(d) ~(p ∧ q)
Hint:
(~p ∧ q) ∨ ~q = (~p ∨ ~q) ∧ (q ∨ ~q)
= (~p ∨ ~q) ∧ t
= ~p ∨ ~q
= ~(p ∧ q)
Question 9.
Which of the following is always true?
(a) ~(p → q) ≡ ~q → ~p
(b) ~(p ∨ q) ≡ ~p ∨ ~q
(c) ~(p → q) ≡ p ∧ ~q
(d) ~(p ∧ q) ≡ ~p ∧ ~q
Answer:
(c) ~(p → q) ≡ p ∧ ~q
Question 10.
~(p ∨ q) ∨ (~p ∧ q) is logically equivalent to
(a) ~p
(b) p
(c) q
(d) ~q
Answer:
(a) ~p
Hint:
~(p ∨ q) ∨ (~p ∧ q) ≡ (~p ∧ ~q) ∨ (~p ∧ q)
≡ ~p ∧ (~q ∨ q)
≡ ~p ∧ t
≡ ~p
Question 11.
If p and q are two statements, then (p → q) ↔ (~q → ~p) is
(a) contradiction
(b) tautology
(c) neither (a) nor (b)
(d) none of these
Answer:
(b) tautology
Question 12.
If p is the sentence ‘This statement is false’, then
(a) truth value of p is T
(b) truth value of p is F
(c) p is both true and false
(d) p is neither true nor false
Answer:
(d) p is neither true nor false
![]()
Question 13.
Conditional p → q is equivalent to
(a) p → ~q
(b) ~p ∨ q
(c) ~p → ~q
(d) p ∨ ~q
Answer:
(b) ~p ∨ q
Question 14.
Negation of the statement ‘This is false or That is true’ is
(a) That is true or This is false
(b) That is true and This is false
(c) This is true and That is false
(d) That is false and That is true
Answer:
(c) This is true and That is false
Question 15.
If p is any statement, then (p ∨ ~p) is a
(a) contingency
(b) contradiction
(c) tautology
(d) none of them
Answer:
(c) tautology
(II) Fill in the blanks:
Question 1.
The statement q → p is called as the ___________ of the statement p → q.
Answer:
Converse
Question 2.
Conjunction of two statements p and q is symbolically written as
Answer:
p ∧ q
Question 3.
If p ∨ q is true, then truth value of ~p ∨ ~q is ___________
Answer:
False
Question 4.
Negation of ‘some men are animal’ is ___________
Answer:
All men are not animal.
OR
No men are animals.
Question 5.
Truth value of if x = 2, then x2 = -4 is ___________
Answer:
False
Question 6.
Inverse of statement pattern p → q is given by ___________
Answer:
~p → ~q
![]()
Question 7.
p ↔ q is false when p and q have ___________ truth values.
Answer:
Different
Question 8.
Let p : The problem is easy. r : It is not challenging. Then verbal form of ~p → r is ___________
Answer:
If the problem is not easy, then it is not challenging.
Question 9.
Truth value of 2 + 3 = 5 if and only if -3 > -9 is ___________
Answer:
T [Hint: T ↔ T = T]
(III) State whether each of the following is True or False:
Question 1.
Truth value of 2 + 3 < 6 is F.
Answer:
False
Question 2.
There are 24 months in a year is a statement.
Answer:
True
Question 3.
p ∧ q has truth value F if both p and q have truth value F.
Answer:
False
Question 4.
The negation of 10 + 20 = 30 is, it is false that 10 + 20 ≠ 30.
Answer:
False
Question 5.
Dual of (p ∧ ~q) ∨ t is (p ∨ ~q) ∨ c.
Answer:
False
![]()
Question 6.
Dual of ‘John and Ayub went to the forest’ is ‘John or Ayub went to the forest.’
Answer:
True
Question 7.
‘His birthday is on 29th February’ is not a statement.
Answer:
True
Question 8.
x2 = 25 is true statement.
Answer:
False
Question 9.
The truth value of ‘√5 is not an irrational number’ is T.
Answer:
False
Question 10.
p ∧ t = p.
Answer:
True
(IV) Solve the following:
Question 1.
State which of the following sentences are statements in logic:
(i) Ice cream Sundaes are my favourite.
Solution:
It is a statement.
(ii) x + 3 = 8, x is variable.
Solution:
It is a statement.
(iii) Read a lot to improve your writing skill.
Solution:
It is an imperative sentence, hence it is not a statement.
(iv) z is a positive number.
Solution:
It is an open sentence, hence it is not a statement.
(v) (a + b)2 = a2 + 2ab + b2 for all a, b ∈ R.
Solution:
It is a statement.
(vi) (2 + 1)2 = 9.
Solution:
It is a statement.
(vii) Why are you sad?
Solution:
It is an interrogative sentence, hence it is not a statement.
![]()
(viii) How beautiful the flower is!
Solution:
It is an exclamatory sentence, hence it is not a statement.
(ix) The square of any odd number is even.
Solution:
It is a statement.
(x) All integers are natural numbers.
Solution:
It is a statement.
(xi) If x is a real number, then x2 ≥ 0.
Solution:
It is a statement.
(xii) Do not come inside the room.
Solution:
It is an imperative sentence, hence it is not a statement.
(xiii) What a horrible sight it was!
Solution:
It is an exclamatory sentence, hence it is not a statement.
Question 2.
Which of the following sentences are statements? In case of a statement, write down the truth value:
(i) What is a happy ending?
Solution:
It is an interrogative sentence, hence it is not a statement.
(ii) The square of every real number is positive.
Solution:
It is a statement that is false, hence its truth value is F.
![]()
(iii) Every parallelogram is a rhombus.
Solution:
It is a statement that is true, hence its truth value is T.
(iv) a2 – b2 = (a + b)(a – b) for all a, b ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is T.
(v) Please carry out my instruction.
Solution:
It is an imperative sentence, hence it is not a statement.
(vi) The Himalayas is the highest mountain range.
Solution:
It is a statement that is true, hence its truth value is T.
(vii) (x – 2)(x – 3) = x2 – 5x + 6 for all x ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is T.
(viii) What are the causes of rural unemployment?
Solution:
It is an interrogative sentence, hence it is not a statement.
(ix) 0! = 1.
Solution:
It is a statement that is true, hence its truth value is T.
(x) The quadratic equation ax2 + bx + c = 0 (a ≠ 0) always has two real roots.
Solution:
It is a statement that is false, hence its truth value is F.
Question 3.
Assuming the first statement as p and second as q, write the following statements in symbolic form:
(i) The Sun has set and Moon has risen.
Solution:
Let p : The Sun has set.
q : Moon has risen.
Then the symbolic form of the given statement is p ∧ q.
(ii) Mona likes Mathematics and Physics.
Solution:
Let p : Mona likes Mathematics.
q : Mona likes Physics.
Then the symbolic form of the given statement is p ∧ q.
(iii) 3 is a prime number if 3 is a perfect square number.
Solution:
Let p : 3 be a prime number.
q : 3 is a perfect square number.
Then the symbolic form of the given statement is p ↔ q.
(iv) Kavita is brilliant and brave.
Solution:
Let p : Kavita is brilliant.
q : Kavita is brave.
Then the symbolic form of the given statement is p ∧ q.
![]()
(v) If Kiran drives a car, then Sameer will walk.
Solution:
Let p : Kiran drives a car.
q : Sameet will walk.
Then the symbolic form of the given statement is p → q.
(vi) The necessary condition for the existence of a tangent to the curve of the function is continuity.
Solution:
The given statement can be written as:
‘If the function is continuous, then the tangent to the curve exists.’
Let p : The function is continuous.
q : Tangent to the curve exists.
Then the symbolic form of the given statement is p → q.
(vii) To be brave is necessary and sufficient condition to climb Mount Everest.
Solution:
Let p : To be brave.
q : Climb Mount Everest.
Then the symbolic form of the given statement is p ↔ q.
(viii) x3 + y3 = (x + y)3, iff xy = 0.
Solution:
Let p : x3 + y3 = (x + y)3.
q : xy = 0.
Then the symbolic form of the given statement is p ↔ q.
(ix) The drug is effective though it has side effects.
Solution:
Let p : The drug is effective.
q : It has side effects.
Then the symbolic form of the given statement is p ∧ q.
(x) If a real number is not rational, then it must be irrational.
Solution:
Let p : A real number is not rational.
q : It must be irrational.
Then the symbolic form of the given statement is p → q.
(xi) It is not true that Ram is tall and handsome.
Solution:
Let p : Ram is tall.
q : Ram is handsome.
Then the symbolic form of the given statement is ~(p ∧ q).
(xii) Even though it is not cloudy, it is still raining.
Solution:
The given statement is equivalent to:
It is not cloudy and it is still raining,
Let p : It is not cloudy.
q : It is still raining.
Then the symbolic form of the given statement is p ∧ q.
(xiii) It is not true that intelligent persons are neither polite nor helpful.
Solution:
Let p : Intelligent persons are neither polite nor helpful.
Then the symbolic form of the given statement is ~p.
(xiv) If the question paper is not easy, then we shall not pass.
Solution:
Let p : The question paper is not easy.
q : We shall not pass.
Then the symbolic form of the given statement is p → q.
Question 4.
If p : Proof is lengthy.
q : It is interesting.
Express the following statements in symbolic form:
(i) Proof is lengthy and it is not interesting.
(ii) If the proof is lengthy, then it is interesting.
(iii) It is not true that the proof is lengthy but it is interesting.
(iv) It is interesting iff the proof is lengthy.
Solution:
The symbolic form of the given statements are:
(i) p ∧ ~q
(ii) p → q
(iii) ~(p ∧ q)
(iv) q ↔ p
![]()
Question 5.
Let p : Sachin win the match.
q : Sachin is a member of the Rajya Sabha.
r : Sachin is happy.
Write the verbal statement for each of the following:
(i) (p ∧ q) ∨ r
Solution:
Sachin wins the match and he is a member of the Rajya Sabha or Sachin is happy.
(ii) p → r
Solution:
If Sachin wins the match, then he is happy.
(iii) ~p ∨ q
Solution:
Sachin does not win the match or he is a member of the Rajya Sabha.
(iv) p → (q ∨ r)
Solution:
If Sachin wins the match, then he is a member of the Rajya Sabha or he is happy.
(v) p → q
Solution:
If Sachin wins the match, then he is a member of the Rajya Sabha.
(vi) (p ∧ q) ∧ ~r
Solution:
Sachin wins the match and he is a member of the Rajya Sabha but he is not happy.
(vii) ~(p ∨ q) ∧ r
Solution:
It is false that Sachin wins the match or he is a member of the Rajya Sabha but he is happy.
Question 6.
Determine the truth values of the following statements:
(i) 4 + 5 = 7 or 9 – 2 = 5.
Solution:
Let p : 4 + 5 = 7.
q : 9 – 2 = 5.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are F.
∴ the truth value of p ∨ q is F. …….[F ∨ F ≡ F]
(ii) If 9 > 1, then x2 – 2x + 1 = 0 for x = 1.
Solution:
Let p : 9 > 1.
q : x2 – 2x + 1 = 0 for x = 1.
Then the symbolic form of the given statement is p → q.
The truth values of both p and q are T.
∴ the truth value of p → q is T. …..[T → T ≡ T]
(iii) x + y = 0 is the equation of a straight line if and only if y2 = 4x is the equation of the parabola.
Solution:
Let p : x + y = 0 is the equation of a straight line.
q : y2 = 4x is the equation of the parabola.
Then the symbolic form of the given statement is p ↔ q.
The truth values of both p and q are T.
∴ the truth value of p ↔ q is T. …..[T ↔ T ≡ T]
![]()
(iv) It is not true that 2 + 3 = 6 or 12 + 3 = 5.
Solution:
Let p : 2 + 3 = 6.
q : 12 + 3 = 5.
Then the symbolic form of the given statement is ~(p ∨ q).
The truth values of both p and q are F.
∴ the truth value of ~(p ∨ q) is T. …..[~(F ∨ F) ≡ ~F ≡ T]
Question 7.
Assuming the following statements
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth values of the following:
(i) Stock prices are not high or stocks are rising.
Solution:
p and q are true, i.e. T.
∴ ~p and ~q are false, i.e. F.
The given statement in symbolic form is ~p ∨ q.
Since, ~T ∨ T ≡ F ∨ T ≡ T, the given statement is true.
Hence, its truth value is ‘T’.
(ii) Stock prices are high and stocks are rising if and only if stock prices are high.
Solution:
The given statement in symbolic form is (p ∧ q) ↔ p.
Since (T ∧ T) ↔ T ≡ T ↔ T ≡ T, the given statement is true.
Hence, its truth value is ‘T’.
(iii) If stock prices are high, then stocks are not rising.
Solution:
The given statement in symbolic form is p → ~q.
Since, T → ~T ≡ T → F ≡ F, the given statement is false.
Hence, its truth value is ‘F’.
(iv) It is false that stocks are rising and stock prices are high.
Solution:
The given statement in symbolic form is ~(q ∧ p).
Since, ~(T ∧ T) ≡ ~T ≡ F, the given statement is false.
Hence, its truth value is ‘F’.
(v) Stock prices are high or stocks are not rising iff stocks are rising.
Solution:
The given statement in symbolic form is (p ∨ ~q) ↔ q.
Since (T ∨ ~T) ↔ T ≡ (T ∨ F) ↔ T
≡ T ↔ T
≡ T, the given statement is true.
Hence, its truth value is ‘T’.
Question 8.
Rewrite the following statements without using conditional:
[Hint: P → q ≡ ~p ∨ q]
(i) If price increases, then demand falls.
(ii) If demand falls, then the price does not increase.
Solution:
Since, p → q ≡ ~p ∨ q, the given statements can be written as:
(i) Price does not increase or demand falls.
(ii) Demand does not fall or price does not increase.
![]()
Question 9.
If p, q, r are statements with truth values T, T, F respectively, determine the truth values of the following:
(i) (p ∧ q) → ~p
Solution:
Truth values of p, q, r are T, T, F respectively.
(p ∧ q) → ~p ≡ (T ∧ T) → ~T
≡ T → F
≡ F
Hence, the truth value of the given statement is false, i.e. F.
(ii) p ↔ (q → ~p)
Solution:
p ↔ (q → ~p) ≡ T ↔ (T → ~T)
≡ T ↔ (T → F)
≡ T ↔ F
≡ F
Hence, the truth value of the given statement is false, i.e. F.
(iii) (p ∧ ~q) ∨ (~p ∧ q)
Solution:
(p ∧ ~q) ∨ (~p ∧ q) ≡ (T ∧ ~T) ∨ (~T ∧ T)
≡ (T ∧ F) ∨ (F ∧ T)
≡ F ∨ F
≡ F
Hence, the truth value of the given statement is false, i.e. F.
(iv) ~(p ∧ q) → ~(q ∧ p)
Solution:
~(p ∧ q) → ~(q ∧ p) ≡ ~(T ∧ T) → ~(T ∧ T)
≡ ~T → ~T
≡ F → F
≡ T
Hence, the truth value of the given statement is true, i.e. T.
(v) ~[(p → q) ↔ (p ∧ ~q)]
Solution:
~[(p → q) ↔ (p ∧ ~q)]
≡ ~[(T → T) ↔ (T ∧ ~T)]
≡ ~[T ↔ (T ∧ F)]
≡ ~[T ↔ F]
≡ ~F
≡ T.
Hence, the truth value of the given statement is true, i.e. T.
Question 10.
Write the negations of the following:
(i) If ΔABC is not equilateral, then it is not equiangular.
Solution:
Let p : ΔABC is not equilateral.
q : It is not equiangular.
Then the symbolic form of the given statement is p → q.
Since, ~(p → q) ≡ p ∧ ~q, the negation of the given statement is:
‘ΔABC is not equilateral and it is equiangular.’
(ii) Ramesh is intelligent and he is hard working.
Solution:
Let p : Ramesh is intelligent.
q : He is hard working.
Then the symbolic form of the given statement is p ∧ q.
Since, ~(p ∧ q) ≡ ~p ∨ ~q, the negation of the given statement is:
‘Ramesh is not intelligent or he is not hard-working.’
![]()
(iii) A angle is a right angle if and only if it is of measure 90°.
Solution:
Let p : An angle is a right angle.
q : It is of measure 90°.
Then the symbolic form of the given statement is p ↔ q.
Since, ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p), the negation of the given statement is:
‘An angle is a right angle and it is not of measure 90° or an angle is of measure 90° and it is not a right angle.’
(iv) Kanchanjunga is in India and Everest is in Nepal.
Solution:
Let p : Kanchenjunga is in India.
q : Everest is in Nepal.
Then the symbolic form of the given statement is p ∧ q.
Since, ~(p ∧ q) ≡ ~p ∨ ~q, the negation of the given statement is:
‘Kanchenjunga is not in India or Everest is not in Nepal.’
(v) If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Solution:
Let p : x ∈ A ∩ B, q : x ∈ A, r : x ∈ B.
Then the symbolic form of the given statement is P → (q ∧ r)
Since, ~(p → q) ≡ p ∧ ~q and ~(p ∧ q)= ~p ∨ ~q,
the negation of the given statement is:
‘x ∈ A ∩ B and x ∉ A or x ∉ B.
Question 11.
Construct the truth table for each of the following statement patterns:
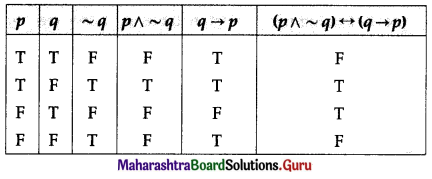
(i) (p ∧ ~q) ↔ (q → p)
Solution:
(p ∧ ~q) ↔ (q → p)
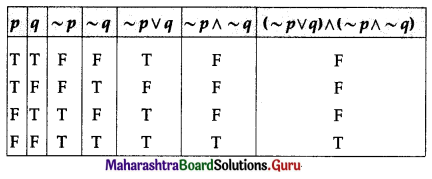
(ii) (~p ∨ q) ∧ (~p ∧ ~q)
Solution:
(~p ∨ q) ∧ (~p ∧ ~q)
(iii) (p ∧ r) → (p ∨ ~q)
Solution:
(p ∧ r) → (p ∨ ~q)

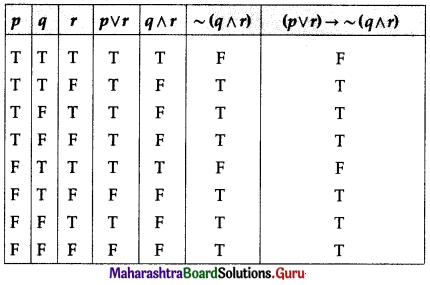
(iv) (p ∨ r) → ~(q ∧ r)
Solution:
(p ∨ r) → ~(q ∧ r)
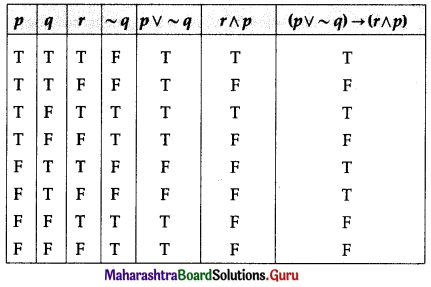
(v) (p ∨ ~q) → (r ∧ p)
Solution:
(p ∨ ~q) → (r ∧ p)
![]()
Question 12.
What is a tautology? What is a contradiction? Show that the negation of a tautology is a contradiction and the negation of a contradiction is a tautology.
Solution:
Tautology: A statement pattern that has all the entries in the last column of its truth table as T is called a tautology.
For example:
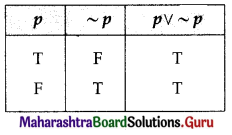
In the above truth table for the statement p ∨ ~p,
we observe that all the entries in the last column are T.
Hence, the statement p ∨ ~p is a tautology.
Contradiction: A statement pattern that has all the entries in the last column of its truth table as F is called a contradiction.
For example:
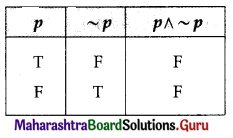
In the above truth table for the statement p ∧ ~p,
we observe that all the entries in the last column are F.
Hence, the statement p ∧ ~p is a contradiction.
To show that the negation of a tautology is a contradiction and vice versa:
A tautology is true on every row of its truth table.
Since, ~T = F and ~F = T, when we negate a tautology, the resulting statement is false on every row of its table.
i.e. the negation of tautology is a contradiction.
Similarly, the negation of a contradiction is a tautology.
Question 13.
Determine whether the following statement patterns is a tautology or a contradiction or a contingency:
(i) [(p ∧ q) ∨ (~p)] ∨ [p ∧ (~q)]
Solution:
[(p ∧ q) ∨ (~p)] ∨ [p ∧ (~q)]
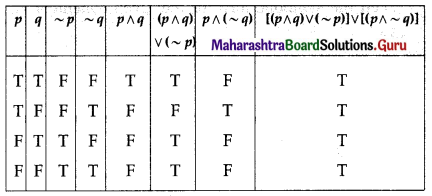
All the entries in the last column of the above truth table are T.
∴ [(p ∧ q) ∨ (~p)] ∨ [p ∧ (~q)] is a tautology.
(ii) [(~p ∧ q) ∧ (q ∧ r)] ∨ (~q)
Solution:
[(~p ∧ q) ∧ (q ∧ r)] ∨ (~q)
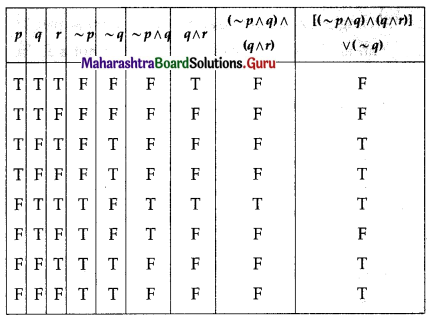
The entries in the last column of the above truth table are neither all T nor all F.
∴ [(~p ∧ q) ∧ (q ∧ r)] ∨ (~q) is a contingency.
(iii) [~(p ∨ q) → p] ↔ [(~p) ∧ (~q)]
Solution:
[~(p ∨ q) → p] ↔ [(~p) ∧ (~q)]
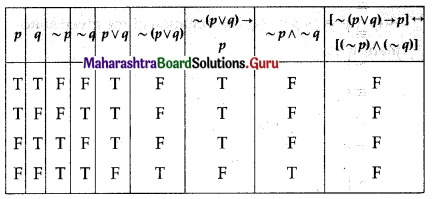
All the entries in the last column of the above truth table are F.
∴ [~(p ∨ q) → p] ↔ [(~p) ∧ (~q)] is a contradiction.
(iv) [~(p ∧ q) → p] ↔ [(~p) ∧ (~q)]
Solution:
[~(p ∧ q) → p] ↔ [(~p) ∧ (~q)]
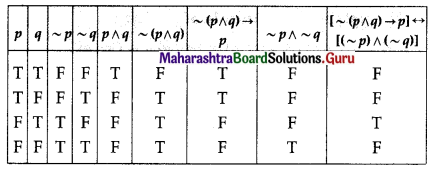
The entries in the last column of the above truth table are neither all T nor all F.
∴ [~(p ∧ q) → p] ↔ [(~p) ∧ (~q)] is a contingency.
(v) [p → (~q ∨ r)] ↔ ~[p → (q → r)]
Solution:
[p → (~q ∨ r)] ↔ ~[p → (q → r)]
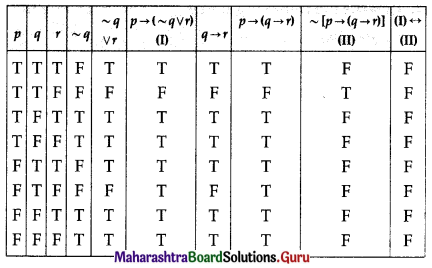
All the entries in the last column of the above truth table are F.
∴ [p → (~q ∨ r)] ↔ ~[p → (q → r)] is a contradiction.
![]()
Question 14.
Using the truth table, prove the following logical equivalences:
(i) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Solution:
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
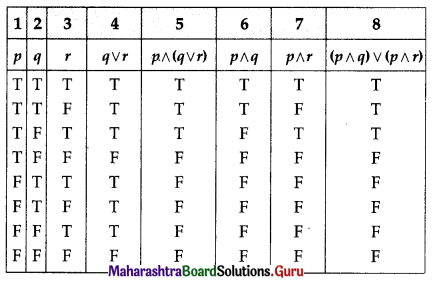
The entries in columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
(ii) [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Solution:
[~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
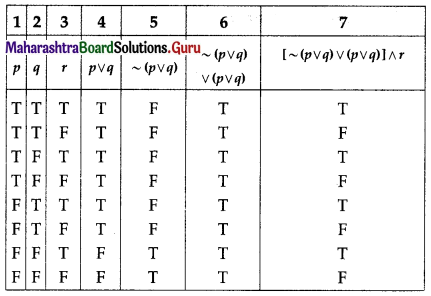
The entries in columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
(iii) p ∧ (~p ∨ q) ≡ p ∧ q
Solution:
p ∧ (~p ∨ q) ≡ p ∧ q
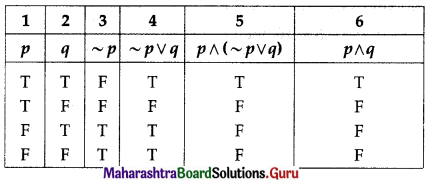
The entries in columns 5 and 6 are identical.
∴ p ∧ (~p ∨ q) ≡ p ∧ q
(iv) p ↔ q ≡ ~(p ∧ ~q) ∧ ~(q ∧ ~p)
Solution:
p ↔ q ≡ ~(p ∧ ~q) ∧ ~(q ∧ ~p)
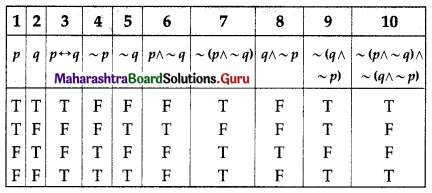
The entries in columns 3 and 10 are identical.
∴ p ↔ q ≡ ~(p ∧ ~q) ∧ ~(q ∧ ~p)
(v) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:
~p ∧ q ≡ (p ∨ q) ∧ ~p
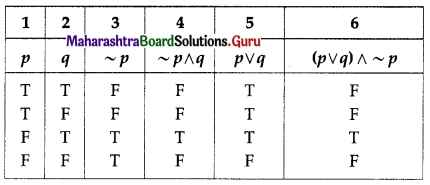
The entries in columns 4 and 6 are identical.
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p
Question 15.
Write the converse, inverse, contrapositive of the following statements:
(i) If 2 + 5 = 10, then 4 + 10 = 20.
Solution:
Let p : 2 + 5 = 10.
q : 4 + 10 = 20.
Then the symbolic form of the given statement is p → q.
Converse: q → p is the converse of p → q
i.e. If 4 + 10 = 20, then 2 + 5 = 10.
Inverse: ~p → ~q is the inverse of p → q
i.e. If 2 + 5 ≠ 10, then 4 + 10 ≠ 20.
Cotrapositive: ~q → ~p is the contrapositive of p → q,
i.e. If 4 +10 ≠ 20, then 2 + 5 ≠ 10.
(ii) If a man is a bachelor, then he is happy.
Solution:
Let p : A man is a bachelor.
q : He is happy.
Then the symbolic form of the given statement is p → q.
Converse: q → p is the converse of p → q
i.e. If a man is happy, then he is a bachelor.
Inverse: ~p → ~q is the inverse of p → q
i.e. If a man is not a bachelor, then he is not happy.
Contrapositive: ~q → ~p is the contrapositive of p → q
i.e., If a man is not happy, then he is not a bachelor.
![]()
(iii) If I do not work hard, then I do not prosper.
Solution:
Let p : I do not work hard.
q : I do not prosper.
Then the symbolic form of the given statement is p → q.
Converse: q → p is the converse of p → q
i.e. If I do not prosper, then I do not work hard.
Inverse: ~p → ~q is the inverse of p → q
i.e. If I work hard, then I prosper.
Contrapositive: ~q → ~p is the contrapositive of p → q
i.e. If I prosper, then I work hard.
Question 16.
State the dual of each of the following statements by applying the principle of duality:
(i) (p ∧ ~q) ∨ (~p ∧ q) ≡ (p ∨ q) ∧ ~(p ∧ q)
(ii) p ∨ (q ∨ r) ≡ ~[(p ∧ q) ∨ (r ∨ s)]
(iii) 2 is an even number or 9 is a perfect square.
Solution:
The duals are given by:
(i) (p ∨ ~q) ∧ (~p ∨ q) ≡ (p ∧ q) ∨ ~(p ∨ q)
(ii) p ∧ (q ∧ r) ≡ ~[(p ∨ q) ∧ (r ∧ s)]
(iii) 2 is an even number and 9 is a perfect square.
Question 17.
Rewrite the following statements without using the connective ‘If … then’:
(i) If a quadrilateral is a rhombus, then it is not a square.
(ii) If 10 – 3 = 7, then 10 × 3 ≠ 30.
(iii) If it rains, then the principal declares a holiday.
Solution:
Since, p → q ≡ ~p ∨ q the given statements can be written as:
(i) A quadrilateral is not a rhombus or it is not a square.
(ii) 10 – 3 ≠ 7 or 10 × 3 ≠ 30.
(iii) It does not rain or the principal declares a holiday.
Question 18.
Write the dual of each of the following:
(i) (~p ∧ q) ∨ (p ∧ ~q) ∨ (~p ∧ ~q)
(ii) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
(iii) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
(iv) ~(p ∨ q) ≡ ~p ∧ ~q.
Solution:
The duals are given by:
(i) (~p ∨ q) ∧ (p ∨ ~q) ∧ (~p ∨ ~q)
(ii) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
(iii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
(iv) ~(p ∧ q) ≡ ~p ∧ ~q
![]()
Question 19.
Consider the following statements:
(i) If D is a dog, then D is very good.
(ii) If D is very good, then D is a dog.
(iii) If D is not very good, then D is not a dog.
(iv) If D is not a dog, then D is not very good.
Identify the pairs of statements having the same meaning. Justify.
Solution:
Let p : D is a dog. and q : D is very good.
Then the given statements in the symbolic form are:
(i) p → q
(ii) q → p
(iii) ~q → ~p
(iv) ~p → ~q
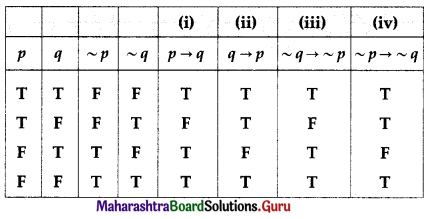
The entries in columns (i) and (iii) are identical. Hence, these statements are equivalent.
∴ the statements (i) and (iii) have the same meaning.
Similarly, the entries in columns (ii) and (iv) are identical. Hence, these statements are equivalent.
∴ the statements (ii) and (iv) have the same meaning.
Question 20.
Express the truth of each of the following statements by Venn diagrams:
(i) All men are mortal.
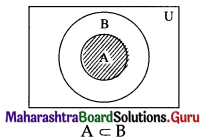
Solution:
Let U : a set of all human being
A : set of all men
B : set of all mortals.
Then the Venn diagram represents the truth of the given statement is as below:
(ii) Some persons are not politicians.
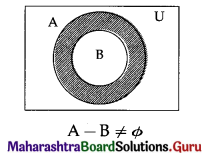
Solution:
Let U : set of all human being
A : set of all persons
B : set of all politicians.
Then the Venn diagram represents the truth of the given statement is as follows:
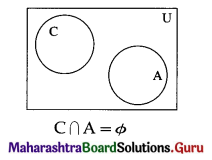
(iii) Some members of the present Indian cricket are not committed.
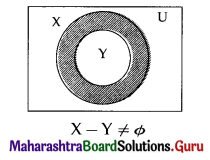
Solution:
Let U : set of all human being
X : set of all members of present Indian cricket
Y : set of all committed members of the present Indian cricket.
Then the Venn diagram represents the truth of the given statement is as below:
![]()
(iv) No child is an adult.
Solution:
Let U : set of all human beings
C : set of all children
A : set of all adults.
Then the Venn diagram represents the truth of the given statement is as below:
Question 21.
If A = {2, 3, 4, 5, 6, 7, 8}, determine the truth value of each of the following statements:
(i) ∃ x ∈ A, such that 3x + 2 > 9.
Solution:
Clearly x = 3, 4, 5, 6, 7, 8 ∈ A satisfy 3x + 2 > 9.
So, the given statement is true, hence its truth value is T.
(ii) ∀x ∈ A, x2 < 18.
Solution:
x = 5, 6, 7, 8 ∈ A do not satisfy x2 < 18.
So the given statement is false, hence its truth value is F.
(iii) ∃x ∈ A, such that x + 3 < 11.
Solution:
Clearly x = 2, 3, 4, 5, 6, 7 ∈ A which satisfy x + 3 < 11.
So, the given statement is True, hence its truth value is T.
(iv) ∀x ∈ A, x2 + 2 ≥ 5.
Solution:
x2 + 2 ≥ 5 for all x ∈ A.
So, the given statement is true, hence its truth value is T.
Question 22.
Write the negations of the following statements:
(i) 7 is a prime number and the Taj Mahal is in Agra.
Solution:
Let p : 7 be a prime number.
q : Taj Mahal is in Agra.
Then the symbolic form of the given statement is p ∧ q.
Since, (p ∧ q) ≡ ~p ∨ ~q,
the negation of the given statement is:
‘7 is not a prime number or Taj Mahal is not in Agra.’
(ii) 10 > 5 and 3 < 8.
Solution:
Let p : 10 > 5.
q : 3 < 8.
Then the symbolic form of the given statement is P ∧ q.
Since, ~(p ∧ q) = ~p ∨ ~q, the negation of the given statement is:
’10 ≤ 5 or 3 ≥ 8′
OR
’10 ≯ 5 or 3 ≮ 8′
![]()
(iii) I will have tea or coffee.
Solution:
The negation of the given statement is:
‘I will not have tea and coffee.’
(iv) ∀n ∈ N, n + 3 > 9.
Solution:
The negation of the given statement is:
‘∃n ∈ N, such that n + 3 ≯ 9.’
OR
‘∃n ∈ N, such that n + 3 ≤ 9.’
(v) ∃x ∈ A, such that x + 5 < 11.
Solution:
The negation of the given statement is:
‘∀x ∈ A, x + 5 ≮ 1.’
OR
‘∀x ∈ A, x + 5 ≥ 11.’