Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives Ex 4.4 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Applications of Derivatives Ex 4.4
Question 1.
The demand function of a commodity at price P is given as D = 40 – \(\frac{5 P}{8}\). Check whether it is increasing or decreasing function.
Solution:
D = 40 – \(\frac{5 P}{8}\)
∴ \(\frac{d D}{d P}=\frac{d}{d P}\left(40-\frac{5 P}{8}\right)\)
= 0 – \(\frac{5}{8}\) × 1
= \(\frac{-5}{8}\)
Hence, the given function is decreasing function.
Question 2.
The price P for demand D is given as P = 183 + 120D – 3D2, find D for which price is increasing.
Solution:
P = 183 + 120D – 3D2
∴ \(\frac{d P}{d D}=\frac{d}{d D}\)(183 + 120D – 3D2)
= 0 + 120 × 1 – 3 × 2D
= 120 – 6D
If price P is increasing, then \(\frac{d P}{d D}\) > 0
∴ 120 – 6D > 0
∴ 120 > 6D
∴ D < 20
Hence, the price is increasing when D < 20.
![]()
Question 3.
The total cost function for production of x articles is given as C = 100 + 600x – 3x2. Find the values of x for which the total cost is decreasing.
Solution:
The cost function is given as
C = 100 + 600x – 3x2
∴ \(\frac{d C}{d D}=\frac{d}{d D}\)(100 + 600x – 3x2)
= 0 + 600 × 1 – 3 × 2x
= 600 – 6x
If the total cost is decreasing, then \(\frac{d C}{d x}\) < 0
∴ 600 – 6x < 0
∴ 600 < 6x
∴ x > 100
Hence, the total cost is decreasing for x > 100.
Question 4.
The manufacturing company produces x items at the total cost of ₹(180 + 4x). The demand function for this product is P = (240 – x). Find x for which
(i) revenue is increasing
(ii) profit is increasing.
Solution:
(i) Let R be the total revenue.
Then R = P.x = (240 – x)x
∴ R = 240x – x2
∴ \(\frac{d R}{d D}=\frac{d}{d D}\)(240x – x2)
= 240 × 1 – 2x
= 240 – 2x
R is increasing, if \(\frac{d R}{d x}\) > 0
i.e. if 240 – 2x > 0
i.e. if 240 > 2x
i.e. if x < 120
Hence, the revenue is increasing, if x < 120.
(ii) Profit π = R – C
∴ π = (240x – x2) – (180 + 4x)
= 240x – x2 – 180 – 4x
= 236x – x2 – 180
∴ \(\frac{d \pi}{d x}=\frac{d}{d x}\)(236x – x2 – 180)
= 236 × 1 – 2x – 0
= 236 – 2x
Profit is increasing, if \(\frac{d \pi}{d x}\) > 0
i.e. if 236 – 2x > 0
i.e. if 236 > 2x
i.e. if x < 118
Hence, the profit is increasing, if x < 118.
![]()
Question 5.
For manufacturing x units, labour cost is 150 – 54x and processing cost is x2. Price of each unit is p = 10800 – 4x2. Find the values of x for which
(i) total cost is decreasing
(ii) revenue is increasing.
Solution:
(i) Total cost C = labour cost + processing cost
∴ C = 150 – 54x + x2
∴ \(\frac{d C}{d x}=\frac{d}{d x}\)(150 – 54x + x2)
= 0 – 54 × 1 + 2x
= -54 + 2x
The total cost is decreasing, if \(\frac{d C}{d x}\) < 0
i.e. if -54 + 2x < 0
i.e. if 2x < 54
i.e. if x < 27
Hence, the total cost is decreasing, if x < 27.
(ii) The total revenue R is given as
R = p.x
R = (10800 – 4x2) x
R = 10800x – 4x3
∴ \(\frac{d R}{d x}=\frac{d}{d x}\)(10800x – 4x3)
= 10800 × 1 – 4 × 3x2
= 10800 – 12x2
The revenue is increasing, if \(\frac{d R}{d x}\) > 0
i.e. if 10800 – 12x2 > 0
i.e. if 10800 > 12x2
i.e. if x2 < 900
i.e. if x < 30 ……[∵ x > 0]
Hence, the revenue is increasing, if x < 30.
Question 6.
The total cost of manufacturing x articles is C = 47x + 300x2 – x4. Find x, for which average cost is
(i) increasing
(ii) decreasing.
Solution:
The total cost is given as C = 47x + 300x2 – x4
∴ the average cost is given by
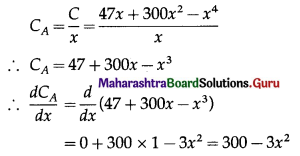
(i) CA is increasing, if \(\frac{d C_{A}}{d x}\) > 0
i.e. if 300 – 3x2 > 0
i.e. if 300 > 3x2
i.e. if x2 < 100
i.e. if x < 10 …..[∵ x > 0]
Hence, the average cost is increasing, if x < 10.
(ii) CA is decreasing, if \(\frac{d C_{A}}{d x}\) < 0
i.e. if 300 – 3x2 < 0
i.e. if 300 < 3x2
i.e. if x2 > 100
i.e. if x > 10 ……[∵ x > 0]
Hence, the average cost is decreasing, if x > 10.
![]()
Question 7.
(i) Find the marginal revenue, if the average revenue is 45 and the elasticity of demand is 5.
Solution:
Given RA = 45 and η = 5
Now, Rm = \(R_{A}\left(1-\frac{1}{\eta}\right)\)
= 45(1 – \(\frac{1}{5}\))
= 45(\(\frac{4}{5}\))
= 36
Hence, the marginal revenue = 36.
(ii) Find the price, if the marginal revenue is 28 and elasticity of demand is 3.
Solution:
Given Rm = 28 and η = 3

Hence, the price = 42.
(iii) Find the elasticity of demand, if the marginal revenue is 50 and price is ₹ 75.
Solution:
Given Rm = 50 and RA = 75

Hence, the elasticity of demand = 3.
Question 8.
If the demand function is D = \(\frac{p+6}{p-3}\), find the elasticity of demand at p = 4.
Solution:
The demand function is

Elasticity of demand is given by

Hence, the elasticity of demand at p = 4 is 3.6
![]()
Question 9.
Find the price for the demand function D = \(\frac{2 p+3}{3 p-1}\), when elasticity of demand is \(\frac{11}{14}\).
Solution:
The demand function is

Elasticity of demand is given by

Question 10.
If the demand function is D = 50 – 3p – p2 elasticity of demand at (i) p = 5 (ii) p = 2. Comment on the result.
Solution:
The demand function is D = 50 – 3p – p2
∴ \(\frac{d D}{d p}=\frac{d}{d p}\)(50 – 3p – p2)
= 0 – 3 × 1 – 2p
= -3 – 2p
Elasticity of demand is given by

(i) When p = 5, then
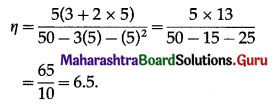
Since, η >1, the demand is elastic.
(ii) When p = 2, then
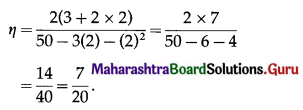
Since, 0 < η < 1, the demand is inelastic.
![]()
Question 11.
For the demand function D = 100 – \(\frac{p^{2}}{2}\), find the elasticity of demand at (i) p = 10 (ii) p = 6 and comment on the results.
Solution:
The demand function is
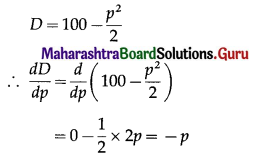
The elasticity of demand is given by
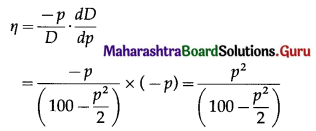
(i) When p = 10, then

Since, η > 1, the demand is elastic.
(ii) When p = 6, then

Since, 0 < η < 1, the demand is inelastic.
Question 12.
A manufacturing company produces, x items at a total cost of ₹(40 + 2x). Their price is given as p = 120 – x. Find the value of x for which
(i) revenue is increasing
(ii) profit is increasing
(iii) Also find an elasticity of demand for price 80.
Solution:
(i) The total revenue R is given by
R = p.x = (120 – x)x
∴ R = 120x – x2
∴ \(\frac{d R}{d x}=\frac{d}{d x}\)(120x – x2)
= 120 × 1 – 2x
= 120 – 2x
If the revenue is increasing, then \(\frac{d R}{d x}\) > 0
∴ 120 – 2x > 0
∴ 120 > 2x
∴ x < 60
Hence, the revenue is increasing when x < 60.
(ii) Profit π = R – C
= (120x – x2) – (40 + 2x)
= 120x – x2 – 40 – 2x
= 118x – x2 – 40
∴ \(\frac{d \pi}{d x}=\frac{d}{d x}\)(118x – x2 – 40)
= 118 × 1 – 2x – 0
= 118 – 2x
If the profit is increasing, then \(\frac{d \pi}{d x}\) > 0
∴ 118 – 2x > 0
∴ 118 > 2x
∴ x < 59
Hence, the profit is increasing when x < 59.
![]()
(iii) p = 120 – x
∴ x = 120 – p
∴ \(\frac{d x}{d p}=\frac{d}{d p}\)(120 – p)
= 0 – 1
= -1
Elasticity of demand is given by
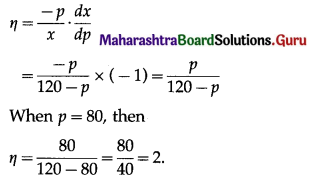
Question 13.
Find MPC, MPS, APC and APS, if the expenditure Ec of a person with income I is given as
Ec = (0.0003)I2 + (0.075)I, when I = 1000.
Solution:
Ec = (0.0003)I2 + (0.075)I
MPC = \(\frac{d E_{c}}{d I}=\frac{d}{d I}\)[(0.0003)I2 + (0.075)I]
= (0.0003)(2I) + (0.075)(1)
= (0.0006)I + 0.075
When I = 1000, then
MPC = (0.0006)(1000) + 0.075
= 0.6 + 0.075
= 0.675.
∴ MPC + MPS = 1
∴ 0.675 + MPS = 1
∴ MPS = 1 – 0.675 = 0.325
Now, APC = \(\frac{E_{c}}{I}=\frac{(0.0003) I^{2}+(0.075) I}{I}\)
= (0.0003)I + (0.075)
When I = 1000, then
APC = (0.0003)(1000) + 0.075
= 0.3 + 0.075
= 0.375
∵ APC + APS = 1
∴ 0.375 + APS = 1
∴ APS = 1 – 0.375 = 0.625
Hence, MPC = 0.675, MPS = 0.325, APC = 0.375, APS = 0.625.