Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives Ex 4.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Applications of Derivatives Ex 4.1
Question 1.
Find the equations of tangent and normal to the following curves at the given point on it:
(i) y = 3x2 – x + 1 at (1, 3)
Solution:
y = 3x2 – x + 1
∴ \(\frac{d y}{d x}=\frac{d}{d x}\) (3x2 – x + 1)
= 3 × 2x – 1 + 0
= 6x – 1
∴ \(\left(\frac{d y}{d x}\right)_{\text {at }(1,3)}\) = 6(1) – 1
= 5
= slope of the tangent at (1, 3).
∴ the equation of the tangent at (1, 3) is
y – 3 = 5(x – 1)
∴ y – 3 = 5x – 5
∴ 5x – y – 2 = 0.
The slope of the normal at (1, 3) = \(\frac{-1}{\left(\frac{d y}{d x}\right)_{\text {at }(1,3)}}=-\frac{1}{5}\)
∴ the equation of the normal at (1, 3) is
y – 3 = \(-\frac{1}{5}\)(x – 1)
∴ 5y – 15 = -x + 1
∴ x + 5y – 16 = 0
Hence, the equations of the tangent and normal are 5x – y – 2 = 0 and x + 5y – 16 = 0 respectively.
![]()
(ii) 2x2 + 3y2 = 5 at (1, 1)
Solution:
2x2 + 3y2 = 5
Differentiating both sides w.r.t. x, we get

= slope of the tangent at (1, 1)
∴ the equation of the tangent at (1, 1) is
y – 1 = \(\frac{-2}{3}\)(x – 1)
∴ 3y – 3 = -2x + 2
∴ 2x + 3y – 5 = 0.
The slope of normal at (1, 1) = \(\frac{-1}{\left(\frac{d y}{d x}\right)_{\text {at }(1,1)}}=\frac{-1}{\left(\frac{-2}{3}\right)}=\frac{3}{2}\)
∴ the equation of the normal at (1, 1) is
y – 1 = \(\frac{3}{2}\)(x – 1)
∴ 2y – 2 = 3x – 3
∴ 3x – 2y – 1 = 0
Hence, the equations of the tangent and normal are 2x + 3y – 5 = 0 and 3x – 2y – 1 = 0 respectively.
(iii) x2 + y2 + xy = 3 at (1, 1)
Solution:
x2 + y2 + xy = 3
Differentiating both sides w.r.t. x, we get
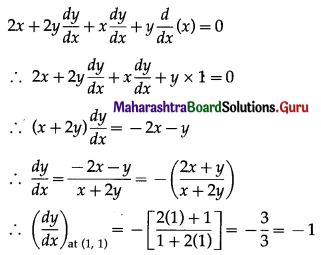
= slope of the tangent at (1, 1)
the equation of the tangent at (1, 1) is
y – 1= -1(x – 1)
∴ y – 1 = -x + 1
∴ x + y = 2
The slope of the normal at (1, 1) = \(\frac{-1}{\left(\frac{d y}{d x}\right)_{a t(1,1)}}\)
= \(\frac{-1}{-1}\)
= 1
∴ the equation of the normal at (1, 1) is y – 1 = 1(x – 1)
∴ y – 1 = x – 1
∴ x – y = 0
Hence, the equations of tangent and normal are x + y = 2 and x – y = 0 respectively.
![]()
Question 2.
Find the equations of the tangent and normal to the curve y = x2 + 5 where the tangent is parallel to the line 4x – y + 1 = 0.
Solution:
Let P(x1, y1) be the point on the curve y = x2 + 5 where the tangent is parallel to the line 4x – y + 1 = 0.
Differentiating y = x2 + 5 w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x}\)(x2 + 5) = 2x + 0 = 2x
\(\left(\frac{d y}{d x}\right)_{\text {at }\left(x_{1}, y_{1}\right)}=2 x_{1}\)
= slope of the tangent at (x1, y1)
Let m1 = 2x1
The slope of the line 4x – y + 1 = 0 is
m2 = \(\frac{-4}{-1}\) = 4
Since, the tangent at P(x1, y1) is parallel to the line 4x – y + 1 = 0,
m1 = m2
∴ 2x1 = 4
∴ x1 = 2
Since, (x1, y1) lies on the curve y = x2 + 5, y1 = \(x_{1}^{2}\) + 5
∴ y1 = (2)2 + 5 = 9 ……[x1 = 2]
∴ the coordinates of the point are (2, 9) and the slope of the tangent = m1 = m2 = 4.
∴ the equation of the tangent at (2, 9) is
y – 9 = 4(x – 2)
∴ y – 9 = 4x – 8
∴ 4x – y + 1 = 0
Slope of the normal = \(\frac{-1}{m_{1}}=-\frac{1}{4}\)
∴ the equation of the normal at (2, 9) is
y – 9 = \(-\frac{1}{4}\)(x – 2)
∴ 4y – 36 = -x + 2
∴ x + 4y – 38 = 0
Hence, the equations of tangent and normal are 4x – y + 1 = 0 and x + 4y – 38 = 0 respectively.
![]()
Question 3.
Find the equations of the tangent and normal to the curve y = 3x2 – 3x – 5 where the tangent is parallel to the line 3x – y + 1 = 0.
Solution:
Let P(x1, y1) be the point on the curve y = 3x2 – 3x – 5 where the tangent is parallel to the line 3x – y + 1 = 0.
Differentiating y = 3x2 – 3x – 5 w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x}\)(3x2 – 3x – 5)
= 3 × 2x – 3 × 1 – 0
= 6x – 3
∴ \(\left(\frac{d y}{d x}\right)_{\text {at }\left(x_{1}, y_{1}\right)}=6 x_{1}-3\)
= slope of the tangent at (x1, y1)
Let m1 = 6x1 – 3
The slope of the line 3x – y + 1 = 0
m2 = \(\frac{-3}{-1}\) = 3
Since, the tangent at P(x1, y1) is parallel to the line 3x – y + 1 = 0,
m1 = m2
∴ 6x1 – 3 = 3
∴ 6x1 = 6
∴ x1 = 1
Since, (x1, y1) lies on the curve y = 3x2 – 3x – 5,
\(y_{1}=3 x_{1}{ }^{2}-3 x_{1}-5\), where x1 = 1
= 3(1)2 – 3(1) – 5
= 3 – 3 – 5
= -5
∴ the coordinates of the point are (1, -5) and the slope of the tangent = m1 = m2 = 3.
∴ the equation of the tangent at (1, -5) is
y – (-5) = 3(x – 1)
∴ y + 5 = 3x – 3
∴ 3x – y – 8 = 0
Slope of the normal = \(-\frac{1}{m_{1}}=-\frac{1}{3}\)
∴ the equation of the normal at (1, -5) is
y – (-5) = \(-\frac{1}{3}\)(x – 1)
∴ 3y + 15 = -x + 1
∴ x + 3y + 14 = 0
Hence, the equations of tangent and normal are 3x – y – 8 = 0 and x + 3y + 14 = 0 respectively.