Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 4 Time Series Miscellaneous Exercise 4 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Time Series Miscellaneous Exercise 4
(I) Choose the correct alternative.
Question 1.
Which of the following can’t be a component of a time series?
(a) Seasonality
(b) Cyclical
(c) Trend
(d) Mean
Answer:
(d) Mean
Question 2.
The first step in time series analysis is to
(a) Perform regression calculations
(b) Calculate a moving average
(c) Plot the data on a graph
(d) Identify seasonal variation
Answer:
(c) Plot the data on a graph
![]()
Question 3.
Time-series analysis is based on the assumption that
(a) Random error terms are normally distributed.
(b) The variable to be forecast and other independent variable are correlated.
(c) Past patterns in the variable to be forecast will continue unchanged into the future.
(d) The data do not exhibit a trend.
Answer:
(c) Past patterns in the variable to be forecast will continue unchanged into the future.
Question 4.
Moving averages are useful in identifying
(a) Seasonal component
(b) Irregular component
(c) Trend component
(d) Cyclical component
Answer:
(c) Trend component
Question 5.
We can use regression line for past data to forecast future data. We then use the line which
(a) Minimizes the sum of squared deviations of past data from the line.
(b) Minimizes the sum of deviations of past data from the line.
(c) Maximizes the sum of squared deviations of past data from the line.
(d) Maximizes the sum of deviation of past data from the line.
Answer:
(a) Minimizes the sum of squared deviations of past data from the line
Question 6.
Which of the following is a major problem for forecasting, especially when using the method of least squares?
(a) The past cannot be known
(b) The future is not entirely certain
(c) The future exactly follows the patterns of the past
(d) The future may not follow the patterns of the past
Answer:
(d) The future may not follow the patterns of the past
![]()
Question 7.
An overall upward or downward pattern in an annual time series would be contained in which component of the time series
(a) Trend
(b) Cyclical
(c) Irregular
(d) Seasonal
Answer:
(a) Trend
Question 8.
The following trend line equation was developed for annual sales from 1984 to 1990 with 1984 as base or zero year. Y1 = 500 + 60X (in 1000 Rs.) The estimated sales for 1984 (in 1000 Rs) is:
(a) ₹ 500
(b) ₹ 560
(c) ₹ 1,040
(d) ₹ 1100
Answer:
(a) ₹ 500
Question 9.
What is a disadvantage of the graphical method of determining a trend line?
(a) Provides quick approximations
(b) Is subject to human error
(c) Provides accurate forecasts
(d) Is too difficult to calculate
Answer:
(b) Is subject to human error
Question 10.
Which component of time series refers to erratic time series movements that follow no recognizable or regular pattern.
(a) Trend
(b) Seasonal
(c) Cyclical
(d) Irregular
Answer:
(a) Trend
(II) Fill in the blanks.
Question 1.
_________ components of time series is indicated by a smooth line.
Answer:
Trend
Question 2.
_________ component of time series is indicated by periodic variation year after year.
Answer:
Seasonal
Question 3.
_________ component of time series is indicated by a long wave spanning two or more years.
Answer:
Cyclical
![]()
Question 4.
_________ component of time series is indicated by up and down movements without any pattern.
Answer:
Irregular
Question 5.
Addictive models of time series _________ independence of its components.
Answer:
assume
Question 6.
Multiplicative models of time series _________ independence of its components.
Answer:
does not assume
Question 7.
The simplest method of measuring the trend of time series is _________
Answer:
graphical method
Question 8.
The method of measuring the trend of time series using only averages is _________
Answer:
moving average method
Question 9.
The complicated but ancient method of measuring the trend of time series is _________
Answer:
least-squares method
Question 10.
The graph of time series clearly shows _________ of it is monotone.
Answer:
trend
(III) State whether each of the following is True or False.
Question 1.
The secular trend component of the time series represents irregular variations.
Answer:
False
![]()
Question 2.
Seasonal variation can be observed over several years.
Answer:
True
Question 3.
Cyclical variation can occur several times in a year.
Answer:
False
Question 4.
Irregular variation is not a random component of time series.
Answer:
False
Question 5.
The additive model of time series does not require the assumptions of independence of its components.
Answer:
False
Question 6.
The multiplicative model of time series does not require the assumption of independence of its components.
Answer:
True
Question 7.
The graphical method of finding trends is very complicated and involves several calculations.
Answer:
False
Question 8.
Moving the average method of finding trends is very complicated and involves several calculations.
Answer:
False
Question 9.
The least-squares method of finding trends is very simple and does not involve any calculations.
Answer:
False
![]()
Question 10.
All three methods of measuring trends will always give the same results.
Answer:
False
(IV) Solve the following problems.
Question 1.
The following table shows the productivity of pig-iron and ferro-alloys (‘000 metric tonnes)
Fit a trend line to the above data by graphical method.
Solution:
Question 2.
Fit a trend line to the data in Problem IV (1) by the method of least squares.
Solution:
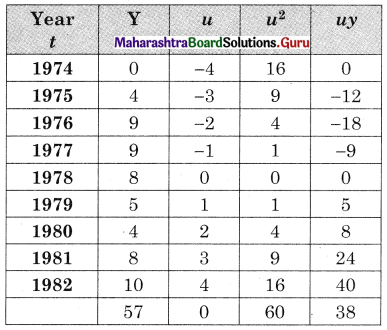
u = \(\frac{t-1978}{1}\), Σy = 57, Σu = 0, Σu2 = 60, Σuy = 38, n = 9
Let the equation of the trend line be
Y = a + bu where u = t – 1978 ……(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu2 ………(iii)
Substituting the values of Σu, n, Σuy, Σu2 in (ii) & (iii) we get
57 = 9a + 0 ∴ a = 6.3333
38 = 0 + b . 60 ∴ b = 0.6333.
∴ The equation of the trend line is
y = 6.3333 + 0.63333u where u = t – 1978
Question 3.
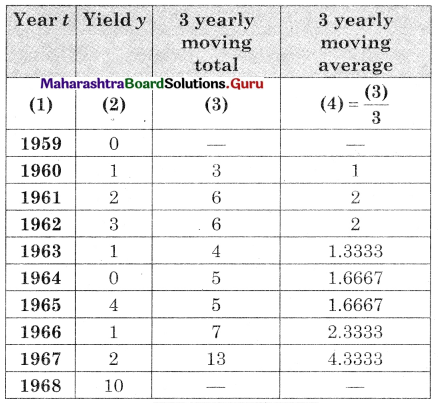
Obtain the trends values for the data on problem IV (1) using 5 yearly moving averages.
Solution:
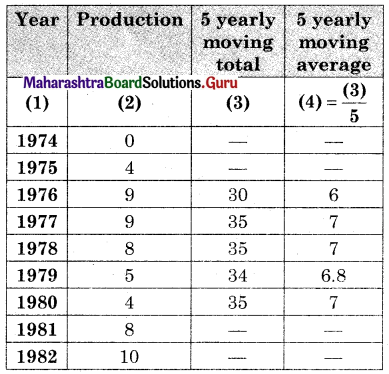
![]()
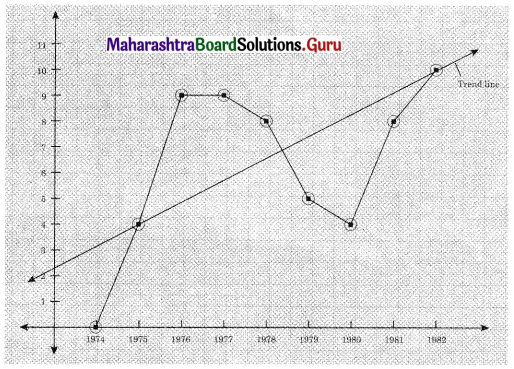
Question 4.
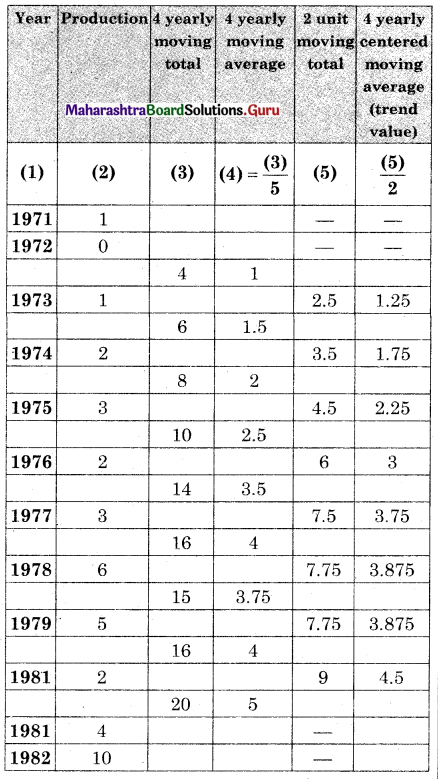
The following table shows the amount of sugar production (in lac tonnes) for the years 1971 to 1982.
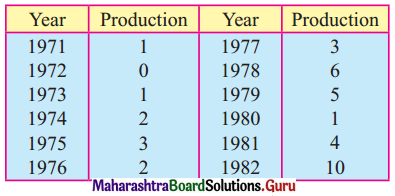
Fit a trend line to the above data by graphical method.
Solution:
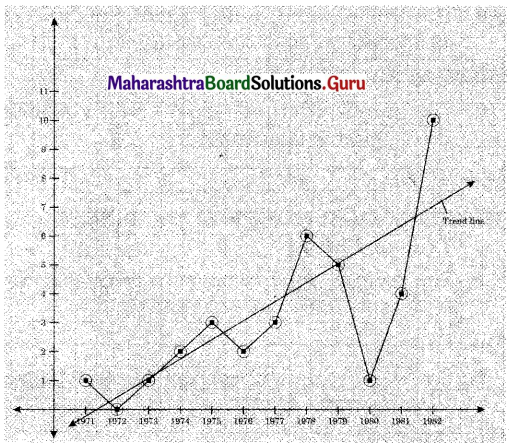
Question 5.
Fit a trend line to data in problem 4 by the method of least squares.
Solution:
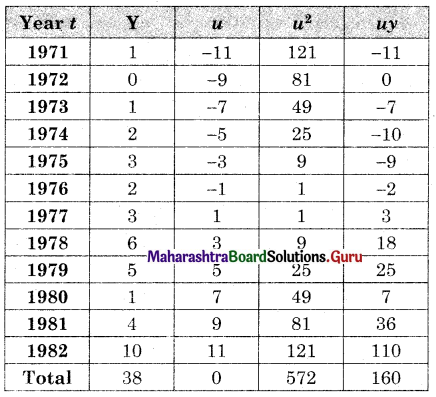
u = \(\frac{t-1976.5}{\frac{1}{2}}\), Σy = 38, Σu = 0, Σu2 = 572, Σuy = 160, n = 12
Let the equation of the trend line be
y = a + bu ……..(i)
where u = \(\frac{t-1976.5}{\frac{1}{2}}\)
u = 2t – 3953
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu2 ……..(iii)
by (ii) 38 = 12o + 0 ∴ a = 3.1867
by (iii) 160 = 0 + b . 572 ∴ b = 0.2797
∴ by (i), Equation of the trend line is
Y = 3.1667 + 0.2797u where u = 2t – 3953.
Question 6.
Obtain trend values for data in Problem 4 using 4-yearly centered moving averages.
Solution:
Question 7.
The percentage of girls’ enrollment in total enrollment for years 1960-2005 is shown in the following table.
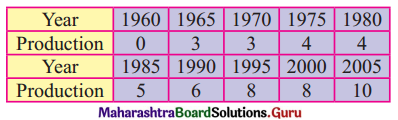
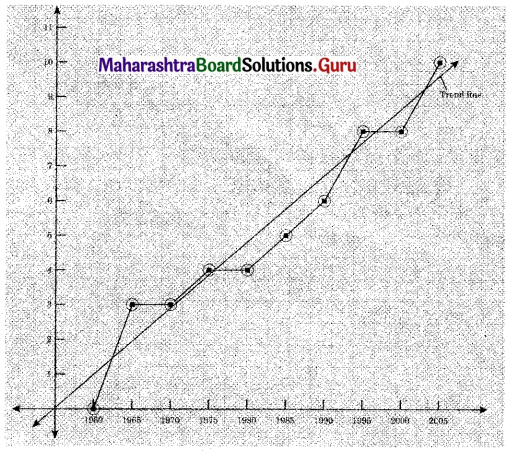
Fit a trend line to the above data by graphical method.
Solution:
Question 8.
Fit a trend line to the data in Problem 7 by the method of least squares.
Solution:
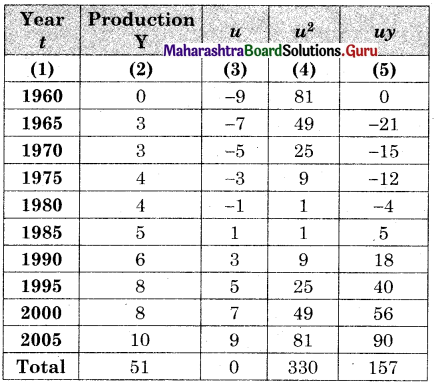
u = \(\frac{t-1980.5}{5}\), Σy = 51, Σu = 0, Σu2 = 330, Σuy = 157, n = 10
Let the equation of the trend line be
Y = a + bu where u = \(\frac{t-1980.5}{5}\) …….(i)
Σy = na + bΣu ……..(ii)
Σuy = aΣu + bΣu2 ……..(iii)
Substituting the values of Σy, Σu, n, Σuy, Σu2 We get
51 = 10a + 0 ∴ a = 5.1
and 157 = 0 + 6.330 ∴ b = 0.4758
by (i) equation of the trend line is
Y = 5.1 + 0.4758u where u = \(\frac{t-1980.5}{5}\)
![]()
Question 9.
Obtain trend values for the data in Problem 7 using 4-yearly moving averages.
Solution:
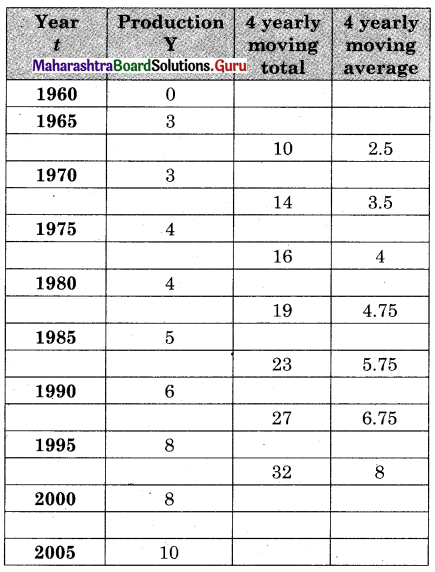
Question 10.
The following data shows the number of boxes of cereal sold in the years 1977 to 1984.
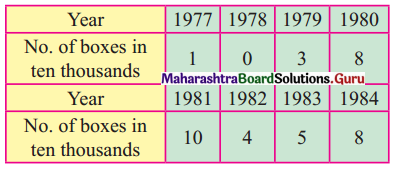
Fit a trend line to the above data by graphical method.
Solution:
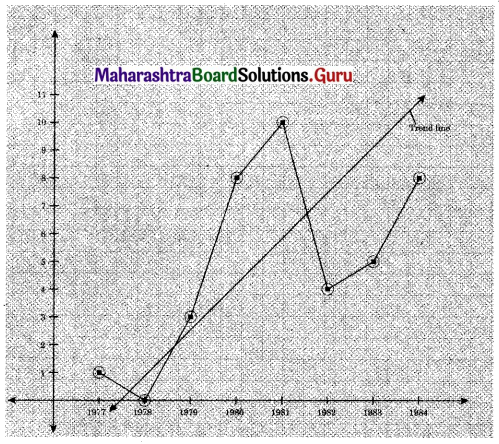
Question 11.
Fit a trend line to data in Problem 10 by the method of least squares.
Solution:
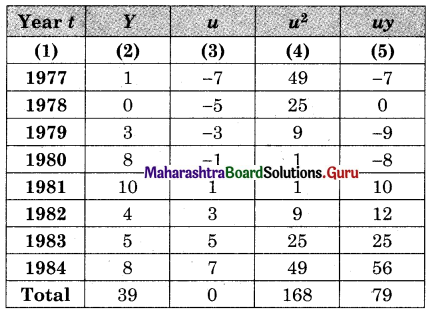
u = \(\frac{t-1980.5}{\frac{1}{2}}\), Σy = 39, Σu = 0, Σu2 = 168, Σuy = 79, n = 8
Let the equation of the trend line by
Y = a + bu
Where u = 2t – 3961 …….(i)
Σy = na + bΣu …….(ii)
Σuy = aΣu + bΣu2 ……..(iii)
Substituting the values of Σy, n, Σu, Σuy, Σu2, in (ii) & (iii)
39 = 8a + 0 ∴ a = 4.875
79 = 0 + b (168) ∴ b = 0.4702
by (i) the equation of the trend line is
Y = 4.875 + 0.4702u Where u = 2t – 3961.
![]()
Question 12.
Obtain trend values for data in Problem 10 using 3-yearly moving averages.
Solution:
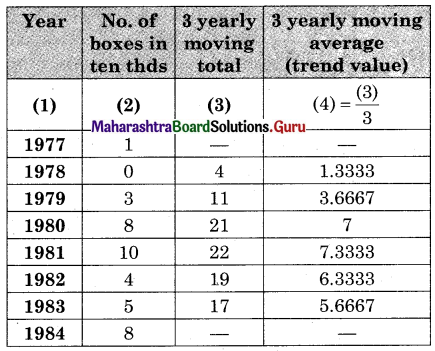
Question 13.
The following table shows the number of trade fatalities (in a state) resulting from drunken driving for the years 1975 to 1983.
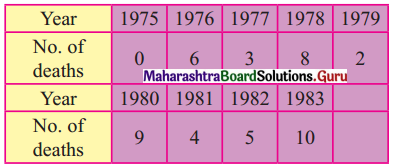
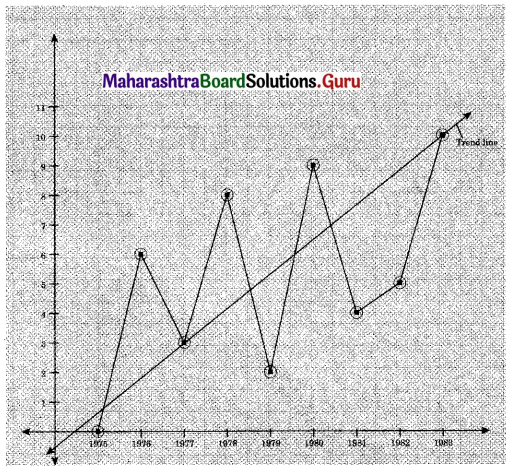
Fit a trend line to the above data by graphical method.
Solution:
Question 14.
Fit a trend line to data in Problem 13 by the method of least squares.
Solution:
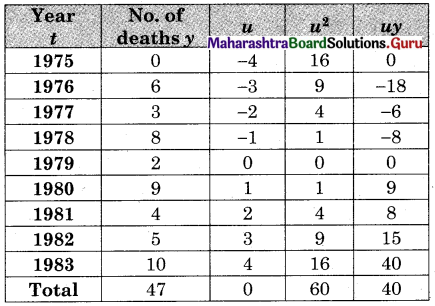
u = \(\frac{t-1979}{1}\), Σy = 47, Σu = 0, Σu2 = 60, Σuy = 40, n = 9
Let the equation of the trends line be
Y = a + bu where u = t – 1979 …….(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu2 ……..(iii)
Substituting values of Σy, n, Σu, Σuy, Σu2 in (ii) & (iii)
We get 47 = 9a + 0 ∴ a = 5.2222
and 40 = 0 + b(60) ∴ b = 0.6667
∴ by (i) the equation of the trend line is
Y = 5.2222 + 0.6667u Where u = t – 1979.
![]()
Question 15.
Obtain trend values for data in Problem 13 using 4-yearly moving averages.
Solution:
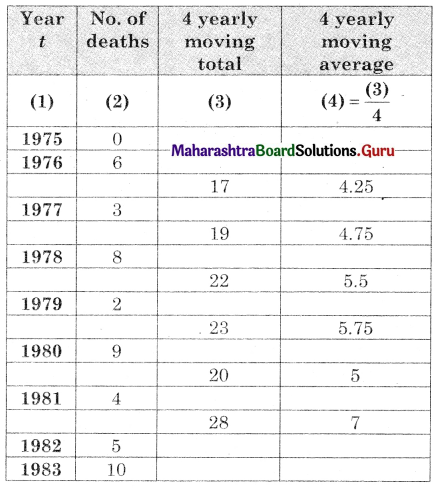
Question 16.
The following table shows the all India infant mortality rates (per ‘000) for the years 1980 to 2000.
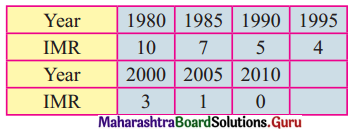
Fit a trend line to the above data by graphical method.
Solution:
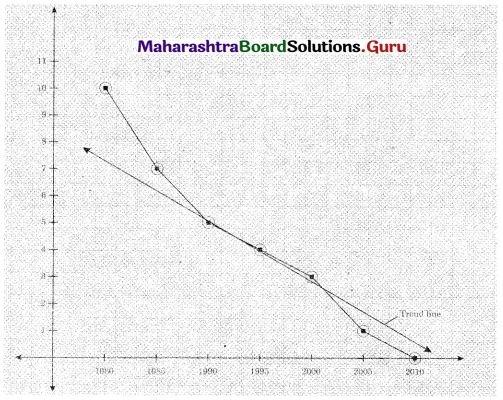
Question 17.
Fit a trend line to data in Problem 16 by the method of least squares.
Solution:
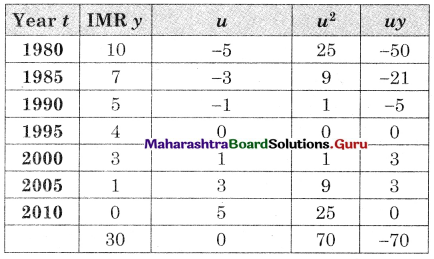
u = \(\frac{t-1995}{5}\), Σy = 30, Σu = 0, Σu2 = 70, Σuy = -70, n = 7
Let the equation of the trend line be
Y = a + bu Where u = \(\frac{t-1995}{5}\) …..(i)
Σy = na + bΣu ……(ii)
Σuy = aΣu + bΣu2 …….(iii)
Substituting values of Σy, n, Σu, Σuy & Σu2 in (ii) & (iii) we get
30 = 7a + 0 ∴ a = 4.2857
-70 = 0 + 6(70) ∴ b = -1
∴ by (i) the equation of the trend line is
y = 4.2857 – 1(u) Where u = \(\frac{t-1995}{5}\)
![]()
Question 18.
Obtain trend values for data in Problem 16 using 3-yearly moving averages.
Solution:
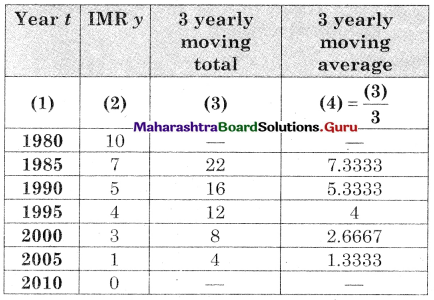
Question 19.
the following table shows the wheat yield (‘000 tonnes) in India for the years 1959 to 1968.
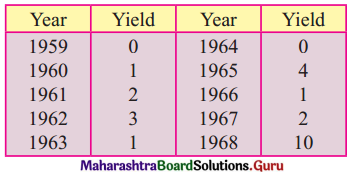
Fit a trend line to the above data by the method of least squares.
Solution:
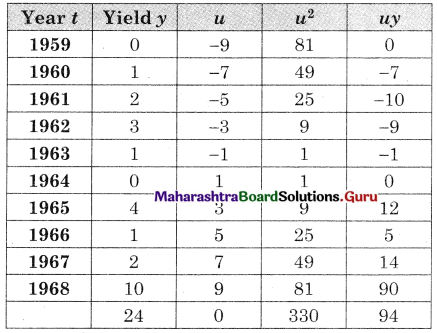
u = \(\frac{t-1963.5}{\frac{1}{2}}\), Σy = 24, Σu = 0, Σu2 = 330, Σuy = 94, n = 10
Let the equation of the trend line be
y = a + bu where u = \(\frac{t-1963.5}{\frac{1}{2}}\) ……(i)
i.e. u = 2t – 3927
Σy = na + bΣu …….(ii)
Σuy = aΣu + Σu2 …..(iii)
Substituting values of Σy, n, Σu, Σuy & Σu2 in (ii) & (iii) we get
24 = 10a + 0 ∴ a = 2.4
94 = 0 + 6.330 ∴ b = 0.2848
∴ Equation of the trend line is
y = 2.4 + (0.2848)u where u = 2t – 3927
![]()
Question 20.
Obtain trend values for data in problem 19 using 3-yearly moving averages.
Solution: