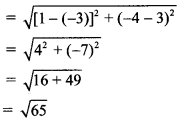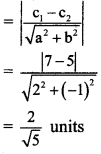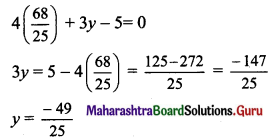Class 11

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 6 Circle Ex 6.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Circle Ex 6.2

Question 1.
Find the centre and radius of each of the following circles:
(i) x² + y² – 2x + 4y – 4 = 0
(ii) x² + y² – 6x – 8y – 24 = 0
(iii) 4x² + 4y² – 24x – 8y – 24 = 0
Solution:
(i) Given equation of the circle is x² + y² – 2x + 4y – 4 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
2g = -2, 2f = 4 and c = -4
⇒ g = -1, f = 2 and c = -4
Centre of the circle = (-g, -f) = (1, -2)
and radius of the circle

(ii) Given equation of the circle is x² + y² – 6x – 8y – 24 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
2g = -6, 2f = -8 and c = -24
⇒ g = -3, f = -4 and c = -24
Centre of the circle = (-g, -f) = (3, 4)
and radius of the circle

(iii) Given equation of the circle is 4x² + 4y² – 24x – 8y – 24 = 0
Dividing throughout by 4, we get x² + y² – 6x – 2y – 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
2g = -6, 2f = -2 and c = -6
⇒ g = -3, f = -1 and c = -6
Centre of the circle = (-g, -f) = (3, 1)
and radius of the circle

Question 2.
Show that the equation 3x² + 3y² + 12x + 18y – 11 = 0 represents a circle.
Solution:
Given equation is 3x² + 3y² + 12x + 18y – 11 = 0
Dividing throughout by 3, we get
x² + y² + 4x + 6y – \(\frac{11}{3}\) = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
2g = 4, 2f = 6, c = \(\frac{-11}{3}\)
⇒ g = 2, f = 3, c = \(\frac{-11}{3}\)
Now, g² + f² – c = (2)² + (3)² – (\(\frac{-11}{3}\))
= 4 + 9 + \(\frac{11}{3}\)
= \(\frac{50}{3}\) > 0
∴ The given equation represents a circle.

Question 3.
Find the equation of the circle passing through the points (5, 7), (6, 6), and (2, -2).
Solution:
Let C(h, k) be the centre of the required circle.
Since the required circle passes through points A(5, 7), B(6, 6), and D(2, -2),
CA = CB = CD = radius

Consider, CA = CD
By distance formula,
\(\sqrt{(\mathrm{h}-5)^{2}+(\mathrm{k}-7)^{2}}=\sqrt{(\mathrm{h}-2)^{2}+[\mathrm{k}-(-2)]^{2}}\)
Squaring both the sides, we get
⇒ (h – 5)² + (k – 7)² = (h – 2)² + (k + 2)²
⇒ h² – 10h + 25 + k² – 14k + 49 = h² – 4h + 4 + k² + 4k + 4
⇒ -10h – 14k + 74 = -4h + 4k + 8
⇒ 6h + 18k – 66 = 0
⇒ h + 3k – 11 = 0 …..(i)
Consider, CB = CD
By distance formula,
\(\sqrt{(h-6)^{2}+(k-6)^{2}}=\sqrt{(h-2)^{2}+[k-(-2)]^{2}}\)
Squaring both the sides, we get
⇒ (h – 6)² + (k – 6)² = (h – 2)² + (k + 2)²
⇒ h² – 12h + 36 + k² – 12k + 36 = h² – 4h + 4 + k² + 4k + 4
⇒ -12h – 12k + 72 = -4h + 4k + 8
⇒ 8h + 16k – 64 = 0
⇒ h + 2k – 8 = 0 ……(ii)
By (i) – (ii), we get k = 3
Substituting k = 3 in (i), we get
h + 3(3) – 11 = 0
⇒ h + 9 – 11 = 0
⇒ h = 2
Centre of the circle is C(2, 3).
radius (r) = CD
= \(\sqrt{(2-2)^{2}+(3+2)^{2}}\)
= \(\sqrt{0+5^{2}}\)
= √25
= 5
The equation of a circle with centre at (h, k) and radius r is given by (x – h)²+ (y – k)² = r²
Here, h = 2, k = 3
The required equation of the circle is
(x – 2)² + (y – 3)² = 5²
⇒ x² – 4x + 4 + y² – 6y + 9 = 25
⇒ x² + y² – 4x – 6y + 4 + 9 – 25 = 0
⇒ x² + y² – 4x – 6y – 12 = 0

Question 4.
Show that the points (3, -2), (1, 0), (-1, -2) and (1, -4) are concyclic.
Solution:
Let the equation of the circle passing through the points (3, -2), (1, 0) and (-1, -2) be
x² + y² + 2gx + 2fy + c = 0 …..(i)
For point (3, -2),
Substituting x = 3 and y = -2 in (i), we get
9 + 4 + 6g – 4f + c = 0
⇒ 6g – 4f + c = -13 ….(ii)
For point (1, 0),
Substituting x = 1 andy = 0 in (i), we get
1 + 0 + 2g + 0 + c = 0
⇒ 2g + c = -1 ……(iii)
For point (-1, -2),
Substituting x = -1 and y = -2, we get
1 + 4 – 2g – 4f + c = 0
⇒ 2g + 4f – c = 5 …….(iv)
Adding (ii) and (iv), we get
8g = -8
⇒ g = -1
Substituting g = -1 in (iii), we get
-2 + c = -1
⇒ c = 1
Substituting g = -1 and c = 1 in (iv), we get
-2 + 4f – 1 = 5
⇒ 4f = 8
⇒ f = 2
Substituting g = -1, f = 2 and c = 1 in (i), we get
x² + y² – 2x + 4y + 1 = 0 ……….(v)
If (1, -4) satisfies equation (v), the four points are concyclic.
Substituting x = 1, y = -4 in L.H.S of (v), we get
L.H.S. = (1)² + (-4)² – 2(1) + 4(-4) + 1
= 1 + 16 – 2 – 16 + 1
= 0
= R.H.S.
Point (1, -4) satisfies equation (v).
∴ The given points are concyclic.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B) Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B)

(I) Select the correct option from the given alternatives.

Question 1.
Given A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 2
\end{array}\right]\), I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) if A – λI is a singular matrix, then ___________
(a) λ = 0
(b) λ² – 3λ – 4 = 0
(c) λ² + 3λ – 4 = 0
(d) λ² – 3λ – 6 = 0
Answer:
(b) λ² – 3λ – 4 = 0
Hint:

Question 2.
Consider the matrices A = \(\left[\begin{array}{ccc}
4 & 6 & -1 \\
3 & 0 & 2 \\
1 & -2 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 4 \\
0 & 1 \\
-1 & 2
\end{array}\right]\), C = \(\left[\begin{array}{l}
3 \\
1 \\
2
\end{array}\right]\). Out of the given matrix products, ___________
(i) (AB)^TC
(ii) C^TC(AB)^T
(iii) C^TAB
(iv) A^TABB^TC
(a) Exactly one is defined
(b) Exactly two are defined
(c) Exactly three are defined
(d) all four are defined
Answer:
(c) Exactly three are defined
Hint:
A is of order 3 × 3, B is of order 3 × 2 and C is of order 3 × 1.
(AB)^TC is of order 2 × 1.
C^TC and (AB)^T are of different orders.
C^TC (AB)^T is not defined.
C^TAB is of order 1 × 2.
A^TABB^TC is of order 3 × 1.

Question 3.
If A and B are square matrices of equal order, then which one is correct among the following?
(a) A + B = B + A
(b) A + B = A – B
(c) A – B = B – A
(d) AB = BA
Answer:
(a) A + B = B + A
Hint:
Matrix addition is commutative.
∴ A + B = B + A

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
a & 2 & b
\end{array}\right]\) is a matrix satisfying the equation AA^T = 9I, where I is the identity matrix of order 3, then the ordered pair (a, b) is equal to ___________
(a) (2, -1)
(b) (-2, 1)
(c) (2, 1)
(d) (-2, -1)
Answer:
(d) (-2, -1)

Question 5.
If A = \(\left[\begin{array}{ll}
\alpha & 2 \\
2 & \alpha
\end{array}\right]\) and |A³| = 125, then α = ___________
(a) ±3
(b) ±2
(c) ±5
(d) 0
Answer:
(a) ±3
Hint:
|A³| = 125
|A|³ = 53 …….[∵ |Aⁿ| = |A|ⁿ, n ∈ N]
∴ |A| = 5
\(\left|\begin{array}{ll}
\alpha & 2 \\
2 & \alpha
\end{array}\right|=5\)
α² – 4 = 5
α² = 9
∴ α = ± 3

Question 6.
If \(\left[\begin{array}{ll}
5 & 7 \\
x & 1 \\
2 & 6
\end{array}\right]-\left[\begin{array}{cc}
1 & 2 \\
-3 & 5 \\
2 & y
\end{array}\right]=\left[\begin{array}{cc}
4 & 5 \\
4 & -4 \\
0 & 4
\end{array}\right]\), then ___________
(a) x = 1, y = -2
(b) x = -1, y = 2
(c) x = 1, y = 2
(d) x = -1, y = -2
Answer:
(c) x = 1, y = 2

Question 7.
If A + B = \(\left[\begin{array}{ll}
7 & 4 \\
8 & 9
\end{array}\right]\) and A – B = \(\left[\begin{array}{ll}
1 & 2 \\
0 & 3
\end{array}\right]\), then the value of A is ___________
(a) \(\left[\begin{array}{ll}
3 & 1 \\
4 & 3
\end{array}\right]\)
(b) \(\left[\begin{array}{ll}
4 & 3 \\
4 & 6
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
6 & 2 \\
8 & 6
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
7 & 6 \\
8 & 12
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{ll}
4 & 3 \\
4 & 6
\end{array}\right]\)

Question 8.
If \(\left[\begin{array}{cc}
x & 3 x-y \\
z x+z & 3 y-w
\end{array}\right]=\left[\begin{array}{ll}
3 & 2 \\
4 & 7
\end{array}\right]\), then ___________
(a) x = 3, y = 7, z = 1, w = 14
(b) x = 3, y = -5, z = -1, w = -4
(c) x = 3, y = 6, z = 2, w = 7
(d) x = -3, y = -7, z = -1, w = -14
Answer:
(a) x = 3, y = 7, z = 1, w = 14

Question 9.
For suitable matrices A, B, the false statement is ___________
(a) (AB)^T = A^TB^T
(B) (A^T)^T = A
(C) (A – B)^T = A^T – B^T
(D) (A + B)^T = A^T + B^T
Answer:
(a) (AB)^T = A^TB^T
Hint:
(AB)^T = B^TA^T

Question 10.
If A = \(\left[\begin{array}{cc}
-2 & 1 \\
0 & 3
\end{array}\right]\) and f(x) = 2x² – 3x, then f(A) = ___________
(a) \(\left[\begin{array}{cc}
14 & 1 \\
0 & -9
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
-14 & 1 \\
0 & 9
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
14 & -1 \\
0 & 9
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-14 & -1 \\
0 & -9
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{cc}
14 & -1 \\
0 & 9
\end{array}\right]\)
Hint:

(II) Answer the following questions.

Question 1.
If A = diag[2, -3, -5], B = diag[4, -6, -3] and C = diag [-3, 4, 1], then find
i. B + C – A
ii. 2A + B – 5C.
Solution:

Question 2.
If f(α) = A = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\), find
i. f(-α)
ii. f(-α) + f(α)
Solution:

Question 3.
Find matrices A and B, where
(i) 2A – B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\) and A + 3B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\)
(ii) 3A – B = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 0 & 5
\end{array}\right]\) and A + 5B = \(\left[\begin{array}{ccc}
0 & 0 & 1 \\
-1 & 0 & 0
\end{array}\right]\)
Solution:
i. Given equations are
2A – B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\) …….(i)

Question 4.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & -2 \\
-1 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & 4 & 1 \\
2 & -1 & -3
\end{array}\right]\), verify
i. (A + 2B^T)^T = A^T + 2B
ii. (3A – 5B^T)^T = 3A^T – 5B.
Solution:

Question 5.
If A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) and A + A^T = I, where I is a unit matrix of order 2 × 2, then find the value of α.
Solution:

Question 6.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & 2 \\
-1 & 0
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & 3 & 2 \\
4 & -1 & -3
\end{array}\right]\), show that AB is singular.
Solution:

Question 7.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 6 \\
1 & 2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
-3 & 2 & -1 \\
-2 & 1 & 0
\end{array}\right]\), show that AB and BA are both singular matrices.
Solution:

Question 8.
If A = \(\left[\begin{array}{ccc}
1 & -1 & 0 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
2 & 2 & -4 \\
-4 & 2 & -4 \\
2 & -1 & 5
\end{array}\right]\), show that BA = 6I.
Solution:

Question 9.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
0 & 3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -2
\end{array}\right]\), verify that |AB| = |A|.|B|.
Solution:

Question 10.
If Aα = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that Aα . Aβ = Aα+β
Solution:

Question 11.
If A = \(\left[\begin{array}{cc}
1 & \omega \\
\omega^{2} & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
\omega^{2} & 1 \\
1 & \omega
\end{array}\right]\), where ω is a complex cube root of unity, then show that AB + BA + A – 2B is a null matrix.
Solution:
ω is the complex cube root of unity.
ω³ = 1
ω³ – 1 = 0
(ω – 1) (ω² + ω + 1) = 0
ω = 1 or ω² + ω + 1 = 0
But, ω is a complex number.
1 + ω + ω² = 0 …….(i)
AB + BA + A – 2B

which is a null matrix.

Question 12.
If A = \(\left[\begin{array}{lrr}
2 & -2 & -4 \\
-1 & 3 & 4 \\
1 & -2 & -3
\end{array}\right]\), show that A² = A.
Solution:

Question 13.
If A = \(\left[\begin{array}{ccc}
4 & -1 & -4 \\
3 & 0 & -4 \\
3 & -1 & -3
\end{array}\right]\), show that A² = I.
Solution:

Question 14.
If A = \(\left[\begin{array}{cc}
3 & -5 \\
-4 & 2
\end{array}\right]\), show that A² – 5A – 14I = 0.
Solution:

Question 15.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
-1 & 2
\end{array}\right]\), show that A – 4A + 3I = 0.
Solution:

Question 16.
If A = \(\left[\begin{array}{cc}
-3 & 2 \\
2 & -4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & x \\
y & 0
\end{array}\right]\) and (A + B)(A – B) = A² – B², find x and y.
Solution:
(A + B)(A – B) = A² – B²
A² – AB + BA – B² = A² – B²
-AB + BA = 0
AB = BA

By equality of matrices, we get
2 – 4x = -3x
∴ x = 2 and 2y = 2x
y = x
∴ y = 2
∴ x = 2, y = 2

Question 17.
If A = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\), show that (A + B)(A – B) ≠ A² – B².
Solution:
We have to prove that
(A + B) . (A – B) ≠ A² – B²
i.e., to prove that A(A – B) + B(A – B) ≠ A² – B²
i.e., to prove that A² – AB + BA – B² ≠ A² – B²
i.e., to prove that AB ≠ BA.

∴ AB ≠ BA

Question 18.
If A = \(\left[\begin{array}{ll}
2 & -1 \\
3 & -2
\end{array}\right]\), find A³.
Solution:

∴ A² = I
Multiplying throughout by A, we get
A³ = A . I
∴ A³ = A

Question 19.
Find x, y if,

Solution:

Question 20.
Find x, y, z if

Solution:

Question 21.
If A = \(\left[\begin{array}{ccc}
2 & 1 & -3 \\
0 & 2 & 6
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & 0 & -2 \\
3 & -1 & 4
\end{array}\right]\), find AB^T and A^TB.
Solution:

Question 22.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
3 & -2 \\
0 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 1 & 0
\end{array}\right]\), show that (AB)^T = B^TA^T.
Solution:

Question 23.
If A = \(\left[\begin{array}{ll}
3 & -4 \\
1 & -1
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), for all n ∈ N.
Solution:

Question 24.
If A = \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{cc}
\cos n \theta & \sin n \theta \\
-\sin n \theta & \cos n \theta
\end{array}\right]\), for all n ∈ N.
Solution:

Question 25.
Two farmers Shantaram and Kantaram cultivate three crops rice, wheat, and groundnut. The sale (in Rupees) of these crops by both the farmers for the month of April and may 2008 is given below,

Find
(i) the total sale in rupees for two months of each farmer for each crop.
(ii) the increase in sales from April to May for every crop of each farmer.
Solution:
(i) Total sale for Shantaram:
For rice = 15000 + 18000 = ₹ 33000.
For wheat = 13000 + 15000 = ₹ 28000.
For groundnut = 12000 + 12000 = ₹ 24000.
Total sale for Kantaram:
For rice = 18000 + 21000 = ₹ 39000
For wheat = 15000 + 16500 = ₹ 31500
For groundnut = 8000 + 16000 = ₹ 24000

Alternate method:
Matrix form

∴ The total sale of April and May of Shantaram in ₹ is ₹ 33000 (rice), ₹ 28000 (wheat), ₹ 24000 (groundnut), and that of Kantaram in ₹ is ₹ 39000(rice), ₹ 31500(wheat), and ₹ 24000 (groundnut).

(ii) Increase in sale from April to May for Shantaram:
For rice = 18000 – 15000 = ₹ 3000
For wheat = 15000 – 13000 = ₹ 2000
For groundnut = 12000 – 12000 = ₹ 0
Increase in sale from April to May for Kantaram:
For rice = 21000 – 18000 = ₹ 3000
For wheat = 16500 – 15000 = ₹ 1500
For groundnut = 16000 – 8000 = ₹ 8000

Alternate method:
Matrix form

∴ The increase in sales for Shantaram from April to May in each crop is ₹ 3000 (rice), ₹ 2000(wheat), 0 (groundnut), and that for Kantaram is ₹ 3000 (rice), ₹ 1500 (wheat), and ₹ 8000 (groundnut).

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 6 Circle Ex 6.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Circle Ex 6.1

Question 1.
Find the equation of a circle with
(i) centre at origin and radius 4.
(ii) centre at (-3, -2) and radius 6.
(iii) centre at (2, -3) and radius 5.
(iv) centre at (-3, -3) passing through point (-3, -6).
Solution:
(i) The equation of a circle with centre at origin and radius ‘r’ is given by
x² + y² = r²
Here, r = 4
∴ The required equation of the circle is x² + y² = 4² i.e., x² + y² = 16.

(ii) The equation of a circle with centre at (h, k) and radius ‘r’ is given by
(x – h)² + (y – k)² = r²
Here, h = -3, k = -2 and r = 6
∴ The required equation of the circle is
[x – (-3)]² + [y – (-2)]² = 6²
⇒ (x + 3)² + (y + 2)² = 36
⇒ x² + 6x + 9 + y² + 4y + 4 – 36 = 0
⇒ x² + y² + 6x + 4y – 23 = 0

(iii) The equation of a circle with centre at (h, k) and radius ‘r’ is given by
(x – h)² + (y – k)² = r²
Here, h = 2, k = -3 and r = 5
The required equation of the circle is
(x – 2)² + [y – (-3)]² = 5²
⇒ (x – 2)² + (y + 3)² = 25
⇒ x² – 4x + 4 + y² + 6y + 9 – 25 = 0
⇒ x² + y² – 4x + 6y – 12 = 0

(iv) Centre of the circle is C (-3, -3) and it passes through the point P (-3, -6).

The equation of a circle with centre at (h, k) and radius ‘r’ is given by
(x – h)² + (y – k)² = r²
Here, h = -3, k = -3, r = 3
The required equation of the circle is
[x – (-3)]² + [y – (-3)]² = 3²
⇒ (x + 3)² + (y + 3)² = 9
⇒ x² + 6x + 9 + y² + 6y + 9 – 9 = 0
⇒ x² + y² + 6x + 6y + 9 = 0

Check:
If the point (-3, -6) satisfies x² + y² + 6x + 6y + 9 = 0, then our answer is correct.
L.H.S. = x² + y² + 6x + 6y + 9
= (-3)² + (-6)² + 6(-3) – 6(-6) + 9
= 9 + 36 – 18 – 36 + 9
= 0
= R.H.S.
Thus, our answer is correct.

Question 2.
Find the centre and radius of the following circles:
(i) x² + y² = 25
(ii) (x – 5)² + (y – 3)² = 20
(iii) \(\left(x-\frac{1}{2}\right)^{2}+\left(y+\frac{1}{3}\right)^{2}=\frac{1}{36}\)
Solution:
(i) Given equation of the circle is
x² + y² = 25
⇒ x² + y² = (5)²
Comparing this equation with x² + y² = r², we get r = 5
Centre of the circle is (0, 0) and radius of the circle is 5.

(ii) Given equation of the circle is
(x – 5)² + (y – 3)² = 20
⇒ (x – 5)² + (y – 3)² = (√20)²
Comparing this equation with (x – h)² + (y – k)² = r², we get
h = 5, k = 3 and r = √20 = 2√5
Centre of the circle = (h, k) = (5, 3)
and radius of the circle = 2√5.

(iii) Given the equation of the circle is

Comparing this equation with (x – h)² + (y – k)² = r², we get
h = \(\frac{1}{2}\), k = \(\frac{-1}{3}\) and r = \(\frac{1}{6}\)
Centre of the circle = (h, k) = (\(\frac{1}{2}\), \(\frac{-1}{3}\)) and radius of the circle = \(\frac{1}{6}\)

Question 3.
Find the equation of the circle with centre
(i) at (a, b) and touching the Y-axis.
(ii) at (-2, 3) and touching the X-axis.
(iii) on the X-axis and passing through the origin having radius 4.
(iv) at (3, 1) and touching the line 8x – 15y + 25 = 0.
Solution:
(i) Since the circle is touching the Y-axis, the radius of the circle is X-co-ordinate of the centre.

∴ r = a
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)² + (y – k)² = r²
Here, h = a, k = b
The required equation of the circle is
⇒ (x – a)² + (y – b)² = a²
⇒ x² – 2ax + a² + y² – 2by + b² = a²
⇒ x² + y² – 2ax – 2by + b² = 0

(ii) Since the circle is touching the X-axis, the radius of the circle is the Y co-ordinate of the centre.

∴ r = 3
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)² + (y – k)² = r²
Here, h = -2, k = 3
The required equation of the circle is
⇒ (x + 2)² + (y – 3)² = 3²
⇒ x² + 4x + 4 + y² – 6y + 9 = 9
⇒ x² + y² + 4x – 6y + 4 = 0

(iii) Let the co-ordinates of the centre of the required circle be C (h, 0).
Since the circle passes through the origin i.e., O(0, 0)
OC = radius
⇒ \(\sqrt{(h-0)^{2}+(0-0)^{2}}=4\)
⇒ h² = 16
⇒ h = ±4

the co-ordinates of the centre are (4, 0) or (-4, 0).
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)² + (y – k)² = r²
Here, h = ± 4, k = 0, r = 4
The required equation of the circle is
⇒ (x – 4)² + (y – 0)² = 4² or (x + 4)² + (y – 0)² = 4²
⇒ x² – 8x + 16 + y² = 16 or x² + 8x + 16 + y² = 16
⇒ x² + y² – 8x = 0 or x² + y² + 8x = 0

(iv) Centre of the circle is C (3, 1).
Let the circle touch the line 8x – 15y + 25 = 0 at point M.

CM = radius (r)
CM = Length of perpendicular from centre C(3, 1) on the line 8x – 15y + 25 = 0

The equation of a circle with centre at (h, k) and radius r is given by
(x – h)² + (y – k)² = r²
Here, h = 3, k = 1 and r = 2
The required equation of the circle is
⇒ (x – 3)² + (y – 1)² = 2²
⇒ x² – 6x + 9 + y² – 2y + 1 = 4
⇒ x² + y² – 6x – 2y + 10 – 4 = 0
⇒ x² + y² – 6x – 2y + 6 = 0

Question 4.
Find the equation of the circle, if the equations of two diameters are 2x + y = 6 and 3x + 2y = 4 and radius is 9.
Solution:

Given equations of diameters are 2x + y = 6 and 3x + 2y = 4.
Let C (h, k) be the centre of the required circle.
Since point of intersection of diameters is the centre of the circle,
x = h, y = k
Equations of diameters become
2h + k = 6 …..(i)
and 3h + 2k = 4 ……..(ii)
By (ii) – 2 × (i), we get
-h = -8
⇒ h = 8
Substituting h = 8 in (i), we get
2(8) + k = 6
⇒ k = 6 – 16
⇒ k = -10
Centre of the circle is C (8, -10) and radius, r = 9
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)² + (y – k)² = r²
Here, h = 8, k = -10
The required equation of the circle is
⇒ (x – 8)² + (y + 10)² = 9²
⇒ x² – 16x + 64 + y² + 20y + 100 = 81
⇒ x² + y² – 16x + 20y + 100 + 64 – 81 = 0
⇒ x² + y² – 16x + 20y + 83 = 0

Question 5.
If y = 2x is a chord of the circle x² + y² – 10x = 0, find the equation of the circle with this chord as diameter.
Solution:

y = 2x is the chord of the given circle.
It satisfies the equation of a given circle.
Substituting y = 2x in x² + y² – 10x = 0, we get
⇒ x² + (2x)² – 10x = 0
⇒ x² + 4x² – 10x = 0
⇒ 5x² – 10x = 0
⇒ 5x(x – 2) = 0
⇒ x = 0 or x = 2
When x = 0, y = 2x = 2(0) = 0
∴ A = (0, 0)
When x = 2, y = 2x = 2 (2) = 4
∴ B = (2, 4)
End points of chord AB are A(0, 0) and B(2, 4).
Chord AB is the diameter of the required circle.
The equation of a circle having (x₁, y₁) and (x₂, y₂) as end points of diameter is given by
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
Here, x₁ = 0, y₁ = 0, x₂ = 2, y₂ = 4
The required equation of the circle is
⇒ (x – 0) (x – 2) + (y – 0) (y – 4 ) = 0
⇒ x² – 2x + y² – 4y = 0
⇒ x² + y² – 2x – 4y = 0

Question 6.
Find the equation of a circle with a radius of 4 units and touch both the co-ordinate axes having centre in the third quadrant. Solution:
The radius of the circle = 4 units
Since the circle touches both the co-ordinate axes and its centre is in the third quadrant,
the centre of the circle is C(-4, -4).

The equation of a circle with centre at (h, k) and radius r is given by (x – h)² + (y – k)² = r²
Here, h = -4, k = -4, r = 4
the required equation of the circle is
⇒ [x – (-4)]² + [y – (-4)]² = 4²
⇒ (x + 4)² + (y + 4)² = 16
⇒ x² + 8x + 16 + y² + 8y + 16 – 16 = 0
⇒ x² + y² + 8x + 8y + 16 = 0

Question 7.
Find the equation of the circle passing through the origin and having intercepts 4 and -5 on the co-ordinate axes.
Solution:
Let the circle intersect X-axis at point A and intersect Y-axis at point B.
the co-ordinates of point A are (4, 0) and the co-ordinates of point B are (0, -5).

Since ∠AOB is a right angle,
AB represents the diameter of the circle.
The equation of a circle having (x₁, y₁) and (x₂, y₂) as end points of diameter is given by
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
Here, x₁ = 4, y₁ = 0, x₂ = 0, y₂ = -5
The required equation of the circle is
⇒ (x – 4) (x – 0) + (y – 0) [y – (-5)] = 0
⇒ x(x – 4) + y(y + 5) = 0
⇒ x² – 4x + y² + 5y = 0
⇒ x² + y² – 4x + 5y = 0

Question 8.
Find the equation of a circle passing through the points (1, -4), (5, 2) and having its centre on line x – 2y + 9 = 0.
Solution:

Let C(h, k) be the centre of the required circle which lies on the line x – 2y + 9 = 0.
Equation of line becomes
h – 2k + 9 = 0 …..(i)
Also, the required circle passes through points A(1, -4) and B(5, 2).
CA = CB = radius
CA = CB
By distance formula,
\(\sqrt{(\mathrm{h}-1)^{2}+[\mathrm{k}-(-4)]^{2}}=\sqrt{(\mathrm{h}-5)^{2}+(\mathrm{k}-2)^{2}}\)
Squaring both the sides, we get
⇒ (h – 1)² + (k + 4)² = (h – 5)² + (k – 2)²
⇒ h² – 2h + 1 + k² + 8k + 16 = h² – 10h + 25 + k² – 4k + 4
⇒ -2h + 8k + 17 = -10h – 4k + 29
⇒ 8h + 12k – 12 = 0
⇒ 2h + 3k – 3 = 0 ……(ii)
By (ii) – (i) × 2, we get
7k = 21
⇒ k = 3
Substituting k = 3 in (i), we get
h – 2(3) + 9 = 0
⇒ h – 6 + 9 = 0
⇒ h = -3
Centre of the circle is C(-3, 3).
radius (r) = CA

The equation of a circle with centre at (h, k) and radius r is given by (x – h)² + (y – k)² = r²
Here, h = -3, k = 3, r = √65
The required equation of the circle is
⇒ [x – (-3)]² + (y – 3)² = (√65)²
⇒ (x + 3)² + (y – 3)² = 65
⇒ x² + 6x + 9 + y² – 6y + 9 – 65 = 0
⇒ x² + y² + 6x – 6y – 47 = 0

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Miscellaneous Exercise 5

(I) Select the correct option from the given alternatives.

Question 1.
If A is (5, -3) and B is a point on the X-axis such that the slope of line AB is -2, then B ≡
(a) (7, 2)
(b) (\(\frac{7}{2}\), 0)
(c) (0, \(\frac{7}{2}\))
(d) (\(\frac{2}{7}\), 0)
Answer:
(b) (\(\frac{7}{2}\), 0)
Hint:
Let B(x, 0) be the point on X-axis.
We have A = (5, -3)
slope of AB = -2
⇒ \(\frac{0-(-3)}{x-5}\) = -2
⇒ 3 = -2(x – 5)
⇒ 3 = -2x + 10
⇒ x = \(\frac{7}{2}\)
Co-ordinates of point B = (\(\frac{7}{2}\), 0)

Question 2.
If the point (1, 1) lies on the line passing through the points (a, 0) and (0, b), then \(\frac{1}{a}+\frac{1}{b}=\)
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{a b}\)
Answer:
(c) 1
Hint:
Line passes through (a, 0), (0, b).
x-intercept = a, y-intercept = b
∴ Equation of line is \(\frac{x}{a}+\frac{y}{b}=1\) …….(i)
Since line (i) passes through (1, 1), (1, 1) satisfies (i)
∴ \(\frac{1}{a}+\frac{1}{b}=1\)

Question 3.
If A(1, -2), B(-2, 3) and C(2, -5) are the vertices of ΔABC, then the equation of median BE is
(a) 7x + 13y + 47 = 0
(b) 13x + 7y + 5 = 0
(c) 7x – 13y + 5 = 0
(d) 13x – 7y – 5 = 0
Answer:
(b) 13x + 7y + 5 = 0
Hint:

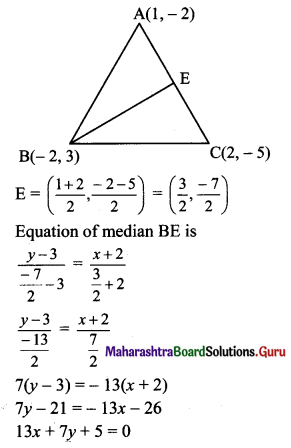
Question 4.
The equation of the line through (1, 2), which makes equal intercepts on the axes, is
(a) x + y = 1
(b) x + y = 2
(c) x + y = 4
(d) x + y = 3
Answer:
(d) x + y = 3
Hint:
Let the equation of required line be
\(\frac{x}{a}+\frac{y}{b}=1\) ……..(i)
Since the line makes equal intercepts on the axes, a = b
\(\frac{x}{a}+\frac{y}{a}=1\)
∴ x + y = a ……(ii)
But, equation (ii) passes through (1, 2).
1 + 2 = a
∴ a = 3
Substituting a = 3 in equation (ii), we get
x + y = 3

Question 5.
If the line kx + 4y = 6 passes through the point of intersection of the two lines 2x + 3y = 4 and 3x + 4y = 5, then k =
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Hint:
Given two lines are
2x + 3y = 4 ……(i)
3x + 4y = 5 …….(ii)
Multiplying (i) by 3 and (ii) by 2 and then subtracting, we get
y = 2
Substituting y = 2 in (i), we get
x = -1
∴ Point of intersection of lines (i) and (ii) is (-1, 2).
Given that the line kx + 4y = 6 passes through (-1, 2).
k(-1) + 4(2) = 6
∴ k = 2

Question 6.
The equation of a line, having inclination 120° with positive direction of X-axis, which is at a distance of 3 units from the origin is
(a) √3x ± y + 6 = 0
(b) √3x + y ± 6 = 0
(c) x + y = 6
(d) x + y = -6
Answer:
(b) √3x + y ± 6 = 0
Hint:

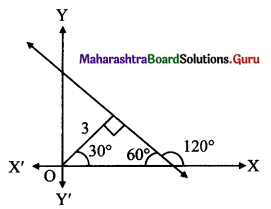
Here, α = 30° and p = 3 units
Equation of line with inclination a and distance from origin as p is
x cos α + y sin α = p
∴ x cos 30° + y sin 30° = ±3
∴ \(\frac{\sqrt{3} x}{2}+\frac{y}{2}=\pm 3\)
∴ √3x + y ± 6 = 0

Question 7.
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) 1
(d) \(\frac{4}{3}\)
Answer:
(d) \(\frac{4}{3}\)
Hint:
Slope of line 3x + y = 3 is -3
∴ Slope of line perpendicular to given line = \(\frac{1}{3}\)
Equation of required line passing through (2, 2) and having slope \(\frac{1}{3}\) is
y – 2 = \(\frac{1}{3}\)(x – 2)
3y – 6 = x – 2
∴ x – 3y + 4 = 0
∴ y-intercept = \(\frac{-4}{-3}=\frac{4}{3}\)

Question 8.
The angle between the line √3x – y – 2 = 0 and x – √3y + 1 = 0 is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Answer:
(b) 30°
Hint:

Question 9.
If kx + 2y – 1 = 0 and 6x – 4y + 2 = 0 are identical lines, then determine k.
(a) -3
(b) \(-\frac{1}{3}\)
(c) \(\frac{1}{3}\)
(d) 3
Answer:
(a) -3
Hint:
Lines kx + 2y – 1 = 0 and 6x – 4y + 2 = 0 are identical.
∴ \(\frac{k}{6}=\frac{2}{-4}=\frac{-1}{2}\)
∴ k = -3

Question 10.
Distance between the two parallel lines y = 2x + 7 and y = 2x + 5 is
(a) \(\frac{\sqrt{2}}{\sqrt{5}}\)
(b) \(\frac{1}{\sqrt{5}}\)
(c) \(\frac{\sqrt{5}}{2}\)
(d) \(\frac{2}{\sqrt{5}}\)
Answer:
(d) \(\frac{2}{\sqrt{5}}\)
Hint:
Here, c₁ = 7, c₂ = 5, a = 2 and b = -1
Distance between parallel lines

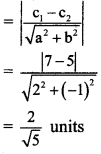
II. Answer the following questions.

Question 1.
Find the value of k:
(a) if the slope of the line passing through the points P(3, 4), Q(5, k) is 9.
(b) the points A(1, 3), B(4, 1), C(3, k) are collinear.
(c) the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3).
Solution:
(a) Given, P(3, 4), Q(5, k) and
Slope of PQ = 9
\(\frac{\mathrm{k}-4}{5-3}\) = 9
\(\frac{\mathrm{k}-4}{2}\) = 9
k – 4 = 18
k = 22

(b) Given, points A(1, 3), B(4, 1) and C(3, k) are collinear.
Slope of AB = Slope of BC
\(\frac{1-3}{4-1}=\frac{k-1}{3-4}\)
\(\frac{-2}{3}=\frac{\mathrm{k}-1}{-1}\)
2 = 3k – 3
k = \(\frac{5}{3}\)

(c) Given, point P(1, k) lies on the line joining A(2, 2) and B(3, 3).
Slope of AB = Slope of BP
\(\frac{3-2}{3-2}=\frac{3-k}{3-1}\)
1 = \(\frac{3-\mathrm{k}}{2}\)
2 = 3 – k
k = 1

Question 2.
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence, find its slope.
Solution:
Given equation is 6x + 3y + 8 = 0, which can be written as
3y = – 6x – 8
y = \(\frac{-6 x}{3}-\frac{8}{3}\)
y = -2x – \(\frac{8}{3}\)
This is of the form y = mx + c with m = -2
y = -2x – \(\frac{8}{3}\) is in slope-intercept form with slope = -2

Question 3.
Find the distance of the origin from the line x = -2.
Solution:
Given equation of line is x = -2
This equation represents a line parallel to Y-axis and at a distance of 2 units to the left of Y-axis.
∴ Distance of the origin from the line is 2 units.

Question 4.
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Solution:
Given equation is 3x + 2y – 6 = 0.
Substituting x = 2 and y = 3 in L.H.S. of given equation, we get
L.H.S. = 3x + 2y – 6
= 3(2) + 2(3) – 6
= 6
≠ R.H.S.
∴ Point A does not lie on the given line.

Question 5.
Which of the following lines passes through the origin?
(a) x = 2
(b) y = 3
(c) y = x + 2
(d) 2x – y = 0
Answer:
(d) 2x – y = 0
Hint:
Any line passing through origin is of the form y = mx or ax + by = 0.
Here in the given option, 2x – y = 0 is in the form ax + by = 0.
∴ Option (d) is the correct answer.

Question 6.
Obtain the equation of the line which is:
(a) parallel to the X-axis and 3 units below it.
(b) parallel to the Y-axis and 2 units to the left of it.
(c) parallel to the X-axis and making an intercept of 5 on the Y-axis.
(d) parallel to the Y-axis and making an intercept of 3 on the X-axis.
Solution:
(a) Equation of a line parallel to X-axis is y = k.
Since the line is at a distance of 3 units below X-axis, k = -3
∴ The equation of the required line is y = -3.

(b) Equation of a line parallel to Y-axis is x = h.
Since the line is at a distance of 2 units to the left of Y-axis, h = -2
∴ The equation of the required line is x = -2.

(c) Equation of a line parallel to X-axis with y-intercept ‘k’ is y = k.
Here, y-intercept = 5
∴ The equation of the required line is y = 5.

(d) Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 3
∴ The equation of the required line is x = 3.

Question 7.
Obtain the equation of the line containing the point:
(i) (2, 3) and parallel to the X-axis.
(ii) (2, 4) and perpendicular to the Y-axis.
Solution:
(i) Equation of a line parallel to X-axis is of the form y = k.
Since the line passes through (2, 3), k = 3
∴ The equation of the required line is y = 3.

(ii) Equation of a line perpendicular to Y-axis
i.e., parallel to X-axis, is of the form y = k.
Since the line passes through (2, 4), k = 4
∴ The equation of the required line is y = 4.

Question 8.
Find the equation of the line:
(a) having slope 5 and containing point A(-1, 2).
(b) containing the point T(7, 3) and having inclination 90°.
(c) through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co-ordinate axes.
Solution:
(a) Given, slope(m) = 5 and the line passes through A(-1, 2).
Equation of the line in slope point form is y – y1 = m(x – x1)
The equation of the required line is
y – 2 = 5(x + 1)
y – 2 = 5x + 5
∴ 5x – y + 7 = 0

(b) Given, Inclination of line = θ = 90°
the required line is parallel to Y-axis.
Equation of a line parallel to Y-axis is of the form x = h.
Since the line passes through (7, 3), h = 7
∴ The equation of the required line is x = 7.

(c) Given equation of the line is 3x + 2y = 2.

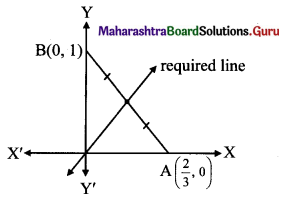
\(\frac{3 x}{2}+\frac{2 y}{2}=1\)
\(\frac{x}{\frac{2}{3}}+\frac{y}{1}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), with a = \(\frac{2}{3}\), b= 1.
The line 3x + 2y = 2 intersects the X-axis at A(\(\frac{2}{3}\), 0) and Y-axis at B(0, 1).
Required line is passing through the midpoint of AB.
Midpoint of AB = \(\left(\frac{\frac{2}{3}+0}{2}, \frac{0+1}{2}\right)=\left(\frac{1}{3}, \frac{1}{2}\right)\)
∴ Required line passes through (0, 0) and \(\left(\frac{1}{3}, \frac{1}{2}\right)\).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-0}{\frac{1}{2}-0}=\frac{x-0}{\frac{1}{3}-0}\)
2y = 3x
∴ 3x – 2y = 0

Question 9.
Find the equation of the line passing through the points S(2, 1) and T(2, 3).
Solution:
The required line passes through the points S(2, 1) and T(2, 3).
Since both the given points have same x co-ordinates i.e. 2
the given points lie on a line parallel to Y-axis.
∴ The equation of the required line is x = 2.

Question 10.
Find the distance of the origin from the line 12x + 5y + 78 = 0.
Solution:
Let p be the perpendicular distance of origin from the line 12x + 5y + 78 = 0.
Here, a = 12, b = 5, c = 78

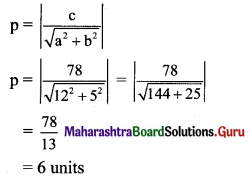
Question 11.
Find the distance between the parallel lines 3x + 4y + 3 = 0 and 3x + 4y + 15 = 0.
Solution:
Equations of the given parallel lines are 3x + 4y + 3 = 0 and 3x + 4y + 15 = 0
Here, a = 3, b = 4, c₁ = 3 and c₂ = 15
∴ Distance between the parallel lines

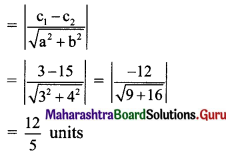
Question 12.
Find the equation of the line which contains the point A(3, 5) and makes equal intercepts on the co-ordinates axes.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) …….(i)
This line passes through A(3, 5).
∴ \(\frac{3}{a}+\frac{5}{b}=1\) ……..(ii)
Since the required line makes equal intercepts on the co-ordinates axes,
a = b …….(iii)
Substituting the value of b in (ii), we get
\(\frac{3}{a}+\frac{5}{a}=1\)
∴ a = 8
∴ b = 8 …… [From (iii)]
Substituting the values of a and b in equation (i), the equation of the required line is
\(\frac{x}{8}+\frac{y}{8}=1\)
∴ x + y = 8

Case II: Line passing through origin.
Slope of line passing through origin and A(3, 5) is
m = \(\frac{5-0}{3-0}=\frac{5}{3}\)
∴ Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is
y = \(\frac{5}{3}\)x
∴ 5x – 3y = 0

Question 13.
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of
(a) the sides
(b) the medians
(c) perpendicular bisectors of sides
(d) altitudes of ?ABC
Solution:
Vertices of ∆ABC are A(1, 4), B(2, 3) and C(1, 6)
(a) Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}\) = \(\frac{x-x_{1}}{x_{2}-x_{1}}\)
Equation of side AB is
\(\frac{y-4}{3-4}=\frac{x-1}{2-1}\)
y – 4 = -1(x – 1)
y – 4 = -x + 1
x + y = 5
Equation of side BC is
\(\frac{y-3}{6-3}=\frac{x-2}{1-2}\)
-1(y – 3) = 3(x – 2)
-y + 3 = 3x – 6
∴ 3x + y = 9
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on a line parallel to Y-axis.
∴ The equation of side AC is x = 1.

(b) Let D, E and F be the midpoints of sides AC and AB respectively of ∆ABC.

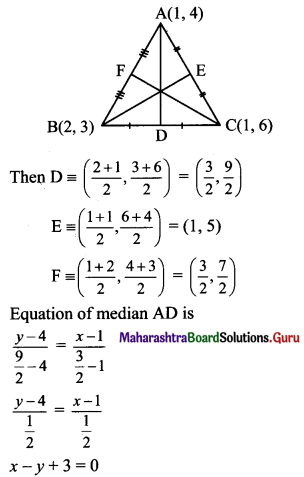
(c) Slope of side BC = \(\left(\frac{6-3}{1-2}\right)=\left(\frac{3}{-1}\right)\) = -3
Slope of perpendicular bisector of BC is \(\frac{1}{3}\) and the line passes through \(\left(\frac{3}{2}, \frac{9}{2}\right)\).
Equation of the perpendicular bisector of side BC is
\(\left(y-\frac{9}{2}\right)=\frac{1}{3}\left(x-\frac{3}{2}\right)\)
3(2y – 9) = (2x – 3)
6y – 27 = 2x – 3
2x – 6y + 24 = 0
∴ x – 3y + 12 = 0
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, perpendicular bisector of side AC is parallel to X-axis.
Since, the perpendicular bisector of side AC passes through E(1, 5).
The equation of perpendicular bisector of side AC is y = 5.
Slope of side AB = \(\left(\frac{3-4}{2-1}\right)\) = -1
Slope of perpendicular bisector of AB is 1 and the line passes through \(\left(\frac{3}{2}, \frac{7}{2}\right)\).
Equation of the perpendicular bisector of side AB is
\(\left(y-\frac{7}{2}\right)=1\left(x-\frac{3}{2}\right)\)
2y – 7 = 2x – 3
2x – 2y + 4 = 0
∴ x – y + 2 = 0

(d) Let AX, BY, and CZ be the altitudes through the vertices A, B and C respectively of ∆ABC.

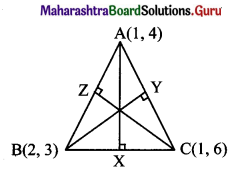
Slope of BC = -3
Slope of AX = \(\frac{1}{3}\) ……[∵ AX ⊥ BC]
Since altitude AX passes through (1, 4) and has slope \(\frac{1}{3}\),
equation of altitude AX is
y – 4 = \(\frac{1}{3}\)(x – 1)
3y – 12 = x – 1
∴ x – 3y + 11 = 0
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, altitude BY is parallel to X-axis.
Since the altitude BY passes through B(2, 3), the equation of altitude BY is y = 3.
Also, slope of AB = -1
Slope of CZ = 1
Since altitude CZ passes through (1, 6) and has slope 1,
equation of altitude CZ is
y – 6 = 1(x – 1)
∴ x – y + 5 = 0

Question 14.
Find the equation of the line which passes through the point of intersection of lines x + y – 3 = 0, 2x – y + 1 = 0 and which is parallel to X-axis.
Solution:
Let u ≡ x + y – 3 = 0 and v ≡ 2x – y + 1 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
(x + y – 3) + k(2x – y + 1) = 0 …..(i)
x + y – 3 + 2kx – ky + k = 0
x + 2kx + y – ky – 3 + k = 0
(1 + 2k)x + (1 – k)y – 3 + k = 0
But, this line is parallel to X-axis
Its slope = 0
⇒ \(\frac{-(1+2 k)}{1-k}=0\)
⇒ 1 + 2k = 0
⇒ k = \(\frac{-1}{2}\)
Substituting the value of k in (i), we get
(x + y – 3) + \(\frac{-1}{2}\) (2x – y + 1) = 0
⇒ 2(x + y – 3) – (2x – y + 1 ) = 0
⇒ 2x + 2y – 6 – 2x + y – 1 = 0
⇒ 3y – 7 = 0, which is the equation of the required line.

Question 15.
Find the equation of the line which passes through the point of intersection of lines x + y + 9 = 0, 2x + 3y + 1 = 0 and which makes x-intercept 1.
Solution:
Let u ≡ x + y + 9 = 0 and v ≡ 2x + 3y + 1 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
(x + y + 9) + k(2x + 3y + 1) = 0 ……(i)
⇒ x + y + 9 + 2kx + 3ky + k = 0
⇒ (1 + 2k)x + (1 + 3k)y + 9 + k = 0
But, x-intercept of this line is 1.
⇒ \(\frac{-(9+\mathrm{k})}{1+2 \mathrm{k}}\)
⇒ -9 – k = 1 + 2k
⇒ k = \(\frac{-10}{3}\)
Substituting the value of k in (i), we get
(x + y + 9) + (\(\frac{-10}{3}\)) (2x + 3y + 1) = 0
⇒ 3(x + y + 9) – 10(2x + 3y + 1) = 0
⇒ 3x + 3y + 27 – 20x – 30y – 10 = 0
⇒ -17x – 27y+ 17 = 0
⇒ 17x + 27y – 17 = 0, which is the equation of the required line.

Question 16.
Find the equation of the line through A(-2, 3) and perpendicular to the line through S(1, 2) and T(2, 5).
Solution:
Slope of ST = \(\frac{5-2}{2-1}\) = 3
Since the required line is perpendicular to ST,
slope of required line = \(\frac{-1}{3}\) and line passes through A(-2, 3)
Equation of the line in slope point form is y – y₁ = m(x – x₁)
The equation of the required line is
y – 3 = \(\frac{-1}{3}\)(x + 2)
⇒ 3(y – 3) = -(x + 2)
⇒ 3y – 9 = -x – 2
⇒ x + 3y = 7

Question 17.
Find the x-intercept of the line whose slope is 3 and which makes intercept 4 on the Y-axis.
Solution:
Equation of a line having slope ‘m’ and y-intercept ‘c’ is y = mx + c
Given, m = 3, c = 4
The equation of the line is y = 3x + 4
3x – y = -4
\(\frac{3 x}{(-4)}-\frac{y}{(-4)}=1\)
\(\frac{x}{\left(\frac{-4}{3}\right)}+\frac{y}{4}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where
x-intercept = a
x-intercept = \(\frac{-4}{3}\)

Alternate Method:

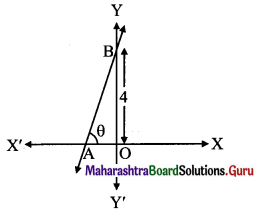
Let θ be the inclination of the line.
Then tan θ = 3 …..[∵ slope = 3 (given)]
\(\frac{\mathrm{OB}}{\mathrm{OA}}=3\)
\(\frac{4}{\mathrm{OA}}=3\)
OA = \(\frac{4}{3}\)
x-intercept = –\(\frac{4}{3}\) as point A is to the left side of Y-axis.

Question 18.
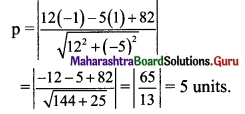
Find the distance of P(-1, 1) from the line 12(x + 6) = 5(y – 2).
Solution:
Given equation of the line is
12(x + 6) = 5(y – 2)
12x + 72 = 5y – 10
12x – 5y + 82 = 0
Let p be the perpendicular distance of the point (-1, 1) from the line 12x – 5y + 82 = 0.

Question 19.
Line through A(h, 3) and B(4,1) intersect the line lx – 9y -19 = 0 at right angle. Find the value of h.
Solution:
Given, A(h, 3) and B(4, 1)
Slope of AB (m₁) = \(\frac{1-3}{4-h}\)
m₁ = \(\frac{2}{h-4}\)
Slope of line 7x – 9y – 19 = 0 is m₂ = \(\frac{7}{9}\)
Since line AB and line 7x – 9y – 19 = 0 are perpendicular to each other,
m₁ × m₂ = -1
\(\frac{2}{h-4} \times \frac{7}{9}=-1\)
14 = 9(4 – h)
14 = 36 – 9h
9h = 22
h = \(\frac{22}{9}\)

Question 20.
Two lines passing through M(2, 3) intersect each other at an angle of 45°. If slope of one line is 2, find the equation of the other line.
Solution:
Let m be the slope of the required line which make an angle of 45° with the other line.
Slope of one of the lines is 2.
tan 45° = \(\left|\frac{\mathrm{m}-2}{1+\mathrm{m}(2)}\right|\)
1 = \(\left|\frac{m-2}{1+2 m}\right|\)
\(\frac{m-2}{1+2 m}=\pm 1\)
\(\frac{\mathrm{m}-2}{1+2 \mathrm{~m}}\) = 1 or \(\frac{\mathrm{m}-2}{1+2 \mathrm{~m}}\) = -1
m – 2 = 1 + 2m or m – 2 = -1 – 2m
m = -3 or 3m = 1
m = -3 or m = \(\frac{1}{3}\)
Required line passes through M(2, 3)
When m = -3, equation of the line is
y – 3 = -3(x – 2)
y – 3 = -3x + 6
∴ 3x + y = 9
When m = \(\frac{1}{3}\), equation of the line is
y – 3 = \(\frac{1}{3}\)(x – 2)
3y – 9 = x – 2
∴ x – 3y + 7 = 0

Question 21.
Find the y-intercept of the line whose slope is 4 and which has x-intercept 5.
Solution:
Given, slope = 4, x-intercept = 5
Since the x-intercept of the line is 5, it passes through (5, 0).
Equation of the line in slope point form is y – y₁ = m(x – x₁)
Equation of the required line is
y – 0 = 4(x – 5)
y = 4x – 20
4x – y = 20
\(\frac{4 x}{20}-\frac{y}{20}=1\)
\(\frac{x}{5}+\frac{y}{(-20)}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where
x-intercept = b, y-intercept = -20

Question 22.
Find the equations of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11 and y = 12.
Solution:
Given, equations of sides of rectangle are x = 8, x = 10, y = 11 and y = 12

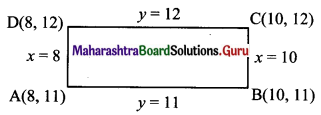
From the above diagram,
Vertices of rectangle are A(8, 11), B(10, 11), C(10, 12) and D(8, 12).
Equation of diagonal AC is
\(\frac{y-11}{12-11}=\frac{x-8}{10-8}\)
\(\frac{y-11}{1}=\frac{x-8}{2}\)
2y – 22 = x – 8
x – 2y + 14 = 0
Equation of diagonal BD is
\(\frac{y-11}{12-11}=\frac{x-10}{8-10}\)
\(\frac{y-11}{1}=\frac{x-10}{-2}\)
-2y + 22 = x – 10
x + 2y = 32

Question 23.
A(1, 4), B(2, 3) and C(1, 6) are vertices of AABC. Find the equation of the altitude through B and hence find the co-ordinates of the point where this altitude cuts the side AC of ∆ABC.
Solution:
Vertices of triangle are A(1, 4), B(2, 3) and C(1, 6).
Let BD be the altitude through the vertex B.

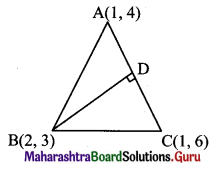
Since both the points A and C have same x co-ordinates i.e. 1
the given points lie on a line parallel to Y-axis.
The equation of the line AC is x = 1 …..(i)
AC is parallel to Y-axis and therefore, altitude BD is parallel to X-axis.
Since the altitude BD passes through B(2, 3), the equation of altitude BD is y = 3 ……(ii)
From (i) and (ii),
Point of intersection of AC and altitude BD is (1, 3).

Question 24.
The vertices of ∆PQR are P(2, 1), Q(-2, 3) and R(4, 5). Find the equation of the median through R.
Solution:

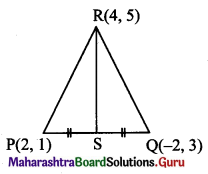
Let S be the midpoint of side PQ.
Then RS is the median through R.
S = \(\left(\frac{2-2}{2}, \frac{3+1}{2}\right)\) = (0, 2)
The median RS passes through the points R(4, 5) and S(0, 2).
∴ Equation of median RS is
\(\frac{y-5}{2-5}=\frac{x-4}{0-4}\)
⇒ \(\frac{y-5}{-3}=\frac{x-4}{-4}\)
⇒ 4(y – 5) = 3(x – 4)
⇒ 4y – 20 = 3x – 12
∴ 3x – 4y + 8 = 0

Question 25.
A line perpendicular to segment joining A(1, 0) and B(2, 3) divides it internally in the ratio 1 : 2. Find the equation of the line. Solution:
Given, A(1, 0), B(2, 3)
Slope of AB = \(\frac{3-0}{2-1}\) = 3
Required line is perpendicular to AB.
Slope of required line = \(\frac{-1}{3}\)
Let point C divide AB in the ratio 1 : 2.

Required line passes through \(\left(\frac{4}{3}, 1\right)\) and has slope = \(\frac{-1}{3}\)
Equation of the line in slope point form is y – y₁ = m(x – x₁)
The equation of the required line is
y – 1 = \(\frac{-1}{3}\left(x-\frac{4}{3}\right)\)
⇒ 3(y – 1) = \(-1\left(x-\frac{4}{3}\right)\)
⇒ 3y – 3 = -x + \(\frac{4}{3}\)
⇒ 9y – 9 = -3x + 4
⇒ 3x + 9y = 13

Question 26.
Find the co-ordinates of the foot of the perpendicular drawn from the point P(-1, 3) to the line 3x – 4y – 16 = 0.
Solution:

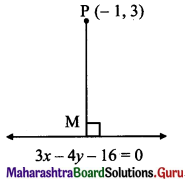
Let M be the foot of perpendicular drawn from P(-1, 3) to the line 3x – 4y – 16 = 0
Slope of the line 3x – 4y – 16 = 0 is \(\frac{-3}{-4}=\frac{3}{4}\)
Since PM ⊥ to line (i),
slope of PM = \(\frac{-4}{3}\)
Equation of PM is
y – 3 = \(\frac{-4}{3}\) (x + 1)
⇒ 3(y – 3) = -4(x + 1)
⇒ 3y – 9 = -4x – 4
∴ 4x + 3y – 5 = 0 ……(ii)
The foot of perpendicular i.e., point M, is the point of intersection of equation (i) and (ii).
By (i) × 3 + (ii) × 4, we get
25x = 68
x = \(\frac{68}{25}\)
Substituting x = \(\frac{68}{25}\) in (ii), we get

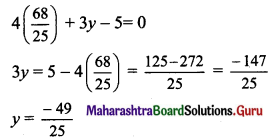
The co-ordinates of the foot of perpendicular M are \(\left(\frac{68}{25}, \frac{-49}{25}\right)\)

Question 27.
Find points on the X-axis whose distance from the line \(\frac{x}{3}+\frac{y}{4}=1\) is 4 units.
Solution:
The equation of line is \(\frac{x}{3}+\frac{y}{4}=1\)
i.e. 4x + 3y – 12 = 0 …..(i)
Let (h, 0) be a point on the X-axis.
The distance of this point from line (i) is 4.
⇒ \(\frac{|4 h+3(0)-12|}{\sqrt{4^{2}+3^{2}}}=4\)
⇒ \(\frac{|4 \mathrm{~h}-12|}{5}=4\)
⇒ |4h – 12| = 20
⇒ 4h – 12 = 20 or 4h – 12 = -20
⇒ 4h = 32 or 4h = -8
⇒ h = 8 or h = -2
∴ The required points are (8, 0) and (-2, 0).

Question 28.
The perpendicular from the origin to a line meets it at (-2, 9). Find the equation of the line.
Solution:

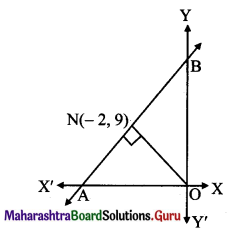
Slope of ON = \(\frac{9-0}{-2-0}=\frac{-9}{2}\)
Since line AB ⊥ ON,
slope of the line AB perpendicular to ON is \(\frac{2}{9}\) and it passes through point N(-2, 9).
Equation of the line in slope point form is y – y₁ = m(x – x₁)
Equation of line AB is
y – 9 = \(\frac{2}{9}\)(x + 2)
⇒ 9(y – 9) = 2(x + 2)
⇒ 9y – 81 = 2x + 4
⇒ 2x – 9y + 85 = 0

Question 29.
P(a, b) is the midpoint of a line segment intercepted between the axes. Show that the equation of the line is \(\frac{x}{a}+\frac{y}{b}=2\).
Solution:
Let the intercepts of a line AB be x₁ and y₁ on the X and Y-axes respectively.
A ≡ (x₁, 0), B = (0, y₁)
P(a, b) is the midpoint of a line segment AB intercepted between the axes.

Question 30.
Find the distance of the line 4x – y = 0 from the point P(4, 1) measured along the line making an angle of 135° with the positive X-axis.
Solution:

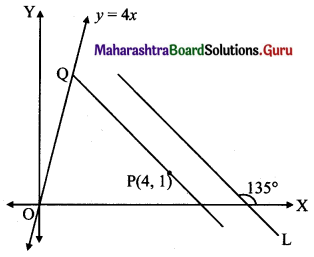
Let a line L make angle 135° with positive X-axis.
Required distance = PQ, where PQ || line L
Slope of PQ = tan 135°
= tan (180° – 45°)
= -tan 45°
= -1
Equation of PQ is
y – 1 = (-1)(x – 4)
y – 1 = -x + 4
x + y = 5 …..(i)
To get point Q we solve the equation 4x – y = 0 with (i)
Substituting y = 4x in (i), we get
5x = 5
x = 1
Substituting x = 1 in (i), we get
1 + y = 5
y = 4
∴ Q = (1, 4)
PQ = \(\sqrt{(4-1)^{2}+(1-4)^{2}}\)
= \(\sqrt{9+9}\)
= 3√2

Question 31.
Show that there are two lines which pass through A(3, 4) and the sum of whose intercepts is zero.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) ……(1)
This line passes through (3, 4)
\(\frac{3}{a}+\frac{4}{b}=1\) …..(ii)
Since the sum of the intercepts of the line is zero,
a + b = 0
a = -b ……(iii)
Substituting the value of a in (ii), we get
\(\frac{3}{-b}+\frac{4}{b}=1\)
\(\frac{1}{b}\) = 1
b = 1
a = -1 ……[From (iii)]
Substituting the values of a and b in (i),
the equation of the required line is
\(\frac{x}{-1}+\frac{y}{1}=1\)
x – y = -1
∴ x – y + 1 = 0

Case II: Line passing through origin.
Slope of line passing through origin and A(3, 4) is
m = \(\frac{4-0}{3-0}=\frac{4}{3}\)
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
The equation of the required line is
y = \(\frac{4}{3}\)x
∴ 4x – 3y = 0
∴ There are two lines which pass through A(3, 4) and the sum of whose intercepts is zero.

Question 32.
Show that there is only one line which passes through B(5, 5) and the sum of whose intercepts is zero.
Solution:
When line is passing through origin, the sum of intercepts made by the line is zero.
Slope of line passing through origin and B(5, 5) is
m = \(\frac{5-0}{5-0}\) = 1
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
The equation of the required line is y = x
∴ x – y = 0
∴ There is only one line which passes through B(5, 5) and the sum of whose intercepts is zero.

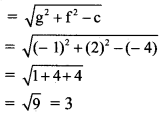
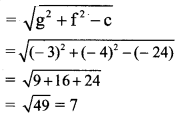
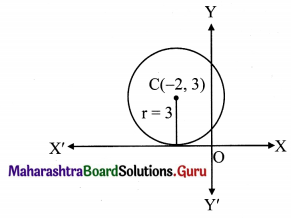
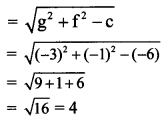
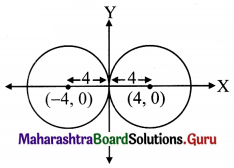
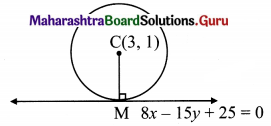
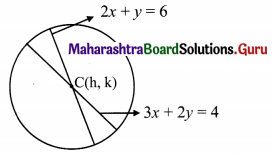
11th Maths Digest Pdf Science, Maharashtra State Board HSC 11th Science Maths Digest Pdf, Maharashtra State Board 11th Maths Book Solutions Pdf, Maharashtra State Board Class 11 Maths Solutions Pdf Part 1 & 2 free download in English Medium and Marathi Medium 2021-2022.

Maharashtra State Board 11th Maths Textbook Solutions Digest Guide

Maharashtra State Board Class 11 Maths Solutions Pdf Part 1

Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement

• Chapter 1 Angle and its Measurement Ex 1.1
• Chapter 1 Angle and its Measurement Ex 1.2
• Chapter 1 Angle and its Measurement Miscellaneous Exercise 1

Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Trigonometry – I

• Chapter 2 Trigonometry – I Ex 2.1
• Chapter 2 Trigonometry – I Ex 2.2
• Chapter 2 Trigonometry – I Miscellaneous Exercise 2

Maharashtra State Board 11th Maths Textbook Chapter 3 Trigonometry – II

• Chapter 3 Trigonometry – II Ex 3.1
• Chapter 3 Trigonometry – II Ex 3.2
• Chapter 3 Trigonometry – II Ex 3.3
• Chapter 3 Trigonometry – II Ex 3.4
• Chapter 3 Trigonometry – II Ex 3.5
• Chapter 3 Trigonometry – II Miscellaneous Exercise 3

11th Science Maths Chapter 4 Determinants and Matrices

• Chapter 4 Determinants and Matrices Ex 4.1
• Chapter 4 Determinants and Matrices Ex 4.2
• Chapter 4 Determinants and Matrices Ex 4.3
• Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(A)
• Chapter 4 Determinants and Matrices Ex 4.4
• Chapter 4 Determinants and Matrices Ex 4.5
• Chapter 4 Determinants and Matrices Ex 4.6
• Chapter 4 Determinants and Matrices Ex 4.7
• Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B)

11th Std State Board Maths Solution Book Pdf Chapter 5 Straight Line

• Chapter 5 Straight Line Ex 5.1
• Chapter 5 Straight Line Ex 5.2
• Chapter 5 Straight Line Ex 5.3
• Chapter 5 Straight Line Ex 5.4
• Chapter 5 Straight Line Miscellaneous Exercise 5

11th State Board Maths Solution Book Pdf Free Download Chapter 6 Circle

• Chapter 6 Circle Ex 6.1
• Chapter 6 Circle Ex 6.2
• Chapter 6 Circle Ex 6.3
• Chapter 6 Circle Miscellaneous Exercise 6

11th Maths Digest Pdf Science Chapter 7 Conic Sections

• Chapter 7 Conic Sections Ex 7.1
• Chapter 7 Conic Sections Ex 7.2
• Chapter 7 Conic Sections Ex 7.3
• Chapter 7 Conic Sections Miscellaneous Exercise 7

11th Maharashtra State Board Maths Solution Book Pdf Part 1 Chapter 8 Measures of Dispersion

• Chapter 8 Measures of Dispersion Ex 8.1
• Chapter 8 Measures of Dispersion Ex 8.2
• Chapter 8 Measures of Dispersion Ex 8.3
• Chapter 8 Measures of Dispersion Miscellaneous Exercise 8

11th Maths Book Solutions State Board Chapter 9 Probability

• Chapter 9 Probability Ex 9.1
• Chapter 9 Probability Ex 9.2
• Chapter 9 Probability Ex 9.3
• Chapter 9 Probability Ex 9.4
• Chapter 9 Probability Ex 9.5
• Chapter 9 Probability Miscellaneous Exercise 9

Maharashtra State Board 11th Maths Book Solutions Pdf Part 2

Maths Digest Std 11 Science Pdf Chapter 1 Complex Numbers

• Chapter 1 Complex Numbers Ex 1.1
• Chapter 1 Complex Numbers Ex 1.2
• Chapter 1 Complex Numbers Ex 1.3
• Chapter 1 Complex Numbers Ex 1.4
• Chapter 1 Complex Numbers Miscellaneous Exercise 1

Maths Solutions for Class 11 State Board Chapter 2 Sequences and Series

• Chapter 2 Sequences and Series Ex 2.1
• Chapter 2 Sequences and Series Ex 2.2
• Chapter 2 Sequences and Series Ex 2.3
• Chapter 2 Sequences and Series Ex 2.4
• Chapter 2 Sequences and Series Ex 2.5
• Chapter 2 Sequences and Series Ex 2.6
• Chapter 2 Sequences and Series Miscellaneous Exercise 2

Std 11 Maths Digest Chapter 3 Permutations and Combination

• Chapter 3 Permutations and Combination Ex 3.1
• Chapter 3 Permutations and Combination Ex 3.2
• Chapter 3 Permutations and Combination Ex 3.3
• Chapter 3 Permutations and Combination Ex 3.4
• Chapter 3 Permutations and Combination Ex 3.5
• Chapter 3 Permutations and Combination Ex 3.6
• Chapter 3 Permutations and Combination Miscellaneous Exercise 3

11 Std Maths Book Pdf Chapter 4 Methods of Induction and Binomial Theorem

• Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1
• Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2
• Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3
• Chapter 4 Methods of Induction and Binomial Theorem Ex 4.4
• Chapter 4 Methods of Induction and Binomial Theorem Ex 4.5
• Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4

State Board 11th Maths Book Answers Chapter 5 Sets and Relations

• Chapter 5 Sets and Relations Ex 5.1
• Chapter 5 Sets and Relations Ex 5.2
• Chapter 5 Sets and Relations Miscellaneous Exercise 5

11th Maths Practical Handbook Pdf Chapter 6 Functions

• Chapter 6 Functions Ex 6.1
• Chapter 6 Functions Ex 6.2
• Chapter 6 Functions Miscellaneous Exercise 6

11th Maths Solution Book Pdf Download Chapter 7 Limits

• Chapter 7 Limits Ex 7.1
• Chapter 7 Limits Ex 7.2
• Chapter 7 Limits Ex 7.3
• Chapter 7 Limits Ex 7.4
• Chapter 7 Limits Ex 7.5
• Chapter 7 Limits Ex 7.6
• Chapter 7 Limits Ex 7.7
• Chapter 7 Limits Miscellaneous Exercise 7

11th Standard State Board Maths Guide Chapter 8 Continuity

• Chapter 8 Continuity Ex 8.1
• Chapter 8 Continuity Miscellaneous Exercise 8

11th Std Maths Guide Free Download Chapter 9 Differentiation

• Chapter 9 Differentiation Ex 9.1
• Chapter 9 Differentiation Ex 9.2
• Chapter 9 Differentiation Miscellaneous Exercise 9

Maharashtra State Board Class 11 Textbook Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(A) Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(A)

I. Select the correct option from the given alternatives.

Question 1.
The determinant D = \(\left|\begin{array}{ccc}
a & b & a+b \\
b & c & b+c \\
a+b & b+c & 0
\end{array}\right|\) = 0, if
(a) a, b, c are in A.P.
(b) a, b, c are in G.P.
(c) a, b, c are in H.P.
(d) α is a root of ax² + 2bx + c = 0
Answer:
(b) a, b, c are in G.P.
Hint:
Applying R₃ → R₃ – (R₁ + R₂), we get
\(\left|\begin{array}{llc}
a & b & a+b \\
b & c & b+c \\
0 & 0 & -(a+2 b+c)
\end{array}\right|=0\)
∴ a[-c(a + 2b + c) – 0] – b[-b(a + 2b + c) – 0] + (a + b) (0 – 0) = 0
∴ (-ac + b²) (a + 2b + c) = 0
∴ -ac + b² = 0 or a + 2b + c = 0
∴ b² = ac
∴ a, b, c are in G.P.

Question 2.
If \(\left|\begin{array}{lll}
x^{k} & x^{k+2} & x^{k+3} \\
y^{k} & y^{k+2} & y^{k+3} \\
z^{k} & z^{k+2} & z^{k+3}
\end{array}\right|\) = (x – y) (y – z) (z – x) \(\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\) then
(a) k = -3
(b) k = -1
(c) k = 1
(d) k = 3
Answer:
(b) k = -1
Hint:

Question 3.
Let D = \(\left|\begin{array}{ccc}
\sin \theta \cdot \cos \phi & \sin \theta \cdot \sin \phi & \cos \theta \\
\cos \theta \cdot \cos \phi & \cos \theta \cdot \sin \phi & -\sin \theta \\
-\sin \theta \cdot \sin \phi & \sin \theta \cdot \cos \phi & 0
\end{array}\right|\) then
(a) D is independent of θ
(b) D is independent of φ
(c) D is a constant
(d) \(\frac{d D}{d}\) at θ = \(\frac{\pi}{2}\) is equal to 0
Answer:
(b) D is independent of φ

Question 4.
The value of a for which the system of equations a³x + (a + 1)y + (a + 2)³ z = 0, ax + (a + 1)y + (a + 2)z = 0 and x + y + z = 0 has a non zero solution is
(a) 0
(b) -1
(c) 1
(d) 2
Answer:
(b) -1
Hint:
The given system of equations will have a non-zero solution, if

Question 5.
\(\left|\begin{array}{lll}
b+c & c+a & a+b \\
q+r & r+p & p+q \\
y+z & z+x & x+y
\end{array}\right|=\)
(a) 2 \(\left|\begin{array}{lll}
c & b & a \\
r & q & p \\
z & y & x
\end{array}\right|\)
(b) 2 \(\left|\begin{array}{lll}
b & a & c \\
q & p & r \\
y & x & z
\end{array}\right|\)
(c) 2 \(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
(d) 2 \(\left|\begin{array}{lll}
a & c & b \\
p & r & q \\
x & z & y
\end{array}\right|\)
Answer:
(c) 2 \(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
Hint:

Question 6.
The system 3x – y + 4z = 3, x + 2y – 3z = -2 and 6x + 5y + λz = -3 has atleast one solution when
(a) λ = -5
(b) λ = 5
(c) λ = 3
(d) λ = -13
Answer:
(a) λ = -5
Hint:
The given system of equations will have more than one solution if

Question 7.
If x = -9 is a root of \(\left|\begin{array}{lll}
x & 3 & 7 \\
2 & x & 2 \\
7 & 6 & x
\end{array}\right|=0\), has other two roots are
(a) 2, -7
(b) -2, 7
(c) 2, 7
(d) -2, -7
Answer:
(c) 2, 7
Hint:

Question 8.
If \(\left|\begin{array}{ccc}
6 i & -3 i & 1 \\
4 & 3 i & -1 \\
20 & 3 & i
\end{array}\right|\) = x + iy, then
(a) x = 3, y = 1
(b) x = 1, y = 3
(c) x = 0, y = 3
(d) x = 0, y = 0
Answer:
(d) x = 0, y = 0

Question 9.
If A(0, 0), B(1, 3) and C(k, 0) are vertices of triangle ABC whose area is 3 sq.units, then the value of k is
(a) 2
(b) -3
(c) 3 or -3
(d) -2 or 2
Answer:
(d) -2 or 2

Question 10.
Which of the following is correct?
(a) Determinant is a square matrix
(b) Determinant is number associated to matrix
(c) Determinant is a number associated with a square matrix
(d) None of these
Answer:
(c) Determinant is a number associated with a square matrix

II. Answer the following questions.

Question 1.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
Solution:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)

= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113

(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)

= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76

Question 2.
Evaluate determinant along second column \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 2 & -2 \\
0 & 1 & -2
\end{array}\right|\)
Solution:

Question 3.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & 3 & 5 \\
400 & 600 & 1000 \\
48 & 47 & 18
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
101 & 102 & 103 \\
106 & 107 & 108 \\
1 & 2 & 3
\end{array}\right|\)
by using properties.
Solution:

Question 4.
Find the minors and cofactors of elements of the determinants.
(i) \(\left|\begin{array}{ccc}
-1 & 0 & 4 \\
-2 & 1 & 3 \\
0 & -4 & 2
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right|\)
Solution:

Question 5.
Find the values of x, if
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
⇒ 1(-10x² + 10x) – 4(5x² + 5) + 20(2x + 2) = 0
⇒ -10x² + 10x – 20x² – 20 + 40x + 40 = 0
⇒ -30x² + 50x + 20 = 0
⇒ 3x² – 5x – 2 = 0 …..[Dividing throughout by (-10)]
⇒ 3x² – 6x + x – 2 = 0
⇒ 3x(x – 2) + 1(x – 2) = 0
⇒ (x – 2) (3x + 1) = 0
⇒ x – 2 = 0 or 3x + 1 = 0
⇒ x = 2 or x = \(-\frac{1}{3}\)

(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
⇒ 1(4 – 16) – 2x(1 – 16) + 4x(1 – 4) = 0
⇒ 1(-12) – 2x(-15) + 4x(-3) = 0
⇒ -12 + 30x – 12x = 0
⇒ 18x = 12
⇒ x = \(\frac{12}{18}=\frac{2}{3}\)

Question 6.
By using properties of determinant, prove that \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:

Question 7.
Without expanding the determinants, show that

Solution:

Question 8.
If \(\left|\begin{array}{lll}
a & 1 & 1 \\
1 & b & 1 \\
1 & 1 & c
\end{array}\right|=0\) then show that \(\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}=1\)
Solution:

Question 9.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
(ii) \(\frac{1}{x}+\frac{1}{y}=\frac{3}{2}, \quad \frac{1}{y}+\frac{1}{z}=\frac{5}{6}, \quad \frac{1}{z}+\frac{1}{x}=\frac{4}{3}\)
(iii) 2x + 3y + 3z = 5, x – 2y + z = -4, 3x – y – 2z = 3
(iv) x + y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
(i) Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1
D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0

Dx = \(\left|\begin{array}{ccc}
1 & -1 & 1 \\
8 & 2 & 3 \\
1 & 1 & -4
\end{array}\right|\)
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40

Dy = \(\left|\begin{array}{ccc}
2 & 1 & 1 \\
1 & 8 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-32 – 3) -1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80

Dz = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 8 \\
3 & 1 & 1
\end{array}\right|\)
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,

∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.

(ii) Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
∴ The given equations become
p + q = \(\frac{3}{2}\)
i.e., 2p + 2q = 3
i.e., 2p + 2q + 0 = 3
q + r = \(\frac{5}{6}\)
i.e., 6q + 6r = 5,
i.e., 0p + 6q + 6r = 5
r + p = \(\frac{4}{3}\)
i.e., 3r + 3p = 4,
i.e., 3p + 0q + 3r = 4
D = \(\left|\begin{array}{lll}
2 & 2 & 0 \\
0 & 6 & 6 \\
3 & 0 & 3
\end{array}\right|\)
= 2(18 – 0) -2(0 – 18) + 0
= 2(18) – 2(-18)
= 36 + 36
= 72 ≠ 0

Dp = \(\left|\begin{array}{lll}
3 & 2 & 0 \\
5 & 6 & 6 \\
4 & 0 & 3
\end{array}\right|\)
= 3(18 – 0) – 2(15 – 24) + 0
= 3(18) – 2(-9)
= 54 + 18
= 72

Dq = \(\left|\begin{array}{lll}
2 & 3 & 0 \\
0 & 5 & 6 \\
3 & 4 & 3
\end{array}\right|\)
= 2(15 – 24) – 3(0 – 18) + 0
= 2(-9) – 3(-18)
= -18 + 54
= 36

Dr = \(\left|\begin{array}{lll}
2 & 2 & 3 \\
0 & 6 & 5 \\
3 & 0 & 4
\end{array}\right|\)
= 2(24 – 0) – 2(0 – 15) + 3(0 – 18)
= 2(24) – 2(-15) + 3(-18)
= 48 + 30 – 54
= 24
By Cramer’s Rule,

∴ x = 1, y = 2 and z = 3 are the solutions of the given equations.

(iii) Given equations are
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3
D = \(\left|\begin{array}{ccc}
2 & 3 & 3 \\
1 & -2 & 1 \\
3 & -1 & -2
\end{array}\right|\)
= 2(4 + 1) – 3(-2 – 3) + 3(-1 + 6)
= 2(5) – 3(-5) + 3(5)
= 10 + 15 + 15
= 40 ≠ 0

Dx = \(\left|\begin{array}{ccc}
5 & 3 & 3 \\
-4 & -2 & 1 \\
3 & -1 & -2
\end{array}\right|\)
= 5(4 + 1) – 3(8 – 3) + 3(4 + 6)
= 5(5) – 3(5) + 3(10)
= 25 – 15 + 30
= 40

Dy = \(\left|\begin{array}{ccc}
2 & 5 & 3 \\
1 & -4 & 1 \\
3 & 3 & -2
\end{array}\right|\)
= 2(8 – 3) – 5(-2 – 3) + 3(3 + 12)
= 2(5) – 5(-5) + 3(15)
= 10 + 25 + 45
= 80

Dz = \(\left|\begin{array}{ccc}
2 & 3 & 5 \\
1 & -2 & -4 \\
3 & -1 & 3
\end{array}\right|\)
= 2(-6 – 4) – 3(3 + 12) + 5(-1 + 6)
= 2(-10) – 3(15) + 5(5)
= -20 -45 + 25
= -40
By Cramer’s Rule,

∴ x = 1, y = 2 and z = -1 are the solutions of the given equations.

(iv) Given equations are
x – y + 2z = 7
3x + 4y – 5z = 5
2x – y + 3z = 12
D = \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right|\)
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0

Dx = \(\left|\begin{array}{ccc}
7 & -1 & 2 \\
5 & 4 & -5 \\
12 & -1 & 3
\end{array}\right|\)
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7) + 1(75) + 2(-53)
= 49 + 75 – 106
= 18

Dy = \(\left|\begin{array}{ccc}
1 & 7 & 2 \\
3 & 5 & -5 \\
2 & 12 & 3
\end{array}\right|\)
= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6

Dz = \(\left|\begin{array}{ccc}
1 & -1 & 7 \\
3 & 4 & 5 \\
2 & -1 & 12
\end{array}\right|\)
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53) + 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,

∴ x = \(\frac{9}{2}\), y = \(\frac{-3}{2}\) and z = \(\frac{1}{2}\) are the solutions of the given equations.

Question 10.
Find the value of k, if the following equations are consistent.
(i) (k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
(ii) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
(iii) (k – 2)x + (k – 1)y = 17, (k – 1)x +(k – 2)y = 18 and x + y = 5
Solution:
(i) Given equations are
(k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
Since these equations are consistent,

⇒ 2(2k + 2 + 2k – 2) – 0 + (k – 1) (4 – 0) = 0
⇒ 2(4k) + (k – 1)4 = 0
⇒ 8k + 4k – 4 = 0
⇒ 12k – 4 = 0
⇒ k = \(\frac{4}{12}=\frac{1}{3}\)

(ii) Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3, i.e., 2x – y – 3 = 0.
Since these equations are consistent,
\(\left|\begin{array}{rrr}
3 & 1 & -2 \\
k & 2 & -3 \\
2 & -1 & -3
\end{array}\right|=0\)
⇒ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ 3(-9) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ -27 + 3k – 6 + 2k + 8 = 0
⇒ 5k – 25 = 0
⇒ k = 5

(iii) Given equations are
(k – 2)x + (k – 1)y = 17
⇒ (k – 2)x + (k – 1)y – 17 = 0
(k – 1)x + (k – 2)y = 18
⇒ (k – 1)x + (k – 2)y – 18 = 0
x + y = 5
⇒ x + y – 5 = 0
Since these equations are consistent,

⇒ -1(-5k + 10 + 18) – 1(-5k + 5 + 18) + 1(k – 1 – k + 2) = 0
⇒ -1(-5k + 28) – 1(-5k + 23) + 1(1) = 0
⇒ 5k – 28 + 5k – 23 + 1 = 0
⇒ 10k – 50 = 0
⇒ k = 5

Question 11.
Find the area of triangle whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
(ii) P(3, 6), Q(-1, 3), R(2, -1)
(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
(i) Here, A(x₁, y₁) = A(-1, 2)
B(x₂, y₂) = B(2, 4)
C(x₃, y₃) = C(0, 0)

Since area cannot be negative,
A(ΔABC) = 4 sq.units

(ii) Here, P(x₁, y₁) = P(3, 6)
Q(x₂, y₂) = Q(-1, 3)
R(x₃, y₃) = R(2, -1)

A(ΔPQR) = \(\frac{25}{2}\) sq.units

(iii) Here, L(x₁, y₁) = L(1, 1)
M(x₂, y₂) = M(-2, 2)
N(x₃, y₃) = N(5, 4)

Since area cannot be negative,
A(ΔLMN) = \(\frac{13}{2}\) sq.units

Question 12.
Find the value of k,
(i) if the area of a triangle is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
(ii) if area of triangle is \(\frac{33}{2}\) square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution:
(i) Here, P(x₁, y₁) = P(k, 0)
Q(x₂, y₂) = Q(4, 0)
R(x₃, y₃) = R(0, 2)
A(ΔPQR) = 4 sq.units

(ii) Here, L(x₁, y₁) = L(3, -5), M(x₂, y₂) = M(-2, k), N(x₃, y₃) = N(1, 4)
A(ΔLMN) = \(\frac{33}{2}\) sq. units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
\(\pm \frac{33}{2}=\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
-2 & k & 1 \\
1 & 4 & 1
\end{array}\right|\)
⇒ \(\pm \frac{33}{2}=\frac{1}{2}\) [3(k – 4) – (-5) (-2 – 1) + 1 (-8 – k)]
⇒ ±33 = 3k – 12 – 15 – 8 – k
⇒ ±33 = 2k – 35
⇒ 2k – 35 = 33 or 2k – 35 = -33
⇒ 2k = 68 or 2k = 2
⇒ k = 34 or k = 1

Question 13.
Find the area of quadrilateral whose vertices are A(0, -4), B(4, 0), C(-4,0), D (0, 4).
Solution:
A(0, -4), B(4, 0), C(-4, 0), D(0, 4)


∴ A(ABDC) = A(ΔABC) + A(ΔBDC)
= 16 + 16
= 32 sq.units

Question 14.
An amount of ₹ 5000 is put into three investments at the rate of interest of 6%, 7%, and 8% per annum respectively. The total annual income is ₹ 350. If the combined income from the first two investments is ₹ 70 more than the income from the third, find the amount of each investment.
Solution:
Let the amount of each investment be ₹ x, ₹ y and ₹ z.
According to the given conditions,
x + y + z = 5000,
6% x + 7% y + 8% z = 350




∴ The amounts of investments are ₹ 1750, ₹ 1500, and ₹ 1750.

Question 15.
Show that the lines x – y = 6, 4x – 3y = 20 and 6x + 5y + 8 = 0 are concurrent. Also, find the point of concurrence.
Solution:
Given equations of the lines are
x – y = 6, i.e., x – y – 6 = 0 ……(i)
4x – 3y = 20, i.e., 4x – 3y – 20 = 0 …..(ii)
6x + 5y + 8 = 0 ……(iii)
The given lines will be concurrent, if

= 1(-24 + 100) – (-1) (32 + 120) – 6(20 + 18)
= 1(76) + 1(152) – 6(38)
= 76 + 152 – 228
= 0
∴ The given lines are concurrent.
To find the point of concurrence, solve any two equations.
Multiplying (i) by 5, we get
5x – 5y – 30 = 0 …….(iv)
Adding (iii) and (iv), we get
11x – 22 = 0
∴ x = 2
Substituting x = 2 in (i), we get
2 – y – 6 = 0
∴ y = -4
∴ The point of concurrence is (2, -4).

Question 16.
Show that the following points are collinear using determinants:
(i) L(2, 5), M(5, 7), N(8, 9)
(ii) P(5,1), Q(1, -1), R(11, 4)
Solution:
(i) Here, L(x₁, y₁) = L(2, 5)
M(x₂, y₂) = M(5, 7)
N(X₃ y₃) = N(8, 9)
If A(ΔLMN) = 0, then the points L, M, N are collinear.

∴ The points L, M, N are collinear.

(ii) Here, P(x₁, y₁) = P(5, 1)
Q(x₂, y₂) = Q(1, -1)
R(x₃, y₃) = R(11, 4)
If A(ΔPQR) = 0, then the points P, Q, R are collinear.

∴ The points P, Q, R are collinear.

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 10 States of Matter Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 10 States of Matter

1. Select and write the most appropriate alternatives from the given choices.

Question A.
The unit of viscosity is
a. dynes
b. newton
c. gram
d. poise
Answer:
d. poise

Question B.
Which of the following is true for 2 moles of an ideal gas?
a. PV = nRT
b. PV = RT
c. PV = 2RT
d. PV = T
Answer:
c. PV = 2RT

Question C.
Intermolecular forces in liquid are
a. greater than gases
b. less than solids
c. both a and b
d. greater than solids
Answer:
c. both a and b

Question D.
Interactive forces are ………. in ideal gas.
a. nil
b. small
c. large
d. same as that of real gases
Answer:
a. nil

Question E.
At constant temperature the pressure of 22.4 dm³ volume of an ideal gas was increased from 10⁵ kPa to 210 kPa, New volume could be-
a. 44.8 dm³
b. 11.2 dm³
c. 22.4 dm³
d. 5.6 dm³
Answer:
b. 11.2 dm³

2. Answer in one sentence.

Question A.
Name the term used for mixing of different gases by random molecular motion and ferquent collision.
Answer:
The mixing of different gases by random molecular motion and frequent collision is called diffusion.

Question B.
The pressure that each individual gas would exert if it were alone in the container, what do we call it as ?
Answer:
The pressure that each individual gas would exert if it were alone in the container is called as partial pressure.

Question C.
When a gas is heated the particles move more quickly. What is the change in volume of a heated gas if the pressure is kept constant ?
Answer:
The volume of the gas increases on heating if pressure is kept constant.

Question D.
A bubble of methane gas rises from the bottom of the North sea. What will happen to the size of the bubble as it rises to the surface ?
Answer:
According to Boyle’s law, the size of the bubble of methane gas increases as it rises to the surface.

Question E.
Convert the following temperatures from degree celcius to kelvin.
a. -15° C
b. 25° C
c. -197° C
d. 273° C
Answer:
a. T(K) = t°C +273.15
∴ T(K) = -15 °C + 273.15 = 258.15 K
b. T(K) = t°C +273.15
∴ T(K) = 25 °C + 273.15 = 298.15 K
c. T(K) = t°C + 273.15
∴ T(K) = -197 °C + 273.15 = 76.15 K
d. T(K) = t°C + 273.15
∴ T(K) = 273 °C + 273.15 = 546.15 K

Question F.
Convert the following pressure values into Pascals.
a. 10 atmosphere
b. 1 kPa.
c. 107000 Nm^-2
d. 1 atmosphere
Answer:
a. 10 atmosphere:
1 atm = 101325 Pa
∴ 10 atm = 1013250 Pa
= 1.01325 × 10⁶ Pa

b. 1 kPa:
1 kPa = 1000 Pa

c. 107000 N m^-2:
1 N m^-2 = 1 Pa
∴ 107000 Nm^-2 = 107000 Pa
= 1.07 × 10⁵ Pa

d. 1 atmosphere:
1 atm = 101325 Pa
= 1.01325 × 10⁵ Pa

Question G.
Convert:
a. Exactly 1.5 atm to pascals
b. 89 kPa to newton per square metre (N m^-2)
c. 101.325 kPa to bar
d. -100 °C to Kelvin
e. 0.124 torr to standard atmosphere
Answer:
a. Exactly 1.5 atm to pascals:
1 atm = 101325 Pa
∴ 1.5 atm = 1.5 × 101325
= 151987.5 Pa

b. 89 kPa to newton per square metre (N m^-2):
1 Pa = 1 N m^-2 and 1 Pa = 10^-3 kPa
∴ 10^-3 kPa = 1 N m^-2
∴ 89 kPa = \(\frac{1 \times 89}{10^{-3}}\) N m^-2 = 89000 N m^-2

c. 101.325 kPa to bar:
1 bar = 1.0 × 10⁵ Pa
= 1.0 × 10² k Pa
∴ 100 kPa = 1 bar
∴ 101.325 kPa = \(\frac{1 \times 101.325}{100}\)
= 1.01325 bar

d. -100 °C to Kelvin:
T(K) = t °C + 273.15
∴ T(K) = (- 100 °C) + 273.15 = 173.15 K

e. 0.124 torr to standard atmosphere:
1 atm = 760 torr
∴ 1 torr = \(\frac {1}{760}\)atm
∴ 0.124 torr = 0.124 × \(\frac {1}{760}\)
= 1.632 × 10^-4 atm

Question H.
If density of a gas is measured at constant temperature and pressure then which of the following statement is correct ?
a. Density is directly proportional to molar mass of the gas.
b. Greater the density greater is the molar mass of the gas.
c. If density, temperature and pressure is given ideal gas equation can be used to find molar mass.
d. All the above statements are correct.
Answer:
d. All the above statements are correct.

Question I.
Observe the following conversions.

Which of the above reactions is in accordance with the priciple of stoichiometry ?
Answer:
Both the reactions are in accordance with the principle of stoichiometry.
In the first reaction, both the reactants are completely consumed to form product according to reaction stoichiometry.
1 mol hydrogen + 1 mol chlorine → 2 mol hydrogen chloride
In the second reaction, chlorine is the limiting reagent and it is completely consumed to form hydrogen chloride. Excess hydrogen remains unreacted at the end of the reaction. This reaction also follows principle of stoichiometry.
2 mol hydrogen + 1 mol chlorine → 2 mol hydrogen chloride + 1 mol hydrogen

Question J.
Hot air balloons float in air because of the low density of the air inside the balloon. Explain this with the help of an appropriate gas law.

Answer:
The working of hot air balloon can be explained with the help of Charles’ law. According to Charles’ law, at constant pressure, the volume of a fixed amount of a gas varies directly with the temperature. This means that as the temperature increases, the air inside the balloon expands and occupies more volume. Thus, hot air inside the balloon is less dense than the surrounding cold air. This causes the hot air balloon to float in air.

3. Answer the following questions.

Question A.
Identify the gas laws from the following diagrams.

Answer:
a. Boyle’s law
b. Charles’ law
c. Avogadro’s law [Note: Assuming, T constant]

Question B.
Consider a sample of a gas in a cylinder with a movable piston.

Show digramatically the changes in the position of piston, if
a. Pressure is increased from 1.0 bar to 2.0 bar at constant temperature.
b. Temperature is decreased from 300 K to 150 K at constant pressure
c. Temperature is decreased from 400 K to 300 K and pressure is decreased from 4 bar to 3 bar.
Answer:

Thus, the volume of the gas remains the same.
Hence, there will be no change in the position of the piston.

Question D.
List the characteristic physical properties of the gases.
Answer:
Characteristic physical properties of the gases:

• Gases are lighter than solids and liquids (i.e., possess lower density).
• Gases do not possess a fixed volume and shape. They occupy entire space available and take the shape of the container.
• Gas molecules are widely separated and are in continuous, random motion. Therefore, gases exert pressure equally in all directions due to collision of gas molecules, on the walls of the container.
• In case of gases, intermolecular forces are weakest.
• Gases possess the property of diffusion, which is a spontaneous homogeneous inter mixing of two or more gases.
• Gases are highly compressible.

Question E.
Define the terms:
a. Polarizability
b. Hydrogen bond
c. Aqueous tension
d. Dipole moment
Answer:
a. Polarizability is defined as the ability of an atom or a molecule to form momentary dipoles, that means, the ability of the atom or molecule to become polar by redistributing its electrons.

b. The electrostatic force of attraction between positively polarised hydrogen atom of one molecule and a highly electronegative atom (which may be negatively charged) of other molecule is called as hydrogen bond.

c. The pressure exerted by saturated water vapour is called aqueous tension.

d. Dipole moment (p) is the product of the magnitude of the charge (Q) and the distance between the centres of positive and negative charge (r). It is designated by a Greek Letter (p) and its unit is Debye (D).

Question F.
Would it be easier to drink water with a straw on the top of the Mount Everest or at the base ? Explain.
Answer:
When you drink through a straw, the pressure inside the straw reduces (as the air is withdraw by mouth) and the liquid is pushed up to your mouth by atmospheric pressure. Thus, drinking with a straw makes use of pressure difference to force the liquid into your mouth. So, if the pressure difference is less it will be difficult to drink through a straw. On the top of the Mount Everest, atmospheric pressure is very low. Hence, it will be difficult to drink water with a straw on the top of Mount Everest as compared to at the base.

Question G.
Identify type of the intermolecular forces in the following compounds.
a. CH₃ – OH
b. CH₂ = CH₂
c. CHCl₃
d. CH₂Cl₂
Answer:
a. Hydrogen bonding (dipole-dipole attraction) and London dispersion forces
b. London dispersion forces
c. Dipole-dipole interactions and London dispersion forces
d. Dipole-dipole interactions and London dispersion forces

Question H.
Name the types of intermolecular forces present in Ar, Cl₂, CCl₄ and HNO₃.
Answer:
a. Ar: London dispersion forces
b. Cl₂: London dispersion forces
c. CCl₄: London dispersion forces
d. HNO₃: Flydrogen bonding (dipole-dipole attraction) and London dispersion forces.

Question I.
Match the pairs of the following :

	A		B
a.	Boyle’s law	i.	At constant pressure and volume
b.	Charles’ law	ii.	At constant temperature
		iii.	At constant pressure

Answer:
a – ii,
b – iii

Question J.
Write the statement for :
(a) Boyle’s law
(b) Charles’ law
Answer:
a. Statement of Boyle’s law: For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of the gas is inversely proportional to the volume (V) of the gas.
OR
At constant temperature, the pressure of fixed amount (number of moles) of a gas varies inversely with its volume.

b. Statement for Charles’ law:
‘At constant pressure, the volume of a fixed mass of a gas is directly proportional to its temperature in Kelvin.

Question K.
Differentiate between Real gas and Ideal gas.
Answer:
Ideal gas:

1. Strictly obeys Boyle’s and Charles’ law.
   \(\frac{\mathrm{PV}}{\mathrm{nRT}}\) = 1
2. Molecules are perfectly elastic.
3. No attraction or repulsion between the gas molecules i.e. collision without loss of kinetic energy (K.E.)
4. Actual volume of the gas molecules is negligible as compared to total volume of the gas.
5. Ideal gases cannot be liquified even at low temperature but continues to obey Charles’ law and finally occupies zero volume at 0 K.
6. Practically, ideal gas does not exist.

Real gas:

1. Shows deviation from Boyle’s and Charles’ law at high pressure and temperature, i.e. obeys Boyle’s law and Charles’ law at low pressure and high temperature. \(\frac{\mathrm{PV}}{\mathrm{nRT}}\) ≠ 1
2. Molecules are not perfectly elastic.
3. Intermolecular attraction is present, hence collision takes place with loss of kinetic energy.
4. Actual volume of individual gas molecule is significant at high pressure and low- temperature.
5. Real gases undergo liquefaction at low’ temperature when cooled and compressed.
6. Gases that exist in nature like H₂, O₂, CO₂, N₂, He, etc. are real gases.

4. Answer the following questions

Question A.
State and write mathematical expression for Dalton’s law of partial pressure and explain it with suitable example.
Answer:
i. Statement: The total pressure of a mixture of two or more non-reactive gases is the sum of the partial pressures of the individual gases in the mixture.
ii. Explanation:
Dalton’s law can be mathematically expressed as:
P_Total = P₁ + P₂ + P₃ …(at constant T and V)
where, P_Total is the total pressure of the mixture and P₁, P₂, P₃, … are the partial pressures of individual gases 1, 2, 3, … in the mixture.
For example, consider two non-reactive gases A and B. On mixing the two gases, pressure exerted by individual gas A in the mixture of both the gases is called partial pressure of gas A (say P₁). Likewise, partial pressure of gas B is P₂. According to Dalton’s law, total pressure of the mixture of gas A and B at constant T and V will be given as:
P_Total = P₁ + P₂

iii. Schematic illustration of Dalton’s law of partial pressures:

Question B.
Derive an Ideal gas equation. Mention the terms involved in it. Also write how it is utilised to obtain combined gas law.
Answer:
According to Boyle’s law,
V ∝ \(\frac{1}{\mathrm{P}}\) (at constant T and n) ……….(1)
According to Charles’ law,
V ∝ T (at constant P and n) ……(2)
According to Avogadro’s law,
V ∝ n (at constant P and T) ……(3)
Combining relations (1), (2) and (3), we get
V ∝ \(\frac{\mathrm{nT}}{\mathrm{P}}\)
Converting this proportionality into an equation by introducing a constant of proportionality (‘R’ known as gas constant), we get
∴ V = \(\frac{\mathrm{nRT}}{\mathrm{P}}\)
On rearranging the above equation, we get
PV = nRT
where,
P = Pressure of gas,
V = Volume of gas,
n = number of moles of gas,
R = Gas constant,
T = Absolute temperature of gas.
This is the ideal gas equation or equation of state.
[Note: In the ideal gas equation, R is called gas constant or universal gas constant, whose value is same for all the gases. In this equation, if three variables are known, fourth can be calculated. The equation describes the state of an ideal gas. Hence, it is also called as equation of state.]

The ideal gas equation is written as PV = nRT …(1)
On rearranging equation (1), we get,

The ideal gas equation used in this form is called combined gas law.

Question C.
With the help of graph answer the following –

At constant temperature,
a. Graph shows relation between pressure and volume. Represent the relation mathematically.
b. Identify the law.
c. Write the statement of law.
Answer:
a. P ∝ \(\frac{1}{\mathrm{~V}}\)
b. The graph represents Boyle’s law as it gives relation between pressure and volume at constant temperature.
c. Statement of Boyle’s law: For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of the gas is inversely proportional to the volume (V) of the gas.
OR
At constant temperature, the pressure of fixed amount (number of moles) of a gas varies inversely with its volume.

Question D.
Write Postulates of kinetic theory of gases.
Answer:
Postulates of kinetic theory of gases:

• Gases consist of tiny particles (molecules or atoms).
• On an average, gas molecules remain far apart from each other. Therefore, the actual volume of the gas molecules is negligible as compared to the volume of the container. Hence, gases are highly compressible.
• The attractive forces between the gas molecules are negligible at ordinary temperature and pressure. As a result, gas expands to occupy entire volume of the container.
• Gas molecules are in constant random motion and move in all possible directions in straight lines. They collide with each other and with the walls of the container.
• Pressure of the gas is due to the collision of gas molecules with the walls of the container.
• The collisions of the gas molecules are perfectly elastic in nature, which means that the total energy of the gaseous particle remains unchanged after collision.
• The different gas molecules move with different velocities at any instant and hence have different kinetic energies. However, the average kinetic energy of the gas molecules is directly proportional to the absolute temperature.

Question E.
Write a short note on
a. Vapour pressure.
b. Surface tension
c. Viscosity.
Answer:
a. Vapour pressure:

• Molecules of liquid have tendency to escape from its surface to form vapour above it. This called evaporation.
• When a liquid is placed in a closed container, the liquid undergoes evaporation and vapours formed undergo condensation.
• At equilibrium, the rate of evaporation and rate of condensation are equal.
• The pressure exerted by the vapour in equilibrium with the liquid is known as saturated vapour pressure or simply vapour pressure.
• Vapour pressure is measured by means of a manometer.
• The most common unit for vapour pressure is torr. 1 torr = 1 mm Hg.

[Note: i. The vapour pressure of water is also called aqueous tension.
ii. Water has a vapour pressure of approximately 20 torr at room temperature.]

b. Surface tension:

• The particles in the bulk of liquid are uniformly attracted in all directions and the net force acting on the molecules present inside the bulk is zero.
• But the molecules at the surface experience a net attractive force towards the interior of the liquid, or the forces acting on the molecules on the surface are imbalanced.
• Therefore, liquids have tendency to minimize their surface area and the surface acts as a stretched membrane.
• The force acting per unit length perpendicular to the line drawn on the surface of liquid is called surface tension.
• Unit: Surface tension is measured in SI unit, N m^-1 and is denoted by Greek letter ‘γ’

c. Viscosity:
i. Liquids (fluids) have tendency to flow.
ii. Viscosity measures the magnitude of internal friction in a liquid or fluid to flow as measured by the force per unit area resisting uniform flow.
iii. Different layers of a liquid flow with different velocity. This called laminar flow. Here, the layers of molecules in the immediate contact of the fixed surface remains stationary. The subsequent layers slip over one another. Strong intermolecular forces obstruct the layers from slipping over one another, resulting in a friction between the layers.
iv. Viscosity is defined as the force of friction between the successive layers of a flowing liquid. It is also the resistance to the flow of a liquid.
v. When a liquid flow through a tube, the central layer has the highest velocity, whereas the layer along the inner wall in the tube remains stationary. This is a result of the viscosity of a liquid. Hence, a velocity gradient exists across the cross-section of the tube.

vi. Viscosity is expressed in terms of coefficient of viscosity, ‘η’ (Eta). The SI unit of viscosity coefficient is N s m^-2 (newton second per square meter). In CGS system, the unit (η) is measured in poise.
1 poise = 1 g cm^-1 s^-1 = 10^-1 kg m^-1 s^-1

5. Solve the following

Question A.
A balloon is inflated with helium gas at room temperature of 25 °C and at 1 bar pressure when its initial volume is 2.27L and allowed to rise in air. As it rises in the air external pressure decreases and the volume of the gas increases till finally it bursts when external pressure is 0.3bar. What is the limit at which volume of the balloon can stay inflated ?
Answer:
Given: P₁ = Initial pressure = 1 bar
V₁ = Initial volume = 2.27 L
P₂ = Final pressure = 0.3 bar
To find: V₂ = Final volume
Formula: P₁V₁ = P₂V₂ (at constant n and T)
Calculation: According to Boyle’s law,
P₁V₁ = P₂V₂ (at constant n and T)
∴ V₂ = \(\frac{P_{1} V_{1}}{P_{2}}=\frac{1 \times 2.27}{0.3}\) = 7.566667 L ≈ 7.567 L
Ans: The balloon can stay inflated below the volume of 7.567 L.

Question B.
A syringe has a volume of 10.0 cm³ at pressure 1 atm. If you plug the end so that no gas can escape and push the plunger down, what must be the final volume to change the pressure to 3.5 atm?

Answer:
Given: P₁ = Initial pressure = 1 atm
V₁ = Initial volume = 10.0 cm³
P₂ = Final pressure = 3.5 atm
To find: V₂ = Final volume
Formula: P₁V₁ = P₂V₂ (at constant n and T)
Calculation: According to Boyle’s law,
P₁V₁ = P₂V₂ (at constant n and T)
∴ V₂ = \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{P}_{2}}=\frac{1 \times 10.0}{3.5}\)
= 2.857 L
Ans: The final volume of the gas in the syringe is 2.857 L.

Question C.
The volume of a given mass of a gas at 0°C is 2 dm³. Calculate the new volume of the gas at constant pressure when
a. The temperature is increased by 10°C.
b.The temperature is decreased by 10°C.
Answer:
Given: T₁ = Initial temperature = 0 °C = 0 + 273.15 = 273.15 K,
V₁ = Initial volume = 2 dm³
a. T₂ = Final temperature = 273.15 K + 10 = 283.15 K
b. T₂ = Final temperature = 273.15 K – 10 = 263.15 K
To find: V₂ = Final volume in both the cases
Formula: \(\frac{\mathrm{V}_{\mathrm{l}}}{\mathrm{T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
Calculation: According to Charles’ law,

Ans: The new volume of a given mass of gas is:
a. 2.073 dm³
b. 1.927 dm³

Question D.
A hot air balloon has a volume of 2800 m³ at 99 °C. What is the volume if the air cools to 80 °C?

Answer:
Given: V₁ = Initial volume = 2800 m³, T₁ = Initial temperature = 99 °C = 99 + 273.15 = 372.15 K,
T₂ = Final temperature = 80 °C = 80 + 273.15 K = 353.15 K
To find: V₂ = Final volume
Formula: = \(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
Calculation: According to Charles’ law,
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
∴ \(\mathrm{V}_{2}=\frac{\mathrm{V}_{1} \mathrm{~T}_{2}}{\mathrm{~T}_{1}}=\frac{2800 \times 353.15}{372.15}=\mathbf{2 6 5 7 \mathrm { m } ^ { 3 }}\)
Ans: The volume of the balloon when the air cools to 80 °C is 2657 m³.

Question E.
At 0 °C, a gas occupies 22.4 liters. How nuch hot must be the gas in celsius and in kelvin to reach volume of 25.0 literes?
Answer:
V₁ = Initial volume of the gas = 22.4 L,
T₁ = Initial temperature = 0 + 273.15 = 273.15 K,
V₂ = Final volume = 25.0 L
To find: T₂ = Final temperature in Celsius and in Kelvin

Ans: The temperature of the gas must be 31.7 °C or 304.9 K.

Question F.
A 20 L container holds 0.650 mol of He gas at 37 °C at a pressure of 628.3 bar. What will be new pressure inside the container if the volume is reduced to 12 L. The temperature is increased to 177 °C and 1.25 mol of additional He gas was added to it?
Answer:
Given: V₁ = Initial volume = 20 L, n₁ = Initial number of moles = 0.650 mol
P₁ = Initial pressure = 628.3 bar
T₁ = Initial temperature = 37 °C = 37 + 273.15 K = 310.15 K
n₂ = Final number of moles = 0.650 + 1.25 = 1.90 mol, V₂ = Final volume = 12 L
T₂ = Final temperature = 177 °C = 177 + 273.15 K = 450.15 K, R = 0.0821 L atm K^-1 mol^-1
To find: P₂ = Final pressure
Formula: PV = nRT
Calculation: According to ideal gas equation,
P₂V₂ = n₂RT₂.
∴ \(\mathrm{P}_{2}=\frac{\mathrm{n}_{2} \mathrm{RT}_{2}}{\mathrm{~V}_{2}}=\frac{1.90 \times 0.0821 \times 450.15}{12}=\mathbf{5 . 8 5 2} \mathrm{atm}\)
Ans: The final pressure of the gas is 5.852 atm.
[Note: In the above numerical, converting the pressure value to different units, we get: 5.852 atm = 4447.52 torr = 5.928 bar]

Question G.
Nitrogen gas is filled in a container of volume 2.32 L at 32 °C and 4.7 atm pressure. Calculate the number of moles of the gas.
Answer:
Given: V = 2.32 L, P = 4.7 atm, T = 32 °C = 32 + 273.15 K = 305.15 K
R = 0.0821 L atm K^-1 mol^-1
To find: n = number of moles of gas
Formula: PV = nRT
Calculation: According to ideal gas equation,
PV = nRT
∴ \(\mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{4.7 \times 2.32}{0.0821 \times 305.15}=\mathbf{0 . 4 3 5} \mathrm{moles}\)
Ans: Number of moles of N₂ gas in the given volume is 0.435 moles.

Question H.
At 25 °C and 760 mm of Hg pressure a gas occupies 600 mL volume. What will be its pressure at the height where temperature is 10 °C and volume of the gas 640 mL ?
Answer:
Given: V₁ = Initial volume = 600 mL, V₂ = Final volume = 640 mL
P₁ = Initial pressure = 760 mm Hg
T₁ = Initial temperature = 25 °C = 25 + 273.15 K = 298.15 K
T₂ = Final temperature = 10 °C = 10 + 273.15 K = 283.15 K
P₂ = Final pressure
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: According to combined gas law.

Ans: The final pressure of a gas is 676.654 mm Hg.

Question I.
A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5g neon. If pressure of the mixture of the gases in the cylinder is 25 bar. What is the partial pressure of dioxygen and neon in the mixture?
Answer:
Given: m_O2 = 70.6 g, m_Ne = 167.5 g,
P_Total = 25 bar
To find: Partial pressure of each gas
Formula: P₁ = x₁ × P_Total
Calculation: Determine number of moles (n) of each gas using formula: n = \(\frac{\mathrm{m}}{\mathrm{M}}\)

Ans: The partial pressure of dioxygen and neon are 5.2 bar and 19.8 bar respectively.

Question J.
Calculate the pressure in atm of 1.0 mole of helium in a 2.0 dm³ container at 20.0 °C.
Answer:
Given: n = number of moles = 1.0 mol, V = volume = 2.0 dm³
T = Temperature = 20.0 °C = 20.0 + 273.15 K = 293.15 K
R = 0.0821 L atm K^-1 mol^-1
To find: Pressure (P)
Formula: PV = nRT
Calculation: According to ideal gas equation,

Ans: The pressure of the given helium gas is 12.03 atm.

Question K.
Calculate the volume of 1 mole of a gas at exactly 20 °C at a pressure of 101.35 kPa.
Answer:
Given: n = number of moles = 1 mol, P = pressure = 101.35 kPa = 1.00025 atm ≈ 1 atm
T = Temperature = 20 °C = 20 + 273.15 K = 293.15 K
R = 0.0821 dm³ atm K^-1 mol^-1
To find: Volume (V)
Formula: PV = nRT
Calculation: According to ideal gas equation,
PV = nRT

Ans: The volume of the given gas is 24.07 dm³.

Question L.
Calculate the number of molecules of methane in 0.50 m³ of the gas at a pressure of 2.0 × 10² kPa and a temperature of exactly 300 K.
Answer:
V = 0.5 m³, P = 2.0 × 10² kPa = 2.0 × 10⁵ Pa
T = 300 K, R = 8.314 J K^-1 mol^-1
To find: Number of molecules of methane gas
Formula: PV = nRT
Calculation: According to ideal gas equation,
n = \(\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{2.0 \times 10^{5} \times 0.5}{8.314 \times 300}=40 \mathrm{~mol}\)
Number of molecules = n × NA = 40 × 6.022 × 10²³ = 2.4088 × 10²³ ≈ 2.409 × 10²⁵
Ans: The number of molecules of methane gas present is 2.409 × 10²⁵ molecules.

11th Chemistry Digest Chapter 10 States of Matter Intext Questions and Answers

Do you know? (Textbook Page No. 140)

Question 1.
Consider three compounds: H₂S, H₂Se and H₂O. Identify which has the highest boiling point. Justify.
Answer:
Among the three compounds H₂O, H₂S and H₂Se, the first one, H₂O has the smallest molecular mass. But it has the highest B.P. of 100 °C. B.P. of H₂S is -60 °C and of H₂Se is -41.25 °C. The extraordinary high B.P. of H₂O is due to very strong hydrogen bonding even though it has the lowest molecular mass.

Can you tell? (Textbook Page No. 140)

Question i.
What are the various components present in the atmosphere?
Answer:
Various components present in the atmosphere are as follows:
a. Nitrogen (78%)
b. Oxygen (21%)
c. Carbon dioxide and other gases (0.03%)
d. Inert gases (mainly argon) (0.97%)
e. Traces of water vapour

Question ii.
Name five elements and five compounds those exist as gases at room temperature.
Answer:
Five elements and five compounds that exist as gases at room temperature are as follows:

No.	Elements
a.	Nitrogen
b.	Oxygen
c.	Hydrogen
d.	Chlorine
e.	Argon

No.	Compounds
a.	Carbon dioxide
b.	Carbon monoxide
c.	Nitrogen dioxide
d.	Sulphur dioxide
e.	Methane

Just think. (Textbook Page No. 140)

Question 1.
What is air?
Answer:

• Air is a mixture of various gases.
• One cannot see air but can feel the cool breeze.
• The composition of air by volume is around 78 percent N₂, 21 percent O₂ and 1 percent other gases including CO₂.

Use your brainpower. (Textbook Page No. 141)

Question 1.
Find the unit in which car-tyre pressure is measured.
Answer:
Car-tyre pressure is measured in the units of pounds per square inch (psi) or Newton per metre square (N m^-2).

Do you know? (Textbook Page No. 142)

Question 1.
How does a bicycle pump work?
Answer:
A bicycle pump works on Boyle’s law. Pushing a bicycle pump squashes the same number of particles into a smaller volume. This squashing means particles hit the walls of the pump more often, increasing the pressure. The increased pressure of a gas can be felt on palm by pushing in the piston of a bicycle pump.

Internet my friend (Textbook Page No. 143)

Question 1.
i. Watch Boyle’s law experiment.
ii. Find applications of Boyle’s law.
iii. Try to study how Boyle’s law helps in ‘scuba-diving’ i.e., importance of Boyle’s law in scuba diving an exhilarating sport.
Answer:
i. Students can refer to ‘Boyle’s law experiment’ on YouTube channel of ‘Socratica’.
ii. a. Syringes: When the plunger of a syringe is pulled back out, it causes the volume of the gas inside it to increase due to the reduction of pressure. This creates a vacuum in the syringe, which is constantly trying to adjust the pressure back to normal. However, since the only substance available, such as the blood or medication, is on the other side of the needle, this liquid is sucked into the vacuum, increasing the pressure and decreasing the volume of the gas. When we push the plunger back down, the pressure again increases, lowering the volume inside the syringe, and pushing the fluid out.

b. Respiration: Boyle’s law is essential for the human breathing process. When person breathes in, his/her lung volume increases and the pressure within decreases. Since air always moves from areas of high pressure to areas of low pressure, air is drawn into the lungs. The opposite happens when person exhales. Since the lung volume decreases, the pressure within increases, forcing the air out of the lungs

c. Storage of Gases: Many industries store gases under high pressure. This allows the gas to be stored at a low volume, saving plenty of storage space.
[Note: Students are expected to search more on the internet about various other applications of Boyle’s law on their own.]

iii. Importance of Boyle’s law in scuba diving:
a. Boyle’s law affects scuba diving in many ways.
b. It explains the role of pressure in the aquatic environment.
c. As divers descend, the water pressure surrounding them increases, causing air in their body and equipment to have a smaller volume. As the divers ascend, water pressure decreases, causing their body and equipment to expand to acquire a greater volume.
d. Furthermore, it is crucial that scuba divers never attempt to hold their breath when immersed in water.
e. According to Boyle’s law, if divers attempt this when they ascend to a body of water of less pressure, then the air that is trapped in their lungs will over-expand and rupture. This is known as Pulmonary Barotrauma. Thus, it is important for scuba divers to exhale as they ascend because the external pressure increases.
f. Also, if a diver returns to the surface too quickly, dissolved gases in the blood expand and form bubbles, which can get stuck in capillaries and organs (causing the ‘bends’).
[Note: Students are expected to collect additional information their own.]

Just think. (Textbook Page No. 144)

Question i.
Why does bicycle tyre burst during summer?
Answer:

• According to Charles’ law, at constant pressure, the volume of a fixed amount of a gas varies directly with the temperature. This means that as the temperature increases, the volume also increases.
• During summer, the temperature of the surrounding air is high. Due to the high temperature, the air inside the tyre gets heated. This will increase the volume of the tyres and it will burst.

Question ii.
Why do the hot air balloons fly high?
Answer:

• According to Charles’ law, at constant pressure, gases expand on heating and become less dense. Thus, hot air is less dense than cold air.
• In a hot air balloon, the air inside it is heated by a burner. Upon heating, the air inside the balloon expands and becomes lighter (less dense) than the cooler air on the outside. This causes the hot air balloon to fly high in air.

Just think. (Textbook Page No. 145)

Question 1.
i. List out various real-life examples of Charles’ law.
ii. Refer and watch Charles’ law experiments.
Answer:
i. Few real-life examples of Charles’ law:
a. Helium balloon: If we fill a helium balloon in a warm or hot room, and then take it into a cold room, it shrinks up and will look like it has lost some of the air inside it. This shows that gases expand on heating and contract on cooling.
b. A bottle of deodorant: If we expose a bottle of deodorant to sunlight and high temperatures, the air molecules inside the bottle will expand which can lead to the bursting of the deodorant bottle. This is another example of Charles’ law.
c. Basketball: You may have noticed that a basketball has less responsive bounce during winter than in summer. This yet another example of Charles’ law. When a basketball is inflated, the air pressure inside it is set to a fixed value. As the temperature falls, the volume of the gas inside the ball also decreases proportionally.
[Note: Students are expected to collect additional real-life examples on their own,]

ii. pi [Note: Students can scan the adjacent QR code to visualize Charles’ law with the aid of a relevant video.]

Use your brainpower. (Textbook Page No. 146)

Question 1.
Why does the pressure in the automobile tyres change during hot summer or winter season?
Answer:

• According to Gay-Lussac’s law, at constant volume, pressure of a fixed amount of a gas is directly proportional to its absolute temperature.
• During hot summer, the temperature of automobile tyre increases faster. Consequently, the air inside the tyre gets heated and the gas molecules starts moving faster.
• As the volume of the tyre remains constant, the pressure inside it increases.
• During winter, the temperature of automobile tyre decreases. Consequently, the air inside the tyre gets cooled and the gas molecules starts moving much slower and the pressure inside the tyre decreases.

Just think. (Textbook Page No. 149)

Question 1.
Do all pure gases and mixtures of gases obey the gas laws?
Answer:
Yes, the gas laws are also applicable to the mixtures of gases. The measurable properties of a mixture of the gases such as pressure, temperature, volume, and amount of gaseous mixture are all related by an ideal gas law.

Just think. (Textbook Page No. 150)

Question 1.
Where is Dalton’s law applicable?
Answer:
Air is a gaseous mixture of different gases. Dalton’s law is useful for the study of various phenomena in air, for example, air pollution.

Just think. (Textbook Page No. 155)

Question 1.
What makes the oil rise through the wick in an oil lamp?
Answer:
In an oil lamp, oil rises through the wick due to the capillary action. Such a capillary rise of oil is due to the surface tension of oil. The wick acts as a capillary tube. When the wick is placed in oil, the attractive forces between the oil and the inner wall of the capillary (wick) pull the oil up through the wick.

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 9 Elements of Group 13, 14 and 15 Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 9 Elements of Group 13, 14 and 15

1. Choose the correct option.

Question A.
Which of the following is not an allotrope of carbon?
a. buckyball
b. diamond
c. graphite
d. emerald
Answer:
d. emerald

Question B.
………… is inorganic graphite.
a. borax
b. diborane
c. boron nitride
d. colemanite
Answer:
c. boron nitride

Question C.
Haber’s process is used for the preparation of ………….
a. HNO3
b. NH3
c. NH2CONH2
d. NH4OH
Answer:
b. NH3

Question D.
Thallium shows a different oxidation state because ……………
a. of inert pair effect
b. it is an inner transition element
c. it is metal
d. of its high electronegativity
Answer:
a. of inert pair effect

Question E.
Which of the following shows the most prominent inert pair effect?
a. C
b. Si
c. Ge
d. Pb
Answer:
d. Pb

2. Identify the group 14 element that best fits each of the following description.

A. Non-metallic element
B. Form the most acidic oxide
C. They prefer +2 oxidation state.
D. Forms strong π bonds.
Answer:
i. Carbon (C)
ii. Carbon
iii. Tin (Sn) and lead (Pb)
iv. Carbon

3. Give reasons.

A. Ga³⁺ salts are better reducing agent while Tl³⁺ salts are better oxidising agent.
B. PbCl₄ is less stable than PbCl₂
Answer:
A. i. Both gallium (Ga) and thallium (Tl) belong to group 13.
ii. Ga is lighter element compared to thallium Tl. Therefore, its +3 oxidation state is stable. Thus, Ga+ loses two electrons and get oxidized to Ga³⁺. Hence, Ga+ salts are better reducing agent.
iii. Thallium is a heavy element. Therefore, due to the inert pair effect, Tl forms stable compounds in +1 oxidation state. Thus, Tl³⁺ salts get easily reduced to Tl¹⁺ by accepting two electrons. Hence, Tl³⁺ salts are better oxidizing agent.
[Note: This question is modified so as to apply the appropriate textual concept.]

B. i. Pb has electronic configuration [Xe] 4f¹⁴ 5d¹⁰ 6s² 6p².
ii. Due to poor shielding of 6s² electrons by inner d and f electrons, it is difficult to remove 6s² electrons (inert pair).
iii. Thus, due to inert pair effect, +2 oxidation state is more stable than +4 oxidation state.
Hence, PbCl₄ is less stable than PbCl₂.

4. Give the formula of a compound in which carbon exhibit an oxidation state of

A. +4
B. +2
C. -4
Answer:
A. CCl₄
B. CO
C. CH₄

5. Explain the trend of the following in group 13 elements :

A. atomic radii
B. ionization enthalpy
C. electron affinity
Answer:
A. Atomic radii:

• In group 13, on moving down the group, the atomic radii increases from B to Al.
• However, there is an anomaly observed in the atomic radius of gallium due to the presence of 3d electrons. These inner 3d electrons offer poor shielding effect and thus, valence shell electrons of Ga experience greater nuclear attraction. As a result, atomic radius of gallium is less than that of aluminium.
• However, the atomic radii again increases from Ga to Tl.
• Therefore, the atomic radii of the group 13 elements varies in the following order:
  B < Al > Ga < In < Tl

B. Ionization enthalpy:

• Ionization enthalpies show irregular trend in the group 13 elements.
• As we move down the group, effective nuclear charge decreases due to addition of new shells in the atom of the elements which leads to increased screening effect. Thus, it becomes easier to remove valence shell electrons and hence, ionization enthalpy decreases from B to Al as expected.
• However, there is a marginal difference in the ionization enthalpy from Al to Tl.
• The ionization enthalpy increases slightly for Ga but decreases from Ga to In.
  In case of Ga, there are 10 d-electrons in its inner electronic configuration which shield the nuclear charge less effectively than the s and p-electrons and therefore, the outer electron is held fairly strongly by the nucleus. As a result, the ionization enthalpy increases slightly.
• Number of d electrons and extent of screening effect in indium is same as that in gallium. However, the atomic size increases from Ga to In. Due to this, the first ionization enthalpy of In decreases.
• The last element Tl has 10 d-electrons and 14 f-electrons in its inner electronic configuration which exert still smaller shielding effect on the outer electrons. Consequently, its first ionization enthalpy increases considerably.

C. Electron affinity:
a. Electron affinity shows irregular trend. It first increases from B to A1 and then decreases. The less electron affinity of boron is due to its smaller size. Adding an electron to the 2p orbital in boron leads to a greater repulsion than adding an electron to the larger 3p orbital of aluminium.

b. From Al to Tl, electron affinity decreases. This is because, nuclear charge increases but simultaneously the number of shells in the atoms also increases. As a result, the effective nuclear charge decreases down the group resulting in increased atomic size and thus, it becomes difficult to add an electron to a larger atom. The electron affinity of Ga and In is same.
Note: Electron affinity of group 13 elements:

6. Answer the following

Question A.
What is hybridization of Al in AlCl₃?
Answer:
Al is sp² hybridized in AlCl₃.

Question B.
Name a molecule having banana bond.
Answer:
Diborane (B₂H₆)

7. Draw the structure of the following

Question A.
Orthophosphoric acid
Answer:

Question B.
Resonance structure of nitric acid
Answer:

8. Find out the difference between

Question A.
Diamond and Graphite
Answer:
Diamond:

1. It has a three-dimensional network structure.
2. In diamond, each carbon atom is sp³ hybridized.
3. Each carbon atom in diamond is linked to four other carbon atoms.
4. Diamond is poor conductor of electricity due to absence of free electrons.
5. Diamond is the hardest known natural substance.

Graphite:

1. It has a two-dimensional hexagonal layered structure.
2. In graphite, each carbon atom is sp² hybridized.
3. Each carbon atom in graphite is linked to three other carbon atoms.
4. Graphite is good conductor of electricity due to presence of free electrons in its structure.
5. Graphite is soft and slippery.

Question B.
White phosphorus and Red phosphorus
Answer:
White phosphorus:

1. It consists of discrete tetrahedral P₄ molecules.
2. It is less stable and more reactive.
3. It exhibits chemiluminescence.
4. It is poisonous.

Red phosphorus:

1. It consists chains of P₄ molecules linked together by covalent bonds.
2. It is stable and less reactive.
3. It does not exhibit chemiluminescence.
4. It is nonpoisonous.

9. What are silicones? Where are they used?
Answer:
i. a. Silicones are organosilicon polymers having R₂SiO (where, R = CH₃ or C₆H₅ group) as a repeating unit held together by

b. Since the empirical formula R₂SiO (where R = CH₃ or C₆H₅ group) is similar to that of ketones (R₂CO), these compounds are named as silicones.

ii. Applications: They are used as

• insulating material for electrical appliances.
• water proofing of fabrics.
• sealant.
• high temperature lubricants.
• for mixing in paints and enamels to make them resistant to high temperature, sunlight and chemicals.

10. Explain the trend in oxidation state of elements from nitrogen to bismuth.
Answer:

• Group 15 elements have five valence electrons (ns² np³). Common oxidation states are -3, +3 and +5. The range of oxidation state is from -3 to +5.
• Group 15 elements exhibit positive oxidation states such as +3 and +5. Due to inert pair effect, the stability of +5 oxidation state decreases and +3 oxidation state increases on moving down the group.
• Group 15 elements show tendency to donate electron pairs in -3 oxidation state. This tendency is maximum for nitrogen.
• The group 15 elements achieve +5 oxidation state only through covalent bonding.
  e. g. NH₃, PH₃, ASH₃, SbH₃, and BiH₃ contain 3 covalent bonds. PCl₅ and PF₅ contain 5 covalent bonds.

11. Give the test that is used to detect borate radical is qualitative analysis.
Answer:
i. Borax when heated with ethyl alcohol and concentrated H₂SO₄, produces volatile vapours of triethyl borate, which bum with green edged flame.

ii. The above reaction is Used as a test for the detection and removal of borate radical \(\left(\mathrm{BO}_{3}^{3-}\right)\) in qualitative analysis.

12. Explain structure and bonding of diborane.
Answer:

• Electronic configuration of boron is 1s² 2s² 2p¹. Thus, it has only three valence electrons.
• In diborane, each boron atom is sp³ hybridized. Three of such hybrid orbitals are half filled while the fourth sp3 hybrid orbital remains vacant.
• The two half-filled sp³ hybrid orbitals of each B atom overlap with 1s orbitals of two terminal H atoms and form four B – H covalent bonds. These bonds are also known as two-centred-two-electron (2c-2e) bonds.
• When ‘1s’ orbital of each of the remaining two H atoms simultaneously overlap with half-filled hybrid orbital of one B atom and the vacant hybrid orbital of the other B atom, it produces two three-centred-two- electron bonds (3c-2e) or banana bonds.
• Hydrogen atoms involved in (3c-2e) bonds are the bridging H atoms i.e., H atoms in two B – H – B bonds.
• In diborane, two B atoms and four terminal H atoms lie in one plane, while the two bridging H atoms lie symmetrically above and below this plane.

13. A compound is prepared from the mineral colemanite by boiling it with a solution of sodium carbonate. It is white crystalline solid and used for inorganic qualitative analysis.

a. Name the compound produced.
b. Write the reaction that explains its formation.
Answer:
a. Borax
b. Borax is obtained from its mineral colemanite by boiling it with a solution of sodium carbonate.

14. Ammonia is a good complexing agent. Explain.
Answer:
i. The lone pair of electrons on nitrogen atom facilitates complexation of ammonia with transition metal ions. Thus, ammonia is a good complexing agent as it forms complex by donating its lone pair of electrons.

ii. This reaction is used for the detection of metal ions such as Cu²⁺ and Ag⁺.

15. State true or false. Correct the false statement.

A. The acidic nature of oxides of group 13 increases down the graph.
B. The tendency for catenation is much higher for C than for Si.
Answer:
A. False
The acidic nature of oxides of group 13 decreases down the group. It changes from acidic through amphoteric to basic.
B. True

16. Match the pairs from column A and B.

	Column A		Column B
i.	BCl3	a.	Angular molecule
ii.	SiO2	b.	Linear covalent molecule
iii.	CO2	c.	Tetrahedral molecule
		d.	Planar trigonal molecule

Answer:
i – d,
ii – c,
iii – b

17. Give the reactions supporting basic nature of ammonia.
Answer:
In the following reactions ammonia reacts with acids to form the corresponding ammonium salts which indicates basic nature of ammonia.

18. Shravani was performing inorganic qualitative analysis of a salt. To an aqueous solution of that salt, she added silver nitrate. When a white precipitate was formed. On adding ammonium hydroxide to this, she obtained a clear solution. Comment on her observations and write the chemical reactions involved.
Answer:
i. When silver nitrate (AgNO₃) is added to an aqueous solution of salt sodium chloride (NaCl), a white precipitate of silver chloride (AgCl) is formed.

ii. On adding ammonium hydroxide (NH₄OH) to this, the white precipitate of silver chloride gets dissolved and thus, a clear solution is obtained.

11th Chemistry Digest Chapter 9 Elements of Group 13, 14 and 15 Intext Questions and Answers

Can you recall? (Textbook Page No. 123)

Question 1.
If the valence shell electronic configuration of an element is 3s² 3p¹, in which block of the periodic table is it placed?
Answer:
The element having valence shell electronic configuration 3s² 3p¹ must be placed in the p-block of the periodic table as its last electron enters in p-subshell (3p).

Can you recall? (Textbook Page No. 127)

Question 1.
What is common between diamond and graphite?
Answer:
Both diamond and graphite are made up of carbon atoms as they are two allotropes of carbon.

Can you recall? (Textbook Page No. 129)

Question i.
Which element from the following pairs has higher ionization enthalpy?
B and TI, N and Bi
Answer:
Among B and Tl, boron has higher ionization enthalpy while, among N and Bi, nitrogen has higher ionization enthalpy.

Question ii.
Does boron form covalent compound or ionic?
Answer:
Yes, boron forms covalent compound.

Try this. (Textbook Page No. 131)

Question 1.
Find out the structural formulae of various oxyacids of phosphorus.
Answer:

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 8 Elements of Group 1 and 2 Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 8 Elements of Group 1 and 2

1. Explain the following

Question A.
Hydrogen shows similarity with alkali metals as well as halogens.
Answer:

• The electronic configuration of hydrogen is 1s¹ which is similar to the outer electronic configuration of alkali metals of group 1 i.e., ns¹.
• However, 1s¹ also resembles the outer electronic configuration of group 17 elements i.e., ns² np⁵.
• By adding one electron to H, it will attain the electronic configuration of the inert gas He which is 1s^2, and by adding one electron to ns² np⁵ we get ns² np⁶ which is the outer electronic configuration of the remaining inert gases.
• Therefore, some chemical properties of hydrogen are similar to those of alkali metals while some resemble halogens.

Hence, hydrogen shows similarity with alkali metals as well as halogens.

Question B.
Standard reduction potential of alkali metals have high negative values.
Answer:

• The general outer electronic configuration of alkali metals is ns¹.
• They readily lose one valence shell electron to achieve stable noble gas configuration and hence, they are highly electropositive and are good reducing agents.

Hence, standard reduction potentials of alkali metals have high negative values.

Question C.
Alkaline earth metals have low values of electronegativity; which decrease down the group.
Answer:

• Electronegativity represents attractive force exerted by the nucleus on shared electrons.
• The general outer electronic configuration of alkaline earth metals is ns². They readily lose their two valence shell electrons to achieve stable noble gas configuration. They are electropositive and hence, they have low values of electronegativity.

Question D.
Sodium dissolves in liquid ammonia to form a solution which shows electrical conductivity.
Answer:
i. Sodium dissolves in liquid ammonia giving deep blue coloured solutions which is electrically conducting in nature.
Na + (x + y) NH₃ → [Na(NH₃)_x]+ + [e(NH₃)_y]^–
ii. Due to formation of ions, the solution shows electrical conductivity.

Question E.
BeCl₂ is covalent while MgCl₂ is ionic.
Answer:

• Be²⁺ ion has very small ionic size and therefore, it has very high charge density.
• Due to this, it has high tendency to distort the electron cloud around the negatively charged chloride ion (Cl^–) which is larger in size.
• This results in partial covalent character of the bond in BeCl₂.
• Mg²⁺ ion has very less tendency to distort the electron cloud of Cl^– due to the bigger size of Mg²⁺ as compared to Be²⁺.

Hence, BeCl₂ is covalent while MgCl₂ is ionic.

Question F.
Lithium floats an water while sodium floats and catches fire when put in water.
Answer:

• When lithium and sodium react with water, hydrogen gas is released. Due to these hydrogen gas bubbles, lithium and sodium floats on water.
  eg. 2Na + 2H₂O → 2Na⁺ + 2OH^– + H₂↑
• The reactivity of group 1 metals increases with increasing atomic radius and lowering of ionization enthalpy down the group.
• Thus, sodium having lower ionization enthalpy, is more reactive than lithium.
• Hence, lithium reacts slowly while sodium reacts vigorously with water.
• Since the reaction of sodium with water is highly exothermic, it catches fire when put in water.

2. Write balanced chemical equations for the following.

Question A.
CO₂ is passed into concentrated solution of NaCl, which is saturated with NH₃.
Answer:

Question B.
A 50% solution of sulphuric acid is subjected to electrolyte oxidation and the product is hydrolysed.
Answer:

Question C.
Magnesium is heated in air.
Answer:

Question D.
Beryllium oxide is treated separately with aqueous HCl and aqueous NaOH solutions.
Answer:
Beryllium oxide (BeO) is an amphoteric oxide and thus, it reacts with both acid (HCl) as well as base (NaOH) to give the corresponding products.
i. \(\mathrm{BeO}+\underset{(\text { Acid })}{2 \mathrm{HCl}} \longrightarrow \mathrm{BeCl}_{2}+\mathrm{H}_{2} \mathrm{O}\)
ii. \(\mathrm{BeO}+\underset{(\text { Base })}{2 \mathrm{NaOH}} \longrightarrow \mathrm{Na}_{2} \mathrm{BeO}_{2}+\mathrm{H}_{2} \mathrm{O}\)

3. Answer the following questions

Question A.
Describe the diagonal relationship between Li and Mg with the help of two illustrative properties.
Answer:
a. The relative placement of these elements with similar properties in the periodic table is across a diagonal and is called diagonal relationship.
b. Lithium is placed in the group 1 and period 2 of the modem periodic table. It resembles with magnesium which is placed in the group 2 and period 3.

ii. Li and Mg show similarities in many of their properties.
e. g.
a. Reaction with oxygen:
1. Group 1 elements except lithium, react with oxygen present in the air to form oxides (M₂O) as well as peroxides (M₂O₂) and superoxides (MO₂) on further reaction with excess of oxygen.
2. This anomalous behaviour of lithium is due to its resemblance with magnesium as a result of diagonal relationship.
3. As group 2 elements form monoxides i.e., oxides, lithium also form monoxides.

b. Reaction with nitrogen:
1. All the group 1 elements react only with oxygen present in the air to form oxides while group 2 elements react with both nitrogen and oxygen present in the air forming corresponding oxides and nitrides.
2. However, lithium reacts with oxygen as well as nitrogen present in the air due to its resemblance with magnesium.

Question B.
Describe the industrial production of dihydrogen from steam. Also write the chemical reaction involved.
Answer:
Three stages are involved in the industrial production of dihydrogen from steam.
i. Stage 1:
a. Reaction of steam on hydrocarbon or coke (C) at 1270 K temperature in presence of nickel catalyst gives water-gas which is a mixture of carbon monoxide and hydrogen.
1. Reaction of steam with hydrocarbon:

2. Reaction of steam with coke or carbon (C):

b. Sawdust, scrapwood, etc. can also be used in place of carbon.

ii. Stage 2:
Water-gas shift reaction: When carbon monoxide in the water-gas reacts with steam in the presence of iron chromate (FeCrO₄) as catalyst, it gets transformed into carbon dioxide. This is called water-gas shift reaction.

iii. Stage 3: In the last stage, carbon dioxide is removed by scrubbing with sodium arsenite solution.

Question C.
A water sample, which did not give lather with soap, was found to contain Ca(HCO₃)₂ and Mg(HCO₃)₂. Which chemical will make this water give lather with soap? Explain with the help of chemical reactions.
Answer:

• Soap does not lather in hard water due to presence of the soluble salts of calcium and magnesium in it. So, the given water sample is hard water.
• Hardness of hard water can be removed by removal of these calcium and magnesium salts.
• Sodium carbonate is used to make hard water soft as it precipitates out the soluble calcium and magnesium salts in hard water as carbonates. Thus, it will make water give lather with soap.
  e.g. Ca(HCO₃)_2(aq) + Na₂CO_3(aq) → CaCO_3(s) + 2NaHCO_3(aq)

Question D.
Name the isotopes of hydrogen. Write their atomic composition schematically and explain which of these is radioactive ?
Answer:
i. Hydrogen has three isotopes i.e., hydrogen \(\left({ }_{1}^{1} \mathrm{H}\right)\), deuterium \(\left({ }_{1}^{2} \mathrm{H}\right)\) and tritium \(\left({ }_{1}^{3} \mathrm{H}\right)\) with mass numbers 1, 2 and 3 respectively.
ii. They all contain one proton and one electron but different number of neutrons in the nucleus.
iii. Atomic composition of isotopes of hydrogen:

iv. Tritium is a radioactive nuclide with half-life period 12.4 years and emits low energy β^– particles.
v. Schematic representation of isotopes of hydrogen is as follows:

4. Name the following

Question A.
Alkali metal with smallest atom.
Answer:
Lithium (Li)

Question B.
The most abundant element in the universe.
Answer:
Hydrogen (H)

Question C.
Radioactive alkali metal.
Answer:
Francium (Fr)

Question D.
Ions having high concentration in cell sap.
Answer:
Potassium ions (K⁺)

Question E.
A compound having hydrogen, aluminium and lithium as its constituent elements.
Answer:
Lithium aluminium hydride (LiAlH₄)

5. Choose the correct option.

Question A.
The unstable isotope of hydrogen is …..
a. H-1
b. H-2
c. H-3
d. H-4
Answer:
c. H-3

Question B.
Identify the odd one.
a. Rb
b. Ra
c. Sr
d. Be
Answer:
a. Rb

Question C.
Which of the following is Lewis acid ?
a. BaCl₂
b. KCl
c. BeCl₂
d. LiCl
Answer:
c. BeCl₂

Question D.
What happens when crystalline Na₂CO₃ is heated ?
a. releases CO₂
b. loses H₂O
c. decomposes into NaHCO₃
d. colour changes.
Answer:
b. loses H₂O

Activity :

1. Collect the information of preparation of dihydrogen and make a chart.
2. Find out the s block elements compounds importance/uses.
Answer:
1.

2. Uses of s-block elements:
Group 1 elements (alkali metals):
a. Lithium: Lithium is widely used in batteries.
b. Sodium:

• Liquid sodium metal is used as a coolant in fast breeder nuclear reactors.
• Sodium is also used as an important reagent in the Wurtz reaction.
• It is used in the manufacture of sodium vapour lamp.

c. Potassium:

• Potassium has a vital role in biological system.
• Potassium chloride (KCl) is used as a fertilizer.
• Potassium hydroxide (KOH) is used in the manufacture of soft soaps and also as an excellent absorbent of carbon dioxide.
• Potassium superoxide (KO₂) is used as a source of oxygen.

d. Caesium: Caesium is used in devising photoelectric cells.

Group 2 elements (alkaline earth metals):
a. Magnesium: Magnesium hydroxide [Mg(OH)₂] in its suspension form is used as an antacid.
b. Calcium: Compounds of calcium such as limestone and gypsum are used as constituents of cement and mortar.
c. Barium: BaSO₄ being insoluble in H₂O and opaque to X-rays is used as ‘barium meal’ to scan the X-ray of human digestive system.
[Note: Students are expected to collect additional information about preparation of dihydrogen and uses of s-block elements on their own.]

11th Chemistry Digest Chapter 8 Elements of Group 1 and 2 Intext Questions and Answers

Can you recall? (Textbook Page No. 110)

Question 1.
Which is the first element in the periodic table?
Answer:
Hydrogen is the first element in the periodic table.

Question 2.
What are isotopes?
Answer:
Many elements exist naturally as a mixture of two or more types of atoms or nuclides. These individual nuclides are called isotopes of that element. Isotopes of an element have the same atomic number (number of protons) but different atomic mass numbers due to different number of neutrons in their nuclei.

Question 3.
Write the formulae of the compounds of hydrogen formed with sodium and chlorine.
Answer:
Hydrogen combines with sodium to form sodium hydride (NaH) while it reacts with chlorine to form hydrogen chloride (HCl).

Can you tell? (Textbook Page No. 110)

Question 1.
In which group should hydrogen be placed? In group 1 or group 17? Why?
Answer:

• Hydrogen contains one valence electron in its valence shell and thus, its valency is one. Therefore, hydrogen resembles alkali metals (group 1 elements) as they also contain one electron in their valence shell (alkali metals tend to lose their valence electron).
• However, hydrogen also shows similarity with halogens (group 17 elements) as their valency is also one because halogens tend to accept one electron in their valence shell.
• Due to this unique behaviour, it is difficult to assign any definite position to hydrogen in the modem periodic table.

Just think! (Textbook Page No. 112)

Question 1.
\(2 \mathrm{Na}_{(\mathrm{s})}+\mathrm{H}_{2(\mathrm{~g})} \stackrel{\Delta}{\longrightarrow} 2 \mathrm{NaH}_{(\mathrm{s})}\)
In the above chemical reaction which element does undergo oxidation and which does undergo reduction?
Answer:
i. Redox reaction can be described as electron transfer as shown below:
2Na_(s) + H_2(g) → 2Na⁺ + 2H^–
ii. Charge development suggests that each sodium atom loses one electron to form Na⁺ and each hydrogen atom gains one electron to form H. This can be represented as follows:

iii. Na is oxidised to NaH by loss of electrons while the elemental hydrogen is reduced to NaH by a gain of electrons.

Can you recall? (Textbook Page No. 113)

Question i.
What is the name of the family of reactive metals having valency one?
Answer:
The family of reactive metals having valency one is known as alkali metals (group 1).

Question ii.
What is the name of the family of reactive metals having valency two?
Answer:
The family of reactive metals having valency two is known as alkaline earth metals (group 2).

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 7 Modern Periodic Table Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 7 Modern Periodic Table

1. Explain the following

Question A.
The elements Li, B, Be and N have the electronegativities 1.0, 2.0, 1.5, and 3.0, respectively on the Pauling scale.
Answer:

• Li, B, Be and N belong to the same period.
• As we move across a period from left to right in the periodic table, the effective nuclear charge increases steadily and therefore, electronegativity increases.

Hence, the elements Li, B, Be and N have the electronegativities 1.0, 2.0, 1.5, and 3.0, respectively on the Pauling scale.

Question B.
The atomic radii of Cl, I and Br are 99, 133 and 114 pm, respectively.
Answer:

• Cl, I and Br belong to group 17 (halogen group) in the periodic table.
• As we move down the group from top to bottom in the periodic table, a new shell gets added in the atom of the elements.
• As a result, the effective nuclear charge decreases due to increase in the atomic size as well as increased shielding effect.
• Therefore, the valence electrons experience less attractive force from the nucleus and are held less tightly resulting in the increased atomic radius.
• Thus, their atomic radii increases in the following order down the group.
  Cl (99 pm) < Br (114 pm) < I (133 pm)

Hence, the atomic radii of Cl, I and Br are 99, 133 and 114 pm, respectively.

Question C.
The ionic radii of F^– and Na⁺ are 133 and 98 pm, respectively.
Answer:

• F^– and Na⁺ are isoelectronic ions as they both have 10 electrons.
• However, the nuclear charge on F^– is +9 while that of Na⁺ is +11.
• In isoelectronic species, larger nuclear charge exerts greater attraction on the electrons and thus, the radius of that isoelectronic species becomes smaller.

Thus, F^– has larger ionic radii (133 pm) than Na⁺ (98 pm).

Question D.
₁₃Al is a metal, ₁₄Si is a metalloid and ₁₅P is a nonmetal.
Answer:

• Electronic configuration of Al is [Ne] 3s² 3p¹, ₁₄Si is [Ne] 3s² 3p² and that of ₁₅P is [Ne] 3s² 3p³.
• Metals are characterized by the ability to form compounds by loss of valence electrons.
• ‘Al’ has 3 valence electrons, thus shows tendency to lose 3 valence electrons to complete its octet. Hence, Al is a metal.
• Nonmetals are characterized by the ability to form compounds by gain of valence electrons in valence shell.
• ‘P’ has 5 valence electrons thus, shows tendency to gain 3 electrons to complete its octet. Hence, ‘P’ is a nonmetal.
• Si has four valence electrons, thus it can either lose/gain electrons to complete its octet. Hence, behaves as a metalloid.

Question E.
Cu forms coloured salts while Zn forms colourless salts.
Answer:

• Electronic configuration of ₂₉CU is [Ar] 3d¹⁰4s¹ while that of Zn is [Ar] 3d¹⁰4s².
• Electronic configuration of Cu in its +1 oxidation state is [Ar] 3d¹⁰ while that in +2 oxidation state is [Ar] 3d⁹.
• Therefore, Cu contains partially filled d orbitals in +2 oxidation state and thus, Cu²⁺ salts are coloured.
• However, Zn has completely filled d orbital which is highly stable and hence, it does not form coloured ions.

Hence, Cu forms coloured salts while Zn forms colourless salts.

2. Write the outer electronic configuration of the following using orbital notation method. Justify.
A. Ge (belongs to period 4 and group 14)
B. Po (belongs to period 6 and group 16)
C. Cu (belongs to period 4 and group 11)
Answer:
A. a. Ge belongs to period 4. Therefore, n = 4.
b. Group 14 indicates that the element belongs to the p-block of the modem periodic table.
c. The general outer electronic configuration of group 14 elements is ns² np².
d. Thus, the outer electronic configuration of Ge is 4s² 4p².

B. a. Po belongs to period 6. Therefore, n = 6.
b. Group 16 indicates that the element belongs to the p-block of the modem periodic table.
c. The general outer electronic configuration of group 16 elements is ns² np⁴.
d. Thus, the outer electronic configuration of Po is 6s² 6p⁴.

C. a. Cu belongs to period 4. Therefore, n = 4.
b. Group 11 indicates that the element belongs to the d-block of the modem periodic table.
c. The general outer electronic configuration of the d-block elements is ns^0-2(n-1)d^1-10.
d. The expected configuration of Cu is 4s²3d⁹. However, the observed configuration of Cu is 4s¹3d¹⁰. This is due to the extra stability associated with completely filled d-subshell. Thus, the outer electronic configuration of Cu is 4s¹3d¹⁰.

3. Answer the following

Question A.
La belongs to group 3 while Hg belongs to group 12 and both belong to period 6 of the periodic table. Write down the general outer electronic configuration of the ten elements from La to Hg together using orbital notation method.
Answer:
i. La and Hg both belongs to period 6. Therefore, n = 6.
ii. Elements of group 3 to group 12 belong to the d-block of the modem periodic table.
iii. The general outer electronic configuration of the d-block elements is ns^0-2 (n -1 )^1-10.
iv. Therefore, the outer electronic configuration of all ten elements from La to Hg is as given in the table below.

[Note: There are 14 elements between La and Hf which are called lanthanides. Therefore, after La, electrons are filled in 4f subshell of lanthanide elements. Once all the 14 elements of lanthanide series are filled, next electron enters 5d subshell of Hf. Hence, the outer electronic configurations of Hf to Hg often include completely filled 4f subshell. For example, the electronic configuration of Hf ‘5d²6s²’ can also be written as ‘4f¹⁴5d²6s²’.]

Question B.
Ionization enthalpy of Li is 520 kJ mol^-1 while that of F is 1681 kJ mol^-1. Explain.
Answer:

• Both Li and F belong to period 2.
• Across a period, the screening effect is the same while the effective nuclear charge increases.
• As a result, the outer electron is held more tightly and therefore, the ionization enthalpy increases across a period.
• Hence, F will have higher ionization enthalpy than Li.

Thus, ionization enthalpy of Li is 520 kJ mol^-1 while that of F is 1681 kJ mol^-1.

Question C.
Explain the screening effect with a suitable example.
Answer:
i. In a multi-electron atom, the electrons in the inner shells tend to prevent the attractive influence of the nucleus from reaching the outermost electron.
ii. Thus, they act as a screen or shield between the nuclear attraction and outermost or valence electrons. This effect of the inner electrons on the outer electrons is known as screening effect or shielding effect.
iii. Across a period, screening effect due to inner electrons remains the same as electrons are added to the same shell.
iv. Down the group, screening effect due to inner electrons increases as a new valence shell is added.
e.g. Potassium (19K) has electronic configuration 1s²2s²2p⁶3s²3p⁶4s¹.
K has 4 shells and thus, the valence shell electrons are effectively shielded by the electrons present in the inner three shells. As a result of this, valence shell electron (4s¹) in K experiences much less effective nuclear charge and can be easily removed.

Question D.
Why the second ionization enthalpy is greater than the first ionization enthalpy ?
Answer:
The second ionization enthalpy (Δ_iH₂) is greater than the first ionization enthalpy (Δ_iH₁) as it involves removal of electron from the positively charged species.

Question E.
Why the elements belonging to the same group do have similar chemical properties ?
Answer:

• Chemical properties of elements depend upon their valency.
• Elements belonging to the same group have the same valency.

Hence, the elements belonging to the same group show similar chemical properties.

Question F.
Explain : electronegativity and electron gain enthalpy. Which of the two can be measured experimentally?
Answer:
i. The ability of a covalently bonded atom to attract the shared electrons toward itself is called electronegativity (EN). Electronegativity cannot be measured experimentally. However, various numerical scales to express electronegativity were developed by many scientists. Pauling scale of electronegativity is the one used most widely.

ii. Electron gain enthalpy is a quantitative measure of the ease with which an atom adds an electron forming the anion and is expressed in kJ mol^-1. Thus, it is an experimentally measurable quantity.

4. Choose the correct option

Question A.
Consider the elements B, Al, Mg and K predict the correct order of metallic character :
a. B > Al > Mg > K
b. Al > Mg > B > K
c. Mg > Al > K > B
d. K > Mg > Al > B
Answer:
d. K > Mg > Al > B

Question B.
In modern periodic table, the period number indicates the :
a. atomic number
b. atomic mass
c. principal quantum number
d. azimuthal quantum number
Answer:
c. principal quantum number

Question C.
The lanthanides are placed in the periodic table at
a. left hand side
b. right hand side
c. middle
d. bottom
Answer:
d. bottom

Question D.
If the valence shell electronic configuration is ns²np⁵, the element will belong to
a. alkali metals
b. halogens
c. alkaline earth metals
d. actinides
Answer:
b. halogens

Question E.
In which group of elements of the modern periodic table are halogen placed ?
a. 17
b. 6
c. 4
d. 2
Answer:
a. 17

Question F.
Which of the atomic number represent the s-block elements ?
a. 7, 15
b. 3, 12
c. 6, 14
d. 9, 17
Answer:
b. 3, 12

Question G.
Which of the following pairs is NOT isoelectronic ?
a. Na⁺ and Na
b. Mg²⁺ and Ne
c. Al³⁺ and B³⁺
d. P3^– and N^3-
Answer:
b. Mg²⁺ and Ne

Question H.
Which of the following pair of elements has similar properties ?
a. 13, 31
b. 11, 20
c. 12, 10
d. 21, 33
Answer:
a. 13, 31

5. Answer the following questions

Question A.
The electronic configuration of some elements are given below:
a. 1s²
b. 1s²2s²2p⁶
In which group and period of the periodic table they are placed ?
Answer:
a. 1s²
Here n = 1. Therefore, the element belongs to the 1st period.
The outer electronic configuration 1s² corresponds to the maximum capacity of 1s, the complete duplet. Therefore, the element is placed at the end of the 1st period in the group 18 of inert gases in the modem periodic table,

b. 1s²2s²2p⁶
Here n = 2. Therefore, the element belongs to the 2nd period.
The outer electronic configuration 2s²2p⁶ corresponds to complete octet. Therefore, the element is placed in the 2nd period of group 18 in the modem periodic table.

Question B.
For each of the following pairs, indicate which of the two species is of large size :
a. Fe²⁺ or Fe³⁺
b. Mg²⁺ or Ca²⁺
Answer:
a. Fe²⁺ has a larger size than Fe³⁺.
b. Ca²⁺ has a larger size than Mg²⁺.

Question C.
Select the smaller ion form each of the following pairs:
a. K⁺, Li⁺
b. N^3-, F^–
Answer:
i. Li⁺ has smaller ionic radius than K⁺
ii. F^– has smaller ionic radius than N^3-.

Question D.
With the help of diagram answer the questions given below:

a. Which atom should have smaller ionization enthalpy, oxygen or sulfur?
b. The lithium forms +1 ions while berylium forms +2 ions ?
Answer:
Sulfur should have smaller ionization energy than oxygen.
a. Lithium has electronic configuration 1s²2s¹ while that of beryllium is 1s²2s².
b. Li can achieve a noble gas configuration by losing one electron while Be can do so by losing two electrons. Hence, lithium forms +1 ions while beryllium forms +2 ions.

Question E.
Define : a. Ionic radius
b. Electronegativity
Answer:
a. Ionic radius: Ionic radius is defined as the distance of valence shell of electrons from the centre of the nucleus in an ion.

b. Electronegativity: The ability of a covalently bonded atom to attract the shared electrons toward itself is called electronegativity (EN).

Question F.
Compare chemical properties of metals and non-metals.
Answer:
i. Metals (like alkali metals) react vigorously with oxygen to form oxides which reacts with water to form strong bases.
e. g. Sodium (Na) reacts with oxygen to form Na₂O which produces NaOH on reaction with water.

ii. Nonmetals (like halogens) react with oxygen to form oxides which on reaction with water form strong acids.
e.g. Chlorine reacts with oxygen to form Cl₂O₇ which produces HClO₄ on reaction with water.

Question G.
What are the valence electrons ? For s-block and p-block elements show that number of valence electrons is equal to its group number.
Answer:

• Electrons present in the outermost shell of the atom of an element are called valence electrons.
• 3Li is an s-block element and its electronic configuration is 1s²2s¹. Since it has one valence electron, it is placed in group 1.
• Therefore, for s-block elements, group number = number of valence electrons.
• However, for p-block elements, group number = 18 – number of electrons required to attain complete octet.
• 7N is a p-block element and its electronic configuration is 1s²2s²2p³. Since it has five electrons in its valence shell, it is short of three electrons to complete its octet.
• Therefore, its group number = 18 – 3 = 15.

Question H.
Define ionization enthalpy. Name the factors on which ionisation enthalpy depends? How does it vary down the group and across a period?
Answer:
i. The energy required to remove an electron from the isolated gaseous atom in its ground state is called ionization enthalpy (Δ_iH).
Ionization enthalpy is the quantitative measure of tendency of an element to lose electron and expressed in kJ mol^-1.

ii. Ionization energy depends on the following factors

• Size (radius) of an atom
• Nuclear charge
• The shielding or screening effect of inner electrons
• Nature of electronic configuration

iii. Variation of ionization energy down the group: On moving down the group, the ionization enthalpy decreases. This is because electron is to be removed from the larger valence shell. Screening due to core electrons goes on increasing and the effective nuclear charge decreases down the group. As a result, the removal of the outer electron becomes easier down the group.

iv. Variation of ionization energy across a period: The screening effect is the same while the effective nuclear charge increases across a period. As a result, the outer electron is held more tightly and hence, the ionization enthalpy increases across a period. Therefore, the alkali metal shows the lowest first ionization enthalpy while the inert gas shows the highest first ionization enthalpy across a period.

Note: First ionization enthalpy values of elements of group 1.

Note: First ionization enthalpy values of elements of period 2.

Question I.
How the atomic size vary in a group and across a period? Explain with suitable example.
Answer:
i. Variation in atomic size down the group:
a. As we move down the group from top to bottom in the periodic table, the atomic size increases with the increase in atomic number.
b. This is because, as the atomic number increases, nuclear charge increases but simultaneously the number of shells in the atoms also increases.
c. Asa result, the effective nuclear charge decreases due to increase in the size of the atom and shielding effect increases down the group. Thus, the valence electrons experience less attractive force from nucleus and are held less tightly.
d. Hence, the atomic size increases in a group from top to bottom.

e. g.

• In group 1, as we move from top to bottom i.e., from Li to Cs, a new shell gets added in the atom of the elements and the electrons are added in this new shell.
• As a result of this, the effective nuclear charge goes on decreasing and screening effect goes on increasing down a group.
• Therefore, the atomic size is the largest for Cs and is the smallest for Li in group 1.

[Note: Atomic radii of Li and Cs are 152 pm and 262 pm respectively.]

ii. Variation in atomic size across a period:
a. As we move across a period from left to right in the periodic table, the atomic size of an element decreases with the increase in atomic number.
b. This is because, as the atomic number increases, nuclear charge increases gradually but addition of electrons takes place in the same shell.
c. Therefore, as we move across a period, the effective nuclear charge increases but screening effect caused by the core electrons remains the same.
d. As a result of this, attraction between the nucleus and the valence electrons increases. Therefore, valence electrons are more tightly bound and hence, the atomic radius goes on decreasing along a period resulting in decrease in atomic size.

e. g.

• In the second period, as we move from left towards right i.e., from Li to F, the electrons are added in the second shell of all the elements in second period (except noble gas Ne).
• As a result of this, the effective nuclear charge goes on increasing from Li to F, however, screening effect remains the same.
• Therefore, the atomic size is the largest for Li (alkali metal) and is the smallest for F (halogen).

[Note: Atomic radii of Li and F are 152 pm and 64 pm respectively.]

Question J.
Give reasons.
a. Alkali metals have low ionization energies.
b. Inert gases have exceptionally high ionization energies.
c. Fluorine has less electron affinity than chlorine.
d. Noble gases possess relatively large atomic size.
Answer:
a. i. Across a period, the screening effect is the same while the effective nuclear charge increases.
ii. As a result, the outer electron is held more tightly and hence, the ionization enthalpy increases across a period.
iii. Since the alkali metals are present in the group 1 of the modem periodic table, they have low ionization energies.

b. i. Across a period, the screening effect is the same and the effective nuclear charge increases.
ii. As a result, the outer electron is held more tightly and hence, the ionization enthalpy increases across a period.
iii. Inert gases are present on the extreme right of the periodic table i.e., in group 18. Also, inert gases have stable electronic configurations i.e., complete octet or duplet. Due to this, they are extremely stable and it is very difficult to remove electrons from their valence shell.
Hence, inert gases have exceptionally high ionization potential.

c. The less electron affinity of fluorine is due to its smaller size. Adding an electron to the 2p orbital in fluorine leads to a greater repulsion than adding an electron to the larger 3p orbital of chlorine.
Hence, fluorine has less electron affinity than chlorine.

d. i. Noble gases have completely filled valence shell i.e., complete octet (except He with complete duplet).
ii. Since their valence shell contains eight electrons, they experience greater electronic repulsion and this results in increased atomic size (atomic radii) of the noble gas elements.
Hence, noble gases possess

Question K.
Consider the oxides Li₂O, CO₂, B₂O₃.
a. Which oxide would you expect to be the most basic?
b. Which oxide would be the most acidic?
c. Give the formula of an amphoteric oxide.
Answer:
a. Li₂O is the most basic oxide.
b. CO₂ is the most acidic oxide.
c. Formula of an amphoteric oxide: Al₂O₃.
[Note: Both B₂O₃ and CO₂ are acidic oxides. But CO₂ is more acidic oxide as compared to B₂O₃. Hence, CO₂ is most acidic oxide amongst the given.]

Activity :

Question 1.
Prepare a wall mounting chart of the modern periodic table.
Answer:
Students can scan the adjacent Q.R. Code to visualise the modern periodic table and are expected to prepare the chart on their own.

11th Chemistry Digest Chapter 7 Modern Periodic Table Intext Questions and Answers

Can you recall? (Textbook Page No. 93)

Question 1.
What was the basis of classification of elements before the knowledge of electronic structure of atom?
Answer:
Elements were classified on the basis of their physical properties before the knowledge of electronic structure of atom.

Question 2.
Name the scientists who made the classification of elements in the nineteenth century.
Answer:
Dmitri Mendeleev, John Newlands and Johann Doberiener were the scientists who made the classification of elements based on their atomic mass in the nineteenth century.

Question 3.
What is Mendeleev’s periodic law?
Answer:
Mendeleev’s periodic law: “The physical and chemical properties of elements are the periodic function of their atomic masses

Question 4.
How many elements are discovered until now?
Answer:
Including manmade elements, total 118 elements are discovered until now.

Question 5.
How many horizontal rows and vertical columns are present in the modern periodic table?
Answer:
The modem periodic table consists of seven horizontal rows called periods numbered from 1 to 7 and eighteen vertical columns called groups numbered from 1 to 18.

Just think. (Textbook Page No. 93)

Question 1.
How many days pass between two successive full moon nights?
Answer:
29.5 days i.e., approximately 30 days pass between two successive full moon nights.

Question 2.
What type of motion does a pendulum exhibit?
Answer:
A pendulum exhibits periodic motion since it traces the same path after regular interval of time.

Question 3.
Give some other examples of periodic events.
Answer:
Following are some other examples of periodic events:

• Motion of earth around the sun.
• Rotation of earth around its own axis.
• Day and night.

Can you recall? (Textbook Page No. 95)

Question i.
What does the principal quantum number ‘n’ and azimuthal quantum number ‘l’ of an electron belonging to an atom represent?
Answer:
The principal quantum number ‘n’ represents the outermost or valence shell of an element (which corresponds to period number) while azimuthal quantum number ‘l’ constitutes a subshell belonging to the shell for the given ‘n’.

Question ii.
Which principle is followed in the distribution of electrons in an atom?
Answer:
The distribution of electrons in an atom is according to the following three principles:

1. Aufbau principle
2. Pauli’s exclusion principle
3. Hund’s rule of maximum multiplicity

[Note: According to aufbau principle, electrons are filled in the subshells in the increasing order of their energies which follows the following order: s < p < d < f.]