Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Miscellaneous Exercise 2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Miscellaneous Exercise 2
(I) Select the correct answer from the given alternative:
Question 1.
The common ratio for the G.P. 0.12, 0.24, 0.48, is
(A) 0.12
(B) 0.2
(C) 0.02
(D) 2
Answer:
(D) 2
![]()
Question 2.
The tenth term of the geometric sequence is \(\frac{1}{4}, \frac{-1}{2}, 1,-2, \ldots\) is
(A) 1024
(B) \(\frac{1}{1024}\)
(C) -128
(D) \(\frac{-1}{128}\)
Answer:
(C) -128
Hint:

Question 3.
If for a G.P. \(\frac{t_{6}}{t_{3}}=\frac{1458}{54}\) then r = ?
(A) 3
(B) 2
(C) 1
(D) -1
Answer:
(A) 3
Hint:
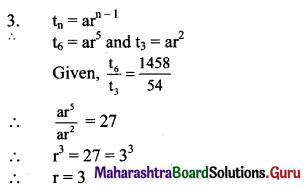
Question 4.
Which term of the geometric progression 1, 2, 4, 8, ….. is 2048.
(A) 10th
(B) 11th
(C) 12th
(D) 13th
Answer:
(C) 12th
Hint:
Here, a = 1, r = 2
nth term of geometric progression = arn-1
∴ arn-1 = 2048
2n-1 = 211
n – 1 = 11
∴ n = 12
Question 5.
If the common ratio of the G.P. is 5, the 5th term is 1875, the first term is
(A) 3
(B) 5
(C) 15
(D) -5
Answer:
(A) 3
Question 6.
The sum of 3 terms of a G.P. is \(\frac{21}{4}\) and their product is 1, then the common ratio is
(A) 1
(B) 2
(C) 4
(D) 8
Answer:
(C) 4
Hint:
Let three terms be \(\frac{a}{r}\), a, ar
According to the given conditions,
\(\frac{a}{r}\) + a + ar = \(\frac{21}{4}\) …..(i)
and \(\frac{a}{r}\) × a × ar = 1,
i.e., a3 = 1
∴ a = 1
∴ from equation (i), we get
\(\frac{1}{r}\) + 1 + r = \(\frac{21}{4}\)
By solving this, we get r = 4.
![]()
Question 7.
Sum to infinity of a G.P. 5, \(-\frac{5}{2}, \frac{5}{4},-\frac{5}{8}, \frac{5}{16}, \ldots\) is
(A) 5
(B) \(-\frac{1}{2}\)
(C) \(\frac{10}{3}\)
(D) \(\frac{3}{10}\)
Answer:
(C) \(\frac{10}{3}\)
Hint:
Here, a = 5, r = \(\frac{-1}{2}\), |r| < 1
∴ Sum to the infinity = \(\frac{a}{1-r}=\frac{5}{1+\frac{1}{2}}=\frac{10}{3}\)
Question 8.
The tenth term of H.P. \(\frac{2}{9}, \frac{1}{7}, \frac{2}{19}, \frac{1}{12}, \ldots\) is
(A) \(\frac{1}{27}\)
(B) \(\frac{9}{2}\)
(C) \(\frac{5}{2}\)
(D) 27
Answer:
(A) \(\frac{1}{27}\)
Hint:

Question 9.
Which of the following is not true, where A, G, H are the AM, GM, HM of a and b respectively, (a, b > 0)
(A) A = \(\frac{a+b}{2}\)
(B) G = \(\sqrt{a b}\)
(C) H = \(\frac{2 a b}{a+b}\)
(D) A = GH
Answer:
(D) A = GH
![]()
Question 10.
The G.M. of two numbers exceeds their H.M. by \(\frac{6}{5}\), the A.M. exceeds G.M. by \(\frac{3}{2}\) the two numbers are
(A) 6, \(\frac{15}{2}\)
(B) 15, 25
(C) 3, 12
(D) \(\frac{6}{5}\), \(\frac{3}{2}\)
Answer:
(C) 3, 12
Hint:


(II) Answer the following:
Question 1.
In a G.P., the fourth term is 48 and the eighth term is 768. Find the tenth term.
Solution:

Question 2.
Find the sum of the first 5 terms of the G.P. whose first term is 1 and the common ratio is \(\frac{2}{3}\).
Solution:
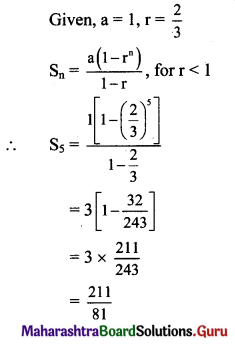
Question 3.
For a G.P. a = \(\frac{4}{3}\) and t7 = \(\frac{243}{1024}\), find the value of r.
Solution:

Question 4.
For a sequence, if \(t_{n}=\frac{5^{n-2}}{7^{n-3}}\), verify whether the sequence is a G.P. If it is a G.P., find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P.
if \(\frac{\mathrm{t}_{\mathrm{n}+1}}{\mathrm{t}_{\mathrm{n}}}\) = constant for all n ∈ N.

![]()
Question 5.
Find three numbers in G.P. such that their sum is 35 and their product is 1000.
Solution:
Let the three numbers in G.P. be \(\frac{a}{r}\), a, ar.
According to the given conditions,
\(\frac{a}{r}\) + a + ar = 35
a(\(\frac{1}{r}\) + 1 + r) = 35 …..(i)
Also, (\(\frac{a}{r}\))(a)(ar) = 1000
a3 = 1000
∴ a = 10
Substituting the value of a in (i), we get

Hence, the three numbers in G.P. are 20, 10, 5, or 5, 10, 20.
Question 6.
Find five numbers in G.P. such that their product is 243 and the sum of the second and fourth numbers is 10.
Solution:
Let the five numbers in G.P. be \(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\).
According to the given condition,


Question 7.
For a sequence, Sn = 4(7n – 1), verify that the sequence is a G.P.
Solution:

∴ The given sequence is a G.P.
Question 8.
Find 2 + 22 + 222 + 2222 + … upto n terms.
Solution:
Sn = 2 + 22 + 222 +… upto n terms
= 2(1 + 11 + 111 + ….. upto n terms)
= \(\frac{2}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{2}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) + …… upto n terms]
= \(\frac{2}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + ….. n times)]
Since 10, 100, 1000, ….. n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10,

![]()
Question 9.
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666,…
Solution:
0.6, 0.66, 0.666, 0.6666, …
∴ t1 = 0.6
t2 = 0.66 = 0.6 + 0.06
t3 = 0.666 = 0.6 + 0.06 + 0.006
Hence, in general
tn = 0.6 + 0.06 + 0.006 + …..upto n terms.
The terms are in G.P. with
a = 0.6, r = \(\frac{0.06}{0.6}\) = 0.1
∴ tn = the sum of first n terms of the G.P.

Question 10.
Find \(\sum_{r=1}^{n}\left(5 r^{2}+4 r-3\right)\)
Solution:

Question 11.
Find \(\sum_{r=1}^{n} r(r-3)(r-2)\)
Solution:

Question 12.
Find \(\sum_{r=1}^{n} \frac{1^{2}+2^{2}+3^{2}+\ldots+r^{2}}{2 r+1}\)
Solution:
We know that

Question 13.
Find \(\sum_{r=1}^{n} \frac{1^{3}+2^{3}+3^{3}+\ldots r^{3}}{(r+1)^{2}}\)
Solution:

![]()
Question 14.
Find 2 × 6 + 4 × 9 + 6 × 12 + ….. upto n terms.
Solution:
2, 4, 6, ….. are in A.P.
∴ rth term = 2 + (r – 1) 2 = 2r
6, 9, 12, ….. are in A.P.
∴ rth term = 6 + (r – 1)(3) = (3r + 3)
∴ 2 × 6 + 4 × 9 + 6 × 12 + ….. to n terms

= n(n + 1) [2n + 1 + 3]
= 2n(n + 1)(n + 2)
Question 15.
Find 2 × 5 × 8 + 4 × 7 × 10 + 6 × 9 × 12 + …… upto n terms.
Solution:
2, 4, 6,… are in A.P.
∴ rth term = 2 + (r – 1) 2 = 2r
5, 7, 9, … are in A.P.
∴ rth term = 5 + (r – 1) (2) = (2r + 3)
8, 10, 12, … are in A.P.
∴ rth term = 8 + (r – 1) (2) = (2r + 6)
2 × 5 × 8 + 4 × 7 × 10 + 6 × 9 × 12 + ….. to n terms

= 2n (n + 1) [n(n + 1) + 3(2n + 1) + 9]
= 2n (n + 1)(n2 + 7n + 12)
= 2n (n + 1) (n + 3) (n + 4)
Question 16.
Find \(\frac{1^{2}}{1}+\frac{1^{2}+2^{2}}{2}+\frac{1^{2}+2^{2}+3^{2}}{3}+\ldots\) upto n terms.
Solution:

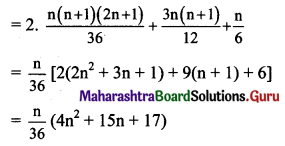
Question 17.
Find 122 + 132 + 142 + 152 + ….. 202
Solution:
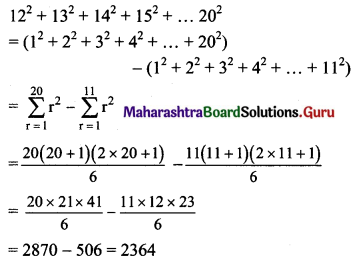
Question 18.
If \(\frac{1+2+3+4+5+\ldots \text { upto } \mathrm{n} \text { terms }}{1 \times 2+2 \times 3+3 \times 4+4 \times 5+\ldots \text { upto } \mathrm{n} \text { terms }}=\frac{3}{22}\), Find the value of n.
Solution:

![]()
Question 19.
Find (502 – 492) + (482 – 472) + (462 – 452) +… + (22 – 12).
Solution:

Question 20.
If \(\frac{1 \times 3+2 \times 5+3 \times 7+\ldots \text { upto } \mathrm{n} \text { terms }}{1^{3}+2^{3}+3^{3}+\ldots \text { upto } \mathrm{n} \text { terms }}=\frac{5}{9}\), find the value of n.
Solution:


Question 21.
For a G.P. if t2 = 7, t4 = 1575, find a.
Solution:

Question 22.
If for a G.P. t3 = \(\frac{1}{3}\), t6 = \(\frac{1}{81}\) find r.
Solution:

Question 23.
Find \(\sum_{r=1}^{n}\left(\frac{2}{3}\right)^{r}\).
Solution:

Question 24.
Find k so that k – 1, k, k + 2 are consecutive terms of a G.P.
Solution:
Since k – 1, k, k + 2 are consecutive terms of a G.P.,
\(\frac{k}{k-1}=\frac{k+2}{k}\)
k2 = k2 + k – 2
k – 2 = 0
∴ k = 2
Question 25.
If for a G.P. first term is (27)2 and the seventh term is (8)2, find S8.
Solution:

Question 26.
If pth, qth and rth terms of a G.P. are x, y, z respectively. Find the value of \(x^{q-r} \cdot y^{r-p} \cdot z^{p-q}\).
Solution:
Let a be the first term and R be the common ratio of the G.P.

Question 27.
Which 2 terms are inserted between 5 and 40 so that the resulting sequence is G.P.
Solution:
Let the required numbers be G1 and G2.
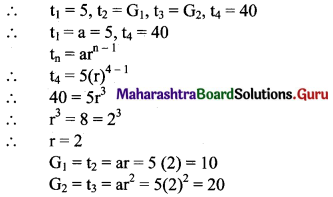
∴ For the resulting sequence to be in G.P. we need to insert numbers 10 and 20.
![]()
Question 28.
If p, q, r are in G.P. and \(\mathrm{p}^{1 / \mathrm{x}}=\mathrm{q}^{1 / \mathrm{y}}=\mathrm{r}^{1 / \mathrm{z}}\), verify whether x, y, z are in A.P. or G.P. or neither.
Solution:

Question 29.
If a, b, c are in G.P. and ax2 + 2bx + c = 0 and px2 + 2qx + r = 0 have common roots, then verify that pb2 – 2qba + ra2 = 0.
Solution:
a, b, c are in G.P.
∴ b2 = ac
ax2 + 2bx + c = 0 becomes

Question 30.
If p, q, r, s are in G.P., show that (p2 + q2 + r2)(q2 + r2 + s2) = (pq + qr + rs)2.
Solution:
p, q, r, s are in G.P.

Question 31.
If p, q, r, s are in G.P., show that (pn + qn), (qn + rn), (rn + sn) are also in G.P.
Solution:
p, q, r, s are in G.P.
Let the common ratio be R
∴ let p = \(\frac{a}{R^{3}}\), q = \(\frac{a}{R}\), r = aR and s = aR3
To show that (pn + qn), (qn + rn), (rn + sn) are in G.P,
i.e., we have to show

![]()
Question 32.
Find the coefficient x6 in the expression of e2x using series expansion.
Solution:

Question 33.
Find the sum of infinite terms of \(1+\frac{4}{5}+\frac{7}{25}+\frac{10}{125}+\frac{13}{625}+\ldots\)
Solution:

