Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 7 Conic Sections Ex 7.3 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 7 Conic Sections Ex 7.3
Question 1.
Find the length of the transverse axis, length of conjugate axis, the eccentricity, the co-ordinates of foci, equations of directrices, and the length of the latus rectum of the hyperbolae.
(i) \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
(ii) \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=-1\)
(iii) 16x2 – 9y2 = 144
(iv) 21x2 – 4y2 = 84
(v) 3x2 – y2 = 4
(vi) x2 – y2 = 16
(vii) \(\frac{y^{2}}{25}-\frac{x^{2}}{9}=1\)
(viii) \(\frac{y^{2}}{25}-\frac{x^{2}}{144}=1\)
(ix) \(\frac{x^{2}}{100}-\frac{y^{2}}{25}=1\)
(x) x = 2 sec θ, y = 2√3 tan θ
Solution:
(i) Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 25 and b2 = 16
⇒ a = 5 and b = 4
Length of transverse axis = 2a = 2(5) = 10
Length of conjugate axis = 2b = 2(4) = 8
We know that

(ii) Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=-1\)
\(\frac{y^{2}}{16}-\frac{x^{2}}{25}=1\)
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b2 = 16 and a2 = 25
⇒ b = 4 and a = 5
Length of transverse axis = 2b = 2(4) = 8
Length of conjugate axis = 2a = 2(5) = 10
Co-ordinates of vertices are B(0, b) and B’ (0, -b)
i.e., B(0, 4) and B'(0, -4)
We know that

![]()
(iii) Given equation of the hyperbola is 16x2 – 9y2 = 144.
\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 9 and b2 = 16
⇒ a = 3 and b = 4
Length of transverse axis = 2a = 2(3) = 6
Length of conjugate axis = 2b = 2(4) = 8
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}=\frac{\sqrt{9+16}}{3}=\frac{\sqrt{25}}{3}=\frac{5}{3}\)
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S(3(\(\frac{5}{3}\)), 0) and S'(-3(\(\frac{5}{3}\)), 0)
i.e., S(5, 0) and S'(-5, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\)
= \(\pm \frac{3}{\left(\frac{5}{3}\right)}\)
= \(\pm \frac{9}{5}\)
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(16)}{3}=\frac{32}{3}\)
(iv) Given equation of the hyperbola is 21x2 – 4y2 = 84.
\(\frac{x^{2}}{4}-\frac{y^{2}}{21}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 4 and b2 = 21
⇒ a = 2 and b = √21
Length of transverse axis = 2a = 2(2) = 4
Length of conjugate axis = 2b = 2√21
We know that

(v) Given equation of the hyperbola is 3x2 – y2 = 4.
\(\frac{x^{2}}{\left(\frac{4}{3}\right)}-\frac{y^{2}}{4}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = \(\frac{4}{3}\) and b2 = 4

(vi) Given equation of the hyperbola is x2 – y2 = 16.
\(\frac{x^{2}}{16}-\frac{y^{2}}{16}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 16 and b2 = 16
⇒ a = 4 and b = 4
Length of transverse axis = 2a = 2(4) = 8
Length of conjugate axis = 2b = 2(4) = 8
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}=\frac{\sqrt{16+16}}{4}=\frac{\sqrt{32}}{4}=\frac{4 \sqrt{2}}{4}=\sqrt{2}\)
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S (4√2, 0) and S’ (-4√2, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\)
⇒ x = \(\pm \frac{4}{\sqrt{2}}\)
⇒ x = ± 2√2
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(16)}{4}\) = 8
![]()
(vii) Given equation of the hyperbola is \(\frac{y^{2}}{25}-\frac{x^{2}}{9}=1\).
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b2 = 25 and a2 = 9
⇒ b = 5 and a = 3
Length of transverse axis = 2b = 2(5) = 10
Length of conjugate axis = 2a = 2(3) = 6
Co-ordinates of vertices are B(0, b) and B’ (0, -b),
i.e., B(0, 5) and B’ (0, -5)
We know that

(viii) Given equation of the hyperbola is \(\frac{y^{2}}{25}-\frac{x^{2}}{144}=1\).
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b2 = 25 and a2 = 144
⇒ b = 5 and a = 12
Length of transverse axis = 2b = 2(5) = 10
Length of conjugate axis = 2a = 2(12) = 24
Co-ordinates of vertices are B(0, b) and B’ (0, -b),
i.e., B(0, 5) and B’ (0, -5)
We know that

(ix) Given equation of the hyperbola is \(\frac{x^{2}}{100}-\frac{y^{2}}{25}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 100 and b2 = 25
⇒ a = 10 and b = 5
Length of transverse axis = 2a = 2(10) = 20
Length of conjugate axis = 2b = 2(5) = 10
We know that

(x) Given equation of the hyperbola is x = 2 sec θ, y = 2√3 tan θ.
Since sec2 θ – tan2 θ = 1,
\(\left(\frac{x}{2}\right)^{2}-\left(\frac{y}{2 \sqrt{3}}\right)^{2}=1\)
\(\frac{x^{2}}{4}-\frac{y^{2}}{12}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 4 and b2 = 12
⇒ a = 2 and b = 2√3
Length of transverse axis = 2a = 2(2) = 4
Length of conjugate axis = 2b = 2(2√3) = 4√3
We know that
e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}\) = \(\frac{\sqrt{4+12}}{2}\) = 2
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S(2(2), 0) and S'(-2(2), 0),
i.e., S(4, 0) and S'(-4, 0)
Equations of the directrices are x = ±\(\frac{a}{e}\).
⇒ x = ±\(\frac{2}{2}\)
⇒ x = ±1
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(12)}{2}\) = 12
![]()
Question 2.
Find the equation of the hyperbola with centre at the origin, length of the conjugate axis as 10, and one of the foci as (-7, 0).
Solution:
Given, one of the foci of the hyperbola is (-7, 0).
Since this focus lies on the X-axis, it is a standard hyperbola.
Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of conjugate axis = 2b
Given, length of conjugate axis = 10
⇒ 2b = 10
⇒ b = 5
⇒ b2 = 25
Co-ordinates of focus are (-ae, 0)
ae = 7
⇒ a2e2 = 49
Now, b2 = a2(e2 – 1)
⇒ 25 = 49 – a2
⇒ a2 = 49 – 25 = 24
The required equation of hyperbola is \(\frac{x^{2}}{24}-\frac{y^{2}}{25}=1\)
Question 3.
Find the eccentricity of the hyperbola, which is conjugate to the hyperbola x2 – 3y2 = 3
Solution:
Given, equation of hyperbola is x2 – 3y2 = 3.
\(\frac{x^{2}}{3}-\frac{y^{2}}{1}=1\)
Equation of the hyperbola conjugate to the above hyperbola is \(\frac{y^{2}}{1}-\frac{x^{2}}{3}=1\)
Comparing this equation with \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\), we get
b2 = 1 and a2 = 3
Now, a2 = b2(e2 – 1)
⇒ 3 = 1(e2 – 1)
⇒ 3 = e – 1
⇒ e2 = 4
⇒ e = 2 …..[∵ e > 1]
![]()
Question 4.
If e and e’ are the eccentricities of a hyperbola and its conjugate hyperbola respectively, prove that \(\frac{1}{e^{2}}+\frac{1}{\left(e^{\prime}\right)^{2}}=1\).
Solution:
Let e be the eccentricity of a hyperbola


Question 5.
Find the equation of the hyperbola referred to its principal axes:
(i) whose distance between foci is 10 and eccentricity is \(\frac{5}{2}\)
(ii) whose distance between foci is 10 and length of the conjugate axis is 6.
(iii) whose distance between directrices is \(\frac{8}{3}\) and eccentricity is \(\frac{3}{2}\).
(iv) whose length of conjugate axis = 12 and passing through (1, -2).
(v) which passes through the points (6, 9) and (3, 0).
(vi) whose vertices are (±7, 0) and endpoints of the conjugate axis are (0, ±3).
(vii) whose foci are at (±2, 0) and eccentricity is \(\frac{3}{2}\).
(viii) whose lengths of transverse and conjugate axes are 6 and 9 respectively.
(ix) whose length of transverse axis is 8 and distance between foci is 10.
Solution:
(i) Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Given, eccentricity (e) = \(\frac{5}{2}\)
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a(\(\frac{5}{2}\)) = 5
⇒ a = 2
⇒ a2 = 4

![]()
(ii) Let the required equation of hyperbola be \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of conjugate axis = 2b
Given, length of conjugate axis = 6
⇒ 2b = 6
⇒ b = 3
⇒ b2 = 9
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a2e2 = 25
Now, b2 = a2 (e2 – 1)
⇒ b2 = a2 e2 – a2
⇒ 9 = 25 – a2
⇒ a2 = 25 – 9
⇒ a2 = 16
The required equation of hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\)
(iii) Let the required equation of hyperbola be \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\)
Given, eccentricity (e) = \(\frac{3}{2}\)
Distance between directrices = \(\frac{2a}{e}\)
Given, distance between directrices = \(\frac{8}{3}\)
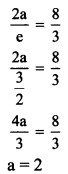

(iv) Let the required equation of hyperbola be
\(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\) ……(i)
Length of conjugate axis = 2b
Given, length of conjugate axis = 12
⇒ 2b = 12
⇒ b = 6 …..(ii)
⇒ b2 = 36
The hyperbola passes through (1, -2)
Substituting x = 1 and y = -2 in (i), we get

![]()
(v) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) ……(i)
The hyperbola passes through the points (6, 9) and (3, 0).

(vi) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Co-ordinates of vertices are (±a, 0).
Given that, co-ordinates of vertices are (±7, 0)
∴ a = 7
Endpoints of the conjugate axis are (0, b) and (0, -b).
Given, the endpoints of the conjugate axis are (0, ±3).
∴ b = 3
The required equation of hyperbola is \(\frac{x^{2}}{7^{2}}-\frac{y^{2}}{3^{2}}=1\)
i.e., \(\frac{x^{2}}{49}-\frac{y^{2}}{9}=1\)
(vii) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) ……(i)
Given, eccentricity (e) = \(\frac{3}{2}\)
Co-ordinates of foci are (±ae, 0).
Given co-ordinates of foci are (±2, 0)
ae = 2
⇒ a(\(\frac{3}{2}\)) = 2
⇒ a = \(\frac{4}{3}\)
⇒ a2 = \(\frac{16}{9}\)
(viii) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of transverse axis = 2a
Given, length of transverse axis = 6
⇒ 2a = 6
⇒ a = 3
⇒ a2 = 9
Length of conjugate axis = 2b
Given, length of conjugate axis = 9
⇒ 2b = 9
⇒ b = \(\frac{9}{2}\)
⇒ b2 = \(\frac{81}{4}\)
The required equation of hyperbola is
\(\frac{x^{2}}{9}-\frac{y^{2}}{\left(\frac{81}{4}\right)}=1\)
i.e., \(\frac{x^{2}}{9}-\frac{4 y^{2}}{81}=1\)
![]()
(ix) Let the required equation of hyperbola be
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Length of transverse axis = 2a
Given, length of transverse axis = 8
⇒ 2a = 8
⇒ a = 4
⇒ a2 = 16
Distance between foci = 2ae
Given, distance between foci = 10
⇒ 2ae = 10
⇒ ae = 5
⇒ a2e2 = 25
Now, b2 = a2 (e2 – 1)
⇒ b2 = a2 e2 – a2
⇒ b2 = 25 – 16 = 9
The required equation of hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\)
Question 6.
Find the equation of the tangent to the hyperbola.
(i) 3x2 – y2 = 4 at the point (2, 2√2).
(ii) 3x2 – y2 = 12 at the point (4, 6)
(iii) \(\frac{x^{2}}{144}-\frac{y^{2}}{25}=1\) at the point whose eccentric angle is \(\frac{\pi}{3}\).
(iv) \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\) at the point in a first quadrant whose ordinate is 3.
(v) 9x2 – 16y2 = 144 at the point L of the latus rectum in the first quadrant.
Solution:








Question 7.
Show that the line 3x – 4y + 10 = 0 is a tangent to the hyperbola x2 – 4y2 = 20. Also, find the point of contact.
Solution:
Given equation of the hyperbola is x2 – 4y2 = 20
\(\frac{x^{2}}{20}-\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 20 and b2 = 5
Given equation of line is 3x – 4y + 10 = 0.
y = \(\frac{3 x}{4}+\frac{5}{2}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{3}{4}\) and c = \(\frac{5}{2}\)
For the line y = mx + c to be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we must have

![]()
Question 8.
If the line 3x – 4y = k touches the hyperbola \(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\), then find the value of k.
Solution:
Given equation of the hyperbola is
\(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\)
\(\frac{x^{2}}{5}-\frac{y^{2}}{\frac{5}{4}}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 5, b2 = \(\frac{5}{4}\)
Given equation of line is 3x – 4y = k
y = \(\frac{3}{4} x-\frac{\mathrm{k}}{4}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{3}{4}\), c = \(-\frac{\mathrm{k}}{4}\)
For the line y = mx + c to be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we must have
c2 = a2 m2 – b2
⇒ \(\left(\frac{-\mathrm{k}}{4}\right)^{2}=5\left(\frac{3}{4}\right)^{2}-\frac{5}{4}\)
⇒ \(\frac{\mathrm{k}^{2}}{16}=\frac{5}{16}(9-4)\)
⇒ \(\frac{\mathrm{k}^{2}}{16}=\frac{5}{16}(5)\)
⇒ k2 = 25
⇒ k = ±5
Alternate method:
Given equation of the hyperbola is
\(\frac{x^{2}}{5}-\frac{4 y^{2}}{5}=1\) …….(i)
Given equation of the line is 3x – 4y = k
y = \(\frac{3 x-\mathrm{k}}{4}\)
Substituting this value ofy in (i), we get
\(\frac{x^{2}}{5}-\frac{4}{5}\left(\frac{3 x-\mathrm{k}}{4}\right)^{2}=1\)
⇒ \(\frac{x^{2}}{5}-\frac{4}{5}\left(\frac{9 x^{2}-6 k x+k^{2}}{16}\right)=1\)
⇒ 4x2 – (9x2 – 6kx + k2) = 20
⇒ 4x2 – 9x2 + 6kx – k2 = 20
⇒ -5x2 + 6kx – k2 = 20
⇒ 5x2 – 6kx + (k2 + 20) = 0 …..(ii)
Since, the given line touches the given hyperbola.
The quadratic equation (ii) in x has equal roots.
(-6k)2 – 4(5)(k2 + 20) = 0
⇒ 36k2 – 20k2 – 400 = 0
⇒ 16k2 = 400
⇒ k2 = 25
⇒ k = ±5
Question 9.
Find the equations of the tangents to the hyperbola \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\) making equal intercepts on the co-ordinate axes.
Solution:
Given equation of the hyperbola is \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\).
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 25 and b2 = 9
Since the tangents make equal intercepts on the co-ordinate axes,
∴ m = -1
Equations of tangents to the hyperbola \(\frac{x^{2}}{\mathrm{a}^{2}}-\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
⇒ y = -x ± \(\sqrt{25(-1)^{2}-9}\)
⇒ y = -x ± √16
⇒ x + y = ±4
![]()
Question 10.
Find the equations of the tangents to the hyperbola 5x2 – 4y2 = 20 which are parallel to the line 3x + 2y + 12 = 0.
Solution:
Given equation of the hyperbola is 5x2 – 4y2 = 20
\(\frac{x^{2}}{4}-\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 4 and b2 = 5
Slope of the line 3x + 2y + 12 = 0 is \(-\frac{3}{2}\)
Since the given line is parallel to the tangents,
Slope of the required tangents (m) = \(-\frac{3}{2}\)
Equations of tangents to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
