Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.2
Question 1.
For the following G.P.s, find Sn.
(i) 3, 6, 12, 24, ……..
Solution:

(ii) p, q, \(\frac{\mathbf{q}^{2}}{\mathbf{p}}, \frac{\mathbf{q}^{3}}{\mathbf{p}^{2}}, \ldots\)
Solution:

![]()
(iii) 0.7, 0.07, 0.007, …….
Solution:

(iv) √5, -5, 5√5, -25, …….
Solution:

Question 2.
For a G.P.
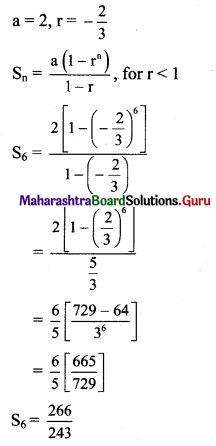
(i) a = 2, r = \(-\frac{2}{3}\), find S6.
Solution:
(ii) If S5 = 1023, r = 4, find a.
Solution:

Question 3.
For a G.P.
(i) If a = 2, r = 3, Sn = 242, find n.
Solution:
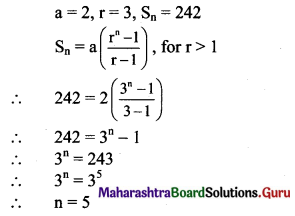
![]()
(ii) For a G.P. sum of the first 3 terms is 125 and the sum of the next 3 terms is 27, find the value of r.
Solution:

Question 4.
For a G.P.
(i) If t3 = 20, t6 = 160, find S7.
Solution:
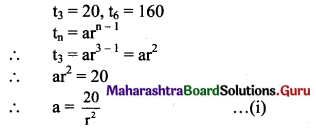

(ii) If t4 = 16, t9 = 512, find S10.
Solution:

Question 5.
Find the sum to n terms
(i) 3 + 33 + 333 + 3333 + …..
Solution:
Sn = 3 + 33 + 333 +….. upto n terms
= 3(1 + 11 + 111 +….. upto n terms)
= \(\frac{3}{9}\)(9 + 99 + 999 + ….. upto n terms)
= \(\frac{3}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{3}{9}\)[(10 + 100 + 1000 + … upto nterms) – (1 + 1 + 1 + ….. n times)]
But 10, 100, 1000, ….. n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10
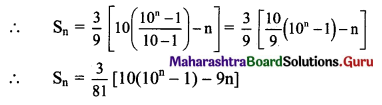
![]()
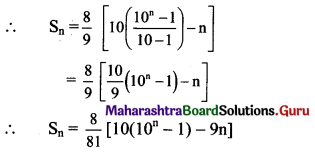
(ii) 8 + 88 + 888 + 8888 + …..
Solution:
Sn = 8 + 88 + 888 + … upto n terms
= 8(1 + 11 + 111 + … upto n terms)
= \(\frac{8}{9}\)(9 + 99 + 999 + … upto n terms)
= \(\frac{8}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{8}{9}\)[(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10
Question 6.
Find the sum to n terms
(i) 0.4 + 0.44 + 0.444 + …..
Solution:
Sn = 0.4 + 0.44 + 0.444 + ….. upto n terms
= 4(0.1 + 0.11 +0.111 + …. upto n terms)
= \(\frac{4}{9}\)(0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{4}{9}\)[(1 – 0.1) + (1 – 0.01) + (1 – 0.001) … upto n terms]
= \(\frac{4}{9}\)[(1 + 1 + 1 + …n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P. with
a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

(ii) 0.7 + 0.77 + 0.777 + ……
Solution:
Sn = 0.7 + 0.77 + 0.777 + … upto n terms
= 7(0.1 + 0.11 + 0.111 + … upton terms)
= \(\frac{7}{9}\)(0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{7}{9}\)[(1 – 0.1) + (1 – 0.01) + (1 – 0.001) +… upto n terms]
= \(\frac{7}{9}\)[(1 + 1 + 1 +… n times) – (0.1 + 0.01 + 0.001 +… upto n terms )]
But 0.1, 0.01, 0.001, … n terms are in G.P. with
a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

Question 7.
Find the sum to n terms of the sequence
(i) 0.5, 0.05, 0.005, …..
Solution:

(ii) 0.2, 0.02, 0.002, ……
Solution:

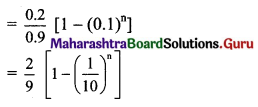
![]()
Question 8.
For a sequence, if Sn = 2(3n – 1), find the nth term, hence showing that the sequence is a G.P.
Solution:

Question 9.
If S, P, R are the sum, product, and sum of the reciprocals of n terms of a G.P, respectively, then verify that \(\left[\frac{S}{R}\right]^{n}\) = P2.
Solution:
Let a be the 1st term and r be the common ratio of the G.P.
∴ the G.P. is a, ar, ar2, ar3, …, arn-1


Question 10.
If Sn, S2n, S3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that Sn(S3n – S2n) = (S2n – Sn)2.
Solution:
Let a and r be the 1st term and common ratio of the G.P. respectively.


Question 11.
Find
(i) \(\sum_{r=1}^{10}\left(3 \times 2^{r}\right)\)
Solution:

(ii) \(\sum_{r=1}^{10} 5 \times 3^{r}\)
Solution:

![]()
Question 12.
The value of a house appreciates 5% per year. How much is the house worth after 6 years if its current worth is Rs. 15 Lac. [Given: (1.05)5 = 1.28, (1.05)6 = 1.34]
Solution:
The value of a house is Rs. 15 Lac.
Appreciation rate = 5% = \(\frac{5}{100}\) = 0.05
Value of house after 1st year = 15(1 + 0.05) = 15(1.05)
Value of house after 6 years = 15(1.05) (1.05)5
= 15(1.05)6
= 15(1.34)
= 20.1 lac.
Question 13.
If one invests Rs. 10,000 in a bank at a rate of interest 8% per annum, how long does it take to double the money by compound interest? [(1.08)5 = 1.47]
Solution:
Amount invested = Rs. 10000
Interest rate = \(\frac{8}{100}\) = 0.08
amount after 1st year = 10000(1 + 0.08) = 10000(1.08)
Value of the amount after n years
= 10000(1.08) × (1.08)n-1
= 10000(1.08)n
= 20000
∴ (1.08)n = 2
∴ (1.08)5 = 1.47 …..[Given]
∴ n = 10 years, (approximately)