Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.3 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.3
Question 1.
A bag contains 3 red marbles and 4 blue marbles. Two marbles are drawn at random without replacement. If the first marble drawn is red, what is the probability that the second marble is blue?
Solution:
Total number of marbles = 3 + 4 = 7
Let event A: The first marble drawn is red.
∴ P(A) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{7} \mathrm{C}_{1}}=\frac{3}{7}\)
Let event B: The second marble drawn is blue.
Since the first red marble is not replaced in the bag, we now have 6 marbles out of which 4 are blue.
∴ Probability that the second marble is blue under the condition that the first red marble is not replaced in the bag = P(B/A) = \(\frac{{ }^{4} \mathrm{C}_{1}}{{ }^{6} \mathrm{C}_{1}}=\frac{4}{6}=\frac{2}{3}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{2}{3} \times \frac{3}{7}\)
= \(\frac{2}{7}\)
Alternate Method:
Total number of marbles = 3 + 4 = 7
Two marbles are drawn at random without replacement.
∴ n(S) = \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) = 7 × 6 = 42
Let event A: The first marble is red and second marble is blue.
First red marble can be drawn from 3 red marbles in \({ }^{3} \mathrm{C}_{1}\) ways and second blue marble can be drawn from 4 blue marbles in \({ }^{4} \mathrm{C}_{1}\) ways.
∴ n(A) = \({ }^{3} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{1}\) = 3 × 4 = 12
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{12}{42}=\frac{2}{7}\)
![]()
Question 2.
A box contains 5 green pencils and 7 yellow pencils. Two pencils are chosen at random from the box without replacement. What is the probability that both are yellow?
Solution:
Total number of pencils = 5 + 7 = 12
Let event A: The first pencil chosen is yellow.
∴ P(A) = \(\frac{{ }^{7} \mathrm{C}_{1}}{{ }^{12} \mathrm{C}_{1}}=\frac{7}{12}\)
Let event B: The second pencil chosen is yellow.
Since the first yellow pencil is not replaced in the box, we now have 11 pencils, out of which 6 are yellow.
∴ Probability that the second pencil is yellow under the condition that the first yellow pencil is not replaced in the box = P(B/A)
= \(\frac{{ }^{6} C_{1}}{{ }^{11} C_{1}}\)
= \(\frac{6}{11}\)
Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{6}{11} \times \frac{7}{12}\)
= \(\frac{7}{22}\)
Question 3.
In a sample of 40 vehicles, 18 are red, 6 are trucks, of which 2 are red. Suppose that a randomly selected vehicle is red. What is the probability it is a truck?
Solution:
One vehicle is selected from 40 vehicles.
Let event A: The selected vehicle is red.
There are total of 18 red vehicles.
∴ P(A) = \(\frac{{ }^{18} \mathrm{C}_{1}}{{ }^{40} \mathrm{C}_{1}}=\frac{18}{40}=\frac{9}{20}\)
Let event B: The selected vehicle is a truck.
There are total of 6 trucks.
Since 2 trucks are red, they are common between A and B.
∴ P(A ∩ B) = \(\frac{{ }^{2} \mathrm{C}_{1}}{{ }^{40} \mathrm{C}_{1}}=\frac{2}{40}=\frac{1}{20}\)
∴ Probability that the selected vehicle is a truck under the condition that it is red = P(B/A)
= \(\frac{P(A \cap B)}{P(A)}\)
= \(\frac{\frac{1}{20}}{\frac{9}{20}}\)
= \(\frac{1}{9}\)
![]()
Question 4.
From a pack of well-shuffled cards, two cards are drawn at random. Find the probability that both the cards are diamonds when
(i) the first card drawn is kept aside.
(ii) the first card drawn is replaced in the pack.
Solution:
In a pack of 52 cards, there are 13 diamond cards.
Let event A: The first card drawn is a diamond card.
∴ P(A) = \(\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{13}{52}=\frac{1}{4}\)
(i) Let event B: The second card drawn is a diamond card.
Since the first diamond card is kept aside, we now have 51 cards, out of which 12 are diamond cards.
Probability that the second card is a diamond card under the condition that the first diamond card is kept aside in the pack = P(B/A) = \(\frac{{ }^{12} \mathrm{C}_{1}}{{ }^{51} \mathrm{C}_{1}}=\frac{12}{51}=\frac{4}{17}\)
∴ Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{1}{4} \times \frac{4}{17}\)
= \(\frac{1}{17}\)
(ii) Let event B: The second card drawn is a diamond card.
Since the first diamond card is replaced in the pack, we now again have 52 cards, out of which 13 are diamond cards.
∴ Probability that the second card is a diamond card under the condition that the first diamond card is replaced in the pack = P(B/A) = \(\frac{{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{1}}=\frac{13}{52}=\frac{1}{4}\)
Required probability = P(A ∩ B)
= P(B/A) . P(A)
= \(\frac{1}{4} \times \frac{1}{4}\)
= \(\frac{1}{16}\)
Question 5.
A, B, and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are \(\frac{3}{4}\), \(\frac{1}{2}\) and \(\frac{5}{8}\). Find the probability that the target
(a) is hit exactly by one of them.
(b) is not hit by any one of them.
(c) is hit.
(d) is exactly hit by two of them.
Solution:
Let event A: A can hit the target,
event B: B can hit the target,
event C: C can hit the target.

Since A, B, C are independent events,
A’, B’, C’ are also independent events.
(a) Let event W: Target is hit exactly by one of them.

(b) Let event X: Target is not hit by any one of them.
∴ P(X) = P(A’ ∩ B’ ∩ C’)
= P(A’) P(B’) P(C’)
= \(\frac{1}{4} \times \frac{1}{2} \times \frac{3}{8}\)
= \(\frac{3}{64}\)
![]()
(c) Let event Y: Target is hit.
∴ P(Y) = 1 – P(target is not hit by any one of them)
= 1 – \(\frac{3}{64}\)
= \(\frac{61}{64}\)
(d) Let event Z: Target is hit by exactly two of them.

Question 6.
The probability that a student X solves a problem in dynamics is \(\frac{2}{5}\) and the probability that student Y solves the same problem is \(\frac{1}{4}\). What is the probability that
(i) the problem is not solved?
(ii) the problem is solved?
(iii) the problem is solved exactly by one of them?
Solution:
Let event A: Student X solves the problem in dynamics,
event B: Student Y solves the problem in dynamics.
∴ P(A) = \(\frac{2}{5}\), P(B) = \(\frac{1}{4}\)
∴ P(A’) = 1 – P(A) = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
P(B’) = 1 – P(B) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
Since A and B are independent events,
A’ and B’ are also independent events.
(i) Let event C: Problem is not solved.
∴ P(C) = P(A’ ∩ B’)
= P(A’) . P(B’)
= \(\frac{3}{5} \times \frac{3}{4}\)
= \(\frac{9}{20}\)
(ii) Let event D: Problem is solved.
Problem can be solved if at least one of the two students solves the problem.
∴ P(D) = P(at least one student solves the problem)
= 1 – P(no student solves the problem)
= 1 – P(A’ ∩ B’)
= 1 – P(A’) P(B’)
= 1 – \(\frac{3}{5} \times \frac{3}{4}\)
= 1 – \(\frac{9}{20}\)
= \(\frac{11}{20}\)
(iii) Let event E: The problem is solved exactly by one of them.
∴ P(E) = P(A’ ∩ B) ∪ P(A ∩ B’)
= P(A’) . P(B) + P(A) . P(B’)
= \(\left(\frac{3}{5} \times \frac{1}{4}\right)+\left(\frac{2}{5} \times \frac{3}{4}\right)\)
= \(\frac{3}{20}+\frac{6}{20}\)
= \(\frac{9}{20}\)
Question 7.
A speaks truth in 80% of the cases and B speaks truth in 60% of the cases. Find the probability that they contradict each other in narrating an incident.
Solution:
Let event A : A speaks the truth,
event B : B speaks the truth.
∴ P(A) = \(\frac{80}{100}=\frac{4}{5}\)
and P(B) = \(\frac{60}{100}=\frac{3}{5}\)
P(A’) = 1 – P(A) = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
and P(B’) = 1 – P(B) = 1 – \(\frac{3}{5}\) = \(\frac{2}{5}\)
∴ P(A and B contradict each other) = P(A speaks the truth and B lies) + P (A lies and B speaks the truth)
= P(A ∩ B’) + P(A’ ∩ B)
= P(A) P(B’) + P(A’) P(B)
= \(\left(\frac{4}{5} \times \frac{2}{5}\right)+\left(\frac{1}{5} \times \frac{3}{5}\right)\)
= \(\frac{8}{25}+\frac{3}{25}\)
= \(\frac{11}{25}\)
![]()
Question 8.
Two hundred patients who had either Eye surgery or Throat surgery were asked whether they were satisfied or unsatisfied regarding the result of their surgery. The following table summarizes their response.
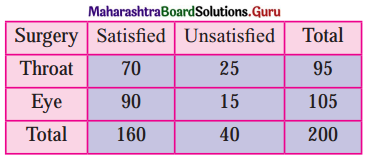
If one person from the 200 patients is selected at random, determine the probability
(a) that the person was satisfied given that the person had Throat surgery.
(b) that person was unsatisfied given that the person had eye surgery.
(c) the person had Throat surgery given that the person was unsatisfied.
Solution:
(a) Let event A: The patient was satisfied,
event B: The patient had throat surgery.
Given, n(S) = 200
n(A ∩ B) = 70
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{70}{200}\)
n(B) = 95
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{95}{200}\)
∴ Required probability = P(A / B)
= \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{\left(\frac{70}{200}\right)}{\left(\frac{95}{200}\right)}\)
= \(\frac{70}{95}\)
= \(\frac{14}{19}\)
Check:
Reduce the sample space to the set of throat patients only.
n(S) = 95
Let E : Patient had satisfactory throat surgery.
n(E) = 70
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{70}{95}=\frac{14}{19}\)
(b) Let event C : The patient was unsatisfied,
event D : The patient had a eye surgery.
Given, n(S) = 200
n(C ∩ D) = 15
∴ P(C ∩ D) = \(\frac{n(C \cap D)}{n(S)}=\frac{15}{200}\)
n(D) = 105
∴ P(D) = \(\frac{105}{200}\)
Required probability = P(C / D)
= \(\frac{P(C \cap D)}{P(D)}\)
= \(\frac{\left(\frac{15}{200}\right)}{\left(\frac{105}{200}\right)}\)
= \(\frac{1}{7}\)
(c) Let event F : The patient had a throat surgery,
event G : The patient was unsatisfied.
Given, n(S) = 200
n(F ∩ G) = 25
∴ P(F ∩ G) = \(\frac{n(F \cap G)}{n(S)}=\frac{25}{200}\)
n(G) = 40
∴ P(G) = \(\frac{n(G)}{n(S)}=\frac{40}{200}\)
∴ Required probability = P(F / G)
= \(\frac{P(F \cap G)}{P(G)}\)
= \(\frac{\left(\frac{25}{200}\right)}{\left(\frac{40}{200}\right)}\)
= \(\frac{5}{8}\)
![]()
Question 9.
Two dice are thrown together. Let A be the event ‘getting 6 on the first die’ and B be the event ‘getting 2 on the second die’. Are events A and B independent?
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: Getting 6 on the first die.
∴ A = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
Let event B : Gettting 2 on the second die.
∴ B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
∴ n(B) = 6
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
Now, A ∩ B = {(6, 2)}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{1}{36}\) …..(i)
P(A) × P(B) = \(\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}\) ……..(ii)
From (i) and (ii), we get
P(A ∩ B) = P(A) × P(B)
∴ A and B are independent events.
Question 10.
The probability that a man who is 45 years old will be alive till he becomes 70 is \(\frac{5}{12}\). The probability that his wife who is 40 years old will be alive till she becomes 65 is \(\frac{3}{8}\). What is the probability that, 25 years hence,
(a) the couple will be alive?
(b) exactly one of them will be alive?
(c) none of them will be alive?
(d) at least one of them will be alive?
Solution:
Let event A: The man will be alive till 70.
∴ P(A) = \(\frac{5}{12}\)
Let event B: The wife will be alive till 65.
∴ P(B) = \(\frac{3}{8}\)
∴ P(A’) = 1 – P(A) = 1 – \(\frac{5}{12}\) = \(\frac{7}{12}\)
P(B’) = 1 – P(B) = 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)
Since A and B are independent events,
A’ and B’ are also independent events.
(a) Let event C : Both man and his wife will be alive.
∴ P(C) = P(A ∩ B) = P(A) . P(B)
= \(\frac{5}{12} \times \frac{3}{8}\)
= \(\frac{5}{32}\)
(b) Let event D: Exactly one of them will be alive.
∴ P(D) = P(A’ ∩ B) + P(A ∩ B’)
= P(A’) . P(B) + P(A) . P(B’)
= \(\left(\frac{7}{12} \times \frac{3}{8}\right)+\left(\frac{5}{12} \times \frac{5}{8}\right)\)
= \(\frac{21}{96}+\frac{25}{96}\)
= \(\frac{23}{48}\)
(c) Let event E: None of them will be alive.
∴ P(E) = P(A’ ∩ B’) = P(A’) . P(B’)
= \(\frac{7}{12} \times \frac{5}{8}\)
= \(\frac{35}{96}\)
(d) Let event F: At least one of them will be alive.
∴ P(F) = 1 – P(none of them will be alive)
= 1 – \(\frac{35}{96}\)
= \(\frac{61}{96}\)
![]()
Question 11.
A box contains 10 red balls and 15 green balls. Two balls are drawn in succession without replacement. What is the probability that,
(a) the first is red and the second is green?
(b) one is red and the other is green?
Solution:
Total number of balls = 10 + 15 = 25
(a) Let event A: First ball drawn is red.
∴ P(A) = \(\frac{{ }^{10} \mathrm{C}_{1}}{{ }^{25} \mathrm{C}_{1}}=\frac{10}{25}=\frac{2}{5}\)
Let event B: Second ball drawn is green.
Since the first red ball is not replaced in the box, we now have 24 balls, out of which 15 are green.
∴ Probability that the second ball is green under the condition that the first red ball is not replaced in the box = P(B/A) = \(\frac{{ }^{15} \mathrm{C}_{1}}{{ }^{24} \mathrm{C}_{1}}=\frac{15}{24}=\frac{5}{8}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{2}{5} \times \frac{5}{8}\)
= \(\frac{1}{4}\)
(b) To find the probability that one ball is red and the other is green, there are two possibilities:
First ball is red and second ball is green.
OR
The first ball is the green and the second ball is red.
From above, we get
P(First ball is red and second ball is green) = \(\frac{1}{4}\)
Similarly,
P(First ball is green and second ball is red) = \(\frac{{ }^{15} \mathrm{C}_{1}}{{ }^{25} \mathrm{C}_{1}} \times \frac{{ }^{10} \mathrm{C}_{1}}{{ }^{24} \mathrm{C}_{1}}=\frac{15}{25} \times \frac{10}{24}=\frac{1}{4}\)
∴ Required probability = P(First ball is red and second ball is green) + P(First ball is green and second ball is red)
= \(\frac{1}{4}\) + \(\frac{1}{4}\)
= \(\frac{1}{2}\)
Question 12.
A bag contains 3 yellow and 5 brown balls. Another bag contains 4 yellow and 6 brown balls. If one ball is drawn from each bag, what is the probability that,
(a) both the balls are of the same colour?
(b) the balls are of a different colours?
Solution:
(a) Let event A: A yellow ball is drawn from each bag.
Probability of drawing one yellow ball from total 8 balls of first bag and that of drawing one yellow ball out of total 10 balls of second bag is
P(A) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{8} \mathrm{C}_{1}} \times \frac{{ }^{4} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}\) = \(\frac{3}{8} \times \frac{4}{10}=\frac{3}{20}\)
Let event B: A brown ball is drawn from each bag.
Probability of drawing one brown ball out of total 8 balls of first bag and that of drawing one brown ball out of total 10 balls of second bag is
P(B) = \(\frac{{ }^{5} \mathrm{C}_{1}}{{ }^{8} \mathrm{C}_{1}} \times \frac{{ }^{6} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}\) = \(\frac{5}{8} \times \frac{6}{10}=\frac{3}{8}\)
Since both the events are mutually exclusive events,
P(A ∩ B) = 0
∴ P(both the balls are of the same colour) = P(both are of yellow colour) or P(both are of brown colour)
= P(A) + P(B)
= \(\frac{3}{20}+\frac{3}{8}\)
= \(\frac{21}{40}\)
(b) P(both the balls are of different colour) = 1 – P(both the balls are of the same colour)
= 1 – \(\frac{21}{40}\)
= \(\frac{19}{40}\)
![]()
Question 13.
An urn contains 4 black, 5 white, and 6 red balls. Two balls are drawn one after the other without replacement. What is the probability that at least one of them is black?
Solution:
Total number of balls in the um = 4 + 5 + 6 = 15
Two balls are drawn from 15 balls without replacement.
∴ n(S) = \({ }^{15} \mathrm{C}_{1} \times{ }^{14} \mathrm{C}_{1}\) = 15 × 14 = 210
Let event A: At least one ball is black.
i.e., the first ball is black, and the second ball is non-black or the first ball is non-black and the second ball is black, or both the first and second balls are black.
∴ n(A) = \({ }^{4} \mathrm{C}_{1} \times{ }^{11} \mathrm{C}_{1}+{ }^{11} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{1}+{ }^{4} \mathrm{C}_{1} \times{ }^{3} \mathrm{C}_{1}\)
= 4 × 11 + 11 × 4 + 4 × 3
= 100
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{100}{210}=\frac{10}{21}\)
Check:
Required probability = 1 – P(no black ball in two balls)
= 1 – \(\frac{{ }^{11} C_{2}}{{ }^{15} C_{2}}=1-\frac{11 \times 10}{15 \times 14}=1-\frac{11}{21}=\frac{10}{21}\)
Question 14.
Three fair coins are tossed. What is the probability of getting three heads given that at least two coins show heads?
Solution:
When three fair coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
∴ n(S) = 8
Let event A: Getting three heads.
∴ A = {HHH}
Let event B: Getting at least two heads.
∴ B = {HHT, HTH, THH, HHH}
∴ n(B) = 4
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{8}\)
Now, A ∩ B = {HHH}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{1}{8}\)
∴ Probability of getting three heads, given that at least two coins show heads, is given by
P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\)
= \(\frac{\frac{1}{8}}{\frac{4}{8}}\)
= \(\frac{1}{4}\)
Question 15.
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards are drawn are face cards?
Solution:
In a pack of52 cards, there are 12 face cards.
Let event A: The first card drawn is a face card.
∴ P(A) = \(\frac{{ }^{12} C_{1}}{{ }^{52} C_{1}}=\frac{12}{52}=\frac{3}{13}\)
Let event B: The second card drawn is a face card.
Since the first card is not replaced in the pack, we now have 51 cards, out of which 11 are face cards.
∴ Probability that the second card is a face card under the condition that the first card is not replaced in the pack = P(B/A) = \(\frac{{ }^{11} C_{1}}{{ }^{51} C_{1}}=\frac{11}{51}\)
∴ Required probability = P(A ∩ B) = P(B/A) . P(A)
= \(\frac{11}{51} \times \frac{3}{13}\)
= \(\frac{11}{221}\)
![]()
Question 16.
Bag A contains 3 red and 2 white balls and bag B contains 2 red and 5 white balls. A bag is selected at random, a ball is drawn and put into the other bag, and then a ball is drawn from that bag. Find the probability that both the balls are drawn are of the same colour.
Solution:
Let event C1: The first ball drawn is red and from bag A,
event D1: The first ball drawn is white and from bag A,
event E1: The first ball drawn is red and from bag B,
event F1: The first ball drawn is white and from bag B,
event C2: Second ball drawn is red and from bag B,
event D2: Second ball drawn is white and from bag B,
event E2: Second ball drawn is red and from bag A,
event F2: Second ball drawn is white and from bag A,
event G: Selecting bag A in the first place,
event H: Selecting bag B in the first place.
P(G) = P(H) = \(\frac{1}{2}\)
Let event X: Both the balls drawn are of same colour.
∴ P(X) = P(G) × P (X/G) + P(H) × P(X/H) …….(i)
If bag A is selected in first place, then In bag A, we have 5 balls, out of which 3 are red.
Probability of getting first red ball from bag A = P(C1) = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{5} \mathrm{C}_{1}}=\frac{3}{5}\)
Since first red ball is put into the bag B, we now have 8 balls in bag B, out of which 3 are red.
∴ Probability of getting second red ball from bag B.
P(C2/C1) = \(\frac{{ }^{3} C_{1}}{{ }^{8} C_{1}}=\frac{3}{8}\)
Similarly, probability of getting first white ball from bag A = P(D1) = \(\frac{{ }^{2} C_{1}}{{ }^{5} C_{1}}=\frac{2}{5}\)
and probability of getting second white ball form bag B = P(D2/D1) = \(\frac{{ }^{6} C_{1}}{{ }^{8} C_{1}}=\frac{6}{8}\)
∴ P(X/G) = P(C1) P(C2/C1) + P(D1) P(D2/D1)
= \(\frac{3}{5} \times \frac{3}{8}+\frac{2}{5} \times \frac{6}{8}\)
= \(\frac{21}{40}\) …..(ii)
Similarly, P(X/H) = P(E1) P(E2/E1) + P(F1) P(F2/F1)
= \(\frac{2}{7} \times \frac{4}{6}+\frac{5}{7} \times \frac{3}{6}\)
= \(\frac{23}{42}\) ………(iii)
From (i), (ii), (iii),
Required probability = \(\frac{1}{2} \times \frac{21}{40}+\frac{1}{2} \times \frac{23}{42}\)
= \(\frac{3604}{6720}\)
= \(\frac{901}{1680}\)
Question 17.
Activity: A bag contains 3 red and 5 white balls. Two balls are drawn at random one after the other without replacement. Find the probability that both the balls are white.
Solution:
Let, event A: The first ball drawn is white
event B: Second ball drawn is white.
P(A) = \(\frac{5}{8}\)
After drawing the first ball, without replacing it into the bag a second ball is drawn from the remaining 7 balls.
∴ P(B/A) = \(\frac{4}{7}\)
∴ P(Both balls are white) = P(A ∩ B)
= P(A) . P(B/A)
= \(\frac{5}{8}\) × \(\frac{4}{7}\)
= \(\frac{5}{14}\)
![]()
Question 18.
A family has two children. Find the probability that both the children are girls, given that at least one of them is a girl.
Solution:
A family has two children.
∴ Sample space S = {BB, BG, GB, GG}
∴ n(S) = 4
Let event A: At least one of the children is a girl.
∴ A = {GG, GB, BG}
∴ n(A) = 3
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{4}\)
Let event B: Both children are girls.
∴ B = {GG}
∴ n(B) = 1
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{4}\)
Also, A ∩ B = B
∴ P(A ∩ B) = P(B) = \(\frac{1}{4}\)
∴ Required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{\frac{1}{4}}{\frac{3}{4}}\)
= \(\frac{1}{3}\)