Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Miscellaneous Exercise 5 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Miscellaneous Exercise 5
(I) Select the correct option from the given alternatives.
Question 1.
If A is (5, -3) and B is a point on the X-axis such that the slope of line AB is -2, then B ≡
(a) (7, 2)
(b) (\(\frac{7}{2}\), 0)
(c) (0, \(\frac{7}{2}\))
(d) (\(\frac{2}{7}\), 0)
Answer:
(b) (\(\frac{7}{2}\), 0)
Hint:
Let B(x, 0) be the point on X-axis.
We have A = (5, -3)
slope of AB = -2
⇒ \(\frac{0-(-3)}{x-5}\) = -2
⇒ 3 = -2(x – 5)
⇒ 3 = -2x + 10
⇒ x = \(\frac{7}{2}\)
Co-ordinates of point B = (\(\frac{7}{2}\), 0)
![]()
Question 2.
If the point (1, 1) lies on the line passing through the points (a, 0) and (0, b), then \(\frac{1}{a}+\frac{1}{b}=\)
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{a b}\)
Answer:
(c) 1
Hint:
Line passes through (a, 0), (0, b).
x-intercept = a, y-intercept = b
∴ Equation of line is \(\frac{x}{a}+\frac{y}{b}=1\) …….(i)
Since line (i) passes through (1, 1), (1, 1) satisfies (i)
∴ \(\frac{1}{a}+\frac{1}{b}=1\)
Question 3.
If A(1, -2), B(-2, 3) and C(2, -5) are the vertices of ΔABC, then the equation of median BE is
(a) 7x + 13y + 47 = 0
(b) 13x + 7y + 5 = 0
(c) 7x – 13y + 5 = 0
(d) 13x – 7y – 5 = 0
Answer:
(b) 13x + 7y + 5 = 0
Hint:
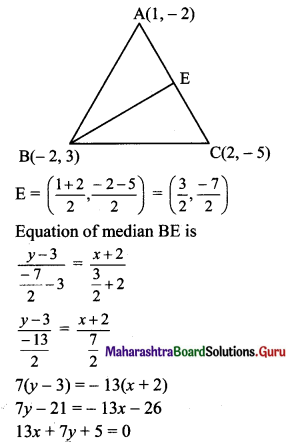
Question 4.
The equation of the line through (1, 2), which makes equal intercepts on the axes, is
(a) x + y = 1
(b) x + y = 2
(c) x + y = 4
(d) x + y = 3
Answer:
(d) x + y = 3
Hint:
Let the equation of required line be
\(\frac{x}{a}+\frac{y}{b}=1\) ……..(i)
Since the line makes equal intercepts on the axes, a = b
\(\frac{x}{a}+\frac{y}{a}=1\)
∴ x + y = a ……(ii)
But, equation (ii) passes through (1, 2).
1 + 2 = a
∴ a = 3
Substituting a = 3 in equation (ii), we get
x + y = 3
Question 5.
If the line kx + 4y = 6 passes through the point of intersection of the two lines 2x + 3y = 4 and 3x + 4y = 5, then k =
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Hint:
Given two lines are
2x + 3y = 4 ……(i)
3x + 4y = 5 …….(ii)
Multiplying (i) by 3 and (ii) by 2 and then subtracting, we get
y = 2
Substituting y = 2 in (i), we get
x = -1
∴ Point of intersection of lines (i) and (ii) is (-1, 2).
Given that the line kx + 4y = 6 passes through (-1, 2).
k(-1) + 4(2) = 6
∴ k = 2
![]()
Question 6.
The equation of a line, having inclination 120° with positive direction of X-axis, which is at a distance of 3 units from the origin is
(a) √3x ± y + 6 = 0
(b) √3x + y ± 6 = 0
(c) x + y = 6
(d) x + y = -6
Answer:
(b) √3x + y ± 6 = 0
Hint:
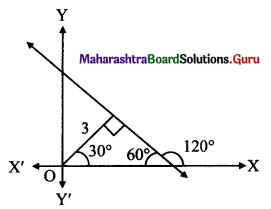
Here, α = 30° and p = 3 units
Equation of line with inclination a and distance from origin as p is
x cos α + y sin α = p
∴ x cos 30° + y sin 30° = ±3
∴ \(\frac{\sqrt{3} x}{2}+\frac{y}{2}=\pm 3\)
∴ √3x + y ± 6 = 0
Question 7.
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) 1
(d) \(\frac{4}{3}\)
Answer:
(d) \(\frac{4}{3}\)
Hint:
Slope of line 3x + y = 3 is -3
∴ Slope of line perpendicular to given line = \(\frac{1}{3}\)
Equation of required line passing through (2, 2) and having slope \(\frac{1}{3}\) is
y – 2 = \(\frac{1}{3}\)(x – 2)
3y – 6 = x – 2
∴ x – 3y + 4 = 0
∴ y-intercept = \(\frac{-4}{-3}=\frac{4}{3}\)
Question 8.
The angle between the line √3x – y – 2 = 0 and x – √3y + 1 = 0 is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Answer:
(b) 30°
Hint:

Question 9.
If kx + 2y – 1 = 0 and 6x – 4y + 2 = 0 are identical lines, then determine k.
(a) -3
(b) \(-\frac{1}{3}\)
(c) \(\frac{1}{3}\)
(d) 3
Answer:
(a) -3
Hint:
Lines kx + 2y – 1 = 0 and 6x – 4y + 2 = 0 are identical.
∴ \(\frac{k}{6}=\frac{2}{-4}=\frac{-1}{2}\)
∴ k = -3
![]()
Question 10.
Distance between the two parallel lines y = 2x + 7 and y = 2x + 5 is
(a) \(\frac{\sqrt{2}}{\sqrt{5}}\)
(b) \(\frac{1}{\sqrt{5}}\)
(c) \(\frac{\sqrt{5}}{2}\)
(d) \(\frac{2}{\sqrt{5}}\)
Answer:
(d) \(\frac{2}{\sqrt{5}}\)
Hint:
Here, c1 = 7, c2 = 5, a = 2 and b = -1
Distance between parallel lines
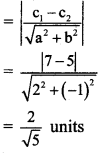
II. Answer the following questions.
Question 1.
Find the value of k:
(a) if the slope of the line passing through the points P(3, 4), Q(5, k) is 9.
(b) the points A(1, 3), B(4, 1), C(3, k) are collinear.
(c) the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3).
Solution:
(a) Given, P(3, 4), Q(5, k) and
Slope of PQ = 9
\(\frac{\mathrm{k}-4}{5-3}\) = 9
\(\frac{\mathrm{k}-4}{2}\) = 9
k – 4 = 18
k = 22
(b) Given, points A(1, 3), B(4, 1) and C(3, k) are collinear.
Slope of AB = Slope of BC
\(\frac{1-3}{4-1}=\frac{k-1}{3-4}\)
\(\frac{-2}{3}=\frac{\mathrm{k}-1}{-1}\)
2 = 3k – 3
k = \(\frac{5}{3}\)
(c) Given, point P(1, k) lies on the line joining A(2, 2) and B(3, 3).
Slope of AB = Slope of BP
\(\frac{3-2}{3-2}=\frac{3-k}{3-1}\)
1 = \(\frac{3-\mathrm{k}}{2}\)
2 = 3 – k
k = 1
![]()
Question 2.
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence, find its slope.
Solution:
Given equation is 6x + 3y + 8 = 0, which can be written as
3y = – 6x – 8
y = \(\frac{-6 x}{3}-\frac{8}{3}\)
y = -2x – \(\frac{8}{3}\)
This is of the form y = mx + c with m = -2
y = -2x – \(\frac{8}{3}\) is in slope-intercept form with slope = -2
Question 3.
Find the distance of the origin from the line x = -2.
Solution:
Given equation of line is x = -2
This equation represents a line parallel to Y-axis and at a distance of 2 units to the left of Y-axis.
∴ Distance of the origin from the line is 2 units.
Question 4.
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Solution:
Given equation is 3x + 2y – 6 = 0.
Substituting x = 2 and y = 3 in L.H.S. of given equation, we get
L.H.S. = 3x + 2y – 6
= 3(2) + 2(3) – 6
= 6
≠ R.H.S.
∴ Point A does not lie on the given line.
Question 5.
Which of the following lines passes through the origin?
(a) x = 2
(b) y = 3
(c) y = x + 2
(d) 2x – y = 0
Answer:
(d) 2x – y = 0
Hint:
Any line passing through origin is of the form y = mx or ax + by = 0.
Here in the given option, 2x – y = 0 is in the form ax + by = 0.
∴ Option (d) is the correct answer.
Question 6.
Obtain the equation of the line which is:
(a) parallel to the X-axis and 3 units below it.
(b) parallel to the Y-axis and 2 units to the left of it.
(c) parallel to the X-axis and making an intercept of 5 on the Y-axis.
(d) parallel to the Y-axis and making an intercept of 3 on the X-axis.
Solution:
(a) Equation of a line parallel to X-axis is y = k.
Since the line is at a distance of 3 units below X-axis, k = -3
∴ The equation of the required line is y = -3.
![]()
(b) Equation of a line parallel to Y-axis is x = h.
Since the line is at a distance of 2 units to the left of Y-axis, h = -2
∴ The equation of the required line is x = -2.
(c) Equation of a line parallel to X-axis with y-intercept ‘k’ is y = k.
Here, y-intercept = 5
∴ The equation of the required line is y = 5.
(d) Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 3
∴ The equation of the required line is x = 3.
Question 7.
Obtain the equation of the line containing the point:
(i) (2, 3) and parallel to the X-axis.
(ii) (2, 4) and perpendicular to the Y-axis.
Solution:
(i) Equation of a line parallel to X-axis is of the form y = k.
Since the line passes through (2, 3), k = 3
∴ The equation of the required line is y = 3.
(ii) Equation of a line perpendicular to Y-axis
i.e., parallel to X-axis, is of the form y = k.
Since the line passes through (2, 4), k = 4
∴ The equation of the required line is y = 4.
Question 8.
Find the equation of the line:
(a) having slope 5 and containing point A(-1, 2).
(b) containing the point T(7, 3) and having inclination 90°.
(c) through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co-ordinate axes.
Solution:
(a) Given, slope(m) = 5 and the line passes through A(-1, 2).
Equation of the line in slope point form is y – y1 = m(x – x1)
The equation of the required line is
y – 2 = 5(x + 1)
y – 2 = 5x + 5
∴ 5x – y + 7 = 0
![]()
(b) Given, Inclination of line = θ = 90°
the required line is parallel to Y-axis.
Equation of a line parallel to Y-axis is of the form x = h.
Since the line passes through (7, 3), h = 7
∴ The equation of the required line is x = 7.
(c) Given equation of the line is 3x + 2y = 2.
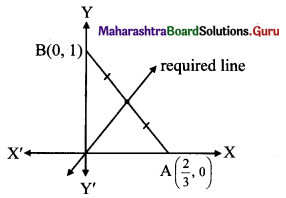
\(\frac{3 x}{2}+\frac{2 y}{2}=1\)
\(\frac{x}{\frac{2}{3}}+\frac{y}{1}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), with a = \(\frac{2}{3}\), b= 1.
The line 3x + 2y = 2 intersects the X-axis at A(\(\frac{2}{3}\), 0) and Y-axis at B(0, 1).
Required line is passing through the midpoint of AB.
Midpoint of AB = \(\left(\frac{\frac{2}{3}+0}{2}, \frac{0+1}{2}\right)=\left(\frac{1}{3}, \frac{1}{2}\right)\)
∴ Required line passes through (0, 0) and \(\left(\frac{1}{3}, \frac{1}{2}\right)\).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-0}{\frac{1}{2}-0}=\frac{x-0}{\frac{1}{3}-0}\)
2y = 3x
∴ 3x – 2y = 0
Question 9.
Find the equation of the line passing through the points S(2, 1) and T(2, 3).
Solution:
The required line passes through the points S(2, 1) and T(2, 3).
Since both the given points have same x co-ordinates i.e. 2
the given points lie on a line parallel to Y-axis.
∴ The equation of the required line is x = 2.
Question 10.
Find the distance of the origin from the line 12x + 5y + 78 = 0.
Solution:
Let p be the perpendicular distance of origin from the line 12x + 5y + 78 = 0.
Here, a = 12, b = 5, c = 78
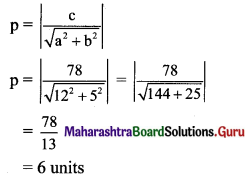
Question 11.
Find the distance between the parallel lines 3x + 4y + 3 = 0 and 3x + 4y + 15 = 0.
Solution:
Equations of the given parallel lines are 3x + 4y + 3 = 0 and 3x + 4y + 15 = 0
Here, a = 3, b = 4, c1 = 3 and c2 = 15
∴ Distance between the parallel lines
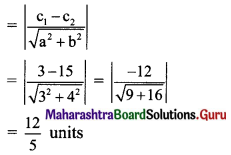
Question 12.
Find the equation of the line which contains the point A(3, 5) and makes equal intercepts on the co-ordinates axes.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) …….(i)
This line passes through A(3, 5).
∴ \(\frac{3}{a}+\frac{5}{b}=1\) ……..(ii)
Since the required line makes equal intercepts on the co-ordinates axes,
a = b …….(iii)
Substituting the value of b in (ii), we get
\(\frac{3}{a}+\frac{5}{a}=1\)
∴ a = 8
∴ b = 8 …… [From (iii)]
Substituting the values of a and b in equation (i), the equation of the required line is
\(\frac{x}{8}+\frac{y}{8}=1\)
∴ x + y = 8
![]()
Case II: Line passing through origin.
Slope of line passing through origin and A(3, 5) is
m = \(\frac{5-0}{3-0}=\frac{5}{3}\)
∴ Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is
y = \(\frac{5}{3}\)x
∴ 5x – 3y = 0
Question 13.
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of
(a) the sides
(b) the medians
(c) perpendicular bisectors of sides
(d) altitudes of ?ABC
Solution:
Vertices of ∆ABC are A(1, 4), B(2, 3) and C(1, 6)
(a) Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}\) = \(\frac{x-x_{1}}{x_{2}-x_{1}}\)
Equation of side AB is
\(\frac{y-4}{3-4}=\frac{x-1}{2-1}\)
y – 4 = -1(x – 1)
y – 4 = -x + 1
x + y = 5
Equation of side BC is
\(\frac{y-3}{6-3}=\frac{x-2}{1-2}\)
-1(y – 3) = 3(x – 2)
-y + 3 = 3x – 6
∴ 3x + y = 9
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on a line parallel to Y-axis.
∴ The equation of side AC is x = 1.
(b) Let D, E and F be the midpoints of sides AC and AB respectively of ∆ABC.
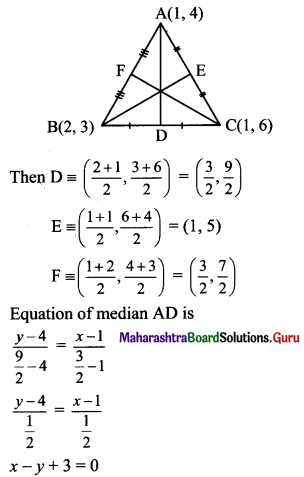

(c) Slope of side BC = \(\left(\frac{6-3}{1-2}\right)=\left(\frac{3}{-1}\right)\) = -3
Slope of perpendicular bisector of BC is \(\frac{1}{3}\) and the line passes through \(\left(\frac{3}{2}, \frac{9}{2}\right)\).
Equation of the perpendicular bisector of side BC is
\(\left(y-\frac{9}{2}\right)=\frac{1}{3}\left(x-\frac{3}{2}\right)\)
3(2y – 9) = (2x – 3)
6y – 27 = 2x – 3
2x – 6y + 24 = 0
∴ x – 3y + 12 = 0
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, perpendicular bisector of side AC is parallel to X-axis.
Since, the perpendicular bisector of side AC passes through E(1, 5).
The equation of perpendicular bisector of side AC is y = 5.
Slope of side AB = \(\left(\frac{3-4}{2-1}\right)\) = -1
Slope of perpendicular bisector of AB is 1 and the line passes through \(\left(\frac{3}{2}, \frac{7}{2}\right)\).
Equation of the perpendicular bisector of side AB is
\(\left(y-\frac{7}{2}\right)=1\left(x-\frac{3}{2}\right)\)
2y – 7 = 2x – 3
2x – 2y + 4 = 0
∴ x – y + 2 = 0
(d) Let AX, BY, and CZ be the altitudes through the vertices A, B and C respectively of ∆ABC.
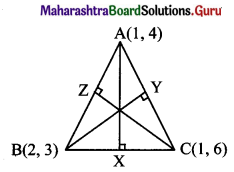
Slope of BC = -3
Slope of AX = \(\frac{1}{3}\) ……[∵ AX ⊥ BC]
Since altitude AX passes through (1, 4) and has slope \(\frac{1}{3}\),
equation of altitude AX is
y – 4 = \(\frac{1}{3}\)(x – 1)
3y – 12 = x – 1
∴ x – 3y + 11 = 0
Since both the points A and C have same x co-ordinates i.e. 1
the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, altitude BY is parallel to X-axis.
Since the altitude BY passes through B(2, 3), the equation of altitude BY is y = 3.
Also, slope of AB = -1
Slope of CZ = 1
Since altitude CZ passes through (1, 6) and has slope 1,
equation of altitude CZ is
y – 6 = 1(x – 1)
∴ x – y + 5 = 0
![]()
Question 14.
Find the equation of the line which passes through the point of intersection of lines x + y – 3 = 0, 2x – y + 1 = 0 and which is parallel to X-axis.
Solution:
Let u ≡ x + y – 3 = 0 and v ≡ 2x – y + 1 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
(x + y – 3) + k(2x – y + 1) = 0 …..(i)
x + y – 3 + 2kx – ky + k = 0
x + 2kx + y – ky – 3 + k = 0
(1 + 2k)x + (1 – k)y – 3 + k = 0
But, this line is parallel to X-axis
Its slope = 0
⇒ \(\frac{-(1+2 k)}{1-k}=0\)
⇒ 1 + 2k = 0
⇒ k = \(\frac{-1}{2}\)
Substituting the value of k in (i), we get
(x + y – 3) + \(\frac{-1}{2}\) (2x – y + 1) = 0
⇒ 2(x + y – 3) – (2x – y + 1 ) = 0
⇒ 2x + 2y – 6 – 2x + y – 1 = 0
⇒ 3y – 7 = 0, which is the equation of the required line.
Question 15.
Find the equation of the line which passes through the point of intersection of lines x + y + 9 = 0, 2x + 3y + 1 = 0 and which makes x-intercept 1.
Solution:
Let u ≡ x + y + 9 = 0 and v ≡ 2x + 3y + 1 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
(x + y + 9) + k(2x + 3y + 1) = 0 ……(i)
⇒ x + y + 9 + 2kx + 3ky + k = 0
⇒ (1 + 2k)x + (1 + 3k)y + 9 + k = 0
But, x-intercept of this line is 1.
⇒ \(\frac{-(9+\mathrm{k})}{1+2 \mathrm{k}}\)
⇒ -9 – k = 1 + 2k
⇒ k = \(\frac{-10}{3}\)
Substituting the value of k in (i), we get
(x + y + 9) + (\(\frac{-10}{3}\)) (2x + 3y + 1) = 0
⇒ 3(x + y + 9) – 10(2x + 3y + 1) = 0
⇒ 3x + 3y + 27 – 20x – 30y – 10 = 0
⇒ -17x – 27y+ 17 = 0
⇒ 17x + 27y – 17 = 0, which is the equation of the required line.
Question 16.
Find the equation of the line through A(-2, 3) and perpendicular to the line through S(1, 2) and T(2, 5).
Solution:
Slope of ST = \(\frac{5-2}{2-1}\) = 3
Since the required line is perpendicular to ST,
slope of required line = \(\frac{-1}{3}\) and line passes through A(-2, 3)
Equation of the line in slope point form is y – y1 = m(x – x1)
The equation of the required line is
y – 3 = \(\frac{-1}{3}\)(x + 2)
⇒ 3(y – 3) = -(x + 2)
⇒ 3y – 9 = -x – 2
⇒ x + 3y = 7
![]()
Question 17.
Find the x-intercept of the line whose slope is 3 and which makes intercept 4 on the Y-axis.
Solution:
Equation of a line having slope ‘m’ and y-intercept ‘c’ is y = mx + c
Given, m = 3, c = 4
The equation of the line is y = 3x + 4
3x – y = -4
\(\frac{3 x}{(-4)}-\frac{y}{(-4)}=1\)
\(\frac{x}{\left(\frac{-4}{3}\right)}+\frac{y}{4}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where
x-intercept = a
x-intercept = \(\frac{-4}{3}\)
Alternate Method:
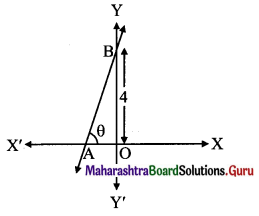
Let θ be the inclination of the line.
Then tan θ = 3 …..[∵ slope = 3 (given)]
\(\frac{\mathrm{OB}}{\mathrm{OA}}=3\)
\(\frac{4}{\mathrm{OA}}=3\)
OA = \(\frac{4}{3}\)
x-intercept = –\(\frac{4}{3}\) as point A is to the left side of Y-axis.
Question 18.
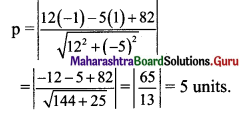
Find the distance of P(-1, 1) from the line 12(x + 6) = 5(y – 2).
Solution:
Given equation of the line is
12(x + 6) = 5(y – 2)
12x + 72 = 5y – 10
12x – 5y + 82 = 0
Let p be the perpendicular distance of the point (-1, 1) from the line 12x – 5y + 82 = 0.
Question 19.
Line through A(h, 3) and B(4,1) intersect the line lx – 9y -19 = 0 at right angle. Find the value of h.
Solution:
Given, A(h, 3) and B(4, 1)
Slope of AB (m1) = \(\frac{1-3}{4-h}\)
m1 = \(\frac{2}{h-4}\)
Slope of line 7x – 9y – 19 = 0 is m2 = \(\frac{7}{9}\)
Since line AB and line 7x – 9y – 19 = 0 are perpendicular to each other,
m1 × m2 = -1
\(\frac{2}{h-4} \times \frac{7}{9}=-1\)
14 = 9(4 – h)
14 = 36 – 9h
9h = 22
h = \(\frac{22}{9}\)
![]()
Question 20.
Two lines passing through M(2, 3) intersect each other at an angle of 45°. If slope of one line is 2, find the equation of the other line.
Solution:
Let m be the slope of the required line which make an angle of 45° with the other line.
Slope of one of the lines is 2.
tan 45° = \(\left|\frac{\mathrm{m}-2}{1+\mathrm{m}(2)}\right|\)
1 = \(\left|\frac{m-2}{1+2 m}\right|\)
\(\frac{m-2}{1+2 m}=\pm 1\)
\(\frac{\mathrm{m}-2}{1+2 \mathrm{~m}}\) = 1 or \(\frac{\mathrm{m}-2}{1+2 \mathrm{~m}}\) = -1
m – 2 = 1 + 2m or m – 2 = -1 – 2m
m = -3 or 3m = 1
m = -3 or m = \(\frac{1}{3}\)
Required line passes through M(2, 3)
When m = -3, equation of the line is
y – 3 = -3(x – 2)
y – 3 = -3x + 6
∴ 3x + y = 9
When m = \(\frac{1}{3}\), equation of the line is
y – 3 = \(\frac{1}{3}\)(x – 2)
3y – 9 = x – 2
∴ x – 3y + 7 = 0
Question 21.
Find the y-intercept of the line whose slope is 4 and which has x-intercept 5.
Solution:
Given, slope = 4, x-intercept = 5
Since the x-intercept of the line is 5, it passes through (5, 0).
Equation of the line in slope point form is y – y1 = m(x – x1)
Equation of the required line is
y – 0 = 4(x – 5)
y = 4x – 20
4x – y = 20
\(\frac{4 x}{20}-\frac{y}{20}=1\)
\(\frac{x}{5}+\frac{y}{(-20)}=1\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where
x-intercept = b, y-intercept = -20
Question 22.
Find the equations of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11 and y = 12.
Solution:
Given, equations of sides of rectangle are x = 8, x = 10, y = 11 and y = 12
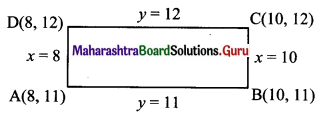
From the above diagram,
Vertices of rectangle are A(8, 11), B(10, 11), C(10, 12) and D(8, 12).
Equation of diagonal AC is
\(\frac{y-11}{12-11}=\frac{x-8}{10-8}\)
\(\frac{y-11}{1}=\frac{x-8}{2}\)
2y – 22 = x – 8
x – 2y + 14 = 0
Equation of diagonal BD is
\(\frac{y-11}{12-11}=\frac{x-10}{8-10}\)
\(\frac{y-11}{1}=\frac{x-10}{-2}\)
-2y + 22 = x – 10
x + 2y = 32
![]()
Question 23.
A(1, 4), B(2, 3) and C(1, 6) are vertices of AABC. Find the equation of the altitude through B and hence find the co-ordinates of the point where this altitude cuts the side AC of ∆ABC.
Solution:
Vertices of triangle are A(1, 4), B(2, 3) and C(1, 6).
Let BD be the altitude through the vertex B.
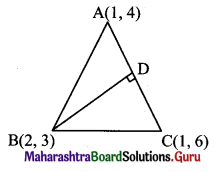
Since both the points A and C have same x co-ordinates i.e. 1
the given points lie on a line parallel to Y-axis.
The equation of the line AC is x = 1 …..(i)
AC is parallel to Y-axis and therefore, altitude BD is parallel to X-axis.
Since the altitude BD passes through B(2, 3), the equation of altitude BD is y = 3 ……(ii)
From (i) and (ii),
Point of intersection of AC and altitude BD is (1, 3).
Question 24.
The vertices of ∆PQR are P(2, 1), Q(-2, 3) and R(4, 5). Find the equation of the median through R.
Solution:
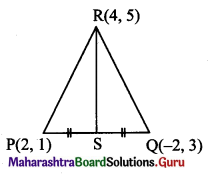
Let S be the midpoint of side PQ.
Then RS is the median through R.
S = \(\left(\frac{2-2}{2}, \frac{3+1}{2}\right)\) = (0, 2)
The median RS passes through the points R(4, 5) and S(0, 2).
∴ Equation of median RS is
\(\frac{y-5}{2-5}=\frac{x-4}{0-4}\)
⇒ \(\frac{y-5}{-3}=\frac{x-4}{-4}\)
⇒ 4(y – 5) = 3(x – 4)
⇒ 4y – 20 = 3x – 12
∴ 3x – 4y + 8 = 0
Question 25.
A line perpendicular to segment joining A(1, 0) and B(2, 3) divides it internally in the ratio 1 : 2. Find the equation of the line. Solution:
Given, A(1, 0), B(2, 3)
Slope of AB = \(\frac{3-0}{2-1}\) = 3
Required line is perpendicular to AB.
Slope of required line = \(\frac{-1}{3}\)
Let point C divide AB in the ratio 1 : 2.

Required line passes through \(\left(\frac{4}{3}, 1\right)\) and has slope = \(\frac{-1}{3}\)
Equation of the line in slope point form is y – y1 = m(x – x1)
The equation of the required line is
y – 1 = \(\frac{-1}{3}\left(x-\frac{4}{3}\right)\)
⇒ 3(y – 1) = \(-1\left(x-\frac{4}{3}\right)\)
⇒ 3y – 3 = -x + \(\frac{4}{3}\)
⇒ 9y – 9 = -3x + 4
⇒ 3x + 9y = 13
Question 26.
Find the co-ordinates of the foot of the perpendicular drawn from the point P(-1, 3) to the line 3x – 4y – 16 = 0.
Solution:
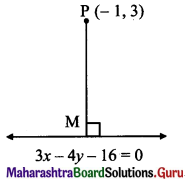
Let M be the foot of perpendicular drawn from P(-1, 3) to the line 3x – 4y – 16 = 0
Slope of the line 3x – 4y – 16 = 0 is \(\frac{-3}{-4}=\frac{3}{4}\)
Since PM ⊥ to line (i),
slope of PM = \(\frac{-4}{3}\)
Equation of PM is
y – 3 = \(\frac{-4}{3}\) (x + 1)
⇒ 3(y – 3) = -4(x + 1)
⇒ 3y – 9 = -4x – 4
∴ 4x + 3y – 5 = 0 ……(ii)
The foot of perpendicular i.e., point M, is the point of intersection of equation (i) and (ii).
By (i) × 3 + (ii) × 4, we get
25x = 68
x = \(\frac{68}{25}\)
Substituting x = \(\frac{68}{25}\) in (ii), we get
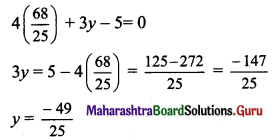
The co-ordinates of the foot of perpendicular M are \(\left(\frac{68}{25}, \frac{-49}{25}\right)\)
![]()
Question 27.
Find points on the X-axis whose distance from the line \(\frac{x}{3}+\frac{y}{4}=1\) is 4 units.
Solution:
The equation of line is \(\frac{x}{3}+\frac{y}{4}=1\)
i.e. 4x + 3y – 12 = 0 …..(i)
Let (h, 0) be a point on the X-axis.
The distance of this point from line (i) is 4.
⇒ \(\frac{|4 h+3(0)-12|}{\sqrt{4^{2}+3^{2}}}=4\)
⇒ \(\frac{|4 \mathrm{~h}-12|}{5}=4\)
⇒ |4h – 12| = 20
⇒ 4h – 12 = 20 or 4h – 12 = -20
⇒ 4h = 32 or 4h = -8
⇒ h = 8 or h = -2
∴ The required points are (8, 0) and (-2, 0).
Question 28.
The perpendicular from the origin to a line meets it at (-2, 9). Find the equation of the line.
Solution:
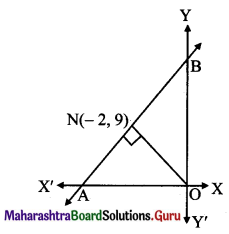
Slope of ON = \(\frac{9-0}{-2-0}=\frac{-9}{2}\)
Since line AB ⊥ ON,
slope of the line AB perpendicular to ON is \(\frac{2}{9}\) and it passes through point N(-2, 9).
Equation of the line in slope point form is y – y1 = m(x – x1)
Equation of line AB is
y – 9 = \(\frac{2}{9}\)(x + 2)
⇒ 9(y – 9) = 2(x + 2)
⇒ 9y – 81 = 2x + 4
⇒ 2x – 9y + 85 = 0
Question 29.
P(a, b) is the midpoint of a line segment intercepted between the axes. Show that the equation of the line is \(\frac{x}{a}+\frac{y}{b}=2\).
Solution:
Let the intercepts of a line AB be x1 and y1 on the X and Y-axes respectively.
A ≡ (x1, 0), B = (0, y1)
P(a, b) is the midpoint of a line segment AB intercepted between the axes.

Question 30.
Find the distance of the line 4x – y = 0 from the point P(4, 1) measured along the line making an angle of 135° with the positive X-axis.
Solution:
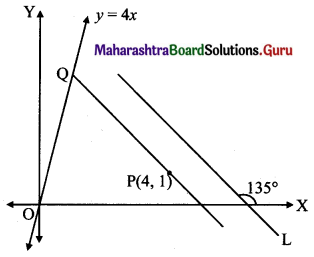
Let a line L make angle 135° with positive X-axis.
Required distance = PQ, where PQ || line L
Slope of PQ = tan 135°
= tan (180° – 45°)
= -tan 45°
= -1
Equation of PQ is
y – 1 = (-1)(x – 4)
y – 1 = -x + 4
x + y = 5 …..(i)
To get point Q we solve the equation 4x – y = 0 with (i)
Substituting y = 4x in (i), we get
5x = 5
x = 1
Substituting x = 1 in (i), we get
1 + y = 5
y = 4
∴ Q = (1, 4)
PQ = \(\sqrt{(4-1)^{2}+(1-4)^{2}}\)
= \(\sqrt{9+9}\)
= 3√2
![]()
Question 31.
Show that there are two lines which pass through A(3, 4) and the sum of whose intercepts is zero.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) ……(1)
This line passes through (3, 4)
\(\frac{3}{a}+\frac{4}{b}=1\) …..(ii)
Since the sum of the intercepts of the line is zero,
a + b = 0
a = -b ……(iii)
Substituting the value of a in (ii), we get
\(\frac{3}{-b}+\frac{4}{b}=1\)
\(\frac{1}{b}\) = 1
b = 1
a = -1 ……[From (iii)]
Substituting the values of a and b in (i),
the equation of the required line is
\(\frac{x}{-1}+\frac{y}{1}=1\)
x – y = -1
∴ x – y + 1 = 0
Case II: Line passing through origin.
Slope of line passing through origin and A(3, 4) is
m = \(\frac{4-0}{3-0}=\frac{4}{3}\)
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
The equation of the required line is
y = \(\frac{4}{3}\)x
∴ 4x – 3y = 0
∴ There are two lines which pass through A(3, 4) and the sum of whose intercepts is zero.
![]()
Question 32.
Show that there is only one line which passes through B(5, 5) and the sum of whose intercepts is zero.
Solution:
When line is passing through origin, the sum of intercepts made by the line is zero.
Slope of line passing through origin and B(5, 5) is
m = \(\frac{5-0}{5-0}\) = 1
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
The equation of the required line is y = x
∴ x – y = 0
∴ There is only one line which passes through B(5, 5) and the sum of whose intercepts is zero.