Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1
Prove by the method of induction, for all n ∈ N.
Question 1.
2 + 4 + 6 + …… + 2n = n(n + 1)
Solution:
Let P(n) = 2 + 4 + 6 + …… + 2n = n(n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(1 + 1) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 4 + 6 + ….. + 2k = k(k + 1) ……(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 4 + 6 + …… + 2(k + 1) = (k + 1) (k + 2)
L.H.S. = 2 + 4 + 6 + …+ 2(k + 1)
= 2 + 4 + 6+ ….. + 2k + 2(k + 1)
= k(k + 1) + 2(k + 1) …..[From (i)]
= (k + 1).(k + 2)
= R.H.S.
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 4 + 6 + …… + 2n = n(n + 1) for all n ∈ N.
![]()
Question 2.
3 + 7 + 11 + ……… to n terms = n(2n + 1)
Solution:
Let P(n) = 3 + 7 + 11 + ……… to n terms = n(2n +1), for all n ∈ N.
But 3, 7, 11, …. are in A.P.
∴ a = 3 and d = 4
Let tn be the nth term.
∴ tn = a + (n – 1)d = 3 + (n – 1)4 = 4n – 1
∴ P(n) = 3 + 7 + 11 + ……. + (4n – 1) = n(2n + 1)
Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 1[2(1)+ 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 3 + 7 + 11 + ….. + (4k – 1) = k(2k + 1) …..(i)
Sept III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
3 + 7 + 11 + …+ [4(k + 1) – 1] = (k + 1)(2k + 3)
L.H.S. = 3 + 7 + 11 + …… + [4(k + 1) – 1]
= 3 + 7 + 11 + ….. + (4k – 1) + [4(k+ 1) – 1]
= k(2k + 1) + (4k + 4 – 1) …..[From (i)]
= 2k2 + k + 4k + 3
= 2k2 + 2k + 3k + 3
= 2k(k + 1) + 3(k + 1)
= (k + 1) (2k + 3)
= R.H.S.
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 3 + 7 + 11 + ….. to n terms = n(2n + 1) for all n ∈ N.
Question 3.
12 + 22 + 32 +…..+ n2 = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let P(n) = 12 + 22 + 32 +…..+ n2 = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 12 = 1
RHS = \(\frac{1(1+1)[2(1)+1]}{6}=\frac{6}{6}\) = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 12 + 22 + 32 +…+ k2 = \(\frac{k(k+1)(2 k+1)}{6}\) …..(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 12 + 22 + 32 + …+ n2 = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.
![]()
Question 4.
12 + 32 + 52 + ….. + (2n – 1)2 = \(\frac{n}{3}\) (2n – 1)(2n + 1)
Solution:
Let P(n) = 12 + 32 + 52+…..+ (2n – 1)2 = \(\frac{n}{3}\) (2n – 1)(2n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 12 = 1
R.H.S. = \(\frac{1}{3}\) [2(1) – 1][2(1) + 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 12 + 32 + 52 +….+(2k – 1)2 = \(\frac{k}{3}\) (2k – 1)(2k + 1) …….(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 12 + 32 + 52 + …+ (2n – 1)2 = \(\frac{n}{3}\) (2n – 1)(2n + 1) for all n ∈ N.
Question 5.
13 + 33 + 53 + ….. to n terms = n2 (2n2 – 1)
Solution:
Let P(n) = 13 + 33 + 53 + …. to n terms = n2 (2n2 – 1), for all n ∈ N.
But 1, 3, 5, are in A.P.
∴ a = 1, d = 2
Let tn be the nth term.
tn = a + (n – 1) d = 1 + (n – 1) 2 = 2n – 1
∴ P(n) = 13 + 33 + 53 +…..+ (2n – 1)3 = n2 (2n2 – 1)
Step I:
Put n = 1
L.H.S. = 13 = 1
R.H.S. = 12 [2(1)2 – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 13 + 33 + 53 +…+ (2k – 1)3 = k2 (2k2 – 1) …..(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 13 + 33 + 53 + … to n terms = n2 (2n2 – 1) for all n ∈ N.
![]()
Question 6.
1.2 + 2.3 + 3.4 +… + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2)
Solution:
Let P(n) = 1.2 + 2.3 + 3.4 +….+n(n + 1) = \(\frac{n(n+1)(n+2)}{3}\), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 1.2 = 2
R.H.S. = \(\frac{1}{3}\) (1 + 1)(1 + 2) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 1.2 + 2.3 + 3.4 + ….. + k(k + 1) = \(\frac{k}{3}\) (k + 1)(k + 2) ……(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.2 + 2.3 + 3.4 + … + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2), for all n ∈ N.
Question 7.
1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n2 + 6n – 1)
Solution:
Let P(n) = 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n2 + 6n -1), for all n ∈ N.
But first factor in each term, i.e., 1, 3, 5,… are in A.P. with a = 1 and d = 2.
∴ nth term = a + (n – 1)d = 1 + (n – 1) 2 = (2n – 1)
Also, second factor in each term,
i.e., 3, 5, 7, … are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1) d = 3 + (n – 1) 2 = (2n + 1)
∴ nth term, tn = (2n – 1) (2n + 1)
∴ P(n) ≡ 1.3 + 3.5 + 5.7 + …. + (2n – 1) (2n + 1) = \(\frac{n}{3}\) (4n2 + 6n – 1)
Step I:
Put n = 1
L.H.S. = 1.3 = 3
R.H.S. = \(\frac{1}{3}\) [4(1)2 + 6(1) – 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is trae for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 1.3 + 3.5 + 5.7 +….+ (2k – 1)(2k + 1) = \(\frac{k}{3}\) (4k2 + 6k – 1) ……(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n2 + 6n – 1) for all n ∈ N.
![]()
Question 8.
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
Solution:
Let P(n) ≡ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = \(\frac{1}{1.3}=\frac{1}{3}\)
R.H.S. = \(\frac{1}{2(1)+1}=\frac{1}{3}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 k-1)(2 k+1)}=\frac{k}{2 k+1}\) …..(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.
Question 9.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\)
Solution:
Let P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.
But first factor in each term of the denominator,
i.e., 3, 5, 7, ….. are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1)d = 3 + (n – 1) 2 = (2n + 1)
Also, second factor in each term of the denominator,
i.e., 5, 7, 9, … are in A.P. with a = 5 and d = 2.
∴ nth term = a + (n – 1) d = 5 + (n – 1) 2 = (2n + 3)
∴ nth term, tn = \(\frac{1}{(2 n+1)(2 n+3)}\)
P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 n+1)(2 n+3)}\) = \(\frac{n}{3(2 n+3)}\)
Step I:
Put n = 1
L.H.S. = \(\frac{1}{3.5}=\frac{1}{15}\)
R.H.S. = \(\frac{1}{3[2(1)+3]}=\frac{1}{3(2+3)}=\frac{1}{15}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 k+1)(2 k+3)}\) = \(\frac{k}{3(2 k+3)}\) ….(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
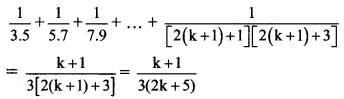

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.
![]()
Question 10.
(23n – 1) is divisible by 7.
Solution:
(23n – 1) is divisible by 7 if and only if (23n – 1) is a multiple of 7.
Let P(n) ≡ (23n – 1) = 7m, where m ∈ N.
Step I:
Put n = 1
∴ 23n – 1 = 23(1) – 1 = 23 – 1 = 8 – 1 = 7
∴ (23n – 1) is a multiple of 7.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
i.e., 23k – 1 is a multiple of 7.
∴ 23k – 1 = 7a, where a ∈ N
∴ 23k = 7a + 1 ……(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
23(k+1) – 1 = 7b, where b ∈ N.
∴ P(k + 1) = 23(k+1) – 1
= 23k+3 – 1
= 23k . (23) – 1
= (7a + 1)8 – 1 …..[From (i)]
= 56a + 8 – 1
= 56a + 7
= 7(8a + 1)
7b, where b = (8a + 1) ∈ N
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (24n – 1) is divisible by 7, for all n ∈ N.
Question 11.
(24n – 1) is divisible by 15.
Solution:
(24n – 1) is divisible by 15 if and only if (24n – 1) is a multiple of 15.
Let P(n) ≡ (24n – 1) = 15m, where m ∈ N.
Step I:
Put n = 1
∴ 24(1) – 1 = 16 – 1 = 15
∴ (24n – 1) is a multiple of 15.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 24k – 1 = 15a, where a ∈ N
∴ 24k = 15a + 1 …..(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
∴ 24(k+1) – 1 = 15b, where b ∈ N
∴ P(k + 1) = 24(k+1) – 1 = 24k+4 – 1
= 24k . 24 – 1
= 16 . (24k) – 1
= 16(15a + 1) – 1 …..[From (i)]
= 240a + 16 – 1
= 240a + 15
= 15(16a + 1)
= 15b, where b = (16a + 1) ∈ N
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (24n – 1) is divisible by 15, for all n ∈ N.
![]()
Question 12.
3n – 2n – 1 is divisible by 4.
Solution:
(3n – 2n – 1) is divisible by 4 if and only if (3n – 2n – 1) is a multiple of 4.
Let P(n) ≡ (3n – 2n – 1) = 4m, where m ∈ N.
Step I:
Put n = 1
∴ (3n – 2n – 1) = 3(1) – 2(1) – 1 = 0 = 4(0)
∴ (3n – 2n – 1) is a multiple of 4.
∴ P(n) is tme for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 3k – 2k – 1 = 4a, where a ∈ N
∴ 3k = 4a + 2k + 1 ….(i)
Step III:
We have to prove that P(n) is tme for n = k + 1,
i.e., to prove that
3(k+1) – 2(k + 1) – 1 = 4b, where b ∈ N
P(k + 1) = 3k+1 – 2(k + 1) – 1
= 3k . 3 – 2k – 2 – 1
= (4a + 2k + 1) . 3 – 2k – 3 …….[From (i)]
= 12a + 6k + 3 – 2k – 3
= 12a + 4k
= 4(3a + k)
= 4b, where b = (3a + k) ∈ N
∴ P(n) is tme for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is tme for all n ∈ N.
∴ 3n – 2n – 1 is divisible by 4, for all n ∈ N.
Question 13.
5 + 52 + 53 + ….. + 5n = \(\frac{5}{4}\) (5n – 1)
Solution:
Let P(n) ≡ 5 + 52 + 53 +…..+ 5n = \(\frac{5}{4}\) (5n – 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 5
R.H.S. = \(\frac{5}{4}\) (51 – 1) = 5
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ 5 + 52 + 53 + ….. + 5k = \(\frac{5}{4}\) (5k – 1) …….(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 5 + 52 + 53 + … + 5n = \(\frac{5}{4}\) (5n – 1), for all n ∈ N.
![]()
Question 14.
(cos θ + i sin θ)n = cos (nθ) + i sin (nθ)
Solution:
Let P(n) ≡ (cos θ + i sin θ)n = cos nθ + i sin nθ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = (cos θ + i sin θ)1 = cos θ + i sin θ
R.H.S. = cos[(1)θ] + i sin[(1)θ] = cos θ + i sin θ
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Step II:
Let us assume that P(n) is true for n = k.
∴ (cos θ + i sin θ)k = cos kθ + i sin kθ …….(i)
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
(cos θ + i sin θ)k+1 = cos (k + 1)θ + i sin (k + 1)θ
L.H.S. = (cos θ + i sin θ)k+1
= (cos θ + i sin θ)k . (cos θ + i sin θ)
= (cos kθ + i sin kθ) . (cos θ + i sin θ) ……[From (i)]
= cos kθ cos θ + i sin θ cos kθ + i sin kθ cosθ – sin kθ sin θ ……[∵ i2 = -1]
= (cos kθ cos θ – sin k θ sin θ) + i(sin kθ cos θ + cos kθ sin θ)
= cos(kθ + θ) + i sin(kθ + θ)
= cos(k + 1) θ + i sin (k + 1) θ
= R.H.S.
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (cos θ + i sin θ)n = cos (nθ) + i sin (nθ), for all n ∈ N.
Question 15.
Given that tn+1 = 5 tn+4, t1 = 4, prove by method of induction that tn = 5n – 1.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation tn+1 = 5 tn+4, t1 = 4 and R.H.S. a general statement tn = 5n – 1.
Step I:
Put n = 1
L.H.S. = 4
R.H.S. = 51 – 1 = 4
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S. = t2 = 5t1 + 4 = 24
R.H.S. = t2 = 52 – 1 = 24
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 2.
Step II:
Let us assume that P(n) is true for n = k.
∴ tk+1 = 5 tk+4 and tk = 5k – 1
Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that tk+1 = 5k+1 – 1
Since tk+1 = 5 tk+4 and tk = 5k – 1 …..[From Step II]
tk+1 = 5 (5k – 1) + 4 = 5k+1 – 1
∴ P(n) is true for n = k + 1.
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ tn = 5n – 1, for all n ∈ N.
![]()
Question 16.
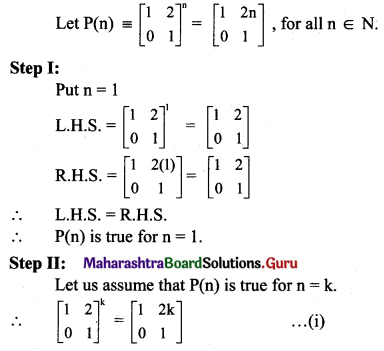
Prove by method of induction
\(\left(\begin{array}{ll}
1 & 2 \\
0 & 1
\end{array}\right)^{n}=\left(\begin{array}{cc}
1 & 2 n \\
0 & 1
\end{array}\right) \forall n \in N\)
Solution: