Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.2
I. Evaluate the following limits:
Question 1.
\(\lim _{z \rightarrow 2}\left[\frac{z^{2}-5 z+6}{z^{2}-4}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow-3}\left[\frac{x+3}{x^{2}+4 x+3}\right]\)
Solution:

![]()
Question 3.
\(\lim _{y \rightarrow 0}\left[\frac{5 y^{3}+8 y^{2}}{3 y^{4}-16 y^{2}}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow-2}\left[\frac{-2 x-4}{x^{3}+2 x^{2}}\right]\)
Solution:


Question 5.
\(\lim _{x \rightarrow 3}\left[\frac{x^{2}+2 x-15}{x^{2}-5 x+6}\right]\)
Solution:

II. Evaluate the following limits:
Question 1.
\(\lim _{u \rightarrow 1}\left[\frac{u^{4}-1}{u^{3}-1}\right]\)
Solution:
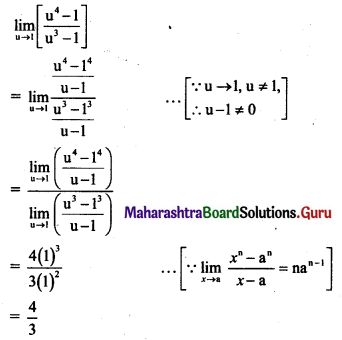
Question 2.
\(\lim _{x \rightarrow 3}\left[\frac{1}{x-3}-\frac{9 x}{x^{3}-27}\right]\)
Solution:
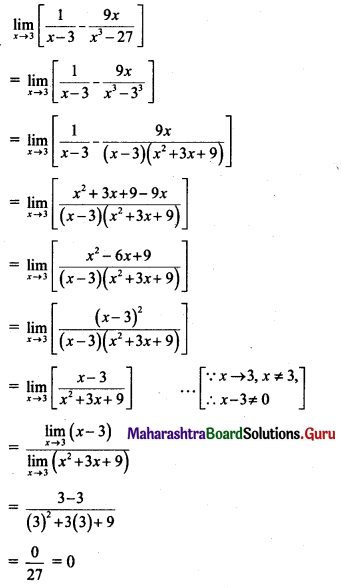
![]()
Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-4 x^{2}+4 x}{x^{2}-1}\right]\)
Solution:

Question 4.
\(\lim _{\Delta x \rightarrow 0}\left[\frac{(x+\Delta x)^{2}-2(x+\Delta x)+1-\left(x^{2}-2 x+1\right)}{\Delta x}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow \sqrt{2}}\left[\frac{x^{2}+x \sqrt{2}-4}{x^{2}-3 x \sqrt{2}+4}\right]\)
Solution:
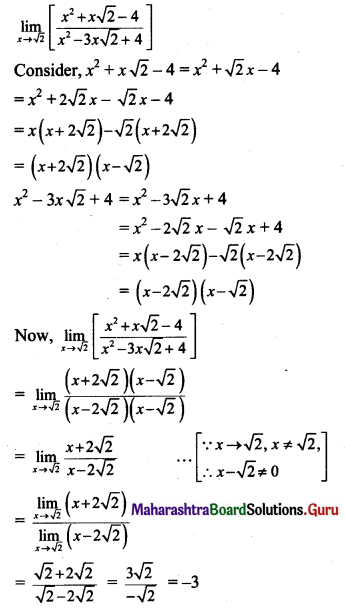
![]()
Question 6.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-7 x+6}{x^{3}-7 x^{2}+16 x-12}\right]\)
Solution:
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-7 x+6}{x^{3}-7 x^{2}+16 x-12}\right]\)
As x → 2, numerator and denominator both tend to zero
∴ x – 2 is a factor of both.
To find the other factor for both of them, by synthetic division
Consider, Numerator = x3 + 0x2 – 7x + 6

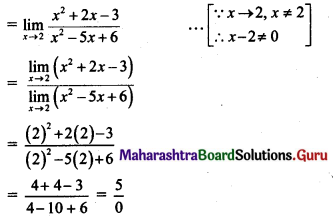
∴ The limit does not exist
III. Evaluate the following limits:
Question 1.
\(\lim _{y \rightarrow \frac{1}{2}}\left[\frac{1-8 y^{3}}{y-4 y^{3}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 1}\left[\frac{x-2}{x^{2}-x}-\frac{1}{x^{3}-3 x^{2}+2 x}\right]\)
Solution:

![]()
Question 3.
\(\lim _{x \rightarrow 1}\left[\frac{x^{4}-3 x^{2}+2}{x^{3}-5 x^{2}+3 x+1}\right]\)
Solution:
\(\lim _{x \rightarrow 1}\left[\frac{x^{4}-3 x^{2}+2}{x^{3}-5 x^{2}+3 x+1}\right]\)
As x → 1, numerator and denominator both tend to zero
∴ x – 1 is a factor of both.
To find the factor of numerator and denominator by synthetic division
Consider, numerator = x4 + 0x3 – 3x2 + 0x + 2


Question 4.
\(\lim _{x \rightarrow 1}\left[\frac{x+2}{x^{2}-5 x+4}+\frac{x-4}{3\left(x^{2}-3 x+2\right)}\right]\)
Solution:


![]()
Question 5.
\(\lim _{x \rightarrow a}\left[\frac{1}{x^{2}-3 a x+2 a^{2}}+\frac{1}{2 x^{2}-3 a x+a^{2}}\right]\)
Solution:

