Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.3 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 3 Permutations and Combination Ex 3.3
Question 1.
Find n, if nP6 : nP3 = 120 : 1.
Solution:
nP6 : nP3 = 120 : 1
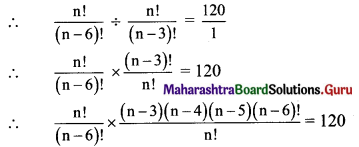
∴ (n – 3) (n – 4) (n – 5) = 120
∴ (n – 3) (n – 4) (n – 5) = 6 × 5 × 4
Comparing on both sides, we get
n – 3 = 6
∴ n = 9
![]()
Question 2.
Find m and n, if (m+n)P2 = 56 and (m-n)P2 = 12.
Solution:
(m+n)P2 = 56
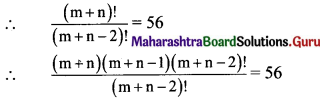
(m + n) (m + n – 1) = 56
Let m + n = t
t(t – 1) = 56
t2 – t – 56 = 0
(t – 8) (t + 7) = 0
t = 8 or t = -7
m + n = 8 or m + n = -7
But m + n ≠ -7
∴ m + n = 8 ……(i)
Also, (m-n)P2 = 12
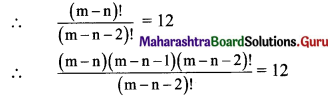
(m – n) (m – n – 1) = 12
Let m – n = a
a(a – 1) = 12
a2 – a – 12 = 0
(a – 4)(a + 3) = 0
a = 4 or a = -3
m – n = 4 or m – n = -3
But m – n ≠ -3
∴ m – n = 4 ……(ii)
Adding (i) and (ii), we get
2m = 12
∴ m = 6
Substituting m = 6 in (ii), we get
6 – n = 4
∴ n = 2
Question 3.
Find r, if 12Pr-2 : 11Pr-1 = 3 : 14.
Solution:
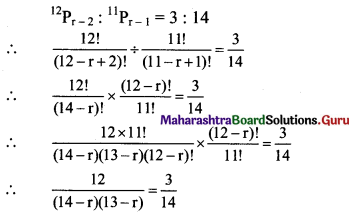
(14 – r)(13 – r) = 8 × 7
Comparing on both sides, we get
14 – r = 8
∴ r = 6
Question 4.
Show that (n + 1) (nPr) = (n – r + 1) [(n+1)Pr]
Solution:

![]()
Question 5.
How many 4 letter words can be formed using letters in the word MADHURI, if (a) letters can be repeated (b) letters cannot be repeated.
Solution:
There are 7 letters in the word MADHURI.
(a) A 4 letter word is to be formed from the letters of the word MADHURI and repetition of letters is allowed.
∴ 1st letter can be filled in 7 ways.
2nd letter can be filled in 7 ways.
3rd letter can be filled in 7 ways.
4th letter can be filled in 7 ways.
∴ Total no. of ways a 4-letter word can be formed = 7 × 7 × 7 × 7 = 2401
(b) When repetition of letters is not allowed, the number of 4-letter words formed from the letters of the word MADHURI is 7P4 = \(\frac{7 !}{(7-4) !}=\frac{7 \times 6 \times 5 \times 4 \times 3 !}{3 !}\) = 840
Question 6.
Determine the number of arrangements of letters of the word ALGORITHM if
(a) vowels are always together.
(b) no two vowels are together.
(c) consonants are at even positions.
(d) O is the first and T is the last letter.
Solution:
There are 9 letters in the word ALGORITHM.
(a) When vowels are always together.
There are 3 vowels in the word ALGORITHM (i.e., A, I, O).
Let us consider these 3 vowels as one unit.
This unit with 6 other letters is to be arranged.
∴ The number of arrangement = 7P7 = 7! = 5040
3 vowels can be arranged among themselves in 3P3 = 3! = 6 ways.
∴ Required number of arrangements = 7! × 3!
= 5040 × 6
= 30240
(b) When no two vowels are together.
There are 6 consonants in the word ALGORITHM,
they can be arranged among themselves in 6P6 = 6! = 720 ways.
Let consonants be denoted by C.
_C _C_ C _C_C_C
There are 7 places marked by ‘_’ in which 3 vowels can be arranged.
∴ Vowels can be arranged in 7P3 = \(\frac{7 !}{(7-3) !}=\frac{7 \times 6 \times 5 \times 4 !}{4 !}\) = 210 ways.
∴ Required number of arrangements = 720 × 210 = 151200
![]()
(c) When consonants are at even positions.
There are 4 even places and 6 consonants in the word ALGORITHM.
∴ 6 consonants can be arranged at 4 even positions in 6P4 = \(\frac{6 !}{(6-4) !}=\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\) = 360 ways.
Remaining 5 letters (3 vowels and 2 consonants) can be arranged in odd position in 5P5 = 5! = 120 ways.
∴ Required number of arrangements = 360 × 120 = 43200
(d) When O is the first and T is the last letter.
All the letters of the word ALGORITHM are to be arranged among themselves such that arrangement begins with O and ends with T.
∴ Position of O and T are fixed.
∴ Other 7 letters can be arranged between O and T among themselves in 7P7 = 7! = 5040 ways.
∴ Required number of arrangements = 5040
Question 7.
In a group photograph, 6 teachers and principal are in the first row and 18 students are in the second row. There are 12 boys and 6 girls among the students. If the middle position is reserved for the principal and if no two girls are together, find the number of arrangements.
Solution:
In 1st row, 6 teachers can be arranged among themselves in 6P6 = 6! ways.
In the 2nd row, 12 boys can be arranged among themselves in 12P12 = 12! ways.
No two girls are together.
So, there are 13 places formed by 12 boys in which 6 girls occupy any 6 places in 13P6 ways.
∴ Required number of arrangements

Question 8.
Find the number of ways so that letters of the word HISTORY can be arranged as
(a) Y and T are together
(b) Y is next to T
(c) there is no restriction
(d) begin and end with a vowel
(e) end in ST
(f) begin with S and end with T
Solution:
There are 7 letters in the word HISTORY
(a) When ‘Y’ and ‘T’ are together.
Let us consider ‘Y’ and ‘T’ as one unit.
This unit with other 5 letters are to be arranged.
∴ The number of arrangement of one unit and 5 letters = 6P6 = 6! = 720
Also, ‘Y’ and ‘T’ can be arranged among themselves in 2P2 = 2! = 2 ways.
∴ A total number of arrangements when Y and T are always together = 6! × 2!
= 120 × 2
= 1440
![]()
(b) When ‘Y’ is next to ‘T’.
Let us take this (‘Y’ next to ‘T’) as one unit.
This unit with 5 other letters is to be arranged.
∴ The number of arrangements of 5 letters and one unit = 6P6 = 6! = 720
Also, ‘Y’ has to be always next to ‘T’.
∴ They can be arranged among themselves in 1 way only.
∴ Total number of arrangements possible when Y is next to T = 720 × 1 = 720
(c) When there is no restriction.
7 letters can be arranged among themselves in 7P7 = 7! ways.
∴ The total number of arrangements possible if there is no restriction = 7!
(d) When begin and end with a vowel.
There are 2 vowels in the word HISTORY.
All other letters of the word HISTORY are to be arranged between 2 vowels such that the arrangement begins and ends with a vowel.
The other 5 letters can be filled between the two vowels in 5P5 = 5! = 120 ways.
Also, 2 vowels can be arranged among themselves at first and last places in 2P2 = 2! = 2 ways.
∴ Total number of arrangements when the word begins and ends with vowel = 120 × 2 = 240
(e) When a word ends in ST.
As the arrangement ends with ST,
the remaining 5 letters can be arranged among themselves in 5P5 = 5! = 120 ways.
∴ Total number of arrangements when the word ends with ST = 120
(f) When a word begins with S and ends with T.
As arrangement begins with S and ends with T,
the remaining 5 letters can be arranged between S and T among themselves in 5P5 = 5! = 120 ways.
Total number of arrangements when the word begins with S and ends with T = 120
![]()
Question 9.
Find the number of arrangements of the letters in the word SOLAPUR so that consonants and vowels are placed alternately.
Solution:
There are 4 consonants S, L, P, R, and 3 vowels A, O, U in the word SOLAPUR.
Consonants and vowels are to be alternated.
∴ Vowels must occur in even places and consonants in odd places.
∴ 3 vowels can be arranged at 3 even places in 3P3 = 3! = 6 ways.
Also, 4 consonants can be arranged at 4 odd places in 4P4 = 4! = 24 ways.
Required number of arrangements = 6 × 24 = 144
Question 10.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 4, 5, 6, 8 if
(a) digits can be repeated.
(b) digits cannot be repeated.
Solution:
(a) A 4 digit number is to be made from the digits 1, 2, 4, 5, 6, 8 such that digits can be repeated.
∴ Unit’s place digit can be filled in 6 ways.
10’s place digit can be filled in 6 ways.
100’s place digit can be filled in 6 ways.
1000’s place digit can be filled in 6 ways.
∴ Total number of numbers that can be formed = 6 × 6 × 6 × 6 = 1296
(b) A 4 different digit number is to be made from the digits 1, 2, 4, 5, 6, 8 without repetition of digits.
∴ 4 different digits are to be arranged from 6 given digits which can be done in 6P4 ways.
∴ Total number of numbers that can be formed
= \(\frac{6 !}{(6-4) !}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\)
= 360
Question 11.
How many numbers can be formed using the digits 0, 1, 2, 3, 4, 5 without repetition so that resulting numbers are between 100 and 1000?
Solution:
A number between 100 and 1000 that can be formed from the digits 0, 1, 2, 3, 4, 5 is of 3 digits, and repetition of digits is not allowed.
∴ 100’s place can be filled in 5 ways as it is a non-zero number.
10’s place digits can be filled in 5 ways.
Unit’s place digit can be filled in 4 ways.
∴ Total number of ways the number can be formed = 5 × 5 × 4 = 100
Question 12.
Find the number of 6-digit numbers using the digits 3, 4, 5, 6, 7, 8 without repetition. How many of these numbers are (a) divisible by 5 (b) not divisible by 5
Solution:
A number of 6 different digits is to be formed from the digits 3, 4, 5, 6, 7, 8 which can be done in 6P6 = 6! = 720 ways.
(a) If the number is to be divisible by 5,
the unit’s place digit can be 5 only.
∴ it can be arranged in 1 way only.
The other 5 digits can be arranged among themselves in 5P5 = 5! = 120 ways.
∴ Required number of numbers divisible by 5 = 1 × 120 = 120
![]()
(b) If the number is not divisible by 5,
unit’s place can be any digit from 3, 4, 6, 7, 8.
∴ it can be arranged in 5 ways.
Other 5 digits can be arranged in 5P5 = 5! = 120 ways.
∴ Required number of numbers not divisible by 5 = 5 × 120 = 600
Question 13.
A code word is formed by two different English letters followed by two non-zero distinct digits. Find the number of such code words. Also, find the number of such code words that end with an even digit.
Solution:
There is a total of 26 alphabets.
A code word contains 2 English alphabets.
∴ 2 alphabets can be filled in 26P2
= \(\frac{26 !}{(26-2) !}\)
= \(\frac{26 \times 25 \times 24 !}{24 !}\)
= 650 ways.
Also, alphabets to be followed by two distinct non-zero digits from 1 to 9 which can be filled in
9P2 = \(\frac{9 !}{(9-2) !}=\frac{9 \times 8 \times 7 !}{7 !}\) = 72 ways.
∴ Total number of a code words = 650 × 72 = 46800.
To find the number of codewords end with an even integer.
2 alphabets can be filled in 650 ways.
The digit in the unit’s place should be an even number between 1 to 9, which can be filled in 4 ways.
Also, 10’s place can be filled in 8 ways.
∴ Total number of codewords = 650 × 4 × 8 = 20800
Question 14.
Find the number of ways in which 5 letters can be posted in 3 post boxes if any number of letters can be posted in a post box.
Solution:
There are 5 letters and 3 post boxes and any number of letters can be posted in all three post boxes.
∴ Each letter can be posted in 3 ways.
∴ Total number of ways 5 letters can be posted = 3 × 3 × 3 × 3 × 3 = 243
![]()
Question 15.
Find the number of arranging 11 distinct objects taken 4 at a time so that a specified object (a) always occurs (b) never occurs
Solution:
There are 11 distinct objects and 4 are to be taken at a time.
(a) The number of permutations of n distinct objects, taken r at a time, when one particular object will always occur is \(\mathbf{r} \times{ }^{(\mathbf{n}-1)} \mathbf{P}_{(\mathbf{r}-1)}\)

∴ In 2880 permutations of 11 distinct objects, taken 4 at a time, one particular object will always occur.
(b) When one particular object will not occur, then 4 objects are to be arranged from 10 objects which can be done in 10P4 = 10 × 9 × 8 × 7 = 5040 ways.
∴ In 5040 permutations of 11 distinct objects, taken 4 at a time, one particular object will never occur.
Question 16.
In how many ways can 5 different books be arranged on a shelf if
(i) there are no restrictions
(ii) 2 books are always together
(iii) 2 books are never together
Solution:
(i) 5 books arranged in 5P5 = 5! = 120 ways.
(ii) 2 books are together.
Let us consider two books as one unit. This unit with the other 3 books can be arranged in 4P4 = 4! = 24 ways.
Also, two books can be arranged among themselves in 2P2 = 2 ways.
∴ Required number of arrangements = 24 × 2 = 48
(iii) Say books are B1, B2, B3, B4, B5 are to be arranged with B1, B2 never together.
B3, B4, B5 can be arranged among themselves in 3P3 = 3! = 6 ways.
B3, B4, B5 create 4 gaps in which B1, B2 are arranged in 4P2 = 4 × 3 = 12 ways.
∴ Required number of arrangements = 6 × 12 = 72
![]()
Question 17.
3 boys and 3 girls are to sit in a row. How many ways can this be done if
(i) there are no restrictions.
(ii) there is a girl at each end.
(iii) boys and girls are at alternate places.
(iv) all-boys sit together.
Solution:
3 boys and 3 girls are to be arranged in a row.
(i) When there are no restrictions.
∴ Required number of arrangements = 6! = 720
(ii) When there is a girl at each end.
3 girls can be arranged at two ends in
3P2 = \(\frac{3 !}{1 !}\) = 3 × 2 = 6 ways.
And remaining 1 girl and 3 boys can be arranged between the two girls in 4P4 = 4! = 24 ways.
∴ Required number of arrangements = 6 × 24 = 144
(iii) Boys and girls are at alternate places.
We can first arrange 3 girls among themselves in 3P3 = 3! = 6 ways.
Let girls be denoted by G.
G – G – G –
There are 3 places marked by ‘-’ where 3 boys can be arranged in 3! = 6 ways.
∴ Total number of such arrangements = 6 × 6 = 36
OR
Similarly, we can first arrange 3 boys in 3! = 6 ways
and then arrange 3 girls alternately in 3! = 6 ways.
∴ Total number of such arrangements = 6 × 6 = 36
∴ Required number of arrangements = 36 + 36 = 72
![]()
(iv) All boys sit together.
Let us consider all boys as one group.
This one group with the other 3 girls can be arranged 4P4 = 4! = 24 ways.
Also, 3 boys can be arranged among themselves in 3P3 = 3! = 6 ways.
∴ Required number of arrangements = 24 × 6 = 144