Maharashtra Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4

(I) Select the correct answers from the given alternatives.

Question 1.
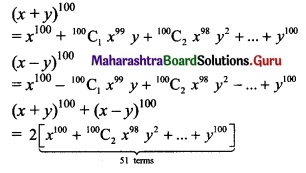
The total number of terms in the expression of (x + y)¹⁰⁰ + (x – y)¹⁰⁰ after simplification is:
(A) 50
(B) 51
(C) 100
(D) 202
Answer:
(B) 51
Hint:

Question 2.
The middle term in the expansion of (1 + x)²ⁿ will be:
(A) (n – 1)^th
(B) n^th
(C) (n + 1)^th
(D) (n + 2)^th
Answer:
(C) (n + 1)^th
Hint:
(1 + x)²ⁿ has (2n + 1) terms.
∴ (n + 1 )^th term is the middle term.

Question 3.
In the expansion of (x² – 2x)¹⁰, the coefficient of x¹⁶ is
(A) -1680
(B) 1680
(C) 3360
(D) 6720
Answer:
(C) 3360
Hint:
(x² – 2x)¹⁰ = x¹⁰ (x – 2)¹⁰
To get the coefficient of x¹⁶ in (x² – 2x)¹⁰,
we need to check coefficient of x⁶ in (x – 2)¹⁰
∴ Required coefficient = ¹⁰C₆ (-2)⁴
= 210 × 16
= 3360

Question 4.
The term not containing x in expansion of \((1-x)^{2}\left(x+\frac{1}{x}\right)^{10}\) is
(A) ¹¹C₅
(B) ¹⁰C₅
(C) ¹⁰C₄
(D) ¹⁰C₇
Answer:
(A) ¹¹C₅
Hint:

Question 5.
The number of terms in expansion of (4y + x)⁸ – (4y – x)⁸ is
(A) 4
(B) 5
(C) 8
(D) 9
Answer:
(A) 4
Hint:

Question 6.
The value of ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + …. + ¹⁴C₁₁ is
(A) 2¹⁴ – 1
(B) 2¹⁴ – 14
(C) 2¹²
(D) 2¹³ – 14
Answer:
(D) 2¹³ – 14
Hint:

Question 7.
The value of ¹¹C₂ + ¹¹C₄ + ¹¹C₆ + ¹¹C₈ is equal to
(A) 2¹⁰ – 1
(B) 2¹⁰ – 11
(C) 2¹⁰ + 12
(D) 2¹⁰ – 12
Answer:
(D) 2¹⁰ – 12
Hint:

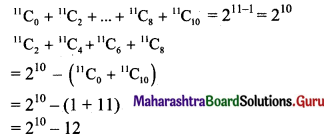
Question 8.
In the expansion of (3x + 2)⁴, the coefficient of the middle term is
(A) 36
(B) 54
(C) 81
(D) 216
Answer:
(D) 216
Hint:
(3x + 2)⁴ has 5 terms.
∴ (3x + 2)⁴ has 3rd term as the middle term.
The coefficient of the middle term

= 6 × 9 × 4
= 216

Question 9.
The coefficient of the 8th term in the expansion of (1 + x)¹⁰ is:
(A) 7
(B) 120
(C) ¹⁰C₈
(D) 210
Answer:
(B) 120
Hint:
r = 7
t₈ = ¹⁰C₇ x⁷ = ¹⁰C₃ x⁷
∴ Coefficient of 8th term = ¹⁰C₃ = 120

Question 10.
If the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are the same, then the value of a is
(A) \(-\frac{7}{9}\)
(B) \(-\frac{9}{7}\)
(C) \(\frac{7}{9}\)
(D) \(\frac{9}{7}\)
Answer:
(D) \(\frac{9}{7}\)
Hint:

(II) Answer the following.

Question 1.
Prove by the method of induction, for all n ∈ N.
(i) 8 + 17 + 26 + ….. + (9n – 1) = \(\frac{n}{2}\) (9n + 7)
Solution:
Let P(n) ≡ 8 + 17 + 26 +…..+(9n – 1) = \(\frac{n}{2}\) (9n + 7), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 8
R.H.S. = \(\frac{1}{2}\) [9(1) + 7] = 8
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 8 + 17 + 26 +…..+ (9k – 1) = \(\frac{k}{2}\) (9k + 7) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., 8 + 17 + 26 + …… + [9(k + 1) – 1]

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 8 + 17 + 26 +…..+ (9n – 1) = \(\frac{n}{2}\) (9n + 7) for all n ∈ N.

(ii) 1² + 4² + 7² + …… + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1)
Solution:
Let P(n) = 1² + 4² + 7² + ….. + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S.= 1² = 1
R.H.S.= \(\frac{1}{2}\) [6(1)² – 3(1) – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 4² + 7² +…..+ (3k – 2)² = \(\frac{k}{2}\) (6k² – 3k – 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 4² + 7² + … + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1) for all n ∈ N.

(iii) 2 + 3.2 + 4.2² + …… + (n + 1) 2^n-1 = n . 2ⁿ
Solution:
Let P(n) ≡ 2 + 3.2 + 4.2² +…..+ (n + 1) 2^n-1 = n.2ⁿ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(2¹) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 3.2 + 4.2² + ….. + (k + 1) 2^k-1 = k.2^k …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 3.2 + 4.2² +….+ (k + 2) 2^k = (k + 1) 2^k+1

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 3.2 + 4.2² +……+ (n + 1) 2^n-1 = n.2ⁿ for all n ∈ N.

(iv) \(\frac{1}{3.4 .5}+\frac{2}{4.5 .6}+\frac{3}{5.6 .7}+\ldots+\frac{n}{(n+2)(n+3)(n+4)}\) = \(\frac{n(n+1)}{6(n+3)(n+4)}\)
Solution:

Question 2.
Given that t_n+1 = 5t_n – 8, t₁ = 3, prove by method of induction that t_n = 5^n-1 + 2.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation t_n+1 = 5t_n – 8, t₁ = 3
and R.H.S. a general statement t_n = 5^n-1 + 2.
Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 5^1-1 + 2 = 1 + 2 = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S = t₂ = 5t₁ – 8 = 5(3) – 8 = 7
R.H.S. = t₂ = 5^2-1 + 2 = 5 + 2 = 7
∴ L.H.S. = R.H.S.
∴ P(n) is tme for n = 2.

Step II:
Let us assume that P(n) is true for n = k.
∴ t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
t_k+1 = 5^k+1-1 + 2 = 5^k + 2
t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2 ……[From Step II]
∴ t_k+1 = 5(5^k-1 + 2) – 8 = 5^k + 2
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n = 5^n-1 + 2, for all n ∈ N.

Question 3.
Prove by method of induction
\(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.
Solution:


Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.

Question 4.
Expand (3x² + 2y)⁵
Solution:
Here, a = 3x², b = 2y, n = 5.
Using binomial theorem,

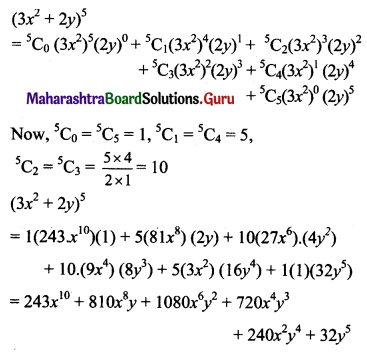
Question 5.
Expand \(\left(\frac{2 x}{3}-\frac{3}{2 x}\right)^{4}\)
Solution:

Question 6.
Find third term in the expansion of \(\left(9 x^{2}-\frac{y^{3}}{6}\right)^{4}\)
Solution:

Question 7.
Find tenth term in the expansion of \(\left(2 x^{2}+\frac{1}{x}\right)^{12}\)
Solution:

Question 8.
Find the middle term(s) in the expansion of
(i) \(\left(\frac{2 a}{3}-\frac{3}{2 a}\right)^{6}\)
Solution:
Here, a = \(\frac{2 a}{3}\), b = \(\frac{-3}{2 a}\), n = 6.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{6+2}{2}=4\)
∴ Middle term is t4, for which r = 3.

∴ The Middle term is -20.

(ii) \(\left(x-\frac{1}{2 y}\right)^{10}\)
Solution:
Here, a = x, b = \(-\frac{1}{2 y}\), n = 10.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{10+2}{2}=6\)
∴ Middle term is t6, for which r = 5

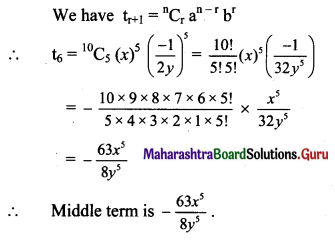
(iii) (x² + 2y²)⁷
Solution:
Here, a = x², b = 2y², n = 7.
Now, n is odd.
∴ \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}=4, \frac{\mathrm{n}+3}{2}=\frac{7+3}{2}=5\)
∴ Middle terms are t₄ and t₅, for which r = 3 and r = 4 respectively.

∴ Middle terms are 280x⁸y⁶ and 560x⁶y⁸.

(iv) \(\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

Question 9.
Find the coefficients of
(i) x⁶ in the expantion of \(\left(3 x^{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

(ii) x⁶⁰ in the expansion of \(\left(\frac{1}{x^{2}}+x^{4}\right)^{18}\)
Solution:

Question 10.
Find the constant term in the expansion of
(i) \(\left(\frac{4 x^{2}}{3}+\frac{3}{2 x}\right)^{9}\)
Solution:

(ii) \(\left(2 x^{2}-\frac{1}{x}\right)^{12}\)
Solution:

Question 11.
Prove by method of induction
(i) log_a xⁿ = n log_a x, x > 0, n ∈ N
Solution:

(ii) 15^2n-1 + 1 is divisible by 16, for all n ∈ N.
Solution:
15^2n-1 + 1 is divisible by 16, if and only if (15^2n-1 + 1) is is a multiple of 16.
Let P(n) ≡ 15^2n-1 + 1 = 16m, where m ∈ N.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 15^2n-1 + 1 is divisible by 16, for all n ∈ N.

(iii) 5²ⁿ – 2²ⁿ is divisible by 3, for all n ∈ N.
Solution:

Question 12.
If the coefficient of x¹⁶ in the expansion of (x² + ax)¹⁰ is 3360, find a.
Solution:

Question 13.
If the middle term in the expansion of \(\left(x+\frac{b}{x}\right)^{6}\) is 160, find b.
Solution:

∴ 160 = \(\frac{6 \times 5 \times 4 \times 3 !}{3 \times 2 \times 1 \times 3 !} \times b^{3}\)
∴ 160 = 20b³
∴ 8 = b³
∴ b = 2

Question 14.
If the coefficients of x² and x³ in theexpansion of (3 + kx)⁹ are equal, find k.
Solution:

Question 15.
If the constant term in the expansion of \(\left(x^{3}+\frac{\mathrm{k}}{x^{8}}\right)^{11}\) is 1320, find k.
Solution:

Question 16.
Show that there is no term containing x⁶ in the expansion of \(\left(x^{2}-\frac{3}{x}\right)^{11}\).
Solution:

Question 17.
Show that there is no constant term in the expansion of \(\left(2 x-\frac{x^{2}}{4}\right)^{9}\)
Solution:

Question 18.
State, first four terms in the expansion of \(\left(1-\frac{2 x}{3}\right)^{-1 / 2}\)
Solution:

Question 19.
State, first four terms in the expansion of \((1-x)^{-1 / 4}\).
Solution:

Question 20.
State, first three terms in the expansion of \((5+4 x)^{-1 / 2}\)
Solution:

Question 21.
Using the binomial theorem, find the value of \(\sqrt[3]{995}\) upto four places of decimals.
Solution:

Question 22.
Find approximate value of \(\frac{1}{4.08}\) upto four places of decimals.
Solution:

Question 23.
Find the term independent of x in the expansion of (1 – x²) \(\left(x+\frac{2}{x}\right)^{6}\).
Solution:

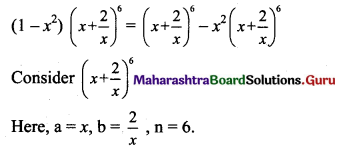
Question 24.
(a + bx) (1 – x)⁶ = 3 – 20x + cx² + …, then find a, b, c.
Solution:

Question 25.
The 3rd term of (1 + x)ⁿ is 36x². Find 5th term.
Solution:

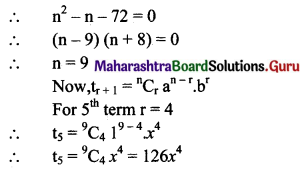
Question 26.
Suppose (1 + kx)ⁿ = 1 – 12x + 60x² – …… find k and n.
Solution: