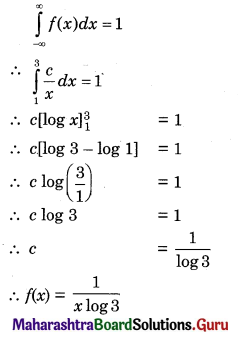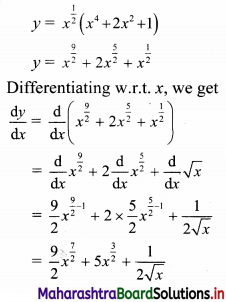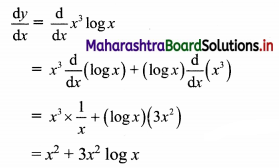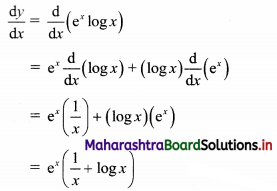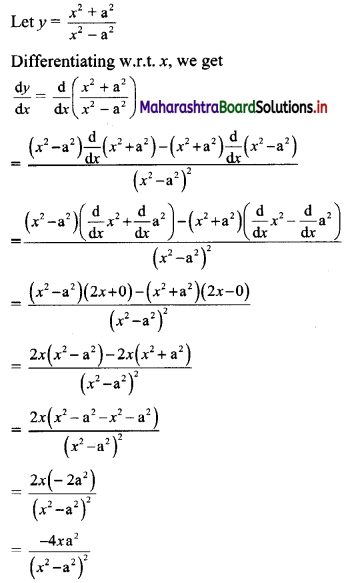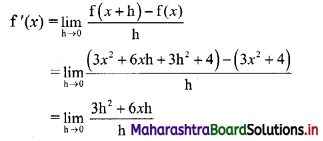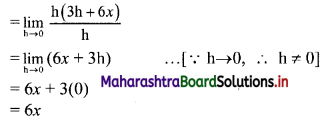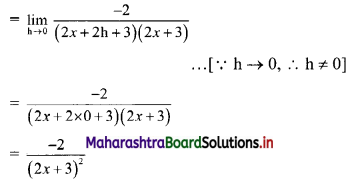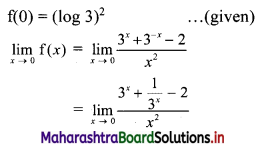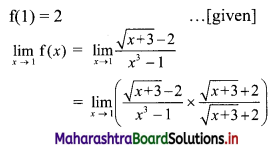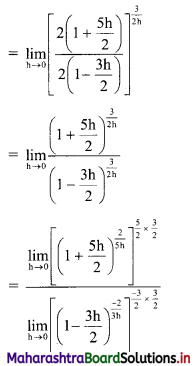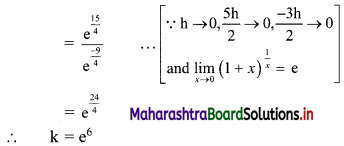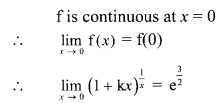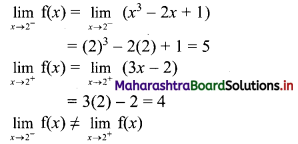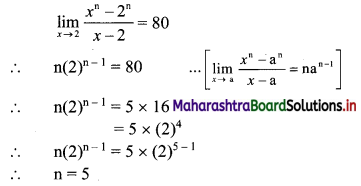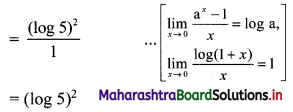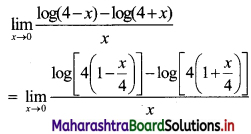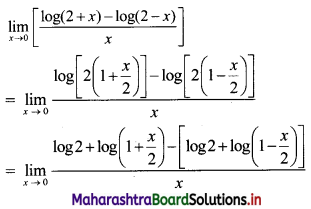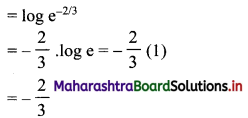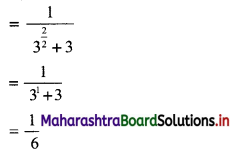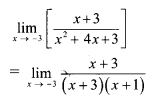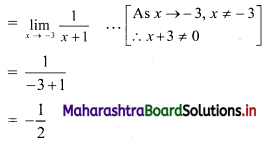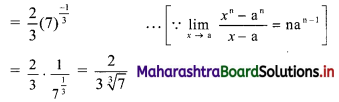Bhagya

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.2

Question 1.
Check whether each of the following is p.d.f.
(i) \(f(x)= \begin{cases}x & \text { for } 0 \leq x \leq 1 \\ 2-x & \text { for } 1<x \leq 2\end{cases}\)
Solution:
Given function is
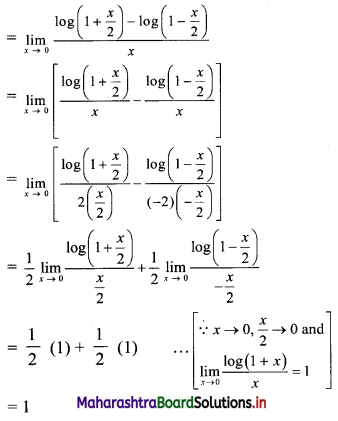
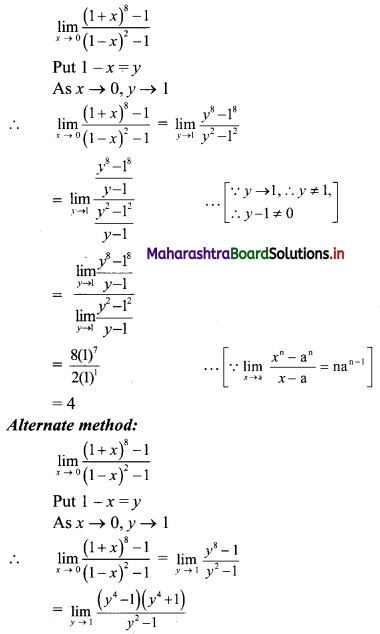
f(x) = x, 0 ≤ x ≤ 1
Each f(x) ≥ 0, as x ≥ 0.


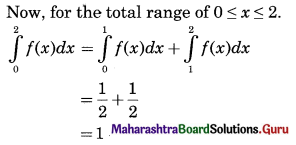
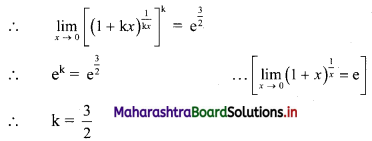
∴ The given function is a p.d.f. of x.

(ii) f(x) = 2 for 0 < x < 1
Solution:
Given function is
f(x) = 2 for 0 < x < 1 Each f(x) > 0,

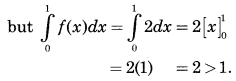
∴ The given function is not a p.d.f.

Question 2.
The following is the p.d.f. of a r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
Find (i) P(X < 1.5), (ii) P(1 < X < 2), (iii) P(X > 2)
Solution:

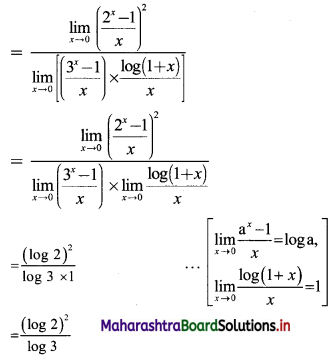
Question 3.
It is felt that error in measurement of reaction temperature (in Celsius) in an experiment is a continuous r.v. with p.d.f.
\(f(x)= \begin{cases}\frac{x^{3}}{64} & \text { for } 0 \leq x \leq 4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Verify whether f(x) is a p.d.f.
(ii) Find P(0 < X ≤ 1).
(iii) Find the probability that X is between 1 and 3.
Solution:
(i) f(x) is p.d.f. of r.v. X if
(a) f(x) ≥ 0, ∀ x ∈ R
(b) \(\int_{0}^{4} f(x) d x\) = 1

Question 4.
Find k, if the following function represents the p.d.f. of a r.v. X.
(i) \(f(x)= \begin{cases}k x & \text { for } 0<x<2 \\ 0 & \text { otherwise }\end{cases}\)
Also find P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)]
Solution:

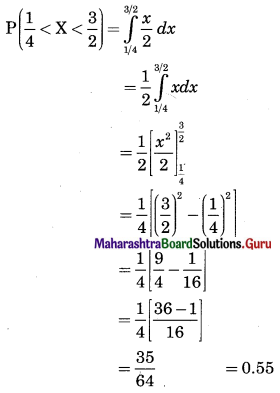
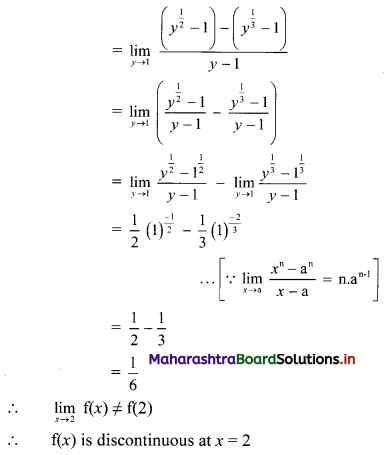
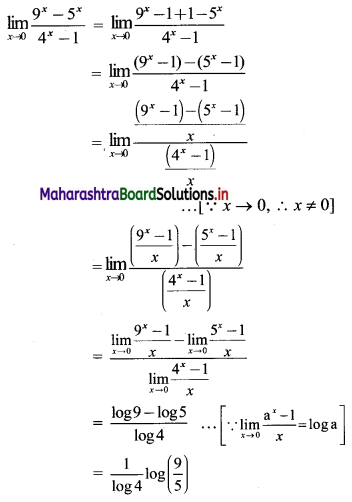
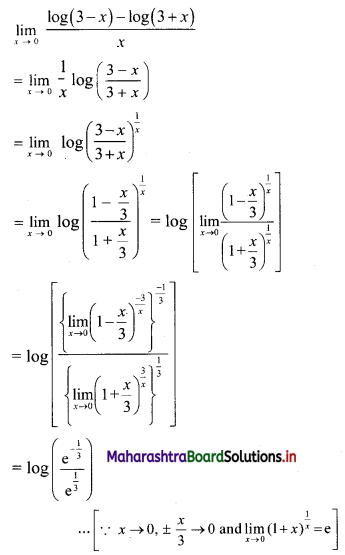
(ii) \(f(x)= \begin{cases}k x(1-x) & \text { for } 0<x<1 \\ 0 & \text { otherwise }\end{cases}\)
Also find (a) P[\(\frac{1}{4}\) < X < \(\frac{1}{2}\)], (b) P[X < \(\frac{1}{2}\)]
Solution:
We know that

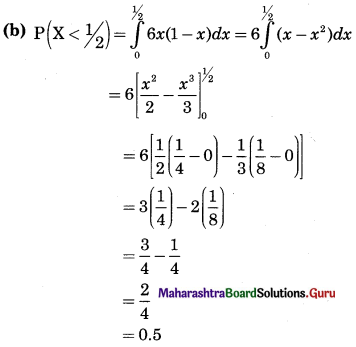
Question 5.
Let X be the amount of time for which a book is taken out of the library by a randomly selected student and suppose that X has p.d.f.
\(f(x)= \begin{cases}0.5 x & \text { for } 0 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Calculate (i) P(X ≤ 1), (ii) P(0.5 ≤ X ≤ 1.5), (iii) P(X ≥ 1.5).
Solution:
Given p.d.f. of X is f(x) = 0.5x for 0 ≤ x ≤ 2
∴ Its c.d.f. F(x) is given by

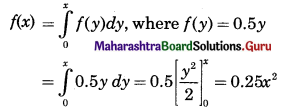
(i) P(X < 1) = F(1)
= 0.25(1)²
= 0.25

(ii) P(0.5 < X < 1.5) = F(1.5) – F(0.5)
= 0.25(1.5)² – 0.25(0.5)²
= 0.25[2.25 – 0.25]
= 0.25(2)
= 0.5

(iii) P(X ≥ 1.5) = 1 – P(X ≤ 1.5)
= 1 – F(1.5)
= 1 – 0.25(1.5)²
= 1 – 0.25(2.25)
= 1 – 0.5625
= 0.4375

Question 6.
Suppose X is the waiting time (in minutes) for a bus and its p.d.f. is given by
\(f(x)=\left\{\begin{array}{cl}
\frac{1}{5} & \text { for } 0 \leq x \leq 5 \\
0 & \text { otherwise }
\end{array}\right.\)
Find the probability that (i) waiting time is between 1 and 3 minutes, (ii) waiting time is more than 4 minutes.
Solution:
p.d.f. of r.v. X is given by
f(x) = \(\frac{1}{5}\) for 0 ≤ x ≤ 5
This is a constant function.
(i) Probability that waiting time X is between 1 and 3 minutes

(ii) Probability that waiting time X is more than 4 minutes

Question 7.
Suppose error involved in making a certain measurement is a continuous r.v. X with p.d.f.
\(f(x)= \begin{cases}k\left(4-x^{2}\right) & \text { for }-2 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Compute (i) P(X > 0), (ii) P(-1 < X < 1), (iii) P(X < -0.5 or X > 0.5)
Solution:
Since given f(x) is a p.d.f. of r.v. X
Since -2 ≤ x ≤ 2
∴ x² ≤ 4
∴ 4 – x² ≥ 0
∴ k(4 – x²) ≥ 0
∴ k ≥ 0 [∵ f(x) ≥ 0]

Question 8.
Following is the p.d.f. of a continuous r.v. X.
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) Find an expression for the c.d.f. of X.
(ii) Find F(x) at x = 0.5, 1.7, and 5.
Solution:
The p.d.f. of a continuous r.v. X is
\(f(x)= \begin{cases}\frac{x}{8} & \text { for } 0<x<4 \\ 0 & \text { otherwise }\end{cases}\)
(i) c.d.f. of continuous r.v. X is given by

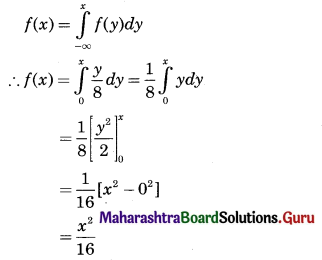
(ii) F(0.5) = \(\frac{(0.5)^{2}}{16}=\frac{0.25}{16}=\frac{1}{64}\) = 0.015
F(1.7) = \(\frac{(1.7)^{2}}{16}=\frac{2.89}{16}\) = 0.18
For any of x greater than or equal to 4, F(x) = 1
∴ F(5) = 1

Question 9.
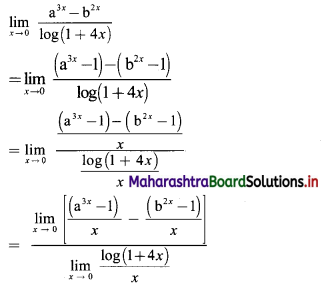
The p.d.f. of a continuous r.v. X is
\(f(x)=\left\{\begin{array}{cl}
\frac{3 x^{2}}{8} & \text { for } 0<x<2 \\
0 & \text { otherwise }
\end{array}\right.\)
Determine the c.d.f. of X and hence find (i) P(X < 1), (ii) P(X < -2), (iii) P(X > 0), (iv) P(1 < X < 2).
Solution:
The p.d.f. of a continuous r.v. X is

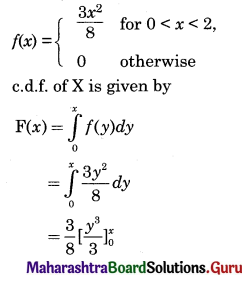
Question 10.
If a r.v. X has p.d.f.
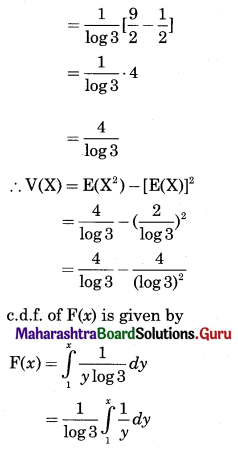
\(f(x)= \begin{cases}\frac{c}{x} & \text { for } 1<x<3, c>0 \\ 0 & \text { otherwise }\end{cases}\)
Find c, E(X) and V(X). Also find f(x).
Solution:
The p.d.f. of r.v. X is
f(x) = \(\frac{c}{x}\), 1 < x < 3, c > 0
For p.d.f. of X, we have

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Differentiation Ex 9.2

I. Differentiate the following functions w.r.t. x.

Question 1.
\(\frac{x}{x+1}\)
Solution:

Question 2.
\(\frac{x^{2}+1}{x}\)
Solution:

Question 3.
\(\frac{1}{e^{x}+1}\)
Solution:

Question 4.
\(\frac{e^{x}}{e^{x}+1}\)
Solution:

Question 5.
\(\frac{x}{\log x}\)
Solution:

Question 6.
\(\frac{2^{x}}{\log x}\)
Solution:

Question 7.
\(\frac{\left(2 e^{x}-1\right)}{\left(2 e^{x}+1\right)}\)
Solution:

Question 8.
\(\frac{(x+1)(x-1)}{\left(e^{x}+1\right)}\)
Solution:

II. Solve the following examples:

Question 1.
The demand D for a price P is given as D = \(\frac{27}{P}\), find the rate of change of demand when the price is 3.
Solution:
Demand, D = \(\frac{27}{P}\)
Rate of change of demand = \(\frac{dD}{dP}\)

When price P = 3,
Rate of change of demand,
\(\left(\frac{\mathrm{dD}}{\mathrm{dP}}\right)_{\mathrm{P}=3}=\frac{-27}{(3)^{2}}=-3\)
∴ When price is 3, Rate of change of demand is -3.

Question 2.
If for a commodity; the price-demand relation is given as D = \(\frac{P+5}{P-1}\). Find the marginal demand when the price is 2.
Solution:

Question 3.
The demand function of a commodity is given as P = 20 + D – D². Find the rate at which price is changing when demand is 3.
Solution:
Given, P = 20 + D – D²
Rate of change of price = \(\frac{dP}{dD}\)
= \(\frac{d}{dD}\)(20 + D – D²)
= 0 + 1 – 2D
= 1 – 2D
Rate of change of price at D = 3 is
\(\left(\frac{\mathrm{dP}}{\mathrm{dD}}\right)_{\mathrm{D}=3}\) = 1 – 2(3) = -5
∴ Price is changing at a rate of -5, when demand is 3.

Question 4.
If the total cost function is given by; C = 5x³ + 7x² + 7; find the average cost and the marginal cost when x = 4.
Solution:
Total cost function, C = 5x³ + 7x² + 7
Average cost = \(\frac{C}{x}\)

When x = 4, Marginal cost = \(\left(\frac{\mathrm{dC}}{\mathrm{d} x}\right)_{x=4}\)
= 15(4)² + 4(4)
= 240 + 16
= 256
∴ the average cost and marginal cost at x = 4 are \(\frac{359}{4}\) and 256 respectively.

Question 5.
The total cost function of producing n notebooks is given by
C = 1500 – 75n + 2n² + \(\frac{n^{3}}{5}\)
Find the marginal cost at n = 10.
Solution:
The total cost function,


∴ Marginal cost at n = 10 is 25.

Question 6.
The total cost of ‘t’ toy cars is given by C = 5(2t) + 17. Find the marginal cost and average cost at t = 3.
Solution:
Total cost of ‘t’ toy cars, C = 5(2t) + 17

∴ at t = 3, the Marginal cost is 40 log 2 and the Average cost is 19.

Question 7.
If for a commodity; the demand function is given by, D = \(\sqrt{75-3 P}\). Find the marginal demand function when P = 5.
Solution:
Demand function, D = \(\sqrt{75-3 P}\)
Now, Marginal demand = \(\frac{dD}{dP}\)

Question 8.
The total cost of producing x units is given by C = 10e^2x, find its marginal cost and average cost when x = 2.
Solution:

Question 9.
The demand function is given as P = 175 + 9D + 25D². Find the revenue, average revenue, and marginal revenue when demand is 10.
Solution:
Given, P = 175 + 9D + 25D²
Total revenue, R = P.D
= (175 + 9D + 25D²)D
= 175D + 9D² + 25D³
Average revenue = P = 175 + 9D + 25D²
Marginal revenue = \(\frac{dR}{dD}\)
= \(\frac{d}{dD}\) (175D + 9D² + 25D³)
= 175 \(\frac{d}{dD}\) (D) + 9 \(\frac{d}{dD}\) (D²) + 25 \(\frac{d}{dD}\) (D³)
= 175(1) + 9(2D) + 25(3D²)
= 175 + 18D + 75D²
When D = 10,
Total revenue = 175(10) + 9(10)² + 25(10)³
= 1750 + 900 + 25000
= 27650
Average revenue = 175 + 9(10) + 25(10)²
= 175 + 90 + 2500
= 2765
Marginal revenue = 175 + 18(10) + 75(10)²
= 175 + 180 + 7500
= 7855
∴ When Demand = 10,
Total revenue = 27650, Average revenue = 2765, Marginal revenue = 7855.

Question 10.
The supply S for a commodity at price P is given by S = P² + 9P – 2. Find the marginal supply when the price is 7.
Solution:
Given, S = P² + 9P – 2

∴ The marginal supply is 23, at P = 7.

Question 11.
The cost of producing x articles is given by C = x² + 15x + 81. Find the average cost and marginal cost functions. Find marginal cost when x = 10. Find x for which the marginal cost equals the average cost.
Solution:
Given, cost C = x² + 15x + 81

If marginal cost = average cost, then
2x + 15 = x + 15 + \(\frac{81}{x}\)
∴ x = \(\frac{81}{x}\)
∴ x² = 81
∴ x = 9 …..[∵ x > 0]

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Differentiation Ex 9.1

I. Find the derivatives of the following functions w.r.t. x.

Question 1.
x¹²
Solution:
Let y = x¹²
Differentiating w.r.t. x, we get

Question 2.
x^-9
Solution:
Let y = x^-9
Differentiating w.r.t. x, we get

Question 3.
\(x^{\frac{3}{2}}\)
Solution:
Let y = \(x^{\frac{3}{2}}\)
Differentiating w.r.t. x, we get

Question 4.
7x√x
Solution:

Question 5.
3⁵
Solution:
Let y = 3⁵
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x} 3^{5}=0\) …..[3⁵ is a constant]

II. Differentiate the following w.r.t. x.

Question 1.
x⁵ + 3x⁴
Solution:
Let y = x⁵ + 3x⁴
Differentiating w.r.t. x, we get

Question 2.
x√x + log x – e^x
Solution:
Let y = x√x + log x – e^x
= \(x^{\frac{3}{2}}+\log x-e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
\(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Solution:
Let y = \(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Differentiating w.r.t. x, we get

Question 4.
\(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Solution:
Let y = \(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Differentiating w.r.t. x, we get

Question 5.
\(\sqrt{x}\left(x^{2}+1\right)^{2}\)
Solution:
Let y = \(\sqrt{x}\left(x^{2}+1\right)^{2}\)

III. Differentiate the following w.r.t. x.

Question 1.
x³ log x
Solution:
Let y = x³ log x
Differentiating w.r.t. x, we get

Question 2.
\(x^{\frac{5}{2}} e^{x}\)
Solution:
Let y = \(x^{\frac{5}{2}} e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
e^x log x
Solution:
Let y = e^x log x
Differentiating w.r.t. x, we get

Question 4.
x³ . 3^x
Solution:
Let y = x³ . 3^x
Differentiating w.r.t. x, we get

IV. Find the derivatives of the following w.r.t. x.

Question 1.
\(\frac{x^{2}+a^{2}}{x^{2}-a^{2}}\)
Solution:

Question 2.
\(\frac{3 x^{2}+5}{2 x^{2}-4}\)
Solution:

Question 3.
\(\frac{\log x}{x^{3}-5}\)
Solution:

Question 4.
\(\frac{3 e^{x}-2}{3 e^{x}+2}\)
Solution:

Question 5.
\(\frac{x \mathrm{e}^{x}}{x+\mathrm{e}^{x}}\)
Solution:

V. Find the derivatives of the following functions by the first principle:

Question 1.
3x² + 4
Solution:
Let f(x) = 3x² + 4
∴ f(x + h) = 3(x + h)² + 4
= 3(x² + 2xh + h²) + 4
= 3x² + 6xh + 3h² + 4
By first principle, we get

Question 2.
x√x
Solution:
Let f(x) = x√x
∴ f(x + h) = \((x+h)^{\frac{3}{2}}\)
By first principle, we get

Question 3.
\(\frac{1}{2 x+3}\)
Solution:
Let f(x) = \(\frac{1}{2 x+3}\)
∴ f(x + h) = \(\frac{1}{2(x+\mathrm{h})+3}=\frac{1}{2 x+2 \mathrm{~h}+3}\)
By first principle, we get

Question 4.
\(\frac{x-1}{2 x+7}\)
Solution:
Let f(x) = \(\frac{x-1}{2 x+7}\)
∴ f(x + h) = \(\frac{x+\mathrm{h}-1}{2(x+\mathrm{h})+7}=\frac{x+\mathrm{h}-1}{2 x+2 \mathrm{~h}+7}\)
By first principle, we get

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Continuity Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 8 Continuity Miscellaneous Exercise 8

I. Discuss the continuity of the following functions at the point(s) or in the interval indicated against them.

Question 1.
If f(x) = 2x² – 2x + 5 for 0 ≤ x < 2
= \(\frac{1-3 x-x^{2}}{1-x}\) for 2 ≤ x < 4
= \(\frac{7-x^{2}}{x-5}\) for 4 ≤ x ≤ 7 on its domain.
Solution:
The domain of f is [0, 5) ∪ (5, 7]
We observe that x = 5 is not included in the domain as f is not defined at x = 5
a. For 0 ≤ x < 2
f(x) = 2x² – 2x + 5
It is a polynomial function and is continuous at all point in [0, 2)

b. For 2 < x < 4
f(x) = \(\frac{1-3 x-x^{2}}{1-x}\)
It is a rational function and is continuous everwhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 1
But x = 1 does not lie in the interval.
f(x) is continuous at all points in (2, 4)

c. For 4 < x ≤ 7, x ≠ 5
i.e. for x ∈ [4, 5) ∪ (5, 7]
∴ f(x) = \(\frac{7-x^{2}}{x-5}\)
It is a rational function and is continuous everywhere except possibly at points where its denominator becomes zero.
Denominator becomes zero at x = 5
But x = 5 ∉ [4, 5) ∪ (5, 7]
∴ f is continuous at all points in (4, 7] – {5}.

d. Since the definition of function changes around x = 2, x = 4 and x = 7
∴ there is disturbance in behaviour of the function.
So we examine continuity at x = 2, 4, 7 separately.
Continuity at x = 2:
\(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{-}}\left(2 x^{2}-2 x+5\right)\)
= 2(2)² – 2(2) + 5
= 8 – 4 + 5
= 9

∴ f is continuous at x = 2

e. Continuity at x = 4:

∴ f is continuous at x = 4

Question 2.
f(x) = \(\frac{3^{x}+3^{-x}-2}{x^{2}}\) for x ≠ 0
= (log 3)² for x = 0 at x = 0
Solution:


∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 3.
f(x) = \(\frac{5^{x}-e^{x}}{2 x}\) for x ≠ 0
= \(\frac{1}{2}\) (log 5 – 1) for x = 0 at x = 0
Solution:

∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 4.
f(x) = \(\frac{\sqrt{x+3}-2}{x^{3}-1}\) for x ≠ 1
= 2 for x = 1, at x = 1
Solution:


∴ \(\lim _{x \rightarrow 1} \mathrm{f}(x) \neq \mathrm{f}(1)\)
∴ f is discontinuous at x = 1

Question 5.
f(x) = \(\frac{\log x-\log 3}{x-3}\) for x ≠ 3
= 3 for x = 3, at x = 3
Solution:

(II) Find k if following functions are continuous at the points indicated against them.

Question 1.
f(x) = \(\left(\frac{5 x-8}{8-3 x}\right)^{\frac{3}{2 x-4}}\) for x ≠ 2
= k for x = 2 at x = 2
Solution:

Question 2.
f(x) = \(\frac{45^{x}-9^{x}-5^{x}+1}{\left(k^{x}-1\right)\left(3^{x}-1\right)}\) for x ≠ 0
= \(\frac{2}{3}\) for x = 0, at x = 0
Solution:

Question 3.
f(x) = \((1+k x)^{\frac{1}{x}}\), for x ≠ 0
= \(e^{\frac{3}{2}}\), for x = 0, at x = 0
Solution:

III. Find a and b if following functions are continuous at the point indicated against them.

Question 1.
f(x) = x² + a, for x ≥ 0
= 2\(\sqrt{x^{2}+1}\) + b, for x < 0 and
f(1) = 2, is continuous at x = 0
Solution:

Question 2.
f(x) = \(\frac{x^{2}-9}{x-3}\) + a, for x > 3
= 5, for x = 3
= 2x² + 3x + b, for x < 3
is continuous at x = 3
Solution:

Question 3.
f(x) = \(\frac{32^{x}-1}{8^{x}-1}\) + a, for x > 0
= 2, for x = 0
= x + 5 – 2b, for x < 0
is continuous at x = 0
Solution:

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Continuity Ex 8.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 8 Continuity Ex 8.1

Question 1.
Examine the continuity of
(i) f(x) = x³ + 2x² – x – 2 at x = -2
Solution:
f(x) = x³ + 2x² – x – 2
Here f(x) is a polynomial function and hence it is continuous for all x ∈ R.
∴ f(x) is continuous at x = -2

(ii) f(x) = \(\frac{x^{2}-9}{x-3}\) on R
Solution:
f(x) = \(\frac{x^{2}-9}{x-3}\); x ∈ R
f(x) is a rational function and is continuous for all x ∈ R, except at the points where denominator becomes zero.
Here, denominator x – 3 = 0 when x = 3.
∴ Function f is continuous for all x ∈ R, except at x = 3, where it is not defined.

Question 2.
Examine whether the function is continuous at the points indicated against them.
(i) f(x) = x³ – 2x + 1, for x ≤ 2
= 3x – 2, for x > 2, at x = 2
Solution:

∴ Function f is discontinuous at x = 2

(ii) f(x) = \(\frac{x^{2}+18 x-19}{x-1}\) for x ≠ 1
= 20, for x = 1, at x = 1
Solution:

∴ f(x) is continuous at x = 1

Question 3.
Test the continuity of the following functions at the points indicated against them.
(i) f(x) = \(\frac{\sqrt{x-1}-(x-1)^{\frac{1}{3}}}{x-2}\) for x ≠ 2
= \(\frac{1}{5}\) for x = 2, at x = 2
Solution:

(ii) f(x) = \(\frac{x^{3}-8}{\sqrt{x+2}-\sqrt{3 x-2}}\) for x ≠ 2
= -24 for x = 2, at x = 2
Solution:

(iii) f(x) = 4x + 1 for x ≤ \(\frac{8}{3}\)
= \(\frac{59-9 x}{3}\), for x > \(\frac{8}{3}\), at x = \(\frac{8}{3}\)
Solution:

(iv) f(x) = \(\frac{x^{3}-27}{x^{2}-9}\) for 0 ≤ x < 3
= \(\frac{9}{2}\), for 3 ≤ x ≤ 6, at x = 3
Solution:

Question 4.
(i) If f(x) = \(\frac{24^{x}-8^{x}-3^{x}+1}{12^{x}-4^{x}-3^{x}+1}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, find k.
Solution:
Function f is continuous at x = 0

(ii) If f(x) = \(\frac{5^{x}+5^{-x}-2}{x^{2}}\), for x ≠ 0
= k for x = 0
is continuous at x = 0, find k.
Solution:
Function f is continuous at x = 0

(iii) For what values of a and b is the function
f(x) = ax + 2b + 18 for x ≤ 0
= x² + 3a – b for 0 < x ≤ 2 = 8x – 2 for x > 2,
continuous for every x?
Solution:
Function f is continuous for every x.
∴ Function f is continuous at x = 0 and x = 2
As f is continuous at x = 0.
∴ \(\lim _{x \rightarrow 0^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 0^{+}} \mathrm{f}(x)\)
∴ \(\lim _{x \rightarrow 0^{-}}(a x+2 b+18)=\lim _{x \rightarrow 0^{+}}\left(x^{2}+3 a-b\right)\)
∴ a(0) + 2b + 18 = (0)2 + 3a – b
∴ 3a – 3b = 18
∴ a – b = 6 …..(i)
Also, Function f is continous at x = 2
∴ \(\lim _{x \rightarrow 2^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 2^{-}} \mathrm{f}(x)\)
∴ \(\lim _{x \rightarrow 2^{-}}\left(x^{2}+3 a-b\right)=\lim _{x \rightarrow 2^{-}}(8 x-2)\)
∴ (2)² + 3a – b = 8(2) – 2
∴ 4 + 3a – b = 14
∴ 3a – b = 10 …..(ii)
Subtracting (i) from (ii), we get
2a = 4
∴ a = 2
Substituting a = 2 in (i), we get
2 – b = 6
∴ b = -4
∴ a = 2 and b = -4

(iv) For what values of a and b is the function
f(x) = \(\frac{x^{2}-4}{x-2}\) for x < 2
= ax² – bx + 3 for 2 ≤ x < 3
= 2x – a + b for x ≥ 3
continuous in its domain.
Solution:
Function f is continuous for every x on R.
∴ Function f is continuous at x = 2 and x = 3.
As f is continuous at x = 2.
∴ \(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{+}} f(x)\)

∴ 2 + 2 = a(2)² – b(2) + 3
∴ 4 = 4a – 2b + 3
∴ 4a – 2b = 1 …..(i)
Also function f is continuous at x = 3
∴ \(\lim _{x \rightarrow 3^{-}} f(x)=\lim _{x \rightarrow 3^{+}} f(x)\)
∴ \(\lim _{x \rightarrow 3^{-}}\left(a x^{2}-b x+3\right)=\lim _{x \rightarrow 3^{+}}(2 x-a+b)\)
∴ a(3)² – b(3) + 3 = 2(3) – a + b
∴ 9a – 3b + 3 = 6 – a + b
∴ 10a – 4b = 3 …..(ii)
Multiplying (i) by 2, we get
8a – 4b = 2 …..(iii)
Subtracting (iii) from (ii), we get
2a = 1
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (i), we get
4(\(\frac{1}{2}\)) – 2b = 1
∴ 2 – 2b = 1
∴ 1 = 2b
∴ b = \(\frac{1}{2}\)
∴ a = \(\frac{1}{2}\) and b = \(\frac{1}{2}\)

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Miscellaneous Exercise 7 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Miscellaneous Exercise 7

I.

Question 1.
If \(\lim _{x \rightarrow 2} \frac{x^{n}-2^{n}}{x-2}=80\) then find the value of n.
Solution:

II. Evaluate the following Limits:

Question 1.
\(\lim _{x \rightarrow a} \frac{(x+2)^{\frac{5}{3}}-(a+2)^{\frac{5}{3}}}{x-a}\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0} \frac{(1+x)^{n}-1}{x}\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{(x-2)}{2 x^{2}-7 x+6}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 1}\left[\frac{x^{3}-1}{x^{2}+5 x-6}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 3}\left[\frac{x-3}{\sqrt{x-2}-\sqrt{4-x}}\right]\)
Solution:

Question 6.
\(\lim _{x \rightarrow 4}\left[\frac{3-\sqrt{5+x}}{1-\sqrt{5-x}}\right]\)
Solution:

Question 7.
\(\lim _{x \rightarrow 0}\left[\frac{5^{x}-1}{x}\right]\)
Solution:

Question 8.
\(\lim _{x \rightarrow 0}\left(1+\frac{x}{5}\right)^{\frac{1}{x}}\)
Solution:

Question 9.
\(\lim _{x \rightarrow 0}\left[\frac{\log (1+9 x)}{x}\right]\)
Solution:

Question 10.
\(\lim _{x \rightarrow 0} \frac{(1-x)^{5}-1}{(1-x)^{3}-1}\)
Solution:

Question 11.
\(\lim _{x \rightarrow 0}\left[\frac{a^{x}+b^{x}+c^{x}-3}{x}\right]\)
Solution:

Question 12.
\(\lim _{x \rightarrow 0} \frac{e^{x}+e^{-x}-2}{x^{2}}\)
Solution:

Question 13.
\(\lim _{x \rightarrow 0}\left[\frac{x\left(6^{x}-3^{x}\right)}{\left(2^{x}-1\right) \cdot \log (1+x)}\right]\)
Solution:

Question 14.
\(\lim _{x \rightarrow 0}\left[\frac{a^{3 x}-a^{2 x}-a^{x}+1}{x^{2}}\right]\)
Solution:

Question 15.
\(\lim _{x \rightarrow 0}\left[\frac{\left(5^{x}-1\right)^{2}}{x \cdot \log (1+x)}\right]\)
Solution:

Question 16.
\(\lim _{x \rightarrow 0}\left[\frac{a^{4 x}-1}{b^{2 x}-1}\right]\)
Solution:

Question 17.
\(\lim _{x \rightarrow 0}\left[\frac{\log 100+\log (0.01+x)}{x}\right]\)
Solution:

Question 18.
\(\lim _{x \rightarrow 0}\left[\frac{\log (4-x)-\log (4+x)}{x}\right]\)
Solution:

Question 19.
Evaluate the limit of the function if exist at x = 1 where,
\(f(x)= \begin{cases}7-4 x & x<1 \\ x^{2}+2 & x \geq 1\end{cases}\)
Solution:

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Ex 7.4 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Ex 7.4

I. Evaluate the following:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{9^{x}-5^{x}}{4^{x}-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{5^{x}+3^{x}-2^{x}-1}{x}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 0}\left[\frac{\log (2+x)-\log (2-x)}{x}\right]\)
Solution:

II. Evaluate the following:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{3^{x}+3^{-x}-2}{x^{2}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{3+x}{3-x}\right]^{\frac{1}{x}}\)
Solution:

Question 3.
\(\lim _{x \rightarrow 0}\left[\frac{\log (3-x)-\log (3+x)}{x}\right]\)
Solution:

III. Evaluate the following:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{a^{3 x}-b^{2 x}}{\log (1+4 x)}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{\left(2^{x}-1\right)^{2}}{\left(3^{x}-1\right) \cdot \log (1+x)}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 0}\left[\frac{15^{x}-5^{x}-3^{x}+1}{x^{2}}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 2}\left[\frac{3^{\frac{x}{2}}-3}{3^{x}-9}\right]\)
Solution:

IV. Evaluate the following:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{(25)^{x}-2(5)^{x}+1}{x^{2}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{(49)^{x}-2(35)^{x}+(25)^{x}}{x^{2}}\right]\)
Solution:

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Ex 7.3 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Ex 7.3

I. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt{6+x+x^{2}}-\sqrt{6}}{x}\right]\)
Solution:

Question 2.
\(\lim _{y \rightarrow 0}\left[\frac{\sqrt{1-y^{2}}-\sqrt{1+y^{2}}}{y^{2}}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{\sqrt{2+x}-\sqrt{6-x}}{\sqrt{x}-\sqrt{2}}\right]\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow a}\left[\frac{\sqrt{a+2 x}-\sqrt{3 x}}{\sqrt{3 a+x}-2 \sqrt{x}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 2}\left[\frac{x^{2}-4}{\sqrt{x+2}-\sqrt{3 x-2}}\right]\)
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 1}\left[\frac{x^{2}+x \sqrt{x}-2}{x-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt{1+x^{2}}-\sqrt{1+x}}{\sqrt{1+x^{3}}-\sqrt{1+x}}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 4}\left[\frac{x^{2}+x-20}{\sqrt{3 x+4}-4}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-8}{\sqrt{x+2}-\sqrt{3 x-2}}\right]\)
Solution:

IV. Evaluate the following limits:

Question 1.
\(\lim _{y \rightarrow 2}\left[\frac{2-y}{\sqrt{3-y}-1}\right]\)
Solution:

Question 2.
\(\lim _{z \rightarrow 4}\left[\frac{3-\sqrt{5+z}}{1-\sqrt{5-z}}\right]\)
Solution:

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Ex 7.2 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Ex 7.2

I. Evaluate the following limits:

Question 1.
\(\lim _{z \rightarrow 2}\left[\frac{z^{2}-5 z+6}{z^{2}-4}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow-3}\left[\frac{x+3}{x^{2}+4 x+3}\right]\)
Solution:

Question 3.
\(\lim _{y \rightarrow 0}\left[\frac{5 y^{3}+8 y^{2}}{3 y^{4}-16 y^{2}}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow-2}\left[\frac{-2 x-4}{x^{3}+2 x^{2}}\right]\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{u \rightarrow 1}\left[\frac{u^{4}-1}{u^{3}-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 3}\left[\frac{1}{x-3}-\frac{9 x}{x^{3}-27}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-4 x^{2}+4 x}{x^{2}-1}\right]\)
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow-2}\left[\frac{x^{7}+x^{5}+160}{x^{3}+8}\right]\)
Solution:

Question 2.
\(\lim _{y \rightarrow \frac{1}{2}}\left[\frac{1-8 y^{3}}{y-4 y^{3}}\right]\)
Solution:

Question 3.
\(\lim _{v \rightarrow \sqrt{2}}\left[\frac{v^{2}+v \sqrt{2}-4}{v^{2}-3 v \sqrt{2}+4}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 3}\left[\frac{x^{2}+2 x-15}{x^{2}-5 x+6}\right]\)
Solution:

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Ex 7.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Ex 7.1

I. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 3}\left[\frac{\sqrt{x+6}}{x}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 2}\left[\frac{x^{-3}-2^{-3}}{x-2}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 5}\left[\frac{x^{3}-125}{x^{5}-3125}\right]\)
Solution:

Question 4.
If \(\lim _{x \rightarrow 1}\left[\frac{x^{4}-1}{x-1}\right]=\lim _{x \rightarrow a}\left[\frac{x^{3}-a^{3}}{x-a}\right]\), find all possible values of a.
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 7}\left[\frac{(\sqrt[3]{x}-\sqrt[3]{7})(\sqrt[3]{x}+\sqrt[3]{7})}{x-7}\right]\)
Solution:

Question 2.
If \(\lim _{x \rightarrow 5}\left[\frac{x^{k}-5^{k}}{x-5}\right]=500\), find all possible values of k.
Solution:

Question 3.
\(\lim _{x \rightarrow 0}\left[\frac{(1-x)^{8}-1}{(1-x)^{2}-1}\right]\)
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt[3]{1+x}-\sqrt{1+x}}{x}\right]\)
Solution:

Question 2.
\(\lim _{y \rightarrow 1}\left[\frac{2 y-2}{\sqrt[3]{7+y}-2}\right]\)
Solution:

Question 3.
\(\lim _{z \rightarrow a}\left[\frac{(z+2)^{\frac{3}{2}}-(a+2)^{\frac{3}{2}}}{z-a}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 5}\left[\frac{x^{3}-125}{x^{2}-25}\right]\)
Solution: