Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Differentiation Ex 9.1
I. Find the derivatives of the following functions w.r.t. x.
Question 1.
x12
Solution:
Let y = x12
Differentiating w.r.t. x, we get
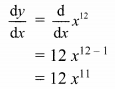
Question 2.
x-9
Solution:
Let y = x-9
Differentiating w.r.t. x, we get
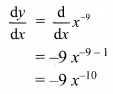
![]()
Question 3.
\(x^{\frac{3}{2}}\)
Solution:
Let y = \(x^{\frac{3}{2}}\)
Differentiating w.r.t. x, we get
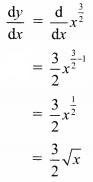
Question 4.
7x√x
Solution:

Question 5.
35
Solution:
Let y = 35
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x} 3^{5}=0\) …..[35 is a constant]
II. Differentiate the following w.r.t. x.
Question 1.
x5 + 3x4
Solution:
Let y = x5 + 3x4
Differentiating w.r.t. x, we get

![]()
Question 2.
x√x + log x – ex
Solution:
Let y = x√x + log x – ex
= \(x^{\frac{3}{2}}+\log x-e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
\(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Solution:
Let y = \(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Differentiating w.r.t. x, we get

Question 4.
\(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Solution:
Let y = \(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Differentiating w.r.t. x, we get

Question 5.
\(\sqrt{x}\left(x^{2}+1\right)^{2}\)
Solution:
Let y = \(\sqrt{x}\left(x^{2}+1\right)^{2}\)
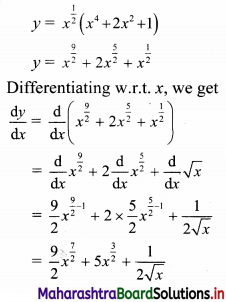
III. Differentiate the following w.r.t. x.
Question 1.
x3 log x
Solution:
Let y = x3 log x
Differentiating w.r.t. x, we get
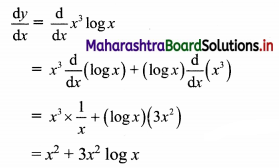
![]()
Question 2.
\(x^{\frac{5}{2}} e^{x}\)
Solution:
Let y = \(x^{\frac{5}{2}} e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
ex log x
Solution:
Let y = ex log x
Differentiating w.r.t. x, we get
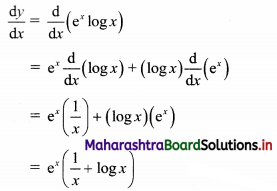
Question 4.
x3 . 3x
Solution:
Let y = x3 . 3x
Differentiating w.r.t. x, we get

IV. Find the derivatives of the following w.r.t. x.
Question 1.
\(\frac{x^{2}+a^{2}}{x^{2}-a^{2}}\)
Solution:
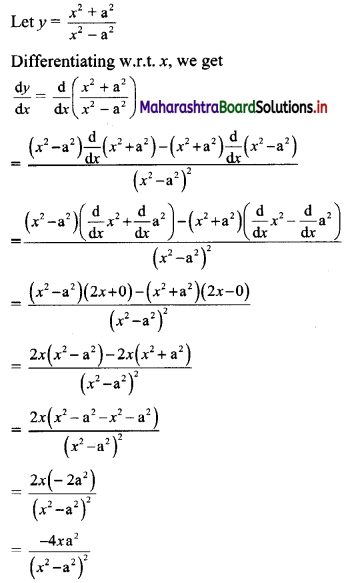
Question 2.
\(\frac{3 x^{2}+5}{2 x^{2}-4}\)
Solution:


![]()
Question 3.
\(\frac{\log x}{x^{3}-5}\)
Solution:

Question 4.
\(\frac{3 e^{x}-2}{3 e^{x}+2}\)
Solution:


Question 5.
\(\frac{x \mathrm{e}^{x}}{x+\mathrm{e}^{x}}\)
Solution:

V. Find the derivatives of the following functions by the first principle:
Question 1.
3x2 + 4
Solution:
Let f(x) = 3x2 + 4
∴ f(x + h) = 3(x + h)2 + 4
= 3(x2 + 2xh + h2) + 4
= 3x2 + 6xh + 3h2 + 4
By first principle, we get
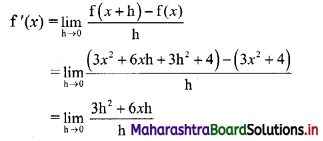
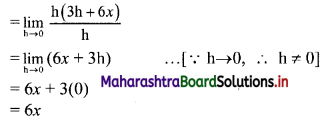
![]()
Question 2.
x√x
Solution:
Let f(x) = x√x
∴ f(x + h) = \((x+h)^{\frac{3}{2}}\)
By first principle, we get

Question 3.
\(\frac{1}{2 x+3}\)
Solution:
Let f(x) = \(\frac{1}{2 x+3}\)
∴ f(x + h) = \(\frac{1}{2(x+\mathrm{h})+3}=\frac{1}{2 x+2 \mathrm{~h}+3}\)
By first principle, we get

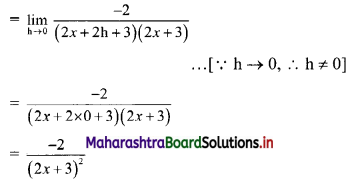
![]()
Question 4.
\(\frac{x-1}{2 x+7}\)
Solution:
Let f(x) = \(\frac{x-1}{2 x+7}\)
∴ f(x + h) = \(\frac{x+\mathrm{h}-1}{2(x+\mathrm{h})+7}=\frac{x+\mathrm{h}-1}{2 x+2 \mathrm{~h}+7}\)
By first principle, we get
