Bhagya

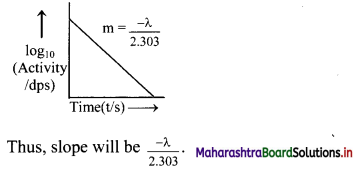
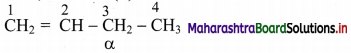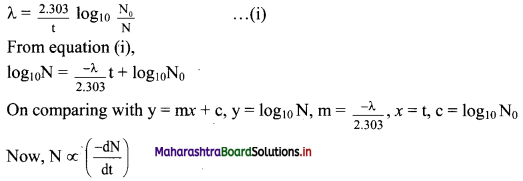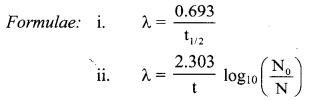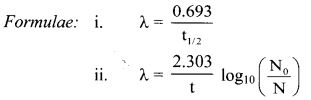Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 11 Electric Current Through Conductors Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 11 Electric Current Through Conductors

Question 1.
Define current. State its formula and SI unit.
Answer:

1. Current is defined as the rate of flow of electric charge.
2. Formula: I = \(\frac {q}{t}\)
3. SI unit: ampere (A)

Question 2.
Derive an expression for a current generated due to the flow of charged particles
Answer:
i. Consider an imaginary gas of both negatively and positively charged particles moving randomly in various directions across a plane P.

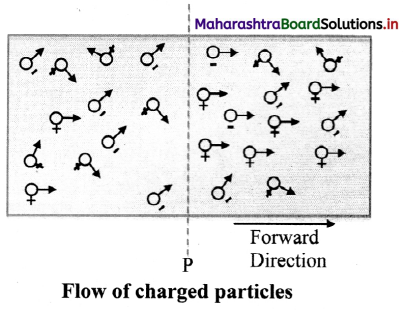
ii. In a time interval t, let the amount of positive charge flowing in the forward direction be q⁺ and the amount of negative charge flowing in the forward direction be q^–. Thus, the net charge flowing in the forward direction is q = q⁺ – q^–

iii. Let I be the current varying with time. Let ∆q be the amount of net charge flowing across the plane P from time t to t + At, i.e. during the time interval ∆t.

iv. Then the current is given by
I(t) = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathrm{q}}{\Delta \mathrm{t}}\)
Flere, the current is expressed as the limit of the ratio (∆q/∆t) as ∆t tends to zero.

Question 3.
Match the amount of current generated A given in column – II with the sources given in column -I.

Answer:

Question 4.
Which are the most common units of current used in semiconductor devices?
Answer:

1. milliampere (mA)
2. microampere (µA)
3. nanoampere (nA)

Question 5.
Six ampere current flows through a bulb. Find the number of electrons that should flow through the bulb in a time of 4 hrs.
Answer:
Given: I = 6 A, t = 4 hrs = 4 × 60 × 60 s
To find: Number of electrons (N)
Formula: I = \(\frac {q}{t}\) = \(\frac {Ne}{t}\)
Calculation: As we know, e = 1.6 × 10^-19 C
From formula,
N = \(\frac {It}{e}\) = \(\frac {6×4×60×60}{1.6×10^{-19}}\) 6x4x60x60 = 5.4 × 10²³

Question 6.
Explain flow of current in different conductor.
Answer:

1. A current can be generated by positively or negatively charged particles.
2. In an electrolyte, both positively and negatively charged particles take part in the conduction.
3.  In a metal, the free electrons are responsible for conduction. These electrons flow and generate a net current under the action of an applied electric field.
4. As long as a steady field exists, the electrons continue to flow in the form of a steady current.
5. Such steady electric fields are generated by cells and batteries.

Question 7.
State the sign convention used to show the flow of electric current in a circuit.
Answer:
The direction of the current in a circuit is drawn in the direction in which positively charged particles would move, even if the current is constituted by the negatively charged particles, (electrons), which move in the direction opposite to that the electric field.

Question 8.
Explain the concept of drift velocity with neat diagrams.
Answer:
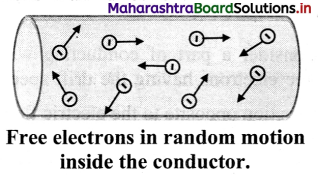
i. When no current flows through a copper rod, the free electrons move in random motion. Therefore, there is no net motion of these electrons in any direction.

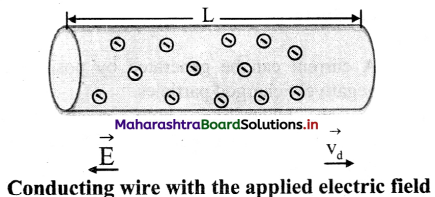
ii. If an electric field is applied along the length of the copper rod, a current is set up in the rod. The electrons inside rod still move randomly, but tend to ‘drift’ in a particular direction.

iii. Their direction is opposite to that of the applied electric field.

iv. The electrons under the action of the applied electric field drift with a drift speed v_d.

Question 9.
What is current density? State its SI unit.
Answer:
i. Current density at a point in a conductor is the amount of current flowing per unit area of the conductor.
Current density, J = \(\frac {I}{A}\)
where, I = Current
A = Area of cross-section

ii. SI unit: A/m²

Question 10.
A metallic wire of diameter 0.02 m contains 10 free electrons per cubic metre. Find the drift velocity for free electrons, having an electric current of 100 amperes flowing through the wire.
(Given: charge on electron = 1.6 × 10^-19C)
Answer:
Given: e = 1.6 × 10^-19 C, n = 10²⁸ electrons/m³,
D = 0.02 m, r = D/2 = 0.01 m,
I = 100 A
To find: Drift velocity (v_d)
Formula: v_d = \(\frac {I}{nAe}\)
Calculation: From formula,
v_d = \(\frac {I}{nπr^2e}\)
∴ v_d = \(\frac {100}{10^{28}×3.142×10^{-4}×1.6×10^{-19}}\)
= \(\frac {10^{-3}}{3.142×1.6}\)
= 1.989 × 10^-4 m/s

Question 11.
A copper wire of radius 0.6 mm carries a current of 1 A. Assuming the current to be uniformly distributed over a cross sectional area, find the magnitude of current density. Answer:
Given: r = 0.6 mm = 0.6 × 10^-3 m, I = 1 A
To find: Current density (J)
Formula: J = \(\frac {I}{A}\)
Calculation: From formula,
J = \(\frac {1}{3.142×(0.6)^2×10^{-6}}\)
= 0.884 × 10⁶ A/m²

Question 12.
A metal wire of radius 0.4 mm carries a current of 2 A. Find the magnitude of current density if the current is assumed to be uniformly distributed over a cross sectional area.
Answer:
Given: r = 0.4 mm = 0.4 × 10^-3 m, I = 2 A
To find: Current density (J)
Formula: J = \(\frac {I}{A}\)
Calculation: From formula,
J = \(\frac {2}{3.142×(0.4)^2×10^{-6}}\)
= 3.978 × 10⁶ A/m²

Question 13.
State and explain ohm’s law.
Answer:
Statement: The current I through a conductor is directly proportional to the potential difference V applied across its two ends provided the physical state of the conductor is unchanged.
Explanation:
According to ohm’s law,
I ∝ V
∴ V = IR or R = \(\frac {V}{I}\)
where, R is proportionality constant and is called the resistance of the conductor.

Question 14.
Draw a graph showing the I-V curve for a good conductor and ideal conductor.
Answer:

Question 15.
Define one ohm.
Answer:
If potential difference of 1 volt across a conductor produces a current of 1 ampere through it, then the resistance of the conductor is one ohm.

Question 16.
Define conductance. State its SI unit.
Answer:

1. Reciprocal of resistance is called conductance.
   C = \(\frac {I}{R}\)
2. S.I unit statement or Ω^-1

Question 17.
Explain the concept of electrical conduction in a conductor.
Answer:

1. Electrical conduction in a conductor is due to mobile charge carriers (electrons).
2. These conduction electrons are free to move inside the volume of the conductor.
3. During their random motion, electrons collide with the ion cores within the conductor. Assuming that electrons do not collide with each other these random motions average out to zero.
4. On application of an electric field E, the motion of the electron is a combination of the random motion of electrons due to collisions and that due to the electric field \(\vec{E}\).
5. The electrons drift under the action of the field \(\vec{E}\) and move in a direction opposite to the direction of the field \(\vec{E}\). In this way electrons in a conductor conduct electricity.

Question 18.
Derive expression for electric field when an electron of mass m is subjected to an electric field (E).
Answer:
i. Consider an electron of mass m subjected to an electric field E. The force experienced by the electron will be \(\vec{F}\) = e\(\vec{E}\).

ii. The acceleration experienced by the electron will then be
\(\vec{a}\) = \(\frac {e\vec{E}}{m}\) …………. (1)

iii. The drift velocities attained by electrons before and after collisions are not related to each other.

iv. After the collision, the electron will move in random direction, but will still drift in the direction opposite to \(\vec{E}\).

v. Let τ be the average time between two successive collisions.

vi. Thus, at any given instant of time, the average drift speed of the electron will be,
v_d = a τ = \(\frac {eEτ}{m}\) ………………(From 1)
v_d = \(\frac {eEτ}{m}\) = \(\frac {J}{ne}\) ……………(2) [∵ v_d = \(\frac {J}{ne}\)]

vii. Electric field is given by,
E = (\(\frac {m}{e^2nτ}\))J ………… (from 2)
= ρJ = [∵ ρ = \(\frac {m}{ne^2τ}\)]
where, ρ is resistivity of the material.

Question 19.
A Flashlight uses two 1.5 V batteries to provide a steady current of 0.5 A in the filament. Determine the resistance of the glowing filament.
Answer:
Given: For each battery, V₁ = V₂ = 1.5 volt,
I = 0.5 A
To find: Resistance (R)
Formula: V = IR
Calculation: Total voltage, V = V₁ + V₂ = 3 volt
From formula,
R = \(\frac {V}{I}\) = \(\frac {3}{0.5}\) = 6.0 Ω

Question 20.
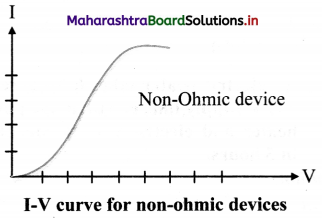
State an expression for resistance of non-ohmic devices and draw I-V curve for such devices.
Answer:
i. Resistance (R) of a non-ohmic device at a particular value of the potential difference V is given by,
R = \(\lim _{\Delta I \rightarrow 0} \frac{\Delta V}{\Delta I}=\frac{d V}{d I}\)
where, ∆V = potential difference between the
two values of potential V – \(\frac {∆V}{2}\) to V + \(\frac {∆V}{2}\),
and ∆I = corresponding change in the current.

Question 21.
Derive an expression for decrease in potential energy when a charge flows through an external resistance in a circuit.
Answer:
i. Consider a resistor AB connected to a cell in a circuit with current flowing from A to B.

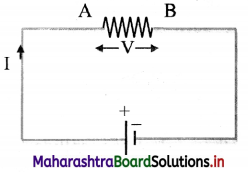
ii. The cell maintains a potential difference V between the two terminals of the resistor, higher potential at A and lower at B.

iii. Let Q be the charge flowing in time ∆t through the resistor from A to B.

iv. The potential difference V between the two points A and B, is equal to the amount of work (W) done to carry a unit positive charge from A to B.
∴ V = \(\frac {W}{Q}\)

v. The cell provides this energy through the charge Q, to the resistor AB where the work is performed.

vi. When the charge Q flows from the higher potential point A to the lower potential point B, there is decrease in its potential energy by an amount
∆U = QV = I∆tV
where I is current due to the charge Q flowing in time ∆t.

Question 22.
Prove that power dissipated across a resistor is responsible for heating up the resistor. Give an example for it.
OR
Derive an expression for the power dissipated across a resistor in terms of its resistance R.
Answer:
i. When a charge Q flows from the higher potential point to the lower potential point, its potential energy decreases by an amount,
∆U = QV = I∆tV
where I is current due to the charge Q flowing in time ∆t.

ii. By the principle of conservation of energy, this energy is converted into some other form of energy.

iii. In the limit as ∆t → 0, \(\frac {dU}{dt}\) = IV
Here, \(\frac {dU}{dt}\) is power, the rate of transfer of energy ans is given by p = \(\frac {dU}{dt}\) = IV
Hence, power is transferred by the cell to the resistor or any other device in place of the resistor, such as a motor, a rechargeable battery etc.

iv. Due to the presence of an electric field, the free electrons move across a resistor and their kinetic energy increases as they move.

v. When these electrons collide with the ion cores, the energy gained by them is shared among the ion cores. Consequently, vibrations of the ions increase, resulting in heating up of the resistor.

vi. Thus, some amount of energy is dissipated in the form of heat in a resistor.

vii. The energy dissipated per unit time is actually the power dissipated which is given by,
P = \(\frac {V^2}{R}\) = I²R
Hence, it is the power dissipation across a resistor which is responsible for heating it up.

viii. For example, the filament of an electric bulb heats upto incandescence, radiating out heat and light.

Question 23.
Calculate the current flowing through a heater rated at 2 kW when connected to a 300 V d. c. supply.
Answer:
Given: P = 2 kW = 2000 W, V = 300 V
To find: Current (I)
Formula: P = IV
Calculation: From formula,
I = \(\frac {P}{V}\) = \(\frac {2000}{300}\) = 6.67 A

Question 24.
An electric heater takes 6 A current from a 230 V supply line, calculate the power of the heater and electric energy consumed by it in 5 hours.
Answer:
Given: I = 6 A, V = 230 V, t = 5 hours
To find: Power (P), Energy consumed
Formulae: i. P = IV
ii. Energy consumed = power × time
Calculation: From formula (i),
P = 6 × 230
= 1380 W = 1.38 kW
From formula (ii),
Energy consumed = 1.38 × 5 = 6.9 kWh
= 6.9 units

Question 25.
When supplied a voltage of 220 V, an electric heater takes 6 A current. Calculate the power of heater and electric energy consumed by its in 2 hours?
Answer:
Given: I = 6 A, V = 220 volt, t = 2 hour
To find: i. Power of heater (P)
ii. Electric energy consumed (E)
Formulae: i. P = IV
ii. Electric energy consumed
= Power × time
Calculation: From formula (i),
P = 6 × 220 = 1320 W = 1.32 kW
From formula (ii),
Electric energy consumed
= 1.32 × 2 = 2.64 kWh = 2.64 units

Question 26.
Explain the colour code system for resistors with an example.
Answer:
i. In colour code system, resistors has 4 bands on it.

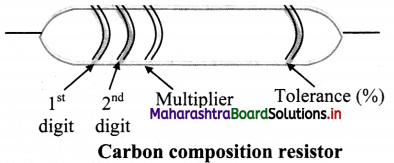
ii. In the four band resistor, the colour code of the first two bands indicate two numbers and third band often called decimal multiplier.

iii. The fourth band separated by a space from the three value bands, indicates tolerance of the resistor.

iv. Following table represents the colour code of carbon resistor.

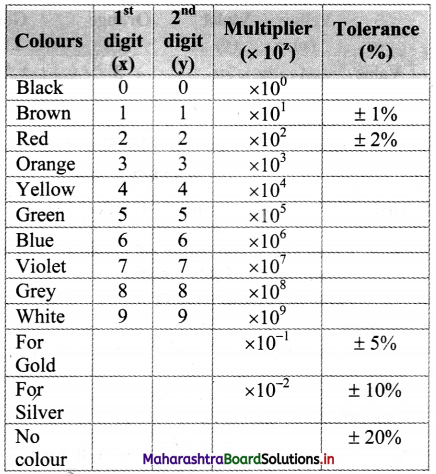
v. Example:
Let the colours of the rings of a resistor starting from one end be brown, red and orange and gold at the other end. To determine resistance of resistor we have,
x = 1, y = 2, z = 3 (From colour code table)
∴ Resistance = xy × 10^z Ω ± tolerance
= 12 × 10³ Ω ± 5%
= 12 kΩ ± 5%
[Note: To remember the colours in order learn the Mnemonics: B.B. ROY of Great Britain had Very Good Wife]

Question 27.
Explain the concept of rheostat.
Answer:

1. A rheostat is an adjustable resistor used in applications that require adjustment of current or resistance in an electric circuit.
2. The rheostat can be used to adjust potential difference between two points in a circuit, change the intensity of lights and control the speed of motors, etc.
3. Its resistive element can be a metal wire or a ribbon, carbon films or a conducting liquid, depending upon the application.
4. In hi-fi equipment, rheostats are used for volume control.

Question 28.
Explain series combination of resistors.
Answer:
i. In series combination, resistors are connected in single electrical path. Hence, the same electric current flows through each resistor in a series combination.

ii. Whereas, in series combination, the supply voltage between two resistors R₁ and R₂ is divided into V₁ and V₂ respectively.

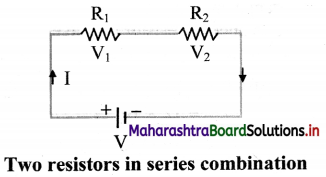
iii. According to Ohm’s law,
R₁ = \(\frac {V_1}{I}\), R₂ = \(\frac {v_2}{I}\)
Total Voltage, V = V₁ + V₂
= I(R₁ + R₂)
∴ V = I R_s
Thus, the equivalent resistance of the series circuit is, R_s = R₁ + R₂

iv. When a number of resistors are connected in series, the equivalent resistance is equal to the sum of individual resistances.
For ‘n’ number of resistors,
R_s = R₁ + R₂ + R₂ + ………….. + R_n = \(\sum_{i=1}^{i=n} R_{i}\)

Question 29.
Explain parallel combination of resistors.
Answer:
i. In parallel combination, the resistors are connected in such a way that the same voltage is applied across each resistor.

ii. A number of resistors are said to be connected in parallel if all of them are connected between the same two electrical points each having individual path.

iii. In parallel combination, the total current I is divided into I, and I2 as shown in the circuit diagram.

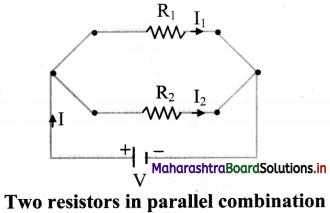
iv. Since voltage V across them remains the same,
I = I₁ + I₂
where I₁ is current flowing through R₁ and I₂ is current flowing through R₂.

v. When Ohm’s law is applied to R₁,
V = I₁R₁
i.e. I₁ = \(\frac {V}{R_1}\) ………(1)
When Ohm’s law applied to R2,
V = I₂R₂
i.e., I₂ = \(\frac {V}{R_2}\) …………(2)

vi. Total current is given by,
I = I₁ + I₂
∴ I = \(\frac {V}{R_1}\) + \(\frac {V}{R_2}\) ………[From (1) and (2)]
Since, I = \(\frac {V}{R_p}\)
∴ \(\frac {V}{R_p}\) = \(\frac {V}{R_1}\) + \(\frac {V}{R_2}\)
∴ \(\frac {1}{R_p}\) = \(\frac {1}{R_1}\) + \(\frac {1}{R_2}\)
Where, R_p is the equivalent resistance in parallel combination.

vii. If ‘n’ number of resistors R₁, R₂, R₃, ………….. R_n are connected in parallel, the equivalent resistance of the combination is given by
\(\frac {1}{R_p}\) = \(\frac {1}{R_1}\) + \(\frac {1}{R_2}\) + \(\frac {1}{R_3}\) ……….. + \(\frac {1}{R_n}\) = \(\sum_{i=1}^{\mathrm{i}=\mathrm{n}} \frac{1}{\mathrm{R}}\)
Thus, when a number of resistors are connected in parallel, the reciprocal of the equivalent resistance is equal to the sum of the reciprocals of individual resistances.

Question 30.
Colour code of resistor is Yellow-Violet- Orange-Gold. Find its value.
Answer:

Value of resistance: xy × 10^z Ω ± tolerance
∴ Value of resistance = 47 × 10³ Ω ± 5%
= 47 kΩ ± 5%

Question 31.
From the given value of resistor, find the colour bands of this resistor.
Value of resistor: 330 Ω
Answer:
Value = 330 Ω = 33 × 10¹ Ω = xy × 10^z Ω

ii. Given: Green – Blue – Red – Gold

Question 32.
Evaluate resistance for the following colour-coded resistors:
i. Yellow – Violet – Black – Silver
ii. Green – Blue – Red – Gold
ill. Brown – Black – Orange – Gold
Answer:
i. Given: Yellow – Violet – Black – Silver
To find: Value of resistance
Formula: Value of resistance
= (xy × 10^z ± T%)Ω

Hence x = 4, y = 7, z = 0, T = 10%
Value of resistance = (xy ×10^z ± T%) Ω
= (47 × 10° ± 10%) Ω
Value of resistance = 47 Ω ± 10%

To find: Value of resistance
Formula: Value of resistance
= (xy × 10^z ± T%) Ω
Calculation:

Hence x = 5, y = 6, z = 2, T = 5%
Value of resistance = (xy × 10^z ± T%) Q
= 56 × 102 Ω ± 5%
= 5.6 k Ω ± 5%

iii. Given: Brown – Black – Orange – Gold
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10^z ± T%) Ω
Calculation:

Hence x = 1, y = 0, z = 3, T = 5%
Value of resistance = (xy × 10^z ± T%) Ω
= 10 × 10³ Ω ± 5%
= 10 kΩ ± 5%

Question 33.
Calculate
i. total resistance and
ii. total current in the following circuit.
R₁ = 3 Ω, R₂ = 6 Ω, R₃ = 5 Ω, V = 14 V

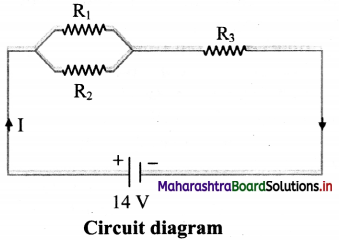
Answer:
i. R₁ and R₂ are connected in parallel. This combination (R_p) is connected in series with R₃.
∴ Total resistance, R_T = R_p + R₃
R_p = \(\frac {R_1R_2}{R_1+R_2}\) = \(\frac {3×6}{3+6}\) = 2 Ω
∴ R_T = 2+ 5 = 7 Ω

ii. Total current: I = \(\frac {V}{R_T}\) = \(\frac {14}{7}\) = 2 A

Question 34.
State the factors affecting resistance of a conductor.
Answer:
Factors affecting resistance of a conductor:

1. Length of conductor
2. Area of cross-section
3. Nature of material

Question 35.
Derive expression for specific resistance of a material.
Answer:
At a particular temperature, the resistance (R) of a conductor of uniform cross section is
i. directly proportional to its length (l),
i.e., R ∝ l ……….. (1)

ii. inversely proportional to its area of cross section (A),
R ∝ \(\frac {1}{A}\) ……….. (1)
From equations (1) and (2),
R = ρ\(\frac {l}{A}\)
where ρ is a constant of proportionality and it is called specific resistance or resistivity of the material of the conductor at a given temperature.

iii. Thus, resistivity is given by,
ρ = \(\frac {RA}{l}\)

Question 36.
State SI unit of resistivity.
Answer:
SI unit of resistivity is ohm-metre (Ω m).

Question 37.
What is conductivity? State its SI unit.
Answer:
i. Reciprocal of resistivity is called as conductivity of a material.
Formula: σ = \(\frac {1}{ρ}\)
ii. SI unit: (\(\frac {1}{ohm m}\)) or siemens/metre

Question 38.
Explain the similarities between R = \(\frac {V}{I}\) and ρ = \(\frac {E}{J}\)
Answer:

1. Resistivity (ρ) is a property of a material, while the resistance (R) refers to a particular object.
2. The electric field \(\vec{E}\) at a point is specified in a material with the potential difference across the resistance and the current density \(\vec{J}\) in a material is specified instead of current I in the resistor.
3. For an isotropic material, resistivity is given by ρ = \(\frac {E}{J}\)
   For a particular resistor, the resistance R given by, R = \(\frac {V}{I}\)

Question 39.
State expression for current density in terms of conductivity.
Answer:
Current density, \(\vec{J}\) = \(\frac {1}{ρ}\) \(\vec{E}\) = σ \(\vec{E}\)
where, ρ = resistivity of the material
E = electric field intensity
σ = conductivity of the material

Question 40.
Calculate the resistance per metre, at room temperature, of a constantan (alloy) wire of diameter 1.25 mm. The resistivity of constantan at room temperature is 5.0 × 10^-7 Ωm.
Answer:
Given: ρ = 5.0 × 10^-7 Ω m, d = 1.25 × 10^-3 m,
∴ r = 0.625 × 10^-3 m
To find: Resistance per metre (\(\frac {R}{l}\))
Formula: ρ = \(\frac {RA}{l}\)
Calculation:
From formula,
\(\frac{\mathrm{R}}{l}=\frac{\rho}{\mathrm{A}}=\frac{\rho}{\pi \mathrm{r}^{2}}\)
= \(\frac{5 \times 10^{-7}}{3.142 \times\left(0.625 \times 10^{-3}\right)^{2}}\)
= \(\frac{5}{3.142 \times 0.625^{2}} \times 10^{-1}\)
= { antilog [log 5 – log 3.142 -2 log 0.625]} × 10^-1
= {antilog [ 0.6990 – 0.4972 -2(1.7959)]} × 10^-1
= {antilog [0.2018- 1.5918]} × 10^-1
= {antilog [0.6100]} × 10^-1
= 4.074 × 10^-1
∴ \(\frac {R}{l}\) ≈ 0.41 Ω m^-1

Question 41.
A negligibly small current is passed through a wire of length 15 m and uniform cross-section 6 × 10^-7 m², and its resistance is measured to be 5 Ω. What is the resistivity of the material at the temperature of the experiment?
Answer:
Given: l = 15 m, A = 6.0 × 10^-7 m², R = 5 Ω
To find: Resistivity (ρ)
Formula: ρ = \(\frac {RA}{l}\)
Calculation: From formula,
ρ = \(\frac {5×6×10^{-7}}{15}\)
∴ ρ = 2 × 10^-7 Ω m

Question 42.
A constantan wire of length 50 cm and 0.4 mm diameter is used in making a resistor. If the resistivity of constantan is 5 × 10^-7m, calculate the value of the resistor.
Answer:
Given: l = 50 cm = 0.5 m,
d = 0.4 mm = 0.4 × 10^-3 m,
r = 0.2 × 10^-3 m, p = 5 × 10^-7 Ωm
To Find: Value of resistor (R)
Formula: ρ = \(\frac {RA}{l}\)
Calculation: from formula,

Question 43.
The resistivity of nichrome is 10^-6 Ωm. What length of a uniform wire of this material and of 0.2 mm diameter will have a resistance of 200 ohm?
Answer:
Given: ρ = 10^-6 Ω m, d = 0.2 mm,
∴ r = 0.1 mm = 0.1 × 10^-3 m, R = 200 Ω
To find: Length (l)
Formula: R = \(\frac {ρl}{A}\) = \(\frac {ρl}{πr^2}\)
Calculation: From formula,
l = \(\frac {πr^2}{ρ}\)
∴ l = \(\frac{200 \times 3.142 \times\left(0.1 \times 10^{-3}\right)^{2}}{10^{-6}}\) = 6 284 m

Question 44.
A wire of circular cross-section and 30 ohm resistance is uniformly stretched until its new length is three times its original length. Find its resistance.
Answer:
Given: R₁ = 30 ohm,
l₁ = original length, A₁ = original area,
l₂ = new length, A₂ = new area
l₂= 3l₁
To find: Resistance (R₂)
Formula: R= ρ\(\frac {l}{A}\)
Calculation: From formula,

The volume of wire remains the same in two cases, we have

Question 45.
Define temperature coefficient of resistivity. State its SI unit.
Answer:
i. The temperature coefficient of resistivity is defined as the increase in resistance per unit original resistance at the chosen reference temperature, per degree rise in temperature.
α = \(\frac{\rho-\rho_{0}}{\rho_{0}\left(T-T_{0}\right)}\)
= \(\frac{\mathrm{R}-\mathrm{R}_{0}}{\mathrm{R}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)
For small difference in temperatures,
α = \(\frac {1}{R_0}\) \(\frac {dR}{dT}\)

ii. SI unit: °C^-1 (per degree Celsius) or K^-1 (per kelvin).

Question 46.
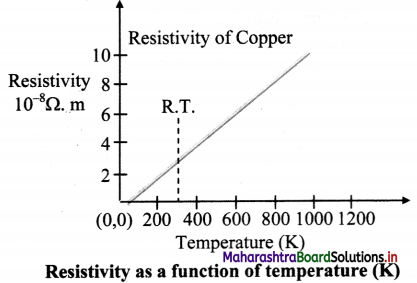
Give expressions for variation of resistivity and resistance with temperature. Represent graphically the temperature dependence of resistivity of copper.
Answer:
i. Resistivity is given by,
ρ = ρ₀ [1 + α (T – T₀)] where,
T₀ = chosen reference temperature
ρ₀ = resistivity at the chosen temperature
α = temperature coefficient of resistivity
T = final temperature

ii. Resistance is given by,
R = R₀ [1+ α (T – T₀)]
Where,
T₀ = chosen reference temperature
R₀ = resistance at the chosen temperature
α = temperature coefficient of resistance
T = final temperature

iii. For example, for copper, the temperature dependence of resistivity can be plotted as shown:

Question 47.
What is super conductivity?
Answer:

1. The resistivity of a metal decreases as the temperature decreases.
2. In case of some metals and metal alloys, the resistivity suddenly drops to zero at a particular temperature (T_c), this temperature is called critical temperature.
3. Super conductivity is the phenomenon where resistivity of a material becomes zero at particular temperature.
4. For example, mercury loses its resistance completely to zero at 4.2 K.

Question 48.
A piece of platinum wire has resistance of 2.5 Ω at 0 °C. If its temperature coefficient of resistance is 4 × 10^-3/°C. Find the resistance of the wire at 80 °C.
Answer:
Given: R₀ = 2.5 Ω
α = 4 × 10^-3/°C = 0.004/°C
T = 80 °C
To find: Resistance at 80 °C (R_T)
Formula: R_T = R₀(l + α T)
Calculation: From formula,
R_T = 2.5 [1+ (0.004 × 80)]
= 2.5(1 + 0.32)
R_T = 2.5 × 1.32
R_T = 3.3 Ω

Question 49.
The resistance of a tungsten filament at 150 °C is 133 ohm. What will be its resistance at 500 °C? The temperature coefficient of resistance of tungsten is 0.0045 per °C.
Answer:
Given: Let resistance at 150 °C be R₁ and resistance at 500 °C be R₂
Thus,
R₁= 133 Ω, α = 0.0045 °C^-1
To find: Resistance (R₂)
Formula: R_T = R₀ (1 + α∆T)
Calculation:
From formula,
R₁ = R₀ (1 + α × 150)
∴ 133 = R₀(1 + 0.0045 × 150) ……….(i)
R₂ = R₀ (1 + α × 500)
∴ R₂ = R₀(1 + 0.0045 × 500) ………(ii)
Dividing equation (ii) by (i), we get
\(\frac{\mathrm{R}_{2}}{133}=\frac{1+(0.0045 \times 500)}{1+(0.0045 \times 150)}=\frac{3.25}{1.675}\)
∴ R₂ = \(\frac {3.25}{1.675}\) × 133 = 258 Ω

Question 50.
A silver wire has resistance of 2.1 Ω at 27.5 °C. If temperature coefficient of silver is 3.94 × 10^-3/°C, find the silver wire resistance at 100 °C.
Answer:
Given: R₁ = 2.1 Ω, T₁ = 27.5 °C,
α = 3.94 × 10^-3/°C, T₂ = 100 °C
To find: Resistance (R₂)
Formula: R_T = R_o (1 + αT)
Calculation:
From the formula,
R₁ = R₀(1 + α × 27.5) ……….. (i)
R₂ = R₀(l + α × 100) ………….. (ii)
Dividing equation (i) by (ii), we get,
\(\frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}=\frac{1+\left(3.94 \times 10^{-3} \times 27.5\right)}{1+\left(3.94 \times 10^{-3} \times 100\right)}\)
\(\frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}=\frac{1.10835}{1.394}\) = 0.795
∴ R₂ = \(\frac{\mathrm{R}_{1}}{0.795}=\frac{2.1}{0.795}\) = 2.641 Ω

Question 51.
At what temperature would the resistance of a copper conductor be double its resistance at 0 °C?
(a for copper = 3.9 × 10^-3/°C)
Answer:
Given: Let the resistance of the conductor at 0°C be R₀
R₁ = R₀ at T₁ = 0°C
R₂ = 2R₀ at T₂ = T
To find: Final temperature (T)
Formula: α = \(\frac {R_2-R_1}{R_1(T_2-T_1)}\)
Calculation: From formula,
α = \(\frac {2R_0-R_0}{R_1(T_2-T_1)}\) = \(\frac {1}{T}\)
∴ T = \(\frac {1}{α}\) = \(\frac {1}{3.9×10^{-3}}\) ≈ 256 °C

Question 52.
A conductor has resistance of 15 Ω at 10 °C and 18 Ω at 400 °C. Find the temperature coefficient of resistance of the material.
Answer:
Given: R₁ = 15 Ω, T₁ = 10 °C, R₂ = 18 Ω,
T₂ = 400 °C
To find: Temperature coefficient of resistance (α)
Formula: R_T = R₀ (1 + αT)
Calculation:
From formula,
R₁ = R₀ (1 + α × 10) ……..(i)
R₂ = R₀ (1 + α × 400) …….(ii)
Dividing equation (i) by (ii), we get,
\(\frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}=\frac{1+(\alpha \times 10)}{1+(\alpha \times 400)}\)
∴ \(\frac{15}{18}=\frac{1+10 \alpha}{1+400 \alpha}\)
∴ 18 + 180 α = 15 + 6000 α
∴ 5820 α = 3
∴ α = \(\frac {3}{5820}\) = 5.155 × 10^-4/°C

Question 53.
Write short note on e.m.f. devices.
Answer:

1. When charges flow through a conductor, a potential difference get established between the two ends of the conductor.
2. For a steady flow of charges, this potential difference is required to be maintained across the two ends of the conductor.
3. There is a device that does so by doing work on the charges, thereby maintaining the potential difference. Such a device is called an emf device and it provides the emf E.
4. The charges move in the conductor due to the energy provided by the emf device. This energy is supplied by the e.m.f. device on account of its work done.
5. Power cells, batteries, Solar cells, fuel cells, and even generators, are some examples of emf devices.

Question 54.
Explain working of a circuit when connected to emf device.
Answer:
i. A circuit is formed with connecting an emf device and a resistor R. Flere, the emf device keeps the positive terminal (+) at a higher electric potential than the negative terminal (-)

ii. The emf is represented by an arrow from the negative terminal to the positive terminal.

iii. When the circuit is open, there is no net flow of charge carriers within the device.

iv. When connected in a circuit, the positive charge carriers move towards the positive terminal which acts as cathode inside the emf device.

v. Thus, the positive charge carriers move from the region of lower potential energy, to the region of higher potential energy.

vi. Consider a charge dq flowing through the cross section of the circuit in time dt.

vii. Since, same amount of charge dq flows throughout the circuit, including the emf device. Hence, the device must do work dW on the charge dq, so that the charge enters the negative terminal (low potential terminal) and leaves the positive terminal (higher potential terminal).

viii. Therefore, e.m.f. of the emf device is,
E = \(\frac {dW}{dq}\)
The SI unit of emf is joule/coulomb (J/C).

Question 55.
What is an ideal e.m.f. device?
Answer:

1. In an ideal e.m.f. device, there is no internal resistance to the motion of charge carriers.
2. The emf of the device is then equal to the potential difference across the two terminals of the device.

Question 56.
What is a real e.m.f. device?
Answer:

1. In a real emf device, there is an internal resistance to the motion of charge carriers.
2. If such a device is not connected in a circuit, there is no current through it.

Question 57.
Derive an expression for current flowing through a circuit when an external resistance is connected to a real e.m.f. device.
Answer:

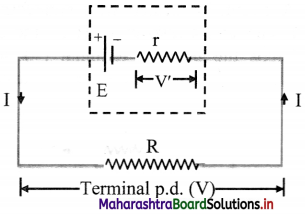
i. If a current (I) flows through an emf device, there is an internal resistance (r) and the emf (E) differs from the potential difference across its two terminals (V).
V = E – Ir ……… (1)

ii. The negative sign is due to the fact that the current I flows through the emf device from the negative terminal to the positive terminal.

iii. By the application of Ohm’s law,
V = IR …….(2)
From equations (1) and (2),
IR = E – Ir
∴ \(\frac {E}{R+r}\)

Question 58.
Explain the conditions for maximum current.
Answer:

1. Current in a circuit is given by, I = \(\frac {E}{R+r}\)
2. Maximum current can be drawn from the emf device, only when R = 0, i.e.
   I_max = \(\frac {E}{R}\)
3. I_max is the maximum allowed current from an emf device (or a cell) which decides the maximum current rating of a cell or a battery.

Question 59.
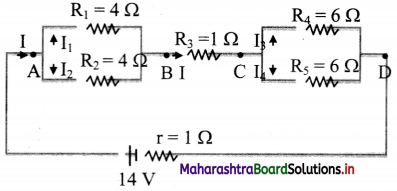
A network of resistors is connected to a 14 V battery with internal resistance 1 Q as shown in the circuit diagram.
i. Calculate the equivalent resistance,
ii. Current in each resistor,
iii. Voltage drops V_AB, V_BC and V_DC.

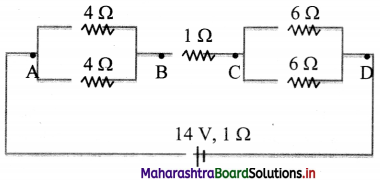
Answer:

For equivalent resistance (R_eq):
R_AB is given as,
\(\frac{1}{\mathrm{R}_{\mathrm{AB}}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\)
∴ R_AB = 2 Ω
R_BC = R₃ = 1 Ω
Also, R_CD is given as,
\(\frac{1}{\mathrm{R}_{\mathrm{CD}}}=\frac{1}{\mathrm{R}_{4}}+\frac{1}{\mathrm{R}_{5}}=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}\)
∴ R_CD = 3 Ω
∴ R_eq = R_AB + R_BC + R_CD
= 2 + 1 + 3 = 6Ω

ii. Current through each resistor:
Total current, I = \(\frac{\mathrm{E}}{\mathrm{R}_{\mathrm{eq}}+\mathrm{r}}\) = \(\frac {14}{6+1}\) = 2 A
Across AB, as, R₁ = R₂
V₁ = V₂
∴I₁ × 4 = I₂ × 4
∴ I₁ = I₂
But, I₁ + I₂ = I
∴ 2I₁ = I
∴ I₁ = I₂ =1 A ….(∵I = 2 A)
Similarly, as R₄ = R₅
I₃ = I₄ = 1 A
Current through resistor BC is same as I.
∴ I_BC = 2 A

iii. Voltage drops across AB, BC and CD:
V_AB = IR_AB = 2 × 2 = 4 V
V_BC = IR_BC = 2 × 1 = 2 V
V_CD = IR_CD = 2 × 3 = 6 V

Question 60.
i. Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
ii. If the combination is connected to a battery of e.m.f. 20 V and negligible internal resistance, determine the current through each resistor and the total current drawn from the battery.
Answer:
Given: R₁ = 2Ω, R₂ = 4 Ω, R₃ = 5 Ω,
V = 20 V
To Find: i. Total resistance (R)
ii. Current through each resistor (I₁, I₂, I₃ respectively)
iii. Total current (I)
Formulae:
i. \(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}\)
ii. V = IR
iii. Total current, I = I₁ +I₂ + I₃
Calculation
From formula (i):
\(\frac{1}{R}=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{19}{20}\)
∴ R = \(\frac {20}{19}\) Ω
From formula (ii):

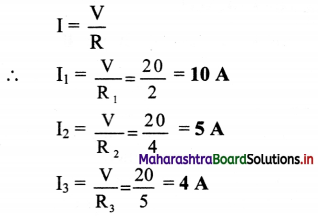
From formula (iii):
I = 10 + 5 + 4
∴ I = 19 A

Question 61.
i. Three resistors 1 Ω, 2 Ω and 3 Ω are combined in series. What is the total resistance of the combination?
ii. If the combination is connected to a battery of e.m.f. 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Answer:
Given: R₁ = 1Ω, R₂ = 2 Ω, R₃ = 3 Ω,
V = 12 V
To Find: i. Total resistance (R)
ii. P.D Across R₁, R₂, R₃ (V₁, V₂, V₃ respectively)
Formulae:
i. R_s = R₁ + R₂ + R₃
ii. V = IR
Calculation
From formula (i):
Rs = l + 2 + 3 = 6 Ω
From formula (ii),
1 = \(\frac {V}{R}\) = \(\frac {12}{6}\) = 2A
∴ V₁ = IR₁ = 2 × 1 = 2 V
∴ V₂ = IR₂ = 2 × 2 = 4 V
∴ V₃ = IR₃ = 2 × 3 = 6 V

Question 62.
A voltmeter is connected across a battery of emf 12 V and internal resistance of 10 Ω. If the voltmeter resistance is 230 Ω, what reading will be shown by the voltmeter? Answer:
Given: E = 12 volt, r = 10 Ω, R = 230 Ω
To find: Reading shown by voltmeter (V)
Formula: i. I = \(\frac {E}{R+r}\)
ii. V = E – Ir
Calculation
From formula (i),
I = \(\frac{12}{230+10}=\frac{12}{240}=\frac{1}{20} \mathrm{~A}\)
From formula (ii),
V= 12 – \(\frac {1}{20}\) × 10 = 12 – 0.5
= 11.5 volt

Question 63.
A battery of e.m.f. 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Answer:
Given: E = 10 V, r = 3 Ω, I = 0.5 A
To find: i. Resistance of resistor (R)
ii. Terminal voltage of battery (V)
Formula: I = \(\frac {E}{R+r}\)
Calculation: From formula, R = \(\frac {E}{I}\) – r
∴ R = \(\frac {10}{0.5}\)– 3 = 17 Ω
∴ V = IR = 0.5 × 17 = 8.5 volt

Question 64.
How many cells each of 1.5 V/500 mA rating would be required in series-parallel combination to provide 1500 mA at 3 V?
Answer:
21 = ………… = 1.5 V (given)
I₁ = I₂ = …………… = 500 mA (given)
1500 mA at 3 V is required.
To determine required number of cells:
For series V = V₁ + V₂ + ………….., and current remains same.
For parallel I = I₁ + I₂ + ………, and voltage remains same.
To achieve battery output of 3V, the cells should be connected in series.
If n are the number of cells connected in series, then
V = V₁ + V₂ + …………. + V_n
∴ V = nV₁
∴ 3 = n × 1.5
∴ n = 2 cells in series
The series combination of two cells in series will give a current 500 mA.
To achieve output of 1500 mA, the number of batteries (n) connected in parallel, each one having output 3V is,
I = I₁ + I₂ + ………. + I_n
∴ I = nI₁
∴ 1500 = n × 500
∴ n = 3 batteries each of two cells
∴ No of cells required are 2 × 3 = 6 .
∴ Number of cells = 6
The six cells must be connected as shown

Question 65.
Explain the concept of series combination of cells.
Answer:
i. In a series combination, cells are connected in single electrical path, such that the positive terminal of one cell is connected to the negative terminal of the next cell, and so on.

ii. The terminal voltage of batteiy/cell is equal to the sum of voltages of individual cells in series. Example: Given figure shows two 1.5 V cells connected in series. This combination provides total voltage,
V = 1.5 V + 1.5 V = 3 V.

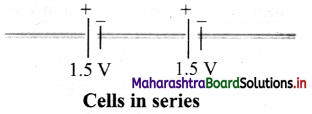
iii. The equivalent emf of n number of cells in series combination is the algebraic sum of their individual emf.
\(\sum_{i} \mathrm{E}_{\mathrm{i}}\) = E₁ + E₂ + E₂+ …….. + E_n

iv. The equivalent internal resistance of n cells in a series combination is the sum of their individual internal resistance.
\(\sum_{i} \mathrm{r}_{\mathrm{i}}\) = r₁ + r₂ + r₃ + ……… + r_n

Question 66.
State advantages of cells in series.
Answer:

1. The cells connected in series produce a larger resultant voltage.
2. Cells which are damaged can be easily identified, hence can be easily replaced.

Question 67.
Explain combination of cells in parallel. Ans:
Answer:
i. Consider two cells which are connected in parallel. Here, positive terminals of all the cells are connected together and the negative terminals of all the cells are connected together.

ii. In parallel connection, the current is divided among the branches i.e. I₁ and I₂ as shown in figure.

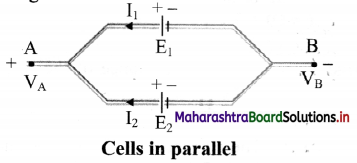
iii. Consider points A and B having potentials V_A and V_B, respectively.

iv. For the first cell the potential difference across its terminals is, V = V_A – V_B = E₁ – I₁ r₁
∴ I₁ = \(\frac {E_1V}{r_1}\) ………. (1)

v. Point A and B are connected exactly similarly to the second cell.
Hence, considering the second cell,
V = V_A – V_B = E₂ – I₂r₂
∴ I₂ = \(\frac {E_2V}{r_2}\) ………. (2)

vi. Since, I = I₁ + I₂ ………….. (3)
Combining equations (1), (2) and (3),

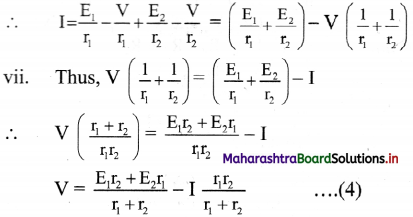
viii. If we replace the cells by a single cell connected between points A and B with the emf E_eq and the internal resistance r_eq then,
V = E_eq– Ir_eq
From equations (4) and (5),

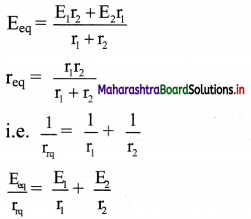
ix. For n number of cells connected in parallel with emf E₁, E₂, E₃, ………….., E_n and internal resistance r₁, r₂, r₃, …………, r_n
\(\frac{1}{\mathrm{r}_{\mathrm{rq}}}=\frac{1}{\mathrm{r}_{1}}+\frac{1}{\mathrm{r}_{2}}+\frac{1}{\mathrm{r}_{3}}+\ldots \ldots \ldots+\frac{1}{\mathrm{r}_{\mathrm{n}}}\)
and \(\frac{\mathrm{E}_{\mathrm{eq}}}{\mathrm{r}_{\mathrm{rq}}}=\frac{\mathrm{E}_{1}}{\mathrm{r}_{1}}+\frac{\mathrm{E}_{2}}{\mathrm{r}_{2}}+\ldots \ldots \ldots+\frac{\mathrm{E}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}}\)

Question 68.
State advantages and disadvantages of cells in parallel.
Answer:
Advantages:
For cells connected in parallel in a circuit, the circuit will not break open even if a cell gets damaged or open.

Disadvantages:
The voltage developed by the cells in parallel connection cannot be increased by increasing number of cells present in circuit.

Question 69.
State the basic categories of electrical cells.
Answer:
Electrical cells can be divided into several categories like primary cell, secondary cell, fuel cell, etc.

Question 70.
Write short note on primary cell.
Answer:

1. A primary cell cannot be charged again. It can be used only once.
2. Dry cells, alkaline cells are different examples of primary cells.
3. Primary cells are low cost and can be used easily. But these are not suitable for heavy loads.

Question 71.
Write short note on secondary cell.
Answer:

1. The secondary cells are rechargeable and can be reused.
2. The chemical reaction in a secondary cell is reversible.
3. Lead acid cell and fuel cell are some examples of secondary cells.
4. Lead acid battery is used widely in vehicles and other applications which require high load currents.
5. Solar cells are secondary cells that convert solar energy into electrical energy.

Question 72.
Write short note on fuel cells vehicles.
Answer:

1. Fuel cells vehicles (FCVs) are electric vehicles that use fuel cells instead of lead acid batteries to power the vehicles.
2. Hydrogen is used as a fuel in fuel cells. The by product after its burning is water.
3. This is important in terms of reducing emission of greenhouse gases produced by traditional gasoline fuelled vehicles.
4. The hydrogen fuel cell vehicles are thus more environment friendly.

Question 73.
What can be concluded from the following observations on a resistor made up of certain material? Calculate the power drawn in each case.

Answer:
i. As the ratio of voltage and current different readings are same, hence ohm’s is valid i.e., V = IR.

ii. Electric power is given by, P = IV
∴ (a) P₁ = 0.2 × 1.6 = 0.32 watt
(b) P₂ = 0.4 × 3.2 = 1.28 watt
(c) P₃ = 0.6 × 4.8 = 2.88 watt
(d) P₄ = 0.8 × 6.4 = 5.12 watt

Question 74.
Answer the following questions from the circuit given below. [S₁, S₂, S₃, S₄, S₅ ⇒ Switches]. Calculate the current (I) flowing in the following cases:
i. S₁, S₄ → open; S₂, S₃, S₅ → closed.
ii. S₂, S₅ → open; S₁, S₃, S₄ → closed.
iii. S₃ → open; S₁, S₂, S₄, S₅ → closed.

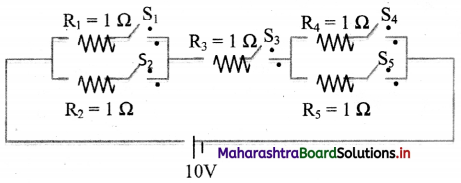
Answer:
i. Here, the circuit can be represented as,

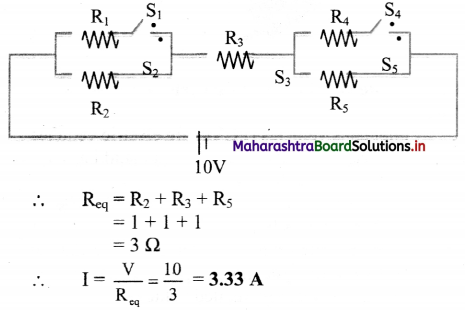
ii. Here, the circuit can be represented as,

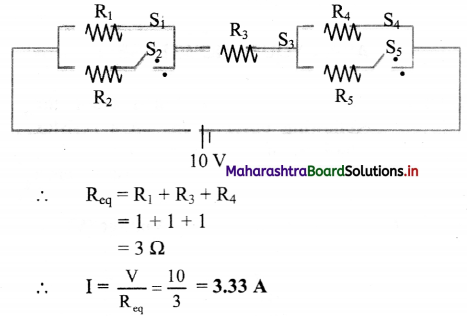
iii. Here, the circuit can be represented as,

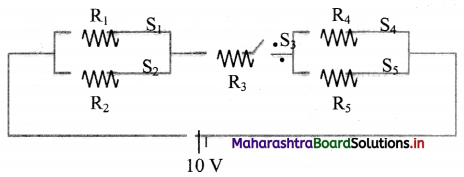
∴ As switch S3 is open, no current will flow in the circuit.

Question 75.
An electric circuit with a carton resistor and an electric bulb (60 watt, 300 Ω) are connected in series with a 230 V source.

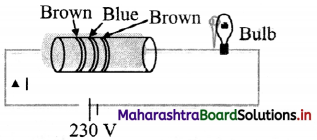
i. Calculate the current flowing through the circuit.
ii. If the electric bulb of 60 watt is replaced by an electric bulb (80 watt, 300 Ω), will it glow? Justify your answer.
Answer:
Resistance of carbon resistor (R₁)
= 16 × 10 Ω = 160 Ω ….(using colour code)
Resistance of bulb (R₂) = 300 Ω
∴ Current through the circuit = \(\frac{V}{R_{1}+R_{2}}\)
∴ I = \(\frac{230}{(160+300)}=\frac{230}{460}\) = 0.5 A

ii. Power drawn through electric bulb
= I²R₂ = (0.5)² × 300 = 75 watt
Hence, if the bulb is replaced by 80 watt bulb, it will not glow.

Question 76.
From the graph given below, which of the two temperatures is higher for a metallic wire? Justify your answer.

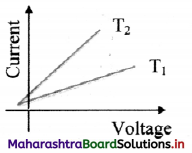
Answer:
As R = \(\frac {V}{I}\)

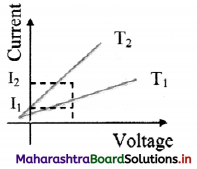
For constant V,
I₂ > I₁
∴ R₁ > R₂
Now, for metallic wire,
R ∝ T
∴ T₁ > T₂
T₁ is greater than T₂.

Question 77.
If n identical cells, each of emf E and internal resistance r, are connected in series, write an expression for the terminal p.d. of the combination and hence show that this is nearly n times that of a single cell.
Answer:
i. Let n identical cells, each of emf E and internal resistance r, be connected in series. Let the current supplied by this combination to an external resistance R be I.

ii. The equivalent emf of the combination,
E_eq = E + E + …….. (n times) = nE

iii. The equivalent internal resistance of the combination,
r_eq= r + r + … (n times)
= nr

iv. The terminal p.d. of the combination is
V = E_eq – Ir_eq = nE – Inr = n (E – Ir)
∴ V = n × terminal p.d. of a single cell
Thus, the terminal p.d. of the series combination is n times that of a single cell.

Question 78.
If n identical cells, each of emf E and internal resistance r, are connected in parallel, derive an expression for the current supplied by this combination to external resistance R. Prove that the combination supplies current almost n times the current supplied by a single cell, when the external resistance R is much smaller than the internal resistance of the parallel combination of the cells.
Answer:
i. Consider n identical cells, each of emf E and internal resistance r, connected in parallel.

ii. Let the current supplied by the combination to the external resistance R be I.
In this case, the equivalent emf of the combination is E.

iii. The equivalent internal resistance r’ of the combination is,
\(\frac{1}{\mathrm{r}^{\prime}}=\frac{1}{\mathrm{r}}+\frac{1}{\mathrm{r}}\) + …………. (n terms)
∴ \(\frac{1}{\mathrm{r}^{\prime}}=\frac{\mathrm{n}}{\mathrm{r}} \Rightarrow \mathrm{r}^{\prime} \frac{\mathrm{n}}{\mathrm{r}}\)

iv. But V = IR is the terminal p.d. across each cell.

v. Hence, the current supplied by each cell,
I = \(\frac {E-V}{r}\)

vi. This gives the current supplied by the combination to the external resistance as
I = \(\frac {E-V}{r}\) + \(\frac {E-V}{r}\) + …….. (n terms) = n(\(\frac {E-V}{r}\))
Thus, current I = n × current supplied by a single cell
This proves that, the current supplied by the combination is n times the current supplied by a single cell.

Multiple Choice Questions

Question 1.
The drift velocity of the free electrons in a conductor is independent of
(A) length of the conductor.
(B) cross-sectional area of conductor.
(C) current.
(D) electric charge.
Answer:
(A) length of the conductor.

Question 2.
The direction of drift velocity in a conductor is
(A) opposite to that of applied electric field.
(B) opposite to the flow of positive charge.
(C) in the direction of the flow of electrons,
(D) all of these.
Answer:
(D) all of these.

Question 3.
The drift velocity of free electrons in a conductor is vd, when the current is flowing in it. If both the radius and current are doubled, the drift velocity will be
(A) \(\frac {v_d}{8}\)
(B) \(\frac {v_d}{4}\)
(C) \(\frac {v_d}{2}\)
(D) v_d
Answer:
(C) \(\frac {v_d}{2}\)

Question 4.
The drift velocity vd of electrons varies with electric field strength E as
(A) v_d ∝ E
(B) v_d ∝ \(\frac {1}{E}\)
(C) v_d ∝ E^1/2
(D) v_d × E^{\(\frac {1}{1/2}\)}
Answer:
(A) v_d ∝ E

Question 5.
When a current I is set up in a wire of radius r, the drift speed is v_d. If the same current is set up through a wire of radius 2r, then the drift speed will be
(A) v_d/4
(B) v_d/2
(C) 2v_d
(D) 4v_d
Answer:
(A) v_d/4

Question 6.
When potential difference is applied across an electrolyte, then Ohm’s law is obeyed at
(A) zero potential
(B) very low potential
(C) negative potential
(D) high potential.
Answer:
(D) high potential.

Question 7.
A current of 1.6 A is passed through an electric lamp for half a minute. If the charge on the electron is 1.6 × 10^-19 C, the number of electrons passing through it is
(A) 1 × 10¹⁹
(B) 1.5 × 10²⁰
(C) 3 × 10¹⁹
(D) 3 × 10²⁰
Answer:
(D) 3 × 10²⁰

Question 8.
The SI unit of the emf of a cell is
(A) V/m
(B) V/C
(C) J/C
(D) C/J
Answer:
(C) J/C

Question 9.
The unit of specific resistance is
(A) Ω m^-1
(B) Ω^-1 m^-1
(C) Ω m
(D) Ω m^-2
Answer:
(C) Ω m

Question 10.
If the length of a conductor is halved, then its conductivity will be
(A) doubled
(B) halved
(C) quadrupled
(D) unchanged
Answer:
(D) unchanged

Question 11.
The resistance of a metal conductor increases with temperature due to
(A) change in current carriers.
(B) change in the dimensions of the conductor.
(C) increase in the number of collisions among the current carriers.
(D) increase in the rate of collisions between the current carriers and the vibrating atoms of the conductor.
Answer:
(D) increase in the rate of collisions between the current carriers and the vibrating atoms of the conductor.

Question 12.
The resistivity of Nichrome is 10^-6 Ω-m. The wire of this material has radius of 0.1 mm with resistance 100 Ω, then the length will be
(A) 3.142 m
(B) 0.3142 m
(C) 3.142 cm
(D) 31.42 m
Answer:
(A) 3.142 m

Question 13.
Given a current carrying wire of non-uniform cross-section. Which of the following is constant throughout the length of the wire?
(A) Current, electric field and drift speed
(B) Drift speed only
(C) Current and drift speed
(D) Current only
Answer:
(D) Current only

Question 14.
A cell of emf E and internal resistance r is connected across an external resistance R (R >> r). The p.d. across R is A 1
(A) \(\frac {E}{R+r}\)
(B) E(I – \(\frac {r}{R}\))
(C) E(I + \(\frac {r}{R}\))
(D) E (R + r)
Answer:
(B) E(I – \(\frac {r}{R}\))

Question 15.
The e.m.f. of a cell of negligible internal resistance is 2 V. It is connected to the series combination of 2 Ω, 3 Ω and 5 Ω resistances. The potential difference across 3 Ω resistance will be
(A) 0.6 V
(B) 10 V
(C) 3 V
(D) 6 V
Answer:
(A) 0.6 V

Question 16.
A P.D. of 20 V is applied across a conductance of 8 mho. The current in the conductor is
(A) 2.5 A
(B) 28 A
(C) 160 A
(D) 45 A
Answer:
(C) 160 A

Question 17.
If an increase in length of copper wire is 0.5% due to stretching, the percentage increase in its resistance will be
(A) 0.1%
(B) 0.2%
(C) 1 %
(D) 2 %
Answer:
(C) 1 %

Question 18.
If a certain piece of copper is to be shaped into a conductor of minimum resistance, its length (L) and cross-sectional area A shall be respectively
(A) L/3 and 4 A
(B) L/2 and 2 A
(C) 2L and A2
(D) L and A
Answer:
(A) L/3 and 4 A

Question 19.
A given resistor has the following colour scheme of the various strips on it: Brown, black, green and silver. Its value in ohm is
(A) 1.0 × 104 ± 10%
(B) 1.0 × 105 ± 10%
(C) 1.0 × 106 + 10%
(D) 1.0 × 107 ± 10%
Answer:
(C) 1.0 × 106 + 10%

Question 20.
A given carbon resistor has the following colour code of the various strips: Orange, red, yellow and gold. The value of resistance in ohm is
(A) 32 × 104 ± 5%
(B) 32 × 104 ± 10%
(C) 23 × 105 ± 5%
(D) 23 × 105 ± 10%
Answer:
(A) 32 × 104 ± 5%

Question 21.
A typical thermistor can easily measure a change in temperature of the order of
(A) 10^-3 °C
(B) 10^-2 °C
(C) 10² °C
(D) 10³ °C
Answer:
(A) 10^-3 °C

Question 22.
Thermistors are usually prepared from
(A) non-metals
(B) metals
(C) oxides of non-metals
(D) oxides of metals
Answer:
(D) oxides of metals

Question 23.
On increasing the temperature of a conductor, its resistance increases because
(A) relaxation time decreases.
(B) mass of the electron increases.
(C) electron density decreases.
(D) all of the above.
Answer:
(A) relaxation time decreases.

Question 24.
Which of the following is used for the formation of thermistor?
(A) copper oxide
(B) nickel oxide
(C) iron oxide
(D) all of the above
Answer:
(D) all of the above

Question 25.
Emf of a cell is 2.2 volt. When resistance R = 5 Ω is connected in series, potential drop across the cell becomes 1.8 volt. Value of internal resistance of the cell is
(A) 10/9 Ω
(B) 7/12 Ω
(C) 9/10 Ω
(D) 12/7 Ω
Answer:
(A) 10/9 Ω

Question 26.
A strip of copper, another of germanium are cooled from room temperature to 80 K. The resistance of
(A) copper strip decreases germanium decreases. and that of
(B) copper strip decreases germanium increases. and that of
(C) Both the strip increases.
(D) copper strip increases germanium decreases. and that of
Answer:
(B) copper strip decreases germanium increases. and that of

Question 27.
The terminal voltage of a cell of emf E on short circuiting will be
(A) E
(B) \(\frac {E}{2}\)
(C) 2E
(D) zero
Answer:
(D) zero

Question 28.
If a battery of emf 2 V with internal resistance one ohm is connected to an external circuit of resistance R across it, then the terminal p.d. becomes 1.5 V. The value of R is
(A) 1 Ω
(B) 1.5 Ω
(C) 2 Ω
(D) 3 Ω
Answer:
(D) 3 Ω

Question 29.
A hall is used 5 hours a day for 25 days in a month. It has 6 lamps of 100 W each and 4 fans of 150 W. The total energy consumed for the month is
(A) 1500 kWh
(B) 150 kWh
(C) 15 kWh
(D) 1.5 kWh
Answer:
(B) 150 kWh

Question 30.
The internal resistance of a cell of emf 2 V is 0.1 Ω. It is connected to a resistance of 3.9 Ω. The voltage across the cell will be
(A) 0.5 V
(B) 1.5 V
(C) 1.95 V
(D) 2 V
Answer:
(C) 1.95 V

Question 31.
The emf of a cell is 12 V. When it sends a current of 1 A through an external resistance, the p.d. across the terminals reduces to 10 V. The internal resistance of the cell is
(A) 0.1 Ω
(B) 0.5 Ω
(C) 1 Ω
(D) 2 Ω
Answer:
(D) 2 Ω

Question 32.
Three resistors, 8 Ω, 4 Ω and 10 Ω connected in parallel as shown in figure, the equivalent resistance is

(A) \(\frac {19}{40}\) Ω
(B) \(\frac {40}{19}\) Ω
(C) \(\frac {80}{19}\) Ω
(D) \(\frac {34}{23}\) Ω
Answer:
(B) \(\frac {40}{19}\) Ω

Question 33.
A potential difference of 20 V is applied across the ends of a coil. The amount of heat generated in it is 800 cal/s. The value of resistance of the coil will be
(A) 12 Ω
(B) 1.2 Ω
(C) 0.12 Ω
(D) 0.012 Ω
Answer:
(C) 0.12 Ω

Question 34.
In a series combination of cells, the effective internal resistance will
(A) remain the same.
(B) decrease.
(C) increase.
(D) be half that of the 1st cell.
Answer:
(C) increase.

Question 35.
The terminal voltage across a cell is more than its e.m.f., if another cell of
(A) higher e.m.f. is connected parallel to it.
(B) less e.m.f. is connected parallel to it.
(C) less e.m.f. is connected in series with it.
(D) higher e.m.f. is connected in series with it.
Answer:
(A) higher e.m.f. is connected parallel to it.

Question 36.
A 100 W, 200 V bulb is connected to a 160 volt supply. The actual power consumption would be
(A) 64 W
(B) 125 W
(C) 100 W
(D) 80 W
Answer:
(A) 64 W

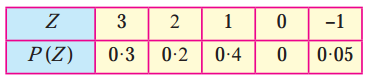
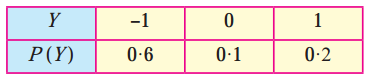
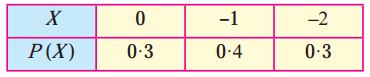
Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 10 Electrostatics Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 10 Electrostatics

Question 1.
Explain: Atoms are electrically neutral.
Answer:

1. The matter is made up of atoms which in turn consists of elementary particles proton, neutron, and electron.
2. A proton is considered to be positively charged and an electron to be negatively charged.
3. Neutron is electrically neutral i.e., it has no charge.
4. An atomic nucleus is made up of protons and neutrons and hence is positively charged.
5. Negatively charged electrons surround the nucleus so as to make an atom electrically neutral.

Question 2.
What do the below diagrams show?

Answer:

1. Figure (a) shows insulated conductor.
2. Figure (b) shows that positive charge is neutralized by electron from Earth.
3. Figure (c) shows that earthing is removed, negative charge still stays in conductor due to positive charged rod.
4. Figure (d) shows that when rod is removed, negative charge is distributed over the surface of the conductor.

Question 3.
Explain concept of charging by conduction.
Answer:

1. When certain dissimilar substances, like fur and amber or comb and dry hair, are rubbed against each other, electrons get transferred to the other substance making them charged.
2. The substance receiving electrons develops a negative charge while the other is left with an equal amount of positive charge.
3. This can be called charging by conduction as charges are transferred from one body to another.

Question 4.
Explain concept of charging by induction.
Answer:

1. If an uncharged conductor is brought near a charged body, (not in physical contact) the nearer side of the conductor develops opposite charge to that on the charged body and the far side of the conductor develops charge similar to that on the charged body. This is called induction.
2. This happens because the electrons in a conductor are free and can move easily in presence of charged body.
3. A charged body attracts or repels electrons in a conductor depending on whether the charge on the body is positive or negative respectively.
4. Positive and negative charges are redistributed and are accumulated at the ends of the conductor near and away from the charged body.
5. In induction, there is no transfer of charges between the charged body and the conductor. So when the charged body is moved away from the conductor, the charges in the conductor are free again.

Question 5.
Explain the concept of additive nature of charge.
Answer:

1. Electric charge is additive, similar to mass. The total electric charge on an object is equal to the algebraic sum of all the electric charges distributed on different parts of the object.
2. It may be pointed out that while taking the algebraic sum, the sign (positive or negative) of the electric charges must be taken into account.
3. Thus, if two bodies have equal and opposite charges, the net charge on the system of the two bodies is zero.
4. This is similar to that in case of atoms where the nucleus is positively charged and this charge is equal to the negative charge of the electrons making the atoms electrically neutral.

Question 6.
State the analogy between the additive property of charge with that of mass.
Answer:

1. The masses of the particles constituting an object are always positive, whereas the charges distributed on different parts of the object may be positive or negative.
2. The total mass of an object is always positive whereas, the total charge on the object may be positive, zero or negative.

Question 7.
What is quantization of charge?
Answer:

1. Protons (+ve) and electrons (-ve) are the charged particles constituting matter, hence the charge on an object must be an integral multiple of ± e i.e., q = ± ne, where n is an integer.
2. Charge on an object can be increased or decreased in multiples of e.
3. It is because, during the charging process an integral number of electrons can be transferred from one body to the other body. This is known as quantization of charge or discrete nature of charge.

Question 8.
Explain with an example why quantization of charge is not observed practically.
Answer:
i. The magnitude of the elementary electric charge (e), is extremely small. Due to this, the number of elementary charges involved in charging an object becomes extremely large.

ii. For example, when a glass rod is rubbed with silk, a charge of the order of one µC (10^-6 C) appears on the glass rod or silk. Since elementary charge e = 1.6 × 10^-19 C. the number of elementary charges on the glass rod (or silk) is given by
n = \(\frac {10^{-6}C}{1.6×10^{-19}C}\) = 6.25 × 10¹²
Since, it is tremendously large number, the quantization of charge is not observed and one usually observes a continuous variation of charge.

Question 9.
The total charge of an isolated system is always conserved. Explain with an example.
Answer:

1. When a glass rod is rubbed with silk, it becomes positively charged and silk becomes negatively charged.
2. The amount of positive charge on glass rod is found to be exactly the same as negative charge on silk.
3. Thus, the systems of glass rod and silk together possesses zero net charge after rubbing.
   Hence, the total charge of an isolated system is always conserved.

Question 10.
Explain the conclusion when charges are brought close to each other.
Answer:

1. Unlike charges attract each other.
2. Like charges repel each other.

Question 11.
How much positive and negative charge is present in 1 g of water? How many electrons are present in it?
(Given: molecular mass of water is 18.0 g)
Answer:
Molecular mass of water is 18 gram, that means the number of molecules in 18 gram of water is 6.02 × 10²³
∴ Number of molecules in lgm of water = \(\frac {6.02×10^{23}}{18}\)
One molecule of water (H₂O) contains two hydrogen atoms and one oxygen atom. Thus, the number of electrons in ILO is sum of the number of electrons in H₂ and oxygen. There are 2 electrons in H₂ and 8 electrons in oxygen.
∴ Number of electrons in H₂O = 2 + 8 = 10
Total number of protons / electrons in one gram of water
= \(\frac {6.02×10^{23}}{18}\) × 10 = 3.344 × 10²³
Total positive charge
= 3.344 × 10²³ × charge on a proton
= 3.344 × 10²³ × 1.6 × 10^-19C
= 5.35 × 10⁴ C
This positive charge is balanced by equal amount of negative charge so that the water molecule is electrically neutral.
∴ Total negative charge = 5.35 × 10⁴C

Question 12.
Define point charge. Which law explains the interaction between charges at rest?
Answer:

1. A point charge is a charge whose dimensions are negligibly small compared to its distance from another bodies.
2. Coulomb’s law explains the interaction between charges at rest.

Question 13.
State and explain Coulomb’s law of electric charge in scalar form.
Answer:
Coulomb’s law:
The force of attraction or repulsion between two point charges at rest is directly proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them. This force acts along the line joining the two charges.
Explanation:
i. Let q₁ and q₂ be the two point charges at rest with each other and separated by a distance r. F is the magnitude of electrostatic force of attraction or repulsion between them.

ii. According to Coulomb’s law.
F ∝ \(\frac {q_1q_2}{r^2}\)
∴ F = K\(\frac {q_1q_2}{r^2}\)
where, K is the constant of proportionality which depends upon the units of F, q₁, q₂, r and medium in which charges are placed.

Question 14.
State conditions for electrostatic force to be attractive or repulsive.
Answer:

1. The force between the two charges will be attractive, if the charges are unlike (one positive and one negative).
2. The force between the two charges will be repulsive, if the charges are similar (both positive or both negative).

Question 15.
Prove that relative permittivity is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.
Answer:
i. The force between the two charges placed in a medium is given by,
F_med = \(\frac {1}{4πε}\) (\(\frac {q_1q_2}{r^2}\)) …………. (1)
where, ε is called the absolute permittivity of the medium.

ii. The force between the same two charges placed in free space or vacuum at distance r is given by,
F_vac = \(\frac {1}{4πε_0}\) (\(\frac {q_1q_2}{r^2}\)) …………. (1)
Dividing equation (2) by equation (1),

Hence, relative permittivity is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.

Question 16.
If relative permittivity of water is 80 then derive the relation between F_water and F_vacuum. What can be concluded from it?
Answer:
i. The force between two point charges q₁ and q₂ placed at a distance r in a medium of relative permittivity ε_r, is given by
F_med = \(\frac{1}{4 \pi \varepsilon_{0} \varepsilon_{r}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) …………. (1)
If the medium is vacuum,
F_vac = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) …………. (2)

ii. Dividing equation (2) by equation (1),
\(\frac{\mathrm{F}_{\mathrm{vac}}}{\mathrm{F}_{\text {med }}}\) = ε_r
For water, ε_r = 80 ……….. (given)
∴ F_water = \(\frac {F_{vac}}{80}\)

iii. This means that when two point charges are placed some distance apart in water, the force between them is reduced to (\(\frac {1}{80}\))^th of the force between the same two charges placed at the same distance in vacuum.

iv. Thus, it is concluded that a material medium reduces the force between charges by a factor of er, its relative permittivity.

Question 17.
Give conversions of micro-coulomb, nano-coulomb and pico-coulomb to coulomb.
Answer:
1 microcoulomb (µC) = 10^-6 C
1 nanocoulomb (nC) = 10^-9 C
1 picocoulomb (pC) = 10^-12 C

Question 18.
Explain Coulomb’s law in vector form.
Answer:
i. Let q₁ and q₂ be the two similar point charges situated at points A and B and let \(\vec{r}\)₁₂ be the distance of separation between them.

ii. The force \(\vec{F}\)₂₁ exerted on q₂ by q₁ is given by,
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{12}\right|^{2}} \times \hat{\mathrm{r}}_{12}\)
where, \(\hat{r}\)₁₂ is the unit vector from A to B.
\(\vec{F}\)₂₁ acts on q₂ at B and is directed along BA, away from B.

iii. Similarly, the force \(\vec{F}\)₁₂ exerted on q₁ by q₂ is given by, \(\vec{F}\)₁₂ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{12}\right|^{2}} \times \hat{\mathrm{r}_{21}}\)
where, \(\hat{r}\)₂₁ is the unit vector from B to A. \(\vec{F}\)₁₂ acts on q₁ at A and is directed along BA, away from A.

iv. The unit vectors \(\hat{r}\)₁₂ and \(\hat{r}\)₂₁ are oppositely directed i.e., \(\hat{r}\)₁₂ = –\(\hat{r}\)₂₁
Hence, \(\vec{F}\)₂₁ = –\(\vec{F}\)₁₂
Thus, the two charges experience force of equal magnitude and opposite in direction.

v. These two forces form an action-reaction pair.

vi. As \(\vec{F}\)₂₁ and \(\vec{F}\)₁₂ act along the line joining the two charges, the electrostatic force is a central force.

Question 19.
State similarities and differences of gravitational and electrostatic forces.
Answer:
i. Similarities:
a. Both forces obey inverse square law:
F ∝ \(\frac{1}{r^2}\)
b. Both are central forces and they act along the line joining the two objects.

ii. Differences:
a. Gravitational force between two objects is always attractive while electrostatic force between two charges can be either attractive or repulsive depending on the nature of charges.
b. Gravitational force is about 36 orders of magnitude weaker than the electrostatic force.

Question 20.
Charge on an electron is 1.6 × 10^-19 C. How many electrons are required to accumulate a charge of one coulomb?
Answer:
1 electron = 1.6 × 10^-19 C
∴ 1 C = \(\frac{1}{1.6 \times 10^{-19}}\) electrons
= 0.625 × 10¹⁹ electrons
……. (Taking reciprocal from log table)
= 6.25 × 10¹⁸ electrons
Hence, 6.25 × 10¹⁸ electrons are required to accumulate a charge of one coulomb.

Question 21.
What is the force between two small charge spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Given: q₁ = 2 × 10^-7 C, q₂ = 3 × 10^-7 C
r = 30 cm = \(\frac {30}{100}\) m = 0.3 m
To find: Force (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,
F = \(\frac{9 \times 10^{9} \times 2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^{2}}\)
∴ F = 6 × 10^-3 N

Question 22.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge -0.8 µC in air is 0.2 N. (i) What is the distance between the two spheres? (ii) What is the force on the second sphere due to the first?
Answer:
i. Given: q₁ = 0.4 µC = 0.4 × 10^-6 C,
q₂ = -0.8 µC = -0.8 × 10^-6 C, F = 0.2 N
To find: i. Distance (r)
ii. Force on second sphere (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:
i. From formula,
r² = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{F}\)
r² = \(\frac{9 \times 10^{9} \times 0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}\)
= 0.0144
∴ r = \(\sqrt{0.0144}\) = 0.12 m
∴ r = 12 cm

ii. The force on the second sphere due to the first is also 0.2 N and is attractive in nature.

Question 23.
i. Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion, if the charge on each is 6.5 × 10^-7 C? The radii of A and B are negligible compared to the distance of separation,
ii. What is the force of repulsion if each sphere is charged double the above amount and the distance between them is halved?
Answer:
Given: q₁ = 6.5 × 10^-7 C q₂ = 6.5 × 10^-7 C
r = 50 cm = 0.50 m
To find: Force of repulsion (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:
From formula,
F = \(\frac{9 \times 10^{9} \times 6.5 \times 10^{-7} \times 6.5 \times 10^{-7}}{(0.50)^{2}}\)
F = 1.52 × 10^-2 N

ii. When each charge is doubled and the distance between them is reduced to half, then
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\left(2 q_{1}\right)\left(2 q_{2}\right)}{(r / 2)^{2}}\)
= 16 × \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\) = 16 × 1.52 × 10^-2
∴ F = 0.24 N

Question 24.
Calculate and compare the electrostatic and gravitational forces between two protons which are 10^-15 m apart. Value of G = 6.674 × 10^-11 m³ kg^-1 s^-2 and mass of the porton is 1.67 × 10^-27 kg.
Answer:
Given: G = 6.674 × 10^-11 m³ kg^-1 s^-2
m_p = 1.67 × 10^-27 kg.
q_p = 1.67 × 10^-19 C, r = 10^-15
To find:
i. Electrostatic Force (F_E)
ii. Gravitational Force (F_G)
Formula: i. F_E = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
ii. F_E = \(\frac {Gm_1m_2}{r^2}\)
Calculation:
From formula (i),
\(\mathrm{F}_{\mathrm{E}}=9 \times 10^{9} \times \frac{1.6 \times 10^{-19} \times 1.6 \times 10^{-19}}{\left(10^{-15}\right)^{2}}\)
= 9 × 1.6 × 1.6 × 10
= 90 × 1.6 × 1.6
= antilog [log 90 + log 1.6 + log 1.6]
= antilog [1.9542 + 0.2041 + 0.2041]
= antilog [2.3624]
= 2.303 × 10² N
From formula (ii),
\(\mathrm{F}_{\mathrm{G}}=6.674 \times 10^{-11} \times \frac{1.67 \times 10^{-27} \times 1.67 \times 10^{-27}}{\left(10^{-15}\right)^{2}}\)
= 6.674 × 1.67 × 1.67 × 10^-35
= {antilog [log 6.674 + log 1.67 + log 1.67]} × 10^-35
= {antilog [0.8244 + 0.2227 + 0.2227]} × 10^-35
= {antilog [1.2698]} × 10^-35
= 1.861 × 10¹ × 10^-35
= 1.861 × 10^-34 N
Now,
\(\frac{\mathrm{F}_{\mathrm{E}}}{\mathrm{F}_{\mathrm{G}}}=\frac{2.303 \times 10^{2}}{1.861 \times 10^{-34}}\)
= {antilog [log 2.303 – log 1.861]} × 10³⁶
= {antilog [0.3623 – 0.2697]} × 10³⁶
= {antilog [0.0926]}
= 1.238 × 10³⁶
∴ F_E ≈ 10³⁶ × F_G

Question 25.
State and explain principle of superposition.
Answer:
Statement: When a number of charges are interacting, the resultant force on a particular charge is given by the vector sum of the forces exerted by individual charges.
Explanation:
i. Consider a number of point charges q₁, q₂, q₃ ……………… kept at points A₁, A₂, A₃ ………….. as shown in figure.

ii. The force exerted on the charge q₁ by q₂ is \(\vec{F}\)₁₂ The value of \(\vec{F}\)₁₂ is calculated by ignoring the presence of other charges. Similarly, force \(\vec{F}\)₁₃, \(\vec{F}\)₁₄ can be found, using the Coulomb’s law.

iii. Total force \(\vec{F}\)₁ on charge qi is the vector sum of all such forces.
\(\vec{F}\)₁ = \(\vec{F}\)₁₂ + \(\vec{F}\)₁₃ + \(\vec{F}\)₁₄ + …………..
\( =\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{21}\right|^{2}} \times \hat{\mathrm{r}}_{21}+\frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\left|\mathrm{r}_{31}\right|^{2}} \times \hat{\mathrm{r}}_{31}+\ldots .\right]\)

where \(\hat{r}\)₂₁, \(\hat{r}\)₃₁ are unit vectors directed to q₁ from q₂, q₃ respectively and r₂₁, r₃₁, r₄₁ are the distances from q₁ to q₂, q₃ respectively.

iv. If q₁, q₂, q₃ ……., q_n are the point charges then the force \(\vec{F}\) exerted by these charges on a test charge q₀ is given by,
\(\vec{F}\)_test = \(\vec{F}\)₁ = \(\vec{F}\)₂ + \(\vec{F}\)₃ + …. + \(\vec{F}\)_n
= \(\sum_{\mathrm{n}=1}^{\mathrm{n}} \mathrm{F}_{\mathrm{n}}=\frac{1}{4 \pi \varepsilon_{0}} \sum_{\mathrm{n}=1}^{\mathrm{n}} \frac{\mathrm{q}_{0} \mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}^{2}} \hat{\mathrm{r}}_{\mathrm{n}}\)
Where, \(\hat{r}\)_n, is a unit vector directed from the nth charge to the test charge q₀ and r₂ is the
separation between them, \(\vec{r}\)_n = r_n \(\hat{r}\)_n

Question 26.
Three charges of 2 µC, 3 µC and 4 µC are placed at points A, B and C respectively, as shown in the figure. Determine the force on A due to other charges.
(Given: AB = 4 cm, BC = 3 cm)

Answer:

Using pythagoras theorem
AC = \(\sqrt {AB^2+BC^2}\)
= \(\sqrt {4^2+3^2}\)
AC = 5 cm
Magnitude of force \(\vec{F}\)_AB on A due to B is,

In ∆ABC 4
cos θ = \(\frac {4}{5}\)
θ = cos^-1 (\(\frac {4}{5}\)) = 36.87°
Forces acting points A are

= 59.36 N
Direction of resultant force is 36.87° (north of west)

[Note: The question given above is modified considering minimum requirement of data needed to solve the problem.]

Question 27.
There are three charges of magnitude 3 pC, 2 pC and 3 pC located at three corners A, B and C of a square ABCD of each side measuring 2 m. Determine the net force on 2 pC charge.
Answer:
Given: q₁ = 3 µC, q₂ = 2 µC, q₃ = 3 µC, r = 2 m
To find: Net force on q₂ (R)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:

From the formula,
Force on q₂ because of q₁

Net force on q₂ is the resultant force of \(\vec{F}\)₂₁ and \(\vec{F}\)₂₃ which is given by,
R = \(\sqrt{\mathrm{F}_{21}^{2}+\mathrm{F}_{23}^{2}}\)
= \(\sqrt{\left(1.35 \times 10^{-2}\right)^{2}+\left(1.35 \times 10^{-2}\right)^{2}}\)
∴ R = 1.91 × 10^-2 N

Question 28.
Explain the concept of electric field.
Answer:

1. The space around a charge gets modified when a test charge is brought in that region, it experiences a coulomb force. The region around a charged object in which coulomb force is experienced by another charge is called electric field.
2. Mathematically, electric field is defined as the force experienced per unit charge.
3. The coulomb force acts across an empty space (vacuum) and does not need any intervening medium for its transmission.
4. The electric field exists around a charge irrespective of the presence of other charges.
5. Since the coulomb force is a vector, the electric field of a charge is also a vector and is directed along the direction of the coulomb force, experienced by a test charge.

Question 29.
Define electric field. State its SI unit and dimensions.
Answer:

1. Electric field is the force experienced by a test charge in presence of the given charge at the given distance from it.
   \(\vec{E}\) = \(\lim _{q \rightarrow 0} \frac{\vec{F}}{q}\)
2. SI unit: newton per coulomb (N/C) or volt per metre (V/m).
3. Dimensions: [L M T^-3 A^-1]

Question 30.
Establish relation between electric field intensity and electrostatic force.
Answer:
i. Let Q and q be two charges separated by a distance r.
The coulomb force between them is given by \(\vec{F}\) = \(\frac {1}{4πε_0}\) \(\frac {Qq}{r^2}\) \(\hat{r}\)
where, \(\hat{r}\) is the unit vector along the line joining Q to q.

ii. Therefore, electric field due to charge Q is given \(\vec{F}\) = \(\frac{\vec{F}}{\mathrm{q}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)

iii. Electric field at a point is useful to estimate the force experienced by a charge at that point.

Question 31.
State an expression for electric field on the surface of the sphere due to a positive point charge placed at its centre.
Answer:
The magnitude of electric field at a distance r from a point charge Q is same at all points on the surface of a sphere of radius r as shown in figure.

ii. Magnitude of electric field is given by,
E = \(\frac {1}{4πε_0}\) \(\frac {Q}{r^2}\)
iii. Its direction is along the radius of the sphere, pointing away from its centre if the charge is positive.

Question 32.
Derive expression for electric field intensity due to a point charge in a material medium.
Answer:
i. Consider a point charge q placed at point O in a medium of dielectric constant K as shown in figure.

ii. Consider the point P in the electric field of point charge at distance r from q. A test charge q0 placed at the point P will experience a force which is given by the Coulomb’s law,
\(\vec{F}\) = \(\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{qq}_{0}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
where \(\hat{r}\) is the unit vector in the direction of force i.e., along OP.

iii. By the definition of electric field intensity,
\(\vec{F}\) = \(\frac{\vec{F}}{\mathrm{q}_{0}}=\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
The direction of \(\vec{E}\) will be along OP when q is positive and along PO when q is negative.

iv. The magnitude of electric field intensity in a medium is given by, E = \(\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)

v. For air or vacuum, K = 1 then
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)

Question 33.
Show graphical representation of variation of coulomb force and electric field due to point charge with distance.
Answer:
Electrostatic force: F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\)
Electric field: E : \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
The coulomb force (F) between two charges and electric field (E) due to a charge both follow the inverse square law.
(F ∝ 1/r², E ∝ 1/r²)

Question 34.
What is non-uniform electric field?
Answer:
A field whose magnitude and direction is not the same at all points.
For example, field due to a point charge. In this case, the magnitude of field is same at distance r from the point charge in any direction but the direction of the field is not same.

Question 35.
Derive relation between electric field (E) and electric potential (V).
Answer:
i. A pair of parallel plates is connected as shown in the figure. The electric field between them is uniform

ii. A potential difference V is applied between two parallel plates separated by a distance ‘d’.

iii. The electric field between them is directed from plate A to plate B.

iv. A charge +q placed between the plates experiences a force F due to the electric field.

v. If the charge is moved against the direction of field, i.e., towards the positive plate, some amount of work is done on it.

vi. If the charge is moved +q from the negative plate B to the positive plate A, then the work done against the field is W = Fd; where ‘d’ is the separation between the plates.

vii. The potential difference V between the two plates is given by W = V_q,
but W = Fd
∴ Vq = Fd
∴ \(\frac {F}{q}\) = \(\frac {V}{d}\) = E
∴ Electric field can be defined as E = V/d.

Question 36.
What are electric lines of force?
Answer:
i. An electric line of force is an imaginary curve drawn in such a way that the tangent at any given point on this curve gives the direction of the electric field at that point.

ii. If a test charge is placed in an electric field it would be acted upon by a force at every point in the field and will move along a path.

iii. The path along which the unit positive charge moves is called a line of force.

iv. A line of force is defined as a curve such that the tangent at any point to this curve gives the direction of the electric field at that point.

v. The density of field lines indicates the strength of electric fields at the given point in space.

Question 37.
State the characteristics of electric lines of force.
Answer:

1. The lines of force originate from a positively charged object and end on a negatively charged object.
2. The lines of force neither intersect nor meet each other, as it will mean that electric field has two directions at a single point.
3. The lines of force leave or terminate on a conductor normally.
4. The lines of force do not pass through conductor i.e., electric field inside a conductor is always zero, but they pass through insulators.
5. Magnitude of the electric field intensity is proportional to the number of lines of force per unit area of the surface held perpendicular to the field.
6. Electric lines of force are crowded in a region where electric intensity is large.
7. Electric lines of force are widely separated from each other in a region where electric intensity is small
8. The lines of force of an uniform electric field are parallel to each other and are equally spaced.

Question 38.
Find the distance from a charge of 4 µC placed in air which produces electric field of intensity 9 × 10³ N/C.
Answer:
Given: K = 1, E = 9 × 10³ N/C
q = 4 µC = 4 × 10^-6
To Find: Distance (r)
Formula: E = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{r^{2}}\)
Calculation from formula
9 × 10³ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{4 \times 10^{-6}}{r^{2}}\)
∴ 9 × 10³ = 9 × 10⁹ \(\frac{4 \times 10^{-6}}{\mathrm{r}^{2}}\)
∴ r² = 4
∴ r = 2 m

Question 39.
What is the magnitude of a point charge chosen so that the electric field 50 cm away has magnitude 2.0 N/C?
Answer:
Given: r = 50 cm – 0.5 m, E = 2 N/C,
To find: Magnitude of charge (q)
Formula: E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\)
Calculation from formula

Question 40.
Three point charges are placed at the vertices of a right angled isosceles triangle as shown in the given figure. What is the magnitude and direction of the resultant electric field at point P which is the mid point of its hypotenuse?

Answer:
Electric field at P due to the charges at A, B and C are shown in the figure.

Let \(\vec{E}\)_A be the field at P due to charge at A and \(\vec{E}\)_c be the field at P due to charge at C.
Since P is the midpoint of AC and the fields at A and C are equal in magnitudes and are opposite in direction, E_A = – E_C .
i.e., \(\vec{E}\)_A + \(\vec{E}\)_C = 0.
Thus, the field at P is only to the charge at B and is given by,

Question 41.
A simplified model of hydrogen atom consists of an electron revolving about a proton at a distance of 5.3 × 10^-11 m. The charge on a proton is +1.6 × 10^-19 C. Calculate the intensity of the electric field due to proton at this distance. Also find the force between electron and proton.
Answer:
Given: r = 5.3 × 10^-11 m
q = 1.6 × 10^-19 C
To Find: i. Intensity of electric field (E)
ii. Force (F)
Formula: i. E = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
ii. E = \(\frac {F}{q}\)
Calculation from formula (i)
E = 9 × 10⁹ × \(\frac{1.6 \times 10^{-19}}{\left(5.3 \times 10^{-11}\right)^{2}}\)
= 5.126 × 10¹¹ N/C
Force between electron and proton,
Force between electron and proton,
F = E × q_e ….[From formula (ii)]
= 5.126 × 10^-11 × -1.6 × 10^-19
= -8.201 × 10⁸ N

Question 42.
The force exerted by an electric field on a charge of +10 µC at a point is 16 × 10^-4 N. What is the intensity of the electric field at the point?
Answer:
Given: q = 10 µC= 10 × 10^-6 C, F = 16 × 10^-4 N
To find: Electric field intensity (E)
Formula: E = \(\frac {F}{q}\)
Calculation: From formula,
E = \(\frac {16×10^{-4}}{10×10^{-6}}\) = 160 N/C

Question 43.
What is the force experienced by a test charge of 0.20 µC placed in an electric field of 3.2 × 10⁶ N/C?
Answer:
Given: q₀ = 0.20 µC = 0.2 × 10⁶ C,
E = 3.2 × 10⁶ N/C
To find: Force (F)
Formula: E = \(\frac {F}{q_0}\)
Calculation: From formula,
F = Eq₀
∴ F = 3.2 × 10⁶ × 0.2 × 10^-6 = 0.64 N

Question 44.
Gap between two electrodes of the spark-plug used in an automobile engine is 1.25 mm. If the potential of 20 V is applied across the gap, what will be the magnitude of electric field between the electrodes?
Answer:
Given: V = 20 V
d = 1.25 mm = 1.25 × 10^-3 m
To Find: Magnitude of electric field (E)
Formula: E = \(\frac {V}{d}\)
Calculation: From formula,
E = \(\frac {20}{1.25×10^{-3}}\)
= 1.6 × 10⁴ V/m

Question 45.
If 100 joules of work must be done to move electric charge equal to 4 C from a place, where potential is -10 volt to another place where potential is V volt, find the value of V.
Answer:
Given: q₀ = 4 C,
V_A = -10 volt,
V_B = V volt,
W_AB = 100 J
To Find: Potential (V)
Formula: V_B – V_A = \(\frac {W_{AB}}{q_0}\)
Calculation: From formula,
V – (-10) = \(\frac {100}{4}\) = 25
∴ V + 10 = 25
∴ V = 15 volt

Question 46.
Find the work done when a point charge of 2.0 pC is moved from a point at a potential of -10 V to a point at which the potential is zero.
Answer:
V_A = -10V,
V_B = 0,
q = 2 × 10^-6 C
To Find: Work done (W)
Formula: V_BA = \(\frac {W}{q}\)
Calculation: From formula,
W = V_BA × q
= (V_B – V_A) × q
= (0 + 10) × 2 × 10^-6
= 20 × 10^-6 J
∴ W = 2 × 10^-5 J

Question 47.
Explain the term: Electric flux
Answer:
i. The number of lines of force per unit area is the intensity of the electric field \(\vec{E}\).

ii. When the area is inclined at an angle θ with the direction of electric field, the electric flux can be calculated as follows.
Let the angle between electric field \(\vec{E}\), and area vector \(\vec{dS}\) be θ, then the electric flux passing through are dS is given by
dø = (component of dS along \(\vec{E}\)) × (area of \(\vec{dS}\))
dø = EdS cos θ
dø = \(\vec{E}\) .\(\vec{dS}\)
Total flux through the entire surface .
ø = ∫dø = \( \int_{S} \vec{E} \cdot d \vec{S}=\vec{E} \cdot \vec{S}\)

iii. The SI unit of electric flux can be calculated using,
ø = \(\vec{E}\). \(\vec{S}\) = (V/m) m² = V m
[Note: Area vector is a vector whose magnitude is equal to area and is directed normal to its surface]

Question 48.
The electric flux through a plane surface of area 200 cm² in a region of uniform electric field 20 N/C is 0.2 N m²/C. Find the angle between electric field and normal to the surface.
Answer:
Given: ds = 200 cm² = 2 × 10^-2 m², E = 20 N/C,
ø = 0.2 N m²/C
To find: Angle between electric field and normal (θ)
Formula: ø = Eds cos θ
Calculation:
From formula,
cos θ = \(\frac {ø}{Eds}\) = \(\frac {0.2}{20×2×10^{-2}}\) = \(\frac {1}{2}\)
∴ θ = cos^-1 (\(\frac {1}{2}\))
∴ θ = 60°

Question 49.
A charge of 5.0 C is kept at the centre of a sphere of radius 1 m. What is the flux passing through the sphere? How will this value change if the radius of the sphere is doubled?
Answer:
Given: q = 5C, r = 1 m
To find: Flux (ø)
Formulae: i. E = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
ii. ø = E × A = E (4πr²)
Calculation: From formula (i),
E = 9 × 10⁹ × \(\frac {5}{1^2}\)
= 4.5 × 10¹⁰ N/C
From formula (ii),
ø = E × 4 π r²
= 4.5 × 10¹⁰ × 4 × 3.14 × 1²
ø = 5.65 × 10¹¹ Vm
This value of flux will not change if radius of sphere is doubled. Though radius of sphere will increase, increased distance will reduce the electric field intensity. As E ∝ \(\frac {1}{r^2}\) and A × r² net variation in total flux will not be observed.

Question 50.
State and prove Gauss’ law of electrostatics.
Answer:
Statement:
The flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by Eo.
\(\int \vec{E} \cdot \overrightarrow{\mathrm{dS}}=\frac{\mathrm{Q}}{\varepsilon_{0}}\)
where Q is the total charge within the surface.

Proof:
i. Consider a closed surface of any shape which encloses number of positive electric charges.

ii. Imagine a small charge +q present at a point O inside closed surface. Imagine an infinitesimal area dS of the given irregular closed surface.

iii. The magnitude of electric field intensity at point P on dS due to charge +q at point O is, E = \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{\mathrm{q}}{\mathrm{r}^{2}}\right)\) ………… (1)

iv. The direction of E is away from point O. Let θ be the angle subtended by normal drawn to area dS and the direction of E

v. Electric flux passing through area (dø)
= Ecosθ dS
= \(\frac{\mathrm{q}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}\) cosθ dS ………….. (from 1)
= \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_{0}}\right)\left(\frac{\mathrm{d} \mathrm{S} \cos \theta}{\mathrm{r}^{2}}\right)\)
But, dω = \(\frac {dS cos θ}{r^2}\)
where, dco is the solid angle subtended by area dS at a point O.
∴ dø = \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_{0}}\right)\) dω …………. (2)

vi. Total electric flux crossing the given closed surface can be obtained by integrating equation (2) over the total area.
\(\phi_{\mathrm{E}}=\int_{\mathrm{s}} \mathrm{d} \phi=\int_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dS}}=\int \frac{\mathrm{q}}{4 \pi \varepsilon_{0}} \mathrm{~d} \omega=\frac{\mathrm{q}}{4 \pi \varepsilon_{0}} \int \mathrm{d} \omega\)

vii. But ∫dω = 4π = solid angle subtended by entire closed surface at point O.
Total Flux = \(\frac {q}{4πε_0}\) (4π)
∴ ø_E = \(\int_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dS}}=\frac{+\mathrm{q}}{\varepsilon_{0}}\)

viii. This is true for every electric charge enclosed by a given closed surface.
Total flux due to charge q₁, over the given closed surface = + \(\frac {q_1}{ε_0}\)
Total flux due to charge q₂, over the given closed surface = + \(\frac {q_2}{ε_0}\)
Total flux due to charge q_n, over the given closed surface = +\(\frac {q_n}{ε_0}\)

ix. According to the superposition principle, the total flux c|> due to all charges enclosed within the given closed surface is
\(\phi_{\mathrm{E}}=\frac{\mathrm{q}_{1}}{\varepsilon_{0}}+\frac{\mathrm{q}_{2}}{\varepsilon_{0}}+\frac{\mathrm{q}_{3}}{\varepsilon_{0}}+\ldots+\frac{\mathrm{q}_{\mathrm{n}}}{\varepsilon_{0}}=\sum_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{n}} \frac{\mathrm{q}_{\mathrm{i}}}{\varepsilon_{0}}=\frac{\mathrm{Q}}{\varepsilon_{0}}\)

Question 51.
With a help of diagram, state the direction of flux due to positive charge, negative charge and charge outside a closed surface.
Answer:

Positive sign indicates that the flux is directed outwards, away from the charge.

If the charge is negative, the flux will be is directed inwards.

If a charge is outside the closed surface, the net flux through it will be zero.

Question 52.
Explain: Electric flux is independent of shape and size of closed surface.
Answer:
i. The net flux crossing an enclosed surface is equal to \(\frac {q}{ε_0}\) where q is the net charge inside the closed surface.

ii. Consider a charge +q at the centre of concentric circles as shown in figure below.

As the charge inside the sphere is unchanged, the flux passing through a sphere of any radius is the same.

iii. Thus, if the radius of the sphere is increased by a factor of 2, the flux passing through is surface remains unchanged.

iv. As shown in figure same number of lines of force cross both the surfaces.
Hence, total flux is independent of shape of the closed surface radius of the sphere and size of closed surface.

Question 53.
Define the following terms with the help of a diagram.
i. Electric dipole
ii. Dipole axis
iii. Axial line
iv. Equatorial line
Answer:
i. Electric dipole: A pair of equal and opposite charges separated by a finite distance is called an electric dipole.

ii. Dipole axis: Line joining the two charges is called the dipole axis.

iii. Axial line: A line passing through the dipole axis is called axial line.

iv. Equatorial line: A line passing through the centre of the dipole and perpendicular to the axial line is called the equatorial line.

AB : Electric dipole Line joining
AB: Dipole axis
X-Y : Axial line
P-Q : Equatorial line

Question 54.
What are polar molecules? Explain with examples.
Answer:

1. Polar molecules are the molecules in which the centre of positive charge and the negative charge is naturally separated.
2. Molecules of water, ammonia, sulphur dioxide, sodium chloride etc. have an inherent separation of centres of positive and negative charges. Such molecules are called polar molecules.

Question 55.
What are non-polar molecules? Explain with examples.
Answer:
i. Non-polar molecules are the molecules in which the centre of positive charge and the negative charge is one and the same. They do not have a permanent electric dipole. When an external electric field is applied to such molecules, the centre of positive and negative charge are displaced and a dipole is induced.

ii. Molecules such as H₂, CI₂, CO₂, CH₄, etc., have their positive and negative charges effectively centred at the same point and are called non-polar molecules.

Question 56.
Derive expression for couple acting on an electric dipole in a uniform electric field.
Answer:
i. Consider an electric dipole placed in a uniform electric field E. The axis of electric dipole makes an angle θ with the direction of electric field.

ii. The force acting on charge – q at A is \(\vec{F}\)_A = -q\(\vec{E}\) in the direction of\(\vec{E}\) and the force acting on charge +q at B is \(\vec{F}\)_B = + q \(\vec{E}\) in the direction opposite to \(\vec{E}\).

iii. Since \(\vec{F}\)_A = –\(\vec{F}\)_B, the two equal and opposite forces separated by a distance form a couple.

iv. Moment of the couple is called torque and is defined by \(\vec{τ}\) = \(\vec{d}\) × \(\vec{F}\) where, d is the perpendicular distance between the two equal and opposite forces.

v. Magnitude of Torque = Magnitude of force × Perpendicular distance
∴ Torque on the dipole (\(\vec{τ}\)) = \(\vec{BA}\) × q\(\vec{E}\)
= 2lqE sin θ
but p = q2l
∴ τ = pEsin θ
∴ In vector form \(\vec{τ}\) = \(\vec{d}\) × \(\vec{E}\)

vi. If θ = 90° sin θ = 1, then τ = pE
When the axis of electric dipole is perpendicular to uniform electric field, torque of the couple acting on the electric dipole is maximum, i.e., τ = pE.

vii. If θ = 0 then τ = 0, this is the minimum torque on the dipole. Torque tends to align its axis along the direction of electric field.

Question 57.
Derive expression for electric intensity at a point on the axis of an electric dipole.
Answer:
i. Consider an electric dipole consisting of two charges -q and +q separated by a distance 2l.

ii. Let P be a point at a distance r from the centre C of the dipole.

iii. The electric intensity \(\vec{E}\)_a at P due to the dipole is the vector sum of the field due to the charge -q at A and +q at B.

iv. Electric field intensity at P due to the charge -q at A = \(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(-q)}{(r+l)^{2}} \hat{\mathrm{u}}_{\mathrm{pD}}\),
where, \(\hat{u}\)_PD is unit vector directed along \(\vec{PD}\)

v. Electric intensity at P due to charge +q at B
\(\vec{E}\)_B = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{(\mathrm{r}-l)^{2}} \hat{\mathrm{u}}_{\mathrm{PQ}}\)
where, \(\hat{u}\)_PQ is a unit vector directed along \(\vec{PQ}\)
The magnitude of \(\vec{E}\)_B is greater than that of \(\vec{E}\)_A since BP < AP

vi. Resultant field \(\vec{E}\)_a at P on the axis, due to the dipole is
\(\vec{E}\)_a = \(\vec{E}\)_B + E\(\vec{E}\)_A

vii. The magnitude of \(\vec{E}\)_a is given by

ix. |\(\vec{E}\)_a| is directed along PQ, which is the direction of the dipole moment \(\vec{p}\) i.e., from the negative to the positive charge, parallel to the axis.

x. If r >> l, l² can be neglected compared to r²,
|\(\vec{E}\)_a| = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\)

The field will be along the direction of the dipole moment \(\vec{p}\).

Question 58.
Drive expression for electric intensity at a point on the equator of an electric dipole.
Answer:
i. Electric field at point P due to charge -q at A is \(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(-\mathrm{q})}{(\mathrm{AP})^{2}} \hat{\mathrm{u}}_{\mathrm{PA}}\)
where, \(\hat{u}\)_PA is a unit vector directed along \(\vec{PA}\)

ii. Similarly, electric field at P due to charge +q at B is
\(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{(\mathrm{BP})^{2}} \hat{\mathrm{u}}_{\mathrm{BP}}\)
where \(\hat{u}\)_BP is a unit vector directed along \(\vec{BP}\)

iii. Electric field at P is the sum of E_A and E_B
∴ \(\vec{E}\)_eq = \(\vec{E}\)_A + \(\vec{E}\)_B

iv. Consider ∆ACP
(AP)² = (PC)² + (AC)² = r² + l² = (BP)²

v. The resultant of fields \(\vec{E}\)_A and \(\vec{E}\)_B acting at point P can be calculated by resolving these vectors E\(\vec{E}\)_A and E\(\vec{E}\)_B along the equatorial line and along a direction perpendicular to it.

vi. Let the Y-axis coincide with the equator of the dipole X-axis will be parallel to dipole axis and the origin is at point P as shown.

vii. The Y-components of E_A and E_B are E_Asin θ and E_B sin θ respectively. They are equal in magnitude but opposite in direction and cancel each other. There is no contribution from them towards the resultant.

viii. The X-components of E_A and E_B are E_Acos θ and E_Bcos θ respectively. They are of equal magnitude and are in the same direction.
∴ |\(\vec{E}\)_eq| = E_A cos θ + E_B cos θ From equation (3),
|\(\vec{E}\)_eq| = 2E_A cos θ

x. The direction of this field is along –\(\vec{P}\) (anti-parallel to \(\vec{P}\)).

Question 59.
An electric dipole of length 2.0 cm is placed with its axis making an angle of 30° with a uniform electric field of 10⁵ N/C as shown in figure. If it experiences a torque of 10√3 N m, calculate the magnitude of charge on dipole.

Answer:
Given: 2l = 2 cm = 2 × 10² m
E = 10⁵ N/C, τ = 10√3 Nm, θ = 30°
To find: Charge (q)
Formula: τ = q E 2 l sin θ
Calculation: From Formula.
q = \(\frac{τ}{\mathrm{E} \times 2 l \times \sin \theta}\)
= \(\frac{10 \sqrt{3}}{10^{5} \times 2 \times 10^{-2} \times \sin 30^{\circ}}\)
= 1.732 × 10^-2 C

Question 60.
Explain the concept of continuous charge distribution.
Answer:
i. A system of charges can be considered as a continuous charge distribution, if the charges are located very close together, compared to their distances from the point where the intensity of electric field is to be found out.

ii. Thus, the charge distribution is said to be continuous for a system of closely spaced charges. It is treated equivalent to a total charge which is continuously distributed along a line or a surface or a volume.

Question 61.
Explain linear charge density.
Answer:
Consider charge q uniformly distributed along a linear conductor of length l, then the linear charge density (λ) is given as,
λ = \(\frac {q}{l}\)
For example, charge distributed uniformly on a straight thin rod or a thin nylon thread. If the charge is not distributed uniformly over the length of thin conductor then charge dq on small element of length dl can be written as dq = λ dl.

Question 62.
Explain surface charge density.
Answer:
i. Consider a charge q uniformly distributed over a surface of area A then the surface charge density c is given as
σ = \(\frac {q}{A}\)
For example, charge distributed uniformly on a thin disc or a synthetic cloth. If the charge is not distributed uniformly over the surface of a conductor, then charge dq on small area element dA can be written as dq = σ dA.

ii. SI unit of σ is (C / m²)

Question 63.
Explain volume charge density.
Answer:
i. Consider a charge q uniformly distributed throughout a volume V, then the volume charge density ρ is given as
ρ = \(\frac {q}{V}\)
For example, charge on a plastic sphere or a plastic cube. If the charge is not distributed uniformly over the volume of a material, then charge dq over small volume element dV can be written as dq = ρ dV.

ii. S.I. unit of p is (C/m³)
[Note: Electric field due to a continuous charge distribution can be calculated by adding electric fields due to all these small charges.]

Question 64.
Explain the concept of static charge.
Answer:

1. Static charges can be created whenever there is a friction between an insulator and other object.
2. For example, when an insulator like rubber or ebonite is rubbed against a cloth, the friction between them causes electrons to be transferred from one to the other.
3. This property of insulators is used in many applications such as photocopier, inkjet printer, painting metal panels, electrostatic precipitation/separators etc.

Question 65.
Explain the disadvantage of static charge.
Answer:

1. When charge transferred from one body to other is very large, sparking can take place. For example, lightning in sky.
2. Sparking can be dangerous while refuelling your vehicle.
3. One can get static shock, if charge transferred is large.
4. Dust or dirt particles gathered on computer or TV screens can catch static charges and can be troublesome.

Question 66.
State the precautions against static charge.
Answer:

1. Home appliances should be grounded.
2. Avoid using rubber soled footwear.
3. Keep your surroundings humid (dry air can retain static charges).

Question 67.
Two charged particles having charge 3 × 10^-8 C each are joined by an insulating string of length 2 m. Find the tension in the string when the system is kept on a smooth horizontal table.
Answer:
Tension (T) in the string is the force of repulsion (F) between the two charges.
According to Coulomb’s law,
F = \(\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}\)
= \(\frac{9 \times 10^{9} \times 3 \times 10^{-8} \times 3 \times 10^{-8}}{2^{2}}\)
F = 2.025 × 10^-6 N
Hence, tension in the string is 2.025 × 10^-6 N.

Question 68.
A free pith ball of mass 5 gram carries a positive charge of 0.6 × 10^-7 C. What is the nature and magnitude of charge that should be given to second ball fixed 6 cm vertically below the former pith ball so that the upper pith bath is stationary?
Answer:
Let +q₂ be the charge on lower pith ball.
Now, the upper pith ball become stationary only when its weight acting downward is balanced by the upward force of repulsion between two pith balls,
i.e., F_E = mg
∴ \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) = mg
∴ \(\frac{9 \times 10^{9} \times 0.6 \times 10^{-7} \times \mathrm{q}_{2}}{\left(6 \times 10^{-2}\right)^{2}}\) = 5 × 10^-3 × 9.8
∴ q₂ = 3.27 × 10^-7C
Hence, the second pith ball carries a positive charge of 3.27 × 10^-7C.

Question 69.
A water drop of mass 11.0 mg and having a charge of 1.6 × 10^-6 C stays suspended in a room. What will be the magnitude and direction of electric Held in the room?
Answer:
As the drop is suspended,
Force (F) due to electric field balances the weight of the drop.
∴ F = mg ………….. (1)
Here, m = 11.0 mg
= 11 × 10^-6 kg,
q = 1.6 × 10^-6 C
Electric field is given by,
E = \(\frac {F}{q}\)
= \(\frac {mg}{q}\)
= \(\frac {11×10^{-6}×9.8}{1.6×10^{-6}}\)
E = 67.4 N/C
As upward force balances the weight, hence direction of electric field must be vertically upwards.

Question 70.
A charged metallic sphere A is suspended by a nylon thread. Another charged metallic sphere B held by an insulating handle is brought close to A such that the distance between their centres is 10 cm, as shown in figure (a). The resulting repulsion of A is noted (for example, by shining a beam of light and measuring the deflection of its shadow on a screen.) Spheres A and B are touched by uncharged spheres C and D respectively, as shown in figure (b). C and D are then removed and B is brought closer to A to a distance of 5.0 cm between their centres, as shown in figure (c). What is the expected repulsion of A on the basis of Coulomb’s law? Spheres A and C and spheres B and D have identical sizes. Ignore the sizes of A and B comparison to the separation between their centres.

Answer:
Let the original charge on sphere A be q and that on B be q’. At a distance r between their centres, the magnitude of the electrostatic force on each is given by
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{qq}^{\prime}}{\mathrm{r}^{2}}\)

Neglecting the sizes of spheres, A and B in comparison to r. When an identical but uncharged sphere C touches A, the charges redistribute on A and C and, by symmetry, each sphere carries a charge q/2. Similarly, after D touches B, the redistributed charge on each is q’/2. Now, if the separation between A and B is halved, the magnitude of the electrostatic force on each is
F’ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(\mathrm{q} / 2)\left(\mathrm{q}^{\prime} / 2\right)}{(\mathrm{r} / 2)^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\left(\mathrm{qq}^{\prime}\right)}{\mathrm{r}^{2}}\) = F

Thus, the electrostatic force on A, due to B, remains unaltered.

Multiple Choice Questions

Question 1.
Force between two charges separated by a certain distance in air is F. If each charge is doubled and the distance between them is also doubled, force would be
(A) F
(B) 2 F
(O’ 4 F
(D) F/4
Answer:
(A) F

Question 2.
For what order of distance is Coulomb7 s law true?
(A) For all distances.
(B) Distances greater than 10^-13 m.
(C) Distances less than 10^-13 m.
(D) Distance equal to 10^-13 m.
Answer:
(B) Distances greater than 10^-13 m.

Question 3.
The permittivity of medium is 26.55 × 10^-12 C²/Nm². The dielectric constant of the medium will be
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(B) 3

Question 4.
A glass rod when rubbed with a piece of fur acquires a charge of magnitude 3.2 µC. The number of electrons transferred is
(A) 2 × 10^-13 from fur to glass
(B) 5 × 10¹² from glass to fur
(C) 2 × 10¹³ from glass to fur
(D) 5 × 10¹² from fur to glass
Answer:
(A) 2 × 10^-13 from fur to glass

Question 5.
Choose the correct answer.
(A) Total charge present in the universe is constant.
(B) Total positive charge present in the universe is constant.
(C) Total negative charge present in the universe is constant.
(D) Total number of charged particles present in the universe is constant.
Answer:
(A) Total charge present in the universe is constant.

Question 6.
If a charge is moved against the Coulomb force of an electric field,
(A) work is done by the electric field
(B) energy is used from some outside source
(C) the strength of the field is decreased
(D) the energy of the system is decreased
Answer:
(B) energy is used from some outside source

Question 7.
Two point charges +4 µC and +2 µC repel each other with a force of 8 N. If a charge of -4 µC is added to each of these charges, the force would be
(A) zero
(B) 8 N
(C) 4 N
(D) 12 N
Answer:
(A) zero

Question 8.
The electric field intensity at a point 2 m from an isolated point charge is 500 N/C. The electric potential at the point is
(A) 0 V
(B) 2.5 V
(C) 250 V
(D) 1000 V
Answer:
(D) 1000 V

Question 9.
The dimensional formula of electric field intensity is
(A) [M¹E¹T^-2A^-1]
(B) [M¹L¹T^-3A^-1]
(C) [M^-1L²T^-3A^-1]
(D) [M¹L²T^-3A^-2]
Answer:
(B) [M¹L¹T^-3A^-1]

Question 10.
A force of 2.25 N acts on a charge of 15 × 10^-4C. Calculate the intensity of electric field at that point.
(A) 1500 NC^-1
(B) 150 NC^-1
(C) 15000NC^-1
(D) 2500 NC^-1
Answer:
(A) 1500 NC^-1

Question 11.
A point charge q produces an electric field of magnitude 2 N C^-1 at a point distant 0.25 m from it. What is the value of charge?
(A) 1.39 × 10^-11 C
(B) 1.39 × 10¹¹ C
(C) 13.9 × 10^-11 C
(D) 13.9 × 10¹¹ C
Answer:
(A) 1.39 × 10^-11 C

Question 12.
The electric intensity in air at a point 20 cm from a point charge Q coulombs is 4.5 × 10⁵ N/ C. The magnitude of Q is
(A) 20 µC
(B) 200 µC
(C) 10 µC
(D) 2 µC
Answer:
(D) 2 µC

Question 13.
The charge on the electron is 1.6 × 10^-19 C. The number of electrons need to be removed from a metal sphere of 0.05 m radius so as to acquire a charge of 4 × 10^-15 C is
(A) 1.25 × 10⁴
(B) 1.25 × 10³
(C) 2.5 × 10³
(D) 2.5 × 10⁴
Answer:
(D) 2.5 × 10⁴

Question 14.
Electric lines of force about a positive point charge and negative point charge are respectively .
(A) circular, clockwise
(B) radially outward, radially inward
(C) radially inward, radially outward
(D) circular, anticlockwise
Answer:
(B) radially outward, radially inward

Question 15.
Which of the following is NOT the property of equipotential surfaces?
(A) They do not intersect each other.
(B) They are concentric spheres for uniform electric field.
(C) Potential at all points on the surface has constant value.
(D) Separation of equipotential surfaces increases with decrease in electric field.
Answer:
(B) They are concentric spheres for uniform electric field.

Question 16.
In a uniform electric field, a charge of 3 C experiences a force of 3000 N. The potential difference between two points 1 cm apart along the electric lines of force will be
(A) 10 V
(B) 3 V
(C) 0.1 V
(D) 20 V
Answer:
(A) 10 V

Question 17.
Gauss’ law helps in
(A) determination of electric field due to symmetric charge distribution.
(B) determination of electric potential due to symmetric charge distribution.
(C) determination of electric flux.
(D) situations where Coulomb’s law fails.
Answer:
(A) determination of electric field due to symmetric charge distribution.

Question 18.
The electric flux over a sphere of radius 1.0 m is ø. If the radius of the sphere is doubled without changing the charge, the flux will be
(A) 4ø
(B) 2ø
(C) ø
(D) 8ø
Answer:
(C) ø

Question 19.
Gauss’ theorem states that total normal electric induction over a closed surface in an electric field is equal to
(A) \( \frac{1}{\varepsilon} \sum \mathrm{q}_{\mathrm{n}}\)
(B) ^εΣ q_n
(C) Σ q_n
(D) q₁ × q₂ × q₃ × ……… q_n
Answer:
(C) Σ q_n

Question 20.
Number of lines of induction starting from a conductor holding + q charge surrounded by a medium of permittivity ε is
(A) q and they leave the surface in normal direction.
(B) q and they leave the surface in any direction.
(C) q/ε and they leave the surface normally at every point.
(D) q/ε and they leave the surface in any direction.
Answer:
(C) q/ε and they leave the surface normally at every point.

Question 21.
An electric dipole of moment p is placed in the position of stable equilibrium in a uniform electric field of intensity E. The torque required to rotate, when the dipole makes an angle 0 with the initial position is
(A) pE cosθ
(B) pE sinθ
(C) pE tanθ
(D) pE cotθ
Answer:
(B) pE sinθ

Question 22.
Four coulomb charge is uniformly distributed on 2 km long wire. Its linear charge density is
(A) 2 C/m
(B) 4 C/m
(C) 4 × 10³ C/m
(D) 2 × 10^-3 C/m
Answer:
(D) 2 × 10^-3 C/m

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry

Question 1.
Define chemistry.
Answer:
Chemistry is the study of matter, its physical and chemical properties, and the physical and chemical changes it undergoes under different conditions.

Question 2.
Why is chemistry called a central science?
Answer:

1. Knowledge of chemistry is required in the studies of physics, biological sciences, applied sciences, and earth and space sciences.
2. Chemistry is involved in every aspect of day-to-day life, i.e. the air we breathe, the food we eat, the fluids we drink, our clothing, transportation and fuel supplies, etc.

Hence, chemistry is called a central science.

Question 3.
Give reason: Although chemistry has ancient roots, it has developed as modern science.
Answer:
Technological development in sophisticated instruments has expanded knowledge of chemistry which, now, has been used in applied sciences such as medicine, dentistry, engineering, agriculture, and daily home use products. Hence, due to development and advancement in science and technology, chemistry has developed as modem science.

Question 4.
How is chemistry traditionally classified?
Answer:
Chemistry is traditionally classified into five branches:

• Organic chemistry
• Inorganic chemistry
• Physical chemistry
• Biochemistry
• Analytical chemistry

Question 5.
Explain the following terms:
i. Organic chemistry
ii. Inorganic chemistry
iii. Physical chemistry
Answer:
i. Organic chemistry: It deals with properties and reactions of compounds of carbon.
ii. Inorganic chemistry: It deals with the study of all the compounds which are not organic.
iii. Physical chemistry: It deals with the study of properties of matter, the energy changes and the theories, laws and principles that explain the transformation of matter from one form to another. It also provides basic framework for all the other branches of chemistry.

Question 6.
Distinguish between
i. Mixtures and pure substances
ii. Mixtures and compounds
Answer:
i.

ii.

Question 7.
What is the difference between element and compound?
Answer:
Elements cannot be broken down into simpler substances while compounds can be broken down into simpler substances by chemical changes.

Question 8.
Explain: States of matter
Answer:
There are three different states of matter as follows:

1. Solid: Particles are held tightly in perfect order. They have definite shape and volume.
2. Liquid: Particles are close to each other but can move around within the liquid.
3. Gas: Particles are far apart as compared to that of solid and liquid.

These three states of matter can be interconverted by changing the conditions of temperature and pressure.

Question 9.
Explain: Physical and chemical properties
Answer:
i. Physical properties: These are properties which can be measured or observed without changing the identity or the composition of the substance. e.g. Colour, odour, melting point, boiling point, density, etc.

ii. Chemical properties: These are properties in which substances undergo change in chemical composition. e.g. Coal bums in air to produce carbon dioxide, magnesium wire bums in air in the presence of oxygen to form magnesium oxide, etc.

Question 10.
How are properties of matter measured?
Answer:

• Measurement involves comparing a property of matter with some fixed standard which is reproducible and unchanging.
• Properties such as mass, length, area, volume, time, etc. are quantitative in nature and can be measured.
• A quantitative measurement is represented by a number followed by units in which it is measured.
• These units are arbitrarily chosen on the basis of universally accepted standards. e.g. Length of class room can be expressed as 10 m. Here, 10 is the number and ‘m’ is the unit ‘metre’ in which the length is measured.

Question 11.
Define: Units
Answer:
The arbitrarily decided and universally accepted standards are called units.
e.g. Metre (m), kilogram (kg).

Question 12.
What are the various systems in which units are expressed?
Answer:
Units are expressed in various systems like CGS (centimetre for length, gram for mass and second for time), FPS (foot, pound, second) and MKS (metre, kilogram, second) systems, etc.

Question 13.
What are SI units? Name the fundamental SI units.
Answer:
SI Units: In 1960, the general conference of weights and measures proposed revised metric system, called International system of Units i.e. SI system (abbreviated from its French name).
The seven fundamental SI units are as given below:

[Note: Units for other quantities such as speed, volume, density, etc. can be derived from fundamental SI units.]

Question 14.
What is the basic unit of mass in the SI system?
Answer:
The basic unit of mass in the SI system is kilogram (kg).

Question 15.
Name the following:
i. Full form of CGS unit system
ii. Full form of FPS unit system
iii. The SI unit of length
iv. Symbol used for Candela unit
v. SI unit of electric current
vi. SI unit of electric current
Answer:
i. Centimetre Gram Second
ii. Foot Pound Second
iii. Metre (m)
iv. Cd
v. Kelvin (K)
vi. Ampere (A)

Question 16.
Give reason: The mass of a body is more fundamental property than its weight.
Answer:

• Mass is an inherent property of matter and is the measure of the quantity of matter of a body.
• The mass of a body does not vary with respect to its position.
• On the other hand, the weight of a body is a result of the mass and gravitational attraction
• Weight varies because the gravitational attraction of the earth for a body varies with the distance from the centre of the earth.

Hence, the mass of a body is more fundamental property than its weight.

Question 17.
How is gram related to the SI unit kilogram?
Answer:
The SI unit kilogram (kg) is related to gram (g) as 1 kg = 1000 g= 10³ g.
[Note: ‘Gram’ is used for weighing small quantities of chemicals in the laboratories.
Other commonly used quantity is ‘milligram’. 1 kg = 1000 g = 10⁶ mg]

Question 18.
Why are fractional units of the SI units of length often used? Give two examples of the fractional units of length. How are they related to the SI unit of length?
Answer:
i. Some properties such as the atomic radius, bond length, wavelength of electromagnetic radiation, etc. are very small and therefore, fractional units of the SI unit of length are often used to express these properties.
ii. Fractional units of length: Nanometre (nm), picometre (pm), etc.
iii. Nanometre (nm) and picometre (pm) are related to the SI unit of length (m) as follows:
1 nm = 10^-9 m, 1 pm = 10^-12 m

Question 19.
Define: Volume
Answer:
Volume is the amount of space occupied by a three-dimensional object. It does not depend on shape.

Question 20.
State the common unit used for the measurement of volume of liquids and gases.
Answer:
The common unit used for the measurement of volume of liquids and gases is litre (L).

Question 21.
How is the SI unit of volume expressed?
Answer:
The SI unit of volume is expressed as (metre)³ or m³.

Question 22.
Name some glassware that are used to measure the volume of liquids and solutions.
Answer:

• Graduated cylinder
• Burette
• Pipette

Question 23.
What is a volumetric flask used for in laboratory?
Answer:
A volumetric flask is used to prepare a known volume of a solution in laboratory.

Question 24.
What is density of a substance? How is it measured?
Answer:
Density:

• Density of a substance is its mass per unit volume. It is the characteristic property of any substance.
• It is determined in the laboratory by measuring both the mass and the volume of a sample.
• The density is calculated by dividing mass by volume.

Question 25.
How is the SI unit of density derived? State CGS unit of density.
Answer:
i. The SI unit of density is derived as follows:
Density = \(\frac{\text { SI unit mass }}{\text { SI unit volume }}\)
= \(\frac{\mathrm{kg}}{\mathrm{m}^{3}}\)
= kg m^-3

ii. CGS unit of density: g cm^-3
[Note: The CGS unit, g cm^-3 is equivalent to \(\frac{\mathrm{g}}{\mathrm{mL}}\) or g mL^-1.]

Question 26.
State three common scales of temperature measurement.
Answer:

1. Degree Celsius (°C)
2. Degree Fahrenheit (°F)
3. Kelvin (K)

Question 27.
State the temperatures in Fahrenheit scale that corresponds to 0 °C and 100 °C.
Answer:
The temperature that corresponds to 0 °C is 32 °F and the temperature that corresponds to 100 °C is 212 °F.

Question 28.
Write the expression showing the relationship between:
i. Degree Fahrenheit and Degree Celsius
ii. Kelvin and Degree Celsius
Answer:
i. The relationship between degree Fahrenheit and degree Celsius is expressed as,
°F = \(\frac {9}{5}\) (°C) + 32
ii. The relationship between Kelvin and degree Celsius is expressed as,
K = °C + 273.15

Question 29.
Convert the following degree Fahrenheit temperature to degree Celsius.
i. 50 °F ii. 10 °F
Answer:
Given: Temperature in degree Fahrenheit = 50 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 50 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
50 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(50-32) \times 5}{9}\)
= 10 °C

ii. Given: Temperature in degree Fahrenheit = 10 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 10 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
10 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(10-32) \times 5}{9}\)
= -12.2 °C
Ans: i. The temperature 50 °F corresponds to 10 °C.
ii. The temperature 10 °F corresponds to -12.2 °C.

Question 30.
What is a chemical combination?
Answer:

• The process in which the elements combine with each other to form compounds is called chemical combination.
• The process of chemical combination is governed by five basic laws which were discovered before the knowledge of molecular formulae.

Question 31.
State and explain the law of definite proportions.
Answer:
Law of definite proportions:
i. The law states that “A given compound always contains exactly the same proportion of elements by weight”.
ii. French chemist, Joseph Proust worked with two samples of cupric carbonate; one of which was naturally occurring cupric carbonate and other was synthetic sample. He found the composition of elements present in both the samples was same as shown below:

iii. Thus, irrespective of the source, a given compound always contains same elements in the same proportion.

Question 32.
State and explain the law of multiple proportions.
Answer:
Law of multiple proportions:
i. John Dalton (British scientist) proposed the law of multiple proportions in 1803.
ii. It has been observed that two or more elements may combine to form more than one compound.
iii. The law states that, “ When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers”.
e.g. Hydrogen and oxygen combine to form two compounds, water and hydrogen peroxide.

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of hydrogen (2 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.

Question 33.
Show that NO and NO₂ satisfy the law of multiple proportions.
Answer:
Nitrogen and oxygen combine to form two compounds, nitric oxide (NO) and nitrogen dioxide (NO₂).

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of nitrogen (14 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 34.
Show that carbon monoxide and carbon dioxide satisfy the law of multiple proportions.
Answer:
Chemical reaction of carbon with oxygen gives two compounds, carbon monoxide (CO) and carbon dioxide (CO₂).

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of carbon (12 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 35.
Show that SO₂ and SO₃ satisfy the law of multiple proportions.
Answer:
Chemical reaction of sulphur with oxygen gives two compounds, sulphur dioxide (SO₂) and sulphur trioxide (SO₃).

Here, the two masses of oxygen (32 g and 48 g) which combine with the fixed mass of sulphur (32 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 32 : 48 or 2 : 3.
This is in accordance with the law of multiple proportions.

Question 36.
State and explain Gay Lussac’s law of gaseous volume with two examples.
Answer:
Gay Lussac’s law:
i. Gay Lussac proposed the law of gaseous volume in 1808.
ii. Gay Lussac’s law states that, “ When gases combine or are produced in a chemical reaction, they do so in a simple ratio by volume, provided all gases are at same temperature and pressure
e.g. a. Under identical conditions of temperature and pressure, 100 mL of hydrogen gas combine with 50 mL of oxygen gas to produce 100 mL of water vapour.

Thus, the simple ratio of volumes is 2 : 1 : 2.

b. Under identical conditions of temperature and pressure, 1 L of nitrogen gas combine with 3 L of hydrogen gas to produce 2 L of ammonia gas.

Thus, the simple ratio of volumes is 1 : 3 : 2.

Question 37.
Give two examples which support the Gay Lussac’s law of gaseous volume.
Answer:
i. Under identical conditions of temperature and pressure, 1 L of hydrogen gas reacts with 1 L of chlorine gas to produce 2 L of hydrogen chloride gas.

Thus, the ratio of volumes is 1 : 1 : 2
This is in accordance with Gay Lussac’s law.

ii. Under identical conditions of temperature and pressure, 200 mL sulphur dioxide combine with 100 mL oxygen to form 200 mL sulphur trioxide.

Thus, the ratio of volumes is 2 : 1 : 2.
This is in accordance with Gay Lussac’s law.

Question 38.
Match the following:

Answer:
i – d,
ii – c,
iii – a,
iv – b

Question 39.
32 g of oxygen reacts with some carbon to make 56 grams of carbon monoxide. Find out how much mass must have been used.
Answer:
Given: Mass of oxygen (reactant) = 32 g, mass of carbon monoxide (product) = 56 g
To find: Mass of oxygen (reactant)
Calculation: 12 g of carbon combine with 16 g oxygen to form 28 g of carbon monoxide as follows:

Hence, (2 × 12 = 24 g) of carbon will combine with (2 × 16 = 32 g) of oxygen to give (2 × 28 = 56 g) carbon monoxide.
Ans: Mass of carbon used = 24 g

Question 40.
Calculate the mass of sulphur trioxide produced by burning 64 g of sulphur in excess of oxygen. (Average atomic mass: S = 32 u, O = 16 u).
Solution:
Given: Mass of sulphur (reactant) = 64 g
To find: Mass of sulphur dioxide (product)
Calculation: 32 g of sulphur combine with 48 g oxygen to form 80 g of sulphur trioxide as follows:

Hence, (2 × 32 = 64 g) of sulphur will combine with (2 × 48 = 96 g) of oxygen to give (2 × 80 = 160 g) sulphur trioxide.
Ans: Mass of sulphur trioxide produced = 160 g

Question 41.
Explain Dalton’s atomic theory.
Answer:
John Dalton published “A New System of chemical philosophy” in the year of 1808. He proposed the following features, which later became famous as Dalton’s atomic theory.

• Matter consists of tiny, indivisible particles called atoms.
• All the atoms of a given elements have identical properties including mass. Atoms of different elements differ in mass.
• Compounds are formed when atoms of different elements combine in a fixed ratio.
• Chemical reactions involve only the reorganization of atoms. Atoms are neither created nor destroyed in a chemical reaction.

Dalton’s atomic theory could explain all the laws of chemical combination.

Question 42.
Give reason: Dalton’s atomic theory explains the law of conservation of mass.
Answer:

• The law of conservation of mass states that, “Mass can neither be created nor destroyed” during chemical combination of matter.
• According to Dalton’s atomic theory, chemical reactions involve only the reorganization of atoms. Therefore, the total number of atoms in the reactants and products should be same and mass is conserved during a reaction.

Hence, Dalton’s atomic theory explains the law of conservation of mass.

Question 43.
Give reason: Dalton’s atomic theory explains the law of multiple proportion.
Answer:

• The law of multiple proportion states that, “When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers
• According to Dalton’s atomic theory, compounds are formed when atoms of different elements combine in fixed ratio.

Hence, Dalton’s atomic theory explains the law of multiple proportion.

Question 44.
Define: Atomic mass unit (amu).
Answer:
Atomic mass unit or amu is defined as a mass exactly equal to one twelth of the mass of one carbon-12 atom.

Question 45.
How is relative atomic mass of an atom measured?
Answer:

• The mass of a single atom is extremely small, i.e. the mass of a hydrogen atom is 1.6736 × 10^-24 g. Hence, it is not possible to weigh a single atom.
• In the present system, mass of an atom is determined relative to the mass of an atom of carbon-12 as the standard. This was decided in 1961 by international agreement.
• The atomic mass of carbon-12 is assigned as 12.00000 atomic mass unit (amu).
• The masses of all other elements are determined relative to the mass of an atom of carbon-12 (C-12).
• The atomic masses are expressed in amu which is exactly equal to one twelth of the mass of one carbon-12 atom.
• The value of 1 amu is equal to 1.6605 × 10^-24 g.

Question 46.
What is meant by Unified Mass unit?
Answer:

• Presently, instead of amu, Unified Mass has now been accepted as the unit of atomic mass.
• It is called Dalton and its symbol is ‘u’ or ‘Da’.

Question 47.
What is average atomic mass?
Answer:
The atomic mass of an element which exists as mixture of two or more isotopes is the average of atomic masses of its isotopes. This is called average atomic mass.

Question 48.
Define: Molecular mass
Answer:
Molecular mass of a substance is the sum of average atomic masses of the atoms of the elements which constitute the molecule.
OR
Molecular mass of a substance is the mass of one molecule of that substance relative to the mass of one carbon-12 atom.

Question 49.
How is molecular mass of a substance calculated? Give example.
Answer:
Molecular mass is calculated by multiplying average atomic mass of each element by the number of its atoms and adding them together.
e.g. Molecular mass of carbon dioxide (CO₂) is calculated as follows:
Molecular mass of CO₂ = (1 × average atomic mass of C) + (2 × average atomic mass of O)
= (1 × 12.0 u) + (2 × 16.0 u)
= 44.0 u

Question 50.
Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g. What is the atomic mass of hydrogen in u?
Solution:
Given: Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g.
To find: Atomic mass of hydrogen in u
Calculation: 1.66056 × 10^-24 g = 1 u
∴ 1.6736 × 10^-24 g = x
x = \(\frac{1.6736 \times 10^{-24} \mathrm{~g}}{1.66056 \times 10^{-24} \mathrm{~g} / \mathrm{u}}\) = 1.008u
Ans: The atomic mass of hydrogen in u = 1.008 u

Question 51.
The mass of an atom of one carbon atom is 12.011 u. What is the mass of 20 atoms of the same isotope?
Solution:
Mass of l atom of carbon = 12.011 u
∴ Mass of 20 atoms of same carbon isotope = 20 × 12.011 u = 240.220 u
Ans: The mass of 20 atoms of same carbon isotope = 240.220 u

Question 52.
Calculate the average atomic mass of neon using the following data:

Solution:
Average atomic mass of Neon (Ne)

Ans: Average atomic mass of neon = 20.1707 u

Question 53.
Calculate the average atomic mass of argon from the following data:

Solution:
Average atomic mass of argon (Ar)

Ans: Average atomic mass of argon = 39.974 g mol^-1

Question 54.
Calculate the molecular mass of the following in u:
i. H₂O ii. C₆H₅Cl iii. H₂SO₄
Solution:
i. Molecular mass of H₂O = (2 × Average atomic mass of H) + (1 × Average atomic mass of O)
= (2 × 1.0u) + (1 × 16.0 u)
= 18 u

ii. Molecular mass of C₆H₅Cl = (6 × Average atomic mass of C) + (5 × Average atomic mass of H) + (1 × Average atomic mass of Cl)
= (6 × 12.0 u) + (5 × 1.0 u) + (1 × 35.5 u)
= 112.5 u

iii. Molecular mass of H₂SO₄ = (2 × Average atomic mass of H) + (1 × Average atomic mass of S) + (4 × Average atomic mass of O)
= (2 × 1.0 u) + (1 × 32.0 u) + (1 × 16.0 u)
= 98 u
Ans: i. The molecular mass of H₂O = 18 u
ii. The molecular mass of C₆H₅Cl = 112.5 u
iii. The molecular mass of H₂SO₄ = 98 u

Question 55.
Find the mass of 1 molecule of oxygen (O₂) in amu (u) and in grams.
Solution:
Molecular mass of O₂ = 2 × 16 u
∴ Mass of 1 molecule = 32 u
∴ Mass of 1 molecule of O₂= 32 × 1.66056 × 10^-24 g = 53.1379 × 10^-24 g
Ans: Mass of 1 molecule in amu = 32 u
Mass of 1 molecule in grams = 53.1379 × 10^-24 g

Question 56.
Find the formula mass of
i. NaCl ii. Cu(NO₃)₂
Solution:
i. Formula mass of NaCl
= Average atomic mass of Na + Average atomic mass of Cl
= 23.0 u + 35.5 u = 58.5 u

ii. Formula mass of Cu(NO₃)₂
= Average atomic mass of Cu + 2 × (Average atomic mass of N + Average atomic mass of three O)
= 63.5 + 2 × [14 + (3 × 16)] = 187.5 u
Ans: i. Formula mass of NaCl = 58.5 u
ii. Formula mass of Cu(NO₃)₂ = 187.5 u

Question 57.
Find the formula mass of
i. KCl
ii. AgCl
Atomic mass of K = 39 u, Ag =108 u and Cl = 35.5 u.
Solution:
i. Formula mass of KCl
= Average atomic mass of K + Average atomic mass of Cl
= 39 u + 35.5 u = 74.5 u

ii. Formula mass of AgCl
= Average atomic mass of Ag + Average atomic mass of Cl
= 108 + 35.5 = 143.5 u
Ans: i. Formula mass of KCl = 74.5 u
ii. Formula mass of AgCl = 143.5 u

Question 58.
Calculate the number of moles and molecules of urea present in 5.6 g of urea.
Solution:
Given: Mass of urea = 5.6 g
To find: The number of moles and molecules of urea
Formulae: i. Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
ii. Number of molecules = Number of moles × Avogadro’s constant
Mass of urea = 5.6 g
Molecular mass of urea, NH₂CONH₂
= (2 × Average atomic mass of N) + (4 × Average atomic mass of H) + (1 × Average atomic mass of C) + (1 × average atomic mass of O)
= (2 × 14 u) + (4 × 1 u) + (1 × 12 u) + (1 × 16 u) = 60 u
∴ Molar mass of urea = 60 g mol^-1
∴ Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{5.6 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 0.09333 mol

[Calculation using log table:
\(\frac{5.6}{60}\)
= Antilog₁₀ [log₁₀ (5.6) – log₁₀ (60)]
= Antilog₁₀ [0.7482 – 1.7782]
= Antilog₁₀ [latex]\overline{2} .9700[/latex]
= 0.09333]

Now,
Number of molecules of urea
= Number of moles × Avogadro’s constant
= 0.09333 mol × 6.022 × 10²³ molecules/mol
= 0.5616 × 10²³ molecules (by using log table)
= 5.616 × 10²² molecules
Ans: Number of moles of urea = 0.0933 mol
Number of molecules of urea = 5.616 × 10²² molecules

[Calculation using log table:
0.09333 × 6.022
= Antilog₁₀ [log₁₀ (0.09333) + log₁₀ (6.022)]
= Antilog₁₀ [\(\overline{2} .9698\) + 0.7797]
= Antilog₁₀ [latex]\overline{1} .7495[/latex]
= 0.5616]

Question 59.
Calculate the number of atoms in each of the following:
i. 64 u of oxygen (O)
ii. 42 g of nitrogen (N)
Solution:
i. 64 u of oxygen (O) = x atoms
Atomic mass of oxygen (O) = 16 u
∴ Mass of one oxygen atom = 16 u
∴ x = \(\frac{64 \mathrm{u}}{16 \mathrm{u}}\) = 4 atoms

ii. 42 g of nitrogen (N)
Atomic mass of nitrogen = 14 u
∴ Molar mass of nitrogen = 14 g mol^-1
Now,
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{42 \mathrm{~g}}{14 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 3 mol
Now,
Number of atoms = Number of moles × Avogadro’s constant
= 3 mol × 6.022 × 10²³ atoms/mol
= 18.07 × 10²³ atoms
= 1.807 × 10²⁴ atoms
Ans: i. Number of oxygen atoms in 64 u = 4 atoms
ii. Number of nitrogen atoms in 42 g = 1.807 × 10²⁴ atoms

Question 60.
Calculate the number of atoms in each of the following.
i. 52 moles of Argon (Ar)
ii. 52 u of Helium (He)
iii. 52 g of Helium (He)
Solution:
i. 52 moles of Argon
1 mole Argon atoms = 6.022 × 10²³ atoms of Ar
∴ Number of atoms = 52 mol × 6.022 × 10²³ atoms/mol
= 313.144 × 10²³ atoms of Argon

ii. 52 g of He
Molar mass of He = mass of 1 atom of He = 4.0 u
4.0 u = 1 He
∴ 52 u = x
∴ x = 52 u × \(\frac{1 \text { atom of He }}{4.0 \mathrm{u}}\) = 13 atoms of He

iii. 52 g of He
Molar mass of He = 4.0 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{52 \mathrm{~g}}{4.0 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 13 mol
Number of atoms of He = Number of moles × Avogadro’s constant
= 13 mol × 6.022 × 10²³ atoms/mol
= 78.286 × 10²³ atoms of He
Ans. i. Number of argon atoms in 52 moles = 313.144 × 10²³ atoms of Argon
ii. Number of helium atoms in 52 u = 13 atoms of He
iii. Number of helium atoms in 52 g = 78.286 × 10²³ atoms of He

Question 61.
Calculate the number of atoms of ‘C’, ‘H’ and ‘O’ in 72.5 g of isopropanol, C₃H₇OH (molar mass 60 g mol^-1).
Solution:
Mass of isopropanol(C₃H₇OH) = 72.5 g
The number of atoms of C, H, O
Calculation: Molecular formula of isopropanol, is C₃H₇OH.
Molar mass of C₃H₇OH = 60 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{72.5 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 1.208 mol
∴ Moles of isopropanol = 1.21 mol
Number of atoms = Number of moles × Avogadro’s constant
Now, 1 molecule of isopropanol has total 12 atoms, out of which 8 atoms are of H, 3 of C and 1 of O.
∴ Number of C atoms in 72.5 g isopropanol = (3 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 2.182 × 10²⁴ atoms of carbon
∴ Number of ‘H’ atoms in 72.5 g isopropanol = (8 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 5.819 × 10²⁴ atoms of hydrogen
∴ Number of ‘O’ atoms in 72.5 g isopropanol = (1 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 7.274 × 10²³ atoms of oxygen
Ans. 72.5g of isopropanol contain 2.182 ×10²⁴ atoms of H and 7.274 × 10²³ atoms of O.

Question 62.
Calculate the number of moles and molecules of ammonia (NH₃) gas in a volume 67.2 dm³ of it measured at STP.
Solution:
Given: Volume of ammonia at STP = 67.2 dm³
To find: Number of moles and molecules of ammonia
Formulae: i. Number of moles of a gas (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
ii. Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
Calculation: Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Number of moles (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
Number of moles of NH₃ = \(\frac{67.2 \mathrm{dm}^{3}}{22.4 \mathrm{dm}^{3} \mathrm{~mol}^{-1}}\)
Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
3.0 mol × 6022 × 10²³ molecules mol^-1
= 18.066 × 10²³ molecules
Ans: Number of moles of ammonia = 3.0 mol
Number of molecules of ammonia = 18.066 × 10²³ molecules

Question 63.
3.40 g of ammonia at STP occupies volume of 4.48 dm³. Calculate molar mass of ammonia.
Solution:
Given: Mass of ammonia = 3.40 g
Volume at STP = 4.48 dm³
To Find: Molar mass of ammonia
Calculation: Let ‘x’ grams be the molar mass of NH₃.
Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Volume occupied by 3.40 g of NH₃ at S.T.P = 4.48 dm³
Volume occupied by ‘x’ g of NH3 at S.T.P = 22.4 dm³
∴ x = \(\frac{22.4 \times 3.40}{4.48}\) = 17.0 g mol^-1
Ans: Molar mass of ammonia is 17.0 g mol^-1.

Question 64.
Veg puffs from a particular bakery have an average mass of 27.0 g, whereas egg puffs from the same bakery have an average mass of 40 g.
i. Suppose a person buys 1 kg of veg puff from the bakery. Calculate the number of veg puffs he receives.
ii. Determine the mass of egg puffs (in kg) that will contain the same number of eggs puffs as in one kilogram of veg puffs.
Solution:
i. Mass of a veg puff = 27.0 g = 0.027 kg
∴ Number of veg puffs in 1 kg = 1 / 0.027 = 37
ii. One kilogram of veg puffs contains 37 veg puffs.
Mass of 37 egg puffs = 37 × 0.040 = 1.48 kg
Ans: i. 37 veg puffs in 1 kg of puff.
ii. Mass of 37 egg puffs is 1.48 kg

Multiple Choice Questions:

1. The branch of chemistry which deals with carbon compounds is called ……………. chemistry.
(A) organic
(B) inorganic
(C) carbon
(D) bio
Answer:
(A) organic

2. A/an is a simple combination of two or more substances in which the constituent substances retain their separate identities.
(A) compound
(B) mixture
(C) element
(D) All of these
Answer:
(B) mixture

3. Which one of the following is NOT a mixture?
(A) Paint
(B) Gasoline
(C) Liquefied Petroleum Gas (LPG)
(D) Distilled water
Answer:
(D) Distilled water

4. The sum of the masses of reactants and products is equal in any physical or chemical reaction. This is in accordance with ………………
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of reciprocal proportion
Answer:
(C) law of conservation of mass

5. A sample of calcium carbonate (CaCO₃) has the following percentage composition: Ca = 40 %; C = 12 %; O = 48 %. If the law of definite proportions is true, then the weight of calcium in 4 g of a sample of calcium
carbonate from another source will be ……………..
(A) 0.016 g
(B) 0.16 g
(C) 1.6 g
(D) 16 g
Answer:
(C) 1.6 g

6. Two elements, A and B, combine to form two compounds in which ‘a’ g of A combines with ‘b₁’ and ‘b₂’g of B respectively. According to law of multiple proportion ………………
(A) b₁ = b₂
(B) b₁ and b₂ bear a simple whole number ratio
(C) a and b₁ bear a whole number ratio
(D) no relation exists between b₁ and b₂
Answer:
(B) b₁ and b₂ bear a simple whole number ratio

7. At constant temperature and pressure, two litres of hydrogen gas react with one litre of oxygen gas to produce two litres of water vapour. This is in accordance with ……………….
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of gaseous volumes
Answer:
(D) law of gaseous volumes

8. One mole of oxygen molecule weighs …………….
(A) 8 g
(B) 32 g
(C) 16 g
(D) 6.022 × 10²³ g
Answer:
(B) 32 g

9. The mass of 0.002 mol of glucose (C₆H₁₂O₆) is ………………
(A) 0.20 g
(B) 0.36 g
(C) 0.50 g
(D) 1.80 g
Answer:
(B) 0.36 g

10. Which of the following is CORRECT?
(A) 1 mole of oxygen atoms contains 6.0221367 × 10²³ atoms of oxygen.
(B) 1 mole of water molecules contains 6.0221367 × 10²³ molecules of water.
(C) 1 mole of sodium chloride contains 6.0221367 × 10²³ formula units of NaCl.
(D) All of these
Answer:
(D) All of these

11. 180 g of glucose (C₆H₁₂O₆) contains ……………. carbon atoms.
(A) 1.8 × 10²³
(B) 1.8 × 10²⁴
(C) 3.6 × 10²³
(D) 3.6 × 10²⁴
Answer:
(C) 3.6 × 10²³

12. The number of molecules present in 8 g of oxygen gas is …………….
(A) 6.022 × 10²³
(B) 3.011 × 10²³
(C) 12.044 × 10²³
(D) 1.505 × 10²³
Answer:
(D) 1.505 × 10²³

13. The number of molecules in 22.4 cm³of ozone gas at STP is ……………….
(A) 6.022 × 10²⁰
(B) 6.022 × 10²³
(C) 22.4 × 10²⁰
(D) 22.4 × 10²³
Answer:
(A) 6.022 × 10²⁰

14. 11.2 cm³ of hydrogen gas at STP, contains …………….. moles.
(A) 0.0005
(B) 0.01
(C) 0.029
(D) 0.5
Answer:
(A) 0.0005

15. The mass of 224 mL of hydrogen gas at STP is
(A) 0.02 g
(B) 0.224 g
(C) 2.24 g
(D) 20.0 g
Answer:
(A) 0.02 g

16. 4.4 g of an unknown gas occupies 2.24 L of volume under STP conditions. The gas may be ………………
(A) CO₂
(B) CO
(C) O₂
(D) SO₂
Answer:
(A) CO₂