Maharashtra Board Class 11 Physics Important Questions Chapter 10 Electrostatics

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 10 Electrostatics Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 10 Electrostatics

Question 1.
Explain: Atoms are electrically neutral.
Answer:

1. The matter is made up of atoms which in turn consists of elementary particles proton, neutron, and electron.
2. A proton is considered to be positively charged and an electron to be negatively charged.
3. Neutron is electrically neutral i.e., it has no charge.
4. An atomic nucleus is made up of protons and neutrons and hence is positively charged.
5. Negatively charged electrons surround the nucleus so as to make an atom electrically neutral.

Question 2.
What do the below diagrams show?

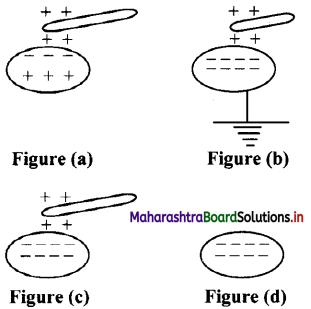
Answer:

1. Figure (a) shows insulated conductor.
2. Figure (b) shows that positive charge is neutralized by electron from Earth.
3. Figure (c) shows that earthing is removed, negative charge still stays in conductor due to positive charged rod.
4. Figure (d) shows that when rod is removed, negative charge is distributed over the surface of the conductor.

Question 3.
Explain concept of charging by conduction.
Answer:

1. When certain dissimilar substances, like fur and amber or comb and dry hair, are rubbed against each other, electrons get transferred to the other substance making them charged.
2. The substance receiving electrons develops a negative charge while the other is left with an equal amount of positive charge.
3. This can be called charging by conduction as charges are transferred from one body to another.

Question 4.
Explain concept of charging by induction.
Answer:

1. If an uncharged conductor is brought near a charged body, (not in physical contact) the nearer side of the conductor develops opposite charge to that on the charged body and the far side of the conductor develops charge similar to that on the charged body. This is called induction.
2. This happens because the electrons in a conductor are free and can move easily in presence of charged body.
3. A charged body attracts or repels electrons in a conductor depending on whether the charge on the body is positive or negative respectively.
4. Positive and negative charges are redistributed and are accumulated at the ends of the conductor near and away from the charged body.
5. In induction, there is no transfer of charges between the charged body and the conductor. So when the charged body is moved away from the conductor, the charges in the conductor are free again.

Question 5.
Explain the concept of additive nature of charge.
Answer:

1. Electric charge is additive, similar to mass. The total electric charge on an object is equal to the algebraic sum of all the electric charges distributed on different parts of the object.
2. It may be pointed out that while taking the algebraic sum, the sign (positive or negative) of the electric charges must be taken into account.
3. Thus, if two bodies have equal and opposite charges, the net charge on the system of the two bodies is zero.
4. This is similar to that in case of atoms where the nucleus is positively charged and this charge is equal to the negative charge of the electrons making the atoms electrically neutral.

Question 6.
State the analogy between the additive property of charge with that of mass.
Answer:

1. The masses of the particles constituting an object are always positive, whereas the charges distributed on different parts of the object may be positive or negative.
2. The total mass of an object is always positive whereas, the total charge on the object may be positive, zero or negative.

Question 7.
What is quantization of charge?
Answer:

1. Protons (+ve) and electrons (-ve) are the charged particles constituting matter, hence the charge on an object must be an integral multiple of ± e i.e., q = ± ne, where n is an integer.
2. Charge on an object can be increased or decreased in multiples of e.
3. It is because, during the charging process an integral number of electrons can be transferred from one body to the other body. This is known as quantization of charge or discrete nature of charge.

Question 8.
Explain with an example why quantization of charge is not observed practically.
Answer:
i. The magnitude of the elementary electric charge (e), is extremely small. Due to this, the number of elementary charges involved in charging an object becomes extremely large.

ii. For example, when a glass rod is rubbed with silk, a charge of the order of one µC (10^-6 C) appears on the glass rod or silk. Since elementary charge e = 1.6 × 10^-19 C. the number of elementary charges on the glass rod (or silk) is given by
n = \(\frac {10^{-6}C}{1.6×10^{-19}C}\) = 6.25 × 10¹²
Since, it is tremendously large number, the quantization of charge is not observed and one usually observes a continuous variation of charge.

Question 9.
The total charge of an isolated system is always conserved. Explain with an example.
Answer:

1. When a glass rod is rubbed with silk, it becomes positively charged and silk becomes negatively charged.
2. The amount of positive charge on glass rod is found to be exactly the same as negative charge on silk.
3. Thus, the systems of glass rod and silk together possesses zero net charge after rubbing.
   Hence, the total charge of an isolated system is always conserved.

Question 10.
Explain the conclusion when charges are brought close to each other.
Answer:

1. Unlike charges attract each other.
2. Like charges repel each other.

Question 11.
How much positive and negative charge is present in 1 g of water? How many electrons are present in it?
(Given: molecular mass of water is 18.0 g)
Answer:
Molecular mass of water is 18 gram, that means the number of molecules in 18 gram of water is 6.02 × 10²³
∴ Number of molecules in lgm of water = \(\frac {6.02×10^{23}}{18}\)
One molecule of water (H₂O) contains two hydrogen atoms and one oxygen atom. Thus, the number of electrons in ILO is sum of the number of electrons in H₂ and oxygen. There are 2 electrons in H₂ and 8 electrons in oxygen.
∴ Number of electrons in H₂O = 2 + 8 = 10
Total number of protons / electrons in one gram of water
= \(\frac {6.02×10^{23}}{18}\) × 10 = 3.344 × 10²³
Total positive charge
= 3.344 × 10²³ × charge on a proton
= 3.344 × 10²³ × 1.6 × 10^-19C
= 5.35 × 10⁴ C
This positive charge is balanced by equal amount of negative charge so that the water molecule is electrically neutral.
∴ Total negative charge = 5.35 × 10⁴C

Question 12.
Define point charge. Which law explains the interaction between charges at rest?
Answer:

1. A point charge is a charge whose dimensions are negligibly small compared to its distance from another bodies.
2. Coulomb’s law explains the interaction between charges at rest.

Question 13.
State and explain Coulomb’s law of electric charge in scalar form.
Answer:
Coulomb’s law:
The force of attraction or repulsion between two point charges at rest is directly proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them. This force acts along the line joining the two charges.
Explanation:
i. Let q₁ and q₂ be the two point charges at rest with each other and separated by a distance r. F is the magnitude of electrostatic force of attraction or repulsion between them.

ii. According to Coulomb’s law.
F ∝ \(\frac {q_1q_2}{r^2}\)
∴ F = K\(\frac {q_1q_2}{r^2}\)
where, K is the constant of proportionality which depends upon the units of F, q₁, q₂, r and medium in which charges are placed.

Question 14.
State conditions for electrostatic force to be attractive or repulsive.
Answer:

1. The force between the two charges will be attractive, if the charges are unlike (one positive and one negative).
2. The force between the two charges will be repulsive, if the charges are similar (both positive or both negative).

Question 15.
Prove that relative permittivity is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.
Answer:
i. The force between the two charges placed in a medium is given by,
F_med = \(\frac {1}{4πε}\) (\(\frac {q_1q_2}{r^2}\)) …………. (1)
where, ε is called the absolute permittivity of the medium.

ii. The force between the same two charges placed in free space or vacuum at distance r is given by,
F_vac = \(\frac {1}{4πε_0}\) (\(\frac {q_1q_2}{r^2}\)) …………. (1)
Dividing equation (2) by equation (1),

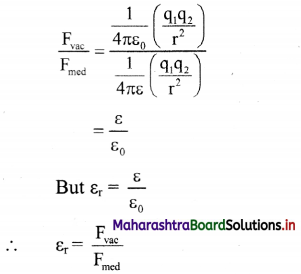
Hence, relative permittivity is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.

Question 16.
If relative permittivity of water is 80 then derive the relation between F_water and F_vacuum. What can be concluded from it?
Answer:
i. The force between two point charges q₁ and q₂ placed at a distance r in a medium of relative permittivity ε_r, is given by
F_med = \(\frac{1}{4 \pi \varepsilon_{0} \varepsilon_{r}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) …………. (1)
If the medium is vacuum,
F_vac = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) …………. (2)

ii. Dividing equation (2) by equation (1),
\(\frac{\mathrm{F}_{\mathrm{vac}}}{\mathrm{F}_{\text {med }}}\) = ε_r
For water, ε_r = 80 ……….. (given)
∴ F_water = \(\frac {F_{vac}}{80}\)

iii. This means that when two point charges are placed some distance apart in water, the force between them is reduced to (\(\frac {1}{80}\))^th of the force between the same two charges placed at the same distance in vacuum.

iv. Thus, it is concluded that a material medium reduces the force between charges by a factor of er, its relative permittivity.

Question 17.
Give conversions of micro-coulomb, nano-coulomb and pico-coulomb to coulomb.
Answer:
1 microcoulomb (µC) = 10^-6 C
1 nanocoulomb (nC) = 10^-9 C
1 picocoulomb (pC) = 10^-12 C

Question 18.
Explain Coulomb’s law in vector form.
Answer:
i. Let q₁ and q₂ be the two similar point charges situated at points A and B and let \(\vec{r}\)₁₂ be the distance of separation between them.

ii. The force \(\vec{F}\)₂₁ exerted on q₂ by q₁ is given by,
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{12}\right|^{2}} \times \hat{\mathrm{r}}_{12}\)
where, \(\hat{r}\)₁₂ is the unit vector from A to B.
\(\vec{F}\)₂₁ acts on q₂ at B and is directed along BA, away from B.

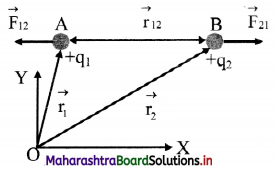
iii. Similarly, the force \(\vec{F}\)₁₂ exerted on q₁ by q₂ is given by, \(\vec{F}\)₁₂ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{12}\right|^{2}} \times \hat{\mathrm{r}_{21}}\)
where, \(\hat{r}\)₂₁ is the unit vector from B to A. \(\vec{F}\)₁₂ acts on q₁ at A and is directed along BA, away from A.

iv. The unit vectors \(\hat{r}\)₁₂ and \(\hat{r}\)₂₁ are oppositely directed i.e., \(\hat{r}\)₁₂ = –\(\hat{r}\)₂₁
Hence, \(\vec{F}\)₂₁ = –\(\vec{F}\)₁₂
Thus, the two charges experience force of equal magnitude and opposite in direction.

v. These two forces form an action-reaction pair.

vi. As \(\vec{F}\)₂₁ and \(\vec{F}\)₁₂ act along the line joining the two charges, the electrostatic force is a central force.

Question 19.
State similarities and differences of gravitational and electrostatic forces.
Answer:
i. Similarities:
a. Both forces obey inverse square law:
F ∝ \(\frac{1}{r^2}\)
b. Both are central forces and they act along the line joining the two objects.

ii. Differences:
a. Gravitational force between two objects is always attractive while electrostatic force between two charges can be either attractive or repulsive depending on the nature of charges.
b. Gravitational force is about 36 orders of magnitude weaker than the electrostatic force.

Question 20.
Charge on an electron is 1.6 × 10^-19 C. How many electrons are required to accumulate a charge of one coulomb?
Answer:
1 electron = 1.6 × 10^-19 C
∴ 1 C = \(\frac{1}{1.6 \times 10^{-19}}\) electrons
= 0.625 × 10¹⁹ electrons
……. (Taking reciprocal from log table)
= 6.25 × 10¹⁸ electrons
Hence, 6.25 × 10¹⁸ electrons are required to accumulate a charge of one coulomb.

Question 21.
What is the force between two small charge spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Given: q₁ = 2 × 10^-7 C, q₂ = 3 × 10^-7 C
r = 30 cm = \(\frac {30}{100}\) m = 0.3 m
To find: Force (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,
F = \(\frac{9 \times 10^{9} \times 2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^{2}}\)
∴ F = 6 × 10^-3 N

Question 22.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge -0.8 µC in air is 0.2 N. (i) What is the distance between the two spheres? (ii) What is the force on the second sphere due to the first?
Answer:
i. Given: q₁ = 0.4 µC = 0.4 × 10^-6 C,
q₂ = -0.8 µC = -0.8 × 10^-6 C, F = 0.2 N
To find: i. Distance (r)
ii. Force on second sphere (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:
i. From formula,
r² = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{F}\)
r² = \(\frac{9 \times 10^{9} \times 0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}\)
= 0.0144
∴ r = \(\sqrt{0.0144}\) = 0.12 m
∴ r = 12 cm

ii. The force on the second sphere due to the first is also 0.2 N and is attractive in nature.

Question 23.
i. Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion, if the charge on each is 6.5 × 10^-7 C? The radii of A and B are negligible compared to the distance of separation,
ii. What is the force of repulsion if each sphere is charged double the above amount and the distance between them is halved?
Answer:
Given: q₁ = 6.5 × 10^-7 C q₂ = 6.5 × 10^-7 C
r = 50 cm = 0.50 m
To find: Force of repulsion (F)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:
From formula,
F = \(\frac{9 \times 10^{9} \times 6.5 \times 10^{-7} \times 6.5 \times 10^{-7}}{(0.50)^{2}}\)
F = 1.52 × 10^-2 N

ii. When each charge is doubled and the distance between them is reduced to half, then
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\left(2 q_{1}\right)\left(2 q_{2}\right)}{(r / 2)^{2}}\)
= 16 × \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\) = 16 × 1.52 × 10^-2
∴ F = 0.24 N

Question 24.
Calculate and compare the electrostatic and gravitational forces between two protons which are 10^-15 m apart. Value of G = 6.674 × 10^-11 m³ kg^-1 s^-2 and mass of the porton is 1.67 × 10^-27 kg.
Answer:
Given: G = 6.674 × 10^-11 m³ kg^-1 s^-2
m_p = 1.67 × 10^-27 kg.
q_p = 1.67 × 10^-19 C, r = 10^-15
To find:
i. Electrostatic Force (F_E)
ii. Gravitational Force (F_G)
Formula: i. F_E = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
ii. F_E = \(\frac {Gm_1m_2}{r^2}\)
Calculation:
From formula (i),
\(\mathrm{F}_{\mathrm{E}}=9 \times 10^{9} \times \frac{1.6 \times 10^{-19} \times 1.6 \times 10^{-19}}{\left(10^{-15}\right)^{2}}\)
= 9 × 1.6 × 1.6 × 10
= 90 × 1.6 × 1.6
= antilog [log 90 + log 1.6 + log 1.6]
= antilog [1.9542 + 0.2041 + 0.2041]
= antilog [2.3624]
= 2.303 × 10² N
From formula (ii),
\(\mathrm{F}_{\mathrm{G}}=6.674 \times 10^{-11} \times \frac{1.67 \times 10^{-27} \times 1.67 \times 10^{-27}}{\left(10^{-15}\right)^{2}}\)
= 6.674 × 1.67 × 1.67 × 10^-35
= {antilog [log 6.674 + log 1.67 + log 1.67]} × 10^-35
= {antilog [0.8244 + 0.2227 + 0.2227]} × 10^-35
= {antilog [1.2698]} × 10^-35
= 1.861 × 10¹ × 10^-35
= 1.861 × 10^-34 N
Now,
\(\frac{\mathrm{F}_{\mathrm{E}}}{\mathrm{F}_{\mathrm{G}}}=\frac{2.303 \times 10^{2}}{1.861 \times 10^{-34}}\)
= {antilog [log 2.303 – log 1.861]} × 10³⁶
= {antilog [0.3623 – 0.2697]} × 10³⁶
= {antilog [0.0926]}
= 1.238 × 10³⁶
∴ F_E ≈ 10³⁶ × F_G

Question 25.
State and explain principle of superposition.
Answer:
Statement: When a number of charges are interacting, the resultant force on a particular charge is given by the vector sum of the forces exerted by individual charges.
Explanation:
i. Consider a number of point charges q₁, q₂, q₃ ……………… kept at points A₁, A₂, A₃ ………….. as shown in figure.

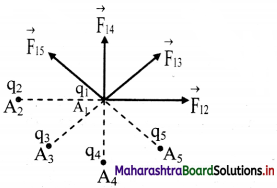
ii. The force exerted on the charge q₁ by q₂ is \(\vec{F}\)₁₂ The value of \(\vec{F}\)₁₂ is calculated by ignoring the presence of other charges. Similarly, force \(\vec{F}\)₁₃, \(\vec{F}\)₁₄ can be found, using the Coulomb’s law.

iii. Total force \(\vec{F}\)₁ on charge qi is the vector sum of all such forces.
\(\vec{F}\)₁ = \(\vec{F}\)₁₂ + \(\vec{F}\)₁₃ + \(\vec{F}\)₁₄ + …………..
\( =\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\left|\mathrm{r}_{21}\right|^{2}} \times \hat{\mathrm{r}}_{21}+\frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\left|\mathrm{r}_{31}\right|^{2}} \times \hat{\mathrm{r}}_{31}+\ldots .\right]\)

where \(\hat{r}\)₂₁, \(\hat{r}\)₃₁ are unit vectors directed to q₁ from q₂, q₃ respectively and r₂₁, r₃₁, r₄₁ are the distances from q₁ to q₂, q₃ respectively.

iv. If q₁, q₂, q₃ ……., q_n are the point charges then the force \(\vec{F}\) exerted by these charges on a test charge q₀ is given by,
\(\vec{F}\)_test = \(\vec{F}\)₁ = \(\vec{F}\)₂ + \(\vec{F}\)₃ + …. + \(\vec{F}\)_n
= \(\sum_{\mathrm{n}=1}^{\mathrm{n}} \mathrm{F}_{\mathrm{n}}=\frac{1}{4 \pi \varepsilon_{0}} \sum_{\mathrm{n}=1}^{\mathrm{n}} \frac{\mathrm{q}_{0} \mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}^{2}} \hat{\mathrm{r}}_{\mathrm{n}}\)
Where, \(\hat{r}\)_n, is a unit vector directed from the nth charge to the test charge q₀ and r₂ is the
separation between them, \(\vec{r}\)_n = r_n \(\hat{r}\)_n

Question 26.
Three charges of 2 µC, 3 µC and 4 µC are placed at points A, B and C respectively, as shown in the figure. Determine the force on A due to other charges.
(Given: AB = 4 cm, BC = 3 cm)

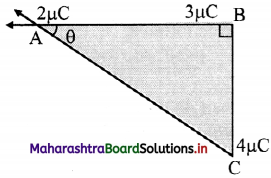
Answer:

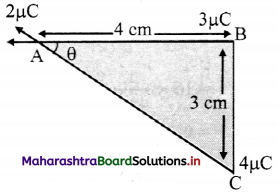
Using pythagoras theorem
AC = \(\sqrt {AB^2+BC^2}\)
= \(\sqrt {4^2+3^2}\)
AC = 5 cm
Magnitude of force \(\vec{F}\)_AB on A due to B is,

In ∆ABC 4
cos θ = \(\frac {4}{5}\)
θ = cos^-1 (\(\frac {4}{5}\)) = 36.87°
Forces acting points A are

= 59.36 N
Direction of resultant force is 36.87° (north of west)

[Note: The question given above is modified considering minimum requirement of data needed to solve the problem.]

Question 27.
There are three charges of magnitude 3 pC, 2 pC and 3 pC located at three corners A, B and C of a square ABCD of each side measuring 2 m. Determine the net force on 2 pC charge.
Answer:
Given: q₁ = 3 µC, q₂ = 2 µC, q₃ = 3 µC, r = 2 m
To find: Net force on q₂ (R)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation:

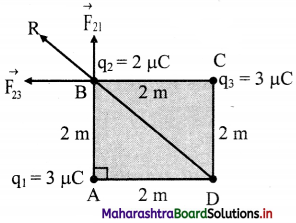
From the formula,
Force on q₂ because of q₁

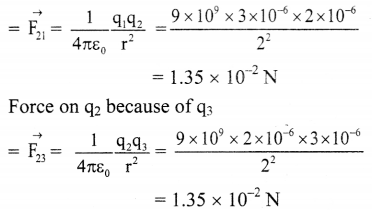
Net force on q₂ is the resultant force of \(\vec{F}\)₂₁ and \(\vec{F}\)₂₃ which is given by,
R = \(\sqrt{\mathrm{F}_{21}^{2}+\mathrm{F}_{23}^{2}}\)
= \(\sqrt{\left(1.35 \times 10^{-2}\right)^{2}+\left(1.35 \times 10^{-2}\right)^{2}}\)
∴ R = 1.91 × 10^-2 N

Question 28.
Explain the concept of electric field.
Answer:

1. The space around a charge gets modified when a test charge is brought in that region, it experiences a coulomb force. The region around a charged object in which coulomb force is experienced by another charge is called electric field.
2. Mathematically, electric field is defined as the force experienced per unit charge.
3. The coulomb force acts across an empty space (vacuum) and does not need any intervening medium for its transmission.
4. The electric field exists around a charge irrespective of the presence of other charges.
5. Since the coulomb force is a vector, the electric field of a charge is also a vector and is directed along the direction of the coulomb force, experienced by a test charge.

Question 29.
Define electric field. State its SI unit and dimensions.
Answer:

1. Electric field is the force experienced by a test charge in presence of the given charge at the given distance from it.
   \(\vec{E}\) = \(\lim _{q \rightarrow 0} \frac{\vec{F}}{q}\)
2. SI unit: newton per coulomb (N/C) or volt per metre (V/m).
3. Dimensions: [L M T^-3 A^-1]

Question 30.
Establish relation between electric field intensity and electrostatic force.
Answer:
i. Let Q and q be two charges separated by a distance r.
The coulomb force between them is given by \(\vec{F}\) = \(\frac {1}{4πε_0}\) \(\frac {Qq}{r^2}\) \(\hat{r}\)
where, \(\hat{r}\) is the unit vector along the line joining Q to q.

ii. Therefore, electric field due to charge Q is given \(\vec{F}\) = \(\frac{\vec{F}}{\mathrm{q}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)

iii. Electric field at a point is useful to estimate the force experienced by a charge at that point.

Question 31.
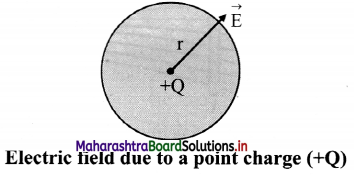
State an expression for electric field on the surface of the sphere due to a positive point charge placed at its centre.
Answer:
The magnitude of electric field at a distance r from a point charge Q is same at all points on the surface of a sphere of radius r as shown in figure.

ii. Magnitude of electric field is given by,
E = \(\frac {1}{4πε_0}\) \(\frac {Q}{r^2}\)
iii. Its direction is along the radius of the sphere, pointing away from its centre if the charge is positive.

Question 32.
Derive expression for electric field intensity due to a point charge in a material medium.
Answer:
i. Consider a point charge q placed at point O in a medium of dielectric constant K as shown in figure.

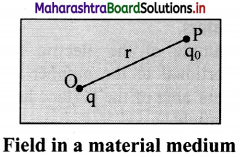
ii. Consider the point P in the electric field of point charge at distance r from q. A test charge q0 placed at the point P will experience a force which is given by the Coulomb’s law,
\(\vec{F}\) = \(\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{qq}_{0}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
where \(\hat{r}\) is the unit vector in the direction of force i.e., along OP.

iii. By the definition of electric field intensity,
\(\vec{F}\) = \(\frac{\vec{F}}{\mathrm{q}_{0}}=\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
The direction of \(\vec{E}\) will be along OP when q is positive and along PO when q is negative.

iv. The magnitude of electric field intensity in a medium is given by, E = \(\frac{1}{4 \pi \varepsilon_{0} \mathrm{~K}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)

v. For air or vacuum, K = 1 then
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)

Question 33.
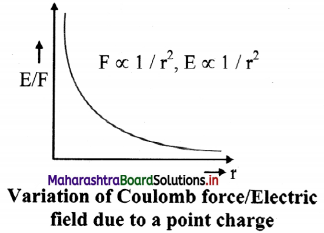
Show graphical representation of variation of coulomb force and electric field due to point charge with distance.
Answer:
Electrostatic force: F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\)
Electric field: E : \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
The coulomb force (F) between two charges and electric field (E) due to a charge both follow the inverse square law.
(F ∝ 1/r², E ∝ 1/r²)

Question 34.
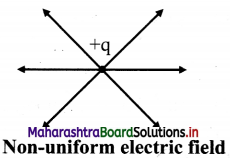
What is non-uniform electric field?
Answer:
A field whose magnitude and direction is not the same at all points.
For example, field due to a point charge. In this case, the magnitude of field is same at distance r from the point charge in any direction but the direction of the field is not same.

Question 35.
Derive relation between electric field (E) and electric potential (V).
Answer:
i. A pair of parallel plates is connected as shown in the figure. The electric field between them is uniform

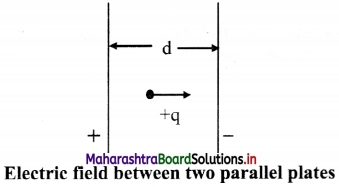
ii. A potential difference V is applied between two parallel plates separated by a distance ‘d’.

iii. The electric field between them is directed from plate A to plate B.

iv. A charge +q placed between the plates experiences a force F due to the electric field.

v. If the charge is moved against the direction of field, i.e., towards the positive plate, some amount of work is done on it.

vi. If the charge is moved +q from the negative plate B to the positive plate A, then the work done against the field is W = Fd; where ‘d’ is the separation between the plates.

vii. The potential difference V between the two plates is given by W = V_q,
but W = Fd
∴ Vq = Fd
∴ \(\frac {F}{q}\) = \(\frac {V}{d}\) = E
∴ Electric field can be defined as E = V/d.

Question 36.
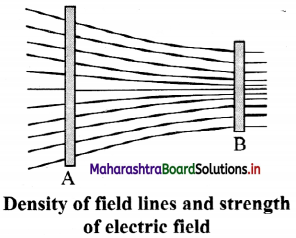
What are electric lines of force?
Answer:
i. An electric line of force is an imaginary curve drawn in such a way that the tangent at any given point on this curve gives the direction of the electric field at that point.

ii. If a test charge is placed in an electric field it would be acted upon by a force at every point in the field and will move along a path.

iii. The path along which the unit positive charge moves is called a line of force.

iv. A line of force is defined as a curve such that the tangent at any point to this curve gives the direction of the electric field at that point.

v. The density of field lines indicates the strength of electric fields at the given point in space.

Question 37.
State the characteristics of electric lines of force.
Answer:

1. The lines of force originate from a positively charged object and end on a negatively charged object.
2. The lines of force neither intersect nor meet each other, as it will mean that electric field has two directions at a single point.
3. The lines of force leave or terminate on a conductor normally.
4. The lines of force do not pass through conductor i.e., electric field inside a conductor is always zero, but they pass through insulators.
5. Magnitude of the electric field intensity is proportional to the number of lines of force per unit area of the surface held perpendicular to the field.
6. Electric lines of force are crowded in a region where electric intensity is large.
7. Electric lines of force are widely separated from each other in a region where electric intensity is small
8. The lines of force of an uniform electric field are parallel to each other and are equally spaced.

Question 38.
Find the distance from a charge of 4 µC placed in air which produces electric field of intensity 9 × 10³ N/C.
Answer:
Given: K = 1, E = 9 × 10³ N/C
q = 4 µC = 4 × 10^-6
To Find: Distance (r)
Formula: E = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{r^{2}}\)
Calculation from formula
9 × 10³ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{4 \times 10^{-6}}{r^{2}}\)
∴ 9 × 10³ = 9 × 10⁹ \(\frac{4 \times 10^{-6}}{\mathrm{r}^{2}}\)
∴ r² = 4
∴ r = 2 m

Question 39.
What is the magnitude of a point charge chosen so that the electric field 50 cm away has magnitude 2.0 N/C?
Answer:
Given: r = 50 cm – 0.5 m, E = 2 N/C,
To find: Magnitude of charge (q)
Formula: E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\)
Calculation from formula

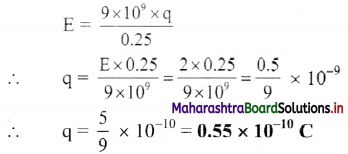
Question 40.
Three point charges are placed at the vertices of a right angled isosceles triangle as shown in the given figure. What is the magnitude and direction of the resultant electric field at point P which is the mid point of its hypotenuse?

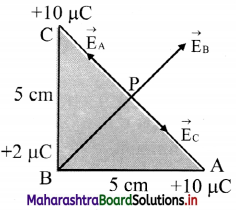
Answer:
Electric field at P due to the charges at A, B and C are shown in the figure.

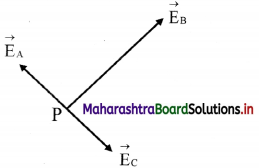
Let \(\vec{E}\)_A be the field at P due to charge at A and \(\vec{E}\)_c be the field at P due to charge at C.
Since P is the midpoint of AC and the fields at A and C are equal in magnitudes and are opposite in direction, E_A = – E_C .
i.e., \(\vec{E}\)_A + \(\vec{E}\)_C = 0.
Thus, the field at P is only to the charge at B and is given by,

Question 41.
A simplified model of hydrogen atom consists of an electron revolving about a proton at a distance of 5.3 × 10^-11 m. The charge on a proton is +1.6 × 10^-19 C. Calculate the intensity of the electric field due to proton at this distance. Also find the force between electron and proton.
Answer:
Given: r = 5.3 × 10^-11 m
q = 1.6 × 10^-19 C
To Find: i. Intensity of electric field (E)
ii. Force (F)
Formula: i. E = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
ii. E = \(\frac {F}{q}\)
Calculation from formula (i)
E = 9 × 10⁹ × \(\frac{1.6 \times 10^{-19}}{\left(5.3 \times 10^{-11}\right)^{2}}\)
= 5.126 × 10¹¹ N/C
Force between electron and proton,
Force between electron and proton,
F = E × q_e ….[From formula (ii)]
= 5.126 × 10^-11 × -1.6 × 10^-19
= -8.201 × 10⁸ N

Question 42.
The force exerted by an electric field on a charge of +10 µC at a point is 16 × 10^-4 N. What is the intensity of the electric field at the point?
Answer:
Given: q = 10 µC= 10 × 10^-6 C, F = 16 × 10^-4 N
To find: Electric field intensity (E)
Formula: E = \(\frac {F}{q}\)
Calculation: From formula,
E = \(\frac {16×10^{-4}}{10×10^{-6}}\) = 160 N/C

Question 43.
What is the force experienced by a test charge of 0.20 µC placed in an electric field of 3.2 × 10⁶ N/C?
Answer:
Given: q₀ = 0.20 µC = 0.2 × 10⁶ C,
E = 3.2 × 10⁶ N/C
To find: Force (F)
Formula: E = \(\frac {F}{q_0}\)
Calculation: From formula,
F = Eq₀
∴ F = 3.2 × 10⁶ × 0.2 × 10^-6 = 0.64 N

Question 44.
Gap between two electrodes of the spark-plug used in an automobile engine is 1.25 mm. If the potential of 20 V is applied across the gap, what will be the magnitude of electric field between the electrodes?
Answer:
Given: V = 20 V
d = 1.25 mm = 1.25 × 10^-3 m
To Find: Magnitude of electric field (E)
Formula: E = \(\frac {V}{d}\)
Calculation: From formula,
E = \(\frac {20}{1.25×10^{-3}}\)
= 1.6 × 10⁴ V/m

Question 45.
If 100 joules of work must be done to move electric charge equal to 4 C from a place, where potential is -10 volt to another place where potential is V volt, find the value of V.
Answer:
Given: q₀ = 4 C,
V_A = -10 volt,
V_B = V volt,
W_AB = 100 J
To Find: Potential (V)
Formula: V_B – V_A = \(\frac {W_{AB}}{q_0}\)
Calculation: From formula,
V – (-10) = \(\frac {100}{4}\) = 25
∴ V + 10 = 25
∴ V = 15 volt

Question 46.
Find the work done when a point charge of 2.0 pC is moved from a point at a potential of -10 V to a point at which the potential is zero.
Answer:
V_A = -10V,
V_B = 0,
q = 2 × 10^-6 C
To Find: Work done (W)
Formula: V_BA = \(\frac {W}{q}\)
Calculation: From formula,
W = V_BA × q
= (V_B – V_A) × q
= (0 + 10) × 2 × 10^-6
= 20 × 10^-6 J
∴ W = 2 × 10^-5 J

Question 47.
Explain the term: Electric flux
Answer:
i. The number of lines of force per unit area is the intensity of the electric field \(\vec{E}\).

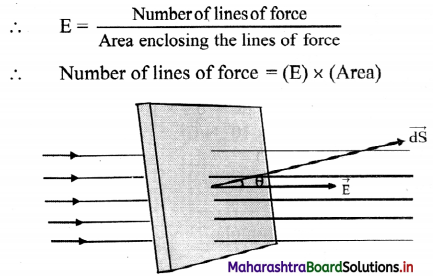
ii. When the area is inclined at an angle θ with the direction of electric field, the electric flux can be calculated as follows.
Let the angle between electric field \(\vec{E}\), and area vector \(\vec{dS}\) be θ, then the electric flux passing through are dS is given by
dø = (component of dS along \(\vec{E}\)) × (area of \(\vec{dS}\))
dø = EdS cos θ
dø = \(\vec{E}\) .\(\vec{dS}\)
Total flux through the entire surface .
ø = ∫dø = \( \int_{S} \vec{E} \cdot d \vec{S}=\vec{E} \cdot \vec{S}\)

iii. The SI unit of electric flux can be calculated using,
ø = \(\vec{E}\). \(\vec{S}\) = (V/m) m² = V m
[Note: Area vector is a vector whose magnitude is equal to area and is directed normal to its surface]

Question 48.
The electric flux through a plane surface of area 200 cm² in a region of uniform electric field 20 N/C is 0.2 N m²/C. Find the angle between electric field and normal to the surface.
Answer:
Given: ds = 200 cm² = 2 × 10^-2 m², E = 20 N/C,
ø = 0.2 N m²/C
To find: Angle between electric field and normal (θ)
Formula: ø = Eds cos θ
Calculation:
From formula,
cos θ = \(\frac {ø}{Eds}\) = \(\frac {0.2}{20×2×10^{-2}}\) = \(\frac {1}{2}\)
∴ θ = cos^-1 (\(\frac {1}{2}\))
∴ θ = 60°

Question 49.
A charge of 5.0 C is kept at the centre of a sphere of radius 1 m. What is the flux passing through the sphere? How will this value change if the radius of the sphere is doubled?
Answer:
Given: q = 5C, r = 1 m
To find: Flux (ø)
Formulae: i. E = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
ii. ø = E × A = E (4πr²)
Calculation: From formula (i),
E = 9 × 10⁹ × \(\frac {5}{1^2}\)
= 4.5 × 10¹⁰ N/C
From formula (ii),
ø = E × 4 π r²
= 4.5 × 10¹⁰ × 4 × 3.14 × 1²
ø = 5.65 × 10¹¹ Vm
This value of flux will not change if radius of sphere is doubled. Though radius of sphere will increase, increased distance will reduce the electric field intensity. As E ∝ \(\frac {1}{r^2}\) and A × r² net variation in total flux will not be observed.

Question 50.
State and prove Gauss’ law of electrostatics.
Answer:
Statement:
The flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by Eo.
\(\int \vec{E} \cdot \overrightarrow{\mathrm{dS}}=\frac{\mathrm{Q}}{\varepsilon_{0}}\)
where Q is the total charge within the surface.

Proof:
i. Consider a closed surface of any shape which encloses number of positive electric charges.

ii. Imagine a small charge +q present at a point O inside closed surface. Imagine an infinitesimal area dS of the given irregular closed surface.

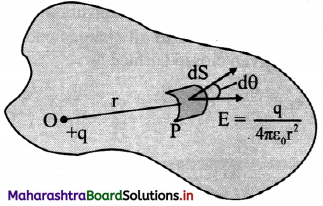
iii. The magnitude of electric field intensity at point P on dS due to charge +q at point O is, E = \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{\mathrm{q}}{\mathrm{r}^{2}}\right)\) ………… (1)

iv. The direction of E is away from point O. Let θ be the angle subtended by normal drawn to area dS and the direction of E

v. Electric flux passing through area (dø)
= Ecosθ dS
= \(\frac{\mathrm{q}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}\) cosθ dS ………….. (from 1)
= \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_{0}}\right)\left(\frac{\mathrm{d} \mathrm{S} \cos \theta}{\mathrm{r}^{2}}\right)\)
But, dω = \(\frac {dS cos θ}{r^2}\)
where, dco is the solid angle subtended by area dS at a point O.
∴ dø = \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_{0}}\right)\) dω …………. (2)

vi. Total electric flux crossing the given closed surface can be obtained by integrating equation (2) over the total area.
\(\phi_{\mathrm{E}}=\int_{\mathrm{s}} \mathrm{d} \phi=\int_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dS}}=\int \frac{\mathrm{q}}{4 \pi \varepsilon_{0}} \mathrm{~d} \omega=\frac{\mathrm{q}}{4 \pi \varepsilon_{0}} \int \mathrm{d} \omega\)

vii. But ∫dω = 4π = solid angle subtended by entire closed surface at point O.
Total Flux = \(\frac {q}{4πε_0}\) (4π)
∴ ø_E = \(\int_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dS}}=\frac{+\mathrm{q}}{\varepsilon_{0}}\)

viii. This is true for every electric charge enclosed by a given closed surface.
Total flux due to charge q₁, over the given closed surface = + \(\frac {q_1}{ε_0}\)
Total flux due to charge q₂, over the given closed surface = + \(\frac {q_2}{ε_0}\)
Total flux due to charge q_n, over the given closed surface = +\(\frac {q_n}{ε_0}\)

ix. According to the superposition principle, the total flux c|> due to all charges enclosed within the given closed surface is
\(\phi_{\mathrm{E}}=\frac{\mathrm{q}_{1}}{\varepsilon_{0}}+\frac{\mathrm{q}_{2}}{\varepsilon_{0}}+\frac{\mathrm{q}_{3}}{\varepsilon_{0}}+\ldots+\frac{\mathrm{q}_{\mathrm{n}}}{\varepsilon_{0}}=\sum_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{n}} \frac{\mathrm{q}_{\mathrm{i}}}{\varepsilon_{0}}=\frac{\mathrm{Q}}{\varepsilon_{0}}\)

Question 51.
With a help of diagram, state the direction of flux due to positive charge, negative charge and charge outside a closed surface.
Answer:

Positive sign indicates that the flux is directed outwards, away from the charge.

If the charge is negative, the flux will be is directed inwards.

If a charge is outside the closed surface, the net flux through it will be zero.

Question 52.
Explain: Electric flux is independent of shape and size of closed surface.
Answer:
i. The net flux crossing an enclosed surface is equal to \(\frac {q}{ε_0}\) where q is the net charge inside the closed surface.

ii. Consider a charge +q at the centre of concentric circles as shown in figure below.

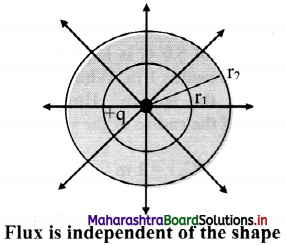
As the charge inside the sphere is unchanged, the flux passing through a sphere of any radius is the same.

iii. Thus, if the radius of the sphere is increased by a factor of 2, the flux passing through is surface remains unchanged.

iv. As shown in figure same number of lines of force cross both the surfaces.
Hence, total flux is independent of shape of the closed surface radius of the sphere and size of closed surface.

Question 53.
Define the following terms with the help of a diagram.
i. Electric dipole
ii. Dipole axis
iii. Axial line
iv. Equatorial line
Answer:
i. Electric dipole: A pair of equal and opposite charges separated by a finite distance is called an electric dipole.

ii. Dipole axis: Line joining the two charges is called the dipole axis.

iii. Axial line: A line passing through the dipole axis is called axial line.

iv. Equatorial line: A line passing through the centre of the dipole and perpendicular to the axial line is called the equatorial line.

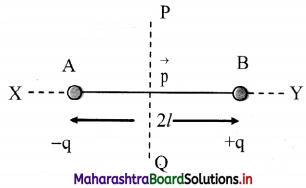
AB : Electric dipole Line joining
AB: Dipole axis
X-Y : Axial line
P-Q : Equatorial line

Question 54.
What are polar molecules? Explain with examples.
Answer:

1. Polar molecules are the molecules in which the centre of positive charge and the negative charge is naturally separated.
2. Molecules of water, ammonia, sulphur dioxide, sodium chloride etc. have an inherent separation of centres of positive and negative charges. Such molecules are called polar molecules.

Question 55.
What are non-polar molecules? Explain with examples.
Answer:
i. Non-polar molecules are the molecules in which the centre of positive charge and the negative charge is one and the same. They do not have a permanent electric dipole. When an external electric field is applied to such molecules, the centre of positive and negative charge are displaced and a dipole is induced.

ii. Molecules such as H₂, CI₂, CO₂, CH₄, etc., have their positive and negative charges effectively centred at the same point and are called non-polar molecules.

Question 56.
Derive expression for couple acting on an electric dipole in a uniform electric field.
Answer:
i. Consider an electric dipole placed in a uniform electric field E. The axis of electric dipole makes an angle θ with the direction of electric field.

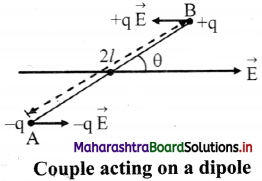
ii. The force acting on charge – q at A is \(\vec{F}\)_A = -q\(\vec{E}\) in the direction of\(\vec{E}\) and the force acting on charge +q at B is \(\vec{F}\)_B = + q \(\vec{E}\) in the direction opposite to \(\vec{E}\).

iii. Since \(\vec{F}\)_A = –\(\vec{F}\)_B, the two equal and opposite forces separated by a distance form a couple.

iv. Moment of the couple is called torque and is defined by \(\vec{τ}\) = \(\vec{d}\) × \(\vec{F}\) where, d is the perpendicular distance between the two equal and opposite forces.

v. Magnitude of Torque = Magnitude of force × Perpendicular distance
∴ Torque on the dipole (\(\vec{τ}\)) = \(\vec{BA}\) × q\(\vec{E}\)
= 2lqE sin θ
but p = q2l
∴ τ = pEsin θ
∴ In vector form \(\vec{τ}\) = \(\vec{d}\) × \(\vec{E}\)

vi. If θ = 90° sin θ = 1, then τ = pE
When the axis of electric dipole is perpendicular to uniform electric field, torque of the couple acting on the electric dipole is maximum, i.e., τ = pE.

vii. If θ = 0 then τ = 0, this is the minimum torque on the dipole. Torque tends to align its axis along the direction of electric field.

Question 57.
Derive expression for electric intensity at a point on the axis of an electric dipole.
Answer:
i. Consider an electric dipole consisting of two charges -q and +q separated by a distance 2l.

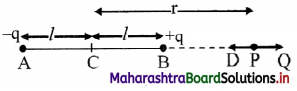
ii. Let P be a point at a distance r from the centre C of the dipole.

iii. The electric intensity \(\vec{E}\)_a at P due to the dipole is the vector sum of the field due to the charge -q at A and +q at B.

iv. Electric field intensity at P due to the charge -q at A = \(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(-q)}{(r+l)^{2}} \hat{\mathrm{u}}_{\mathrm{pD}}\),
where, \(\hat{u}\)_PD is unit vector directed along \(\vec{PD}\)

v. Electric intensity at P due to charge +q at B
\(\vec{E}\)_B = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{(\mathrm{r}-l)^{2}} \hat{\mathrm{u}}_{\mathrm{PQ}}\)
where, \(\hat{u}\)_PQ is a unit vector directed along \(\vec{PQ}\)
The magnitude of \(\vec{E}\)_B is greater than that of \(\vec{E}\)_A since BP < AP

vi. Resultant field \(\vec{E}\)_a at P on the axis, due to the dipole is
\(\vec{E}\)_a = \(\vec{E}\)_B + E\(\vec{E}\)_A

vii. The magnitude of \(\vec{E}\)_a is given by

ix. |\(\vec{E}\)_a| is directed along PQ, which is the direction of the dipole moment \(\vec{p}\) i.e., from the negative to the positive charge, parallel to the axis.

x. If r >> l, l² can be neglected compared to r²,
|\(\vec{E}\)_a| = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\)

The field will be along the direction of the dipole moment \(\vec{p}\).

Question 58.
Drive expression for electric intensity at a point on the equator of an electric dipole.
Answer:
i. Electric field at point P due to charge -q at A is \(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(-\mathrm{q})}{(\mathrm{AP})^{2}} \hat{\mathrm{u}}_{\mathrm{PA}}\)
where, \(\hat{u}\)_PA is a unit vector directed along \(\vec{PA}\)

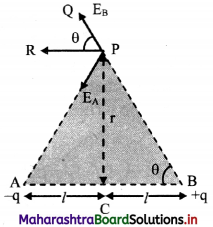
ii. Similarly, electric field at P due to charge +q at B is
\(\vec{E}\)_A = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{(\mathrm{BP})^{2}} \hat{\mathrm{u}}_{\mathrm{BP}}\)
where \(\hat{u}\)_BP is a unit vector directed along \(\vec{BP}\)

iii. Electric field at P is the sum of E_A and E_B
∴ \(\vec{E}\)_eq = \(\vec{E}\)_A + \(\vec{E}\)_B

iv. Consider ∆ACP
(AP)² = (PC)² + (AC)² = r² + l² = (BP)²

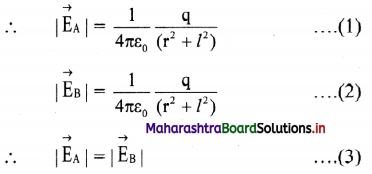
v. The resultant of fields \(\vec{E}\)_A and \(\vec{E}\)_B acting at point P can be calculated by resolving these vectors E\(\vec{E}\)_A and E\(\vec{E}\)_B along the equatorial line and along a direction perpendicular to it.

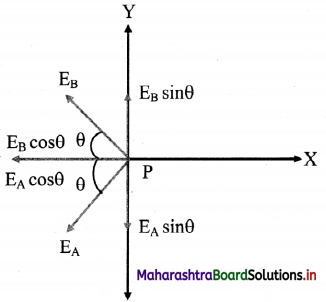
vi. Let the Y-axis coincide with the equator of the dipole X-axis will be parallel to dipole axis and the origin is at point P as shown.

vii. The Y-components of E_A and E_B are E_Asin θ and E_B sin θ respectively. They are equal in magnitude but opposite in direction and cancel each other. There is no contribution from them towards the resultant.

viii. The X-components of E_A and E_B are E_Acos θ and E_Bcos θ respectively. They are of equal magnitude and are in the same direction.
∴ |\(\vec{E}\)_eq| = E_A cos θ + E_B cos θ From equation (3),
|\(\vec{E}\)_eq| = 2E_A cos θ

x. The direction of this field is along –\(\vec{P}\) (anti-parallel to \(\vec{P}\)).

Question 59.
An electric dipole of length 2.0 cm is placed with its axis making an angle of 30° with a uniform electric field of 10⁵ N/C as shown in figure. If it experiences a torque of 10√3 N m, calculate the magnitude of charge on dipole.

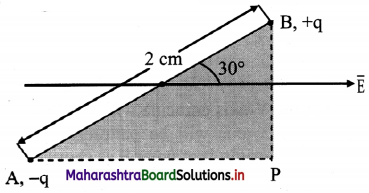
Answer:
Given: 2l = 2 cm = 2 × 10² m
E = 10⁵ N/C, τ = 10√3 Nm, θ = 30°
To find: Charge (q)
Formula: τ = q E 2 l sin θ
Calculation: From Formula.
q = \(\frac{τ}{\mathrm{E} \times 2 l \times \sin \theta}\)
= \(\frac{10 \sqrt{3}}{10^{5} \times 2 \times 10^{-2} \times \sin 30^{\circ}}\)
= 1.732 × 10^-2 C

Question 60.
Explain the concept of continuous charge distribution.
Answer:
i. A system of charges can be considered as a continuous charge distribution, if the charges are located very close together, compared to their distances from the point where the intensity of electric field is to be found out.

ii. Thus, the charge distribution is said to be continuous for a system of closely spaced charges. It is treated equivalent to a total charge which is continuously distributed along a line or a surface or a volume.

Question 61.
Explain linear charge density.
Answer:
Consider charge q uniformly distributed along a linear conductor of length l, then the linear charge density (λ) is given as,
λ = \(\frac {q}{l}\)
For example, charge distributed uniformly on a straight thin rod or a thin nylon thread. If the charge is not distributed uniformly over the length of thin conductor then charge dq on small element of length dl can be written as dq = λ dl.

Question 62.
Explain surface charge density.
Answer:
i. Consider a charge q uniformly distributed over a surface of area A then the surface charge density c is given as
σ = \(\frac {q}{A}\)
For example, charge distributed uniformly on a thin disc or a synthetic cloth. If the charge is not distributed uniformly over the surface of a conductor, then charge dq on small area element dA can be written as dq = σ dA.

ii. SI unit of σ is (C / m²)

Question 63.
Explain volume charge density.
Answer:
i. Consider a charge q uniformly distributed throughout a volume V, then the volume charge density ρ is given as
ρ = \(\frac {q}{V}\)
For example, charge on a plastic sphere or a plastic cube. If the charge is not distributed uniformly over the volume of a material, then charge dq over small volume element dV can be written as dq = ρ dV.

ii. S.I. unit of p is (C/m³)
[Note: Electric field due to a continuous charge distribution can be calculated by adding electric fields due to all these small charges.]

Question 64.
Explain the concept of static charge.
Answer:

1. Static charges can be created whenever there is a friction between an insulator and other object.
2. For example, when an insulator like rubber or ebonite is rubbed against a cloth, the friction between them causes electrons to be transferred from one to the other.
3. This property of insulators is used in many applications such as photocopier, inkjet printer, painting metal panels, electrostatic precipitation/separators etc.

Question 65.
Explain the disadvantage of static charge.
Answer:

1. When charge transferred from one body to other is very large, sparking can take place. For example, lightning in sky.
2. Sparking can be dangerous while refuelling your vehicle.
3. One can get static shock, if charge transferred is large.
4. Dust or dirt particles gathered on computer or TV screens can catch static charges and can be troublesome.

Question 66.
State the precautions against static charge.
Answer:

1. Home appliances should be grounded.
2. Avoid using rubber soled footwear.
3. Keep your surroundings humid (dry air can retain static charges).

Question 67.
Two charged particles having charge 3 × 10^-8 C each are joined by an insulating string of length 2 m. Find the tension in the string when the system is kept on a smooth horizontal table.
Answer:
Tension (T) in the string is the force of repulsion (F) between the two charges.
According to Coulomb’s law,
F = \(\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}\)
= \(\frac{9 \times 10^{9} \times 3 \times 10^{-8} \times 3 \times 10^{-8}}{2^{2}}\)
F = 2.025 × 10^-6 N
Hence, tension in the string is 2.025 × 10^-6 N.

Question 68.
A free pith ball of mass 5 gram carries a positive charge of 0.6 × 10^-7 C. What is the nature and magnitude of charge that should be given to second ball fixed 6 cm vertically below the former pith ball so that the upper pith bath is stationary?
Answer:
Let +q₂ be the charge on lower pith ball.
Now, the upper pith ball become stationary only when its weight acting downward is balanced by the upward force of repulsion between two pith balls,
i.e., F_E = mg
∴ \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) = mg
∴ \(\frac{9 \times 10^{9} \times 0.6 \times 10^{-7} \times \mathrm{q}_{2}}{\left(6 \times 10^{-2}\right)^{2}}\) = 5 × 10^-3 × 9.8
∴ q₂ = 3.27 × 10^-7C
Hence, the second pith ball carries a positive charge of 3.27 × 10^-7C.

Question 69.
A water drop of mass 11.0 mg and having a charge of 1.6 × 10^-6 C stays suspended in a room. What will be the magnitude and direction of electric Held in the room?
Answer:
As the drop is suspended,
Force (F) due to electric field balances the weight of the drop.
∴ F = mg ………….. (1)
Here, m = 11.0 mg
= 11 × 10^-6 kg,
q = 1.6 × 10^-6 C
Electric field is given by,
E = \(\frac {F}{q}\)
= \(\frac {mg}{q}\)
= \(\frac {11×10^{-6}×9.8}{1.6×10^{-6}}\)
E = 67.4 N/C
As upward force balances the weight, hence direction of electric field must be vertically upwards.

Question 70.
A charged metallic sphere A is suspended by a nylon thread. Another charged metallic sphere B held by an insulating handle is brought close to A such that the distance between their centres is 10 cm, as shown in figure (a). The resulting repulsion of A is noted (for example, by shining a beam of light and measuring the deflection of its shadow on a screen.) Spheres A and B are touched by uncharged spheres C and D respectively, as shown in figure (b). C and D are then removed and B is brought closer to A to a distance of 5.0 cm between their centres, as shown in figure (c). What is the expected repulsion of A on the basis of Coulomb’s law? Spheres A and C and spheres B and D have identical sizes. Ignore the sizes of A and B comparison to the separation between their centres.

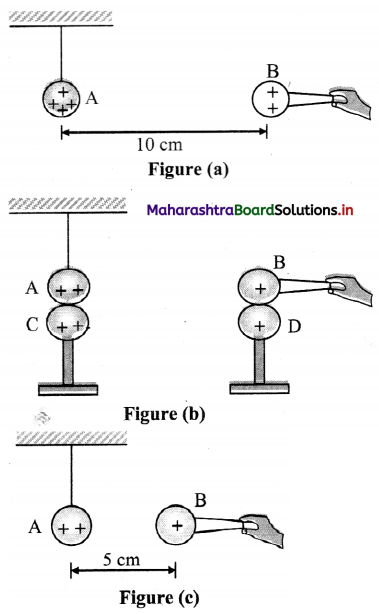
Answer:
Let the original charge on sphere A be q and that on B be q’. At a distance r between their centres, the magnitude of the electrostatic force on each is given by
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{qq}^{\prime}}{\mathrm{r}^{2}}\)

Neglecting the sizes of spheres, A and B in comparison to r. When an identical but uncharged sphere C touches A, the charges redistribute on A and C and, by symmetry, each sphere carries a charge q/2. Similarly, after D touches B, the redistributed charge on each is q’/2. Now, if the separation between A and B is halved, the magnitude of the electrostatic force on each is
F’ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(\mathrm{q} / 2)\left(\mathrm{q}^{\prime} / 2\right)}{(\mathrm{r} / 2)^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\left(\mathrm{qq}^{\prime}\right)}{\mathrm{r}^{2}}\) = F

Thus, the electrostatic force on A, due to B, remains unaltered.

Multiple Choice Questions

Question 1.
Force between two charges separated by a certain distance in air is F. If each charge is doubled and the distance between them is also doubled, force would be
(A) F
(B) 2 F
(O’ 4 F
(D) F/4
Answer:
(A) F

Question 2.
For what order of distance is Coulomb7 s law true?
(A) For all distances.
(B) Distances greater than 10^-13 m.
(C) Distances less than 10^-13 m.
(D) Distance equal to 10^-13 m.
Answer:
(B) Distances greater than 10^-13 m.

Question 3.
The permittivity of medium is 26.55 × 10^-12 C²/Nm². The dielectric constant of the medium will be
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(B) 3

Question 4.
A glass rod when rubbed with a piece of fur acquires a charge of magnitude 3.2 µC. The number of electrons transferred is
(A) 2 × 10^-13 from fur to glass
(B) 5 × 10¹² from glass to fur
(C) 2 × 10¹³ from glass to fur
(D) 5 × 10¹² from fur to glass
Answer:
(A) 2 × 10^-13 from fur to glass

Question 5.
Choose the correct answer.
(A) Total charge present in the universe is constant.
(B) Total positive charge present in the universe is constant.
(C) Total negative charge present in the universe is constant.
(D) Total number of charged particles present in the universe is constant.
Answer:
(A) Total charge present in the universe is constant.

Question 6.
If a charge is moved against the Coulomb force of an electric field,
(A) work is done by the electric field
(B) energy is used from some outside source
(C) the strength of the field is decreased
(D) the energy of the system is decreased
Answer:
(B) energy is used from some outside source

Question 7.
Two point charges +4 µC and +2 µC repel each other with a force of 8 N. If a charge of -4 µC is added to each of these charges, the force would be
(A) zero
(B) 8 N
(C) 4 N
(D) 12 N
Answer:
(A) zero

Question 8.
The electric field intensity at a point 2 m from an isolated point charge is 500 N/C. The electric potential at the point is
(A) 0 V
(B) 2.5 V
(C) 250 V
(D) 1000 V
Answer:
(D) 1000 V

Question 9.
The dimensional formula of electric field intensity is
(A) [M¹E¹T^-2A^-1]
(B) [M¹L¹T^-3A^-1]
(C) [M^-1L²T^-3A^-1]
(D) [M¹L²T^-3A^-2]
Answer:
(B) [M¹L¹T^-3A^-1]

Question 10.
A force of 2.25 N acts on a charge of 15 × 10^-4C. Calculate the intensity of electric field at that point.
(A) 1500 NC^-1
(B) 150 NC^-1
(C) 15000NC^-1
(D) 2500 NC^-1
Answer:
(A) 1500 NC^-1

Question 11.
A point charge q produces an electric field of magnitude 2 N C^-1 at a point distant 0.25 m from it. What is the value of charge?
(A) 1.39 × 10^-11 C
(B) 1.39 × 10¹¹ C
(C) 13.9 × 10^-11 C
(D) 13.9 × 10¹¹ C
Answer:
(A) 1.39 × 10^-11 C

Question 12.
The electric intensity in air at a point 20 cm from a point charge Q coulombs is 4.5 × 10⁵ N/ C. The magnitude of Q is
(A) 20 µC
(B) 200 µC
(C) 10 µC
(D) 2 µC
Answer:
(D) 2 µC

Question 13.
The charge on the electron is 1.6 × 10^-19 C. The number of electrons need to be removed from a metal sphere of 0.05 m radius so as to acquire a charge of 4 × 10^-15 C is
(A) 1.25 × 10⁴
(B) 1.25 × 10³
(C) 2.5 × 10³
(D) 2.5 × 10⁴
Answer:
(D) 2.5 × 10⁴

Question 14.
Electric lines of force about a positive point charge and negative point charge are respectively .
(A) circular, clockwise
(B) radially outward, radially inward
(C) radially inward, radially outward
(D) circular, anticlockwise
Answer:
(B) radially outward, radially inward

Question 15.
Which of the following is NOT the property of equipotential surfaces?
(A) They do not intersect each other.
(B) They are concentric spheres for uniform electric field.
(C) Potential at all points on the surface has constant value.
(D) Separation of equipotential surfaces increases with decrease in electric field.
Answer:
(B) They are concentric spheres for uniform electric field.

Question 16.
In a uniform electric field, a charge of 3 C experiences a force of 3000 N. The potential difference between two points 1 cm apart along the electric lines of force will be
(A) 10 V
(B) 3 V
(C) 0.1 V
(D) 20 V
Answer:
(A) 10 V

Question 17.
Gauss’ law helps in
(A) determination of electric field due to symmetric charge distribution.
(B) determination of electric potential due to symmetric charge distribution.
(C) determination of electric flux.
(D) situations where Coulomb’s law fails.
Answer:
(A) determination of electric field due to symmetric charge distribution.

Question 18.
The electric flux over a sphere of radius 1.0 m is ø. If the radius of the sphere is doubled without changing the charge, the flux will be
(A) 4ø
(B) 2ø
(C) ø
(D) 8ø
Answer:
(C) ø

Question 19.
Gauss’ theorem states that total normal electric induction over a closed surface in an electric field is equal to
(A) \( \frac{1}{\varepsilon} \sum \mathrm{q}_{\mathrm{n}}\)
(B) ^εΣ q_n
(C) Σ q_n
(D) q₁ × q₂ × q₃ × ……… q_n
Answer:
(C) Σ q_n

Question 20.
Number of lines of induction starting from a conductor holding + q charge surrounded by a medium of permittivity ε is
(A) q and they leave the surface in normal direction.
(B) q and they leave the surface in any direction.
(C) q/ε and they leave the surface normally at every point.
(D) q/ε and they leave the surface in any direction.
Answer:
(C) q/ε and they leave the surface normally at every point.

Question 21.
An electric dipole of moment p is placed in the position of stable equilibrium in a uniform electric field of intensity E. The torque required to rotate, when the dipole makes an angle 0 with the initial position is
(A) pE cosθ
(B) pE sinθ
(C) pE tanθ
(D) pE cotθ
Answer:
(B) pE sinθ

Question 22.
Four coulomb charge is uniformly distributed on 2 km long wire. Its linear charge density is
(A) 2 C/m
(B) 4 C/m
(C) 4 × 10³ C/m
(D) 2 × 10^-3 C/m
Answer:
(D) 2 × 10^-3 C/m