Maharashtra Board Class 11 Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry

Question 1.
Define chemistry.
Answer:
Chemistry is the study of matter, its physical and chemical properties, and the physical and chemical changes it undergoes under different conditions.

Question 2.
Why is chemistry called a central science?
Answer:

1. Knowledge of chemistry is required in the studies of physics, biological sciences, applied sciences, and earth and space sciences.
2. Chemistry is involved in every aspect of day-to-day life, i.e. the air we breathe, the food we eat, the fluids we drink, our clothing, transportation and fuel supplies, etc.

Hence, chemistry is called a central science.

Question 3.
Give reason: Although chemistry has ancient roots, it has developed as modern science.
Answer:
Technological development in sophisticated instruments has expanded knowledge of chemistry which, now, has been used in applied sciences such as medicine, dentistry, engineering, agriculture, and daily home use products. Hence, due to development and advancement in science and technology, chemistry has developed as modem science.

Question 4.
How is chemistry traditionally classified?
Answer:
Chemistry is traditionally classified into five branches:

• Organic chemistry
• Inorganic chemistry
• Physical chemistry
• Biochemistry
• Analytical chemistry

Question 5.
Explain the following terms:
i. Organic chemistry
ii. Inorganic chemistry
iii. Physical chemistry
Answer:
i. Organic chemistry: It deals with properties and reactions of compounds of carbon.
ii. Inorganic chemistry: It deals with the study of all the compounds which are not organic.
iii. Physical chemistry: It deals with the study of properties of matter, the energy changes and the theories, laws and principles that explain the transformation of matter from one form to another. It also provides basic framework for all the other branches of chemistry.

Question 6.
Distinguish between
i. Mixtures and pure substances
ii. Mixtures and compounds
Answer:
i.

	Mixtures	Pure substances
a.	Mixtures have no definite chemical composition.	Pure substances have a definite chemical composition.
b.	Mixtures have no definite properties.	Pure substances always have the same properties regardless of their origin.
e.g.	Paint (mixture of oils, pigment, additive), concrete (a mixture of sand, cement, water), etc.	Pure metal, distilled water, etc.

ii.

	Mixtures	Compounds
a.	Mixtures have no definite chemical composition.	Compounds are made up of two or more elements in fixed proportion.
b.	The constituents of a mixture can be easily separated by physical method.	The constituents of a compound cannot be easily separated by physical method.
e.g.	Paint (mixture of oils, pigment, additive), concrete (a mixture of sand, cement, water), etc.	Water, table salt, sugar, etc.

Question 7.
What is the difference between element and compound?
Answer:
Elements cannot be broken down into simpler substances while compounds can be broken down into simpler substances by chemical changes.

Question 8.
Explain: States of matter
Answer:
There are three different states of matter as follows:

1. Solid: Particles are held tightly in perfect order. They have definite shape and volume.
2. Liquid: Particles are close to each other but can move around within the liquid.
3. Gas: Particles are far apart as compared to that of solid and liquid.

These three states of matter can be interconverted by changing the conditions of temperature and pressure.

Question 9.
Explain: Physical and chemical properties
Answer:
i. Physical properties: These are properties which can be measured or observed without changing the identity or the composition of the substance. e.g. Colour, odour, melting point, boiling point, density, etc.

ii. Chemical properties: These are properties in which substances undergo change in chemical composition. e.g. Coal bums in air to produce carbon dioxide, magnesium wire bums in air in the presence of oxygen to form magnesium oxide, etc.

Question 10.
How are properties of matter measured?
Answer:

• Measurement involves comparing a property of matter with some fixed standard which is reproducible and unchanging.
• Properties such as mass, length, area, volume, time, etc. are quantitative in nature and can be measured.
• A quantitative measurement is represented by a number followed by units in which it is measured.
• These units are arbitrarily chosen on the basis of universally accepted standards. e.g. Length of class room can be expressed as 10 m. Here, 10 is the number and ‘m’ is the unit ‘metre’ in which the length is measured.

Question 11.
Define: Units
Answer:
The arbitrarily decided and universally accepted standards are called units.
e.g. Metre (m), kilogram (kg).

Question 12.
What are the various systems in which units are expressed?
Answer:
Units are expressed in various systems like CGS (centimetre for length, gram for mass and second for time), FPS (foot, pound, second) and MKS (metre, kilogram, second) systems, etc.

Question 13.
What are SI units? Name the fundamental SI units.
Answer:
SI Units: In 1960, the general conference of weights and measures proposed revised metric system, called International system of Units i.e. SI system (abbreviated from its French name).
The seven fundamental SI units are as given below:

No.	Base physical quantity	SI unit	Symbol
i.	Length	Metre	k
ii.	Mass	Kilogram	kg
iii.	Time	Second	s
iv.	Temperature	Kelvin	K
v.	Amount of substance	Mole	mol
vi.	Electric current	Ampere	A
vii.	Luminous intensity	Candela	cd

[Note: Units for other quantities such as speed, volume, density, etc. can be derived from fundamental SI units.]

Question 14.
What is the basic unit of mass in the SI system?
Answer:
The basic unit of mass in the SI system is kilogram (kg).

Question 15.
Name the following:
i. Full form of CGS unit system
ii. Full form of FPS unit system
iii. The SI unit of length
iv. Symbol used for Candela unit
v. SI unit of electric current
vi. SI unit of electric current
Answer:
i. Centimetre Gram Second
ii. Foot Pound Second
iii. Metre (m)
iv. Cd
v. Kelvin (K)
vi. Ampere (A)

Question 16.
Give reason: The mass of a body is more fundamental property than its weight.
Answer:

• Mass is an inherent property of matter and is the measure of the quantity of matter of a body.
• The mass of a body does not vary with respect to its position.
• On the other hand, the weight of a body is a result of the mass and gravitational attraction
• Weight varies because the gravitational attraction of the earth for a body varies with the distance from the centre of the earth.

Hence, the mass of a body is more fundamental property than its weight.

Question 17.
How is gram related to the SI unit kilogram?
Answer:
The SI unit kilogram (kg) is related to gram (g) as 1 kg = 1000 g= 10³ g.
[Note: ‘Gram’ is used for weighing small quantities of chemicals in the laboratories.
Other commonly used quantity is ‘milligram’. 1 kg = 1000 g = 10⁶ mg]

Question 18.
Why are fractional units of the SI units of length often used? Give two examples of the fractional units of length. How are they related to the SI unit of length?
Answer:
i. Some properties such as the atomic radius, bond length, wavelength of electromagnetic radiation, etc. are very small and therefore, fractional units of the SI unit of length are often used to express these properties.
ii. Fractional units of length: Nanometre (nm), picometre (pm), etc.
iii. Nanometre (nm) and picometre (pm) are related to the SI unit of length (m) as follows:
1 nm = 10^-9 m, 1 pm = 10^-12 m

Question 19.
Define: Volume
Answer:
Volume is the amount of space occupied by a three-dimensional object. It does not depend on shape.

Question 20.
State the common unit used for the measurement of volume of liquids and gases.
Answer:
The common unit used for the measurement of volume of liquids and gases is litre (L).

Question 21.
How is the SI unit of volume expressed?
Answer:
The SI unit of volume is expressed as (metre)³ or m³.

Question 22.
Name some glassware that are used to measure the volume of liquids and solutions.
Answer:

• Graduated cylinder
• Burette
• Pipette

Question 23.
What is a volumetric flask used for in laboratory?
Answer:
A volumetric flask is used to prepare a known volume of a solution in laboratory.

Question 24.
What is density of a substance? How is it measured?
Answer:
Density:

• Density of a substance is its mass per unit volume. It is the characteristic property of any substance.
• It is determined in the laboratory by measuring both the mass and the volume of a sample.
• The density is calculated by dividing mass by volume.

Question 25.
How is the SI unit of density derived? State CGS unit of density.
Answer:
i. The SI unit of density is derived as follows:
Density = \(\frac{\text { SI unit mass }}{\text { SI unit volume }}\)
= \(\frac{\mathrm{kg}}{\mathrm{m}^{3}}\)
= kg m^-3

ii. CGS unit of density: g cm^-3
[Note: The CGS unit, g cm^-3 is equivalent to \(\frac{\mathrm{g}}{\mathrm{mL}}\) or g mL^-1.]

Question 26.
State three common scales of temperature measurement.
Answer:

1. Degree Celsius (°C)
2. Degree Fahrenheit (°F)
3. Kelvin (K)

Question 27.
State the temperatures in Fahrenheit scale that corresponds to 0 °C and 100 °C.
Answer:
The temperature that corresponds to 0 °C is 32 °F and the temperature that corresponds to 100 °C is 212 °F.

Question 28.
Write the expression showing the relationship between:
i. Degree Fahrenheit and Degree Celsius
ii. Kelvin and Degree Celsius
Answer:
i. The relationship between degree Fahrenheit and degree Celsius is expressed as,
°F = \(\frac {9}{5}\) (°C) + 32
ii. The relationship between Kelvin and degree Celsius is expressed as,
K = °C + 273.15

Question 29.
Convert the following degree Fahrenheit temperature to degree Celsius.
i. 50 °F ii. 10 °F
Answer:
Given: Temperature in degree Fahrenheit = 50 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 50 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
50 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(50-32) \times 5}{9}\)
= 10 °C

ii. Given: Temperature in degree Fahrenheit = 10 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 10 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
10 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(10-32) \times 5}{9}\)
= -12.2 °C
Ans: i. The temperature 50 °F corresponds to 10 °C.
ii. The temperature 10 °F corresponds to -12.2 °C.

Question 30.
What is a chemical combination?
Answer:

• The process in which the elements combine with each other to form compounds is called chemical combination.
• The process of chemical combination is governed by five basic laws which were discovered before the knowledge of molecular formulae.

Question 31.
State and explain the law of definite proportions.
Answer:
Law of definite proportions:
i. The law states that “A given compound always contains exactly the same proportion of elements by weight”.
ii. French chemist, Joseph Proust worked with two samples of cupric carbonate; one of which was naturally occurring cupric carbonate and other was synthetic sample. He found the composition of elements present in both the samples was same as shown below:

Cupric carbonate	% of copper	% of carbon	% of oxygen
Natural sample	51.35	9.74	38.91
Synthetic sample	51.35	9.74	38.91

iii. Thus, irrespective of the source, a given compound always contains same elements in the same proportion.

Question 32.
State and explain the law of multiple proportions.
Answer:
Law of multiple proportions:
i. John Dalton (British scientist) proposed the law of multiple proportions in 1803.
ii. It has been observed that two or more elements may combine to form more than one compound.
iii. The law states that, “ When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers”.
e.g. Hydrogen and oxygen combine to form two compounds, water and hydrogen peroxide.

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of hydrogen (2 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.

Question 33.
Show that NO and NO₂ satisfy the law of multiple proportions.
Answer:
Nitrogen and oxygen combine to form two compounds, nitric oxide (NO) and nitrogen dioxide (NO₂).

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of nitrogen (14 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 34.
Show that carbon monoxide and carbon dioxide satisfy the law of multiple proportions.
Answer:
Chemical reaction of carbon with oxygen gives two compounds, carbon monoxide (CO) and carbon dioxide (CO₂).

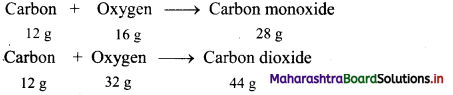
Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of carbon (12 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 35.
Show that SO₂ and SO₃ satisfy the law of multiple proportions.
Answer:
Chemical reaction of sulphur with oxygen gives two compounds, sulphur dioxide (SO₂) and sulphur trioxide (SO₃).

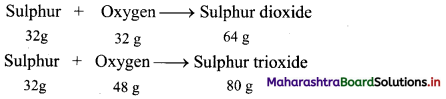
Here, the two masses of oxygen (32 g and 48 g) which combine with the fixed mass of sulphur (32 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 32 : 48 or 2 : 3.
This is in accordance with the law of multiple proportions.

Question 36.
State and explain Gay Lussac’s law of gaseous volume with two examples.
Answer:
Gay Lussac’s law:
i. Gay Lussac proposed the law of gaseous volume in 1808.
ii. Gay Lussac’s law states that, “ When gases combine or are produced in a chemical reaction, they do so in a simple ratio by volume, provided all gases are at same temperature and pressure
e.g. a. Under identical conditions of temperature and pressure, 100 mL of hydrogen gas combine with 50 mL of oxygen gas to produce 100 mL of water vapour.

Thus, the simple ratio of volumes is 2 : 1 : 2.

b. Under identical conditions of temperature and pressure, 1 L of nitrogen gas combine with 3 L of hydrogen gas to produce 2 L of ammonia gas.

Thus, the simple ratio of volumes is 1 : 3 : 2.

Question 37.
Give two examples which support the Gay Lussac’s law of gaseous volume.
Answer:
i. Under identical conditions of temperature and pressure, 1 L of hydrogen gas reacts with 1 L of chlorine gas to produce 2 L of hydrogen chloride gas.

Thus, the ratio of volumes is 1 : 1 : 2
This is in accordance with Gay Lussac’s law.

ii. Under identical conditions of temperature and pressure, 200 mL sulphur dioxide combine with 100 mL oxygen to form 200 mL sulphur trioxide.

Thus, the ratio of volumes is 2 : 1 : 2.
This is in accordance with Gay Lussac’s law.

Question 38.
Match the following:

	Law		Statement
i.	Law of definite proportions	a.	When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers
ii.	Gay Lussac’s law	b.	Equal volumes of all gases at the same temperature and pressure contain equal number of molecules
iii.	Law of multiple proportions	c.	When gases combine or are produced in a chemical reaction they do so in a simple ratio by volume, provided all gases are at same temperature and pressure
iv.	Avogadro’s law	d.	A given compound always contains exactly the same proportion of elements by weight

Answer:
i – d,
ii – c,
iii – a,
iv – b

Question 39.
32 g of oxygen reacts with some carbon to make 56 grams of carbon monoxide. Find out how much mass must have been used.
Answer:
Given: Mass of oxygen (reactant) = 32 g, mass of carbon monoxide (product) = 56 g
To find: Mass of oxygen (reactant)
Calculation: 12 g of carbon combine with 16 g oxygen to form 28 g of carbon monoxide as follows:

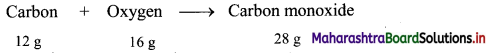
Hence, (2 × 12 = 24 g) of carbon will combine with (2 × 16 = 32 g) of oxygen to give (2 × 28 = 56 g) carbon monoxide.
Ans: Mass of carbon used = 24 g

Question 40.
Calculate the mass of sulphur trioxide produced by burning 64 g of sulphur in excess of oxygen. (Average atomic mass: S = 32 u, O = 16 u).
Solution:
Given: Mass of sulphur (reactant) = 64 g
To find: Mass of sulphur dioxide (product)
Calculation: 32 g of sulphur combine with 48 g oxygen to form 80 g of sulphur trioxide as follows:

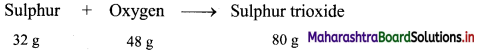
Hence, (2 × 32 = 64 g) of sulphur will combine with (2 × 48 = 96 g) of oxygen to give (2 × 80 = 160 g) sulphur trioxide.
Ans: Mass of sulphur trioxide produced = 160 g

Question 41.
Explain Dalton’s atomic theory.
Answer:
John Dalton published “A New System of chemical philosophy” in the year of 1808. He proposed the following features, which later became famous as Dalton’s atomic theory.

• Matter consists of tiny, indivisible particles called atoms.
• All the atoms of a given elements have identical properties including mass. Atoms of different elements differ in mass.
• Compounds are formed when atoms of different elements combine in a fixed ratio.
• Chemical reactions involve only the reorganization of atoms. Atoms are neither created nor destroyed in a chemical reaction.

Dalton’s atomic theory could explain all the laws of chemical combination.

Question 42.
Give reason: Dalton’s atomic theory explains the law of conservation of mass.
Answer:

• The law of conservation of mass states that, “Mass can neither be created nor destroyed” during chemical combination of matter.
• According to Dalton’s atomic theory, chemical reactions involve only the reorganization of atoms. Therefore, the total number of atoms in the reactants and products should be same and mass is conserved during a reaction.

Hence, Dalton’s atomic theory explains the law of conservation of mass.

Question 43.
Give reason: Dalton’s atomic theory explains the law of multiple proportion.
Answer:

• The law of multiple proportion states that, “When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers
• According to Dalton’s atomic theory, compounds are formed when atoms of different elements combine in fixed ratio.

Hence, Dalton’s atomic theory explains the law of multiple proportion.

Question 44.
Define: Atomic mass unit (amu).
Answer:
Atomic mass unit or amu is defined as a mass exactly equal to one twelth of the mass of one carbon-12 atom.

Question 45.
How is relative atomic mass of an atom measured?
Answer:

• The mass of a single atom is extremely small, i.e. the mass of a hydrogen atom is 1.6736 × 10^-24 g. Hence, it is not possible to weigh a single atom.
• In the present system, mass of an atom is determined relative to the mass of an atom of carbon-12 as the standard. This was decided in 1961 by international agreement.
• The atomic mass of carbon-12 is assigned as 12.00000 atomic mass unit (amu).
• The masses of all other elements are determined relative to the mass of an atom of carbon-12 (C-12).
• The atomic masses are expressed in amu which is exactly equal to one twelth of the mass of one carbon-12 atom.
• The value of 1 amu is equal to 1.6605 × 10^-24 g.

Question 46.
What is meant by Unified Mass unit?
Answer:

• Presently, instead of amu, Unified Mass has now been accepted as the unit of atomic mass.
• It is called Dalton and its symbol is ‘u’ or ‘Da’.

Question 47.
What is average atomic mass?
Answer:
The atomic mass of an element which exists as mixture of two or more isotopes is the average of atomic masses of its isotopes. This is called average atomic mass.

Question 48.
Define: Molecular mass
Answer:
Molecular mass of a substance is the sum of average atomic masses of the atoms of the elements which constitute the molecule.
OR
Molecular mass of a substance is the mass of one molecule of that substance relative to the mass of one carbon-12 atom.

Question 49.
How is molecular mass of a substance calculated? Give example.
Answer:
Molecular mass is calculated by multiplying average atomic mass of each element by the number of its atoms and adding them together.
e.g. Molecular mass of carbon dioxide (CO₂) is calculated as follows:
Molecular mass of CO₂ = (1 × average atomic mass of C) + (2 × average atomic mass of O)
= (1 × 12.0 u) + (2 × 16.0 u)
= 44.0 u

Question 50.
Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g. What is the atomic mass of hydrogen in u?
Solution:
Given: Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g.
To find: Atomic mass of hydrogen in u
Calculation: 1.66056 × 10^-24 g = 1 u
∴ 1.6736 × 10^-24 g = x
x = \(\frac{1.6736 \times 10^{-24} \mathrm{~g}}{1.66056 \times 10^{-24} \mathrm{~g} / \mathrm{u}}\) = 1.008u
Ans: The atomic mass of hydrogen in u = 1.008 u

Question 51.
The mass of an atom of one carbon atom is 12.011 u. What is the mass of 20 atoms of the same isotope?
Solution:
Mass of l atom of carbon = 12.011 u
∴ Mass of 20 atoms of same carbon isotope = 20 × 12.011 u = 240.220 u
Ans: The mass of 20 atoms of same carbon isotope = 240.220 u

Question 52.
Calculate the average atomic mass of neon using the following data:

Isotope	Atomic mass	Natural Abundance
20Ne	19.9924 u	90.92%
21Ne	20.9940 u	0.26 %
22Ne	21.9914 u	8.82 %

Solution:
Average atomic mass of Neon (Ne)

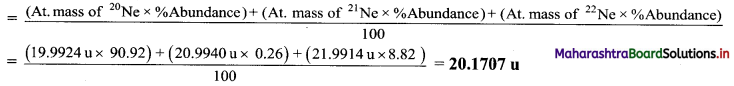
Ans: Average atomic mass of neon = 20.1707 u

Question 53.
Calculate the average atomic mass of argon from the following data:

Isotope	Isotopic mass (g mol-1)	Abundance
36Ar	35.96755	0.337%
38Ar	37.96272	0.063%
40Ar	39.9624	99.600%

Solution:
Average atomic mass of argon (Ar)

Ans: Average atomic mass of argon = 39.974 g mol^-1

Question 54.
Calculate the molecular mass of the following in u:
i. H₂O ii. C₆H₅Cl iii. H₂SO₄
Solution:
i. Molecular mass of H₂O = (2 × Average atomic mass of H) + (1 × Average atomic mass of O)
= (2 × 1.0u) + (1 × 16.0 u)
= 18 u

ii. Molecular mass of C₆H₅Cl = (6 × Average atomic mass of C) + (5 × Average atomic mass of H) + (1 × Average atomic mass of Cl)
= (6 × 12.0 u) + (5 × 1.0 u) + (1 × 35.5 u)
= 112.5 u

iii. Molecular mass of H₂SO₄ = (2 × Average atomic mass of H) + (1 × Average atomic mass of S) + (4 × Average atomic mass of O)
= (2 × 1.0 u) + (1 × 32.0 u) + (1 × 16.0 u)
= 98 u
Ans: i. The molecular mass of H₂O = 18 u
ii. The molecular mass of C₆H₅Cl = 112.5 u
iii. The molecular mass of H₂SO₄ = 98 u

Question 55.
Find the mass of 1 molecule of oxygen (O₂) in amu (u) and in grams.
Solution:
Molecular mass of O₂ = 2 × 16 u
∴ Mass of 1 molecule = 32 u
∴ Mass of 1 molecule of O₂= 32 × 1.66056 × 10^-24 g = 53.1379 × 10^-24 g
Ans: Mass of 1 molecule in amu = 32 u
Mass of 1 molecule in grams = 53.1379 × 10^-24 g

Question 56.
Find the formula mass of
i. NaCl ii. Cu(NO₃)₂
Solution:
i. Formula mass of NaCl
= Average atomic mass of Na + Average atomic mass of Cl
= 23.0 u + 35.5 u = 58.5 u

ii. Formula mass of Cu(NO₃)₂
= Average atomic mass of Cu + 2 × (Average atomic mass of N + Average atomic mass of three O)
= 63.5 + 2 × [14 + (3 × 16)] = 187.5 u
Ans: i. Formula mass of NaCl = 58.5 u
ii. Formula mass of Cu(NO₃)₂ = 187.5 u

Question 57.
Find the formula mass of
i. KCl
ii. AgCl
Atomic mass of K = 39 u, Ag =108 u and Cl = 35.5 u.
Solution:
i. Formula mass of KCl
= Average atomic mass of K + Average atomic mass of Cl
= 39 u + 35.5 u = 74.5 u

ii. Formula mass of AgCl
= Average atomic mass of Ag + Average atomic mass of Cl
= 108 + 35.5 = 143.5 u
Ans: i. Formula mass of KCl = 74.5 u
ii. Formula mass of AgCl = 143.5 u

Question 58.
Calculate the number of moles and molecules of urea present in 5.6 g of urea.
Solution:
Given: Mass of urea = 5.6 g
To find: The number of moles and molecules of urea
Formulae: i. Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
ii. Number of molecules = Number of moles × Avogadro’s constant
Mass of urea = 5.6 g
Molecular mass of urea, NH₂CONH₂
= (2 × Average atomic mass of N) + (4 × Average atomic mass of H) + (1 × Average atomic mass of C) + (1 × average atomic mass of O)
= (2 × 14 u) + (4 × 1 u) + (1 × 12 u) + (1 × 16 u) = 60 u
∴ Molar mass of urea = 60 g mol^-1
∴ Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{5.6 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 0.09333 mol

[Calculation using log table:
\(\frac{5.6}{60}\)
= Antilog₁₀ [log₁₀ (5.6) – log₁₀ (60)]
= Antilog₁₀ [0.7482 – 1.7782]
= Antilog₁₀ [latex]\overline{2} .9700[/latex]
= 0.09333]

Now,
Number of molecules of urea
= Number of moles × Avogadro’s constant
= 0.09333 mol × 6.022 × 10²³ molecules/mol
= 0.5616 × 10²³ molecules (by using log table)
= 5.616 × 10²² molecules
Ans: Number of moles of urea = 0.0933 mol
Number of molecules of urea = 5.616 × 10²² molecules

[Calculation using log table:
0.09333 × 6.022
= Antilog₁₀ [log₁₀ (0.09333) + log₁₀ (6.022)]
= Antilog₁₀ [\(\overline{2} .9698\) + 0.7797]
= Antilog₁₀ [latex]\overline{1} .7495[/latex]
= 0.5616]

Question 59.
Calculate the number of atoms in each of the following:
i. 64 u of oxygen (O)
ii. 42 g of nitrogen (N)
Solution:
i. 64 u of oxygen (O) = x atoms
Atomic mass of oxygen (O) = 16 u
∴ Mass of one oxygen atom = 16 u
∴ x = \(\frac{64 \mathrm{u}}{16 \mathrm{u}}\) = 4 atoms

ii. 42 g of nitrogen (N)
Atomic mass of nitrogen = 14 u
∴ Molar mass of nitrogen = 14 g mol^-1
Now,
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{42 \mathrm{~g}}{14 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 3 mol
Now,
Number of atoms = Number of moles × Avogadro’s constant
= 3 mol × 6.022 × 10²³ atoms/mol
= 18.07 × 10²³ atoms
= 1.807 × 10²⁴ atoms
Ans: i. Number of oxygen atoms in 64 u = 4 atoms
ii. Number of nitrogen atoms in 42 g = 1.807 × 10²⁴ atoms

Question 60.
Calculate the number of atoms in each of the following.
i. 52 moles of Argon (Ar)
ii. 52 u of Helium (He)
iii. 52 g of Helium (He)
Solution:
i. 52 moles of Argon
1 mole Argon atoms = 6.022 × 10²³ atoms of Ar
∴ Number of atoms = 52 mol × 6.022 × 10²³ atoms/mol
= 313.144 × 10²³ atoms of Argon

ii. 52 g of He
Molar mass of He = mass of 1 atom of He = 4.0 u
4.0 u = 1 He
∴ 52 u = x
∴ x = 52 u × \(\frac{1 \text { atom of He }}{4.0 \mathrm{u}}\) = 13 atoms of He

iii. 52 g of He
Molar mass of He = 4.0 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{52 \mathrm{~g}}{4.0 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 13 mol
Number of atoms of He = Number of moles × Avogadro’s constant
= 13 mol × 6.022 × 10²³ atoms/mol
= 78.286 × 10²³ atoms of He
Ans. i. Number of argon atoms in 52 moles = 313.144 × 10²³ atoms of Argon
ii. Number of helium atoms in 52 u = 13 atoms of He
iii. Number of helium atoms in 52 g = 78.286 × 10²³ atoms of He

Question 61.
Calculate the number of atoms of ‘C’, ‘H’ and ‘O’ in 72.5 g of isopropanol, C₃H₇OH (molar mass 60 g mol^-1).
Solution:
Mass of isopropanol(C₃H₇OH) = 72.5 g
The number of atoms of C, H, O
Calculation: Molecular formula of isopropanol, is C₃H₇OH.
Molar mass of C₃H₇OH = 60 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{72.5 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 1.208 mol
∴ Moles of isopropanol = 1.21 mol
Number of atoms = Number of moles × Avogadro’s constant
Now, 1 molecule of isopropanol has total 12 atoms, out of which 8 atoms are of H, 3 of C and 1 of O.
∴ Number of C atoms in 72.5 g isopropanol = (3 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 2.182 × 10²⁴ atoms of carbon
∴ Number of ‘H’ atoms in 72.5 g isopropanol = (8 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 5.819 × 10²⁴ atoms of hydrogen
∴ Number of ‘O’ atoms in 72.5 g isopropanol = (1 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 7.274 × 10²³ atoms of oxygen
Ans. 72.5g of isopropanol contain 2.182 ×10²⁴ atoms of H and 7.274 × 10²³ atoms of O.

Question 62.
Calculate the number of moles and molecules of ammonia (NH₃) gas in a volume 67.2 dm³ of it measured at STP.
Solution:
Given: Volume of ammonia at STP = 67.2 dm³
To find: Number of moles and molecules of ammonia
Formulae: i. Number of moles of a gas (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
ii. Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
Calculation: Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Number of moles (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
Number of moles of NH₃ = \(\frac{67.2 \mathrm{dm}^{3}}{22.4 \mathrm{dm}^{3} \mathrm{~mol}^{-1}}\)
Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
3.0 mol × 6022 × 10²³ molecules mol^-1
= 18.066 × 10²³ molecules
Ans: Number of moles of ammonia = 3.0 mol
Number of molecules of ammonia = 18.066 × 10²³ molecules

Question 63.
3.40 g of ammonia at STP occupies volume of 4.48 dm³. Calculate molar mass of ammonia.
Solution:
Given: Mass of ammonia = 3.40 g
Volume at STP = 4.48 dm³
To Find: Molar mass of ammonia
Calculation: Let ‘x’ grams be the molar mass of NH₃.
Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Volume occupied by 3.40 g of NH₃ at S.T.P = 4.48 dm³
Volume occupied by ‘x’ g of NH3 at S.T.P = 22.4 dm³
∴ x = \(\frac{22.4 \times 3.40}{4.48}\) = 17.0 g mol^-1
Ans: Molar mass of ammonia is 17.0 g mol^-1.

Question 64.
Veg puffs from a particular bakery have an average mass of 27.0 g, whereas egg puffs from the same bakery have an average mass of 40 g.
i. Suppose a person buys 1 kg of veg puff from the bakery. Calculate the number of veg puffs he receives.
ii. Determine the mass of egg puffs (in kg) that will contain the same number of eggs puffs as in one kilogram of veg puffs.
Solution:
i. Mass of a veg puff = 27.0 g = 0.027 kg
∴ Number of veg puffs in 1 kg = 1 / 0.027 = 37
ii. One kilogram of veg puffs contains 37 veg puffs.
Mass of 37 egg puffs = 37 × 0.040 = 1.48 kg
Ans: i. 37 veg puffs in 1 kg of puff.
ii. Mass of 37 egg puffs is 1.48 kg

Multiple Choice Questions:

1. The branch of chemistry which deals with carbon compounds is called ……………. chemistry.
(A) organic
(B) inorganic
(C) carbon
(D) bio
Answer:
(A) organic

2. A/an is a simple combination of two or more substances in which the constituent substances retain their separate identities.
(A) compound
(B) mixture
(C) element
(D) All of these
Answer:
(B) mixture

3. Which one of the following is NOT a mixture?
(A) Paint
(B) Gasoline
(C) Liquefied Petroleum Gas (LPG)
(D) Distilled water
Answer:
(D) Distilled water

4. The sum of the masses of reactants and products is equal in any physical or chemical reaction. This is in accordance with ………………
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of reciprocal proportion
Answer:
(C) law of conservation of mass

5. A sample of calcium carbonate (CaCO₃) has the following percentage composition: Ca = 40 %; C = 12 %; O = 48 %. If the law of definite proportions is true, then the weight of calcium in 4 g of a sample of calcium
carbonate from another source will be ……………..
(A) 0.016 g
(B) 0.16 g
(C) 1.6 g
(D) 16 g
Answer:
(C) 1.6 g

6. Two elements, A and B, combine to form two compounds in which ‘a’ g of A combines with ‘b₁’ and ‘b₂’g of B respectively. According to law of multiple proportion ………………
(A) b₁ = b₂
(B) b₁ and b₂ bear a simple whole number ratio
(C) a and b₁ bear a whole number ratio
(D) no relation exists between b₁ and b₂
Answer:
(B) b₁ and b₂ bear a simple whole number ratio

7. At constant temperature and pressure, two litres of hydrogen gas react with one litre of oxygen gas to produce two litres of water vapour. This is in accordance with ……………….
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of gaseous volumes
Answer:
(D) law of gaseous volumes

8. One mole of oxygen molecule weighs …………….
(A) 8 g
(B) 32 g
(C) 16 g
(D) 6.022 × 10²³ g
Answer:
(B) 32 g

9. The mass of 0.002 mol of glucose (C₆H₁₂O₆) is ………………
(A) 0.20 g
(B) 0.36 g
(C) 0.50 g
(D) 1.80 g
Answer:
(B) 0.36 g

10. Which of the following is CORRECT?
(A) 1 mole of oxygen atoms contains 6.0221367 × 10²³ atoms of oxygen.
(B) 1 mole of water molecules contains 6.0221367 × 10²³ molecules of water.
(C) 1 mole of sodium chloride contains 6.0221367 × 10²³ formula units of NaCl.
(D) All of these
Answer:
(D) All of these

11. 180 g of glucose (C₆H₁₂O₆) contains ……………. carbon atoms.
(A) 1.8 × 10²³
(B) 1.8 × 10²⁴
(C) 3.6 × 10²³
(D) 3.6 × 10²⁴
Answer:
(C) 3.6 × 10²³

12. The number of molecules present in 8 g of oxygen gas is …………….
(A) 6.022 × 10²³
(B) 3.011 × 10²³
(C) 12.044 × 10²³
(D) 1.505 × 10²³
Answer:
(D) 1.505 × 10²³

13. The number of molecules in 22.4 cm³of ozone gas at STP is ……………….
(A) 6.022 × 10²⁰
(B) 6.022 × 10²³
(C) 22.4 × 10²⁰
(D) 22.4 × 10²³
Answer:
(A) 6.022 × 10²⁰

14. 11.2 cm³ of hydrogen gas at STP, contains …………….. moles.
(A) 0.0005
(B) 0.01
(C) 0.029
(D) 0.5
Answer:
(A) 0.0005

15. The mass of 224 mL of hydrogen gas at STP is
(A) 0.02 g
(B) 0.224 g
(C) 2.24 g
(D) 20.0 g
Answer:
(A) 0.02 g

16. 4.4 g of an unknown gas occupies 2.24 L of volume under STP conditions. The gas may be ………………
(A) CO₂
(B) CO
(C) O₂
(D) SO₂
Answer:
(A) CO₂