Bhagya

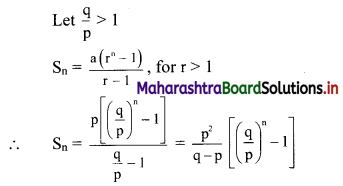
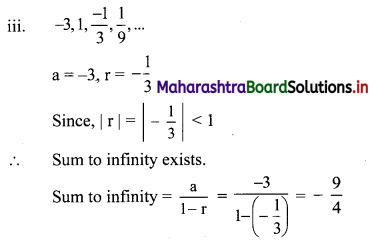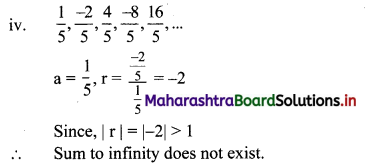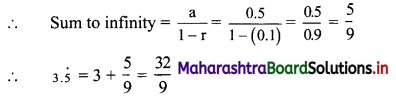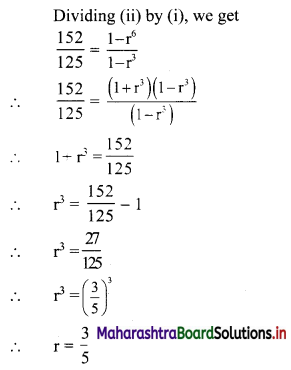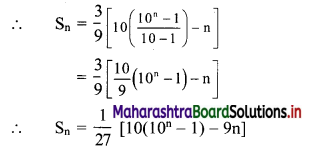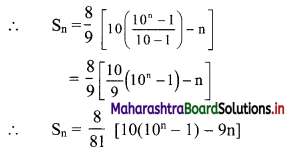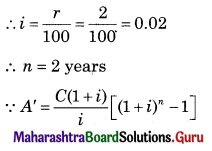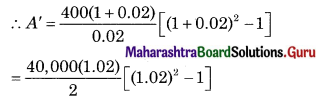Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Determinants Miscellaneous Exercise 6 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Determinants Miscellaneous Exercise 6

Question 1.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
Solution:

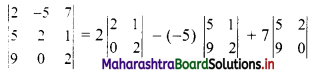
= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113

(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
Solution:

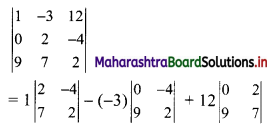
= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76

Question 2.
Find the value(s) of x, if
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
∴ 1(-10x² + 10x) – 4(5x² + 5) + 20(2x + 2) = 0
∴ -10x² + 10x – 20x² – 20 + 40x + 40 = 0
∴ -30x² + 50x + 20 = 0
∴ 3x² – 5x – 2 = 0 ……[Dividing throughout by (-10)]
∴ 3x² – 6x + x – 2 = 0
∴ 3x(x – 2) + 1(x – 2) = 0
∴ (x – 2) (3x + 1) = 0
∴ x – 2 = 0 or 3x + 1 = 0
∴ x = 2 or x = \(-\frac{1}{3}\)

(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
∴ 1(4 – 16) – 2x(1 – 16) + 4x(1 – 4) = 0
∴ 1(-12) – 2x(-15) + 4x(-3) = 0
∴ -12 + 30x – 12x = 0
∴ 18x = 12
∴ x = \(\frac{2}{3}\)

Question 3.
By using properties of determinants, prove that \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|=0\).
Solution:

Question 4.
Without expanding the determinants, show that

Solution:

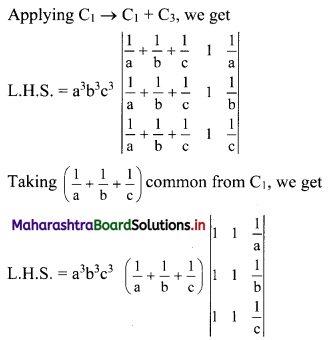
Question 5.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
Solution:
Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1
D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0
D_x = \(\left|\begin{array}{ccc}
1 & -1 & 1 \\
8 & 2 & 3 \\
1 & 1 & -4
\end{array}\right|\)
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40
D_y = \(\left|\begin{array}{ccc}
2 & 1 & 1 \\
1 & 8 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-32 – 3) – 1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80
D_z = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 8 \\
3 & 1 & 1
\end{array}\right|\)
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,
x = \(\frac{D_{x}}{D}=\frac{-40}{-40}\) = 1
y = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
z = \(\frac{\mathrm{D}_{z}}{\mathrm{D}}=\frac{-40}{-40}\) = 1
∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.

(ii) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=-2\), \(\frac{1}{x}-\frac{2}{y}+\frac{1}{z}=3\), \(\frac{2}{x}-\frac{1}{y}+\frac{3}{z}=-1\)
Solution:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
The given equations become
p + q + r = -2
p – 2q + r = 3
2p – q + 3r = -1
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -2 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(-6 + 1) – 1(3 – 2) + 1(-1 + 4)
= -5 – 1 + 3
= -3
D_p = \(\left|\begin{array}{rrr}
-2 & 1 & 1 \\
3 & -2 & 1 \\
-1 & -1 & 3
\end{array}\right|\)
= -2(-6 + 1) – 1(9 + 1) + 1(-3 – 2)
= 10 – 10 – 5
= -5
D_q = \(\left|\begin{array}{ccc}
1 & -2 & 1 \\
1 & 3 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(9 + 1) + 2(3 – 2) + 1(-1 – 6)
= 10 + 2 – 7
= 5
D_r = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
1 & -2 & 3 \\
2 & -1 & -1
\end{array}\right|\)
= 1(2 + 3) – 1(-1 – 6) – 2(-1 + 4)
= 5 + 7 – 6
= 6
By Cramer’s Rule,
p = \(\frac{\mathrm{D}_{\mathrm{p}}}{\mathrm{D}}=\frac{-5}{-3}=\frac{5}{3}\)
q = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
r = \(\frac{D_{2}}{D}=\frac{-40}{-40}\) = 1
∴ x = \(\frac{3}{5}\), y = \(\frac{-3}{5}\), z = \(\frac{-1}{2}\) are the solutions of the given equations.

(iii) x – y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
Given equations are
x – y + 2z = 1
3x + 4y – 5z = 5
2x – y + 3z = 12
D = \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right|\)
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0
D_x = \(\left|\begin{array}{ccc}
7 & -1 & 2 \\
5 & 4 & -5 \\
12 & -1 & 3
\end{array}\right|\)
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7)+ 1(75) +2(-53)
= 49 + 75 – 106
= 18
D_y = \(\left|\begin{array}{ccc}
1 & 7 & 2 \\
3 & 5 & -5 \\
2 & 12 & 3
\end{array}\right|\)
= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6
D_z = \(\left|\begin{array}{ccc}
1 & -1 & 7 \\
3 & 4 & 5 \\
2 & -1 & 12
\end{array}\right|\)
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53)+ 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,
x = \(\frac{\mathrm{D}_{x}}{\mathrm{D}}=\frac{18}{4}=\frac{9}{2}\)
y = \(\frac{D_{y}}{D}=\frac{-6}{4}=\frac{-3}{2}\)
z = \(\frac{D_{z}}{D}=\frac{2}{4}=\frac{1}{2}\)
∴ x = \(\frac{9}{2}\), y = \(\frac{-3}{2}\) and z = \(\frac{1}{2}\) are the solutions of the given equations.

Question 6.
Find the value(s) of k, if the following equations are consistent.
(i) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
Solution:
Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3 i.e. 2x – y – 3 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{rrr}
3 & 1 & -2 \\
k & 2 & -3 \\
2 & -1 & -3
\end{array}\right|=0\)
∴ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
∴ 3(-9) – 1 (-3k + 6) – 2(-k – 4) = 0
∴ -27 + 3k – 6 + 2k + 8 = 0
∴ 5k – 25 = 0
∴ k = 5

(ii) kx + 3y + 4 = 0, x + ky + 3 = 0, 3x + 4y + 5 = 0
Solution:
Given equations are
kx + 3y + 4 = 0
x + ky + 3 = 0
3x + 4y + 5 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{lll}
\mathrm{k} & 3 & 4 \\
1 & \mathrm{k} & 3 \\
3 & 4 & 5
\end{array}\right|=0\)
∴ k(5k – 12) – 3(5 – 9) + 4(4 – 3k) = 0
∴ 5k² – 12k + 12 + 16 – 12k = 0
∴ 5k² – 24k + 28 = 0
∴ 5k² – 10k – 14k + 28 = 0
∴ 5k(k – 2) – 14(k – 2) = 0
∴ (k – 2) (5k – 14) = 0
∴ k – 2 = 0 or 5k – 14 = 0
∴ k = 2 or k = \(\frac{14}{5}\)

Question 7.
Find the area of triangles whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
Solution:
Here, A(x₁, y₁) ≡ A(-1, 2), B(x₂, y₂) ≡ B(2, 4), C(x₃, y₃) ≡ C(0, 0)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(∆ABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
-1 & 2 & 1 \\
2 & 4 & 1 \\
0 & 0 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [-1(4 – 0) – 2(2 – 0) + 1(0 – 0)]
= \(\frac{1}{2}\) (-4 – 4)
= \(\frac{1}{2}\) (-8)
= -4
Since, area cannot be negative.
∴ A(∆ABC) = 4 sq.units

(ii) P(3, 6), Q(-1, 3), R(2, -1)
Solution:
Here, P(x₁, y₁) ≡ P(3, 6), Q(x₂, y₂) ≡ Q(-1, 3), R(x₃, y₃) ≡ R(2, -1)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆PQR) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & 6 & 1 \\
-1 & 3 & 1 \\
2 & -1 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [3(3 + 1) – 6(-1 – 2) + 1(1 – 6)]
= \(\frac{1}{2}\) [3(4) – 6(-3) + 1(-5)]
= \(\frac{1}{2}\) (12 + 18 – 5)
∴ A(∆PQR) = \(\frac{25}{2}\) sq.units

(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
Here, L(x₁, y₁) ≡ L(1, 1), M(x₂, y₂) ≡ M(-2, 2), N(x₃, y₃) ≡ N(5, 4)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆LMN) = \(\frac{1}{2}\left|\begin{array}{rrr}
1 & 1 & 1 \\
-2 & 2 & 1 \\
5 & 4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [1(2 – 4) -1(-2 – 5) + 1(-8 – 10)]
= \(\frac{1}{2}\) [1(-2) – 1(-7) + 1(-18)]
= \(\frac{1}{2}\) (-2 + 7 – 18)
= \(\frac{-13}{2}\)
Since, area cannot be negative.
∴ A(∆LMN) = \(\frac{13}{2}\) sq.units

Question 8.
Find the value of k,
(i) if the area of ∆PQR is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
Solution:
Here, P(x₁, y₁) ≡ P(k, 0), Q(x₂, y₂) ≡ Q(4, 0), R(x₃, y₃) ≡ R(0, 2)
A(∆PQR) = 4 sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\left|\begin{array}{lll}
k & 0 & 1 \\
4 & 0 & 1 \\
0 & 2 & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\) [k(0 – 2) – 0 + 1(8 – 0)]
∴ ±8 = -2k + 8
∴ 8 = -2k + 8 or -8 = -2k + 8
∴ -2k = 0 or 2k = 16
∴ k = 0 or k = 8

(ii) if area of ∆LMN is \(\frac{33}{2}\) square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution:
Here, L(x₁, y₁) ≡ L(3, -5), M(x₂, y₂) ≡ M(-2, k), N(x₃, y₃) ≡ N(1, 4)
A(∆LMN) = \(\frac{33}{2}\) sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ \(\pm \frac{33}{2}=\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
-2 & \mathrm{k} & 1 \\
1 & 4 & 1
\end{array}\right|\)
∴ ±\(\frac{33}{2}\) = \(\frac{1}{2}\) [3(k – 4) – (-5) (-2 – 1) + 1(-8 – k)]
∴ ±33 = 3k – 12 – 15 – 8 – k
∴ 33 = 2k – 35
∴ 2k – 35 = 33 or 2k – 35 = -33
∴ 2k = 68 or 2k = 2
∴ k = 34 or k = 1

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.4 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Sequences and Series Ex 4.4

Question 1.
Verify whether the following sequences are H.P.
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Solution:
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
Here, the reciprocal sequence is 3, 5, 7, 9, …
∴ t₁ = 3, t₂ = 5, t₃ = 7, …..
∵ t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = 2, constant
∴ The reciprocal sequence is an A.P.
∴ the given sequence is H.P.

(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
Here, the reciprocal sequence is 3, 6, 9, 12 …
∴ t₁ = 3, t₂ = 6, t₃ = 9, t₄ = 12, …
∵ t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = 3, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.

(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Here, the reciprocal sequence is 7, 9, 11, 13, 15, ……
∴ t₁ = 7, t₂ = 9, t₃ = 11, t₄ = 13, …..
∵ t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = 2, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.

Question 2.
Find the nth term and hence find the 8th term of the following H.P.s:
(i) \(\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, \frac{1}{11}, \ldots \ldots \ldots\)
(ii) \(\frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{5}, \frac{1}{10}, \frac{1}{15}, \frac{1}{20}, \cdots \cdots \cdots\)
Solution:

Question 3.
Find A.M. of two positive numbers whose G.M. and H.M. are 4 and \(\frac{16}{5}\).
Solution:
G.M. = 4, H.M. = \(\frac{16}{5}\)
∵ (G.M.)² = (A.M.) (H.M.)
∴ 16 = A.M. × \(\frac{16}{5}\)
∴ A.M. = 5

Question 4.
Find H.M. of two positive numbers whose A.M. and G.M. are \(\frac{15}{2}\) and 6.
Solution:
A.M. = \(\frac{15}{2}\), G.M. = 6
Now, (G.M.)² = (A.M.) (H.M.)
∴ 6² = \(\frac{15}{2}\) × H.M.
∴ H.M. = 36 × \(\frac{2}{15}\)
∴ H.M. = \(\frac{24}{5}\)

Question 5.
Find G.M. of two positive numbers whose A.M. and H.M. are 75 and 48.
Solution:
A.M. = 75, H.M. = 48
(G.M.)² = (A.M.) (H.M.)
∵ (G.M.)² = 75 × 48
∵ (G.M.)² = 25 × 3 × 16 × 3
∵ (G.M.)² = 5² × 4² × 3²
∴ G.M. = 5 × 4 × 3
∴ G.M. = 60

Question 6.
Insert two numbers between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.
Solution:
Let the required numbers be \(\frac{1}{\mathrm{H}_{1}}\) and \(\frac{1}{\mathrm{H}_{2}}\).
∴ \(\frac{1}{7}, \frac{1}{\mathrm{H}_{1}}, \frac{1}{\mathrm{H}_{2}}, \frac{1}{13}\) are in H.P.
∴ 7, H₁, H₂ and 13 are in A.P.
∴ t₁ = a = 7 and t₄ = a + 3d = 13
∴ 7 + 3d = 13
∴ 3d = 6
∴ d = 2
∴ H₁ = t₂ = a + d = 7 + 2 = 9
and H₂ = t₃ = a + 2d = 7 + 2(2) = 11
∴ \(\frac{1}{9}\) and \(\frac{1}{11}\) are the required numbers to be inserted between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.

Question 7.
Insert two numbers between 1 and -27 so that the resulting sequence is a G.P.
Solution:
Let the required numbers be G₁ and G₂.
∴ 1, G₁, G₂, -27 are in G.P.
∴ t₁ = 1, t₂ = G₁, t₃ = G₂, t₄ = -27
∴ t₁ = a = 1
t_n = ar^n-1
∴ t₄ = (1) r^4-1
∴ -27 = r³
∴ r³ = (-3)³
∴ r = -3
∴ G₁ = t₂ = ar = 1(-3) = -3
∴ G₂ = t₃ = ar = 1(-3)² = 9
∴ -3 and 9 are the required numbers to be inserted between 1 and -27 so that the resulting sequence is a G.P.

Question 8.
Find two numbers whose A.M. exceeds their G.M. by \(\frac{1}{2}\) and their H.M. by \(\frac{25}{26}\).
Solution:
Let a, b be the two numbers.


∴ a + b = 13
∴ b = 13 – a …….(iii)
and ab = 36
∴ a(13 – a) = 36 …… [From (iii)]
∴ a² – 13a + 36 = 0
∴ (a – 4)(a – 9) = 0
∴ a = 4 or a = 9
When a = 4, b = 13 – 4 = 9
When a = 9, b = 13 – 9 = 4
∴ the two numbers are 4 and 9.

Question 9.
Find two numbers whose A.M. exceeds G.M. bv 7 and their H.M. by \(\frac{63}{5}\).
Solution:
Let a, b be the two numbers.

∴ a + b = 70
∴ b = 70 – a …..(ii)
∴ G = A – 7 = 35 – 7 = 28 …….[From (i)]
∴ √ab = 28
∴ ab = 28² = 784
∴ a(70 – a) = 784 ……[From (ii)]
∴ 70a – a² = 784
∴ a² – 70a + 784 = 0
∴ a² – 56a – 14a + 784 = 0
∴ (a – 56) (a – 14) = 0
∴ a = 14 or a = 56
When a = 14, b = 70 – 14 = 56
When a = 56, b = 70 – 56 = 14
∴ the two numbers are 14 and 56.

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.3 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Sequences and Series Ex 4.3

Question 1.
Determine whether the sum to infinity of the following G.P’.s exist. If exists, find it.
(i) \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \ldots\)
(ii) \(2, \frac{4}{3}, \frac{8}{9}, \frac{16}{27}, \ldots\)
(iii) \(-3,1, \frac{-1}{3}, \frac{1}{9}, \ldots\)
(iv) \(\frac{1}{5}, \frac{-2}{5}, \frac{4}{5}, \frac{-8}{5}, \frac{16}{5}, \ldots\)
Solution:

Question 2.
Express the following recurring decimals as a rational number.
(i) \(0 . \overline{32}\)
(ii) 3.5
(iii) \(4 . \overline{18}\)
(iv) \(0.3 \overline{45}\)
(v) \(3.4 \overline{56}\)
Solution:
(i) \(0 . \overline{32}\) = 0.323232…..
= 0.32 + 0.0032 + 0.000032 + …..
Here, 0.32, 0.0032, 0.000032, … are in G.P. with a = 0.32 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.
∴ Sum to infinity = \(\frac{a}{1-r}\)

(ii) 3.5 = 3.555… = 3 + 0.5 + 0.05 + 0.005 + …
Here, 0.5, 0.05, 0.005, … are in G.P. with a = 0.5 and r = 0.1
Since, |r| = |0.1| < 1
∴ Sum to infinity exists.

(iii) \(4 . \overline{18}\) = 4.181818…..
= 4 + 0.18 + 0.0018 + 0.000018 + …..
Here, 0.18, 0.0018, 0.000018, … are in G.P. with a = 0.18 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

(iv) 0.345 = 0.3454545…..
= 0.3 + 0.045 + 0.00045 + 0.0000045 + …..
Here, 0.045, 0.00045, 0.0000045, … are in G.P. with a = 0.045, r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

(v) \(3.4 \overline{56}\) = 3.4565656 …..
= 3.4 + 0.056 + 0.00056 + 0.0000056 + ….
Here, 0.056, 0.00056, 0.0000056, … are in G.P. with a = 0.056 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

Question 3.
If the common ratio of a G.P. is \(\frac{2}{3}\) and sum of its terms to infinity is 12. Find the first term.
Solution:
r = \(\frac{2}{3}\), sum to infinity = 12 … [Given]
Sum to infinity = \(\frac{a}{1-r}\)
∴ 12 = \(\frac{a}{1-\frac{2}{3}}\)
∴ a = 12 × \(\frac{1}{3}\)
∴ a = 4

Question 4.
If the first term of a G.P. is 16 and sum of its terms to infinity is \(\frac{176}{5}\), find the common ratio.
Solution:
a = 16, sum to infinity = \(\frac{176}{5}\) … [Given]
Sum to infinity = \(\frac{a}{1-r}\)
∴ \(\frac{176}{5}=\frac{16}{1-r}\)
∴ \(\frac{11}{5}=\frac{1}{1-r}\)
∴ 11 – 11r = 5
∴ 11r = 6
∴ r = \(\frac{6}{11}\)

Question 5.
The sum of the terms of an infinite G.P. is 5 and the sum of the squares of those terms is 15. Find the G.P.
Solution:
Let the required G.P. be a, ar, ar², ar³, …..
Sum to infinity of this G.P. = 5
∴ 5 = \(\frac{a}{1-r}\)
∴ a = 5(1 – r) ……(i)
Also, the sum of the squares of the terms is 15.

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.2 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Sequences and Series Ex 4.2

Question 1.
For the following G.P.’s, find S_n.
(i) 3, 6, 12, 24, …..
(ii) \(\mathbf{p}, \mathbf{q}, \frac{\mathbf{q}^{2}}{\mathbf{p}}, \frac{\mathbf{q}^{3}}{\mathbf{p}^{2}}, \ldots\)
Solution:

Question 2.
For a G.P., if
(i) a = 2, r = \(-\frac{2}{3}\), find S₆.
(ii) S₅ = 1023, r = 4, find a.
Solution:

Question 3.
For a G. P., if
(i) a = 2, r = 3, S_n = 242, find n.
(ii) sum of the first 3 terms is 125 and the sum of the next 3 terms is 27, find the value of r.
Solution:
(i) a = 2, r = 3, S_n = 242
Sn = \(a\left(\frac{r^{n}-1}{r-1}\right)\), for r > 1

Question 4.
For a G. P.,
(i) if t₃ = 20, t₆ = 160, find S₇.
(ii) if t₄ = 16, t₉ = 512, find S₁₀.
Solution:
(i) t₃ = 20, t₆ = 160
t_n = ar^n-1
∴ t₃ = ar^3-1 = ar²
∴ ar² = 20
∴ a = \(\frac{20}{\mathrm{r}^{2}}\) ……(i)

Question 5.
Find the sum to n terms:
(i) 3 + 33 + 333 + 3333 + ……
(ii) 8 + 88 + 888 + 8888 + ……..
Solution:
(i) S_n = 3 + 33 + 333 +….. upto n terms
= 3(1 + 11 + 111 +….. upto n terms)
= \(\frac{3}{9}\)(9 + 99 + 999 + … upto n terms)
= \(\frac{3}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{3}{9}\)[(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P.
with a = 10, r = \(\frac{100}{10}\) = 10

(ii) S_n = 8 + 88 + 888 + … upto n terms
= 8(1 + 11 + 111 + … upto n terms)
= \(\frac{8}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{8}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{8}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10

Question 6.
Find the sum to n terms:
(i) 0.4 + 0.44 + 0.444 + ……
(ii) 0.7 + 0.77 + 0.777 + …..
Solution:
(i) S_n = 0.4 + 0.44 + 0.444 + ….. upto n terms
= 4(0.1 + 0.11 + 0.111 + …. upto n terms)
= \(\frac{4}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{4}{9}\) [(i – 0.1) + (1 – 0.01) + (1 – 0.001) … upto n terms]
= \(\frac{4}{9}\) [(1 + 1 + 1 + …n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1
∴ S_n = \(\frac{4}{9}\left\{\mathrm{n}-0.1\left[\frac{1-(0.1)^{\mathrm{n}}}{1-0.1}\right]\right\}\)

(ii) S_n = 0.7 + 0.77 + 0.777 + … upto n terms
= 7(0.1 + 0.11 + 0.111 + … upto n terms)
= \(\frac{7}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{7}{9}\) [(1 – 0.1) + (1 – 0.01) + (1 – 0.001) +… upto n terms]
= \(\frac{7}{9}\) [(1 + 1 + 1 +… n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

Question 7.
Find the nth terms of the sequences:
(i) 0.5, 0.55, 0.555,…..
(ii) 0.2, 0.22, 0.222,…..
Solution:
(i) Let t₁ = 0.5, t₂ = 0.55, t₃ = 0.555 and so on.
t₁ = 0.5
t₂ = 0.55 = 0.5 + 0.05
t₃ = 0.555 = 0.5 + 0.05 + 0.005
∴ t_n = 0.5 + 0.05 + 0.005 + … upto n terms
But 0.5, 0.05, 0.005, … upto n terms are in G.P. with a = 0.5 and r = 0.1
∴ t_n = the sum of first n terms of the G.P.

(ii) Let t₁ = 0.2, t₂ = 0.22, t₃ = 0.222 and so on
t₁ = 0.2
t₂ = 0.22 = 0.2 + 0.02
t₃ = 0.222 = 0.2 + 0.02 + 0.002
∴ t_n = 0.2 + 0.02 + 0.002 + … upto n terms
But 0.2, 0.02, 0.002, … upto n terms are in G.P. with a = 0.2 and r = 0.1
∴ t_n = the sum of first n terms of the G.P.

Question 8.
For a sequence, if S_n = 2(3^n-1), find the nth term, hence showing that the sequence is a G.P.
Solution:

Question 9.
If S, P, R are the sum, product and sum of the reciprocals of n terms of a G.P. respectively, then verify that \(\left(\frac{\mathbf{S}}{\mathbf{R}}\right)^{\mathbf{n}}\) = P².
Solution:
Let a be the 1st term and r be the common ratio of the G.P.
∴ the G.P. is a, ar, ar², ar³, …, ar^n-1

Question 10.
If S_n, S_2n, S_3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that S_n (S_3n – S_2n) = (S_2n – S_n)².
Solution:
Let a and r be the 1st term and common ratio of the G.P. respectively.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.1

Question 1.
Let X represent the difference between a number of heads and the number of tails obtained when a coin is tossed 6 times. What are the possible values of X?
Solution:
∵ A coin is tossed 6 times
S = {6H and 0T, 5H and 1T, 4H and 2T, 3H and 3T, 2H and 4T, 1H and 5T, 0H and 6T}
X: Difference between no. of heads and no. of tails.
X = 6 – 0 = 6
X = 5 – 1 = 4
X = 4 – 2 = 2
X = 3 – 3 = 0
X = 2 – 4 = -2
X = 1 – 5 = -4
X = 0 – 6 = -6
X = {-6, -4, -2, 0, 2, 4, 6}

Question 2.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes the number of black balls drawn. What are the possible values of X?
Solution:
S : Two bolts are drawn from the Urn
S = {RR, RB, BR, BB}
X : No. of black balls
∴ X = {0, 1, 2}

Question 3.
Determine whether each of the following is a probability distribution. Give reasons for your answer.
(i)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.4 + 0.4 + 0.2
= 1
∴ The function is a p.m.f.

(ii)

Solution:
Here, p(3) = -0.1 < 0
∴ P(X = x) ≯ 0, ∀ x
∴ The function is not a p.m.f.

(iii)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.1 + 0.6 + 0.3
= 1
∴ The function is a p.m.f.

(iv)

Solution:
Here, P(Z = z) ≥ 0, ∀ z and
\(\sum_{x=-1}^{3} \mathrm{P}(\mathrm{Z}=z)\) = p(-1) + p(0) + p(1) + p(2) + p(3)
= 0.05 + 0 + 0.4 + 0.2 + 0.3
= 0.95
≠ 1
∴ The function is not a p.m.f.

(v)

Solution:
Here, P(Y = y) ≥ 0, ∀ y and
\(\sum_{x=-1}^{2} \mathrm{P}(\mathrm{Y}=y)\) = p(-1) + p(0) + p(1)
= 0.1 + 0.6 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.

(vi)

Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{0} \mathrm{P}(X=x)\) = p(-2) + p(-1) + p(0)
= 0.3 + 0.4 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.

Question 4.
Find the probability distribution of
(i) number of heads in two tosses of a coin,
(ii) number of trails in three tosses of a coin,
(iii) number of heads in four tosses of a coin.
Solution:
(i) S: Coin is tossed two times
S = {HH, HT, TH, TT}
n(S) = 4
X: No. of heads
Range of X = {0, 1, 2}
p.m.f. Table

(ii) S: 3 coin are tossed
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
X: No. of heads
Range of X = {0, 1, 2, 3}
p.m.f. Table

(iii) S: Four coin are tossed
S = {HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
n(S) = 16
X: No. of heads
Range of X = {0, 1, 2, 3, 4}
p.m.f. Table

Question 5.
Find the probability distribution of the number of successes in two tosses of a die if successes are defined as getting a number greater than 4.
Solution:
S = A die is tossed 2 times
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
X = No. getting greater than 4
Range of X = {0, 1, 2}
p(0) = \(\frac{16}{36}=\frac{4}{9}\)
p(1) = \(\frac{16}{36}=\frac{4}{9}\)
p(2) = \(\frac{4}{36}=\frac{1}{9}\)

Question 6.
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
Solution:
Total no. of bulbs = 30
No. of defective bulbs = 6
A sample of 4 bulbs are drawn from 30 bulbs.
∴ n(S) = \({ }^{30} \mathrm{C}_{4}\)
∴ No. of non-defective bulbs = 24
Let X = No. of defective bulbs drawn in sample of 4 bulbs.

Question 7.
A coin is biased so that the head is 3 times as likely to occur as the tail. Find the probability distribution of a number of tails in two tosses.
Solution:
Here, the head is 3 times as likely to occur as the tail.
i.e., If 4 times coin is tossed, 3 times there will be a head and 1 time there will be the tail.
∴ p(H) = \(\frac{3}{4}\) and p(T) = \(\frac{1}{4}\)
Let X : No. of tails in two tosses.
And coin is tossed twice.
∴ X = {0, 1, 2}
For X = 0,
p(0) = p(both heads)
= p(H) × p(H)
= \(\frac{3}{4} \times \frac{3}{4}\)
= \(\frac{9}{16}\)
For X = 1,
p(1) = p(HT or TH)
= p(HT) + p(TH)
= p(H) × p(T) + p(T) × p(H)
= \(\frac{3}{4} \times \frac{1}{4}+\frac{1}{4} \times \frac{3}{4}\)
= \(\frac{6}{16}\)
For X = 2,
p(2) = p(both tails)
= p(T) × p(T)
= \(\frac{1}{4} \times \frac{1}{4}\)
= \(\frac{1}{16}\)
The probability distribution of the number of tails in two tosses is

Question 8.
A random variable X has the following probability distribution:

Determine (i) k, (ii) P(X < 3), (iii) P(0 < X < 3), (iv) P(X > 4).
Solution:
(i) It is a p.m.f. of r.v. X
∴ Σp(x) = 1
∴ p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) = 1
∴ k + 2k + 2k + 3k + k² + 2k² + (7k² + k) = 1
∴ 10k² + 9k = 1
∴ 10k² + 9k – 1 = 0
∴ 10k² + 10k – k – 1 = 0
∴ 10k(k + 1) – (k + 1) = 0
∴ (10k – 1)(k + 1) = 0
∴ 10k – 1 = 0 or k + 1 = 0
∴ k = \(\frac{1}{10}\) or k = -1
but k = -1 is not accepted
∴ k = \(\frac{1}{2}\) is accepted

(ii) P(X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iii) P(0 < X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iv) P(X > 4) = p(5) + p(6) + p(7)
= k² + 2k² + (7k² + k)
= 10k² + k
= \(10\left(\frac{1}{10}\right)^{2}+\frac{1}{10}\)
= \(\frac{2}{10}\)
= \(\frac{1}{5}\)

Question 9.
Find expected value and variance of X using the following p.m.f.

Solution:

E(X) = Σxp = -0.05
V(X) = Σx²p – (Σxp)²
= 2.25 – (-0.05)²
= 2.25 – 0.0025
= 2.2475

Question 10.
Find expected value and variance of X, the number on the uppermost face of a fair die.
Solution:
S : A fair die is thrown
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
X: No obtained on uppermost face of die
Range of X = {1, 2, 3, 4, 5, 6}

E(X) = Σxp = \(\frac{21}{6}=\frac{7}{2}\) = 3.5
V(X) = Σx²p – (Σxp)²
= \(\frac{91}{6}\) – (3.5)²
= 15.17 – 12.25
= 2.92

Question 11.
Find the mean of the number of heads in three tosses of a fair coin.
Solution:
S : A coin is tossed 3 times
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Range of X = {0, 1, 2, 3}

∴ Mean = E(X) = Σxp = \(\frac{12}{8}=\frac{3}{2}\) = 1.5

Question 12.
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Solution:
S : Two dice are thrown
S = {(1, 1), (1, 2), (1, 3), ……, (6, 6)}
n(S) = 36
Range of X = {0, 1, 2}
First 6 positive integers are 1, 2, 3, 4, 5, 6
X = Larger two numbers selected
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36

∴ E(X) = Σxp = \(\frac{12}{36}=\frac{1}{3}\)

Question 13.
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers. Find E(X).
Solution:
First 6 positive integers are 1, 2, 3, 4, 5, 6
X : The larger of the selected two numbers
S = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
n(S) = 30

E(X) = Σxp = \(\frac{140}{30}=\frac{14}{3}\) = 4.67

Question 14.
Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance of X.
Solution:
S : Two fair dice are rolled
S = {(1, 1), (1, 2), (1, 4), ……, (6, 6)}
n(S) = 36
X : Sum of the two numbers.
Range of X = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}


V(X) = Σx²p – (Σxp)²
= \(\frac{1952}{36}-\left(\frac{252}{36}\right)^{2}\)
= 54.22 – (7)²
= 5.22
SD(X) = √V(X) = √5.22 = 2.28

Question 15.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. If X denotes the age of a randomly selected student, find the probability distribution of X. Find the mean and variance of X.
Solution:

Question 16.
70% of the member’s favour and 30% oppose a proposal in a meeting. The random variable X takes the value 0 if a member opposes the proposal and the value 1 if a member is in favour. Find E(X) and V(X).
Solution:

E(X) = Σxp = 0.7
V(X) = Σx²p – (Σxp)²
= 0.7 – (0.7)²
= 0.7 – 0.49
= 0.21

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Sequences and Series Ex 4.1

Question 1.
Verify whether the following sequences are G.P. If so, write tn.
(i) 2, 6, 18, 54, ……
(ii) 1, -5, 25, -125, …….
(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)
(iv) 3, 4, 5, 6, ……
(v) 7, 14, 21, 28, …..
Solution:
(i) 2, 6, 18, 54, …….
t₁ = 2, t₂ = 6, t₃ = 18, t₄ = 54, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=3\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 2, r = 3
t_n= ar^n-1
∴ t_n = 2(3^n-1)

(ii) 1, -5, 25, -125, ……
t₁ = 1, t₂ = -5, t₃ = 25, t₄ = -125, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=-5\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 1, r = -5
t_n = ar^n-1
∴ t_n = (-5)^n-1

(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)

Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.

(iv) 3, 4, 5, 6,……
t₁ = 3, t₂ = 4, t₃ = 5, t₄ = 6, …..
Here, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}=\frac{4}{3}, \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}}=\frac{5}{4}, \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}=\frac{6}{5}\)
Since, \(\frac{t_{2}}{t_{1}} \neq \frac{t_{3}}{t_{2}} \neq \frac{t_{4}}{t_{3}}\)
∴ the given sequence is not a geometric progression.

(v) 7, 14, 21, 28, …..
t₁ = 7, t₂ = 14, t₃ = 21, t₄ = 28, …..
Here, \(\frac{t_{2}}{t_{1}}=2, \frac{t_{3}}{t_{2}}=\frac{3}{2}, \frac{t_{4}}{t_{3}}=\frac{4}{3}\)
Since, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}} \neq \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}} \neq \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}\)
∴ the given sequence is not a geometric progression.

Question 2.
For the G.P.,
(i) if r = \(\frac{1}{3}\), a = 9, find t₇.
(ii) if a = \(\frac{7}{243}\), r = \(\frac{1}{3}\), find t₃.
(iii) if a = 7, r = -3, find t₆.
(iv) if a = \(\frac{2}{3}\), t₆ = 162, find r.
Solution:

Question 3.
Which term of the G. P. 5, 25, 125, 625, ….. is 510?
Solution:

Question 4.
For what values of x, \(\frac{4}{3}\), x, \(\frac{4}{27}\) are in G. P.?
Solution:

Question 5.
If for a sequence, \(t_{n}=\frac{5^{n-3}}{2^{n-3}}\), show that the sequence is a G. P. Find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P., if \(\frac{t_{n}}{t_{n-1}}\) = constant, for all n ∈ N

∴ the sequence is a G. P. with common ratio \(\frac{5}{2}\)
First term, t₁ = \(\frac{5^{\mathrm{l}-3}}{2^{1-3}}=\frac{2^{2}}{5^{2}}=\frac{4}{25}\)

Question 6.
Find three numbers in G. P. such that their sum is 21 and sum of their squares is 189.
Solution:
Let the three numbers in G. P. be \(\frac{a}{\mathrm{r}}\), a, ar.
According to the first condition,



∴ the three numbers are 12, 6, 3 or 3, 6, 12.
Check:
First condition:
12, 6, 3 are in G.P. with r = \(\frac{1}{2}\)
12 + 6 + 3 = 21
Second condition:
12² + 6² + 3² = 144 + 36 + 9 = 189
Thus, both the conditions are satisfied.

Question 7.
Find four numbers in G. P. such that sum of the middle two numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\).
According to the second condition,
\(\frac{\mathrm{a}}{\mathrm{r}^{3}}\left(\frac{\mathrm{a}}{\mathrm{r}}\right)(\mathrm{ar})\left(\mathrm{ar}^{3}\right)=1\)
∴ a⁴ = 1
∴ a = 1
According to the first condition,

Question 8.
Find five numbers in G. P. such that their product is 1024 and the fifth term is square of the third term.
Solution:
Let the five numbers in G. P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the given conditions,

When a = 4, r = -2
\(\frac{a}{r^{2}}\) = 1, \(\frac{a}{r}\) = -2, a = 4, ar = -8, ar² = 16
∴ the five numbers in G.P. are 1, 2, 4, 8, 16 or 1, -2, 4, -8, 16.

Question 9.
The fifth term of a G. P. is x, eighth term of the G. P. is y and eleventh term of the G. P. is z. Verify whether y² = xz.
Solution:

Question 10.
If p, q, r, s are in G. P., show that p + q, q + r, r + s are also in G.P.
Solution:
p, q, r, s are in G.P.

∴ p + q, q + r, r + s are in G.P.

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Miscellaneous Exercise 3 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 3 Complex Numbers Miscellaneous Exercise 3

Question 1.
Find the value of \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}\)
Solution:

Question 2.
Find the value of √-3 × √-6.
Solution:
√-3 × √-6 = √3 × √-1 + √6 × √-1
= √3i × √6i
= √18i²
= -3√2 ……[∵ i² = -1]

Question 3.
Simplify the following and express in the form a + ib.
(i) 3 + √-64
(ii) (2i³)²
(iii) (2 + 3i) (1 – 4i)
(iv) \(\frac{5}{2}\) i(-4 – 3i)
(v) (1 + 3i)2 (3 + i)
(vi) \(\frac{4+3 i}{1-i}\)
(vii) \(\left(1+\frac{2}{i}\right)\left(3+\frac{4}{i}\right)(5+i)^{-1}\)
(viii) \(\frac{\sqrt{5}+\sqrt{3} i}{\sqrt{5}-\sqrt{3} i}\)
(ix) \(\frac{3 i^{5}+2 i^{7}+i^{9}}{i^{6}+2 i^{8}+3 i^{18}}\)
(x) \(\frac{5+7 i}{4+3 i}+\frac{5+7 i}{4-3 i}\)
Solution:
(i) 3 + √-64
= 3 + √64 . √-1
= 3 + 8i

(ii) (2i³)²
= 4i⁶
= 4(i²)³
= 4(-1)³ …..[∵ i² = -1]
= -4
= -4 + 0i

(iii) (2 + 3i)(1 – 4i) = 2 – 8i + 3i – 12i²
= 2 – 5i – 12(-1) ……[∵ i² = -1]
= 14 – 5i

(iv) \(\frac{5}{2}\) i(-4 – 3i)
= \(\frac{5}{2}\) (-4i – 3i²)
= \(\frac{5}{2}\) [-4i – 3(-1)] ……[∵ i² = -1]
= \(\frac{5}{2}\) (3 – 4i)
= \(\frac{15}{2}\) – 10i

(v) (1 + 3i)² (3 + i)
= (1 + 6i + 9i²) (3 + i)
= (1 + 6i – 9)(3 + i) ……[∵ i² = -1]
= (-8 + 6i)(3 + i)
= -24 – 8i + 18i + 6i²
= -24 + 10i + 6(-1)
= -24 + 10i – 6
= -30 + 10i

Question 4.
Solve the following equations for x, y ∈ R:
(i) (4 – 5i) x + (2 + 3i) y = 10 – 7i
(ii) (1 – 3i) x + (2 + 5i) y = 1 + i
(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
(iv) (x + iy) (5 + 6i) = 2 + 3i
(v) 2x + i⁹ y (2 + i) = x i⁷ + 10 i¹⁶
Solution:
(i) (4 – 5i) x + (2 + 3i)y = 10 – 7i
∴ (4x + 2y) + (3y – 5x) i = 10 – 7i
Equating real and imaginary parts, we get
4x + 2y = 10
i.e., 2x + y = 5 …….(i)
and 3y – 5x = -7 ……..(ii)
Equation (i) × 3 – equation (ii) gives
11x = 22
∴ x = 2
Putting x = 2 in (i), we get
2(2) + y = 5
∴ y = 1
∴ x = 2 and y = 1

(ii) (1 – 3i) x + (2 + 5i) y = 7 + i
∴ (x + 2y) + (-3x + 5y)i = 7 + i
Equating real and imaginary parts, we get
x + 2y = 7 ……..(i)
and -3x + 5y = 1 ……..(ii)
Equation (i) × 3 + equation (ii) gives
11y = 22
∴ y = 2
Putting y = 2 in (i), we get
x + 2(2) = 7
∴ x = 3
∴ x = 3 and y = 2

(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
∴ x + iy = (7 – i)(2 + 3i)
∴ x + iy = 14 + 21i – 2i – 3i²
∴ x + iy = 14 + 19i – 3(-1) …..[∵ i² = -1]
∴ x + iy = 17 + 19i
Equating real and imaginary parts, we get
x = 17 and y = 19

(iv) (x + iy)(5 + 6i) = 2 + 3i

Equating real and imaginary parts, we get
x = \(\frac{28}{61}\) and y = \(\frac{3}{61}\)

(v) 2x + i⁹ y (2 + i) = x i⁷ + 10 i¹⁶
∴ 2x + (i⁴)² . i . y (2 + i) = x (i²)³ . i + 10 . (i⁴)⁴
∴ 2x + (1)² . iy (2 + i) = x (-1)³ . i + 10 (1)⁴ ……[∵ i² = -1, i⁴ = 1]
∴ 2x + 2yi + yi² = -xi + 10
∴ 2x + 2yi – y + xi = 10
∴ (2x – y) + (x + 2y)i = 10 + 0.i
Equating real and imaginary parts, we get
2x – y = 10 ……(i)
and x + 2y = 0 ……..(ii)
Equation (i) × 2 + equation (ii) gives
5x = 20
∴ x = 4
Putting x = 4 in (i), we get
2(4) – y = 10
∴ y = 8 – 10
∴ y = -2
∴ x = 4 and y = -2

Question 5.
Find the value of:
(i) x³ + 2x² – 3x + 21, if x = 1 + 2i
(ii) x³ – 5x² + 4x + 8, if x = \(\frac{10}{3-i}\)
(iii) x³ – 3x² + 19x – 20, if x = 1 – 4i
Solution:
(i) x = 1 + 2i
∴ x – 1 = 2i
∴ (x – 1)² = 4i²
∴ x² – 2x + 1 = -4 ……[∵ i² = -1]
∴ x² – 2x + 5 = 0 ……(i)

∴ x³ + 2x² – 3x + 21
= (x² – 2x + 5)(x + 4) + 1
= 0.(x + 4) + 1 ……[From (i)]
= 0 + 1
= 1
∴ x³ + 2x² – 3x + 21 = 1

(ii) x = \(\frac{10}{3-i}\)

x³ – 5x² + 4x + 8
= (x² – 6x + 10)(x + 1) – 2
= 0 . (x + 1) – 2 ……[From (i)]
= 0 – 2
∴ x³ – 5x² + 4x + 8 = -2

(iii) x = 1 – 4i
∴ x – 1 = -4i
∴ (x – 1)² = 16i²
∴ x² – 2x + 1 = -16 ……[∵ i² = -1]
∴ x² – 2x + 17 = 0 ……(i)

∴ x³ – 3x² + 19x – 20
= (x² – 2x + 17) (x – 1) – 3
= 0 . (x – 1) – 3 ….[From (i)]
= 0 – 3
= -3
∴ x³ – 3x² + 19x – 20 = -3

Question 6.
Find the square roots of:
(i) -16 + 30i
(ii) 15 – 8i
(iii) 2 + 2√3i
(iv) 18i
(v) 3 – 4i
(vi) 6 + 8i
Solution:
(i) Let \(\sqrt{-16+30 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
-16 + 30i = a² + b²i² + 2abi
∴ -16 + 30i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = -16 and 2ab = 30
∴ a² – b² = -16 and b = \(\frac{15}{a}\)
∴ a² – \(\left(\frac{15}{a}\right)^{2}\) = -16
∴ a² – \(\frac{225}{a^{2}}\) = -16
∴ a⁴ – 225 = – 16a²
∴ a⁴ + 16a² – 225 = 0
∴ (a² + 25)(a² – 9) = 0
∴ a² = -25 or a² = 9
But a ∈ R, a² ≠ -25
∴ a² = 9
∴ a = ±3
When a = 3, b = \(\frac{15}{3}\) = 5
When a = -3, b = \(\frac{15}{-3}\) = -5
∴ \(\sqrt{-16+30 \mathrm{i}}\) = ±(3 + 5i)

(ii) Let \(\sqrt{15-8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
15 – 8i = a² + b²i² + 2abi
∴ 15 – 8i = (a² – b²) + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 15 and 2ab = -8
∴ a² – b² = 15 and b = \(\frac{-4}{a}\)
∴ a² – (\(\left(\frac{-4}{a}\right)^{2}\)) = 15
∴ a² – \(\frac{16}{a^{2}}\) = 15
∴ a⁴ – 16 = 15a²
∴ a⁴ – 15a² – 16 = 0
∴ (a² – 16)(a² + 1) = 0
∴ a² = 16 or a² = -1
But a ∈ R, a² ≠ -1
∴ a² = 16
∴ a = ±4
When a = 4, b = \(\frac{-4}{4}\) = -1
When a = -4, b = \(\frac{-4}{-4}\) = 1
\(\sqrt{15-8 i}\) = ±(4 – i)

(iii) Let \(\sqrt{2+2 \sqrt{3} i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
2 – 2√3i = a² + b²i² + 2abi
∴ 2 – 2√3i = a² – b² + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 2 and 2ab = 2√3
∴ a² – b² = 2 and b = \(\frac{\sqrt{3}}{\mathrm{a}}\)
∴ a² – \(\left(\frac{\sqrt{3}}{a}\right)^{2}\) = 2
∴ a² – \(\frac{3}{a^{2}}\) = 2
∴ a⁴ – 3 = 2a²
∴ a⁴ – 2a² – 3 = 0
∴ (a² – 3)(a² + 1) = 0
∴ a² = 3 or a² = -1
But a ∈ R, a² ≠ -1
∴ a² = 3
∴ a = ±√3
When a = √3 , b = \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1
When a = -√3 , b = \(\frac{\sqrt{3}}{-\sqrt{3}}\) = -1
∴ \(\sqrt{2+2 \sqrt{3} i}\) = ±(√3 + i)

(iv) Let \(\sqrt{18 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
18i = a² + b²i² + 2abi
∴ 0 + 18i = a² – b² + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 0 and 2ab = 18
∴ a² – b² = 0 and b = \(\frac{9}{\mathrm{a}}\)
∴ a² – \(\left(\frac{9}{a}\right)^{2}\) = 0
∴ a² – \(\frac{81}{a^{2}}\) = 0
∴ a⁴ – 81 = 0
∴ (a² – 9) (a² + 9) = 0
∴ a² = 9 or a² = -9
But a ∈ R, a² ≠ -9
∴ a² = 9
∴ a = ±3
When a = 3, b = \(\frac{9}{3}\) = 3
When a = 3, b = \(\frac{9}{-3}\) = -3
∴ \(\sqrt{18 \mathrm{i}}\) = ±3(1 + i)

(v) Let \(\sqrt{3-4 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
3 – 4i = a² + b²i² + 2abi
∴ 3 – 4i = a² – b² + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 3 and 2ab = -4
∴ a² – b² = 3 and b = \(\frac{-2}{a}\)
∴ a² – \(\left(-\frac{2}{a}\right)^{2}\) = 3
∴ a² – \(\frac{4}{a^{2}}\) = 3
∴ a⁴ – 4 = 3a²
∴ a⁴ – 3a² – 4 = 0
∴ (a² – 4)(a² + 1) = 0
∴ a² = 4 or a² = -1
But, a ∈ R, a² ≠ -1
∴ a² = 4
∴ a = ±2
When a = 2, b = \(\frac{-2}{2}\) = -1
When a = -2, b = \(\frac{-2}{-2}\) = 1
∴ \(\sqrt{3-4 i}\) = ±(2 – i)

(vi) Let \(\sqrt{6+8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
6 + 8i = a² + b²i² + 2abi
∴ 6 + 8i = a² – b² + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 6 and 2ab = 8
∴ a² – b² = 6 and b = \(\frac{4}{\mathrm{a}}\)
∴ a² – \(\left(\frac{4}{a}\right)^{2}\) = 6
∴ a² – \(\frac{16}{a^{2}}\) = 6
∴ a⁴ – 16 = 6a²
∴ a⁴ – 6a² – 16 = 0
∴ (a² – 8)(a² + 2) = 0
∴ a² = 8 or a² = -2
But a ∈ R, a² ≠ -2
∴ a² = 8
∴ a = ±2√2
When a = 2√2, b = \(\frac{4}{2 \sqrt{2}}\) = √2
When a = -2√2, b = \(\frac{4}{-2 \sqrt{2}}\) = -√2
∴ \(\sqrt{6+8 i}\) = ±(2√2 + √2i) = ±√2(2 + i)

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Ex 2.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Insurance and Annuity Ex 2.1

Question 1.
Find the premium on a property worth ₹ 25,00,000 at 3% if
(i) the property is fully insured
(ii) the property is insured for 80% of its value.
Solution:
Case-1
Property value = ₹ 25,00,000
Rate of Premium = 3%
Policy Value = ₹ 25,00,000
∴ Amount of Premium = 3% × 25,00,000 = ₹ 75,000
Case-2
Property Value = ₹ 25,00,000
Policy value = 80% × 25,00,000 = ₹ 20,00,000
Rate of Premium = 3%
∴ Amount of Premium = 3% × 20,00,000 = ₹ 60,000

Question 2.
A shop is valued at ₹ 3,60,000 for 75% of its value. If the rate of premium is 0.9%, find the premium paid by the owner of the shop. Also, find the agents commission if the agent gets commission at 15% of the premium.
Solution:
Property Value = ₹ 3,60,000
Policy Value = 75% × 3,60,000 = ₹ 2,70,000
Rate of Premium = 0.9%
∴ Amount of Premium = 0.9% × 2,70,000 = ₹ 2,430
Rate of Commission = 15%
∴ Amount of Commission = 15% × 2,430 = ₹ 364.5

Question 3.
A person insures his office valued at ₹ 5,00,000 for 80% of its value. Find the rate of premium if he pays ₹ 13,000 as premium. Also, find agent’s commission at 11%.
Solution:
Property Value = ₹ 5,00,000
Policy Value = 80% × 5,00,000 = ₹ 4,00,000
Amount of Premium = ₹ 13000
Let the rate of Premium be x%
Amount of premium = Rate × Policy Value
∴ 13000 = x% × 4,00,000
∴ \(\frac{13,000}{4,00,000}=\frac{x}{100}\)
∴ \(\frac{13,000 \times 100}{4,00,000}\) = x
∴ x = 3.25%
Rate of commission = 11%
∴ Amount of Commission = 11% × 13,000 = ₹ 1,430

Question 4.
A building is insured for 75% of its value. The annual premium at 0.70 percent amounts to ₹ 2625. If the building is damaged to the extent of 60% due to fire, how much can be claimed under the policy?
Solution:
Let the Property Value of building be ₹ x
Policy Value = 75% × x = 0.75x
Rate of Premium = 0.70%
Amount of Policy = Rate × Policy Value
2625 = 0.70% × 0.75x
\(\frac{2625}{0.75}\) = 0.70% × x
3520 = \(\frac{0.70}{100}\) × x
\(\frac{3500 \times 100}{0.70}\) = x
x = ₹ 5,00,000
∴ Damage = 60% × Property Value
= \(\frac{60}{100}\) × 5,00,000
= ₹ 3,00,000
∴ Policy Value = 0.75 × 3,00,000 = ₹ 2,25,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,25,000}{5,00,000}\) × 3,00,000
= ₹ 1,35,000

Question 5.
A stock worth ₹ 7,00,000 was insured for ₹ 4,50,000. Fire burnt stock worth ₹ 3,00,000 completely and damaged there remaining stock to the extent of 75% of its value. What amount can be claimed undertaken policy?
Solution:
Property Value = ₹ 7,00,000
Policy Value = ₹ 4,50,000
Complete Loss = 3,00,000
Partial loss = 75% × [7,00,000 – 3,00,000]
= \(\frac{75}{100}\) × 4,00,000
= ₹ 3,00,000
∴ Total loss = ₹ 3,00,000 + ₹ 3,00,000 = ₹ 6,00,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{4,50,000}{7,00,000}\) × 6,00,000
= ₹ 3,85,714.29

Question 6.
A cargo of rice was insured at 0.625 % to cover 80% of its value. The premium paid was ₹ 5,250. If the price of rice is ₹ 21 per kg. find the quantity of rice (in kg) in the cargo.
Solution:
Let Property Value be ₹ x
Policy Value = 80% × x = ₹ 0.8x
Rate of Policy = 0.625%
Amount of Premium = Rate × Policy value
∴ 5250 = 0.625% × 0.8x
∴ 5250 = 0.005x
∴ x = \(\frac{5250}{0.005}\)
∴ x = ₹ 10,50,000
Rate of Rice = ₹ 21/kg
∴ Quantity of Rice (in kg) = \(\frac{\text { Total value }}{\text { Rate of Rice }}\)
= \(\frac{10,50,000}{21}\)
= 50,000 kgs

Question 7.
60,000 articles costing ₹ 200 per dozen were insured against fire for ₹ 2,40,000. If 20% of the articles were burnt and 7,200 of the remaining articles were damaged to the extent of 80% of their value, find the amount that can be claimed under the policy.
Solution:
No of articles = 60,000
Cost of articles = ₹ 200/dozen
∴ Property of Value = \(\frac{60,000}{12}\) × 200 = ₹ 1o,oo,ooo
∴ Policy Value = ₹ 2,40,000
Complete Loss = 20% × 10,00,000 = ₹ 2,00,000
Partial loss = \(\frac{7200}{12}\) × 200 × 80% = ₹ 96,000
∴ Total loss = 2,00,000 + 96,000 = ₹ 2,96,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,40,000}{10,00,000}\) × 2,96,000
= ₹ 71,040

Question 8.
The rate of premium is 2% and other expenses are 0.075%. A cargo worth ₹ 3,50,100 is to be insured so that all its value and the cost of insurance will be recovered in the event of total loss.
Solution:
Let the Policy Value of Cargo be ₹ 100 which includes insurance and other expenses
∴ Property Value = 100 – [2 + 0.075] = ₹ 97.925
If Policy Value is ₹ 100, then Property Value is ₹ 97.925
If Property Value is ₹ 3,50,100
Then policy Value = \(\frac{100 \times 3,50,100}{97.925}\) = ₹ 3,57,518.51

Question 9.
A property worth ₹ 4,00,000 is insured with three companies. A, B, and C. The amounts insured with these companies are ₹ 1,60,000, ₹ 1,00,000 and ₹ 1,40,000 respectively. Find the amount recoverable from each company in the event of a loss to the extent of ₹ 9,000.
Solution:
Property Value = ₹ 4,00,000
Loss = ₹ 9,000
Total Value of Policies = 1,60,000 + 1,00,000 + 1,40,000 = ₹ 4,00,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
Claim of company A = \(\frac{1,60,000}{40,000}\) × 9,000 = ₹ 3,600
Claim of company B = \(\frac{1,00,000}{4,00,000}\) × 9,000 = ₹ 2,250
Claim of company C = \(\frac{1,40,000}{4,00,000}\) × 9,000 = ₹ 3,150

Question 10.
A car valued at ₹ 8,00,000 is insured for ₹ 5,00,000. The rate of premium is 5% less 20%. How much will the owner bear including the premium if value of the ear is reduced to 60% of its original value.
Solution:
Property Value = ₹ 8,00,000
Policy Value = ₹ 5,00,000
Rate of Premium = 5% less 20%
= 5% – 20% × 5%
= (5 – 1)%
= 4%
Amount of Premium = 4% × 5,00,000 = ₹ 20,000
Loss = [100 – 60]% × Property Value
= 40% × 8,00,000
= ₹ 3,20,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{5,00,000}{8,00,000}\) × 3,20,000
= ₹ 2,00,000
Loss bear by owner = Loss – claim + Premium
= 3,20,000 – 2,00,000 + 20,000
= ₹ 1,40,000

Question 11.
A shop and a godown worth ₹ 1,00,000 and ₹ 2,00,000 respectively were insured through an agent who was paid 12% of the total premium. If the shop was insured for 80% and the godown for 60% of their respective values, find the agent’s commission, given that the rate of premium was 0.80% less 20%.
Solution:
Rate of Premium = 0.80% Less 20%
= 0.80% – 20% × 0.80%
= (0.80 – 0.16)%
= 0.64%
For Shop
Property Value = ₹ 1,00,000
Policy Value = 80% × 1,00,000 = ₹ 80,000
Premium = 0.64% × 80,000 = ₹ 512
For Godown
Property Value = ₹ 2,00,000
Policy Value = 60% × 2,00,000 = ₹ 1,20,000
Premium = 0.64% × 1,20,000 = ₹ 768
∴ Total Premium = 512 + 768 = ₹ 1,280
Rate of Commission = 12%
∴ Agent Commission = 12% × 1,280 = ₹ 153.6

Question 12.
The rate of premium on a policy of ₹ 1,00,000 is ₹ 56 per thousand per annum. A rebate of ₹ 0.75 per thousand is permitted if the premium is paid annually. Find the net amount of premium payable if the policy holder pays the premium annually.
Solution:
Policy Value = ₹ 1,00,000
Rate of Premium = ₹ 56 per thousand p.a
Rate of Rebate = ₹ 0.75 per thousand p.a
Premium is paid annually
∴ Net rate of = 56 – 0.75 = ₹ 55.25 per thousand p.a.
∴ Net Amount ot Premium = \(\frac{1,00,000}{1000}\) × 55.25 = ₹ 5,525

Question 13.
A warehouse valued at ₹ 40,000 contains goods worth ₹ 2,40,000. The warehouse is insured against fire for ₹ 16,000 and the goods to the extent of 90% of their value. Goods worth ₹ 80,000 are completely destroyed, while the remaining goods are destroyed to 80% of their value due to a fire. The damage to the warehouse is to the extent of ₹ 8,000. Find the total amount that can be claimed.
Solution:
For Warehouse
Property Value = ₹ 40,000
Policy Value = ₹ 16,000
Loss = ₹ 8,000
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{16,000}{40,000}\) × 8,000
= ₹ 3,200
For Goods
Property Value = ₹ 2,40,000
Policy Value = 90% × 2,40,000 = ₹ 2,16,000
Complete Loss = 80,000
Partial Loss = 80% × (2,16,000 – 80,000)
= 80% × 1,36,000
= ₹ 1,08,800
Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{2,16,000}{24,000}\) × 1,08,800
= ₹ 97,920
∴ Total Claim = 3,200 + 97,920 = ₹ 1,01,120

Question 14.
A person takes a life policy for ₹ 2,00,000 for a period of 20 years. He pays premium for 10 years during which bonus was declared at an average rate of ₹ 20 per year per thousand. Find the paid up value of the policy if he discontinuous paying premium after 10 years.
Solution:
Policy Value = ₹ 2,00,000
Rate of Bonus = ₹ 20 Per thousand p.a.
Total Bonus = \(\frac{2,00,000 \times 20}{1,000}\) = ₹ 4,000
∴ Bonus for 10 years = 4,000 × 10 = ₹ 40,000
Period of Policy = 20 years
∴ Amount of Premium = \(\frac{2,00,000}{20}\) = ₹ 10,000 p.a.
∴ Total Premium for 10 years = 10,000 × 10 = ₹ 1,00,000
∴ Paid up Value of Policy = Total premium + Total Bonus
= 1,00,000 + 40,000
= ₹ 1,40,000

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1

(I) Choose the correct alternative.

Question 1.
An agent who gives a guarantee to his principal that the party will pay the sale price of goods is called
(a) Auctioneer
(b) Del Credere Agent
(c) Factor
(d) Broker
Answer:
(b) Del Credere Agent

Question 2.
An agent who is given the possession of goods to be sold is known as
(a) Factor
(b) Broker
(c) Auctioneer
(d) Del Credere Agent
Answer:
(a) Factor

Question 3.
The date on which the period of the bill expires is called
(a) Legal Due Date
(b) Grace Date
(c) Nominal Due Date
(d) Date of Drawing
Answer:
(c) Nominal Due Date

Question 4.
The payment date after adding 3 days of grace period is known as
(a) The legal due date
(b) The nominal due date
(c) Days of grace
(d) Date of drawing
Answer:
(a) The legal due date

Question 5.
The sum due is also called as
(a) Face value
(b) Present value
(c) Cash value
(d) True discount
Answer:
(a) Face value

Question 6.
P is the abbreviation of
(a) Face value
(b) Present worth
(c) Cash value
(d) True discount
Answer:
(b) Present worth

Question 7.
Banker’s gain is the simple interest on
(a) Banker’s discount
(b) Face Value
(c) Cash value
(d) True discount
Answer:
(d) True discount

Question 8.
The marked price is also called as
(a) Cost price
(b) Selling price
(c) List price
(d) Invoice price
Answer:
(c) List price

Question 9.
When only one discount is given then
(a) List price = Invoice price
(b) Invoice price = Net selling price
(c) Invoice price = Cost price
(d) Cost price = Net selling price
Answer:
(b) Invoice price = Net selling price

Question 10.
The difference between the face value and present worth is called
(a) Banker’s discount
(b) True discount
(c) Banker’s gain
(d) Cash value
Answer:
(b) True discount

(II) Fill in the blanks.

Question 1.
A person who draws the bill is called ____________
Answer:
Drawee

Question 2.
An ____________ is an agent who sells the goods by auction.
Answer:
Auctioneer

Question 3.
Trade discount is allowed on the ____________ price.
Answer:
Catalogue/List

Question 4.
The banker’s discount is also called ____________.
Answer:
Commercial Discount

Question 5.
The banker’s discount is always ____________ than the true discount.
Answer:
higher

Question 6.
The diffrence between the banker’s discount and the true discount is called ____________.
Answer:
bankers gain

Question 7.
The date by which the buyer is legally allowed to pay the amount is known as ____________.
Answer:
legal due date

Question 8.
A ____________ is an agent who brings together the buyer and the seller.
Answer:
broker

Question 9.
If buyer is allowed both trade and cash discounts, ____________ discount is fist calculated on ____________ price.
Answer:
Trade, Catalogue/List

Question 10.
____________ = List price (catalogue Price) – Trade Discount.
Answer:
Invoice Price

(III) State whether each of the following is True or False.

Question 1.
A broker is an agent who gives a guarantee to the seller that the buyer will pay the sale price of goods.
Answer:
False

Question 2.
A cash discount is allowed on the list price.
Answer:
False

Question 3.
Trade discount is allowed on catalogue price.
Answer:
True

Question 4.
The buyer is legally allowed 6 days grace period.
Answer:
False

Question 5.
The date on which the period of the bill expires is called the nominal due date.
Answer:
True

Question 6.
The difference between the banker’s discount and true discount is called sum due.
Answer:
False

Question 7.
The banker’s discount is always lower than the true discount.
Answer:
False

Question 8.
The banker’s discount is also called a commercial discount.
Answer:
True

Question 9.
In general cash, the discount is more than trade discount.
Answer:
False

Question 10.
A person can get both, trade discount and a cash discount.
Answer:
True

(IV) Solve the following problems.

Question 1.
A salesman gets a commission of 6.5% on the total sales made by him and a bonus of 1% on sales over ₹ 50,000. Find his total income on a turnover of ₹ 75,000.
Solution:
Rate of commission = 6.5% on the total sales
∴ Commission on a turnover of ₹ 75,000
= \(\frac{6.5}{100}\) × 75,000
= ₹ 4,875
Rate of bonus = 1% on sales over ₹ 50,000
∴ Amount of bonus = \(\frac{1}{100}\) × (75,000 – 50,000) = ₹ 250
∴ Total income of the sales man = ₹ 4,875 + ₹ 250 = ₹ 5,125

Question 2.
A shop is sold at 30% profit, the amount of brokerage at the rate of \(\frac{3}{4}\)% amounts to ₹ 73,125. Find the cost of the shop.
Solution:
Rate of brokerage = \(\frac{3}{4}\)%
Amount of brokerage = ₹ 73,125
Let the selling price of the shop be ₹ 100 then the brokerage = ₹ \(\frac{3}{4}\)
Thus, if the amount of brokerage is ₹ \(\frac{3}{4}\) then the selling price of the shop is ₹ 100
If the amount of brokerage is ₹ 73,125, then the selling price of the shop is = 73125 × \(\frac{4}{3}\) × 100 = ₹ 97,50,000
The shop is sold at 30% profit
∴ If the cost of the shop is ₹ 100, then it is sold at ₹ 130
Thus, if the shop is sold at ₹ 130, then its cost price is ₹ 100
If the shop is sold at ₹ 97,50,000 then its cost price is = \(\frac{97,50,000 \times 100}{130}\) = ₹ 75,00,000
Then, the cost of the shop is ₹ 75,00,000

Question 3.
A merchant gives 5% commission and 1.5% delcredere to his agents. If the agent sells goods worth ₹ 30,600 how much does he get? How much does the merchant receive?
Solution:
Rate of commission = 5%
Total sales = ₹ 30,600
Amount of commission = \(\frac{5}{100}\) × 30,600
Rate of delcredere = 1.5%
= \(\frac{1.5}{100}\) × 30,600
= ₹ 459
Thus, the agents gets 1,530 + 459 = ₹ 1,989
And the merchant receives = 30,600 – 1,989 = ₹ 28,611

Question 4.
After deducting commission at 7\(\frac{1}{2}\)% on first ₹ 50,000 and 5% on the balance of sales made by him, an agent remits ₹ 93,750 to his principal. Find the value of goods sold by him.
Solution:
Rate of commission = 7\(\frac{1}{2}\)% on first ₹ 50,000
= \(\frac{7.5}{100}\) × 50,000
= ₹ 3,750
Let the total sales be ₹ x
Rate of commission on the balance sales = 5%
Commission on the balance sales = \(\frac{5}{100}\) × (x – 50000) = \(\frac{x}{20}\) – 2,500
Total commission = 3750 + \(\frac{x}{20}\) – 2,500 = \(\frac{x}{20}\) + 1,250
Now, the amount to be remitted to the principal = Value of goods sold – Commission of the agent
= x – (\(\frac{x}{20}\) + 1250)
= \(\frac{19x}{20}\) – 1250
The agents remits ₹ 93,750 to his principal
∴ \(\frac{19x}{20}\) – 1,250 = 93,750
∴ \(\frac{19x}{20}\) = 95,000
∴ x = ₹ 1,00,000
Thus, the value of the goods sold by the agent is ₹ 1,00,000

Question 5.
The present worth of ₹ 11,660 due 9 months hence is ₹ 11,000. Find the rate of interest.
Solution:
Given, PW = ₹ 11,000, SD = ₹ 11,660
n = \(\frac{9}{12}\) year = \(\frac{3}{4}\) year
We have,

∴ The rate of interest is 8% p.a.

Question 6.
An article is marked at ₹ 800, a trader allows a discount of 2.5% and gains 20% on the cost. Find the cost price of the article?
Solution:
Marked price of the article = ₹ 800
Rate of discount = 2.5%
Amount of discount = \(\frac{2.5}{100}\) × 800 = ₹ 20
∴ Selling price of the article = 800 – 20 = ₹ 780
Now, given, gain = 20%
Let cost price of the article be ₹ 100, then
The selling price of the article is ₹ 120
Thus if cost price of the articles is ₹ x
Then the selling price is ₹ 780
∴ x = \(\frac{780 \times 100}{120}\)
∴ x = 650
∴ Cost price of the article is ₹ 650

Question 7.
A salesman is paid a fixed monthly salary plus commission on the sales. If on sale of ₹ 96,000 and ₹ 1,08,000 in two successive months he receives in all ₹ 17,600 and ₹ 18,800 respectively. Find his monthly salary and rate of commission paid to him.
Solution:
Let the monthly salary of the salesman be ₹ x
And the rate of commission be y%
Income = monthly salary + commission on the sales
17600 = x + \(\frac{y}{100}\) × 96,000
∴ 17600 = x + 960y ………(1)
and 18800 = x + \(\frac{y}{100}\) × 108000
∴ 18,800 = x + 1080y ………(2)
Subtracting equation (1) from equation (2), we get
1,200 = 120y
∴ y = 10
Substituting y = 10 in (1), we get
17,600 = x + 960(10)
∴ x = 17,600 – 9,600 = 8,000
∴ Salary of the salesman = ₹ 8,000
Rate of commission = 10%

Question 8.
A merchant buys some mixers at a 15% discount on catalogue price. The catalogue price is ₹ 5,500 per price of the mixer. The freight charges amount to 2\(\frac{1}{2}\)% on the catalogue price. The merchant sells each mixer at a 5% discount on the catalogue price. His net profit is ₹ 41,250, Find the number of mixers.
Solution:
Catalogue price of a mixer = ₹ 5,500
Trade discount = 15% on catalogue price
= \(\frac{15}{100}\) × 5,500
= ₹ 825
Freight charges = 2\(\frac{1}{2}\)% of the catalogue price
= \(\frac{5}{2} \times \frac{1}{100} \times 5,500\)
= ₹ 137.5
∴ Cost price of a mixer for the merchant = 5,500 – 825 + 137.5 = 4,812,5
Catalogue price = ₹ 5,500
Rate of discount = 5%
∴ Selling price of one mixer = 5500 – \(\frac{5}{100}\) × 5,500 = ₹ 5,225
∴ Profit on one mixer = 5,225 – 4,812.5 = ₹ 412.5
Now, total profit = ₹ 41,250
∴ Number of mixers = \(\frac{41,250}{412.5}\) = 100
Thus the number of mixers is 100.

Question 9.
A bill is drawn for ₹ 7,000 on 3rd May for 3 months and is discounted on 25th May at 5.5% Find the present worth.
Solution:
Face value of the bill = ₹ 7,000
Date of drawing = 3rd May
Period = 3 months
Normal due date = 3rd August
Legal due date = 6th August
Rate of interest = 5.5%
Date of discounting = 25th May
Unexpired period (number of days from date of discounting to legal due date)

∴ Bankers discount = 7,000 × \(\frac{73}{365} \times \frac{5.5}{100}\) = ₹ 77
Also PW = SD – BD
= 7,000 – 77
= ₹ 6,923
∴ Present worth is ₹ 6,923

Question 10.
A bill was drawn on 14th April 2005 for ₹ 3,500 and was discounted on 6th July 2005 at 5% per annum. The banker paid ₹ 3,465 for the bill. Find the period of the bill.
Solution:
Face value of the bill = ₹ 3,500
Date of drawing = 14/04/2005
Date of discount = 06/07/2005
Rate of interest = 5%
Cash value = ₹ 3,465
Bankers discount = Face value – Cash value
= 3,500 – 3,465
= ₹ 35
Let the unexpired days be n days
∴ BD = \(\frac{\mathrm{FV} \times n \times r}{365 \times 100}\)
∴ 35 = \(\frac{3,500 \times n \times 5}{365 \times 100}\)
∴ n = 73 days
Thus, legal due date is 73 days from the date of discounting

∴ Legal due date = 17/09/2005
∴ Nominal due date = 14/09/2005
∴ The period of the bill is 5 months

Question 11.
The difference between true discount and banker’s discount on 6 months hence at 4% p.a. is ₹ 80. Find the true discount, banker’s discount, and amount of the bill.
Solution:
BG = BD – TD
∴ BG = ₹ 80
Also BG = \(\frac{\mathrm{TD} \times n \times r}{100}\)
∴ 80 = \(\frac{\mathrm{TD} \times 6 \times 4}{12 \times 100}\)
∴ TD = \(\frac{80 \times 100}{2}\)
∴ TD = ₹ 4,000
Now BD = TD + BG
= 4,000 + 80
= ₹ 4,080
Also, BD = \(\frac{\mathrm{FV} \times n \times r}{100}\)
∴ 4,080 = \(\frac{\mathrm{FV} \times 6 \times 4}{12 \times 100}\)
∴ FV = \(\frac{4,080 \times 100}{2}\)
∴ FV = ₹ 2,04,000
Amount of the bill = ₹ 2,04,000

Question 12.
A manufacturer makes a clear profit of 30% on the cost after allowing a 35% discount. If the cost of production rises by 20%, by what percentage should he reduce the rate of discount so as to make the same rate of profit keeping his list prices unaltered.
Solution:
Rate of discount = 35%
Let the list price be ₹ 100.
Then discount at 35% = ₹ 35
∴ Net selling price = 100 – 35 = ₹ 65 ……..(1)
The manufacturer makes a clear profit of 30% on the cost after allowing a 35% Discount.
Let the cost be ₹ 100.
Then selling price at 30% profit is 100 + 30 = ₹ 130.
Thus, if the net selling price is ₹ 130, then the cost price is ₹ 100.
But, the net selling price is ₹ 130, then the cost price is ₹ 65 ……[from (1)]
∴ The cost price is \(\frac{65}{130} \times 100\) = ₹ 50
Hence, we have,

Now, the cost of production has increased by 20%.
Let the old cost price be ₹ 100.
∴ The new cost price is ₹ 120.
But, the old cost price is ₹ 50.
∴ The new cost price is = \(\frac{50}{100} \times 120\) = ₹ 60.
The old net price is ₹ 65.
Now 20% of ₹ 65 = \(\frac{20}{100} \times 65\) = ₹ 13
∴ New net price = 65 + 13 = ₹ 78
Hence, we have

Now, 100 – 78 = ₹ 22
Thus, the rate of discount should be reduced by 22%, The original rate of discount is 35%.
Hence, the reduction in discount should be (35 – 22)% = 13%
so as to make the same rate of profit, keeping the list price unaltered.

Question 13.
A trader offers a 25% discount on the catalogue price of the radio and yet makes a 20% profit. If he gains ₹ 160 per radio, what must be the catalogue price of the radio?
Solution:
Rate of discount = 25% on the catalogue price of a radio.
Let the catalogue price of the radio be ₹ 100.
Then, the discount on a radio = ₹ 25.
Net selling price = 100 – 25 = ₹ 75.
He makes a profit of 20%.
Let the cost price be ₹ 100.
Then, at 20% profit, net selling price = ₹ 120.
Thus, if net SP is ₹ 120, then cost price is ₹ 100.
But, the net SP is ₹ 75.
∴ The cost price is \(\frac{75}{120}\) × 100 = \(\frac{750}{12}\) = ₹ 62.50
∴ Profit on a radio set = 75 – 62.5 = ₹ 12.50
Thus, if the profit on a radio set is ₹ 12.50 then its catalogue price is ₹ 100.
But the profit on a radio set is ₹ 160.
∴ The catalogue price of radio = \(\frac{160}{12.50}\) × 100
= 12.80 × 100
= ₹ 1,280
∴ Thus, the catalogue price of the radio is ₹ 1280

Question 14.
A bill of ₹ 4,800 was drawn on 9th March 2006 at 6 months and was discounted on 19th April 2006 for 6\(\frac{1}{4}\)% p.a. How much does the banker charge and how much does the holder receive?
Solution:
Face value of the bill = ₹ 4.800
Date of drawing = 09/03/2006
Period of the bill = 6 months
Normal due date = 09/09/2006
Legal due date = 12/09/2006
Rate of discount = 6\(\frac{1}{4}\)% = 6.25%
Now, for the unexpired

Thus the banker charges ₹ 120
Amount received by the holder = 4,800 – 120 = ₹ 4,680

Question 15.
A bill of ₹ 65,700 drawn on July 10 for 6 months was discounted for ₹ 65,160 at 5% p.a. On what day was the bill discounted?
Solution:
BD = FV – Cash value
= 65,700 – 65,160
= ₹ 540
Let the unexpired days be x days
BD = \(\frac{\mathrm{FV} \times n \times r}{100}\)
∴ 540 = \(\frac{65,700 \times x \times 5}{365 \times 100}\)
∴ x = 60 days
The unexpired days = 60 days
Date-of drawing = 10th July
Period of the bill = 6 months
Nominal due date = 10th January (next year)
Legal due date = 13th January (next year)
Then the date of discount is 60 days before, the legal due date

∴ The date of discounting is 14th November

Question 16.
An agent sold a car and charged a 3% commission on the sale value. If the owner of the car received ₹ 48,500, find the sale value of the car. If the agent charged 2% from the buyer, find his total remuneration.
Solution:
Let the sale value of the car be ₹ x
Rate of commission of the agent = 3%
Since the owner received ₹ 48,500 after agent has charged his commission
x – \(\frac{3 x}{100}\) = 48500
∴ \(\frac{97 x}{100}\) = 48500
∴ x = \(\frac{48,500 \times 100}{97}\)
∴ x = ₹ 50,000
∴ Sale value of the car = ₹ 50,000
Against commission received from the owner = \(\frac{3}{100}\) × 50,000 = ₹ 1500
Against commission received from the buyer = \(\frac{2}{100}\) × 50,000 = ₹ 1000
∴ Agents total remuneration = 1,500 + 1,000 = ₹ 2,500

Question 17.
An agent is paid a commission of 4% on cash sales and 6% on credit sales made by him. If on the sale of ₹ 51,000 the agent claims a total commission of ₹ 2,700, find the sales made by him for cash and on credit.
Solution:
Total sales = ₹ 51,000
Let eash sales be ₹ x
∴ Credit sales = ₹ (51,000 – x)
Agent’s commission on cash sales = 4%
= \(\frac{4}{100}\) × x
= \(\frac{4x}{100}\)
Commission on credit sales = 6%
= \(\frac{6}{100}\)(51,000 – x)
Given total commission = ₹ 2,700

∴ Cash sales = ₹ 18,000
∴ Credit sales = 51,000 – 18,000 = ₹ 33,000

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Ex 2.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Insurance and Annuity Ex 2.2

Question 1.
Find the accumulated (future) value of annuity of ₹ 800 for 3 year at interest rate 8% compounded annually. [Given: (1.08)³ = 1.2597]
Solution:
∵ C = ₹ 800
∵ n = 3 years
∵ r = 8% p.a.

∴ A = 10,000[(1.08)³ – 1]
∴ A = 10,000[1.2597 – 1]
∴ A = 10,000 × 0.2597
∴ A = ₹ 2,597

Question 2.
A person invested ₹ 5,000 every year in finance company that offered him interest compounded at 10% p.a., what is the amount accumulated after 4 years? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ C = ₹ 5,000
∵ r = 10% p.a.

= 50,000[(1.1)⁴ – 1]
= 50,000[1.4641 – 1]
= 50,000 × 0.4641
= ₹ 23,205

Question 3.
Find the amount accumulated after 2 years if a sum of ₹ 24,000 is invested every six months at 12% p.a. compounded half yearly. [Given: (1.06)⁴ = 1.2625]
Solution:
∵ C = ₹ 24,000
∵ n = 2 years
But invested half yearly
∴ n = 2 × 2 = 4
∵ r = 12% p.a. compounded half yearly

= 4,00,000[(1.06)⁴ – 1]
= 4,00,000[1.2625 – 1]
= 4,00,000 × 0.2625
= ₹ 1,05,000

Question 4.
Find the accumulated value after 1 year of an annuity immediate in which ₹ 10,000 are invested every quarter at 16% p.a. compounded quarterly. [Given: (1.04)⁴ = 1.1699]
Solution:
∵ C = ₹ 10,000
∵ n = 1 year
But invested every quarterly
∴ n = 1 × 4 = 4
∴ r = 16% p.a. compounded quarterly

= 2,50,000 [1.1699 – 1]
= 2,50,000 × 0.1699
= ₹ 42,475

Question 5.
Find the present value of an annuity immediate of ₹ 36,000 p.a. for 3 years at 9% p.a. compounded annually. [Given: (1.09)^-3 = 0.7722]
Solution:
∵ C = ₹ 36,000
∵ n = 3 years
∵ r = 9% p.a.

= 4,00,000 × 0.2278
= ₹ 91,120

Question 6.
Find the present value of ordinary annuity of ₹ 63,000 p.a. for 4 years at 14% p.a. compounded annually. [Given: (1.14)^-4 = 0.5921]
Solution:
∵ C = ₹ 63,000
∵ n = 4 years
∵ r = 14% p.a.

= 4,50,000[1 – 0.5921]
= 4,50,000 × 0.4079
= ₹ 1,83,555

Question 7.
A lady plans to save for her daughter’s marriage. She wishes to accumulate a sum of ₹ 4,64,100 at the end of 4 years. What amount should she invest every year if she get an interest of 10%p.a. compounded annually? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ A = ₹ 4,64,100
∵ n = 4 years
∵ r = 10% p.a.

∴ 46,410 = C[1.4641 – 1]
∴ 46,410 = C × 0.4641
∴ \(\frac{46,410}{0.4641}\) = C
∴ C = ₹ 1,00,000

Question 8.
A person wants to create a fund of ₹ 6,96,150 after 4 years at the time of his retirement. He decides to invest a fixed amount at the end of every year in a bank that offers him interest of 10% p.a. compounded annually. What amount should he invest every year? [Given: (1.1)⁴ = 1.4641]
Solution:
∵ A = ₹ 6,96,150
∵ n = 4 years
∵ r = 10% p.a

∴ 69,615 = C[1.4641 – 1]
∴ 69,615 = C × 0.4641
∴ \(\frac{69,615}{0.4641}\) = C
∴ C = ₹ 1,50,000

Question 9.
Find the rate of interest compounded annually if an annuity immediate at ₹ 20,000 per year amounts to ₹ 2,60,000 in 3 years.
Solution:
∵ C = ₹ 20,000
∵ A = ₹ 2,60,000
∵ n = 3 years

∴ 13i = 3i + 3 i² + i³
∴ 13i = i(3 + 3i + i²)
∴ 13 = 3 + i + i²
∴ i² + 3i + 3 – 13 = 0
∴ i² + 3i – 10 = 0
∴ (i + 5) (i – 2) = 0
∴ i + 5 = 0 or i – 2 = 0
∴ i = -5 or i = 2
∵ Rate of interest cannot be negative
∴ i = 2 is accepted
∴ \(\frac{r}{100}\) = 2
∴ r = 200% p.a.

Question 10.
Find the number of years for which an annuity of ₹ 500 is paid at the end of every years, if the accumulated amount works out to be ₹ 1,655 when interest is compounded annually at 10% p.a.
Solution:
∵ C = 7500
∵ A = 71,655
∵ r = 10% p.a.


∴ 0.331 + 1 = (1.1)ⁿ
∴ 1.331 = (1.1)ⁿ
∴ (1.1)³ = (1.1)ⁿ
∴ n = 3 years

Question 11.
Find the accumulated value of annuity due of ₹ 1,000 p.a. for 3 years at 10% p.a. compounded annually. [Given: (1.1)³ = 1.331]
Solution:
∵ C = ₹ 1,000
∵ n = 3 years
∵ r = 10% p.a.

∴ A’ = 10,000 × 1.1[(1.1)³ – 1]
∴ A’ = 11,000 [1.331 – 1]
∴ A’ = 11,000 × 0.331
∴ A’ = ₹ 3,641

Question 12.
A person plans to put ₹ 400 at the beginning of each year for 2 years in a deposit that gives interest at 2% p.a. compounded annually. Find the amount that will be accumulated at the end of 2 years. [Given: (1.02)² = 1.0404]
Solution:
∵ C = ₹ 400
∵ r = 2% p.a.


= 20,000 (1.02) (1.0404 – 1)
= 20,400 [0.0404]
= ₹ 824.16

Question 13.
Find the present value of an annuity due of ₹ 600 to be paid quarterly at 32% p.a. compounded quarterly. [Given (1.08)^-4 = 0.7350]
Solution:
∵ C = ₹ 600
∵ n = 1 year
∴ But invested every quarterly
∴ n = 1 × 4 = 4
∵ r = 32% p.a. compounded quarterly

= 7,500(1.08) [1 – 0.7350]
= 8,100 [0.2650]
= ₹ 2,146.5

Question 14.
An annuity immediate is to be paid for some years at 12% p.a. The present value of the annuity is ₹ 10,000 and the accumulated value is ₹ 20,000. Find the amount of each annuity payment.
Solution:
∵ r = 12% p.a.
∴ i = \(\frac{r}{100}=\frac{12}{100}\) = 0.12
∵ P = ₹ 10,000
∵ A = ₹ 20,000
∵ \(\frac{1}{P}-\frac{1}{A}=\frac{i}{C}\)

∴ C = 0.12 × 20,000
∴ C = ₹ 2,400

Question 15.
For an annuity immediate paid for 3 years with interest compounded at 10% p.a. the present value is ₹ 24,000. What will be the accumulated value after 3 years? [Given (1.1)³ = 1.331]
Solution:
∵ n = 3 years
∵ P = ₹ 24,000
∵ r = 10% p.a.
∴ i = \(\frac{r}{100}=\frac{10}{100}\) = 0.1
∵ A = P(1 + i)ⁿ
∴ A = 24,000 [1 + 0.1]³
∴ A = 24,000 × (1.1)³
∴ A = 24,000 × 1.331
∴ A = ₹ 31,944

Question 16.
A person sets up a sinking fund in order to have ₹ 1,00,000 after 10 years. What amount should be deposited bi-annually in the account that pays him 5% p.a. compounded semi-annually? [Given: (1.025)²⁰ = 1.675]
Solution:
∴ A = ₹ 1,00,000
∴ n = 10 years
But, invested half yearly
∴ n = 10 × 2 = 20
∵ r = 5% p.a. compounded half yearly
∴ r = \(\frac{r}{2}=\frac{5}{2}\) = 2.5%
∴ i = \(\frac{r}{100}=\frac{2.5}{100}\) = 0.025

∴ 2,500 = C[1.675 – 1]
∴ 2,500 = C × 0.675
∴ \(\frac{2,500}{0.675}\) = C
∴ C = ₹ 3,703.70