Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.2 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Sequences and Series Ex 4.2
Question 1.
For the following G.P.’s, find Sn.
(i) 3, 6, 12, 24, …..
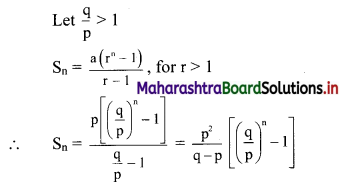
(ii) \(\mathbf{p}, \mathbf{q}, \frac{\mathbf{q}^{2}}{\mathbf{p}}, \frac{\mathbf{q}^{3}}{\mathbf{p}^{2}}, \ldots\)
Solution:

Question 2.
For a G.P., if
(i) a = 2, r = \(-\frac{2}{3}\), find S6.
(ii) S5 = 1023, r = 4, find a.
Solution:

![]()
Question 3.
For a G. P., if
(i) a = 2, r = 3, Sn = 242, find n.
(ii) sum of the first 3 terms is 125 and the sum of the next 3 terms is 27, find the value of r.
Solution:
(i) a = 2, r = 3, Sn = 242
Sn = \(a\left(\frac{r^{n}-1}{r-1}\right)\), for r > 1

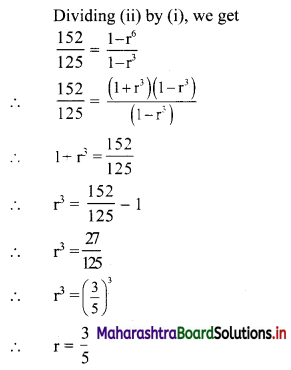
Question 4.
For a G. P.,
(i) if t3 = 20, t6 = 160, find S7.
(ii) if t4 = 16, t9 = 512, find S10.
Solution:
(i) t3 = 20, t6 = 160
tn = arn-1
∴ t3 = ar3-1 = ar2
∴ ar2 = 20
∴ a = \(\frac{20}{\mathrm{r}^{2}}\) ……(i)


Question 5.
Find the sum to n terms:
(i) 3 + 33 + 333 + 3333 + ……
(ii) 8 + 88 + 888 + 8888 + ……..
Solution:
(i) Sn = 3 + 33 + 333 +….. upto n terms
= 3(1 + 11 + 111 +….. upto n terms)
= \(\frac{3}{9}\)(9 + 99 + 999 + … upto n terms)
= \(\frac{3}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{3}{9}\)[(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P.
with a = 10, r = \(\frac{100}{10}\) = 10
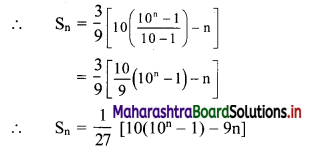
(ii) Sn = 8 + 88 + 888 + … upto n terms
= 8(1 + 11 + 111 + … upto n terms)
= \(\frac{8}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{8}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{8}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10
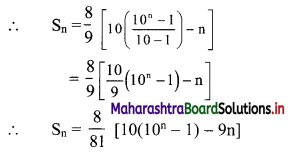
![]()
Question 6.
Find the sum to n terms:
(i) 0.4 + 0.44 + 0.444 + ……
(ii) 0.7 + 0.77 + 0.777 + …..
Solution:
(i) Sn = 0.4 + 0.44 + 0.444 + ….. upto n terms
= 4(0.1 + 0.11 + 0.111 + …. upto n terms)
= \(\frac{4}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{4}{9}\) [(i – 0.1) + (1 – 0.01) + (1 – 0.001) … upto n terms]
= \(\frac{4}{9}\) [(1 + 1 + 1 + …n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1
∴ Sn = \(\frac{4}{9}\left\{\mathrm{n}-0.1\left[\frac{1-(0.1)^{\mathrm{n}}}{1-0.1}\right]\right\}\)

(ii) Sn = 0.7 + 0.77 + 0.777 + … upto n terms
= 7(0.1 + 0.11 + 0.111 + … upto n terms)
= \(\frac{7}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{7}{9}\) [(1 – 0.1) + (1 – 0.01) + (1 – 0.001) +… upto n terms]
= \(\frac{7}{9}\) [(1 + 1 + 1 +… n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

Question 7.
Find the nth terms of the sequences:
(i) 0.5, 0.55, 0.555,…..
(ii) 0.2, 0.22, 0.222,…..
Solution:
(i) Let t1 = 0.5, t2 = 0.55, t3 = 0.555 and so on.
t1 = 0.5
t2 = 0.55 = 0.5 + 0.05
t3 = 0.555 = 0.5 + 0.05 + 0.005
∴ tn = 0.5 + 0.05 + 0.005 + … upto n terms
But 0.5, 0.05, 0.005, … upto n terms are in G.P. with a = 0.5 and r = 0.1
∴ tn = the sum of first n terms of the G.P.

(ii) Let t1 = 0.2, t2 = 0.22, t3 = 0.222 and so on
t1 = 0.2
t2 = 0.22 = 0.2 + 0.02
t3 = 0.222 = 0.2 + 0.02 + 0.002
∴ tn = 0.2 + 0.02 + 0.002 + … upto n terms
But 0.2, 0.02, 0.002, … upto n terms are in G.P. with a = 0.2 and r = 0.1
∴ tn = the sum of first n terms of the G.P.

Question 8.
For a sequence, if Sn = 2(3n-1), find the nth term, hence showing that the sequence is a G.P.
Solution:

Question 9.
If S, P, R are the sum, product and sum of the reciprocals of n terms of a G.P. respectively, then verify that \(\left(\frac{\mathbf{S}}{\mathbf{R}}\right)^{\mathbf{n}}\) = P2.
Solution:
Let a be the 1st term and r be the common ratio of the G.P.
∴ the G.P. is a, ar, ar2, ar3, …, arn-1


![]()
Question 10.
If Sn, S2n, S3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that Sn (S3n – S2n) = (S2n – Sn)2.
Solution:
Let a and r be the 1st term and common ratio of the G.P. respectively.

