Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.1
Question 1.
Find the principal solutions of the following equations :
(i) cos θ= \(\frac{1}{2}\)
Solution:
We know that, cos\(\frac{\pi}{3}\) = \(\frac{1}{2}\) and cos (2π – θ) = cos θ
∴ cos\(\frac{\pi}{3}\) = cos(2π – \(\frac{\pi}{3}\)) = cos\(\frac{5 \pi}{3}\)
∴ cos\(\frac{\pi}{3}\) = cos\(\frac{5 \pi}{3}\) = \(\frac{1}{2}\), where
0 < \(\frac{\pi}{3}\) < 2π and 0 < \(\frac{5 \pi}{3}\) < 2π
∴ cos θ = \(\frac{1}{2}\) gives cos θ = cos\(\frac{\pi}{3}\) = cos\(\frac{5 \pi}{3}\)
∴ θ = \(\frac{\pi}{3}\) and θ = \(\frac{5 \pi}{3}\)
Hence, the required principal solutions are
θ = \(\frac{\pi}{3}\) and θ = \(\frac{5 \pi}{3}\)
(ii) sec θ = \(\frac{2}{\sqrt{3}}\)
Solution:
(iii) cot θ = \(\sqrt {3}\)
Solution:
The given equation is cot θ = \(\sqrt {3}\) which is same as tan θ = \(\frac{1}{\sqrt{3}}\).
We know that,
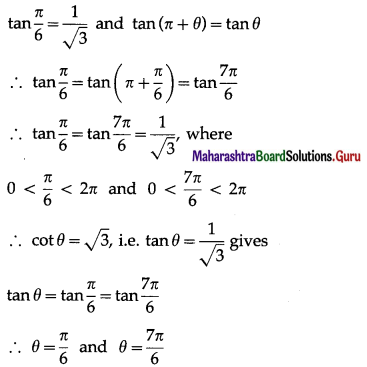
Hence, the required principal solution are
θ = \(\frac{\pi}{6}\) and θ = \(\frac{7 \pi}{6}\).
![]()
(iv) cot θ = 0.
Solution:
Question 2.
Find the principal solutions of the following equations:
(i) sinθ = \(-\frac{1}{2}\)
Solution:
We know that,
sin\(\frac{\pi}{6}\) = \(\frac{1}{2}\) and sin (π + θ) = -sinθ,
sin(2π – θ) = -sinθ

Hence, the required principal solutions are
θ = \(\frac{7\pi}{6}\) and θ = \(\frac{11 \pi}{6}\).
(ii) tanθ = -1
Solution:
We know that,
tan\(\frac{\pi}{4}\) = 1 and tan(π – θ) = -tanθ,
tan(2π – θ) = -tanθ
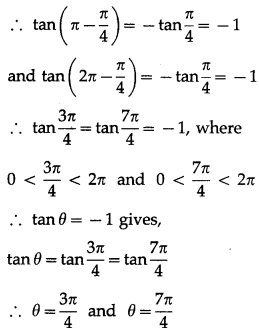
Hence, the required principal solutions are
θ = \(\frac{3\pi}{4}\) and θ = \(\frac{7 \pi}{4}\).
![]()
(iii) \(\sqrt {3}\) cosecθ + 2 = 0.
Solution:
Question 3.
Find the general solutions of the following equations :
(i) sinθ = \(\frac{1}{2}\)
Solution:
(i) The general solution of sin θ = sin ∝ is
θ = nπ + (-1 )n∝, n ∈ Z
Now, sinθ = \(\frac{1}{2}\) = sin\(\frac{\pi}{6}\) …[∵ sin\(\frac{\pi}{6}\) = \(\frac{1}{2}\)]
∴ the required general solution is
θ = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ Z.
(ii) cosθ = \(\frac{\sqrt{3}}{2}\)
Solution:
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
Now, cosθ = \(\frac{\sqrt{3}}{2}\) = cos\(\frac{\pi}{6}\) …[∵ cos\(\frac{\pi}{6}\) = \(\frac{\sqrt{3}}{2}\)]
∴ the required general solution is
θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z.
![]()
(iii) tanθ = \(\frac{1}{\sqrt{3}}\)
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z
Now, tan θ = \(\frac{1}{\sqrt{3}}\) = tan\(\frac{\pi}{6}\) …[tan\(\frac{\pi}{6}\) = \(\frac{1}{\sqrt{3}}\)]
∴ the required general solution is
θ = nπ + \(\frac{\pi}{6}\) , n ∈ Z.
(iv) cotθ = 0.
Solution:
The general solution of tan θ = tan ∝ is
θ = nπ + ∝, n ∈ Z
Now, cot θ = 0 ∴ tan θ does not exist
∴ tanθ = tan\(\frac{\pi}{2}\) [∵ tan\(\frac{\pi}{2}\) does not exist]
∴ the required general solution is
θ = nπ + \(\frac{\pi}{2}\), n ∈ Z.
![]()
Question 4.
Find the general solutions of the following equations:
(i) secθ = \(\sqrt {2}\)
Solution:
The general solution of cos θ = cos ∝ is
θ = nπ ± ∝, n ∈ Z.
Now, secθ = \(\sqrt {2}\) ∴ cosθ = \(\frac{1}{\sqrt{2}}\)
∴ cosθ = cos\(\frac{\pi}{4}\) ….[cos\(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)]
∴ the required general solution is
θ = 2nπ ± \(\frac{\pi}{4}\), n ∈ Z.
(ii) cosecθ = –\(\sqrt {2}\)
Solution:
The general solution of sinθ = sin∝ is

(iii) tanθ = -1
Solution:
The general solution of tanθ = tan∝ is

![]()
Question 5.
Find the general solutions of the following equations :
(i) sin 2θ = \(\frac{1}{2}\)
Solution:
The general solution of sin θ = sin ∝ is
θ = nπ + (-1)n∝, n ∈ Z

(ii) tan \(\frac{2 \theta}{3}\) = \(\sqrt {3}\)
Solution:
The general solution of tan θ = tan ∝ is
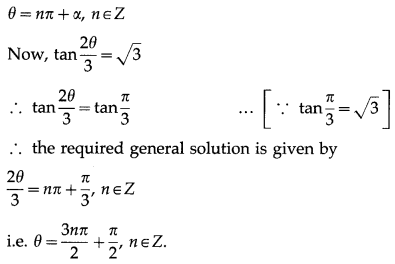
![]()
(iii) cot 4θ = -1
Solution:
The general solution of tan θ = tan ∝ is

Question 6.
Find the general solutions of the following equations :
(i) 4 cos2θ = 3
Solution:
The general solution of cos2θ = cos2 ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 cos2θ = 3

(ii) 4 sin2θ = 1
Solution:
The general solution of sin2θ = sin2 ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 sin2θ = 3

![]()
(iii) cos 4θ = cos 2θ
Solution:
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
∴ the general solution of cos 4θ = cos 2θ is given by
4θ = 2nπ ± 2θ, n ∈ Z
Taking positive sign, we get
4θ = 2nπ + 2θ, n ∈ Z
∴ 2θ = 2nπ, n ∈ Z
∴ θ = nπ, n ∈ Z
Taking negative sign, we get
4θ = 2nπ – 2θ, n ∈ Z
∴ 6θ = 2nπ, n ∈ Z
∴ θ = \(\frac{n \pi}{3}\), n ∈ Z
Hence, the required general solution is
θ = \(\frac{n \pi}{3}\), n ∈ Z or ∴ θ = nπ, n ∈ Z.
Alternative Method:
cos 4θ = cos 2θ
∴ cos4θ – cos 20 = 0
∴ -2sin\(\left(\frac{4 \theta+2 \theta}{2}\right)\)∙sin\(\left(\frac{4 \theta-2 \theta}{2}\right)\) = 0
∴ sin3θ∙sinθ = 0
∴ either sin3θ = 0 or sin θ = 0
The general solution of sin θ = 0 is
θ = nπ, n ∈ Z.
∴ the required general solution is given by
3θ = nπ, n ∈ Z or θ = nπ, n ∈ Z
i.e. θ = \(\frac{n \pi}{3}\), n ∈ Z or θ = nπ, n ∈ Z.
Question 7.
Find the general solutions of the following equations :
(i) sinθ = tanθ
Solution:
sin θ = tan θ
∴ sin θ = \(\frac{\sin \theta}{\cos \theta}\)
∴ sin θ cos θ = sin θ
∴ sin θ cos θ – sinθ = 0
∴ sin θ (cos θ – 1) = θ
∴ either sinθ = 0 or cosθ – 1 = 0
∴ either sin θ = 0 or cos θ = 1
∴ either sinθ = 0 or cosθ = cosθ …[∵ cos0 = 1]
The general solution of sinθ = 0 is θ = nπ, n ∈ Z and cos θ = cos ∝ is θ = 2nπ ± ∝, where n ∈ Z.
∴ the required general solution is given by
θ = nπ, n ∈ Z or θ = 2nπ ± 0, n ∈ Z
∴ θ = nπ, n ∈ Z or θ = 2nπ, n ∈ Z.
![]()
(ii) tan3θ = 3tanθ
Solution:
tan3θ = 3tanθ
∴ tan3θ – 3tanθ = 0
∴ tan θ (tan2θ – 3) = 0
∴ either tan θ = 0 or tan2θ – 3 = 0
∴ either tanθ = 0 or tan2θ = 3
∴ either tan θ = 0 or tan2θ = (\(\sqrt {3}\) )3
∴ either tan θ = 0 or tan2θ = (tan\(\frac{\pi}{3}\))3 …[tan\(\frac{\pi}{3}\) = \(\sqrt {3}\)]
∴ either tanθ = 0 or tan2θ = tan2\(\frac{\pi}{3}\)
The general solution of
tanθ = 0 is θ = nπ, n ∈ Z and
tan2θ = tan2∝ is θ = nπ ± ∝, n ∈ Z.
∴ the required general solution is given by
θ = nπ, n ∈ Z or θ = nπ ± \(\frac{\pi}{3}\), n ∈ Z.
(iii) cosθ + sinθ = 1.
Solution:
cosθ + sinθ = 1


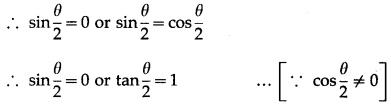
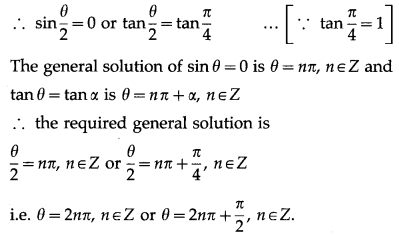
Question 8.
Which of the following equations have solutions ?
(i) cos 2θ = -1
Solution:
cos 2θ = -1
Since -1 ≤ cos θ ≤ 1 for any θ,
cos 2θ = -1 has solution.
![]()
(ii) cos2θ = -1
Solution:
cos2θ = -1
This is not possible because cos2θ ≥ 0 for any θ.
∴ cos2θ = -1 does not have any solution.
(iii) 2 sinθ = 3
Solution:
2 sin θ = 3 ∴ sin θ = \(\frac{3}{2}\)
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 2 sin θ = 3 does not have any solution.
![]()
(iv) 3 tanθ = 5
Solution:
3tanθ = 5 ∴ tanθ = \(\frac{5}{3}\)
This is possible because tan θ is any real number.
∴ 3tanθ = 5 has solution.