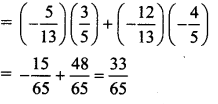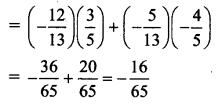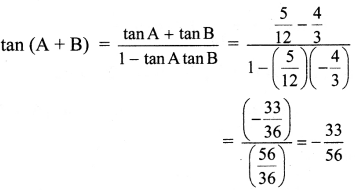Uncategorized

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Ex 5.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Ex 5.2

Question 1.
Find the slope of each of the lines which passes through the following points:
i. A(2, -1), B(4,3)
ii. C(- 2,3), D(5, 7)
iii. E(2,3), F(2, – 1)
iv. G(7,1), H(- 3,1)
Solution:
i. Here, A = (2, -1) andB = (4, 3)
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-(-1)}{4-2}=\frac{4}{2}\) = 2

ii. Here, C = (-2, 3) and D = (5, 7)
Slope of line CD = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{7-3}{5-(-2)}=\frac{4}{7}\)

iii. Here, E s (2, 3) and F = (2, -1)
Slope of line EF = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-1-3}{2-2}=\frac{-4}{0}\), which ix not defined.

Alternate Method:
Points E and F have same x co-ordinates i.e. 2.
Points E and F lie on a line parallel to Y-axis.
∴ The slope of EF is not defined.

iv. Here, G = (7, 1) and H = (-3, 1)
Slope of line GH = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-1}{-3-7}\) = o

Alternate Method:
Points G and H have same y co-ordinate i.e. 1.
∴ Points G and H lie on a line parallel to the
X-axis.
∴ The slope of GH is 0.

Question 2.
If the x and x-intercepts of line L are 2 and 3 respectively, then find the slope of line L.
Solution:
Given, x-intercept of line L is 2 and y-intercept of line L is 3
∴ The line L intersects X-axis at (2, 0) and Y-axis at (0,3).
∴ The line L passes through (2, 0) and (0, 3).
Slope of line L = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{0-2}=\frac{-3}{2}\)

Question 3.
Find the slope of the line whose inclination is 30°.
Solution:
Given, inclination (θ) = 30°
∴ Slope of the line = tanθ = tan30° = \(\frac{1}{\sqrt{3}}\)

Question 4.
Find the slope of the line whose inclination is \(\frac{\pi}{4}\)
Solution:
Given, inclination (0) = \(\frac{\pi}{4}\)
∴ Slope of the line = tan θ = tan\(\frac{\pi}{4}\) = 1

Question 5.
A line makes intercepts 3 and 3 on the co-ordinate axes. Find the inclination of the line.
Solution:
Given, x-intercept of line is 3 and y-intercept of line is 3
∴ The line intersects X-axis at (3, 0) and Y-axis at (0, 3).
∴ The line passes through (3, 0) and (0,3).
∴ Slope of line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{0-3}\) = -1
But, slope of a line = tan θ
∴ tan θ = – 1
= – tan \(\frac{\pi}{4}\)
= tan(π-\(\frac{\pi}{4}\) ) …[v tan(π – θ) = -tan θ]
tan θ = tan \(\frac{3\pi}{4}\)
θ = \(\frac{3\pi}{4}\)
The inclination of the line is \(\frac{3\pi}{4}\).
[Note: Answer given in the textbook is ‘-1 However, as per our calculation it is \(\frac{3\pi}{4}\)]

Question 6.
Without using Pythagoras theorem, show that points A (4, 4), B (3, 5) and C (- 1, – 1) are the vertices of a right-angled triangle.
Solution:
Given, A(4,4), B(3, 5), C (-1, -1).
Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-4}{3-4}\) = – 1
Slope of BC = \(\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}\)
Slope of AC = \(\frac{-1-4}{-1-4}\) = 1
Slope of AB x slope of AC = – 1 x 1 = – 1
∴ side AB ⊥ side AC
∴ ∆ABC is a right angled triangle right angled at A.
∴ The given points are the vertices of a right angled triangle.

Question 7.
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise.
Solution:

Since the line makes an angle of 45° with positive direction of Y-axis in anticlockwise direction,
Inclination of the line (0) = (90° + 45°)
∴ Slope of the line = tan(90° + 45°)
= – cot 45°
= -1

Question 8.
Find the value of k for which the points P(k, -1), Q(2,1) and R(4,5) are collinear.
Solution:
Given, points P(k, – 1), Q (2, 1) and R(4, 5) are collinear.
∴ Slope of PQ = Slope of QR .
∴ \(\frac{1-(-1)}{2-k}=\frac{5-1}{4-2}\)
∴ \(\frac{2}{2-k}=\frac{4}{2}\)
∴ 4 = 4 (2 – k)
∴ 1 = 2 – k
∴ k = 2 – 1 = 1

Question 9.
Find the acute angle between the X-axis and the line joining the points A(3, -1) and B(4, – 2).
Solution:
Given, A (3, – 1) and B (4, – 2)
Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-(-1)}{4-3}\) = – 1
But, slope of a line = tan θ
∴ tan θ = – 1
= – tan 45°
= tan (180° -45°)
… [∵ tan (180° – θ) = -tan θ]
= tan 135°
∴ θ = 135°

Let α be the acute angle that line AB makes with X-axis.
Then, α + 0 = 180°
α = 180°- 135° = 45°
∴ The acute angle between the X-axis and the line joining the points A and B is 45°.

Question 10.
A line passes through points A(xi, y0 and B(h, k). If the slope of the line is m, then show that k – y₁ = m (h – x₁).
Solution:
Given, A(x₁, y₁), B(h, k) and
slope of line AB = m
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
∴ m = \(\frac{\mathrm{k}-y_{1}}{\mathrm{~h}-x_{1}}\)
∴ k – y₁ = m (h – x₁)

Question 11.
If the points A(h, 0), B(0, k) and C(a, b) lie on a line, then show that \(\frac{a}{h}+\frac{b}{k}\) = 1. ‘
Solution:
Given, A(h, 0), B(0, k) and C(a, b)
Since the points A, B and C lie on a line, they are collinear.
∴ Slope of AB = slope of BC

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.3

Question 1.
Solve the following linear equations by using Cramer’s Rule.
x+y + z = 6, x – y + z = 2,.x + 2y – z = 2
x + y – 2z = -10,
2x +y – 3z = -19, 4x + 6y + z = 2
x + z = 1, y + z = 1, x + y = 4
\(\frac{-2}{x}-\frac{1}{y}-\frac{3}{z}\) = 3, \(\frac{2}{x}-\frac{3}{y}+\frac{1}{z}\) = -13 and \(\frac{2}{x}-\frac{3}{z}\) = -11
Solution:
Given equations are
x + y + z = 6,
x – y + z = 2,
x + 2y – z = 2.
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 2 & -1
\end{array}\right|\)
1 2 -1 = 1(1 -2) – 1(-1 – 1) + 1(2 + 1)
= 1 (-1)-1 (-2)+ 1(3)
= -1 + 2 + 3
= 4 ≠ 0

D_x = \(\left|\begin{array}{ccc}
6 & 1 & 1 \\
2 & -1 & 1 \\
2 & 2 & -1
\end{array}\right|\)
= 6(1 – 2) – 1(-2 – 2) + 1(4 + 2)
= 6(-1) -1 (-4) + 1(6)
= -6 + 4 + 6
= 4

D_y = \(\left|\begin{array}{ccc}
1 & 6 & 1 \\
1 & 2 & 1 \\
1 & 2 & -1
\end{array}\right|\)
= 1(-2 – 2) – 6(-l – 1) + 1(2 = 1 (- 4) – 6 (- 2) + 1(0)
= -4+12 + 0 = 8

D_z = \(\left|\begin{array}{ccc}
1 & 1 & 6 \\
1 & -1 & 2 \\
1 & 2 & 2
\end{array}\right|\)
= l(-2 – 4) – 1(2 – 2) + 6(2 + 1)
= l(-6)-l(0) + 6(3)
= -6 + 0+18 = 12

By Cramer’s Rule,

∴ x = 1, y = 2 and z = 3 are the solutions of the given equations.

ii. Given equations are x+y- 2z = -10,
2x + y – 3z = -19,
Ax + 6y + z = 2.
D = \(\left|\begin{array}{ccc}
1 & 1 & -2 \\
2 & 1 & -3 \\
4 & 6 & 1
\end{array}\right|\)
= 1(1 + 18)- 1(2+ 12)-2(12-4)
= 1(19)-1(14)-2(8)
= 19-14-16 = -11 ≠ 0

D_x = \(\left|\begin{array}{ccc}
-10 & 1 & -2 \\
-19 & 1 & -3 \\
2 & 6 & 1
\end{array}\right|\)
= -10(1 + 18) – 1(-19 + 6) – 2(- 114 – 2)
= -10(19)- 1(-13) -2(-l 16)
= -190+ 13 + 232 = 55

D_y = \(\left|\begin{array}{ccc}
1 & -10 & -2 \\
2 & -19 & -3 \\
4 & 2 & 1
\end{array}\right|\)
= 1(-19 + 6) – (-10)(2 + 12) – 2(4 + 76) = 1(-13) + 10(14) – 2(80)
= -13 + 140-160 = -33

D_z = \(\left|\begin{array}{ccc}
1 & 1 & -10 \\
2 & 1 & -19 \\
4 & 6 & 2
\end{array}\right|\)
= 1(2+ 114)-1(4+ 76)-10(12-4)
= 1(116)-1(80)-10(8)
= 116-80-80 .
= -44
By Cramer’s Rule,

∴ x = -5, y = 3 and z = 4 are the solutions of the given equations.
[Note: The question has been modified]

iii. Given equations are
x + z = 1, i.e.,x + 0y + z = 1,
y + z = 1, i.e., 0x + y + z = 1,
x + y = 4, i.e., x + y + 0z = 4.
D = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 0
\end{array}\right|\)
= 1(0 – 1) – 0 + 1(0 – 1)
= 1(-1)+1(-1)
= -1-1 = -2 ≠ 0
D_x = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 0
\end{array}\right|\)
= 1(0 – 1) – 0 + 1(1 -4) = l(-l)+l(-3)
= -1 – 3
= -4

D_y = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
0 & 1 & 1 \\
1 & 4 & 0
\end{array}\right|\)
= 1(0 – 4) – 1(0 – 1) + 1(0 – 1)
= 1(-4) – 1(-1) + 1(-1)
= -4 + 1 – 1
= -4

D_z = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 4
\end{array}\right|\)
= 1(4 – 1) – 0 + 1(0 – 1)
= 1(3) + 1(-1)
= 3 – 1
= 2

By Cramer’s Rule,

∴ x = 2, y = 2 and z = -1 are the solutions of the given equations.

Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
∴ The given equations become
-2p – q – 3r = 3, i.e., 2p + q + 3r = -3,
2p-3q + r = -13,
2p – 3r = -11, i.e., 2p + 0q – 3r = -11.
D = \(\left|\begin{array}{ccc}
2 & 1 & 3 \\
2 & -3 & 1 \\
2 & 0 & -3
\end{array}\right|\)
= 2(9 – 0) – 1(-6 – 2) + 3(0 + 6)
= 2(9) – 1(-8) + 3(6)
= 18 + 8 + 18
= 44 ≠ 0

D_P = \(\left|\begin{array}{ccc}
-3 & 1 & 3 \\
-13 & -3 & 1 \\
-11 & 0 & -3
\end{array}\right|\)
= -3(9 – 0) – 1(39 + 11) + 3(0 – 33)
= -3(9) – 1(50) + 3(-33)
= -27 – 50 – 99
= -176

D_q = \(\left|\begin{array}{ccc}
2 & -3 & 3 \\
2 & -13 & 1 \\
2 & -11 & -3
\end{array}\right|\)
= 2(39 + 11)- (-3)(-6 – 2) + 3(-22 + 26)
= 2(50) + 3(-8) + 3(4)
= 100 – 24 + 12
= 88

D_r = \(\left|\begin{array}{ccc}
2 & 1 & -3 \\
2 & -3 & -13 \\
2 & 0 & -11
\end{array}\right|\)
= 2(33 – 0) – 1(-22 + 26) – 3(0 + 6)
= 2(33) – 1(4) – 3(6)
= 66 – 4 – 18
= 44

By Cramer’s Rule,

∴ x = \(\frac/{-1}{4}\), y = \(\frac{1}{2}\) z = 1 are the solutions of the given equations.

Question 2.
The sum of three numbers is 15. If the second number is subtracted from the sum of first and third numbers, then we get 5. When the third number is subtracted from the sum of twice the first number and the second number, we get 4. Find the three numbers.
Solution:
Let the three numbers be x, y and z.
According to the given conditions, x + y + z = 15,
x + z-y = 5, i.e., x – y + z = 5,
2x + y – z = 4.
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -1 & 1 \\
2 & 1 & -1
\end{array}\right|\)
= 1(1 – 1) – 1(-1 – 2) + 1(1 + 2)
= 1(0) – 1(-3) + 1(3)
= 0 + 3 + 3
= 6 ≠ 0

D_x = \(\left|\begin{array}{ccc}
15 & 1 & 1 \\
5 & -1 & 1 \\
4 & 1 & -1
\end{array}\right|\)
= 15(1 – 1) – 1(-5 – 4) + 1(5 + 4)
= 15(0) – 1(-9) + 1(9)
= 0 + 9 + 9
= 18

D_y = \(\left|\begin{array}{ccc}
1 & 15 & 1 \\
1 & 5 & 1 \\
2 & 4 & -1
\end{array}\right|\)
= 1(-5 – 4) – 15(-1 – 2) + 1(4 – 10)
= 1(-9) – 15(-3) + 1(-6)
= -9 + 45 – 6 = 30

D_z = \(\left|\begin{array}{ccc}
1 & 1 & 15 \\
1 & -1 & 5 \\
2 & 1 & 4
\end{array}\right|\)
= 1(-4 – 5) – 1(4 – 10) + 15(1 + 2)
= 1(-9) – 1(-6) + 15(3)
= -9 + 6 + 45
= 42
By Cramer’s Rule,

∴ The three numbers are 3, 5 and 7.

Question 3.
Examine the consistency of the following equations.
i. 2x – y + 3 = 0, 3x + y – 2 = 0, 11x + 2y – 3 = 0
ii. 2x + 3y – 4 = 0, x + 2y = 3, 3x + 4y + 5 = 0
iii. x + 2y – 3 = 0,7x + 4y – 11 = 0,2x + 4y – 6 = 0
Solution:
i. Given equations are 2x – y + 3 = 0,
3x + y – 2 = 0,
11x + 2y – 3 = 0.
D = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
3 & 1 & -2 \\
11 & 2 & -3
\end{array}\right|\)
= 2(-3 + 4) – (-l)(-9 + 22) + 3(6-11)
= 2(1)+1(13)+ 3(-5)
= 2 + 13-15 = 0
∴ The given equations are consistent.

ii. Given equations are 2x + 3y – 4 = 0,
x + 2y = 3, i.e., x + 2y – 3 = 0,
3x + 4y + 5 = 0.
\(\left|\begin{array}{ccc}
2 & 3 & -4 \\
1 & 2 & -3 \\
3 & 4 & 5
\end{array}\right|\)
= 2(10 + 12) – 3(5 + 9) – 4(4 – 6)
= 2 (22) – 3(14) – 4(-2)
= 44 – 42 + 8
= 10 ≠ 0
∴ The given equations are not consistent.

iii. Given equations are x + 2y – 3 =
7x + 4y – 11 =0,
2x + 4y – 6 = 0.
\(\left|\begin{array}{ccc}
1 & 2 & -3 \\
7 & 4 & -11 \\
2 & 4 & -6
\end{array}\right|\)
= 1(-24 + 44) – 2(-42 + 22) – 3(28 – 8)
= 1(20) – 2(-20) – 3(20)
= 20 + 40 – 60
= 0
∴ The given equations are consistent.

Question 4.
Find k, if the following equations are consistent.
i. 2x + 3y-2 = 0,2x + 4y-k = 0,x-2j + 3k = 0
ii. kx + 3,y +1 = 0, x + 2y+1 = 0, x + y = 0
Solution:
i. Given equations are 2x + 3y – 2 = 0,
2x + 4y – k = 0,
x – 2y + 3k = 0.
Since these equations are consistent,
\(\left|\begin{array}{ccc}
2 & 3 & -2 \\
2 & 4 & -k \\
1 & -2 & 3 k
\end{array}\right|\) = 0
∴ 2(12k – 2k) – 3(6k + k) – 2(- 4 – 4) = 0
∴ 2(10k) – 3(7k) – 2(- 8) = 0
∴ 20k – 21k + 16 = 0
∴ k = 16

Given equations are are
kx + 3y + 1 = 0,
x + 2y +1=0,
x + y = 0, i.e., x + y + 0 = 0.
Since these equations are consistent,
\(\left|\begin{array}{lll}
k & 3 & 1 \\
1 & 2 & 1 \\
1 & 1 & 0
\end{array}\right|\) = 0
∴ k(0 – 1) – 3(0 – 1) + 1(1 – 2) = 0
∴ k(-1) – 3(-1) + 1(-1) = 0
∴ -k + 3 – 1 = 0
∴ k = 2.

Question 5.
Find the area of triangle whose vertices are
i. A (5,8), B (5,0), C (1,0)
ii. P(3/2, 1), Q(4,2), R(4, -1/2)
iii. M (0, 5), N (- 2, 3), T (1, – 4)
Solution:
i. Here, A(x₁, y₁) ≡ A(5, 8), B(x₂, y₂) = B(5, 0), C(x₃, y₃) = C(1,0)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(ΔABC) = \(\frac{1}{2}\left|\begin{array}{lll}
5 & 8 & 1 \\
5 & 0 & 1 \\
1 & 0 & 1
\end{array}\right|\)
= \(\frac{1}{2}\)[5(0 – 0) – 8(5 – 1) + 1(0 – 0)]
= \(\frac{1}{2}\)[0 – 8(4) + 0]
= \(\frac{1}{2}\)(-32)
= -16
Since area cannot be negative,
A(ΔABC) = 16 sq. units

ii. Here, P(x₁, y₁) ≡ P(3/2, 1), Q(x₂, y₂) ≡ Q(4, 2), R(x₃, y₃) ≡ R(4,-\(\frac{1}{2}\) )


Since area cannot be negative
A(ΔPQR) = 25/8 sq. units

iii. Here, M(x₁, y₁) ≡ M(0, 5), N(x₂, y₂) ≡ N(-2, 3)
T(x₃, y₃) ≡ T(1, -4)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(ΔMNT) = \(\frac{1}{2}\left|\begin{array}{ccc}
0 & 5 & 1 \\
-2 & 3 & 1 \\
1 & -4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [ 0 – 5 (-2 -1) + 1 (8 – 3)]
= \(\frac{1}{2}\)[-5 (-3) + 1(5)]
= \(\frac{1}{2}\) (15 + 5)
= \(\frac{1}{2}\) (20)
= 10 sq. units

Question 6.
Find the area of quadrilateral whose vertices are A (- 3,1), B (- 2, – 2), C (1,4), D (3, – 1).
Solution:
A(-3, 1), B(-2, -2), C(l, 4), D(3, -1)

A(□ ABDC) = A(ΔABD) + A(ΔADC)
Area of triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(ΔABD) = \(\frac{1}{2}\left|\begin{array}{ccc}
-3 & 1 & 1 \\
-2 & -2 & 1 \\
3 & -1 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [-3 (-2 + 1) – 1(-2 – 3) + 1(2 + 6)
= \(\frac{1}{2}\) [-3(-1) – 1(-5) + 1(8)]
= \(\frac{1}{2}\) (3 + 5 + 8)
= \(\frac{1}{2}\) (16)
∴ A(ΔABD) = 8 sq. units
A(ΔADC) = \(\frac{1}{2}\left|\begin{array}{ccc}
-3 & 1 & 1 \\
3 & -1 & 1 \\
1 & 4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [-3(-1-4) – 1(3 – 1) + 1(12 + 1)]
= \(\frac{1}{2}\) [-3(-5) – 1(2) + 1(13)]
= \(\frac{1}{2}\) [15 – 2 + 13]
= \(\frac{1}{2}\) (26)
∴ A(ΔADC) = 13 sq. units
∴ A(□ ABDC) = A(ΔABD) + A(ΔADC)
= 8 + 13
= 21 sq. units

Question 7.
Find the value of k, if the area of triangle whose vertices are P (k, 0), Q (2,2), R (4,3) is \(\frac{3}{2}\) sq. units.
Solution:
Here, P(x₁, y₁) ≡ P(k, 0), Q(x₂, y₂) ≡ Q(2, 2), R(x₃, y₃) ≡ R(4,3)
∴ A(ΔPQR) = \(\frac{3}{2}\) sq. units
Area if triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ \(\pm \frac{3}{2}=\frac{1}{2}\left|\begin{array}{lll}
k & 0 & 1 \\
2 & 2 & 1 \\
4 & 3 & 1
\end{array}\right|\)
∴ ± \( [k(2 – 3) – 0 + 1 (6 – 8)]
∴ ± [latex\frac{3}{2}=\frac{1}{2}\) (-k -2)
∴ ± 3 = -k – 2
∴ 3 = -k – 2 or -3 = -k – 2
∴ k = -5 or k = 1

Question 8.
Examine the collinearity of the following set of points:
i. A (3, – 1), B (0, – 3), C (12, 5)
ii. P (3, – 5), Q (6,1), R (4, 2)
iii. L(0,1/2), M(2,-1), N(-4, 7/2)
Solution:
i. Here, A(x₁, y₁) ≡ A(3, -1), B(x₂, y₂) ≡ B(0, -3), C(x₃, y₃) ≡ C(12, 5)
If A(∆ABC) = 0, then the points A, B, C are collinear.
∴ A(∆ABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & -1 & 1 \\
0 & -3 & 1 \\
12 & 5 & 1
\end{array}\right|\)
= \(\frac{1}{2}\)[3(-3 – 5) – (-1) (0 – 12) + 1(0 + 36)]
= \(\frac{1}{2}\)[3(-8)+ 1(-12)+ 1(36)]
= \(\frac{1}{2}\)(-24 – 12 + 36)
= 0
∴ The points A, B, C are collinear.

ii. Here, P(x₁, y₁) ≡ P(3, -5), Q(x₂, y₂) ≡ Q(6, 1), R(x₃, y₃) ≡ R(4,2)
∴ If A(∆PQR) = 0, then the points P,Q, R are collinear
∴ A(∆PQR) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
6 & 1 & 1 \\
4 & 2 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [3(1-2) – (-5)(6 – 4) + 1(12 – 4)]
= \(\frac{1}{2}\) [3(-1) + 5(2) + 1(8)]
= \(\frac{1}{2}\)(-3 + 10 + 8)= \(\frac{15}{2}\) ≠ 0
∴ The points P, Q, R are non-collinear.

iii. Here, L(x₁, y₁) ≡ L(0,1/2), M(x₂, y₂) ≡ M(2, -1), N(x₃, y₃) ≡ N(-4, 7/2)
If A(∆LMN) = 0, then the points L, M, N are collinear.
∴ A(∆LMN) = \(\frac{1}{2}\left|\begin{array}{ccc}
0 & \frac{1}{2} & 1 \\
2 & -1 & 1 \\
-4 & \frac{7}{2} & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [0 – ]\(\frac{1}{2}\) (2 + 4) + 1(7 – 4)]
= \(\frac{1}{2}\)[ –\(\frac{1}{2}\) (6) + 1(3)]
= \(\frac{1}{2}\) (-3 + 3) = 0
∴ The points L, M, N are collinear.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Ex 3.5

Question 1.
In Δ ABC, A + B + C = π, show that
cos2A + cos2B + cos2C = – 1 – 4 cosA cosB cosC
Solution:
L.H.S. = cos 2A + cos 2B + cos 2C
= \(2 \cdot \cos \left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right) \cdot \cos \left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)+\cos 2 \mathrm{C}\)
= 2.cos(A + B).cos (A – B) + 2cos²C – 1
In ΔABC, A + B + C = π
∴ A + B = π – C
∴ cos(A + B) = cos(π – C)
∴ cos(A + B) = – cosC ………….(i)

∴ L.H.S. = – 2.cos C.cos (A – B) + 2.cos²C – 1 …[From(i)]
= – 1 – 2.cosC.[cos(A – B) – cosC]
= – 1 – 2.cos C.[cos(A – B) + cos(A + B)]
… [From (i)]
= – 1 – 2.cos C.(2.cos A.cos B)
= – 1 – 4.cos A.cos B.cos C = R.H.S.

Question 2.
sin A + sin B + sin C = 4 cos A/2 cos B/2 cos C/2
Solution:

Question 3.
cos A + Cos B + Cos C = 4 cos A/2 cos B/2 cos C/2
= \(2 \cdot \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cdot \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)-\left(1-2 \sin ^{2} \frac{\mathrm{C}}{2}\right)\)
Solution:
L.H.S. = sin A + sin B + sin C
= \(2 \cdot \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cdot \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)-\left(1-2 \sin ^{2} \frac{\mathrm{C}}{2}\right)\)
In Δ ABC, A + B + C = π ,
∴ A + B = π – C

Question 4.
sin² A + sin² B – sin² C = 2 sin A sin B cos C
Solution:
We know that, sin² = \(\frac{1-\cos 2 \theta}{2}\)
L.H.S.
= sin² + sin² B + sin² C

= 1 – cos(A + B). cos(A – B) – sin²C
= (1 – sin² C ) – cos (A + B). cos (A – B)
= cos² C – cos(A + B). cos(A – B)
∴ cos(A + B) = cos(it — C)
∴ cos(A + B) = — cos C …(i)
∴ L.H.S. = cos²C + cos C.cos(A – B)
… [From (i)]
= cos C[cos C + cos(A – B)]
= cos C[- cos(A + B) + cos(A – B)]
… [From (i)]
= cos C[cos (A-B) – cos(A + B)]
= cos C(2 sin A.sin B)
= 2 sin A.sin B. cos C
= R.H.S.
[Note: The question has been modified.]

Question 5.
\(\sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}-\sin ^{2} \frac{C}{2}\) = \(1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\)
Solution:

Question 6.
tan \(\frac{\mathbf{A}}{2}\) tan \(\frac{\mathbf{B}}{2}\) tan \(\frac{\mathbf{B}}{2}\) tan \(\frac{\mathbf{C}}{2}\) tan \(\frac{\mathbf{C}}{2}\) tan \(\frac{\mathbf{A}}{2}\) = 1
Solution:
In Δ ABC,
A + B + C = π
∴ A + B = π – C

Question 7.
\(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2}\)
Solution:
In Δ ABC,
A + B + C = π
∴ A + B = π – C

Question 8.
tan 2A + tan 2B + tan 2C = tan 2A tan 2B + tan 2C
Solution:
In Δ ABC,
A + B + C = π
∴ 2A + 2B + 2C = 2π
∴ 2A + 2B = 2π – 2C
tan(2A + 2B) = tan(2n — 2C)
\(\frac{\tan 2 \mathrm{~A}+\tan 2 \mathrm{~B}}{1-\tan 2 \mathrm{~A} \cdot \tan 2 \mathrm{~B}}\) = -tan 2C
∴ tan2A+tan2B=—tan2C.(1-tan2A.tan2B)
∴ tan 2A + tan 2B = – tan2C+ tan2A.tan2B.tan2C
∴ tan 2A + tan 2B + tan 2C = tan2A.tan2B.tan2C

Question 9.
cos² A + cos² B – cos² C = 1 – 2 sin A sin B sin C
Solution:
we know that cos²θ = \(\frac{1+\cos 2 \theta}{2}\)
L.H.S.
= cos² A + cos² B + cos² C

= 1 + cos (A + B).cos(A — B) – cos2 C
In ΔABC,
A + B + C = π
A + B = π — C
cos(A + B) = cos(π — C)
cos(A + B) = -cosC ………….. (i)
L.H.S. = 1 — cos C.cos(A — B) — cos² C
…[From(i)]
= 1 — cos C.[cos(A — B) + cos C]
= 1 — cos C.[cos(A — B) — cos(A + B)]
.. .[From (i)]
= 1 — cos C.(2.sin A.sin B)
= 1 — 2.sinA.sin B.cos C
= R.H.S.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Ex 3.4

Question 1.
Express the following as a sum or difference of two trigonometric functions.
i. 2sin 4x cos 2x
ii. 2sin \(\frac{2 \pi}{3}\) cos \(\frac{\pi}{2}\)
iii. 2cos 4θ cos 2θ
iv. 2cos 35° cos 75°
Solution:
i. 2sin 4x cos 2x = sin(4x + 2x ) + sin (4x – 2x)
= sin 6x + sin 2x

ii.

[Note: Answer given in the textbook is sin \(\frac{7 \pi}{12}\) + sin \(\frac{\pi}{12}\) However, as per our calculation it is sin \(\frac{7 \pi}{6}\) + sin \(\frac{\pi}{6}\)

iii. 2cos 4θ cos 2θ = cos(4θ + 2θ)+cos (4θ – 2θ)
= cos 6θ + cos 2θ

iv. 2cos 35° cos75°
= cos(35° + 75°) + cos (35° – 75°)
= cos 110° + cos (-40)°
= cos 110° + cos 40° … [∵ cos(-θ) = cos θ]

Question 2.
Prove the following:
i. \(\frac{\sin 2 x+\sin 2 y}{\sin 2 x-\sin 2 y}=\frac{\tan (x+y)}{\tan (x-y)}\)
Solution:

ii. sin 6x + sin 4x – sin 2x = 4 cos x sin 2x cos 3x
Solution:
L.H.S. = sin 6x + sin 4x — sin 2x
= 2sin \(\left(\frac{6 x+4 x}{2}\right)\) cos \(\left(\frac{6 x-4 x}{2}\right)\) – 2 sin x cos x
= 2 sin 5x cos x — 2 sin x cos x
= 2 cos x (sin 5x — sin x)
= 2 cos \(\left[2 \cos \left(\frac{5 x+x}{2}\right) \sin \left(\frac{5 x-x}{2}\right)\right]\)
= 2 cos x (2 cos 3x sin 2x)
= 4 cos x sin 2x cos 3x
= R.H.S.
[Note: The question has been modified.]

iii. \(\frac{\sin x-\sin 3 x+\sin 5 x-\sin 7 x}{\cos x-\cos 3 x-\cos 5 x+\cos 7 x}\) = cot 2x
Solution:

iv. sin 18° cos 39° + sin 6° cos 15° = sin 24° cos 33°
Solution:
L.H.S. = sin 18°.cos 39° + sin 6°.cos 15°
= \(\frac{1}{2}\) (2 cos 39°sin 18° + 2.cos 15°.sin 6°)
= \(\frac{1}{2}\)[sin(39° + 18°) — sin(39° — 18°) + sin (15° + 6°) — sin (15° — 6°)]
= \(\frac{1}{2}\)(sin57° – sin21° + sin 21°- sin9°)
= \(\frac{1}{2}\)(sin57° – sin9°)
= \(\frac{1}{2}\) x 2. cos \(\left(\frac{57^{\circ}+9^{\circ}}{2}\right) \cdot \sin \left(\frac{57^{\circ}-9^{\circ}}{2}\right)\)
= cos 33° .sin 24°
= sin 24°. cos 33°
= R.H.S.

v. cos 20° cos 40° cos 60°cos 80° = 1/16
Solution:
L.H.S. = cos 20°.cos 40°.cos 60°.cos 80°
= cos 20°.cos 40°.\(\frac{1}{2}\) .cos 80°
= \(\frac{1}{2 \times 2}\)(2 cos 40°.cos 20°).cos 80°
= \(\frac{1}{4}\)[cos(40° + 20°) + cos(40°- 20°)].cos80°
= \(\frac{1}{4}\)(cos 60° + cos 20°) cos 80°
=\(\frac{1}{4}\)cos 60°. cos 80° + \(\frac{1}{4}\) cos 20°. cos 80°
= \(\frac{1}{4}\left(\frac{1}{2}\right) \cos 80^{\circ}+\frac{1}{2 \times 4}\left(2 \cos 80^{\circ} \cos 20^{\circ}\right)\)
= \(\frac{1}{8}\) cos 80° + \(\frac{1}{8}\)[cos (80° + 20°) + cos (80° — 20°)]
= \(\frac{1}{8}\)cos 80° + \(\frac{1}{8}\)(cos 100° + cos 60°)
= \(\frac{1}{8}\) cos 80° + \(\frac{1}{8}\)cos 100° + \(\frac{1}{8}\)cos 60°
= \(\frac{1}{8}\) cos 80° = \(\frac{1}{8}\) cos (180° – 80°) + \(\frac{1}{8} \times \frac{1}{2}\)
= \(\frac{1}{8}\) cos 80° – \(\frac{1}{8}\) cos 80° + \(\frac{1}{16}\) … [∵ cos (180 – θ) = – cos θ]
= \(\frac{1}{16}\) = R.H.S

vi. sin 20° sin 40° sin 60° sin 80° = 3/16
Solution:

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest अपठित बोध Notes, Questions and Answers.

Maharashtra State Board 12th Hindi अपठित बोध

कृतिपत्रिका के प्रश्न 4 (इ) के लिए अपठित परिच्छेद क्र. 1

प्रश्न. निम्नलिखित अपठित परिच्छेद पढ़कर सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का वचन बदलकर लिखिए :
(1) मशीन – …………………………………….
(2) कक्षा – …………………………………….
(3) कपड़े – …………………………………….
(4) आवश्यकता – …………………………………….
उत्तर :
(1) मशीन – मशीनें
(2) कक्षा – कक्षाएँ
(3) कपड़े – कपड़ा
(4) आवश्यकता – आवश्यकताएँ।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘गृहिणी की सुघड़ता’ विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
स्त्री की सुघड़ता उसके सौंदर्य के साथ-साथ उसके अच्छे व्यवहार और उसके अच्छे कामों से आँकी जाती है। सुघड़ गृहिणी अपने सद्व्यवहार और अपने काम से सबका दिल जीत लेती है। घर को सुव्यवस्थित रखना, बच्चों का उचित पालन-पोषण और उनकी शिक्षा-दीक्षा का प्रबंध करना, उनको अच्छे संस्कार देना, बुजुर्गों तथा अतिथियों की देखभाल तथा उनका सम्मान करना, सभी रिश्तेदारों से अच्छे संबंध बनाए रखना तथा सामाजिक व्यवहार निभाना आदि जिम्मेदारियाँ गृहिणी के ही हिस्से में आती हैं।

स्त्रियों के संबंध में सुघड़ता एक आवश्यक गुण है। सुघड़ स्त्री न केवल अपने परिवारजनों की बल्कि अपने समाज, जान-पहचानवालो और रिश्तेदारों की भी प्रशंसा की पात्र बन जाती है। लोगों द्वारा जगहजगह पर उसके उदाहरण दिए जाते हैं। इस प्रकार की सुघड़ता से उसका आत्मविश्वास बढ़ता हैं।

अपठित परिच्छेद क्र. 2
प्रश्न. निम्नलिखित अपठित परिच्छेद पढ़कर सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) सूर्य = …………………………………….
(2) गति = …………………………………….
(3) आकाश = …………………………………….
(4) आँख = …………………………………….
उत्तर :
(1) सूर्य = रवि
(2) गति = रफ्तार
(3) आकाश = गगन
(4) आँख = नयन।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘सौरमंडल’ विषय पर 40 से 50 शब्दों में अपने १ विचार लिखिए।
उत्तर :
सूर्य के चारों ओर चक्कर लगाने वाले ग्रहों, धूमकेतुओं, उल्काओं और अन्य आकाशीय पिंडों के समूह को ‘सौरमंडल’। कहते है। ये सभी एक-दूसरे में गुरुत्वाकर्षण बल द्वारा बँधे हुए हैं। सौरमंडल में 8 ग्रह हैं – बुध, शुक्र, पृथ्वी, मंगल, बृहस्पति, शनि, युरेनस और नेपच्यून।

ग्रहों के उपग्रह भी होते हैं, जो अपने ग्रहों की परिक्रमा करते हैं। सूर्य हमारी आकाशगंगा से लगभग 30,000 प्रकाश वर्ष दूरी पर स्थित है। सूर्य आकाशगंगा के चारों ओर 250 किमी प्रति सेकंड की गति से परिक्रमा कर रहा है। सूर्य अपने अक्ष पर पूरब से पश्चिम की ओर घूमता है।

सूर्य हमारी पृथ्वी से 13 लाख गुना बड़ा है। बुध, शुक्र, शनि, बृहस्पति और मंगल इन पाँचों ग्रहों को बिना दूरबीन के भी देखा जा सकता है। सूर्य हमारे सौरमंडल का सबसे बड़ा पिंड है।

अपठित परिच्छेद क्र. 3
प्रश्न. निम्नलिखित अपठित परिच्छेद पढ़कर सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
परिच्छेद में प्रयुक्त उपसर्गयुक्त शब्दों से मूल शब्द और उपसर्ग को अलग-अलग करके लिखिए :
(1) निर्विवाद
(2) अनिश्चित।
उत्तर :
(1) निर्विवाद = निर् + विवाद।
(2) अनिश्चित = अ + निश्चित।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘जीवन-यापन के लिए समय से उचित व्यवसाय का चुनाव आवश्यक’ विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
दुनिया में दो तरह के मनुष्य होते हैं एक वे जो समाज में पारंपरिक रूप से किसी धंधे वाले परिवार से जुड़े हैं – जैसे किसान, लोहार, सुनार, नाई, धोबी आदि। इनके बच्चों को अकसर पारंपरिक कार्य सीखने का मौका मिल जाता है। इसी तरह छोटे-मोटे दुकानदार, कारखाना मालिक तथा बड़े-बड़े उद्योगपतियों का अपना व्यवसाय होता है।

इनके बच्चों को भी जन्म से ही अपने पारिवारिक व्यवसाय की जानकारी होती है और बड़े होने पर उनमें से अनेक अपने पारिवारिक धंधों से जुड़ जाते हैं। विशेष परेशानी उन लोगों को होती है, जो गरीब तबके से आते हैं और पढ़ने-लिखने के बाद भी उन्हें यह नहीं सूझता कि पढ़ाई के बाद व्यवसाय के अवसर कहाँ हैं, जहाँ वे हाथ-पाँव मारें। फिर भी इनमें से कुछ को किन्हीं कारणों से जीवन-यापन के अवसर उपलब्ध हो जाते हैं।

पर अधिकांश लोगों को यह सौभाग्य प्राप्त नहीं हो पाता। मजबूरी में उन्हें अपनी रुचि-अरुचि का ध्यान न रखते हुए कुछ-न-कुछ करने के लिए बाध्य होना पड़ता है। कुछ लोग हिम्मत हारकर बैठ जाते हैं और माता-पिता के लिए बोझ बन जाते हैं। ऐसे लोगों को यह बात समझनी चाहिए कि जीवन-यापन के लिए कुछ-न-कुछ तो करना ही होगा, तभी उद्धार होगा। इसलिए उन्हें हारकर बैठने के बजाय, सदा प्रयासरत रहना चाहिए। प्रयास करने से कोई-न-कोई राह अवश्य मिलती है।

अपठित परिच्छेद क्र. 4
प्रश्न. निम्नलिखित अपठित परिच्छेद पढ़कर सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) दुर्लभ x ………………………………
(2) कोमल x ………………………………
(3) सरल x ………………………………
(4) सजीव x ………………………………
उत्तर :
(1) दुर्लभ x सुलभ
(2) कोमल x कठोर
(3) सरल x कठिन
(4) सजीव x निर्जीव

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘पशुओं के प्रति दयाभाव’ विषय पर 40 से 50 शब्दों में अपने विचार लिखिए :
उत्तर :
मनुष्यों की तरह ही पशु भी सृष्टि के आदि काल से पृथ्वी पर रहते आए हैं। पहले मनुष्य और पशु दोनों जंगलों में रहते थे। जब मनुष्य समूह बनाकर एक स्थान पर स्थायी रूप से रहने लगा और खेती करने लगा, तो उसने अपनी आवश्यकता के अनुसार अनेक पशुओं को पालतू बना लिया और उनसे काम लेने लगा। आज भी यह परंपरा जारी है। पर अनेक लोग पशुओं के साथ क्रूरता का व्यवहार करते हैं। वे जानवरों से आवश्यकता से अधिक काम लेते हैं।

उन्हें शारीरिक रूप से प्रताड़ित करते हैं। अपने मनोरंजन के लिए निरीह जंगली जानवरों की हत्या करते हैं। लोगों को अपनी इस प्रवृत्ति से बाज आना जाहिए। हमें इन मूक प्राणियों के प्रति दया की भावना रखनी चाहिए और पशुओं के साथ होने वाले अत्याचार को रोकना चाहिए।

अपठित परिच्छेद क्र. 5
प्रश्न. निम्नलिखित अपठित परिच्छेद पढ़कर सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) रसायन – ……………………………….
(2) वस्तु – ……………………………….
(3) धरती – ……………………………….
(4) तेल – ……………………………….
उत्तर :
(1) रसायन – पुल्लिंग
(2) वस्तु – स्त्रीलिंग
(3) धरती – स्त्रीलिंग
(4) तेल – पुल्लिंग।

कृति 3 : (अभिव्यक्ति)

प्रश्न 1.
‘ध्वनि प्रदूषण’ विषय पर 40 से 50 शब्दों में अपने विचार लिखिए।
उत्तर :
पर्यावरण में अनेक प्रकार के प्रदूषण हैं। ध्वनि प्रदूषण उनमें से एक है। ध्वनि प्रदूषण आधुनिक जीवन और बढ़ते हुए औद्योगीकरण का भयानक परिणाम है। इसके कुछ मुख्य स्रोत सड़क पर यातायात, परिवहन (ट्रक, बस, ऑटो, बाइक आदि) के द्वारा उत्पन्न शोर, भवन, सङक, बाँध, फ्लाई ओवर, हाइ-वे, स्टेशन आदि के निर्माण के समय बुलडोजर, डंपिंग ट्रक, लोडर आदि के कारण उत्पन्न शोर, औद्योगिक शोर, दैनिक जीवन में घरेलू उपकरणों का प्रयोग आदि हैं। ध्वनि प्रदूषण स्वास्थ्य के लिए बहुत हानिकारक है।

उच्च स्तर के ध्वनि प्रदूषण के कारण लोगों के व्यवहार में चिड़चिड़ापन आ जाता है। तेज आवाज बेहरेपन और कान की अन्य जटिल समस्याओं का कारण बनती है। ध्वनि प्रदूषण चिंता, बेचैनी, थकान, सिरदर्द, घबराहट आदि का भी कारण बनता है। दिन-प्रति-दिन बढ़ता ध्वनि प्रदूषण मनुष्यों की काम करने की क्षमता, गुणवत्ता तथा एकाग्रता को बुरी तरह प्रभावित कर रहा है।

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Ex 3.1

Question 1.
Find the values of:
i. sin 150°
ü. cos 75°
iii. tan 105°
iv. cot 225°
Solution:
i. sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
\(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
[Note: Answer given in the textbook is \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\) However, as per our calculation it is \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

ii. cos 75° = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

iii. tan 105° = tan (60° +45°)

iv. cot 225°

Question 2.
Perove the following:
i. \(\cos \left(\frac{\pi}{2}-x\right) \cos \left(\frac{\pi}{2}-y\right) -\sin \left(\frac{\pi}{2}-x\right) \sin \left(\frac{\pi}{2}-y\right)=-\cos (x+y)\)
Solution:
L.H.S

= -(cos x cos y – sin x sin y)
= – cos (x+y)
= R.H.S

ii. \(\tan \left(\frac{\pi}{4}+\theta\right)=\frac{1+\tan \theta}{1-\tan \theta}\)
L.H.S =\(\tan \left(\frac{\pi}{4}+\theta\right)\)

R.H.S.
[Note : The question has been modified.]

iii. \(\left(\frac{1+\tan x}{1-\tan x}\right)^{2}=\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}\)
Solution:

iv. sin [(n+1)A] . sin [(n+2)A] + cos [(n+1)A] . cos [(n+2)A] = cos A
Solution:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let(n+2)Aaand(n+l)Ab …(i)
∴ L.H.S. = cos a. cos b + sin a. sin b
= cos (a — b)
= cos [(n + 2)A — (n + I )A]
…[From (i)]
cos[(n+2 – n – 1)A]
= cos A
= R.H.S.

v. \(\sqrt{2} \cos \left(\frac{\pi}{4}-\mathrm{A}\right)=\cos \mathrm{A}+\sin \mathrm{A}\)
Solution:

vi. \(\frac{\cos (x-y)}{\cos (x+y)}=\frac{\cot x \cot y+1}{\cot x \cot y-1}\)
Solution:

vii. cos (x + y). cos (x – y) = cos²y – sin²x
Solution:
L.H.S. = cos(x + y). cos(x – y)
= (cos x cos y – sin x sin y). (cos x cos y + sin x sin y)
= cos² x cos²y – sin²x sin²y
…[∵ (a – b) (a + b) = a² – b²]
= (1 – sin²x) cos²y – sin²x (1 – cos²y)
…[∵ sin²e + cos²0 = 1]
= cos²y – cos²y sin²x – sin²x + sin²x cos²y
= cos²y – sin²x
=R.H.S.

viii.\(\frac{\tan 5 A-\tan 3 A}{\tan 5 A+\tan 3 A}=\frac{\sin 2 A}{\sin 8 A}\)
Solution:

ix. tan 8θ – tan 5θ – tan 3θ = tan 8θ tan 5θ tan 3θ
Solution:
Since, 8θ = 5θ + 3θ
∴ tan 8θ = tan (5θ + 3θ)
∴ tan 8θ = \(\frac{\tan 5 \theta+\tan 3 \theta}{1-\tan 5 \theta \tan 3 \theta}\)
∴ tan 8θ (1 – tan 5θ.tan 3θ) = tan 5θ + tan 3θ
∴ tan 8θ – tan8θ.tan5θ.tan3θ = tan5θ + tan 3θ
∴ tan 8θ – tan 5θ – tan 3θ = tan 8θ.tan 5θ.tan 3θ

x. tan 50° = tan 40° + 2tan 10°
Solution:
Since, 50° = 10° +40°
∴ tan 50° = tan (10° + 40°)
∴ \(\frac{\tan 10^{\circ}+\tan 40^{\circ}}{1-\tan 10^{\circ} \tan 40^{\circ}}\)
∴ tan 50° (1 – tan 10° tan 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan 50° = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan (90° – 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° cot 40°
= tan 10° + tan 40° …[∵ tan (90° – θ) = cot θ]
∴ tan 50° – tan 10° tan 40°. \(\frac{1}{\tan 40^{\circ}}\) = tan 10° + tan 40°
∴ tan 50° – tan 10°. 1 = tan 10° + tan 40°
∴ tan 50° = tan 40° + 2 tan 10°

xi. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\) = tan 72°
Solution:
\(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\)
Dividing numerator and cos 27°, we get denominator by cos 27°, we get

= tan (45° + 27°)
= tan 72° = R.H.S

xii. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}=\tan 72^{\circ}\)
Solution:
Since 45° = 10° + 35°,
tan 45° = tan (10° +35°)
∴ \(\frac{\tan 10^{\circ}+\tan 35^{\circ}}{1-\tan 10^{\circ} \tan 35^{\circ}}\)
∴ 1 – tan 10° tan 35o = tan 10° + tan 35°
∴ tan 10° + tan 35° + tan 10° tan 35° = 1

xiii. tan 10° + tan 35° + tan 10°. tan 35° = 1
Solution:

xiv. \(\frac{\cos 15^{\circ}-\sin 15^{\circ}}{\cos 15^{\circ}+\sin 15^{\circ}}=\frac{1}{\sqrt{3}}\)
Solution:
Dividing numerator and cos 15°, we get

= tan (45° + 15°)
= tan 30° = \(\frac{1}{\sqrt{3}}\) = R.H.S

Question 3.
If sin A = \(-\frac{5}{13}\),π < A < \(\frac{3 \pi}{2}\) and cos B = \(\frac{3}{5}, \frac{3 \pi}{2}\) < B < 2π, find
i. sin (A+B)
ii. cos (A-B)
iii. tan (A + B)
Solution:
Given, sin A = \(-\frac{5}{13}\)
We know that,
cos² A = 1 – sin²A = \(1-\left(-\frac{5}{13}\right)^{2}=1-\frac{25}{169}=\frac{144}{169}\)
∴ cos A = \(\pm \frac{12}{13}\)
Since, π < A < \(\frac{3 \pi}{2}\)
∴ ‘A’ lies in the 3rd quadrant.
∴ cos A<0
cos A = \(\frac{-12}{13}\)
Also,cos B = \(\frac{3}{5}\)
∴ sin²B = 1 – cos²B = \(1-\left(\frac{3}{5}\right)^{2}=1-\frac{9}{25}=\frac{16}{25}\)
∴ sin B = \(\pm \frac{4}{5}\)
Since, \(\frac{3 \pi}{2}\) < B < 2π
∴ ‘B’ lies in the 4th quadrant.
∴ sin B<0
Sin B = \(\frac{-4}{5}\)

i. sin (A + B) = sin A cos B+cos A sin B

ii. cos (A -B) = cos A cos B + sin A sin B

iii.

Question 4.
If tan A = \(\frac{5}{6}\) , tan B = \(\frac{1}{11}\) prove that A + B = \(\frac{\pi}{4}\)
Solution:
Given tan A = \(\frac{5}{6}\), tan B = \(\frac{1}{11}\)

∴ tan (A + B) = tan \(\frac{\pi}{4}\)
∴ A + B = \(\frac{\pi}{4}\)

Balbharti Maharashtra State Board Hindi Yuvakbharati 12th Digest Chapter 5.2 वृंद के दोहे Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 12th Hindi Yuvakbharati Solutions Chapter 5.2 वृंद के दोहे

12th Hindi Guide Chapter 5.2 वृंद के दोहे Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

आकलन

प्रश्न 1.
(अ) कारण लिखिए :
(a) सरस्वती के भंडार को अपूर्व कहा गया है :- ………………………………………..
(b) व्यापार में दूसरी बार छल-कपट करना असंभव होता है :- ………………………………………..
उत्तर :
(a) सरस्वती के भंडार को जैसे-जैसे खर्च किया जाता रहता है, वैसे-वैसे वह अधिक से अधिक लोगों तक पहुँचता रहता है अर्थात उसमें वृद्धि होती रहती है। इसलिए सरस्वती के भंडार को अपूर्व कहा गया है।
(b) व्यापार में पहली बार किया गया छल-कपट सामने वाले पक्ष को समझते देर नहीं लगती। दूसरी बार वह सतर्क हो जाता है। इसलिए व्यापार में दूसरी बार छल-कपट करना असंभव होता है।

(आ) सहसंबंध जोड़िए :
(a) काग निबौरी लेत गुन बिन बड़पन कोइ – (b) ऊँचे बैठे ना लहैं,
(b) कोकिल अंबहि लेत है। – (b) बैठो देवल सिखर पर, वायस गरुड़ न होइ।
उत्तर :
(a) ऊँचे बैठे ना लहैं, गुन बिन बड़पन कोइ। – (b) बैठो देवल सिखर पर वायस गरुड़ न होइ।।
(b) कोकिल अंबहि लेत है, – (b) काग निबौरी लेत।

शब्दसंपदा

प्रश्न 2.
निम्नलिखित शब्दों के लिए विलोम शब्द लिखिए :
(१) आदर – ………………………………………..
(२) अस्त – ………………………………………..
(३) कपूत – ………………………………………..
(४) पतन – ………………………………………..
उत्तर :
(1) आदर x अनादर
(2) अस्त x उदय
(3) कपूत x सपूत
(4) पतन x उत्थान।

अभिव्यक्ति

प्रश्न 3.
(अ) चादर देखकर पैर फैलाना बुद्धिमानी कहलाती है’, इस विषय पर अपने विचार व्यक्त कीजिए।
उत्तर :
चादर देखकर पैर फैलाने का अर्थ है, जितनी अपनी क्षमता हो उतने में ही काम चलाना। यह अर्थशास्त्र का साधारण नियम है। सामान्य व्यक्तियों से लेकर बड़ी-बड़ी कंपनियाँ भी इस नियम का पालन करती हैं। जो लोग इस नियम के आधार पर अपना कार्य करते हैं, उनके काम सुचारु रूप से चलते हैं।

जो लोग बिना सोचे-विचारे किसी काम की शुरुआत कर देते हैं और अपनी क्षमता का ध्यान नहीं रखते, उनके सामने आगे चलकर आर्थिक संकट उपस्थित हो जाता है। इसके कारण काम ठप हो जाता है। इसलिए समझदारी इसी में है कि अपनी क्षमता का अंदाज लगाकर ही कोई कार्य शुरू किया जाए। इससे कार्य आसानी से पूरा हो जाता है। चादर देखकर पैर फैलाने में ही बुद्धिमानी होती है।

(आ) ‘ज्ञान की पूँजी बढ़ानी चाहिए’, इस विषय पर अपने विचार लिखिए।
उत्तर :
ज्ञान मनुष्य की अमूल्य पूँजी है। बचपन से मृत्यु तक मनुष्य विभिन्न स्रोतों से ज्ञान की प्राप्ति करता रहता है। बचपन में उसे अपने माता-पिता, अपने शिक्षकों, गुरुजनों तथा मिलने-जुलने वालों से ज्ञान की प्राप्ति होती है। ज्ञान का भंडार अथाह है। कुछ ज्ञान हमें स्वाभाविक रूप से मिल जाता है, पर कुछ के लिए हमें स्वयं प्रयास करना पड़ता है। ज्ञान किसी एक की धरोहर नहीं है। ज्ञान हमारे चारों तरफ बिखरा पड़ा है।

उसे देखने की दृष्टि की जरूरत होती है। संतों, महात्माओं तथा मनीषियों के व्याख्यानों, हितोपदेशों, नीतिकथाओं, बोधकथाओं तथा विभिन्न धर्मों के महान ग्रंथों में ज्ञान का भंडार है। हर मनुष्य अपनी क्षमता और आवश्यकता के अनुसार अपने ज्ञान की पूँजी में वृद्धि करता रहता है। भगवान महावीर, बुद्ध तथा महात्मा गांधी जैसे महापुरुष अपनी ज्ञान की पूँजी तथा अपने कार्यों के बल पर जनसामान्य के पूज्य बन गए हैं। इसलिए मनुष्य को सदा अपने ज्ञान की पूँजी बढ़ाते रहना चाहिए।

रसास्वादन

प्रश्न 4.
जीवन के अनुभवों और वास्तविकता से परिचित कराने वाले वृंद जी के दोहों का रसास्वादन कीजिए।
उत्तर :
कवि वृंद ने अपने लोकप्रिय छंद दोहों के माध्यम से सीधे-सादे ढंग से जीवन के अनुभवों से परिचित कराया है तथा। जीवन का वास्तविक मार्ग दिखाया है।

कवि व्यावहारिक ज्ञान देते हुए कहते हैं कि मनुष्य को अपनी आर्थिक क्षमता को ध्यान में रखकर किसी काम की शुरुआत करनी चाहिए। तभी सफलता मिल सकती है। इसी तरह व्यापार करने वालों को सचेत करते हुए उन्होंने कहा है कि वे व्यापार में छल-कपट का सहारा न लें। इससे वे अपना ही नुकसान करेंगे। वे कहते हैं कि।

किसी का सहारा मिलने के भरोसे मनुष्य को हाथ पर हाथ धरकर निष्क्रिय नहीं बैठ जाना चाहिए। मनुष्य को अपना काम तो करते ही रहना चाहिए। इसी तरह से वे कुटिल व्यक्तियों के मुँह न लगने की उपयोगी सलाह देते हैं, वह उस समय आपको कुछ ऐसा भला-बुरा सुना सकता है, जो आपको प्रिय न लगे।

अपने आप को बड़ा बताने से कोई बड़ा नहीं हो जाता। जिसमें बड़प्पन के गुण होते हैं उसी को लोग बड़ा मनुष्य मानते हैं। गुणों के बारे में उनका कहना है कि जिसके अंदर जैसा गुण होता है, उसे वैसा ही लाभ मिलता है। कोयल को मधुर आम मिलता है और कौवे को कड़वी निबौली। बिना सोचे विचार किया गया कोई काम अपने लिए ही नुकसानदेह होता है। वे कहते हैं कि बच्चे के अच्छे-बुरे होने के लक्षण पालने में ही दिखाई दे जाते हैं, ठीक उसी तरह जैसे किसी पौधे के पत्तों को देखकर उसकी प्रगति का पता चल जाता है।

कवि एक अनूठी बात बताते हुए कहते हैं कि संसार की किसी भी चीज को खर्च करने पर उसमें कमी आती है, पर ज्ञान एक ऐसी चीज है, जिसके भंडार को जितना खर्च किया जाए वह उतना ही बढ़ता जाता है। उसकी एक विशेषता यह भी है कि यदि उसे खर्च न किया जाए तो वह नष्ट होता जाता है।

कवि ने विविध प्रतीकों की उपमाओं के द्वारा अपनी बात को अत्यंत प्रभावशाली ढंग से व्यक्त किया है। दोहों का प्रसाद गुण उनकी बात को स्पष्ट करने में सहायक होता है।

साहित्य संबंधी सामान्य ज्ञान

प्रश्न 5.
(अ) वृंद जी की प्रमुख रचनाएँ – ………………………………………..
उत्तर :
वृंद जी की प्रमुख रचनाएँ इस प्रकार हैं : वृंद सतसई, समेत शिखर छंद, भाव पंचाशिका, पवन पचीसी, हितोपदेश, यमक सतसई, वचनिका तथा सत्यस्वरूप आदि।

(आ) दोहा छंद की विशेषता – ………………………………………..
उत्तर :
दोहा अर्ध सम मात्रिक छंद है। इसके चार चरण होते हैं। दोहे के प्रथम और तृतीय (विषम) चरण में 13 – 13 मात्राएँ होती हैं तथा द्वितीय और चतुर्थ (सम) चरणों में 11 – 11 मात्राएँ होती हैं। दोहे के प्रत्येक चरण के अंत में लघु वर्ण आता है।

अलंकार

जिस प्रकार स्वर्ण आदि के आभूषणों से शरीर की शोभा बढ़ती है उसी प्रकार जिन साधनों से काव्य की सुंदरता में वृद्धि होती है; वहाँ अलंकार की उत्पत्ति होती है।

मुख्य रूप से अलंकार के तीन भेद हैं –

• शब्दालंकार,
• अर्थालंकार,
• उभयालंकार

ग्यारहवीं कक्षा की युवकभारती पाठ्यपुस्तक में हमने ‘शब्दालंकार’ का अध्ययन किया है। यहाँ हम अर्थालंकार का अध्ययन करेंगे।

रूपक : जहाँ प्रस्तुत अथवा उपमेय पर उपमान अर्थात अप्रस्तुत का आरोप होता है अथवा उपमेय या उपमान को एकरूप मान लिया जाता है; वहाँ रूपक अलंकार होता है अर्थात एक वस्तु के साथ दूसरी वस्तु को इस प्रकार रखना कि दोनों अभिन्न मालूम हों, दोनों में अंतर दिखाई न पड़े।

उदा. –
(१) उधो, मेरा हृदयतल था एक उद्यान न्यारा।
शोभा देतीं अमित उसमें कल्पना-क्यारियाँ भी।।
(२) पायो जी मैंने राम रतन धन पायो।
(३) चरण-सरोज पखारन लागा।
(४) सिंधु-सेज पर धरा-वधू।
अब तनिक संकुचित बैठी-सी।।

उपमा : जहाँ पर किसी एक वस्तु की तुलना दूसरी लोक प्रसिद्ध वस्तु से रूप, रंग, गुण, धर्म या आकार के आधार पर की जाती हो; वहाँ उपमा अलंकार होता है अर्थात जहाँ उपमेय की तुलना उपमान से की जाए; वहाँ उपमा अलंकार उत्पन्न होता है।
उदा. –
(१) चरण-कमल-सम कोमल।
(२) राधा-वदन चंद सो सुंदर।
(३) जियु बिनु देह, नदी बिनु वारी।
तैसे हि अनाथ, पुरुष बिनु नारी।।
(४) ऊँची-नीची सड़क, बुढ़िया के कूबड़-सी।
नंदनवन-सी फूल उठी, छोटी-सी कुटिया मेरी।
(५) मोती की लड़ियों से सुंदर, झरते हैं झाग भरे निर्झर।
(६) पीपर पात सरस मन डोला।

Hindi Yuvakbharati 12th Digest Chapter 5.2 वृंद के दोहे Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए।
पद्यांश क्र.1
प्रश्न. निम्नलिखित पद्यांशपढ़करदी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :
(1) आँखों की तुलना की गई है इससे – ……………………………………
(2) काम शुरू करने से पहले इसके बारे में सोचना बहुत जरूरी होता है – ……………………………………
(3) दूसरे की आशा के भरोसे यह बंद नहीं करना चाहिए – ……………………………………
(4) पद्यांश में प्रयुक्त पानी रखने के काम आने वाला मिट्टी का बरतन – ……………………………………
उत्तर :
(1) आरसी (आईने) से।
(2) अपनी पहुँच (क्षमता)।
(3) कोशिश करना।
(4) गगरी।

प्रश्न 2.
पद्यांश में प्रयुक्त दो कहावतें :
(1) …………………………………………….
(2) …………………………………………….
उत्तर :
(1) तेते पाँव पसारिए, जेती लांबी सौर। (अर्थ : जितना सामर्थ्य हो उतना ही खर्च करना चाहिए।)
(2) काठ की हँड़िया बार-बार नही चढ़ती। (अर्थ : धोखा बार-बार नहीं दिया जा सकता।)

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों को शुद्ध रूप में लिखिए :
(1) सुरसति – ……………………………….
(2) अपूरब – ……………………………….
(3) गुन – ……………………………….
(4) सिखर – ……………………………….
उत्तर :
(1) सुरसति – सरस्वती
(2) अपूरब – अपूर्व
(3) गुन – गुण
(4) सिखर – शिखर।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए :
(1) आरसी – ……………………………….
(2) सौर – ……………………………….
(3) काठ – ……………………………….
(4) वायस – ……………………………….
उत्तर :
(1) आरसी – स्त्रीलिंग
(2) सौर – स्त्रीलिंग
(3) काठ – पुल्लिंग
(4) वायस – पुल्लिंग।

प्रश्न 3.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए :
(1) बढ़ना x ……………………………….
(2) कपट x ……………………………….
(3) गन x ……………………………….
(4) आशा x ……………………………….
उत्तर :
(1) बढ़ना x घटना
(2) कपट x निष्कपट
(3) गुन x अवगुन
(4) आशा x निराशा।

पद्यांश क्र.2
प्रश्न. निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
कारण लिखिए :
(1) नीच को छेड़ना नहीं चाहिए – ………………………………………………
(2) उच्च पद पर आसीन का पतन निश्चित है – ………………………………………………
उत्तर :
(1) नीच को छेड़ना नहीं चाहिए – क्योंकि नीच को छेड़ना कीचड़ है में पत्थर डालने के समान है, जिससे कीचड़ उछलकर अपने ऊपर ही आता है।
(2) उच्च पद पर आसीन का पतन निश्चित है – कोई कितने ही उच्च पद पर क्यों न हो, किसी न किसी दिन किसी कारण से अथवा सेवा निवृत्त होने पर उसे अपने पद से नीचे उतरना ही पड़ता है।

प्रश्न 2.
सहसंबंध जोड़िए:
(1) होनहार बिरवान के, (1) काग निबौरी लेत।
(2) अपनी पहुँच बिचारि कै, करतब करिए दौर। (2) बैठो देवल सिखर पर वायस गरुड़ न होइ।।
उत्तर :
(1) होनहार बिरवान के, (1) होत चीकने पात।
(1) अपनी पहुँच बिचारि कै, करतब करिए दौर। (2) तेते पाँव पसारिए, जेती लांबी सौर।।

प्रश्न 3.
उत्तर लिखिए :
(1) सूर्य इस समय तपता है – ………………………………………………
(2) नबौरियों का आदर करने वाला – ………………………………………………
(3) यह कार्य अपने लिए हानिकारक होता है – ………………………………………………
(4) चिकने पात इनके होते हैं – ………………………………………………
उत्तर :
(1) मध्याह्न में।
(2) काग।
(3) अविवेक के साथ किया गया कार्य।
(4) होनहार पौधों के।

प्रश्न 4.
लिखिए :

उत्तर :

कृति 2 : (शब्द संपदा)

(2) निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(1) पाथर (पत्थर) = ………………………………………………
(2) भान (भानु) = ………………………………………………
(3) कोकिल = ………………………………………………
(4) मात = ………………………………………………
उत्तर :
(1) पाथर (पत्थर) = पाषाण
(2) भान (भानु) = सूर्य
(3) कोकिल = कोयल
(4) मात = शरीर।

रसास्वादन मुद्दों के आधार पर
(कृतिपत्रिका के प्रश्न 2 (इ) के लिए

प्रश्न 1.
निम्नलिखित मुद्दों के आधार पर वृंद के दोहे’ का रसास्वादन कीजिए :
उत्तर :
(1) रचना का शीर्षक : वृंद के दोहे।
(2) रचनाकार : वृंद। (पूरा नाम : वृंदावनदास)
(3) कविता की केंद्रीय कल्पना : प्रस्तूत दोहों में कई नीतिपरक बातों की सीख दी गई है। इस तरह कविता की केंद्रीय कल्पना नीतिपरक बातें हैं।
(4) रस-अलंकार :

(5) प्रतीक विधान : कवि वृंद के दोहों मे समझाने के लिए कई प्रतीकों का सुंदर उपयोग किया है। कविता में प्रयुक्त इन प्रतीकों में नयना, सौर (चादर), काठ की हाँड़ी, वायस, गरुड़, गागरि, पाथर, कोकिल, अंबा, निबौली, कुल्हाड़ी तथा बिरवान आदि प्रतीकों का समावेश है।

(6) कल्पना : अनेक नीति-परक उपयोगी बातें दोहों का विषय।

(7) पसंद की पंक्तियाँ तथा प्रभाव : कविता की पसंद की पंक्तियाँ इस प्रकार हैं :
सुरसति के भंडार की, बड़ी अपूरब बात।
ज्यौं खरचै त्यौं-त्यौं बढ़े, बिन खरचे घटि जात।
इन पंक्तियों से ज्ञान के भंडार की विपुलता तथा उसके विशेष गुण की महत्ता की जानकारी होती है।

(8) कविता पसंद आने का कारण : संसार में कोई वस्तु ऐसी नहीं है, जो किसी को देने से कम न होती हो। लेकिन ज्ञान का भंडार निराला है। इस ज्ञान को जितना खर्च किया जाए, उतना ही अधिक बढ़ता है। इतना ही नहीं, यदि इसे दूसरों को न दिया जाए और अपने ही पास जमा करके रहने दिया जाए, तो यह नष्ट हो जाता है।

व्याकरण

अलंकार :

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त अलंकार पहचानकर उनके नाम लिखिए :

(1) जान पड़ता है नेत्र देख बड़े-बड़े
हीरकों में गोल नीलम है जड़े

(2) करत-करत अभ्यास के जड़मति होत सुजान।
रसरी आवत जात से, सिल पर पड़त निसान।

(3) पत्रा ही तिरर्थ पाइयो, वाँ घर के चहुँ पास।
नितप्रति पूनो ही रह्यो आनन ओप उजास।

(4) ओ अकूल की उज्जवल हास।
अरी अतल की पुलकित श्वास।
महानंद की मधुर उमंग।
चिर शाश्वत की अस्थिर लास।

(5) सठ सुधरहि सत संगति पाई।
पारस परसि कुधातु सुहाई।
उत्तर :
(1) उत्प्रेक्षा अलंकार
(2) दृष्टांत अलंकार
(3) अतिशयोक्ति अलंकार
(4) रूपक अलंकार
(5) दृष्टांत अलंकार।

रस

प्रश्न 1.
निम्नलिखित काव्य पंक्तियों में प्रयुक्त रस पहचानकर लिखिए :
(1) कहा कैकेयी ने सक्रोध
दूर हट! दूर हट! निर्बोध!
द्विजिव्हे रस में विष मत घोल।

(2) कबहूँ ससि माँगत आरि करें, कबहूँ प्रतिबिंब निहारि डरै।
कबहूँ करताल बजाइ कै नाचत, मातु सबै मन मोद मरे।।
कबहूँ रिसिआइ कहैं हठि कै, पुनि लेत सोई जेहि लागि रैं।
अवेधेस के बालक, चारि सदा, तुलसी मन मंदिर में बिहरै।।

(3) दूलह श्री रघुनाथ बने, दुलही सिय सुंदर मंदिर माहीं।
गावति गीत सबै मिलि सुंदर, वेद जुवा जुरि विप्र पढ़ाहीं।
राम को रूप निहारति जानकी, कंकन के नग की परछाहीं।
यातै सबै सुधि भूल गई कर टेकि रही पल, टारति नाहीं।। (तुलसीदास-कवितावली)

(4) मेरे तो गिरधर गोपाल दूसरो न कोई।
जाके सिर मोर मुकुट, मेरो पति सोई।
साधुन संग बैठि-बैठि, लोक लाज खोई।
अब तो बात फैलि गई जानत सब कोई।
अँसुवन जल सींचिं-सींचि प्रेम बेलि बोई।
मीरा को लगन लागी होनी होइ सो होई।

(5) लीन्हौं उखारि पहार विसाल, चल्यो तेहि काल बिलंब न लायो।
मारुत नंदन मारुत को, मन को, खगराज को वेग लजायो।
तीखी तुरा तुलसी कहती पै हिए उपमा को समाउ न आयौ।
मानो प्रत्यच्छ परब्बत की नभ लीक लसी कपि यों धुकि धायौ।
उत्तर :
(1) रौद्र रस
(2) वात्सल्य रस
(3) शृंगार रस
(4) भक्ति रस
(5) अद्भुत रस।

मुहावरे

निम्नलिखित मुहावरों के अर्थ लिखकर वाक्य में प्रयोग कीजिए :

(1) ओखली में सिर देना।
अर्थ : जानबूझ कर जोखिम उठाना।
वाक्य : आदिवासियों का वह नेता अपने भाइयों के हित की लड़ाई लड़ने के लिए ओखली में सिर देने के लिए हमेशा तैयार रहता था।

(2) डूबती नैया पार लगाना।
अर्थ : कष्टों से छुटकारा देना।
वाक्य : सेठ जी ने अपने कर्मचारी को कर्ज से छुटकारा दिलाकर उसकी डूबती नैया पार करा दी।

(3) तलवे चाटना।
अर्थ : खुशामद करना।
वाक्य : अपना काम करवाने के लिए बड़े-बड़े लोगों को भी अधिकारियों के तलवे चाटने पड़ते हैं।

(4) पेट काटना।
अर्थ : भूखा रहना।
वाक्य : रमेश को अपनी सीमित आय में अपने दोनों बच्चों को पेट काटकर पढ़ाना पड़ा था।

(5) हाथ खींचना।
अर्थ : साथ न देना।
वाक्य : बेटे के हाथ खींच लेने के बाद रघु को गृहस्थी चलाना भारी पड़ रहा है।

काल परिवर्तन

प्रश्न 1.
सूचना के अनुसार काल परिवर्तन कर वाक्य फिर से लिखिए :
(1) होनहार पौधों के पत्ते चिकने होते हैं। (सामान्य भविष्यकाल)
(2) कोयल आम का स्वाद लेती है। (अपूर्ण भूतकाल)
(3) आईना भला-बुरा बता देता है। (पूर्ण वर्तमानकाल)
(4) काठ की हाँडी दुबारा नहीं चढ़ेगी। (सामान्य वर्तमानकाल)
(5) मंदिर के शिखर पर कौआ बैठा है। (पूर्ण भूतकाल)
उत्तर :
(1) होनहार पौधों के पत्ते चिकने होंगे।
(2) कोयल आम का स्वाद ले रही थी।
(3) आईने ने भला-बुरा बता दिया है।
(4) काठ की हाँडी दुबारा नहीं चढ़ती।
(5) मंदिर के शिखर पर कौआ बैठा था।

वाक्य शुद्धिकरण

प्रश्न 1.
निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए :
(1) मैं मेरा काम दूसरे से करवाता है।
(2) सारे विद्यालय के विद्यार्थी पढ़ने में तेज है।
(3) पशु का झुंड देखकर मैं डर गए।
(4) वह अपनी पाँव पर खुद कुल्हाड़ी मारता हैं।
(5) मध्याह्न के सूर्य तपते है।
उत्तर :
(1) मैं अपना काम दूसरे से करवाता हूँ।
(2) विद्यालय के सारे विद्यार्थी पढ़ने में तेज हैं।
(3) पशुओं का झुंड देखकर मैं डर गया।
(4) वह अपने पाँव पर खुद कुल्हाड़ी मारता है।
(5) मध्याह्न का सूर्य तपता है।

वृंद के दोहे Summary in Hindi

वृंद के दोहे कवि का परिचय

वृंद के दोहे कवि का नाम : वृंद। पूरा नाम : वृंदावनदास। (जन्म 1643; निधन 1723.)

वृंद के दोहे प्रमुख कृतियाँ : वृंद सतसई, समेत शिखर छंद, भाव पंचाशिका, पवन पचीसी, हितोपदेश संधि, यमक सतसई, वचनिका, सत्यस्वरूप, बारहमासा आदि।

वृंद के दोहे विशेषता : रीतिकालीन परंपरा के अंतर्गत आपका नाम आदर के साथ लिया जाता है। आपकी रचनाएँ रीतिबद्ध परंपरा में महत्त्वपूर्ण स्थान रखती हैं। आपने काव्य के विविध प्रकारों में रचनाएँ रची हैं। आपके नीतिपरक दोहे जनसाधारण में बहुत प्रसिद्ध हैं। विधा दोहा छंद। रीतिकालीन काव्य परंपरा में दोहा छंद का विशेष स्थान रहा है। दोहा अर्ध सम मात्रिक छंद है। इसके प्रत्येक चरण के अंत में लघुवर्ण आता है। इसके चार चरण होते हैं, प्रथम और तृतीय चरण में 13 – 13 मात्राएँ होती हैं तथा द्वितीय और चतुर्थ चरण में 11 – 11 मात्राएँ होती हैं।

वृंद के दोहे विषय प्रवेश : कवि वृंद अपने दोहों के माध्यम से अपनी सरल-सुबोध भाषा में अत्यंत उपयोगी एवं व्यावहारिक बातों से परिचित करते हैं। प्रस्तुत दोहों में उन्होंने विद्या की विशेषता, आँखों की पहचानने की शक्ति, अपनी क्षमता के अनुरूप काम करने, व्यापार करने के सही ढंग, गुण के अनुसार आदर पाने, नीच को न छेड़ने तथा पालने में ही बच्चे के लक्षण दिख जाने आदि नीतिपरक बातें बताई हैं।

वृंद के दोहे दोहों का सरल अर्थ

1. कवि वृंद कहते हैं कि माँ सरस्वती के ज्ञान की बात बहुत अनूठी और अपूर्व है। इस ज्ञान के भंडार को जितना खर्च किया जाए अर्थात जितना बाँटा जाए उतना ही बढ़ता है। यदि ज्ञान को बाँटा न जाए, तो इसमें कमी आती जाती है। कवि वृंद कहते हैं कि आँखें हित और अहित की सारी बातें उसी तरह बता देती हैं, जैसे निर्मल आईने से अच्छी और बुरी दोनों तरह की बातों का पता चल जाता है।
2. कवि कहते हैं कि हमारी जितनी क्षमता हो, उसी के अनुसार हमें अपने कार्य का फैलाव करना चाहिए। कवि उदाहरण देते हुए कहते हैं कि हमारी चादर की लंबाई जितनी हो, हमें उतने ही पाँव फैलाने चाहिए। यदि हम ऐसा नहीं करते, तो हम अपना कार्य पूरा नहीं कर सकते।
3. कवि कहते हैं कि व्यापार यानी लेन-देन में हमें छल-कपट का सहारा नहीं लेना चाहिए। यदि हम एक बार छल-कपट से काम लेते हैं, तो दूसरी बार हम व्यापारी अथवा ग्राहक से लेन-देन नहीं कर सकते। कवि काठ की हाँडी का उदाहरण देते हुए कहते हैं कि जिस प्रकार काठ की हाँडी एक बार ही आग पर चढ़ाई जा सकती है, दूसरी बार वह काम में नहीं आ सकती, उसी प्रकार छल-कपट से व्यापार में एक ही बार किसी को धोखा दिया जा सकता है, दूसरी बार यह तरीका काम में नहीं लाया जा सकता।
4. कवि कहते हैं कि बिना गुण के किसी व्यक्ति को उच्च स्थान पर बैठने मात्र से बड़प्पन नहीं मिलता। वे कहते हैं कि जिस प्रकार मंदिर के ऊँचे शिखर पर बैठने मात्र से कौआ गरुड़ नहीं हो जाता, उसी प्रकार गुणों से रहित कोई व्यक्ति बड़प्पन का अधिकारी नहीं हो सकता।
5. कवि कहते हैं कि मनुष्य को किसी के सहारे की आशा में खुद प्रयत्न करना छोड़ नहीं देना चाहिए। क्या बादल घिर जाने पर उससे मिलने वाले विपुल जल की उम्मीद में कोई पानी रखने का अपना जलपात्र यानी गगरी फोड़कर फेंक देता है?
6. कवि कहते हैं कि नीच अर्थात बुरे आदमी को कभी कुछ (बुरा भला) कहकर छेड़ना नहीं चाहिए। क्योंकि जैसे कीचड़ में पत्थर फेंकने पर कीचड़ की गंदगी अपने ही ऊपर आती है, उसी तरह बुरे आदमी को कही गई बातों के बदले उसके द्वारा कहे गए अपशब्द हमें सुनने पड़ते हैं।
7. जिस व्यक्ति को उच्च पद प्राप्त होता है, उसका भी एक-नएक दिन पतन होना निश्चित है। जिस प्रकार मध्याह्न का सूर्य उस समय बहुत तपता है, पर उसे भी एक समय अस्त हो जाना पड़ता है।
8. जिस व्यक्ति को जिस चीज के गुणों के बारे में जानकारी होती है वह उसे ही सम्मान देता है। जैसे कोयल आम का स्वाद लेती है और कौआ निबौरियाँ ही खाता है।
9. कवि कहते हैं कि अविवेक के साथ किया गया कार्य स्वयं के लिए हानिकारक सिद्ध होता है। ठीक उसी तरह जैसे कोई मूर्ख अपनी अविवेकता से कोई कार्य कर अपने पाँव पर अपने हाथ से कुल्हाड़ी मार लेता है।
10. कवि कहते हैं कि पालने में बच्चे के शरीर के लक्षण देखकर उसके अच्छे-बुरे होने का पता चल जाता है। जैसे किसी पौधे के चिकने और स्वस्थ पत्ते देखकर उसके होनहार होने के लक्षण दिखाई देते हैं।

वृंद के दोहे शब्दार्थ

• सरसुति = सरस्वती, विद्या की देवी
• सौर = चादर
• लहैं = लेना
• उद्यम = प्रयत्न
• पाथर = पत्थर
• अंबहि = आम
• करतब = कार्य
• काठ = लकड़ी
• वायस = कौआ
• पयोद = बादल
• तिहि = उसे
• निबौरी = नीम का फल

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest Chapter 12 पैंजण Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati Solutions Chapter 12 पैंजण

11th Marathi Digest Chapter 12 पैंजण Textbook Questions and Answers

कृती

1. योग्य पर्याय निवडून वाक्ये पूर्ण करा.

प्रश्न अ.
आजी जखमांना ऊब देऊन राज करायची! म्हणजे
(१) आजी जखमांना औषधपाणी करून काम करायची.
(२) रूढींचा त्रास सहन करत स्वयंपाकघरापुरती वावरायची.
(३) जखमारूपी संकटांना सहन करून आनंदात राहायची.
उत्तरः
आजी जखमांना ऊब देऊन राज करायची ! म्हणजे – जखमारूपी संकटांना सहन करून आनंदात राहायची.

प्रश्न आ.
सारे दुर्लक्षून ती राजराणीसारखी भिरभिरायची! म्हणजे
(१) राजाच्या राणीसारखा सन्मान तिला मिळायचा.
(२) राजाच्या राणीचा तोरा मिरवायची.
(३) रूढींच्या मर्यादेत राहून घरापुरत्या निर्णयात सहभागी होण्यात धन्यता मानायची.
उत्तर :
सारे दुर्लक्षून राजाराणीसारखी भिरभिरायची ! म्हणजे – रूढींच्या मर्यादेत राहून घरापुरत्या निर्णयात सहभागी होण्यात धन्यता मानायची.

प्रश्न इ.
मिळणाऱ्या स्वातंत्र्यासाठी मी सारे सहन करते. म्हणजे
(१) घराबाहेर पडण्याच्या स्वातंत्र्यासाठी कौटुंबिक, सामाजिक बंधने सहन करते.
(२) स्वातंत्र्य मिळाले म्हणून इतर दु:खं सहन करते.
(३) ऐच्छिक वेषभूषेसाठी सारे सहन करते.
उत्तर :
मिळणाऱ्या स्वातंत्र्यासाठी मी सारे सहन करते. म्हणजे – घराबाहेर पडण्याच्या स्वातंत्र्यासाठी कौटुंबिक, सामाजिक बंधने सहन करते.

प्रश्न ई.
पायच होऊ देत आता… घट्ट, मजबूत, पोलादी पुढल्या का होईना शतकाआधी! म्हणजे
(१) पुढचे शतक येण्यापूर्वी स्वयंपूर्ण आणि समर्थ बनू दे.
(२) पुढल्या शतकाआधी पाय जमिनीवर राहू दे.
(३) पुढल्या शतकाआधी काटे कमकुवत होऊ दे.
उत्तर :
पुढल्या का होईना शतकाआधी! पायच होऊ देत आता… घट्ट, मजबूत, पोलादी. म्हणजे – पुढचे शतक येण्यापूर्वी स्वयंपूर्ण आणि समर्थ बनू दे.

2.
प्रश्न अ.
खालील ओळींतील संकल्पना स्पष्ट करा.
(१) नादाच्या भुलभुलैय्यातून बाहेर न पडणे.
उत्तर :
संसाराचाही एक नाद असतो. आपल्या पुरुषप्रधान संस्कृतीत संसाराचा नाद बाईलाच शिकवला जातो. त्याची रीतभात सांभाळण्यात बाईचा जन्म जातो. जे आपल्याला पढवलं गेलं त्याच्या पलीकडे जाऊन स्वतंत्र व्यक्ती म्हणून जगण्याची हिंमत बाईने दाखवली तर तिची अवहेलना केली जाते. शक्यतो अशी हिंमत करणाऱ्या स्त्रिया अभावानेच आढळतात. आपल्या संसाराच्या जबाबदाऱ्या पेलताना आपलं पिचणं हा भूलभुलैय्या प्रमाण मानून बाई जगते. त्यात अडकते. त्यातून बाहेर पडत नाही.

(२) पण सारे दुर्लक्षून राजराणीसारखे भिरभिरणे.
उत्तर:
प्राचीन काळापासून कौटुंबिक बंधनात अडकलेली स्त्री शिक्षणाचा परीस स्पर्श होता बदलली. पण तिच्यात झालेले परिवर्तन हे पुन्हा घरापुरतंच मर्यादित राहिलं. तिला स्वयंपाकघरातून गच्चीपर्यंत हिंडण्याचे स्वातंत्र्य दिले गेले. पण ते मिळाल्यामुळे आनंदित झालेली स्त्री अनेक ओझी, बंधनं स्वीकारतच राहिली. आमच्या घरी हे चालत नाही, ते चालत नाही म्हणून घराचं कौतुक सांगताना ती थकली नाही. पण एकीकडे आपल्याला दुसरे कोणतेच स्वातंत्र्य नाही याकडे दुर्लक्ष करून ती मिळालेल्या स्वातंत्र्याचा आनंद घेऊ लागली.

(३) मिळणाऱ्या स्वातंत्र्यासाठी सारे सहन करणे.
उत्तर :
कवयित्री ही आपल्या आजी, आईला घरात मिळणाऱ्या वागणुकीविषयी कवितेतून भाष्य करते तेव्हा त्या दोघींपेक्षा आपण जास्त सुखी आहोत असं तिला वाटतं. कवयित्री पैंजण, तोरड्या आपल्या पायात घालत नाही. काही बंधनं तिनं झुगारली पण तिनं चपला, बूट, सँडल जवळ केल्या. घर, अंगणाबाहेर पडली.

चपला, बूट, सँडल हे आधुनिकतेचे प्रतीक. आपल्या घराबाहेर पडताना कवयित्रीने या चपला, बूट, सँडल धारण केले. पण तेही तिच्या पायांना साथ देऊ शकले नाहीत. जगताना घराबाहेरची अनेक संकटे ती पेलू लागली. घरात राहताना घरातील संकटे, बंधने तर बाहेर पडली तरी घराबाहेरची संकटे होतीच. पण आर्थिक, निवड स्वातंत्र्यासाठी, स्वतःचे हक्क मिळवण्यासाठी त्या सर्वच संकटांकडे ती दुर्लक्ष करू लागली. पण व्रण तर उमटत राहिले पायांवर, मनावर.

प्रश्न आ.
खालील तक्ता पूर्ण करा.

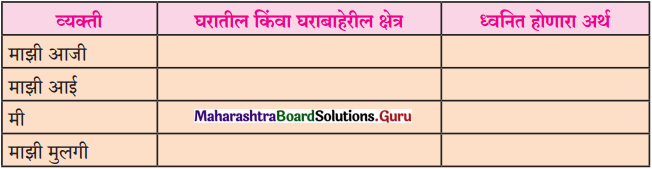
उत्तरः

प्रश्न इ.
खालील तक्ता पूर्ण करा.

उत्तरः

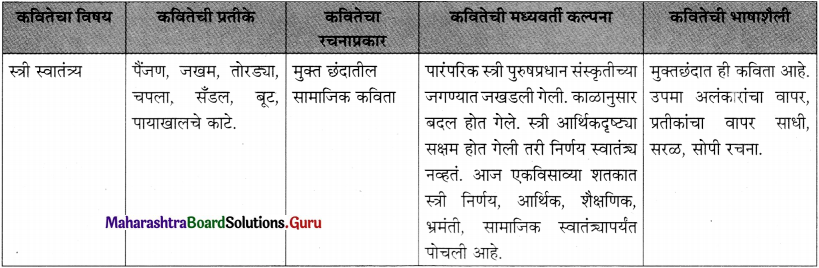
3. काव्यसौंदर्य.

प्रश्न अ.
‘चपला घसरतात, सँडल बोचतात, बूट चावतात पण मिळणाऱ्या स्वातंत्र्यासाठी मी सारे सहन करते,’ या ओळींतील विचारसौंदर्य स्पष्ट करा.
उत्तर :
कवयित्री नीलम माणगावे यांच्या पैंजण कवितेत स्त्री स्वातंत्र्याचा विचार मांडला आहे. प्राचीन काळातील स्त्रीचे जगणे ते आधुनिक काळातील स्त्रीचे जगणे यांतील फरक कवयित्री स्पष्ट करते. यात चार पिढ्यांमधील स्त्रीमधील बदलत गेलेले स्वरूप कवयित्री कथन करते.

आजी, आई, मी, मुलगी या चार अवस्थांपैकी मी जी आहे तिचे वर्णन करताना कवयित्री सांगते की ही स्त्री चपला, पायात पैंजण, तोरड्या घालत नाही. तिच्या पायातील चपला घसरतात, सँडल बोचतात, बूट चावतात हे सर्व त्रासदायक असते. या पायताणांचा त्रास होऊन पायाला या गोष्टी बोचत असतात.

कोणतीही एक चप्पल /सँडल कायमस्वरूपी नाही. त्या बदलत जातात पण त्या ज्या पायाला वेदना होतात ते पाय तेच असतात. कामाला ते पाय वणवण फिरतात. पण त्यामुळे तिला बाहेर पडता येतं. तिला काही निर्णय घेता येतात. तिला थोडं आर्थिक स्वातंत्र्य मिळतं पण त्यात ती पूर्णतः पिचूनही जाते.

प्रश्न आ.
‘अगं पायाखालचे काटे मोडण्यासारखे पायच होऊ देत आता… घट्ट, मजबूत, पोलादी’, या ओळींतील अर्थसौंदर्य स्पष्ट करा.
उत्तर :
पुरुषसत्ताक समाजरचनेमध्ये स्त्री आज स्वतःचे स्वतंत्र जग निर्माण करत आहे. आपल्या जीवनातील दुःख दूर करायची असतील तर पुरुषांनी हात दिला तर पुढे जाऊ असा विचार आजची स्त्री करत नाही. ती स्वसामर्थ्यावर विश्वास ठेऊन पुढे जाण्याचा विचार करत आहे. आताच्या काळातील स्त्रीने आपल्या केश, वेशभूषेत कमालीचा बदल केला आहे, इतकेच काय तर आजच्या स्त्रीने दागदागिन्यांचा अव्हेर करत मुक्तपणे जगायला सुरुवात केली आहे.

कवयित्रीच्या मुलीलाही पैंजण, तोरड्या नको आहेत. तिला पायाचे रक्षण करण्याकरता चपला, बूट वगैरेही नको आहेत. त्यांचं घसरणंसदधा तिला नकोय. तिच्या पायाखाली संस्कतीचे, बंधनाचे काटे येणार. ते बोचणारच. ते काटे मोडन काढण्यासाठी तिला तिचे पाय घट्ट, मजबूत, पोलादी करायचे आहेत. स्वत:ला इतकं मजबूत घडवायचंय की कोणाच्या आधाराशिवाय तिला पुढं जाता यायला हवं.

प्रश्न इ.
आजीच्या आणि आईच्या कौटुंबिक वातावरणात झालेला फरक कोणकोणत्या प्रतीकांतून वर्णन केला आहे ते स्पष्ट करा.
उत्तर :
कवयित्री नीलम माणगावे यांच्या पैंजण कवितेत स्त्रियांच्या चार पिढ्या आणि त्यांचे संघर्ष, त्यातून त्यांनी मिळवलेले स्वातंत्र्य याचा विचार मांडला आहे.

कवयित्री या कवितेत मी म्हणून अभिव्यक्त होताना आपल्या आजी आणि आईच्या वाट्याला आलेल्या भोगवट्याचे चित्रण करते. आजी आपल्या पायात दोन किलो वजनाचे पैंजण घालून सम्राज्ञीसारखी ठुमकत फिरायची. त्या ओझ्याने तिचे पाय ठणकून यायचे, जखमा व्हायच्या, रक्त वहायचं पण नादाच्या मोहापायी ते सर्व ती सहन करायची. आपल्या जखमांना ऊब देऊन ती राज करायची. निदान राज करत असलेलं भासवायची.

संसाराचा गाडा हे पैंजणाचे प्रतीक मानले तर ‘रांधा, वाढा, उष्टी काढा’, एकत्र कुटुंब, त्यांचे मान अपमान, जबाबदाऱ्या या सगळ्यांत तिचं आयुष्य पिचून गेलं, तिच्या पायांना सवयच झाली अनेक जखमा सोसायची. पण त्याच्या विरोधात कधी तक्रार नाही केली. जे आहे त्यात समाधान मानण्याची तयारी होती. कवयित्रीच्या आईने पैंजण घालणे सोडून दिले. नाजूक हलक्या तोरड्या घालायला सुरुवात केली. घरातील सर्वच ठिकाणी ती हिंडू फिरू शकायची.

मधून तोरड्या टोचल्या की साडीचे काठ फाटायचे, दोरे लोंबायचे पण तरीही आपल्याला निदान मुक्तपणे फिरता येते याचा आनंद असायचा. या दोन्ही घरांतील फरक स्पष्ट करण्याकरता काही प्रतीकांचा वापर केला आहे. पैंजण – घरातील प्रचंड जबाबदाऱ्या, स्वयंपाक घरातून माजघरात – केवळ मर्यादित विश्व, सम्राज्ञी – एक प्रकारे गुलामच पण तरी स्वयंपाकघर, माजघरात हुकूमशाही, नादाचा भूलभुलैय्या – संसाराचा जीव, जखमांना ऊब – मनातील जखमा बाजूला, आईच्या पायातील तोरड्या – नाजूक, हलक्या-म्हणजे आजीपेक्षा कमी जबाबदारी, स्वयंपाकघर, माजघर, सोपा, अंगण, माडी, गच्ची या सर्व ठिकाणी हिंडंण्याची मुभा, राजा राणी – निदान आपल्याला घरातल्या सर्व ठिकाणी फिरता येतंय, त्यांच्यावर अधिकार गाजवता येतो त्याचा आनंद.

4. अभिव्यक्ती.

प्रश्न अ.
कवितेत वर्णन केलेली आजी व आजची आजी यांच्यात कालपरत्वे झालेला बदल स्वभाषेत स्पष्ट करा.
उत्तर :
पूर्वीच्या काळी स्त्रीचा वावर तिच्या घरापुरता मर्यादित होता.अनेक अलंकार धारण करून, नऊवारी साडी नेसून पहाटे चारपासून ते रात्रीपर्यंत, एकत्र कुटुंबाच्या सर्वच जबाबदाऱ्या पेलाव्या लागायच्या. घरातल्या स्वयंपाकघरातच ती राणी असायची पण घरातील बाकीच्या कोणत्याच गोष्टीमध्ये तिला विचारात घेतलं जात नसे. अहोरात्र तिच्या कष्टाच्या बदल्यात तिला कोणत्याच प्रकारचे सुख मिळत नव्हते.

अर्थात स्त्रियांना अशाच पद्धतीने वाढवले जात असे. ती स्वतंत्र व्यक्ती आहे म्हणून तिला शिकवले जात नसे. पण आजची आजी मात्र बदलली आहे. ती कमवणारी असल्यामुळे तिची स्वत:ची मतं आहेत. ती आपल्या नातवंडांना शिक्षणात मदत करणारी आहे.

चूल-मूल या संकल्पनांना तिनं कालबाह्य ठरवलेलं आहे. सौभाग्य अलंकार, केशभूषा या बाबतीत तिनं कात टाकली आहे. आपल्या नातीला वाढवताना ती तिचा माणूस म्हणून विचार करते आहे. त्यामुळे आजची आजी प्रगल्भ आहे.

प्रश्न आ.
स्त्रीच्या भविष्यकालीन प्रगत रूपांविषयी तुमच्या कल्पना स्पष्ट करा.
उत्तर :
आजची स्त्री स्वतंत्र आहे असं पूर्णार्थाने म्हणता येणार नाही पण ती मात्र सगळ्या पारंपरिक विचारांना बाजूला सारून पुढे जाताना दिसत आहे.

आजचे दहावी, बारावीचे निकाल पाहता मुलींच्या संख्येत वाढ होताना दिसत आहे. यामध्ये पुढील काळात मुली शिक्षण, करिअर यात पुढेच जाणार आहेत. त्यांची सहनशीलता, कष्ट करण्याची वृत्ती, भविष्यकाळाचा विचार करण्याची वृत्ती, एकाच वेळी चार गोष्टींचा साकल्याने विचार करण्याची पद्धत यामुळे पुढचा काळ मुलींच्या हाती असणार आहे. ती सर्वच बंधनांना झुगारून पुढे जाईल.

आपल्यावर होणाऱ्या आणि त्याकरता न्यायालय धाव घेत न बसता योग्य ती शिक्षा दयायला ती स्वत: समर्थ असेल. पुरुषापेक्षा ती नक्कीच वरचढ असेल. शहरामध्ये बदलत असलेले चित्र हळूहळू ग्रामीण भागापर्यंत पोचेल आणि तिथेही हे बदल होतील. गरज आहे पुरुष आणि स्त्री यांच्या समानतेची.

दोन्ही बाजूंनी एकमेकांना समजून घेण्याची. पण त्याकरता संवाद होणं आवश्यक आहे. पुरुषांच्या बरोबरीने काम करताना स्त्रियांनाही अनेक अडचणींना सामोरं जावं लागणार आहे. पण त्या या संघर्षातून पुढेच जातील कारण त्यांनी त्यांची मनं घट्ट केली आहेत.पुरुषाने स्त्रियांना समजून घेण्याच्या कक्षा रुंदावल्या पाहिजेत.

5. रसग्रहण.

प्रश्न 1.
‘पैंजण’ या कवितेचे रसग्रहण करा.
उत्तरः
कवयित्री नीलम माणगावे यांनी ‘पैंजण’ या कवितेत स्त्रियांच्या प्रगतीच्या प्रवासात कशी आणि कोणती स्थित्यंतरे झाली याचे वर्णन केले आहे. प्राचीन काळातील स्त्री ते आताच्या काळातील स्त्री यांचे प्रगतीच्या वाटेवरचे टप्पे पाहता स्त्रीने स्वत:चे स्वातंत्र्य मिळवले. तिचा आत्मविकास तिने केलेला आहे. या कवितेची रचना मुक्तबंधात करताना काही प्रतिमांचा, उपमांचा वापर कवयित्रीने केलेला आहे.

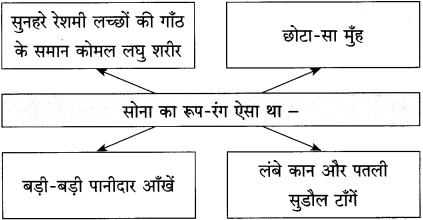
कवयित्री अगदी पारंपरिक स्त्रीचा उल्लेख करताना आजी म्हणून करते: आजी तिच्या काळात दोन दोन किलो वजनाचे पैंजण घालून स्वयंपाकघरातून माजघरात, माजघरातून स्वयंपाकघरात एखादया सम्राज्ञीसारखी फिरायची. आजीला केवळ या दोन ठिकाणी फिरण्याचे स्वातंत्र्य होतं;

पण या दोन्ही ठिकाणी आपण आपला अधिकार गाजवू शकतो याची जाणीव तिला होती. अखंड कुटुंब, त्याच्या जबाबदाऱ्या पेलताना तिला मिळणारा मान तिला महत्त्वाचा वाटत होता. आपल्या घरात आपण सम्राज्ञी असल्यासारखी वावरायची. तिच्या पायातल्या पैंजणांमुळे तिचे पाय भरून यायचे, दुखायचे, खुपायचे. घोटे काळे ठिक्कर पडायचे. या जबाबदाऱ्यांमुळे जास्तीची कामे पडायची, अखंड आयुष्य घरातील दोन खोल्यात जगायला लागायचं.

पण त्या संसाराचा, जबाबदाऱ्यांचा नादच इतका की त्यामुळे आपलं माणूसपण भरडलं जातं याचे भानच नसायचं, पैंजणाखाली फडके बांधून जखमांना बरं करत करत आजी जगायची, संसाराचा भार पेलताना थकून जायची, अपमान गिळायची, अत्याचार सहन करायची. पण संसारात या जखमा सहन कराव्या लागणारच याची जाणीव ठेवून ती आहे त्यात सुख मानायची.

यामध्ये पैंजण या अलंकाराचा वापर करून कवयित्रीने तिच्या पायातील बेड्यांचा उल्लेख केला आहे. या बंधनांनी त्रास झाला, जखमा झाल्या तरी तोंड दाबून बुक्क्यांचा मार ती सहन करत होती.

कवयित्री आपल्या आधीच्या पिढीतल्या स्त्रियांवरील बंधने कथन करताना आईचा उल्लेख करते. आईने पैंजण सोडून नाजूक, हलक्या तोरड्या घातल्या. तिला आईचं दुखणं ठाऊक होतं, तोरड्या घातल्यामुळे आता आपल्या पायाला कमी जाच होईल असं तिला वाटलं. पाय दुखले, खुपले चिघळले नाहीत.

मग तिला स्वयंपाकघर ते गच्चीपर्यंत हिंडण्याची मुभा मिळाली. आपल्या अगोदरच्या पिढीला हे स्वातंत्र्य नव्हतं त्यामुळे तिला आनंदच झाला. या तोरड्यांचा त्रास व्हायचाच. अधून मधून साडीचे काठ फाटायचे, दोरे लोंबकळायचे पण तरीही आपल्याला घरातील काहीजण विचारतात, काही हक्क आपल्याकरता आहेत याच्या जाणिवेने ती सारा जाच, दुखणं दुर्लक्षून ती स्वत:च्या घरात राणी असल्यासारखी भिरभिरायची. इथं भिरभिरणं या क्रियापदामधूनच ती स्थिर कुठेही नसायची याची जाणीव कवयित्री करून देते.

स्वत:च्या काळातील स्त्रीचा उल्लेख करताना ती म्हणते की अडकणं, बोचणं, चिघळणं, फाटणं काहीच नको म्हणून पैंजण, तोरड्यांना कवयित्रीने अगदी हद्दपार केलं.

हलक्या अशा चपळाईने सँडल घालता घालता घरच नव्हे तर अंगणही ओलांडून कवयित्रीने घराच्या बाहेर पाऊल टाकलं. पण कधीतरी चपला, बूट, सँडलही बोचतात. घराच्या बाहेर पडताना पायाच्या सुरक्षिततेसाठी या पायताणांचा वापर ती करते. परंतु या पायताणांचा त्रास ती सहन करते. आपल्याला मिळणाऱ्या स्वातंत्र्यासाठी घरात असतानाही काही गोष्टींच्या वेदना होत्याच. ती बाहेर पडली तेव्हा वेदना सहन कराव्या लागत आहेत.

पण आपल्याला घराबाहेर मिळणारे सन्मान, स्वातंत्र्य याकरता तिने सारे दुःख सहन केले. आताच्या मुलींच्या स्वातंत्र्याबाबत भाष्य करताना कवयित्री म्हणते की माझी मुलगी पैंजण, तोरड्या तर घालणार नाही. चप्पल, बूट, सँडलही नको, कोणतीच बंधने, त्यातून होणारी घुसमट आताच्या मुलीला, स्त्रीला नकोय.

त्या सगळ्याच्या पलिकडे जाऊन केवळ आपल्या सामर्थ्याने तिला पुढे जायचे आहे. पाय पोलादी करायचे आहेत, कारण कोणत्याही वेदना पोचल्या तरी त्या सहन करण्याची तयारी आहे. पुढच्या शतकाआधी हे व्हावं असं तिला वाटतं.

प्रकल्प.
स्त्रियांच्या प्रगतीसंदर्भातील विविध घटनांचे अर्थपूर्ण कोलाज तयार करा.

प्रश्न 1.
म्हणींचा शोध घ्या. (तिरपा, आडवा, वरून खाली किंवा खालून वर)

उत्तर :
(१) बळी तो कान पिळी
(२) पालथ्या घड्यावर पाणी
(३) शक्तीपेक्षा युक्ती श्रेष्ठ
(४) दिव्याखाली अंधार
(५) अति तेथे माती

11th Marathi Book Answers Chapter 12 पैंजण Additional Important Questions and Answers

कृती : २ खालील पठित पदय पंक्तीच्या आधारे दिलेल्या सुचनेनुसार कृती करा.

कृती-१. चौकट पूर्ण करा

प्रश्न 1.
पैंजणाचे वजन :
उत्तर :
दोन किलो

प्रश्न 2.
आजीचं ठुमकणं :
उत्तर :
सम्राज्ञीसारखे

कृती-२. आकृतीबंध पूर्ण करा.

प्रश्न अ.

उत्तर :
a. जखम व्हायची
b. जखम चिघळायची
c. रक्त वाहायचे

प्रश्न ब.
सम्राज्ञीसारखं फिरण्याची जागा : –

उत्तर :
a. स्वयंपाकघर
b. माजघर

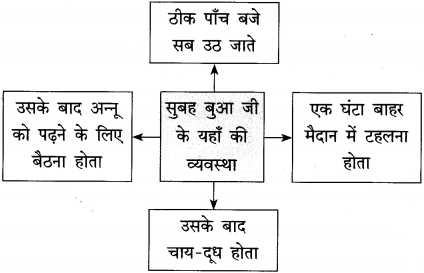
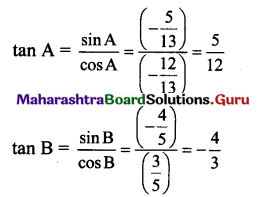
दोन दोन किलो वजनाचे ……………………………………………………………………………………………………………………… राज करायची ! (पाठ्यपुस्तक पृष्ठ क्र. ५३)

कृती-३.

प्रश्न 1.
स्वयंपाकघरातून माजघरात,
माजघरातून स्वयंपाकघरात
‘एखादया सम्राज्ञी
सारखी ठुमकत फिरायची!’
यातील तुम्हांला जाणवलेला अर्थ स्पष्ट करा.
उत्तर :
जुन्या काळातील आजीचं अस्तित्व घरापुरतं मर्यादित होतं. घरामध्येही केवळ स्वयंपाकघर, माजघर या ठिकाणीच तिचं अस्तित्व होतं. जे आहे त्यात जुळवून घेण्याचा प्रयत्न त्या काळच्या स्त्रिया करत होत्या. आजीला घरातील स्वयंपाक स्वातंत्र्य होतं. ते सणासुदीला माजघरात वावरण्याचे स्वातंत्र्य होतं.

या दोन खोल्यांव्यतिरिक्त कोणत्याही ठिकाणी तिला जाण्याचे स्वातंत्र्य नव्हतं. पण या ठिकाणी आपल्याला फिरता येतंय. तिथे आपले हक्क चालतायत याच्या अल्प आनंदात एखादया सम्राज्ञीसारखी ती ठुमकत फिरायची. त्या काळात कुटुंब मोठी असायची घरातील ज्येष्ठ स्त्रीला मान असायचा पण निर्णय स्वातंत्र्य नसायचे. त्याबद्दल तिला खेदही वाटत नसायचा.

प्रश्न 2.
आजीला घरात मिळणाऱ्या वागणुकीबद्दल तुमचे मत लिहा.
उत्तर :
माझी आजी गावात राहते. पूर्वी आमच्याकडे एकत्र कुटुंबपद्धती होती. त्यावेळी आजी घरात मोठी सून होती. तिच्यावर बऱ्याच जबाबदाऱ्या असायच्या. कधी तिला माहेरीसुद्धा जायला मिळायचे नाही. पै-पाहुणा घरात आला की सर्वांचे हवे-नको ते पाहण्यात ती मग्न असायची. बाबा-आत्याच्या लहानपणी तिने त्यांना खूप वेळही दिला नाही. पण घरातले सर्वच जण तिचा खूप आदर करत. आगोदर कोणत्याच कार्यात तिचा विचार विचारात घेतला जात नसायचा.

पण जसजसे तिचे वय वाढत गेले तसतसं तिच्या मायेची निर्णयक्षमतेची, समंजसपणाची ख्याती घरभर पसरली तेव्हा तिच्या मतांचा आदर केला जाऊ लागला. माझ्या सर्व काकुंना तिने फार प्रेमानं वागवलं आणि आईचा सासू म्हणून कधी जाच केला नाही.

सर्वांना समजून घेण्यात ती कधीच कमी पडली नाही. त्यामुळे घर दुभंगलं नाही. तिने खूप खस्ता खाल्ल्या घराच्या जबाबदाऱ्या पेलताना; पण आज मात्र ‘काका-काकू, आत्या-मामा, पणजीदेखील तिला फार जपतात. ती सर्वांसाठी प्रेम बरसणारी आहे. तिला खरोखर सन्मानाने वागवले जाते.

पैंजण Summary in Marathi

पैंजण प्रस्तावनाः

नीलम माणगावे कवयित्री लेखिका, संपादिका, बालसाहित्यकार म्हणून परिचित असलेल्या लेखिका. त्यांची आजवर ६० पुस्तके प्रकाशित झाली आहेत. आकाशवाणीवरून त्यांनी कौटुंबिक श्रुतिकालेखन केलं आहे. त्यांच्या कवितांचा गाभा स्त्री हा असतो. स्त्रीवादी जाणीवा त्यांच्या कवितेतून प्रकट झालेल्या दिसतात. बाईपणाची वेदना, कल्लोळ, असोशी कवितेच्या मूळ गाभा असलेल्या दिसतात. कवितेची भाषा सहज, सोपी आहे. अलंकारांचा, प्रतीक, प्रतिमांचा सोस नसलेली त्यांची कविता असल्यामुळे ती सहज उलगडत जाते. गुलदस्ता , ‘शतकाच्या उंबरठ्यावर ‘जाग’ हे कविता संग्रह ‘तीच माती तेच आकाश’, ‘शांते तू जिंकलीस’, ‘निर्भया लढते आहे’ हे कथासंग्रह, अनेक पुरस्कारांनी सन्मानित केले गेले आहे.

पैंजण कवितेचा आशय :

कवयित्री नीलम माणगावे यांच्या पैंजण या कवितेत स्त्रीच्या प्रगतीचा आलेखच मांडण्याचा प्रयत्न केला आहे. कवयित्री प्राचीन ते अर्वाचीन काळात स्त्रियांच्या जगण्यात जे बदल झाले आहेत त्याचे वर्णन करीत आहे.

प्राचीन काळातील स्त्री तिला कवयित्री आजी म्हणू पाहते. ही आजी दोन दोन किलो वजनाचे पैंजण घालून स्वयंपाकघरातून माजघरात आणि माजघरातून स्वयंपाकघरात सम्राज्ञीसारखी ठुमकत फिरायची. त्या पैंजणांनी तिचे पाय सुजायचे. ते ओझं सहन व्हायचं नाही . तिचे पायाचे घोटे काळे ठिक्कर पडायचे. कधी जखम झाली तरी तिने पैंजण काढले नाहीत. पैंजणाच्या नादात ती इतकी अडकली की त्या भूलभुलैय्यातून बाहेर न पडता पैंजणाखाली फडके बांधून ती सारे निभवायची. आनंद मानायची.

कवयित्री आपल्या अगोदरच्या स्त्रीच्या पिढीबाबत बोलताना आपल्या आईचा उल्लेख करते. आईने पैंजण घालणे सोडून दिले. नाजूक, हलक्या, तोरड्या घालायला सुरुवात केली. आपल्याच तोऱ्यात ती स्वयंपाकघरापासून ते गच्चीपर्यंत मनमुराद फिरायची. आपल्या आईला जितकं स्वातंत्र्य मिळालं नाही तितकं आपल्याला मिळालं याचा आनंद तिच्या मनी होता. तोरड्या तिच्या पायाला टोचायच्या त्यामुळे साडीचे काठ फाटायचे, दोरे लोंबायचे पण सर्व दुर्लक्षून ती राजाराणीसारखी भिरभिरायची. आनंदात जगायची. आपण या घरात राजाची राणी आहोत या भ्रमात ती असायची.

कवयित्री जेव्हा आपल्या पिढीबद्दल बोलते तेव्हा ती स्वत:चे उदाहरण देते. पैंजण, तोरड्या घालणं तिनं केव्हाच सोडलं. हलक्याशा सँडल, बूट, चपला घालता घालता घरच नाही तर अंगण ओलांडन तिनं घराबाहेर पाऊल टाकलं पण कधी कधी याच चप्पल. बट. सँडल. यांचा त्रास होतो. त्याच्याही जखमा पायाला सोसाव्या लागतात. पण आपण घराबाहेर जातो, पैसे कमवतो, चार लोकांमध्ये आपल्याला सन्मान मिळतो. काही गोष्टीत आपली मतं विचारली जातात, त्याची दखल घेतली जाते याचा आनंद इतका असतो की झालेल्या जखमांकडे ती दुर्लक्ष करते.

कवयित्रीची मुलगी तर त्याही पुढचा विचार करते. पैंजण, तोरड्या तर नकोतच तिला. चप्पल, बूट, सँडलही नको. त्यांचं पकडणं, घसरणं नकोच.

पायाखालचे काटे मोडण्याइतपत पायच पोलादी, मजबूत, घट्ट व्हायला हवेत, पुढच्या शतका आधी हे झालं तर उत्तमच आहे.

पैंजण समानार्थी शब्द / पर्यायी शब्द :

पैंजण – पायातील दागिना (a silver ornament (for the ankles), माजघर – घराचा मध्यभाग, वापरायची खोली (the central portion of a house), सम्राज्ञी – राज्यावर हक्क असणारी राणी (queen), ठुमकत – नादाचा एक प्रकार, (लचकत, मुरडत) भूलभुलैय्या – चक्रव्यूह (circular, confusing military array), फडके – कपडा (cloth), तोरड्या – पायातील कडे(Ornaments for the nakles), पोलादी – पोलाद हा मजबूत धातू आहे. त्यापासून तयार झालेले विशेषण(firm, stern), ऊब – उष्णता (warmness) हद्दपार – सीमेच्या बाहेर(deported).

Balbharti Maharashtra State Board Marathi Yuvakbharati 11th Digest व्याकरण शब्दसिद्धी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board 11th Marathi Yuvakbharati Solutions व्याकरण शब्दसिद्धी

11th Marathi Guide व्याकरण शब्दसिद्धी Textbook Questions and Answers

शब्दसिद्धी

भाषा व्यवहारामध्ये म्हणजेच लिहिताना वा बोलताना आपण नानाविध शब्दांचा वापर करतो. आपल्या भाषिक व्यवहारातील सर्वच शब्द आपल्या मूळ मराठी भाषेतील असतीलच असे नाही. बऱ्याचदा मूळ भाषेतील शब्दांपासून आपण नवनवीन शब्द बनतो. केव्हा केव्हा इतर भाषेतील शब्दांचाही स्वाभाविकपणे आपण वापर करतो. बऱ्याचदा तो शब्द दुसऱ्या भाषेतील आहे हेही आपल्या लक्षात येत नाही.

इतर भाषेतीलही काही शब्द मराठीत असे रुळले आहेत की त्यांचे वेगळेपणही बऱ्याचदा लक्षात न घेता तो आपल्याच भाषेतील शब्द आहे या पद्धतीने आपण त्याचा वापर करत असतो. यासाठीच आपल्या भाषेतील मूळ शब्द कोणते? आपल्या भाषेत रुळलेले कोणते शब्द आपण इतर भाषांमधून जसेच्या तसे घेतले आहेत वा कोणत्या शब्द रूपात कसा बदल केला आहे हे समजून घेणे भाषेच्या अभ्यासात अत्यंत महत्त्वाचे आहे.

भाषेतील शब्द कसा बनतो वा सिद्ध होतो या प्रक्रियेलाच शब्दसिद्धी असे म्हणतात.

काही उपसर्गघटित शब्द :

उपसर्ग व त्याचा अर्थ	उपसर्गघटित साधित शब्दांची उदाहरणे
अति (= फार / पलीकडे)	अतिशय, अतिरेक, अतिक्रम, अतिलोभी, अतिसार इ.
आ (= पासून / पर्यंत / पलीकडे)	आजन्म, आमरण, आक्रमण, आक्रोश इ.
सु (= चांगले / सोपे)	सुग्रास, सुभाषित, सुकर, सुगम, सुशिक्षित इ.
अव (= हीन / कमी)	अवघड, अवजड, अवकळा, अवदसा, अवलक्षण इ.
दर (= प्रत्येक)	दररोज, दरसाल, दरमहा, दरमजल, दरशेकडा इ.
आड (= लहान / गौण)	आडनाव, आडवाट, आडकाठी, आडवळण, आडदांड इ.
दुर्, दुस् (= वाईट / दुष्ट)	दुर्गुण, दुर्दशा, दुर्जन, दुर्लभ, दुराचरण, दुर्लक्ष इ.
प्रति (= उलट / फिरून)	प्रतिकार, प्रतिबिंब, प्रतिदिन, प्रतिकूल, प्रत्येक इ.
वि (= विशेष / शिवाय)	विख्यात, विज्ञान, विधवा, विसंगती, विपत्ती इ.
भर (= मुख्य / पूर्ण)	भरधाव, भरजरी, भरदिवसा, भरचौकात, भरलोकात, भरपेट इ.
अनु (= मागून / सारखे)	अनुकरण, अनुक्रम, अनुभव, अनुवाद, अनुमती इ.
उत् (= श्रेष्ठ / उंच)	उत्कर्ष, उन्नती, उत्तीर्ण, उत्तम, उत्प्रेक्षा इ.
अभि (= पूर्वी/ जवळ)	अभिनय, अभिनंदन, अभिरुची, अभिप्राय, अभिमुख इ.
गैर (= वाचून / विना)	गैरहजर, गैरशिस्त, गैरसमज, गैरसोय, गैरहिशोबी इ.
सर (= मुख्य)	सरकार, सरपंच, सरहद्द, सरदार, सरनौबत इ.
बे (= वाचून / शिवाय / रहित)	बेडर, बेअब्रू, बेदम, बेईमान, बेइज्जत, बेशरम, इ.
ना (= अभाव)	नाउमेद, नाराज, नापसंत, नालायक, नाकबूल इ.
प्र (= अधिक / पुढे)	प्रताप, प्रबल, प्रगती, प्रवाह, प्रदोष, प्रस्थान, प्रसिद्ध इ.
बद (= वाईट)	बदनाम, बदसूर, बदफैली, बदलौकिक इ.
हर (= प्रत्येक)	हररोज, हरघडी, हरदम, हरकाम,

काही प्रत्ययघटित शब्द

1. कृदन्ते / धातुसाधिते : धातूस कृतप्रलय लागून तयार होणारे नवीन शब्द.

प्रत्यय	धातुसाधित शब्द (उदाहरणे)
अक	लेखक, पाचक, रक्षक, भक्षक, गायक, वाहक इ.
अनीय	श्रवणीय, मननीय, रमणीय, वंदनीय, पूजनीय इ.
आई	खोदाई, चराई, उजळाई, शिलाई, अंगाई इ.
रा	लाजरा, बुजरा, हसरा, कापरा, दुखरा इ.
ऊन	करून, देऊन, बसून, हसून इ.
अना	प्रार्थना, वेदना, कल्पना, तुलना, वंदना इ.
ण	धरण, जळण, तळण, चढण, भांडण, लोळण इ.
तव्य	कर्तव्य, तालव्य, भवितव्य इ.
आळू	झोपाळू, लाजाळू, कनवाळू, विसराळू इ.
णावळ	खाणावळ, जेवणावळ, धुणावळ, लिहिणावळ इ.

2. तद्धिते / शब्दसाधितेः धातूखेरीज अन्यशब्दांना प्रत्यय लागून तयार होणारे नवीन शब्द

प्रत्यय	शब्द साधिते (उदाहरणे)
इक	कायिक, वाचिक, मानसिक, धार्मिक, लौकिक इ.
कर	सुखकर, खेळकर, खोडकर, दिनकर, प्रभाकर इ.
की	माणुसकी, भावकी, गावकी, शेतकी, उनाडकी इ.
खोर	भांडखोर, चिडखोर, चहाडखोर, चेष्टेखोर, मस्तीखोर इ.
दार	दुकानदार, फौजदार, जमिनदार, इमानदार, धारदार, डौलदार इ.
कट	तेलकट, मातकट, धुरकट, मळकट, पोरकट इ.
गर, गार	सौदागर, जादूगार, गुन्हेगार, माहितगार, कामगार इ.
खाना	कारखाना, तोफखाना, दवाखाना, हत्तीखाना, दारूखाना इ.
नामा	करारनामा, हुकूमनामा, पंचनामा, जाहीरनामा इ.
आई	लढाई, नवलाई, दांडगाई, शिष्टाई, खोदाई. इ.