Important Questions

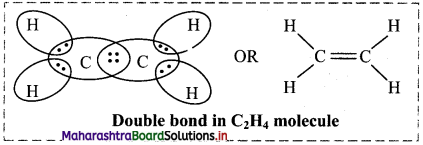
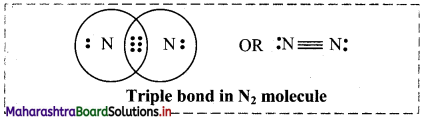
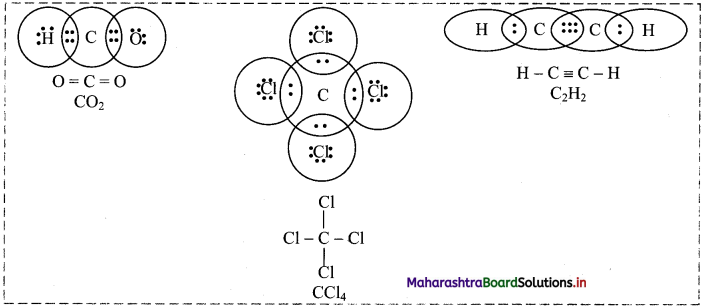
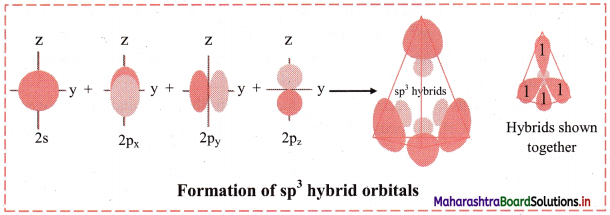
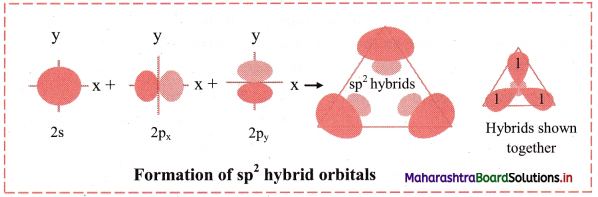
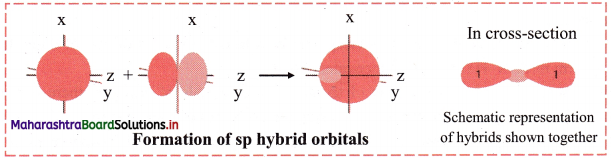
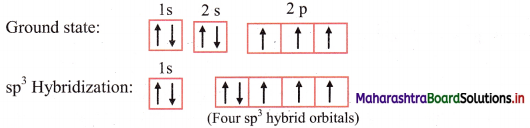
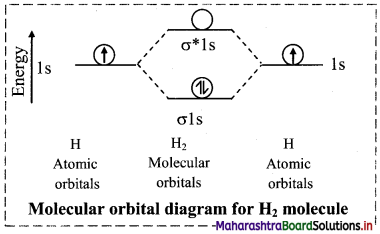
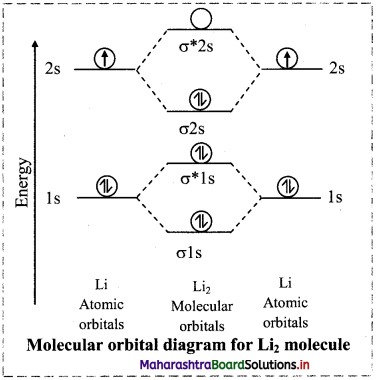
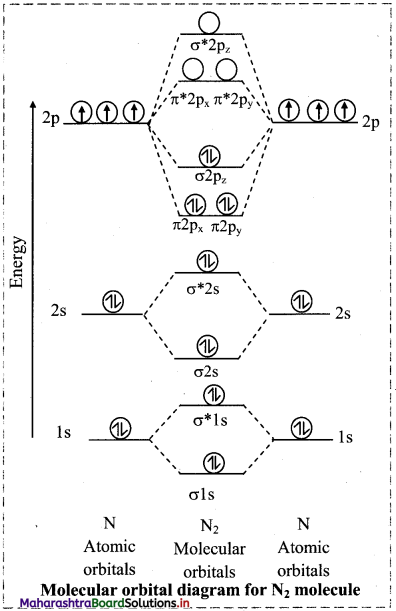
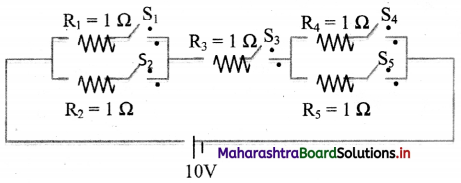
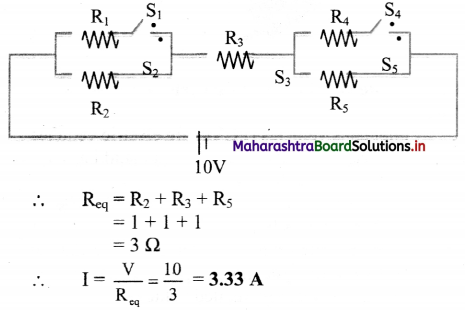
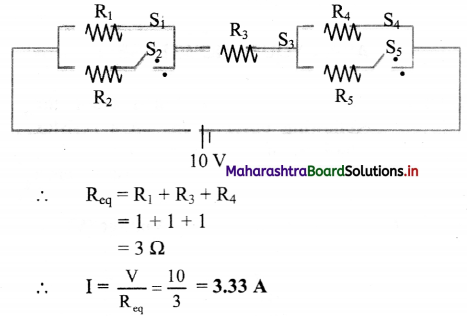
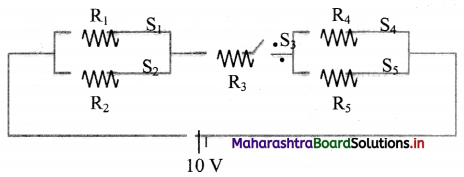
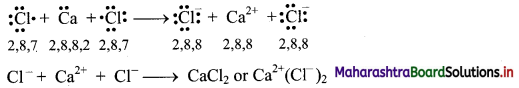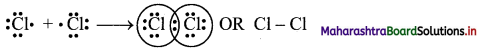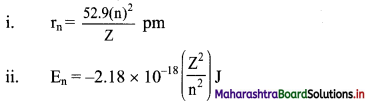Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 6 Redox Reactions Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 6 Redox Reactions

Question 1.
What does the term ‘redox’ refer to?
Answer:
Redox is an abbreviation used for the terms ‘oxidation and reduction’.

Question 2.
Give examples of naturally occurring redox reactions.
Answer:

1. Respiration
2. Rusting
3. Combustion of fuel

Question 3.
Define Oxidant/Oxidising agent.
Answer:
A reagent/substance which itself undergoes reduction and causes oxidation of another species is called oxidant/oxidising agent.

Question 4.
Define: Reductant/Reducing agent
Answer:
A reagent/substance which itself undergoes oxidation bringing about the reduction of another species is called reductant/reducing agent.

Question 5.
Explain redox reaction giving an example.
Answer:
Oxidation and reduction reactions occur simultaneously. Therefore, the oxidation-reduction reaction is also referred to as a redox reaction.

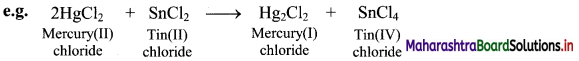
In the above reaction, HgCl₂ is reduced to Hg₂Cl₂ and SnCl₂ is oxidised to SnCl₄. Hence, it is a redox reaction.

Question 6.
Explain redox reaction in terms of electron transfer.
Answer:
i. Redox reaction can be described in terms of electron transfer as shown below:
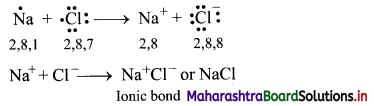
2Mg_(s) + O_2(g) → Mg²⁺ + 2O^2-
ii. Charge development suggests that each magnesium atom loses two electrons to form Mg²⁺ and each oxygen atom gains two electrons to form O^2-. This can be represented as follows:

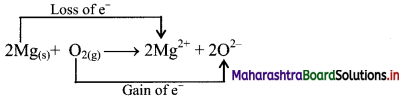
iii. When Mg is oxidised to MgO, the neutral Mg atom loses electrons to form Mg²⁺ in MgO while the elemental oxygen gains electrons and forms O^2- in MgO.
iv. Each of the above steps represents a half reaction which involves electron transfer (loss or gain).
v. Sum of these two half reactions or the overall reaction is a redox reaction.

Question 7.
Justify the following reaction as redox reaction in terms of electron transfer.
Mg + F₂ → MgF₂
Answer:
i. Redox reaction can be described in terms of electron transfer as shown below:
Mg_(s) + F_2(g) → Mg²⁺ + 2F^–
ii. Charge development suggests that magnesium atom loses two electrons to form Mg²⁺ and each fluorine atom gains one electron to form F^–. This can be represented as follows:

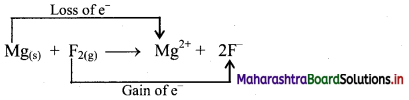
iii. When Mg is oxidised to MgF₂, the neutral Mg atom loses electrons to form Mg²⁺ in MgF₂ while the elemental fluorine gains electrons and forms F^–in MgF₂.
iv. Each of the above steps represents a half reaction which involves electron transfer (loss or gain).
v. Sum of these two half reactions or the overall reaction is a redox reaction.

Question 8.
Justify that the reaction 2Na_(s) + H_2(g) → 2NaH_(s) is a redox reaction.
Answer:
Redox reaction can be described as electron transfer as shown below:
2Na_(s) + H_2(g) → 2Na⁺ + 2H^–
ii. Charge development suggests that each sodium atom loses one electron to form Na⁺ and each hydrogen atom gains one electron to form H^–. This can be represented as follows:

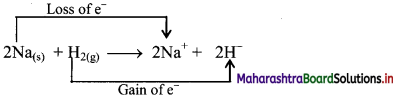
iii. When Na is oxidised to NaH, the neutral Na atom loses one electron to form Na⁺ in NaH while the elemental hydrogen gains one electron and forms H^– in NaH.
iv. Each of the above steps represents a half reaction which involves electron transfer (loss or gain).
v. Sum of these two half reactions or the overall reaction is a redox reaction.

Question 9.
Define the terms oxidation and reduction in terms of electron transfer.
Answer:
i. The half reaction involving loss of electrons is called oxidation reaction.

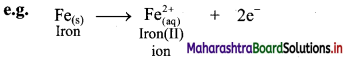
ii. The half reaction involving gain of electrons is called reduction reaction.

Question 10.
Define the terms oxidant and reductant in terms of electron transfer.
Answer:

1. Oxidant: Oxidant or oxidising agent is an electron acceptor.
2. Reductant: Reductant or reducing agent is an electron donor.

Question 11.
Identify oxidising and reducing agents in the following reaction.
\(\mathrm{Fe}_{(s)}+\mathrm{Cu}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Fe}_{(\mathrm{aq})}^{2+}+\mathrm{Cu}_{(\mathrm{s})}\)
Answer:
Fe_(s) acts as a reducing agent as it donates electrons while \(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) acts as an oxidising agent as it accepts electrons.

Question 12.
Define: Displacement reaction.
Answer:
A reaction in which an ion (or an atom) in a compound is replaced by an ion (or an atom) of another element is called displacement reaction.
e.g. X + YZ → XZ + Y

Question 13.
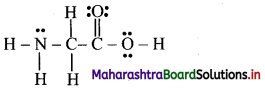
Draw structure and assign oxidation number to each atom in:
i. Br₃O₈
ii. C₃O₂
Answer:
i. Br₃O₈

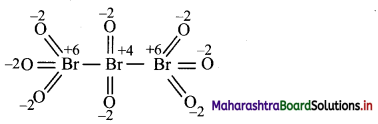
ii. C₃O₂

Question 14.
Deduce the oxidation number of S in the following species:
i. SO₂
ii. \(\mathrm{SO}_{4}^{2-}\)
Answer:
i. SO₂ is a neutral molecule.
∴ Sum of oxidation numbers of all atoms of SO₂ = 0
∴ (Oxidation number of S) + 2 × (Oxidation number of O) = 0
∴ Oxidation number of S + 2 × (- 2) = 0
∴ Oxidation number of S in SO₂ = 0 – (- 4)
∴ Oxidation number of S in SO₂ = +4

ii. \(\mathrm{SO}_{4}^{2-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms of \(\mathrm{SO}_{4}^{2-}\) = – 2
∴ (Oxidation number of S) + 4 × (Oxidation number of O) = – 2
∴ Oxidation number of S in \(\mathrm{SO}_{4}^{2-}\) = – 2 – 4 × (-2) = – 2 + 8
∴ Oxidation number of S in \(\mathrm{SO}_{4}^{2-}\) = +6

Question 15.
Assign oxidation number to each element in the following compounds or ions.
i. KMnO₄
ii. K₂Cr₂O₇
iii. Ca₃(PO₄)₂
Answer:
i. KMnO₄
Oxidation number of K = +1
Oxidation number of O = -2
KMnO₄ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of K) + (Oxidation number of Mn) + 4 × (Oxidation number of O) = 0
∴ (+1) + Oxidation number of Mn + 4 × (-2) = 0
∴ Oxidation number of Mn + 1 – 8 = 0
∴ Oxidation number of Mn – 7 = 0
∴ Oxidation number of Mn in KMnO₄ = +7

ii. K₂Cr₂O₇
Oxidation number of K = +1
Oxidation number of O = -2
K₂Cr₂O₇ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of K) + 2 × (Oxidation number of Cr) + 7 × (Oxidation number of O) = 0
∴ 2 × (+1) + 2 × (Oxidation number of Cr) + 7 × (-2) = 0
∴ 2 × (Oxidation number of Cr) + 2 – 14 = 0
∴ 2 × (Oxidation number of Cr) – 12 = 0
∴ 2 × (Oxidation number of Cr) = +12
∴ Oxidation number of Cr = +12/2
∴ Oxidation number of Cr in K₂Cr₂O₇ = +6

iii. Ca₃(PO₄)₂
Oxidation number of Ca = +2 (∵ Ca is alkaline earth metal.)
Oxidation number of O = -2
Ca₃(PO₄)₂ is a neutral molecule.
Sum of the oxidation numbers of all atoms = 0
∴ 3 × (Oxidation number of Ca) + 2 × (Oxidation number of P) + 8 × (Oxidation number of O) = 0
∴ 3 × (+2)+ 2 × (Oxidation number of P)+ 8 × (-2) = 0
∴ 2 × (Oxidation number of P) + 6 – 16 = 0
∴ 2 × (Oxidation number of P) – 10 = 0
∴ 2 × (Oxidation number of P) = +10
∴ Oxidation number of P = +10/2
∴ Oxidation number of P in Ca₃(PO₄)₂ = +5

Question 16.
Assign oxidation number to the atoms other than O and H in the following species.
i. \(\mathrm{SO}_{3}^{2-}\)
ii. \(\mathrm{BrO}_{3}^{-}\)
iii. \(\mathrm{ClO}_{4}^{-}\)
iv. \(\mathrm{NH}_{4}^{+}\)
v. \(\mathrm{NO}_{3}^{-}\)
vi. \(\mathrm{NO}_{2}^{-}\)
vii. SO₃
viii. N₂O₅
Answer:
The oxidation number of O atom bonded to a more electropositive atom is -2 and that of H atom bonded to electronegative atom is +1. Sum of the oxidation numbers of all atoms in ionic species is equal to charge it carries and that for neutral molecule is zero. Using these values, the oxidation numbers of atoms of the other elements in a given polyatomic species are calculated as follows:
i. \(\mathrm{SO}_{3}^{2-}\)
(Oxidation number of S) + 3 × (Oxidation number of O) = – 2
∴ Oxidation number of S + 3 × (-2) = – 2
∴ Oxidation number of S – 6 = – 2
∴ Oxidation number of S = – 2 + 6
∴ Oxidation number of S in \(\mathrm{SO}_{3}^{2-}\) = +4

ii. \(\mathrm{BrO}_{3}^{-}\)
(Oxidation number of Br) + 3 × (Oxidation number of O) = -1
∴ Oxidation number of Br + 3 × (-2) = – 1
∴ Oxidation number of Br – 6 = – 1
∴ Oxidation number of Br = – 1 + 6
Oxidation number of Br in \(\mathrm{BrO}_{3}^{-}\) = +5

iii. \(\mathrm{ClO}_{4}^{-}\)
(Oxidation number of Cl) + 4 × (Oxidation number of O) = – 1
∴ Oxidation number of Cl + 4 × (-2) = – 1
∴ Oxidation number of Cl – 8 = – 1
∴ Oxidation number of Cl = – 1 + 8
∴ Oxidation number of Cl in \(\mathrm{ClO}_{4}^{-}\) = +7

iv. \(\mathrm{NH}_{4}^{+}\)
(Oxidation number of N) + 4 × (Oxidation number of H) = + 1
∴ Oxidation number of N + 4 × (+1) = +1
∴ Oxidation number of N + 4 = + 1
∴ Oxidation number of N = + 1 – 4
∴ Oxidation number of N in \(\mathrm{NH}_{4}^{+}\) = -3

v. \(\mathrm{NO}_{3}^{-}\)
(Oxidation number of N) + 3 × (Oxidation number of O) = – 1
∴ Oxidation number of N + 3 × (-2) = – 1
∴ Oxidation number of N – 6 = – 1
∴ Oxidation number of N = – 1 + 6
∴ Oxidation number of N in \(\mathrm{NO}_{3}^{-}\) = +5

vi. \(\mathrm{NO}_{2}^{-}\)
(Oxidation number of N) + 2 × (Oxidation number of O) = – 1
∴ Oxidation number of N + 2 × (-2) = – 1
∴ Oxidation number of N – 4 = – 1
∴ Oxidation number of N = – 1 + 4
∴ Oxidation number of N in \(\mathrm{NO}_{2}^{-}\) = +3

vii. SO₃
(Oxidation number of S) + 3 × (Oxidation number of O) = 0
∴ Oxidation number of S + 3 × (-2) = 0
∴ Oxidation number of S – 6 = 0
∴ Oxidation number of S = 0 + 6
∴ Oxidation number of S in SO₃ = +6

viii. N₂O₅
2 × (Oxidation number of N) + 5 × (Oxidation number of O) = 0
∴ 2 × (Oxidation number of N) + 5 × (-2) = 0
∴ 2 × (Oxidation number of N) – 10 = 0
∴ 2 × (Oxidation number of N) = 0 + 10
∴ Oxidation number of N = 10/2
∴ Oxidation number of N in N₂O₅ = +5

Question 17.
Find the oxidation numbers of the underlined species in the following compounds or ions.

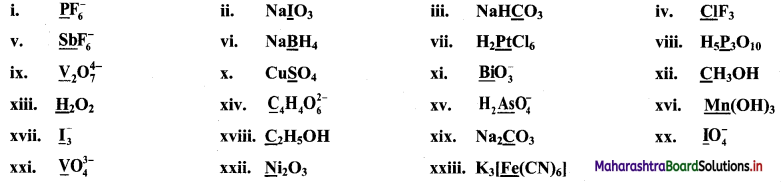
Answer:
i. P\(\mathrm{F}_{6}^{-}\)
Oxidation number of F = -1
P\(\mathrm{F}_{6}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ (Oxidation number of P) + 6 × (Oxidation number of F) = – 1
∴ Oxidation number of P + 6 × (-1) = -1
∴ Oxidation number of P – 6 = – 1
Oxidation number of P in P\(\mathrm{F}_{6}^{-}\) = +5

ii. NaIO₃
Oxidation number of Na = +1
Oxidation number of O = -2
NaIO₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
(Oxidation number of Na) + (Oxidation number of I) + 3 × (Oxidation number of O) = 0
(+1) + (Oxidation number of I) + 3 × (-2) = 0
Oxidation number of I + 1 – 6 = 0
Oxidation number of I in NaIO₃ = +5

iii. NaHCO₃
Oxidation number of Na = +1
Oxidation number of H = +1
Oxidation number of O = -2
NaHCO₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of Na) + (Oxidation number of H) + (Oxidation number of C) + 3 × (Oxidation number of O) = 0
∴ (+1) + (+1) + (Oxidation number of C) + 3 × (-2) = 0
∴ Oxidation number of C + 2 – 6 = 0
∴ Oxidation number of C in NaHCO₃ = +4

iv. ClF₃
Oxidation number of F = -1
ClF₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of Cl) + 3 × (Oxidation number of F) = 0
∴ Oxidation number of Cl + 3 × (-1) = 0
∴ Oxidation number of Cl in ClF₃ = +3

v. Sb\(\mathrm{F}_{6}^{-}\)
Oxidation number of F = -1
Sb\(\mathrm{F}_{6}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ (Oxidation number of Sb) + 6 × (Oxidation number of F) = – 1
∴ Oxidation number of Sb + 6 × (-1) = -1
∴ Oxidation number of Sb in Sb\(\mathrm{F}_{6}^{-}\) = +5

vi. NaBH₄
Oxidation number of Na =+1
Oxidation number of H = -1 (for Hydride)
NaBH₄ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of Na) + (Oxidation number of B) + 4 × (Oxidation number of H) = 0
∴ (+1) + (Oxidation number of B) + 4 × (-1) = 0
∴ Oxidation number of B + 1 – 4 = 0
∴ Oxidation number of B in NaBH₄ = +3

vii. H₂PtCl₆
Oxidation number of H = +1
Oxidation number of Cl = -1
H₂PtCl₆ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of H) + (Oxidation number of Pt) + 6 × (Oxidation number of Cl) = 0
∴ 2 × (+1) + (Oxidation number of Pt) + 6 × (-1) = 0
(Oxidation number of Pt) + 2 – 6 = 0
∴ Oxidation number of Pt in H₂PtCl₆ = +4

viii. H₅P₃O₁₀
Oxidation number of H = +1
Oxidation number of O = -2
H₅P₃O₁₀ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 5 × (Oxidation number of H) + 3 × (Oxidation number of P) +10 × (Oxidation number of O) = 0
∴ 5 × (+1) + 3 × (Oxidation number of P) + 10 × (-2) = 0
∴ 3 × (Oxidation number of P) + 5 – 20 = 0
Oxidation number of P = +\(\frac {15}{3}\)
∴ Oxidation number of P in H₅P₃O₁₀ = +5

ix. V₂\(\mathrm{O}_{7}^{4-}\)
Oxidation number of O = -2
V₂\(\mathrm{O}_{7}^{4-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 4
∴ 2 × (Oxidation number of V) + 7 × (Oxidation number of O) = – 4
∴ 2 × (Oxidation number of V) + 7 × (-2) = – 4
∴ 2 × (Oxidation number of V) = – 4 + 14
∴ Oxidation number of V = +\(\frac {10}{2}\)
∴ Oxidation number of V in V₂\(\mathrm{O}_{7}^{4-}\) = +5

x. CuSO₄
Oxidation number of Cu = +2
Oxidation number of O = -2
CuSO₄ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of Cu) + (Oxidation number of S) + 4 × (Oxidation number of O) = 0
∴ (+2) + Oxidation number of S + 4 × (-2) = 0
∴ Oxidation number of S + 2 – 8 = 0
∴ Oxidation number of S in CuSO₄ = +6

xi. Bi\(\mathrm{O}_{3}^{-}\)
Oxidation number of O = -2
Bi\(\mathrm{O}_{3}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ (Oxidation number of Bi) + 3 × (Oxidation number of O) = – 1
∴ Oxidation number of Bi + 3 × (-2) = – 1
∴ Oxidation number of Bi = – 1 + 6
∴ Oxidation number of Bi in Bi\(\mathrm{O}_{3}^{-}\) = +5

xii. CH₃OH
Oxidation number of H = +1
Oxidation number of O = -2
CH₃OH is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of C) + 4 × (Oxidation number of H) + (Oxidation number of O) = 0
∴ (Oxidation number of C) + 4 × (+1) + (-2) = 0
∴ Oxidation number of C + 2 = 0
∴ Oxidation number of C in CH₃OH = -2

xiii. H₂O₂
Oxidation number of O = -1 (for peroxide)
H₂O₂ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of H) + 2 × (Oxidation number of O) = 0
∴ 2 × (Oxidation number of H) + 2 × (-1) = 0
∴ Oxidation number of H = +\(\frac {2}{2}\)
∴ Oxidation number of H in H₂O₂ = +1

xiv. C₄H₄\(\mathrm{O}_{6}^{2-}\)
Oxidation number of H = +1
Oxidation number of O = -2
C₄H₄\(\mathrm{O}_{6}^{2-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 2
∴ 4 × (Oxidation number of C) + 4 × (Oxidation number of H) + 6 × (Oxidation number of O) = – 2
∴ 4 × (Oxidationnumber of C) + 4 × (+1) +6 × (-2) = -2
∴ 4 × (Oxidation number of C) + 4 – 12 = -2
∴ 4 × (Oxidation number of C) = – 2 + 8
∴ Oxidation number of C = +\(\frac {6}{4}\)
∴ Oxidation number of C in C₄H₄\(\mathrm{O}_{6}^{2-}\) = +1.5

xv. H₂As\(\mathrm{O}_{4}^{-}\)
Oxidation number of H = +1
Oxidation number of O = -2
H₂As\(\mathrm{O}_{4}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ 2 × (Oxidation number of H) + (Oxidation number of As) + 4 × (Oxidation number of O) = -1
∴ 2 × (+1) + Oxidation number of As + 4 × (-2) = – 1
∴ Oxidation number of As + 2 – 8 = – 1
∴ Oxidation number of As = – 1 + 6
∴ Oxidation number of As in H₂As\(\mathrm{O}_{4}^{-}\) = +5

xvi. Mn(OH)₃
Oxidation number of O = -2
Oxidation number of H = +1
Mn(OH)₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ (Oxidation number of Mn) + 3 × (Oxidation number of O) + 3 × (Oxidation number of H) = 0
∴ Oxidation number of Mn + 3 × (-2) + 3 × (+1) = 0
∴ Oxidation number of Mn – 6 + 3 = 0
∴ Oxidation number of Mn in Mn(OH)₃ = +3

xvii. \(\mathrm{I}_{3}^{-}\)
\(\mathrm{I}_{3}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ 3 × Oxidation number of I = – 1
∴ Oxidation number of I in \(\mathrm{I}_{3}^{-}\) = –\(\frac {1}{3}\)

xviii. C₂H₅OH
Oxidation number of O = -2
Oxidation number of H = +1
C₂H₅OH is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of C) + 6 × (Oxidation number of H) + (Oxidation number of O) = 0
∴ 2 × (Oxidationnumberof C) + 6 × (+1) + (-2) = 0
∴ 2 × (Oxidation number of C) = – 4
∴ Oxidation number of C = –\(\frac {4}{2}\)
∴ Oxidation number of C in C₂H₅OH = -2

xix. Na₂CO₃
Oxidation number of Na = +1
Oxidation number of O = -2
Na₂CO₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of Na) + (Oxidation number of C) + 3 × (Oxidation number of O) = 0
∴ 2 × (+1) + (Oxidation number of C) + 3 × (-2) = 0
∴ Oxidation number of C + 2 – 6 = 0
∴ Oxidation number of C in Na₂CO₃ = +4

xx. I[latex]\mathrm{O}_{4}^{-}[/latex]
Oxidation number of O = -2
I\(\mathrm{O}_{4}^{-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 1
∴ (Oxidation number of I) + 4 × (Oxidation number of O) = – 1
∴ Oxidation number of I + 4 × (-2) = – 1
∴ Oxidation number of I = -1 +8
∴ Oxidation number of I in I\(\mathrm{O}_{4}^{-}\) = +7

xxi. V\(\mathrm{O}_{4}^{3-}\)
Oxidation number of O = -2
V\(\mathrm{O}_{4}^{3-}\) is an ionic species.
∴ Sum of the oxidation numbers of all atoms = – 3
∴ (Oxidation number of V) + 4 × (Oxidation number of O) = – 3
∴ Oxidation number of V + 4 × (-2) = – 3
∴ Oxidation number of V = -3 + 8
∴ Oxidation number of V in V\(\mathrm{O}_{4}^{3-}\) = +5

xxii. Ni₂O₃
Oxidation number of O = -2
Ni₂O₃ is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 2 × (Oxidation number of Ni) + 3 × (Oxidation number of O) = 0
∴ 2 × (Oxidation number of Ni) + 3 × (-2) = 0
∴ 2 × (Oxidation number of Ni) = +6
∴ Oxidation number of Ni = +\(\frac {6}{2}\)
∴ Oxidation number of Ni in Ni₂O₃ = +3

xxiii. K₃[Fe(CN)₆]
Oxidation number of K = +1
Oxidation number of CN group = -1
K₃[Fe(CN)₆] is a neutral molecule.
∴ Sum of the oxidation numbers of all atoms = 0
∴ 3 × (Oxidation number of K) + (Oxidation number of Fe) + 6 × (Oxidation number of CN group) = 0
∴ 3 × (+1) + Oxidation number of Fe + 6 × (-1) = O
∴ Oxidation number of Fe + 3 – 6 = 0
∴ Oxidation number of Fe in K₃[Fe(CN)₆] = +3

Question 18.
Define: Stock notation.
Answer:
Representation in which oxidation number of an atom is denoted by Roman numeral in parentheses after the chemical symbol is called Stock notation. This name was given after the German scientist, Alfred Stock. e.g. Au¹⁺Cl^1- → Au(I)Cl

Question 19.
What is the use of Stock notation?
Answer:
The Stock notation is used to specify the oxidation number of the metal.

Question 20.
How will you write Stock notations for the following compounds?
i. AuCl₃
ii. SnCl₄
iii. SnCl₂
iv. MnO₂
Answer:
i. AuCl₃: The charge on each element is \(\mathrm{Au}^{3+} \mathrm{Cl}_{3}^{1-}\). Hence, the stock notation is Au(III)Cl₃.
ii. SnCl₄: The charge on each element is \(\mathrm{Sn}^{4+} \mathrm{Cl}_{4}^{1-}\). Hence, the stock notation is Sn(IV)Cl₄.
iii. SnCl₂: The charge on each element is \(\mathrm{Sn}^{2+} \mathrm{Cl}_{2}^{1-}\). Hence, the stock notation is Sn(II)Cl₂.
iv. MnO₂: The charge on each element is \(\mathrm{Mn}^{4+} \mathrm{O}_{2}^{2-}\). Hence, the stock notation is Mn(IV)O₂.

Question 21.
Write the formula for each of the following ionic compounds:
i. Nickel(III) oxide
ii. Tin(IV) chloride
iii. Bismuth(V) chloride
iv. Cobalt(III) chloride
v. Lead(IV) oxide
vi. Chromium(II) chloride
Answer:
i. Ni₂O₃
ii. SnCl₄
iii. BiCl₅
iv. CoCl₃
v. PbO₂
vi. CrCl₂

Question 22.
Define the terms oxidation and reduction in terms of oxidation number.
Answer:
i. Oxidation is an increase in the oxidation number of an element in a given substance.
e.g. Fe_(s) → \(\mathrm{Fe}_{(\mathrm{aq})}^{2+}\)
ii. Reduction is a decrease in the oxidation number of an element in a given substance. e.g. \(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) → Cu_(s)

Question 23.
Define the terms oxidant and reductant in terms of oxidation number.
Answer:

1. Oxidant: Oxidant or oxidising agent is a substance which increases the oxidation number of an element in a given substance, and itself undergoes decrease in oxidation number of a constituent element in it.
2. Reductant: Reductant or reducing agent is a substance that lowers the oxidation number of an element in a given substance, and itself undergoes an increase in the oxidation number of a constituent element in it.

Question 24.
Identify whether the following reaction is redox or NOT. State oxidant and reductant therein.

Answer:
i. Write oxidation number of all the atoms of reactants and products.

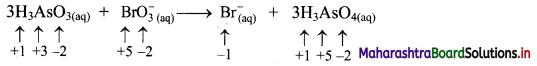
ii. Identify the species that undergoes change in oxidation number.

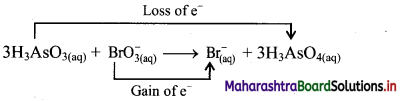
iii. The oxidation number of As increases from +3 to +5 and that of Br decreases from +5 to -1. Because oxidation number of one species increases and that of the other decreases, the reaction is a redox reaction.
iv. The oxidation number of As increases by loss of electrons and therefore, As is a reducing agent and itself is oxidised. On the other hand, the oxidation number of Br decreases and therefore, Br is an oxidising agent and itself is reduced by gain of electrons.
Result:
a. The given reaction is a redox reaction.
b. Oxidant/oxidising agent: \(\mathrm{BrO}_{3}^{-}\)
c. Reductant/reducing agent: H3AsO3

Question 25.
For the reaction, \(\mathrm{SeO}_{3(\mathrm{aq})}^{2-}+\mathrm{Cl}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq})}^{-} \longrightarrow \mathrm{SeO}_{4(\mathrm{aq})}^{2-}+2 \mathrm{Cl}_{(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(l)}\), complete the following table.

Oxidising agent	————–
Reducing agent	————–
Oxidised species	————–
Reduced species	————–

Answer:

Oxidising agent	Cl2(g)
Reducing agent	\(\mathrm{Se} \mathrm{O}_{3(\mathrm{aq})}^{2-}\)
Oxidised species	\(\mathrm{Se} \mathrm{O}_{4(\mathrm{aq})}^{2-}\)
Reduced species	\(2 \mathrm{Cl}_{(\mathrm{aq})}^{-}\)

Question 26.
Using oxidation number concept, identify the redox reactions, identify oxidizing and reducing agents in case of redox reactions.

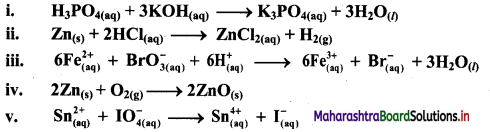
Answer:
i. H₃PO_4(aq) + 3KOH_(aq) → K₃PO_4(aq) + 3H₂O_(l)
a. Write oxidation number of all the atoms of reactants and products

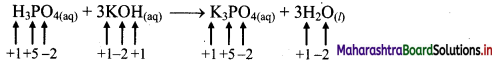
b. Since, the oxidation numbers of all the species remain same, this is NOT a redox reaction.

Result:
The given reaction is NOT a redox reaction.

ii. Zn_(s) + 2HCl_(aq) → ZnCl₂(_(aq)) + H_2(g)
a. Write oxidation number of all the atoms of reactants and products.

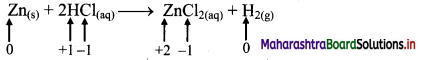
b. Identify the species that undergoes change in oxidation number.

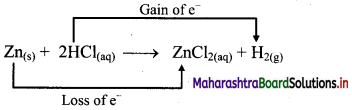
c. The oxidation number of Zn increases from 0 to +2 and that of H decreases from +1 to 0. Because oxidation number of one species increases and that of other decreases, the reaction is redox reaction.
d. The oxidation number of Zn increases by loss of electrons and therefore, Zn is a reducing agent and itself is oxidized. On the other hand, the oxidation number of H decreases by gain of electrons and therefore, H is oxidising an agent and itself is reduced by gain of electrons.

Result:

1. The given reaction is a redox reaction.
2. Oxidant/oxidising agent: HCl
3. Reductant/reducing agent: Zn

iii.

c. The oxidation number of Fe increases from +2 to +3 and that of Br decreases from +5 to -1. Because oxidation number of one species increases and that of the other decreases, the reaction is a redox reaction.
d. The oxidation number of Fe increases by loss of electrons and therefore, Fe is a reducing agent and itself is oxidized. On the other hand, the oxidation number of Br decreases by gain of electrons and therefore, Br is an oxidising an agent and itself is reduced.

Result:

1. The given reaction is a redox reaction.
2. Oxidant/oxidising agent: \(\mathrm{BrO}_{3}^{-}\)
3. Reductant/reducing agent: Fe²⁺

iv. 2Zn_(s) + O_2(g) → 2ZnO_(s)
a. Write oxidation number of all the atoms of reactants and products.

b. Identify the species that undergoes change in oxidation number.

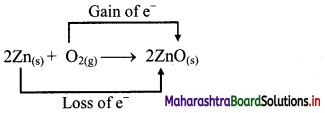
c. The oxidation number of Zn increases from 0 to +2 and that of O decreases from 0 to -2. Because oxidation number of one species increases and that of the other decreases, the reaction is a redox reaction.
d. The oxidation number of Zn increases by loss of electrons and therefore, Zn is a reducing agent and itself is oxidized. On the other hand, the oxidation number of O decreases by gain of electrons and therefore, O is an oxidising agent and itself is reduced.

Result:

1. The given reaction is a redox reaction.
2. Oxidant/oxidising agent: O₂
3. Reductant/reducing agent: Zn

v. \(\mathrm{Sn}_{(a q)}^{2+}+\mathrm{IO}_{4(2 q)}^{-} \longrightarrow \mathrm{Sn}_{(aq)}^{4+}+\mathrm{I}_{(a \mathrm{q})}^{-}\)
a. Write oxidation number of all the atoms of reactants and products.

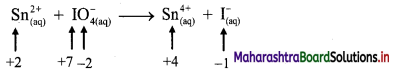
b. Identify the species that undergoes change in oxidation number.

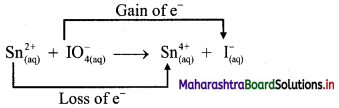
c. The oxidation number of Sn increases from +2 to +4 and that of I decreases from +7 to -1. Because oxidation number of one species increases and that of the other decreases, the reaction is a redox reaction.
d. The oxidation number of Sn increases by loss of electrons and therefore, Sn is a reducing agent and itself is oxidized. On the other hand, the oxidation number of I decreases by gain of electrons and therefore, I is an oxidising agent and itself is reduced.

Result:

1. The given reaction is a redox reaction.
2. Oxidant/oxidising agent: Sn²⁺
3. Reductant/reducing agent: \(\mathrm{IO}_{4}^{-}\)

Question 27.
Name two methods used to balance redox reactions.
Answer:

1. Oxidation number method
2. Half reaction method or ion electrode method

Question 28.
Describe the steps involved in balancing redox reactions by the oxidation number method.
Answer:
i. Step 1: Write the unbalanced equation for redox reaction. Balance the equation for all atoms in the reactions, except H and O. Identify the atoms which undergo change in oxidation number and by how much. Draw the bracket to connect atoms of the elements that changes the oxidation number.

ii. Step 2: Show an increase in oxidation number per atom of the oxidised species and hence, the net increase in oxidation number. Similarly, show a decrease in the oxidation number per atom of the reduced species and the net decrease in oxidation number. Determine the factors which will make the total increase and decrease equal. Insert the coefficients into the equation.

iii. Step 3: Balance oxygen atoms by adding H₂O to the side containing less O atoms, one H₂O is added for one O atom. Balance H atoms by adding H⁺ ions to the side having less H atoms.

iv. Step 4: If the reaction occurs in basic medium, then add OH^– ions equal to the number of H⁺ ions added in step 3, on both the sides of equation. The H⁺ and OH^– ions on same side of reactions are combined to give H₂O molecules.

v. Step 5: Check the equation with respect to both, the number of atoms of each element and the charges. It is balanced.
Note: For acidic medium, step 4 is omitted.

Question 29.
Using the oxidation number method write the net ionic equation for the reaction of potassium permanganate, KMnO₄, with ferrous sulphate, FeSO₄.
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+\mathrm{Fe}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+\mathrm{Fe}_{(\mathrm{aq})}^{3+}\)
Answer:
Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+\mathrm{Fe}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+\mathrm{Fe}_{(\mathrm{aq})}^{3+}\)

Step 2: Assign oxidation number to Mn and Fe, and calculate the increase and decrease in the oxidation number and make them equal.

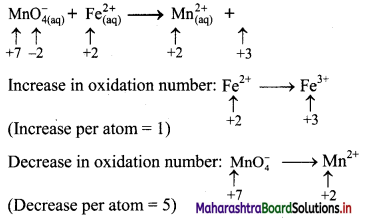
To make the net increase and dicrease equal, we must take 5 atoms of Fe²⁺
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+5 \mathrm{Fe}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+5 \mathrm{Fe}_{(\mathrm{aq})}^{3+}\)

Step 3: Balance the ‘O’ atoms by adding 4H₂O to the right-hand side.
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+5 \mathrm{Fe}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+5 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 4: The medium is acidic. To make the charges and hydrogen atoms on the two sides equal, add 8H⁺ on the left-hand side.
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+5 \mathrm{Fe}_{(\mathrm{aq})}^{2+}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+5 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 5: Check the two sides for balance of charges and atoms. The net ionic equation obtained in step 4 is the balanced equation.
Hence, balanced equation:
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+5 \mathrm{Fe}_{(\mathrm{aq})}^{2+}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Mn}_{(\mathrm{aq})}^{2+}+5 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Question 30.
Balance the following reaction by oxidation number method.
CuO + NH₃ → Cu + N₂ + H₂O
Answer:
Step 1: Write skeletal equation and balance the elements other than O and H.
CuO + 2NH₃ → Cu + N₂ + H₂O
Step 2: Assign oxidation number to Cu and N. Calculate the increase and decrease in the oxidation number and make them equal.

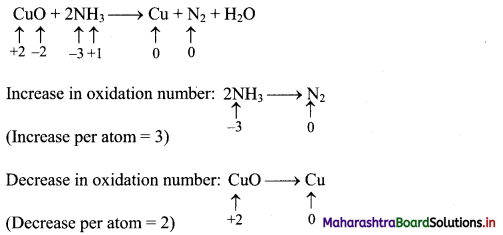
To make the net increase and decrease equal, we must take 3 atoms of Cu and 2 atoms of N. (There are already 2 N atoms.)
3CuO + 2NH₃ → 3Cu + N₂ + H₂O
Step 3: Balance ‘O’ atoms by adding 3H₂O to the right-hand side.
3CuO + 2NH₃ → 3Cu + N₂ + 3H₂O
Step 4: Charges are already balanced.
Step 5: Check two sides for balance of atoms and charges. The equation obtained in step 3 is balanced.
Hence, balanced equation: 3CuO + 2NH₃ → 3Cu + N₂ + 3H₂O

Question 31.
Balance the following redox equation by oxidation number method. The reactions occur in acidic medium.

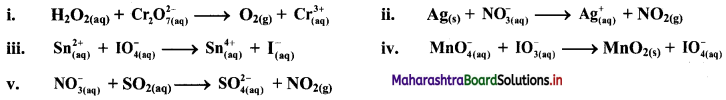
Answer:
i. \(\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7 \text { (aq) }}^{2-} \longrightarrow \mathrm{O}_{2(\mathrm{~g})}+\mathrm{Cr}_{(\mathrm{aq})}^{3+}\)
Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7 \text { (aq) }}^{2-} \longrightarrow \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}\)

Step 2: Assign oxidation number to O and Cr. Calculate the increase and decrease in the oxidation number and make them equal.

Since there are two Cr atoms, the net decrease in oxidation number is 6. In order to make the net increase and decrease equal, we must take 6 atoms of O i.e., 3H₂O₂.
\(3 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-} \longrightarrow 3 \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}\)

Step 3: Balance ‘O’ atoms by adding 7H₂O to the right-hand side.
\(3 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-} \longrightarrow 3 \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}+7 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 4: The medium is acidic. To make the charges and hydrogen atoms on the two sides equal, add 8H⁺ on the left-hand side.
\(3 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 3 \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}+7 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 5: Check two sides for balance of atoms and charges.
Hence, balanced equation:
\(3 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 3 \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}+7 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

ii. \(\mathrm{Ag}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{q})}^{-} \longrightarrow \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{NO}_{2(\mathrm{~g})}\)

Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{Ag}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{q})}^{-} \longrightarrow \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{NO}_{2(\mathrm{~g})}\)

Step 2: Assign oxidation number to Ag and N. Calculate the increase and decrease in the oxidation number and make them equal.

Because net increase is equal to net decrease, multiplying coefficients are not required.

Step 3: Balance ‘O’ atoms by adding H₂O to the right-hand side.
\(\mathrm{Ag}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{NO}_{2(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 4: The medium is acidic. To make the charges and hydrogen atoms on the two sides equal, add 2H⁺ on the left-hand side.
\(\mathrm{Ag}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-}+2 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{NO}_{2(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)
Thus, the equation is balanced with respect to the atoms as well as charges.

Step 5: Check two sides for balance of atoms and charges.
Hence, balanced equation: \(\mathrm{Ag}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-}+2 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{NO}_{2(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)

iii. \(\mathrm{Sn}_{(\mathfrak{a q})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-} \longrightarrow \mathrm{Sn}_{(\mathrm{aq})}^{4+}+\mathrm{I}_{(\mathrm{aq})}^{-}\)

Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{Sn}_{(\mathfrak{a q})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-} \longrightarrow \mathrm{Sn}_{(\mathrm{aq})}^{4+}+\mathrm{I}_{(\mathrm{aq})}^{-}\)

Step 2: Assign oxidation number to Sn and I. Calculate the increase and decrease in the oxidation number and make them equal.

To make the net increase and decrease equal, we must take 4 atoms of Sn.
\(4 \mathrm{Sn}_{(\mathrm{aq})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-} \longrightarrow 4 \mathrm{Sn}_{(\mathrm{aq})}^{4+}+\mathrm{I}_{(\mathrm{aq})}^{-}\)

Step 3: Balance ‘O’ atoms by adding 4H₂O to the right-hand side.
\(4 \mathrm{Sn}_{(\mathrm{aq})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-} \longrightarrow 4 \mathrm{Sn}_{(\text {aq })}^{4+}+\mathrm{I}_{(\text {aq })}^{-}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 4: The medium is acidic. To make the charges and hydrogen atoms on the two sides equal, add 8H⁺ on the left-hand side.
\(4 \mathrm{Sn}_{(\mathrm{aq})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 4 \mathrm{Sn}_{(\mathrm{aq})}^{4+}+\mathrm{I}_{(\mathrm{aq})}^{-}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 5: Check two sides for balance of atoms and charges.
Hence, balanced equation: \(4 \mathrm{Sn}_{(\mathrm{aq})}^{2+}+\mathrm{IO}_{4(\mathrm{aq})}^{-}+8 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 4 \mathrm{Sn}_{(\mathrm{aq})}^{4+}+\mathrm{I}_{(\mathrm{aq})}^{-}+4 \mathrm{H}_{2} \mathrm{O}_{(l)}\)

iv. \(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+\mathrm{IO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{MnO}_{2(\mathrm{~s})}+\mathrm{IO}_{4(\mathrm{aq})}^{-}\)

Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{MnO}_{4(\mathrm{aq})}^{-}+\mathrm{IO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{MnO}_{2(\mathrm{~s})}+\mathrm{IO}_{4(\mathrm{aq})}^{-}\)

Step 2: Assign oxidation number to Mn and I. Calculate the increase and decrease in the oxidation number and make them equal.


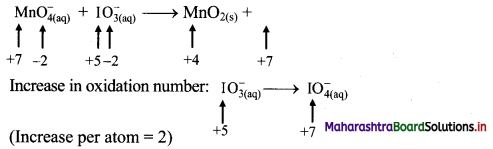
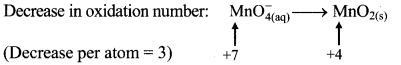
To make the net increase and decrease equal, we must take 2 atoms of Mn and 3 atoms of I.
\(2 \mathrm{MnO}_{4(a q)}^{-}+3 \mathrm{IO}_{3(\mathrm{aq})}^{-} \longrightarrow 2 \mathrm{MnO}_{2(\mathrm{~s})}+3 \mathrm{IO}_{4(\mathrm{aq})}^{-}\)

Step 3: Balance ‘O’ atoms by adding 1H₂O to the right-hand side.
\(2 \mathrm{MnO}_{4(\mathrm{aq})}^{-}+3 \mathrm{IO}_{3(\mathrm{aq})}^{-} \longrightarrow 2 \mathrm{MnO}_{2(\mathrm{~s})}+3 \mathrm{IO}_{4(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 4: The medium is acidic. To make the charges and hydrogen atoms on the two sides equal, add 2H on the left-hand side.
\(2 \mathrm{MnO}_{4(\mathrm{aq})}^{-}+3 \mathrm{IO}_{3(\mathrm{aq})}^{-}+2 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 2 \mathrm{MnO}_{2(\mathrm{~s})}+3 \mathrm{IO}_{4(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)

Step 5: Check two sides for balanced of atoms and charges.
Hence, balanced equation: \(2 \mathrm{MnO}_{4(\mathrm{aq})}^{-}+3 \mathrm{IO}_{3(\mathrm{aq})}^{-}+2 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 2 \mathrm{MnO}_{2(\mathrm{~s})}+3 \mathrm{IO}_{4(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(l)}\)

Question 32.
Balance the following redox equation in basic medium by oxidation number method:

Answer:
i. \(\mathrm{Zn}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{NH}_{3(\mathrm{aq})}+\mathrm{Zn}(\mathrm{OH})_{6(\mathrm{aq})}^{2-}\)

Step 1: Write skeletal equation and balance the elements other than 0 and H.
\(\mathrm{Zn}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{NH}_{3(\mathrm{aq})}+\mathrm{Zn}(\mathrm{OH})_{6(\mathrm{aq})}^{2-}\)

Step 2: Assign oxidation number to Zn and N. Calculate the increase and decrease in the oxidation number and make them equal.

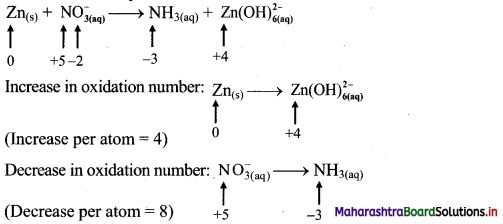
To make the net increase and decrease equal, we must take 2 atoms of Zn.
\(2 \mathrm{Zn}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{NH}_{3(\mathrm{aq})}+2 \mathrm{Zn}(\mathrm{OH})_{6(\mathrm{aq})}^{2-}\)

Step 3: Balance ‘O’ atoms by adding 9H₂O to the left-hand side.
\(2 \mathrm{Zn}_{(\mathrm{s})}+\mathrm{NO}_{3(\mathrm{aq})}^{-}+9 \mathrm{H}_{2} \mathrm{O}_{(l)} \longrightarrow \mathrm{NH}_{3(\mathrm{aq})}+2 \mathrm{Zn}(\mathrm{OH})_{6(\mathrm{aq})}^{2-}\)

Step 4: The medium is basic. To make hydrogen atoms on the two sides equal, add 3H on the right-hand side.

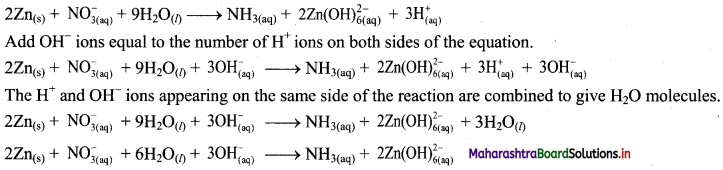
Step 5: Check two sides for balance of atoms and charges.
Hence, balanced equation:

ii. \(\mathrm{MnCl}_{2(\mathrm{aq})}+\mathrm{HO}_{2(\mathrm{aq})}^{-} \longrightarrow \mathrm{Mn}(\mathrm{OH})_{3(\mathrm{~s})}+\mathrm{Cl}_{(\mathrm{aq})}^{-}\)

Step 1: Write skeletal equation and balance the elements other than O and H.
\(\mathrm{MnCl}_{2(\mathrm{aq})}+\mathrm{HO}_{2(\mathrm{aq})}^{-} \longrightarrow \mathrm{Mn}(\mathrm{OH})_{3(\mathrm{~s})}+\mathrm{Cl}_{(\mathrm{aq})}^{-}\)

Step 2: Assign oxidation number to Mn and O. Calculate the increase and decrease in the oxidation number and make them equal.

iii. Cu(OH)_2(s) + N₂H_4(aq) → Cu_(s) + N_2(g)
Step 1: Write skeletal equation and balance the elements other that O and H.
Cu(OH)_2(s) + N₂H_4(aq) → Cu_(s) + N_2(g)
Step 2: Assign oxidation number to Cu and N. Calculate the increase and decrease in the oxidation number and make them equal.


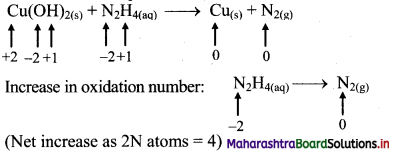
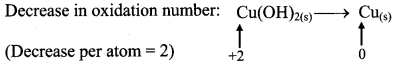
To make the net increase and decrease equal, we must take 2 atoms of Cu.
2Cu(OH)_2(s) + N₂H_4(aq) → 2Cu_(s) + N_2(g)
Step 3: Balance ‘O’ atoms by adding 4H20 to the right-hand side.
2Cu(OH)_2(s) + N₂H_4(aq) → 2Cu_(s) + N_2(g) + 4H₂O_(l)
Step 4: The equation is balanced for both atoms as well as charges.
Step 5: Check two sides for balance of atoms and charges.
Hence, balanced equation: 2Cu(OH)_2(s) + N₂H_4(aq) → 2Cu_(s) + N_2(g) + 4H₂O_(l)

Question 33.
Describe the steps involved in balancing redox reactions by ion electron method (Half reaction method).
Answer:
In this method two half equations are balanced separately and then added together to give balanced equation. Following steps are involved.

• Step 1: Write unbalanced equation for the redox reaction, assign oxidation number to all the atoms in the reactants and products. Divide the equation into two half equations. One half equation involves increase in oxidation number and another involves decrease in oxidation number (Write two half equations separately).
• Step 2: Balance the atoms except O and H in each half equation. Balance oxygen atom by adding H₂O to the side with less O atoms.
• Step 3: Balance H atoms by adding H⁺ ions to the side having less H atoms.
• Step 4: Balance the charges by adding appropriate number of electrons to the right side of oxidation half equation and to the left of reduction half equation.
• Step 5: Multiply half equation by suitable factors to equalize the number of electrons in two half equations. Add two half equations and cancel the number of electrons on both sides of equation.
• Step 6: If the reaction occurs in basic medium then add OH^– ions, equal to number of H⁺ ions on both sides of equation. The H⁺ and OH^– ions on same side of equation combine to give H₂O molecules.
• Check that the equation is balanced in both, the atoms and the charges.

Question 34.
Balance the following unbalanced equation (in acidic medium) by ion electron method (half reaction method).
\(\mathrm{Mn}_{(\mathrm{aq})}^{2+}+\mathrm{ClO}_{3(\mathrm{qq})}^{-} \longrightarrow \mathrm{MnO}_{2(\mathrm{~s})}+\mathrm{ClO}_{2(\mathrm{aq})}\)
Answer:
Step 1: Write imbalanced equation for the redox reaction. Assign oxidation number to all the atoms in reactants and products. Divide the equation into two half equations.

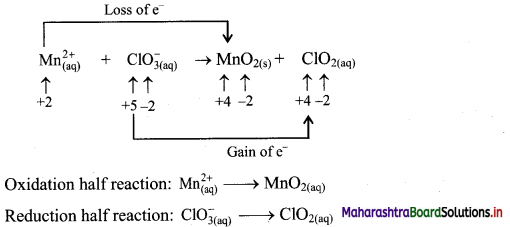
Step 2: Balance the atoms except O and H in each half equation. Balance half equations for O atoms by adding H₂O to the side with less O atoms. Add 2H₂O to left side of oxidation half equation and 1H₂O to the right side of reduction half equation.

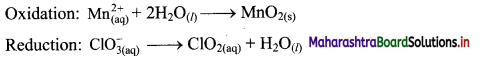
Step 3: Balance H atoms by adding H+ ions to the side with less H. Hence add 4H⁺ ions to the right side of oxidation half equation and 2H⁺ ions to the left side of reduction half equation.

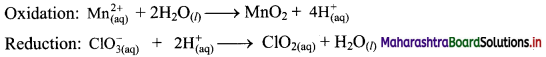
Step 4: Now add 2 electrons to the right side of oxidation half equation and 1 electron to the left side of reduction half equation to balance the charges.

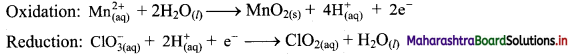
Step 5: Multiply reduction half equation by 2 to equalize number of electrons in two half equations. Then add two half equation.

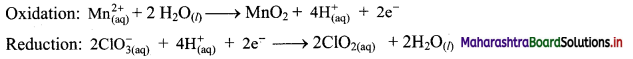
Add two half equations:
\(\mathrm{Mn}_{(\mathrm{aq})}^{2+}+2 \mathrm{ClO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{MnO}_{2(\mathrm{~s})}+2 \mathrm{ClO}_{2(\mathrm{aq})}\)
The equation is balanced in terms of number of atoms and the charges.
Hence, balanced equation: \(\mathrm{Mn}_{(\mathrm{aq})}^{2+}+2 \mathrm{ClO}_{3(\mathrm{aq})}^{-} \longrightarrow \mathrm{MnO}_{2(\mathrm{~s})}+2 \mathrm{ClO}_{2(\mathrm{aq})}\)

Question 35.
Balance the following unbalanced equation by ion electron method (half reaction method).
\(\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+\mathrm{ClO}_{4(\mathrm{aq})}^{-} \longrightarrow \mathrm{ClO}_{2(\mathrm{aq})}^{-}+\mathrm{O}_{2(\mathrm{~g})}\)
Answer:
Step 1: Write unbalanced equation for the redox reaction. Assign oxidation number to all the atoms in reactants and products. Divide the equation into two half equations.

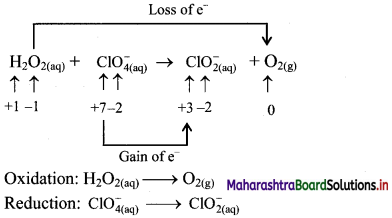
Step 2: Balance the atoms except O and H in each half equation. Balance the half equation for O atoms by adding H₂O to the side with less O atoms. Hence, add 2H₂O to the right side of reduction half equation and none to the oxidation half equation

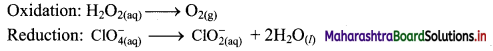
Step 3: Balance H atoms by adding H⁺ ions to the side with less H. Hence add 2H⁺ ions to the right side of oxidation half equation and 4H⁺ ions to the left side of reduction half equation.

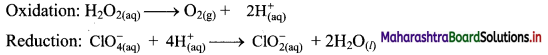
Step 4: Add 2 electrons to the right side of oxidation half equation and 4 electrons to the left side of reduction half equation to balance the charges.

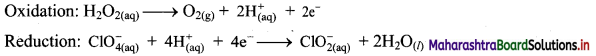
Step 5: Multiply oxidation half equation by 2 to equalize the number of electrons and then add two half equations.

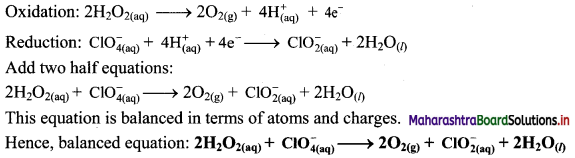
Question 36.
Balance the following redox equations by ion-electron (half reaction method).

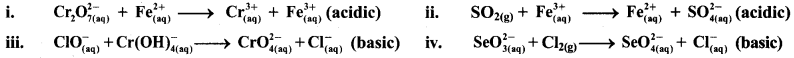
Answer:
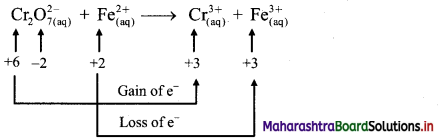
i. \(\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-}+\mathrm{Fe}_{(\mathrm{aq})}^{2+} \longrightarrow \mathrm{Cr}_{(\mathrm{aq})}^{3+}+\mathrm{Fe}_{(\mathrm{aq})}^{3+}(\text { acidic })\)
Step 1: Write unbalanced equation for the redox reaction. Assign oxidation number to all the atoms in reactants and products. Divide the equation into two half equations.

Step 2: Balance the atoms except O and H in each half equation. Balance half equation for O atoms by adding 7H₂O to the right side of reduction half equation.

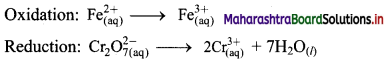
Step 3: Balance H atoms by adding H+ ions to the side with less H. Hence, add 14H⁺ ions to the left side of reduction half equation.

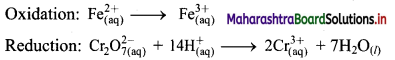
Step 4: Now add 1 electron to the right side of oxidation half equation and 6 electrons to the left side of reduction half equation to balance the charges.

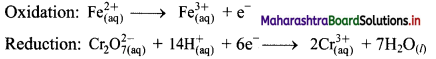
Step 5: Multiply oxidation half equation by 6 to equalize number of electrons in two half equations. Then add two half equation.

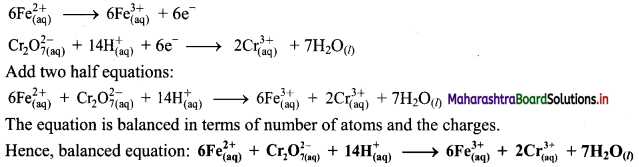
ii. \(\mathrm{SO}_{2(\mathrm{~g})}+\mathrm{Fe}_{(\mathrm{aq})}^{3+} \longrightarrow \mathrm{Fe}_{(\mathrm{aq})}^{2+}+\mathrm{SO}_{4(\mathrm{aq})}^{2-}(\text { acidic })\)
Step 1 : Write unbalanced equation for the redox reaction. Assign oxidation number to all the atoms in reactants and products in them. Divide the equation into two half equations.

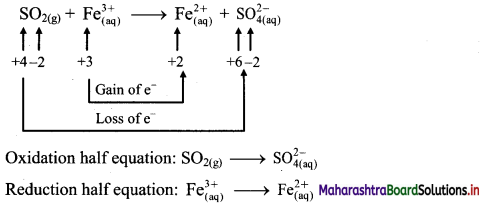
Step 2: Balance the atoms except O and H in each half equation. Balance half equation for O atoms by adding 2H₂O to the left side of oxidation half equation.

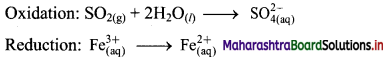
Step 3: Balance H atoms by adding H⁺ ions to the side with less H. Hence, add 4H⁺ ions to the right side of oxidation half equation.

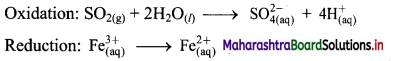
Step 4: Now add 2 electrons to the right side of oxidation half equation and 1 electron to the left side of reduction half equation to balance the charges.

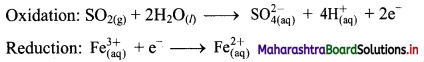
Step 5: Multiply reduction half equation by 2 to equalize number of electrons in two half equations. Then add two half equation.

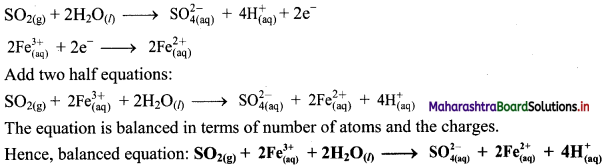
iii. \(\mathrm{ClO}_{(\mathrm{aq})}^{-}+\mathrm{Cr}(\mathrm{OH})_{4(\mathrm{aq})}^{-} \longrightarrow \mathrm{CrO}_{4(\mathrm{aq})}^{2-}+\mathrm{Cl}_{(\mathrm{aq})}^{-} \text {(basic) }\)
Step 1: Write unbalanced equation for the redox reaction: Assign oxidation number to all the atoms in reactants and products. Divide the equation into two half equations.

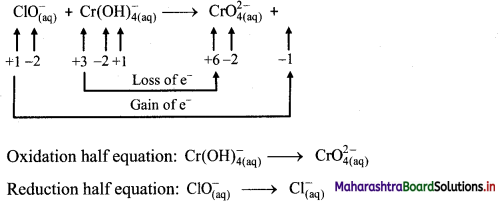
Step 2: Balance the atoms except O and H in each half equation. Balance half equation for O atoms by adding 1H₂O to the right side of reduction half equation.

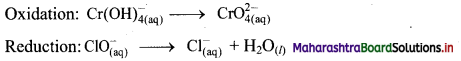
Step 3: Balance H atoms by adding H⁺ ions to the side with less H. Hence, add 4H⁺ ions to the right side of oxidation half equation and 2H⁺ ions to the left side of reduction half equation.

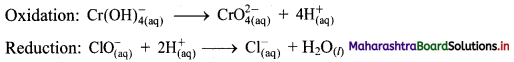
Step 4: Now add 3 electrons to the right side of oxidation half equation and 2 electrons to the left side of reduction half equation to balance the charges.

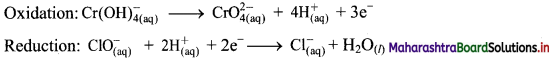
Step 5: Multiply oxidation half equation by 2 and reduction half equation by 3 to equalize number of electrons in two half equations. Then add two half equation.

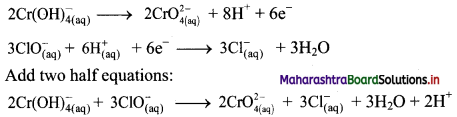
Step 6: The reaction takes place in basic medium. 20H^– ions, equal to the number of H⁺ ions (2H⁺ ions) are added on both sides of the equation.

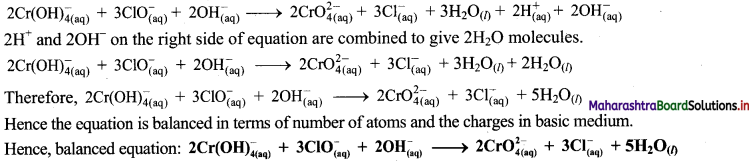
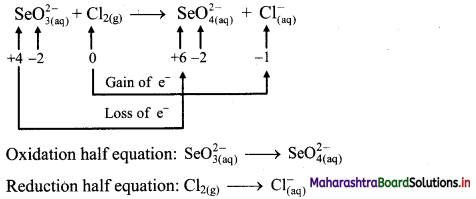
iv. \(\mathrm{SeO}_{3(\mathrm{aq})}^{2-}+\mathrm{Cl}_{2(\mathrm{~g})} \longrightarrow \mathrm{SeO}_{4(a q)}^{2-}+\mathrm{Cl}_{(\mathrm{aq})}^{-} \text {(basic) }\)
Step 1: Write unbalanced equation for the redox reaction. Assign oxidation number to all the atoms in reactants and products in them. Divide the equation into two half equations.

Step 2: Balance the atoms except O and H in each half equation. Balance half equation for O atoms by adding H₂O to the left side of oxidation half equation.

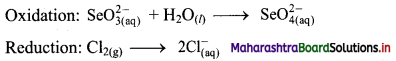
Step 3: Balance H atoms by adding H⁺ ions to the side with less H. Hence, add 2H⁺ ions to the right side of oxidation half equation.

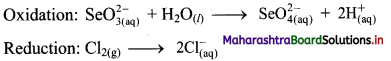
Step 4: Now add 2 electrons to the right side of oxidation half equation and 2 electrons to the left side of reduction half equation to balance the charges.

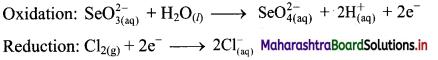
Step 5: There is equal number of electrons in two half equations. Add two half equation.

Question 37.
Explain displacement reaction in terms of redox reaction by giving example.
Answer:
i. Displacement reaction can be looked upon as redox reaction. Consider the following displacement reaction.

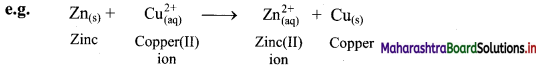
ii. Here, Zn gets oxidized to Zn²⁺ ion and Cu²⁺ ions get reduced to metallic Cu. A direct transfer of electron from zinc atom to cupric ions takes place in this case.

Question 38.
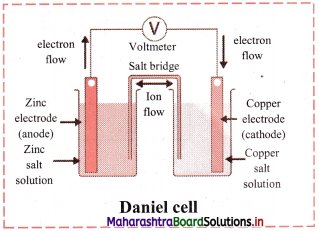
Explain construction of Daniel cell.
Answer:

• The zinc and copper plates are connected by an electric wire through a switch and voltmeter.
• The solution in two containers are connected by salt bridge (U-shaped glass tube containing a gel of KCl or NH₄NO₃ in agar-agar).
• When switch is on, electrical circuit is complete as indicated by the deflection in the voltmeter.
• The circuit has two parts, one in the form of electrical wire which allows the flow of electrons and the other in the form of two solutions joined by salt bridge. In solution part of the circuit, the electric current is carried by movement of ions.

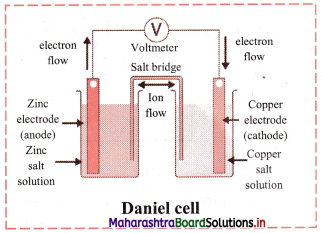
Question 39.
Explain working of Daniel cell.
Answer:
i. When a circuit is complete, the zinc atoms on zinc plates spontaneously lose electrons which are picked up in the external circuit.
ii. The electrons flow from the zinc plate to copper plate through wire.
iii. Cu²⁺ ions in the second container receive these electrons through the copper plate and are reduced to copper atoms which get deposited on the copper plate.
iv. Here, zinc plate acts as anode (negative electrode) and the copper plate acts as cathode (positive electrode).

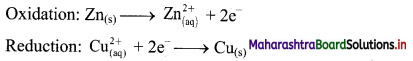
v. Thus, when two half reactions, namely, oxidation and reduction, are allowed to take place in separate containers and provision is made for completing the electrical circuit, electron transfer take place through the circuit.
vi. This results in flow of electric current in the circuit as indicated by deflection in voltmeter.
vii. Thus, in Daniel cell, electricity is generated by redox reaction.

Question 40.
Draw a neat and labelled diagram of Daniel cell.
Answer:

Question 41.
Chalcopyrite (CuFeS₂) is a common ore of copper. Since it has low concentration of copper, the ore is first concentrated through froth floatation process. The concentrated ore is then heated strongly with silicon dioxide (silica) and oxygen in a furnace. The product obtained, copper(I) sulphide, is further converted to copper (99.5% pure) with a final blast of air (O₂) during which sulphur dioxide is released as a by-product.
i. Write a balanced reaction for the extraction of copper from copper(I) sulphide.
ii. Which species undergoes an increase in the oxidation state?
iii. Which species accepts electrons?
Answer:
i. Cu₂S + O₂ → 2Cu + SO₂
ii. Sulphur undergoes an increase in the oxidation state from -2 (in Cu₂S) to +4 (in SO₂).
iii. Copper accepts one electron and undergoes a decrease in the oxidation state from +1(in Cu₂S) to 0 (in Cu). Oxygen accepts two electrons and undergoes a decrease in the oxidation state from 0 (in O₂) to -2 (in SO₂).

Question 42.
Consider the elements: Cs, Ne, I and F
i. Identify the element that exhibits only negative oxidation state.
ii. Identify the element that exhibits only positive oxidation state.
iii. Identify the element that exhibits both negative as well as positive oxidation state.
iv. Identify the element that exhibits neither the negative nor the positive oxidation state.
Answer:
i. F: It is most electronegative. It shows only a negative oxidation state of -1.
ii. Cs: Alkali metals have only one electron in their valence shell and hence, exhibits only positive (+1) oxidation state.
iii. I: Because of the presence of 7 electrons in its valence shell, I shows negative oxidation state of -1 (to have stable noble gas configuration) and positive oxidation numbers of +1, +3, +5 and +7 because of the presence of d-orbitals.
iv. Ne: It is an inert gas and therefore, does not exhibit negative or positive oxidation state.

Multiple Choice Questions

1. Loss of electrons means ………….
(A) reduction
(B) oxidation
(C) precipitation
(D) complexometry
Answer:
(B) oxidation

2. Reduction involves ……………
(A) gain of electrons
(B) addition of oxygen
(C) increase in oxidation number
(D) loss of electron
Answer:
(A) gain of electrons

3. Which of the following statement is INCORRECT?
(A) Oxidant is a substance which increases the oxidation number of other substance.
(B) Reductant is a substance which decreases the oxidation number of other substance.
(C) The oxidation number of oxidant decreases.
(D) In oxidation, there is decrease in oxidation number.
Answer:
(D) In oxidation, there is decrease in oxidation number.

4. Which of the following is an example of oxidation process?

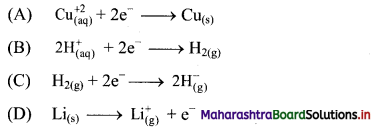
Answer:
(D) \(\mathrm{Li}_{(\mathrm{s})} \longrightarrow \mathrm{Li}_{(\mathrm{g})}^{+}+\mathrm{e}^{-}\)

5. Which is the best description of the behaviour of chlorine in the reaction?
H₂O + Cl₂ → HOCl + HCl
(A) Neither oxidized not reduced
(B) Both oxidised and reduced
(C) Oxidised only
(D) Reduced only
Answer:
(B) Both oxidised and reduced

6. In the reaction,
\(\begin{array}{r} 3 \mathrm{Br}_{2}+6 \mathrm{CO}_{3}^{2-}+3 \mathrm{H}_{2} \mathrm{O} \longrightarrow \ 5 \mathrm{Br}^{-}+\mathrm{BrO}_{3}^{-}+6 \mathrm{HCO}_{3}^{-} \end{array}\) …………..
(A) Br₂ is oxidised and carbonate is reduced
(B) bromine is reduced and water is oxidised
(C) bromine is neither reduced nor oxidised
(D) bromine is both reduced and oxidised
Answer:
(D) bromine is both reduced and oxidised

7. A chemical reaction in which oxidation and reduction processes takes place simultaneously is known as ………… reaction.
(A) redox
(B) precipitation
(C) complexometric
(D) titration
Answer:
(A) redox

8. Which of the following is a redox reaction?
(A) NaCl + KNO₃ → NaNO₃ + KCl
(B) CaC₂O₄ + 2HCl → CaCl₂ + H₂C₂O₄
(C) Mg(OH)₂ + 2NH₄Cl → MgCl₂ + 2NH₄OH
(D) Zn + 2AgCN → 2Ag + Zn(CN)₂
Answer:
(D) Zn + 2AgCN → 2Ag + Zn(CN)₂

9. Oxidation number of metal ion is always …………..
(A) positive
(B) negative
(C) zero
(D) non zero
Answer:
(A) positive

10. The oxidation number of oxygen in peroxide is …………..
(A) -2
(B) -1
(C) +1
(D) +2
Answer:
(B) -1

11. The oxidation number of oxygen is …………. in oxygen difluoride.
(A) -2
(B) -1
(C) +2
(D) +1
Answer:
(C) +2

12. Oxidation number of carbon in CH₂F₂ is ………….
(A) +1
(B) -1
(C) 0
(D) +2
Answer:
(C) 0

13. In calcium hydride (CaH₂), the oxidation number of hydrogen is ………….
(A) +1
(B) -1
(C) +2
(D) -2
Answer:
(B) -1

14. The element with atomic number 9 can exhibit oxidation state of …………..
(A) +1
(B) +3
(C) -1
(D) +5
Answer:
(C) -1

15. The highest and lowest oxidation states possible for Te (group 16) are ……………
(A) +6, -2
(B) +6, 0
(C) +4, -4
(D) +6, -6
Answer:
(A) +6, -2

16. What is the oxidation state of S in Na₂S₂ ?
(A) +1
(B) -2
(C) -1
(D) 0
Answer:
(C) -1

17. The oxidation state of S in S₂O₈^2- is ………….
(A) +2
(B) + 4
(C) +6
(D) + 7
Answer:
(D) + 7

18. The oxidation state of phosphorus in Ba(H₂PO₂)₂ is …………..
(A) +3
(B) +2
(C) +1
(D) -1
Answer:
(C) +1

19. Amongst the following, identify the species having an atom with +6 oxidation state.
(A) \(\mathrm{MnO}_{4}^{-}\)
(B) \(\mathrm{Cr}(\mathrm{OH})_{3}^{6-}\)
(C) \(\mathrm{NiF}_{6}^{2-}\)
(D) CrO₂Cl₂
Answer:
(D) CrO₂Cl₂

20. In which of the following compounds, the oxidation number of carbon is NOT zero?
(A) (CHCl)₂
(B) HCHO
(C) CH₃COOH
(D) CH₂Cl₂
Answer:
(C) CH₃COOH

21. The oxidation number of S in S₈, S₂F₂ and H₂S respectively are ………….
(A) 0, +1, -2
(B) +2, +1, -2
(C) 0, +1, +2
(D) +2, +1, -2
Answer:
(A) 0, +1, -2

22. The coefficients x, y, and z in the following balanced equation
xZn + \(\mathrm{yNO}_{3}^{-}\) + 10H+ → zZn²⁺ + \(\mathrm{NH}_{4}^{+}\) + 3H₂O are …………..
(A) 4, 1, 4
(B) 2, 2, 2
(C) 4, 2, 4
(D) 4, 4, 4
Answer:
(A) 4, 1, 4

23. For the redox reaction:
\(\mathrm{MnO}_{4}{ }^{-}+\mathrm{C}_{2} \mathrm{O}_{4}^{2-}+\mathrm{H}^{+} \longrightarrow \mathrm{Mn}^{2+}+\mathrm{CO}_{2}+\mathrm{H}_{2} \mathrm{O}\)
The CORRECT coefficients of the reactants in the balanced reaction are ……………

Answer:
(A)

24. In the reaction
3CuO + 2NH₃ → N₂ + 3H₂O + 3Cu
the change of NH₃ to N₂ involve ……………..
(A) loss of 6 electrons per mol of N₂
(B) loss of 3 electrons per mol of N₂
(C) gain of 6 electrons per mole N₂
(D) gain of 3 electrons per mole N₂
Answer:
(A) loss of 6 electrons per mol of N₂

25. When KMnO₄ acts as an oxidizing agent and ultimately forms \(\mathrm{MnO}_{4}^{2-}\), MnO₂, Mn₂O_3, and Mn²⁺, then the number of electrons transferred in each case is …………..
(A) 4, 3, 1, 5
(B) 1, 5, 3, 7
(C) 1, 3, 4, 5
(D) 3, 5, 7, 1
Answer:
(C) 1, 3, 4, 5

26. In electrochemical cell, the magnitude and direction of the electrode potential depends on which of the following?
(A) Nature of metal and ions
(B) Concentration of ions
(C) Temperature
(D) All of these
Answer:
(D) All of these

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 5 Chemical Bonding Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 5 Chemical Bonding

Question 1.
Explain the electronic theory of valence.
Answer:
Electronic theory of valence:

• The electronic theory of valence was proposed by Kossel and Lewis in 1916.
• They gave a logical explanation of valence which was based on the inertness of noble gases (that is, the octet rule developed by Lewis).
• According to Lewis, the atom can be pictured in terms of a positively charged ‘kernel’ (the nucleus plus inner electrons) and outer shell that can accommodate a maximum of eight electrons. This octet of electrons represents a stable electronic arrangement.
• Thus, according to this theory, during the formation of a chemical bond, each atom loses, gains or shares outer electrons so that it achieves stable octet.
• The formation of NaCl involves transfer of one electron from sodium (Na) to chlorine (Cl). Na⁺ and Cl^– ions are formed which are held together by chemical bond. The formation of H₂, F₂, Cl₂, HCl, etc., involves sharing of a pair of electrons between the atoms. In both cases, each atom attains a stable outer octet of electrons.

Question 2.
Give the significance of octet rule. Explain why this rule is not valid for H and Li atoms.
Answer:
i. Significance: Octet rule is found to be very useful:

• in explaining the normal valence of elements
• in the study of the chemical combination of atoms leading to the formation of molecules.

ii. Octet rule is not valid for H and Li atoms. According to octet rule, during the formation of a chemical bond, each atom loses, gains or shares electrons so that it achieves stable octet (eight electrons in the valence shell). However, H and Li atoms tend to have only two electrons in their valence shell similar to that of Helium (1s²), which called duplet. Hence, octet rule is not valid for H and Li atoms.

Question 3.
Define ionic bond.
Answer:
The bond formed by complete transfer of one or more electrons from an electropositive atom to an electronegative atom, leading to formation of ions which are held together by electrostatic attraction is called ionic bond or electrovalent bond.

Question 4.
Explain the formation of ionic bond in sodium chloride (NaCl).
Answer:
Formation of sodium chloride (NaCl):
i. The electronic configurations of sodium and chlorine are:
Na (Z = 11): 1s² 2s² 2p⁶ 3s¹ or (2, 8, 1)
Cl (Z = 17): 1s² 2s² 2p⁶ 3s² 3p⁵ or (2, 8, 7)
ii. Sodium has one electron in its valence shell. It has tendency to lose one electron to acquire the electronic configuration of the nearest inert gas, neon (2, 8).
iii. Chlorine has seven electrons in its valence shell. It has tendency to gain one electron and thereby acquire the electronic configuration of the nearest inert gas, argon (2, 8, 8).
iv. During the combination of sodium and chlorine atoms, the sodium atom transfers its valence electron to the chlorine atom.
v. Sodium atom changes into Na+ ion while the chlorine atom changes into Cl^– ion. The two ions are held together by strong electrostatic force of attraction.
vi. The formation of ionic bond between Na and Cl can be shown as follows:

Question 5.
Explain the formation of ionic bonds in calcium chloride (CaCl₂).
Answer:
Formation of calcium chloride (CaCl₂):
i. The electronic configurations of calcium and chlorine are:
Na (Z = 11): 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² or (2, 8, 8, 2)
Cl (Z = 17): 1s² 2s² 2p⁶ 3s² 3p⁵ or (2, 8, 7)
ii. Calcium has two electrons in its valence shell. It has tendency to lose two electrons to acquire the electronic configuration of the nearest inert gas, argon (2, 8, 8).
iii. Chlorine has seven electrons in its valence shell. It has tendency to gain one electron and thereby acquire the electronic configuration of the nearest inert gas, argon (2, 8, 8).
iv. During the combination of calcium and chlorine atoms, the calcium atom transfers its valence electrons to two chlorine atoms.
v. Calcium atom changes into Ca²⁺ ion while the two chlorine atoms change into two Cl^– ions. These ions are held together by strong electrostatic force of attraction.
vi. The formation of ionic bond(s) between Ca and Cl can be shown as follows:

Question 6.
What are ionic solids?
Answer:
Ionic solids are solids which contain cations and anions held together by ionic bonds.
e.g. Sodium chloride (NaCl), Calcium chloride (CaCl₂)

Question 7.
Define lattice enthalpy.
Answer:
Lattice enthalpy of an ionic solid is defined as the energy required to completely separate one mole of solid ionic compound into the gaseous components.
Note: Lattice enthalpy values of some ionic compounds:

Compound	Lattice enthalpy kJ mol–1
LiCl	853
NaCl	788
BeF2	3020
CaCl2	2258
AlCl3	5492

Question 8.
Arrange NaCl, CaCl₂ and AlCl₃ in increasing order of lattice enthalpy (positive value). Justify your answer.
Answer:
Compounds having cations with higher charge have large lattice enthalpy (higher positive value) than compounds having cations with lower charge.
Hence, the correct order is NaCl < CaCl₂ < AlCl₃.

Question 9.
Lattice enthalpy of LiF is more than that of NaF. Explain.
Answer:
As the size of the cation decrease, lattice enthalpy increases. Li⁺ ion is smaller than Na⁺ ion. Hence, lattice enthalpy of LiF is more than that of NaF.

Question 10.
Define covalent bond.
Answer:
The attractive force which exists due to the mutual sharing of electrons between the two atoms of similar electronegativity or having small difference in electronegativities is called a covalent bond.

Question 11.
Explain the formation of covalent bond in H₂ molecule.
Answer:
Formation of H₂ molecule:
i. The electronic configuration of H atom is 1s¹.
ii. It needs one more electron to complete its valence shell.
iii. When two hydrogen atoms approach each other at a certain internuclear distance, they share their valence electrons.
iv. The shared pair of electrons belongs equally to both the hydrogen atoms. The two atoms are said to be linked by a single covalent bond and a H₂ molecule is formed.

Question 12.
Explain the formation of covalent bond in Cl₂ molecule.
Answer:
Formation of Cl₂ molecule:
i. The electronic configuration of Cl atom is [Ne] 3s² 3p⁵.
ii. It needs one more electron to complete its valence shell.
iii. When two chlorine atoms approach each other at a certain internuclear distance, they share their valence electrons. In the process, both the atoms attain the valence shell of octet of nearest noble gas, argon.
iv. The shared pair of electrons belongs equally to both the chlorine atoms. The two atoms are said to be linked by a single covalent bond and a Cl₂ molecule is formed.

Question 13.
What are the important features of covalent bond?
Answer:

• Each covalent bond is formed as a result of sharing of electron pair between the two atoms.
• When a covalent bond is formed, each combining atom contributes one electron to the shared pair.
• The combining atoms attain the outer shell noble gas configuration as a result of the sharing of electrons.

Question 14.
Explain the types of covalent bond with suitable examples.
Answer:
The three types of covalent bonds are as follows.
i. Single bond: When two combining atoms share one electron pair, the covalent bond between them is called single bond.
Single bond is observed in number of molecules.
e.g. H₂, Cl₂, water molecule, etc.

ii. Double bond: When two combining atoms share two pairs of electrons, the covalent bond between them is called a double bond, e.g. Double bond is present in C₂H₄ molecule

iii. Triple bond: When two combining atoms share three pairs of electrons, the covalent bond between them is called a triple bond, e.g. Triple bond is present in N₂ molecule.

Note: Formation of covalent bonds in CO₂, CCl₄ and C₂H₂:

Question 15.
Distinguish between ionic bond and covalent bond.
Answer:
Ionic bond:

1. It is formed by the transfer of electrons from one atom to another.
2. It is formed by the transfer of electrons from one atom to another.
3. In this, oppositely charged ions are formed.
4. There are no multiple ionic bonds.
5. This bond usually exists between metal and non-metal atoms.
6. e.g. NaCl, CaCl₂

Covalent bond:

1. It is formed by sharing of electrons.
2. Atoms are held together due to shared pair of electrons.
3. In this, oppositely charged ions are not formed.
4. Covalent bonds may be single or double or triple bonds.
5. This bond usually exists between non-metal atoms.
6. e.g. H₂, Cl₂

Question 16.
What are the steps to write Lewis dot structure?
Answer:
Steps to write Lewis dot structures:

• Add the total number of valence electrons of combining atoms in the molecule.
• In anions, add one electron for each negative charge.
• In cations, subtract one electron from valence electrons for each positive charge.
• Write skeletal structure of the molecule to show the atoms and number of valence electrons forming the single bond between the atoms.
• Add remaining electron pairs to complete the octet of each atom.
• If octet is not complete form multiple bonds between the atoms such that octet of each atom is complete.
• In polyatomic atoms and ions, the least electronegative atom is the central atom.
  e.g. In \(\mathrm{SO}_{4}^{2-}\) ion, ‘S’ is the central atom and in \(\mathrm{NO}_{3}^{-}\), ‘N’ is the central atom.
• After writing the number of electrons as shared pairs forming single bonds, the remaining electron pairs are used either for multiple bonds or they remain as lone pairs.

Question 17.
Write the Lewis structure of nitrite ion, \(\mathrm{NO}_{2}^{-}\).
Answer:
Step I: Count the total number of valence electrons of nitrogen atom, oxygen atom and one electron of additional negative charge.
Valence shell configuration of nitrogen and oxygen are:
N ⇒ (2s² 2p³), O ⇒ (2s² 2p⁴)
The total electrons available are:
5 + (2 × 6) + 1 = 18 electrons
Step II: The skeletal structure of \(\mathrm{NO}_{2}^{-}\) is written as O N O
Step III: Draw a single bond i.e., one shared electron pair between the nitrogen and each oxygen atoms. Then distribute the remaining electrons to achieve noble gas configuration for each atom. This does not complete the octet of nitrogen.

Hence, there is a multiple bond between nitrogen and one of the oxygen atoms (a double bond). The remaining two electrons constitute a lone pair on nitrogen.
Following are Lewis dot structures of \(\mathrm{NO}_{2}^{-}\).

Question 18.
Write the Lewis structure of CO molecule.
Answer:
Step I: Count number of electrons of carbon and oxygen atoms. The valence shell configuration of carbon and oxygen atoms are: 2s² 2p² and 2s² 2p⁴, respectively. The valence electrons available are:
4 + 6=10
Step II: The skeletal structure of CO is written as
C O
Step III: Draw a single bond (One shared electron pair) between C and O and complete the octet on O. The remaining two electrons is a lone pair on C.

The octet on carbon is not complete. Hence, there is a multiple bond between C and O (a triple bond between C and O atom). This satisfies the octet rule for carbon and oxygen atoms.
The Lewis structure of CO molecule is:

Question 19.
Explain the term formal charge.
Answer:
i. Formal charge is the charge assigned to an atom in a molecule, assuming that all electrons are shared equally between atoms, regardless of their relative electronegativities.
ii. While determining the best Lewis structure per molecule, the structure is chosen such that the formal charge is as close to zero as possible.
iii. The structure having the lowest formal charge has the lowest energy.
iv. Formal charge is assigned to an atom based on electron dot structures of the molecule/ion.
v. Formal charge on an atom in a Lewis structure of a polyatomic species can be determined using the following formula:

Question 20.
Explain the calculation of the formal charge on oxygen atoms in case of O₃ (ozone) molecule.
Answer:
i. Lewis dot structure of O₃ (ozone) molecule is:

Three oxygen atoms are present in the O₃ molecule and are labelled as 1, 2 and 3.
ii. Formal charges on oxygen atoms labelled as 1, 2, 3 are calculated as shown below:

iii. On the basis of the formal charge values, O₃ is shown as

[Note: Indicating the charges on the atoms in the Lewis structure helps in keeping track of the valence electrons in the molecule. Formal charges help in the selection of the lowest energy structure from a number of possible Lewis structures for a given species.]

Question 21.
CO₂ can be represented by following three structures:

Calculate the formal charge on each atom in all the three structures of CO₂ molecule. Identify the structure with lowest energy.
Answer: Formal charges on atoms labelled as 1, 2, 3 are calculated as shown below:
Structure (I):

Structure (II):

Structure (III):

While determining the best Lewis structure per molecule, the structure is chosen such that the formal charge is as close to zero as possible. The structure having the lowest formal charge has the lowest energy.

In structure (I), the formal charge on each atom is 0 while in structures (II) and (III) formal charge on carbon is 0 while oxygens have formal charge -1 or +1. Hence, the possible structure with the lowest energy will be structure (I). Thus, formal charges help in the selection of the lowest energy structure from a number of possible Lewis structures for a given species.

Question 22.
Find out the formal charges on S, C and N.
(S = C = N)^– ; (S – C ≡ N)^– ; (S ≡ C – N)^–
Answer:
Step I:
Write Lewis dot diagrams for the structures:

Step II:
Assign formal charges for all the atoms:
F.C. = V.E. – N.E. – 1/2 (B.E.)
Structure A:
Formal charge on S = 6 – 4 – 1/2(4) = 0
Formal charge on C = 4 – 0 – 1/2 (8) = 0
Formal charge on N = 5 – 4 – 1/2 (4) = -1
Structure B:
Formal charge on S = 6 – 6 – 1/2(2) = -1
Formal charge on C = 4 – 0 – 1/2 (8) = 0
Formal charge on N = 5 – 2 – 1/2 (6) = 0
Structure C:
Formal charge on S = 6 – 2 – 1/2(6) = +1
Formal charge on C = 4 – 0 – 1/2(8) = 0
Formal charge on N = 5 – 6 – 1/2(2) = -2

Question 23.
Give the limitations of octet rule:
Answer:
Limitations of octet rule:
i. Octet rule does not explain stability of some molecules.
The octet rule is based on the inert behaviour of noble gases, which have their octet complete i.e., have eight electrons in their valence shell. It is very useful to explain the structures and stability of organic molecules. However, there are many molecules whose existence cannot be explained by the octet theory. The central atoms in these molecules does not have eight electrons in their valence shell, and yet they are stable.
Such molecules can be categorized as having:
a. Incomplete octet
b. Expanded octet
c. Odd electrons

a. Molecules with incomplete octet: e.g. BF₃, BeCl₂, LiCl
In these covalent molecules, the atoms B, Be and Li have less than eight electrons in their valence shell but these molecules are stable.
Li in LiCl has only two electrons, Be in BeCl₂ has four electrons while B in BF₃ has six electrons in the valence shell.

b. Molecules with expanded octet: Some molecules like SF₆, PCl₅, H₂SO₄ have more than eight electrons around the central atom.

c. Odd electron molecules:
Some molecules like NO (nitric oxide) and NO₂ (nitrogen dioxide) do not obey the octet rule. These molecules, have odd number of valence electrons.

ii. The observed shape and geometry of a molecule, cannot be explained, by the octet rule.
iii. Octet rule fails to explain the difference in energies of molecules, though all the covalent bonds are formed in an identical manner, that is, by sharing a pair of electrons. The rule fails to explain the differences in reactivities of different molecules.
Note: Sulphur also forms many compounds in which octet rule is obeyed. For example, in sulphur dichloride, the sulphur atom has eight electrons around it.

Question 24.
State the basic idea on which VSEPR theory was proposed by Sidgwick and Powell.
Answer:
Valence Shell Electron Pair Repulsion (VSEPR) theory is based on the basic idea that the electron pairs on the atoms shown in the Lewis diagram repel each other. In the real molecule, they arrange themselves in such a way that there is minimum repulsion between them.

Question 25.
Give the rules of VSEPR Theory.
Answer:
Rules of VSEPR Theory:
i. Electron pairs arrange themselves in such a way that repulsion between them is minimum.
ii. The molecule acquires minimum energy and maximum stability.
iii. Lone pair of electrons also contribute in determining the shape of the molecule.
iv. Repulsion of other electron pairs by the lone pair (L.P.) stronger than that of bonding pair (B.P.).
Trend for repulsion between electron pair is as follows:
L.P. – L.P. > L.P. – B.P. > B.P. – B.P.
Lone pair-Lone pair repulsion is maximum because this electron pair is under the influence of only one nucleus while the bonded pair is shared between two nuclei.
Thus, the number of lone pair and bonded pair of electrons decide the shape of the molecules. Molecules having no lone pair of electrons have a regular geometry.

Note:
i. Electron pair geometry: The arrangement of electrons around the central atom is called as electron pair geometry. These electron pairs may be shared in a covalent bond or they may be lone pairs.
ii. Geometry of some molecules (having no lone pair of electrons):


iii. Geometry of some molecules (having one or more lone pairs of electrons):

Question 26.
Match the following:

	Molecule		Shape
i.	SbF5	a.	Trigonal bipyramidal
ii.	SO2	b.	Bent
iii.	SF4	c.	Square pyramidal
iv.	IF5	d.	See-saw

Answer:
i – a,
ii – b,
iii – d,
iv – c

Question 27.
Complete the following table:

Answer:

Question 28.
Explain geometry of NH₃ molecule according to VSEPR theory.
Answer:

• In NH₃ molecule, the central atom nitrogen has five electrons in its valence shell. On bond formation with three hydrogen atoms, there are 8 electrons in the valence shell of nitrogen. Out of these, three pairs are bond pairs (N – H covalent bonds) and one forms lone pair. The expected geometry is tetrahedral and bond angle is 109° 28′.
• There are two types of repulsions between the electron pairs: Lone pair – bond pair and bond pair – bond pair
• The lone pair – bond pair repulsions are stronger and the bonded pairs are pushed inwards. Thus, reducing the bond angle to 107°18′ and shape of the molecule becomes trigonal pyramidal.

Diagram:

Question 29.
Explain geometry of H₂O molecule according to VSEPR theory.
Answer:

• In H₂O molecule, the central atom oxygen has six electrons in its valence shell. On bond formation with two hydrogen atoms, there are 8 electrons in the valence shell of oxygen. Out of these, two pairs are bond pairs and two are lone pairs.
• Due to lone pair – lone pair repulsion, the lone pairs are pushed towards the bond pairs and bond pair – lone pair repulsions become stronger thereby reducing the H-O-H bond angle from 109° 28′ to 104° 35′ and the geometry of the molecule becomes angular (bent).

Diagram:

Question 30.
Write the postulates of Valence Bond Theory.
Answer:
Postulates of Valence Bond Theory:

• A covalent bond is formed when the half-filled valence orbital of one atom overlaps with the half-filled valence orbital of another atom.
• The electrons in the half-filled valence orbitals must have opposite spins.
• During bond formation, the half-filled orbitals overlap and the opposite spins of the electrons get neutralized. The increased electron density decreases the nuclear repulsion and energy is released during overlapping of the orbitals.
• Greater the extent of overlap, stronger is the bond formed. However, complete overlap of orbitals does not take place due to intemuclear repulsions.
• If an atom possesses more than one unpaired-electrons, then it can form more than one bond. So, number of bonds formed will be equal to the number of half-filled orbitals in the valence shell i.e., number of unpaired electrons.
• The distance at which the attractive and repulsive forces balance each other is the equilibrium distance between the nuclei of the bonded atoms. At this distance, the total energy of the two bonded atoms is minimum and stability of the molecule is maximum.
• Electrons which are paired in the valence shell cannot participate in bond formation. However, in an atom if there is one or more vacant orbital present then these electrons can unpair and participate in bond formation provided the energies of the filled and vacant orbitals differ slightly from each other.
• During bond formation, the ‘s’ orbital which is spherical can overlap in any direction. The ‘p’ orbitals can overlap only in the x, y or z directions. Similarly, ‘d’ and ‘f orbitals are oriented in certain directions in space and overlap only in these directions. Thus, the covalent bond is directional in nature.

Note: In order to explain the covalent bonding, Heitler and London developed the valence bond theory on the basis of wave mechanics. This theory was further extended by Pauling and Slater.

Question 31.
Explain the formation of hydrogen molecule with the help of potential energy curve.
OR
Explain the formation of H₂ on the basis of VBT.
Answer:
Formation of H₂ on the basis of VBT:

• Hydrogen atom has electronic configuration 1s¹. It contains one unpaired electron in its valence shell.
• When the two hydrogen atoms containing unpaired electrons with opposite spins are separated by a large distance, they can neither attract nor repel each other (there are no interactions between them). The energy of the system is the sum of the potential energies of the two atoms which is arbitrarily taken as zero.
• When the two atoms approach each other, attractive and repulsive forces begin to operate on them. Experimentally, it has been found that during formation of hydrogen molecule, the magnitude of the newly developed attractive forces contributes more than the newly developed repulsive forces. As a result, the potential energy of the system begins to decrease.
• As the atoms come closer to one another the energy of the system decreases. The overlap of the atomic orbitals increases only up to a certain distance between the two nuclei, where the attractive and repulsive forces balance each other and the system attains minimum energy. At this stage, a stable bond is formed between the two atoms.
• If the distance between the two atoms is decreased further, the repulsive forces exceed the attractive forces and the energy of the system increases and stability decreases.
• When two hydrogen atoms with electrons having parallel spin approach each other, the potential energy of the system increases and bond formation does not take place.

Question 32.
Define:
i. Sigma overlap
ii. pi overlap
Answer:
i. Sigma overlap (σ bond): When two half-filled orbitals of two atoms overlap along the internuclear axis, it is called as sigma overlap or sigma bond.
ii. pi overlap (π bond): When two half-filled orbitals of two atoms overlap side-ways (laterally), it is called as π overlap or π bond.

Question 33.
Explain with example:
i. s-s σ overlap
ii. p-p σ overlap
iii. s-p a overlap
Answer:
i. s-s σ overlap:
a. The overlap between two half-filled s orbitals of two different atoms containing unpaired electrons with opposite spins is called s-s overlap.
e.g. Formation of H₂ molecule by s-s overlap:
Hydrogen atom (Z = 1) has electronic configuration: 1s¹. The 1s¹ orbitals of two hydrogen atoms overlap along the internuclear axis to form a σ bond between the atoms in H₂ molecule.
b. Diagram:

ii. p-p σ overlap:
a. This type of overlap takes place when two p orbitals from different atoms overlap along the internuclear axis.
e.g. Formation of F₂ molecule by p-p overlap:
Fluorine atom (Z = 9) has electronic configuration 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{2}\) \(2 \mathrm{p}_{\mathrm{y}}^{2}\) \(2 \mathrm{p}_{\mathrm{z}}^{1}\).
During the formation of F₂ molecule, half-filled 2p_z orbital of one F atom overlaps with similar half-filled 2p_z orbital containing electron with opposite spin of another F atom axially and a p-p σ bond is formed.
b. Diagram:

iii. s-p σ overlap:
a. In this type of overlap one half filled s orbital of one atom and one half filled p orbital of another orbital overlap along the internuclear axis.
e.g. Formation of HF molecule by s-p overlap:
Hydrogen atom (Z = 1) has electronic configuration: 1s¹ and fluorine atom (Z = 9) has electronic configuration 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{2}\) \(2 \mathrm{p}_{\mathrm{y}}^{2}\) \(2 \mathrm{p}_{\mathrm{z}}^{1}\). During the formation of HF molecule, half-filled 1s orbital of hydrogen atom overlaps coaxially with half-filled 2p_z orbital of fluorine atom with opposite electron spin and an s-p σ bond is formed.
b. Diagram:

Question 34.
Explain the formation of π bond with diagram.
OR
Explain π overlap with diagram.
Answer:

• When two half-filled p orbitals of two atoms overlap side-ways (laterally), it is called π overlap and the bond formed is called π bond.
• π bond is perpendicular to the intemuclear axis.

Diagram:

Question 35.
Identify the type of bond formed:


Answer:
i. σ bond
ii. π bond
iii. σ bond
iv. σ bond

Question 36.
Explain divalency of beryllium, though number of unpaired electrons in a beryllium atom is zero.
Answer:
Beryllium (Z = 4) has electronic configuration 1s² 2s² in its ground state.
When one of the 2s electrons of Be is promoted to the vacant 2p orbital, the electronic configuration of Be in its excited state becomes 1s² 2s¹ \(2 \mathrm{p}_{\mathrm{x}}^{1}\). This is called formation of an excited state and it has two unpaired electrons. Hence, though the number of unpaired electrons in the ground state of Be atom is zero, beryllium shows divalency.

Question 37.
Define the term hybridization.
Answer:
Hybridization is defined as the process of mixing of valence orbitals of same atom and recasting them into equal number of new equivalent orbitals (hybrid orbitals).

Question 38.
Explain in detail the steps involved in hybridization.
Answer:
Steps involved in hybridization:
i. Formation of the excited state:
a. The paired electrons in the ground state are uncoupled and one electron is promoted to the vacant orbital having slightly higher energy.
b. Now, total number of half-filled orbitals is equal to the valency of the element in the stable compound, e.g. In BeF₂, valency of Be is two. In the excited state, one electron from 2s orbital is uncoupled and promoted to 2p orbital.

ii. Mixing and recasting:

• In this step, the two ‘s’ and ‘p’ orbitals having slightly different energies mix with each other.
• Redistribution of electron density and energy takes place and two new orbitals having exactly same shape and energy are formed.
• These new orbitals arrange themselves in space in such a way that there is minimum repulsion and maximum separation between them. e.g. During formation of sp hybrid orbitals as in Be, the two sp hybrid orbitals form an angle of 180° with each other.

Question 39.
List the important conditions required for hybridization.
Answer:
Conditions for hybridization:

• Orbitals belonging to the same atom can participate in hybridization.
• Orbitals having nearly same energy can undergo hybridization.

[Note: 2s and 2p orbitals of the same atom undergo hybridization but 3s and 2p orbitals of the same atom do not.]

Question 40.
Enlist the characteristic features of hybrid orbitals.
Answer:
Characteristic features of hybrid orbitals:

• Number of hybrid orbitals formed is exactly the same as the participating atomic orbitals.
• They have same energy and shape.
• Hybrid orbitals are oriented in space in such a way that there is minimum repulsion and thus are directional in nature.
• The hybrid orbitals are different in shape from the participating atomic orbitals, but they bear the characteristics of the atomic orbitals from which they are derived.
• Each hybrid orbitals can hold two electrons with opposite spins.
• A hybrid orbital has two lobes on the two sides of the nucleus. One lobe is large and the other small.
• Covalent bonds formed by hybrid orbitals are stronger than those formed by pure orbitals, because the hybrid orbital has electron density concentrated on the side with a larger lobe and the other is small allowing greater overlap of the orbitals.

Question 41.
Explain with diagrams:
i. sp³ hybridization
ii. sp² hybridization
iii. sp hybridization
Answer:
i. sp³ hybridization:
In this type, one s and three p orbitals having comparable energy mix and recast to form four sp³ hybrid orbitals, ‘s’ orbital is spherically symmetrical while the p_x, p_y, p_z, orbitals have two lobes and are directed along x, y and z axes, respectively.

The four sp³ hybrid orbitals formed are equivalent in energy and shape. They have one large lobe and one small lobe. They are at an angle of 109° 28′ with each other in space and point towards the comers of a tetrahedron. CH₄, NH₃, H₂O are examples where the orbitals on central atom undergo sp³ hybridization.

Diagram:

ii. sp² hybridization:
This hybridization involves the mixing of one s and two p orbitals to give three sp² hybrid orbitals of same energy and shape. The three orbitals are maximum apart and oriented at an angle of 120° and are in one plane. The third p orbital does not participate in hybridization and remains at right angles to the plane of the sp² hybrid orbitals. BF₃, C₂H₄ molecules are examples of sp² hybridization.
Diagram:

iii. sp hybridization:
In this type, one s and one p orbital undergo mixing and recasting to form two sp hybrid orbitals of same energy and shape. The two hybrid orbitals are placed at an angle of 180°. Other two p orbitals do not participate in hybridization and are at right angles to the hybrid orbitals. For example, BeCl₂ and acetylene molecule (HC ≡ CH).
Diagram:

Question 42.
Explain the formation of an ammonia molecule on the basis of hybridization.
Answer:
Formation of an ammonia (NH₃) molecule on the basis of sp³ hybridization:
i. Ammonia molecule (NH₃) has one nitrogen atom and three hydrogen atoms.
ii. The ground state electronic configuration of nitrogen (Z = 7) is 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{1}\) \(2 \mathrm{p}_{\mathrm{y}}^{1}\) \(2 \mathrm{p}_{\mathrm{z}}^{1}\)
Electronic configuration of nitrogen:

iii. The ground state electronic configuration explains the observed valency of nitrogen in NH₃ which is three.
iv. The 2s, 2p_x, 2p_y and 2p_z orbitals of nitrogen atom mix and recast to form four sp³ hybrid orbitals of equivalent energy. These orbitals are tetrahedrally oriented in space. One of the sp³ hybrid orbital contains a lone pair of electrons.
v. Three half-filled sp³ hybrid orbitals of N atom overlap axially with half-filled 1s orbital of three different hydrogen atoms to form three N-H (sp³-s) sigma covalent bonds.
vi. Since, there is one lone pair of electrons in one of the sp³ hybrid orbitals of nitrogen, there is repulsion between lone pair and bonding pair of electrons. As a result, the H-N-H bond angle is reduced from regular tetrahedral angle 109° 28′ to 107° 18′. Geometry of NH₃ molecule is pyramidal or distorted tetrahedral.

Question 43.
Explain the formation of water (H₂O) molecule on the basis of hybridization.
Answer:
Formation of water (H₂O) molecule on the basis of sp³ hybridization:
i. Water molecule (H₂O) has one oxygen atom and two hydrogen atoms.
ii. The ground state electronic configuration of oxygen (Z = 8) is 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{2}\) \(2 \mathrm{p}_{\mathrm{y}}^{1}\) \(2 \mathrm{p}_{\mathrm{z}}^{1}\).
Electronic configuration of oxygen:

iii. The ground state electronic configuration explains the observed valency of oxygen in H₂O molecule which is 2.
iv. The 2s, 2p_x, 2p_y and 2p_z orbitals of oxygen atom mix and recast to form four sp³ hybrid orbitals of equivalent energy. These orbitals are tetrahedrally oriented in space. Two of the sp hybrid orbitals contain lone pair of electrons.
v. Two half-filled sp³ hybrid orbitals of O atom overlap axially with half-filled 1s orbitals of two different hydrogen atoms to fonn two O-H (sp³-s) sigma covalent bonds.
vi. Since, there are two lone pairs of electrons in two of the sp³ hybrid orbitals of oxygen, there is repulsion between lone pair and bonding pair of electrons. As a result, the H-O-H bond angle is reduced from regular tetrahedral angle 109°28′ to 104°35′. The geometry of H₂O molecule is angular or V shaped.

Diagram:

Question 44.
Explain the formation of an ethene molecule on the basis of hybridization.
Answer:
Formation of an ethene (ethylene) molecule on the basis of sp² hybridization:
i. Ethene molecule (C₂H₄) has two carbon atoms and four hydrogen atoms.
ii. The ground state electronic configuration of C (Z = 6) is 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{1}\) \(2 \mathrm{p}_{\mathrm{y}}^{1}\) \(2 \mathrm{p}_{\mathrm{z}}^{0}\).
Electronic configuration of carbon:

iii. One electron from 2s orbital of each carbon atom is excited to the 2p_z orbital. Then each carbon atom undergoes sp2 hybridization.
iv. One ’s’ orbital and two ‘p’ orbitals on carbon hybridize to form three sp² hybrid orbitals of equal energy and symmetry.
v. Two sp² hybrid orbitals overlap axially two ‘s’ orbitals of hydrogen to form sp²-s σ bond. The unhybridized ‘p’ orbitals on the two carbon atoms overlap laterally to form a π bond. Thus, the C₂H₄ molecule has four sp²-s σ bonds, one sp²-sp² σ bond and one p-p π bond.
vi. Each H-C-H and H-C-C bond angle in ethene molecule is 120°. All the six atoms in ethene (ethylene) molecule are in one plane. Geometry of the molecule at each carbon atom is trigonal planar.

Question 45.
Explain the formation of boron trifluoride on the basis of hybridization.
Answer:
Formation of boron trifluoride on the basis of sp² hybridization:
i. Boron trifluoride (BF₃) has one boron atom and three fluorine atoms.
ii. Observed valency of boron in BF₃ molecule is three and its geometry is trigonal planar. This can be explained on the basis of sp² hybridization.
iii. The ground state electronic configuration of B (Z = 5) is 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{1}\) \(2 \mathrm{p}_{\mathrm{y}}^{0}\) \(2 \mathrm{p}_{\mathrm{z}}^{0}\).
Electronic configuration of boron:

iv. One electron from 2s orbital of boron atom is uncoupled and promoted to vacant 2p_y orbital.
v. The three orbitals i.e. 2s, 2p_x of and 2p_y of boron undergoes sp² hybridization to form three sp² hybrid orbitals of equivalent energy, which are oriented along the three comers of an equilateral triangle making an angle of 120°.
vi. Each sp² hybrid orbital of boron atom having unpaired electron overlaps axially with half-filled 2p_z orbital of fluorine atom containing electron with opposite spin to form three B-F sigma bonds by sp²-p type of overlap.
vii. Each F-B-F bond angle in BF₃ molecule is 120°. The geometry of BF₃ molecule is trigonal planar.

Diagram:

Question 46.
Explain the formation of an acetylene molecule on the basis of hybridization.
Answer:
Formation of acetylene (ethyne) molecule on the basis of sp hybridization:
i. Acetylene molecule (C₂H₂) has two carbon atoms and two hydrogen atoms.
ii. The ground state electronic configuration of C (Z = 6) is 1s² 2s² \(2 \mathrm{p}_{\mathrm{x}}^{1}\) \(2 \mathrm{p}_{\mathrm{y}}^{1}\) \(2 \mathrm{p}_{\mathrm{z}}^{0}\).
Electronic configuration of carbon:

iii. Each carbon atom undergoes sp hybridization. One s and one p orbitals mix and recast to give two sp hybrid orbitals arranged at 180° to each other.
iv. Out of the two sp hybrid orbitals of carbon atom, one overlaps axially with s orbital of hydrogen while the other sp hybrid orbital overlaps with sp hybrid orbital of other carbon atom to form the sp-sp σ bond. The C H σ bond is formed by sp-s overlap.
v. The remaining two unhybridized p orbitals overlap laterally to form two p-p π bonds. So, there are three bonds between the two carbon atoms: one C-C σ bond (sp-sp) overlap, two C-C π bonds (p-p) overlap. There are two sp-s σ bonds in acetylene (one between each C and H).
vi. Each H-C-C bond angle in ethyne molecule is 180°. All the four atoms in ethyne molecule are in a straight line. The geometry of acetylene molecule is linear.

Diagram:

Question 47.
Explain the formation of BeCl₂.
Answer:
Formation of BeCl₂:
i. BeCl₂ molecule has one Be atom and two chlorine atoms.
ii. Electronic configuration of Be is 1s² 2s² \(2 \mathrm{p}_{\mathrm{z}}^{0}\).
Electronic configuration of beryllium:

iii. The 2s and 2p_z orbitals undergo sp hybridization to form two sp hybrid orbitals oriented at 180° with each other. 2p_z orbitals of two chlorine atoms overlap with the sp hybrid orbitals to form two sp-p σ bonds.
Cl – Be – Cl bond angle is 180°. The geometry of the molecule is linear.

Diagram:

Question 48.
Match the following:

	Molecule		Hybridization and bond angle
i.	Water	a.	Sp2, 120°
ii.	Boron trifluoride	b.	Sp3, 104.5°
iii.	Beryllium fluoride	c.	Sp3, 109.5°
iv.	Methane	d.	Sp, 180°

Answer:
i – b
ii – a
iii – d
iv – c

Question 49.
Give the importance of valence bond theory.
Answer:
Valence Bond theory introduced five new concepts in chemical bonding:

• Delocalization of electron over the two nuclei
• Shielding effect of electrons
• Covalent character of bond
• Partial ionic character of a covalent bond
• The concept of resonance and connection between resonance energy and molecular stability

Question 50.
What are the limitations of valence bond theory?
Answer:
Limitations of valence bond theory:

• Valence Bond theory explains only the formation of covalent bond in which a shared pair of electrons comes from two bonding atoms. However, it offers no explanation for the formation of a coordinate covalent bond in which both the electrons are contributed by one of the bonded atoms.
• Oxygen molecule is expected to be diamagnetic according to this theory. The two atoms in oxygen molecule should have completely filled electronic shells which give no unpaired electrons to the molecule making it diamagnetic. However, experimentally the molecule is found to be paramagnetic having two unpaired electrons. Thus, this theory fails to explain paramagnetism of oxygen molecule.
• Valence bond theory does not explain the bonding in electron deficient molecules like B₂H₆ in which the central atom possesses a smaller number of electrons than required for an octet of electron.

Question 51.
What are the two ways in which two atomic orbitals combine to form molecular orbitals (MOs)?
Answer:
Two atomic orbitals can combine in two ways to form molecular orbitals:
i. By addition of their wave functions.
ii. By subtraction of their wave functions.
Addition of the atomic orbtials wave functions results in formation of a molecular orbital which is lower in energy than atomic orbitals and is termed as Bonding Molecular Orbital (BMO). Subtraction of the atomic orbitals results in the formation of a molecular orbital which is higher in energy than the atomic orbitals and is termed as Antibonding Molecular Orbital (AMO).

Question 52.
State True or False. Correct the false statement.
i. According to MO theory, the formation of molecular orbitals from atomic orbitals is expressed in terms of Linear Combination of Atomic Orbitals (LCAO).
ii. An MO contains maximum two electrons with opposite spins.
iii. Interference of electron waves of combining atoms can only be constructive.
iv. In bonding molecular orbital, the large electron density is observed between the nuclei of the bonding atoms than the individual atomic orbitals.
v. In the antibonding molecular orbital, the electron density is nearly zero between the nuclei.
Answer:
i. True
ii. True
iii. False
Interference of electron waves of combining atoms can be constructive or destructive.
iv. True
v. True

Question 53.
What are the conditions required for linear combination of atomic orbitals to form molecular orbitals?
Answer:
The following conditions are required for the linear combination of atomic orbitals (LCAO) to form molecular orbitals:
i. The combining atomic orbitals must have comparable energies.
So, Is orbitals of one atom can combine with 1 s orbital of another atom but not with 2s orbital, because energy of 2s orbital is much higher than that of 1 s orbital.

ii. The combining atomic orbitals must have the same symmetry along the molecular axis. Conventionally, z axis is taken as the internuclear axis. So even if atomic orbitals have same energy but their symmetry is not same they cannot combine. For example, 2s orbital of an atom can combine only with 2p_z orbital of another atom, and not with 2p_x or 2p_y orbital of that atom because the symmetries are not same. p_z is symmetrical along z axis while px is symmetrical along x axis.

iii. The combining atomic orbitals must overlap to the maximum extent. Greater the overlap, greater is the electron density between the nuclei and so stronger is the bond formed.

Question 54.
Explain and draw an energy level diagram obtained by the linear combination of two 1s atomic orbitals.
Answer:
The s-orbitals are spherically symmetrical along x, y and z axis. Two Is atomic orbitals combine to form σ 1s (bonding molecular orbital) and σ*1s (antibonding molecular orbital). Both the a bonding and σ* antibonding orbitals are symmetrical along the bond axis.
Diagram:

[Note: If we consider ‘z’ to be internuclear axis then linear combination of p_z orbitals from two atoms can form σ 2p_z bonding σ*(2p_z) molecular orbitals.]

Question 55.
Explain the formation of π and π* molecular orbitals with the help of a diagram.
Answer:
When the atomic orbitals overlap laterally, a pi (π) molecular orbital is formed.
The px and py orbitals are not symmetrical along the bond axis. They have a positive lobe above the axis and negative lobe below the axis. Hence, linear combination of such orbitals leads to the formation of molecular orbitals with positive and negative lobes above and below the bond axis. These are designed as π bonding and π antibonding orbitals. The electron density in such π orbitals is concentrated above and below the bond axis. The π molecular orbitals has a node between the nuclei.
Diagram:

Question 56.
Write the increasing order of energies of molecular orbitals in various diatomic molecules of second row elements.
Answer:
The increasing order of energies of molecular orbitals for molecules (except O₂ and F₂) is:
σ1s < σ*1s < σ2s < σ*2s < (π2p_x = π2p_y) < σ2p_z < (π*2p_x = π*2p_y) < σ*2p_z
The increasing order of energy of molecular orbitals for diatomic molecules like O₂ and F₂ is:
σ1s < σ*1s < σ2s < σ*2s < σ2p_z < (π2p_x = π2p_y) < (π*2p_x = π*2p_y) < σ*2p_z

Question 57.
Explain briefly the information provided by the electronic configuration of molecules.
Answer:
The electronic configuration of molecules provides the following information:

• Stability of molecules: If the number of electrons in bonding MOs is greater than the number in antibonding MOs the molecule is stable.
• Magnetic nature of molecules: If all MOs in a molecule are completely filled with two electrons each, the molecule is diamagnetic (i.e., repelled) by magnetic field. However, if at least one MO is half-filled with one electron, the molecule is paramagnetic (i. e., attracted by magnetic field).
• Bond order of molecule: The bond order of the molecule can be calculated from the number of electrons in bonding MOs (N_b) and antibonding MOs (N_a).

Question 58.
What are the key ideas of MO theory?
OR
What are the salient features of MO theory?
Answer:
Key ideas of MO Theory:

• MOs in molecules are similar to AOs of atoms. Molecular orbital describes region of space in the molecule representing the probability of an electron.
• MOs are formed by combining AOs of different atoms. The number of MOs formed is equal to the number of AOs combined.
• Atomic orbitals of comparable energies and proper symmetry combine to form molecular orbitals.
• MOs those are lower in energy than the starting AOs are bonding MOs and those higher in energy are antibonding MOs.
• The electrons are filled in MOs beginning with the lowest energy.
• Only two electrons occupy each molecular orbital and they have opposite spins, that is, their spins are paired.
• The bond order of the molecule can be calculated from the number of bonding and antibonding electrons.

Question 59.
Explain the formation of the following molecules on the basis of MOT. Also find the bond order.
i. H₂
ii. Li₂
iii. N₂
iv. O₂
v. F₂
Answer:
i. Hydrogen molecule (H₂):

a. Hydrogen atom (Z = 1) has electronic configuration as 1s¹.
b. Hydrogen atom contains one electron, hence hydrogen molecule which is diatomic contains two electrons.
c. Linear combination of two 1s atomic orbitals gives rise to two molecular orbitals σ1s and σ*1s.
d. The two electrons from the hydrogen atoms occupy the σ1s molecular orbital and σ*1s remains vacant.
e. Thus, electronic configuration of H₂ molecule is σ1s².
f. Since, no unpaired electron is present in hydrogen molecule, it is diamagnetic.
g. There are no electrons in the antibonding molecular orbital (σ*1s).
h. The bond order of H₂ molecule is
Bond order = \(\frac{\mathrm{N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}}{2}=\frac{2-0}{2}\) = 1
Thus, a single covalent bond is present between two hydrogen atoms.
[Note: The bond length is 74 pm and the bond dissociation energy is 438 kJ mol^-1.]

ii. Lithium molecule (Li₂):

a. Lithium atom (Z = 3) has electronic configuration as 1s² 2s¹.
b. Lithium atom has 3 electrons, hence Li₂ molecule has 6 electrons.
c. Linear combination of four atomic orbitals gives rise to four molecular orbitals namely σ1s, σ*1s, σ2S and σ*2s.
d. The electronic configuration of Li₂ molecule is (σ1s)² (σ*1s)² (σ2s)².
e. Since no unpaired electron is present in lithium molecule, it is diamagnetic.
f. Bond order of Li₂ molecule
\(=\frac{\mathrm{N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}}{2}=\frac{4-2}{2}=1\)
Thus, a single covalent bond is present between two Li atoms. Hence, Li₂ is a stable molecule.

iii. Nitrogen molecule (N₂):

a. Nitrogen atom (Z = 7) has electronic configuration as 1s² 2s² 2p³.
b. Nitrogen atom contains 7 electrons, hence nitrogen molecule contains 14 electrons.
c. Linear combination of atomic orbitals gives rise to different molecular orbitals.
d. The electronic configuration of N₂ molecule is
N₂: (σ1s)² (σ*1s)² (σ2s)² (σ*2s)² (π2p_x)² (π2p_y)² (σ2p_z)²
e. Since N₂ molecule does not have unpaired electron, it is diamagnetic.
f. Bond order of N₂ molecule
\(=\frac{\mathrm{N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}}{2}=\frac{10-4}{2}=3\)
Thus, there are three bonds in N₂ molecule.

Question 60.
Study the following tables showing bond enthalpies of single and multiple bonds.

Bond	ΔaH/kJ mol-1
C-H	400-415
N-H	390
O-H	460-464
C-C	345
C-N	290-315
C-O	355-380
C-Cl	330

Bond	ΔaH/kJ mol-1
C-Br	275
O-O	175-184
C=C	610-630
C≡C	835
C=O	724-757
C≡N	854

i. Among single bonds, which bond is the strongest?
ii. How is bond enthalpy related to bond strength?
Answer:
i. Among single bonds, O-H bond is the strongest.
ii. Larger the bond enthalpy, stronger is the bond.

Question 61.
Write a short note on bond length.
Answer:
Bond length:

• Bond length is defined as the equilibrium distance between the nuclei of two covalently bonded atoms in a molecule.
• Each atom of the bonded pair contributes to the bond length.
• Bond length depends upon the size of atoms and multiplicity of bonds. It increases with increase in size of atom and decreases with increase in multiplicity of bond.
  e.g. C – C single bond is longer than C ≡ C triple bond.
• Bond lengths are measured by X-ray and electron diffraction techniques.

Question 62.
Cl-Cl covalent bond length is smaller than Br-Br covalent bond length. Explain.
Answer:
Bond length increases with increase in size of atom. Cl atom is smaller than Br atom. Hence, Cl-Cl covalent bond length is smaller than Br-Br covalent bond length.

Question 63.
Arrange the following bonds in decreasing order of bond strength: C-N, C=N, C≡N
Answer:
C≡N > C=N > C-N
Note: Average bond lengths for some single, double and triple bonds:

Type of bond	Covalent bond length (pm)
O-H	96
C-H	107
N-O	136
C-O	143
C-N	143
C-C	154
C=C	121
N=O	122
C=C	133
C=N	138
C≡N	116
C≡C	120

Type of bond	Covalent bond length (pm)
H2(H-H)	74
F2(F-F)	144
Cl2(Cl-Cl)	199
Br2(Br-Br)	228
I2(I-I)	267
N2(N≡N)	109
O2(O-O)	121
HF (H-F)	92
HCl (H-Cl)	127
HBr (H-Br)	141
HI (H-I)	160

Question 64.
Write a short note on bond order.
Answer:
i. According to the Lewis theory, bond order is given by the number of bonds between the two atoms in a molecule.
e.g. a. In hydrogen molecule, bond order between hydrogen atoms is one as one electron pair is shared.
b. In oxygen molecule, bond order between oxygen atoms is two as two electron pairs are shared.
c. In acetylene molecule, bond order between two carbon atoms is three as three electron pairs are shared.

ii. The isoelectronic molecules and ions have identical bond orders.
e.g. a. The bond order of F₂ and \(\mathrm{O}_{2}{ }^{2-}\) is one.
b. The bond order of N₂, CO and NO⁺ is 3.

iii. As the bond order increases, the bond enthalpy increases and bond length decreases.
iv. With the help of bond order, the stability of a molecule can be predicted.
[Note: N₂ molecule has bond enthalpy of 946 kJ mol^-1. It is one of the highest for diatomic molecules.]

Question 65.
Explain how polarity (ionic character) is developed in a covalent bond.
Answer:
i. Covalent bonds are formed between two atoms of the same or different elements.
ii. When a covalent bond is formed between atoms of same element such as H-H, F-F, Cl-Cl, etc., the shared pair of electrons is attracted equally to both atoms and is situated midway between two atoms. Such covalent bond is termed as nonpolar covalent bond.
iii. When a covalent bond is formed between two atoms of different elements that have different electronegativities, the shared electron pair does not remain at the centre. The electron pair is pulled towards the more electronegative atom resulting in the separation of charges. This give rise to dipole. The more electronegative atom acquires a partial -ve charge and the other atom gets a partial +ve charge. Such a bond is called as polar covalent bond. The examples of polar molecules include HF, HC1, etc.

Fluorine is more electronegative than hydrogen, therefore, the shared electron pair is more attracted towards fluorine and the atoms acquire partial +ve and -ve charges, respectively.
iv. Polarity of the covalent bond increases as the difference in the electronegativity between the bonded atoms increases. When the difference in electronegativities of combining atom is about 1.7, ionic percentage in the covalent bond is 50%.

Question 66.
Define and explain the term dipole moment.
Answer:
i. Dipole moment (μ) is the product of the magnitude of charge and distance between the centres of +ve and -ve charges.
ii. It is given by, µ = Q × r
where, Q = charge, r = distance of separation.
iii. Unit of dipole moment is Debye (D).
iv. Dipole moment being a vector quantity is represented by a small arrow with the tail on the positive centre and head pointing towards the negative centre.

Note: 1 D = 3.33564 × 10^-30 C m
where C is coulomb and m is meter.

Question 67.
Dipole moment in case of BeF2 is zero. Explain.
Answer:

• Dipole moment is a vector quantity. Therefore, the resultant dipole moment of a molecule is the vector sum of dipole moments of various bonds in the molecule.
• In BeF₂ molecule, Be-F bond is polar and has a bond dipole moment.
• BeF₂ is a linear molecule with two Be-F bonds oriented at 180° (opposite to each other).
• The two bond dipoles are equal in magnitude and act in opposite direction to cancel each other. Therefore, the net dipole moment in case of BeF₂ is zero.

Question 68.
Dipole moment in case of BF₃ is zero. Explain.
Answer:
i. Dipole moment is a vector quantity. Therefore, the resultant dipole moment of a molecule is the vector sum of dipole moments of various bonds in the molecule.
ii. In BF₃ molecule, B-F bond is polar and has a bond dipole moment.
iii. Also, in BF₃, the three B-F bonds are oriented at an angle of 120° to one another.
iv. The resultant of any two bond moments is equal in magnitude and opposite in direction to that of third. Hence, the net sum is zero and the dipole moment of tetra-atomic BF₃ molecule is zero.

Question 69.
Dipole moment of H₂O is higher than that of NH₃. Explain.
Answer:
In both NH₃ and H₂O, the central atom undergoes sp³ hybridization. In both the molecules, the orbital dipole due to the lone pair increases the effect of resultant dipole moment. However, in NH₃, nitrogen has only one lone pair while in H₂O, oxygen has two lone pairs. Hence, dipole moment of H₂O is higher than that of NH₃.

Question 70.
Dipole moment of NF₃ is less than that of NH₃, even though N-F bond is more polar than N-H bond. Explain.
Answer:

• Both NH₃ and NF₃ have pyramidal structure with a lone pair on the N atom. In NF₃, F is more electronegative than N while in NH₃, N is more electronegative.
• In NH₃, the orbital dipole due to the lone pair is in the same direction as the resultant dipole moment of N-H bonds, whereas in NF₃ the orbital dipole is in the direction opposite to the resultant dipole moment of three N-F bonds.
• The orbital dipole because of lone pair decreases the effect of the resultant N-F bond moments, which results in the low dipole moment of NF₃ (0.8 × 10^-30 C m) as compared to NH₃ (4.90 × 10^-30 C m).

Question 71.
CHCl₃ is polar. Explain.
Answer:
In CHCl₃, the dipoles are not equal and do not cancel each other. Hence, CHCl₃ is polar with a non-zero dipole moment.

Note: Dipole moments and geometry of some molecules are given in the following table:

Question 72.
Explain Fajan’s rule with suitable examples.
Answer:
Fajan’s rule:
i. Smaller the size of the cation and larger the size of the anion, greater is the covalent character of the ionic bond. For example, Li⁺ Cl^– is more covalent than Na⁺Cl. Similarly, Li⁺I^– is more covalent than Li⁺Cl^–.

ii. Greater the charge on cation, more is covalent character of the ionic bond. For example, covalent character of AlCl₃, MgCl₂ and NaCl decreases in the following order Al³⁺(Cl^–)₃ > Mg²⁺(Cl^–)₂ > Na⁺ Cl^–

iii. A cation with the outer electronic configuration of the s²p⁶d¹⁰ type possesses greater polarising power compared to the cation having the same size and same charge but having outer electronic configuration of s²p⁶ type.

This is because d electrons of the s²p⁶d¹⁰ shell screen nuclear charge less effectively compared to s and p electrons of s²p⁶ shell. Hence, the effective nuclear charge in a cation having s²p⁶d¹⁰ configuration is greater than that of the one having s²p⁶ configuration. For example: Cu⁺Cl^– is more covalent than Na⁺Cl^–. Here,
(Cu⁺ = 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰; Na⁺ = 1s² 2s² 2p⁶)

Question 73.
Explain resonance with respect to \(\mathrm{CO}_{3}^{2-}\) ion.
Answer:
i. Three structures written for \(\mathrm{CO}_{3}^{2-}\) as follows:

ii. Each structure differs from the other only in the position of electrons without changing positions of the atoms. None of these individual structures is adequate to explain the properties of \(\mathrm{CO}_{3}^{2-}\).
iii. The actual structure of \(\mathrm{CO}_{3}^{2-}\) is a combination of three Lewis structures and is called as the resonance hybrid.
iv. Energy of the resonance hybrid structure is less than the energy of any single canonical form. Hence, resonance stabilizes certain polyatomic molecules or ions.
v. The average of all resonating structures contributes to overall bonding characteristic features of the molecule or ion.

Question 74.
Explain O₃ molecule is the resonance hybrid.
Answer:
Ozone is a resonance hybrid of structures I and II. The structures I and II are canonical forms while structure III is a resonance hybrid. The energy of structure III is less than that of I and II.

Question 75.
Define resonance energy.
Answer:
Resonance energy is defined as the difference in energy of the most stable contributing structure and the resonating forms.

Question 76.
Write the resonance structures of \(\mathrm{NO}_{3}^{-}\) ion.
Answer:
Resonance structures of \(\mathrm{NO}_{3}^{-}\) :

Question 77.
A student represents the Lewis dot structure of AlCl₃ molecule as shown below:

i. Is the representation correct? Justify your answer.
ii. If the chlorine atoms are replaced by bromine atoms, what will be the number of electrons present in the valence shell of aluminium?
Answer:
i. No, the representation is incorrect. There will be no lone pair of electrons on aluminium.
ii. The number of electrons present in the valence shell of aluminium will be six.

Question 78.
Below is an incomplete Lewis structure for glycine. Complete the following Lewis structure and answer the following questions. (Hint: Add lone pairs and multiple bonds to the structure below to give each atom a formal charge of zero.)

i. How many lone pairs of electrons are present on N-atom in the structure?
ii. How many pi bonds are present in the structure?
iii. How many sigma bonds are present in the structure?
Answer:
The correct Lewis structure is:

i. The number of lone pairs of electrons on N-atom is 1.
ii. The number of pi bonds in the structure is 1.
iii. The number of sigma bonds in the structure is 9.

Question 79.
Consider the following four species and answer the below given questions.
\(\mathrm{O}_{2}^{-}\), O₂ \(\mathrm{O}_{2}^{+}\), \(\mathrm{O}_{2}^{2-}\)
i. What is the bond order of \(\mathrm{O}_{2}^{+}\) ?
ii. Which species is least stable?
Answer:
i. Electronic configuration of \(\mathrm{O}_{2}^{+}\) can be given as:
(σ1s)² (σ*1s)² (σ2s)² (σ*2s)² (σ2p_z)² (π2p_x)² (π2p_y)² (π*2p_x)¹ (π*2p_y)⁰
∴ Bond order = \(\frac {1}{2}\) (10 – 5) = 2.5

ii. Stability of the molecule or species ∝ Bond order
Bond order decreases as: \(\mathrm{O}_{2}^{+}\) > O₂ > \(\mathrm{O}_{2}^{-}\) > \(\mathrm{O}_{2}^{2-}\)
∴ Stability decreases as: \(\mathrm{O}_{2}^{+}\) > O₂ > \(\mathrm{O}_{2}^{-}\) > \(\mathrm{O}_{2}^{2-}\)
Hence, least stable species is \(\mathrm{O}_{2}^{2-}\).

Multiple Choice Questions

1. The CORRECT Lewis structure of CO molecule is:

Answer:

2. Which of the following molecule does NOT obey octet rule?
(A) BF₃
(B) CO₂
(C) H₂O
(D) N₂
Answer:
(A) BF₃

3. In BF₃, bond angle is .
(A) 90°
(B) 109°
(C) 120°
(D) 180°
Answer:
(C) 120°

4. Identify the geometry represented by the following diagram.

(A) Trigonal bipyramidal
(B) T-shape
(C) square planar
(D) square pyramidal
Answer:
(D) square pyramidal

5. The geometry of H₂S is ………….
(A) tetrahedral
(B) angular
(C) linear
(D) trigonal planar
Answer:
(B) angular

6. What will be the shape of molecule whose central atom is associated with 3 bonds and one lone pair?
(A) Trigonal pyramidal
(B) Tetrahedral
(C) Square planar
(D) Triangular planar
Answer:
(A) Trigonal pyramidal

7. Pair of molecules having identical geometry is …………..
(A) BF₃, NH₃
(B) BF₃, AlF₃
(C) BeF₂, H₂O
(D) BCl₃, PCl₃
Answer:
(B) BF₃, AlF₃

8. Which of the following molecule has bent shape?
(A) PCl₃
(B) OF₂
(C) BH₃
(D) BeBr2
Answer:
(B) OF₂

9. Which of the following is INCORRECT?
(A) The strength of the bond depends on the extent of overlap of the atomic orbitals.
(B) The extent of overlap depends on the shape and size of the atomic orbitals.
(C) The energy of the bonded atoms is more than that of the free atoms.
(D) During overlap of atomic orbitals, the electron density increases in between the two nuclei.
Answer:
(C) The energy of the bonded atoms is more than that of the free atoms.

10. In the potential energy curve for hydrogen molecule, the maximum stability is achieved when …………..
(A) potential energy of the system is maximum
(B) potential energy of the system is minimum
(C) force of repulsion become greater than force of attraction
(D) no bond formation takes place
Answer:
(B) potential energy of the system is minimum

11. In acetylene, C-C σ bond is formed by …………. overlap.
(A) sp²-sp²
(B) sp-sp
(C) sp-s
(D) p-p
Answer:
(B) sp-sp

12. The formation of O-H bonds in a water molecule involves …………. overlap.
(A) sp³-s
(B) sp¹-s
(C) sp-p
(D) sp³-p
Answer:
(A) sp³-s

13. The molecular orbital shown in the diagram can be described as ………….

(A) σ
(B) σ*
(C) π*
(D) π
Answer:
(C) π*

14. The bond order of lithium molecule is ………….
(A) one
(B) two
(C) three
(D) four
Answer:
(A) one

15. The bond order in N₂ molecule is …………
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
(C) 3

16. The bond energies of F₂, Cl₂, Br₂ and I₂ are 37, 58, 46, and 36 kcal/mol respectively. The strongest bond is present in …………..
(A) Br₂
(B) I₂
(C) Cl₂
(D) F₂
Answer:
(C) Cl₂

17. The common features among the species CO and NO⁺ are: ……………
(A) isoelectronic species and bond order 3
(B) isoelectronic species and bond order 2
(C) odd electron species and unstable
(D) odd electron species and bond order 1
Answer:
(A) isoelectronic species and bond order 3

18. Which of the following is CORRECT for H₂O ?

	H=O bond	H2O molecule
(A)	polar	nonpolar
(B)	nonpolar	polar
(C)	polar	polar
(D)	nonpolar	nonpolar

Answer:
(C)

19. Each of the following molecules has a non-zero dipole moment EXCEPT:
(A) NF₃
(B) BF₃
(C) SO₂
(D) LiH
Answer:
(B) BF₃

20. Which of the following compounds is non-polar?
(A) HCl
(B) CH₂Cl₂
(C) CHCl₃
(D) CCl₄
Answer:
(D) CCl₄

21. The dipole moment of …………..
(A) NF₃ is higher than that of NH₂
(B) BF₃ is higher than that of NH₃
(C) H₂S is higher than that of H₂O
(D) HCl is higher than that of HBr
Answer:
(D) HCl is higher than that of HBr

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 4 Structure of Atom Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 4 Structure of Atom

Question 1.
Complete the information about the properties of subatomic particles in the following table:

Answer:

Question 2.
What are three important subatomic particles of an atom?
Answer:
Electron, proton and neutron are the three important subatomic particles of an atom.

Question 3.
Write a short note on discovery of electron.
Answer:

• In the year 1897, J J. Thomson studied the properties of cathode rays through a cathode ray tube experiment and found that the cathode rays are a stream of very small, negatively charged particles.
• These particles are 1837 times lighter than a hydrogen atom and are present in all atoms.
• These particles were later named as electrons.

Question 4.
Draw labelled diagram of Rutherford’s α-particle scattering experiment.
Answer:

Question 5.
Write a short note on discovery of proton.
Answer:

• After the discovery of nucleus in an atom, Rutherford found that the fast moving α-particles transmuted nitrogen into oxygen with simultaneous liberation of hydrogen.
  \({ }_{7}^{14} \mathrm{~N}+{ }_{2}^{4} \alpha \longrightarrow{ }_{8}^{17} \mathrm{O}+{ }_{1}^{1} \mathrm{H}\)
• He further showed that other elements could also be transmuted similarly and hydrogen was always emitted in the process.
• Based on these observations, he proposed that the hydrogen nucleus must be contained inside nuclei of all the elements. Hence, he renamed hydrogen nucleus as proton.

Question 6.
Write a short note on discovery of neutron.
Answer:

• In 1920, Ernest Rutherford proposed the existence of an electrically neutral and massive particle in the nucleus of an atom in order to account for the disparity in atomic number and atomic mass of an element.
• In 1932, James Chadwick measured the velocity of protons ejected from paraffin by an unidentified radiation from beryllium (Be).
• From that he determined the mass of the particles of this unidentified neutral radiation, which was found to be almost same as that of the mass of a proton.
• He named this neutral particle as ‘neutron’, which was earlier predicted by Rutherford.

Question 7.
State true or false. Correct the false statement.
i. An electron is 1837 times lighter than a proton.
ii. In Rutherford’s experiment of scattering of α-particles by thin gold foil, most of the α-particles
bounced back.
iii. Cathode rays are a stream of very small, positively charged particles.
Answer:
i. True
ii. False,
In Rutherford’s experiment of scattering of α-particles by thin gold foil, very few α-particles bounced back.
iii. False,
Cathode rays are a stream of very small, negatively charged particles.

Question 8.
Explain the term: Atomic number
Answer:

• Atomic number is defined as the number of protons present in the nucleus of an atom of a particular element.
• Atomic number is represented by Z.
• An atom is electrically neutral. Hence, the number of protons equals to the number of electrons. In other words, the atomic number of an atom is equal to the number of electrons.

∴ Atomic Number (Z) = Number of protons = Number of electrons

Question 9.
Give reason: The approximate atomic mass in Daltons is numerically equal to the number of nucleons in the atom.
Answer:

• The electrons possess negligible mass. They do not contribute much to the mass of an atom.
• Therefore, the entire mass of an atom is supposed to be present in the nucleus which consists of protons and neutrons, which are collectively called as nucleons.

Hence, approximate atomic mass in Daltons is numerically equal to the number of nucleons in the atom.

Question 10.
Explain: Atomic mass number.
Answer:

• The sum of the total number of protons and neutrons present in the nucleus of an atom is called the atomic mass number of that atom.
• Atomic mass number is represented by A
• Mass number (A) = Number of protons (Z) + Number of neutrons (N) = Total number of nucleons
  ∴ A = Z + N OR N = A – Z

Question 11.
How is an atom of an element ‘X’ having atomic number ‘Z’ and atomic mass number ‘A’ represented?
Answer:
An atom of an element ‘X’ having atomic number ‘Z’ and atomic mass number ‘A’ is represented as: \({ }_{Z}^{A} X\)

Question 12.
What is a nuclide?
Answer:
The atom or nucleus having a unique composition as specified by \({ }_{Z}^{A} X\) is called as a nuclide.

Question 13.
If an element ‘X’ has 6 protons and 8 neutrons, then write its representation.
Answer:
The representation of the given element is \({ }_{6}^{14} \mathrm{X}\).

Question 14.
Three elements Q, R and T have mass number 40. Their atoms contain 22, 21 and 20 neutrons respectively. Represent their atomic composition with appropriate symbol.
Answer:
Mass number (A) = Number of protons (Z) + Number of neutrons (N) .
A = Z + N
∴ Z = A – N
For the given three elements, A = 40. Values of their atomic numbers Z, are calculated from the given values of the number of neutrons, N, using the above formula.
For Q: Z = A – N = 40 – 22 = 18
For R: Z = A – N = 40 – 21 = 19
For T: Z = A – N = 40 – 20 = 20
Now, atomic composition of an element (X) is represented as \({ }_{Z}^{A} X\).
The atomic compositions of the three elements are written as follows:
\({ }_{18}^{40} \mathrm{Q}\), \({ }_{19}^{40} \mathrm{R}\), \({ }_{20}^{40} \mathrm{T}\)

Question 15.
Find out the number of protons, electrons and neutrons in the nuclide \({ }_{18}^{40} \mathrm{Ar}\).
Solution:
For the given nuclide,
Atomic number, Z = 18, Mass number, A = 40
Number of protons = Number of electrons = Z = 18
Number of neutrons (N) = A – Z = 40 – 18 = 22
Ans: Number of protons = 18, Number of electrons = 18, Number of neutrons = 22

Question 16.
How many protons, electrons and neutrons are there in the following nuclei?
i. \({ }_{8}^{17} \mathrm{O}\)
ii. \({ }_{12}^{25} \mathrm{Mg}\)
iii. \({ }_{35}^{80} \mathrm{Br}\)
Solution:
i. \({ }_{8}^{17} \mathrm{O}\)
Atomic number, Z = 8, Mass number, A = 17
Number of protons = Number of electrons = Z = 8
Number of neutrons (N) = A – Z = 17 – 8 = 9
Ans: Number of protons = 8, Number of electrons = 8, Number of neutrons = 9

ii. \({ }_{12}^{25} \mathrm{Mg}\)
Atomic number, Z = 12, Mass number, A = 25
Number of protons = Number of electrons = Z = 12
Number of neutrons (N) = A – Z = 25 – 12 = 13
Ans: Number of protons = 12, Number of electrons = 12, Number of neutrons = 13

iii. \({ }_{35}^{80} \mathrm{Br}\)
Atomic number, Z = 35, Mass number, A = 80
Number of protons = Number of electrons = Z = 35
Number of neutrons (N) = A – Z = 80 – 35 = 45
Ans: Number of protons = 35, Number of electrons = 35, Number of neutrons = 45

Question 17.
Define isotopes.
Answer:
Isotopes are defined as the atoms of an element having the same number ofprotons but different number of neutrons in their nuclei.
e.g. \({ }_{6}^{12} \mathrm{C}\), \({ }_{6}^{13} \mathrm{C}\) and \({ }_{6}^{14} \mathrm{Br}\) are isotopes.

Question 18.
Complete the information about the isotopes of carbon in the following table:

Answer:

Question 19.
Define isobars.
Answer:
Isobars are defined as the atoms of different elements having the same mass number but different atomic number.
e.g. \({ }_{6}^{14} \mathrm{C}\) and \({ }_{7}^{14} \mathrm{N}\) are isobars.

Question 20.
Complete the following table:

Answer:

Question 21.
The two natural isotopes of chlorine viz. \({ }_{17}^{35} \mathrm{Cl}\) and \({ }_{17}^{37} \mathrm{Cl}\) exist in relative abundance of 3 : 1. Find out the average atomic mass of chlorine.
Solution:
Given: Isotopes of chlorine \({ }_{17}^{35} \mathrm{Cl}\) and \({ }_{17}^{37} \mathrm{Cl}\).
Ratio of relative abundance of these isotopes is 3 : 1.
To find: Average atomic mass of chlorine
Calculation: From the relative abundance 3 : 1, it is understood that out of 4 chlorine atoms, 3 atoms have mass 35 and 1 atom has mass 37.
Therefore, the average atomic mass of chlorine = \(\frac{3 \times 35+1 \times 37}{4}\) = 35.5
∴ Average atomic mass of chlorine = 35.5 u
Ans: The average atomic mass of chlorine is 35.5 u.

Question 22.
Find out the average atomic mass of lithium (Li) from the following data:

Isotope	Atomic mass (u)	Abundance
6Li	6.015	7.59%
7Li	7.016	92.41%

Solution:
Given: Three isotopes of lithium along with respective atomic mass and % abundance.
To find: Average atomic mass of lithium
Calculation:

Ans: Average atomic mass of lithium is 6.940 u.

Question 23.
Certain results were obtained when scientists studied the interactions of radiation with matter. What were the two results, utilized by Neils Bohr to overcome the drawbacks of Rutherford model?
Answer:
The two results utilized by Neils Bohr to overcome the drawbacks of Rutherford model were:

• Wave particle duality of electromagnetic radiation
• Line emission spectra of hydrogen

Question 24.
Explain in short the wave particle duality of light (electromagnetic radiation).
Answer:
Wave particle duality of light (electromagnetic radiation):

• Light has both particle and wave like nature.
  Phenomena such as diffraction and interference of light could be explained by treating light as electromagnetic wave.
• However, the black-body radiation or photoelectric effect could not be explained by wave nature of light. This could be accounted for by considering particle nature of light. Thus, both phenomena could be explained only by accepting that light has dual behaviour.
• When light interacts with matter it behaves as a stream of particles (called photons) and when light propagates, it behaves as an electromagnetic wave.

Question 25.
Observe the following figure of an electromagnetic wave and answer the questions given below:

i. What does ‘x’ represent?
ii. What does ‘y’ represent?
Answer:
i. ‘x’ represents amplitude of the wave.
ii. ‘y’ represents wavelength of the wave.

Question 26.
Define and explain the following terms:
i. Wavelength (λ).
ii. Frequency (ν)
iii. Wavenumber (\(\bar{v}\))
iv. Amplitude (A)
v. Velocity (c)
Answer:
i. Wavelength (λ):

• The distance between two consecutive crests or two consecutive troughs in a wave is called wavelength.
• It is represented by Greek letter λ (lambda).
• The SI unit for wavelength is metre (m).

Note: The other units include Angstrom, nanometre, picometer (1 pm = 10^-12 m) and micron (1µ = 10^-6 m).
1Å = 10^-8 cm = 10^-10 m
1nm = 10^-9 m = 10Å

ii. Frequency (ν):

• The number of waves that pass a given point in one second is called frequency.
• It is represented by Greek letter ‘ν’ (nu).
• The SI unit of frequency is Hertz (Hz) or s^-1.

Note: 1 Hz = 1 cycle per second (1 cps)
The units, kilo Hertz (kHz) and mega Hertz (mHz) are commonly used.
1 kHz = 10³ Hz = 10³ cps
1 mHz = 10⁶ Hz = 10⁶ cps

iii. Wavenumber (\(\bar{v}\)):

• The number of wavelengths per unit length is called the wavenumber.
• It is represented by \(\bar{v}\) (nu bar).
• The commonly used unit for wavenumber is cm^-1 while its SI unit is m^-1.
• Wavenumber of a wave is related to the wavelength as follows:
  \(\bar{v}\) = \(\frac{1}{\lambda}\)

iv. Amplitude (A):

• The height of a crest or the depth of a trough from the line of propagation of the wave is called
  amplitude.
• It is represented by letter ‘A’.
• The square of the amplitude represents the intensity (brightness) of the radiation.

v. Velocity (c):

• The distance travelled by a wave in one second is called the velocity of the wave.
• It is denoted by letter c.
• It is the product of the frequency and wavelength. Hence, c = νλ
• The velocity of all types of electromagnetic radiations (in space or in vacuum) is the same and it is equal to the velocity of light (3 × 10¹⁰ cm s^-1 or 3 × 10⁸ m s^-1. However, they may have different wavelengths and frequencies.

Question 27.
Write a short note on quantum theory of radiation.
Answer:
i. Max Planck put forward a theory known as Planck’s quantum theory to explain black-body radiation.
ii. According to this theory, the energy of electromagnetic radiation depends upon the frequency and not the amplitude.
iii. The smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation is called as ‘quantum’.
iv. The energy (E) of each quantum of radiation is directly proportional to its frequency (ν).
i.e., E ∝ ν ; E = hν
where, h = Planck’s constant = 6.626 × 10^-34 J s.

Question 28.
Parameters of blue and red light are 400 nm and 750 nm respectively. Which of the two is of higher energy?
Answer:
400 nm and 750 nm are the wavelengths of blue and red light respectively. Energy of radiation is given by the expression E = hν and the frequency (ν), of radiation is related to the wavelength by the expression.
ν = \(\frac{c}{\lambda}\)
∴ E = \(\frac{\mathrm{hc}}{\lambda}\)
Therefore, shorter the wavelength, λ, larger the frequency, ν, and higher the energy, E. Thus, blue light which has shorter λ (400 nm) than red light (750 nm) has higher energy.

Question 29.
What is an emission spectrum?
Answer:

• When a substance is irradiated with electromagnetic radiation, it absorbs energy. Atoms, molecules or ions, which have absorbed radiation are said to be ‘excited’. Heating can also result in an excited state.
• The excited species emits the absorbed energy in the form of radiation. This process is called emission of radiation and the recorded spectrum of this emitted radiation is called ‘emission spectrum’.

Question 30.
Give some examples of commonly used light sources that work on atomic emission.
Answer:
Examples are fluorescent tube, sodium vapor lamp, neon sign and halogen lamp.

Question 31.
Write a short note on emission spectrum of hydrogen. Also, list all the five series of lines in the hydrogen spectrum.
Answer:
i. When electric discharge is passed through gaseous hydrogen, it emits radiation. The recorded spectrum of this emitted radiation is called hydrogen emission spectrum.

ii. This spectrum falls in different regions of electromagnetic radiation and it is comprised of a series of lines corresponding to different frequencies. That is, the spectrum was discontinuous.

iii. In the year, 1885, Balmer expressed the wave numbers of the emission lines in the visible region of electromagnetic spectrum by the formula:
\(\overline{\mathrm{v}}=109677\left[\frac{1}{2^{2}}-\frac{1}{\mathrm{n}^{2}}\right] \mathrm{cm}^{-1}\)
where, n = 3, 4, 5,…
These lines are known as Balmer series.

iv. Rydberg found that other series of lines could be described by the following formula:
\(\bar{v}=109677\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right] \mathrm{cm}^{-1}\)
where, 109677 cm^-1 is called Rydberg constant for hydrogen (R_H).

v. Different series of emission spectral lines for hydrogen are as follows:

Series	n1	n2	Region
Lyman	1	2, 3, 4, ….	Ultraviolet
Balmer	2	3, 4, 5, ….	Visible
Paschen	3	4, 5, 6, ….	Infrared
Bracket	4	5, 6, 7, ….	Infrared
Pfund	5	6, 7, 8,….	Infrared

Question 32.
Observe the emission spectrum of hydrogen and answer the following questions.

i. Is the spectrum continuous?
ii. In which region of electromagnetic radiation does the Paschen series belong?
iii. Which series falls in the visible region of electromagnetic radiation?
Answer:
i. The spectra is not continuous and comprises of a series of lines corresponding to different frequencies.
ii. Paschen series falls in the infrared region of electromagnetic radiation.
iii. Balmer series falls partly in the visible region of electromagnetic radiation.

Question 33.
Give the expression to calculate wavenumber of the emission lines in the Balmer series.
Answer:
\(\bar{v}=109677\left[\frac{1}{2^{2}}-\frac{1}{\mathrm{n}^{2}}\right] \mathrm{cm}^{-1}\)
where, n = 3, 4, 5, ….

Question 34.
Visible light has wavelengths ranging from 400 nm (violet) to 750 nm (red). Express these wavelengths in terms of frequency (Hz). (1 nm = 10^-9 m)
Solution:
Given: Wavelengths: λ₁ = 400 nm (for violet light), λ₂ = 750 nm (for red light)
To find: Frequencies: ν₁, ν₂
Formula: ν = \(\frac{c}{\lambda}\)
Calculation: i. Wavelength of violet light, λ₁ = 400 nm = 400 × 10^-9 m
Frequency, ν = \(\frac{c}{\lambda}\) where c is speed of light = 3.0 × 10⁸ ms^-1
∴ ν₁ = \(\frac{3.0 \times 10^{8} \mathrm{~ms}^{-1}}{400 \times 10^{-9} \mathrm{~m}}\) = 7.50 × 10¹⁴ Hz
ii. Wavelength of red light, λ₂ = 750 nm = 750 × 10^-9 m
Frequency, ν = \(\frac{c}{\lambda}\)
∴ ν₂ = \(\frac{3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{750 \times 10^{-9} \mathrm{~m}}\) = 4.00 × 10¹⁴ Hz
Ans: The frequency of violet light is 7.50 × 10¹⁴ Hz and that of red light is 4.00 × 10¹⁴ Hz.

Question 35.
Yellow light emitted from a lamp has a wavelength of 580 nm. Find the frequency and wavenumber of this light.
Solution:
Given: Wavelength (λ) = 580 nm
To find: Frequency (ν), Wave number \(\bar{v}\)
Formulae : \(v=\frac{c}{\lambda}, \bar{v}=\frac{1}{\lambda}\)
Calculation: Wavelength of yellow light (λ) = 580 nm = 580 × 10^-9 m [1 nm = 10^-9 m]
We know that frequency (ν) is related to wavelength as: ν = \(\frac{c}{\lambda}\)
where, c, velocity of light = 3.0 × 10^-8 m s^-1
∴ ν = \(\frac{3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{580 \times 10^{-9} \mathrm{~m}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)
Again, Wave number, \(\bar{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-9} \mathrm{~m}}=1.72 \times 10^{6} \mathrm{~m}^{-1}\)
Ans: Frequency = 5.17 × 10¹⁴ s^-1 and wave number = 1.72 × 10⁶ m^-1

Question 36.
Calculate the energy of a photon of radiation having wavelength 300 nm. [h = 6.63 × 10^-34 J s]
Solution:
Given: Wavelength (λ) = 300 nm
To find: Energy of a photon (E)
Formulae: E = \(\frac{\mathrm{hc}}{\lambda}\)
Calculation: From formula,
E = \(\frac{6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{300 \times 10^{-9} \mathrm{~m}}=6.63 \times 10^{-19} \mathrm{~J}\)
Ans: Energy of a photon is 6.63 × 10^-19 J.

Question 37.
Explain briefly the results of Bohr’s theory for hydrogen atom.
Answer:
i. The stationary states for electrons are numbered n = 1, 2, 3……. These integers are known as principal quantum numbers.
ii. The radii of the stationary states are r_n = n² a₀, where a₀ = 52.9 pm (picometer). Thus, the radius of the first stationary state, called the Bohr radius is 52.9 pm.
iii. The most important property associated with the electron is the energy of its stationary state. It is given by the formula:
E_n = -R_H (1/n²), where n = 1, 2, 3, …..
R_H is the Rydberg constant for hydrogen and its value in joules is 2.18 × 10^-18 J.
The lowest energy state is called the ground state. Energy of the ground state (n = 1) is:
E₁ = -2.18 × 10^-18 × 1/1² = -2.18 × 10^-18 J
Energy of the stationary state corresponding to n = 2 is
E₂ = -2.18 × 10^-18 × (1/(2)²) = -0.545 × 10^-18 J.
iv. Bohr theory can be applied to hydrogen like species. For example, He⁺, Li²⁺, Be³⁺ and so on. Energies and radii of the stationary states associated with these species are given by:

where, Z is the atomic number. From the above expressions, it can be seen that the energy decreases (becomes more negative) and radius becomes smaller as the value of Z increases.
v. Velocities of electrons can also be calculated from the Bohr theory. Qualitatively, it is found that the magnitude of velocity of an electron increases with increase of Z and decreases with increase in the principal quantum number (n).

Question 38.
How many electrons are present in \({ }_{1}^{2} \mathrm{H}\), ₂He and He⁺ ? Which of these are hydrogen-like species?
Answer:
Hydrogen-like species contain only one electron.
Consider \({ }_{1}^{2} \mathrm{H}\):
Number of protons = Number of electrons = 1
Consider ₂He:
Number of protons = Number of electrons = 2
Consider He⁺:
Number of electrons = (Number of electrons in He – 1) = 2 – 1 = 1
Thus, \({ }_{1}^{2} \mathrm{H}\) and He⁺ are hydrogen-like species.
[Note: Bohr’s theory is applicable to hydrogen atom and hydrogen-like species, which contain only one electron.]

Question 39.
Describe how the line spectrum of hydrogen is explained by Bohr theory.
Answer:
i. According to second postulate of Bohr theory, radiation is emitted when an electron moves from an outer orbit of higher principal quantum number (n_i) to an inner orbit of lower principal quantum number (n_f). The energy difference (ΔE) between the initial and final orbit of the electronic transition corresponds to the energy of the emitted radiation.
ii. From the third postulate of Bohr theory, ΔE can be expressed as
ΔE = E_i – E_f …….(1)
iii. According to the results derived from Bohr theory, the energy (E_n) of an orbit is related to its principal quantum number ‘n’ by the equation:
E = \(-\mathrm{R}_{\mathrm{H}}\left(\frac{1}{\mathrm{n}^{2}}\right)\) ……(2)
iv. On combining these two equations, we get:

v. Substituting the value of R_H in joules, we get

vi. This expression can be rewritten in the terms of wavenumber of the emitted radiation in the following steps:
(ΔE) J = (h) J s × (ν) Hz
and

This equation appears like the Rydberg equation, where, n_f = n₁ and n_i = n₂.
In other words, Bohr theory successfully accounts for the empirical Rydberg equation for the line emission spectrum of hydrogen.

Question 40.
Observe the following diagram showing electronic transition in the hydrogen spectrum.

i. Electron jumps from higher energy level to n = 1. Which series does it correspond to?
ii. Electron jumps from higher energy level to n = 4. Which series does it correspond to?
iii. Which transition will give second line of Balmer series?
Answer:
i. When electron jumps from higher energy level to n = 1, it corresponds to Lyman series.
ii. When electron jumps from higher energy level to n = 1, it corresponds to Bracket series.
iii. When electron jumps from n = 4 to n = 1, the second line of Balmer series is observed.

Question 41.
Explain de Broglie’s equation.
Answer:
de Broglie’s equation:

• de Broglie proposed (in 1924) that matter should exhibit a dual behaviour. That is, every object which possesses a mass and velocity behaves both as a particle and as a wave. An electron has mass and velocity. This means that an electron should have momentum (p), a property of particle as well as wavelength (λ), a property of wave.
• According to de Broglie, the wavelength λ of a particle of mass m moving with a velocity v is
  λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) where, h is Planck’s constant.
• The quantity mv gives the momentum of the particles.
  λ = \(\frac{\mathrm{h}}{\mathrm{p}}\) where, p represents the momentum of the particle.
• de Broglie’s prediction was confirmed by diffraction experiments (a wave property).

[Note: According to de Broglie’s equation, the wavelength of a moving particle is inversely proportional to its mass. Therefore, heavier particles have much smaller wavelength than lighter particles like electrons.]

Question 42.
Write a note on Heisenberg’s uncertainty principle.
Answer:
i. Uncertainty principle was proposed by Wemer Heisenberg in 1927. It can be stated as “It is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron ”.
ii. If Δx is the uncertainty in the determination of the position of a very small moving particle and Δpx is the uncertainty in the determination of its momentum, then
Δx Δp_x ≥ \(\frac{\mathrm{h}}{4 \pi}\) …….(1) where h is Planck’s constant
iii. The above equation can alternatively be stated as,
Δx × m × Δv_x ≥ \(\frac{\mathrm{h}}{4 \pi}\), because Δp_x = m × Δv_x ……..(2)
where Δv_x is the uncertainty in the determination of velocity and m is the mass of the particle.

Question 43.
Calculate the radius and energy associated with the first orbit of He.
Solution:
Given: n = 1
To find: Radius and energy associated with the first orbit of He⁺
Formulae:

Calculation: He⁺ is a hydrogen-like species having Z = 2.
Using formula (i),
Radius of the first orbit of He⁺ = r₁ = \(\frac{52.9 \times(1)^{2}}{2} \mathrm{pm}\)
= 26.45 pm
Using formula (ii),
Energy of the first orbit of He⁺ = E₁ = -2.18 × 10^-18 \(\left(\frac{2^{2}}{1^{2}}\right) \mathrm{J}\)
= -8.72 × 10^-18 J
Ans: Radius of the first orbit of He⁺ is 26.45 pm and energy of the first orbit of He⁺ is -8.72 × 10^-18 J.

Question 44.
What is the wavelength of the photon emitted during the transition from the orbit of n = 5 to that of n = 2 in hydrogen atom?
Solution:
Given: n_i = 5, n_f = 2
To find: Wavelength of the photon emitted

Ans: Wavelength of the photon emitted is 434 nm.

Question 45.
Calculate the mass of a hypothetical particle having wavelength 5894 A and velocity 1.0 × 10⁸ ms^-1.
Solution:
Given: Wavelength (λ) = 5894 Å, Velocity (ν) = 1.0 × 10⁸ ms^-1
To find: Mass of a particle
Formula: λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) or m = \(\frac{\mathrm{h}}{\lambda \mathrm{v}}\) (according to de-Broglie equation)
Calculation: m = \(\frac{\mathrm{h}}{\lambda \mathrm{v}}\)
∴ m = \(\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}}{\left(5894 \times 10^{-10} \mathrm{~m}\right) \times\left(1.0 \times 10^{8} \mathrm{~ms}^{-1}\right)}\)
= 1.124 × 10^-35 kg
Ans: Mass of a particle is 1.124 × 10^-35 kg.

[Calculation using log table:
\(\frac{6.626 \times 10^{-34}}{5894 \times 10^{-10} \times 1.0 \times 10^{8}}=\frac{6.626}{5894} \times 10^{-32}\)
= Antilog₁₀ [log₁₀ 6.626 – log₁₀ 5894] × 10^-32
= Antilog₁₀ [0.8213 – 3.7704] × 10^-32
= Antilog₁₀ [latex]\overline{3} .0509[/latex] × 10^-32 = 1.124 × 10^-35]

Question 46.
Write a short note on Schrodinger equation.
Answer:
Schrodinger equation or wave equation:
i. Schrodinger developed the fundamental equation of quantum mechanics which incorporates wave particle duality of matter. The Schrodinger equation or wave equation is written as:
It \(\hat{\mathbf{H}}\)ψ = Eψ
Here \(\hat{\mathbf{H}}\) is a mathematical operator called Hamiltonian, ψ (psi) is the wave function and E is the total energy of the system.

ii. When Schrodinger equation is solved for an electron in hydrogen atom, the possible values of energy states (E) that the electron may have along with the corresponding wave function (ψ) are obtained. As a consequence of solving this equation, a set of three quantum numbers characteristic of the quantized energy levels and the corresponding wave functions are obtained. These are: Principal quantum number (n), azimuthal quantum number (l) and magnetic quantum number (m_l).

iii. The solution of Schrodinger wave equation led to three quantum numbers and successfully predicted features of hydrogen atom emission spectrum.

iv. Splitting of spectral lines in multi-electron atomic emission spectra could not be explained through such model. These were explained by George Uhlenbeck and Samuel Goudsmit (1925) who proposed the presence of the fourth quantum number called electron spin quantum number, m_s.

Question 47.
Write a short note on magnetic orbital quantum number (m_l).
Answer:
Magnetic orbital quantum number (m_l):

• Magnetic orbital quantum number describes the relative spatial orientation of the orbitals in a given subshell.
• It is denoted by m; and it has values from -l to +l through zero, giving total values or total orientations equal to (2l + 1).
• For s-subshell, 1 = 0, hence, m_l = 0. Thus, s-subshell contains only one orbital.
• For p-subshell, l = 1, hence, m_l = +1, 0, -1. Thus, p-subshell contains three orbitals having distinct orientations.

Question 48.
If n = 2, what are the values of quantum number l and m_l ?
Answer:
For a given n, l = 0 to (n – 1) and for given l, m_l = -l…., 0…. + l
Therefore, the possible values of l and ml for n = 2 are:

Value of n	Value of l	Value of ml
2	0	ml = 0
	1	ml = -1 ml = 0 ml = +1

Question 49.
What are the values of m_l for f-subshell?
Answer:
For f-subshell, l = 3. Therefore, m_l has seven values: + 3, + 2, + 1, 0, -1, -2, -3.

Question 50.
How many orbitals make the N-shell? What is the subshell wise distribution of orbitals in the N-shell?
Answer:
For N-shell principal quantum number n = 4
∴ Total number of orbitals in N-shell = n² = 4² = 16. The total number of subshells in N-shell = n = 4.
The four subshells with their azimuthal quantum numbers and the constituent number of orbitals are as shown below:

Azimuthal quantum number (l)	Symbol of subshell	Number of orbitals (2l + 1)
l = 0	s	(2 × 0) + 1 = 1
l = 1	P	(2 × 1) + 1 = 3
l = 2	d	(2 × 2) + 1 = 5
l = 3	f	(2 × 3) + 1 = 7

Question 51.
Complete the following flow chart:

Answer:

Question 52.
Write a short note on electron spin quantum number.
Answer:
Electron spin quantum number (m_s):

• Electron spin quantum number describes the spin state of the electron in an orbital. It is designated as ms.
• An electron spins around its axis and this imparts spin angular momentum to it.
• The two orientations which the spin angular momentum of an electron can take up give rise to the spin states which can be distinguished from each other by the spin quantum number, m_s, which can be either +1/2 or -1/2.
• The two spin states are represented by two arrows, ↑ (pointing up) and ↓ (pointing down) and thus have opposite spins.

Question 53.
An atom has two electrons in its 4s orbital. Write the values of the four quantum numbers for each of them.
Answer:
For the 4s orbital, 4 stands for the principal quantum number n; s stands for the subshell s having the value of azimuthal quantum number, l = 0. In the ‘s’ subshell, there is only one orbital and has magnetic quantum number, ml = 0. The two electrons in this orbital have opposite spins. Thus, the four quantum numbers of two electrons in 4s orbital are:

Question 54.
Write a short note on probability density of electron.
Answer:
i. The probability of finding an electron at a given point in an atom is proportional to the square of the wave function at that point (ψ²).
ii. According to Max Born, the square of wave function at a point in an atom is the probability density of the electron at that point.
The following figure shows the probability density diagrams of Is and 2s atomic orbitals. These diagrams appear like a cloud.
The electron cloud of 2s orbital shows one node, which is a region with nearly zero probability density and displays the change of sign for its corresponding wavefunction.
Diagram:

Question 55.
What is meant by the term ‘boundary surface diagram’?
Answer:
A boundary surface is drawn in space for an orbital such that the value of probability density (ψ²) is constant and encloses a region where the probability of finding electron is typically more than 90%. Such a boundary surface diagram is a good representation of shape of an orbital.
e.g. Boundary surface diagram of Is and 2s orbitals are spherical in shape.

Question 56.
Describe the shape of s orbital.
Answer:
Shape of s orbital:

• For each value of principal quantum number ‘n’, there is only one s-orbital.
• For s-orbital, l = 0 and m_l = 0, hence s-orbital has only one orientation i.e., the probability of finding the electrons is same in all directions. Thus, s-orbital is spherically symmetrical around the nucleus.
• The value of n determines the size of an orbital. With increase in the value of n, the size of the s-orbital increases.

Diagram:

Question 57.
Describe the shape of 2p orbitals.
Answer:
Shape of 2p orbitals:
i. For p orbital, l = 1. For l = 1, m_l = +1, 0, -1. Thus, p orbitals have three orientations.
ii. Each orbital has two lobes on the two sides of a nodal plane passing through the nucleus.
iii. Shape of 2p orbitals resembles a dumbbell.
iv. The size and energy of the three 2p orbitals are the same. However, their orientations in space are different. The lobes of the three 2p orbitals are along the x, y and z axes. Accordingly, the corresponding orbitals are designated as 2p_x, 2p_y and 2p_z. The size and energy of the orbitals in p subshell increase with the increase of principal quantum number.
Diagram:

Question 58.
Describe the shape of 3d orbitals.
Answer:
Shape of 3d orbitals:

• For d orbital, l = 2. For l = 2, m_l = +2, +1, 0, -1, -2. Thus, d orbitals have five orientations.
• They are designated as d_xy, d_yz, d_zx, d_x²-y² and d_z.
• Shape of 3d orbitals are shown in the following figure. The first three have double dumb-bell shape. They lie in xy, yz and xz plane, respectively. The d_x²-y² is also dumb-bell shaped and lies along the x and y axes. d_z² is dumb-bell shaped along z axis with a dough-nut shaped ring of high electron density around the nucleus in xy plane.
• In spite of difference in their shapes, the five d orbitals are equivalent in energy. The shapes of 4d, 5d, 6d…….. orbitals are similar to those of 3d orbitals, but their respective size and energies are large or they are said to be more diffused.

Diagram:

Question 59.
Explain (n + l) rule with respect to energies of orbitals.
Answer:
The lower the sum (n + l) for an orbital, the lower is its energy. If two orbitals have the same (n + l) values, then the orbital with the lower value of n is of lower energy. This is called the (n + l) rule.

Question 60.
What are the two methods of representing electronic configuration of an atom?
Answer:
The two methods of representing electronic configuration of an atom are:
i. Orbital notation: ns^a np^b nd^c …..
In the orbital notation method, a shell is represented by the principal quantum number (n) followed by respective symbol of the subshell. The number of electrons occupying that subshell being written as superscript on right side of the symbol.

ii. Orbital diagram:
In the orbital diagram method, each orbital in a subshell is represented by a box and the electrons represented by an arrow (↑ for up spin and ↓ for down spin) are placed in the respective boxes. In this method, all the four quantum numbers of electron are accounted for.

Note: Consider two electrons in 3s orbital:

Question 61.
Complete the following table:

Answer:

Question 62.
Explain condensed orbital notation of electronic configuration of an atom.
Answer:

• The orbital notation of electronic configuration of an element with high atomic number comprises a long train of symbols of orbitals with an increasing order of energy.
• It can be condensed by dividing it into two parts: Inner or core part of electronic configuration and outer electronic configuration.
• Electronic configuration of the preceding inert gas is a part of the electronic configuration of any element. In the condensed orbital notation, it is implied by writing symbol of that inert gas in a square bracket. It is core part of the electronic configuration of that element. The outer electronic configuration is specific to a particular element and written immediately after the bracket.
• For example, the orbital notation of potassium ‘K (Z = 19) is Is² 2s² 2p⁶ 3s² 3p⁶ 4s¹’. Its core part is the electronic configuration of the preceding inert gas argon ‘Ar: 1s² 2s² 2p⁶ 3s² 3p⁶, while ‘4s¹’ is an outer part. Therefore, the condensed orbital notation of electronic configuration of potassium is ‘K: [Ar] 4s².’

Note: Electronic configuration of the elements with atomic numbers 1 to 30 is as follows:

Question 63.
Write electronic configuration of ₁₈Ar and ₁₉K using orbital notation and orbital diagram method.
Answer:
From the atomic numbers, it is understood that 18 electrons are to be filled in Ar atom and 19 electrons are to be filled in K atom. These are to be filled in the orbitals according to the Aufbau principle. The electronic configuration of these atoms can be represented as:

Question 64.
Write condensed orbital notation of electronic configuration of the following elements:
i. Fluorine (Z = 9)
ii. Scandium (Z = 21)
iii. Cobalt (Z = 27)
iv. Zinc (Z = 30)
Answer:

No.	Element	Condensed orbital notation
i.	Fluorine (Z = 9)	[He] 2s2 2p5
ii.	Scandium (Z = 21)	[Ar] 4s2 3d1
iii.	Cobalt (Z = 27)	[Ar] 4s2 3d7
iv.	Zinc (Z = 30)	[Ar] 4s2 3d10

Question 65.
Find out one dinegative anion and one unipositive cation which are isoelectronic with Ne atom. Write their electronic configuration using orbital notations and orbital diagram method.
Answer:
Atomic number (Z) of Ne is 10. Therefore, Ne and its isoelectronic species contain 10 electrons each. The dinegative anionic species, isoelectronic with Ne is obtained by adding two electrons to the atom with Z = 8. This is O^2- ion.
The unipositive cationic species, isoelectronic with Ne is obtained by removing one electron from an atom with Z = 11. It is Na⁺ ion.
These species and their electronic configurations are shown below:

Question 66.
A student pictorially represented the electronic configuration of cobalt (Z = 27) in ground state as shown in the following figure.

i. Is this the correct representation?
ii. Identify the rules of electron filling that are violated (if any) in the above answer and give the correct representation.
Answer:
i. No, the electronic configuration of cobalt in ground state is incorrectly represented.
ii. The mles of electron filling that are violated in the above diagram are Pauli’s exclusion principle and Hund’s rule. The correct electronic configuration is:

Question 67.
With reference to the representative model of the gold foil experiment, answer the following questions:

i. What evidence regarding an atom do lines A, B and C provide?
ii. How does Rutherford’s model contradict Thomson’s plum-pudding model?
iii. What results would you expect from the experiment if Thomson’s plum-pudding model was correct?
Answer:
i. Line A – Most of the space inside the atom is empty because most of the α-particles passed through the gold foil without getting deflected.
Line B – The nucleus is positively charged since some α-particles were deflected at small angles.
Line C – The nucleus contains most of the atoms mass since few α-particles were deflected backward, i.e. toward the radioactive source.

ii. According to plum-pudding model, an atom was considered a positively charged sphere with negatively charged electrons embedded in it. However, Rutherford’s gold foil experiment proved that an atom consists of large empty space with positive charge concentrated only at the centre (nucleus) and negatively charged electrons revolve around the nucleus in various orbits.

iii. If Thomson’s plum-pudding model was correct, then in the gold foil experiment we would not expect to see any significant deflection of the α-particles, i.e., Most α-particles would pass through the foil with very small or no deflections.

Question 68.
Complete the following table:

Answer:

Multiple Choice Questions

1. Which of the following statements about the electron is INCORRECT?
(A) It is a negatively charged particle.
(B) The mass of electron is equal to the mass of neutron.
(C) It is a basic constituent of all atoms.
(D) It is a constituent of cathode rays.
Answer:
(B) The mass of electron is equal to the mass of neutron.

2. The isotopes of an element differ in
(A) the number of neutrons in the nucleus
(B) the charge on the nucleus
(C) the number of extra-nuclear electrons
(D) both the nuclear charge and the number of extra-nuclear electrons
Answer:
(A) the number of neutrons in the nucleus

3. The difference between U²³⁵ and U²³⁸ atoms is that U²³⁸ contains ………….
(A) 3 more protons
(B) 3 more protons and 3 more electrons
(C) 3 more neutrons and 3 more electrons
(D) 3 more neutrons
Answer:
(D) 3 more neutrons

4. The number of electrons, protons and neutrons in ³¹P^3- ion is respectively ……………
(A) 15, 15, 16
(B) 15, 16, 15
(C) 18, 15, 16
(D) 15, 16, 18
Answer:
(C) 18, 15, 16

5. In vacuum, the speed of all types of electromagnetic radiation is equal to ………….
(A) 3.0 × 10⁶ m s^-1
(B) 3.0 × 10⁸ m s^-1
(C) 3.0 × 10¹⁰ m s^-1
(D) 3.0 × 10¹² m s^-1
Answer:
(B) 3.0 × 10⁸ m s^-1

6. In the electromagnetic spectrum, the ultraviolet region is around ………….. Hz.
(A) 10⁶
(B) 10¹⁰
(C) 10¹⁶
(D) 10²⁶
Answer:
(C) 10¹⁶

7. In hydrogen spectrum, the series of lines appearing in ultraviolet region of electromagnetic spectrum are called ………….
(A) Lyman series
(B) Balmer series
(C) Pfund series
(D) Brackett series
Answer:
(A) Lyman series

8. The energy of electron in the n^th Bohr orbit of H-atom is …………

Answer:
(C) \(-\frac{2.18 \times 10^{-18}}{\mathrm{n}^{2}} \mathrm{~J}\)

9. Which of the following is a hydrogen-like species?
(A) He²⁺
(B) Be³⁺
(C) Li⁺
(D) H⁺
Answer:
(B) Be³⁺

10. The de Broglie wavelength associated with a particle of mass 10^-6 kg moving with a velocity of 10 m s^-1 is ………..
(A) 6.63 × 10^-22 m
(B) 6.63 × 10^-29 m
(C) 6.63 × 10^-31 m
(D) 6.63 × 10^-34 m
Answer:
(B) 6.63 × 10^-29 m

11. An orbital is designated by …………. quantum numbers while an electron in an atom is designated by …………. quantum numbers.
(A) two, three
(B) three, two
(C) four, two
(D) three, four
Answer:
(D) three, four

12. In a multi-electron atom, the energy of the orbital depends on two quantum numbers: ……….
(A) n and ms
(B) n and ml
(C) ml and ms
(D) n and l
Answer:
(D) n and l

13. The number of subshells in a shell is equal to ………..
(A) n
(B) n²
(C) n – 1
(D) l + 1
Answer:
(A) n

14. The maximum number of electrons in a subshell for which l = 3 is …………..
(A) 14
(B) 10
(C) 8
(D) 4
Answer:
(A) 14

15. Which of the following is INCORRECT?
(A) A nodal plane has ψ² very close to zero.
(B) The value of ψ² at any finite distance from the nucleus is always zero.
(C) A boundary surface diagram enclosing 100 % probability density cannot be drawn.
(D) A boundary surface diagram is a good representation of shape of an orbtial.
Answer:
(B) The value of ψ² at any finite distance from the nucleus is always zero.

16. p_z-Orbital has ……….. nodal plane/planes.
(A) zero
(B) one
(C) two
(D) three
Answer:
(B) one

17. Which of the following pairs of d-orbitals will have electron density along the axis?
(A) d_xy, d_x²-y²
(B) d_z², d_xz
(C) d_xz, d_yz
(D) d_z², d_x²-y²
Answer:
(D) d_z², d_x²-y²

18. The two electrons have the following set of quantum numbers:
P = 3, 2, -2, +\(\frac {1}{2}\)
Q = 3, 0, 0, +\(\frac {1}{2}\)
Which of the following statement is TRUE?
(A) P and Q have same energy
(B) P has greater energy than Q
(C) P has lesser energy than Q
(D) P and Q represent same electron
Answer:
(B) P has greater energy than Q

19. For 3d orbital, the values of n and l are ………… respectively.
(A) 0, 3
(B) 3, 2
(C) 3, 0
(D) 3, 3
Answer:
(B) 3, 2

20. For the electron present in 1 s orbital of helium atom, the correct set of values of quantum numbers is ………..
(A) 1, 0, 0, +1/2
(B) 1, 1, 0, +1/2
(C) 1, 1, 1, +1/2
(D) 2, 0, 0, +1/2
Answer:
(A) 1, 0, 0, +1/2

21. The ground state electronic configuration for chromium atom (Z = 24) is …………
(A) [Ar] 3d⁵ 4s¹
(B) [Ar] 3d⁴ 4s²
(C) [Ar] 3d⁸
(D) [Ar] 4s¹ 4p⁵
Answer:
(A) [Ar] 3d⁵ 4s¹

22. The electronic configuration of Ni²⁺ is ……….. (Atomic number of Ni = 28)
(A) [Ar] 4s² 3d⁶
(B) [Ar] 4s¹ 3d⁸
(C) [Ar] 3d⁸
(D) [Ar] 4s² 3d⁸
Answer:
(C) [Ar] 3d⁸

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 3 Basic Analytical Techniques Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 3 Basic Analytical Techniques

Question 1.
Give reason: Purification of a chemical substance is important before investigating its composition and properties.
Answer:

• Chemical substances occur in nature in the impure stage.
• Also, chemical substances synthesized in the laboratory are obtained in crude and impure form.
• Impurities present in the chemical substances may interfere with the properties to be determined (e.g. melting point or boiling point).
• Therefore, before investigating the composition and properties of a given chemical substance, it is important to obtain it in pure form.

Question 2.
What are the different types of impurities that a solid may contain?
Answer:
A solid substance may contain two types of impurities:

• Impurities that are soluble in the same solvent as the main substance.
• Impurities that are not soluble in the same solvent as the main substance.

Question 3.
For which of the following cases, is the process of filtration feasible? Why?
Case 1: A solid substance containing impurities that are soluble in the same solvent as the main substance.
Case 2: A solid substance containing impurities that are not soluble in the same solvent as the main substance.
Answer:
Impurities which are not soluble in the same solvent as the main compound can be separated by a simple process called filtration. Hence, for ‘Case 2’, filtration is more feasible.

Question 4.
Describe the process of filtration with a neat and labelled diagram.
Answer:
i. Impurities which are not soluble in the same solvent as the main compound can be separated by a simple process called filtration.
ii. Procedure:
a. A circular piece of filter paper is folded to form a cone and fitted in the funnel.
b. The funnel is fixed on a stand and a beaker is kept below.
c. The mixture which has to be purified is added to a suitable solvent in which the main compound dissolves.
d. The paper is made moist, and the solution to be filtered is poured on the filter paper.
e. Diagram:

iii. The insoluble part remaining on the filter paper is called residue and the liquid which pass through the filter paper and collected in the beaker is called filtrate.
iv. This process is similar to separating tea leaves from decoction of tea or sand from mixture of sand and water.

Question 5.
Why is safety bottle used when filtration is carried out under suction?
Answer:
The safety bottle is used to prevent sucking of the filtrate into suction pump.

Question 6.
Name the steps involved in the process of crystallization.
Answer:
Steps involved in the process of crystallization:

• Preparation of a saturated solution
• Hot filtration
• Cooling of the filtrate
• Filtration

Question 7.
How is saturated solution of the crude solid prepared?
Answer:

• A saturated solution of the crude solid is prepared by boiling it in a small but sufficient quantity of a suitable solvent.
• The main solute from the sample of the crude solid dissolves to form a saturated solution on boiling.

[Note: The solution is not saturated with respect to the soluble impurities, as they are in small proportion.]

Question 8.
Explain the following steps with respect to the process of crystallization.
i. Preparation of a saturated solution
ii. Hot filtration
iii. Cooling of the filtrate
iv. Filtration
Answer:
i. Preparation of a saturated solution:

• A saturated solution of the crude solid is prepared by boiling it in a small but sufficient quantity of a suitable solvent.
• On doing so the main solute forms an almost saturated solution, but the solution is not saturated with respect to the soluble impurities, as they are in small proportion.

ii. Hot filtration: The hot saturated solution is quickly filtered to remove undissolved impurities as residue. Filtration under suction can be employed for rapid filtration.

iii. Cooling of the filtrate:

• The hot filtrate is allowed to cool.
• On cooling, the filtrate becomes supersaturated with respect to the main dissolved solute because solubility of a substance decreases with lowering of temperature.
• The excess quantity of the dissolved solute comes out of the solution in the form of crystals.
• The dissolved impurities, however, do not supersaturate the solution, as their quantity is small.
• These continue to stay in the solution in dissolved state even on cooling. Therefore, the separated crystals are free from soluble impurities.

iv. Filtration:

• The crystals obtained on cooling are further purified by filtration to remove insoluble impurities.
• The filtrate obtained is called as mother liquor.
• The crystals obtained after filtration are free from soluble as well as insoluble impurities.

Question 9.
Name the common solvents used in the process of crystallization.
Answer:
The commonly used solvents are water, ethyl alcohol, methyl alcohol, acetone, ether or their combinations.

Question 10.
Describe the process of crystallization of common salt from impure sample with the help of a diagram.
Answer:

• Impure sample of a common salt is added to the required quantity of water and stirred with a glass rod.
• More amount of salt is added and the solution is heated till no more salt dissolves.
• The hot saturated solution is filtered off to remove insoluble impurities while the filtrate is collected in an evaporating dish.
• The filtrate is allowed to cool which results in the formation crystals of pure salt (NaCl) leaving behind the soluble impurities.
• The crystals are filtered and dried.

The diagram is as follows:

Question 11.
Which solvent is used for the purification of copper sulphate and benzoic acid?
Answer:
The solvent used for the purification of copper sulphate and benzoic acid is water.

Question 12.
Define: Fractional crystallization
Answer:
Fractional crystallization is a process wherein two or more soluble substances having widely different solubilities in the same solvent at same temperature are separated by crystallization.

Question 13.
Give a brief description of the principle of fractional crystallization.
Answer:
Fractional crystallization is based on the differences in solubilities of two or more compounds in the same solvent at the same temperature. That is, the substance which is least soluble crystallizes out first and the most soluble substance crystallizes out last.
e.g. Mixture of two solutes A and B can be purified by fractional crystallization as follows:

• Preparation of a saturated solution: Mixture of two solutes A and B are dissolved in a suitable hot solvent to prepare a saturated solution.
• Hot filtration: The hot saturated solution is filtered to remove insoluble impurities.
• Cooling of the filtrate: Hot filtrate is allowed to cool. On cooling, the solute which is least soluble crystallizes out first leaving behind the most soluble substance in the mother liquor.
• Filtration: The crystals formed are filtered, washed with solvent and dried. Crystals obtained will be of a solute which is least soluble in a given solvent.
• Concentration of a mother liquor: The mother liquor is concentrated by evaporating the solvent. These crystals are filtered and dried to obtain the second purified component (which was more soluble in given solvent).

Question 14.
Which type of impure liquids can be purified by the process of distillation?
Answer:
Distillation technique can be employed for the purification of

• volatile liquids from non-volatile impurities.
• liquids having sufficient difference in their boiling point.

Question 15.
Explain the construction of simple distillation unit using neat labelled diagram.
Answer:
i. The apparatus used for simple distillation is shown in the figure below:

ii. It consists of round bottom flask fitted with a cork having a thermometer.
iii. The flask has a sidearm through which it is connected to a condenser.
iv. The condenser has a jacket with two outlets through which water is circulated.
v. The liquid to be distilled is taken in the round bottom flask fixed by clamp.
vi. The flask is placed in a water bath or oil bath or sometimes wire gauze is kept on a stand as shown in the figure.

Question 16.
State the principle involved and describe the process to separate acetone and water from their mixture.
Answer:
i. Acetone and water can be separated from their mixture by simple distillation.

ii. Principle: Acetone and water are two miscible liquids having an appreciable difference (more than 30 K) in their boiling points. Acetone boils at 56 °C while boiling point of water is 100 °C. When the mixture of acetone and water is heated and temperature of the mixture reaches 56 °C acetone will distil out first. Once all acetone distils out, and when the temperature rises to 100 °C water will distil out.

iii. Process to separate acetone and water from their mixture:

• Take the mixture of water and acetone in the distillation flask.
• Heat the flask on a water bath carefully. At 56 °C acetone will distil out, collect it in receiver.
• After all acetone distilled, change the receiver. Discard a few mL of the liquid. As the temperature reaches 100 °C water will begin to distil. Collect this in another receiver.

Question 17.
What is the advantage of fractional distillation over simple distillation?
Answer:
If in a mixture, the difference in boiling points of two liquids is not appreciable/large, they cannot be separated using simple distillation. To separate such liquids, fractional distillation is used.

Question 18.
Label the following diagram and explain the process by giving example.

Answer:
The labelled diagram is as follows:

i. In fractional distillation, vapours first pass through the fractionating column.
ii. Vapours of more volatile liquid with lower boiling point rise up more than the vapours of liquid having higher boiling point.
e.g.

• Suppose we have a mixture of two liquid ‘A’ and ‘B’ having boiling points 363 K and 373 K respectively.
• ‘A’ is more volatile and ‘B’ is less volatile. As the mixture is heated, vapours of ‘A’ along with a little vapours of ‘B’ rise up and come in contact with the large surface of the fractionating column.
• Vapours of ‘B’ condense rapidly into the distillation flask. While passing through the fractionating column, there is an exchange between the ascending vapours and descending liquid. The vapours of ‘B’ are scrubbed off by the descending liquid, this makes the vapours richer in ‘A’.
• This process is repeated each time the vapours and liquid come in contact with the surface in the fractionating column.
• Rising vapours become richer in ‘A’ and escape through the fractionating column and reach the condenser while the liquid in the distillation flask is richer in ‘B.
• The separated components are further purified by repeating the process.

Question 19.
Give two examples of a mixture that can be separated by fractional distillation.
Answer:

1. Mixture of acetone (b.p. 329 K) and methyl alcohol (b.p. 337.7 K)
2. Mixture of acetone (b.p. 329 K) and benzene (b.p. 353 K)

Question 20.
Give one industrial application of fractional distillation.
Answer:
Fractional distillation is used in petroleum industry to separate different fractions of crude oil.

Question 21.
Write a short note on distillation under reduced pressure.
Answer:

• Liquids having very high boiling points or which decompose on heating are purified by the method of distillation under reduced pressure.
• In this method, the liquid is made to boil at a temperature lower than its normal boiling point by reducing the pressure on its surface.
• The external pressure is reduced using a water pump or vacuum pump, e.g. Glycerol can be separated from soap by using this method.

Question 22.
Write the principle of solvent extraction and explain the process with labelled diagram.
Answer:
Principle: Extraction of compound takes place based on the difference in solubility of compound in two liquids.

• In this process, the solute distributes itself between two immiscible liquids. From the aqueous phase the solute gets extracted in the organic phase.
• On shaking for a few times with small volumes of organic phase, most of the solute gets extracted into the organic phase.
• Then solute is then recovered from organic solvent either by evaporation of organic solvent or distillation.

Diagram:

Question 23.
Write a short note on continuous extraction method.
Answer:

• During solvent extraction, if the solute is found to be less soluble in organic phase, then continuous extraction method is employed.
• In this method, the same amount of organic solvent is used repeatedly for extraction.
• This ensures that the most of the solute gets extracted in the organic phase.
• This technique involves continuous distillation of the solvent within the same assembly. Hence, the use of large quantity of organic solvent is avoided.

Question 24.
Match the following:

	Process		Used in the purification/separation of
i.	Crystallization	a.	Acetone and benzene
ii.	Simple distillation	b.	Benzoic acid and water
iii.	Fractional distillation	c.	Impure copper sulphate
iv.	Solvent extraction	d.	Acetone and water

Answer:
i – c,
ii – d,
iii – a,
iv – b

Question 25.
What is chromatography? Explain the principle behind it.
Answer:
Chromatography is a technique used to separate components of a mixture, and also purify compounds.
Principle: The principle of separation of substances in chromatography is based on the distribution of the solutes in two phases, i.e., stationary phase and mobile phase.

• Chromatography uses two phases for separation.
• This technique is based on the difference in rates at which components in the mixture move through the stationary phase under the influence of the mobile phase.
• In this technique, first the mixture of components is loaded at one end of the stationary phase and then the mobile phase is allowed to move over the stationary phase. The mobile phase can be a pure solvent or a mixture of solvents.
• Depending on the relative affinity of the components toward the stationary phase and mobile phase, they remain on the surface of the stationary phase or move along with the mobile phase, and gradually get separated.

Question 26.
Give a brief description of column chromatography with an illustration.
Answer:
Column chromatography involves the separation of components over a column of stationary phase. The stationary phase material can be alumina, silica gel.
Procedure:

• A slurry of the stationary phase material is filled in a long glass tube provided with a stopcock at the bottom and a glass wool plug at the lower end.
• The mixture to be separated is dissolved in a suitable solvent and then it is loaded on top of adsorbent column.
• A suitable mobile phase which could be a single solvent or a mixture of solvents is then poured over the adsorbent column.
• The mixture along with the mobile phase slowly moves down the column.
• The solutes get adsorbed on the stationary phase and depending on the degree to which they are adsorbed, they get separated from each other.
• The component which is readily adsorbed are retained on the column and others move down the column to various distances forming distinct bands.
• The component which is less strongly adsorbed is desorbed first and leaves the column first, while the strongly adsorbed component is eluted later.
• The solutions of these components are collected separately.
• These different components can be recovered by evaporating the solvent.

Question 27.
How is TLC plate or chromplate prepared?
Answer:
TLC plate or chromplate is prepared by applying a thin layer (0.2 mm thick) of adsorbent silica gel or alumina spread over a glass plate.

Question 28.
Describe the process of thin layer chromatography (TLC) and separation of components in it.
Answer:
i. Process:

• A thin layer (about 0.2 mm thick) of an adsorbent like silica gel or alumina is spread over a thin glass plate (called chromplate or TLC plate). This plate acts as a stationary phase.
• With the help of a capillary tube, the solution of the mixture to be separated is spotted at above 2 cm (on base line) from one end of the TLC plate.
• The TLC plate is then placed in a closed jar containing a suitable solvent (mobile phase or eluant).
• As the mobile phase rises up the plate, the components of the mixture move up along with the mobile phase to different distances depending upon their degree of adsorption, thus resulting in complete separation.

ii. Separation of components:

• If the components are coloured, they appear as separated coloured spots on the plate.
• If the components are not coloured but have property of fluorescence, they can be visualised under UV light, or the plate can be kept in a chamber containing a few iodine crystals. The Iodine vapours are adsorbed by the components and the spots appear brown.
• Amino acids are visualised by spraying the plate with a solution of ninhydrin. This is known as spraying agent.

Question 29.
Name the physical state each of stationary phase and mobile phase in partition chromatography.
Answer:
In partition chromatography, both stationary and mobile phases are in liquid state.

Question 30.
State the principle of partition chromatography.
Answer:
Partition chromatography is based on continuous differential partitioning of components of a mixture between stationary and mobile phases.

Question 31.
Describe the process of paper chromatography.
Answer:
Process of paper chromatography:

• The mixture of the compound to be analysed is dissolved in a suitable solvent and spotted on the chromatography paper about 2 cm from one end of the paper using a glass capillary.
• The paper is then suspended in a chamber containing the mobile phase.
• The mobile phase rises up the paper and flows over the spot, due to capillary action.
• Different solutes are retained differently on the paper depending on their selective partitioning between the two phases. The paper strip so developed, is known as chromatogram.

Question 32.
Name the following:
i. A glass plate coated with a thin layer of silica gel.
ii. A spraying agent used for the visualization of amino acids.
Answer:
i. Chromplate/TLC plate
ii. Ninhydrin

Question 33.
Write a short note on R_f value.
Answer:
i. In chromatography, migration of the solute relative to the solvent front gives an idea about the relative retention of the solutes (or components of t the mixture) on the stationary phase.
ii. The relative adsorption of solutes is expressed in terms of its R_f value.
The symbol R_f stands for Retardation Factor.

Question 34.
In a chemical laboratory, Priyal was asked to isolate an organic compound from its aqueous solution. She added ethyl acetate to the given sample, separated the organic layer and kept it for evaporation. At the end of her practical, Priyal found few crystals in the beaker which she kept for evaporation. Answer the following questions:
i. In the above passage, which method was used by Priyal for separation? State its principle.
ii. Why do you think the organic compound dissolved in ethyl acetate?
iii. Illustrate the method of separation used in the passage with an example.
Answer:
i. Method used: Solvent extraction method.
Principle: Extraction of compound takes place based on the difference in solubility of compound in two liquids,

• In this process, the solute distributes itself between two immiscible liquids. From the aqueous phase the solute gets extracted in the organic phase.
• On shaking for a few times with small volumes of organic phase, most of the solute gets extracted into the organic phase.
• Then solute is then recovered from organic solvent either by evaporation of organic solvent or distillation.

ii. An organic compound (non-polar) dissolves in organic solvents (non-polar) because of the dipole-dipole interactions in between them (like dissolves like). Water is a polar solvent and it is unlikely that the covalent constituents of the organic substance is strong enough to break the ionic bonds. Any substance dissolves in other because it is able to break the bonds between the solvent molecules and form weak bonds with the solvent molecules. Hence, the organic compound will be more soluble in ethyl acetate as compared to water and this helps in its isolation from aqueous solution.

iii. An example for the separation of organic compound using solvents extraction method is: Benzoic acid in water can be extracted from its aqueous solution by using benzene.

Question 35.

Based on the above diagram, answer the following questions:
i. Name the chromatographic technique involved.
ii. From the developed chromatogram, state which has the highest and which has the lowest R_f value?
iii. Based on the TLC, which component would elute out at the end of a column chromatography?
iv. Mention two applications of TLC method.
Answer:
i. Thin layer chromatography
ii. Based on the developed chromatogram, spot ‘x’ has the highest Rf value while spot ‘z’ the lowest Rf value.
iii. Based on the TLC, spot ‘z’ being strongly adsorbed will elute at the end of a column chromatography.
iv. Applications of TLC are:

• Separation of plant pigments from its mixture.
• Separation of impurities from a given organic compound.
• Separation of different amino acid.

Multiple Choice Questions

1. If a crude solid is made of mainly one substance and has some impurities then it is purified by ……………..
(A) crystallization
(B) distillation
(C) extraction
(D) sublimation
Answer:
(A) crystallization

2. Impure common salt can be purified by ……………
(A) crystallization
(B) distillation
(C) extraction
(D) sublimation
Answer:
(A) crystallization

3. Which of the following solvents is most commonly used for the crystallization of copper sulphate?
(A) Water
(B) Acetone
(C) Ether
(D) Methanol
Answer:
(A) Water

4. In distillation of liquid, water condenser is used ……………
(A) to boil the liquid
(B) to collect the liquid
(C) to condense hot vapours of the liquid
(D) to adsorb the liquid
Answer:
(C) to condense hot vapours of the liquid

5. Separation of binary mixture of acetone and methyl alcohol is done by ……………
(A) simple distillation
(B) fractional distillation
(C) fractional crystallization
(D) re-crystallization
Answer:
(B) fractional distillation

6. Which of the following method is used to separate different fractions of crude oil?
(A) Solvent extraction
(B) Simple distillation
(C) Fractional distillation
(D) TLC
Answer:
(C) Fractional distillation

7. The method used to separate a given organic compound present in aqueous solution by shaking with a suitable solvent in which the compound is more soluble than water is called ……………….
(A) simple distillation
(B) fractional distillation
(C) solvent extraction
(D) crystallization
Answer:
(C) solvent extraction

8. Adsorption chromatography is a chromatographic technique based on the principle of ……………
(A) differential adsorption
(B) differential solubility
(C) differential extraction
(D) all of these
Answer:
(A) differential adsorption

9. The stationary phase and mobile phase in TLC are ……………. respectively.
(A) solid and liquid
(B) solid and gas
(C) liquid and solid
(D) liquid and liquid
Answer:
(A) solid and liquid

10. Which of.the following is most commonly used for the visualization of amino acids in chromatography?
(A) Ultraviolet light
(B) Spraying agent
(C) Sunlight
(D) X-rays
Answer:
(B) Spraying agent

11. The stationary phase and mobile phase in partition chromatography are ………….. respectively.
(A) solid and liquid
(B) solid and gas
(C) liquid and solid
(D) liquid and liquid
Answer:
(D) liquid and liquid

12. Paper chromatography is based on the principle of …………….
(A) adsorption
(B) partition
(C) solubility
(D) volatility
Answer:
(B) partition

13. In paper chromatography, the mobile phase rises up the chromatography paper due to ………………
(A) evaporation of volatile solvent
(B) capillary action
(C) gravitational force
(D) differential adsorption
Answer:
(B) capillary action

14. Which of the following is a type of partition chromatography?
(A) Column chromatography
(B) Thin layer chromatography
(C) Paper chromatography
(D) Both (B) and (C)
Answer:
(C) Paper chromatography

15. The principle of differential adsorption is applicable for which of the following chromatographic technique?
(A) Column chromatography
(B) Thin layer chromatography
(C) Paper chromatography
(D) Both (A) and (B)
Answer:
(D) Both (A) and (B)

16. Which of the following method will give clean separation of a sample of chloroform (organic liquid) and water in a short time span?
(A) TLC
(B) Distillation under reduced pressure
(C) Solvent extraction
(D) Simple distillation
Answer:
(C) Solvent extraction

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 2 Introduction to Analytical Chemistry Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 2 Introduction to Analytical Chemistry

Question 1.
Explain the statement: Analytical chemistry provides physical or chemical information about a sample.
Answer:

• Analytical chemistry facilitates the investigation of the chemical composition of substances.
• It uses the instruments and methods to separate, identify and quantify a sample under study.

Thus, analytical chemistry provides chemical or physical information about a sample.

Question 2.
What is the difference between qualitative analysis and quantitative analysis?
Answer:

1. Qualitative analysis deals with the detection of the presence or absence of elements in compounds and of chemical compounds in mixtures.
2. Quantitative analysis deals with the determination of the relative proportions of elements in compounds and of chemical compounds in mixtures.

Question 3.
Explain the importance of chemical analysis.
Answer:

• Chemical analysis is one of the most important methods of monitoring the composition of raw materials, intermediates and finished products, and also the composition of air in streets and premises of industrial plants.
• In agriculture, chemical analysis is used to determine the composition of soils and fertilizers.
• In medicine, it is used to determine the composition of medicinal preparations.

Question 4.
Write a note on the applications of analytical chemistry.
Answer:

• Analytical chemistry has applications in forensic science, engineering and industry.
• Analytical chemistry is also useful in the field of agriculture and pharmaceutical industry.
• Industrial process as a whole and the production of new kinds of materials are closely associated with analytical chemistry.

Question 5.
What is semi-microanalysis?
Answer:

• When the amount of a solid or liquid sample taken for analysis is a few grams, the analysis is called semi-microanalysis.
• It is of two types: qualitative and quantitative analysis.

Question 6.
What does classical qualitative analysis method include?
Answer:
Classical qualitative analysis method includes separation and identification of compounds.

• Separations may be done by methods such as precipitation, extraction and distillation.
• Identification may be based on differences in colour, odour, melting point, boiling point, and reactivity.

Question 7.
Name two methods of classical quantitative analysis.
Answer:

1. Volumetric analysis (Titrimetric analysis)
2. Gravimetric analysis (i.e., decomposition, precipitation)

Question 8.
What are the two stages involved in the chemical analysis of a sample?
Answer:
The chemical analysis of a sample is carried out mainly in two stages: by the dry method and by the wet method. In dry method, the sample under test is not dissolved and in wet method, the sample under test is first dissolved and then analysed to determine its composition.

Question 9.
Explain: Qualitative analysis of organic compounds
Answer:

• The majority of organic compounds are composed of a relatively small number of elements.
• The most important ones are: carbon, hydrogen, oxygen, nitrogen, sulphur, halogen, phosphorus.
• Elementary qualitative analysis is concerned with the detection of the presence of these elements.
• The identification of an organic compound involves tests such as detection of functional group, determination of melting/boiling points, etc.

Question 10.
What does qualitative analysis of inorganic compounds involve?
Answer:
The qualitative analysis of simple inorganic compounds involves detection and confirmation of cationic and anionic species (basic and acidic radical) in them.

Question 11.
Explain: Chemical methods of quantitative analysis
Answer:

• Quantitative analysis of organic compounds involves methods such as determination of percentage of constituent elements, concentrations of a known compound in the given sample, etc.
• Quantitative analysis of simple inorganic compounds involves methods such as gravimetric analysis (i.e., decomposition, precipitation, etc.) and the titrimetric or volumetric analysis (i.e., progress of reaction between two solutions till its completion).
• The quantitative analytical methods involve measurement of quantities such as mass and volume using some equipment/apparatus such as weighing machine, burette, etc.

Question 12.
Why is accurate measurement crucial in science?
Answer:

• The accuracy of measurement is of a great concern in analytical chemistry. This is because faulty equipment, poor data processing or human error can lead to inaccurate measurements. Also, there can be intrinsic errors in the analytical measurement.
• When measurements are not accurate, this provides incorrect data that can lead to wrong conclusions. For example, if a laboratory experiment requires a specific amount of a chemical, then measuring the wrong amount may result in an unsafe or unexpected outcome.
• Hence, the numerical data obtained experimentally are treated mathematically to reach some quantitative conclusion.
• Also, an analytical chemist has to know how to report the quantitative analytical data, indicating the extent of the accuracy of measurement, perform the mathematical operation and properly express the quantitative error in the result.

Question 13.
Why are scientific notations (exponential notations) used?
Answer:
A chemist has to deal with numbers as large as 602,200,000,000,000,000,000,000 for the molecules of 2 g of hydrogen gas or as small as 0.00000000000000000000000166 g. that is, mass of a H atom. To avoid the writing of so many zeros in mathematical operations, scientific notations i.e. exponential notations are used.

Question 14.
How are numbers expressed in scientific notations (exponential notations)?
Answer:
In scientific notations, numbers are expressed in the form of N × 10ⁿ, where ‘n’ is an exponent with positive or negative values and N can have a value between 1 to 10.
e.g. i. The number, 602,200,000,000,000,000,000,000 is expressed as 6.022 × 10²³.
ii. The mass of a H atom, 0.00000000000000000000000166 g is expressed as 1.66 × 10^-24 g.
iii. The number 123.546 is written as 1.23546 × 10².
iv. The number 0.00015 is written as 1.5 × 10^-4.

Question 15.
Express the following quantities in scientific notations (exponential notations).
i. 0.0345
ii . 0.08
iii. 653.00
iv. 34.768
Answer:
i. 0.0345 = 3.45 × 10^-2
ii. 0.08 = 8 × 10^-2
iii. 653.00 = 6.5300 × 10²
iv. 34.768 = 3.4768 × 10¹

Question 16.
Define: Accuracy of measurement
Answer:
Nearness of the measured value to the true value is called the accuracy of measurement.

Question 17.
Explain with the help of a diagram how accuracy depends upon the sensitivity or least count of the measuring equipment.
Answer:
A burette reading of 10.2 mL is as shown in the diagram below:

• For all the three situations in the above figure, the reading would be noted is 10.2 mL.
• It means that there is an uncertainty about the digit appearing after the decimal point in the reading 10.2 mL because the least count of the burette is 0.1 mL.
• The meaning of the reading 10.2 mL is that the true value of the reading lies between 10.1 mL and 10.3 mL.
• This is indicated by writing 10.2 ± 0.1 mL.
• Here, the burette reading has an error of ± 0.1 mL.
• Smaller the error, higher is the accuracy.

Question 18.
How is absolute error calculated?
Answer:
Absolute error is calculated by subtracting true value from observed value.
Absolute error = Observed value – Tme value

Question 19.
Explain the term: Relative error
Answer:

1. Relative error is the ratio of an absolute error to the true value.
2. Relative error is generally a more useful quantity than absolute error.
3. Relative error is expressed as a percentage and can be calculated as follows:
   Relative error = \(\frac{\text { Absolute error }}{\text { True value }} \times 100 \%\)

Question 20.
Explain the term: Precision in measurement
Answer:

• Multiple readings of the same quantity are noted to minimize the error.
• If the multiple readings of the same quantity match closely, they are said to have high precision.
• High precision implies reproducibility of the readings.
• High precision is a prerequisite for high accuracy.
• Precision is expressed in terms of deviation (i.e. absolute deviation and relative deviation).

Question 21.
Explain the following terms with respect to precise measurement:
i. Absolute deviation
ii. Mean absolute deviation
iii. Relative deviation
Answer:
i. Absolute deviation: An absolute deviation is the modulus of the difference between an observed value and the arithmetic mean for the set of several measurements made in the same way. It is a measure of absolute error in the repeated observation. It is expressed as follows:
Absolute deviation = |Observed value – Mean|

ii. Mean absolute deviation: Arithmetic mean of all the absolute deviations is called the mean absolute deviation in the measurements.

iii. Relative deviation: The ratio of mean absolute deviation to its arithmetic mean is called relative deviation. It is expressed as follows:
Relative deviation = \(\frac{\text { Mean absolute deviation }}{\text { Mean }}\) × 100%

Question 22.
Explain the need of significant figures in measurement.
Answer:

• Uncertainty in measured value leads to uncertainty in calculated result.
• Uncertainty in a value is indicated by mentioning the number of significant figures in that value. e.g. Consider, the column reading 10.2 ± 0.1 mL recorded on a burette having the least count of 0.1 mL. Here, it is said that the last digit ‘2’ in the reading is uncertain, its uncertainty is ±0.1 mL. On the other hand, the figure ‘10’ is certain.
• The significant figures in a measurement or result are the number of digits known with certainty plus one uncertain digit.
• In a scientific experiment, a result is obtained by doing calculation in which values of a number of quantities measured with equipment of different least counts are used.

Question 23.
How many significant figures are present in the following measurements?
i. 4.065 m
ii. 0.32 g
iii. 57.98 cm³
iv. 0.02 s
v. 4.0 × 10^-4 km
vi. 604.0820 kg
vii. 307.100 × 10^-5 cm
Answer:
i. 4
ii. 2
iii. 4
iv. 1
v. 2
vi. 7
vii. 6

Question 24.
How many significant figures are present in each of the following?
i. 45.0
ii. 0.001
iii. 2.10 × 10^-8
iv. 340000
v. 0.0100
vi. 7890320
vii. 100.00
viii. 100
Answer:
i. 3
ii. 1
iii. 3
iv. 2
v. 3
vi. 6
vii. 5
viii. 1

Question 25.
State the rules used to round off a number to the required number of significant figures.
Answer:
The following rules are used to round off a number to the required number of significant figures:

• If the digit following the last digit to be kept is less than five, the last digit is left unchanged, e.g. 46.32 rounded off to two significant figures is 46.
• If the digit following the last digit to be kept is five or more, the last digit to be kept is increased by one. e.g. 52.87 rounded to three significant figures is 52.9.

Question 26.
Round off each of the following to the number of significant digits indicated:
i. 1.223 to two digits
ii. 12.56 to three digits
iii. 122.17 to four digits
iv. 231.5 to three digits
Answer:
i. 1.223 to two digits = 1.2
This is because the third digit is less than 5, so we drop it and all the other digits to its right.
ii. 12.56 to three digits = 12.6
This is because the fourth digit is greater than 5, so we drop it and add 1 to the third digit.
iii. 122.17 to four digits = 122.2
This is because the fifth digit is greater than 5, so we drop it and add 1 to the fourth digit.
iv. 231.5 to three digits = 232
This is because the fourth digit is 5, so we drop it and add 1 to the third digit.

Question 27.
Add 5.55 × 10⁴ and 6.95 × 10³ and express the result in scientific notation.
Solution:
To perform addition operation, first the numbers are written in such a way that they have the same exponent. The coefficients are then added.
(5.55 × 10⁴) + (6.95 × 10³)= (5.55 × 10⁴) + (0.695 × 10⁴)
= (5.55 +0.695) × 10⁴
= 6.245 × 10⁴

Question 28.
Add 1.77 × 10² and 2.23 × 10³ and express the result in scientific notation.
Solution:
To perform addition operation, first the numbers are written in such a way that they have the same exponent. The coefficients are then added.
(1.77 × 10²) + (2.23 × 10³) = (0.177 × 10³) + (2.23 × 10³)
= (0.177 + 2.23) × 10³
= 2.407 × 10³

Question 29.
Subtract 5.8 × 10^-3 from 3.5 × 10^-2 and express result in scientific notation.
Solution:
To perform subtraction operation, first the numbers are written in such a way that they have the same exponent. Then subtraction of coefficients can be done.
(3.5 × 10^-2)- (5.8 × 10^-3) = (3.5 × 10^-2) – (0.58 × 10^-2)
= (3.5 – 0.58) × 10^-2
= 2.92 × 10^-2

Question 30.
Subtract 6.90 × 10^-5 from 5.11 × 10^-4 and express the result in scientific notation.
Solution:
To perform subtraction operation, first the numbers are written in such a way that they have the same exponent. Then subtraction of coefficients can be done.
(5.11 × 10^-4) – (6.90 × 10^-5) = (5.11 × 10^-4) – (0.690 × 10^-4)
= (5.11 – 0.690) × 10^-4
= 4.42 × 10^-4

Question 31.
Perform following calculations and express results in scientific notations (exponential notations),
i. (1.5 × 10^-6) – (5.8 × 10^-7)
ii. (9.8 × 10^-3) – (8.8 × 10^-3)
iii. (6.5 × 10^-8) – (5.5 × 10^-9)
Solution:
To perform subtraction operation, first the numbers are written in such a way that they have the same exponent. Then subtraction of coefficients can be done.
i. (1.5 × 10^-6) – (5.8 × 10^-7) = (1.5 × 10^-6) – (0.58 × 10^-6)
= (1.5 – 0.58) × 10^-6
= 0.92 × 10^-6
= 9.2 × 10^-7

ii. (9.8 × 10^-3) – (8.8 × 10^-3) = (9.8 – 8.8) × 10^-3
= 1.0 × 10^-3

iii. (6.5 × 10^-8) – (5.0 × 10^-9) = (6.5 × 10^-8) – (0.50 × 10^-8)
= (6.5 – 0.50) × 10^-8
= 6.0 × 10^-8

Question 32.
Multiply 5.6 × 10⁵ and 6.9 × 10⁸ and express result in scientific notation.
Solution:
(5.6 × 10⁵) × (6.9 × 10⁸) = (5.6 × 6.9) (10⁵⁺⁸)
= 38.64 × 10¹³
= 3.864 × 10¹⁴

Question 33.
Multiply 9.8 × 10^-2 and 2.5 × 10^-6 and express result in scientific notation.
Solution:
(9.8 × 10^-2) × (2.5 × 10^-6) = (9.8 × 2.5) (10^-2+(-6))
= (9.8 × 2.5) × (10^-2-6)
= 24.5 × 10^-8
= 2.45 × 10^-7

Question 34.
Perform following calculations and express results in scientific notations (exponential notations).
i. (2.5 × 10^-6) × (1.8 × 10^-7)
ii. (4.5 × 10^-3) × (1.8 × 10³)
iii. (8.5 × 10⁷) × (3.5 × 10⁹)
Solution:
i. (2.5 × 10^-6) × (1.8 × 10^-7) = (2.5 × 1.8) (10^-6+(-7))
= (2.5 × 1.8) × (10^-6-7)
= 4.5 × 10^-13

ii. (4.5 × 10-3) × (1.8 × 103) = (4.5 × 1.8) (10^-3+3)
= (4.5 × 1.8) × (10⁰)
= 8.1

iii. (8.5 × 10⁷) × (3.5 × 10⁹) = (8.5 × 3.5) (10⁷⁺⁹)
= (8.5 × 3.5) × 10¹⁶
= 29.75 × 10¹⁶
= 2.975 × 10¹⁷
[Note: To express number in scientific notation, the number has to be greater than or equal to 10 or less than 1. The number, 8.1 is greater than 1, but less than 10 and hence, it cannot be expressed in scientific notation.]

Question 35.
In laboratory experiment, 10 g potassium chlorate sample on decomposition gives following data: The sample contains 3.8 g of oxygen and the actual mass of oxygen in the quantity of potassium chlorate is 3.92 g. Calculate absolute error and relative error.
Solution:
The observed value is 3.8 g and accepted (true) value is 3.92 g.
i. Absolute error = Observed value – True value
= 3.8 – 3.92
= -0.12 g

[Note: The negative sign indicates that experimental result is lower than the true value.]
Ans: i. Absolute error = -0.12 g
ii. Relative error = -3.06%

Question 36.
12.15 g of magnesium gives 20.20 g of magnesium oxide on burning. The actual mass of magnesium oxide that should be produced is 20.15 g. Calculate absolute error and relative error.
Solution:
The observed value is 20.20 g and accepted (true) value is 20.15 g.
i. Absolute error = Observed value – True value
= 20.20 – 20.15
= 0.05 g

Ans: i. Absolute error = 0.05 g
ii. Relative error = 0.25 %

Question 37.
The three identical samples of potassium chlorate are decomposed. The mass of oxygen is determined to be 3.87 g, 3.95 g and 3.89 g for the set. Calculate absolute deviation and relative deviation.
Solution:
Mean = \(\frac{3.87+3.95+3.89}{3}\) = 3.90

Sample	Mass of oxygen	Absolute deviation = | Observed value – Mean |
1	3.87 g	0.03 g
2	3.95 g	0.05 g
3	3.89 g	0.01 g

Ans: i. Absolute deviation in each observation = 0.03 g, 0.05 g, 0.01 g
Relative deviation = 0.8%

Question 38.
In repeated measurements in volumetric analysis, the end-points were observed as 11.15 mL, 11.17 mL, 11.11 mL and 11.17 mL. Calculate mean absolute deviation and relative deviation.
Solution:
Mean = \(\frac{11.15+11.17+11.11+11.17}{4}\) = 11.15

Measurement	End-point	Absolute deviation = |Observed value – Mean|
1	11.15 mL	0
2	11.17 mL	0.02 mL
3	11.11 mL	0.04 mL
4	11.17 mL	0.02 mL

Ans: i. Mean absolute deviation = ±0.02 mL
ii. Relative deviation = 0.2%

Question 39.
Calculate the mass percentages of H, P and O in phosphoric acid if atomic masses are H = 1, P = 31 and O = 16.
Solution:
Atomic mass of H = 1, P = 31 and 0=16
The mass percentage of hydrogen, phosphorus, oxygen in H₃PO₄
Formula:

Calculation: Molecular formula of phosphoric acid: H₃PO₄
∴ Molar mass of H₃PO₄ = 3 × (1) + 1 × (31) + 4 × (16)
= 3 + 31 + 64
= 98 g mol^-1
Percentage of H = \(\frac {3}{98}\) × 100 = 3.06%
Percentage of P = \(\frac {31}{98}\) × 100 = 31.63%
Percentage of O = \(\frac {64}{98}\) × 100 = 65.31%
Ans: Mass percentage of H, P and O in phosphoric acid are 3.06%, 31.63% and 65.31% respectively.

Question 40.
Calculate the percentage composition of the elements in HNO₃ (H = 1, N = 14, O = 16).
Solution:
Atomic mass of H = 1, N = 14 and O = 16
The mass percentage of H, N and O in HNO₃
Formula:

Calculation: Molecular formula of HNO₃
∴ Molar mass = 1 × (1) + 1 × (14) + 3 × (16) = 1 + 14 + 48 = 63 g mol^-1
∴ Percentage of H = \(\frac {1}{63}\) × 100 = 1.59%
Percentage of N = \(\frac {14}{63}\) × 100 = 22.22%
Percentage of O = \(\frac {48}{63}\) × 100 = 76.19%
Ans: Mass percentage of H, N and O in HNO₃ are 1.59%, 22.22% and 76.19% respectively.

Question 41.
A compound contains 4.07% hydrogen, 24.27% carbon and 71.65% chlorine by mass. Its molar mass is 98.96 g mol^-1. What is its empirical formula and molecular formula? Atomic masses of hydrogen, carbon and chlorine are 1.008,12.000 and 35.453 u, respectively
Solution:
Given: Percentage of H, C and Cl = 4.07% , 24.27% and 71.65% by mass respectively.
To find: Empirical formula and molecular formula
Calculation: Step I:
Check whether the sum of all the percentages is 100.
4.07 + 24.27 + 71.65 = 99.99 ≈ 100
Therefore, no need to consider presence of oxygen atom in the molecule.

Step II:
Conversion of mass percent to grams. Since we are having mass percent, it is convenient to use 100 g of the compound as the starting material. Thus, in the 100 g sample of the above compound, 4.07 g hydrogen 24.27 g carbon and 71.65 g chlorine are present.

Step III:
Convert into number of moles of each element. Divide the masses obtained above by respective atomic masses of various elements.
Moles of hydrogen = \(\frac{4.07 \mathrm{~g}}{1.008 \mathrm{~g}}\) = 4.04 mol
Moles of carbon = \(\frac{24.27 \mathrm{~g}}{12.000 \mathrm{~g}}\) = 2.0225 mol
Moles of chlorine = \(\frac{71.65 \mathrm{~g}}{35.453 \mathrm{~g}}\) = 2.021 mol

Steps IV:
Divide the mole values obtained above by the smallest value among them.

Hence, the ratio of number of moles of 2 : 1 : 1 for H : C : Cl.
In case the ratios are not whole numbers, then they may be converted into whole number by multiplying by the suitable coefficient.

Step V:
Write empirical formula by mentioning the numbers after writing the symbols of respective elements. CH₂Cl is thus, the empirical formula of the above compound.

Step VI:
Writing molecular formula
a. Determine empirical formula mass: Add the atomic masses of various atoms present in the empirical formula.
For CH₂Cl, empirical formula mass = 12.000 + 2 × 1.008 + 35.453 = 49.469 g mol^-1
b. Divide molar mass by empirical formula mass

c. Multiply empirical formula by r obtained above to get the molecular formula:
Molecular formula = r × empirical formula
∴ Molecular formula is 2 × CH₂Cl i.e. C₂H₄Cl₂.
Ans: The empirical formula of the compound is CH₂Cl and the molecular formula of the compound is C₂H₄Cl₂.
[Note: The question is modified to include the determination of molecular formula of the compound.]

Question 42.
A compound with molar mass 159 was found to contain 39.62% copper and 20.13% sulphur. Suggest molecular formula for the compound (Atomic masses: Cu = 63, S = 32 and O = 16).
Solution:
Given: Atomic mass of Cu = 63, S = 32, and O = 16
Percentage of copper and sulphur = 39.62% and 20.13% respectively.
To find: The molecular formula of the compound
Calculation: % copper + % sulphur = 39.62 + 20.13 = 59.75
This is less than 100 %. Hence, compound contains adequate oxygen so that the total percentage of elements is 100%.
Hence, % of oxygen = 100 – 59.75 = 40.25%

Hence, empirical formula is CuSO₄.
Empirical formula mass = 63 + 32 +16 × 4 = 159 g mol^-1
Hence,
Molar mass = Empirical formula mass
∴ Molecular formula = Empirical formula = CuSO₄
Ans: Molecular formula of the compound = CuSO₄

Question 43.
An inorganic compound contained 24.75% potassium and 34.75% manganese and some other common elements. Give the empirical formula of the compound. (K = 39 u, Mn = 54.9 u, O = 16 u)
Solution:
Given: Atomic mass of K = 39 u, Mn = 59 u, and O = 16 u.
Percentage of potassium and manganese = 24.75 % and 34.75% respectively
To find: The empirical formula of the given inorganic compound
Calculation: Percentage of potassium = 24.75%
Percentage of manganese = 34.75%
Total percentage = 59.50%
∴ Remaining must be that of oxygen
∴ Percentage of oxygen = 100 – 59.50 = 40.50%
Moles of K = \(\frac{\% \text { of } \mathrm{K}}{\text { Atomic mass of } \mathrm{K}}=\frac{24.75}{39}\) = 0.635 mol

Empirical formula = KMnO₄
Ans: The empirical formula of given inorganic compound is KMnO₄.

Question 44.
An organic compound contains 40.92% carbon by mass, 4.58% hydrogen and 54.50% oxygen. Determine the empirical formula of the compound.
Solution:
Given: Percentage mass of carbon = 40.92%; Percentage mass of hydrogen = 4.58%
Percentage mass of oxygen = 54.50%
To find: The empirical formula of compound
Calculation:

∴ Ratio = 1 : 1.34 : 1
Multiply by 3 to get whole number
∴ Ratio = 3 : 4.02 : 3 ≈ 3 : 4 : 3
∴ The empirical formula of the compound is C₃H₄O₃.
Ans: Empirical formula of the compound is C₃H₄O₃.

Question 45.
Define stoichiometric calculations.
Answer:
Calculations based on a balanced chemical equation are known as stoichiometric calculations.

Question 46.
Give reason: Balanced chemical equation is useful in solving problems based on chemical equations.
Answer:
Balanced chemical equation is symbolic representation of a chemical reaction. It provides the following information, which is useful in solving problems based on chemical equations:

• It indicates the number of moles of the reactants involved in a chemical reaction and the number of moles of the products formed.
• It indicates the relative masses of the reactants and products linked with a chemical change, and
• It indicates the relationship between the volume/s of the gaseous reactants and products, at STP.

Hence, balanced chemical equation is useful in solving problems based on chemical equations.

Question 47.
What are different types of stoichiometric problems? Write steps involved in solving stoichiometric problems.
Answer:
i. Generally, problems based on stoichiometry are of the following types:

• Problems based on mass-mass relationship
• Problems based on mass-volume relationship
• Problems based on volume-volume relationship.

ii. Steps involved in problems based on stoichiometric calculations:

• Write down the balanced chemical equation representing the chemical reaction.
• Write the number of moles and the relative masses or volumes of the reactants and products below the respective formulae.
• Relative masses or volumes should be calculated from the respective formula mass referring to the condition of STP.
• Apply the unitary method to calculate the unknown factors) as required by the problem.

Question 48.
Calculate the mass of carbon dioxide and water formed on complete combustion of 24 g of methane gas. (Atomic masses, C = 12 u, H = 1 u, O = 16 u)
Solution:
Mass of methane consumed in reaction = 24 g
Atomic mass: C = 12 u, H = 1 u, O = 16 u
To find: Mass of carbon dioxide and water formed
Calculation: The balanced chemical equation is,

Hence, 16 g of CH₄ on complete combustion will produce 44 g of CO₂.
∴ 24 g of CH₄ = \(\frac {24}{16}\) × 44 = 66 g of CO₂
Similarly, 16 g of CH₄ will produce 36 g of water.
∴ 24 g of CH₄ = \(\frac {24}{16}\) × 36 = 54 g of water
Ans: Mass of carbon dioxide and water formed respectively are 66 g and 54 g.

Question 49.
How much CaO will be produced by decomposition of 5 g CaCO₃?
Solution:
Given: Mass of CaCO₃ consumed in reaction = 5 g
To find: Mass of CaO produced
Calculation: Calcium carbonate decomposes according to the balanced equation,

So, 100 g of CaCO₃ produce 56 g of CaO.

Ans: Mass of CaO produced = 2.8 g

Question 50.
How many litres of oxygen at STP are required to burn completely 2.2 g of propane, C₃H₈ ?
Solution:
Given: Mass of propane used up in reaction = 2.2 g
To find: Volume of oxygen required at STP
Calculation:
The balanced chemical equation for the combustion of propane is,

(∵ 1 mol of ideal gas occupies 22.4 L of volume at STP)
Thus, 44 g of propane require 112 litres of oxygen at STP for complete combustion.
∴ 2.2 g of propane will require
\(\frac {112}{44}\) × 2.2 = 5.6 litres of O₂ at STP for complete combustion.
Ans: Volume of O₂ (at STP) required to bum 2.2 g propane = 5.6 litres

Question 51.
A piece of zinc weighing 0.635 g when treated with excess of dilute H₂SO₄ liberated 200 cm³ hydrogen at STP. Calculate the percentage purity of the zinc sample.
Solution:
Given: Mass of zinc = 0.635 g, volume of H₂ liberated = 200 cm³
To find: % purity of zinc sample
Calculation: The relevant balanced chemical equation is,
Zn + H₂SO₄ → ZnSO₄ + H₂
It indicates that 22.4 L of hydrogen at STP = 65 g of Zn.
(where, atomic mass of Zn = 65 u)
∴ 0.200 L of hydrogen at STP
= \(\frac{65 \mathrm{~g}}{22.4 \mathrm{~L}}\) × 200 L
= 0.5803 g of Zn
∴ Percentage purity of Zn = \(\frac{0.5803}{0.635}\) × 100
= 91.37 % (by using log tables)
Ans: Percentage purity of Zn sample = 91.37%

[Calculation using log table:
\(\frac{65 \times 0.200}{22.4}\)
= Antilog₁₀ [log₁₀ (65) + log₁₀ (0.200) – log₁₀ (22.4)]
= Antilog₁₀ [1.8129 + \(\overline{1} .3010\) – 1.3502]
= Antilog₁₀ [latex]\overline{1} .7637[/latex] = 0.5803
\(\frac{0.5803}{0.635} \times 100=\frac{58.03}{0.635}\)
= Antilog₁₀ [log₁₀ (58.03) – log₁₀ (0.635)]
= Antilog₁₀ [1.7636 – \(\overline{1} .8028\)]
= Antilog₁₀ [1.9608] = 91.37]

Question 52.
Explain with the help of a chemical reaction how limiting reagent works.
Answer:

• Consider the formation of nitrogen dioxide (NO₂) from nitric oxide (NO) and oxygen.
  2NO_(g) + O_2(g) → 2NO_2(g)
• Suppose initially, we take 8 moles of NO and 7 moles of O₂.
• To determine the limiting reagent, calculate the number of moles NO₂ produced from the given initial quantities of NO and O₂. The limiting reagent will yield the smaller amount of the product.
• Starting with 8 moles of NO, the number of NO₂ produced is,
  8 mol NO × \(\frac{2 \mathrm{~mol} \mathrm{NO}_{2}}{2 \mathrm{~mol} \mathrm{NO}}\) = 8 mol NO₂
• Starting with 7 moles of O₂, the number of moles NO₂ produced is,
  7 mol O₂ × \(\frac{2 \mathrm{~mol} \mathrm{NO}_{2}}{1 \mathrm{~mol} \mathrm{NO}}\) = 14 mol NO₂
• Since, 8 moles NO result in a smaller amount of NO₂, NO is the limiting reagent, and O₂ is the excess reagent, before reaction has started.

Question 53.
Urea [(NH₂)₂CO] is prepared by reacting ammonia with carbon dioxide.
2NH_3(g) + CO_2(g) → (NH₂)₂CO_(aq) + H₂O_(l)
In one process, 637.2 g of NH₃ are treated with 1142 g of CO₂.
i. Which of the two reactants is the limiting reagent?
ii. Calculate the mass of (NH₂)₂CO formed.
iii. How much excess reagent (in grams) is left at the end of the reaction?
Solution:
i. If 637.2 g of NH₃ react completely, calculate the number of moles of (NH₂)₂CO, that could be produced, by the following relation.
Mass of NH₃ → Moles of NH₃ → Moles of (NH₂)₂CO

If 1142 g of CO₂ react completely, calculate the number of moles of (NH₂)₂CO, that could be produced, by the following relation.
Mass of CO₂ → Moles of CO₂ → Moles of (NH₂)₂CO

Since NH₃ produces smaller amount of (NH₂)₂CO, the limiting reagent is NH₃.

iii. Starting with 18.71 moles of (NH₂)₂CO, we can determine the mass of CO₂ that reacted using the mole ratio from the balanced equation and the molar mass of CO₂ by the following relation.
Moles of (NH₂)₂CO → Moles of CO₂ → Grams of CO₂

The amount of CO₂ remaining = 1142 g – 823.4 g = 318.6 g ≈ 319 g CO₂ remaining
Ans: i. Limiting reagent = NH₃
ii. Mass of (NH₂)₂CO produced = 1124 g
iii. Mass of CO₂ remaining = 319 g

Question 54.
6 g of H₂ reacts with 32 g of O₂ to yield water. Which is the limiting reactant? Find the mass of water produced and the amount of excess reagent left.
Solution:
i. The reaction is: 2H_2(g) + O_2(g) → 2H₂O_(l)
If 6 g of H₂ react completely, calculate the number of moles of H₂O, that could be produced, by the following relation.
Mass of H₂ → Moles of H₂ → Moles of H₂O

If 32 g of O₂ react completely, calculate the number of moles of H₂O, that could be produced, by the following relation.
Mass of O₂ → Moles of O₂ → Moles of H₂O

Since O₂ produces smaller amount of H₂O, the limiting reagent is O₂.

iii. Starting with 2 moles of H₂O, we can determine the mass of H₂ that reacted using the mole ratio from the balanced equation and the molar mass of H₂ by the following relation.
Moles of H₂O → Moles of H₂ → Grams of H₂

The amount of H₂ remaining = 6g – 4g = 2g H₂ remaining
Ans: i. Limiting reagent = O₂
ii. Mass of H₂O produced = 36 g
iii. Mass of H₂ remaining = 2 g

Question 55.
Name different ways to express the concentration of a solution (or the amount of substance in a given volume of solution).
Answer:

• Mass percent or weight percent (w/w %)
• Mole fraction
• Molarity (M)
• Molality (m)

Question 56.
State the formula to obtain mass percent.
Answer:
Mass percent (w/w %) = \(\frac{\text { Mass of Solute }}{\text { Massof solution }} \times 100\)

Question 57.
Why is molality NOT affected by temperature?
Answer:

• Molality is the number of moles of solute present in 1 kg of solvent. Therefore, molality is mass dependent.
• Mass remains unaffected with temperature.

Hence, molality is not affected by temperature.

Question 58.
State TRUE or FALSE. Correct the statement if false.
i. A majority of reactions in the laboratory are carried out in in gaseous forms.
ii. Molarity is the most widely used to express the concentration of solution.
iii. Molality of a solution changes with temperature.
Answer:
i. False
A majority of reactions in the laboratory are carried out in solution forms.
ii. Tme
iii. False
Molality of a solution does not change with temperature.

Question 59.
A solution is prepared by adding 2 g of a substance A to 18 g of water. Calculate the mass percent of the solute.
Solution:
Given: Mass of substance = 2 g, mass of water = 18 g
To find: Mass % of solute

Ans: Mass percent of A = 10 % w/w

Question 60.
Calculate the molarity of NaOH in the solution prepared by dissolving its 4 g in enough water to form 250 mL of the solution.
Solution:
Given: Mass of solute (NaOH) = 4 g, volume of solution = 250 mL = 0.250 L
To find: Molarity of the solution

Ans: Molarity of the NaOH solution = 0.4 M

Question 61.
The density of 3 M solution of NaCl is 1.25 g mL^-1. Calculate molality of the solution.
Solution:
Given: Molarity of the solution = 3 M, density of the solution = 1.25 g mL^-1
To find: Molality of the solution
Formula:

Calculation: Molarity = 3 mol L^-1
∴ Mass of NaCl in 1 L solution = 3 × 58.5 = 175.5 g
Mass of 1 L solution = 1000 × 1.25 = 1250 g (∵ Density = 1.25 g mL^-1)
Mass of water in solution = 1250 – 175.5 = 1074.5 g = 1.0745 kg

Ans: Molality of the NaCl solution = 2.790 m

[Calculation using log table:
\(\frac{3}{1.0745}\)
= Antilog₁₀ [log₁₀ (3) – log₁₀ (1.0745)]
= Antilog₁₀ [0.4771 – 0.0315]
= Antilog₁₀ [0.4456] = 2.790]

Question 62.
Calculate the molarity of 1.8 g HNO₃ dissolved in 250 mL aqueous solution.
Solution:
Mass of HNO₃ = 1.8 g,
volume of solution = 250 mL = 0.250 L
To find: Molarity
Formulae:

Calculation: Molar mass of HNO₃ = 63 g mol^-1
Using formula (i),

Ans: Molarity of the HNO₃ solution = 0.114 M

Question 63.
What volume in mL of a 0.1 M H₂SO₄ solution will contain 0.5 moles of H₂SO₄?
Solution:
Given: Molarity of H₂SO₄ solution = 0.1 M
Moles of H₂SO₄ = 0.5 mol
To find: Volume of H₂SO₄ solution

= 5 L
= 5000 L
Ans: Volume of a 0.1 M H₂SO₄ solution = 5000 mL

Question 64.
A mixture has 18 g water and 414 g ethanol. What are the mole fractions of water and ethanol?
Solution:
Given: Mass of water = 18 g, mass of ethanol = 414 g
To find: Mole fractions of water and ethanol
Formulae:


Ans: Mole fraction of water = 0.1
Mole fraction of ethanol = 0.9

Question 65.
Explain in brief: Use of graphs in analytical chemistry.
Answer:
i. Analytical chemistry often involves deducing some relation between two or more properties of matter under study.
ii. For example, the relation between temperature and volume of a given amount of gas.
iii. A set of experimentally measured values of volume and temperature of a definite mass of a gas upon plotting on a graph paper appears as in the figure below:

iv. When the points are directly connected, a zig zag pattern results as shown below:

From the above pattern, no meaningful result can be deduced.
v. A smooth curve (or average curve) passing through these points can be drawn as shown below. This straight line is consistent with the V ∝ T .

vi. While fitting the points into a smooth curve, all the plotted points should be evenly distributed. This can be verified mathematically, by drawing a perpendicular from each point to the curve. The perpendicular represents deviation of each point from the curve. Take sum of all the perpendiculars on side of the line and sum of all the perpendiculars on another side of the line separately. If the two sums are equal (or nearly equal), the curve drawn shows the experimental points in the best possible representation

Question 66.
1.5 g of an impure sample of sodium sulphate dissolved in water was treated with excess of barium chloride solution when 1.74 g of BaSO₄ was obtained as dry precipitate. Calculate the percentage purity of the sample.
Solution:

The chemical equation representing the reaction is:

To calculate the mass of Na₂SO₄ from which 1.74 g of BaSO₄ is obtained:
233 g of BaSO₄ is produced from 142 g of Na₂SO₄.
∴ Mass of Na₂SO₄ from which 1.74 g of BaSO₄ would be obtained = \(\frac {142}{233}\) × 1.74 = 1.06 g
∴ The mass of pure Na₂SO₄ present in 1.5 g of impure sample = 1.06 g
To calculate the percentage purity of the impure sample:
1.5 g of impure sample contains 1.06 g of pure Na₂SO₄
∴ 100 g of the impure sample will contain = \(\frac{1.06}{1.5}\) × 100 = 70.67 g of pure Na₂SO₄
Ans: Percentage purity of the sample is 70.67 %.

Question 67.
Calculate the amount of lime Ca(OH)₂, required to remove hardness of 50,000 L of well water which has been found to contain 1.62 g of calcium bicarbonate per 10 L .
Solution:
Calculation of total Ca(HCO₃)₂ present:
10 L of water contains 1.62 g of Ca(HCO₃)
∴ 50,000 L of water will contain \(\frac{1.62}{10}\) × 50,000 = 8100 g of Ca(HCO₃)
Calculation of lime required:
The balanced equation for the reaction:

∴ 162 g of Ca(HCO₃) requires 74 g of lime.
Mass of lime required by 8100 g of Ca(HCO₃) = \(\frac {74}{162}\) × 8100 g = 3700 g = 3.7 kg
Ans: The amount of lime required to remove hardness of 50,000 L of well water, with 1.62 g of calcium bicarbonate per 10 L, is 3.7 kg.

Multiple Choice Questions

1. The number of significant figures in 0.0110 is …………….
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(B) 3

2. For the following measurements in which the true value is 4.0 g, find the CORRECT statement.

Student	Readings (g)
A	4.01	3.99
B	4.05	3.95

(A) Results of both the students are neither accurate nor precise.
(B) Results of student A are both precise and accurate.
(C) Results of student A are neither precise nor accurate.
(D) Results of student B are both precise and accurate.
Answer:
(B) Results of student A are both precise and accurate.

3. 18.238 is rounded off to four significant figures as ………….
(A) 18.20
(B) 18.23
(C) 18.2360
(D) 18.24
Answer:
(D) 18.24

4. The % of H₂O in Fe(CNS)₃.3H₂O is ……………..
(A) 34
(B) 11
(C) 19
(D) 46
Answer:
(C) 19

5. The molecular mass of an organic compound is 78 g mol^-1. Its empirical formula is CH. The molecular formula is ………….
(A) C₂H₄
(B) C₂H₂
(C) C₆H₆
(D) C₄H₄
Answer:
(C) C₆H₆

6. The percentage of oxygen in NaOH is ……………
(A) 40%
(B) 60%
(C) 8%
(D) 10%
Answer:
(A) 40%

7. 1.2 g of Mg (At. mass 24) will produce MgO equal to …………….
(A) 0.05 mol
(B) 0.03 mol
(C) 0.01 mol
(D) 0.02 mol
Answer:
(A) 0.05 mol

8. …………. reagent is the reactant that reacts completely but limits further progress of the reaction.
(A) Oxidizing
(B) Reducing
(C) Limiting
(D) Excess
Answer:
(C) Limiting

9. If a solution is made up of 1 mol ethanol and 9 mol water, then mole fraction of water in the solution is ……………
(A) 0.1
(B) 0.5
(C) 0.9
(D) 1.0
Answer:
(C) 0.9

10. 0.9 glucose (C₆H₁₂O₆) is present in 1 L of solution. Find molarity.
(A) 5 M
(B) 50 M
(C) 0.005 M
(D) 0.5 M
Answer:
(C) 0.005 M

11. Molality of a solution is the ……………
(A) number of moles of solute present in 1 kg of solvent
(B) number of moles of solute present in 1 L of solution
(C) mass of solute present in 1 kg of solvent
(D) number of moles of solute present in 1 kg of solution
Answer:
(A) number of moles of solute present in 1 kg of solvent

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry

Question 1.
Define chemistry.
Answer:
Chemistry is the study of matter, its physical and chemical properties, and the physical and chemical changes it undergoes under different conditions.

Question 2.
Why is chemistry called a central science?
Answer:

1. Knowledge of chemistry is required in the studies of physics, biological sciences, applied sciences, and earth and space sciences.
2. Chemistry is involved in every aspect of day-to-day life, i.e. the air we breathe, the food we eat, the fluids we drink, our clothing, transportation and fuel supplies, etc.

Hence, chemistry is called a central science.

Question 3.
Give reason: Although chemistry has ancient roots, it has developed as modern science.
Answer:
Technological development in sophisticated instruments has expanded knowledge of chemistry which, now, has been used in applied sciences such as medicine, dentistry, engineering, agriculture, and daily home use products. Hence, due to development and advancement in science and technology, chemistry has developed as modem science.

Question 4.
How is chemistry traditionally classified?
Answer:
Chemistry is traditionally classified into five branches:

• Organic chemistry
• Inorganic chemistry
• Physical chemistry
• Biochemistry
• Analytical chemistry

Question 5.
Explain the following terms:
i. Organic chemistry
ii. Inorganic chemistry
iii. Physical chemistry
Answer:
i. Organic chemistry: It deals with properties and reactions of compounds of carbon.
ii. Inorganic chemistry: It deals with the study of all the compounds which are not organic.
iii. Physical chemistry: It deals with the study of properties of matter, the energy changes and the theories, laws and principles that explain the transformation of matter from one form to another. It also provides basic framework for all the other branches of chemistry.

Question 6.
Distinguish between
i. Mixtures and pure substances
ii. Mixtures and compounds
Answer:
i.

	Mixtures	Pure substances
a.	Mixtures have no definite chemical composition.	Pure substances have a definite chemical composition.
b.	Mixtures have no definite properties.	Pure substances always have the same properties regardless of their origin.
e.g.	Paint (mixture of oils, pigment, additive), concrete (a mixture of sand, cement, water), etc.	Pure metal, distilled water, etc.

ii.

	Mixtures	Compounds
a.	Mixtures have no definite chemical composition.	Compounds are made up of two or more elements in fixed proportion.
b.	The constituents of a mixture can be easily separated by physical method.	The constituents of a compound cannot be easily separated by physical method.
e.g.	Paint (mixture of oils, pigment, additive), concrete (a mixture of sand, cement, water), etc.	Water, table salt, sugar, etc.

Question 7.
What is the difference between element and compound?
Answer:
Elements cannot be broken down into simpler substances while compounds can be broken down into simpler substances by chemical changes.

Question 8.
Explain: States of matter
Answer:
There are three different states of matter as follows:

1. Solid: Particles are held tightly in perfect order. They have definite shape and volume.
2. Liquid: Particles are close to each other but can move around within the liquid.
3. Gas: Particles are far apart as compared to that of solid and liquid.

These three states of matter can be interconverted by changing the conditions of temperature and pressure.

Question 9.
Explain: Physical and chemical properties
Answer:
i. Physical properties: These are properties which can be measured or observed without changing the identity or the composition of the substance. e.g. Colour, odour, melting point, boiling point, density, etc.

ii. Chemical properties: These are properties in which substances undergo change in chemical composition. e.g. Coal bums in air to produce carbon dioxide, magnesium wire bums in air in the presence of oxygen to form magnesium oxide, etc.

Question 10.
How are properties of matter measured?
Answer:

• Measurement involves comparing a property of matter with some fixed standard which is reproducible and unchanging.
• Properties such as mass, length, area, volume, time, etc. are quantitative in nature and can be measured.
• A quantitative measurement is represented by a number followed by units in which it is measured.
• These units are arbitrarily chosen on the basis of universally accepted standards. e.g. Length of class room can be expressed as 10 m. Here, 10 is the number and ‘m’ is the unit ‘metre’ in which the length is measured.

Question 11.
Define: Units
Answer:
The arbitrarily decided and universally accepted standards are called units.
e.g. Metre (m), kilogram (kg).

Question 12.
What are the various systems in which units are expressed?
Answer:
Units are expressed in various systems like CGS (centimetre for length, gram for mass and second for time), FPS (foot, pound, second) and MKS (metre, kilogram, second) systems, etc.

Question 13.
What are SI units? Name the fundamental SI units.
Answer:
SI Units: In 1960, the general conference of weights and measures proposed revised metric system, called International system of Units i.e. SI system (abbreviated from its French name).
The seven fundamental SI units are as given below:

No.	Base physical quantity	SI unit	Symbol
i.	Length	Metre	k
ii.	Mass	Kilogram	kg
iii.	Time	Second	s
iv.	Temperature	Kelvin	K
v.	Amount of substance	Mole	mol
vi.	Electric current	Ampere	A
vii.	Luminous intensity	Candela	cd

[Note: Units for other quantities such as speed, volume, density, etc. can be derived from fundamental SI units.]

Question 14.
What is the basic unit of mass in the SI system?
Answer:
The basic unit of mass in the SI system is kilogram (kg).

Question 15.
Name the following:
i. Full form of CGS unit system
ii. Full form of FPS unit system
iii. The SI unit of length
iv. Symbol used for Candela unit
v. SI unit of electric current
vi. SI unit of electric current
Answer:
i. Centimetre Gram Second
ii. Foot Pound Second
iii. Metre (m)
iv. Cd
v. Kelvin (K)
vi. Ampere (A)

Question 16.
Give reason: The mass of a body is more fundamental property than its weight.
Answer:

• Mass is an inherent property of matter and is the measure of the quantity of matter of a body.
• The mass of a body does not vary with respect to its position.
• On the other hand, the weight of a body is a result of the mass and gravitational attraction
• Weight varies because the gravitational attraction of the earth for a body varies with the distance from the centre of the earth.

Hence, the mass of a body is more fundamental property than its weight.

Question 17.
How is gram related to the SI unit kilogram?
Answer:
The SI unit kilogram (kg) is related to gram (g) as 1 kg = 1000 g= 10³ g.
[Note: ‘Gram’ is used for weighing small quantities of chemicals in the laboratories.
Other commonly used quantity is ‘milligram’. 1 kg = 1000 g = 10⁶ mg]

Question 18.
Why are fractional units of the SI units of length often used? Give two examples of the fractional units of length. How are they related to the SI unit of length?
Answer:
i. Some properties such as the atomic radius, bond length, wavelength of electromagnetic radiation, etc. are very small and therefore, fractional units of the SI unit of length are often used to express these properties.
ii. Fractional units of length: Nanometre (nm), picometre (pm), etc.
iii. Nanometre (nm) and picometre (pm) are related to the SI unit of length (m) as follows:
1 nm = 10^-9 m, 1 pm = 10^-12 m

Question 19.
Define: Volume
Answer:
Volume is the amount of space occupied by a three-dimensional object. It does not depend on shape.

Question 20.
State the common unit used for the measurement of volume of liquids and gases.
Answer:
The common unit used for the measurement of volume of liquids and gases is litre (L).

Question 21.
How is the SI unit of volume expressed?
Answer:
The SI unit of volume is expressed as (metre)³ or m³.

Question 22.
Name some glassware that are used to measure the volume of liquids and solutions.
Answer:

• Graduated cylinder
• Burette
• Pipette

Question 23.
What is a volumetric flask used for in laboratory?
Answer:
A volumetric flask is used to prepare a known volume of a solution in laboratory.

Question 24.
What is density of a substance? How is it measured?
Answer:
Density:

• Density of a substance is its mass per unit volume. It is the characteristic property of any substance.
• It is determined in the laboratory by measuring both the mass and the volume of a sample.
• The density is calculated by dividing mass by volume.

Question 25.
How is the SI unit of density derived? State CGS unit of density.
Answer:
i. The SI unit of density is derived as follows:
Density = \(\frac{\text { SI unit mass }}{\text { SI unit volume }}\)
= \(\frac{\mathrm{kg}}{\mathrm{m}^{3}}\)
= kg m^-3

ii. CGS unit of density: g cm^-3
[Note: The CGS unit, g cm^-3 is equivalent to \(\frac{\mathrm{g}}{\mathrm{mL}}\) or g mL^-1.]

Question 26.
State three common scales of temperature measurement.
Answer:

1. Degree Celsius (°C)
2. Degree Fahrenheit (°F)
3. Kelvin (K)

Question 27.
State the temperatures in Fahrenheit scale that corresponds to 0 °C and 100 °C.
Answer:
The temperature that corresponds to 0 °C is 32 °F and the temperature that corresponds to 100 °C is 212 °F.

Question 28.
Write the expression showing the relationship between:
i. Degree Fahrenheit and Degree Celsius
ii. Kelvin and Degree Celsius
Answer:
i. The relationship between degree Fahrenheit and degree Celsius is expressed as,
°F = \(\frac {9}{5}\) (°C) + 32
ii. The relationship between Kelvin and degree Celsius is expressed as,
K = °C + 273.15

Question 29.
Convert the following degree Fahrenheit temperature to degree Celsius.
i. 50 °F ii. 10 °F
Answer:
Given: Temperature in degree Fahrenheit = 50 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 50 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
50 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(50-32) \times 5}{9}\)
= 10 °C

ii. Given: Temperature in degree Fahrenheit = 10 °F
To find: Temperature in degree Celsius
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 10 °F in the formula,
°F = \(\frac {9}{5}\) (°C) + 32
10 = \(\frac {9}{5}\) (°C) + 32
°C = \(\frac{(10-32) \times 5}{9}\)
= -12.2 °C
Ans: i. The temperature 50 °F corresponds to 10 °C.
ii. The temperature 10 °F corresponds to -12.2 °C.

Question 30.
What is a chemical combination?
Answer:

• The process in which the elements combine with each other to form compounds is called chemical combination.
• The process of chemical combination is governed by five basic laws which were discovered before the knowledge of molecular formulae.

Question 31.
State and explain the law of definite proportions.
Answer:
Law of definite proportions:
i. The law states that “A given compound always contains exactly the same proportion of elements by weight”.
ii. French chemist, Joseph Proust worked with two samples of cupric carbonate; one of which was naturally occurring cupric carbonate and other was synthetic sample. He found the composition of elements present in both the samples was same as shown below:

Cupric carbonate	% of copper	% of carbon	% of oxygen
Natural sample	51.35	9.74	38.91
Synthetic sample	51.35	9.74	38.91

iii. Thus, irrespective of the source, a given compound always contains same elements in the same proportion.

Question 32.
State and explain the law of multiple proportions.
Answer:
Law of multiple proportions:
i. John Dalton (British scientist) proposed the law of multiple proportions in 1803.
ii. It has been observed that two or more elements may combine to form more than one compound.
iii. The law states that, “ When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers”.
e.g. Hydrogen and oxygen combine to form two compounds, water and hydrogen peroxide.

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of hydrogen (2 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.

Question 33.
Show that NO and NO₂ satisfy the law of multiple proportions.
Answer:
Nitrogen and oxygen combine to form two compounds, nitric oxide (NO) and nitrogen dioxide (NO₂).

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of nitrogen (14 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 34.
Show that carbon monoxide and carbon dioxide satisfy the law of multiple proportions.
Answer:
Chemical reaction of carbon with oxygen gives two compounds, carbon monoxide (CO) and carbon dioxide (CO₂).

Here, the two masses of oxygen (16 g and 32 g) which combine with the fixed mass of carbon (12 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 16 : 32 or 1 : 2.
This is in accordance with the law of multiple proportions.

Question 35.
Show that SO₂ and SO₃ satisfy the law of multiple proportions.
Answer:
Chemical reaction of sulphur with oxygen gives two compounds, sulphur dioxide (SO₂) and sulphur trioxide (SO₃).

Here, the two masses of oxygen (32 g and 48 g) which combine with the fixed mass of sulphur (32 g) in these two compounds bear a simple ratio of small whole numbers, i.e. 32 : 48 or 2 : 3.
This is in accordance with the law of multiple proportions.

Question 36.
State and explain Gay Lussac’s law of gaseous volume with two examples.
Answer:
Gay Lussac’s law:
i. Gay Lussac proposed the law of gaseous volume in 1808.
ii. Gay Lussac’s law states that, “ When gases combine or are produced in a chemical reaction, they do so in a simple ratio by volume, provided all gases are at same temperature and pressure
e.g. a. Under identical conditions of temperature and pressure, 100 mL of hydrogen gas combine with 50 mL of oxygen gas to produce 100 mL of water vapour.

Thus, the simple ratio of volumes is 2 : 1 : 2.

b. Under identical conditions of temperature and pressure, 1 L of nitrogen gas combine with 3 L of hydrogen gas to produce 2 L of ammonia gas.

Thus, the simple ratio of volumes is 1 : 3 : 2.

Question 37.
Give two examples which support the Gay Lussac’s law of gaseous volume.
Answer:
i. Under identical conditions of temperature and pressure, 1 L of hydrogen gas reacts with 1 L of chlorine gas to produce 2 L of hydrogen chloride gas.

Thus, the ratio of volumes is 1 : 1 : 2
This is in accordance with Gay Lussac’s law.

ii. Under identical conditions of temperature and pressure, 200 mL sulphur dioxide combine with 100 mL oxygen to form 200 mL sulphur trioxide.

Thus, the ratio of volumes is 2 : 1 : 2.
This is in accordance with Gay Lussac’s law.

Question 38.
Match the following:

	Law		Statement
i.	Law of definite proportions	a.	When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers
ii.	Gay Lussac’s law	b.	Equal volumes of all gases at the same temperature and pressure contain equal number of molecules
iii.	Law of multiple proportions	c.	When gases combine or are produced in a chemical reaction they do so in a simple ratio by volume, provided all gases are at same temperature and pressure
iv.	Avogadro’s law	d.	A given compound always contains exactly the same proportion of elements by weight

Answer:
i – d,
ii – c,
iii – a,
iv – b

Question 39.
32 g of oxygen reacts with some carbon to make 56 grams of carbon monoxide. Find out how much mass must have been used.
Answer:
Given: Mass of oxygen (reactant) = 32 g, mass of carbon monoxide (product) = 56 g
To find: Mass of oxygen (reactant)
Calculation: 12 g of carbon combine with 16 g oxygen to form 28 g of carbon monoxide as follows:

Hence, (2 × 12 = 24 g) of carbon will combine with (2 × 16 = 32 g) of oxygen to give (2 × 28 = 56 g) carbon monoxide.
Ans: Mass of carbon used = 24 g

Question 40.
Calculate the mass of sulphur trioxide produced by burning 64 g of sulphur in excess of oxygen. (Average atomic mass: S = 32 u, O = 16 u).
Solution:
Given: Mass of sulphur (reactant) = 64 g
To find: Mass of sulphur dioxide (product)
Calculation: 32 g of sulphur combine with 48 g oxygen to form 80 g of sulphur trioxide as follows:

Hence, (2 × 32 = 64 g) of sulphur will combine with (2 × 48 = 96 g) of oxygen to give (2 × 80 = 160 g) sulphur trioxide.
Ans: Mass of sulphur trioxide produced = 160 g

Question 41.
Explain Dalton’s atomic theory.
Answer:
John Dalton published “A New System of chemical philosophy” in the year of 1808. He proposed the following features, which later became famous as Dalton’s atomic theory.

• Matter consists of tiny, indivisible particles called atoms.
• All the atoms of a given elements have identical properties including mass. Atoms of different elements differ in mass.
• Compounds are formed when atoms of different elements combine in a fixed ratio.
• Chemical reactions involve only the reorganization of atoms. Atoms are neither created nor destroyed in a chemical reaction.

Dalton’s atomic theory could explain all the laws of chemical combination.

Question 42.
Give reason: Dalton’s atomic theory explains the law of conservation of mass.
Answer:

• The law of conservation of mass states that, “Mass can neither be created nor destroyed” during chemical combination of matter.
• According to Dalton’s atomic theory, chemical reactions involve only the reorganization of atoms. Therefore, the total number of atoms in the reactants and products should be same and mass is conserved during a reaction.

Hence, Dalton’s atomic theory explains the law of conservation of mass.

Question 43.
Give reason: Dalton’s atomic theory explains the law of multiple proportion.
Answer:

• The law of multiple proportion states that, “When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers
• According to Dalton’s atomic theory, compounds are formed when atoms of different elements combine in fixed ratio.

Hence, Dalton’s atomic theory explains the law of multiple proportion.

Question 44.
Define: Atomic mass unit (amu).
Answer:
Atomic mass unit or amu is defined as a mass exactly equal to one twelth of the mass of one carbon-12 atom.

Question 45.
How is relative atomic mass of an atom measured?
Answer:

• The mass of a single atom is extremely small, i.e. the mass of a hydrogen atom is 1.6736 × 10^-24 g. Hence, it is not possible to weigh a single atom.
• In the present system, mass of an atom is determined relative to the mass of an atom of carbon-12 as the standard. This was decided in 1961 by international agreement.
• The atomic mass of carbon-12 is assigned as 12.00000 atomic mass unit (amu).
• The masses of all other elements are determined relative to the mass of an atom of carbon-12 (C-12).
• The atomic masses are expressed in amu which is exactly equal to one twelth of the mass of one carbon-12 atom.
• The value of 1 amu is equal to 1.6605 × 10^-24 g.

Question 46.
What is meant by Unified Mass unit?
Answer:

• Presently, instead of amu, Unified Mass has now been accepted as the unit of atomic mass.
• It is called Dalton and its symbol is ‘u’ or ‘Da’.

Question 47.
What is average atomic mass?
Answer:
The atomic mass of an element which exists as mixture of two or more isotopes is the average of atomic masses of its isotopes. This is called average atomic mass.

Question 48.
Define: Molecular mass
Answer:
Molecular mass of a substance is the sum of average atomic masses of the atoms of the elements which constitute the molecule.
OR
Molecular mass of a substance is the mass of one molecule of that substance relative to the mass of one carbon-12 atom.

Question 49.
How is molecular mass of a substance calculated? Give example.
Answer:
Molecular mass is calculated by multiplying average atomic mass of each element by the number of its atoms and adding them together.
e.g. Molecular mass of carbon dioxide (CO₂) is calculated as follows:
Molecular mass of CO₂ = (1 × average atomic mass of C) + (2 × average atomic mass of O)
= (1 × 12.0 u) + (2 × 16.0 u)
= 44.0 u

Question 50.
Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g. What is the atomic mass of hydrogen in u?
Solution:
Given: Mass of an atom of hydrogen in gram is 1.6736 × 10^-24 g.
To find: Atomic mass of hydrogen in u
Calculation: 1.66056 × 10^-24 g = 1 u
∴ 1.6736 × 10^-24 g = x
x = \(\frac{1.6736 \times 10^{-24} \mathrm{~g}}{1.66056 \times 10^{-24} \mathrm{~g} / \mathrm{u}}\) = 1.008u
Ans: The atomic mass of hydrogen in u = 1.008 u

Question 51.
The mass of an atom of one carbon atom is 12.011 u. What is the mass of 20 atoms of the same isotope?
Solution:
Mass of l atom of carbon = 12.011 u
∴ Mass of 20 atoms of same carbon isotope = 20 × 12.011 u = 240.220 u
Ans: The mass of 20 atoms of same carbon isotope = 240.220 u

Question 52.
Calculate the average atomic mass of neon using the following data:

Isotope	Atomic mass	Natural Abundance
20Ne	19.9924 u	90.92%
21Ne	20.9940 u	0.26 %
22Ne	21.9914 u	8.82 %

Solution:
Average atomic mass of Neon (Ne)

Ans: Average atomic mass of neon = 20.1707 u

Question 53.
Calculate the average atomic mass of argon from the following data:

Isotope	Isotopic mass (g mol-1)	Abundance
36Ar	35.96755	0.337%
38Ar	37.96272	0.063%
40Ar	39.9624	99.600%

Solution:
Average atomic mass of argon (Ar)

Ans: Average atomic mass of argon = 39.974 g mol^-1

Question 54.
Calculate the molecular mass of the following in u:
i. H₂O ii. C₆H₅Cl iii. H₂SO₄
Solution:
i. Molecular mass of H₂O = (2 × Average atomic mass of H) + (1 × Average atomic mass of O)
= (2 × 1.0u) + (1 × 16.0 u)
= 18 u

ii. Molecular mass of C₆H₅Cl = (6 × Average atomic mass of C) + (5 × Average atomic mass of H) + (1 × Average atomic mass of Cl)
= (6 × 12.0 u) + (5 × 1.0 u) + (1 × 35.5 u)
= 112.5 u

iii. Molecular mass of H₂SO₄ = (2 × Average atomic mass of H) + (1 × Average atomic mass of S) + (4 × Average atomic mass of O)
= (2 × 1.0 u) + (1 × 32.0 u) + (1 × 16.0 u)
= 98 u
Ans: i. The molecular mass of H₂O = 18 u
ii. The molecular mass of C₆H₅Cl = 112.5 u
iii. The molecular mass of H₂SO₄ = 98 u

Question 55.
Find the mass of 1 molecule of oxygen (O₂) in amu (u) and in grams.
Solution:
Molecular mass of O₂ = 2 × 16 u
∴ Mass of 1 molecule = 32 u
∴ Mass of 1 molecule of O₂= 32 × 1.66056 × 10^-24 g = 53.1379 × 10^-24 g
Ans: Mass of 1 molecule in amu = 32 u
Mass of 1 molecule in grams = 53.1379 × 10^-24 g

Question 56.
Find the formula mass of
i. NaCl ii. Cu(NO₃)₂
Solution:
i. Formula mass of NaCl
= Average atomic mass of Na + Average atomic mass of Cl
= 23.0 u + 35.5 u = 58.5 u

ii. Formula mass of Cu(NO₃)₂
= Average atomic mass of Cu + 2 × (Average atomic mass of N + Average atomic mass of three O)
= 63.5 + 2 × [14 + (3 × 16)] = 187.5 u
Ans: i. Formula mass of NaCl = 58.5 u
ii. Formula mass of Cu(NO₃)₂ = 187.5 u

Question 57.
Find the formula mass of
i. KCl
ii. AgCl
Atomic mass of K = 39 u, Ag =108 u and Cl = 35.5 u.
Solution:
i. Formula mass of KCl
= Average atomic mass of K + Average atomic mass of Cl
= 39 u + 35.5 u = 74.5 u

ii. Formula mass of AgCl
= Average atomic mass of Ag + Average atomic mass of Cl
= 108 + 35.5 = 143.5 u
Ans: i. Formula mass of KCl = 74.5 u
ii. Formula mass of AgCl = 143.5 u

Question 58.
Calculate the number of moles and molecules of urea present in 5.6 g of urea.
Solution:
Given: Mass of urea = 5.6 g
To find: The number of moles and molecules of urea
Formulae: i. Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
ii. Number of molecules = Number of moles × Avogadro’s constant
Mass of urea = 5.6 g
Molecular mass of urea, NH₂CONH₂
= (2 × Average atomic mass of N) + (4 × Average atomic mass of H) + (1 × Average atomic mass of C) + (1 × average atomic mass of O)
= (2 × 14 u) + (4 × 1 u) + (1 × 12 u) + (1 × 16 u) = 60 u
∴ Molar mass of urea = 60 g mol^-1
∴ Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{5.6 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 0.09333 mol

[Calculation using log table:
\(\frac{5.6}{60}\)
= Antilog₁₀ [log₁₀ (5.6) – log₁₀ (60)]
= Antilog₁₀ [0.7482 – 1.7782]
= Antilog₁₀ [latex]\overline{2} .9700[/latex]
= 0.09333]

Now,
Number of molecules of urea
= Number of moles × Avogadro’s constant
= 0.09333 mol × 6.022 × 10²³ molecules/mol
= 0.5616 × 10²³ molecules (by using log table)
= 5.616 × 10²² molecules
Ans: Number of moles of urea = 0.0933 mol
Number of molecules of urea = 5.616 × 10²² molecules

[Calculation using log table:
0.09333 × 6.022
= Antilog₁₀ [log₁₀ (0.09333) + log₁₀ (6.022)]
= Antilog₁₀ [\(\overline{2} .9698\) + 0.7797]
= Antilog₁₀ [latex]\overline{1} .7495[/latex]
= 0.5616]

Question 59.
Calculate the number of atoms in each of the following:
i. 64 u of oxygen (O)
ii. 42 g of nitrogen (N)
Solution:
i. 64 u of oxygen (O) = x atoms
Atomic mass of oxygen (O) = 16 u
∴ Mass of one oxygen atom = 16 u
∴ x = \(\frac{64 \mathrm{u}}{16 \mathrm{u}}\) = 4 atoms

ii. 42 g of nitrogen (N)
Atomic mass of nitrogen = 14 u
∴ Molar mass of nitrogen = 14 g mol^-1
Now,
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{42 \mathrm{~g}}{14 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 3 mol
Now,
Number of atoms = Number of moles × Avogadro’s constant
= 3 mol × 6.022 × 10²³ atoms/mol
= 18.07 × 10²³ atoms
= 1.807 × 10²⁴ atoms
Ans: i. Number of oxygen atoms in 64 u = 4 atoms
ii. Number of nitrogen atoms in 42 g = 1.807 × 10²⁴ atoms

Question 60.
Calculate the number of atoms in each of the following.
i. 52 moles of Argon (Ar)
ii. 52 u of Helium (He)
iii. 52 g of Helium (He)
Solution:
i. 52 moles of Argon
1 mole Argon atoms = 6.022 × 10²³ atoms of Ar
∴ Number of atoms = 52 mol × 6.022 × 10²³ atoms/mol
= 313.144 × 10²³ atoms of Argon

ii. 52 g of He
Molar mass of He = mass of 1 atom of He = 4.0 u
4.0 u = 1 He
∴ 52 u = x
∴ x = 52 u × \(\frac{1 \text { atom of He }}{4.0 \mathrm{u}}\) = 13 atoms of He

iii. 52 g of He
Molar mass of He = 4.0 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{52 \mathrm{~g}}{4.0 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 13 mol
Number of atoms of He = Number of moles × Avogadro’s constant
= 13 mol × 6.022 × 10²³ atoms/mol
= 78.286 × 10²³ atoms of He
Ans. i. Number of argon atoms in 52 moles = 313.144 × 10²³ atoms of Argon
ii. Number of helium atoms in 52 u = 13 atoms of He
iii. Number of helium atoms in 52 g = 78.286 × 10²³ atoms of He

Question 61.
Calculate the number of atoms of ‘C’, ‘H’ and ‘O’ in 72.5 g of isopropanol, C₃H₇OH (molar mass 60 g mol^-1).
Solution:
Mass of isopropanol(C₃H₇OH) = 72.5 g
The number of atoms of C, H, O
Calculation: Molecular formula of isopropanol, is C₃H₇OH.
Molar mass of C₃H₇OH = 60 g mol^-1
Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{72.5 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 1.208 mol
∴ Moles of isopropanol = 1.21 mol
Number of atoms = Number of moles × Avogadro’s constant
Now, 1 molecule of isopropanol has total 12 atoms, out of which 8 atoms are of H, 3 of C and 1 of O.
∴ Number of C atoms in 72.5 g isopropanol = (3 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 2.182 × 10²⁴ atoms of carbon
∴ Number of ‘H’ atoms in 72.5 g isopropanol = (8 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 5.819 × 10²⁴ atoms of hydrogen
∴ Number of ‘O’ atoms in 72.5 g isopropanol = (1 × 1.208) mol × 6.022 × 10²³ atoms/mol
= 7.274 × 10²³ atoms of oxygen
Ans. 72.5g of isopropanol contain 2.182 ×10²⁴ atoms of H and 7.274 × 10²³ atoms of O.

Question 62.
Calculate the number of moles and molecules of ammonia (NH₃) gas in a volume 67.2 dm³ of it measured at STP.
Solution:
Given: Volume of ammonia at STP = 67.2 dm³
To find: Number of moles and molecules of ammonia
Formulae: i. Number of moles of a gas (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
ii. Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
Calculation: Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Number of moles (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
Number of moles of NH₃ = \(\frac{67.2 \mathrm{dm}^{3}}{22.4 \mathrm{dm}^{3} \mathrm{~mol}^{-1}}\)
Number of molecules = Number of moles × 6.022 × 10²³ molecules mol^-1
3.0 mol × 6022 × 10²³ molecules mol^-1
= 18.066 × 10²³ molecules
Ans: Number of moles of ammonia = 3.0 mol
Number of molecules of ammonia = 18.066 × 10²³ molecules

Question 63.
3.40 g of ammonia at STP occupies volume of 4.48 dm³. Calculate molar mass of ammonia.
Solution:
Given: Mass of ammonia = 3.40 g
Volume at STP = 4.48 dm³
To Find: Molar mass of ammonia
Calculation: Let ‘x’ grams be the molar mass of NH₃.
Molar volume of a gas = 22.4 dm³ mol^-1 at STP.
Volume occupied by 3.40 g of NH₃ at S.T.P = 4.48 dm³
Volume occupied by ‘x’ g of NH3 at S.T.P = 22.4 dm³
∴ x = \(\frac{22.4 \times 3.40}{4.48}\) = 17.0 g mol^-1
Ans: Molar mass of ammonia is 17.0 g mol^-1.

Question 64.
Veg puffs from a particular bakery have an average mass of 27.0 g, whereas egg puffs from the same bakery have an average mass of 40 g.
i. Suppose a person buys 1 kg of veg puff from the bakery. Calculate the number of veg puffs he receives.
ii. Determine the mass of egg puffs (in kg) that will contain the same number of eggs puffs as in one kilogram of veg puffs.
Solution:
i. Mass of a veg puff = 27.0 g = 0.027 kg
∴ Number of veg puffs in 1 kg = 1 / 0.027 = 37
ii. One kilogram of veg puffs contains 37 veg puffs.
Mass of 37 egg puffs = 37 × 0.040 = 1.48 kg
Ans: i. 37 veg puffs in 1 kg of puff.
ii. Mass of 37 egg puffs is 1.48 kg

Multiple Choice Questions:

1. The branch of chemistry which deals with carbon compounds is called ……………. chemistry.
(A) organic
(B) inorganic
(C) carbon
(D) bio
Answer:
(A) organic

2. A/an is a simple combination of two or more substances in which the constituent substances retain their separate identities.
(A) compound
(B) mixture
(C) element
(D) All of these
Answer:
(B) mixture

3. Which one of the following is NOT a mixture?
(A) Paint
(B) Gasoline
(C) Liquefied Petroleum Gas (LPG)
(D) Distilled water
Answer:
(D) Distilled water

4. The sum of the masses of reactants and products is equal in any physical or chemical reaction. This is in accordance with ………………
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of reciprocal proportion
Answer:
(C) law of conservation of mass

5. A sample of calcium carbonate (CaCO₃) has the following percentage composition: Ca = 40 %; C = 12 %; O = 48 %. If the law of definite proportions is true, then the weight of calcium in 4 g of a sample of calcium
carbonate from another source will be ……………..
(A) 0.016 g
(B) 0.16 g
(C) 1.6 g
(D) 16 g
Answer:
(C) 1.6 g

6. Two elements, A and B, combine to form two compounds in which ‘a’ g of A combines with ‘b₁’ and ‘b₂’g of B respectively. According to law of multiple proportion ………………
(A) b₁ = b₂
(B) b₁ and b₂ bear a simple whole number ratio
(C) a and b₁ bear a whole number ratio
(D) no relation exists between b₁ and b₂
Answer:
(B) b₁ and b₂ bear a simple whole number ratio

7. At constant temperature and pressure, two litres of hydrogen gas react with one litre of oxygen gas to produce two litres of water vapour. This is in accordance with ……………….
(A) law of multiple proportion
(B) law of definite composition
(C) law of conservation of mass
(D) law of gaseous volumes
Answer:
(D) law of gaseous volumes

8. One mole of oxygen molecule weighs …………….
(A) 8 g
(B) 32 g
(C) 16 g
(D) 6.022 × 10²³ g
Answer:
(B) 32 g

9. The mass of 0.002 mol of glucose (C₆H₁₂O₆) is ………………
(A) 0.20 g
(B) 0.36 g
(C) 0.50 g
(D) 1.80 g
Answer:
(B) 0.36 g

10. Which of the following is CORRECT?
(A) 1 mole of oxygen atoms contains 6.0221367 × 10²³ atoms of oxygen.
(B) 1 mole of water molecules contains 6.0221367 × 10²³ molecules of water.
(C) 1 mole of sodium chloride contains 6.0221367 × 10²³ formula units of NaCl.
(D) All of these
Answer:
(D) All of these

11. 180 g of glucose (C₆H₁₂O₆) contains ……………. carbon atoms.
(A) 1.8 × 10²³
(B) 1.8 × 10²⁴
(C) 3.6 × 10²³
(D) 3.6 × 10²⁴
Answer:
(C) 3.6 × 10²³

12. The number of molecules present in 8 g of oxygen gas is …………….
(A) 6.022 × 10²³
(B) 3.011 × 10²³
(C) 12.044 × 10²³
(D) 1.505 × 10²³
Answer:
(D) 1.505 × 10²³

13. The number of molecules in 22.4 cm³of ozone gas at STP is ……………….
(A) 6.022 × 10²⁰
(B) 6.022 × 10²³
(C) 22.4 × 10²⁰
(D) 22.4 × 10²³
Answer:
(A) 6.022 × 10²⁰

14. 11.2 cm³ of hydrogen gas at STP, contains …………….. moles.
(A) 0.0005
(B) 0.01
(C) 0.029
(D) 0.5
Answer:
(A) 0.0005

15. The mass of 224 mL of hydrogen gas at STP is
(A) 0.02 g
(B) 0.224 g
(C) 2.24 g
(D) 20.0 g
Answer:
(A) 0.02 g

16. 4.4 g of an unknown gas occupies 2.24 L of volume under STP conditions. The gas may be ………………
(A) CO₂
(B) CO
(C) O₂
(D) SO₂
Answer:
(A) CO₂

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 14 Semiconductors Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 14 Semiconductors

Question 1.
What are the factors on which the electrical conductivity of any solid depends?
Answer:
Electrical conduction in a solid depends on its temperature, the number of charge carriers, how easily these carries can move inside a solid (mobility), its crystal structure, types, and the nature of defects present in a solid.

Question 2.
Why are metals good conductors of electricity?
Answer:
Metals are good conductors of electricity due to a large number of free electrons (≈ 10²⁸ per m³) present in them.

Question 3.
Give the formula for the electrical conductivity of a solid and give the significance of the terms involved.
Answer:
The electrical conductivity (σ) of a solid is given by a = nqµ,
where n = charge carrier density (number of charge carriers per unit volume)
q = charge on the carriers
µ = mobility of carriers

Question 4.
Explain in brief temperature dependence of electrical conductivity of metals and semiconductors with the help of graph.
Answer:
i. The electrical conductivity of a metal decreases with increase in its temperature.

ii. When the temperature of a semiconductor is increased, its electrical conductivity also increases

Question 5.
Mention the broad classification of semiconductors along with examples.
Answer:
A broad classification of semiconductors can be:

1. Elemental semiconductors: Silicon, germanium
2. Compound Semiconductors: Cadmium sulphide, zinc sulphide, etc.
3. Organic Semiconductors: Anthracene, doped pthalocyanines, polyaniline etc.

Question 6.
What are some electrical properties of semiconductors?
Answer:

1. Electrical properties of semiconductors are different from metals and insulators due to their unique conduction mechanism.
2. The electronic configuration of the elemental semiconductors plays a very important role in their electrical properties.
3. They are from the fourth group of elements in the periodic table.
4. They have a valence of four.
5. Their atoms are bonded by covalent bonds. At absolute zero temperature, all the covalent bonds are completely satisfied in a single crystal of pure semiconductor like silicon or germanium.

Question 7.
Explain in detail the distribution of electron energy levels in an isolated atom with the help of an example.
Answer:

1. An isolated atom has its nucleus at the centre which is surrounded by a number of revolving electrons. These electrons are arranged in different and discrete energy levels.
2. Consider the electronic configuration of sodium (atomic number 11) i.e, 1s², 2s², 2p⁶, 3s¹. The outermost level 3s can take one more electron but it is half filled in sodium,
3. The energy levels in each atom are filled according to Pauli’s exclusion principle which states that no two similar spin electrons can occupy the same energy level.
4. That means any energy level can accommodate only two electrons (one with spin up state and the other with spin down state)
5. Thus, there can be two states per energy level.
6. Figure given below shows the allowed energy levels of a sodium atom by horizontal lines. The curved lines represent the potential energy of an electron near the nucleus due to Coulomb interaction.
   

Question 8.
Explain formation of energy bands in solid sodium with neat labelled energy band diagrams.
Answer:
i. For an isolated sodium atom (atomic number 11) the electronic configuration is given as 1s², 2s², 2p⁶, 3s¹. The outermost level 3s is half filled in sodium.

ii. The energy levels are filled according to Pauli’s exclusion principle.

iii. Consider two sodium atoms close enough so that outer 3s electrons can be considered equally to be part of any atom.

iv. The 3s electrons from both the sodium atoms need to be accommodated in the same level.

v. This is made possible by splitting the 3 s level into two sub-levels so that the Pauli’s exclusion principle is not violated. Figure given below shows the splitting of the 3 s level into two sub levels.

vi. When solid sodium is formed, the atoms come close to each other such that distance between them remains of the order of 2 – 3 Å. Therefore, the electrons from different atoms interact with each other and also with the neighbouring atomic cores.

vii. The interaction between the outer most electrons is more due to overlap while the inner most electrons remain mostly unaffected. Each of these energy levels is split into a large number of sub levels, of the order of Avogadro’s number due to number of atoms in solid sodium is of the order of this number.

viii. The separation between the sublevels is so small that the energy levels appear almost continuous. This continuum of energy levels is called an energy band. The bands are called 1 s band, 2s band, 2p band and so on. Figure shows these bands in sodium metal.

Question 9.
Explain concept of valence band and conduction band in solid crystal.
Answer:
A. Valence band (V.B):

1. The topmost occupied energy level in an atom is the valence level. The energy band formed by valence energy levels of atoms in a solid is called the valence band.
2. In metallic conductors, the valence electrons are loosely attached to the nucleus. At ordinary room temperature, some valence electrons become free. They do not leave the metal surface but can move from atom to atom randomly.
3. Such free electrons are responsible for electric current through conductors.

B. Conduction band (C.B):

1. The immediately next energy level that electrons from valence band can occupy is called conduction level. The band formed by conduction levels is called conduction band.
2. It is the next permitted energy band beyond valence band.
3. In conduction band, electrons move freely and conduct electric current through the solids.
4. An insulator has empty conduction band.

Question 10.
Draw neat labelled diagram showing energy bands in sodium. Why broadening of higher bands is different than that of the lower energy bands?
Answer:

Broadening of valence and higher bands is more since interaction of these electrons is stronger than the inner most electrons.

Question 11.
State the conditions when electrons of a semiconductor can take part in conduction.
Answer:

1. All the energy levels in a band, including the topmost band, in a semiconductor are completely occupied at absolute zero.
2. At some finite temperature T, few electrons gain thermal energy of the order of kT, where k is the Boltzmann constant.
3. Electrons in the bands between the valence band cannot move to higher band since these are already occupied.
4. Only electrons from the valence band can be excited to the empty conduction band, if the thermal energy gained by these electrons is greater than the band gap.
5. Electrons can also gain energy when an external electric field is applied to a solid. Energy gained due to electric field is smaller, hence only electrons at the topmost energy level gain such energy and participate in electrical conduction.

Question 12.
Define 1 eV.
Answer:
1 eV is the energy gained by an electron while it overcomes a potential difference of one volt. 1 eV= 1.6 × 10^-19 J.

Question 13.
C, Si and Ge have same lattice structure. Why is C insulator while Si and Ge intrinsic semiconductors?
Answer:

1. The 4 valence electrons of C, Si or Ge lie respectively in the second, third and fourth orbit.
2. Energy required to take out an electron from these atoms (i.e., ionisation energy E_g) will be least for Ge, followed by Si and highest for C.
3. Hence, number of free electrons for conduction in Ge and Si are significant but negligibly small for

Question 14.
What is intrinsic semiconductor?
Answer:
A pure semiconductor is blown as intrinsic semiconductor.

Question 15.
Explain characteristics and structure of silicon using a neat labelled diagram.
Answer:

1. Silicon (Si) has atomic number 14 and its electronic configuration is 1s² 2s² 2p⁶ 3s² 3p².
2. Its valence is 4.
3. Each atom of Si forms four covalent bonds with its neighbouring atoms. One Si atom is surrounded by four Si atoms at the comers of a regular tetrahedron as shown in the figure.
   

Question 16.
Describe in detail formation of holes in ii. intrinsic semiconductor.
Answer:
i. In intrinsic semiconductor at absolute zero temperature, all valence electrons are tightly bound to respective atoms and the covalent bonds are complete.

ii. Electrons are not available to conduct electricity through the crystal because they cannot gain enough energy to get into higher energy levels.

iii. At room temperature, however, a few covalent bonds are broken due to heat energy produced by random motion of atoms. Some of the valence electrons can be moved to the conduction band. This creates a vacancy in the valence band as shown in figure.

iv. These vacancies of electrons in the valence band are called holes. The holes are thus absence of electrons in the valence band and they carry an effective positive charge.

Question 17.
How does electric conduction take place inside a pure silicon?
Answer:

1. There are two different types of charge carriers in a pure semiconductor. One is the electron and the other is the hole or absence of electron.
2. Electrical conduction takes place by transportation of both carriers or any one of the two carriers in a semiconductor.
3. When a semiconductor is connected in a circuit, electrons, being negatively charged, move towards positive terminal of the battery.
4. Holes have an effective positive charge, and move towards negative terminal of the battery. Thus, the current through a semiconductor is carried by two types of charge carriers moving in opposite directions.
5. Figure given below represents the current through a pure silicon.
   

Question 18.
Why do holes not exist in conductor?
Answer:

1. In case of semiconductors, there is one missing electron from one of the covalent bonds.
2. The absence of electron leaves an empty space called as hole; each hole carries an effective positive charge.
3. In case of an conductor, number of free electrons are always available for conduction. There is no absence of electron in it. Hence holes do not exist in conductor.

Question 19.
What is the need for doping an intrinsic semiconductor?
Answer:
The electric conductivity of an intrinsic semiconductor is very low at room temperature; hence no electronic devices can be fabricated using them. Addition of a small amount of a suitable impurity to an intrinsic semiconductor increases its conductivity appreciably. Hence, intrinsic semiconductors are doped with impurities.

Question 20.
Explain what is doping.
Answer:

1. The process of adding impurities to an intrinsic semiconductor is called doping.
2. The impurity atoms are called dopants which may be either trivalent or pentavalent. The parent atoms are called hosts.
3. The dopant material is so selected that it does not disturb the crystal structure of the host.
4. The size and the electronic configuration of the dopant should be compatible with that of the host.
5. Doping is expressed in ppm (parts per million), i.e., one impurity atom per one million atoms of the host.
6. Doping significantly increases the concentration of charge carriers.

Question 21.
What is extrinsic semiconductors?
Answer:
The semiconductor with impurity is called a doped semiconductor or an extrinsic semiconductor.

Question 22.
Draw neat diagrams showing schematic electronic structure of:
i. A pentavalent atom [Antimony (Sb)]
ii. A trivalent atom [Boron (B)]
Answer:

[Note: Electronic structure of antimony is drawn as per its electronic configuration in accordance with Modern Periodic Table.]

Question 23.
With the help of neat diagram, explain the structure of n-type semiconductor in detail.
Answer:
i. When silicon or germanium crystal is doped with a pentavalent impurity such as phosphorus, arsenic, or antimony we get n-type semiconductor.

ii. When a dopant atom of 5 valence electrons occupies the position of a Si atom in the crystal lattice, 4 electrons from the dopant form bonds with 4 neighbouring Si atoms and the fifth electron from the dopant remains very weakly bound to its parent atom

iii. To make this electron free even at room temperature, very small energy is required. It is 0.01 eV for Ge and 0.05 eV for Si.

iv. As this semiconductor has large number of electrons in conduction band and its conductivity is due to negatively charged carriers, it is called n-type semiconductor.

v. The n-type semiconductor also has a few electrons and holes produced due to the thermally broken bonds.

vi. The density of conduction electrons (n_e) in a doped semiconductor is the sum total of the electrons contributed by donors and the thermally generated electrons from the host.

vii. The density of holes (n_h) is only due to the thermally generated holes of the host Si atoms.

viii. Thus, the number of free electrons exceeds the number of holes (n_e >> n_h). Thus, in n-type semiconductor electrons are the majority carriers and holes are the minority carriers.

Question 24.
What are some features of n-type semiconductor?
Answer:

1. These are materials doped with pentavalent impurity (donors) atoms.
2. Electrical conduction in these materials is due to majority charge carriers i.e., electrons.
3. The donor atom loses electrons and becomes positively charged ions.
4. Number of free electrons is very large compared to the number of holes, n_e >> n_h. Electrons are majority charge carriers.
5. When energy is supplied externally, negatively charged free electrons (majority charges carries) and positively charged holes (minority charges carries) are available for conduction.

Question 25.
With the help of neat diagram, explain the structure of p-type semiconductor in detail.
Answer:
i. When silicon or germanium crystal is doped with a trivalent impurity such as boron, aluminium or indium, we get a p-type semiconductor.

ii. The dopant trivalent atom has one valence electron less than that of a silicon atom. Every trivalent dopant atom shares its three electrons with three neighbouring Si atoms to form covalent bonds. But the fourth bond between silicon atom and its neighbour is not complete.

iii. The incomplete bond can be completed by another electron in the neighbourhood from Si atom.

iv. The shared electron creates a vacancy in its place. This vacancy or the absence of electron is a hole.

v. Thus, a hole is available for conduction from each acceptor impurity atom.

vi. Holes are majority carriers and electrons are minority carriers in such materials. Acceptor atoms are negatively charged ions and majority carriers are holes. Therefore, extrinsic semiconductor doped with trivalent impurity is called a p-type semiconductor.

vii. For a p-type semiconductor, n_h >> n_e^.

Question 26.
What are some features of p-type semiconductors?
Answer:

1. These are materials doped with trivalent impurity atoms (acceptors).
2. Electrical conduction in these materials is due to majority charge carriers i.e., holes.
3. The acceptor atoms acquire electron and become negatively charged-ions.
4. Number of holes is very large compared to the number of free electrons. n_h >> n_e. Holes are majority charge carriers.
5. When energy is supplied externally, positively charged holes (majority charge carriers) and negatively charged free electrons (minority charge carriers) are available for conduction.

Question 27.
What are donor and acceptor impurities?
Answer:

1. Every pentavalent dopant atom which donates one electron for conduction is called a donor impurity.
2. Each trivalent atom which can accept an electron is called an acceptor impurity.

Question 28.
Explain the energy levels of both donor and acceptor impurities with a schematic band structure.
Answer:
i. The free electrons donated by the donor impurity atoms occupy energy levels which are in the band gap and are close to the conduction band.

ii. The vacancies of electrons or the extra holes are created in the valence band due to addition of acceptor impurities. The impurity levels are created just above the valence band in the band gap.

Question 29.
Distinguish between p-type and n-type semiconductor.
Answer:

p-type semiconductor	n-type semiconductor
1. The impurity of some trivalent element like B, Al, In, etc. is mixed with semiconductor.	The impurity of some pentavalent element like P, As, Sb, etc. is mixed
2. The impurity atom accepts one electron hence the impurities	The impurity atom donates – one electron, hence the impurities added are known as donor impurities.
3. The holes are majority charge carriers and electrons are minority charge carriers.	The electrons are j majority charge carriers and holes are minority charge carriers.
4. The acceptor energy level is close to the valence band and far away from conduction band.	Donor energy level is close to the conduction band and far away from valence band.

Question 30.
What is the charge on a p-type and n-type semiconductor?
Answer:
n-type as well as p-type semiconductors are electrically neutral.

Question 31.
Explain the transportation of holes inside a p-type semiconductor.
Answer:
i. Consider a p-type semiconductor connected to terminals of a battery as shown.

ii. When the circuit is switched on, electrons at 1 and 2 are attracted to the positive terminal of the battery and occupy nearby holes at x and y. This creates holes at the positions 1 and 2 previously occupied by electrons.

iii. Next, electrons at 3 and 4 move towards the positive terminal and create holes in their previous positions.

iv. But, the holes are captured at the negative terminal by the electrons supplied by the battery.

v. In this way, holes are transported from one place to other and density of holes is kept constant so long as the battery is working.

Question 32.
A pure Si crystal has 4 × 10²⁸ atoms m^-3. It is doped by 1 ppm concentration of antimony. Calculate the number of electrons and holes. Given n₁ = 1.2 × 10¹⁶/m³.
Answer:
As, the atom is doped with 1 ppm concentration of antimony (Sb).
1 ppm = 1 parts per one million atoms. = 1/10⁶
∴ no. of Si atoms = \(\frac {Total no. of Si atoms}{10^6}\)
= \(\frac {4×10^{28}}{10^6}\) = 4 × 10²² m^-3
i.e., total no. of extra free electrons (n_e)
= 4 × 10²² m^-3
n_i² = n_e n_h
∴ n_h = \(\frac {n_i^2}{n_e}\) = \(\frac {(1.2×10^{16})^2}{4×10^{22}}\)
= \(\frac {144×10^{30}{4×10^{22}}\)
= 36 × 10^-8
= 3.6 × 10⁹ m^-3.

Question 33.
A pure silicon crystal at temperature of 300 K has electron and hole concentration 1.5 × 10¹⁶ m^-3 each. (n_e = n_h). Doping bv indium increases n_h to 4.5 × 10²² m^-3. Calculate ne for the doped silicon crystal.
Answer:
Given: At 300 K, n_i = n_e = n_h = 1.5 × 10¹⁶ m^-3
After doping n_h = 4.5 × 10²² m^-3
To find: Number density of electrons (n_e)
Formula: n_i² = n_e nn_h
Calculation From formula:
n_e = \(\frac {n_i^2}{n_h}\) = \(\frac {(1.5×10^{16})^2}{4×10^{22}}\)
= \(\frac {255×10^{30}{45×10^{21}}\)
= 5 × 10^-9 m^-3.

Question 34.
A Ge specimen is doped with A/. The concentration of acceptor atoms is ~10²¹ atoms/m³. Given that the intrinsic concentration of electron-hole pairs is ~10 ¹⁹/m³, calculate the concentration of electrons in the specimen.
Answer:
Given: At room temperature,
n_i = n_e = n_h = 10¹⁹ m^-3
After doping n_h = 10²¹ m^-3
To find: Number density of electrons (nc)
Formulae: n_i² = n_en_h
Calculation: From formula,
n_e = \(\frac {n_i^2}{n_h}\) = \(\frac {(10^{19})^2}{10^{21}}\)
= \(\frac {255×10^{30}{45×10^{21}}\)
= 10¹⁷ m^-3.

Question 35.
A semiconductor has equal electron and hole concentration of 2 × 10⁸ m^-3. On doping with a certain impurity, the electron concentration increases to 4 × 10¹⁰ m^-3, then calculate the new hole concentration of the semiconductor.
Answer:
Given: n_i = 2 × 10⁸ m^-3, n = 4 × 10¹⁰ m^-3
After doping n_h = 10²¹ m^-3
To find: Number density of holes (n_h)
Formulae: n_i ²= n_en_h
Calculation: From formula.
n_h = \(\frac {n_i^2}{n_e}\) = \(\frac {(2×10^{8})^2}{4×10^{10}}\) = 10⁶ m^-3

Question 36.
What is a p-n junction?
Answer:
When n-type and p-type semiconductor materials are fused together, the junction formed is called as p-n junction.

Question 37.
Explain the process of diffusion in p-n junction.
Answer:
i. The transfer of electrons and holes across the p-n junction is called diffusion.

ii. When an n-type and a p-type semiconductor materials are fused together, initially, the number of electrons in the n-side of a junction is very large compared to the number of electrons on the p-side. The same is true for the number of holes on the p-side and on the n-side.

iii. Thus, a large difference in density of carriers exists on both sides of the p-n junction. This difference causes migration of electrons from the n-side to the p-side of the

iv. They fill up the holes in the p-type material and produce negative ions.

v. When the electrons from the n-side of a junction migrate to the p-side, they leave behind positively charged donor ions on the n- side. Effectively, holes from the p-side migrate into the n-region.

vi. As a result, in the p-type region near the junction there are negatively charged acceptor ions, and in the n-type region near the junction there are positively charged donor ions.

vii. The extent up to which the electrons and the holes can diffuse across the junction depends on the density of the donor and the acceptor ions on the n-side and the p-side respectively, of the junction.

Question 38.
Define potential barrier.
Answer:
The diffusion of carriers across the junction and resultant accumulation of positive and negative charges across the junction builds a potential difference across the junction. This potential difference is called the potential barrier.

Question 39.
Draw neat labelled diagrams for potentials barrier and depletion layer in a p-n junction.
Answer:

Question 40.
Explain in brief electric field across a p-n junction with a neat labelled diagram.
Answer:

1. When p-type semiconductor is fused with n-type semiconductor, a depletion region is developed across the junction.
2. The n-side near the boundary of a p-n junction becomes positive with respect to the p-side because it has lost electrons and the p-side has lost holes.
3. Thus, the presence of impurity ions on both sides of the junction establishes an electric field across this region such that the n-side is at a positive voltage relative to the p-side.
   

Question 41.
What is the need of biasing a p-n junction?
Answer:

1. Due to potential barrier across depletion region, charge carriers require extra energy to overcome the barrier.
2. A suitable voltage needs to be applied to the junction externally, so that these charge carriers can overcome the potential barrier and move across the junction.

Question 41.
Explain the mechanism of forward biased p-n junction.
Answer:

1. In forward bias, a p-n junction is connected in an electric circuit such that the p-region is connected to the positive terminal and the n-region is connected to the negative terminal of an external voltage source.
2. The external voltage effectively opposes the built-in potential of the junction. The width of potential barrier is thus reduced.
3. Also, negative charge carriers (electrons) from the n-region are pushed towards the junction.
4. A similar effect is experienced by positive charge carriers (holes) in the p-region and they are pushed towards the junction.
5. Both the charge carriers thus find it easy to cross over the barrier and contribute towards the electric current.
   

Question 42.
Explain the mechanism of reverse biased p-n junction.
Answer:
i. In reverse biased, the p-region is connected to the negative terminal and the n-region is connected to the positive terminal of the external voltage source. This external voltage effectively adds to the built-in potential of the junction. The width of potential barrier is thus increased.

ii. Also, the negative charge carriers (electrons) from the n-region are pulled away from the junction.

iii. Similar effect is experienced by the positive charge carriers (holes) in the p-region and they are pulled away from the junction.

iv. Both the charge carriers thus find it very difficult to cross over the barrier and thus do not contribute towards the electric current.

Question 43.
State some important features of the depletion region.
Answer:

1. It is formed by diffusion of electrons from n-region to the p-region. This leaves positively charged ions in the n-region.
2. The p-region accumulates electrons (negative charges) and the n-region accumulates the holes (positive charges).
3. The accumulation of charges on either sides of the junction results in forming a potential barrier and prevents flow of charges.
4. There are no charges in this region.
5. The depletion region has higher potential on the n-side and lower potential on the p-side of the junction.

Question 44.
What is p-n junction diode? Draw its circuit symbol.
Answer:
A p-n junction, when provided with metallic connectors on each side is called a junction diode

Question 45.
Explain asymmetrical flow of current in p-n junction diode in detail.
Answer:

i. The barrier potential is reduced in forward biased mode and it is increased in reverse biased mode.

ii. Carriers find it easy to cross the junction in forward bias and contribute towards current because the barrier width is reduced and they are pushed towards the junction and gain extra energy to cross the junction.

iii. The current through the diode in forward bias is large and of the order of a few milliamperes (10^-3 A) for a typical diode.

iv. When connected in reverse bias, width of the potential barrier is increased and the carriers are pushed away from the junction so that very few carriers can cross the junction and contribute towards current.

v. This results in a very small current through a reverse biased diode. The current in reverse biased diode is of the order of a few microamperes (10^-6 A).

vi. When the polarity of bias voltage is reversed, the width of the depletion layer changes. This results in asymmetrical current flow through a diode as shown in figure.

Question 46.
What is knee voltage?
Answer:
In forward bias mode, the voltage for which the current in a p-n junction diode rises sharply is called knee voltage.

Question 47.
What is a forward current in case of zero biased p-n junction diode?
Answer:
When the diode terminals are shorted together, some holes (majority carriers) in the p-side have enough thermal energy to overcome the potential barrier. Such carriers cross the barrier potential and contribute to current. This current is known as the forward current.

Question 48.
Define reverse current in zero biased p-n junction diode.
Answer:
When the diode terminals are shorted together some holes generated in the n-side (minority carriers), move across the junction and contribute to current. This current is known as the reverse current.

Question 49.
Explain the I-V characteristics of a reverse biased junction diode.
Answer:
i. The positive terminal of the external voltage is connected to the cathode (n-side) and negative terminal to the anode (p-side) across the diode.

ii. In case of reverse bias the width of the depletion region increases and the p-n junction behaves like a high resistance.

iii. Practically no current flows through it with an increase in the reverse bias voltage. However, a very small leakage current does flow through the junction which is of the order of a few micro amperes, (µA).

iv. When the reverse bias voltage applied to a diode is increased to sufficiently large value, it causes the p-n junction to overheat. The overheating of the junction results in a sudden rise in the current through the junction. This is because covalent bonds break and a large number of carries are available for conduction. The diode thus no longer behaves like a diode. This effect is called the avalanche breakdown.

v. The reverse biased characteristic of a diode is shown in figure.

Question 50.
Explain zero biased junction diode.
Answer:
i. When a diode is connected in a zero bias condition, no external potential energy is applied to the p-n junction.

li. The potential barrier that exists in a junction prevents the diffusion of any more majority carriers across it. However, some minority carriers (few free electrons in the p-region and few holes in the n-region) drift across the junction.

iii. An equilibrium is established when the majority carriers are equal in number (n_e = n_h) and both moving in opposite directions. The net current flowing across the junction is zero. This is a state of‘dynamic equilibrium’.

iv. The minority carriers are continuously generated due to thermal energy.

v. When the temperature of the p-n junction is raised, this state of equilibrium is changed.

vi. This results in generating more minority carriers and an increase in the leakage current. An electric current, however, cannot flow through the diode because it is not connected in any electric circuit

Question 51.
What is dynamic equilibrium?
Answer:
An equilibrium is established when the majority carriers are equal in number (n_e = n_h) and both moving in opposite directions. The net current flowing across the junction is zero. This is a state of‘dynamic equilibrium’.

Question 52.
Draw a neat diagram and state I-V characteristics of an ideal diode.
Answer:
An ideal diode offers zero resistance in forward biased mode and infinite resistance in reverse biased mode.

Question 53.
What do you mean by static resistance of a diode?
Answer:
Static (DC) resistance:

1. When a p-n junction diode is forward biased, it offers a definite resistance in the circuit. This resistance is called the static or DC resistance (R_g) of a diode.
2. The DC resistance of a diode is the ratio of the DC voltage across the diode to the DC current flowing through it at a particular voltage.
3. It is given by, R_g = \(\frac {V}{I}\)

Question 54.
Explain dynamic resistance of a diode.
Answer:

1. The dynamic (AC) resistance of a diode, r_g, at a particular applied voltage, is defined as
   r_g = \(\frac {∆V}{∆I}\)
2. The dynamic resistance of a diode depends on the operating voltage.
3. It is the reciprocal of the slope of the characteristics at that point.

Question 55.
Draw a graph representing static and dynamic resistances of a diode.
Answer:

Question 56.
Refer to the figure as shown below and find the resistance between point A and B when an ideal diode is (i) forward biased and (ii) reverse biased.

Answer:
We know that for an ideal diode, the resistance is zero when forward biased and infinite when reverse biased.
i. Figure (a) shows the circuit when the diode is forward biased. An ideal diode behaves as a conductor and the circuit is similar to two resistances in parallel.

∴ R_AB = (30 × 30)/(30 +30) = 900/60 = 15 Ω

ii. Figure (b) shows the circuit when the diode is reverse biased.

It does not conduct and behaves as an open switch along path ACB. Therefore, R_AB = 30 Ω. the only resistance in the circuit along the path ADB.

Question 57.
State advantages of semiconductor devices.
Answer:

1. Electronic properties of semiconductors can be controlled to suit our requirement.
2. They are smaller in size and light weight.
3. They can operate at smaller voltages (of the order of few mV) and require less current (of the order of pA or mA), therefore, consume lesser power.
4. Almost no heating effects occur, therefore these devices are thermally stable.
5. Faster speed of operation due to smaller size.
6. Fabrication of ICs is possible.

Question 58.
State disadvantages of semiconductor devices.
Answer:

1. They are sensitive to electrostatic charges.
2. Not very useful for controlling high power.
3. They are sensitive to radiation.
4. They are sensitive to fluctuations in temperature.
5. They need controlled conditions for their manufacturing.
6. Very few materials are semiconductors.

Question 59.
Explain applications of semiconductors.
Answer:
i. Solar cell:

1. It converts light energy into electric energy.
2. t is useful to produce electricity in remote areas and also for providing electricity for satellites, space probes and space stations.

ii. Photo resistor: It changes its resistance when light is incident on it.

iii. Bi-polar junction transistor:

1. These are devices with two junctions and three terminals.
2. A transistor can be a p-n-p or n-p-n transistor.
3. Conduction takes place with holes and electrons.
4. Many other types of transistors are designed and fabricated to suit specific requirements.
5. They are used in almost all semiconductor devices.

iv. Photodiode: It conducts when illuminated with light.

v. LED (Light Emitting Diode):

1. It emits light when current passes through it.
2. House hold LED lamps use similar technology.
3. They consume less power, are smaller in size and have a longer life and are cost effective.

vi. Solid State Laser: It is a special type of LED. It emits light of specific frequency. It is smaller in size and consumes less power.

vii. Integrated Circuits (ICs): A small device having hundreds of diodes and transistors performs the work of a large number of electronic circuits.

Question 60.
Explain any four application of p-n junction diode.
Answer:
1. Solar cell:

1. It converts light energy into electric energy.
2. It is useful to produce electricity in remote areas and also for providing electricity for satellites, space probes and space stations.

ii. Photodiode: It conducts when illuminated with light.

iii. LED (Light Emitting Diode):

1. It emits light when current passes through it.
2. House hold LED lamps use similar technology.
3. They consume less power, are smaller in size and have a longer life and are cost effective.

iv. Solid State Laser: It is a special type of LED. It emits light of specific frequency. It is smaller in size and consumes less power.

Question 61.
What is thermistor?
Answer:
Thermistor is a temperature sensitive resistor. Its resistance changes with change in its temperature.

Question 62.
What are different ty pes of thermistor and what are their applications?
Answer:
There are two types of thermistor:
i. NTC (Negative Thermal Coefficient) thermistor: Resistance of a NTC thermistor decreases with increase in its temperature. Its temperature coefficient is negative. They are commonly used as temperature sensors and also in temperature control circuits.

ii. PTC (Positive Thermal Coefficient) thermistor: Resistance of a PTC thermistor increases with increase in its temperature. They are commonly used in series with a circuit. They are generally used as a reusable fuse to limit current passing through a circuit to protect against over current conditions, as resettable fuses.

Question 63.
How are thermistors fabricated?
Answer:
Thermistors are made from thermally sensitive metal oxide semiconductors. Thermistors are very sensitive to changes in temperature.

Question 64.
Enlist any two features of thermistor.
Answer:

1. A small change in surrounding temperature causes a large change in their resistance.
2. They can measure temperature variations of a small area due to their small size.

Question 65.
Write a note on:
i. Electric devices
ii. Electronic devices
Answer:
i. Electric devices:

1. These devices convert electrical energy into some other form.
2. Examples: Fan, refrigerator, geyser etc. Fan converts electrical energy into mechanical energy. A geyser converts it into heat energy.
3. They use good conductors (mostly metals) for conduction of electricity.
4. Common working range of currents for electric circuits is milliampere (mA) to ampere.
5. Their energy consumption is also moderate to high. A typical geyser consumes about 2.0 to 2.50 kW of power.
6. They are moderate to large in size and are costly.

ii. Electronic devices:

1. Electronic circuits work with control or sequential changes in current through a cell.
2. A calculator, a cell phone, a smart watch or the remote control of a TV set are some of the electronic devices.
3. Semiconductors are used to fabricate such devices.
4. Common working range of currents for electronic circuits it is nano-ampere to µA.
5. They consume very low energy. They are very compact, and cost effective.

Question 66.
Can we take one slab of p-type semiconductor and physically join it to another n-type semiconductor to get p-n junction?
Answer:

1. No. Any slab, howsoever flat, will have roughness much larger than the inter-atomic crystal spacing (~2 to 3 Å).
2. Hence, continuous contact at the atomic level will not be possible. The junction will behave as a discontinuity for the flowing charge carriers.

Question 67.
What is Avalanche breakdown and zener breakdown?
Answer:
i. Avalanche breakdown: In high reverse bias, minority carriers acquire sufficient kinetic energy and collide with a valence electron. Due to collisions the covalent bond breaks. The valence electron enters conduction band. A breakdown occurring in such a manner is avalanche breakdown. It occurs with lightly doped p-n junctions.

ii. Zener breakdown: It occurs in specially designed and highly doped p-n junctions, viz., zener diodes. In this case, covalent bonds break directly due to application of high electric field. Avalanche breakdown voltage is higher than zener voltage.

Question 68.
Indicators on platform, digital clocks, calculators make use of seven LEDs to indicate a number. How do you think these LEDs might be arranged?
Answer:
i. The indicators on platforms, digital clocks, calculators are made using seven LEDs arranged in such a way that when provided proper signal they light up displaying desired alphabet or number.

ii. This arrangement of LEDs is called Seven Segment Display.

Multiple Choice Questions

Question 1.
The number of electrons in the valence shell of semiconductor is ……………
(A) less than 4
(B) equal to 4
(C) more than 4
(D) zero
Answer:
(B) equal to 4

Question 2.
If the temperature of semiconductor is increased, the number of electrons in the valence band will ……………….
(A) decrease
(B) remains same
(C) increase
(D) either increase or decrease
Answer:
(A) decrease

Question 3.
When N-type semiconductor is heated, the ……………..
(A) number of electrons and holes remains same.
(B) number of electrons increases while that of holes decreases.
(C) number of electrons decreases while that of holes increases.
(D) number of electrons and holes increases equally.
Answer:
(D) number of electrons and holes increases equally.

Question 4.
In conduction band of solid, there is no electron at room temperature. The solid is ……………
(A) semiconductors
(B) insulator
(C) conductor
(D) metal
Answer:
(B) insulator

Question 5.
In the crystal of pure Ge or Si, each covalent bond consists of …………..
(A) 1 electron
(B) 2 electrons
(C) 3 electrons
(D) 4 electrons
Answer:
(B) 2 electrons

Question 6.
A pure semiconductor is ……………..
(A) an extrinsic semiconductor
(B) an intrinsic semiconductor
(C) p-type semiconductor
(D) n-type semiconductor
Answer:
(B) an intrinsic semiconductor

Question 7.
For an extrinsic semiconductor, the valency of the donor impurity is …………..
(A) 2
(B) 1
(C) 4
(D) 5
Answer:
(D) 5

Question 8.
In a semiconductor, acceptor impurity is
(A) antimony
(B) indium
(C) phosphorous
(D) arsenic
Answer:
(B) indium

Question 9.
What are majority carriers in a semiconductor?
(A) Holes in n-type and electrons in p-type.
(B) Holes in n-type and p-type both.
(C) Electrons in n-type and p-type both.
(D) Holes in p-type and electrons in n-type.
Answer:
(D) Holes in p-type and electrons in n-type.

Question 10.
When a hole is produced in P-type semiconductor, there is ……………….
(A) extra electron in valence band.
(B) extra electron in conduction band.
(C) missing electron in valence band.
(D) missing electron in conduction band.
Answer:
(C) missing electron in valence band.

Question 11.
The number of bonds formed in p-type and n-type semiconductors are respectively
(A) 4,5
(B) 3,4
(C) 4,3
(D) 5,4
Answer:
(B) 3,4

Question 12.
The movement of a hole is brought about by the valency being filled by a ………………..
(A) free electrons
(B) valence electrons
(C) positive ions
(D) negative ions
Answer:
(B) valence electrons

Question 13.
The drift current in a p-n junction is
(A) from the p region to n region.
(B) from the n region to p region.
(C) from n to p region if the junction is forward biased and from p to n region if the junction is reverse biased.
(D) from p to n region if the junction is forward biased and from n to p region if the junction is reverse biased.
Answer:
(B) from the n region to p region.

Question 14.
If a p-n junction diode is not connected to any circuit, then
(A) the potential is same everywhere.
(B) potential is not same and n-type side has lower potential than p-type side.
(C) there is an electric field at junction direction from p-type side to n-type side.
(D) there is an electric field at the junction directed from n-type side to p-type side.
Answer:
(D) there is an electric field at the junction directed from n-type side to p-type side.

Question 15.
In an unbiased p-n junction, holes diffuse from the p-region to n-region because
(A) free electrons in the n-region attract them.
(B) they move across the junction by the potential difference.
(C) hole concentration in p-region is more as compared to n-region.
(D) all the above.
Answer:
(C) hole concentration in p-region is more as compared to n-region.

Question 16.
The width of depletion region ……………
(A) becomes small in forward bias of diode
(B) becomes large in forward bias of diode
(C) is not affected upon by the bias
(D) becomes small in reverse bias of diode
Answer:
(A) becomes small in forward bias of diode

Question 17.
For p-n junction in reverse bias, which of the following is true?
(A) There is no current through P-N junction due to majority carriers from both regions.
(B) Width of potential barriers is small and it offers low resistance.
(C) Current is due to majority carriers.
(D) Both (B) and (C)
Answer:
(A) There is no current through P-N junction due to majority carriers from both regions.

Question 18.
In the circuit shown below Di and D2 are two silicon diodes. The current in the circuit is …………….

(A) 2 A
(B) 2 mA
(C) 0.8 mA
(D) very small (approx 0)
Answer:
(D) very small (approx 0)

Question 19.
For an ideal junction diode,
(A) forward bias resistance is infinity.
(B) forward bias resistance is zero.
(C) reverse bias resistance is infinity.
(D) both (B) and (C).
Answer:
(D) both (B) and (C).