Maharashtra Board Class 11 Physics Important Questions Chapter 12 Magnetism

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 12 Magnetism Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 12 Magnetism

Question 1.
What are some commonly known facts about magnetism?
Answer:
Some commonly known facts about magnetism:

1. Every magnet regardless of its size and shape has two poles called the north pole and the south pole.
2. Isolated magnetic monopoles do not exist. If a magnet is broken into two or more pieces then each piece behaves like an independent magnet with a somewhat weaker magnetic field.
3. Like magnetic poles repel each other, whereas unlike poles attract each other.
4. When a bar magnet/ magnetic needle is suspended freely or is pivoted, it aligns itself in the geographically north-south direction.

Question 2.
What are some properties of magnetic lines of force?
Answer:

1. Magnetic lines of force originate from the north pole and end at the south pole.
2. The magnetic lines of force of a magnet or a solenoid form closed loops. This is in contrast to the case of an electric dipole, where the electric lines of force originate from the positive charge and end on the negative charge.
3. The direction of the net magnetic field \(\vec{B}\) at a point is given by the tangent to the magnetic line of force at that point.
4. The number of lines of force crossing per unit area decides the magnitude of a magnetic field \(\vec{B}\).
5. The magnetic lines of force do not intersect. This is because had they intersected, the direction of the magnetic field would not be unique at that point.

Question 3.
What is magnetic flux? What is unit of magnetic flux in SI system?
Answer:

1. The number of lines of force per unit area is called magnetic flux (ø).
2. SI unit of magnetic flux (ø) is weber (Wb).

Question 4.
How do we determine strength of magnetic field at a given point due to a magnet? Write down units of magnetic field in SI and CGS system and their interconversion.
Answer:
i. Density of lines of force i.e., the number of lines of force per unit area around a particular point determines the strength of the magnetic field at that point.

ii. The magnitude of magnetic field strength B at a point in a magnetic field is given by,
Magnetic Field = \(\frac {magnetic flux}{area}\)
i.e., B = \(\frac {ø}{A}\)

iii. SI unit of magnetic field (B) is expressed as weber/m² or Tesla.

iv. 1 Tesla = 10⁴ Gauss

Question 5.
What is the unit of magnetic intensity?
Answer:
SI unit: weber/m² or Tesla.

Question 6.
Explain the pole strength and magnetic dipole moment of a bar magnet.
Answer:
i. The bar magnet said to have pole strength +q_m and -q_m near the north and south poles respectively.

ii. As bar magnet has two poles with equal and opposite pole strength, it is called as a magnetic dipole.

iii. The two poles are separated by a distance equal to 2l.

iv. The product of pole strength and the magnetic length is called as magnetic dipole moment.
∴ \(\vec{m}\) = q_m (2\(\vec{l}\))
where, 2\(\vec{l}\) is a vector from south pole to north pole.

Question 7.
State the SI units of pole strength and magnetic dipole moment.
Answer:

1. SI unit of pole strength (q_m) is Am.
2. SI unit of magnetic dipole moment (m) is Am².

Question 8.
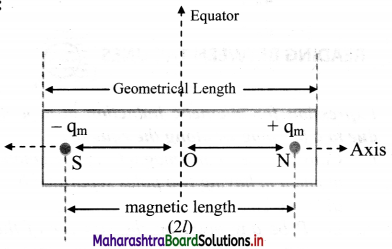
Draw neat labelled diagram for a bar magnet.
Answer:

Question 9.
Define and explain the following terms in case of a bar magnet:
i. Axis
ii. Equator
iii. Magnetic length
Answer:
i. Axis: It is the line passing through both the poles of a bar magnet. There is only one axis for a given bar magnet.

ii. Equator:

• A line passing through the centre of a magnet and perpendicular to its axis is called magnetic equator.
• The plane containing all equators is called the equatorial plane.
• The locus of points, on the equatorial plane, which are equidistant from the centre of the magnet is called the equatorial circle.
• The popularly known ‘equator’ of the planet is actually an ‘equatorial circle’. Such a circle with any diameter is an equator.

iii. Magnetic length (2l)
It is the distance between the two poles of a magnet.
Magnetic length (2l) = \(\frac {5}{6}\) × Geometric length.

Question 10.
State the expression for magnetic induction at a point due to a very short bar magnet along its axis.
Answer:
For very short bar magnet, the magnetic induction at point on the axis is given as,
\(\overrightarrow{\mathrm{B}}_{\mathrm{axis}}=\frac{\mu_{0}}{4 \pi} \frac{2 \overrightarrow{\mathrm{m}}}{\mathrm{r}^{3}}\)

Question 11.
State the expression for the magnetic induction at any point along the equator of a very short bar magnet.
Answer:
For very short bar magnet, the magnetic induction at point on the equator is given as,
\(\overrightarrow{\mathrm{B}}_{\text {equator }}=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{\mathrm{m}}}{\mathrm{r}^{3}}\)

Question 12.
Show that the magnitude of magnetic induction at a point on the axis of a short bar magnet is twice the magnitude of magnetic induction at a point on the equator at the same distance.
Answer:
i. Magnitude of magnetic induction at a point along the axis of a short magnet is given by,
\(\mathrm{B}_{\mathrm{axis}}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^{3}}\) ………….. (1)

ii. Magnitude of magnetic induction at a point on equatorial line is given by
\(\mathrm{B}_{\text {equator }}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{m}}{\mathrm{r}^{3}}\) …………… (2)

iii. Dividing equation (1) by (2), we get,
\(\frac{\mathrm{B}_{\mathrm{axis}}}{\mathrm{B}_{\mathrm{eq}}}=\frac{\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^{3}}}{\frac{\mu_{0}}{4 \pi} \frac{\mathrm{m}}{\mathrm{r}^{3}}}\)
∴ \(\frac{B_{\text {axis }}}{B_{e q}}\) = 2
∴ B_axis = 2B_eq

Question 13.
Derive an expression for the magnetic field due to a bar magnet at an arbitrary point.
Answer:
i. Consider a bar magnet of magnetic moment \(\vec{m}\) with centre at O as shown in figure and let P be any point in its magnetic field.

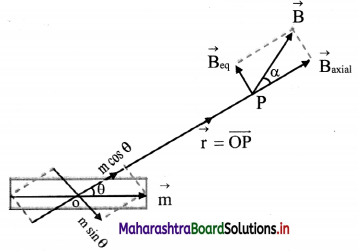
ii. Magnetic moment \(\vec{m}\) is resolved into components along \(\vec{r}\) and perpendicular to \(\vec{r}\).

iii. For the component m cos θ along \(\vec{r}\), the point P is an axial point.

iv. For the component m sinθ perpendicular to \(\vec{r}\), the point P is an equatorial point at the same distance \(\vec{r}\).

v. For a point on the axis, B_a = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{\mathrm{r}^{3}}\)
Here
B_a = \(\frac{\mu_{0}}{4 \pi} \frac{2 m \cos \theta}{r^{3}}\) ………….. (1)
directed along m cosθ.

vi. For point on equator,
B_a = \(\frac{\mu_{o}}{4 \pi} \frac{m \sin \theta}{r^{3}}\) …………. (2)
directed opposite to m sin θ

vii. Thus, the magnitude of the resultant magnetic field B, at point P is given by

viii. Let a be the angle made by the direction of \(\vec{B}\) with \(\vec{r}\). Then, by using equation (1) and equation (2),
tan α = \(\frac {B_{eq}}{B_a}\) = \(\frac {1}{2}\) (tan θ)
The angle between directions of \(\vec{B}\) and \(\vec{m}\) is then (θ + a).

Question 14.
A bar magnet of magnetic moment 5.0 Am² has the poles 20 cm apart. Calculate the pole strength.
Solution:
Given: m = 5.0 Am², 2l = 20 cm = 0.20 m
To find: Pole strength (q_m)
Formula: q_m = \(\frac {m}{2l}\)
Calculation:
From formula.
q_m = \(\frac {5.0}{0.20}\) = 25 Am

Question 15.
A bar magnet has magnetic moment 3.6 Am² and pole strength 10.8 Am. Determine its magnetic length and geometric length.
Answer:
Given: m = 3.6 Am², q_m = 10.8 Am
To find:
i. Magnetic length
ii. Geometric length
Formulae:
i. Magnetic length = \(\frac {m}{q_m}\)
ii. Geometric length = \(\frac {6}{5}\) × magnetic length.
Calculation: From formula (i),
Magnetic length = \(\frac {3.6}{10.8}\) = 0.33 m
From formula (ii),
Geometric length = \(\frac {6}{5}\) × 0.33
= 0.396 m ≈ 0.4 m

Question 16.
A short magnetic dipole has magnetic moment 0.5 A m². Calculate its magnetic field at a distance of 20 cm from the centre of magnetic dipole on (i) the axis (ii) the equatorial line (Given µ₀ = 4π × 10^-7 SI units)
Answer:
Given: m = 0.5 Am², r = 20 cm = 20 × 10^-2 m
To Find: i. Magnetic field on the axial point (B_a)
ii. Magnetic field on the equatorial point (B_eq)
Formulae:
i. B_a = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{r^{3}}\)
ii. B_a = 2B_eq
Calculation: From formula (i),
B_a = 10^-7 × \(\frac{2 \times 0.5}{(0.2)^{3}}\)
= \(\frac{10^{-7}}{8 \times 10^{-3}}\)
= 0.125 × 10^-4
∴ B_a = 1.25 × 10^-5 Wb/m²
From formula (ii),
B_eq = \(\frac {B_a}{2}\) = \(\frac {1.25×10^{-5}}{2}\)
= 0.625 × 10^-5 Wb/m²

Question 17.
A short bar magnet has a magnetic moment of 0.48 JT^-1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (i) the axis (ii) the equatorial lines (normal bisector) of the magnet.
Answer:
Given: m = 0.48 JT^-1, r = 10 cm = 0.1 m
To find:
i. Magnetic induction along axis (B_a)
ii. Magnetic induction along equator (B_eq)
Formulae:
i. B_a = \(\frac {µ_0}{4π}\) \(\frac {2m}{r^3}\)
ii. B_a = 2 B_eq
Calculation: From formula (i),
B_a = 10^-7 × \(\frac {2×0.48}{10^{-3}}\)
∴ B_a = 0.96 × 10^-4 T along S-N direction
From formula (ii),
B_eq = \(\frac {0.96×106{-4}}{2}\)
∴ B_eq = 0.48 × 10^-4 T along N-S direction

Question 18.
Define the following magnetic parameters.
i. Magnetic axis
ii. Magnetic equator
iii. Magnetic Meridian
Answer:
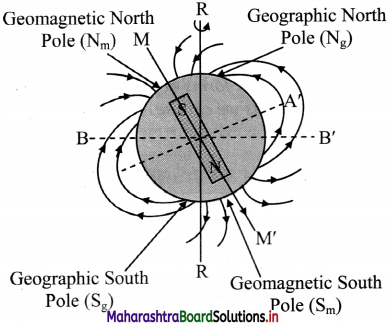
i. Magnetic axis: The Earth is considered to be a huge magnetic dipole. The straight line joining the two poles is called the magnetic axis.

ii. Magnetic equator: A great circle in the plane perpendicular to magnetic axis is magnetic equatorial circle.

iii. Magnetic Meridian: A plane perpendicular to surface of the Earth (Vertical plane) and passing through the magnetic axis is magnetic meridian. Direction of resultant magnetic field of the Earth is always along or parallel to magnetic meridian.

Question 19.
Draw neat labelled diagram representing the Earth as a magnet.
Answer:

Question 20.
Define magnetic declination.
Answer:
Angle between the geographic and the magnetic meridian at a place is called magnetic declination (α).

Question 21.
Draw a neat labelled diagram showing the magnetic declination at a place.
Answer:

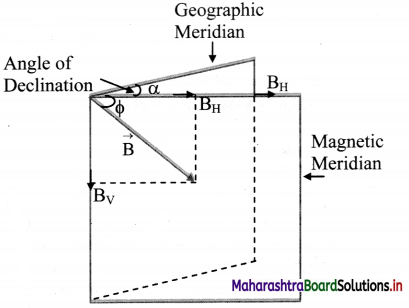
Question 22.
Draw a neat labelled diagram for angle of dip.
Answer:

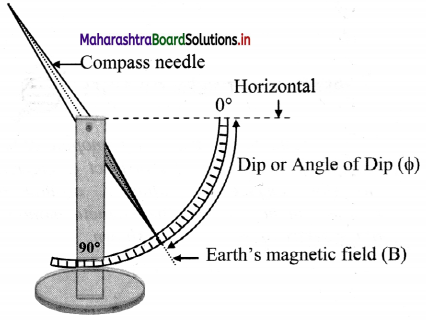
Write a short note on Earth’s magnetic field. Mention the extreme values of magnetic field at magnetic poles and magnetic equator.
Ans:
i. Magnetic force experienced per unit pole strength is magnetic field \(\vec{B}\) at that place.

ii. This field can be resolved in components along the horizontal (\(\vec{B}_H\)) and along vertical (\(\vec{B}_v\)).

iii. The two components are related with the angle of dip (ø) as, B_H = B cos ø, B_v = B sin ø
\(\frac {B_v}{B_H}\) = tan ø
B² = B\(_v^2\) + B\(_H^2\)
∴ B = \( \sqrt{\mathrm{B}_{\mathrm{V}}^{2}+\mathrm{B}_{\mathrm{H}}^{2}}\)

iv. At the magnetic North pole: \(\vec{B}\) = \(\vec{B}\)_v, directed upward, \(\vec{B}\)_H = 0 and ø = 90°.

v. At the magnetic south pole: \(\vec{B}\) = \(\vec{B}\)_v, directed downward, \(\vec{B}\)_H = 0 and ø = 270°.

vi. Anywhere on the magnetic equator (magnetic great circle): B = B_H along South to North, \(\vec{B}\)_v = 0 and ø = 0

Question 23.
What are magnetic maps?
Answer:
Magnetic elements of the Earth (B_H, α and ø) vary from place to place and also with time. The maps providing these values at different locations are called magnetic maps.

Question 24.
Define following terms in case of magnetic maps:
i. Isomagnetic charts
ii. Isodynamic lines
iii. Isogonic lines
iv. Aclinic lines
Answer:
i. Isomagnetic charts: Magnetic maps drawn by joining places with the same value of a particular element are called isomagnetic charts.
ii. Isodynamic lines: Lines joining the places of equal horizontal components (B_H) on magnetic maps are known as isodynamic lines.
iii. Isogonic lines: Lines joining the places of equal declination (α) on magnetic maps are called isogonic lines.
iv. Aclinic lines: Lines joining the places of equal inclination or dip (ø) on magnetic maps are called aclinic lines.

Question 25.
Magnetic equator and geographical equator of the earth are same. Is this true or false?
Answer:
False. Magnetic equator and geographical equator of the earth are not same. By definition, they are different. Magnetic declination is the angle between magnetic equator and geographical equator of the earth.

Question 26.
Earth’s magnetic field at the equator is approximately 4 × 10^-5 T. Calculate Earth’s dipole moment. (Radius of Earth = 6.4 × 10⁶ m, µ₀ = 4π × 10^-7 SI units)
Answer:
Consider earth’s magnetic field as due to a bar magnet at the centre of earth, held along the polar axis of earth.
∴ B_eq = \(\frac {µ_0}{4π}\) \(\frac {m}{r^3}\) ……….. (where, R = radius of earth)
∴ m = \(\frac{\mathrm{B}_{\mathrm{eq}} \times \mathrm{R}^{3}}{\mu_{0} / 4 \pi}\) = \(\frac{4 \times 10^{-5} \times\left(6.4 \times 10^{6}\right)^{3}}{10^{-7}}\)
= 4 × (6.4)³ × 10²⁰
= 1048 × 10²⁰
∴ M = 1.048 × 10²³ Am²

Question 27.
At a given place on the Earth, a bar magnet of magnetic moment \(\vec{m}\) is kept horizontal in the East-West direction. P and Q are the two neutral points due to magnetic field of this magnet and \(\vec{B}\)_H is the horizontal component of the Earth’s magnetic field.
i. Calculate the angles between position vectors of P and Q with the direction of \(\vec{m}\).
ii. Points P and Q are 1 m from the centre of the bar magnet and B_H = 3.5 × 10^-5 T. Calculate magnetic dipole moment of the bar magnet.
Neutral point is that point where the resultant magnetic field is zero.
Answer:
i. The direction of magnetic field \(\vec{B}\) due to the bar magnet is opposite to \(\vec{B}\)_H at the neutral points P and Q such that (θ + α) = 90° at P and (θ + α) = 270° at Question
∴ tan α = \(\frac {1}{2}\) tan θ
∴ tan θ = 2 tan α
= 2 tan (90 – θ) and 2 tan (270 – θ)
∴ tan θ = ± 2 cot θ
∴ tan²θ = 2 …….. (1)
∴ tanθ = ±√2
∴ θ = tan^-1 (±√2)
∴ θ = 54°44′ and 180° – 54° 44° = 125°16′

ii. For magnetic dipole moment of the bar magnet:
From equation (2), tan² θ = 2
∴ sec² θ = 1 + tan² θ = 1 + 2 = 3
∴ cos² θ = \(\frac {1}{3}\)
r = 1 m and B = B_H = 3.5 × 10^-5 T ……. (Given)
we have,

Question 28.
A bar magnet is cut into two equal parts vertically and half part of a bar magnet is kept on the other such that opposite poles align each other. Calculate the magnetic moment of the combination, if m is the magnetic moment of the original magnet.
Answer:
When bar magnet is cut into two equal parts, then magnetic moment of each part becomes half of the original directed from S to N pole.
∴ Magnetic moment of the combination = \(\frac {m}{2}\) – \(\frac {m}{2}\) = 0
∴ The net magnetic moment of the combination is zero.

Question 29.
Answer the following questions regarding earth’s magnetism:
i. Which direction would a compass needlepoint to, if located right on the geomagnetic north or south pole?
ii. Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
Answer:
i. At the poles, earth’s magnetic field is exactly vertical. As the compass needle is free to rotate in a horizontal plane only, it may point out in any direction.
ii. The earth’s magnetic field is only approximately a dipole field. Hence the local N-S poles may lie oriented in different directions. This is possible due to deposits of magnetised minerals in the earth’s crust.

Choose the correct option.

Question 1.
The ratio of magnetic induction along the axis to magnetic induction along the equator of a magnet is
(A) 1 : 1
(B) 1 : 2
(C) 2 : 1
(D) 4 : 1
Answer:
(C) 2 : 1

Question 2.
Magnetic field lines
(A) do not intersect each other.
(B) intersect each other at 45°.
(C) intersect each other at 90°.
(D) intersect each other at 60°.
Answer:
(A) do not intersect each other.

Question 3.
The points A and B are situated perpendicular to the axis of 2 cm long bar magnet at large distances x and 3 x from the centre on opposite sides. The ratio of magnetic fields at A and B will be approximately equal to
(A) 27 : 1
(B) 1 : 27
(C) 9 : 1
(D) 1 : 9
Answer:
(A) 27 : 1

Question 4.
A compass needle is placed at the magnetic pole. It
(A) points N – S.
(B) points E – W.
(C) becomes vertical.
(D) may stay in any direction.
Answer:
(D) may stay in any direction.

Question 5.
Magnetic lines of force originate from …………… pole and end at …………….. pole outside the magnet.
(A) north, north
(B) north, south
(C) south, north
(D) south, south
Answer:
(B) north, south

Question 6.
Two isolated point poles of strength 30 A-m and 60 A-m are placed at a distance of 0.3 m. The force of repulsion between them is
(A) 2 × 10^-3 N
(B) 2 × 10^-4 N
(C) 2 × 10⁵ N
(D) 2 × 10^-5 N
Answer:
(A) 2 × 10^-3 N

Question 7.
The magnetic dipole moment has dimensions of
(A) current × length.
(B) charge × time × length.
(C) current × area.
(D) \(\frac {current}{area}\)
Answer:
(C) current × area.

Question 8.
A large magnet is broken into two pieces so that their lengths are in the ratio 2:1. The pole strengths of the two pieces will have the ratio
(A) 2 : 1
(B) 1 :2
(C) 4 : 1
(D) 1 : 1
Answer:
(A) 2 : 1

Question 9.
The magnetic induction B and the force F on a pole of strength m are related by
(A) B = m F
(B) F = nIABm
(C) F = m B
(D) F = \(\frac {m}{B}\)
Answer:
(C) F = m B

Question 10.
A magnetic dipole has magnetic length 10 cm and pole strength 100 Am. Its magnetic dipole moment is ………………. Am².
(A) 1000
(B) 500
(C) 10
(D) 5
Answer:
(C) 10

Question 11.
The geometric length of a bar magnet having half magnetic length 5 cm is …………… cm.
(A) 12
(B) 10
(C) 6
(D) 4.2
Answer:
(A) 12

Question 12.
The angle of dip at the equator is
(A) 90°
(B) 45°
(C) 30°
(D) 0°
Answer:
(D) 0°

Question 13.
The angle of dip at the magnetic poles of the earth is
(A) 90°
(B) 45°
(C) 30°
(D) 0°
Answer:
(A) 90°