Important Questions

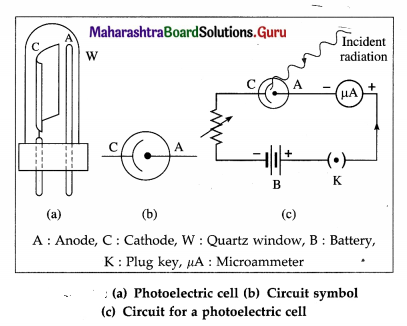
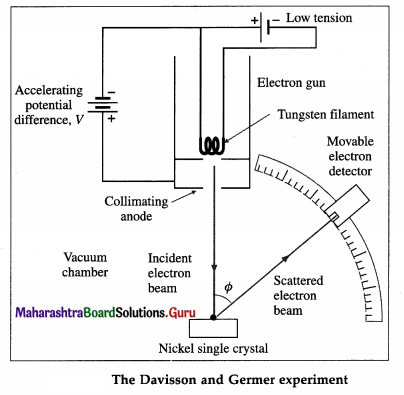
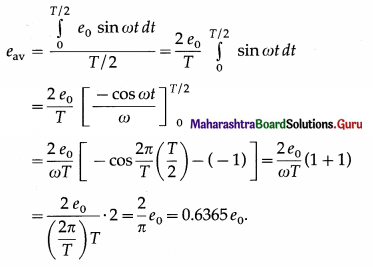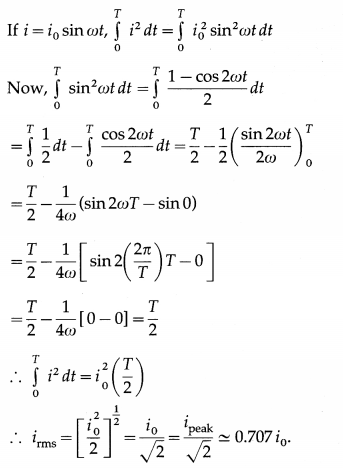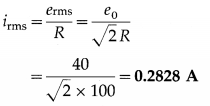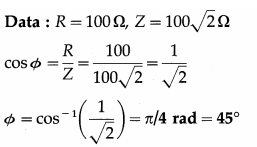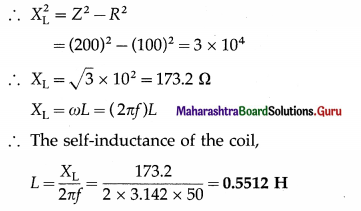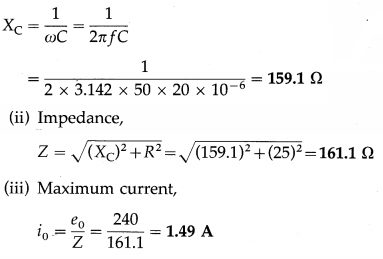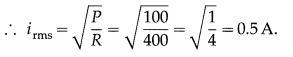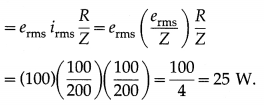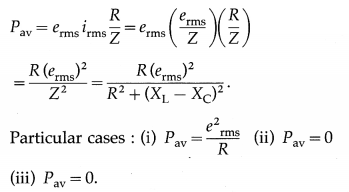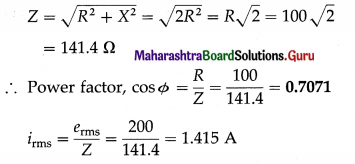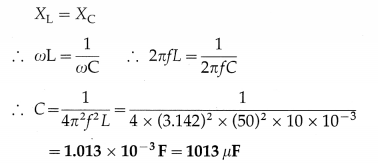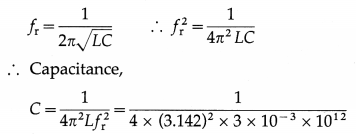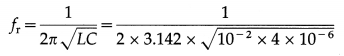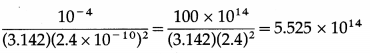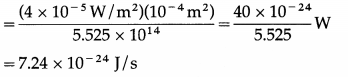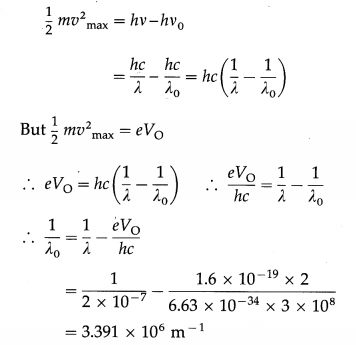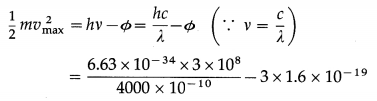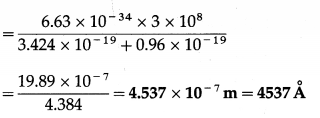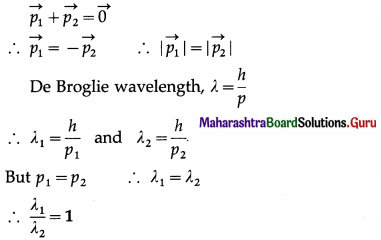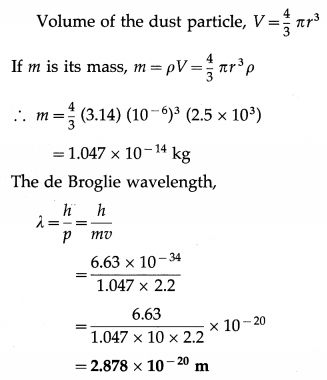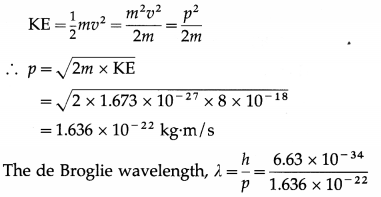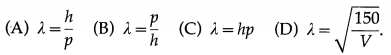Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 12 Electromagnetic Induction Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 12 Electromagnetic Induction

Question 1.
Describe Faraday’s magnet and coil experiment. What conclusion can be drawn from the experiment?
Answer:
Faraday’s magnet and coil experiment:

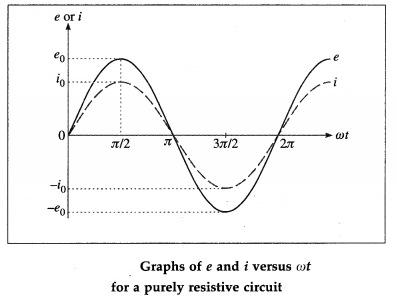
1. The terminals of a copper coil of several turns are connected to a sensitive galvanometer.
   
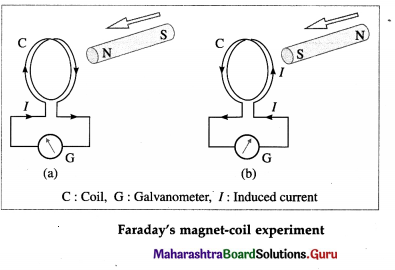
2. A bar magnet is moved swiftly towards the coil with its N-pole facing the coil. As long as the magnet is in motion, the galvanometer shows a deflection [from figure (a)].
3. If the magnet is now moved swiftly away from the coil, again the galvanometer shows a deflection, but now in the opposite direction.
4. The galvanometer shows a deflection when the experiment is repeated with the S-pole of the magnet facing the coil [from figure (b)]. However, the effect of bringing the S-pole towards the coil is the same as that of taking the N-pole away from the coil and vice versa.
5. The same results are obtained when the magnet is held still and the coil is moved towards or away from the magnet.

Conclusion : A current is induced in an electric circuit whenever the magnetic flux linked with the circuit keeps on changing as a result of relative motion of a magnet and the circuit.

Question 2.
Describe Faraday’s coil-coil experiment. What conclusion can be drawn from the experiment?
Answer:
Faraday’s coil-coil experiment:
(1) A copper coil P of several turns is connected in series to a rheostat, a tap key and a battery. The terminals of another copper coil Q of several turns are connected to a sensitive galvanometer. The coils are placed close to each other such that when a current is passed through coil P by closing the key K, the magnetic flux through P is linked with coil Q.

(2) On closing the key K, the rise of current in coil P changes the flux linked with the coil Q nearby as shown by a momentary deflection (throw) of the galvanometer G, from below figure. A similar deflection in the same direction is seen if the key closed and either coil is moved swiftly towards the other.

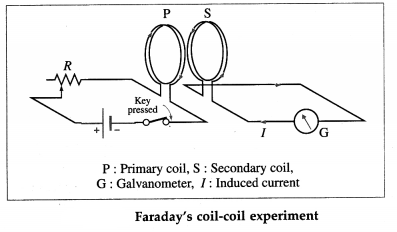
(3) On releasing the tap key, the current in the coil P does not reduce to zero instantaneously. With the decreasing flux through its turns, and a consequent decrease in the flux linked with coil Q, there is an opposite throw of the galvanometer. A similar deflection in the same direction is seen if the key is kept closed and either coil is moved swiftly away from the other.

Conclusion : A current is induced in an electric circuit whenever the magnetic flux linked with the circuit keeps on changing, either as a result of changing current in a nearby circuit or due to relative motion between them.

Question 3.
Will an induced current be always produced in a coil whenever there is a change of magnetic flux linked with it ?
Answer:
Yes, provided the coil is in a closed circuit.

Question 4.
What is the basis of Lena’s law of electromagnetic Induction?
Answer:
Law of conservation of energy is the basis of Lenz’s law of electromagnetic inductIon.

Question 5.
Express Faraday-Lena’s law of electromagnetic induction in an equation form.
Answer:
Suppose dΦ_m Is the change in the magnetic flux through a coil or circuit in time dt. Then, by
Faraday’s second law of electromagnetic induction, the magnitude of the einf Induced is
e ∝ \(\frac{d \Phi_{\mathrm{m}}}{d t}\) or e = k\(\frac{d \Phi_{\mathrm{m}}}{d t}\)
where dΦ_m/dt is the rate of change of magnetic flux
linked with the coil and k is a constant of proportionality. The Sl units of e (the volt) and dΦ_m df (the weber per second) are so selected that the constant of proportionality, k, becomes unity. Combining Faraday’s law and Lents law of electromagnetic induction, the induced emf
e = – \(\frac{d \Phi_{\mathrm{m}}}{d t}\)
where the minus sign is Included to indicate the polarity of the induced emf as given by Lents law. This polarity simply determines the direction of the induced current in a dosed loop. If a coil has N tightly wound loops, the induced emf will be N times greater than for a single loop, so that
e = – N \(\frac{d \Phi_{\mathrm{m}}}{d t}\)
where \(\frac{d \Phi_{\mathrm{m}}}{d t}\) is the rate of change of magnetic flux through one loop.

Question 6.
State the causes of induced current and explain them on the basis of Lena’s law.
Answer:
According to Lena’s law, the direction of the induced emf or current is such as to oppose the change that produces it. The change that induces a current may be
(i) the motion of a conductor in a magnetic field or
(ii) the change of the magnetic flux through a stationary circuit.
In the first case, the direction of induced emf in the moving conductor Is such that the direction of the side-thrust exerted on the conductor by the magnetic field is opposite in direction to its motion. The motion of the conductor is, therefore, opposed.

In the second case, the induced current sets up a magnetic field of its own which within the area bounded by the circuit is (a) opposite to the original magnetic field if this field is increasing, but (b) is in the same direction as the original field, if the field is decreasing. Thus, it is the change in magnetic flux through the circuit (not the flux itself) which is opposed by the induced current.

Question 7.
In one version of Faraday’s coil-coil experiment, the two coils are wound on the same iron ring as shown, where closing and opening the switch induces a current in the other coil. How do the multiple-loop coils and iron ring enhance the observation of induced emf?

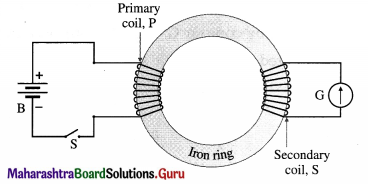
Answer:
The magnetic flux through a coil is directly proportional to the number of turns a coil has. Hence, with multiloop coils in Faraday’s coil-coil experiment, the induced emf is directly proportional to N. Also, the permeability of iron being many orders of magnitude greater than air, the magnetic field lines of the primary coil P are confined to the iron ring and almost all the flux is linked with the secondary coil S. Thus, increased flux and better flux linkage enhances the magnitude of the induced emf.

Question 8.
A circular conducting loop in a uniform magnetic field is stretched to an elongated ellipse as shown below. The magnetic field points into the page. Will an emf be induced in the loop? If so, state why and give the direction of the induced current.

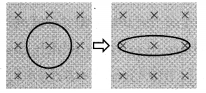
Answer:
Looking in the direction of the magnetic field, there will be an induced current in the clockwise sense.

For the same perimeter, the area of a circle is greater than that of an ellipse. Hence, stretching the loop reduces the inward flux through its plane. To oppose this decreasing flux, a current is induced in the clockwise sense so that the field due to the induced current is into the plane of the diagram.

Question 9.
A bar magnet is dropped vertically through a thick copper ring as shown. What is the direction of the force exerted by the coil on the magnet? Explain.

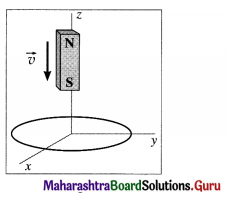
Answer:
The magnetic flux through the loop increases when the magnet approaches the loop, and decreases after the magnet has passed through. The induced current in the loop opposes the cause producing the change in flux which, in this case, is the falling magnet. Therefore, the motion of the magnet’ is opposed, first with a repulsion and then with an attraction. The force, in both cases, is upward in the + z-direction.

The magnetic dipole moment of the falling magnet is directed up. Therefore, looking down the z-axis, the induced current is clockwise when the magnet is approaching the loop, so that the magnetic moment of the loop points down; subsequently, as the magnet recedes, the induced current is anticlockwise.

Question 10.
Briefly explain the jumping ring experiment.
Answer:
Elihu Thompson’s jumping ring experiment is an outstanding demonstration of Faraday’s laws and Lenz’s law of electromagnetic induction. The apparatus consists of a cylindrical laminated iron- cored solenoid. A conducting non-magnetic ring, usually copper or aluminium, is placed over the extended vertical core of the solenoid. When an alternating current is passed through the solenoid, the ring is thrown off high into the air.

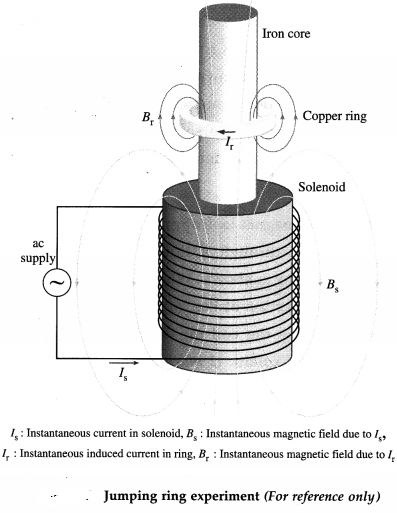
Due to ac, the magnetic field of the solenoid changes continuously. This induces eddy current in the ring. By Lenz’s law, the magnetic field produced by the induced eddy current in the ring opposes the changing magnetic field of the solenoid. Consequently, the two magnetic fields repel each other, making the ring jump.

The iron core increases the magnetic field of the solenoid. Often, the ring is cooled with liquid nitrogen. The colder the ring, the less is its resistance and greater the eddy current in it. More current means a greater magnetic field and even higher jumps.

Question 11.
Explain what you understand by magnetic flux.
Answer:
The total number of magnetic lines of force passing normally through a given area in a magnetic field, is called the magnetic flux through that area.

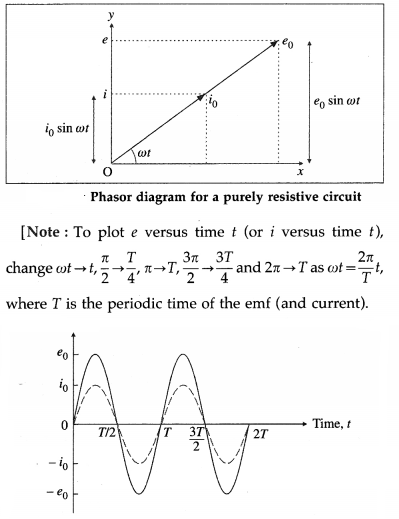
Consider a very small area dA in a uniform magnetic field of induction \(\vec{B}\). The area dA can be represented by a vector \(\overrightarrow{d A}\) perpendicular to it.

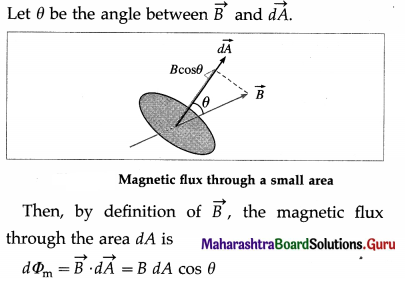
[Note : The area vector is perpendicular to the sur-face, so it can point either up and to the right as shown or down and to the left. Although either choice is acceptable, choosing the direction that is closest to the magnetic field is convenient and usually the one we choose.]

Question 12.
How do you find the magnetic flux through a finite area A ?
Answer:
Consider a small area element \(\overrightarrow{d A}\) of a finite area A bounded by contour C, from below figure. Suppose this area is situated in a magnetic field \(\vec{B}\).

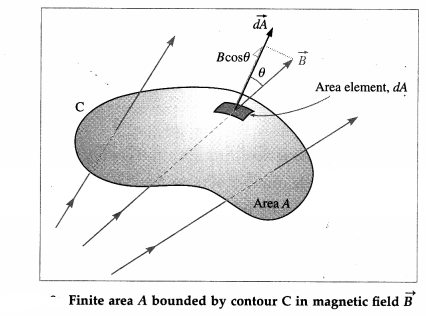
In general, the magnetic field may not be uniform over the area A. Then, the magnetic flux through the area element is dΦ_m = \(\vec{B} \cdot \overrightarrow{d A}\) = B (dA) cos θ
where θ is the angle between \(\vec{B}\) and \(\overrightarrow{d A}\), so that the flux through the area A is
Φ_m = \(\int d \Phi_{\mathrm{m}}=\int_{A} \vec{B} \cdot \overrightarrow{d A}=\int_{A}\) B(dA)cos θ
The integration is over the entire area A. \(\vec{B}\) can be taken out of the integral if and. only if \(\vec{B}\) is the same everywhere over A, in which case,
Φ_m = \(\int_{A}\) B (dA) cos θ = B cos θ \(\int_{A}\) dA = BA cos θ
where \(\int_{A}\) dA is just the total area A.

Question 13.
State an expression for the magnetic flux through a loop of finite area A inside a uniform magnetic field \(\vec{B}\). Hence discuss Faraday’s second law, given that the magnetic flux varies with time.
Answer:
Consider a conducting loop of finite area A, situated in a uniform magnetic field \(\vec{B}\). We choose the direction of the area vector \(\vec{A}\) that is closest to the magnetic field. For the area vector in below figure, the fingers of the right hand must be turned in the sense of the arrow on the contour of the loop.

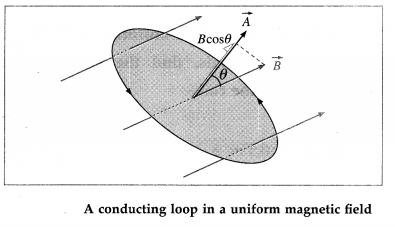
Since \(\vec{B}\) is the same everywhere over A, the flux through the area A is
Φ_m = BA cos θ
where θ is the angle between \(\vec{B}\) and \(\vec{A}\).
Faraday’s discovery was that the rate of change of flux dΦ_m/ dt is related to the work done on taking a unit positive charge around the contour in the reverse direction. This work done is just the induced emf. Accordingly we express Faraday’s second law of electromagnetic induction as
|e| = \(\frac{d \Phi_{\mathrm{m}}}{d t}=\frac{d}{d t}\) (BA cos θ)
If B, A and θ are all constants in time, no emf is induced in the loop. An emf will be induced if at least one of these parameters changes with time. B and A may change in magnitude; the loop may turn, thereby changing θ.

Question 14.
When is the magnetic flux through an area element (i) maximum (ii) zero? Explain.
Answer:
When an area element dA is placed in a magnetic field \(\vec{B}\), the magnetic flux through the element is
dΦ_m = B(dA) cos θ …………. (1)
where 8 is the angle between \(\vec{B}\) and the area vector \(\overrightarrow{d A}\).
(i) The maximum value of cos θ = 1 when θ = 0. Thus, from Eq. (1), the magnetic flux is maximum, dΦ_m = B(dA), when the magnetic induction is in the direction of the area vector.
(ii) The minimum value of cos θ = 0 when θ = 90°. Then, the magnetic flux is minimum, dΦ_m = 0, when the magnetic induction is perpendicular to the area vector.

Question 15.
State the SI units and dimensions of
(i) magnetic induction
(ii) magnetic flux.
Answer:
(i) Magnetic induction, B :
SI unit : the tesla (T) : 1 T = 1 Wb / m²
Dimensions: [B] = [MT^-2I^-1].

(ii) Magnetic flux, Φ_m:
SI unit : the weber (Wb)
Dimensions : [Φ_m] = [B][A]
= [MT^-2I^-1][L²] = [ML²T^-2I^-1]

Question 16.
State the relation between the SI units volt and weber.
Answer:
1 volt = 1 weber per second (1 V = 1 Wb/s).

Question 17.
Explain how Lenz’s law is incorporated into Faraday’s second law of electromagnetic induction by introducing a minus sign.
Answer:
Consider a conducting loop of area A in a uniform external magnetic field \(\vec{B}\) with its plane perpendicular to the field, i.e., its area vector \(\vec{A}\) is parallel to \(\vec{B}\) , from below figure. We choose the x-axis along \(\vec{B}\), so that \(\vec{B}=B \hat{i}\) and \(\vec{A}=A \hat{i}\).

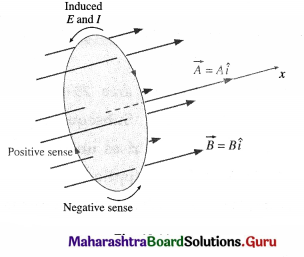
Suppose the magnitude of the magnetic induction increases with time. Then, \(\vec{A}\) remaining constant, the induced emf by Faraday-Lenz’s second law of electromagnetic induction is
e = \(-\frac{d \Phi_{\mathrm{m}}}{d t}=-\frac{d}{d t}(B A)=-A \frac{d B}{d t}\) ………….. (1)
Since we have assumed that B is increasing with time, dB / dt is a positive quantity. Also, A = |\(\vec{A}\)| is positive by definition. Hence, the right hand side of Eq. (1) is a negative quantity.

The right hand rule for area vector fixes the positive sense of circulation around the loop as the clockwise sense. Then, by Lenz’s law the induced current in the loop is in the anticlockwise sense. The sense of the induced emf is the same as the sense of the current it drives. With the clockwise sense fixed as positive, the anticlockwise sense of the induced current is negative. Hence, the sense of e is also negative. That is, the left hand side of Eq. (1) is indeed a negative quantity. Thus, introducing a minus sign in Faraday’s second law incorporates Ienz’s law into Faraday’s law.

18. Solve the following
Question 1.
A coil of effective area 25 m² is placed in a field-free region. Subsequently, a uniform magnetic field that rises uniformly from zero to 1.25 T in 0.15 s is applied perpendicular to the plane of the coil. What is the magnitude of the emf induced in the coil?
Solution:
Data : NA = 25 m², B_f = 1.25 T, B_i = 0, A t = 0.15 s
Initial magnetic flux, Φ_i = 0 (∵ B_i = 0)
Final magnetic flux, Φ_f = NAB_f
e = –\(\frac{d \Phi}{d t}=-\frac{\left(\Phi_{\mathrm{f}}-\Phi_{\mathrm{i}}\right)}{d t}\)

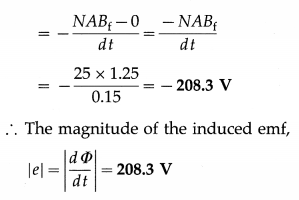
Question 2.
A rectangular coil of length 0.5 m and breadth 0.4 m has resistance of 5 Ω. The coil is placed in a magnetic field of induction 0.05 T and its direction is perpendicular to the plane of the coil. If the magnetic induction is uniformly reduced to zero in 5 milliseconds, find the emf and current induced in the coil.
Solution:
Data : l =0.5 m, b = 0.4 m, R = 5Ω, B = 0.05 T, B_f = 0, dt = 5 × 10^-3 s
Area of the coil, A = lb = 0.5 × 0.4 = 0.2 m²
Initial magnetic flux, Φ_i = AB_i
= 0.02 × 0.05 = 0.01 Wb
Final magnetic flux, Φ_f = 0 (∵ B_f = 0)

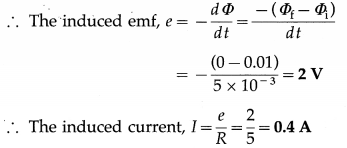
Question 3.
A square wire loop with sides 0.5 m is placed with its plane perpendicular to a magnetic field. The resistance of the loop is 5 Ω. Find at what rate the magnetic induction should be changed so that a current of 0.1 A is induced in the loop.
Solution:
Data : l = 0.5 m, R = 5 Ω, I = 0.1 A
A = l² = 0.5 × 0.5 = 0.25 m²
The magnitude of the induced emf,
|e| = \(\frac{d \Phi}{d t}=\frac{d}{d t}\) (BA) = A \(\frac{d B}{d t}\)
since the area (A) of the coil is constant. The induced current, I = \(\frac{|e|}{R}=\frac{A}{R} \frac{d B}{d t}\)
∴ The time rate of change of magnetic induction,
\(\frac{d B}{d t}=\frac{I R}{A}=\frac{0.1 \times 5}{0.25}\) = 2 T/s

Question 4.
The magnetic flux through a loop of resistance 0.1 Ω is varying according to the relation Φ = 6t² + 7t + 1, where Φ is in mihiweber and t is in second. What is the emf induced in the loop at t = 1 s and the magnitude of the current?
Solution:
Data: R = 0.1 Ω, Φ_m = 6t² + 7t + 1 mWb, t = 1 s
(i) The induced emf, |e| = \(\frac{d \Phi_{\mathrm{m}}}{d t}\) = \(\frac{d}{d t}\)(6t² + 7t + 1)
= (12t + 7) mV
= 12(1) + 7 = 19 mV

(ii) The magnitude of the current = \(\frac{|e|}{R}\)
= \(\frac{19 \mathrm{mV}}{0.1 \Omega}\) = 190 mA

Question 5.
A wire 88 cm long is bent into a circular loop and kept with its plane perpendicular to a magnetic field of induction 2.5 Wb/m². Within 0.5 second, the coil is changed to a square and the magnetic induction is increased by 0.5 Wb/m². Calculate the emf induced in the wire.
Solution:
Data: l = 88 cm, B_i = 2.5 Wb/m², B_f = 3 Wb/m², ∆t = 0.5 s
For the circular loop, l = 2πr
∴ r = \(\frac{l}{2 \pi}=\frac{88}{2 \times(22 / 7)}\) = 14 cm = 0.14 m
Area of the circular loop, A_i = πr²
= \(\frac{22}{7}\) (0.14)² = 0.0616 m²
Initial magnetic flux, Φ_i = A_iB_i
= 0.0616 × 2.5 = 0.154 Wb
For the square loop, length of each side
= \(\frac{88}{4}\) cm = 22 cm = 0.22 m 4
Area of the square loop, A_f = (0.22)²
= 0.0484 m²
∴ Final magnetic flux, Φ_f = A_fB_f
= 0.0484 × 3 = 0.1452 Wb
Induced emf, e = – \(\frac{\Phi_{\mathrm{f}}-\Phi_{1}}{\Delta t}=\frac{\Phi_{1}-\Phi_{\mathrm{f}}}{\Delta t}\)
∴ e = \(\frac{0.154-0.1452}{0.5}\) = 8.8 × 10^-3 × 2
= 1.76 × 10^-2 V

Question 6.
A 1000 turn, 20 cm diameter coil is rotated in the Earth’s magnetic field of strength 5 × 10^-5 T. The plane of the coil was initially perpendicular t0 the Earth’s field and is rotated to be parallel to the field in 10 ms? Find the average emf induced.
Solution:
Data: N = 1000, d = 0.2 m, B = 5 × 10^-5 T,
∆t = 10 ms = 10^-2 s
Radius of coil, r = d/2 = 10^-1 m
Induced emf, e = -N \(\frac{\Delta \Phi_{\mathrm{m}}}{\Delta t}=-N \frac{\Phi_{\mathrm{f}}-\Phi_{1}}{\Delta t}\)
Initial area, A_i = πr² and initial flux,
NΦ_i = NBA_i NB (πr²)
Final flux, Φ_f = 0, since the plane of the coil is parallel to the field lines.

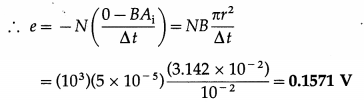
Question 7.
A television loop antenna has diameter of 11 cm. The magnetic field of the TV signal is uniform, normal to the plane of the loop and changing at the rate of 0.16 T/s. What is the magnitude of the emf induced in the antenna?
Solution:

Question 8.
The magnetic field through a wire loop, of radius 12 cm and resistance 8.5 Ω, changes with time as shown in the graph below. The magnetic field is uniform and perpendicular to the plane of the loop. Calculate the emf induced in the loop as a function of time. Hence, find the induced emf in the time interval (a) t = 0 to t = 2 s (b) t = 2 s to t = 4s (c) t = 4s to t = 6s.

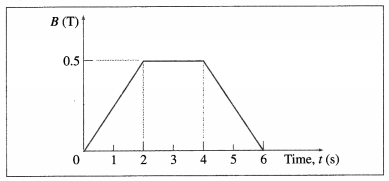
Solution :
Data : r = 0.12 m, R = 8.5 Ω

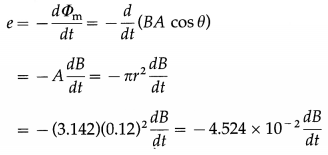
This is the emf induced in the loop as a function of time.
\(\frac{d B}{d t}\) is the slope of the B-t graph

Question 19.
What is motional emf?
Answer:
An emf induced in a conductor or circuit moving in a magnetic field is called motional emf.

Question 20.
Determine the motional emf induced in a straight conductor moving in a uniform magnetic field with constant velocity.
Answer:
Consider a straight wire AB resting on a pair of conducting rails separated by a distance l lying wholly in a plane perpendicular to a uniform magnetic field \(\vec{B}\). \(\vec{B}\) points into the page and the rails are stationary relative to the field and are connected to a stationary resistor R.

Suppose an external agent moves the rod to the right with a constant speed v, perpendicular to its length and to \(\vec{B}\). As the rod moves through a distance dx = vdt in time dt, the area of the loop ABCD increases by dA = ldx = lv dt.

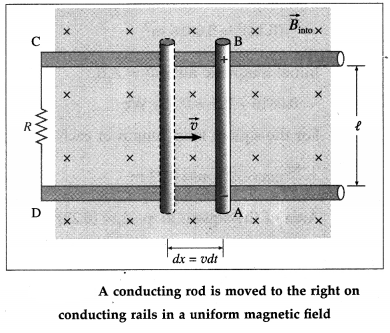
Therefore, in time dt, the increase in the magnetic flux through the loop,
dΦ_m = BdA = Blvdt
By Faraday’s law of electromagnetic induction, the magnitude of the induced emf
e = \(\frac{d \Phi_{\mathrm{m}}}{d t}=\frac{B l v d t}{d t}\) = Blv

Question 21.
Determine the motional emf induced in a straight conductor moving in a uniform magnetic field with constant velocity on the basis of Lorentz force.
Answer:
Consider a straight rod or wire PQ of length l, lying wholly in a plane perpendicular to a uniform magnetic field of induction B , as shown in below figure; \(\vec{B}\) points into the page.

Suppose an external agent moves the wire to the right with a constant velocity \(\vec{v}\) perpendicular to its length and to \(\vec{B}\). The free electrons in the wire experience a Lorentz force \(\vec{F}\) ( = q\(\vec{v}\) × \(\vec{B}\)).

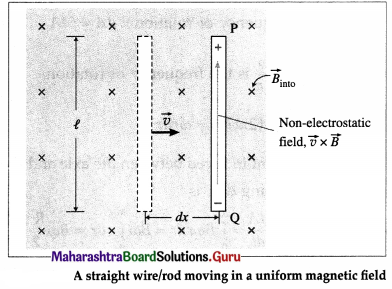
According to the right-hand rule for cross products, the Lorentz force on negatively charged electrons is downward. The Lorentz force \(\vec{F}\) moves the free electrons in the wire from P to Q so that P becomes positive with respect to Q. Thus, there will be a separation of the charges to the two ends of the wire until an electric field builds up to oppose further motion of the charges.

In moving the electrons a distance l along the wire, the work done by the Lorentz force is
W = Fl = (qvB sin θ) l = qvBl
since the angle between \(\vec{v}\) and \(\vec{B}\), θ = 90°. Since electrical work done per unit charge is emf, the induced emf in the wire is
e = \(\frac{W}{q}\) = vB l
Alternatively, the electric field due to the separation of charges is \(\vec{F} / q=\vec{v} \times \vec{B}\). Since \(\vec{v}\) is perpendicular to B, the magnitude of the field = vB.
Electric field = \(\frac{\text { p.d. }(e) \text { between } \mathrm{P} \text { and } \mathrm{Q}}{\text { distance } \mathrm{PQ}(l)}\)
Therefore, the p.d. or emf induced in the wire PQ is e = v B l

Question 22.
Determine the motional emf induced in a straight conductor rotating in a uniform magnetic field with constant angular velocity.
Answer:
Suppose a rod of length l is rotated anticlockwise, around an axis through one end and perpendicular to its length, in a plane perpendicular to a uniform magnetic field of induction \(\vec{B}\), as shown in below figure; \(\vec{B}\) points into the page. Let the constant angular speed of the rod be ω.

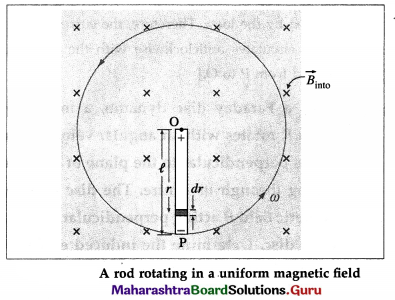
Consider an infinitesimal length element dr at a distance r from the rotation axis. In one rotation, the area traced by the element is dA = 2πrdr. Therefore, the time rate at which the element traces out the area is
\(\frac{d A}{d t}\) = frequency of rotation × dA = f dA
where f = \(\frac{\omega}{2 \pi}\) is the frequency of rotation.
∴ \(\frac{d A}{d t}=\frac{\omega}{2 \pi}\) (2πrdr) = ωr dr
Therefore, the magnitude of the induced emf in the element is
|de| = \(\frac{d \Phi_{\mathrm{m}}}{d t}=B \frac{d A}{d t}\) = B ωr dr
Since the emfs in all the elements of the rod will be in series, the total emf induced across the ends of the rotating rod is
|e| = \(\int d e=\int_{0}^{l} B \omega r d r=B \omega \int_{0}^{l} r d r=B \omega \frac{l^{2}}{2}\)
For anticlockwise rotation in B pointing into the page, the pivot point O\(\vec{B}\) is at a higher potential.

[Note : To understand the polarity of the emf across the ends of the rod, imagine that the rod slides along a wire that forms a circular arc MPN of radius /, as shown below. Assume that the resistor R furnishes all of the resistance in the closed loop. As 9 increases, so does the inward flux through the loop due to \(\vec{B}\).

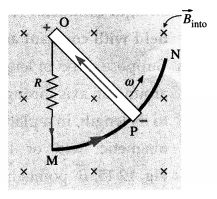
To counteract this increase, the magnetic field due to the induced current must be directed out of the page in the region enclosed by the loop. Therefore, the current in the loop POMP circulates anticlockwise with the motional emf directed from P to O.]

23. Solve the following
Question 1.
A straight metal wire slides to the right at a constant 5 m/s along a pair of parallel metallic rails 25 cm apart. A 10 Ω resistor connects the rails on the left end. The entire setup lies wholly inside a uniform magnetic field of strength 0.5 T, directed into the page. Find the magnitude and direction of the induced current in the circuit.
Solution:
Data : v = 5 m/s, l = 0.25 m, R = 10 Ω, B = 0.5T
The induced current,
i = \(\frac{e}{R}=\frac{B l v}{R}=\frac{(0.5)(0.25)(5)}{10}\) = 0.0625 A
Since the magnetic flux into the page through the | closed conducting loop increases, the induced current in the loop must be anticlockwise. Alternatively, Fleming’s right hand rule gives the direction of induced current in the moving wire from bottom to top.

Question 2.
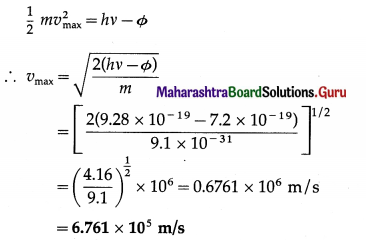
A straight conductor (rod) of length 0.3 m is rotated about one end at a constant 6280 rad/s in a plane normal to a uniform magnetic field of induction 5 × 10^-5 T. Calculate the emf induced between its ends.
Solution:
Data : l = 0.3 m, ω = 6280 rad/s, B = 5 × 10^-5 T In one rotation, the rod traces out a circle of radius l, i.e., an area, A = πl². Therefore, the time rate at which the rod traces out the area is

Question 3.
A metal rod 1/\(\sqrt{\pi}\) m long rotates about one of its ends in a plane perpendicular to a magnetic field of induction 4 × 10^-3 T. Calculate the number of revolutions made by the rod per second if the emf induced between the ends of the rod is 16 m V.
Solution :
Data : r = l = \(\frac{1}{\sqrt{\pi}}\) m, B = 4 × 10^-3 T, |e| = 16 mV = 16 × 10^-3 V
In one rotation, the rod traces out a circle of radius Z, i.e., an area, A = πl²
Therefore, the time rate at which the rod traces out the area is

Question 4.
A cycle wheel with 10 spokes, each of length 0. 5 m, is moved at a speed of 18 km/h in a plane normal to the Earth’s magnetic induction of 3.6 × 10^-5 T. Calculate the emf induced between
(i) the axle and the rim of the cycle wheel
(ii) ends of a single spoke and ten spokes.
Solution:
Data : r = l = 0.5 m, v = 18 km/h = \(\frac{18000}{3600}\) = 5 m/s,

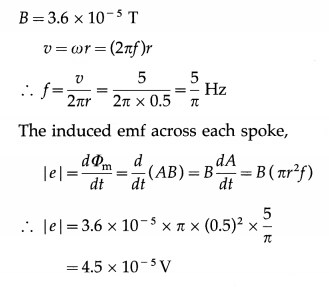
Since the spokes have common ends (the axle and wheel rim), they are connected in parallel. Hence,
the emf induced between the end of a single spoke and the other common end of ten spokes is also 4.5 × 10^-5 V.

Since the total emf of this parallel combination of identical emfs e is equal to a single emf e, the emf induced between the axle and wheel rim is equal to 4.5 × 10^-5 V.

Question 24.
Briefly describe with necessary diagrams the experimental setup to investigate the phenomenon of electromagnetic induction for a magnet swinging through a coil.
Answer:
Apparatus: A permanent magnet is mounted at the centre of the arc of a semicircular aluminium frame of radius 50 cm. The whole frame is pivoted at its centre and can oscillate freely in its plane, from figure (a). Movable weights m₁ and m₂ on the radial arms of the frame can be symmetrically positioned to adjust the period of oscillation from about 1.5s to 3s. The magnet can freely pass through a copper coil of about 10000 turns.

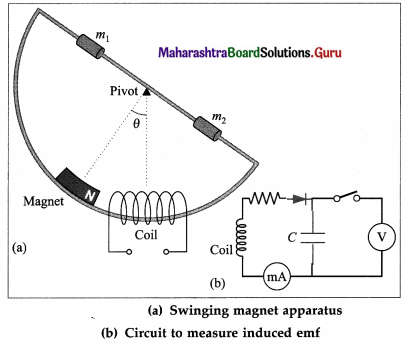
When the magnet swings through and out of the coil, the magnetic flux through the coil changes, inducing an emf. The amplitude of the swing can be read from the graduations on the arc. Since the induced emf will be small, it may be measured by connecting the terminals of the coils to a CRO (cathode-ray oscilloscope, or they may be connected to a 100 pF capacitor through a diode, from figure (b), and the voltage across the capacitor is measured. The resistor in series with the diode helps to adjust the capacitor charging time ( = RC).

[Note : Real-time graphs can be captured using a datalogger connected to a computer. The datalogger uses rotary motion, voltage and magnetic field sensors to measure the angle, the induced voltage and the magnetic flux, respectively.]

Question 25.
In the experiment to investigate the phenomenon of electromagnetic induction for a magnet swinging through a coil, relate the graphical representations (flux-time and voltage-time) with the motion of the magnet.
Answer:
In the demonstration of a magnet swinging through a coil, a voltage is induced in the coil as the magnet swings through it. For the discussion, we assume the length of the magnet to be smaller (about half) than the length of the coil and the North pole of the magnet swings into the coil from the left. (The polarity of the induced voltage pulse depends on the polarity of the magnet.)

We take the magnetic flux linked with the coil to be nearly zero when the magnet is high up away from the coil. As the magnet moves through it the coil and recedes, the magnetic field through the coil increases to its maximum and then decreases. There is a substantial magnetic field at the coil only when it is very near the magnet. Moreover, the speed of the magnet is maximum when it is at the centre of the coil, since it is then at the mean position of its oscillation. Thus the magnetic field changes quite slowly when the magnet is far away and rapidly as it approaches the coil, from figure (a).

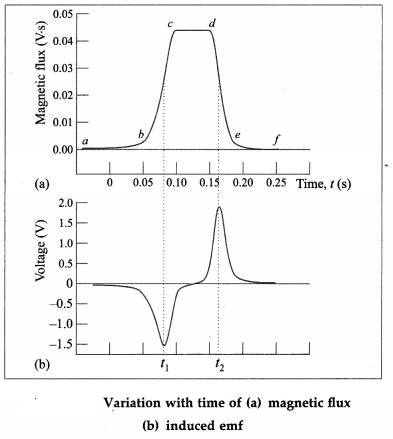
The flux through the coil increases as the north pole approaches the left end of the coil, and reaches a maximum when the magnet is exactly midway in the coil, as shown by the portion be in from figure (a). By Lenz’s law, the induced emf will produce a leftward flux that will seek to oppose the increasing magnetic flux of the magnet through the coil.

The interval cd, when the flux is maximum but remains constant and induced emf is zero, corresponds to the situation where the magnet is wholly inside the coil.

Once the magnet swings past the centre of the coil, the flux through the coil starts to decrease-the interval de. To reinforce the decreasing flux of the magnet through the coil, a rightward flux is now induced, thereby flipping the polarity of the induced emf.

If we use a coil that is shorter than the magnet, the time interval cd for which the induced emf remains zero would have been shorter. The times f₁ and f₂ in from figure (a) are the points of inflection of the curve, and in from figure (b) are obviously the minimum and maximum of the induced emf, respectively. The sequence of two pulses, one negative and one positive, occurs during just half a cycle. On the return swing of the magnet, they are repeated in the same order.

Question 26.
In the experiment to investigate the phenomenon of electromagnetic induction for a magnet swinging through a coil, show that the peak induced emf is directly proportional to the speed of the magnet (or show that the peak induced emf is directly proportional to the angular amplitude and inversely proportional to the time period).
Answer:
In the experiment, a magnet is swung through a coil in a radius R. The angular position θ of the magnet is measured from the vertical, the mean position of the swing. The angular amplitude is θ₀.

The kinetic energy of the system is \(\frac{1}{2}\) Iω² and the potential energy (relative to the lowest position of the magnet) is MgR(1 – cos θ), where M is mass of the system. Conservation of energy gives, for small θ,

as required. The rate of change of flux through the coil is essentially proportional to the velocity of the magnet as it passes through the coil. By choosing different amplitudes of oscillation of the magnet, we can alter this velocity.

Question 27.
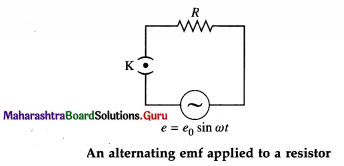
What is an ac generator? State the principle of an ac generator.
Answer:
An electric generator or dynamo converts mechanical energy into electric energy, just the opposite of what an electric motor does.

Principle : An AC generator works on electro-magnetic induction : When a coil of wire rotates between two poles of a permanent magnet such that the magnetic flux through the coil changes periodically with time due to a change in the angle between the area vector and the magnetic field, an alternating emf is induced in the coil causing a current to pass when the circuit is closed.

Question 28.
Briefly describe the construction of a simple ac generator. Obtain an expression for the emf induced in a coil rotating with a uniform angular velocity in a uniform magnetic field. Show graphically the variation of the emf with time (t). OR Describe the construction of a simple ac generator and explain its working.
Answer:
Construction : A simplified diagram of an ac generator is shown in below figure 12.18. It consists of many loops of wire wound on an armature that can rotate in a magnetic field. When the armature is turned by some mechanical means, an emf is generated in the rotating coil.

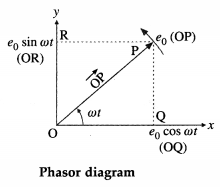
Consider the coil to have N turns, each of area A, and rotated with a constant angular speed ω – about an axis in the plane of the coil and perpendicular to a uniform magnetic field \(\vec{B}\), as shown in the figure. The frequency of rotation of the coil is f = ω / 2π.

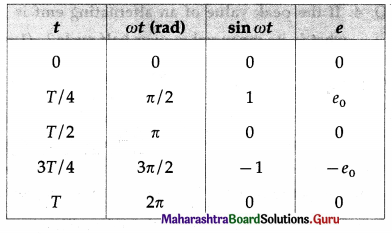
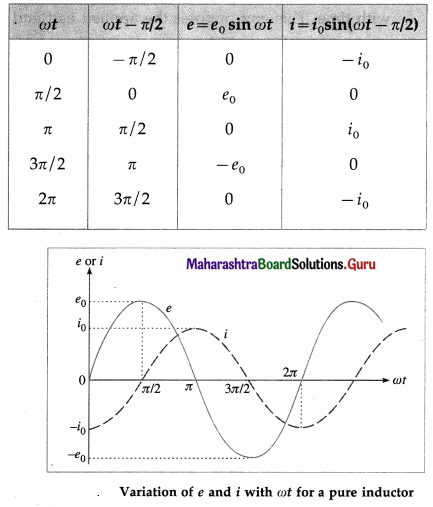
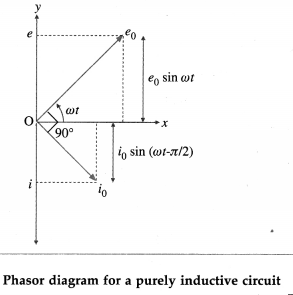
Working : The angle 9 between the magnetic field \(\vec{B}\) and the area of the coil \(\vec{A}\) at any instant t is θ = ωt (assuming θ = 0° at t = 0). At this position, the magnetic flux through the coil is
Φ_m = \(N \vec{B} \cdot \vec{A}\) = NBA cos θ = NBA cos ωt

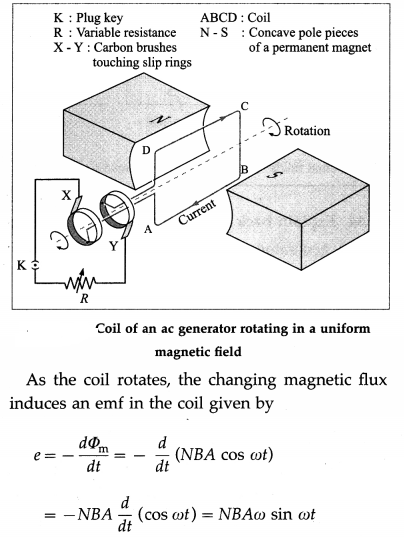
∴ e = e₀ sin ωt, where e₀ = NBAω.
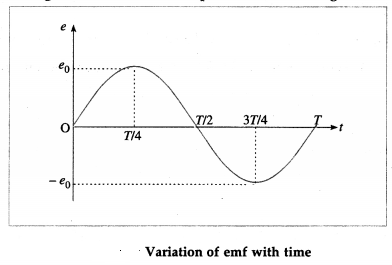
Therefore the induced emf varies as sin cot and is called sinusoidally alternating emf. In one rotation of the coil, sin cot varies between +1 and – 1 and hence the induced emf varies between +e₀ and -e₀. The maximum value e₀ of an alternating emf is called the peak value or amplitude of the emf.

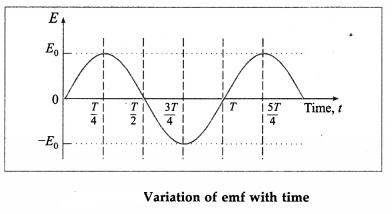
The sinusoidal variation of emf with time t is shown in above figure. The emf changes direction at the end of every half rotation of the coil. The frequency of the alternating emf is equal to the frequency/of rotation of the coil. The period of the alternating emf is T = \(\frac{1}{f}\)

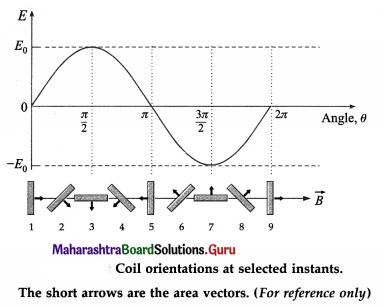
Imagine looking at the coil of the ac generator from the slip rings along the rotation axis in Fig. 12.18. The magnetic flux, rate of change of flux and sign of the induced emf are shown in the table below for the different orientations of the coil as in below figure.

Coil orientation	Flux Φm	dΦm/dt	Induced emf
1	Positive maximum	Momentarily zero (constant flux)	Zero
2	Positive	Decreasing (negative)	Positive
3	Zero	Decreasing (negative)	Positive
4	Negative	Decreasing (negative)	Positive
5	Negative maximum	Momentarily zero (constant flux)	Zero
6	Negative	Increasing (positive)	Negative
7	Zero	Increasing (positive)	Negative
8	Positive	Increasing (positive)	Negative
9	Return to positive maximum	Momentarily zero (constant flux)	Zero

Question 29.
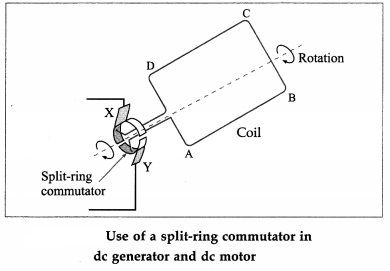
How does a dc generator differ from an ac generator?
Answer:
A dc generator is much like an ac generator, except that the slip rings at the ouput are replaced by a split-ring commutator, just as in a dc motor.

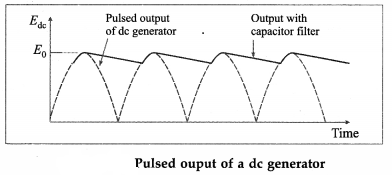
The output of a dc generator is a pulsating dc as shown in Fig. 12.22. For a smoother output, a capacitor filter is connected in parallel with the output (see below figure for reference).

Question 30
Explain back emf in a motor.
Answer:
A generator converts mechanical energy into electrical energy, whereas a motor converts electrical energy into mechanical energy. Also, motors and generators have the same construction. When the coil of a motor is rotated by the input emf, the changing magnetic flux through the coil induces an emf, consistent with Faraday’s law of induction. A motor thus acts as a generator whenever its coil rotates. According to Lenz’s law, this induced emf opposes any change, so that the input emf that powers the motor is opposed by the motor’s self-generated emf. This self-generated emf is called a back emf because it opposes the change producing it.

Question 31.
A motor draws more current when it starts than when it runs at its full (i.e., operating) speed. Explain.
OR
When a pump or refrigerator (or other large motor) starts up, lights in the same circuit dim briefly.
Answer:
The back emf is effectively the generator output of a motor, and is proportional to the angular velocity co of the motor. Hence, when the motor is first turned on, the back emf is zero and the coil receives the full input voltage. Thus, the motor draws maximum current when it is first turned on. As the motor speeds up, the back emf grows, always opposing the driving emf, and reduces the voltage across the coil and the amount of current it draws. This explains why a motor draws more current when it first comes on, than when it runs at its normal operating speed.

The effect is noticeable when a high power motor, like that of a pump, refrigerator or washing machine is first turned on. The large initial current causes the voltage at the outlets in the same circuit to drop. Due to the IR drop produced in feeder lines by the large current drawn by the motor, lights in the same circuit dim briefly.

[Note : A motor is designed to run at a certain speed for a given applied voltage. A mechanical overload on the motor slows it down appreciably. If the rotation speed is reduced, the back emf will not be as high as designed for and the current will increase. At too low speed, the large current can even burn its coil. On the other hand, if there is no mechanical load on the motor, its angular velocity will increase until the back emf is nearly equal to the driving emf. Then, the motor uses only enough energy to overcome friction.]

Question 32.
What is back torque in a generator?
Answer:
In an electric generator, the mechanical rotation of the armature induces an emf in its coil. This is the output emf of the generator. Under no-load condition, there is no current although the output emf exists, and it takes little effort to rotate the armature.

However, when a load current is drawn, the situation is similar to a current-carrying coil in an external magnetic field. Then, a torque is exerted, and this torque opposes the rotation. This is called back torque or counter torque.

Because of the back torque, the external agent has to apply a greater torque to keep the generator running. The greater the load current, the greater is the back torque.

33. Solve the following 
Question 1.
An ac generator spinning at a rate of 750 rev/min produces a maximum emf of 45 V. At what angular speed does this generator produce a maximum emf of 102 V ?
Solution:
Data : e₁ = 45 V, f₁ = 750 rpm, e₂ = 102 V
e = NABω = NAB(2πf) ∴ e ∝ f
∴\(\frac{e_{2}}{e_{1}}=\frac{f_{2}}{f_{1}}\)
∴ f₂ = \(\frac{e_{2}}{e_{1}}\) × f₁ = \(\frac{102}{45}\) × 750 = 1700 rpm
This is the required frequency of the generator coil.

Question 2.
An ac generator has a coil of 250 turns rotating at 60 Hz in a magnetic field of \(\frac{0.6}{\pi}\) T. What must be the area of each turn of the coil to produce a maximum emf of 180 V ?
Solution:
Data : N = 250, f = 60 Hz, B = \(\frac{0.6}{\pi}\) T
e₀ = NABω = NAB (2πf)
∴ A = \(\frac{e_{0}}{N B 2 \pi f}=\frac{180}{(250)(0.6 / \pi)(2 \pi \times 60)}=\frac{18}{25 \times 72}\)
= 10^-2 m²
This must be the area of each turn of the coil.

Question 3.
A dynamo attached to a bicycle has a 200 turn coil, each of area 0.10 m². The coil rotates half a revolution per second and is placed in a uniform magnetic field of 0.02 T. Find the maximum voltage generated in the coil.
Solution:
Data : N = 200, A = 0.1 m², f = 0.5 Hz, B = 0.02T
e₀ = NABω = NAB (2πf)
Therefore, the maximum voltage generated,
e₀ = (200)(0.1)(0.02)(2 × 3.142 × 0.5) = 1.26 V

Question 4.
A motor has a coil resistance of 5 Ω. If it draws 8.2 A when running at full speed and connected to a 220 V line, how large is the back emf ?
Solution:
Data : R = 5 Ω, I = 8.2 A, e_appIied = 220 V
e_appIied – e_back =IR = 0
∴ e_back = _appIied – IR = 220 – (8.2)(5)
= 220 – 42 = 178 V

Question 5.
The back emf in a motor is 100 V when operating . at 2500 rpm. What would be the back emf at 1800 rpm? Assume the magnetic field remains unchanged.
Solution:
Data : e₁ = 100 V, f₁ = 2500 rpm, f₂ = 1800 rpm
The back emf is proportional to the angular speed.
∴ \(\frac{e_{2}}{e_{1}}=\frac{f_{2}}{f_{1}}\)
∴ e₂ = \(\frac{f_{2}}{f_{1}}\) × e₁ = \(\frac{1800}{2500}\) × 100 = 72V
This is the back emf at lower speed.

Question 6.
The armature windings of a dc motor have a resistance of 10 Ω. The motor is connected to a 220 V line, and when the motor reaches full speed at normal load, the back emf is 160 V. Calculate
(a) the current when the motor is just starting up
(b) the current at full speed,
(c) What will be the current if the load causes it to run at half speed ?
Solution:
Data : R = 10 Ω, e_appIied = 220 V, e_back = 160 V,
f₂ = f₁/2 .
e_appIied – e_back – IR = 0
(a) At start up, back emf is zero.
∴ I_start = \(\frac{e_{\text {applied }}}{R}=\frac{220}{10}\) = 22 A

(b) At full speed,
I_normal = \(\frac{e_{\text {applied }}-e_{\text {back }}}{R}=\frac{220-160}{10}=\frac{60}{10}\) = 6 A

(c) Back emf is proprtional to rotational speed. Thus, if the motion is running at half the speed, back emf is half the original value, i.e., 80 V. Therefore, at half speed,
I₂ = \(\frac{e_{\text {applied }}-e_{2}}{R}=\frac{220-80}{10}=\frac{140}{10}\) = 14 A

Question 34.
Find an expression for the power expended in pulling a conducting loop out of a magnetic field.
Answer:
When an external agent produces a relative motion between a conducting loop and an external magnetic field, a magnetic force resists the motion, requiring the applied force to do positive work. The work done is transferred to the material of the loop as thermal energy because of the electrical resistance of the material to the current that is induced by the motion.

Proof : Consider a rectangular wire loop ABCD of width l, with its plane perpendicular to a uniform magnetic field of induction \(\vec{B}\). The loop is being pulled out of the magnetic field at a constant speed v, as shown in below figure (a).

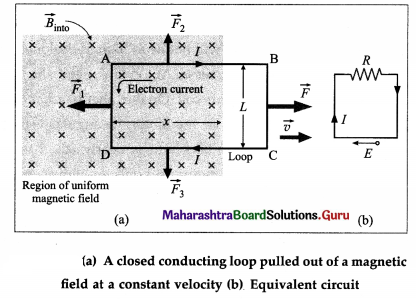
At any instant, let x be the length of the part of the loop in the magnetic field. As the loop moves to the right through a distance dx = vdt in time dt, the area of the loop inside the field changes by dA = ldx = lvdt. And, the change in the magnetic flux dΦ_m through the loop is
dΦ_m = BdA = Blvdt ………….. (1)
Then, the time rate of change of magnetic flux is
\(\frac{d \Phi_{\mathrm{m}}}{d t}=\frac{B l v d t}{d t}\) = B l v ……………. (2)
By Faraday’s second law, the magnitude of the induced emf is
|e| = \(\frac{d \Phi_{\mathrm{m}}}{d t}\) = B l v ………….. (3)

Due to the motion of the loop, the tree electrons (charge, e) in the wire inside the field experience Lorentz force \(e \vec{v} \times \vec{B}\). In the wire PQ this force moves the Free electrons 1mm P to Q making them travel in the anticlockwise sense around the 1oop. Therefore, the induced conventional current I is in the clockwise sense, as shown.

From figure (b) shows the equivalent circuit of the loop, where the induced emf e is a distributed emf and R is the total resistance of the loop.
∴ I = \(\frac{|e|}{R}=\frac{B l v}{R}\) …………… (4)
Now, a straight current carrying conductor of length L in a magnetic held experiences a torce
\(\vec{F}=I \vec{L} \times \vec{B}\)
whose direction can be found using Fleming’s Left hand rule.

Accordingly, forces \(\vec{F}_{2}\) and \(\vec{F}_{3}\) on wires AH and CD, respectively, are equal in magnitude (= Ix8), opposite in direction and have the same line of action- Hence, they balance each other. There is no torce on the wire BC as it hes outside the field.

The force \(\vec{F}_{1}\) on the wire AD has magnitude F₁ = IlB and Is directed towards the left. To move the loop with constant velocity \(\vec{v}\), an external force \(\vec{F}=-\vec{F}_{1}\) must be applied. Therefore, in magnitude,

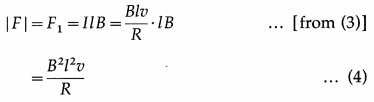
Because B, l and R are constants a force of constant magnitude F is required to move the loop at constant speed v.

Thus, the power or the rate of doing work by the external agent is
P = \(\vec{F} \cdot \vec{v}\) = Fv = \(\frac{B^{2} l^{2} v^{2}}{R}\) ………….. (5)

Question 35.
Why and where are eddy currents undesirable ? How are they minimized ?
Answer:
Eddy currents result in generation of heat (energy loss) in the cores of transformers, motors, induction coils, etc.

To minimize the eddy currents, instead of a solid metal block, cores are made of thin insulated metal strips or laminae.

Question 36.
If a magnet is dropped through a long thick- walled vertical copper tube, it attains a constant velocity after some time. Explain.
Answer:
Every thin transverse section of a thick-walled vertical copper tube is an annular disc. The downward motion of the magnet causes increased magnetic flux through such conducting discs. By Lenz’s . law, the induced or eddy current around the discs produces a magnetic field of its own to oppose the change in flux due to the magnet’s motion.

Initially, as the magnet falls under gravity, its speed increases. But, quickly the vertically upward force on the magnet due to the induced current becomes equal in magnitude to the gravitational force on the magnet and the net force on the magnet becomes zero. The subsequent motion of the magnet is at this constant terminal speed.

Question 37.
Describe in brief an experiment to demonstrate that eddy currents oppose the cause producing them.
Answer:
Apparatus : A strong electromagnet; two thick copper discs (4″ dia, \(\frac{1}{4}\)” thick), each attached to a rod about 30″ long. One of the discs has several vertical slots, about 80 % of the way up. The pendulums can be suspended from a lab stand by a pivot mount and made to oscillate between closely-spaced pole pieces of the electromagnet.

Experiment: When the electromagnet is not turned on, both the pendulums swing freely with some damping due to air resistance. When the electromagnet is turned on, the slotted pendulum still swings, although a little more damped, but the solid pendulum practically stops dead between the pole pieces of the magnet immediately.

Conclusion : As the pendulums enter or exit the magnetic field, the changing magnetic flux sets up eddy currents in the discs. The sense of the eddy currents is so as to produce a torque that opposes the rotation of the discs about their pivot. This opposing torque produces a breaking action, damping the oscillations.

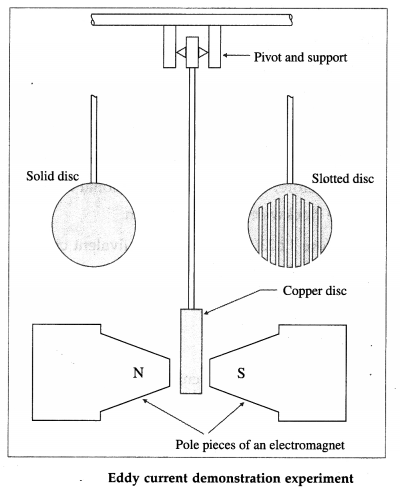
In the case of the solid disc, the continuous volume of the disc offers large unbroken path to the swirling electrons. Thus, the eddy current builds up to a large magnitude. The thicker the disc, the larger is the eddy current and, consequently, the larger the damping.

In the case of the slotted disc, the vertical slots do not allow large eddy current and, consequently, the damping is small.

Question 38.
A solid conducting plate swings like a pendulum about a pivot into a region of uniform magnetic field, as shown in the diagram. As it enters and leaves the field, show and explain the directions of the eddy current induced in the plate and the force on the plate.

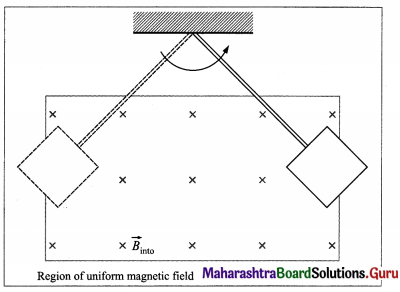
Answer:
Figure shows the eddy currents in the conducting plate as it enters and leaves the magnetic field. In both cases, it experiences a force \(\vec{F}\) opposing its motion. As the plate enters from the left, the magnetic flux through the plate increases. This sets up an eddy current in the anticlockwise direction, as shown. Since only the right-hand side of the current loop is inside the field, by Fleming’s right hand rule (FRH rule), an unopposed force acts on it to the left. There is no eddy current once the plate is completely inside the uniform field. When the plate leaves the field on the right, the decreasing flux causes an eddy current in the clockwise direction. The damping magnetic force on the current is to the left, further slowing the motion.

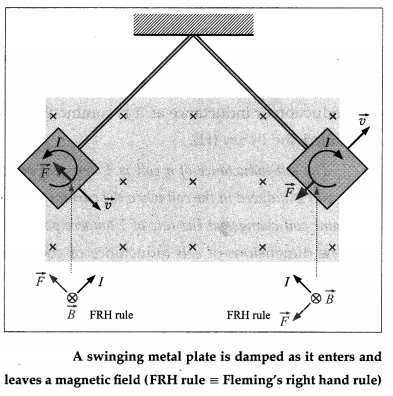
The eddy current in the plate results in mechanical energy being dissipated as thermal energy. Each time the plate enters and leaves the field, a part of its mechanical energy is transformed into thermal energy. After a few swings, the mechanical energy becomes zero and the motion comes to a stop with the warmed-up plate hanging vertically.

39. Solve the following 
Question 1.
A metal rod of resistance of 15 Ω is moved to the right at a constant 60 cm/s along two parallel conducting rails-25 cm apart and shorted at one end. A magnetic field of magnitude 0.35 T points into the page, (a) What are the induced emf and current in the rod? (b) At what rate is thermal energy generated?
Solution:
Data: R = 15Ω, v = 0.6 m/s, l = 0.25m, B = 0.35T
(a) Induced emf, e = Blv = (0.35)(0.25)(0.6)
= 0.0525 V = 52.5 mV
The current in the rod, I = \(\frac{e}{\mathrm{R}}=\frac{52.5}{15}\) = 3 5 mA

(b) Power dissipated, P = eI = 0.0525 × 3.5 × 10^-4
= 0.184 mW

Question 2.
A conducting rod 10 cm long is being pulled along horizontal, frictionless conducting rails at a con-stant 5 m/s. The rails are shorted at one end with a metal strip. There is a uniform magnetic field of strength 1.2 T out of the page in the region in which the rod moves. If the resistance of the rod is 0.5 Ω, what is the power of the external agent pulling the rod? Assume that the resistance of the rails is negligibly small.
Solution:
Data: l = 0.1 m, B = 1.2T, v = 5 m/s. R = 0.5 Ω
Power, P = \(\frac{(B l v)^{2}}{R}=\frac{(1.2 \times 0.1 \times 5)^{2}}{0.5}\) = 0.72 W

Question 40.
Explain the concept of self induction.
Answer:
Consider an isolated coil or circuit in which there is a current I. The current produces a magnetic flux linked with the coil.

The magnetic flux linked with the coil can be changed by varying the current in the coil itself, e.g., by breaking and closing the circuit. This produces a self-induced emf in the coil, called a back emf because it opposes the change producing it. It sets up an induced current in the coil itself in the same direction as the original current opposing its decrease when the key K is suddenly opened. When the key K is closed, the induced current is opposite to the conventional current, opposing its increase.

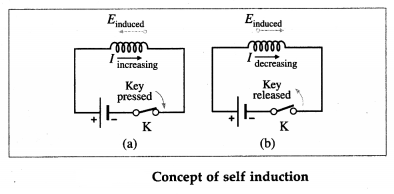
When the current through a coil changes continuously, e.g., by a time-varying applied emf, the magnetic flux linked with the coil also goes on changing.

The production of induced emf in a coil, due to the changes of current in the same coil, is called self induction.

Question 41.
Explain and define the self inductance of a coil.
OR
Define the coefficient of self induction.
Answer:
When the current through a coil goes on changing, the magnetic flux linked with the coil also goes on changing. The magnetic flux (NΦ_m) linked with the coil at any instant is directly proportional to the current (I) through the coil at that instant.
NΦ_m ∝ I
∴ NΦ_m = LI
where L is a constant, dependent on the geometry of the coil, called the self inductance or the coefficient, of self induction of the coil.
The self-induced emf in the coil is

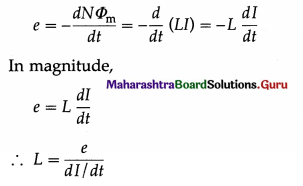
Definition : The self inductance or the coefficient of self induction of a coil is defined as the emf induced in the coil per unit time rate of change of current in the same coil. OR (using L = NΦ_m/I), the self inductance of a coil is the ratio of magnetic flux linked with the coil to the current in it.

Question 42.
State and define the SI unit of self inductance. Give its dimensions.
OR
Write the SI unit and dimensions of the coefficient of self induction.
Answer:
The SI unit of self inductance or coefficient of self induction or inductance as it is commonly called is called the henry (H).

The self-inductance of a coil is 1 henry, if an emf of 1 volt is induced in the coil when the current through the same coil changes at the rate of 1 ampere per second.

The dimensions of self inductance or coefficient of self induction are [ML²T^-2I^-2].
1 henry = 1 H = 1 V/A.s = 1 T.m²/A

[ Note : The unit henry is named in honour of Joseph Henry (1797-1878) US physicist.]

Question 43.
What is an inductor?
Answer:
An inductor is a coil of wire with significant self inductance. If the coil is wound on a nonmagnetic cylinder or former, such as ceramic or plastic, it is called an air-core inductor; its circuit symbol is . If the cod is wound on a magnetic former. such as laminated iron or ferrite. it Is called an iron core inductor; its circuit symbol is .

Question 44.
Current passes through a coil shown from left to right. In which direction is th induced emf. if the current is (a) increasing with time (b) decreasing in time?

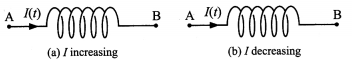
Answer:
From Lent’s law, the induced emf must oppose the diange in the magnetic flux. (a) When the current mcreases to the right, so is the magnetic flux. To oppose the increasing flux to the tight. the induced emi Is to the left. i.e.. the point A is at a positive potential relative to point B.

(b) When the current to the right is decreasing the induced emf acts to boost up the flux to the right and points to the tight, so that the point A is at a negative potential relative to point B.

Question 45.
Derive an expression for the energy stored in the magnetic field of an inductor.
OR
Derive an expression for the electrical work done in establishing a steady current in a coil of self inductance L.
Answer:
Consider an inductor of sell inductance L connected in a circuit When the circuit is dosed, the current in the circuit increases and so does the magnetic flux linked with the coiL At any instant the magnitude of the induced emf is
e = L \(\frac{d i}{d t}\)
The power consumed in the inductor is
P = ei = L \(\frac{d i}{d t}\) ∙ i
[Alternatively, the work done in moving a charge dq against this emf e is
dw = edq = L \(\frac{d i}{d t}\) ∙ dq = Li ∙ di (∵ \(\frac{d q}{d t}\) = i)
This work done is stored in the magnetic field of the inductor. dw = du.]

The total energy stored In the magnetic field when the current increases from 0 to I In a time interval from 0 to t can be determined by integrating this expression :
U_m = \(\int_{0}^{t} P d t=\int_{0}^{I} L i d i=L \int_{0}^{I} i d i=\frac{1}{2} L I^{2}\)
which is the required expression for the stored magnetic energy.
[Note: Compare this with the electric energy stored in a capacitor, U_e = \(\frac{1}{2}\)CV²]

Question 46.
State the expression for the energy stored in’the magnetic field of an inductor. Hence, define its self inductance.
Answer:
When a steady current is passed through an inductor of self inductance L the energy stored in the
magnetic field of the inductor is U_m = \(\frac{1}{2}\)Li²]. Therefore, for unit current, L = 2U_m

Hence, we may define the self inductance of a coil as numerically equal to twice the energy stored in its magnetic field for unit current through the inductor.

Question 47.
What is the role of an inductor in an ac circuit ?
Answer:
As a circuit element, an inductor slows down changes in the current in the circuit. Thus, it provides an electrical inertia and is said to act as a ballast. In a non-inductive coil (L ≅ 0), electrical energy is converted into heat due to ohmic resistance of the coil (Joule heating). On the other hand, an inductive coil or an inductor stores part of the energy in the magnetic field of its coils when the current through it is increasing; this energy is released when the current is decreasing. Thus, an inductor limits an alternating current more efficiently than a non-inductive coil or a pure resistor.

Question 48.
State the expressions for the effective or equivalent inductance of a combination of a number of inductors connected (a) in series (b) in parallel. Assume that their mutual inductance can be ignored.
Answer:
We assume that the inductors are so far apart that their mutual inductance is negligible.
(a) For a series combination of a number of inductors, L₁, L₂, L₃, …, the equivalent inductance is
L_series = L₁ + L₂ + L₃+ ……..

(b) For a parallel combination of a number of inductors, L₁, L₂, L₃, …, the equivalent inductance is
\(\frac{1}{L_{\text {parallel }}}=\frac{1}{L_{1}}+\frac{1}{L_{2}}+\frac{1}{L_{3}}+\ldots\)

Question 49.
Obtain an expression for the self inductance of a solenoid.
Answer:
Consider a long air-cored solenoid of length Z, diameter d and N turns of wire. We assume that the length of the solenoid is much greater than its diameter so that the magnetic field inside the solenoid may considered to be uniform, that is, end effects in the solenoid can be ignored. With a steady current I in the solenoid, the magnetic field within the solenoid is
B = µ₀nI ………….. (1)
where n = N/l is the number of turns per unit length. So the magnetic flux through one turn is
Φ_m = BA = µ₀nIA ……….. (2)
Hence, the self inductance of the solenoid,
L = \(\frac{N \Phi_{\mathrm{m}}}{I}\) =(nl)µ₀nA = µ₀n²lA = µ₀n² V ………….. (3)
= µ₀n²l\(\frac{\pi d^{2}}{4}\) …………. (4)
where V = lA is the interior volume of the solenoid. Equation (3) or (4) gives the required expression.

[Note: It is evident thatthe self inductance of a long solenoid depends only on its physical properties – such as the number of turns of wire per unit length and the volume, and not on the magnetic field or the current. This is true for inductors in general.] .

Question 50.
State the expression for the self inductance of a solenoid. Hence show that the SI unit of magnetic permeability is the henry per metre.
Answer:
The self inductance of an air-cored long solenoid of volume V and number of turns per unit length n is L = µ₀n²V. Since [n²] = [L^-2], n²V has the dimension of length. The SI unit of the L being the henry, the SI unit of magnetic permeability (µ₀) is the henry per metre (H / m). .
µ₀ = 4π × 10^-7 H/m = 4π × 10^-7 T∙m/A

Question 51.
Derive an expression for the self inductance of a narrow air-cored toroid of circular cross section.
Answer:
Consider a narrow air-cored toroid of circular cross section of radius r, central radius R and number of turns N. So that, assuming r << R, the magnetic field in the toroidal cavity is considered to be uniform, equal to
B = \(\frac{\mu_{0} N I}{2 \pi R}\) = µ₀nI ………….. (1)
where n = \(\frac{N}{2 \pi R}\) is the number of turns of the wire 2nR per unit length. The area of cross section, A = πr².
The magnetic flux through one turn is
Φ_m = BA = µ₀nIA ………… (2)
Hence, the self inductance of the toroid,
L = \(\frac{N \Phi_{\mathrm{m}}}{I}\) = (2πRn) µ₀nA = µ₀2πRn²A = µ₀n²V …………… (3)
= \(\frac{\mu_{0} N^{2} r^{2}}{2 R}\) ………….. (4)
where V = 2πRA is the volume of the toroidal cavity. Equation (3) or (4) gives the required expression.

Question 52.
Obtain an expression for the energy density of a magnetic field.
Answer:
Consider a short length ¡ near the middle of a long, tightly wound solenoid, of cross-sectional area A, number of turns per unit length n and carrying a steady current I. For such a solenoid, the magnetic field is approximately uniform everywhere inside and zero outside. So, the magnetic energy U_m stored by this length l of the solenoid lies entirely within the volume Al.

The magnetic field inside the solenoid is
B = µ₀nI …………… (1)
and if L be the inductance of length l of the solenoid,
L = µ₀ n²lA …………… (2)
The stored magnetic energy,
U_m = \(\frac{1}{2}\)LI² …………. (3)
and the energy density of the magnetic field (energy per unit volume) is

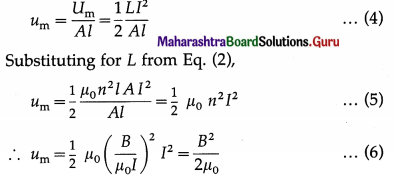
Equation (6) gives the magnetic energy density in vacuum at any point in a magnetic field of induction B, irrespective of how the field is produced.

[Note : Compare Eq.(6) with the electric energy density in vacuum at any point in an electric field of intensity
e, u_e = \(\frac{1}{2}\) ε₀e². Both u_e and u_m are proportional to the square of the appropriate field magnitude.]

Question 53.
Determine the magnetic energy stored per unit length of a coaxial cable, represented by two coaxial cylindrical shells of radii a (inner) and b (outer), and carrying a current I. Hence derive an expression for the self inductance of the coaxial cable of length l.
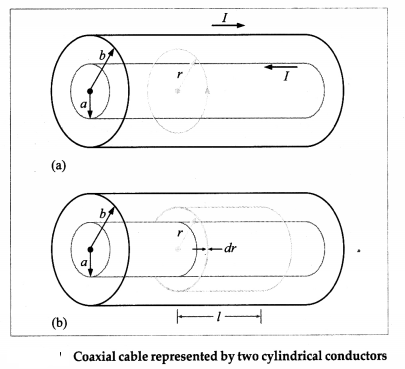
Answer:
Figure (a) shows a coaxial cable represented by two hollow, concentric cylindrical conductors along which there is electric current in opposite directions. The magnetic field between the conductors can be found by applying Ampere’s law to the dashed path of radius r{a < r < b) in figure (a). Because of the cylindrical symmetry, B is constant along the path, and
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = B (2πr) = u₀I
∴ B = \(\frac{\mu_{0} I}{2 \pi r}\) ……………… (1)

A similar application of Ampere’s law for r > b and r < a, shows that B = 0 in both the regions. Therefore, all the magnetic energy is stored between the two conductors of the cable.
The energy density of the magnetic field is
u_m = \(\frac{B^{2}}{2 \mu_{0}}\) …………….. (2)
Therefore, substituting for B from Eq. (1) into Eq. (2), the magnetic energy stored in a cylindrical shell of radius r, thickness dr and length l is
dU_m = u_mdV = u_m(2πr ∙ dr ∙ l)

Equating the right hand sides of Eqs. (4) and (6),

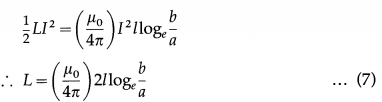
54. Solve the following
Question 1.
A coil of self inductance 5 H is connected in series with a switch and a battery. After the switch is closed, the steady state value of the current is 5 A. The switch is then suddenly opened, causing the current to drop to zero in 0.2 s. Find the emf developed across the inductor (coil) as the switch is opened.
Solution:
Data : L = 5 H, I_i = 5 A, I_f = 0, ∆t = 0.2 s
The rate of change of current,
\(\frac{d I}{d t}=\frac{I_{\mathrm{f}}-I_{\mathrm{i}}}{\Delta t}=\frac{0-5}{0.2}\) = – 25 A/s
∴ The induced emf,
e = -L \(\frac{d I}{d t}\) = -5(-25) = 125 V

Question 2.
A toroidal coil has an inductance of 47 mH. Find the maximum self-induced emf in the coil when the current in it is reversed from 15 A to -15 A in 0.01 s.
Solution:
Data : L = 4.7 × 10^-2 H, I_i = 15A, I_i = -15 A,
∆f = 0.01 s
The rate of change of current,
\(\frac{d I}{d t}=\frac{I_{\mathrm{f}}-I_{\mathrm{i}}}{\Delta t}=\frac{(-15)-15}{0.01}\) = – 3000 A/s
∴ The maximum self-induced emf,
e = – L \(\frac{d I}{d t}\) (4.7 × 10^-2) (- 3000) = 141 V

Question 3.
An emf of 2 V is induced in a closely-wound coil of 50 turns when the current through it increases uniformly from O to 5 A in 0.1 s. (a) What is the self inductance of the coil? (b) What is the flux through each turn of the coil for a steady current at 5A?
Solution:
Data : e = 2 V, N = 50, I_i = 0, I_f = 5A, ∆t = 0.1 s
(a) The rate of change of current

This is the flux through each turn.

Question 4.
At the instant the current through a coil is 0.2 A, the energy stored in its magnetic field is 6 mJ. What is the self indudance of the coil ?
Solution:
Data: I = 0.2A, U_m = 6 × 10^-3 J
U_m = \(\frac{1}{2}\) LI²
Therefore, self inductance of the coil is

Question 5.
A coil of self inductance 3 H and resistance 100 Ω carries a steady current of 2 A. (a) What is the energy stored in the magnetic field of the coil? (b) What is the energy per second dissipated in the resistance of the coil ?
Solution:
Data : L = 3 H, R = 100 Ω, I = 2 A
(a) Magnetic energy stored,
U_m = \(\frac{1}{2}\) LI² = \(\frac{1}{2}\) (3) (2)² = 6 J

(b) Power dissipated in the resistance of the coil,
P = I²R = (2)²(100) = 400 W

Question 6.
A 10 H inductor carries a current of 25 A. Flow much ice at 0 °C could be melted by the energy stored in the magnetic field of the inductor ? [Latent heat of fusion of ice, L_f = 335 J/g]
Solution:
Data : L = 10 H, Z = 25 A, L_f = 335 J/g
Magnetic energy stored,
U_m = \(\frac{1}{2}\) LI² = \(\frac{1}{2}\) (10) (25)² = 3125 J
Heat energy required to melt ice at 0 °C of mass m,
H = mL_f
Equating H with U_m,
m = \(\frac{U_{\mathrm{m}}}{L_{\mathrm{f}}}=\frac{3125}{335}\) = 9.328 g
Therefore, 9.328 g of ice could be melted by the energy stored.

Question 7.
A solenoid 40 cm long has a cross-sectional area of 0.9 cm2 and is tightly wound with wire of diameter 1 mm. Calculate the self inductance of the solenoid.
Solution:
Data : D = 1 mm, l = 40 cm = 0.4 m, A = 0.9 cm² = 9 × 10^-5 m², I_i = 10 A, I_f = 0, ∆t = 0.1 s,
μ₀ = 4π × 10^-7 H/m
The number of turns per unit length,
n = \(\frac{1}{1 \mathrm{~mm}}\) = 1 mm^-1 = 10³ m^-1
Self inductance of the solenoid,
L = μ₀n²lA = (4π × 10^-7)(10³)²(0.4)(9 × 10^-5)
= 16 × 9 × 3.142 × 10^-7 = 4.524 × 10^-5 H

Question 8.
A solenoid of 1000 turns is wound with wire of diameter 0.1 cm and has a self inductance of 2.4 π × 10^-5 H. Find (a) the cross-sectional area of the solenoid (b) the magnetic flux through one turn of the solenoid when a current of 3 A flows through it.
Solution:
Data: N = 1000, D = 0.1 cm, L = 2.4π × 10^-5 H,
I = 3A, μ₀ = 4π × 10^-7 H/m
The number of turns per unit length.
n = \(\frac{1}{1 \mathrm{~mm}}\) = 1 mm^-1 = 10³ m^-1
and the length of the solenoid,
l = ND = 1000 × 0.1 = 100 cm = 1 m
L = μ₀n²lA

(a) The area of cross section,
A = \(\frac{L}{\mu_{0} n^{2} l}=\frac{2.4 \pi \times 10^{-5}}{\left(4 \pi \times 10^{-7}\right)\left(10^{3}\right)^{2}(1)}=\frac{24 \pi}{4 \pi} \times 10^{-5}\)
= 6 × 10^-5 m²

(b) Magnetic flux through one turn,
Φ_m = BA = (μ₀nI)A
= (4π × 10^-7)(10³)(3)(6 × 10^-5)
= 72π × 10^-9 Wb

Question 9.
A toroid of circular cross section of radius 0.05 m has 2000 windings and a self inductance of 0.04 H. What is (a) the current through the windings when the energy in its magnetic field is 2 × 10^-6 J (b) the central radius of the toroid ?
Solution:
Data : r = 0.05 m, N = 2000, L = 0.04 H,
U_m = 2 × 10^-6 J, μ₀ = 4π × 10^-7 H/m
(a) U_m = \(\frac{1}{2}\) LI²
Therefore, the current in the windings,

Question 10.
A coaxial cable, whose outer radius is five times its inner radius, is carrying a current of 1.5 A. What is the magnetic field energy stored in a 2 m length of the cable ?
Solution:
Data : b/a = 5, I = 1.5A, l = 2m, \(\frac{\mu_{0}}{4 \pi}\) = 10^-7 H/m
The total magnetic energy in a given length of a current-carrying coaxial cable,
U_m = \(\left(\frac{\mu_{0}}{4 \pi}\right) I^{2} l \log _{e} \frac{b}{a}\)
Therefore, the required magnetic energy is
U_m = (10^-7)(1.5)²(2)log_e5
= 4.5 × 10⁷ × 2.303 × log₁₀5
= 4.5 × 10^-7 × 2.303 × 0.6990 = 7.24 × 10^-7 J

Question 55.
Explain the concept/phenomenon of mutual induction.
OR
Explain and define mutual inductance of a coil with respect to another coil.
OR
Define the coefficient of mutual induction.
Answer:

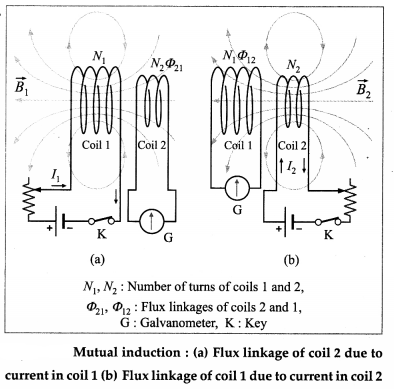
The production of induced emf in a coil due to the change of current in the same coil is called self induction.

In above figure (a), a current I₁ in coil 1 sets up a magnetic flux Φ₂₁ through one turn of a neighbouring coil 2, magnetically linking the two coils. Then, the flux through the N₂ turns of coil 2, i.e., the flux linkage of coil 2, is N₂Φ₂₁.
N₂Φ₂₁ ∝ I₁
∴ N₂Φ₂₁ = M₂₁I₁ …………. (1)
where the constant of proportionality, M₂₁, is called the coefficient of mutual induction of coil 2 with respect to coil 1. If the current I₁ in coil 1 changes with time, the varying flux linkage induces an emf e₂ in coil 2.
e₂ = – \(\frac{d}{d t}\) (N₂Φ₂₁) = – M₂₁ \(\frac{d I_{1}}{d t}\) …………. (2)
Similarly, if we interchange the roles of the two coils and set up a current I₂ in coil 2 [from figure (b)], Then, the flux linkage of N1 turns of coil 1 is N₁Φ₁₂ and
N₁Φ₁₂ = M₁₂I₂ ………… (3)
where M₁₂ is the coefficient of mutual induction of coil 1 with respect to coil 2. And, for a varying current I₂(t), the induced emf in coil 1 is

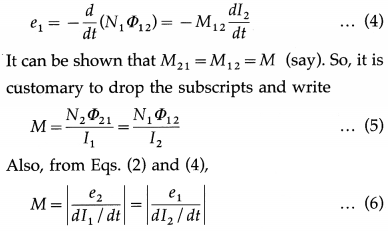
We define mutual inductance using Eq. (5) or Eq. (6).

The mutual inductance or the coefficient of mutual induction of two magnetically linked coils is equal to the flux linkage of one coil per unit current in the neighbouring coil.
OR
The mutual inductance or the coefficient of mutual induction of two magnetically linked coils is numerically equal to the emf induced in one coil (secondary) per unit time rate of change of current in the neighbouring coil (primary).

Question 56.
State and define the SI unit of mutual inductance. Give its dimensions.
Answer:
The SI unit of mutual inductance is called the henry (H).

The mutual inductance of a coil (secondary) with respect to a magnetically linked neighbouring coil (primary) is one henry if an emf of 1 volt is induced in the secondary coil when the current in the primary coil changes at the rate of 1 ampere per second.

The dimensions of mutual inductance are [ML²T^-2I^-2] (the same as those of self inductance).

Question 57.
Two coils A and B have mutual inductance 2 × 10^-2 H. If the current in the coil A is 5 sin (10πt) ampere, find the maximum emf induced in the coil B.
Ans;
The emf induced in the coil B,
|e_B| = M \(\frac{d I_{\mathrm{A}}}{d t}\)
=(2 × 10^-2)[5 cos (10πt)] × 10π
∴ |e_B|_max = π volts.

Question 58.
A long solenoid, of radius R, has n turns per unit length. An insulated coil C of IV turns is wound over it as shown. Show that the mutual inductance for the coil-solenoid combination is given by M = μ₀πR²nN.

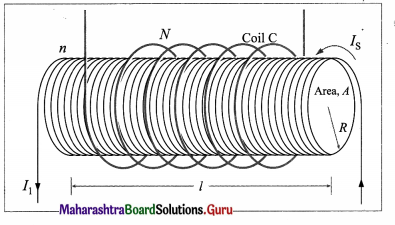
Answer:
We assume the solenoid to be ideal and that all the flux from the solenoid passes through the outer coil C. For a steady current Is through the solenoid, the uniform magnetic field inside the solenoid is
B = μ₀nI_s ……………… (1)
Then, the magnetic flux through each turn of the coil due to the current in the solenoid is
Φ_CS = BA = (μ₀nI_s)(πR²) ………….. (2)
Thus, their mutual inductance is
M = \(\frac{N \Phi_{\mathrm{CS}}}{I_{\mathrm{S}}}\) = μ₀πR²nN ………….. (3)
Equation (2) is true as long as the magnetic field of the solenoid is entirely contained within the cross section of the coil C. Hence, M does not depend on the shape, size, or possible lack of close packing of the coil.

Question 59.
A solenoid of N₁ turns has length l₁ and radius R₁, and a second smaller solenoid of N₂ turns has length l₂ and radius R₂. The smaller solenoid is placed coaxially and completely inside the larger solenoid. What is their mutual inductance ?
Answer:
Assuming the larger solenoid to be ideal, the magnetic field within it may be considered uniform, so the flux through the small solenoid due to the larger solenoid is also uniform. Assuming a current I₁ in the larger solenoid, the magnitude of the magnetic field at points within the small solenoid due to the larger one is
B₁ = μ₀\(\frac{N_{1}}{l_{1}}\) I₁
Then, the flux Φ₂₁ through each turn of the small coil is
Φ₂₁ = B₁A₂
where is A₂ = πR²₂, the area enclosed by the turn. Thus, the flux linkage in the small solenoid with its N₂ turns is
N₂Φ₂₁ = N₂B₁A₂
Thus, their mutual inductance is
M = \(\frac{N_{2} \Phi_{21}}{I_{1}}=N_{2}\left(\mu_{0} \frac{N_{1}}{l_{1}}\right)\left(\pi R_{2}^{2}\right)=\mu_{0} \pi \frac{N_{1} N_{2}}{l_{1}} R_{2}^{2}\)
which is the required expression.

Question 60.
What is meant by coefficient of magnetic coupling?
Answer:
For two inductively coupled coils, the fraction of the magnetic flux produced by the current in one coil (primary) that is linked with the other coil (secondary) is called the coefficient of magnetic coupling between the two coils.

The coupling coefficient K shows how good the coupling between the two coils is; 0 ≤ K ≤ 1. In the ideal case when all the flux of the primary passes through the secondary, K=l. For coils which are not coupled, K = 0. Two coils are tightly coupled if K > 0.5 and loosely coupled if K < 0.5.

[ Note ; For iron-core coupled circuits, the value of K may be as high as 0.99, for air-core coupled circuits, K varies between 0.4 to 0.8. ]

Question 61.
State the factors which magnetic coupling coefficient of two coils depends on.
Answer:
The coefficient of magnetic coupling between two coils depends on

1. the permeability of the core on which the coils are wound
2. the distance between the coils
3. the angle between the coil axes.

Question 62.
When is the magnetic coupling coefficient of two coils (i) maximum (ii) minimum?
Answer:
The coefficient of magnetic coupling between two coils is

1. maximum when the coils are wound on the same ferrite (iron) core such that the flux linkage is maximum,
2. minimum for air-cored coils with the coil axes perpendicular.

Question 63.
Show that the mutual inductance for a pair of inductively coupled coils/circuits of self inductances L₁ and L₂ is given by M = K\(\sqrt{L_{1} L_{2}}\), where K is the coupling coefficient.
Answer:
Consider a pair of inductively coupled coils having N₁ and N₂ turns, shown in figure

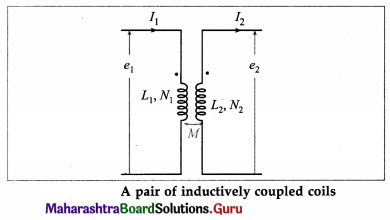
A current l₁(t) sets up a flux N₁Φ₁(t) in coil 1 and induces a current l₂(t) and flux N₂Φ₂(t) in coil 2. Then, the self inductances of the coils are

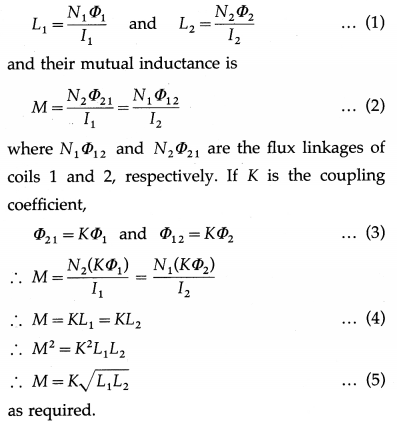
Alternate method :
Consider a pair of inductively coupled coils shown in above figure.We assume that I₁(t), I₂(t) are zero at t = 0. as also the magnetic energy of the system.
The induced emfs are

The net energy Input to the system shown in figure at time t is given by

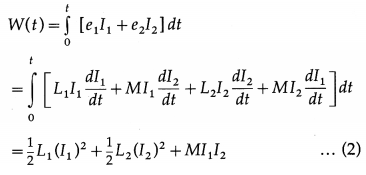
If one current enters a dot marked terminal while the other leaves a dot marked terminal, Eq. (2) becomes
W(t) = \(\frac{1}{2}\) L₁(I₁)² + \(\frac{1}{2}\) L₂(I₁)² – MI₁I₂ …………. (3)
The net electrical energy input to the system is non-negative, W(t) ≥ 0. We rearrange Eq.(3) as

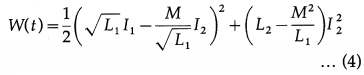
The first term in the parenthesis on the right hand side of Eq. (4) is positive for all values of I₁ and I₂ Thus, for the second term also to be non-negative,

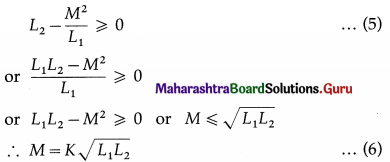
where the coupling coefficient K is a non-negtive number, 0 ≤ K ≤ 1, and is independent of the reference directions of the currents in the coils.

Question 64.
What is a transformer?
State the principle of working of a transformer.
Answer:
A transformer is an electrical device which uses mutual induction to transform electrical power at one alternating voltage into electrical power at another alternating voltage (usually different), without change of frequency of the voltage.

Principle : A transformer works on the principle that a changing current through one coil creates a changing magnetic flux through an adjacent coil which in turn induces an emf and a current in the second coil.

Question 65.
What are step-up and step-down transformers?
Answer:

1. Step-up transformer : It increases the amplitude of the alternating emf, i.e., it changes a low voltage alternating emf into a high voltage alternating emf with a lower current.
2. Step-down transformer : It decreases the amplitude of the alternating emf, i.e., it changes a high voltage alternating emf into a low voltage alternating emf with a higher current.

Question 66.
Describe the construction and working of a transformer with a neat labelled diagram.
Answer:
Construction : A transformer consists of two coils, primary and secondary, wound on two arms of a rectangular frame called the core.
(1) Primary coil : It consists of an insulated copper wire wound on one arm of the core. Input voltage is applied at the ends of this coil.

In a step-up transformer, thick copper wire is used for primary coil. In a step-down transformer, thin copper wire is used for primary coil.

(2) Secondary coil : It consists of an insulated copper wire wound on the other arm of the core. The output voltage is obtained at the ends of this coil.

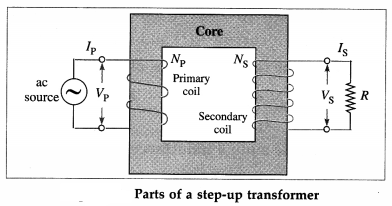
In a step-up transformer, thin copper wire is used for secondary coil. In a step-down transformer, thick copper wire is used for secondary coil.

(3) Core : It consists of thin rectangular frames of soft iron stacked together, but insulated from each other. A core prepared by stacking thin sheets rather than using a single thick sheet helps reduce eddy currents.

Working : When the terminals of the primary coil are connected to a source of an alternating emf (input voltage), there is an alternating current through it. The alternating current produces a time varying magnetic field in the core of the transformer. The magnetic flux associated with the secondary coil thus varies periodically with time according to the current in the primary coil. Therefore, an alternating emf (output voltage) is induced in the secondary coil.

Question 67.
Derive the relationship \(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}=\frac{I_{\mathrm{S}}}{I_{\mathrm{P}}}\) for a transformer.
Answer:
An alternating emf VP from an ac source is applied across the primary coil of a transformer. This sets up an alternating current IP in the primary circuit and also produces an alternating magnetic flux through the primary coil such that
V_P = -N_P \(\frac{d \Phi_{\mathrm{P}}}{d t}\),
where N_P is the number of turns of the primary coil and Φ_P is the magnetic flux through each turn.

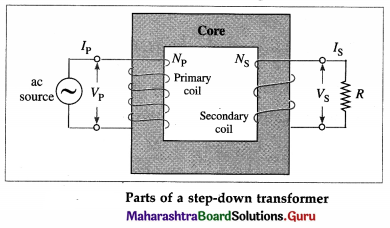
Assuming an ideal transformer (i.e., there is no leakage of magnetic flux), the same magnetic flux links both the primary and the secondary coils,
i. e., Φ_P = Φ_S
As a result, the alternating emf induced in the secondary coil,
V_S = = N_S \(\frac{d \Phi_{\mathrm{S}}}{d t}\) = – N_S \(\frac{d \Phi_{\mathrm{P}}}{d t}\)

where N_S is the number of turns of the secondary coil. If the secondary circuit is completed by a resistance R, the secondary current is I_S = V_S/R, assuming the resistance of the coil to be far less than R. Ignoring power losses, the power delivered to the primary coil equals that taken out of the secondary coil, so V_PI_P = V_SI_S.
∴ \(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}=\frac{I_{\mathrm{S}}}{I_{\mathrm{P}}}\)
which is the required expression.

Question 68.
Derive the relation \(\frac{V_{\mathrm{S}}}{V_{\mathrm{P}}}=\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) for a transformer. Hence, explain a step-up and a step-down trans-former. Also, show that \(\frac{I_{P}}{I_{\mathrm{S}}}=\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\)
OR
Derive expressions for the emf and current for a transformer in terms of the turns ratio.
Answer:
An alternating emf VP from an ac source is applied across the primary coil of a transformer, shown in figure.

This sets up an alternating current fP in the primary circuit and also produces an alternating magnetic flux through the primary coil such that
V_P = -N_P \(\frac{d \Phi_{\mathrm{P}}}{d t}\) ………….. (1)
where N_P is the number of turns of the primary coil and Φ_P is the magnetic flux through each turn.

Assuming an ideal transformer (i.e., there is no leakage of magnetic flux), the same magnetic flux links both the primary and the secondary coils, i.e., Φ_P = Φ_S.
As a result, the alternating emf induced in the secondary coil,
V_S = – N_S \(\frac{d \Phi_{\mathrm{S}}}{d t}\) = – N_S \(\frac{d \Phi_{\mathrm{P}}}{d t}\) ……………… (2)
where N_S is the number of turns of the secondary coil.
From Eqs. (1) and (2),
\(\frac{V_{\mathrm{S}}}{V_{\mathrm{P}}}=\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) or V_S = V_P \(\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) …………… (3)

Case (1) i If N_S > N_P, V_S > V_P. Then, the trans-former is called a step-up transformer.
Case (2) : If N_S < N_P, V_S < V_P. Then the transformer is called a step-down transformer.

Ignoring power losses, the power delivered to the primary coil equals that taken out of the secondary coil, so that V_PI_P = V_SI_S …………. (4)
From Eqs. (3) and (4),
\(\frac{I_{\mathrm{P}}}{I_{\mathrm{S}}}=\frac{V_{\mathrm{S}}}{V_{\mathrm{P}}}=\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\)

Question 69.
What is the turns ratio of a transformer? What can you say about its value for a (1) step-up transformer (2) step-down transformer?
Answer:
The ratio of the number of turns in the secondary coil (N_S) to that in the primary coil (N_P) is called the turns ratio of a transformer.
The turns ratio \(\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) > 1 for a step-up transformer.
The turns ratio \(\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) < 1 for a step-down transformer.

Question 70.
State any two factors on which the maximum value of the alternating emf induced in the secondary coil of a transformer depends.
Answer:
The maximum value of the alternating emf induced in the secondary coil of a transformer depends on

1. the ratio of the number of turns of the secondary coil to that of the primary coil
2. the maximum value of the alternating emf applied to the primary coil
3. the core of the transformer.

Question 71.
The primary coil of a transformer has 100 turns and the secondary coil has 200 turns. If the peak value of the alternating emf applied to the primary coil is 100 V, what is the peak value of the alternating emf obtained across the secondary coil?
Answer:

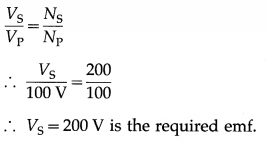
Question 72.
Distinguish between a step-up and a step-down transformers. (Any two points)
Answer:

Step-up transformer	Step-down transformer
1. The output voltage is more than the input voltage.	1. The output voltage is less than the input voltage.
2. The number of turns of the secondary coil is more than that of the primary coil.	2. The number of turns of the secondary coil is less than that of the primary coil.
3. The output current is less than the input current.	3. The output current is more than that of the input current.
4. The primary coil is made of thicker copper wire than the secondary coil.	4. The secondary coil is made of thicker copper wire than the primary coil.

72. Solve the following
Question 1.
When a current changes from 4 A to 12 A in 0.5 s in the primary coil, an induced emf of 50 mV is generated in the secondary coil. What is the mutual inductance between the two coils ? What will be the emf induced in the secondary, if the current in the primary changes from 3 A to 9 A in 0.02 s ?
Solution:
Data : I_i1 =4 A, I_f1 = 12 A, ∆t₁ = 0.5 s, ∆t₂ = 0.02 s

Question 2.
A plane coil of lo turns is tightly wound around a solenoid of diameter 2 cm having 400 turns per centimeter. The relative permeability of the core is 800. Calculate the mutual inductance.
Solution:
Data: N = 10, R = 1 cm = 10^-2 m,
n = 400 cm^-1 = 4 × 10⁴ m^-1, k = 800,
μ₀ = 4π × 10⁴ H/m
Mutual inductance,
M = kμ₀πR²nN
=(800)(4π × 10^-7)[π × (10²)²](4 × 10⁴)(10)
= 0.1264 H

Question 3.
Two coils of 100 turns and 200 turns have self inductances 25 mH and 40 mH, respectively. Their mutual inductance is 3 mH. If a 6 mA current in the first coil is changing at the rate of 4 A/s, calculate (a) 2 that links the first coil (b) self induced emf in the first coil (c) Φ₂₁ that links the second coil (d) mutually induced emf in the second coil.
Solution:
Data : N₁ = 100, N₂ = 200, L₁ = 25 mH, L₂ = 40 mH,
I₁ = 6 mA, dI₁ /dt = 4 A/s
(a) The flux per unit turn in coil 1,
Φ₂₁ = \( \frac{L_{1} I_{1}}{N_{1}}=\frac{\left(25 \times 10^{-3}\right)\left(6 \times 10^{-3}\right)}{100}\)
= 1.5 × 10^-6 Wb =1.5 μ Wb

(b) The magnitude of the self induced emf in coil 1 is
L₁ = \(\frac{d I_{1}}{d t}\) = (25 × 10^-3)(4) = 0.1 V

(c) The flux per unit turn in coil 2,
Φ₂₁ = \(\frac{M I_{1}}{N_{2}}=\frac{\left(3 \times 10^{-3}\right)\left(6 \times 10^{-3}\right)}{200}\)
= 90 × 10^-9 Wb = 90 nWb

(d) The mutually induced emf in coil 2 is
e₂₁ = M \(\frac{d I_{1}}{d t}\) = (3 × 10^-3)(4) = 12 × 10^-3 V
= 12 mV

Question 4.
The coefficient of mutual induction between primary and secondary coils is 2 H. Calculate the induced emf if a current of 4A is cut off in 2.5 × 10^-4 second.
Solution:
Data : M = 2 H, dI = – 4 A, dt = 2.5 × 10^-4 s
The induced emf, e = – M \(\frac{d I}{d t}=-\frac{2 \times(-4)}{2.5 \times 10^{-4}}\)
= \(\frac{8}{2.5}\) × 10⁴ = 3.2 × 10⁴ V

Question 5.
A current of 10 A in the primary of a transformer is reduced to zero at the uniform rate in 0.1 second. If the mutual inductance be 3 H, what is the emf induced in the secondary and change in the magnetic flux per turn in the secondary if it has 50 turns?
Solution:

This gives the change in the magnetic flux per turn in the secondary.

Question 6.
The primary and secondary coils of a transformer, assumed to be ideal, have 20 and 300 turns of wire, respectively. If the primary voltage is VP = 10 sincot (in volt), what is the maximum voltage in the secondary coil?
Solution:
Data : N_P = 20, N_S = 300, V_P = 10 sin ωt V
V_S = \(\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) V_P
= \(\frac{300}{20}\) × 10 sin ωt
= 150 sin ωt V
This is of the form V₀ sin ωt, where V₀ is the peak (or maximum) voltage.
∴ The maximum voltage in the secondary coil is 150 V.

Question 7.
A transformer converts 200 V ac to 50 V ac. The secondary has 50 turns and the load across it draws 300 mA current. Calculate (i) the number of turns in the primary (ii) the power consumed.
Solution:
Data: V_P = 200 V, V_S = 50 V, N_S = 50, I_S = 300mA = 0.3 A
(i) \(\frac{N_{\mathrm{P}}}{N_{\mathrm{S}}}=\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\)
∴ The number of turns in the primary,
N_P = N_S\(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\)
= 50 × \(\frac{200}{50}\) = 200

(ii) Power consumed = V_SI_S = 50 × 0.3 = 15 W

Question 8.
A resistance of 3 Ω is connected to the secondary coil of 60 turns of an ideal transformer. Calculate the current (peak value) in the resistor if the primary has 1200 turns and is connected to 240 V (peak) ac supply. Assume that all the magnetic flux in the primary coil passes through the secondary coil and that there are no other losses.
Solution:
Data : R = 3 Ω, N_S = 60, N_P = 1200, V_P = 240 V
V_S = \(\frac{N_{\mathrm{S}}}{N_{\mathrm{P}}}\) × V_P
= \(\frac{60}{1200}\) × 240 = 12 V (peak)
∴ The peak value of the current in the resistor in the transformer secondary coil is
I_S = \(\frac{V_{\mathrm{S}}}{R}=\frac{12}{3}\) = 4 A

Question 9.
The primary of a transformer has 40 turns and works on 100 V and 100 W. Find the number of turns in the secondary to step up the voltage to 400 V. Also calculate the current in the secondary and primary.
Solution :
Data : N_P = 40, V_P = 100 V, P_P = 100 W, V_S = 400 V

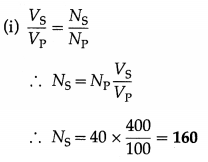
This gives the number of turns in the secondary coil.

(ii) Assuming P_S = P_S = 100 W,
V_SI_S = 100 W
∴ I_S = \(\frac{100}{V_{\mathrm{S}}}=\frac{100}{400}\) = 0.25 A
This gives the current in the secondary coil.

(iii) V_P . I_P = P_P ∴ I_P = \(\frac{P_{\mathrm{P}}}{V_{\mathrm{P}}}=\frac{100}{100}\) = 1 A
This gives the current in the primary coil.

Question 10.
A transformer converts 400 volt ac to 100 volt ac The secondary of the transformer has 50 turns and the load across it draws a current of 600 mA. What is the current in the primary, the power consumed and the number of turns in the primary?
Solution:
Data : V_P = 400 V. V_S = 100 V, N_S = 50, I_S = 0.6 A
Assuming no power loss. P_PV_P = I_SV_S
∴ The current in the primary,

Question 11.
A step down transformer works on 220 V a mains. What is the efficiency of the transformer when a bulb of 100 Wf20 V is connected to the a mains and the current in the primary is 0.5 A ?
Solution:
Data: V_P = 220V, V_S = 20V, P_S = 100W, I_P = 0.5 A
The Input power. P_P = I_PV_P = (0.5)220) = 110 W
The output power, P_S = 100 W
∴ The efficiency of the transformer
= \(\frac{\text { output power }}{\text { input power }}=\frac{100}{110}\) = 0.9091 or 90.91%

Multiple Choice Questions

Question 1.
A circular loop is placed in a uniform magnetic field. The total number of magnetic field lines passing normally through the plane of the coil is called
(A) the displacement current
(B) the eddy current
(C) the self inductance
(D) the magnetic flux
Answer:
(D) the magnetic flux

Question 2.
According to Lenz’s law, the direction of the induced current in a closed conducting loop is such that the induced magnetic field attempts to
(A) maintain the original magnetic flux through the loop
(B) maximize the magnetic flux through the loop
(C) maintain the magnetic flux through the loop to zero
(D) minimize the magnetic flux through the loop.
Answer:
(A) maintain the original magnetic flux through the loop

Question 3.
A metallic conductor AB moves across a magnetic field as shown in the following figure.

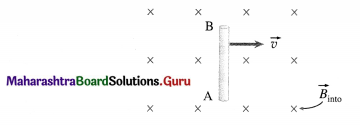
Which of the following statements is correct?
(A) The free electrons experience a magnetic force and move to the lower part of the conductor.
(B) The free electrons experience a magnetic force and move to the upper part of the conductor.
(C) The positive and negative charges experience a magnetic force and move, respectively, to the upper and lower parts of the conductor.
(D) The moving conductor gives rise to an emf but there is no separation of charges as they are bound in the solid structure.
Answer:
(A) The free electrons experience a magnetic force and move to the lower part of the conductor.

Question 4.
A bar magnet moves vertically down, approaching a circular conducting loop in the x-y plane. The direction of the induced current in the loop (looking down the z-axis) is

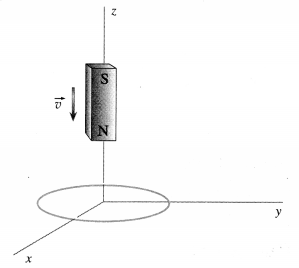
(A) anticlockwise
(B) clockwise
(C) alternating
(D) along negative z-axis.
Answer:
(A) anticlockwise

Question 5.
A moving conductor AB of length 1 makes a sliding electrical contacts at its ends with two parallel conducting rails. The rails are joined at the left edge (CD) by a resistance R to form a complete circuit.

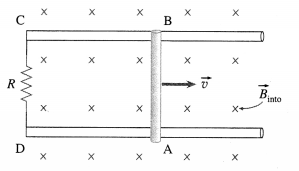
The rate at which the magnetic flux through the area bounded by the circuit changes is
(A) Bv
(B) Bl/v
(C) Bvl
(D) Bv/l.
Answer:
(C) Bvl

Question 6.
A metre gauge train is heading north with speed 54 km/h in the Earth’s magnetic field 3 × 10^-4 T. The emf induced across the axle joining the wheels is
(A) 0.45 mV
(B) 4.5 mV
(C) 45 mV
(D) 450 mV.
Answer:
(B) 4.5 mV

Question 7.
A conducting rod of length l rotates about one of its ends in a uniform magnetic field \(\vec{B}\) with a constant angular speed ω. If the plane of rotation is perpendicular to \(\vec{B}\), the emf induced between the ends of the rod is
(A) \(\frac{1}{2}\)Bωl2
(B) πl²Bω
(C) Bωl²
(D) 2Bωl².
Answer:
(A) \(\frac{1}{2}\)Bωl2

Question 8.
A circular conducting loop of area 100 cm2 and resistance 3 Ω is placed in a magnetic field with its plane perpendicular to the field. If the field is spatially uniform but varies with time t (in second) as B(f) = 1.5 cos ωt tesla, the peak value of the current is
(A) 3 mA
(B) 5ω mA
(C) 300ω mA
(D) 500 mA.
Answer:
(B) 5ω mA

Question 9.
In a simple rectangular-loop ac generator, the time rate of change of magnetic flux is a maximum when
(A) the induced emf has a minimum value
(B) the plane of the coil is parallel to the magnetic field
(C) the plane of the coil is perpendicular to the magnetic field
(D) the emf varies sinusoidally with time.
Answer:
(B) the plane of the coil is parallel to the magnetic field

Question 10.
A simple generator has a 300 loop square coil of side 20 cm turning in a field of 0.7 T. How fast must it turn to produce a peak output of 210 V ?
(A) 25 rps
(B) 4 rps
(C) 2.5 rps
(D) 0.4 rps
Answer:
(B) 4 rps

Question 11.
A rectangular loop generator of 100 turns, each of area 1000 cm², rotates in a uniform field of 0.02 π tesla with an angular velocity of 60 π rad/s. The maximum value of \(\frac{d \Phi_{\mathrm{m}}}{d t}\) is
(A) 12π V
(B) 12π² Wb
(C) 6π² V
(D) 12π² V.
Answer:
(D) 12π² V.

Question 12.
A 250 loop circular coil of area 16π² cm² rotates at 100 rev/s in a uniform magnetic field of 0.5 T. The rms voltage output of the generator is nearly
(A) 200\(\sqrt {2}\) V
(B) 20\(\sqrt {2}\) V
(C) 400 V
(D) 2\(\sqrt {2}\) MV.
Answer:
(A) 200\(\sqrt {2}\) V

Question 13.
Two tightly wound solenoids have the same length and circular cross-sectional area, but the wire of solenoid 1 is half as thick as solenoid 2. The ratio of their inductances is
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) 4
Answer:
(D) 4

Question 14.
The wire of a tightly wound solenoid is unwound and used to make another tightly wound solenoid of twice the diameter. The inductance changes by a factor of
(A) 4
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
(B) 2

Question 15.
The back emf of a dc motor is 108 V when it is connected to a 120 V line and reaches full speed against its normal load. What will be its back emf if a change in load causes the motor to run at half speed ?
(A) 66 V
(B) 12 V
(C) 60 V
(D) 54 V
Answer:
(D) 54 V

Question 16.
A single rectangular loop of wire, of dimensions 0.8 m × 0.4 m and resistance 0.2 Ω, is in a region of uniform magnetic field of 0.5 T in a plane perpendicular to the field. It is pulled along its length at a constant velocity of 5 m/s. Once one of its shorter side is just outside the field, the force required to pull the loop out of the field is

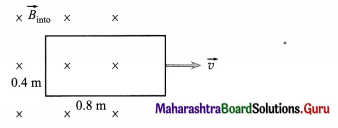
(A) 0.2 N
(B) 0.5 N
(C) 1 N
(D) 2 N.
Answer:
(C) 1 N

Question 17.
A pivoted bar with slots falls through a magnetic field. The bar falls the quickest if it is made of [Assume identical plate and slot dimensions. Ignore air resistance.]

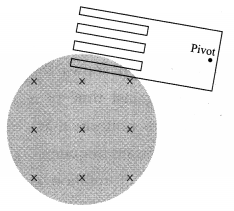
(A) copper
(B) a ferromagnetic
(C) aluminium
(D) plastic
Answer:
(D) plastic

Question 18.
Eddy currents are also called
(A) Maxwell currents
(B) Faraday currents
(C) displacement currents
(D) Foucault currents
Answer:
(D) Foucault currents

Question 19.
At a given instant the current and self-induced emf (e) in an inductor are directed as shown. If e = 60 V,
which of the following is true?

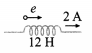
(A) The current is increasing at 2 A/s. 12 H
(B) The current is decreasing at 5 A/s.
(C) The current is increasing at 5 A/s.
(D) The current is decreasing at 6 A/s.
Answer:
(C) The current is increasing at 5 A/s.

Question 20.
A metal ring is placed in a region of uniform magnetic field such that the plane of the ring is perpendicular to the direction of the field. The field strength is increasing at a constant rate. Which of the following graphs best shows the variation with time t of the induced current I in the ring ?

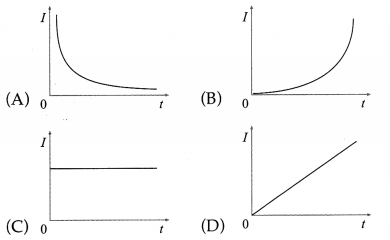
Answer:
(C)

Question 21.
At a given instant, the current through a 60 mH inductor is 50 mA and increasing at 100 mA/ s. The energy stored at that instant is
(A) 150 µJ
(B) 75 µJ
(C) 0.6 mJ
(D) 0.3 mJ
Answer:
(B) 75 µJ

Question 22.
The magnetic field within an air-cored solenoid is 0.8 T. If the solenoid is 40 cm long and 2 cm in diameter, the energy stored in its magnetic field is
(A) 32 J
(B) 3.2 J
(C) 6.4 kJ
(D) 64 kJ
Answer:
(A) 32 J

Question 23.
The adjacent graph shows the E induced emf against time of a coil rotated in a uniform magnetic field at a certain frequency. 0;
If the frequency of rotation is reduced to one half of its initial value, which one of the following graphs correctly shows the new variation of the induced emf with time.

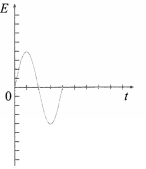
[All the graphs are drawn to the same scale.]

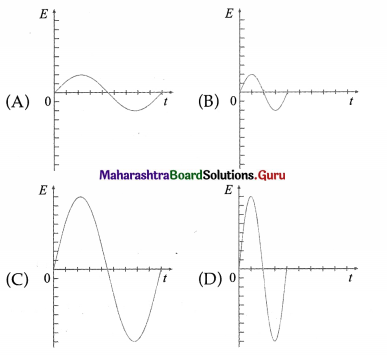
Answer:
(A)

Question 24.
A transformer has 320 turns primary coil and 120 turns secondary coil. Which of the following statements is true ?
(A) It changes current by a factor of \(\frac{8}{3}\) and is a step-up transformer.
(B) It is a step-down transformer and changes current by a factor of \(\frac{8}{3}\).
(C) It changes current by a factor of \(\frac{8}{3}\) and is a step-up transformer.
(D) It is a step-down transformer and changes current by a factor of \(\frac{8}{3}\).
Answer:
(B) It is a step-down transformer and changes current by a factor of \(\frac{8}{3}\).

Question 25.
Input power at 11000 V is fed to a step-down transformer which has 4000 turns in its primary winding. In order to get output power at 220 V, the number of turns in the secondary must be
(A) 20
(B) 80
(C) 400
(D) 800.
Answer:
(B) 80

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 6 Social Responsibilities of Business Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 6 Social Responsibilities of Business

Select the correct options and rewrite the sentence

Question 1.
Business organisation should not create profit.
(a) reasonable
(b) secret
(c) maximum
Answer:
(b) secret

Question 2.
Business organisation should avoid creation of ……………….
(a) trade unions
(b) consumers’ cell
(c) monopoly
Answer:
(c) monopoly

Question 3.
Business organisation is a part of ……………….
(a) industry
(b) government
(c) society
Answer:
(c) society

Question 4.
To maintain industrial peace is the responsibility of organisation towards ……………….
(a) customers
(b) employees
(c) society
Answer:
(b) employees

Question 5.
Ultimate goal of business must be satisfaction of …………………
(a) shareholders
(b) consumers
(c) owners
Answer:
(b) consumers

Question 6.
Location of industries should be in ……………….. zones.
(a) residential
(b) industrial
(c) commercial
Answer:
(b) industrial

Question 7.
To maintain safety of investment is responsibility of business towards …………………
(a) community
(b) investors
(c) employees
Answer:
(b) investors

Question 8.
In modern business environment, …………….. provides more opportunities and challenges.
(a) privatisation
(b) globalisation
(c) specialisation
Answer:
(b) globalisation

Match the pairs

Question 1.

Group A	Group B
(A) Responsibility to owners	(1) Negotiations with management
(B) Anti-social activity	(2) Pollution control
(C) Business ethics	(3) Good working condition
(D) Responsibility towards community	(4) Branch of philosophy
(E) Trade union	(5) Earning foreign exchange
	(6) Creating goodwill
	(7) To help small scale industry
	(8) Confidentiality
	(9) Provide often sales services
	(10) Smuggling

Answer:

Group A	Group B
(A) Responsibility to owners	(6) Creating goodwill
(B) Anti-social activity	(10) Smuggling
(C) Business ethics	(8) Confidentiality
(D) Responsibility towards community	(2) Pollution control
(E) Trade union	(1) Negotiations with management

Give one word/phrase/term for the following statement

Question 1.
Code of conduct followed by the business to regulate their behaviour.
Answer:
Business Ethics

Question 2.
Latest trend towards quality control.
Answer:
International Standard Organisation (ISO).

Question 3.
Process of integration of national economy with world economy.
Answer:
Globalisation

Question 4.
An association of employees who have come together to improve their wages, conditions of employment by means of collective bargaining.
Answer:
Trade Union

Question 5.
Responsibility of business organisation, towards environment, towards sustainable development including health and well-being of society.
Answer:
Corporate Social Responsibility (CSR)

Question 6.
Indian philosopher who had promoted concept of social responsibility in ancient times.
Answer:
Chanakya

Question 7.
Running efficient business is the responsibility of business towards this group.
Answer:
Owners.

State whether following statement are true or false

Question 1.
Business ethics are applicable to all business organisations.
Answer:
True

Question 2.
Every business organisation should undertake Research and Development.
Answer:
True

Question 3.
Business ethics can be considered as a tool for social development.
Answer:
False.

Question 4.
A business unit is a part of society.
Answer:
True

Question 5.
Business should not disclose their records to investors.
Answer:
False

Question 6.
Providing career opportunities to employees is the responsibility of business.
Answer:
True

Question 7.
Management should avoid worker’s participation while making decisions.
Answer:
False

Question 8.
Business organisation is not liable to control pollution.
Answer:
False

Question 9.
Ethics is a branch of politics.
Answer:
False

Question 10.
Business organisation can use natural resources as they want.
Answer:
False

Question 11.
Business organisation can participate in solving complex social problems.
Answer:
True

Complete the sentences

Question 1.
Business ethics is a branch of ……………..
Answer:
Social science

Question 2.
……………… should be printed on every product.
Answer:
Maximum Retail Price

Question 3.
Business and society are ……………….
Answer:
interdependent

Question 4.
The ……………….. protects the rights of employees.
Answer:
trade union

Question 5.
All companies shall spend, in every financial year, at least ……………… of the average net profits of the company.
Answer:
2%.

Answer in one sentence

Question 1.
In ancient times who preached and promoted ethical principles while doing business ?
Answer:
Philosophers like Chanakya from India and pre-Christian era philosophers in West, preached and promoted ethical principles while doing business.

Question 2.
Which points are to be considered by the business regarding investment by the investors ?
Answer:

1. Fair returns on investment,
2. Safety of investment,
3. Steady appreciation of business are the points to be considered by the business regarding investment made by investors.

Question 3.
Why is it necessary for the business to provide job security to their employees ?
Answer:
Security of job provides mental peace and employees can work with full dedication and concentration which will raise their morale and ; loyalty towards the organisation.

Question 4.
What should be banned by management to protect the interest of employees ?
Answer:
Management and Trade Union should agree to ban strikes and lockouts to protect the interest of both the parties.

Question 5.
What are 4 R’s in waste prevention techniques?
Answer:
Waste prevention techniques are commonly summarized in 4 ‘R’s:

1. Reduction in waste
2. Reuse of waste if practicable
3. Recycle of waste which cannot be reduced or reused.
4. Recover materials or energy from waste, if it cannot be reduced, reused or recycled.

Question 6.
Which companies has to comply with provisions related to CSR under Section 135 of Indian Companies Act 2013 ?
Answer:
Under Section 135 of India Companies Act 2013, the companies having net worth of 1500 Cr or more or turnover of 1000 Cr or more or net profit of 15 Cr or more during any financial year shall be required to comply with provision related to CSR.

Question 7.
How much amount companies are required to spend in pursuance of their CSR policy ?
Answer:
All companies shall spend, in every financial year, at least 2% of the average net profits of the company made during the three immediately preceding financial years, in pursuance of its CSR Policy.

Question 8.
What are penalties for Non-compliance of CSR activities ?
Answer:
Penalties for non-complying the duty of CSR would attract a fine of not less than Rs 50,000 which may extend to Rs 25,00,000 and every officer of the company in default shall be punishable with imprisonment for a term which may extend to 3 years; or with fine which shall not be less than Rs 50,000 which may extend to Rs 5,00,000 or with both.

Attempt the following

Question 1.
Explain the responsibilities of business organisations towards owners.
Answer:
The responsibilities of business organisations towards the owners are explained as follows:
(1) Reasonable profit : The business organisations must earn adequate (reasonable) profit for further growth and expansion. It brings financial stability.

(2) Exploring business opportunities : Opportunity refers to the scope available to the business enterprise to grow, expand and diversify the business. Businessmen should be watchful to find and explore such opportunities. They should take advantage of and exploit every possible opportunity. It is very essential for success of the business.

(3) Optimum use of capital : The business organisations are expected to use available capital more carefully and efficiently. Business risk should be carefully and properly considered. Management should take extra care for the safety of the capital.

(4) Minimise wastage : Management should provide due attention throughout the business to avoid or minimise the wastage of time, money, manpower and other resources. This in turn facilitates business enterprise to maximise its profitability.

(5) Efficient business : Business organisations are expected to make use of available resources up to their optimum level. Efficient use of resources ultimately increases efficiency, productivity and profitability.

(6) Fair practices on stock exchange : The business organisations should avoid all sorts of unfair practices on stock exchange such as insider trading, providing wrong and secret information about the affairs of the company, etc. Artificial increase or decrease in share prices put the common investors to loss.

(7) Expansion and diversification : The business unit must always develop, expand and diversify its business to strengthen and consolidate its position. It should always undertake research and development activities to face competition more successfully.

(8) Periodic information : It is obligatory for a business organisation to provide complete and accurate information in respect to financial position. It should disclose information through reports, circulars, etc.

(9) Effective use of owners’ funds : The company is expected to use the shareholders’ i.e. owners’ funds in the most profitable manner. It helps the organisation to give short term and long term returns in proper time.

(10) Creating goodwill : In order to get respect and trust in the (share) market, the management is expected to develop and maintain good public image of its company.

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 5 Emerging Modes of Business Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 5 Emerging Modes of Business

Select the correct options and rewrite the sentence

Question 1.
Wedding Planning is an example of ……………….
(a) corporate organisation
(b) outsourcing
(c) buying and selling of goods
Answer:
(b) outsourcing

Question 2.
……………… is the trading aspect of e-business where it connects buyers and sellers on the internet.
(a) Outsourcing
(b) e-commerce
(c) e-mail
Answer:
(b) e-commerce

Question 3.
An electronic facility of transferring funds through the internet is ………………. transfer.
(a) cash
(b) net banking
(c) credit
Answer:
(b) net banking

Question 4.
Credit or Debit Cards are popularly known as ………………. ‘Money’.
(a) Paper
(b) Plastic
(c) Polymer
Answer:
(b) Plastic

Question 5.
In e-business payments have to be made ……………….
(a) in cash
(b) credit
(c) online
Answer:
(c) online

Question 6.
The transactions under ………………. are between one business firm and other business firm.
(a) C2C
(b) B2C
(c) B2B
Answer:
(c) B2B

Match the pairs

Question 1.

Group A	Group B
(A) Outsourcing	(1) Consumer to consumer
(B) B2A	(2) Exist everywhere
(C) KPO	(3) First step
(D) C2A	(4) Business to Consumer
(E) LPO	(5) Electronic business
	(6) BPO
	(7) RTO
	(8) Efficient business
	(9) Exist only in cyberspace
	(10) Last step

Answer:

Group A	Group B
(A) Outsourcing	(8) Efficient business
(B) B2A	(5) Electronic business
(C) KPO	(6) BPO
(D) C2A	(1) Consumer to consumer
(E) LPO	(7) RTO

Give one word/phrase/term for the following statement

Question 1.
Name the term which is used by even common man effectively while collecting the needed s information quickly.
Answer:
Internet

Question 2.
Name the electronic facility of transferring funds through the internet.
Answer:
Net banking transfer

Question 3.
The form of electronic currency that exists only in cyberspace.
Answer:
Digital cash

Question 4.
The outsourcing of peripheral activities of the organisation to an external organisation to minimise cost.
Answer:
Business Process Outsourcing (BPO)

Question 5.
The trading aspect of e-business that connects buyers and sellers on the internet.
Answer:
e-commerce.

State whether following statement are true or false

Question 1.
Credit cards are used for online payment.
Answer:
True

Question 2.
In online transactions ‘Account’ is password protected.
Answer:
True

Question 3.
Online transactions are done without the help of internet.
Answer:
False

Question 4.
BPO enables optimum utilisation of scarce resources.
Answer:
True

Find the odd one

Question 1.
C2B, B2A, A2U, C2A.
Answer:
A2U

Question 2.
Off shore, Seashore, On shore, Near shore
Answer:
Seashore.

Complete the sentences

Question 1.
Use of Internet has considerably reduced the dependence on
Answer:
Paper work

Question 2.
includes more knowledge based and specialised work.
Answer:
KPO

Question 3.
The concept of e-business was coined in 90s by
Answer:
IBM.

Correct the underlined word and rewrite the sentence:

Question 1.
BPO is more complex than KPO.
Answer:
less

Question 2.
Traditional business lacks personal touch.
Answer:
e-business

Question 3.
E-commerce is superset of E-business.
Answer:
subset

Question 4.
E-business is narrower concept than s e-commerce.
Answer:
broader

Question 5.
E-commerce is more appropriate in B2B transaction.
Answer:
B2C.

Distinguish between

Question 1.
BPO and LPO
Answer:

	BPO	LPO
1. Meaning	BPO implies the outsourcing of non-primary peripheral activities of the organisation to an external organisation to decrease cost and increase efficiency of parent organisation.	LPO is a type of KPO that renders legal services ranging from drafting legal documents, performing legal research to offering legal advice for certain money consideration.
2. Degree of complexity	BPO is comparatively less complex.	LPO is relatively more complex.
3. Requirement	BPO requires process expertise.	LPO requires legal (law) expertise.
4. Talent required in employees	BPO requires personnel having good communication having legal (law) knowledge.	LPO requires professionally qualified personnel skills.
5. Focus	BPO focus on low level process.	LPO focus on high level process.
6. Outcome	BPO gives a company the ability to get access to skilled and trained manpower at low rate.	LPO allows organisations to access high level talent and niche expertise that does not exist within the firm.

Question 2.
KPO and LPO
Answer:

	KPO	LPO
1. Meaning	KPO is a form of outsourcing in which knowledge related and information related work are outsourced to third party service providers to help in value addition and to get cost benefits.	LPO is a type of KPO that renders legal services ranging from drafting legal documents, performing legal research to offering legal advice for certain money consideration.
2. Requirement	KPO requires knowledge expertise.	LPO requires legal (law) expertise.
3. Talent required in employees	KPO requires professionally qualified personnel having technical knowledge.	LPO requires professionally qualified personnel having legal (law) knowledge.
4. Nature	KPO is a subset of BPO which involves outsource of core functions of the parent company.	LPO is a type of KPO that is specific to legal services.
5. Sources of services	Business organisations mostly hire services from skilled employees supplied by KPO service providers.	In-house, legal department mostly hire services from law firms situated in foreign country to minimise cost.
6. Problems	Lack of communication due to legal, language and cultural barriers may create complications	LPO gets affected adversely by geographical hurdles between law firm and client organisation.

 

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 3 Entrepreneurship Development Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 3 Entrepreneurship Development

Select the correct options and rewrite the sentences

Question 1.
The term entrepreneur was first used by ………………
(a) J. Schumpeter
(b) R. Cantilon
(c) A.H. Cole
Answer:
(b) R. Cantilon

Question 2.
13 functions of an entrepreneur were enumerated by ………………
(a) J. Scumpeter
(b) R. Cantilon
(c) Kilby Peter
Answer:
(c) Kilby Peter

Question 3.
The inner urge of a person to do something is ………………
(a) initiative
(b) hard work
(c) creativity
Answer:
(a) initiative

Question 4.
Entrepreneurial ……………… is measured in terms of the individual’s attitude towards opportunity recognition.
(a) value
(b) attitude
(c) motivation
(b) attitude

Question 5.
The basic elements of the process of ……………… are motive, behaviour and goal.
(a) value
(b) motivation
(c) attitude
Answer:
(b) motivation

Question 6.
EDP was first introduced in ……………… in 1970.
(a) Maharashtra
(b) Andhra Pradesh
(c) Gujarat
Answer:
(c) Gujarat

Give one word/phrase/term which can substitute each one of the following

Question 1.
A process of setting up a new business organisation.
Answer:
Entrepreneurship

Question 2.
A combination of knowledge, skills, motive, attitude and habits.
Answer:
Competence

Question 3.
A scheme of instructions which is planned, systematic, consistent, pervasive and monitored to measure its effectiveness.
Answer:
Training

Question 4.
The fourth factor of production.
Answer:
Entrepreneurs.

Answer in one sentence

Question 1.
What is Entrepreneurship Development Programme (EDP)?
Answer:
An Entrepreneurship Development Programme is a device to help a person In strengthening his entrepreneurial motive and In acquiring skills and capabilities necessary for playing his entrepreneurial role efficiently.

Question 2.
Who is Intrapreneur?
Answer:
An intrapreneur is an employee who has the authority and support of his company/employer to implement his own innovative and creative ideas.

Question 3.
What is Training?
Answer:
Training is a scheme of instructions which is planned systematic, consistent, pervasive and monitored to measure its effectiveness.

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 2 Functions of Management Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 2 Functions of Management

Select the correct options and rewrite the sentences

Question 1.
Planning is …………… function.
(a) advanced
(b) basic
(c) end
Answer:
(b) basic

Question 2.
Division of work is involved in ……………… function.
(a) Planning
(b) Organising
(c) Directing
Answer:
(b) Organising

Question 3.
Directing is initiated at ……………….. level.
(a) Top
(b) Middle
(c) Lower
Answer:
(a) Top

Question 4.
Staffing function is a ……………… activity.
(a) basic
(b) continuous
(c) neutral
Answer:
(b) continuous

Question 5.
A process to establish harmony among different activities to achieve desired results is called ………………..
(a) Controlling
(b) Co-ordinating
(c) Co-operation
Answer:
(b) Co-ordinating

Question 6.
Unification, integration and synchronization of the efforts of group members so as to achieve common goals is a ……………… function.
(a) Planning
(b) Organising
(c) Co-ordinating
Answer:
(c) Co-ordinating

Question 7.
Staffing is concerned with ……………….
(a) physical factor
(b) financial factor
(c) human factor
Answer:
(c) human factor

Question 8.
Controlling measures the ……………… of actual performance from the standard performance.
(a) action
(b) deviation
(c) objective
Answer:
(b) deviation

Question 9.
Directing is a responsibility of ……………… at all levels.
(a) Manager
(b) Worker
(c) People
Answer:
(a) Manager

Question 10.
Physical, financial and human resources to develop productive relationship is a ………………. function.
(a) Organising
(b) Directing
(c) Staffing
Answer:
(a) Organising

Match the pairs

Question 1.

Group A	Group B
(A) Planning	(1) Individual Taste
(B) Organising	(2) Goodwill
(C) Staffing	(3) Bridges the gap between where we are now and where we want to go
(D) Co-ordinating	(4) All the people are employed
(E) Controlling	(5) Not directly related to Human Beings
	(6) Identify and Grouping the work to be performed
	(7) Corrective Action taking
	(8) Right People at Right Jobs
	(9) Taking action against employees
	(10) Aims only at Organisational Goals

Answer:

Group A	Group B
(A) Planning	(3) Bridges the gap between where we are now and where we want to go
(B) Organising	(6) Identify and Grouping the work to be performed
(C) Staffing	(8) Right People at Right Jobs
(D) Co-ordinating	(2) Goodwill
(E) Controlling	(7) Corrective Action taking

Question 2.

Group A	Group B
(A) Planning	(1) Unimportant management function
(B) Organising	(2) Increases productivity
(C) Staffing	(3) Goal-oriented /Basic function
(D) Co-ordinating	(4) Manager
(E) Controlling	(5) Departmentalisation
	(6) Following orders
	(7) Human Resource Development
	(8) Worker
	(9) Chain of action
	(10) Deviations in performance

Answer:

Group A	Group B
(A) Planning	(3) Goal-oriented /Basic function
(B) Organising	(5) Departmentalisation
(C) Staffing	(7) Human Resource Development
(D) Co-ordinating	(9) Chain of action
(E) Controlling	(10) Deviations in performance

Give one word/phrase/term for the following statements

Question 1.
One of the functions of management is considered as a base for all functions.
Answer:
Planning function

Question 2.
The function of management, which identifies and divides the work of the organisation.
Answer:
Organising function

Question 3.
A process where standards are set, actual performance is measured and corrective action is taken.
Answer:
Controlling function

Question 4.
An end function where the performance is evaluated in accordance with plan.
Answer:
Controlling function

Question 5.
An orderly arrangement of group efforts to provide unity of action to achieve common goals.
Answer:
Co-ordinating function

Question 6.
A process of taking steps to bring actual results and desired results closer together.
Answer:
Controlling function

Question 7.
A function which provides instructions from top level management to the lower level.
Answer:
Directing function.

Complete the sentences

Question 1.
A few philosophers called ………………. as ‘Life spark of an Enterprise’.
Answer:
Directing

Question 2.
……………….. is an integral part of direction function.
Answer:
Supervision

Question 3.
……………….. is a hidden force that binds all other functions of management.
Answer:
Co-ordination.

Explain the following terms/concepts

Question 1.
Co-ordination
Answer:
Co-ordination is the integration and synchronisation of the efforts of a group of employees so as to provide unity of action for organisational goals. It is a hidden force which binds all other functions of management. Different activities of different departments are integrated and harmonised in achieving desired goal of an organisation. Thus, co-ordination between different functions and all levels of employee is the heart of success of an organisation.

Question 2.
Controlling
Answer:
Controlling is the process of bringing about conformity of performance with actual planned action. It helps is taking timely corrective measures to bring the actual and desired results close to each other. Controlling helps in formatting future plan also. It is required in all types of organisation and at all levels of management.

Distinguish between

Question 1.
Planning and Staffing
Answer:

	Planning	Staffing
1. Meaning	Planning refers to a process of deciding in advance what to do, where to do, how to do, when to do and who is to do it.	Staffing is a process of recruitment through which competent employees are selected, properly trained, effectively developed, suitably rewarded.
2. Objective	The objective of planning is to set the goals and choose the means to achieve those goals.	The objective of the staffing is to obtain the most competent and efficient staff to improve the overall performance.
3. Area of function	Planning involves setting objectives, identifying alternative courses of actions and selecting best plain for the organisation.	Staffing involves selection, recruitment, training, development, promotion, transfer, etc. of employees
4. Factors	In planning function, internal as well as external factors are considered to set the targets.	In staffing function, only internal factors such as human factor, finance, workload, etc. are considered.
5. Resources	Planning is related with those resources which are required for achieving the targets.	Staffing is related with human resources only.
6. Levels of management	Usually, overall planning for entire organisation is done by the top level management.	Usually, function of staffing is undertaken by the middle level management.

 

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 9 Depository System Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 9 Depository System

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Dematerialization removes the problem of _____________ handling of securities.
(a) Physical
(b) Public
(c) Social
Answer:
(a) Physical

Question 2.
The National Securities Depository Limited (NSDL) was established in the year _____________
(a) 1995
(b) 1996
(c) 1997
Answer:
(b) 1996

Question 3.
The process of converting shares from the electronic form into physical form is called _____________
(a) Rematerialization
(b) Dematerialization
(c) Depository
Answer:
(a) Rematerialisation

Question 4.
An agent of the depository is _____________
(a) Depository Participant (DP)
(b) Depository Officer (DO)
(c) Beneficial Owner (BO)
Answer:
(a) Depository Participant (DP)

Question 5.
An intermediary between the investors and depository is _____________
(a) Depository Participant
(b) SEBI
(c) Chief Executive Officer (CEO)
Answer:
(a) Depository Participant (DP)

Question 6.
An investor has to open _____________ with the Depository Participant for handling shares in electronic form.
(a) Demat A/c
(b) Securities
(c) Depository A/c
Answer:
(a) Demat A/c

Question 7.
Depository Participant is an agent of _____________
(a) Investor
(b) Securities and Exchange Board of India
(c) Depository
Answer:
(a) Investor

Question 8.
_____________ is a process by which share certificates of investors are converted into an electronic form.
(a) Dematerialization
(b) Rematerialization
(c) Depository
Answer:
(a) Dematerialization

Question 9.
Dematerialization is a process in which share in physical form is converted into _____________
(a) Electronic form
(b) Paper form
(c) Computer form
Answer:
(a) Electronic form

Question 10.
The provisions regarding dematerialization of securities are made in _____________
(a) Law
(b) Memorandum of Articles
(c) Articles of Association
Answer:
(c) Articles of Association

Question 11.
Demat account holder can _____________ any person of his choice.
(a) Elect
(b) Nominate
(c) Choose
Answer:
(b) Nominate

Question 12.
All depository participants are to be registered with _____________
(a) Registrar of companies
(b) Securities and Exchange Board of India (SEBI)
(c) Depository
Answer:
(b) Securities and Exchange Board of India (SEBI)

Question 13.
An institution which records share certificate in the electronic form is known as _____________
(a) Stock exchange
(b) Depository
(c) Depository Participant
Answer:
(b) Depository

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Dematerialization	(a) State of being interchangeable
(2) Rematerialisation	(b) Register with Depository
(3) Fungibility	(c) Demat Request Form
(4) Issuer	(d) Transferor informs DP
(5) Sale of Shares	(e) Transferee intimates the DP
(6) Purchase of Shares	(f) Remat Request Form
	(g) Broker

Answer:

Group ‘A’	Group ‘B’
(1) Dematerialization	(c) Demat Request Form
(2) Rematerialisation	(f) Remat Request Form
(3) Fungibility	(a) State of being interchangeable
(4) Issuer	(b) Register with Depository
(5) Sale of Shares	(d) Transferor informs DP
(6) Purchase of Shares	(e) Transferee intimates the DP

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
The year in which the Depository act was passed.
Answer:
1996

Question 2.
The largest institution in India which gives Depository services.
Answer:
NSDL (National Security Depository limited)

Question 3.
The year in which National Security Depository Limited (NSDL) Started functioning.
Answer:
1996

Question 4.
Investor in whose name Demat account is opened.
Answer:
Beneficial owner (ISIN)

Question 5.
An account to be opened by an investor for handling shares in electronic form.
Answer:
Demat A/c

1D. State whether the following statements are true or false.

Question 1.
CDSL is the oldest Depository in India.
Answer:
False

Question 2.
An investor can keep his Securities with his savings bank account.
Answer:
False

Question 3.
ISIN number is given to the Depository Participant.
Answer:
False

Question 4.
Dealing in Demated Securities is a time-consuming process.
Answer:
True

Question 5.
Settlement of cash is easy in case of rematerialized Securities.
Answer:
False

Question 6.
For Dematerialized Securities Company has to be registered with the Depository.
Answer:
True

1E. Find the odd one.

Question 1.
Physical, Electronic, Capital
Answer:
Capital

Question 2.
Off Market Trade, Market Trade, Clearing blouse.
Answer:
Clearing House

1F. Complete the sentences.

Question 1.
An agent of Depository is called as _____________
Answer:
Depository Participant

Question 2.
An investor who opens an account with the Depository participant is known as _____________
Answer:
Beneficial Owner

Question 3.
An account through which the Securities are held in electronic form is called as _____________
Answer:
Demat A/c

Question 4.
For converting physical Securities into electronic Securities an investor has to submit _____________
Answer:
Demat Request Form (DRF)

Question 5.
For converting electronic Securities into physical certificates an investor has to submit _____________
Answer:
Remat Request Form (RRF)

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(a) Depository Participant	(1) ……………………….
(b) ……………………	(2) Holds securities electronically
(c) Issuer	(3) ………………………
(d) …………………….	(4) Investor

(Beneficial owner, Depository, Links investor and depository, Company issuing securities)
Answer:

Group ‘A’	Group ‘B’
(a) Depository Participant	(1) Links investor and depository
(b) Depository	(2) Holds securities electronically
(c) Issuer	(3) Company issuing securities
(d) Beneficial owner	(4) Investor

1H. Answer in one sentence.

Question 1.
Who is the Beneficial Owner?
Answer:
The investor in whose name Securities are credited to his Demat A/c is the ‘Beneficial Owner’.

Question 2.
What are the two modes of holding securities?
Answer:
The two modes of holding securities are:

• Physical
• Electronic

Question 3.
When and where was the world’s first depository system set up?
Answer:
The world’s first depository system was set up in Germany in 1947.

Question 4.
What is Corporate Action?
Answer:
When the investor accounts get automatically credited/debited for securities in case of change initiated by the company is called Corporate Action.

Question 5.
Who is the Issuer?
Answer:
The issuer is the company that issues securities in the dematerialized form.

Question 6.
What is the full form of IPO?
Answer:
IPO means Initial Public Offer.

2. Explain the following terms/concepts.

Question 1.
Depository
Answer:

• It is an organization like the Central Bank where securities are held in electronic form at the investor’s request.
• It also provides different services related to different transactions in such securities.
• It is responsible for the safe-keeping of the investor’s securities.
• There is no direct access of investors with the Depository.
• It works as a link between the company and investors.

Question 2.
Depository Participant (DP)
Answer:

• Depository Participant is an agent of Depository who is registered under the SEBI Act.
• He acts as a link between the Depository and the investor.

Question 3.
Beneficial Owner (BO)
Answer:

• The BO is the investor of securities who have accepted the services of a Depository Participant.
• The BO can also be called Client of Depository and DP. BO is given a unique account number in which securities are held.

Question 4.
Off Market Trade
Answer:

• Trade settled between two parties i.e. transferor or transferee on certain agreed terms without the involvement of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Off Market Trade’.
• For e.g. Legacy transfers, gifts, shifting of securities between a client and a sub-broker, etc.

Question 5.
Market Trade
Answer:
Trade settled between two parties i.e. transferor or transferee with the help of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Market Trade’.

3. Study the following case/situation and express your opinion.

1. KPCL Bank is a well-established banking institution. Now, it got registered as a Depository Participant.

Question (a).
Under which act did KPCL Bank got registered as a DP?
Answer:
Under SEBI Act, KPCL Bank got registered as a DP.

Question (b).
KPCL Bank as an intermediary will be a link between whom?
Answer:
KPCL Bank as an intermediary will be a link between the Depository and the investor.

Question (c).
Name the two depositories in India, of whom KPCL Bank can be a DP (Agent).
Answer:
NSDL and CDSL.

2. Mr.K wants to rematerialize his 50 shares of PQR Ltd.

Question (a).
Which form he is required to fill as a written request to the DP?
Answer:
He is required to fill Remat Request Form (RRF).

Question (b).
Does he have to fill instrument of transfer if he wishes to transfer the same after remit?
Answer:
Yes. He needs to fill instrument of transfer if he wishes to transfer the same after remit.

Question (c).
Does he have to quote certificate no. and distinctive no. if he wishes to transfer his shares after it is in remat form?
Answer:
Yes, he has to quote certificate no. and distinctive no. if he wishes to transfer his shares after it is in Remat form.

3. Mariam is a broker working with Abacus Co.

Question (a).
Who is the depositor?
Answer:
Abacus Co is the depositor.

Question (b).
Who is the depository participant?
Answer:
Mariam is a depositor participant.

Question (c).
Mariam should be registered with whom?
Answer:
Mariam being the broker must be registered with SEBI and comply with SEBI norms.

4. Distinguish between the following.

Question 1.
Depository and Depository Participant.
Answer:

Points	Depository	Depository Participant
1. Meaning	A depository is an entity that helps the investor to buy or sell securities online.	A depository participant is a link between companies and investors.
2. Types	There are two depositories functional in India. They are NSDL and CDSL.	Various depository participants are linked to NSDL and CDSL.
3. Who can be?	A Depository may be organizations, banks, or institutions.	A Depository Participant can be a bank, financial institution, a broker.
4. Registered	Depositories must be registered as a company under the Companies Act and obtain a Certificate of Commencement of business from SEBI.	Depository Participants should be registered under the SEBI Act.

Question 2.
NSDL and CDSL
Answer:

Points	NSDL	CDSL
1. Full Form	NSDL means National Securities Depository Ltd.	CDSL means Central Depository Services India Ltd.
2. Formed	NSDL was formed in 1996	CDSL was formed in 1999
3. Works for	NSDL mainly works for National Stock Exchange (NSE)	CDSL mainly works for the Bombay Stock Exchange(BSE)
4. Registered	Depositories must be registered as a company under the Companies Act and obtain a Certificate of Commencement of business from SEBI.	Depository Participants should be registered under the SEBI Act.

5. Answer the brief.

Question 1.
What are the two ways of holding securities?
Answer:
There are two ways of holding the securities:
(i) Physical mode:
Securities are held in physical form i.e. paper form. Holding securities in physical form is riskier as it can be torn, misplaced, stolen, damaged, etc. It also consumes a lot of time in storing and handling certificates and documents. Transfer and Transmission of shares is a time-consuming process.

(ii) Electronic/Dematerialized:
In this system, securities are held in electronic or dematerialized form. Holding securities in electronic form is a safe and secure way. It saves a lot of time in storing and handling certificates and documents. Transfer and Transmission of shares is a time-saving process. The electronic system is a much faster and easier system of holding securities.

Question 2.
Explain Depository System. State its importance.
Answer:
A depository system is a system, where securities are held in electronic form. The transfer and settlement of securities are done electronically. On behalf of shareholders, the Depository System maintains accounts of the shareholder, enables transfer, collects dividends, bonus shares, etc.

It is also known as, ‘Scripless trading system’. The Depository Act was passed in the year 1996 under which the depository system was introduced. NSDL and CDSL are the two depositories operating in India.

Importance of Depository System:

• Depository plays a very important role in the smooth functioning of the capital market.
• Reduced paperwork: The aim of the depository system is to reduce the paperwork. It is scriptless system.
• Use of Technology: Paperless trading is possible as it uses the technology. It facilitates electronic transfer.
• Elimination of Storage and handing: As it is a scriptless system storing and handing of certificates work gets eliminated.
• Reduces cost and efforts: Depository system the cost and efforts involved in storage and handling of physical certificates.

Question 3.
Explain the various concepts/terms related to Depository System:
Answer:
(i) Dematerialization:
It is the process in which share certificates are converted into electronic form. The client has to open a DEMAT account with the help of DP.

(ii) Fungibility:
Fungibility means interchangeable. Financial assets may or may not be fungible. The shares in depositories are fungible. They don’t have distinctive numbers for identification.

(iii) Rematerialization:
Rematerialization is the process in which shares are reconverted into physical form.

(iv) International Securities Identification Number:
ISIN is an identification number given to a security of an issuer company at the time of issuing such security for the first time in the depository system. ISIN consists of a 12 (Twelve) digit alpha-numeric code which is divided into 3 (Three) parts. For Govt, securities allotment of ISIN is done by the RBI & for others by NSDL. It is accepted globally.

Question 4.
How many depositories are established in India, under the Depository Act of 1996?
Answer:
There are two depositories established in India under the Depository Act of 1996:
(i) NSDL (National Security Depository Limited):

• NSDL is the first and the largest depository in India established in November 1996.
• It is established by IDBI (Industrial Development Bank of India), Unit Trust of India (UTI), and National Stock Exchange (NSE).
• NSDL has its headquarters in Mumbai.
• It is registered under the Companies Act as a Public Limited Company.
• Investors, Stock Exchanges, Banks, Clearing Members, etc. receive a variety of services from NSDL.
• Services provided by NSDL include account maintenance, dematerialization, rematerialization, settlement of trades through market transfers and off-market transfer, nomination, transmission, distribution of noncash corporate actions, dividend distributions, facility of freezing, or locking of investors’ accounts, Investor grievances, etc.

(ii) CDSL (Central Depository Services Limited:

• CDSL began its operations in February 1999.
• It was promoted by the Bombay Stock Exchange jointly with several banks.
• The headquarters of CDSL is in Mumbai.
• CDSL also offers Demat services like NSDL across the country and has a wide DP network.
• NSDL and CDSL have played a great role in the success of the Depository System in India.

6. Justify the following statements.

Question 1.
The depository system has some advantages to the Investor.
Answer:

• The depository system holds certificates of the Investor in an electronic form.
• Safety is ensured as the entire system functions under the Depository Act and is monitored by SEBI.
• The investor even can freeze his account to avoid fraud.
• Investors can easily transfer the securities in electronic form.
• The investor receives a statement of account periodically which keeps him updated.
• Investors can raise easy loans against the Dematerialized securities.
• A nomination facility is also available for investors.
• Dividend, Bonus Shares, Right Issue, Redemption amount gets automatically credited to Investors account.
• Thus, it is rightly justified that Depository systems have some advantages to the investor.

Question 2.
An investor can raise loan against dematerialized securities.
Answer:

• Investors can take a loan against securities (shares, debentures, bonds, mutual fund units) that are held in their Demat accounts.
• The time required for the documentation process to take loans is less.
• In order to raise a loan against dematerialized securities, both the borrower and lender should have Demat accounts with the same depository
• The Demat accounts can be held with the same or different depository participant (DP).
• Thus, it is rightly said that investors can raise loans against dematerialized securities.

Question 3.
Better and quicker services of the Depository system attract investment from abroad.
Answer:

• Paperless trading is a boon for company management.
• Automatic and transparent screen-based trading in securities, shorter settlement periods have improved liquidity in investment in securities.
• The transfer process under the depository system is prompt and free from defects.
• The company is able to know the particulars of beneficial owners and their holdings periodically.
• Thus, it is rightly said that Better and quicker services of the Depository system attract investment from abroad.

Question 4.
It is necessary for the Beneficial Owner to open a DEMAT account with the DP.
Answer:

• The beneficial Owner is the investor of the company.
• For holding the securities in electronic form, it is necessary to open a DEMAT account.
• DEMAT account can be opened with the help of DP.
• The BO can also be called a client of Depository and DP.
• BO has to pay charges to the DP for availing the services of DP.
• BO is entitled to all rights, benefits and is subject to all liabilities with respect to securities.
• BO is given a unique account number in which securities are held.
• Thus, it is rightly said that it is necessary for the Beneficial Owner to open a DEMAT account with the DP.

7. Answer the following questions.

Question 1.
What is the procedure for the Transfer of Securities under the Depository System in case of the sale of shares?
Answer:
When shares are sold the Transferor (Investor) has to inform his DP by issuing Delivery Instruction Slip (DIS) duly filled and signed with the details of the security sold. At the end of the transaction, the said securities are debited from his Demat Account.

Transfer of shares can be done in two ways:
(i) Off Market Trade:
Trade settled between two parties i.e. transferor or transferee on certain agreed terms without the involvement of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Off Market Trade’. For e.g. Legacy transfers, gifts, shifting of securities between a client and a sub-broker, etc.

Procedure:

• Seller i.e. the transferor gives instructions to the DP to transfer securities from the seller’s account to the buyer’s account.
• The buyer i.e. transferee will get securities credited to his account through his DP. DP will transfer the securities only after receiving confirmation from the depository.
• The transferee will directly pay the money to the transferor.

Diagrammatic presentation:

(ii) Market Trade:
Trade settled between two parties i.e. transferor or transferee with the help of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Market Trade’.

Procedure:

• The Seller i.e. the transferor gives instruction to his DP. The securities are then transferred from Transferor’s account to the Transferor’s Broker account.
• From the Transferor’s Brokers account securities are transferred to the clearinghouse of the Stock Exchange.
• On the pay-out day, securities move from the clearinghouse to the account of the broker of the transferee.
• After instructions and confirmation from Depository, securities are transferred to the buyer’s account.

8. Attempt the following.

Question 1.
Explain the process of Dematerialisation?
Answer:
Dematerialization is the process of converting physical certificates into electronic form/mode. When an investor opts for a depository system, he has to approach a Depository participant, who is the authorized agent of the depository. The investor needs to surrender his share certificate to the company through a depository participants. On confirmation from the company and Depository DP arranges to credit investors account with an equivalent number of shares.

Following steps are involved in the process of Dematerialisation:

• Submission of DRF by Investor: The investor has to submit the DRF (Demat Request Form) in triplicate and original certificates to DP.
• Entry in the system and forwarding request to Depository: DP enters the details of Demat request in the system and sends it to the Depository.
• Forwarding Copy to the Issuer: DP sends the physical certificates and copy of DRF to the Issuer i.e. Company
• Verification by the Issuer: The Issuer (Company) verifies and confirms to Depository about dematerializing of the securities.
• Updating records by the Depository: Depository records the request in the system and forwards it to the Issuer Company.
• Intimation to the DP: Depositor credits the dematerialized securities to the beneficiary/investors Demat A/c and informs the DP.
• Intimation to the investor: A statement of account is issued to the Investor periodically. It contains all the details of the investor.

Question 2.
Explain the functioning of the depository under the IPO scheme.
Answer:
IPO is the first sale of shares by a privately owned company to the general public. A public company can raise capital by making an appeal to the general public to purchase shares of the company by issuing a prospectus.

The process of IPO is as follows:

• Submission of Application: The investor (applicant/BO) has to submit an application for securities to the issuer company.
• Verification with Depository: The details of the investor are verified by the company with Depository.
• Report by Depository: After verification depository submits the investors report to the issuer company
• Details of Allotment: The issuer company submits the details of allotment to the depository for updating their records.
• Crediting the account: The depository credits the account of the beneficial owner with a specific number of securities.
• Intimation to the DP: Depository then informs the Depository Participant (DP) about the details of the beneficial owner account.
• Intimation to the BO: Depository Participant informs the beneficial owner (investor) about his investment through Statement of Accounts.

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 1 Principles of Management Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 1 Principles of Management

Select the correct options and rewrite the sentences

Question 1.
Technique of study of ………………. concentrates on the body movements of the worker.
(a) Motion
(b) Time
(c) Organization
Answer:
(a) Motion

Question 2.
14 principles of management are developed by ………………
(a) F. W. Taylor
(b) Henry Fayol
(c) Peter Drucker
Answer:
(b) Henry Fayol

Question 3.
Management principles influence ……………..
(a) human behaviour
(b) organization
(c) government
Answer:
(a) human behaviour

Question 4.
Management principles are …………….. in nature.
(a) constant
(b) universal
(c) limited
Answer:
(b) universal

Question 5.
Management principles establish ……………….. relationship.
(a) social
(b) legal
(c) cause and effect
Answer:
(c) cause and effect

Question 6.
‘One-plan-one head’ is stated in ……………….
(a) Principle of Direction
(b) Principle of Unity of Command
(c) Scalar Chain
Answer:
(a) Principle of Direction

Question 7.
Principle that focuses on complete change in the attitude of the employees is known as the Principles of …………………
(a) Attitude Change
(b) Scientific Management
(c) Mental Revolution
Answer:
(c) Mental Revolution

Match the pairs

Question 1.

Group A	Group B
(A) Division of work	(1) Direct communication
(B) Authority	(2) Adhering to rules
(C) Fair  remuneration	(3) Specialisation
(D) Discipline	(4) Long chain of communication
(E) Gang Plank	(5) Right wages to the employees
	(6) Responsibility
	(7) No confidence in management policies
	(8) Allotting work to any employee
	(9) Exploitation of workers
	(10) Misuse of power

Answer:

Group A	Group B
(A) Division of work	(3) Specialisation
(B) Authority	(6) Responsibility
(C) Fair  remuneration	(5) Right wages to the employees
(D) Discipline	(2) Adhering to rules
(E) Gang Plank	(1) Direct communication

Give one word/phrase/term for the following statements

Question 1.
Father of Scientific Management.
Answer:
Fredrick Winslow Taylor

Question 2.
The principle of management which says unity is strength.
Answer:
Principle of Esprit de corps

Question 3.
The principle of management explaining about fair payment to workers.
Answer:
Principle of Remuneration

Question 4.
The statements which disclose fundamental truth of management.
Answer:
Principle of Management

Question 5.
Principle of management which states that there should be balance between the authority and responsibility.
Answer:
Principle of Authority and Responsibility

Question 6.
Principle of management which states that every employee should receive orders and instructions from one boss only.
Answer:
Principle of Unity of Command.

State whether the following statements are True or False

Question 1.
Management principles are applicable to all types of organisation.
Answer:
True

Question 2.
Employees can be motivated by following the principle of fair remuneration.
Answer:
True

Question 3.
The goal of organisation must not be sacrificed for individual goal.
Answer:
True

Question 4.
F. W. Taylor recommended total six foremen to control the various aspects of production.
Answer:
False.

Find the odd one

Question 1.
Principle of Unity of Direction, Principle of Centralisation, Principle of Order, Time Study.
Answer:
Time Study

Question 2.
Standardisation of tools and equipment, Science – not rule of thumb, Mental Revolution, Division of Responsibility.
Answer:
Standardisation of tools and equipment

Question 3.
Scientific task setting, Scientific selection and training. Principle of Stability of Tenure, Differential Piece – Rate Wage Plan.
Answer:
Principle of stability of tenure

Justify the following statements

Question 1.
Principles of management improve the efficiency of employees.
Answer:
(1) Principles of management if used and applied by the organisation in right direction, they help to improve understanding and the overall efficiency of the employees. Principles of management advocate planned activities and : systematic organisation of men, materials, methods, machinery, etc. which in turn help to improve and increase the efficiency of employees.

(2) Principles of management guide the managers about handling the human resource, reducing the wastage, co-ordinating the activities of different departments, etc. This helps to improve the productivity in the organisation and consequently efficiency of employees. Principles of management also help to develop the objective approach.

(3) Application and use of principles of management leads to specialisation, increased productivity and efficiency. It boosts the morale of employees. These principles help to co-ordinate and control various activities of the organisation and also motivate the employees to perform more efficiently and effectively.

(4) Principle of fair remuneration indicates the management to pay adequate wages and other incentives to the employees. This goes a long way to increase the morale of employees who in turn would put their best efforts to perform their duties more efficiently. Principles of management also help to understand social responsibilities and to carry out research and development activities to improve the efficiency of employees.

Question 2.
Principles of management are applicable to all types of organisations.
Answer:
(1) Principles of management are the statements of fundamental truth which act as guidelines for managerial decision-making and actions. They establish cause and effect relationship. They are evolved through observation, analysis and experiments.

(2) However, managers can suitably modify the principles of management keeping in mind the requirements of the organisation.

(3) Principles of management are also helpful in achieving and attaining social and cultural goals. They are also directed to maximising profit without ignoring social values.

(4) Thus, Principles of management are universal in nature. They are applicable to all types of organisations irrespective of the type, size or nature of the organisations.

Attempt the following

Question 1.
Explain the significance of management principles.
Answer:
The significance of management principles is explained as follows:
(1) Provides useful insight to manager : The study of management principles helps the manager to understand the organisation, its situations and problems. They act as guidelines to find out the ‘ solutions to the problems and handle the situation accordingly. The use and application of these principles help the manager to know the manner in which they should act in different situations, Timely guidance provided by the management principles reduces the wastage of resources and help to achieve goals in exact manner.

(2) Helpful in efficient utilisation of resources : The two resources used in the organisations Eire classified as physiCEd resources such as materials, machine, money, etc. and human resources i.e. manpower. The main function of management is to mEiintain proper balance between these resources by putting them to optimum use and control the wastage of resources. It uses different techniques Emd management principles and maintains discipline and healthy working environment. This helps to establish cordial relation between management and employees. This in turn increases the efficiency level of employees.

(3) Scientific decisions : Scientific decisions in relation to business organisation implies systematic and balanced decision. Management principles train and help the manager to tackle the situation tactfully instead of using trial and error method. Managers get an idea to analyse the situation systematically, to search alternative options and their results with the use of management principles.

(4) Understanding social responsibility : A business is a part of the society. It makes use of the resources of the society and therefore, it has to perform some social responsibilities. Management principles guide the managers to understand and perform social responsibilities so that management can focus on providing quality products at reasonable prices, avoiding unfair trade practices and artificial monopolistic situations in the market, fair remuneration to employees, heEdthy working environment, standard tools and equipment, etc.

(5) Encourage Research and Development : Principles of management are evolutionary in nature and have evolved with passage of time. They have undergone certain changes on account of changes in the business world. They are modified and developed over the years to suit the current trends. They stress on scientific study, research and development in the organisation. Research and Development always works to find out new techniques in the field of production, marketing, finance, human resources, etc.

(6) Helps to co-ordinate and control : Principles of management serve as guidelines for better co-ordination and control. These principles help the mEmagers in this challenge to co-ordinate the activities of different departments. Managers can easily exercise control over the performance of their employees. The proper use of these principles helps to achieve the given target easily.

(7) Develops objective approach : By using various principles of management, the manager can develop an objective approach. The manager can find out and identify opportunities, root causes of the problems and can provide appropriate solutions on it in right direction. This approach also helps to build confidence in the minds of the managers.

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 13 AC Circuits Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 13 AC Circuits

Question 1.
Write an expression for an alternating emf that varies sinusoidally with time. Show graphically variation of emf with time.
Answer:
An alternating emf that varies sinusoidally with time is given by e = e₀ sin ωt, where e₀ is the maximum value of the emf, called the peak value, and co is the angular frequency of the emf.
ω = 2πf = \(\frac{2 \pi}{T}\), where f is the frequency of the emf, expressed in Hz, and T is the periodic time of the emf, expressed in second.

Using these data, we can plot e versus t

Question 2.
An alternating emf is given by e = 2.20 sin ωt (in volt). What will be its value at time t = \(\frac{T}{12}\)?
Answer:
e = 220 sin[latex]\frac{2 \pi}{T}\left(\frac{T}{12}\right)[/latex]= 220 sin(\(\frac{\pi}{6}\))
= 220 \(\left(\frac{1}{2}\right)\) = 110 v.

Question 3.
What is the average or mean value of an alternating emf? Obtain the expression for it. (2 marks)
Answer:
The average or mean value of an alternating emf is defined as its average value over half cycle (because the average value over one cycle is zero) and is given as

Question 4.
If the peak value of an alternating emf is 10 V, what is its mean value over half cycle?
Answer:
e_av = 0.6365 e₀ = 0.6365(10) = 6.365 V
Note: In general, when e = e₀ sin ωt, the correspond ing current is j = i sin (ωt + α), where α is the phase difference between emf e and current j. ¿z may be positive or negative or zero.

i₀ is the peak value of the current and i_av (over half cycle)
= \(\frac{2}{\pi}\) i₀ = 0.6365 i₀].

Question 5.
What is the rms value of an alternating current? Find the relation between the rms value and peak value of an alternating current that varies sinusoidaily with time.
Answer:
The root mean square (rms) value of an alternating current i is, by definition,
i_rms = \(\left[\frac{\int_{0}^{I} i^{2} d t}{T}\right]^{\frac{1}{2}}\), where T is the periodic time, i.e., time for one cycle.

[Note: i_rms is also called the effective value or virtual value of the alternating current. In one cycle, the heat produced in a resistor by i = i₀ sin ωt is the same as that produced by a direct current (dc) equal to i_rms]

Question 6.
What is the relation between i,, (over half cycle) and i_rms?
Answer:
i_av (over half cycle) = \(\frac{2}{\pi}\) i₀, and i_rms = \(\frac{i_{0}}{\sqrt{2}}\)
∴ i_av (over half cycle) = \(\left(\frac{2}{\pi}\right)\left(\sqrt{2} i_{\mathrm{rms}}\right)=\frac{2 \sqrt{2}}{\pi} i_{\mathrm{rms}}\)

Question 7.
If i_rms = 3.142 A, what is i_av (over half cycle)?
Answer:
i_av (over half cycle) = \(\frac{2 \sqrt{2}}{\pi}\) i_rms
= \(\frac{(2)(1.414)}{3.142}\)(3.142) = 2.828 A
[Note: i_av (over half cycle) < i_rms]

Question 8.
For e = e₀ sin ωt, what is
(i) e_av (over half cycle)
(ii) r_rms
Answer:
For e = e₀ sin ωt, e_av (over half cycle) = \(\frac{2}{\pi}\) e₀ and e_rms = \(\frac{e_{0}}{\sqrt{2}}\)

9. Solve the following:
Question 1.
An alternating emf is given by e = 220 sin 314.2 t (in volt). Find its
(i) peak value
(ii) rms value
(iii) average value over half cycle
(iv) frequency
(iv) period
(vi) value at \(\frac{T}{4}\) .
Solution:
Data: e = 220 sin314.2t (in volt), t = \(\frac{T}{4}\)
(i) Comparing the given equation with e = e₀ sin ωt, we get, peak value, e₀ = 220V.

(ii) e_rms = e₀/\(\sqrt{2}\) = 155.6 V

(iii) e_av (over half cycle) = \(\frac{2}{\pi}\)e₀ = \(\frac{2(220)}{3.142}\) = 140V

(iv) ω = 2πf= 314.2 ∴ The frequency,
f = \(\frac{\omega}{2 \pi}=\frac{314.2}{2(3.142)}\) = 50 Hz

(v) The period, T = \(=\frac{1}{f}=\frac{1}{50}\) = 0.02 same

(vi) e = 220 sin(\(\frac{2 \pi}{T} \cdot \frac{T}{4}\)) = 220 sin \(\frac{\pi}{2}\) = 220 v

Question 2.
The peak value of AC through a resistor of 10 Ω is 10 mA. What is the voltage across the resistor at time
Solution:

This is the required voltage.

Question 3.
The peak value of AC through a resistor of 100 Ω is 2A If the frequency of AC is 50Hz, find the heat produced in the resistor in one cycle.
Solution:
Data: R = 100 Ω, i₀ = 2A, f = 50 Hz
H = \(\frac{R i_{0}^{2}}{2 f}=\frac{100(2)^{2}}{2(50)}\) = 4 J
This is the required quantity.

Question 10.
What is a phasor?
Answer:
A phasor is a rotating vector that represents a quantity varying sinusoidally with time.

Question 11.
What is a phasor diagram ? Illustrate it with an example.
Answer:
A diagram that represents a phasor is called phasor diagram. Consider an alternating emf e = e₀ sin ωt. The phasor representing it is inclined to the horizontal axis at an angle cot and rotates in an anticlockwise direction as shown in below figure.

The length (OP) of the arrow \(\overrightarrow{\mathrm{OP}}\) represents the peak value (maximum value), e₀, of the emf.
For e = e₀ sin ωt, the projection of \(\overrightarrow{\mathrm{OP}}\) on the y-axis gives the instantaneous value of the emf.

In above figure, OR = e₀ sin ωt.
For e = ₀ sin ωt, the projection of \(\overrightarrow{\mathrm{OP}}\) on the x-axis gives the instantaneous value of the emf.
In above figure, OQ = e₀ sin ωt.
Phasor diagrams are useful in adding harmonically varying quantities.

Question 12.
An alternating emf e = e₀ sin ωt is applied to a resistor of resistance R. Write the expression for the current through the resistor. Show the variation of emf and current with ωt. Draw a phasor diagram to show emf and current.
Answer:
Below figure shows an alternating emf e = e₀ sin ωt applied to a resistor of resistance R.

e₀ is the peak value and co is the angular frequency of the emf. The instantaneous current through the resistor is i = i₀ sin ωt, where i₀ is the peak value of the current.
Here, i and e are always in phase.
For ωt = 0, sin ωt = 0,e = 0,i = 0;
for ωt = π/2, sin ωt = 1, e = e₀, i = i₀;
for ωt = π, sin ωt = 0, e = 0, i = 0;
for ωt = 3π/2, sin ωt = -1, e= – e₀, i= -i₀;
for ωt = 2π, sin ωt = 0, e = 0, i = 0.
Below figure shows variation of e and i with cot.

Below figure shows phasors of e and i

Variation of e and i with time t for a purely resistive AC circuit

Question 13.
If the peak value of the alternating emf applied to a resistor of 100Ω is 100 V, what is the rms current through the resistor?
Answer:
The rms current through the resistor,
i_rms = \(\frac{i_{0}}{\sqrt{2}}=\frac{e_{0}}{R \sqrt{2}}=\frac{100}{100 \sqrt{2}}\) = 0.7071 A

Question 14.
An alternating emf e = e₀ sin ωt is applied to a pure inductor of inductance L. Show variation of the emf and current with ωt.
Answer:
Here, e = e₀ sin ωt and i = i₀ sin (ωt – π/2), where i₀ = e₀/ωL.

[Note : A pure inductor ≡ an ideal inductor.]

Question 15.
Draw a Phasor diagram showing e and i in the case of a purely inductive circuit.
Answer:
In this case, e = e₀ sin ωt and i = i₀ sin (ωt – \(\frac{\pi}{2}\)),
where i₀ = \(\frac{e_{0}}{\omega L}\) and L is the inductance of the inductor. In this case, the current j lags behind the emf e by a phase angle of \(\frac{\pi}{2}\) rad.

Question 16.
Explain the term inductive reactance. Show graphically variation of inductive reactance with the frequency of the applied alternating emf.
Answer:
When an alternating emf e = e₀ sin ωt is applied to a pure inductor of inductance L, the current in the
circuit is i = i₀ sin (ωt – \(\frac{\pi}{2}\)), where i₀ = \(\frac{\pi}{2}\), where i₀ = \(\frac{e_{0}}{\omega L}\) In the case of a pure resistor of resistance R, i = i₀ sin ωt for e = e₀ sin ωt, and i₀ = \(\frac{e_{0}}{R}\)

Comparison of Eqs. i₀ = \(\frac{e_{0}}{\omega L}\) and i₀ = \(\frac{e_{0}}{R}\) shows that ωL is the resistance offered by the inductor to the applied alternating emf. It is called the reactance. It increases linearly with the frequency because ωL = 2πfL. This is illustrated in the following figure. ωL is denoted by X_L.

[Note : Reactance has the same dimensions and unit as resistance.]

Question 17.
What is the reactance of a pure inductor with inductance 10H if the frequency of the applied alternating emf is 50 Hz?
Answer:
The reactance of the inductor,
X_L = ωL = 2πfL = 2(3.142)(50)(10) = 3142 Ω
[Note : In a DC circuit, f = 0 ∴ X_L = 2πfL = 0.]

Question 18.
How does a pure inductor behave when the frequency of the applied alternating emf is
(i) very high
(ii) very low?
Answer:
Inductive reactance = 2πfL.
(i) If the frequency (f) of the applied emf is very high, the inductive reactance (for reasonable value of inductance L) will be very high. Hence, the current through the inductor will be very low (for reasonable value of peak emf). Hence, it will practically block AC.

(ii) For very low f, 2πfL is low and hence the inductor will behave as a good conductor.

Question 19.
The capacitance of an ideal capacitor is 2 μF. What is its reactance if the frequency of the applied alternating emf is 1000 Hz?
Answer:
The reactance of the capacitor =

Question 20.
How does a pure (an ideal) capacitor behave when the frequency of the applied alternating emf is very low?
Answer:
Capacitive reactance = \(\frac{1}{2 \pi f C}\)
If the frequency (f) of the applied emf is very low, the capacitive reactance (for reasonable value of capacitance C) will be very high and hence the current through the circuit will be very low (for reasonable value of peak emf).

Question 21.
What will be the current through an ideal capacitor if it is connected across a 2 V battery ?
Answer:
In a DC circuit, the frequency (f) of the applied emf is zero.
∴ Capacitive reactance, \(\frac{1}{2 \pi f C}\) = ∞
∴ The current through the capacitor will be zero.
(Note : The capacitor blocks DC and acts as an open circuit while it passes AC of high frequency.]

Question 22.
An alternating emf is applied to an LR circuit. Assuming the expression for the current, obtain the expressions for the applied emf and the effective resistance of the circuit. Assume the inductor and resistor to be ideal. Draw the phasor diagram showing the emf and current.
Answer:
Below figure shows a source of alternating emf (e), key K, ideal inductor of inductance L and ideal resistor of resistance R connected to form a closed series circuit. Ignoring the resistance of the source andthekey,wehave,e = Ri + L\(\frac{d i}{d t}\) …………… (1)
where Ri is the potential difference across R and L\(\frac{d i}{d t}\) is the potential difference across L.

where e₀ = Zi₀ is the peak value of the applied emf.
Z = \(\frac{e_{0}}{i_{0}}=\sqrt{R^{2}+\omega^{2} L^{2}}\) is the effective resistance of the circuit. It is called the impedance. Here, the emf leads the current by phase angle Φ.

Question 23.
(a) What is the impedance of an LR circuit if R = 40 Ω and X_L = 30 Ω ?
(b) What is the peak current if the peak emf is 10 V, R = 0 and X_L = 30 Ω?
Ans.
(a) The impedance, Z = \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}}\)
= \(\sqrt{1600+900}=\sqrt{2500}\) = 50 Ω.
(b) i₀ = \(\frac{e_{0}}{X_{\mathrm{L}}}=\frac{10}{30}=\frac{1}{3}\) A = 0.3333 A.

Question 24.
An alternating emf is applied to a CR circuit. Obtain an expression for the phase difference between the emf and the current. Also obtain the expression for the effective resistance of the cir-cuit. Assume the capacitor and resistor to be ideal. Draw the phasor diagram showing the emf and current.
Answer:
Below figure shows a source of alternating emf (e), key K, ideal capacitor of capacitance C and ideal resistor of resistance R to form a closed series circuit. Ignoring the resistance of the source and the key, we have,

where C is the time independent constant of integration which must be zero as j oscillates about zero when e oscillates about zero.
∴ e = R i₀ sin ωt – \(\frac{i_{0}}{\omega C}\) cos ωt
Let Z = \(\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}\), R = Z cos and \(\frac{1}{\omega C}\) = Z sin Φ
∴ e = i₀Z (cos Φ sin ωt – sin Φ cos ωt)
= Zi₀ (sin ωt cos Φ – cos ωt sin Φ)
= Zi₀ sin (ωt – Φ) = e₀ sin (ωt – Φ), where e₀ = Zi₀ is the peak emf. Here, the emf lags behind the current by phase angle Φ.

Question 25.
(a) What is the impedance of a CR circuit if R = 30 Ω and X_C = 40 Ω?
(b) What is the peak current if the peak emf is 10 V, R = 0 and X_C = 40 Ω ?
Ans.
(a) The impedance, Z = \(\sqrt{R^{2}+X_{\mathrm{C}}^{2}}=\sqrt{900+1600}\)
= \(\sqrt{2500}\) = 50
(b) The peak current i₀ = \(\frac{e_{0}}{X_{C}}=\frac{10}{40}\) = 0.25 A.

Question 26.
What is meant by the term impedance? State the formula for it in the case of an LCR series circuit.
Answer:
In an AC circuit containing resistance and inductance and / or capacitance, the effective resistance offered by the circuit to the flow of current is called impedance. It is denoted by Z.
For an LCR series circuit,
Z = \(\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}\) where
ω = 2πf is the angular frequency and f is the frequency of AC.
[Note: Here, in the absence of a capacitor.
Z = \(\sqrt{R^{2}+\omega^{2} L^{2}}\), and in the absence of an inductor,
Z = \(\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}\)].

Question 27.
Draw the impedance triangle for a series LCR AC circuit and write the expressions for the im-pedance and the phase difference between the emf and the current.
Answer:

28. Solve the following :
Question 1.
An alternating emf e = 40 sin (120 πt) (in volt) is applied across a 100 Ω resistor. Calculate the rms current through the resistor and the frequency of the applied emf.
Solution:
Data : e = 40 sin (120 πt) V, R = 100 Ω
The equation of a sinusoidally alternating emf is e = e₀ sin ωt
where e₀ is the peak value of the emf.
Comparing the given expression with this, we get, e₀ = 40 V
∴ The rms current,

Comparing e = 40 sin (120 πt) with
e = e₀ sin ωt, we get,
ω = 2πf= 120 π
∴ f = 60 Hz
This is the frequency of the applied emf.

Question 2.
In problem (1) above, what is the period of the AC?
Solution:
The period of the AC,
T = \(\frac{1}{f}=\frac{1}{60}\) s ≈ 0.01667 s

Question 3.
An alternating emf of frequency 50 Hz is applied a series combination of an inductor (L = 2 H) and a resistor (R = 100 Ω). What is the impedance of the circuit?
Solution:
Data : f = 50 Hz, L = 0.2 H, R = 100 Ω
The inductive reactance, X_L = 2πfL
= 2(3.142)(50)(0.2) = 62.84 Ω
The impedance of the circuit, Z = \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}}\)
= \(\sqrt{(100)^{2}+(62.84)^{2}}=\sqrt{10000+3949}=\sqrt{13949}\)
= 118.1 Ω

Question 4.
An alternating emf is applied to a series combination of an inductor and a resistor (R = 100 Ω). If the impedance of the circuit is 100\(\sqrt {2}\) Ω, what is the phase difference between the emf and the current?
Solution:

This is the phase difference between the emf and the current.

Question 5.
When 100 V dc is applied across a coil, a current of 1 A flows through it. When 100 V ac of frequency 50 Hz is applied to the same coil, only 0.5 A current flows through it. Calculate the resistance, impedance and self-inductance of the coil.
Solution:
Data : V_dc = 100 V, I_dc = 1 A, V_rms = 100 V,
f = 50 Hz, I_rms = 0.5 A
(i) The resistance of the coil,
R = \(\frac{V_{\mathrm{dc}}}{I_{\mathrm{dc}}}=\frac{100}{1}\) = 100 Ω

(ii) The impedance of the coil,
Z = \(\frac{V_{\mathrm{rms}}}{I_{\mathrm{rms}}}=\frac{100}{0.5}\) = 200 Ω
Z² = R² + X²_L

Question 6.
A 20 µF capacitor is connected in series with a 25 Ω resistor and a source of alternating emf, 240 V (peak)/50 Hz. Calculate the capacitive reactance, circuit impedance and the maximum current in the circuit.
Solution:
Data : C = 20 µF = 20 × 10^-6 F, k = 25 Ω, e₀ = 240 V, f = 50 Hz
(i) Capacitive reactance,

Question 7.
A 25 µF capacitor, 0.1 H inductor and 25 Ω resistor are connected in series with an ac source of emf e = 220 sin 314t volt. What is the expression for the instantaneous value of the current?
Solution:
Data : C = 25 µF = 25 × 10^-6 F, L = 0.1 H,
R = 25 Ω, e = 220 sin 314t volt
The equation of a sinusoidally alternating emf is e = e₀ sin ωt, where e₀ is the peak emf. Comparing the given expression with this, we get,
e₀ = 220 V, ω = 314 rad/s
∴ Inductive reactance,
X_L = ωL = 314 × 0.1 = 31.4 Ω and capacitive reactance,
X_C = \(\frac{1}{\omega C}=\frac{1}{314 \times 25 \times 10^{-6}}\) = 127.4 Ω
∴ The reactance of the circuit,
|X_L – X_C| = 96 Ω (capacitive, ∵ X_C > X_L)

∴ Φ = – 75°24′
i. e., the applied emf lags behind the current by 75°24′.
The instantaneous value of the current is i = i₀ sin (ωt + Φ)
∴ i = 1.569 sin (314 f + 75°24′) ampere

Question 8.
An alternating emf of peak value 110 V and frequency 50 Hz is connected across an LCR series circuit with R = 100 Ω, L = 10 mH and C = 25 µF. Calculate the inductive reactance, capacitive reactance and impedance of the circuit.
Solution:
Data : e₀ = 110 V, f = 50 Hz, R = 100 Ω,
L = 10 mH = 10 × 10^-3 H, C = 25 µF = 25 × 10^-6 F
(i) Inductive reactance,
X_L = ωL = 2πfL
= 2 × 3.142 × 50 × 10 × 10^-3 = 3.142 Ω

(ii) Capacitive reactance,

Question 29.
An alternating emf with rms value 100 V is applied to a pure resistor of resistance 100 Ω. What is the power consumed over one cycle ?
Answer:
The power consumed over one cycle = e_rms i_rms
= e_rms \(\left(\frac{e_{\mathrm{rms}}}{R}\right)\) = (100) \(\left(\frac{100}{100}\right)\) = 100 W.

Question 30.
An alternating emf is applied to a pure resistor of 400 Ω. If the power consumed over one cycle is 100 W, what is the rms current through the resistor?
Answer:
P_av = R (i_rms)²

Question 31.
An alternating emf with e_rms = 100 V is applied to a series LR circuit with R = 100 Ω and Z = 200 Ω What is the average power consumed over one cycle?
Answer:
The average power consumed over one cycle

Question 32.
An alternating emf with e_rms = 60 V is applied to a series CR circuit with R = 100 \(\sqrt {3}\) Ω and capacitive reactance 100 V 3Q. What is the average power consumed over one cycle ?
Answer:
The average power consumed over one cycle

Question 33.
State the expression for the average power consumed over one cycle in the case of a series LCR AC circuit. What happens if the circuit is purely
(i) resistive
(ii) inductive
(iii) capacitive?
Answer:
Average power consumed over one cycle in the case of a series LCR AC circuit,

Question 34.
In the case of a series LCR AC circuit, what is the power factor if
(i) the resistance is far greater than the reactance
(ii) the resistance is far less than the reactance?
Answer:
Power factor, cos Φ = \(\frac{R}{\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}}\)
(i) For R >> (X_L – X_C), cos Φ ≅ 1
(ii) For R >> (X_L – X_e), cos Φ ≅ zero.

35. Solve the following.
Question 1.
An alternating emf e = 200 sin ωt (in volt) is connected to a 1000 Ω resistor. Calculate the rms current through the resistor and the average power dissipated in it in one cycle.
Solution:
Data: e = 200 sin ωt V, R = 1000 Ω
The equation of a sinusoidally alternating emf is e = e₀ sin ωt, where e₀ is the peak value of the emf.
Comparing the given expression with this, we get
∴ Peak current, i₀ = \(\frac{e_{0}}{R}=\frac{200}{1000}\) = 0.2 A
∴ rms current, i_rms = \(\frac{i_{0}}{\sqrt{2}}=\frac{0.2}{\sqrt{2}}\) = 0.1414 A
The average power dissipated in the resistor in one cycle,
P_av = e_rms i_rms = \(\frac{e_{0} i_{0}}{2}=\frac{200 \times 0.2}{2}\) = 20 W

Question 2.
A circuit has a resistance and a reactance, each equal to 100 Ω Find its power factor. If the rms value of the applied voltage is 200 V, what is the average power consumed by the circuit?
Solution:
Data : R = 100 Ω, X = 100 Ω, V_rms = 200 V

∴ The average power, P = e_rms i_rms cos Φ
= 200 × 1.415 × 0.7071 = 200 W

Question 3.
A dc ammeter and an ac hot-wire ammeter are connected to a circuit in series. When a direct current is passed through the circuit, the dc ammeter shows 6A. When a pure alternating current is passed, the ac ammeter shows 8 A. What will be the reading of each ammeter if the direct and alternating currents pass simultaneously through the circuit?
Solution:
Data: i_dc = 6 A, i_rms(ac) = 8A
A dc ammeter measures the average value of a current passing through it. Since the average value of an alternating current over one cycle is zero, when the direct and alternating currents are siniultaneously passed, the dc ammeter will read 6 A which is the dc part.

An ac hot-wire ammeter measures the effective value of a current using the heating effect of an electric current. When the direct and alternating currents are simultaneously passed through the ac ammeter, the average power dissipated is
P_av = i²_dcR + i²_rms = i²_eff R
where R is the resistance of the heating element of the ac ammeter.
∴ i_eff = \(\sqrt{i_{\mathrm{dc}}^{2}+i_{\mathrm{rms}}^{2}}\)
= \(\sqrt{(6)^{2}+(8)^{2}}\) = 10 A
Thus, the ac ammeter will read 10 A.

Question 4.
An alternating emf e = 100 sin [2π(1000) t] (in volt) is applied to a series LCR circuit with resistance 300 Ω, inductance 0.1 H and capacitance 1 µF. Find the power factor and the average power consumed over one cycle.
Solution:
Data: e = 100 sin[2π (1000)t] (in volt), R = 300 Ω L = 0.1H, C = 1 µF = 1 × 10^-6 F
Comparing e = e₀ sin 2πft with the given equation,
we get e₀ = 100 V, f = 1000 Hz
∴ X_L = 2πfL = 2(3.142)(1000)(0.1) = 628.4 Ω

= 4.835 W

Question 5.
An ac circuit with a 10 Ω resistor, 0.1 H inductor and 50 µF capacitor is connected across a 200 V/50 Hz supply. Compute
(i) the power factor
(ii) the average power dissipated in the circuit.
Solution:
Data : R = 10 Ω, L = 0.1 H, e_rms = 200 V, C = 50 µF = 50 × 10^-6 F, f = 50 Hz
(i) X_L = ωL = (2πf)L
= 2 × 3.142 × 50 × 0.1
= 31.42 Ω


[Note: An alternating emf is usually specified by giving its rms value.]

Question 36.
How are oscillations produced using an inductor and a capacitor?
Answer:
Consider a charged capacitor of capacitance C, with an initial charge q₀, connected to an ideal inductor of inductance L through a key K. We assume that the circuit does not include any resistance or a source of emf. At first, the energy stored in the electric field in the dielectric medium between the plates of the capacitor is U_E = \(\frac{1}{2} \frac{q_{o}^{2}}{C^{\prime}}\), while the energy stored in the magnetic field in the inductor is zero.

When the key is closed, the capacitor begins to discharge through the inductor and there is a clockwise current in the circuit, as shown in below figure (a). Let q and i are the instantaneous values of charge on the capacitor and current in the circuit, respectively.

As q decreases, i increases : i = – dq/dt. Thus, the energy U_B = \(\frac{1}{2}\) Li² stored in the magnetic field of the inductor increases from zero. Since the circuit is free of resistance, energy is not dissipated in the form of heat, so that the decrease in the energy stored in the capacitor appears as the increase in energy stored in the inductor. As the current reaches its maximum value i(y the capacitor is fully discharged and all the energy is stored in the inductor, from figure (b).

Although q = 0 at this instant, dq/dt is nonzero. The current in the inductor then continues to transfer charge from the top plate of the capacitor to its bottom plate, as in from figure (c). The electric field in the capacitor builds up again, but now in the opposite sense, as energy flows back into it from the inductor. Eventually, all the energy of the magnetic field of the inductor is transferred back into the electric field of the capacitor, which is now fully charged, from figure (d).

The capacitor then begins to discharge with an anticlockwise current until the energy is completely back with the inductor. The magnetic field in the inductor is in the opposite sense and becomes maximum when the current reaches its maximum minimum value – i₀. Subsequently, the current in the inductor charges the capacitor once again until the capacitor is fully charged and back to its original condition.

In the absence of an energy dissipative resistance (ideal condition), this cycle continues indefinitely. When the magnitude of the current is maximum, the energy is stored completely in the magnetic field. When the energy is stored entirely in the electric field, the current is zero. The current varies sinusoidally with time between i₀ and – i₀. The frequency of this electrical oscillation in the LC circuit is determined by the values of L and C.

[Notes : (1) Electrical oscillations in an LC circuit are analogous to the oscillations of an ideal mechanical oscillator. An LC circuit with resistance is analogous to a damped mechanical oscillator, while one with a source of alternating emf is analogous to a forced mechanical oscillator. (2) With suitable choices of L and C, it is possible to obtain frequencies ranging from 10 Hz to 10 GHz. (3) In practice, LC oscillations are damped because an inductor has some resistance (R) and hence Joule heat (izRt) is developed in it. The amplitude of oscillations goes on decreasing with time and becomes zero eventually. Also, part of energy stored in the inductor and capacitor is radiated in the form of electromagnetic waves. Working of radio and TV transmitters is based on such radiation.]

Question 37.
Explain electrical resonance in an LCR series circuit. Deduce the expression for the resonant frequency of the circuit.
Answer:
Suppose a sinusoidally alternating emf e, of peak value e₀ and frequency f, is applied to a circuit containing an inductor of inductance L, a resistor of resistance R and a capacitor of capacitance C, all in series, from figure (a) The inductive reactance, X_L, and the capacitive reactance, X_C, are
X_L = ωL and X_C = \(\frac{1}{\omega C}\)
where ω = 2πf.
The rms values i_rms and e_rms of current and emf are proportional to one another.
i_rms = \(\frac{e_{\mathrm{rms}}}{\mathrm{Z}}\)
where Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\) = the impedance of the circuit.

The impedance Z drops to a minimum at the frequency f_r for which the inductive and capacitive reactances are equal (and opposite, in a phasor diagram); i.e., when

At this frequency, Z = R and the phase angle Φ = 0, i.e., the combination behaves like a pure
resistance, and the current and emf are in phase. If R is small, the loss is small. Then, the current may be very large. At any other frequency, the impedance is greater than R. If a mixture of frequencies is applied to the circuit, the current only builds up to a large value for frequencies near the one to which the circuit is ‘tuned’, as given by Eq. (5). The resonance curve, from figure (b), shows the variation of the rms current with frequency. This is an example of electrical resonance. Equations (3) or (4) give the resonance condition and f_ris called the resonant frequency of the LCR series circuit.

At the resonant frequency, the potential differences across the capacitor and inductor are equal in magnitude but in exact antiphase; the current is in quadrature, i.e., 900 out of phase with them. The energy stored in the electric field of the capacitor changes periodically as the square of the potential difference across it; while the energy stored in the magnetic field of the inductor changes periodically as the square of the current. At moments when the potential difference across the capacitor is a maximum and the current through the inductor zero, there is then a maximum of energy stored in the electric field of the capacitor. At moments the potential difference across the capacitor is zero and the current through the inductor a maximum, there is then a maximum of energy stored in the magnetic field of the inductor.

At resonance, the total energy stored in the L-C system is constant, and is simply passed back and forth between the electric and magnetic fields. When the resonant current is first building up, this energy is drawn from the ac supply. After that, the supply only needs to make up the energy lost as heat in the resistor.

Question 38.
State the characteristics of a series LCR AC resonance circuit.
Answer:
Characteristics of a series LCR AC resonance circuit:

1. Resonance occurs when inductive reactance (X_L = 2πfL) equals capacitive reactance j (X_C = \(\frac{1}{2 \pi f C}\)). Resonant frequency, f_r = \(\frac{1}{2 \pi \sqrt{L C}}\).
2. Impedance is minimum and the circuit is purely resistive.
3. Current is maximum.
4. Frequencies, other than the resonant frequency (f_r) are rejected. Only f_r is accepted. Hence, it is called the acceptor circuit.

Question 39.
In LCR series circuit, what is the condition for current resonance ?
Answer:
In LCR series circuit, the condition for current resonance is ωL = \(\frac{1}{\omega C}\) or f = \(\frac{1}{2 \pi \sqrt{L C}},\), where L is the inductance, C is the capacitance and / is the frequency of the applied alternating emf.

Question 40.
In LCR series circuit, what is the
(i) reactance and
(ii) impedance at current resonance?
Answer:
In LCR series circuit, at current resonance,

1. reactance is zero and
2. impedance equals resistance R.

Question 41.
A series LCR circuit has resistance 5 Ω and reactance, for a certain frequency, is 10\(\sqrt {2}\) Ω, what is the impedance of the circuit?
Answer:
Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}=\sqrt{(5)^{2}+(10 \sqrt{2})^{2}}\)
= \(\sqrt{25+200}=\sqrt{225}\) = 15 Ω is the impedance of the circuit.

Question 42.
In LCR series circuit, what is the
(i) power factor and
(ii) phase difference between the emf and current, at resonance.
Answer:
At resonance,

1. the power factor is 1 and
2. the phase difference between the emf and current is zero.

Question 43.
What is an acceptor circuit ? State its use.
Answer:
An acceptor circuit is a series LCR resonant circuit used in communications and broadcasting to selec-tively pass a current for a signal of only the desired frequency.

The resonance curve of a series LCR resonant circuit with a small resistance exhibits a very sharp peak at a certain frequency called the resonant frequency f_r. For an alternating signal of this frequency, the impedance of the circuit is minimum, equal to R, and the current is maximum. That is, the circuit has a selective property as it prefers to pass a signal of frequency f_r and reject those of other frequencies.

Use : An acceptor circuit is used in a radio or television receiver to accept the signal of a desired broadcasting station or channel from all the signals that arrive concurrently at its antenna. Tuning a receiver means adjusting the acceptor circuit to be resonant at a desired frequency.

Question 44.
Explain electrical resonance in an LC parallel circuit. Deduce the expression for the resonant frequency of the circuit.
Answer:
Consider a capacitor of capacitance C, and an inductor of large self-inductance L and negligible resistance, connected in parallel across a source of sinusoidally alternating emf from below figure. Let the instantaneous value of the applied emf be
e = e₀ sin ωt

Let i_L and i_C be the instantaneous currents through the inductor and capacitor respectively.
As the current in the inductor lags behind the emf in phase by π/2 radian,
i_L = \(\frac{e_{0}}{X_{\mathrm{L}}} \sin \left(\omega t-\frac{\pi}{2}\right)=-\frac{e_{0}}{X_{\mathrm{L}}} \cos \omega t\)
where X_L is the inductive reactance.
As the current in the capacitor leads the emf by a phase angle of π/2 radian,
i_C = \(\frac{e_{0}}{X_{C}}\) sin (ωt + π/2) = \(\frac{e_{0}}{X_{C}}\) cos ωt
where X_C is the capacitive reactance.
The instantaneous current drawn from the source is
i = i_L + i_C = e₀ \(\left(\frac{1}{X_{\mathrm{C}}}-\frac{1}{X_{\mathrm{L}}}\right)\) cos ωt
If X_L = X_C, i = 0. Thus, no current is drawn from the source if X_L = X_C. In such a case, alternating current goes on circulating in the LC loop, though no current is supplied by the source. This condition is called parallel resonance and the frequency of ac at which it occurs is called the resonant frequency (f_r).
The condition for resonance is
X_L = X_C

In practice, every inductor possesses some resistance and hence even at resonance, some current is drawn from the source. Also, the resonant frequency is different from that for zero resistence.

The resonance curve shows the variation of current (i) and impedance with the frequency of the ac supply, from figure (b). At resonance the current supplied by the source is minimum and the impedance of the circuit is maximum.

Question 45.
State the characteristics of a parallel LC AC resonance circuit.
Answer:
Characteristics of a parallel LC AC resonance circuit:

1. Resonance occurs when inductive reactance (X_L = 2πfL) equals capacitive reactance (X_C = \(\frac{1}{2 \pi f C}\))
   Resonant frequency, f_r = \(\frac{1}{2 \pi \sqrt{L C}}\)
2. Impedance is maximum.
3. Current is minimum.
4. The circuit rejects f_r but allows the current to flow for other frequencies. Hence, it is called a rejector circuit.

Question 46.
What is a rejector circuit? State its use.
Answer:
A rejector circuit is a parallel LC resonant circuit used in communications and broadcasting as well as filter circuits to selectively reject a signal of a certain frequency.

The resonance curve of a parallel resonant circuit with a finite resistance of its inductor windings exhibits a sharp minimum at a certain frequency called the resonant frequency f_r. For an alternating signal of this frequency, the impedance of the circuit is maximum and the current is minimum. That is, the circuit has a selective property to reject a signal of frequency f_r while passing those of other frequencies.

Use : A rejector circuit is used at the output stage of a radiowave transmitter.

Question 47.
Distinguish between an acceptor circuit and a rejector circuit. (Any two points)
Answer:

Acceptor circuit	Rejector circuit
1. An acceptor circuit is a 1. series LCR resonant circuit.	1. A rejector circuit is a parallel LC resonant circuit.
2. For such a circuit with a 2. small resistance, the reson­ance curve has a sharp peak at the resonant frequency, i.e., at this frequency, the impedance is minimum so that the current is maxi­mum.	2. With a small resistance of its inductor windings, the res­onance curve has a sharp minimum at the resonant frequency, i.e., at this fre­quency, the impedance is maximum so that the cur­rent is minimum.
3. It selectively passes a signal 3. of frequency equal to the resonant frequency.	3. It selectively rejects a signal of frequency equal to the resonant frequency.

Question 48.
In an LC parallel circuit, under what condition, does the impedance become maximum?
Answer:
In an LC parallel circuit, the Impedance becomes maximum when ωL = \(\frac{1}{\omega C}\) or f = \(\frac{1}{2 \pi \sqrt{L C}^{\prime}}\) where f is the frequency 0f the applied alternating emf, L is the inductance and C is the capacitance.

Question 49.
Explain the terme sharpness of resonance and Q factor (quality factor).
Answer:
In a series LCR Ac circuit, the amplitude of the current, i.e., the peak value of the current, is
i₀ = \(\frac{e_{0}}{\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}}\)
If the angular frequency, n changed. at resonance.
ω_rL = \(\frac{1}{\omega_{\mathrm{r}} C}\) giving ω_r = \(\frac{1}{\sqrt{L C}}\)
For ω different from ω_r, the amplitude of i is less than the maximum value of i₀. which is \(\frac{e_{0}}{R}\).

Contider the value of ω for which i₀ = \(\frac{\left(i_{0}\right)_{\max }}{\sqrt{2}}\)
= \(\frac{e_{0}}{R \sqrt{2}}\) that the power dissipated by the circuit is half the maximum power. This ω is called the half power angular frequency. There are two such values of ω on either side of ω_r as shown in below figure.

circuit. \(\frac{\omega_{\mathrm{r}}}{2 \Delta \omega}\) is a measure of the sharpness of resonance If It is high, resonance is sharp; if it is low, resonance is not sharp.

The sharpness of resonance Is measured by a coefficient called the quality or Q fader of the cicuit.

The Q factor of a series LCR resonant circuit is defined as the ratio of the resonant angular frequency to the diference in two angular frequencies taken on both sides of the angular resonant ‘frequency such that at each angular frequency the current amplitude becomes \(\frac{1}{\sqrt{2}}\) times the value at resonant frequency.
∴ Q = \(\frac{\omega_{\mathrm{r}}}{\omega_{2}-\omega_{1}}=\frac{\omega_{\mathrm{r}}}{2 \Delta \omega}=\frac{\text { resonant frequency }}{\text { bandwidth }}\)

Q-factor is a dimensionless quantity. The larger the Q-factor, the smaller is the bandwidth i.e., the sharper is the peak in the current It means the series resonant circuit is more selective in this case. from figure shows that the lower angular frequency side of the resonance curve is dominated by the capacitive reactance, the higher angular frequency side is dominated by the inductive reactance and resonance occurs ¡n the middle. This follows from the formulae, X_L = ωL and X_C = \(\frac{1}{\omega C}\). The higher the ω, the greater ¡s X_L and smaller is X_C. At ω = ω_r, X_L = X_C.

Question 50.
What Is the natural frequency of LC circuit with inductance 1H and capacitance µF?
Answer:

Question 51.
What is a choke coil? What is it used for? Explain.
Answer:
A choke coil is an inductor of high inductance. It consists of a large number of turns of thick insulated copper wire wound closely over a soft iron laminated cure- Average power consumed by it over one cycle is P_av = r_rms i_rms cos Φ, where the power factor cos Φ = \(\frac{R}{\sqrt{R^{2}+\omega^{2} L^{2}}}\)

For ωL >> R. cos Φ is very low implying power consumption is reduced. The energy loss due to hysteresis in iron core is reduced by using a soft Iron core.

In an AC circuit a choke coil is used instead of a resistor to reduce power consumption In case of a pure resistor P_av is high as it is e_rms i_rms.

Question 52.
What is the approximate value of the power factor of a choke coil with R = 10 Ω and reactance = 100Ω ?
Answer:

53. Solve the following 
Question 1.
A coil of resistance S D and self-inductance 0.2 H is connected in series with a variable capacitor across a 30 V_(rms) 50 Hz supply. At what capacitance will resonance occur? Find the corresponding current.
Solution:
Data: R = 5 Ω. L = 0.2 H, e_rms = 30 V. f = 50 Hz
Let C be the capacitance of the capacitor at resonance.
(i) At resonance,

Question 2.
An ac circuit consists of a resistor of 5 0 and an inductor of 10 mH connected In series with a 50 V
(peak)/50 Hz supply. What capacitance should be connected in series with the circuit to obtain maximum current? What will be the maximum current?
Solution:
Data: R = 50 Ω, L = 10 mH = 10 × 10^-3 H, e₀ = 50 V, f = 50 Hz
(i) Maximum current is obtained at resonance.
The condition for resonance is

(ii) At resonance, Z = R
∴ Maximum current,
i₀ = \(\frac{e_{0}}{Z}=\frac{e_{0}}{R}=\frac{50}{5}\) = 10 A

Question 3.
An LCR series combination has R = 10 Ω, L = 1 mH and C = 2 µF. Determine (i) the resonant frequency (ii) the current in the circuit (iii) voltages across L and C, when an alternating voltage of rms value 10 mV operating at the resonant frequency is applied to the series combination.
Solution:
Data : R = 10 Ω, L = 1 mH = 10^-3 H, C = 2 × 10^-6 F, e_rms = 10 mV = 10^-2 V

Question 4.
In a parallel resonant circuit, the inductance of the coil is 3 mH and resonant frequency is 1000 kHz. What is the capacitance of the capacitor in the circuit?
Solution:
Data : L = 3 mH = 3 × 10^-3 Hz, f_r = 1000 kHz = 1000 × 10³ = 10⁶ Hz

= 8.441 × 10^-12 F or 8.441 pF

Question 5.
An ac circuit consists of an inductor of inductance 125 mH connected in parallel with a capacitor of capacity 50 µF. Determine the resonant frequency.
Solution :
Data : L = 125 mH = 0.125 H, C = 50 µF = 50 × 10^-6 F
Resonant frequency,

= 63.65 Hz

Question 6.
An ac voltage of rms value 1V is applied to a parallel combination of inductor L = 10mH and capacitor C = 4 µF. Calculate the resonant frequency and the current through each branch at resonance.
Solution:
Data : e_rms = 1 V, L = 10 mH = 10^-2H, C = 4 µF = 4 × 10^-6 F
(i) Resonant frequency,

= 795.7 Hz

(ii) At resonance, the currents through the inductor and capacitor are in exact antiphase but equal in magnitude : i_L = i_C.
∴ i_C = \(\frac{e_{\mathrm{rms}}}{X_{\mathrm{C}}}\) = (2πf_rC) e_rms
= (2 × 3.142 × 795.7 × 4 × 10^-6)(1) = 0.02A

Multiple Choice Questions

Question 1.
The motor of an electric fan has a self inductance of 10 H, and is connected to a 50-Hz ac supply in series with a capacitor. If maximum power transfer occurs when X_L = X_C, the capacitance of the capacitor is
(A) 0.5 µF
(B) 1 µF
(C) 10 µF
(D) 100 µF.
Answer:
(B) 1 µF

Question 2.
The reactance of a coil is 157 Ω. On connecting the coil across a source of frequency 100 Hz, the current lags behind the emf by 45°. The inductance of the coil is
(A) 0.25 H
(B) 0.5 H
(C) 4 H
(D) 314 H.
Answer:
(A) 0.25 H

Question 3.
In a series LCR circuit, the power factor at resonance is
(A) zero
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{\sqrt{2}}\)
(D) 1.
Answer:
(D) 1.

Question 4.
The current in an LC circuit at resonance is called
(A) the displacement current
(B) the idle current
(C) the wattless current
(D) the apparent current.
Answer:
(C) the wattless current

Question 5.
In a series LCR circuit at resonance, the applied emf and current are
(A) out of phase
(B) in phase
(C) differ in phase by \(\frac{\pi}{4}\) radian
(D) differ in phase by \(\frac{\pi}{2}\) radian.
Answer:
(B) in phase

Question 6.
In a series LCR circuit, R = 3 Ω, X_L = 8 Ω and X_C = 4 Ω. The impedance of the circuit is
(A) 3 Ω
(B) 7 Ω
(C) 5 Ω
(D) 25 Ω
Answer:
(C) 5 Ω

Question 7.
A sinusoidal emf of peak value 150\(\sqrt {2}\) V is applied to a series LCR circuit in which R = 3 Ω and Z = 5 Ω. The rms current in the circuit is
(A) 30 A
(B) 30\(\sqrt {2}\) A
(C) 50 A
(D) 50\(\sqrt {2}\) A.
Answer:
(A) 30 A

Question 8.
In a series LCR circuit, R = 3 Ω, Z = 5 Ω, i_rms = 40 A and power factor = 0.6. The average power dissipated in the circuit is
(A) 2880 W
(B) 4800 W
(C) 8000 W
(D) 9600 W.
Answer:
(A) 2880 W

Question 9.
A parallel LC resonant circuit is used as
(A) a filter circuit
(B) a tuning circuit in a television receiver
(C) a transformer
(D) a rectifier.
Answer:
(A) a filter circuit

Question 10.
A senes LCR resonant circuit is used as
(A) a potential divider
(B) a tuning circuit in a television receiver
(C) a source of wattless current
(D) a radiowave trasmitter.
Answer:
(B) a tuning circuit in a television receiver

Question 11.
If AC voltage is applied to a pure capacitor. then voltage acrose the capacitor .
(A) leads the current by phase angle (\(\frac{\pi}{2}\)) rad
(B) leads the current by phase angle π rad
(C) lags behind the current by phase angle (\(\frac{\pi}{2}\)) rad
(D) lags behind the current by phase angle π rad.
Answer:
(C) lags behind the current by phase angle (\(\frac{\pi}{2}\)) rad

Question 12.
In a series LCR circuit at resonance, the phase difference between the current and emf of the source is
(A) π rad
(B) \(\frac{\pi}{2}\) rad
(C) \(\frac{\pi}{4}\) rad
(D) zero rad.
Answer:
(D) zero rad.

Question 13.
For e = e₀ sin ωt, (average) over one cycle is

Answer:
(D) \(\frac{2}{\pi} e_{0}\)

Question 14.
For i = i₀ sin ωt. i_rms/i_av is

Answer:
(A) \(\frac{\pi}{2 \sqrt{2}}\)

Question 15.
If i = 10sin(314t) [in ampere). i_av =
(A) 6.365 A
(B) 10/\(\sqrt{2}\) A
(C) 10/π A
(D) 5A.
Answer:
(A) 6.365 A

Question 16.
If e = 10 sin(400t) [in volt]. e_rms =
(A) \(\frac{10}{\pi}\) V
(B) \(\frac{10 \sqrt{2}}{\pi}\) V
(C) 5V
(D) 7.07V
Answer:
(D) 7.07V

Question 17.
In a purely resistive circuit, the heat produced by a sinusoidally varying AC over a complete cycle is given by H =

Answer:
(C) \(R\left(i_{\mathrm{rms}}\right)^{2} \cdot \frac{2 \pi}{\omega}\)

Question 18.
In a purely inductive AC circuit, i₀ =
(A) \(\frac{e_{0}}{L}\)
(B) \(\frac{e_{0}}{\omega L}\)
(C) \(\frac{e_{0}}{f L}\)
(D) ωLe₀.
Answer:
(B) \(\frac{e_{0}}{\omega L}\)

Question 19.
In a purely capacitive AC circuit, i₀ =
(A) e₀/C
(B) ωCe₀
(C) e₀/ωC
(D),fCe₀.
Answer:
(B) ωCe₀

Question 20.
The impedance of a series LCR circuit is
(A) R + (X_L – X_C)
(B) R + (X_C – X_L)
(C) \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\)
(D) \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}-X_{\mathrm{C}}^{2}}\)
Answer:
(C) \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}\)

Question 21.
In a purely inductive circuit, P_av =

Answer:
(C) Zero

Question 22.
In a series LCR AC circuit, power factor is

Answer:
(D) \(\frac{R}{Z}\)

Question 23.
The Q factor of an LCR series resonant circuit is
(A) resonant frequency/bandwidth
(B) bandwidth / resonant frequency
(C) ω_r/(ω₁ + ω₂)
(D) (ω₁ + ω₂)/ ω_r
Answer:
(A) resonant frequency/bandwidth

Question 24.
The power factor for a choke coil is

Answer:
(A) \(\frac{R}{\sqrt{R^{2}+\omega^{2} L^{2}}}\)

Question 25.
The power factor for a purely resistive AC circuit is
(A) 0.5
(B) 1
(C) \(\frac{1}{\pi}\)
(D) \(\frac{\pi}{2}\)
Answer:
(B) 1

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 7 Correspondence with Debentureholders Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 7 Correspondence with Debentureholders

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Debenture holders receive ______________ as a proof of their investment in the company.
(a) Share Certificate
(b) Debenture Certificate
(c) Share Warrant
Answer:
(b) Debenture Certificate

Question 2.
______________ have no right to attend company’s meetings.
(a) Shareholders
(b) Directors
(c) Debenture holders
Answer:
(c) Debentureholders

Question 3.
______________ have priority in the repayment of the capital at the time of winding up of the company.
(a) Debenture holders
(b) Shareholders
(c) Secretary
Answer:
(a) Debenture holders

Question 4.
Debentures are secured through charge on the ______________ of the company.
(a) Liability
(b) Profits
(c) Assets
Answer:
(c) Assets

Question 5.
The fund created for the redemption of debentures is known as ______________
(a) DRRF
(b) DHFL
(c) IEPF
Answer:
(a) DRRF

Question 6.
Debentures are repaid on maturity by using debenture ______________ reserve.
(a) Redemption
(b) Depreciation
(c) General
Answer:
(a) Redemption

Question 7.
Debenture holder has the right to inspect ______________
(a) Partnership Deed
(b) Memorandum of Association
(c) Trust Deed
Answer:
(c) Trust Deed

Question 8.
From the date of request, trust deed should be provided by the company with in ______________
(a) 14 days
(b) 7 days
(c) 21 days
Answer:
(b) 7 days

Question 9.
Communication in writing means ______________
(a) Correspondence
(b) Motion
(c) Voting
Answer:
(a) Correspondence

Question 10.
Debentures are issued after passing resolution at ______________
(a) Board Meeting
(b) General Meeting
(c) Committee Meeting
Answer:
(a) Board Meeting

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Courtesy	(a) Wrong Publicity
(2) Prompt Response	(b) True and Real Facts
(3) Transparency	(c) Politeness
(4) Conciseness	(d) Up to date information
(5) Precise Information	(e) Reply without delay
(6) Secretary	(f) Irrelevant Information
(7) Goodwill	(g) Hide Information
	(h) Confidential Officer
	(i) False and incorrect Information
	(j) Rude and harsh wording
	(k) Brief and to the point
	(l) Delay in replying
	(m) Good image of the company
	(n) Disclose Secrets

Answer:

Group ‘A’	Group ‘B’
(1) Courtesy	(c) Politeness
(2) Prompt Response	(e) Reply without delay
(3) Transparency	(b) True and Real Facts
(4) Conciseness	(k) Brief and to the point
(5) Precise Information	(d) Up to date information
(6) Secretary	(h) Confidential Officer
(7) Goodwill	(m) Good image of the company

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
Capital raised by the company by issuing debentures.
Answer:
Debenture Capital

Question 2.
Rate of interest on debentures.
Answer:
Fixed

Question 3.
Debentures are secured by a charge of the assets of the company.
Answer:
Secured Debentures

Question 4.
Debentures are redeemable after a certain period of time.
Answer:
Redeemable Debentures

Question 5.
The Debenture holder has a right to inspect and obtain copies of this deed.
Answer:
Trust Deed

Question 6.
Debenture holder who gets interested through interest coupons.
Answer:
Bearer Debenture holder

Question 7.
The Debentures are issued to the public by issuing this document.
Answer:
Prospectus

Question 8.
The type of Debentures which can be converted into equity shares.
Answer:
Convertible Debentures

1D. State whether the following statements are true or false.

Question 1.
Debenture holders are the creditors of the company.
Answer:
True

Question 2.
Debenture holders enjoy normal voting rights.
Answer:
False

Question 3.
Debentures can be issued to more than 500 people without appointing Debenture Trustee.
Answer:
False

Question 4.
Debenture Certificate is issued within 6 months from the date of allotment of debentures.
Answer:
True

Question 5.
Secretary is the confidential officer of the company.
Answer:
True

1E. Find the odd one.

Question 1.
Courtesy, Transparency, Enclosure
Answer:
Enclosure

Question 2.
Conciseness, Accuracy, Inside address
Answer:
Inside address

Question 3.
Convertible Debentures, Secured Debentures, Cumulative Preference Shares.
Answer:
Cumulative Preference Share

1F. Complete the sentences.

Question 1.
Convertible Debentures are converted into ______________ on the maturity.
Answer:
Equity shares

Question 2.
Redeemable Debentures are ______________ on the date of maturity.
Answer:
Repaid

Question 3.
Registered Debenture holders get interest through ______________
Answer:
Interest Warrant

Question 4.
Bearer Debenture holders get interest through ______________
Answer:
Interest Coupons

Question 5.
Secured Debentures are secured by ______________ on the assets of the company.
Answer:
Charge

Question 6.
Being the creditors, due ______________ should be given to the Debenture holders while corresponding.
Answer:
Respect

Question 7.
The secretary should follow the ______________ of the Companies Act, 2013 .
Answer:
Statutory Provisions

Question 8.
As a Confidential Officer of the company, the secretary should not disclose any important and ______________ information related to the company while corresponding.
Answer:
Secret

Question 9.
The information provided by the secretary must be factual and ______________
Answer:
True

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(a) Interest Warrant	(1) …………………..
(b) ………………………..	(2) Interest Coupons
(c) …………………………	(3) Secured Debenture

(Bearer Debentures, Registered Debentures, Charge on the assets)
Answer:

Group ‘A’	Group ‘B’
(a) Interest Warrant	(1) Registered Debentures
(b) Bearer Debentures	(2) Interest Coupons
(c) Charge on the assets	(3) Secured Debenture

1H. Answer in one sentence.

Question 1.
Who is appointed when the issue of debentures exceeds more than 500 people?
Answer:
Debenture trustees are appointed when the issue of debentures exceeds more than 500 people.

Question 2.
Debenture Certificate should be issued within how many months from the date of allotment of Debentures?
Answer:
Debenture Certificate should be issued within 6 months from the date of allotment of Debentures.

Question 3.
Which debentures are converted into equity shares?
Answer:
Convertible Debentures are converted into equity shares.

Question 4.
Who has to communicate the decisions of the management and other information to the Debenture holders?
Answer:
The secretary has to communicate the decisions of the management and other information to the debenture holders.

Question 5.
Which fund is created for Redemption of Debentures?
Answer:
A Debenture Redemption Reserve Fund is created for Redemption of Debentures.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Debentures carry a fluctuating rate of interest as a return on investment in debentures.
Answer:
Debentures carry a fixed rate of interest as a return on investment in debentures.

Question 2.
Debenture Capital is the owned capital of a company.
Answer:
Debenture Capital is the borrowed capital of a company.

1J. Arrange in proper order.

Question 1.
Redemption of Debentures, Debenture Redemption Reserve Fund, Debenture Redemption Form.
Answer:
Debenture Redemption Reserve Fund, Debenture Redemption Form, Redemption of Debentures

2. Study the case/situation and express your opinion.

1. As a secretary of Velon Industries Limited.

Question (a).
Give any three circumstances where the company will have to correspond with the debenture holders.
Answer:
Secretary will correspond with the debenture holder under the following circumstances:

• Allotment Letter to debenture holders.
• Payment of Interest.
• Redemption of debentures.

Question (b).
What precautions should be taken while drafting the letters?
Answer:
As a secretary, one should be polite, transparency should be maintained and the image of the company should be kept in mind while drafting the letters.

Question (c).
Board Resolution is necessary for the payment of interest?
Answer:
Yes, Board Resolution is necessary for the payment of interest.

2. Disha Industries Ltd. Allots debentures to Mr. Vijay Mittal.

Question (A).
Which letter will be sent to Mr. Vijay Mittal?
Answer:
Letter of Allotment of Debentures will be sent to Mr. Vijay Mittal.

Question (b).
Why does Vijay Mittal preserve the Allotment Letter?
Answer:
Mr. Vijay Mittal preserves the allotment letter because he will receive a Debenture Certificate in exchange for the allotment letter.

Question (c).
What details does the letter contain?
Answer:
The letter contains the details of the issue of debentures i.e number of debentures applied, numbers of debentures allotted, distinctive numbers of debentures, amount received, types of debentures, rate of interest, maturity date, etc.

3. Rolta India Limited wants to pay interest to the debenture holders.

Question (a).
Which resolution is required for the payment of interest to debenture holders?
Answer:
Board Resolution is required for the payment of interest to the debenture holders.

Question (b).
Can the company pay interest in the next year as in the current year company has incurred a loss?
Answer:
No, the company has to pay the interest as it does not depend upon the profits of the company.

Question (c).
How can the company pay interest to the debenture holders?
Answer:
The company can pay interest to debenture holders by the way of interest warrant and electronic mode i.e. ECS and NEFT.

3. Answer in brief.

Question 1.
What is a debenture? Explain Debenture Capital.
Answer:
Debentures is an instrument in writing, acknowledging a debt under a common seal of a company.

• Debenture represents the borrowed capital of a company.
• The debenture is an acknowledgment of debt.
• The debenture holder is a creditor of the company.
• Compared to equity shares, debenture capital is considered safe and secured capital.
• Debentures are repaid on the expiry of a fixed period at the winding up of the company before equity shares are repaid.
• A debenture may be secured, unsecured, redeemable, convertible, non-convertible, etc
• Secured debentures have a charge on the assets of the company.
• Redeemable debentures are repaid on the expiry of a fixed period.
• Convertible debentures are converted into equity shares on the expiry of a fixed period.
• Non-convertible debentures cannot be converted into equity shares but are repaid on the expiry of the fixed period.

Question 2.
State any four precautions to be taken while drafting letters to the debenture holders.
Answer:
The following precautions are to be kept in mind by the secretary while corresponding with the debentures.
(i) Transparency:

• Transparency with debenture holders has to be maintained.
• It is necessary to disclose correct and accurate information of the company, favourable as well as the adverse credit rating of the company, etc. in correspondence.

(ii) Politeness (Courtesy):

• As debenture holders are the creditors of the company, proper respect should be given to them in correspondence.
• The use of words in the letter should be proper which depicts respect to the debenture holders.
• Rude and harsh words should be strictly avoided.

(iii) Conciseness:

• Letters to the debenture holders should be brief and to the point.
• Unnecessary information should be avoided.

(iv) Accuracy/Precise information:

• The secretary should provide precise and up-to-date information to debenture holders.
• The information must be true and correct.

Question 3.
When does a secretary enter into correspondence with debenture holders?
Answer:

1. Debenture holders are creditors of the company.
2. Therefore, they do not participate in the management of the company.
3. They do not enjoy voting rights.
4. Whatever decisions are taken by the management, are communicated to them by the secretary.
5. A secretary has to enter into correspondence with the debenture holders under the following circumstances:
   • Informing the applicant about allotment of debentures.
   • Informing about payment of interest through
     • Interest warrant
     • Electronic payment of Interest
   • Letter of conversion of debentures into equity shares.
   • Letter for the redemption of debentures.

4. Justify the following statements.

Question 1.
Debenture holders are the creditors of the company.
Answer:

• Debenture represents borrowed capital of the company.
• It is an acknowledgment of debt issued by the company under its common seal.
• The person buying the debenture is known as the ‘Debenture holder’.
• Debenture holders are the creditors of the company.
• They provide loans to the company and hence, enjoy fixed-rate interest as a return on their investment.
• Debentures are secured and redeemable. They are repaid after a certain period of time, i.e. on the maturity date.
• Thus, it is rightly justified that, debenture holders are the creditors of the company.

Question 2.
The company secretary should follow legal provisions while corresponding with Debenture holders.
Answer:

• Debenture holders are the creditors of the company and hence, the secretary has to correspond with Debenture holders on different occasions.
• The secretary should follow the statutory provisions of the Companies Act, 2013 and other relevant laws while corresponding with Debenture holders.
• Secretary should be cautious and careful while corresponding with debenture holders on legal matters. He should be aware of legal consequences.
• Non-compliance with legal provisions can result in legal consequences, creating problems for the company.
• Thus, it is rightly justified that, the company secretary should follow legal provisions while corresponding with debenture holders.

Question 3.
Interest is a debt.
Answer:

• Debenture capital is the borrowed capital of the company.
• Debenture holders are the creditors of the company receiving the fixed rate of interest.
• The company pays the interest through interest warrant and electronic mode i.e. Electronic Clearing System (ECS) or National Electronic Fund Transfer (NEFT).
• Interest is to be paid compulsorily even if the company makes a loss. It does not depend upon the profits of the company.
• Thus, it is rightly justified that, interest is debt.

5. Attempt the following.

Question 1.
Explain the different types of letters written to the debenture holders.
Answer:
Secretary has to communicate with the management and the debenture holders for various reasons. This communication is done by drafting letters to the debenture holders. A secretary should be very cautious and careful while corresponding with debenture holders of the company. Following are the circumstances when the secretary corresponds with the debenture holders.

(i) Debenture Allotment Letter.

• An allotment Letter is sent to the debenture holders when the company allows debentures to the applicant.
• Allotment Letter is preserved by the debenture holder till he receives Debenture Certificate in exchange for this letter.
• Allotment Letter contains details of the issue of debentures, i.e. name of debenture holder, debentures issued, face value, types of debentures, rate of interest, etc.

(ii) Payment of Interest Letter.

• Interest is paid to the debenture holders through:
  • Interest Warrant
  • Electronically
• Payment of Interest Letter contains details such as a number of debentures, distinctive numbers, the gross amount of interest payable, TDS deducted, the net amount of interest payable, etc.
• Board Resolution is required for the payment of interest on debentures.

(iii) Conversion of Debentures Letter.

• Debentures are converted into equity shares.
• Conversion of Debenture Letter is issued only when the company receives Letter of Option.
• After conversion, a share certificate is issued.
• Approval of shareholders is necessary by passing a special resolution at Extra-Ordinary General Meeting.
• Only after receiving the shareholders’ approval, letter of conversion of debentures is sent to debenture holders.

(iv) Redemption of Debentures Letter.

• Debentures are redeemed after a specific period.
• Debenture Redemption Reserve Fund (DRRF) is created for the redemption of debentures.
• Debenture Redemption Form (DRF) is sent along with the letter.
• This letter informs that their debentures have become due for redemption.

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 14 Dual Nature of Radiation and Matter Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 14 Dual Nature of Radiation and Matter

Question 1.
Explain Planck’s idea of quantization of energy.
Answer:
Max Planck, in 1900, put forward the idea of quantization of energy to explain the blackbody radiation spectrum. He proposed that atoms behave as tiny oscillators and emit electromagnetic radiation, not continuously but as little packets of energy called quanta. He assumed that the energy associated with a quantum of radiation (now called a photon) is proportional to the frequency v of the oscillator. Thus, E = nhv, where n = 1, 2, 3, 4, … etc., and h is a universal constant, now called Planck’s constant. For n = 1, E = hv. A quantum of radiation is emitted when there is a transition from higher quantized level of energy of an oscillator to lower quantized level.

[Note : Historically, various terms have been used to denote a particle of light; quantum of electromagnetic radiation ≡ photon ≡ packet of energy ≡ atom of energy ≡ quantum of radiation ≡ bundle of energy. Interaction between two charged particles involves exchange of photons. The photon has zero rest mass, no charge, unit spin and travels in free space at a speed of 2.99792458 × 10⁸ m/s exact by definition. There is no conservation law for photons, i.e., they can be produced / absorbed.]

Question 2.
What was Hertz’s observation regarding emission of electrons from a metal surface?
Answer:
During his experiments on electromagnetic waves in 1887, Heinrich Rudolph Hertz (1857-94), Ger-man physicist, noticed that electric sparks occurred more readily when one of the electrodes of his spark-gap transmitter was exposed to ultraviolet radiation. This discovery was called the Hertz effect and is now known as the photoelectric effect.

Although Hertz did not follow up his discovery, others quickly established that the cause of the sparking ease was due to emission of negatively charged particles from the electrode irradiated. These particles were identified as electrons after the discovery of the electron in 1897.

Question 3.
Draw a neat labelled diagram to illustrate photoelectric effect.
Answer:

[Note : Positive metal ions and atoms are not shown in the figure.]

Question 4.
What were the investigations of Hallwachs and Lenard regarding photoelectric effect?
Answer:
Wilhelm Hallwachs (1859-1922), German physicist, found that a metal plate irradiated with ultraviolet radiation lost its charge more rapidly when the plate is negatively charged than when it is neutral or positive.

Investigations of photoelectric effect by Phillipp Lenard (1862-1947), German physicist, showed that

1. electron emission occurs only with radiations below a critical wavelength, i.e., above a critical frequency.
2. kinetic energy of the emitted electrons increases as wavelength decreases i.e., frequency increases but is independent of the intensity of radiation which determines the rate of emission of electrons (the number of electrons emitted per unit time).

Question 5.
What is a photosensitive surface?
Answer:
The surface which emits electrons when illuminated by electromagnetic radiation of appropriate frequency is called photosensitive surface.
[Note : The material that exhibits photoelectric effect is called photosensitive material.]

Question 6.
Why are alkali metals most suitable as photo-sensitive surfaces?
Answer:
The alkali metals e.g., caesium, potassium and sodium emit photoelectrons even when visible radiation (light) is incident on them. Hence, they are most suitable as photosensitive surfaces.

Question 7.
With a neat diagram, describe the apparatus to study the characteristics of photoelectric effect.
Answer:
Apparatus : A photoelectric cell G consists of the emitting electrode E (emitter) of the material being studied and the collecting electrode C (collector). The electrodes are sealed in an evacuated glass envelope provided with quartz window W that allows the passage of UV radiation and visible light. Monochromatic light of variable frequency from a suitable source S (such as a carbon arc) passes through a pair of polarizers P (permitting a change in the intensity of radiation) and falls on the emitter.

The electric circuit, as shown in below figure, allows the collector potential to be varied from positive through zero to negative with respect to the emitter, and permits the measurement of potential difference and current between the electrodes. When the collector is made negative, the voltmeter is connected in reverse.

[ Note : The radiation coming out of a filter is not truly monochromatic, it lies in the wavelength range between λ and λ + ∆λ that depends on the source and the filter. ]

Question 8.
In the experiment to study photoelectric effect, describe the effects of the frequency and intensity of the incident radiation on the photoelectric current, for a given emitter material and potential difference across the photoelectric cell.
Answer:
The emitter of the photoelectric cell is irradiated with monochromatic light whose frequency and intensity can be varied continuously and measured. Initially, the collector is made positive with respect to the emitter, so that photoelectrons ejected move quickly from the emitter to the collector. About 10 V is sufficient to do this. The photoelectric current as a function of intensity and frequency of incident radiation is studied.

(1) Effect of frequency : Keeping the light intensity and the accelerating potential difference V constant, the frequency of the incident radiation is varied from that of far-UV to red. It is found that for every material (usually, a metal) irradiated there is a limiting frequency below which no photoelectrons are emitted irrespective of the intensity of the radiation. This frequency, v₀, called the threshold frequency or cut-off frequency, is a characteristic of the material irradiated.

The graph of photoelectric current against frequency is shown in below figure; A and B represent two different metals. The photoelectric current is not the same in the two cases, because the intensity of light is different for different frequencies.

(2) Effect of intensity : With an emitter of a given material, the light intensity is varied by keeping the frequency v (≥ v₀) of the light and the accelerating potential difference V constant. It is found that the rate of electron emission, as indicated by the photoelectric current, is proportional to the light intensity. The graph of photoelectric current against light intensity is a straight line through (0, 0), below figure; if we vary either the frequency of the light or the material irradiated, only the slope of the line changes. No electrons are emitted in the absence of incident radiation.

[Note : The dark current, i.e., the current observed in the absence of light, is extremely low. Hence, it is ignored.]

Question 9.
In the experiment to study photoelectric effect, describe the variation of the photoelectric current as a function of the potential difference across the photoelectric cell, for incident radiation of (1) a given frequency above the threshold but different intensities (2) a given intensity but different frequencies above the threshold.
Answer:
(1) The potential difference (p.d.) across the photo-electric cell is varied keeping both the frequency v (≥ threshold frequency v₀) and the intensity of the light constant. Starting with the collector at about 10 V positive, we reduce this potential to zero and then run it negative.

When the p.d. across the tube is 10 V or more, all the emitted electrons are accelerated and travel across the tube, constituting the saturation current for a given light intensity; an increase in the potential of the collector does not cause an increase in current. As the collector potential is reduced from positive values through zero to negative values, the tube current reduces because of the applied retarding potential. In this case, some electrons stop and turn back before they can reach the collector. Eventually the potential difference is large enough to stop the current completely. This is called the stopping potential or cut-off potential VQ. The product of the stopping potential and electronic charge, V₀e, is equal to the maximum kinetic energy that an electron can have at the time of emission.
V₀e = KE_max \(\frac{1}{2}\)v²_max

In above figure, I₁ and I₂ are two intensities of the incident radiation for the same frequency v ( > v₀); I₂ = 2I₀. Doubling the intensity of light doubles the current at each potential, as in I₂, but V₀ is independent of I.

(2) The above experiment is repeated with different light frequencies for a given emitter material and light intensity. It is found that the stopping potential increases linearly with the frequency in below figure. Therefore, when photoejection occurs for frequencies above v₀, the maximum kinetic energy of the photoelectrons increases linearly with the frequency of the radiation.

[Note : It was shown by Hughes that the stopping potential depends linearly on the frequency of incident radiation. Lawrence and Beams established that the time interval between arrival of a photon on a metal surface and emission of an electron is less than 3 × 10^-9 sc.]

Question 10.
What is the effect of the intensity of incident radiation on the stopping potential in photo-electric emission?
Answer:
V₀ is independent of intensity.

Question 11.
In the experiment to study photoelectric effect, discuss the effect and significance of extremely weak radiation of frequency greater than the threshold frequency for the emitter material.
Answer:
The emitter of the photoelectric cell is irradiated with monochromatic light whose frequency is greater than the threshold frequency for the emitter material. The collector is kept at 10 V positive with respect to the emitter, so that photoelectrons ejected move quickly from the emitter to the collector.

The light is made extremely dim (i.e., the intensity is extremely weak). In this case, the number of ‘ photoelectrons emitted per unit time is very small (and special techniques are required to detect them); but, however few, they are emitted almost instantaneously and with the same maximum kinetic energy as for bright light of the same frequency.

According to the wave theory of light, wave trains of pulsating electromagnetic field spread out from the source. Dim light corresponds to waves of small amplitudes and small energy. If dim light spreads over a surface, conservation of energy requires that the electrons must store energy over long periods of time, which can be several hours, before gathering enough energy to become free of the metal. The fact that photoelectrons appear immediately, within about 10^-9 s, can be explained only by assuming that the light energy is not spread over the surface uniformly as required by the wave theory, but falls on the surface in concentrated bundles.

Question 12.
Define (1) threshold frequency (2) threshold wavelength (3) stopping potential.
Answer:
(1) The threshold frequency for a given metal surface is the characteristic minimum frequency of the incident radiation below which no photoelectrons are emitted from that metal surface (whatever may be the intensity of incident light).

(2) The threshold wavelength for a given metal surface is the characteristic maximum wavelength of the incident radiation above which no photoelectrons are emitted from that metal surface (whatever may be the intensity of incident light).

(3) The stopping potential is the value of the retarding potential difference that is just sufficient to stop the most energetic photoelectrons emitted from reaching the collector so that the photoelectric current in a photocell reduces to zero.

[Note : The threshold wavelength λ₀ = c/v₀, where c is the speed of light in free space and v₀ is the threshold frequency for the metal.]

Question 13.
State the characteristics of photoelectric effect.
Answer:
Characteristics of photoelectric effect:
(1) For every metal surface there is a limiting frequency of incident radiation below which no photoelectrons are emitted from that metal surface. This frequency, called the threshold frequency, is characteristic of the metal irradiated.

(2) The time rate of emission of photoelectrons in-creases in direct proportion to the intensity, of incident radiation.

(3) The photoelectrons have different speeds at the time of emission ranging from zero to a certain maximum value, which is characteristic for a given metal for a given frequency of the incident radiation. The maximum kinetic energy of the photoelectrons at the time of emission is independent of the intensity but increases linearly with the frequency of the incident radiation.

(4) For incident radiation of frequency greater than or equal to the threshold frequency for a given metal surface, photoelectric emission from the surface is almost instantaneous, even under extremely weak irradiation.

Question 14.
Can we get photoemission with an intense beam of radio waves ? Is photoemission possible at all frequencies ?
Answer:
The frequency of the incident radiation and not its intensity is the criterion for photoelectric effect. The lowest frequency of electromagnetic waves that can cause photoemission is about 4.6 × 10¹⁴ Hz (for the alkali metal caesium). Since radio waves have frequencies 1 GHz or lower, they cannot cause photoemission.

Only alkali metals are photosensitive to visible light; other metals are photosensitive only to far ultraviolet radiations.

Question 15.
Explain how wave theory of light fails to explain the characteristics of photoelectric effect.
OR
Explain the failure of wave theory of light to account for the observations from experiments on photoelectric effect.
Answer:
According to the wave theory of light, electromagnetic waves carry the energy stored in oscillating electric and magnetic fields. When enough energy is absorbed by an electron in a substance, it should be liberated as a photoelectron. Frequency of light does not come into picture in this case. Hence, there should not be any threshold frequency for emission of electrons. But it is found that there exists threshold frequency and it depends on the metal.

Experimentally, the maximum kinetic energy of photoelectrons increases linearly with the frequency of light. This cannot be accounted by the wave theory of light.

If a source of light is weak or far away from a metal surface, emission of an electron will not be almost instantaneous. The electron may have to wait for several hours/days for absorption of enough energy from the incident light as by the wave theory of light, energy is spread over the wavefront. But experimentally, for an appropriate frequency of incident light, photoelectric effect is almost instantaneous.

Only one observation, photoelectric current ∝ intensity of incident light can be accounted by the wave theory of light.

Question 16.
Give Einstein’s explanation of the photoelectric effect.
Answer:
Max Planck put forward the quantum theory in 1900 to explain blackbody spectrum. In the theory, he proposed that the electromagnetic radiation emitted by the body consists of discrete concentrated bundles of energy, each equal to hv, where h is a universal constant (now called Planck’s constant) and v is the frequency of the radiation.

Einstein put forth (1905) that these energy quanta, called light quanta/later called photons, interact with matter much like a particle. When a photon collides with an electron in an atom, the electron absorbs whole of the photon energy hv in a single collision or nothing. The electron uses this energy (1) to liberate itself from the atom, (2) to overcome the potential energy barrier at the surface thus liberating itself from the metal, and (3) retains the remaining part as its kinetic energy. Different electrons need different energies in the first two processes. There are some electrons which use minimum energy in the two processes, and hence come out of the metal with maximum kinetic energy. The minimum energy required, in the form of electromagnetic radiation, to free an electron from a metal is called the photoelectric work function Φ of that metal. Thus, for the most energetic photoelectrons at the time of emission,
maximum kinetic energy of the electron = photon energy – photoelectric work function
∴ \(\frac{1}{2}\)\(m v_{\max }^{2}\) = hv – Φ ∴ hv = Φ + \(\frac{1}{2}\)\(m v_{\max }^{2}\)
The above equation is called Einstein’s photo-electric equation.

Light interacts with matter as concentrated bundles of energy rather than energy spread over a Huygens type wavefront. Even under weak irradiation, an electron absorbs a photon’s energy in a single collision. But the rate of incident photons in dim light being less, the chances of such absorption diminish and consequently the photoelectric current diminishes. However, a photoelectron is emitted as soon as a photon is absorbed.

[Note : Albert Einstein (1879-1955), German-Swiss- US theoretical physicist, gave his photoelectric equation in 1905. In the period 1912-1916, Robert Andrews Millikan (1868 -1953), US physicist, was the first to obtain the precise experimental data from which the straight-line graphs, like the one shown in Fig. 14.6, were plotted for various metals. Einstein’s theoretically predicted equation-clearly having the right form for a straight-line graph-was thus verified.]

Question 17.
Define photoelectric work function of a metal.
Answer:
The photoelectric work function of a metal is defined as the minimum photon energy that ejects an electron from the metal.
It is equal to hv₀, where h is Planck’s constant and v0 is the threshold frequency for the metal.

Question 18.
Write Einstein’s photoelectric equation and explain its various tends. How does the equation explain the various features of the photoelectric effect?
Answer:
Einstein’s photoelectric equation :
hv = Φ + \(\frac{1}{2}\)\(m v_{\max }^{2}\) ………… (1)
where h ≡ Planck’s constant, v ≡ frequency of the electromagnetic radiation, hv ≡ energy of the photon incident on a metal surface, Φ ≡ photo-electric work function, i.e., the minimum energy of light quantum required to liberate an electron from the metal surface, v_max and – \(\frac{1}{2}\)\(m v_{\max }^{2}\) ≡ the maximum speed and maximum kinetic energy of the photoelectrons at the time of emission. Φ = hv₀, where v₀ is the threshold frequency for the metal.

Explanation of the characteristics of photoelectric effect:
(1) From the above equation we find that for photoejection, hv ≥ Φ. That is, hv_min = hv₀ must be equal to Φ. Hence, photoelectric effect is observed only if hv ≥ hv₀, i.e., v ≥ v₀. This shows the existence of a threshold frequency v₀ for which photoelectrons are just liberated from a metal surface (with zero kinetic energy). Since different metals differ in electronic configuration, the work function hv₀ and, therefore, frequency v₀ are different and characteristic of different metals.

(2) In this particle model of light,’ intensity of incident radiation’ stands for the number of photons incident on a metal per unit surface area per unit time. As the number of photons incident on a metal per unit surface area per unit time increases, there is a greater likelihood of a photon being absorbed by any electron. Therefore, the time rate of photoejection and hence photoelectric current increases linearly with the intensity of the incident radiation (v ≥ v₀).

(3) From Eq. (1), \(\frac{1}{2}\)\(m v_{\max }^{2}\), = hv – Φ= h(v – v₀)
This shows that the maximum kinetic energy in-creases linearly with the frequency v of the incident photon (v ≥ v₀) and does not depend on the time rate at which photons are incident on a metal surface.

(4) As the incident energy is concentrated in the form of a photon, and not spread over a wavefront, it is expected that an electron is emitted from the metal surface as soon as a photon (v ≥ v₀) is absorbed. This is in agreement with the experimental observation.

[ Note : The frequency v that appears in the formula E = hv is the frequency of the oscillating electric field / magnetic field in the electromagnetic wave. ]

Question 19.
Obtain the dimensions of Planck’s constant.
Answer:
The energy of a photon of frequency v is E = hv, where h is the Planck’s, constant.
∴ [h] = \(\frac{[E]}{[v]}=\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~T}^{-1}}\) = ML²T^-1

Question 20.
Is the kinetic energy of all photoelectrons the same when emitted from a certain metal ? Explain.
Answer:
No. Explanation : Depending upon the position and state of an electron in a metal when it absorbs an incident photon, a photoelectron can have kinetic energy ranging from 0 to a certain maximum value equal to the photon energy minus the work function of the metal. Hence, the emitted photoelectrons have this range of kinetic energies.

Question 21.
In photoelectric effect, what does the stopping potential depend upon ?
Answer:
In photoelectric effect, the stopping potential depends upon the energy of the incident photon and the work function for the metal irradiated (or upon the frequency/wavelength of the incident radiation and the threshold frequency/wavelength for the metal irradiated).

Question 22.
What does the maximum kinetic energy (or the maximum speed) of a photoelectron depend on?
Answer:
The maximum kinetic energy (or the maximum speed) of a photoelectron depends upon the energy of the incident photon and the work function for the metal irradiated (or upon the frequency /wavelength of the incident radiation and the threshold frequency/wavelength for the metal irradiated).

Question 23.
In photoelectric effect, if a graph of stopping potential versus frequency of the incident radiation is plotted, what does the intercept on the frequency axis (v corresponding to V_o = 0) represent?
Answer:
The intercept on the frequency axis (v corresponding to V_o = 0) represents the threshold frequency for the metal.

Question 24.
State the equation that relates the threshold wavelength (λ_o), the wavelength of incident radiation (λ) and the maximum speed of a photo-electron (v_max).
Answer:
\(\frac{h c}{\lambda}=\frac{h c}{\lambda_{0}}+\frac{1}{2} m v_{\max }^{2}\) is the required equation, where h is Planck’s constant, c is the speed of light in vacuum (free space) and m is the mass of the electron.

Question 25.
What is the energy of a photon (quantum of radiation) of frequency 6 × 10¹⁴ Hz?
[h = 6.63 × 10^-34 J∙s]
Answer:
hv = (6.63 × 10^-34)(6 × 10¹⁴)
= 3.978 × 10^-19 J is the energy of the photon.

Question 26.
If the total energy of a radiation of frequency 10¹⁴ Hz is 6.63 J, calculate the number of photons in the radiation.
Answer:
E = nhv, where hv is the energy of a photon in a radiation of frequency v and n is the number of photons in the radiation.
∴ n = \(\frac{E}{h v}=\frac{6.63}{\left(6.63 \times 10^{-34}\right)\left(10^{14}\right)}\) = 10²⁰

Question 27.
If in a photoelectric experiment, the stopping potential is 1.5 volts, what is the maximum kinetic energy of a photoelectron ? [e = 1.6 × 10^-19 C]
Answer:
\(\frac{1}{2}\)\(m v_{\max }^{2}\) = V_se = ( 1.5)(1.6 × 10^-19)
= 2.4 × 10^-19 J is the required kinetic energy.

Question 28.
What is the photoelectric work function for a metal if the threshold wavelength for the metal is 3.315 × 10^-7 m?
[h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s]
Answer:
Photoelectric work function for the metal =

Question 29.
Explain the utilization of energy absorbed by an electron in a metal during its collision with a photon.
Answer:
When a photon collides with an atomic electron inside an emitter metal, the electron absorbs whole of the photon energy in a single shot or nothing. The electron uses the absorbed energy (1) to liberate itself from the atom, (2) to overcome the potential energy barrier at the surface thus liberating itself from the metal, and (3) retains the remaining part as its kinetic energy.

30. Solve the following :
(h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s, e = 1.6 × 10^-19 J, m (electron) = 9.1 × 10^-31 kg)

Question 1.
Find the energy of a photon if
(i) the frequency of radiation is 100 MHz
(ii) the wavelength of radiation is 10000 Å.
Solution:
Data : h = 6.63 × 10^-34 J∙s, v = 100 MHz = 100 × 10⁶ Hz, λ = 10000 Å = 10⁶ m, c = 3 × 10⁸ m/s
(i) The energy of a photon, E = hv
= (6.63 × 10^-34)(100 × 10⁶) = 6.63 × 10^-26 J

(ii) The energy of a photon, E = \(\frac{h c}{\lambda}\)
= \(\frac{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{10^{-6}}\) = 1.989 × 10^-19 J

Question 2.
A monochromatic source emits light of wavelength 6000 Å. If the power of the source is 10 W, find the number of photons emitted by it per second assuming that 1% of electric energy is converted into light.
Solution:
Data : λ = 6000 Å = 6 × 10^-7 m ,h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s, electric energy converted into light per second = \(\frac{1}{100}\) × 10W = 0.1J/s

Question 3.
Radiation of intensity 4 × 10^-5 W/m² is incident uniformly on a metal surface with work function 2.4 eV and area 1 cm². Assume that the radius of a metal atom is 2.4 Å and photoelectrons are ejected only from the surface of the metal. On the basis of the wave theory of light, how long will it take for an electron to be ejected from the metal surface ? (Assume one free electron/metal atom.)
Solution:
Data : Power/area = 4 × 10^-5 W/m², Φ = 2.4 eV = 2.4 × 1.6 × 10^-19 J = 3.84 × 10^-19 J, A = 1 cm² = 10^-4 m², r = 2.4 Å = 2.4 × 10^-10 m
Number of metal atoms on the surface = \(\frac{A}{\pi r^{2}}\)

For a single free electron, radiant energy incident per unit time

Ignoring reflection/scattering of light, time needed to absorb energy equal to 3.84 × 10^-19 J is
\(\frac{3.84 \times 10^{-19} \mathrm{~J}}{7.24 \times 10^{-24} \mathrm{~J} / \mathrm{s}}\) = 5.304 × 10⁴ s = 53040s
= 14 hours 44 minutes.

Question 4.
The energy of a photon is 2 eV. Find its frequency and wavelength.
Solution:
Data : E = 2 eV = 2 × 1.6 × 10^-19 J, c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J∙s
(i) Frequency,

= 6.217 × 10^-7 = 6.217 × 10^-7 × 10¹⁰ Å
= 6217 Å = 621.7 nm

Question 5.
Find the wave number of a photon having an energy of 2.072 eV. [Given : e, c, h]
Solution:
Data : e = 1.6 × 10^-19 C, c = 3 × 10⁸ m / s, h = 6.63 × 10^-34 J∙s,
E = 2.072 eV = 2.072 × 1.6 × 10^-19 J
E = hv = \(\frac{h c}{\lambda}\)
Wave number, \(\frac{1}{\lambda}=\frac{E}{h c}\)
= \(\frac{2.072 \times 1.6 \times 10^{-19}}{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}\) = 1.666 × 10⁶ m^-1

Question 6.
Calculate the energy of a photon, in joule and eV, in a light of wavelength 5000 Å.
Solution :
Data : λ = 5000 Å = 5000 × 10^-10 m = 5 × 10^-7 m, c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J∙s
Energy of a photon, E = hv = \(\frac{h c}{\lambda}\)

Question 7.
The photoelectric work function for a metal surface is 2.3 eV. 1f the light of wavelength 6800 Å is incident on the surface of the metal, find the threshold frequency and the incident frequency. Will there be an emission of photoelectrons or not? [Given : c, h]
Solution:
Data: c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J.s, Φ = 2.3 eV = 2.3 × 1.6 × 10^-19 J, λ = 6800 Å = 6.8 × 10^-7 m
(i) Threshold frequency (v₀) : Φ = hv₀
∴ v₀ = \(\frac{\phi}{h}=\frac{2.3 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}}\) = 5.550 × 10¹⁴ Hz

(ii) Incident frequency (v) : c = vλ
∴ v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{6.8 \times 10^{-7}}\) = 4.412 × 10¹⁴ Hz

(iii) Thus, v <v₀
As the frequency of the incident orange light is less than the threshold frequency there will be no emission of photoelectrons.

Question 8.
If the work function of a metal is 3 eV, calculate the threshold wavelength of that metal. [Given : c, h, 1 eV = 1.6 × 10^-19 J]
Solution:
Data : Φ = 3 eV, c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J.s, 1 eV = 1.6 × 10^-19 J
∴ Φ = 3 × 1.6 × 10^-19 J

Question 9.
The photoelectric work function of copper is 4.7 eV. What are the threshold frequency and wavelength for photoemission from a copper surface? [1 eV = 1.6 × 10^-19 J]
Solution :
Data : Φ = 4.7 eV, 1 eV = 1.6 × 10^-19 J, c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J.s

Question 10.
The work functions for potassium and caesium are 2.25 eV and 2.14 eV respectively. Will the photoelectric effect occur for either of these elements
(i) with incident light of wavelength 5650 Å
(ii) with light of wavelength 5180 Å?
Solution:
Data : Φ (potassium) = 2.25 eV,
Φ (caesium) = 2.14 eV, λ₁ = 5650 Å = 5.650 × 10^-7 m, λ₂ = 5180 Å = 5.180 × 10^-7 m, h = 6.63 × 10^-34 J.s, c = 3 × 10⁸ m/s
Φ (potassium) = 2.25 eV
= 2.25 × 1.6 × 10^-19 J =3.6 × 10^-19 J
Φ (caesium) = 2.14 eV = 2.14 × 1.6 × 10^-19 J
= 3.424 × 10^-19 J
Photon energy, E = \(\frac{h c}{\lambda}\)

(i) For λ₁ = 5650 Å
E₁ = \(\frac{h c}{\lambda_{1}}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{5.650 \times 10^{-7}}\)
= 3.52 × 10^-19 J
This is greater than Φ (caesium), but less than Φ (potassium). Hence, photoelectric effect will occur in case of caesium, but not in case of potassium.

(ii) For λ₂ = 5180 Å
E₂ = \(\frac{h c}{\lambda_{2}}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{5.180 \times 10^{-7}}\)
= 3.84 × 10^-19 J
This is greater than 0 for potassium and for caesium. Hence, photoelectric effect will occur in both the cases.

Question 11.
Photoemission just occurs from a lead surface when radiation of wavelength 3000 Å is incident on it. Find the maximum kinetic energy of the photoelectrons when the surface is irradiated by UV radiation of wavelength 2500 Å.
Solution:
Data : λ₀ = 3000 Å = 3 × 10^-7 m, λ = 2500 Å = 2.5 × 10^-7 m, h = 6.63 × 10^-34 J∙s,c = 3 × 10⁸ m/s
According to Einstein’s photoelectric equation, the maximum kinetic energy of the photoelectrons

Question 12.
The photoelectric work function for a metal is 4.2 eV. If the stopping potential is 3 V, find the threshold wavelength and the maximum kinetic energy of emitted electrons. [Given : c, h, e]
Solution :
Data : e = 1.6 × 10^-19 C, c = 3 × 10⁸ m/s, Φ = 4.2 eV = 4.2 × 1.6 × 10^-19 J = 6.72 × 10^-19 J, h = 6.63 × 10^-34 J∙s, v₀ = 3 V
(i) Threshold wavelength.

= 2.960 × 10^-7 m or 2960 Å

(ii) Maximum kinetic energy of emitted electrons,
KE_max = eV₀ = (1.6 × 10^-19)(3) = 4.8 × 10^-19 J

Question 13.
Radiation of wavelength 2 × 10^-7 m is incident on the cathode of a photocell. The current in the photocell is reduced to zero by a stopping potential of 2 V. Find the threshold wavelength for the cathode.
Solution:
Data : λ = 2 × 10^-19 m, V₀ = 2 V, e = 1.6 × 10^-19 C, h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s
According to Einstein’s photoelectric equation,

∴ The threshold wavelength, λ₀ = 2.948 × 10^-7 m

Question 14.
The photoelectric current in a photoelectric cell can be reduced to zero by a stopping potential of 1.8 volts. Monochromatic light of wavelength 2200 Å is incident on the cathode. Find the maximum kinetic energy of the photoelectrons in joule. [Charge on the electron = 1.6 × 10^-19 C]
Solution:
Data: V₀ = 1.8 V, e = 1.6 × 10^-7 C .
The maximum kinetic energy of the photoelectrons,
KE_max = eV₀
= (1.6 × 10^-19) (1.8) = 2.88 × 10^-19 J

Question 15.
The photoelectric work function of a metal is 3 eV. Find the maximum kinetic energy and maximum speed of photoelectrons when radiation of wavelength 4000 Å is incident on the metal surface.
Solution:
Data : Φ = 3 eV = 3 × 1.6 × 10^-19 J, c = 3 × 10⁸ m / s, λ = 4000 Å = 4000 × 10^-10 m, h = 6.63 × 10^-34 J∙s, m = 9.1 × 10^-31 kg
(i) According to Einstein’s photoelectric equation, the maximum kinetic energy of photoelectrons,

= 1.725 × 10^-20 J

= 1.947 × 10⁵ m/s

Question 16.
The work function of tungsten is 4.50 eV. Calculate the speed of the fastest electron ejected from tungsten surface when light whose photon energy is 5.80eV shines on the surface.
Solution:
Data : Φ = 4.50 eV = 4.50 × 1.6 × 10^-19 J = 7.2 × 10^-19 J,
hv = 5.80eV = 5.80 × 1.6 × 10^-19 J = 9.28 × 10^-19 J,
m = 9.1 × 10^-31 kg

This is the speed of the fastest electron ejected.

Question 17.
If the work function for a certain metal is 1.8 eV,
(i) what is the stopping potential for electrons ejected from the metal when light of 4000 Å shines on the metal
(ii) what is the maximum speed of the ejected electrons?
Solution:
Data: Φ = 1.8eV, λ = 4000 Å = 4 × 10^-7 m,
h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s,
m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C

This is the maximum speed of the ejected electrons.

Question 18.
The work function of caesium is 2.14 eV. Find
(i) the threshold frequency for caesium
(ii) the wavelength of the incident light if photocurrent is brought to zero by a stopping potential of 0.60 V.
Solution:
Data : Φ = 2.14eV = 2.14 × 1.6 × 10^-19 J = 3.424 × 10^-19 J, V_O = 0.60 V,h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s, e = 1.6 × 10^-19C
(i) Φ = hv₀
∴ The threshold frequency, v₀ = \(\frac{\phi}{h}\)
= \(\frac{3.424 \times 10^{-19}}{6.63 \times 10^{-34}}\) = 5.164 × 10¹⁴ Hz

(ii) V_Oe = 0.6 × 1.6 × 10^-19 = 0.96 × 10^-19 J
\(\frac{h c}{\lambda}\) – Φ = V_Oe ∴ \(\frac{h c}{\lambda}\) = Φ + V_Oe
∴ λ = \(\frac{h c}{\phi+V_{\mathrm{O}} e}\)

This is the required wavelength of the incident light.

Question 19.
The threshold wavelength for photoemission from silver is 3800 Å. Calculate the maximum kinetic energy in eV of photoelectrons emitted when ultraviolet radiation of wavelength 2600 Å falls on it. Also calculate the corresponding stop-ping potential. [1 eV = 1.6 × 10^-19 J]
Solution:
Data : λ₀ = 3800 A = 3.8 × 10^-7 m,
λ = 2600 Å = 2.6 × 10^-7 m, c = 3 × 10⁸ m/s, h = 6.63 × 10^-34 J∙s, 1 eV = 1.6 × 10^-19 J
(i) According to Einstein’s photoelectric equation, the maximum kinetic energy of photoelectrons emitted,

Question 20.
When a surface is irradiated with light of wavelength 4950 Å, a photocurrent appears. The current vanishes if a retarding potential greater than 0.6 V is applied across the phototube. When a different source of light is used, it is found that the critical retarding potential is 1.1 V. Find the work function of the emitting surface and the wavelength of light from the second source.
Solution :
Data : λ₁ = 4.95 × 10^-7 m, V_O1 = 0.6 V, V_O2 = 1.1 V, h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s, e = 1.6 × 10^-19 C

∴ The wavelength of light from the second source,

Question 21.
The work function for the surface of aluminium is 4.2 eV. What potential difference will be required to stop the most energetic electrons emitted by light of wavelength 2000 Å? What should be the wavelength of the incident light for which the stopping potential is zero?
Solution:
Data: Φ = 4.2eV, λ₁ = 2 × 10^-7 m,V_O2 = 0,
h = 6.63 × 10^-34 J∙s, c = 3 × 10⁸ m/s, e = 1.6 × 10^-19 C

Question 22.
Radiation of wavelength 3000 Å falls on a metal surface having work function 2.3 eV. Calculate the maximum speed of ejected electrons.
Solution:
Data : λ = 3000 Å = 3 × 10^-7 m, h = 6.63 × 10^-34 J∙s, Φ = 2.3 eV = 2.3 × 1.6 × 10^-19 J, c = 3 × 10⁸ m/s, m = 9.1 × 10^-31 kg

Question 23.
If the total energy of radiation of frequency 10¹⁴ Hz is 6.63 J, calculate the number of photons in the radiation. [Planck’s constant = 6.63 × 10^-34 J∙s]
Solution:
Data: v = 10¹⁴ Hz, h = 6.63 × 10^-34 J∙s
The energy of a photon in a radiation of frequency v is hv.
∴ E = nhv,
so that the number of photons in the radiation is
n = \(\frac{E}{h v}\)
= \(\frac{6.63}{\left(6.63 \times 10^{-34}\right)\left(10^{14}\right)}\) = 10²⁰

Question 31.
Explain wave-particle duality of electromagnetic radiation.
Answer:
A particle is an object with a definite position in space at a given instant and having mass (or momentum), while a wave is a periodically repeated pattern in space and time, generally described by its velocity of propagation, wavelength and amplitude. It is a characteristic of a wave that it is not localized, i.e., it is spread over a region. Thus, these two concepts are contradictory and classical physics treats particles and waves as separate.

Under suitable circumstances, light and all other types of electromagnetic radiation exhibit typical ‘ wave phenomena like polarization, interference and diffraction. On the other hand, radiation exhibits a particle-like nature when it interacts with matter, as in the photoelectric effect and the Compton effect (scattering of X-rays by electrons in matter). It is emitted or absorbed only in terms of quanta of energy. This is the concept of photon : a particle with energy E = hv, where v is the frequency of the radiation and Planck’s constant h connects v and E, respectively the wave and particle aspects.

We see, therefore, that radiation exhibits a dual character. The synthesis of these two contradictory descriptions is called wave-particle duality of electromagnetic radiation.
[Notes : (1) Arthur Holly Compton (1892-1962), US physicist, discovered the effect, now known as the Compton effect, in 1923. (2) Planck’s constant h is also called the elementary quantum of action. Like e and c, it is one of the fundamental constants of nature.]

Question 32.
What is Compton effect? State the formula for the Compton shift and obtain its maximum value.
Answer:
When a high energy X-ray photon or γ-ray photon is scattered by an electron that is (almost) free, the photon loses energy and the electron gains energy shown in figure. This effect was discovered by A.H. Compton in 1923. It is now known as the Compton effect. This effect exhibits particle nature of electro-magnetic radiation.

If X is the wavelength of the incident photon, λ is the wavelength of the scattered photon, θ is the angle through which the photon is scattered, m₀ is the rest mass of an electron, c is the speed of light in free space and h is Plank’s constant, then, the wavelength shift, called the Compton shift is given by

[Note : In a collision between a low energy photon and a high energy electron, scattering results in loss in the energy of the electron and gain in the energy of the photon. This effect is known as the inverse Compton effect.]

Question 33.
What is the implication of Einstein’s interpretation of the photoelectric effect?
OR
What is the significance of the photoelectric effect?
Answer:
The phenomena of interference and polarization exhibit the wave nature of light, and James Clerk Maxwell (1831 – 79), British physicist, had established by 1865 that light is, and propagates as, an electromagnetic wave.

In his interpretation of the photoelectric effect in 1905, Einstein proposed that electromagnetic radiation behaves as a series of small packets or quanta of energy, later called photons. If the frequency of radiation is v, each photon has energy hv and momentum hv/c, where c is the speed of light in free space. Einstein’s photoelectric equation was verified experimentally by Robert Andrews Millikan (1868-1953), US physicist, in 1916.

A very strong additional evidence in support of the quantum theory of radiation was the discovery (in 1923) and explanation of the inelastic scattering of X-rays or γ-rays by electrons in matter by Arthur Holly Compton (1892-1962), US physicist. This inelastic scattering in which a photon transfers part of its energy to an electron is known as the Compton effect. It is similar to the Raman effect. The Compton effect shows particle nature of electro-magnetic radiation.

Since energy and momentum are considered in classical physics as characteristic properties of particles, the photoelectric effect and Compton effect exhibit the particle nature of radiation. But, to describe the photon energy, the quantum theory needs the frequency of the radiation, which is necessarily an attribute associated with a wave in classical physics. Thus, radiation exhibits the dual, seemingly contradictory, characters of particle and wave. In an experiment, we need to use only one of the descriptions, not both at the same time.

[Note : The momentum p and energy £ of a photon are related by the equation, p = E/c, where c is the speed of light in free space.]

Question 34.
Give a brief summary of the quantum theory of radiation.
OR
What is the photon picture of electromagnetic radiation?
Answer:
Quantum theory of radiation (The photon picture of electromagnetic radiation) :
(1) In its interaction with matter, electromagnetic radiation behaves as particles or quanta of energy. A quantum of energy is called a photon.

(2) If the frequency of radiation is v, irrespective of the intensity of radiation, each photon has energy hv and momentum hv/c, where c is the speed of light in free space.

(3) Intensity of radiation corresponds to the number of photons incident per unit time per unit surface area.

(4) Photons are electrically neutral and have zero rest mass.

(5) A photonRarticle collision (such as a photon-electron collision) obeys (he principles of conservation of energy arid momentum. However, in such a collision, an incident photon may be absorbed and/or a new photon may be created, so that the number of photons may not be conserved. For example, a γ-ray photon of energy greater than 1.02 MeV can produce an electron-positron pair in the presence of a heavy nucleus such as lead. In this case, the photon disappears and two particles (electron and positron) are produced. The total energy and momentum are conserved.

[Note: Photons have unit spin. Photons are influenced by gravitational field. A gravitational field can change the path and/or frequency/wavelength of a photon. Even after more than a century of its introduction, the concept of photon is not fully understood.]

Question 35.
What is the momentum of a photon of energy 3 × 10^-19 J? [c = 3 × 10⁸ m/s]
Answer:
Momentum of a photon = \(\frac{E}{c}=\frac{3 \times 10^{-19}}{3 \times 10^{8}}\)
= 10^-27 kg∙m/s .

Question 36.
What is the momentum of a photon of wave length 3.315 × 10^-7 m? [h = 6.63 × 10^-34J∙s]
Answer:
Momentum of a photon \(\frac{h}{\lambda}=\frac{6.63 \times 10^{-34}}{3.315 \times 10^{-7}}\)
= 2 × 10^-27 kg∙m/s .

37. Solve the following :

Question 1.
Find the momentum of a photon if the wavelength of the radiation is 6630 Å.
Solution:
Data : λ = 6.63 × 10^-7 m, h = 6.63 × 10^-34 J∙s
Energy of a photon, E = hv
c = λv
The momentum of a photon,

Question 2.
Find the momentum of a photon of energy 3 eV.
Solution :
Data : e = 1.602 × 10^-19 C,
E = 3 eV = 3 × 1.6 × 10^-19 J, c = 3 × 10⁸ m/s
The momentum of the photon,
p = \(\frac{E}{c}=\frac{3 \times 1.6 \times 10^{-19}}{3 \times 10^{8}}\) = 1.6 × 10^-27 kg∙m/s

Question 3.
Find the energy of a photon with momentum 2 × 10^-27 kg∙m/s.
Solution :
Data : p = 2 × 10^-27 kg∙m/s
The energy of the photon,
E = pc = (2 × 10^-27)(3 × 10⁸) = 6 × 10^-19 J
= \(\frac{6 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 3.75 eV

Question 38.
What is a photocell or photoelectric cell?
Describe its construction and working with a neat labelled diagram.
Answer:
A photocell or photoelectric cell is a device in which light energy is converted into electrical energy by photoelectric effect.

Construction : One form of the photoelectric cell shown in figure consists of a highly evacuated or gas-filled glass tube, an emitter (cathode) and a collector (anode). The light enters through a quartz window W and falls on the semicylindrical cathode C coated with a photosensitive metal. The anode is in the form of a straight wire of platinum or nickel, coaxial with the cathode.

If the cell is required to respond to the visible part of the spectrum, the cathode is coated with potassium or rubidium and the quartz window is replaced by glass. If the UV radiation only is to be used, cadmium is used as the sensitive surface. The cell is either highly evacuated (for accurate photometry) or filled with an inert gas at low pressure (if a larger current is desired).

Working : A photocell is connected in series with a battery and a variable resistance. The collector is kept at a positive potential with respect to the emitter. When UV radiation or visible light of frequency greater than the threshold frequency for the emitter surface is incident on the emitter, the ejected photoelectrons are focused by the cylindrical emitter (cathode) towards the collector (anode).

The photoelectrons collected by the collector constitute a photocurrent which may be measured by a microammeter in series with the photocell, as in an exposure meter or lux meter. Otherwise, the photocurrent is used to operate a relay circuit as in an alarm, or to drive the coils of a speaker as in reading an optical sound track in a cine film. The photocurrent becomes zero when the incident light is cut off.

Question 39.
State any four applications of a photoelectric cell.
OR
Explain any two applications of photoelectric effect.
Answer:
Applications of a photoelectric cell :
(1) In an exposure meter used for photography: A photographic film must be exposed to correct amount of light which, for a given film speed and lens aperture, depends on the exposure time. An exposure meter consists of a photocell, battery and microammeter connected in series. When the meter is directed towards an object, light reflected by the object enters the photocell and the photocurrent is directly proportional to the intensity of this light.
Usually, the microammeter scale is calibrated to read the exposure time directly.

(2) As a lux meter : A lux meter is used to measure the illumination and is similar in working to an exposure meter, except that the scale is calibrated to read the illumination in lux.

(3) In a burglar alarm as a ‘normally closed’ light- activated switch : It consists of a photocell, battery, relay system and a small directed light source. The radiation from the source falls on the photocell. If the light beam is interrupted by an intruder, the photoelectric current stops. This activates the relay system which sets off an alarm.

(4) In an optical reader of sound track in a cine film : The sound track of a cine film is recorded on one side of the positive film that is run in a cinema hall. The track consists of a dark wavy patch modulated by the recorded sound. Light from the projector lamp also passes through the sound track and falls on a photocell behind. The photocurrent is proportional to the transmitted light intensity and changes according to the recorded sound wave. The photocurrent is amplified and is used to drive the loudspeaker.

(5) A photocell can be used to switch on or off street lights.

Question 40.
Name any two instruments in which photo-electric effect is used.
Answer:
Exposure meter used in photography and lux meter.

Question 41.
State the de Broglie hypothesis and the de Broglie equation.
Answer:
De Broglie hypothesis : Louis de Broglie (1892-1987), French physicist, proposed (in 1924) that the wave-particle duality may not be unique to light but a universal characteristic of nature, so that a particle of matter in motion also has a wave or periodicity associated with it which becomes evident when the magnitude of Planck’s constant h cannot be ignored.

De Broglie equation : A particle of mass m moving with a speed v should under suitable experimental conditions exhibit the characteristics of a wave of wavelength
λ = \(\frac{h}{m v}=\frac{h}{p}\)
where p = mv = momentum of the particle.
The relation λ = h/p is called the de Broglie equation, and the wavelength λ associated with a particle momentum is called its de Broglie wavelength. The corresponding waves are termed as matter waves or de Broglie waves or Schrodinger waves.

[Note: This hypothesis was revolutionary at that time and accepted by others because Einstein supported it. Erwin Schrodinger (1887-1961), Austrian physicist, formulated a wave equation for matter waves.]

Question 42.
Explain the concept of de Broglie waves or matter waves.
Answer:
According to de Broglie, a particle of mass m moving with a speed v should, under suitable experimental conditions, exhibit the characteristics of a wave of wavelength
λ = \(\frac{h}{m v}=\frac{h}{p}\) … ………. (1)
where p = mv ≡ momentum of the particle and h is Planck’s constant.

This dual character of matter contained in Eq. (1) is usually referred to as the wave nature of matter or matter waves. They are a set of waves that represent the behaviour of particles under appropriate conditions. It does not, however, mean that the particles themselves are oscillating in space.

Interpretation of matter waves by Max Born (1882-1970), German bom British physicist, is that they are waves of probability, since the square of their amplitude at a given point is linked to the likelihood of finding the particle there. Hence, the wavelength λ may be regarded as a measure of the degree to which the energy is localized. If λ is exceedingly small, the energy is very localized and the particle character of the object is dominant. On the other hand, if λ is very large, the energy is distributed over a large volume; under these circumstances, the wave behaviour is dominant.

The wave nature of material particles such as the electron, neutron and helium atom has been established experimentally beyond doubt.

Question 43.
Derive an expression for the de Broglie wavelength associated with an electron accelerated from rest through a potential difference V. Consider the nonrelativistic case.
Answer:
Consider an electron accelerated from rest through a potential difference V. Let v be the final speed of the electron. We consider the nonrelativistic case, v << c, where c is the speed of light in free space. The kinetic energy acquired by the electron is
\(\frac{1}{2}\) mv² = \(\frac{1}{2m}\) (mv)² = eV ………. (1)
where e and m are the electronic charge and mass (nonrelativistic).

Therefore, the electron momentum,
p = mv = \(\sqrt{2 m e V}\) ………… (2)
The de Broglie wavelength associated with the electron is
λ = \(\frac{h}{p}\) ………….. (3)
where h is Planck’s constant.
From Eqs. (2) and (3),
λ = \(\frac{h}{\sqrt{2 m e V}}\)
Equation (4) gives the required expression.
[Note : Substituting the values of h = 6.63 × 10^-34 J-s, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C in Eq. (4), we obtain λ = \(\sqrt{150 / V}\) × 10^-10 m = \(\sqrt{150 / V}\) Å = \(12.25 / \sqrt{V}\) Å, where V is in volt. Therefore, electrons accelerated from rest through 150 volts have a de Broglie wavelength of 1 Å. This corresponds to the X-ray region of the electromagnetic spectrum.]

Question 44.
Derive an expression for the de Broglie wavelength.
Answer:
For the particle-like aspects of electromagnetic radiation, we consider radiation to consist of particles whose motion is governed by the wave propagation properties of certain associated waves.

To determine the wavelength of such waves, consider a beam of electromagnetic radiation of frequency v whose quanta have energy E.
E = hv
where h is the Planck constant.
For a quantum of radiation of momentum p, by Einstein’s theory,
E = pc
where c is the speed of propagation of the radiation in free space.
∴ pc = hv
∴ p\(\frac{c}{v}\) = h
The wavelength X of the associated wave governing the motion of the quanta is given by the relation
λ = c/v.
∴ pλ = h ∴ λ = \(\frac{h}{p}\)
V ’
This is the required expression.

Question 45.
What is the de Broglie wavelength associated with a particle having momentum 10^-26 kg∙m/s? [h = 6.63 × 10^-34 J∙s]
Answer:
The de Broglie wavelength associated with the particle,
λ = \(\frac{h}{p}=\frac{6.63 \times 10^{-34}}{10^{-26}}\) = 6.63 × 10^-8 m

Question 46.
With a neat labelled diagram, describe the Davisson and Germer experiment in support of the concept of matter waves.
Answer:
Davisson and Germer experiment (1927) :
The experimental arrangement, as shown in below figure, consists of an electron gun, a crystal holder and an electron detector enclosed in a vacuum chamber. In the electron gun, electrons emitted by a heated metallic filament (cathode) are accelerated by a potential difference V between the cathode and the anode, and emerge through a small hole in the anode. The electron gun directs a narrow collimated beam of electrons at a nickel crystal. Scattered electrons are detected by a movable detector.

The angle Φ between the incident and scattered beams is the scattering angle. Polar graphs of the number of scattered electrons as a function of angle Φ are plotted for different values of the accelerating voltage.

It is found that the electrons are scattered at a certain angle more than at others. Also, the number of scattered electrons in this direction is maximum for a certain kinetic energy of the incident electrons.

The detector registered a maximum at a scattering angle Φ = 50° for V = 54 V from figure. This electron diffraction can be understood only on the basis of de Broglie’s matter wave model. The de Broglie wavelength of the electrons accelerated from rest through a p.d. of 54 V is λ = \(\sqrt{150 / 54}\) Å = 1.67 Å
The wavelength calculated from the diffraction effect is 1.65 Å, nearly 1.67 Å.
[ Note : Clinton Joseph Davisson (1881 -1958), US physicist. Lester Halbert Germer (1896-1971), US physicist.]

47. Solve the following

Question 1.
(2) Find the momentum of the electron having de Brogue wavelength of 0.5 Å.
Solution:
Data: λ = 0.5Å = 5 × 10^-11 m, h = 6.63 × 10^-34 J∙s
The momentum of the electron, .
p = \(\frac{h}{\lambda}=\frac{6.63 \times 10^{-34}}{5 \times 10^{-11}}\) = 1.326 × 10^-23 kg∙m/s

Question 2.
A cracker of mass M at rest explodes in two parts of masses m₁ and m₂ with non-zero velocities. Find the ratio of the de Broglie wavelengths of the two particles.
Solution:
The cracker has zero momentum before explosion. By the principle of conservation of momentum, after the explosion,

Question 3.
Calculate the de Brogue wavelength of a proton if it is moving with the speed of 2 × 10⁵ m/s. [m^p = 1.673 × 10^-27 kg]
Solution:
Data: m^p = 1673 × 10^-27 kg, v = 2 × 10⁵ m/s, h = 6.63 × 10^-34 J∙s
De Brogue wavelength, λ = \(\frac{h}{p}=\frac{h}{m v}\)
∴ λ = \(\frac{6.63 \times 10^{-34}}{\left(1.673 \times 10^{-27}\right)\left(2 \times 10^{5}\right)}\)
= 1.981 × 10^-12 m

Question 4.
Calculate the de Brogue wavelength of an electron moving with \(\frac{1}{300}\) of the speed of light in vacuum. [Take m (electron) = 9.11 × 10^-28 g]
Solution:

Question 5.
Find the de Broglie wavelength of a dust particle of radius 1 μm and density 2.5 g/cm³ drifting at 2.2 m/s. (Take π = 3.14)
Solution:
Data : r = 1 μm = 10^-6 m, h = 6.63 × 10^-34 J∙s, ρ = 2.5 g/cm³ = 2.5 × 10³ kg/m³, v = 2.2 m/s,

Question 6.
Find the de Broglie wavelength associated with a car (mass = 1000 kg) moving at 20 m/s.
Solution:
Data : m = 1000 kg, v = 20 m/s,h = 6.63 × 10^-34 J∙s
The de Broglie wavelength,
λ = \(\frac{h}{p}=\frac{h}{m v}=\frac{6.63 \times 10^{-34}}{(1000)(20)}\) = 3.315 × 10^-38 m

Question 7.
What is the de Broglie wavelength of an electron accelerated from rest through 25000 volts ?
Solution:
Data: V = 25 × 10³ V, e = 1.6 × 10^-19 C, m_e = 9.11 × 10^-31 kg, h = 6.63 × 10^-34 J∙s
Kinetic energy of the electron,
E = eV
=(1.6 × 10^-19)(25 × 10³ V)
=4 × 10^-15 j
The momentum of the electron,

I Note : Here, the kinetic energy of the electron, 25 keV, is far less than the electron’s rest mass energy (m0c²) which is about 0.51 MeV. Hence, it is a nonrelativistic case.]

Question 8.
Find the de Broglie wavelength of a proton accelerated from rest by a potential difference of 50 V. [m_p = 1.673 × 10^-27 kg]
Solution:
Data : m_p = 1.673 × 10^-27 kg, h = 6.63 × 10^-34 J∙s, KE = 50 eV = 50 × 1.6 × 10^-19 J = 8 × 10^-18 J
The kinetic energy of the proton,

= 4.053 × 10^-12 m = 0.04053 A

Question 9.
A moving electron and a photon have the same de Brogue wavelength. Show that the electron possesses more energy than that carried by the photon.
Solution:
The de Brogue wavelength, λ = \(\frac{h}{p}\)
If an electron and a photon have the same de Brogue wavelength, they must have the same momentum, p.
For the photon, E_p = hv = \(\frac{h c}{\lambda}=\left(\frac{h}{\lambda}\right) c\) = pc … (1)
For the electron, mass m = \(\frac{m_{0}}{\sqrt{1-v^{2} / c^{2}}}\)
where m₀ is the rest mass of the electron and y is its speed.
∴ \(m^{2}\left(\frac{c^{2}-v^{2}}{c^{2}}\right)=m_{0}^{2}\)
∴ m²c⁴ – m²v²c² = \(m_{0}^{2} c^{4}\)
∴ (m²c⁴ = (m₀c²)² + p²c² (where p = mv)
∴ \(E_{\mathrm{e}}^{2}\) = (m₀c²)² + p²c²
where E_e = mc² = m₀c² + K is the total energy of the electron, m₀c² being he rest mass energy and K, the kinetic energy.
∴ E_e = \(\sqrt{\left(m_{0} c^{2}\right)^{2}+p^{2} c^{2}}\) …………. (2)
From Eqs. (1) and (2), we have E_e > E_p.
[Note : The result m = \(\frac{m_{0}}{\sqrt{1-v^{2} / c^{2}}}\) was obtained by Einstein in 1905.]

Multiple Choice Questions

Question 1.
The energy of a photon of wavelength λ is

Answer:
(D) \(\frac{h c}{\lambda}\)

Question 2.
The number of photoelectrons emitted
(A) varies inversely with the frequency of radiation
(B) varies directly with the frequency of radiation
(C) varies inversely with the intensity of radiation
(D) varies directly with the intensity of radiation.
Answer:
(D) varies directly with the intensity of radiation.

Question 3.
A metal emits no electrons if the incident light energy falls below certain threshold. For photo-emission, you would decrease
(A) the intensity of light
(B) the frequency of light
(C) the wavelength of light
(D) the collector potential.
Answer:
(C) the wavelength of light

Question 4.
When light of wavelength 5000 Å falls on a metal surface whose photoelectric work function is 1.9 eV, the kinetic energy of the most energetic photoelectrons is
(A) 0.59 eV
(B) 1.39 eV
(C)1.59eV
(D)2.59eV.
Answer:
(A) 0.59 eV

Question 5.
The threshold wavelengths for photoemission of two metals A and B are 300 nm and 600 nm, respectively. The ratio Φ_A/Φ_B of their photoelectric work functions is
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) 4.
Answer:
(C) 2

Question 6.
The photoelectric threshold wavelength of a certain metal is 3315 Å. Its work function is
(A) 6 × 10^-19 J
(B) 7.286 × 10^-19 J
(C) 9 × 10^-19 J
(D) 9.945 × 10^-19 J.
Answer:
(A) 6 × 10^-19 J

Question 7.
The photoelectric work function of a certain metal is 2.5 eV. If the metal is separately irradiated with photons of energy 3 eV and 4.5 eV, the ratio of the respective stopping potentials is
(A) 1
(B) \(\frac{2}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{1}{5}\)
Answer:
(B) \(\frac{2}{3}\)

Question 8.
Sodium and copper have photoelectric work functions 2.3 eV and 4.7 eV, respectively. The ratio λ_0Na/λ_oCu 0f the threshold wavelengths for photoemission is about
(A) 1 : 4
(B) 1 : 2
(C) 2 : 1
(D) 4 : 1.
Answer:
(C) 2 : 1

Question 9.
When light of wavelength A falls on the cathode of a photocell, the kinetic energy of the most energetic photoelectrons emitted is £. If light of wavelength λ/2 is used, what can be said about the new value E’?
(A) E’ = E/2
(B) E’ = E
(C) E’ = 2E
(D) E’ > 2E.
Answer:
(D) E’ > 2E.

Question 10.
Electrons are ejected from a metallic surface when light with a wavelength of 6250 Å is used. If light of wavelength 4500 Å is used instead,
(A) there may not be any photoemission
(B) the photoelectric current will increase
(C) the stopping potential will increase
(D) the stopping potential will decrease.
Answer:
(C) the stopping potential will increase

Question 11.
UV radiation of energy 6.2 eV falls on molybdenum surface whose photoelectric work function is 4.2 eV. The kinetic energy of the fastest photoelectrons is
(A) 3.2 × 10^-19 J
(B) 3.52 × 10^-19 J
(C) 6.72 × 10^-19 J
(D) 9.92 × 10^-19 J.
Answer:
(A) 3.2 × 10^-19 J

Question 12.
In a photocell, increasing the intensity of light increases
(A) the stopping potential
(B) the photoelectric current
(C) the energy of the incident photons
(D) the maximum kinetic energy of the photo-electrons.
Answer:
(B) the photoelectric current

Question 13.
In a photocell, doubling the intensity of the incident light (v > v₀) doubles the
(A) stopping potential
(B) threshold frequency
(C) saturation current
(D) threshold wavelength.
Answer:
(C) saturation current

Question 14.
In the usual notation, the momentum of a photon is
(A) hvc
(B) \(\frac{h v}{c}\)
(C) \(\frac{h \lambda}{c}\)
(D) hλc.
Answer:
(B) \(\frac{h v}{c}\)

Question 15.
The momentum of a photon with λ = 3315 Å is
(A) 2 × 10^-27 kg∙m/s
(B) 5 × 10^-27 kg∙m/s
(C) 2 × 10^-41 kg∙m/s
(D) 5 × 10^-41 kg∙m/s.
Answer:
(A) 2 × 10^-27 kg∙m/s

Question 16.
Let p and E denote the linear momentum and energy of emitted photon, respectively. If the wavelength of incident radiation is increased,
(A) both p and E decrease
(B) p increases and E decreases
(C) p decreases and E increases
(D) both p and E decrease.
Answer:
(C) p decreases and E increases

Question 17.
When radiations of wavelength λ₁ and λ₂ are incident on a certain photosensitive material, the energies of electron ejected are E₁ and E₂ respectively, such that E₁ > E₂. Then, Planck’s constant h is [c = speed of light]

Answer:
(C) \(\frac{\left(E_{1}-E_{2}\right) \lambda_{1} \cdot \lambda_{2}}{c\left(\lambda_{2}-\lambda_{1}\right)}\)

Question 18.
If the frequency of incident light falling on a photosensitive material is doubled, then the kinetic energy of the emitted photoelectron will be
(A) the same as its initial value
(B) two times its initial value
(C) more than two times its initial value
(D) less than two times its initial value.
Answer:
(C) more than two times its initial value

Question 19.
The kinetic energy of emitted photoelectrons is independent of
(A) the frequency of incident radiation
(B) the intensity of incident radiation
(C) the wavelength of incident radiation
(D) the collector plate potential.
Answer:
(B) the intensity of incident radiation

Question 20.
In a photon-electron collision
(A) only total energy is conserved
(B) only total momentum is conserved
(C) both total energy and total momentum are conserved
(D) both total momentum and total energy are not conserved.
Answer:
(C) both total energy and total momentum are conserved

Question 21.
The de Broglie equation for the wavelength of matter waves is

Answer:
(A) λ = \(\frac{h}{p}\)

Question 22.
The momentum associated with a photon is given by
(A) hv
(B) \(\frac{h v}{c}\)
(C) hE
(D) hλ
Answer:
(B) \(\frac{h v}{c}\)

Question 23.
The momentum of a photon of de Broglie wave-length 5000 Å is [h = 6.63 × 10^-34 J∙s]
(A) 1.326 × 10^-28 kg∙m/s
(B) 7.54 × 10^-28 kg∙m/s
(C) 1.326 × 10^-27 kg∙m/s
(D) 7.54 × 10^-27 kg∙m/s.
Answer:
(C) 1.326 × 10^-27 kg∙m/s

Question 24.
The de Broglie wavelength of a 100-m sprinter of mass 66 kg running at a speed of 10 m/s is about
[h = 6.63 × 10^-34 J∙s]
(A) 10^-34 m
(B) 10^-33 m
(C) 10^-32 m
(D) 10^-31 m.
Answer:
(C) 10^-32 m

Question 25.
Which of the following particles moving with the same speed has the longest de Broglie wavelength?
(A) Proton
(B) Neutron
(C) α-particle
(D) β-particle
Answer:
(D) β-particle

Question 26.
If p and E are respectively the momentum and energy of a photon, the speed of the photon is given by
(A) p∙E
(B) E/p
(C) (E/p)²
(D) \(\sqrt{E / p}\)
Answer:
(B) E/p

Question 27.
If the kinetic energy of a free electron is doubled, its de Broglie wavelength
(A) decreases by a factor of 2
(B) increases by a factor of 2
(C) decreases by a factor of \(\sqrt {2}\)
(D) increases by a factor of \(\sqrt {2}\).
Answer:
(C) decreases by a factor of \(\sqrt {2}\)

Question 28.
The de Broglie wavelength of an a-particle accelerated from rest through a potential difference V is λ. In order to have the same de Broglie wavelength, a proton must be accelerated from rest through a potential difference of .
(A) V
(B) 2V
(C) 4V
(D) 8V.
Answer:
(D) 8V.

Question 29.
If a photon has the same wavelength as the de Broglie wavelength of an electron, they have the same
(A) velocity
(B) energy
(C) momentum
(D) angular momentum.
Answer:
(C) momentum

Question 35.
The de Broglie wavelength of a grain of sand, of mass 1 mg, blown by a wind at the speed of 20 m/s is [h = 6.63 × 10^-34 J∙s]
(A) 33.15 × 10^-36m
(B) 33.15 × 10^-33 m
(C) 33.15 × 10^-30 m
(D) 33.15 × 10^-30 m.
Answer:
(C) 33.15 × 10^-30 m