Prasanna

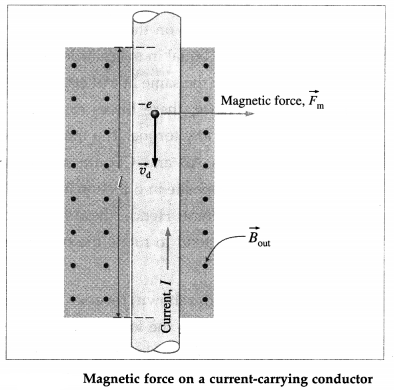
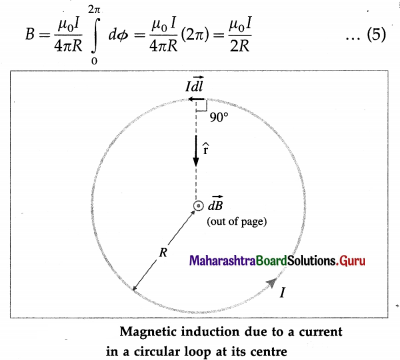
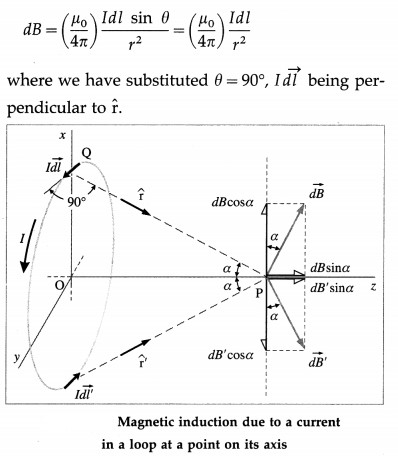
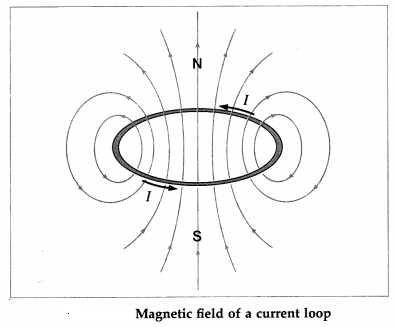
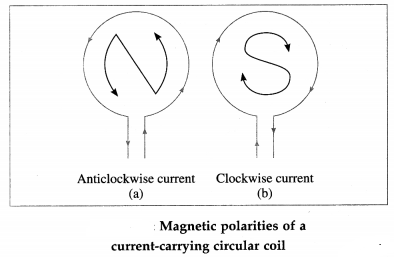
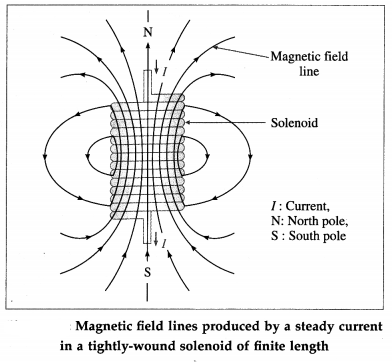
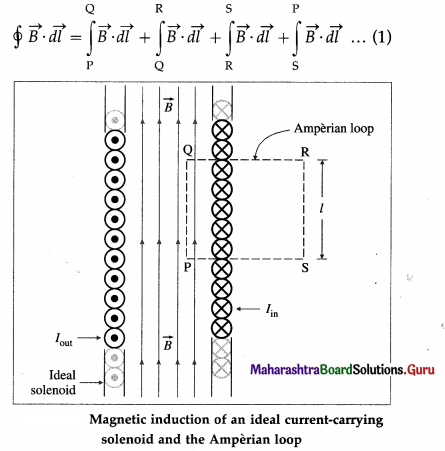
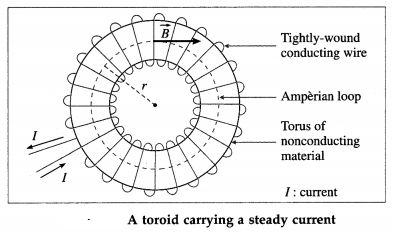
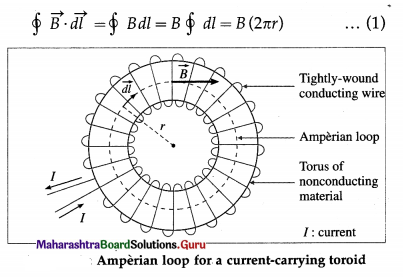
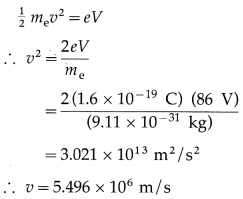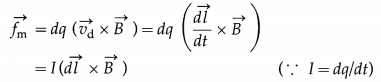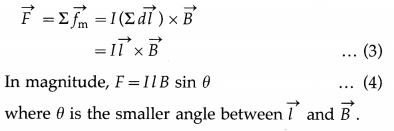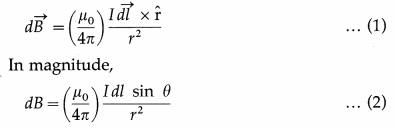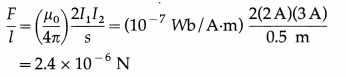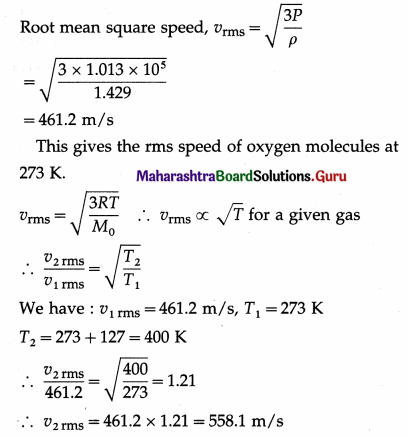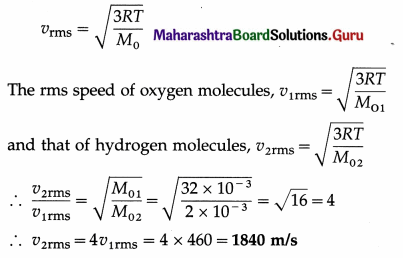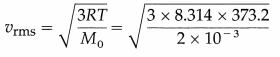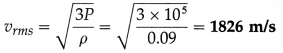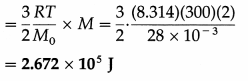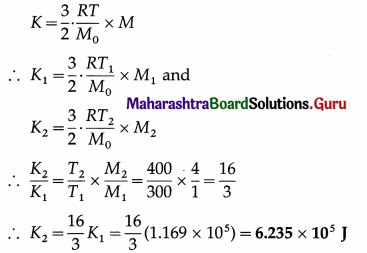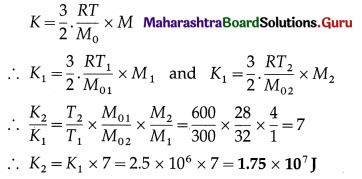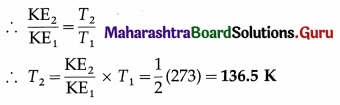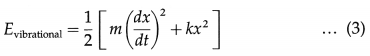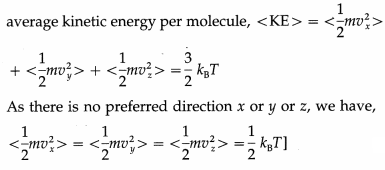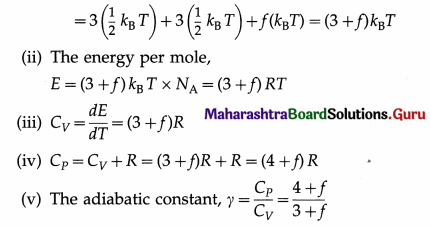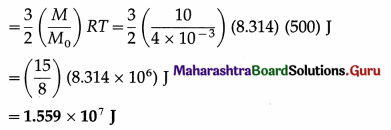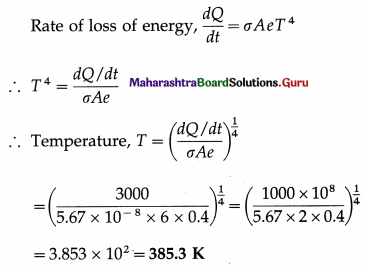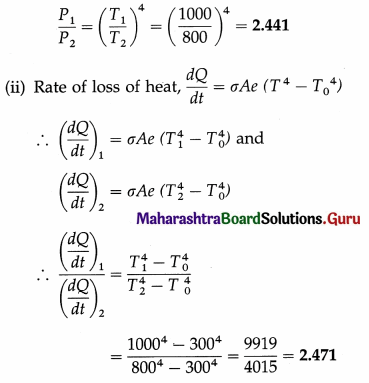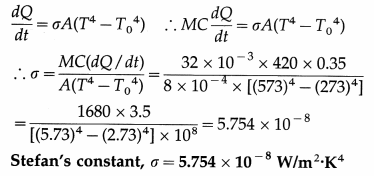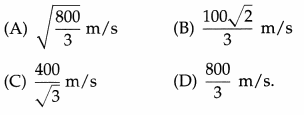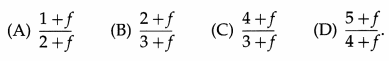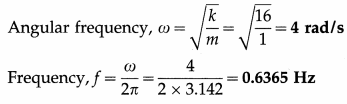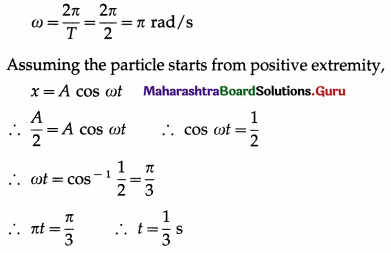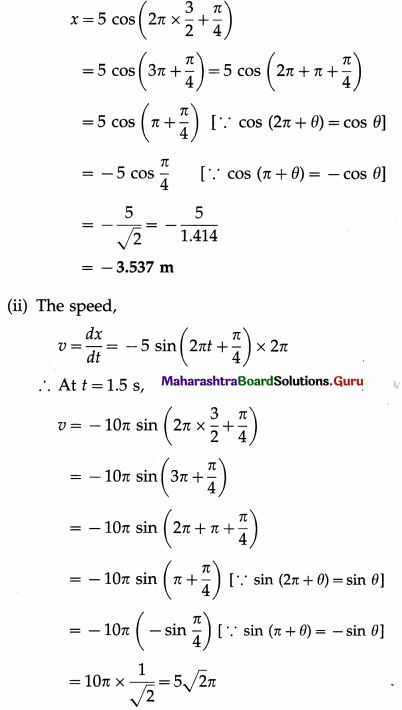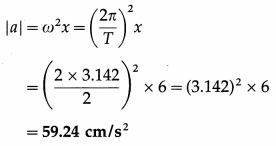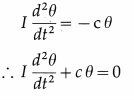Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 9 Current Electricity Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 9 Current Electricity

Question 1.
Define the following terms:

1. Electrical circuit
2. Junction
3. Loop
4. Branch
5. Electrical network.

Answer:

1. Electrical circuit: An electrical circuit, in general, consists of a number of electrical components such as an electrical cell, a plug key (or a switch), a resistor, a current meter (a milliammeter or an ammeter), a voltmeter, etc., connected together to form a conducting path.
2. Junction: A point in an electrical circuit where two or more conductors are joined together is called a junction.
3. Loop: A closed conducting path in an electrical network is called a loop or mesh.
4. Branch: A branch is any part of an electrical network that lies between two junctions.
5. Electrical network: An electrical network consists of a number of electrical components connected together to form a system of inter-related circuits.

Question 2.
State Kirchhoff’s first law or current law or junction law.
Answer:
The algebraic sum of the currents at a junction is zero in an electrical network, i.e. \(\sum_{i=1}^{n}\) I_i = 0, where I_i is
the current in the i^th conductor at a junction having n conductors.

Question 3.
What is the sign convention used for Kirchhoff’s first law? Explain with an example.
Answer:
A current arriving at a junction is considered positive while a current leaving a junction is considered negative.

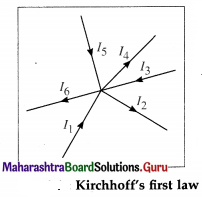
Consider a junction in a circuit where six current carrying conductors meet. Currents I₁, I₃ and I₅ are considered positive as they arrive at the junction.
Currents I₂, I₄ and I₆ are considered negative as they leave the junction.

Using Kirchhoff’s current law, \(\sum_{i=1}^{6}\) I_i = 0, we get,
I₁ – I₂ + I₃ – I₄ + I₅ – I₆ = 0
∴ I₁ + I₃ + I₅ = I₂ + I₄ + I₆
Thus the total current flowing towards the junction is equal to the total current flowing away from the junction.

[Note : As the current is the time rate of flow of charge, it follows that the net charge entering the junction in a given time equals the net charge leaving the junction in the same time. Thus, this law (current law/junction law) is based on the conservation of charge. ]

Question 4.
State Kirchhoff’s second law or voltage law or loop law.
Ans. The algebraic sum of the potential differences (products of current and resistance) and the electromotive forces (emf’s) in a closed loop is zero. Σ IR + Σ E = 0

Question 5.
What is the sign convention used for Kirchhoff’s second law ? Explain with an example.
Answer:
(1) While tracing a loop, if we traverse a resistor along the direction of conventional current, the potential difference across the resistor is considered negative. If we traverse the resistor opposite to the direction of conventional current, the potential difference across the resistor is considered positive.

(2) While tracing a loop within the source, if we travel from the negative terminal of the source (cell) to the positive terminal of the source (cell), the emf of the source (cell) is considered positive.

On the contrary, if we travel from the positive terminal of the source (cell) to the negative terminal of the source (cell), the emf of the source (cell) is considered negative.

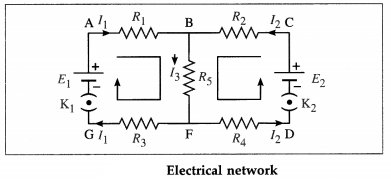
Consider the electrical network shown in above figure.
Tracing loop ABFGA in the clockwise direction, we get,
– I₁R₁ – I₃R₅ – I₁R₃ + E₁ = 0
∴ E₁ = I₁R₁ + I₃R₅ + I₁R₃
Tracing loop BFDCB in the anticlockwise direction, we get,
– I₃R₅ – I₂R₄ + E₂ – I₂R₂ = 0
∴ E₂ = I₂R₂ + I₃R₅ + I₂R₄

[Notes : (1) We may as well consider loop ABCDFGA and write the corresponding equation. (2) As the emf of a cell is the energy provided by the cell per unit charge in circulating the charge and the potential difference across a resistance is the work done per unit charge, it follows that this law (voltage law /loop law) is based on the conservation of energy.]

Question 6.
What is the basis of Kirchhoff’s current law and voltage law?
Answer:
Kirchhoff’s current law is consistent with the conservation of electric charge while the voltage law is consistent with the law of conservation of energy.

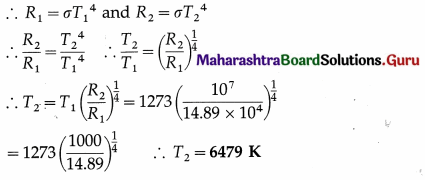
7. Solve the following

Question 1.
Determine the current flowing through the galvanometer shown in the figure below.

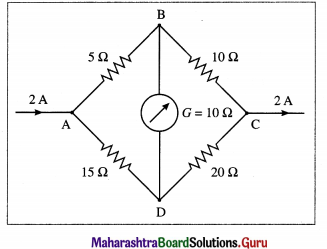
Solution:

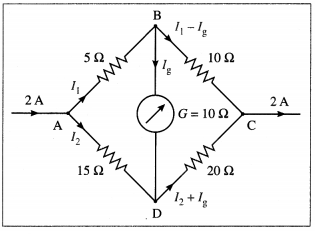
To find I_g we apply Kirchhoff’s voltage law.
Loop ABDA :
– 5I₁ – 10I_g + 15I₂ = 0
∴ – 5I₁ + 15I₂ = 10I_g
∴ -I₁ + 3I₂ = 2I_g ………….. (1)
Loop BCDB :
-10(I₁ – I_g) + 20 (I₂ + I_g) + 10I_g = 0
∴ – 10I₁ + 10I_g + 20I₂ + 20I_g + 10I_g = 0
∴ I₁ – 2I₂ = 4I_g …………. (2)
Adding Eqs. (1) and (2), we get, I₂ = 6 I_g …………. (3)
Substituting for Z2 from Eq. (3) in Eq. (2).
∴ I₁ = 12I_g + 4I_g = 16I_g
Now, I₁ + I₂ = 2 A by the data.
∴ 16I_g + 6I_g = 2A
∴ 22I_g = 2A
∴ I_g = \(\frac{2}{22}\) A = \(\frac{1}{11}\) A from B to D
This is the current flowing through the galvanometer.

Question 8.
State the factors on which the resistance Of a material depends.
Answer:
The resistance of a material depends upon tem-perature, strain, humidity, etc.

[Note : Depending upon the factors stated above, resistance may vary from near zero to thousands of megaohm.]

Question 9.
What are the applications of Wheatstone’s metre bridge?
Answer:

1. Wheatstone’s metre bridge is used for measuring the values of very low resistance precisely.
2. It can also be used to measure the quantities such as strain galvanometer, resistance, capacitance of a capacitor, inductance of an inductor, impedence of a combination of a resistor, capacitor and inductor and the internal resistance of a cell.

Question 10.
What is the balance point in Kelvin’s method to measure the resistance of a galvanometer?
Answer:
Kelvin’s method of determination of the galvanometer resistance is an equal deflection method. The balance point in Kelvin’s method is a point on the wire for which the bridge network is balanced and the galvanometer shows no change in deflection.

Question 11.
Why is Kelvin’s method to measure the resistance of a galvanometer called an equal deflection method?
Answer:
In Kelvin’s method of determination of the galvanometer resistance using a Wheatstone metre bridge, the galvanometer is connected in one gap of the bridge and a variable known resistance is connected in the other gap. The junction of the two gaps (say, B) is connected directly to a pencil jockey.

The jockey is tapped along the wire to locate the equipotential balance point D when the galvanometer shows no change in deflection.

Since the galvanometer shows the same deflection on making or breaking the contact between the jockey and the wire, the method is an equal deflection method.

12. Solve the following :

Question 1.
Four resistances 5 Ω, 10 Ω, 15 Ω and X (unknown) are connected in the cyclic order so as to form a Wheatstone network. Determine X if the network is balanced.
Solution:
Data : P = 5 Ω, Q = 10 Ω, R = 15 Ω

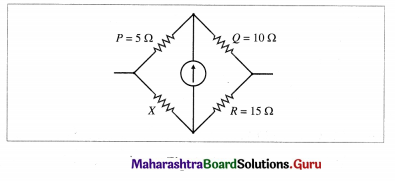
Since the network is balanced,
\(\frac{P}{Q}=\frac{X}{R}\)
∴ \(\frac{5}{10}=\frac{X}{15}\)
∴ X = 15 × \(\frac{5}{10}\) = 7.5 Ω

Question 2.
Resistances P = 10 Ω, Q = 15 Ω, S = 50 Ω and R = 25 Ω are connected in order in the arms AB, BC, CD and DA respectively of a Wheatstone network ABCD. A cell is connected between A and C. What resistance has to be connected in parallel to S to balance the network?
Solution:
Data : P = 10 Ω, Q = 15 Ω, S = 50 Ω and R = 25 Ω
Let x = resistance to be connected in parallel to S to balance the network. The resistance of the parallel combination of S and x is \(\frac{S x}{S+x}\) .
For the balanced network,

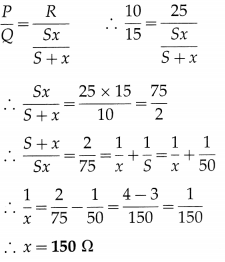
Question 3.
Four resistances 4 Ω, 8 Ω, X and 6 Ω are connected in the cyclic order so as to form Wheatstone’s network. If the network is balanced, find X.
Solution:
Data : P = 4Ω, Q = 8 Ω, R = X and S = 6 Ω
Since the network is balanced,
∴ \(\frac{P}{Q}=\frac{S}{R}\)
∴ X = 6\(\frac{8}{4}\) = 12 Ω

Question 4.
Four resistances 4 Ω, 4 Ω, 4 Ω and 12 Ω form a Wheatstone network. Find the resistance which connected across the 12 Ω resistance will balance the network.
Solution:
The resistance in each of the three arms of the network is 4 Ω. Hence, to balance the network, the resistance in the fourth arm must also be 4 Ω.

Hence, the resistance (R) to be connected across. i.e., in parallel to, the 12 Ω resistance should be such that their equivalent resistance is 4Ω.

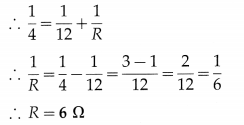
Question 5.
Four resistances 80 Ω, 40 Ω, 10 Ω and 15 Ω are connected to form Wheatstone’s network ABCD as shown in the following figure.

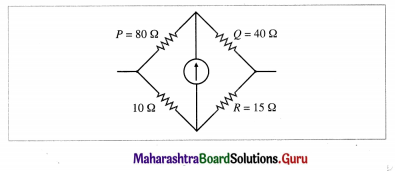
What resistance must be connected in the branch containing 10 Ω to balance the network?
Solution:
Data : P = 80 Ω, Q = 40 Ω, 10 Ω and R = 15 Ω are connected as shown in above figure.
When the network is balanced,
\(\frac{P}{Q}=\frac{S}{R}\)
∴ \(\frac{80}{40}=\frac{S}{15}\)
∴ S = 15 × 2 = 30 Ω
Let X be the resistance to be connected in series with 10 Ω, so as to obtain 30 Ω.
∴ X + 10 = 30
∴ X = 20 Ω

Question 6.
An unknown resistance is placed in the left gap and resistance of 50 ohms is placed in the right gap of a meter bridge. The null point is obtained at 40 cm from the left end. Determine the unknown resistance.
Solution:
Data : R =50 C in the right gap, l_X =40 cm
\(\)
Now, l_R = 100 – l_X = 100 – 40 = 60 cm
∴ \(\frac{X}{50}=\frac{40}{60}\)
∴ X = 50 × \(\frac{2}{3}\) = \(\frac{100}{3}\) = 33.33 Ω
This is the unknown resistance.

Question 7.
Two resistances X and Y in the two gaps of a metre bridge give a null point dividing the wire in the ratio 2 : 3. If each resistance is increased by 30 Ω, the new null point divides the wire in the ratio 5 : 6, calculate each resistance.
Solution:
From the data, we have in the first case,
\(\frac{X}{Y}=\frac{l_{X}}{l_{Y}}=\frac{2}{3}\)
∴ 3X = 2Y ……….. (1)
and in the second case, \(\frac{X+30}{Y+30}=\frac{l_{X+30}}{l_{Y+30}}=\frac{5}{6}\)
∴ 6X + 180 = 5Y + 150
∴ 6X – 5Y = -30
∴ 6X = 5Y – 30
∴ 2(3X) = 5Y – 30 …………. (2)
Substituting the value of 3X from Eq. (1) in Eq. (2),
we get,
2(2Y) = 5Y – 30
∴ Y = 30 Ω
∴ X = \(\frac{2}{3}\)Y = 20 Ω

Question 8.
In a metre bridge experiment, with a resistance R₁ in the left gap and a resistance X in the right gap, the null point is obtained at 40 cm from the left end of the wire. With a resistance R₂ in the left gap and the same resistance X in the right gap, the null point is obtained at 50 cm from the left end of the wire. Where will be the null point if R₁ and R₂ are connected first in series and then in parallel in the left gap, the right gap still containing X?
Solution:
From the data in the example, we have:
When R₁ is connected in the left gap and X in the right gap, l_R1 = 40 cm, and with R₂ in the left gap, l_R2 50 cm.
∴ In the first case,
l_X = 100 – l_R1 = 100 – 40 = 60cm

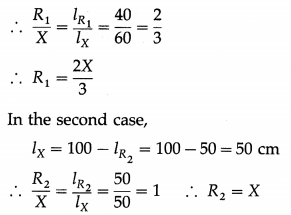
(i) When R₁ and R₂ are connected in series, the effective resistance is
R_S = R₁ + R₂ = \(\frac{2 X}{3}\) + X = \(\frac{5 X}{3}\)
Let the corresponding null point be at a distance l₁ from the left end of the wire.

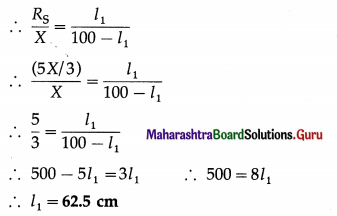
(ii) When R₁ and R₁ are connected in parallel, the effective resistance is
R_P = \(\frac{R_{1} R_{2}}{R_{1}+R_{2}}=\frac{\frac{2 X}{3} \times X}{\frac{2 X}{3}+X}=\frac{2 X}{5}\)
Let the corresponding null point be at a distance l₂ Erom the left end of the wire.

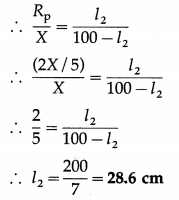
With the same resistance X in the right gap, the null points will be at 62.5 cm and 28.6 cm from the left end of the wire for the series and parallel combinations respectively of R₁ and R₂ in the left gap.

Question 9.
A uniform wire is cut into two pieces such that one piece is twice as long as the other. The two pieces are connected in parallel in the left gap of a metre bridge. When a resistance of 20 Ω is connected in the right gap, the null point is obtained at 60 cm from the right end of the bridge wire. Find the resistance of the wire before it was cut into two pieces.
Solution:
Let R_w be the resistance of the wire before it was cut into two pieces. Let L₁, L₂ and X₁, X₂ be the lengths and resistance of the two pieces.

∴ The original resistance of the wire is
R_w = X₁ + X₂ = 40 + 20 = 60 Ω

Question 10.
Two resistances, 20 Ω and 30 Ω, are connected across the two gaps of a metre bridge as shown in the following figure.

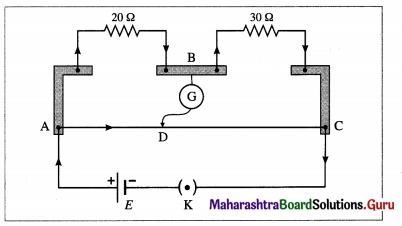
The bridge wire has diameter 0.5 mm and resistance 2 Ω. The emf of the cell is 2 V. Assume that the internal resistance of the cell is zero. Calculate (I) the resistivity (specific resistance) of the material of the bridge wire (ii) the current provided by the cell when the bridge is balanced.
Solution:
Data: R₁ = 20 Ω, R₂ = 30 Ω. I_g = 0, R (wire) = 2 Ω,
r (wire) = 0.25 mm = 2.5 x iO m (as the diameter of the wire is 0.5mm), l = 1 m, E = 2V

Question 11.
Two diametrically opposite points of a metal ring are connected to two tenninals of the left gap of a metre bridge. A resistance of 11 Ω is connected in the right gap. If the null point is obtained at 45 cm from the left end, find the resistance of the metal ring.
Solution:
Data: R = 11 Ω, L_X = 45 cm
∴ L_R = 100 – L_X = 100 – 45 = 55cm
Let \(\frac{X}{2}\) be the resistance of each half of the metal ring. Therefore the resistance in the left gap is the effective resistance of the parallel combination of \(\frac{X}{2}\) and \(\frac{X}{2}\)

The resistance of the metal ring is 36 Ω

Question 12.
In a metre bridge experiment, the resistances R and X are connected in the left and right gap, respectively, and the null point is obtained at 33.7 cm from the left end. When a resistance of 12 Ω is connected in parallel to X, the null point is obtained at 51.9 cm from the left end. Calculate R and X.
Solution:
(1) In the first case,
l_R = 33.7 cm, l_X = 100 – 33.7 = 66.3 cm
∴ \(\frac{X}{R}=\frac{l_{X}}{l_{R}}=\frac{66.3}{33.7}\) …………….. (1)

(2) In the second case,
l_R = 51.9 cm, l_X = 100 – 51.9 = 48.1 cm
X’ = X || 12 Ω = \(\frac{12 X}{12+X}\)
∴ \(\frac{X^{\prime}}{R}=\frac{48.1}{51.9}\) ……………. (2)
Dividing Eq. (1) by Eq. (2), we get,

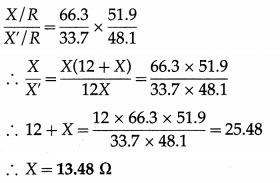
Then, from Eq. (1),
R = 13.48 × \(\frac{33.7}{66.3}\) = 6.852 Ω

Question 13.
What is the SI unit of potential gradient?
Answer:
The SI unit of potential gradient is the \(\frac{\text { volt }}{\text { metre }}\left(\frac{\mathrm{V}}{\mathrm{m}}\right)\).

Question 14.
Explain how two cells are connected so as to
(i) assist each other
(ii) oppose each other. Write the formulae for the corresponding effective emf.
Answer:
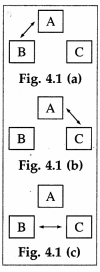
Consider two cells connected so that the positive terminal of the first cell is connected to the negative terminal of the second cell as shown in figure (a). The emf’s of the two cells are added up and the effective emf of the combination of the two cells is E₁ + E₂. This method of connecting two cells is called the sum method. Here, the cells assist each other.

Consider two cells connected so that their negative terminals are connected together or their positive terminals are connected together as shown in figure (b).

In this case their emf’s oppose each other and the effective emf of the combination of the two cells is E₁ – E₂(E₁ > E₂ assumed). This method of connecting two cells is called the difference method.

Question 15.
What is the internal resistance of the cell ?
Answer:
The internal resistance of a cell is the resistance offered by the electrolyte and electrodes in the cell.

Question 16.
Explain how a potentiometer is used as a voltage divider.
Answer:
A potentiometer can be used as a voltage divider to continuously change the output voltage of a voltage supply. As shown in the below figure, potential difference V is set up between points A and B of a potentiometer wire. One end of a device is connected to positive point A and the other other end is connected to a slider that can move along wire AB. The voltage V divides in proportion of lengths l₁ and l₂ as shown in figure.

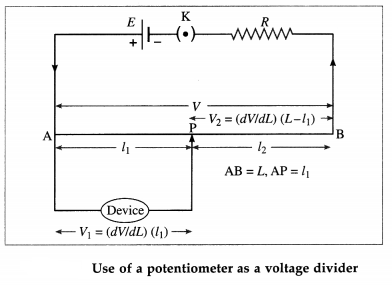
By using the slider we can change the output voltage from 0 to V.

Question 17.
State the precautions which must be taken in using a potentiometer.
Answer:
Precautions to be taken in using a potentiometer:

1. The potential difference across the potentiometer wire must be greater than the emf or potential difference to be balanced. Hence, in comparing emfs, the driver emf E > E₁, E₂ (direct method) or E > E₁ + E₂ (combination method).
2. The positive terminal of the cell with emf E1 and that with emf E₂, or their combination, must be connected to the higher potential terminal of the potentiometer.
3. The potentiometer wire must be of uniform cross section and homogeneous.
4. The potentiometer wire should be long and have a high resistivity and low temperature coefficient of resistance.

Question 18.
State the advantages of a potentiometer over a voltmeter.
Answer:
Advantages of a potentiometer over a voltmeter :
(1) The cell, whose emf is being measured, draws no current from the circuit at the null point. Thus, the potentiometer measures the open-circuit potential difference across its terminals, or the emf E. A voltmeter will measure the terminal potential difference, V, of the cell in a closed circuit. This is because the resistance of a voltmeter is high but not infinite and hence the voltmeter is not ideal.

(2) By setting up a suitably small potential gradient along a long potentiometer wire, any small voltage can be measured. Increasing the length of the wire effectively decreases the potential gradient, and increases both the precision and accuracy of measurement.

(3) The adjustment of a potentiometer is a ‘null’ method which does not, in any way, depend on the calibration of the galvanometer. The galvanometer is used only to detect the current, not to measure it. The accuracy of a voltmeter is limited by its calibration.

(4) Since a potentiometer can measure both the emf and terminal potential difference of a cell, the internal resistance of the cell can be found.

19. Solve the following

Question 1.
In a potentiometer circuit. E = 2 V, r = 2 Ω, R_wire = 10 Ω, R_ext = 1988 Ω and L = 4 m (in the usual notation). What is the potential gradient along the wire ?
Solution:

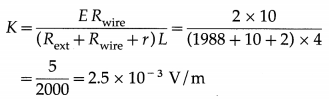
The potential gradient along the wire is 2.5 × 10^-3 V/m

Question 2.
A potentiometer wire has length 2 m and resistance 10 Ω. It is connected in series with a resistance 990 Ω and a cell of emf 2 V. Calculate the potential gradient along the wire.
Solution:
Data : L 10 m, R = 10 Ω, R_ext = 990 Ω, E =2 V
The current in the circuit is
I = \(\frac{E}{R+R_{\text {ext }}}=\frac{2}{10+990}=\frac{2}{1000}\) = 2 × 10^-3 A
The potential difference across the wire is
V = IR = 2 × 10^-3 × 10 = 2 × 10^-2 V
∴ The potential gradient along the wire
= \(\frac{V}{L}=\frac{2 \times 10^{-2}}{2}\) = 10^-2 V/m

Question 3.
A potentiometer wire 4 m long has a resistance of 4 Ω. What resistance must be connected in series with the wire and a cell of emf 2 V having internal resistance of 2 Ω to get a potential drop of 10^-3 V/cm along the wire?
Solution:
Data: L = 4 m, R = 4 Ω, E = 2 V, r = 2 Ω
The required potential drop per unit length of the wire is
10^-4 V/cm = \(\frac{10^{-3} \mathrm{~V}}{10^{-2} \mathrm{~m}}\) = 0.1 V/m
Let R_S be the series resistance for which the desired potential drop is obtained.
The current in the circuit is

Question 4.
A potentiometer wire of length 5 m is connected to a battery. For a certain cell having negligible internal resistance, the null point is obtained at 250 cm. If the length of the potentiometer wire is increased by 1 m, where will be the new position of the null point?
Solution:
Data : L₁ = 5m, L₂ = 6m, l₁ = 250 cm
E = (\(\frac{V}{L}\))l
where V/L is the potential gradient and l is the balancing length.
∴ E₁= (\(\frac{V}{L_{1}}\))l₁ = (\(\frac{V}{L_{2}}\))₂
l₂ = (\(\frac{L_{2}}{L_{1}}\)) × l₁ = \(\frac{6}{5}\) × 250 = 300 cm

Question 5.
A potentiometer wire, of length 4 m and resistance 8 Ω, is connected in series with a battery of emf 2 V and negligible internal resistance. If the emf of the cell balances against a length of 217 cm of the potentiometer wire, find the emf of the cell. When the cell is shunted by a resistance of 15 Ω, the balancing length is reduced by 17 cm. Find the internal resistance of the cell.
Solution:
Data: L = 4 m, R = 8 Ω, E = 2V, r = 0,
R(shunt) = 15 Ω, l = 217 cm = 2.17 m,
l₁ = 217 – 17 = 200 cm = 2 m

Question 6.
Two cells of emf’s E₁ and E₂ (E₁ > E₂) are connected in a potentiometer circuit so as to assist each other. The null point is obtained at 8.125 m from the high potential end of the potentiometer wire. When the cell with emf E₂ is connected so as to oppose the emf E₁, the null point is obtained at 1.25 m from the same end. Compare the emf’s of the two cells.
Solution:
Data : l₁ = 8.125 m (cells assisting), l₂ = 1.25 m (cells opposing)
E₁ + E₂ = Kl₁ and E₁ – E₂ = Kl₂
where K is the potential gradient.

Question 7.
A cell balances against a length of 200 cm on a potentiometer wire when it is shunted by a resistance of 8 Ω. The balancing length reduces by 40 cm when it is shunted by a resistance of 4 Ω. Calculate the balancing length when the cell is in an open circuit. Also calculate the internal resistance of the cell.
Solution:
Data : Part I : R = 8 Ω, l₂ = 200 cm;
Part II : R = 4 Ω, l₂ = 160 cm

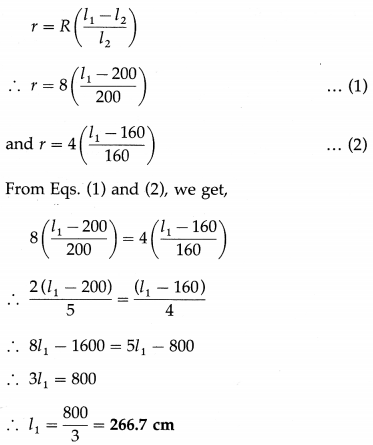
This is the balancing length when the cell is in open circuit. The internal resistance of the cell,

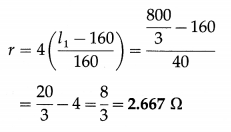
Question 8.
When a resistance of 12 Ω is connected across a cell, its terminal potential difference is balanced by 120 cm of a potentiometer wire. When a resistance of 18 Ω is connected across the same cell, the balancing length is 150 cm. Find the balancing length when the cell is in open circuit. Also calculate the internal resistance of the cell.
Solution:
Data : Part I : R = 12 Ω, l₂ = 120 cm;
Part II : R = 18 Ω, l₂ = 150 cm

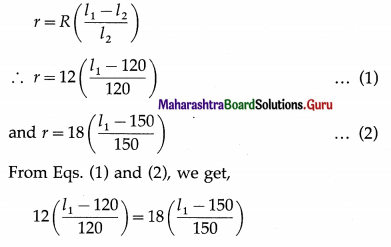
∴ \(\frac{l_{1}-120}{10}=\frac{6\left(l_{1}-150\right)}{50}\)
∴ 5 (l₁ – 120) = 6(l₁ -150)
∴ 5l₁ – 600 = 6l₁ – 900
∴ l₁ = 300 cm
This is the balancing length when the cell is in open circuit.
∴ r = \(12\left(\frac{l_{1}-120}{120}\right)=\frac{300-120}{10}=\frac{180}{10}\) = 18 Ω
This is the internal resistance of the cell a unit

Question 20.
What is a galvanometer?
Answer:
A galvanometer is a device used to detect weak electric currents in a circuit. The current may be of the order of a few microamperes, or even a few nanoamperes.

Question 21.
State the principle of working of a moving coil galvanometer.
Answer:
A current-carrying coil suspended in a magnetic field experiences a torque which rotates the plane of the coil and tends to maximize the magnetic flux through the coil. The torque due to the spring or the suspension fibre to which the coil is attached tends to restore the coil to its initial position. In equilibrium, the coil comes to rest and its deflection is proportional to the current through the coil.

Question 22.
Explain the basic construction of a galvanometer.
Answer:
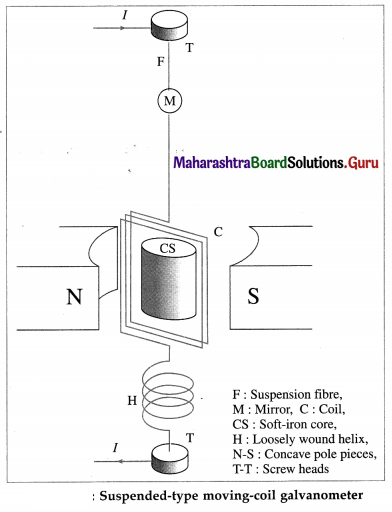
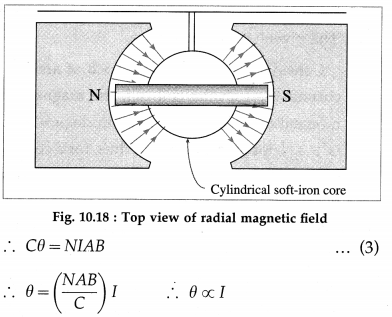
A galvanometer consists of a coil of a large number of turns of fine insulated copper wire wound on a rectangular nonconducting, nonmagnetic frame. The coil is pivoted (or suspended) between cylindrically concave pole pieces of a horseshoe strong permanent magnet. The coil swings freely around a cylindrical soft iron core fitted between the pole pieces. The deflection of the coil can be read with a pointer attached to it. The position of the pointer on the scale provided depends on the current passing through the galvanometer (or the potential difference across it). A galvanometer can be used as an ammeter or a voltmeter with a suitable modification.

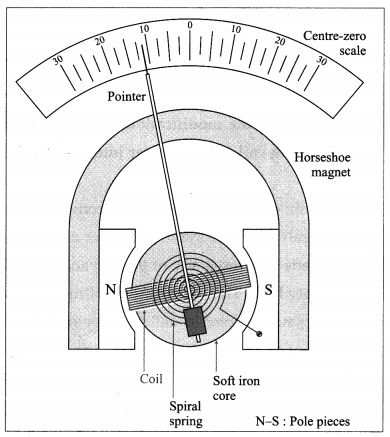
[Note : A table galvanometer has a resistance of about 50 Ω and can carry a current up to about 1 mA.]

Question 23.
What are the modifications necessary to convert a moving-coil galvanometer (MCG) into an ammeter?
Answer:
To convert a moving-coil galvanometer (MCG) into an ammeter, the following modifications are necessary :

1. The effective current capacity of the MCG must be increased to a desired higher value.
2. A galvanometer when connected in series with a resistance, should not decrease the current through the resistance. Hence, the effective resistance of the galvanometer must be decreased by connecting an appropriate low resistance across it. An ideal ammeter should have zero resistance.
3. It must be protected from the damages which are likely to occur due to the passage of an excess electric current.

Question 24.
State the function of the shunt in modifying a galvonometer to an ammeter.
Answer:
Functions of the shunt:

1. It lowers the effective resistance of the ammeter
2. It is used to divert to a large part of total current by providing an alternate path and thus it protects the instrument from damage.
3. With a shunt of proper value, a galvanometer can be modified into an ammeter of practically any desired range.

Question 25.
Explain how a moving-coil galvanometer is converted into an ammeter. Derive the necessary formula.
Answer:
A moving-coil galvanometer is converted into an ammeter by reducing its effective resistance by connecting a low resistance S across the coil. Such a parallel low resistance is called a shunt since it shunts a part of the current around the coil, shown in below figure. That makes it possible to increase the range of currents over which the meter is useful.

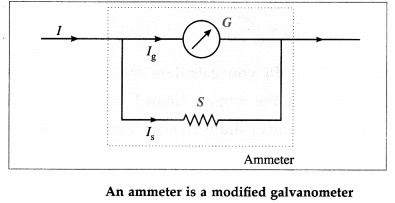
Let I be the maximum current to be measured and I_g the current for which the galvanometer of resistance G shows a full-scale deflection. Then, the shunt resistance S should be such that the remaining current I – I_g = I_s is shunted through it.

In the parallel combination, the potential difference across the galvanometer = the potential difference across the shunt
∴ I_g G = I_s S
= (I – I_g)S
∴ S = (\(\frac{I_{\mathrm{g}}}{I-I_{\mathrm{g}}}\)) C
This is the required resistance of the shunt. The scale of the galvanometer is then calibrated so as to read the current in ampere or its submultiples (mA. µA) directly.

[Notes :
(1) Thick bars of manganin are used for shunts because manganin has a very small temperature coefficient of resistivity.
(2) The fraction of the current passing through the galvanometer and shunt are, respectively,
\(\frac{I_{g}}{I}=\frac{S}{S+G}\) and \(\frac{I_{g}}{I}=\frac{G}{S+G}\)
(3) On the right hand side of Eq. (1), dividing both the numerator and denominator by I_g, we get,
S = \(\frac{1}{\left(I / I_{\mathrm{g}}\right)-1}\) ∙ G = \(\frac{G}{p-1}\)
where p = I/Ig is the range-multiplying factor, i.e., the current range of the galvanometer can be increased by a factor p by connecting a shunt whose resistance is smaller than the galvanometer resistance by a factor p – 1.
∴ p = \(\frac{G+S}{S}\)
If R_A is the resistance of the ammeter,
R_A = \(\frac{G S}{G+S}=\frac{G}{p}\)]

Question 26.
How do you calculate the shunt required to increase the range p times?
Answer:
The value of shunt resistance required to convert a galvanometer into an ammeter is given by,
S = (\(\frac{I_{\mathrm{g}}}{I-I_{\mathrm{g}}}\)) G
If the current I is p times the current I_g, then I = pI_g. Using this in the above expression, we get,
S = \(\frac{G I_{\mathrm{g}}}{p I_{\mathrm{g}}-I_{\mathrm{g}}}\) OR S = \(\frac{G}{p-1}\)
This is the required shunt resistance to increase the range p times.

Question 27.
What is the current flowing through the shunt resistance?
Answer:

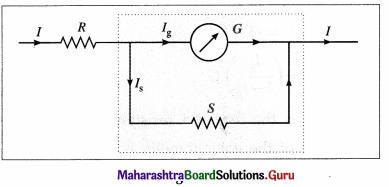
If I_S is the current through the shunt resistance, then the remaining current (I – I_S) will flow through the galvanometer.

Now, the potential difference across the galvanometer = the potential difference across the shunt
∴ G(I – I_S) = S I_S
∴ GI – GI_S = S I_S
∴ SI_S + GI_S = G I
∴ I_S = (\(\frac{G}{S+G}\))I
This is the current flowing through the shunt resistance.

Question 28.
What are the modifications required to convert a moving-coil galvanometer into a voltmeter?
Answer:
The modifications required to convert a moving- coil galvanometer into a voltmeter are as follows :

1. The effective resistance of the galvanometer should be very high. This is because a voltmeter requires a very small current to deflect its pointer. If a larger current than this flows through the voltmeter, the voltmeter is said to load the circuit and it will record a much smaller voltage drop.
2. The voltage measuring capacity (range) should be increased to a desired value.
3. It must be protected from damages which are likely to occur due to an excess applied potential difference.

Question 29.
Explain how a moving-coil galvanometer is converted into a voltmeter. Derive the necessary formula.
Answer:
A moving-coil galvanometer is converted into a voltmeter by increasing its effective resistance by connecting a high resistance Rs in series with the galvanometer, shown in figure. The series resistance is also useful for changing the range of any given voltmeter.

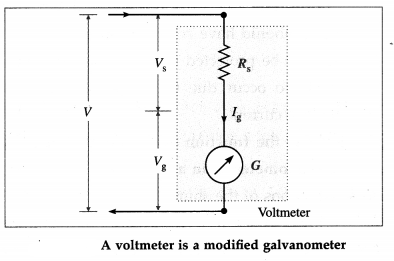
Let G be the resistance of the galvanometer coil and I_g the current required for a full-scale deflection.

Let V be the maximum potential difference to be measured. The value of the series resistance R_S should be such that when the potential difference applied across the instrument is V, the current through the galvanometer is I_g.

In the series combination, the potential difference V gets divided across the galvanometer (resistance, G) and the resistance R_S :
V = I_gG + I_gR_S = I_g(G + R_S)
∴ R_S = \(\frac{V}{I_{\mathrm{g}}}\) – G
This is the required value of the series resistance. The scale of the galvanometer is then calibrated so as to read the potential difference in volt or its submultiples, e.g., mV, directly.

[Notes :
(1) A series multiplier is made of manganin wire because manganin has a very small temperature coefficient of resistivity.
(2) The maximum potential difference V_g that can be dropped across the galvanometer is V_g = I_g G. Therefore, the above expression for the series resistance may be rewritten as
R_s = \(\frac{V G}{I_{\mathrm{g}} G}\) – G
= \(\frac{V G}{V_{\mathrm{g}}}\) – G = G(p – 1)
where p = V/V_g is the range-multiplying factor, i.e., the voltage range of the galvanometer can be increased by a factor of p by connecting a series resistance which is (p – 1) times the galvanometer resistance.
∴ p = \(\frac{V}{V_{g}}=\frac{\left(R_{\mathrm{S}}+G\right) I_{\mathrm{g}}}{G I_{\mathrm{g}}}=\frac{R_{\mathrm{S}}+G}{G}\)
Since the resistance of the voltmeter is R_v = R_S + G,
p = \(\frac{R_{\mathrm{V}}}{G}\)
∴R_v = G_p]

Question 30.
State the functions of the series resistance in modifying a galvanometer into a voltmeter.
Answer:
Functions of the series, resistance:

1. It increases the effective resistance of the voltmeter.
2. It drops off a larger fraction of the measured potential difference thus protecting the sensitive meter movement of the basic galvanometer.
3. With resistance of proper value, a galvanometer can be modified to a voltmeter of desired range. .

Question 31.
Distinguish between an ammeter and a voltmeter
Answer:

Ammeter	Voltmeter
1. It measures current.	1. It measures potential difference.
2. It is connected in series with a resistance.	2. It is connected in parallel to a resistance.
3. An ammeter should have very low resistance (ideally zero).	3. A voltmeter should have very high resistance (ideally infinite).
4. Its range can be increased by decreasing the value of shunt resistance.	4. Its range can be increased by increasing the value of series resistance.
5. The resistance of an ammeter is RA =	5. The resistance of a voltmeter is Rv = G + Rs = Gp.

32. Solve the following

Question 1.
Calculate the value of the shunt which when connected across a galvanometer of resistance 38 Ω will allow 1/20th of the current to pass through the galvanometer.
Solution:
Data : G = 38 Ω, I_g / I = \(\frac{1}{20}\)

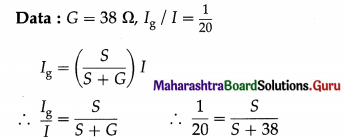
∴ S + 38 = 20 S
∴ 19 S = 38
∴ S = 2 Ω
This is the required value of the shunt.

Question 2.
A galvanometer is shunted by 1/r of its resistance. Find the fraction of the total current passing through the galvanometer.
Solution:
Let G be the resistance of the galvanometer, I the total current and I_g the current through the galvanometer when it is shunted. The resistance of the shunt is

The fraction \(\frac{1}{1+r}\) of the total current passes through the galvanometer.
[Note : The fraction of the current through the shunt = \(\frac{I_{\mathrm{S}}}{I}=1-\frac{I_{\mathrm{g}}}{I}=\frac{r}{1+r}\)]

Question 3.
A resistance of 3 Ω is connected in parallel to a galvanometer of resistance 297 Ω. Find the fraction of the current passing through the galvanometer.
Solution:
Data : G = 297 Ω, S = 3 Ω
I_g = \(\frac{S}{S+G}\) ∙ I
∴ \(\frac{I_{\mathrm{g}}}{I}=\frac{S}{S+G}=\frac{3}{3+297}=\frac{3}{300}\) = 0.01
This is the fraction of the current through the galvanometer.

[Note: The fraction of the current through the shunt
= \(\frac{I_{\mathrm{S}}}{I}\) = 1 – 0.01 = 0.99]

Question 4.
The combined resistance of a galvanometer of resistance 1000Ωand its shunt is 25 Ω. Calculate the value of the shunt.
Solution:
Data: G = 1000 Ω, R_A =25 Ω

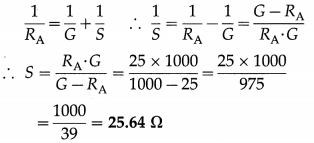
This is the value of the shunt.

Question 5.
A galvanometer with a coil of resistance 40 Ω gives a full scale deflection for a current of 5 mA. How will you convert it into an ammeter of range 0 – 5 A?
Solution:
Data: G = 40 Ω, I_g = 5 mA = 5 × 10^-3 A, I = 5 A
To convert a galvanometer into an ammeter, a shunt (i.e., low resistance in parallel) should be connected with the galvanometer coil. The required shunt resistance,
S = (\(\frac{I_{\mathrm{g}}}{I-I_{\mathrm{g}}}\)) G = (\(\frac{5 \times 10^{-3}}{5-5 \times 10^{-3}}\)) × 40
= \(\frac{200}{4995}\) = 0.04 Ω

Question 6.
A galvanometer has a resistance of 16 Ω and gives a full scale deflection when a current of 20 mA is passed through it. The only shunt resistance available is 0.04 Ω which is not sufficient to convert the galvanometer to an ammeter to measure up to 10 A. What resistance should be connected in series with the coil of the galvanometer so that the range of the ammeter is 10 A ?
Solution:
Data: G =16 Ω, I_g = 20 mA = 0.02 A,
S = 0.04 Ω, I = 10 A
Let X be the resistance to be connected in series with the coil of the galvanometer.
The fraction of the current through the galvanometer is \(\frac{I_{\mathrm{g}}}{I}\).

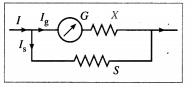
\(\frac{I_{\mathrm{g}}}{I}=\frac{S}{(G+X)+S}\)
∴ (G + X) + S = \(\frac{I}{I_{\mathrm{g}}}\) × S = \(\frac{10}{0.02}\) × 0.04 = 20
∴ X = 20 – (16 + 0.04) = 3.96 Ω
Alternate method:
Let G’ = G + X = 16 + X
The range multiplying factor,
p = \(\frac{I}{I_{\mathrm{g}}}=\frac{10}{0.02}\) = 500
Then, S = \(\frac{G^{\prime}}{p-1}\)
∴ G’= 16 + X = S(p – 1)
= 0.04(500 – 1) = 19.96 Ω
∴ X = 19.96 – 16 = 3.96 Ω

Question 7.
A galvanometer of resistance 100 C gives a full scale deflection for a current of 2 mA. How will you use it to measure (i) current up to 2 A (ii) voltage up to 10 V?
Solution:
Data : G = 100 Ω, I_g = 2 mA = 2 × 10^-3 A, I = 2 A, V = 10 V

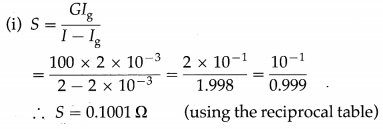
A resistance of 0.1001 Ωshould be connected in parallel to the coil of the galvanometer to measure current up to 2 A.

(ii) R_s = \(\frac{V}{I_{\mathrm{g}}}\) – G
= \(\frac{10}{2 \times 10^{-3}}\) – 100 = 5000 – 100 = 4900 Ω
A resistance of 4900 Ω should be connected in series with the coil of the galvanometer to measure voltage up to 10 V.

Question 8.
Calculate the value of resistance needed to convert a moving-coil galvanometer of 60 Ω which gives a full scale deflection for a current of 50 mA into (i) an ammeter of range 0 – 5 A (ii) a voltmeter of range 0 – 50 V.
Solution:
Data : G = 60 Ω, I_g = 50 mA = 5 × 10^-2 A, I = 5 A, V = 50 V

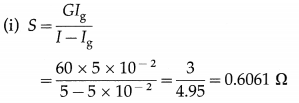
A resistance of 0.6061 Ω should be connected in parallel to the coil of the galvanometer to measure current up to 5 A.

(ii) R_s = \(\frac{V}{I_{\mathrm{g}}}\) – G
= \(\frac{50}{5 \times 10^{-2}}\) – 60
= 1000 – 60 = 940 Ω
A resistance of 940 Ω should be connected in series with the coil of the galvanometer to measure voltage up to 50 V.

Question 9.
A voltmeter of resistance 500 Ω can measure a maximum voltage of 5 V. How can it be made to measure a maximum voltage of 100 V? Solution:
Data : G = 500 Ω, V_g = 5 V, V = 100 V
To increase the range of the voltmeter by a factor p = \(\frac{V}{V_{\mathrm{g}}}\), a resistance R should be connected in series with it.
R_s = G(p – 1) = 500(\(\frac{100}{5}\) – 1) = 9500 Ω

Question 10.
A moving-coil galvanometer of resistance 200 ohms gives a full scale deflection of 100 divisions for a current of 50 milliamperes. How will you convert it into an ammeter to read 2 amperes for 20 divisions?
Solution:
Data : G = 200 Ω, I_g = 50 mA = 50 × 10^-3 A
The total number of scale divisions is 100. The ammeter has to read 20 divisions for a current of 2 A. Hence, for 100 divisions, the current must be I = 10 A.

To convert the galvanometer into an ammeter, a shunt must be connected in parallel to the galvanometer coil. The required shunt resistance,

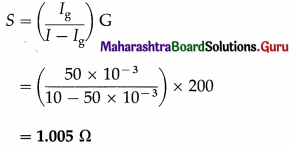
Question 11.
A galvanometer of resistance 50 Ω has a current sensitivity of 5 div/mA. The instrument has 25 divisions. How will you convert it into a voltmeter of range 0 – 50 V ?
Solution:
Data : G = 50 Ω, V = 50 V
For a current of 1 mA, the galvanometer shows a deflection of 5 divisions. Hence, for a full scale deflection (i.e. deflection of 25 divisions), the current passing through the galvanometer should be 5 mA.

∴ I_g = 5mA = 5 × 10^-3 A

To convert the galvanometer into a voltmeter, a high resistance must be connected in series with the galvanometer coil. This series multiplier,
R_s = \(\frac{V}{I_{\mathrm{g}}}\) – G = \(\frac{50}{5 \times 10^{-3}}\) – 50
= 9950 Ω

Multiple Choice Questions

Question 1.
For a Wheatstone network shown in the following figure, I_g = 0 when .

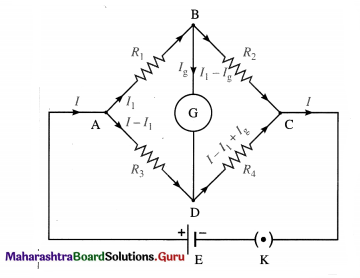
(A) E = 0
(B)V_B = V_D
(C) V_B > V_D
(D) V_B < V_D
Answer:
(B)V_B = V_D

Question 2.
A potentiometer wire is 100 cm long and a constant potential difference is maintained across it. Two cells are connected in series, first to support one another and then in opposite direction. The balance points are obtained at 50 cm and 10 cm from the positive end of the wire in the two cases. The ratio of emfs is
(A) 5 : 4
(B) 3 : 4
(C) 3 : 2
(D) 5 : 1
Answer:
(C) 3 : 2

Question 3.
When the current in a potentiometer wire decreases, the potential gradient
(A) decreases
(B) increases
(C) remains the same provided the resistance and the length of the wire remain the same
(D) remains the same, irrespective of the resistance . of the wire and its length.
Answer:
(A) decreases

Question 4.
In the circuit given below the current through the 6 Ω resistor will be

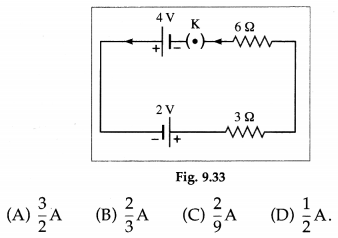
Answer:
(B) \(\frac{2}{3}\) A

Question 5.
The accuracy of a potentiometer wire can be increased by
(A) increasing its length
(B) decreasing its length
(C) using a cell of higher emf
(D) using a cell of lower emf.
Answer:
(A) increasing its length

Question 6.
A cell of emf 1.1 V and internal resistance r is connected across an external resistor of resistance R = 10 r. The potential difference across the resistor is
(A) 0.1 V
(B) 0.9 V
(C) 1.0 V
(D) 1.1 V.
Answer:
(C) 1.0 V

Question 7.
When a metal conductor connected in the left gap of a metre bridge is heated, the null point
(A) will shift towards right
(B) will shift towards left
(C) will remain unchanged
(D) will shift towards right or left depending upon the resistivity of the metal.
Answer:
(A) will shift towards right

Question 8.
In using a Wheatstone’s bridge to accurately measure an unknown resistance, a calibrated known variable resistor is varied until
(A) the change in the galvanometer reading is zero
(B) a change in the value of the variable resistor produces no change in the galvanometer reading
(C) the potential difference across the unknown resistance is zero
(D) the potential difference across the galvanometer is zero.
Answer:
(D) the potential difference across the galvanometer is zero.

Question 9.
In a Wheatstone network, the resistances in cyclic order are P = 10 Ω, Q = 5 Ω, S = 4 Ω and R = 4 Ω. Then, for the bridge to balance,
(A) 5 Ω should be connected in parallel to Q = 5 Ω
(B) 10 Ω should be connected in series with Q = 5 Ω
(C) 5 Ω should be connected in series with P = 10 Ω
(D) 10 Ω should be connected in parallel to P = 10 Ω
Answer:
(D) 10 Ω should be connected in parallel to P = 10 Ω

Question 10.
Two resistors, R₁ and R, are connected in the left gap and the right gap of a metre bridge, and the balancing length is obtained at 20 cm from the left. On inter-changing the resistors in the two gaps, the balancing length shifts by
(A) 20 cm
(B) 40 cm
(C) 60 cm
(D) 80 cm.
Answer:
(C) 60 cm

Question 11.
An instrument which can measure terminal potential difference as well as electromotive force (emf) is
(A) Wheatstone’s metre bridge
(B) a voltmeter
(C) a potentiometer
(D) a galvanometer
Answer:
(C) a potentiometer

Question 12.
A 10 m long wire of resistance 2012 is connected in series with a resistance of 10 Ω and a battery of emf 3 V and negligible internal resistance. The potential gradient, in µV / mm, along the wire is
(A) 2
(B) 20
(C) 200
(D) 2000
Answer:
(C) 200

Question 13.
A 10 m long potentiometer wire has a resistance of 20 Ω. If it is connected in series with a resistance of 55 Ω and a cell of emf 4 V and internal resistance 5 Ω, the potential gradient along the wire is
(A) 0.1 V/m
(B) 0.08 V/m
(C) 0.01 V/m
(D) none of these.
Answer:
(A) 0.1 V/m

Question 14.
A potential gradient of 6 × 10^-3 V/ mm is set up on a potentiometer wire which has a resistance of 2 Ω/m. Two emfs 2.5 V and 1.3 V, once assisting and then opposing each other, are balanced on the wire. The balancing lengths in the two cases are in the ratio
(A) 19 : 2
(B) 19 : 6
(C) 25 : 13
(D) 2:1.
Answer:
(B) 19 : 6

Question 15.
A potentiometer wire, having a resistance of 5 Ω and length 10 m, is connected in series a cell of emf 5 V and an external resistance of 495 Ω. A potential difference of 1.5 mV will balance against a length of
(A) 3 cm
(B) 30 cm
(C) 3 m
(D) none of these.
Answer:
(B) 30 cm

Question 16.
A load resistance R is connected across a cell of emf E and internal resistance r. If the closed-circuit p.d. across the terminals of the cell is V, the internal resistance of the cell is
(A) (E – V) R
(B) (V – E)R
(C) \(\frac{E-V}{V} R\)
(D) \(\frac{E-V}{V}\)
Answer:
(C) \(\frac{E-V}{V} R\)

Question 17.
The open-circuit potential difference across the terminals of a cell balances on 150 cm of a potentiometer wire. When the cell is shunted by a 4.9 Ω resistor, the balancing length reduces to 147 cm. The internal resistance of the cell is
(A) 0.01 Ω
(B) 0.05 Ω
(C) 0.1 Ω
(D) 1 Ω
Answer:
(C) 0.1 Ω

Question 18.
To convert a galvanometer into an ammeter
(A) a high resistance is connected in parallel to the galvanometer
(B) a high resistance is connected in series with the galvanometer
(C) a low resistance is connected in parallel to the galvanometer
(D) a low resistance value is connected in series with the galvanometer.
Answer:
(C) a low resistance is connected in parallel to the galvanometer

Question 19.
To convert a galvanometer into a voltmeter
(A) a high resistance is connected in parallel to the galvanometer
(B) a high resistance is connected in series with the galvanometer
(C) a low resistance is connected in parallel to the galvonometer
(D) a low resistance is connected in series with the galvonometer.
Answer:
(B) a high resistance is connected in series with the galvanometer

Question 20.
An ideal ammeter has
(A) a moderate resistance
(B) a high resistance
(C) an infinite resistance
(D) zero resistance
Answer:
(D) zero resistance

Question 21.
An ideal voltmeter has
(A) a low resistance
(B) a high resistance
(C) an infinite resistance
(D) zero resistance
Answer:
(C) an infinite resistance

Question 22.
The fraction of the total current passing through the galvanometer is

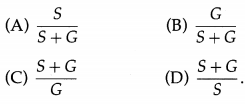
Answer:
(A) \(\frac{S}{S+G}\)

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 10 Magnetic Fields due to Electric Current Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 10 Magnetic Fields due to Electric Current

Question 1.
What is the magnetic effect of electric current?
Answer:
An electric current produces a magnetic field around it. This phenomenon is known as the magnetic effect of electric current. It was discovered by Hans Christian Oersted.

It was Ampere who first speculated that all magnetic effects are attributable to electric charges in motion (electric current). It takes a moving electric charge to produce a magnetic field, and it takes another moving electric charge to “feel” a magnetic field.

[Note : Hans Christian Oersted (1777-1851), Danish physicist, discovered electromagnetism in 1820. The oersted, the CGS unit of magnetic field strength, is named after him.]

Question 2.
Describe the magnetic field near a current in a long, straight wire. State the expression for the magnetic induction near a straight infinitely long current-carrying wire.
Answer:
Suppose a point P is at a distance a from a straight, infinitely long, wire carrying a current I, as shown in figure.

It can be shown that the magnitude of the total magnetic induction at P is given by the expression
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I}{a}\)
That is, the magnitude B is inversely proportional to the distance from the wire. Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the conductor; the direction of \(\vec{B}\) is everywhere tangential to such a circle. Thus, the magnetic field lines around the current in the straight wire is a family of circles centred on the wire. The magnitude of the field B depends only on the current and the perpendicular distance a of the point from the wire.

Question 3.
Explain the use of right hand grip rule to give the direction of magnetic field in the vicinity of a straight current-carrying conductor.
OR
State the right hand rule for the direction of the magnetic field due to a straight current-carrying wire.
Answer:
Right hand [grip] rule : If a straight current-carrying wire is grasped by the right hand, so that the extended thumb points in the direction of the current, the direction of the magnetic induction is the same as the direction of the fingers which are curled around the wire.

Question 4.
State the factors which the magnetic force on a charge depends upon. Hence state the expression for the Lorentz force on a charge due to an electric field as well as a magnetic field.
Hence discuss the magnetic force on a charged particle which is
(i) moving parallel to the magnetic field
(ii) stationary.
Answer:
A charge q moving with a velocity \(\vec{v}\) through a magnetic field of induction \(\vec{B}\) experiences a magnetic force perpendicular both to \(\vec{B}\) and \(\vec{v}\) . Experimental observations show that the magnitude of the force is proportional to the magnitude of \(\vec{B}\), the speed of the particle, the charge q and the sine of the angle θ between \(\vec{v}\) and \(\vec{B}\). That is, the magnetic force, F_m = qvB sin θ
∴ F_m = q(\(\vec{v}\) × \(\vec{B}\))
Therefore, at every instant \(\vec{F}_{\mathrm{m}}\) acts in a direction perpendicular to the plane of \(\vec{v}\) and \(\vec{B}\).

If the moving charge is negative, the direction of the force \(\vec{F}_{\mathrm{m}}\) acting on it is opposite to that given by the right-handed screw rule for the cross-product \(\vec{v}\) × \(\vec{B}\).

If the charged particle moves through a region of space where both electric and magnetic fields are present, both fields exert forces on the particle.

The force due to the electric field \(\vec{E}\) is \(\vec{F}_{\mathrm{e}}=q \vec{E}\).

The total force on a moving charge in electric and magnetic fields is called the Lorentz force :
\(\vec{F}=\vec{F}_{\mathrm{e}}+\vec{F}_{\mathrm{m}}=q(\vec{E}+\vec{v} \times \vec{B})\)
Special cases :
(i) \(\vec{v}\) is parallel or antiparallel to \(\vec{B}\): In this case, F_m = qvB sin 0° = 0. That is, the magnetic force on the charge is zero.
(ii) The charge is stationary (v = 0) : In this case, even if q ≠ 0 and B ≠ 0, F_m = q(0)B sin θ = 0. That is, the magnetic force on a stationary charge is zero.

Question 5.
Explain why the magnetic force on a charged particle cannot change the linear speed and the kinetic energy of the particle.
OR
One implication of the Lorentz force law is that magnetic force does no work. Justify.
Answer:
The magnetic force on a particle carrying a charge q and moving with a velocity \(\vec{v}\) in a magnetic field of induction \(\vec{B}\) is \(\vec{F}_{\mathrm{m}}=q \vec{v} \times \vec{B}\). At every instant, \(\vec{F}_{\mathrm{m}}\) is perpendicular to the linear velocity \(\vec{v}\), and \(\vec{B}\). Therefore, a non-zero magnetic force may change the direction of the velocity and the dot product

But \(\vec{F}_{\mathrm{m}} \cdot \vec{v}\) is the power, i.e., the time rate of doing work. Hence, the work done by the magnetic force in every short displacement of the particle is zero. The work done by a force produces a change in kinetic energy. Zero work means no change in kinetic energy. Thus, although the magnetic force changes the direction of the velocity \(\vec{v}\), it cannot change the linear speed and the kinetic energy of the particle.

Question 6.
Define the SI unit of magnetic induction from Lorentz force.
Answer:
The SI unit of magnetic induction is the tesla.
We can define the unit from the velocity-dependent part of the Lorentz force that acts on a charge in motion parallel to a magnetic field.

Definition : The magnitude of magnetic induction is said to be 1 tesla when a charge of 1 coulomb experiences a force of 1 N when it moves at 1 m/s in a magnetic field in a direction perpendicular to the direction of the field.

1 tesla (T) = 1 N’s/Gm = 1 N/A-m.
[Notes : (1) Since the ampere and not the coulomb is the fundamental unit, the tesla is defined from the expression for the force on a current-carrying conductor in a magnetic field when placed perpendicular to the direction of the field (see Unit 10.5, Q. 29): The magnitude of magnetic induction is said to be 1 tesla when a conductor of length 1 metre and carrying a current of 1 ampere experiences a force oflN when it is placed with its length perpendicular to the direction of the magnetic field. (2) The unit is named after Nikola Tesla (1870 -1943), Croatia-born US electrical engineer, inventor of the AC induction motor.]

Question 7.
Name a non-SI unit of magnetic induction. State its relation to the SI unit of magnetic induction.
Answer:
A CGS unit of magnetic induction of historical interest is the gauss, symbol G. However, since the magnetic flux and the magnetic flux density (magnetic induction, B) are defined by similar equations in the CGS system and the SI, this non-SI unit is accepted for use with SI.

1 G = 10^-4 T

[Note : The unit gauss is named after Karl Friedrich Gauss (1777 -1855), German mathematician, who strongly promoted in 1832 the use of the French decimal or metric system, with the metre and the kilogram and the astronomical second, as a coherent system of units for physical sciences. Gauss was the first to make absolute measurements of the Earth’s magnetic field in terms of a decimal system based on the three mechanical units millimetre, gram and second for, respectively, the quantities length, mass and time.]

Question 8.
Explain cyclotron motion and cyclotron formula.
Answer:
Suppose a particle of mass m and charge q enters a region of uniform magnetic field of induction \(\vec{B}\). In below figure, \(\vec{B}\) points into the page. The magnetic force \(\vec{F}_{\mathrm{m}}\) on the particle is always perpendicular to the velocity of the particle, \(\vec{v}\). Assuming the charged particle started moving in a plane perpendicular to \(\vec{B}\), its motion in the magnetic field is a uniform circular motion, with the magnetic force providing the centripetal acceleration.

where p = mv is the linear momentum of the particle. Equation (1) is known as the cyclotron formula because it describes the motion of a particle in a cyclotron-the first of the modern particle accelerators.

Question 9.
Explain the condition under which a charged particle will travel through a uniform magnetic field in a helical path.
OR
Describe the general motion of charged particle in a uniform magnetic field.
Answer:
Suppose a particle of mass m and charge q starts in a region of uniform magnetic field of induction \(\vec{B}\) with a velocity \(\vec{v}\) which has a non-zero component v_|| in the direction of \(\vec{B}\), From below figure. The magnetic force \(\vec{F}_{\mathrm{m}}\) on the particle is always perpendicular to \(\vec{v}\) and provides a centripetal acceleration such that

The parallel component of the motion \(\vec{v}_{\|}\) is unaffected by the magnetic field, so that the motion of the particle is a composite motion: an UCM with speed v_⊥ -the speed perpendicular to \(\vec{B}\) and a translation with a constant speed v_||. Therefore, the particle moves in a helix. Thus, the perpendicular component v_⊥ determines the radius of the helix while the parallel component v_|| determines the pitch x of the helix, i.e., the distance between adjacent turns. x = v_||/ T.

[Notes : (1) At non-relativistic speeds (v much less than the speed of light), the period T is independent of the speed of the particle. For all particles with the same charge-to-mass ratio (q/ m), faster particles move in larger circles than the slower ones, but all take the same time T to complete one revolution. (2) Looking in the direction of \(\vec{B}\), a positive charge always revolves anticlockwise, and a negative charge always clockwise.]

Question 10.
State under what conditions will a charged particle moving through a uniform magnetic field travel in
(i) a straight line
(ii) a circular path
(iii) a helical path.
Ans.
(i) A charged particle travels undeviated through a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is parallel or antiparallel to \(\vec{B}\). In this case, the magnetic force on the charge is zero.
(ii) A charged particle travels in a circular path within a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is perpendicular to \(\vec{B}\).
(iii) A charged particle travels in a helical path through a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is inclined at an angle θ to \(\vec{B}\), 0 < θ < 90°. In this case, the component of \(\vec{v}\) parallel to \(\vec{B}\) is unaffected by the magnetic field. The radius and pitch of the helix are determined respectively by the perpendicular and parallel components of \(\vec{v}\).

Question 11.
A particle of charge q enters a region of uniform magnetic field \(\vec{B}\) (pointing into the page). The field deflects the particle a distance d above the original line of flight, as shown in below figure. Is the charge positive or negative ? Find the momentum of the particle in terms of a, d, B and q.

Answer:
Since \(\vec{v} \times \vec{B}\) points upward, and that is also the direction of the magnetic force \(\vec{F}_{\mathrm{m}}\), q must be positive.
Using the Pythagorean theorem to find R in terms of a and d,

[Note: A similar solved question in the textbook, Example 10.2, is wrong. The acceleration qvB/m is the centripetal acceleration whose magnitude remains constant but direction changes continuously. Hence, it cannot be used in a kinematical equation to calculate s. The final expression for p arrived at in the textbook is therefore not correct.]

Question 12.
An ion of mass re and charge q is accelerated from rest through a potential difference V and enters a region of uniform magnetic field of induction B. Within the region, the ion moves in a semidrcle and strikes a photographic plate which lies along the diameter of the semicircle at a distance D from the point of entry. Show that the mass of the ion is given by m = \(k \frac{q D^{2} B^{2}}{V}\)
Answer:
Consider positive ions of charge q and mass m accelerated from rest to a speed r’ by an accelerating potential V. Then, the kinetic energy of the ions is

On entering a region of uniform magnetic field of induction B (see above figure for reference), the Ions travel in a semicircular path in a plane normal to the field with a radius
R = \(\frac{m v}{q B}\)
∴ m²v² = q²B²R² ………….. (2)
From Eq. (1) m²v² = 2qVm ………….. (3)
Equating the right hand sides of Eqs. (2) and (3),
2qVm = q²B²R²
∴ m = \(\frac{q B^{2} R^{2}}{2 V}\)
Since R = \(\frac{D}{2}\),
m = \(\frac{q B^{2} D^{2}}{8 V}\) = k\(\frac{q B^{2} D^{2}}{V}\)
where k = \(\frac{1}{8}\), Equation (4) Is the required expression.

[Note : This is especially the working of a mass spectrometer which Is used to measure the mass of an ion. A mass spectrometer is so sensitive it is used to measure isotopic masses. If the isotopes of an element carry the same charge, they acquire the same energy when accelerator through the same pd. But within the magnetic field, they travel in different semicircles depending on their masses and strike a detector or photographic plate at different D.]

Question 13.
A particle of charge q and momentum p enters a region of uniform magnetic field B travelling at right angles to the field, and is deflected through a right angle as shown. Obtain an expression for the length of the particle’s path In terms of q, p and B.

Answer:
A particle of charge q and momentum p enters a region of uniform magnetic field B travelling at right angles to the field. Within the field, the particle travels in a circular path of radius
R = \(\frac{p}{q B}\) ………. (1)
From the diagram, the length s of the particle’s path in the field is one quarter of the circumference,
∴ s = \(\frac{2 \pi R}{4}=\frac{\pi}{2} \frac{p}{q B}\) ………….. (2)
This is the required expression.

Question 14.
What is a cyclotron? State its principle of working.
Answer:
A cyclotron is a cyclic magnetic resonance accelerator in which an alternating potential difference of a few kV is used to accelerate light positive ions such as protons, deuterons, α-particles, etc., but not electrons, to very high energies of the order of a few MeV. It was developed by E. O. Lawrence and M. S. Livingston in 1932.

Principle: The cyclotron employs the principle of synchronous acceleration to accelerate charged particles which describe a spiral path at right angles to a constant magnetic field and make multiple passes through the same alternating p.d., whose frequency is the same as the frequency of revolution of the particles. .

Question 15.
Describe the construction of the cyclotron with a neat labelled diagram.
Answer:
Construction of the cyclotron: Two hollow D-shaped chambers that are open at their straight edges form the electrodes. They are called the dees. The dees are separated by a small gap, as shown in below figure, and a high-frequency (10⁶ Hz to 10⁷ Hz) alternating p.d. (of the order of 10⁴ V to 10⁵ V) is applied between them. The whole system is placed in an evacuated chamber between the poles of a large and strong electromagnet (B ≡ ≅ 1 T to 2T).

The ions to be accelerated are produced in an ion source; a hydrogen tube gives protons, heavy hydrogen or deuterium gives deuterons while helium gives x-particles, etc. The positive ions are injected near the centre and are accelerated each time they

cross the gap between the does. At the edge of one of the does, an electrostatic deflector deflects the spiralling particles out of the system to strike a target.

Question 16.
Explain the working of the cyclotron with a neat labelled diagram.
Answer:
The dees of the cyclotron are separated by a small gap and a high-frequency alternating p.d. is applied between them. Light positive ions are injected into the system near the centre.

Suppose a positive ion of charge q and mass m is injected when D₁ is positive and D₂ is negative. The positive ion will accelerate towards D₂. Inside the dees there is no electric field. Hence, inside D₂ it has a constant speed v. The magnetic force of magnitude qvB makes it move in a semicircular path through D₂. The radius r of its orbit is given by equating the centripetal force to the magnetic force.

Let t be the time spent by the ion to describe the semicircular path.

If t is also half the period of oscillation T of the alternating p.d., the ion will be in resonance with the electric field in the gap. That is, the ion will emerge from D₂ at the instant D₁ becomes negative and will be accelerated towards D₁. As the ion gains speed in the gap, its path in D₁ has greater radius. This process repeats after every half cycle of the alternating p.d. and the ion is accelerated each time it crosses the gap between the dees.

The radius of the path of the charged particles increases proportionately with their speed, the period of revolution remains constant.

After a large number of revolutions, the ion reaches the edge of the system where a negatively charged electrostatic deflector plate deflects it out of the system towards the target.

Question 17.
State the functions of the electric and magnetic fields in a cyclotron.
Answer:
The function of the electric field in the gap between the dees of a cyclotron is to accelerate the positively charged particles while that of the magnetic field in the dees is to deflect the particles in semicircular paths so that they return to the gap in a fixed time interval to reuse the alternating electric field.

Question 18.
Show that for a given positive ion species in a cyclotron,
(i) the radius of their circular path inside a dee is directly proportional to their speed
(ii) the time spent in a dee (or the cyclotron frequency or the magnetic resonance frequency) is independent of the radius of their path and speed
(iii) the maximum ion energy obtainableis directly proportional to the square of the magnetic induction.
Answer:
Consider positive ions of charge q and mass m injected in a cyclotron. In the electric-field-free region inside a dee, the ions are acted upon only by the uniform magnetic field. Hence, inside a dee the ions travel in a semicircular path with a constant speed y, in a plane normal to the field. If B is the induction of the magnetic field, the magnetic force of magnitude qvB provides the centripetal force.
∴\(\frac{m v^{2}}{r}\) = qvB
∴ r = \(\frac{m v}{q B}\) …………. (1)
Thus, for given q, m and B,
r ∝ v
If t be the time spent in a dee by the ion to describe a semicircular path of radius r,
t = \(\frac{\pi r}{v}=\frac{\pi}{v} \times \frac{m v}{q B}\)
∴ t = \(\frac{\pi m}{q B}\) …………. (2)
Thus, t is independent of r and y, i.e., it takes the ions exactly the same time t to travel the semicircular paths inside the dees irrespective of the radius of the path and the speed of the ions so long a the mass in is constant. This is the critical characteristic of operation of the cyclotron.

The periodic time of an ion in its circular path is
T = 2t = \(\frac{2 \pi m}{q B}\) ………….. (3)

The frequency of revolution,
f = \(\frac{1}{T}=\frac{q B}{2 \pi m}\) …………. (4)
is called the cyclotron frequency or the magnetic resonance frequency. The frequency is independent of r and y for a given ion species and remains constant so long as the mass m is constant.

If R is the maximum radius of the path, the same as the radius of the dee, just before the ions are deflected out of the accelerator,
V_max = \(\frac{q B R}{m}\) …………. (5)
so that KE_max = \(\frac{q^{2} B^{2} R^{2}}{2 m}\) (in joule)
= \(\frac{q^{2} B^{2} R^{2}}{2 e m}\) (in eV) …………… (6)
Thus, for a given ion species and dees of given radius,
KE_max ∝ B²

Question 19.
What is meant by cyclotron frequency?
Answer:
The cyclotron frequency, or the magnetic resonance frequency, is the frequency of revolution of a charged particle of charge per unit mass \(\frac{q}{m}\) in a magnetic field of induction B inside a cyclotron. The cyclotron frequency, f = \(\frac{q B}{2 \pi m}\). The frequency of the alternating voltage applied to the dees of the cyclotron should be equal to the cyclotron frequency.

Question 20.
What is resonance condition in a cyclotron ?
OR
What should be the frequency of the alternating voltage applied between the dees of a cyclotron?
Answer:
The frequency of the alternating voltage between the dees of a cyclotron should be equal to the cyclotron frequency so that a positive ion exiting a dee always sees an accelerating potential difference to the other dee. This equality of the frequencies is called the resonance condition.

Question 21.
State any two limitations of a cyclotron.
Answer:
Limitations of a cyclotron :

1. It cannot be used to accelerate electrons. Because electrons have a very small mass, they quickly achieve relativistic speeds, i.e., speeds at which their mass increases significantly with increase in speed. Then they cannot remain synchronous with the alternating electric field between the dees.
2. For higher energies, with a given magnetic field strength, the exit radius and thus the dees must be large. It is difficult to produce a uniform magnetic field over a large area.
3. Even protons, deuterons, a-particles, etc., cannot be accelerated to very high energy, say of the order of 500 MeV, using a cyclotron with a fixed cyclotron frequency.
4. No particle accelerator can accelerate uncharged particles, such as neutrons.

Question 22.
Does the time spent by a charged particle inside a dee of a cyclotron depend upon its speed and the radius of its path ? Why ?
Answer:
The time spent by a charged particle to describe a semicircular path of radius r inside a dee of a cyclotron is independent of the radius of the path and the speed v so long as the mass m of the particle is constant. This is true for any charged particle of mass m and carrying a charge q, and is the critical characteristic of operation of the cyclotron.
r = \(\frac{m v}{q B}\)
So that the time spent in a dee,
t = \(\frac{\pi r}{v}=\frac{\pi}{v} \times \frac{m v}{q B}=\frac{\pi m}{q B}\)
which is independent of r and v.

Question 23.
The frequency of revolution of the charged particles in a cyclotron does not depend upon their speed. Why?
Answer:
The time t spent by a charged particle, of mass m and carrying a charge q, inside a dee of a cyclotron is independent of the radius of the path and the speed of the particle so long as m is constant. Then, the periodic time of the charged particle in its nearly circular path is T = 2t, and the frequency of revolution,
f = \(\frac{1}{T}=\frac{1}{2 t}=\frac{q B}{2 \pi m}\)
are also independent of the radius and the speed.

Question 24.
What are the factors on which the cyclotron frequency depends?
Answer:
The cyclotron frequency depends upon

1. the magnetic induction and
2. the specific charge (the ratio charge/mass) of the charged particles.

Question 25.
What are the factors on which the maximum kinetic energy acquired by a charged particle in the cyclotron depends?
Answer:
The maximum kinetic energy acquired by a charged particle in the cyclotron depends upon

1. the magnetic induction
2. the specific charge (the ratio charge/mass) of the charged particles and
3. the radius of the dees.

Question 26.
In a certain cyclotron, the cyclotron frequency for acceleration of protons is 10⁸ Hz. What will be its value if the magnetic induction is doubled ?
Answer:
As the cyclotron frequency is directly proportional to the magnetic induction, the new frequency will be 2 × 10⁸ Hz. .

27. Solve the following :

Question 1.
An alpha particle (carrying a positive charge q = 3.2 × 10^-19 C) enters a region of uniform magnetic field of induction \(\vec{B}=(0.5 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})\) T with a velocity \(\vec{v}=(4 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}+\hat{\mathrm{k}})\) × 10² m/s. What is the force \(\vec{F}\) on the alpha particle?
Solution:

Question 2.
The magnetic field and electric field in a region in space are \(\vec{B}=B \hat{\mathrm{i}}\) and \(\vec{E}=E \hat{\mathrm{i}}\). A particle of charge q moves into the region with velocity \(\vec{v}=v \hat{\mathrm{j}}\). Find the magnitude and direction of the Lorentz force on the charged particle if q = 1 C,B = 1 T,E = 3 V/m and v = 4 m/s,
Solution:
Data : q = 1 C, B = 1 T, E = 3 V/m, v = 4 m/s
The Lorentz force on the charged particle is

Question 3.
An electron is accelerated from rest through 86 V and then enters a region of uniform magnetic induction of magnitude 1.5 T. What is the maximum value of the magnetic force the electron can experience?
[m_e = 9.11 × 10^-31 kg, e = 1.6 × 10^-19 C]
Solution:
Data : V= 86 V, B = 1.5 T, m_e = 9.11 × 10^-31 kg, e = 1.6 × 10^-19 C
Since the electron is accelerated from rest, the kinetic energy acquired by it is

The maximum value of the magnetic force on the electron is
F_m = evB
= (1.6 × 10^-19 C) (5.496 × 10⁶ m/s) (1.5 T)
= 1.319 × 10^-12 N or 1.319 pN

Question 4.
A cosmic ray proton enters the Earth’s magnetic field in a direction perpendicular to the field. If the speed of the proton is 2 × 10⁷ m/s and B = 1.6 × 10^-6 T, find the force exerted on the proton by the magnetic field. [Charge on a proton, e = 1.6 × 10^-19 C]
Solution :
Data : v = 2 × 10⁷ m/s, B = 1.6 × 10^-6 T, e = 1.6 × 10^-19 C
The magnetic force on the proton is
F_m = evB (∵ \(\vec{v} \perp \vec{B}\))
= (1.6 × 10^-19 C)(2 × 10⁷ m/s)(1.6 × 10^-6 T)
= 5.12 × 10^-18 N

[Note : The Earth’s magnetic field traps the charged particles in doughnut-shaped regions outside the atmosphere. These regions are called Van Allen radiation belts. Near the poles, charged particles from these belts enter the atmosphere and produce the awesome shimmering curtains of light called the aurora borealis (northern ! lights) and aurora australis (southern lights).]

Question 5.
A charged particle moves with velocity 3 × 10⁶ m/s at right angles to a uniform magnetic field of induction 0.005 T. Find the magnitude of the charge if the particle experiences a force of 2 × 10^-2 N.
Solution:
Data : v = 3 × 10⁶ m/s, B = 5 × 10^-3 T,
F_m = 2 × 10^-2 N
F_m = qvB (∵ \(\vec{v} \perp \vec{B}\))
∴ The charge on the particle,

Question 6.
An electron in a TV picture tube moves horizontally with a speed 2 × 10⁷ m/s. It is deflected upward by a horizontal magnetic field of induction 10^-3 T. Find the magnitude of the force acting on the electron due to the action of the magnetic field.
Solution:
Data : e = 1.6 × 10^-19 C, v = 2 × 10⁷ m/s,
B = 10^-3 T
The magnitude of the magnetic force,
F_m = evB (∵ \(\vec{v} \perp \vec{B}\))
= (1.6 × 10^-19 C)(2 × 10⁷ m/s) (10^-3 T)
= 3.2 × 10^-15 N = 3.2 fN

Question 7.
The first practical cyclotron developed by Lawrence and Livingston in 1932 had dees of radius 12 cm and produced protons of about 1 MeV energy.
Calculate (i) the applied magnetic induction
(ii) the frequency of the accelerating electric field.
[m^p = 1.67 × 10^-27 kg, q = 1.6 × 10^-19 C
Solution:
Data: R = 0.12 m, m^p = 1.67 × 10^-27 kg,
q = 1.6 × 10^-19 C,
KE_max = 1 MeV =(1 × 10⁶)(1.6 × 10^-19)
= 1.6 × 10^-13 J

Question 8.
In a cyclotron, for the same B and R, show that the maximum kinetic energy of α-particles is twice that of deuterons.
Solution:
Data: Let E_α and E_d denote the maximum kinetic energies of α-particIes (He⁺⁺ ions) and deuterons
(D⁺ ions). For an α-partic1e,
q = +2e and m ≅ 4m^p and for a deuteron,
q = +e and m ≅ 2m^p
where e is the elementary charge and m^p is the proton mass.
In a cyclotron, the maximum kinetic energy of the ions obtainable with dec radius R and magnetic field induction B is

Question 28.
Derive an expression for the magnetic force experienced by a straight current-carrying conductor placed in a uniform magnetic field.
Discuss the cases when the force is maximum and minimum.
State the expressions for the force experienced by a current-carrying
(i) conductor of arbitrary shape
(ii) closed circuit (conducting loop).
Answer:
Consider a straight current-carrying conductor placed in a region of uniform magnetic field of induction \(\vec{B}\) pointing out of the page, as shown in below figure by the evenly placed dots. Let the length of the conductor inside the field be l and the current in it be I.

In metallic conductors, electrons are the charge carriers. The direction of conventional current is, however, taken to be that of flow of positive charge which is opposite to the electron current.

Let dq be the positive charge passing through an element of the conductor of length dl in time dt.
\(\overrightarrow{d l}\) has the same direction as that of the current.
Then, I = \(\overrightarrow{d l}\)/dt ………….. (1)
and drift velocity,\(\overrightarrow{v_{\mathrm{d}}}\) = \(\overrightarrow{d l}\)/dt ……….. (2)
The magnetic force on the charge dq is

The charge dq is constrained to remain within the conductor. Hence, the conductor itself experiences this force. The force on the entire part of the conductor within the region of the magnetic field is

Case 1 : When the conductor is parallel to the magnetic field, \(\vec{l}\) is parallel or antiparallel to \(\vec{B}\) according as the current is in the direction of \(\vec{B}\) or opposite to it; then θ = 0° or θ = 180°, so that sin θ = 0. Hence, in either of these two cases, F = 0.

Case 2 : The maximum value of the force is F_max = IlB, when sin θ = 1, that is, when the conductor lies at right angles to \(\vec{B}\) (θ = 90°).
(i) For a current-carrying wire of arbitrary shape in a uniform field,
\(\vec{F}=\int \vec{f}_{\mathrm{m}}=I\left(\int \overrightarrow{d l}\right) \times \vec{B}\) …………. (5)
(ii) For a current-carrying conducting loop (closed circuit) in a uniform field,
\(\vec{F}=\int \vec{f}_{\mathrm{m}}=I(\oint \overrightarrow{d l} \times \vec{B})\) ………….. (6)
But for a closed loop of arbitrary shape, the integral is zero.
∴ \(\vec{F}\) = 0
[Notes : (1) While the direction of \(\vec{F}\) can be found from the cross product of \(\vec{l}\) and \(\vec{B}\), there is a handy rule due to Sir John Ambrose Fleming (1849-1945), British physicist and electrical engineer.

Fleming’s left hand rule : If the forefinger and the middle finger of the left hand are stretched out to point in the directions of the magnetic field and the current, respectively, then the outstretched thumb indicates the direction of the magnetic force on the current-carrying straight conductor, from below figure.]

(2) Equation (3) is usually used to define the unit of magnetic field induction, the tesla. See the note to Q. 6. (3) B cannot be taken out of the integral in Eq. (6).]

Question 29.
A straight conductor of length 0.5 m and carrying a current of 2 A is placed in a magnetic field of induction 2 Wb/m² at right angles to the length of the conductor. What is the magnetic force on the conductor?
Answer:
F = IlB
= (2A) (0.5m) (2 Wb/m²)
= 2 N is the force on the conductor.

Question 30.
A rectangular loop of wire hanging vertically with one end in a uniform magnetic field \(\vec{B}\), supports a small block of mass m. \(\vec{B}\) points into the page in the shaded region of below figure. For what current I in the loop would the magnetic force exactly balance the downward gravitational force?

Answer:
The magnetic force on the horizontal segment of the loop inside the field must be upward to balance the downward gravitational force. With \(\vec{B}\) pointing into the page, the current in that segment must be toward the right so that \(\vec{F}=\vec{L} \times \vec{B}\) on that segment points upward. That is, the current in the loop must be clockwise.
Taking L = a, F = IaB
∴ IaB = mg
∴ I = \(\frac{m g}{a B}\)
is the required expression for the current.

Question 31.
Explain with a neat labelled diagram how the magnetic forces on a current loop produce rotary motion as in an electric motor.
Answer:
Consider a current-carrying rectangular loop ABCD, within a uniform magnetic field \frac{m g}{a B}, from below figure. Lead wires and commutator are not shown for simplicity. The coil is free to rotate about a fixed axis. Suppose the sides AB and CD are perpendicular to the field direction.

The magnetic force on each segment act at the centre of mass of that segment. The direction of the force on each segment can be found using the right hand rule for the cross product or from Fleming’s left hand rule.

The magnetic forces on the short sides AD and CB are, in general, equal in magnitude, opposite in direction and have the same line of action along the rotation axis. Hence, these forces cancel out and does not produce any torque. The magnetic forces on the long sides AB and CD are also equal in magnitude and opposite in direction but their lines of action are different. Hence, these forces constitute a couple and tend to rotate the coil about the central axis.

A commutator (not shown) reverses the direction of the current through the loop every half-revolution so that the torque always acts in the same direction.

Question 32.
Derive an expression for the net torque on a rectangular current-carrying loop placed in a uniform magnetic field with its rotation axis
perpendicular to the field.
Answer:
Consider a rectangular loop ABCD of length l, breadth b and carrying a current I, placed in a uniform magnetic field of induction \(\vec{B}\) with its rotation axis perpendicular to \(\vec{B}\), from figure (a). To define the orientation of the loop in the magnetic field, we use a normal vector \(\hat{n}\) that is perpendicular to the plane of the loop. The direction of \(\hat{n}\) is given by a right hand rule: If the fingers of right hand are curled in the direction of current in the loop, the outstretched thumb is the direction of \(\hat{n}\). Suppose the normal vector \(\hat{n}\) of the loop makes an arbitrary angle with \(\vec{B}\), as shown in figure (b).

In the side view, Fig. 10.15 (b), the sides CD, DA, AB and BC have been labelled as 1, 2, 3 and 4, respectively. In this view, the current in side 1 (CD) is out of the page as shown by a ⊙ while that in side 3 (AB) is into the page shown by a ⊗.

For side 2 (AD) and side 4 (BC), the length of the conductor \(|\vec{L}|\) = b and the angle between \(\vec{L}\) and \(\vec{B}\) is (90° – θ). Hence, the forces on sides 2 and 4 are equal in magnitude :

F₂ = F₄ = IbB sin(90° – θ) = IbB cosθ

However, \(\vec{F}_{2}\) is directed out of the page while \(\vec{F}_{4}\) is into, and because their common line of action is through the centre of the loop, their net torque is zero. For side 1 (CD) and side 3 (AB), \(|\vec{L}|\) = I and \(\vec{L}\) is perpendicular to \(\vec{B}\). Hence, the forces \(\vec{F}_{1}\), and F\(\vec{F}_{3}\) have the same magnitude : F₁ = F₃ = IlB

But their lines of action being different, they constitute a couple.

Moment arm of the couple = b sin θ
∴ Torque exerted by the couple = force of the couple x moment arm of couple
∴ τ = (IlB)(b sin θ)
in the clockwise sense in figure (b). The torque tends to rotate the loop so as to align its normal vector h with the direction of the magnetic field.
∴ τ = I(lb)B sin θ = MB sinθ
where A = lb is the area of the loop. For a rectangular coil of N turns in place of a single-turn loop,
τ = NIAB sin θ
This is the required expression for the net torque. The torque has maximum magnitude for θ = 90°, that is when \(\hat{n}\) is perpendicular to \(\vec{B}\) or, in other words, the plane of the coil is parallel to the field.
τ_max = NIAB

Question 33.
Describe the construction of a suspended-type moving-coil galvanometer with a neat labelled diagram.
Answer:
A permanent fixed-magnet, suspended-type moving-coil galvanometer is shown in below figure. It consists of a coil of a large number of turns of fine insulated copper wire wound on a rectangular, nonconducting, non-magnetic frame. The coil is suspended between the cylindrically concave pole pieces of a horseshoe permanent magnet by a fine phosphor-bronze wire F from an adjustable screw- head. The other terminal of the coil is connected to a loosely-wound wire helix H. The coil swings freely around a cylindrical soft-iron core CS fitted between the pole pieces.

The suspension F and the helix H serve as the two current leads to the coil. The suspension fibre also provides the restoring torque when the coil is rotated from its normal position. The cylindrically concave pole pieces together with the soft-iron core make the magnetic field radial in the annular region in which the vertical sides of the coil move. The soft-iron core also concentrates the magnetic field (i.e., increases the magnetic induction) in the annular region.

The angle of deflection is observed with a beam of light reflected from a small mirror M fixed to the suspension fibre. The reflected beam is observed on a ground-glass scale arranged about a metre from the instrument, the light beam serving as a weightless pointer.

[Note : The diagram given in the textbook (Fig. 10.13) has serious errors, notably, the missing suspension fibre by which the coil is hung. The metal fibre (made of phosphor bronze), which bears the weight of the coil, is also the current lead to the coil and provides the restoring torque. The Tower suspension shown in the textbook is actually a loose wire which merely provides an exit lead to the current but does not exert any torque on the coil.]

Question 34.
State the principle of working of a moving- coil galvanometer (suspended-coil type).
Answer:
Principle : A current-carrying coil suspended in a magnetic field experiences a torque which rotates the plane of the coil and tends to maximize the magnetic flux through the coil.

The deflection of the coil in a moving-coil gal-vanometer is linearly related to the current through it and, therefore, can be used to measure current in terms of the deflection.

Question. 35.
With the help of neat diagrams, describe the working of a moving-coil galvanometer.
Answer:
Consider a rectangular coil-of length Z, breadth b and N turns – carrying a current I suspended in a uniform magnetic field of induction \(\vec{B}\).

The magnetic forces on the horizontal sides of the coil have the same line of action and do not exert any torque. The magnetic forces on the vertical sides constitute a couple and exert a deflecting torque. If the plane of the coil is parallel to \(\vec{B}\), the magnitude of the deflecting torque is maximum equal to
τ_d = NIAB …………… (1)
where A = lb is the area of each turn of the coil. This torque rotates the coil.

In a moving-coil galvanometer, the coil swings in a radial magnetic field produced by the combination of the cylindrically concave pole pieces and the soft-iron core. Hence, the plane of the coil is always parallel to the field lines, as shown in Fig. 10.18. Therefore, the deflecting torque is constant and maximum as given by Eq. (1).

The rotation of the coil twists the suspension fibre which exerts a restoring torque on the coil. The restoring torque is proportional to the angle of twist θ.
τ_r = Cθ …………… (2)
where C is the torque constant, i.e., torque per unit angle of twist. C depends on the dimensions and the elasticity of the suspension fibre.

The coil eventually comes to rest in the position where the restoring torque equals the deflecting torque in magnitude. Therefore, in the equilibrium position,
τ_r = τ_d

since N, A, B and C are constant. Thus, the deflection of the coil is directly proportional to the current in it.

Question 36.
A coil suspended freely in a radial magnetic field rotates through 30° when a current of 30 /(A is passed through it. Through what angle will it rotate if the current is doubled and the magnetic induction is halved?
Answer:
The angle of rotation, θ ∝ IB (in the usual notation)
As I₂B₂ = (2I₁)\(\left(\frac{B_{1}}{2}\right)\) = I₁B₁, the angle of rotation will be the same, i.e., 30°.

Question 37.
What is the advantage of a radial magnetic field in a moving-coil galvanometer and how is it produced?
Answer:

1. Advantage of radial magnetic field in a moving- coil galvanometer:
   • As the coil rotates, its plane is always parallel to the field. That way, the deflecting torque is always a maximum depending only on the current in the coil, but not on the position of the coil.
   • The restoring torque is proportional to the deflection so that a radial field makes the deflection proportional to the current. The instrument then has a linear scale, i.e., the divisions of the scale are evenly spaced. This makes it particularly straight forward to calibrate and to read.
2. Producing radial magnetic field :
   • The pole pieces of the permanent magnet are made cylindrically concave, concentric with the axis of the coil.
   • A soft iron cylinder is centred between the pole pieces so that it forms a narrow cylindrical gap in which the sides of the coil can move. Together, they produce a radial magnetic, field; that is, the magnetic lines of force in the gap are along radii to the central axis.

Question 38.
What will happen if the magnetic field in a moving-coil galvanometer is not radial?
Answer:
Suppose the magnetic field is uniform but not radial. Then, when the coil comes to rest after rotation through an angle θ, NIAB cos θ = Cθ (in usual notations).
∴ I ∝ \(\frac{\theta}{\cos \theta}\)
as N, A, B and C are constants in a particular case. Thus, the current is not directly proportional to the deflection. Hence, we cannot have a linear scale for measurement.

Question 39.
Explain the use of a soft iron core in a moving- coil galvanometer.
Answer:
In a moving-coil galvanometer, the pole pieces of the permanent magnet are made cylindrically concave, coaxial with the coil. A soft iron core is fixed centrally between the pole pieces so that it partly fills the space inside the coil and forms a narrow cylindrical gap in which the sides of the coil can move.
(1) The soft iron core, together with the concave pole pieces produces a radially uniform magnetic field, i.e., the magnetic lines of force in the gap are along radii to the central axis. This makes the deflection of the coil proportional to the current in it. The instrument then has a linear scale which is particularly straightforward to calibrate and to read.

(2) The permeability of iron being more than that of air, the magnetic lines of force pass through the soft iron core. By making the cylindrical gap as narrow as possible then increases the magnetic induction in the gap. This increases the deflecting torque on the coil and the sensitivity of the instrument.

Question 40.
Why does not the Earth’s magnetic field affect the working of a moving-coil galvanometer?
Answer:
The coil of a moving-coil galvanometer rotates in the magnetic field of a permanent magnet. The magnetic induction of the permanent magnet is many orders of magnitude (typically 10⁴ times) stronger than that of the Earth. Hence, the Earth’s magnetic field does not affect the working of the galvanometer.

Question 41.
Explain the magnetic dipole moment of a current loop. State its magnitude and direction.
Answer:
The responses of a current-carrying coil to an external magnetic field is identical to that of a magnetic dipole (or a bar magnet). Like a magnetic dipole, a current-carrying coil placed in a magnetic field \(\vec{B}\) experiences a torque. In that sense, the coil is said to be a magnetic dipole. To account for a torque τ on the coil due to the magnetic field, we assign a magnetic dipole moment \(\vec{\mu}\) to the coil, such that
\(\vec{\tau}=\vec{\mu} \times \vec{B}=N I \vec{A} \times \vec{B}\)

where \(\vec{\mu}=N I \vec{A}\). Here, N is the number of turns in the coil, I is the current through the coil and A is the area enclosed by each turn of the coil. The direction of \(\vec{\mu}\) is that of the area vector \(\vec{A}\), given by a right hand rule shown in below figure. If the fingers of right hand are curled in the direction of current in the loop, the outstretched thumb is the direction of \(\vec{A}\) and \(\vec{\mu}\). In magnitude, μ = NIA.
The torque tends to align \(\vec{\mu}\) along \(\vec{B}\).

Question 42.
State if the following statement is true : “The magnetic dipole moment of a current-carrying coil of given geometry is constant.” Justify your answer.
Answer:
The given statement is false.
Consider a coil of N turns, each of area A. If the current through the coil is I, the magnetic dipole moment of the coil is, in magnitude, μ = NIA. That is, μ ∝ I, for given N and A. Thus, for a coil of given geometry, its magnetic dipole moment varies with the current through it.

Question 43.
In analogy with an electric dipole, state an expression for the magnetic potential energy of an magnetic dipole in a uniform magnetic field. Discuss the orientations of the dipole moment for the maximum and minimum of potential energy.
Answer:
Consider an electric dipole of dipole moment \(\vec{p}\) placed in a uniform electric field \(\vec{p}\) making an angle Φ with \(\vec{p}\). The torque \(\vec{\tau}=\vec{p} \times \vec{E}\) tends to rotate the dipole and align it with \(\vec{E}\).

If the dipole was initially parallel to \(\vec{E}\), its potential energy is minimum. We arbitrarily assign U₀ = 0 to the minimum potential energy for this position. Then, at a position where \(\vec{p}\) makes an angle θ with \(\vec{E}\), the potential energy of the dipole is
U_θ = -pE cos θ = –\(\vec{p} \cdot \vec{E}\).
A current-carrying coil placed in a magnetic field \(\vec{B}\) experiences a torque,
\(\vec{\tau}=\vec{\mu} \times \vec{B}\) …………. (1)
where \(\vec{\mu}\) is the magnetic dipole moment of the coil. In analogy with an electric dipole, the potential energy of a magnetic dipole is
U_θ = – μB cos θ = – \(\vec{\mu} \cdot \vec{B}\) ……….. (2)
U_θ is also known as orientation energy.
A magnetic dipole has its lowest energy ( = – μB cos 0 = – μB) when its dipole moment is lined up with the magnetic field, and has its highest energy ( = – μBcos 180° = + μB) when is directed opposite the field.

44. Solve the following :
Question 1.
A straight current-carrying conductor 30 cm long carries a current of 5 A. It is placed in a uniform magnetic field of induction 0.2 T, with its length making an angle of 60° with the direction of the field. Find the force acting on the conductor.
Solution:
Data : l = 30 cm = 0.3 m, I = 5 A, B = 0.2 T, θ = 60°
The magnitude of the force on the conductor,
F = I\(|\vec{l} \times \vec{B}|\) = IlB sin θ
= (5 A) (0.3 m) (0.2 T) sin 60°
= 0.3 × 0.866 = 0.2598 N
The direction of the force is given by the cross product rule.

Question 2.
A conductor of length 25 cm is placed (i) parallel (ii) perpendicular (iii) inclined at an angle 30°, to a uniform magnetic field of induction 2 T. If 1 C of charge passes through it in 5 s, calculate the force experienced by the conductor in each case.
Solution:
Data : l = 25 cm = 0.25 m, θ₁ = 0°, θ₂ = 90°, θ₃ = 30°, B = 2 T, q = 1 C, f = 5 s
The current in the conductor,
I = \(\frac{q}{t}=\frac{1 \mathrm{C}}{5 \mathrm{~s}}\) = 0.2 A
The magnitude of the force on the conductor,
F = I\(|\vec{l} \times \vec{B}|\) = IlB sin θ
(i) θ₁ =0° A ∴ sin θ₁ = 0 ∴ F = 0 N
(ii) θ₂ = 9O° ∴ sin θ₂ = 1
∴ F = IlB = (0.2 A)(0.25 m)(2 T)
= 0.1 N
(iii) θ₃ = 30° ∴ sin θ₃ = 0.5
∴ F = IlB sin θ₃ = (0.1 N) (0.5) = 0.05 N
The direction of \(\vec{F}\) in each case is given by the cross product rule.

Question 3.
A horizontal straight wire is in a uniform magnetic field which is horizontal and at right angles to the length of the wire. The part of the wire that lies in the field has a length 2 m and mass 1 gram. If the magnetic induction is 1 mT, find the current that should be passed through the wire to balance it.
Solution:
Data : l = 2 m, m = 1 g = 10^-3 kg, g = 9.8 m/s²,
B = 1 mT = 10^-3 T
To balance the wire, the upward magnetic force must be equal in magnitude to the downward force due to gravity.

Question 4.
A circular loop of radius 10 cm is carrying a current of 0.1 A. Calculate its magnetic moment.
Solution:
Data : R = 10 cm = 0.1m, N = 1, I = 0.1 A
The magnetic moment,
μ = NIA = NI(πR²)
= (1) (0.1 A) (3.142) (0.1 m)²
= 3.142 × 10^-3 A∙m²

Question 5.
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Å. If the frequency of revolution of an electron is 9 × 10⁹ MHz, calculate the equivalent magnetic moment. [e = 1.6 × 10^-19 C]
Solution : .
Data : r = 0.53 Å = 0.53 × 10^-10 m,
f = 9 × 10⁹ MHz = 9 × 10¹⁵ Hz, e = 1.6 × 10^-19 C
Magnetic moment, M₀ = IA = efπr²
= 1.6 × 10^-19 × 9 × 10¹⁵ × 3.142 × (0.53 × 10^-10)²
= 14.4 × 3.142 × (0.53)² × 10^-19 × 10¹⁵ × 10^-20
= 1.272 × 10^-23 A∙m²

Question 6.
A rectangular coil of 10 turns, each of area 0.05 m², is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 /(A is passed through it.

(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
(iii) What is the minimum torque experienced by the coil?
SoLution:
Data: N = 10, A = 0.05 m², B = 0.01 T, I = 30 μA = 3 × 10^-5 A
(i) The magnetic moment,
μ = NIA = 10(3 × 10^-5 A)(0.05 m²)
=1.5 × 10^-5 A∙m² = 15 μA∙m²

(ii) The maximum torque experienced by the coil (when its plane is parallel to \(\vec{B}\)) is
τ_max = MB
= (1.5 × 10^-5 A∙m²)(0.01 T)
= 1.5 × 10^-7 N∙m

(iii) The minimum torque experienced by the coil (when its plane is perpendicular to \(\vec{B}\)) is
τ_min = 0

Question 7.
A coil has 300 turns, each of area 0.05 m2. (i) Find the current through the coil for which the magnetic moment of the coil will be 4.5 A-m2. (ii) It is placed in a uniform magnetic field of induction 0.2 T with its magnetic moment making an angle of 30° with \(\vec{B}\). Calculate the magnitude of the torque experienced by the coil. (3 marks)
Solution:
Data : N = 300, A = 0.05 m², M = 4.5 A ∙ m², B = 0.2 T, θ = 30°
(i) M = NIA
∴ The current in the coil,
I = \(\frac{M}{N A}=\frac{4.5}{300 \times 0.05}\) = 0.3 A

(ii) The magnitude of the torque,
τ = MB sin θ = 4.5 × 0.2 × sin 30°
= 0.9 × \(\frac{1}{2}\) = 0.45 N∙m

Question 8.
A rectangular coil of 10 turns, each of area 0.05 m², is suspended freely in a radial magnetic field of 0.01 Wb/m². If the torsional constant of the suspension fibre is 5 × 10^-9 N∙m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
Solution:
Data : A = 0.05 m², B = 0.01 Wb/m², N = 10, C = 5 × 10^-9 N∙m per degree,
I = 30 μA = 30 × 10^-6 A,
I = \(\left(\frac{C}{N A B}\right) \theta\)
∴ The deflection of the coil,
θ = \(\frac{N I A B}{C}=\frac{10 \times 30 \times 10^{-6} \times 0.05 \times 0.01}{5 \times 10^{-9}}\) = 30°

Question 9.
A moving-coil galvanometer has coil of area 10 cm² and 100 turns. It is suspended by a fibre of torque constant 10^-8 N∙m/degree in a radial magnetic field of induction 0.05 Wb/m². Find the angle through which the coil will be deflected when a current of 16 μA passes through it.
Solution:
Data ; A = 10^-3 m², N = 100, C = 10^-8 N∙m/degree, B = 0.05 Wb/m², 7 = 1.6 × 10^-5 A
I = \(\left(\frac{C}{N A B}\right) \theta\)
∴ The deflection of the coil,
θ = \(\frac{N I A B}{C}=\frac{(100)\left(1.6 \times 10^{-5}\right)\left(10^{-3}\right)(0.05)}{10^{-8}}\) = 8

Question 10.
A bar magnet of moment 7.5 A∙m² experiences a torque of magnitude 1.5 × 10^-4 N∙m when placed inclined at 30° in a uniform magnetic field. Find the magnitude of the magnetic induction of the field.
Solution:
Data : μ = 7.5 A∙m², τ = 1.5 × 10^-4 N∙m, θ = 30° T = μB sin θ
∴ The magnitude of the magnetic induction,

Question 11.
A circular coil, having 200 turns each of area 2.5 × 10^-4 m², carries a current of 200 μA. Initially, the coil is at rest in a magnetic field of induction 0.8 T, with its magnetic dipole moment aligned with the field. Find the work an external agent has to do to rotate the coil through (i) 90° from its initial position (ii) further 90°.
Solution:
Data : N = 200, A = 2.5 × 10^-4 m², B = 0.8T,
I = 200 μA = 2 × 10^-4 A, θ = 90°
W = ∆U =U_θ – U₀
(i) The work done to rotate through 90°,
W = U_90° – U_0° = – μB cos 90° – (- μB cos 0°)
= 0 + μB = (NIA)B (∵ μ = NIA)
= (200)(2 × 10^-4)(2.5 × 10^-4)(0.8)
= 8 × 10^-6 J = 8 μJ

(ii) The work done to rotate further through 90°, so that the dipole moment is antiparallel to the field,
W = U_80° – U_90° = – μB cos 180° – (- μB cos 90°)
= μB + 0 = (NIA)B = 8 μJ

Question 12.
A magnetic dipole of moment 0.025 J/T is free to rotate in a uniform magnetic field of induction 50 mT. When released from rest in the magnetic field, the dipole rotates to align with the field. At the instant the dipole moment is parallel to the field, its kinetic energy is 625 μJ. What was the initial angle between the dipole moment and the magnetic field?
Solution:
Data: μ = 0.025J/T, B = 50mT = 5 × 10^-2 T,
∆K = 625 pJ = 6.25 × 10^-4 J
Change in potential energy,
∆U =U_θ – U₀ = – μB cos 0° – (- μ8 cos θ)
= – μB(1 – cos θ)
By the principle of conservation of energy,
∆K + ∆U = 0
∴ ∆K = – ∆U = μB(1 – cos θ)
∴ (2.5 × 10^-2)(5 × 10^-2)(1 – cos θ) = 6.25 × 10^-4
∴ (1 – cos θ) = 0.5 ∴ cos θ = 0.5
The initial angle between the dipole moment and the magnetic field,
θ = 60° .

Question 45.
State the Bio-Savart law (Laplace law) for the magnetic induction produced by a current el-ement. Express it in vector form.
Answer:
Consider a very short segment of length dl of a wire carrying a current I. The product I\(\overrightarrow{d l}\) is called a current element; the direction of the vector \(\overrightarrow{d l}\) is along the wire in the direction of the current.

Biot-Savart law (Laplace law) : The magnitude of the incremental magnetic induction \(\overrightarrow{d B}\) produced by a current element I\(\overrightarrow{d l}\) at a distance r from it is directly proportional to the magnitude Idl of the current element, the sine of the angle between the current element I \(\overrightarrow{d l}\) and the unit vector \(\hat{r}\) directed from the current element toward the point in question, and inversely proportional to the square of the distance of the point from the current element; the magnetic induction is directed perpendicular to both I \(\overrightarrow{d l}\) and \(\hat{r}\) as per the cross product rule.

of free space. Equations (1) and (2) are called Biot-Savart law.

The incremental magnetic induction \(\overrightarrow{d B}\) is given by the right-handed screw rule of vector crossproduct I\(\overrightarrow{d l} \times \hat{\mathbf{r}}\). In below figure, the current element I \(\overrightarrow{d l}\) and \(\hat{r}\) are in the plane of the page, so that \(\overrightarrow{d B}\) points out of the page at point P shown by ⊙; at the point Q, \(\overrightarrow{d B}\) points into the page shown by ⊗.

The magnetic induction \(\vec{B}\) at the point due to the entire wire is, by the principle of superposition, the vector sum of the contributions \(\overrightarrow{d B}\) from all the current elements making up the wire.
From Eq. (2),
\(\vec{B}=\int \overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \int \frac{I \vec{d} \times \hat{\mathrm{r}}}{r^{2}}\)
[Notes : (1) The above law is based on experiments by Jean Baptiste Biot (1774-1862) and Felix Savart (1791-1841), French physicists. From their observations Laplace deduced the law mathematically. (2) The Biot- Savart law plays a similar role in magnetostatics as Coulomb’s law does in electrostatics.]

Question 46.
Using Biot-Savart’s law, obtain the expression for the magnetic induction near a straight infinite ly long current-carrying wire.
Answer:
Suppose a point P is at a distance a from a straight, infinitely long, wire carrying a current I, as shown in below figure. The incremental magnetic induction \(d \vec{B}\) at the point P due to a current element, \(I \overrightarrow{d l}\) is

At the point P, \(d \vec{B}\) is directed perpendicular to the plane of the figure and into of the page as given by the right hand rule for the direction of \(\overrightarrow{d l} \times \hat{\mathbf{r}}\).

At point P, \(d \vec{B}\) has this same direction for all the current elements into which the wire can be divided. Thus, we can find the magnitude of the magnetic field produced at P by the current elements in the lower half of the infinitely long wire by integrating dB in Eq. (2), from 0 to ∞.

Now consider a current element in the upper half of the wire, one that is as far above P as I\(\overrightarrow{d l}\) is below P. By symmetry, the magnetic field produced at P by this current element has the same magnitude and direction as that from I \overrightarrow{d l} in above figure. Thus, the magnetic field produced by the upper half of the wire is exactly the same as that produced by the lower half. Hence, the magnitude of the total magnetic field at P is

That is, the magnitude B is inversely proportional to the distance from the wire. Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the conductor; the direction of \(\vec{B}\) is everywhere tangential to such a circle. Thus, the magnetic field lines around the current in the straight wire is a family of circles centred on the wire.

[Notes : (1) The magnetic field at P due to either only the lower half or the upper half of the infinite wire in figure is half the value in Eq. (5); that is, for a semi-infinite wire,

Question 47.
Show that currents in two long, straight, parallel wires exert forces on each other. Derive the expression for the force.
OR
Derive an expression for the force per unit length between two infinitely long parallel conductors carrying current and hence define the ampere.
Answer:
When two currents pass in adjacent parallel straight conductors, we may think of each of the currents as being situated in the magnetic field caused by the other current. This results in a force on each conductor.

Consider two infinitely long, straight, parallel wires, each of length ¡ a distance s apart in vacuum, as shown in figure (a). The magnetic field around the wire 1, carrying a current I₁ has an induction of magnitude
B₁ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1}}{s}\)
Wire 2, with a current I₂ in the same direction as I₁, is situated in this field. The direction of the field
with induction \(\overrightarrow{B_{1}}\) at the position of wire 2, given by the right hand Igripi rule, is perpendicular to the plane of the two conductors, as shown. Hence, the force \(\overrightarrow{F_{2}}\) on wire 2 has a magnitude
F₂ = I₂lB₁ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2} l}{s}\) ……………… (1)
and is, by Fleming’s left hand rule, towards wire 1. Similarly, the magnetic induction \(\overrightarrow{B_{2}}\) at the position of wire 1 has a magnitude
B₂ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{2}}{s}\)
and is also directed perpendicular to the plane of the wires. Hence, the force on wire 1 has a magnitude
F₁ = I₁lB₂ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2} l}{s}\) ……………… (2)
directed towards wire 2. Thus, the two currents attract each other. \(\vec{F}_{1}=-\vec{F}_{2} \), i.e., they are equal in magnitude and opposite in direction.

Ampere found that the wires attracted each other when the currents in them were in the same direction [from figure (a )], and repelled each other when they were in the opposite directions [from figure (b)].

From the Eq. (2), the force per unit length acting on each wire is
\(\frac{F}{l}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2}}{s}\)
Using SI units, μ₀/4π = 10^-7 N / A² and, if I₁ = I₂ = 1 A and s = 1 m, then
\(\frac{F}{l}\) = 2 × 10^-7 N / m
In SI, this equation is the defining relation for the ampere.

Definition: The ampere is that constant current which if maintained in two infinitely long straight parallel wires, and placed one metre apart in vacuum, would cause each conductor to experience a force per unit length of 2 × 10^-7 newton per metre. [Note : 1 Wb/A∙m = 1 T∙m/A = l N/A².]

Question 48.
Two very long and straight parallel conductors separated by 0.5 m in vacuum carry currents 2 A and 3 A respectively. What is the force per unit length of a conductor? [\(\frac{\mu_{0}}{4 \pi}\) = 10^-7 Wb/A∙m]
Answer:
The force per unit length on each conductor,

Question 49.
Obtain an expression for the magnetic induction produced by a current in a wire in the shape of a circular arc at its centre of curvature. Hence obtain an expression for the magnetic induction at the centre of a circular coil carrying a current.
Answer:
Consider a wire in the shape of a circular arc of radius of curvature R and carrying a current I. The unit vector \(\hat{\mathrm{r}}\) from each current element I\(\overrightarrow{d l}\) towards

the centre of the loop is perpendicular to I\(\overrightarrow{d l}\), i.e., the angle θ between them is 90°. The direction of the incremental magnetic induction \(\overrightarrow{d B}\) due to each current element is in the same direction, viz., perpendicular to the plane of the loop, and out of the plane of the figure for the sense of the current shown in above figure.

Since every current element is equidistant from the centre of curvature C, the magnetic field at C due to each current element in the arc by Biot-Savart’s law is

If the arc subtends an angle 0 at its centre of curvature C, the total field at C due to all the elements on the arc is

where Φ is in radian.
The magnitude of the total induction \(\vec{B}\) at the centre of a circular coil is, from Eq. (3),

If a circular coil has N turns, each of radius r and carries a current I, the magnetic induction at its centre has a magnitude
B = \(\frac{\mu_{0} N I}{2 R}\) …………… (6)

Question 50.
Derive an expression for the magnetic induction at a point on the axis of a circular coil carrying a current.
OR
A circular coil of N turns, each of radius R, carries a current I. Derive the expression for the magnitude of the magnetic induction on the axis of the coil at a distance z. Hence obtain the expression for the magnitude of the magnetic induction for z » R.
Answer:
Consider a circular, conducting loop of radius R in the xy-plane, whose centre is at the origin. For any point P on the z-axis (which is also the axis of the loop), the current element I \(\overrightarrow{d l}\) is perpendicular to the unit vector \(\hat{\mathbf{r}}\) directed from the current element to point P. The incremental magnetic induction, \(\overrightarrow{d B}\), due to a current element at Q lies in the plane QOP, in the direction of I \(\overrightarrow{d l} \times \vec{r}\), as shown in below figure. In magnitude,

Each element of the loop has its diametrically opposed companion I \(\overrightarrow{d l}\) on the other side of the loop, both of equal segment length dl. Point P is equidistant from the two elements, that is, r = r’. Therefore, the two contributions \(\overrightarrow{d B}\) and \(\overrightarrow{d B}^{\prime}\) have equal magnitudes, and their vertical components, dB cos α and dB’cos α, are oppositely directed. Thus, they will add to zero when all the \(\overrightarrow{d B}\) contributions are summed, and there can be no vertical component of the resultant induction \(\vec{B}\). However, the horizontal components are of like direction and will sum to a definite value and hence \(\vec{B}\) will have only a horizontal z-component. For the magnitude of \(\vec{B}\), we need to add only the z-components of the \(\overrightarrow{d B}\) vectors :

For values of z that are much larger than the radius R, we may ignore the value of R in the denominator above and write
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I A}{z^{3}}\) (for z >> R) …………… (2)
For a circular coil of N turns Eqs. (1) and (2) are, respectively,
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 N I A}{\left(R^{2}+z^{2}\right)^{\frac{3}{2}}}\) and B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 N I A}{z^{3}}\)

Question 51.
How is the magnetic field of a small current loop identical to that of a short magnetic dipole? Explain.
OR
Explain the equivalence of the fields of a current-carrying circular coil and a magnetic dipole.
Answer:
An electric current in a circular loop establishes a magnetic field similar in every respect to the field of a magnetic dipole (or a bar magnet).

Consider a circular conducting ioop of radius R, axis along the x-axis and carrying a current I. The area of the loop is A = πR²and \(\vec{A}\) has the direction given by right hand rule. The axial magnetic induction of the current loop at a distance x from its centre is
\(\vec{B}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I \vec{A}}{\left(R^{2}+x^{2}\right)^{3 / 2}}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 \vec{\mu}}{\left(R^{2}+x^{2}\right)^{3 / 2}}\)
where \(\vec{M}=I \vec{A}\) is the magnetic moment of the current loop and μ₀ is the permeability of free space. For x >> R, ignoring R² in comparison with X²,
\(\vec{B}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 \vec{\mu}}{x^{3}}\)
This equation also gives the magnetic induction on the axis of a short magnetic dipole (or a bar magnet) of magnetic moment \(\vec{\mu}\).

For a magnetic dipole, the dipole moment is directed from the south pole of the dipole to its north pole. For a current loop, the magnetic dipole moment has the direction of the axial field of the current loop as given by the right-hand rule.

When an observer looking at a current carrying circular loop finds the direction of the current anticlockwise, the face of the loop towards the observer acts as the north pole. When an observer looking at a current-carrying circular loop finds the direction of the current clockwise, the face of the loop towards the observer acts as the south pole. This rule is known as the clock rule.

Question 52.
State the expressions for the axial fields of an electric dipole and a small current-loop.
Answer:
The axial far field of an electric dipole of electric dipole moment \(\vec{p}\) at an axial point r is
\(\vec{E}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \vec{p}}{r^{3}}\)
The axial magnetic field far from a small current-loop is
\(\vec{B}=\frac{\mu_{0}}{4 \pi} \frac{2 \vec{\mu}}{r^{3}}\)
where \(\vec{\mu}=I \vec{A}\) is the magnetic dipole moment of the loop, I is the current in the loop and \(\vec{A}\) is the area vector given by the right-hand rule. The axial field of an electric dipole, \(\vec{E}\) is in the direction of the dipole moment \(\vec{p}\). On the axis of a current loop, the magnetic field \(\vec{B}\) is in the direction of the dipole moment \(\vec{\mu}\).

53. Solve the following
Question 1.
(1) Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10A. Calculate the force per metre on each conductor, if the currents are in the same direction and in the opposite direction.
Solution:
Data: s = 0.4 m, I₁ = 5A, I₂ = 10A
μ₀/4π = 10^-7 N/A²
The force per unit length acting on each conductor is
\(\frac{F}{l}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2}}{s}\)
= (10^-7 N/A²) \(\frac{2(5 \mathrm{~A})(10 \mathrm{~A})}{0.4 \mathrm{~m}}\)
= 2.5 × 10^-5 N/m (= 25 μN/m)
This force is attractive if the currents are in the same direction and repulsive if the currents are in the opposite directions.

Question 2.
Two wires 12 m long and 10 cm apart carry the same current. Find the current through each wire if the force per unit length on each wire is 0.001 N/m.
Solution:
Data : l = 12 m, s = 10 cm = 0.1 m,
I₁ = I₂ = I, \(\frac{F}{l}\) = 0.001 N/m

The current through each wire is 10\(\sqrt {5}\) A.

Question 3.
The wire shown below carries a current of 2 A. The curved segment is a quadrant of radius 10 cm while the straight segments are along radii. Find the magnitude and direction of the magnetic induction at the centre O of the quadrant by the entire wire.

Solution:
Data : I = 2 A, R = 10 cm = 10^-1 m
The point O lies along the straight segments AB and CD. Hence, the magnetic induction \(\vec{B}\) produced by each of them is zero.

Since θ = 90°, the magnitude of the magnetic induction due to the current in quadrant BC is \(\frac{1}{4}\)th of that produced at the centre of a loop.

Question 4.
A flat coil of 70 turns has a diameter of 20 cm and carries a current of 5 A. Find the magnitude of the magnetic induction at (a) the centre of the coil (b) a point on the axis 20 cm from the centre of the coil.
Solution:
Data : N = 70, R = 10 cm = 0.1 m, I = 5 A, z = 0.2 m, μ₀ = 4π × 10^-7 T∙m/A
(a) At the centre of the coil:
The magnitude of the magnetic induction,

Question 5.
(12) A current of 10 A passes through a coil having 5 turns and produces a magnetic field of magnitude 0.5 × 10^-4 T at the centre of the coil. Calculate the diameter of the coil.
Solution:
Data: I = 10A, N = 5, B = 5 × 10^-5 T,
μ₀/4π = 10^-7 T∙m/A
B = \(\frac{\mu_{0} N I}{2 R}\)
∴ The diameter of the coil,
2R = \(\frac{\mu_{0} N I}{B}=\frac{\left(4 \pi \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} / \mathrm{A}\right)(5)(10 \mathrm{~A})}{5 \times 10^{-5} \mathrm{~T}}\)
= 4 × 3.142 × 10^-1 = 1.257 m

Question 6.
Calculate the magnitude of the magnetic induction due to a circular coil of 400 turns and radius 0.05 m, carrying a current of 5 A, at a point on the axis of the coil at a distance 0.1 m.
Solution:
Data : N = 400, R = 0.05 m = 5 × 10^-2 m,
I = 5 A, z = 0.1 m, μ₀/4π = 10^-7 T∙m/A
The magnitude of the magnetic induction,

Question 7.
A circular coil of wire has 100 turns. The radius of the coil is 50 cm. It is desired to have a magnetic induction of 80 μT at the centre of the coil. What should be the current through the coil ?
Solution:
Data: N = 100, R = 50 cm = 0.5 m,
B = 80 μT = 8 × 10^-5 T, μ₀/4π = 10^-7 T∙m/A

Question 54.
State and explain Ampere’s circuital law.
OR
State Ampere’s circuital law.
Answer:
Ampere’s circuital law : In free space, the line integral of magnetic induction around a closed path in a magnetic field is equal to p0 times the net steady current enclosed by the path.
In mathematical form,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀I …………. (1)
where \(\vec{B}\) is the magnetic induction at any point on the path in vacuum, \(\overrightarrow{d l}\) is the length element of the path, I is the net steady current enclosed and p0 is the permeability of free space.

Explanation : Below figure shows two wires carrying currents I₁ and I₂ in vacuum. The magnetic induction \(\vec{B}\) at any point is the net effect of these currents.

To find the magnitude B of the magnetic induction :
(i) We construct an imaginary closed curve around the conductors, called an Amperian loop, and imagine it divided into small elements of length dl. The direction of \(\overrightarrow{d l}\) is the direction along which the loop is traced.

(ii) We assign signs to the currents using the right hand rule : If the fingers of the right hand are curled in the direction in which the loop is traced, then a current in the direction of the outstretched thumb is taken to be positive while a current in the opposite direction is taken to be negative.

For each length element of the Amperian loop, \(\vec{B} \cdot \overrightarrow{d l}\) gives the product of the length dl of the element and the component of \(\vec{B}\) parallel to \(\overrightarrow{d l}\). If θ is the angle between \(\overrightarrow{d l}\) and \(\vec{B}\),
\(\vec{B} \cdot \overrightarrow{d l}\) = (B cos θ) dl
Then, the line integral,
\(\oint \vec{B} \cdot \overrightarrow{d l}=\oint\) Bcosθ dl ……………(2)
For the case shown in figure, the net current I through the surface bounded by the loop is
I = I₂ – I₁
∴ \(\oint\) Bcosθ dl = μ₀ I
= μ₀(I₂ – I₁) ……………. (3)
Equation (3) can be solved only when B is uniform and hence can be taken out of the integral.

[Note : Ampere’s law in magnetostatics plays the part of Gauss’s law of electrostatics. In particular, for currents with appropriate symmetry, Ampere’s law in integral form offers an efficient way of calculating the magnetic field. Like Gauss’s law, Ampere’s law is always true (for steady currents), but it is useful only when the symmetry of the problem enables B to be taken out of the integral \(\oint \vec{B} \cdot \overrightarrow{d l}\). The current configurations that can be handled by Ampere’s law are infinite straight conductor, infinite plane, infinite solenoid and toroid.]

Question 55.
Using Ampere’s law, obtain an expression for the magnetic induction near a current-carrying straight, infinitely long wire.
Answer:
Consider a point P at a distance a from a straight, infinitely long wire carrying a current I in free space, from figure (a). Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the wire. We, therefore, choose an Amperian loop a circle of radius a centred on the wire with its plane perpendicular to the wire, as shown in from figure (b).

since cos θ = 1 and B has the same value around the path. \(\oint\) dl gives the circumference of the circular loop.

In the figure, the Amperian loop is traced in the anticlockwise sense, so that the current I is taken as positive in accordance with the right hand rule.
By Ampere’s law,

This is the required expression.

Question 56.
What is a solenoid? With a neat labelled diagram, describe the magnetic field produced by a current-carrying solenoid.
Answer:
A solenoid is a long wire wound in the form of a helix. An ideal solenoid is tightly wound and infinitely long, i.e., its turns are closely spaced and the solenoid is very long compared to its crosssectional radius.

Each turn of a solenoid acts approximately as a circular loop. Suppose the solenoid carries a steady current I. The net magnetic field due to the current in the solenoid is the vector sum of the fields due to the current in all the turns. In the case of a tightly- wound solenoid of finite length, Fig. 10.39, the magnetic field lines are approximately parallel only near the centre of the solenoid, indicating a nearly uniform field there. However, close to the ends, the field lines diverge from one end and converge at the other end. This field distribution is similar to that of a bar magnet. Thus, one end of the solenoid behaves like the north pole of a magnet and the opposite end behaves like the south pole. The field outside is very weak near the midpoint.

For an ideal solenoid, the magnetic field inside is reasonably uniform over the cross section and parallel to the axis throughout the volume enclosed by the solenoid. The field outside is negligible in this case.

Question 57.
Using Ampere’s law, derive an expression for the magnetic induction inside an ideal solenoid carrying a steady current.
Answer:
An ideal solenoid is tightly wound and infinitely long. Let n be the number of turns of wire per unit length and I be the steady current in the solenoid.

For an ideal solenoid, the magnetic induction \(\vec{B}\) inside is reasonably uniform over the cross section and parallel to the axis throughout the volume enclosed by the solenoid; \(\vec{B}\) outside is negligible.

As an Amperian loop, we choose a rectangular path PQRS of length l parallel to the solenoid axis, from below figure. The width of the rectangle is taken to be sufficiently large so that the side RS is far from the solenoid where \(\vec{B}\) = 0. The line integral of the magnetic induction around the Amperian loop in the sense PQRSP is


Thus, from Eqs. (1), (2), (3) and (4),
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = Bl ……….. (5)
The total current enclosed by the Amperian loop is
I_encl = current through each turn × number of turns enclosed by the loop
= I × nl = nlI ……… (6)
By Ampere’s law,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀I_encl (in vacuum)
Therefore, from Eq.s (5) and (6),
Bl = μ₀ nlI
∴ B = μ₀nI …………. (7)
This is the required expression.

[Notes : (1) The field inside an ideal solenoid is uniform-it doesn’t depend on the distance from the axis. In this sense, the solenoid is to magnetostatics what the parallel-plate capacitor is to electrostatics; a simple device for producing strong uniform fields. (2) At an axial point at the end of a long solenoid, B = \(\frac{1}{2}\) μ₀nI]

Question 58.
What is the magnetic field (i) outside (ii) inside a long air-cored current-carrying solenoid ?
Answer:
For an ideal solenoid, the magnetic field induction outside is negligible, nearly zero. Inside the solenoid, the field lines are parallel to the axis of the solenoid and the magnitude of the magnetic induction, B = μ₀nI, where μ₀ is the permeability of free space, n is the number of turns of wire per unit length and I is the steady current in the solenoid.

Question 59.
What is a toroid? With a neat diagram, describe the magnetic field produced by a toroid carrying a steady current.
Answer:
A toroid is a toroidal solenoid. An ideal toroid consists of a long conducting wire wound tightly around a torus, a doughnut-shaped ring, made of a nonconducting material.

In an ideal toroid carrying a steady current, the magnetic field in the interior of the toroid is tangential to any circle concentric with the axis of the toroid and has the same value on this circle (the dashed line in above figure). Also, the magnitude of the magnetic induction external to the toroid is negligible.

Question 60.
Using Ampere’s law, derive an expression for the magnetic induction inside an ideal toroid carrying a steady current.
Answer:
An ideal toroid consists of a long conducting wire wound tightly around a torus made of a non-conducting material. When a steady current is passed through it, the magnetic induction \(\vec{B}\) in the interior of the toroid is tangent to any circle concentric with y the axis of the toroid and has the same value on this circle.

Suppose the toroid has N turns of wire and I is the current in its coil. As our Amperian loop, we choose a circle of radius r concentric with the axis of the toroid, as shown in figure. Since \(\vec{B}\) has the same value on this circle and is tangential to it, we go around this path in the direction of \(\vec{B}\) so that \(\vec{B}\) and \(\overrightarrow{d l}\) are parallel. Then, the line integral of the magnetic induction around the Amperian loop is

The net current enclosed by the Amperean loop is
I_encl = current through each turn × number of turns enclosed by the loop
= I × N = NI …………….. (2)
By Ampere’s law,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀ I_encl (in free space)
Therefore, from Eqs. (1) and (2),
B (2πr) = μ₀NI
∴ B = \(\frac{\mu_{0}}{2 \pi} \frac{N I}{r}\) …………… (3)
This is the required expression.

61. Solve the following

Question 1.
Four long parallel wires are arranged at the four comers of a square ABCD of side 20 cm. Each wire carries a current of 5 A. Currents in the conductors 1 and 2, at comers A and B, are out of the page while those in the conductors 3 and 4, at comers C and D, are into the page. What is the magnitude of the magnetic induction at the centre of the square?
Solution:
Data : 2l = 20 cm = 0.2 m, I = 5 A
If each side of the square array is 2l, then from geometry, the centre of the square O is a distance \(\sqrt {2}\)l from each corner. Since each wire carries the same current, B₁ = B₂ = B₃ = B₄. Using the right hand [grip] rule, the directions of the magnetic inductions due to conductors 1 and 3 are along OB, while those due to conductors 2 and 4 are along OC, as shown.

This is also the magnitude of the magnetic induc-tion along OC, B₂ + B₄.

Their components parallel to AD (or BC) are oppositely directed and cancel out. Therefore, the total induction at the centre of the square has a magnitude equal to the sum of the components parallel to AB (or DC).

The magnitude of the magnetic induction at the centre of the square is 2 × 10^-5 T.

Question 2.
Two long straight parallel wires in vacuum are 4 m apart and carry currents of 2 A and 6 A in the same direction. Find the neutral point, i.e., the point at which the resultant magnetic induction is zero.
Solution:
Data: I₁ =2 A, I₂ = 6 A, a =4 m
The currents through the wires are in the same direction. Therefore, the two magnetic inductions \(\overrightarrow{B_{1}}\) and \(\overrightarrow{B_{2}}\) will have opposite directions at any point between the two wires. Hence, the point must lie between the two wires. For the resultant magnetic induction to be zero, we must have B₁ = B₂. Let the corresponding point (the neutral point) be at a distance a₁ from the first wire and a₂ from the second wire.

The neutral point lies at a distance of 1 m from the wire carrying a current of 2 A.

Question 3.
A solenoid 1.5 m long and 4 cm in diameter has – 10 turns/cm. A current of 5 A is passing through it. Calculate the magnetic induction (i) inside (ii) at one end on the axis of the solenoid.
Solution:
Data : L = 1.5 m, r = 2 cm, n = 10 turns/cm = 10³ turns/metre, I = 5 A, μ₀ = 4π × 10^-7 T∙m/A
Since the diameter is very small compared to its length, we approximate the solenoid to be long, i.e., an ideal solenoid.

(i) At an axial point well inside a long solenoid,
B = μ₀nI
= (4π × 10^-7 )(10³)(5) = 2 × 3.142 × 10^-3
= 6.284 × 10^-3 T

(ii) At an axial point at the end of a long solenoid,
B = \(\frac{1}{2}\) μ₀nI
= \(\frac{1}{2}\) (6.284 × 10^-3) = 3.142 × 10^-3 T

Question 4.
A toroidally wound coil has an inner radius of 15 cm, an outer radius of 20 cm and is wound with 1500 turns of wire. What is the magnitude of the magnetic induction at the centre of the coil when the current in the winding is 10 A ?
Solution:
Data : Central radius, r = \(\frac{1}{2}\) (15 + 20) = 17.5 cm
= 0.175 m, N = 1500, I = 10 A, \(\frac{\mu_{0}}{4 \pi}\) = 10^-7 T∙m/A
The magnetic induction,
B = \(\frac{\mu_{0} N I}{2 \pi r}=\frac{\mu_{0}}{4 \pi} \frac{2 N I}{r}=10^{-7} \times \frac{2 \times 1500 \times 10}{0.175}\)
= 1.714 × 10^-2 T

Multiple Choice Questions

Question 1.
A doubly ionized helium nucleus (charge = 3.2 × 10^-19 C) enters a region of uniform magnetic field with a velocity (10³ m/s)\(\hat{\mathbf{i}}\). The magnetic induction in the region is 20 mT directed towards the positive x-axis. The force on the ion is
(A) (6.4 × 10^-18 N) \(\hat{\mathrm{j}}\)
(B) (6.4 × 10^-18 N) \(\hat{\mathrm{k}}\)
(C) zero
(D) none of these.
Answer:
(C) zero

Question 2.
In a cyclotron, charged particles are accelerated by
(A) the electrostatic deflector plate
(B) the electric field in the dees
(C) the magnetic field in the dees
(D) the p.d. across the gap between the dees.
Answer:
(D) the p.d. across the gap between the dees.

Question 3.
Cyclotron cannot accelerate
(A) protons
(B) neutrons
(C) α-particles
(D) deuterons.
Answer:
(B) neutrons

Question 4.
If R is the radius of the dees and B the magnitude of the magnetic field induction in which positive charges (q) of mass m escape from the cyclotron, then their maximum speed v_max is
(A) \(\frac{q R}{B m}\)
(B) \(\frac{q m}{B R}\)
(C) \(\frac{q B R}{m}\)
(D) \(\frac{m}{q B R}\)
Answer:
(C) \(\frac{q B R}{m}\)

Question 5.
A charged particle moving with a velocity \(\vec{v}\) enters a region of uniform magnetic field \(\vec{B}\). If the velocity has a component parallel to \(\vec{B}\), which of the following quantities is independent of \(\overrightarrow{\mid v} \mid\)?
(A) Period T of its circular motion
(B) Pitch p of its helical path
(C) Radius r of its helical path
(D) Both p and T
Answer:
(A) Period T of its circular motion

Question 6.
A charged particle moving with a velocity \(\vec{v}\) enters a region of uniform magnetic field \(\vec{B}\) such that the pitch of the resulting helical motion is equal to the radius of the helix. The angle between \(\vec{v}\) and \(\vec{B}\) is
(A) tan^-1 2π
(B) sin^-1 2π
(C) tan^-1 \(\frac{1}{2 \pi}\left(\frac{q B}{m}\right)^{2}\)
(D) tan^-1 2π\(2 \pi\left(\frac{q B}{m}\right)^{2}\).
Answer:
(A) tan^-1 2π

Question 7.
The following four cases show a positive charge moving into a magnetic field \(\vec{B}\) with velocity \(\vec{v}\). In which of the cases are the forces opposite in direction?

(A) (iii) and (iv)
(B) (i) and (ii)
(C) (i) and (iii)
(D) (ii) and (iv)
Answer:
(B) (i) and (ii)

Question 8.
A charged particle enters a uniform magnetic field initially travelling perpendicular to the field lines and is bent in a circular arc of radius R. If the particle had the same charge but double the mass and were travelling twice as fast, the radius of its circular arc would be
(A) 2R
(B) 4R
(C) R
(D) \(\frac{1}{4}\)R.
Answer:
(B) 4R

Question 9.
A straight wire along the y-axis carries a current of 4 A. The wire is placed in a uniform magnetic field (0.02 T) \((\hat{\mathrm{i}}+\hat{\mathrm{j}})\). If the current in the wire is directed towards the negative y-axis, the force per unit length on the wire is
(A) zero
(B) – (0.08 N/m) \(\hat{\mathrm{k}}\)
(C) (0.08 N/m) \((\hat{\mathrm{i}}-\hat{\mathrm{j}})\)
(D) (0.08 N/m) \(\hat{\mathrm{k}}\)
Answer:
(D) (0.08 N/m) \(\hat{\mathrm{k}}\)

Question 10.
A 30-turn coil of diameter 2 cm carries a current of 10 mA. When it is placed in a uniform magnetic field of 0.05 T, the magnitude of the maximum torque that could be exerted on the coil by the magnetic field is
(A) 1.88 × 10^-5 N∙m
(B) 4.7 × 10^-6 N∙m
(C) 4.7 × 10^-7 N∙m
(D) 1.88 × 10^-8 N∙m.
Answer:
(B) 4.7 × 10^-6 N∙m

Question 11.
A circular loop of area \(\sqrt{2}\) cm² and carrying a current of 10 μA is placed in a magnetic field \(\vec{B}\) with its plane parallel to \(\vec{B}\) (B = 15 mT). When the loop has rotated through an angle of 45°, the magnitude of the torque exerted on this loop is
(A) zero
(B) 15 × 10^-12 N∙m
(C) 15 × 10^-8 N∙m
(D) 15 × 10^-2 N∙m
Answer:
(B) 15 × 10^-12 N∙m

Question 12.
A current loop of magnetic dipole moment 0.1 A-m2 is oriented with the plane of the loop perpendicular to a uniform 1.50 T magnetic field, as shown. The torque that the magnetic field exerts on the current loop is

(A) 0.15 N∙m
(B) 0.075 N∙m
(C) -0.075 N∙m
(D) -0.15 N∙m.
Answer:
(B) 0.075 N∙m

Question 13.
A rectangular coil of dipole moment fi, free to rotate, is placed in a uniform magnetic field B with its plane parallel to the magnetic lines of force. Then, the coil will
(A) rotate to maximize the magnetic flux through its plane
(B) rotate to minimize the magnetic flux through its plane
(C) not experience any torque
(D) experience a constant torque equal to μB.
Answer:
(C) not experience any torque

Question 14.
When a current is passed through a suspended moving-coil galvanometer, the deflection of the coil is arrested by
(A) the elastic torsion of the suspension fibre
(B) the elastic winding of the helical spring
(C) the friction at the point of suspension
(D) the changing magnetic flux through the coil.
Answer:
(A) the elastic torsion of the suspension fibre

Question 15.
When a current is passed through a suspended moving-coil galvanometer, the deflection of the coil is 9. Then, in the usual notation, the expression \(\frac{\mu B}{\theta}\) is
(A) the torsion constant of the helical spring
(B) the magnetic dipole moment of the current-carrying coil
(C) the current through the coil
(D) the torsion constant of the suspension fibre.
Answer:
(D) the torsion constant of the suspension fibre.

Question 16.
The magnetic potential energy of a coil of dipole moment \(\vec{\mu}\) and area vector \(\vec{A}\) placed in a magnetic \(\vec{B}\) is maximum for which of the following cases ?

Answer:
(C) \(\vec{B} \uparrow \downarrow \vec{A}\)

Question 17.
Two points, A and B, are at distances r_A and r_B from a long, straight, current-carrying conductor. If r_B = 2 r_A, the magnitudes of the magnetic inductions at the two points are related by
(A )B_A = B_B
(B) B_A = 2B_B
(C) B_A = 4B_B
(D) B_B = 2B_A
Answer:
(B) B_A = 2B_B

Question 18.
Two long, straight, parallel wires are 5 cm apart and carry currents I₁ and I₂ in the same direction. If 2I₁ = 3I₂, then at a point P, 2 cm from wire 2,

Answer:
(B) \(\overrightarrow{B_{1}}=-\overrightarrow{B_{2}}\)

Question 19.
A wire of length L is first formed into a loop of one turn and then as a loop of two turns. The same current I is passed through the wire in the two cases. The ratio of the magnitude of the magnetic field induction at the centre of the single-turn loop to that at the centre of the double-turn loop is
(A) 4
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
(D) \(\frac{1}{4}\)

Question 20.
Two circular coils 1 and 2 have both their radii and number of turns in the ratio 1 : 2. If the currents in them are in the ratio 2: 1, the magnitudes of the magnetic inductions at the centres of the coils are in the ratio
(A) 1 : 1
(B) 2 : 1
(C) 1 : 2
(D) 1 : 8.
Answer:
(B) 2 : 1

Question 21.
Three straight, parallel wires are coplanar and perpendicular to the plane of the page. The currents I₁ and I₃ are directed out of the page. If the wire 3 experiences no force due to the currents I₁ and I₂, then the current in the wire 2 is

(A) I₂ = 2I₁ and directed into the page
(B) I₂ = 0.5I₁ and directed into the page
(C) I₂ = 2I₁ and directed out of the page
(D) I₂ = 0.5I₁ and directed out of the page.
Answer:
(B) I₂ = 0.5I₁ and directed into the page

Question 22.
Two diametrically opposite points of a uniform metal ring (radius, R) are connected to the terminals of a battery. If the current drawn from the battery is I, the magnetic induction at the centre of the ring has a magnitude
(A) \(\frac{\mu_{0} I}{R}\)
(B) \(\frac{\mu_{0} I}{2R}\)
(C) \(\frac{\mu_{0} I}{4R}\)
(D) zero
Answer:
(D) zero

Question 23.
Two circular coaxial coils, each of N turns and radius R, are separated by a distance R. They carry equal currents I in the same direction. If the magnetic induction at P, on the common axis and midway between the coils, due to the left hand coil is B, then the total induction at P is

(A) 2B
(B) B
(C) \(\frac{1}{2}\) B
(D) zero.
Answer:
(A) 2B

Question 24.
A toroid with a circular cross section has a current I in its windings. The total number of windings is N. The total current through an Amperian loop of radius r equal to the mean radius of the toroid is
(A) zero
(B) I
(C) NI
(D) \(\frac{N I}{2 \pi r}\)
Answer:
(C) NI

Question 25.
A very long solenoid has 8400 windings and a length of 7 m. If the field inside is 2ir x iO T, the current in the windings is about
[μ₀/4π = 10^-7 T∙m/A]
(A) 0.42 A
(B) 0.83 A
(C) 4.2 A
(D) 8.3 A.
Answer:
(C) 4.2 A

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 3 Kinetic Theory of Gases and Radiation Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 3 Kinetic Theory of Gases and Radiation

Question 1.
What is an ideal or perfect gas ? Explain.
Answer:
An ideal or perfect gas is a gas which obeys the gas laws (Boyle’s law, Charles’ law and Gay-Lussac’s law) at all pressures and temperatures. An ideal gas cannot be liquefied by application of pressure or lowering the temperature.

A molecule of an ideal gas is an ideal particle having only mass and velocity. Its structure and size are ignored. Also, intermolecular forces are zero except during collisions.

Question 2.
Derive the ideal gas equation, PV = nRT.
OR
Derive the equation of state for an ideal gas
Answer:
Let P₁, V₁ and T₁ be the pressure, volume and absolute temperature (thermodynamic temperature) of n moles of a gas (assumed to be ideal).
Suppose the gas is heated at constant pressure (P₁) so that its temperature becomes T and volume becomes V₂. Then by Charles’ law,\(\frac{V_{2}}{V_{1}}\) = \(\frac{T}{T_{1}}\).
∴ T = \(\frac{V_{2}}{V_{1}}\)T₁ … (1)
Now, suppose that the gas is heated at constant volume (V₂) so that its temperature becomes T₂ and pressure becomes P₂. Then by Gay—Lussac’s law,
\(\frac{P_{2}}{P_{1}}\) = \(\frac{T_{2}}{T}\)
∴ T = \(\frac{P_{1}}{P_{2}}\)T₂ … (2)
From equations (1) and (2), we get,
\(\frac{V_{2}}{V_{1}}\)T₁ = \(\frac{P_{1}}{P_{2}}\)T₂
∴ \(\frac{P_{2} V_{2}}{T_{2}}\) = \(\frac{P_{1} V_{1}}{T_{1}}\)
When pressure and temperature are constant, V ∝ n. Hence, in general, we can write \(\frac{P V}{T}\) = nR, where R is a proportionality constant, called the universal gas constant.
Thus, PV = nRT for an ideal gas. This is the equation of state for an ideal gas.

[ Note : By Boyle’s law, for a fixed mass of gas at constant temperature, PV = constant. Writing PV ∝ nT, we get PV = nRT.]

Question 3.
Express the ideal gas equation in terms of
(i) the Avogadro number
(ii) The Boltzmann constant.
Answer:
In the usual notation, PV = nRT;
(i) Now, the number of moles, n = \(\frac{N}{N_{\mathrm{A}}}\), where N is the number of molecules corresponding to n moles of the gas and N_A is the Avogadro number.
∴ PV = \(\frac{N}{N_{\mathrm{A}}}\)RT

(ii) PV = \(\frac{N}{N_{\mathrm{A}}}\)RT = N(\(\frac{R}{N_{\mathrm{A}}}\))T
= Nk_BT, where k_B = \(\frac{R}{N_{\mathrm{A}}}\) is the Boltzmann constant.

Question 4.
Express the ideal gas equation in terms of the density of the gas.
Answer:
In the usual notation, PV = nRT. Now, the number of moles n = \(\frac{M}{M_{0}}\), where M is the mass of the gas M₀ corresponding to n moles and M₀ is the molar mass of the gas.

is the density of the gas.

Notes :

(1) Charles’ law : At a constant pressure, the volume of a fixed mass of gas is directly proportional to its absolute temperature (thermodynamic temperature).
If V is the volume of n moles of an ideal gas at a pressure P and T denotes its absolute temperature, P and n remaining constant,
V ∝ T or \(\frac{V}{T}\) = constant

The law was deduced experimentally in 1787 by Jacques Alexandre Cesar Charles (1746 -1823), French physicist.

From Charles’ law, V = KT, where K is a constant which depends on the mass and pressure. If M and ρ are the mass and mass per unit volume of a gas, V = M/ρ.

Charles’ law was properly established only after the publication in 1802 of more accurate experimental results by Joseph Gay-Lussac (1778-1850), French chemist. Hence, the law is also known as Gay-Lussac’s law.

(2) The Boltzmann constant is the ratio of the molar gas constant (R) to the Avogadro constant (Avogadro number) (NA). Its symbol is k_B or k.
k_B = 1.380 648 8(13) × 10^-23 JK^-1

It is a fundamental physical constant relating the average energy of a molecule (at the microscopic level) with temperature (a state variable, at the macroscopic level). It can be called the gas constant per molecule. It is named after Ludwig Eduard Boltzmann (1844-1906), Austrian physicist.

Question 5.
State the basic assumptions of the kinetic theory of gases.
Answer:
The basic assumptions of the kinetic theory of an ideal gas :

1. A gas of a pure material consists of an extremely large number of identical molecules.
2. A gas molecule behaves as an ideal particle, i.e., it has mass but its structure and size can be ignored as compared with the intermolecular separation in a dilute gas and the dimensions of the container.
3. The molecules are in constant random motion with various velocities and obey Newton’s laws of motion.
4. Intermolecular forces can be ignored on the average so that the only forces between the molecules and the walls of the container are contact forces during collisions. It follows that between successive collisions, a gas molecule travels in a straight line with constant speed.
5. The collisions are perfectly elastic conserving total momentum and kinetic energy, and the duration of a collision is very small compared to the time interval between successive collisions.

Notes :

(1) The walls of the container holding the gas are assumed to be rigid and infinitely massive so that they do not move. (2) Assumption (2) allows us to ignore intermolecular collisions because if they are truly point like (i.e., of negligible extent) they cannot make contact with each other. Therefore, the only collisions we consider are those with the walls of the container. If these collisions are perfectly elastic [by assumption (5)], they only change the direction of the velocity of a gas molecule and a gas molecule possesses only kinetic energy by assumption
(4). The kinetic theory of gases was developed by Daniel Bernoulli (1700 – 82), Swiss mathematician, Rudolf Clausius (1822 – 88), German theoretical physicist, James Clerk Maxwell (1831-79), British physicist, Ludwig Eduard Boltzmann, Josiah Willard Gibbs (1839-1903), US physical chemist.]

Question 6.
Distinguish between an ideal gas and a real gas.
Answer:

Ideal Gas	Real Gas
1. Molecules of an ideal gas behave as ideal particles, i.e., they are like geometrical points without size and structure.	1. Molecules of a real gas have finite size and structure.
2. Molecules of an ideal gas have only translational motion.	2. Polyatomic molecules have in general, translational, vibrational and rotational motion.
3. There are no intermolecular forces in this case.	3. Intermolecular forces are non-zero in this case.
4. An ideal gas cannot be liquefied.	4. A real gas can be liquefied and also solidified in many cases, by application of pressure and reducing temperature.
5. There are no intermolecular collisions in this case.	5. There are intermolecular collisions in this case, and under normal conditions the collision frequency is very high.
6. In the absence of intermolecular forces, the internal energy of the gas is only kinetic.	6. Due to the intermolecular forces, the internal energy of the gas is (potential energy + kinetic energy.)

Question 7.
The pressure exerted by a certain mass of enclosed gas at 300 K is 5 × 10⁴ Pa. What will be the pressure exerted by the gas at 600 K if the volume of the gas is kept constant ?
Answer:
Here, P ∝ T ∴\(\frac{P_{2}}{P_{1}}\) = \(\frac{T_{2}}{T_{1}}\) = \(\frac{600}{300}\) = 2
∴ P₂ = 2P₁ = 2 × 5 × 10⁴ Pa = 10⁵ Pa is the required pressure.

Question 8.
Solve the following :

Question 1.
16 g of oxygen occupy 0.025 m3 at 27 °C. Find the pressure exerted by it.
[Molar mass of oxygen = 32 g/mol, universal gas constant R = 8.3 J/mol.K]
Solution :
Data : M = 16 g, M₀ = 32 g/mol, V = 0.025 m³,
T = 27 °C = (273 + 27) K = 300 K,R = 8.3 J/mol.K
PV = nRT, where number of moles, n = \(\frac{M}{M_{0}}\)
∴ The pressure exerted by the gas,

[Note : 1 Pa = 1 N/m²]

Question 2.
Two tanks of equal volume contain equal masses of oxygen and nitrogen at 127 °C. Find the ratio of
(i) the number of molecules of the gases
(ii) the pressure exerted by the gases in the two tanks. [Molar mass of oxygen = 32 g/mol, molar mass of nitrogen = 28 g/mol]
Solution :
Data : M₀ = M_N (equal masses of the two gases), equal volumes and the same temperature,
M₀₁ (Oxygen) = 32 g/ mol,
M₀₂(nitrogen) = 28 g/mol
Let N₁ and N₂ be the number of molecules of oxygen and nitrogen, n₁ and n₂ the respective number of moles, and N_A the Avogadro number.

This is the ratio of the number of oxygen-molecules to that of nitrogen.

(ii) Using the ideal gas equation, PV = nRT,
P₁ = n₁\(\frac{R T}{V}\) and P₂ = n₂\(\frac{R T}{V}\) … (3)
since the gases occupy the same volume V and are at the same temperature T.

This is the corresponding pressure ratio.

Question 3.
A room is to be prepared for a birthday party filled with helium balloons. Some balloons are filled to occupy 0.240 m³ when the pressure inside them is 0.038 atm and the constant temperature of the room is 70 °F. With what pressure should the larger balloons be filled with helium so that they occupy 0.400 m³ ?
Solution :
Data : V₁ = 0.240 m³, P₁ = 0.038 atm, temperature = 70 °F, V₂ = 0.400 m³
At constant temperature, by Boyle’s law,
P₂V₂ = P₁V₁
∴ Hence, the pressure of helium inside the larger balloons,
∴ P₂ = \(\frac{P_{1} V_{1}}{V_{2}}\) = \(\frac{(0.038)(0.240)}{0.400}\)
= 0.038 × 0.6 = 0.0228 atm

Question 4.
Determine the pressure exerted by 4 grams of hydrogen occupying a volume of 16 litres at 10 °C. (R = 8.314 J/mol.K, molar mass of hydrogen = 2 g/mol)
Solution :
Data : Mass of hydrogen = 4 grams,
V = 16 litres = 16 × 10^-3 m³,
T = 273 + 10 = 283 K, M₀ = 2 g/mol,
R = 8.314 J/mol.K
Number of moles (n) = \(\frac{\text { mass }}{M_{0}}\) = \(\frac{4}{2}\) = 2
PV = nRT ∴ P = \(\frac{n R T}{V}\) = \(\frac{2 \times 8.314 \times 283}{16 \times 10^{-3}}\)
P = 2.941 × 10⁵ N/m²
This is the pressure exerted by the gas.

Question 5.
Find the number of molecules per m3 of a gas at STP.
[Given : 1 atmosphere = 1.013 × 10⁵ N/m² N_A = 6.022 × 10²³ per mole, R = 8.314 J/mol.K]
Solution :
Data : P = 1.013 × 10⁵ N/m²,
N_A = 6.022 × 10²³ per mole,
R = 8.314 J/mol.K, T = 273 K
Number of molecules per m³,

= 2.688 × 10²⁵ molecules/m³
[ Note : STP means Standard temperature (0°C) and pressure (1 atmosphere).]

Question 6.
Explain the concept of free path of a gas molecule. Define free path and mean free path. State the expression for mean free path.
Answer:
Molecules of a real gas’ are not point like particles. For simplicity, molecules are assumed to be spherical. Because of their finite size, two molecules collide with each other when they come within a molecular diameter of each other, strictly speaking, within the sphere of influence of each molecule.
The molecular collisions, though perfectly elastic, result in significant changes in the speeds and

directions of motion of the molecules. Hence, every molecule follows a zigzag path, with abrupt changes in its speed and direction of motion at short and random time intervals. This is called Brownian motion.

Free path : The straight line path of a molecule, i.e., the distance covered by it between successive collisions, is called a free path.

Mean free path : The average distance travelled by a gas molecule between successive collisions, the average being taken over a large number of free paths (or collisions) is called the mean free path.

Maxwell, on the basis of the law of distribution of molecular speeds, obtained the formula for the mean free path (λ) as λ = \(\frac{1}{\sqrt{2} \pi d^{2}(N / V)}\), where N is the number of molecules in volume V of the gas and d is the diameter of a molecule.

[Note : Brownian motion is named after Robert Brown (1773-1858), British botanist, who, in 1827, observed under the microscope the random movement of pollen grains suspended in water. ]

Question 7.
Express the mean free path of a gas molecule in terms of pressure and temperature.
Answer:
In the usual notation, the mean free path of a gas molecule,

Question 8.
Express the mean free path of a gas molecule in terms of the density of the gas
Answer:
In the usual notation, the mean free path of a gas molecule,
λ = \(\frac{1}{\sqrt{2} \pi d^{2}(N / V)}\)
Density, ρ, of the gas = \(\frac{\text { mass }}{\text { volume }}\)
= \(\frac{m N}{V}\), where m is the molecular mass.
∴ \(\frac{N}{V}\) = \(\frac{\rho}{m}\)
∴ λ = \(\frac{m}{\sqrt{2} \pi d^{2} \rho}\)

Question 9.
State the factors on which the mean free path of a gas molecule depends.
Answer:
The mean free path of a gas molecule depends upon the number of molecules per unit volume of the gas and molecular diameter.

Question 10.
What happens to the mean free path of a gas molecule if there is

1. increase in temperature at constant pressure
2. increase in pressure at constant temperature?

Answer:

1. The mean free path increases,
2. The mean free path decreases.

Question 9.
Solve the following :

Question 1.
Calculate the mean free path of a gas molecule if the molecular diameter is 5A and the number of molecules per unit volume of the gas is 2 × 10²⁴ per m³. Compare it with molecular diameter.
Solution :
Data : d = 5Å = 5 × 10^-10m, \(\frac{N}{V}\) = 2 × 10²⁴ per m³

[Note : 1Å = 10^-10m, 1 nm = 10^-9 m = 10 Å]

Question 2.
If the mean free path of a gas molecule under certain conditions is 5000Å and the molecular speed is 500 mIs, find
(i) the time interval between successive collisions
(ii) the collision frequency (number of collisions per unit time) of a gas molecule.
Solution :
Data : λ = 5000 Å = 5000 × 10^-10 m
= 5 × 10^-7 m, v = 500 m/s
(i) speed (v) = \(\frac{\text { distance }(\lambda)}{\text { time }(T)}\)
∴ The time interval between successive collisions of a gas molecule, T = \(\frac{\lambda}{v}\)
= \(\frac{5 \times 10^{-7} \mathrm{~m}}{500 \mathrm{~m} / \mathrm{s}}\) = 10^-9 s

(ii) The collision frequency (number of collisions per unit time) of a gas molecule,
f = \(\frac{1}{T}\) = \(\frac{1}{10^{-9} \mathrm{~s}}\) = 10⁹ collisions per second

Question 3.
Calculate the mean free path of a gas molecule with diameter 4 Å if the pressure of the gas is 1.013 × 10⁵ N/m² and the temperature is 27° C. (The Boltzmann constant, k_B = 1.38 × 10^-23 J/K)
Solution :
Data : d = 4 Å = 4 × 10^-10m, P = 1.013 × 10⁵ N/m², T = (273 + 27) K = 300 K_B = 1.38 × 10^-23 J/K
The mean free path of a gas molecule,

Question 4.
Find the mean free path of a gas molecule if the diameter of a molecule is 4 A, the mass of a molecule is 5.316 × 10^-26 kg and density of the gas is 1.429 kg/m³.
Solution :
Data : d = 4 Å = 4 × 10^-10 m, m = 5.316 × 10^-26 kg, ρ = 1.429 kg/m³
The mean free path of a gas molecule,

Question 5.
The mean free path of a gas molecule is 60 nm when the density of the gas is 1.2 kg/m³. What will be the mean free path if the density is reduced to 0.8 kg/m³ ?
Solution :
Data : λ₁ = 60 nm, ρ₁ = 1.2 kg/m3, ρ₂ = 0.8 kg/m³
λ = \(\frac{m}{\sqrt{2} \pi d^{2} \rho}\)
∴ \(\frac{\lambda_{2}}{\lambda_{1}}\) = \(\frac{\rho_{1}}{\rho_{2}}\) as m and d are not changed.
∴ λ₂ = \(\lambda_{1} \frac{\rho_{1}}{\rho_{2}}\) = 60\(\left(\frac{1.2}{0.8}\right)\) nm = 90 nm
This is the required quantity.

Question 10.
What is the origin of pressure exerted by a gas on the walls of a container?
Answer:
The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on a wall by all the molecules, per unit wall area, is the gas pressure on the wall.

Question 11.
Define
(1) the mean (or average) speed
(2) the mean square speed
(3) the root-mean-square speed of gas molecules. State the expressions for the same.
Answer:
(1) Mean (or average) speed of molecules of a gas : The mean speed of gas molecules is defined as the arithmetic mean of the speeds of all molecules of the gas at a given temperature.

(2) Mean square speed of molecules of a gas : The mean square speed of gas molecules is defined as the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.

(3) Root-mean-square speed of molecules of a gas : The root-mean-square (rms) speed of gas molecules is defined as the square root of the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.

If there are N molecules in an enclosed pure gas and v₁, v₂, v₃, …, v_N are the speeds of different molecules,

1. the mean speed, \(\bar{v}\) = \(\frac{v_{1}+v_{2}+\ldots+v_{N}}{N}\)
2. the mean square speed,
   \(\overline{v^{2}}\) = \(\frac{v_{1}^{2}+v_{2}^{2}+\ldots+v_{N}^{2}}{N}\)
3. the rms speed, v_rms = \(\sqrt{\overline{v^{2}}}\)

[Note : The mean square velocity is numerically equal to the mean square speed. Similarly, the rms velocity is numerically equal to the rms speed. But in random motion, the mean velocity would be statistically zero, but the mean speed cannot be zero. ]

Question 12.
On the basis of the kinetic theory of gases, derive an expression for the pressure exerted by the gas.
Answer:
The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on the wall by all the molecules, per unit wall area, is the gas pressure on the wall.

Consider a very dilute gas at a steady-state temperature enclosed in a cubical container of side L. The coordinate axes are aligned with the edges of this cube, as shown in above figure. Suppose that there are N molecules in the container, each of mass m. Consider a molecule moving with velocity \(\).
\(\overrightarrow{v_{1}}\) = \(v_{1 x} \hat{\mathbf{i}}\) + \(v_{1 y} \hat{\mathrm{j}}\) + \(v_{1 z} \hat{\mathbf{k}}\) …. (1)

where v, v_1x and v_1z are the velocity components along the x-, y- and z-axes, respectively, so that
\(v_{1}^{2}\) = \(v_{1 x}^{2}\) + \(v_{1 y}^{2}\) + \(v_{1 z}^{2}\)
The change in momentum of the molecule on collision with the right wall
= final momentum – initial momentum
= (-m|v_1x|) – m|v_1x| = -2m|v_1x|
Assuming the collision to be elastic, the change in momentum of the right wall due to this collision is 2m|v_1x|.

Since the distance between the right and left walls is L, the time between successive collisions with the right wall is,
∆t = \(\frac{2 L}{\left|v_{1 x}\right|}\)
Therefore, the frequency with which the molecule collides with the right wall is \(\frac{\left|v_{1 x}\right|}{2 L}\).

∴ Rate of change of momentum of the right wall = (change in momentum in one collision)
(frequency of collision)
= (2m|v_1x|).\(\frac{\left|v_{1 x}\right|}{2 L}\) = \(\frac{m v_{1 x}^{2}}{L}\) …. (2)
By Newton’s second law of motion, this is the force f_1x exerted by the molecule on the right wall.
Thus, the net force on the right wall by all the N molecules is
F_x = f_1x + f_2x + … + f_Nx

The pressure P_x exerted by all the molecules on a wall perpendicular to the x-axis is

where V = L³ is the volume of the container.

As pressure is the same in all directions,

By definition, the mean square speed of the gas molecules is

where v_rms is the root-mean-square speed of molecules of the gas at a given temperature. Equation (12) gives the pressure exerted by an ideal gas in terms of its density and the root-mean-square speed of its molecules.

Question 13.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is \(\frac{3}{2}\)P.
Answer:
According to the kinetic theory of gases, the pressure P exerted by the gas is
P = \(\frac{1}{3} \rho v_{r m s}^{2}\) = \(\frac{1}{3} \frac{M}{V} v_{\mathrm{rms}}^{2}\)
where v_rms is the rms speed (root-mean-square speed) of the gas molecules; M, V and ρ are the mass, volume and density of the gas, respectively.

Thus, the kinetic energy per unit volume of an ideal gas is \(\frac{3}{2}\)P.

Question 14.
What is the kinetic energy per unit volume of a gas if the gas pressure is 10⁵ N/m²?
Answer:
Kinetic energy per unit volume of a gas
= \(\frac{3}{2}\)P = \(\frac{3}{2}\) × 10⁵ = 1.5 × 10⁵ J/m³.

Question 15.
Assuming the expression for the pressure exerted by an ideal gas, prove that (1) the kinetic energy per mole of the gas = \(\frac{3}{2}\)RT (2) the rms speed of a gas molecule, u_rms = \(\sqrt{3 R T / M_{0}}\).
OR
Assuming the expression for the pressure exerted by an ideal gas, show that the rms speed of a gas molecule is directly proportional to the square root of its absolute temperature.
OR
Show that the rms velocity of gas molecules is directly proportional to the square root of its absolute temperature.
Answer:
According to the kinetic theory of gases, the pressure P exerted by a gas is
ρ = \(\frac{1}{3} \rho v_{\mathrm{rms}}^{2}\) = \(\frac{1}{3} \frac{M}{V} v_{\mathrm{rms}}^{2}\)
∴ PV = \(\frac{1}{3} m v_{\mathrm{rms}}^{2}\)
where v_rms is the rms speed (root-mean-square speed) of the gas molecules; M, V and ρ are the mass,
volume and density of the gas, respectively. If there are n moles of the gas and M₀ is the molar mass,
M = nM₀, so that PV = \(\frac{1}{3} n M_{0} v_{\mathrm{rms}}^{2}\) … (1)
The equation of state of an ideal gas is
PV = nRT … (2)
where T is the absolute temperature of the gas and R is the molar gas constant.
From Eqs. (1) and (2), we get,

where the term on the left-hand side is the kinetic energy of one mole of the gas.
∴ Kinetic energy per mole of the gas = \(\frac{3}{2}\)RT… (5)
From Eq. (3),

In Eq. (6), R and M0 are constant so that v_rms ∝ \(\sqrt{T}\). Thus, the rms speed of a gas molecule is directly proportional to the square root of the absolute temperature of the gas.

Question 16.
The rms speed of oxygen molecules at a certain temperature is 400 m/s. What is the rms speed of nitrogen molecules at the same temperature ?
[M₀₁ (oxygen) = 32 × 10^-3 kg/mol,
M₀₂ (nitrogen) = 28 × 10^-3 kg/mol]
Answer:

Question 17.
The kinetic energy per unit mass of a certain gas at 300 K is 1.3 × 10⁵ J/kg. What will be the kinetic energy per unit mass of the gas at 600 K ?
Answer:
KE per unit mass of a gas (KE/M) ∝ T

This is the required quantity.

Question 18.
Prove that the kinetic energy per molecule of an ideal gas is \(\frac{3}{2}\)K_BT.
Give the interpretation of temperature according to the kinetic theory of gases.
Answer:
Consider n moles of an ideal gas in a container of volume V. If m is the mass of a gas molecule and v_rms is the root-mean-square speed of the gas molecules then, by the kinetic theory, the pressure exerted by the gas is

Therefore, the kinetic energy per molecule of an ideal gas is directly proportional to its absolute temperature.

This equation is the relation between the kinetic per molecule of a gas and the absolute temperature which is the macroscopic parameter of the gas. The absolute temperature of a gas is a measure of the kinetic energy per molecule of the gas. This result is called the kinetic intepretation of temperature, i.e., the interpretation of temperature according to the kinetic theory of gases.

Question 19.
The rms speed of molecules of a certain gas at 300 K is 400 m/s. What will be the rms speed if the gas is heated to 600 K?
Answer:

gives the required rms speed.

Question 20.
State Boyle’s law. Deduce it on the basis of the kinetic theory of an ideal gas.
OR
Deduce Boyle’s law using the expression for pressure exerted by an ideal gas.
Answer:
Boyle’s law : At a constant temperature, the pressure exerted by a fixed mass of gas is inversely proportional to its volume. If P and V denote the pressure and volume of a fixed mass of gas, then, PV = constant at a constant temperature, for a fixed mass of gas.
According to the kinetic theory of gases, the pressure exerted by the gas is
P = \(\frac{1}{3} \frac{N m v_{\mathrm{rms}}^{2}}{V}\)
where N is the number of molecules of the gas, m is the mass of a single molecule, v_rms is the rms speed of the molecules and V is the volume occupied by the gas.
∴ PV = (\(\frac{1}{2}\)mv²rms) × \(\frac{2}{3}\) N
= (KE of a gas molecule) \(\frac{2}{3}\) N … (1)

For a fixed mass of gas, N is constant. Further, intermolecular forces are ignored so that the corresponding potential energy of the gas molecules may be assumed to be zero. Therefore, \(\frac{1}{2} m v_{\mathrm{rms}}^{2}\) is the total energy of a gas molecule and N\(\left(\frac{1}{2} m v_{\mathrm{rms}}^{2}\right)\) is the total energy of the gas molecules, which is proportional to the absolute temperature of the gas. Then, the right-hand side of EQ. (1) will be constant if its temperature is constant. Hence, it follows that PV = constant for a fixed mass of gas at constant temperature, which is Boyle’s law.

Question 21.
Solve the following :

Question 1.
The speeds of five molecules are 200 m/s, 300 m/s, 400 m/s, 500 m/s and 600 m/s respectively. Find
(i) the mean speed
(ii) the mean square speed
(iii) the root mean square speed of the molecules.
Solution :
Data : v₁ = 200 m/s, v₂ = 300 m/s, v₃ = 400 m/s,. v₅ = 500 m/s, v₆ = 600 m/s
(i) Mean speed,

Question 2.
Find the number of molecules in 1 cm³ of oxygen at a pressure of 105 N/m² if the rms speed of oxygen molecules is 426 m/s. What is the temperature of the gas? (Mass of an oxygen molecule = 5.28 × 10^-26 kg, k_B = 1.38 × 10^-23 J/K)
Solution :
Data : m = 5.28 × 10^-26 kg, v_rms = 426 m/s,
V = 1 cm³ = 10^-6 m³, P = 10⁵ Pa, k_B = 1.38 × 10^-23 J/K

This is the number of molecules in 1 cm3 of oxygen under given conditions.

(ii) PV = nRT

This is the required temperature.

Question 3.
A cylinder filled with hydrogen at 400 K exerts a pressure of 3 atmospheres. If hydrogen is replaced by an equal mass of helium at the same temperature, find the
(i) relative number of molecules of hydrogen and helium occupying the cylinder
(ii) pressure exerted by helium. (Molar mass of hydrogen = 2 g/mol, molar mass of helium = 4 g/mol)
Solution:
Let the subscript 1 refer to hydrogen and the subscript 2 to helium.
From the data in the example,
T = 400 K, P₁ = 3 atmospheres, molar mass of hydrogen, M₁ = 2 g/mol
Molar mass of helium, M₂ = 4 g/mol
∴ \(\frac{M_{2}}{M_{1}}\) = \(\frac{4}{2}\) = 2

(i) Since both the gases have the same mass, N₁m₁ = N₂m₂, where is the mass of a molecule of hydrogen and m2 is the mass of a molecule of helium.

∴ P₂ = \(\frac{2}{3}\) × \(\frac{N_{2}}{V}\) × \(\left(\frac{1}{2} m_{2} v_{2 \mathrm{rms}}^{2}\right)\)
As the temperature is the same in both the cases, the average kinetic energy of gas molecules will be the same in both the cases.

Pressure exerted by helium,
P₂ = 1.5 atmospheres

Question 4.
Calculate the rms speed of oxygen molecules at 127 °C. (Density of oxygen at STP = 1.429 kg/m³ and one atmosphere = 1.013 × 10⁵ N/m²)
Solution:
By the data, ρ = 1.429 kg/m³,
P = 1.013 × 10⁵N/m²

The root mean square speed of oxygen molecules at 127° C = 558.1 m/s.

Question 5.
At what temperature will helium molecules have the same rms speed as that of hydrogen molecules at STP ? (Molar mass of hydrogen = 2 g/mol, molar mass of helium = 4 g/mol)
Solution :
Data : M₀₁ (hydrogen) = 2 g/mol
M₀₂ (helium) = 4 g/mol, T₁ (hydrogen) = 273 K,
v_rms (hydrogen) = v_2rms (helium)

The temperature of helium = 546 K = 273 °C

Question 6.
Compute the temperature at which the rms speed of nitrogen molecules is 831 m/s. [Universal gas constant, R = 8310 J/kmol K, molar mass of nitrogen = 28 kg/kmol]
Solution :
Data : v_rms = 831 m/s, R = 8310 J/kmol.K,
M₀ = 28 kg/kmol

This is the required temperature.

Question 7.
If the rms speed of oxygen molecules at STP is 460 m/s, determine the rms speed of hydrogen molecules at STP. [Molar mass of oxygen = 32 g/mol, molar mass of hydrogen = 2 g/mol]
Solution :
Data : v_rms (oxygen) = 460 m/s, same temperature, M₀₁ (oxygen) = 32 × 10^-3 kg/mol,
M₀₂ (hydrogen) = 2 × 10^-3 kg/mol

This is the rms speed of hydrogen molecules at STP.

Question 8.
Calculate the rms speed of helium atoms at 27 °C. [Density of helium at STP = 0.1785 kg/m3, one atmosphere = 1.013 × 10⁵ Pa]
Solution :
Data : ρ = 0.1785 kg/m³, P = 1.013 × 10⁵ Pa,
T₀ = 273 K, T = (273 + 27) = 300 K
The rms speed of helium atoms at STP,

Question 9.
Determine the pressure of oxygen at 0°C if the density of oxygen at STP = 1.44 kg/m³ and the rms speed of the molecules at STP = 456.4 m/s.
Solution :
Data : ρ = 1.44 kg/m³, v_rms = 456.4 m/s
The pressure of oxygen,
P = \(\frac{1}{3} \rho v_{\mathrm{rms}}^{2}\)
= \(\frac{1}{2}\)(1.44)(456.4)² = 9.98 × 10⁴ Pa

Question 10.
Calculate the rms speed of hydrogen molecules at 373.2K. [Molar mass of hydrogen, M₀ = 2 × 10^-3 kg/mol, R = 8.314 J/mol.K]
Solution :
Data : T = 373.2 K, M₀ = 2 × 10^-3 kg/mol,
R = 8.314 J/mol.K
The rms speed of hydrogen molecules,

= 2157 m/s = 2.157 km/s

Question 11.
Find the rms speed of hydrogen molecules if its pressure is 10⁵ Pa and density is 0.09 kg/m³.
Solution :
Data : ρ = 0.09 kg/m³, P = 10⁵ Pa
The rms speed of hydrogen molecules,

Question 12.
The temperature of matter in interstellar space has an average value of about 3 K. Find the rms speed of a proton in the space. [m_p = 1.673 × 10^-27 kg, k_B = 1.38 × 10^-23 J/K]
Solution :
Data : T = 3 K, mp = 1.673 × 10^-27 kg, k_B = 1.38 × 10^-23 J/K
The rms speed of a proton in interstellar space,

Question 13.
Find the temperature at which
(i) the rms speed
(ii) the average kinetic energy of the molecules of an ideal gas are double their respective values at STP.
Solution:
Data : T₀ = 273 K, v = 2v₀ (rms speeds),
KE = 2KE₀ (average kinetic energies)
(i) v_rms ∝ \(\sqrt{\mathrm{T}}\) for a given gas.
∴\(\frac{v}{v_{\mathrm{o}}}\) = \(\sqrt{\frac{T}{T_{0}}}\)
∴\(\sqrt{\frac{T}{T_{0}}}\) = 2
∴ Temperature, T = 4T₀ = 4 × 273 = 1092 K

(ii) Average Kinetic Energy ∝ T
∴ \(\frac{\mathrm{KE}}{\mathrm{KE}_{0}}\) = \(\frac{T}{T_{0}}\)
∴ Temperature, T = 2T₀ = 2 × 273 = 546 K

Question 14.
At what temperature is the rms speed of an argon atom equal to that of a helium atom at – 20 °C ? [Atomic mass of Ar = 39.9 amu, atomic mass of He = 4.0 amu]
Solution :
Data : T₁ = -20 °C = 273 – 20 = 253 K,
M₀₁ (He) = 4 amu, M₀₂ (Ar) = 39.9 amu

∴ T₂ = \(\frac{M_{02}}{M_{01}}\) T₁ = \(\frac{39.9}{4} \times 253\)
= 2523 K
This is the required temperature.

Question 15.
Calculate the kinetic energy
(i) per mole
(ii) per unit mass
(iii) per molecule of nitrogen at STP. [Molar mass of nitrogen = 28 × 10^-3 kg/mol, R = 8.314 J/mol.K, k_B = 1.38 × 10^-23 J/K]
Solution :
Data : T = 273 K, M₀ = 28 × 10^-3 kg/mol,
R = 8.314 J/mol.K, k_B = 1.38 × 10^-23 J/K
(i) The KE per mole = \(\frac{3}{2}\)RT
= \(\frac{3}{2}\)(8.314)(273) = 3.404 × 10³ J/mol

(ii) The KE per unit mass = \(\frac{3}{2} \frac{R T}{M_{0}}\)
= \(\frac{3}{2} \cdot \frac{(8.314)(273)}{28 \times 10^{-3}}\) = 1.216 × 10⁵ J/kg

(iii) The KE per molecule

Question 16.
Calculate the average molecular kinetic energy
(i) per kilomole
(ii) per kilogram of oxygen at 27 °C. [R = 8310 J/kmol.K, Avogadro’s number = 6.02 × 10²⁶ molecules/kmol]
Solution :
Data : T = 273 + 27 = 300 K, M₀ = 32 kg / kmol,
R = 8310 J/kmol.K
(i) The average molecular kinetic energy per kilomole of oxygen
= \(\frac{3}{2}\) RT = \(\frac{3}{2}\) (8310) (300)
= 4155 × 900 = 3739 × 1000
= 3.739 × 10⁶ J/kmol

(ii) The average molecular kinetic energy per unit mass of oxygen

Question 17.
Calculate the kinetic energy of 10 grams of argon molecules at 127 °C. [Universal gas constant R = 8310 J/kmol.K, atomic weight of argon = 40]
Solution:
Data : M = 10 g = 10 × 10^-3 kg, T = 273 + 127 = 400 K,R = 8310 J/kmol.K, M₀ = 40 kg/kmol Kinetic energy per unit mass

= 15 × 8310 = 1.247 × 10⁵ J/kg
∴ The kinetic energy of 1 × 10^-3 kg of argon at 127°C = 1.247 × 10⁵ × 10 × 10^-3
= 1247 J

Question 18.
Calculate the kinetic energy of 2 kg of nitrogen at 300 K. [Molar mass of nitrogen = 28 × 10^-3 kg/mol, R = 8.314 J/mol.K]
Solution :
Data : Mass of nitrogen, M = 2 kg, T = 300 K,
M₀ = 28 × 10^-3 kg/mol, R = 8.314 J/mol.K
Kinetic energy per kg = \(\frac{3}{2} \frac{R T}{M_{0}}\)
∴ The kinetic energy of 2 kg of nitrogen

Question 19.
The kinetic energy of 1 kg of oxygen at 300 K is 1.169 × 10⁵ J. Find the kinetic energy of 4 kg of oxygen at 400 K.
Solution :
Data : Masses of oxygen, M₁ = 1 kg and M₂ = 4 kg, T₁ = 300 K, T₂ = 400 K, kinetic energy,
K₁ = 1.169 × 10⁵ J
Kinetic energy of a given mass (M) of a gas,

This is the kinetic energy of 4 kg of oxygen at 400 K.

Question 20.
The kinetic energy per unit mass of nitrogen at 300 K is 2.5 × 10⁶J/kg. Find the kinetic energy of 4 kg of oxygen at 600 K. [Molar mass of nitrogen = 28 kg/kmol, molar mass of oxygen = 32 kg/kmol]
Solution:
Data : T₁ = 300 K, K₁ = 2.5 × 10⁶ J/kg,
M₁ (nitrogen) = 1 kg, M₂(oxygen) = 4 kg,
M₀₁ (nitrogen) = 28 kg/kmol, T₂ = 600 K,
M₀₂(oxygen) = 32 kg/kmol
Kinetic energy of a given mass M of a gas,

This is the required quantity.

Question 21.
The pressure of a gas in a 0.1 litre container is 200 kPa and the KE per molecule is 6 × 10^-21J. Find the number of gas molecules in the container. How many moles are in the container? [Avogadro number = 6.022 × 10²³ mol^-1]
Solution:
Data : V = 0.1 litre = 10^-4 m³, P = 200 kPa
= 2 × 10⁵ Pa, KE per molecule = 6 × 10^-21 J,
N_A = 6.022 × 10²³ mol^-1
The KE per molecule of a gas = \(\frac{3}{2}\)k_BT

Question 22.
At what temperature will the average kinetic energy of a gas be exactly half of its value at NTP ?
Solution :
Data : KE₂/KE₁ = 1/2, T₁ = 273K
Average molecular kinetic energy per mole of the gas = \(\frac{3}{2}\)RT

This is the required temperature.

Question 23.
Find the kinetic energy per unit volume of nitrogen at a pressure of 76 cm of mercury. Hence, find the kinetic energy of 10 cm³ of the gas under the same condition. Take ρ (mercury) = 13.6 g/cm³ and g = 9.8 m/s².
Solution :
Data :h = 76 cm = 0.76 m, ρ = 13.6 g/cm³ = 13.6 × 10³ kg/m³, g = 9.8 m/s²,
V = 10 cm³ = 10 × 10^-6 cm³

(i) The kinetic energy per unit volume of nitrogen

(ii) The kinetic energy of 10 cm³ of the gas = \(\frac{3}{2}\) PV= (1.519 × 10⁵) (10 × 10^-6)
= 1.519 J

Question 22.
What is meant by degrees of freedom ? Explain the degrees of freedom for
(i) an atom
(ii) a diatomic molecule.
Answer:
The concept of degrees of freedom as used in the kinetic theory specifies the number of independent ways in which an atom or molecule can take up energy. It depends only on the possibilities of motion of the atom or molecule.

Gas molecules of all types have x-, y- and z-components of velocity that are entirely independent of one another. Thus, they have three ways to move in translation, i.e., three degrees of translational freedom.

An atom (or a monatomic molecule, i.e., a molecule containing a single atom, e.g., He) treated as a point mass, has no rotational motion. Hence, it has only three degrees of translational freedom.

A diatomic molecule, in addition to translation, can rotate about axes perpendicular to the line connecting the atoms, as shown in below figure, but not about that line itself. Therefore, it has only two degrees of rotational freedom.

Further, the two atoms may oscillate alternately toward and away from one another along the line joining them, as if connected by a spring. As a, i harmonic oscillator can have potential energy as well as kinetic energy, a diatomic molecule is regarded to have two degrees of vibrational freedom. Thus, at high enough temperatures, a diatomic molecule has seven degrees of freedom : three of translation, and two each of rotation and vibration.

Notes :

(1) That a monatomic gas molecule does not have rotational energy, and that a diatomic molecule does not have a third rotational degree of freedom corresponding to rotation about the line joining the atoms, are explained by quantum theory.

(2) Also according to quantum theory, rotational and oscillatory motions begin at certain higher temperatures. For a molecule of a diatomic gas (like hydrogen), only translation is possible at very low temperatures (below about 100 K). As the temperature increases, rotational motion can begin; so that, at room temperature, a diatomic molecule has only five degrees of freedom-behaving like a pair of atoms rigidly connected like a dumbbell. Oscillatory motion can begin only at quite high temperatures substantially above room temperature (usually of the order of thousands of kelvin).

Question 23.
Derive Mayer’s relation between the molar specific heat of a gas at constant pressure and that at constant volume.
OR
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
Answer:
Consider a cylinder of volume V containing n moles of an ideal gas at pressure P, fitted with a piston of area A. Suppose, the gas is heated at constant pressure which raises its temperature by dT. The gas exerts a total force F = PA on the piston which moves outward a small distance dx.

dW = Fdx = PAdx = PdV … (1)
where Adx = dV is the increase in volume of the gas during the expansion. dW is the work done by the gas on the surroundings as a result of the expansion. If the heat supplied to the gas is dQ_P and the increase in its internal energy is dE then, by the first law of thermodynamics,
dQ_P = dE + dW=dE + PdV
If C_P is the molar specific heat capacity of the gas at constant pressure, dQ_P = nC_P dT.
∴ nC_PdT = dE + PdV …(2)

On the other hand, if the gas was heated at constant volume (instead of at constant pressure) from the initial state such that its temperature increases by the same amount dT, then dW=0. Since the internal energy of an ideal gas depends only on the temperature, the increase in internal would again be dE. If dQv was the heat supplied to the gas in this case, by the first law of thermodynamics and the definition of molar specific heat capacity at constant volume (C_V),

This is Mayer’s relation between C_P and C_V.

Here, heat and work are expressed in the same units. If heat is expressed in calorie or kilo calorie and work is expressed in erg or joule, the above relation becomes
C_P – C_V = \(\frac{R}{J}\) …. (7)
Where J is the mechanical equivalent of heat.

Question 24.
Express Mayer’s relation in terms of the principal specific heats, S_P and S_V.
Answer:
Mayer’s relation : C_P – C_V = R. Let M₀ = molar mass of the gas, S_P = specific heat of the gas at constant pressure and S_V = specific heat of the gas at constant volume.

Now, C_P = M₀S_P and C_V = M₀S_V
∴ M₀S_p – M₀S_V = R
∴ S_P – S_V = \(\frac{R}{M_{0}}\) when heat and work are expressed
in the same units. If heat is expressed in calorie or kilo calorie and work is expressed in erg or joule, we
get,
S_p – S_v = \(\frac{R}{M_{0} J}\), where J is the mechanical equivalent of heat.

Question 25.
Explain : Each translational and rotational degree of freedom contributes only one quadratic term to the energy but one vibrational mode contributes two quadratic terms.
Answer:
With three translational degrees of freedom, the average translational energy per molecule of a gas is

where m is the mass of the molecule and v_x, v_y and v_z are the x-, y- and z-components of the molecular velocity.

A diatomic molecule has two rotational degrees of freedom. If ω₁ and ω₂ are the angular speeds about the two axes and I₁ and I₂ are the corresponding moments of inertia, the rotational energy of a diatomic molecule,

A diatomic molecule is regarded to have two degrees of vibrational freedom for the vibrational mode in which the two atoms vibrate relative to, and without affecting, the centre of mass of the molecule. Comparing this system with a vibrating body of mass m connected to a spring of force constant k, the vibrational energy has two terms corresponding to the kinetic and potential energies :

where x is the displacement from the mean position.

From Eqs. (1), (2) and (3), each translational and rotational degree of freedom contributes only one quadratic term to the average energy of a gas molecule while one vibrational mode contributes two quadratic terms.

[ Note : For a gas at an absolute temperature T, the

Question 26.
Explain the degrees of freedom a polyatomic molecule can have. Hence write the expressions for
(i) the energy per molecule
(ii) the energy per mole
(iii) C_V
(iv) C_P
(v) the adiabatic constant, for a polyatomic gas.
Answer:
A polyatomic molecule has three degrees of translational freedom like any particle. Each molecule can also rotate about its centre of mass with an angular velocity components along each of the three axes. Therefore, each molecule has three degrees of rotational freedom. Additionally, if the molecule is soft at high enough temperatures, it can vibrate easily with many different frequencies, say, f, because there are many interatomic bonds. Hence, it has 2f degrees of vibrational freedom. Then, according to the law of equipartition of energy, for each degree of freedom of translation and rotation,
the molecule has the average energy \(\frac{1}{2}\)k_BT, but for each frequency of vibration the average energy is k_BT, since each vibration involves potential energy and kinetic energy. k_B is the Boltzmann constant and T is the thermodynamic temperature.
(i) The energy per molecule

[Note : As /increases, y decreases.]

Question 27.
The top of a cloud of smoke holds together for hours. Why?
Answer:
According to the law of equipartition of energy, the smoke particles have the same average kinetic energy of random motion as the air molecules. But smoke particles have a much larger mass than air molecules and therefore move slowly, i.e., the average speed of diffusion of smoke particles is small. Hence, in the absence of significant turbulence in the atmosphere, a smoke cloud is relatively stable.

Question 28.
Solve the following :

Question 1.
Find the kinetic energy per molecule of a monatomic gas at 300 K.
Solution :
Data : T = 300 K, k_B = 1.38 × 10^-23 J/K
The kinetic energy per molecule of the gas
= \(\frac{3}{2}\)k_BT
= \(\frac{3}{2}\) (1.38 × 10^-23) (300) J/molecule
= (4.5) (1.38 × 10^-21) J/molecule
= 6.21 × 10^-21 J/molecule
[Note : Here, the number of degrees of freedom is 3.]

Question 2.
Find the kinetic energy of two moles of a mon-atomic gas at 400 K.
Solution :
Data : n = 2, T = 400 K, R = 8.314 J/mol.K
The kinetic energy of two moles of the gas
= \(\frac{3}{2}\)nRT = \(\frac{3}{2}\)(2) (8.314) (400) J
= (12) (8.314 × 10²) J
= 9.977 × 10³ J.

Question 3.
Find the kinetic energy of 10 kg of a monatomic gas at 500 K if the molar mass of the gas is 4 × 10^-3 kg/mol.
Solution :
Data : M = 10 kg, M₀ = 4 × 10^-3 kg/mol, T = 500 K, R = 8.314 J/mol.K.
The kinetic energy of 10 kg of the gas

Question 4.
Find the kinetic energy per molecule of a diatomic gas at 300 K.
Solution :
Data : T = 300 K, k_B = 1.38 × 10^-23 J/K
The kinetic energy per molecule of the gas
= \(\frac{5}{2}\) k_BT = \(\frac{5}{2}\)(1.38 × 10^-23) (300) J/molecule
= (7.5) (1.38 × 10^-23) J/molecule
= 1.035 × 10^-22 J/molecule.
[Note : Here, the number of degrees of freedom is 5.]

Question 5.
Find the kinetic energy of four moles of a diatomic gas at 400 K.
Solution :
Data : n = 4, T = 400 K, R = 8.314 J/mol.K
The kinetic energy of four moles of the gas
= \(\frac{5}{2}\)nRT = \(\left(\frac{5}{2}\right)\) (8.314) (400) J
= (40)(8.314 × 10²) J
= 3.326 × 10⁴ J

Question 6.
Find the kinetic energy of 56 kg of a diatomic gas at 500 K if the molar mass of the gas is 28 × 10^-3 kg/mol.
Solution :
Data : M = 56 kg, M₀ = 28 × 10^-3 kg/mol, T = 500 K, R = 8.314 J/mol.K
The kinetic energy of 56 kg of the gas

= 25(8.314 × 10⁵)
= 2.079 × 10⁷ J

Question 7.
When two kilocalories of heat are supplied to a system, the internal energy of the system increases by 5030 J and the work done by the gas against the external pressure is 3350 J. Calculate J, the mechanical equivalent of heat.
Solution :
Data : From the data in the example,
dQ = 2 kcal, dE = 5030 J, dW = 3350 J.
dQ = \(\frac{d E+d W}{J}\), where J = mechanical equivalent of heat

Question 8.
Find the increase in the internal energy of a gas of mass 10 grams when it is heated from 300 K to 305 K.
Given : S_V = 0.16 kcal/kg.K, J = 4186 J/kcal
Solution :
Data : M = 10 grams = 10 × 10^-3 kg,
S_V = 0.16 kcal/kg.K, J = 4186 J/kcal
Rise in the temperature of the gas,
∆T = 305 – 300 = 5K
∆E = J S_V M∆T = (4186)(0.16)(10 × 10^-3) × (5) J
= 33.49 J
The increase in the internal energy of the gas, ∆E = 33.49 J

Question 9.
The molar specific heat of helium at constant volume is 12.5 J/mol.K. Find its molar specific heat at constant pressure. Take R = 8.31 J/mol.K.
Solution :
Data : C_V = 12.5 J/mol.K, R = 8.31 J/mol.K
The molar specific heat of helium at constant press-ure,
C_P = C_V + R = (12.5 + 8.31) J/mol.K
= 20.81 J/mol.K.

Question 10.
Find the principal specific heats of helium and hence the universal gas constant. Given : C_P = 20.81 J/mol.K, C_V = 12.5 J/mol.K. M₀ (He) = 4 × 10^-3 kg/mol.
Solution :
Data : C_P = 20.81 J/mol.K, C_V = 12.5 J/mol.K,
M₀ = 4 × 10^-3 kg/mol.
(i) The specific heat of helium at constant pressure,

[Note : R = C_P – C_V = (20.81 – 12.5) J/mol.K = 8.31 J/mol.K. The difference between the two values of R is due to the approximation involved in calculation.]

Question 11.
The molar specific heat of nitrogen at constant volume is 4.952 cal/mol.K and that at constant pressure is 6.933 cal/mol.K. Find the mechanical equivalent of heat. Take R = 8.31 J/mol.K.
Solution :
Data : C_V = 4.952 cal/mol.K, C_P = 6.933 cal/mol.K, R = 8.31 J/mol.K

Question 29.
Name and define the modes of heat transfer.
Answer:
The three modes of heat transfer are conduction, convection and radiation.

1. Conduction is the mode of heat transfer within a body or between two bodies in contact, from a region of high temperature to a region of lower temperature without the migration of the particles of the medium.
2. Convection is the mode of heat transfer from one part of a fluid to another by the migration of the particles of the fluid.
3. Radiation is the mode of heat transfer by electromagnetic waves / quanta.

Question 30.
What is thermal radiation or heat radiation? State its characteristic properties.
Answer:
Radiation is the mode of heat transfer or in general, energy transfer by electromagnetic waves / quanta. Thermal radiation or heat radiation is the radiation produced by thermal agitation of the particles of a body, and its spectrum, i.e., frequency distribution or wavelength distribution, is continuous from the far infrared to the extreme ultraviolet region depending on the temperature of the body.

Properties :

1. Thermal radiations are electromagnetic waves/ quanta extending from the far infrared to the extreme ultraviolet region. In this spectrum, the infrared waves (wavelengths ranging from about 700 nm to about 1 mm) are sensed as heat.
2. They have the same speed in free space as that of light, nearly 3 × 10⁸ m/s, which makes radiation the most rapid mode of heat transfer.
3. They exhibit all the optical phenomena of light, viz., reflection, absorption, refraction, interference, diffraction and polarization.
4. Radiation incident on a body is, in general, partly reflected, partly, absorbed and partly transmitted.
5. Thermal radiation obeys the inverse-square law of intensity, i.e., the intensity at a point is inversely proportional to the square of its distance from a point source of radiation.

Question 31.
Define the coefficients of absorption, reflection and transmission. Obtain the relation between them.
Answer:

1. The coefficient of absorption or absorptive power or absorptivity of a body is the ratio of the quantity of radiant energy absorbed by the body to the quantity of radiant energy incident on the body in the same time.
2. The coefficient of reflection or reflectance or reflective power of the surface of a body is the ratio of the quantity of radiant energy reflected by the surface to the quantity of radiant energy incident on the surface in the same time.
3. The coefficient of transmission or transmittance or transmissive power of a body is the ratio of the quantity of radiant energy transmitted by the body to the quantity of radiant energy incident on the body in the same time.

Let Q be the quantity of radiant energy incident on a body and Q_a, Q_r and Q_t be the quantities of radiant energy absorbed, reflected and transmitted by the body respectively, in the same time. Since the total energy is conserved, we have,

Hence, a + r + t = 1
This is the required relation.

[Note : The coefficients of absorption, reflection and transmission are, respectively, the measures of the ability of the body or material to absorb, reflect or transmit radiation.

They are dimensionless quantities and have no units. They depend on the material and physical conditions of the body as well as on the frequency of the incident radiation.]

Question 32.
If for a certain body, under certain conditions, the coefficient of absorption is 0.2 and the coefficient of reflection is 0.5, what will be the coefficient of transmission ?
Answer:
In the usual notation, a + r +1 = 1
Hence, the coefficient of transmission of the body = 1 – (a + r) = 1 – (0.2 + 0.5) = 1 – 0.7 = 0.3.

Question 33.
Give four exmaples of

1. athermanous substance
2. diathermanous substances.

Answer:

1. Water, wood, iron, copper, moist air, benzene are athermanous substances.
2. Quartz, sodium chloride, hydrogen, oxygen, dry air, carbon tetrachloride are diathermanous substances.

Question 34.
A substance may be athermanous or diathermanous for certain wavelength ranges while good absorber for other wavelength ranges. Explain.
Answer:
For interaction of light with matter, it is necessary to consider the atomic nature of matter. Interaction of an atom with light depends on the frequency or equivalently on the photon energy.

An atom absorbs light if the photon’s energy equals one of the excitation energies of the atom. In the dense atomic neighbourhood of ordinary gases at pressures above 100 Pa, solids and liquids, the discrete atomic energy states widen into bands. Thus, bulk matter, depending on its nature, possesses absorption bands in specific regions within the electromagnetic frequency spectrum.

Radiant energy of other frequencies is elastically scattered so that the material is transparent at these frequencies.

[Note : Colourless, transparent materials have their absorption bands outside the visible region of the spectrum, which is why they are, in fact, colourless and transparent. Glasses have absorption bands in the ultraviolet region (~ 100 nm-200 nm), where they become opaque. At even longer wavelengths of radiowaves glass is again transparent. In comparison, a stained glass has absorption band in the visible region where it absorbs out a particular range of frequencies, transmitting the complementary colour. Semiconductors, such as ZnSe, CdTe, GaAs and Ge, which are opaque in the visible region of the spectrum are highly transparent in the infrared region (2 µm to 30 µm).]

Question 35.
In Fery’s blackbody, the hole is the blackbody but not the inner coated or outer sphere alone. Explain.
Answer:
Any space which is almost wholly closed – e.g., an empty closed tin can with a tiny hole punched-approximates to a blackbody. The hole is a good absorber and looks black because any light which enters through it is almost completely absorbed after multiple reflections inside. This absorption is quickened in Fery’s blackbody by the inner coat of lampblack. Thus, the hole acts as a perfect absorber.

Also, the relative intensities of radiation at different wavelengths is determined only by the temperature of the blackbody, not by the nature of its surfaces. This is so because the radiation coming out from a small part of the inner surface is made up of

1. the radiation emitted by that area
2. the radiation from other parts reflected at that area. Since the hole in Fery’s blackbody is very small, the radiations from the inner surface are well mixed up by reflection before they can escape. Hence, when Fery’s blackbody is placed in a high-temperature bath of fused salts, the hole serves as the source of blackbody radiation.

The outer surface of Fery’s blackbody is made highly reflective and lampblack too has a small coefficient of reflection. Hence, neither of them alone is a blackbody.

Question 36.
What is
(i) a cavity radiator
(ii) cavity radiation?
Answer:
(i) A cavity radiator is a block of material with internal cavity. The inner and outer surfaces of the block are connected by a small hole. Most of the radiant energy entering the block through the hole cannot escape from the hole. The block, therefore, acts almost like a blackbody.

(ii) When the cavity radiator is heated to high temperature, radiation coming out from the hole resembles blackbody radiation. It is called cavity radiation. It depends only on the temperature of the radiator and not on the shape and size of the cavity as well as the material of the walls of the cavity.

Question 37.
‘If r = 1, then it is a white body’. Is this true ? Explain.
Answer:
No.
Since a + r + t = l,a = 0 and t = 0 for r = 1. Therefore, by Kirchhoff’s law, e = a = 0 which is impossible as every body at temperature above 0 K does emit radiant energy, and T = 0 K is impossible.

A blackbody being a full radiator, when heated to high enough temperature it would emit thermal radiation at all the wavelengths and thus appear white. A perfect reflector (r = 1), on the other hand, is a poor emitter and thus would not necessarily appear white when heated.

Question 38.
State and explain Prevost’s theory of exchange of heat.
Answer:
In 1792, Pierre Prevost put forward a theory of exchange of heat. According to this theory, all bodies at all temperatures above the absolute zero temperature (0 K) radiate thermal energy to the surroundings and at the same time receive radiant energy from the surroundings. Thus, there is continuous exchange of radiant energy between a body and its surroundings.

The quantity of radiant energy (thermal energy) emitted by a body per unit time depends upon the nature of the emitting surface, the area of the surface and the temperature of the surface. The quantity of radiant energy absorbed by a body per unit time depends upon the nature of the absorbing surface, the area of the surface and the time rate at which the radiant energy is incident on the body.

If the time rate of emission of thermal energy is greater than the time rate of absorption of thermal energy, the temperature of the body falls. If the emission rate is less than the absorption rate, the temperature of the body increases. If the emission rate equals the absorption rate, the temperature of the body remains constant.

[Note : A body appears red if its temperature is around 800 °C, and white hot if its temperature is around 3000 °C]

Question 39.
Define
(1) emissive power or radiant power
(2) coefficient of emission of a body
Answer:
(1) Emissive power or radiant power of a body (symbol, R) : The emissive power or radiant power of a body at a given temperature is defined as the quantity of radiant energy emitted by the body per unit time per unit surface area of the body at that temperature.

(2) Coefficient of emission (or emissivity) of a body (symbol, e) : The coefficient of emission (or emissivity) of a body is defined as the ratio of the emissive power of the body (R) to the emissive power of a perfect blackbody (R_b) at the same temperature as that of the body.
e = \(\frac{R}{R_{\mathrm{b}}}\)

[Note : The SI unit and dimensions of emissive power are the watt per square metre (W/m² Or Js^-1m^-2) and [M¹L°T^-3]. The coefficient of emission is a dimensionless and unitless quantity. For a perfect blackbody, e = 1 and for a perfect reflector, e = 0.]

Question 40.
If the emissive power of a certain body at a certain temperature is 2000 W/m² and the emissive power of a perfect blackbody at the same temperature is 10000 W/m², what is the coefficient of emission of the body?
Answer:
The coefficient of emission of the body,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{2000}{1000}\) = 0.2

Question 41.
State the characteristics of blackbody radiation spectrum.
Answer:
Characteristics of blackbody radiation spectrum :

1. The emissive power R_λ for every wavelength λ increases with increasing temperature.
2. Each curve has a characteristic form with a maximum for R_λ at a certain wavelength λ_m.
3. λ_m depends on the absolute temperature of the body and, with increasing temperature, shifts towards shorter wavelengths, i.e., towards the ultraviolet end of the spectrum.
4. λ_mT = a constant.
5. The area under each curve gives the total radiant power per unit area of a blackbody at that temperature and is proportional to T⁴, (Stefan-Boltzmann law).

Notes :

1. Experimental work on the distribution of energy in blackbody radiation, was carried out by German physicists Otto Lummer (1860-1925), Wilhelm Wien (1864-1928) and Ernst Pringsheim (1859-1917).
2. Explanation of the radiation spectrum, given by Wien on the basis of thermodynamics could account only for the short wavelength region. The formula obtained by Rayleigh and Jeans, on the basis of the equipartition of energy could account only for long wavelength region. Planck’s empirical formula, put forward in 1900, could account for the entire spectrum.

Question 42.
State the significance of Wien’s displacement law.
Answer:
Significance :

1. It can be used to estimate the surface temperature of stars.
2. It explains the common observation of the change of colour of a solid on heating-from dull red (longer wavelengths) to yellow (smaller wavelengths) to white (all wavelengths in the visible region).

Question 43.
Explain the Stefan-Boltzmann law.
Answer:
The power per unit area radiated from the surface of a blackbody at an absolute temperature T is its emissive power or radiant power R_b at that temperature. According to the Stefan-Boltzmann law,
R_b ∝ T⁴ ∴ R_b = σT⁴
where the constant a is called Stefan’s constant.

If A is the surface area of the body, its radiant power, i.e., energy radiated per unit time, is AσT⁴.

[Note : This law was deduced by Josef Stefan (1835-93), Austrian physicist, from the experimental results obtained by John Tyndall (1820-93), British physicist. The theoretical derivation of this law is due to Boltzmann in 1884. Hence, the law is known as the Stefan- Boltzmann law.

Question 44.
What is the emissive power of a perfect black-body at 1000 K? (σ = 5.67 × 10^-8 W/m².K⁴)
Answer:
R_b = σT⁴ = 5.67 × 10^-8 × (10³)⁴
= 5.67 × 10⁴\(\frac{\mathrm{W}}{\mathrm{m}^{2}}\) is the required emissive power.

Question 45.
In the above case (Question 43), if the body is not a perfect blackbody and e = 0.1, what will be the emissive power?
Answer:
R = eRh = 0.1 × 5.67 × 104 = 5.67 × 10³\(\frac{\mathrm{W}}{\mathrm{m}^{2}}\)

Question 46.
Derive an expression for the net rate of loss of heat per unit area by a perfect blackbody in a cooler surroundings.
Answer:
Consider a perfect blackbody at absolute temperature T. We assume its surroundings also to act as a perfect blackbody at absolute temperature T₀, where T₀ < T.

The power per unit area radiated from the surface of a blackbody at temperature T is its emissive power R_b at that temperature. According to the Stefan-Boltzmann law,
R_b = σT⁴
where σ is the Stefan constant.
At the same time, the body absorbs radiant energy from the surroundings. The radiant energy absorbed per unit time per unit area by the black-body is \(\sigma T_{0}^{4}\).

Therefore, the net rate of loss of radiant energy per unit area by the blackbody is σ(T⁴ – \(T_{0}^{4}\)).

[Note : If the body at temperature T has emissivity e < 1, (i.e., it is not a perfect blackbody) the net rate of loss of radiant energy per unit area is eσ(T⁴ – \(T_{0}^{4}\)).]

Question 47.
Compare the rates of radiation of energy by a metal sphere at 600 K and 300 K.
Answer:

Question 48.
Solve the following :

Question 1.
Radiant energy is incident on a body at the rate of 2000 joules per minute. If the reflection coefficient of the body is 0.1 and its transmission coefficient is 0.2, find the radiant energy
(i) absorbed
(ii) reflected
(iii) transmitted by the body in 2 minutes.
Solution :
Data : r = 0.1, t = 0.2
a + r + t = 1
∴ a = 1 – r – f = 1 – 0.1 – 0.2 = 0.7
Radiant energy incident per minute on the body is 2000 J. Hence, in 2 minutes, the radiant energy (Q) incident on the body is 4000 J. Let Q_a, Q_r and Q_t be the quantities of radiant energy absorbed, reflected and transmitted in 2 minutes by the body, respectively.

Question 2.
Heat is incident at the rate of 10 watts on a completely opaque body having emissivity 0.8. Find the quantity of radiant heat reflected by it in 1 minute.
Answer:
Data : e = 0.8, time =1 min =60 s, \(\frac{d Q}{d t}\)= 10 W
For a completely opaque body, t =0.
Also, a = e = 0.8
a + r + t = 1
∴ 0.8 + r + 0 = 1
∴ r = 1 – 0.8 = 0.2
Total radiant heat incident on the body in 1 minute
Q = \(\left(\frac{d Q}{d t}\right)\) × time = 10 × 60 = 600J
∴ The quantity of radiant heat reflected by the body in 1 minute is
Q_r = rQ = 0.2 × 600 = 120J

Question 3.
A metal cube of side 2 cm emits 672 J of heat in 100 s at a certain temperature. Calculate its emissive power (radiant power) at that temperature.
Solution :
Data : L = 2 cm = 2 × 10^-2 m, Q = 672 J, t = 100 s
The surface area of the cube is
A = 6L² = 6(2 × 10^-2)² = 24 × 10^-4 m²
The energy radiated by the cube is Q = RAt
where R ≡ emissive power (radiant power).

Question 4.
The energy of 6000 J is radiated in 5 minutes by a body of surface area 100 cm². Find the emissive power (radiant power) of the body.
Solution :
Data : Q = 6000 J, t = 5 minutes = 5 × 60 s = 300 s,
A = 10 cm² = 10 × 10^-4 m² = 10^-3 m²

Emissive power (radiant power), R = \(\frac{Q}{A t}\)
= \(\frac{6000}{10^{-3} \times 300}\)
= 2000 J/m².s 2000 W/m²

Question 5.
An ordinary body A and a perfect blackbody B are maintained at the same temperature. If the radiant power of A is 2 × 10⁴ W/m² and that of B is 5 × 10⁴ W/m², what is the coefficient of emission (emissivity) of A ?
Solution :
Data : R = 2 × 10⁴ W/m², R_b = 5 × 10⁴ W/m²
The coefficient of emission (emissivity) of A,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{2 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}}{5 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}}\) = 0.4

Question 6.
A body of surface area 100 cm² radiates energy 3000 J in 10 minutes at a certain constant temperature. The radiant power of a perfect blackbody maintained at the same temperature is 2500 W/m². Find the the radiant power and emissivity of the body.
Solution:
Data : A = 100 cm² = 100 × 10^-4m² = 10^-2m², t = 10 minutes = 10 × 60 s = 600 s, Q = 3000 J.
R_b = 2500 W/m².

(i) The radiant power of the body,
R = \(\frac{Q}{A t}\) = \(\frac{3000 \mathrm{~J}}{\left(10^{-2} \mathrm{~m}^{2}\right)(600 \mathrm{~s})}\)
= 5 × 10² W/m²

(ii) The emissivity of the body,
e = \(\frac{R}{R_{\mathrm{b}}}\) = \(\frac{500 \mathrm{~W} / \mathrm{m}^{2}}{2500 \mathrm{~W} / \mathrm{m}^{2}}\) = 0.2

Question 7.
For a certain body, the coefficient of absorption (absorptive power, absorptivity) is 0.4. The body is maintained at a constant temperature. The radiant power of a perfect blackbody maintained at the same temperature is 5 × 10⁴ W/m². Find the radiant power of the body at that temperature.
Solution:
Data: a = 0.4, R_b = 5 × 10⁴ W/m²
As the emissivity, e = a,
we have, e = 0.4
∴ R = eR_b = (0.4) (5 × 10⁴ W/m²)
= 2 × 10⁴ W/m²
This is the required quantity.

Question 8.
Calculate the wavelength in angstrom at which the emissive power is maximum for a blackbody heated to 3727 °C.
[Wien’s constant, b = 2.898 × 10^-3 m.K]
Solution :
Data : T = 3727 °C = 3727 + 273 = 4000 K,
b = 2.898 × 10^-3 m.K

Question 9.
The maximum radiant power of the Sun is at wavelength 500 nm. The Wien displacement law constant is 2.898 × 10^-3 m.K. Estimate the temperature of the surface of the Sun. Assume the Sun to be a blackbody radiator.
Solution :
Data : λ_m = 500 nm = 5 × 10⁷ m, b = 2.898 × 10^-3 m.K
By Wien’s displacement law,
λ_mT = b
∴ The estimated surface temperature of the Sun,

Question 10.
What is the peak wavelength of the radiation emitted by a blackbody at 35 °C ? [Wien’s displace-ment law constant, b = 2.898 × 10^-3 m.K]
Solution :
Data : t = 35 °C, b = 2.898 × 10^-3 m.K
The absolute temperature of the blackbody,
T = t + 273 = 35 + 273 = 308 K
By Wien’s displacement law, λ_mT = b
∴ The peak wavelength,

Question 11.
Calculate the emissive power of a perfect black-body at 127°C.
Solution:
Data: T = 127°C = (127 + 273) K = 400 K,
= 5.67 × 10^-8 W/m².K⁴
Emissive power, R_b = σT⁴
= 5.67 × 10^-8 × (400)⁴
= 1.452 × 10³ W/m²

Question 12.
What is the temperature at which a blackbody radiates heat at the rate of 1 kilowatt per square metre?
Solution :
Data : R_b = 1 kW/m² = 1000 W/m²,
σ = 5.67 × 10^-8 W/m²K⁴
R_b = σT⁴
∴ Temperature, T = \(\left(\frac{R_{\mathrm{b}}}{\sigma}\right)^{1 / 4}\)

Question 13.
A perfect blackbody, maintained at 27 °C, radiates energy at the rate of 551.1 W. Find the surface area of the body.
Solution :
Data : dQ/dt = 551.1 W,
T = 27 °C = (27 + 273) K = 300 K,
σ = 5.67 × 10^-8 W/m².K⁴
Let A be the surface area of the body. Energy radiated per unit time,

Question 14.
Calculate the energy radiated in two minutes by a perfect black sphere of radius 2 cm, maintained at 427 °C.
Solution :
Data : T = 427 °C = (427 + 273) K = 700 K, r = 2 cm = 0.02 m, σ = 5.67 × 10^-8 W/m².K⁴, t = 2 minutes = 120 seconds
∴ A = 4πr² = 4 × 3.142 × (0.02)² = 5.027 × 10^-3 m²
Energy radiated in time t = AσT⁴t
∴ Energy radiated in 120 seconds
= 5.027 × 10^-3 × 5.67 × 10^-8 × (700)⁴ × 120 J
= 8.212 × 10³ J

Question 15.
The temperature of the filament of a 100 watt electric lamp is 2727 °C. Calculate its emissivity if the length of the filament is 8 cm and its radius is 0.5 mm.
Solution :

Question 16.
A 60 watt electric bulb loses its energy entirely by radiation from the surface of its filament. If the surface area of the filament is 4 cm² and its coefficient of emission is 0.4, calculate the temperature of the filament.
Solution :

Question 17.
Energy is emitted from a hole in an electric furnace at the rate of 20 watts when the furnace is at 227 °C. Find the area of the hole.
Solution :
Data : T = 227 °C = (227 + 273) K = 500 K,
P = 20 W, σ = 5.67 × 10^-8 W/m².K⁴
Let A be the area at the hole. Then,
P = AσT⁴

Question 18.
A body of surface area 10 cm2 and temperature 727 °C emits 300 J of energy per minute. Find its emissivity.
Solution :
Data : A = 10 cm² = 10 × 10^-4m² = 10^-3m²,
T = 273 + 727 = 1000 K, Q = 300 J,

Question 19.
A pinhole is made in a hollow sphere of radius 5 cm whose inner wall is at 727 °C. Find the power radiated per unit area. [Stefan’s constant, a = 5.7 × 10^-8J/m².s.K⁴, emissivity (e) = 0.2]
Solution :
Data : r = 5 × 10^-2m, T = 727 + 273 = 1000 K, e = 0.2,
σ = 5.7 × 10^-2 J/m².s.K⁴
The power radiated per unit area, i.e., emissive power,
R = eσT⁴
= (0.2) (5.7 × 10^-8) (10³)⁴
= 1.14 × 10^-8 × 10¹² = 1.14 × 10⁴ W/m²

Question 20.
A body of surface area 400 cm² and absorption coefficient 0.5 radiates energy 1.5 kcal in 2 minutes when the temperature of the body is kept constant. Find the temperature of the body. (Given : J = 4186 J/kcal, σ = 5.67 × 10^-8 J/s.m.K⁴)
Solution :
Data : A = 400 cm² = 400 × 10^-4 4 m²
= 4 × 10^-2 m², absorption coefficient, a = 0.8
But a = e ∴ e = 0.8, J = 4186 J/kcal
Q = 1.5 kcal = 1.5 × 4186 J = 6279 J,
t = 2 minutes = 120 s, σ = 5.67 × 10^-8 J/s.m. K⁴
Energy radiated, Q = σ AeT⁴t
∴ 6279 = (5.67 × 10^-8) × (4 × 10^-2) × 0.8 × T⁴ × 120
∴ T⁴ = \(\frac{6279 \times 10^{8}}{21.77}\) = 288.4 × 10⁸
∴ T = 4.121 × 10² K
This is the temperature of the body.

Question 21.
The filament of an evacuated light bulb has length 10 cm, diameter 0.2 mm and emissivity 0.2. Calculate the power it radiates at 2000 K. (a = 5.67 × 10^-8 W/m².K⁴)
Solution :
Data : 1 = 10 cm = 0.1 m, d = 0.2 mm
∴ r = 0.1 mm = 0.1 × 10^-3 m, e = 0.2,
T = 2000 K, σ = 5.67 × 10^-3 W/m².K⁴
Surface area of the filament, A = 2πrl

This is the required quantity.

Question 22.
A body of surface area 10 cm² and temperature 727 °C emits 300 J of energy per minute. Find its emissivity.
Solution :
Data : A = 10 cm² = 10 × 10^-4 m² = 10^-3 m²,
T = 273 + 727 = 1000 K, Q = 300 J,
t = 1 minute = 60 s, σ = 5.67 × 10^-8 J/m².s.K⁴
Q = σAeT⁴t

Question 23.
A metal cube of each side of length 1 m loses all its energy at the rate of 3000 watts. If the emissivity of the material of the cube is 0.4, estimate its temperature.
Solution :
Data : L = 1 m, e = 0.4, \(\frac{d Q}{d t}\) = 3000 W, dt
a = 5.67 × 10^-8 W/m².K⁴
Surface area of the cube, A = 6L² = 6 m²

Question 24.
Assuming the Stefan-Boltzmann law, compare the rate of radiation from a metal ball at 727 °C with its rate of radiation at 527 °C. Also compare its rate of loss of heat at the two temperatures, if the temperature of the surroundings is 27 °C. Solution :
Data : T₀ = 273 + 27 = 300 K,
T₁ = 273 + 727 = 1000 K, T₂ = 273 + 527 = 800 K
(i) Rate of radiation (radiant power),
P = σAeT⁴
If P₁ and P₂ are the radiant powers at the temperatures T₁ and T₂, respectively,

Question 25.
A black body at 1000°c radiates 14.89 watt per square centimetre of its surface. The surfaceof a certain star radiates 10 kW per square centimetre. Assuming that the star’s surface behaves as a perfect blackbody, estimate its temperature.
Solution:
Data: T₁ = 273 + 1000 = 1273K,
R₁ = 14.89 watt/cm² = 14.89 × 10⁴ watt/m²,
R₂ = 10 kW/cm² = 10⁷ watt/cm²
Emissive power of a blackbody, R = σT⁴

∴ This is the temperature of the star’s surface.

Question 26.
A blackbody with initial temperature of 300 °C is allowed to cool inside an evacuated enclosure surrounded by melting ice at the rate of 0.35 °C/second. If the mass, specific heat and surface area of the body are 32 grams, 0.10 cal/g °C and 8 cm² respectively, calculate Stefan’s constant. (Take J = 4200 j/kcal.)
Solution :
Data : T = 273 + 300 = 573 K, T₀ = 273 K,
\(\frac{d Q}{d t}\) = 0.35 °C/s = 0.35 K/s, at
M = 32 g = 32 × 10^-3 kg, A = 8 cm² = 8 × 10^-4 m² C = 0.10 cal/g.°C = 0.10 kcal/kg.K = 420 j/kg.K
since J = 4200 J/kcal

Question 27.
A blackbody at 327 °C, when suspended in a black enclosure at 27 °C, loses heat at a certain rate. Find the temperature of the body at which its rate of loss of heat by radiation will be half of the above rate. Assume that the other conditions remain unchanged.
Solution :
Data : T₁ = 273 + 327 = 600 K, T₀ = 273 + 27 = 300 K,

Question 49.
Choose the correct option.

Question 1.
The rms speed of a gas molecule is directly proportional to
(A) its absolute temperature
(B) the square root of its absolute temperature
(C) the square of its absolute temperature
(D) its molar mass.
Answer:
(B) the square root of its absolute temperature

Question 2.
Temperature remaining constant, if you double the number of molecules in a box, the pressure will
(A) remain unchanged
(B) double
(C) become one-half
(D) quadruple.
Answer:
(B) double

Question 3.
The pressure P of an ideal gas having volume V is \(\frac{2 E}{3 V}\). Then E is
(A) translational kinetic energy
(B) rotational kinetic energy
(C) vibrational kinetic energy
(D) potential energy.
Answer:
(A) translational kinetic energy

Question 4.
According to the kinetic theory of gases, at a given temperature, molecules of all gases have the same
(A) rms speed
(B) momentum
(C) energy
(D) most probable speed.
Answer:
(C) energy

Question 5.
The kinetic energy per molecule of a gas at temperature T is
(A) \(\frac{3}{2} R T\)
(B) \(\frac{3}{2} k_{\mathrm{B}} T\)
(C) \(\frac{2}{3} R T\)
(D) \(\frac{3}{2} \frac{R T}{M_{0}}\)
Answer:
(B) \(\frac{3}{2} k_{\mathrm{B}} T\)

Question 6.
When the temperature of an enclosed gas is increased by 2 °C, its pressure increases by 0.5%. The initial temperature of the gas was
(A) 250 K
(B) 275 K
(C) 300 K
(D) 400 K.
Answer:
(D) 400 K.

Question 6.
For a given gas at 800 K, the rms speed of the ‘ molecules is
(A) four times the rms speed at 200 K
(B) half the rms speed at 200 K
(C) twice the rms speed at 200 K
(D) twice the rms speed at 400 K.
Answer:
(C) twice the rms speed at 200 K

Question 7.
If the absolute temperature of a gas becomes three times the initial absolute temperature, the rms speed of the gas molecules
(A) becomes \(\frac{1}{3}\) times the initial rms speed
(B) becomes \(\frac{1}{\sqrt{3}}\) times the initial rms speed
(C) becomes \(\sqrt{3}\) times the initial rms speed
(D) becomes 3 times the initial rms speed.
Answer:
(C) becomes \(\sqrt{3}\) times the initial rms speed

Question 8.
An ideal gas occupies 2 m³ at a pressure of 2 atm. Taking 1 atm = 10⁵ Pa, the energy density of the gas is
(A) 3 × 10⁵ J/m³
(B) 1.5 × 10⁵ J/m³
(C) 300 J/m³
(D) 150 J/m³.
Answer:
(A) 3 × 10⁵ J/m³

Question 9.
An ideal gas is confined to a cylinder with a movable piston. As it is heated to twice its initial absolute temperature, the gas is allowed to expand freely against the atmospheric pressure. The average thermal energy of the molecules
(A) quadruples
(B) doubles
(C) increases by a factor of \(\sqrt{2}\)
(D) remains unchanged.
Answer:
(B) doubles

Question 10.
Equal volumes of hydrogen and oxygen (relative molar masses 2 and 32, respectively) in separate containers are equimolar and exert equal pressure. The rms speeds of hydrogen and oxygen molecules are in the ratio
(A) 1 : 32
(B) 1 : 16
(C) 1 : 4
(D) 4 : 1.
Answer:
(D) 4 : 1.

Question 11.
At what temperature will the rms velocity of a gas molecule be double its value at NTP ?
A) 273 °C
(B) 546 °C
(C) 819 °C
(D) 1092 °C.
Answer:
(C) 819 °C

Question 12.
The rms speed of the molecules of a gas is 200 m/s at 27 °C and 1 atmosphere pressure. The rms speed at 127 °C and double the pressure is

Answer:
(C) \(\frac{400}{\sqrt{3}}\) m/s

Question 13.
The temperature at which helium molecules have the same rms speed as hydrogen molecules at STP is
[M_oH = M_oHe = 4g/mol]
A) 1092 K
(B) 546 K
(C) 300 K
(D) 273 K.
Answer:
(B) 546 K

Question 14.
The number of degrees of freedom for a rigid diatomic molecule is
(A) 3
(B) 5
(C) 6
(D) 7
Answer:
(B) 5

Question 15.
For polyatomic molecules having / vibrational modes, the ratio of two specific heats is

Answer:
(C) \(\frac{4+f}{3+f}\)

Question 16.
A nonlinear triatomic molecule has …… degree(s) of freedom of rotational motion.
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
(D) 3

Question 17.
The wavelength range of thermal radiation is
(A) from 4000 Å to 7000 Å
(B) from 7700 Å to 4 × 10⁶ Å
(C) from 10⁶ Å to 10⁸ Å
(D) from 4 × 10^-12 Å to 4 × 10⁸ Å.
Answer:
(B) from 7700 Å to 4 × 10⁶ Å

Question 18.
The coefficient of reflection of a perfectly opaque body is 0.16. Its coefficient of emission is
(A) 0.94
(B) 0.84
(C) 0.74
(D) 0.64.
Answer:
(B) 0.84

Question 19.
Which of the following materials is diathermanous ?
(A) Wax
(B) Glass
(C) Quartz
(D) Porcelain
Answer:
(C) Quartz

Question 20.
Which of the following substances is opaque to radiant energy?
(A) Carbon tetrachloride
(B) Sodium chloride
(C) Benzene
(D) Potassium bromide
Answer:
(C) Benzene

Question 21.
The substance which allows heat radiations to pass through it is
(A) iron
(B) water vapour
(C) wood
(D) dry air.
Answer:
(D) dry air.

Question 22.
A perfect blackbody is the one that
(A) absorbs all incident radiation
(B) reflects all incident radiation
(C) transmits all incident radiation
(D) both reflects and transmits incident radiation.
Answer:
(A) absorbs all incident radiation

Question 23.
The conical projection in Fery’s blackbody is
(A) used to support the spheres
(B) used to transmit incident radiation to outer sphere
(C) used to prevent reflected radiation to escape outside
(D) used for all of the above purposes.
Answer:
(C) used to prevent reflected radiation to escape outside

Question 24.
The emissive power of a body is
(A) the energy emitted by the body in a given time
(B) the radiant energy emitted by the body per unit area of the body
(C) the radiant energy emitted by the body per unit time
(D) the radiant energy emitted by the body per unit time per unit area of the body.
Answer:
(D) the radiant energy emitted by the body per unit time per unit area of the body.

Question 25.
The dimensions of emissive power are
(A) [M¹L^-2T^-3]
(B) [M¹L²T^-3]
(C) [M¹L⁰T^-3]
(D) [M¹L^0-2]
Answer:
(C) [M¹L⁰T^-3]

Question 26.
The emissive power per wavelength interval R_λ of a blackbody at an absolute temperature T₁ is maximum at λ₁ = 1.1 µm. At an absolute temperature T₂, its R_λ is maximum at λ₂ = 0.55 µm. Then, \(\frac{T_{1}}{T_{2}}\) is equal to
(A) \(\frac{1}{2}\)
(B) 1
(C) 2
(D) 4.
Answer:
(A) \(\frac{1}{2}\)

Question 27.
The temperature of the photosphere of the Sun is about 6000 K. Wien’s displacement law constant is 2.898 × 10^-3 m.K. The photosphere has maximum emissive power at wavelength
(A) 483 nm
(B) 496.7 nm
(C) 4830 nm
(D) 4967 nm.
Answer:
(A) 483 nm

Question 28.
A sphere and a cube made of the same metal have equal volumes, identical surface characteristics and are at the same temperature. If they are allowed to cool in identical surroundings, the ratio of their rates of loss of heat will be
(A) \(\frac{4 \pi}{3}\) : 1
(B) 1 : 1
(C) \(\left(\frac{\pi}{6}\right)^{\frac{2}{3}}\) : 1
(D) \(\left(\frac{\pi}{6}\right)^{\frac{1}{3}}\) : 1
Answer:
(D) \(\left(\frac{\pi}{6}\right)^{\frac{1}{3}}\) : 1

Question 29.
If the absolute temperature of a blackbody is increased by a factor 3, the energy radiated by it per unit time per unit area will increase by a factor of
(A) 9
(B) 27
(C) 81
(D) 243.
Answer:
(C) 81

Question 30.
Two spheres P and Q, having radii 8 cm and 2 cm, and of the same surface characteristics are maintained at 127 °C and 527 °C, respectively. The ratio of the radiant powers of P to Q is
(A) 0.0039
(B) 0.0156
(C) 1
(D) 2.
Answer:
(C) 1

Question 31.
Two copper spheres of radii 6 cm and 12 cm, respectively, are suspended in an evacuated enclosure. Each of them is at a temperature of 15 °C above the surroundings. The ratio of their rate of loss of heat is
(A) 2 : 1
(B) 1 : 4
(C) 1 : 8
(D) 8 : 1.
Answer:
(B) 1 : 4

Question 32.
The peak of the radiation spectrum of a blackbody occurs at 2 µn. Taking Wien’s displacement law constant as 2.9 × 10^-3 m.K, the approximate temperature of the blackbody is
(A) 15 K
(B) 150 K
(C) 750 K
(D) 1500 K.
Answer:
(D) 1500 K.

Question 33.
The light from the Sun is found to have a maximum intensity near the wavelength of 470 nm. Assuming the surface of the Sun as a blackbody, the temperature of the Sun is [Wien’s constant b = 2.898 × 10^-3 m.K]
(A) 5800 K
(B) 6050 K
(C) 6166 K
(D) 6500 K.
Answer:
(C) 6166 K

Question 34.
The amount of energy radiated per unit time by a body does not depend upon the
(A) nature of its surface
(B) area of its surface
(C) mass of the body
(D) temperature difference of the surface and surroundings.
Answer:
(C) mass of the body

Question 35.
Two gases exert pressure in the ratio 3 : 2 and their densities are in the ratio 2 : 3. Then the ratio of their rms speeds is
(A) 2 : 3
(B) 3 : 2
(C) 2 : 1
(D) 1 : 2.
Answer:
(B) 3 : 2

Question 36.
Find the wavelength at which a blackbody radiates maximum energy, if its temperature is 427 °C.
[Wien’s constant b = 2.898 × 10^-3 m.K]
(A) 0.0414 × 10^-6 m
(B) 4.14 × 10^-6 m
(C) 41.4 × 10^-6 m
(D) 414 × 10^-6 m
Answer:
(B) 4.14 × 10^-6 m

Question 37.
If the total kinetic energy per unit volume of gas enclosed in a container is E, the pressure exerted by the gas is
(A) E
(B) \(\frac{3}{2}\)E
(C) \(\sqrt{3}\)E
(D) \(\frac{2}{3}\)E.
Answer:
(D) \(\frac{2}{3}\)E.

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics

Question 1.
What is temperature? Explain.
Answer:
The temperature of a body is a quantitative measure of the degree of hotness or coolness of the body. According to the kinetic theory of gases, it is a measure of the average kinetic energy per molecule of the gas. Temperature difference determines the direction of flow of heat from one body to another or from one part of the body to the other. Its SI unit is the kelvin (K).

Question 2.
What is heat ? Explain.
Answer:
When two bodies are in thermal contact with each other, there is a transfer of energy from the body at higher temperature to the body at lower temperature. The energy in transfer is called the heat. Also when two parts of a body are at different temperatures, there is a transfer of energy from the part at higher temperature to the other part. The SI unit of heat is the joule.

[Note : Count Rumford [Benjamin Thompson] (1753-1814) Anglo-American adventurer, social reformer, inventor and physicist, measured the relation between work and heat. When he visited Arsenal in Munich, he found that tremendous amount of heat was produced in a short time when a brass cannon was being bored. He found that even with a blunt borer a lot of heat can be produced from a piece of metal. At that time it was thought that heat consists of a fluid called caloric. Rumford’s experiments showed that caloric did not exist and heat is the motion of the particles of a body. He measured the relation beween work done and corresponding heat produced. The result was not accurate, but important in development of thermodynamics.]

Question 3.
What is thermodynamics ?
Answer:
Thermodynamics is the branch of physics that deals with the conversion of energy (including heat) from one form into another, the direction of energy transfer between a system and its environment with the resulting variation in temperature, in general, or changes of state, and the availability of energy to do mechanical work.

Question 4.
What is meant by thermal equilibrium ? What is meant by the expression “two systems are in thermal equilibrium” ?
Answer:
A system is in a state of thermal equilibrium if there is no transfer of heat (energy) between the various parts of the system or between the system and its surroundings.

Two systems are said to be in thermal equilibrium when they are in thermodynamic states such that, if they are separated by a diathermic (heat conducting) wall, the combined system would be in thermal equilibrium, i.e., there would be no net transfer of heat (energy) between them.
[Note :It is the energy in transfer that is called the heat.]

Question 5.
State the zeroth law of thermodynamics.
Answer:
Zeroth law of thermodynamics : If two systems are each in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.

[Note :The zeroth law is fundamental to the other laws of thermodynamics. That this law is assumed by the other laws of thermodynamics was realized much later. This law has no single discoverer. It was given the status of a law, following the suggestion by R. H. Fowler (in 1931), only after the first, second and third laws were named.]

Question 6.
Explain the zeroth law of thermodynamics.
Answer:
Consider three systems A, B and C. Suppose A and B are in thermal equilibrium, and A and C are also in thermal equilibrium. Then B and C are also in thermal equlibrium. Thus, A, B and C are at the same temperature and A works as a thermometer.

[Note: The arrows in the figure indicate energy exchange]

Question 7.
Define internal energy.
Answer:
Internal energy of a system is defined as the sum of the kinetic energies of the atoms and molecules belonging to the system, and the potential energies associated with the interactions between these constituents (atoms and molecules).
[Note : Internal energy does not include the potential energy and kinetic energy of the system as a whole. In the case of an ideal gas, internal energy is purely kinetic. In the case of real gases, liquids and solids, internal energy is the sum of potential and kinetic energies. For an ideal gas, internal energy depends on temperature only. In other cases, internal energy depends on temperature, as well as on pressure and volume. According to quantum theory, internal energy never becomes zero. Even at OK. particles have energy called zero-point energy.]

Question 8.
What is the internal energy of one mole of argon and oxygen ?
Answer:
Argon is a monatamic gas. In this case, with three degrees of freedom, the average kinetic energy per molecule = \(\left(\frac{3}{2}\right)\)k_BT, where k_B is the Boltzmann constant and T is the absolute (thermodynamic) temperature of the gas. Hence, the internal energy of one mole of argon = N_A\(\left(\frac{3}{2} k_{\mathrm{B}} T\right)\) = \(\frac{3}{2}\)RT, where N_A is the Avogadro number and R = N_Ak_B is the universal gas constant. Oxygen is a diatomic gas. In this case, with five degrees of freedom at moderate temperatures, the internal energy of one mole of
oxygen = \(\frac{3}{2}\)RT.

Question 9.
Find the internal energy of one mole of argon at 300 K. (R = 8.314 J/mol.K)
Answer:
The internal energy of one mole of argon at 300 K
= \(\frac{3}{2}\)RT = \(\frac{3}{2}\)(8.314)(300) J = 3741 J.

Question 10.
The internal energy of one mole of nitrogen at 300 K is 6235 J. What is the internal energy of one mole of nitrogen at 400 K ?
Answer:

This is the required quantity.
[Note : In chapter 3, the symbol E was used for internal energy.]

Question 11.
Explain the term thermodynamic system.
Answer:
A thermodynamic system is a collection of objects that can form a unit which may have ability to Surrounding

exchange energy with its surroundings. Everything outside the system is called its surroundings or environment. For example, a gas enclosed in a container is a system, the container is the boundary and the atmosphere is the environment.

Question 12.
Explain classification of thermodynamic systems.
Answer:
Depending upon the exchange of energy and matter with the environment, thermodynamic systems are classified as open, closed or isolated.

A system that can freely exchange energy and matter with its environment is called an open system. Example : water boiling in an open vessel.

A system that can freely exchange energy but not matter with its environment is called a closed system. Example : water boiling in a closed vessel.

A system that cannot exchange energy as well as matter with its environment is called an isolated system. In practice it is impossible to realize an isolated system as every object at a temperature above 0 K emits energy in the form of radiation, and no object can ever attain 0 K.

For many practical purposes, a thermos flask containing a liquid can be considered an isolated system.

These three types are illustrated in above figure.

Question 13.
What is a thermodynamic process? Give an exmple.
Answer:
A process in which the thermodynamic state of a system is changed is called a thermodynamic process.
Example : Suppose a container is partially filled with water and then closed with a lid. If the container is heated, the temperature of the water starts rising and after some time the water starts boiling. The steam produced exerts pressure on the walls of the container, Here, there is a change in the pressure, volume and temperature of the water, i.e. there is a change in the thermodynamic state of the system.

Question 14.
Explain the relation between heat and internal energy.
Answer:
Suppose a system consists of a glass filled with water at temperature T_S. Let T_E be the temperature of the environment (surroundings) such as the surrounding air in the room. There is a continuous exchange of energy between the system and the surroundings.

If T_S > T_E, the net effect of energy exchange is the net transfer of internal energy from the system to the environment till thermal equilibrium is reached, i.e., T_S and T_E became equal. This internal energy in transit is called heat (Q). The change in the temperature of the environment is usually negligible compared with the change in the temperature of the system.

For T_S < T_E, there is energy exchange between the
system and the environment, but no net transfer of
energy.

For T_S = T_E, there is energy exchange between the system and the environment, but no net transfer of energy.

Thus, the net transfer of energy takes place only when there is temperature difference.

Question 15.
Explain how the internal energy of a system can be changed.
Answer:
Consider a system (S) consisting of some quantity of gas enclosed in a cylinder fitted with a movable, massless, and frictionless piston.

Suppose the gas is heated using a burner (source of heat, environment). Let T_S = temperature of the system (gas) and T_E = temperature of the environment.

Here, T_E > T_S. Hence, there will be a net flow of energy (heat) from the environment to the system causing the increase in the internal energy of the system.

The internal energy of the gas (system) can also be increased by quickly pushing the piston inward so that the gas is compressed.

The work done on the gas raises the temperature of the gas. Thus, there is increase in the internal energy of the gas. If the gas pushes the piston outward, the work is done by the gas on the environment and the gas cools as its internal energy becomes less.

Question 16.
On the basis of the kinetic theory of gases, explain
(i) positive work done by a system
(ii) negative work done by a system.
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.

During expansion of the gas, molecules colliding with the piston lose momentum to it. This exerts force and hence pressure on the piston, moving it outward through a finite distance. Here, the gas does a positive work on the piston. There is increase in the volume of the gas. The work done by the piston on the gas is negative.

During compression of the gas, molecules colliding with the piston gain momentum from it. The piston moving inward through a finite distance exerts force on the gas. Here, the gas does a negative work on the piston. There is decrease in the volume of the gas.

The work done by the piston on the gas is positive.

Question 17.
Obtain an expression for the work done by a gas.
OR
Show that the work done by a gas is given by
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.

During expansion of the gas, molecules colliding with the piston impart momentum to the piston. The time rate of change of momentum is the force, F exerted by the gas on the piston. If dx is the displacement of the piston, the work done by the gas, dW = F dx. If A is the area of cross section of the piston, the pressure exerted by the gas, P = \(\frac{F}{A}\).

Hence, the work done, dW = PAdx = PdV where dV = Adx is the increase in the volume of the gas. Here, dx is the infinitesimal displacement of the piston and dV is the infinitesimal increase in the volume of the gas.

If V_i is the initial volume of the gas, and V_f is the final volume, the total work done by the gas in moving the piston is given by W = \(\int_{V_{i}}^{V_{\mathrm{f}}} P d V\).

Question 18.
State the first law of thermodynamics. Express it in mathematical form.
Answer:
First law of thermodynamics : The change in the internal energy of a system (∆U) is the difference between the heat supplied to the system (Q) and the work done by the system on its surroundings (W).
Mathematically, ∆ U = Q – W, which is the same as Q = ∆ U + W.

Notes :

1. if Q is positive, it means heat is added to the system. If Q is negative, it means heat is given out by the system or removed from the system,
2. If ∆U is positive, it means there is increase in the internal energy of the system. If ∆ U is negative, it means there is decrease in the internal energy of the system,
3. If W is positive, it means it is the work done by the system on its surroundings. Negative W means work is done on the system by the surroundings,
4. The first law of thermodynamics is largely due to Joule. It is essentially the law of conservation of energy applied to the systems that are not isolated, i.e., the systems that can exchange energy with the surroundings. Thermodynamics was developed in 1850 by Rudolf Clausius (1822-88) German theoretical physicist, His ideas were developed in 1851 by William Thomson [Lord Kelvin] (1824-1907), British physicist and electrical engineer,
5. Q = ∆ U + W. Here, all quantities are expressed in the same units, e.g., cal or joule. If Q and A U are expressed in heat unit (cal, kcal) and W is expressed in mechanical unit (erg, joule) then the above equation takes the form Q = ∆ U + \(\frac{W}{J}\), where J is the mechanical equivalent of heat.]

Question 19.
What is the property of a system or a system variable ?
Answer:
The property of a system or a system variable is any measurable or observable characteristic or property of the system when the system remains in equilibrium.

Question 20.
Name the macroscopic variables of a system.
Answer:
Pressure, volume, temperature, density, mass, specific volume, amount of substance (expressed in mole) are macroscopic variables of a system.
Notes : The quantities specified above are not totally independent, e.g.,

1. density = mass/volume
2. specific volume (volume per unit mass) = 1/density.

Question 21.
What is an intensive variable ? Give examples.
Answer:
A variable that does not depend on the size of the system is called an intensive variable.
Examples : pressure, temperature, density.

Question 22.
What is an extensive variable ? Give examples.
Answer:
A variable that depends on the size of the system is called an extensive variable.
Examples : internal energy, mass.

Question 23.
What is mechanical equilibrium ?
Answer:
A system is said to be in mechanical equilibrium when there are no unbalanced forces within the system and between the system and its surroundings.
OR
A system is said to be in mechanical equilibrium when the pressure in the system is the same throughout and does not change with time.
[Note : The constituents of a system, atoms, molecules, ions, etc, are never at rest. Within a system, even in the condition of equilibrium, statistical fluctuations do occur, but the time of observation is usually very large so that these fluctuations can be ignored.]

Question 24.
What is chemical equilibrium ?
Answer:
A system is said to be in chemical equilibrium when there are no chemical reactions going on within the system.
OR
A system is said to be in chemical equilibrium when its chemical composition is the same throughout the system and does not change with time.
[Note : In this case, in the absence of concentration gradient, there is no diffusion, i.e., there is no transport of matter from one part of the system to the other.]

Question 25.
What is thermal equilibrium ?
Answer:
A system is said to be in thermal equilibrium when its temperature is uniform throughout the system and does not change with time.

Question 26.
Give two examples of thermodynamic systems not in equilibrium.
Answer:

1. When an inflated balloon is punctured, the air inside it suddenly expands and escapes into the atmosphere. During the rapid expansion, there is no uniformity of pressure, temperature and density.
2. When water is heated, there is no uniformity of pressure, temperature and density. If the vessel is open, some water molecules escape to the atmosphere.

Question 27.
What is the equation of state ? Explain.
Answer:
The mathematical relation between the state variables (pressure, volume, temperature, amount of the substance) is called the equation of state.

In the usual notation, the equation of state for an ideal gas is PV = nRT.

For a fixed mass of gas, the number of moles, n, is constant. R is the universal gas constant. Thus, out of pressure (P), volume (V) and thermodynamic temperature (T), only two (any two) are independent.

Question 28.
Draw P-V diagram for positive work at constant pressure.

Answer:
In this case, during the expansion, the work done by the gas, W = \(\int_{V_{1}}^{V_{2}} P d V\) = P(V₂ – V₁) is positive as V₂ > V₁.

Question 29.
What is a thermodynamic process ? Explain.
Answer:
A procedure by which the initial state of a system changes to its final state is called a thermodynamic process. During the process/ there may be

1. addition of heat to the system
2. removal of heat from the system
3. change in the temperature of the system
4. change in the volume of the system
5. change in the pressure of the system.

Question 30.
What is a quasistatic process ?
Answer:
A quasistatic process is an idealised process which occurs infinitely slowly such that at all times the system is infinitesimally close to a state of thermodynamic equilibrium. Although the conditions for such a process can never be rigorously satisfied in practice, any real process which does not involve large accelerations or large temperature gradients is a reasonable approximation to a quasistatic process.

Question 31.
Draw a diagram to illustrate that the work done by a system depends on the process even when the initial and final states are the same.

Answer:
In the above diagram, the initial state of a gas is characterized by (P_i, V_i) [corresponding to point A] and the final state of the gas is characterized by (P_f, V_f) [corresponding to point B]. Path 1 corresponds to constant temperature. Path 2 corresponds to the combination AC [P constant] + CB [V constant]. Path 3 corresponds to the combination AD [V constant] + DB [P constant]. The work done by the gas (W) is the area under the curve and is different in each case.

Question 32.
What is a reversible process? What is an irreversible process? Give four examples of an irreversible process. Explain in detail.
Answer:
A reversible process is one which is performed in such a way that, at the conclusion of the process, both the system and its local surroundings are restored to their initial states, without producing any change in the rest of the universe.

A process may take place reversibly if it is quasistatic and there are no dissipative effects. Such a process cannot be realized in practice.

A process which does not fulfill the rigorous requirements of reversibility is said to be an irreversible process. Thus, in this case, the system and the local surroundings cannot be restored to their initial states without affecting the rest of the universe. All natural processes are irreversible.
Examples of irreversible process :

1. When two bodies at different temperatures are brought in thermal contact, they attain the same temperature after some time due to energy exchange. Later, they never attain their initial temperatures.
2. Free expansion of a gas.
3. A gas seeping through a porous plug.
4. Collapse of a soap film after it is pricked.
5. All chemical reactions.
6. Diffusion of two dissimilar inert gases.
7. Solution of a solid in water.
8. Osmosis.

[Note : A free expansion is an adiabatic process, i.e., a process in which no heat is added to the system or removed from the system. Consider a gas confined by a valve to one half of a double chamber with adiabatic walls while the other half is evacuated.

When the gas is in thermal equilibrium, the gas is allowed to expand to fill the entire chamber by opening the valve.
No interaction takes place and hence there are no local surroundings. While rushing into a vacuum, the gas does not meet any pressure and hence no work is done by the gas. The gas only changes state isothermally from a volume V_i to a larger volume V_f.]

To restore the gas to its initial state, it would have to be compressed isothermally to the volume V_i; an amount of work W would have to done on the gas by some mechanical device and an equal amount of heat would have to flow out of the gas into a reservoir. If the mechanical device and the reservoir are to be left unchanged, the heat would have to be extracted from the reservoir and converted completely into work. Since this last step is impossible, the process of free expansion is irreversible.

It can be shown that the diffusion of two dissimilar inert gases is equivalent to two independent free expansions. It follows that diffusion is irreversible.]

Question 33.
What are the causes of irreversibility?
Answer:

1. Some processes such as a free expansion of a gas or an explosive chemical reaction or burning of a fuel take the system to non-equilibrium states.
2. Most processes involve dissipative forces such as friction and viscosity (internal friction in fluids). These forces can be minimized, but cannot be eliminated.

Question 34.
What is an isothermal process? Obtain an expression for the work done by a gas in an isothermal process.
Answer:
A process in which changes in pressure and volume of a system take place at a constant temperature is called an isothermal process.

Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. Let P_i, V_i and T be the initial pressure, volume and absolute temperature respectively of the gas. Consider an isothermal expansion (or compression) of the gas in which P_f, V_f and T are respectively the final pressure, volume and absolute

temperature of the gas. Assuming the gas to behave as an ideal gas, we have, its equation of state :
PV = nRT = constant as T = constant, R is the universal gas constant. The work done by the gas,

Notes :

1. The above expression for W can be written in various forms such as W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_iV_i ln \(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_fV_f\(\left(\frac{V_{f}}{V_{\mathrm{i}}}\right)\), etc.
2. W is positive if V_f > V_i (expansion). W is negative if V_f < V_i (contraction).
3. At constant temperature, change in internal energy, ∆ U = 0.
   ∴ Q = ∆ U + W = W.
4. Isothermal process shown in P- V diagram is also called an isotherm.
5. Melting of ice is an isothermal process.

Question 35.
What is an isobaric process? Obtain the expressions for the work done, change in internal energy and heat supplied in an isobaric process in the case of a gas.
Answer:
A process in which pressure remains constant is called an isobaric process. Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. We assume that the gas behaves as an ideal gas so that we can use the equation of state PV = nRT.

Consider an isobaric expansion (or compression) of the gas in which the volume of the gas changes from V_i to V_f and the temperature of the gas changes from T_i to T_f when the pressure (P) of the gas is kept constant. The work done by the gas,

Now, PV_i = nRT_i and PV_f = nRT_f
∴ PV_f – PV_i = nRT_f – nRT_i
∴ P(V_f – V_i) = nR(T_f – T_i)
∴ from Eq. (1), W = nR(T_f – T_i) … (2)
The change in the internal energy of the gas,
∆ U = nC_v(T_f – T_i) …(3)
where C_v is the molar specific heat of the gas at constant volume.
From Eqs. (2) and (3), we have, the heat supplied to the gas,
Q = ∆ U + W = nC_v(T_f – T_i) + nR(T_f – T_i)
= n(C_v + R)(T_f – T_i)
∴ Q = _nC_p(T_f – T_i) …(4)
Where C_p ( = C_v + R) is the molar specific heat of the gas at constant pressure.
[Note : P-V curve for an isobaric process is called an isobar.

Question 36.
What is an isochoric process ? Write the expressions for the work done, change in internal energy and heat supplied in this case. Also draw the corresponding P-V diagram.
Answer:
A process that takes place at constant volume is called an isochoric process (or isometric process).

As there is no change in volume in this case, the work done (W) by the system on its environment is zero. The change in the internal energy.
∆ U = _nC_v (T_f – T_i) and heat supplied,
Q = ∆ U = _nC_v(T_f – T_i)

Question 37.
What is an adiabatic process ? Obtain expressions for the work done by a system (an ideal gas) in an adiabatic process. Also draw the corresponding P-V diagram.
Answer:
A process during which there is no transfer of heat (energy) from the system to the surroundings or from the surroundings to the system is called an adiabatic process.

It can be shown that if an ideal gas is subjected to an adiabatic process, then,
PV^γ = constant = C, where γ, is \(\frac{C_{P}}{C_{V}}\). γ is called the adiabatic ratio. C_P is the molar specific heat of the gas at constant pressure and C_V is the molar specific heat at constant volume.
Let P_i = initial pressure, P_i final pressure V_f = initial volume and V_f = final volume of the gas taken through an adiabatic process.

Now, P_iV_i = nRT_i and P_fV_f = nRT_f, where n is the number of moles of the gas, T_i is the initial temperature of the gas, T_f is the final temperature of the gas and R is the universal gas constant.

[Note: We have Q = ∆ U + W = 0 in an adiabatic process.
∴ W= -∆ U = -nC_v(T_f – T_i)_nC_v(T_i – T_f)]

Question 38.
What is a cyclic process? Explain with a diagram.
Answer:
A thermodynamic process in which the system returns to its initial state is called a cyclic process. This is illustrated in below figure. Path 1 shows how the state of the system (ideal gas) is changed from (P_i, V_i) [point A] to (P_f, V_f) [point B], Path 2 shows the return of the system from point B to point A. As the system returns to its initial state, the total change in its internal energy is zero. Hence, according to the first law of thermodynamics, heat supplied,

Q = ∆ U + W = 0 + W = W. The area enclosed by the cycle in P-V plane gives the work done (W) by the system.

Question 39.
Explain the term free expansion of a gas.
Answer:
When a balloon is ruptured suddenly, or a tyre is punctured suddenly, the air inside the balloon/ tyre rushes out rapidly to the atmosphere. This process (expansion of air inside the balloon/tyre) is so quick that there is no time for transfer of heat from the system to the surroundings or from the surroundings to the system. Such an adiabatic expansion is called free expansion. It is characterized by Q = W = 0, implying ∆ U = 0. Free expansion is an uncontrolled change and the system is not in thermodynamic equilibrium. Free expansion cannot be illustrated with a P-V diagram as only the initial state and final state are known.

Question 40.
Solve the following :

Question 1.
A gas enclosed in a cylinder fitted with a movable, massless and frictionless piston is expanded so that its volume increases from 5 L to 6 L at a constant pressure of 1.013 × 10⁵ Pa. Find the work done by the gas in this process.
Solution :
Data : P = 1.013 × 10⁵ Pa, V_i = 5L = 5 × 10^-3 m³,
v_f = 6L = 6 × 10^-3 m³
The work done by the gas, in this process,
W = P(V_f – V_i)
= (1.013 × 10⁵)(6 × 10^-3 – 5 × 10^-3)J
= 1.013 × 10²J

Question 2.
The initial pressure and volume of a gas enclosed in a cylinder are respectively 1 × 10⁵ N/m² and 5 × 10^-3 m³. If the work done in compressing the gas at constant pressure is 100 J. Find the final volume of the gas.
Solution :
Data : P = 1 × 10⁵ N/m², V_i = 5 × 10^-3 m³,
W= -100 J
W = P(V_f – V_i) ∴ V_f – V_i = \(\frac{W}{P}\)
∴ V_f = V_i + \(\frac{W}{P}\) = 5 × 10^-3 + \(\frac{(-100)}{\left(1 \times 10^{5}\right)}\)
= 5 × 10^-3 -1 × 10^-3 = 4 × 10^-3 m³
This is the final volume of the gas.

Question 3.
If the work done by a system on its surroundings is 100 J and the increase in the internal energy of the system is 100 cal, what must be the heat supplied to the system? (Given : J = 4.186J/cal)
Solution :
Data : W = 100 J, ∆ U = 100 cal, J = 4.186 J / cal
The heat supplied to the system,
Q = ∆ U + W = (100 cal) (4.186 J/cal) + 100 J
= 418.6J + 100J = 518.6 J

Question 4.
Ten litres of water are boiled at 100°C, at a pressure of 1.013 × 10⁵ Pa, and converted into steam. The specific latent heat of vaporization of water is 539 cal/g. Find
(a) the heat supplied to the system
(b) the work done by the system
(c) the change in the internal energy of the system. 1 cm³ of water on conversion into steam, occupies 1671 cm³ (J = 4.186 J/cal)
Solution :
Data : P = 1.013 × 10⁵ Pa, V (water) = 10 L = 10 × 10^-3 m³, V(steam) = 1671 × 10 × 10^-3 m³, L = 539 cal/g = 539 × 10³ \(\frac{\mathrm{cal}}{\mathrm{kg}}\) = 539 × 10³ × 4.186\(\frac{\mathrm{J}}{\mathrm{kg}}\) as J = 4.186 J/cal, mass of the water (M) = volume × density = 10 × 10^-3 m³ × 10³ kg/m³ = 10 kg

(a) Q = ML = (10) (5.39 × 4.186 × 10⁵) J
= 2.256 × 10⁷J
This is the heat supplied to the system

(b) W = P∆V = (1.013 × 10⁵) (1671 – 1) × 10^-2J
= (1.013) (1670) × 10³ J = 1.692 × 10⁶ J
This is the work done by the system.

(c) ∆ U = Q – W = 22.56 × 10⁶ – 1.692 × 10⁶
= 2.0868 × 107J
This is the change (increase) in the internal energy of the system.

Question 5.
Find the heat needed to melt 100 grams of ice at 0°C, at a pressure of 1.013 × 10⁵ N/m². What is the work done in this process ? What is the change in the internal energy of the system ?
Given : Specific latent heat of fusion of ice = 79.71 cal/g, density of ice = 0.92 g/cm³, density of water = 1 g/cm³,1 cal = 4.186 J.
Solution :

1. The heat needed to melt the ice, Q = ML = (0.1) (3.337 × 10⁵) J = 3.337 × 10⁴ J
2. The work done, W = P(V_Water – V_ice)
   = (1.013 × 10⁵) (100 – 108.7) × 10^-6J = -0.8813J
3. The change in the internal energy,
   ∆ U = Q – W = 3.337 × 10⁴ J + 0.8813 J
   = 3370.8813 J

Question 6.
Find the work done by the gas when it is taken through the cycle shown in the following figure. (1 L = 10^-3 m³)
Solution :

∴ W_ABCDA = W_AB + W_BC + W_CD + W_DA
= 2000J + 0 – 1000J + 0 = 1000J

Question 7.
A gas with adiabatic constant γ = 1.4, expands adiabatically so that the final pressure becomes half the initial pressure. If the initial volume of the gas 1 × 10^-2 m³, find the final volume.
Solution:

This is the final volume of the gas.

Question 8.
In an adiabatic compression of a gas with γ = 1.4, the initial temperature of the gas is 300 K and the final temperature is 360 K. If the initial volume of the gas is 2 × 10^-3 m³, find the final volume.
Solution:
Data: γ = 1.4, T_i = 300 K, T_f = 360 K
∴ T_f/T_i = 1.2, V_i = 2 × 10^-3 m³

This is the final volume of the gas.

Question 9.
In an adiabatic compression of a gas with γ = 1.4, the final pressure is double the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature.
Solution:
Data: γ = 1.4, P_f = 2P_i, T_i = 300 K

∴ log \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = 0.2857 log 2 = 0.2857 (0.3010) = 0.086
∴ \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = antilog 0.086 = 1.219
∴ T_f = 1219T_i
= (1.219) (300) = 365.7 K
This is the final temperature of the gas.

Question 10.
In an adiabatic compression of a gas the final volume of the gas is 80% of the initial volume. If the initial temperature of the gas is 27 °C, find the final temperature of the gas. Take γ = 5/3.
Solution :
Data: V_f = 0.8 V_i ∴ \(\frac{V_{\mathrm{i}}}{V_{\mathrm{f}}}\) = \(\frac{10}{8}\) = 1.25,
∴ T_i = 27 °C = (273 + 27) K = 300 K, γ = \(\frac{5}{3}\)

∴ x = antilog 0.0646 = 1.161
∴ T_f = (300) (1.161) = 348.3 K
= (348.3 – 273)°C = 75.3 °C
This is the final temperature of the gas.

Question 11.
In an adiabatic expansion of a gas, the final volume of the gas is double the initial volume. If the initial pressure of the gas is 105 Pa, find the final pressure of the gas. (γ = 5/3)
Solution :

Let 2^5/3 = x ∴ \(\frac{5}{3}\)log 2 = log x
∴ log x = \(\left(\frac{5}{3}\right)\) (0.3010) = 0.5017
∴ x = antilog 0.5017 = 3.175
∴ P_f = \(\frac{10^{5}}{3.175}\) = 3.15 × 10⁴ Pa
This is the final pressure of the gas.

Question 12.
In an adiabatic process, the final pressure of the gas is half the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature of the gas. (Take γ = \(\frac{5}{3}\))
Solution :

This is the final temperature of the gas.

Question 13.
In an adiabatic process, the pressure of the gas drops from 1 × 10⁵ N/m² to 5 × 10⁴ N/m² and the temperature drops from 27 °C to – 46 °C. Find the adiabatic ratio for the gas.
Solution :


This is the adiabatic ratio (γ) for the gas.
[Note : This value (1.673) is slightly more than 5/3 (the value for a monatomic gas) due to error in measurement of pressure and temperature.]

Question 14.
Two moles of a gas expand isothermally at 300 K. If the initial volume of the gas is 23 L and the final volume is 46 L, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data ; n = 2, T = 300 K, V, = 23 L = 23 × 10^-3 m³, V_f = 46 L = 46 × 10^-3 m³, R = 8.314 J/mol.K
The work done by the gas on its surroundings,
W = nRT ln \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\) = 2.303 nRT log₁₀ \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\)
= (2.303) (2) (8.314) (300) log₁₀ \(\left(\frac{46 \times 10^{-3}}{23 \times 10^{-3}}\right)\)
= (4.606) (8.314) (300) log\(\begin{array}{r}
2 \\
10
\end{array}\)
= (4.606) (8.314) (300) (0.3010)
= 3458J

Question 15.
Four moles of a gas expand isothermally at 300 K. If the final pressure of the gas is 80% of the initial pressure, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data : n = 4, T = 300 K, P_f = 0.8 P_i
∴ \(\frac{P_{i}}{P_{f}}\) = \(\frac{10}{8}\), R = 8.314 j/mol.K
The work done by the gas on its surroundings,
W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\)
= (4) (8.314) (300) 2.303 log₁₀ \(\left(\frac{10}{8}\right)\)
= 2.3 × 10⁴ log₁₀ (1.25) = 2.3 × 10⁴ × 0.0969
= 2.229 × 10³J

Question 16.
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure so that the rise in temperature is 10 K. Find the increase in the internal energy of the gas.
Solution :
Data : C_v = 12.47 J/mol.k, n = 2, T_f – T_i = 10 K
The increase in the internal energy of the gas,
∆ U = _nC_v (T_f – T_i)
= (2) (12.47) (10) J
= 249.4 J

Question 17.
The molar specific heat of Ar at constant volume is 12.47 J/mol.K. Two moles of Ar are heated at constant pressure so that the rise in temperature is 20 K. Find the work done by the gas on its surroundings and the heat supplied to the gas. Take R = 8.314 J/mol.K.
Solution :
Data : C_v = 12.47 j/mol.K, n = 2,T_f – T_i = 20 K,
R = 8.314 J/mol.K

1. W = nR (T_f – T_i) = (2) (8.314) (20) J = 332.6 J
   This is the work done by the gas on its surroundings.
2. Q = _nC_v(T_f – T_i) + W = (2) (12.47) (20) + 332.6
   = 498.8 + 332.6 = 831.4 J
   This is the heat supplied to the gas.

Question 18.
The molar specific heat of a gas at constant pressure is 29.11 J/mol.k. Two moles of the gas are heated at constant pressure so that the rise in temperature is 40 K. Find the heat supplied to the gas.
Solution :
Data : C_P = 29.11 J/mol.K, n = 2, T_f – T_i = 40 K.
The heat supplied to the gas,
Q = _nC_P (T_f – T_i) = (2) (29.11) (40) J
= 2329 J

Question 19.
The molar specific heat of a gas at constant volume is 20.8 J/mol.k. Two moles of the gas are heated at constant volume so that the rise in temperature is 10 K. Find the heat supplied to the gas.
Solution :
Data : C_v = 20.8 J/mol.K, n = 2, T_f – T_i = 10 K.
The heat supplied to the gas,
Q = _nC_v (T_f – T_i) = (2) (20.8) (10) J
= 416J

Question 20.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 10⁵ Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 10⁴ Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Take γ = 5/3.
Solution :
Data : H = 2, P_i = 1.013 × 10⁵ Pa, P_f = 3.191 × 10⁴ Pa,
V_i = 22.4 L = 22.4 × 10^-3 m³,
V_f = 44.8 L = 44.8 × 10^-3 m³, γ = 5/3

Question 21.
In an adiabatic expansion of 2 moles of a gas, the temperature of the gas decreases from 37°C to 27°C. Find the work done by the gas on its surroundings. Take γ = 5/3 and R = 8.314 J/mol.K
Answer:
Data: n =2, T_i = (273 + 37) = 310 K,
T_f = (273 + 27)K = 300K, γ = 5/3,
R = 8.314 J/mol.K.
The work done by the gas on its surroundings,

Question 22.
A resistor of resistance 200 Ω carries a current of 2 A for 10 minutes. Assuming that almost all the heat produced in the resistor is transferred to water (mass = 5 kg, specific heat capacity = 1 kcal/kg), and the work done by the water against the external pressure during the expansion of water can be ignored, find the rise in the temperature of the water. (J = 4186 J/cal)
Solution :
Data : I = 2 A, R = 200 Ω, t = 10 min = 10 × 60 s = 600 s, M = 5 kg, S = (1 kcal/kg) (4186 J/kcal)
= 4186 J/kg
Q = ∆ U + W = MS ∆T + W \(\simeq\) MS ∆T ignoring W.
Also, Q = I²Rt ∴ I²RT = MS∆T
∴ The rise in the temperature of water = ∆T = \(\frac{I^{2} R t}{M S}\)
= \(\frac{(2)^{2}(200)(600)}{(5)(4186)}\)°C = 22.93°C

Question 23.
The initial pressure, volume and temperature of a gas are respectively 1 × 10⁵ Pa, 2 × 10^-2 m³ and 400 K. The temperature of the gas is reduced from 400 K to 300 K at constant volume. Then the gas is compressed at constant temperature so that its volume becomes 1.5 × 10^-2 m³.
Solution:
Data : P_A = 1 × 10⁵ Pa, V_A = 2 × 10^-2 m³, T_A = 400 K, V_B = v_A = 2 × 10^-2 m³, T_B = 300 K, T_C = T_B = 300 K, V_C = 1.5 x 10× 10^-2 m³, Also, P_C = P_A = 1 × 10⁵ Pa as the gas returns to its initial state.

Question 24.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat of the gas at
(i) constant volume
(ii) constant pressure.
(R = 8.314 J/mol. K)
Solution :
Data : r = 5/3, R = 8.314 J/mol.K

This is the required quantity.
(ii) C_P = _γC_V = \(\left(\frac{5}{3}\right)\)(12.47) = 20.78 J/mol.

Question 41.
What is a heat engine ?
Answer:
A heat engine is a device in which a system is taken through cyclic processes that result in converting part of heat supplied by a hot reservoir into work (mechanical energy) and releasing the remaining part to a cold reservoir. At the end of every cycle involving thermodynamic changes, the system is returned to the initial state.
[Note : Automobile engine is a heat engine.]

Question 42.
What does a heat engine consist of ?
OR
What are the elements (parts) of a typical heat engine?
Answer:
The following are the parts of a typical heat engine :

(1) Working substance : It can be

1. a mixture of fuel vapour and air in a gasoline (petrol) engine or diesel engine
2. steam in a steam engine. The working substance is called a system.

(2) Hot and cold reservoirs : The hot reservoir is a source of heat that supplies heat to the working substance at constant temperature T_H. The cold reservoir, also called the sink, takes up the heat released by the working substance at constant temperature T_C < T_H.

(3) Cylinder and piston : The working substance is enclosed in a cylinder fitted with (ideally) a movable, massless, and frictionless piston. The walls of the cylinder are nonconducting, but the base is conducting. The piston is nonconducting. The piston is connected to a crankshaft so that the work done by the working substance (mechanical energy) can be transferred to the environment.

Question 43.
What are the two basic types of heat engines?
Answer:
(i) External combustion engine in which the working substance is heated externally as in a steam engine.
(ii) Internal combustion engine in which the working substance is heated internally as in a petrol engine or diesel engine.
[Note : A steam engine was invented by Thomas New-comen (1663-1729), English engineer. The first practical steam engine was constructed in 1712. The modem steam engine was invented in 1790 by James Watt (1736-1819), British instrument maker and engineer. A hot-air type engine was developed by Robert Stirling (1790-1878), Scottish engineer and clergyman.

A four-stroke internal combustion engine was devised by Nikolaus August Otto (1832-1891), German engineer. A compression-ignition internal combustion engine was devised by Rudolph (Christian Karl) Diesel (1858 – 1913), German engineer.]

Question 44.
State the basic steps involved in the working of a heat engine.
Answer:

1. The working substance absorbs heat (Q_H) from a hot reservoir at constant temperature. T_H. It is an isothermal process Q_H is positive.
2. Part of the heat absorbed by the working substance is converted into work (W), i.e. mechanical energy. In this case, there is a change in the volume of the substance.
3. The remaining heat (|Q_C| = |Q_H| – W) is transferred to a cold reservoir at constant temperature T_C < T_H. Q_C is negative.

Question 45.
Draw a neat labelled energy flow diagram of a heat engine.
Answer:

Question 46.
Define thermal efficiency of a heat engine.
Answer:
The thermal efficiency, η of a heat engine is defined W as η = \(\frac{W}{Q_{H}}\), where W is the work done (output) by Q_H the working substance and Q_H is the amount of heat absorbed (input) by it.
[Note : η has no unit and dimensions or its dimensions are [M°L°T°].]

Question 47.
Draw a neat labelled P-V diagram for a typical heat engine.
Answer:

Here, T_H is the temperature at which the work is done by the gas and T_c is the temperature at which the work is done on the gas. The area of the loop ABCDA is the work output.

Question 48.
Solve the following :

Question 1.
Find the thermal efficiency of a heat engine if in one cycle the work output is 3000 J and the heat input is 10000 J.
Solution :
Data : W = 3000 J, Q_H = 10000 J
The thermal efficiency of the engine,
η = \(\frac{W}{Q_{\mathrm{H}}}\) = \(\frac{3000 \mathrm{~J}}{10000 \mathrm{~J}}\) = 0.3 = 30%

Question 2.
The thermal efficiency of a heat engine is 25%. If in one cycle the heat absorbed from the hot reservoir is 50000 J, what is the heat rejected to the cold reservoir in one cycle ?
Solution :
Data : η = 25% = 0.25, Q_H = 50000 J W
η = \(\frac{W}{Q_{\mathrm{H}}}\)
∴ W = _ηQ_H = (0.25)(50000)J = 12500J
Now, W = Q_H – |Q_C|
∴ |Q_C| = Q_H – W
= (50000 – 12500) J
= 37500J
This is the heat rejected to the cold reservoir in one cycle.
[Notes : Q_C = – 37500 J]

Question 49.
What is a refrigerator?
Answer:
A refrigerator is a device that uses work to transfer energy in the form of heat from a cold reservoir to a hot reservoir as it continuously repeats a thermodynamic cycle. Thus, it is a heat engine that runs in the backward direction.

Question 50.
With a neat labelled energy flow diagram, explain the working of a refrigerator.
Answer:
A refrigerator performs a cycle in a direction opposite to that of a heat engine, the net result being absorption of some energy as heat from a reservoir at low temperature, a net amount of work done on the system and the rejection of a larger amount

of energy as heat to a reservoir at a higher temperature. The working substance undergoing the refrigeration cycle is called a refrigerant. The refrigerant (such as ammonia or Freon) is a saturated liquid at a high pressure and at as low a temperature as can be obtained with air or water cooling.

The refrigeration cycle comprises the following processes :

1. Throttling process : The saturated liquid refrigerant passes from the condenser through a narrow opening from a region of constant high pressure to a region of constant lower pressure almost adiabatically. It is a property of saturated liquids (not gases) that a throttling process produces cooling and partial vaporization.
2. Isothermal, isobaric vaporization-with the heat of vaporization being supplied by the materials or the region to be cooled : Heat Q_c is absorbed by the refrigerant at the low temperature T_C, thereby cooling the materials of the cold reservoir.
3. Adiabatic compression of the refrigerant by an electrical compressor, thereby raising its temperature above T_H.
4. Isobaric cooling and condensation in the condenser at T_H : In the condenser, the vapour is cooled until it condenses and is completely liquefied, i. e., heat Q_H is rejected to the surroundings which is the hot reservoir.

Question 51.
Draw a neat labelled schematic diagram of transferring heat from a cold region to a hot region.
Answer:

Question 52.
What is refrigeration?
Answer:
Refrigeration is artificial cooling of a space or substance of a system and/or maintaining its temperature below the ambient temperature.

Question 53.
Draw a neat labelled diagram to illustrate schematics of a refrigerator.
Answer:

Question 54.
What are the steps through which a refrigerant goes in one complete cycle of refrigeration ?
Answer:
In one complete cycle of refrigeration, the refrigerant, a liquid such as fluorinated hydrocarbon, goes through the following steps :

1. The refrigerant in the closed tube passes through the nozzle and expands, into a low-pressure area. This adiabatic expansion results in reduction in pressure and temperature of the fluid and the fluid turns into a gas.
2. The cold gas is in thermal contact with the inner compartment of the fridge. Here it absorbs heat at constant pressure from the contents of the fridge.
3. The gas passes to a compressor where it does work in adiabatic compression. This raises its temperature and converts it back into a liquid.
4. The hot liquid passes through the coils on the outside of the refrigerator and releases heat to the air outside in an isobaric compression process.
   The compressor, driven by an external source of energy, does work on the refrigerant during each cycle.

Question 55.
Explain the energy flow in a refrigerator and define the coefficient of performance of a refrigerator.
Answer:
In a refrigerator, Q_C is the heat absorbed by the working substance (refrigerant) at a lower temperature T_C, W is the work done on the working substance, and Q_H is the heat rejected at a higher temperature T_H. The absorption of heat is from the contents of the refrigerator and rejection of heat is to the atmosphere. Here, Q_C is positive and W and Q_H are negative. In one cycle, the total change in the internal energy of the working substance is zero.
∴ Q_H + Q_C = W ∴ Q_H = W – Q_C
∴ -Q_H = Q_C – W
Now, Q_H < 0, W < 0 and Q_C > 0
∴ |Q_H| = |Q_C| + |W|
The coefficient of performance (CoP), K, or quality factor, or Q value of a refrigerator is defined as

[Note: K does not have unit and dimensions or its dimensions are [M°L°T°.]

Question 56.
How does an air conditioner differ from a refrigerator? Define the coefficient of performance of an air conditioner and express it in terms of heat current.
Answer:
The working of an air conditioner is exactly similar to that of a refrigerator, but the volume of the chamber/room cooled by an air conditioner is far greater than that in a refrigerator. The evaporator coils of an air conditioner are inside the room, and the condenser outside the room. A fan inside the air conditioner circulates cool air in the room.

The coefficient of performance, K, of an air conditioner is defined as K = \(|\frac{Q_{\mathrm{C}}}{W}|\), where Q_C is the heat absorbed and W is the work done. The time rate of heat removed is the heat current, H = \(\frac{\left|Q_{C}\right|}{t}\), where t is the time in which heat |Q_C|, is removed.

where H = |Q_C|/t is the heat current and P( = |W|/t) is the time rate of doing work, i.e., power.

Question 57.
What is a heat pump ?
Answer:
A heat pump is a device used to heat a building by cooling the air outside it. It works like a refrigerator but cooling outside space and heating inside space. In this case, the evaporator coils are outside the building to absorb heat from the air. The condenser coils are inside the building to release the heat to warm the building.

Question 58.
Solve the following :

Question 1.
In a refrigerator, in one cycle, the external work done on the working substance is 20% of the energy extracted from the cold reservoir. Find the coefficient of performance of the refrigerator.
Solution :
Data: |W| = 0.2|Q_C|
The coefficient of performance of the refrigerator,
K = |\(\frac{Q_{C}}{W}\)| = \(\frac{\left|Q_{C}\right|}{0.2\left|Q_{C}\right|}\)
= 5

Question 2.
The coefficient of performance of a room air conditioner is 3. If the rate of doing work is 2kW, find the heat current.
Solution :
Data : K = 3, P = 2000 W
K = \(\frac{H}{P}\)
∴ Heat current, H = KP = (3) (2000) W
= 6000 W = 6kW

Question 59.
State and explain the limitations of the first law of thermodynamics.
Answer:

1. The first law of thermodynamics is essentially the principle of conservation of energy as there is a close relation between work and energy. We find that there is a net transfer of energy (heat) from a body at higher temperature to a body at lower temperature. The net transfer of energy from a body at lower temperature to a body at higher temperature is not observed though consistent with the first law of thermodynamics.
2. If two containers, one containing nitrogen and the other containing oxygen, are connected to allow diffusion, they mix readily. They never get separated into the respective containers though there is no violation of the first law of thermodynamics.
3. It is not possible to design a heat engine with 100% efficiency, though there is no restriction imposed by the first law of thermodynamics.
4. At room temperature, ice absorbs heat from the surrounding air and melts. The process in the opposite direction is not observed, though consistent with energy conservation. These examples suggest that there is some other law operative in nature that determines the direction of a process

Question 60.
State the two forms of the second law of thermodynamics.
Answer:
Second law of thermodynamics :

1. It is impossible to extract an amount of heat Q_H from a hot reservoir and use it all to do work W. Some amount of heat Q_C must be exhausted (given out) to a cold reservoir. This prohibits the possibility of a perfect heat engine.
   This statement is called the first form or the engine law or the engine statement or the Kelvin-Planck statement of the second law of thermodynamics.
2. It is not possible for heat to flow from a colder body to a warmer body without any work having been done to accomplish this. This prohibits the possibility of a perfect refrigerator.
   This statement is called the second form or the Clausius statement of the second law of thermodynamics.

Notes :

1. Max Planck (Karl Ernst Ludwig) (1858-1947) German physicist, put forward quantum therory of radiation.
2. Rudolf Clausius (1822-88) German theoretical physicist, made significant contribution to thermodynamics.

Question 61.
Draw neat labelled diagrams to illustrate
(i) energy flow diagram for engine statement.
(ii) energy flow diagram for a perfect refrigerator.
Answer:

Question 62.
State the difference between a reversible process and an irreversible process.
OR
Distinguish between a reversible process and an irreversible process.
Answer:
A reversible process is a bidirectional process, i.e., its path in P-V plane is the same in either direction. In contrast, an irreversible process is a undirectional process, i.e., it can take place only in one direction.

A reversible process consists of a very large number of infinitesimally small steps so that the system is all the time in thermodynamic equilibrium with its environment. In contrast an irreversible process may occur so rapidly that it is never in thermodynamic equilibrium with its environment.

Question 63.
Draw a neat labelled diagram of a Carnot cycle and describe the processes occurring in a Carnot engine. Write the expression for the efficiency of a Carnot engine.
Answer:
Basically, two processes occur in a Carnot engine :

(1) Exchange of heat with the reservoirs : In isothermal expansion AB, the working substance takes in heat Q_H from a lot reservoir (source) at constant temperature T_H. In isothermal compression CD, the working substance gives out heat Q_C to a cold reservoir (sink) at constant temperature T_C.

(2) Doing work : In adiabatic expansion BC, the working substance does work on the environment and in adiabatic compression DA, work is done on the working substance by the environment.
All processes are reversible. It can be shown that \(\frac{\left|Q_{C}\right|}{Q_{\mathrm{H}}}\) = \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\). Hence, the efficiency of a Carnot engine,

Question 64.
What is a Carnot refrigerator? State the expressions for the coefficient of performance of a Carnot refrigerator.
Answer:
A Carnot refrigerator is a Carnot engine operated in the reverse direction. Here, heat Q_C is absorbed from a cold reservoir at temperature T_C, work W is provided externally, and heat Q_H is given out to a hot reservoir at temperature T_H.
The coefficient of performance of a Carnot refrigerator is

[Note: K is large if T_H-T_C is small. It means a large quantity of heat can be removed from the body at lower temperature to the body at higher temperature by doing small amount of work. K is small if T_H – T_C is large.
It means a small quantity of heat can be removed from the body at lower temperature to the body at higher temperature even with large amount of work.]

Question 65.
Solve the following :

Question 1.
A Carnot engine receives 6 × 10⁴ J from a reservoir at 600 K, does some work, and rejects some heat to a reservoir at 500 K. Find the
(i) the heat rejected by the engine
(ii) the work done by the engine
(iii) the efficiency of the engine.
Solution :
Data : Q_H = 6 × 10⁴J, T_H = 600K, T_C = 500K
(i) The heat rejected by the engine

Question 2.
A Carnot engine operates between 27 °C and 87 °C. Find its efficiency.
Solution :
Data : T_C = 27 °C = (273 + 27) K = 300 K,
T_H = 87 °C = (273 + 87) = 360 K
The efficiency of the engine,

Question 3.
The coefficient of performance of a Carnot refrigerator is 4. If the temperature of the hot reservoir is 47 °C, find the temperature of the cold reservoir.
Solution :
Data : K = 4, T_H = 47°C = (273 + 47) K = 320
K = \(\frac{T_{\mathrm{c}}}{T_{\mathrm{H}}-T_{\mathrm{c}}}\) ∴ KT_H – KT_c = T_c
∴ KT_H = (1 + K)T_c
∴ T_c = \(\frac{K T_{\mathrm{H}}}{1+K}\) = \(\frac{(4)(320)}{1+4}\)K = (0.8)(320)K
= 256K = (256 – 273)°C = – 17°C
This is the temperature of the cold reservoir.

[Note : A hot-air type engine consisting of two cylinders, was developed by Robert Stirling (1790 -1878), a Scottish engineer and clergyman. He developed the concept in 1816 and obtained a patent for his design in 1827. Some engines were made in 1844. He also used helium and hydrogen in some engines developed thereafter. Stirling engines are used in submarines and spacecrafts.]

Question 66.
Draw a neat labelled diagram of a Sterling cycle and describe the various processes taking place in a Sterling engine.

Answer:
The working substance can be air or helium or hydrogen or nitrogen. All processes are reversible.

1. AB is isothermal expansion, at temperature T_H, in which heat Q_H is absorbed from the source and useful work is done by the working substance.
2. BC is isochoric process in which some heat is released by the gas (working substance) to the refrigerator and the gas cools to temperature T_c < T_H.
3. CD is isothermal compression, at temperature T_c, in which heat Q_c is rejected to the coolant (sink).
4. DA is isochoric process in which heat is taken in by the gas and its temperature rises to T_H.

[Note : Stirling engine operated in reverse direction is used in the field of cryogenics to obtain extremely low – temperatures to liquefy air or other gases.]

Question 67.
Refer above figure and answer the following questions.
(i) What is the work done in process AB ?
(ii) What is the change in internal energy and heat released in process BC ?
Answer:
(i) In this case, the change in the internal energy is zero, as the temperature of the gas remains constant. Hence, the work done, W = heat absorbed, Q_H.

(ii) In this case, the change in the internal energy, ∆ U = _nC_V (T_C – T_H), where n = number of moles of the gas used in the Stirling engine and C_V = molar specific heat of the gas. As W = 0 at constant volume, heat released’= ∆ U.

Question 68.
Choose the correct option :

Question 1.
According to the first law of thermodynamics, in the usual notation,
(A) Q = ∆U + W
(B) Q = ∆U – W
(C) Q = W – ∆U
(D) Q= -(∆ U + W).
Answer:
(A) Q = ∆U + W

Question 2.
In an isothermal process, in the usual notation,
(A) PV = constant
(B) V/T = constant
(C) P/T = constant
(D) Q = 0.
Answer:
(A) PV = constant

Question 3.
In an isothermal process, in the usual notation,
(A) W = nRT (V_f/V_i)
(B) W = ∆ U
(C) W = Q
(D) W = 0.
Answer:
(C) W = Q

Question 4.
In an adiabatic process, in the usual notation,
(A) TV^γ = constant
(B) PT^γ = constant
(C) W = 0
(D) PV^γ = constant.
Answer:
(D) PV^γ = constant.

Question 5.
In an isobaric process, in the usual notation,
(A) W = P (V_f – V_i)
(B) W = Q
(C) W = – ∆U
(D) ∆T = 0.
Answer:
(A) W = P (V_f – V_i)

Question 6.
In an adiabatic process, in the usual notation,
(A) ∆ P = 0
(B) ∆ V = 0
(C) Q = 0
(D) ∆U = 0.
Answer:
(C) Q = 0

Question 7.
In an isothermal process, in the usual notation,
(A) W = P(V_f – V_i)
(B) W = 0
(C) W = V(P_f – P_i)
(D) W = nRT In(V_f/V_i).
Answer:
(D) W = nRT In(V_f/V_i).

Question 8.
In an isobaric process, in the usual notation,
(A) W = _nC_V (T_f – T_i)
(B) Q = _nC_P (T_f – T_i)
(C) ∆U = nR(T_f – T_i)
(D) W = 0.
Answer:
(B) Q = _nC_P (T_f – T_i)

Question 9.
In the usual notation, the isothermal work, W =
(A) P(V_f – V_i)
(B) nRT(P_i/ P_f)
(C) nRT ln(P_i/P_f)
(D) nRT(P_f/P_i).
Answer:
(C) nRT ln(P_i/P_f)

Question 10.
If Q and ∆u are expressed in cal and W is expressed in joule, then,
(A) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(B) Q = ∆U – (W/J)
(C) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(D) Q = ∆U + (W/J)
Answer:
(D) Q = ∆U + (W/J)

Question 11.
In an adiabatic process, in the usual notation, W =

Answer:
(A) \(\frac{P_{\mathrm{i}} V_{\mathrm{i}}-P_{\mathrm{f}} V_{\mathrm{f}}}{\gamma-1}\)

Question 12.
In a cyclic process,
(A) ∆U = Q
(B) Q = 0
(C) W = 0
(D) W = Q
Answer:
(D) W = Q

Question 13.
The efficiency of a heat engine is given by η =
(A) Q_H/W
(B) W/Q_c
(C) W/Q_H
(D) Q_c/W.
Answer:
(C) W/Q_H

Question 14.
In a cyclic process, the area enclosed by the loop in the P – V plane corresponds to
(A) ∆U
(B) W
(C) Q – W
(D) W – Q.
Answer:
(B) W

Question 15.
The efficiency of a Carnot engine is given by K =
(A) T_c/(T_H – T_c)
(B) (T_H – T_c)/T_c
(C) T_H/(T_H – T_c)
(D) (T_H – T_c)/T_H
Answer:
(A) T_c/(T_H – T_c)

Question 16.
The coefficient of performance of a Carnot refrigerator is given by K =
(A) T_c(T_H-T_c)
(B) (T_H-T_c)/T_c
(C) T_H/(T_H-T_c)
(D) (T_H-T_c)/T_H.
Answer:
(A) T_c(T_H-T_c)

Question 17.
The efficiency of a Carnot engine working between T_H = 400 K and T_c = 300 K is
(A) 75%
(B) 25%
(C) 1/3
(D) 4/7.
Answer:
(B) 25%

Question 18.
If a Carnot engine receives 5000 J from a hot reservoir and rejects 4000 J to a cold reservoir, the efficiency of the engine is
(A) 25%
(B) 10%
(C) 1/9
(D) 20%.
Answer:
(D) 20%.

Question 19.
If a Carnot refrigerator works between 250 K and 300 K, its coefficient of performance =
(A) 6
(B) 1.2
(C) 5
(D) 10.
Answer:
(C) 5

Question 20.
The coefficient of performance of a Carnot refrigerator is 4. If T_c = 250 K, then T_H =
(A) 625 K
(B) 310 K
(C) 312.5 K
(D) 320 K.
Answer:
(C) 312.5 K

Question 21.
The coefficient of performance of a Carnot refrigerator working between T_H and T_c is K and the efficiency of a Carnot engine working between the same T_H and T_c is η. Then
(A) ηk = \(\frac{Q_{\mathrm{H}}}{Q_{\mathrm{c}}}\)
(B) η/k = Q_c/Q_H
(C) η/k = Q_H/Q_c
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)
Answer:
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)

Question 22.
The internal energy of one mole of organ is
(A) \(\frac{5}{2}\)RT
(B) RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 23.
The internal energy of one mole of oxygen is
(A) \(\frac{5}{2}\)RT
(B) 5RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 24.
The internal energy of one mole of nitrogen at 300 K is about 6225 J. Its internal energy at 400 K will be about
(A) 8300J
(B) 4670J
(C) 8500J
(D) 8000J.
Answer:
(A) 8300J

Question 25.
The adiabatic constant γ for argan is
(A) 4/3
(B) 7/5
(C) 6/5
(D) 5/3.
Answer:
(D) 5/3.