Maharashtra Board Class 12 Physics Important Questions Chapter 10 Magnetic Fields due to Electric Current

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 10 Magnetic Fields due to Electric Current Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 10 Magnetic Fields due to Electric Current

Question 1.
What is the magnetic effect of electric current?
Answer:
An electric current produces a magnetic field around it. This phenomenon is known as the magnetic effect of electric current. It was discovered by Hans Christian Oersted.

It was Ampere who first speculated that all magnetic effects are attributable to electric charges in motion (electric current). It takes a moving electric charge to produce a magnetic field, and it takes another moving electric charge to “feel” a magnetic field.

[Note : Hans Christian Oersted (1777-1851), Danish physicist, discovered electromagnetism in 1820. The oersted, the CGS unit of magnetic field strength, is named after him.]

Question 2.
Describe the magnetic field near a current in a long, straight wire. State the expression for the magnetic induction near a straight infinitely long current-carrying wire.
Answer:
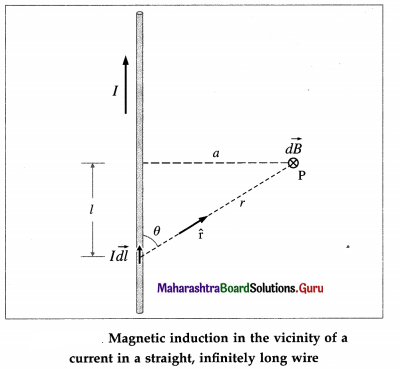
Suppose a point P is at a distance a from a straight, infinitely long, wire carrying a current I, as shown in figure.

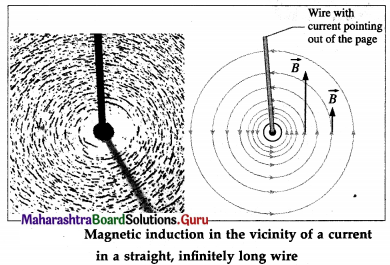
It can be shown that the magnitude of the total magnetic induction at P is given by the expression
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I}{a}\)
That is, the magnitude B is inversely proportional to the distance from the wire. Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the conductor; the direction of \(\vec{B}\) is everywhere tangential to such a circle. Thus, the magnetic field lines around the current in the straight wire is a family of circles centred on the wire. The magnitude of the field B depends only on the current and the perpendicular distance a of the point from the wire.

Question 3.
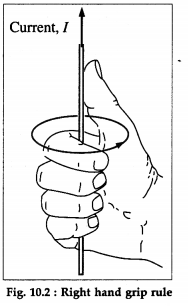
Explain the use of right hand grip rule to give the direction of magnetic field in the vicinity of a straight current-carrying conductor.
OR
State the right hand rule for the direction of the magnetic field due to a straight current-carrying wire.
Answer:
Right hand [grip] rule : If a straight current-carrying wire is grasped by the right hand, so that the extended thumb points in the direction of the current, the direction of the magnetic induction is the same as the direction of the fingers which are curled around the wire.

Question 4.
State the factors which the magnetic force on a charge depends upon. Hence state the expression for the Lorentz force on a charge due to an electric field as well as a magnetic field.
Hence discuss the magnetic force on a charged particle which is
(i) moving parallel to the magnetic field
(ii) stationary.
Answer:
A charge q moving with a velocity \(\vec{v}\) through a magnetic field of induction \(\vec{B}\) experiences a magnetic force perpendicular both to \(\vec{B}\) and \(\vec{v}\) . Experimental observations show that the magnitude of the force is proportional to the magnitude of \(\vec{B}\), the speed of the particle, the charge q and the sine of the angle θ between \(\vec{v}\) and \(\vec{B}\). That is, the magnetic force, F_m = qvB sin θ
∴ F_m = q(\(\vec{v}\) × \(\vec{B}\))
Therefore, at every instant \(\vec{F}_{\mathrm{m}}\) acts in a direction perpendicular to the plane of \(\vec{v}\) and \(\vec{B}\).

If the moving charge is negative, the direction of the force \(\vec{F}_{\mathrm{m}}\) acting on it is opposite to that given by the right-handed screw rule for the cross-product \(\vec{v}\) × \(\vec{B}\).

If the charged particle moves through a region of space where both electric and magnetic fields are present, both fields exert forces on the particle.

The force due to the electric field \(\vec{E}\) is \(\vec{F}_{\mathrm{e}}=q \vec{E}\).

The total force on a moving charge in electric and magnetic fields is called the Lorentz force :
\(\vec{F}=\vec{F}_{\mathrm{e}}+\vec{F}_{\mathrm{m}}=q(\vec{E}+\vec{v} \times \vec{B})\)
Special cases :
(i) \(\vec{v}\) is parallel or antiparallel to \(\vec{B}\): In this case, F_m = qvB sin 0° = 0. That is, the magnetic force on the charge is zero.
(ii) The charge is stationary (v = 0) : In this case, even if q ≠ 0 and B ≠ 0, F_m = q(0)B sin θ = 0. That is, the magnetic force on a stationary charge is zero.

Question 5.
Explain why the magnetic force on a charged particle cannot change the linear speed and the kinetic energy of the particle.
OR
One implication of the Lorentz force law is that magnetic force does no work. Justify.
Answer:
The magnetic force on a particle carrying a charge q and moving with a velocity \(\vec{v}\) in a magnetic field of induction \(\vec{B}\) is \(\vec{F}_{\mathrm{m}}=q \vec{v} \times \vec{B}\). At every instant, \(\vec{F}_{\mathrm{m}}\) is perpendicular to the linear velocity \(\vec{v}\), and \(\vec{B}\). Therefore, a non-zero magnetic force may change the direction of the velocity and the dot product

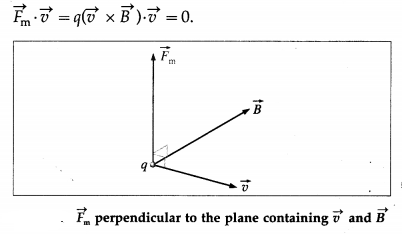
But \(\vec{F}_{\mathrm{m}} \cdot \vec{v}\) is the power, i.e., the time rate of doing work. Hence, the work done by the magnetic force in every short displacement of the particle is zero. The work done by a force produces a change in kinetic energy. Zero work means no change in kinetic energy. Thus, although the magnetic force changes the direction of the velocity \(\vec{v}\), it cannot change the linear speed and the kinetic energy of the particle.

Question 6.
Define the SI unit of magnetic induction from Lorentz force.
Answer:
The SI unit of magnetic induction is the tesla.
We can define the unit from the velocity-dependent part of the Lorentz force that acts on a charge in motion parallel to a magnetic field.

Definition : The magnitude of magnetic induction is said to be 1 tesla when a charge of 1 coulomb experiences a force of 1 N when it moves at 1 m/s in a magnetic field in a direction perpendicular to the direction of the field.

1 tesla (T) = 1 N’s/Gm = 1 N/A-m.
[Notes : (1) Since the ampere and not the coulomb is the fundamental unit, the tesla is defined from the expression for the force on a current-carrying conductor in a magnetic field when placed perpendicular to the direction of the field (see Unit 10.5, Q. 29): The magnitude of magnetic induction is said to be 1 tesla when a conductor of length 1 metre and carrying a current of 1 ampere experiences a force oflN when it is placed with its length perpendicular to the direction of the magnetic field. (2) The unit is named after Nikola Tesla (1870 -1943), Croatia-born US electrical engineer, inventor of the AC induction motor.]

Question 7.
Name a non-SI unit of magnetic induction. State its relation to the SI unit of magnetic induction.
Answer:
A CGS unit of magnetic induction of historical interest is the gauss, symbol G. However, since the magnetic flux and the magnetic flux density (magnetic induction, B) are defined by similar equations in the CGS system and the SI, this non-SI unit is accepted for use with SI.

1 G = 10^-4 T

[Note : The unit gauss is named after Karl Friedrich Gauss (1777 -1855), German mathematician, who strongly promoted in 1832 the use of the French decimal or metric system, with the metre and the kilogram and the astronomical second, as a coherent system of units for physical sciences. Gauss was the first to make absolute measurements of the Earth’s magnetic field in terms of a decimal system based on the three mechanical units millimetre, gram and second for, respectively, the quantities length, mass and time.]

Question 8.
Explain cyclotron motion and cyclotron formula.
Answer:
Suppose a particle of mass m and charge q enters a region of uniform magnetic field of induction \(\vec{B}\). In below figure, \(\vec{B}\) points into the page. The magnetic force \(\vec{F}_{\mathrm{m}}\) on the particle is always perpendicular to the velocity of the particle, \(\vec{v}\). Assuming the charged particle started moving in a plane perpendicular to \(\vec{B}\), its motion in the magnetic field is a uniform circular motion, with the magnetic force providing the centripetal acceleration.

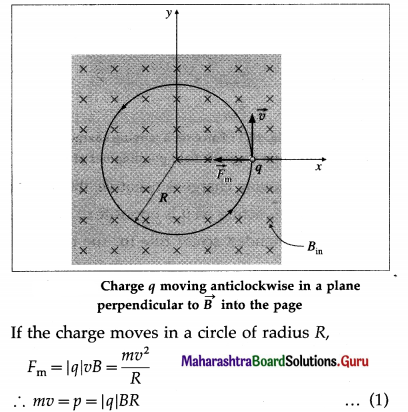
where p = mv is the linear momentum of the particle. Equation (1) is known as the cyclotron formula because it describes the motion of a particle in a cyclotron-the first of the modern particle accelerators.

Question 9.
Explain the condition under which a charged particle will travel through a uniform magnetic field in a helical path.
OR
Describe the general motion of charged particle in a uniform magnetic field.
Answer:
Suppose a particle of mass m and charge q starts in a region of uniform magnetic field of induction \(\vec{B}\) with a velocity \(\vec{v}\) which has a non-zero component v_|| in the direction of \(\vec{B}\), From below figure. The magnetic force \(\vec{F}_{\mathrm{m}}\) on the particle is always perpendicular to \(\vec{v}\) and provides a centripetal acceleration such that

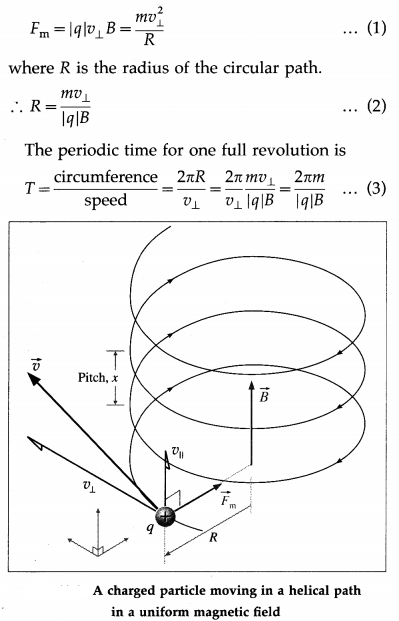
The parallel component of the motion \(\vec{v}_{\|}\) is unaffected by the magnetic field, so that the motion of the particle is a composite motion: an UCM with speed v_⊥ -the speed perpendicular to \(\vec{B}\) and a translation with a constant speed v_||. Therefore, the particle moves in a helix. Thus, the perpendicular component v_⊥ determines the radius of the helix while the parallel component v_|| determines the pitch x of the helix, i.e., the distance between adjacent turns. x = v_||/ T.

[Notes : (1) At non-relativistic speeds (v much less than the speed of light), the period T is independent of the speed of the particle. For all particles with the same charge-to-mass ratio (q/ m), faster particles move in larger circles than the slower ones, but all take the same time T to complete one revolution. (2) Looking in the direction of \(\vec{B}\), a positive charge always revolves anticlockwise, and a negative charge always clockwise.]

Question 10.
State under what conditions will a charged particle moving through a uniform magnetic field travel in
(i) a straight line
(ii) a circular path
(iii) a helical path.
Ans.
(i) A charged particle travels undeviated through a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is parallel or antiparallel to \(\vec{B}\). In this case, the magnetic force on the charge is zero.
(ii) A charged particle travels in a circular path within a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is perpendicular to \(\vec{B}\).
(iii) A charged particle travels in a helical path through a magnetic field \(\vec{B}\), if its velocity \(\vec{v}\) is inclined at an angle θ to \(\vec{B}\), 0 < θ < 90°. In this case, the component of \(\vec{v}\) parallel to \(\vec{B}\) is unaffected by the magnetic field. The radius and pitch of the helix are determined respectively by the perpendicular and parallel components of \(\vec{v}\).

Question 11.
A particle of charge q enters a region of uniform magnetic field \(\vec{B}\) (pointing into the page). The field deflects the particle a distance d above the original line of flight, as shown in below figure. Is the charge positive or negative ? Find the momentum of the particle in terms of a, d, B and q.

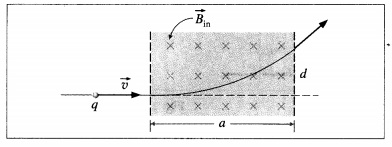
Answer:
Since \(\vec{v} \times \vec{B}\) points upward, and that is also the direction of the magnetic force \(\vec{F}_{\mathrm{m}}\), q must be positive.
Using the Pythagorean theorem to find R in terms of a and d,

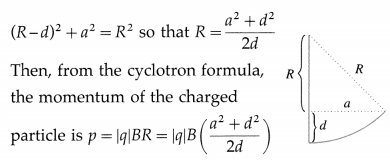
[Note: A similar solved question in the textbook, Example 10.2, is wrong. The acceleration qvB/m is the centripetal acceleration whose magnitude remains constant but direction changes continuously. Hence, it cannot be used in a kinematical equation to calculate s. The final expression for p arrived at in the textbook is therefore not correct.]

Question 12.
An ion of mass re and charge q is accelerated from rest through a potential difference V and enters a region of uniform magnetic field of induction B. Within the region, the ion moves in a semidrcle and strikes a photographic plate which lies along the diameter of the semicircle at a distance D from the point of entry. Show that the mass of the ion is given by m = \(k \frac{q D^{2} B^{2}}{V}\)
Answer:
Consider positive ions of charge q and mass m accelerated from rest to a speed r’ by an accelerating potential V. Then, the kinetic energy of the ions is

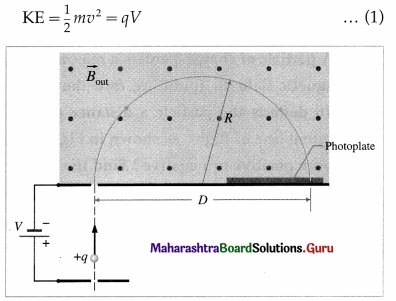
On entering a region of uniform magnetic field of induction B (see above figure for reference), the Ions travel in a semicircular path in a plane normal to the field with a radius
R = \(\frac{m v}{q B}\)
∴ m²v² = q²B²R² ………….. (2)
From Eq. (1) m²v² = 2qVm ………….. (3)
Equating the right hand sides of Eqs. (2) and (3),
2qVm = q²B²R²
∴ m = \(\frac{q B^{2} R^{2}}{2 V}\)
Since R = \(\frac{D}{2}\),
m = \(\frac{q B^{2} D^{2}}{8 V}\) = k\(\frac{q B^{2} D^{2}}{V}\)
where k = \(\frac{1}{8}\), Equation (4) Is the required expression.

[Note : This is especially the working of a mass spectrometer which Is used to measure the mass of an ion. A mass spectrometer is so sensitive it is used to measure isotopic masses. If the isotopes of an element carry the same charge, they acquire the same energy when accelerator through the same pd. But within the magnetic field, they travel in different semicircles depending on their masses and strike a detector or photographic plate at different D.]

Question 13.
A particle of charge q and momentum p enters a region of uniform magnetic field B travelling at right angles to the field, and is deflected through a right angle as shown. Obtain an expression for the length of the particle’s path In terms of q, p and B.

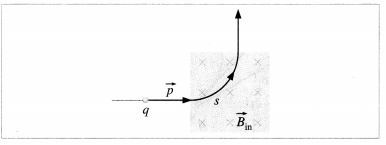
Answer:
A particle of charge q and momentum p enters a region of uniform magnetic field B travelling at right angles to the field. Within the field, the particle travels in a circular path of radius
R = \(\frac{p}{q B}\) ………. (1)
From the diagram, the length s of the particle’s path in the field is one quarter of the circumference,
∴ s = \(\frac{2 \pi R}{4}=\frac{\pi}{2} \frac{p}{q B}\) ………….. (2)
This is the required expression.

Question 14.
What is a cyclotron? State its principle of working.
Answer:
A cyclotron is a cyclic magnetic resonance accelerator in which an alternating potential difference of a few kV is used to accelerate light positive ions such as protons, deuterons, α-particles, etc., but not electrons, to very high energies of the order of a few MeV. It was developed by E. O. Lawrence and M. S. Livingston in 1932.

Principle: The cyclotron employs the principle of synchronous acceleration to accelerate charged particles which describe a spiral path at right angles to a constant magnetic field and make multiple passes through the same alternating p.d., whose frequency is the same as the frequency of revolution of the particles. .

Question 15.
Describe the construction of the cyclotron with a neat labelled diagram.
Answer:
Construction of the cyclotron: Two hollow D-shaped chambers that are open at their straight edges form the electrodes. They are called the dees. The dees are separated by a small gap, as shown in below figure, and a high-frequency (10⁶ Hz to 10⁷ Hz) alternating p.d. (of the order of 10⁴ V to 10⁵ V) is applied between them. The whole system is placed in an evacuated chamber between the poles of a large and strong electromagnet (B ≡ ≅ 1 T to 2T).

The ions to be accelerated are produced in an ion source; a hydrogen tube gives protons, heavy hydrogen or deuterium gives deuterons while helium gives x-particles, etc. The positive ions are injected near the centre and are accelerated each time they

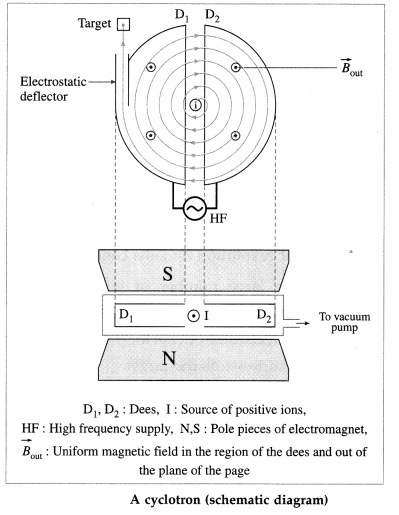
cross the gap between the does. At the edge of one of the does, an electrostatic deflector deflects the spiralling particles out of the system to strike a target.

Question 16.
Explain the working of the cyclotron with a neat labelled diagram.
Answer:
The dees of the cyclotron are separated by a small gap and a high-frequency alternating p.d. is applied between them. Light positive ions are injected into the system near the centre.

Suppose a positive ion of charge q and mass m is injected when D₁ is positive and D₂ is negative. The positive ion will accelerate towards D₂. Inside the dees there is no electric field. Hence, inside D₂ it has a constant speed v. The magnetic force of magnitude qvB makes it move in a semicircular path through D₂. The radius r of its orbit is given by equating the centripetal force to the magnetic force.

Let t be the time spent by the ion to describe the semicircular path.

If t is also half the period of oscillation T of the alternating p.d., the ion will be in resonance with the electric field in the gap. That is, the ion will emerge from D₂ at the instant D₁ becomes negative and will be accelerated towards D₁. As the ion gains speed in the gap, its path in D₁ has greater radius. This process repeats after every half cycle of the alternating p.d. and the ion is accelerated each time it crosses the gap between the dees.

The radius of the path of the charged particles increases proportionately with their speed, the period of revolution remains constant.

After a large number of revolutions, the ion reaches the edge of the system where a negatively charged electrostatic deflector plate deflects it out of the system towards the target.

Question 17.
State the functions of the electric and magnetic fields in a cyclotron.
Answer:
The function of the electric field in the gap between the dees of a cyclotron is to accelerate the positively charged particles while that of the magnetic field in the dees is to deflect the particles in semicircular paths so that they return to the gap in a fixed time interval to reuse the alternating electric field.

Question 18.
Show that for a given positive ion species in a cyclotron,
(i) the radius of their circular path inside a dee is directly proportional to their speed
(ii) the time spent in a dee (or the cyclotron frequency or the magnetic resonance frequency) is independent of the radius of their path and speed
(iii) the maximum ion energy obtainableis directly proportional to the square of the magnetic induction.
Answer:
Consider positive ions of charge q and mass m injected in a cyclotron. In the electric-field-free region inside a dee, the ions are acted upon only by the uniform magnetic field. Hence, inside a dee the ions travel in a semicircular path with a constant speed y, in a plane normal to the field. If B is the induction of the magnetic field, the magnetic force of magnitude qvB provides the centripetal force.
∴\(\frac{m v^{2}}{r}\) = qvB
∴ r = \(\frac{m v}{q B}\) …………. (1)
Thus, for given q, m and B,
r ∝ v
If t be the time spent in a dee by the ion to describe a semicircular path of radius r,
t = \(\frac{\pi r}{v}=\frac{\pi}{v} \times \frac{m v}{q B}\)
∴ t = \(\frac{\pi m}{q B}\) …………. (2)
Thus, t is independent of r and y, i.e., it takes the ions exactly the same time t to travel the semicircular paths inside the dees irrespective of the radius of the path and the speed of the ions so long a the mass in is constant. This is the critical characteristic of operation of the cyclotron.

The periodic time of an ion in its circular path is
T = 2t = \(\frac{2 \pi m}{q B}\) ………….. (3)

The frequency of revolution,
f = \(\frac{1}{T}=\frac{q B}{2 \pi m}\) …………. (4)
is called the cyclotron frequency or the magnetic resonance frequency. The frequency is independent of r and y for a given ion species and remains constant so long as the mass m is constant.

If R is the maximum radius of the path, the same as the radius of the dee, just before the ions are deflected out of the accelerator,
V_max = \(\frac{q B R}{m}\) …………. (5)
so that KE_max = \(\frac{q^{2} B^{2} R^{2}}{2 m}\) (in joule)
= \(\frac{q^{2} B^{2} R^{2}}{2 e m}\) (in eV) …………… (6)
Thus, for a given ion species and dees of given radius,
KE_max ∝ B²

Question 19.
What is meant by cyclotron frequency?
Answer:
The cyclotron frequency, or the magnetic resonance frequency, is the frequency of revolution of a charged particle of charge per unit mass \(\frac{q}{m}\) in a magnetic field of induction B inside a cyclotron. The cyclotron frequency, f = \(\frac{q B}{2 \pi m}\). The frequency of the alternating voltage applied to the dees of the cyclotron should be equal to the cyclotron frequency.

Question 20.
What is resonance condition in a cyclotron ?
OR
What should be the frequency of the alternating voltage applied between the dees of a cyclotron?
Answer:
The frequency of the alternating voltage between the dees of a cyclotron should be equal to the cyclotron frequency so that a positive ion exiting a dee always sees an accelerating potential difference to the other dee. This equality of the frequencies is called the resonance condition.

Question 21.
State any two limitations of a cyclotron.
Answer:
Limitations of a cyclotron :

1. It cannot be used to accelerate electrons. Because electrons have a very small mass, they quickly achieve relativistic speeds, i.e., speeds at which their mass increases significantly with increase in speed. Then they cannot remain synchronous with the alternating electric field between the dees.
2. For higher energies, with a given magnetic field strength, the exit radius and thus the dees must be large. It is difficult to produce a uniform magnetic field over a large area.
3. Even protons, deuterons, a-particles, etc., cannot be accelerated to very high energy, say of the order of 500 MeV, using a cyclotron with a fixed cyclotron frequency.
4. No particle accelerator can accelerate uncharged particles, such as neutrons.

Question 22.
Does the time spent by a charged particle inside a dee of a cyclotron depend upon its speed and the radius of its path ? Why ?
Answer:
The time spent by a charged particle to describe a semicircular path of radius r inside a dee of a cyclotron is independent of the radius of the path and the speed v so long as the mass m of the particle is constant. This is true for any charged particle of mass m and carrying a charge q, and is the critical characteristic of operation of the cyclotron.
r = \(\frac{m v}{q B}\)
So that the time spent in a dee,
t = \(\frac{\pi r}{v}=\frac{\pi}{v} \times \frac{m v}{q B}=\frac{\pi m}{q B}\)
which is independent of r and v.

Question 23.
The frequency of revolution of the charged particles in a cyclotron does not depend upon their speed. Why?
Answer:
The time t spent by a charged particle, of mass m and carrying a charge q, inside a dee of a cyclotron is independent of the radius of the path and the speed of the particle so long as m is constant. Then, the periodic time of the charged particle in its nearly circular path is T = 2t, and the frequency of revolution,
f = \(\frac{1}{T}=\frac{1}{2 t}=\frac{q B}{2 \pi m}\)
are also independent of the radius and the speed.

Question 24.
What are the factors on which the cyclotron frequency depends?
Answer:
The cyclotron frequency depends upon

1. the magnetic induction and
2. the specific charge (the ratio charge/mass) of the charged particles.

Question 25.
What are the factors on which the maximum kinetic energy acquired by a charged particle in the cyclotron depends?
Answer:
The maximum kinetic energy acquired by a charged particle in the cyclotron depends upon

1. the magnetic induction
2. the specific charge (the ratio charge/mass) of the charged particles and
3. the radius of the dees.

Question 26.
In a certain cyclotron, the cyclotron frequency for acceleration of protons is 10⁸ Hz. What will be its value if the magnetic induction is doubled ?
Answer:
As the cyclotron frequency is directly proportional to the magnetic induction, the new frequency will be 2 × 10⁸ Hz. .

27. Solve the following :

Question 1.
An alpha particle (carrying a positive charge q = 3.2 × 10^-19 C) enters a region of uniform magnetic field of induction \(\vec{B}=(0.5 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})\) T with a velocity \(\vec{v}=(4 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}+\hat{\mathrm{k}})\) × 10² m/s. What is the force \(\vec{F}\) on the alpha particle?
Solution:

Question 2.
The magnetic field and electric field in a region in space are \(\vec{B}=B \hat{\mathrm{i}}\) and \(\vec{E}=E \hat{\mathrm{i}}\). A particle of charge q moves into the region with velocity \(\vec{v}=v \hat{\mathrm{j}}\). Find the magnitude and direction of the Lorentz force on the charged particle if q = 1 C,B = 1 T,E = 3 V/m and v = 4 m/s,
Solution:
Data : q = 1 C, B = 1 T, E = 3 V/m, v = 4 m/s
The Lorentz force on the charged particle is

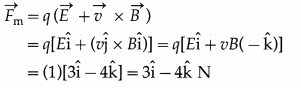
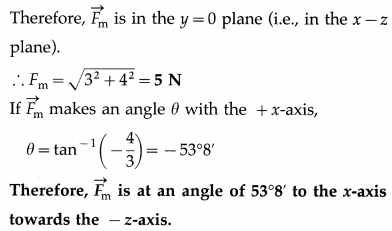
Question 3.
An electron is accelerated from rest through 86 V and then enters a region of uniform magnetic induction of magnitude 1.5 T. What is the maximum value of the magnetic force the electron can experience?
[m_e = 9.11 × 10^-31 kg, e = 1.6 × 10^-19 C]
Solution:
Data : V= 86 V, B = 1.5 T, m_e = 9.11 × 10^-31 kg, e = 1.6 × 10^-19 C
Since the electron is accelerated from rest, the kinetic energy acquired by it is

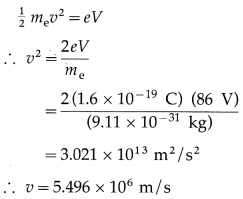
The maximum value of the magnetic force on the electron is
F_m = evB
= (1.6 × 10^-19 C) (5.496 × 10⁶ m/s) (1.5 T)
= 1.319 × 10^-12 N or 1.319 pN

Question 4.
A cosmic ray proton enters the Earth’s magnetic field in a direction perpendicular to the field. If the speed of the proton is 2 × 10⁷ m/s and B = 1.6 × 10^-6 T, find the force exerted on the proton by the magnetic field. [Charge on a proton, e = 1.6 × 10^-19 C]
Solution :
Data : v = 2 × 10⁷ m/s, B = 1.6 × 10^-6 T, e = 1.6 × 10^-19 C
The magnetic force on the proton is
F_m = evB (∵ \(\vec{v} \perp \vec{B}\))
= (1.6 × 10^-19 C)(2 × 10⁷ m/s)(1.6 × 10^-6 T)
= 5.12 × 10^-18 N

[Note : The Earth’s magnetic field traps the charged particles in doughnut-shaped regions outside the atmosphere. These regions are called Van Allen radiation belts. Near the poles, charged particles from these belts enter the atmosphere and produce the awesome shimmering curtains of light called the aurora borealis (northern ! lights) and aurora australis (southern lights).]

Question 5.
A charged particle moves with velocity 3 × 10⁶ m/s at right angles to a uniform magnetic field of induction 0.005 T. Find the magnitude of the charge if the particle experiences a force of 2 × 10^-2 N.
Solution:
Data : v = 3 × 10⁶ m/s, B = 5 × 10^-3 T,
F_m = 2 × 10^-2 N
F_m = qvB (∵ \(\vec{v} \perp \vec{B}\))
∴ The charge on the particle,

Question 6.
An electron in a TV picture tube moves horizontally with a speed 2 × 10⁷ m/s. It is deflected upward by a horizontal magnetic field of induction 10^-3 T. Find the magnitude of the force acting on the electron due to the action of the magnetic field.
Solution:
Data : e = 1.6 × 10^-19 C, v = 2 × 10⁷ m/s,
B = 10^-3 T
The magnitude of the magnetic force,
F_m = evB (∵ \(\vec{v} \perp \vec{B}\))
= (1.6 × 10^-19 C)(2 × 10⁷ m/s) (10^-3 T)
= 3.2 × 10^-15 N = 3.2 fN

Question 7.
The first practical cyclotron developed by Lawrence and Livingston in 1932 had dees of radius 12 cm and produced protons of about 1 MeV energy.
Calculate (i) the applied magnetic induction
(ii) the frequency of the accelerating electric field.
[m^p = 1.67 × 10^-27 kg, q = 1.6 × 10^-19 C
Solution:
Data: R = 0.12 m, m^p = 1.67 × 10^-27 kg,
q = 1.6 × 10^-19 C,
KE_max = 1 MeV =(1 × 10⁶)(1.6 × 10^-19)
= 1.6 × 10^-13 J

Question 8.
In a cyclotron, for the same B and R, show that the maximum kinetic energy of α-particles is twice that of deuterons.
Solution:
Data: Let E_α and E_d denote the maximum kinetic energies of α-particIes (He⁺⁺ ions) and deuterons
(D⁺ ions). For an α-partic1e,
q = +2e and m ≅ 4m^p and for a deuteron,
q = +e and m ≅ 2m^p
where e is the elementary charge and m^p is the proton mass.
In a cyclotron, the maximum kinetic energy of the ions obtainable with dec radius R and magnetic field induction B is

Question 28.
Derive an expression for the magnetic force experienced by a straight current-carrying conductor placed in a uniform magnetic field.
Discuss the cases when the force is maximum and minimum.
State the expressions for the force experienced by a current-carrying
(i) conductor of arbitrary shape
(ii) closed circuit (conducting loop).
Answer:
Consider a straight current-carrying conductor placed in a region of uniform magnetic field of induction \(\vec{B}\) pointing out of the page, as shown in below figure by the evenly placed dots. Let the length of the conductor inside the field be l and the current in it be I.

In metallic conductors, electrons are the charge carriers. The direction of conventional current is, however, taken to be that of flow of positive charge which is opposite to the electron current.

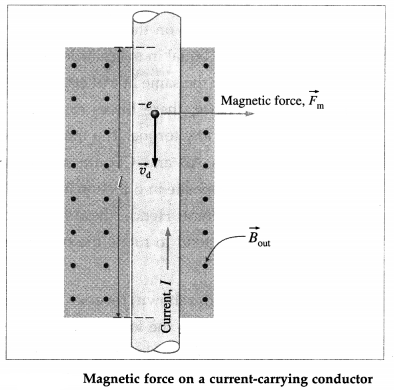
Let dq be the positive charge passing through an element of the conductor of length dl in time dt.
\(\overrightarrow{d l}\) has the same direction as that of the current.
Then, I = \(\overrightarrow{d l}\)/dt ………….. (1)
and drift velocity,\(\overrightarrow{v_{\mathrm{d}}}\) = \(\overrightarrow{d l}\)/dt ……….. (2)
The magnetic force on the charge dq is

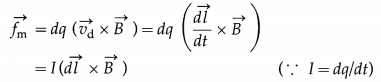
The charge dq is constrained to remain within the conductor. Hence, the conductor itself experiences this force. The force on the entire part of the conductor within the region of the magnetic field is

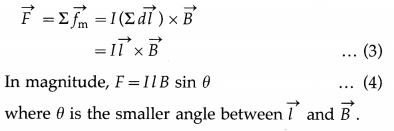
Case 1 : When the conductor is parallel to the magnetic field, \(\vec{l}\) is parallel or antiparallel to \(\vec{B}\) according as the current is in the direction of \(\vec{B}\) or opposite to it; then θ = 0° or θ = 180°, so that sin θ = 0. Hence, in either of these two cases, F = 0.

Case 2 : The maximum value of the force is F_max = IlB, when sin θ = 1, that is, when the conductor lies at right angles to \(\vec{B}\) (θ = 90°).
(i) For a current-carrying wire of arbitrary shape in a uniform field,
\(\vec{F}=\int \vec{f}_{\mathrm{m}}=I\left(\int \overrightarrow{d l}\right) \times \vec{B}\) …………. (5)
(ii) For a current-carrying conducting loop (closed circuit) in a uniform field,
\(\vec{F}=\int \vec{f}_{\mathrm{m}}=I(\oint \overrightarrow{d l} \times \vec{B})\) ………….. (6)
But for a closed loop of arbitrary shape, the integral is zero.
∴ \(\vec{F}\) = 0
[Notes : (1) While the direction of \(\vec{F}\) can be found from the cross product of \(\vec{l}\) and \(\vec{B}\), there is a handy rule due to Sir John Ambrose Fleming (1849-1945), British physicist and electrical engineer.

Fleming’s left hand rule : If the forefinger and the middle finger of the left hand are stretched out to point in the directions of the magnetic field and the current, respectively, then the outstretched thumb indicates the direction of the magnetic force on the current-carrying straight conductor, from below figure.]

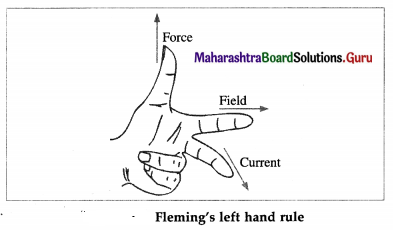
(2) Equation (3) is usually used to define the unit of magnetic field induction, the tesla. See the note to Q. 6. (3) B cannot be taken out of the integral in Eq. (6).]

Question 29.
A straight conductor of length 0.5 m and carrying a current of 2 A is placed in a magnetic field of induction 2 Wb/m² at right angles to the length of the conductor. What is the magnetic force on the conductor?
Answer:
F = IlB
= (2A) (0.5m) (2 Wb/m²)
= 2 N is the force on the conductor.

Question 30.
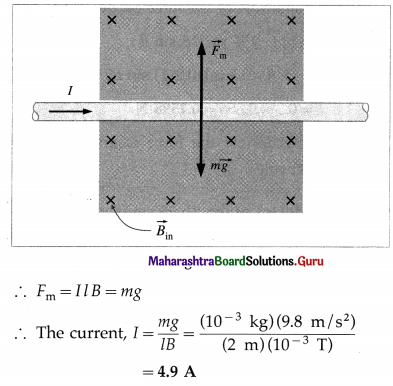
A rectangular loop of wire hanging vertically with one end in a uniform magnetic field \(\vec{B}\), supports a small block of mass m. \(\vec{B}\) points into the page in the shaded region of below figure. For what current I in the loop would the magnetic force exactly balance the downward gravitational force?

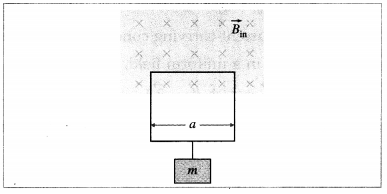
Answer:
The magnetic force on the horizontal segment of the loop inside the field must be upward to balance the downward gravitational force. With \(\vec{B}\) pointing into the page, the current in that segment must be toward the right so that \(\vec{F}=\vec{L} \times \vec{B}\) on that segment points upward. That is, the current in the loop must be clockwise.
Taking L = a, F = IaB
∴ IaB = mg
∴ I = \(\frac{m g}{a B}\)
is the required expression for the current.

Question 31.
Explain with a neat labelled diagram how the magnetic forces on a current loop produce rotary motion as in an electric motor.
Answer:
Consider a current-carrying rectangular loop ABCD, within a uniform magnetic field \frac{m g}{a B}, from below figure. Lead wires and commutator are not shown for simplicity. The coil is free to rotate about a fixed axis. Suppose the sides AB and CD are perpendicular to the field direction.

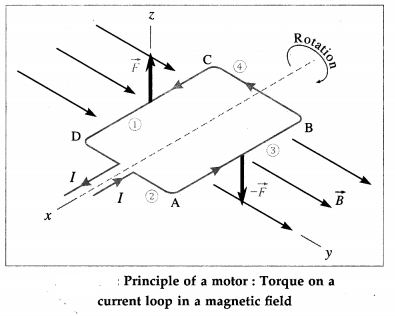
The magnetic force on each segment act at the centre of mass of that segment. The direction of the force on each segment can be found using the right hand rule for the cross product or from Fleming’s left hand rule.

The magnetic forces on the short sides AD and CB are, in general, equal in magnitude, opposite in direction and have the same line of action along the rotation axis. Hence, these forces cancel out and does not produce any torque. The magnetic forces on the long sides AB and CD are also equal in magnitude and opposite in direction but their lines of action are different. Hence, these forces constitute a couple and tend to rotate the coil about the central axis.

A commutator (not shown) reverses the direction of the current through the loop every half-revolution so that the torque always acts in the same direction.

Question 32.
Derive an expression for the net torque on a rectangular current-carrying loop placed in a uniform magnetic field with its rotation axis
perpendicular to the field.
Answer:
Consider a rectangular loop ABCD of length l, breadth b and carrying a current I, placed in a uniform magnetic field of induction \(\vec{B}\) with its rotation axis perpendicular to \(\vec{B}\), from figure (a). To define the orientation of the loop in the magnetic field, we use a normal vector \(\hat{n}\) that is perpendicular to the plane of the loop. The direction of \(\hat{n}\) is given by a right hand rule: If the fingers of right hand are curled in the direction of current in the loop, the outstretched thumb is the direction of \(\hat{n}\). Suppose the normal vector \(\hat{n}\) of the loop makes an arbitrary angle with \(\vec{B}\), as shown in figure (b).

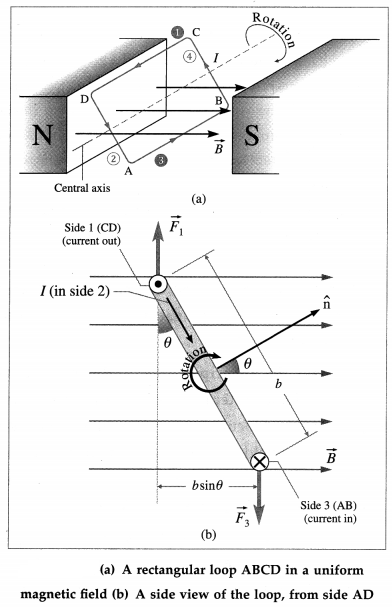
In the side view, Fig. 10.15 (b), the sides CD, DA, AB and BC have been labelled as 1, 2, 3 and 4, respectively. In this view, the current in side 1 (CD) is out of the page as shown by a ⊙ while that in side 3 (AB) is into the page shown by a ⊗.

For side 2 (AD) and side 4 (BC), the length of the conductor \(|\vec{L}|\) = b and the angle between \(\vec{L}\) and \(\vec{B}\) is (90° – θ). Hence, the forces on sides 2 and 4 are equal in magnitude :

F₂ = F₄ = IbB sin(90° – θ) = IbB cosθ

However, \(\vec{F}_{2}\) is directed out of the page while \(\vec{F}_{4}\) is into, and because their common line of action is through the centre of the loop, their net torque is zero. For side 1 (CD) and side 3 (AB), \(|\vec{L}|\) = I and \(\vec{L}\) is perpendicular to \(\vec{B}\). Hence, the forces \(\vec{F}_{1}\), and F\(\vec{F}_{3}\) have the same magnitude : F₁ = F₃ = IlB

But their lines of action being different, they constitute a couple.

Moment arm of the couple = b sin θ
∴ Torque exerted by the couple = force of the couple x moment arm of couple
∴ τ = (IlB)(b sin θ)
in the clockwise sense in figure (b). The torque tends to rotate the loop so as to align its normal vector h with the direction of the magnetic field.
∴ τ = I(lb)B sin θ = MB sinθ
where A = lb is the area of the loop. For a rectangular coil of N turns in place of a single-turn loop,
τ = NIAB sin θ
This is the required expression for the net torque. The torque has maximum magnitude for θ = 90°, that is when \(\hat{n}\) is perpendicular to \(\vec{B}\) or, in other words, the plane of the coil is parallel to the field.
τ_max = NIAB

Question 33.
Describe the construction of a suspended-type moving-coil galvanometer with a neat labelled diagram.
Answer:
A permanent fixed-magnet, suspended-type moving-coil galvanometer is shown in below figure. It consists of a coil of a large number of turns of fine insulated copper wire wound on a rectangular, nonconducting, non-magnetic frame. The coil is suspended between the cylindrically concave pole pieces of a horseshoe permanent magnet by a fine phosphor-bronze wire F from an adjustable screw- head. The other terminal of the coil is connected to a loosely-wound wire helix H. The coil swings freely around a cylindrical soft-iron core CS fitted between the pole pieces.

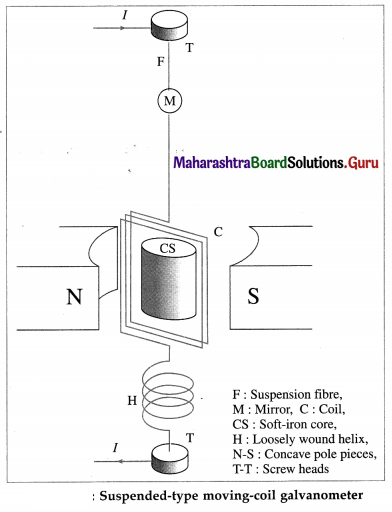
The suspension F and the helix H serve as the two current leads to the coil. The suspension fibre also provides the restoring torque when the coil is rotated from its normal position. The cylindrically concave pole pieces together with the soft-iron core make the magnetic field radial in the annular region in which the vertical sides of the coil move. The soft-iron core also concentrates the magnetic field (i.e., increases the magnetic induction) in the annular region.

The angle of deflection is observed with a beam of light reflected from a small mirror M fixed to the suspension fibre. The reflected beam is observed on a ground-glass scale arranged about a metre from the instrument, the light beam serving as a weightless pointer.

[Note : The diagram given in the textbook (Fig. 10.13) has serious errors, notably, the missing suspension fibre by which the coil is hung. The metal fibre (made of phosphor bronze), which bears the weight of the coil, is also the current lead to the coil and provides the restoring torque. The Tower suspension shown in the textbook is actually a loose wire which merely provides an exit lead to the current but does not exert any torque on the coil.]

Question 34.
State the principle of working of a moving- coil galvanometer (suspended-coil type).
Answer:
Principle : A current-carrying coil suspended in a magnetic field experiences a torque which rotates the plane of the coil and tends to maximize the magnetic flux through the coil.

The deflection of the coil in a moving-coil gal-vanometer is linearly related to the current through it and, therefore, can be used to measure current in terms of the deflection.

Question. 35.
With the help of neat diagrams, describe the working of a moving-coil galvanometer.
Answer:
Consider a rectangular coil-of length Z, breadth b and N turns – carrying a current I suspended in a uniform magnetic field of induction \(\vec{B}\).

The magnetic forces on the horizontal sides of the coil have the same line of action and do not exert any torque. The magnetic forces on the vertical sides constitute a couple and exert a deflecting torque. If the plane of the coil is parallel to \(\vec{B}\), the magnitude of the deflecting torque is maximum equal to
τ_d = NIAB …………… (1)
where A = lb is the area of each turn of the coil. This torque rotates the coil.

In a moving-coil galvanometer, the coil swings in a radial magnetic field produced by the combination of the cylindrically concave pole pieces and the soft-iron core. Hence, the plane of the coil is always parallel to the field lines, as shown in Fig. 10.18. Therefore, the deflecting torque is constant and maximum as given by Eq. (1).

The rotation of the coil twists the suspension fibre which exerts a restoring torque on the coil. The restoring torque is proportional to the angle of twist θ.
τ_r = Cθ …………… (2)
where C is the torque constant, i.e., torque per unit angle of twist. C depends on the dimensions and the elasticity of the suspension fibre.

The coil eventually comes to rest in the position where the restoring torque equals the deflecting torque in magnitude. Therefore, in the equilibrium position,
τ_r = τ_d

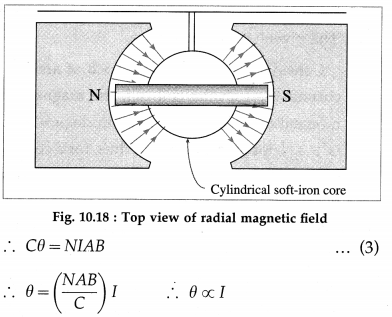
since N, A, B and C are constant. Thus, the deflection of the coil is directly proportional to the current in it.

Question 36.
A coil suspended freely in a radial magnetic field rotates through 30° when a current of 30 /(A is passed through it. Through what angle will it rotate if the current is doubled and the magnetic induction is halved?
Answer:
The angle of rotation, θ ∝ IB (in the usual notation)
As I₂B₂ = (2I₁)\(\left(\frac{B_{1}}{2}\right)\) = I₁B₁, the angle of rotation will be the same, i.e., 30°.

Question 37.
What is the advantage of a radial magnetic field in a moving-coil galvanometer and how is it produced?
Answer:

1. Advantage of radial magnetic field in a moving- coil galvanometer:
   • As the coil rotates, its plane is always parallel to the field. That way, the deflecting torque is always a maximum depending only on the current in the coil, but not on the position of the coil.
   • The restoring torque is proportional to the deflection so that a radial field makes the deflection proportional to the current. The instrument then has a linear scale, i.e., the divisions of the scale are evenly spaced. This makes it particularly straight forward to calibrate and to read.
2. Producing radial magnetic field :
   • The pole pieces of the permanent magnet are made cylindrically concave, concentric with the axis of the coil.
   • A soft iron cylinder is centred between the pole pieces so that it forms a narrow cylindrical gap in which the sides of the coil can move. Together, they produce a radial magnetic, field; that is, the magnetic lines of force in the gap are along radii to the central axis.

Question 38.
What will happen if the magnetic field in a moving-coil galvanometer is not radial?
Answer:
Suppose the magnetic field is uniform but not radial. Then, when the coil comes to rest after rotation through an angle θ, NIAB cos θ = Cθ (in usual notations).
∴ I ∝ \(\frac{\theta}{\cos \theta}\)
as N, A, B and C are constants in a particular case. Thus, the current is not directly proportional to the deflection. Hence, we cannot have a linear scale for measurement.

Question 39.
Explain the use of a soft iron core in a moving- coil galvanometer.
Answer:
In a moving-coil galvanometer, the pole pieces of the permanent magnet are made cylindrically concave, coaxial with the coil. A soft iron core is fixed centrally between the pole pieces so that it partly fills the space inside the coil and forms a narrow cylindrical gap in which the sides of the coil can move.
(1) The soft iron core, together with the concave pole pieces produces a radially uniform magnetic field, i.e., the magnetic lines of force in the gap are along radii to the central axis. This makes the deflection of the coil proportional to the current in it. The instrument then has a linear scale which is particularly straightforward to calibrate and to read.

(2) The permeability of iron being more than that of air, the magnetic lines of force pass through the soft iron core. By making the cylindrical gap as narrow as possible then increases the magnetic induction in the gap. This increases the deflecting torque on the coil and the sensitivity of the instrument.

Question 40.
Why does not the Earth’s magnetic field affect the working of a moving-coil galvanometer?
Answer:
The coil of a moving-coil galvanometer rotates in the magnetic field of a permanent magnet. The magnetic induction of the permanent magnet is many orders of magnitude (typically 10⁴ times) stronger than that of the Earth. Hence, the Earth’s magnetic field does not affect the working of the galvanometer.

Question 41.
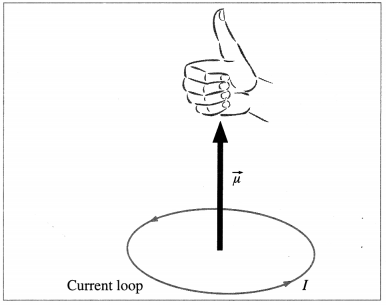
Explain the magnetic dipole moment of a current loop. State its magnitude and direction.
Answer:
The responses of a current-carrying coil to an external magnetic field is identical to that of a magnetic dipole (or a bar magnet). Like a magnetic dipole, a current-carrying coil placed in a magnetic field \(\vec{B}\) experiences a torque. In that sense, the coil is said to be a magnetic dipole. To account for a torque τ on the coil due to the magnetic field, we assign a magnetic dipole moment \(\vec{\mu}\) to the coil, such that
\(\vec{\tau}=\vec{\mu} \times \vec{B}=N I \vec{A} \times \vec{B}\)

where \(\vec{\mu}=N I \vec{A}\). Here, N is the number of turns in the coil, I is the current through the coil and A is the area enclosed by each turn of the coil. The direction of \(\vec{\mu}\) is that of the area vector \(\vec{A}\), given by a right hand rule shown in below figure. If the fingers of right hand are curled in the direction of current in the loop, the outstretched thumb is the direction of \(\vec{A}\) and \(\vec{\mu}\). In magnitude, μ = NIA.
The torque tends to align \(\vec{\mu}\) along \(\vec{B}\).

Question 42.
State if the following statement is true : “The magnetic dipole moment of a current-carrying coil of given geometry is constant.” Justify your answer.
Answer:
The given statement is false.
Consider a coil of N turns, each of area A. If the current through the coil is I, the magnetic dipole moment of the coil is, in magnitude, μ = NIA. That is, μ ∝ I, for given N and A. Thus, for a coil of given geometry, its magnetic dipole moment varies with the current through it.

Question 43.
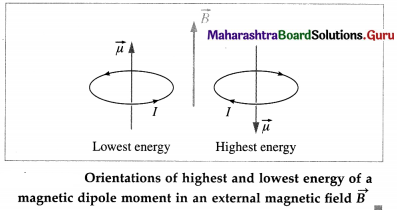
In analogy with an electric dipole, state an expression for the magnetic potential energy of an magnetic dipole in a uniform magnetic field. Discuss the orientations of the dipole moment for the maximum and minimum of potential energy.
Answer:
Consider an electric dipole of dipole moment \(\vec{p}\) placed in a uniform electric field \(\vec{p}\) making an angle Φ with \(\vec{p}\). The torque \(\vec{\tau}=\vec{p} \times \vec{E}\) tends to rotate the dipole and align it with \(\vec{E}\).

If the dipole was initially parallel to \(\vec{E}\), its potential energy is minimum. We arbitrarily assign U₀ = 0 to the minimum potential energy for this position. Then, at a position where \(\vec{p}\) makes an angle θ with \(\vec{E}\), the potential energy of the dipole is
U_θ = -pE cos θ = –\(\vec{p} \cdot \vec{E}\).
A current-carrying coil placed in a magnetic field \(\vec{B}\) experiences a torque,
\(\vec{\tau}=\vec{\mu} \times \vec{B}\) …………. (1)
where \(\vec{\mu}\) is the magnetic dipole moment of the coil. In analogy with an electric dipole, the potential energy of a magnetic dipole is
U_θ = – μB cos θ = – \(\vec{\mu} \cdot \vec{B}\) ……….. (2)
U_θ is also known as orientation energy.
A magnetic dipole has its lowest energy ( = – μB cos 0 = – μB) when its dipole moment is lined up with the magnetic field, and has its highest energy ( = – μBcos 180° = + μB) when is directed opposite the field.

44. Solve the following :
Question 1.
A straight current-carrying conductor 30 cm long carries a current of 5 A. It is placed in a uniform magnetic field of induction 0.2 T, with its length making an angle of 60° with the direction of the field. Find the force acting on the conductor.
Solution:
Data : l = 30 cm = 0.3 m, I = 5 A, B = 0.2 T, θ = 60°
The magnitude of the force on the conductor,
F = I\(|\vec{l} \times \vec{B}|\) = IlB sin θ
= (5 A) (0.3 m) (0.2 T) sin 60°
= 0.3 × 0.866 = 0.2598 N
The direction of the force is given by the cross product rule.

Question 2.
A conductor of length 25 cm is placed (i) parallel (ii) perpendicular (iii) inclined at an angle 30°, to a uniform magnetic field of induction 2 T. If 1 C of charge passes through it in 5 s, calculate the force experienced by the conductor in each case.
Solution:
Data : l = 25 cm = 0.25 m, θ₁ = 0°, θ₂ = 90°, θ₃ = 30°, B = 2 T, q = 1 C, f = 5 s
The current in the conductor,
I = \(\frac{q}{t}=\frac{1 \mathrm{C}}{5 \mathrm{~s}}\) = 0.2 A
The magnitude of the force on the conductor,
F = I\(|\vec{l} \times \vec{B}|\) = IlB sin θ
(i) θ₁ =0° A ∴ sin θ₁ = 0 ∴ F = 0 N
(ii) θ₂ = 9O° ∴ sin θ₂ = 1
∴ F = IlB = (0.2 A)(0.25 m)(2 T)
= 0.1 N
(iii) θ₃ = 30° ∴ sin θ₃ = 0.5
∴ F = IlB sin θ₃ = (0.1 N) (0.5) = 0.05 N
The direction of \(\vec{F}\) in each case is given by the cross product rule.

Question 3.
A horizontal straight wire is in a uniform magnetic field which is horizontal and at right angles to the length of the wire. The part of the wire that lies in the field has a length 2 m and mass 1 gram. If the magnetic induction is 1 mT, find the current that should be passed through the wire to balance it.
Solution:
Data : l = 2 m, m = 1 g = 10^-3 kg, g = 9.8 m/s²,
B = 1 mT = 10^-3 T
To balance the wire, the upward magnetic force must be equal in magnitude to the downward force due to gravity.

Question 4.
A circular loop of radius 10 cm is carrying a current of 0.1 A. Calculate its magnetic moment.
Solution:
Data : R = 10 cm = 0.1m, N = 1, I = 0.1 A
The magnetic moment,
μ = NIA = NI(πR²)
= (1) (0.1 A) (3.142) (0.1 m)²
= 3.142 × 10^-3 A∙m²

Question 5.
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Å. If the frequency of revolution of an electron is 9 × 10⁹ MHz, calculate the equivalent magnetic moment. [e = 1.6 × 10^-19 C]
Solution : .
Data : r = 0.53 Å = 0.53 × 10^-10 m,
f = 9 × 10⁹ MHz = 9 × 10¹⁵ Hz, e = 1.6 × 10^-19 C
Magnetic moment, M₀ = IA = efπr²
= 1.6 × 10^-19 × 9 × 10¹⁵ × 3.142 × (0.53 × 10^-10)²
= 14.4 × 3.142 × (0.53)² × 10^-19 × 10¹⁵ × 10^-20
= 1.272 × 10^-23 A∙m²

Question 6.
A rectangular coil of 10 turns, each of area 0.05 m², is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 /(A is passed through it.

(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
(iii) What is the minimum torque experienced by the coil?
SoLution:
Data: N = 10, A = 0.05 m², B = 0.01 T, I = 30 μA = 3 × 10^-5 A
(i) The magnetic moment,
μ = NIA = 10(3 × 10^-5 A)(0.05 m²)
=1.5 × 10^-5 A∙m² = 15 μA∙m²

(ii) The maximum torque experienced by the coil (when its plane is parallel to \(\vec{B}\)) is
τ_max = MB
= (1.5 × 10^-5 A∙m²)(0.01 T)
= 1.5 × 10^-7 N∙m

(iii) The minimum torque experienced by the coil (when its plane is perpendicular to \(\vec{B}\)) is
τ_min = 0

Question 7.
A coil has 300 turns, each of area 0.05 m2. (i) Find the current through the coil for which the magnetic moment of the coil will be 4.5 A-m2. (ii) It is placed in a uniform magnetic field of induction 0.2 T with its magnetic moment making an angle of 30° with \(\vec{B}\). Calculate the magnitude of the torque experienced by the coil. (3 marks)
Solution:
Data : N = 300, A = 0.05 m², M = 4.5 A ∙ m², B = 0.2 T, θ = 30°
(i) M = NIA
∴ The current in the coil,
I = \(\frac{M}{N A}=\frac{4.5}{300 \times 0.05}\) = 0.3 A

(ii) The magnitude of the torque,
τ = MB sin θ = 4.5 × 0.2 × sin 30°
= 0.9 × \(\frac{1}{2}\) = 0.45 N∙m

Question 8.
A rectangular coil of 10 turns, each of area 0.05 m², is suspended freely in a radial magnetic field of 0.01 Wb/m². If the torsional constant of the suspension fibre is 5 × 10^-9 N∙m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
Solution:
Data : A = 0.05 m², B = 0.01 Wb/m², N = 10, C = 5 × 10^-9 N∙m per degree,
I = 30 μA = 30 × 10^-6 A,
I = \(\left(\frac{C}{N A B}\right) \theta\)
∴ The deflection of the coil,
θ = \(\frac{N I A B}{C}=\frac{10 \times 30 \times 10^{-6} \times 0.05 \times 0.01}{5 \times 10^{-9}}\) = 30°

Question 9.
A moving-coil galvanometer has coil of area 10 cm² and 100 turns. It is suspended by a fibre of torque constant 10^-8 N∙m/degree in a radial magnetic field of induction 0.05 Wb/m². Find the angle through which the coil will be deflected when a current of 16 μA passes through it.
Solution:
Data ; A = 10^-3 m², N = 100, C = 10^-8 N∙m/degree, B = 0.05 Wb/m², 7 = 1.6 × 10^-5 A
I = \(\left(\frac{C}{N A B}\right) \theta\)
∴ The deflection of the coil,
θ = \(\frac{N I A B}{C}=\frac{(100)\left(1.6 \times 10^{-5}\right)\left(10^{-3}\right)(0.05)}{10^{-8}}\) = 8

Question 10.
A bar magnet of moment 7.5 A∙m² experiences a torque of magnitude 1.5 × 10^-4 N∙m when placed inclined at 30° in a uniform magnetic field. Find the magnitude of the magnetic induction of the field.
Solution:
Data : μ = 7.5 A∙m², τ = 1.5 × 10^-4 N∙m, θ = 30° T = μB sin θ
∴ The magnitude of the magnetic induction,

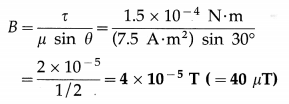
Question 11.
A circular coil, having 200 turns each of area 2.5 × 10^-4 m², carries a current of 200 μA. Initially, the coil is at rest in a magnetic field of induction 0.8 T, with its magnetic dipole moment aligned with the field. Find the work an external agent has to do to rotate the coil through (i) 90° from its initial position (ii) further 90°.
Solution:
Data : N = 200, A = 2.5 × 10^-4 m², B = 0.8T,
I = 200 μA = 2 × 10^-4 A, θ = 90°
W = ∆U =U_θ – U₀
(i) The work done to rotate through 90°,
W = U_90° – U_0° = – μB cos 90° – (- μB cos 0°)
= 0 + μB = (NIA)B (∵ μ = NIA)
= (200)(2 × 10^-4)(2.5 × 10^-4)(0.8)
= 8 × 10^-6 J = 8 μJ

(ii) The work done to rotate further through 90°, so that the dipole moment is antiparallel to the field,
W = U_80° – U_90° = – μB cos 180° – (- μB cos 90°)
= μB + 0 = (NIA)B = 8 μJ

Question 12.
A magnetic dipole of moment 0.025 J/T is free to rotate in a uniform magnetic field of induction 50 mT. When released from rest in the magnetic field, the dipole rotates to align with the field. At the instant the dipole moment is parallel to the field, its kinetic energy is 625 μJ. What was the initial angle between the dipole moment and the magnetic field?
Solution:
Data: μ = 0.025J/T, B = 50mT = 5 × 10^-2 T,
∆K = 625 pJ = 6.25 × 10^-4 J
Change in potential energy,
∆U =U_θ – U₀ = – μB cos 0° – (- μ8 cos θ)
= – μB(1 – cos θ)
By the principle of conservation of energy,
∆K + ∆U = 0
∴ ∆K = – ∆U = μB(1 – cos θ)
∴ (2.5 × 10^-2)(5 × 10^-2)(1 – cos θ) = 6.25 × 10^-4
∴ (1 – cos θ) = 0.5 ∴ cos θ = 0.5
The initial angle between the dipole moment and the magnetic field,
θ = 60° .

Question 45.
State the Bio-Savart law (Laplace law) for the magnetic induction produced by a current el-ement. Express it in vector form.
Answer:
Consider a very short segment of length dl of a wire carrying a current I. The product I\(\overrightarrow{d l}\) is called a current element; the direction of the vector \(\overrightarrow{d l}\) is along the wire in the direction of the current.

Biot-Savart law (Laplace law) : The magnitude of the incremental magnetic induction \(\overrightarrow{d B}\) produced by a current element I\(\overrightarrow{d l}\) at a distance r from it is directly proportional to the magnitude Idl of the current element, the sine of the angle between the current element I \(\overrightarrow{d l}\) and the unit vector \(\hat{r}\) directed from the current element toward the point in question, and inversely proportional to the square of the distance of the point from the current element; the magnetic induction is directed perpendicular to both I \(\overrightarrow{d l}\) and \(\hat{r}\) as per the cross product rule.

of free space. Equations (1) and (2) are called Biot-Savart law.

The incremental magnetic induction \(\overrightarrow{d B}\) is given by the right-handed screw rule of vector crossproduct I\(\overrightarrow{d l} \times \hat{\mathbf{r}}\). In below figure, the current element I \(\overrightarrow{d l}\) and \(\hat{r}\) are in the plane of the page, so that \(\overrightarrow{d B}\) points out of the page at point P shown by ⊙; at the point Q, \(\overrightarrow{d B}\) points into the page shown by ⊗.

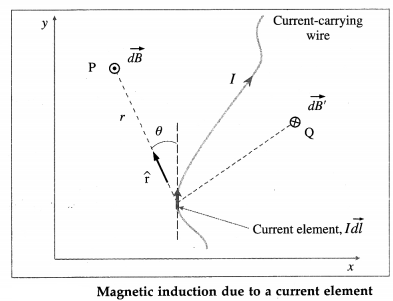
The magnetic induction \(\vec{B}\) at the point due to the entire wire is, by the principle of superposition, the vector sum of the contributions \(\overrightarrow{d B}\) from all the current elements making up the wire.
From Eq. (2),
\(\vec{B}=\int \overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \int \frac{I \vec{d} \times \hat{\mathrm{r}}}{r^{2}}\)
[Notes : (1) The above law is based on experiments by Jean Baptiste Biot (1774-1862) and Felix Savart (1791-1841), French physicists. From their observations Laplace deduced the law mathematically. (2) The Biot- Savart law plays a similar role in magnetostatics as Coulomb’s law does in electrostatics.]

Question 46.
Using Biot-Savart’s law, obtain the expression for the magnetic induction near a straight infinite ly long current-carrying wire.
Answer:
Suppose a point P is at a distance a from a straight, infinitely long, wire carrying a current I, as shown in below figure. The incremental magnetic induction \(d \vec{B}\) at the point P due to a current element, \(I \overrightarrow{d l}\) is

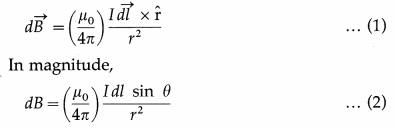
At the point P, \(d \vec{B}\) is directed perpendicular to the plane of the figure and into of the page as given by the right hand rule for the direction of \(\overrightarrow{d l} \times \hat{\mathbf{r}}\).

At point P, \(d \vec{B}\) has this same direction for all the current elements into which the wire can be divided. Thus, we can find the magnitude of the magnetic field produced at P by the current elements in the lower half of the infinitely long wire by integrating dB in Eq. (2), from 0 to ∞.

Now consider a current element in the upper half of the wire, one that is as far above P as I\(\overrightarrow{d l}\) is below P. By symmetry, the magnetic field produced at P by this current element has the same magnitude and direction as that from I \overrightarrow{d l} in above figure. Thus, the magnetic field produced by the upper half of the wire is exactly the same as that produced by the lower half. Hence, the magnitude of the total magnetic field at P is

That is, the magnitude B is inversely proportional to the distance from the wire. Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the conductor; the direction of \(\vec{B}\) is everywhere tangential to such a circle. Thus, the magnetic field lines around the current in the straight wire is a family of circles centred on the wire.

[Notes : (1) The magnetic field at P due to either only the lower half or the upper half of the infinite wire in figure is half the value in Eq. (5); that is, for a semi-infinite wire,

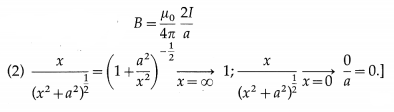
Question 47.
Show that currents in two long, straight, parallel wires exert forces on each other. Derive the expression for the force.
OR
Derive an expression for the force per unit length between two infinitely long parallel conductors carrying current and hence define the ampere.
Answer:
When two currents pass in adjacent parallel straight conductors, we may think of each of the currents as being situated in the magnetic field caused by the other current. This results in a force on each conductor.

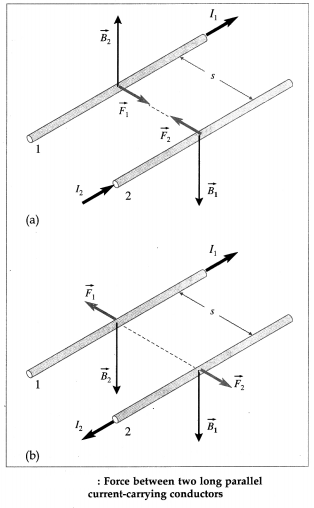
Consider two infinitely long, straight, parallel wires, each of length ¡ a distance s apart in vacuum, as shown in figure (a). The magnetic field around the wire 1, carrying a current I₁ has an induction of magnitude
B₁ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1}}{s}\)
Wire 2, with a current I₂ in the same direction as I₁, is situated in this field. The direction of the field
with induction \(\overrightarrow{B_{1}}\) at the position of wire 2, given by the right hand Igripi rule, is perpendicular to the plane of the two conductors, as shown. Hence, the force \(\overrightarrow{F_{2}}\) on wire 2 has a magnitude
F₂ = I₂lB₁ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2} l}{s}\) ……………… (1)
and is, by Fleming’s left hand rule, towards wire 1. Similarly, the magnetic induction \(\overrightarrow{B_{2}}\) at the position of wire 1 has a magnitude
B₂ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{2}}{s}\)
and is also directed perpendicular to the plane of the wires. Hence, the force on wire 1 has a magnitude
F₁ = I₁lB₂ = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2} l}{s}\) ……………… (2)
directed towards wire 2. Thus, the two currents attract each other. \(\vec{F}_{1}=-\vec{F}_{2} \), i.e., they are equal in magnitude and opposite in direction.

Ampere found that the wires attracted each other when the currents in them were in the same direction [from figure (a )], and repelled each other when they were in the opposite directions [from figure (b)].

From the Eq. (2), the force per unit length acting on each wire is
\(\frac{F}{l}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2}}{s}\)
Using SI units, μ₀/4π = 10^-7 N / A² and, if I₁ = I₂ = 1 A and s = 1 m, then
\(\frac{F}{l}\) = 2 × 10^-7 N / m
In SI, this equation is the defining relation for the ampere.

Definition: The ampere is that constant current which if maintained in two infinitely long straight parallel wires, and placed one metre apart in vacuum, would cause each conductor to experience a force per unit length of 2 × 10^-7 newton per metre. [Note : 1 Wb/A∙m = 1 T∙m/A = l N/A².]

Question 48.
Two very long and straight parallel conductors separated by 0.5 m in vacuum carry currents 2 A and 3 A respectively. What is the force per unit length of a conductor? [\(\frac{\mu_{0}}{4 \pi}\) = 10^-7 Wb/A∙m]
Answer:
The force per unit length on each conductor,

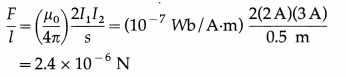
Question 49.
Obtain an expression for the magnetic induction produced by a current in a wire in the shape of a circular arc at its centre of curvature. Hence obtain an expression for the magnetic induction at the centre of a circular coil carrying a current.
Answer:
Consider a wire in the shape of a circular arc of radius of curvature R and carrying a current I. The unit vector \(\hat{\mathrm{r}}\) from each current element I\(\overrightarrow{d l}\) towards

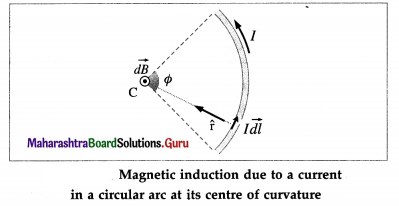
the centre of the loop is perpendicular to I\(\overrightarrow{d l}\), i.e., the angle θ between them is 90°. The direction of the incremental magnetic induction \(\overrightarrow{d B}\) due to each current element is in the same direction, viz., perpendicular to the plane of the loop, and out of the plane of the figure for the sense of the current shown in above figure.

Since every current element is equidistant from the centre of curvature C, the magnetic field at C due to each current element in the arc by Biot-Savart’s law is

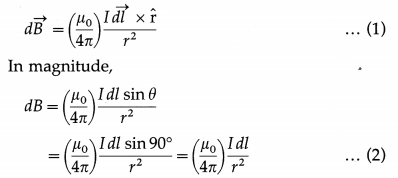
If the arc subtends an angle 0 at its centre of curvature C, the total field at C due to all the elements on the arc is

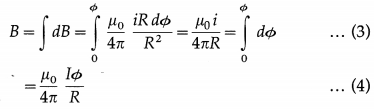
where Φ is in radian.
The magnitude of the total induction \(\vec{B}\) at the centre of a circular coil is, from Eq. (3),

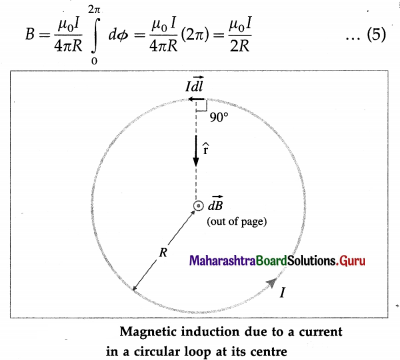
If a circular coil has N turns, each of radius r and carries a current I, the magnetic induction at its centre has a magnitude
B = \(\frac{\mu_{0} N I}{2 R}\) …………… (6)

Question 50.
Derive an expression for the magnetic induction at a point on the axis of a circular coil carrying a current.
OR
A circular coil of N turns, each of radius R, carries a current I. Derive the expression for the magnitude of the magnetic induction on the axis of the coil at a distance z. Hence obtain the expression for the magnitude of the magnetic induction for z » R.
Answer:
Consider a circular, conducting loop of radius R in the xy-plane, whose centre is at the origin. For any point P on the z-axis (which is also the axis of the loop), the current element I \(\overrightarrow{d l}\) is perpendicular to the unit vector \(\hat{\mathbf{r}}\) directed from the current element to point P. The incremental magnetic induction, \(\overrightarrow{d B}\), due to a current element at Q lies in the plane QOP, in the direction of I \(\overrightarrow{d l} \times \vec{r}\), as shown in below figure. In magnitude,

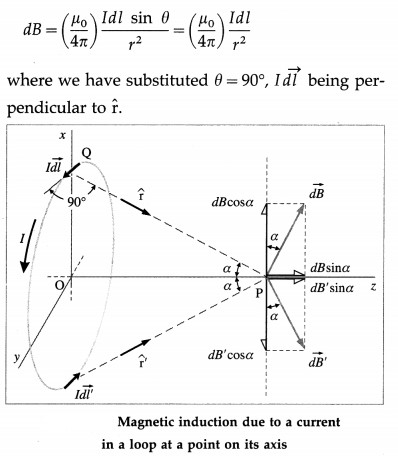
Each element of the loop has its diametrically opposed companion I \(\overrightarrow{d l}\) on the other side of the loop, both of equal segment length dl. Point P is equidistant from the two elements, that is, r = r’. Therefore, the two contributions \(\overrightarrow{d B}\) and \(\overrightarrow{d B}^{\prime}\) have equal magnitudes, and their vertical components, dB cos α and dB’cos α, are oppositely directed. Thus, they will add to zero when all the \(\overrightarrow{d B}\) contributions are summed, and there can be no vertical component of the resultant induction \(\vec{B}\). However, the horizontal components are of like direction and will sum to a definite value and hence \(\vec{B}\) will have only a horizontal z-component. For the magnitude of \(\vec{B}\), we need to add only the z-components of the \(\overrightarrow{d B}\) vectors :

For values of z that are much larger than the radius R, we may ignore the value of R in the denominator above and write
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I A}{z^{3}}\) (for z >> R) …………… (2)
For a circular coil of N turns Eqs. (1) and (2) are, respectively,
B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 N I A}{\left(R^{2}+z^{2}\right)^{\frac{3}{2}}}\) and B = \(\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 N I A}{z^{3}}\)

Question 51.
How is the magnetic field of a small current loop identical to that of a short magnetic dipole? Explain.
OR
Explain the equivalence of the fields of a current-carrying circular coil and a magnetic dipole.
Answer:
An electric current in a circular loop establishes a magnetic field similar in every respect to the field of a magnetic dipole (or a bar magnet).

Consider a circular conducting ioop of radius R, axis along the x-axis and carrying a current I. The area of the loop is A = πR²and \(\vec{A}\) has the direction given by right hand rule. The axial magnetic induction of the current loop at a distance x from its centre is
\(\vec{B}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I \vec{A}}{\left(R^{2}+x^{2}\right)^{3 / 2}}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 \vec{\mu}}{\left(R^{2}+x^{2}\right)^{3 / 2}}\)
where \(\vec{M}=I \vec{A}\) is the magnetic moment of the current loop and μ₀ is the permeability of free space. For x >> R, ignoring R² in comparison with X²,
\(\vec{B}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 \vec{\mu}}{x^{3}}\)
This equation also gives the magnetic induction on the axis of a short magnetic dipole (or a bar magnet) of magnetic moment \(\vec{\mu}\).

For a magnetic dipole, the dipole moment is directed from the south pole of the dipole to its north pole. For a current loop, the magnetic dipole moment has the direction of the axial field of the current loop as given by the right-hand rule.

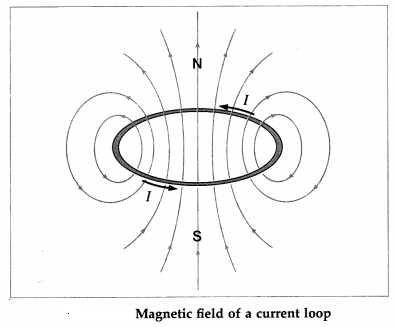
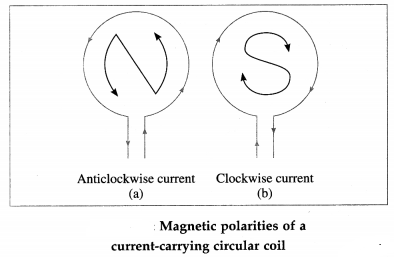
When an observer looking at a current carrying circular loop finds the direction of the current anticlockwise, the face of the loop towards the observer acts as the north pole. When an observer looking at a current-carrying circular loop finds the direction of the current clockwise, the face of the loop towards the observer acts as the south pole. This rule is known as the clock rule.

Question 52.
State the expressions for the axial fields of an electric dipole and a small current-loop.
Answer:
The axial far field of an electric dipole of electric dipole moment \(\vec{p}\) at an axial point r is
\(\vec{E}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \vec{p}}{r^{3}}\)
The axial magnetic field far from a small current-loop is
\(\vec{B}=\frac{\mu_{0}}{4 \pi} \frac{2 \vec{\mu}}{r^{3}}\)
where \(\vec{\mu}=I \vec{A}\) is the magnetic dipole moment of the loop, I is the current in the loop and \(\vec{A}\) is the area vector given by the right-hand rule. The axial field of an electric dipole, \(\vec{E}\) is in the direction of the dipole moment \(\vec{p}\). On the axis of a current loop, the magnetic field \(\vec{B}\) is in the direction of the dipole moment \(\vec{\mu}\).

53. Solve the following
Question 1.
(1) Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10A. Calculate the force per metre on each conductor, if the currents are in the same direction and in the opposite direction.
Solution:
Data: s = 0.4 m, I₁ = 5A, I₂ = 10A
μ₀/4π = 10^-7 N/A²
The force per unit length acting on each conductor is
\(\frac{F}{l}=\left(\frac{\mu_{0}}{4 \pi}\right) \frac{2 I_{1} I_{2}}{s}\)
= (10^-7 N/A²) \(\frac{2(5 \mathrm{~A})(10 \mathrm{~A})}{0.4 \mathrm{~m}}\)
= 2.5 × 10^-5 N/m (= 25 μN/m)
This force is attractive if the currents are in the same direction and repulsive if the currents are in the opposite directions.

Question 2.
Two wires 12 m long and 10 cm apart carry the same current. Find the current through each wire if the force per unit length on each wire is 0.001 N/m.
Solution:
Data : l = 12 m, s = 10 cm = 0.1 m,
I₁ = I₂ = I, \(\frac{F}{l}\) = 0.001 N/m

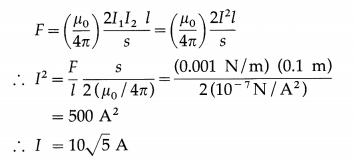
The current through each wire is 10\(\sqrt {5}\) A.

Question 3.
The wire shown below carries a current of 2 A. The curved segment is a quadrant of radius 10 cm while the straight segments are along radii. Find the magnitude and direction of the magnetic induction at the centre O of the quadrant by the entire wire.

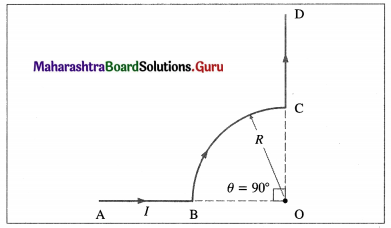
Solution:
Data : I = 2 A, R = 10 cm = 10^-1 m
The point O lies along the straight segments AB and CD. Hence, the magnetic induction \(\vec{B}\) produced by each of them is zero.

Since θ = 90°, the magnitude of the magnetic induction due to the current in quadrant BC is \(\frac{1}{4}\)th of that produced at the centre of a loop.

Question 4.
A flat coil of 70 turns has a diameter of 20 cm and carries a current of 5 A. Find the magnitude of the magnetic induction at (a) the centre of the coil (b) a point on the axis 20 cm from the centre of the coil.
Solution:
Data : N = 70, R = 10 cm = 0.1 m, I = 5 A, z = 0.2 m, μ₀ = 4π × 10^-7 T∙m/A
(a) At the centre of the coil:
The magnitude of the magnetic induction,

Question 5.
(12) A current of 10 A passes through a coil having 5 turns and produces a magnetic field of magnitude 0.5 × 10^-4 T at the centre of the coil. Calculate the diameter of the coil.
Solution:
Data: I = 10A, N = 5, B = 5 × 10^-5 T,
μ₀/4π = 10^-7 T∙m/A
B = \(\frac{\mu_{0} N I}{2 R}\)
∴ The diameter of the coil,
2R = \(\frac{\mu_{0} N I}{B}=\frac{\left(4 \pi \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} / \mathrm{A}\right)(5)(10 \mathrm{~A})}{5 \times 10^{-5} \mathrm{~T}}\)
= 4 × 3.142 × 10^-1 = 1.257 m

Question 6.
Calculate the magnitude of the magnetic induction due to a circular coil of 400 turns and radius 0.05 m, carrying a current of 5 A, at a point on the axis of the coil at a distance 0.1 m.
Solution:
Data : N = 400, R = 0.05 m = 5 × 10^-2 m,
I = 5 A, z = 0.1 m, μ₀/4π = 10^-7 T∙m/A
The magnitude of the magnetic induction,

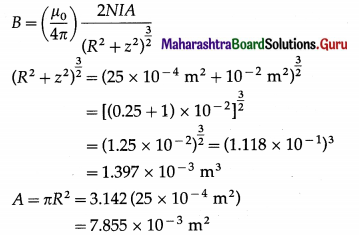
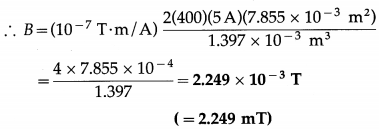
Question 7.
A circular coil of wire has 100 turns. The radius of the coil is 50 cm. It is desired to have a magnetic induction of 80 μT at the centre of the coil. What should be the current through the coil ?
Solution:
Data: N = 100, R = 50 cm = 0.5 m,
B = 80 μT = 8 × 10^-5 T, μ₀/4π = 10^-7 T∙m/A

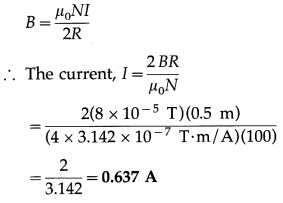
Question 54.
State and explain Ampere’s circuital law.
OR
State Ampere’s circuital law.
Answer:
Ampere’s circuital law : In free space, the line integral of magnetic induction around a closed path in a magnetic field is equal to p0 times the net steady current enclosed by the path.
In mathematical form,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀I …………. (1)
where \(\vec{B}\) is the magnetic induction at any point on the path in vacuum, \(\overrightarrow{d l}\) is the length element of the path, I is the net steady current enclosed and p0 is the permeability of free space.

Explanation : Below figure shows two wires carrying currents I₁ and I₂ in vacuum. The magnetic induction \(\vec{B}\) at any point is the net effect of these currents.

To find the magnitude B of the magnetic induction :
(i) We construct an imaginary closed curve around the conductors, called an Amperian loop, and imagine it divided into small elements of length dl. The direction of \(\overrightarrow{d l}\) is the direction along which the loop is traced.

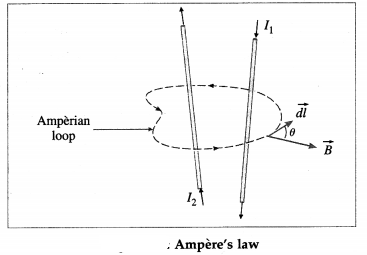
(ii) We assign signs to the currents using the right hand rule : If the fingers of the right hand are curled in the direction in which the loop is traced, then a current in the direction of the outstretched thumb is taken to be positive while a current in the opposite direction is taken to be negative.

For each length element of the Amperian loop, \(\vec{B} \cdot \overrightarrow{d l}\) gives the product of the length dl of the element and the component of \(\vec{B}\) parallel to \(\overrightarrow{d l}\). If θ is the angle between \(\overrightarrow{d l}\) and \(\vec{B}\),
\(\vec{B} \cdot \overrightarrow{d l}\) = (B cos θ) dl
Then, the line integral,
\(\oint \vec{B} \cdot \overrightarrow{d l}=\oint\) Bcosθ dl ……………(2)
For the case shown in figure, the net current I through the surface bounded by the loop is
I = I₂ – I₁
∴ \(\oint\) Bcosθ dl = μ₀ I
= μ₀(I₂ – I₁) ……………. (3)
Equation (3) can be solved only when B is uniform and hence can be taken out of the integral.

[Note : Ampere’s law in magnetostatics plays the part of Gauss’s law of electrostatics. In particular, for currents with appropriate symmetry, Ampere’s law in integral form offers an efficient way of calculating the magnetic field. Like Gauss’s law, Ampere’s law is always true (for steady currents), but it is useful only when the symmetry of the problem enables B to be taken out of the integral \(\oint \vec{B} \cdot \overrightarrow{d l}\). The current configurations that can be handled by Ampere’s law are infinite straight conductor, infinite plane, infinite solenoid and toroid.]

Question 55.
Using Ampere’s law, obtain an expression for the magnetic induction near a current-carrying straight, infinitely long wire.
Answer:
Consider a point P at a distance a from a straight, infinitely long wire carrying a current I in free space, from figure (a). Because of the axial symmetry about the straight wire, the magnetic induction has the same magnitude B at all points on a circle in a transverse plane and centred on the wire. We, therefore, choose an Amperian loop a circle of radius a centred on the wire with its plane perpendicular to the wire, as shown in from figure (b).

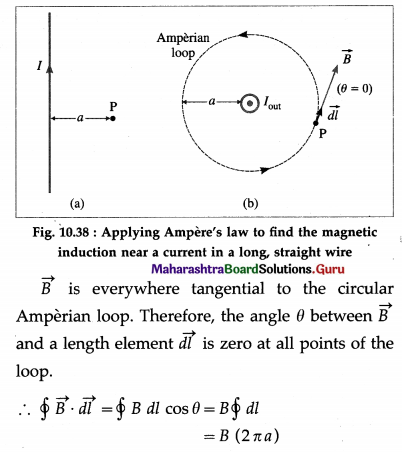
since cos θ = 1 and B has the same value around the path. \(\oint\) dl gives the circumference of the circular loop.

In the figure, the Amperian loop is traced in the anticlockwise sense, so that the current I is taken as positive in accordance with the right hand rule.
By Ampere’s law,

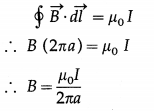
This is the required expression.

Question 56.
What is a solenoid? With a neat labelled diagram, describe the magnetic field produced by a current-carrying solenoid.
Answer:
A solenoid is a long wire wound in the form of a helix. An ideal solenoid is tightly wound and infinitely long, i.e., its turns are closely spaced and the solenoid is very long compared to its crosssectional radius.

Each turn of a solenoid acts approximately as a circular loop. Suppose the solenoid carries a steady current I. The net magnetic field due to the current in the solenoid is the vector sum of the fields due to the current in all the turns. In the case of a tightly- wound solenoid of finite length, Fig. 10.39, the magnetic field lines are approximately parallel only near the centre of the solenoid, indicating a nearly uniform field there. However, close to the ends, the field lines diverge from one end and converge at the other end. This field distribution is similar to that of a bar magnet. Thus, one end of the solenoid behaves like the north pole of a magnet and the opposite end behaves like the south pole. The field outside is very weak near the midpoint.

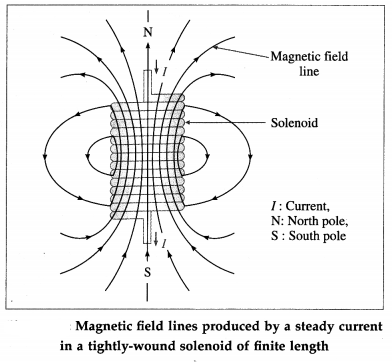
For an ideal solenoid, the magnetic field inside is reasonably uniform over the cross section and parallel to the axis throughout the volume enclosed by the solenoid. The field outside is negligible in this case.

Question 57.
Using Ampere’s law, derive an expression for the magnetic induction inside an ideal solenoid carrying a steady current.
Answer:
An ideal solenoid is tightly wound and infinitely long. Let n be the number of turns of wire per unit length and I be the steady current in the solenoid.

For an ideal solenoid, the magnetic induction \(\vec{B}\) inside is reasonably uniform over the cross section and parallel to the axis throughout the volume enclosed by the solenoid; \(\vec{B}\) outside is negligible.

As an Amperian loop, we choose a rectangular path PQRS of length l parallel to the solenoid axis, from below figure. The width of the rectangle is taken to be sufficiently large so that the side RS is far from the solenoid where \(\vec{B}\) = 0. The line integral of the magnetic induction around the Amperian loop in the sense PQRSP is


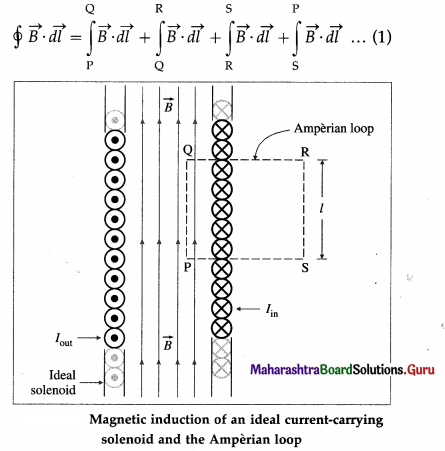
Thus, from Eqs. (1), (2), (3) and (4),
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = Bl ……….. (5)
The total current enclosed by the Amperian loop is
I_encl = current through each turn × number of turns enclosed by the loop
= I × nl = nlI ……… (6)
By Ampere’s law,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀I_encl (in vacuum)
Therefore, from Eq.s (5) and (6),
Bl = μ₀ nlI
∴ B = μ₀nI …………. (7)
This is the required expression.

[Notes : (1) The field inside an ideal solenoid is uniform-it doesn’t depend on the distance from the axis. In this sense, the solenoid is to magnetostatics what the parallel-plate capacitor is to electrostatics; a simple device for producing strong uniform fields. (2) At an axial point at the end of a long solenoid, B = \(\frac{1}{2}\) μ₀nI]

Question 58.
What is the magnetic field (i) outside (ii) inside a long air-cored current-carrying solenoid ?
Answer:
For an ideal solenoid, the magnetic field induction outside is negligible, nearly zero. Inside the solenoid, the field lines are parallel to the axis of the solenoid and the magnitude of the magnetic induction, B = μ₀nI, where μ₀ is the permeability of free space, n is the number of turns of wire per unit length and I is the steady current in the solenoid.

Question 59.
What is a toroid? With a neat diagram, describe the magnetic field produced by a toroid carrying a steady current.
Answer:
A toroid is a toroidal solenoid. An ideal toroid consists of a long conducting wire wound tightly around a torus, a doughnut-shaped ring, made of a nonconducting material.

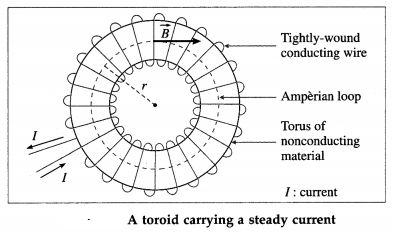
In an ideal toroid carrying a steady current, the magnetic field in the interior of the toroid is tangential to any circle concentric with the axis of the toroid and has the same value on this circle (the dashed line in above figure). Also, the magnitude of the magnetic induction external to the toroid is negligible.

Question 60.
Using Ampere’s law, derive an expression for the magnetic induction inside an ideal toroid carrying a steady current.
Answer:
An ideal toroid consists of a long conducting wire wound tightly around a torus made of a non-conducting material. When a steady current is passed through it, the magnetic induction \(\vec{B}\) in the interior of the toroid is tangent to any circle concentric with y the axis of the toroid and has the same value on this circle.

Suppose the toroid has N turns of wire and I is the current in its coil. As our Amperian loop, we choose a circle of radius r concentric with the axis of the toroid, as shown in figure. Since \(\vec{B}\) has the same value on this circle and is tangential to it, we go around this path in the direction of \(\vec{B}\) so that \(\vec{B}\) and \(\overrightarrow{d l}\) are parallel. Then, the line integral of the magnetic induction around the Amperian loop is

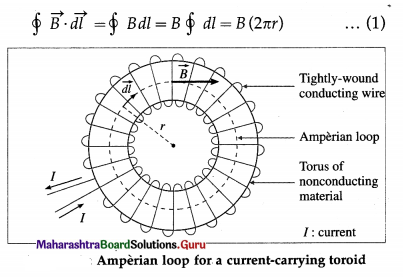
The net current enclosed by the Amperean loop is
I_encl = current through each turn × number of turns enclosed by the loop
= I × N = NI …………….. (2)
By Ampere’s law,
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = μ₀ I_encl (in free space)
Therefore, from Eqs. (1) and (2),
B (2πr) = μ₀NI
∴ B = \(\frac{\mu_{0}}{2 \pi} \frac{N I}{r}\) …………… (3)
This is the required expression.

61. Solve the following

Question 1.
Four long parallel wires are arranged at the four comers of a square ABCD of side 20 cm. Each wire carries a current of 5 A. Currents in the conductors 1 and 2, at comers A and B, are out of the page while those in the conductors 3 and 4, at comers C and D, are into the page. What is the magnitude of the magnetic induction at the centre of the square?
Solution:
Data : 2l = 20 cm = 0.2 m, I = 5 A
If each side of the square array is 2l, then from geometry, the centre of the square O is a distance \(\sqrt {2}\)l from each corner. Since each wire carries the same current, B₁ = B₂ = B₃ = B₄. Using the right hand [grip] rule, the directions of the magnetic inductions due to conductors 1 and 3 are along OB, while those due to conductors 2 and 4 are along OC, as shown.

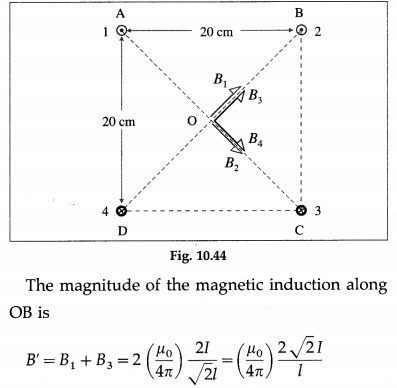
This is also the magnitude of the magnetic induc-tion along OC, B₂ + B₄.

Their components parallel to AD (or BC) are oppositely directed and cancel out. Therefore, the total induction at the centre of the square has a magnitude equal to the sum of the components parallel to AB (or DC).

The magnitude of the magnetic induction at the centre of the square is 2 × 10^-5 T.

Question 2.
Two long straight parallel wires in vacuum are 4 m apart and carry currents of 2 A and 6 A in the same direction. Find the neutral point, i.e., the point at which the resultant magnetic induction is zero.
Solution:
Data: I₁ =2 A, I₂ = 6 A, a =4 m
The currents through the wires are in the same direction. Therefore, the two magnetic inductions \(\overrightarrow{B_{1}}\) and \(\overrightarrow{B_{2}}\) will have opposite directions at any point between the two wires. Hence, the point must lie between the two wires. For the resultant magnetic induction to be zero, we must have B₁ = B₂. Let the corresponding point (the neutral point) be at a distance a₁ from the first wire and a₂ from the second wire.

The neutral point lies at a distance of 1 m from the wire carrying a current of 2 A.

Question 3.
A solenoid 1.5 m long and 4 cm in diameter has – 10 turns/cm. A current of 5 A is passing through it. Calculate the magnetic induction (i) inside (ii) at one end on the axis of the solenoid.
Solution:
Data : L = 1.5 m, r = 2 cm, n = 10 turns/cm = 10³ turns/metre, I = 5 A, μ₀ = 4π × 10^-7 T∙m/A
Since the diameter is very small compared to its length, we approximate the solenoid to be long, i.e., an ideal solenoid.

(i) At an axial point well inside a long solenoid,
B = μ₀nI
= (4π × 10^-7 )(10³)(5) = 2 × 3.142 × 10^-3
= 6.284 × 10^-3 T

(ii) At an axial point at the end of a long solenoid,
B = \(\frac{1}{2}\) μ₀nI
= \(\frac{1}{2}\) (6.284 × 10^-3) = 3.142 × 10^-3 T

Question 4.
A toroidally wound coil has an inner radius of 15 cm, an outer radius of 20 cm and is wound with 1500 turns of wire. What is the magnitude of the magnetic induction at the centre of the coil when the current in the winding is 10 A ?
Solution:
Data : Central radius, r = \(\frac{1}{2}\) (15 + 20) = 17.5 cm
= 0.175 m, N = 1500, I = 10 A, \(\frac{\mu_{0}}{4 \pi}\) = 10^-7 T∙m/A
The magnetic induction,
B = \(\frac{\mu_{0} N I}{2 \pi r}=\frac{\mu_{0}}{4 \pi} \frac{2 N I}{r}=10^{-7} \times \frac{2 \times 1500 \times 10}{0.175}\)
= 1.714 × 10^-2 T

Multiple Choice Questions

Question 1.
A doubly ionized helium nucleus (charge = 3.2 × 10^-19 C) enters a region of uniform magnetic field with a velocity (10³ m/s)\(\hat{\mathbf{i}}\). The magnetic induction in the region is 20 mT directed towards the positive x-axis. The force on the ion is
(A) (6.4 × 10^-18 N) \(\hat{\mathrm{j}}\)
(B) (6.4 × 10^-18 N) \(\hat{\mathrm{k}}\)
(C) zero
(D) none of these.
Answer:
(C) zero

Question 2.
In a cyclotron, charged particles are accelerated by
(A) the electrostatic deflector plate
(B) the electric field in the dees
(C) the magnetic field in the dees
(D) the p.d. across the gap between the dees.
Answer:
(D) the p.d. across the gap between the dees.

Question 3.
Cyclotron cannot accelerate
(A) protons
(B) neutrons
(C) α-particles
(D) deuterons.
Answer:
(B) neutrons

Question 4.
If R is the radius of the dees and B the magnitude of the magnetic field induction in which positive charges (q) of mass m escape from the cyclotron, then their maximum speed v_max is
(A) \(\frac{q R}{B m}\)
(B) \(\frac{q m}{B R}\)
(C) \(\frac{q B R}{m}\)
(D) \(\frac{m}{q B R}\)
Answer:
(C) \(\frac{q B R}{m}\)

Question 5.
A charged particle moving with a velocity \(\vec{v}\) enters a region of uniform magnetic field \(\vec{B}\). If the velocity has a component parallel to \(\vec{B}\), which of the following quantities is independent of \(\overrightarrow{\mid v} \mid\)?
(A) Period T of its circular motion
(B) Pitch p of its helical path
(C) Radius r of its helical path
(D) Both p and T
Answer:
(A) Period T of its circular motion

Question 6.
A charged particle moving with a velocity \(\vec{v}\) enters a region of uniform magnetic field \(\vec{B}\) such that the pitch of the resulting helical motion is equal to the radius of the helix. The angle between \(\vec{v}\) and \(\vec{B}\) is
(A) tan^-1 2π
(B) sin^-1 2π
(C) tan^-1 \(\frac{1}{2 \pi}\left(\frac{q B}{m}\right)^{2}\)
(D) tan^-1 2π\(2 \pi\left(\frac{q B}{m}\right)^{2}\).
Answer:
(A) tan^-1 2π

Question 7.
The following four cases show a positive charge moving into a magnetic field \(\vec{B}\) with velocity \(\vec{v}\). In which of the cases are the forces opposite in direction?

(A) (iii) and (iv)
(B) (i) and (ii)
(C) (i) and (iii)
(D) (ii) and (iv)
Answer:
(B) (i) and (ii)

Question 8.
A charged particle enters a uniform magnetic field initially travelling perpendicular to the field lines and is bent in a circular arc of radius R. If the particle had the same charge but double the mass and were travelling twice as fast, the radius of its circular arc would be
(A) 2R
(B) 4R
(C) R
(D) \(\frac{1}{4}\)R.
Answer:
(B) 4R

Question 9.
A straight wire along the y-axis carries a current of 4 A. The wire is placed in a uniform magnetic field (0.02 T) \((\hat{\mathrm{i}}+\hat{\mathrm{j}})\). If the current in the wire is directed towards the negative y-axis, the force per unit length on the wire is
(A) zero
(B) – (0.08 N/m) \(\hat{\mathrm{k}}\)
(C) (0.08 N/m) \((\hat{\mathrm{i}}-\hat{\mathrm{j}})\)
(D) (0.08 N/m) \(\hat{\mathrm{k}}\)
Answer:
(D) (0.08 N/m) \(\hat{\mathrm{k}}\)

Question 10.
A 30-turn coil of diameter 2 cm carries a current of 10 mA. When it is placed in a uniform magnetic field of 0.05 T, the magnitude of the maximum torque that could be exerted on the coil by the magnetic field is
(A) 1.88 × 10^-5 N∙m
(B) 4.7 × 10^-6 N∙m
(C) 4.7 × 10^-7 N∙m
(D) 1.88 × 10^-8 N∙m.
Answer:
(B) 4.7 × 10^-6 N∙m

Question 11.
A circular loop of area \(\sqrt{2}\) cm² and carrying a current of 10 μA is placed in a magnetic field \(\vec{B}\) with its plane parallel to \(\vec{B}\) (B = 15 mT). When the loop has rotated through an angle of 45°, the magnitude of the torque exerted on this loop is
(A) zero
(B) 15 × 10^-12 N∙m
(C) 15 × 10^-8 N∙m
(D) 15 × 10^-2 N∙m
Answer:
(B) 15 × 10^-12 N∙m

Question 12.
A current loop of magnetic dipole moment 0.1 A-m2 is oriented with the plane of the loop perpendicular to a uniform 1.50 T magnetic field, as shown. The torque that the magnetic field exerts on the current loop is

(A) 0.15 N∙m
(B) 0.075 N∙m
(C) -0.075 N∙m
(D) -0.15 N∙m.
Answer:
(B) 0.075 N∙m

Question 13.
A rectangular coil of dipole moment fi, free to rotate, is placed in a uniform magnetic field B with its plane parallel to the magnetic lines of force. Then, the coil will
(A) rotate to maximize the magnetic flux through its plane
(B) rotate to minimize the magnetic flux through its plane
(C) not experience any torque
(D) experience a constant torque equal to μB.
Answer:
(C) not experience any torque

Question 14.
When a current is passed through a suspended moving-coil galvanometer, the deflection of the coil is arrested by
(A) the elastic torsion of the suspension fibre
(B) the elastic winding of the helical spring
(C) the friction at the point of suspension
(D) the changing magnetic flux through the coil.
Answer:
(A) the elastic torsion of the suspension fibre

Question 15.
When a current is passed through a suspended moving-coil galvanometer, the deflection of the coil is 9. Then, in the usual notation, the expression \(\frac{\mu B}{\theta}\) is
(A) the torsion constant of the helical spring
(B) the magnetic dipole moment of the current-carrying coil
(C) the current through the coil
(D) the torsion constant of the suspension fibre.
Answer:
(D) the torsion constant of the suspension fibre.

Question 16.
The magnetic potential energy of a coil of dipole moment \(\vec{\mu}\) and area vector \(\vec{A}\) placed in a magnetic \(\vec{B}\) is maximum for which of the following cases ?

Answer:
(C) \(\vec{B} \uparrow \downarrow \vec{A}\)

Question 17.
Two points, A and B, are at distances r_A and r_B from a long, straight, current-carrying conductor. If r_B = 2 r_A, the magnitudes of the magnetic inductions at the two points are related by
(A )B_A = B_B
(B) B_A = 2B_B
(C) B_A = 4B_B
(D) B_B = 2B_A
Answer:
(B) B_A = 2B_B

Question 18.
Two long, straight, parallel wires are 5 cm apart and carry currents I₁ and I₂ in the same direction. If 2I₁ = 3I₂, then at a point P, 2 cm from wire 2,

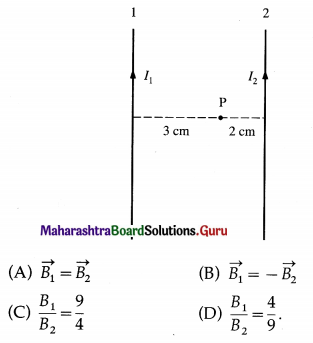
Answer:
(B) \(\overrightarrow{B_{1}}=-\overrightarrow{B_{2}}\)

Question 19.
A wire of length L is first formed into a loop of one turn and then as a loop of two turns. The same current I is passed through the wire in the two cases. The ratio of the magnitude of the magnetic field induction at the centre of the single-turn loop to that at the centre of the double-turn loop is
(A) 4
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
(D) \(\frac{1}{4}\)

Question 20.
Two circular coils 1 and 2 have both their radii and number of turns in the ratio 1 : 2. If the currents in them are in the ratio 2: 1, the magnitudes of the magnetic inductions at the centres of the coils are in the ratio
(A) 1 : 1
(B) 2 : 1
(C) 1 : 2
(D) 1 : 8.
Answer:
(B) 2 : 1

Question 21.
Three straight, parallel wires are coplanar and perpendicular to the plane of the page. The currents I₁ and I₃ are directed out of the page. If the wire 3 experiences no force due to the currents I₁ and I₂, then the current in the wire 2 is

(A) I₂ = 2I₁ and directed into the page
(B) I₂ = 0.5I₁ and directed into the page
(C) I₂ = 2I₁ and directed out of the page
(D) I₂ = 0.5I₁ and directed out of the page.
Answer:
(B) I₂ = 0.5I₁ and directed into the page

Question 22.
Two diametrically opposite points of a uniform metal ring (radius, R) are connected to the terminals of a battery. If the current drawn from the battery is I, the magnetic induction at the centre of the ring has a magnitude
(A) \(\frac{\mu_{0} I}{R}\)
(B) \(\frac{\mu_{0} I}{2R}\)
(C) \(\frac{\mu_{0} I}{4R}\)
(D) zero
Answer:
(D) zero

Question 23.
Two circular coaxial coils, each of N turns and radius R, are separated by a distance R. They carry equal currents I in the same direction. If the magnetic induction at P, on the common axis and midway between the coils, due to the left hand coil is B, then the total induction at P is

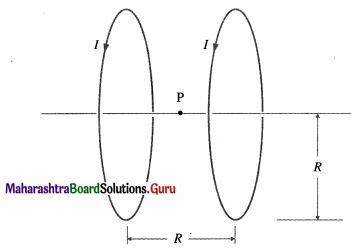
(A) 2B
(B) B
(C) \(\frac{1}{2}\) B
(D) zero.
Answer:
(A) 2B

Question 24.
A toroid with a circular cross section has a current I in its windings. The total number of windings is N. The total current through an Amperian loop of radius r equal to the mean radius of the toroid is
(A) zero
(B) I
(C) NI
(D) \(\frac{N I}{2 \pi r}\)
Answer:
(C) NI

Question 25.
A very long solenoid has 8400 windings and a length of 7 m. If the field inside is 2ir x iO T, the current in the windings is about
[μ₀/4π = 10^-7 T∙m/A]
(A) 0.42 A
(B) 0.83 A
(C) 4.2 A
(D) 8.3 A.
Answer:
(C) 4.2 A