Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics

Question 1.
What is temperature? Explain.
Answer:
The temperature of a body is a quantitative measure of the degree of hotness or coolness of the body. According to the kinetic theory of gases, it is a measure of the average kinetic energy per molecule of the gas. Temperature difference determines the direction of flow of heat from one body to another or from one part of the body to the other. Its SI unit is the kelvin (K).

Question 2.
What is heat ? Explain.
Answer:
When two bodies are in thermal contact with each other, there is a transfer of energy from the body at higher temperature to the body at lower temperature. The energy in transfer is called the heat. Also when two parts of a body are at different temperatures, there is a transfer of energy from the part at higher temperature to the other part. The SI unit of heat is the joule.

[Note : Count Rumford [Benjamin Thompson] (1753-1814) Anglo-American adventurer, social reformer, inventor and physicist, measured the relation between work and heat. When he visited Arsenal in Munich, he found that tremendous amount of heat was produced in a short time when a brass cannon was being bored. He found that even with a blunt borer a lot of heat can be produced from a piece of metal. At that time it was thought that heat consists of a fluid called caloric. Rumford’s experiments showed that caloric did not exist and heat is the motion of the particles of a body. He measured the relation beween work done and corresponding heat produced. The result was not accurate, but important in development of thermodynamics.]

Question 3.
What is thermodynamics ?
Answer:
Thermodynamics is the branch of physics that deals with the conversion of energy (including heat) from one form into another, the direction of energy transfer between a system and its environment with the resulting variation in temperature, in general, or changes of state, and the availability of energy to do mechanical work.

Question 4.
What is meant by thermal equilibrium ? What is meant by the expression “two systems are in thermal equilibrium” ?
Answer:
A system is in a state of thermal equilibrium if there is no transfer of heat (energy) between the various parts of the system or between the system and its surroundings.

Two systems are said to be in thermal equilibrium when they are in thermodynamic states such that, if they are separated by a diathermic (heat conducting) wall, the combined system would be in thermal equilibrium, i.e., there would be no net transfer of heat (energy) between them.
[Note :It is the energy in transfer that is called the heat.]

Question 5.
State the zeroth law of thermodynamics.
Answer:
Zeroth law of thermodynamics : If two systems are each in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.

[Note :The zeroth law is fundamental to the other laws of thermodynamics. That this law is assumed by the other laws of thermodynamics was realized much later. This law has no single discoverer. It was given the status of a law, following the suggestion by R. H. Fowler (in 1931), only after the first, second and third laws were named.]

Question 6.
Explain the zeroth law of thermodynamics.
Answer:
Consider three systems A, B and C. Suppose A and B are in thermal equilibrium, and A and C are also in thermal equilibrium. Then B and C are also in thermal equlibrium. Thus, A, B and C are at the same temperature and A works as a thermometer.

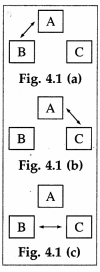
[Note: The arrows in the figure indicate energy exchange]

Question 7.
Define internal energy.
Answer:
Internal energy of a system is defined as the sum of the kinetic energies of the atoms and molecules belonging to the system, and the potential energies associated with the interactions between these constituents (atoms and molecules).
[Note : Internal energy does not include the potential energy and kinetic energy of the system as a whole. In the case of an ideal gas, internal energy is purely kinetic. In the case of real gases, liquids and solids, internal energy is the sum of potential and kinetic energies. For an ideal gas, internal energy depends on temperature only. In other cases, internal energy depends on temperature, as well as on pressure and volume. According to quantum theory, internal energy never becomes zero. Even at OK. particles have energy called zero-point energy.]

Question 8.
What is the internal energy of one mole of argon and oxygen ?
Answer:
Argon is a monatamic gas. In this case, with three degrees of freedom, the average kinetic energy per molecule = \(\left(\frac{3}{2}\right)\)k_BT, where k_B is the Boltzmann constant and T is the absolute (thermodynamic) temperature of the gas. Hence, the internal energy of one mole of argon = N_A\(\left(\frac{3}{2} k_{\mathrm{B}} T\right)\) = \(\frac{3}{2}\)RT, where N_A is the Avogadro number and R = N_Ak_B is the universal gas constant. Oxygen is a diatomic gas. In this case, with five degrees of freedom at moderate temperatures, the internal energy of one mole of
oxygen = \(\frac{3}{2}\)RT.

Question 9.
Find the internal energy of one mole of argon at 300 K. (R = 8.314 J/mol.K)
Answer:
The internal energy of one mole of argon at 300 K
= \(\frac{3}{2}\)RT = \(\frac{3}{2}\)(8.314)(300) J = 3741 J.

Question 10.
The internal energy of one mole of nitrogen at 300 K is 6235 J. What is the internal energy of one mole of nitrogen at 400 K ?
Answer:

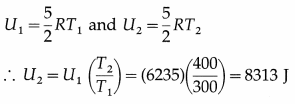
This is the required quantity.
[Note : In chapter 3, the symbol E was used for internal energy.]

Question 11.
Explain the term thermodynamic system.
Answer:
A thermodynamic system is a collection of objects that can form a unit which may have ability to Surrounding

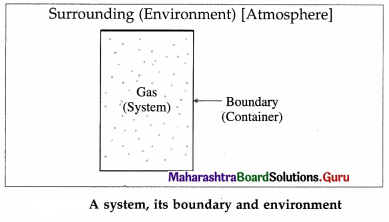
exchange energy with its surroundings. Everything outside the system is called its surroundings or environment. For example, a gas enclosed in a container is a system, the container is the boundary and the atmosphere is the environment.

Question 12.
Explain classification of thermodynamic systems.
Answer:
Depending upon the exchange of energy and matter with the environment, thermodynamic systems are classified as open, closed or isolated.

A system that can freely exchange energy and matter with its environment is called an open system. Example : water boiling in an open vessel.

A system that can freely exchange energy but not matter with its environment is called a closed system. Example : water boiling in a closed vessel.

A system that cannot exchange energy as well as matter with its environment is called an isolated system. In practice it is impossible to realize an isolated system as every object at a temperature above 0 K emits energy in the form of radiation, and no object can ever attain 0 K.

For many practical purposes, a thermos flask containing a liquid can be considered an isolated system.

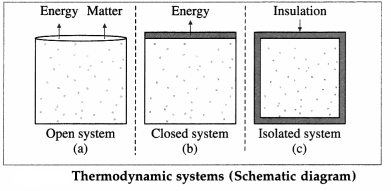
These three types are illustrated in above figure.

Question 13.
What is a thermodynamic process? Give an exmple.
Answer:
A process in which the thermodynamic state of a system is changed is called a thermodynamic process.
Example : Suppose a container is partially filled with water and then closed with a lid. If the container is heated, the temperature of the water starts rising and after some time the water starts boiling. The steam produced exerts pressure on the walls of the container, Here, there is a change in the pressure, volume and temperature of the water, i.e. there is a change in the thermodynamic state of the system.

Question 14.
Explain the relation between heat and internal energy.
Answer:
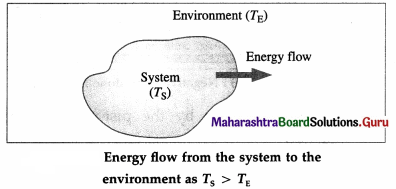
Suppose a system consists of a glass filled with water at temperature T_S. Let T_E be the temperature of the environment (surroundings) such as the surrounding air in the room. There is a continuous exchange of energy between the system and the surroundings.

If T_S > T_E, the net effect of energy exchange is the net transfer of internal energy from the system to the environment till thermal equilibrium is reached, i.e., T_S and T_E became equal. This internal energy in transit is called heat (Q). The change in the temperature of the environment is usually negligible compared with the change in the temperature of the system.

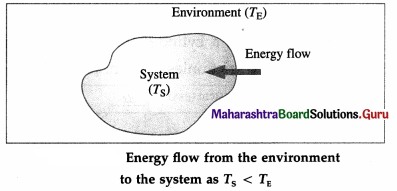
For T_S < T_E, there is energy exchange between the
system and the environment, but no net transfer of
energy.

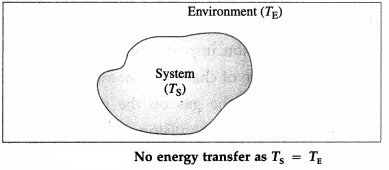
For T_S = T_E, there is energy exchange between the system and the environment, but no net transfer of energy.

Thus, the net transfer of energy takes place only when there is temperature difference.

Question 15.
Explain how the internal energy of a system can be changed.
Answer:
Consider a system (S) consisting of some quantity of gas enclosed in a cylinder fitted with a movable, massless, and frictionless piston.

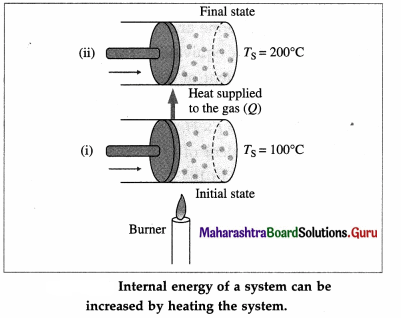
Suppose the gas is heated using a burner (source of heat, environment). Let T_S = temperature of the system (gas) and T_E = temperature of the environment.

Here, T_E > T_S. Hence, there will be a net flow of energy (heat) from the environment to the system causing the increase in the internal energy of the system.

The internal energy of the gas (system) can also be increased by quickly pushing the piston inward so that the gas is compressed.

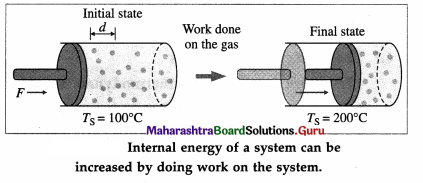
The work done on the gas raises the temperature of the gas. Thus, there is increase in the internal energy of the gas. If the gas pushes the piston outward, the work is done by the gas on the environment and the gas cools as its internal energy becomes less.

Question 16.
On the basis of the kinetic theory of gases, explain
(i) positive work done by a system
(ii) negative work done by a system.
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.

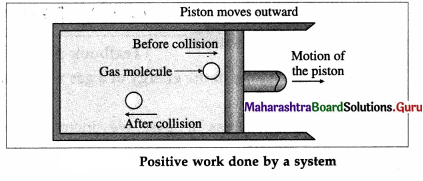
During expansion of the gas, molecules colliding with the piston lose momentum to it. This exerts force and hence pressure on the piston, moving it outward through a finite distance. Here, the gas does a positive work on the piston. There is increase in the volume of the gas. The work done by the piston on the gas is negative.

During compression of the gas, molecules colliding with the piston gain momentum from it. The piston moving inward through a finite distance exerts force on the gas. Here, the gas does a negative work on the piston. There is decrease in the volume of the gas.

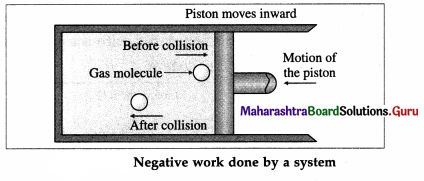
The work done by the piston on the gas is positive.

Question 17.
Obtain an expression for the work done by a gas.
OR
Show that the work done by a gas is given by
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.

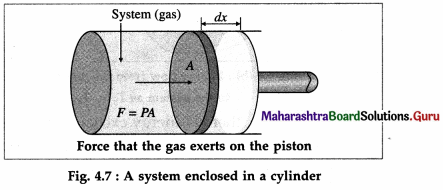
During expansion of the gas, molecules colliding with the piston impart momentum to the piston. The time rate of change of momentum is the force, F exerted by the gas on the piston. If dx is the displacement of the piston, the work done by the gas, dW = F dx. If A is the area of cross section of the piston, the pressure exerted by the gas, P = \(\frac{F}{A}\).

Hence, the work done, dW = PAdx = PdV where dV = Adx is the increase in the volume of the gas. Here, dx is the infinitesimal displacement of the piston and dV is the infinitesimal increase in the volume of the gas.

If V_i is the initial volume of the gas, and V_f is the final volume, the total work done by the gas in moving the piston is given by W = \(\int_{V_{i}}^{V_{\mathrm{f}}} P d V\).

Question 18.
State the first law of thermodynamics. Express it in mathematical form.
Answer:
First law of thermodynamics : The change in the internal energy of a system (∆U) is the difference between the heat supplied to the system (Q) and the work done by the system on its surroundings (W).
Mathematically, ∆ U = Q – W, which is the same as Q = ∆ U + W.

Notes :

1. if Q is positive, it means heat is added to the system. If Q is negative, it means heat is given out by the system or removed from the system,
2. If ∆U is positive, it means there is increase in the internal energy of the system. If ∆ U is negative, it means there is decrease in the internal energy of the system,
3. If W is positive, it means it is the work done by the system on its surroundings. Negative W means work is done on the system by the surroundings,
4. The first law of thermodynamics is largely due to Joule. It is essentially the law of conservation of energy applied to the systems that are not isolated, i.e., the systems that can exchange energy with the surroundings. Thermodynamics was developed in 1850 by Rudolf Clausius (1822-88) German theoretical physicist, His ideas were developed in 1851 by William Thomson [Lord Kelvin] (1824-1907), British physicist and electrical engineer,
5. Q = ∆ U + W. Here, all quantities are expressed in the same units, e.g., cal or joule. If Q and A U are expressed in heat unit (cal, kcal) and W is expressed in mechanical unit (erg, joule) then the above equation takes the form Q = ∆ U + \(\frac{W}{J}\), where J is the mechanical equivalent of heat.]

Question 19.
What is the property of a system or a system variable ?
Answer:
The property of a system or a system variable is any measurable or observable characteristic or property of the system when the system remains in equilibrium.

Question 20.
Name the macroscopic variables of a system.
Answer:
Pressure, volume, temperature, density, mass, specific volume, amount of substance (expressed in mole) are macroscopic variables of a system.
Notes : The quantities specified above are not totally independent, e.g.,

1. density = mass/volume
2. specific volume (volume per unit mass) = 1/density.

Question 21.
What is an intensive variable ? Give examples.
Answer:
A variable that does not depend on the size of the system is called an intensive variable.
Examples : pressure, temperature, density.

Question 22.
What is an extensive variable ? Give examples.
Answer:
A variable that depends on the size of the system is called an extensive variable.
Examples : internal energy, mass.

Question 23.
What is mechanical equilibrium ?
Answer:
A system is said to be in mechanical equilibrium when there are no unbalanced forces within the system and between the system and its surroundings.
OR
A system is said to be in mechanical equilibrium when the pressure in the system is the same throughout and does not change with time.
[Note : The constituents of a system, atoms, molecules, ions, etc, are never at rest. Within a system, even in the condition of equilibrium, statistical fluctuations do occur, but the time of observation is usually very large so that these fluctuations can be ignored.]

Question 24.
What is chemical equilibrium ?
Answer:
A system is said to be in chemical equilibrium when there are no chemical reactions going on within the system.
OR
A system is said to be in chemical equilibrium when its chemical composition is the same throughout the system and does not change with time.
[Note : In this case, in the absence of concentration gradient, there is no diffusion, i.e., there is no transport of matter from one part of the system to the other.]

Question 25.
What is thermal equilibrium ?
Answer:
A system is said to be in thermal equilibrium when its temperature is uniform throughout the system and does not change with time.

Question 26.
Give two examples of thermodynamic systems not in equilibrium.
Answer:

1. When an inflated balloon is punctured, the air inside it suddenly expands and escapes into the atmosphere. During the rapid expansion, there is no uniformity of pressure, temperature and density.
2. When water is heated, there is no uniformity of pressure, temperature and density. If the vessel is open, some water molecules escape to the atmosphere.

Question 27.
What is the equation of state ? Explain.
Answer:
The mathematical relation between the state variables (pressure, volume, temperature, amount of the substance) is called the equation of state.

In the usual notation, the equation of state for an ideal gas is PV = nRT.

For a fixed mass of gas, the number of moles, n, is constant. R is the universal gas constant. Thus, out of pressure (P), volume (V) and thermodynamic temperature (T), only two (any two) are independent.

Question 28.
Draw P-V diagram for positive work at constant pressure.

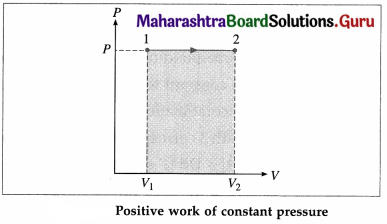
Answer:
In this case, during the expansion, the work done by the gas, W = \(\int_{V_{1}}^{V_{2}} P d V\) = P(V₂ – V₁) is positive as V₂ > V₁.

Question 29.
What is a thermodynamic process ? Explain.
Answer:
A procedure by which the initial state of a system changes to its final state is called a thermodynamic process. During the process/ there may be

1. addition of heat to the system
2. removal of heat from the system
3. change in the temperature of the system
4. change in the volume of the system
5. change in the pressure of the system.

Question 30.
What is a quasistatic process ?
Answer:
A quasistatic process is an idealised process which occurs infinitely slowly such that at all times the system is infinitesimally close to a state of thermodynamic equilibrium. Although the conditions for such a process can never be rigorously satisfied in practice, any real process which does not involve large accelerations or large temperature gradients is a reasonable approximation to a quasistatic process.

Question 31.
Draw a diagram to illustrate that the work done by a system depends on the process even when the initial and final states are the same.

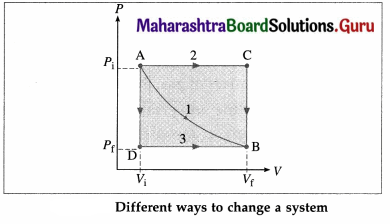
Answer:
In the above diagram, the initial state of a gas is characterized by (P_i, V_i) [corresponding to point A] and the final state of the gas is characterized by (P_f, V_f) [corresponding to point B]. Path 1 corresponds to constant temperature. Path 2 corresponds to the combination AC [P constant] + CB [V constant]. Path 3 corresponds to the combination AD [V constant] + DB [P constant]. The work done by the gas (W) is the area under the curve and is different in each case.

Question 32.
What is a reversible process? What is an irreversible process? Give four examples of an irreversible process. Explain in detail.
Answer:
A reversible process is one which is performed in such a way that, at the conclusion of the process, both the system and its local surroundings are restored to their initial states, without producing any change in the rest of the universe.

A process may take place reversibly if it is quasistatic and there are no dissipative effects. Such a process cannot be realized in practice.

A process which does not fulfill the rigorous requirements of reversibility is said to be an irreversible process. Thus, in this case, the system and the local surroundings cannot be restored to their initial states without affecting the rest of the universe. All natural processes are irreversible.
Examples of irreversible process :

1. When two bodies at different temperatures are brought in thermal contact, they attain the same temperature after some time due to energy exchange. Later, they never attain their initial temperatures.
2. Free expansion of a gas.
3. A gas seeping through a porous plug.
4. Collapse of a soap film after it is pricked.
5. All chemical reactions.
6. Diffusion of two dissimilar inert gases.
7. Solution of a solid in water.
8. Osmosis.

[Note : A free expansion is an adiabatic process, i.e., a process in which no heat is added to the system or removed from the system. Consider a gas confined by a valve to one half of a double chamber with adiabatic walls while the other half is evacuated.

When the gas is in thermal equilibrium, the gas is allowed to expand to fill the entire chamber by opening the valve.
No interaction takes place and hence there are no local surroundings. While rushing into a vacuum, the gas does not meet any pressure and hence no work is done by the gas. The gas only changes state isothermally from a volume V_i to a larger volume V_f.]

To restore the gas to its initial state, it would have to be compressed isothermally to the volume V_i; an amount of work W would have to done on the gas by some mechanical device and an equal amount of heat would have to flow out of the gas into a reservoir. If the mechanical device and the reservoir are to be left unchanged, the heat would have to be extracted from the reservoir and converted completely into work. Since this last step is impossible, the process of free expansion is irreversible.

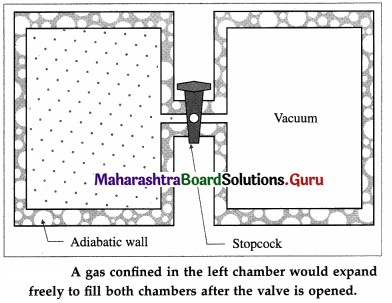
It can be shown that the diffusion of two dissimilar inert gases is equivalent to two independent free expansions. It follows that diffusion is irreversible.]

Question 33.
What are the causes of irreversibility?
Answer:

1. Some processes such as a free expansion of a gas or an explosive chemical reaction or burning of a fuel take the system to non-equilibrium states.
2. Most processes involve dissipative forces such as friction and viscosity (internal friction in fluids). These forces can be minimized, but cannot be eliminated.

Question 34.
What is an isothermal process? Obtain an expression for the work done by a gas in an isothermal process.
Answer:
A process in which changes in pressure and volume of a system take place at a constant temperature is called an isothermal process.

Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. Let P_i, V_i and T be the initial pressure, volume and absolute temperature respectively of the gas. Consider an isothermal expansion (or compression) of the gas in which P_f, V_f and T are respectively the final pressure, volume and absolute

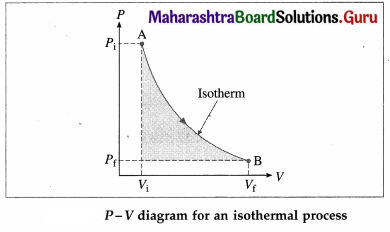
temperature of the gas. Assuming the gas to behave as an ideal gas, we have, its equation of state :
PV = nRT = constant as T = constant, R is the universal gas constant. The work done by the gas,

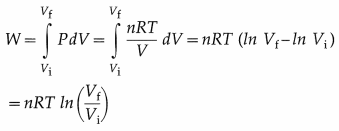
Notes :

1. The above expression for W can be written in various forms such as W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_iV_i ln \(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_fV_f\(\left(\frac{V_{f}}{V_{\mathrm{i}}}\right)\), etc.
2. W is positive if V_f > V_i (expansion). W is negative if V_f < V_i (contraction).
3. At constant temperature, change in internal energy, ∆ U = 0.
   ∴ Q = ∆ U + W = W.
4. Isothermal process shown in P- V diagram is also called an isotherm.
5. Melting of ice is an isothermal process.

Question 35.
What is an isobaric process? Obtain the expressions for the work done, change in internal energy and heat supplied in an isobaric process in the case of a gas.
Answer:
A process in which pressure remains constant is called an isobaric process. Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. We assume that the gas behaves as an ideal gas so that we can use the equation of state PV = nRT.

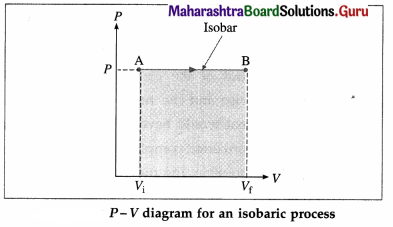
Consider an isobaric expansion (or compression) of the gas in which the volume of the gas changes from V_i to V_f and the temperature of the gas changes from T_i to T_f when the pressure (P) of the gas is kept constant. The work done by the gas,

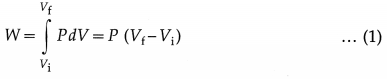
Now, PV_i = nRT_i and PV_f = nRT_f
∴ PV_f – PV_i = nRT_f – nRT_i
∴ P(V_f – V_i) = nR(T_f – T_i)
∴ from Eq. (1), W = nR(T_f – T_i) … (2)
The change in the internal energy of the gas,
∆ U = nC_v(T_f – T_i) …(3)
where C_v is the molar specific heat of the gas at constant volume.
From Eqs. (2) and (3), we have, the heat supplied to the gas,
Q = ∆ U + W = nC_v(T_f – T_i) + nR(T_f – T_i)
= n(C_v + R)(T_f – T_i)
∴ Q = _nC_p(T_f – T_i) …(4)
Where C_p ( = C_v + R) is the molar specific heat of the gas at constant pressure.
[Note : P-V curve for an isobaric process is called an isobar.

Question 36.
What is an isochoric process ? Write the expressions for the work done, change in internal energy and heat supplied in this case. Also draw the corresponding P-V diagram.
Answer:
A process that takes place at constant volume is called an isochoric process (or isometric process).

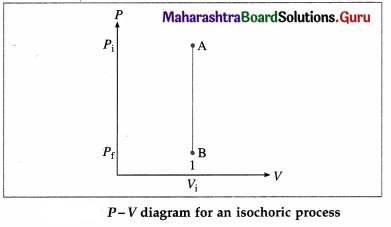
As there is no change in volume in this case, the work done (W) by the system on its environment is zero. The change in the internal energy.
∆ U = _nC_v (T_f – T_i) and heat supplied,
Q = ∆ U = _nC_v(T_f – T_i)

Question 37.
What is an adiabatic process ? Obtain expressions for the work done by a system (an ideal gas) in an adiabatic process. Also draw the corresponding P-V diagram.
Answer:
A process during which there is no transfer of heat (energy) from the system to the surroundings or from the surroundings to the system is called an adiabatic process.

It can be shown that if an ideal gas is subjected to an adiabatic process, then,
PV^γ = constant = C, where γ, is \(\frac{C_{P}}{C_{V}}\). γ is called the adiabatic ratio. C_P is the molar specific heat of the gas at constant pressure and C_V is the molar specific heat at constant volume.
Let P_i = initial pressure, P_i final pressure V_f = initial volume and V_f = final volume of the gas taken through an adiabatic process.

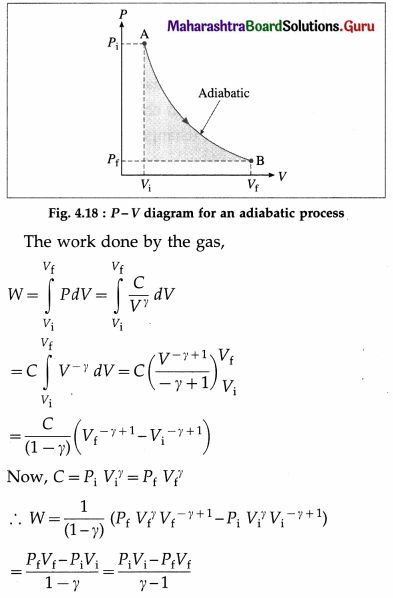
Now, P_iV_i = nRT_i and P_fV_f = nRT_f, where n is the number of moles of the gas, T_i is the initial temperature of the gas, T_f is the final temperature of the gas and R is the universal gas constant.

[Note: We have Q = ∆ U + W = 0 in an adiabatic process.
∴ W= -∆ U = -nC_v(T_f – T_i)_nC_v(T_i – T_f)]

Question 38.
What is a cyclic process? Explain with a diagram.
Answer:
A thermodynamic process in which the system returns to its initial state is called a cyclic process. This is illustrated in below figure. Path 1 shows how the state of the system (ideal gas) is changed from (P_i, V_i) [point A] to (P_f, V_f) [point B], Path 2 shows the return of the system from point B to point A. As the system returns to its initial state, the total change in its internal energy is zero. Hence, according to the first law of thermodynamics, heat supplied,

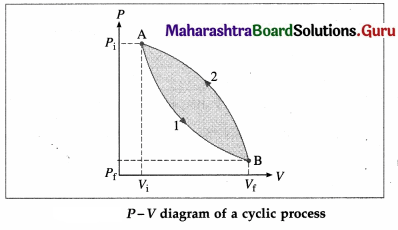
Q = ∆ U + W = 0 + W = W. The area enclosed by the cycle in P-V plane gives the work done (W) by the system.

Question 39.
Explain the term free expansion of a gas.
Answer:
When a balloon is ruptured suddenly, or a tyre is punctured suddenly, the air inside the balloon/ tyre rushes out rapidly to the atmosphere. This process (expansion of air inside the balloon/tyre) is so quick that there is no time for transfer of heat from the system to the surroundings or from the surroundings to the system. Such an adiabatic expansion is called free expansion. It is characterized by Q = W = 0, implying ∆ U = 0. Free expansion is an uncontrolled change and the system is not in thermodynamic equilibrium. Free expansion cannot be illustrated with a P-V diagram as only the initial state and final state are known.

Question 40.
Solve the following :

Question 1.
A gas enclosed in a cylinder fitted with a movable, massless and frictionless piston is expanded so that its volume increases from 5 L to 6 L at a constant pressure of 1.013 × 10⁵ Pa. Find the work done by the gas in this process.
Solution :
Data : P = 1.013 × 10⁵ Pa, V_i = 5L = 5 × 10^-3 m³,
v_f = 6L = 6 × 10^-3 m³
The work done by the gas, in this process,
W = P(V_f – V_i)
= (1.013 × 10⁵)(6 × 10^-3 – 5 × 10^-3)J
= 1.013 × 10²J

Question 2.
The initial pressure and volume of a gas enclosed in a cylinder are respectively 1 × 10⁵ N/m² and 5 × 10^-3 m³. If the work done in compressing the gas at constant pressure is 100 J. Find the final volume of the gas.
Solution :
Data : P = 1 × 10⁵ N/m², V_i = 5 × 10^-3 m³,
W= -100 J
W = P(V_f – V_i) ∴ V_f – V_i = \(\frac{W}{P}\)
∴ V_f = V_i + \(\frac{W}{P}\) = 5 × 10^-3 + \(\frac{(-100)}{\left(1 \times 10^{5}\right)}\)
= 5 × 10^-3 -1 × 10^-3 = 4 × 10^-3 m³
This is the final volume of the gas.

Question 3.
If the work done by a system on its surroundings is 100 J and the increase in the internal energy of the system is 100 cal, what must be the heat supplied to the system? (Given : J = 4.186J/cal)
Solution :
Data : W = 100 J, ∆ U = 100 cal, J = 4.186 J / cal
The heat supplied to the system,
Q = ∆ U + W = (100 cal) (4.186 J/cal) + 100 J
= 418.6J + 100J = 518.6 J

Question 4.
Ten litres of water are boiled at 100°C, at a pressure of 1.013 × 10⁵ Pa, and converted into steam. The specific latent heat of vaporization of water is 539 cal/g. Find
(a) the heat supplied to the system
(b) the work done by the system
(c) the change in the internal energy of the system. 1 cm³ of water on conversion into steam, occupies 1671 cm³ (J = 4.186 J/cal)
Solution :
Data : P = 1.013 × 10⁵ Pa, V (water) = 10 L = 10 × 10^-3 m³, V(steam) = 1671 × 10 × 10^-3 m³, L = 539 cal/g = 539 × 10³ \(\frac{\mathrm{cal}}{\mathrm{kg}}\) = 539 × 10³ × 4.186\(\frac{\mathrm{J}}{\mathrm{kg}}\) as J = 4.186 J/cal, mass of the water (M) = volume × density = 10 × 10^-3 m³ × 10³ kg/m³ = 10 kg

(a) Q = ML = (10) (5.39 × 4.186 × 10⁵) J
= 2.256 × 10⁷J
This is the heat supplied to the system

(b) W = P∆V = (1.013 × 10⁵) (1671 – 1) × 10^-2J
= (1.013) (1670) × 10³ J = 1.692 × 10⁶ J
This is the work done by the system.

(c) ∆ U = Q – W = 22.56 × 10⁶ – 1.692 × 10⁶
= 2.0868 × 107J
This is the change (increase) in the internal energy of the system.

Question 5.
Find the heat needed to melt 100 grams of ice at 0°C, at a pressure of 1.013 × 10⁵ N/m². What is the work done in this process ? What is the change in the internal energy of the system ?
Given : Specific latent heat of fusion of ice = 79.71 cal/g, density of ice = 0.92 g/cm³, density of water = 1 g/cm³,1 cal = 4.186 J.
Solution :

1. The heat needed to melt the ice, Q = ML = (0.1) (3.337 × 10⁵) J = 3.337 × 10⁴ J
2. The work done, W = P(V_Water – V_ice)
   = (1.013 × 10⁵) (100 – 108.7) × 10^-6J = -0.8813J
3. The change in the internal energy,
   ∆ U = Q – W = 3.337 × 10⁴ J + 0.8813 J
   = 3370.8813 J

Question 6.
Find the work done by the gas when it is taken through the cycle shown in the following figure. (1 L = 10^-3 m³)
Solution :

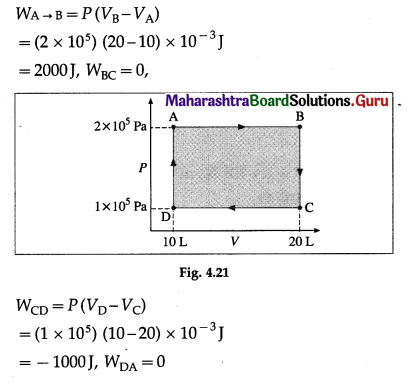
∴ W_ABCDA = W_AB + W_BC + W_CD + W_DA
= 2000J + 0 – 1000J + 0 = 1000J

Question 7.
A gas with adiabatic constant γ = 1.4, expands adiabatically so that the final pressure becomes half the initial pressure. If the initial volume of the gas 1 × 10^-2 m³, find the final volume.
Solution:

This is the final volume of the gas.

Question 8.
In an adiabatic compression of a gas with γ = 1.4, the initial temperature of the gas is 300 K and the final temperature is 360 K. If the initial volume of the gas is 2 × 10^-3 m³, find the final volume.
Solution:
Data: γ = 1.4, T_i = 300 K, T_f = 360 K
∴ T_f/T_i = 1.2, V_i = 2 × 10^-3 m³

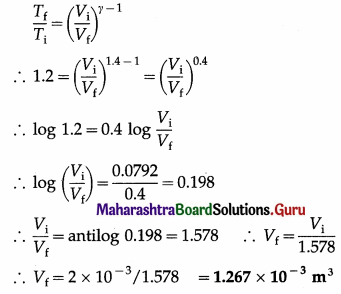
This is the final volume of the gas.

Question 9.
In an adiabatic compression of a gas with γ = 1.4, the final pressure is double the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature.
Solution:
Data: γ = 1.4, P_f = 2P_i, T_i = 300 K

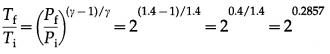
∴ log \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = 0.2857 log 2 = 0.2857 (0.3010) = 0.086
∴ \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = antilog 0.086 = 1.219
∴ T_f = 1219T_i
= (1.219) (300) = 365.7 K
This is the final temperature of the gas.

Question 10.
In an adiabatic compression of a gas the final volume of the gas is 80% of the initial volume. If the initial temperature of the gas is 27 °C, find the final temperature of the gas. Take γ = 5/3.
Solution :
Data: V_f = 0.8 V_i ∴ \(\frac{V_{\mathrm{i}}}{V_{\mathrm{f}}}\) = \(\frac{10}{8}\) = 1.25,
∴ T_i = 27 °C = (273 + 27) K = 300 K, γ = \(\frac{5}{3}\)

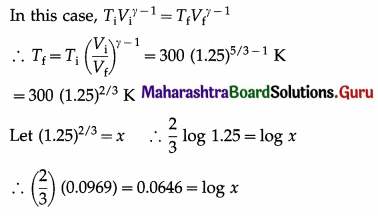
∴ x = antilog 0.0646 = 1.161
∴ T_f = (300) (1.161) = 348.3 K
= (348.3 – 273)°C = 75.3 °C
This is the final temperature of the gas.

Question 11.
In an adiabatic expansion of a gas, the final volume of the gas is double the initial volume. If the initial pressure of the gas is 105 Pa, find the final pressure of the gas. (γ = 5/3)
Solution :

Let 2^5/3 = x ∴ \(\frac{5}{3}\)log 2 = log x
∴ log x = \(\left(\frac{5}{3}\right)\) (0.3010) = 0.5017
∴ x = antilog 0.5017 = 3.175
∴ P_f = \(\frac{10^{5}}{3.175}\) = 3.15 × 10⁴ Pa
This is the final pressure of the gas.

Question 12.
In an adiabatic process, the final pressure of the gas is half the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature of the gas. (Take γ = \(\frac{5}{3}\))
Solution :

This is the final temperature of the gas.

Question 13.
In an adiabatic process, the pressure of the gas drops from 1 × 10⁵ N/m² to 5 × 10⁴ N/m² and the temperature drops from 27 °C to – 46 °C. Find the adiabatic ratio for the gas.
Solution :


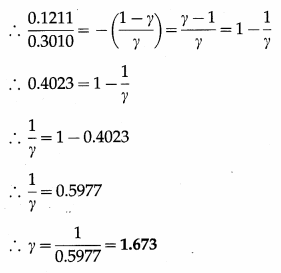
This is the adiabatic ratio (γ) for the gas.
[Note : This value (1.673) is slightly more than 5/3 (the value for a monatomic gas) due to error in measurement of pressure and temperature.]

Question 14.
Two moles of a gas expand isothermally at 300 K. If the initial volume of the gas is 23 L and the final volume is 46 L, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data ; n = 2, T = 300 K, V, = 23 L = 23 × 10^-3 m³, V_f = 46 L = 46 × 10^-3 m³, R = 8.314 J/mol.K
The work done by the gas on its surroundings,
W = nRT ln \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\) = 2.303 nRT log₁₀ \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\)
= (2.303) (2) (8.314) (300) log₁₀ \(\left(\frac{46 \times 10^{-3}}{23 \times 10^{-3}}\right)\)
= (4.606) (8.314) (300) log\(\begin{array}{r}
2 \\
10
\end{array}\)
= (4.606) (8.314) (300) (0.3010)
= 3458J

Question 15.
Four moles of a gas expand isothermally at 300 K. If the final pressure of the gas is 80% of the initial pressure, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data : n = 4, T = 300 K, P_f = 0.8 P_i
∴ \(\frac{P_{i}}{P_{f}}\) = \(\frac{10}{8}\), R = 8.314 j/mol.K
The work done by the gas on its surroundings,
W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\)
= (4) (8.314) (300) 2.303 log₁₀ \(\left(\frac{10}{8}\right)\)
= 2.3 × 10⁴ log₁₀ (1.25) = 2.3 × 10⁴ × 0.0969
= 2.229 × 10³J

Question 16.
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure so that the rise in temperature is 10 K. Find the increase in the internal energy of the gas.
Solution :
Data : C_v = 12.47 J/mol.k, n = 2, T_f – T_i = 10 K
The increase in the internal energy of the gas,
∆ U = _nC_v (T_f – T_i)
= (2) (12.47) (10) J
= 249.4 J

Question 17.
The molar specific heat of Ar at constant volume is 12.47 J/mol.K. Two moles of Ar are heated at constant pressure so that the rise in temperature is 20 K. Find the work done by the gas on its surroundings and the heat supplied to the gas. Take R = 8.314 J/mol.K.
Solution :
Data : C_v = 12.47 j/mol.K, n = 2,T_f – T_i = 20 K,
R = 8.314 J/mol.K

1. W = nR (T_f – T_i) = (2) (8.314) (20) J = 332.6 J
   This is the work done by the gas on its surroundings.
2. Q = _nC_v(T_f – T_i) + W = (2) (12.47) (20) + 332.6
   = 498.8 + 332.6 = 831.4 J
   This is the heat supplied to the gas.

Question 18.
The molar specific heat of a gas at constant pressure is 29.11 J/mol.k. Two moles of the gas are heated at constant pressure so that the rise in temperature is 40 K. Find the heat supplied to the gas.
Solution :
Data : C_P = 29.11 J/mol.K, n = 2, T_f – T_i = 40 K.
The heat supplied to the gas,
Q = _nC_P (T_f – T_i) = (2) (29.11) (40) J
= 2329 J

Question 19.
The molar specific heat of a gas at constant volume is 20.8 J/mol.k. Two moles of the gas are heated at constant volume so that the rise in temperature is 10 K. Find the heat supplied to the gas.
Solution :
Data : C_v = 20.8 J/mol.K, n = 2, T_f – T_i = 10 K.
The heat supplied to the gas,
Q = _nC_v (T_f – T_i) = (2) (20.8) (10) J
= 416J

Question 20.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 10⁵ Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 10⁴ Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Take γ = 5/3.
Solution :
Data : H = 2, P_i = 1.013 × 10⁵ Pa, P_f = 3.191 × 10⁴ Pa,
V_i = 22.4 L = 22.4 × 10^-3 m³,
V_f = 44.8 L = 44.8 × 10^-3 m³, γ = 5/3

Question 21.
In an adiabatic expansion of 2 moles of a gas, the temperature of the gas decreases from 37°C to 27°C. Find the work done by the gas on its surroundings. Take γ = 5/3 and R = 8.314 J/mol.K
Answer:
Data: n =2, T_i = (273 + 37) = 310 K,
T_f = (273 + 27)K = 300K, γ = 5/3,
R = 8.314 J/mol.K.
The work done by the gas on its surroundings,

Question 22.
A resistor of resistance 200 Ω carries a current of 2 A for 10 minutes. Assuming that almost all the heat produced in the resistor is transferred to water (mass = 5 kg, specific heat capacity = 1 kcal/kg), and the work done by the water against the external pressure during the expansion of water can be ignored, find the rise in the temperature of the water. (J = 4186 J/cal)
Solution :
Data : I = 2 A, R = 200 Ω, t = 10 min = 10 × 60 s = 600 s, M = 5 kg, S = (1 kcal/kg) (4186 J/kcal)
= 4186 J/kg
Q = ∆ U + W = MS ∆T + W \(\simeq\) MS ∆T ignoring W.
Also, Q = I²Rt ∴ I²RT = MS∆T
∴ The rise in the temperature of water = ∆T = \(\frac{I^{2} R t}{M S}\)
= \(\frac{(2)^{2}(200)(600)}{(5)(4186)}\)°C = 22.93°C

Question 23.
The initial pressure, volume and temperature of a gas are respectively 1 × 10⁵ Pa, 2 × 10^-2 m³ and 400 K. The temperature of the gas is reduced from 400 K to 300 K at constant volume. Then the gas is compressed at constant temperature so that its volume becomes 1.5 × 10^-2 m³.
Solution:
Data : P_A = 1 × 10⁵ Pa, V_A = 2 × 10^-2 m³, T_A = 400 K, V_B = v_A = 2 × 10^-2 m³, T_B = 300 K, T_C = T_B = 300 K, V_C = 1.5 x 10× 10^-2 m³, Also, P_C = P_A = 1 × 10⁵ Pa as the gas returns to its initial state.

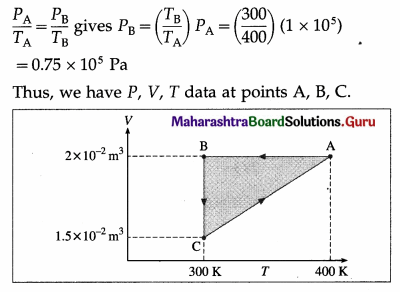
Question 24.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat of the gas at
(i) constant volume
(ii) constant pressure.
(R = 8.314 J/mol. K)
Solution :
Data : r = 5/3, R = 8.314 J/mol.K

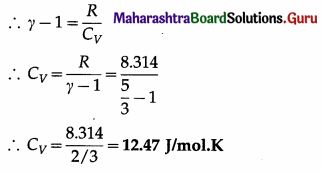
This is the required quantity.
(ii) C_P = _γC_V = \(\left(\frac{5}{3}\right)\)(12.47) = 20.78 J/mol.

Question 41.
What is a heat engine ?
Answer:
A heat engine is a device in which a system is taken through cyclic processes that result in converting part of heat supplied by a hot reservoir into work (mechanical energy) and releasing the remaining part to a cold reservoir. At the end of every cycle involving thermodynamic changes, the system is returned to the initial state.
[Note : Automobile engine is a heat engine.]

Question 42.
What does a heat engine consist of ?
OR
What are the elements (parts) of a typical heat engine?
Answer:
The following are the parts of a typical heat engine :

(1) Working substance : It can be

1. a mixture of fuel vapour and air in a gasoline (petrol) engine or diesel engine
2. steam in a steam engine. The working substance is called a system.

(2) Hot and cold reservoirs : The hot reservoir is a source of heat that supplies heat to the working substance at constant temperature T_H. The cold reservoir, also called the sink, takes up the heat released by the working substance at constant temperature T_C < T_H.

(3) Cylinder and piston : The working substance is enclosed in a cylinder fitted with (ideally) a movable, massless, and frictionless piston. The walls of the cylinder are nonconducting, but the base is conducting. The piston is nonconducting. The piston is connected to a crankshaft so that the work done by the working substance (mechanical energy) can be transferred to the environment.

Question 43.
What are the two basic types of heat engines?
Answer:
(i) External combustion engine in which the working substance is heated externally as in a steam engine.
(ii) Internal combustion engine in which the working substance is heated internally as in a petrol engine or diesel engine.
[Note : A steam engine was invented by Thomas New-comen (1663-1729), English engineer. The first practical steam engine was constructed in 1712. The modem steam engine was invented in 1790 by James Watt (1736-1819), British instrument maker and engineer. A hot-air type engine was developed by Robert Stirling (1790-1878), Scottish engineer and clergyman.

A four-stroke internal combustion engine was devised by Nikolaus August Otto (1832-1891), German engineer. A compression-ignition internal combustion engine was devised by Rudolph (Christian Karl) Diesel (1858 – 1913), German engineer.]

Question 44.
State the basic steps involved in the working of a heat engine.
Answer:

1. The working substance absorbs heat (Q_H) from a hot reservoir at constant temperature. T_H. It is an isothermal process Q_H is positive.
2. Part of the heat absorbed by the working substance is converted into work (W), i.e. mechanical energy. In this case, there is a change in the volume of the substance.
3. The remaining heat (|Q_C| = |Q_H| – W) is transferred to a cold reservoir at constant temperature T_C < T_H. Q_C is negative.

Question 45.
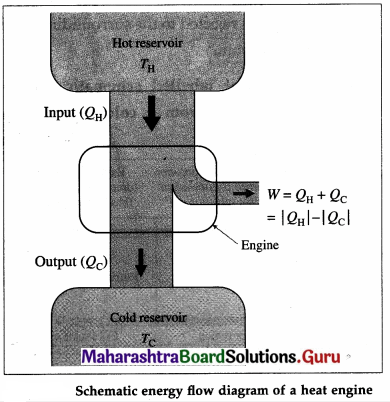
Draw a neat labelled energy flow diagram of a heat engine.
Answer:

Question 46.
Define thermal efficiency of a heat engine.
Answer:
The thermal efficiency, η of a heat engine is defined W as η = \(\frac{W}{Q_{H}}\), where W is the work done (output) by Q_H the working substance and Q_H is the amount of heat absorbed (input) by it.
[Note : η has no unit and dimensions or its dimensions are [M°L°T°].]

Question 47.
Draw a neat labelled P-V diagram for a typical heat engine.
Answer:

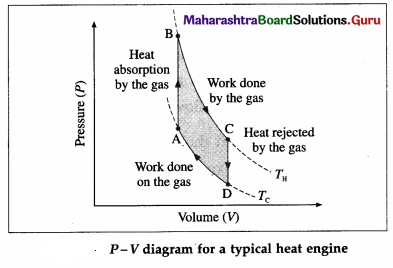
Here, T_H is the temperature at which the work is done by the gas and T_c is the temperature at which the work is done on the gas. The area of the loop ABCDA is the work output.

Question 48.
Solve the following :

Question 1.
Find the thermal efficiency of a heat engine if in one cycle the work output is 3000 J and the heat input is 10000 J.
Solution :
Data : W = 3000 J, Q_H = 10000 J
The thermal efficiency of the engine,
η = \(\frac{W}{Q_{\mathrm{H}}}\) = \(\frac{3000 \mathrm{~J}}{10000 \mathrm{~J}}\) = 0.3 = 30%

Question 2.
The thermal efficiency of a heat engine is 25%. If in one cycle the heat absorbed from the hot reservoir is 50000 J, what is the heat rejected to the cold reservoir in one cycle ?
Solution :
Data : η = 25% = 0.25, Q_H = 50000 J W
η = \(\frac{W}{Q_{\mathrm{H}}}\)
∴ W = _ηQ_H = (0.25)(50000)J = 12500J
Now, W = Q_H – |Q_C|
∴ |Q_C| = Q_H – W
= (50000 – 12500) J
= 37500J
This is the heat rejected to the cold reservoir in one cycle.
[Notes : Q_C = – 37500 J]

Question 49.
What is a refrigerator?
Answer:
A refrigerator is a device that uses work to transfer energy in the form of heat from a cold reservoir to a hot reservoir as it continuously repeats a thermodynamic cycle. Thus, it is a heat engine that runs in the backward direction.

Question 50.
With a neat labelled energy flow diagram, explain the working of a refrigerator.
Answer:
A refrigerator performs a cycle in a direction opposite to that of a heat engine, the net result being absorption of some energy as heat from a reservoir at low temperature, a net amount of work done on the system and the rejection of a larger amount

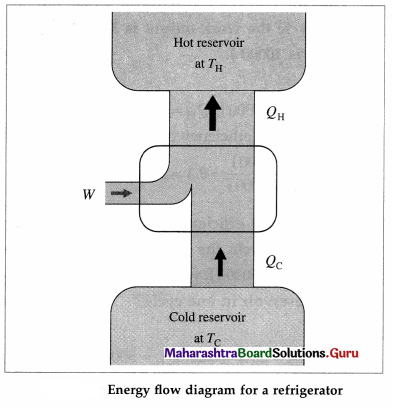
of energy as heat to a reservoir at a higher temperature. The working substance undergoing the refrigeration cycle is called a refrigerant. The refrigerant (such as ammonia or Freon) is a saturated liquid at a high pressure and at as low a temperature as can be obtained with air or water cooling.

The refrigeration cycle comprises the following processes :

1. Throttling process : The saturated liquid refrigerant passes from the condenser through a narrow opening from a region of constant high pressure to a region of constant lower pressure almost adiabatically. It is a property of saturated liquids (not gases) that a throttling process produces cooling and partial vaporization.
2. Isothermal, isobaric vaporization-with the heat of vaporization being supplied by the materials or the region to be cooled : Heat Q_c is absorbed by the refrigerant at the low temperature T_C, thereby cooling the materials of the cold reservoir.
3. Adiabatic compression of the refrigerant by an electrical compressor, thereby raising its temperature above T_H.
4. Isobaric cooling and condensation in the condenser at T_H : In the condenser, the vapour is cooled until it condenses and is completely liquefied, i. e., heat Q_H is rejected to the surroundings which is the hot reservoir.

Question 51.
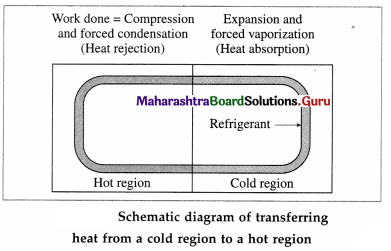
Draw a neat labelled schematic diagram of transferring heat from a cold region to a hot region.
Answer:

Question 52.
What is refrigeration?
Answer:
Refrigeration is artificial cooling of a space or substance of a system and/or maintaining its temperature below the ambient temperature.

Question 53.
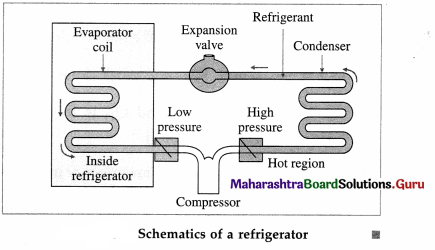
Draw a neat labelled diagram to illustrate schematics of a refrigerator.
Answer:

Question 54.
What are the steps through which a refrigerant goes in one complete cycle of refrigeration ?
Answer:
In one complete cycle of refrigeration, the refrigerant, a liquid such as fluorinated hydrocarbon, goes through the following steps :

1. The refrigerant in the closed tube passes through the nozzle and expands, into a low-pressure area. This adiabatic expansion results in reduction in pressure and temperature of the fluid and the fluid turns into a gas.
2. The cold gas is in thermal contact with the inner compartment of the fridge. Here it absorbs heat at constant pressure from the contents of the fridge.
3. The gas passes to a compressor where it does work in adiabatic compression. This raises its temperature and converts it back into a liquid.
4. The hot liquid passes through the coils on the outside of the refrigerator and releases heat to the air outside in an isobaric compression process.
   The compressor, driven by an external source of energy, does work on the refrigerant during each cycle.

Question 55.
Explain the energy flow in a refrigerator and define the coefficient of performance of a refrigerator.
Answer:
In a refrigerator, Q_C is the heat absorbed by the working substance (refrigerant) at a lower temperature T_C, W is the work done on the working substance, and Q_H is the heat rejected at a higher temperature T_H. The absorption of heat is from the contents of the refrigerator and rejection of heat is to the atmosphere. Here, Q_C is positive and W and Q_H are negative. In one cycle, the total change in the internal energy of the working substance is zero.
∴ Q_H + Q_C = W ∴ Q_H = W – Q_C
∴ -Q_H = Q_C – W
Now, Q_H < 0, W < 0 and Q_C > 0
∴ |Q_H| = |Q_C| + |W|
The coefficient of performance (CoP), K, or quality factor, or Q value of a refrigerator is defined as

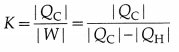
[Note: K does not have unit and dimensions or its dimensions are [M°L°T°.]

Question 56.
How does an air conditioner differ from a refrigerator? Define the coefficient of performance of an air conditioner and express it in terms of heat current.
Answer:
The working of an air conditioner is exactly similar to that of a refrigerator, but the volume of the chamber/room cooled by an air conditioner is far greater than that in a refrigerator. The evaporator coils of an air conditioner are inside the room, and the condenser outside the room. A fan inside the air conditioner circulates cool air in the room.

The coefficient of performance, K, of an air conditioner is defined as K = \(|\frac{Q_{\mathrm{C}}}{W}|\), where Q_C is the heat absorbed and W is the work done. The time rate of heat removed is the heat current, H = \(\frac{\left|Q_{C}\right|}{t}\), where t is the time in which heat |Q_C|, is removed.

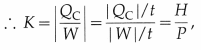
where H = |Q_C|/t is the heat current and P( = |W|/t) is the time rate of doing work, i.e., power.

Question 57.
What is a heat pump ?
Answer:
A heat pump is a device used to heat a building by cooling the air outside it. It works like a refrigerator but cooling outside space and heating inside space. In this case, the evaporator coils are outside the building to absorb heat from the air. The condenser coils are inside the building to release the heat to warm the building.

Question 58.
Solve the following :

Question 1.
In a refrigerator, in one cycle, the external work done on the working substance is 20% of the energy extracted from the cold reservoir. Find the coefficient of performance of the refrigerator.
Solution :
Data: |W| = 0.2|Q_C|
The coefficient of performance of the refrigerator,
K = |\(\frac{Q_{C}}{W}\)| = \(\frac{\left|Q_{C}\right|}{0.2\left|Q_{C}\right|}\)
= 5

Question 2.
The coefficient of performance of a room air conditioner is 3. If the rate of doing work is 2kW, find the heat current.
Solution :
Data : K = 3, P = 2000 W
K = \(\frac{H}{P}\)
∴ Heat current, H = KP = (3) (2000) W
= 6000 W = 6kW

Question 59.
State and explain the limitations of the first law of thermodynamics.
Answer:

1. The first law of thermodynamics is essentially the principle of conservation of energy as there is a close relation between work and energy. We find that there is a net transfer of energy (heat) from a body at higher temperature to a body at lower temperature. The net transfer of energy from a body at lower temperature to a body at higher temperature is not observed though consistent with the first law of thermodynamics.
2. If two containers, one containing nitrogen and the other containing oxygen, are connected to allow diffusion, they mix readily. They never get separated into the respective containers though there is no violation of the first law of thermodynamics.
3. It is not possible to design a heat engine with 100% efficiency, though there is no restriction imposed by the first law of thermodynamics.
4. At room temperature, ice absorbs heat from the surrounding air and melts. The process in the opposite direction is not observed, though consistent with energy conservation. These examples suggest that there is some other law operative in nature that determines the direction of a process

Question 60.
State the two forms of the second law of thermodynamics.
Answer:
Second law of thermodynamics :

1. It is impossible to extract an amount of heat Q_H from a hot reservoir and use it all to do work W. Some amount of heat Q_C must be exhausted (given out) to a cold reservoir. This prohibits the possibility of a perfect heat engine.
   This statement is called the first form or the engine law or the engine statement or the Kelvin-Planck statement of the second law of thermodynamics.
2. It is not possible for heat to flow from a colder body to a warmer body without any work having been done to accomplish this. This prohibits the possibility of a perfect refrigerator.
   This statement is called the second form or the Clausius statement of the second law of thermodynamics.

Notes :

1. Max Planck (Karl Ernst Ludwig) (1858-1947) German physicist, put forward quantum therory of radiation.
2. Rudolf Clausius (1822-88) German theoretical physicist, made significant contribution to thermodynamics.

Question 61.
Draw neat labelled diagrams to illustrate
(i) energy flow diagram for engine statement.
(ii) energy flow diagram for a perfect refrigerator.
Answer:

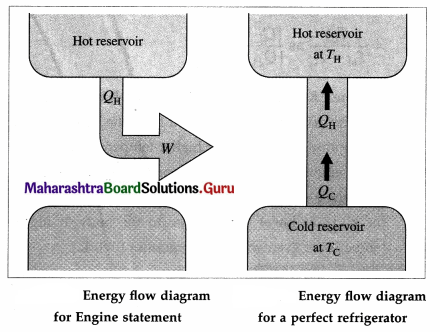
Question 62.
State the difference between a reversible process and an irreversible process.
OR
Distinguish between a reversible process and an irreversible process.
Answer:
A reversible process is a bidirectional process, i.e., its path in P-V plane is the same in either direction. In contrast, an irreversible process is a undirectional process, i.e., it can take place only in one direction.

A reversible process consists of a very large number of infinitesimally small steps so that the system is all the time in thermodynamic equilibrium with its environment. In contrast an irreversible process may occur so rapidly that it is never in thermodynamic equilibrium with its environment.

Question 63.
Draw a neat labelled diagram of a Carnot cycle and describe the processes occurring in a Carnot engine. Write the expression for the efficiency of a Carnot engine.
Answer:
Basically, two processes occur in a Carnot engine :

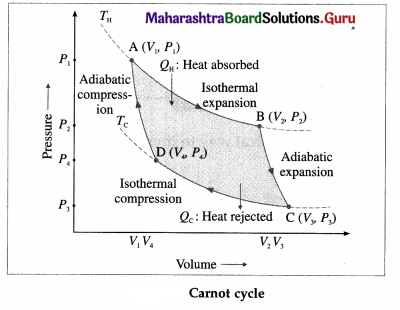
(1) Exchange of heat with the reservoirs : In isothermal expansion AB, the working substance takes in heat Q_H from a lot reservoir (source) at constant temperature T_H. In isothermal compression CD, the working substance gives out heat Q_C to a cold reservoir (sink) at constant temperature T_C.

(2) Doing work : In adiabatic expansion BC, the working substance does work on the environment and in adiabatic compression DA, work is done on the working substance by the environment.
All processes are reversible. It can be shown that \(\frac{\left|Q_{C}\right|}{Q_{\mathrm{H}}}\) = \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\). Hence, the efficiency of a Carnot engine,

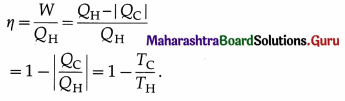
Question 64.
What is a Carnot refrigerator? State the expressions for the coefficient of performance of a Carnot refrigerator.
Answer:
A Carnot refrigerator is a Carnot engine operated in the reverse direction. Here, heat Q_C is absorbed from a cold reservoir at temperature T_C, work W is provided externally, and heat Q_H is given out to a hot reservoir at temperature T_H.
The coefficient of performance of a Carnot refrigerator is

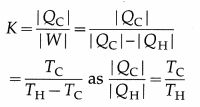
[Note: K is large if T_H-T_C is small. It means a large quantity of heat can be removed from the body at lower temperature to the body at higher temperature by doing small amount of work. K is small if T_H – T_C is large.
It means a small quantity of heat can be removed from the body at lower temperature to the body at higher temperature even with large amount of work.]

Question 65.
Solve the following :

Question 1.
A Carnot engine receives 6 × 10⁴ J from a reservoir at 600 K, does some work, and rejects some heat to a reservoir at 500 K. Find the
(i) the heat rejected by the engine
(ii) the work done by the engine
(iii) the efficiency of the engine.
Solution :
Data : Q_H = 6 × 10⁴J, T_H = 600K, T_C = 500K
(i) The heat rejected by the engine

Question 2.
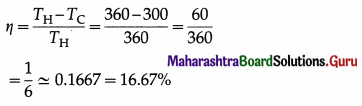
A Carnot engine operates between 27 °C and 87 °C. Find its efficiency.
Solution :
Data : T_C = 27 °C = (273 + 27) K = 300 K,
T_H = 87 °C = (273 + 87) = 360 K
The efficiency of the engine,

Question 3.
The coefficient of performance of a Carnot refrigerator is 4. If the temperature of the hot reservoir is 47 °C, find the temperature of the cold reservoir.
Solution :
Data : K = 4, T_H = 47°C = (273 + 47) K = 320
K = \(\frac{T_{\mathrm{c}}}{T_{\mathrm{H}}-T_{\mathrm{c}}}\) ∴ KT_H – KT_c = T_c
∴ KT_H = (1 + K)T_c
∴ T_c = \(\frac{K T_{\mathrm{H}}}{1+K}\) = \(\frac{(4)(320)}{1+4}\)K = (0.8)(320)K
= 256K = (256 – 273)°C = – 17°C
This is the temperature of the cold reservoir.

[Note : A hot-air type engine consisting of two cylinders, was developed by Robert Stirling (1790 -1878), a Scottish engineer and clergyman. He developed the concept in 1816 and obtained a patent for his design in 1827. Some engines were made in 1844. He also used helium and hydrogen in some engines developed thereafter. Stirling engines are used in submarines and spacecrafts.]

Question 66.
Draw a neat labelled diagram of a Sterling cycle and describe the various processes taking place in a Sterling engine.

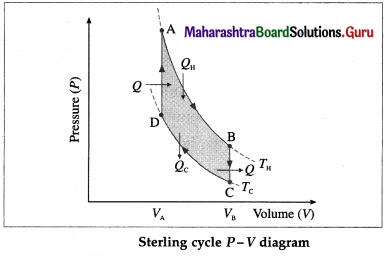
Answer:
The working substance can be air or helium or hydrogen or nitrogen. All processes are reversible.

1. AB is isothermal expansion, at temperature T_H, in which heat Q_H is absorbed from the source and useful work is done by the working substance.
2. BC is isochoric process in which some heat is released by the gas (working substance) to the refrigerator and the gas cools to temperature T_c < T_H.
3. CD is isothermal compression, at temperature T_c, in which heat Q_c is rejected to the coolant (sink).
4. DA is isochoric process in which heat is taken in by the gas and its temperature rises to T_H.

[Note : Stirling engine operated in reverse direction is used in the field of cryogenics to obtain extremely low – temperatures to liquefy air or other gases.]

Question 67.
Refer above figure and answer the following questions.
(i) What is the work done in process AB ?
(ii) What is the change in internal energy and heat released in process BC ?
Answer:
(i) In this case, the change in the internal energy is zero, as the temperature of the gas remains constant. Hence, the work done, W = heat absorbed, Q_H.

(ii) In this case, the change in the internal energy, ∆ U = _nC_V (T_C – T_H), where n = number of moles of the gas used in the Stirling engine and C_V = molar specific heat of the gas. As W = 0 at constant volume, heat released’= ∆ U.

Question 68.
Choose the correct option :

Question 1.
According to the first law of thermodynamics, in the usual notation,
(A) Q = ∆U + W
(B) Q = ∆U – W
(C) Q = W – ∆U
(D) Q= -(∆ U + W).
Answer:
(A) Q = ∆U + W

Question 2.
In an isothermal process, in the usual notation,
(A) PV = constant
(B) V/T = constant
(C) P/T = constant
(D) Q = 0.
Answer:
(A) PV = constant

Question 3.
In an isothermal process, in the usual notation,
(A) W = nRT (V_f/V_i)
(B) W = ∆ U
(C) W = Q
(D) W = 0.
Answer:
(C) W = Q

Question 4.
In an adiabatic process, in the usual notation,
(A) TV^γ = constant
(B) PT^γ = constant
(C) W = 0
(D) PV^γ = constant.
Answer:
(D) PV^γ = constant.

Question 5.
In an isobaric process, in the usual notation,
(A) W = P (V_f – V_i)
(B) W = Q
(C) W = – ∆U
(D) ∆T = 0.
Answer:
(A) W = P (V_f – V_i)

Question 6.
In an adiabatic process, in the usual notation,
(A) ∆ P = 0
(B) ∆ V = 0
(C) Q = 0
(D) ∆U = 0.
Answer:
(C) Q = 0

Question 7.
In an isothermal process, in the usual notation,
(A) W = P(V_f – V_i)
(B) W = 0
(C) W = V(P_f – P_i)
(D) W = nRT In(V_f/V_i).
Answer:
(D) W = nRT In(V_f/V_i).

Question 8.
In an isobaric process, in the usual notation,
(A) W = _nC_V (T_f – T_i)
(B) Q = _nC_P (T_f – T_i)
(C) ∆U = nR(T_f – T_i)
(D) W = 0.
Answer:
(B) Q = _nC_P (T_f – T_i)

Question 9.
In the usual notation, the isothermal work, W =
(A) P(V_f – V_i)
(B) nRT(P_i/ P_f)
(C) nRT ln(P_i/P_f)
(D) nRT(P_f/P_i).
Answer:
(C) nRT ln(P_i/P_f)

Question 10.
If Q and ∆u are expressed in cal and W is expressed in joule, then,
(A) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(B) Q = ∆U – (W/J)
(C) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(D) Q = ∆U + (W/J)
Answer:
(D) Q = ∆U + (W/J)

Question 11.
In an adiabatic process, in the usual notation, W =

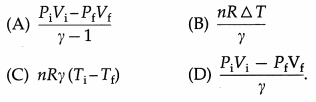
Answer:
(A) \(\frac{P_{\mathrm{i}} V_{\mathrm{i}}-P_{\mathrm{f}} V_{\mathrm{f}}}{\gamma-1}\)

Question 12.
In a cyclic process,
(A) ∆U = Q
(B) Q = 0
(C) W = 0
(D) W = Q
Answer:
(D) W = Q

Question 13.
The efficiency of a heat engine is given by η =
(A) Q_H/W
(B) W/Q_c
(C) W/Q_H
(D) Q_c/W.
Answer:
(C) W/Q_H

Question 14.
In a cyclic process, the area enclosed by the loop in the P – V plane corresponds to
(A) ∆U
(B) W
(C) Q – W
(D) W – Q.
Answer:
(B) W

Question 15.
The efficiency of a Carnot engine is given by K =
(A) T_c/(T_H – T_c)
(B) (T_H – T_c)/T_c
(C) T_H/(T_H – T_c)
(D) (T_H – T_c)/T_H
Answer:
(A) T_c/(T_H – T_c)

Question 16.
The coefficient of performance of a Carnot refrigerator is given by K =
(A) T_c(T_H-T_c)
(B) (T_H-T_c)/T_c
(C) T_H/(T_H-T_c)
(D) (T_H-T_c)/T_H.
Answer:
(A) T_c(T_H-T_c)

Question 17.
The efficiency of a Carnot engine working between T_H = 400 K and T_c = 300 K is
(A) 75%
(B) 25%
(C) 1/3
(D) 4/7.
Answer:
(B) 25%

Question 18.
If a Carnot engine receives 5000 J from a hot reservoir and rejects 4000 J to a cold reservoir, the efficiency of the engine is
(A) 25%
(B) 10%
(C) 1/9
(D) 20%.
Answer:
(D) 20%.

Question 19.
If a Carnot refrigerator works between 250 K and 300 K, its coefficient of performance =
(A) 6
(B) 1.2
(C) 5
(D) 10.
Answer:
(C) 5

Question 20.
The coefficient of performance of a Carnot refrigerator is 4. If T_c = 250 K, then T_H =
(A) 625 K
(B) 310 K
(C) 312.5 K
(D) 320 K.
Answer:
(C) 312.5 K

Question 21.
The coefficient of performance of a Carnot refrigerator working between T_H and T_c is K and the efficiency of a Carnot engine working between the same T_H and T_c is η. Then
(A) ηk = \(\frac{Q_{\mathrm{H}}}{Q_{\mathrm{c}}}\)
(B) η/k = Q_c/Q_H
(C) η/k = Q_H/Q_c
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)
Answer:
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)

Question 22.
The internal energy of one mole of organ is
(A) \(\frac{5}{2}\)RT
(B) RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 23.
The internal energy of one mole of oxygen is
(A) \(\frac{5}{2}\)RT
(B) 5RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 24.
The internal energy of one mole of nitrogen at 300 K is about 6225 J. Its internal energy at 400 K will be about
(A) 8300J
(B) 4670J
(C) 8500J
(D) 8000J.
Answer:
(A) 8300J

Question 25.
The adiabatic constant γ for argan is
(A) 4/3
(B) 7/5
(C) 6/5
(D) 5/3.
Answer:
(D) 5/3.