Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 5 Oscillations Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 5 Oscillations

Question 1.
Define :
(1) periodic motion
(2) oscillatory motion. Give two examples.
Answer:
(1) Periodic motion : A motion that repeats itself at definite intervals of time is said to be a periodic motion.
Examples : The motion of the hands of a clock, the motion of the Earth around the Sun.

(2) Oscillatory motion : A periodic motion in which a body moves back and forth over the same path, straight or curved, between alternate extremes is said to be an oscillatory motion.
Examples : The motion of a taut string when plucked, the vibrations of the atoms in a molecule, the oscillations of a simple pendulum.
[Note : The oscillatory motion of a particle is also called a harmonic motion when its position, velocity and acceleration can be expressed in terms of a periodic, sinusoidal functions-sine or cosine, of time.

Question 2.
With a neat diagram, describe a spring-and-block oscillator.
Answer:
Consider a spring-and-block oscillator as shown in below figure in which the block slides on a frictionless horizontal surface. The spring has a relaxed length when the block is at rest at the position O.

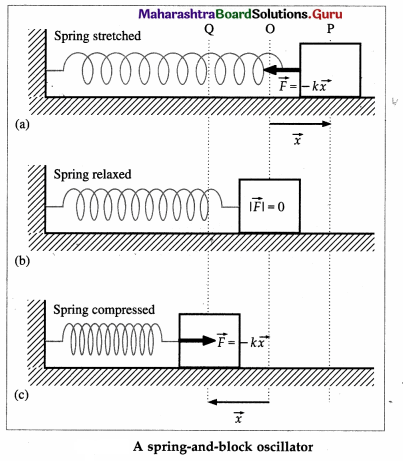
The block is then displaced to P by an amount x measured from the equilibrium position O. Upon releasing, the unbalanced force \(\vec{F}\) = –\(k \vec{x}\) toward left accelerates the block and its speed increases. As x gets smaller, |\(\vec{F}\)| and the acceleration decrease proportionately.

k is the elastic constant of the spring called the force constant or spring constant.

At the instant the block passes through the point O, | \(\vec{F}\) | = 0 because x = 0; although there is no acceleration, the speed is maximum.

As soon as the block passes O going to the left, the force on the block and its acceleration increases to the right, because the spring is now compressed. Eventually, the block is brought to rest momentarily at the point Question Then on, the subsequent motion is the same as the motion from P to Q, with all directions reversed.

The acceleration of the block is \(\vec{a}\) = \(\frac{\vec{F}}{m}\) = –\(\frac{k}{m} \vec{x}\) where m is the mass of the block. This shows that the acceleration is also proportional to the displacement and its direction is opposite to that of the displacement, i.e., the force and acceleration are both directed towards the mean or equilibrium position. The motion repeats causing the block to oscillate about equilibrium or mean position O. This oscillatory motion along a straight path is called linear simple harmonic motion (SHM).

The points P and Q are called the extreme positions or the turning points of the motion. One oscillation is a complete to-and-fro motion of the oscillating body (block, in this case) along its path (the motion from O to P, P to Q and Q to O), i.e., two consecutive passages of the body through the point O in the same direction.

Question 3.
In linear SHM, what can you say about the restoring force when the speed of the particle is

1. zero
2. maximum ?

Answer:
The restoring force is

1. maximum
2. zero.

Question 4.
Define period or periodic time, frequency, amplitude and path length of simple harmonic motion (SHM).
Answer:

1. Period or periodic time of SHM : The time taken by a particle performing simple harmonic motion to complete one oscillation is called the period or periodic time of SHM.
2. Frequency of SHM : The number of oscillations performed per unit time by a particle executing SHM is called the frequency of SHM.
3. Amplitude of SHM : The magnitude of the maximum displacement of a particle performing SHM from its mean position is called the amplitude of SHM.
4. Path length of SHM : The length of the path over which a particle performs SHM is twice the amplitude of the motion and is called the path length or range of the SHM.
   [Note : The frequency of SHM is equal to the reciprocal of the period of SHM.]

Question 5.
Obtain the differential equation of linear simple harmonic motion.
Answer:
When a particle performs linear SHM, the force acting on the particle is always directed towards the mean position. The magnitude of the force is directly proportional to the magnitude of the displacement of the particle from the mean position. Thus, if \(\vec{F}\) is the force acting on the particle when its displacement from the mean position is \(\vec{x}\), \(\vec{F}\) = -k\(\vec{x}\) … (1)
where the constant k, the force per unit displacement, is called the force constant. The minus sign indicates that the force and the displacement are oppositely directed.
The velocity of the particle is \(\frac{d \vec{x}}{d t}\) and its acceleration is \(\frac{d^{2} \vec{x}}{d t^{2}}\).
Let m be the mass of the particle.
Force = mass × acceleration
∴ \(\vec{F}\) = m\(\frac{d^{2} \vec{x}}{d t^{2}}\)
Hence, from Eq. (1),
m\(\frac{d^{2} \vec{x}}{d t^{2}}\) = -k\(\vec{x}\)
∴ \(\frac{d^{2} \vec{x}}{d t^{2}}\) + \(\frac{k}{m} \vec{x}\) = 0 … (2)
This is the differential equation of linear SHM.

Question 6.
Obtain the dimensions of force constant in SHM.
Answer:

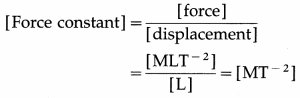
[Note : The SI unit of force constant is the newton per metre (N/m) while the cgs unit is the dyne per centimetre (dyn/cm).]

Question 7.
State the differential equation of linear SHM. Hence, obtain the expressions for the acceleration, velocity and displacement of a particle performing linear SHM.
Answer:
The differential equation of linear SHM is
\(\frac{d^{2} \vec{x}}{d t^{2}}\) + \(\frac{k}{m} \vec{x}\) = 0
where m = mass of the particle performing SHM, \(\frac{d^{2} \vec{x}}{d t^{2}}\) = acceleration of the particle when its displacement from the mean position is \(\vec{x}\) and k = force constant. For linear motion, we can write the differential equation in scalar form :
\(\frac{d^{2} x}{d t^{2}}\) + \(\frac{k}{m}\)x = 0
Let \(\frac{k}{m}\) = ω², a constant
∴ \(\frac{d^{2} x}{d t^{2}}\) + ω²x = 0
∴ Acceleration, a = \(\frac{d^{2} x}{d t^{2}}\) = ω²
The minus sign shows that the acceleration and the displacement have opposite directions. Writing v = \(\frac{d x}{d t}\) as the velocity of the particle.

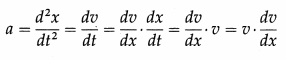
Hence, EQ. (1) can be written as
v\(\frac{d v}{d x}\) = -ω²x dx
∴ vdv = -ω²x dx
Integrating this expression, we get,
\(\frac{v^{2}}{2}\) = –\(\frac{-\omega^{2} x^{2}}{2}\) + C
where the constant of integration C is found from a boundary condition.

At an extreme position (a turning point of the motion), the velocity of the particle is zero. Thus, v = 0 when x = ± A, where A is the amplitude.

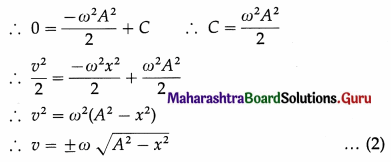
This equation gives the velocity of the particle in terms of the displacement, x. The velocity towards right is taken to be positive and that towards left as negative.
Since, v = dx/dt, we can write Eq. (2) as follows :

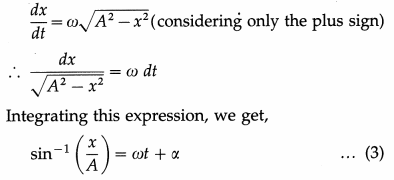
where the constant of integration, α, is found from the initial conditions, i.e., the displacement and the velocity of the particle at time t = 0.
From Eq. (3), we have
\(\frac{x}{A}\) = sin (ωt + α)
∴ Displacement as a function of time is,
x = A sin (ωt + α)

Question 8.
From the definition of linear SHM, derive an expression for the angular frequency of a body performing linear SHM.
Answer:
When a body of mass m performs linear SHM, the restoring force on it is always directed towards the mean position and its magnitude is directly proportional to the magnitude of the displacement of the body from the mean position. Thus, if \(\vec{F}\) is the force acting on the body when its displacement from the mean position is \(\vec{x}\),
\(\vec{F}\) = m\(\) = – k\(\vec{x}\)
where the constant k, the force per unit displacement, is the force constant.
Let \(\frac{k}{m}\) = ω², a constant. m
∴ Acceleration, a = –\(\frac{k}{m}\)x = -ω²x
∴ The angular frequency
ω = \(\sqrt{\frac{k}{m}}\) = \(\sqrt{\left|\frac{a}{x}\right|}\)
= \(\sqrt{\text { acceleration per unit displacement }}\)

Question 9.
What is the displacement of a particle at any position, performing linear SHM ?
Answer:
The displacement of a particle performing linear SHM is a specified distance of the particle from the mean position in a specified direction along its path. The general expression for the displacement is x = A sin (ωt + α), where A and ω are respectively the amplitude or maximum displacement and the angular frequency of the motion, and α is the initial phase.

Question 10.
Assuming the general expression for displacement of a particle in SHM, obtain the expressions for the displacement when the particle starts from
(i) the mean position
(ii) an extreme position.
Answer:
The general expression for the displacement of a particle in SHM at time t is x = A sin (ωt + α) … (1) where A is the amplitude and re is a constant in a particular case.
∴ ωt + α = sin^-1\(\frac{x}{A}\) …. (2)
(i) When the particle starts from the mean position, x = 0 at t = 0. Then, from Eq. (2),
α = sin^-1 0 = 0 or π … (3)
Substituting for α into Eq. (1),
x = A sin ωt for α = 0 and x = – A sin ωt for α = π
∴ x = ±A sin ωt … (4)
where the plus sign is taken if the particle’s initial velocity is to the right, while the minus sign is taken when the initial velocity is to the left.

(ii) x = ±A at t = 0 when the particle starts from the right or left extreme position, respectively. Then, from Eq. (2),

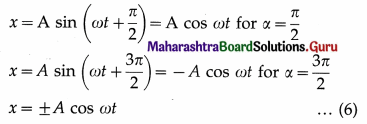
where the plus sign is taken when the particle starts from the positive extreme, while the minus sign is taken when the particle starts from the negative extreme.

Question 11.
At what position is the acceleration of a particle in SHM maximum? What is its magnitude? At what position is the acceleration minimum ? What is its magnitude ?
Answer:
The magnitude of the acceleration of a particle performing SHM is
a = ω²x … (1)
where ω is a constant related to the system.
From Eq. (1), the acceleration has a maximum value a_max when displacement x is maximum, |x| = A, i.e., the particle is at the extreme positions.
∴ a_max = ω²A
Also from EQ. (1), the acceleration has a minimum value when x is minimum, x = 0, i.e., the particle is at the mean position.
∴ a_min = 0

Question 12.
At what position is the velocity of a particle in SHM maximum ? What is its magnitude ? At what position is the velocity minimum? What is its magnitude?
Answer:
The velocity of a particle in SHM is
v = ω\(\sqrt{A^{2}-x^{2}}\) … (1)
where ω is a constant related to the system and A is the amplitude of SHM.
From EQ. (1) it is clear that the velocity is maximum when A² – x² is maximum, that is when displacement x = 0, i.e., the particle is at the mean position.
∴ v_max = ωA
Also from Eq. (1), the velocity is minimum when A² – x² is minimum, equal to zero. This occurs when x is maximum, x = ± A, i.e., the particle is at the extreme positions.
∴ v_min = 0

Question 13.
For a particle performing linear SHM, show that its average speed over one oscillation is \(\frac{2 \omega A}{\pi}\), where A is the amplitude of SHM.
OR
Show that the average speed of a particle performing SHM in one oscillation is \(\frac{2}{\pi}\) × maximum speed.
Answer:
During one oscillation, a particle performing SHM covers a total distance equal to 4A, where A is the amplitude of SHM. The time taken to cover this distance is the period (T) of SHM.

Question 14.
A body of mass 200 g performs linear SHM with period 2πs. What is the force constant ?
Answer:
Force constant, k = mω² = m\(\left(\frac{2 \pi}{T}\right)^{2}\)
= 0.2kg × \(\left(\frac{2 \pi}{2 \pi \mathrm{s}}\right)^{2}\) = 0.2N/m.

Question 15.
Derive expressions for the period of SHM in terms of
(1) angular frequency
(2) force constant
(3) acceleration.
Answer:
The general expression for the displacement (x) of a particle performing SHM is x = A sin (ωt + α)
(1) Let T be the period of the SHM and x₁ the displacement after a further time interval T. Then
x₁ = A sin [ω(t + T) + α]
= A sin (ωt + ωT + α)
= A sin (ωt + α + ωT)
Since T ≠ 0, for x₁ to be equal to x, we must have (ωT)_min = 2π.
Hence, the period (T) of SHM is T = 2π/ω
This is the expression for the period in terms of the constant co, the angular frequency.

(2) If m is the mass of the particle and k is the force constant, ω = \(\sqrt{k / m}\).
∴T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{\sqrt{k / m}}\) = 2π \(\sqrt{\frac{m}{k}}\)

(3) The acceleration of a particle performing SHM has a magnitude a = ω²x
∴ ω = \(\sqrt{a / x}\)

Question 16.
A small uniform cylinder floats upright to a depth d in a liquid. If it is depressed slightly and released, find its period of oscillations.
Answer:
Consider a cylinder, of length L, area of cross section A and density ρ, floating in a liquid of density σ. If the cylinder floats up to depth d in the liquid, then by the law of floatation, the weight of the cylinder equals the weight of the liquid displaced, i.e.,
ALρg = Adσg
∴ L = dσ/p … (1)
Let the cylinder be pushed down by a distance y. Then, the weight of the liquid displaced by the cylinder of length y will exert a net upward force on the cylinder :
F = Ayσg,
which produces an acceleration,

Question 17.
How does the frequency of an SHM vary with

1. the force constant k
2. the mass of the particle performing SHM ?

Answer:
The frequency of a particle of mass m performing
SHM is f = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\).

1. ∴ f ∝\(\sqrt{k}\)
   Thus, the frequency of an SHM is directly proportional to the square root of the force constant of the motion.
2. ∴ f ∝ \(\frac{1}{\sqrt{m}}\)
   Thus, the frequency of an SHM is inversely proportional to the square root of the mass of the particle performing SHM.

Question 18.
In linear SHM, at what position of the particle is the acceleration of the particle half the maximum acceleration?
Answer:
In linear SHM, | a | ∝ | x | ∴ a = \(\frac{a_{\max }}{2}\) when | x | = \(\frac{A}{2}\), where A is the amplitude of SHM.

Question 19.
If the displacement of a particle in SHM is given by x = 0.1 sin (6πrt) metre, what is the frequency of motion ?
Answer:
Comparison of the given equation with
x = A sin (2πft) gives 2πf = 6π rad/s.
∴ Frequency of motion,/= 3 Hz

Question 20.
If the displacement of a particle in SHM is given by x = 0.1 cos (100t) metre, what is the maximum speed of the particle ?
Answer:
Comparison of the given equation with
x = A cos (ωt) gives A = 0.1 m and ω = 100 rad/s.
∴ Maximum speed of the particle = ωA
= 1000 × 0.1 = 10 m/s

Question 21.
A body of mass m tied to a spring performs SHM with period 2 seconds. If the mass is increased by 3m, what will be the period of SHM ?
Answer:

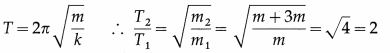
∴ T₂ = 2T₁ = 2 × 2 = 4 seconds gives the required period of SHM.

Question 22.
A particle executing SHM has velocities v₁ and v₂ when at distances x₁ and x₂ respectively from the mean position. Show that its period is T = 2π\(\sqrt{\frac{x_{1}^{2}-x_{2}^{2}}{v_{2}^{2}-v_{1}^{2}}}\) and the amplitude of SHM is A = \(\sqrt{\frac{v_{2}^{2} x_{1}^{2}-v_{1}^{2} x_{2}^{2}}{v_{2}^{2}-v_{1}^{2}}}\)
Answer:
If A is the amplitude and co is the angular frequency, V₁ = ω\(\sqrt{A^{2}-x_{1}^{2}}\) … (1)
and v₂ = ω\(\sqrt{A^{2}-x_{2}^{2}}\) … (2)

Question 23.
Explain
(i) a series combination
(ii) a parallel combination of springs. Obtain the spring constant in each case.
Answer:
(i) Series combination of springs : When two light springs obeying Hooke’s law are connected as shown in below figure and both the springs experience the same force applied to the free end of the combination, they are said to be connected in series.

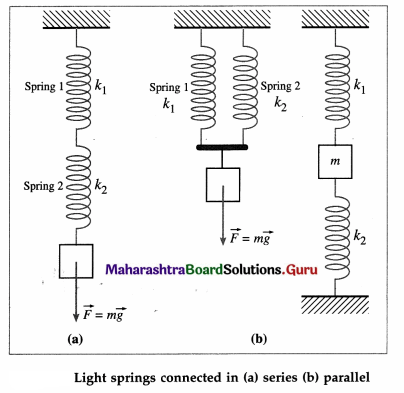
Consider two springs, 1 and 2, with respective spring constants k₁ and k₂ connected in series and supporting a load F = mg so that the springs are extended. Since the same force acts on each spring, by Hooke’s law,
F = k₁x₁ (for spring 1) and F = k₂x₂ (for spring 2) The system of two springs in series is equivalent to a single spring, of spring constant k_S such that F = k_Sx, where the total extension x of the combination is the sum x₁ + x₂ of their elongations.
x = x₁ + x₂
∴ \(\frac{F}{k_{\mathrm{S}}}\) = \(\frac{F}{k_{1}}\) + \(\frac{F}{k_{2}}\) ∴ \(\frac{1}{k_{\mathrm{S}}}\) = \(\frac{1}{k_{1}}\) + \(\frac{1}{k_{2}}\)
For a series combination of N such springs, of spring constants, k₁, k₂, k₃, … k_N

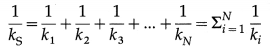
(ii) Parallel combination of springs : When two light springs obeying Hooke’s law are connected via a thin vertical rod as shown, they are said to be connected in parallel. If a constant force \(\vec{F}\) is exerted on the rod such that the rod remains perpendicular to the direction of the force, the springs undergo the same extension.

Consider two springs, 1 and 2, with respective spring constants k₁ and k₂ connected in series and supporting a load F = mg so that the springs are extended. The two springs stretch by the same amount x but share the load.
F = F₁ + F₂
The system of two springs in parallel is equivalent to a single spring, of spring constant kF such that F = k_PX,
∴ k_Px = k₁x + k₂x ∴ k_P = k₁ + k₂
For a parallel combination of N such springs, of spring constants k₁, k₂, k₃, … k_N
k_P = k₁ + k₂ + k₃ + … + k_N = \(\Sigma_{i=1}^{N} k_{i}\)
Therefore, for a parallel combination of N identical light springs, each of spring constant k, k_P = Nk

Question 24.
Solve the following :

Question 1.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate
(i) the angular frequency
(ii) the frequency of oscillation.
Solution :
Data : m = 1 kg, k = 16 N/m

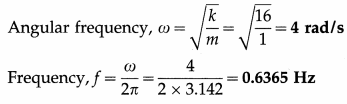
Question 2.
Calculate the time taken by a body performing SHM of period 2 seconds to cover half the amplitude starting from an extreme position.
Solution :
Data : T = 2 s, x₀ = + A (initially at positive extremity), x = \(\frac{A}{2}\)

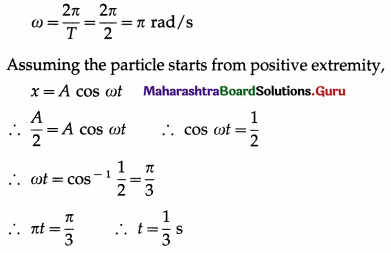
∴ Starting from the positive extremity, the particle takes \(\frac{1}{3}\) s to cover a distance equal to half the amplitude.

Question 3.
A 3 kg block, attached to a spring, performs linear SHM with the displacement given by x = 2 cos (50t) m. Find the spring constant of the spring.
Solution :
Data : m = 3 kg, x = 2 cos (50t) m
Comparing the given equation with x = A cos ωt,
ω = 50 rad/s
ω² = k/m
∴ The spring constant,
k = mω² = (3)(50)²
= 3 × 2500 = 7500 N/m

Question 4.
A body oscillates in SHM according to the equation x = 5 cos (2πt + \(\frac{\pi}{4}\)), where x and t are
in SI units. Calculate the
(i) displacement and
(ii) speed of the body at t = 1.5 s.
Solution:
Data: x = cos \(\left(2 \pi t+\frac{\pi}{4}\right)\), t = 1.5 s
(i) The displacement at t = 1.5 s is

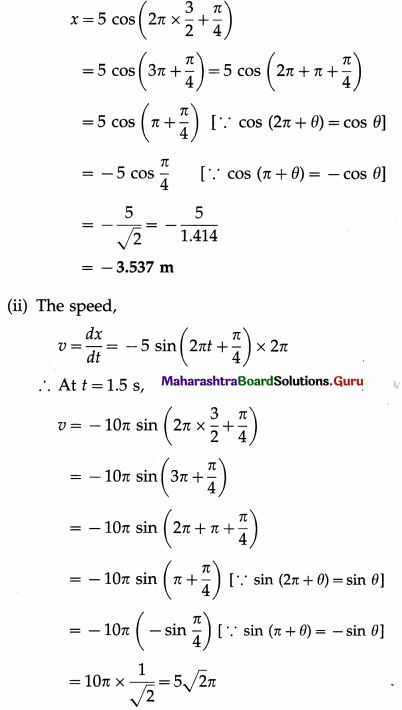
= 5(1.414)(3.142) = 22.21 m/s

Question 5.
The equation of motion of a particle executing SHM is x = a sin \(\left(\frac{\pi}{6} t\right)\) + b cos \(\left(\frac{\pi}{6} t\right)\), where a = 3 cm and b = 4 cm. Express this equation in the form x = A sin \(\left(\frac{\pi}{6} t+\phi\right)\). Hence, find A and φ.
Solution:
Let a = A cos φ and b = A sin φ, so that

Question 6.
A particle performs SHM of amplitude 10 cm. Its maximum velocity during oscillations is 100 cm/s. What is its displacement, when the velocity is 60 cm/s?
Solution :
Data : A = 10 cm, v_max = 100 cm/s, v = 60 cm/s
v_max = ωA = 100 cm/s

Question 7.
A body of mass M attached to a spring oscillates with a period of 2 seconds. If the mass is increased by 2 kg, the period increases by 1 second. Find the initial mass, assuming that Hooke’s law is obeyed.
Answer:
Data : m₁ = M, T₁ = 2 s, m₂ = M + 2 kg, T₂ = 2s + 1 s = 3s

Question 8.
A load of 100 g increases the length of a light spring by 10 cm. Find the period of its linear SHM if it is allowed to oscillate freely in the vertical direction. What will be the period if the load is increased to 400 g? [g = 9.8 m/s²]
Solution :
Data :m = 100 g = 100 × 10^-3 kg, x = 10 cm = 0.1 m g = 9.8 m/s², m₁ = 400 g = 400 × 10^-3 kg
(1) Stretching force F = mg
Now F = kx (numerically), where k is the force constant.
∴ mg = kx

Question 9.
A particle in SHM has a period of 2 seconds and an amplitude of 10 cm. Calculate its acceleration when it is at 4 cm from its positive extreme position.
Solution :
Data : T = 2s, A = 10 cm, A – x = 4 cm
∴ x = 10 cm – 4 cm = 6 cm

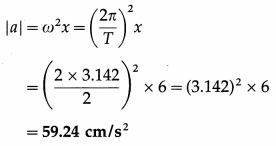
Question 10.
A particle executes SHM with amplitude 5 cm and period 2 s. Find the speed of the particle at a point where its acceleration is half the maximum acceleration.
Solution :
Data: A = 5 cm = 5 × 10^-2 m, T = 2s,

Question 11.
The periodic time of a linear harmonic oscillator is 2π seconds, with maximum displacement of 1 cm. If the particle starts from an extreme position, find the displacement of the particle after π/3 seconds.
Solution :
Data : T = 2π s, A = 1 cm, t = π/3
ω = \(\frac{2 \pi}{T}\) = \(\frac{2 \pi}{2 \pi}\) = 1 rad/s
x = A cos ωt (∵ particle starts from extreme position)
= (1) cos\(\left(1 \times \frac{\pi}{3}\right)\) = cos \(\left(1 \times \frac{\pi}{3}\right)\) = cos \(\frac{\pi}{3}\) = \(\frac{1}{2}\) cm

Question 12.
A particle performs SHM of period 12 seconds and amplitude 8 cm. If initially the particle is at the positive extremity, how much time will it take to cover a distance of 6 cm from that position?
Solution :
Data : T = 12 s, A = 8 cm
∴ ω = 2π/T = π/6 rad/s
When the particle covers a distance of 6 cm from the positive extremity, its displacement measured from the mean position is x = 8 – 6 = 2 cm.
As the particle starts from the positive extreme position, its displacement is

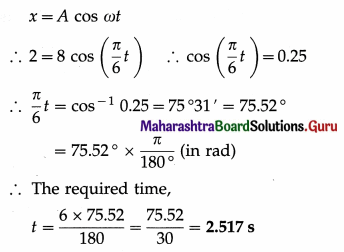
Question 13.
A particle executes SHM with amplitude 10 cm and period 10 s. Find the velocity and acceleration of the particle at a distance of 5 cm from the equilibrium position.
Solution :
Data : A = 10 cm = 0.1 m, T = 10 s, x = ± 5 cm = ± 0.05 m

Question 14.
A body performs SHM on a path 0.12 m long. Its velocity at the centre of the path is 0.12 m/s. Find the period of SHM. Also find the magnitude of the velocity of the body at \(\sqrt{3}\) × 10^-2 m from the centre of the path.
Solution :
The path length of the SHM is the range 2 A, and the velocity at the centre of the path, i.e., at the equilibrium position, is the maximum velocity v_max.
Data : 2A = 0.12 m, v_max = 0.12 m/s,
x = ± \(\sqrt{3}\) × 10^-2 m

Question 15.
A particle of mass 2 g executes SHM with a period of 12 s and amplitude 10 cm. Find the acceleration of the particle and the restoring force on the particle when it is 2 cm from its mean position. Also find the maximum velocity of the particle.
Solution :
Data : m = 2g = 2 × 10^-3 kg, T = 12 s,
A = 10 cm = 0.1 m, x = ±2 cm = ±2 × 10^-2 m

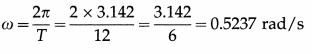
The acceleration of the particle, a = ω² = (0.5237)² (± 2 × 10^-2)
= ± 0.2743 × 2 × 10^-2 = ± 5.486 × 10^-3 m/s²
The restoring force on the particle at that position, F = ma = ± (2 × 10^-2) (5.486 × 10^-3)
= ±1.097 × 10^-5 N
The maximum velocity of the particle, v_max = ωA = 0.5237 × 0.1 5.237 × 10^-2 m/s

Question 16.
The maximum velocity of a particle performing linear SHM is 0.16 m/s. If its maximum acceleration is 0.64 m/s², calculate its period.
Solution :
Data : v_max = 0.16 m/s, a_max = 0.64 m/s²
v_max = ωA and a_max = ω²A

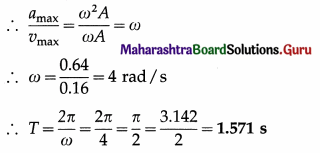
Question 17.
A particle performing linear SHM has maximum velocity of 25 cm/s and maximum acceleration of 100 cm/s². Find the amplitude and period of oscillation, [π = 3.142]
Solution :
Data : v_max = 25 cm/s, a_max = 100 cm/s²

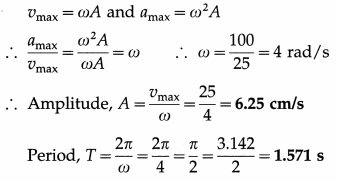
Question 18.
A particle performing linear SHM has a period of 6.28 seconds and path length of 20 cm. What is the velocity when its displacement is 6 cm from the mean position?
Solution :
Data : T = 6.28 s, 2A = 20 cm ∴ A = 10 cm, x = 6 cm

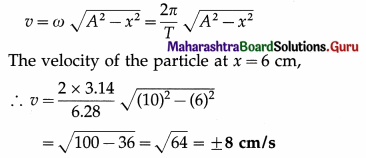
Question 19.
A uniform wooden rod floats vertically in water with 14 cm of its length immersed in the water. If it is depressed slightly and released, find its period of oscillations.
Solution :
Data : d = 14 cm = 0.14 m

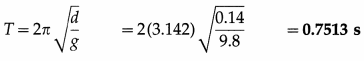
Question 20.
A particle performs UCM. The diameter of the circle is 4 cm. What is the amplitude of linear SHM that is the projection of the UCM on a diameter?
Answer:
Amplitude of linear SHM = radius of the circle = 2 cm.

Question 21.
A particle performs UCM with period 2n seconds along a circle of diameter 10 cm. What is the maximum speed of its shadow on a diameter of the circle ?
Answer:
Maximum speed, v_max = ωA = \(\frac{2 \pi}{T}\)A
= \(\frac{2 \pi}{2 \pi}\) × 5 × 10^-2 = 5 × 10^-2 m/s.

Question 22.
See Question 20 above. What is the maximum acceleration of the shadow ?
Answer:
Maximum acceleration, a_max = ω²A = \(\left(\frac{2 \pi}{T}\right)^{2}\) A
= \(\left(\frac{2 \pi}{2 \pi}\right)^{2}\) × 5 × 10^-2 = 5 × 10^-2 m/s².

Question 23.
What do you understand by the phase and epoch of an SHM ?
Answer:
(1) Phase of simple harmonic motion (SHM) represents the state of oscillation of the particle performing SHM, i.e., it gives the displacement of the particle, its direction of motion from its equilibrium position and the number of oscillations completed.

The displacement of a particle in SHM is given by x = A sin (ωt + α). The angle (ωt + α) is called the phase angle or simply the phase of SHM. The SI unit of phase angle is the radian (symbol, rad).

(2) Epoch of simple harmonic motion (SHM) represents the initial phase of the particle performing SHM, i.e., it gives the displacement of the particle and its direction of motion at time t = 0.

If x₀ is the initial position of the particle, i.e., the position at time t = 0, x₀ = A sin α or α = sin^-1 (x₀/A). The angle α, therefore, determines the initial state of the particle. Hence, the angle α is the epoch or initial phase or phase constant of SHM.
[Note : The symbol for the unit radian is rad, not superscripted c.]

Question 25.
Solve the following.

Question 1.
The differential equation for a particle performing linear SHM is \(\frac{d^{2} x}{d t^{2}}\) = – 4x. If the amplitude is 0.5 m and the initial phase is π/6 radian, obtain the expression for the displacement and find the velocity of the particle at x = 0.3 m.
Solution:
Data : A = 0.5 m, α = π/6 rad
(1) \(\frac{d^{2} x}{d t^{2}}\) = -4x
Comparing this equation with the general equation \(\frac{d^{2} x}{d t^{2}}\) = – ω²x, we get,
ω² = 4 or ω = 2 rad/s
Now, x = A sin (ωt + α)
Substituting the values of A, ω and α, the expression for the displacement for the given SHM is
x = 0.5 sin (2t + π/6) m

(2) The velocity of the particle at x = 0.3 m is v = ± ω \(\sqrt{A^{2}-x^{2}}\)
= ± 2 \(\sqrt{(0.5)^{2}-(0.3)^{2}}\) = ± 0.8 m/s

Question 2.
The displacement of a particle performing linear SHM is given by x = 6 sin (3πt + \(\frac{5 \pi}{6}\)) metre. Find
the amplitude, frequency and the phase constant of the motion.
Solution :
Data : x = 6 sin (3πt + \(\frac{5 \pi}{6}\)) metre
Comparing this equation with x = A sin (ωt + α), we get:

1. Amplitude, A = 6 m
2. ω = 3π rad / s
   ∴ Frequency, f = \(\frac{\omega}{2 \pi}\) = \(\frac{3 \pi}{2 \pi}\) = 1.5 Hz 5%
3. Phase constant, α = \(\frac{5 \pi}{6}\) rad

Question 3.
The equation of linear SHM is a: = 10 sin (4πt + \(\frac{1}{24}\)) cm. Find the amplitude, period and phase constant of the motion. Also, find the phase angle \(\frac{1}{24}\) second after the start.
Solution:
Data : x = 10 sin\(\left(4 \pi t+\frac{\pi}{6}\right)\) + cm, f = \(\frac{1}{24}\) s

(1) Comparing the given equation with x = A sin (ωt +α), we get,
A = 10 cm, ω = 4π rad/s, α = \(\frac{\pi}{6}\) rad
∴

1. Amplitude, A = 10 cm
2. Period, T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{4 \pi}\) = 0.5 s
3. Phase constant, α = \(\frac{\pi}{6}\) rad

(2) Phase angle = (ωt + α) = 4πt + \(\frac{\pi}{6}\)
The phase angle \(\frac{1}{24}\) second after the start is obtained by substituting t = \(\frac{1}{24}\) in the above expression.
∴ Phase angle = 4πt + \(\frac{\pi}{6}\) = (4π × \(\frac{1}{24}\)) + \(\frac{\pi}{6}\)
= \(\frac{\pi}{6}\) + \(\frac{\pi}{6}\) = \(\frac{\pi}{3}\) rad

Question 4.
Describe the state of oscillation of a particle if the phase angle of SHM is rad.
Solution :
Data : θ = \(\frac{25 \pi}{4}\) rad
θ = \(\frac{25 \pi}{4}\) = 6π + \(\frac{\pi}{4}\) = 3(2π) rad + \(\frac{\pi}{4}\) rad
The first term indicates that the particle has completed 3 oscillations. The second term indicates that the displacement of the particle in the 4th oscillation is A sin \(\frac{\pi}{4}\) = + \(\frac{1}{\sqrt{2}}\)A, where A is the amplitude of the SHM, and moving towards the positive extreme.

Question 5.
A particle in linear SHM is in its 5th oscillation. If its displacement at that instant is –\(\frac{1}{2}\) A and
is moving toward the mean position, determine its phase at that instant.
Solution :
Data : x = –\(\frac{1}{2}\) A, 5th oscillation
A sin θ₁ = –\(\frac{1}{2}\)A ∴ θ₁ = sin^-1\(\left(-\frac{1}{2}\right)\) = π – \(\frac{\pi}{6}\) rad
As the particle is in its 5th oscillation, its phase is
θ = 2 × 2π + θ₁ = 4π + (π – \(\frac{\pi}{6}\)) = 5π – \(\frac{\pi}{6}\) = \(\frac{29 \pi}{6}\) rad

Question 6.
The amplitude and periodic time of SHM are 5 cm and 6 s, respectively. What is the phase at a distance of 2.5 cm from the mean position?
Solution :
Data : A = 5 cm, T = 6 s, x = 2.5 cm
Since the particle starts from the mean position, its epoch, α = 0.
∴ The equation of motion is x = A sin ωt
∴ The required phase of the particle,
ω = sin^-1\(\frac{x}{A}\)
= sin^-1\(\frac{2.5}{5}\) = sin^-1 \(\frac{1}{2}\) = \(\frac{\pi}{6}\) rad

Question 26.
State the expressions for the displacement, velocity and acceleration of a particle performing linear SHM, starting from the mean position towards the positive extreme position. Hence, draw their graphs with respect to time. Draw your conclusions from the graphs.
OR
Represents graphically the displacement, velocity and acceleration against time for a particle performing linear SHM when it starts from the mean position.
Answer:
Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where co is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are

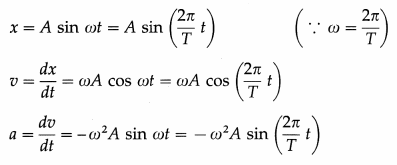
as the initial phase α = 0

Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.

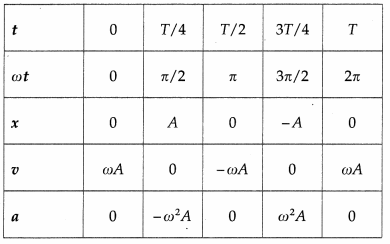
Using the values in the table we can plot graphs of displacement, velocity and acceleration with time.

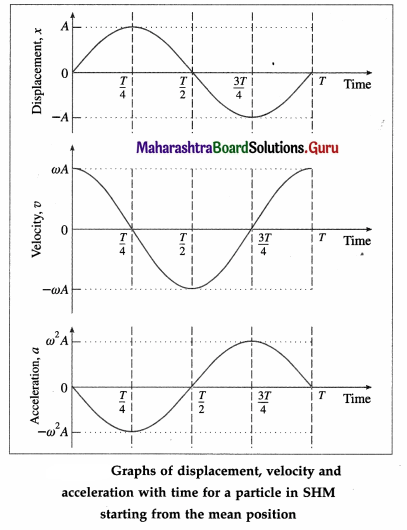
Conclusions :

1. The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting at the mean position, the x-t and a-t graph are sine curves. The v-t graph is a cosine curve.
2. There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
3. There is a phase difference of n radians between x and a.

Question 27.
State the expressions for the displacement, velocity and acceleration of a particle performing linear SHM, starting from the positive extreme position. Hence, draw their graphs with respect to time. Draw your conclusions from the graphs.
OR
A particle performs linear SHM starting from the positive extreme position. Plot the graphs of its displacement, velocity and acceleration against time.
Answer:
Consider a particle performing linear SHM with amplitude A and period T = 2π/ω, starting from the positive extreme position, where ω is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant (t) are
x = A cos ωt = A cos\(\left(\frac{2 \pi}{T} t\right)\) (∵ ω = \(\frac{2 \pi}{T}\))
v = – ωA sin ωt = -ωA sin \(\left(\frac{2 \pi}{T} t\right)\)
a = – ω²A sin ωt = -ω²A cos \(\left(\frac{2 \pi}{T} t\right)\)

Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.

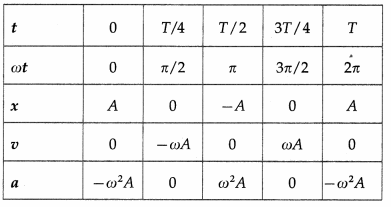
Using these values, we can plot graphs showing the variation of displacement, velocity and acceleration with time.

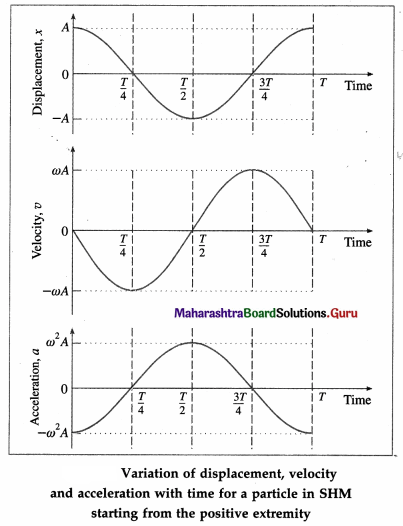
Conclusions :

1. The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x-t and a-t graphs are cosine curves; the v-t graph is a sine curve.
2. There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
3. There is a phase difference of π radians between x and a.

Explanations :
(1) v-t graph : It is a sine curve, i.e., the velocity is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π/2 rad between a and v.

v is minimum (equal to zero) at the extreme positions (i.e., at x = ± A) and v is maximum ( = ± ωA) at the mean position (x = 0).

(2) a-t graph : It is a cosine curve, i.e., the acceleration is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π rad between v and a. a is minimum (equal to zero) at the mean position (x = 0) and a is maximum ( = \(\mp\)ω²A) at the extreme positions (x = ± A).

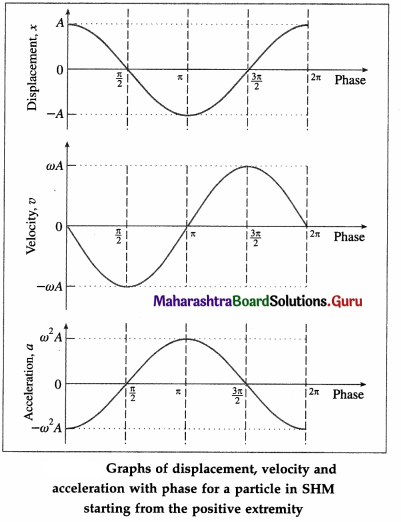
Question 28.
Discuss analytically the composition of two SHMs of the same period and parallel to each other (along the same path). Find the resultant amplitude when the phase difference is
(1) zero
(2) \(\frac{\pi}{3}\) rad
(3) \(\frac{\pi}{2}\) rad
(4) π rad.
Answer:
Let a particle be subjected to two parallel linear SHMs of the same period along the same path and the same mean position, represented by
x₁ = A₁ sin (ωt + α) and x₂ = A₂ sin (ωt + β),
where A₁ and A₂ are the amplitudes, and α and β are the initial phases of the two SHMs.

According to the principle of superposition, the displacement of the particle at any instant t is the algebraic sum x = x₁ + x₂.
∴ x = A₁ sin (ωt + α) + A₂ sin (ωt + β)
= A₁ sin ωt cos α + A₁ cos ωt sin α + A₂ cos ωt sin β
= (A₁ cos α + A₂ cos β) sin ωt + (A₁ sin α + A₂sin β) cos ωt
Let A₁ cos α + A₂ cos β = R cos δ …. (1)
and A₁ sin α + A₂ sin β = R sin δ …. (2)
∴ x = R cos δ sin ωt + R sin δ cos ωt
∴ x = R cos(ωt + δ) ….. (3)

Equation (3), which gives the displacement of the particle, shows that the resultant motion is also simple harmonic, along the same path as the SHMs superposed, with the same mean position, and amplitude R and initial phase δ but having the same period as the individual SHMs.

Amplitude R of the resultant motion : The resultant amplitude R is found by squaring and adding Eqs. (1) and (2).

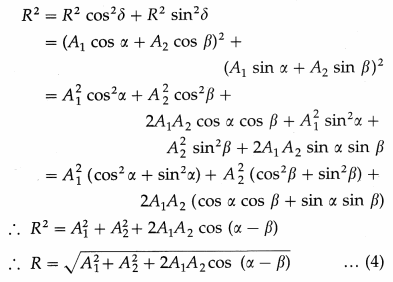
Initial phase S of the resultant motion : The initial phase of the resultant motion is found by dividing Eq. (2) by Eq. (1).

Notes :

1. Since the displacements due to the super-posed linear SHMs are along the same path, their vector sum can be replaced by the algebraic sum.
2. To determine δ uniquely, we need to know both sin δ and cos δ.

Question 29.
Solve the following :

Question 1.
Two parallel SHMs are given by x₁ = 20 sin (8πt) cm and x₂ = 10 sin (8πt + π/2) cm. Find the amplitude and the epoch of the resultant SHM.
Solution :
Data : x₁ = 20 sin (8πt) cm = A₁ sin (ωt + α), x₂ = 10 sin (8πt + π/2) cm = A₂ sin (ωt + β)
∴ A₁ = 20 cm, A₂ = 10 cm, α = 0, β = π/2
(1) Resultant amplitude,

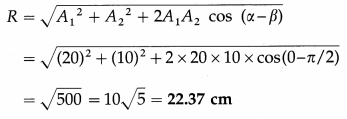
(2) Initial phase of resultant SHM,

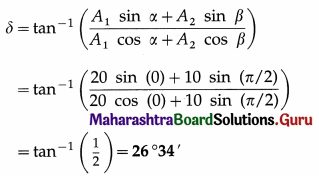
Question 2.
The displacement of a particle performing SHM is given by x = [5 sin πt + 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\) cm. Determine the amplitude, period and initial phase of the motion.
Solution :
Data : x = [5 sin πt + 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\)] cm
The given expression for displacement may be written as the superposition of two parallel SHMs of the same period as x = x₁ + x₂, where x₁ = 5 sin πt cm = A₁ sin (ωt + α) and
x₂ = 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\) cm = A₂ sin (ωt + β)
∴ A₁ = 5 cm, A₂ = 12 cm, ω = π rad/s, α = 0, β = \(\frac{\pi}{2}\) rad.

Question 3.
An SHM is given by the equation x = [8 sin (4πt) + 6 cos (4πt)] cm. Find its
(1) amplitude
(2) initial phase
(3) period
(4) frequency.
Solution:
Data : x = [8 sin (4πt) + 6 cos (4πt)] cm
x = 8 sin (4πt) + 6 cos (4πt)
= 8 sin (4πt) + 6 sin \(\left(4 \pi t+\frac{\pi}{2}\right)\)
Thus, x is the superposition of two parallel SHMs of the same period : x = x₁ + x₂, where
x₁ = 8 sin (4πt) cm = A₁ sin (ωt + α) and
x₂ = 6 sin \(\left(4 \pi t+\frac{\pi}{2}\right)\) = A₂ sin (ωt + β)
∴ A₁ = 8 cm, A₂ = 6cm, ω = 4π rad/s, α = 0,
β = \(\frac{\pi}{2}\) rad

Question 30.
Show that the total energy of a particle performing linear SHM is directly proportional to
(1) the square of the amplitude
(2) the square of the frequency.
Answer:
For a particle of mass m executing SHM with angular frequency ω and amplitude A, its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)mω²(A² – x²) … (1)
and PE = \(\frac{1}{2}\)mω²x² … (2)
Then, the total energy,
E = PE + KE
= \(\frac{1}{2}\)mω²x² + \(\frac{1}{2}\)mω²(A² – x²)
= \(\frac{1}{2}\)mω²A² …. (3)
Therefore, total energy of the particle is

1. directly proportional to the mass (E ∝ m),
2. directly proportional to the square of the amplitude (E ∝ A²)
3. proportional to the square of the frequency
   (E ∝f²), as f = ω/2π

Question 31.
State the expression for the total energy of SHM in terms of acceleration.
Answer:
The total energy of a particle of mass m performing SHM with angular frequency ω, E = \(\frac{1}{2}\)mω²A²
The maximum acceleration of the particle, a_max = ω²A²
E = \(\frac{1}{2}\) mAa_max is the required expression.

Question 32.
State the expressions for the kinetic energy and potential energy of a particle performing SHM. Find their values at
(i) an extreme position
(ii) the mean position.
Using the expressions for the kinetic energy and potential energy of a particle in simple harmonic motion at any position, show that
(i) at the mean position, total energy = kinetic energy
(ii) at an extreme position, total energy = potential energy.
Answer:
For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency ω = \(\sqrt{k / m}\), its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)k(A² – x²) and
PE = \(\frac{1}{2}\)kx²
and total energy, E = \(\frac{1}{2}\)kA²
(i) At the mean position, x = 0,
KE = \(\frac{1}{2}\)kA² = E and PE = 0

(ii) At an extreme position, x = ±A, KE = 0 and PE = \(\frac{1}{2}\)kA² = E

That is, the energy transfers back and forth between kinetic energy and potential energy, while the total mechanical energy of the oscillating particle remains constant. The total energy is entirely kinetic energy at the mean position and entirely potential energy at the extremes.

Question 33.
State the expressions for the kinetic energy (KE) and potential energy (PE) at a displacement x for a particle performing linear SHM. Find
(i) the displacement at which KE is equal to PE
(ii) the KE and PE when the particle is halfway to a extreme position.
Answer:
For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency ω = \(\sqrt{k / m}\), its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)E (A² – x²) and
PE = \(\frac{1}{2}\)kx²
and total energy, E = \(\frac{1}{2}\)kA²

∴ At x = ±\(\frac{A}{2}\), the energy is 25% potential energy and 75% kinetic energy.

Question 34.
The maximum potential energy (PE) of a particle in SHM is 2 × 10^-4 J. What will be the PE of the particle when its displacement from the mean position is half the amplitude of SHM ?
Answer:
(PE)_max = \(\frac{1}{2}\)kA², PE = \(\frac{1}{2}\)kx²
∴ PE = (PE)_max \(\left(\frac{x}{A}\right)^{2}\) = 2 × 10^-4J × \(\left(\frac{1}{2}\right)^{2}\)
= 5 × 10^-5 J is the required answer.

Question 35.
A particle performs linear SHM of amplitude 10 cm. At what displacement of the particle from its mean position will the potential energy (PE) of the particle be 1 % of the maximum PE ?
Answer:

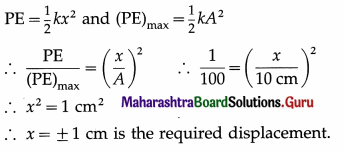
Question 36.
Represent graphically the variations of KE, PE and TE of a particle performing linear SHM with respect to its displacement.
Answer:

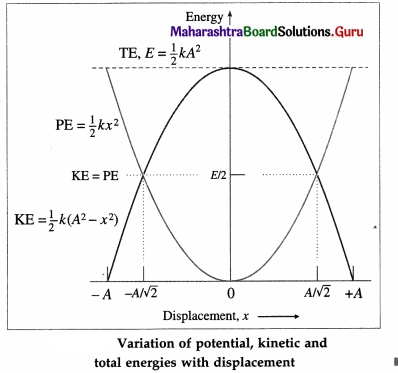
Question 37.
Represent graphically the variation of potential energy, kinetic energy and total energy of a particle performing SHM with time.
Answer:
Consider a particle performing SHM, with amplitude A and period T = \(\frac{2 \pi}{\omega}\) starting from the mean position towards the positive extreme position; ω = \(\sqrt{\frac{k}{m}}\) is the appropriate constant related to the system. The total energy of the particle is E = \(\frac{1}{2}\)kA². Its displacement (x), potential energy (PE) and kinetic energy (KE) at any instant are given by
x = A sin ωt

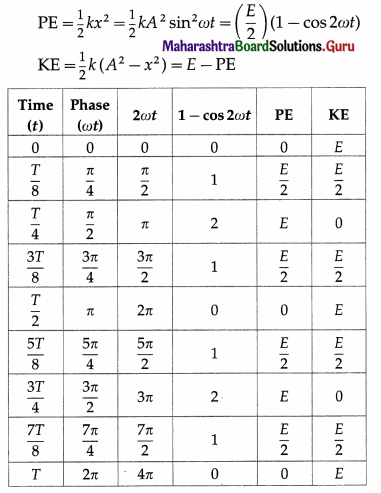
Using the values in the table, we can plot graphs of PE, KE and total energy with times as follows:

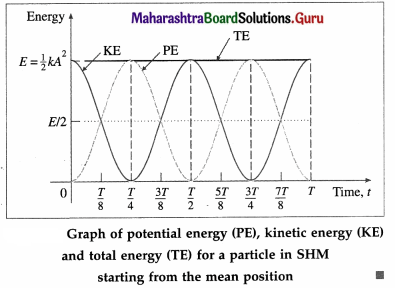
Question 38.
Solve the following :

Question 1.
A particle of mass 10 g is performing SHM. Its kinetic energies are 4.7 J and 4.6 J when the displacements are 4 cm and 6 cm, respectively. Compute the period of oscillation.
Answer:
Data : m = 0.01 kg, KE₁ = 4.7 J, x₁ = 4 × 10^-2 m, KE₂ = 4.6 J, x₂ = 6 × 10^-2 m
Since the total energy of a particle in SHM is constant,

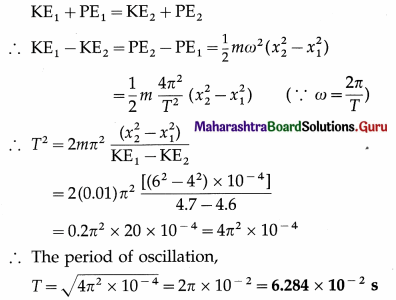
Question 2.
The total energy of a particle of mass 100 grams performing SHM is 0.2 J. Find its maximum velocity and period if the amplitude is 2\(\sqrt{2}\) cm.
Solution :
Data : m = 100 g = 0.1 kg, E = 0.2 J,
A = 2\(\sqrt{2}\) cm = 2\(\sqrt{2}\) × 10^-2 m
(i) The total energy,

Question 3.
An object of mass 0.5 kg performs SHM with force constant 10 N/m and amplitude 3 cm.
(i) What is the total energy of the object?
(ii) What is its maximum speed ?
(iii) What is its speed at x = 2 cm?
(iv) What are its kinetic and potential energies at x = 2 cm ?
Solution :
Data : m = 0.5 kg, A: = 10 N/m,
A = 3 cm = 3 × 10^-2m, x = 2 cm = 2 × 10^-2m

Question 4.
When the displacement in SHM is one-third of the amplitude, what fraction of the total energy is potential and what fraction is kinetic?
Solution :
Data : x = A/3

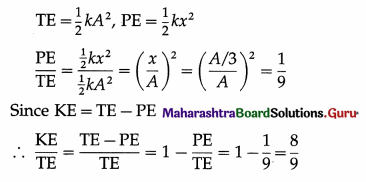
Therefore, \(\frac{1}{9}\) th of the total energy is potential and \(\frac{8}{9}\)th of the total energy is kinetic.

Question 5.
A particle executes SHM with a period of 8 s. Find the time in which half the total energy is potential.
Solution :
Data : T = 8 s, PE = \(\frac{1}{2}\)E
ω = \(\frac{2 \pi}{T}\) = \(\frac{2 \pi}{8}\) = \(\frac{\pi}{4}\) rad/s
The total energy, E = \(\frac{1}{2}\)kA² and the potential
energy = \(\frac{1}{2}\)kx²
Therefore, from the data,

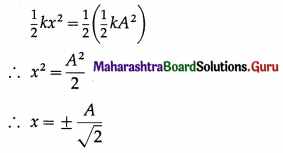
Assuming that the particle starts from the mean position, the equation of motion is
x = A sin ωt

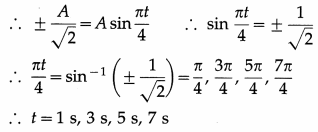
Therefore, in one oscillation, the particle’s potential energy is half the total energy 1 s, 3 s, 5 s and 7 s after passing through the mean position.

Question 39.
Define practical simple pendulum.
Answer:
Practical simple pendulum is defined as a small heavy sphere, called the bob, suspended by a light and inextensible string from a rigid support.

Question 40.
Under what conditions can we consider the oscillations of a simple pendulum to be linear simple harmonic?
Answer:
The oscillations of a simple pendulum are approximately linear simple harmonic only if

1. the amplitude of oscillation is very small compared to its length
2. the oscillations are in a single vertical plane.

Question 41.
What is the effect of mass and amplitude on the period of a simple pendulum ?
Answer:
The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum. This is the law of mass.
The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small. This is the law of isochronism. If the amplitude is large, the motion is periodic but not simple harmonic.

Question 42.
From the definition of linear SHM, derive an expression for the angular frequency of a body performing linear SHM.
Answer:
When a body of mass m performs linear SHM, the restoring force on it is always directed towards the mean position and its magnitude is directly proportional to the magnitude of the displacement of the body from the mean position. Thus, if \(\vec{F}\) is the force acting on the body when its displacement from the mean position is \(\vec{x}\),
\(\vec{F}\) = m\(\vec{a}\) = – kx\(\vec{x}\)
where the constant k, the force per unit displacement, is called the force constant.
Let \(\frac{k}{m}\) = ω², a constant.
∴ Acceleration, a = –\(\frac{k}{m}\) = – ω²x
∴ The angular frequency,

Question 43.
A simple pendulum is set into oscillations in a uniformly travelling car along a horizontal road. What happens to its period if the car takes a sudden turn towards the left ?
Answer:
The equilibrium position of the string makes an angle θ = tan^-1(a_c/g) with the vertical due to the centrifugal force to the right.
The centripetal acceleration, a_c, is horizontal and towards the left. The acceleration due to gravity is vertically downward.
∴ g_eff = \(\sqrt{g^{2}+a_{\mathrm{c}}^{2}}\)
so that the period of oscillation T = \(2 \pi \sqrt{L / g_{\text {eff }}}\)
∴ As the car takes a sudden left turn, the period of oscillation decreases.

Question 44.
Define a seconds pendulum. Find an expression for its length at a given place. Show that the length of a seconds pendulum has a fixed value at a given place.
Answer:
(1) Seconds pendulum: A simple pendulum of period two seconds is called a seconds pendulum.

(2) The period of a simple pendulum is
T = \(2 \pi \sqrt{\frac{L}{g}}\)
For a seconds pendulum, T = 2s.
∴ 2 = \(2 \pi \sqrt{\frac{L}{g}}\) ∴ L = \(\frac{g}{\pi^{2}}\)
This expression gives the length of the seconds pendulum at a place where acceleration due to gravity is g.

(3) At a given place, the value of g is constant.
∴ L = g/π² = a fixed value, at a given place.

[Note : Because the effective gravitational acceleration varies from place to place, the length of a seconds pendulum should be changed in direct proportion. Since the effective gravitational acceleration increases from the equator to the poles, so should the length of a seconds pendulum be increased.]

Question 45.
Two simple pendulums have lengths in the ratio 1 : 9. What is the ratio of their periods at a given place ?
Answer:

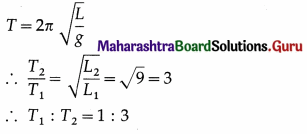
Question 46.
If the length of a seconds pendulum is doubled, what will be the new period?
Answer:

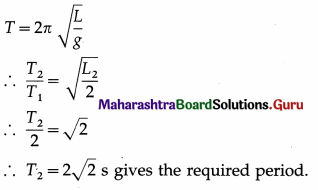
Question 47.
Distinguish between a simple pendulum and a conical pendulum.
Answer:

Simple pendulum	Conical pendulum
1. The oscillations of the bob are in a vertical plane.	1. The bob performs UCM in a horizontal plane and the string traces out a cone of constant semivertical angle.
2. The energy of the bob transfers back and forth between kinetic energy and potential energy, while its total mech­anical energy remains con­stant.	2. The gravitational PE of the bob being constant may be taken to be zero. The total mechanical energy remains constant and is entirely kin­etic.
3. The period depends on the 3. length of the string and the acceleration due to gravity. T =2π\(\sqrt{L / g}\)	3. The period depends on the length of the string, the ac­celeration due to gravity and cosine of the semiverti­cal angle. T =2π\(\sqrt{L \cos \theta / g}\)

Question 48.
Solve the following.

Question 1.
A simple pendulum of length 1 m has a bob of mass 10 g and oscillates freely with an amplitude of 2 cm. Find its potential energy at the extreme position. [g = 9.8 m/s²]
Solution :
Data : L = 1 m, m = 10 g = 10 × 10^-3 kg = 10^-2 kg, g = 9.8 m/s², A = 2 cm = 0.02 m
Period of a simple pendulum, T = \(2 \pi \sqrt{\frac{L}{g}}\)

Question 2.
The period of oscillation of a simple pendulum increases by 20% when the length of the pendulum is increased by 44 cm. Find its
(i) initial length
(ii) initial period of oscillation at a place where g is 9.8 m/s².
Solution:
Let T and L be the initial period and length of the pendulum. Let T₁ and L₁ be the final period and length.
Data : T₁ = T + 0.2 T = 1.2 T, L₁ = L + 0.44 m

Squaring and cross-multiplying, we get,
L + 0.44 = 1.44 L
∴ 0. 44 L = 0.44
∴ L = \(\frac{0.44}{0.44}\) = 1 m
∴ T = 2π\(\sqrt{\frac{L}{g}}\) = 2 × 3.142 × \(\sqrt{\frac{1}{9.8}}\)
= 2.007 s

Question 3.
Calculate the length of a seconds pendulum at a place where g = 9.81 m/s².
Answer:
Data : T = 2 s, g = 9.81 m/s²
Period of a simple pendulum, T = \(2 \pi \sqrt{\frac{L}{g}}\)
For a seconds pendulum, 2 = \(2 \pi \sqrt{\frac{L}{g}}\)
∴ The length of the seconds pendulum,
L = \(\frac{g}{\pi^{2}}\) = \(\frac{9.81}{(3.142)^{2}}\) = 0.9937

Question 4.
A clock regulated by a seconds pendulum keeps correct time. During summer the length of the pendulum increases to 1.01 m. How much will the clock gain or lose in one day ? [g = 9.8 m/s²]
Solution:
Data: L = 1.01 m, g = 9.8 m/s²

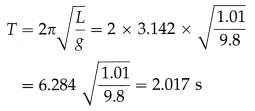
The period of a seconds pendulum is 2 seconds. Hence, the given pendulum clock will lose 0.017 s in 2.017 s during summer.
∴ Time lost in 24 hours
= \(\frac{24 \times 3600 \times 0.017}{2.017}\)s = 728.1 s
The given pendulum clock will lose 728.1 seconds per day during summer.

Question 5.
A small drop of mercury oscillates simple harmonically inside a watch glass whose radius of curvature is 2.5 m. Find the period of the motion. [g = 9.8m/s²]
Solution :
Data : R = 2.5 m, g = 9.8 m/s²
Consider a small drop of mercury on a watch glass of radius of curvature R.

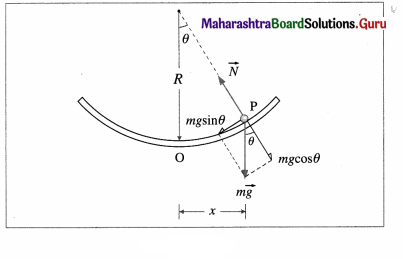
Away from its equilibrium position O, its weight \(m \vec{g}\) is resolved into two perpendicular components : mg cos θ normal to the concave surface and mg sin θ tangential to the surface, mg cos θ is balanced by the normal reaction (\(\vec{N}\)) of the surface while mg sin θ constitutes the restoring force that brings the drop back to O. If θ is small and in radian,
restoring force, F = ma = – mg sin θ
= – mg θ
= -mg\(\frac{x}{R}\)
∴ The acceleration per unit displacement, |\(\frac{a}{x}\)| = \(\frac{g}{R}\)
∴ The period of the motion, T = \(\frac{2 \pi}{\sqrt{|a / x|}}\) = \(2 \pi \sqrt{\frac{R}{g}}\)
Data : R = 2.5 m, g = 9.8 m/s²
∴ The period of oscillation is
T = 2 × 3.142\(\sqrt{\frac{2.5}{9.8}}\) = 6.284 × 0.5051 = 3.174 s.

Question 49.
Explain angular or torsional oscillations.
Hence obtain the differential equation of the motion.
Answer:
Suppose a disc is suspended from its centre by a wire or a twistless thread such that the disc remains horizontal, as shown in below figure. The rest position of

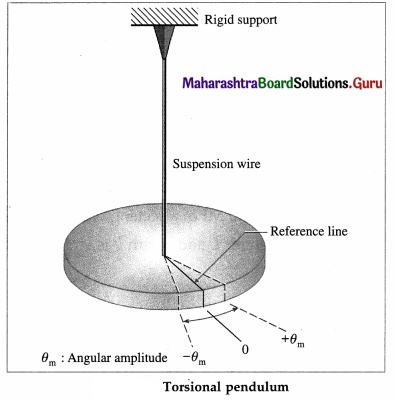
the disc is marked by a reference line. When the disc is rotated in the horizontal plane by a small angular displacement 0 = 0m from its rest position (θ = θ_m), the suspension wire is twisted. When the disc is released, it oscillates about the rest position in angular or torsional oscillation with angular amplitude θ_m.

The device is called a torsional pendulum and the springiness or elasticity of the motion is associated with the twisting of the suspension wire. The twist in either direction stores potential energy in the wire and provides an alternating restoring torque, opposite in direction to the angular displacement. The motion is governed by this torque.

If the magnitude of the restoring torque (τ) is proportional to the angular displacement (θ), τ ∝ (-θ) or τ = – cθ … (1)
where the constant of proportionality c is called the torsion constant, that depends on the length, diameter and material of the suspension wire. In this case, the oscillations will be simple harmonic.

Let I be the moment of inertia (MI) of the oscillating disc.
Torque = MI × angular acceleration
τ = Iα = I\(\frac{d^{2} \theta}{d t^{2}}\)
Hence, from EQ. (1),

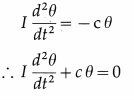
This is the differential equation of angular SHM.
[Note : Angular displacement being a dimensionless quantity, the SI unit of torsion constant is the same as that of torque = the newton-metre (N-m)]

Question 50.
Define angular SHM. State the differential equation of angular SHM. Hence derive an expression for the period of angular SHM in terms of
(i) the torsion constant
(ii) the angular acceleration.
Answer:
Definition : Angular SHM is defined as the oscillatory motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.
The differential equation of angular SHM is
I\(\frac{d^{2} \theta}{d t^{2}}\) + c θ = 0 … (1)
where I = moment of inertia of the
where I = moment of inertia of the oscillating body,
\(\frac{d^{2} \theta}{d t^{2}}\) = angular acceleration of the body when its angular displacement is θ, and c = torsion constant of the suspension wire,

Question 51.
Solve the following :

Question 1.
A bar magnet of moment 10 A.m² is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 39 μT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 10°.
Solution :
Data : μ = 10 A.m², Bh = 3.9 × 10^-5 T, θ = 10°
The magnitude of the torque is τ = – μB_h sin θ = (10)(3.9 × 10^-5) sin 10°
= (3.9 × 10^-4)(0.1736) = 6.770 × 10^-5 N.m

Question 2.
A disc, of radius 12 cm and mass 250 g, is suspended horizontally by a long wire at its centre. Its period T₁ of angular SHM is measured to be 8.43 s. An irregularly shaped object X is then hung from the same wire and its period T₂ is found to be 4.76 s. What is the rotational inertia of object X about its suspension axis ?
Solution:
Data : R = 0.12 m, M = 0.25 kg, T, = 8.43 s, T₂ = 4.76 s
The MI of the disc about the rotation axis (perpendicular through its centre) is = \(\frac{1}{2}\) MR²

Question 52.
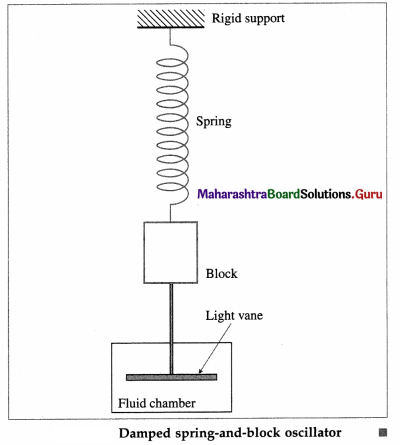
What is meant by damped oscillations ? Draw a neat, labelled diagram of a damped spring-and-block oscillator.
Answer:
Oscillations of gradually decreasing amplitude are called damped oscillations. Oscillations of a system in the presence of dissipative frictional forces are damped.

The dissipative damping force removes energy from the system which requires external periodic force to continue.

Below Figure shows a spring-and-block oscillator attached with a light vane that moves in a fluid with viscosity. When the system is set into oscillation, the amplitude decreases for each oscillation due to the viscous drag on the vane.

Question 53.
Write the differential equation of motion for an oscillator in the presence of a damping force directly proportional to the velocity. Under what condition is the motion oscillatory? Hence, discuss the frequency, amplitude and energy of the damped oscillations.
OR
Oscillations in the presence of a force proportional to the velocity are periodic but not simple harmonic. Explain.
OR
The presence of a damping force changes the character of a simple harmonic motion. Explain this qualitatively.
Answer:
Consider the oscillations of a body in the presence of a dissipative frictional force such as viscous drag or fluid friction. Such a force is proportional to the velocity of the body and is in a direction opposite to that of the velocity. If the fluid flow past the body is streamline, then by Stokes’ law, the resistive force is
f = -βv = -β\(\frac{d x}{d t}\)… (1)
where v = \(\frac{d x}{d t}\) is the velocity and β is a positive constant of proportionality called the damping constant.
The linear restoring force on the oscillator is F = -kx … (2)
where k is the force constant. If m is the mass of the oscillator and its acceleration is \(\frac{d^{2} x}{d t^{2}}\)

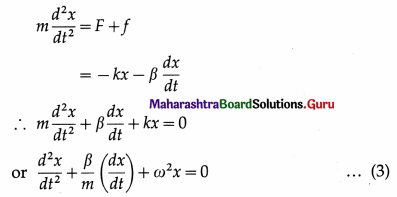
where ω² = \(\frac{k}{m}\). Equation (3) is the differential equation of the oscillator in presence of a resistive force directly proportional to the velocity.
The solution of the above differential equation obtained using standard mathematical technique is

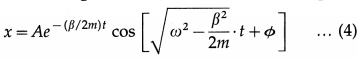
where constants A and φ can be determined in the usual way from the initial conditions. In writing this solution, it is assumed β is less than 2mω, i.e., the resistive term is relatively small.

In Eq. (4),
(1) the harmonic term, cos \(\left[\sqrt{\omega^{2}-\frac{\beta^{2}}{2 m}} t+\phi\right]\), that the motion is oscillatory with angular frequency ω’ = \(\sqrt{\omega^{2}-\frac{\beta^{2}}{4 m^{2}}}\) if β is less than 2mω. The harmonic term can also be written in terms of a sine function with the same ω’.
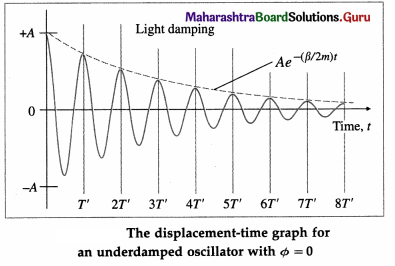
(2) A’ = Ae^-(β/2m)t is the amplitude of the oscillation. The exponential factor e^-(β/2m)t steadily decreases the amplitude of the motion, making it approach zero for large t. Hence, the motion is said to be damped oscillation or damped harmonic motion.
(3) the total energy, \(\frac{1}{2}\)m(ω’)², decays exponentially with time as the amplitude decreases. The energy is dissipated in the form of heat by the damping force.
(4) the period of the damped oscillations is

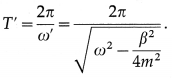
∴ T is greater than 2π/ω.
Thus, the motion is periodic but not simple harmonic because the amplitude steadily decreases.

Notes :

1. The energy decreases faster than the amplitude.
2. For β < 2mω, the larger the value of β, the faster the amplitude decreases. The condition is called underdamping.
3. When β = 2mω = \(2 \sqrt{k m}\) km, ω’ = 0, i.e., the system no longer oscillates. When displaced and released, it returns to its equilibrium position without oscillation. The condition is called critical damping.
4. If β > 2mω, the system is said to overdamped or dead beat. Again, the system does not oscillate but returns to equilibrium position more slowly than for critical damping.
5. All practical cases of so called free oscillations, such as that of a simple pendulum or a tuning fork, are damped. We also encounter damped oscillations in electrical circuits containing inductance, capacitance and resistance due to resistive losses. While in many cases it is desirable to minimize damping, in ammeters and voltmeters the oscillations of the pointer are designed to be dead beat.

Question 54.
Solve the following.

Question 1.
For a damped spring-and-block oscillator, the mass of the block is 0.2 kg, the spring constant is 90 N/m and the damping constant is 0.06 kg/s. Calculate
(i) the period of oscillation
(ii) the time taken for its amplitude to become half its initial value.
Solution :
Data : m = 0.2 kg, k = 90 N/m, β = 0.06 kg/s
(i) The period of the damped oscillation is

(ii) The amplitude of the damped oscillation is
A’ = Ae^-(β/2m)t
If the amplitude becomes half the initial amplitude A at time f,

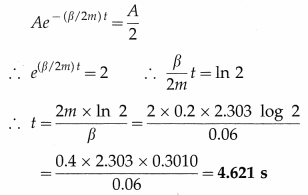
Question 2.
A steel sphere of mass 0.02 kg attains a terminal speed vi = 0.5 m/s when dropped into a tall cylinder of oil. The same sphere is then attached to the free end of an ideal vertical spring of spring constant 8 N/m. The sphere is immersed in the same oil and set into vertical oscillation. Find
(i) the damping constant
(ii) the angular frequency of the damped SHM.
(iii) Hence, write the equation for displacement of the damped SHM as a function of time, assuming that the initial amplitude is 10 cm. [g = 10 m/s²]
Solution :
Data : m = 0.02 kg, v_t = 0.5 m/s, k = 8 N/m,
A = 10 cm = 0.1 m, g = 10 m/s²
When the sphere falls with terminal velocity in oil, the resultant force on it is zero. Therefore, the
The equation of motion of the damped oscillation is resistive force and its weight are equal in magnitude and opposite in direction.
∴ |F_r| = βv_t = mg
where β is the damping constant.
∴ β = \(\frac{m g}{v_{\mathrm{t}}}\) = \(\frac{0.02 \times 10}{0.5}\) = 0.4 kg/s
The angular frequency of the damped oscillation in oil,

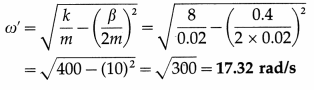
The equation of motion of the damped oscillation is
x = Ae^(β/2m)t cos(w’t + φ)
∴ x = (0.1 m)e^-(0.4/004)t cos (17.32t + φ)
x = (0.1 m) e^-10t cos(17.32t + φ)

Question 55.
Explain
(1) free vibrations
(2) forced vibrations.
Answer:
(1) Free vibrations : A body capable of vibrations is said to perform free vibrations when it is disturbed from its equilibrium position and left to itself.

In the absence of dissipative forces such as friction due to surrounding air and internal forces, the total energy and hence the amplitude of vibrations of the body remains constant. The frequencies of the free vibrations of a body are called its natural frequencies and depend on the body itself.

In the absence of a maintaining force, in practice, the total energy and hence the amplitude decreases due to dissipative forces and the vibration is said to be damped. The frequency of damped vibrations is less than the natural frequency.

(2) Forced vibrations : The vibrations of a body in response to an external periodic force are called forced vibrations.

The external force supplies the necessary energy to make up for the dissipative losses. The frequency of the forced vibrations is equal to the frequency of the external periodic force.

The amplitude of the forced vibrations depends upon the mass of the vibrating body, the amplitude of the external force, the difference between the natural frequency and the frequency of the periodic force, and the extent of damping.

Question 56.
Distinguish between free vibrations and forced vibrations.
Answer:

Free vibrations	Forced vibrations
1. Free vibrations are pro­duced when a body is disturbed from its equilibrium position and released. Ex. Simple pendulum.	1. Forced vibrations are pro­duced by an external periodic force. Ex. Musical instrument having a sounding board.
2. The frequency of free vibra­tions depends on the body and is called its natural frequency.	2. The frequency of forced vi­brations is equal to that of the external periodic force.
3. The energy of the body remains constant only in the absence of friction, air resis­tance, etc.	3. The energy of the body is maintained constant by the external periodic force.

Question 57.
Explain resonance.
Answer:
Resonance : If a body is made to vibrate by an external periodic force, whose frequency is equal to the natural frequency (or nearly so) of the body, the body vibrates with maximum amplitude. This phenomenon is called resonance.

The corresponding frequency is called the resonant frequency.

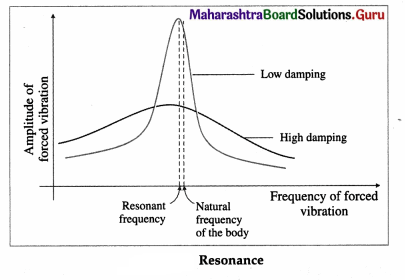
For low damping, the amplitude of vibrations has a sharp maximum at resonance, as shown. The flatter curve without a pronounced maximum is for high damping.

Suppose several pendulums-A, B, C, D and E are coupled to a heavier pendulum Z, by suspending them from a stretched cord, and that only the length of C is the same as that of Z. When Z is set into oscillation perpendicular to the cord PQ, the others are also set into forced oscillations in parallel vertical planes. Their amplitudes vary but those of A, B, D and E never become very large because the frequency of Z is not the same as the natural frequency of any of them. On the other hand, C will be in resonant oscillation and its amplitude will be large.

Question 58.
The differential equation of SHM for a seconds pendulum is
(A) \(\frac{d^{2} x}{d t^{2}}\) + x = 0
(B) \(\frac{d^{2} x}{d t^{2}}\) + πx = 0
(C) \(\frac{d^{2} x}{d t^{2}}\) + 4πx = 0
(D) \(\frac{d^{2} x}{d t^{2}}\) + π²x = 0.
Answer:
(D) \(\frac{d^{2} x}{d t^{2}}\) + π²x = 0.

Question 59.
The phase change of a particle performing SHM between successive passages through the mean position is
(A) 2π rad
(B) π rad
(C) \(\frac{\pi}{2}\) rad
(D) \(\frac{\pi}{4}\) rad.
Answer:
(B) π rad

Question 60.
If the equation of motion of a particle performing SHM is x = 0.028 cos (2.8πt + π) (all quantities in SI units), the frequency of the motion is
(A) 0.7 Hz
(B) 1.4 Hz
(C) 2.8 Hz
(D) 14 Hz.
Answer:
(B) 1.4 Hz

Question 61.
A spring-and-block system constitutes a simple harmonic oscillator. To double the frequency of oscillation, the mass of the block must be ….. the initial mass.
(A) \(\frac{1}{4}\) times
(B) half
(C) double
(D) 4 times
Answer:
(A) \(\frac{1}{4}\) times

Question 62.
A horizontal spring-and-block system consists of a block of mass 1 kg, resting on a frictionless surface, and an ideal spring. A force of 10 N is required to compress the spring by 10 cm. The spring constant of the spring is
(A) 100 N.m^-1
(B) 10N.m^-1
(C) N.m^-1
(D) 0.1 N.m^-1.
Answer:
(C) N.m^-1

Question 63.
A vertical spring-and-block system has a block of mass 10 g and oscillates with a period 1 s. The period of SHM of a block of mass 90 g, suspended from the same spring, is
(A) \(\frac{1}{9}\)s
(B) \(\frac{1}{3}\)s
(C) 3 s
(D) 9 s.
Answer:
(C) 3 s

Question 64.
A simple harmonic oscillator has an amplitude A and period T. The time required by the oscillator to cover the distance from x = A to x = \(\frac{A}{2}\) is
(A) \(\frac{T}{2}\)
(B) \(\frac{T}{3}\)
(C) \(\frac{T}{4}\)
(D) \(\frac{T}{6}\)
Answer:
(D) \(\frac{T}{6}\)

Question 65.
The period of SHM of a particle with maximum velocity 50 cm/s and maximum acceleration 10 cm/s² is
(A) 31.42 s
(B) 6.284 s
(C) 3.142 s
(D) 0.3142 s.
Answer:
(C) 3.142 s

Question 66.
A particle executing SHM of amplitude 5 cm has an acceleration of 27 cm/s² when it is 3 cm from the mean position. Its maximum velocity is
(A) 15 cm/s
(B) 30 cm/s
(C) 45 cm/s
(D) 60 cm/s.
Answer:
(A) 15 cm/s

Question 67.
A particle performs linear SHM with a period of 6 s, starting from the positive extremity. At time t = 7 s, its displacement is 3 cm. The amplitude of the motion is
(A) 4 cm
(B) 6 cm
(C) 8 cm
(D) 12 cm.
Answer:
(B) 6 cm

Question 68.
A spring-and-block oscillator with an ideal spring of force constant 180 N/m oscillates with a frequency of 6 Hz. The mass of the block is, approximately,
(A) \(\frac{1}{8}\) kg
(B) \(\frac{1}{4}\) kg
(C) 4 kg
(D) 8 kg.
Answer:
(A) \(\frac{1}{8}\) kg

Question 69.
A particle executing linear SHM has velocities v₁ and v₂ at distances x₁ and x₂, respectively, from the mean position. The angular velocity of the particle is

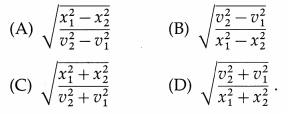
Answer:
(B) \(\sqrt{\frac{v_{2}^{2}-v_{1}^{2}}{x_{1}^{2}-x_{2}^{2}}}\)

Question 70.
A particle executes linear SHM with period 12 s. To traverse a distance equal to half its amplitude from the equilibrium position, it takes
(A) 6s
(B) 4s
(C) 2s
(D) 1s.
Answer:
(D) 1s

Question 71.
The minimum time taken by a particle in SHM with period T to go from an extreme position to a point half way to the equilibrium position is
A. \(\frac{T}{12}\)
B. \(\frac{T}{8}\)
C. \(\frac{T}{6}\)
D. \(\frac{T}{4}\)
Answer:
C. \(\frac{T}{6}\)

Question 72.
In simple harmonic motion, the acceleration of a particle is zero when its
(A) velocity is zero
(B) displacement is zero
(C) both velocity and displacement are zero
(D) both velocity and displacement are maximum.
Answer:
(B) displacement is zero

Question 73.
The acceleration of a particle performing SHM is 3m/s² at a distance of 3 cm from the mean position.
The periodic time of the motion is
(A) 0.02 π s
(B) 0.04 π s
(C) 0.2 π s
(D) 2 π s.
Answer:
(C) 0.2 π s

Question 74.
A particle performing linear SHM with a frequency n is confined within limits x = ±A. Midway between an extremity and the equilibrium position, its speed is
(A) \(\sqrt{6}\)nA
(B) \(\sqrt{3}\)πnA
(C) \(\sqrt{6}\)πnA
(D) \(\sqrt{12}\)πnA
Answer:
(B) \(\sqrt{3}\)πnA

Question 75.
The total energy of a particle executing SHM is proportional to
(A) the frequency of oscillation
(B) the square of the amplitude of motion
(C) the velocity at the equilibrium position
(D) the displacement from the equilibrium position.
Answer:
(B) the square of the amplitude of motion

Question 76.
Two spring-and-block oscillators oscillate harmonically with the same amplitude and a constant phase difference of 90°. Their maximum velocities are v and v + x. The value of x is
(A) 0
(B) \(\frac{v}{3}\)
(C) 2
(D) \(\frac{v}{\sqrt{2}}\).
Answer:
(A) 0

Question 77.
If the length of a simple pendulum is increased to 4 times its initial length, its frequency of oscillation will
(A) reduce to half its initial frequency
(B) increase to twice its initial frequency
(C) reduce to \(\frac{1}{4}\) th its initial frequency
(D) increase to 4 times its initial frequency.
Answer:
(A) reduce to half its initial frequency

Question 78.
If the length of a simple pendulum is doubled keeping its amplitude constant, its energy will be
(A) unchanged
(B) doubled
(C) halved
(D) increased to four times the initial energy.
Answer:
(C) halved

Question 79.
The amplitude of oscillations of a simple pendulum of period T and length L is increased by 5%. The new period of the pendulum will be
(A) T/8
(B) T/4
(C) T/2
(D) T.
Answer:
(D) T.

Question 80.
In 20 s, two simple pendulums, P and Q, complete 9 and 7 oscillations, respectively, on the Earth. On the
Moon, where the acceleration due to gravity is \(\frac{1}{6}\)th that on the Earth, their periods are in the ratio (A) 8 : 1
(B) 9 : 7
(C) 7 : 9
(D) 3 : 14.
Answer:
(C) 7 : 9

Question 81.
If T is the time period of a simple pendulum in an elevator at rest, its time period in a freely falling elevator will be
(A) \(\frac{T}{\sqrt{2}}\)
(B) \(\sqrt{2}\)T
(C) 2T
(D) infinite.
Answer:
(D) infinite.

Question 82.
A seconds pendulum is suspended in an elevator moving with a constant speed in the downward direction. The periodic time (T) of that pendulum is
(A) less than two seconds
(B) equal to two seconds
(C) greater than two seconds
(D) very much greater than two seconds.
Answer:
(B) equal to two seconds

Question 83.
The total work done by a restoring force in simple harmonic motion of amplitude A and angular frequency ω, in one oscillation is
(A) \(\frac{1}{2}\)mA²ω²
(B) zero
(C) mA²ω²
(D) \(\frac{1}{2}\)mAω.
Answer:
(B) zero

Question 84.
Two particles perform linear simple harmonic motion along the same path of length 2A and period T as shown in the graph below. The phase difference between them is

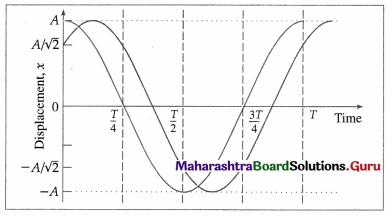
(A) zero rad
(B) \(\frac{\pi}{4}\) rad
(C) \(\frac{\pi}{2}\) rad
(D) \(\frac{3 \pi}{4}\) rad
Answer:
(B) \(\frac{\pi}{4}\) rad

Question 85.
The average displacement over a period of SHM is
(A = amplitude of SHM)
(A) 0
(B) A
(C) 2A
(D) 4A.
Answer:
(A) 0

Question 86.
Two springs of force constants k₁ and k₂(k₁ > k₂) are stretched by the same force. If W₁ and W₂ be the work done in stretching the springs, then
(A) W₁ = W₂
(B) W₁ < W₂
(C) W₁ > W₂
(D) W₁ = W₂ = 0.
Answer:
(B) W₁ < W₂

Question 87.
Two bar magnets of identical size have magnetic moments M_A and M_B. If the magnet A oscillates at twice the frequency of magnet B, then
(A) M_A = 2M_B
(B) M_A = 8M_B
(C) M_A = 4M_B
(D) M_B = 8M_A.
Answer:
(C) M_A = 4M_B

Question 88.
A magnet is suspended to oscillate in the horizontal plane. It makes 20 oscillations per minute at a place where the dip angle is 30° and 15 oscillations per minute where the dip angle is 60°. The ratio of the Earth’s total magnetic field at the two places is
(A) 3\(\sqrt{3}\) : 16
(B) 16 : 9\(\sqrt{3}\)
(C) 4 : 9\(\sqrt{3}\)
(D) 9 : 16\(\sqrt{3}\).
Answer:
(B) 16 : 9\(\sqrt{3}\)