Bhagya

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.4

I. Evaluate the following limits:

Question 1.
\(\lim _{\theta \rightarrow 0}\left[\frac{\sin (m \theta)}{\tan (n \theta)}\right]\)
Solution:

Question 2.
\(\lim _{\theta \rightarrow 0}\left[\frac{1-\cos 2 \theta}{\theta^{2}}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 0}\left[\frac{x \cdot \tan x}{1-\cos x}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 0}\left(\frac{\sec x-1}{x^{2}}\right)\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{1-\cos (n x)}{1-\cos (m x)}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow \frac{\pi}{6}}\left[\frac{2-{cosec} x}{\cot ^{2} x-3}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow \frac{\pi}{4}}\left[\frac{\cos x-\sin x}{\cos 2 x}\right]\)
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{\cos (a x)-\cos (b x)}{\cos (c x)-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow \pi}\left[\frac{\sqrt{1-\cos x}-\sqrt{2}}{\sin ^{2} x}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow \frac{\pi}{4}}\left[\frac{\tan ^{2} x-\cot ^{2} x}{\sec x-{cosec} x}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow \frac{\pi}{6}}\left[\frac{2 \sin ^{2} x+\sin x-1}{2 \sin ^{2} x-3 \sin x+1}\right]\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Permutations and Combination Ex 3.2

Question 1.
Evaluate:
(i) 8!
Solution:
8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320

(ii) 10!
Solution:
10!
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 3628800

(iii) 10! – 6!
Solution:
10! – 6!
= 10 × 9 × 8 × 7 × 6! – 6!
= 6! (10 × 9 × 8 × 7 – 1)
= 6! (5040 – 1)
= 6 × 5 × 4 × 3 × 2 × 1 × 5039
= 3628080

(iv) (10 – 6)!
Solution:
(10 – 6)!
= 4!
= 4 × 3 × 2 × 1
= 24

Question 2.
Compute:
(i) \(\frac{12 !}{6 !}\)
Solution:
\(\frac{12 !}{6 !}=\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 !}{6 !}\)
= 12 × 11 × 10 × 9 × 8 × 7
= 665280

(ii) \(\left(\frac{12}{6}\right) !\)
Solution:
\(\left(\frac{12}{6}\right) !\)
= 2!
= 2 × 1
= 2

(iii) (3 × 2)!
Solution:
(3 × 2)!
= 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720

(iv) 3! × 2!
Solution:
3! × 2!
= 3 × 2 × 1 × 2 × 1
= 12

(v) \(\frac{9 !}{3 ! 6 !}\)
Solution:
\(\frac{9 !}{3 ! 6 !}=\frac{9 \times 8 \times 7 \times 6 !}{(3 \times 2 \times 1) \times 6 !}=84\)

(vi) \(\frac{6 !-4 !}{4 !}\)
Solution:
\(\frac{6 !-4 !}{4 !}=\frac{6 \times 5 \times 4 !-4 !}{4 !}=\frac{4 !(6 \times 5-1)}{4 !}=29\)

(vii) \(\frac{8 !}{6 !-4 !}\)
Solution:
\(\frac{8 !}{6 !-4 !}=\frac{8 \times 7 \times 6 \times 5 \times 4 !}{6 \times 5 \times 4 !-4 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4 !}{4 !(6 \times 5-1)}\)
= \(\frac{1680}{29}\)
= 57.93

(viii) \(\frac{8 !}{(6-4) !}\)
Solution:
\(\frac{8 !}{(6-4) !}=\frac{8 !}{2 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\)
= 20160

Question 3.
Write in terms of factorials
(i) 5 × 6 × 7 × 8 × 9 × 10
Solution:
5 × 6 × 7 × 8 × 9 × 10 = 10 × 9 × 8 × 7 × 6 × 5
Multiplying and dividing by 4!, we get
= \(\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 !}{4 !}\)
= \(\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 !}\)
= \(\frac{10 !}{4 !}\)

(ii) 3 × 6 × 9 × 12 × 15
Solution:
3 × 6 × 9 × 12 × 15
= 3 × (3 × 2) × (3 × 3) × (3 × 4) × (3 × 5)
= (3⁵) (5 × 4 × 3 × 2 × 1)
= 3⁵ (5!)

(iii) 6 × 7 × 8 × 9
Solution:
6 × 7 × 8 × 9 = 9 × 8 × 7 × 6
Multiplying and dividing by 5!, we get
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 !}{5 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 !}\)
= \(\frac{9 !}{5 !}\)

(iv) 5 × 10 × 15 × 20
Solution:
5 × 10 × 15 × 20
= (5 × 1) × (5 × 2) × (5 × 3) × (5 × 4)
= (5⁴) (4 × 3 × 2 × 1)
= (5⁴) (4!)

Question 4.
Evaluate: \(\frac{n !}{r !(n-r) !}\) for
(i) n = 8, r = 6
(ii) n = 12, r = 12
(iii) n = 15, r = 10
(iv) n = 15, r = 8
Solution:

Question 5.
Find n, if
(i) \(\frac{n}{8 !}=\frac{3}{6 !}+\frac{1 !}{4 !}\)
Solution:

(ii) \(\frac{n}{6 !}=\frac{4}{8 !}+\frac{3}{6 !}\)
Solution:

(iii) \(\frac{1 !}{n !}=\frac{1 !}{4 !}-\frac{4}{5 !}\)
Solution:

(iv) (n + 1)! = 42 × (n -1)!
Solution:
(n + 1)! = 42(n – 1)!
∴ (n + 1) n (n – 1)! = 42(n – 1)!
∴ n² + n = 42
∴ n² + n – 42 = 0
∴ (n + 7)(n – 6) = 0
∴ n = -7 or n = 6
But n ≠ -7 as n ∈ N
∴ n = 6

(v) (n + 3)! = 110 × (n + 1)!
Solution:
(n + 3)! = (110) (n + 1)!
∴ (n + 3)(n + 2)(n + 1)! = 110(n + 1)!
∴ (n + 3) (n + 2) = (11) (10)
Comparing on both sides, we get
n + 3 = 11
∴ n = 8

Question 6.
Find n, if:
(i) \(\frac{(17-n) !}{(14-n) !}=5 !\)
Solution:

∴ (17 – n) (16 – n) (15 – n) = 6 × 5 × 4
Comparing on both sides, we get
17 – n = 6
∴ n = 11

(ii) \(\frac{(15-n) !}{(13-n) !}=12\)
Solution:
\(\frac{(15-n) !}{(13-n) !}=12\)
∴ \(\frac{(15-n)(14-n)(13-n) !}{(13-n) !}=12\)
∴ (15 – n) (14 – n) = 4 × 3
Comparing on both sides, we get
∴ 15 – n = 4
∴ n = 11

(iii) \(\frac{n !}{3 !(n-3) !}: \frac{n !}{5 !(n-5) !}=5: 3\)
Solution:

∴ 12 = (n – 3)(n – 4)
(n – 3)(n – 4) = 4 × 3
Comparing on both sides, we get
n – 3 = 4
∴ n = 7

(iv) \(\frac{n !}{3 !(n-3) !}: \frac{n !}{5 !(n-7) !}=1: 6\)
Solution:

∴ 120 = (n – 3)(n – 4) (n – 5)(n – 6)
∴ (n – 3)(n – 4) (n – 5)(n – 6) = 5 × 4 × 3 × 2
Comparing on both sides, we get
n – 3 = 5
∴ n = 8

(v) \(\frac{(2 n) !}{7 !(2 n-7) !}: \frac{n !}{4 !(n-4) !}=24: 1\)
Solution:


(2n – 1)(2n – 3)(2n – 5) = \(\frac{24 \times 7 \times 6 \times 5}{16}\)
∴ (2n – 1)(2n – 3)(2n – 5) = 9 × 7 × 5
Comparing on both sides. We get
∴ 2n – 1 = 9
∴ n = 5

Question 7.
Show that \(\frac{n !}{r !(n-r) !}+\frac{n !}{(r-1) !(n-r+1) !}=\frac{(n+1) !}{r !(n-r+1) !}\)
Solution:

Question 8.
Show that \(\frac{9 !}{3 ! 6 !}+\frac{9 !}{4 ! 5 !}=\frac{10 !}{4 ! 6 !}\)
Solution:

Question 9.
Show that \(\frac{(2 n) !}{n !}\) = 2n (2n – 1)(2n – 3)…5.3.1
Solution:

Question 10.
Simplify
(i) \(\frac{(2 n+2) !}{(2 n) !}\)
Solution:

(ii) \(\frac{(n+3) !}{\left(n^{2}-4\right)(n+1) !}\)
Solution:

(iii) \(\frac{1}{n !}-\frac{1}{(n-1) !}-\frac{1}{(n-2) !}\)
Solution:

(iv) n[n! + (n – 1)!] + n²(n – 1)! + (n + 1)!
Solution:

(v) \(\frac{n+2}{n !}-\frac{3 n+1}{(n+1) !}\)
Solution:

(vi) \(\frac{1}{(n-1) !}+\frac{1-n}{(n+1) !}\)
Solution:

(vii) \(\frac{1}{n !}-\frac{3}{(n+1) !}-\frac{n^{2}-4}{(n+2) !}\)
Solution:

(viii) \(\frac{n^{2}-9}{(n+3) !}+\frac{6}{(n+2) !}-\frac{1}{(n+1) !}\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.3

I. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt{6+x+x^{2}}-\sqrt{6}}{x}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 3}\left[\frac{\sqrt{2 x+3}-\sqrt{4 x-3}}{x^{2}-9}\right]\)
Solution:

Question 3.
\(\lim _{y \rightarrow 0}\left[\frac{\sqrt{1-y^{2}}-\sqrt{1+y^{2}}}{y^{2}}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 2}\left[\frac{\sqrt{2+x}-\sqrt{6-x}}{\sqrt{x}-\sqrt{2}}\right]\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow a}\left[\frac{\sqrt{a+2 x}-\sqrt{3 x}}{\sqrt{3 a+x}-2 \sqrt{x}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 2}\left[\frac{x^{2}-4}{\sqrt{x+2}-\sqrt{3 x-2}}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{\sqrt{1+\sqrt{2+x}}-\sqrt{3}}{x-2}\right]\)
Solution:

Question 4.
\(\lim _{y \rightarrow 0}\left[\frac{\sqrt{a+y}-\sqrt{a}}{y \sqrt{a+y}}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 0}\left(\frac{\sqrt{x^{2}+9}-\sqrt{2 x^{2}+9}}{\sqrt{3 x^{2}+4}-\sqrt{2 x^{2}+4}}\right)\)
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 1}\left[\frac{x^{2}+x \sqrt{x}-2}{x-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt{1+x^{2}}-\sqrt{1+x}}{\sqrt{1+x^{3}}-\sqrt{1+x}}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 4}\left[\frac{x^{2}+x-20}{\sqrt{3 x+4}-4}\right]\)
Solution:

Question 4.
\(\lim _{z \rightarrow 4}\left[\frac{3-\sqrt{5+z}}{1-\sqrt{5-z}}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 0}\left(\frac{3}{x \sqrt{9-x}}-\frac{1}{x}\right)\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 1 Complex Numbers Ex 1.4

Question 1.
Find the value of
(i) ω¹⁸
(ii) ω²¹
(iii) ω^-30
(iv) ω^-105
Solution:

Question 2.
If ω is the complex cube root of unity, show that
(i) (2 – ω)(2 – ω²) = 7
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
L.H.S. = (2 – ω)(2 – ω²)
= 4 – 2ω² – 2ω + ω³
= 4 – 2(ω² + ω) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
= R.H.S.

(ii) (1 + ω – ω²)⁶ = 64
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(iii) (1 + ω)³ – (1 + ω²)³ = 0
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(iv) (2 + ω + ω²)³ – (1 – 3ω + ω²)³ = 65
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(v) (3 + 3ω + 5ω²)⁶ – (2 + 6ω + 2ω²)³ = 0
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(vi) \(\frac{a+b \omega+c \omega^{2}}{c+a \omega+b \omega^{2}}\) = ω²
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(vii) (a + b) + (aω + bω²) + (aω² + bω) = 0
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(viii) (a – b)(a – bω)(a – bω²) = a³ – b³
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

(ix) (a + b)² + (aω + bω²)² + (aω²+ bω)² = 6ab
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1

Question 3.
If ω is the complex cube root of unity, find the value of
(i) ω + \(\frac{1}{\omega}\)
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
\(\omega+\frac{1}{\omega}=\frac{\omega^{2}+1}{\omega}=\frac{-\omega}{\omega}=-1\)

(ii) ω² + ω³ + ω⁴
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
ω² + ω³ + ω⁴
= ω²(1 + ω + ω²)
= ω²(0)
= 0

(iii) (1 + ω²)³
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(1 + ω²)³
= (-ω)³
= -ω³
= -1

(iv) (1 – ω – ω²)³ + (1 – ω + ω²)³
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(1 – ω – ω²)³ + (1 – ω + ω²)³
= [1 – (ω + ω²)]³ + [(1 + ω²) – ω]³
= [1 – (-1)]² + (-ω – ω)³
= 2³ + (-2ω)³
= 8 – 8ω³
= 8 – 8(1)
= 0

(v) (1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸)
Solution:
ω is the complex cube root of unity.
ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸)
= (1 + ω)(1 + ω²)(1 + ω)(1 + ω²) …..[∵ ω³ = 1, ω⁴ = ω]
= (-ω²)(-ω)(-ω²)(-ω)
= ω⁶
= (ω³)²
= (1)²
= 1

Question 4.
If α and β are the complex cube roots of unity, show that
(i) α² + β² + αβ = 0
(ii) α⁴ + β⁴ + α^-1β^-1 = 0
Solution:
α and β are the complex cube roots of unity.

Question 5.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are complex cube roots of unity, show that xyz = a³ + b³.
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.
∴ α = \(\frac{-1+i \sqrt{3}}{2}\) and β = \(\frac{-1-i \sqrt{3}}{2}\)

Question 6.
Find the equation in cartesian coordinates of the locus of z if
(i) |z| = 10
Solution:
Let z = x + iy
|z| = 10
|x + iy| = 10
\(\sqrt{x^{2}+y^{2}}\) = 10
∴ x² + y² = 100

(ii) |z – 3| = 2
Solution:
Let z = x + iy
|z – 3| = 2
|x + iy – 3| = 2
|(x – 3) + iy| = 2
\(\sqrt{(x-3)^{2}+y^{2}}\) = 2
∴ (x – 3)² + y² = 4

(iii) |z – 5 + 6i| = 5
Solution:
Let z = x + iy
|z – 5 + 6i| = 5
|x + iy – 5 + 6i| = 5
|(x – 5) + i(y + 6)| = 5
\(\sqrt{(x-5)^{2}+(y+6)^{2}}\) = 5
∴ (x – 5)² + (y + 6)² = 25

(iv) |z + 8| = |z – 4|
Solution:
Let z = x + iy
|z + 8| = |z – 4|
|x + iy + 8| = |x + iy – 4|
|(x + 8) + iy | = |(x – 4) + iy|
\(\sqrt{(x+8)^{2}+y^{2}}=\sqrt{(x-4)^{2}+y^{2}}\)
(x + 8)² + y² = (x – 4)² + y²
x² + 16x + 64 + y² = x² – 8x + 16 + y²
16x + 64 = -8x + 16
24x + 48 = 0
∴ x + 2 = 0

(v) |z – 2 – 2i | = |z + 2 + 2i|
Solution:
Let z = x + iy
|z – 2 – 2i| = |z + 2 + 2i|
|x + iy – 2 – 2i | = |x + iy + 2 + 2i |
|(x – 2) + i(y – 2)| = |(x + 2) + i(y + 2)|
\(\sqrt{(x-2)^{2}+(y-2)^{2}}=\sqrt{(x+2)^{2}+(y+2)^{2}}\)
(x – 2)² + (y – 2)² = (x + 2)² + (y + 2)²
x²– 4x + 4 + y² – 4y + 4 = x² + 4x + 4 + y² + 4y + 4
-4x – 4y = 4x + 4y
8x + 8y = 0
x + y = 0
y = -x

(vi) \(\frac{|z+3 i|}{|z-6 i|}=1\)
Solution:
Let z = x + iy

x² + (y + 3)² = x² + (y – 6)²
y² + 6y + 9 = y² – 12y + 36
18y – 27 = 0
2y – 3 = 0

Question 7.
Use De Moivre’s theorem and simplify the following:
(i) \(\frac{(\cos 2 \theta+i \sin 2 \theta)^{7}}{(\cos 4 \theta+i \sin 4 \theta)^{3}}\)
Solution:

(ii) \(\frac{\cos 5 \theta+i \sin 5 \theta}{(\cos 3 \theta-i \sin 3 \theta)^{2}}\)
Solution:

(iii) \(\frac{\left(\cos \frac{7 \pi}{13}+i \sin \frac{7 \pi}{13}\right)^{4}}{\left(\cos \frac{4 \pi}{13}-i \sin \frac{4 \pi}{13}\right)^{6}}\)
Solution:

Question 8.
Express the following in the form a + ib, a, b ∈ R, using De Moivre’s theorem.
(i) (1 – i)⁵
Solution:

(ii) (1 + i)⁶
Solution:

(iii) (1 – √3 i)⁴
Solution:

(iv) (-2√3 – 2i)⁵
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.2

I. Evaluate the following limits:

Question 1.
\(\lim _{z \rightarrow 2}\left[\frac{z^{2}-5 z+6}{z^{2}-4}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow-3}\left[\frac{x+3}{x^{2}+4 x+3}\right]\)
Solution:

Question 3.
\(\lim _{y \rightarrow 0}\left[\frac{5 y^{3}+8 y^{2}}{3 y^{4}-16 y^{2}}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow-2}\left[\frac{-2 x-4}{x^{3}+2 x^{2}}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 3}\left[\frac{x^{2}+2 x-15}{x^{2}-5 x+6}\right]\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{u \rightarrow 1}\left[\frac{u^{4}-1}{u^{3}-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 3}\left[\frac{1}{x-3}-\frac{9 x}{x^{3}-27}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-4 x^{2}+4 x}{x^{2}-1}\right]\)
Solution:

Question 4.
\(\lim _{\Delta x \rightarrow 0}\left[\frac{(x+\Delta x)^{2}-2(x+\Delta x)+1-\left(x^{2}-2 x+1\right)}{\Delta x}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow \sqrt{2}}\left[\frac{x^{2}+x \sqrt{2}-4}{x^{2}-3 x \sqrt{2}+4}\right]\)
Solution:

Question 6.
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-7 x+6}{x^{3}-7 x^{2}+16 x-12}\right]\)
Solution:
\(\lim _{x \rightarrow 2}\left[\frac{x^{3}-7 x+6}{x^{3}-7 x^{2}+16 x-12}\right]\)
As x → 2, numerator and denominator both tend to zero
∴ x – 2 is a factor of both.
To find the other factor for both of them, by synthetic division
Consider, Numerator = x³ + 0x² – 7x + 6


∴ The limit does not exist

III. Evaluate the following limits:

Question 1.
\(\lim _{y \rightarrow \frac{1}{2}}\left[\frac{1-8 y^{3}}{y-4 y^{3}}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 1}\left[\frac{x-2}{x^{2}-x}-\frac{1}{x^{3}-3 x^{2}+2 x}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 1}\left[\frac{x^{4}-3 x^{2}+2}{x^{3}-5 x^{2}+3 x+1}\right]\)
Solution:
\(\lim _{x \rightarrow 1}\left[\frac{x^{4}-3 x^{2}+2}{x^{3}-5 x^{2}+3 x+1}\right]\)
As x → 1, numerator and denominator both tend to zero
∴ x – 1 is a factor of both.
To find the factor of numerator and denominator by synthetic division
Consider, numerator = x⁴ + 0x³ – 3x² + 0x + 2

Question 4.
\(\lim _{x \rightarrow 1}\left[\frac{x+2}{x^{2}-5 x+4}+\frac{x-4}{3\left(x^{2}-3 x+2\right)}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow a}\left[\frac{1}{x^{2}-3 a x+2 a^{2}}+\frac{1}{2 x^{2}-3 a x+a^{2}}\right]\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 6 Functions Ex 6.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Functions Ex 6.2

Question 1.
If f(x) = 3x + 5, g(x) = 6x – 1, then find
(i) (f + g) (x)
(ii) (f – g) (2)
(iii) (fg) (3)
(iv) (f/g) (x) and its domain
Solution:
f(x) = 3x + 5, g (x) = 6x – 1
(i) (f + g) (x) = f (x) + g (x)
= 3x + 5 + 6x – 1
= 9x + 4

(ii) (f – g) (2) = f(2) – g(2)
= [3(2) + 5] – [6(2) – 1]
= 6 + 5 – 12 + 1
= 0

(iii) (fg) (3) = f (3) g(3)
= [3(3) + 5] [6(3) – 1]
= (14) (17)
= 238

(iv) \(\left(\frac{\mathrm{f}}{\mathrm{g}}\right)(x)=\frac{\mathrm{f}(x)}{\mathrm{g}(x)}=\frac{3 x+5}{6 x-1}, x \neq \frac{1}{6}\)
Domain = R – {\(\frac{1}{6}\)}

Question 2.
Let f: (2, 4, 5} → {2, 3, 6} and g: {2, 3, 6} → {2, 4} be given by f = {(2, 3), (4, 6), (5, 2)} and g = {(2, 4), (3, 4), (6, 2)}. Write down gof.
Solution:
f = {(2, 3), (4, 6), (5, 2)}
∴ f(2) = 3, f(4) = 6, f(5) = 2
g ={(2, 4), (3, 4), (6, 2)}
∴ g(2) = 4, g(3) = 4, g(6) = 2
gof: {2, 4, 5} → {2, 4}
(gof) (2) = g(f(2)) = g(3) = 4
(gof) (4) = g(f(4)) = g(6) = 2
(gof) (5) = g(f(5)) = g(2) = 4
∴ gof = {(2, 4), (4, 2), (5, 4)}

Question 3.
If f(x) = 2x² + 3, g(x) = 5x – 2, then find
(i) fog
(ii) gof
(iii) fof
(iv) gog
Solution:
f(x) = 2x² + 3, g(x) = 5x – 2
(i) (fog) (x) = f(g(x))
= f(5x – 2)
= 2(5x – 2)² + 3
= 2(25x² – 20x + 4) + 3
= 50x² – 40x + 11

(ii) (gof) (x) = g(f(x))
= g(2x² + 3)
= 5(2x + 3) – 2
= 10x² + 13

(iii) (fof) (x) = f(f(x))
= f(2x² + 3)
= 2(2x² + 3)² + 3
= 2(4x⁴ + 12x² + 9) + 3
= 8x⁴ + 24x² + 21

(iv) (gog) (x) = g(g(x))
= g(5x – 2)
= 5(5x – 2) – 2
= 25x – 12

Question 4.
Verify that f and g are inverse functions of each other, where
(i) f(x) = \(\frac{x-7}{4}\), g(x) = 4x + 7
(ii) f(x) = x³ + 4, g(x) = \(\sqrt[3]{x-4}\)
(iii) f(x) = \(\frac{x+3}{x-2}\), g(x) = \(\frac{2 x+3}{x-1}\)
Solution:
(i) f(x) = \(\frac{x-7}{4}\)
Replacing x by g(x), we get
f[g(x)] = \(\frac{g(x)-7}{4}=\frac{4 x+7-7}{4}\) = x
g(x) = 4x + 7
Replacing x by f(x), we get
g[f(x)] = 4f(x) + 7 = 4(\(\frac{x-7}{4}\)) + 7 = x
Here, f[g(x)] = x and g[f(x)] = x.
∴ f and g are inverse functions of each other.

(ii) f(x) = x³ + 4
Replacing x by g(x), we get
f[g(x)] = [g(x)]³ + 4
= \((\sqrt[3]{x-4})^{3}+4\)
= x – 4 + 4
= x
g(x) = \(\sqrt[3]{x-4}\)
Replacing x by f(x), we get
g[f(x)] = \(\sqrt[3]{f(x)-4}=\sqrt[3]{x^{3}+4-4}=\sqrt[3]{x^{3}}\) = x
Here, f[g(x)] = x and g[f(x)] = x
∴ f and g are inverse functions of each other.

(iii) f(x) = \(\frac{x+3}{x-2}\)
Replacing x by g(x), we get

Here, f[g(x)] = x and g[f(x)] = x.
∴ f and g are inverse functions of each other.

Question 5.
Check if the following functions have an inverse function. If yes, find the inverse function.
(i) f(x) = 5x²
(ii) f(x) = 8
(iii) f(x) = \(\frac{6 x-7}{3}\)
(iv) f(x) = \(\sqrt{4 x+5}\)
(v) f(x) = 9x³ + 8
(vi) f(x) =
Solution:
(i) f(x) = 5x² = y (say)

For two values (x₁ and x₂) of x, values of the function are equal.
∴ f is not one-one.
∴ f does not have an inverse.

(ii) f(x) = 8 = y (say)
For every value of x, the value of the function f is the same.
∴ f is not one-one i.e. (many-one) function.
∴ f does not have the inverse.

(iii) f(x) = \(\frac{6 x-7}{3}\)
Let f(x₁) = f(x₂)
∴ \(\frac{6 x_{1}-7}{3}=\frac{6 x_{2}-7}{3}\)
∴ x₁ = x₂
∴ f is a one-one function.
f(x) = \(\frac{6 x-7}{3}\) = y (say)
∴ x = \(\frac{3y+7}{6}\)
∴ For every y, we can get x
∴ f is an onto function.
∴ x = \(\frac{3y+7}{6}\) = f^-1 (y)
Replacing y by x, we get
f-1 (x) = \(\frac{3x+7}{6}\)

(iv) f(x) = \(\sqrt{4 x+5}, x \geq \frac{-5}{4}\)
Let f(x₁) = f(x₂)
∴ \(\sqrt{4 x_{1}+5}=\sqrt{4 x_{2}+5}\)
∴ x₁ = x₂
∴ f is a one-one function.
f(x) = \(\sqrt{4 x+5}\) = y, (say) y ≥ 0
Squaring on both sides, we get
y² = 4x + 5
∴ x = \(\frac{y^{2}-5}{4}\)
∴ For every y we can get x.
∴ f is an onto function.
∴ x = \(\frac{y^{2}-5}{4}\) = f^-1 (y)
Replacing y by x, we get
f^-1 (x) = \(\frac{x^{2}-5}{4}\)

(v) f(x) 9x³ + 8
Let f(x₁) = f(x₂)
∴ \(9 x_{1}^{3}+8=9 x_{2}^{3}+8\)
∴ x₁ = x₂
∴ f is a one-one function.
∴ f(x) = 9x³ + 8 = y, (say)
∴ x = \(\sqrt[3]{\frac{y-8}{9}}\)
∴ For every y we can get x.
∴ f is an onto function.
∴ x = \(\sqrt[3]{\frac{y-8}{9}}\) = f^-1 (y)
Replacing y by x, we get
f^-1 (x) = \(\sqrt[3]{\frac{x-8}{9}}\)

(vi) f(x) = x + 7, x < 0
= 8 – x, x ≥ 0

We observe from the graph that for two values of x, say x₁, x₂ the values of the function are equal.
i.e. f(x₁) = f(x₂)
∴ f is not one-one (i.e. many-one) function.
∴ f does not have inverse.

Question 6.
If f(x) = , then find
(i) f(3)
(ii) f(2)
(iii) f(0)
Solution:
f(x) = x² + 3, x ≤ 2
= 5x + 7, x > 2
(i) f(3) = 5(3) + 7
= 15 + 7
= 22

(ii) f(2) = 2² + 3
= 4 + 3
= 7

(iii) f(0) = 0² + 3 = 3

Question 7.
If f(x) = , then find
(i) f(-4)
(ii) f(-3)
(iii) f(1)
(iv) f(5)
Solution:
f(x) = 4x – 2, x ≤ -3
= 5, -3 < x < 3
= x², x ≥ 3
(i) f(-4) = 4(-4) – 2
= -16 – 2
= -18

(ii) f(-3) = 4(-3) – 2
= -12 – 2
= -14

(iii) f(1) = 5

(iv) f(5) = 5² = 25

Question 8.
If f(x) = 2 |x| + 3x, then find
(i) f(2)
(ii) f(-5)
Solution:
f(x) = 2 |x| + 3x
(i) f(2) = 2|2| + 3(2)
= 2 (2) + 6 ….. [∵ |x| = x, x > 0]
= 10

(ii) f(-5) = 2 |-5| + 3(-5)
= 2(5) – 15 …..[∵ |x| = -x, x < 0]
= 10 – 15
= -5

Question 9.
If f(x) = 4[x] – 3, where [x] is greatest integer function of x, then find
(i) f(7.2)
(ii) f(0.5)
(iii) \(f\left(-\frac{5}{2}\right)\)
(iv) f(2π), where π = 3.14
Solution:
f(x) = 4[x] – 3
(i) f(7.2) = 4 [7.2] – 3
= 4(7) – 3 ………[∵ 7 ≤ 7.2 < 8, [7.2] = 7]
= 25

(ii) f(0.5) = 4[0.5] – 3
= 4(0) – 3 ………[∵ 0 ≤ 0.5 < 1, [0.5] = 0]
= -3

(iii) \(f\left(-\frac{5}{2}\right)\) = f(-2.5)
= 4[-2.5] – 3
= 4(-3) – 3 …….[∵-3 ≤ -2.5 ≤ -2, [-2.5] = -3]
= -15

(iv) f(2π) = 4[2π] – 3
= 4[6.28] – 3 …..[∵ π = 3.14]
= 4(6) – 3 …….[∵ 6 ≤ 6.28 < 7, [6.28] = 6]
= 21

Question 10.
If f(x) = 2{x} + 5x, where {x} is fractional part function of x, then find
(i) f(-1)
(ii) f(\(\frac{1}{4}\))
(iii) f(-1.2)
(iv) f(-6)
Solution:
f(x) = 2{x} + 5x
(i) {-1} = -1 – [-1] = -1 + 1 = 0
∴ f(-1) = 2 {-1} + 5(-1)
= 2(0) – 5
= -5

(ii) {\(\frac{1}{4}\)} = \(\frac{1}{4}\) – [latex]\frac{1}{4}[/latex] = \(\frac{1}{4}\) – 0 = \(\frac{1}{4}\)
f(\(\frac{1}{4}\)) = 2{\(\frac{1}{4}\)} + 5(\(\frac{1}{4}\))
= 2(\(\frac{1}{4}\)) + \(\frac{5}{4}\)
= \(\frac{7}{4}\)
= 1.75

(iii) {-1.2} = -1.2 – [-1.2] = -1.2 + 2 = 0.8
f(-1.2) = 2{-1.2} + 5(-1.2)
= 2(0.8) + (-6)
= -4.4

(iv) {-6} = -6 – [-6] = -6 + 6 = 0
f(-6) = 2{-6} + 5(-6)
= 2(0) – 30
= -30

Question 11.
Solve the following for x, where |x| is modulus function, [x] is the greatest integer function, {x} is a fractional part function.
(i) |x + 4| ≥ 5
(ii) |x – 4| + |x – 2| = 3
(iii) x² + 7|x| + 12 = 0
(iv) |x| ≤ 3
(v) 2|x| = 5
(vi) [x + [x + [x]]] = 9
(vii) {x} > 4
(viii) {x} = o
(ix) {x} = 0.5
(x) 2{x} = x + [x]
Solution:
(i) |x + 4| ≥ 5
The solution of |x| ≥ a is x ≤ -a or x ≥ a
∴ |x + 4| ≥ 5 gives
∴ x + 4 ≤ -5 or x + 4 ≥ 5
∴ x ≤ -5 – 4 or x ≥ 5 – 4
∴ x ≤ -9 or x ≥ 1
∴ The solution set = (-∞, – 9] ∪ [1, ∞)

(ii) |x – 4| + |x – 2| = 3 …..(i)
Case I: x < 2
Equation (i) reduces to
4 – x + 2 – x = 3 …….[x < 2 < 4, x – 4 < 0, x – 2 < 0]
∴ 6 – 3 = 2x
∴ x = \(\frac{3}{2}\)

Case II: 2 ≤ x < 4
Equation (i) reduces to
4 – x + x – 2 = 3
∴ 2 = 3 (absurd)
There is no solution in [2, 4)

Case III: x ≥ 4
Equation (i) reduces to
x – 4 + x – 2 = 3
∴ 2x = 6 + 3 = 9
∴ x = \(\frac{9}{2}\)
∴ x = \(\frac{3}{2}\), \(\frac{9}{2}\) are solutions.
The solution set = {\(\frac{3}{2}\), \(\frac{9}{2}\)}

(iii) x² + 7|x| + 12 = 0
∴ (|x|)² + 7|x| + 12 = 0
∴ (|x| + 3) (|x| + 4) = 0
∴ There is no x that satisfies the equation.
The solution set = { } or Φ

(iv) |x| ≤ 3 The solution set of |x| ≤ a is -a ≤ x ≤ a
∴ The required solution is -3 ≤ x ≤ 3
∴ The solution set is [-3, 3]

(v) 2|x| = 5
∴ |x| = \(\frac{5}{2}\)
∴ x = ±\(\frac{5}{2}\)

(vi) [x + [x + [x]]] = 9
∴ [x + [x] + [x] ] = 9 …….[[x + n] = [x] + n, if n is an integer]
∴ [x + 2[x]] = 9
∴ [x] + 2[x] = 9 …..[[2[x] is an integer]]
∴ [x] = 3
∴ x ∈ [3, 4)

(vii) {x} > 4
This is a meaningless statement as 0 ≤ {x} < 1
∴ The solution set = { } or Φ

(viii) {x} = 0
∴ x is an integer
∴ The solution set is Z.

(ix) {x} = 0.5
∴ x = ….., -2.5, -1.5, -0.5, 0.5, 1.5, …..
∴ The solution set = {x : x = n + 0.5, n ∈ Z}

(x) 2{x} = x + [x]
= [x] + {x} + [x] ……[x = [x] + {x}]
∴ {x} = 2[x]
R.H.S. is an integer
∴ L.H.S. is an integer
∴ {x} = 0
∴ [x] = 0
∴ x = 0

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Ex 7.1

I. Evaluate the following limits:

Question 1.
\(\lim _{z \rightarrow-3}\left[\frac{\sqrt{Z+6}}{Z}\right]\)
Solution:

Question 2.
\(\lim _{y \rightarrow-3}\left[\frac{y^{5}+243}{y^{3}+27}\right]\)
Solution:

Question 3.
\(\lim _{z \rightarrow-5}\left[\frac{\left(\frac{1}{z}+\frac{1}{5}\right)}{z+5}\right]\)
Solution:

II. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 3}\left[\frac{\sqrt{2 x+6}}{x}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 2}\left[\frac{x^{-3}-2^{-3}}{x-2}\right]\)
Solution:

Question 3.
\(\lim _{x \rightarrow 5}\left[\frac{x^{3}-125}{x^{5}-3125}\right]\)
Solution:

Question 4.
If \(\lim _{x \rightarrow 1}\left[\frac{x^{4}-1}{x-1}\right]=\lim _{x \rightarrow a}\left[\frac{x^{3}-a^{3}}{x-a}\right]\), find all possible values of a.
Solution:

III. Evaluate the following limits:

Question 1.
\(\lim _{x \rightarrow 1}\left[\frac{x+x^{2}+x^{3}+\ldots \ldots \ldots+x^{n}-n}{x-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 7}\left[\frac{(\sqrt[3]{x}-\sqrt[3]{7})(\sqrt[3]{x}+\sqrt[3]{7})}{x-7}\right]\)
Solution:

Question 3.
If \(\lim _{x \rightarrow 5}\left[\frac{x^{k}-5^{k}}{x-5}\right]\) = 500, find all possible values of k.
Solution:

Question 4.
\(\lim _{x \rightarrow 0}\left[\frac{(1-x)^{8}-1}{(1-x)^{2}-1}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 0}\left[\frac{\sqrt[3]{1+x}-\sqrt{1+x}}{x}\right]\)
Solution:

Question 6.
\(\lim _{y \rightarrow 1}\left[\frac{2 y-2}{\sqrt[3]{7+y}-2}\right]\)
Solution:

Question 7.
\(\lim _{z \rightarrow a}\left[\frac{(z+2)^{\frac{3}{2}}-(a+2)^{\frac{3}{2}}}{z-a}\right]\)
Solution:

Question 8.
\(\lim _{x \rightarrow 7}\left[\frac{x^{3}-343}{\sqrt{x}-\sqrt{7}}\right]\)
Solution:

Question 9.
\(\lim _{x \rightarrow 1}\left(\frac{x+x^{3}+x^{5}+\ldots+x^{2 n-1}-n}{x-1}\right)\)
Solution:

IV. In the following examples, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.

Question 1.
\(\lim _{x \rightarrow 2}(2 x+3)=7\)
Solution:
We have to find some δ so that
\(\lim _{x \rightarrow 2}(2 x+3)=7\)
Here a = 2, l = 1 and f(x) = 2x + 3
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |(2x + 3) – 7| < ∈
∴ |2x + 4| < ∈
∴ 2(x – 2)|< ∈
∴ |x – 2| < \(\frac{\epsilon}{2}\)
∴ δ ≤ \(\frac{\epsilon}{2}\) such that
|2x + 4| < δ ⇒ |f(x) – 7| < ∈

Question 2.
\(\lim _{x \rightarrow-3}(3 x+2)=-7\)
Solution:
We have to find some δ so that
\(\lim _{x \rightarrow-3}(3 x+2)=-7\)
Here a = -3, l = -7 and f(x) = 3x + 2
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |3x + 2 – (-7)| < ∈
∴ |3x + 9| < ∈
∴ |3(x + 3)| < ∈
∴ |x + 3| < \(\frac{\epsilon}{3}\)
∴ δ < \(\frac{\epsilon}{3}\) such that
|x + 3| ≤ δ ⇒ |f(x) + 7| < ∈

Question 3.
\(\lim _{x \rightarrow 2}\left(x^{2}-1\right)=3\)
Solution:
We have to find some δ > 0 such that
\(\lim _{x \rightarrow 2}\left(x^{2}-1\right)=3\)
Here, a = 2, l = 3 and f(x) = x² – 1
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |(x² – 1) – 3| < ∈
∴ |x² – 4| < ∈
∴ |(x + 2)(x – 2)| < ∈ …..(i)
We have to get rid of the factor |x + 2|
As |x – 2| < δ
-δ < x – 2 < δ
∴ 2 – δ < x < 2 + δ
Since δ can be assumed as very small, let us choose δ < 1
∴ 1 < x < 3
∴ 3 < x + 2 < 5 …..(Adding 2 throughout)
∴ |x + 2| < 5
∴ |(x + 2)(x – 2)| < 5|x – 2| ……(ii)
From (i) and (ii), we get
5|x – 2|< ∈
∴ x – 2 < \(\frac{\epsilon}{5}\)
If δ = \(\frac{\epsilon}{5}\), |x – 2| < δ ⇒ |x² – 4| < ∈
∴ We choose δ = min{\(\frac{\epsilon}{5}\), 1} then
|x – 2| < δ ⇒ |f(x) – 3| < ∈

Question 4.
\(\lim _{x \rightarrow 1}\left(x^{2}+x+1\right)=3\)
Solution:
We have to find some δ > 0 such that
\(\lim _{x \rightarrow 1}\left(x^{2}+x+1\right)=3\)
Here a = 1, l = 3 and f(x) = x² + x + 1
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |x² + x + 1 – 3| < ∈
∴ |x² + x – 2| < ∈
∴ |(x + 2)(x – 1)| < ∈ …..(i)
We have to get rid of the factor |x + 2|
As |x – 1| < δ
-δ < x – 1 < δ
∴ 1 – δ < x < 1 + δ
Since δ can be assumed as very small, let us choose δ < 1
∴ 0 < x < 2
∴ 2 < x + 2 < 4
∴ |x + 2| < 4
∴ |(x + 2)(x – 1)|< 4 |x – 1| …..(ii)
From (i) and (ii), we get
4|x – 1| < ∈
∴ |x – 1| < \(\frac{\epsilon}{4}\)
If δ = \(\frac{\epsilon}{4}\),
|x – 1| < δ ⇒ x² + x – 2 < ∈
∴ We choose δ = min{\(\frac{\epsilon}{4}\), 1} then
|x – 1| < δ ⇒ |f(x) – 3| < ∈

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1

Prove by the method of induction, for all n ∈ N.

Question 1.
2 + 4 + 6 + …… + 2n = n(n + 1)
Solution:
Let P(n) = 2 + 4 + 6 + …… + 2n = n(n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(1 + 1) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 4 + 6 + ….. + 2k = k(k + 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 4 + 6 + …… + 2(k + 1) = (k + 1) (k + 2)
L.H.S. = 2 + 4 + 6 + …+ 2(k + 1)
= 2 + 4 + 6+ ….. + 2k + 2(k + 1)
= k(k + 1) + 2(k + 1) …..[From (i)]
= (k + 1).(k + 2)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 4 + 6 + …… + 2n = n(n + 1) for all n ∈ N.

Question 2.
3 + 7 + 11 + ……… to n terms = n(2n + 1)
Solution:
Let P(n) = 3 + 7 + 11 + ……… to n terms = n(2n +1), for all n ∈ N.
But 3, 7, 11, …. are in A.P.
∴ a = 3 and d = 4
Let t_n be the nth term.
∴ t_n = a + (n – 1)d = 3 + (n – 1)4 = 4n – 1
∴ P(n) = 3 + 7 + 11 + ……. + (4n – 1) = n(2n + 1)

Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 1[2(1)+ 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 3 + 7 + 11 + ….. + (4k – 1) = k(2k + 1) …..(i)

Sept III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
3 + 7 + 11 + …+ [4(k + 1) – 1] = (k + 1)(2k + 3)
L.H.S. = 3 + 7 + 11 + …… + [4(k + 1) – 1]
= 3 + 7 + 11 + ….. + (4k – 1) + [4(k+ 1) – 1]
= k(2k + 1) + (4k + 4 – 1) …..[From (i)]
= 2k² + k + 4k + 3
= 2k² + 2k + 3k + 3
= 2k(k + 1) + 3(k + 1)
= (k + 1) (2k + 3)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 3 + 7 + 11 + ….. to n terms = n(2n + 1) for all n ∈ N.

Question 3.
1² + 2² + 3² +…..+ n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let P(n) = 1² + 2² + 3² +…..+ n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 1² = 1
RHS = \(\frac{1(1+1)[2(1)+1]}{6}=\frac{6}{6}\) = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 2² + 3² +…+ k² = \(\frac{k(k+1)(2 k+1)}{6}\) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 2² + 3² + …+ n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.

Question 4.
1² + 3² + 5² + ….. + (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1)
Solution:
Let P(n) = 1² + 3² + 5²+…..+ (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 1² = 1
R.H.S. = \(\frac{1}{3}\) [2(1) – 1][2(1) + 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 3² + 5² +….+(2k – 1)² = \(\frac{k}{3}\) (2k – 1)(2k + 1) …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 3² + 5² + …+ (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1) for all n ∈ N.

Question 5.
1³ + 3³ + 5³ + ….. to n terms = n² (2n² – 1)
Solution:
Let P(n) = 1³ + 3³ + 5³ + …. to n terms = n² (2n² – 1), for all n ∈ N.
But 1, 3, 5, are in A.P.
∴ a = 1, d = 2
Let tn be the nth term.
t_n = a + (n – 1) d = 1 + (n – 1) 2 = 2n – 1
∴ P(n) = 1³ + 3³ + 5³ +…..+ (2n – 1)³ = n² (2n² – 1)

Step I:
Put n = 1
L.H.S. = 1³ = 1
R.H.S. = 1² [2(1)² – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1³ + 3³ + 5³ +…+ (2k – 1)³ = k² (2k² – 1) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1³ + 3³ + 5³ + … to n terms = n² (2n² – 1) for all n ∈ N.

Question 6.
1.2 + 2.3 + 3.4 +… + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2)
Solution:
Let P(n) = 1.2 + 2.3 + 3.4 +….+n(n + 1) = \(\frac{n(n+1)(n+2)}{3}\), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = 1.2 = 2
R.H.S. = \(\frac{1}{3}\) (1 + 1)(1 + 2) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1.2 + 2.3 + 3.4 + ….. + k(k + 1) = \(\frac{k}{3}\) (k + 1)(k + 2) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.2 + 2.3 + 3.4 + … + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2), for all n ∈ N.

Question 7.
1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n – 1)
Solution:
Let P(n) = 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n -1), for all n ∈ N.
But first factor in each term, i.e., 1, 3, 5,… are in A.P. with a = 1 and d = 2.
∴ nth term = a + (n – 1)d = 1 + (n – 1) 2 = (2n – 1)
Also, second factor in each term,
i.e., 3, 5, 7, … are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1) d = 3 + (n – 1) 2 = (2n + 1)
∴ nth term, t_n = (2n – 1) (2n + 1)
∴ P(n) ≡ 1.3 + 3.5 + 5.7 + …. + (2n – 1) (2n + 1) = \(\frac{n}{3}\) (4n² + 6n – 1)

Step I:
Put n = 1
L.H.S. = 1.3 = 3
R.H.S. = \(\frac{1}{3}\) [4(1)² + 6(1) – 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is trae for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1.3 + 3.5 + 5.7 +….+ (2k – 1)(2k + 1) = \(\frac{k}{3}\) (4k² + 6k – 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n – 1) for all n ∈ N.

Question 8.
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
Solution:
Let P(n) ≡ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = \(\frac{1}{1.3}=\frac{1}{3}\)
R.H.S. = \(\frac{1}{2(1)+1}=\frac{1}{3}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 k-1)(2 k+1)}=\frac{k}{2 k+1}\) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.

Question 9.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\)
Solution:
Let P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.
But first factor in each term of the denominator,
i.e., 3, 5, 7, ….. are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1)d = 3 + (n – 1) 2 = (2n + 1)
Also, second factor in each term of the denominator,
i.e., 5, 7, 9, … are in A.P. with a = 5 and d = 2.
∴ nth term = a + (n – 1) d = 5 + (n – 1) 2 = (2n + 3)
∴ nth term, t_n = \(\frac{1}{(2 n+1)(2 n+3)}\)
P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 n+1)(2 n+3)}\) = \(\frac{n}{3(2 n+3)}\)

Step I:
Put n = 1
L.H.S. = \(\frac{1}{3.5}=\frac{1}{15}\)
R.H.S. = \(\frac{1}{3[2(1)+3]}=\frac{1}{3(2+3)}=\frac{1}{15}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 k+1)(2 k+3)}\) = \(\frac{k}{3(2 k+3)}\) ….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that


∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.

Question 10.
(2³ⁿ – 1) is divisible by 7.
Solution:
(2³ⁿ – 1) is divisible by 7 if and only if (2³ⁿ – 1) is a multiple of 7.
Let P(n) ≡ (2³ⁿ – 1) = 7m, where m ∈ N.

Step I:
Put n = 1
∴ 2³ⁿ – 1 = 2³⁽¹⁾ – 1 = 2³ – 1 = 8 – 1 = 7
∴ (2³ⁿ – 1) is a multiple of 7.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
i.e., 2^3k – 1 is a multiple of 7.
∴ 2^3k – 1 = 7a, where a ∈ N
∴ 2^3k = 7a + 1 ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2^3(k+1) – 1 = 7b, where b ∈ N.
∴ P(k + 1) = 2^3(k+1) – 1
= 2^3k+3 – 1
= 2^3k . (2³) – 1
= (7a + 1)8 – 1 …..[From (i)]
= 56a + 8 – 1
= 56a + 7
= 7(8a + 1)
7b, where b = (8a + 1) ∈ N
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 7, for all n ∈ N.

Question 11.
(2⁴ⁿ – 1) is divisible by 15.
Solution:
(2⁴ⁿ – 1) is divisible by 15 if and only if (2⁴ⁿ – 1) is a multiple of 15.
Let P(n) ≡ (2⁴ⁿ – 1) = 15m, where m ∈ N.

Step I:
Put n = 1
∴ 2⁴⁽¹⁾ – 1 = 16 – 1 = 15
∴ (2⁴ⁿ – 1) is a multiple of 15.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2^4k – 1 = 15a, where a ∈ N
∴ 2^4k = 15a + 1 …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
∴ 2^4(k+1) – 1 = 15b, where b ∈ N
∴ P(k + 1) = 2^4(k+1) – 1 = 2^4k+4 – 1
= 2^4k . 2⁴ – 1
= 16 . (2^4k) – 1
= 16(15a + 1) – 1 …..[From (i)]
= 240a + 16 – 1
= 240a + 15
= 15(16a + 1)
= 15b, where b = (16a + 1) ∈ N
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 15, for all n ∈ N.

Question 12.
3ⁿ – 2n – 1 is divisible by 4.
Solution:
(3ⁿ – 2n – 1) is divisible by 4 if and only if (3ⁿ – 2n – 1) is a multiple of 4.
Let P(n) ≡ (3ⁿ – 2n – 1) = 4m, where m ∈ N.

Step I:
Put n = 1
∴ (3ⁿ – 2n – 1) = 3⁽¹⁾ – 2(1) – 1 = 0 = 4(0)
∴ (3ⁿ – 2n – 1) is a multiple of 4.
∴ P(n) is tme for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 3^k – 2k – 1 = 4a, where a ∈ N
∴ 3^k = 4a + 2k + 1 ….(i)

Step III:
We have to prove that P(n) is tme for n = k + 1,
i.e., to prove that
3^(k+1) – 2(k + 1) – 1 = 4b, where b ∈ N
P(k + 1) = 3^k+1 – 2(k + 1) – 1
= 3^k . 3 – 2k – 2 – 1
= (4a + 2k + 1) . 3 – 2k – 3 …….[From (i)]
= 12a + 6k + 3 – 2k – 3
= 12a + 4k
= 4(3a + k)
= 4b, where b = (3a + k) ∈ N
∴ P(n) is tme for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is tme for all n ∈ N.
∴ 3ⁿ – 2n – 1 is divisible by 4, for all n ∈ N.

Question 13.
5 + 5² + 5³ + ….. + 5ⁿ = \(\frac{5}{4}\) (5ⁿ – 1)
Solution:
Let P(n) ≡ 5 + 52 + 53 +…..+ 5n = \(\frac{5}{4}\) (5n – 1), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = 5
R.H.S. = \(\frac{5}{4}\) (5¹ – 1) = 5
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 5 + 5² + 5³ + ….. + 5^k = \(\frac{5}{4}\) (5^k – 1) …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 5 + 5² + 5³ + … + 5ⁿ = \(\frac{5}{4}\) (5ⁿ – 1), for all n ∈ N.

Question 14.
(cos θ + i sin θ)ⁿ = cos (nθ) + i sin (nθ)
Solution:
Let P(n) ≡ (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = (cos θ + i sin θ)¹ = cos θ + i sin θ
R.H.S. = cos[(1)θ] + i sin[(1)θ] = cos θ + i sin θ
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ (cos θ + i sin θ)^k = cos kθ + i sin kθ …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
(cos θ + i sin θ)^k+1 = cos (k + 1)θ + i sin (k + 1)θ
L.H.S. = (cos θ + i sin θ)^k+1
= (cos θ + i sin θ)^k . (cos θ + i sin θ)
= (cos kθ + i sin kθ) . (cos θ + i sin θ) ……[From (i)]
= cos kθ cos θ + i sin θ cos kθ + i sin kθ cosθ – sin kθ sin θ ……[∵ i² = -1]
= (cos kθ cos θ – sin k θ sin θ) + i(sin kθ cos θ + cos kθ sin θ)
= cos(kθ + θ) + i sin(kθ + θ)
= cos(k + 1) θ + i sin (k + 1) θ
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (cos θ + i sin θ)ⁿ = cos (nθ) + i sin (nθ), for all n ∈ N.

Question 15.
Given that t_n+1 = 5 t_n+4, t₁ = 4, prove by method of induction that t_n = 5ⁿ – 1.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation t_n+1 = 5 t_n+4, t₁ = 4 and R.H.S. a general statement t_n = 5ⁿ – 1.
Step I:
Put n = 1
L.H.S. = 4
R.H.S. = 5¹ – 1 = 4
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S. = t₂ = 5t₁ + 4 = 24
R.H.S. = t₂ = 5² – 1 = 24
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 2.

Step II:
Let us assume that P(n) is true for n = k.
∴ t_k+1 = 5 t_k+4 and t_k = 5^k – 1

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that t_k+1 = 5^k+1 – 1
Since t_k+1 = 5 t_k+4 and t_k = 5^k – 1 …..[From Step II]
t_k+1 = 5 (5^k – 1) + 4 = 5^k+1 – 1
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n = 5ⁿ – 1, for all n ∈ N.

Question 16.
Prove by method of induction
\(\left(\begin{array}{ll}
1 & 2 \\
0 & 1
\end{array}\right)^{n}=\left(\begin{array}{cc}
1 & 2 n \\
0 & 1
\end{array}\right) \forall n \in N\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 1 Complex Numbers Ex 1.3

Question 1.
Find the modulus and amplitude for each of the following complex numbers:
(i) 7 – 5i
Solution:
Let z = 7 – 5i
a = 7, b = -5
i.e. a > 0, b < 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{7^{2}+(-5)^{2}}=\sqrt{49+25}=\sqrt{74}\)
Here, (7, -5) lies in 4th quadrant.

(ii) √3 + √2 i
Solution:
Let z = √3 + √2 i
a = √3, b = √2,
i.e. a > 0, b > 0

(iii) -8 + 15i
Solution:
Let z = -8 + 15i
a = -8, b = 15 , i.e. a < 0, b > 0

(iv) -3(1 – i)
Solution:
Let z = -3(1 – i) = -3 + 3i
a = -3, b = 3 , i.e. a < 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{(-3)^{2}+3^{2}}=\sqrt{9+9}\) = 3√2
Here, (-3, 3) lies in 2nd quadrant.
amp(z) = π – \(\tan ^{-1}\left|\frac{b}{a}\right|\)

(v) -4 – 4i
Solution:
Let z = -4 – 4i
a = -4, b = -4 , i.e. a < 0, b < 0

(vi) √3 – i
Solution:
Let z = √3 – i
a = √3, b = -1, i.e. a > 0, b < 0

(vii) 3
Solution:
Let z = 3 + 0i
a = 3, b = 0
z is a real number, it lies on the positive real axis.
|z|= \(\sqrt{a^{2}+b^{2}}=\sqrt{3^{2}+0^{2}}=\sqrt{9+0}\) = 3
and amp (z) = 0

(viii) 1 + i
Solution:
Let z = 1 + i
a = 1, b = 1, i.e. a > 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{1^{2}+1^{2}}=\sqrt{1+1}=\sqrt{2}\)
Here, (1, 1) lies in 1st quadrant.
amp (z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(1)=\frac{\pi}{4}\)

(ix) 1 + i√3
Solution:
Let z = 1 + i√3
a = 1, b = √3, i.e. a > 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{1^{2}+(\sqrt{3})^{2}}=\sqrt{1+3}=2\)
Here, (1, √3) lies in 1st quadrant.
amp (z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(\sqrt{3})=\frac{\pi}{3}\)

(x) (1 + 2i)² (1 – i)
Solution:
Let z = (1 + 2i)² (1 – i)
= (1 + 4i + 4i²) (1 – i)
= [1 + 4i + 4(-1)] (1 – i) ….[∵ i² = -1]
= (-3 + 4i) (1 – i)
= -3 + 3i + 4i – 4i²
= -3 + 7i – 4(-1)
= -3 + 7i + 4
∴ z = 1 + 7i
∴ a = 1, b = 7, i. e. a > 0, b > 0
∴ |z| = \(\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}=\sqrt{1^{2}+7^{2}}=\sqrt{1+49}=5 \sqrt{2}\)
Here, (1, 7) lies in 1st quadrant.
∴ amp(z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(7)\)

Question 2.
Find real values of θ for which \(\left(\frac{4+3 i \sin \theta}{1-2 i \sin \theta}\right)\) is purely real.
Solution:

Question 3.
If z = 3 + 5i, then represent the z, \(\overline{\mathbf{z}}\), -z, \(\overline{\mathbf{-z}}\) in Argand’s diagram.
Solution:
z = 3 + 5i
\(\overline{\mathbf{z}}\) = 3 – 5i
-z = – 3 – 5i
\(\overline{\mathbf{-z}}\)= -3 + 5i
The above complex numbers will be represented by the points
A (3, 5), B (3, -5), C (-3, -5) , D (-3, 5) respectively as shown below:

Question 4.
Express the following complex numbers in polar form and exponential form.
(i) -1 + √3 i
Solution:
Let z = – 1 + √3
a = -1, b = √3

(ii) -i
Solution:
Let z = -i = 0 – i
a = 0, b = -1
z lies on negative imaginary Y-axis.
|z| = r = \(\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}=\sqrt{0^{2}+(-1)^{2}}\) = 1 and
θ = amp z = 270° = \(\frac{3 \pi}{2}\)
The polar form of z = r (cos θ + i sin θ)
= 1 (cos 270° + i sin 270°)
= 1 (cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\))
The exponential form of z = \(r e^{i \theta}=e^{\frac{3 \pi}{2} i}\)

(iii) -1
Solution:
Let z = -1 = -1 + 0.i
a = -1, b = 0
z lies on negative real X-axis.
|z| = r = \(\sqrt{a^{2}+b^{2}}=\sqrt{(-1)^{2}+0^{2}}\) = 1 and
θ = amp z = 180° = π
The polar form of z = r (cos θ + i sin θ)
= 1 (cos 180° + i sin 180°)
= 1 (cos π + i sin π)
The exponential form of z = \(r e^{i \theta}=e^{\pi i}\)

(iv) \(\frac{1}{1+i}\)
Solution:

(v) \(\frac{1+2 i}{1-3 i}\)
Solution:

(vi) \(\frac{1+7 \mathbf{i}}{(2-\mathbf{i})^{2}}\)
Solution:

Question 5.
Express the following numbers in the form x + iy:
(i) \(\sqrt{3}\left(\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}\right)\)
Solution:

(ii) \(\sqrt{2} \cdot\left(\cos \frac{7 \pi}{4}+i \sin \frac{7 \pi}{4}\right)\)
Solution:

(iii) \(7\left(\cos \left(-\frac{5 \pi}{6}\right)+i \sin \left(-\frac{5 \pi}{6}\right)\right)\)
Solution:

(iv) \(e^{\frac{\pi}{3} i}\)
Solution:

(v) \(e^{\frac{-4 \pi}{3} i}\)
Solution:

(vi) \([latex]e^{\frac{5 \pi}{6} i}\)[/latex]
Solution:

Question 6.
Find the modulus and argument of the complex number \(\frac{1+2 i}{1-3 i}\).
Solution:

Question 7.
Convert the complex number \(\mathrm{z}=\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}\) in the polar form.
Solution:

Question 8.
For z = 2 + 3i, verify the following:
(i) \(\overline{(\bar{z})}=z\)
Solution:
z = 2 + 3i
∴ \(\bar{z}\) = 2 – 3i
∴ \(\overline{\bar{z}}\) = 2 + 3i = z

(ii) \(\overline{z \bar{z}}=|z|^{2}\)
Solution:
z\(\bar{z}\) = (2 + 3i) (2 – 3i)
= 4 – 9i²
= 4 – 9(-1) …..[∵ i² = -1]
= 13
|z|² = \(\left(\sqrt{2^{2}+3^{2}}\right)^{2}\)
= 2² + 3²
= 4 + 9
= 13
∴ \(\overline{z \bar{z}}=|z|^{2}\)

(iii) (z + \(\bar{z}\)) is real
Solution:
(z + \(\bar{z}\)) = (2 + 3i) + (2 – 3i)
= 2 + 3i + 2 – 3i
= 4, which is a real number.
∴ z + \(\bar{z}\) is real.

(iv) z – \(\bar{z}\) = 6i
Solution:
z – \(\bar{z}\) = (2 + 3i) – (2 – 3i)
= 2 + 3i – 2 + 3i
= 6i

Question 9.
z₁ = 1 + i, z₂ = 2 – 3i, verify the following:
(i) \(\overline{Z_{1}+Z_{2}}=\overline{Z_{1}}+\overline{Z_{2}}\)
Solution:

(ii) \(\overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
Solution:

(iii) \(\overline{Z_{1} \cdot Z_{2}}=\overline{Z_{1}} \cdot \overline{Z_{2}}\)
Solution:

(iv) \(\overline{\left(\frac{\mathbf{z}_{1}}{\mathbf{z}_{2}}\right)}=\frac{\overline{\mathbf{z}}_{1}}{\overline{\mathbf{z}}_{2}}\)
Solution:

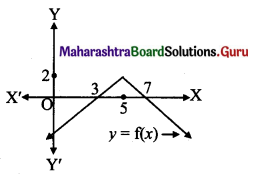
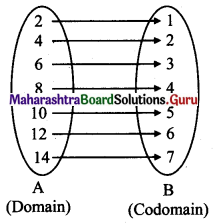
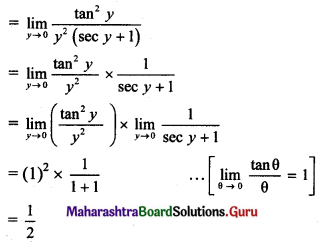
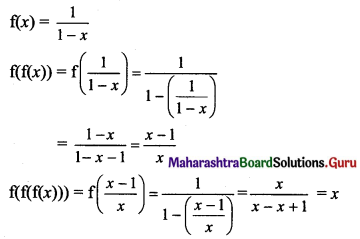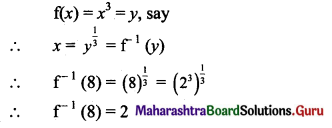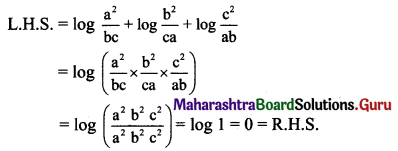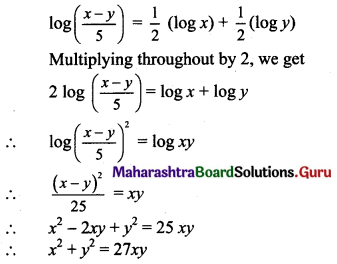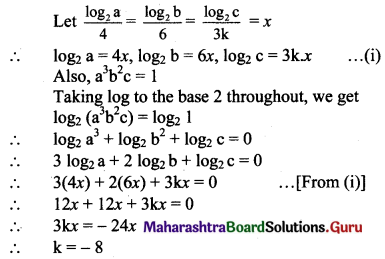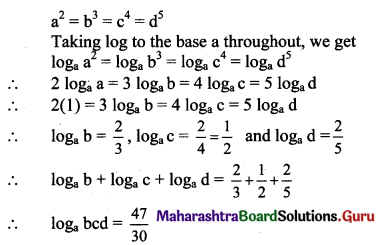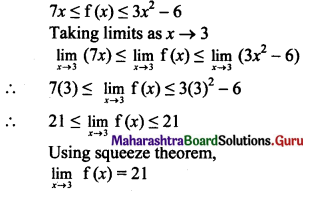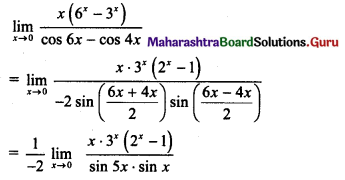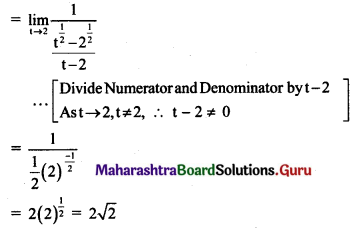Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Permutations and Combination Ex 3.1

Question 1.
A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl?
Solution:
There are 30 boys and 20 girls.
A teacher can select any boy as a class monitor from 30 boys in 30 different ways and he can select any girl as a class monitor from 20 girls in 20 different ways.
∴ by the fundamental principle of addition, the total number of ways a teacher can select a class monitor = 30 + 20 = 50
Hence, there are 50 different ways to select a class monitor.

Question 2.
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
Solution:
A signal is generated from 2 flags and there are 4 flags of different colours available.
∴ 1st flag can be any one of the available 4 flags.
∴ It can be selected in 4 ways.
Now, 2nd flag is to be selected for which 3 flags are available for a different signal.
∴ 2nd flag can be anyone from these 3 flags.
∴ It can be selected in 3 ways.
∴ By using the fundamental principle of multiplication, total no. of ways a signal can be generated = 4 × 3 = 12
∴ 12 different signals can be generated.

Question 3.
How many two-letter words can be formed using letters from the word SPACE, when repetition of letters (i) is allowed (ii) is not allowed
Solution:
A two-letter word is to be formed out of the letters of the word SPACE.
(i) When repetition of the letters is allowed 1st letter can be selected in 5 ways.
2nd letter can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, the total number of 2-letter words = 5 × 5 = 25

(ii) When repetition of the letters is not allowed 1st letter can be selected in 5 ways.
2nd letter can be selected in 4 ways.
∴ By using the fundamental principle of multiplication, the total number of 2-letter words = 5 × 4 = 20

Question 4.
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits (i) are allowed (ii) are not allowed?
Solution:
A three-digit number is to be formed from the digits 0, 1, 3, 5, 6.
(i) When repetition of digits is allowed,
100’s place digit should be a non-zero number.
Hence, it can be anyone from digits 1, 3, 5,6.
∴ 100’s place digit can be selected in 4 ways.
10’s and unit’s place digit can be zero and digits can be repeated.
∴ 10’s place digit can be selected in 5 ways and the unit’s place digit can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, the total number of three-digit numbers = 4 × 5 × 5 = 100

(ii) When repetition of digits is not allowed,
100’s place digit should be a non-zero number.
Hence, it can be anyone from digits 1, 3, 5, 6.
∴ 100’s place digit can be selected in 4 ways.
10’s and unit’s place digit can be zero and digits can’t be repeated.
∴ 10’s place digit can be selected in 4 ways and the unit’s place digit can be selected in 3 ways.
∴ By using the fundamental principle of multiplication, the total number of two-digit numbers = 4 × 4 × 3 = 48

Question 5.
How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?
Solution:
A 3-digit number is to be formed from the digits 2, 3, 4, 5, 6 where digits can be repeated.
∴ Unit’s place digit can be selected in 5 ways.
10’s place digit can be selected in 5 ways.
100’s place digit can be selected in 5 ways.
∴ By using fundamental principle of multiplication, total number of 3-digit numbers = 5 × 5 × 5 = 125

Question 6.
A letter lock contains 3 rings and each ring contains 5 letters. Determine the maximum number of false trails that can be made before the lock is opened.
Solution:
A letter lock has 3 rings, each ring containing 5 different letters.
∴ A letter from each ring can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, a total number of trials that can be made = 5 × 5 × 5 = 125.
Out of these 124 wrong attempts are made and in the 125th attempt, the lock gets opened.
∴ A maximum number of false trials = 124.

Question 7.
In a test, 5 questions are of the form ‘state, true or false. No student has got all answers correct. Also, the answer of every student is different. Find the number of students who appeared for the test.
Solution:
Every question can be answered in 2 ways. (True or False)
∴ By using the fundamental principle of multiplication, the total number of set of answers possible = 2 × 2 × 2 × 2 × 2 = 32.
Since One of them is the case where all questions are answered correctly,
The number of wrong answers = 32 – 1 = 31.
Since no student has answered all the questions correctly, the number of students who appeared for the test are 31.

Question 8.
How many numbers between 100 and 1000 have 4 in the unit’s place?
Solution:
Numbers between 100 and 1000 are 3-digit numbers.
A 3-digit number is to be formed from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, where the unit place digit is 4.
Unit’s place digit is 4.
∴ it can be selected in 1 way only.
10’s place digit can be selected in 10 ways.
For a 3-digit number, 100’s place digit should be a non-zero number.
∴ 100’s place digit can be selected in 9 ways.
∴ By using the fundamental principle of multiplication,
total numbers between 100 and 1000 which have 4 in the units place = 1 × 10 × 9 = 90.

Question 9.
How many numbers between 100 and 1000 have the digit 7 exactly once?
Solution:
Numbers between 100 and 1000 are 3-digit numbers.
A 3-digit number is to be formed from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, where exactly one of the digits is 7.
When 7 is in unit’s place:
Unit’s place digit is 7.
∴ it can be selected in 1 way only.
10’s place digit can be selected in 9 ways.
100’s place digit can be selected in 8 ways.
Total numbers which have 7 in unit’s place = 1 × 9 × 8 = 72.

When 7 is in 10’s place:
Unit’s place digit can be selected in 9 ways.
10’s place digit is 7.
∴ it can be selected in 1 way only.
100’s place digit can be selected in 8 ways.
∴ A total number of numbers which have 7 in 10’s place = 9 × 1 × 8 = 72.

When 7 is in 100’s place:
Unit’s place digit can be selected in 9 ways.
10’s place digit can be selected in 9 ways.
100’s place digit is 7.
∴ it can be selected in 1 way only.
∴ Total numbers which have 7 in 100’s place = 9 × 9 × 1 = 81.
∴ Total numbers between 100 and 1000 having digit 7 exactly once = 72 + 72 + 81 = 225

Question 10.
How many four-digit numbers will not exceed 7432 if they are formed using the digits 2, 3, 4, 7 without repetition?
Solution:
Between any set of digits, the greatest number is possible when digits are arranged in descending order.
∴ 7432 is the greatest number, formed from the digits 2, 3, 4, 7.
Since a 4-digit number is to be formed from the digits 2, 3, 4, 7, where repetition of the digit is not allowed,
1000’s place digit can be selected in 4 ways,
100’s place digit can be selected in 3 ways,
10’s place digit can be selected in 2 ways,
Unit’s place digit can be selected in 1 way.
∴ Total number of numbers not exceeding 7432 that can be formed with the digits 2, 3, 4, 7 = Total number of four-digit numbers possible from the digits 2, 3, 4, 7
= 4 × 3 × 2 × 1
= 24

Question 11.
If numbers are formed using digits 2, 3, 4, 5, 6 without repetition, how many of them will exceed 400?
Solution:
Case I: Number of three-digit numbers formed from 2, 3, 4, 5, 6, greater than 400.
100’s place can be filled by any one of the numbers 4, 5, 6.
100’s place digit can be selected in 3 ways.
Since repetition is not allowed, 10’s place can be filled by any one of the remaining four numbers.
∴ 10’s place digit can be selected in 4 ways.
Unit’s place digit can be selected in 3 ways.
∴ Total number of three-digit numbers formed = 3 × 4 × 3 = 36

Case II: Number of four-digit numbers formed from 2, 3, 4, 5, 6.
Since repetition of digits is not allowed,
1000’s place digit can be selected in 5 ways.
100’s place digit can be selected in 4 ways.
10’s place digit can be selected in 3 ways.
Unit’s place digit can be selected in 2 ways.
∴ Total number of four-digit numbers formed = 5 × 4 × 3 × 2 = 120

Case III: Number of five-digit numbers formed from 2, 3, 4, 5, 6.
Similarly, since repetition of digits is not allowed,
Total number of five digit numbers formed = 5 × 4 × 3 × 2 × 1 = 120.
∴ Total number of numbers that exceed 400 = 36 + 120 + 120 = 276

Question 12.
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
Solution:
Case I: 2-digit numbers more than 13, less than 20, formed from the digits 0, 1, 2, 5, 7, 8.
10’s place digit is 1.
∴ it can be selected in 1 way only.
Unit’s place can be filled by any one of the numbers 5, 7, 8.
∴ Unit’s place digit can be selected in 3 ways.
∴ Total number of such numbers = 1 × 3 = 3.

Case II: 2-digit numbers more than 20 formed from 0, 1, 2, 5, 7, 8.
10’s place can be filled by any one of the numbers 2, 5, 7, 8.
∴ 10’s place digit can be selected in 4 ways.
Since repetition is allowed, the unit’s place can be filled by one of the remaining 6 digits.
∴ Unit’s place digit can be selected in 6 ways.
∴ Total number of such numbers = 4 × 6 = 24.

Case III: 3-digit numbers formed from 0, 1, 2, 5, 7, 8.
Similarly, since repetition of digits is allowed, the total number of such numbers = 5 × 6 × 6 = 180.
All cases are mutually exclusive.
∴ Total number of required numbers = 3 + 24 + 180 = 207

Question 13.
A school has three gates and four staircases from the first floor to the second floor. How many ways does a student have to go from outside the school to his classroom on the second floor?
Solution:
A student can go inside the school from outside in 3 ways and from the first floor to the second floor in 4 ways.
∴ A number of ways to choose gates = 3.
The number of ways to choose a staircase = 4.
By using the fundamental principle of multiplication,
number of ways in which a student has to go from outside the school to his classroom = 4 × 3 = 12

Question 14.
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated?
Solution:
Here, repetition of digits is not allowed.
For a number to be divisible by 5,
unit’s place digit should be 0 or 5.
Case I: when unit’s place is 0
Unit’s place digit can be selected in 1 way.
10’s place digit can be selected in 5 ways.
100’s place digit can be selected in 4 ways.
1000’s place digit can be selected in 3 ways.
10000’s place digit can be selected in 2 ways.
∴ Total number of numbers = 1 × 5 × 4 × 3 × 2 = 120.

Case II: when the unit’s place is 5
Unit’s place digit can be selected in 1 way.
10000’s place should be a non-zero number.
∴ It can be selected in 4 ways.
1000’s place digit can be selected in 4 ways.
100’s place digit can be selected in 3 ways.
10’s place digit can be selected in 2 ways.
∴ Total number of numbers = 1 × 4 × 4 × 3 × 2 = 96
∴ Total number of required numbers = 120 + 96 = 216