Bhagya

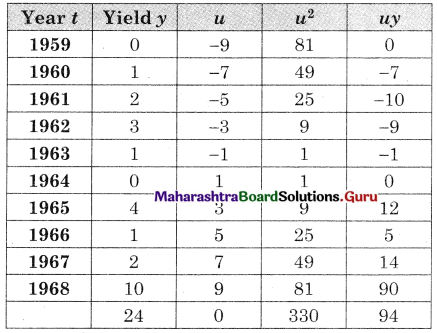
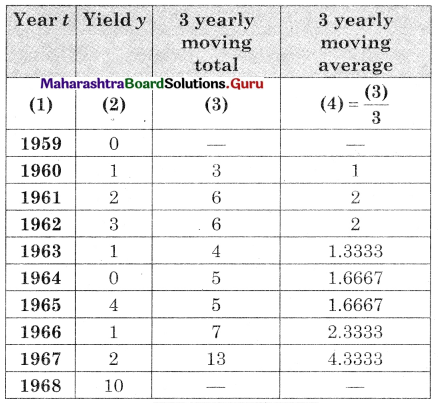
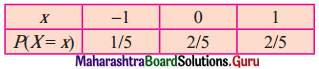
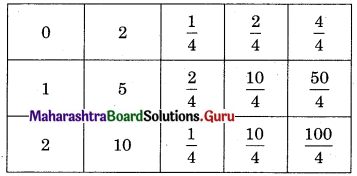
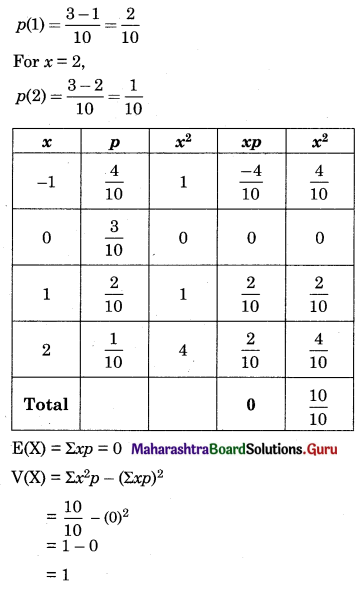
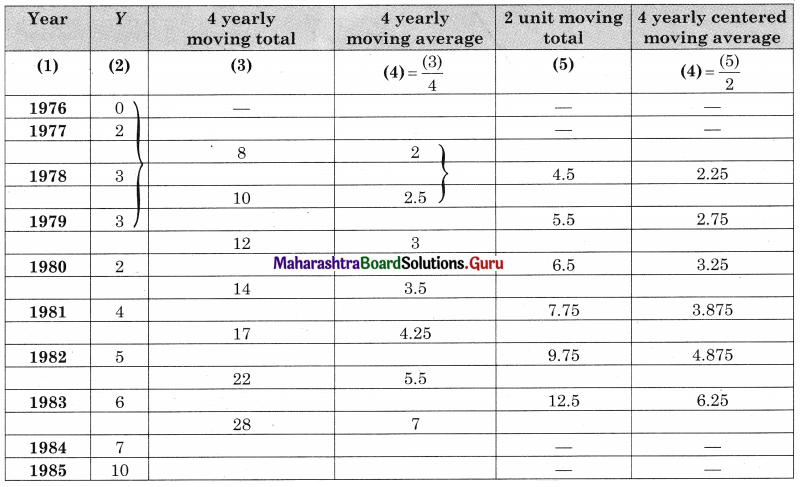
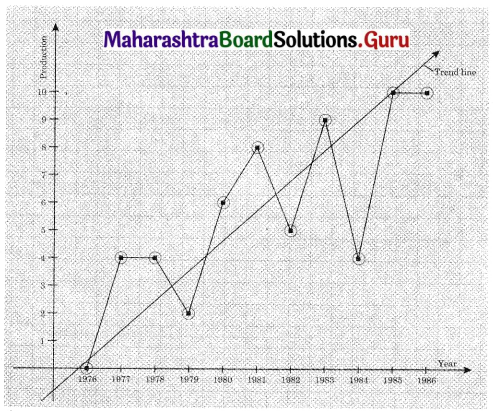
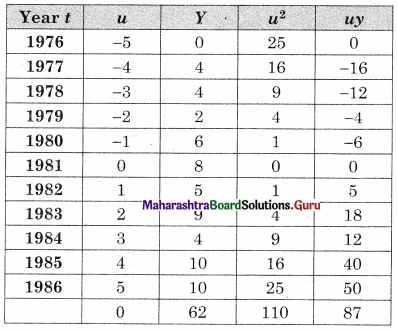
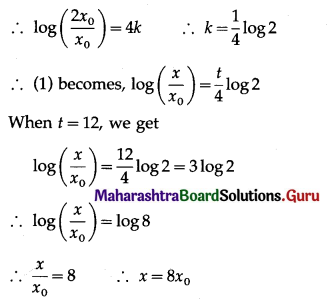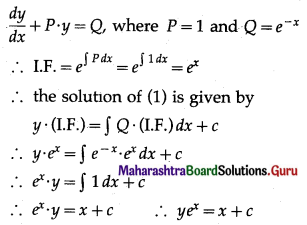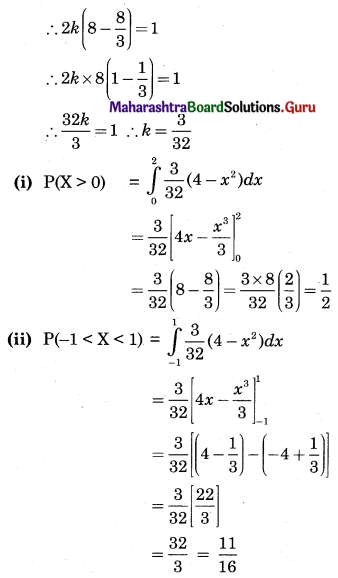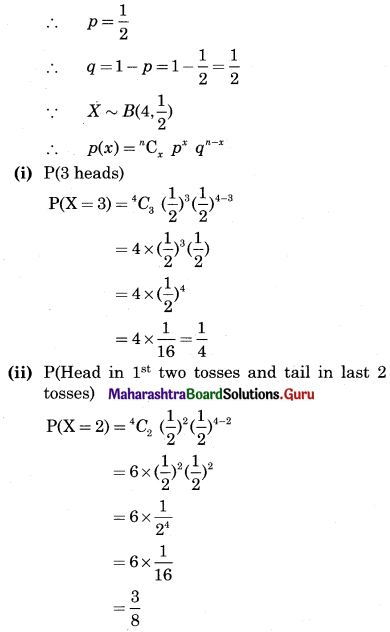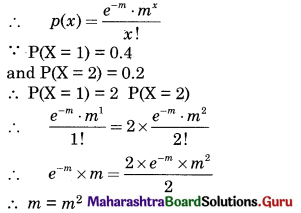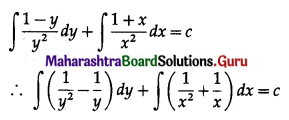Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7

(I) Choose the correct alternative.

Question 1.
In sequencing, an optimal path is one that minimizes ___________
(a) Elapsed time
(b) Idle time
(c) Both (a) and (b)
(d) Ready time
Answer:
(c) Both (a) and (b)

Question 2.
If job A to D have processing times as 5, 6, 8, 4 on first machine and 4, 7, 9, 10 on second machine then the optimal sequence is:
(a) CDAB
(b) DBCA
(c) BCDA
(d) ABCD
Answer:
(b) DBCA

Question 3.
The objective of sequence problem is
(a) to find the order in which jobs are to be made
(b) to find the time required for the completing all the job on hand
(c) to find the sequence in which jobs on hand are to be processed to minimize the total time required for processing the jobs
(d) to maximize the cost
Answer:
(c) to find the sequence in which jobs on hand are to be processed to minimize the total time required for processing the jobs

Question 4.
If there are n jobs and m machines, then there will be ___________ sequences of doing the jobs.
(a) mn
(b) m(n!)
(c) n^m
(d) (n!)^m
Answer:
(d) (n!)^m

Question 5.
The Assignment Problem is solved by
(a) Simple method
(b) Hungarian method
(c) Vector method
(d) Graphical method
Answer:
(b) Hungarian method

Question 6.
In solving 2 machine and n jobs sequencing problem, the following assumption is wrong
(a) No passing is allowed
(b) Processing times are known
(c) Handling times is negligible
(d) The time of passing depends on the order of machining
Answer:
(d) The time of passing depends on the order of machining

Question 7.
To use the Hungarian method, a profit maximization assignments problem requires
(a) Converting all profit to opportunity losses
(b) A dummy person or job
(c) Matrix expansion
(d) Finding the maximum number of lines to cover all the zeros in the reduced matrix
Answer:
(a) Converting all profits to opportunity losses

Question 8.
Using the Hungarian method the optimal assignment obtained for the following assignment problem to minimize the total cost is:

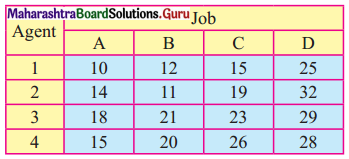
(a) 1 – C, 2 – B, 3 – D, 4 – A
(b) 1 – B, 2 – C, 3 – A, 4 – D
(c) 1 – A, 2 – B, 3 – C, 4 – D
(d) 1 – D, 2 – A, 3 – B, 4 – C
Answer:
(a) 1 – C, 2 – B, 3 – D, 4 – A

Question 9.
The assignment problem is said to be unbalanced if
(a) Number of rows is greater than the number of columns
(b) Number of rows is lesser than number of columns
(c) Number of rows is equal to the number of columns
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 10.
The assignment problem is said to be balanced if
(a) Number of rows is greater than the number of columns
(b) Number of rows is lesser than number of columns
(c) Number of rows is equal to the number of columns
(d) If the entry of rows is zero
Answer:
(c) Number of rows is equal to number of columns

Question 11.
The assignment problem is said to be balanced if it is a
(a) Square matrix
(b) Rectangular matrix
(c) Unit matrix
(d) Triangular matrix
Answer:
(a) Square matrix

Question 12.
In an assignment problem if the number of rows is greater than the number of columns then
(a) Dummy column is added
(b) Dummy row is added
(c) Row with cost 1 is added
(d) Column with cost 1 is added
Answer:
(a) Dummy column is added

Question 13.
In a 3 machine and 5 jobs problem, the least of processing times on machines A, B, and C are 5, 1 and 3 hours and the highest processing times are 9, 5 and 7 respectively, then it can be converted to a 2 machine problem if the order of the machines is:
(a) B – A – C
(b) A – B – C
(c) C – B – A
(d) Any order
Answer:
(b) A – B – C

Question 14.
The objective of an assignment problem is to assign
(a) Number of jobs to equal number of persons at maximum cost
(b) Number of jobs to equal number of persons at minimum cost
(c) Only the maximize cost
(d) Only to minimize cost
Answer:
(b) Number of jobs to equal number of persons at minimum cost

(II) Fill in the blanks.

Question 1.
An assignment problem is said to be unbalanced when ___________
Answer:
the number of rows is not equal to the number of columns

Question 2.
When the number of rows is equal to the Number of columns then the problem is said to be ___________ assignment problem.
Answer:
balanced

Question 3.
For solving assignment problem the matrix should be a ___________
Answer:
square matrix

Question 4.
If the given matrix is not a ___________ matrix, the assignment problem is called an unbalanced problem.
Answer:
square

Question 5.
A dummy row(s) or column(s) with the cost elements as ___________ the matrix of an unbalanced assignment problem as a square matrix.
Answer:
zero

Question 6.
The time interval between starting the first job and completing the last, job including the idle time (if any) in a particular order by the given set of machines is called ___________
Answer:
Total elapsed time

Question 7.
The time for which a machine j does not have a job to process to the start of job i is called ___________
Answer:
Idle time

Question 8.
The maximization assignment problem is transformed to minimization problem by subtracting each entry in the table from the ___________ value in the table.
Answer:
maximum

Question 9.
When the assignment problem has more than one solution, then it is ___________ optimal solution.
Answer:
multiple

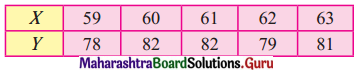
Question 10.
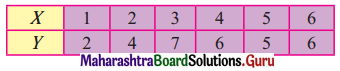
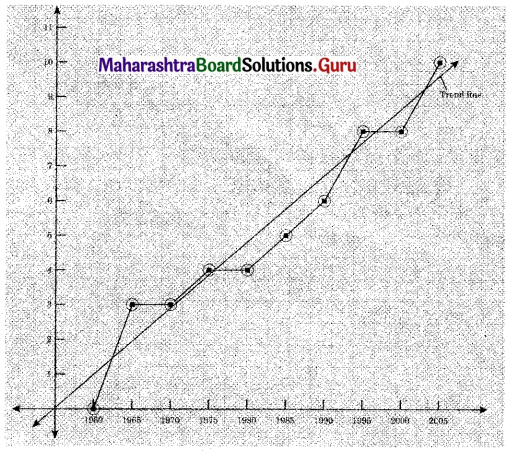
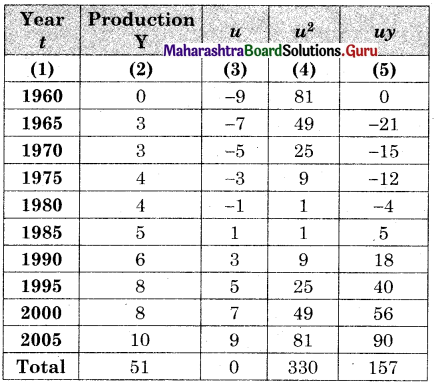
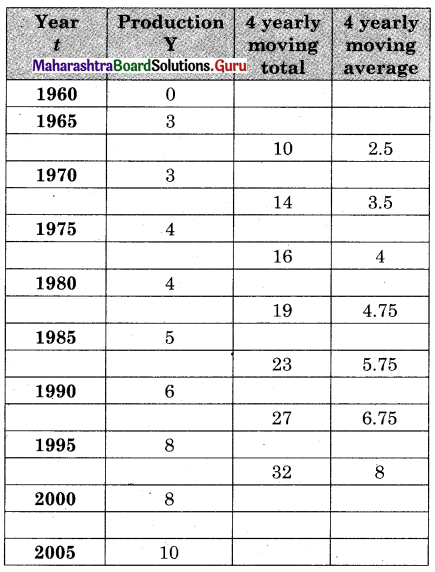
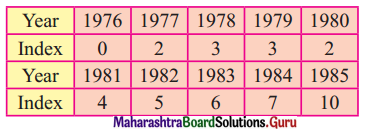
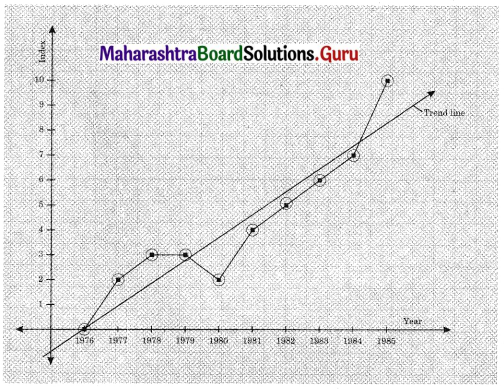
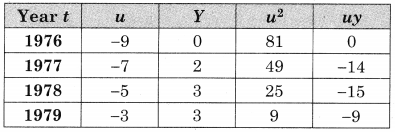
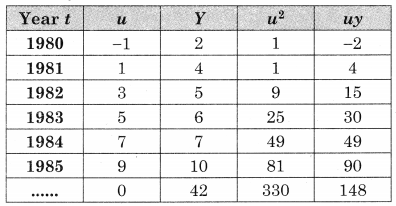
The time required for printing four books A, B, C, and D is 5, 8, 10, and 7 hours. While its data entry requires 7, 4, 3, and 6 hrs respectively. The sequence that minimizes total elapsed time is ___________
Answer:
A – D – B – C

(III) State whether each of the following is True or False.

Question 1.
One machine – one job is not an assumption in solving sequencing problems.
Answer:
False

Question 2.
If there are two least processing times for machine A and machine B, priority is given for the processing time which has the lowest time of the adjacent machine.
Answer:
True

Question 3.
To convert the assignment problem into a maximization problem, the smallest element in the matrix is deducted from all other elements.
Answer:
False

Question 4.
The Hungarian method operates on the principle of matrix reduction, whereby the cost table is reduced to a set of opportunity costs.
Answer:
True

Question 5.
In a sequencing problem, the processing times are dependent on the order of processing the jobs on machines.
Answer:
False

Question 6.
The optimal assignment is made in the Hungarian method to cells in the reduced matrix that contain a Zero.
Answer:
True

Question 7.
Using the Hungarian method, the optimal solution to an assignment problem is fund when the minimum number of lines required to cover the zero cells in the reduced matrix equals the number of people.
Answer:
True

Question 8.
In an assignment problem, if a number of columns are greater than the number of rows, then a dummy column is added.
Answer:
False

Question 9.
The purpose of a dummy row or column in an assignment problem is to obtain a balance between a total number of activities and a total number of resources.
Answer:
True

Question 10.
One of the assumptions made while sequencing n jobs on 2 machines is: two jobs must be loaded at a time on any machine.
Answer:
False

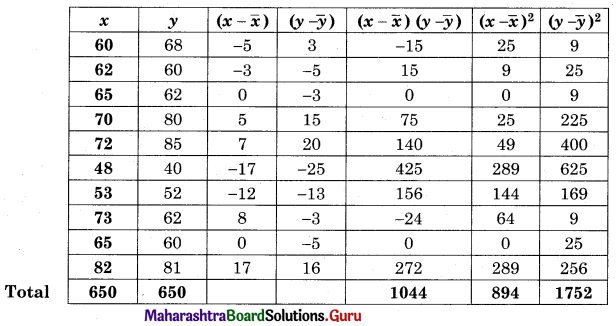
(IV) Solve the following problems.

Part – I

Question 1.
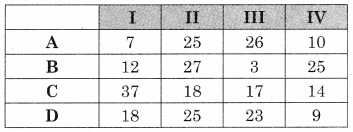
A plant manager has four subordinates, and four tasks to be performed. The subordinates differ in efficiency and the tasks differ in their intrinsic difficulty. This estimate of the times each man would take to perform each task is given in the effectiveness matrix below.

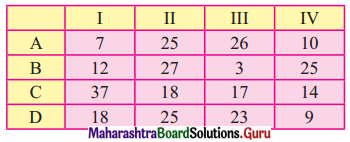
How should the tasks be allocated, one to a man, as to minimize the total man-hours?
Solution:
The hr matrix is given by

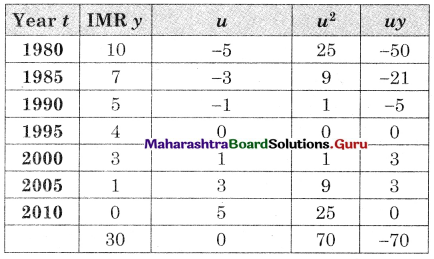
Subtracting row minimum from all values in that row we get

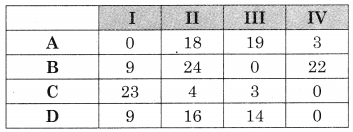
Subtracting column minimum from all values in that column we get

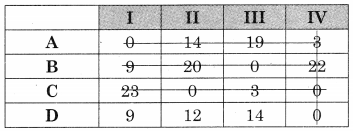
The minimum no. of lines covering ail the zeros (4) is equal to the order of the matrix (4)
∴ The assignment is possible.

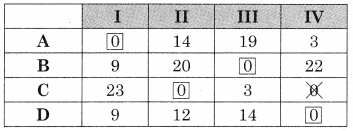
The assignment is
A → I, B → III, C → II, D → IV
For the minimum hrs. take the corresponding value from the hr matrix.
Minimum hrs = 7 + 3 + 18 + 9 = 37 hrs

Question 2.
A dairy plant has five milk tankers, I, II, III, IV & V. These milk tankers are to be used on five delivery routes A, B, C, D & E. The distances (in kms) between the dairy plant and the delivery routes are given in the following distance matrix.

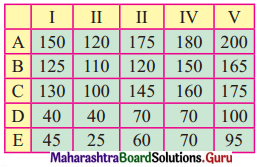
How should the milk tankers be assigned to the chilling centre so as to minimize the distance travelled?
Solution:
The distance matrix is given by

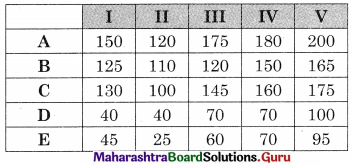
Subtracting row minimum from all values in that row we get

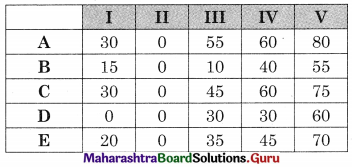
Subtracting column minimum from each value in that column we get

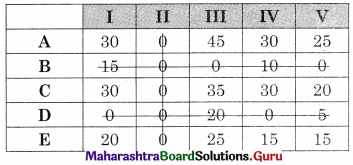
The number of lines covering all the zeros (3) is less than the order of the matrix (5) so the assignment is not possible. The modification is required.
The minimum uncovered value (15) is subtracted from uncovered values and added to the values at the intersection. The numbers on the lines remain the same. We get

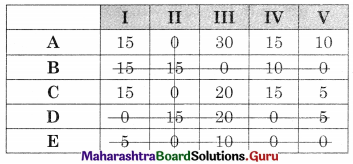
The minimum lines covering all the zeros (4) are less than the order of the matrix (5) so the assignment is not possible. The modification is required the minimum uncovered value (5) is subtracted from uncovered values and added to the values at the intersection. The numbers on the lines remain the same we get

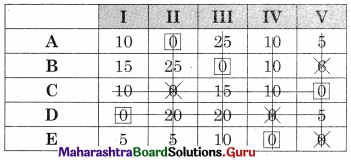
The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) So assignment is possible.
The assignment is
A → II, B → III, C → V, D → I, E → IV
Total minimum distance is = 120 + 120 + 175 + 40 + 70 = 525 kms.

Question 3.
Solve the following assignment problem to maximize sales:

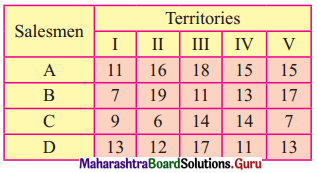
Solution:
As it is a maximization problem so we need to convert it into a minimization problem.
Subtracting all the values from the maximum value (19) we get

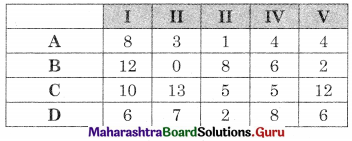
Also, it is an unbalanced problem so we need to add a dummy row (E) with all values zero, we get

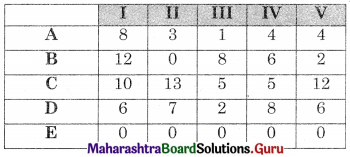
Subtracting row minimum from all values in that row we get

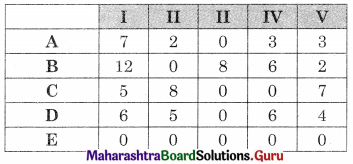
Subtracting column minimum from all values in that column we get the same matrix

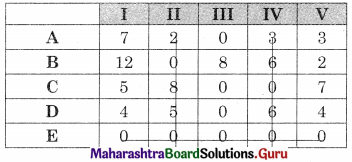
The minimum number of lines covering all the zero (4) is less than the order of the matrix (5) So assignment is not possible. The modification is required. The minimum uncovered value (2) is subtracted from the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

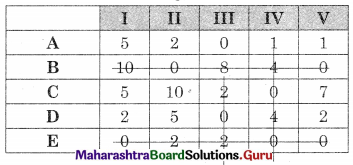
The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so the assignment is not possible. The modification is required. The minimum uncovered value (1) is subtracted from the uncovered value and added to the values at the intersection. The values on the lines remain the same. We get

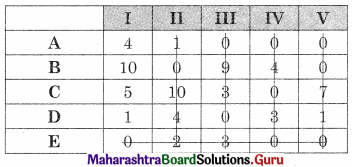
The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

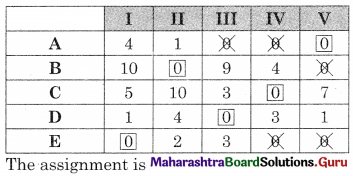
The assignment is
A → V, B → II, C → IV, D → III, E → I
No salesman goes to I as E is a dummy row.
For the maximum value take the corresponding values from the original matrix.
We get Maximum value = 15 + 19 + 14 + 17 + 0 = 65 units

Question 4.
The estimated sales (tons) per month in four different cities by five different managers are given below:

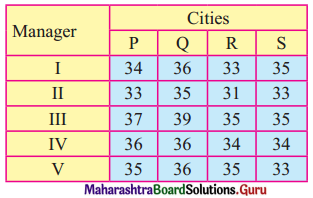
Find out the assignment of managers to cities in order to maximize sales.
Solution:
This is a maximizing problem. To convert it into minimizing problem subtract all the values of the matrix from the maximum (largest) value (39) we get

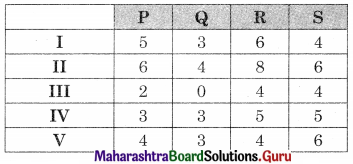
Also as it is an unbalanced problem so we have to add a dummy column (T) with all the values as zero. We get

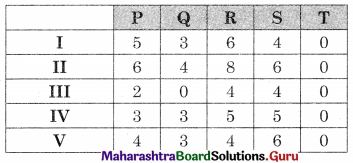
Subtracting row minimum from all values in that row we get the same matrix
Subtracting column minimum from all values in that column we get

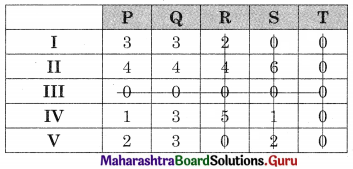
The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so assignments are not possible. The modification is required. The minimum uncovered value (1) is subtracted from the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

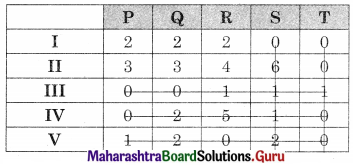
The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

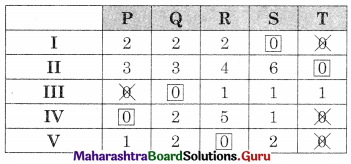
So I → S, II → T, III → Q, IV → P, V → R.
As T is dummy manager II is not given any city.
To find the maximum sales we take the corresponding value from the original matrix
Total maximum sales = 35 + 39 + 36 + 35 = 145 tons

Question 5.
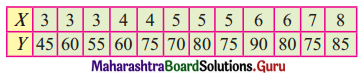
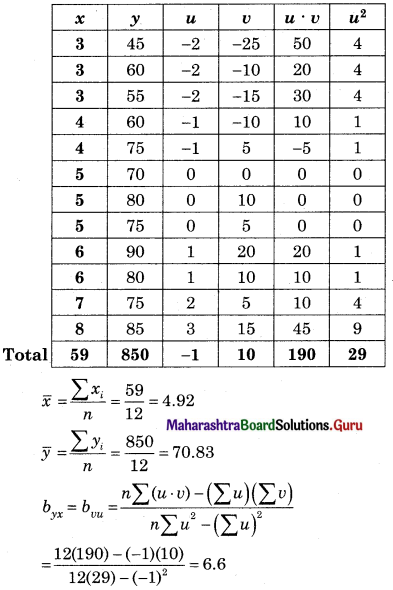
Consider the problem of assigning five operators to five machines. The assignment costs are given in the following table.

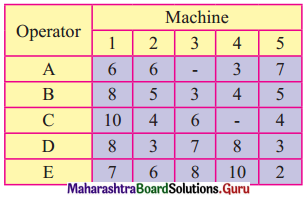
Operator A cannot be assigned to machine 3 and operator C cannot be assigned to machine 4. Find the optimal assignment schedule.
Solution:
This is a restricted assignment problem, so we assign a very high cost (oo) to the prohibited cells we get

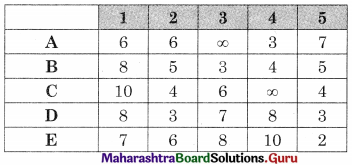
Subtracting row minimum from all values in that row we get.

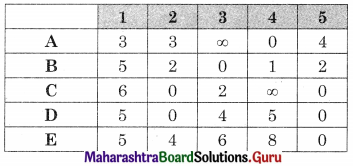
Subtracting column minimum from all values in that column we get

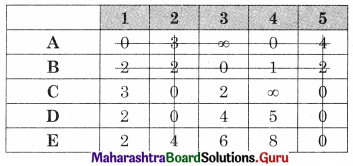
As the minimum number of lines covering all the zeros (4) is equal to the order of the matrix (5) so the assignment is not possible. The modification is required. The minimum uncovered value (2) is subtracted from all the uncovered values and added to the values at the intersection. The values on the lines remain the same. We get

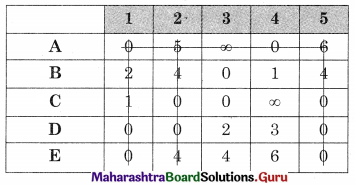
As the minimum number of lines covering all the zeros (5) is equal to the order of the matrix, assignment is the possible

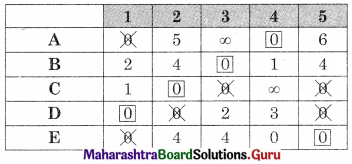
So A → 4, B → 3, C → 2, D → 1, E → 5
For the minimum cost take the corresponding values from the cost matrix we get
Total minimum cost = 3 + 3 + 4 + 3 + 7 = 20 units

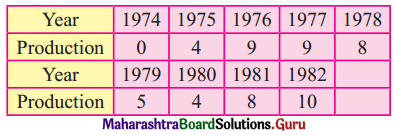
Question 6.
A chartered accountant’s firm has accepted five new cases. The estimated number of days required by each of their five employees for each case are given below, where-means that the particular employee can not be assigned the particular case. Determine the optimal assignment of cases of the employees so that the total number of days required to complete these five cases will be minimum. Also, find the minimum number of days.

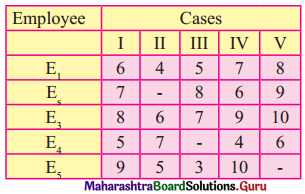
Solution:
This is a restricted assignment problem so we assign a very high cost (∞) to all the prohibited cells. The day matrix becomes

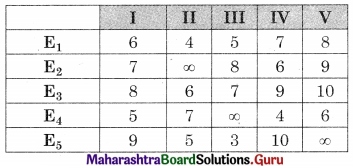
Subtracting row minimum from all values in that row we get

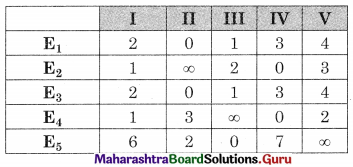
Subtracting column minimum from all values in that column we get

The minimum number of lines covering all the zeros (4) is less than the order of the matrix (5) so the assignment is not possible, The modification is required. The minimum uncovered value (1) is subtracted from all the uncovered values and added to the values at the intersection. The values on the lines remain the same, we get

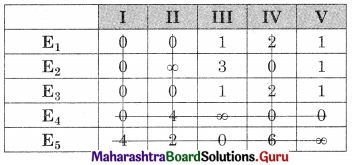
The minimum number of lines covering all the zeros (5) is equal to the order of the matrix (5) so the assignment is possible.

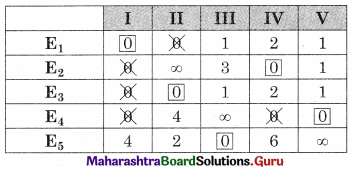
So E₁ → I, E₂ → IV, E₃ → II, E₄ → V, E₅ → III
To find the minimum number of days we take the corresponding values from the day matrix.
Total minimum number of days = 6 + 6 + 6 + 6 + 3 = 27 days

Part – II

Question 1.
A readymade garments manufacture has to process 7 items through two stages of production, namely cutting and sewing. The time taken in hours for each of these items in different stages are given below:

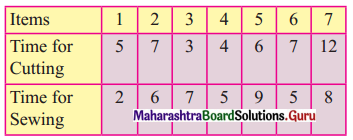
Find the sequence in which these items are to be processed through these stages so as to minimize the total processing time. Also, find the idle time of each machine.
Solution:
Let A = cutting and B = sewing. So we have

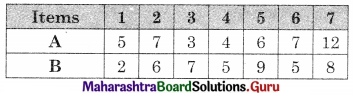
Observe min {A, B} = 2 for item 1 for B.

The problem reduces to

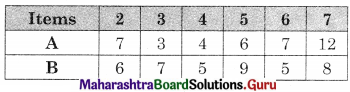
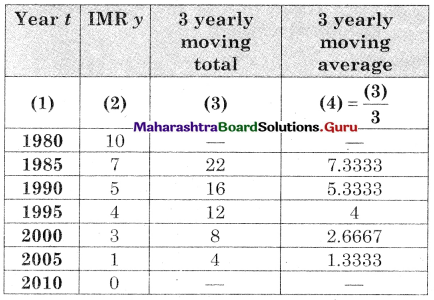
Now min {A, B} = 3 for item 3 for A

The problem reduces to

New min {A , B} = 4 for item 4 for A.

The problem reduces to

Now min(A, B} = 5 for item 6 for B

The problem reduces to

Now min {A, B} = 6 for item 5 for A and item 2 for B

Now only 7 is left
∴ The optimal sequence is

Worktable

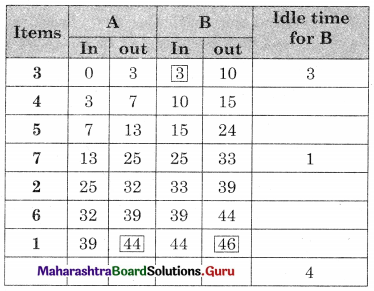
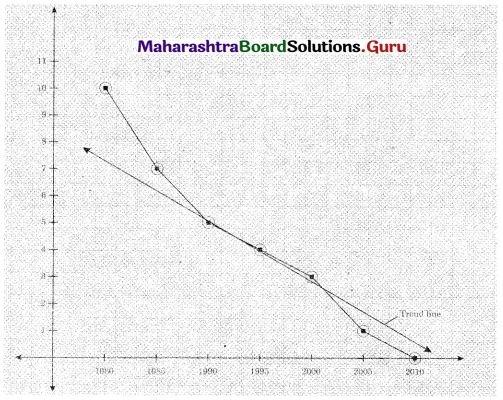
Total elapsed time = 46 hrs
Idle time for A (cutting) = 46 – 44 = 2 hrs
Idle time for B (Sewing) = 4 hrs

Question 2.
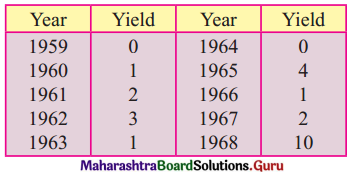
Five jobs must pass through a lathe and a surface grinder, in that order. The processing times in hours are shown below. Determine the optimal sequence of the jobs. Also, find the idle time of each machine.

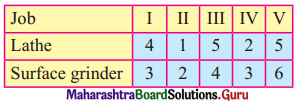
Solution:
Let A = lathe and B = surface grinder. We have

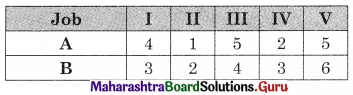
Observe min {A, B} = 1 for job II for A

The problem reduces to

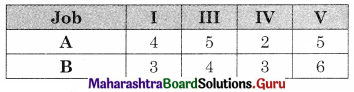
Now min {A, B} = 2 for job IV for A

The problem reduces to

Now min {A, B} = 3 for job I for B

The problem reduces to

Now min {A, B} = 5 for jobs III and V for A
∴ We have two options

or

We take the first one.
Worktable

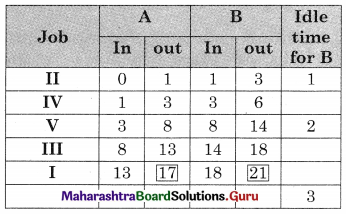
Total elapsed time = 21 hrs
Idle time for A (lathe) = 21 – 17 = 4 hrs
Idle time for B (surface grinder) = 3 hrs

Question 3.
Find the sequence that minimizes the total elapsed time to complete the following jobs. Each job is processed in order AB.

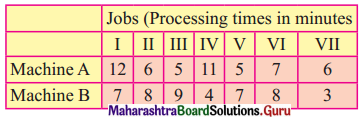
Determine the sequence for the jobs so as to minimize the processing time. Find the total elapsed time and the idle time for both machines.
Solution:
Observe min {A, B} = 3 for job VII on B.

The problem reduces to

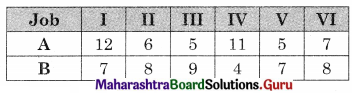
Now min {A, B} = 4 for job IV on B.

The problem reduces to

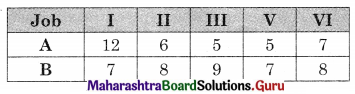
Now min {A, B} = 5 for job III & V on A. we have two options

or

We take the first one
The problem reduces to

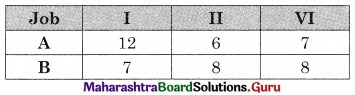
Now min {A, B} = 5 for job II on A

The problem reduces to

Now min {A, B} = 7 for a job I on B and for job VI on A
∴ The optional sequence is

Worktable

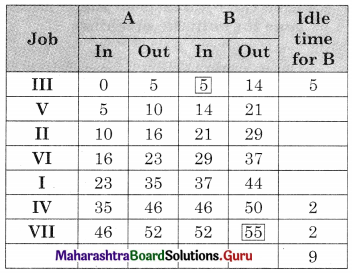
Total elapsed time = 55 units
Idle time for A = 55 – 52 = 3 units
Idle time for B = 9 units.

Question 4.
A toy manufacturing company has five types of toys. Each toy has to go through three machines A, B, C in the order ABC. The time required in hours for each process is given in the following table.

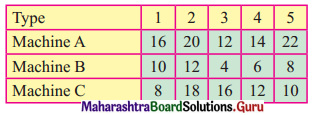
Solve the problem for minimizing the total elapsed time.
Solution:
Min A = 12, Max B = 12
As min A ≥ max B.
The problem can be converted into two machine problems.
Let G and H be two fictitious machines such that G = A + B and H = B + C, We get

Now min {G, H} = 16 for type 3 on G

The problem reduces to

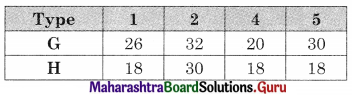
Min (G, H} = 18 for type 1, 4 & 5 on H
We have more than one option, we take

Now only type 2 is left.
∴ The optional sequence is

Worktable

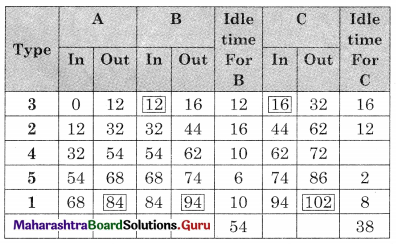
Total elapsed time = 102 hours
Idle time for A = 102 – 84 = 18 hours
Idle time for B = 54 + (102 – 94) = 62 hours
Idle time for C = 38 hours

Question 5.
A foreman wants to process 4 different jobs on three machines: a shaping machine, a drilling machine, and a tapping, the sequence of operations being shaping-drilling-tapping. Decide the optimal sequence for the four jobs to minimize the total elapsed time. Also, find the total elapsed time and the idle time for every machine.

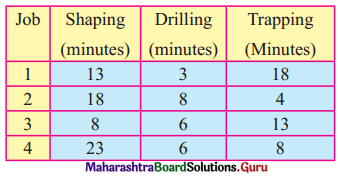
Solution:
The time matrix is

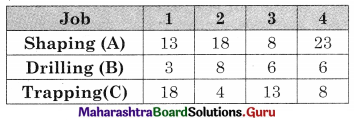
Min A = 8, Max B = 8, as min A ≥ max B.
The problem can be converted into a two-machine problem.
Let G and H be two fictitious machines such that
G = A + B and H = B + C we get

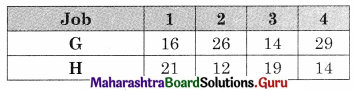
Observe min (G, H} = 12 for job 2 on H

The problem reduces to

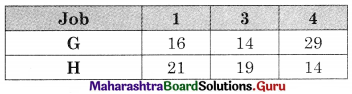
Now min {G, H} = 14 for job 3 on G and job 4 on H

Now only job 1 is left.
∴ The optimal sequence is

Worktable

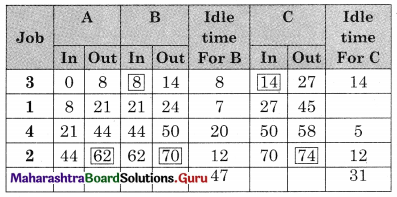
Total elapsed time = 74 min
Idle time for A (shapping) = 74 – 62 = 12 min
Idle time for B (Drilling) = 47 + (74 – 70) = 51 min
Idle time for C (trapping) = 31 min

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

(I) Choose the correct option from the given alternatives:

Question 1.
The order and degree of \(\left(\frac{d y}{d x}\right)^{3}-\frac{d^{3} y}{d x^{3}}+y e^{x}=0\) are respectively.
(a) 3, 1
(b) 1, 3
(c) 3, 3
(d) 1, 1
Answer:
(a) 3, 1

Question 2.
The order and degree of \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]^{\frac{2}{3}}=8 \frac{d^{3} y}{d x^{3}}\) are respectively
(a) 3, 1
(c) 3, 3
(b) 1, 3
(d) 1, 1
Answer:
(c) 3, 3

Question 3.
The differential equation of y = k₁ + \(\frac{k_{2}}{x}\) is
(a) \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
(d) \(x \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
Answer:
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)

Question 4.
The differential equation of y = k₁ e^x + k₂ e^-x is
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
(b) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}+y \frac{d y}{d x}=0\)
(d) \(\frac{d^{2} y}{d x^{2}}+y=0\)
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)

Question 5.
The solution of \(\frac{d y}{d x}\) = 1 is
(a) x + y = c
(b) xy = c
(c) x² + y² = c
(d) y – x = c
Answer:
(d) y – x = c

Question 6.
The solution of \(\frac{d y}{d x}+\frac{x^{2}}{y^{2}}=0\) is
(a) x³ + y³ = 7
(b) x² + y² = c
(c) x³ + y³ = c
(d) x + y = c
Answer:
(c) x³ + y³ = c

Question 7.
The solution of x \(\frac{d y}{d x}\) = y log y is
(a) y = ae^x
(b) y = be^2x
(c) y = be^-2x
(d) y = e^ax
Answer:
(d) y = e^ax

Question 8.
Bacterial increases at a rate proportional to the number present. If the original number M doubles in 3 hours, then the number of bacteria will be 4M in
(a) 4 hours
(b) 6 hours
(c) 8 hours
(d) 10 hours
Answer:
(b) 6 hours

Question 9.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is
(a) x
(b) -x
(c) e^x
(d) e^-x
Answer:
(c) e^x

Question 10.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is e^-x, then its solution is
(a) ye^-x = x + c
(b) ye^x = x + c
(c) ye^x = 2x + c
(d) ye^-x = 2x + c
Answer:
(a) ye^-x = x + c

(II) Fill in the blanks:

Question 1.
The order of highest derivative occurring in the differential equation is called ________ of the differential equation.
Answer:
order

Question 2.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called ________ of the differential equation.
Answer:
degree

Question 3.
A solution of differential equation that can be obtained from the general solution by giving particular values to the arbitrary constants is called _________ solution.
Answer:
particular

Question 4.
Order and degree of a differential equation are always _________ integers.
Answer:
positive

Question 5.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is _________
Answer:
e^-x

Question 6.
The differential equation by eliminating arbitrary constants from bx + ay = ab is _________
Answer:
\(\frac{d^{2} y}{d x^{2}}=0\)

(III) State whether each of the following is True or False:

Question 1.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is e^-x.
Answer:
True

Question 2.
The order and degree of a differential equation are always positive integers.
Answer:
True

Question 3.
The degree of a differential equation is the power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any.
Answer:
True

Question 4.
The order of highest derivative occurring in the differential equation is called the degree of the differential equation.
Answer:
False

Question 5.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called the order of the differential equation.
Answer:
False

Question 6.
The degree of the differential equation \(e^{\frac{d y}{d x}}=\frac{d y}{d x}+c\) is not defined.
Answer:
True

(IV) Solve the following:

Question 1.
Find the order and degree of the following differential equations:
(i) \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given differential equation is \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
∴ \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3}=\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3
∴ order = 3 and degree = 3

(ii) \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
Solution:
The given differential equation is \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ order = 1, degree = 2.

Question 2.
Verify that y = log x + c is a solution of the differential equation \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\).
Solution:
y = log x + c
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{1}{x}+0=\frac{1}{x}\)
∴ x\(\frac{d y}{d x}\) = 1
Differentiating again w.r.t. x, we get
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \times 1=0\)
∴ \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
This shows that y = log x + c is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)

Question 3.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = 1 + x + y + xy
Solution:
\(\frac{d y}{d x}\) = 1 + x + y + xy
∴ \(\frac{d y}{d x}\) = (1 + x) + y(1 + x) = (1 + x)(1 + y)
∴ \(\frac{1}{1+y}\) dy = (1 + x) dx
Integrating, we get
∫\(\frac{1}{1+y}\) dy = ∫(1 + x) dx
∴ log|1 + y| = x + \(\frac{x^{2}}{2}\) + c
This is the general solution.

(ii) \(e^{d y / d x}=x\)
Solution:

∴ from (1), the general solution is
y = x log x – x + c, i.e. y = x(log x – 1) + c.

(iii) dr = ar dθ – θ dr
Solution:
dr = ar dθ – θ dr
∴ dr + θ dr = ar dθ
∴ (1 + θ) dr = ar dθ
∴ \(\frac{d r}{r}=\frac{a d \theta}{1+\theta}\)
On integrating, we get
\(\int \frac{d r}{r}=a \int \frac{d \theta}{1+\theta}\)
∴ log |r| = a log |1 + θ| + c
This is the general solution.

(iv) Find the differential equation of the family of curves y = e^x (ax + bx²), where a and b are arbitrary constants.
Solution:
y = e^x (ax + bx²)
ax + bx² = ye^-x …….(1)
Differentiating (1) w.r.t. x twice and writing \(\frac{d y}{d x}\) as y₁ and \(\frac{d^{2} y}{d x^{2}}\) as y₂, we get


This is the required differential equation.

Question 4.
Solve \(\frac{d y}{d x}=\frac{x+y+1}{x+y-1}\) when x = \(\frac{2}{3}\) and y = \(\frac{1}{3}\).
Solution:

Question 5.
Solve y dx – x dy = -log x dx.
Solution:
y dx – x dy = -log x dx
∴ y dx – x dy + log x dx = 0
∴ x dy = (y + log x) dx
∴ \(\frac{d y}{d x}=\frac{y+\log x}{x}=\frac{y}{x}+\frac{\log x}{x}\)
∴ \(\frac{d y}{d x}-\frac{1}{x} \cdot y=\frac{\log x}{x}\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 6.
Solve y log y \(\frac{d x}{d y}\) + x – log y = 0.
Solution:

Question 7.
Solve (x + y) dy = a² dx
Solution:

Question 8.
Solve \(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\)
Solution:
\(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\) ……..(1)
This is a linear differential equation of the form

This is the general solution.

Question 9.
The rate of growth of the population is proportional to the number present. If the population doubled in the last 25 years and the present population is 1 lakh, when will the city have a population of 400000?
Solution:
Let P be the population at time t years.
Then the rate of growth of the population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\)= k dt
On integrating, we get
\(\int \frac{d P}{P}=k \int d t\)
∴ log P = kt + c
The population doubled in 25 years and present population is 1,00,000.
∴ initial population was 50,000
i.e. when t = 0, P = 50000
∴ log 50000 = k × 0 + c
∴ c = log 50000
∴ log P = kt + log 50000
When t = 25, P = 100000
∴ log 100000 = k × 25 + log 50000
∴ 25k = log 100000 – log 50000 = log(\(\frac{100000}{50000}\))
∴ k = \(\frac{1}{25}\) log 2
∴ log P = \(\frac{t}{25}\) log 2 + log 50000
If P = 400000, then
log 400000 = \(\frac{t}{25}\) log 2 + log 50000
∴ log 400000 – log 50000 = \(\frac{t}{25}\) log 2
∴ log(\(\frac{400000}{50000}\)) = \(\log (2)^{t / 25}\)
∴ log 8 = \(\log (2)^{t / 25}\)
∴ 8 = \((2)^{t / 25}\)
∴ \((2)^{t / 25}\) = (2)³
∴ \(\frac{t}{25}\) = 3
∴ t = 75
∴ the population will be 400000 in (75 – 25) = 50 years.

Question 10.
The resale value of a machine decreases over a 10 years period at a rate that depends on the age of the machine. When the machine is x years old, the rate at which its value is changing is ₹ 2200(x – 10) per year. Express the value of the machine as a function of its age and initial value. If the machine was originally worth ₹ 1,20,000 how much will it be worth when it is 10 years old?
Solution:
Let V be the value of the machine after x years.
Then rate of change of the value is \(\frac{d V}{d x}\) which is 2200(x – 10)
∴ \(\frac{d V}{d x}\) = 2200(x – 10)
∴ dV = 2200(x – 10) dx
On integrating, we get
∫dV = 2200∫(x – 10) dx
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + c
Initially, i.e. at x = 0, V = 120000
∴ 120000 = 2200 × 0 + c = c
∴ c = 120000
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + 120000 …….(1)
This gives value of the machine in terms of initial value and age x.
We have to find V when x = 10.
When x = 10, from (1)
V = 2200[\(\frac{100}{2}\) – 100] + 120000
= 2200 [-50] + 120000
= -110000 + 120000
= 10000
Hence, the value of the machine after 10 years will be ₹ 10000.

Question 11.
Solve y² dx + (xy + x²) dy = 0
Solution:

Question 12.
Solve x²y dx – (x³ + y³) dy = 0
Solution:

Question 13.
Solve yx \(\frac{d y}{d x}\) = x² + 2y²
Solution:

Question 14.
Solve (x + 2y³) \(\frac{d y}{d x}\) = y
Solution:
(x + 2y³) \(\frac{d y}{d x}\) = y
∴ x + 2y³ = y \(\frac{d x}{d y}\)

This is the general solution.

Question 15.
Solve y dx – x dy + log x dx = 0
Solution:
y dx – x dy + log x dx = 0
∴ (y + log x) dx = x dy


This is the general solution.

Question 16.
Solve \(\frac{d y}{d x}\) = log x dx
Solution:
\(\frac{d y}{d x}\) = log x dx
∴ dy = log x dx
On integrating, we get
∫dy = ∫log x . 1 dx
∴ y = (log x) ∫1 dx – \(\int\left[\left\{\frac{d}{d x}(\log x)\right\} \cdot \int 1 d x\right] d x\)
∴ y = (log x) . x – \(\int \frac{1}{x} \cdot x d x\)
∴ y = x log x – ∫1 dx
∴ y = x log x – x + c
This is the general solution.

Question 17.
y log y \(\frac{d x}{d y}\) = log y – x
Solution:

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Ex 3.1

Question 1.
The HRD manager of the company wants to find a measure which he can use to fix the monthly income of persons applying for the job in the production department. As an experimental project. He collected data of 7 persons from that department referring to years of service and their monthly incomes.

(i) Find the regression equation of income on years of service.
(ii) What initial start would you recommend for a person applying for the job after having served in a similar capacity in another company for 13 years?
Solution:


(i) Regression equation of Y on X is (Y – \(\bar{y}\)) = b_yx (x – \(\bar{x}\))
(Y – 8) = 0.75(x – \(\bar{x}\))
Y = 0.75x + 2
(ii) When x = 13
Y = 0.75(13) + 2 = 11.75
Recommended income for the person is ₹ 11750.

Question 2.
Calculate the regression equations of X on Y and Y on X from the following date:

Solution:


Regression equation of X on Y is (X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 14) = 1(Y – 8)
X – 14 = Y – 8
X = Y + 6
Regression equation Y on X is (Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 8) = 0.87(X – 14)
Y – 8 = 0.87X – 12.18
Y = 0.87X – 4.18

Question 3.
For a certain bivariate data on 5 pairs of observations given
Σx = 20, Σy = 20, Σx² = 90, Σy² = 90, Σxy = 76
Calculate (i) cov(x, y), (ii) b_yx and b_xy, (iii) r
Solution:


Sine byx and bxy are negative, r = -0.4

Question 4.
From the following data estimate y when x = 125

Solution:
Let u = x – 122, v = y – 14

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 13.5) = -0.21(x – 121.5)
Y – 13.5 = -0.21x + 25.52
Y = -0.21x + 39.02
When x = 125
Y = -0.21(125) + 39.02
= -26.25 + 39.02
= 12.77

Question 5.
The following table gives the aptitude test scores and productivity indices of 10 works selected at workers selected randomly.

Obtain the two regression equation and estimate
(i) The productivity index of a worker whose test score is 95.
(ii) The test score when productivity index is 75.
Solution:


Regression equation of Y on X,
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{y}\))
(Y – 65) = 1.16 (x – 65)
Y – 65 = 1.16x – 75.4
Y = 1.16x – 10.4
(i) When x = 95
Y = 1.16(95) – 10.4
= 110.2 – 10.4
= 99.8
Regression equation of X on Y,
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 65) = 0.59(y – 65)
(X – 65) = 0.59y – 38.35
X = 0.59y + 26.65
(ii) When y = 75
x = 0.59(75) + 26.65
= 44.25 + 26.65
= 70.9

Question 6.
Compute the appropriate regression equation for the following data.

Solution:
Since x is the independent variable, and y is the dependent variable,
we need to find regression equation of y on x


Regression equation of y on x is (y – \(\bar{y}\)) = b_yx (x – \(\bar{x}\))
(y – 10) = -13.4(x – 6)
y – 10 = -1.34x + 8.04
y = -1.34x + 18.04

Question 7.
The following are the marks obtained by the students in Economic (X) and Mathematics (Y)

Find the regression equation of Y and X.
Solution:
Let u = x – 61, v = y – 80

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 80.4) = 0.3(x – 61)
Y – 80.4 = 0.3x – 18.3
Y = 0.3x + 62.1

Question 8.
For the following bivariate data obtain the equation of two regressions lines:

Solution:


Regression equation of Y on X
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 9) = 2(x – 3)
Y – 9 = 2x – 6
Y = 2x + 3
Regression equation of X on Y
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 3) = 0.5(y – 9)
(X – 3) = 0.5y – 4.5
X = 0.5y – 1.5

Question 9.
Find the following data obtain the equation of two regression lines:

Solution:


Regression of Y on X,
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 8) = 0.65(x – 6)
Y – 8 = -0.65x + 3.9
Y = -0.65x + 11.9
Regression of X on Y
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 6) = -1.3(y – 8)
(X – 6) = -1.3y + 10.4
X = -1.3y + 16.4

Question 10.
For the following data, find the regression line of Y on X

Hence find the most likely value of y when x = 4
Solution:

(Y – 3) = 2(x – 2)
Y – 3 = 2x – 4
Y = 2x – 1
When x = 4
Y = 2(4) – 1
= 8 – 1
= 7

Question 11.
Find the following data, find the regression equation of Y on X, and estimate Y when X = 10.

Solution:

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 5) = (0.63)(x – 3.5)
Y – 5 = 0.63x – 2.2
Y = 0.63x + 2.8
When x = 10
Y = 0.63(10) + 2.8
= 6.3 + 2.8
= 9.1

Question 12.
The following sample gave the number of hours of study (X) per day for an examination and marks (Y) obtained by 12 students.

Obtain the line of regression of marks on hours of study.
Solution:
Let u = x – 5, v = y – 70

∴ Equation of marks on hours of study is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 70.83) = 6.6(x – 4.92)
Y – 70.83 = 6.6x – 32.47
∴ Y = 6.6x + 38.36

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 4 Time Series Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Time Series Miscellaneous Exercise 4

(I) Choose the correct alternative.

Question 1.
Which of the following can’t be a component of a time series?
(a) Seasonality
(b) Cyclical
(c) Trend
(d) Mean
Answer:
(d) Mean

Question 2.
The first step in time series analysis is to
(a) Perform regression calculations
(b) Calculate a moving average
(c) Plot the data on a graph
(d) Identify seasonal variation
Answer:
(c) Plot the data on a graph

Question 3.
Time-series analysis is based on the assumption that
(a) Random error terms are normally distributed.
(b) The variable to be forecast and other independent variable are correlated.
(c) Past patterns in the variable to be forecast will continue unchanged into the future.
(d) The data do not exhibit a trend.
Answer:
(c) Past patterns in the variable to be forecast will continue unchanged into the future.

Question 4.
Moving averages are useful in identifying
(a) Seasonal component
(b) Irregular component
(c) Trend component
(d) Cyclical component
Answer:
(c) Trend component

Question 5.
We can use regression line for past data to forecast future data. We then use the line which
(a) Minimizes the sum of squared deviations of past data from the line.
(b) Minimizes the sum of deviations of past data from the line.
(c) Maximizes the sum of squared deviations of past data from the line.
(d) Maximizes the sum of deviation of past data from the line.
Answer:
(a) Minimizes the sum of squared deviations of past data from the line

Question 6.
Which of the following is a major problem for forecasting, especially when using the method of least squares?
(a) The past cannot be known
(b) The future is not entirely certain
(c) The future exactly follows the patterns of the past
(d) The future may not follow the patterns of the past
Answer:
(d) The future may not follow the patterns of the past

Question 7.
An overall upward or downward pattern in an annual time series would be contained in which component of the time series
(a) Trend
(b) Cyclical
(c) Irregular
(d) Seasonal
Answer:
(a) Trend

Question 8.
The following trend line equation was developed for annual sales from 1984 to 1990 with 1984 as base or zero year. Y1 = 500 + 60X (in 1000 Rs.) The estimated sales for 1984 (in 1000 Rs) is:
(a) ₹ 500
(b) ₹ 560
(c) ₹ 1,040
(d) ₹ 1100
Answer:
(a) ₹ 500

Question 9.
What is a disadvantage of the graphical method of determining a trend line?
(a) Provides quick approximations
(b) Is subject to human error
(c) Provides accurate forecasts
(d) Is too difficult to calculate
Answer:
(b) Is subject to human error

Question 10.
Which component of time series refers to erratic time series movements that follow no recognizable or regular pattern.
(a) Trend
(b) Seasonal
(c) Cyclical
(d) Irregular
Answer:
(a) Trend

(II) Fill in the blanks.

Question 1.
_________ components of time series is indicated by a smooth line.
Answer:
Trend

Question 2.
_________ component of time series is indicated by periodic variation year after year.
Answer:
Seasonal

Question 3.
_________ component of time series is indicated by a long wave spanning two or more years.
Answer:
Cyclical

Question 4.
_________ component of time series is indicated by up and down movements without any pattern.
Answer:
Irregular

Question 5.
Addictive models of time series _________ independence of its components.
Answer:
assume

Question 6.
Multiplicative models of time series _________ independence of its components.
Answer:
does not assume

Question 7.
The simplest method of measuring the trend of time series is _________
Answer:
graphical method

Question 8.
The method of measuring the trend of time series using only averages is _________
Answer:
moving average method

Question 9.
The complicated but ancient method of measuring the trend of time series is _________
Answer:
least-squares method

Question 10.
The graph of time series clearly shows _________ of it is monotone.
Answer:
trend

(III) State whether each of the following is True or False.

Question 1.
The secular trend component of the time series represents irregular variations.
Answer:
False

Question 2.
Seasonal variation can be observed over several years.
Answer:
True

Question 3.
Cyclical variation can occur several times in a year.
Answer:
False

Question 4.
Irregular variation is not a random component of time series.
Answer:
False

Question 5.
The additive model of time series does not require the assumptions of independence of its components.
Answer:
False

Question 6.
The multiplicative model of time series does not require the assumption of independence of its components.
Answer:
True

Question 7.
The graphical method of finding trends is very complicated and involves several calculations.
Answer:
False

Question 8.
Moving the average method of finding trends is very complicated and involves several calculations.
Answer:
False

Question 9.
The least-squares method of finding trends is very simple and does not involve any calculations.
Answer:
False

Question 10.
All three methods of measuring trends will always give the same results.
Answer:
False

(IV) Solve the following problems.

Question 1.
The following table shows the productivity of pig-iron and ferro-alloys (‘000 metric tonnes)

Fit a trend line to the above data by graphical method.
Solution:

Question 2.
Fit a trend line to the data in Problem IV (1) by the method of least squares.
Solution:

u = \(\frac{t-1978}{1}\), Σy = 57, Σu = 0, Σu² = 60, Σuy = 38, n = 9
Let the equation of the trend line be
Y = a + bu where u = t – 1978 ……(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ………(iii)
Substituting the values of Σu, n, Σuy, Σu² in (ii) & (iii) we get
57 = 9a + 0 ∴ a = 6.3333
38 = 0 + b . 60 ∴ b = 0.6333.
∴ The equation of the trend line is
y = 6.3333 + 0.63333u where u = t – 1978

Question 3.
Obtain the trends values for the data on problem IV (1) using 5 yearly moving averages.
Solution:

Question 4.
The following table shows the amount of sugar production (in lac tonnes) for the years 1971 to 1982.

Fit a trend line to the above data by graphical method.
Solution:

Question 5.
Fit a trend line to data in problem 4 by the method of least squares.
Solution:

u = \(\frac{t-1976.5}{\frac{1}{2}}\), Σy = 38, Σu = 0, Σu² = 572, Σuy = 160, n = 12
Let the equation of the trend line be
y = a + bu ……..(i)
where u = \(\frac{t-1976.5}{\frac{1}{2}}\)
u = 2t – 3953
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ……..(iii)
by (ii) 38 = 12o + 0 ∴ a = 3.1867
by (iii) 160 = 0 + b . 572 ∴ b = 0.2797
∴ by (i), Equation of the trend line is
Y = 3.1667 + 0.2797u where u = 2t – 3953.

Question 6.
Obtain trend values for data in Problem 4 using 4-yearly centered moving averages.
Solution:

Question 7.
The percentage of girls’ enrollment in total enrollment for years 1960-2005 is shown in the following table.

Fit a trend line to the above data by graphical method.
Solution:

Question 8.
Fit a trend line to the data in Problem 7 by the method of least squares.
Solution:

u = \(\frac{t-1980.5}{5}\), Σy = 51, Σu = 0, Σu² = 330, Σuy = 157, n = 10
Let the equation of the trend line be
Y = a + bu where u = \(\frac{t-1980.5}{5}\) …….(i)
Σy = na + bΣu ……..(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting the values of Σy, Σu, n, Σuy, Σu² We get
51 = 10a + 0 ∴ a = 5.1
and 157 = 0 + 6.330 ∴ b = 0.4758
by (i) equation of the trend line is
Y = 5.1 + 0.4758u where u = \(\frac{t-1980.5}{5}\)

Question 9.
Obtain trend values for the data in Problem 7 using 4-yearly moving averages.
Solution:

Question 10.
The following data shows the number of boxes of cereal sold in the years 1977 to 1984.

Fit a trend line to the above data by graphical method.
Solution:

Question 11.
Fit a trend line to data in Problem 10 by the method of least squares.
Solution:

u = \(\frac{t-1980.5}{\frac{1}{2}}\), Σy = 39, Σu = 0, Σu² = 168, Σuy = 79, n = 8
Let the equation of the trend line by
Y = a + bu
Where u = 2t – 3961 …….(i)
Σy = na + bΣu …….(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting the values of Σy, n, Σu, Σuy, Σu², in (ii) & (iii)
39 = 8a + 0 ∴ a = 4.875
79 = 0 + b (168) ∴ b = 0.4702
by (i) the equation of the trend line is
Y = 4.875 + 0.4702u Where u = 2t – 3961.

Question 12.
Obtain trend values for data in Problem 10 using 3-yearly moving averages.
Solution:

Question 13.
The following table shows the number of trade fatalities (in a state) resulting from drunken driving for the years 1975 to 1983.

Fit a trend line to the above data by graphical method.
Solution:

Question 14.
Fit a trend line to data in Problem 13 by the method of least squares.
Solution:

u = \(\frac{t-1979}{1}\), Σy = 47, Σu = 0, Σu² = 60, Σuy = 40, n = 9
Let the equation of the trends line be
Y = a + bu where u = t – 1979 …….(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting values of Σy, n, Σu, Σuy, Σu² in (ii) & (iii)
We get 47 = 9a + 0 ∴ a = 5.2222
and 40 = 0 + b(60) ∴ b = 0.6667
∴ by (i) the equation of the trend line is
Y = 5.2222 + 0.6667u Where u = t – 1979.

Question 15.
Obtain trend values for data in Problem 13 using 4-yearly moving averages.
Solution:

Question 16.
The following table shows the all India infant mortality rates (per ‘000) for the years 1980 to 2000.

Fit a trend line to the above data by graphical method.
Solution:

Question 17.
Fit a trend line to data in Problem 16 by the method of least squares.
Solution:

u = \(\frac{t-1995}{5}\), Σy = 30, Σu = 0, Σu² = 70, Σuy = -70, n = 7
Let the equation of the trend line be
Y = a + bu Where u = \(\frac{t-1995}{5}\) …..(i)
Σy = na + bΣu ……(ii)
Σuy = aΣu + bΣu² …….(iii)
Substituting values of Σy, n, Σu, Σuy & Σu² in (ii) & (iii) we get
30 = 7a + 0 ∴ a = 4.2857
-70 = 0 + 6(70) ∴ b = -1
∴ by (i) the equation of the trend line is
y = 4.2857 – 1(u) Where u = \(\frac{t-1995}{5}\)

Question 18.
Obtain trend values for data in Problem 16 using 3-yearly moving averages.
Solution:

Question 19.
the following table shows the wheat yield (‘000 tonnes) in India for the years 1959 to 1968.

Fit a trend line to the above data by the method of least squares.
Solution:

u = \(\frac{t-1963.5}{\frac{1}{2}}\), Σy = 24, Σu = 0, Σu² = 330, Σuy = 94, n = 10
Let the equation of the trend line be
y = a + bu where u = \(\frac{t-1963.5}{\frac{1}{2}}\) ……(i)
i.e. u = 2t – 3927
Σy = na + bΣu …….(ii)
Σuy = aΣu + Σu² …..(iii)
Substituting values of Σy, n, Σu, Σuy & Σu² in (ii) & (iii) we get
24 = 10a + 0 ∴ a = 2.4
94 = 0 + 6.330 ∴ b = 0.2848
∴ Equation of the trend line is
y = 2.4 + (0.2848)u where u = 2t – 3927

Question 20.
Obtain trend values for data in problem 19 using 3-yearly moving averages.
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.6 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.6

Question 1.
In a certain culture of bacteria, the rate of increase is proportional to the number present. If it is found that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours.
Solution:
Let x be the number of bacteria in the culture at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, let x = x₀
∴ log x₀ = k × 0 + c
∴ c = log x₀
∴ log x = kt + log x₀
∴ log x – log x₀ = kt
∴ log(\(\frac{x}{x_{0}}\)) = kt ……(1)
Since the number doubles in 4 hours, i.e. when t = 4, x = 2x₀

∴ the number of bacteria will be 8 times the original number in 12 hours.

Question 2.
If the population of a town increases at a rate proportional to the population at that time. If the population increases from 40 thousand to 60 thousand in 40 years, what will be the population in another 20 years? (Given: \(\sqrt{\frac{3}{2}}\) = 1.2247)
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, k is a constant
∴ \(\frac{d P}{P}\) = k dt
Integrating, we get
∫\(\frac{d P}{P}\) = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 40000
∴ log 40000 = 0 + c
∴ c = log 40000
∴ log P = kt + log 40000
∴ log P – log 40000 = kt
∴ log(\(\frac{P}{40000}\)) = kt ………(1)
When t = 40, P = 60000

∴ population after 60 years will be 73482.

Question 3.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after \(\frac{5}{2}\) hours. [Given: √2 = 1.414]
Solution:
Let x be the number of bacteria at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, x = 1000
∴ log 1000 = k × 0 + c
∴ c = log 1000
∴ log x = kt + log 1000
∴ log x – log 1000 = kt
∴ log(\(\frac{x}{1000}\)) = kt …….(1)
Now, when t = 1, x = 2 × 1000 = 2000

∴ number of bacteria after \(\frac{5}{2}\) hours = 5656.

Question 4.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 30,000 to 40,000.
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant.
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
∫\(\frac{1}{P}\)dP = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 30000
∴ log 30000 = k x 0 + c
∴ c = log 30000
∴ log P = kt + log 30000
∴ log P – log 30000 = kt

∴ the population of the city at time t = 30000\(\left(\frac{4}{3}\right)^{\frac{t}{40}}\).

Question 5.
The rate of depreciation \(\frac{d V}{d t}\) of a machine is inversely proportional to the square of t + 1, where V is the value of the machine t years after it was purchased. The initial value of the machine was ₹ 8,00,000 and its value decreased ₹ 1,00,000 in the first year. Find the value after 6 years.
Solution:
Let V be the value of the machine at the end of t years.
Then \(\frac{d V}{d t}\), the rate of depreciation, is inversly proportional to (t + 1)².

Initially, i.e. when t = 0, V = 800000
∴ 800000 = \(\frac{k}{1}\) + c = k + c ………(1)
Now, when t = 1, V = 800000 – 100000 = 700000
∴ 700000 = \(\frac{k}{1+1}\) + c = \(\frac{k}{2}\) + c ……(2)
Subtracting (2) from (1), we get
100000 = \(\frac{1k}{2}\)
∴ k = 200000
∴ from (1), 800000 = 200000 + c
∴ c = 600000 200000
∴ V = \(\frac{200000}{t+1}\) + 600000
When t = 6,
V = \(\frac{200000}{7}\) + 600000
= 28571.43 + 600000
= 628571.43 ~ 628571
Hence, the value of the machine after 6 years will be ₹ 6,28,571.

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.5

Solve the following differential equations.

Question 1.
\(\frac{d y}{d x}+y=e^{-x}\)
Solution:
\(\frac{d y}{d x}+y=e^{-x}\) …….(1)
This is the linear differential equation of the form

This is the general solution.

Question 2.
\(\frac{d y}{d x}\) + y = 3
Solution:
\(\frac{d y}{d x}\) + y = 3
This is the linear differential equation of the form

This is the general solution.

Question 3.
x\(\frac{d y}{d x}\) + 2y = x² . log x.
Solution:
x\(\frac{d y}{d x}\) + 2y = x² . log x
∴ \(\frac{d y}{d x}+\left(\frac{2}{x}\right) \cdot y=x \cdot \log x\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 4.
(x + y)\(\frac{d y}{d x}\) = 1
Solution:
(x + y) \(\frac{d y}{d x}\) = 1
∴ \(\frac{d x}{d y}\) = x + y
∴ \(\frac{d x}{d y}\) – x = y
∴ \(\frac{d x}{d y}\) + (-1) x = y ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 5.
y dx + (x – y²) dy = 0
Solution:
y dx + (x – y²) dy = 0
∴ y dx = -(x – y²) dy
∴ \(\frac{d x}{d y}=-\frac{\left(x-y^{2}\right)}{y}=-\frac{x}{y}+y\)
∴ \(\frac{d x}{d y}+\left(\frac{1}{y}\right) \cdot x=y\) ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 6.
\(\frac{d y}{d x}\) + 2xy = x
Solution:
\(\frac{d y}{d x}\) + 2xy = x ………(1)
This is the linear differential equation of the form

This is the general solution.

Question 7.
(x + a) \(\frac{d y}{d x}\) = -y + a
Solution:
(x + a) \(\frac{d y}{d x}\) + y = a
∴ \(\frac{d y}{d x}+\left(\frac{1}{x+a}\right) y=\frac{a}{x+a}\) ……..(1)
This is the linear differential equation of the form

This is the general solution.

Question 8.
dy + (2y) dx = 8 dx
Solution:
dy + (2y) dx = 8 dx
∴ \(\frac{d y}{d x}\) + 2y = 8 …….(1)
This is the linear differential equation of the form

This is the general solution.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Miscellaneous Exercise 8

(I) Choose the correct alternative.

Question 1.
F(x) is c.d.f. of discreter r.v. X whose p.m.f. is given by P(x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\), for x = 0, 1, 2, 3, 4 & P(x) = 0 otherwise then F(5) = __________
(a) \(\frac{1}{16}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{1}{4}\)
(d) 1
Answer:
(d) 1

Question 2.
F(x) is c.d.f. of discrete r.v. X whose distribution is

then F(-3) = __________
(a) 0
(b) 1
(c) 0.2
(d) 0.15
Answer:
(a) 0

Question 3.
X : number obtained on uppermost face when a fair die is thrown then E(X) = __________
(a) 3.0
(b) 3.5
(c) 4.0
(d) 4.5
Answer:
(b) 3.5

Question 4.
If p.m.f. of r.v. X is given below.

then Var(X) = __________
(a) p²
(b) q²
(c) pq
(d) 2pq
Answer:
(d) 2pq

Question 5.
The expected value of the sum of two numbers obtained when two fair dice are rolled is __________
(a) 5
(b) 6
(c) 7
(d) 8
Answer:
(c) 7

Question 6.
Given p.d.f. of a continuous r.v. X as
f(x) = \(\frac{x^{2}}{3}\) for -1 < x < 2
= 0 otherwise then F(1) =
(a) \(\frac{1}{9}\)
(b) \(\frac{2}{9}\)
(c) \(\frac{3}{9}\)
(d) \(\frac{4}{9}\)
Answer:
(b) \(\frac{2}{9}\)

Question 7.
X is r.v. with p.d.f.
f(x) = \(\frac{k}{\sqrt{x}}\), 0 < x < 4
= 0 otherwise then E(X) = __________
(a) \(\frac{1}{3}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{2}{3}\)
(d) 1
Answer:
(b) \(\frac{4}{3}\)

Question 8.
If X follows B(20, \(\frac{1}{10}\)) then E(X) = __________
(a) 2
(b) 5
(c) 4
(d) 3
Answer:
(a) 2

Question 9.
If E(X) = m and Var(X) = m then X follows __________
(a) Binomial distribution
(b) Possion distribution
(c) Normal distribution
(d) none of the above
Answer:
(b) Possion distribution

Question 10.
If E(X) > Var(X) then X follows __________
(a) Binomial distribution
(b) Possion distribution
(c) Normal distribution
(d) none of the above
Answer:
(a) Binomial distribution

(II) Fill in the blanks.

Question 1.
The values of discrete r.v. are generally obtained by __________
Answer:
counting

Question 2.
The values of continuous r.v. are generally obtained by __________
Answer:
measurement

Question 3.
If X is dicrete random variable takes the values x₁, x₂, x₃, …… x_n then \(\sum_{i=1}^{n} p\left(x_{i}\right)\) = __________
Answer:
1

Question 4.
If f(x) is distribution function of discrete r.v. X with p.m.f. p(x) = \(\frac{x-1}{3}\) for x = 1, 2, 3, and p(x) = 0 otherwise then F(4) = __________
Answer:
1

Question 5.
If f(x) is distribution function of discrete r.v. X with p.m.f. p(x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\) for x = 0, 1, 2, 3, 4, and p(x) = 0 otherwise then F(-1) = __________
Answer:
0

Question 6.
E(X) is considered to be __________ of the probability distribution of X.
Answer:
centre of gravity

Question 7.
If X is continuous r.v. and f(x_i) = P(X ≤ x_i) = \(\int_{-\infty}^{x_{i}} f(x) d x\) then f(x) is called __________
Answer:
Cumulative Distribution Function

Question 8.
In Binomial distribution probability of success ________ from trial to trial.
Answer:
remains constant/independent

Question 9.
In Binomial distribution, if n is very large and probability success of p is very small such that np = m (constant) then ________ distribution is applied.
Answer:
Possion

(III) State whether each of the following is True or False.

Question 1.
If P(X = x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\) for x = 0, 1, 2, 3, 4, then F(5) = \(\frac{1}{4}\) when f(x) is c.d.f.
Answer:
False

Question 2.

If F(x) is c.d.f. of discrete r.v. X then F(-3) = 0.
Answer:
True

Question 3.
X is the number obtained on the uppermost face when a die is thrown the E(X) = 3.5.
Answer:
True

Question 4.
If p.m.f. of discrete r.v.X is

then E(X) = 2p.
Answer:
True

Question 5.
The p.m.f. of a r.v. X is p(x) = \(\frac{2 x}{n(n+1)}\), x = 1, 2,……n
= 0 otherwise,
Then E(X) = \(\frac{2 n+1}{3}\)
Answer:
True

Question 6.
If f(x) = kx (1 – x) for 0 < x < 1
= 0 otherwise then k = 12
Answer:
False

Question 7.
If X ~ B(n, p) and n = 6 and P(X = 4) = P(X = 2) then p = \(\frac{1}{2}\).
Answer:
True

Question 8.
If r.v. X assumes values 1, 2, 3,………, n with equal probabilities then E(X) = \(\frac{(n+1)}{2}\)
Answer:
True

Question 9.
If r.v. X assumes the values 1, 2, 3,………, 9 with equal probabilities, E(X) = 5.
Answer:
True

(IV) Solve the following problems.

Part – I

Question 1.
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
(i) An economist is interested in knowing the number of unemployed graduates in the town with a population of 1 lakh.
Solution:
X = No. of unemployed graduates in a town.
∵ The population of the town is 1 lakh
∴ X takes finite values
∴ X is a Discrete Random Variable
∴ Range of = {0, 1, 2, 4, …. 1,00,000}

(ii) Amount of syrup prescribed by a physician.
Solution:
X : Amount of syrup prescribed.
∴ X Takes infinite values
∴ X is a Continuous Random Variable.

(iii) A person on a high protein diet is interested in the weight gained in a week.
Solution:
X : Gain in weight in a week.
X takes infinite values
∴ X is a Continuous Random Variable.

(iv) Twelve of 20 white rats available for an experiment are male. A scientist randomly selects 5 rats and counts the number of female rats among them.
Solution:
X : No. of female rats selected
X takes finite values.
∴ X is a Discrete Random Variable.
Range of X = {0, 1, 2, 3, 4, 5}

(v) A highway safety group is interested in the speed (km/hrs) of a car at a checkpoint.
Solution:
X : Speed of car in km/hr
X takes infinite values
∴ X is a Continuous Random Variable.

Question 2.
The probability distribution of a discrete r.v. X is as follows.

(i) Determine the value of k.
(ii) Find P(X ≤ 4), P(2 < X < 4), P(X ≥ 3).
Solution:
(i) Assuming that the given distribution is a p.m.f. of X
∴ Each P(X = x) ≥ 0 for x = 1, 2, 3, 4, 5, 6
k ≥ 0
ΣP(X = x) = 1 and
k + 2k + 3k + 4k + 5k + 6k = 1
∴ 21k = 1 ∴ k = \(\frac{1}{21}\)

(ii) P(X ≤ 4) = 1 – P(X > 4)
= 1 – [P(X = 5) + P(X = 6)]
= 1 – [latex]\frac{5}{21}+\frac{6}{21}[/latex]
= 1 – \(\frac{11}{21}\)
= \(\frac{10}{21}\)
P(2 < X < 6) = p(3) + p(4) + p(5)
= 3k + 4k + 5k
= \(\frac{3}{21}+\frac{4}{21}+\frac{5}{21}\)
= \(\frac{12}{21}\)
= \(\frac{4}{7}\)

(iii) P(X ≥ 3) = p(3) + p(4) + p(5) + p(6)
= 3k + 4k + 5k + 6k

Question 3.
Following is the probability distribution of an r.v. X.

Find the probability that
(i) X is positive.
(ii) X is non-negative.
(iii) X is odd.
(iv) X is even.
Solution:
(i) P(X is positive)
P(X = 0) = p(1) + p(2) + p(3)
= 0.25 + 0.15 + 0.10
= 0.50

(ii) P(X is non-negative)
P(X ≥ 0) = p(0) + p(1) + p(2) + p(3)
= 0.20 + 0.25 + 0.15 + 0.10
= 0.70

(iii) P(X is odd)
P(X = -3, -1, 1, 3)
= p(- 3) +p(-1) + p(1) + p(3)
= 0.05 + 0.15 + 0.25 + 0.10
= 0.55

(iv) P(X is even)
= 1 – P(X is odd)
= 1 – 0.55
= 0.45

Question 4.
The p.m.f of a r.v. X is given by
\(P(X=x)= \begin{cases}\left(\begin{array}{l}
5 \\
x
\end{array}\right) \frac{1}{2^{5}}, & x=0,1,2,3,4,5 . \\
0 & \text { otherwise }\end{cases}\)
Show that P(X ≤ 2) = P(X ≥ 3).
Solution:
For x = 0, 1, 2, 3, 4, 5

Question 5.
In the following probability distribution of an r.v. X

Find a and obtain the c.d.f. of X.
Solution:
Given distribution is p.m.f. of r.v. X
ΣP(X = x) = 1
∴ p(1) + p(2) + p(3) + p(4) + p(5) = 1

Question 6.
A fair coin is tossed 4 times. Let X denote the number of heads obtained. Identify the probability distribution of X and state the formula for p.m.f. of X.
Solution:
A fair coin is tossed 4 times
∴ Sample space contains 16 outcomes
Let X = Number of heads obtained
∴ X takes the values x = 0, 1, 2, 3, 4.
∴ The number of heads obtained in a toss is an even

Question 7.
Find the probability of the number of successes in two tosses of a die, where success is defined as (i) number greater than 4 (ii) six appearing in at least one toss.
Solution:
S : A die is tossed two times
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
(i) X : No. is greater than 4
Range of X = {0, 1, 2}

(ii) X : Six appears on aleast one die.
Range of X = {0, 1, 2}

Question 8.
A random variable X has the following probability distribution.

Determine (i) k, (ii) P(X < 3), (iii) P(X > 6), (iv) P(0 < X < 3).
Solution:
(i) It is a p.m.f. of r.v. X
Σp(x) = 1
p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) = 1
k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
9k + 10k² = 1
10k² + 9k – 1 = 0
10k² +10k – k – 1 = 0
∴ 10k(k + 1) – 1(k + 1) = 0
∴ (10k – 1) (k + 1) = 0
∴ 10k – 1 = 0r k + 1 = 0
∴ k = \(\frac{1}{10}\) or k = -1
k = -1 is not accepted, p(x) ≥ 0, ∀ x ∈ R
∴ k = \(\frac{1}{10}\)

(ii) P(X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iii) P(X > 6) = p(7)
= 7k² + k
= \(7\left(\frac{1}{10}\right)^{2}+\frac{1}{10}\)
= \(\frac{7}{100}+\frac{1}{10}\)
= \(\frac{17}{100}\)

(iv) P(0 < X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

Question 9.
The following is the c.d.f. of a r.v. X.

Find the probability distribution of X and P(-1 ≤ X ≤ 2).
Solution:

P(-1 ≤ X ≤ 2) = p(-1) + p(0) + p(1) + p(2)
= 0.2 + 0.15 + 0.10 + 0.10
= 0.55

Question 10.
Find the expected value and variance of the r.v. X if its probability distribution is as follows.
(i)

Solution:

(ii)

Solution:
E(X) = Σx . p(x)

(iii)

Solution:

(iv)

Solution:

= 1.25
S.D. of X = σ_x = √Var(X)
= √1.25
= 1.118

Question 11.
A player tosses two coins. He wins ₹ 10 if 2 heads appear, ₹ 5 if 1 head appears, and ₹ 2 if no head appears. Find the expected value and variance of the winning amount.
Solution:
S : Two fair coin are tossed
S = {HH, HT, TT, TH}
n(S) = 4
∴ Range of X = {0, 1, 2}
∴ Let Y = amount received corresponds to values of X

Expected winning amount
E(Y) = Σpy = \(\frac{22}{4}\) = ₹ 5.5
V(Y) = Σpy² – (Σpy)²
= \(\frac{154}{4}\) – (5.5)²
= 38.5 – 30.25
= ₹ 8.25

Question 12.
Let the p.m.f. of the r.v. X be
\(p(x)= \begin{cases}\frac{3-x}{10} & \text { for } x=-1,0,1,2 \\ 0 & \text { otherwise }\end{cases}\)
Calculate E(X) and Var(X).
Solution:

Question 13.
Suppose error involved in making a certain measurement is a continuous r.v. X with p.d.f.
\(f(x)= \begin{cases}k\left(4-x^{2}\right) & \text { for }-2 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Compute (i) P(X > 0), (ii) P(-1 < X < 1), (iii) P(X < -0.5 or X > 0.5)
Solution:
We know that

Question 14.
The p.d.f. of the r.v. X is given by
\(f(x)= \begin{cases}\frac{1}{2 a} & \text { for } 0<x<2 a \\ 0 & \text { otherwise }\end{cases}\)
Show that P(X < \(\frac{a}{2}\)) = P(X > \(\frac{3a}{2}\))
Solution:

Question 15.
Determine k if
\(f(x)= \begin{cases}k e^{-\theta x} & \text { for } 0 \leq x<\infty, \theta>0 \\ 0 & \text { otherwise }\end{cases}\)
is the p.d.f. of the r.v. X. Also find P(X > \(\frac{1}{\theta}\)). Find M if P(0 < X < M) = \(\frac{1}{2}\)
Solution:
We know that

Question 16.
The p.d.f. of the r.v. X is given by
\(f_{x}(x)=\left\{\begin{array}{l}
\frac{k}{\sqrt{x}}, 0<x<4 \\
0, \text { otherwise }
\end{array}\right.\)
Determine k, c.d.f. of X and hence find P(X ≤ 2) and P(X ≥ 1).
Solution:
We know that

Question 17.
Let X denote the reaction temperature (in °C) of a certain chemical process. Let X be a continuous r.v. with p.d.f.
\(f(x)= \begin{cases}\frac{1}{10}, & -5 \leq x \leq 5 \\ 0, & \text { otherwise }\end{cases}\)
Compute P(X < 0).
Solution:
Given p.d.f. is f(x) = \(\frac{1}{10}\), for -5 ≤ x ≤ 5
Let its c.d.f. F(x) be given by

Part – II

Question 1.
Let X ~ B(10, 0.2). Find (i) P(X = 1) (ii) P(X ≥ 1) (iii) P(X ≤ 8)
Solution:
X ~ B(10, 0.2)
n = 10, p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
(i) P(X = 1) = ¹⁰C₁ (0.2)¹ (0.8)⁹ = 0.2684

(ii) P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – ¹⁰C₀ (0.2)⁰ (0.8)¹⁰
= 1 – 0.1074
= 0.8926

(iii) P(X ≤ 8) = 1 – P(x > 1)
= 1 – [p(9) + p(10)]
= 1 – [¹⁰C₉ (0.2)⁹ (0.8)¹ + ¹⁰C₁₀ (0.2)¹⁰]
= 1 – 0.00000041984
= 0.9999

Question 2.
Let X ~ B(n, p) (i) If n = 10 and E(X) = 5, find p and Var(X), (ii) If E(X) = 5 and Var(X) = 2.5, find n and p.
Solution:
X ~ B(n, p)
(i) n = 10, E(X) = 5
∴ np = 5
∴ 10p = 5
∴ p = \(\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
V(X) = npq
= 10 × \(\frac{1}{2}\) × \(\frac{1}{2}\)
= 2.5

(ii) E(X) = 5, V(X) = 2.5
∴ np = 5, ∴ npq = 2.5
∴ 5q = 2.5
∴ q = \(\frac{2.5}{5}\) = 0.5, p = 1 – 0.5 = 0.5
But np = 5
∴ n(0.5) = 5
∴ n = 10

Question 3.
If a fair coin is tossed 4 times, find the probability that it shows (i) 3 heads, (ii) head in the first 2 tosses, and tail in the last 2 tosses.
Solution:
n : No. of times a coin is tossed
∴ n = 4
X : No. of heads
P : Probability of getting heads

Question 4.
The probability that a bomb will hit the target is 0.8. Find the probability that, out of 5 bombs, exactly 2 will miss the target.
Solution:
X : No. of bombs miss the target
p : Probability that bomb miss the target
∴ q = 0.8
∴ p = 1 – q = 1 – 0.8 = 0.2
n = No. of bombs = 5
∴ X ~ B(5, 0.2)
∴ p(x) = ⁿC_x p^x q^n-x
P(X = 2) = ⁵C₂ (0.2)² (0.8)^5-2
= 10 × 0.04 × (0.8)³
= 10 × 0.04 × 0.512
= 0.4 × 0.512
= 0.2048

Question 5.
The probability that a lamp in the classroom will burn is 0.3. 3 lamps are fitted in the classroom. The classroom is unusable if the number of lamps burning in it is less than 2. Find the probability that the classroom can not be used on a random occasion.
Solution:
X : No. of lamps not burning
p : Probability that the lamp is not burning
∴ q = 0.3
∴ p = 1 – q = 1 – 0.3 = 0.7
n = No. of lamps fitted = 3
∴ X ~ B(3, 0.7)
∴ p(x) = ⁿC_x p^x q^n-x
P(classroom cannot be used)
P(X < 2) = p(0) + p(1)
= ³C₀ (0.7)⁰ (0.3)^3-0 + ³C₁ (0.7)¹ (0.3)^3-1
= 1 × 1 × (0.3)³ + 3 × 0.7 × (0.3)²
= (0.3)2 [0.3 + 3 × 0.7]
= 0.09 [0.3 + 2.1]
= 0.09 [2.4]
= 0.216

Question 6.
A large chain retailer purchases an electric device from the manufacturer. The manufacturer indicates that the defective rate of the device is 10%. The inspector of the retailer randomly selects 4 items from a shipment. Find the probability that the inspector finds at most one defective item in the 4 selected items.
Solution:
X : No. of defective items
n : No. of items selected = 4
p : Probability of getting defective items
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
P(At most one defective item)
P(X ≤ 1) = p(0) + p(1)
= ⁴C₀ (0.1)⁰ (0.9)^4-0 + ⁴C₁ (0.1)¹ (0.9)^4-1
= 1 × 1 × (0.9)⁴ + 4 × 0.1 × (0.9)³
= (0.9)3 [0.9 + 4 × 0.1]
= (0.9)3 × [0.9 + 0.4]
= 0.729 × 1.3
= 0.9477

Question 7.
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Solution:
p = 0.6, q = 1 – 0.6 = 0.4, n = 4
x = 2
∴ p(x) = ⁿC_x p^x q^n-x
P(X = 2) = ⁴C₂ (0.6)² (0.4)² = 0.3456

Question 8.
An examination consists of 5 multiple choice questions, in each of which the candidate has to decide which one of 4 suggested answers is correct. A completely unprepared student guesses each answer randomly. Find the probability that this student gets 4 or more correct answers.
Solution:
n : No. of multiple-choice questions
∴ n = 5
X : No. of correct answers
p : Probability of getting correct answer
∵ There are 4 options out of which one is correct
∴ p = \(\frac{1}{4}\)
∴ q = 1 – p = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
∵ X ~ B(5, \(\frac{1}{4}\))
∴ p(x) = ⁿC_x p^x q^n-x
P(Four or more correct answers)
P(X ≥ 4) = p(4) + p(5)

Question 9.
The probability that a machine will produce all bolts in a production run with in the specification is 0.9. A sample of 3 machines is taken at random. Calculate the probability that all machines will produce all bolts in a production run within the specification.
Solution:
n : No. of samples selected
∴ n = 3
X : No. of bolts produce by machines
p : Probability of getting bolts
∴ p = 0.9
∴ q = 1 – p = 1 – 0.9 = 0.1
∴ X ~ B(3, 0.9)
∴ p(x) = ⁿC_x p^x q^n-x
P(Machine will produce all bolts)
P(X = 3) = ³C₃ (0.9)³ (0.1)^3-3
= 1 × (0.9)³ × (0.1)⁰
= 1 × (0.9)³ × 1
= (0.9)³
= 0.729

Question 10.
A computer installation has 3 terminals. The probability that anyone terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that (i) 0 (ii) 1 terminal requires attention during a week.
Solution:
n : No. of terminals
∴ n = 3
X : No. of terminals need attention
p : Probability of getting terminals need attention
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
∵ X ~ B(3, 0.1)
∴ p(x) = ⁿC_x p^x q^n-x
(i) P(No attention)
∴ P(X = 0) = ³C₀ × (0.1)⁰ (0.9)^3-1
= 1 × 1 × (0.9)³
= 0.729

(ii) P(One terminal need attention)
∴ P(X = 1) = ³C₁ (0.1)¹ (0.9)^3-1
= 3 × 0.1 × (0.9)²
= 0.3 × 0.81
= 0.243

Question 11.
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics, (i) Calculate the probabilities of obtaining an answer yes from all of the selected students, (ii) Find the probability that the visitor obtains the answer yes from at least 3 students.
Solution:
X : No. of students like mathematics
p: Probability that students like mathematics
∴ p = 0.8
∴ q = 1 – p = 1 – 0.8 = 0.2
n : No. of students selected
∴ n = 4
∵ X ~ B(4, 0.8)
∴ p(x) = ⁿC_x p^x q^n-x
(i) P(All students like mathematics)
∴ P(X = 4) = ⁴C₄ (0.8)⁴ (0.2)^4-4
= 1 × (0.8)⁴ × (0.2)⁰
= 1 × (0.8)⁴ × 1
= 0.4096

(ii) P(Atleast 3 students like mathematics)
∴ P(X ≥ 3) = p(3) + p(4)
= ⁴C₃ (0.8)³ (0.2)^4-3 + 0.4096
= 4 × (0.8)³ (0.2)¹ + 0.4096
= 0.8 × (0.8)³ + 0.4096
= (0.8)⁴ × 0.4096
= 0.4096 + 0.4096
= 0.8192

Question 12.
It is observed that it rains on 10 days out of 30 days. Find the probability that
(i) it rains on exactly 3 days of a week.
(ii) it rains at most 2 days a week.
Solution:
X : No. of days it rains in a week
p : Probability that it rains
∴ p = \(\frac{10}{30}=\frac{1}{3}\)
∴ q = 1 – p = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
n : No. of days in a week
∴ n = 7
∴ X ~ B(7, \(\frac{1}{3}\))
(i) P(Rains on Exactly 3 days of a week)

(ii) P(Rains on at most 2 days of a week)
∴ P(X ≤ 2) = p(0) + p(1) + p(2)

Question 13.
If X follows Poisson distribution such that P(X = 1) = 0.4 and P(X = 2) = 0.2, find variance of X.
Solution:
X : Follows Possion Distribution

∴ m = 1
∴ Mean = m = Variance of X = 1

Question 14.
If X has Poisson distribution with parameter m, such that
\(\frac{P(X=x+1)}{P(X=x)}=\frac{m}{x+1}\)
find probabilities P(X = 1) and P(X = 2), when X follows Poisson distribution with m = 2 and P(X = 0) = 0.1353.
Solution:
Given that the random variable X follows the Poisson distribution with parameter m = 2
i.e. X ~ P(2)
Its p.m.f. is satisfying the given equation.
\(\frac{P(X=x+1)}{P(X=x)}=\frac{m}{x+1}\)
When x = 0,
\(\frac{\mathrm{P}(\mathrm{X}=1)}{\mathrm{P}(\mathrm{X}=0)}=\frac{2}{0+1}\)
P(X = 1) = 2P(X = 0)
= 2(0.1353)
= 0.2706
When x = 1,
\(\frac{\mathrm{P}(\mathrm{X}=2)}{\mathrm{P}(\mathrm{X}=1)}=\frac{2}{1+1}\)
P(X = 2) = P(X = 1) = 0.2706

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.4

Solve the following differential equations:

Question 1.
x dx + 2y dy = 0
Solution:
x dx + 2y dy = 0
Integrating, we get
∫x dx + 2 ∫y dy = c₁
∴ \(\frac{x^{2}}{2}+2\left(\frac{y^{2}}{2}\right)=c_{1}\)
∴ x² + 2y² = c, where c = 2c₁
This is the general solution.

Question 2.
y² dx + (xy + x²) dy = 0
Solution:
y² dx + (xy + x²) dy = 0
∴ (xy + x²) dy = -y² dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get



This is the general solution.

Question 3.
x²y dx – (x³ + y³) dy = 0
Solution:
x²y dx – (x³ + y³) dy = 0
∴ (x³ + y³) dy = x²y dx
∴ \(\frac{d y}{d x}=\frac{x^{2} y}{x^{3}+y^{3}}\) ……(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)


This is the general solution.

Question 4.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:



This is the general solution.

Question 5.
(x² – y²) dx + 2xy dy = 0
Solution:
(x² – y²) dx + 2xy dy = 0
∴ 2xy dy = -(x² – y²) dx = (y² – x²) dx
∴ \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\) ………(1)

Question 6.
xy\(\frac{d y}{d x}\) = x² + 2y²
Solution:

Question 7.
x²\(\frac{d y}{d x}\) = x² + xy – y²
Solution:

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 4 Time Series Ex 4.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Time Series Ex 4.1

Question 1.
The following data gives the production of bleaching powder (in ‘000 tonnes) for the years 1962 to 1972.

Fit a trend line by graphical method to the above data.
Solution:

Question 2.
Use the method of least squares to fit a trend line to the data in problem 1 above. Also, obtain the trend value for the year 1975.
Solution:


n = 11, let the trend line the
y = a + bu ……..(I)
Σy = na + bΣu ……..(i)
Σuy = aΣu + bΣu² ………(ii)
Substituting the values of Σy, Σu, Σuy, & Σu², we get
46 = 11a + 0
∴ a = 4.18 And
114 = 0 + b(110)
∴ b = 1.04
By (I) the equation of the trends line is
y = 4.18 + 1.04u
Where u = t – 1967 ……..(iii)
For the year 1975 we have u = 8
Substituting in (iii) we get
Y= 4.18 + 1.04(8) = 12.5
Trend value for the year 1975 is 12.5 (in ‘000 tonnes).

Question 3.
Obtain the trend line for the above data using 5 yearly moving averages.
Solution:

Question 4.
The following table shows the index of industrial production for the period from 1976 to 1985, using the year 1976 as the base year.

Fit a trend line to the above data by graphical method.
Solution:

Question 5.
Fit a trend line to the data in problem 4 above by the method of least squares. Also, obtain the trend value for the index of industrial production for the year 1987.
Solution:


u = \(\frac{t-1980.5}{\frac{1}{2}}\), n = 10, Σu = 0, Σy = 42, Σu² = 330, Σuy = 148
Let the trend line be y = a + bu ……(i)
where u = \(\frac{t-1980.5}{\frac{1}{2}}\)
i.e. u = 2t – 3961
Σy = na + bΣu ……(ii)
Σuy = aΣu + bΣu² ……….(iii)
Substituting the values of Σy, n, Σu, Σuy & Σu² We get
42 = 10a + 0
∴ a = 4.2 and
148 = 0 + 5.330
∴ b = 0.4485
∴ by (i) the equation of the trends line is
Y = 4.2 + 0.4485u ………(iv)
where u = 2t – 3961
For the year 1987,
u = 13 by (iv) we have
Y = 4.2 + 0.4485(13) = 10.0305
∴ The trend value for the year 1987 is 10.0305

Question 6.
Obtain the trend values for the data in problem 4 using 4-yearly centered moving averages.
Solution:

Question 7.
The following table gives the production of steel (in millions of tonnes) for the years 1976 to 1986.

Fit a trend line to the above data by the graphical method.
Solution:

Question 8.
Fit a trend line to the data in Problem 7 by the method of least squares. Also, obtain the trend value for the year 1990.
Solution:

u = \(\frac{t-1981}{1}\), n = 10, Σu = 0, ΣY = 62, Σu² = 110, Σuy = 87
Let the equation of the trend line be
Y = a + bu
where u = t – 1981 ……(i)
ΣY = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ………(iii)
Substituting the values of Σy, n, Σu, Σuy, Σu² in (ii) & (iii)
62 = 11a + 0
∴ a = 5.6364 And
87 = 0 + 5(110)
∴ b = 0.7909
∴ by (i) equation of the trend line is y = 5.6364 + 0.7909u
Where u = t – 1981
For the year 1990,
u = 9
∴ y = 5.6364 + 0.7909(9)
∴ y = 12.7545 (in million tonnes)

Question 9.
Obtain the trend values for the above data using 3-yearly moving averages.
Solution:

Question 10.
The following table shows the production of gasoline in the U.S.A. for the years 1962 to 1976.

(i) Obtain trend values for the above data using 5-yearly moving averages.
(ii) Plot the original time series and trend values obtained above on the same graph.
Solution:
(i)

(ii)

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.3

Question 1.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = x²y + y
Solution:
\(\frac{d y}{d x}\) = x²y + y
∴ \(\frac{d y}{d x}\) = y(x² + 1)
∴ \(\frac{1}{y}\) dy = (x² + 1) dx
Integrating, we get
∫\(\frac{1}{y}\) dy = ∫(x² + 1) dx
∴ log |y|= \(\frac{x^{3}}{3}\) + x + c
This is the general solution.

(ii) \(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)
Solution:
\(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)

This is the general solution.

(iii) (x² – yx²) dy + (y² + xy²) dx = 0
Solution:
(x² – yx²) dy + (y² + xy²) dx = 0
∴ x²(1 – y) dy + y²(1 + x) dx = 0
∴ \(\frac{1-y}{y^{2}} d y+\frac{1+x}{x^{2}} d x=0\)
Integrating, we get


This is the general solution.

(iv) \(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)
Solution:
\(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)

∴ 2y² log |x + 1| = 2cy² – 1 is the required solution.

Question 2.
For each of the following differential equations find the particular solution:
(i) (x – y²x) dx – (y + x²y) dy = 0, when x = 2, y = 0.
Solution:
(x – y²x) dx – (y + x²y) dy = 0
∴ x(1 – y²) dx – y(1 + x²) dy = 0

∴ the general solution is
log |1 + x²| + log |1 – y²| = log c, where c₁ = log c
∴ log |(1 + x²)(1 – y²) | = log c
∴ (1 + x²)(1 – y²) = c
When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x²)(1 – y²) = 5.

(ii) (x + 1) \(\frac{d y}{d x}\) -1 = 2e^-y, when y = 0, x = 1.
Solution:

∴ log |2 + e^y| = log |c(x + 1)|
∴ 2 + e^y = c(x + 1)
This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = \(\frac{3}{2}\)
∴ the particular solution is
2 + e^y = \(\frac{3}{2}\)(x + 1)
∴ 4 + 2e^y = 3x + 3
∴ 3x – 2e^y – 1 = 0

(iii) y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0, when x = e, y = e².
Solution:

∴ from (1), the general solution is
log |x log x| – log |y| = log c, where c₁ = log c
∴ log |\(\frac{x \log x}{y}\)| = log c
∴ \(\frac{x \log x}{y}\) = c
∴ x log x = cy
This is the general solution.
Now, y = e², when x = e
e log e = ce²
1 = ce ……[∵ log e = 1]
c = \(\frac{1}{e}\)
∴ the particular solution is x log x = (\(\frac{1}{e}\)) y
∴ y = e^x log x

(iv) \(\frac{d y}{d x}\) = 4x + y + 1, when y = 1, x = 0.
Solution:
\(\frac{d y}{d x}\) = 4x + y + 1
Put 4x + y + 1 = v

∴ log |v + 4| = x + c
∴ log |4x + y + 1 + 4| = x + c
i.e. log |4x + y + 5| = x + c
This is the general solution.
Now, y = 1 when x = 0
∴ log|0 + 1 + 5| = 0 + c,
i.e. c = log 6
∴ the particular solution is
log |4x + y + 5| = x + log 6
∴ \(\log \left|\frac{4 x+y+5}{6}\right|\) = x