Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.1
Question 1.
The following table gives income (X) and expenditure (Y) of 25 families:
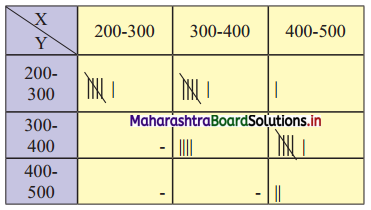
Find
(i) Marginal frequency distributions of income and expenditure.
(ii) Conditional frequency distribution of X when Y is between 300 – 400.
(iii) Conditional frequency distribution of Y when X is between 200 – 300.
(iv) How many families have their income ₹ 300 and more and expenses ₹ 400 and less?
Solution:
The bivariate frequency distribution table for Income (X) and Expenditure (Y) is as follows:
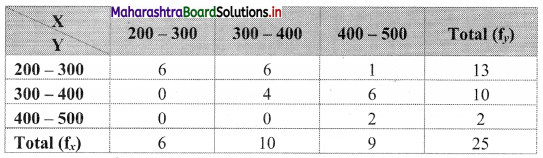
(i) Marginal frequency distribution of income (X):

Marginal frequency distribution of expenditure ( Y):

(ii) Conditional frequency distribution of X when Y is between 300 – 400:

(iii) Conditional frequency distribution of Y when X is between 200 – 300:

(iv) The cells 300 – 400 and 400 – 500 are having income ₹ 300 and more and the cells 200 – 300 and 300 – 400 are having expenditure ₹ 400 and less.
Now, the following table indicates the number of families satisfying the above condition.
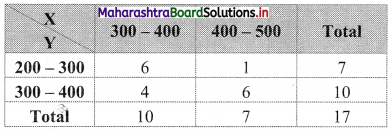
∴ There are 17 families with income ₹ 300 and more and expenditure ₹ 400 and less.
![]()
Question 2.
Two dice are thrown simultaneously 25 times. The following pairs of observations are obtained.
(2, 3) (2, 5) (5, 5) (4, 5) (6, 4) (3, 2) (5, 2) (4, 1) (2, 5) (6, 1) (3, 1) (3, 3) (4, 3) (4, 5) (2, 5) (3, 4) (2, 5) (3, 4) (2, 5) (4, 3) (5, 2) (4, 5) (4, 3) (2, 3) (4, 1)
Prepare a bivariate frequency distribution table for the above data. Also, obtain the marginal distributions.
Solution:
Let X = Observation on 1st die
Y = Observation on 2nd die
Now, the minimum value of X is 1 and the maximum value is 6.
Also, the minimum value of Y is 1 and the maximum value is 6.
A bivariate frequency distribution can be prepared by taking X as row and Y as a column.
Bivariate frequency distribution is as follows:
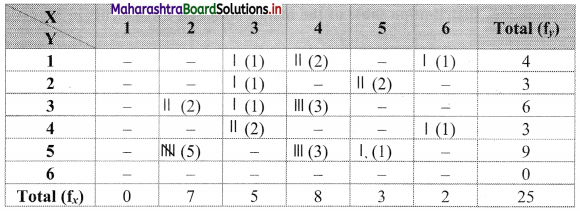
Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Question 3.
Following data gives the age of husbands (X) and age of wives (Y) in years. Construct a bivariate frequency distribution table and find the marginal distributions.
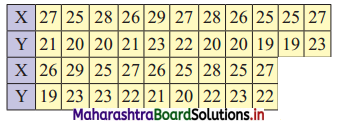
Find conditional frequency distribution of age of husbands when the age of wife is 23 years.
Solution:
Given, X = Age of Husbands (in years)
Y = Age of Wives (in years)
Now, the minimum value of X is 25 and the maximum value is 29.
Also, the minimum value of Y is 19 and the maximum value is 23.
Bivariate frequency distribution is as follows:
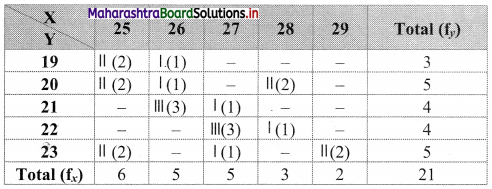
Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of X when Y is 23:

![]()
Question 4.
Construct a bivariate frequency distribution table of the marks obtained by students in Statistics (X) and English (Y).

Construct a bivariate frequency distribution table for the above data by taking class intervals 20 – 30, 30 – 40, …. etc. for both X and Y. Also find the marginal distributions and conditional frequency distribution of Y when X lies between 30 – 40.
Solution:
Given, X = Marks in Statistics
Y = Marks in English
A bivariate frequency table can be prepared by taking class intervals 20 – 30, 30 – 40,…, etc for both X and Y.
Bivariate frequency distribution is as follows:
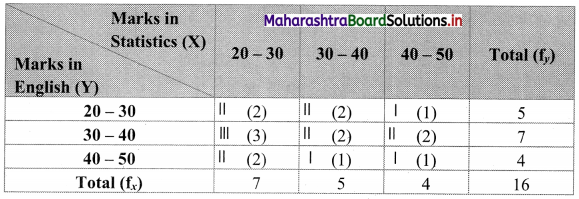
Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of Y when X lies between 30 – 40:

![]()
Question 5.
Following data gives height in cms (X) and weight in kgs (Y) of 20 boys. Prepare a bivariate frequency table taking class intervals 150 – 154, 155 – 159,…etc. for X and 35 – 39, 40 – 44,…, etc for Y. Also, find
(i) Marginal frequency distributions.
(ii) Conditional frequency distribution of Y when 155 ≤ X ≤ 159.
(152,40) (160,54) (163,52) (150,35) (154,36) (160,49) (166,54) (157,38)
(159,43) (153,48) (152,41) (158,51) (155,44) (156,47) (156,43) (166,53)
(160,50) (151,39) (153,50) (158,46)
Solution:
Given X = Height in cms.
Y = Weight in kgs.
Bivariate frequency table can be prepared by taking class intervals 150 – 154, 155 – 159, …, etc for X and 35 – 39, 40 – 44,…etc for Y.
The bivariate frequency distribution table is as follows:
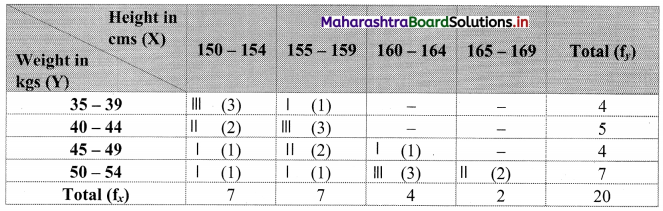
Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of Y when 155 ≤ X ≤ 159:
