Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.2 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.2
Question 1.
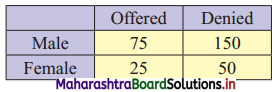
The following table shows the classification of applications for secretarial and for sales positions according to gender. Calculate the value of ϰ2 statistic.
Solution:
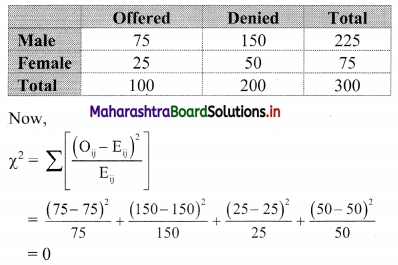
Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{225 \times 100}{300}\) = 75
E12 = \(\frac{225 \times 200}{300}\) = 150
E21 = \(\frac{75 \times 100}{300}\) = 25
E22 = \(\frac{75 \times 200}{300}\) = 50
Table of expected frequencies.
![]()
Question 2.
200 teenagers were asked which takeaway food do they prefer – French fries, burgers, or pizza. The results were-
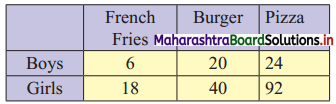
Compute ϰ2 statistic.
Solution:
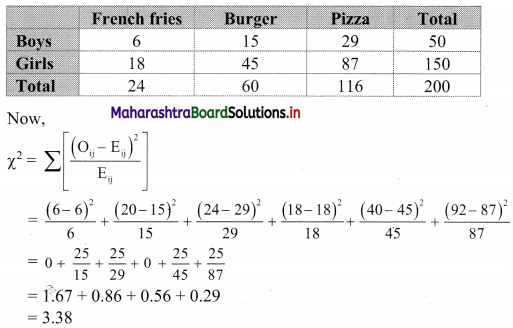
Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E11 = \(\frac{50 \times 24}{200}\) = 6
E12 = \(\frac{50 \times 60}{200}\) = 15
E13 = \(\frac{50 \times 116}{200}\) = 29
E21 = \(\frac{150 \times 24}{200}\) = 18
E22 = \(\frac{150 \times 60}{200}\) = 45
E23 = \(\frac{150 \times 116}{200}\) = 87
Table of expected frequencies.
Question 3.
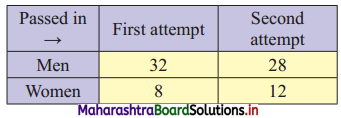
A sample of men and women who had passed their driving test either in 1st attempt or in 2nd attempt
were surveyed. Compute ϰ2 statistic.
Solution:
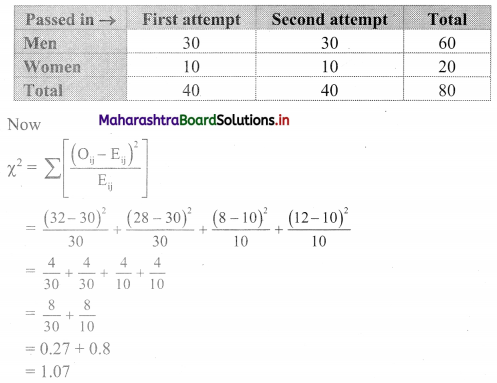
Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{60 \times 40}{80}\) = 30
E12 = \(\frac{60 \times 40}{80}\) = 30
E21 = \(\frac{20 \times 40}{80}\) = 10
E22 = \(\frac{20 \times 40}{80}\) = 10
Table of expected frequencies.
![]()
Question 4.
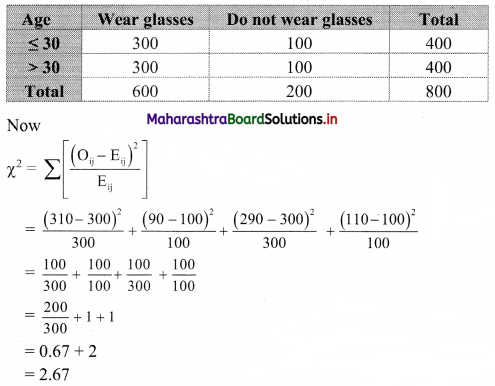
800 people were asked whether they wear glasses for reading with the following results.
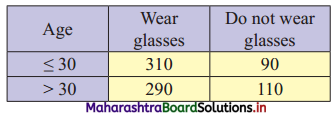
Compute the ϰ2 square statistic.
Solution:
Table of observed frequencies.

Expected frequencies are given by
Eij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E11 = \(\frac{400 \times 600}{800}\) = 300
E12 = \(\frac{400 \times 200}{800}\) = 100
E21 = \(\frac{400 \times 600}{800}\) = 300
E22 = \(\frac{400 \times 200}{800}\) = 100
Table of expected frequencies.
Question 5.
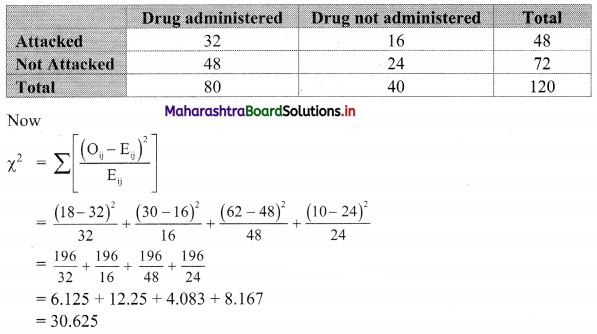
Out of a sample of 120 persons in a village, 80 were administered a new drug for preventing influenza, and out of the 18 were attacked by influenza. Out of those who are not administered the new drug, 10 persons were not attacked by influenza:
(i) Prepare a two-way table showing frequencies.
(ii) Compute the ϰ2 square statistic.
Solution:
(i) The given data can be arranged in the following table.

The observed frequency table can be prepared as follows:

(ii) Expected frequencies are given by
Eij = \(\frac{R_{i} \times C_{j}}{N}\)
E11 = \(\frac{48 \times 80}{120}\) = 32
E12 = \(\frac{48 \times 40}{120}\) = 16
E21 = \(\frac{72 \times 80}{120}\) = 48
E22 = \(\frac{72 \times 40}{120}\) = 24
Table of expected frequencies.