Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Skewness Miscellaneous Exercise 3 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 3 Skewness Miscellaneous Exercise 3
Question 1.
For u distribution, mean = 100, mode = 80 and S.D. = 20. Find Pearsonian coefficient of skewness Skp.
Solution:
Given, Mean = 100, Mode = 80, S.D. = 20
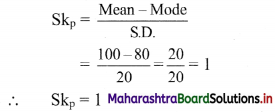
Question 2.
For a distribution, mean = 60, median = 75 and variance = 900. Find Pearsonian coefficient of skewness Skp.
Solution:
Given. Mean = 60, Median = 75, Variance = 900
∴ S.D. = √Variance = √900 = 30

![]()
Question 3.
For a distribution, Q1 = 25, Q2 = 35 and Q3 = 50. Find Bowley’s coefficient of skewness Skb.
Solution:
Given Q1 = 25, Q2 = 35, Q3 = 50
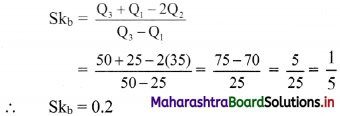
Question 4.
For a distribution Q3 – Q2 = 40, Q2 – Q1 = 60. Find Bowlev’s coefficient of skewness Skb.
Solution:
Given, Q3 – Q2 = 40, Q2 – Q1 = 60

Question 5.
For a distribution, Bowley’s coefficient of skewness is 0.6. The sum of upper and lower quartiles is 100 and median is 38. Find the upper and lower quartiles.
Solution:
Given, Skb = 0.6, Q3 + Q1 = 100,
Median = Q2 = 38
Skb = \(\frac{Q_{3}+Q_{1}-2 Q_{2}}{Q_{3}-Q_{1}}\)
∴ 0.6 = \(\frac{100-2(38)}{Q_{3}-Q_{1}}\)
∴ 0.6(Q3 – Q1) = 100 – 76 = 24
∴ Q3 – Q1 = 40 ….(i)
Q3 + Q1 = 100 …..(ii) (given)
Adding (i) and (ii), we get
2Q3 = 140
∴ Q3 = 70
Substituting the value of Q3 in (ii), we get
70 + Q1 = 100
∴ Q1 = 100 – 70 = 30
∴ upper quartile = 70 and lower quartile = 30
![]()
Question 6.
For a frequency distribution, the mean is 200, the coefficient of variation is 8% and Karl Pearsonian’s coefficient of skewness is 0.3. Find the mode and median of the distribution.
Solution:
Mean = \(\bar{x}\) = 200
Coefficient of variation, C.V. = 8%, Skp = 0.3
C.V. = \(\frac{\sigma}{\bar{x}} \times 100\), where σ = standard deviation
∴ 8 = \(\frac{\sigma}{200} \times 100\)
∴ σ = \(\frac{8 \times 200}{100}\) = 16
Now, Skp = \(\frac{\text { Mean – Mode }}{\text { S.D. }}\)
∴ 0.3 = \(\frac{200-\text { Mode }}{16}\)
∴ 0.3 × 16 = 200 – Mode
∴ Mode = 200 – 4.8 = 195.2
Since, Mean – Mode = 3(Mean – Median)
∴ 200 – 195.2 = 3(200 – Median)
∴ 4.8 = 600 – 3Median
∴ 3Median = 600 – 4.8 = 595.2
∴ Median = 198.4
Question 7.
Calculate Karl Pearsonian’s coefficient of skewness Skp from the follow ing data:
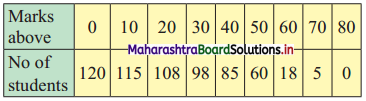
Solution:
The given table is the cumulative frequency table of more than type.
From this table, we have to prepare the frequency distribution table and then calculate the value of Skp.
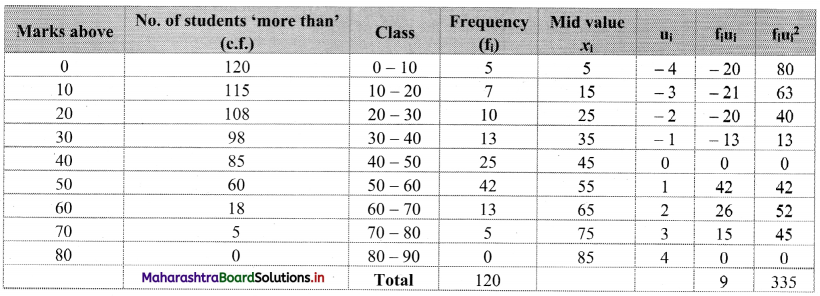
Construct the following table:
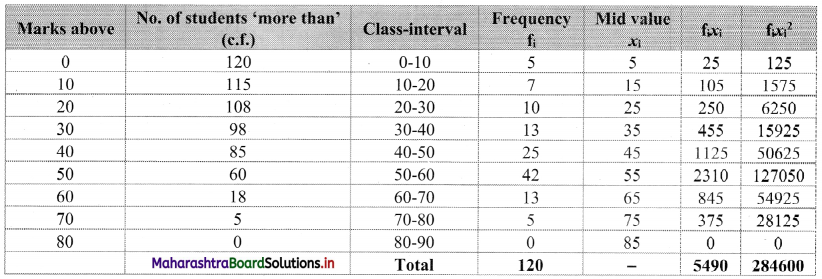
From the table, N = 120, Σfixi = 5490 and \(\sum \mathrm{f}_{\mathrm{i}} x_{\mathrm{i}}^{2}\) = 284600
Mean = \(\bar{x}=\frac{\sum f_{i} x_{i}}{N}=\frac{5490}{120}\) = 45.75
Maximum frequency 42 is of the class 50 – 60
∴ Mode lies in the class 50 – 60
∴ L = 50, f1 = 42, f0 = 25, f2 = 13, h = 10

Alternate Method:
Let u = \(\frac{x-45}{10}\)
\(\overline{\mathrm{u}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\mathrm{N}}=\frac{9}{120}\) = 0.075
∴ \(\bar{x}\) = 45 + 10(\(\bar{u}\))
= 45 + 10(0.075)
= 45 + 0.75
= 45.75
Var(u) = \(\sigma_{u}^{2}=\frac{\sum f_{i} u_{i}{ }^{2}}{N}-(\bar{u})^{2}\)
= \(\frac{335}{120}\) – (0.075)2
= 2.7917 – 0.0056
= 2.7861
Var(X) = h2 × Var(u)
= 100 × 2.7861
= 278.61
S.D. = √278.61 = 16.6916
Maximum frequency 42 is of the class 50 – 60.
∴ Mode lies in the class 50 – 60.
∴ L = 50, f1 = 42, f0 = 25, f2 = 13, h = 10

![]()
Question 8.
Calculate Bowley’s coefficient of skewness Skb from the following data.
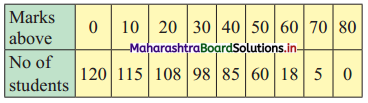
Solution:
To calculate Bowley’s coefficient of skewness Skb, we construct the following table:
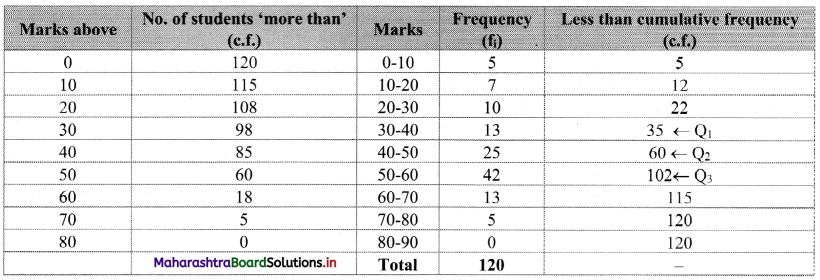
Here, N = 120
Q1 class = class containing the \(\left(\frac{N}{4}\right)^{t h}\) observation
∴ \(\frac{N}{4}=\frac{120}{4}\) = 30
Cumulative frequency which is just greater than (or equal to) 30 is 35.
∴ Q1 lies in the class 30-40.
∴ L = 30, h = 10, f = 13, c.f. = 22

Q2 class = class containing the \(\left(\frac{N}{2}\right)^{t h}\) observation
∴ \(\frac{\mathrm{N}}{2}=\frac{120}{2}\) = 60
Cumulative frequency which is just greater than (or equal to) 60 is 60.
∴ Q2 lies in the class 40-50.
∴ L = 40, h = 10, f = 25, c.f. = 35
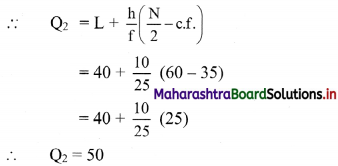
Q3 class = class containing the \(\left(\frac{3 \mathrm{~N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{3 \mathrm{~N}}{4}=\frac{3 \times 120}{4}\) = 90
Cumulative frequency which is just greater than (or equal to) 90 is 102.
∴ Q3 lies in the class 50 – 60
∴ L = 50, h = 10, f = 42, c.f. = 60
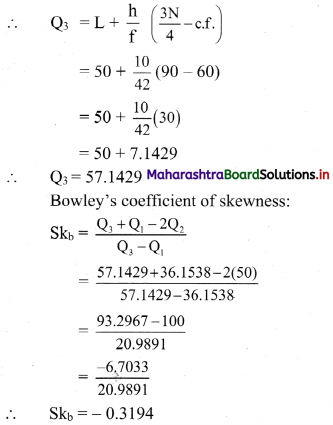
Question 9.
Find Skp for the following set of observations:
18, 27, 10, 25, 31, 13, 28
Solution:
The given data can be arranged in ascending order as follows:
10, 13, 18, 25, 27, 28, 31
Here, n = 7
∴ Median = value of \(\left(\frac{n+1}{2}\right)^{\text {th }}\) observation
= value of \(\left(\frac{7+1}{2}\right)^{\text {th }}\) observation
= value of 4th observation
= 25
For finding standard deviation, we construct the following table:
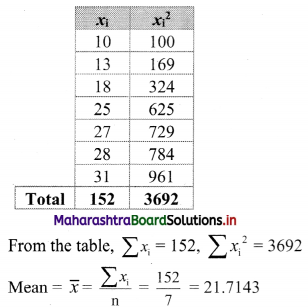

![]()
Question 10.
Find Skb for the following set of observations:
18, 27, 10, 25, 31, 13, 28
Solution:
The given data can be arranged in ascending order as follows:
10, 13, 18, 25, 27, 28, 31
Here, n = 7
∴ Q1 = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{7+1}{4}\right)^{\text {th }}\) observation
= value of 2nd observation
∴ Q1 = 13
Q2 = value of 2\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{7+1}{4}\right)^{\text {th }}\) observation
= value of (2 × 2)th observation
= value of 4th observation
∴ Q2 = 25
Q3 = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{7+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 2)th observation
= value of 6th observation
∴ Q3 = 28
Coefficient of skewness,

∴ Skb = -0.6