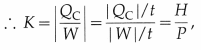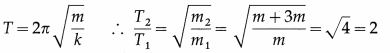Important Questions – Page 14 – Maharashtra Board Solutions

Maharashtra Board Class 12 Secretarial Practice Important Questions Chapter 11 Financial Market

July 3, 2024July 2, 2024 by Bhagya

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 11 Financial Market Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 11 Financial Market

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
A ___________ is an institution that facilitates exchange of financial instruments.
(a) Capital Market
(b) Financial Market
(c) Money Market
Answer:
(b) Financial Market

Question 2.
The ___________ market contributes to the national growth by ensuring a continuous flow of surplus funds to deficit units.
(a) Financial
(b) Money
(c) Secondary
Answer:
(a) Financial

Question 3.
The market which provides short term funds is ___________
(a) Capital Market
(b) Sold Market
(c) Money Market
Answer:
(c) Money Market

Question 4.
The maturity period of commercial bills is ___________ days.
(a) 90
(b) 92
(c) 96
Answer:
(a) 90

Question 5.
___________ are debt instruments that are issued by corporate houses for raising short term financial resources.
(a) Commercial papers
(b) Treasury bills
(c) Government securities
Answer:
(a) Commercial papers

Question 6.
The maturity period of Treasury bill is ___________ days.
(a) 192
(b) 182
(c) 172
Answer:
(b) 182

Question 7.
The debt instruments which are issued by the corporate houses to raise funds from the money market is ___________
(a) Certificate of deposit
(b) Preference shares
(c) Commercial papers
Answer:
(c) Commercial papers

Question 8.
___________ deals in medium and long term funds.
(a) Capital Market
(b) Gold Market
(c) Money Market
Answer:
(a) Capital Market

Question 9.
The repurchase rate which is also known as the official bank rate is ___________ rate.
(a) Repo
(b) Credit
(c) Interest
Answer:
(a) Repo

Question 10.
___________ bills enjoy a high degree of liquidity.
(a) Treasury
(b) Commercial
(c) Publicity
Answer:
(a) Treasury

Question 11.
___________ is also known as new issue market.
(a) Primary Market
(b) Secondary Market
(c) Financial Market
Answer:
(a) Primary Market

Question 12.
The Market which is also known as the government securities market is ___________ market.
(a) Primary
(b) Secondary
(c) Gilt-edged
Answer:
(c) Gilt-edged

Question 13.
A market where existing securities are resold or traded is called ___________ market.
(a) Commodity
(b) Secondary
(c) Primary
Answer:
(b) Secondary

Question 14.
A financial market is a link between investor and ___________
(a) borrowers
(b) creditors
(c) capitalists
Answer:
(a) borrowers

Question 15.
___________ plays an important role in the financial system of a country.
(a) Capital Market
(b) Money Market
(c) Financial Market
Answer:
(a) Capital Market

Question 16.
The market which provides short term fund is ___________
(a) Capital Market
(b) Gold Market
(c) Money Market
Answer:
(c) Money Market

Question 17.
The market which deals in medium-term and long-term credit or fund is called ___________
(a) Money Market
(b) Capital Market
(c) Gold Market
Answer:
(b) Capital Market

Question 18.
A security market in which new issues of securities (i.e. shares and debentures) are arranged or organized is called ___________ market.
(a) Primary
(b) Secondary
(c) Bullion
Answer:
(a) Primary

Question 19.
In Money Market, funds can be traded for a maximum period of ___________ year/s.
(a) one
(b) five
(c) two
Answer:
(a) one

Question 20.
The debt instruments which are issued by the corporate houses to raise funds from the money market is ___________
(a) Certificate of deposit
(b) Preference shares
(c) Commercial Papers
Answer:
(c) Commercial Papers

Question 21.
___________ is the most common method to meet the credit needs of trade and industry.
(a) Commercial papers
(b) Treasury bills
(c) Commercial bills
Answer:
(c) Commercial bills

Question 22.
The liquidity is ___________ in case of commercial bills.
(a) high
(b) low
(c) constant
Answer:
(a) high

Question 23.
The repurchase rate which is also known as the official bank rate is ___________ rate.
(a) Repo
(b) Credit
(c) Interest
Answer:
(a) Repo

Question 24.
The market which is also known as the government securities market is ___________ market.
(a) Primary
(b) Secondary
(c) Gilt-edged
Answer:
(c) Gilt-edged

Question 25.
Under ___________ the shares of a company are sold among the selected group of persons.
(a) Right issue
(b) Private placement
(c) Public issue
Answer:
(b) Private placement

Question 26.
A market where existing securities are resold or traded is called ___________ market.
(a) commodity
(b) secondary
(c) primary
Answer:
(b) secondary

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Treasury bill	(a) Primary market
(2) Commercial bill	(b) Long term credit
(3) New Issue	(c) Mobilization of funds
(4) Stock Exchange	(d) Promissory note
(5) Financial Market	(e) Short term credit
	(f) Secondary market
	(g) Central Government
	(h) Deals only with brokers
	(i) New banking institution
	(j) Mutual Fund

Answer:

Group ‘A’	Group ‘B’
(1) Treasury bill	(d) Promissory note
(2) Commercial bill	(e) Short term credit
(3) New Issue	(a) Primary market
(4) Stock Exchange	(f) Secondary market
(5) Financial Market	(c) Mobilization of funds

Question 2.

Group ‘A’	Group ‘B’
(1) Money Market	(a) Most common method to meet credit needs
(2) Commercial bills	(b) Primary Market
(3) Repo rate	(c) Interest
(4) Gilt-edged market	(d) Government securities market
(5) Secondary market	(e) Official bank rate
	(f) Treasury bills
	(g) Financial market
	(h) Short term funds are borrowed and lent
	(i) Stock exchange
	(j) Fewer applications than expected

Answer:

Group ‘A’	Group ‘B’
(1) Money Market	(h) Short term funds are borrowed and lent
(2) Commercial bills	(a) Most common method to meet credit needs
(3) Repo rate	(e) Official bank rate
(4) Gilt-edged market	(d) Government securities market
(5) Secondary market	(i) Stock exchange

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
A market that provides long-term funds.
Answer:
Capital Market

Question 2.
An intermediary between the lender and borrower.
Answer:
Financial Market

Question 3.
A market where short-term funds are borrowed and lent.
Answer:
Money Market

Question 4.
A debt instrument issued by the corporate house for raising the short-term funds from the money market.
Answer:
Commercial Paper

Question 5.
Short-term instrument issued by a commercial bank and special financial institution.
Answer:
Certificate of deposit

Question 6.
A type of bill in the nature of promissory note issued by the government.
Answer:
Treasury bill

Question 7.
A market for borrowing and lending long-term capital is required by the business enterprises.
Answer:
Capital Market

Question 8.
The market deals in the issue of new securities.
Answer:
Primary Market

Question 9.
The government securities market is for government and semi-government securities.
Answer:
Gilt-edged Security Market

Question 10.
The equity shares of the companies are issued to the existing equity shareholders.
Answer:
Right Issue

Question 11.
A marketplace where the existing securities are bought and sold.
Answer:
Secondary Market

Question 12.
The place where buying and selling of securities take place.
Answer:
Stock Exchange

Question 13.
The institution which regulates business in the stock exchange.
Answer:
SEBI

Question 14.
A market for financial assets which are close substitutes for money.
Answer:
Money Market

Question 15.
A market where short-term funds are borrowed and lent.
Answer:
Money Market

Question 16.
A market for borrowing and lending long-term capital is required by the business enterprises.
Answer:
Capital Market

Question 17.
A debt instrument issued by the corporate house for raising the short-term funds from the money market.
Answer:
Commercial Paper

Question 18.
The negotiable term deposit certificates are issued by the financial institutions at discount, at market rate, or at par.
Answer:
Certificate of deposit

Question 19.
A type of bill in the nature of promissory note issued by the government.
Answer:
Treasury Bill

Question 20.
The bill is issued by the government for raising short-term funds to bridge the gap between receipts and expenditure.
Answer:
Treasury Bill

Question 21.
A market where productive capital is raised and made available for industrial purposes.
Answer:
Capital Market

Question 22.
A market for government and semi-government securities.
Answer:
Gilt-edged Market

Question 23.
The market is utilized for raising fresh capital in the form of shares and debentures.
Answer:
Primary Market

Question 24.
The equity shares of the companies are issued to the existing equity shareholders.
Answer:
Right Issue

Question 25.
The most popular method of raising long-term securities by offering them to the public by using a prospectus.
Answer:
Public Issue

Question 26.
A marketplace where the existing securities are bought and sold.
Answer:
Secondary/Stock Market

1D. State whether the following statements are true or false.

Question 1.
Money market Facilitates mobilization of funds.
Answer:
False

Question 2.
Repo Rate is known as an official bank Rate.
Answer:
True

Question 3.
The financial market does not contribute towards nations’ growth and development.
Answer:
False

Question 4.
Commercial bill is a common method to meet long term needs of industry.
Answer:
False

Question 5.
Reverse Repo Rate is similar to Repo Rate.
Answer:
False

Question 6.
MMMF is a part of the capital market.
Answer:
False

Question 7.
The financial market brings together borrowers and lenders.
Answer:
True

Question 8.
Certificate of deposit is a part of the money market.
Answer:
True

1E. Find the odd one.

Question 1.
91 days, 182 days, 365 days
Answer:
365 days

Question 2.
Share, debentures, MMMF’s
Answer:
MMMF’s

Question 3.
Treasury Bill, certificate of deposit, bond
Answer:
Bond

Question 4.
Share, debenture, commercial paper
Answer:
Commercial paper

Question 5.
SEBI, RBI, SIDBI
Answer:
SIDBI

Question 6.
Commercial paper, certificate of deposit, bond
Answer:
Bond

Question 7.
Preference share, Equity shares, commercial bill
Answer:
Commercial Bill

1F. Complete the sentences.

Question 1.
Financial Assets are exchanged in a ___________
Answer:
Financial Market

Question 2.
___________ is dealing with second hand issue.
Answer:
Secondary Market

Question 3.
Money Market is Regulated by ___________
Answer:
RBI

Question 4.
The instruments of ___________ can easily converted into cash.
Answer:
Money Market

Question 5.
___________ is an unsecured promissory note issued by companies.
Answer:
Commercial Paper

Question 6.
Secondary market is commonly called as ___________
Answer:
Stock Exchange

Question 7.
___________ Market increases liquidity of fund in the economy.
Answer:
Money

Question 8.
___________ is dealing with mobilisation of fund.
Answer:
Capital Market

Question 9.
Derivative market is specially designed to ___________
Answer:
derivatives

Question 10.
___________ are the intermediary of primary market.
Answer:
Underwriters

Question 11.
___________ is also known as new issue market.
Answer:
Primary Market

Question 12.
___________ are the intermediary of Secondary Market.
Answer:
Security brokers

Question 13.
In ___________ risk factor is very less.
Answer:
Money Market

Question 14.
Government security market is also called as ___________
Answer:
Gilt Edged Market

Question 15.
Private companies deal their securities in ___________
Answer:
Industrial Security Market

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(1) ………………….	(a) Promissory note
(2) …………………	(b) short term credit
(3) New Issue	(c) ……………….
(4) Stock Exchange	(d) ………………

(Commercial bill, Treasury bill, Secondary market, Primary market)
Answer:

Group ‘A’	Group ‘B’
(1) Treasury Bill	(a) Promissory note
(2) Commercial Bill	(b) short term credit
(3) New Issue	(c) Primary Market
(4) Stock Exchange	(d) Secondary Market

Question 2.

Group ‘A’	Group ‘B’
(1) Financial Market	(a) ………………….
(2) Money Market	(b) …………………
(3) ………………….	(c) Primary Market
(4) ………………….	(d) Commercial Paper
(5) Capital Market	(e) …………………

(Financial Securities, Short Term, Neiv issue, unsecured promissory note, long term)
Answer:

Group ‘A’	Group ‘B’
(1) Financial Market	(a) Financial Securities
(2) Money Market	(b) Short term
(3) New Issue	(c) Primary Market
(4) Unsecured promissory Note	(d) Commercial Paper
(5) Capital Market	(e) Long Term

Question 3.

Group ‘A’	Group ‘B’
(1) ………………….	(a) Gilt-edged Market
(2) …………………	(b) Repo Rate
(3) Commercial bills	(c) ……………………
(4) Money market	(d) …………………..

(Short term, most common method to meet credit needs, official bank rate, Government securities)
Answer:

Group ‘A’	Group ‘B’
(1) Government securities	(a) Gilt-edged Market
(2) Official Bank Rate	(b) Repo Rate
(3) Commercial bills	(c) Most common method to meet credit needs
(4) Money market	(d) short term

1H. Answer in one sentence.

Question 1.
What is Repo Rate?
Answer:
This is a rate at which commercial banks borrow money from the central bank (RBI).

Question 2.
What is a Secondary Market?
Answer:
It is the market where existing securities are resold. It is also called as the stock market.

Question 3.
What is a Treasury bill?
Answer:
It is a short-term security issued by RBI on behalf of the Central Government of India to meet government short-term fund requirements.

Question 4.
What is commercial paper?
Answer:
Commercial paper is an unsecured debt instrument issued by companies to build short-term finance.

Question 5.
What is the Gilt-edged market?
Answer:
The gilt-edged market is the market where government securities are traded. This market deals in government and semi-government securities.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Treasury bills are issued by companies.
Answer:
Commercial papers are issued by companies.

Question 2.
Capital Market builds finance for the short term.
Answer:
Money Market builds finance for the short term.

Question 3.
Gilt edge market deals with corporate securities.
Answer:
Industrial Securities Market deals with corporate securities.

Question 4.
The government uses commercial bills to build short-term finance.
Answer:
Treasury Bills uses commercial bills to build short-term finance.

Question 5.
Mutual Fund deals in Money Market.
Answer:
Money Market Mutual Fund deals in Money Market.

Question 6.
The minimum value of the commercial paper is 6 lakhs.
Answer:
The minimum value of the commercial paper is 5 lakhs.

Question 7.
Trade Bills are unsecured negotiable promissory notes issued by Banks.
Answer:
Certificate of deposits is an unsecured negotiable promissory note issued by Banks.

Question 8.
Underwriters are the intermediary of the secondary market.
Answer:
Security Brokers are the intermediary of the secondary market.

Question 9.
Direct Investment took place in the secondary market.
Answer:
Indirect Investment took place in the secondary market.

Question 10.
In the primary market security price is fixed by Demand and supply.
Answer:
In the Secondary market security price is fixed by Demand and supply.

Question 11.
Primary Market the parties dealing in this market are the only investors.
Answer:
Secondary Market the parties dealing in this market are the only investors.

1J. Arrange in proper order.

Question 1.
Arrange the given instruments by using minimum amount Criteria:
(a) Certificate of deposit
(b) Commercial paper
(c) Treasury Bill
Answer:
(a) Treasury Bill
(b) Certificate of deposit
(c) Commercial paper

Question 2.
Arrange the following instruments on the basis of ‘Year of the beginning’:
(a) Commercial papers
(b) Certificate of deposits
(c) Treasury bills
Answer:
(a) Treasury bills [1990]
(b) Certificate of deposits [1989]
(c) Commercial papers [1917]

Question 3.
Arrange the following securities on the basis of redemption:
(a) Preference shares
(b) Equity shares
(c) Debentures
Answer:
(a) Debentures
(b) Preference shares
(c) Equity shares

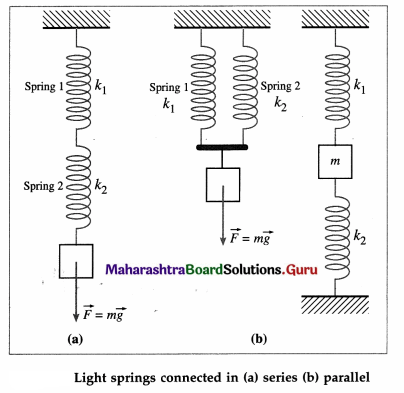
2. Explain the following terms/concepts.

Question 1.
Private Placement
Answer:
Private placement means when a company offers its securities to a selected group of persons identified by the board excluding qualified institutional buyers and employees not exceeding 200. This helps the company to raise funds quickly and economically

Question 2.
Government Securities
Answer:

The marketable debt issued by the government, semi-government which represents claims on the government is known as ‘Government Securities’.
These securities are safe as payment of interest & repayment of principal amount are guaranteed.

Question 3.
Repo Rate
Answer:

Repo is an agreement where the seller of a security agrees to buy it back from the lender at a higher price on a future date.
This agreement is made between RBI and commercial banks. Here, commercial banks borrow from RBI.

Question 4.
Reverse Repo Rate
Answer:

Reverse Repo rate is the rate at which RBI borrows from commercial banks.
Reverse Repo rate is always less than Repo Rate.

Question 5.
Gilt-edged market
Answer:
The gilt-edged market is the market where government securities are traded. This market deals in government and semi-government securities.

Question 6.
Money Market Mutual Fund
Answer:
Money Market Mutual Funds (MMMFs):
A Mutual Fund which invests in Money market instruments like Call Money, Repos, T-bills, CDs, etc. is called as MMMFs. This type of Mutual Fund invests in debt instruments that mature in less than 1 year and have low risk. Individuals and corporates are allowed to invest in MMMFs.

3. Study the following case/situation and express your opinion.

1. M/s. Radheshyam company wants short-term loans (Borrowing) to meet its working capital needs. Hence as an expert advice M/s. Radheshyam on the following matters.

Question (a).
Can a company select a capital market to complete its working capital needs?
Answer:
No, Company cannot select a capital market to meet working capital requirements. A company should go for the money market.

Question (b).
If a company selects the money market, the names of the instruments through which short-term finance can be build up?
Answer:
If company select money market option, it can build up finance through Trade bill, commercial papers and MMMF’s.

Question (c).
Is completion of working capital needs important to Radhaeshyam Company?
Answer:
Yes, completion of working capital needs important to Radheshyam company. Because working capital needs are daily needs of the business. Once it is completed production cycle can work better.

2. Government of India wants short-term finance to deal with the short-term deficit condition. Advice the government on the following.

Question (a).
Name of the instrument through which government can build up short-term finance?
Answer:
Treasury bill is the best option to build short-term finance for the Government. It can be issued for 91 days, 182 days, and 364 days.

Question (b).
What will be the minimum amount of investment in the Treasury bill?
Answer:
The minimum amount of investment in treasury bills is ₹ 25,000.

Question (c).
Method of issue of Treasury bill.
Answer:
Treasury bills are issued at discount and repaid at par. Hence it is also caused as a ‘zero’ coupon bond.

4. Distinguish between the following.

Question 1.
Commercial Bills and Treasury Bills
Answer:

Points	Commercial Bills	Treasury Bills
1. Meaning	Commercial Bills are the money market instruments that are created to fulfill the credit needs of Trade and Industry.	Treasury bills are the money market instruments that are created to fulfill the credit needs of the government.
2. Nature of instrument	They are in the form of a bill of Exchange.	They are in the form of promissory notes.
3. Maturity Period	The maturity period is 3 months/90 days.	The maturity period of treasury bills is 91 days, 182 days, 364 days.
4. Borrower	Blue Chip companies or big business organizations are the borrowers.	Government is the borrower.
5. Development of market	The commercial bill market has not much developed in the money market.	Treasury bills have developed in the money market due to government support.

Question 2.
Repo Rate and Reverse Repo Rate
Answer:

Points	Repo Rate	Reverse Repo Rate
1. Meaning	It is the interest rate at which the central bank repurchases the Government Securities.	It is the interest rate at which commercial banks repurchase the Government Securities.
2. Level	Repo Rate is always higher than Reverse Repo Rate.	Reverse Repo rate is always lower than Repo Rate.
3. Initiative	It is carried out by the central bank.	It is carried out by a commercial bank.
4. Current Rate	The current Repo Rate as of February 2020 is 5.15%.	The current Reverse Repo Rate as of February 2020 is 4.90%.
5. Lender and Borrower	Here, the lender is RBI and Borrower is a commercial Bank.	Here, the lender is a commercial Bank and Borrower is RBI.
6. Borrower’s objective	Its main objective is to manage short-term deficiency of funds.	Its main objective is to reduce the overall supply of money in the economy.

5. Answer in brief.

Question 1.
Write a note on the importance of the financial market.
Answer:
Role: A financial market is of great use for a country as it helps the economy in the following ways:
(i) Saving Mobilization:
Obtaining funds from surplus units such a households individuals, public sector units, central government, etc and channelizing their funds or productive purposes.

(ii) Investments:
The financial market plays an important role in arranging to invest funds thus, collected in those units which are in need of the funds.

(iii) National Growth:
The financial market contributes to the national growth by ensuring a continuous flow of surplus funds to deficit units.

(iv) Entrepreneurship Growth:
Financial markets contribute to the development of the entrepreneurial class by making available the necessary financial resources.

(v) Industrial Development:
The components of financial markets help towards accelerated growth of industrial and economic development of a country thus, contributing to raising the standard of living and the society’s wellbeing.

(vi) Capital formation:
The capital market brings together borrowers and lenders. It attracts saving from people and directs it towards the institutions where it is needed. It generates capital for the business.

Question 2.
Explain constituents of Capital Market.
Answer:
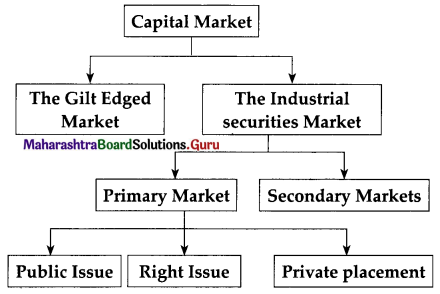
The capital market is divided into two segments:

Gilt Edged Market
Industrial Securities Market

(i) Gilt Edged Market:
It is also known as the government securities market, which is a market for government and semi-government securities.
Features of this market are:

Guaranteed return on investment
No speculation on securities
Major institutions are LIC, PF, and commercial banks.
The heavy volume of transactions
Institutional-based investors.

(ii) Industrial Securities Market:
It is a market for industrial securities such as bonds, equities, etc. It comprises two segments.

Primary Market
Secondary Market

Primary Market:
It is also known as New Issue Market. The market is utilized for raising fresh capital in the form of shares and debentures. It helps to accelerate economic and industrial development.

Modes of raising capital in the Primary Market:
(i) Public Issue/Prospectus:
Securities are issued to the general public. This is the most popular method of raising long-term funds. In this method, securities are offered to the public by issuing a prospectus.

(ii) Rights Issue:
The equity shares of a company are issued to the existing equity shareholders in the form of rights issues. In this issue, additional securities are offered to the existing shareholders.

(iii) Private Placement:
Under the private placement, the shares of a company are sold among the selected group of persons. There are three categories of participants in the primary market i.e. issuers of securities, investors, and intermediaries.

Secondary Market:
It is a market where existing securities are sold or traded. This market is also known as the stock market. The secondary market consists of recognized stock exchanges operating under rules, bye-laws, and regulations duly approved by the government.

Question 3.
Write a note on Participants in the Money Market.
Answer:
Some important participants in the money market:
(i) Reserve Bank of India:
It is the most important participant in the money market. Through the money market, RBI regulates the money supply and implements its monetary policy. It issues government securities on behalf of the government and also underwrites them. It acts as an intermediary and regulator of the market.

(ii) Central and State Government:
Central Government is a borrower in the Money Market, through the issue of Treasury Bills (T-Bills). The T-Bills are issued through the Reserve Bank of India (RBI). The T-Bills represent zero risk instruments. Due to its risk-free nature banks, corporate, etc. buy the T-Bills and lend to the government as a part of its short-term borrowing program. The state government issues bonds called State Development Loans.

(iii) Public Sector Undertakings (PSU):
Many listed government companies can issue commercial paper in order to obtain its working capital.

(iv) Scheduled Commercial Banks:
Scheduled commercial banks are very big borrowers and lenders in the money market. They borrow and lend in call money market, short notice market, Repo and Reverse Repo market.

(v) Insurance Companies:
Both, the general and life insurance companies are usual lenders in the money market. They invest more in capital market instruments. Their role in the money market is limited.

(vi) Mutual Funds:
Mutual Funds offer varieties of schemes for the different investment objectives of the public. Mutual funds schemes are liquid schemes. These schemes have the investment objective of investing in money market instruments.

6. Justify the following statements.

Question 1.
Primary Market is known as the New issue market.
Answer:

The primary market is that security market where fresh securities are raised in the form of shares and debentures.
This market is mainly utilized for raising long-term funds.
Funds are raised in this market through various modes such as public issue/prospectus, right issue, and private placement.
Moreover, the primary market is also beneficial for capital formation in the country which in turn accelerates its economic and industrial development.
Thus, the Primary market is known as New Issue Market.

Question 2.
The gilt-edged market is known as the government securities market.
Answer:

A gilt-edged market is a market where government and semi-government securities are traded. Therefore, it is also known as the government securities market.
In such a market, mostly gilt-edged securities are traded. These are the stocks and bonds issued by the Central or State Government.
These securities are considered safe investments as payment of interest and repayment of principal amount on them are guaranteed by the government. Also, there is no speculation on such securities.
In the Gilt-edged market, the major participants are public corporations such as Life Insurance Corporation (LIC), Provident Fund (PF), and commercial banks.
The government securities are mostly in the form of stock certificates, promissory notes, and government bonds.
Thus, the gilt-edged market is known as the government securities market.

Question 3.
Repo rate is known as the official bank Rate.
Answer:

Repo rate refers to the discounted interest rate at which the Central Bank repurchases the government securities.
Such transaction is mainly carried out to reduce short-term liquidity in the system.
Here, the Central Bank has the sole power to adjust (increase or decrease) the repo rate so as to control the money supply in an economy.
Additionally, the transactions are mainly carried out between the Central Bank and Commercial Banks at a repo rate.
Due to all the above reasons, the repo rate is known as the official bank rate.

Question 4.
Capital Market facilitates the mobilization of funds.
Answer:

The money market is a place where short-term funds are borrowed and lent.
It is a market for financial assets that are close substitutes for money.
The instruments dealt in the money market are liquid and can be easily converted into cash at a low transaction cost.
Due to this, the money market fails to facilitate the mobilization of funds.
On the other hand, the Capital market, a market for long-term instruments, facilitates the mobilization of funds.
In this market, the instruments such as bonds, debentures, equity shares, and stocks having long or indefinite maturity periods are traded.
Thus, mobilization of funds is facilitated by the capital market rather than the money market.

7. Answer the following questions.

Question 1.
Explain the role and importance of the financial market in the development of an economy.
Answer:
Role: A financial market is of great use for a country as it helps the economy in the following ways:
(i) Saving Mobilization:
Obtaining funds from surplus units such as households, individuals, public sector units, Central Government, etc and channelizing their funds or productive purposes.

(ii) Investments:
The financial market plays an important role in arranging to invest funds thus, collected in those units which are in need of the funds.

(iii) National Growth:
The financial market contributes to national growth by ensuring a continuous flow of surplus funds to deficit units.

(iv) Entrepreneurship Growth:
Financial markets contribute to the development of the entrepreneurial class by making available the necessary financial resources.

(vii) Employment Generation:
The capital market is contributed towards the generation of capital. It supports the development of small and large businesses. It creates employment opportunities for the public.

(viii) Productive use of funds:
The financial market allows productive use of the fund. An excess fund of investors is used by the borrowers for productive purposes.

Question 2.
Explain constituents of the Indian capital market.
Answer:
Maharashtra Board Class 12 Secretarial Practice Important Questions Chapter 11 Financial Market 7 Q2

(i) The Gilt Edged Market: It is also known as the government securities market, which is a market for government and semi-government securities. Features of this market are:

Guaranteed return on investment
No speculation on securities
Major institutions are LIC, PF, and commercial banks.
The heavy volume of transactions
Institutional-based investors.

(ii) Industrial Securities Market: It is a market for industrial securities such as bonds, equities, etc. It comprises two segments.

Primary Market
Secondary Market

(A) Primary Market: It is also known as New Issue Market. The market is utilized for raising fresh capital in the form of shares and debentures. The industrial sectors usually approach this market for raising fresh capital. This is usually a long-term fund. The primary market is useful for capital formation in the country and accelerates economic and industrial development.

(iii) Private Placement:
Under the private placement, the shares of a company are sold among the selected group of persons. There are three categories of participants in the primary market. They are the issuers of securities, investors, and intermediaries.

(B) Secondary Market: It is a market where existing securities are sold or traded. This market is also known as the stock market. The secondary market consists of recognized stock exchanges operating under rules, bye-laws, and regulations duly approved by the government.

A stock exchange is defined under section 2(3) of the Securities Contracts (Regulations)
Act 1956 as “An association, organization or body of individuals, whether incorporated or not established for the purpose of assisting, regulating or controlling of business in buying, selling or dealing in securities.”

Functions of Secondary Market:

To facilitate liquidity and marketability of securities.
To contribute to the economic growth through mobilization of funds to the most efficient channels.
To provide an instant valuation of securities dealt at the stock exchange.
To ensure a measure of safety and fair dealing to protect investor’s interests.

8. Attempt the following.

Question 1.
Explain features of the Indian Money Market?
Answer:
A money market is a place where short-term funds are borrowed and lent. The Instruments dealt with within this market are liquid financial assets.
The features of the money market are as follows:
(i) No Fixed Place for Trading of Securities/Shares:
In the money market, there is no definite place to carry out lending and borrowing operations of securities or shares.

(ii) Involvement of Brokers:
Dealings in such a market can be conducted with or without the participation of brokers.
Companies, banks, etc. may directly deal in the money market.

(iii) Financial Assets:
The financial assets that are dealt in the money market are close substitutes for money as these assets can be easily converted into cash without any loss in value.

(iv) Organisations Involved:
The main organizations dealing in the money market in India are the Reserve Bank of India (RB), State governments, banks, corporate investors, etc.

(v) Nature of the Market:
It is not a single market but a collection of markets for different instruments such as commercial bills, commercial papers, certificates of deposits, government securities, etc.

(vi) Term of Finance:
The funds can be borrowed or lent for a maximum period of one year.

(vii) Source of Short Term Funds:
The money market provides a place or a system whereby short-term (for a period of less than one year) funds can be easily borrowed or lent.

Question 2.
Explain important participants of the Indian Money Market.
Answer:
Some important participants in the Indian Money Market are:
(i) Reserve Bank of India:
It is the most important participant in the money market. Through the money market, RBI regulates the money supply and implements its monetary policy. It issues government securities on behalf of The Government and also underwrites them. It acts as an intermediary and regulator of the market.

(iii) Public Sector Undertakings (PSU):
Many listed government companies can issue commercial paper in order to obtain their working capital.

(iv) Scheduled Commercial Banks:
Scheduled commercial banks are very big borrowers and lenders in the money market. They borrow and lend in the call money market, short notice market, Repo and Reverse Repo market.

(vii) Non-Banking Finance Companies (NBFCs): NBFCs use their surplus funds to invest in government securities, bonds, etc. (Example of NBFC – Unit Trust of India)

(viii) Corporates:
Corporates borrow by issuing commercial papers which are nothing but short-term promissory notes. They are the lender to the banks when they buy the certificate of deposit issued by the banks.

(ix) Primary Dealers:
Their main role is to promote transactions in government securities. They buy as well as underwrite the government securities.

Maharashtra State Board Class 11 Secretarial Practice Important Questions and Answers

July 3, 2024July 2, 2024 by Bhagya

Maharashtra State Board HSC 11th Secretarial Practice Important Questions and Answers

Maharashtra Board 11th HSC Important Questions

Maharashtra Board Class 12 Secretarial Practice Important Questions Chapter 12 Stock Exchange

July 3, 2024July 2, 2024 by Bhagya

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 12 Stock Exchange Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 12 Stock Exchange

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
The Securities Contracts (Regulation) Act was passed in the year _____________
(a) 1956
(b) 1947
(c) 1971
Answer:
(a) 1956

Question 2.
SEBI was established in the year _____________
(a) 1988
(b) 1987
(c) 1986
Answer:
(a) 1988

Question 3.
The Oldest Stock Exchange in Asia is _____________
(a) BSE
(b) NSE
(c) LSE
Answer:
(a) BSE

Question 4.
The BSE switched to electronic trading system in _____________
(a) 1988
(b) 1995
(c) 1956
Answer:
(b) 1995

Question 5.
Stock Exchange is also formed/termed as _____________
(a) Local Market
(b) Super Market
(c) Stock Market
Answer:
(c) Stock Market

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) SEBI	(a) Sensex
(2) Stock Exchange	(b) Primary market
(3) Nifty	(c) Auction
(4) Bear	(d) Made up of 50 listed companies
(5) SENSEX	(e) Optimistic about rising in prices of securities
	(f) Pessimistic about fall in prices of securities
	(g) Purchase and sale of shares
	(h) Machinery regulating Stock Exchanges
	(i) BSE
	(j) NSE

Answer:

Group ‘A’	Group ‘B’
(1) SEBI	(h) Machinery regulating Stock Exchanges
(2) Stock Exchange	(g) Purchase and sale of shares
(3) Nifty	(d) Made up of 50 listed companies
(4) Bear	(f) Pessimistic about fall in prices of securities
(5) SENSEX	(i) BSE

Question 2.

Group ‘A’	Group ‘B’
(1) Bull	(a) A Secondary Market for Securities
(2) Stag	(b) Auction
(3) Broker	(c) Invests in Primary Market
(4) Stock Exchange	(d) Mandiwala
(5) NSE	(e) Deals on behalf of his client
	(f) A broker optimistic about rising in prices of securities
	(g) A broker pessimistic about fall in prices of securities
	(h) 1992
	(i) 1988
	(j) 1996

Answer:

Group ‘A’	Group ‘B’
(1) Bull	(f) A broker optimistic about rising in prices of securities
(2) Stag	(c) Invests in Primary Market
(3) Broker	(e) Deals on behalf of his client
(4) Stock Exchange	(a) A Secondary Market for Securities
(5) NSE	(h) 1992

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
He/She acts as a link between Jobber and the investor.
Answer:
broker

Question 2.
The securities contract (Regulation) Act 1956, provides the functioning, licensing of this institution.
Answer:
Stock Exchange

Question 3.
The first listed Stock Exchange in India.
Answer:
BSE

Question 4.
The professional speculator in the Stock Exchange.
Answer:
Jobber

Question 5.
An intermediary between investor and broker.
Answer:
Jobber

Question 6.
The single and most important institution in the secondary market for securities.
Answer:
Stock Exchange

1D. State whether the following statements are True or False.

Question 1.
Stock Exchange in India is regulated by SEBI.
Answer:
True

Question 2.
Stock Exchange is also called a Primary Market.
Answer:
False

Question 3.
The NSE is the first listed Stock Exchange in India.
Answer:
False

Question 4.
The objective of SEBI is to protect the interests of companies.
Answer:
False

Question 5.
The securities market is an organised market in India.
Answer:
True

Question 6.
Stock Exchanges reflect the financial progress of a country.
Answer:
True

Question 7.
There is no control on Stock Exchange.
Answer:
False

Question 8.
Stock Exchange is a place for buying and selling securities.
Answer:
True

Question 9.
Insider trading is legally permitted.
Answer:
False

1E. Find the odd one.

Question 1.
BSE, NSE, LSE
Answer:
LSE

Question 2.
Crash, Bull, Bear
Answer:
Crash

Question 3.
Sensex, Rally, Nifty
Answer:
Rally

1F. Complete the sentences.

Question 1.
A bear broker whose expectations have gone wrong and makes a loss in dealings is called _____________
Answer:
Lame duck

Question 2.
SEBI has its headquarters in _____________
Answer:
Mumbai

Question 3.
The NSE (National Stock Exchange of India) was incorporated in the year _____________
Answer:
1992

Question 4.
SEBI regulates capital markets in _____________
Answer:
India

Question 5.
A smart speculator, who quickly judges market trends thereby makes profits is _____________
Answer:
a wolf

Question 6.
The instructions are given by an investor to the broker to buy or sell a security when it reaches a certain price is called _____________
Answer:
stop-loss

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(a) Oldest Stock Exchange in India	(1) ……………………….
(b) ………………..	(2) Stock Exchange

(BSE, Secondary Market)
Answer:

Group ‘A’	Group ‘B’
(a) Oldest Stock Exchange in India	(1) BSE
(b) Secondary Market	(2) Stock Exchange

1H. Answer in one sentence.

Question 1.
What is SEBI?
Answer:
SEBI is a statutory body under the SEBI Act, 1992, which regulates and controls the activities of the stock exchanges and protects the interest of investors.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
NSE is the oldest Stock Exchange in Asia.
Answer:
BSE is the oldest Stock Exchange in Asia.

Question 2.
Insider Trading is the practice of buying and selling securities within the same trading day before the closing of markets on that day.
Answer:
Day Trading is the practice of buying and selling securities within the same trading day before the closing of markets on that day.

Question 3.
The sensitive index called Sensex is made up of the 50 largest and actively traded stocks of listed companies.
Answer:
The sensitive index called Sensex is made up of the 30 largest and actively traded stocks of listed companies.

Question 4.
Investors can deal in their securities through a Jobber.
Answer:
Investors can deal in their securities through a broker.

Question 5.
In India, Bear is known as Tejiwala.
Answer:
In India, Bear is known as Mandiwala.

2. Explain the following terms/concepts.

Question 1.
Insider Trading
Answer:
Insider trading is the trading of a public listed company’s securities by an individual with access to non-public information about the company. It is illegal as it is unfair to other investors who do not have access to the information.

Question 2.
Sensex
Answer:
It is the Index of the BSE that was created in 1986, which represents the increase or decrease in prices of stocks of a selected group of companies. The sensitive Index called Sensex is made up of the 30 largest and actively traded stocks of listed companies.

Question 3.
Nifty
Answer:
It is the index of the NSE created in 1996 made up of 50 listed companies. It includes all the 30 Sensex stocks.

Question 4.
Crash
Answer:
If the Sensex or Nifty moves in a downward direction, it is called a crash. Bears are active during this period.

Question 5.
Stop-loss
Answer:
It is instruction or order given by an investor to the broker to buy or sell a security when it reaches a certain price. This instruction is given by the investor when he wants to avoid losses when the prices fall below the stop price.

3. Study the following case/situation and express your opinion.

1. Ajay is a licensed member of the Stock Exchange Arnav his client wants to purchase securities. Answer the questions from the above situation.

Question (a).
By what term/name will Ajay be known?
Answer:
Ajay will be known as ‘Broker’.

Question (b).
How did Ajay become/acquire the term?
Answer:
Ajay acquired the term as ‘Broker’ by registering himself with the Stock Exchange as it is required for the purpose of trading in the Stock Exchange.

Question (c).
How did the transaction between them take place?
Answer:
The transaction between Ajay and Arnav was validated by a note given by Ajay to his client Arnav. This note is called contract note which both Ajay and Arnav had a copy of each immediately after their transaction within 24 hours.

2. Anurag is an employee of the Stock Exchange who passes sensitive information relating to likely high growth in profits of ‘sun’ company to his relative Jyoti. Jyoti thus buys shares at low prices. But due to the Corona Virus spread and lockdown and worldwide panic, the Sensex is moving swiftly in a downward direction. Answer the following queries.

Question (a).
Describe the nature of the term that describes Jyoti’s actions?
Answer:
The term that describes Jyoti’s actions is known as ‘Insider trading’ means trading due to non-public sensitive information about ‘SUN’ Company.

Question (b).
Is Jyoti’s action normal? Why?
Answer:
Jyoti’s action which is based on insider information is illegal. It is unfair to other investors who do not have access to the information.

Question (c).
What is this downward direction called?
Answer:
If the Sensex/ Nifty moves in a downward direction it is called a ‘CRASH’.

3. Moon Co-Ltd. listed its shares in Bombay Stock Exchange (BSE). Due to the COVID-19 pandemic, the Stock Exchanges in India came crashing down. Answer the queries.

Question (a).
What do you mean by the term Stock Exchange Crash?
Answer:
If the Sensex or Nifty moves in the downward direction, it is called a crash.

Question (b).
What is the Index of BSE called?
Answer:
The index of BSE is called Sensex which represents the increase or decrease in prices of stocks of a selected group of companies.

Question (c).
The Index of BSE comprises of how many companies.
Answer:
The index of BSE or Sensitive index called Sensex is made up of the 30 largest and actively traded stocks of listed companies. It was created in 1986.

4. Keith Bionics Ltd. a newly formed company makes a public issue of shares for the first time to raise capital funds. It also gets itself listed for the first time with BSE. Answer the queries.

Question (a).
What is Keith Bionics’ first time issue termed as/called?
Answer:
The public issue of shares or other securities by the new company ‘Keith Bionics Ltd/is termed as/called ‘Initial Public Offer (IPO)’.

Question (b).
What do you mean by listing with BSE?
Answer:
Listing means an agreement signed by Keith Bionics Ltd. with BSE so that its share and securities get a platform to be bought and sold in BSE multiple times.

Question (c).
What is the advantage of listing to Keith Bionics Ltd.?
Answer:
Because of listing with BSE the shares and securities of Keith Bionics Ltd. can be bought and sold (traded) in BSE repeatedly thus providing marketability along with liquidity for this company’s share.

4. Distinguish between the following.

Question 1.
Bull and Bear
Answer:

Points	Bull	Bear
1. Meaning	A speculator who purchases the securities with the intention to sell them at a higher price later is called the Bull.	A speculator who sells the securities when the prices of securities start falling is called the Bear.
2. Functions	A bull buys securities at a lesser price and sells them at a maximum higher price to make the maximum possible profit.	A bear buys securities at a lesser price and sells them at a little higher price to make a desirable profit and to avoid selling at a still lower prices in the future.
3. Expectation	A bull always anticipates that the prices of securities will rise further in the future.	A bear always anticipates that the prices of securities will fall further in the future.
4. Other names	A bull is also called ‘Tejiwala’. This is because he always anticipates the price to rise.	A bear is also called ‘Mandiwala’. This is because he always expects the price to fall.
5. Nature/View of future	A bull takes an optimistic view of the future.	A bear takes a pessimistic view of the future.

5. Answer in brief.

Question 1.
Explain the management and organizational structure of the Stock Exchange in India.
Answer:
(i) Management of Stock Exchange:

The Executive committee of the stock exchange looks after the overall activities and management of the stock exchange.
The composition, powers, and the name of the executive committee differ from exchange to exchange.
There are other supporting committees to assist the executive committee like an advisory committee, listing committee, etc.

(ii) Organization Structure of Stock Exchanges in India:
In India, the stock exchange may be organized in one of the following three forms:

Voluntary non-profit making organization.
Companies with liability limited by shares.
Companies with liability limited by guarantee.

The Securities Contract (Regulations) Act 1956, provides rules for their functioning, licensing, recognition, and controlling speculations.

(iii) Membership of Stock Exchange:
The eligibility criteria for membership may differ from stock exchange to stock exchange.

6. Justify the following statements.

Question 1.
Stock Exchange is a Secondary Market.
Answer:

The stock exchange is a specific place where the trading of securities is arranged in an organized method.
In the primary market, new securities are floated by the issuing companies and direct contact with the public at large is established for selling of the securities.
A stock exchange is the single most important institution in the secondary market for securities.
It is the place where already issued and outstanding shares are bought and sold, repeatedly.
Thus, it is rightly said that Stock Exchange is a secondary market which is an organized market in India.

Question 2.
The objective of SEBI is to protect the interest of investors.
Answer:

The Securities and Exchange Board of India was set up on 12th April 1988, the main purpose of setting up SEBI was to develop and regulate stock exchange in India.
The objectives of SEBI are to protect the interest of the investors.
To bring professionalism in the working of intermediaries in the capital markets, i.e., brokers, mutual funds, stock exchanges, Demat depositories, etc. is also an objective of SEBI.
Objectives of SEBI also include creating a good financial climate, so that companies can raise long-term funds through the issue of securities – shares and debentures.
Thus, it is rightly said that the objective of SEBI is to protect the interest of investors.

Question 3.
Insider trading is considered illegal.
Answer:

Insider trading refers to the trading of shares on the stock exchanges with sensitive information, which is not yet published.
The insiders include managers, directors, other employees, auditors, etc., who have a hold over sensitive information and accordingly buy or sell on the Stock Exchanges.
For instance, if the sensitive information relates to likely high growth in profits of the company, then the insiders may buy the shares at a low price and when the information is published, the share price may shoot up considerably resulting in the insiders selling and making huge profits.
Insider trading is restricted by SEBI.
Thus, insider trading is considered illegal.

7. Answer the following questions.

Question 1.
What is Stock Exchange? Explain the organizational structure and features of the Stock Exchange.
Answer:
Stock Exchange is a place where securities are purchased and sold in an organized manner. It is also known as Stock Market, Share Market, Share Bazaar, or Secondary Market. The Securities Exchange Board of India regulates the stock exchange.

Organization Structure of Stock Exchanges in India:
In India, the stock exchange may be organized in one of the following three forms:

Voluntary Non-Profit making organization
Companies with liability limited by shares
Companies with liability limited by guarantee

The Securities Regulation Act 1956 provides rules for functioning, licensing, recognition, and controlling the stock exchanges.

Features of Stock Exchange:
(i) Market for Securities:
Stock exchange deals with securities. Securities include equity shares, preference shares, debentures, government securities, and bonds, etc. It is a trading place where corporate securities and government securities are traded.

(ii) Second Hand Securities:
Stock exchange includes trading of securities that are already issued by the companies. In other words, second-hand securities are bought and sold among investors in the stock exchange.

(iii) Listed Securities:
Only listed securities can be traded on a stock exchange. Listing of securities provides protection of the investor’s interests. The company also has to strictly follow the rules laid down by the stock exchange.

(iv) Organised and Regulated Market:
The stock exchange is an organized market of securities. All the listed companies have to follow the rules and regulations laid down by the stock exchange.

(v) Specific Location:
The stock exchange is a place where securities are traded. It is a marketplace where brokers and intermediaries meet to conduct dealings in securities. Now, the stock exchange has also been digitalized.

(vi) Only Members can trade:
The stock exchange is only open to its members who are known as brokers. Brokers act as agents between members or their authorized agents on behalf of the investors.

Question 2.
Explain the importance of the Stock Exchange.
OR
State/Explain the role of the Stock Exchange.
Answer:
The stock exchange’s role is vital for the economic development of a nation. It is briefly stated as follows:
(i) Assist in raising funds:
Stock Exchanges’ enables companies to raise long-term funds which can be utilized for expansion and modernization and also for the purpose of setting up new projects.

(ii) Facilitates listing of shares:
The companies that issue shares to the public can get their shares listed in one or more stock exchanges thus, enabling them to raise long-term funds through the issue of shares.

(iii) Facilitates trading of shares:
The stock exchanges facilitate the trading of shares between sellers and buyers thus, brings liquidity to the shares. Sellers can sell shares and realize cash when in need of funds or whenever they want to book profits.

(iv) Generate Employment:
Stock Exchanges generate employment facilities in the country as a number of brokers, sub-brokers, agents, and others employment. Stock Exchanges also facilitate indirect employment in the various sectors.

(v) Facilitates Capital Formation:
Stock Exchanges encourage investors to invest in the primary and secondary stock markets. By investments, money is saved. These savings leads to investment in shares and other securities thus, leading to capital formation.

(vi) Stimulates Industrial Development:
The stock exchanges facilitate mobilization of long-term funds through the issue of shares and debentures which are utilized by companies for Expansion and Modernization, Setting up of new projects.
Thus enhancing and improving industrial development in the country.

(vii) Facilitates Regional Development:
The stock exchanges facilitate regional development through companies that generate long-term funds due to them. Thus, utilizing the funds generated for the development of backward regions by setting up new units.

(viii) Provides Investment Opportunity:
The stock exchanges provide additional opportunities for investors to invest in shares. Usually, returns from stock markets are much higher as compares to traditional forms of investment, provided investment is done in good companies that provide good returns to investors.

(ix) Provides revenue to the government.
The stock exchanges provide revenue to the government either directly or indirectly. The stock exchanges pay tax on the revenue earned by them, an investor who invests in stock markets are subject to capital gains tax. The companies also pay their taxes thus, providing revenue to the government.

(x) Promotes efficient management of listed companies:
Stock Exchanges indirectly promote the efficiency of the management of listed companies. Listed companies have to perform well for their own interest and that of their shareholders. The efficiency of the listed company is reflected in the share prices on stock markets. Higher the efficiency, higher is the performance and as such higher the prices of the shares on the stock markets.

8. Attempt the following.

Question 1.
Write about the major Stock Exchanges in India.
Answer:
Following are the two most important Stock Exchanges in India.
(i) Bombay Stock Exchange BSE:

Bombay Stock Exchanges commonly referred to as the BSE is a stock exchange located on Dalai Street, Mumbai.
It is the 11th largest Stock Exchange in the world by market capitalization. Established in 1875, BSE is Asia’s first Stock Exchange and is the first listed Stock Exchange in India.
At that time it was called ‘The Native Share and Stock Broker’s Association. (NSSBA). Approximately over 5000 companies are listed in the BSE.
It is now a demutualized and corporatized entity registered under the Companies Act 1956.
(e) The BSE switched to an electronic trading system in 1995. This automated, screen-based trading platform is called BSE-On-Line Trading (BOLT).
BSE is the first exchange in India and second in the world to obtain ISO 9001:2000 certifications.
The BSE has also introduced a centralized
exchange-based internet system, bsewebx.co.in to enable investors anywhere in the world to trade on the BSE platform.
It operates one of the most respected capital market educational institutes in the country (The BSE Institute Ltd). BSE also provides depository services through its Central Depository Services Ltd. CDSL arm.

(ii) National Stock Exchange (NSE):

NSE was set up by a group of leading Indian Financial Institutions in 1992 as a company and was recognized as a Stock Exchange in 1993 under the Securities Contracts (Regulation) Act, 1956.
It started trading activities in 1994.
It is the largest and most modem stock exchange in India.
The NSE is located in Mumbai. It was the first demutualized electronic exchange in India.
NSE was the first exchange in the country to provide a modern, fully automated screen-based electronic trading system that offered easy trading facilities to investors.
The main index of NSE is the NIFTY which was launched in 1996.

Features:

It has nationwide coverage.
There is transparency in dealings.
Investors can check the exact price at which the transaction took place.
The index of NSE is called The broader 50 share – NIFTY.

Objectives:

Establishing nationwide trading facilities for all types of securities.
Ensuring equal access to investors all over the country through an appropriate communication network.
Meeting informational benchmarks and standards.
Enabling shorter settlement cycles.

Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics

July 2, 2024July 1, 2024 by Prasanna

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 4 Thermodynamics

Question 1.
What is temperature? Explain.
Answer:
The temperature of a body is a quantitative measure of the degree of hotness or coolness of the body. According to the kinetic theory of gases, it is a measure of the average kinetic energy per molecule of the gas. Temperature difference determines the direction of flow of heat from one body to another or from one part of the body to the other. Its SI unit is the kelvin (K).

Question 2.
What is heat ? Explain.
Answer:
When two bodies are in thermal contact with each other, there is a transfer of energy from the body at higher temperature to the body at lower temperature. The energy in transfer is called the heat. Also when two parts of a body are at different temperatures, there is a transfer of energy from the part at higher temperature to the other part. The SI unit of heat is the joule.

[Note : Count Rumford [Benjamin Thompson] (1753-1814) Anglo-American adventurer, social reformer, inventor and physicist, measured the relation between work and heat. When he visited Arsenal in Munich, he found that tremendous amount of heat was produced in a short time when a brass cannon was being bored. He found that even with a blunt borer a lot of heat can be produced from a piece of metal. At that time it was thought that heat consists of a fluid called caloric. Rumford’s experiments showed that caloric did not exist and heat is the motion of the particles of a body. He measured the relation beween work done and corresponding heat produced. The result was not accurate, but important in development of thermodynamics.]

Question 3.
What is thermodynamics ?
Answer:
Thermodynamics is the branch of physics that deals with the conversion of energy (including heat) from one form into another, the direction of energy transfer between a system and its environment with the resulting variation in temperature, in general, or changes of state, and the availability of energy to do mechanical work.

Question 4.
What is meant by thermal equilibrium ? What is meant by the expression “two systems are in thermal equilibrium” ?
Answer:
A system is in a state of thermal equilibrium if there is no transfer of heat (energy) between the various parts of the system or between the system and its surroundings.

Two systems are said to be in thermal equilibrium when they are in thermodynamic states such that, if they are separated by a diathermic (heat conducting) wall, the combined system would be in thermal equilibrium, i.e., there would be no net transfer of heat (energy) between them.
[Note :It is the energy in transfer that is called the heat.]

Question 5.
State the zeroth law of thermodynamics.
Answer:
Zeroth law of thermodynamics : If two systems are each in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.

[Note :The zeroth law is fundamental to the other laws of thermodynamics. That this law is assumed by the other laws of thermodynamics was realized much later. This law has no single discoverer. It was given the status of a law, following the suggestion by R. H. Fowler (in 1931), only after the first, second and third laws were named.]

Question 6.
Explain the zeroth law of thermodynamics.
Answer:
Consider three systems A, B and C. Suppose A and B are in thermal equilibrium, and A and C are also in thermal equilibrium. Then B and C are also in thermal equlibrium. Thus, A, B and C are at the same temperature and A works as a thermometer.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 1
[Note: The arrows in the figure indicate energy exchange]

Question 7.
Define internal energy.
Answer:
Internal energy of a system is defined as the sum of the kinetic energies of the atoms and molecules belonging to the system, and the potential energies associated with the interactions between these constituents (atoms and molecules).
[Note : Internal energy does not include the potential energy and kinetic energy of the system as a whole. In the case of an ideal gas, internal energy is purely kinetic. In the case of real gases, liquids and solids, internal energy is the sum of potential and kinetic energies. For an ideal gas, internal energy depends on temperature only. In other cases, internal energy depends on temperature, as well as on pressure and volume. According to quantum theory, internal energy never becomes zero. Even at OK. particles have energy called zero-point energy.]

Question 8.
What is the internal energy of one mole of argon and oxygen ?
Answer:
Argon is a monatamic gas. In this case, with three degrees of freedom, the average kinetic energy per molecule = \(\left(\frac{3}{2}\right)\)k_BT, where k_B is the Boltzmann constant and T is the absolute (thermodynamic) temperature of the gas. Hence, the internal energy of one mole of argon = N_A\(\left(\frac{3}{2} k_{\mathrm{B}} T\right)\) = \(\frac{3}{2}\)RT, where N_A is the Avogadro number and R = N_Ak_B is the universal gas constant. Oxygen is a diatomic gas. In this case, with five degrees of freedom at moderate temperatures, the internal energy of one mole of
oxygen = \(\frac{3}{2}\)RT.

Question 9.
Find the internal energy of one mole of argon at 300 K. (R = 8.314 J/mol.K)
Answer:
The internal energy of one mole of argon at 300 K
= \(\frac{3}{2}\)RT = \(\frac{3}{2}\)(8.314)(300) J = 3741 J.

Question 10.
The internal energy of one mole of nitrogen at 300 K is 6235 J. What is the internal energy of one mole of nitrogen at 400 K ?
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 2
This is the required quantity.
[Note : In chapter 3, the symbol E was used for internal energy.]

Question 11.
Explain the term thermodynamic system.
Answer:
A thermodynamic system is a collection of objects that can form a unit which may have ability to Surrounding
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 3
exchange energy with its surroundings. Everything outside the system is called its surroundings or environment. For example, a gas enclosed in a container is a system, the container is the boundary and the atmosphere is the environment.

Question 12.
Explain classification of thermodynamic systems.
Answer:
Depending upon the exchange of energy and matter with the environment, thermodynamic systems are classified as open, closed or isolated.

A system that can freely exchange energy and matter with its environment is called an open system. Example : water boiling in an open vessel.

A system that can freely exchange energy but not matter with its environment is called a closed system. Example : water boiling in a closed vessel.

A system that cannot exchange energy as well as matter with its environment is called an isolated system. In practice it is impossible to realize an isolated system as every object at a temperature above 0 K emits energy in the form of radiation, and no object can ever attain 0 K.

For many practical purposes, a thermos flask containing a liquid can be considered an isolated system.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 4
These three types are illustrated in above figure.

Question 13.
What is a thermodynamic process? Give an exmple.
Answer:
A process in which the thermodynamic state of a system is changed is called a thermodynamic process.
Example : Suppose a container is partially filled with water and then closed with a lid. If the container is heated, the temperature of the water starts rising and after some time the water starts boiling. The steam produced exerts pressure on the walls of the container, Here, there is a change in the pressure, volume and temperature of the water, i.e. there is a change in the thermodynamic state of the system.

Question 14.
Explain the relation between heat and internal energy.
Answer:
Suppose a system consists of a glass filled with water at temperature T_S. Let T_E be the temperature of the environment (surroundings) such as the surrounding air in the room. There is a continuous exchange of energy between the system and the surroundings.

If T_S > T_E, the net effect of energy exchange is the net transfer of internal energy from the system to the environment till thermal equilibrium is reached, i.e., T_S and T_E became equal. This internal energy in transit is called heat (Q). The change in the temperature of the environment is usually negligible compared with the change in the temperature of the system.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 5

For T_S < T_E, there is energy exchange between the
system and the environment, but no net transfer of
energy.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 6
For T_S = T_E, there is energy exchange between the system and the environment, but no net transfer of energy.

Thus, the net transfer of energy takes place only when there is temperature difference.

Question 15.
Explain how the internal energy of a system can be changed.
Answer:
Consider a system (S) consisting of some quantity of gas enclosed in a cylinder fitted with a movable, massless, and frictionless piston.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 8
Suppose the gas is heated using a burner (source of heat, environment). Let T_S = temperature of the system (gas) and T_E = temperature of the environment.

Here, T_E > T_S. Hence, there will be a net flow of energy (heat) from the environment to the system causing the increase in the internal energy of the system.

The internal energy of the gas (system) can also be increased by quickly pushing the piston inward so that the gas is compressed.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 9
The work done on the gas raises the temperature of the gas. Thus, there is increase in the internal energy of the gas. If the gas pushes the piston outward, the work is done by the gas on the environment and the gas cools as its internal energy becomes less.

Question 16.
On the basis of the kinetic theory of gases, explain
(i) positive work done by a system
(ii) negative work done by a system.
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 10
During expansion of the gas, molecules colliding with the piston lose momentum to it. This exerts force and hence pressure on the piston, moving it outward through a finite distance. Here, the gas does a positive work on the piston. There is increase in the volume of the gas. The work done by the piston on the gas is negative.

During compression of the gas, molecules colliding with the piston gain momentum from it. The piston moving inward through a finite distance exerts force on the gas. Here, the gas does a negative work on the piston. There is decrease in the volume of the gas.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 11
The work done by the piston on the gas is positive.

Question 17.
Obtain an expression for the work done by a gas.
OR
Show that the work done by a gas is given by
Answer:
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 12
During expansion of the gas, molecules colliding with the piston impart momentum to the piston. The time rate of change of momentum is the force, F exerted by the gas on the piston. If dx is the displacement of the piston, the work done by the gas, dW = F dx. If A is the area of cross section of the piston, the pressure exerted by the gas, P = \(\frac{F}{A}\).

Hence, the work done, dW = PAdx = PdV where dV = Adx is the increase in the volume of the gas. Here, dx is the infinitesimal displacement of the piston and dV is the infinitesimal increase in the volume of the gas.

If V_i is the initial volume of the gas, and V_f is the final volume, the total work done by the gas in moving the piston is given by W = \(\int_{V_{i}}^{V_{\mathrm{f}}} P d V\).

Question 18.
State the first law of thermodynamics. Express it in mathematical form.
Answer:
First law of thermodynamics : The change in the internal energy of a system (∆U) is the difference between the heat supplied to the system (Q) and the work done by the system on its surroundings (W).
Mathematically, ∆ U = Q – W, which is the same as Q = ∆ U + W.

Notes :

if Q is positive, it means heat is added to the system. If Q is negative, it means heat is given out by the system or removed from the system,
If ∆U is positive, it means there is increase in the internal energy of the system. If ∆ U is negative, it means there is decrease in the internal energy of the system,
If W is positive, it means it is the work done by the system on its surroundings. Negative W means work is done on the system by the surroundings,
The first law of thermodynamics is largely due to Joule. It is essentially the law of conservation of energy applied to the systems that are not isolated, i.e., the systems that can exchange energy with the surroundings. Thermodynamics was developed in 1850 by Rudolf Clausius (1822-88) German theoretical physicist, His ideas were developed in 1851 by William Thomson [Lord Kelvin] (1824-1907), British physicist and electrical engineer,
Q = ∆ U + W. Here, all quantities are expressed in the same units, e.g., cal or joule. If Q and A U are expressed in heat unit (cal, kcal) and W is expressed in mechanical unit (erg, joule) then the above equation takes the form Q = ∆ U + \(\frac{W}{J}\), where J is the mechanical equivalent of heat.]

Question 19.
What is the property of a system or a system variable ?
Answer:
The property of a system or a system variable is any measurable or observable characteristic or property of the system when the system remains in equilibrium.

Question 20.
Name the macroscopic variables of a system.
Answer:
Pressure, volume, temperature, density, mass, specific volume, amount of substance (expressed in mole) are macroscopic variables of a system.
Notes : The quantities specified above are not totally independent, e.g.,

density = mass/volume
specific volume (volume per unit mass) = 1/density.

Question 21.
What is an intensive variable ? Give examples.
Answer:
A variable that does not depend on the size of the system is called an intensive variable.
Examples : pressure, temperature, density.

Question 22.
What is an extensive variable ? Give examples.
Answer:
A variable that depends on the size of the system is called an extensive variable.
Examples : internal energy, mass.

Question 23.
What is mechanical equilibrium ?
Answer:
A system is said to be in mechanical equilibrium when there are no unbalanced forces within the system and between the system and its surroundings.
OR
A system is said to be in mechanical equilibrium when the pressure in the system is the same throughout and does not change with time.
[Note : The constituents of a system, atoms, molecules, ions, etc, are never at rest. Within a system, even in the condition of equilibrium, statistical fluctuations do occur, but the time of observation is usually very large so that these fluctuations can be ignored.]

Question 24.
What is chemical equilibrium ?
Answer:
A system is said to be in chemical equilibrium when there are no chemical reactions going on within the system.
OR
A system is said to be in chemical equilibrium when its chemical composition is the same throughout the system and does not change with time.
[Note : In this case, in the absence of concentration gradient, there is no diffusion, i.e., there is no transport of matter from one part of the system to the other.]

Question 25.
What is thermal equilibrium ?
Answer:
A system is said to be in thermal equilibrium when its temperature is uniform throughout the system and does not change with time.

Question 26.
Give two examples of thermodynamic systems not in equilibrium.
Answer:

When an inflated balloon is punctured, the air inside it suddenly expands and escapes into the atmosphere. During the rapid expansion, there is no uniformity of pressure, temperature and density.
When water is heated, there is no uniformity of pressure, temperature and density. If the vessel is open, some water molecules escape to the atmosphere.

Question 27.
What is the equation of state ? Explain.
Answer:
The mathematical relation between the state variables (pressure, volume, temperature, amount of the substance) is called the equation of state.

In the usual notation, the equation of state for an ideal gas is PV = nRT.

For a fixed mass of gas, the number of moles, n, is constant. R is the universal gas constant. Thus, out of pressure (P), volume (V) and thermodynamic temperature (T), only two (any two) are independent.

Question 28.
Draw P-V diagram for positive work at constant pressure.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 13
Answer:
In this case, during the expansion, the work done by the gas, W = \(\int_{V_{1}}^{V_{2}} P d V\) = P(V₂ – V₁) is positive as V₂ > V₁.

Question 29.
What is a thermodynamic process ? Explain.
Answer:
A procedure by which the initial state of a system changes to its final state is called a thermodynamic process. During the process/ there may be

addition of heat to the system
removal of heat from the system
change in the temperature of the system
change in the volume of the system
change in the pressure of the system.

Question 30.
What is a quasistatic process ?
Answer:
A quasistatic process is an idealised process which occurs infinitely slowly such that at all times the system is infinitesimally close to a state of thermodynamic equilibrium. Although the conditions for such a process can never be rigorously satisfied in practice, any real process which does not involve large accelerations or large temperature gradients is a reasonable approximation to a quasistatic process.

Question 31.
Draw a diagram to illustrate that the work done by a system depends on the process even when the initial and final states are the same.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 14
Answer:
In the above diagram, the initial state of a gas is characterized by (P_i, V_i) [corresponding to point A] and the final state of the gas is characterized by (P_f, V_f) [corresponding to point B]. Path 1 corresponds to constant temperature. Path 2 corresponds to the combination AC [P constant] + CB [V constant]. Path 3 corresponds to the combination AD [V constant] + DB [P constant]. The work done by the gas (W) is the area under the curve and is different in each case.

Question 32.
What is a reversible process? What is an irreversible process? Give four examples of an irreversible process. Explain in detail.
Answer:
A reversible process is one which is performed in such a way that, at the conclusion of the process, both the system and its local surroundings are restored to their initial states, without producing any change in the rest of the universe.

A process may take place reversibly if it is quasistatic and there are no dissipative effects. Such a process cannot be realized in practice.

A process which does not fulfill the rigorous requirements of reversibility is said to be an irreversible process. Thus, in this case, the system and the local surroundings cannot be restored to their initial states without affecting the rest of the universe. All natural processes are irreversible.
Examples of irreversible process :

When two bodies at different temperatures are brought in thermal contact, they attain the same temperature after some time due to energy exchange. Later, they never attain their initial temperatures.
Free expansion of a gas.
A gas seeping through a porous plug.
Collapse of a soap film after it is pricked.
All chemical reactions.
Diffusion of two dissimilar inert gases.
Solution of a solid in water.
Osmosis.

[Note : A free expansion is an adiabatic process, i.e., a process in which no heat is added to the system or removed from the system. Consider a gas confined by a valve to one half of a double chamber with adiabatic walls while the other half is evacuated.

When the gas is in thermal equilibrium, the gas is allowed to expand to fill the entire chamber by opening the valve.
No interaction takes place and hence there are no local surroundings. While rushing into a vacuum, the gas does not meet any pressure and hence no work is done by the gas. The gas only changes state isothermally from a volume V_i to a larger volume V_f.]

To restore the gas to its initial state, it would have to be compressed isothermally to the volume V_i; an amount of work W would have to done on the gas by some mechanical device and an equal amount of heat would have to flow out of the gas into a reservoir. If the mechanical device and the reservoir are to be left unchanged, the heat would have to be extracted from the reservoir and converted completely into work. Since this last step is impossible, the process of free expansion is irreversible.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 15
It can be shown that the diffusion of two dissimilar inert gases is equivalent to two independent free expansions. It follows that diffusion is irreversible.]

Question 33.
What are the causes of irreversibility?
Answer:

Some processes such as a free expansion of a gas or an explosive chemical reaction or burning of a fuel take the system to non-equilibrium states.
Most processes involve dissipative forces such as friction and viscosity (internal friction in fluids). These forces can be minimized, but cannot be eliminated.

Question 34.
What is an isothermal process? Obtain an expression for the work done by a gas in an isothermal process.
Answer:
A process in which changes in pressure and volume of a system take place at a constant temperature is called an isothermal process.

Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. Let P_i, V_i and T be the initial pressure, volume and absolute temperature respectively of the gas. Consider an isothermal expansion (or compression) of the gas in which P_f, V_f and T are respectively the final pressure, volume and absolute
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 16
temperature of the gas. Assuming the gas to behave as an ideal gas, we have, its equation of state :
PV = nRT = constant as T = constant, R is the universal gas constant. The work done by the gas,

Notes :

The above expression for W can be written in various forms such as W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_iV_i ln \(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\) = P_fV_f\(\left(\frac{V_{f}}{V_{\mathrm{i}}}\right)\), etc.
W is positive if V_f > V_i (expansion). W is negative if V_f < V_i (contraction).
At constant temperature, change in internal energy, ∆ U = 0.
∴ Q = ∆ U + W = W.
Isothermal process shown in P- V diagram is also called an isotherm.
Melting of ice is an isothermal process.

Question 35.
What is an isobaric process? Obtain the expressions for the work done, change in internal energy and heat supplied in an isobaric process in the case of a gas.
Answer:
A process in which pressure remains constant is called an isobaric process. Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. We assume that the gas behaves as an ideal gas so that we can use the equation of state PV = nRT.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 18
Consider an isobaric expansion (or compression) of the gas in which the volume of the gas changes from V_i to V_f and the temperature of the gas changes from T_i to T_f when the pressure (P) of the gas is kept constant. The work done by the gas,
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 19
Now, PV_i = nRT_i and PV_f = nRT_f
∴ PV_f – PV_i = nRT_f – nRT_i
∴ P(V_f – V_i) = nR(T_f – T_i)
∴ from Eq. (1), W = nR(T_f – T_i) … (2)
The change in the internal energy of the gas,
∆ U = nC_v(T_f – T_i) …(3)
where C_v is the molar specific heat of the gas at constant volume.
From Eqs. (2) and (3), we have, the heat supplied to the gas,
Q = ∆ U + W = nC_v(T_f – T_i) + nR(T_f – T_i)
= n(C_v + R)(T_f – T_i)
∴ Q = _nC_p(T_f – T_i) …(4)
Where C_p ( = C_v + R) is the molar specific heat of the gas at constant pressure.
[Note : P-V curve for an isobaric process is called an isobar.

Question 36.
What is an isochoric process ? Write the expressions for the work done, change in internal energy and heat supplied in this case. Also draw the corresponding P-V diagram.
Answer:
A process that takes place at constant volume is called an isochoric process (or isometric process).
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 20
As there is no change in volume in this case, the work done (W) by the system on its environment is zero. The change in the internal energy.
∆ U = _nC_v (T_f – T_i) and heat supplied,
Q = ∆ U = _nC_v(T_f – T_i)

Question 37.
What is an adiabatic process ? Obtain expressions for the work done by a system (an ideal gas) in an adiabatic process. Also draw the corresponding P-V diagram.
Answer:
A process during which there is no transfer of heat (energy) from the system to the surroundings or from the surroundings to the system is called an adiabatic process.

It can be shown that if an ideal gas is subjected to an adiabatic process, then,
PV^γ = constant = C, where γ, is \(\frac{C_{P}}{C_{V}}\). γ is called the adiabatic ratio. C_P is the molar specific heat of the gas at constant pressure and C_V is the molar specific heat at constant volume.
Let P_i = initial pressure, P_i final pressure V_f = initial volume and V_f = final volume of the gas taken through an adiabatic process.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 21
Now, P_iV_i = nRT_i and P_fV_f = nRT_f, where n is the number of moles of the gas, T_i is the initial temperature of the gas, T_f is the final temperature of the gas and R is the universal gas constant.

[Note: We have Q = ∆ U + W = 0 in an adiabatic process.
∴ W= -∆ U = -nC_v(T_f – T_i)_nC_v(T_i – T_f)]

Question 38.
What is a cyclic process? Explain with a diagram.
Answer:
A thermodynamic process in which the system returns to its initial state is called a cyclic process. This is illustrated in below figure. Path 1 shows how the state of the system (ideal gas) is changed from (P_i, V_i) [point A] to (P_f, V_f) [point B], Path 2 shows the return of the system from point B to point A. As the system returns to its initial state, the total change in its internal energy is zero. Hence, according to the first law of thermodynamics, heat supplied,
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 23
Q = ∆ U + W = 0 + W = W. The area enclosed by the cycle in P-V plane gives the work done (W) by the system.

Question 39.
Explain the term free expansion of a gas.
Answer:
When a balloon is ruptured suddenly, or a tyre is punctured suddenly, the air inside the balloon/ tyre rushes out rapidly to the atmosphere. This process (expansion of air inside the balloon/tyre) is so quick that there is no time for transfer of heat from the system to the surroundings or from the surroundings to the system. Such an adiabatic expansion is called free expansion. It is characterized by Q = W = 0, implying ∆ U = 0. Free expansion is an uncontrolled change and the system is not in thermodynamic equilibrium. Free expansion cannot be illustrated with a P-V diagram as only the initial state and final state are known.

Question 40.
Solve the following :

Question 1.
A gas enclosed in a cylinder fitted with a movable, massless and frictionless piston is expanded so that its volume increases from 5 L to 6 L at a constant pressure of 1.013 × 10⁵ Pa. Find the work done by the gas in this process.
Solution :
Data : P = 1.013 × 10⁵ Pa, V_i = 5L = 5 × 10^-3 m³,
v_f = 6L = 6 × 10^-3 m³
The work done by the gas, in this process,
W = P(V_f – V_i)
= (1.013 × 10⁵)(6 × 10^-3 – 5 × 10^-3)J
= 1.013 × 10²J

Question 2.
The initial pressure and volume of a gas enclosed in a cylinder are respectively 1 × 10⁵ N/m² and 5 × 10^-3 m³. If the work done in compressing the gas at constant pressure is 100 J. Find the final volume of the gas.
Solution :
Data : P = 1 × 10⁵ N/m², V_i = 5 × 10^-3 m³,
W= -100 J
W = P(V_f – V_i) ∴ V_f – V_i = \(\frac{W}{P}\)
∴ V_f = V_i + \(\frac{W}{P}\) = 5 × 10^-3 + \(\frac{(-100)}{\left(1 \times 10^{5}\right)}\)
= 5 × 10^-3 -1 × 10^-3 = 4 × 10^-3 m³
This is the final volume of the gas.

Question 3.
If the work done by a system on its surroundings is 100 J and the increase in the internal energy of the system is 100 cal, what must be the heat supplied to the system? (Given : J = 4.186J/cal)
Solution :
Data : W = 100 J, ∆ U = 100 cal, J = 4.186 J / cal
The heat supplied to the system,
Q = ∆ U + W = (100 cal) (4.186 J/cal) + 100 J
= 418.6J + 100J = 518.6 J

Question 4.
Ten litres of water are boiled at 100°C, at a pressure of 1.013 × 10⁵ Pa, and converted into steam. The specific latent heat of vaporization of water is 539 cal/g. Find
(a) the heat supplied to the system
(b) the work done by the system
(c) the change in the internal energy of the system. 1 cm³ of water on conversion into steam, occupies 1671 cm³ (J = 4.186 J/cal)
Solution :
Data : P = 1.013 × 10⁵ Pa, V (water) = 10 L = 10 × 10^-3 m³, V(steam) = 1671 × 10 × 10^-3 m³, L = 539 cal/g = 539 × 10³ \(\frac{\mathrm{cal}}{\mathrm{kg}}\) = 539 × 10³ × 4.186\(\frac{\mathrm{J}}{\mathrm{kg}}\) as J = 4.186 J/cal, mass of the water (M) = volume × density = 10 × 10^-3 m³ × 10³ kg/m³ = 10 kg

(a) Q = ML = (10) (5.39 × 4.186 × 10⁵) J
= 2.256 × 10⁷J
This is the heat supplied to the system

(b) W = P∆V = (1.013 × 10⁵) (1671 – 1) × 10^-2J
= (1.013) (1670) × 10³ J = 1.692 × 10⁶ J
This is the work done by the system.

(c) ∆ U = Q – W = 22.56 × 10⁶ – 1.692 × 10⁶
= 2.0868 × 107J
This is the change (increase) in the internal energy of the system.

Question 5.
Find the heat needed to melt 100 grams of ice at 0°C, at a pressure of 1.013 × 10⁵ N/m². What is the work done in this process ? What is the change in the internal energy of the system ?
Given : Specific latent heat of fusion of ice = 79.71 cal/g, density of ice = 0.92 g/cm³, density of water = 1 g/cm³,1 cal = 4.186 J.
Solution :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 24

The heat needed to melt the ice, Q = ML = (0.1) (3.337 × 10⁵) J = 3.337 × 10⁴ J
The work done, W = P(V_Water – V_ice)
= (1.013 × 10⁵) (100 – 108.7) × 10^-6J = -0.8813J
The change in the internal energy,
∆ U = Q – W = 3.337 × 10⁴ J + 0.8813 J
= 3370.8813 J

Question 6.
Find the work done by the gas when it is taken through the cycle shown in the following figure. (1 L = 10^-3 m³)
Solution :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 25
∴ W_ABCDA = W_AB + W_BC + W_CD + W_DA
= 2000J + 0 – 1000J + 0 = 1000J

Question 7.
A gas with adiabatic constant γ = 1.4, expands adiabatically so that the final pressure becomes half the initial pressure. If the initial volume of the gas 1 × 10^-2 m³, find the final volume.
Solution:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 26
This is the final volume of the gas.

Question 8.
In an adiabatic compression of a gas with γ = 1.4, the initial temperature of the gas is 300 K and the final temperature is 360 K. If the initial volume of the gas is 2 × 10^-3 m³, find the final volume.
Solution:
Data: γ = 1.4, T_i = 300 K, T_f = 360 K
∴ T_f/T_i = 1.2, V_i = 2 × 10^-3 m³
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 27
This is the final volume of the gas.

Question 9.
In an adiabatic compression of a gas with γ = 1.4, the final pressure is double the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature.
Solution:
Data: γ = 1.4, P_f = 2P_i, T_i = 300 K
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 28
∴ log \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = 0.2857 log 2 = 0.2857 (0.3010) = 0.086
∴ \(\frac{T_{\mathrm{f}}}{T_{\mathrm{i}}}\) = antilog 0.086 = 1.219
∴ T_f = 1219T_i
= (1.219) (300) = 365.7 K
This is the final temperature of the gas.

Question 10.
In an adiabatic compression of a gas the final volume of the gas is 80% of the initial volume. If the initial temperature of the gas is 27 °C, find the final temperature of the gas. Take γ = 5/3.
Solution :
Data: V_f = 0.8 V_i ∴ \(\frac{V_{\mathrm{i}}}{V_{\mathrm{f}}}\) = \(\frac{10}{8}\) = 1.25,
∴ T_i = 27 °C = (273 + 27) K = 300 K, γ = \(\frac{5}{3}\)
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 29
∴ x = antilog 0.0646 = 1.161
∴ T_f = (300) (1.161) = 348.3 K
= (348.3 – 273)°C = 75.3 °C
This is the final temperature of the gas.

Question 11.
In an adiabatic expansion of a gas, the final volume of the gas is double the initial volume. If the initial pressure of the gas is 105 Pa, find the final pressure of the gas. (γ = 5/3)
Solution :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 30
Let 2^5/3 = x ∴ \(\frac{5}{3}\)log 2 = log x
∴ log x = \(\left(\frac{5}{3}\right)\) (0.3010) = 0.5017
∴ x = antilog 0.5017 = 3.175
∴ P_f = \(\frac{10^{5}}{3.175}\) = 3.15 × 10⁴ Pa
This is the final pressure of the gas.

Question 12.
In an adiabatic process, the final pressure of the gas is half the initial pressure. If the initial temperature of the gas is 300 K, find the final temperature of the gas. (Take γ = \(\frac{5}{3}\))
Solution :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 31
This is the final temperature of the gas.

Question 13.
In an adiabatic process, the pressure of the gas drops from 1 × 10⁵ N/m² to 5 × 10⁴ N/m² and the temperature drops from 27 °C to – 46 °C. Find the adiabatic ratio for the gas.
Solution :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 32

This is the adiabatic ratio (γ) for the gas.
[Note : This value (1.673) is slightly more than 5/3 (the value for a monatomic gas) due to error in measurement of pressure and temperature.]

Question 14.
Two moles of a gas expand isothermally at 300 K. If the initial volume of the gas is 23 L and the final volume is 46 L, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data ; n = 2, T = 300 K, V, = 23 L = 23 × 10^-3 m³, V_f = 46 L = 46 × 10^-3 m³, R = 8.314 J/mol.K
The work done by the gas on its surroundings,
W = nRT ln \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\) = 2.303 nRT log₁₀ \(\left(\frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}\right)\)
= (2.303) (2) (8.314) (300) log₁₀ \(\left(\frac{46 \times 10^{-3}}{23 \times 10^{-3}}\right)\)
= (4.606) (8.314) (300) log\(\begin{array}{r}
2 \\
10
\end{array}\)
= (4.606) (8.314) (300) (0.3010)
= 3458J

Question 15.
Four moles of a gas expand isothermally at 300 K. If the final pressure of the gas is 80% of the initial pressure, find the work done by the gas on its surroundings. (R = 8.314 J/mol.K)
Solution :
Data : n = 4, T = 300 K, P_f = 0.8 P_i
∴ \(\frac{P_{i}}{P_{f}}\) = \(\frac{10}{8}\), R = 8.314 j/mol.K
The work done by the gas on its surroundings,
W = nRT ln\(\left(\frac{P_{\mathrm{i}}}{P_{\mathrm{f}}}\right)\)
= (4) (8.314) (300) 2.303 log₁₀ \(\left(\frac{10}{8}\right)\)
= 2.3 × 10⁴ log₁₀ (1.25) = 2.3 × 10⁴ × 0.0969
= 2.229 × 10³J

Question 16.
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure so that the rise in temperature is 10 K. Find the increase in the internal energy of the gas.
Solution :
Data : C_v = 12.47 J/mol.k, n = 2, T_f – T_i = 10 K
The increase in the internal energy of the gas,
∆ U = _nC_v (T_f – T_i)
= (2) (12.47) (10) J
= 249.4 J

Question 17.
The molar specific heat of Ar at constant volume is 12.47 J/mol.K. Two moles of Ar are heated at constant pressure so that the rise in temperature is 20 K. Find the work done by the gas on its surroundings and the heat supplied to the gas. Take R = 8.314 J/mol.K.
Solution :
Data : C_v = 12.47 j/mol.K, n = 2,T_f – T_i = 20 K,
R = 8.314 J/mol.K

W = nR (T_f – T_i) = (2) (8.314) (20) J = 332.6 J
This is the work done by the gas on its surroundings.
Q = _nC_v(T_f – T_i) + W = (2) (12.47) (20) + 332.6
= 498.8 + 332.6 = 831.4 J
This is the heat supplied to the gas.

Question 18.
The molar specific heat of a gas at constant pressure is 29.11 J/mol.k. Two moles of the gas are heated at constant pressure so that the rise in temperature is 40 K. Find the heat supplied to the gas.
Solution :
Data : C_P = 29.11 J/mol.K, n = 2, T_f – T_i = 40 K.
The heat supplied to the gas,
Q = _nC_P (T_f – T_i) = (2) (29.11) (40) J
= 2329 J

Question 19.
The molar specific heat of a gas at constant volume is 20.8 J/mol.k. Two moles of the gas are heated at constant volume so that the rise in temperature is 10 K. Find the heat supplied to the gas.
Solution :
Data : C_v = 20.8 J/mol.K, n = 2, T_f – T_i = 10 K.
The heat supplied to the gas,
Q = _nC_v (T_f – T_i) = (2) (20.8) (10) J
= 416J

Question 20.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 10⁵ Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 10⁴ Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Take γ = 5/3.
Solution :
Data : H = 2, P_i = 1.013 × 10⁵ Pa, P_f = 3.191 × 10⁴ Pa,
V_i = 22.4 L = 22.4 × 10^-3 m³,
V_f = 44.8 L = 44.8 × 10^-3 m³, γ = 5/3
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 34

Question 21.
In an adiabatic expansion of 2 moles of a gas, the temperature of the gas decreases from 37°C to 27°C. Find the work done by the gas on its surroundings. Take γ = 5/3 and R = 8.314 J/mol.K
Answer:
Data: n =2, T_i = (273 + 37) = 310 K,
T_f = (273 + 27)K = 300K, γ = 5/3,
R = 8.314 J/mol.K.
The work done by the gas on its surroundings,
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 35

Question 22.
A resistor of resistance 200 Ω carries a current of 2 A for 10 minutes. Assuming that almost all the heat produced in the resistor is transferred to water (mass = 5 kg, specific heat capacity = 1 kcal/kg), and the work done by the water against the external pressure during the expansion of water can be ignored, find the rise in the temperature of the water. (J = 4186 J/cal)
Solution :
Data : I = 2 A, R = 200 Ω, t = 10 min = 10 × 60 s = 600 s, M = 5 kg, S = (1 kcal/kg) (4186 J/kcal)
= 4186 J/kg
Q = ∆ U + W = MS ∆T + W \(\simeq\) MS ∆T ignoring W.
Also, Q = I²Rt ∴ I²RT = MS∆T
∴ The rise in the temperature of water = ∆T = \(\frac{I^{2} R t}{M S}\)
= \(\frac{(2)^{2}(200)(600)}{(5)(4186)}\)°C = 22.93°C

Question 23.
The initial pressure, volume and temperature of a gas are respectively 1 × 10⁵ Pa, 2 × 10^-2 m³ and 400 K. The temperature of the gas is reduced from 400 K to 300 K at constant volume. Then the gas is compressed at constant temperature so that its volume becomes 1.5 × 10^-2 m³.
Solution:
Data : P_A = 1 × 10⁵ Pa, V_A = 2 × 10^-2 m³, T_A = 400 K, V_B = v_A = 2 × 10^-2 m³, T_B = 300 K, T_C = T_B = 300 K, V_C = 1.5 x 10× 10^-2 m³, Also, P_C = P_A = 1 × 10⁵ Pa as the gas returns to its initial state.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 36

Question 24.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat of the gas at
(i) constant volume
(ii) constant pressure.
(R = 8.314 J/mol. K)
Solution :
Data : r = 5/3, R = 8.314 J/mol.K
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 37
This is the required quantity.
(ii) C_P = _γC_V = \(\left(\frac{5}{3}\right)\)(12.47) = 20.78 J/mol.

Question 41.
What is a heat engine ?
Answer:
A heat engine is a device in which a system is taken through cyclic processes that result in converting part of heat supplied by a hot reservoir into work (mechanical energy) and releasing the remaining part to a cold reservoir. At the end of every cycle involving thermodynamic changes, the system is returned to the initial state.
[Note : Automobile engine is a heat engine.]

Question 42.
What does a heat engine consist of ?
OR
What are the elements (parts) of a typical heat engine?
Answer:
The following are the parts of a typical heat engine :

(1) Working substance : It can be

a mixture of fuel vapour and air in a gasoline (petrol) engine or diesel engine
steam in a steam engine. The working substance is called a system.

(2) Hot and cold reservoirs : The hot reservoir is a source of heat that supplies heat to the working substance at constant temperature T_H. The cold reservoir, also called the sink, takes up the heat released by the working substance at constant temperature T_C < T_H.

(3) Cylinder and piston : The working substance is enclosed in a cylinder fitted with (ideally) a movable, massless, and frictionless piston. The walls of the cylinder are nonconducting, but the base is conducting. The piston is nonconducting. The piston is connected to a crankshaft so that the work done by the working substance (mechanical energy) can be transferred to the environment.

Question 43.
What are the two basic types of heat engines?
Answer:
(i) External combustion engine in which the working substance is heated externally as in a steam engine.
(ii) Internal combustion engine in which the working substance is heated internally as in a petrol engine or diesel engine.
[Note : A steam engine was invented by Thomas New-comen (1663-1729), English engineer. The first practical steam engine was constructed in 1712. The modem steam engine was invented in 1790 by James Watt (1736-1819), British instrument maker and engineer. A hot-air type engine was developed by Robert Stirling (1790-1878), Scottish engineer and clergyman.

A four-stroke internal combustion engine was devised by Nikolaus August Otto (1832-1891), German engineer. A compression-ignition internal combustion engine was devised by Rudolph (Christian Karl) Diesel (1858 – 1913), German engineer.]

Question 44.
State the basic steps involved in the working of a heat engine.
Answer:

The working substance absorbs heat (Q_H) from a hot reservoir at constant temperature. T_H. It is an isothermal process Q_H is positive.
Part of the heat absorbed by the working substance is converted into work (W), i.e. mechanical energy. In this case, there is a change in the volume of the substance.
The remaining heat (|Q_C| = |Q_H| – W) is transferred to a cold reservoir at constant temperature T_C < T_H. Q_C is negative.

Question 45.
Draw a neat labelled energy flow diagram of a heat engine.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 38

Question 46.
Define thermal efficiency of a heat engine.
Answer:
The thermal efficiency, η of a heat engine is defined W as η = \(\frac{W}{Q_{H}}\), where W is the work done (output) by Q_H the working substance and Q_H is the amount of heat absorbed (input) by it.
[Note : η has no unit and dimensions or its dimensions are [M°L°T°].]

Question 47.
Draw a neat labelled P-V diagram for a typical heat engine.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 39
Here, T_H is the temperature at which the work is done by the gas and T_c is the temperature at which the work is done on the gas. The area of the loop ABCDA is the work output.

Question 48.
Solve the following :

Question 1.
Find the thermal efficiency of a heat engine if in one cycle the work output is 3000 J and the heat input is 10000 J.
Solution :
Data : W = 3000 J, Q_H = 10000 J
The thermal efficiency of the engine,
η = \(\frac{W}{Q_{\mathrm{H}}}\) = \(\frac{3000 \mathrm{~J}}{10000 \mathrm{~J}}\) = 0.3 = 30%

Question 2.
The thermal efficiency of a heat engine is 25%. If in one cycle the heat absorbed from the hot reservoir is 50000 J, what is the heat rejected to the cold reservoir in one cycle ?
Solution :
Data : η = 25% = 0.25, Q_H = 50000 J W
η = \(\frac{W}{Q_{\mathrm{H}}}\)
∴ W = _ηQ_H = (0.25)(50000)J = 12500J
Now, W = Q_H – |Q_C|
∴ |Q_C| = Q_H – W
= (50000 – 12500) J
= 37500J
This is the heat rejected to the cold reservoir in one cycle.
[Notes : Q_C = – 37500 J]

Question 49.
What is a refrigerator?
Answer:
A refrigerator is a device that uses work to transfer energy in the form of heat from a cold reservoir to a hot reservoir as it continuously repeats a thermodynamic cycle. Thus, it is a heat engine that runs in the backward direction.

Question 50.
With a neat labelled energy flow diagram, explain the working of a refrigerator.
Answer:
A refrigerator performs a cycle in a direction opposite to that of a heat engine, the net result being absorption of some energy as heat from a reservoir at low temperature, a net amount of work done on the system and the rejection of a larger amount
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 40
of energy as heat to a reservoir at a higher temperature. The working substance undergoing the refrigeration cycle is called a refrigerant. The refrigerant (such as ammonia or Freon) is a saturated liquid at a high pressure and at as low a temperature as can be obtained with air or water cooling.

The refrigeration cycle comprises the following processes :

Throttling process : The saturated liquid refrigerant passes from the condenser through a narrow opening from a region of constant high pressure to a region of constant lower pressure almost adiabatically. It is a property of saturated liquids (not gases) that a throttling process produces cooling and partial vaporization.
Isothermal, isobaric vaporization-with the heat of vaporization being supplied by the materials or the region to be cooled : Heat Q_c is absorbed by the refrigerant at the low temperature T_C, thereby cooling the materials of the cold reservoir.
Adiabatic compression of the refrigerant by an electrical compressor, thereby raising its temperature above T_H.
Isobaric cooling and condensation in the condenser at T_H : In the condenser, the vapour is cooled until it condenses and is completely liquefied, i. e., heat Q_H is rejected to the surroundings which is the hot reservoir.

Question 51.
Draw a neat labelled schematic diagram of transferring heat from a cold region to a hot region.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 41

Question 52.
What is refrigeration?
Answer:
Refrigeration is artificial cooling of a space or substance of a system and/or maintaining its temperature below the ambient temperature.

Question 53.
Draw a neat labelled diagram to illustrate schematics of a refrigerator.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 42

Question 54.
What are the steps through which a refrigerant goes in one complete cycle of refrigeration ?
Answer:
In one complete cycle of refrigeration, the refrigerant, a liquid such as fluorinated hydrocarbon, goes through the following steps :

The refrigerant in the closed tube passes through the nozzle and expands, into a low-pressure area. This adiabatic expansion results in reduction in pressure and temperature of the fluid and the fluid turns into a gas.
The cold gas is in thermal contact with the inner compartment of the fridge. Here it absorbs heat at constant pressure from the contents of the fridge.
The gas passes to a compressor where it does work in adiabatic compression. This raises its temperature and converts it back into a liquid.
The hot liquid passes through the coils on the outside of the refrigerator and releases heat to the air outside in an isobaric compression process.
The compressor, driven by an external source of energy, does work on the refrigerant during each cycle.

Question 55.
Explain the energy flow in a refrigerator and define the coefficient of performance of a refrigerator.
Answer:
In a refrigerator, Q_C is the heat absorbed by the working substance (refrigerant) at a lower temperature T_C, W is the work done on the working substance, and Q_H is the heat rejected at a higher temperature T_H. The absorption of heat is from the contents of the refrigerator and rejection of heat is to the atmosphere. Here, Q_C is positive and W and Q_H are negative. In one cycle, the total change in the internal energy of the working substance is zero.
∴ Q_H + Q_C = W ∴ Q_H = W – Q_C
∴ -Q_H = Q_C – W
Now, Q_H < 0, W < 0 and Q_C > 0
∴ |Q_H| = |Q_C| + |W|
The coefficient of performance (CoP), K, or quality factor, or Q value of a refrigerator is defined as
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 43
[Note: K does not have unit and dimensions or its dimensions are [M°L°T°.]

Question 56.
How does an air conditioner differ from a refrigerator? Define the coefficient of performance of an air conditioner and express it in terms of heat current.
Answer:
The working of an air conditioner is exactly similar to that of a refrigerator, but the volume of the chamber/room cooled by an air conditioner is far greater than that in a refrigerator. The evaporator coils of an air conditioner are inside the room, and the condenser outside the room. A fan inside the air conditioner circulates cool air in the room.

The coefficient of performance, K, of an air conditioner is defined as K = \(|\frac{Q_{\mathrm{C}}}{W}|\), where Q_C is the heat absorbed and W is the work done. The time rate of heat removed is the heat current, H = \(\frac{\left|Q_{C}\right|}{t}\), where t is the time in which heat |Q_C|, is removed.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 44
where H = |Q_C|/t is the heat current and P( = |W|/t) is the time rate of doing work, i.e., power.

Question 57.
What is a heat pump ?
Answer:
A heat pump is a device used to heat a building by cooling the air outside it. It works like a refrigerator but cooling outside space and heating inside space. In this case, the evaporator coils are outside the building to absorb heat from the air. The condenser coils are inside the building to release the heat to warm the building.

Question 58.
Solve the following :

Question 1.
In a refrigerator, in one cycle, the external work done on the working substance is 20% of the energy extracted from the cold reservoir. Find the coefficient of performance of the refrigerator.
Solution :
Data: |W| = 0.2|Q_C|
The coefficient of performance of the refrigerator,
K = |\(\frac{Q_{C}}{W}\)| = \(\frac{\left|Q_{C}\right|}{0.2\left|Q_{C}\right|}\)
= 5

Question 2.
The coefficient of performance of a room air conditioner is 3. If the rate of doing work is 2kW, find the heat current.
Solution :
Data : K = 3, P = 2000 W
K = \(\frac{H}{P}\)
∴ Heat current, H = KP = (3) (2000) W
= 6000 W = 6kW

Question 59.
State and explain the limitations of the first law of thermodynamics.
Answer:

The first law of thermodynamics is essentially the principle of conservation of energy as there is a close relation between work and energy. We find that there is a net transfer of energy (heat) from a body at higher temperature to a body at lower temperature. The net transfer of energy from a body at lower temperature to a body at higher temperature is not observed though consistent with the first law of thermodynamics.
If two containers, one containing nitrogen and the other containing oxygen, are connected to allow diffusion, they mix readily. They never get separated into the respective containers though there is no violation of the first law of thermodynamics.
It is not possible to design a heat engine with 100% efficiency, though there is no restriction imposed by the first law of thermodynamics.
At room temperature, ice absorbs heat from the surrounding air and melts. The process in the opposite direction is not observed, though consistent with energy conservation. These examples suggest that there is some other law operative in nature that determines the direction of a process

Question 60.
State the two forms of the second law of thermodynamics.
Answer:
Second law of thermodynamics :

It is impossible to extract an amount of heat Q_H from a hot reservoir and use it all to do work W. Some amount of heat Q_C must be exhausted (given out) to a cold reservoir. This prohibits the possibility of a perfect heat engine.
This statement is called the first form or the engine law or the engine statement or the Kelvin-Planck statement of the second law of thermodynamics.
It is not possible for heat to flow from a colder body to a warmer body without any work having been done to accomplish this. This prohibits the possibility of a perfect refrigerator.
This statement is called the second form or the Clausius statement of the second law of thermodynamics.

Notes :

Max Planck (Karl Ernst Ludwig) (1858-1947) German physicist, put forward quantum therory of radiation.
Rudolf Clausius (1822-88) German theoretical physicist, made significant contribution to thermodynamics.

Question 61.
Draw neat labelled diagrams to illustrate
(i) energy flow diagram for engine statement.
(ii) energy flow diagram for a perfect refrigerator.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 45

Question 62.
State the difference between a reversible process and an irreversible process.
OR
Distinguish between a reversible process and an irreversible process.
Answer:
A reversible process is a bidirectional process, i.e., its path in P-V plane is the same in either direction. In contrast, an irreversible process is a undirectional process, i.e., it can take place only in one direction.

A reversible process consists of a very large number of infinitesimally small steps so that the system is all the time in thermodynamic equilibrium with its environment. In contrast an irreversible process may occur so rapidly that it is never in thermodynamic equilibrium with its environment.

Question 63.
Draw a neat labelled diagram of a Carnot cycle and describe the processes occurring in a Carnot engine. Write the expression for the efficiency of a Carnot engine.
Answer:
Basically, two processes occur in a Carnot engine :
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 46
(1) Exchange of heat with the reservoirs : In isothermal expansion AB, the working substance takes in heat Q_H from a lot reservoir (source) at constant temperature T_H. In isothermal compression CD, the working substance gives out heat Q_C to a cold reservoir (sink) at constant temperature T_C.

(2) Doing work : In adiabatic expansion BC, the working substance does work on the environment and in adiabatic compression DA, work is done on the working substance by the environment.
All processes are reversible. It can be shown that \(\frac{\left|Q_{C}\right|}{Q_{\mathrm{H}}}\) = \(\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}\). Hence, the efficiency of a Carnot engine,
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 47

Question 64.
What is a Carnot refrigerator? State the expressions for the coefficient of performance of a Carnot refrigerator.
Answer:
A Carnot refrigerator is a Carnot engine operated in the reverse direction. Here, heat Q_C is absorbed from a cold reservoir at temperature T_C, work W is provided externally, and heat Q_H is given out to a hot reservoir at temperature T_H.
The coefficient of performance of a Carnot refrigerator is
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 48
[Note: K is large if T_H-T_C is small. It means a large quantity of heat can be removed from the body at lower temperature to the body at higher temperature by doing small amount of work. K is small if T_H – T_C is large.
It means a small quantity of heat can be removed from the body at lower temperature to the body at higher temperature even with large amount of work.]

Question 65.
Solve the following :

Question 1.
A Carnot engine receives 6 × 10⁴ J from a reservoir at 600 K, does some work, and rejects some heat to a reservoir at 500 K. Find the
(i) the heat rejected by the engine
(ii) the work done by the engine
(iii) the efficiency of the engine.
Solution :
Data : Q_H = 6 × 10⁴J, T_H = 600K, T_C = 500K
(i) The heat rejected by the engine
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 49

Question 2.
A Carnot engine operates between 27 °C and 87 °C. Find its efficiency.
Solution :
Data : T_C = 27 °C = (273 + 27) K = 300 K,
T_H = 87 °C = (273 + 87) = 360 K
The efficiency of the engine,
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 50

Question 3.
The coefficient of performance of a Carnot refrigerator is 4. If the temperature of the hot reservoir is 47 °C, find the temperature of the cold reservoir.
Solution :
Data : K = 4, T_H = 47°C = (273 + 47) K = 320
K = \(\frac{T_{\mathrm{c}}}{T_{\mathrm{H}}-T_{\mathrm{c}}}\) ∴ KT_H – KT_c = T_c
∴ KT_H = (1 + K)T_c
∴ T_c = \(\frac{K T_{\mathrm{H}}}{1+K}\) = \(\frac{(4)(320)}{1+4}\)K = (0.8)(320)K
= 256K = (256 – 273)°C = – 17°C
This is the temperature of the cold reservoir.

[Note : A hot-air type engine consisting of two cylinders, was developed by Robert Stirling (1790 -1878), a Scottish engineer and clergyman. He developed the concept in 1816 and obtained a patent for his design in 1827. Some engines were made in 1844. He also used helium and hydrogen in some engines developed thereafter. Stirling engines are used in submarines and spacecrafts.]

Question 66.
Draw a neat labelled diagram of a Sterling cycle and describe the various processes taking place in a Sterling engine.
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 51
Answer:
The working substance can be air or helium or hydrogen or nitrogen. All processes are reversible.

AB is isothermal expansion, at temperature T_H, in which heat Q_H is absorbed from the source and useful work is done by the working substance.
BC is isochoric process in which some heat is released by the gas (working substance) to the refrigerator and the gas cools to temperature T_c < T_H.
CD is isothermal compression, at temperature T_c, in which heat Q_c is rejected to the coolant (sink).
DA is isochoric process in which heat is taken in by the gas and its temperature rises to T_H.

[Note : Stirling engine operated in reverse direction is used in the field of cryogenics to obtain extremely low – temperatures to liquefy air or other gases.]

Question 67.
Refer above figure and answer the following questions.
(i) What is the work done in process AB ?
(ii) What is the change in internal energy and heat released in process BC ?
Answer:
(i) In this case, the change in the internal energy is zero, as the temperature of the gas remains constant. Hence, the work done, W = heat absorbed, Q_H.

(ii) In this case, the change in the internal energy, ∆ U = _nC_V (T_C – T_H), where n = number of moles of the gas used in the Stirling engine and C_V = molar specific heat of the gas. As W = 0 at constant volume, heat released’= ∆ U.

Question 68.
Choose the correct option :

Question 1.
According to the first law of thermodynamics, in the usual notation,
(A) Q = ∆U + W
(B) Q = ∆U – W
(C) Q = W – ∆U
(D) Q= -(∆ U + W).
Answer:
(A) Q = ∆U + W

Question 2.
In an isothermal process, in the usual notation,
(A) PV = constant
(B) V/T = constant
(C) P/T = constant
(D) Q = 0.
Answer:
(A) PV = constant

Question 3.
In an isothermal process, in the usual notation,
(A) W = nRT (V_f/V_i)
(B) W = ∆ U
(C) W = Q
(D) W = 0.
Answer:
(C) W = Q

Question 4.
In an adiabatic process, in the usual notation,
(A) TV^γ = constant
(B) PT^γ = constant
(C) W = 0
(D) PV^γ = constant.
Answer:
(D) PV^γ = constant.

Question 5.
In an isobaric process, in the usual notation,
(A) W = P (V_f – V_i)
(B) W = Q
(C) W = – ∆U
(D) ∆T = 0.
Answer:
(A) W = P (V_f – V_i)

Question 6.
In an adiabatic process, in the usual notation,
(A) ∆ P = 0
(B) ∆ V = 0
(C) Q = 0
(D) ∆U = 0.
Answer:
(C) Q = 0

Question 7.
In an isothermal process, in the usual notation,
(A) W = P(V_f – V_i)
(B) W = 0
(C) W = V(P_f – P_i)
(D) W = nRT In(V_f/V_i).
Answer:
(D) W = nRT In(V_f/V_i).

Question 8.
In an isobaric process, in the usual notation,
(A) W = _nC_V (T_f – T_i)
(B) Q = _nC_P (T_f – T_i)
(C) ∆U = nR(T_f – T_i)
(D) W = 0.
Answer:
(B) Q = _nC_P (T_f – T_i)

Question 9.
In the usual notation, the isothermal work, W =
(A) P(V_f – V_i)
(B) nRT(P_i/ P_f)
(C) nRT ln(P_i/P_f)
(D) nRT(P_f/P_i).
Answer:
(C) nRT ln(P_i/P_f)

Question 10.
If Q and ∆u are expressed in cal and W is expressed in joule, then,
(A) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(B) Q = ∆U – (W/J)
(C) \(\frac{Q}{J}\) = \(\frac{\Delta U}{J}\) + W
(D) Q = ∆U + (W/J)
Answer:
(D) Q = ∆U + (W/J)

Question 11.
In an adiabatic process, in the usual notation, W =
Maharashtra Board Class 12 Physics Important Questions Chapter 4 Thermodynamics 52
Answer:
(A) \(\frac{P_{\mathrm{i}} V_{\mathrm{i}}-P_{\mathrm{f}} V_{\mathrm{f}}}{\gamma-1}\)

Question 12.
In a cyclic process,
(A) ∆U = Q
(B) Q = 0
(C) W = 0
(D) W = Q
Answer:
(D) W = Q

Question 13.
The efficiency of a heat engine is given by η =
(A) Q_H/W
(B) W/Q_c
(C) W/Q_H
(D) Q_c/W.
Answer:
(C) W/Q_H

Question 14.
In a cyclic process, the area enclosed by the loop in the P – V plane corresponds to
(A) ∆U
(B) W
(C) Q – W
(D) W – Q.
Answer:
(B) W

Question 15.
The efficiency of a Carnot engine is given by K =
(A) T_c/(T_H – T_c)
(B) (T_H – T_c)/T_c
(C) T_H/(T_H – T_c)
(D) (T_H – T_c)/T_H
Answer:
(A) T_c/(T_H – T_c)

Question 16.
The coefficient of performance of a Carnot refrigerator is given by K =
(A) T_c(T_H-T_c)
(B) (T_H-T_c)/T_c
(C) T_H/(T_H-T_c)
(D) (T_H-T_c)/T_H.
Answer:
(A) T_c(T_H-T_c)

Question 17.
The efficiency of a Carnot engine working between T_H = 400 K and T_c = 300 K is
(A) 75%
(B) 25%
(C) 1/3
(D) 4/7.
Answer:
(B) 25%

Question 18.
If a Carnot engine receives 5000 J from a hot reservoir and rejects 4000 J to a cold reservoir, the efficiency of the engine is
(A) 25%
(B) 10%
(C) 1/9
(D) 20%.
Answer:
(D) 20%.

Question 19.
If a Carnot refrigerator works between 250 K and 300 K, its coefficient of performance =
(A) 6
(B) 1.2
(C) 5
(D) 10.
Answer:
(C) 5

Question 20.
The coefficient of performance of a Carnot refrigerator is 4. If T_c = 250 K, then T_H =
(A) 625 K
(B) 310 K
(C) 312.5 K
(D) 320 K.
Answer:
(C) 312.5 K

Question 21.
The coefficient of performance of a Carnot refrigerator working between T_H and T_c is K and the efficiency of a Carnot engine working between the same T_H and T_c is η. Then
(A) ηk = \(\frac{Q_{\mathrm{H}}}{Q_{\mathrm{c}}}\)
(B) η/k = Q_c/Q_H
(C) η/k = Q_H/Q_c
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)
Answer:
(D) ηk = \(\frac{Q_{c}}{Q_{H}}\)

Question 22.
The internal energy of one mole of organ is
(A) \(\frac{5}{2}\)RT
(B) RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 23.
The internal energy of one mole of oxygen is
(A) \(\frac{5}{2}\)RT
(B) 5RT
(C) \(\frac{3}{2}\)RT
(D) 3RT.
Answer:
(C) \(\frac{3}{2}\)RT

Question 24.
The internal energy of one mole of nitrogen at 300 K is about 6225 J. Its internal energy at 400 K will be about
(A) 8300J
(B) 4670J
(C) 8500J
(D) 8000J.
Answer:
(A) 8300J

Question 25.
The adiabatic constant γ for argan is
(A) 4/3
(B) 7/5
(C) 6/5
(D) 5/3.
Answer:
(D) 5/3.

Maharashtra Board Class 11 History Important Questions Chapter 4 Vedic Period

July 2, 2024July 1, 2024 by Bhagya

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 4 Vedic Period Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 4 Vedic Period

1A. Choose the correct alternative and write the complete sentences.

Question 1.
____________ was composed in India around 1500 B.C.E.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

Question 2.
In the year 1583, an Italian merchant ____________ came to Kochi, Kerala.
(a) Vasco da Gama
(b) Filippo Sassetti
(c) Albuquerque
(d) Ferdinand
Answer:
(b) Fillippo Sassetti

Question 3.
The texts of the four Vedas are known as the ____________
(a) Aranyaka
(b) Brahmanas
(c) Samhitas
(d) Upanishads
Answer:
(c) Samhitas

Question 4.
The verses in the Rigveda are known as ____________
(a) Ruchas
(b) Suktas
(c) Mandala
(d) Mantras
Answer:
(a) Ruchas

Question 5.
The Vedic society was organised into four classes known as ____________
(a) Ashramas
(b) Varnas
(c) Javas
(d) Mahajanapadas
Answer:
(b) Varnas

Question 6.
____________ mentioned as the Lord of Urvara.
(a) Agni
(b) Varun
(c) Indra
(d) Pushan
Answer:
(b) Varun

Question 7.
The chariot makers in the Vedic Period were known as ____________
(a) Rathakara
(b) Taksham
(c) Kulal
(d) Vaya
Answer:
(a) Rathakara

Question 8.
The verses in ____________ is known on ‘Rueha’.
(a) Samaveda
(b) Rigveda
(c) Atharvaveda
(d) Yajurveda
Answer:
(b) Rigveda

Question 9.
The ____________ is regarded as the text that is fundamental in development of Indian music.
(a) Rigveda
(b) Samaveda
(c) Yajurveda
(d) Atharvaveda
Answer:
(b) Samaveda

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Rigveda	Suktas (hymns)
(b) Yajurveda	Explanation of the sacrificial rituals
(c) Samaveda	Rules of reciting mantras
(d) Atharvaveda	Rules of grammar

Answer:
(d) Atharvaveda – Charms and medicines for various problems and diseases

Question 2.

Set ‘A’	Set ‘B’
(a) Shatdru	Sutlej
(b) Asikni	Chinab
(c) Parushi	Bias
(d) Vitasta	Jhelum

Answer:
(c) Parushi – Ravi

Question 3.

Set ‘A’	Set ‘B’
(a) Kubha	Kabul
(b) Gomati	Gomal
(c) Suvastu	Swat
(d) ‘God’s Country	Devraya Desh

Answer:
(d) ‘God’s Country’ – Devnirmit Desh

1C. Find the odd one out.

Question 1.
Deities of the Vedic period:
(a) Indra
(b) Varun
(c) Ashwins
(d) Rathakara
Answer:
(d) Rathakara

Question 2.
Rivers of the Saptasindhu:
(a) Shatdru
(b) Vipas
(c) Asikni
(d) Cauvery
Answer:
(d) Cauvery

Question 3.
The Vedas:
(a) Rigveda
(b)Yajurveda
(c) Upanishad
(d) Atharvaveda
Answer:
(c) Upanishad

Question 4.
Terms associated with the textile industry:
(a) Tantum
(b) Otum
(c) Shuttle
(d) Uran
Answer:
(d) Uran

2A. Write the names of historical places, persons, and events.

Question 1.
Asiatic Society of Bengal in 1784.
Answer:
Sir William Jones

Question 2.
Tribal Settlements.
Answer:
Krishtya

Question 3.
Earthen Jars in Marathi.
Answer:
Rahatgadage

Question 4.
Vedic name for carpenters.
Answer:
Takshan

Question 5.
Vedic name for the weaver.
Answer:
Vaya

Question 6.
Two well-known epics.
Answer:
Ramayana and Mahabharata

Question 7.
River transport.
Answer:
Navya

2B. Choose the correct reason and complete the sentence.

Question 1.
The Rigvedic culture is the culture of the ____________
(a) Early Vedic period
(b) Late Vedic Period
(c) Post Vedic Period
(d) Pre Vedic period
Answer:
(a) Early Vedic period

Question 2.
The Atharvaveda contains information about ____________
(a) Science, Technology and Inventions.
(b) Charms and medicines for various problems and diseases.
(c) Day-to-day life.
(d) The norms of statesmanship.
Answer:
(b) Charms and medicines for various problems and diseases.

Question 3.
The ____________ also mentions trade by exchange, negotiations, and traders travelling far and wide to earn profits.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

2C. Write the correct chronological order.

Question 1.
(a) Brahmanas
(b) Aryamka
(c) Vedas
(d) Upanishada
Answer:
(a) Vedas
(b) Brahmanas
(c) Aryamka
(d) Upanishads

Question 2.
(a) Grihasthashram
(b) Vanaprasthashram
(c) Brahmacharyashram
(d) Sanyasashram
Answer:
(a) Brahmacharyashram
(b) Grihasthashram
(c) Vanaprasthashram
(d) Sanyasashram

Question 3.
(a) Vedic Literature and Social organisation of Vedic Times
(b) Vedic literature, Linguistics, and Archaeology
(c) Later Vedic Period
(d) The Early Vedic Culture
Answer:
(a) Vedic literature, Linguistics, and Archaeology
(b) Vedic Literature and Social organisation of Vedic Times
(c) The Early Vedic Culture
(d) Later Vedic Period

3. Complete the concept maps.

Question 1.
Maharashtra Board Class 11 History Important Questions Chapter 4 Vedic Period 3 Q1
Answer:

Question 2.
Maharashtra Board Class 11 History Important Questions Chapter 4 Vedic Period 3 Q2
Answer:

Question 3.
Maharashtra Board Class 11 History Important Questions Chapter 4 Vedic Period 3 Q3
Answer:

4. Explain the following concepts.

Question 1.
Varna System.
Answer:

The Vedic society was organized into four classes known as ‘Varna’, namely, Brahmana, Kshatriya, Vaishya, and Shudra.
The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
In the later Vedic period, the varna system lost its flexibility.
Also, the caste system got rooted firmly by this period.
In the beginning, the varna or the caste was decided by one’s occupation.
Later it came to be determined on the basis of birth.

5. Explain the statement with reasons.

Question 1.
It became impossible to change one’s Varna and caste in which he/she was born.
Answer:

The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
In the later Vedic period, the varna system lost its flexibility.
Also, the caste system got rooted firmly by this period.
In the beginning, the varna or the caste was decided by one’s occupation.
Later it came to be determined on the basis of birth.
Hence it became impossible to change one’s varna and caste, in which he/she was born.

Question 2.
Vedic literature is supposed to be the earliest literature of India.
Answer:

The language of Vedic Literature in Sanskrit and it is one of the oldest languages.
Vid’ in Sanskrit means to know and ‘Ved’ means knowledge.
The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.
The texts of these four Vedas are known as the ‘Samhitas’.
Thus, the Vedic literature is supposed to be the earliest literature of India.

Question 3.
Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.
Answer:

The Yajurveda offers an explanation of the sacrificial rituals.
It explains when and how the mantras should be used.
A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra.
Thus, the Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

6. State your opinion.

Question 1.
Later Vedic Period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.
Answer:

Later Vedic Period is dated to around 1000-600 B.C.E. The information about this period is gathered from the treatises written in that period.
The material culture as reflected in the epics, Ramayana and Mahabharata was studied with the help of archaeological evidence.
A picture of the migration in the Later Vedic period can be gathered from the Saptasindhu region toward the east and its geographic markers from the literature of that period.
Thus, this period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.

7. Answer the following questions in detail.

Question 1.
Write a note on Vedic literature in detail.
Answer:

Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit.
The four Vedas form the core of Vedic literature, i.e., Rigveda, Yajurveda, Samaveda and Atharvaveda.
The texts of these four Vedas are known as ‘Samhitas’ vid in Sanskrit means ‘to know’ and Veda means ‘knowledge.
The Rigveda contains Suktas (hymns) composed to eulogize the deities.
The verses in the Rigveda are known as ‘Rucha’. A number of Ruchas strung together to make a Sukta (hymn).
Many Suktas make one Mandala. The Yajurveda offers explanations of rituals.
It explains how and when mantras are to be used. The Samaveda is a text that gives the rules of reciting mantras in a musical form.
The Atharvaveda is about day-to-day life. It contains information about charms and medicines.

Question 2.
Write a note on the Later Vedic period in detail.
Answer:

The Later Vedic period is dated around 1000-600 B.C.E. The treatises of the period give information about this period.
This period saw the spread of Later Vedic from the foothills of the Himalayas in the north to the Vindhyas in the south.
A story in the Satapatha Brahmana bears evidence of the Later Vedic period settling and bringing land under cultivation from west to east.
The Later Vedic period saw a gradual formation of the confederacies of the Vedic villages. They were known as ‘Janapadas’.
Generally, the seniors and the elites in a Janapada collectively took social decisions.
They functioned like oligarchic states. These slowly expanded into Mahajanapadas.

Question 3.
Write about the following:
(a) Varna System
(b) Ashrama System
Answer:
(a) Varna System:

The Vedic society was organised into four classes known as “Varna’ namely Brahmana Kshatriya, Vaishya, and Shudra.
The Varna system is mentioned in the 10th Mandala (chapter) of the Rigveda.
In the Later Vedic period, the varna system became rigid. Also, the caste system got firmly rooted.
In the beginning, the varna or the caste was decided by one’s occupation later it came to be determined on the basis of birth.

(b) Ashrama System: The Ashrama System of the Vedic period was divided into four stages namely Brahmacharya Ashram, Grihastha Ashram, Vanaprastha Ashrama, and Sanyasa Ashrama.

In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
In the third stage, one was expected to retire from the active life of a householder.
It was also desirable that one should stay away from human settlement, renounce all family bonds, accept a wandering life, etc.
A Sanyasi was to give up all worldly attachments and not be permitted to settle at one place for a longer time.

8. Answer the following questions with the help of given points.

Question 1.
Write a note on Ashrama System with the help of stages involved in it.
Answer:
The Ashrama System of the Vedic culture lays down the norms of living an ideal life by dividing the span of human life into four successive stages, namely Brahmacharyashram, Grihasthashram, Vanaprasthashram, and Sanyasashram.

In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
In the third stage, one was expected to retire from the active life of the householder and if the need is to give advice to the younger people. It was also desirable that one should stay away from human settlement.
In the fourth and the last stage one was expected to renounce all the family bonds, accept a wandering life, and go away. A Sanyasi was not permitted to settle at one place for a longer time.

Question 2.
Write a note on Vedic Literature:
(a) Rigveda
(b) Yajurveda
(c) Samaveda
(d) Atharvaveda
Answer:
Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit. The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.

(a) Rigveda: The Rigveda contains Suktas (hymns) composed to eulogize the deities. The verses in Rigveda are known as ‘Rucha’. A number of Ruchas strung together makes a Sukta (hymn). Many Suktas make one Mandala.

(b) Yajurveda: The Yajurveda offers an explanation of the sacrificial rituals. It explains when and how the mantras should be used. A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra. The Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

(c) Samaveda: The Samaveda is a text that gives the rules of reciting mantras in a musical form. The Samaveda is regarded as the text that is fundamental in the development of Indian music.

(d) Atharvaveda: The Atharvaveda is about day-to-day life. It contains information about charms and medicines for various problems and diseases. It also talks about the norms of statesmanship.

Maharashtra Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India

July 2, 2024July 1, 2024 by Bhagya

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 3 Chalcolithic Villages in India

1A. Choose the correct alternative and write the complete sentences.

Question 1.
___________ culture at Balathal is dated to 4000 B.C.E.
(a) Ahar
(b) Jorwe
(c) Ganeshwar-Jodhpura
(d) Malwa
Answer:
(a) Ahar

Question 2.
Ahar culture is also known as ___________ culture.
(a) Jorwe
(b) Kayatha
(c) Banas
(d) Savalda
Answer:
(c) Banas

Question 3.
___________ is a site situated on the bank of the river known as Chhoti Kali Sindh.
(a) Savalda
(b) Navadatoli
(c) Malwa
(d) Kayatha
Answer:
(d) Kayatha

Question 4.
___________ was known as ‘Rangpur’.
(a) Maharashtra
(b) Gujarat
(c) Madhya Pradesh
(d) Rajasthan
Answer:
(b) Gujarat

Question 5.
Savalda is in ___________ district.
(a) Satara
(b) Ratnagiri
(c) Dhule
(d) Pune
Answer:
(c) Dhule

Question 6.
The culture in south Gujarat is known as ___________ culture.
(a) Pravhas
(b) Nevase
(c) Malwa
(d) Rangpur
Answer:
(a) Pravhas

Question 7.
The age when huge stone slabs were used is known as ___________ age.
(a) Palaeolithic
(b) Mesolithic
(c) Neolithic
(d) Megalithic
Answer:
(d) Megalithic

Question 8.
The archaeological evidence shows that ___________ was a centre of mass production of pottery.
(a) Gilund
(b) Khethri
(c) Balathal
(d) Baras
Answer:
(c) Balathal

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Malwa Culture	1600-1400 B.C.E.
(b) Megalithic circles in India	1500-500 B.C.E
(c) Early Jorwe Culture	1400-1000 B.C.E.
(d) Late Jorwe Culture	1000-800 B.C.E.

Answer:
(d) Late Jorwe Culture – 1000-700 B.C.E.

Question 2.

Set ‘A’	Set ‘B’
(a) Early Harappan phase	3950-2600 B.C.E.
(b) Mature (urban) phase	2500-1800 B.C.E.
(c) Savalda culture	2000-1800 B.C.E.
(d) Post-Harappan phase	1900-900 B.C.E.

Answer:
(b) Mature (urban) phase – 2600-1900 B.C.E.

1C. Find the odd one out.

Question 1.
Ahar, Kayatha, Malwa, Mohenjodaro.
Answer:
Mohenjodaro

Question 2.
Early Harappan phase, Mature (Urban) phase, Pre Harappan Phase, Post-Harappan phase.
Answer:
Pre Harappan Phase

Question 3.
Malwa Culture, Early Jorwe Culture, Late Jorwe Culture, Post Late Jorwe Culture.
Answer:
Post-Late Jorwe Culture

Question 4.
Odisha, Todas, Kurumbas, Nagas.
Answer:
Nagas

Question 5.
Takalghat, Mahuzari, Khasis, Khapa.
Answer:
Khasis

Question 6.
Godavari, Inamgaon, Tapi, Bhima.
Answer:
Inamgaon

2A. Write the names of historical places, persons, and events.

Question 1.
A tributary of the river Banas
Answer:
Ahar

Question 2.
The culture found at Khetri
Answer:
Ganeshwar-Jodhpura

Question 3.
Pottery found in river beds
Answer:
Ochre coloured pottery

Question 4.
An important site of Malwa culture on the banks of Narmada
Answer:
Navadatoli

Question 5.
Tribes in Odisha
Answer:
Bodos

Question 6.
Furnace discovered near Nagpur
Answer:
Naikund

2B. Choose the correct reason and complete the sentence.

Question 1.
Ochre Coloured Pottery (OCP) and copper hoards are supposed to belong ___________
(a) one and the same culture
(b) one and the another culture
(c) similar culture
(d) different culture
Answer:
(a) one and the same culture

Question 2.
People of the Mature Harappan and the Late Harappan culture had the knowledge of ___________
(a) designs include motifs like sun, moon, fish, deer, and peacock
(b) wheel-made pottery
(c) the technology of making copper objects
(d) excavations of copper artifacts
Answer:
(b) wheel-made pottery

Question 3.
Kayatha culture was contemporary to the ___________
(a) Dholavira region
(b) Mohenjodaro
(c) Banas culture
(d) Harappan Civilisation
Answer:
(d) Harappan Civilisation

Question 4.
Ahar culture at Balathal is dated to ___________
(a) 400 B.C.E
(b) 40 B.C.E
(c) 4000 B.C.E
(d) 40000 B.C.E
Answer:
(c) 4000 B.C.E

2C. Write the correct chronological order.

Question 1.
(a) Malwa culture – 1800 B.C.
(b) Early Jorwe culture – 1400 B.C.
(c) Ahar culture – 4000 B.C.E.
(d) Savalda culture – 2000 B.C.E.
Answer:
(a) Ahar culture – 4000 B.C.E.
(b) Savalda culture – 2000 B.C.E.
(c) Malwa culture – 1800 B.C.E.
(d) Early Jorwe culture – 1400 B.C.E.

Question 2.
(a) Late Jorwe Culture – 1000-700 B.C.E.
(b) Kutch – Saurashtra was abandoned by 1900 B.C.E.
(c) Early Jorwe Culture – 1400-1000 B.C.E.
(d) Malwa Culture – 1600-1400 B.C.E.
Answer:
(a) Kutch – Saurashtra were abandoned by 1900 B.C.E.
(b) Malwa Culture – 1600-1400 BCE
(c) Early Jorwe Culture – 1400-1000 B.C.E.
(d) Late Jorwe Culture – 1000-700 B.C.E.

Question 3.
(a) Mature (urban) phase – 2600-1900 B.C.E.
(b) ‘Ahar’ culture at Balathal – 4000 B.C.E.
(c) Post-Harappan phase – 1900-900 B.C.E.
(d) Early Harappan phase – 3950-2600 B.C.E.
Answer:
(a) ‘Ahar’ culture at Balathal – 4000 B.C.E.
(b) Early Harappan phase – 3950-2600 B.C.E.
(c) Mature (urban) phase – 2600-1900 B.C.E.
(d) Post-Harappan phase – 1900-900 B.C.E.

3. Complete the concept maps.

Question 1.
Maharashtra Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India 3 Q1
Answer:

Question 2.
Maharashtra Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India 3 Q2
Answer:

Question 3.
Maharashtra Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India 3 Q3
Answer:

Question 4.
Maharashtra Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India 3 Q4
Answer:

4. Write short notes.

Question 1.
Ochre coloured pottery
Answer:

Initially, the Ochre Coloured Pottery (OCP) was mostly found in river beds.
Generally, the potsherds of OCP are found in worn-out, rounded, and brittle conditions as they remained in flowing water for a long time.
A number of sites of the OCP are found in Punjab, Haryana, Rajasthan, and the western region of Uttar Pradesh.
The OCP culture in Rajasthan is dated about 3000 B.C.E.

Question 2.
Jorwe Pottery
Answer:

Jorwe pots are well baked giving a metallic sound and designs on these pots are painted in brown.
They are red in colour with designs painted in black.
Jorwe pottery includes shapes like spouted pots, carinated bowls, and troughs (carination is the central ridge on the pot), lota, globular jars, etc.
The Late Jorwe people made pots of the same shapes, but without any decoration.

5. Explain the statements with reasons.

Question 1.
There were two chalcolithic cultures in Gujarat, in the post-Harappan period.
Answer:

In the post-Harappan period, there were two chalcolithic cultures in Gujarat.
The culture in south Gujarat was known as ‘Prabhas’ culture and the one in northeastern Gujarat was known as ‘Rangpur’ culture.
The pottery of these chalcolithic cultures was akin to Late Harappan pottery with regards to the colour, shapes, and designs.
These cultures existed till 1800-1200 B.C.E.

Question 2.
Savalda people and The Harappans in Saurashtra had trade relations.
Answer:

There was a cultural contact between the Savalda people and the Harappans in Saurashtra.
Its evidence has been found at the site of Kaothe in Dhule district.
The artifacts made of chank shells found at Kaothe confirm that the Savalda people and The Harappans in Saurashtra had trade relations.

6. State your opinion.

Question 1.
Kayatha culture was contemporary to the Harappan civilisation.
Answer:

The people of Kayatha culture subsisted on agriculture and animal husbandry.
They mainly used handmade pots and microliths.
Artifacts like copper axes and bangles, necklaces made of beads of steatite were found in the Kayatha houses.
People of Kayatha culture and Harappan culture seem to have been in contact much before the rise of the Harappan cities.

Question 2.
Ochre Coloured Pottery (OCP) and copper hoards are supposed to belong to one and the same culture.
Answer:

The Copper Hoards found in India come from various regions, such as Uttar Pradesh, Bihar, Bengal, Odisha, and Madhya Pradesh.
The copper objects found in these hoards indicate that the artisans who fashioned them were very highly skilled.
The archaeological sites of OCP and the find-spots of the copper hoards often seem to be situated in the same vicinity, not very distant from each other.
Hence, OCP and copper hoards are supposed to belong to one and the same culture.

7. Answers the following questions in detail.

Question 1.
Write a note on ‘Jorwe’ pottery.
Answer:

Jorwe pots are well baked giving a metallic sound. They are red in colour with designs painted in black.
Jorwe pottery includes shapes like spouted pots, carinated bowls, and troughs, lota, globular jars, etc.
The late Jorwe people made pots of the same shapes but without any decoration.
Potters kilns were found in both Malwa and Early Jorwe periods.
They were round in shape. The kiln of the early Jowre period was larger and of greater capacity.
In the late Jorwe period potters did not have a specially built kiln. They baked their pots directly on the ground.
Inamgaon was the centre of pottery production which supplied pottery to the surrounding villages.

Question 2.
Discuss the Megalithic period in India.
Answer:

A nomadic people around 700 B.C.E. erected stone circles by using huge slabs of rock.
The space within these circles was used to bury dead people.
These circles are known as Megaliths. The period of these Megaliths is known as the ‘Megalithic Age’.
They were used for various purposes, but mainly they contain the remains of the dead.
They were the memorials of the dead. Such megalithic circles have been found in many parts of the world.
A few tribes in India practice it even today. For instance; the Bodos in Odisha, Todas, and Kurumbas in South India.
Nagas and Khasis in Northeast India. Most of these circles in India are dated to 1500-500 B.C.E.
Perhaps these people were from South India. The Megalithic circles in Maharashtra belong to the Iron Age. They are dated to 1000-400 B.C.E.
In Maharashtra, Megalithic burials have been found in the Vidarbha region especially in the districts of Nagpur, Chandrapur, and Bhandara.
Megalithic people used horses for transport and travel. They were instrumental in introducing the ‘Iron Age’ in ancient India.

8. Answer the following questions with the help of given points.

Question 1.
Write a note with the help of the following points:
(a) ‘Ahar’ or ‘Banas’ Culture
(b) Ganeshwar – Jodhpur Culture
(c) Kayatha Culture
(d) Malwa Culture
Answer:
(a) ‘Ahar’ or ‘Banas’ Culture: The chalcolithic cultures in India generally belong to the post- Harappan period. However, the ‘Ahar’ or ‘Banas’ culture in the Mewad region of Rajasthan was contemporary to the Harappan civilisation. Balathal and Gilund near Udaipur are the important sites of Ahar culture. ‘Ahar’ culture at Balathal is dated to 4000 B.C.E and was first discovered at Ahar near Udaipur, so it was named as ‘Ahar’ culture.

(b) Ganeshwar-Jodhpura Culture: Many sites of the culture known as ‘Ganeshwar-Jodhpura’ culture have been found in the vicinity of the copper mines at Khetri. The settlements there are earlier than the Harappan civilisation. During the excavations at Ganeshwar copper artifacts like arrowheads, spearheads, harpoons, bangles, chisels, and also pottery was found. The people of Ganeshwar-Jodhpura culture supplied copper objects to the Harappans.

(c) Kayatha Culture: Kayatha is a site situated on the banks of the river known as Chhoti Kali Sindh, at a distance of 25 kilometers from Ujjain in Madhya Pradesh. Kayatha culture was contemporary to the Harappan civilisation. The people of Kayatha culture subsisted on agriculture and animal husbandry.

(d) Malwa Culture: The name ‘Malwa’ obviously tells us that this culture originated and spread first in the Malwa region. It existed in Madhya Pradesh during 1800-1200 B.C.E. ‘Navadatoli’ situated on the river Narmada, on the opposite bank of Maheshwar, is an important site of Malwa culture. The other important sites are Eran (District Sagar) and Nagda (District Ujjain). They were surrounded by protective walls.

Maharashtra Board 12th OCM Important Questions Chapter 8 Marketing

July 1, 2024June 30, 2024 by Prasanna

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 8 Marketing Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 8 Marketing

Select the correct options and rewrite the sentence

Question 1.
In …………….. there are few sellers selling homogeneous products or differentiated products in the market.
(a) Monopoly
(b) Duopoly
(c) Oligopoly
Answer:
(c) Oligopoly

Question 2.
The process of classification of products according to similar characteristics and/or quality is known as ………………
(a) Standardisation
(b) Grading
(c) Branding
Answer:
(b) Grading

Question 3.
The market which uses Information Technology for buying and selling of product or service is known as ………………….
(a) Exchange concept of market
(b) Digital concept of market
(c) Place concept of market
Answer:
(b) Digital concept of market

Question 4.
The market for semi-processed or semifinished goods is called ……………………
(a) Primary Market
(b) Secondary Market
(c) Terminal Market
Answer:
(b) Secondary Market

Question 5.
……………….. helps to avoid breakage, damage and destruction of product.
(a) Packaging
(b) Grading
(c) Branding
Answer:
(a) Packaging

Question 6.
……………… gives a special identity to the product.
(a) Grading
(b) Packaging
(c) Branding
Answer:
(c) Branding

Match the pairs

Question 1.

Group A	Group B
(A) Regulated Market	1. Market of consumer goods
(B) Capital Market	2. Monopoly
(C) Tool of Marketing	3. Provides employment
(D) Marketing Mix	4. Stock Exchange
(E) Promotion	5. Market not controlled by regulation
	6. Provides quality products
	7. 4 Ps
	8. Packaging and labelling
	9. Process of informing customers about producer
	10. Borrowing and lending long term capital

Answer:

Group A	Group B
(A) Regulated Market	4. Stock Exchange
(B) Capital Market	10. Borrowing and lending long term capital
(C) Tool of Marketing	8. Packaging and labelling
(D) Marketing Mix	7. 4 Ps
(E) Promotion	9. Process of informing customers about producer

Question 2.

Group A	Group B
(A) Customer Support Service	(1) Creates good design of product
(B) Label	(2) To identity Need/ Want of Consumers
(C) Product Development	(3) Provides Information
(D) Marketing Research	(4) After Sales Services
(E) Trademark	(5) Movement of finished goods
	(6) Storage of goods
	(7) Registered Brands
	(8) King of Market
	(9) Distribution Channel
	(10) Decreases Distribution cost

Answer:

Group A	Group B
(A) Customer Support Service	(4) After Sales Services
(B) Label	(3) Provides Information
(C) Product Development	(1) Creates good design of product
(D) Marketing Research	(2) To identity Need/ Want of Consumers
(E) Trademark	(7) Registered Brands

Give one word/phrase/term for the following statements

Question 1.
The market for the commodities which are sold within geographical limits of a region.
Answer:
Local Market

Question 2.
The market for agricultural and forest products.
Answer:
Primary Market

Question 3.
Where there is single seller or producer who controls the market.
Answer:
Monopoly

Question 4.
Market situation where there is single buyer of a commodity or service.
Answer:
Monopsony

Question 5.
Market where lEirge number of buyers and sellers buy and sell their homogeneous products.
Answer:
Perfect Market.

Question 6.
The process of identifying the needs Emd wants of consumers in the market.
Answer:
Marketing Research

Question 7.
The tool of market that helps to publicise the product to the consumer.
Answer:
Promotion

Question 8.
Putting the right product at the right time, at the right place, at the right price.
Answer:
MEirketing Mix

Question 9.
Slip attached to the product which provides all the information regEirding product and its producer.
Answer:
Labelling

Question 10.
Function of determining standards and ensuring uniformity in the product.
Answer:
Standardisation

Question 11.
The market for the commodities which are sold within country.
Answer:
National Market

Question 12.
The market for commodities which are produced in one country and sold in other countries.
Answer:
International Market

Question 13.
A type of market which has very short time existence.
Answer:
Very Short Period s Market

Question 14.
A market in which the activities of buying and selling is undertaken in large quantities at cheaper rate.
Answer:
Wholesale Market

Question 15.
A market where goods are sold to ultimate consumers.
Answer:
Terminal Market.

State whether following the statements are True or False

Question 1.
Monopsony refers to a market situation where there is a single seller of a commodity or service.
Answer:
False

Question 2.
Product development is one time process.
Answer:
False

Question 3.
Marketing follows customer oriented approach.
Answer:
True

Question 4.
Commodity Exchanges, Stock Exchanges, Foreign ExchEmges are examples of unregulated or raw market.
Answer:
False

Question 5.
Effective utilisation of channel of distribution can help in reducing the cost price of product.
Answer:
True.

Find the odd one

Question 1.
Local market, International market, Terminal j market, National market
Answer:
Terminal market

Question 2.
Very short period market, Perfect market, Short period market, Long period market
Answer:
Perfect market

Question 3.
Monopoly, Monopsony, Oligopoly, Imperfect market
Answer:
Imperfect market.

Complete the sentences

Question 1.
…………….. is a part and parcel of modern day’s life.
Answer:
Marketing

Question 2.
…………….. is the king of the market.
Answer:
Customer

Question 3.
Market which uses Information Technology for buying and selling of goods or services is called ………………..
Answer:
Digital market

Question 4.
Market for goods, materials, consumer and industrial goods is called ………………….
Answer:
Commodity market

Question 5.
………………. market refers to the markets regulated by statutory provisions of the country.
Answer:
Regulated

Question 6.
In …………………. there are two sellers, selling either a homogenous product or differentiated products.
Answer:
Duopoly

Question 7.
…………………. involves collecting raw materials from different sources and bringing them at one place for production.
Answer:
Assembling.

Correct the underlined word and rewrite the sentence

Question 1.
Transportation creates time utility.
Answer:
Perfect market refers to a market situation which is characterised by large number of buyers and sellers who buy and sell their homogeneous products.

Question 2.
Imperfect market refers to a market situation which is characterised by large number of buyers and sellers who buy and sell their homogeneous products.
Answer:
Warehousing creates time utility.

Question 3.
Producer is the king of the market.
Answer:
Consumer is the king of the market.

Question 4.
Retail market refers to the market of bulk purchase and sale of goods.
Answer:
Wholesale market refers to the market of bulk purchase- and sale of goods.

Question 5.
Determining the right price is the result of product development.
Answer:
Determining the right price is the result of marketing research.

Arrange in proper order

Question 1.
Terminal market, Primary market, Secondary market.
Answer:
Primary market, Secondary market, Terminal market.

Distinguish between

Question 1.
Marketing and Selling
Answer:

	Taiga Region	Tundra Region
1. Meaning	Marketing refers to a process in which needs are identified or created, products offered and delivered to the consumers.	Selling refers to a process of processing orders from customers and delivering the products to them.
2. Concept	As compared to selling, marketing is wider concept. It comprises of selling and other functions.	As compared to marketing, selling is narrower concept. It is part and parcel of marketing concept.
3. Essential	Fulfilling the needs and satisfaction of the consumers are the essence of the marketing concept.	Transfer of title and possession of the products from one person to another are the essence of selling.
4. Orientation	Marketing is consumer oriented. It stresses more on consumers and the maximisation of their satisfaction.	Selling is product oriented. It stresses more on the product and its efficiency.
5. Views	Marketing views (looks at) the customers as they are the centre of all activities of marketing.	Selling views (looks at) the customers as a last link in the activities of selling.
6. Activity	Marketing is an indirect activity.	Selling is a direct activity.

Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations

July 1, 2024June 30, 2024 by Prasanna

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 5 Oscillations Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 5 Oscillations

Question 1.
Define :
(1) periodic motion
(2) oscillatory motion. Give two examples.
Answer:
(1) Periodic motion : A motion that repeats itself at definite intervals of time is said to be a periodic motion.
Examples : The motion of the hands of a clock, the motion of the Earth around the Sun.

(2) Oscillatory motion : A periodic motion in which a body moves back and forth over the same path, straight or curved, between alternate extremes is said to be an oscillatory motion.
Examples : The motion of a taut string when plucked, the vibrations of the atoms in a molecule, the oscillations of a simple pendulum.
[Note : The oscillatory motion of a particle is also called a harmonic motion when its position, velocity and acceleration can be expressed in terms of a periodic, sinusoidal functions-sine or cosine, of time.

Question 2.
With a neat diagram, describe a spring-and-block oscillator.
Answer:
Consider a spring-and-block oscillator as shown in below figure in which the block slides on a frictionless horizontal surface. The spring has a relaxed length when the block is at rest at the position O.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 1
The block is then displaced to P by an amount x measured from the equilibrium position O. Upon releasing, the unbalanced force \(\vec{F}\) = –\(k \vec{x}\) toward left accelerates the block and its speed increases. As x gets smaller, |\(\vec{F}\)| and the acceleration decrease proportionately.

k is the elastic constant of the spring called the force constant or spring constant.

At the instant the block passes through the point O, | \(\vec{F}\) | = 0 because x = 0; although there is no acceleration, the speed is maximum.

As soon as the block passes O going to the left, the force on the block and its acceleration increases to the right, because the spring is now compressed. Eventually, the block is brought to rest momentarily at the point Question Then on, the subsequent motion is the same as the motion from P to Q, with all directions reversed.

The acceleration of the block is \(\vec{a}\) = \(\frac{\vec{F}}{m}\) = –\(\frac{k}{m} \vec{x}\) where m is the mass of the block. This shows that the acceleration is also proportional to the displacement and its direction is opposite to that of the displacement, i.e., the force and acceleration are both directed towards the mean or equilibrium position. The motion repeats causing the block to oscillate about equilibrium or mean position O. This oscillatory motion along a straight path is called linear simple harmonic motion (SHM).

The points P and Q are called the extreme positions or the turning points of the motion. One oscillation is a complete to-and-fro motion of the oscillating body (block, in this case) along its path (the motion from O to P, P to Q and Q to O), i.e., two consecutive passages of the body through the point O in the same direction.

Question 3.
In linear SHM, what can you say about the restoring force when the speed of the particle is

zero
maximum ?

Answer:
The restoring force is

maximum
zero.

Question 4.
Define period or periodic time, frequency, amplitude and path length of simple harmonic motion (SHM).
Answer:

Period or periodic time of SHM : The time taken by a particle performing simple harmonic motion to complete one oscillation is called the period or periodic time of SHM.
Frequency of SHM : The number of oscillations performed per unit time by a particle executing SHM is called the frequency of SHM.
Amplitude of SHM : The magnitude of the maximum displacement of a particle performing SHM from its mean position is called the amplitude of SHM.
Path length of SHM : The length of the path over which a particle performs SHM is twice the amplitude of the motion and is called the path length or range of the SHM.
[Note : The frequency of SHM is equal to the reciprocal of the period of SHM.]

Question 5.
Obtain the differential equation of linear simple harmonic motion.
Answer:
When a particle performs linear SHM, the force acting on the particle is always directed towards the mean position. The magnitude of the force is directly proportional to the magnitude of the displacement of the particle from the mean position. Thus, if \(\vec{F}\) is the force acting on the particle when its displacement from the mean position is \(\vec{x}\), \(\vec{F}\) = -k\(\vec{x}\) … (1)
where the constant k, the force per unit displacement, is called the force constant. The minus sign indicates that the force and the displacement are oppositely directed.
The velocity of the particle is \(\frac{d \vec{x}}{d t}\) and its acceleration is \(\frac{d^{2} \vec{x}}{d t^{2}}\).
Let m be the mass of the particle.
Force = mass × acceleration
∴ \(\vec{F}\) = m\(\frac{d^{2} \vec{x}}{d t^{2}}\)
Hence, from Eq. (1),
m\(\frac{d^{2} \vec{x}}{d t^{2}}\) = -k\(\vec{x}\)
∴ \(\frac{d^{2} \vec{x}}{d t^{2}}\) + \(\frac{k}{m} \vec{x}\) = 0 … (2)
This is the differential equation of linear SHM.

Question 6.
Obtain the dimensions of force constant in SHM.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 2
[Note : The SI unit of force constant is the newton per metre (N/m) while the cgs unit is the dyne per centimetre (dyn/cm).]

Question 7.
State the differential equation of linear SHM. Hence, obtain the expressions for the acceleration, velocity and displacement of a particle performing linear SHM.
Answer:
The differential equation of linear SHM is
\(\frac{d^{2} \vec{x}}{d t^{2}}\) + \(\frac{k}{m} \vec{x}\) = 0
where m = mass of the particle performing SHM, \(\frac{d^{2} \vec{x}}{d t^{2}}\) = acceleration of the particle when its displacement from the mean position is \(\vec{x}\) and k = force constant. For linear motion, we can write the differential equation in scalar form :
\(\frac{d^{2} x}{d t^{2}}\) + \(\frac{k}{m}\)x = 0
Let \(\frac{k}{m}\) = ω², a constant
∴ \(\frac{d^{2} x}{d t^{2}}\) + ω²x = 0
∴ Acceleration, a = \(\frac{d^{2} x}{d t^{2}}\) = ω²
The minus sign shows that the acceleration and the displacement have opposite directions. Writing v = \(\frac{d x}{d t}\) as the velocity of the particle.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 3
Hence, EQ. (1) can be written as
v\(\frac{d v}{d x}\) = -ω²x dx
∴ vdv = -ω²x dx
Integrating this expression, we get,
\(\frac{v^{2}}{2}\) = –\(\frac{-\omega^{2} x^{2}}{2}\) + C
where the constant of integration C is found from a boundary condition.

At an extreme position (a turning point of the motion), the velocity of the particle is zero. Thus, v = 0 when x = ± A, where A is the amplitude.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 4
This equation gives the velocity of the particle in terms of the displacement, x. The velocity towards right is taken to be positive and that towards left as negative.
Since, v = dx/dt, we can write Eq. (2) as follows :
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 5
where the constant of integration, α, is found from the initial conditions, i.e., the displacement and the velocity of the particle at time t = 0.
From Eq. (3), we have
\(\frac{x}{A}\) = sin (ωt + α)
∴ Displacement as a function of time is,
x = A sin (ωt + α)

Question 8.
From the definition of linear SHM, derive an expression for the angular frequency of a body performing linear SHM.
Answer:
When a body of mass m performs linear SHM, the restoring force on it is always directed towards the mean position and its magnitude is directly proportional to the magnitude of the displacement of the body from the mean position. Thus, if \(\vec{F}\) is the force acting on the body when its displacement from the mean position is \(\vec{x}\),
\(\vec{F}\) = m\(\) = – k\(\vec{x}\)
where the constant k, the force per unit displacement, is the force constant.
Let \(\frac{k}{m}\) = ω², a constant. m
∴ Acceleration, a = –\(\frac{k}{m}\)x = -ω²x
∴ The angular frequency
ω = \(\sqrt{\frac{k}{m}}\) = \(\sqrt{\left|\frac{a}{x}\right|}\)
= \(\sqrt{\text { acceleration per unit displacement }}\)

Question 9.
What is the displacement of a particle at any position, performing linear SHM ?
Answer:
The displacement of a particle performing linear SHM is a specified distance of the particle from the mean position in a specified direction along its path. The general expression for the displacement is x = A sin (ωt + α), where A and ω are respectively the amplitude or maximum displacement and the angular frequency of the motion, and α is the initial phase.

Question 10.
Assuming the general expression for displacement of a particle in SHM, obtain the expressions for the displacement when the particle starts from
(i) the mean position
(ii) an extreme position.
Answer:
The general expression for the displacement of a particle in SHM at time t is x = A sin (ωt + α) … (1) where A is the amplitude and re is a constant in a particular case.
∴ ωt + α = sin^-1\(\frac{x}{A}\) …. (2)
(i) When the particle starts from the mean position, x = 0 at t = 0. Then, from Eq. (2),
α = sin^-1 0 = 0 or π … (3)
Substituting for α into Eq. (1),
x = A sin ωt for α = 0 and x = – A sin ωt for α = π
∴ x = ±A sin ωt … (4)
where the plus sign is taken if the particle’s initial velocity is to the right, while the minus sign is taken when the initial velocity is to the left.

(ii) x = ±A at t = 0 when the particle starts from the right or left extreme position, respectively. Then, from Eq. (2),
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 6
where the plus sign is taken when the particle starts from the positive extreme, while the minus sign is taken when the particle starts from the negative extreme.

Question 11.
At what position is the acceleration of a particle in SHM maximum? What is its magnitude? At what position is the acceleration minimum ? What is its magnitude ?
Answer:
The magnitude of the acceleration of a particle performing SHM is
a = ω²x … (1)
where ω is a constant related to the system.
From Eq. (1), the acceleration has a maximum value a_max when displacement x is maximum, |x| = A, i.e., the particle is at the extreme positions.
∴ a_max = ω²A
Also from EQ. (1), the acceleration has a minimum value when x is minimum, x = 0, i.e., the particle is at the mean position.
∴ a_min = 0

Question 12.
At what position is the velocity of a particle in SHM maximum ? What is its magnitude ? At what position is the velocity minimum? What is its magnitude?
Answer:
The velocity of a particle in SHM is
v = ω\(\sqrt{A^{2}-x^{2}}\) … (1)
where ω is a constant related to the system and A is the amplitude of SHM.
From EQ. (1) it is clear that the velocity is maximum when A² – x² is maximum, that is when displacement x = 0, i.e., the particle is at the mean position.
∴ v_max = ωA
Also from Eq. (1), the velocity is minimum when A² – x² is minimum, equal to zero. This occurs when x is maximum, x = ± A, i.e., the particle is at the extreme positions.
∴ v_min = 0

Question 13.
For a particle performing linear SHM, show that its average speed over one oscillation is \(\frac{2 \omega A}{\pi}\), where A is the amplitude of SHM.
OR
Show that the average speed of a particle performing SHM in one oscillation is \(\frac{2}{\pi}\) × maximum speed.
Answer:
During one oscillation, a particle performing SHM covers a total distance equal to 4A, where A is the amplitude of SHM. The time taken to cover this distance is the period (T) of SHM.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 7

Question 14.
A body of mass 200 g performs linear SHM with period 2πs. What is the force constant ?
Answer:
Force constant, k = mω² = m\(\left(\frac{2 \pi}{T}\right)^{2}\)
= 0.2kg × \(\left(\frac{2 \pi}{2 \pi \mathrm{s}}\right)^{2}\) = 0.2N/m.

Question 15.
Derive expressions for the period of SHM in terms of
(1) angular frequency
(2) force constant
(3) acceleration.
Answer:
The general expression for the displacement (x) of a particle performing SHM is x = A sin (ωt + α)
(1) Let T be the period of the SHM and x₁ the displacement after a further time interval T. Then
x₁ = A sin [ω(t + T) + α]
= A sin (ωt + ωT + α)
= A sin (ωt + α + ωT)
Since T ≠ 0, for x₁ to be equal to x, we must have (ωT)_min = 2π.
Hence, the period (T) of SHM is T = 2π/ω
This is the expression for the period in terms of the constant co, the angular frequency.

(2) If m is the mass of the particle and k is the force constant, ω = \(\sqrt{k / m}\).
∴T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{\sqrt{k / m}}\) = 2π \(\sqrt{\frac{m}{k}}\)

(3) The acceleration of a particle performing SHM has a magnitude a = ω²x
∴ ω = \(\sqrt{a / x}\)
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 8

Question 16.
A small uniform cylinder floats upright to a depth d in a liquid. If it is depressed slightly and released, find its period of oscillations.
Answer:
Consider a cylinder, of length L, area of cross section A and density ρ, floating in a liquid of density σ. If the cylinder floats up to depth d in the liquid, then by the law of floatation, the weight of the cylinder equals the weight of the liquid displaced, i.e.,
ALρg = Adσg
∴ L = dσ/p … (1)
Let the cylinder be pushed down by a distance y. Then, the weight of the liquid displaced by the cylinder of length y will exert a net upward force on the cylinder :
F = Ayσg,
which produces an acceleration,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 9

Question 17.
How does the frequency of an SHM vary with

the force constant k
the mass of the particle performing SHM ?

Answer:
The frequency of a particle of mass m performing
SHM is f = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\).

∴ f ∝\(\sqrt{k}\)
Thus, the frequency of an SHM is directly proportional to the square root of the force constant of the motion.
∴ f ∝ \(\frac{1}{\sqrt{m}}\)
Thus, the frequency of an SHM is inversely proportional to the square root of the mass of the particle performing SHM.

Question 18.
In linear SHM, at what position of the particle is the acceleration of the particle half the maximum acceleration?
Answer:
In linear SHM, | a | ∝ | x | ∴ a = \(\frac{a_{\max }}{2}\) when | x | = \(\frac{A}{2}\), where A is the amplitude of SHM.

Question 19.
If the displacement of a particle in SHM is given by x = 0.1 sin (6πrt) metre, what is the frequency of motion ?
Answer:
Comparison of the given equation with
x = A sin (2πft) gives 2πf = 6π rad/s.
∴ Frequency of motion,/= 3 Hz

Question 20.
If the displacement of a particle in SHM is given by x = 0.1 cos (100t) metre, what is the maximum speed of the particle ?
Answer:
Comparison of the given equation with
x = A cos (ωt) gives A = 0.1 m and ω = 100 rad/s.
∴ Maximum speed of the particle = ωA
= 1000 × 0.1 = 10 m/s

Question 21.
A body of mass m tied to a spring performs SHM with period 2 seconds. If the mass is increased by 3m, what will be the period of SHM ?
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 10
∴ T₂ = 2T₁ = 2 × 2 = 4 seconds gives the required period of SHM.

Question 22.
A particle executing SHM has velocities v₁ and v₂ when at distances x₁ and x₂ respectively from the mean position. Show that its period is T = 2π\(\sqrt{\frac{x_{1}^{2}-x_{2}^{2}}{v_{2}^{2}-v_{1}^{2}}}\) and the amplitude of SHM is A = \(\sqrt{\frac{v_{2}^{2} x_{1}^{2}-v_{1}^{2} x_{2}^{2}}{v_{2}^{2}-v_{1}^{2}}}\)
Answer:
If A is the amplitude and co is the angular frequency, V₁ = ω\(\sqrt{A^{2}-x_{1}^{2}}\) … (1)
and v₂ = ω\(\sqrt{A^{2}-x_{2}^{2}}\) … (2)
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 111

Question 23.
Explain
(i) a series combination
(ii) a parallel combination of springs. Obtain the spring constant in each case.
Answer:
(i) Series combination of springs : When two light springs obeying Hooke’s law are connected as shown in below figure and both the springs experience the same force applied to the free end of the combination, they are said to be connected in series.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 12
Consider two springs, 1 and 2, with respective spring constants k₁ and k₂ connected in series and supporting a load F = mg so that the springs are extended. Since the same force acts on each spring, by Hooke’s law,
F = k₁x₁ (for spring 1) and F = k₂x₂ (for spring 2) The system of two springs in series is equivalent to a single spring, of spring constant k_S such that F = k_Sx, where the total extension x of the combination is the sum x₁ + x₂ of their elongations.
x = x₁ + x₂
∴ \(\frac{F}{k_{\mathrm{S}}}\) = \(\frac{F}{k_{1}}\) + \(\frac{F}{k_{2}}\) ∴ \(\frac{1}{k_{\mathrm{S}}}\) = \(\frac{1}{k_{1}}\) + \(\frac{1}{k_{2}}\)
For a series combination of N such springs, of spring constants, k₁, k₂, k₃, … k_N
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 13

(ii) Parallel combination of springs : When two light springs obeying Hooke’s law are connected via a thin vertical rod as shown, they are said to be connected in parallel. If a constant force \(\vec{F}\) is exerted on the rod such that the rod remains perpendicular to the direction of the force, the springs undergo the same extension.

Consider two springs, 1 and 2, with respective spring constants k₁ and k₂ connected in series and supporting a load F = mg so that the springs are extended. The two springs stretch by the same amount x but share the load.
F = F₁ + F₂
The system of two springs in parallel is equivalent to a single spring, of spring constant kF such that F = k_PX,
∴ k_Px = k₁x + k₂x ∴ k_P = k₁ + k₂
For a parallel combination of N such springs, of spring constants k₁, k₂, k₃, … k_N
k_P = k₁ + k₂ + k₃ + … + k_N = \(\Sigma_{i=1}^{N} k_{i}\)
Therefore, for a parallel combination of N identical light springs, each of spring constant k, k_P = Nk

Question 24.
Solve the following :

Question 1.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate
(i) the angular frequency
(ii) the frequency of oscillation.
Solution :
Data : m = 1 kg, k = 16 N/m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 14

Question 2.
Calculate the time taken by a body performing SHM of period 2 seconds to cover half the amplitude starting from an extreme position.
Solution :
Data : T = 2 s, x₀ = + A (initially at positive extremity), x = \(\frac{A}{2}\)
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 15
∴ Starting from the positive extremity, the particle takes \(\frac{1}{3}\) s to cover a distance equal to half the amplitude.

Question 3.
A 3 kg block, attached to a spring, performs linear SHM with the displacement given by x = 2 cos (50t) m. Find the spring constant of the spring.
Solution :
Data : m = 3 kg, x = 2 cos (50t) m
Comparing the given equation with x = A cos ωt,
ω = 50 rad/s
ω² = k/m
∴ The spring constant,
k = mω² = (3)(50)²
= 3 × 2500 = 7500 N/m

Question 4.
A body oscillates in SHM according to the equation x = 5 cos (2πt + \(\frac{\pi}{4}\)), where x and t are
in SI units. Calculate the
(i) displacement and
(ii) speed of the body at t = 1.5 s.
Solution:
Data: x = cos \(\left(2 \pi t+\frac{\pi}{4}\right)\), t = 1.5 s
(i) The displacement at t = 1.5 s is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 16
= 5(1.414)(3.142) = 22.21 m/s

Question 5.
The equation of motion of a particle executing SHM is x = a sin \(\left(\frac{\pi}{6} t\right)\) + b cos \(\left(\frac{\pi}{6} t\right)\), where a = 3 cm and b = 4 cm. Express this equation in the form x = A sin \(\left(\frac{\pi}{6} t+\phi\right)\). Hence, find A and φ.
Solution:
Let a = A cos φ and b = A sin φ, so that
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 17

Question 6.
A particle performs SHM of amplitude 10 cm. Its maximum velocity during oscillations is 100 cm/s. What is its displacement, when the velocity is 60 cm/s?
Solution :
Data : A = 10 cm, v_max = 100 cm/s, v = 60 cm/s
v_max = ωA = 100 cm/s
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 18

Question 7.
A body of mass M attached to a spring oscillates with a period of 2 seconds. If the mass is increased by 2 kg, the period increases by 1 second. Find the initial mass, assuming that Hooke’s law is obeyed.
Answer:
Data : m₁ = M, T₁ = 2 s, m₂ = M + 2 kg, T₂ = 2s + 1 s = 3s
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 19

Question 8.
A load of 100 g increases the length of a light spring by 10 cm. Find the period of its linear SHM if it is allowed to oscillate freely in the vertical direction. What will be the period if the load is increased to 400 g? [g = 9.8 m/s²]
Solution :
Data :m = 100 g = 100 × 10^-3 kg, x = 10 cm = 0.1 m g = 9.8 m/s², m₁ = 400 g = 400 × 10^-3 kg
(1) Stretching force F = mg
Now F = kx (numerically), where k is the force constant.
∴ mg = kx
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 20

Question 9.
A particle in SHM has a period of 2 seconds and an amplitude of 10 cm. Calculate its acceleration when it is at 4 cm from its positive extreme position.
Solution :
Data : T = 2s, A = 10 cm, A – x = 4 cm
∴ x = 10 cm – 4 cm = 6 cm
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 21

Question 10.
A particle executes SHM with amplitude 5 cm and period 2 s. Find the speed of the particle at a point where its acceleration is half the maximum acceleration.
Solution :
Data: A = 5 cm = 5 × 10^-2 m, T = 2s,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 22

Question 11.
The periodic time of a linear harmonic oscillator is 2π seconds, with maximum displacement of 1 cm. If the particle starts from an extreme position, find the displacement of the particle after π/3 seconds.
Solution :
Data : T = 2π s, A = 1 cm, t = π/3
ω = \(\frac{2 \pi}{T}\) = \(\frac{2 \pi}{2 \pi}\) = 1 rad/s
x = A cos ωt (∵ particle starts from extreme position)
= (1) cos\(\left(1 \times \frac{\pi}{3}\right)\) = cos \(\left(1 \times \frac{\pi}{3}\right)\) = cos \(\frac{\pi}{3}\) = \(\frac{1}{2}\) cm

Question 12.
A particle performs SHM of period 12 seconds and amplitude 8 cm. If initially the particle is at the positive extremity, how much time will it take to cover a distance of 6 cm from that position?
Solution :
Data : T = 12 s, A = 8 cm
∴ ω = 2π/T = π/6 rad/s
When the particle covers a distance of 6 cm from the positive extremity, its displacement measured from the mean position is x = 8 – 6 = 2 cm.
As the particle starts from the positive extreme position, its displacement is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 23

Question 13.
A particle executes SHM with amplitude 10 cm and period 10 s. Find the velocity and acceleration of the particle at a distance of 5 cm from the equilibrium position.
Solution :
Data : A = 10 cm = 0.1 m, T = 10 s, x = ± 5 cm = ± 0.05 m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 24

Question 14.
A body performs SHM on a path 0.12 m long. Its velocity at the centre of the path is 0.12 m/s. Find the period of SHM. Also find the magnitude of the velocity of the body at \(\sqrt{3}\) × 10^-2 m from the centre of the path.
Solution :
The path length of the SHM is the range 2 A, and the velocity at the centre of the path, i.e., at the equilibrium position, is the maximum velocity v_max.
Data : 2A = 0.12 m, v_max = 0.12 m/s,
x = ± \(\sqrt{3}\) × 10^-2 m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 25

Question 15.
A particle of mass 2 g executes SHM with a period of 12 s and amplitude 10 cm. Find the acceleration of the particle and the restoring force on the particle when it is 2 cm from its mean position. Also find the maximum velocity of the particle.
Solution :
Data : m = 2g = 2 × 10^-3 kg, T = 12 s,
A = 10 cm = 0.1 m, x = ±2 cm = ±2 × 10^-2 m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 26
The acceleration of the particle, a = ω² = (0.5237)² (± 2 × 10^-2)
= ± 0.2743 × 2 × 10^-2 = ± 5.486 × 10^-3 m/s²
The restoring force on the particle at that position, F = ma = ± (2 × 10^-2) (5.486 × 10^-3)
= ±1.097 × 10^-5 N
The maximum velocity of the particle, v_max = ωA = 0.5237 × 0.1 5.237 × 10^-2 m/s

Question 16.
The maximum velocity of a particle performing linear SHM is 0.16 m/s. If its maximum acceleration is 0.64 m/s², calculate its period.
Solution :
Data : v_max = 0.16 m/s, a_max = 0.64 m/s²
v_max = ωA and a_max = ω²A
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 27

Question 17.
A particle performing linear SHM has maximum velocity of 25 cm/s and maximum acceleration of 100 cm/s². Find the amplitude and period of oscillation, [π = 3.142]
Solution :
Data : v_max = 25 cm/s, a_max = 100 cm/s²
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 28

Question 18.
A particle performing linear SHM has a period of 6.28 seconds and path length of 20 cm. What is the velocity when its displacement is 6 cm from the mean position?
Solution :
Data : T = 6.28 s, 2A = 20 cm ∴ A = 10 cm, x = 6 cm
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 29

Question 19.
A uniform wooden rod floats vertically in water with 14 cm of its length immersed in the water. If it is depressed slightly and released, find its period of oscillations.
Solution :
Data : d = 14 cm = 0.14 m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 30

Question 20.
A particle performs UCM. The diameter of the circle is 4 cm. What is the amplitude of linear SHM that is the projection of the UCM on a diameter?
Answer:
Amplitude of linear SHM = radius of the circle = 2 cm.

Question 21.
A particle performs UCM with period 2n seconds along a circle of diameter 10 cm. What is the maximum speed of its shadow on a diameter of the circle ?
Answer:
Maximum speed, v_max = ωA = \(\frac{2 \pi}{T}\)A
= \(\frac{2 \pi}{2 \pi}\) × 5 × 10^-2 = 5 × 10^-2 m/s.

Question 22.
See Question 20 above. What is the maximum acceleration of the shadow ?
Answer:
Maximum acceleration, a_max = ω²A = \(\left(\frac{2 \pi}{T}\right)^{2}\) A
= \(\left(\frac{2 \pi}{2 \pi}\right)^{2}\) × 5 × 10^-2 = 5 × 10^-2 m/s².

Question 23.
What do you understand by the phase and epoch of an SHM ?
Answer:
(1) Phase of simple harmonic motion (SHM) represents the state of oscillation of the particle performing SHM, i.e., it gives the displacement of the particle, its direction of motion from its equilibrium position and the number of oscillations completed.

The displacement of a particle in SHM is given by x = A sin (ωt + α). The angle (ωt + α) is called the phase angle or simply the phase of SHM. The SI unit of phase angle is the radian (symbol, rad).

(2) Epoch of simple harmonic motion (SHM) represents the initial phase of the particle performing SHM, i.e., it gives the displacement of the particle and its direction of motion at time t = 0.

If x₀ is the initial position of the particle, i.e., the position at time t = 0, x₀ = A sin α or α = sin^-1 (x₀/A). The angle α, therefore, determines the initial state of the particle. Hence, the angle α is the epoch or initial phase or phase constant of SHM.
[Note : The symbol for the unit radian is rad, not superscripted c.]

Question 25.
Solve the following.

Question 1.
The differential equation for a particle performing linear SHM is \(\frac{d^{2} x}{d t^{2}}\) = – 4x. If the amplitude is 0.5 m and the initial phase is π/6 radian, obtain the expression for the displacement and find the velocity of the particle at x = 0.3 m.
Solution:
Data : A = 0.5 m, α = π/6 rad
(1) \(\frac{d^{2} x}{d t^{2}}\) = -4x
Comparing this equation with the general equation \(\frac{d^{2} x}{d t^{2}}\) = – ω²x, we get,
ω² = 4 or ω = 2 rad/s
Now, x = A sin (ωt + α)
Substituting the values of A, ω and α, the expression for the displacement for the given SHM is
x = 0.5 sin (2t + π/6) m

(2) The velocity of the particle at x = 0.3 m is v = ± ω \(\sqrt{A^{2}-x^{2}}\)
= ± 2 \(\sqrt{(0.5)^{2}-(0.3)^{2}}\) = ± 0.8 m/s

Question 2.
The displacement of a particle performing linear SHM is given by x = 6 sin (3πt + \(\frac{5 \pi}{6}\)) metre. Find
the amplitude, frequency and the phase constant of the motion.
Solution :
Data : x = 6 sin (3πt + \(\frac{5 \pi}{6}\)) metre
Comparing this equation with x = A sin (ωt + α), we get:

Amplitude, A = 6 m
ω = 3π rad / s
∴ Frequency, f = \(\frac{\omega}{2 \pi}\) = \(\frac{3 \pi}{2 \pi}\) = 1.5 Hz 5%
Phase constant, α = \(\frac{5 \pi}{6}\) rad

Question 3.
The equation of linear SHM is a: = 10 sin (4πt + \(\frac{1}{24}\)) cm. Find the amplitude, period and phase constant of the motion. Also, find the phase angle \(\frac{1}{24}\) second after the start.
Solution:
Data : x = 10 sin\(\left(4 \pi t+\frac{\pi}{6}\right)\) + cm, f = \(\frac{1}{24}\) s

(1) Comparing the given equation with x = A sin (ωt +α), we get,
A = 10 cm, ω = 4π rad/s, α = \(\frac{\pi}{6}\) rad
∴

Amplitude, A = 10 cm
Period, T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{4 \pi}\) = 0.5 s
Phase constant, α = \(\frac{\pi}{6}\) rad

(2) Phase angle = (ωt + α) = 4πt + \(\frac{\pi}{6}\)
The phase angle \(\frac{1}{24}\) second after the start is obtained by substituting t = \(\frac{1}{24}\) in the above expression.
∴ Phase angle = 4πt + \(\frac{\pi}{6}\) = (4π × \(\frac{1}{24}\)) + \(\frac{\pi}{6}\)
= \(\frac{\pi}{6}\) + \(\frac{\pi}{6}\) = \(\frac{\pi}{3}\) rad

Question 4.
Describe the state of oscillation of a particle if the phase angle of SHM is rad.
Solution :
Data : θ = \(\frac{25 \pi}{4}\) rad
θ = \(\frac{25 \pi}{4}\) = 6π + \(\frac{\pi}{4}\) = 3(2π) rad + \(\frac{\pi}{4}\) rad
The first term indicates that the particle has completed 3 oscillations. The second term indicates that the displacement of the particle in the 4th oscillation is A sin \(\frac{\pi}{4}\) = + \(\frac{1}{\sqrt{2}}\)A, where A is the amplitude of the SHM, and moving towards the positive extreme.

Question 5.
A particle in linear SHM is in its 5th oscillation. If its displacement at that instant is –\(\frac{1}{2}\) A and
is moving toward the mean position, determine its phase at that instant.
Solution :
Data : x = –\(\frac{1}{2}\) A, 5th oscillation
A sin θ₁ = –\(\frac{1}{2}\)A ∴ θ₁ = sin^-1\(\left(-\frac{1}{2}\right)\) = π – \(\frac{\pi}{6}\) rad
As the particle is in its 5th oscillation, its phase is
θ = 2 × 2π + θ₁ = 4π + (π – \(\frac{\pi}{6}\)) = 5π – \(\frac{\pi}{6}\) = \(\frac{29 \pi}{6}\) rad

Question 6.
The amplitude and periodic time of SHM are 5 cm and 6 s, respectively. What is the phase at a distance of 2.5 cm from the mean position?
Solution :
Data : A = 5 cm, T = 6 s, x = 2.5 cm
Since the particle starts from the mean position, its epoch, α = 0.
∴ The equation of motion is x = A sin ωt
∴ The required phase of the particle,
ω = sin^-1\(\frac{x}{A}\)
= sin^-1\(\frac{2.5}{5}\) = sin^-1 \(\frac{1}{2}\) = \(\frac{\pi}{6}\) rad

Question 26.
State the expressions for the displacement, velocity and acceleration of a particle performing linear SHM, starting from the mean position towards the positive extreme position. Hence, draw their graphs with respect to time. Draw your conclusions from the graphs.
OR
Represents graphically the displacement, velocity and acceleration against time for a particle performing linear SHM when it starts from the mean position.
Answer:
Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where co is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 31
as the initial phase α = 0

Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 32
Using the values in the table we can plot graphs of displacement, velocity and acceleration with time.

Conclusions :

The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting at the mean position, the x-t and a-t graph are sine curves. The v-t graph is a cosine curve.
There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
There is a phase difference of n radians between x and a.

Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 34

Question 27.
State the expressions for the displacement, velocity and acceleration of a particle performing linear SHM, starting from the positive extreme position. Hence, draw their graphs with respect to time. Draw your conclusions from the graphs.
OR
A particle performs linear SHM starting from the positive extreme position. Plot the graphs of its displacement, velocity and acceleration against time.
Answer:
Consider a particle performing linear SHM with amplitude A and period T = 2π/ω, starting from the positive extreme position, where ω is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant (t) are
x = A cos ωt = A cos\(\left(\frac{2 \pi}{T} t\right)\) (∵ ω = \(\frac{2 \pi}{T}\))
v = – ωA sin ωt = -ωA sin \(\left(\frac{2 \pi}{T} t\right)\)
a = – ω²A sin ωt = -ω²A cos \(\left(\frac{2 \pi}{T} t\right)\)

Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 35
Using these values, we can plot graphs showing the variation of displacement, velocity and acceleration with time.

Conclusions :

The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x-t and a-t graphs are cosine curves; the v-t graph is a sine curve.
There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
There is a phase difference of π radians between x and a.

Explanations :
(1) v-t graph : It is a sine curve, i.e., the velocity is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π/2 rad between a and v.

v is minimum (equal to zero) at the extreme positions (i.e., at x = ± A) and v is maximum ( = ± ωA) at the mean position (x = 0).

(2) a-t graph : It is a cosine curve, i.e., the acceleration is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π rad between v and a. a is minimum (equal to zero) at the mean position (x = 0) and a is maximum ( = \(\mp\)ω²A) at the extreme positions (x = ± A).
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 37

Question 28.
Discuss analytically the composition of two SHMs of the same period and parallel to each other (along the same path). Find the resultant amplitude when the phase difference is
(1) zero
(2) \(\frac{\pi}{3}\) rad
(3) \(\frac{\pi}{2}\) rad
(4) π rad.
Answer:
Let a particle be subjected to two parallel linear SHMs of the same period along the same path and the same mean position, represented by
x₁ = A₁ sin (ωt + α) and x₂ = A₂ sin (ωt + β),
where A₁ and A₂ are the amplitudes, and α and β are the initial phases of the two SHMs.

According to the principle of superposition, the displacement of the particle at any instant t is the algebraic sum x = x₁ + x₂.
∴ x = A₁ sin (ωt + α) + A₂ sin (ωt + β)
= A₁ sin ωt cos α + A₁ cos ωt sin α + A₂ cos ωt sin β
= (A₁ cos α + A₂ cos β) sin ωt + (A₁ sin α + A₂sin β) cos ωt
Let A₁ cos α + A₂ cos β = R cos δ …. (1)
and A₁ sin α + A₂ sin β = R sin δ …. (2)
∴ x = R cos δ sin ωt + R sin δ cos ωt
∴ x = R cos(ωt + δ) ….. (3)

Equation (3), which gives the displacement of the particle, shows that the resultant motion is also simple harmonic, along the same path as the SHMs superposed, with the same mean position, and amplitude R and initial phase δ but having the same period as the individual SHMs.

Amplitude R of the resultant motion : The resultant amplitude R is found by squaring and adding Eqs. (1) and (2).
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 38
Initial phase S of the resultant motion : The initial phase of the resultant motion is found by dividing Eq. (2) by Eq. (1).

Notes :

Since the displacements due to the super-posed linear SHMs are along the same path, their vector sum can be replaced by the algebraic sum.
To determine δ uniquely, we need to know both sin δ and cos δ.

Question 29.
Solve the following :

Question 1.
Two parallel SHMs are given by x₁ = 20 sin (8πt) cm and x₂ = 10 sin (8πt + π/2) cm. Find the amplitude and the epoch of the resultant SHM.
Solution :
Data : x₁ = 20 sin (8πt) cm = A₁ sin (ωt + α), x₂ = 10 sin (8πt + π/2) cm = A₂ sin (ωt + β)
∴ A₁ = 20 cm, A₂ = 10 cm, α = 0, β = π/2
(1) Resultant amplitude,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 40

(2) Initial phase of resultant SHM,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 41

Question 2.
The displacement of a particle performing SHM is given by x = [5 sin πt + 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\) cm. Determine the amplitude, period and initial phase of the motion.
Solution :
Data : x = [5 sin πt + 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\)] cm
The given expression for displacement may be written as the superposition of two parallel SHMs of the same period as x = x₁ + x₂, where x₁ = 5 sin πt cm = A₁ sin (ωt + α) and
x₂ = 12 sin \(\left(\pi t+\frac{\pi}{2}\right)\) cm = A₂ sin (ωt + β)
∴ A₁ = 5 cm, A₂ = 12 cm, ω = π rad/s, α = 0, β = \(\frac{\pi}{2}\) rad.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 42

Question 3.
An SHM is given by the equation x = [8 sin (4πt) + 6 cos (4πt)] cm. Find its
(1) amplitude
(2) initial phase
(3) period
(4) frequency.
Solution:
Data : x = [8 sin (4πt) + 6 cos (4πt)] cm
x = 8 sin (4πt) + 6 cos (4πt)
= 8 sin (4πt) + 6 sin \(\left(4 \pi t+\frac{\pi}{2}\right)\)
Thus, x is the superposition of two parallel SHMs of the same period : x = x₁ + x₂, where
x₁ = 8 sin (4πt) cm = A₁ sin (ωt + α) and
x₂ = 6 sin \(\left(4 \pi t+\frac{\pi}{2}\right)\) = A₂ sin (ωt + β)
∴ A₁ = 8 cm, A₂ = 6cm, ω = 4π rad/s, α = 0,
β = \(\frac{\pi}{2}\) rad
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 43

Question 30.
Show that the total energy of a particle performing linear SHM is directly proportional to
(1) the square of the amplitude
(2) the square of the frequency.
Answer:
For a particle of mass m executing SHM with angular frequency ω and amplitude A, its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)mω²(A² – x²) … (1)
and PE = \(\frac{1}{2}\)mω²x² … (2)
Then, the total energy,
E = PE + KE
= \(\frac{1}{2}\)mω²x² + \(\frac{1}{2}\)mω²(A² – x²)
= \(\frac{1}{2}\)mω²A² …. (3)
Therefore, total energy of the particle is

directly proportional to the mass (E ∝ m),
directly proportional to the square of the amplitude (E ∝ A²)
proportional to the square of the frequency
(E ∝f²), as f = ω/2π

Question 31.
State the expression for the total energy of SHM in terms of acceleration.
Answer:
The total energy of a particle of mass m performing SHM with angular frequency ω, E = \(\frac{1}{2}\)mω²A²
The maximum acceleration of the particle, a_max = ω²A²
E = \(\frac{1}{2}\) mAa_max is the required expression.

Question 32.
State the expressions for the kinetic energy and potential energy of a particle performing SHM. Find their values at
(i) an extreme position
(ii) the mean position.
Using the expressions for the kinetic energy and potential energy of a particle in simple harmonic motion at any position, show that
(i) at the mean position, total energy = kinetic energy
(ii) at an extreme position, total energy = potential energy.
Answer:
For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency ω = \(\sqrt{k / m}\), its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)k(A² – x²) and
PE = \(\frac{1}{2}\)kx²
and total energy, E = \(\frac{1}{2}\)kA²
(i) At the mean position, x = 0,
KE = \(\frac{1}{2}\)kA² = E and PE = 0

(ii) At an extreme position, x = ±A, KE = 0 and PE = \(\frac{1}{2}\)kA² = E

That is, the energy transfers back and forth between kinetic energy and potential energy, while the total mechanical energy of the oscillating particle remains constant. The total energy is entirely kinetic energy at the mean position and entirely potential energy at the extremes.

Question 33.
State the expressions for the kinetic energy (KE) and potential energy (PE) at a displacement x for a particle performing linear SHM. Find
(i) the displacement at which KE is equal to PE
(ii) the KE and PE when the particle is halfway to a extreme position.
Answer:
For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency ω = \(\sqrt{k / m}\), its kinetic and potential energies are respectively,
KE = \(\frac{1}{2}\)E (A² – x²) and
PE = \(\frac{1}{2}\)kx²
and total energy, E = \(\frac{1}{2}\)kA²
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 44
∴ At x = ±\(\frac{A}{2}\), the energy is 25% potential energy and 75% kinetic energy.

Question 34.
The maximum potential energy (PE) of a particle in SHM is 2 × 10^-4 J. What will be the PE of the particle when its displacement from the mean position is half the amplitude of SHM ?
Answer:
(PE)_max = \(\frac{1}{2}\)kA², PE = \(\frac{1}{2}\)kx²
∴ PE = (PE)_max \(\left(\frac{x}{A}\right)^{2}\) = 2 × 10^-4J × \(\left(\frac{1}{2}\right)^{2}\)
= 5 × 10^-5 J is the required answer.

Question 35.
A particle performs linear SHM of amplitude 10 cm. At what displacement of the particle from its mean position will the potential energy (PE) of the particle be 1 % of the maximum PE ?
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 45

Question 36.
Represent graphically the variations of KE, PE and TE of a particle performing linear SHM with respect to its displacement.
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 46

Question 37.
Represent graphically the variation of potential energy, kinetic energy and total energy of a particle performing SHM with time.
Answer:
Consider a particle performing SHM, with amplitude A and period T = \(\frac{2 \pi}{\omega}\) starting from the mean position towards the positive extreme position; ω = \(\sqrt{\frac{k}{m}}\) is the appropriate constant related to the system. The total energy of the particle is E = \(\frac{1}{2}\)kA². Its displacement (x), potential energy (PE) and kinetic energy (KE) at any instant are given by
x = A sin ωt
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 47
Using the values in the table, we can plot graphs of PE, KE and total energy with times as follows:

Question 38.
Solve the following :

Question 1.
A particle of mass 10 g is performing SHM. Its kinetic energies are 4.7 J and 4.6 J when the displacements are 4 cm and 6 cm, respectively. Compute the period of oscillation.
Answer:
Data : m = 0.01 kg, KE₁ = 4.7 J, x₁ = 4 × 10^-2 m, KE₂ = 4.6 J, x₂ = 6 × 10^-2 m
Since the total energy of a particle in SHM is constant,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 49

Question 2.
The total energy of a particle of mass 100 grams performing SHM is 0.2 J. Find its maximum velocity and period if the amplitude is 2\(\sqrt{2}\) cm.
Solution :
Data : m = 100 g = 0.1 kg, E = 0.2 J,
A = 2\(\sqrt{2}\) cm = 2\(\sqrt{2}\) × 10^-2 m
(i) The total energy,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 50

Question 3.
An object of mass 0.5 kg performs SHM with force constant 10 N/m and amplitude 3 cm.
(i) What is the total energy of the object?
(ii) What is its maximum speed ?
(iii) What is its speed at x = 2 cm?
(iv) What are its kinetic and potential energies at x = 2 cm ?
Solution :
Data : m = 0.5 kg, A: = 10 N/m,
A = 3 cm = 3 × 10^-2m, x = 2 cm = 2 × 10^-2m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 51

Question 4.
When the displacement in SHM is one-third of the amplitude, what fraction of the total energy is potential and what fraction is kinetic?
Solution :
Data : x = A/3
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 52
Therefore, \(\frac{1}{9}\) th of the total energy is potential and \(\frac{8}{9}\)th of the total energy is kinetic.

Question 5.
A particle executes SHM with a period of 8 s. Find the time in which half the total energy is potential.
Solution :
Data : T = 8 s, PE = \(\frac{1}{2}\)E
ω = \(\frac{2 \pi}{T}\) = \(\frac{2 \pi}{8}\) = \(\frac{\pi}{4}\) rad/s
The total energy, E = \(\frac{1}{2}\)kA² and the potential
energy = \(\frac{1}{2}\)kx²
Therefore, from the data,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 53
Assuming that the particle starts from the mean position, the equation of motion is
x = A sin ωt

Therefore, in one oscillation, the particle’s potential energy is half the total energy 1 s, 3 s, 5 s and 7 s after passing through the mean position.

Question 39.
Define practical simple pendulum.
Answer:
Practical simple pendulum is defined as a small heavy sphere, called the bob, suspended by a light and inextensible string from a rigid support.

Question 40.
Under what conditions can we consider the oscillations of a simple pendulum to be linear simple harmonic?
Answer:
The oscillations of a simple pendulum are approximately linear simple harmonic only if

the amplitude of oscillation is very small compared to its length
the oscillations are in a single vertical plane.

Question 41.
What is the effect of mass and amplitude on the period of a simple pendulum ?
Answer:
The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum. This is the law of mass.
The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small. This is the law of isochronism. If the amplitude is large, the motion is periodic but not simple harmonic.

Question 42.
From the definition of linear SHM, derive an expression for the angular frequency of a body performing linear SHM.
Answer:
When a body of mass m performs linear SHM, the restoring force on it is always directed towards the mean position and its magnitude is directly proportional to the magnitude of the displacement of the body from the mean position. Thus, if \(\vec{F}\) is the force acting on the body when its displacement from the mean position is \(\vec{x}\),
\(\vec{F}\) = m\(\vec{a}\) = – kx\(\vec{x}\)
where the constant k, the force per unit displacement, is called the force constant.
Let \(\frac{k}{m}\) = ω², a constant.
∴ Acceleration, a = –\(\frac{k}{m}\) = – ω²x
∴ The angular frequency,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 55

Question 43.
A simple pendulum is set into oscillations in a uniformly travelling car along a horizontal road. What happens to its period if the car takes a sudden turn towards the left ?
Answer:
The equilibrium position of the string makes an angle θ = tan^-1(a_c/g) with the vertical due to the centrifugal force to the right.
The centripetal acceleration, a_c, is horizontal and towards the left. The acceleration due to gravity is vertically downward.
∴ g_eff = \(\sqrt{g^{2}+a_{\mathrm{c}}^{2}}\)
so that the period of oscillation T = \(2 \pi \sqrt{L / g_{\text {eff }}}\)
∴ As the car takes a sudden left turn, the period of oscillation decreases.

Question 44.
Define a seconds pendulum. Find an expression for its length at a given place. Show that the length of a seconds pendulum has a fixed value at a given place.
Answer:
(1) Seconds pendulum: A simple pendulum of period two seconds is called a seconds pendulum.

(2) The period of a simple pendulum is
T = \(2 \pi \sqrt{\frac{L}{g}}\)
For a seconds pendulum, T = 2s.
∴ 2 = \(2 \pi \sqrt{\frac{L}{g}}\) ∴ L = \(\frac{g}{\pi^{2}}\)
This expression gives the length of the seconds pendulum at a place where acceleration due to gravity is g.

(3) At a given place, the value of g is constant.
∴ L = g/π² = a fixed value, at a given place.

[Note : Because the effective gravitational acceleration varies from place to place, the length of a seconds pendulum should be changed in direct proportion. Since the effective gravitational acceleration increases from the equator to the poles, so should the length of a seconds pendulum be increased.]

Question 45.
Two simple pendulums have lengths in the ratio 1 : 9. What is the ratio of their periods at a given place ?
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 56

Question 46.
If the length of a seconds pendulum is doubled, what will be the new period?
Answer:
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 57

Question 47.
Distinguish between a simple pendulum and a conical pendulum.
Answer:

Simple pendulum	Conical pendulum
1. The oscillations of the bob are in a vertical plane.	1. The bob performs UCM in a horizontal plane and the string traces out a cone of constant semivertical angle.
2. The energy of the bob transfers back and forth between kinetic energy and potential energy, while its total mechanical energy remains constant.	2. The gravitational PE of the bob being constant may be taken to be zero. The total mechanical energy remains constant and is entirely kinetic.
3. The period depends on the 3. length of the string and the acceleration due to gravity. T =2π\(\sqrt{L / g}\)	3. The period depends on the length of the string, the acceleration due to gravity and cosine of the semivertical angle. T =2π\(\sqrt{L \cos \theta / g}\)

Question 48.
Solve the following.

Question 1.
A simple pendulum of length 1 m has a bob of mass 10 g and oscillates freely with an amplitude of 2 cm. Find its potential energy at the extreme position. [g = 9.8 m/s²]
Solution :
Data : L = 1 m, m = 10 g = 10 × 10^-3 kg = 10^-2 kg, g = 9.8 m/s², A = 2 cm = 0.02 m
Period of a simple pendulum, T = \(2 \pi \sqrt{\frac{L}{g}}\)
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 58

Question 2.
The period of oscillation of a simple pendulum increases by 20% when the length of the pendulum is increased by 44 cm. Find its
(i) initial length
(ii) initial period of oscillation at a place where g is 9.8 m/s².
Solution:
Let T and L be the initial period and length of the pendulum. Let T₁ and L₁ be the final period and length.
Data : T₁ = T + 0.2 T = 1.2 T, L₁ = L + 0.44 m
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 59
Squaring and cross-multiplying, we get,
L + 0.44 = 1.44 L
∴ 0. 44 L = 0.44
∴ L = \(\frac{0.44}{0.44}\) = 1 m
∴ T = 2π\(\sqrt{\frac{L}{g}}\) = 2 × 3.142 × \(\sqrt{\frac{1}{9.8}}\)
= 2.007 s

Question 3.
Calculate the length of a seconds pendulum at a place where g = 9.81 m/s².
Answer:
Data : T = 2 s, g = 9.81 m/s²
Period of a simple pendulum, T = \(2 \pi \sqrt{\frac{L}{g}}\)
For a seconds pendulum, 2 = \(2 \pi \sqrt{\frac{L}{g}}\)
∴ The length of the seconds pendulum,
L = \(\frac{g}{\pi^{2}}\) = \(\frac{9.81}{(3.142)^{2}}\) = 0.9937

Question 4.
A clock regulated by a seconds pendulum keeps correct time. During summer the length of the pendulum increases to 1.01 m. How much will the clock gain or lose in one day ? [g = 9.8 m/s²]
Solution:
Data: L = 1.01 m, g = 9.8 m/s²
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 60
The period of a seconds pendulum is 2 seconds. Hence, the given pendulum clock will lose 0.017 s in 2.017 s during summer.
∴ Time lost in 24 hours
= \(\frac{24 \times 3600 \times 0.017}{2.017}\)s = 728.1 s
The given pendulum clock will lose 728.1 seconds per day during summer.

Question 5.
A small drop of mercury oscillates simple harmonically inside a watch glass whose radius of curvature is 2.5 m. Find the period of the motion. [g = 9.8m/s²]
Solution :
Data : R = 2.5 m, g = 9.8 m/s²
Consider a small drop of mercury on a watch glass of radius of curvature R.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 61
Away from its equilibrium position O, its weight \(m \vec{g}\) is resolved into two perpendicular components : mg cos θ normal to the concave surface and mg sin θ tangential to the surface, mg cos θ is balanced by the normal reaction (\(\vec{N}\)) of the surface while mg sin θ constitutes the restoring force that brings the drop back to O. If θ is small and in radian,
restoring force, F = ma = – mg sin θ
= – mg θ
= -mg\(\frac{x}{R}\)
∴ The acceleration per unit displacement, |\(\frac{a}{x}\)| = \(\frac{g}{R}\)
∴ The period of the motion, T = \(\frac{2 \pi}{\sqrt{|a / x|}}\) = \(2 \pi \sqrt{\frac{R}{g}}\)
Data : R = 2.5 m, g = 9.8 m/s²
∴ The period of oscillation is
T = 2 × 3.142\(\sqrt{\frac{2.5}{9.8}}\) = 6.284 × 0.5051 = 3.174 s.

Question 49.
Explain angular or torsional oscillations.
Hence obtain the differential equation of the motion.
Answer:
Suppose a disc is suspended from its centre by a wire or a twistless thread such that the disc remains horizontal, as shown in below figure. The rest position of
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 62
the disc is marked by a reference line. When the disc is rotated in the horizontal plane by a small angular displacement 0 = 0m from its rest position (θ = θ_m), the suspension wire is twisted. When the disc is released, it oscillates about the rest position in angular or torsional oscillation with angular amplitude θ_m.

The device is called a torsional pendulum and the springiness or elasticity of the motion is associated with the twisting of the suspension wire. The twist in either direction stores potential energy in the wire and provides an alternating restoring torque, opposite in direction to the angular displacement. The motion is governed by this torque.

If the magnitude of the restoring torque (τ) is proportional to the angular displacement (θ), τ ∝ (-θ) or τ = – cθ … (1)
where the constant of proportionality c is called the torsion constant, that depends on the length, diameter and material of the suspension wire. In this case, the oscillations will be simple harmonic.

Let I be the moment of inertia (MI) of the oscillating disc.
Torque = MI × angular acceleration
τ = Iα = I\(\frac{d^{2} \theta}{d t^{2}}\)
Hence, from EQ. (1),
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 63
This is the differential equation of angular SHM.
[Note : Angular displacement being a dimensionless quantity, the SI unit of torsion constant is the same as that of torque = the newton-metre (N-m)]

Question 50.
Define angular SHM. State the differential equation of angular SHM. Hence derive an expression for the period of angular SHM in terms of
(i) the torsion constant
(ii) the angular acceleration.
Answer:
Definition : Angular SHM is defined as the oscillatory motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.
The differential equation of angular SHM is
I\(\frac{d^{2} \theta}{d t^{2}}\) + c θ = 0 … (1)
where I = moment of inertia of the
where I = moment of inertia of the oscillating body,
\(\frac{d^{2} \theta}{d t^{2}}\) = angular acceleration of the body when its angular displacement is θ, and c = torsion constant of the suspension wire,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 64

Question 51.
Solve the following :

Question 1.
A bar magnet of moment 10 A.m² is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 39 μT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 10°.
Solution :
Data : μ = 10 A.m², Bh = 3.9 × 10^-5 T, θ = 10°
The magnitude of the torque is τ = – μB_h sin θ = (10)(3.9 × 10^-5) sin 10°
= (3.9 × 10^-4)(0.1736) = 6.770 × 10^-5 N.m

Question 2.
A disc, of radius 12 cm and mass 250 g, is suspended horizontally by a long wire at its centre. Its period T₁ of angular SHM is measured to be 8.43 s. An irregularly shaped object X is then hung from the same wire and its period T₂ is found to be 4.76 s. What is the rotational inertia of object X about its suspension axis ?
Solution:
Data : R = 0.12 m, M = 0.25 kg, T, = 8.43 s, T₂ = 4.76 s
The MI of the disc about the rotation axis (perpendicular through its centre) is = \(\frac{1}{2}\) MR²
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 65

Question 52.
What is meant by damped oscillations ? Draw a neat, labelled diagram of a damped spring-and-block oscillator.
Answer:
Oscillations of gradually decreasing amplitude are called damped oscillations. Oscillations of a system in the presence of dissipative frictional forces are damped.

The dissipative damping force removes energy from the system which requires external periodic force to continue.

Below Figure shows a spring-and-block oscillator attached with a light vane that moves in a fluid with viscosity. When the system is set into oscillation, the amplitude decreases for each oscillation due to the viscous drag on the vane.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 66

Question 53.
Write the differential equation of motion for an oscillator in the presence of a damping force directly proportional to the velocity. Under what condition is the motion oscillatory? Hence, discuss the frequency, amplitude and energy of the damped oscillations.
OR
Oscillations in the presence of a force proportional to the velocity are periodic but not simple harmonic. Explain.
OR
The presence of a damping force changes the character of a simple harmonic motion. Explain this qualitatively.
Answer:
Consider the oscillations of a body in the presence of a dissipative frictional force such as viscous drag or fluid friction. Such a force is proportional to the velocity of the body and is in a direction opposite to that of the velocity. If the fluid flow past the body is streamline, then by Stokes’ law, the resistive force is
f = -βv = -β\(\frac{d x}{d t}\)… (1)
where v = \(\frac{d x}{d t}\) is the velocity and β is a positive constant of proportionality called the damping constant.
The linear restoring force on the oscillator is F = -kx … (2)
where k is the force constant. If m is the mass of the oscillator and its acceleration is \(\frac{d^{2} x}{d t^{2}}\)
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 67
where ω² = \(\frac{k}{m}\). Equation (3) is the differential equation of the oscillator in presence of a resistive force directly proportional to the velocity.
The solution of the above differential equation obtained using standard mathematical technique is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 68
where constants A and φ can be determined in the usual way from the initial conditions. In writing this solution, it is assumed β is less than 2mω, i.e., the resistive term is relatively small.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 69
In Eq. (4),
(1) the harmonic term, cos \(\left[\sqrt{\omega^{2}-\frac{\beta^{2}}{2 m}} t+\phi\right]\), that the motion is oscillatory with angular frequency ω’ = \(\sqrt{\omega^{2}-\frac{\beta^{2}}{4 m^{2}}}\) if β is less than 2mω. The harmonic term can also be written in terms of a sine function with the same ω’.
(2) A’ = Ae^-(β/2m)t is the amplitude of the oscillation. The exponential factor e^-(β/2m)t steadily decreases the amplitude of the motion, making it approach zero for large t. Hence, the motion is said to be damped oscillation or damped harmonic motion.
(3) the total energy, \(\frac{1}{2}\)m(ω’)², decays exponentially with time as the amplitude decreases. The energy is dissipated in the form of heat by the damping force.
(4) the period of the damped oscillations is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 70
∴ T is greater than 2π/ω.
Thus, the motion is periodic but not simple harmonic because the amplitude steadily decreases.

Notes :

The energy decreases faster than the amplitude.
For β < 2mω, the larger the value of β, the faster the amplitude decreases. The condition is called underdamping.
When β = 2mω = \(2 \sqrt{k m}\) km, ω’ = 0, i.e., the system no longer oscillates. When displaced and released, it returns to its equilibrium position without oscillation. The condition is called critical damping.
If β > 2mω, the system is said to overdamped or dead beat. Again, the system does not oscillate but returns to equilibrium position more slowly than for critical damping.
All practical cases of so called free oscillations, such as that of a simple pendulum or a tuning fork, are damped. We also encounter damped oscillations in electrical circuits containing inductance, capacitance and resistance due to resistive losses. While in many cases it is desirable to minimize damping, in ammeters and voltmeters the oscillations of the pointer are designed to be dead beat.

Question 54.
Solve the following.

Question 1.
For a damped spring-and-block oscillator, the mass of the block is 0.2 kg, the spring constant is 90 N/m and the damping constant is 0.06 kg/s. Calculate
(i) the period of oscillation
(ii) the time taken for its amplitude to become half its initial value.
Solution :
Data : m = 0.2 kg, k = 90 N/m, β = 0.06 kg/s
(i) The period of the damped oscillation is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 71
(ii) The amplitude of the damped oscillation is
A’ = Ae^-(β/2m)t
If the amplitude becomes half the initial amplitude A at time f,

Question 2.
A steel sphere of mass 0.02 kg attains a terminal speed vi = 0.5 m/s when dropped into a tall cylinder of oil. The same sphere is then attached to the free end of an ideal vertical spring of spring constant 8 N/m. The sphere is immersed in the same oil and set into vertical oscillation. Find
(i) the damping constant
(ii) the angular frequency of the damped SHM.
(iii) Hence, write the equation for displacement of the damped SHM as a function of time, assuming that the initial amplitude is 10 cm. [g = 10 m/s²]
Solution :
Data : m = 0.02 kg, v_t = 0.5 m/s, k = 8 N/m,
A = 10 cm = 0.1 m, g = 10 m/s²
When the sphere falls with terminal velocity in oil, the resultant force on it is zero. Therefore, the
The equation of motion of the damped oscillation is resistive force and its weight are equal in magnitude and opposite in direction.
∴ |F_r| = βv_t = mg
where β is the damping constant.
∴ β = \(\frac{m g}{v_{\mathrm{t}}}\) = \(\frac{0.02 \times 10}{0.5}\) = 0.4 kg/s
The angular frequency of the damped oscillation in oil,
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 73
The equation of motion of the damped oscillation is
x = Ae^(β/2m)t cos(w’t + φ)
∴ x = (0.1 m)e^-(0.4/004)t cos (17.32t + φ)
x = (0.1 m) e^-10t cos(17.32t + φ)

Question 55.
Explain
(1) free vibrations
(2) forced vibrations.
Answer:
(1) Free vibrations : A body capable of vibrations is said to perform free vibrations when it is disturbed from its equilibrium position and left to itself.

In the absence of dissipative forces such as friction due to surrounding air and internal forces, the total energy and hence the amplitude of vibrations of the body remains constant. The frequencies of the free vibrations of a body are called its natural frequencies and depend on the body itself.

In the absence of a maintaining force, in practice, the total energy and hence the amplitude decreases due to dissipative forces and the vibration is said to be damped. The frequency of damped vibrations is less than the natural frequency.

(2) Forced vibrations : The vibrations of a body in response to an external periodic force are called forced vibrations.

The external force supplies the necessary energy to make up for the dissipative losses. The frequency of the forced vibrations is equal to the frequency of the external periodic force.

The amplitude of the forced vibrations depends upon the mass of the vibrating body, the amplitude of the external force, the difference between the natural frequency and the frequency of the periodic force, and the extent of damping.

Question 56.
Distinguish between free vibrations and forced vibrations.
Answer:

Free vibrations	Forced vibrations
1. Free vibrations are produced when a body is disturbed from its equilibrium position and released. Ex. Simple pendulum.	1. Forced vibrations are produced by an external periodic force. Ex. Musical instrument having a sounding board.
2. The frequency of free vibrations depends on the body and is called its natural frequency.	2. The frequency of forced vibrations is equal to that of the external periodic force.
3. The energy of the body remains constant only in the absence of friction, air resistance, etc.	3. The energy of the body is maintained constant by the external periodic force.

Question 57.
Explain resonance.
Answer:
Resonance : If a body is made to vibrate by an external periodic force, whose frequency is equal to the natural frequency (or nearly so) of the body, the body vibrates with maximum amplitude. This phenomenon is called resonance.

The corresponding frequency is called the resonant frequency.
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 74
For low damping, the amplitude of vibrations has a sharp maximum at resonance, as shown. The flatter curve without a pronounced maximum is for high damping.

Suppose several pendulums-A, B, C, D and E are coupled to a heavier pendulum Z, by suspending them from a stretched cord, and that only the length of C is the same as that of Z. When Z is set into oscillation perpendicular to the cord PQ, the others are also set into forced oscillations in parallel vertical planes. Their amplitudes vary but those of A, B, D and E never become very large because the frequency of Z is not the same as the natural frequency of any of them. On the other hand, C will be in resonant oscillation and its amplitude will be large.

Question 58.
The differential equation of SHM for a seconds pendulum is
(A) \(\frac{d^{2} x}{d t^{2}}\) + x = 0
(B) \(\frac{d^{2} x}{d t^{2}}\) + πx = 0
(C) \(\frac{d^{2} x}{d t^{2}}\) + 4πx = 0
(D) \(\frac{d^{2} x}{d t^{2}}\) + π²x = 0.
Answer:
(D) \(\frac{d^{2} x}{d t^{2}}\) + π²x = 0.

Question 59.
The phase change of a particle performing SHM between successive passages through the mean position is
(A) 2π rad
(B) π rad
(C) \(\frac{\pi}{2}\) rad
(D) \(\frac{\pi}{4}\) rad.
Answer:
(B) π rad

Question 60.
If the equation of motion of a particle performing SHM is x = 0.028 cos (2.8πt + π) (all quantities in SI units), the frequency of the motion is
(A) 0.7 Hz
(B) 1.4 Hz
(C) 2.8 Hz
(D) 14 Hz.
Answer:
(B) 1.4 Hz

Question 61.
A spring-and-block system constitutes a simple harmonic oscillator. To double the frequency of oscillation, the mass of the block must be ….. the initial mass.
(A) \(\frac{1}{4}\) times
(B) half
(C) double
(D) 4 times
Answer:
(A) \(\frac{1}{4}\) times

Question 62.
A horizontal spring-and-block system consists of a block of mass 1 kg, resting on a frictionless surface, and an ideal spring. A force of 10 N is required to compress the spring by 10 cm. The spring constant of the spring is
(A) 100 N.m^-1
(B) 10N.m^-1
(C) N.m^-1
(D) 0.1 N.m^-1.
Answer:
(C) N.m^-1

Question 63.
A vertical spring-and-block system has a block of mass 10 g and oscillates with a period 1 s. The period of SHM of a block of mass 90 g, suspended from the same spring, is
(A) \(\frac{1}{9}\)s
(B) \(\frac{1}{3}\)s
(C) 3 s
(D) 9 s.
Answer:
(C) 3 s

Question 64.
A simple harmonic oscillator has an amplitude A and period T. The time required by the oscillator to cover the distance from x = A to x = \(\frac{A}{2}\) is
(A) \(\frac{T}{2}\)
(B) \(\frac{T}{3}\)
(C) \(\frac{T}{4}\)
(D) \(\frac{T}{6}\)
Answer:
(D) \(\frac{T}{6}\)

Question 65.
The period of SHM of a particle with maximum velocity 50 cm/s and maximum acceleration 10 cm/s² is
(A) 31.42 s
(B) 6.284 s
(C) 3.142 s
(D) 0.3142 s.
Answer:
(C) 3.142 s

Question 66.
A particle executing SHM of amplitude 5 cm has an acceleration of 27 cm/s² when it is 3 cm from the mean position. Its maximum velocity is
(A) 15 cm/s
(B) 30 cm/s
(C) 45 cm/s
(D) 60 cm/s.
Answer:
(A) 15 cm/s

Question 67.
A particle performs linear SHM with a period of 6 s, starting from the positive extremity. At time t = 7 s, its displacement is 3 cm. The amplitude of the motion is
(A) 4 cm
(B) 6 cm
(C) 8 cm
(D) 12 cm.
Answer:
(B) 6 cm

Question 68.
A spring-and-block oscillator with an ideal spring of force constant 180 N/m oscillates with a frequency of 6 Hz. The mass of the block is, approximately,
(A) \(\frac{1}{8}\) kg
(B) \(\frac{1}{4}\) kg
(C) 4 kg
(D) 8 kg.
Answer:
(A) \(\frac{1}{8}\) kg

Question 69.
A particle executing linear SHM has velocities v₁ and v₂ at distances x₁ and x₂, respectively, from the mean position. The angular velocity of the particle is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 76
Answer:
(B) \(\sqrt{\frac{v_{2}^{2}-v_{1}^{2}}{x_{1}^{2}-x_{2}^{2}}}\)

Question 70.
A particle executes linear SHM with period 12 s. To traverse a distance equal to half its amplitude from the equilibrium position, it takes
(A) 6s
(B) 4s
(C) 2s
(D) 1s.
Answer:
(D) 1s

Question 71.
The minimum time taken by a particle in SHM with period T to go from an extreme position to a point half way to the equilibrium position is
A. \(\frac{T}{12}\)
B. \(\frac{T}{8}\)
C. \(\frac{T}{6}\)
D. \(\frac{T}{4}\)
Answer:
C. \(\frac{T}{6}\)

Question 72.
In simple harmonic motion, the acceleration of a particle is zero when its
(A) velocity is zero
(B) displacement is zero
(C) both velocity and displacement are zero
(D) both velocity and displacement are maximum.
Answer:
(B) displacement is zero

Question 73.
The acceleration of a particle performing SHM is 3m/s² at a distance of 3 cm from the mean position.
The periodic time of the motion is
(A) 0.02 π s
(B) 0.04 π s
(C) 0.2 π s
(D) 2 π s.
Answer:
(C) 0.2 π s

Question 74.
A particle performing linear SHM with a frequency n is confined within limits x = ±A. Midway between an extremity and the equilibrium position, its speed is
(A) \(\sqrt{6}\)nA
(B) \(\sqrt{3}\)πnA
(C) \(\sqrt{6}\)πnA
(D) \(\sqrt{12}\)πnA
Answer:
(B) \(\sqrt{3}\)πnA

Question 75.
The total energy of a particle executing SHM is proportional to
(A) the frequency of oscillation
(B) the square of the amplitude of motion
(C) the velocity at the equilibrium position
(D) the displacement from the equilibrium position.
Answer:
(B) the square of the amplitude of motion

Question 76.
Two spring-and-block oscillators oscillate harmonically with the same amplitude and a constant phase difference of 90°. Their maximum velocities are v and v + x. The value of x is
(A) 0
(B) \(\frac{v}{3}\)
(C) 2
(D) \(\frac{v}{\sqrt{2}}\).
Answer:
(A) 0

Question 77.
If the length of a simple pendulum is increased to 4 times its initial length, its frequency of oscillation will
(A) reduce to half its initial frequency
(B) increase to twice its initial frequency
(C) reduce to \(\frac{1}{4}\) th its initial frequency
(D) increase to 4 times its initial frequency.
Answer:
(A) reduce to half its initial frequency

Question 78.
If the length of a simple pendulum is doubled keeping its amplitude constant, its energy will be
(A) unchanged
(B) doubled
(C) halved
(D) increased to four times the initial energy.
Answer:
(C) halved

Question 79.
The amplitude of oscillations of a simple pendulum of period T and length L is increased by 5%. The new period of the pendulum will be
(A) T/8
(B) T/4
(C) T/2
(D) T.
Answer:
(D) T.

Question 80.
In 20 s, two simple pendulums, P and Q, complete 9 and 7 oscillations, respectively, on the Earth. On the
Moon, where the acceleration due to gravity is \(\frac{1}{6}\)th that on the Earth, their periods are in the ratio (A) 8 : 1
(B) 9 : 7
(C) 7 : 9
(D) 3 : 14.
Answer:
(C) 7 : 9

Question 81.
If T is the time period of a simple pendulum in an elevator at rest, its time period in a freely falling elevator will be
(A) \(\frac{T}{\sqrt{2}}\)
(B) \(\sqrt{2}\)T
(C) 2T
(D) infinite.
Answer:
(D) infinite.

Question 82.
A seconds pendulum is suspended in an elevator moving with a constant speed in the downward direction. The periodic time (T) of that pendulum is
(A) less than two seconds
(B) equal to two seconds
(C) greater than two seconds
(D) very much greater than two seconds.
Answer:
(B) equal to two seconds

Question 83.
The total work done by a restoring force in simple harmonic motion of amplitude A and angular frequency ω, in one oscillation is
(A) \(\frac{1}{2}\)mA²ω²
(B) zero
(C) mA²ω²
(D) \(\frac{1}{2}\)mAω.
Answer:
(B) zero

Question 84.
Two particles perform linear simple harmonic motion along the same path of length 2A and period T as shown in the graph below. The phase difference between them is
Maharashtra Board Class 12 Physics Important Questions Chapter 5 Oscillations Important Questions 77
(A) zero rad
(B) \(\frac{\pi}{4}\) rad
(C) \(\frac{\pi}{2}\) rad
(D) \(\frac{3 \pi}{4}\) rad
Answer:
(B) \(\frac{\pi}{4}\) rad

Question 85.
The average displacement over a period of SHM is
(A = amplitude of SHM)
(A) 0
(B) A
(C) 2A
(D) 4A.
Answer:
(A) 0

Question 86.
Two springs of force constants k₁ and k₂(k₁ > k₂) are stretched by the same force. If W₁ and W₂ be the work done in stretching the springs, then
(A) W₁ = W₂
(B) W₁ < W₂
(C) W₁ > W₂
(D) W₁ = W₂ = 0.
Answer:
(B) W₁ < W₂

Question 87.
Two bar magnets of identical size have magnetic moments M_A and M_B. If the magnet A oscillates at twice the frequency of magnet B, then
(A) M_A = 2M_B
(B) M_A = 8M_B
(C) M_A = 4M_B
(D) M_B = 8M_A.
Answer:
(C) M_A = 4M_B

Question 88.
A magnet is suspended to oscillate in the horizontal plane. It makes 20 oscillations per minute at a place where the dip angle is 30° and 15 oscillations per minute where the dip angle is 60°. The ratio of the Earth’s total magnetic field at the two places is
(A) 3\(\sqrt{3}\) : 16
(B) 16 : 9\(\sqrt{3}\)
(C) 4 : 9\(\sqrt{3}\)
(D) 9 : 16\(\sqrt{3}\).
Answer:
(B) 16 : 9\(\sqrt{3}\)

Maharashtra Board 12th OCM Important Questions Chapter 7 Consumer Protection

July 1, 2024June 30, 2024 by Prasanna

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 7 Consumer Protection Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 7 Consumer Protection

Select the correct options and rewrite the sentence

Question 1.
Any person who does not agree with the decision of the State Commission can appeal to the ……………….
(a) Supreme Court
(b) High Court
(c) National Commission
Answer:
(c) National Commission

Question 2.
Right to ………………… restricts monopolistic tendencies in the market.
(a) Information
(b) Choose
(c) Safety
Answer:
(b) Choose

Question 3.
………………. is referred to as ‘People’s Court.’
(a) Lok Adalat
(b) Public Interest Litigation
(c) Consumer Welfare Fund
Answer:
(a) Lok Adalat

Question 4.
State Consumer Dispute Redressal Commission is popularly known as ……………….
(a) National Commission
(b) State Commission
(c) District Forum
Answer:
(b) State Commission

Question 5.
……………… is the President of State Commission.
(a) District Court Judge
(b) Supreme Court Judge
(c) High Court Judge
Answer:
(c) High Court Judge

Question 6.
……………… is celebrated as ‘National Consumer Day’.
(a) 15th March
(b) 24th December
(c) 26th January
Answer:
(b) 24th December

Question 7.
National Commission entertains complaints where the values of goods or services paid as consideration exceeds Rs ………………..
(a) 50 lakh
(b) 1 crore
(c) 10 crore
Answer:
(c) 10 crore

Match the pairs

Question 1.

Group A	Group B
(A) District Judge	(1) 2019
(B) Right to Redressal	(2) Duty of seller
(C) Consumer Protection Act	(3) President of District Commission
(D) Creating Consumer Awareness	(4) Supreme Court
(E) Lok Adalat	(5) Seek legal remedy in the court
	(6) Use of media
	(7) Settlement of disputes by mutual compromise
	(8) 2010
	(9) President of National Commission
	(10) Selecting best quality product

Answer:

Group A	Group B
(A) District Judge	(3) President of District Commission
(B) Right to Redressal	(5) Seek legal remedy in the court
(C) Consumer Protection Act	(1) 2019
(D) Creating Consumer Awareness	(6) Use of media
(E) Lok Adalat	(7) Settlement of disputes by mutual compromise

Give one word/phrase/term for the following statement

Question 1.
The right of a consumer which allows him to express his views.
Answer:
Right to be Heard

Question 2.
The right of a consumer which creates an awareness in him about his rights.
Answer:
Right to Consumer Education

Question 3.
Non-profit and non-political independent groups working for a definite cause.
Answer:
Non-Government Organisations (NGOs)

Question 4.
The right which demands that inferior quality goods or defective products are not brought in the market at all.
Answer:
Right to Safety

Question 5.
The court established by Government to settle consumer disputes by mutual compromise.
Answer:
Lok Adalat/People’s Court.

State whether the following statements are True or False

Question 1.
The Consumer Protection Act was passed in the interest of the sellers.
Answer:
False

Question 2.
Order issued by District Forum on a complaint is final.
Answer:
False

Question 3.
24th December is observed as International Consumer Rights Day every year.
Answer:
False.

Find the odd one

Question 1.
Right to Safety, Right to Travel, Right to Information, Right to Choose.
Answer:
Right to Travel

Question 2.
Right to be Heard, Right to Represent, Right to Redress, Right to Adult Education.
Answer:
Right to Adult Education.

Complete the sentences

Question 1.
The primary objective of consumer movement is to protect ………………. rights.
Answer:
consumers

Question 2.
An appeal against the order of State Commission may be made to the National Commission within ………………. days.
Answer:
30

Question 3.
A District Commission shall be established by ………………..
Answer:
State Government.

Select the correct option and complete the following table

(High Court Judge, Four, Consumer Organisations, does not exceeds Rs one crore, 2019, created by the Department of Consumer Affairs, 15th March, Lok Adalat, Public Interest Litigation, 24th December)

Group A	Group B
1 Janahit Yachika	—————-
2. Consumer Welfare Fund	——————-

Answer:

Group A	Group B
1 Janahit Yachika	Public Interest Litigation
2. Consumer Welfare Fund	Created by the department of consumer Affairs.

Justify the following statements

Question 1.
Order issued by the District Commission on a complaint is final.
Answer:
(1) The main objective of the Consumer Protection Act, 1986 is expeditious and inexpensive settlement of consumer disputes. In order to achieve this objective, the Act provides the three tier quasi-judicial consumer disputes redressal machinery at district, state and national level.

(2) A consumer redressal agency established by the state government in each district to give relief or settle the disputes of consumers who complain against manufacturers or traders is called a ‘District Commission’. It consists of a president and two other members to be appointed by the state government.

(3) The District Commission has a jurisdiction over a particular district. As per amendments made to the Consumer Protection Act, 1986, it has the jurisdiction to entertain complaints where the value of goods or services, including compensation, if any, does not exceed Rs one crore.

(4) The justice or order given by the District Commission is binding on both the parties. However, if any person is not satisfied with the order of District Commission he can appeal against such order to the State Commission within 45 days of the order. Thus, order issued by the District Commission on a complaint is not final.

Question 2.
Lok Adalat can rightly be described as ‘People’s Court’.
Answer:
(1) Lok Adalat, i.e. People’s Court is established by the government to settle the disputes by compromise. It is a mock court held by the State authority, District authority, Supreme Court Legal Service Committee, High Court Legal Service Committee or Taluka Legal Service Committee.

(2) Lok Adalat accepts the cases pending in regular courts to settle them by compromise. For this, both the parties to the case should agree to transfer the case to Lok Adalat from regular court. Even on the application of one of the parties, the court transfers the case to Lok Adalat, if the court feels that there are chances for a compromise.

(3) In Lok Adalat, if a matter cannot be settled through a compromise, then it is returned to regular court. The order passed or resolution of disputes by Lok Adalat is given statutory recognition.

(4) Lok Adalat is one of the several ways to resolve the consumers’ problems or grievances. Some organisations such as Railways, MSEDCL, MSRTC, Telephone Exchanges, Insurance Companies in public sector regularly hold Lok Adalat to resolve consumers’ problems through compromise.

Maharashtra Board Class 12 Secretarial Practice Important Questions Chapter 10 Dividend and Interest

July 1, 2024June 30, 2024 by Bhagya

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 10 Dividend and Interest Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 10 Dividend and Interest

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Dividend is a part of ______________ distributed to the shareholders.
(a) Profit
(b) Reserve
(c) Unpaid Capital
Answer:
(a) Profit

Question 2.
Dividend is an income on investment in ______________
(a) Debentures
(b) Loan
(c) Shares
Answer:
(c) shares

Question 3.
Unpaid or Unclaimed dividend shall be transferred to ‘Investors Education and Protection Fund’ on expiry of ______________ years.
(a) Three
(b) Seven
(c) Five
Answer:
(b) Seven

Question 4.
The dividend declared between two Annual General Meetings is known as ______________ dividend.
(a) Interim
(b) Final
(c) Annual
Answer:
(a) Interim

Question 5.
The ______________ recommends the final dividend.
(a) Shareholders
(b) Board of Directors
(c) Promoters
Answer:
(b) Board of Directors

Question 6.
______________ is the dividend declared at the Annual General Meeting.
(a) Interim dividend
(b) Final dividend
(c) Unpaid dividend
Answer:
(b) Final Dividend

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Dividend coupon	(a) Return of investment of shareholders
(2) Dividend warrant	(b) Declared at Annual General Meeting
(3) Dividend	(c) Share certificate holder
(4) Final Dividend	(d) Share warrant holder
(5) Interim Dividend	(e) Return on debentures
	(f) Declared between two Annual General Meetings
	(g) Bonus Shares
	(h) Declared at an extraordinary general meeting
	(i) Special resolution
	(j) Debenture certificate holder

Answer:

Group ‘A’	Group ‘B’
(1) Dividend coupon	(d) Share warrant holder
(2) Dividend warrant	(c) Share certificate holder
(3) Dividend	(a) Return of investment of shareholders
(4) Final Dividend	(b) Declared at Annual General Meeting
(5) Interim Dividend	(f) Declared between two Annual General Meetings

Question 2.

Group ‘A’	Group ‘B’
(1) Interim dividend	(a) Cannot be paid in kind
(2) Dividend account	(b) Cannot be paid out of reserves
(3) Declaration of dividend	(c) Owners of the company
(4) Interest	(d) Board of Directors
(5) Listed Company	(e) Schedule Bank
	(f) Dividend as a per-share basis only
	(g) IEPF
	(h) Debenture holders
	(i) Rate of dividend is high
	(j) Shareholder’ approval

Answer:

Group ‘A’	Group ‘B’
(1) Interim dividend	(b) Cannot be paid out of reserves
(2) Dividend account	(e) Schedule Bank
(3) Declaration of dividend	(j) Shareholder’ approval
(4) Interest	(h) Debenture holders
(5) Listed Company	(f) Dividend as a per-share basis only

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
A dividend remaining unpaid to shareholders even after the expiry of 30 days of its declaration.
Answer:
Unpaid dividend

Question 2.
People who recommend the rate of dividend.
Answer:
Board of directors

1D. State whether the following statements are true or false.

Question 1.
The final dividend is paid on the actual profits that arrived after the closure of books of accounts.
Answer:
True

Question 2.
The interim dividend is declared before the preparation of the final accounts of the company.
Answer:
True

Question 3.
The higher the risk, the lower is the interest.
Answer:
False

Question 4.
Auditors’ opinions should be taken before declaring an Interim dividend.
Answer:
True

Question 5.
‘Unpaid Dividend Account’ is opened in a private Bank by the company.
Answer:
False

1E. Find the odd one.

Question 1.
Equity Shares, Preference Shares, Deposit Holders
Answer:
Deposit Holders

Question 2.
Interest, Dividend warrant, Dividend Mandate
Answer:
Interest

Question 3.
Unpaid/Unclaimed Account, IEPF, Deposits
Answer:
Deposits

Question 4.
ECS, NEFT, Cash
Answer:
Cash

1F. Complete the sentences.

Question 1.
Dividend can be paid out of ______________
Answer:
capital profits

Question 2.
Dividend which is approved by shareholders should pass ______________
Answer:
ordinary resolution

Question 3.
The dividend declared by company but not been paid or claimed by 9 shareholders is called ______________
Answer:
unpaid/ unclaimed dividend

Question 4.
Rate of interest is expressed as annual percentage of ______________
Answer:
principal

Question 5.
______________ is paid to the creditor of the company.
Answer:
Interest

Question 6.
Any amount in ‘Unpaid Dividend A/c’ for 7 years should be transferred to ______________
Answer:
IEPF

1G. Answer in one sentence.

Question 1.
Who declares the final dividend?
Answer:
The final dividend is declared by shareholders.

Question 2.
Which are the two types of dividend?
Answer:
The two types of dividends are (a) Interim and (b) Final.

Question 3.
Name the electronic mode of payment of dividends.
Answer:
The electronic mode of payment of dividends is ECS (Electronic Clearing Services), NEFT (National Electronic Fund Transfer).

Question 4.
What is the full form of IEPF?
Answer:
IEPF means Investors Education and Protection Fund.

1H. Correct the underlined word/s and rewrite the following sentences.

Question 1.
The dividend is payable in kind.
Answer:
The dividend is payable in cash.

Question 2.
Unclaimed/Unpaid dividends should be transferred to Dividend Account.
Answer:
Unclaimed/ Unpaid dividends should be transferred to Unpaid Dividend Account.

Question 3.
The interim dividend rate is higher than the Final Dividend.
Answer:
The interim dividend rate is lower than the Final Dividend.

Question 4.
The rate of dividend is expressed as an annual percentage of the principal.
Answer:
The rate of interest is expressed as the annual percentage of the principal.

Question 5.
Dividends cannot be declared out of reserves.
Answer:
A dividend cannot be declared out of capital.

Question 6.
The dividend is declared at the Board Meeting.
Answer:
The dividend is declared at the Annual General Meeting.

Question 7.
The dividend Mandate should be sent to the registered address of the shareholder.
Answer:
A dividend Warrant should be sent to the registered address of the shareholder

Question 8.
Interest is a charge on capital profits.
Answer:
Interest is a charge on profits.

Question 9.
Interest is paid to the owners of the company.
Answer:
The dividend is paid to the owners of the company.

1I. Arrange in Proper Order.

Question 1.
(a) Declaration of Dividend
(b) Sources of Dividend
(c) Payment of Dividend
Answer:
(a) Sources of dividend
(b) Declaration of Dividend
(c) Payment of Dividend

Question 2.
(a) Payment of dividend to shareholder’s banker
(b) Dividend Mandate
(c) Company authorizes
Answer:
(a) Dividend Mandate
(b) Company authorizes
(c) Payment of dividend to shareholder’s banker

2. Explain the following terms/concepts.

Question 1.
Dividend Warrant.
Answer:
It is an instrument sent by the company to the shareholder. It is a document that reflects shareholder is entitled to receive a dividend or not. It contains the name and address of the registered shareholder. In other words, it is the order of payment in which dividend is paid.

3. Study the following case/situation and express your opinion.

1. VMCL Co. Ltd. decides to pay the final dividend.

Question (a).
Is the rate of final dividend lower than interim dividend which is already paid by them?
Answer:
No, as the interim dividend is a part of the first half of the profit, its rate is lower than the final dividend.

Question (b).
Who has the authority to declare the final dividend?
Answer:
The Board of Directors has the authority to declare the final dividend.

Question (c).
Can it be paid out of capital profit?
Answer:
Yes, the final dividend can be paid out of capital profits, if it fulfills certain statutory conditions. For eg. Capital profits should be released in cash.

2. Mr. Dutch has given a loan to the VMCL Co.

Question (a).
What is Mr. Dutch to VMCL Co.?
Answer:
Mr. Dutch is the creditor for the VMCL Co.

Question (b).
What will Mr. Dutch receive in return?
Answer:
Mr. Dutch will receive interest in return.

Question (c).
Will Mr. Dutch receive interest even if the company is in loss?
Answer:
Yes, Mr. Dutch will receive interest even if the company incurs loss because it is not linked with profits or loss of the company.

3. Mr. B is the shareholder who wants to get dividend credited directly in his bank account.

Question (a).
What form is Mr. B required to fill to get the dividend credited directly into this account?
Answer:
“Dividend Mandate” is the prescribed form required to fill to get dividends credited directly into this account.

Question (b).
If Mr. B has sold his partial shares, will he receive the dividend?
Answer:
No, If Mr. B has sold his partial shares, he will be receiving dividend on the remaining shares.

Question (c).
What is the benefit of Dividend Mandate?
Answer:
The benefit of dividend mandate is it saves time, cost and efforts.

4. Answer in brief.

Question 1.
Explain different modes of payment of dividend.
Answer:
Dividend is either paid in cash or by cheque or warrant or by electronic mode. Dividend is paid to the shareholders. Following are the modes of payment of dividend:
(i) Dividend Warrant:
It is a cheque sent by a company to a shareholder for payment of dividend to the registered address of the shareholder.

(ii) Dividend Mandate:
A shareholder can also receive dividend directly in the bank account for which the shareholder has to send a request to the company in the prescribed form called ‘Dividend Mandate’. Dividend mandate authorizes the company to pay dividend directly to shareholder’s bank account.

(iii) Electronic Mode:
Company can also use electronic mode to pay dividends.
It is mandatory for the listed company to use electronic mode of payment approved by RBI such as ECS (Electronic Clearing Services), NEFT (National Electronic Fund Transfer).
Banks should also make necessary arrangements with other banks in collaboration for paying dividend through Dividend Warrants at par.

5. Justify the following statements.

Question 1.
Dividend cannot be paid on calls i.e. in advance.
Answer:

Dividend is an unconditional payment made out of company’s profit.
It is paid out of current profits or profits of the previous financial year.
Dividend once approved and declare by shareholders cannot be cancelled.
Once the Annual Accounts of previous year has been approved in AGM the dividend of the previous year cannot be declared.
Thus, it is rightly said that dividend cannot be paid on calls i.e. in advance.

Question 2.
Dividend can be declared even if a company suffers loss in that particular period.
Answer:

Dividend is paid out of company’s profit i.e. out of current profits, profit of any previous year, out of capital profits and money provided by central or state government.
Every year the company transfer part of its profit to different reserves.
Dividend may be declared from capital profit i.e. selling company’s assets.
Company may utilise accumulated profit and reserves in absence of profit.
Government also provides funds to company under certain schemes.
Thus, it is rightly said that dividend can be declared, even if a company suffers loss in that particular period.

Question 3.
The rate of interim dividend is lesser than final dividend.
Answer:

Final dividend is declared at the end of the financial year whereas Interim dividend is declared between two annual general meetings.
Interim dividend is declared when the company makes good profit in the first half of the financial year.
Interim dividend is declared twice in a year.
Hence the rate of dividend is lower than final dividend.
Thus, it is rightly said that the rate of interim dividend is lesser than final dividend. OR Interest is paid to the creditor of the company.

Question 4.
Payment of interest does not require the passing of a resolution at any meeting.
OR
Resolution need not be passed for payment of interest.
Answer:

Interest is the liability of the company.
It is to be paid to the creditors: of the company.
It is paid every year irrespective of the profits earned by the company every year. It is a charge on profit.
The rate of interest is fixed and pre-determined. Thus, it is rightly said that payment of interest does not require the passing of a resolution at any meeting. OR Resolution need not be passed for payment of interest.

6. Answer the following questions.

Question 1.
Explain legal provisions for the payment of dividends.
Answer:
The term dividend is derived from the Latin word ‘Dividendum’ which means that which is to be divided. A dividend is the portion of the company’s earnings distributed to the shareholders decided and managed by the company’s board of directors. Dividend is a share in distributable profits of the company. A shareholder is entitled to receive the dividend when it is formally declared by the company.

Legal provisions for payment of Dividend are as follows:

According to the provisions of Companies Act 2013, no dividend shall be payable except by way of cash.
Dividend can also be paid through cheque, warrant or by any electronic mode, to the shareholder.
In case of Joint holding of shares dividend, warrant should be sent to the registered address of the first-named joint shareholder as per the Register of Members or to the other joint shareholder whose name has been given to the company.
Company must pay dividend within 30 days from the date of its declaration.
Dividend is payable only to the registered shareholders of the company. Preference shareholders are entitled to receive the dividend before the equity shareholders as per the terms of issue of the preference share.
Dividend will be paid as per the statements furnished by the depository in case of shares held in electronic form. Whereas the shares held in the physical form, will receive dividend as per the names appearing in the Company’s Register of Members.
Default:
- Default is paying a dividend in the given time result in-
- Punishment to every Director of the company.
- Company will be liable to pay the interest at the rate of 12% p.a. till the default continues.

Question 2.
Explain the rules pertaining to the Unpaid/Unclaimed Account.
Answer:
Dividend declared by the company but neither paid to nor claimed by a shareholder within 30 days of its declaration is termed as Unpaid and Unclaimed Dividend. Following rules govern the Unpaid/Unclaimed Dividend:

Unpaid/’Unclaimed should be transferred to ‘Unpaid Dividend Account’ opened in a scheduled Bank by the company.
This transfer should be within 7 (seven) days of the end of 30 days within which payment was to be made. In other words, this transfer should happen within 37 (Thirty-seven) days from the declaration of dividend.
Within 90 (Ninety) days of the transfer of amount in the ‘Unpaid Dividend Account’, the company is required to publish a statement mentioning the name, address and unpaid amount payable to the shareholder. This statement is to be published on the company’s website or any other website approved by the Central Government.
If any person claims the dividend to the company after a long time, then the company is liable to pay the unpaid or unclaimed dividend to the person.
Any amount in the Unpaid Dividend Account of a company that remains unpaid/ unclaimed for a period of 7 (seven) years from the date of such a transfer shall be, transferred by the company to ‘Investors Education and Protection Fund (IEPF).
The claimant of money will have to follow the procedures and submit necessary documents to get a claim from IEPF.

7. Attempt the following.

Question 1.
Explain the legal provisions for the sources of dividends.
Answer:
The term dividend is derived from Latin word ‘Dividendum’ which means that which is to be divided. A dividend is the portion of the company’s earnings distributed to the shareholders decided and managed by the company’s board of directors.
Dividend is a share in distributable profits of the company. Shareholder is entitled to receive the dividend when it is formally declared by the company.

Legal provisions for the sources of dividend
(i) Company can pay dividend for the financial year out of the following:

Current Profits i.e. profits earned by the company for the current year, after providing for depreciation and transfer to Reserves.
Out of profits of the company of any previous financial year, after providing for depreciation.
The money provided by the Central or State Government to pay dividends.

(ii) Dividend can be paid out of Capital Profits:

Capital profits are realized in cash
It mentioned in Articles of Association of the company
It remains as profits after revaluation of all Assets and Liabilities.

(iii) Dividend cannot be paid out of Capital.

(iv) Dividend can be paid out of free reserves of the company.

Question 2.
Explain the legal provisions of the listed company regarding the declaration of dividends.
Answer:
When a company lists its shares on Stock Exchange, additional listing agreements are to be followed which are as follows:

Stock exchange should be informed. If the securities are listed 2 days prior to the Board meeting in which recommendation of final dividend is to be considered.
Stock Exchange should be informed immediately regarding the declaration of dividend as soon as the Board meeting gets over.
Notice of closing book should be informed at least 7 (seven) working days before the closure to the stock exchange.
Transfer Register and Register of Members should be closed.
Electronic Clearing Services (FCS) or National Electronic Fund Transfer (NEFT) mode should be used for the payment of dividends.
The listed company has to pay the dividend on a per-share basis only.