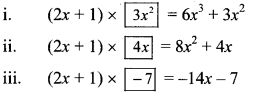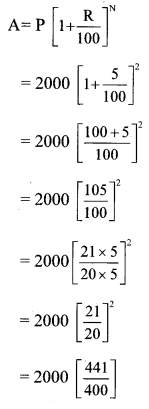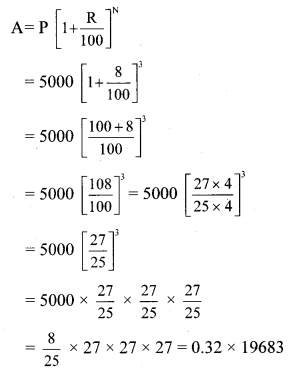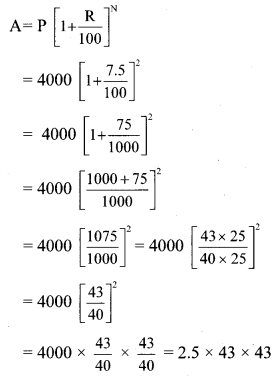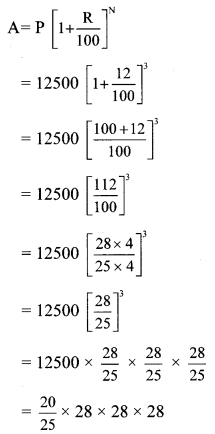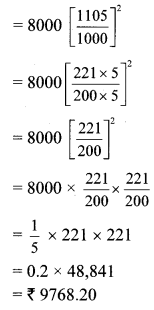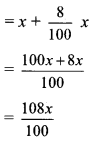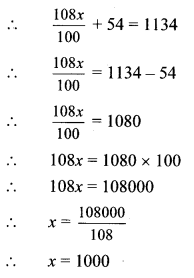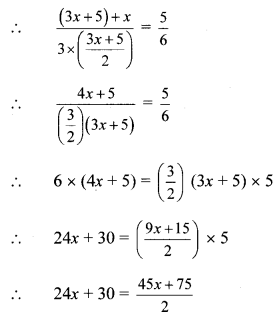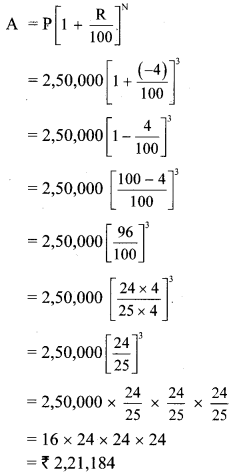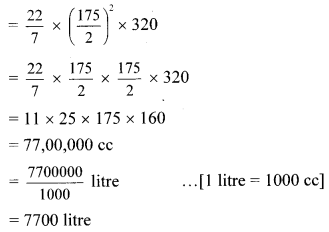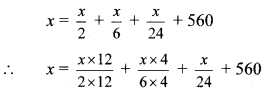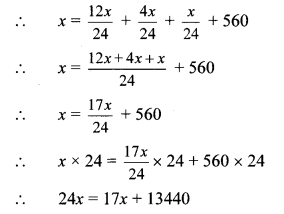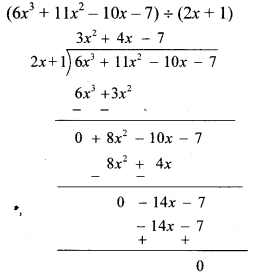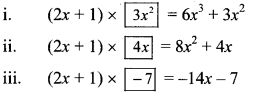Class 8

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.3 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.3 8th Std Maths Answers Chapter 15 Area

Question 1.
In the given figure, ☐ABCD is a trapezium, side AB || side DC, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area ☐ABCD.

Solution:
☐ABCD is a trapezium, side AB || side DC,
l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm,
Area of a trapezium = \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A (☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC)] x l(AD)
= \(\frac { 1 }{ 2 }\) x (13 + 9) x 8
= \(\frac { 1 }{ 2 }\) x 22 x 8
= 11 x 8
= 88 sq.cm
∴ The area of ☐ABCD is 88 sq. cm.
[Note: The question is modified.]

Question 2.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Solution:
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x (8.5 + 11.5) x 4.2
= \(\frac { 1 }{ 2 }\) x 20 x 4.2
= 10 x 4.2
= 42 sq. cm
∴ The area of the trapezium is 42 sq. cm.

Question 3.
☐PQRS is an isosceles trapezium. l(PQ) = 7 cm, seg PM ⊥ seg SR, l(SM) = 3 cm. Distance between two parallel sides is 4 cm, find the area of ☐PQRS.

Solution:
☐PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In ☐PMNQ,
seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ ☐PMNQ is a rectangle.

Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]² = [l(PM)]² + [l(SM)]² … [Pythagoras theorem]
∴ [l(PS)]² = (4)² + (3)²
∴ [l(PS)]² = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm
…[Taking square root of both sides]
☐PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]² = [l(QN)]² + [l(NR)]²
… [Pythagoras theorem]
∴ (5)² = (4)² + [l(NR)]²
∴ 25 = 16 + [l(NR)]²
∴ [l(NR)]² = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm
…[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3
= 13 cm
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐PQRS) = \(\frac { 1 }{ 2 }\) x [l(PQ) + l(SR)] x l(PM)
= \(\frac { 1 }{ 2 }\) x (7+ 13) x 4
= \(\frac { 1 }{ 2 }\) x 20 x 4
= 40 sq.cm
∴ The area of ☐PQRS is 40 sq. cm.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.2 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.2 8th Std Maths Answers Chapter 15 Area

Question 1.
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 15 cm and 24 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 15 × 24
= 15 × 12
= 180 sq.cm
∴ The area of the rhombus is 180 sq. cm.

Question 2.
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 16.5 × 14.2
= 16.5 × 7.1
= 117.15 sq cm
∴ The area of the rhombus is 117.15 sq. cm.

Question 3.
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution:
Let ₹ABCD be the rhombus. Diagonals AC and BD intersect at point E.

l(AC) = 48 cm …(i)
l(AE) = \(\frac { 1 }{ 2 }l(AC)\) …[Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) × 48 …[From (i)]
= 24 cm …(ii)
Perimeter of rhombus = 100 cm …[Given]
Perimeter of rhombus = 4 × side
∴ 100 = 4 × l(AD)
∴ l(AD) = \(\frac { 100 }{ 4 }\) = 25 cm …(iii)
In ∆ADE,
m∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
∴ [l(AD)]² = [l(AE)]² + [l(DE)]² … [Pythagoras theorem]
∴ (25)² = (24)² + l(DE)² … [From (ii) and (iii)]
∴ 625 = 576 + l(DE)²
∴ l(DE)² = 625 – 576
∴ l(DE)² = 49
∴ l(DE) = √49
… [Taking square root of both sides]
l(DE) = 7 cm …(iv)
l(DE) = \(\frac { 1 }{ 2 } l(BD)\) ….[Diagonals of a rhombus bisect each other]
∴ 7 = \(\frac { 1 }{ 2 } l(BD)\) …[From (iv)]
∴ l(BD) = 7 × 2
= 14 cm …(v)
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × l(AC) × l(BD)
= \(\frac { 1 }{ 2 }\) × 48 × 14 … [From (i) and (v)]
= 48 × 7
= 336 sq.cm
∴ The area of the quadrilateral is 336 sq.cm.

Question 4.
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq.cm, find its perimeter.
Solution:
Let ₹ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and A(₹ABCD) = 240 sq. cm .. .(ii)

Area of the rhombus = \(\frac { 1 }{ 2 }\) × product of lengths of diagonal
∴ 240 = \(\frac { 1 }{ 2 }\) × l(AC) x l(BD) …[From (ii)]
∴ 240 = \(\frac { 1 }{ 2 }\) × 30 × l(BD) …[From (i)]
∴ l(BD) = \(\frac { 240\times 2 }{ 30 }\)
∴ l(BD) = 8 × 2 = 16 cm …(iii)
Diagonals of a rhombus bisect each other.
∴ l(AE) = \(\frac { 1 }{ 2 }l(AC)\)
= \(\frac { 1 }{ 2 }\) × 30 … [From (i)]
= 15 cm …(iv)
and l(DE) = \(\frac { 1 }{ 2 }l(BD)\)
= \(\frac { 1 }{ 2 }\) × 16
= 8 cm
In ∆ADE,
m∠AED = 90°
…[Diagonals of a rhombus are perpendicular to each other]
∴[l(AD)]² = [l(AE)]² + [l(DE)]²
…[Pythagoras theorem]
∴l(AD)² = (15)² + (8)² … [From (iv) and (v)]
= 225 + 64
∴l(AD)² = 289
∴l(AD) = √289
…[Taking square root of both sides]
∴l(AD) = 17 cm
Perimeter of rhombus = 4 × side
= 4 × l(AD)
= 4 × 17
= 68 cm
∴The perimeter of the rhombus is 68 cm.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.1 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.1 8th Std Maths Answers Chapter 15 Area

Question 1.
If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
Solution:
Given, base = 18 cm, height = 11 cm
Area of a parallelogram = base × height
= 18 × 11
= 198 sq.cm
∴ Area of the parallelogram is 198 sq.cm.

Question 2.
If area of a parallelogram is 29.6 sq. cm and its base is 8 cm, find its height.
Solution:
Given, area of a parallelogram = 29.6 sq.cm,
base = 8 cm
Area of a parallelogram = base × height
∴ 29.6 = 8 × height
∴ height = \(\frac { 29.6 }{ 8 }\) = 3.7 cm
∴ Height of the parallelogram is 3.7 cm.

Question 3.
Area of a parallelogram is 83.2 sq.cm. If its height is 6.4 cm, find the length of its base.
Solution:
Given, area of a parallelogram = 83.2 sq.cm, height = 6.4 cm
Area of a parallelogram = base × height
∴ 83.2 = base × 6.4
∴ base = \(\frac { 83.2 }{ 6.4 }\) = 13 cm
∴ The length of the base of the parallelogram is 13 cm.

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.1 Intext Questions and Activities

Question 1.
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = base × height (Textbook pg. no.94)

Solution:
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = Area of a rectangle = length × breadth = base × height

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 14.1 8th Std Maths Answers Solutions Chapter 14 Compound Interest.

Practice Set 14.1 8th Std Maths Answers Chapter 14 Compound Interest

Practice Set 14.1 Class 8 Question 1.
Find the amount and the compound interest.

No	Principal (Rs)	Rate (p.c.p.a.)	Duration (years)
i.	2000	5	2
ii.	5000	8	3
iii.	4000	7.5	2

Solution:
i. Here P = Rs 2000, R = 5 p.c.p.a. and N = 2 years

= 5 × 441
∴ A = Rs 2205
I = Amount (A) – Principal (P)
= 2205 – 2000
= Rs 205
∴ The amount is Rs 2205 and the compound interest is Rs 205.

ii. Here, P = Rs 5000, R = 8 p.c.p.a. and N = 3 years

∴ A = Rs 6298.56
I = Amount (A) – Principal (P)
= 6298.56 – 5000
= Rs 1298.56
∴ The amount is Rs 6298.56 and the compound interest is Rs 1298.56.

iii. Here, P = Rs 4000, R = 7.5 p.c.p.a. and N = 2 years

∴A = Rs 4622.50
I = Amount (A) – Principal (P)
= 4622.50 – 4000
= Rs 622.50
∴The amount is Rs 4622.50 and the compound interest is Rs 622.50.

Compound Interest Practice Set 14.1 Question 2.
Sameerrao has taken a loan of Rs 12500 at the rate of 12 p.c.p.a. for 3 years. If the interest is compounded annually then how many rupees should he pay to clear his loan?
Solution:
Here, P = Rs 12,500, R = 12 p.c.p.a. and
N = 3 years

= 0.8 × 28 × 28 × 28
= Rs 17,561.60
Sameerrao should pay Rs 17,561.60 to clear his loan.

8th Standard Maths Practice Set 14.1 Question 3.
To start a business Shalaka has taken a loan of Rs 8000 at a rate of \(10\frac { 1 }{ 2 }\) p.c.p.a. After two years how much compound interest will she have to pay?
Solution:
Here, P = Rs 8000, N = 2 years and


I = Amount (A) – Principal (P)
= 9768.20 – 8000
= Rs 1768.20
∴ After two years Shalaka will have to pay Rs 1768.20 as compound interest.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.2 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Practice Set 12.2 8th Std Maths Answers Chapter 12 Equations in One Variable

Equation In One Variable Practice Set 12.2 Question 1.
Mother is 25 years older than her son. Find son’s age, if after 8 years ratio of son’s age to mother’s age will be \(\frac { 4 }{ 9 }\).
Solution:
Let the son’s present age be x years.
∴ Mother’s present age = (x + 25) years
After 8 years,
Son’s age = (x + 8) years
Mother’s age = (x + 25 + 8) = (x + 33) years
Since, the ratio of the son’s age to mother’s age after 8 years is \(\frac { 4 }{ 9 }\).
∴ \(\frac{x+8}{x+33}=\frac{4}{9}\)
∴ 9 (x + 8) = 4 (x + 33)
∴ 9x + 72 = 4x + 132
∴ 9x – 4x = 132 – 72
∴ 5x = 60
∴ x = \(\frac { 60 }{ 5 }\)
∴ x = 12
∴ Son’s present age is 12 years.

8th Std Maths Practice Set 12.2 Question 2.
The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent to \(\frac { 1 }{ 2 }\) . Find the fraction.
Solution:
Let the numerator of the fraction be x.
The denominator of a fraction is greater than its numerator by 12.
∴ Denominator of the fraction = (x + 12)
∴ The required fraction = \(\frac { x }{ x+12 }\)
For the new fraction,
numerator is decreased by 2.
∴ The new numerator = (x – 2)
Also, denominator is increased by 7.
∴ The new denominator = (x + 12) + 7
= (x + 19)
Since, the new fraction is equivalent to \(\frac { 1 }{ 2 }\).
∴ \(\frac{x-2}{x+19}=\frac{1}{2}\)
∴ 2(x – 2) = 1(x + 19)
∴ 2x – 4 = x + 19
∴ 2x – x = 19 + 4
∴ x = 23
∴ The required fraction = \(\frac{x}{x+12}=\frac{23}{23+12}=\frac{23}{35}\)
∴ The required fraction is \(\frac { 23 }{ 35 }\)

Practice Set 12.2 Class 8 Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.

∴ Weight of copper in the brass utensil = \(\left(\frac{13}{7} x\right)\) gm
The weight of the brass utensil = 700 gm
∴ \(\frac { 13 }{ 7 }x+x=700\)
∴ \(\frac { 13 }{ 7 }x\) x × 7 + x × 7 = 700 × 7
∴ 13x + 7x = 4900
∴ 20x = 4900
∴ \(x=\frac { 4900 }{ 20 }\)
∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Practice Set 12.2 8th Class Question 4.
Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let the three consecutive whole numbers be (x – 1), x and (x + 1).
∴ Sum of the three numbers
= (x – 1) + x + (x + 1)
= 3x
Given that, the sum of the three numbers is greater than 45 and less than 54.
When the sum of the three numbers is 45,
3x = 45
∴ x = \(\frac { 45 }{ 3 }\)
∴ x = 15
When the sum of the three numbers is 54,
∴ 3x = 54
∴ x = \(\frac { 54 }{ 3 }\)
∴ x = 18
∴ the value of x is greater than 15 and less than 18.
∴ the value of x is either 16 or 17

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17

Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.

Practice Set 12.2 8th Standard Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x

	Digit in units place	Digit in tens place	Number
Original Number	x	2x	(2x × 10) + x = 20x + x = 21x
New Number	2x	x	(x × 10) + 2x = 10x + 2x = 12x

Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = \(\frac { 66 }{ 33 }\)
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.

8th Standard Maths Practice Set 12.2 Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ \(x=\frac { 33000 }{ 300 }\)
∴ x = 110
∴ 110 tickets of Rs 100 were sold.

8th Maths Practice Set 12.2 Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.

Raju Sold A Bicycle to Amit at 8 Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x

Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134

∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Class 8 Maths Practice Set 12.2 Question 9.
A cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Let the number of runs required by the cricket player to score in the third match be x.
Number of runs scored by the player in first match = 180
Number of runs scored in second match = 257
∴ Total runs scored by the player = 180 + 257 + x = 437 + x
Average of runs in the three matches = \(\frac { 437+x }{ 3 }\)
Since, the average of runs should be 230.
\(\frac { 437+x }{ 3 }=230\)
∴ 437 + x = 230 × 3
∴ 437 + x = 690
∴ x = 690 – 437
∴ x = 253
∴ The cricket player should score 253 runs in the third match.

8th Class Math Practice Set 12.2 Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
∴ Anil’s present age = \(\left(\frac{3 x+5}{2}\right)\) years
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.

∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = \(\frac { 15 }{ 3 }\)
∴ x = 5
∴ Viru’s present age is 5 years.

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.2 Intext Questions and Activities

8th Math Practice Set 12.2 Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.1 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Practice Set 12.1 8th Std Maths Answers Chapter 12 Equations in One Variable

Equation in One Variable Practice Set 12.1 Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.

Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.

Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.

ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.

Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.

Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.

iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.

Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.

Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.

iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.

Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.

Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.

Practice Set 12.1 Question 2.
Solve the following equations:
i. 17p – 2 = 49
ii. 2m + 7 = 9
iii. 3x + 12 = 2x – 4
iv. 5 (x – 3) = 3 (x + 2)
v. \(\frac { 9x }{ 8 }+1=10\)
vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)
vii. 13x – 5 = \(\frac { 3 }{ 2 }\)
viii. 3 (y + 8) = 10 (y – 4) + 8
ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
x. \(\frac{y-4}{3}+3 y=4\)
xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51
∴ \(\frac{17 p}{17}=\frac{51}{17}\) …[Dividing both the sides by 17]
p = 3

ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2
∴ \(\frac{2 m}{2}=\frac{2}{2}\) [Dividing both the sides by 2]
∴ m = 1

iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16

iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21
∴ \(\frac{2 x}{2}=\frac{21}{2}\) …[Dividing both the sides by 2]
∴ \(x=\frac{21}{2}\)

v. \(\frac { 9x }{ 8 }+1=10\)

vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)

vii. 13x – 5 = \(\frac { 3 }{ 2 }\)

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56
∴ \(\frac{-7 y}{-7}=\frac{-56}{-7}\)…[Dividing both the sides by – 7]
∴ y = 8

ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
∴\(\frac{x-9}{x-5} \times 7(x-5)=\frac{5}{7} \times 7(x-5)\)
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38
∴\(\frac{2 x}{2}=\frac{38}{2}\) …[Dividing both the sides by 2]
∴x = 19

x. \(\frac{y-4}{3}+3 y=4\)
∴\(\frac{y-4}{3} \times 3+3 y \times 3=4 \times 3\)
…[Multiplying both the sides by 3]
∴y – 4 + 9y = 12
∴10y – 4 = 12
∴10y – 4 + 4=12 + 4
…[Adding 4 on both the sides]
∴10y = 16
∴\(\frac{10 y}{10}=\frac{16}{10}\)…[Dividing both the sides by 10]
∴y = \(\frac { 8 }{ 5 }\)

xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
∴\(\frac{b+(b+1)+(b+2)}{4} \times 4=21 \times 4\)
…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.1 Intext Questions and Activities

Std 8 Maths Practice Set 12.1 Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __

ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __

iii. [latex]\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × __ = 4 ×__
∴x = __

iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5

ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9

iii. \(\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12

iv. 4x = 24
∴ \(\frac{4 x}{[4]}=\frac{24}{[4]}\)
… [Dividing both the sides by 4]
∴x = 6

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.3 8th Std Maths Answers Solutions Chapter 11 Statistics.

Practice Set 11.3 8th Std Maths Answers Chapter 11 Statistics

Exercise 11.3 Class 8 Question 1.
Show the following information by a percentage bar graph.

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75

Solution:

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75
Percentage of students securing grade A	75%	60%	25%	20%
Percentage of students not securing grade A	25%	40%	75%	80%

Statistics for Class 8 Question 2.
Observe the following graph and answer the questions.

1. State the type of the bar graph.
2. How much percent is the Tur production to total production in Ajita’s farm?
3. Compare the production of Gram in the farms of Yash and Ravi and state whose percentage of production is more and by how much?
4. Whose percentage production of Tur is the least?
5. State production percentages of Tur and Gram in Sudha’s farm.

Solution:

1. The given graph is a percentage bar graph.
2. Percent of tur production to the total production in Ajita’s farm is 60%.
3. Production of Gram in the farm of Yash = 50%
   Production of Gram in the farm of Ravi = 30%
   ∴ Difference in the production = 50% – 30% =20%
   ∴ Yash’s production of Gram is more and by 20%.
4. Sudha’s percentage production of Tur is the least.
5. Production percentages of Tur and Gram in Sudha’s farm are 40% and 60% respectively.

8th Standard Statistics Question 3.
The following data is collected in a survey of some students of 10th standard from some schools. Draw the percentage bar graph of the data.

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24

Solution:

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24
Total number of students	150	80	50	40
Percentage of students having inclination towards science stream	60%	75%	50%	40%
Percentage of students having inclination towards commerce stream	40%	25%	50%	60%

Maharashtra Board Class 8 Maths Chapter 11 Statistics Practice Set 11.3 Intext Questions and Activities

Statistics 8th Class Question 1.
Compare and discuss a percentage bar diagram and a subdivided bar diagram. Use it to learn the graphs in the subjects like Science, Geography. (Textbook pg, no. 74)
Solution:
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.1 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.1 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
Show the following numbers on a number line. Draw a separate number line for each example.
i. \(\frac{3}{2}, \frac{5}{2},-\frac{3}{2}\)
ii. \(\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}\)
iii. \(\frac{-5}{8}, \frac{11}{8}\)
iv. \(\frac{13}{10}, \frac{-17}{10}\)
Solution:
i. \(\frac{3}{2}, \frac{5}{2},-\frac{3}{2}\)

Here, the denominator of each fraction is 2.
∴ Each unit will be divided into 2 equal parts.

ii. \(\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}\)

Here, the denominator of each fraction is 5.
∴ Each unit will be divided into 5 equal parts.

iii. \(\frac{-5}{8}, \frac{11}{8}\)

Here, the denominator of each fraction is 8.
∴ Each unit will be divided into 8 equal parts.

iv. \(\frac{13}{10}, \frac{-17}{10}\)

Here, the denominator of each fraction is 10.
∴ Each unit will be divided into 10 equal parts.

Question 2.
Observe the number line and answer the questions.

i. Which number is indicated by point B?
ii. Which point indicates the number \(1\frac { 3 }{ 4 }\) ?
iii. State whether the statement, ‘the point D denotes the number \(\frac { 5 }{ 2 }\) is true or false.
Solution:
Here, each emit is divided into 4 equal parts.
i. Point B is marked on the 10th equal part on the left side of O.
∴ The number indicated by point B is \(\frac { -10 }{ 4 }\).

ii.

Point C is marked on the 7th equal part on the right side of O.
∴ The number \(1\frac { 3 }{ 4 }\) is indicated by point C.

iii. True
Point D is marked on the 10th equal part on the right side of O.
∴ D denotes the number \(\frac{10}{4}=\frac{5 \times 2}{2 \times 2}=\frac{5}{2}\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Miscellaneous Exercise 2 8th Std Maths Answers Solutions.

Miscellaneous Exercise 2 8th Std Maths Answers

Question 1.
Questions and their alternative answers are given. Choose the correct alternative answer.
i. Find the circumference of a circle whose area is 1386 cm²? [Chapter 15]
(A) 132 cm²
(B) 132 cm
(C) 42 cm
(D) 21 cm²
Solution:
(B) 132 cm

Hint:
i. Area of the circle = πr²
1386 = \(\frac { 22 }{ 7 }\) x r²
r² = 1386 x \(\frac { 7 }{ 22 }\)
= 63 x 7
= 441
r = √441 … [Taking square root of both sides]
= 21 cm
Circumference of the circle = 2πr
= 2 x \(\frac { 22 }{ 7 }\) x 21
= 132 cm

ii. The side of a cube is 4 m. If it is doubled, how many times will be the volume of the new cube, as compared with the original cube? [Chapter 16]
(A) Two times
(B) Three times
(C) Four times
(D) Eight times
Solution:
(D) Eight times

Hint:
ii. Original volume = (4)³ = 64 cu.m
New side = 8 m
∴ New volume = (8)² = 512 cu.m
Now, \(\frac{\text { new volume }}{\text { original volume }}=\frac{512}{64}\) = 8
original volume 64
∴ volume of new cube will increase 8 times as compared to the volume of original cube.

Question 2.
Pranalee was practicing for a 100 m running race. She ran 100 m distance 20 times. The time required, in seconds, for each attempt was as follows. [Chapter 11]
18, 17, 17, 16,15, 16, 15, 14,16, 15, 15, 17, 15, 16,15, 17, 16, 15, 14,15
Find the mean of the time taken for running.
Solution:

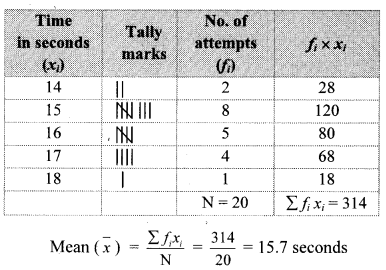
∴ The mean of the time taken for running 100 m race is 15.7 seconds.

Question 3.
∆DEF and ∆LMN are congruent in the correspondence EDF ↔ LMN. Write the pairs of congruent sides and congruent angles in the correspondence. [Chapter 13]
Solution:

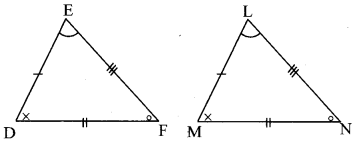
∆EDF ≅ ∆LMN
∴side ED ≅ side LM
side DF ≅ side MN
side EF ≅ side LN
∠E ≅∠L
∠D ≅∠M
∠F ≅∠N

Question 4.
The cost of a machine is Rs 2,50,000. It depreciates at the rate of 4% per annum. Find the cost of the machine after three years. [Chapter 14]
Solution:
Here, P = Cost of the machine = Rs 2,50,000
R = Rate of depreciation = 4%
N = 3 Years
A = Depreciated price of the machine

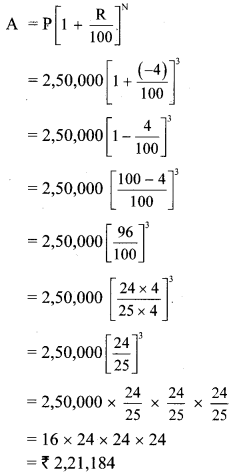
∴The cost of the machine after three years will be Rs 2,21,184.

Question 5.
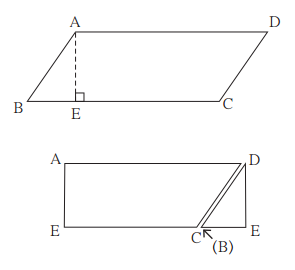
In ☐ABCD, side AB || side DC, seg AE ⊥ seg DC. If l(AB) = 9 cm, l(AE) = 10 cm, A(☐ABCD) = 115 cm² , find l(DC). [Chapter 15]
Solution:
Given, side AB || side DC.
∴ ☐ABCD is a trapezium.

Given, l(AB) = 9 cm, l(AE) = 10 cm,
A(☐ABCD) = 115 cm²
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC) x l(AE)]
∴ 115 = \(\frac { 1 }{ 2 }\) x [9 + l(DC)] x 10
∴ \(\frac { 115 \times 2 }{ 10 }\) = 9 + l(DC)
∴ 23 = 9 + l(DC)
∴ l(DC) = 23 – 9
∴ l(DC) = 14cm

Question 6.
The diameter and height of a cylindrical tank is 1.75 m and 3.2 m respectively. How much is the capacity of tank in litre?
[π = \(\frac { 22 }{ 7 }\)] [Chapter 16]
Solution:
Given: For cylindrical tank:
diameter (d) = 1.75 m, height (h) = 3.2 m
To Find: Capacity of tank in litre
diameter (d) = 1.75 m
= 1.75 x 100
….[∵ 1 m = 100cm]
= 175 cm
∴ radius (r) = \(=\frac{\mathrm{d}}{2}=\frac{175}{2}\) cm
h = 3.2 cm
= 3.2 x 100
= 320 cm
Capacity of tank = Volume of the cylindrical tank
= πr²h

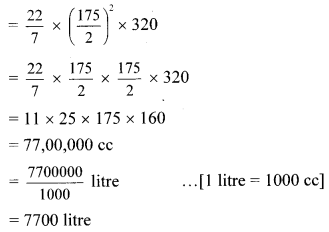
∴ The capacity of the tank is 7700 litre.

Question 7.
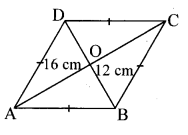
The length of a chord of a circle is 16.8 cm, radius is 9.1 cm. Find its distance from the centre. [Chapter 17]
Solution:

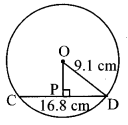
Let CD be the chord of the Circle with centre O.
Draw seg OP ⊥ chord CD
∴l(PD) = \(\frac { 1 }{ 2 }\) l(CD)
…[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(PD) = \(\frac { 1 }{ 2 }\) x 16.8 …[l(CD) = 16.8cm]
∴l(PD) = 8.4 cm …(i)
∴In ∆OPD, m∠OPD = 90°
∴[l(OD)]² = [l(OP)]² + [l(PD)]² …..[Pythagoras theorem]
∴(9.1)² = [l(OP)]² + (8.4)² … [From (i) and l(OD) = 9.1 cm]
∴(9.1)² – (8.4)² = [l(OP)]²
∴(9.1 + 8.4) (9.1 – 8.4) = [l(OP)]²
…[∵ a² – b² = (a + b) (a – b)]
∴17.5 x (0.7) = [l(OP)]²
∴12.25 = [l(OP)]²
i.e., [l(OP)]² = 12.25
∴l(OP) = √12.25
…[Taking square root of both sides]
∴l(OP) = 3.5 cm
∴The distance of the chord from the centre is 3.5 cm.

Question 8.
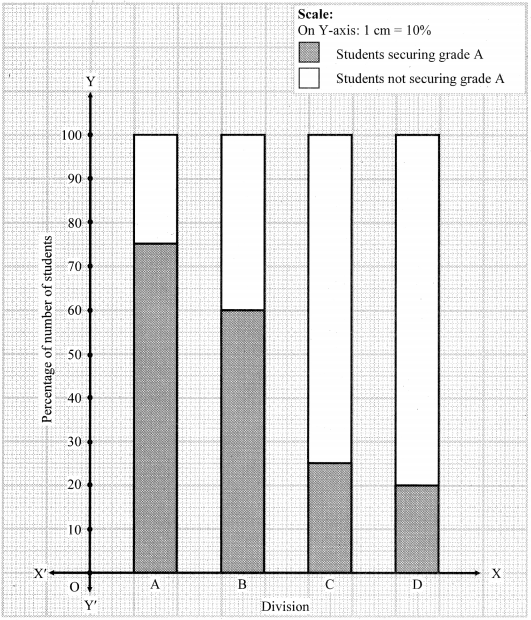
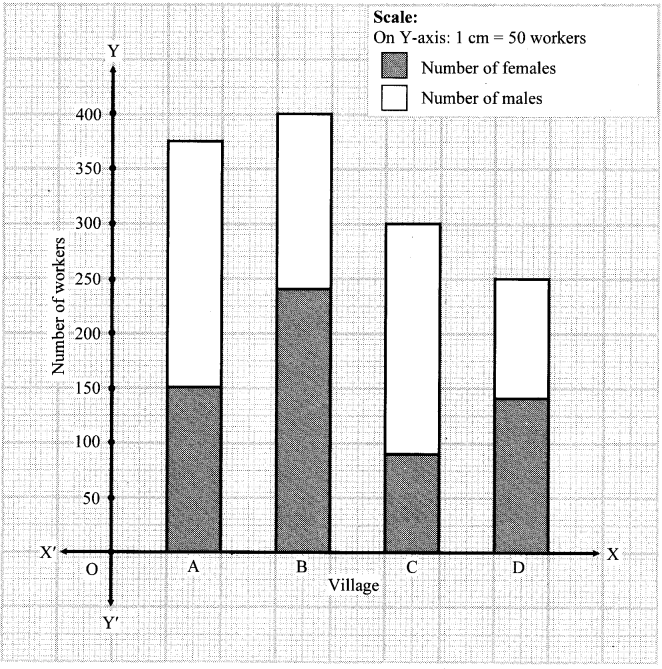
The following tables shows the number of male and female workers, under employment guarantee scheme, in villages A, B, C and D.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110

i. Show the information by a sub-divided bar-diagram.
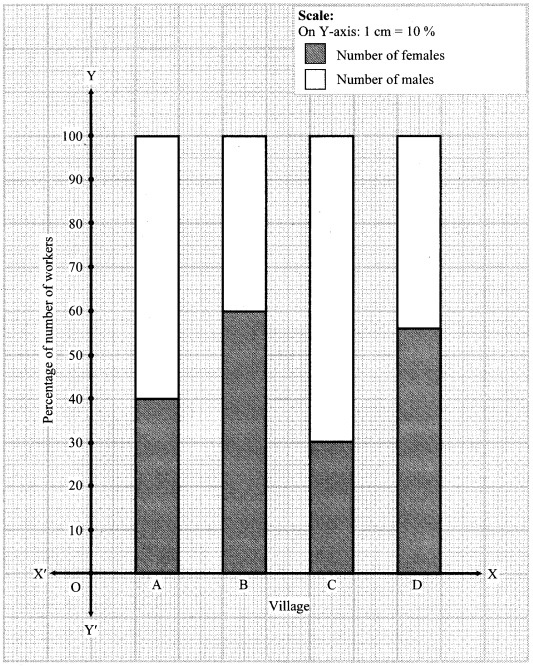
ii. Show the information by a percentage bar diagram. [Chapter 11]
Solution:
i.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250

ii.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250
Percentage of females	40%	60%	30%	56%
Percentage of males	60%	40%	70%	44%

Question 9.
Solve the following equations.
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
iii. 5(1 – 2x) = 9(1 -x)
[Chapter 12]
Solution:
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
∴ 17x + 68 + 8x + 48 = 11x + 55 + 15x + 45
∴ 17x + 8x + 68 + 48 = 11x + 15x + 55 + 45
∴ 25x + 116 = 26x + 100
∴ 25x + 116 – 116 = 26x + 100 – 116
… [Subtracting 116 from both the sides]
∴ 25x = 26x – 16
∴ 25x – 26x = 26x – 16 – 26x
… [Subtracting 26x from both the sides]
∴ -x = -16
∴ \(\frac{-x}{-1}=\frac{-16}{-1}\)
∴ x = 16

ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{3 y \times 2}{2 \times 2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4} \times 4+\frac{y+4}{4} \times 4=5 \times 4-\frac{y-2}{4} \times 4\)
……[Multiplying both the sides by 4]
∴ 6y + y + 4 = 20 – (y – 2)
∴ 7y + 4 = 20 – y + 2
∴ 7y + 4 = 22 – y
∴ 7y + 4 – 4 = 22 – y – 4
…..[Subtracting 4 from both the sides]
∴ 7y = 18 – y
∴ 7y + y = 18 – y + y
…[Adding y on both the sides]
∴ 8y = 18
∴ \(\frac{8 y}{8}=\frac{18}{8}\) … [Dividing both the sides by 8]
∴ \(y=\frac { 9 }{ 4 }\)

iii. 5(1 – 2x) = 9(1 – x)
∴ 5 – 10x = 9 – 9x
∴ 5 – 10x – 5 = 9 – 9x – 5
….[Subtracting 5 from both the sides]
∴ -10x = 4 – 9x
∴ -10x + 9x = 4 – 9x + 9x
… [Adding 9x on both the sides]
∴ -x = 4
∴ -x x (- 1) = 4 x (- 1)
… [Multiplying both the sides by – 1]
∴ x = – 4

Question 10.
Complete the activity according to the given steps.
i. Draw rhombus ABCD. Draw diagonal AC.
ii. Show the congruent parts in the figure by identical marks.
iii. State by which, test and in which correspondence ∆ADC and ∆ABC are congruent.
iv. Give reason to show ∠DCA ≅ ∠BCA, and ∠DAC ≅ ∠BAC
v. State which property of a rhombus is revealed from the above steps. [Chapter 13]
Solution:
a.

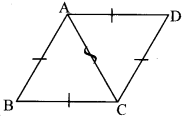
b. In ∆ADC and ∆ABC,
side AD ≅ side AB …..[Sides of a rhombus]
side DC ≅ side BC …..[Sides of a rhombus]
side AC ≅ side AC … [Common side]
∆ADC ≅ ∆ABC … [By SSS test]
∠DCA ≅ ∠BCA …[Corresponding angles of congruent triangles]
∠DAC ≅ ∠BAC …[Corresponding angles of congruent triangles]
From the above steps, property of rhombus revealed is ‘diagonal of a rhombus bisect the opposite angles’.

Question 11.
The shape of a farm is a quadrilateral. Measurements taken of the farm, by naming its corners as P, Q, R, S in order are as follows. l(PQ) = 170 m,
l(QR) = 250 m, l(RS) = 100 m, l(PS) = 240 m, l(PR) = 260 m.
Find the area of the field in hectare (1 hectare = 10,000 sq.m). [Chapter 15]
Solution:

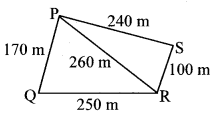
Area of the field = A(∆PQR) + A(∆PSR)
In ∆PQR, a = 170 m, b = 250 m, c = 260 m
Semiperimeter of ∆PQR = s

Area of the field = A(∆PQR) + A(∆PSR)
= 20400 + 12000
= 32400 sq.m
= \(\frac { 32400 }{ 10000 }\)
…[1 hectare = 10,000 sq.m]
= 3.24 hectares
∴ The area of the field is 3.24 hectares.

Question 12.
In a library, 50% of total number of books is of Marathi. The books of English are \(\frac { 1 }{ 3 }\) of Marathi books. The books on Mathematics are 25% of the English books. The remaining 560 books are of other subjects. What is the total number of books in the library? [Chapter 12]
Solution:
Let the total number of books in the library be x
50% of total number of books is of Marathi.
Number of Marathi books = 50% of x
= \(\frac { 50 }{ 100 }x\)
= \(\frac { x }{ 2 }\)
The books of English are \(\frac { 1 }{ 3 }\) of Marathi books.
Number of books of English = \(\frac{1}{3} \times \frac{x}{2}\)
= \(\frac { x }{ 6 }\)
The books on Mathematics are 25% of the English books.
Number of books of Mathematics
= 25% of \(\frac { x }{ 6 }\)
= \(\frac{25}{100} \times \frac{x}{6}\)
= \(\frac { x }{ 24 }\)
Since, there are 560 books of other subjects, the total number of books in the library are


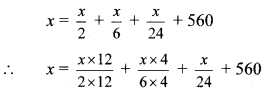
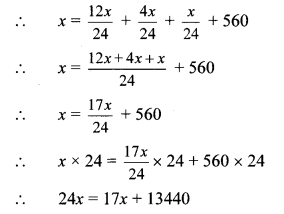
∴ 24x – 17x = 17x + 13440 – 17x
∴ 7x = 13440
∴ \(\frac{7 x}{7}=\frac{13440}{7}\)
∴ x = 1920
∴ The total number of books in the library are 1920.

Question 13.
Divide the polynomial (6x³ + 11x² – 10x – 7) by the binomial (2x + 1). Write the quotient and the remainder. [Chapter 10]
Solution:

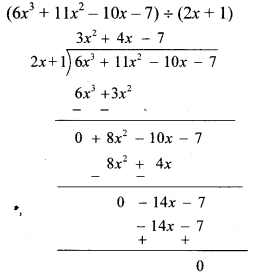
∴ Quotient = 3x² + 4x – 7,
remainder = 0
Explanation:

Maharashtra Board Class 8 Maths Solutions

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.2 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Practice Set 8.2 8th Std Maths Answers Chapter 8 Quadrilateral: Constructions and Types

Question 1.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l(BC) = 4.5 cm.
Solution:

Question 2.
Draw a square WXYZ with side 5.2 cm.
Solution:

Question 3.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
Solution:

Question 4.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Solution:

Let ₹ABCD be the rectangle.
l(BC) = 24cm, l(AC) = 26cm
In ∆ABC,
m∠ABC = 90° …[Angle of a rectangle]
∴[l(AC)]² = [l(AB)]2 + [l(BC)]²
…[Pythagoras theorem]
∴ (26 )² = [l(AB)]² + (24)²
∴(26)² – (24)² = [l(AB)]²
∴(26 + 24) (26 – 24) = [l(AB)]²
…[∵ a² – b² = (a + b)(a – b)]
∴50 x 2 = [l(AB)]²
∴100 = [l(AB)]²
i.e. [l(AB)]² = 100
∴l(AB) = √100
…[Taking square root of both sides]
∴l(AB) =10 cm
∴The length of the other side is 10 cm.

Question 5.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
Solution:
In rhombus ABCD,

l(AC) = 16 cm and l(BD) = 12 cm.
Let the diagonals of rhombus ABCD intersect at point O.
l(AO) = \(\frac { 1 }{ 2 }\) l(AC)
…[Diagonals of a rhombus bisect each other]
∴l(AO) = \(\frac { 1 }{ 2 }\) × 16
∴l(AO) = 8 cm
Also, l(DO) = \(\frac { 1 }{ 2 }\) l(BD)
…[Diagonals of a rhombus bisect each other]
∴l(DO) = \(\frac { 1 }{ 2 }\) × 12
∴l(DO) = 6 cm
In ∆DOA,
m∠DOA = 90°
..[Diagonals of a rhombus are perpendicular to each other]
[l(AD)]² = [l(AO)]² + [l(DO)]²
…[Pythagoras theorem]

= (8)² + (6)²
= 64 + 36
∴[l(AD)]² = 100
∴l(AD) = √100
… [Taking square root of both sides]
∴l(AD) = 10 cm
∴l(AB) = l(BC) = l(CD) = l(AD) = 10 cm
…[Sides of a rhombus are congruent]
Perimeter of rhombus ABCD
= l(AB) + l(BC) + l(CD) + l(AD)
= 10+10+10+10
= 40 cm
∴The side and perimeter of the rhombus are 10 cm and 40 cm respectively.

Question 6.
Find the length of diagonal of a square with side 8 cm.
Solution:
Let ₹XYWZ be the square of side 8cm.

seg XW is a diagonal.
In ∆ XYW,
m∠XYW = 90°
… [Angle of a square]
∴ [l(XW)]² = [l(XY)]² + [l(YW)]²
…[Pythagoras theorem]
= (8)² + (8)²
= 64 + 64
∴ [l(XW)]² = 128
∴ l(XW) = √128
…[Taking square root of both sides]
= √64 × 2
= 8 √2 cm
∴ The length of the diagonal of the square is 8 √2 cm.

Question 7.
Measure of one angle of a rhombus is 50°, find the measures of remaining three angles.
Solution:
Let ₹ABCD be the rhombus.

m∠A = 50°
m∠C = m∠A
….[Opposite angles of a rhombus are congruent]
∴ m∠C = 50°
Also, m∠D = m∠B …(i)
….[Opposite angles of a rhombus are congruent]
In ₹ABCD,
m∠A + m∠B + m∠C + m∠D = 360°
….[Sum of the measures of the angles of a quadrilateral is 360°]
∴ 50° + m∠B + 50° + m∠D = 360°
∴ m∠B + m∠D + 100° = 360°
∴ m∠B + m∠D = 360° – 100°
∴ m∠B + m∠B = 260° …[From (i)]
∴ 2m∠B = 260°
∴ m∠B = \(\frac { 260 }{ 2 }\)
∴ m∠B = 130°
∴ m∠D = m∠B = 130° …[From (i)]
∴ The measures of the remaining angles of the rhombus are 130°, 50° and 130°.

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.2 Intext Questions and Activities

Question 1.
Construct a rectangle PQRS by taking two convenient adjacent sides. Name the point of intersection of diagonals as T. Using divider and ruler, measure the following lengths.
i. lengths of opposite sides, seg QR and seg PS.
ii. lengths of seg PQ and seg SR.
iii. lengths of diagonals PR and QS.
iv. lengths of seg PT and seg TR, which are parts of the diagonal PR.
v. lengths of seg QT and seg TS, which are parts of the diagonal QS.
Observe the measures. Discuss about the measures obtained by your classmates. (Textbook pg. no. 44)
Solution:
Draw a rectangle PQRS such that, l(PQ) = 3 cm and l(QR) = 4 cm.

Steps of construction:
i. As shown in the rough figure, draw seg QR of length 4 cm.
ii. Placing the centre of the protractor at point Q, draw ray QW making an angle of 90° with seg QR.
iii. By taking a distance of 3 cm on the compass and placing it at point Q, draw an arc on ray QW. Name the point as P.
iv. Draw ray PV and ray RU making an angle of 90° with seg PQ and seg QR respectively.
v. Name the point of intersection of ray PV and ray RU as S.
₹PQRS is the required rectangle.

From the figure,
i. l(QR) = l(PS) = 4 cm
ii. l(PQ) = l(SR) = 3 cm
iii. l(PR) = l(QS) = 5 cm
iv. l(PT) = l(TR) = 2.5 cm
v. l(QT) = l(TS) = 2.5 cm

From the above measures, we can say that for any rectangle,
i. Opposite sides are congruent.
ii. Diagonals are congruent.
iii. Diagonals bisect each other.

Question 2.
Draw a square by taking convenient length of side. Name the point of intersection of its diagonals as E. Using the apparatus in a compass box, measure the following lengths.
i. lengths of diagonal AC and diagonal BD.
ii. lengths of two parts of each diagonal made by point E.
iii. all the angles made at the point E.
iv. parts of each angle of the square made by each diagonal, (e.g. ∠ADB and ∠CDB).
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 44)
Solution:
Draw a square ABCD such that its side is 5cm

Steps of construction:
i. As shown in the rough figure, draw seg BC of length 5 cm.
ii. Placing the centre of the protractor at point B, draw ray BP making an angle of 90° with seg BC.
iii. By taking a distance of 5 cm on the compass and placing it at point B, draw an arc on ray BP. Name the point as A.
iv. Placing the centre of the protractor at point C, draw ray CQ making an angle of 90° with seg BC.
v. By taking a distance of 5 cm on the compass and placing it at point C, draw an arc on ray CQ. Name the point as D.
vi. Draw seg AD.
₹ABCD is the required square.

From the figure,
i. l(AC) = l(BD) ≅ 7cm
ii. l(AE) = l(EC) ≅ 3.5cm,
l(BE) = l(ED) ≅ 3.5cm
iii. m∠AED = m∠BEC = m∠CED = m∠BEA = 90°
iv. Angles made by diagonal AC:
m∠BAC = m∠DAC = 45°
m∠BCA = m∠DCA = 45°
Angles made by diagonal BD:
m∠ABD = m∠CBD = 45°
m∠ADB = m∠CDB = 45°

From the above measures, we can say that for any square,
i. Diagonals are congruent.
ii. Diagonals bisect each other.
iii. Diagonals are perpendicular to each other.
iv. Diagonals bisect the opposite angles.

Question 3.
Draw a rhombus EFGH by taking convenient length of side and convenient measure of an angle.
Draw its diagonals and name their point of Intersection as M.
i. Measure the opposite angles of the quadrilateral and angles at the point M.
ii. Measure the two parts of every angle made by the diagonal.
iii. Measure the lengths of both diagonals. Measure the two parts of diagonals made by point M.
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 45)
Solution:
Draw a rhombus EFGH such that its side is 5 cm and m∠F = 60°.

Steps of construction:
i. As shown in the rough figure, draw seg FG of length 5 cm.
ii. Placing the centre of the protractor at point F, draw ray FX making an angle 60° with seg FG.
iii. By taking a distance of 5 cm on the compass and placing it at point F, draw an arc on ray FX. Name the point as E.
iv. By taking a distance of 5 cm on the compass and placing it at point E and point G, draw arcs. Name the point of intersection of arcs as H. ₹EFGH is the required rhombus.

From the figure,
i. Opposite angles:
m∠EFG = m∠GHE = 60°,
m∠FEH = m∠HGF = 120°
Angles at the point M:
m∠EMF = m∠FMG = m∠GMH = m∠HME = 90°

ii. Angles made by diagonal FH:
m∠EFH = m∠GFH = 30° m∠EHF = m∠GHF = 30°
Angles made by diagonal EG:
m∠FEG = m∠HEG = 60° m∠FGE = m∠HGE = 60°

iii. l(FH) ≈ 8.6 cm
l(EG) = 5 cm
l(FM) = l(HM) ≈ 4.3 cm
l(EM) = l(GM) ≈ 2.5 cm

From the above measures, we can say that for any rhombus,
i. Opposite angles are congruent.
ii. Diagonals bisect the opposite angles.
iii. Diagonals bisect each other and they are perpendicular to each other.