Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.2 8th Std Maths Answers Solutions Chapter 15 Area.
Practice Set 15.2 8th Std Maths Answers Chapter 15 Area
Question 1.
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 15 cm and 24 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 15 × 24
= 15 × 12
= 180 sq.cm
∴ The area of the rhombus is 180 sq. cm.
Question 2.
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 16.5 × 14.2
= 16.5 × 7.1
= 117.15 sq cm
∴ The area of the rhombus is 117.15 sq. cm.
Question 3.
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution:
Let ₹ABCD be the rhombus. Diagonals AC and BD intersect at point E.
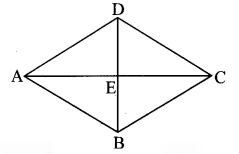
l(AC) = 48 cm …(i)
l(AE) = \(\frac { 1 }{ 2 }l(AC)\) …[Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) × 48 …[From (i)]
= 24 cm …(ii)
Perimeter of rhombus = 100 cm …[Given]
Perimeter of rhombus = 4 × side
∴ 100 = 4 × l(AD)
∴ l(AD) = \(\frac { 100 }{ 4 }\) = 25 cm …(iii)
In ∆ADE,
m∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
∴ [l(AD)]² = [l(AE)]² + [l(DE)]² … [Pythagoras theorem]
∴ (25)² = (24)² + l(DE)² … [From (ii) and (iii)]
∴ 625 = 576 + l(DE)²
∴ l(DE)² = 625 – 576
∴ l(DE)² = 49
∴ l(DE) = √49
… [Taking square root of both sides]
l(DE) = 7 cm …(iv)
l(DE) = \(\frac { 1 }{ 2 } l(BD)\) ….[Diagonals of a rhombus bisect each other]
∴ 7 = \(\frac { 1 }{ 2 } l(BD)\) …[From (iv)]
∴ l(BD) = 7 × 2
= 14 cm …(v)
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × l(AC) × l(BD)
= \(\frac { 1 }{ 2 }\) × 48 × 14 … [From (i) and (v)]
= 48 × 7
= 336 sq.cm
∴ The area of the quadrilateral is 336 sq.cm.
Question 4.
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq.cm, find its perimeter.
Solution:
Let ₹ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and A(₹ABCD) = 240 sq. cm .. .(ii)
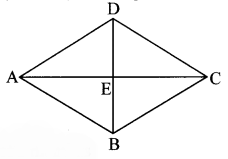
Area of the rhombus = \(\frac { 1 }{ 2 }\) × product of lengths of diagonal
∴ 240 = \(\frac { 1 }{ 2 }\) × l(AC) x l(BD) …[From (ii)]
∴ 240 = \(\frac { 1 }{ 2 }\) × 30 × l(BD) …[From (i)]
∴ l(BD) = \(\frac { 240\times 2 }{ 30 }\)
∴ l(BD) = 8 × 2 = 16 cm …(iii)
Diagonals of a rhombus bisect each other.
∴ l(AE) = \(\frac { 1 }{ 2 }l(AC)\)
= \(\frac { 1 }{ 2 }\) × 30 … [From (i)]
= 15 cm …(iv)
and l(DE) = \(\frac { 1 }{ 2 }l(BD)\)
= \(\frac { 1 }{ 2 }\) × 16
= 8 cm
In ∆ADE,
m∠AED = 90°
…[Diagonals of a rhombus are perpendicular to each other]
∴[l(AD)]² = [l(AE)]² + [l(DE)]²
…[Pythagoras theorem]
∴l(AD)² = (15)² + (8)² … [From (iv) and (v)]
= 225 + 64
∴l(AD)² = 289
∴l(AD) = √289
…[Taking square root of both sides]
∴l(AD) = 17 cm
Perimeter of rhombus = 4 × side
= 4 × l(AD)
= 4 × 17
= 68 cm
∴The perimeter of the rhombus is 68 cm.