Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.3 8th Std Maths Answers Solutions Chapter 15 Area.
Practice Set 15.3 8th Std Maths Answers Chapter 15 Area
Question 1.
In the given figure, ☐ABCD is a trapezium, side AB || side DC, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area ☐ABCD.
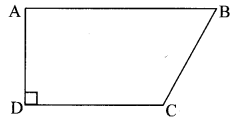
Solution:
☐ABCD is a trapezium, side AB || side DC,
l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm,
Area of a trapezium = \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A (☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC)] x l(AD)
= \(\frac { 1 }{ 2 }\) x (13 + 9) x 8
= \(\frac { 1 }{ 2 }\) x 22 x 8
= 11 x 8
= 88 sq.cm
∴ The area of ☐ABCD is 88 sq. cm.
[Note: The question is modified.]
Question 2.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Solution:
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x (8.5 + 11.5) x 4.2
= \(\frac { 1 }{ 2 }\) x 20 x 4.2
= 10 x 4.2
= 42 sq. cm
∴ The area of the trapezium is 42 sq. cm.
Question 3.
☐PQRS is an isosceles trapezium. l(PQ) = 7 cm, seg PM ⊥ seg SR, l(SM) = 3 cm. Distance between two parallel sides is 4 cm, find the area of ☐PQRS.
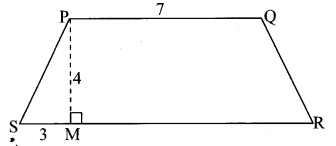
Solution:
☐PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In ☐PMNQ,
seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ ☐PMNQ is a rectangle.
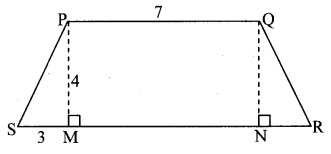
Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]² = [l(PM)]² + [l(SM)]² … [Pythagoras theorem]
∴ [l(PS)]² = (4)² + (3)²
∴ [l(PS)]² = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm
…[Taking square root of both sides]
☐PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]² = [l(QN)]² + [l(NR)]²
… [Pythagoras theorem]
∴ (5)² = (4)² + [l(NR)]²
∴ 25 = 16 + [l(NR)]²
∴ [l(NR)]² = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm
…[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3
= 13 cm
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐PQRS) = \(\frac { 1 }{ 2 }\) x [l(PQ) + l(SR)] x l(PM)
= \(\frac { 1 }{ 2 }\) x (7+ 13) x 4
= \(\frac { 1 }{ 2 }\) x 20 x 4
= 40 sq.cm
∴ The area of ☐PQRS is 40 sq. cm.