Prasanna

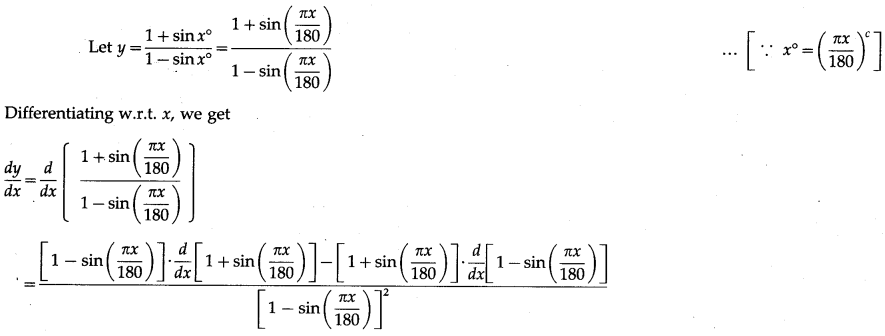
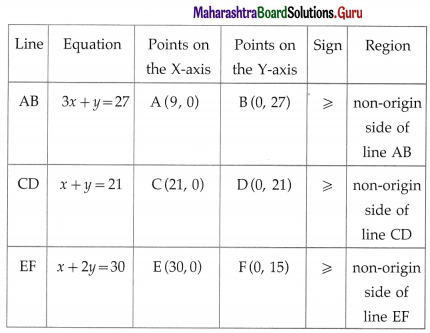
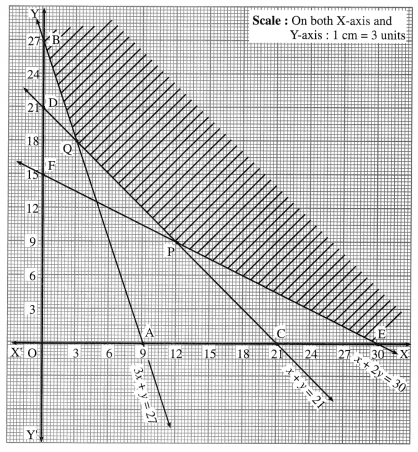
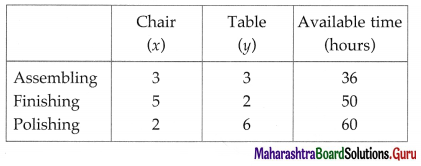
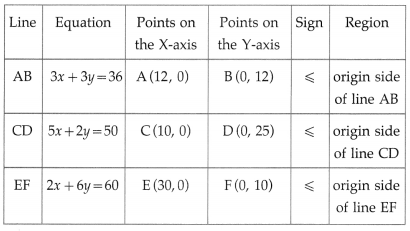
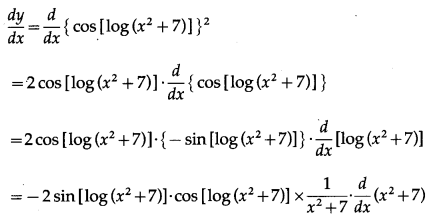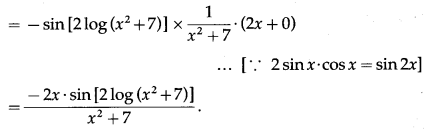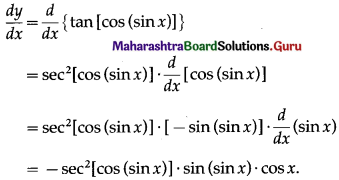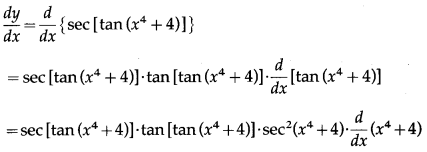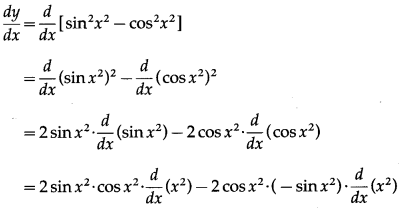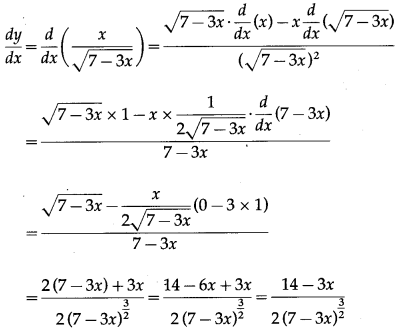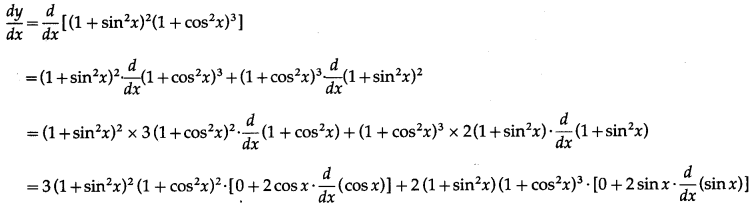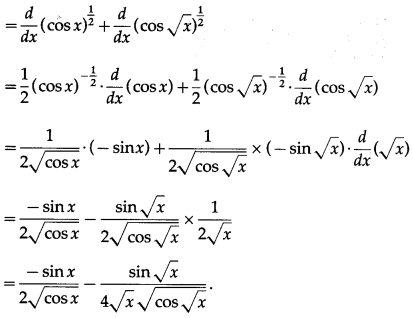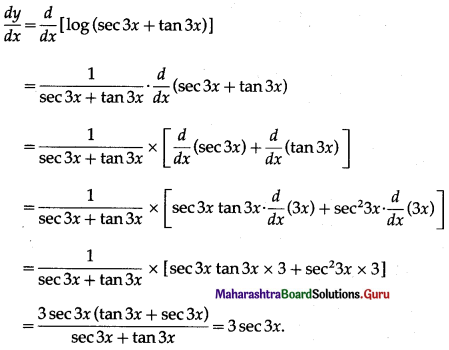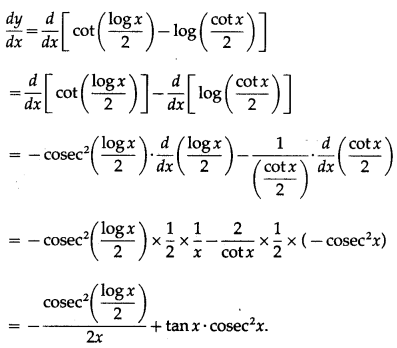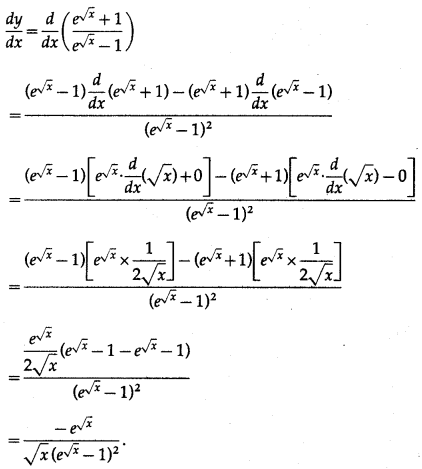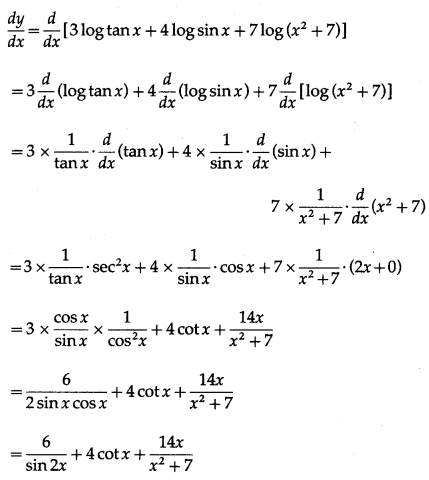Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.6 Science and Spirituality Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 English Kumarbharati Textbook Solutions Unit 2.6 Science and Spirituality

Maharashtra Board Class 10 English Solutions Unit 2.6 Warming Up Questions and Answers

Question 1.
Get into pairs/groups and match the columns:

‘A’	‘B’
(1) Science	(a) The study of the basic nature of knowledge, reality and existence, especially as an academic subject.
(2) Religion	(b) The study of nature of God and religious belief.
(3) Spirituality	(c) The intellectual and practical activities in a systematic study of structure and behaviour of the natural world through experiment and observation.
(4) Philosophy	(d) The belief in and worship of a superhuman controlling power God.
(5) Theology	(e) The quality of being more concerned with the human spirit as opposed to material or physical things.

Answer:

‘A’	‘B’
(1) Science	(c) The intellectual and practical activities in a systematic study of structure and behaviour of the natural world through experiment and observation.
(2) Religion	(d) The belief in and worship of a superhuman controlling power God.
(3) Spirituality	(e) The quality of being more concerned with the human spirit as opposed to material or physical things.
(4) Philosophy	(a) The study of the basic nature of knowledge, reality and existence, especially as an academic subject.
(5) Theology	(b) The study of nature of God and religious belief.

Question 2.
Given below are some incomplete Quotes. Complete them choosing from the words SCIENCE /RELIGION /SPIRITUAL and make them meaningful:

• ………………………….. without religion is lame; without science is blind. ………………………….. has outrun our power, we have guided missiles, but misguided man.
• On a ………………………….. journey, we all have the same destination.
• ………………………….. is meant to awaken man’s love for his Source – God!
• ………………………….. provides a means of with the Creator of Heaven and Earth, in the language of your heart and soul.
• ………………………….. is a beautiful gift to humanity; we should not distort it.

Answer:

• Science, Religion
• Science, Spiritual
• Spiritual
• Religion
• Religion
• Science

Question 3.
What’s the difference between science and technology? Discuss in pairs and tell your answer to the class.
Answer:
We generally assume that science and technology mean almost the same thing. HowSver, there is a difference. The goal of science is the pursuit of knowledge for its own sake while the goal of technology is to turn the scientific knowledge into industrial and commercial use. Simply put, technology is the practical application of science,

Question 4.
Do you think that science and faith are both important in our lives? Why? Discuss in your group and give a small presentation in front of the class.
Answer:
Yes, both science and faith are important in our lives. There is no contradiction between the two. Both genuinely seek the truth. Science explores the truth about the material and physical world. Faith introspects on the spiritual aspects including the Self and the Creator. Science helps us understand the physical structure of the universe, while faith deals with human values and morals. Both complement each other. In the words of Einstein, ‘Science without religion is lame; religion without science is blind.’

Question 5.
We need science

Answer:

Question 6.
Refer to a dictionary to find out the meanings of the following words.

• Spirit- a person’s mind or feelings or soul.
• Spiritual
• Spirituality
• Spiritualism
• Spiritualist

Answer:

• Spiritual – relating to or affecting the human spirit or soul, as opposed to material or physical things
• Spirituality – the quality of being concerned with the human spirit, or soul, as opposed to material or physical things
• Spiritualism – a system of belief or religious practice based on supposed communication with the spirits of the dead, especially through mediums
• Spiritualist – an advocate of the doctrine that the spirit exists as distinct from matter, or that spirit is the only reality

Science and Spirituality Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
(A) Read ‘Part I’ and match the words in Column ‘A’ with associating words given in Column ‘B’.

No	‘A’		‘B’
(i)	Science and faith	(a)	Created by fact and faith
(ii)	Science	(b)	Success of societies
(iii)	Better Planet	(c)	Betterment of humanity
(iv)	Creations and Discoveries	(d)	Believers of science and religions
(v)	Conflict	(e)	Solves questions, discovers truth, conceives inventions

(i) …………………………..
(ii) …………………………..
(iii) …………………………..
(iv) …………………………..
(v) …………………………..
Answer:

‘A’	‘B’
(1) Science and faith	(a) Success of societies
(2) Science	(e) Solves questions, discovers truth, conceives inventions
(3) Better Planet	(a) Created by fact and faith
(4) Creations and Discoveries	(c) Betterment of humanity
(5) Conflict	(d) Believers of science and religions

(B) Read ‘Part II’. Go through the given statements and say whether you agree or disagree to each of them.
(a) The Space Research set up facility was planned at Allapi, Kerala – …………………………..
(b) The person who could help and can be contacted was the Bishop – …………………………..
(c) It was quite easy to relocate so many people and destroy religious institutions for space-research centre – …………………………..
(d) Dr. Kalam joined ISRO in 1970 – …………………………..
(e) Science and spirituality seeks prosperity of the human life – …………………………..
Answer:
(a) Disagree
(b) Agree
(c) centre Disagree
(d) Disagree
(e) Agree

(C) Go through ‘Part III’ and complete the following statements.
(a) The essence of a happy life and a peaceful society lies in one sentence – …………………………..
(b) To keep this planet liveable and the human race thriving, we have to …………………………..
(c) Mahaswamiji’s greatest contribution is the …………………………..
(d) We can remove the  our souls by …………………………..
(e) The narrator, Srijan, realised that through Dr. Kalam’s words of wisdom …………………………..
(f) Mahaswamiji possesses powers that kept him so strong were ………………………….. or
Answer:
(a) The essence of a happy life and a peaceful society lies in one sentence – ‘What can I give’.
(b) To keep this planet liveable and the human race thriving, we have to replace this attitude of ‘what can I take’ with the goodness of
(c) Mahaswamiji’s greatest contribution was the establishment of a free residential education system for more than nine thousand children in the ashram.
(d) We can remove the impurities obscuring our souls by living pure and ethical lives and by serving humanity.
(e) The narrator, Srijan, realized that through Dr Kalam’s words of wisdom he was getting to learn from countless great minds.
(f) The narrator (Srijan) said this to Dr Kalam ‘ while discussing the Mahaswamiji’s 102nd birthday i celebrations.

2. Choose the correct alternative for the given statements.
(A) Dr. Kalam’s father was an …………………………. .
(a) teacher
(b) scientist
(c) farmer
(d) imam.
Answer:
(d) imam.

(B) Dr. Kalam’s friends discussed on …………………………. .
(a) science and technology
(b) discoveries and inventions.
(c) science and spirituality
(d) community’s problems and solutions.
Answer:
(c) science and spirituality

(C) According to Dr. Kalam, the need that is felt more than ever is ………………………….. .
(a) a laboratory to conduct experiments.
(b) a new technology to find results.
(c) a dialogue among cultures, religions and civilizations.
(d) a dialogue between people of different professions.
Answer:
(c) a dialogue among cultures, religions and civilizations.

(D) Dr. Kalam’s father was a symbol of ………………………….. .
(a) trust and faith.
(b) simplicity and divinity
(c) teacher and disciple.
(d) father and friend.
Answer:
(b) simplicity and divinity

(E) Spirituality takes care of ………………………….. .
(a) education, teaching and learning.
(b) science, technology and sci-fi.
(c) confusion, misery or failure.
(d) crime, illiteracy and child labour.
Answer:
(c) confusion, misery or failure.

(F) How can academic brilliance diminish?
(a) by disturbance and frustration.
(b) by going off track
(c) by a coating of dust.
(d) by losing focus and seriousness.
Answer:
(d) by losing focus and seriousness

(G) What was most astonishing about 102 year old Swamiji?
(a) He was a great speaker and orator.
(b) He was a great scientist.
(c) He was a great admirer of technology.
(d) He looked as steady and alert as any other youngster.
Answer:
(d) He looked as steady and alert as any other youngster.

(H) What Dr. Kalam gathered while swimming in silence at the shores of Mahapragyaji?
(a) beautiful sea shores
(b) tree lined beaches
(c) sands of conscience
(d) beautiful sun-set.
Answer:
(c) sands of conscience

Question 3.
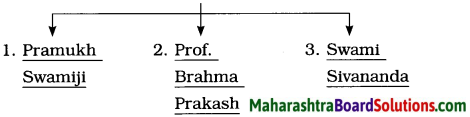
Among the three parts, there are people who touched and influenced the life of Dr. A. P. J. Kalam in one or the other ways. Complete the web chart by writing the names of such people.
Answer:
Kalam In one way or the other were:

Question 4.
Write the significance of the following years, as given in the text.
1960 ……………………………
1970 ……………………………
1980 ……………………………
2009 ……………………………
2012 ……………………………
Answer:
1960 → Is significant as Dr Kalamoined ISRO that year.
1970 → Dr Kalam made his first unsuccessful launch.
1980 → Dr Kalam made his first successful launch.
2009 → The writer graduated from IIMA and met Dr Kalam
2012 → The writer was discussing with Dr Kalam the number of Ph.D’s he (Dr Kalam) had received.

Question 5.
Who said to whom and when?
(a) “Can we give up God’s abode for such a great scientific mission ?”
…………………………………………………………………..
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

(b) “And then God will shine through us.”
…………………………………………………………………..
Answer:
Professor Satish Dhawan to Dr Kalam when ‘ they were talking about academic brilliance.

(c) “I wonder what power Mahaswamiji possesses, that keeps him so strong.”
…………………………………………………………………..
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

Question 6.
Answer the following in your own words, and write in your notebook.
(a) What makes Dr Kalam a humble personality?
Answer:
Even though Dr Kalam was indisputably a great scientist, he had deep faith and espoused the cause of the betterment of humanity. This shows that he was indeed a humble personality.

(b) How were different virtues inculcated in Dr Kalam?
Answer:
Dr Kalam inculcated the virtue of humility from his father who was a boatman. He learnt from his father how simplicity and divinity could go together.

(c) How did the Reverend relate and compare the work that he and Dr Sarabhai did for people?
Answer:
The Reverend said that Dr Sarabhai was a scientist. We benefit from the devices that science has developed in many ways – in our homes and in the fields of medicine and technology. A priest prays for the peace and well-being of his people. Thus both science and spirituality seek the Almighty’s blessing for the prosperity of the human mind and body. In short, both are doing the sameob.

(d) What was so remarkable about Dr Sri Sri Shivakumar Mahaswamiji?
Answer:
The remarkable aspect about Dr Sri Shivakumara Mahaswamiji was that he had dedicated his life to the service of humanity.

(e) Why is there an urgent need to replace ‘What can I take’ with ‘What can I give?
Answer:
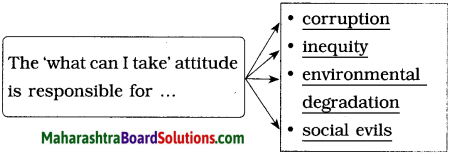
There is an urgent need to replace ‘What can I take’ with ‘What can I give’ for the very survival of humanity. Unless we realize the gravity of the message, this planet will become a hub of environmental degradation, social evils, inequity and corruption. If we do not take up the challenge, our planet will not be liveable and the human race will not prosper.

Question 7.
In your notebook, write a short paragraph on each of the following covering up their profession and personality traits with examples.
(a) Rev. Peter Bernard Pereira
(b) Dr Sri Shivakumar Mahaswamiji
(c) Dr A. P. J. Abdul Kalam
Answer:
(a) His interactions with the great scientist Professor Vikram Sarabhai and the Reverend Peter Bernard Pereira shaped Dr Kalam’s thoughts on religion.
(b) The 102nd birthday celebrations of His Holiness Dr Sri Sri Shivakumara Mahaswamiji.
(c) Dr A P Abdul Kalam was the past President of India. By the way, he was a great scientist, orator and a humanitarian.

8. Write in your own simple words what the following expressions convey in the context they occur in the text.
(a) Faith and fact can, together, create a better planet.
…………………………………………………………………..
Answer:
If people have belief in a greater power! as well as understand the truth of things that exist around them, this world will become a better place for all of us to live in harmony.

(b) Dr Kalam’s own life was nourished by multiple faiths.
…………………………………………………………………..
Answer:
This means that the life of Dr Kalam improved in quality because of the discussion he had with people of different faiths, such as the head priest of a temple who was a Vedic scholar, and a Christian priest.

(c) But there was a major roadblock.
…………………………………………………………………..
Answer:
This expression conveys the fact that something was being planned, but there were serious issues that hindered its progress.

(d) Only when the dust is removed, does the mirror shine and the reflection becomes clear.
…………………………………………………………………..
Answer:
This expression is a comparison between the mind and the mirror. The brilliance of both can be diminished by many factors that act like coatings of dust. However, when that coating is removed, both shine and radiate brilliance.

(e) Through his (Kalam’s) words of wisdom, I was getting to learn from countless great minds.
…………………………………………………………………..
Answer:
This expression first of all conveys the information that Dr Kalam himself was a very well- read person who had acquired his knowledge from innumerable great minds of the past. Further, it conveys that the speaker (Narrator; Srijan) himself received an education from Dr Kalam by association with him.

(f) He gathered the sands of conscience to be our guide, our best friend.
…………………………………………………………………..
Answer:
These words convey the idea that Dr Kalam realized that our own conscience is our guide and! best friend.

(g) ‘What can I take?’ is the thought which is responsible for all the wrong, seen around us.
…………………………………………………………………..
Answer:
These words convey the idea that when people think only in terms of what they can get S from others, it leads to every possible illegal or bad behaviour.

9. (A) From the lesson, pick out one word for each of the following.
(a) increase the speed …………………………
(b) point of view …………………………
(c) nearness in space …………………………
(d) a place of residence …………………………
(e) eager to know everything …………………………
(f) echoed loudly …………………………
(g) giving away much to the needy …………………………
(h) without making a difference …………………………
Answer:
(a) accelerate
(b) perspective
(c) proximity
(d) abode
(e) inquIsitive
(f) reverberated
(g) munificence
(h) indiscriminately

(B) Arrange the following words in the alphabetical order.

• inventions,
• indisputable,
• interactions,
• inequity,
• institutions,
• inquisitive,
• indiscriminately

Answer:

• indiscrimInately,
• Indisputable,
• inequity,
• Inquisitive,
• institutions,
• Interactions,
• Inventions.

(C) Find from the lesson the noun forms of –
1. combine …………………………
2. solve …………………………
3. simple …………………………
4. divine …………………………
5. advance …………………………
6. tranquil …………………………
7. liveable …………………………
8. strong …………………………
Answer:
1. combination
2. solution
3. simplicity
4. divinity
5. advancement
6. tranquillity
7. life
8. strength

Question 10.
Match the word connectors with reference to part I, II, III respectively. Make sentences of each of these connectors.

No	Word		Connector
1.	government	(a)	person
2.	betterment of	(b)	curbs
3.	pure and ethical	(c)	degradation
4.	community’s	(d)	launch
5.	religions	(e)	dialogue
6.	astonishing	(f)	silence
7.	technological	(g)	motivation
8.	frank	(h)	aspect
9.	social	(i)	life
10.	faith	(j)	centre
11.	inquisitive	(k)	officials
12.	academic	(l)	problems
13.	environmental	(m)	humanity
14.	pin-drop	(n)	service
15.	alternate	(o)	bodies
16.	remarkable	(p)	evils
17.	silent	(q)	advancement
18.	famished	(r)	brilliance
19.	unsuccessful	(s)	accommodation
20.	space-research	(t)	discipline

Answer:
(1) Some government officials came to our village to inspect the sanitary conditions.
(2) Gandhiji’s efforts were for the betterment of humanity.
(3) The hermit was revered for living a pure and ethical life.
(4) We formed a core team to look into the community’s problems.
(5) We need religious discipline in order to develop a clear conscience.
(6) The most astonishing aspect of this great king’s personality is his humility.
(7) The district required more skilled manpower for technological advancement.
(8) The teacher had a frank dialogue with the youth about his drug problem.
(9) He left his good secureob in order to dedicate himself to social service.
(10) In order to make progress, people should avoid conservative faith curbs.
(11) To be a good detective, ond must basically be an inquisitive person.
(12) All through his school and college days he displayed academic brilliance.
(13) Plastics are major contributors to environmental degradation.
(14) There was pin-drop silence when the sad news was announced.
(15) The owner was provided alternate accommodation until his flat was renovated.
(16) Lai Bahadur Shastri was a remarkable person.
(17) Our inner beliefs should be the silent motivation to do good to others.
(18) The communal kitchen is a great boon to famished bodies.
(19) At the first attempt it was an unsuccessful launch.
(20) ISRO is a space research centre in Bengaluru.

Question 11.
Simple sentence : subject + verb + object/complement/adverbial: Analysing a simple sentence is done by separating the subject and the predicate. The predicate is further analysed into –
(1) verb + object as in ‘A doctor treats patients’./ ‘He greeted the teacher.’
(2) verb + complement as in ‘They are very tired.’ / ‘I have a cold.’
(3) verb + adverbial as in (He walks slowly. / Raj arrived late. / The thief is hiding there.)

Say whether the predicates in the following sentences have an object/a complement/an adverbial.
(1) There was silence. …………………………
(2) Alexander Bell invented the telephone. …………………………
(3) They have a holiday. …………………………
(4) The dancer danced gracefully. …………………………
(5) The milkman comes daily. …………………………
(6) The hostess served tea. …………………………
(7) The kite soared upwards. …………………………
Answer:
(1) Complement
(2) Object
(3) Complement
(4) Adverbial
(5) Adverbial
(6) Object
(7) Adverbial

Question 12.
(A) Punctuate the following sentences to make them meaningful.
(1) dinesh took a bus that stopped at nanded railway station after crossing somvar peth
(2) dr a p j abdul kalam was the past president of india by the way he was a great scientist orator and a humanitarian
(3) nouns are of different types common proper abstract concrete material
(4) what a lot of noise you all make said the teacher cant you keep quiet for a while
(5) wow how lovely that cake looks they said we cant wait to eat it
Answer”
(1) Dinesh took a bus that stopped at Nanded railway station after crossing Somvar Peth.
(2) Dr A P J Abdul Kalam was the past President of India. By the way, he was a great scientist, orator and a humanitarian.
(3) Nouns are of different types: common, proper, abstract, concrete, material.
(4) “What a lot of noise you all make!” said the teacher, “Can’t you keep quiet for a while?”
(5) “Wow! How lovely that cake looks!” they said, “We can’t wait to eat it.”

(B) Copy the first paragraph on page 92 in your notebook, carefully. Encircle all the punctuation marks with a colored pencil/pen.
“Dear children …………………. ‘amen’.

Question 13.
Project :
Read Dr. A.P.J. Abdul Kalam’s very renowned books ‘Wings of Fire’; and ‘Ignited Minds’, to find the following :
(a) Subject of the book
(b) Special features of the book
(c) Teachings/learnings/moral/message from the book
(d) Your own opinion/idea/comment on the book
Answer:
Dr A. P.. Kalam was the son of an imam, a simple fisherman. He was born in Rameswaram on 15 October 1931. He went on to become the 11th President of India from 2002 to 2007. He was widely acclaimed as the ‘People’s President’. He was particularly fond of children and youth and made himself approachable to them at all times.

He was a student of Physics and aerospace engineering. He was a scientist and science administrator mainly at the Defence Research and Development Organisation (DRDO) and Indian Space Research Organisation (ISRO) for nearly four decades. He was intimately involved in India’s civilian space programme and military missile development efforts.

He is famous as the Missile Man of India for his work on the development of ballistic missile and launch vehicle technology. He also played a pivotal organisational, technical, and political role in India’s Pokhran-II nuclear tests in 1998, the first since the initial nuclear test by India in 1974.

He was the recipient of several prestigious awards, including the Bharat Ratna in 1997, India’s highest civilian honour.

Amongst his writings, the most famous are ‘Transcendence: My Spiritual Experiences with Pramukh Swamiji’, and ‘India 2020’.

While delivering a lecture at the Indian Institute of Management, Shillong, Kalam collapsed and died from an apparent cardiac arrest on 27uly 2015, aged 83. Thousands including national-level dignitaries attended the funeral ceremony held in his hometown of Rameswaram, where he was buried with full state honours.

Question 14.
(A) Draft a speech that you would give at your School Assembly convincing junior students that the secret of true happiness lies in Giving and Sharing more than in Receiving and Taking.

Write it with the appropriate steps in your notebook.
Answer:
Friends,
It is through experience I .have learned that ‘AS’ you give, so you live’.

There was a time in my life when I only wanted things. I was happy only when I received gifts. My main goal in life was to take as many things from others as I could.

But then one day, on the way to market, I saw a beggar boy running along the road. In his hand he held a loaf of bread. He ran to his mother, who was lying on the sidewalk. He sat next to her and started feeding her. It touched me deeply that this boy who must have been hungry himself, found greateroy in feeding his famished mother.

From that day onwards I started giving things to others. If I had two pens and someone wanted one, I would give it to him or her. I asked my mother to give my old clothes to a poor child from a nearby slum. For my birthday celebrations, instead of having a party, I went along with my mother to the temple and fed a line of beggars.

Giving things to others brings me greatoy and happiness. Receiving something gives temporary satisfaction. But reaching out to others and seeing them smile, sharing things with others and making it worthwhile – these are far more precious than any other personal possessions.

Thank you.

(B) Divide your class in two groups and have a Debate on the topic ‘Science and Spirituality can go hand in hand’.
Answer:
For (view):
Both science and spirituality study aspects of our world. Both require mental discipline. Both require belief in certain axioms and truths. Hence both are valid. Science is the body. Spirituality is the mind. Science explores the creations of God. Spirituality delves into the nature of God. Both are two sides of the same coin. Both complement each other.

It is inevitable therefore that science and spirituality go hand in hand.

Against (counterview):

Science requires factual knowledge. It is a component of millions of physical laws. Spirituality is a free bird that soars on the wings- of personal belief. It does not require proof. Only faith. How then can they be considered to be on the same plane? One is concrete; the other abstract. In order to draw upon spirituality, one may conjure up any image in the mind and be satisfied. Science seeks explanation in logical reasoning based upon unlimited past experiences and developed into a truth by considering experiment after experiment.

The two are poles apart and cannot go hand in hand.

Question 15.
State whether the statements are True or False:
Answer:
(a) It is necessary for science and faith to function true to their roles.
(b) Kalam’s status as a great scientist is in dispute.
(c) Both fact and faith are required for a better world.
(d) There is never any conflict between believers in science and believers in religion.
Answer:
(a) True
(b) False
(c) True
(d) False

Question 16.
Why do science and faith have to go hand in hand?
Answer:
Science and faith must go hand in hand for the sake of human good. Science provides focus on human activities while faith gives one a perspective, which is essential for success.

Question 17.
From the passage pick out one word for each of the following:
(a) keeps something within limits
(b) unable to be challenged or doubted
Answer:
(a) curbs
(b) indisputable

Question 18.
Write the noun forms of:
(a) create
(b) coexist
(c) discover
(d) conceive
(e) accelerate.
Answer:
(a) create – creation
(b) coexist – coexistence
(c) discover – discovery
(d) conceive – conception
(e) accelerate – acceleration.

Question 19.
Faith provides perspective. (Rewrite beginning with ‘Perspective’.)
Answer:
Perspective is provided by faith.

Question 20.
Write whether the predicates in the following sentences have an object/a complement/an adverbial: (The answers are given directly and underlined.)
(a) This is indisputable.
(b) Science provides focus.
(c) They will work together.
Answer:
(a) complement
(b) object
(c) adverbial

Question 21.
Fill in the blanks with suitable prepositions: (The answers are given directly and underlined.)
Answer:
Conflict often arises between people who believe in science and people who believe in religion,

Question 22.
Which, according to you, is more important for our planet to survive – science or religion? Give your reasons in brief.
Answer:
According to me, both are important – science \ as well as religion. Science provides us with facts that tell us about our planet. Religion educates us about the proper attitude towards all things created on earth. We need both for our planet to survive. Both go hand in hand.

Question 23.
Complete the following map:
Answer:

Question 24.
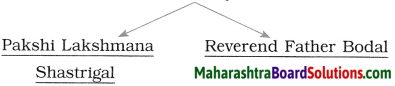
Complete the following based on the passage: (The answers are given directly and underlined.)
Answer:
People who touched and influenced Dr A. P.. Kalam in one way or the other were:

Question 25.
Complete the following.
Answer:

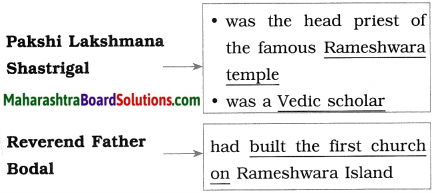
Question 26.
Give evidence from the passage to show that Dr Kalam’s father combined the virtues of ‘simplicity’ and ‘divinity’.
Answer:
Dr Kalam’s father was a boatman. This was the basis for his simplicity. He was also an imam in a mosque and believed strongly in leading a spiritual life. This was the basis of his divinity.

Question 27.
Write from the passage four words that are connected with or related to religions.
Answer:
imam, mosque, Hindu, Christian (priest, temple, Vedic, reverend father, church, divinity, spiritual, spirituality)

Question 28.
Match the words in column ‘A’ with their meanings in column ‘B’:

‘A’	‘B’
(i) remembered	(a) frank
(ii) honest	(b) misery
(iii) clothes	(c) recalled
(iv) sorrow	(d) attire

Answer:

‘A’	‘B’
(i) remembered	(c) recalled;
(ii) honest	(a) frank;
(iii) clothes	(d) attire;
(iv) sorrow	(e) misery.

Question 29.
Write the noun forms of:
(a) solve
(b) frank
(c) believe.
Answer:
(a) Solve – solution
(b) frank – frankness
(c) believe – belief.

Question 30.
(1) Write whether the predicates in the following sentences have an object/a complement/an adverbial:
(a) His father was a boatman.
(b) Father Bodal had built the first church.
Answer:
(a) complement
(b) object

Question 31.
Pick out the auxiliaries and state the mood:
(a) All three of them used to sit and discuss the community’s problems.
(b) Simplicity and divinity could go together.
Answer:
(a) used to – past habit
(b) could – possibility.

Question 32.
Even though his father was a boatman, Dr Kalam went on to become the President of India. (Rewrite using ‘yet’.)
Answer:
Dr Kalam’s father was a boatman, yet” he went on to become the President of India.

Question 33.
Complete the following based on the passage:
Answer:
People who touched and influenced Dr A. P.. Kalam in one way or the other were:

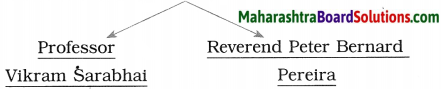
Question 34.
What is the significance of the year 1960 as given in the passage?
Answer:
1960 is significant as Dr Kalamoined ISRO that year.

Question 35.
Complete the following.
Answer:

Question 36.
Write from the passage words that sound the same as:
(a) grate
(b) dew
(c) wood
(d) hear
(e) two
(f) sew.
Answer:
(a) grate – great
(b) dew – due
(c) wood – would
(d) hear – here
(e) two – to
(f) sew – so.

Question 37.
Pick out from the following words that, do not begin with the prefix ‘re-’ religion, reverend, religious, research, relocate, region
Answer:
religion, reverend, religious, region

Question 38.
Match the phrases with one word from the passage:

‘A’	‘B’
(i) which is new and inexperienced	(a) proximity
(ii) a place provided for a particular purpose.	(b) fledgling purpose
(iii) something that causes delay or obstruction	(c) site
(iv) nearness in space	(d) roadblock

Answer:

‘A’	‘B’
(i) which is new and inexperienced	(b) fledgling purpose
(ii) a place provided for a particular purpose.	(c) site
(iii) something that causes delay or obstruction	(d) roadblock
(iv) nearness in space	(a) proximity

Question 39.
Professor Sarabhai and his team had selected a site in Thumba, Kerala. (Pick out the subject of the sentence.)
Answer:
Professor Sarabhai and his team

Question 40.
It was here that he learnt about the true meaning of religious service.
Answer:
Where did he learn about the true meaning of religious service?

Question 41.
It would be impossible to relocate so many people. (Rewrite using ‘not’.)
Answer:
It would not be possible to relocate so many people.

Question 42.
What do you learn from this passage?
Answer:
From this passage, I learn that people belonging to different religions can come together and reach a common understanding to resolve major and sensitive issues. Religious harmony is the theme of this passage.

Question 43.
Complete the following:
(a) Reverend Father Pereira helped to solve the problem of acquiring the site.
(b) Father Pereira described the Church in three ways: (i) his abode (ii) his children’s abode (iii) God’s abode.
Answer:
(a) Reverend Father Pereira
(b) (i) abode
(ii) his children’s
(iii) God’s.

Question 44.
Go through the given statements and say whether you Agree or Disagree with each of them:
Answer:
(a) Science and spirituality seek the prosperity of human life. –
(b) Reverend Pereira absolutely refused to consider Dr Kalam’s request. –
(c) Alternate accommodation was offered only to the fishermen. – Disagree
(d) Everyone present in the church agreed to Reverend Pereira’s plea –
Answer:
(a) Agree
(b) Disagree
(c) Disagree
(d) Agree

Question 45.
Who said to whom and when? ‘Can we give up God’s abode for such a great scientific mission?’
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

Question 46.
Complete the following with the reference to the passage:
(1) We benefit from the devices that science has developed to light up our homes.
(2) We can talk to a large gathering and be heard using a microphone.
(3) Medical science allows doctors to diagnose and treat patients.
(4) Science and technology enhance the overall comfort and quality of human life.
Answer:
(1) to light up our homes.
(2) using a microphone.
(3) diagnose and treat patients.
(4) comfort and quality of human life.

Question 47.
Write one word for:
(a) one who follows a teacher or a leader
(b) eager to know everything
(c) a place of residence
(d) echoed loudly
Answer:
(a) discIple
(b) inquisitive
(c) abode
(d) reverberated

Question 48.
Write from the passage two words that have almost the same meaning as ‘prosperity’:
Answer:
comfort, well-being

Question 49.
Write from the passage two words that indicate noise.
Answer:
reverberated, deafening.

Question 50.
How is it possible? (Rewrite as an assertive sentence.)
Answer:
It is not possible.

Question 51.
I am able to talk to you using this mic. (Rewrite using ‘can’.)
Answer:
I can talk to you using this mic.

Question 52.
The whole church reverberated with the deafening noise of a collective ‘amen’. (Pick out the prepositions.)
Answer:
with, of

Question 53.
Add question tags:
(a) Vikram and I are doing the sameob.
(b) I am able to talk to you using this mic.
Answer:
(a) Vikram and I are doing the sameob, aren’t we?
(b) I am able to talk to you using this mie, aren’t I’

Question 54.
How did the people respond to the appeal made by Reverend Pereira? Would you give the ( same response?
Answer:
The people got up and the whole church reverberated with the deafening noise of a collective ‘amen’. Yes, if I had been part of the gathering, I too would haveoined in with a loud positive response, Considering the importance of the space research centre, I would have been willing to suffer the agony i of relocation.

Question 55.
Complete the following:
(a) We can lead a pure life by serving humanity.
(b) The philosophy of Dr Kalam had an impact on the narrator.
Answer:
(a) serving humanity.
(b) Dr Kalam

Question 56.
Who had directly influenced Dr Kalam’s beliefs?
(a) Professor Satish Dhawan
(b) Srijan
(c) God
(d) countless great minds
Answer:
(a) Professor Satish Dhawan

Question 57.
Who said the following to whom and when? “And then God will shine through us.”
Answer:
Professor Satish Dhawan to Dr Kalam when ‘ they were talking about academic brilliance.

Question 58.
Match the words in column ‘A’ with their opposites in column ‘B’: ‘

‘A’	‘B’
(i) asked	(a) increased
(ii) obscure	(b) impure
(iii) diminished	(c) clear
(iv) pure	(d) responded

Answer:

‘A’	‘B’
(i) asked	(d) responded
(ii) obscure	(c) clear
(iii) diminished	(a) increased
(iv) pure	(b) impure

Question 59.
Choose from the following words/phrases that more or less indicate the meaning of the word ‘wisdom’:
humanity, brilliance, ethical lives, academically accomplished, great minds
Answer:
brilliance, academically accomplished, great minds

Question 60.
Write the noun forms of:
(a) responded
(b) accomplished
(c) different
(d) clear t
(e) pure
Answer:
(a) responded – response
(b) accomplished – accomplishment
(c) different – difference
(d) clear – clarity
(e) pure – purity.

Question 61.
Academic brilliance is no different from the brilliance of a mirror. (Rewrite without ‘no’.)
Answer:
Academic brilliance is similar to the brilliance of a mirror.

Question 62.
God will shine through us. (Add a question tag.)
Answer:
God will shine through us, won’t He?

Question 63.
He had advised me to use my degree and gold medal to transform society. (Pick out the infinitives.)
Answer:
to use, to transform

Question 64.
Name the following based on the passage. The person who touched and influenced the life of Dr APJ Abdul Kalam. –
Answer:
Dr Sri Sri Shivakumara Mahaswamiji.

Question 65.
Find evidence from the passage that indicates that Swamiji:
(a) was dedicated
(b) has inner strength
(c) contributed to the good of the society
(d) was younger than the young generation
Answer:
(a) Who has dedicated his life to the service of humanity.
(b) Swamiji stood on his feet without any support!
(c) his greatest contribution is the establishment of a free residential education. Swamiji feeds thousands of children.
(d) He looked as steady and alert as any other youngster present there.

Question 66.
Complete the following.
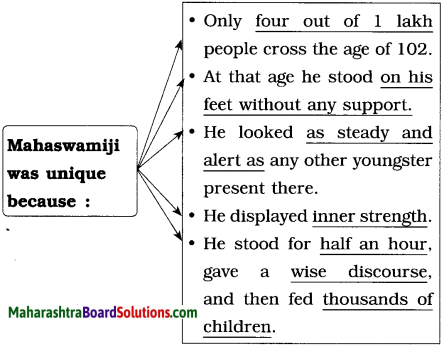
Answer:

Question 67.
Write a short paragraph on Dr Sri Shivakumara Mahaswamiji covering his profession and mentioning his personality traits with examples.
Answer:
Dr Sri Sri Shivakumara Mahaswamiji was a remarkable person. He had dedicated his life to the service of humanity and had established a free residential education system for more than nine thousand children. At the age of 102 he could stand without support, give a wise discourse for half an hour and then go on to feed thousands of children. He looked as steady and alert as any other youngster present there and displayed tremendous amount of inner strength.

Question 68.
Write the opposites of the following words using prefixes (un-, in-, etc.):
(a) invited
(b) remarkable
(c) humanity
(d) wise.
Answer:
(a) invited – uninvited
(b) remarkable – unremarkable
(c) humanity – inhumanity
(d) wise – unwise.

Question 69.
Guess the meanings of:
(i) genetics
(ii) googled?
Answer:
(i) genetics – heredity and the variation of inherited characteristics.
(ii) googled – found out information about the subject on the Google website

Question 70.
Find out the noun forms of the following from the passage:
(a) celebrated ……
(b) contribute …..
(c) educate …
(d) strong ….
Answer:
(a) celebrated – celebration
(b) contribute – contribution
(c) educate – education
(d) strong – strength

Question 71.
This display of inner strength touched Dr Kalam deeply. (Rewrite beginning ‘Dr Kalam
Answer:
Dr Kalam was deeply touched by this display of inner strength.

Question 72.
How many of these four would be able to stand tall for half an hour? (Rewrite as an assertive sentence.)
Answer:
Not many of these four would be able to stand tall for half an hour.

Question 73.
I had googled the subject beforehand. (Identify the tense of the sentence.)
Answer:
Past perfect tense

Question 74.
We were discussing this unusual birthday party. (Add a question tag.)
Answer:
We were discussing this unusual birthday party, weren’t we?

Question 75.
What measures will you take to keep yourself physically and mentally fit?
Answer:
To keep myself physically fit, I will take good care of my diet and eat only healthy foods. I will exercise regularly. To keep myself mentally fit, I will try to have a positive attitude towards life, be cheerful and happy and help others.

Question 76.
Fill in the blanks:
(a) Dr Kalam observed great …………………… in Swami Sivananda.
(b) Dr Kalam’s father believed in the value of …………………. .
(c) Mahaswamiji gives education to famished ……………………, food to famished ………………….. .
(d) The essence of a happy life and a peaceful society lies in one sentence – ……………………. .
Answer:
(a) tranquillity
(b) giving back
(c) minds, bodies
(d) ‘What can i give’

Question 77.
Complete the following based on the passage:
Answer:
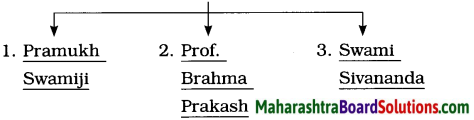
The people who touched and influenced Dr APJ Kalam in one way or the other were:

Question 78.
Complete the following table:

Name of person	Values
(a) Pramukh Swamiji	goodness of action
(b) Professor Brahma Prakash	need for living a pure and ethical life
(c) Father Pereira and Dr Sarabhai	selflessness in service
(d) Swami Sivananda	tranquillity
(e) Dr Kalam’s father	simplicity, the value of giving back
(f) Mahaswamiji	munificence, spirit of giving.

Answer:
(a) Goodness of action
(b) Pure and ethical life
(c) Selflessness in service
(d) Tranquillity
(e) Simplicity, giving back
(f) Munificence

Question 79.
Rearrange the letters to form sensible words:
(a) y e s f i l l e t =
(b) s c e n e c o i n c =
Answer:
(a) y e s f i l l e t = lifestyle
(b) s c e n e c o i n c = conscience

Question 80.
From the lesson write one word for:
Answer:
(a) giving away much to the needy munificence
(b) the basic idea of something essence

Question 81.
Complete the following choosing from the words/phrases given below: [moral sense of right and wrong, purity, characteristic spirit of a culture, principle or belief, simplicity, peace, generosity, spirituality]
(a) A tenet is a principle or belief.
(b) Conscience is a moral sense of right and wrong.
(c) Ethos is the characteristic spirit of a culture.
(d) Tranquillity is peace.
Answer:
(a) Principle or belief.
(b) Moral sense of right and wrong.
(c) Characteristic spirit of a culture.
(d) Peace.

Question 82.
Write the noun forms of:
(a) pure
(b) settle
(c) final.
Answer:
(a) pure – purity
(b) settle – settlement
(c) final – finality.

Question 83.
Activities based on Contextual Grammar:
(1) In giving so much, he becomes strong. (Rewrite using ‘because’.)
Answer:
He becomes strong because he gives so much.

Question 84.
His munificence fuels his strength. (Rewrite beginning with ‘His strength …’.)
Answer:
His strength is fuelled by his munificence.

Question 86.
What was the secret of Mahaswamiji’s fitness even at the age of 102 years?
Answer:
Mahaswamiji was a remarkable man. He lived with the belief of giving selflessly to famished minds and bodies. By giving, he himself became stronger. His spirit of generosity increased his strength and kept him standing tall and active in life.

Question 87.
Fill in the blanks:
(1) Dr Kalam’s message made an impact on the writer because of its gravity and the challenge it posed became his silent motivation.
(2) The truth of humanity lies in the answer to the question ‘What can I give?’
Answer:
(1) gravity, challenge
(2) truth, humanity

Question 88.
What makes society corrupt and unfair?
Answer:
Society becomes corrupt and unfair when humans think they can take indiscriminately from the environment and destroy it or when they think only of what they can take from other humans.

Question 89.
Complete the following with word from the passage:
Answer:

Question 90.
Pick out the adverbs: circumspectiy, indiscriminately, inequity, gravity.
Answer:
circumspectly, indiscriminately

Question 91.
Write what the underlined auxiliaries indicate:
(a) What can I give?
(b) We have to replace this attitude …
Answer:
(a) can – ability, possibility
(b) have to – obligation, compulsion.

Question 92.
The gravity of the message struck me. (Rewrite in the passive voice.)
Answer:
I was struck by the gravity of the message.

Question 93.
What answers do you get when you ask yourself the question ‘What can I give’?
Answer:
When I ask myself the question ‘What can I give’, I get the answer that I can ‘give’ my talents, my proper moral attitudes, my efforts in the service of others, financial help according to my means …!

Question 94.
Punctuate the following sentences to make them meaningful: (Note: 1 sentence will be asked in the activity sheet.)
(1) Spot the errors and rewrite the sentence correctly: We discussing the number of Ph.D’s Dr Kalam received.
(2) Arrange the following words in alphabetical order: inventions, indisputable, interactions, inequity, institutions, inquisitive, indiscriminately.
(3) Identify the type of sentence: Within a year he wants to build scientific facilities near the sea coast.
(4) Rearrange the letters to form two sensible words:
(1) i c e g e n t s
(2) f u n m i n c e i c e
(5) Make a meaningful sentence using the phrase: to come full circle.
(6) Pick out an infinitive and use it in your own sentence: I am able to talk to you using this mic.
(7) Write two smaller words hidden in the given word: perspective
(8) Complete the following word chain with words from the lesson: church, _ _ _ _ _e,
Answer:
(1) We weref discussing the number of Ph.D’s Dr Kalam had received.
(2) indiscriminately, indisputable, inequity, inquisitive, institutions, interactions, inventions
(3) Assertive Sentence
(4) (1) genetics (2) munificence
(6) It is firstanuary, the year has come full circle.
(6) Infinitive: to talk Sentence: The headmaster wants to talk to you about the annual function.!
(7) perspective: price, respect (spice, spite)
(8) church, house, equator, religious, scientist, team, mic, culture

Question 95.
(1) Write a word that sounds the same as ‘there’ and make a sentence.
(2) Prepare a word register of eight words for the word ‘house’.
(3) Rewrite beginning with the underlined part. His team had selected a site in Thumba.
Answer:
(1) Homophone: there – their! Sentence: They wanted admission for their child,
(2) House: apartment, residence, abode, dwelling, home, habitation, domicile, lodging, settlement
(3) A site in Thumba had been selected (by his team).

Question 96.
(1) Underline the modal auxiliary and state its function: They must have come full circle.
(2) Use the word ‘benefit’ as a noun as well as a verb in sentences.
Answer:!
(1) They must have come full circle. Function: past certainty.
(2) (a) Science confers many benefits on mankind, (noun)
(b) The bonus will benefit our family in many ways, (verb)

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.2 Three Questions Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 English Kumarbharati Textbook Solutions Unit 2.2 Three Questions

Maharashtra Board Class 10 English Solutions Unit 2.2 Warming Up Questions and Answers

Question 1.
Expressions in English classified under different heads. Pair up with your partner, guess and match the columns. (Use a dictionary.)

A		B
(1) Principle	(a)	a generally accepted, evident, truth
(2) Quotation	(b)	short striking messages for the public
(3) Moral	(c)	a short witty remark stating the truth
(4) Idioms	(d)	a popular, well-known truth
(5) Slogans	(e)	established expressions which do not convey exactly the same as individual words
(6) One-liners	(f)	words cited from a speech/text of a famous person
(7) Maxims	(g)	a lesson derived from a story or experience
(8) Proverb	(h)	a rule to govern one’s behavior

Answer:

A		B
(1) Principle	(h)	a rule to govern one’s behavior
(2) Quotation	(f)	words cited from a speech/text of a famous person
(3) Moral	(g)	a lesson derived from a story or experience
(4) Idioms	(e)	established expressions which do not convey exactly the same as individual words
(5) Slogans	(b)	short striking messages for the public
(6) One-liners	(c)	a short witty remark stating the truth
(7) Maxims	(d)	a popular, well-known truth
(8) Proverb	(a)	a generally accepted, evident, truth

Question 2.
Read the polite requests/suggestions and complete the gaps in the responses. Make sure they are polite and not repeated.
→ Could you lend me your dictionary?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, here it is.
Refuse (2) I’m sorry, I can’t. I am using it now.

→ Can you please pass the salad?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Sure!
Accept (2) Here you are.

→ May I know the exact time?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Right now It is exactly ten to six.
Accept (2) It’s 10 minutes past 5.

→ Shall we plan a class-picnic?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, let’s!
Refuse (2) Not now; I’m going to my native place for a month.

→ Do you need help?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, please.
Refuse (2) It’s all right, thank you. I can manage.

→ Is it alright if I use your laptop?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, I can spare It for an hour.
Refuse (2) Well… could you wait some time? I have some things I need to complete.

Question 3.
Let’s see if you remember a nursery rhyme you must have sung, as a kid :
Fill in the missing words: ………………..
‘The ……………….. time to be happy is
The to be happy is here.
And the way to be ……………….., is to ……………….. someone
happy And have a little ……………….. right here!’
(happy, make, heaven, now, place)
(You can listen to this song on the internet.)
Answer:
(happy, make, heaven, now, place)
The time to be happy is now.
The place to be happy is here.
And the way to be happy is to make someone happy. And have a little heaven right here!

Three Questions Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Read the story and answer whether the following statements are true or false.
(a) The people convinced the King to make a proclamation. ……………………………..
(b) The hermit spoke usually to everyone. ……………………………..
(c) The King received all answers from the hermit. ……………………………..
(d) The person the King saved and helped was his enemy. ……………………………..
(e) To do good to people is the purpose of our life. ……………………………..
Answer:
(a) True
(b) False
(c) False
(d) True
(e) True

Question 2.
Match the titles with the contents of the proper paragraph.

1	Once a certain king . . . important to do.	a	King gains a friend.
2	Many learned people . . . time for everything.	b	The wounded stranger
3	Equally varied . . . gave the reward to none.	c	King helps the hermit.
4	When the King arrived, . . . my first attention.	d	The stranger begs for pardon.
5	The hermit listened . . . continued to dig.	e	The hermit points out answers.
6	The King turned around . . . gave it to him.	f	Stranger’s vicious intention
7	Meanwhile the sun . . . said the King.	g	Questions remain unanswered.
8	“You do not know … all my life.	h	The king received various answers.
9	The King was very glad . . . the day before.	i	King’s announcement.
10	“Do you not see?” . . . sent into this life!”	j	The King meets the hermit.

Answer:

(1) Once a certain king … important to do.	i	The king’s announcement.
(2) Many learned people … time for everything.	h	The king received various answers.
(3) Equally varied … gave the reward to none.	g	The questions remained unanswered.
(4) When the king arrived, … rriy first attention.	j	The king meets the hermit
(5) The hermit listened … continued to dig.	c	The king helps the hermit.
(6) The king turned round … gave it to him.	b	The wounded stranger.
(7) Meanwhile the sun … said the king.	d	The stranger begs for pardon.
(8) ‘You do not know … all my life.’	f	The stranger’s vicious intentions.
(9) The king was very glad … the day before.	a	The king gains a friend.
(10) ‘Do you not see?’ … sent into his life.	e	The hermit points out answers.

Question 3.
The character traits of the king and hermit are mixed up. Sort them out in the right box.

Answer:
KiNG
impatient. eager to succeed, helpful

HERMIT
feeble, enlightened, patient, convincing, wise

Question 4.
Complete the Tree diagrams associated with the happenings in the story.

Answer:

Question 5.
Write down in your notebook two points for each of the following. How do you know . . .
(a) the learned advisers who came to the court confused the king.
(b) the king was humble.
(c) the king’s enemy was repentant.
(d) the hermit was truly wise.
Answer:
We come to know that the king was humble by the fact that he did not mind doing ordinary work such as digging. He did not use his authority as king to force the hermit to answer his questions. Instead he requested the hermit politely and was ready to go away if the hermit refused to answer his questions.

Question 6.
Choose the correct answer and fill in the blanks.
(a) “Varied” (Paragraph-3) means ……………………
(i) different
(ii) unnecessary
(iii) unequal
(iv) unimportant.
Answer:
(a) different

(b) Many learned people came to the court and gave ……………………
(i) The same answers
(ii) correct answers
(iii) different answers
(iv) wrong answers.
Answer:
(iii) different answers

(c) The synonym of ‘convinced’ is ……………………
(i) persuaded
(ii) happy
(iii) unhappy
(iv) angry.
Answer:
(i) persuaded

(d) The King wanted to know the …………………… time to begin everything.
(i) right
(ii) exact
(iii) proper
(iv) good.
Answer:
(i) right

(e) ‘‘I pray you to answer my question.’’ Here ‘pray’ means ……………………
(i) plead to God
(ii) request
(iii) order
(iv) suggest.
Answer:
(ii) request

(f) Choose an adverb that collocates with “breathed ……………………
(i) hurriedly
(ii) heavily
(iii) hardly
(iv) calmly.
Answer:
(i) heavily

Question 7.
Answer the following questions.
(a) The learned people were sometimes divided in their opinions, different persons giving quite different answers; at other times, none of them gave an answer. They all suggested ways to look for an answer. Point out one example of each.
Answer:
To know the right time for every action: Draw up in advance a table of days, months and years and live strictly according to it. The people the king most needed: Councillors The most important occupation: Science.

(b) Though the hermit did not say anything to the king for some time, he did not ignore the king or treat him rudely in any way. Do you agree? What evidence of his politeness can you point out? What shows that he listened and responded to the king’s words?
Answer:
I agree that though the hermit did not say anything to the king for some time, he did not ignore the king or treat him rudely in any way. His politeness is evident by the fact that he greeted the king. By spitting on his hand before he resumed digging, the hermit indicated that the work he was doing was more important and that the king would have to wait.

(c) The hermit ‘spoke only to common people’; so the king ‘put on simple clothes’. Do you think the king hoped to be mistaken for a common man, or was he just showing that he was a humble person? What shows that the hermit knew him to be the king?
Answer:
The king put on* simple clothes because he did not want the hermit to refuse to answer his questions. The king was aware that the hermit was wise and would know that he was the king and not mistake him for a common person. Out of humility and respect, the king dressed up like a commoner. We know that-the hermit knew that he was the king by the way he returned the king’s greeting.

(d) Did the king behave as an ordinary person, rather than as a ruler, at the hermit’s hut? What shows it? Did he also act as a good, kind person? When did he do so?
Answer:
Like any other ordinary person, the king tended to the wounded man. He even washed the wound and bandaged it many times. When required, he brought and gave the man water to drink. The king went out of his way to be good and kind to the man. All this happened after the wounded man came running, wounded, to the hermit’s hut.

(e) Do you think the hermit knew, beforehand, not only about the king’s arrival but about the ambush by his enemy? Think a little about this and say what you really feel.
Answer:
I think the hermit somehow knew everything before the king arrived. He must have known about the plan of the king’s enemy and so was able to deal with it purposefully when the king arrived. News about the ambush must definitely have come to his ears. Otherwise he would not have been able to answer the king’s questions in such a real and practical way. He was a hermit, a wise man, and nothing of importance would have escaped his consideration.

Question 8.
Consider this list of the different things that happened and rearrange them in the order of time, that is, what happened first, what happened next and so on. Read the related paragraph again if you are uncertain.

(a) The bearded man resolved to kill the king.
(b) The king went alone to see the hermit.
(c) The king executed the bearded man’s brother.
(d) The king spent the night at the hermit’s hut.
(e) The bearded man laid an ambush to kill the king.
(f) The king’s bodyguards recognised and wounded the bearded man.
(g) The bearded man came out of the ambush.
Answer:
(b) The king executed the bearded man’s brother.
(a) The bearded man resolved to kill the king.
(c) The bearded man laid an ambush to kill the king.
(e) The bearded man came out of the ambush.
(d) The king’s bodyguards recognised and wounded the bearded man.
(f) The king spent the night at the hermit’s hut.
(g) The king went alone to see the hermit.

Question 9.
Read the story in your own language, summarize the following aspects of the story in 4 to 5 lines each in your own language. Write it in your notebook.
(a) King’s problem: ……………………
Answer:
The King’s problem was that he wanted someone from his kingdom to give him the answers to three questions.
(1) What was the right time to begin everything?
(2) Who are the right people to listen to?
(3) What was the most important thing to do?

(b) Attempts made to find a solution: ……………………
(c) Climax: ……………………
(d) Solution: ……………………
(e) Message: ……………………
Answer:
The King wanted the answers to three questions. In order to find a solution, he had a proclamation made in his kingdom. He also announced a great reward to anyone who would give him the answers to his questions.

Question 10.
(A) The following compound words from the story are spelt in a jumbled order. Rearrange the letters to make them meaningful.
(1) a r e e t u k d n = ……………………
(2) y o n n a e = ……………………
(3) s t a p s i e m = ……………………
(4) h e e d a r f o n b = ……………………
(5) n e v h i g r e t y = ……………………
(6) h e i l n e w a m = ……………………
(7) d a d e b e r = ……………………
Answer:
(1) a r e e t u k d n = undertake
(2) y o n n a e = anyone
(3) s t a p s i e m = pastimes
(4) h e e d a r f o n b = beforehand
(5) n e v h i g r e t y = everything
(6) h e i l n e w a m = meanwhile
(7) d a d e b e r = bearded

(B) From the story, find the collocations of the following.
(1) …………………… important.
(2) …………………… intently
(3) frail and ……………………
(4) widely ……………………
(5) …………………… time
(6) …………………… blood
(7) simple ……………………
(8) closed ……………………
(9) …………………… asleep
(10) …………………… peace
(11) took ……………………..
Answer:
(1) most important
(2) gazing intently
(3) frail and weak
(4) widely renowned
(5) right time
(6) warm blood
(7) simple clothes
(8) closed eyes
(9) fell asleep.
(10) made peace
(11) took leave

Question 11.
Say whether the Verbs underlined in the sentences are finite (limited by the number or person of the subject) or non-finite (not governed by the subject, number or person).
(1) He decides to go to a hermit.
(2) I have come to you, wise hermit.
(3) He gave the reward to none.
(4) The hermit was digging the ground.
(5) I pray you to answer my questions.
(6) ‘‘ Forgive me.’’
(7) The sun began to sink.
Answer:
(1) decides – finite; to go – non-finite.
(2) have come – finite; to ask, to answer-non- finite.
(3) gave – finite; This sentence has no non-finite verb.
(4) was – finite; digging – non-finite.
(5) pray – finite: to answer – non-finite
(6) forgive – finIte
(7) began – finite; to sink – non-finite.

Question 12.
Narrate an experience of your own that has helped you to realise that ‘Patience is bitter, but its fruit is sweet.’ Write it in your notebook, in about 20 lines.
Answer:
Patience is bitter, but its fruit is sweet!

It was Rousseau who said, ‘Patience is bitter, but its fruit is sweet.’

I realized the truth of this statement when I was in Std. X. It was an important year for me. My school was far from my home. So were my classes. I had to spend a lot of time walking in order to reach either school or classes. This meant a lot of waste of precious time that I could use very well for study.

I was an only child and my father had passed away four years ago. My mother would tell me, ‘Have patience. Things will work out.’ But I really could not understand her.

The rainy months passed by with me trudging anxiously to school or to the classes. If I was lucky, someone would give me a lift, dy studies were suffering.

I was lagging behind in keeping up with homework and revision.

Then one day the postman delivered a letter. Mother read it in excitement.

‘You know what? There’s a good news. Your uncle from the US is coming to visit us. He is your dad’s brother. The last time he saw you was when you were j a baby.’

‘Oh,’ I said, wondering how that could be good for us. On the contrary, I would have to take my uncle visiting and that would take up more of the time I required for earnest study.

The day arrived. My uncle came over. A jolly fellow, full of stories and fun and small delightful gifts. In the afternoon I took his leave saying I had to go to school and then classes.

‘How are you going?’ he asked.
I put my head down and said, ‘Walking’.
‘Come, I’ll take you by autorickshaw,’ he said. And so we went.
‘It’s quite a distance,’ my uncle commented. I nodded silently.
In the evening when I came home, I could not believe my eyes.
There, resting against the wall was the most beautiful bicycle I had ever seen.
Mother and my uncle came out to greet me.
‘This is yours, boy. No more walking long distances for you!’
Tears welled up in my eyes and I ran and hugged my uncle.
‘Thank you so much,’ I said.
Indeed, my patience had been rewarded with sweet fruit!

Question 13.
After reading this story, develop a dialogue with 2 of your classmates about the characters in the story. Besides the tactful introduction to the conversation and write 8 to 10 sets of dialogues.
Answer:
My self: Hey, did you like the story, ‘Three Questions’?

Student 1: Yes, I was particularly impressed with the king. He was very humble. He was eager to know more about life.

My self: Yes, he did not claim that he knew everything just because he was king.

Student 2: I liked the hermit. He was quite a cool character.

My self: He was very wise. He knew beforehand that the king would come to him. He also knew the solution to the king’s problem, even before the incidents occurred.

Student 1: Yes. And the surprising thing is that the king indirectly got the answers to his questions from a long-forgotten enemy.

My self: The story is very cleverly written, woven around these three characters. One seeks answers to questions. One knows the answers to the questions. One is the medium through which the answers are given.

Student 2: If the king’s bodyguards had not attacked the man, he would not have come to the hermit’s hut and met the king.

My self: If the man had not been wounded and the king had not bandaged his wounds and saved his life, the man would not have forgiven him for a cruel wrongdoing in the past.

Student 1: Yes, Leo Tolstoy wanted to give us the message of forgiveness and doing good even to our enemies. Through the three characters in the story and their interactions, the writer brought out his message very well.

My sfelf : Indeed, a well-written story, and one from which we learn such a lot!

Question 14.
From the library or Internet, read the story ‘How much land does a man need?’ by Leo Tolstoy and write a review of the same, covering the following points.
Background of the story
Characters
Plot/Theme
Climax
Message/Moral
Answer:
The climax of the story is that the person whom the king had wronged by executing his brother years ago, finally forgave him. This is because the king had saved his life.

(a) rose got up from a sitting or kneeling position a flower
(b) sink drop downwards go down below the surface of a liquid
(c) bed a garden plot a piece of furniture for resting
(d) rest to cease work in order to relax or sleep the remaining part

By saving the life of the wounded man, who was in fact the king’s enemy, the king passes on to us the message that the most important thing in life is to do good to others, because it is for that purpose alone we were sent into this life.

Question 15.
What final suggestion did the last group of learned men offer regarding the best time?
Answer:
The last group of learned men said that it was impossible for one man to decide correctly the right time for every action and that the king should, instead, have a council of wise people, who would help him to fix the proper time for everything.

Question 16.
Choose the correct question tag from the alternatives and write the complete answer:
He would give a great reward,…
(a) would he?
(b) won’t he?
(c) wouldn’t he?
(d) will he?
Answer:
He would give a great reward, wouldn’t he?

Question 17.
Pick out the finite and non-finite verbs from the sentences:
(1) He always knew the right time to begin everything.
(2) He was right in thinking this way.
Answer:
(1) knew – finite; to begin – non-finite
(2) was – finite; thinking – non-finite.

Question 18.
They all gave different answers. (Rewrite using the opposite of ‘different’.)
Answer:
None of them gave similar answers.

Question 19.
He was convinced that he was right. (Pick out the clauses and name them.)
Answer:
He was convinced – Main clause.
that he was right – Subordinate Noun clause.

Question 20.
What is the right time, according to you?
Answer:
According to me, the right time is the present. Yesterday cannot be undone. Tomorrow cannot be predicted. Therefore, the only right time is today, i.e. the present.

Question 21.
The learned advisers who came to the court confused the king. How do you know?
Answer:
By giving the king’ different answers, the learned advisers who came to the court confused the king. None of the answers given by the advisers was complete or comprehensive. From their answers it is quite clear to me that each one of them dwelt on part of the truth and not the whole truth.

Question 22.
Read the following passage and do the activities:
(1) Arrange these incidents in proper sequence:
(a) The king asked the hermit the three questions.
(b) The king saw that the hermit was digging the ground.
*(c) The king went alone to see the hermit.
(d) The hermit greeted the king.
Answer:
(c) The king went alone to see the hermit.
(b) The king saw that the hermit was digging the ground.
(d) The hermit greeted the king.
(a) The king asked the liermit the three questions.

Question 23.
State whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(a) The hermit was well known. True
(b) The hermit spoke usually to everyone. False
(c) The hermit dug the ground easily False
(d) The hermit was strong. False

Question 24.
Why did the king go to the hermit in disguise?
Answer:
The hermit spoke only to common people. The king knew this. So he wanted to present himself as a common man and elicit answers for his questions. That is why he went to the hermit in disguise.

Question 25.
Write from the passage synonyms for:
(a) famous
(b) weak.
Answer:
(a) renowned
(b) frail.

Question 26.
The following compound words from the passage are spelt in jumbled order. Rearrange the letters to make them meaningful.
Answer:
(i) d ubgyroad = bodyguard
(ii) frawera = warfare

Question 27.
The king was convinced by none of these answers. (Rewrite beginning with ‘None of these answers …’.)
Answer:
None of these answers convinced the king.

Question 28.
State whether the following statements are True or False:
Answer:
(a) The king got irritated with the hermit. False
(b) The hermit answered all the questions of the king. False
(c) It was evening when the king met the hermit. True
(d) The hermit was full of energy. False

Question 29.
Who said to whom?
(a) Let me take the spade and work a while for you.
(b) Now rest a while and let me work a bit.
Answer:
(a) The king said this to the hermit.
(b) The hermit said this to the king.

Question 30.
How did the hermit respond to the king’s questions?
Answer:
The hermit listened to the king but said nothing. He just spat on his hand and continued digging. Later, when the king felt sorry for him, the hermit handed the king the spade to take over. When the king asked his question again, instead of giving an answer, the hermit rose and stretched out his hand for the spade.

Question 31.
In what state was the bearded man when he arrived?
Answer:
The bearded man was wounded. He fainted. He had a large wound in his stomach. The bleeding j would not stop and the wound had to be bandaged and re-bandaged. The bandage was soaked with blood. The bearded man was indeed in a very serious condition when he arrived.

Question 32.
Choose adverbs/adjectives that collocate with these words:
(1) moaning:
(a) profusely
(b) heavily
(c) feebly
(d) sadly.
Answer:
(i) moaning feebly

(ii) blood:
(a) profuse
(b) warm
(c) fresh
(d) bandaged.
Answer:
warm

Question 33.
Complete the following table with meanings from the brackets:
(Meanings: go down below the surface of a liquid, to cease work in order to relax or sleep, a piece of furniture for resting, a garden plot, got up from a sitting or kneeling position, drop downwards, the remaining part, a flower) (The answers are given directly in the table.)
Answer:
Words Meaning in the text Other meaning
(a) rose got up from a sitting or kneeling position a flower
(b) sink drop downwards go down below the surface of a liquid
(c) bed a garden plot a piece of furniture for resting
(d) rest to cease work in order to relax or sleep the remaining part

Question 34.
Pick out the finite and non-finite verbs from the sentences:
(a) The king continued to dig.
Answer:
(a) continued – finite; to dig – non-finite.

Question 35.
‘Here comes someone running,’ said the hermit. (Rewrite in indirect speech.)
Answer:
The hermit said that there came someone running.

Question 36.
He fainted and fell to the ground. (Rewrite using a present participle in place of the underlined word.)
Answer:
Fainting, he fell to the ground.

Question 37.
The blood would not stop flowing. (Rewrite without ‘not’.)
Answer:
The blood flowed continuously.

Question 38.
Say whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(a) The person the king saved and helped was his enemy. True
(b) The hermit helped the king. True
(c) When he awoke, the king immediately realized where he was. False
(d) The king had gone out for a walk. False

Question 39.
Why had the wounded man asked for the king’s pardon?
Answer:
The wounded man had resolved to kill the king. In try ng to do so. he was wounded and the king saved his life. Hence the wounded man asked for the king’s pardon.

Question 40.
Write two points for the following:
The king’s enemy was repentant. How do you know?
Answer:
The king’s enemy tells him that since the king had saved his life, if he (the king) wished it, he would serve him all his life. This shows that he was repentant.

Question 41.
Match the words with their opposites:
Answer:
Answer:
(a) familiar X strange
(b) forget X remember.
(c) firm X weak
(d) everything x nothing.

Question 42.
Forgive me,’ said the beard€d man. (Rewrite In indirect speech.)
Answer:
The bearded man asked him (the king) to forgive him.

Question 43.
What qualities of the king do you notice in this passage?
Answer:
Even though he was king, he did not hesitate to carry the wounded man into the hut. He was humble enough to sleep in a hut next to a wounded man. All this shows, that the king was not proud of his royal position. He was, at heart, kind, considerate and humane.

Question 44.
State whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(1) The hermit pitied the king’s weakness. False
(2) The king received all answers from the hermit. True
(3) The present is the only time when we have power. True
(4) To do good to people is the purpose of our life. True

Question 45.
How did the hermit finally point out the answers to the king’s questions?
Answer:
The hermit finally pointed out the answers to the king’s questions by referring to incidents that the king actually experienced when he visited the hermit. With the help of each incident, the- hermit explained to the king what the most important time was,’ who the most important person was and what the most important action was.

Question 46.
Summarize the following aspect in 4 to 5 lines each in your own words:
(a) The solution.
Answer:
The king finally got the answers to his questions. The most important time was when the king was digging the beds and when he was attending to the wounded man. Otherwise he would not have met the man and the man would have died. The most important action was bandaging the man’s wounds. If the man had died, he would not have made peace with the king. The most important man was the hermit, who made it possible for the king to find the answers to his questions.

Question 47.
Match the following:
‘A’ ‘B’
(1) one who heals – (a) sower
(2) one who lives alone in a forest – (b) physician
(3) one who plants seeds – (c) enemy
(4) one who is actively opposed to you – (d) hermit
Answer:
(1) one who heals – physician
(2) one who lives alone in a forest – hermit
(3) one who plants seeds – sower
(4) one who is actively opposed to you – enemy

Question 48.
He was the most important man. (Rewrite as a question.)
Answer:
Wasn’t he the most important man?

Question 49.
There is only one time that is important. (Rewrite using ‘no’.)
Answer:
There is no other time that is important.

Question 50.
For that purpose alone were you sent into this world. (Rewrite beginning with the subject ‘you’.)
Answer:
You were sent into this world for that purpose alone.

Question 51.
What qualities of the king stand out as he forgave his enemy?
Answer:
As the king forgave his enemy, we see him as a very humane person, as a person who believes in peace and forgiveness and one who shows mercy to even those who would wish to harm him.

Question 52.
(1) Pick out the infinitives in the given sentence and make your own sentence: He would give a reward to anyone who would teach him how he might know the most important thing to do.
(2) Write two compound words from the lesson.
(3) Punctuate the sentence: ive nothing to forgive you for said the king
(4) Make a meaningful sentence using the phrase: to feel sorry for (someone)
(5) Find out two hidden words in the given word: approaching
(6) Spot the error and rewrite the correct sentence: The king convinced none of these answers.
(7) Write the present participle forms of the given verbs: let, beg (run)
(8) Write these words in alphabetical order: beforehand, bearded, breathed, bodyguard.
Answer:
(1) Infinitive: to do Sentence: We were asked to do a simple activity before the session began.
(2) undertake, warfare
(3) T ve nothing to forgive you for,” said the king.
(4) Feeling sorry for the poor man, I gave him some food to eat.
(5) approach, aching
(6) The king was convinced by none of these answers.
(7) letting, begging (running)
(8) bearded, beforehand, bodyguard, breathed.

Question 53.
(1) Rewrite using indirect narration: “O wise one! Could you give me the answer to my three questions?” the king said to the hermit.
(2) Complete the following word chain with words from the lesson:
we . . . . . → . . . . . → . . . . . → . . . . .
(3) Rewrite beginning with the underlined part: The hermit again gave no answer.
(4) Make sentences of your own to show the difference of meaning between the words: ‘pray’ and ‘prey’.
Answer:
(1) Addressing the hermit as the ‘wise one’, the king asked him if he could give him the answer to his three questions.
(2) weak → king → ground → different.
(3) Again no answer was given by the hermit.
(4) (a) Every night the little boy would kneel by his bedside and pray.

(b) The vulture is a bird of prey.
(B) Do as directed (Challenging Activities):
(1) Change to the positive degree: What you did for him was your most important business.
(2) Use the given word as a noun and as a verb: wish
Answer:
(1) No other business of yours was as important as what you did for him.
(2) Word: wish
Sentences: (a) Make a wish and it will come true. (noun)
(b) You may leave if you wish, (verb)

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.1 Animals Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 English Kumarbharati Textbook Solutions Unit 2.1 Animals

Maharashtra Board Class 10 English Solutions Unit 2.1 Warming Up Questions and Answers

Question 1.
Get into pairs and attempt the following :
“The more I learn about people, the more I like my dog.”- Mark Twain. – Discuss with your partner what Mark Twain means from the above quote.

Write in your own words
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
Answer:
‘The more I learn about people, the more I like my dog. – Mark Twain.

Ely the above quote, Mark Twain means that his dog has certain qualities which he finds lacking in human beings. Each day, as he comes across different people and learns more about human nature, the feeling grows within him that humans possess many disagreeable qualities that do not help in improving relationships. As a result, he begins to love his dog more than human beings.

Question 2.
Put the following attributes/abilities given below in the proper circles.
(a) self-control
(b) communicates
(c) love and care
(d) cooks
(e) good manners
(f) has 3600 vision
(g) shows gratitude
(h) lives for more than 150 years
(i) swims
(j) learns computing
(k) worships god
(l) sleeps in standing position
(m) stands up immediately after birth
(n) brings up children
(o) belongs to various species

Answer:

Question 3.
At times, especially when you are frustrated, you wish you were an animal/ a bird/ a fish/ a butterfly and not a human being.

Say which of the above you would choose to transform to and give 3 or 4 reasons for your choice.
I wish I could be a ………………………………………..
…………………………………………………………………….
…………………………………………………………………….
Answer:
When I am frustrated, I wish I could be a bird, so I could fly away from the cause of frustration. At such times, I would like to be far from the noise and crowd on earth and sail in silence across the sky. I would prefer to concentrate on my own thoughts and regain my peace, and the best place for that would be the vast open sky. Flapping my wings would keep me active and busy and help me forget about my worries.

Question 4.
We come across many animals in our vicinity. We have also read about different animals in books. Make a list of all animals that fall under various categories. One is given for you.

Amphibians	Mammals	Wild Animals	Aquatic Animals	Pet Animals
frog	cow	lion	octopus	cat

Answer:

Amphibians	Mammals	Wild Animals	Aquatic Animals	Pet Animals
frog	cow	lion	octopus	cat
toad	bat	tiger	crocodile	dog
salamander	squirrel	bear	alligator	guinea pig
caecilian	mongoose	wolf	hippopotamus	gold fish
		cheetah	turtle
		leopard
		monkey

Animals Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
(A) Match the words given in table A with their meanings in table B.

No	(A) Words		(B) Meaning
(i)	whine	(a)	an offense against the religious or moral law
(ii)	sin	(b)	complain in an annoying way
(iii)	evince	(c)	craze
(iv)	mania	(d)	failing to take proper care
(v)	negligent	(e)	show

Answer:

No	(A) Words		(B) Meanings
(i)	whine	(b)	complain in an annoying way
(ii)	sin	(a)	an offense against the religious or moral law
(iii)	evince	(e)	show
(iv)	mania	(c)	mental illness
(v)	negligent	(d)	failing to take proper care

(B) Find adjectives from the poem which refer to positive and negative thinking

Positive	Negative
1…………………………….	1…………………………….
2…………………………….	2…………………………….
3…………………………….	3…………………………….

Answer:

Positive	Negative
(1) placid	(1) dissatisfied
(2) self-contained	(2) demented
	(3) unhappy

Question 2.
Complete the following.
(a) The poet wishes he could ……………………………….
(b) Animals do not complain about ……………………………….
(c) Animals do not merely discuss ……………………………….
(d) Animals are not crazy about ……………………………….
Answer:
(a) The poet wishes he could turn and live with animals.
(b) Animals do not complain about their condition.
(c) Animals do not merely discuss their duty to God.
(d) Animals are not crazy about owning things.

Question 3.
State whether the following statements are true or false.
(a) Animals are self-reliant. ……………………………….
(b) Animals quarrel for their possessions. ……………………………….
(c) Animals do not worship other animals. ……………………………….
(d) Humans have given up many good qualities. ……………………………….
(e) Animals suffer humiliation. ……………………………….
(f) The poet has retained all his natural virtues. ……………………………….
Answer:
(a) True
(b) False
(c) True
(d) True
(e) False
(f) False

Question 4.
With the help of the poem find the differences between animals and human beings.

Human beings	Animals
Always complain about their condition	Never complain about anything
…………………………………. ………………………………….	…………………………………. ………………………………….

Answer:

Human Beings	Animals
Always complain about their condition.	Never complain about their condition.
Spend sleepless nights regretting their sins.	Don’t regret their sins at all.
Sicken others by discussing their duty to God.	Do not discuss their duty to God.
Always dissatisfied.	Always contented.
Crazy about acquiring possessions.	Never interested in owning things.
Worship other human beings.	Never worship anyone of their kind.
Always unhappy about earthly matters.	Unconcerned about earthly matters.

Question 5.
Read the text again, and complete the web, highlighting the good values/habits which we can learn from animals.

Answer:

Question 6.
Find outlines from the poem that are examples of the following Figures of Speech.

Figures of Speech	Lines
Repetition	…………………………
Alliteration	…………………………
Hyperbole	…………………………

Answer:

Figures of Speech	Lines
Repetition	I stand and look at them long and long They do not sweat and whine … They do not he awake … They do not make … Not one is dissatisfied, not one is demented …
Alliteration	Not one is dissatisfied, not one is demented … … they evince them plainly in their possession.
Hyperbole	… Not one is respectable or unhappy over the whole earth.

Question 7.
Identify the Figures of Speech in the following lines.
(a) I stand and look at them long and long.
………………………………………………………………..

(b) They do not sweat and whine about their condition.
………………………………………………………………..

(c) They do not make me sick discussing their duty to God.
………………………………………………………………..

(d) …… not one is demented with the mania of owning things.
………………………………………………………………..

(e) They bring me tokens of myself.
………………………………………………………………..

(f) No one is respectable or unhappy over the whole earth.
………………………………………………………………..
Answer:
(a) Repetition
(b) Tautology
(c) Alliteration
(d) Hyperbole
(e) Paradox
(f) Hyperbole

Question 8.
Read the poem again and write an appreciation of the poem in a paragraph format with the help of given points. (Refer to page no. 5)
Answer:
Point Format
(for understanding)
The title of the poem : Animals’
The poet : Walt Whitman
Rhyme scheme : free verse (no rhyme scheme)
Figures of speech : Repetition, Alliteration. Tautology, Hyperbole, etc.
The theme/central idea : Animals are better than humans.

Paragraph Format
The poem ‘Animals’ has been penned by Walt Whitman.

The poet has broken away from the conventional use of a rhyme scheme and has written the poem in free verse.

The chief figure of speech used in the poem is Repetition. Lines such as ‘They do not sweat …’. ‘They do not lie awake …’. ‘They do not make me sick …’ make a strong impact, expressing the qualities that humans should possess, but do not. The other figures of speech are Alliteration, Tautology, Hyperbole, etc.

The central idea of the poem is that animals today are better than humans

Question 9.
Divide the class into two groups. One group should offer points in favor of (views) and the other against (counterviews) the topic ‘Life of an animal is better than that of a human being.’

Later use the points to express your own views/counterviews in paragraph format in your notebook.
Answer:
Point Format

View	Counterview
Animals are placid and self-contained.	Animals cannot improve their lot in life.
Animals do not try to set targets or achieve goals. Humans do.	By setting targets, goals are achieved.
Animals do not complain about their condition.	It is only by complaining that one comes to know how things can be improved.
Animals are self-satisfied with their condition, whatever it be.	Humans continuously try to improve their living conditions.
Animals do not worship other things or animals or persons as gods.	Animals have no idea about God. Humans acknowledge a divine Creator.
Animals do not worry about possessions or earthly matters.	Animals have no care about the future of this planet. Humans do.

Question 10.
What craze do animals never display?
Answer:
Animals never display the craze of owning things.

Question 11.
What could have happened to the tokens of the poet’s self?
Answer:
The tokens of the poet’s self might have been lost from the time man resorted to manipulating nature and considered himself apart from it.

Question 12.
What does the poet mean by ‘They bring me tokens of myself?
Answer:
By ‘They bring me tokens of myself the poet means that animals possess and express visible signs of qualities such as innocence and simplicity that he himself (i.e. all human beings) must have possessed.

Question 13.
Give one example of a Rhetorical Question from the poem. Explain.
Answer:
Did I pass that way huge times ago and negligently drop them?
The poet uses a question to assert that we human beings unmindfully discarded the good qualities that we possessed somewhere along the line.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 50 Answers Solutions Chapter 14 Algebraic Formulae – Expansion of Squares.

Algebraic Formulae – Expansion of Squares Class 7 Practice Set 50 Answers Solutions Chapter 14

Question 1.
Expand:
i. (5a + 6b)²
ii. \(\left(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{3}\right)^{2}\)
iii. (2p – 3q)²
iv. \(\left(x-\frac{2}{x}\right)^{2}\)
v. (ax + by)²
vi. (7m – 4)²
vii. \(\left(x+\frac{1}{2}\right)^{2}\)
viii. \(\left(a-\frac{1}{a}\right)^{2}\)
Solution:
i. (5a + 6b)²
Here, A = 5a and B = 6b
(5a + 6b)² = (5a)² + 2 × 5a × 6b + (6b)²
…. [(A + B)² = A² + 2AB + B²]
∴ (5a + 6b)² = 25a² + 60ab + 36b²

ii. \(\left(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{3}\right)^{2}\)
Here A = \(\frac { a }{ 2 }\) and B = \(\frac { b }{ 3 }\)

iii. (2p – 3q)²
Here, a = 2p and b = 3q
(2p – 3q)² = (2p)² – 2 × (2p) × (3q) + (3q)²
…. [(a – b)² = a² – 2ab + b²]
∴ (2p – 3q)² = 4p² – 12pq + 9q²

iv. \(\left(x-\frac{2}{x}\right)^{2}\)
Here a = x and b = \(\frac { 2 }{ x }\)

v. (ax + by)²
Here, A = ax and B = by
(ax + by)² = (ax)² + 2 × ax × by + (by)²
…. [(A + B)² = A² + 2AB + B²]
∴ (ax + by)² = a²x² + 2abxy + b²y²

vi. (7m – 4)²
Here, a = 7m and b = 4
(7m – 4)² = (7m)² – 2 × 7m × 4 + 4²
…. [(a – b)² = a² – 2ab + b²]
∴ (7m – 4)² = 49m² – 56m + 16

vii. \(\left(x+\frac{1}{2}\right)^{2}\)
Here a = x and b = \(\frac { 1 }{ 2 }\)

viii. \(\left(a-\frac{1}{a}\right)^{2}\)
Here A = a and B = \(\frac { 1 }{ a }\)

Question 2.
Which of the options given below is the square of the binomial
(A) \(64-\frac{1}{x^{2}}\)
(B) \(64+\frac{1}{x^{2}}\)
(C) \(64-\frac{16}{x}+\frac{1}{x^{2}}\)
(D) \(64+\frac{16}{x}+\frac{1}{x^{2}}\)
Solution:
(C) \(64-\frac{16}{x}+\frac{1}{x^{2}}\)

Hint:
= \(\left(8-\frac{1}{x}\right)^{2}=8^{2}-2 \times 8 \times \frac{1}{x}+\left(\frac{1}{x}\right)^{2}\) …[(a – b)² = a² – 2ab + b²]
= \(64-\frac{16}{x}+\frac{1}{x^{2}}\)

Question 3.
Of which of the binomials given below is the m²n² + 14mnpq + 49p²q² the expansion?
(A) (m + n) (p + q)
(B) (mn – pq)
(C) (7mn + pq)
(D) (mn + 7pq)
Solution:
(D) (mn + 7pq)

Hint:
Here, square root of the first term = mn
Square root of the last term = 7pq
∴ Required binomial = (mn + 7pq)²

Question 4.
Use an expansion formula to find the values of:
i. (997)²
ii. (102)²
iii. (97)²
iv. (1005)²
Solution:
i. (997)² = (1000 – 3)²
Here, a = 1000 and b = 3
(1000 – 3)² = (1000)² – 2 x 1000 x 3 + 3²
…. [(a – b)² = a² – 2ab + b²]
= 1000000 – 6000 + 9
= 994009
∴ (997)² = 994009

ii. (102)² = (100 + 2)²
Here, a = 100 and b = 2
(100 + 2)² = (100)² + 2 x 100 x 2 + 2²
…. [(a + b)² = a² + 2ab + b²]
= 10000 + 400 + 4
= 10404
∴ (102)² = 10404

iii. (97)² = (100 – 3)²
Here, a = 100 and b = 3
(100 – 3)² = (100)² – 2 x 100 x 3 + 3²
…. [(a – b)² = a² – 2ab + b²]
= 10000 – 600 + 9
= 9409
∴ (97)² = 9409

iv. (1005)² = (1000 + 5)²
Here, a = 1000 and b = 5 (1000 + 5)²
= (1000)² + 2 x 1000 x 5 + 5²
…. [(a + b)² = a² + 2ab + b²]
= 1000000+ 10000 + 25
= 1010025
∴ (1005)² = 1010025

Maharashtra Board Class 7 Maths Chapter 14 Algebraic Formulae – Expansion of Squares Practice Set 50 Intext Questions and Activities

Question 1.
Use the given values to verify the formulae for squares of binomials. (Textbook pg. no. 92)
i. a = -7, b = 8
ii. a = 11,b = 3
iii. a = 2.5,b = 1.2
Solution:
i. (a + b)² = (-7 + 8)²
= 1²
= 1
a² + 2ab + b² = (-7)² + 2 x (-7) x 8 + 8²
= 49 – 112 + 64
= 1
∴(a + b)² = a² + 2ab + b²
(a – b)² = (-7 – 8)²
= (-15)²
= 225
a² – 2ab + b² = (-7)² – 2 x (-7) x 8 + (8)²
= 49 + 112 + 64
= 225
∴(a – b)² = a² – 2ab + b²

ii. (a + b)² = (11 + 3)²
= 14²
= 196
a² + 2ab + b² = 11² + 2 x 11 x 3 + 3²
= 121 + 66 + 9
= 196
∴(a + b)² = a² + 2ab + b²
(a – b)² = (11 – 3)² = 8²
= 64
a² – 2ab + b² = 11² – 2 x 11 x 3 + 3²
= 121 – 66 + 9
= 64
∴(a – b)² = a² – 2ab + b²

iii. (a + b)² = (2.5 + 1.2)²
= 3.7²
= 13.69
a² + 2ab + b² = (2.5)² + 2 x 2.5 x 1.2 + (1.2)²
= 6.25 + 6 + 1.44
= 13.69
∴(a + b)² = a² + 2ab + b²
(a – b)² = (2.5 – 1.2)²
= 1.32
= 1.69
a² – 2ab + b² = (2.5)² – 2 x 2.5 x 1.2 + (1.2)²
= 6.25 – 6 + 1.44
= 1.69
∴(a – b)² = a² – 2ab + b²-

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Miscellaneous Exercise 3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Miscellaneous Exercise 3

I. Select the correct option from the given alternatives.

Question 1.
The value of sin(n + 1) A sin(n + 2) A + cos(n + 1) A cos(n + 2) A is equal to
(a) sin A
(b) cos A
(c) -cos A
(d) sin 2A
Answer:
(b) cos A
Hint:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let (n + 2)A = a and (n + 1)A = b … (i)
∴ L.H.S. = cos a . cos b + sin a . sin b
= cos (a – b)
= cos [(n + 2)A – (n + 1)A] ……..[From (i)]
= cos [(n + 2 – n – 1)A]
= cos A
= R.H.S.

Question 2.
If tan A – tan B = x and cot B – cot A = y, then cot (A – B) = ________
(a) \(\frac{1}{y}-\frac{1}{x}\)
(b) \(\frac{1}{x}-\frac{1}{y}\)
(c) \(\frac{1}{x}+\frac{1}{y}\)
(d) \(\frac{x y}{x-y}\)
Answer:
(c) \(\frac{1}{x}+\frac{1}{y}\)
Hint:

Question 3.
If sin θ = n sin(θ + 2α), then tan(θ + α) is equal to
(a) \(\frac{1+n}{2-n}\) tan α
(b) \(\frac{1-n}{1+n}\) tan α
(c) tan α
(d) \(\frac{1+n}{1-n}\) tan α
Answer:
(d) \(\frac{1+n}{1-n}\) tan α
Hint:

Question 4.
The value of \(\frac{\cos \theta}{1+\sin \theta}\) is equal to ________
(a) \(\tan \left(\frac{\theta}{2}-\frac{\pi}{4}\right)\)
(b) \(\tan \left(-\frac{\pi}{4}-\frac{\theta}{2}\right)\)
(c) \(\tan \left(\frac{\pi}{4}-\frac{\theta}{2}\right)\)
(d) \(\tan \left(\frac{\pi}{4}+\frac{\theta}{2}\right)\)
Answer:
(c) \(\tan \left(\frac{\pi}{4}-\frac{\theta}{2}\right)\)
Hint:

Question 5.
The value of cos A cos (60° – A) cos (60° + A) is equal to ________
(a) \(\frac{1}{2}\) cos 3A
(b) cos 3A
(c) \(\frac{1}{4}\) cos 3A
(d) 4cos 3A
Answer:
(c) \(\frac{1}{4}\) cos 3A
Hint:

Question 6.
The value of \(\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14} \sin \frac{7 \pi}{14} \sin \frac{9 \pi}{14} \sin \frac{11 \pi}{14} \sin \frac{13 \pi}{14}\) is ________
(a) \(\frac{1}{16}\)
(b) \(\frac{1}{64}\)
(c) \(\frac{1}{128}\)
(d) \(\frac{1}{256}\)
Answer:
(b) \(\frac{1}{64}\)
Hint:

Question 7.
If α + β + γ = π, then the value of sin² α + sin² β – sin² γ is equal to ________
(a) 2 sin α
(b) 2 sin α cos β sin γ
(c) 2 sin α sin β cos γ
(d) 2 sin α sin β sin γ
Answer:
(c) 2 sin α sin β cos γ
Hint:
sin² α + sin² β – sin² γ
= \(\frac{1-\cos 2 \alpha}{2}+\frac{1-\cos 2 \beta}{2}-\sin ^{2} \gamma\)
= 1 – \(\frac{1}{2}\) (cos 2α + cos 2β) – 1 + cos² γ
= \(\frac{-1}{2}\) × 2 cos(α + β) cos(α – β) + cos² γ
= cos γ cos (α – β) + cos² γ …..[∵ α + β + γ = π]
= cos γ [cos (α – β) + cos γ]
= cos γ [cos (α – β) – cos (α + β)]
= 2 sin α sin β cos γ

Question 8.
Let 0 < A, B < \(\frac{\pi}{2}\) satisfying the equation 3sin² A + 2sin² B = 1 and 3sin 2A – 2sin 2B = 0, then A + 2B is equal to ________
(a) π
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{4}\)
(d) 2π
Answer:
(b) \(\frac{\pi}{2}\)
Hint:
3 sin 2A – 2sin 2B = 0
sin 2B = \(\frac{3}{2}\) sin 2A …….(i)
3 sin² A + 2 sin² B = 1
3 sin² A = 1 – 2 sin² B
3 sin² A = cos 2B ……(ii)
cos(A + 2B) = cos A cos 2B – sin A sin 2B
= cos A (3 sin² A) – sin A (\(\frac{3}{2}\) sin 2A) …..[From (i) and (ii)]
= 3 cos A sin² A – \(\frac{3}{2}\) (sin A) (2 sin A cos A)
= 3 cos A sin² A – 3 sin² A cos A
= 0
= cos \(\frac{\pi}{2}\)
∴ A + 2B = \(\frac{\pi}{2}\) ……..[∵ 0 < A + 2B < \(\frac{3 \pi}{2}\)]

Question 9.
In ∆ABC if cot A cot B cot C > 0, then the triangle is ________
(a) acute-angled
(b) right-angled
(c) obtuse-angled
(d) isosceles right-angled
Answer:
(a) acute angled
Hint:
cot A cot B cot C > 0
Case I:
cot A, cot B, cot C > 0
∴ cot A > 0, cot B > 0, cot C > 0
∴ 0 < A < \(\frac{\pi}{2}\), 0 < B < \(\frac{\pi}{2}\), 0 < C < \(\frac{\pi}{2}\)
∴ ∆ABC is an acute angled triangle.
Case II:
Two of cot A, cot B, cot C < 0
0 < A, B, C < π and two of cot A, cot B, cot C < 0
∴ Two angles A, B, C are in the 2nd quadrant which is not possible.

Question 10.
The numerical value of tan 20° tan 80° cot 50° is equal to ________
(a) √3
(b) \(\frac{1}{\sqrt{3}}\)
(c) 2√3
(d) \(\frac{1}{2 \sqrt{3}}\)
Answer:
(a) √3
Hint:
L.H.S. = tan 20° tan 80° cot 50°
= tan 20° tan 80° cot (90° – 40°)
= tan 20° tan 80° tan 40°
= tan 20° tan (60° + 20°) tan (60° – 20°)

= tan 3(20°)
= tan 60°
= √3
= R.H.S.

II. Prove the following.

Question 1.
tan 20° tan 80° cot 50° = √3
Solution:
L.H.S. = tan 20° tan 80° cot 50°
= tan 20° tan 80° cot (90° – 40°)
= tan 20° tan 80° tan 40°
= tan 20° tan (60° + 20°) tan (60° – 20°)

= tan 3(20°)
= tan 60°
= √3
= R.H.S.

Question 2.
If sin α sin β – cos α cos β + 1 = 0, then prove that cot α tan β = -1.
Solution:
sin α sin β – cos α cos β + 1 = 0
∴ cos α cos β – sin α sin β = 1
∴ cos (α + β) = 1
∴ α + β = 0 ……[∵ cos 0 = 1]
∴ β = -α
L.H.S. = cot α tan β
= cot α tan(-α)
= -cot α tan α
= -1
= R.H.S.

Question 3.
\(\cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15} \cos \frac{16 \pi}{15}=\frac{1}{16}\)
Solution:

Question 4.
\(\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)=\frac{1}{8}\)
Solution:

Question 5.
cos 12° + cos 84° + cos 156° + cos 132° = \(-\frac{1}{2}\)
Solution:

Question 6.
\(\cos \left(\frac{\pi}{4}+x\right)+\cos \left(\frac{\pi}{4}-x\right)=\sqrt{2} \cos x\)
Solution:

Question 7.
\(\frac{\sin 5 x-2 \sin 3 x+\sin x}{\cos 5 x-\cos x}=\tan x\)
Solution:

Question 8.
sin² 6x – sin² 4x = sin 2x sin 10x
Solution:

Question 9.
cos² 2x – cos² 6x = sin 4x sin 8x
Solution:

Question 10.
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution:

Question 11.
\(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}\)
Solution:

Question 12.
If sin 2A = λ sin 2B, then prove that \(\frac{\tan (A+B)}{\tan (A-B)}=\frac{\lambda+1}{\lambda-1}\)
Solution:

Question 13.
\(\frac{2 \cos 2 A+1}{2 \cos 2 A-1}\) = tan (60° + A) tan (60° – A)
Solution:

Question 14.
tan A + tan (60° + A) + tan (120° + A) = 3 tan 3A
Solution:

Question 15.
3 tan⁶ 10° – 27 tan⁴ 10° + 33 tan² 10° = 1
Solution:

Question 16.
cosec 48° + cosec 96° + cosec 192° + cosec 384° = 0
Solution:
L.H.S. = cosec 48° + cosec 96° + cosec 192° + cosec 384°
= cosec 48° + cosec (180° – 84°) + cosec (180° + 12°) + cosec (360° + 24°)
= cosec 48° + cosec 84° + cosec (-12°) + cosec 24°

Question 17.
3(sin x – cos x)⁴ + 6(sin x + cos x)² + 4(sin⁶ x + cos⁶ x) = 13
Solution:
(sin x – cos x)⁴
= [(sin x – cos x)²]²
= (sin² x + cos² x – 2 sin x cos x)²
= (1 – 2 sin x cosx)²
= 1 – 4 sin x cos x + 4 sin² x cos² x
(sin x + cos x)² = sin² x + cos² x + 2 sin x cos x = 1 + 2 sin x cos x
sin⁶ x + cos⁶ x
= (sin² x)³ + (cos² x)³
= (sin² x + cos² x)³ – 3 sin² x cos² x (sin² x + cos² x) …..[∵ a³ + b³ = (a + b)³ – 3ab(a + b)]
= 1³ – 3 sin² x cos² x (1)
= 1 – 3 sin² x cos² x
L.H.S. = 3(sin x – cos x)⁴ + 6(sin x + cos x)² + 4(sin⁶ x + cos⁶ x)
= 3(1 – 4 sin x cos x + 4 sin² x cos² x) + 6(1 + 2 sin x cos x) + 4(1 – 3 sin² x cos² x)
= 3 – 12 sin x cos x + 12 sin² x cos² x + 6 + 12 sin x cos x + 4 – 12 sin² x cos² x
= 13
= R.H.S.

Question 18.
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
Solution:
We have to prove that,
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
i.e., to prove,
cot A – tan A – 2 tan 2A – 4 tan 4A – 8 cot 8A = 0

∴ cot θ – tan θ = 2 cot 2θ …..(i)
L.H.S. = cot A – tan A – 2 tan 2A – 4 tan 4A – 8 cot 8A
= 2 cot 2A – 2 tan 2A – 4 tan 4A – 8 cot 8A …..[From (i)]
= 2(cot 2A – tan 2A) – 4 tan 4A – 8 cot 8A
= 2 × 2 cot 2(2A) – 4 tan 4A – 8 cot 8A ……[From (i)]
= 4(cot 4A – tan 4A) – 8 cot 8A
= 4 × 2 cot 2(4A) – 8 cot 8A ……[From (i)]
= 8 cot 8A – 8 cot 8A = 0
= R.H.S.
Alternate Method:

Question 19.
If A + B + C = \(\frac{3 \pi}{2}\), then cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C
Solution:

Question 20.
In any triangle ABC, sin A – cos B = cos C. Show that ∠B = \(\frac{\pi}{2}\).
Solution:
sin A – cos B = cos C
∴ sin A = cos B + cos C

A = B – C ………(i)
In ∆ABC,
A + B + C = π
∴ B – C + B + C = π
∴ 2B = π
∴ B = \(\frac{\pi}{2}\)

Question 21.
\(\frac{\tan ^{3} x}{1+\tan ^{2} x}+\frac{\cot ^{3} x}{1+\cot ^{2} x}\) = sec x cosec x – 2 sin x cos x
Solution:

Question 22.
sin 20° sin 40° sin 80° = \(\frac{\sqrt{3}}{8}\)
Solution:
L.H.S. = sin 20°. sin 40°. sin 80°
= sin 20°. sin 40°. sin 80°
= \(\frac{1}{2}\) (2 . sin 40°. sin 20°) . sin 80°
= \(\frac{1}{2}\) [cos(40° – 20°) – cos (40° + 20°)] . sin 80°
= \(\frac{1}{2}\) (cos 20° – cos 60°) sin 80°
= \(\frac{1}{2}\) . cos 20° . sin 80° – \(\frac{1}{2}\) . cos 60° . sin 80°
= \(\frac{1}{2 \times 2}\) (2 sin 80° . cos 20°) – \(\frac{1}{2 \times 2}\) . sin 80°
= \(\frac{1}{4}\) [sin(80° + 20°) + sin (80° – 20°)] – \(\frac{1}{2}\) . sin 80°

Question 23.
sin 18° = \(\frac{\sqrt{5}-1}{4}\)
Solution:
Let θ = 18°
∴ 5θ = 90°
∴ 2θ + 3θ = 90°
∴ 2θ = 90° – 3θ
∴ sin 2θ = sin (90° – 3θ)
∴ sin 2θ = cos 3θ
∴ 2 sin θ cos θ = 4 cos³ θ – 3 cos θ
∴ 2 sin θ = 4 cos² θ – 3 …..[∵ cos θ ≠ 0]
∴ 2 sin θ = 4 (1 – sin² θ) – 3
∴ 2 sin θ = 1 – 4 sin² θ
∴ 4 sin² θ + 2 sin θ – 1 = 0
∴ sin θ = \(\frac{-2 \pm \sqrt{4+16}}{8}\)
= \(\frac{-2 \pm 2 \sqrt{5}}{8}\)
= \(\frac{-1 \pm \sqrt{5}}{4}\)
Since, sin 18° > 0
∴ sin 18°= \(\frac{\sqrt{5}-1}{4}\)

Question 24.
cos 36° = \(\frac{\sqrt{5}+1}{4}\)
Solution:
We know that,
cos 2θ = 1 – 2 sin² θ
cos 36° = cos 2(18°)
= 1 – 2 sin² 18°

∴ cos 36° = \(\frac{\sqrt{5}+1}{4}\)

Question 25.
sin 36° = \(\frac{\sqrt{10-2 \sqrt{5}}}{4}\)
Solution:
We know that, sin² θ = 1 – cos² θ
sin² 36° = 1 – cos² 36°
= 1 – \(\left(\frac{\sqrt{5}+1}{4}\right)^{2}\)
= \(\frac{16-(5+1+2 \sqrt{5})}{16}\)
= \(\frac{10-2 \sqrt{5}}{16}\)
∴ sin 36° = \(\frac{\sqrt{10-2 \sqrt{5}}}{4}\) ……[∵ sin 36° is positive]

Question 26.
\(\sin \frac{\pi^{c}}{8}=\frac{1}{2} \sqrt{2-\sqrt{2}}\)
Solution:

Question 27.
tan \(\frac{\pi}{8}\) = √2 – 1
Solution:

Question 28.
tan 6° tan 42° tan 66° tan 78° = 1
Solution:

Question 29.
sin 47° + sin 61° – sin 11° – sin 25° = cos 7°
Solution:

Question 30.
√3 cosec 20° – sec 20° = 4
Solution:

Question 31.
In ∆ABC, ∠C = \(\frac{2 \pi}{3}\), then prove that cos² A + cos² B – cos A cos B = \(\frac{3}{4}\).
Solution:

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Ex 5.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Ex 5.3

Question 1.
Write the equation of the line:
i. parallel to the X-axis and at a distance of 5 units from it and above it.
ii. parallel to the Y-axis and at a distance of 5 units from it and to the left of it.
iii. parallel to the X-axis and at a distance of 4 units from the point (- 2,3).
Solution:
i. Equation of a line parallel to X-axis is y = k. Since the line is at a distance of 5 units above X-axis, k = 5
∴ The equation of the required line is y = 5.

ii. Equation of a line parallel to Y-axis is x = h. Since the line is at a distance of 5 units to the left of Y-axis, h = -5
∴ The equation of the required line is x = -5.
[Note: Answer given in the textbook is ‘y = -5
However, we found that ‘x = – 5’.]

iii. Equation of a line parallel to the X-axis is of the form y = k (k > 0 or k < 0).
Since the line is at a distance of 4 units from the point (- 2, 3),
k = 4 + 3 = 7 or k = 3- 4 = -1
∴ The equation of the required line is y = 1 or y = – 1.

Question 2.
Obtain the equation of the line:
i. parallel to the X-axis and making an intercept of 3 units on the Y-axis.
ii. parallel to the Y-axis and making an intercept of 4 units on the X-axis.
Solution:
i. Equation of a line parallel to X-axis with y-intercept ‘k’ isy = k.
Here, y-intercept = 3
∴ The equation of the required line is y = 3.

ii. Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 4
∴ The equation of the required line is x = 4.

Question 3.
Obtain the equation of the line containing the point:
i. A(2, – 3) and parallel to the Y-axis.
ii. B(4, – 3) and parallel to the X-axis.
Solution:
i. Equation of a line parallel to Y-axis is of the form x = h.
Since the line passes through A(2, – 3), h = 2
∴ The equation of the required line is x = 2.

ii. Equation of a line parallel to X-axis is of the formy = k.
Since the line passes through B(4, – 3), k = -3
∴ The equation of the required line is y = – 3.

Question 4.
Find the equation of the line:
i. passing through the points A(2, 0) and B(3,4)
ii. passing through the points P(2, 1) and Q(2,-1)
Solution:
i. The required line passes through the points A(2, 0) and B(3,4).
Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
Here, (x₁y₁) = (2,0) and (x₁,y₂) = (3,4)
∴ The equation of the required line is
∴ \(\frac{y-0}{4-0}=\frac{x-2}{3-2}\)
∴ \(\frac{y}{4}=\frac{x-2}{1}\)
∴ y = 4(x – 2)
∴ y = 4x – 8
∴ 4x – y – 8 = 0

ii. The required line passes through the points P(2, 1) and Q(2,-1).
Since both the given points have same
x co-ordinates i.e. 2,
the given points lie on the line x = 2.
∴ The equation of the required line is x = 2.

Question 5.
Find the equation of the line:
i. containing the origin and having inclination 60°.
ii. passing through the origin and parallel to AB, where A is (2,4) and B is (1,7).
iii. having slope 1/2 and containing the point (3, -2)
iv. containing the point A(3, 5) and having slope 2/3
v. containing the point A(4, 3) and having inclination 120°.
vi. passing through the origin and which bisects the portion of the line 3JC + y = 6 intercepted between the co-ordinate axes.
Solution:
i. Given, Inclination of line = θ = 60°
Slope of the line (m) = tan θ = tan 60°
= \(\sqrt{3}\)
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
.‘. The equation of the required line is y = \(\sqrt{3}\) x

ii. Given, A (2, 4) and B (1, 7)
Slope of AB = \(\frac{7-4}{1-2}\) = -3 1-2
Since the required line is parallel to line AB, slope of required line (m) = slope of AB
∴ m = – 3 and the required line passes through the origin.
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is y = – 3x

iii. Given, slope(m) = \(=\frac{1}{2}\) and the line passes through (3, – 2).
Equation of the line in slope point form is
y-y ₁= m(x-x₁)
∴ The equation of the required line is
[y-(- 2)]=\(\frac{1}{2}\)(x-3)
∴ 2(y + 2)=x – 3
∴ 2y + 4 = x – 3
∴ x – 2y – 7 = 0

iv. Given, slope(m) = \(\frac{2}{3}\) and the line passes through (3, 5).
Equation of the line in slope point form is y-y₁ = m(x -x₁)
∴ The equation of the required line is y – 5 = \(\frac{2}{3}\)(x-3)
∴ 3 (y – 5) = 2 (x – 3)
∴ 3y – 15 = 2x – 6
∴ 2x – 3y + 9 = 0

v. Given, Inclination of line = θ = 120°
Slope of the line (m) = tan θ = tan 120°
= tan (90° + 30°)
= – cot 30°
= – \(\sqrt{3}\)
and the line passes through A(4, 3).
Equation of the line in slope point form is y-y₁ = m(x -x₁)
∴ The equation of the required line is
y- 3 = –\(\sqrt{3}\)(x-4)
∴ y – 3 = –\(\sqrt{3}\) x + 4\(\sqrt{3}\)
∴ \(\sqrt{3}\)x + y – 3 -4\(\sqrt{3}\) = 0

vi.

Given equation of the line is 3x +y = 6.
∴ \(\frac{x}{2}+\frac{y}{6}=1\)
This equation is of the form \(\frac{x}{\mathrm{a}}+\frac{y}{\mathrm{~b}}\) = 1,
where a = 2, b = 6
∴ The line 3x + y = 6 intersects the X-axis and Y-axis at A(2, 0) and B(0, 6) respectively. Required line is passing through the midpoint of AB.
∴ Midpoint of AB = ( \(\frac{2+0}{2}, \frac{0+6}{2}\) ) = (1,3)
∴ Required line passes through (0, 0) and (1,3).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-0}{3-0}=\frac{x-0}{1-0}\)
\(\frac{y}{3}=\frac{x}{1}\)
∴ y = 3x
∴ 3x – y = 0

Alternate Method:
Given equation of the line is 3x + y = 6 …(i)
Substitute y = 0 in (i) to get a point on X-axis.
∴ 3x + 0 = 6
∴ x = 2
Substitute x = 0 in (i) to get a point on Y-axis.
∴ 3(0) + 7 = 6
∴ y = 6
∴ The line 3x + y = 6 intersects the X-axis and Y-axis at A(2,0) and B(0,6) respectively.
Let M be the midpoint of AB.
M = \(\left(\frac{2+0}{2}, \frac{0+6}{2}\right)\) = (1,3)
Slope of OM (m) = \(\frac{3-0}{1-0}\) = 3
Equation of OM is of the formy = mx.
∴ The equation of the required line is y = 3x
∴ 3x – y = 0

Question 6.
Line y = mx + c passes through the points A(2,1) and B(3,2). Determine m and c.
Solution:
Given, A(2, 1) and B(3,2)
Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-1}{2-1}=\frac{x-2}{3-2}\)
∴ \(\frac{y-1}{1}=\frac{x-2}{1}\)
∴ y – 1 = x – 2
∴ y = x – 1
Comparing this equation with y = mx + c, we get
m = 1 and c = – 1

Alternate Method:
Points A(2, 1) and B(3, 2) lie on the line y = mx + c.
∴ They must satisfy the equation.
∴ 2m + c = 1 …(i)
and 3m + c = 2 …(ii)
equation (ii) – equation (i) gives m = 1
Substituting m = 1 in (i), we get 2(1) + c = 1
∴ c = 1 – 2 = – 1

Question 7.
Find the equation of the line having inclination 135° and making x-intercept 7.
Solution:
Given, Inclination of line = 0 = 135°
∴ Slope of the line (m) = tan 0 = tan 135°
= tan (90° + 45°)
= – cot 45° = – 1 x-intercept of the required line is 7.
∴ The line passes through (7, 0).
Equation of the line in slope point form is y – y₁ = m(x – x₁)
∴ The equation of the required line is y — 0 = – 1 (x – 7)
∴ y = -x + 7
∴ x + y – 7 = 0

Question 8.
The vertices of a triangle are A(3, 4), B(2, 0) and C(- 1, 6). Find the equations of the lines containing
i. side BC
ii. the median AD
iii. the midpoints of sides AB and BC.
Solution:
Vertices of AABC are A(3, 4), B(2, 0) and C(- 1, 6).
i. Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the side BC is
\(\frac{y-0}{6-0}=\frac{x-2}{-1-2}\)
\(\frac{y}{6}=\frac{x-2}{-3}\)
∴ – 3y = 6x – 12
∴ 6x + 3y – 12 = 0
∴ 2x + y – 4 = 0

ii. Let D be the midpoint of side BC.
Then, AD is the median through A.
∴ D = \(\left(\frac{2-1}{2}, \frac{0+6}{2}\right)=\left(\frac{1}{2}, 3\right)\)
The median AD passes through the points
A(3,4) and D( \(\frac{1}{2}\) , 3)

∴ The equation of the median AD is
\(\frac{y-4}{3-4}=\frac{x-3}{\frac{1}{2}-3}\)
\(\frac{y-4}{-1}=\frac{x-3}{-\frac{5}{2}}\)
\(\frac{5}{2}\)(y-4) = x – 3
∴ 5y – 20 = 2x – 6
∴ 2x – 5y + 14 = 0

iii. Let D and E be the midpoints of side AB and side BC respectively.
The equation of the line DE is

∴ -4(y-2) = 2x-5
∴ 2x + 4y – 13 = 0

Question 9.
Find the x and y-intercepts of the following lines:
i. \(\frac{x}{3}+\frac{y}{2}=1\)
ii. \(\frac{3 x}{2}+\frac{2 y}{3}=1\)
iii. 2x – 3y + 12 = 0
Solution:
i. Given equation of the line is latex]\frac{x}{3}+\frac{y}{2}=1[/latex]
This is of the form \(\frac{x}{a}+\frac{y}{b}\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = 3, y-intercept = 2

ii. Given equation of the line is \(\frac{3 x}{2}+\frac{2 y}{3}\) = 1
∴ \(\frac{x}{\left(\frac{2}{3}\right)}+\frac{y}{\left(\frac{3}{2}\right)}\) = 1
This is of the form = \(\frac{x}{a}+\frac{y}{b}\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = \(\frac{2}{3}\) and y-intercept = \(\frac{3}{2}\)

iii. Given equation of the line is 2x – 3y + 12 = 0
∴ 2x – 3y = – 12
∴ \(\frac{2 x}{(-12)}-\frac{3 y}{(-12)}=1\)
∴ \(\frac{x}{-6}+\frac{y}{4}=1\)
This is of the form \(\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = – 6 and y-intercept = 4

Question 10.
Find equations of the line which contains the point A(l, 3) and the sum of whose intercepts on the co-ordinate axes is zero.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be
\(\frac{x}{a}+\frac{y}{b}=1\) ………..(i)
Since, the sum of the intercepts of the line is zero.
∴ a + b = 0
∴ b = – a
Substituting b = – a in (i), we get
\(\frac{x}{a}+\frac{y}{(-a)}=1\)
x – y = a .. .(ii)
Since, the line passes through A(1, 3).
∴ 1 – 3 = a
∴ a = – 2
Substituting the value of a in (ii), equation of the required line is
∴ x – y = – 2,
∴ x – y + 2 = 0

Case II: Line passing through origin.
Slope of line passing through origin and
A(1, 3) is m = \(\frac{3-0}{1-0}\) = 3
∴ Equation of the line having slope m and passing through origin (0, 0) is / = mx.
∴ The equation of the required line is y = 3x
∴ 3x – y = 0

Question 11.
Find equations of the line containing the point A(3, 4) and making equal intercepts on the co-ordinate axes.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) …………(i)
This line passes through A(3, 4).
∴ \(\frac{3}{a}+\frac{4}{b}=1\)……………..(ii)
Since, the required line make equal intercepts on the co-ordinate axes.
∴ a = b …(iii)
Substituting the value of b in (ii), we get
\(\frac{3}{a}+\frac{4}{a}=1\)
∴ \(\frac{7}{a}=1\)
∴ a = 7
∴ b = 7 …[From (iii)]
Substituting the values of a and b in (i), equation of the required line is
\(\frac{x}{7}+\frac{y}{7}=1\) = 1
∴ x + y = 7

Case II: Line passing through origin.
Slope of line passing through origin and A(3,4) is m = \(=\frac{4-0}{3-0}=\frac{4}{3}\)
∴ Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is 4
y = \(\frac{4}{3}\)x
∴ 4x – 3y = 0

Question 12.
Find the equations of the altitudes of the triangle whose vertices are A(2, 5), B(6, – 1 ) and C(- 4, – 3).
Solution:

A(2, 5), B(6, – 1), C(- 4, – 3) are the vertices of ∆ABC.
Let AD, BE and CF be the altitudes through the vertices A, B and C respectively of ∆ABC.
∴ Slope of AD = -5 …[∵AD ⊥ BC]
Since altitude AD passes through (2, 5) and has slope – 5,
equation of the altitude AD is y – 5 = -5 (x – 2)
∴ y – 5 = – 5x + 10
∴ 5x +y -15 = 0
Now, slope of AC = \(\frac{-3-5}{-4-2}=\frac{-8}{-6}=\frac{4}{3}\)
Slope of BE = \(\frac{-3}{4}\)
…[∵ BE ⊥ AC]
Since altitude BE passes through (6,-1) and has slope \(\frac{-3}{4}\),
equation of the altitude BE is
y-(-1) = \(\frac{-3}{4}\) (x – 6)
∴ 4 (y + 1) = – 3 (x – 6)
∴ 4y + 4 =-3x+ 18
∴ 3x + 4y – 14 = 0
Also, slope of AB = \(\frac{-1-5}{6-2}=\frac{-6}{4}=\frac{-3}{2}\)
∴ Slope of CF = \({2}{3}\) ….[∵ CF ⊥ AB]
Since altitude CF passes through (- 4, – 3) and has slope , \(\frac{2}{3}\)
equation of the altitude CF is
y-(-3) = \(\frac{2}{3}\)[x-(-4)]
∴ 3 (y + 3) = 2 (x + 4)
∴ 3y + 9 = 2x + 8
∴ 2x – 3y – 1 = 0

Question 13.
Find the equations of perpendicular bisectors of sides of the triangle whose vertices are P(-1, 8), Q(4, – 2) and R(- 5, – 3).
Solution:

Let A, B and C be the midpoints of sides PQ, QR and PR respectively of APQR.
A is the midpoint of side PQ.

Slope of perpendicular bisector of PQ is \(\frac{1}{2}\) and it passes through (\(\frac{3}{2}\)), 3).
Equation of the perpendicular bisector of side PQ is
y – 3 = \(\frac{1}{2}\)(x – \(\frac{3}{2}\))
y – 3 = (\(\frac{1}{2}\left(\frac{2 x-3}{2}\right)\))
∴ 4(y – 3) = 2x – 3
∴ 4y – 12 = 2x – 3
∴ 2x – 4y + 9 = 0
B is the midpoint of side QR
∴ B = \(\left(\frac{4-5}{2}, \frac{-2-3}{2}\right)=\left(\frac{-1}{2}, \frac{-5}{2}\right)\)
Slope of side QR = \(\frac{-3-(-2)}{-5-4}=\frac{-1}{-9}=\frac{1}{9}\)
∴ Slope of perpendicular bisector of QR is -9 and it passes through \(\left(-\frac{1}{2},-\frac{5}{2}\right)\)
∴ Equation of the perpendicular bisector of side QR is

∴ 2y + 5 = -18x – 9
∴ 18x + 2y + 14 = 0
∴ 9x + y + 7 = 0
C is the midpoint of side PR.

Equation of the perpendicular bisector of PR is \(y-\frac{5}{2}=-\frac{4}{11}(x+3)\)
∴ \(11\left(\frac{2 y-5}{2}\right)\) =-4(x + 3)
∴ 11(2y – 5) = – 8 (x + 3)
∴ 22y – 55 = – 8x – 24
∴ 8x + 22y -31 = 0

Question 14.
Find the co-ordinates of the orthocentre of the triangle whose vertices are A(2, – 2), B(l, 1) and C(-1,0).
Solution:
Let O be the orthocentre of AABC.
Let AM and BN be the altitudes of sides BC and AC respectively.
Now, slope of BC = \(\frac{0-1}{-1-1}=\frac{-1}{-2}=\frac{1}{2}\)
Slope of AM = -2 ,..[∵ AM ⊥ BC]
Since AM passes through (2, – 2) and has slope -2,
equation of the altitude AM is y – (- 2) = – 2 (x – 2)
∴ y + 2 = -2x + 4
∴ 2x + y – 2 = 0 …(i)

Also, slope of AC = \(\frac{0-(-2)}{-1-2}=\frac{2}{-3}\)
∴ Slope of BN = \(\frac{3}{2}\) …[∵ BN ⊥ AC]
Since BN passes through (1,1) and has slope \(\frac{3}{2}\), equation of the altitude BN is
y – 1 = \(\frac{3}{2}\)(x-1)
∴ 2y – 2 = 3x – 3
∴ 3x – 2y – 1 = 0 …(ii)
To find co-ordinates of orthocentre, we have to solve equations (i) and (ii).
By (i) x 2 + (ii), we get
7x – 5 = 0
∴ x = \(\frac{5}{7}\)
substituting x = \(\frac{5}{7}\) in eq (i), we get
2(\(\frac{5}{7}\)) + y – 2 = 0
∴ y = -2(\(\frac{5}{7}\)) + 2
∴ y = \(\frac{-10+14}{7}=\frac{4}{7}\)
∴ Coordinates of orthocentre O = \(\left(\frac{5}{7}, \frac{4}{7}\right)\)

Question 15.
N(3, – 4) is the foot of the perpendicular drawn from the origin to line L. Find the equation of line L.
Solution:

Slope of ON = \(\frac{-4-0}{3-0}=\frac{-4}{3}\)
Since line L ⊥ ON,
slope of the line L is \(\frac{3}{4}\) and it passes through point N(3, -4).
Equation of the line in slope point form is y – y₁ = m(x – x₁)
Equation of line L is
y-(-4) = \(\frac{3}{4}\)(x-3)
∴ 4(y + 4) = 3(x – 3)
∴ 4y + 16 = 3x – 9
∴ 3x – 4y – 25 = 0

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.1

Question 1.
Differentiate the following w.r.t. x :
(i) (x³ – 2x – 1)⁵
Solution:
Method 1:
Let y = (x³ – 2x – 1)⁵
Put u = x³ – 2x – 1. Then y = u⁵

Method 2:
Let y = (x³ – 2x – 1)⁵
Differentiating w.r.t. x, we get

(ii) \(\left(2 x^{\frac{3}{2}}-3 x^{\frac{4}{3}}-5\right)^{\frac{5}{2}}\)
Solution:
Let y = \(\left(2 x^{\frac{3}{2}}-3 x^{\frac{4}{3}}-5\right)^{\frac{5}{2}}\)
Differentiating w.r.t. x, we get

(iii) \(\sqrt{x^{2}+4 x-7}\)
Solution:

(iv) \(\sqrt{x^{2}+\sqrt{x^{2}+1}}\)
Solution:
Let y = \(\sqrt{x^{2}+\sqrt{x^{2}+1}}\)
Differentiating w.r.t. x, we get

(v) \(\frac{3}{5 \sqrt[3]{\left(2 x^{2}-7 x-5\right)^{5}}}\)
Solution:
Let y = \(\frac{3}{5 \sqrt[3]{\left(2 x^{2}-7 x-5\right)^{5}}}\)
Differentiating w.r.t. x, we get

(vi) \(\left(\sqrt{3 x-5}-\frac{1}{\sqrt{3 x-5}}\right)^{5}\)
Solution:
Let y = \(\left(\sqrt{3 x-5}-\frac{1}{\sqrt{3 x-5}}\right)^{5}\)
Differentiating w.r.t. x, we get

Question 2.
Diffrentiate the following w.r.t. x
(i) cos(x² + a²)
Solution:
Let y = cos(x² + a²)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)[cos(x² + a²)]
= -sin(x² + a²)∙\(\frac{d}{d x}\)x² + a²)
= -sin(x² + a²)∙(2x + 0)
= -2xsin(x² + a²)

(ii) \(\sqrt{e^{(3 x+2)}+5}\)
Solution:
Let y = \(\sqrt{e^{(3 x+2)}+5}\)
Differentiating w.r.t. x, we get

(iii) log[tan(\(\frac{x}{2}\))]
Solution:
Let y = log[tan(\(\frac{x}{2}\))]
Differentiating w.r.t. x, we get

(iv) \(\sqrt{\tan \sqrt{x}}\)
Solution:
Let y = \(\sqrt{\tan \sqrt{x}}\)
Differentiating w.r.t. x, we get

(v) cot³[log (x³)]
Solution:
Let y = cot³[log (x³)]
Differentiating w.r.t. x, we get

(vi) 5^{sin3x+ 3}
Solution:
Let y = 5^{sin3x+ 3}
Differentiating w.r.t. x, we get

(vii) cosec (\(\sqrt{\cos X}\))
Solution:
Let y = cosec (\(\sqrt{\cos X}\))
Differentiating w.r.t. x, we get

(viii) log[cos (x³ – 5)]
Solution:
Let y = log[cos (x³ – 5)]
Differentiating w.r.t. x, we get

(ix) e^{3 sin2x – 2 cos2x}
Solution:
Let y = e^{3 sin2x – 2 cos2x}
Differentiating w.r.t. x, we get

(x) cos²[log (x²+ 7)]
Solution:
Let y = cos²[log (x²+ 7)]
Differentiating w.r.t. x, we get

(xi) tan[cos (sinx)]
Solution:
Let y = tan[cos (sinx)]
Differentiating w.r.t. x, we get

(xii) sec[tan (x⁴ + 4)]
Solution:
Let y = sec[tan (x⁴ + 4)]
Differentiating w.r.t. x, we get

= sec[tan(x⁴ + 4)]∙tan[tan(x⁴ + 4)]∙sec²(x⁴ + 4)(4x³ + 0)
= 4x³sec²(x⁴ + 4)∙sec[tan(x⁴ + 4)]∙tan[tan(x⁴ + 4)].

(xiii) e^{log[(logx)2 – logx2]}
Solution:
Let y = e^{log[(logx)2 – logx2]}
= (log x)² – log x² …[∵ e^{log x} = x]
Differentiating w.r.t. x, we get

(xiv) sin\(\sqrt{\sin \sqrt{x}}\)
Solution:
Let y = sin\(\sqrt{\sin \sqrt{x}}\)
Differentiating w.r.t. x, we get

(xv) log[sec(e^x2)]
Solution:
Let y = log[sec(e^x2)]
Differentiating w.r.t. x, we get

(xvi) log_e²(logx)
Solution:
Let y = log_e²(logx) = \(\frac{\log (\log x)}{\log e^{2}}\)

(xvii) [log{log(logx)}]²
Solution:
let y = [log{log(logx)}]²
Differentiating w.r.t. x, we get

(xviii) sin²x² – cos²x²
Solution:
Let y = sin²x² – cos²x²
Differentiating w.r.t. x, we get

= 2sinx²∙cosx² × 2x + 2sinx²∙cosx² × 2x
= 4x(2sinx²∙cosx²)
= 4xsin(2x²).

Question 3.
Diffrentiate the following w.r.t. x
(i) (x² + 4x + 1)³ + (x³ – 5x – 2)⁴
Solution:
Let y = (x² + 4x + 1)³ + (x³ – 5x – 2)⁴
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)[(x² + 4x + 1)³ + (x³ – 5x – 2)⁴]
= \(\frac{d}{d x}\) = (x² + 4x + 1)³ + \(\frac{d}{d x}\)(x³ – 5x – 2)⁴
= 3(x² + 4x + 1)²∙\(\frac{d}{d x}\)(x² + 4x + 1) + 4(x³ – 5x – 2)⁴∙\(\frac{d}{d x}\)(x³ – 5x – 2)
= 3(x² + 4x + 1)³∙(2x + 4 × 1 + 0) + 4(x³ – 5x – 2)³∙(3x² – 5 × 1 – 0)
= 6 (x + 2)(x² + 4x + 1)² + 4 (3x² – 5)(x³ – 5x – 2)³.
(ii) (1 + 4x)⁵(3 + x − x²)⁸
Solution:
Let y = (1 + 4x)⁵(3 + x − x²)⁸
Differentiating w.r.t. x, we get

= 8 (1 + 4x)⁵ (3 + x – x²)⁷∙(0 + 1 – 2x) + 5 (1 + 4x)⁴ (3 + x – x²)⁸∙(0 + 4 × 1)
= 8 (1 – 2x)(1 + 4x)⁵(3 + x – x²)⁷ + 20(1 + 4x)⁴(3 + x – x²)⁸.

(iii) \(\frac{x}{\sqrt{7-3 x}}\)
Solution:
Let y = \(\frac{x}{\sqrt{7-3 x}}\)
Differentiating w.r.t. x, we get

(iv) \(\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\)
Solution:
Let y = \(\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\left[\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\right]\)

(v) (1 + sin²x)²(1 + cos²x)³
Solution:
Let y = (1 + sin²x)²(1 + cos²x)³
Differentiating w.r.t. x, we get

= 3(1 + sin²x)² (1 + cos²x)²∙[2cosx(-sinx)] + 2 (1 + sin²x)(1 + cos²x)³∙[2sinx-cosx]
= 3 (1 + sin²x)² (1 + cos²x)² (-sin 2x) + 2(1 + sin²x)(1 + cos²x)³(sin 2x)
= sin2x (1 + sin²x) (1 + cos²x)² [-3(1 + sin²x) + 2(1 + cos²x)]
= sin2x (1 + sin²x)(1 + cos²x)²(-3 – 3sin²x + 2 + 2cos²x)
= sin2x (1 + sin²x)(1 + cos²x)² [-1 – 3 sin²x + 2 (1 – sin²x)]
= sin 2x(1 + sin²x)(1 + cos²x)² (-1 – 3 sin²x + 2 – 2 sin²x)
= sin2x (1 + sin²x)(1 + cos²x)²(1 – 5 sin²x).

(vi) \(\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}\)
Solution:
Let y = \(\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}[\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}]\)

(vii) log(sec 3x+ tan 3x)
Solution:
Let y = log(sec 3x+ tan 3x)
Differentiating w.r.t. x, we get

(viii) \(\frac{1+\sin x^{\circ}}{1-\sin x^{\circ}}\)
Solution:

(ix) cot\(\left(\frac{\log x}{2}\right)\) – log\(\left(\frac{\cot x}{2}\right)\)
Solution:
Let y = cot\(\left(\frac{\log x}{2}\right)\) – log\(\left(\frac{\cot x}{2}\right)\)
Differentiating w.r.t. x, we get

(x) \(\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\)
Solution:

(xi) \(\frac{e^{\sqrt{x}}+1}{e^{\sqrt{x}}-1}\)
Solution:
let y = \(\frac{e^{\sqrt{x}}+1}{e^{\sqrt{x}}-1}\)
Differentiating w.r.t. x, we get

(xii) log[tan³x·sin⁴x·(x² + 7)⁷]
Solution:
Let y = log [tan³x·sin⁴x·(x² + 7)⁷]
= log tan³x + log sin⁴x + log (x² + 7)⁷
= 3 log tan x + 4 log sin x + 7 log (x² + 7)
Differentiating w.r.t. x, we get

= 6cosec2x + 4 cotx + \(\frac{14 x}{x^{2}+7}\)

(xiii) log\(\left(\sqrt{\frac{1-\cos 3 x}{1+\cos 3 x}}\right)\)
Solution:

(xiv) log\(\left(\sqrt{\left.\frac{1+\cos \left(\frac{5 x}{2}\right)}{1-\cos \left(\frac{5 x}{2}\right)}\right)}\right.\)
Solution:
Using log\(\left(\frac{a}{b}\right)\) = log a – log b
log a^b = b log a


\(-\frac{5}{2}\)cosec\(\left(\frac{5 x}{2}\right)\)

(xv) log\(\left(\sqrt{\frac{1-\sin x}{1+\sin x}}\right)\)
Solution:

(xvi) log\(\left[4^{2 x}\left(\frac{x^{2}+5}{\sqrt{2 x^{3}-4}}\right)^{\frac{3}{2}}\right]\)
Solution:

(xvii) log\(\left[\frac{e^{x^{2}}(5-4 x)^{\frac{3}{2}}}{\sqrt[3]{7-6 x}}\right]\)
Solution:

(xviii) log\(\left[\frac{a^{\cos x}}{\left(x^{2}-3\right)^{3} \log x}\right]\)
Solution:

(xix) y= (25)^log₅(secx) − (16)^log₄(tanx)
Solution:
y = (25)^log₅(secx) − (16)^log₄(tanx)
= 5^{2log₅(secx)} – 4^{2log₄(tanx)}
= 5^{log₅(sec5x)} – 4^{log₄(tan2x)}
= sec²x – tan²x … [∵ = x]
∴ y = 1
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(1) = 0

(xx) \(\frac{\left(x^{2}+2\right)^{4}}{\sqrt{x^{2}+5}}\)
Solution:
Let y = \(\frac{\left(x^{2}+2\right)^{4}}{\sqrt{x^{2}+5}}\)
Differentiating w.r.t. x, we get

Question 4.
A table of values of f, g, f ‘ and g’ is given

(i) If r(x) = f [g(x)] find r’ (2).
Solution:
r(x) = f[g(x)]
∴ r'(x) = \(\frac{d}{d x}\)f[g(x)]
= f'[g(x)]∙\(\frac{d}{d x}\)[g(x)]
= f'[g(x)∙[g'(x)]
∴ r'(2) = f'[g(2)]∙g'(2)
= f'(6)∙g'(2) … [∵ g(x) = 6, when x = 2]
= -4 × 4 … [From the table]
= -16.

(ii) If R(x) = g[3 + f(x)] find R’ (4).
Solution:
R(x) = g[3 + f(x)]
∴ R'(x) = \(\frac{d}{d x}\){g[3+f(x)]}
= g'[3 + f(x)]∙\(\frac{d}{d x}\)[3 + f(x)]
= g'[3 +f(x)]∙[0 + f'(x)]
= g'[3 + f(x)]∙f'(x)
∴ R'(4) = g'[3 + f(4)]∙f'(4)
= g'[3 + 3]∙f'(4) … [∵ f(x) = 3, when x = 4]
= g'(6)∙f'(4)
= 7 × 5 … [From the table]
= 35.

(iii) If s(x) = f[9− f(x)] find s’ (4).
Solution:
s(x) = f[9− f(x)]
∴ s'(x) = \(\frac{d}{d x}\){f[9 – f(x)]}
= f'[9 – f(x)]∙\(\frac{d}{d x}\)[0 – f(x)]
= f'[9 – f(x)]∙[0 – f'(x)]
= -f'[9 – f(x)] – f'(x)
∴ s'(4) = -f'[9 – f(4)] – f'(4)
= -f'[9 – 3] – f'(4) … [∵ f(x) = 3, when x = 4]
= -f'(6) – f'(4)
= -(-4)(5) … [From the table]
= 20.

(iv) If S(x) = g[g(x)] find S’ (6)
Solution:
S(x) = g[g(x)]
∴ S'(x) = \(\frac{d}{d x}\)g[g(x)]
= g'[g(x)]∙\(\frac{d}{d x}\)[g(x)]
= g'[g(x)]∙g'(x)
∴ S ‘(6) = g'[g'(6)]∙g'(6)
= g'(2)∙g'(6) … [∵ g (x) = 2, when x = 6]
= 4 × 7 … [From the table]
= 28.

Question 5.
Assume that f ‘(3) = -1, g'(2) = 5, g(2) = 3 and y = f[g(x)] then \(\left[\frac{d y}{d x}\right]_{x=2}\) = ?
Solution:
y = f[g(x)]
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\){[g(x)]}

Question 6.
If h(x) = \(\sqrt{4 f(x)+3 g(x)}\), f(1) = 4, g(1) = 3, f ‘(1) = 3, g'(1) = 4 find h'(1).
Solution:
Given f(1) = 4, g(1) = 3, f ‘(1) = 3, g'(1) = 4 …..(1)

Question 7.
Find the x co-ordinates of all the points on the curve y = sin 2x – 2 sin x, 0 ≤ x < 2π where \(\frac{d y}{d x}\) = 0.
Solution:
y = sin 2x – 2 sin x, 0 ≤ x < 2π

= cos2x × 2 – 2cosx
= 2 (2 cos²x – 1) – 2 cosx
= 4 cos²x – 2 – 2 cos x
= 4 cos²x – 2 cos x – 2
If \(\frac{d y}{d x}\) = 0, then 4 cos²x – 2 cos x – 2 = 0
∴ 4cos²x – 4cosx + 2cosx – 2 = 0
∴ 4 cosx (cosx – 1) + 2 (cosx – 1) = 0
∴ (cosx – 1)(4cosx + 2) = 0
∴ cosx – 1 = 0 or 4cosx + 2 = 0
∴ cos x = 1 or cos x = \(-\frac{1}{2}\)
∴ cos x = cos 0

Question 8.
Select the appropriate hint from the hint basket and fill up the blank spaces in the following paragraph. [Activity]
“Let f (x) = x² + 5 and g(x) = e^x + 3 then
f [g(x)] = _ _ _ _ _ _ _ _ and g [f(x)] =_ _ _ _ _ _ _ _.
Now f ‘(x) = _ _ _ _ _ _ _ _ and g'(x) = _ _ _ _ _ _ _ _.
The derivative off [g (x)] w. r. t. x in terms of f and g is _ _ _ _ _ _ _ _.
Therefore \(\frac{d}{d x}\)[f[g(x)]] = _ _ _ _ _ _ _ _ _ and [\(\frac{d}{d x}\)[f[g(x)]]]_{x = 0} = _ _ _ _ _ _ _ _ _ _ _.
The derivative of g[f(x)] w. r. t. x in terms of f and g is _ _ _ _ _ _ __ _ _ _ _.
Therefore \(\frac{d}{d x}\)[g[f(x)]] = _ _ _ _ _ _ _ _ _ and [\(\frac{d}{d x}\)[g[f(x)]]]_{x = 1} = _ _ _ _ _ _ _ _ _ _ _.”
Hint basket : { f ‘[g(x)]·g'(x), 2e^2x + 6e^x, 8, g'[f(x)]·f ‘(x), 2xe^{x2 + 5}, -2e⁶, e^2x + 6e^x + 14, e^{x2 + 5} + 3, 2x, e^x}
Solution:
f[g(x)] = e^2x + 6e^x + 14
g[f(x)] = e^{x2 + 5} + 3
f'(x) = 2x, g’f(x) = e^x
The derivative of f[g(x)] w.r.t. x in terms of and g is f'[g(x)]∙g'(x).
∴ \(\frac{d}{d x}\){f[g(x)]} = 2e^2x + 6e^x and \(\frac{d}{d x}\){f[g(x)]}_{x = 0} = 8
The derivative of g[f(x)] w.r.t. x in terms of f and g is g’f(x)]∙f'(x).
∴ \(\frac{d}{d x}\){g[(f(x)]} = 2xe^{x2 + 5} and
\(\frac{d}{d x}\){g[(f(x)]}_{x = -1} = -2e⁶.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Miscellaneous Exercise 7 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Miscellaneous Exercise 7

I) Select the appropriate alternatives for each of the following :
Question 1.
The value of objective function is maximum under linear constraints _______.
(A) at the centre of feasible region
(B) at (0, 0)
(C) at a vertex of feasible region
(D) the vertex which is of maximum distance from (0, 0)
Solution:
(C) at a vertex of feasible region

Question 2.
Which of the following is correct _______.
(A) every L.P.P. has an optimal solution
(B) a L.P.P. has unique optimal solution
(C) if L.P.P. has two optimal solutions then it has infinite number of optimal solutions
(D) the set of all feasible solution of L.P.P. may not be convex set
Solution:
(C) if L.P.P. has two optimal solutions then it has infinite number of optimal solutions

Question 3.
Objective function of L.P.P. is _______.
(A) a constraint
(B) a function to be maximized or minimized
(C) a relation between the decision variables
(D) equation of a straight line
Solution:
(B) a function to be maximized or minimized

Question 4.
The maximum value of z = 5x + 3y subjected to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y≥ 0 is _______.
(A) 235
(B) \(\frac{235}{9}\)
(C) \(\frac{235}{19}\)
(D) \(\frac{235}{3}\)
Solution:
(C) \(\frac{235}{19}\)

Question 5.
The maximum value of z = 10x + 6y subjected to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y≥ 0. _______.
(A) 56
(B) 65
(C) 55
(D) 66
Solution:
(A) 56

Question 6.
The point at which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is obtained at _______.
(A) (30, 25)
(B) (20, 35)
(C) (35, 20)
(D) (40, 15)
Solution:
(D) (40, 15)

Question 7.
Of all the points of the feasible region, the optimal value ofz obtained at the point lies _______.
(A) inside the feasible region
(B) at the boundary of the feasible region
(C) at vertex of feasible region
(D) outside the feasible region
Solution:
(C) at vertex of feasible region

Question 8.
Feasible region is the set of points which satisfy _______.
(A) the objective function
(B) all of the given constraints
(C) some of the given constraints
(D) only one constraint
Solution:
(B) all of the given constraints

Question 9.
Solution of L.P.P. to minimize z = 2x + 3y such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is _______.
(A) x = 0, y = \(\frac{1}{2}\)
(B) x = \(\frac{1}{2}\), y = 0
(C) x = 1, y = 2
(D) x = \(\frac{1}{2}\), y = \(\frac{1}{2}\)
Solution:
(A) x = 0, y = \(\frac{1}{2}\)

Question 10.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are _______.
(A) (0, 0), (4, 0), (7, 1), (0, 4)
(B) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (0, 4)
(C) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (0, 7)
(D) (0, 0), (4, 0), (3, 1), (0, 7)
Solution:
(B) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (0, 4)

Question 11.
The corner points of the feasible solution are (0, 0), (2, 0), (\(\frac{12}{7}\), \(\frac{3}{7}\)), (0, 1). Then z = 7x + y is maximum at _______.
(A) (0, 0)
(B) (2, 0)
(C) (\(\frac{12}{7}\), \(\frac{3}{7}\))
(D) (0, 1)
Solution:
(B) (2, 0)

Question 12.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1) and (0, \(\frac{7}{3}\) ), the maximum value of z = 4x + 5y is _______.
(A) 12
(B) 13
(C) 35
(D) 0
Solution:
(B) 13

Question 13.
If the corner points of the feasible solution are (0, 10), (2, 2) and (4, 0) then the point of minimum z = 3x + 2y is _______.
(A) (2, 2)
(B) (0, 10)
(C) (4, 0)
(D) (3 ,4)
Solution:
(A) (2, 2)

Question 14.
The half plane represented by 3x + 2y < 8 contains the point _______.
(A) (1, \(\frac{5}{2}\))
(B) (2, 1)
(C) (0, 0)
(D) (5, 1)
Solution:
(C) (0, 0)

Question 15.
The half plane represented by 4x + 3y > 14 contains the point _______.
(A) (0, 0)
(B) (2, 2)
(C) (3, 4)
(D) (1, 1)
Solution:
(C) (3, 4)

II) Solve the following :
Question 1.
Solve each of the following inequations graphically using X Y plane.
(i) 4x – 18 ≥ 0
Solution:
Consider the line whose equation is 4x – 18 ≥ 0 i.e. x = \(\frac{18}{4}=\frac{9}{2}\) = 4.5
This represents a line parallel to Y-axis passing3through the point (4.5, 0)
Draw the line x = 4.5
To find the solution set we have to check the position of the origin (0, 0).
When x = 0, 4x – 18 = 4 × 0 – 18 = -18 > 0
∴ the coordinates of the origin does not satisfy thegiven inequality.
∴ the solution set consists of the line x = 4.5 and the non-origin side of the line which is shaded in the graph.

(ii) -11x – 55 ≤ 0
Solution:
Consider the line whose equation is -11x – 55 ≤ 0 i.e. x = -5
This represents a line parallel to Y-axis passing3through the point (-5, 0)
Draw the line x = – 5
To find the solution set we have to check the position of the origin (0, 0).
When x = 0, -11x – 55 = – 11(0) – 55 = -55 > 0
∴ the coordinates of the origin does not satisfy thegiven inequality.
∴ the solution set consists of the line x = -5 and the non-origin side of the line which is shaded in the graph.

(iii) 5y – 12 ≥ 0
Solution:
Consider the line whose equation is 5y – 12 ≥ 0 i.e. y = \(\frac{12}{5}\)
This represents a line parallel to X-axis passing through the point (o, \(\frac{12}{5}\))
Draw the line y = \(\frac{12}{5}\)
To find the solution set, we have to check the position of the origin (0, 0).
When y = 0, 5y – 12 = 5(0) – 12 = -12 > 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = \(\frac{12}{5}\) and the non-origin side of the line which is shaded in the graph.

(iv) y ≤ -3.5
Solution:
Consider the line whose equation is y ≤ – 3.5 i.e. y = – 3.5
This represents a line parallel to X-axis passing3through the point (0, -3.5)
Draw the line y = – 3.5
To find the solution set, we have to check the position of the origin (0, 0).
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = – 3.5 and the non-origin side of the line which is shaded in the graph.

Question 2.
Sketch the graph of each of following inequations in XOY co-ordinate system.
(i) x ≥ 5y
Solution:

(ii) x + y≤ 0
Solution:

(iii) 2y – 5x ≥ 0
Solution:

(iv) |x + 5| ≤ y
Solution:
|x + 5| ≤ y
∴ -y ≤ x + 5 ≤ y
∴ -y ≤ x + 5 and x + 5 ≤ y
∴ x + y ≥ -5 and x – y ≤ -5
First we draw the lines AB and AC whose equations are
x + y= -5 and x – y = -5 respectively.

The graph of |x + 5| ≤ y is as below:

Question 3.
Find graphical solution for each of the following system of linear inequation.
(i) 2x + y ≥ 2, x – y ≤ 1
Solution:
First we draw the lines AB and AC whose equations are 2x + y = 2 and x – y = 1 respectively.


The solution set of the given system of inequalities is shaded in the graph.

(ii) x + 2y ≥ 4, 2x – y ≤ 6
Solution:

(iii) 3x + 4y ≤ 12, x – 2y ≥ 2, y ≥ -1
Solution:
First we draw the lines AB, CD and ED whose equations are 3x + 4y = 12, x – 2y = 2 and y = -1 respectively.


The solution set of given system of inequation is shaded in the graph.

Question 4.
Find feasible solution for each of the following system of linear inequations graphically.
(i) 2x + 3y ≤ 12, 2x + y ≤ 8, x ≥ 0, y ≥ 0
Solution:

The feasible solution is OCPBO.

(ii) 3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
Solution:

The feasible solution is ACDBA.

Question 5.
Solve each of the following L.P.P.
(i) Maximize z = 5x₁ + 6x₂ subject to 2x₁ + 3x₂ ≤ 18, 2x₁ + x₂ ≤ 12, x₁ ≥ 0, x₂ ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 2x₁ + 3x₂ = 18 and 2x₁ + x₂ = 12 respectively.


The feasible region is OCPBO which is shaded in the graph. The vertices of the feasible region are O(0, 0), C(6, 0), P and B (0,6).
P is the point of intersection of the lines
2x₁ + 3x₂ = 18 ….(1)
and 2x₁ + x₂ = 12
On subtracting, we get
2x₂ = 6 ∴ x₂ = 3
Substituting x₂ = 3 in (2), we get
2x₁ + 3 = 12 ∴ x₂ = 9
∴ P is (\(\frac{9}{2}\), 3)
The values of objective function z = 5x₁ + 6x₂ at these vertices are
z(O) = 5(0) + 6(0) = 0 + 0 = 0
z(C) = 5(6) + 6(0) = 30 + 0 = 30
z(P) = 5(\(\frac{9}{2}\)) + 6(3) = \(\frac{45}{2}\) + 18 = \(\frac{45+36}{2}=\frac{81}{2}\) = 40.5
z(B) = 5(0) + 6(3) = 0 + 18 = 18
Maximum value of z is 40.5 when x₁ = 9/2, y = 3.

(ii) Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21
Question is modified.
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 3x + y = 27 and x + y = 21 respectively.


The feasible region is OAPDO which is shaded region in the graph. The vertices of the feasible region are 0(0, 0), A (9, 0), P and D(0, 21). P is the point of intersection of lines
3x + y = 27 … (1)
and x + y = 21 … (2)
On substracting, we get 2x = 6 ∴ x = 3
Substituting x = 3 in equation (1), we get
9 + y = 27 ∴ y = 18
∴ P = (3, 18)
The values of the objective function z = 4x + 2y at these vertices are
z(O) = 4(0) + 2(0) = 0 + 0 = 0
z(a) = 4(9) + 2(0) = 36 + 0 = 36
z(P) = 4(3) + 2(18) = 12 + 36 = 48
z (D) = 4(0) + 2(21) = 0 + 42 = 42
∴ 2 has minimum value 48 when x = 3, y = 18.

(iii) Maximize z = 6x + 10y subject to 3x + 5y ≤ 10, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 3x + 5y = 10 and 5x + 3y = 15 respectively.


The feasible region is OCPBD which is shaded in the graph.
The vertices of the feasible region are 0(0, 0), C(3, 0), P and B (0, 2).
P is the point of intersection of the lines
3x + 5y = 10 … (1)
and 5x + 3y = 15 … (2)
Multiplying equation (1) by 5 and equation (2) by 3, we get
15x + 25y = 50
15x + 9y = 45
On subtracting, we get
16y = 5 ∴ y = \(\frac{5}{16}\)
Substituting y = \(\frac{5}{16}\) in equation (1), we get
3x + \(\frac{25}{16}\) = 10 ∴ 3x = 10 – \(\frac{25}{16}=\frac{135}{16}\)
∴ x = \(\frac{45}{16}\) ∴ P ≡ \(\left(\frac{45}{16}, \frac{5}{16}\right)\)
The values of objective function z = 6x + 10y at these vertices are
z(O) = 6(0) + 10(0) = 0 + 0 = 0
z(C) = 6(3) + 10(0) = 18 + 0 = 18
z(P) = 6\(\left(\frac{45}{16}\right)\) + 10\(\left(\frac{5}{10}\right)\) = \(\frac{270}{16}+\frac{50}{16}=\frac{320}{16}\) = 20
z(B) = 6(0) + 10(2) = 0 + 20 = 20
The maximum value of z is 20 at P\(\left(\frac{45}{16}, \frac{5}{16}\right)\) and B (0, 2) two consecutive vertices.
∴ z has maximum value 20 at each point of line segment PB where B is (0, 2) and P is \(\left(\frac{45}{16}, \frac{5}{16}\right)\).
Hence, there are infinite number of optimum solutions.

(iv) Maximize z = 2x + 3y subject to x – y ≥ 3, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB whose equation is x – y = 3.


The feasible region is shaded which is unbounded.
Therefore, the value of objective function can be in- j creased indefinitely. Hence, this LPP has unbounded solution.

Question 6.
Solve each of the following L.P.P.
(i) Maximize z = 4x₁ + 3x₂ subject to 3x₁ + x₂ ≤ 15, 3x₁ + 4x₂ ≤ 24, x₁ ≥ 0, x₂ ≥ 0
Solution:
We first draw the lines AB and CD whose equations are 3x₁ + x₂ = 15 and 3x₁ + 4x₂ = 24 respectively.


The feasible region is OAPDO which is shaded in the graph.
The Vertices of the feasible region are 0(0, 0), A(5, 0), P and D(0, 6).
P is the point of intersection of lines.
3x₁ + 4x₂ = 24 … (1)
and 3x₁ + x₂ = 15 … (2)
On subtracting, we get
3x₂ = 9 ∴ x₂ = 3
Substituting x₂ = 3 in (2), we get
3x₁ + 3 = 15
∴ 3x₁ = 12 ∴ x₁ = 4 ∴ P is (4, 3)
The values of objective function z = 4x₁ + 3x₂ at these vertices are
z(O) = 4(0) + 3(0) = 0 + 0 = 0
z(a) = 4(5) + 3(0) = 20 + 0 = 20
z(P) = 4(4) + 3(3) = 16 + 9 = 25
z(D) = 4(0) + 3(6) = 0 + 18 = 18
∴ z has maximum value 25 when x = 4 and y = 3.

(ii) Maximize z = 60x + 50y subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
Solution:
We first draw the lines AB and CD whose equations are x + 2y = 40 and 3x + 2y = 60 respectively.


The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (20, 0), P and B (0, 20).
P is the point of intersection of the lines.
3x + 2y = 60 … (1)
and x + 2y = 40 … (2)
On subtracting, we get
2x = 20 ∴ x = 10
Substituting x = 10 in (2), we get
10 + 2y = 40
∴ 2y = 30 ∴ y = 15 ∴ P is (10, 15)
The values of the objective function z = 60x + 50y at these vertices are
z(O) = 60(0) + 50(0) = 0 + 0 = 0
z(C) = 60(20) + 50(0) = 1200 + 0 = 1200
z(P) = 60(10) + 50(15) = 600 + 750 = 1350
z(B) = 60(0) + 50(20) = 0 + 1000 = 1000 .
∴ z has maximum value 1350 at x = 10, y = 15.

(iii) Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30; x ≥ 0, y ≥ 0
Solution:
We first draw the lines AB, CD and EF whose equations are 3x + y = 27, x + y = 21, x + 2y = 30 respectively.


The feasible region is XEPQBY which is shaded in the graph.
The vertices of the feasible region are E (30,0), P, Q and B (0,27).
P is the point of intersection of the lines
x + 2y = 30 … (1)
and x + y = 21 … (2)
On subtracting, we get
y = 9
Substituting y = 9 in (2), we get
x + 9 = 21 ∴ x = 12
∴ P is (12, 9)
Q is the point of intersection of the lines
x + y = 21 … (2)
and 3x + y = 27 … (3)
On subtracting, we get
2x = 6 ∴ x = 3
Substituting x = 3 in (2), we get
3 + y = 21 ∴ y = 18
∴ Q is (3, 18).
The values of the objective function z = 4x + 2y at these vertices are
z(E) = 4(30) + 2(0) = 120 + 0 = 120
z(P) = 4(12) + 2(9) = 48 + 18 = 66
z(Q) = 4(3) + 2(18) = 12 + 36 = 48
z(B) = 4(0) + 2(27) = 0 + 54 = 54
∴ z has minimum value 48, when x = 3 and y = 18.

Question 7.
A carpenter makes chairs and tables. Profits are ₹140/- per chair and ₹ 210/- per table. Both products are processed on three machines : Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by following table:

Formulate the above problem as L.P.P. Solve it graphically to get maximum profit.
Solution:
Let the number of chairs and tables made by the carpenter be x and y respectively.
The profits are ₹ 140 per chair and ₹ 210 per table.
∴ total profit z = ₹ (140x + 210y) This is the objective function which is to be maximized.
The constraints are as per the following table :

From the table, the constraints are
3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60.
The number of chairs and tables cannot be negative.
∴ x ≥ 0, y ≥ 0
Hence, the mathematical formulation of given LPP is :
Maximize z = 140x + 210y, subject to
3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.
We first draw the lines AB, CD and EF whose equations are 3x + 3y = 36, 5x + 2y = 50 and 2x + 6y = 60 respectively.


The feasible region is OCPQFO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (10, 0), P, Q and F (0, 10).
P is the point of intersection of the lines
5x + 2y = 50 … (1)
and 3x + 3y = 36 … (2)
Multiplying equation (1) by 3 and equation (2) by 2, we get
15x + 6y = 150
6x + 6y = 72
On subtracting, we get 26
9x = 78 ∴ x = \(\frac{26}{3}\)
Substituting x = \(\frac{26}{3}\) in (2), we get
3\(\left(\frac{26}{3}\right)\) + 3y = 36
3y = 1o y = \(\frac{10}{3}\)
Q is the point of intersection of the lines
3x + 3y = 36 … (2)
and 2x + 6y = 60 … (3)
Multiplying equation (2) by 2, we get
6x + 6 y = 72
Subtracting equation (3) from this equation, we get
4x = 12 ∴ x = 3
Substituting x = 3 in (2), we get
3(3) + 3y = 36
∴ 3y = 27 ∴ y = 9
∴ Q is (3, 9).
Hence, the vertices of the feasible region are O (0, 0),
C(10, 0), P\(\left(\frac{26}{3}, \frac{10}{3}\right)\), Q(3, 9) and F(0, 10).
The values of the objective function z = 140x + 210y at these vertices are
z(O) = 140(0) + 210(0) = 0 + 0 = 0
z(C) = 140 (10) + 210(0) = 1400 + 0 = 1400
z(P) = 140\(\left(\frac{26}{3}\right)\) + 210\(\left(\frac{10}{3}\right)\) = \(\frac{3640+2100}{3}=\frac{5740}{3}\) = 1913.33
z(Q) = 140(3) + 210(9) = 420 + 1890 = 2310
z(F) = 140(0) + 210(10) = 0 + 2100 = 2100
∴ z has maximum value 2310 when x = 3 and y = 9 Hence, the carpenter should make 3 chairs and 9 tables to get the maximum profit of ₹ 2310.

Question 8.
A company manufactures bicycles and tricycles, each of which must be processed through two machines A and B. Maximum availability of Machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on Machine A and 3 hours on Machine B. Manufacturing a tricycles requires 4 hours on Machine A and 10 hours on Machine B. If profits are ₹180/- for a bicycle and ₹220/- for a tricycle. Determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Solution:
Let x bicycles and y tricycles are to be manu¬factured. Then the total profit is z = ₹ (180x + 220y)
This is a linear function which is to be maximized. Hence, it is the objective function. The constraints are as per the following table :

From the table, the constraints are
6x + 4y ≤ 120, 3x +10y ≤ 180
Also, the number of bicycles and tricycles cannot be i negative.
∴ x ≥ 0, y ≥ 0.
Hence, the mathematical formulation of given LPP is :
Maximize z = 180x + 220y, subject to
6x + 4y ≤ 120, 3x + 10y ≤ 180, x ≥ 0, y ≥ 0.
First we draw the lines AB and CD whose equations are 6x + 4y = 120 and 3x + 10y = 180 respectively.


The feasible region is OAPDO which is shaded in the graph.
The vertices of the feasible region are O(0, 0), A(20, 0) P and D(0, 18).
P is the point of intersection of the lines
3x + 10y = 180 … (1)
and 6x + 4y = 120 … (2)
Multiplying equation (1) by 2, we get
6x + 20y = 360
Subtracting equation (2) from this equation, we get
16y = 240 ∴ y = 15
∴ from (1), 3x + 10(15) = 180
∴ 3x = 30 ∴ x = 10
∴ P = (10, 15)
The values of the objective function z = 180x + 220y at these vertices are
z(O) = 180(0) + 220(0) = 0 + 0 = 0
z(a) = 180(20) + 220(0) = 3600 + 0 = 3600
z(P) = 180(10) + 220(15) = 1800 + 3300 = 5100
z(D) = 180(0) +220(18) = 3960
∴ the maximum value of z is 5100 at the point (10, 15).
Hence, 10 bicycles and 15 tricycles should be manufactured in order to have the maximum profit of ₹ 5100.

Question 9.
A factory produced two types of chemicals A and B. The following table gives the units of ingredients P and Q (per kg) of chemicals A and B as well as minimum requirements of P and Q and also cost per kg. chemicals A and B :

Find the number of units of chemicals A and B should be produced so as to minimize the cost.
Solution:
Let the factory produce x units of chemical A and y units of chemical B. Then the total cost is z = ₹ (4x + 6y). This is the objective function which is to be minimized.
From the given table, the constraints are
x + 2y ≥ 80, 3x + y ≥ 75.
Also, the number of units x and y of chemicals A and B cannot be negative.
∴ x ≥ 0, y ≥ 0.
∴ the mathematical formulation of given LPP is
Minimize z = 4x + 6y, subject to
x + 2y ≥ 80, 3x + y ≥ 75, x ≥ 0, y ≥ 0.
First we draw the lines AB and CD whose equations are x + 2y = 80 and 3x + y = 75 respectively.


The feasible region is shaded in the graph.
The vertices of the feasible region are A (80, 0), P and D (0, 75).
P is the point of intersection of the lines
x + 2y = 80 … (1)
and 3x + y = 75 … (2)
Multiplying equation (2) by 2, we get
6x + 2 y = 150
Subtracting equation (1) from this equation, we get
5x = 70 ∴ x = 14
∴ from (2), 3(14) + y = 75
∴ 42 + y = 75 ∴ y = 33
∴ P = (14, 33)
The values of the objective function z = 4x + 6y at these vertices are
z(a) = 4(80)+ 6(0) =320 + 0 = 320
z(P) = 4(14)+ 6(33) = 56+ 198 = 254
z(D) = 4(0) + 6(75) = 0 + 450 = 450
∴ the minimum value of z is 254 at the point (14, 33).
Hence, 14 units of chemical A and 33 units of chemical B are to be produced in order to have the j minimum cost of ₹ 254.

Question 10.
A company produces mixers and food processors. Profit on selling one mixer and one food processor is ₹ 2,000/- and ₹ 3,000/- respectively. Both the products are processed through three Machines A, B, C. The time required in hours by each product and total time available in hours per week on each machine are as follows :

How many mixers and food processors should be produced to maximize the profit?
Solution:
Let the company produce x mixers and y food processors.
Then the total profit is z = ₹ (2000x + 3000y)
This is the objective function which is to be maximized. From the given table in the problem, the constraints are 3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60
Also, the number of mixers and food processors cannot be negative,
∴ x ≥ 0, y ≥ 0.
∴ the mathematical formulation of given LPP is
Maximize z = 2000x + 3000y, subject to 3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤60, x ≥ 0, y ≥ 0.
First we draw the lines AB, CD and EF whose equations are 3x + 3y = 36, 5x + 2y = 50 and 2x + 6y = 60 respectively.


The feasible region is OCPQFO which is shaded in the graph.
The vertices of the feasible region are O(0, 0), C(10, 0), P, Q and F(0,10).
P is the point of intersection of the lines
3x + 3y = 36 … (1)
and 5x + 2y = 50 … (2)
Multiplying equation (1) by 2 and equation (2) by 3, we get
6x + 6y = 72
15x + 6y = 150
On subtracting, we get
9x = 78
∴ x = \(\frac{26}{3}\)
∴ from (1), 3\(\left(\frac{26}{3}\right)\) + 3y = 36
∴ 3y = 10
∴ y = \(\frac{10}{3}\)
∴ P = \(\left(\frac{26}{3}, \frac{10}{3}\right)\)
Q is the point of intersection of the lines
3x + 3y = 36 … (1)
and 2x + 6y = 60 … (3)
Multiplying equation (1) by 2, we get
6x + 6y = 72
Subtracting equation (3), from this equation, we get
4x = 12
∴ x = 3
∴ from (1), 3(3) + 3y = 36
∴ 3y = 27
∴ y = 9
∴ Q = (3, 9)
The values of the objective function z = 2000x + 3000y at these vertices are
z(O) = 2000(0) + 3000(0) = 0 + 0 = 0
z(C) = 2000(10) + 3000(0) = 20000 + 0 = 20000
z(P) = 2000\(\left(\frac{26}{3}\right)\) + 3000\(\left(\frac{10}{3}\right)\) = \(\frac{52000}{3}+\frac{30000}{3}=\frac{82000}{3}\)
z(Q) = 2000(3) + 3000(9) = 6000 + 27000 = 33000
z(F) = 2000(0) + 3000(10) = 30000 + 0 = 30000
∴ the maximum value of z is 33000 at the point (3, 9).
Hence, 3 mixers and 9 food processors should be produced in order to get the maximum profit of ₹ 33,000.

Question 11.
A chemical company produces a chemical containing three basic elements A, B, C so that it has at least 16 liters of A, 24 liters of B and 18 liters of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 liters of A, 12 liters of B, 2 liters of C. Each unit of compound II has 2 liters of A, 2 liters of B and 6 liters of C. The cost per unit of compound I is ₹ 800/- and that of compound II is ₹ 640/-. Formulate the problem as L.P.P. and solve it to minimize the cost.
Solution:
Let the company buy x units of compound I and y units of compound II.
Then the total cost is z = ₹(800x + 640y).
This is the objective function which is to be minimized.
The constraints are as per the following table :

From the table, the constraints are
4x + 2y ≥ 16, 12x + 2y ≥ 24, 2x + 6y ≥ 18.
Also, the number of units of compound I and compound II cannot be negative.
∴ x ≥ 0, y ≥ 0.
∴ the mathematical formulation of given LPP is
Minimize z = 800x + 640y, subject to 4x + 2y ≥ 16, 12x + 2y ≥ 24, 2x + 6y ≥ 18, x ≥ 0, y ≥ 0.
First we draw the lines AB, CD and EF whose equations are 4x + 2y = 16, 12x + 2y = 24 and 2x + 6y = 18


The feasible region is shaded in the graph.
The vertices of the feasible region are E(9, 0), P, Q, and D(0, 12).
P is the point of intersection of the lines
2x + 6y = 18 … (1)
and 4x + 2y = 16 … (2)
Multiplying equation (1) by 2, we get 4x + 12y = 36
Subtracting equation (2) from this equation, we get
10y = 20
∴ y = 2
∴ from (1), 2x + 6(2) = 18
∴ 2x = 6
∴ x = 3
∴ P = (3, 2)
Q is the point of intersection of the lines
12x + 2y = 24 … (3)
and 4x + 2y = 16 … (2)
On subtracting, we get
8x = 8 ∴ x = 1
∴ from (2), 4(1) + 2y = 16
∴ 2y = 12 ∴ y = 6
∴ Q = (1, 6)
The values of the objective function z = 800x + 640y at these vertices are
z(E) = 800(9)+ 640(0) =7200 + 0 = 7200
z(P) = 800(3) + 640(2) = 2400 + 1280 = 3680
z(Q) = 800(1) + 640(6) =800 + 3840 =4640
z(D) = 800(0) + 640(12) = 0 + 7680 = 7680
∴ the minimum value of z is 3680 at the point (3, 2).
Hence, the company should buy 3 units of compound I and 2 units of compound II to have the minimum cost of ₹ 3680.

Question 12.
A person makes two types of gift items A and B requires the services of a cutter and a finisher. Gift item A requires 4 hours of cutter’s time and 2 hours of finisher’s time. B requires 2 hours of cutter’s time and 4 hours of finisher’s time. The cutter and finisher have 208 hours and 152 hours available times respectively every month. The profit of one gift item of type A is ₹ 75/- and on gift item B is ₹ 125/-. Assuming that the person can sell all the gift items produced, determine how many gift items of each type should he make every month to obtain the best returns?
Solution:
Let x: number of gift item A
y: number of gift item B
As numbers of the items are never negative
x ≥ 0; y ≥ 0

Total time required for the cutter = 4x + 2y
Maximum available time 208 hours
∴ 4x+ 2y ≤ 208
Total time required for the finisher 2x +4y
Maximum available time 152 hours
2x + 4y ≤ 152
Total Profit is 75x + 125y
∴ L.P.P. of the above problem is
Minimize z = 75x + 125y
Subject to 4x+ 2y ≤ 208
2x + 4y ≤ 152
x ≥ 0; y ≥ 0
Graphical solution

Corner points
Now, Z at
x = (75x + 125y)
O(0, 0) = 75 × 0 + 125 × 0 = 0
A(52,0) = 75 × 52 + 125 × 0 = 3900
B(44, 16) = 75 × 44 + 125 × 16 = 5300
C(0, 38) = 75 × 0 + 125 × 38 = 4750
A person should make 44 items of type A and 16 Uems of type Band his returns are ₹ 5,300.

Question 13.
A firm manufactures two products A and B on which profit earned per unit ₹3/- and ₹4/- respectively. Each product is processed on two machines M₁ and M₂. The product A requires one minute of processing time on M₁ and two minute of processing time on M₂, B requires one minute of processing time on M₁ and one minute of processing time on M₂. Machine M₁ is available for use for 450 minutes while M₂ is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
Solution:
Let the firm manufactures x units of product
A and y units of product B.
The profit earned per unit of A is ₹3 and B is ₹ 4.
Hence, the total profit is z = ₹ (3x + 4y).
This is the linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table :

From the table, the constraints are
x + y ≤ 450, 2x + y ≤ 600
Since, the number of gift items cannot be negative, x ≥ 0, y ≥ o.
∴ the mathematical formulation of LPP is,
Maximize z = 3x + 4y, subject to x + y ≤ 450, 2x + y ≤ 600, x ≥ 0, y ≥ 0.
Now, we draw the lines AB and CD whose equations are x + y = 450 and 2x + y — 600 respectively.


The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O(0, 0), C(300, 0), P and B (0, 450).
P is the point of intersection of the lines
2x + y = 600 … (1)
and x + y = 450 … (2)
On subtracting, we get
∴ x = 150
Substituting x = 150 in equation (2), we get
150 + y = 450
∴ y = 300
∴ P = (150, 300)
The values of the objective function z = 3x + 4y at these vertices are
z(O) = 3(0) + 4(0) = 0 + 0 = 0
z(C) = 3(300) + 4(0) = 900 + 0 = 900
z(P) = 3(150) + 4(300) = 450 + 1200 = 1650
z(B) = 3(0) + 4(450) = 0 + 1800 = 1800
∴ z has the maximum value 1800 when x = 0 and y = 450 Hence, the firm gets maximum profit of ₹ 1800 if it manufactures 450 units of product B and no unit product A.

Question 14.
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20/- per unit of A and ₹ 30/- per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should the manufacture per month to maximize profit? How much is the maximum profit?
Solution:
Let the firm manufactures x units of item A and y units of item B.
Firm can make profit of ₹ 20 per unit of A and ₹ 30 per unit of B.
Hence, the total profit is z = ₹ (20x + 30y).
This is the objective function which is to be maximized. The constraints are as per the following table :

From the table, the constraints are
3x + 2y ≤ 210, 2x + 4y ≤ 300
Since, number of items cannot be negative, x ≥ 0, y ≥ 0.
Hence, the mathematical formulation of given LPP is :
Maximize z = 20x + 30y, subject to 3x + 2y ≤ 210, 2x + 4y ≤ 300, x ≥ 0, y ≥ 0.
We draw the lines AB and CD whose equations are 3x + 2y = 210 and 2x + 4y = 300 respectively.

The feasible region is OAPDO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), A (70, 0), P and D (0, 75).
P is the point of intersection of the lines
2x + 4y = 300 … (1)
and 3x + 2y = 210 … (2)
Multiplying equation (2) by 2, we get
6x + 4y = 420
Subtracting equation (1) from this equation, we get
∴ 4x = 120 ∴ x = 30
Substituting x = 30 in (1), we get
2(30) + 4y = 300
∴ 4y = 240 ∴ y = 60
∴ P is (30, 60)
The values of the objective function z = 20x + 30y at these vertices are
z(O) = 20(0) + 30(0) = 0 + 0 = 0
z(A) = 20(70) + 30(0) = 1400 + 0 = 1400
z(P) = 20(30) + 30(60) = 600 + 1800 = 2400
z(D) = 20(0) + 30(75) = 0 + 2250 = 2250
∴ z has the maximum value 2400 when x = 30 and y = 60. Hence, the firm should manufactured 30 units of item A and 60 units of item B to get the maximum profit of ₹ 2400.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.7 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.7

Question 1.
Find A^T, if
i. A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:
i. A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
∴ A^T = \(\left[\begin{array}{rr}
1 & -4 \\
3 & 5
\end{array}\right]\)

ii. A = \(\left[\begin{array}{ccc}
-4 & 0 & 5
2 & -6 & 1 \\
\end{array}\right]\)
∴ A^T = \(\left[\begin{array}{cc}
2 & -4 \\
-6 & 0 \\
1 & 5
\end{array}\right]\)

[Note: Answer given in the textbook is A^T = \(\left[\begin{array}{cc}
2 & -4 \\
6 & 0 \\
1 & 5
\end{array}\right]\). However, as per our calculation it is A^T = \(\left[\begin{array}{cc}
2 & -4 \\
-6 & 0 \\
1 & 5
\end{array}\right]\). ]

Question 2.
If [a_ij]_3×3 where a_ij = 2(i – j), find A and
A^T. State whether A and A^T are symmetric or skew-symmetric matrices?
Solution:
A = [a_ij]_3×3 = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
Given a_ij = 2 (i — j)
∴ a₁₁ = 2(1-1) = 0,
a₁₂ = 2(1-2) = -2,
a₁₃ = 2(1-3) = -4,
a₂₁ = 2(2-1) = 2,
a₂₂ = 2(2-2) = 0,
a₂₃=2(2-3) = -2,
a₃₁ = 2(3-1) = 4,
a₃₂ = 2(3-2) = 2,
a₃₃=2(3-3) = 0

∴ A^T = -A and A = -A^T
∴ A and A^T both are skew-symmetric matrices.

Questionn 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (2A)^T = 2A^T.
Solution:

From (i) and (ii), we get
(2A)^T = 2A^T

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that (3A)^T = 3A^T.
Solution:

From (i) and (ii), we get
(3A)^T = 3A^T

Question 5.
If A = \(\left[\begin{array}{ccc}
0 & 1+2 i & 1-2 \\
-1-2 i & 0 & -7 \\
2-i & 7 & 0
\end{array}\right]\),
where i = \(\sqrt{-1}\), prove that A^T = – A.
Solution:

Question 6.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\) , B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\) then show that
i. (A + B)^T = AT + B^T
ii. (A – C)^T = A^T – C^T
Solution:

From (i) and (ii), we get
(A + B)^T = AT + B^T
[Note: The question has been modified.]

From (i) and (ii), we get
(A – C)^T = A^T – C^T</sup

Question 7.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\) then find C^T, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:
3A – 2B + C = I
∴ C = I + 2B – 3A

Question 8.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
i. A^T + 4B^T
ii. 5A^T – 5B^T
Solution:

ii. ii. 5A^T – 5B^T = 5(A^T – B^T)

Question 9.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{rrr}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)^T = A^T + 2B^T + 3C^T.
Solution:
A + 2B + 3C

∴ A^T + 2B^T + 3C^T = \(\left[\begin{array}{cc}
5 & 6 \\
8 & 8 \\
2 & -2
\end{array}\right]\)
From (i) and (ii), we get
(A + 2B + 3C)^T = A^T + 2B^T + 3C^T

Question 10.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + B^T)^T = A^T + B.
prove that (A + B^T)^T = A^T + B
Solution:


From (i) and (ii), we get
(A + B^T)^T = A^T + B

Question 11.
Prove that A + A^T is a symmetric and A – A^T is a skew symmetric matrix, where
i. A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

∴ (A + A^T)^T = A + A^T, i.e., A + A^T = (A + A^T)^T
∴ A + A^T is a symmetric matrix.


∴ (A – A^T)^T = – (A – A^T),
i.e., A – A^T = -(A – A^T)^T
∴ A – A^T is skew symmetric matrix.

∴ (A + A^T)^T = A + A^T, i.e., A + A^T = (A + A^T)^T
∴ A + A^T is a symmetric matrix.

∴ (A – A^T)^T = – (A – A^T),
i.e., A – A^T = -(A – A^T)^T
∴ A – A^T is skew symmetric matrix.

Question 12.
Express the following matrices as the sum of a symmetric and a skew symmetric matrix.
i. \(\left[\begin{array}{cc}
4 & -2 \\
3 & -5
\end{array}\right]\)
ii. \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:
A square matrix A can be expressed as the sum of a symmetric and a skew symmetric matrix as
A = \(\frac{1}{2}\) (A + A^T) + \(\frac{1}{2}\) (A – A^T)

P is symmetric matrix …[∵ a_ij = a_ji]
and Q is a skew symmetric matrix [∵ -a_ij = -a_ji]
A = P + Q
A = \(\left[\begin{array}{cc}
4 & \frac{1}{2} \\
\frac{1}{2} & -5
\end{array}\right]+\left[\begin{array}{ll}
0 & \frac{-5}{2} \\
\frac{5}{2} & 0
\end{array}\right]\)

∴ P is symmetric matrix …[∵ a_ij = a_ji]
and Q is a skew symmetric matrix [∵ -a_ij = -a_ji]
∴ A = P + Q
∴ A = \(\left[\begin{array}{cc}
4 & \frac{1}{2} \\
\frac{1}{2} & -5
\end{array}\right]+\left[\begin{array}{ll}
0 & \frac{-5}{2} \\
\frac{5}{2} & 0
\end{array}\right]\)

Question 13.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
i. (AB)^T = B^TA^T
ii. (BA)^T = A^TB^T
Solution:


From (i) and (ii), we get
(AB)^T = B^TA^T

From (i) and (ii) we get
(BA)^T = A^TB^T

Question 14.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that A^TA = I, where I is the unit matrix of order 2.
Solution:


∴ A^TA = I, where I is the unit matrix of order 2.

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Ex 5.4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Ex 5.4

Question 1.
Find the slope, x-intercept, y-intercept of each of the following lines, i. 2x + 3y-6 = 0 ii. 3x-y-9 = 0 iii. x + 2y = 0
Solution:
i. Given equation of the line is 2x + 3y – 6 = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 2, b = 3, c = -6

ii. Given equation of the line is 3x – y – 9 = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 3, b = – 1, c = – 9

iii. Given equation of the line is x + 2y = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 1, b = 2, c = 0

Question 2.
Write each of the following equations in ax + by + c = 0 form.
i. y = 2x – 4
ii. y = 4
iii. \(\frac{x}{2}+\frac{y}{4}=1\)
iv. \(\frac{x}{3}-\frac{y}{2}=0\)
i. y = 2x – 4
∴ 2x – y – 4 = 0 is the equation in ax + by + c = 0 form.

ii. y = 4
∴ 0x + 1y – 4 = 0 is the equation in ax + by + c = 0 form.

iii. \(\frac{x}{2}+\frac{y}{4}=1\)
∴ \(\frac{2 x+y}{4}\)
∴ 2x + y – 4 = 0 is the equation in ax + by + c = 0 form.

iv. \(\frac{x}{3}-\frac{y}{2}=0\)
∴ 2x – 3y = 0
∴ 2x – 3y + 0 = 0 is the equation in ax + by + c = 0 form.
[Note: Answer given in the textbook is ‘2x – 3y – 6 = 0’. However, as per our calculation it is ‘2x-3y + 0 = 0’.]

Question 3.
Show that the lines x – 2y – 7 = 0 and 2x – 4y + 15 = 0 are parallel to each other.
Solution:
Let m₁ be the slope of the line x – 2y – 7 = 0.
∴ m₁ = \(\frac{-\text { coefficient of } x}{\text { coefficient of } y}=\frac{-1}{-2}=\frac{1}{2}\)
Let m₂ be the slope of the line 2x – 4y + 15 = 0.
∴ m₂ = \(\frac{-\text { coefficient of } x}{\text { coefficient of } y}=\frac{-2}{-4}=\frac{1}{2}\)
Since m₁ = m₂
the given lines are parallel to each other.

Question 4.
Show that the lines x – 2y – 7 = 0 and 2x + y + 1 = 0 are perpendicular to each other. Find their point of intersection.
Solution:
Let m₁ be the slope of the line x – 2y – 7 = 0.
∴ m₁ = \(\frac{-\text { coefficient of } x}{\text { coefficient of } y}=\frac{-1}{-2}=\frac{1}{2}\)
Let m₂ be the slope of the line 2x + y + 1 = 0.
∴ m₂ = \(\frac{-\text { coefficient of } x}{\text { coefficient of } y}=\frac{-2}{1}=-2\)
Since m₁ x m₁ = \(\frac{1}{2}\) x (- 2) = -1,
the given lines are perpendicular to each other. Consider,
x – 2y – 7 = 0 …(i)
2x + y + 1 =0 …(ii)
Multiplying equation (ii) by 2, we get
4x + 2y + 2 = 0 …(iii)
Adding equations (i) and (iii), we get
5x – 5 = 0
∴ x = 1
Substituting x = 1 in equation (ii), we get
2 + y + 1 = 0
∴ y = – 3
∴ The point of intersection of the given lines is (1,-3).

Question 5.
If the line 3x + 4y = p makes a triangle of area 24 square units with the co-ordinate axes, then find the value of p.
Solution:
Let the line 3x + 4y = p cuts the X and Y axes at points A and B respectively.
3x + 4y = p

This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\),
where a = \(\frac{p}{3}\) and b = \(\frac{p}{4}\)
∴ A (a, 0) ≡ (\(\frac{p}{3}\), 0) and B ≡ (0, b) = (0, \(\frac{p}{4}\))
∴ OA = \(\frac{p}{3}\) and OB = \(\frac{p}{4}\)
Given, A (∆OAB) = 24 sq. units
∴ \(\left|\frac{1}{2} \times \mathrm{OA} \times \mathrm{OB}\right|=24\)
∴ \(\left|\frac{1}{2} \times \frac{\mathrm{p}}{3} \times \frac{\mathrm{p}}{4}\right|=24\)
∴ p² = 576
∴ p = ± 24

Question 6.
Find the co-ordinates of the foot of the perpendicular drawn from the point A(- 2,3) to the line 3x-y -1 = 0.
Solution:
Let M be the foot of perpendicular drawn from
point A(- 2,3) to the line
3x-y- 1 = 0 …(i)
Slope of the line 3x-y – 1 = 0 is \(\frac{-3}{-1}\) =3.
Since AM ⊥ to line (i),
slope of AM = \(\frac{-1}{3}\)
∴ Equation of AM is
y – 3 = \(\frac{-1}{3}\)(x + 2)

∴ 3(y – 3) = – 1(x + 2)
∴ 3y – 9 = -x – 2
∴ x + 3y – 7 = 0 …………(ii)
The foot of perpendicular i.e., point M, is the point of intersection of equations (i) and (ii).
By (i) x 3 + (ii), we get 10x -10 = 0
∴ x = 1
Substituting x = 1 in (ii), we get
1 + 3y – 7 = 0
∴ 3y = 6
∴ y = 2
∴ The co-ordinates of the foot of the perpendicular Mare (1,2).

Question 7.
Find the co-ordinates of the circumcentre of the triangle whose vertices are A(- 2, 3), B(6, -1), C(4,3),e
Solution:
Here, A(-2, 3), B(6, -1), C(4, 3) are the vertices of ∆ABC.
Let F be the circumcentre of AABC.
Let FD and FE be the perpendicular bisectors of the sides BC and AC respectively.
∴ D and E are the midpoints of side BC and AC respectively.

Since FD passes through (5, 1) and has slope 1/2 equation of FD is
y – 1 = \(\frac{1}{2}\)(x-5)
∴ 2 (y – 1) = x – 5
∴ 2y – 2 = x – 5
∴ x – 2y – 3 = 0 …(i)
Since both the points A and C have same y co-ordinates i.e. 3,
the given points lie on the line y = 3.
Since the equation FE passes through E(1, 3),
the equation of FE is x = 1. .. .(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of x in (i), we get
1 – 2y -3 = 0
∴ y = -1
∴ Co-ordinates of circumcentre F ≡ (1, – 1).

Question 8.
Find the co-ordinates of the orthocentre of the triangle whose vertices are A(3, – 2), B(7,6), C (-1,2).
Solution:
Let O be the orthocentre of ∆ABC.
Let AD and BE be the altitudes on the sides BC and AC respectively.

Slope of side BC = \(\frac{2-6}{-1-7}=\frac{-4}{-8}=\frac{1}{2}\)
∴ Slope of AD = – 2 [∵ AD ⊥ BC]
∴ Equation of line AD is
y – (-2) = (- 2) (x – 3)
∴ y + 2 = -2x + 6
∴ 2x + y -4 = 0 …(i)
Slope of side AC = \(\frac{-2-2}{3-(-1)}=\frac{-4}{4}\) = -1
∴ Slope of BE = 1 …[ ∵ BE ⊥ AC]
∴ Equation of line BE is
y – 6 = 1(x – 7)
∴ y – 6 = x – 1
∴ x = y + 1 …(ii)
Substituting x = y + 1 in (i), we get
2(y + 1) + y – 4 = 0
∴ 2y + 2 + y – 4 = 0
∴ 3y – 2 = 0
∴ y = \(\frac{2}{3} in (ii), we get
Substituting y = [latex]\frac{2}{3}\) in (ii), we get
x = \(\frac{2}{3}+1=\frac{5}{3}\)
∴ Co-ordinates of orthocentre, O = \(\left(\frac{5}{3}, \frac{2}{3}\right)\)

Question 9.
Show that the lines 3 – 4y + 5 = 0, lx – 8y + 5 = 0 and 4JC + 5y – 45 = 0 are concurrent. Find their point of concurrence.
Solution:
The number of lines intersecting at a point are called concurrent lines and their point of intersection is called the point of concurrence. Equations of the given lines are
3x – 4y + 5 = 0 …(i)
7x-8y + 5 = 0 …(ii)
4x + 5y – 45 = 0 …(iii)
By (i) x 2 – (ii), we get
– x + 5 = 0
∴ x = 5
Substituting x = 5 in (i), we get
3(5) – 4y + 5 = 0
∴ -4y = – 20
∴ y = 5
∴ The point of intersection of lines (i) and (ii) is given by (5, 5).
Substituting x = 5 and y = 5 in L.H.S. of (iii), we get
L.H.S. = 4(5) + 5(5) – 45
= 20 + 25 – 45
= 0
= R.H.S.
∴ Line (iii) also passes through (5, 5).
Hence, the given three lines are concurrent and the point of concurrence is (5, 5).

Question 10.
Find the equation of the line whose x-intercept is 3 and which ¡s perpendicular to the line 3x – y + 23 = 0.
Solution:
Slope of the line 3x – y + 23 = 0 is 3.
∴ Slope of the required line perpendicular to
3x – y + 23 = 0 is \(\frac{-1}{3}\)
Since the x-intercept of the required line is 3, it passes through (3, 0).
∴ The equation of the required line is ‘
y – 0 = \(\frac{-1}{3}\)(x – 3)
∴ 3y = x + 3
∴ x + 3y = 3

Question 11.
Find the distance of the origin from the line 7x + 24y – 50 = 0.
Solution:
Let p be the perpendicular distance of origin
fromtheline7x + 24y – 50 = 0
Here, a = 7, b = 24, c = -50

Question 12.
Find the distance of the point A(- 2, 3) from the line 12x – 5y – 13 = 0.
Solution:
Let p be the perpendicular distance of the point A(- 2, 3) from the line 12x – 5y – 13 = 0
Here, a = 12, b = – 5, c = – 13, x₁ = -2, y₁ = 3

Question 13.
Find the distance between parallel lines 4x – 3y + 5 = 0 and 4xr – 3y + 7 = 0.
Solution:
Equations of the given parallel lines are 4x – 3y + 5 = 0 and 4x – 3y + 1 = 0
Here, a = 4, b = – 3, c₁ = 5 and c₂ = 7
∴ Distance between the parallel lines

Question 14.
Find the distance between the parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Solution:
Equations of the given parallel lines are 3x + 2y + 6 = 0 and
9x + 6y – 1 = 0 i.e., 3x + 2y – \(\frac{7}{3}\) =0
Here, a = 3, b = 2, c₁ = 6 and c₂ = \(\frac{-7}{3}\)
∴ Distance between the parallel lines

Question 15.
Find the points on the line x + y – 4 = 0 which are at a unit distance from the line 4JC + 3y = 10.
Solution:
Let P(x₁, y₁) be a point on the line x + y – 4 = o.
∴ x₁ + y₁ – 4 = 0
∴ y₁ = 4 – x₁ …(i)
Also, distance of P from the line 4x + 3y- 10 = 0 is 1

∴ 5 = | x₁ + 2 |
∴ x₁ + 2 = ± 5
∴ x₁ + 2 = 5 or x₁ + 2 = – 5
∴ x₁ = 3 or x₁ = – 7
From (i), when x₁ = 3, y₁ = 1
and when x₁ = -7, y₁ = 11
∴ The required points are (3, 1) and (-7, 11).
[Note: The question has been modified]

Question 16.
Find the equation of the line parallel to the X-axis and passing through the point of intersection of lines x + y – 2 = 0 and 4x + 3y = 10.
Solution:
Let u = x + y – 2 = 0 and v = 4x + 3y – 10 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
∴ (x + y – 2) + k(4x + 3y – 10) = 0 …(i)
∴ x + y – 2 + 4kx + 3ky – 10k = 0
∴ x + 4kx + y + 3ky – 2 – 10k = 0
∴ (1+ 4k)x + (1 + 3k)y – 2 – 10k = 0
But, this line is parallel to X-axis.
∴ Its slope = 0
∴ \(\frac{-(1+4 k)}{1+3 k}\) = 0
∴ 1 + 4k = 0
∴ k = \(\frac{-1}{4}\)
Substituting the value of k in (i), we get
(x + y – 2) + (4x + 3y – 10) = 0
∴ 4(x +y – 2) – (4x + 3y -10 ) = 0
∴ 4x + 4y – 8 – 4x – 3y + 10 = 0
∴ y + 2 = 0, which is the equation of the required line.
[Note: Answer given in the textbook is 5y – 8= 0. However, as per our calculation it is y + 2 = 0.]

Question 17.
Find the equation of the line passing through the point of intersection of lines x + y – 2 = 0 and 2xr – 3y + 4 = 0 and making intercept 3 on the X-axis.
Solution:
Let u ≡ x + y – 2 = 0 and v ≡ 2x – 3y + 4 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
∴ (x +y – 2) + k(2x – 3y + 4) = 0 …(i)
But, x-intercept of line is 3.
∴ It passes through (3, 0).
Substituting x = 3 and y = 0 in (i), we get
(3 + 0 – 2) + k(6 – 0 + 4) = 0
∴ 1 + 10k = 0
k = \(\frac{-1}{10}\)
Substituting the value of k in (i), we get (x + y – 2) + \(\left(\frac{-1}{10}\right)\) (2x – 3y + 4) = 0
∴ 10(x + y – 2) – (2x – 3y + 4) = 0
∴ 10x + 10y -20 — 2x + 3y-4 = 0
∴ 8x + 13y – 24 = 0, which is the equation of the required line.

Question 18.
If A(4, 3), B(0, 0) and C(2, 3) are the vertices of ΔABC, then find the equation of bisector of angle BAC.
Solution:
Let the bisector of ∠ BAC meets BC at point D.
∴ Point D divides seg BC in the ratio l(AB) : l(AC)

∴ 18 (y – 3) = 6 (x – 4)
∴ 3(y – 3) = x – 4
∴ 3y – 9 = x – 4
∴ x – 3y + 5 = 0

Question 19.
D(- 1, 8), E(4, – 2), F(- 5, – 3) are midpoints of sides BC, CA and AB of AABC. Find
i. equations of sides of ΔABC.
ii. co-ordinates of the circumcentre of ΔABC.
Solution:
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of ΔABC.
Given, points D, E and F are midpoints of sides BC, CA and AB respectively of ΔABC.

∴ x₁ + x₂ = -10 …………. (v)
and y₁ + y₂ = – 6 …………(vi)
For x-coordinates:
Adding (i), (iii) and (v), we get
2x₁ + 2x₂ + 2x₃ = – 4
∴ x₁ + x₂ + x₃ = -2 …………..(vii)
Solving (i) and (vii), we get x₁ = 0
Solving (iii) and (vii), we get x₂ = – 10
Solving (v) and (vii), we get x₃ = 8

For y-coordinates:
Adding (ii), (iv) and (vi), we get 2y₁ + 2y₂ + 2y₃ = 6
y₁ + y₂ + y₃ = 3 …….(viii)
Solving (ii) and (viii), we get y₁ = -13
Solving (iv) and (viii), we get y₂ = 7
Solving (vi) and (viii), we get y₃ = 9
∴ Vertices of AABC are A(0, – 13), B(- 10, 7), C(8, 9)

∴ 8(y + 13) = 22x
∴ 4(y + 13) = 11x
∴ 11x – 4y – 52 = 0

ii. Here, A(0, – 13), B(- 10, 7), C(8, 9) are the vertices of ΔABC.
Let F be the circumcentre of AABC.
Let FD and FE be perpendicular bisectors of the sides BC and AC respectively.
D and E are the midpoints of side BC and AC.

∴ Slope of FD = -9 … [ ∵ FD ⊥ BC]
Since FD passes through (-1, 8) and has slope -9, equation of FD is
y – 8 = -9 (x +1)
∴ y – 8 = -9x – 9
∴ y = -9x – 1
Also, slope of AC = \(\frac{-13-9}{0-8}=\frac{11}{4}\)
∴ Slope of FE = \(\frac{-4}{11}\) [ ∵ FE ⊥ AC]
Since FE passes through (4, -2) and has slope -4
\(\frac{-4}{11}\), equation of FE is
(y + 2) = \(\frac{-4}{11}\) (x – 4)
∴ 11(y + 2) = -4(x – 4)
∴ 11y + 22 = – 4x + 16
∴ 4x + 11y = -6 …………(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value ofy in (ii), we get
4x + 11(-9x- 1) = – 6
∴ 4x – 99x -11 = – 6
∴ -95x = 5
∴ x = \(\frac{-1}{19}\)
Substituting the value of x in (i), we get
y = -9(\(\frac{-1}{19}\)) – 1 = \(\frac{-10}{19}\)
∴ Co-ordinates of circumcentre F ≡ \(\left(\frac{-1}{19}, \frac{-10}{19}\right)\)

Question 20.
0(0, 0), A(6, 0) and B(0, 8) are vertices of a triangle. Find the co-ordinates of the incentre of ∆OAB.
Solution:
Let bisector of ∠O meet AB at point D and bisector of ∠A meet BO at point E
∴ Point D divides seg AB in the ratio l(OA): l(OB)
and point E divides seg BO in the ratio l(AB): l(AO)
Let I be the incentre of ∠OAB.

∴ Point D divides AB internally in 6 : 8
i.e. 3 :4

∴ y = x …(i)
Now, by distance formula,
l(AB) = \(\begin{aligned}
&=\sqrt{(6-0)^{2}+(0-8)^{2}} \\
&=\sqrt{36+64}=10
\end{aligned}\)
l(AO) = \(\sqrt{(6-0)^{2}+(0-0)^{2}}\) = 6
∴ Point E divides BO internally in 10 : 6 i.e. 5:3

∴ -2y = x – 6
∴ x + 2y = 6 …(ii)
To find co-ordinates of incentre, we have to solve equations (i) and (ii).
Substituting y = x in (ii), we get
x + 2x = 6
∴ x = 2
Substituting the value of x in (i), we get
y = 2
∴ Co-ordinates of incentre I ≡ (2, 2).

Alternate Method:
Let I be the incentre.
I lies in the 1st quadrant.
OPIR is a square having side length r.
Since OA = 6, OP = r,
PA = 6 – r
Since PA = AQ,
AQ = 6 – r …(i)
Since OB = 8, OR = r,
BR = 8 – r
∴ BR = BQ
∴ BQ = 8 – r …(ii)

AB = BQ + AQ
Also, AB = \(\begin{aligned}
&=\sqrt{\mathrm{OA}^{2}+\mathrm{OB}^{2}} \\
&=\sqrt{6^{2}+8^{2}} \\
&=\sqrt{100}=10
\end{aligned}\)
∴ BQ + AQ= 10
∴ (8 – r) + (6 – r) = 10
∴ 2r = 14- 10 = 4
∴ r = 2
∴ I = (2,2)