Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 14.2 8th Std Maths Answers Solutions Chapter 14 Compound Interest.

Practice Set 14.2 8th Std Maths Answers Chapter 14 Compound Interest

Compound Interest class 8 practice set 14.2 Question 1. On the construction work of a flyover bridge there were 320 workers initially. The number of workers were increased by 25% every year. Find the number of workers after 2 years.
Solution:
Here, P = Initial number of workers = 320
R = Increase in the number of workers per year = 25%
N = 2 years
A = Number of workers after 2 years

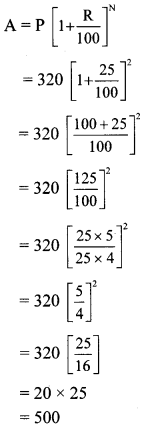
∴ The number of workers after 2 years would be 500.

Question 2.
A shepherd has 200 sheep with him. Find the number of sheeps with him after 3 years if the increase in number of sheeps is 8% every year.
Solution:
Here, P = Present number of sheeps = 200
R = Increase in number of sheeps per year = 8%
N = 3 years
A = Number of sheeps after 3 years

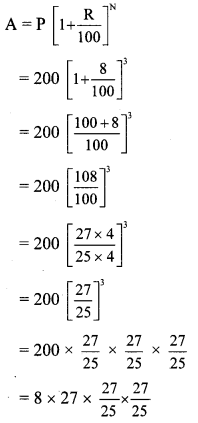
= \(\frac{0.32}{25} \times 27 \times 27 \times 27\)
= 0.0128 × 27 × 27 × 27
= 251.9424
= 252
∴ The number of sheeps with the shepherd after 2 years would be 252 (approx).

8th Class Math Practice Set 14.2 Question 3.
In a forest there are 40,000 trees. Find the expected number of trees after 3 years if the objective is to increase the number at the rate 5% per year.
Solution:
Here, P = Present number of trees in the forest = 40,000
R = Increase in the number of trees per year = 5%
N = 3 years
A = Number of trees after 3 years

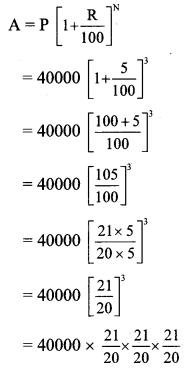
= 5 × 21 × 21 × 21
= 5 × 9261
= 46,305
∴ The expected number of trees in the forest after 3 years is 46,305.

Std 8 Maths Practice Set 14.2 Question 4.
The cost price of a machine is Rs 2,50,000. If the rate of depreciation is 10% per year, find the depreciation in price of the machine after two years.
Solution:
Here, P = Cost price of machine = Rs 2,50,000
R = Rate of depreciation per year = 10%
N = 2 years
A = Depreciated price of the machine after 2 years

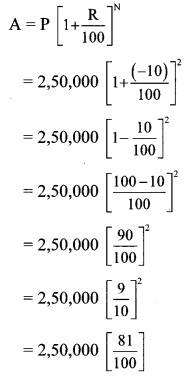
= 2,500 × 81
= Rs 2,02,500
Depreciation in price = Cost price (P) – Depreciated price (A)
= 2,50,000 – 2,02,500
= Rs 47,500
∴ The depreciation in price of the machine after 2 years would be Rs 47,500.

Question 5.
Find the compound interest if the amount of a certain principal after two years is Rs 4036.80 at the rate of 16 p.c.p.a.
Solution:
Here, A = Rs 4036.80, R = 16 p.c.p.a. and N = 2 years
i. \(\mathbf{A}=\mathbf{P}\left[1+\frac{\mathbf{R}}{100}\right]^{N}\)

ii. Interest = Amount (A) – Principal (P)
= 4036.80 – 3000
= Rs 1036.80
∴ The compound interest after 2 years would be Rs 1036.80.

Question 6.
A loan of Rs 15,000 was taken on compound interest. If the rate of compound interest is 12 p.c.p.a. find the amount to settle the loan after 3 years.
Solution:
Here, P = Rs 15,000, R = 12 p.c.p.a, and
N = 3 years

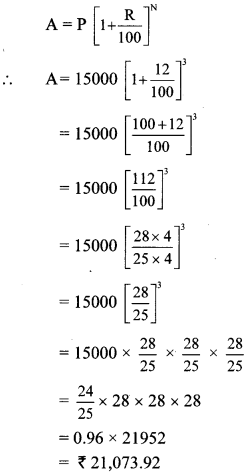
∴ The amount required to settle the loan after 3 years is Rs 21,073.92.

Practice Set 14.2 Class 8 Question 7.
A principal amounts to Rs 13,924 in 2 years by compound interest at 18 p.c.p.a. Find the principal.
Solution:
Here, A = Rs 13,924, R = 18 p.c.p.a., and N = 2 years

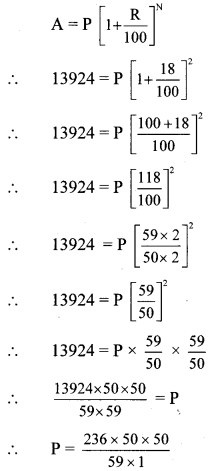
∴ P = 4 x 50 x 50
∴ P = Rs 10,000
∴ The principal is Rs 10,000.

Question 8.
The population of a suburb is 16,000. Find the rate of increase in the population if the population after two years is 17,640.
Solution:
Here, P = Population of a suburb = 16,000
N = 2 years
A = Increase in the population after 2 years = 17,640
R = Rate of increase in population


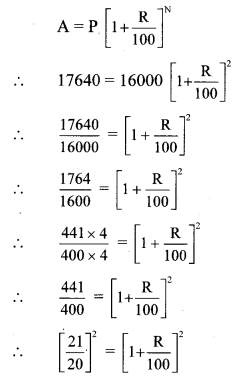
∴5 = R
i.e., R = 5%
∴The rate of increase in the population is 5 p.c.p.a.

Compound Interest Practice Set 14.2 Question 9.
In how many years Rs 700 will amount to Rs 847 at a compound interest rate of 10 p.c.p.a.
Solution:
Here, P = Rs 700, R = 10 p.c.p.a., A = Rs 847

∴Rs 700 will amount to Rs 847 in 2 years.

Practice Set 14.2 Question 10.
Find the difference between simple interest and compound interest on Rs 20,000 in 2 years at 8 p.c.p.a.
Solution:
Here, P = Rs 20,000, R = 8 p.c.p.a.,
N = 2 years
i. Simple interest (I)

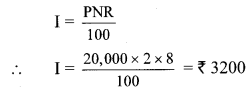
Simple interest (I) = Rs 3200

ii. Compound Interest (I):


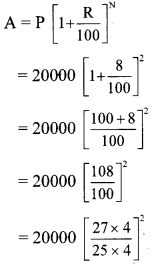
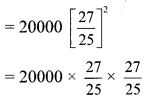
= 32 × 27 × 27
= Rs 23,328
Compound interest (I)
= Amount (A) – Principal (P)
= 23,328 – 20,000
= Rs 3328 ,..(ii)

iii. Difference
= Compound interest – Simple interest
= 3328 – 3200 … [Form (i) and (ii)]
= Rs 128
∴ The difference between compound interest and simple interest is Rs 128.
[Note: The question is modified as per the answer given in the textbook.]

Maharashtra Board Class 8 Maths Chapter 14 Compound Interest Practice Set 14.2 Intext Questions and Activities

8th Standard Maths Practice Set 14.2 Question 1.
Visit the bank nearer to your house and get the information regarding the different schemes and rates of interests. Make a chart and display in your class. (Textbook pg. no. 90)
Solution:
(Students should attempt this activity at their own.)

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.5 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Practice Set 5.5 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals

Question 1.
In the adjoining figure, points X, Y, Z are the midpoints of of ∆ABC respectively, cm. Find the lengths of side AB, side BC and side AC AB = 5 cm, AC = 9 cm and BC = 11c.m. Find the lengths of XY, YZ, XZ.

Solution:
i. AC = 9 cm [Given]
Points X and Y are the midpoints of sides AB and BC respectively. [Given]
∴ XY = \(\frac { 1 }{ 2 }\) AC [Midpoint tfyeprem]
= \(\frac { 1 }{ 2 }\) x 9 = 4.5 cm

ii. AB = 5 cm [Given]
Points Y and Z are the midpoints of sides BC and AC respectively. [Given]
∴ YZ = \(\frac { 1 }{ 2 }\) AB [Midpoint theorem]
= \(\frac { 1 }{ 2 }\) x 5 = 2.5 cm

iii. BC = 11 cm [Given]
Points X and Z are the midpoints of sides AB and AC respectively. [Given]
∴ XZ = \(\frac { 1 }{ 2 }\) BC [Midpoint theorem]
= \(\frac { 1 }{ 2 }\) x 11 = 5.5 cm
l(XY) = 4.5 cm, l(YZ) = 2.5 cm, l(XZ) = 5.5 cm

Question 2.
In the adjoining figure, □PQRS and □MNRL are rectangles. If point M is the midpoint of side PR, then prove that,
i. SL = LR
ii. LN = \(\frac { 1 }{ 2 }\) SQ.

Given: □PQRS and □MNRL are rectangles. M is the midpoint of side PR.
Solution:
Toprove:
i. SL = LR
ii. LN = \(\frac { 1 }{ 2 }\) (SQ)
Proof:
i. □PQRS and □MNRL are rectangles. [Given]
∴ ∠S = ∠L = 90° [Angles of rectangles]
∠S and ∠L form a pair of corresponding angles on sides SP and LM when SR is their transversal.

∴eg ML || seg PS …(i) [Corresponding angles test]
In ∆PRS,
Point M is the midpoint of PR and seg ML || seg PS. [Given] [From (i)]
∴ Point L is the midpoint of seg SR. ……(ii) [Converse of midpoint theorem]
∴ SL = LR

ii. Similarly for ∆PRQ, we can prove that,

Point N is the midpoint of seg QR. ….(iii)
In ∆RSQ,
Points L and N are the midpoints of seg SR and seg QR respectively. [From (ii) and (iii)]
∴ LN = \(\frac { 1 }{ 2 }\)SQ [Midpoint theorem]

Question 3.
In the adjoining figure, ∆ABC is an equilateral triangle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ∆FED is an equilateral triangle.

Given: ∆ABC is an equilateral triangle.
Points F, D and E are midpoints of side AB, side BC, side AC respectively.
To prove: ∆FED is an equilateral triangle.
Solution:
Proof:
∆ABC is an equilateral triangle. [Given]
∴ AB = BC = AC ….(i) [Sides of an equilateral triangle]
Points F, D and E are midpoints of side AB and BC respectively.

∴ FD = \(\frac { 1 }{ 2 }\)AC …..(ii) [Midpoint theorem]
Points D and E are the midpoints of sides BC and AC respectively.

∴ DE = \(\frac { 1 }{ 2 }\)AB …..(iii) [Midpoint theorem]
Points F and E are the midpoints of sides AB and AC respectively.
∴ FE = \(\frac { 1 }{ 2 }\)BC
∴ FD = DE = FE [From (i), (ii), (iii) and (iv) ]
∴ ∆FED is an equilateral triangle.

Question 4.
In the adjoining figure, seg PD is a median of ∆PQR. Point T is the midpoint of seg PD. Produced QT intersects PR at M. Show that \(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\). [Hint: Draw DN || QM]

Solution:
Given: seg PD is a median of ∆PQR. Point T is the midpoint of seg PD.
To Prove: \(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\)
Construction: Draw seg DN ||seg QM such that P-M-N and M-N-R.
Proof:
In ∆PDN,
Point T is the midpoint of seg PD and seg TM || seg DN [Given]
∴ Point M is the midpoint of seg PN. [Construction and Q-T-M]
∴ PM = MN [Converse of midpoint theorem]
In ∆QMR,
Point D is the midpoint of seg QR and seg DN || seg QM [Construction]

∴ Point N is the midpoint of seg MR. [Converse of midpoint theorem]
∴ RN = MN …..(ii)
∴ PM = MN = RN …..(iii) [From (i) and (ii)]
Now, PR = PM + MN + RN [ P-M-R-Q-T-M]
∴ PR = PM + PM + PM [From (iii) ]
∴ PR = 3PM
\(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\)

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.

Practice Set 6.1 Geometry 9th Std Maths Part 2 Answers Chapter 6 Circle

Question 1.
Distance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of a circle.
Given: In a circle with centre O,
OA is radius and AB is its chord,
seg OP ⊥ chord AB, A-P-B
AB = 12 cm, OP =8 cm
To Find: Diameter of the circle
Solution:

i. AP = \(\frac { 1 }{ 2 }\) AB [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
∴ AP = \(\frac { 1 }{ 2 }\) x 12 = 6 cm ….(i)

ii. In ∆OPA, ∠OPA = 90°
∴ OA² = OP² + AP² [Pythagoras theorem]
= 8² + 6² [From (i)]
= 64 + 36
∴ OA² = 100
∴ OA = \(\sqrt { 100 }\) [Taking square root on both sides]
= 10 cm

iii. Radius (r) = 10 cm
∴ Diameter = 2r = 2 x 10 = 20 cm
∴ The diameter of the circle is 20 cm.

Question 2.
Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the centre.
Solution:

Given: In a circle with centre O,
PO is radius and PQ is its chord,
seg OR ⊥ chord PQ, P-R-Q
PQ = 24 cm, diameter (d) = 26 cm
To Find: Distance of the chord from the centre (OR)
Solution:
Radius (OP) = \(\frac { d }{ 2 }\) = \(\frac { 26 }{ 2 }\) = 13 cm ……(i)
∴ PR = \(\frac { 1 }{ 2 }\) PQ [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\) x 24 = 12 cm …..(ii)

ii. In ∆ORP, ∠ORP = 90°
∴ OP²= OR² + PR² [Pythagoras theorem]
∴ 13² = OR² + 12² [From (i) and (ii)]
∴ 169 = OR² + 144
∴ OR² = 169 – 144
∴ OR² = 25
∴ OR = √25 = 5 cm [Taking square root on both sides]
∴ The distance of the chord from the centre of the circle is 5 cm.

Question 3.
Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord.
Given: in a circle with centre A,
PA is radius and PQ is chord,
seg AM ⊥ chord PQ, P-M-Q
AP = 34 cm, AM = 30 cm
To Find: Length of the chord (PQ)
Solution:

I. In ∆AMP, ∠AMP = 90°
∴ AP² = AM² + PM² [Pythagoras theorem]
34² = 30² + PM²
∴ PM² = 34² – 30²
∴ PM² (34 – 30)(34 + 30) [a² – b² = (a – b)(a + b)]
= 4 x 64
∴ PM = \(\sqrt { 4\times64 }\) ………(i) [Taking square root on both sides]
= 2 x 8 = 16cm

ii. Now, PM = \(\frac { 1 }{ 2 }\)(PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
16 = \(\frac { 1 }{ 2 }\)(PQ) [From (i)]
∴ PQ = 16 x 2
= 32cm
∴ The length of the chord of the circle is 32cm.

Question 4.
Radius of a circle with centre O is 41 units. Length of a chord PQ is 80 units, find the distance of the chord from the centre of the circle.
Given: In a circle with centre O,
OP is radius and PQ is its chord,
seg OM ⊥ chord PQ, P-M-Q
OP = 41 units, PQ = 80 units,
To Find: Distance of the chord from the centre of the circle(OM)
Solution:

i. \(\frac { 1 }{ 2 }\)PM = (PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\)(80) = 40 Units ….(i)

ii. In ∆OMP, ∠OMP = 90°
∴ OP² = OM² + PM² [Pythagoras theorem]
∴ 41² = OM² + 40² [From (i)]
∴ OM² = 41² – 40²
= (41 -40) (41 +40) [a² – b² = (a – b) (a + b)]
= (1)(81)
∴ OM² = 81 OM = √81 = 9 units [Taking square root on both sides] [From (i)]
∴ The distance of the chord from the centre of the circle is 9 units.

Question 5.
In the adjoining figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q. Show that AP = BQ.

Given: Two concentric circles having centre O.
To prove: AP = BQ
Construction: Draw seg OM ⊥ chord AB, A-M-B
Solution:
Proof:
For smaller circle,
seg OM ⊥ chord PQ [Construction, A-P-M, M-Q-B]
∴ PM = MQ …..(i) [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
For bigger circle,
seg OM ⊥ chord AB [Construction]
∴ AM = MB [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ AP + PM = MQ + QB [A-P-M, M-Q-B]
∴ AP + MQ = MQ + QB [From (i)]
∴ AP = BQ

Question 6.
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
Solution:

Given: O is the centre of the circle.
seg PQ is the diameter.
Diameter PQ bisects the chords AB and CD in points M and N respectively.
To prove: chord AB || chord CD.
Proof:
Diameter PQ bisects the chord AB in point M [Given]
∴ seg AM ≅ seg BM
∴ seg OM ⊥ chord AB [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠OMA = 90° …..(i)
Also, diameter PQ bisects the chord CD in point N [Given]
∴ seg CN ≅ seg DN
seg ON ⊥ chord CD [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠ONC = 90° …..(ii)
Now, ∠OMA + ∠ONC = 90° + 90° [From (i) and (ii)]
= 180°
But, ∠OMA and ∠ONC form a pair of interior angles on lines AB and CD when seg MN is their transversal.
∴ chord AB || chord CD [Interior angles test]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Practice Set 5.4 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals

Question 1.
In □IJKL, side IJ || side KL, ∠I = 108° and ∠K = 53°, then find the measures of ∠J and ∠L.
Solution:

i. ∠I = 108° [Given]
side IJ || side KL and side IL is their transveral. [Given]
∴ ∠I + ∠L = 180° [Interior angles]
∴ 108° + ∠L = 180°
∴ ∠L = 180° – 108° = 72°

ii. ∠K = 53° [Given]
side IJ || side KL and side JK is their transveral. [Given]
∴ ∠J + ∠K = 180° [Interior angles]
∴ ∠J + 53° = 180°
∴ ∠J= 180°- 53° = 127°
∴ ∠L = 72°, ∠J = 127°

Question 2.
In □ABCD, side BC || side AD, side AB ≅ side DC. If ∠A = 72°, then find the measures of ∠B and ∠D.
Construction: Draw seg BP ⊥ side AD, A – P – D, seg CQ ⊥ side AD, A – Q – D.
Solution:

i. ∠A = 72° [Given]
In □ABCD, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180° [Interior angles]
∴ 72° +∠B = 180°
∴ ∠B = 180° – 72° = 108°

ii. In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQD [Each angle is of measure 90°]
Hypotenuse AB ≅ Hypotenuse DC [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D
∴ ∠D = 72°
∴ ∠B = 108°, ∠D = 72°

Question 3.
In □ABCD, side BC < side AD, side BC || side AD and if side BA ≅ side CD, then prove that ∠ABC = ∠DCB.

Given: side BC < side AD, side BC || side AD, side BA = side CD
To prove: ∠ABC ≅ ∠DCB
Construction: Draw seg BP ⊥ side AD, A – P – D
seg CQ ⊥ side AD, A – Q – D
Solution:
Proof:
In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQB [Each angle is of measure 90°]
Hypotenuse BA ≅ Hypotenuse CD [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D ….(i)
Now, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180°…..(ii) [Interior angles]
Also, side BC || side AD and side CD is their transversal. [Given]
∴ ∠C + ∠D = 180° …..(iii) [Interior angles]
∴ ∠A + ∠B = ∠C + ∠D [From (ii) and (iii)]
∴ ∠A + ∠B = ∠C + ∠A [From (i)]
∴ ∠B = ∠C
∴ ∠ABC ≅ ∠DCB

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Practice Set 5.3 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals

Question 1.
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm, then find BO and if ∠CAD = 35°, then find ∠ACB.
Solution:

i. AC = 8 cm …(i) [Given]
□ABCD is a rectangle [Given]
∴ BD = AC [Diagonals of a rectangle are congruent]
∴ BD = 8 cm [From (i)]
BO = \(\frac { 1 }{ 2 }\) BD [Diagonals of a rectangle bisect each other]
∴ BO = \(\frac { 1 }{ 2 }\) x 8
∴ BO = 4 cm

ii. side AD || side BC and seg AC is their transversal. [Opposite sides of a rectangle are parallel]
∴ ∠ACB = ∠CAD [Alternate angles]
∠ACB = 35° [ ∵∠CAD = 35°]
∴ BO = 4 cm, ∠ACB = 35°

Question 2.
In a rhombus PQRS, if PQ = 7.5 cm, then find QR. If ∠QPS 75°, then find the measures of ∠PQR and ∠SRQ.
Solution:

i. PQ = 7.5 cm [Given]
□PQRS is a rhombus. [Given]
∴ QR = PQ [Sides of a rhombus are congruent]
∴ QR = 7.5 cm

ii. ∠QPS = 75° [Given]
∠QPS + ∠PQR = 180° [Adjacent angles of a rhombus are supplementary]
∴ 75° + ∠PQR = 180°
∴ ∠PQR = 180° – 75°
∴ ∠PQR =105°

iii. ∠SRQ = ∠QPS [Opposite angles of a rhombus]
∴ ∠SRQ = 75°
∴ QR = 7.5 cm, ∠PQR = 105°,
∠SRQ = 75°

Question 3.
Diagonals of a square IJKL intersects at point M. Find the measures of ∠IMJ, ∠JIK and ∠LJK.
Solution:

□IJKL is a square. [Given]
∴ seg IK ⊥ seg JL [Diagonals of a square are perpendicular to each other]
∠ IMJ=90°
∠ JIL 90° ……. (i) [Angle of a square]

ii. ∠JIK = \(\frac { 1 }{ 2 }\)∠JIL [Diagonals of a square bisect the opposite angles]
∠JIK = \(\frac { 1 }{ 2 }\) (90°) [From (i)
∴ ∠JIK = 45°
∠IJK = 90° (ii) [Angle of a square]

iii. ∠LJK = \(\frac { 1 }{ 2 }\)∠IJK [Diagonals of a square bisect the opposite angles]
∠LJK = \(\frac { 1 }{ 2 }\) (90°) [From (ii)]
∴ ∠LJK = 45°
∴ ∠LJK = 90°, ∠JIK = 45°, ∠LJK=45°

Question 4.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its Perimeter.
Solution:

i. Let □ABCD be the rhombus.
AC = 20 cm, BD = 21 cm

ii. In ∆AOB, ∠AOB = 90° [Diagonals of a rhombus are prependicular to each other]
∴ AB² = AO² + BO² [Pythagoras theorem]

iii. Perimeter of □ABCD
= 4 x AB = 4 x 14.5 = 58 cm
∴ The side and perimeter of the rhombus are 14.5 cm and 58 cm respectively.

Question 5.
State with reasons whether the following statements are ‘true’ or ‘false’.
i. Every parallelogram is a rhombus.
ii. Every rhombus is a rectangle,
iii. Every rectangle is a parallelogram.
iv. Every square is a rectangle,
v. Every square is a rhombus.
vi. Every parallelogram is a rectangle.
Answer:
i. False.
All the sides of a rhombus are congruent, while the opposite sides of a parallelogram are congruent.
ii. False.
All the angles of a rectangle are congruent, while the opposite angles of a rhombus are congruent.
iii. True.
The opposite sides of a parallelogram are parallel and congruent. Also, its opposite angles are congruent.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
iv. True.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
All the sides of a square are parallel and congruent. Also, all its angles are congruent.
v. True.
All the sides of a rhombus are congruent. Also, its diagonals are perpendicular bisectors of each other.
All the sides of a square are congruent. Also, its diagonals are perpendicular bisectors of each other.
vi. False.
All the angles of a rectangle are congruent, while the opposite angles of a parallelogram are congruent.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Practice Set 5.1 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals

Question 1.
Diagonals of a parallelogram WXYZ intersect each other at point O. If ∠XYZ∠ = 135°, then measure of ∠XWZ and ∠YZW? If l(OY) = 5 cm, then l(WY) = ?
Solution:

i. ∠XYZ = 135°
□WXYZ is a parallelogram.
∠XWZ = ∠XYZ
∴ ∠XWZ = 135° …..(i)

ii. ∠YZW + ∠XYZ = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠YZW + 135°= 180° [From (i)]
∴ ∠YZW = 180°- 135°
∴ ∠YZW = 45°

iii. l(OY) = 5 cm [Given]
l(OY) = \(\frac { 1 }{ 2 }\) l(WY) [Diagonals of a parallelogram bisect each other]
∴ l(WY) = 2 x l(OY)
= 2 x 5
∴ l(WY) = 10 cm
∴∠XWZ = 135°, ∠YZW = 45°, l(WY) = 10 cm

Question 2.
In a parallelogram ABCD, if ∠A = (3x + 12)°, ∠B = (2x – 32)°, then liptl the value of x and the measures of ∠C and ∠D.
Solution:

□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary],
∴ (3x + 12)° + (2x-32)° = 180°
∴ 3x + 12 + 2x – 32 = 180
∴ 5x – 20 = 180
∴ 5x= 180 + 20
∴ 5x = 200
∴ x = \(\frac { 200 }{ 5 }\)
∴ x = 40

ii. ∠A = (3x + 12)°
= [3(40) + 12]°
=(120 +12)°= 132°
∠B = (2x – 32)°
= [2(40) – 32]°
= (80 – 32)° = 48°
∴ ∠C = ∠A = 132°
∠D = ∠B = 48° [Opposite angles of a parallelogram]
∴ The value of x is 40, and the measures of ∠C and ∠D are 132° and 48° respectively.

Question 3.
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
Solution:

i. Let □ABCD be the parallelogram and the length of AD be x cm.
One side is greater than the other by 25 cm.
∴ AB = x + 25 cm
AD = BC = x cm
AB = DC = (x + 25) cm [Opposite angles of a parallelogram]

ii. Perimeter of □ABCD = 150 cm [Given]
∴ AB + BC + DC + AD = 150
∴ (x + 25) +x + (x + 25) + x – 150
∴ 4x + 50 = 150
∴ 4x = 150 – 50
∴ 4x = 100
∴ x = \(\frac { 100 }{ 4 }\)
∴ x = 25

iii. AD = BC = x = 25 cm
AB = DC = x + 25 = 25 + 25 = 50 cm
∴ The lengths of the sides of the parallelogram are 25 cm, 50 cm, 25 cm and 50 cm.

Question 4.
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
Solution:

i. Let □ABCD be the parallelogram.
The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.
Let the common multiple be x.
∴ ∠A = x° and ∠B = 2x°
∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ x + 2x = 180
∴ 3x = 180
∴ x = \(\frac { 180 }{ 3 }\)
∴ x = 60

ii. ∠A = x° = 60°
∠B = 2x° = 2 x 60° = 120°
∠A = ∠C = 60°
∠B = ∠D= 120° [Opposite angles of a parallelogram]
∴ The measures of the angles of the parallelogram are 60°, 120°, 60° and 120°.

Question 5.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO show that □ABCD is a rhombus.

Given: AO = 5, BO = 12 and AB = 13.
To prove: □ABCD is a rhombus.
Solition:
Proof:
AO = 5, BO = 12, AB = 13 [Given]
AO² + BO² = 5² + 12²
= 25 + 144
∴ AO² + BO² = 169 …..(i)
AB² = 13² = 169 ….(ii)
∴ AB² = AO² + BO² [From (i) and (ii)]
∴ ∆AOB is a right-angled triangle. [Converse of Pythagoras theorem]
∴ ∠AOB = 90°
∴ seg AC ⊥ seg BD …..(iii) [A-O-C]
∴ In parallelogram ABCD,
∴ seg AC ⊥ seg BD [From (iii)]
∴ □ABCD is a rhombus. [A parallelogram is a rhombus perpendicular to each other]

Question 6.
In the adjoining figure, □PQRS and □ABCR are two parallelograms. If ∠P = 110°, then find the measures of all the angles of □ABCR.
Solution:

□PQRS is a parallelogram. [Given]
∴ ∠R = ∠P [Opposite angles of a parallelogram]
∴ ∠R = 110° …..(iii)
□ABCR is a parallelogram. [Given]
∴ ∠A + ∠R= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠A+ 110°= 180° [From (i)]
∴ ∠A= 180°- 110°
∴ ∠A = 70°
∴ ∠C = ∠A = 70°
∴ ∠B = ∠R= 110° [Opposite angles of a parallelogram]
∴ ∠A = 70°, ∠B = 110°,
∴ ∠C = 70°, ∠R = 110°

Question 7.
In the adjoining figure, □ABCD is a parallelogram. Point E is on the ray AB such that BE = AB, then prove that line ED bisects seg BC at point F.

Given: □ABCD is a parallelogram.
BE = AB
To prove: Line ED bisects seg BC at point F i.e. FC = FB
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ seg AB ≅ seg DC …….(i) [Opposite angles of a parallelogram]
seg AB ≅ seg BE ……..(ii) [Given]
seg DC ≅ seg BE ……..(iii) [From (i) and (ii)]
side DC || side AB [Opposite sides of a parallelogram]
i.e. side DC || seg AE and seg DE is their transversal. [A-B-E]
∴ ∠CDE ≅ ∠AED
∴ ∠CDF ≅ ∠BEF …..(iv) [D-F-E, A-B-E]
In ∆DFC and ∆EFB,
seg DC = seg EB [From (iii)]
∠CDF ≅ ∠BEF [From (iv)]
∠DFC ≅ ∠EFB [Vertically opposite angles]
∴ ∆DFC ≅ ∆EFB [SAA test]
∴ FC ≅ FB [c.s.c.t]
∴ Line ED bisects seg BC at point F.

Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Practice Set 5.1 Intext Questions and Activities

Question 1.
Write the following pairs considering □ABCD. (Textbook pg. no 57)

Pairs of adjacent sides:
i. AB, AD
ii. AD, DC
iii. DC, BC
iv. BC, AB

Pairs of adjacent angles:
i. ∠A, ∠B
ii. ∠C, ∠D
iii. ∠B, ∠C
iv. ∠D, ∠A

Pairs of opposite sides:
i. AB, DC
ii. AD, BC

Pairs of opposite angles:
i. ∠A, ∠C
ii. ∠B, ∠D

Question 2.
Complete the following tree diagram. (Textbook pg. no 57)

Question 3.
In the above theorem, to prove ∠DAB ≅ ∠BCD, is any change in the construction needed? If so, how will you write the proof making the change? (Textbook pg. no. 60)

Solution:
Yes
Construction: Draw diagonal BD.
Proof:
side AB || side CD and diagonal BD is their transversal. [Given]
∴ ∠ABD ≅ ∠CDB ……..(i) [Alternate angles]
side BC || side AD and diagonal BD is their transversal. [Given]
∴ ∠ADB ≅ ∠CBD ……..(ii) [Alternate angles]
In ∆DAB and ∆BCD,
∠ABD ≅ ∠CDB [From (i)]
seg BD ≅ seg DB [Common side]
∴ ∠ADB ≅ ∠CBD [From (ii)]
∴ ∆DAB ≅ ∆BCD [ASA test]
∴ ∠DAB ≅ ∠BCD [c.a.c.t.]
Note: ∠DAB s ∠BCD can be proved using the same construction as in the above theorem.
∠BAC ≅ ∠DCA …..(i)
∠DAC ≅ ∠BCA ……(ii)
∴ ∠BAC + ∠DAC ≅ ∠DCA + ∠BCA [Adding (i) and (ii)]
∴ ∠DAB ≅ ∠BCD [Angle addition property]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Practice Set 5.2 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals

Question 1.
In the adjoining figure, □ABCD is a parallelogram, P and Q are midpoints of sides AB and DC respectively, then prove □APCQ is a parallelogram.

Given: □ABCD is a parallelogram. P and Q are the midpoints of sides AB and DC respectively.
To prove: □APCQ is a parallelogram.
Solution:
Proof:
AP = \(\frac { 1 }{ 2 }\) AB …..(i) [P is the midpoint of side AB]
QC = \(\frac { 1 }{ 2 }\) DC ….(ii) [Q is the midpoint of side CD]
□ABCD is a parallelogram. [Given]
∴ AB = DC [Opposite sides of a parallelogram]
∴ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DC [Multiplying both sides by \(\frac { 1 }{ 2 }\)]
∴ AP = QC ….(iii) [From (i) and (ii)]
Also, AB || DC [Opposite angles of a parallelogram]
i.e. AP || QC ….(iv) [A – P – B, D – Q – C]
From (iii) and (iv),
□APCQ is a parallelogram. [A quadrilateral is a parallelogram if its opposite sides is parallel and congruent]

Question 2.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.

Given:
□ABCD is a rectangle.
To prove: Rectangle ABCD is a parallelogram.
Solution:
Proof:
□ABCD is a rectangle.
∴ ∠A ≅ ∠C = 90° [Given]
∠B ≅ ∠D = 90° [Angles of a rectangle]
∴ Rectangle ABCD is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

Question 3.
In the adjoining figure, G is the point of concurrence of medians of ADEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that □GEHF is a parallelogram.

Given: Point G (centroid) is the point of concurrence of the medians of ADEF.
DG = GH
To prove: □GEHF is a parallelogram.
Solution:
Proof:

Let ray DH intersect seg EF at point I such that E-I-F.
∴ seg DI is the median of ∆DEF.
∴ El = FI ……(i)
Point G is the centroid of ∆DEF.
∴ \(\frac { DG }{ GI }\) = \(\frac { 2 }{ 1 }\) [Centroid divides each median in the ratio 2:1]
∴ DG = 2(GI)
∴ GH = 2(GI) [DG = GH]
∴ GI + HI = 2(GI) [G-I-H]
∴ HI = 2(GI) – GI
∴ HI = GI ….(ii)
From (i) and (ii),
□GEHF is a parallelogram [A quadrilateral is a parallelogram, if its diagonals bisect each other]

Question 4.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.

Given: □ABCD is a parallelogram.
Rays AS, BQ, CQ and DS bisect ∠A, ∠B, ∠C and ∠D respectively.
To prove: □PQRS is a rectangle.
Solution:
Proof:
∠BAS = ∠DAS = x° …(i) [ray AS bisects ∠A]
∠ABQ = ∠CBQ =y° ….(ii) [ray BQ bisects ∠B]
∠BCQ = ∠DCQ = u° …..(iii) [ray CQ bisects ∠C]
∠ADS = ∠CDS = v° ….(iv) [ray DS bisects ∠D]
□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ∠ABQ + ∠CBQ = 180° [Angle addition property]
∴ x°+x°+ v° + v° = 180 [From (i) and (ii)]
∴ 2x° + 2v° =180
∴ x + y = 90° ……(v) [Dividing both sides by 2]
Also, ∠A + ∠D= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ADS + ∠CDS = 180° [Angle addition property]
∴ x° + x° + v° + v° = 180°
∴ 2x° + 2v° = 180°
∴ x° + v° = 90° …..(vi) [Dividing both sides by 2]
In ∆ARB,
∠RAB + ∠RBA + ∠ARB = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x° + y° + ∠SRQ = 180° [A – S – R, B – Q – R]
∴ 90° + ∠SRQ = 180° [From (v)]
∴ ∠SRQ = 180°- 90° = 90° …..(vi)
Similarly, we can prove
∠SPQ = 90° …(viii)
In ∆ASD,
∠ASD + ∠SAD + ∠SDA = 180° [Sum of the measures of angles a triangle is 180°]
∴ ∠ASD + x° + v° = 180° [From (vi)]
∴ ∠ASD + 90° = 180°
∴∠ASD = 180°- 90° = 90°
∴ ∠PSR = ∠ASD [Vertically opposite angles]
∴ ∠PSR = 90° …..(ix)
Similarly we can prove
∠PQR = 90° ..(x)
∴ In □PQRS,
∠SRQ = ∠SPQ = ∠PSR = ∠PQR = 90° [From (vii), (viii), (ix), (x)]
∴ □PQRS is a rectangle. [Each angle is of measure 90°]

Question 5.
In the adjoining figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS, then prove that □PQRS is a parallelogram.

Given: □ABCD is a parallelogram.
AP = BQ = CR = DS
To prove: □PQRS is a parallelogram.
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ ∠B = ∠D ….(i) [Opposite angles of a parallelogram]
Also, AB = CD [Opposite sides of a parallelogram]
∴ AP + BP = DR + CR [A-P-B, D-R-C]
∴ AP + BP = DR + AP [AP = CR]
∴ BP = DR ….(ii)
In APBQ and ARDS,
seg BP ≅ seg DR [From (ii)]
∠PBQ ≅ ∠RDS [From (i)]
seg BQ ≅ seg DS [Given]
∴ ∆PBQ ≅ ∆RDS [SAS test]
∴ seg PQ ≅ seg RS …..(iii) [c.s.c.t]
Similarly, we can prove that
∆PAS ≅ ∆RCQ
∴ seg PS ≅ seg RQ ….(iv) [c.s.c.t]
From (iii) and (iv),
□PQRS is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Practice Set 5.2 Intext Questions and Activities

Question 1.
Points D and E are the midpoints of side AB and side AC of ∆ABC respectively. Point F is on ray ED such that ED = DF. Prove that □AFBE is a parallelogram. For this example write ‘given’ and ‘to prove’ and complete the proof. (Text book pg. no. 66)

Given: D and E are the midpoints of side AB and side AC respectively.
ED = DF
To prove: □AFBE is a parallelogram.
Solution:
Proof:
seg AB and seg EF are the diagonals of □AFBE.
seg AD ≅ seg DB [Given]
seg DE ≅ seg DF [Given]
∴ Diagonals of □AFBE bisect each other.
∴ □AFBE is a parallelogram. [ By test of parallelogram]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Problem Set 4 Geometry 9th Std Maths Part 2 Answers Chapter 4 Constructions of Triangles

Question 1.
Construct ∆XYZ, such that XY + XZ = 10.3 cm, YZ = 4.9 cm, ∠XYZ = 45°.
Solution:

As shown in the rough figure draw segYZ = 4.9cm
Draw a ray YT making an angle of 45° with YZ
Take a point W on ray YT, such that YW= 10.3 cm
Now,YX + XW = YW [Y-X-W]
∴ YX + XW=10.3cm …..(i)
Also, XY + X∠10.3cm ……(ii) [Given]
∴ YX + XW = XY + XZ [From (i) and (ii)]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg WZ
∴ The point of intersection of ray YT and perpendicular bisector of seg WZ is point X.

Steps of construction:
i. Draw seg YZ of length 4.9 cm.
ii. Draw ray YT, such that ∠ZYT = 75°.
iii. Mark point W on ray YT such that l(YW) = 10.3 cm.
iv. Join points W and Z.
v. Draw perpendicular bisector of seg WZ intersecting ray YT. Name the point as X.
vi. Join the points X and Z.
Hence, ∆XYZ is the required triangle.

Question 2.
Construct ∆ABC, in which ∠B = 70°, ∠C = 60°, AB + BC + AC = 11.2 cm.
Solution:

i. As shown in the figure, take point D and E on line BC, such that
BD = AB and CE = AC ……(i)
BD + BC + CE = DE [D-B-C, B-C-E]
∴ AB + BC + AC = DE …..(ii)
Also,
AB + BC + AC= 11.2 cm ….(iii) [Given]
∴ DE = 11.2 cm [From (ii) and (iii)]

ii. In ∆ADB
AB = BD [From (i)]
∴ ∠BAD = ∠BDA = x° ….(iv) [Isosceles triangle theorem]
In ∆ABD, ∠ABC is the exterior angle.
∴ ∠BAD + ∠BDA = ∠ABC [Remote interior angles theorem]
x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠ADB = 35°
∴ ∠D = 35°
Similarly, ∠E = 30°

iii. Now, in ∆ADE
∠D = 35°, ∠E = 30° and DE = 11.2 cm
Elence, ∆ADE can be drawn.

iv. Since, AB = BD
∴ Point B lies on perpendicular bisector of seg AD.
Also AC = CE
∴ Point C lies on perpendicular bisector of seg AE.
∴ Points B and C can be located by drawing the perpendicular bisector of AD and AE respectively.
∴ ∆ABC can be drawn.

Steps of construction:
i. Draw seg DE of length 11.2 cm.
ii. From point D draw ray making angle of 35°.
iii. From point E draw ray making angle of 30°.
iv. Name the point of intersection of two rays as A.
v. Draw the perpendicular bisector of seg DA and seg EA intersecting seg DE in B and C respectively.
vi. Join AB and AC.
Hence, ∆ABC is the required triangle.

Question 3.
The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
Solution:

Let the common multiple be x
∴ In ∆ABC,
AB = 2x cm, AC = 3x cm, BC = 4x cm
Perimeter of triangle = 14.4 cm
∴ AB + BC + AC= 14.4
∴ 9x = 14.4
∴ x = \(\frac { 14.4 }{ 9 }\)
∴ x = 1.6
∴ AB = 2x = 2x 1.6 = 3.2 cm
∴ AC = 3x = 3 x 1.6 = 4.8 cm
∴ BC = 4x = 4 x 1.6 = 6.4 cm

Question 4.
Construct ∆PQR, in which PQ – PR = 2.4 cm, QR = 6.4 cm and ∠PQR = 55°.
Solution:

Here, PQ – PR = 2.4 cm
∴ PQ > PR
As shown in the rough figure draw seg QR = 6.4 cm
Draw a ray QT making on angle of 55° with QR
Take a point S on ray QT, such that QS = 2.4 cm.
Now, PQ – PS = QS [Q-S-P]
∴ PQ – PS = 2.4 cm …(i)
Also, PQ – PR = 2.4 cm ….(ii) [Given]
∴ PQ – PS = PQ – PR [From (i) and (ii)]
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg RS
∴ Point P is the intersection of ray QT and the perpendicular bisector of seg RS

Steps of construction:
i. Draw seg QR of length 6.4 cm.
ii. Draw ray QT, such that ∠RQT = 55°.
iii. Take point S on ray QT such that l(QS) = 2.4 cm.
iv. Join the points S and R.
v. Draw perpendicular bisector of seg SR intersecting ray QT.
Name that point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Practice Set 4.3 Geometry 9th Std Maths Part 2 Answers Chapter 4 Constructions of Triangles

Question 1.
Construct ∆PQR, in which ∠Q = 70°, ∠R = 80° and PQ + QR + PR = 9.5 cm.
Solution:

i. As shown in the figure, take point T and S on line QR, such that
QT = PQ and RS = PR ….(i)
QT + QR + RS = TS [T-Q-R, Q-R-S]
∴ PQ + QR + PR = TS …..(ii) [From (i)]
Also,
PQ + QR + PR = 9.5 cm ….(iii) [Given]
∴ TS = 9.5 cm

ii. In ∆PQT
PQ = QT [From (i)]
∴ ∠QPT = ∠QTP = x° ….(iv) [Isosceles triangle theorem]
In ∆PQT, ∠PQR is the exterior angle.
∴ ∠QPT + ∠QTP = ∠PQR [Remote interior angles theorem]
∴ x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠PTQ = 35°
∴ ∠T = 35°
Similarly, ∠S = 40°

iii. Now, in ∆PTS
∠T = 35°, ∠S = 40° and TS = 9.5 cm Hence, ∆PTS can be drawn.

iv. Since, PQ = TQ,
∴ Point Q lies on perpendicular bisector of seg PT.
Also, RP = RS
∴ Point R lies on perpendicular bisector of seg PS.
Points Q and R can be located by drawing the perpendicular bisector of PT and PS respectively.
∴ ∆PQR can be drawn.

Steps of construction:
i. Draw seg TS of length 9.5 cm.
ii. From point T draw ray making angle of 35°.
iii. From point S draw ray making angle of 40°.
iv. Name the point of intersection of two rays as P.
v. Draw the perpendicular bisector of seg PT and seg PS intersecting seg TS in Q and R respectively.
vi. Join PQ and PR.
Hence, ∆PQR is the required triangle.

Question 2.
Construct ∆XYZ, in which ∠Y = 58°, ∠X = 46° and perimeter of triangle is 10.5 cm.
Solution:

i. As shown in the figure, take point W and V on line YX, such that
YW = ZY and XV = ZX ……(i)
YW + YX + XV = WV [W-Y-X, Y-X-V]
∠Y + YX + ∠X = WV ……(ii) [From (i)]
Also,
∠Y + YX + ∠X = 10.5 cm …..(iii) [Given]
∴ WV = 10.5 cm [From (ii) and (iii)]

ii. In ∆ZWY
∠Y = YM [From (i)]
∴ ∠YZW = ∠YWZ = x° …..(iv) [Isosceles triangle theorem]
In ∆ZYW, ∠ZYX is the exterior angle.
∴ ∠YZW + ∠YWZ = ∠ZYX [Remote interior angles theorem]
∴ x + x = 58° [From (iv)]
∴ 2x = 58°
∴ x = 29°
∴ ∠ZWY = 29°
∴ ∠W = 29°
∴ Similarly, ∠V = 23°

iii. Now, in ∆ZWV
∠W = 29°, ∠V = 23° and
WV= 10.5 cm
Hence, ∆ZWV can be drawn.

iv. Since, ZY = YW
∴ Point Y lies on perpendicular bisector of seg ZW.
Also, ZX = XV
∴ Point X lies on perpendicular bisector of seg ZV.
∴ Points Y and X can be located by drawing the perpendicular bisector of ZW and ZV respectively.
∴ ∆XYZ can be drawn.

Steps of construction:
i. Draw seg WV of length 10.5 cm.
ii. From point W draw ray making angle of 29°.
iii. From point V draw ray making angle of 23°.
iv. Name the point of intersection of two rays as Z.
v. Draw the perpendicular bisector of seg WZ and seg VZ intersecting seg WV in Y and X respectively.
vi. Join XY and XX.
Hence, ∆XYX is the required triangle

Question 3.
Construct ∆LMN, in which ∠M = 60°, ∠N = 80° and LM + MN + NL = 11 cm.
Solution:

i. As shown in the figure, take point S and T on line MN, such that
MS = LM and NT = LN …..(i)
MS + MN + NT = ST [S-M-N, M-N-T]
∴ LM + MN + LN = ST …..(ii)
Also,
LM + MN + LN = 11 cm ….(iii)
∴ ST = 11 cm [From (ii) and (iii)]

ii. In ∆LSM
LM = MS
∴ ∠MLS = ∠MSL = x° …..(iv) [isosceles triangle theorem]
In ∆LMS, ∠LMN is the exterior angle.
∴ ∠MLS + ∠MSL = ∠LMN [Remote interior angles theorem]
∴ x + x = 60° [From (iv)]
∴ 2x = 60°
∴ x = 30°
∴ ∠LSM = 30°
∴ ∠S = 30°
Similarly, ∠T = 40°

iii. Now, in ∆LST
∠S = 30°, ∠T = 40° and ST = 11 cm
Hence, ALST can be drawn.

iv. Since, LM = MS
∴ Point M lies on perpendicular bisector of seg LS.
Also LN = NT
∴ Point N lies on perpendicular bisector of seg LT.
∴ Points M and N can be located by drawing the perpendicular bisector of LS and LT respectively.
∴ ∆LMN can be drawn.

Steps of construction:
i. Draw seg ST of length 11 cm.
ii. From point S draw ray making angle of 30°.
iii. From point T draw ray making angle of 40°.
iv. Name the point of intersection of two rays as L.
v. Draw the perpendicular bisector of seg LS and seg LT intersecting seg ST in M and N respectively.
vi. Join LM and LN.
Hence, ∆LMN is the required triangle.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Practice Set 4.2 Geometry 9th Std Maths Part 2 Answers Chapter 4 Constructions of Triangles

Question 1.
Construct ∆XYZ, such that YZ = 7.4 cm, ∠XYZ = 45° and XY – XZ = 2.7 cm.
Solution:

Here, XY – XZ = 2.7 cm
∴ XY > XZ
As shown in the rough figure draw seg YZ = 7.4 cm
Draw a ray YP making an angle of 45° with YZ
Take a point W on ray YP, such that
YW = 2.7 cm.
Now, XY – XW = YW [Y-W-X]
∴ XY – XW = 2.7 cm ….(i)
Also, XY – XZ = 2.7 cm ….(ii) [Given]
∴ XY – XW = XY – XZ [From (i) and (ii)]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg ZW
∴ Point X is the intersection of ray YP and the perpendicular bisector seg ZW

Steps of construction:
i. Draw seg YZ of length 7.4 cm.
ii. Draw ray YP, such that ∠ZYP = 45°.
iii. Mark point W on ray YP such that l(YW) = 2.7 cm.
iv. Join points W and Z.
v. Join the points X and Z.
Hence, ∆XYZ is the required triangle.

Question 2.
Construct ∆PQR, such that QR = 6.5 cm, ∠PQR = 60° and PQ – PR = 2.5 cm.
Solution:

Here, PQ – PR = 2.5 cm
∴ PQ > PR
As shown in the rough figure draw seg QR = 6.5 cm
Draw a ray QT making on angle of 60° with QR
Take a point S on ray QT, such that QS = 2.5 cm.
Now, PQ – PS = QS [Q-S-T]
∴ PQ – PS = 2.5 cm ……(i) [Given]
Also, PQ – PR = 2.5 cm …..(ii) [From (i) and (ii)]
∴ PQ – PS = PQ – PR
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg RS
∴ Point P is the intersection of ray QT and the perpendicular bisector of seg RS

Steps of construction:
i. Draw seg QR of length 6.5 cm.
ii. Draw ray QT, such that ∠RQT = 600.
iii. Mark point S on ray QT such that l(QS) = 2.5 cm.
iv. Join points S and R.
v. Draw perpendicular bisector of seg SR intersecting ray QT. Name the point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.

Question 3.
Construct ∆ABC, such that BC = 6 cm, ∠ABC = 100° and AC – AB = 2.5 cm.

Solution:
Here, AC – AB = 2.5 cm
∴ AC > AB
As shown in the rough figure draw seg BC = 6 cm
Draw a ray BT making an angle of 100° with BC.
Take a point D on opposite ray of BT, :
such that BD 2.5 cm.
Now, AD – AB = BD [A-B-D]
∴ AD – AB = 2.5cm …..(i)
Also, AC – AB = 2.5 cm …..(ii) [Given]
∴ AD – AB = AC – AB [From (i) and (ii)]
∴ AD = AC
∴ Point A is on the perpendicular bisector of seg DC
∴ Point A is the intersection of ray BT and the perpendicular bisector of seg DC

Steps of construction:
i. Draw seg BC of length 6 cm.
ii. Draw ray BT, such that ∠CBT = 100°.
iii. Take point D on opposite ray of BT such that l(BD) = 2.5 cm.
iv. Join the points D and C.
v. Draw the perpendicular bisector of seg DC intersecting ray BT. Name the point as A.
vi. Join the points A and C.
Hence, ∆ABC is the required triangle.