Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.
Problem Set 4 Geometry 9th Std Maths Part 2 Answers Chapter 4 Constructions of Triangles
Question 1.
Construct ∆XYZ, such that XY + XZ = 10.3 cm, YZ = 4.9 cm, ∠XYZ = 45°.
Solution:
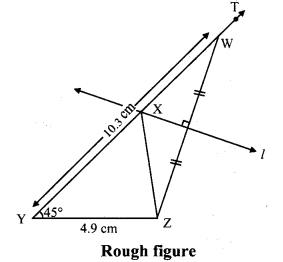
As shown in the rough figure draw segYZ = 4.9cm
Draw a ray YT making an angle of 45° with YZ
Take a point W on ray YT, such that YW= 10.3 cm
Now,YX + XW = YW [Y-X-W]
∴ YX + XW=10.3cm …..(i)
Also, XY + X∠10.3cm ……(ii) [Given]
∴ YX + XW = XY + XZ [From (i) and (ii)]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg WZ
∴ The point of intersection of ray YT and perpendicular bisector of seg WZ is point X.
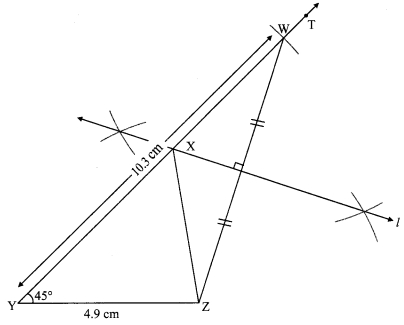
Steps of construction:
i. Draw seg YZ of length 4.9 cm.
ii. Draw ray YT, such that ∠ZYT = 75°.
iii. Mark point W on ray YT such that l(YW) = 10.3 cm.
iv. Join points W and Z.
v. Draw perpendicular bisector of seg WZ intersecting ray YT. Name the point as X.
vi. Join the points X and Z.
Hence, ∆XYZ is the required triangle.
Question 2.
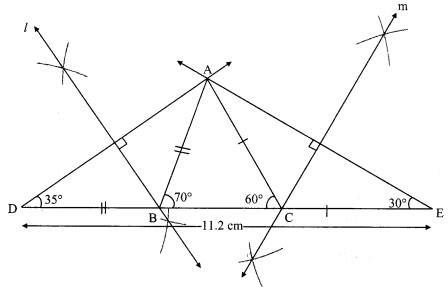
Construct ∆ABC, in which ∠B = 70°, ∠C = 60°, AB + BC + AC = 11.2 cm.
Solution:
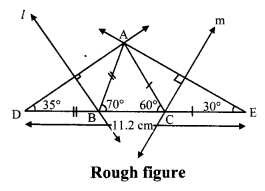
i. As shown in the figure, take point D and E on line BC, such that
BD = AB and CE = AC ……(i)
BD + BC + CE = DE [D-B-C, B-C-E]
∴ AB + BC + AC = DE …..(ii)
Also,
AB + BC + AC= 11.2 cm ….(iii) [Given]
∴ DE = 11.2 cm [From (ii) and (iii)]
ii. In ∆ADB
AB = BD [From (i)]
∴ ∠BAD = ∠BDA = x° ….(iv) [Isosceles triangle theorem]
In ∆ABD, ∠ABC is the exterior angle.
∴ ∠BAD + ∠BDA = ∠ABC [Remote interior angles theorem]
x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠ADB = 35°
∴ ∠D = 35°
Similarly, ∠E = 30°
iii. Now, in ∆ADE
∠D = 35°, ∠E = 30° and DE = 11.2 cm
Elence, ∆ADE can be drawn.
iv. Since, AB = BD
∴ Point B lies on perpendicular bisector of seg AD.
Also AC = CE
∴ Point C lies on perpendicular bisector of seg AE.
∴ Points B and C can be located by drawing the perpendicular bisector of AD and AE respectively.
∴ ∆ABC can be drawn.
Steps of construction:
i. Draw seg DE of length 11.2 cm.
ii. From point D draw ray making angle of 35°.
iii. From point E draw ray making angle of 30°.
iv. Name the point of intersection of two rays as A.
v. Draw the perpendicular bisector of seg DA and seg EA intersecting seg DE in B and C respectively.
vi. Join AB and AC.
Hence, ∆ABC is the required triangle.
Question 3.
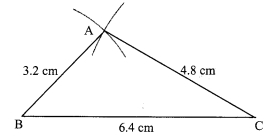
The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
Solution:
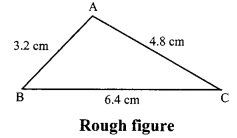
Let the common multiple be x
∴ In ∆ABC,
AB = 2x cm, AC = 3x cm, BC = 4x cm
Perimeter of triangle = 14.4 cm
∴ AB + BC + AC= 14.4
∴ 9x = 14.4
∴ x = \(\frac { 14.4 }{ 9 }\)
∴ x = 1.6
∴ AB = 2x = 2x 1.6 = 3.2 cm
∴ AC = 3x = 3 x 1.6 = 4.8 cm
∴ BC = 4x = 4 x 1.6 = 6.4 cm
Question 4.
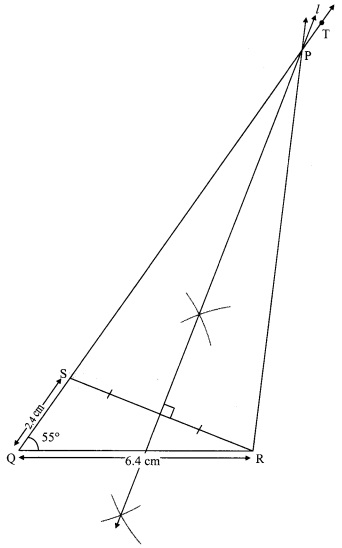
Construct ∆PQR, in which PQ – PR = 2.4 cm, QR = 6.4 cm and ∠PQR = 55°.
Solution:
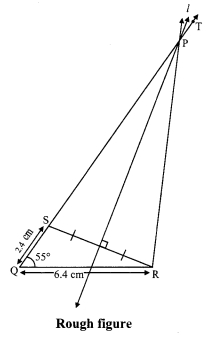
Here, PQ – PR = 2.4 cm
∴ PQ > PR
As shown in the rough figure draw seg QR = 6.4 cm
Draw a ray QT making on angle of 55° with QR
Take a point S on ray QT, such that QS = 2.4 cm.
Now, PQ – PS = QS [Q-S-P]
∴ PQ – PS = 2.4 cm …(i)
Also, PQ – PR = 2.4 cm ….(ii) [Given]
∴ PQ – PS = PQ – PR [From (i) and (ii)]
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg RS
∴ Point P is the intersection of ray QT and the perpendicular bisector of seg RS
Steps of construction:
i. Draw seg QR of length 6.4 cm.
ii. Draw ray QT, such that ∠RQT = 55°.
iii. Take point S on ray QT such that l(QS) = 2.4 cm.
iv. Join the points S and R.
v. Draw perpendicular bisector of seg SR intersecting ray QT.
Name that point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.